最新九年级数学圆的中考试题培训资料
初三数学九上圆所有知识点总结和常考题型练习题

圆知识点一、圆的概念集合形式的概念: 1.圆可以看作是到定点的距离等于定长的点的集合;2.圆的外部: 可以看作是到定点的距离大于定长的点的集合;3.圆的内部: 可以看作是到定点的距离小于定长的点的集合轨迹形式的概念:1.圆:到定点的距离等于定长的点的轨迹就是以定点为圆心, 定长为半径的圆;(补充)2.垂直平分线: 到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线);3.角的平分线: 到角两边距离相等的点的轨迹是这个角的平分线;4、到直线的距离相等的点的轨迹是: 平行于这条直线且到这条直线的距离等于定长的两条直线;5、到两条平行线距离相等的点的轨迹是: 平行于这两条平行线且到两条直线距离都相等的一条直线。
二、点与圆的位置关系1.点在圆内点在圆内;2.点在圆上点在圆上;3.点在圆外点在圆外;三、直线与圆的位置关系1.直线与圆相离无交点;2.直线与圆相切有一个交点;3.直线与圆相交有两个交点;四、垂径定理垂径定理: 垂直于弦的直径平分弦且平分弦所对的弧。
推论1: (1)平分弦(不是直径)的直径垂直于弦, 并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心, 并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径, 垂直平分弦, 并且平分弦所对的另一条弧以上共4个定理, 简称2推3定理:此定理中共5个结论中, 只要知道其中2个即可推出其它3个结论, 即:①AB是直径②AB CD⊥③CE DE=④弧BC=弧BD⑤弧AC=弧AD中任意2个条件推出其他3个结论。
推论2: 圆的两条平行弦所夹的弧相等。
即:在⊙中, ∵∥∴弧AC=弧BD五、圆心角定理圆心角定理: 同圆或等圆中, 相等的圆心角所对的弦相等, 所对的弧相等,弦心距相等。
此定理也称1推3定理, 即上述四个结论中,只要知道其中的1个相等, 则可以推出其它的3个结论,即: ①;②;③OC OF=;④弧BA=弧BD六、圆周角定理1.圆周角定理: 同弧所对的圆周角等于它所对的圆心的角的一半。
压轴题 圆的五种考法(解析版)--九年级数学常考压轴题

压轴题圆的五种考法目录解题知识必备压轴题型讲练类型一、四点共圆类型二、圆中最值问题类型三、定点定长构造辅助圆类型四、定弦定角构造辅助圆类型五、对角互补构造辅助圆压轴能力测评(10题)类型一、四点共圆一.填空题1.(2022秋•大丰区期中)如图,ΔABC中,AD⊥BC,∠B=45°,∠C=30°.以AD为弦的圆分别交AB、AC于E、F两点.点G在AC边上,且满足∠EDG=120°.若CD=4+22,则ΔDEG的面积的最小值是.【分析】连接EF,利用四点共圆和同弧所对的圆周角相等证明EF⎳DG,从而得到SΔEDG=S△EDG,当FG最小时,ΔDFG的面积就最小,作ΔDFG的外接圆O,过O点作OH⊥FG交于点H,连接OF、OG,DO+OH=12+22FG,当DO+OH最小时,FG就最小,当D、O、H三点共线时,DO+OH最小,此时DH⊥FG,在RtΔFHO中,(2FH)2=FH2+(2+2-2FH)2,求出FH=2,可得FG的最小值为22,再求SΔDFG =22+2,即ΔDEG的面积的最小值为22+2.【解答】解:连接EF,AD⊥BC,∠B=45°,∠C=30°,∴∠B=45°,∠DAC=60°,∵∠BAC=105°,∵A、E、F、D四点共圆,∴∠EDF=75°,∵∠EDG=120°,∴∠FDG=45°,∵ED =ED ,∴∠EFD =∠FDG ,∴EF ⎳DG ,∴S ΔEDG =S △EDG ,∵CD =4+22,∠C =30°,∴AC =833+463,AD =433+263,∴AC 边上的高=AD ⋅DC AC=2+2,∴当FG 最小时,ΔDFG 的面积就最小,作ΔDFG 的外接圆O ,过O 点作OH ⊥FG 交于点H ,连接OF 、OG ,∵∠FDG =45°,∴∠FOG =90°,∵OF =GO ,∴ΔFOG 是等腰直角三角形,∵∠FOH =12∠FOG =45°,∴ΔFOH 是等腰直角三角形,∴FH =OH =12FG ,FO =2FH ,∴DO +OH =22FG +12FG =12+22FG ,∴当DO +OH 最小时,FG 就最小,∵DO +OH ≥DH ,∴当D 、O 、H 三点共线时,DO +OH 最小,此时DH ⊥FG ,∴DH =2+2,在Rt ΔFHO 中,(2FH )2=FH 2+(2+2-2FH )2,解得FH =2或FH =4+32,∵OH =2+2=FH +FO ,∴FH =2,∴FG 的最小值为22,∴S ΔDFG =12×22×(2+2)=22+2,∴ΔDEG 的面积的最小值为22+2,故答案为:22+2.【点评】本题考查圆的综合应用,熟练掌握圆心角与圆周角的关系,四点共圆的性质,三角形外接圆的性质是解题的关键.二.解答题2.(2022秋•建湖县期中)如图,在⊙O 的内接四边形ABCD 中,DB =DC ,∠DAE 是四边形ABCD 的一个外角.(1)若∠DAE =75°,则∠DAC =°;(2)过点D 作DE ⊥AB 于E ,判断AB 、AE 、AC 之间的数量关系并证明;(3)若AB =6、AE =2,求BD 2-AD 2的值.【分析】(1)根据四边形外接圆的性质,同弧所对的圆周角相等,可得∠DCB=∠DBC=∠DAC=75°;(2)过点D作DF⊥AC于点F,可证明ΔBDE≅ΔCDF(AAS),ΔADE≅ΔADF(AAS),则AC=AF+FC= AE+BE=AE+AE+AB=2AE+AB;(3)在RtΔBDE中,BD2=64+DE2,在RtΔAED中,AD2=4+ED2,再求解即可.【解答】解:(1)∵四边形ABCD是圆O的内接四边形,∴∠BCD+∠BAD=180°,∵∠DAE是四边形ABCD的一个外角,∴∠DAE=∠BCD,∵BD=CD,∴∠CBD=∠DCB,∵弧CD所对的圆周角分别为∠CAD、∠CBD,∴∠CBD=∠CAD,∵∠DAE=75°,∴∠DCB=∠DBC=∠DAC=75°,故答案为:75;(2)过点D作DF⊥AC于点F,∵DE⊥AB,∴∠DEA=90°,∵∠ABD=∠ACD,BD=CD,∠E=∠DFC=90°,∴ΔBDE≅ΔCDF(AAS),∴DE=DF,AE=CF,∴∠ADE=∠ADF,又∵∠E=∠AFD,AD=AD,∴ΔADE≅ΔADF(AAS),∴AE=AF,∴AC=AF+FC=AE+BE=AE+AE+AB=2AE+AB,即AC=2AE+AB;(3)在RtΔBDE中,BD2=BE2+DE2,在RtΔAED中,AD2=AE2+ED2,∵AB=6,AE=2,∴BE=8,∴BD2=64+DE2,AD2=4+ED2,∴BD2-AD2=60.【点评】本题考查圆的综合应用,熟练掌握同弧所对的圆周角相等,四点共圆的性质,直角三角形勾股定理,三角形全等的判定及性质是解题的关键.3.(2023秋•鄞州区期中)如图,在△ABC 中,点D ,E 为AB ,AC 上的点,BE =CD ,DC ,BE 交于F ,△BDF 与△CEF 的外接圆相交于点G (异于F ),H 1,H 2分别为△ABC 和△ADE 的垂心.证明:(1)GF 平分∠BFC ;(2)H 1,H 2,G 三点共线.(注:利用坐标系、复数解题者不给分)【分析】(1)通过证明△BGE ≅△DGC 得出DG =BG ,然后由BG =DG 推导出∠BFG +∠DFG =180°,再由邻补角的性质得出∠BFG =∠GFC ,即可证明结论;(2)根据题意构造B 、E 、B ′、E ′四点共⊙P ,以及D 、C 、D ′、C ′四点共⊙Q ,然后由相似三角形推导出点H 1、H 2对于⊙P 和⊙Q 等幂,再由根轴的性质得出H 1H 2是PQ 的垂直平分线,最后根据GP =GQ 得到GM ⊥PQ ,进而证得三点共线.【解答】(1)证明:在△BGE 和△DGC 中,∠GBE =∠GDC ,BE =CD ,∠GEB =∠GCD ,∴△BGE ≅△DGC (ASA ).∴DG =BG ,∴BG =DG ,∵DBG +DG =2πR (R 为△BDF 的外接圆半径).∴∠BFG +∠DFG =180°.又∵∠GFC +∠DFG =180°,∴∠BFG =∠GFC ,∴GF 平分∠BFC .(2)证明:连接BH 1、DH 2并延长分别交AC 于B ′、D ′,连接CH 1、EH 2并延长交AB 于C ′、E ′.BE 中点为P ,CD 中点为Q .∵BB ′⊥AC ,EE ′⊥AB ,∴B 、E 、B ′、E ′四点共⊙P .∵DD ′⊥AC ,CC ′⊥AB ,∴D 、C 、D ′、C ′四点共⊙Q .∵∠DE ′H 2=∠ED ′H 2,∠DH 2E ′∽△EH 2D ′,∴△DE ′H2∽△ED ′H 2,∴DH 2:EH 2=E ′H 2:D ′H 2,∴DH 2⋅D ′H 2=EH 2⋅E ′H 2.同理得CH 1⋅C ′H 1=BH 1⋅B ′H 1.∴H 1,H 2在⊙P 和⊙Q 的根轴上.∵⊙P 和⊙Q 的根轴是过两圆的交点的直线.∴H 1,H 2在⊙P 和⊙Q 的公共弦JK 上.又∵BE =CD ,即⊙P 和⊙Q 是等圆,∴四边形PJQK 为菱形.∴H 1H 2是PQ 的垂直平分线,M 为PQ 中点.由(1)知△BGE ≅△DGC ,∵GP 、GQ 分别为△BGE 和△DGC 的对应边上的中线,∴GP =GQ ,∴点G 在PQ 的垂直平分线上.∴H 1,H 2,G 三点共线.【点评】本题考查了全等三角形的判定和性质,圆周角定理,圆幂定理,菱形的性质,等腰三角形的性质等.本题辅助线繁多,综合性强,通过四点共圆判断出H 1、H 2两点对于⊙P 和⊙Q 等幂是解答本题的关键.4.(2022秋•沙坪坝区校级期中)在ΔABC 中,已知AB =AC ,作AM ⊥BC ,D 是AM 上一点,∠DBC =30°,连接BD 、CD ,在BD 上截取DE =AD ,连接AE .(1)如图1所示,若∠BAC =90°,AD =3,求ΔABE 的周长;(2)如图2所示,若分别取AE 、AC 的中点N 、H ,连接MN 、MH ,求证:MN =MH ;(3)如图3所示,∠BAC =90°,BC =2,将AC 沿着直线AP 翻折得到AQ ,连接BQ ,直线BQ 交AP 于点P ,N 为AE 中点,当PN 取得最小值时,请直接写出ΔAPN 的面积.【分析】(1)过点D 作DL ⊥AE 于L ,则∠ALD =∠ELD =90°,由∠DBC =30°,可得BD =2DM ,设DM =x ,则BD =2x ,由勾股定理可得BM =3x ,AM =x +3,可得BM =CM =AM =33+32,AB =2BM =2×33+32=36+322,利用勾股定理可得AL =AD 2-DL 2=(3)2-32 2=32,进而可得AE =2AL =2×32=3,即可求得答案;(2)延长AM 至F ,使MF =AM ,在DF 上截取DT =DE ,连接EF ,ET ,设∠ABM =α,则∠BAM =90°-α,可证得ΔDET 是等边三角形,得出:DT =ET =DE =AD ,∠DTE =60°,再证得ΔABD ≅ΔEFT (SAS ),可得AB =EF =AC ,利用三角形中位线定理可得MN =12EF ,再由直角三角形性质可得MH =12AC ,即可证得结论;(3)连接CP ,先证得点P 在ΔABC 的外接圆⊙M 上,当且仅当点P 为半径MP 经过点N 时,PN 取得最小值,连接DN ,过点N 作NG ⊥AM 于G ,利用解直角三角形可得DM =BM ⋅tan30°=33,AD =DE =1-33,AN =EN =32AD =321-33 ,NG =12AN =12×321-33 =3-14,AG =3NG =3-34,GM =AM -AG =1-3-34=1+34,由勾股定理可得MN =GM 2+NG 2=1+34 2+3-14 2=22,PN =MP -MN =1-22,再利用S ΔAPN S ΔAMN =PN MN=2-1,即可求得答案.【解答】(1)解:过点D 作DL ⊥AE 于L ,则∠ALD =∠ELD =90°,∵∠BAC =90°,AB =AC ,AM ⊥BC ,∴AM =BM =CM ,∠BMD =90°,∠ABM =∠BAM =45°,∵∠DBC =30°,∴BD =2DM ,设DM =x ,则BD =2x ,∴BM =BD 2-DM 2=(2x )2-x 2=3x ,AM =x +3,∴3x =x +3,∴x =3+32,∴BM =CM =AM =33+32,∴AB =2BM =2×33+32=36+322,∵DE =AD ,∴∠DAE =∠DEA ,∵∠DAE +∠DEA =∠BDM =90°-30°=60°,∴∠DAE =∠DEA =30°,∴∠BAE =∠BAM -∠DAE =45°-30°=15°,∵∠ABD =∠ABM -∠DBC =45°-30°=15°,∴∠BAE =∠ABD ,∴AE =BE ,在Rt ΔADL 中,DL =12AD =32,∴AL =AD 2-DL 2=(3)2-322=32,∵DE =AD ,DL ⊥AE ,∴AE =2AL =2×32=3,∴ΔABE 的周长=AB +AE +BE =36+322+3+3=36+32+122;(2)证明:延长AM 至F ,使MF =AM ,在DF 上截取DT =DE ,连接EF ,ET ,设∠ABM =α,则∠BAM =90°-α,∵∠DBC =30°,∴∠BDT =60°,∠ABD =α-30°,BD =2DM ,∵DE =AD ,∴∠AED =∠DAE =30°,∴ΔDET 是等边三角形,∴DT =ET =DE =AD ,∠DTE=60°,∵AF =2(AD +DM )=AT +FT ,∴FT =2DM =BD ,∵∠EDT =∠ETD =60°,∴∠ADB =180°-60°=120°=∠ETF ,在ΔABD 和ΔEFT 中,AD =ET∠ADB =∠ETF BD =FT,∴ΔABD ≅ΔEFT (SAS ),∴AB =EF ,∵AB =AC ,∴EF =AC ,∵N 、M 分别是AE 、AF 的中点,∴MN =12EF ,∵点H 是Rt ΔACM 斜边AC 的中点,∴MH =12AC ,∴MN =MH ;(3)解:如图,连接CP ,由翻折得:∠ACP =∠AQP ,AC =AQ ,∵AB =AC ,∠BAC =90°,BC =2,AM ⊥BC ,∴AB =AQ ,AM =BM =CM =1,∴∠ABP =∠AQB ,∵∠AQB +∠AQP =180°,∴∠ABP +∠ACP =180°,∴点P 在ΔABC 的外接圆⊙M 上,当且仅当点P 为半径MP 经过点N 时,PN 取得最小值,如图,连接DN ,过点N 作NG ⊥AM 于G ,∵∠DBC =30°,∴DM =BM ⋅tan30°=33,∴AD =DE =1-33,∴AN =EN =32AD =321-33,∵∠AGN =90°,∠NAG =30°,∴NG =12AN =12×321-33 =3-14,∴AG =3NG =3-34,∴GM =AM -AG =1-3-34=1+34,在Rt ΔMNG 中,MN =GM 2+NG 2=1+342+3-14 2=22,∴PN =MP -MN =1-22,∴SΔAPNSΔAMN=PNMN=1-2222=2-1,∵SΔAMN=12AM⋅NG=12×1×3-14=3-18,∴SΔAPN=(2-1)SΔAMN=(2-1)×3-18=6-3-2+18.【点评】本题是几何综合题,考查了等腰三角形性质,等腰直角三角形性质,直角三角形性质,等边三角形性质,全等三角形的判定和性质,勾股定理,圆内接四边形的判定,三角形面积等,涉及知识点多,难度大,添加适当的辅助线是解题的关键与难点.5.(2022秋•鼓楼区期中)以下是“四点共圆”的几个结论,你能证明并运用它们吗?Ⅰ.若两个直角三角形有公共斜边,则这两个三角形的4个顶点共圆(图1、2);Ⅱ.若四边形的一组对角互补,则这个四边形的4个顶点共圆(图3);Ⅲ.若线段同侧两点与线段两端点连线的夹角相等,则这两点和线段两端点共圆(图4).(1)在图1、2中,取AC的中点O,根据得OA=OB=OC=OD,即A,B,C,D共圆;(2)在图3中,画⊙O经过点A,B,D(图5).假设点C落在⊙O外,BC交⊙O于点E,连接DE,可得=180°,所以∠BED=,得出矛盾;同理点C也不会落在⊙O内,即A,B,C,D共圆.结论Ⅲ同理可证.(3)利用四点共圆证明锐角三角形的三条高交于一点.已知:如图6,锐角三角形ABC的高BD,CE相交于点H,射线AH交BC于点F.求证:AF是ΔABC的高.(补全以下证明框图,并在图上作必要标注)(4)如图7,点P是ΔABC外部一点,过P作直线AB,BC,CA的垂线,垂足分别为E,F,D,且点D,E,F在同一条直线上.求证:点P在ΔABC的外接圆上.【分析】(1)根据直角三角形斜边中线的性质可得结论;(2)由圆周角的性质可得∠BED+∠A=180°,再结合题干条件,得出矛盾,由此可得出结论;(3)如图,连接DE,由点B、C、D、E四点共圆得∠BDE=∠ECB,由点A、D、H、E四点共圆得∠BDE=∠BAF,从而证明∠BAF+∠ABF=90°即可;(4)连接BP和CP,由点A,E,P,F四点共圆可得,∠BEF=∠BPF,由点C,P,D,F四点共圆可得∠CDF =∠CPF,再由外角的性质及角的和差可得∠BAC=∠BPC,由此可得点A,B,C,P四点共圆,即点P在ΔABC的外接圆上.【解答】解:(1)在图1、2中,取AC的中点O,根据直角三角形斜边上的中线等于斜边的一半,得OA=OB= OC=OD,即A,B,C,D共圆;故答案为:直角三角形斜边上的中线等于斜边的一半;(2)在图3中,画⊙O经过点A,B,D(图5).假设点C落在⊙O外,BC交⊙O于点E,连接DE,可得∠BED+∠A=180°,∴∠BED=180°-∠A,得出矛盾;同理点C也不会落在⊙O内,即A,B,C,D共圆.结论Ⅲ同理可证.故答案为:∠BED+∠A;180°-∠A;(3)如图6,连接DE,由点B、C、D、E四点共圆得∠BDE=∠ECB,由点A、D、H、E四点共圆得∠BDE=∠BAF,∴∠ECB=∠BAF,∵∠BEC=90°,∴∠ECB+∠ABF=90°,∴∠BAF+∠ABF=90°,∴∠BFA=90°,∴AF为ΔABC的边BC上的高.(4)如图7,连接BP和CP,由点A,E,P,F四点共圆可得∠BEF=∠BPF,由点C,P,D,F四点共圆可得∠CDF=∠CPF,∵∠ADE=∠CDF,∴∠ADE=∠CPF,∵∠BAC=∠BEF+∠ADE,∠BPC=∠BPF+∠CPF,∴∠BAC=∠BPC,∴点A,B,C,P四点共圆,即点P在ΔABC的外接圆上.【点评】本题考查了圆的定义,直角三角形斜边上的中线等于斜边一半,圆内接四边形对角互补,圆周角定理,内心的定义.第(3)(4)题解题关键是选取适当的四点证明共圆,再利用圆周角定理证明角相等.类型二、圆中最值问题一.填空题6.(2022秋•长沙期中)如图,⊙O 的半径为1,P A ,PB 为⊙O 的切线,切点为A ,B ,∠APB =60°,点M 为劣弧AB 上一动点,过点M 作⊙O 的切线,分别交P A ,PB 于点E ,F ,EF 的最小值是.【分析】由切线的性质定理,全等三角形的判定和性质,三角形外心的性质,可以求解.【解答】解:连接OA ,OE ,OM ,OF ,OB ,∵P A ,PB 为⊙O 的切线,EF 切⊙O 于M ,∴OA ⊥P A ,OB ⊥PB ,OM ⊥EF ,∵四边形PBOA 内角和是360°,∴∠P +∠AOB =360°-∠P AB -∠PBA =180°,∴∠AOB =180°-∠P =120°,∵OE =OE ,OA =OM ,∴Rt ΔOAE ≅Rt ΔOME (HL ),∴∠AOE =∠MOE ,同理:∠MOF =∠BOF ,∴∠EOF =∠EOM +∠FOM =12∠AOB =60°,设ΔOEF 的外心是点C ,作CH ⊥EF 于H ,连接CO ,CE ,CF ,OM ,∵点C 是ΔOEF 的外心,∴OC =EC =FC ,∴∠CEF =∠CFE ,EH =FH ,∵∠ECF =2∠EOF =120°,∴∠CEF =30°,∴CH =12CE =12OC ,∵OC +CH ≥OM ,∴3CH ≥1,∴CH ≥13,∵tan ∠CEH =CH EH,∴EH =3CH ,∴EF =2EH =23CH ,∴EF ≥233,∴EF 的最小值是233,故答案为:233.【点评】本题考查有关圆的最值问题,关键是掌握切线的性质定理,全等三角形的判定和性质,三角形外心的性二.解答题7.(2022秋•东城区校级期中)对于平面直角坐标系xOy中的图形G和点P给出如下定义;Q为图形G上任意一点,若P,Q两点间距离的最大值和最小值都存在,且最大值是最小值的k倍,则称点P为图形G 的“k分点”.已知点N(3,0),A(1,0),B(0,3),C(1,-1).(1)①在点A,B,C中,线段ON的“2分点”是;②点D(a,0),若点C为线段OD的“二分点”,求a的值;(2)以点O为圆心,r为半径画图,若线段AN上存在⊙O的“二分点”,直接写出r的取值范围.【分析】(1)①分别求出点A、B、C到线段ON的最小值和最大值,看是否满足“2分点”定义即可,②对a的取值分情况讨论:0<a≤1,1<a≤2,a>2和a<0,根据“二分点”的定义可求解,(2)设线段AN上存在⊙O的“二分点”为M(m,0)(1≤m≤3).对r的取值分情况讨论0<r≤1,1<r<3且m<r,1<r<3且m>r,r≥3,根据二分点的定义可求解.【解答】(1)解:①如图,∵点A在ON上,故最小值为0,不符合题意,点B到ON的最小值为OB=3,最大值为BN=32+32=32,∴点B是线段ON的“2分点”,点C到ON的最小值为1,最大值为CN=22+12=5∴点C不是线段ON的“2分点”,故答案为:点B;②当0<a≤1时,点C到OD的最小值为CD=(1-a)2+(-1)2=2-2a+a2,点C到OD的最大值为CO=12+(-1)2=2,∴2=22-2a+a2,即2a2-4a+3=0,∵△<0,故无解,舍去;当1<a≤2时,点C到OD的最小值为1,点C到OD的最大值为CO=12+(-1)2=2,最大值不是最小值的2倍,所以舍去,当a>2时,点C到OD的最小值为1,点C到OD的最大值为CD=(a-1)2+(0-1)2=a2-2a+2,∵点C为线段OD的“二分点”,∴a2-2a+2=2×1,a1=1+3,a2=1-3(舍去),当a<0时,点C到OD的最小值为CO=12+(-1)2=2,点C到OD的最大值为CD=(1-a)2+(-1-0)2=a2-2a+2,∵点C为线段OD的“二分点”,同0<a≤1时,无解,舍去;综上,a=1+3.(2)如图所示,设线段AN上存在⊙O的“二分点”为M(m,0)(1≤m≤3),当0<r≤1时,最小值为:m-r,最大值为:m+r,m,∴2(m-r)=m+r,即r=13∵1≤m≤3,≤r≤1,∴13当1<r<3且m<r时,最小值为:r-m,最大值为r+m,∴2(r-m)=r+m,即r=3m,∵1≤m≤3,∴3≤r≤9,∵1<r<3,∴r不存在,当1<r<3且m>r时,最小值为:m-r,最大值为:m+r,m,∴2(m-r)=r+m,即r=13≤r≤1,∴13∵1<r<3,∴r 不存在.当r ≥3时,最小值为:r -m ,最大值为:m +r ,∴2(r -m )=r +m ,即r =3m ,∴3≤r ≤9.综上所述,r 的取值范围为13≤r ≤1或3≤r ≤9.【点评】本题考查坐标上的两点距离,勾股定理,点到圆的距离.根据题目所给条件,掌握“k 分点”的定义是解题的关键.8.(2022秋•江阴市期中)如图,在平面直角坐标系中,点A 的坐标为(-3,0),点B 在y 轴的正半轴上,且∠ABO =30°,以点B 为圆心,1为半径画⊙B ,与y 轴交于点C (点C 在点B 的下方),点Q 是AB 的中点,点P 是⊙B 上的一个动点,从点C 开始以5度/秒的速度沿圆周逆时针运动一周,设运动时间为t 秒.(1)如图1,连接OQ ,当OQ ⎳BP 时,求t 的值;(2)如图2,点P 在运动过程中,连接AP ,以AP 为边在左侧作等边ΔAPD ,①当t =12秒时,求点D 的坐标;②连接DQ ,当DQ 最大时,求此时t 的值和这个最大值.【分析】(1)如图,过点B 作BP ⎳OQ ,交⊙B 于点P 1,P 2,由平行得出点P 的旋转角,进而可得出时间t ;(2)①将线段AB 绕点A 逆时针旋转60°到线段AB ′,连接B ′D ,易证△AB ′D ≅ΔABP (SAS ),所以B ′D =BP =1,∠AB ′D =∠ABP =90°;过点B ′作B ′N ⊥x 轴于点N ,过点D 作DM ⊥B ′N 于点M ,所以∠M =∠ANB ′=90°,由互余可知,∠MBD ′=∠B ′AN ,所以∠B ′AB =60°,∠BAO =60°,所以∠B ′AN =60°,AN =3,B ′N =3,则MB ′=12,MD =32,进而可得点D 的坐标;②由旋转可知,点D 在以点B ′为圆心,1长为半径的圆上运动,当DQ 最大时,点D ,B ′,Q 三点共线,设⊙B与y 轴的另一个交点为C ′,则C ′(0,4),OC ′=4,由点Q 是AB 的中点可知,Q -32,32,B ′(-23,3),进而可得B ′Q =3,所以DQ =4,易证△AB ′Q ≅ΔABO (SSS ),进而可得ΔADQ ≅△AC ′O (SAS ),所以AD =AC ′,即此时点P 与点C ′重合,所以t =180°5°=36.【解答】解:(1)如图:∵ΔABO 是直角三角形,Q 是AB 中点,∴OQ =QA =QB ,∴∠BOQ =∠ABO =30°,又∵OQ ⎳BP 1,∴∠OBP 1=∠BOQ =30°,∴点P 的轨迹是⊙B 中30°圆心角所对的弧,∴t =30°5°=6,∵当点P 运动到P 1B 延长线与⊙B 的交点P 2时,点P 的轨迹是⊙B 中180°+30°=210°圆心角所对的弧,∴t =210°5°=42.故t 的值为6或42;(2)①如图,∵∠ABO =30°,OA =3,∴OB =3,AB =23,当t =12时,∠CBP =60°,∴∠ABP =90°,将线段AB 绕点A 逆时针旋转60°到线段AB ′,连接B ′D ,由旋转可知,∠BAB ′=60°,AB =AB ′=23,∵ΔADP 是等边三角形,∴∠DAP =60°,AD =AP ,∴∠B ′AD =∠BAP ,∴△AB ′D ≅ΔABP (SAS ),∴B ′D =BP =1,∠AB ′D =∠ABP =90°,过点B ′作B ′N ⊥x 轴于点N ,过点D 作DM ⊥B ′N 于点M ,∴∠M =∠ANB ′=90°,∴∠AB ′N +∠B ′AN =90°,∠MB ′D +∠AB ′N =90°,∴∠MB ′D =∠B ′AN ,∵∠B ′AB =60°,∠BAO =60°,∴∠B ′AN =60°,AN =3,B ′N =3,∴∠MB ′D =60°,∴MB ′=12,MD =32,∴MN =72.∴D -332,72;②由旋转可知,点D 在以点B ′为圆心,1长为半径的圆上运动,∴当DQ 最大时,点D ,B ′,Q 三点共线,如图所示,设⊙B 与y 轴的另一个交点为C ′,∴C ′(0,4),∴OC ′=4,∵点Q 为AB 的中点,∴AQ =BQ =3,AB ′=AB =23,由①可知,B (0,3),∴Q -32,32,B ′(-23,3),∴DQ =4,∴B ′Q =BO ,AQ =BQ =3,AB ′=AB =23,∴△AB ′Q ≅ΔABO (SSS ),∴∠AQB ′=∠AOB =90°,∵DQ =OC ′,AQ =AO ,∴ΔADQ ≅△AC ′O (SAS ),∴AD =AC ′,即此时点P 与点C ′重合,∴t =180°5°=36.综上,t =36,DQ 最大值是4.【点评】本题属于圆的综合题,涉及考查旋转的性质,等边三角形的性质,全等三角形的性质与判定,相似三角形的相似与判定,含30°的直角三角形的三边关系,根据题意得出点D 的轨迹是解题关键.类型三、定点定长构造辅助圆一.填空题9.(2023秋•常州期中)如图,点A ,B 的坐标分别为A (4,0),B (0,4),C 为坐标平面内一点,BC =2,点M 为线段AC 的中点,连接OM ,OM 的最大值为.【分析】先判断出点C 的运动轨迹是在半径为2的⊙B 上,再取OD =OA =4,连接OD ,则OM 是ΔACD 的中位线,OM =12CD ,进而可得OM 最大值时,CD 取最大值,此时D 、B 、C 三点共线,计算即可求出结果.【解答】解:∵C 为坐标平面内一点,BC =2,∴点C 的运动轨迹是在半径为2的⊙B 上,如图,取OD =OA =4,连接OD ,∵点M 为线段AC 的中点,∴OM 是ΔACD 的中位线,∴OM =12CD ,∴OM 最大值时,CD 取最大值,此时D 、B 、C 三点共线,此时在Rt ΔOBD 中,BD =42+42=42,∴CD =2+42,∴OM 的最大值是1+22.故答案为:1+22.【点评】本题考查了坐标和三角形的中位线,定点定长构造辅助圆等,解题关键是确定点C 的运动轨迹.二.解答题10.(2022秋•秀洲区期中)如图,ΔABC 中,AC =BC =4,∠ACB =90°,过点C 任作一条直线CD ,将线段BC 沿直线CD 翻折得线段CE ,直线AE 交直线CD 于点F .(1)小智同学通过思考推得当点E 在AB 上方时,∠AEB 的角度是不变的,请按小智的思路帮助小智完成以下推理过程:∵AC =BC =EC ,∴A 、B 、E 三点在以C 为圆心以AC 为半径的圆上.∴∠AEB =∠ACB =°.(2)若BE =2,求CF 的长.(3)线段AE 最大值为;若取BC 的中点M ,则线段MF 的最小值为.【分析】(1)根据AC =BC =EC ,得A 、B 、E 三点在以C 为圆心以AC 为半径的圆上,根据圆周角定理可知∠AEB 的度数;(2)由ΔEFG 是等腰三角形可求出FG =1,利用勾股定理求出CG 的长,从而得出答案;(3)根据直径是圆中最大的弦知当AE 经过圆心C 时,线段AE 的最大值为2AC =8,取AB 的中点O ,连接OF ,可证∠AFB =90°,则点F 在以AB 为直径的圆O 上,当OF 经过点M 时,MF 最短,此时OF ⊥BC ,从而解决问题.【解答】解:(1)∵AC =BC =EC ,∴A 、B 、E 三点在以C 为圆心以AC 为半径的圆上,∴∠AEB =12∠ACB =45°,故答案为:12,45;(2)由折叠可知,CD 垂直平分BE ,∴BE ⊥CD ,设CD 、BE 交于点G ,则GE =BG =12BE =1,∴∠FGE =90°,∵∠AEB =45°,∴FG =GE =1,在Rt ΔCEG 中,由勾股定理得,CG =CE 2-DE 2=15,∴CF =CG -FG =15-1;当点E 在AB 的下方时,如图,∵AC =BC =EC ,∴A 、B 、E 三点在以C 为圆心以AC 为半径的圆上,∴∠EAB +∠EBA =12∠ACB =45°,即∠BEF =45°,由翻折可知,∠EGF=90°,EG=GB 12BE=1,∴ΔEGF是等腰直角三角形,∴GF=EG=1,在RtΔCEG中,CG=CE2-EG2=42-12=15,∴CF=15+1,综上所述,CF的长为15-1或15+1;(3)∵A,B,E,三点在以C为圆心,以AC为半径的圆上,∴当AE经过圆心C时,线段AE的最大值为2AC=8,在RtΔABC中,AC=BC=4,∠ACB=90°,∴AB=AC2+BC2=42,BM=CM=12BC=2,∠ABC=∠BAC=45°,连接BF,取AB的中点O,连接OF,如图,∵CD垂直平分BE,∠AEB=45°,∴BF=EF,∴∠EBF=∠AEB=45°,∴∠EFB=90°,∴∠AFB=90°,∴OF=12AB=OA=OB=22,∴点F在以点O为圆心,AB为直径的圆上,∵∠ACB=90°,∴点C在⊙O上,∴当OF经过点M时,MF最短,此时OF⊥BC,∴OM=BM⋅tan∠ABC=2×1=2,∴MF=OF-OM=22-2,即线段MF的最小值为22-2,故答案为:8;22-2.【点评】本题是圆的综合题,主要考查了等腰直角三角形的性质,线段垂直平分线的性质,圆周角定理,利用定点定长构造辅助圆是解题的关键.类型四、定弦定角构造辅助圆一.填空题11.(2023春•梁子湖区期中)如图,矩形ABCD的边AB=8,AD=6,M为BC的中点,P是矩形内部一动点,且满足∠ADP=∠P AB,N为边CD上的一个动点,连接PN,MN,则PN+MN的最小值为.【分析】先找出点P 的运动路线为以AD 为直径的圆,设圆心为O ,作点M 关于直线DC 的对称点M ′,连接OM ′交⊙O 于点P ′,可推出M ′P ′的长即为PN +MN 的最小值,再求出M ′P ′的长即可.【解答】解:∵四边形ABCD 是矩形,∴∠BAD =90°,∵∠ADP =∠P AB ,∴∠ADP +∠P AD =∠P AB +∠P AD =∠BAD =90°,∴点P 的运动路线为以AD 为直径的圆,作以AD 为直径的⊙O ,作点M 关于直线DC 的对称点M ′,连接OM ′交⊙O 于点P ′,连接M ′N ,OP ,则OP =OP ′=3,M ′N =MN ,∴PN +MN =PN +M ′N =PN +M ′N +OP -OP ′≥OM ′-OP ′=OM ′-3,∴PN +MN 的最小值为OM ′-3;连接OM ,∵四边形ABCD 是矩形,点O 是AD 的中点,点M 为BC 的中点,∴OD =12AD =12BC =CM =3,OD ⎳CM ,∠ODC =90°,∴四边形OMCD 是矩形,∴OM =DC =AB =8,∵点M 关于直线DC 的对称点M ′,∴M ′M =2MC =6,在Rt △M ′OM 中,由勾股定理,得OM ′=OM 2+M ′M 2=82+62=10,∴PN +MN 的最小值为OM ′-3=10-3=7,故答案为:7.【点评】本题考查轴对称-最短路线问题,矩形的性质,勾股定理,能利用一条线段的长表示两线段的和的最小值是解题的关键.二.解答题小赵同学在学习完“圆”这一章内容后,感觉到一些几何问题,如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.我们把这个过程称为“化隐圆为显圆”.①已知:如图1,OA =OB =OC ,若∠AOB =50°,求∠ACB 的度数.解:若以点O 为圆心,OA 为半径作辅助圆,∠AOB 是⊙O 的圆心角,而∠ACB 是圆周角,从而可容易得到∠ACB = °.②如图2,点P 为正方形ABCD 内一点,且∠BPC =90°,若AB =4,求AP 的最小值.解:∵BC =4,∠BPC =90°,∴点P 在以BC 为直径的圆上,设圆心为点O ,则O 、P 、A 三点共线时AP 最小,最小值为 .(2)【问题解决】①如图3,在平行四边形ABCD 中,已知AB =4,BC =6,∠ABC =60°,点P 是BC 边上一动点(点P 不与B ,C 重合),连接AP ,作点B 关于直线AP 的对称点Q ,则线段QC 的最小值为 .②如图4,△ABC 中,∠BAC =90°,AB =4,AC =3,D 为AC 上一动点,以AD 为直径的⊙O 交BD 于E ,求线段CE 的最小值.(3)【问题拓展】如图5,在平面直角坐标系中,已知两点A (2,3),B (6,7),x 轴上有一动点P ,当∠APB 最大时,直接写出点P 的坐标 .【分析】(1)①利用圆周角定理即可求得答案;②由正方形性质可得:∠ABC =90°,BC =AB =4,OB =12BC =2,由勾股定理得:AO =25,推出点P 在以BC 为直径的⊙O 上,则O 、P 、A 三点共线时AP 最小,即可求得答案;(2)①过点A 作AH ⊥BC 于H ,利用解直角三角形得AH =AB ⋅sin ∠ABC =23,BH =AB ⋅cos ∠ABC =2,CH =BC -BH =4,由勾股定理得AC =27,再由AQ =AB =4,可得点Q 在以A 为圆心AB 为半径的⊙A 上,即当C 、Q 、A 三点共线时QC 最小,QC 的最小值=AC -AQ =27-4;②连接AE ,由AD 是⊙O 的直径,可得∠AED =90°,推出∠AEB =90°,即点E 在以AB 为直径的圆上,进而可得当C 、E 、Q 三点共线时,CE 最小,运用勾股定理即可求得答案;(3)当∠APB 最大时,过A 、B 两点的⊙O ′与x 轴相切,利用待定系数法可得直线AB 的解析式为y =x +1,线段AB 的垂直平分线为y =-x +9,设O ′(m ,-m +9),根据O ′A =O ′B =O ′P ,建立方程求解即可得出答【解答】解:(1)①如图1,以点O为圆心,OA为半径作辅助圆⊙O,∵AB =AB ,∠AOB=50°,∠AOB=25°,∴∠ACB=12故答案为:25.②点P为正方形ABCD内一点,且∠BPC=90°,若AB=4,求AP的最小值.如图②,以BC为直径作⊙O,∵四边形ABCD是正方形,∴∠ABC=90°,BC=AB=4,BC=2,∴OB=12在Rt△ABO中,AO=AB2+OB2=42+22=25,∵BC=4,∠BPC=90°,∴点P在以BC为直径的⊙O上,则O、P、A三点共线时AP最小,∴AP的最小值=AO-OP=25-2,故答案为:25-2.(2)①如图3,过点A作AH⊥BC于H,∵AB=4,BC=6,∠ABC=60°,则AH=AB⋅sin∠ABC=4sin60°=23,BH=AB⋅cos∠ABC=4cos60°=2,∴CH=BC-BH=6-2=4,在Rt△ACH中,AC=AH2+CH2=(23)2+42=27,∵点B与点Q关于直线AP对称,∴AQ=AB=4,∴点Q在以A为圆心AB为半径的⊙A上,∴当C、Q、A三点共线时QC最小,QC的最小值=AC-AQ=27-4,故答案为:27-4.②如图4,连接AE,∵AD是⊙O的直径,∴∠AED=90°,∴∠AEB=180°-∠AED=90°,以AB 为直径作⊙Q ,交⊙O 于E ,当C 、E 、Q 三点共线时,CE 最小,∵△ABC 中,∠BAC =90°,AB =4,AC =3,∴QE =AQ =12AB =2,∴CQ =AC 2+AQ 2=32+22=13,∴CE =CQ -QE =13-2,故线段CE 的最小值为13-2.(3)当∠APB 最大时,过A 、B 两点的⊙O ′与x 轴相切,设直线AB 的解析式为y =kx +b ,把A (2,3),B (6,7)代入,得:2k +b =36k +b =7 ,解得:k =1b =1 ,∴直线AB 的解析式为y =x +1,∵线段AB 的中点坐标为(4,5),圆心O ′在AB 的垂直平分线上,∴线段AB 的垂直平分线为y =-x +9,设O ′(m ,-m +9),∵O ′A =O ′B =O ′P ,∴(m -2)2+(-m +9-3)2=(-m +9)2,解得:m =42-1或m =-42-1(舍去),∴点P 的坐标为(42-1,0),故答案为:42-1.【点评】本题是圆的综合题,考查了圆的有关知识,正方形的性质,平行四边形的性质,解直角三角形等知识,灵活运用这些性质解决问题是解题的关键.13.(2022秋•泗洪县期中)已知:⊙O 和⊙O 外一点P .(1)如图甲,P A 和PB 是⊙O 的两条切线,A 、B 分别为切点,求证:P A =PB .(2)尺规作图:在图乙中,过P 点画⊙O 的两条切线PE 、PF ,E 、F 为切点(要求:保留作图痕迹,不写作法).【分析】(1)如图,连接OP、OA、OB.只要证明RtΔP AO≅RtΔPBO(HL),可得P A=PB.(2)以OP为直径作⊙O′,两圆交于点E、F,直线PE、PF即为所求;【解答】解:(1)如图,连接OP、OA、OB.∵P A、PB是切线,∴P A⊥OA,PB⊥OB,∴∠P AO=∠PBO=90°,在RtΔP AO和RtΔPBO中,OP=OP,OA=OB∴RtΔP AO≅RtΔPBO,∴P A=PB.(2)以OP为直径作⊙O′,两圆交于点E、F,直线PE、PF即为所求;【点评】本题考查切线的性质、全等三角形的判定和性质,直径的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用辅助圆解决问题,属于中考常考题型.类型五、对角互补构造辅助圆14.(2021秋•越秀区校级期中)如图1,在ΔABC中,∠ACB=90°,CD平分∠ACB,且AD⊥BD于点D.(1)判断ΔABD的形状;(2)如图2,在(1)的结论下,若BQ=22,DQ=3,∠BQD=75°,求AQ的长;(3)如图3,在(1)的结论下,若将DB绕着点D顺时针旋转α(0°<α<90°)得到DP,连接BP,作DE⊥BP交AP于点F.试探究AF与DE的数量关系,并说明理由.【分析】(1)由∠ACB+∠ADB=90°+90°=180°,知点A、C、B、D上四点共圆,则∠ACD=∠ABD=45°,即可得出结论;(2)将ΔADQ绕点D顺时针旋转90°得ΔBDE,连接EQ,过点B作EQ的垂线,交EQ的延长线于H,得ΔQDE是等腰直角三角形,从而可解直角三角形BQH,在RtΔBEH中,利用勾股定理得可求出BE的长度,从而解决问题;(3)在AF上截取AM=PF,利用SAS证明ΔADM≅ΔPDF,得∠ADM=∠PDE,DM=DF,可证明ΔMDF、ΔPEF是等腰直角三角形,从而解决问题.【解答】解:(1)∵∠ACB=90°,CD平分∠ACB,∴∠ACD=45°,∵∠ACB+∠ADB=90°+90°=180°,∴点A、C、B、D上四点共圆,∴∠ACD=∠ABD=45°,∴∠BAD=∠ABD=45°,∴ΔABD是等腰直角三角形;(2)将ΔADQ绕点D顺时针旋转90°得ΔBDE,连接EQ,过点B作EQ的垂线,交EQ的延长线于H,∴DQ=DE,∠QDE=90°,AQ=BE,∴ΔQDE是等腰直角三角形,∴∠DQE=45°,∴QE=2DQ=32,∵∠BQD=75°,∴∠BQE=∠BQD+∠DQE=120°,∴∠BQH=60°,BQ=2,BH=6,∴QH=12在RtΔBEH中,由勾股定理得BE=BH2+EH2=(42)2+(6)2=38,∴AQ=BE=38;(3)AF=2DE.,理由如下:如图,在AF上截取AM=PF,∵DA=DP,∴∠DAM=∠DPF,∴ΔADM≅ΔPDF(SAS),∴∠ADM=∠PDE,DM=DF,∵BD=DP,DE⊥BP,∴∠BDE=∠PDE,∴∠ADM=∠BDE,∴ΔMDF是等腰直角三角形,∴∠MFD=45°,MF=2DF,∴∠EFP=45°,∴ΔPEF是等腰直角三角形,∴PF=2EF,∴AF=2DE.【点评】本题主要考查了等腰直角三角形的判定与性质,全等三角形的判定与性质,等腰三角形的性质,含30°角的直角三角形的性质,勾股定理,四点共圆等知识,作辅助线构造全等三角形是解题的关键.15.(2021秋•西城区校级期中)如图,ΔABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.(1)求证:BD=CE;(2)延长ED交BC于点F,求证:F为BC的中点;(3)若ΔABC的边长为1,直接写出EF的最大值.【分析】(1)利用SAS证明ΔBAD≅ΔCAE,即可得出结论;(2)过点C作CG⎳BP交DF的延长线于点G,利用等角对等边可得CG=CE,由(1)ΔBAD≅ΔCAE,得BD=CE,再利用AAS证明ΔBDF≅ΔCGF,从而解决问题;(3)由(2)知∠AFC=∠AEC=90°,则点A,F,C,E四点在以AC为直径的圆上,故EF的最大值为直径.【解答】(1)证明:∵线段AD绕点A逆时针旋转60°得到线段AE,∴ΔADE是等边三角形,∴AD=AE,∠DAE=60°,∵ΔABC是等边三角形,∴AB=AC,∠BAC=60°,∴∠BAC=∠DAE,∴∠BAD=∠CAE,在ΔBAD和ΔCAE中,AB=AC∠BAD=∠CAE AD=AE,∴ΔBAD≅ΔCAE(SAS),∴BD=CE;(2)证明:如图,过点C作CG⎳BP交DF的延长线于点G,∴∠G=∠BDF,∴∠G =30°,由(1)可知,BD =CE ,∠CEA =∠BDA ,∵AD ⊥BP ,∴∠BDA =90°,∴∠CEA =90°,∵∠AED =60°,∴∠CED =30°=∠G ,∴CE =CG ,∴BD =CG ,在ΔBDF 和ΔCGF 中,∠BDF =∠G∠BFD =∠CFG BD =CG,∴ΔBDF ≅ΔCGF (AAS ),∴BF =FC ,即F 为BC 的中点;(3)解:如图,连接AF ,∵ΔABC 是等边三角形,BF =FC ,∴AF ⊥BC ,∴∠AFC =90°,∴∠AFC =∠AEC =90°,∴点A ,F ,C ,E 四点在以AC 为直径的圆上,∴EF 的最大值为直径,即最大值为1.【点评】本题主要考查了等边三角形的性质,全等三角形的判定与性质,四点共圆等知识,作辅助线构造全等三角形是解题的关键.16.(2023秋•东城区校级期中)如图1,在Rt ΔABC 中,∠ABC =90°,BA =BC ,直线MN 是过点A 的直线CD ⊥MN 于点D ,连接BD .(1)观察猜想张老师在课堂上提出问题:线段DC ,AD ,BD 之间有什么数量关系.经过观察思考,小明出一种思路:如图1,过点B 作BE ⊥BD ,交MN 于点E ,进而得出:DC +AD =BD .(2)探究证明将直线MN 绕点A 顺时针旋转到图2的位置写出此时线段DC ,AD ,BD之间的数量关系,并证明(3)拓展延伸在直线MN 绕点A 旋转的过程中,当ΔABD 面积取得最大值时,若CD 长为1,请直接写BD 的长.【分析】(1)由题意:ΔBAE≅ΔBCD,推出AE=CD,BE=BD,推出CD+AD=AD+AE=DE,ΔBDE是等腰直角三角形,推出DE=2BD,可得DC+AD=2BD;(2)结论:AD-DC=2BD.过点B作BE⊥BD,交MN于点E.AD交BC于O.只要证明ΔCDB≅ΔAEB,即可解决问题;(3)如图3中,当点D在线段AB的垂直平分线上且在AB的右侧时,ΔABD的面积最大.【解答】解:(1)如图1中,由题意:ΔBAE≅ΔBCD,∴AE=CD,BE=BD,∴CD+AD=AD+AE=DE,∵ΔBDE是等腰直角三角形,∴DE=2BD,∴DC+AD=2BD,故答案为2.(2)AD-DC=2BD.证明:如图,过点B作BE⊥BD,交MN于点E.AD交BC于O.∵∠ABC=∠DBE=90°,∴∠ABE+∠EBC=∠CBD+∠EBC,∴∠ABE=∠CBD.∵∠BAE+∠AOB=90°,∠BCD+∠COD=90°,∠AOB=∠COD,∴∠BAE=∠BCD,∴∠ABE=∠DBC.又∵AB=CB,∴ΔCDB≅ΔAEB,∴CD=AE,EB=BD,∴△BD为等腰直角三角形,DE=2BD.∵DE=AD-AE=AD-CD,∴AD-CD=2BD.(3)如图3中,易知A、B、C、D四点共圆,当点D在线段AB的垂直平分线上且在AB的右侧时,ΔABD的面积最大.。
初三圆测试题及答案

初三圆测试题及答案一、选择题(每题3分,共30分)1. 圆的半径为r,圆的周长为()。
A. 2πrB. πrC. 2rD. πr²2. 圆的直径为d,圆的面积为()。
A. πd²/4B. πd²C. πr²D. πr²/23. 点P在圆O的内部,则点P到圆心O的距离()。
A. 大于半径B. 等于半径C. 小于半径D. 不确定4. 圆的切线与过切点的半径垂直,切线的长度等于()。
A. 半径B. 直径C. 半径的一半D. 无法确定5. 已知圆的半径为5,圆心到直线的距离为3,那么直线与圆的位置关系是()。
A. 相离B. 相切C. 相交D. 内切6. 圆的内接四边形的对角互补,即()。
A. 对角和为180°B. 对角和为90°C. 对角和为360°D. 对角差为180°7. 圆的外接圆的半径等于()。
A. 边长B. 对角线的一半C. 对角线D. 无法确定8. 圆的内切圆的半径等于()。
A. 边长的一半B. 对角线的一半C. 对边之和的一半D. 无法确定9. 圆的弧长公式为()。
A. L = 2πrθ/360B. L = πrθC. L = rθD. L = 2πr10. 圆的扇形面积公式为()。
A. S = 1/2r²θB. S = r²θC. S = 1/2LD. S = 1/2rL二、填空题(每题2分,共20分)11. 圆的周长公式为C = ____________。
12. 若圆的半径为4,则圆的面积为___________。
13. 圆的切线与半径的关系是___________。
14. 圆的内接正六边形的边长等于___________。
15. 圆的外接正三角形的边长等于___________。
16. 圆的内切圆的半径等于圆的内接正六边形的边长的___________。
17. 圆的弧长公式中θ表示的是___________。
九年级圆知识点及习题(含答案)

圆圆的有关概念与性质1.圆上各点到圆心的距离都等于半径。
2.圆是轴对称图形,任何一条直径所在的直线都是它的对称轴;圆又是中心对称图形,圆心是它的对称中心。
3.垂直于弦的直径平分这条弦,并且平分弦所对的弧;平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧。
4.在同圆或等圆中,如果两个圆心角,两条弧,两条弦,两条弦心距,两个圆周角中有一组量相等,那么它们所对应的其余各组量都分别相等。
5.同弧或等弧所对的圆周角相等,都等于它所对的圆心角的一半。
6.直径所对的圆周角是 90°,90°所对的弦是直径。
7.三角形的三个顶点确定 1 个圆,这个圆叫做三角形的外接圆,三角形的外接圆的圆心叫外心,是三角形三边垂直平分线的交点。
8.与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心是三角形三条角平分线的交点的交点,叫做三角形的内心。
9.圆内接四边形:顶点都在圆上的四边形,叫圆内接四边形.10.圆内接四边形对角互补,它的一个外角等于它相邻内角的对角与圆有关的位置关系1.点与圆的位置关系共有三种:①点在圆外,②点在圆上,③点在圆内;对应的点到圆心的距离d和半径r之间的数量关系分别为:①d > r,②d = r,③d < r.2.直线与圆的位置关系共有三种:①相交,②相切,③相离;对应的圆心到直线的距离d和圆的半径r之间的数量关系分别为:①d < r,②d = r,③d > r.3.圆与圆的位置关系共有五种:①内含,②相内切,③相交,④相外切,⑤外离;两圆的圆心距d和两圆的半径R、r(R≥r)之间的数量关系分别为:①d < R-r,②d = R-r,③ R-r < d < R+ r,④d = R+r,⑤d > R+r.4.圆的切线垂直于过切点的半径;经过直径的一端,并且垂直于这条直径的直线是圆的切线.5.从圆外一点可以向圆引 2 条切线, 切线长 相等,这点与圆心之间的连线 平分 这两条切线的夹角。
人教版九年级数学中考复习圆(含答案)

人教版九年级数学中考复习圆一、选择题(本大题共10小题,每小题4分,满分40分)1.如图,四边形ABCD是☉O的内接正方形,P是CD上不同于点C的任意一点,则∠BPC的大小是()A.22.5°B.30°C.45°D.50°2.如图,AB为☉O的直径,AB=30,点C在☉O上,∠A=24°,则AC的长为()A.9πB.10πC.11πD.12π3.如图,已知☉O为四边形ABCD的外接圆,O为圆心.若∠BCD=120°,AB=AD=2,则☉O的半径长为()A.3√22B.√62C.32D.2√334.在平面直角坐标系中,圆心为坐标原点,☉O的半径为10,则点P(-8,6)与☉O的位置关系为()A.点P在☉O上B.点P在☉O外C.点P在☉O内D.无法确定5.如图,点A,B,C在半径为6的☉O上,AB的长为2π,则∠ACB的大小是()A.20°B.30°C.45°D.60°6.在平面直角坐标系内,以原点O 为圆心,1为半径作圆,点P 在直线y =√3x +2√3上运动,过点P 作该圆的一条切线,切点为A ,则PA 的最小值为( ) A.3 B.2 C.√3 D.√27.如图,正六边形ABCDEF 的边长为2,分别以点A ,D 为圆心,以AB ,DC 为半径作扇形ABF ,扇形DCE.则图中阴影部分的面积是( )A.6√3-43πB.6√3-83πC.12√3-43πD.12√3-83π8.如图,半圆O 的直径AB =10 cm,弦AC =6 cm,D 是BC的中点,则弦AD 的长为( )A.4 cmB.3√5 cmC.4√5 cmD.5√5 cm9.以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( ) A.√28B.√34C.√24D.√3810.如图,AB 是☉O 的直径,C ,D 是☉O 上的点,且O C∥BD,A D 分别与BC ,OC 相交于点E ,F ,则下列结论:①AD ⊥BD ;②∠AOC =∠AEC ;③CB 平分∠ABD ;④AF =DF ;⑤BD =2OF ;⑥△CEF ≌△BED.其中结论一定成立的是( ) A.②④⑤⑥ B.①③⑤⑥ C.②③④⑥D.①③④⑤二、填空题(本大题共4小题,每小题5分,满分20分)11.如图,AB 为☉O 的直径,点C 在☉O 上,且OC ⊥AB ,过点C 的弦CD 与线段OB 相交于点E ,满足∠AEC =65°,连接AD ,则∠BAD = °.x-3交x轴于点A,交y轴于点B,P是x轴上一动点,以点P为圆心,以1个12.如图,直线y=-34单位长度为半径作☉P,当☉P与直线AB相切时,点P的坐标是.13.如图,在Rt△OAB中,∠AOB=45°,AB=2,将Rt△OAB绕点O顺时针旋转90°得到Rt△OCD,则AB扫过的阴影部分的面积为.14.如图,在一个圆柱形铁桶内底面的点A处有一只飞虫,在其上边沿的点B处有一面包残渣.cm,铁桶的底面直径为40 cm,桶高已知C是点B正下方的桶内底面上一点,劣弧AC的长为40π360 cm,则该飞虫从点A到达点B的最短路径为 cm.三、(本大题共2小题,每小题8分,满分16分)15.如图,AB,CD是☉O的直径,弦CE∥AB,CE所对的圆心角的度数为50°,求∠AOC的度数.16.如图,已知AB是☉O的直径,点C,D在☉O上,∠D=60°且AB=6,过点O作OE⊥AC,垂足为E.(1)求OE的长;(2)若OE的延长线交☉O于点F,求阴影部分的面积S.四、(本大题共2小题,每小题8分,满分16分)17.如图,四边形ABCD是☉O的内接四边形,DB平分∠ADC,连接OC,OC⊥BD.(1)求证:AB=CD;(2)若∠A等于66°,求∠ADB的度数.18.如图,☉O为△ABC的内切圆,∠ACB=90°,AO的延长线交BC于点D,AC=4,CD=2,求☉O的半径.五、(本大题共2小题,每小题10分,满分20分)19.如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作☉O,分别与AC,BC相交于点M,N.(1)过点N作☉O的切线NE与AB相交于点E,求证:NE⊥AB;(2)连接MD,求证:MD=NB.20.已知☉O是△ABC的外接圆,∠CAD=∠ABC.(1)如图1,试判断直线AD与☉O的位置关系,并说明理由;(2)如图2,将直线AD沿直线AC翻折后交☉O于点E,连接OA,OE,CE.若∠ABC=30°,求证:四边形ACEO是菱形.六、(本题满分12分)21.如图,已知平面直角坐标系中一条圆弧经过正方形网格的格点A,B,C.(1)用直尺画出该圆弧所在圆的圆心M的位置;(2)若点A的坐标为(0,4),点D的坐标为(7,0),试验证点D是否在经过点A,B,C的圆上;(3)在(2)的条件下,求证:直线CD是☉M的切线.七、(本题满分12分)22.如图,已知点A,B,C,D均在☉O上,AD∥BC,BD平分∠ABC,∠BAD=120°,四边形ABCD的周长为15.(1)求☉O的半径;(2)求图中阴影部分的面积.八、(本题满分14分)23.小平所在的学习小组发现,车辆转弯时,能否顺利通过直角弯道的标准是车辆是否可以行驶到和路的边界夹角是45°的位置(如图1中的位置).例如,图2是某巷子的俯视图,巷子路面宽4 m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE,CE的夹角都是45°时,连接EF,交CD 于点G,若GF的长度至少能达到车身宽度,则车辆能通过.(1)小平认为长8 m、宽3 m的消防车不能通过该直角转弯,请你帮他说明理由;(2)小平提出将拐弯处改为圆弧(MM'和NN'是以O为圆心,分别以OM和ON为半径的弧),长8 m、宽3 m的消防车就可以通过该弯道了,具体方案如图3,其中OM⊥OM',你能帮小平算出,ON 至少为多少时,这种消防车可以通过该巷子?答案一、选择题(本大题共10小题,每小题4分,满分40分)3.如图,四边形ABCD是☉O的内接正方形,P是CD上不同于点C的任意一点,则∠BPC的大小是A.22.5°B.30°C.45°D.50°4.如图,AB为☉O的直径,AB=30,点C在☉O上,∠A=24°,则AC的长为A.9πB.10πC.11πD.12π3.如图,已知☉O为四边形ABCD的外接圆,O为圆心.若∠BCD=120°,AB=AD=2,则☉O的半径长为A.3√22B.√62C.32D.2√334.在平面直角坐标系中,圆心为坐标原点,☉O的半径为10,则点P(-8,6)与☉O的位置关系为A.点P在☉O上B.点P在☉O外C.点P在☉O内D.无法确定5.如图,点A,B,C在半径为6的☉O上,AB的长为2π,则∠ACB的大小是A.20°B.30°C.45°D.60°6.在平面直角坐标系内,以原点O 为圆心,1为半径作圆,点P 在直线y =√3x +2√3上运动,过点P 作该圆的一条切线,切点为A ,则PA 的最小值为 A.3 B.2 C.√3 D.√27.如图,正六边形ABCDEF 的边长为2,分别以点A ,D 为圆心,以AB ,DC 为半径作扇形ABF ,扇形DCE.则图中阴影部分的面积是A.6√3-43πB.6√3-83πC.12√3-43πD.12√3-83π8.如图,半圆O 的直径AB =10 cm,弦AC =6 cm,D 是BC的中点,则弦AD 的长为A.4 cmB.3√5 cmC.4√5 cmD.5√5 cm提示:连接OC ,OD ,作DE ⊥AB 于点E ,OF ⊥AC 于点F.∴∠AFO =∠DEO =90°.∵CD=BD ,∴∠DOB =∠OAC =2∠BAD.∵OA =OD ,∴△AOF ≌△ODE (AAS),∴OE =AF =12AC =3 cm .在Rt△DOE 中,DE =√OD 2−OE 2=4 cm,在Rt△ADE 中,AD =√DE 2+AE 2=4√5 cm . 9.以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是 A.√28B.√34C.√24D.√3810.如图,AB是☉O的直径,C,D是☉O上的点,且O C∥BD,A D分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED.其中结论一定成立的是A.②④⑤⑥B.①③⑤⑥C.②③④⑥D.①③④⑤二、填空题(本大题共4小题,每小题5分,满分20分)11.如图,AB为☉O的直径,点C在☉O上,且OC⊥AB,过点C的弦CD与线段OB相交于点E,满足∠AEC=65°,连接AD,则∠BAD=20°.x-3交x轴于点A,交y轴于点B,P是x轴上一动点,以点P为圆心,以1个12.如图,直线y=-34,0).单位长度为半径作☉P,当☉P与直线AB相切时,点P的坐标是(−7313.如图,在Rt△OAB中,∠AOB=45°,AB=2,将Rt△OAB绕点O顺时针旋转90°得到Rt△OCD,则AB扫过的阴影部分的面积为π.14.如图,在一个圆柱形铁桶内底面的点A处有一只飞虫,在其上边沿的点B处有一面包残渣.cm,铁桶的底面直径为40 cm,桶高已知C是点B正下方的桶内底面上一点,劣弧AC的长为40π360 cm,则该飞虫从点A到达点B的最短路径为40√3 cm.提示:如图,连接AB,OC,OA,AC,作OH⊥AC于点H.设∠AOC=n°.∵AC的长=40π3,∴nπ·20180=40π3,∴n=120.∵OA=OC,OH⊥AC,∴∠COH=∠AOH=60°,CH=AH,∴AC=2CH=2·OC·sin 60°=2×20×√32=20√3(cm).在Rt△ABC中,AB=√BC2+AC2=√602+(20√3)2=40√3(cm),∴该飞虫从点A到达点B的最短路径为40√3 cm.三、(本大题共2小题,每小题8分,满分16分)15.如图,AB,CD是☉O的直径,弦CE∥AB,CE所对的圆心角的度数为50°,求∠AOC的度数.解:连接OE.由已知可得∠COE=50°.∵OC=OE,∴∠OCE=∠OEC=12(180°-50°)=65°.∵CE∥AB,∴∠AOC=∠OCE=65°.16.如图,已知AB是☉O的直径,点C,D在☉O上,∠D=60°且AB=6,过点O作OE⊥AC,垂足为E.(1)求OE的长;(2)若OE的延长线交☉O于点F,求阴影部分的面积S.解:(1)∵∠D =60°,∴∠B =60°.∵AB 是☉O 的直径,∴∠ACB =90°,∠CAB =30°. 又∵AB =6,∴OA =3. ∵OE ⊥AC ,∴OE =12OA =32.(2)连接OC.易得△COE ≌△AFE ,∠COF =60°, ∴阴影部分的面积S =S 扇形FOC =60π×32360=32π.四、(本大题共2小题,每小题8分,满分16分)17.如图,四边形ABCD 是☉O 的内接四边形,DB 平分∠ADC ,连接OC ,OC ⊥BD. (1)求证:AB =CD ;(2)若∠A 等于66°,求∠ADB 的度数.解:(1)∵DB 平分∠ADC ,∴AB =BC . ∵OC ⊥BD ,∴BC =CD . ∴AB=CD ,∴AB =CD. (2)∵四边形ABCD 是☉O 的内接四边形, ∴∠BCD =180°-∠A =114°. ∵BC=CD ,∴BC =CD , ∴∠BDC =12×(180°-114°)=33°. ∵DB 平分∠ADC , ∴∠ADB =∠BDC =33°.18.如图,☉O为△ABC的内切圆,∠ACB=90°,AO的延长线交BC于点D,AC=4,CD=2,求☉O的半径.解:设☉O与AC的切点为M,圆的半径为r.连接OM.∵OM⊥AC,∠ACB=90°,∴OM∥DC,∴∠MOC=∠DCO.又∵∠MCO=∠DCO,∴∠MOC=∠MCO,∴CM=OM=r,由条件易得△AOM∽△ADC,∴OMCD =AMAC,即r2=4−r4,解得r=43.∴☉O的半径是43.五、(本大题共2小题,每小题10分,满分20分)19.如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作☉O,分别与AC,BC相交于点M,N.(1)过点N作☉O的切线NE与AB相交于点E,求证:NE⊥AB;(2)连接MD,求证:MD=NB.证明:(1)连接ON.∵CD是Rt△ABC的斜边AB上的中线,∴AD=CD=DB,∴∠DCB=∠DBC.又∵OC=ON,∴∠DCB=∠ONC,∴∠ONC=∠DBC,∴ON∥AB.∵NE是☉O的切线,ON是☉O的半径,∴∠ONE=90°,∴∠NEB=90°,即NE⊥AB.(2)由(1)可知ON∥AB.BC.又∵OC=OD,∴CN=NB=12∵CD是☉O的直径,∴∠CMD=90°.又∵∠ACB=90°,∴MD∥BC.BC,∵D是AB的中点,∴MD=12∴MD=NB.20.已知☉O是△ABC的外接圆,∠CAD=∠ABC.(1)如图1,试判断直线AD与☉O的位置关系,并说明理由;(2)如图2,将直线AD沿直线AC翻折后交☉O于点E,连接OA,OE,CE.若∠ABC=30°,求证:四边形ACEO是菱形.解:(1)直线AD与☉O相切.理由:作直径AP,连接CP.∵∠APC=∠ABC,∠CAD=∠ABC,∴∠CAD=∠APC.∵AP是☉O的直径,∴∠ACP=90°,∴∠CAP+∠APC=90°,∴∠CAP+∠CAD=90°,即∠DAP=90°,∴AD⊥AP,∴直线AD与☉O相切.(2)连接OC.∵∠ABC=30°,∴∠CAE=∠CAD=∠ABC=30°,∴∠AOC=2∠ABC=60°,∠COE=2∠CAE=60°.∵OA=OC=OE,∴△AOC,△COE都是等边三角形,∴OA=AC=OC,OC=CE=EO,∴OA=AC=CE=EO,∴四边形ACEO是菱形.六、(本题满分12分)21.如图,已知平面直角坐标系中一条圆弧经过正方形网格的格点A,B,C.(1)用直尺画出该圆弧所在圆的圆心M的位置;(2)若点A的坐标为(0,4),点D的坐标为(7,0),试验证点D是否在经过点A,B,C的圆上;(3)在(2)的条件下,求证:直线CD是☉M的切线.解:(1)图略.(2)由点A(0,4),可得小正方形的边长为1,从而点B(4,4),C(6,2),M(2,0),则圆弧所在圆的半径为√22+42=2√5,点D到点M的距离为7-2=5>2√5,所以点D不在经过点A,B,C的圆上.(3)设过点C与x轴垂直的直线与x轴的交点为E,连接MC,作直线CD.由(2)知小正方形的边长为1,所以CE=2,ME=4,ED=1,MD=5.在Rt△CEM中,MC2=ME2+CE2=42+22=20,在Rt△CED中,CD2=ED2+CE2=12+22=5,所以MD2=MC2+CD2,所以∠MCD=90°.因为MC为☉M的半径,所以直线CD是☉M的切线.七、(本题满分12分)22.如图,已知点A,B,C,D均在☉O上,AD∥BC,BD平分∠ABC,∠BAD=120°,四边形ABCD的周长为15.(1)求☉O的半径;(2)求图中阴影部分的面积.解:(1)∵AD∥BC,∠BAD=120°,∴∠ABC=60°.又∵BD 平分∠ABC ,AD ∥BC , ∴∠ABD =∠DBC =∠ADB =30°, ∴AB=AD =CD ,∴AB =AD =CD. ∵四边形ABCD 的周长为15,∴BC +3CD =15. 又∵在Rt△BDC 中,BC =2CD ,∴BC +32BC =15,∴BC =6, ∴☉O 的半径为3.(2)连接OA ,OD ,过点O 作OE ⊥AD 于点E. 在Rt△AOE 中,∠AOE =30°, ∴OE =OA ·cos 30°=3√32, ∴S △AOD =12AD ·OE =12×3×3√32=9√34, ∴S 阴影=S扇形AOD -S △AOD =60π×32360-9√34=6π−9√34. 八、(本题满分14分)23.小平所在的学习小组发现,车辆转弯时,能否顺利通过直角弯道的标准是车辆是否可以行驶到和路的边界夹角是45°的位置(如图1中的位置).例如,图2是某巷子的俯视图,巷子路面宽4 m,转弯处为直角,车辆的车身为矩形ABCD ,CD 与DE ,CE 的夹角都是45°时,连接EF ,交CD 于点G ,若GF 的长度至少能达到车身宽度,则车辆能通过.(1)小平认为长8 m 、宽3 m 的消防车不能通过该直角转弯,请你帮他说明理由;(2)小平提出将拐弯处改为圆弧(MM'和NN '是以O 为圆心,分别以OM 和ON 为半径的弧),长8 m 、宽3 m 的消防车就可以通过该弯道了,具体方案如图3,其中OM ⊥OM',你能帮小平算出,ON 至少为多少时,这种消防车可以通过该巷子?解:(1)作FH ⊥EC ,垂足为H.∵FH =EH =4,∴EF =4√2,且∠GEC =45°. ∵GC =4,∴GE =GC =4,∴GF=4√2-4<3,即GF的长度未达到车身宽度,∴消防车不能通过该直角转弯.(2)若点C,D分别与点M',M重合,则△OGM为等腰直角三角形,如图所示.∴OG=4,OM=4√2,∴OF=ON=OM-MN=4√2-4,∴FG=8-4√2<3,∴点C,D在MM'上.设ON=x,连接OC.在Rt△OCG中,OG=x+3,OC=x+4,CG=4,由勾股定理,得OG2+CG2=OC2,即(x+3)2+42=(x+4)2,解得x=4.5.答:ON至少为4.5 m时,这种消防车可以通过该巷子.。
数学初三圆的试题及答案

数学初三圆的试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是圆的标准方程?A. (x-a)²+(y-b)²=r²B. x²+y²=rC. x²+y²=r²D. (x-a)²+(y-b)²=r答案:A2. 圆心为(2,3),半径为5的圆的方程是什么?A. (x-2)²+(y-3)²=25B. (x-2)²+(y-3)²=5C. x²+y²=25D. x²+y²=5答案:A3. 已知圆C的圆心为(1,1),半径为2,点P(4,3)在圆C上,那么点P 到圆心的距离是多少?A. 2B. 3C. 4D. 5答案:B4. 圆的直径是10,那么它的半径是多少?A. 5B. 10C. 20D. 15答案:A5. 圆心在原点,半径为3的圆的方程是?A. x²+y²=9B. (x-0)²+(y-0)²=3C. x²+y²=3D. (x-3)²+(y-3)²=9答案:A6. 圆的周长公式是?A. C=2πrB. C=πrC. C=2rD. C=r答案:A7. 圆的面积公式是?A. A=πr²B. A=2πrC. A=r²D. A=2r答案:A8. 圆的切线与半径垂直,那么切线与圆心的距离是多少?A. rB. 2rC. πrD. 0答案:A9. 圆的弧长公式是?A. L=rθB. L=2πrC. L=rθ/180D. L=2πrθ/360答案:D10. 圆的扇形面积公式是?A. S=1/2r²θB. S=1/2r²C. S=rθD. S=2πrθ/360答案:D二、填空题(每题4分,共20分)1. 圆心在(-2,4),半径为3的圆的方程是:(x+2)²+(y-4)²=________。
九年级中考总复习《圆》专题培训学校学生用

1九年级中考总复习《圆》专题一、经典中考填空题1. (2012 陕西中考)如图,在半径为 5 的圆 O 中,AB ,CD 是互相垂直的两条弦,垂足为 P , 且 AB =CD =8,则 OP 的长为 。
2.(2012 甘肃兰州中考改编)已知两圆的直径分别是方程x 2 - 6 x + 8 = 0 的两根,两圆圆心距为 3cm ,则这两个圆的位置关系是 。
3.(2012 福建泉州中考)如图,O 是△ABC 内心,过点 O 作 EF//AB,与 AC,BC 分别交于点 E 、F ,则线段 EF 、AE 、BF 的数量关系为。
4.(2012 湖北黄石中考)如图所示,直线 CD 与以线段 AB 为直径的圆相切于点 D 并交 BA 的延长线于点 C ,且 AB=2,AD=1,P 点在切线 CD 上移动。
当∠APB 的度数最大时,则∠APB 的度数为 。
注意:P 与 D 重合时,E 、P 、D 重合,∠APB 最大,等于 90°,此时∠ABP=30°.5.(2012 安徽中考)如图,点 A 、B 、C 、D 在⊙O 上,O 点在∠D 的内部,四边形 OABC 为平 行四边形,则∠OAD+∠OCD= 。
填空第 1 题填空第 3 题填空第 4 题填空第 5 题6.(2012 浙江宁波中考)如图,△ABC 中,∠BAC=60°,∠ABC=45°,AB= 2 2 ,D 是线段BC 上的一个动点,以 AD 为直径画⊙O 分别交 AB ,AC 于 E 、F,连结 EF,则线段 EF 长度的最小 值为 。
填空第 7 题填空第 6 题填空第 8 题7.(2012 甘肃兰州中考)如图,两个同心圆,大圆的半径为5cm ,小圆的半径为 3,若大圆 的弦 AB 与小圆相交,则弦 AB 的取值范围是 。
8.(2012 天津中考)如图,已知正方形ABCD 的边长为 1,以顶点 A 、B 为圆心,1 为半径的 两弧交于点 E ,以顶点 C 、D 为圆心,1 为半径的两弧交于点 F ,则 EF 的长 。
北师大版九年级数学中考总复习九:圆的专题辅导
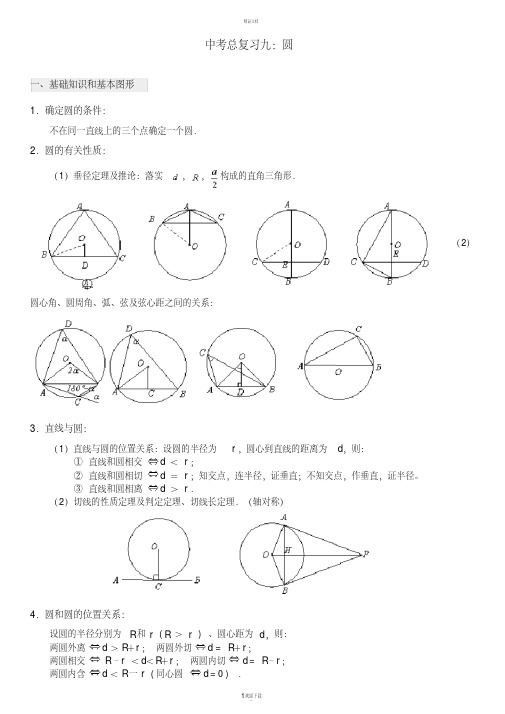
中考总复习九:圆一、基础知识和基本图形1.确定圆的条件:不在同一直线上的三个点确定一个圆.2.圆的有关性质:(1)垂径定理及推论:落实,,构成的直角三角形.(2)圆心角、圆周角、弧、弦及弦心距之间的关系:3.直线与圆:(1)直线与圆的位置关系:设圆的半径为r,圆心到直线的距离为d,则:①直线和圆相交d<r;②直线和圆相切 d =r;知交点,连半径,证垂直;不知交点,作垂直,证半径。
③直线和圆相离 d >r.(2)切线的性质定理及判定定理、切线长定理.(轴对称)4.圆和圆的位置关系:设圆的半径分别为R和r (R >r ) 、圆心距为d,则:两圆外离d>R+r;两圆外切d = R+r;两圆相交 R–r<d<R+r;两圆内切d = R–r;两圆内含d<R一r (同心圆d = 0 ).5.有关圆的计算(1)扇形弧长和扇形面积.(2)三角形的内切圆.(3)圆锥的侧面展开.(4)有关阴影面积.(割补法)二、例题1.如图,⊙O是△ABC的外接圆,⊙O的半径R=2,sin B=,则弦AC的长为______________.分析:如何利用好圆的半径,如何把角B放到一个直角三角形中去运用三角函数值,这就需要作直径,并构造直径所对的圆周角,这样就把角B转化到直角三角形中了。
解答:作直径AO,交圆O于D,连CD利用勾股定理求得: AC=32.如图,分别是的切线,为切点,是⊙O的直径,已知,的度数为().A.B.C.D.分析:本题利用圆心角与圆周角的关系,以及切线长定理解决解答:D3.如图,梯形中,,,,,以为圆心在梯形内画出一个最大的扇形(图中阴影部分)的面积是_____________.分析:要求扇形面积,关键是确定半径和圆心角解答:过A作AE⊥BC于E,可求得∠B为60度,AE=,所以最大扇形面积为4。
4.在中,,.如果圆的半径为,且经过点,那么线段的长等于______________.分析:此题应分类讨论,考虑圆心O在BC上和在BC下两种情况解答:5或35.如图,已知:△ABC是⊙O的内接三角形,AD⊥BC于D点,且AC=5,DC=3,AB=,则⊙O 的直径等于______________.分析:先解三角形,求得∠B为45度,再构造直径AO解答:作直径AO,交圆O于E,连CE可求得∠E=∠B=45度,所以直径AE=6.如图,已知大半圆⊙与小半圆⊙相内切于点B,大半圆的弦MN切小半圆于点D,若MN∥AB,当MN=4时,则此图中的阴影部分的面积是_____________.分析:此题需用到垂径定理和整体带入解答:连接,过作⊥MN于E阴影面积为27.已知:如图,△OBC内接于圆,圆与直角坐标系的x、y轴交于B、A两点,若∠BOC=45°,∠OBC=75°,A点坐标为(0,2).则点B点的坐标为___________;BC的长=__________.解答:连AB、AC,可求得B(),BC=8.如图,⊙O的半径为3cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以cm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为_______s时,BP 与⊙O相切.解答:要考虑到两种情况,5或19.已知:点F在线段AB上,BF为⊙O的直径,点D在⊙O上,BC AD 于点C,BD平分.(1)求证:AC是⊙O的切线;(2)若AD=,AF=,求CD的长.解答:(1)连OD,证明OD//BC(2)利用方程和相似,求得CD=10.如图,AB、CD是⊙O的两条弦,它们相交于点P,连接AD、BD.已知AD=BD=4,PC=6,求CD的长.解答:连AC,利用∽,求得CD=811.如图,点I是△ABC的内心,线段A I的延长线交△ABC的外接圆于点D,交BC边于点E.(1)求证:ID=BD;(2)设△ABC的外接圆的半径为5,I D=6,,,当点A在优弧上运动时,求与的函数关系式,并指出自变量的取值范围.解答:(1)提示:证∠IBD=∠BID(2)(6)12.如图,点是半圆的半径上的动点,作于.点是半圆上位于左侧的点,连结交线段于,且.(1)求证:是⊙O的切线.(2)若⊙O的半径为,,设.①求关于的函数关系式.②当时,求的值.解答:(1)连DO,证OD⊥DP;(2)①连PO,;②,提示:在三角形EBC中求13.二次函数的图象与轴相交于点A、B两点(点A在点B的左边),与轴交于点C,点M是它的顶点.(1)求证:以A为圆心,直径为5的圆与直线CM相离;(2)将(1)中的⊙A的圆心在轴上移动,平移多少个单位,使⊙A与直线CM相切.解答:(1),(2)个单位.。
九年级中考数学考点分类复习——圆

中考数学考点分类复习——圆一、选择题1.下列三个命题:①圆既是轴对称图形,又是中心对称图形;②垂直于弦的直径平分这条弦;③相等圆心角所对的弧相等.其中是真命题的是()A.①②B.②③C.①③D.①②③2.已知⊙O的半径为5,圆心O到点P的距离为4,则点P与⊙O的位置关系是( )A.点P在⊙O内B.点P的⊙O上C.点P在⊙O外D.点P在⊙O上或⊙O外3.如图,⊙O的直径AB垂直于弦CD,∠CAB=36°,则∠BCD的大小是( )A.18° B.36° C.54° D.72°4.若等腰直角三角形的外接圆半径的长为2,则其内切圆半径的长为( )A. 2B.22-2C.2- 2D.2-15.如图,PA,PB为⊙O的切线,A,B分别为切点,∠APB=60∘,点P到圆心O的距离OP=2,则⊙O的半径为( )A.12B.1 C.32D.26.如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C.若∠ABO=20°,则∠C 的度数是( )A.70°B.50°C.45°D.20°7.如图,有一半径是1米的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形,用此扇形铁皮围成一个圆锥,该圆锥的底面圆的半径长为( )A.2米B.22米 C.24米 D.28米8. 如图,△ABC是☉O的内接三角形,下列选项中,能使过点A的直线EF与☉O相切于点A的条件是()A.∠EAB=∠CB.∠B=90∘C.EF⊥ACD.AC是☉O的直径9.如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( )A.10B.8 2C.413D.24110.如图,P 是⊙O 外一点,PA 、PB 分别和⊙O 切于A 、B 两点,C 是AB ︵上任意一点,过C作⊙O 的切线分别交PA 、PB 于D 、E .若△PDE 的周长为12,则PA 的长为( )A .12B .6C .8D .411.如图,AB 与⊙O 相切于点C ,OA =OB ,⊙O 的直径为6 cm ,AB =6 3 cm ,则阴影部分的面积为( )A.()93-π cm 2B.()93-2π cm 2C.()93-3π cm 2D.()93-4π cm 212. 一圆形玻璃被打碎后,其中四块碎片如图所示,若选择其中一块碎片带到商店,配制与原来大小一样的圆形玻璃,选择的是( )A.①B.③C.②D.④13.如图,已知⊙O 的半径是2,点A ,B ,C 在⊙O 上,若四边形OABC 为菱形,则图中阴影部分面积为( )A.23π-2 3B.23π- 3C.43π-2 3D.43π- 3 14. 如图,直线l 1 // l 2,⊙O 与l 1和l 2分别相切于点A 和点B .点M 和点N 分别是l 1和l 2上的动点,MN 沿l 1和l 2平移.⊙O 的半径为1,∠1=60∘.下列结论错误的是( )A.MN =4√33B.l 1和l 2的距离为2C.若∠MON =90∘,则MN 与⊙O 相切D.若MN 与⊙O 相切,则AM =√315.如图,⊙O 的半径为3,四边形ABCD 内接于⊙O ,连接OB ,OD.若∠BOD =∠BCD ,则BD ︵的长为( )A.πB.32π C.2π D.3π 二.填空题16.在Rt △ABC 中,∠C =90°,CA =8,CB =6,则△ABC 内切圆的周长为______.17. △ABC 中,∠C =90∘,AB =4cm ,BC =2cm ,以点A 为圆心,以3.4cm 的长为半径画圆,则点C 在⊙O ________,点B 在⊙O ________.18.扇形的半径是9 cm ,弧长是3π cm ,则此扇形的圆心角为 度.19.如图,已知⊙O 的半径为2,△ABC 内接于⊙O ,∠ACB =135°,则AB =______.20.如图,正六边形ABCDEF 内接于⊙O ,则∠ADF 的度数为 .21.如图,在圆O 中,AB 为直径,AD 为弦,过点B 的切线与AD 的延长线交于点C ,AD =DC ,则∠C =______度.22.如图,PA ,PB 分别与⊙O 相切于点A ,B ,⊙O 的切线EF 分别交PA ,PB 于点E ,F ,切点C 在AB ︵上.若PA 的长为2,则△PEF 的周长是 .23.如图,点A ,B ,C 均在6×6的正方形网格格点上,过A ,B ,C 三点的外接圆除经过A ,B ,C 三点外还能经过的格点数为 .24.如图,AB 是⊙O 的直径,点C 在⊙O 上,过点C 的切线与BA 的延长线交于点D ,点E 在弧BC 上(不与点B 、C 重合),连结BE 、CE .若∠D =40°,则∠BEC =_______度.25.如图,在平面直角坐标系中有一正方形AOBC ,反比例函数y =k x经过正方形AOBC 对角线的交点,半径为6-32的圆内切于△ABC ,则k 的值为 .26. 如图,与相切,切点为,交于点,点是优弧上一点,若,则的度数为________.27. 如图,在⊙O 中,弦AB 、CD 相交于点E ,∠BDC =45∘,∠BED =95∘,则∠C 的度数为________度.28.如图,⊙O 是△ABC 的内切圆,切点分别是D 、E 、F .已知∠A =110°,∠C =30°,则∠DFE 的度数是______.29. 如图,正方形ABCD内接于⊙O,E为DC的中点,直线BE交⊙O于点F,若⊙O的半径为√2,则BF的长为________.30. 如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧DE交AB于E点,若AB=8cm,则图中阴影部分的面积为________cm2.(取准确值)三、解答题31.如图所示,CD是△ABC的中线,AB=2CD,∠B=60∘.求证:△ABC的外接圆的半径为CB.32. 如图所示,AB是⊙O的一条直径,CD是⊙O的一条弦,延长BA与DC的延长线相交于P点,若AB=2PC,∠P=36∘,求∠COD的度数.33.如图,在△ABC中,以AC为直径的⊙O分别交AB,BC于点D,E,连接DE,AD=BD,∠ADE=120°.(1)试判断△ABC的形状,并说明理由;(2)若AC=2,求图中阴影部分的面积.34.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠BCD.(1)求证:CB∥PD;(2)若BC=3,sin∠BPD=35,求⊙O的直径.35.如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,DE⊥AC,垂足为E.(1)判断DE与⊙O的位置关系,并证明你的结论;(2)如果⊙O的直径为9,cos B=13,求DE的长36.如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形,过A 点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于点G.(1)求证:EF是⊙O的切线;(2)求AE的长.37.如图, Rt △ABC 中,∠ABC=90°,以AB 为直径的⊙O 交AC 于点D ,过点D 的切线交BC 于E .(1)求证:12DE BC =;(2)若tanC=25,DE=2,求AD 的长.38.已知,在四边形ABCD 中,E 是对角线AC 上一点,ED =EC ,以AE 为直径的⊙O 与边CD 相切于D , 点B 在⊙O 上,连结OB .(1)求证:DE =OE ;(2)若AB ∥CD ,求证:四边形ABCD 是菱形.39.如图,在ABC ∆中,AB AC =,以AB 为直径作O 交BC 于点D ,过点D 作O 的切线DE 交AC 于点E ,交AB 延长线于点F .(1)求证:DE AC ⊥;(2)若10,8AB AE ==,求BF 的长.40. 如图,正六边形ABCDEF 内接于⊙O ,BE 是⊙O 的直径,连接BF ,延长BA ,过F 作FG ⊥BA ,垂足为G .(1)求证:FG 是⊙O 的切线;(2)已知FG =2√3,求图中阴影部分的面积.41.如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E ,点P 在⊙O 上,PB 与CD 交于点F ,∠PBC=∠C .(1)求证:CB ∥PD ;(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.42.如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.(1)求证:PD是⊙O的切线;(2)求证:△PBD∽△DCA;(3)当AB=6,AC=8时,求线段PB的长.AH ,以点O为圆心,OA的长为半径作⊙O,过43.如图,点O是线段AH上一点,3点H作AH的垂线交⊙O于C,N两点,点B在线段CN的延长线上,连接AB交⊙O于点M,以AB,BC为边作ABCD.(1)求证:AD 是⊙O 的切线;(2)若13OH AH =,求四边形AHCD 与⊙O 重叠部分的面积; (3)若13NH AH =,54BN =,连接MN ,求OH 和MN 的长.44.已知ABC 内接于O ,BAC ∠的平分线交O 于点D ,连接DB ,DC .(1)如图①,当120BAC ∠=时,请直接写出线段AB ,AC ,AD 之间满足的等量关系式: ;(2)如图②,当90BAC ∠=时,试探究线段AB ,AC ,AD 之间满足的等量关系,并证明你的结论;(3)如图③,若BC=5,BD=4,求AD AB AC+ 的值.。
九年级数学专题复习之《圆》的综合训练卷

九年级数学专题复习之《圆》的综合训练卷一.选择题(共10小题)1.如图,矩形ABCD中.AB=3,BC=6,以点B为圆心、BA为半径画弧,交BC于点E,以点D为圆心、DA为半径画弧,交BC于点F,则阴影部分的面积为()A.B.6π﹣C.D.2.如图,点C是半圆O的中点,AB是直径,CF⊥弦AD于点E,交AB于点F,若CE=1,EF=,则BF的长为()A.B.1C.D.3.已知⊙O的半径为2,A为圆内一定点,AO=1.P为圆上一动点,以AP为边作等腰△APG,AP=PG,∠APG=120°,OG的最大值为()A.1+B.1+2C.2+D.2﹣14.如图,⊙O中,弦AB⊥CD,垂足为E,F为的中点,连接AF、BF、AC,AF交CD 于M,过F作FH⊥AC,垂足为G,以下结论:①=;②HC=BF:③MF=FC:④+=+,其中成立的个数是()A.1个B.2个C.3个D.4个5.如图,AB是⊙O的直径,AB=10,P是半径OA上的一动点,PC⊥AB交⊙O于点C,在半径OB上取点Q,使得OQ=CP,DQ⊥AB交⊙O于点D,点C,D位于AB两侧,连接CD交AB于点F,点P从点A出发沿AO向终点O运动,在整个运动过程中,△CFP与△DFQ的面积和的变化情况是()A.一直减小B.一直不变C.先变大后变小D.先变小后变大6.如图,AB是半圆O的直径,点D在半圆O上,AB=2,AD=10,C是弧BD上的一个动点,连接AC,过D点作DH⊥AC于H,连接BH,在点C移动的过程中,BH的最小值是()A.5B.6C.7D.87.如图,已知OA=6,OB=8,BC=2,⊙P与OB、AB均相切,点P是线段AC与抛物线y=ax2的交点,则a的值为()A.4B.C.D.58.如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π,MN=1,则△AMN周长的最小值是()A.3B.4C.5D.69.如图,已知在矩形ABCD中,AB=1,BC=,点P是AD边上的一个动点,连结BP,点C关于直线BP的对称点为C1,当点P运动时,点C1也随之运动.若点P从点A运动到点D,则线段CC1扫过的区域的面积是()A.πB.π+C.D.2π10.如图,半径为1的⊙O与直线l相切于点A,C为⊙O上的一点,CB⊥l于点B,则AB+BC 的最大值是()A.2B.C.D.二.填空题(共10小题)11.已知如图,AB=4,AC=2,∠BAC=60°,所在圆的圆心是点O,∠BOC=60°,分别在、线段AB和AC上选取点P、E、F,则PE+EF+FP的最小值为.12.已知圆锥的侧面积是40π,底面圆直径为2,则圆锥的母线长是.13.如图,在Rt△ABC中,∠ACB=90°,AC=10,BC=8,点D是BC上一点,BC=3CD,点P是线段AC上一个动点,以PD为直径作⊙O,点M为的中点,连接AM,则AM 的最小值为.14.如图,等边△ABC中,AB=2,点D是以A为圆心,半径为1的圆上一动点,连接CD,取CD的中点E,连接BE,则线段BE的最大值与最小值之和为.15.如图,AB是半圆O的直径,点C在半径OA上,过点C做CD⊥AB交半圆O于点D.以CD,CA为边分别向左、下作正方形CDEF,CAGH.过点B作GH的垂线与GH的延长线交于点I,M为HI的中点.记正方形CDEF,CAGH,四边形BCHI的面积分别为S1,S2,S3.(1)若AC:BC=2:3,则的值为;(2)若D,O,M在同条直线上,则的值为.16.如图,直线y=﹣x+m(m>0)与x轴、y轴分别交于点A,B,C是AB的中点,点D 在直线y=﹣2上,以CD为直径的圆与直线AB的另一交点为E,交y轴于点F,G,已知CE+DE=6,FG=2,则CD的长是.17.如图1,▱ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD上的一动点,设PB+ PD的值为a,如图2,⊙O是正方形ABCD的内切圆,AB=4,点P是⊙O上一个动点,设AP+DP的值为b,如图3,MN=4,∠M=75°,MG=3.点O是△MNG内一点,设点O到△MNG三个顶点的距离和的值为c,则a2+b2+c2的最小值为.18.如图,正六边形ABCDEF中,G,H分别是边AF和DE上的点,GF=AB=2,∠GCH =60°,则线段EH长.19.如图,边长为5的圆内接正方形ABCD中,P为CD的中点,连接AP并延长交圆于点E,则DE的长为.20.已知:如图,在矩形ABCD中,AB=6,BC=9,点E是对角线AC上的一点,经过C,D,E三点的⊙O与AD,BC分别交于点F,G,连接ED,EF,EG,延长GE交AD于点H.若当△HEF是等腰三角形时,CE的长为.三.解答题(共10小题)21.如图,O是△ABC的外心,I是△ABC的内心,连AI并延长交BC和⊙O于D、E两点.(1)求证:EB=EI;(2)若AB=4,AC=3,BE=2,求AI的长.22.如图,AB是⊙O的直径,P在AB的延长线上,PD与⊙O相切于点D,C在⊙O上,PC=PD.(1)求证:PC是⊙O的切线;(2)连接AC,若AC=PC,PB=1,求⊙O的半径.23.如图,钝角△ABC中,AB=AC,BC=2,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F.(1)求证:EF⊥AC.(2)连接DF,若∠ABC=30°,且DF∥BC,求⊙O的半径长.24.如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,CD=CE (1)求证:OA=OB;(2)已知AB=4 ,OA=4,求阴影部分的面积.25.已知⊙O为△ABC的外接圆,直线l与⊙O相切于点P,且l∥BC.(1)连接PO,并延长交⊙O于点D,连接AD.证明:AD平分∠BAC;(2)在(1)的条件下,AD交BC于点E,连接CD.若DE=2,AE=6.试求CD的长.26.如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°(1)求∠B的大小;(2)已知圆心O到BD的距离为3,求AD的长.27.如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,连接MB.(1)若BE=8,求⊙O的半径;(2)若∠DMB=∠D,求线段OE的长.28.如图,在Rt△ABC中,∠C=90°,AE平分∠BAC交BC于点E,点D在AB上,DE⊥AE,⊙O是Rt△ADE的外接圆,交AC于点F.(1)求证:BC是⊙O的切线;(2)若⊙O的半径为5,AC=8,求S△BDE.29.如图,在△ABC中,BE是∠ABC的平分线,∠C=90°,点D在AB边上,以DB为直径的半圆O经过点E.(1)求证:AC是⊙O的切线.(2)若BC=3,⊙O的半径为2,求BE的长.30.如图,以Rt△ABC的直角边AB为直径的⊙O交斜边AC于点D,过点D作⊙O的切线与BC交于点E,弦DM与AB垂直,垂足为H.(1)求证:E为BC的中点;(2)若⊙O的面积为12π,两个三角形△AHD和△BMH的外接圆面积之比为3,求△DEC的内切圆面积S1和四边形OBED的外接圆面积S2的比.。
初三圆试题及答案数学

初三圆试题及答案数学初三数学圆的试题及答案如下:1. 已知圆的半径为5,求圆的面积。
答案:圆的面积公式为A=πr²,将半径r=5代入公式,得到A=π×5²=25π。
2. 若点A(3,4)在圆x²+y²=25内,则该圆的直径是多少?答案:点A(3,4)在圆x²+y²=25内,说明该点到圆心的距离小于半径。
圆的半径为5,因此直径为2×5=10。
3. 已知圆的直径为10,求该圆的周长。
答案:圆的周长公式为C=πd,将直径d=10代入公式,得到C=π×10=10π。
4. 已知圆的周长为6π,求该圆的半径。
答案:圆的周长公式为C=2πr,将周长C=6π代入公式,得到6π=2πr,解得r=3。
5. 已知圆的半径为4,求该圆的直径。
答案:圆的直径为半径的2倍,因此直径d=2×4=8。
6. 已知圆的直径为12,求该圆的面积。
答案:圆的半径为直径的一半,即r=12÷2=6。
将半径代入面积公式A=πr²,得到A=π×6²=36π。
7. 若点B(-2,-3)在圆x²+y²=16外,则该圆的半径是多少?答案:点B(-2,-3)在圆x²+y²=16外,说明该点到圆心的距离大于半径。
圆的半径为4,因此该点到圆心的距离大于4。
8. 已知圆的半径为5,求该圆的直径。
答案:圆的直径为半径的2倍,因此直径d=2×5=10。
9. 已知圆的周长为8π,求该圆的半径。
答案:圆的周长公式为C=2πr,将周长C=8π代入公式,得到8π=2πr,解得r=4。
10. 已知圆的直径为8,求该圆的面积。
答案:圆的半径为直径的一半,即r=8÷2=4。
将半径代入面积公式A=πr²,得到A=π×4²=16π。
以上就是初三数学圆的试题及答案,涵盖了圆的面积、周长、半径和直径等基本概念和计算方法。
初三圆的测试题及答案

初三圆的测试题及答案一、选择题(每题3分,共30分)1. 圆的半径为r,直径为d,则d与r的关系是()A. d=2rB. d=rC. d=r/2D. d=r^22. 圆的周长公式是()A. C=πdB. C=2πrC. C=πr^2D. C=2r3. 已知圆的半径为5cm,那么这个圆的面积是多少平方厘米?()A. 25πB. 50πC. 75πD. 100π4. 圆心到圆上任意一点的距离叫做()A. 半径B. 直径C. 周长D. 面积5. 圆的面积公式是()B. A=πr^2C. A=2πrD. A=r^26. 一个圆的直径增加一倍,那么它的面积增加()A. 一倍B. 两倍C. 四倍D. 八倍7. 圆的半径扩大到原来的2倍,周长扩大到原来的()A. 2倍B. 3倍C. 4倍D. 5倍8. 圆的周长和它的直径的比值叫做()A. 半径B. 直径C. 周长D. 圆周率9. 已知一个圆的周长是12.56cm,那么这个圆的半径是多少厘米?()A. 2B. 3C. 4D. 510. 圆的直径是半径的()B. 1/2倍C. 1/4倍D. 4倍二、填空题(每题2分,共20分)1. 圆的周长公式为C=2πr,其中π是一个常数,约等于______。
2. 圆的面积公式为A=πr^2,其中r表示圆的______。
3. 一个圆的半径为4cm,那么它的直径是_______cm。
4. 一个圆的直径为10cm,那么它的半径是_______cm。
5. 圆的周长和它的直径的比值是一个固定的数,这个数叫做______。
6. 如果一个圆的半径扩大到原来的3倍,那么它的面积扩大到原来的______倍。
7. 一个圆的周长是6.28cm,那么它的半径是_______cm。
8. 圆的直径是半径的______倍。
9. 圆的周长是它直径的______倍。
10. 一个圆的半径为6cm,那么它的面积是______平方厘米。
三、解答题(每题10分,共50分)1. 已知一个圆的半径为8cm,求这个圆的周长和面积。
(完整版)中考复习--圆专题(所有知识点和题型汇总,全)

《圆》题型分类资料一.圆的有关概念:1.下列说法:①直径是弦②弦是直径③半圆是弧,但弧不一定是半圆④长度相等的两条弧是等弧,正确的命题有()A. 1 个B.2 个C.3 个D.4 个2.下列命题是假命题的是()A.直径是圆最长的弦B.长度相等的弧是等弧C.在同圆或等圆中,相等的圆心角所对的弧也相等D.如果三角形一边的中线等于这条边的一半,那么这个三角形是直角三角形。
3.下列命题正确的是()A.三点确定一个圆B.长度相等的两条弧是等弧C.一个三角形有且只有一个外接圆D.一个圆只有一个外接三角形4.下列说法正确的是( )A.相等的圆周角所对的弧相等B.圆周角等于圆心角的一半C.长度相等的弧所对的圆周角相等5.下面四个图中的角,为圆心角的是( )D.直径所对的圆周角等于90°A.B.C.D.二.和圆有关的角:1.如图1,点O 是△ABC 的内心,∠A=50 ,则∠BOC=图1 图22.如图2,若AB 是⊙O 的直径,CD 是⊙O 的弦,∠ABD=58°,则∠BCD 的度数为( )A.116°B.64°C. 58°D.32°3.如图3,点O 为优弧AB 所在圆的圆心,∠AOC=108°,点D 在AB 的延长线上,BD=BC,则∠D 的度数为ADOO1 2CDC图 3图 44.如图 4,AB 、AC 是⊙O 的两条切线,切点分别为 B 、C ,D 是优弧 BC 上的一点,已知∠BAC =80°,那么∠BDC =度.5. 如图 5,在⊙O 中, BC 是直径,弦 BA ,CD 的延长线相交于点 P ,若∠P =50°,则∠AOD =.PCBAOBC图 5 图 66. 如图 6,A ,B ,C ,是⊙O 上的三个点,若∠AOC =110°,则∠ABC =°.7. 圆的内接四边形 ABCD 中,∠A :∠B :∠C =2:3:7,则∠D 的度数为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级数学中考专项 圆 一、选择题 1.(北京市西城区)如图,BC 是⊙O 的直径,P 是CB 延长线上一点,PA 切⊙O于点A ,如果PA =3,PB =1,那么∠APC 等于 ( )(A ) 15 (B ) 30 (C ) 45 (D ) 602.(北京市西城区)如果圆柱的高为20厘米,底面半径是高的41,那么这个圆柱的侧面积是 ( )(A )100π平方厘米 (B )200π平方厘米(C )500π平方厘米 (D )200平方厘米3.(北京市西城区)“圆材埋壁”是我国古代著名的数学菱《九章算术》中的一个问题,“今在圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表述是:“如图,CD 为⊙O 的直径,弦AB ⊥CD ,垂足为E ,CE =1寸,AB =寸,求直径CD 的长”.依题意,CD 长为 ( )(A )225寸 (B )13寸 (C )25寸 (D )26寸 4.(北京市朝阳区)已知:如图,⊙O 半径为5,PC 切⊙O 于点C ,PO 交⊙O 于点A ,PA =4,那么PC 的长等于 ( )(A )6 (B )25 (C )210 (D )2145.(北京市朝阳区)如果圆锥的侧面积为20π平方厘米,它的母线长为5厘米,那么此圆锥的底面半径的长等于 ( )(A )2厘米 (B )22厘米 (C )4厘米 (D )8厘米6.(天津市)相交两圆的公共弦长为16厘米,若两圆的半径长分别为10厘米和17厘米,则这两圆的圆心距为 ( )(A )7厘米 (B )16厘米 (C )21厘米 (D )27厘米7.(重庆市)如图,⊙O 为△ABC 的内切圆,∠C =90,AO 的延长线交BC 于点D ,AC =4,DC =1,,则⊙O 的半径等于 ( )(A )54 (B )45 (C )43 (D )65 8.(重庆市)一居民小区有一正多边形的活动场.为迎接“AAPP ”会议在重庆市的召开,小区管委会决定在这个多边形的每个顶点处修建一个半径为2米的扇形花台,花台都以多边形的顶点为圆心,比多边形的内角为圆心角,花台占地面积共为12π平方米.若每个花台的造价为400元,则建造这些花台共需资金 ( )(A )2400元 (B )2800元 (C )3200元 (D )3600元9.(河北省)如图,AB 是⊙O 直径,CD 是弦.若AB =10厘米,CD =8厘米,那么A 、B 两点到直线CD 的距离之和为 ( )(A )12厘米 (B )10厘米 (C )8厘米 (D )6厘米10.(河北省)某工件形状如图所示,圆弧BC 的度数为60,AB =6厘米,点B 到点C 的距离等于AB ,∠BAC = 30,则工件的面积等于 ( )(A )4π (B )6π (C )8π (D )10π11.(沈阳市)如图,PA 切⊙O 于点A ,PBC 是⊙O 的割线且过圆心,PA =4,PB =2,则⊙O 的半径等于 ( )(A )3 (B )4 (C )6 (D )812.(哈尔滨市)已知⊙O 的半径为35厘米,⊙O '的半径为5厘米.⊙O 与⊙O '相交于点D 、E .若两圆的公共弦DE 的长是6厘米(圆心O 、O '在公共弦DE 的两侧),则两圆的圆心距O O '的长为 ( )(A )2厘米 (B )10厘米 (C )2厘米或10厘米 (D )4厘米13.(陕西省)如图,两个等圆⊙O 和⊙O '的两条切线OA 、OB ,A 、B 是切点,则∠AOB 等于 ( )(A ) 30 (B ) 45 (C ) 60 (D )9014.(甘肃省)如图,AB 是⊙O 的直径,∠C = 30,则∠ABD = ( )(A ) 30 (B ) 40 (C ) 50 (D ) 6015.(甘肃省)弧长为6π的弧所对的圆心角为 60,则弧所在的圆的半径为( )(A )6 (B )62 (C )12 (D )1816.(甘肃省)如图,在△ABC 中,∠BAC = 90,AB =AC =2,以AB 为直径的圆交BC 于D ,则图中阴影部分的面积为 ( )(A )1 (B )2 (C )1+4π (D )2-4π 17.(宁夏回族自治区)已知圆的内接正六边形的周长为18,那么圆的面积为 ( )(A )18π (B )9π (C )6π (D )3π18.(山东省)如图,点P 是半径为5的⊙O 内一点,且OP =3,在过点P的所有弦中,长度为整数的弦一共有 ( )(A )2条 (B )3条 (C )4条 (D )5条19.(南京市)如图,正六边形ABCDEF 的边长的上a ,分别以C 、F 为圆心,a 为半径画弧,则图中阴影部分的面积是 ( )(A )261a π (B )231a π (C )232a π (D )234a π20.(杭州市)过⊙O 内一点M 的最长的弦长为6厘米,最短的弦长为4厘米,则OM 的长为 ( )(A )3厘米 (B )5厘米 (C )2厘米 (D )5厘米21.(安徽省)已知圆锥的底面半径是3,高是4,则这个圆锥侧面展开图的面积是 ( )(A )12π (B )15π (C )30π (D )24π22.(安微省)已知⊙O 的直径AB 与弦AC 的夹角为 30,过C 点的切线PC 与AB 延长线交P .PC =5,则⊙O 的半径为 ( )(A )335 (B )635 (C )10 (D )5 23.(福州市)如图:PA 切⊙O 于点A ,PBC 是⊙O 的一条割线,有PA=32,PB =BC ,那么BC 的长是 ( )(A )3 (B )32 (C )3 (D )3224.(河南省)如图,⊙A 、⊙B 、⊙C 、⊙D 、⊙E 相互外离,它们的半径都是1,顺次连结五个圆心得到五边形ABCDE ,则图中五个扇形(阴影部分)的面积之和是 ( )(A )π (B )1.5π (C )2π (D )2.5π25.(四川省)正六边形的半径为2厘米,那么它的周长为 ( )(A )6厘米 (B )12厘米 (C )24厘米 (D )122厘米26.(四川省)一个圆柱形油桶的底面直径为0.6米,高为1米,那么这个油桶的侧面积为 ( )(A )0.09π平方米 (B )0.3π平方米 (C )0.6平方米 (D )0.6π平方米27.(贵阳市)一个形如圆锥的冰淇淋纸筒,其底面直径为6厘米,母线长为5厘米,围成这样的冰淇淋纸筒所需纸片的面积是 ( )(A )66π平方厘米 (B )30π平方厘米 (C )28π平方厘米 (D )15π平方厘米28.(新疆乌鲁木齐)在半径为2的⊙O 中,圆心O 到弦AB 的距离为1,则弦AB 所对的圆心角的度数可以是 ( )(A ) 60 (B ) 90 (C ) 120 (D ) 15029.(新疆乌鲁木齐)将一张长80厘米、宽40厘米的矩形铁皮卷成一个高为40厘米的圆柱形水桶的侧面,(接口损耗不计),则桶底的面积为 ( )(A )π1600平方厘米 (B )1600π平方厘米(C )π6400平方厘米 (D )6400π平方厘米 30.(成都市)如图,已知AB 是⊙O 的直径,弦CD ⊥AB 于点P ,CD =10厘米,AP ∶PB =1∶5,那么⊙O 的半径是 ( )(A )6厘米 (B )53厘米 (C )8厘米 (D )35厘米31.(成都市)在Rt △ABC 中,已知AB =6,AC =8,∠A =90.如果把Rt △ABC 绕直线AC 旋转一周得到一个圆锥,其表面积为S 1;把Rt △ABC 绕直线AB 旋转一周得到另一个圆锥,其表面积为S 2,那么S 1∶S 2等于 ( )(A )2∶3 (B )3∶4 (C )4∶9 (D )5∶1232.(苏州市)如图,⊙O 的弦AB =8厘米,弦CD 平分AB 于点E .若CE =2厘米.ED 长为 ( )(A )8厘米 (B )6厘米 (C )4厘米 (D )2厘米 33.(苏州市)如图,四边形ABCD 内接于⊙O ,若∠BOD =160,则∠BCD = ( )(A ) 160 (B ) 100 (C ) 80 (D ) 2034.(镇江市)如图,正方形ABCD 内接于⊙O ,E 为DC 的中点,直线BE交⊙O 于点F .若⊙O 的半径为2,则BF 的长为 ( )(A )23 (B )22 (C )556 (D )554 35.(扬州市)如图,AB 是⊙O 的直径,∠ACD = 15,则∠BAD 的度数为 ( )(A ) 75 (B ) 72 (C ) 70 (D )6536.(扬州市)已知:点P 直线l 的距离为3,以点P 为圆心,r 为半径画圆,如果圆上有且只有两点到直线l 的距离均为2,则半径r 的取值范围是 ( )(A )r >1 (B )r >2 (C )2<r <3 (D )1<r <537.(绍兴市)边长为a 的正方边形的边心距为 ( )(A )a (B )23a (C )3a (D )2a 38.(绍兴市)如图,以圆柱的下底面为底面,上底面圆心为顶点的圆锥的母线长为4,高线长为3,则圆柱的侧面积为 ( )(A )30π (B )76π (C )20π (D )74π39.(昆明市)如图,扇形的半径OA =20厘米,∠AOB = 135,用它做成一个圆锥的侧面,则此圆锥底面的半径为 ( )(A )3.75厘米 (B )7.5厘米 (C )15厘米 (D )30厘米40.(昆明市)如图,正六边形ABCDEF 中.阴影部分面积为123平方厘米,则此正六边形的边长为 ( )(A )2厘米 (B )4厘米 (C )6厘米 (D )8厘米41.(温州市)已知扇形的弧长是2π厘米,半径为12厘米,则这个扇形的圆心角是 ( )(A ) 60 (B ) 45 (C ) 30 (D ) 2042.(温州市)圆锥的高线长是厘米,底面直径为12厘米,则这个圆锥的侧面积是 ( )(A )48π厘米 (B )24π13平方厘米(C )48π13平方厘米 (D )60π平方厘米43.(温州市)如图,AB 是⊙O 的直径,点P 在BA 的延长线上,PC是⊙O 的切线,C 为切点,PC =26,PA =4,则⊙O 的半径等于 ( )(A )1 (B )2 (C )23 (D )26 44.(常州市)已知圆柱的母线长为5厘米,表面积为28π平方厘米,则这个圆柱的底面半径是( ) (A )5厘米 (B )4厘米 (C )2厘米 (D )3厘米45.(常州市)半径相等的圆内接正三角形、正方形、正六边形的边长之比为 ( )(A )1∶2∶3 (B )3∶2∶1(C )3∶2∶1 (D )1∶2∶346.(广东省)如图,若四边形ABCD 是半径为1和⊙O 的内接正方形,则图中四个弓形(即四个阴影部分)的面积和为 ( )(A )(2π-2)厘米 (B )(2π-1)厘米(C )(π-2)厘米 (D )(π-1)厘米47.(武汉市)如图,已知圆心角∠BOC = 100,则圆周角∠BAC 的度数是( )(A ) 50 (B ) 100 (C ) 130 (D ) 20048.(武汉市)半径为5厘米的圆中,有一条长为6厘米的弦,则圆心到此弦的距离为 ( )(A )3厘米 (B )4厘米 (C )5厘米 (D )6厘米49.已知:Rt △ABC 中,∠C = 90,O 为斜边AB 上的一点,以O 为圆心的圆与边AC 、BC 分别相切于点E 、F ,若AC =1,BC =3,则⊙O 的半径为 ( )(A )21 (B )32 (C )43 (D )54 50.(武汉市)已知:如图,E 是相交两圆⊙M 和⊙O 的一个交点,且ME ⊥NE ,AB 为外公切线,切点分别为A 、B ,连结AE 、BE .则∠AEB 的度数为 ( )(A )145° (B )140° (C )135° (D )130°二、填空题1.(北京市东城区)如图,AB 、AC 是⊙O 的两条切线,切点分别为B 、C ,D 是优弧上的一点,已知∠BAC =80,那么∠BDC =__________度.2.(北京市东城区)在Rt △ABC 中,∠C =90,A B=3,BC =1,以AC 所在直线为轴旋转一周,所得圆锥的侧面展开图的面积是__________.3.(北京市海淀区)如果圆锥母线长为6厘米,那么这个圆锥的侧面积是_______平方厘米4.(北京市海淀区)一种圆状包装的保鲜膜,如图所示,其规格为“20厘米×60米”,经测量这筒保鲜膜的内径1ϕ、外径2ϕ的长分别为3.2厘米、4.0厘米,则该种保鲜膜的厚度约为_________厘米(π取3.14,结果保留两位有效数字).5.(上海市)两个点O 为圆心的同心圆中,大圆的弦AB 与小圆相切,如果AB 的长为24,大圆的半径OA 为13,那么小圆的半径为___________.6.(天津市)已知⊙O 中,两弦AB 与CD 相交于点E ,若E 为AB 的中点,CE ∶ED =1∶4,AB =4,则CD 的长等于___________.7.(重庆市)如图,AB 是⊙O 的直径,四边形ABCD 内接于⊙O ,,,的度数比为3∶2∶4,MN 是⊙O 的切线,C 是切点,则∠BCM 的度数为___________.8.(重庆市)如图,P 是⊙O 的直径AB 延长线上一点,PC 切⊙O于点C ,PC =6,BC ∶AC =1∶2,则AB 的长为___________.9.(重庆市)如图,四边形ABCD 内接于⊙O ,AD ∥BC ,=,若AD =4,BC =6,则四边形ABCD 的面积为__________.10.(山西省)若一个圆柱的侧面积等于两底面积的和,则它的高h 与底面半径r 的大小关系是__________.11.(沈阳市)要用圆形铁片截出边长为4厘米的正方形铁片,则选用的圆形铁片的直径最小要___________厘米.12.(沈阳市)圆内两条弦AB 和CD 相交于P 点,AB 长为7,AB 把CD 分成两部分的线段长分别为2和6,那么=__________.13.(沈阳市)△ABC 是半径为2厘米的圆内接三角形,若BC =23厘米,则∠A 的度数为________.14.(沈阳市)如图,已知OA 、OB 是⊙O 的半径,且OA =5,∠AOB =15 ,AC⊥OB 于C ,则图中阴影部分的面积(结果保留π)S =_________.15.(哈尔滨市)如图,圆内接正六边形ABCDEF 中,AC 、BF 交于点M .则ABM S △∶AFM S △=_________.16.(哈尔滨市)两圆外离,圆心距为25厘米,两圆周长分别为15π厘米和10π厘米.则其内公切线和连心线所夹的锐角等于__________度.17.(哈尔滨市)将两边长分别为4厘米和6厘米的矩形以其一边所在直线为轴旋转一周,所得圆柱体的表面积为_________平方厘米.18.(陕西省)如图,在⊙O 的内接四边形ABCD 中,∠BCD =130 ,则∠BOD的度数是________.19.(陕西省)已知⊙O 的半径为4厘米,以O 为圆心的小圆与⊙O 组成的圆环的面积等于小圆的面积,则这个小圆的半径是______厘米.20.(陕西省)如图,⊙O 1的半径O 1A 是⊙O 2的直径,C 是⊙O 1上的一点,O 1C 交⊙O 2于点B .若⊙O 1的半径等于5厘米,的长等于⊙O 1周长的101,则的长是_________. 21.(甘肃省)正三角形的内切圆与外接圆面积之比为_________.22.(甘肃省)如图,AB =8,AC =6,以AC 和BC 为直径作半圆,两圆的公切线MN 与AB 的延长线交于D ,则BD 的长为_________.23.(宁夏回族自治区)圆锥的母线长为5厘米,高为3厘米,在它的侧面展开图中,扇形的圆心角是_________度.24.(南京市)如图,AB 是⊙O 的直径,弦CD ⊥AB ,垂足是G ,F 是CG 的中点,延长AF 交⊙O 于E ,CF =2,AF =3,则EF 的长是_________.25.(福州市)在⊙O 中,直径AB =4厘米,弦CD ⊥AB 于E ,OE =3,则弦CD 的长为__________厘米.26.(福州市)若圆锥底面的直径为厘米,线线长为5厘米,则它的侧面积为__________平方厘米(结果保留π).27.(河南省)如图,AB 为⊙O 的直径,P 点在AB 的延长线上,PM 切⊙O 于M 点.若OA =a ,PM =3a ,那么△PMB 的周长的__________.28.(长沙市)在半径9厘米的圆中, 60的圆心角所对的弧长为__________厘米.29.(四川省)扇形的圆心角为120 ,弧长为6π厘米,那么这个扇形的面积为_________.30.(贵阳市)如果圆O 的直径为10厘米,弦AB 的长为6厘米,那么弦AB 的弦心距等于________厘米.31.(贵阳市)某种商品的商标图案如图所求(阴影部分),已知菱形ABCD的边长为4,∠A = 60,是以A 为圆心,AB 长为半径的弧,是以B 为圆心,BC 长为半径的弧,则该商标图案的面积为_________.32.(云南省)已知,一个直角三角形的两条直角边的长分别为3厘米、4厘米、以它的直角边所在直角线为轴旋转一周,所得圆锥的表面积是__________.33.(新疆乌鲁木齐)正六边形的边心距与半径的比值为_________.34.(新疆乌鲁木齐)如图,已知扇形AOB 的半径为12,OA ⊥OB ,C 为OA 上一点,以AC 为直径的半圆1O 和以OB 为直径的半圆2O 相切,则半圆1O 的半径为__________.35.(成都市)如图,PA、PB与⊙O分别相切于点A、点B,AC是⊙O的直径,PC交⊙O于点D.已60,AC=2,那么CD的长为________.知∠APB=36.(苏州市)底面半径为2厘米,高为3厘米的圆柱的体积为_________立方厘米(结果保留π).37.(扬州市)边长为2厘米的正六边形的外接圆半径是________厘米,内切圆半径是________厘米(结果保留根号).38.(绍兴市)如图,PT是⊙O的切线,T为切点,PB是⊙O的割线交⊙O于A、B两点,交弦CD于点M,已知:CM=10,MD=2,PA=MB=4,则PT的长等于__________.90,半径OA=1,C是线段AB39.(温州市)如图,扇形OAB中,∠AOB=的中点,CD∥OA,交于点D,则CD=________.40.(常州市)已知扇形的圆心角为150 ,它所对的弧长为20π厘米,则扇形的半径是________厘米,扇形的面积是__________平方厘米.41.(常州市)如图,AB是⊙O直径,CE切⊙O于点C,CD⊥AB,D为垂足,AB=12厘米,∠B=30 ,则∠ECB=__________ ;CD=_________厘米.42.(常州市)如图,DE是⊙O直径,弦AB⊥DE,垂足为C,若AB=6,CE=1,则CD=________,OC=_________.43.(常州市)如果把人的头顶和脚底分别看作一个点,把地球赤道作一个圆,那么身高压2米的汤姆沿着地球赤道环道环行一周,他的头顶比脚底多行________米.44.(海南省)已知:⊙O的半径为1,M为⊙O外的一点,MA切⊙O于点A,MA=1.若AB是⊙O 的弦,且AB=2,则MB的长度为_________.45.(武汉市)如果圆的半径为4厘米,那么它的周长为__________厘米.三、初三数学关于圆方面的习题1.(苏州市)已知:如图,△ABC 内接于⊙O ,过点B 作⊙O 的切线,交CA 的延长线于点E ,∠EBC =2∠C .①求证:AB =AC ; ②若tan ∠ABE =21,(ⅰ)求BCAB的值;(ⅱ)求当AC =2时,AE 的长.2.(广州市)如图,PA 为⊙O 的切线,A 为切点,⊙O 的割线PBC 过点O 与⊙O 分别交于B 、C ,PA =8cm ,PB =4cm ,求⊙O 的半径.3.(河北省)已知:如图,BC 是⊙O 的直径,AC 切⊙O 于点C ,AB 交⊙O 于点D ,若AD ︰DB =2︰3,AC =10,求sin B 的值.4.(北京市海淀区)如图,PC 为⊙O 的切线,C 为切点,PAB 是过O 的割线,CD ⊥AB 于点D ,若tan B =21,PC =10cm ,求三角形BCD 的面积.5.(宁夏回族自治区)如图,在两个半圆中,大圆的弦MN 与小圆相切,D 为切点,且MN ∥AB ,MN =a ,ON 、CD 分别为两圆的半径,求阴影部分的面积.6.(四川省)已知,如图,以△ABC 的边AB 作直径的⊙O ,分别并AC 、BC 于点D 、E ,弦FG ∥AB ,S △CDE ︰S △ABC =1︰4,DE =5cm ,FG =8cm ,求梯形AFGB 的面积.7.(贵阳市)如图所示:PA 为⊙O 的切线,A 为切点,PBC 是过点O 的割线,PA =10,PB =5,求:(1)⊙O 的面积(注:用含π的式子表示); (2)cos ∠BAP 的值.8(2011杭州模拟26)如图,⊙O 是Rt △ABC 的外接圆,∠ABC=90°,点P 是圆外一点,PA 切⊙O 于点A ,且PA=PB . (1)求证:PB 是⊙O 的切线;(2)已知PA=3,BC=1,求⊙O 的半径.9(2011年浙江仙居)(10分)如图,点D 在O ⊙的直径AB 的延长线上,点C 在O ⊙上,CD AC =,0120=∠ACD ,(1)求证:CD 是O ⊙的切线;(2)若O ⊙的半径为2,求图中阴影部分的面积.10、(2011年浙江杭州五模)如图,AB 为⊙O 的直径,点C 在⊙O 上,过点C 作⊙O 的切线交AB 的延长线于点D ,已知∠D =30°.⑴求∠A 的度数;⑵若点F 在⊙O 上,CF ⊥AB ,垂足为E ,CF =34,ABCOE CBOF求图中阴影部分的面积. 参考答案 一、选择题1.B 2.B 3.D 4.D 5.C 6.C 7.A 8.C 9.D 10.B 11.A 12.B 13.C 14.D 15.D 16.A 17.B 18.C 19.C 20.B 21.C 22.A 23.A 24.B 25.B 26.D 27.D 28.C 29.A 30.B 31.A 32.A 33.B 34.C 35.A 36.D 37.B 38.B 39.B 40.B 41.C 42.D 43.A 44.C 45.B 46.C 47.A 48.B 49.C 50.C二、填空题1.50 2.2π 3.18π 4.4105.7-⨯ 5.5 6.5 7.30° 8.9 9.25 10.h =r 11.4212.3或4 13.60°或120° 14.8252425-π 15.1:2 16.30 17.80π或120π 18.100° 19.22 20.π 21.1:4 22.1 23.288 24.4 25.2 26.15π 27.()a 23+ 28.3π 29.27π平方厘米 30.4 31.34 32.24π平方厘米或36π平方厘米 33.2334.435.774 36.12π 37.2,3 38.132 39.213- 40.24,240π 41.60°,33 42.9,4 43.4π 44.1或5 45.8π 三、解答题:1.(1)∵ BE 切⊙O 于点B ,∴ ∠ABE =∠C . ∵ ∠EBC =2∠C ,即 ∠ABE +∠ABC =2∠C , ∴ ∠C +∠ABC =2∠C , ∴ ∠ABC =∠C ,∴ AB =AC . (2)①连结AO ,交BC 于点F , ∵ AB =AC ,∴=,∴ AO ⊥BC 且BF =FC .在Rt △ABF 中,BFAF=tan ∠ABF , 又 tan ∠ABF =tan C =tan ∠ABE =21,∴ BF AF =21,∴ AF =21BF .∴ AB =22BF AF +=2221BF BF +⎪⎭⎫ ⎝⎛=25BF .∴452==BF AB BC AB . ②在△EBA 与△ECB 中,∵ ∠E =∠E ,∠EBA =∠ECB ,∴ △EBA ∽△ECB .∴ ⎪⎩⎪⎨⎧⋅==ECEA BE BC ABEB EA 2,解之,得516EA 2=EA ·(EA +AC ),又EA ≠0,∴511EA =AC ,EA =115×2=1110. 2.设⊙的半径为r ,由切割线定理,得PA 2=PB ·PC , ∴ 82=4(4+2r ),解得r =6(cm ).即⊙O 的半径为6cm .3.由已知AD ︰DB =2︰3,可设AD =2k ,DB =3k (k >0). ∵ AC 切⊙O 于点C ,线段ADB 为⊙O 的割线, ∴ AC 2=AD ·AB ,∵ AB =AD +DB =2k +3k =5k , ∴ 102=2k ×5k ,∴ k 2=10, ∵ k >0,∴ k =10. ∴ AB =5k =510.∵ AC 切⊙O 于C ,BC 为⊙O 的直径, ∴ AC ⊥BC . 在Rt △ACB 中,sin B =51010510==AB AC . 4.解法一:连结AC .∵ AB 是⊙O 的直径,点C 在⊙O 上, ∴ ∠ACB =90°. CD ⊥AB 于点D ,∴ ∠ADC =∠BDC =90°,∠2=90°-∠BAC =∠B .∵ tan B =21, ∴ tan ∠2=21.∴ CBACDB CD CD AD ===21. 设AD =x (x >0),CD =2x ,DB =4x ,AB =5x . ∵ PC 切⊙O 于点C ,点B 在⊙O 上,∴ ∠1=∠B . ∵ ∠P =∠P ,∴ △PAC ∽△PCB , ∴21==CB AC PC PA . ∵ PC =10,∴ PA =5,∵ PC 切⊙O 于点C ,PAB 是⊙O 的割线, ∵ PC 2=PA ·PB ,∴ 102=5(5+5 x ).解得x =3. ∴ AD =3,CD =6,DB =12. ∴ S △BCD =21CD ·DB =21×6×12=36. 即三角形BCD 的面积36cm 2.解法二:同解法一,由△PAC ∽△PCB ,得21==CB AC PC PA . ∵ PA =10,∴ PB =20. 由切割线定理,得PC 2=PA ·PB .∴ PA =201022-PB PC =5,∴ AB =PB -PA =15, ∵ AD +DB =x +4x =15,解得x =3, ∴ CD =2x =6,DB =4x =12. ∴ S △BCD =21CD ·DB =21×6×12=36. 即三角形BCD 的面积36cm 2.5.解:如图取MN 的中点E ,连结OE ,∴ OE ⊥MN ,EN =21MN =21a . 在四边形EOCD 中,∵ CO ⊥DE ,OE ⊥DE ,DE ∥CO , ∴ 四边形EOCD 为矩形. ∴ OE =CD ,在Rt △NOE 中,NO 2-OE 2=EN 2=22⎪⎭⎫⎝⎛a .∴ S 阴影=21π(NO 2-OE 2)=21π·22⎪⎭⎫⎝⎛a =28πa .6.解:∵ ∠CDE =∠CBA ,∠DCE =∠BCA ,∴ △CDE ∽△ABC .∴ 2⎪⎭⎫⎝⎛=∆∆AB DE S S ABC CDE∴AB DE =ABCCDE S S ∆∆=41=21,即215=AB ,解得 AB =10(cm ), 作OM ⊥FG ,垂足为M , 则FM =21FG =21×8=4(cm ), 连结OF , ∵ OA =21AB =21×10=5(cm ). ∴ OF =OA =5(cm ). 在Rt △OMF 中,由勾股定理,得OM =22FM OF -=2245-=3(cm ). ∴ 梯形AFGB 的面积=2FG AB +·OM =2810⨯×3=27(cm 2). 7.⎭⎬⎫的割线⊙是的切线⊙是O PBC O PA )1(⇒PA 2=PB ·PC ⇒PC =20⇒半径为7.5⇒圆面积为π4225(或56.25π)(平方单位).⎭⎬⎫∠=∠∠=∠P P BAP C )2(⇒△ACP ∽△BAP ⇒PB PA AB AC =⇒12=AB AC . 解法一:设AB =x ,AC =2x ,BC 为⊙O 的直径⇒∠CAB =90°,则 BC =5x . ∵ ∠BAP =∠C ,∴ cos ∠BAP =cos ∠C =55252==x x BC AC解法二:设AB =x ,在Rt △ABC 中,AC 2+AB 2=BC 2, 即 x 2+(2x )2=152,解之得 x =35,∴ AC =65,∵ ∠BAP =∠C ,∴ ∴ cos ∠BAP =cos ∠C =5521556==BC AC 必修① 第四章 物质的跨膜运输测试题1.新鲜的叶类蔬菜表面常残留水溶性有机农药。
