圆的知识点初三

合集下载

初三圆的知识点

初三圆的知识点圆是初中数学中的一个重要内容，也是中考的必考知识点之一。

在初三阶段，我们对圆的认识会更加深入和全面。

接下来，让我们一起系统地学习一下初三圆的相关知识点。

一、圆的基本概念1、圆的定义在平面内，到定点的距离等于定长的所有点组成的图形叫做圆。

其中，定点称为圆心，定长称为半径。

2、圆的表示方法通常用符号“⊙”表示圆，后面加上圆心的字母，如⊙O 表示以 O 为圆心的圆。

3、弦与直径连接圆上任意两点的线段叫做弦，经过圆心的弦叫做直径。

直径是圆中最长的弦。

4、弧圆上任意两点间的部分叫做圆弧，简称弧。

弧分为优弧（大于半圆的弧）、劣弧（小于半圆的弧）和半圆。

5、等圆与等弧能够重合的两个圆叫做等圆。

在同圆或等圆中，能够互相重合的弧叫做等弧。

二、圆的基本性质1、圆的对称性圆是轴对称图形，其对称轴是任意一条经过圆心的直线。

圆也是中心对称图形，其对称中心是圆心。

2、垂径定理垂直于弦的直径平分弦且平分弦所对的两条弧。

推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。

3、弧、弦、圆心角的关系在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等。

推论：在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦相等；如果两条弦相等，那么它们所对的圆心角相等，所对的优弧和劣弧分别相等。

4、圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半。

推论 1：同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等。

推论 2：半圆（或直径）所对的圆周角是直角；90°的圆周角所对的弦是直径。

三、圆的位置关系1、点与圆的位置关系设⊙O 的半径为 r，点 P 到圆心的距离 OP ＝ d，则有：点 P 在圆外⇔ d ＞ r；点 P 在圆上⇔ d ＝ r；点 P 在圆内⇔ d ＜ r。

2、直线与圆的位置关系设⊙O 的半径为 r，圆心 O 到直线 l 的距离为 d，则有：直线 l 和⊙O 相离⇔ d ＞ r；直线 l 和⊙O 相切⇔ d ＝ r；直线 l 和⊙O 相交⇔ d ＜ r。

圆知识点总结初三

圆知识点总结初三
一、基础概念
圆：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆。

固定的端点O叫做圆心，线段OA叫做半径。

弧、弦、直径：在圆上，由圆心到圆上任意一点的线段叫做半径，由圆上两点所连成的线段（直径和直径所截得的线段除外），叫做弦，而由圆上两点所截得的线段，叫做直径。

圆周角：顶点在圆上，两边和圆相交的角叫做圆周角。

二、圆的性质
圆的对称性：圆既是中心对称图形，也是轴对称图形。

弦与直径的关系：垂直于弦的直径平分这条弦，并且平分这条弦所对的两条弧。

弦与半径的关系：垂直于弦的半径平分这条弦，并且平分这条弦所对的两条弧。

直径与半径的关系：过圆心且垂直于弦的直径必平分这条弦。

同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等。

垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。

圆心角与圆周角的关系：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等。

圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半。

切线与半径的关系：圆的切线垂直于经过切点的半径。

切线长定理：从圆外一点引圆的两条切线，它们的切线长相等。

三、圆的计算
圆的周长公式：C = 2πr，其中r为圆的半径。

圆的面积公式：S = πr²，其中r为圆的半径。

扇形面积公式：扇形面积= (θ/360)πr²，其中θ为扇形的圆心角（单位为度），r为圆的半径。

关于圆的知识点初三

关于圆的知识点初三
圆是初中数学中的一个重要概念，它是平面几何中的基本图形之一。

在初三阶段，学生需要掌握圆的定义、性质、公式等知识点，下面我们来一一介绍。

一、圆的定义
圆是由平面上所有到定点距离相等的点组成的图形。

这个定点叫做圆心，到圆心的距离叫做半径。

圆的符号是“⚪”。

二、圆的性质
1.圆的直径是圆上任意两点之间的最长线段，它等于半径的两倍。

2.圆的周长是圆上任意两点之间的距离之和，它等于直径乘以π（圆周率）。

3.圆的面积是圆内所有点到圆心的距离之和，它等于半径的平方乘以π。

4.圆的内角和公式为：n个点的圆的内角和为（n-2）×180度。

5.圆的切线与半径垂直。

三、圆的公式
1.圆的周长公式：C=2πr，其中C表示周长，r表示半径，π≈3.14。

2.圆的面积公式：S=πr²，其中S表示面积，r表示半径，π≈
3.14。

四、圆的应用
1.圆的应用非常广泛，比如在建筑设计中，圆形的建筑物往往更加美观；在机械制造中，圆形的零件更容易加工和安装；在地理学中，圆形的地球仪可以更好地展示地球的形状和大小。

2.圆的应用还包括计算圆的周长、面积等问题。

比如，如果知道圆的半径，就可以用圆的周长公式计算出圆的周长；如果知道圆的面积，就可以用圆的面积公式计算出圆的半径。

以上就是关于圆的知识点的介绍，希望对初三学生有所帮助。

在学习圆的过程中，需要多做练习，掌握圆的定义、性质、公式等知识点，才能更好地应用到实际问题中。

初三圆知识点

初三圆的知识点1圆的定义：（1）平面上到定点的距离等于定长的所有点组成的图形叫做圆。

（2)平面上一条线段，绕它的一端旋转360°，留下的轨迹叫圆。

圆心：（1）如定义（1）中，该定点为圆心（2）如定义（2）中，绕的那一端的端点为圆心。

（3）圆任意两条对称轴的交点为圆心。

（4）垂直于圆内任意一条弦且两个端点在圆上的线段的二分点为圆心。

注：圆心一般用字母O表示直径：通过圆心，并且两端都在圆上的线段叫做圆的直径。

直径一般用字母d表示。

半径：连接圆心和圆上任意一点的线段，叫做圆的半径。

半径一般用字母r 表示。

圆的直径和半径都有无数条。

圆是轴对称图形，每条直径所在的直线是圆的对称轴。

在同圆或等圆中：直径是半径的2倍，半径是直径的二分之一.d=2r或r=二分之d。

圆的半径或直径决定圆的大小，圆心决定圆的位置。

圆的周长：围成圆的曲线的长度叫做圆的周长，用字母C表示。

圆的周长与直径的比值叫做圆周率。

圆的周长除以直径的商是一个固定的数，把它叫做圆周率，它是一个无限不循环小数（无理数），用字母π表示。

计算时，通常取它的近似值，π≈3.14。

直径所对的圆周角是直角。

90°的圆周角所对的弦是直径。

圆的面积公式：圆所占平面的大小叫做圆的面积。

πr^2，用字母S表示。

一条弧所对的圆周角是圆心角的二分之一。

在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦心距也相等。

在同圆或等圆中，如果两条弧相等，那么他们所对的圆心角相等，所对的弦相等，所对的弦心距也相等。

在同圆或等圆中，如果两条弦相等，那么他们所对的圆心角相等，所对的弧相等，所对的弦心距也相等。

周长计算公式1.、已知直径：C=πd2、已知半径：C=2πr3、已知周长：D=c\π4、圆周长的一半:1\2周长(曲线)5、半圆的长：1\2周长+直径面积计算公式：1、已知半径：S=πr平方2、已知直径：S=π（d\2）平方3、已知周长：S=π(c\2π)平方点、直线、圆和圆的位置关系1、点和圆的位置关系①点在圆内<=>点到圆心的距离小于半径②点在圆上<=>点到圆心的距离等于半径③点在圆外<=>点到圆心的距离大于半径2.过三点的圆不在同一直线上的三个点确定一个圆。

初三圆的知识点总结图

初三圆的知识点总结图一、圆的基本定义1. 圆的定义- 圆心- 半径- 直径- 圆周2. 圆的表示方法- 用圆心坐标和半径表示- 用方程式表示二、圆的性质1. 圆的对称性- 轴对称- 中心对称2. 圆的内接图形- 弦- 直径- 切线3. 圆的外切图形- 外切正多边形- 外切圆三、圆的计算公式1. 圆的周长计算公式- 周长与直径的关系- 周长与半径的关系2. 圆的面积计算公式- 面积与半径的关系 - 环形面积的计算四、圆的应用1. 圆在几何中的应用- 圆与直线的关系- 圆与圆的关系2. 圆在实际生活中的应用 - 建筑设计- 机械制造- 日常生活中的圆五、圆的相关定理1. 垂径定理- 定理内容- 定理的应用2. 圆周角定理- 定理内容- 定理的应用3. 圆的切线定理- 切线与半径的关系 - 切线与弦的关系六、圆的作图方法1. 用圆规画圆- 步骤说明- 注意事项2. 圆的五等分- 方法介绍- 应用实例七、圆的方程1. 标准圆方程- 方程形式- 参数解释2. 一般圆方程- 方程形式- 参数解释八、圆与坐标系1. 圆的坐标方程- 圆心和半径的坐标表示- 圆与坐标轴的关系2. 圆与直线的交点- 解析方法- 交点求解九、圆的进阶知识1. 圆锥曲线- 椭圆- 双曲线- 抛物线2. 非欧几何中的圆- 球面几何- 双曲几何请根据上述框架在Word文档中创建内容，并添加适当的图表、公式和示例以增强文档的可读性和实用性。

您可以根据实际需要调整各个部分的内容和顺序。

记得在编辑时使用清晰、专业的语言，并确保文档的格式规范、逻辑清晰。

初三圆知识点

初三圆知识点一、圆的定义圆是平面上到给定点距离相等的点的集合。

二、圆的要素1. 圆心：圆心是圆上所有点到该点的距离相等的点。

2. 半径：半径是圆心到圆上任意一点的距离。

3. 圆周：圆周是圆上所有点的集合。

4. 直径：直径是通过圆心，并且两端点都在圆周上的线段。

直径的长度等于圆的半径的两倍。

三、圆的公式1. 圆的周长（C）：C = 2πr (其中，r为半径，π取近似值3.14)2. 圆的面积（A）：A = πr²四、圆的性质1. 圆上任意两点之间的线段都属于圆的直径。

2. 圆上相等弧所对的圆心角相等。

3. 圆上相等弧所对的周角相等。

4. 圆心角的度数等于所对弧所对的周角的一半。

5. 位于同弧上的两个圆周角互补，即它们的和为180度。

6. 圆周角的度数等于其所对弧的度数。

五、圆的相关概念与定理1. 切线：切点在圆上的直线称为圆的切线。

切线与半径垂直。

2. 弦：不经过圆心连接圆上两点的线段称为圆的弦。

3. 弧：圆上两点之间的部分称为圆的弧。

4. 弦长定理：一个弦所对的圆周角等于其所对的弧所对的圆周角的一半。

5. 切线定理：切线与半径所成的角是直角。

6. 弧长定理：同样的角度所对应的弧长和圆心角所对应的圆周角的弧长成正比。

六、圆的应用1. 圆的交点：两条圆的交点是满足位于两个圆的圆周上的点。

2. 圆与直线的关系：直线与圆的关系有切线、相交、内含和外切四种情况。

3. 圆的切线的性质：切线与半径垂直、切线与半径所成的角为直角。

七、例题解析例题1：已知圆的半径为5cm，求圆的周长和面积。

解析：根据圆的公式，圆的周长= 2πr = 2 * 3.14 * 5 = 31.4cm，圆的面积= πr² = 3.14 * 5² = 78.5cm²。

例题2：在圆 O 中，弧 AC = 60度，求相应的弧度。

解析：根据圆的性质，圆周角的度数等于其所对弧的度数，所以弧度为π/3。

例题3：已知圆 O 的直径为12cm，求圆的周长和面积。

初三圆的知识点总结

初三圆的知识点总结圆是初中数学中的重要概念之一，而初三阶段则是圆的学习重点。

在初三阶段，学生需要掌握圆的定义、性质、相关定理和应用。

下面我们来总结一下初三圆的知识点。

一、圆的定义和性质1. 圆的定义圆是由平面上到定点的距离等于定长的所有点构成的集合。

定点叫圆心，定长叫半径。

通常记作圆O，圆心为O，半径为r。

2. 圆的性质（1）圆的直径、半径、弧长和圆心角的关系：一个圆的直径是圆的一条弧上的两个端点，直径等于圆的半径的两倍。

（2）圆的周长公式：圆的周长等于2πr，其中r为圆的半径。

（3）圆的面积公式：圆的面积等于πr²，其中r为圆的半径。

（4）切线定理：在圆上的切线和半径垂直，切点、圆心和切线上的半径构成直角三角形。

二、圆的相关定理1. 圆心角定理定理：在同一个圆或等圆上的圆心角等于其对应弧所对的圆周角的一半。

结论：圆心角相等的弧是等弧。

2. 弧长定理定理：在同一个圆或等圆上，相等圆心角所对的弧相等，反之，相等弧对应的圆心角相等。

3. 弧度和角度定理：弧长与半径之比叫做弧度制下的角度。

1弧度（rad）=57.3°。

结论：弧长l=rθ，其中θ为弧度。

4. 正弦定理和余弦定理正弦定理：在一个三角形ABC中，a/sinA=b/sinB=c/sinC。

余弦定理：在一个三角形ABC中，a²=b²+c²-2bc*cosA。

5. 切线定理定理：在圆上的切线和半径垂直。

6. 切线与弦的关系定理：在圆上，如果一条切线和一条弦相交，那么切线和弦的交点与圆心的连线垂直。

三、圆的相关应用1. 圆的相关应用（1）圆的插值：根据圆的相关性质和定理求出圆的周长、面积及其相关角度。

（2）圆的相关推理：利用圆的性质和相关定理解决与圆相关的问题。

2. 圆的实际应用（1）工程中的车轮和齿轮。

（2）地理中的经纬度。

（3）天文中的星座和行星轨道。

（4）生活中的钟面和圆形的器物。

以上就是初三圆的知识点总结，希望对你的学习有所帮助。

九年级数学圆的知识点总结大全

一、圆的定义和性质1.圆的定义：平面上到定点的距离等于定长的点的集合。

2.圆的要素：圆心、半径、圆周。

3.圆的性质：（1）半径相等的两个圆是同心圆；（2）同圆中，圆心角等于圆周角的1/2；（3）同弧上的两条弦所对的圆心角相等；（4）圆心角相等的弧相等；（5）相等弧所对的弦相等；（6）正多边形的内角和是定值，因此内接于一个圆的正多边形的各个内角相等；（7）直径是弦中最长的。

二、弧与圆周角1.弧的定义：圆上两点间的弧是以这两点为端点的两条互不相交的圆弧中，长的那一段。

2.弧的性质：（1）圆周角所对的弧是唯一确定的；（2）全周角所对的弧是定长的。

3.圆周角的定义：以圆心为端点的两条互不相交的射线所夹的角。

4.圆周角的度量：可以用角的度数来衡量。

三、切线与弦1.切线的定义：切线是与圆只有一个公共点的直线。

2.切线与半径的关系：切线与半径的关系是切线⊥半径。

3.弦的定义：两点之间的线段叫做弦。

4.弦的性质：（1）圆内的弦比它们所对的圆心角小，而且与一个圆心角的两个弧所对的弧一样；（2）相等的弦所对的圆心角相等。

四、相交弦定理1.弦上的点：如果一个点在弦上，则这个点到两个端点的距离相等。

2.相交弦定理：如果两个弦相交于圆内的一个点，则这两个弦上的两个点一定分别在另一个弦上的两侧。

五、余弦定理1.面积的性质：圆内、圆外的面积相等，夹在一个圆内的圆周弧的面积也相等。

2.余弦定理：在一个圆上，任意两条弧所对的圆心角的余弦值相等。

六、正多边形的面积公式1.正六边形的面积：正六边形的面积=3×（边长）²×√3÷22.正八边形的面积：正八边形的面积=2×（边长）²×√23.正十二边形的面积：正十二边形的面积=3×（边长）²×√34. 正十六边形的面积：正十六边形的面积=4×（边长）²×tan(22.5°)。

初三数学圆知识点

初三数学圆知识点一、圆的基本定义1. 圆的定义：平面上所有与定点（圆心）距离相等的点的集合。

2. 圆心（O）：圆的中心点，所有圆上的点到圆心的距离都等于半径。

3. 半径（r）：圆心到圆上任意一点的距离。

4. 直径（d）：圆上任意两点间的最长距离，等于半径的两倍。

5. 弦（c）：圆上任意两点间的线段。

6. 弧（a）：圆上两点间的圆周部分。

7. 优弧：大于半圆的弧。

8. 劣弧：小于半圆的弧。

9. 半圆：圆的一半，由直径两端的点和圆上所有点组成的弧。

二、圆的性质1. 所有半径的长度相等。

2. 直径是半径的两倍。

3. 圆周角定理：圆周上同弧所对的圆周角等于该弧所对的圆心角的一半。

4. 圆内接四边形的对角互补。

5. 切线与半径相交于切点，切线垂直于经过切点的半径。

6. 弦与直径相交于圆心，形成直角。

三、圆的计算公式1. 圆的周长（C）：C = πd = 2πr2. 圆的面积（S）：S = πr²3. 扇形面积：S = (θ/360)πr²，其中θ为扇形的中心角（单位：度）。

4. 弓形面积：S = (θ/360)πr² - (θ/2)r，其中θ为弓形的中心角（单位：度）。

四、圆的应用问题1. 圆与直线的关系：相交、相切、相离。

2. 圆与圆的关系：内含、外离、相交、内切、外切。

3. 圆的切线问题：求切线长度、切点坐标。

4. 圆的弦长问题：给定圆心和半径，求两点间弦的长度。

5. 圆的面积问题：已知圆的周长或直径，求圆的面积。

五、圆的几何构造1. 给定半径，如何画圆。

2. 给定圆心和半径，如何构造圆。

3. 如何通过三点确定一个圆。

4. 如何构造圆的内接正多边形。

六、圆的方程1. 标准圆方程：(x - a)² + (y - b)² = r²，其中(a, b)是圆心坐标，r是半径。

2. 一般圆方程：Ax + By + C = 0，可以通过圆心和半径转换得到。

初三圆的知识点总结

初三圆的知识点总结圆是初中数学中的重要内容，在中考中也占据着重要的地位。

以下是对初三圆的知识点的详细总结。

一、圆的基本概念1、圆的定义在平面内，到定点的距离等于定长的点的集合叫做圆。

定点称为圆心，定长称为半径。

2、圆的表示以点 O 为圆心，r 为半径的圆记作“⊙O，r”。

3、弦连接圆上任意两点的线段叫做弦。

经过圆心的弦叫做直径，直径是圆中最长的弦。

4、弧圆上任意两点间的部分叫做圆弧，简称弧。

大于半圆的弧称为优弧，小于半圆的弧称为劣弧。

5、半圆圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆。

6、等圆能够重合的两个圆叫做等圆。

7、等弧在同圆或等圆中，能够互相重合的弧叫做等弧。

二、圆的性质1、圆的对称性（1）圆是轴对称图形，其对称轴是任意一条通过圆心的直线。

（2）圆是中心对称图形，对称中心为圆心。

2、垂径定理垂直于弦的直径平分弦且平分弦所对的两条弧。

推论：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。

（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧。

（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧。

3、圆心角、弧、弦的关系在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等。

4、圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半。

推论 1：同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等。

推论 2：半圆（或直径）所对的圆周角是直角；90°的圆周角所对的弦是直径。

推论 3：如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。

三、圆的位置关系1、点与圆的位置关系设⊙O 的半径为 r，点 P 到圆心的距离 OP ＝ d，则有：（1）点 P 在圆外⇔ d ＞ r ；（2）点 P 在圆上⇔ d ＝ r ；（3）点 P 在圆内⇔ d ＜ r 。

2、直线与圆的位置关系设⊙O 的半径为 r，圆心 O 到直线 l 的距离为 d，则有：（1）直线 l 和⊙O 相离⇔ d ＞ r ；（2）直线 l 和⊙O 相切⇔ d ＝ r ；（3）直线 l 和⊙O 相交⇔ d ＜ r 。

九年级数学上册圆的知识点总结

九年级数学上册圆的知识点总结一、圆的认识1.圆的定义：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆（或圆可以看做是所有到定点O的距离等于定长的点的集合）2.圆的表示方法：①圆心用字母O表示，半径用字母r表示；②弧用弧长表示，扇形用圆心角表示；③圆是一种曲线图形，圆上任意一点P到圆心的距离OP都等于半径r；④圆心角是指顶点在圆心上的角，圆心角的一边与圆相交，另一边与圆相切或相割；⑤在同圆或等圆中，能够互相重合的弧叫做等弧；⑥半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径。

1.圆的各部分名称及性质：①圆心：将圆对折，两个折痕相交于一点，这一点叫做圆心。

圆心一般用字母O表示。

圆心决定圆的位置。

②半径：连接圆心到圆上任意一点的线段叫做半径。

半径用字母r表示。

圆的半径决定圆的大小。

半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径。

③直径：通过圆心且两个端点都在圆周上的线段叫做圆的直径。

直径用字母d表示。

直径是半径的2倍，同一个圆内所有的直径都相等。

直径是圆中最长的线段。

④弦：连接圆上任意两点的线段叫做弦。

在同一个圆内最长的弦是直径。

直径是最长的弦。

⑤弧：经过圆上任意两点间的部分叫做弧。

在同一个圆内，能够互相重合的弧叫做等弧。

等弧只有在同一个圆里才能出现。

⑥扇形：由一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形。

顶点在圆心上的扇形叫做圆心扇形，顶点在圆周上的扇形叫做圆周扇形。

在同一个圆里，由过一条弧的中点且垂直于这条弧所平分的那条弦与这条弧所组成的图形叫做弓形。

弓形的弧小于半圆的弧，弓形的弦大于半圆的弦。

二、点和圆的三种位置关系1.点和圆的三种位置关系：设⊙O的半径为r，点P到圆心的距离OP为d，则有：①点P在圆外⇔d＞r；②点P在圆上⇔d=r；③点P在圆内⇔d＜r.1.确定圆的条件：不在同一直线上的三个点确定一个圆.常用符号“（1）P （2）r （3）”表示.即要确定一个圆必须知道它的和圆的半径.若已知三点的位置关系是①②③,则可确定一个圆,若位置关系是①③,则可确定无数个圆；若是位置关系②,则不能确定一个圆,应先找出这三点所在直线的垂线段的中垂线,再根据垂径定理作出中垂线,它和三点确定的直线外一点和以该点为圆心,垂线段的长度为半径确定一个唯一的圆.若是位置关系③,则根据从直线外一点向这条直线所作的垂线段最短,确定垂足的位置,再根据垂径定理作出中垂线,它和三点确定的直线外一点和以该点为圆心,垂线段的长度为半径确定一个唯一的圆.若是位置关系①②,则以不共线的三点为三个顶点作三个三角形,这三个三角形的三条边分别两两相交且交点不重合的三个交点为三个圆心,以各顶点到相应交点的距离为半径作三个圆,这三个圆的公共部分即为以不共线的三点确定的圆的三个交点组成的图形,简称“三交圆”.若是位置关系①③,则以不共线的三点为三个顶点作三个三角形,这三个三角形的三条边分别两两相交且交点不重合的三个交点为三个圆心,以各顶点到相应交点的距离为半径作三个圆,这三个圆的公共部分即为以不共线的三点确定的圆的三个交点组成的图形,简称“三交圆”.若是位置关系②③,则不能确定一个唯一的圆.若是位置关系①②③也不能确定一个唯一的确定的唯一的确定的确定的确定的确定的确定的。

初三数学圆的知识点和公式总结

初三数学圆的知识点和公式总结数学圆的知识点和公式总结如下：1. 圆的定义：圆是由平面上所有到一个固定点的距离等于一个常数的点的集合。

2. 圆的要素：- 圆心：到圆上任意一点的距离相等的点，通常用大写字母O表示。

- 圆的半径：连接圆心和圆上任意一点的线段的长度，通常用小写字母r表示。

- 圆的直径：通过圆心的两个点之间的距离的两倍，即2r。

- 圆周：圆上所有的点构成的曲线。

- 圆内部：圆周所围成的区域。

3. 圆的相关公式：- 圆的周长：C=2πr，其中π≈3.14。

- 圆的面积：A=πr²。

- 圆的直径与周长的关系：C=πd，其中d为直径。

- 圆的直径与面积的关系：A=π(d/2)²。

4. 圆与圆的位置关系：- 相离：两个圆没有交点，且两个圆心之间的距离大于两个半径之和。

- 外切：两个圆内切于一个切点，且两个圆心之间的距离等于两个半径之和。

- 相交：两个圆有两个交点，且两个圆心之间的距离小于两个半径之和。

- 内切：一个圆在另一个圆的内部，且两个圆心之间的距离等于两个半径之差。

- 同心：两个圆的圆心重合，半径可以相等也可以不相等。

5. 圆的常用定理：- 弧长公式：弧长L=2πr(θ/360°)，其中θ为所对的圆心角的度数。

- 弦长公式：弦长l=2r*sin(θ/2)，其中θ为所对的圆心角的度数。

- 弧度制与角度制的转换：1弧度=180°/π，1°=π/180弧度。

- 正弦定理：在任意三角形ABC中，a/sinA=b/sinB=c/sinC。

- 余弦定理：在任意三角形ABC中，c²=a²+b²-2ab*cosC。

- 勾股定理：在直角三角形ABC中，a²+b²=c²。

希望以上总结对你有帮助！如有其他问题，请随时提问。

关于圆的知识点初三

关于圆的知识点初三
1. 圆的定义：平面上离定点（圆心）距离相等的点的集合即为圆。

2. 圆的基本元素：圆心、半径。

3. 圆的性质：
（1）圆上任意两点的距离相等；
（2）圆的直径等于其半径的两倍；
（3）通过圆心可以作弦，弦长相等的弦在圆上的两个端点与
圆心三点共线。

4. 圆的相关概念：
（1）圆的周长：圆周的长度，等于直径长（或半径长）的π倍，表示为2πR（或πD）。

（2）圆的面积：圆内的面积，等于半径平方×π，表示为πR²。

（3）圆心角：以圆心为顶点，两边分别为圆弧的角度。

（4）弧长：圆上一段弧对应的圆周长度。

（5）扇形面积：圆心角包围的弧与圆心对应的部分面积。

（6）切线：过圆上一点的直线，与半径形成的角为直角。

（7）切点：切线和圆的交点。

（8）相交弧：两圆相交部分对应的弧。

（9）相切：两个圆只有一个交点。

（10）不相交：两个圆没有交点。

5. 圆的相关定理：
（1）内接圆定理：一个三角形的内切圆，与三角形的三边相切。

（2）外接圆定理：一个三角形的外接圆，通过三角形的三个顶点。

（3）切线定理：从一点到圆的切点的切线与此点到圆心的直线垂直。

（4）圆的每条直径将圆分成两个全等的半圆。

（5）弧与正多边形内角和的关系：正n边形内角和等于圆心角的n倍。

九年级数学圆的知识

九年级数学圆的知识
九年级数学中，圆的知识包括以下内容：
1. 圆的定义：圆是由平面上所有到定点距离相等的点组成的集合。

2. 圆的元素：圆心是圆的中心点，用O表示；半径是圆心到圆上任意一点的距离，用r表示；直径是通过圆心的一条线段，两端点在圆上，直径的长度是半径的两倍。

3. 圆的性质：
- 圆上任意两点与圆心的距离相等。

- 圆上的点与圆心的距离等于半径。

- 圆的直径是最长的线段，且等于半径的两倍。

- 圆的任意弦都可以作为直径，即两端点在圆上的线段。

- 圆的任意弦都可以分成两段，两段长度乘积等于这条弦所对应的弧的长度乘积。

- 圆的周长是圆周上一周的长度，等于2πr，其中π是一个无理数，约等于3.14159。

- 圆的面积是圆内部的所有点组成的区域的大小，等于πr²。

4. 圆的相关定理：
- 弧长定理：圆的弧所对应的圆心角的度数等于弧长所占圆周的度数。

- 弦切定理：在圆上，切线与弦的乘积等于切点外的弦与切点外
的弦的乘积。

- 切线定理：在圆上，切线与切点外的弦的乘积等于切点外的弦与切点外的弦的乘积。

- 弧度制：角度的度数可以转化为弧度制，1°对应π/180弧度。

以上是九年级数学中关于圆的基本知识，还有更深入的内容如圆锥、圆柱、圆台等，这些内容超出了本回答的范围。

初三有关圆的知识点

初三有关圆的知识点一1、圆的有关概念：(1)、确定一个圆的要素是圆心和半径。

(2)①连结圆上任意两点的线段叫做弦。

②经过圆心的弦叫做直径。

③圆上任意两点间的部分叫做圆弧，简称弧。

④小于半圆周的圆弧叫做劣弧。

⑤大于半圆周的圆弧叫做优弧。

⑥在同圆或等圆中，能够互相重合的弧叫做等弧。

⑦顶点在圆上，并且两边和圆相交的角叫圆周角。

⑧经过三角形三个顶点可以画一个圆，并且只能画一个，经过三角形三个顶点的圆叫做三角形的外接圆，三角形外接圆的圆心叫做这个三角形的外心，这个三角形叫做这个圆的内接三角形，外心是三角形各边中垂线的交点;直角三角形外接圆半径等于斜边的一半。

⑨与三角形各边都相切的圆叫做三角形的内切圆，三角形的内切圆的圆心叫做三角形的内心，这个三角形叫做圆外切三角形，三角形的内心就是三角形三条内角平分线的交点。

2、圆的有关性质(1)定理在同圆或等圆中，如果圆心角相等，那么它所对的弧相等，所对的弦相等，所对的弦的弦心距相等。

推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对的其余各组量都分别相等。

(2)垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。

推论1：①平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧。

②弦的垂直平分线经过圆心，并且平分弦所对的两条弧。

③平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧。

推论2：圆的两条平行弦所夹的弧相等。

(3)圆周角定理：一条弧所对的圆周角等于该弧所对的圆心角的一半。

推论1在同圆或等圆中，同弧或等弧所对的圆周角相等，相等的圆周角所对的弧也相等。

推论2半圆或直径所对的圆周角都相等，都等于90 。

90 的圆周角所对的弦是圆的直径。

推论3如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。

(4)切线的判定与性质：判定定理：经过半径的外端且垂直与这条半径的直线是圆的切线。

性质定理：圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点;经过切点切垂直于切线的直线必经过圆心。

初三数学圆知识点大全

初三数学圆知识点大全 1、圆的有关概念：(1)、确定一个圆的要素是圆心和半径。

(2)①连结圆上任意两点的线段叫做弦。

②经过圆心的弦叫做直径。

③圆上任意两点间的部分叫做圆弧，简称弧。

④小于半圆周的圆弧叫做劣弧。

⑤大于半圆周的圆弧叫做优弧。

⑥在同圆或等圆中，能够互相重合的弧叫做等弧。

⑦顶点在圆上，并且两边和圆相交的角叫圆周角。

2、圆的有关性质(1)定理在同圆或等圆中，如果圆心角相等，那么它所对的弧相等，所对的弦相等，所对的弦的弦心距相等。

推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对的其余各组量都分别相等。

(2)垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。

推论1：①平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧。

②弦的垂直平分线经过圆心，并且平分弦所对的两条弧。

③平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧。

推论2：圆的两条平行弦所夹的弧相等。

(3)圆周角定理：一条弧所对的圆周角等于该弧所对的圆心角的一半。

推论1在同圆或等圆中，同弧或等弧所对的圆周角相等，相等的圆周角所对的弧也相等。

推论2半圆或直径所对的圆周角都相等，都等于90 。

90 的圆周角所对的弦是圆的直径。

推论3如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。

(4)切线的判定与性质：判定定理：经过半径的外端且垂直与这条半径的直线是圆的切线。

性质定理：圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点;经过切点切垂直于切线的直线必经过圆心。

初中数学九年级上圆的知识点

初中数学九年级上圆的知识点圆是初中数学九年级上的一个重要知识点，下面将从圆的定义、圆的性质、圆的相关定理以及圆的应用等方面进行论述。

一、圆的定义圆是平面上的重要几何图形之一，是由与一个定点距离相等的所有点构成的集合。

这个定点称为圆心，距离称为半径，用字母r表示。

圆通常用圆的轮廓线表示，在数学表达中用字母O表示。

二、圆的性质1. 圆的任意两点到圆心的距离相等。

这意味着圆上的每一个点到圆心的距离都相等，即圆的半径。

2. 圆的直径是圆上任意两点之间的最长距离。

直径的长度是半径的两倍。

3. 圆的弦是圆上任意两点之间的线段。

弦不一定通过圆心，可以在圆内或圆外。

4. 圆上的切线垂直于半径。

切线是与圆相切的线，与圆的切点处的半径垂直。

三、圆的相关定理1. 弧与角的关系圆上的弧对应的圆心角是两个端点在圆心所对应的角，它们的度数相等。

2. 弧长与圆周角的关系圆的弧长是圆心角所对应的弧所在圆的一部分的长度，弧长等于这个圆心角所对应的圆周角度数的比值。

3. 弦长与弦心角的关系弦上的弦长是弦心角所对应的弦所在圆的一部分的长度，弦长等于这个弦心角所对应的圆周角度数的比值的2倍。

4. 割线定理割线是两个切点之间的线段，割线上的两个切线段长度乘积等于这条割线与这两个切点之间的弦段长度乘积。

四、圆的应用1. 圆的测量圆的周长等于圆周上的任意一段弧长，即C=πd或C=2πr，其中d为直径，r为半径。

圆的面积等于圆内所包围的面积，即S=πr²。

2. 圆的位置关系两个圆之间的位置关系可以分为外切、内切、相交、相离四种情况，通过判断两个圆心的距离与两个圆的半径之间的关系可以确定两个圆的位置关系。

3. 圆的轴对称与旋转对称圆具有轴对称性和旋转对称性，利用这个特性可以解决一些与圆相关的问题。

综上所述，圆是初中数学九年级上的重要知识点，通过对圆的定义、性质、相关定理和应用进行论述，可以帮助同学们更好地理解和掌握圆的知识，提高数学学科的学习成绩。

初三《圆》知识点及定理

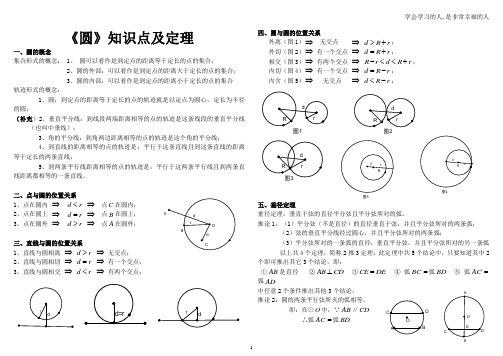
《圆》知识点及定理一、圆的概念集合形式的概念： 1、圆可以看作是到定点的距离等于定长的点的集合；2、圆的外部：可以看作是到定点的距离大于定长的点的集合；3、圆的内部：可以看作是到定点的距离小于定长的点的集合轨迹形式的概念：1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；（补充）2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）；3、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。

二、点与圆的位置关系1、点在圆内⇒d r<⇒点C在圆内；2、点在圆上⇒d r=⇒点B在圆上；3、点在圆外⇒d r>⇒点A在圆外；三、直线与圆的位置关系1、直线与圆相离⇒d r>⇒无交点；2、直线与圆相切⇒d r=⇒有一个交点；3、直线与圆相交⇒d r<⇒有两个交点；四、圆与圆的位置关系外离（图1）⇒无交点⇒d R r>+；外切（图2）⇒有一个交点⇒d R r=+；相交（图3）⇒有两个交点⇒R r d R r-<<+；内切（图4）⇒有一个交点⇒d R r=-；内含（图5）⇒无交点⇒d R r<-；五、垂径定理垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。

推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共4个定理，简称2推3定理：此定理中共5个结论中，只要知道其中2个即可推出其它3个结论，即：①AB是直径②AB CD⊥③CE DE=④弧BC=弧BD⑤弧AC=弧AD中任意2个条件推出其他3个结论。

初三《圆》知识点及定理

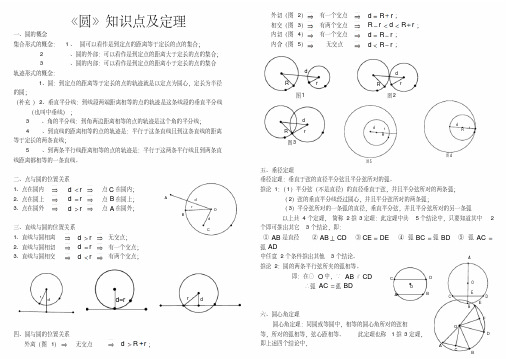
（ 3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧
以上共 4 个定理，简称 2 推 3 定理：此定理中共 5 个结论中，只要知道其中 2
个即可推出其它 3 个结论，即：
① AB 是直径 ② AB CD ③ CE DE ④ 弧 BC 弧 BD ⑤ 弧 AC
弧 AD
中任意 2 个条件推出其他 3 个结论。
即：在⊙ O 中，∵ PB 、 PE 是割线 ∴ PC PB PD PE
十二、两圆公共弦定理圆公共弦定理：两圆圆心的连线垂直并且平分这两个圆的的公共弦。
如图： O1O2 垂直平分 AB 。
即：∵⊙ O1、⊙ O2 相交于 A 、 B 两点
A
O1
O2
B
∴ O1O2 垂直平分 AB
十三、圆的公切线
A B
P
即：∵ PA 、 PB 是的两条切线
即：在⊙ O 中，∵ AB 是直径 ∴ C 90
或∵ C 90 ∴ AB 是直径
B
A
O
∴ PA PB PO 平分 BPA
O
A
N
B O
A
推论 3：若三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。
即：在△ ABC 中，∵ OC OA OB ∴△ ABC 是直角三角形或 C 90
求： EM的长．例 4 如图 23-13 ， AB是⊙ O的直径， PB切⊙ O于点 B， PA交⊙ O于点 C， PF 分别交
AB、BC于 E、D，交⊙ O于 F、G，且 BE、BD恰好是关于 x 的方程
( 其中 m为实数 ) 的两根． (1) 求证： BE＝BD；
(2) 若
，求∠ A 的度数．
dr

初三关于圆的知识点

1.圆的周长C=2πr=πd2.圆的面积S=πr²3.扇形弧长l=nπr/1804.扇形面积S=nπr²/360=rl/25.圆锥侧面积S=πrl〖圆的定义〗几何说：平面上到定点的距离等于定长的所有点组成的图形叫做圆。

定点称为圆心，定长称为半径。

轨迹说：平面上一动点以一定点为中心，一定长为距离运动一周的轨迹称为圆周，简称圆。

集合说：到定点的距离等于定长的点的集合叫做圆。

〖圆的相关量〗圆周率：圆周长度与圆的直径长度的比叫做圆周率，值是3.141592653589793238462643383279502884197169399375105820974944592307816 4062862089986280348253421170679...，通常用π表示，计算中常取3.14为它的近似值(但奥数常取3或3.1416)。

圆弧和弦：圆上任意两点间的部分叫做圆弧，简称弧。

大于半圆的弧称为优弧，小于半圆的弧称为劣弧。

连接圆上任意两点的线段叫做弦。

经过圆心的弦叫做直径。

圆心角和圆周角：顶点在圆心上的角叫做圆心角。

顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角。

内心和外心：过三角形的三个顶点的圆叫做三角形的外接圆，其圆心叫做三角形的外心。

和三角形三边都相切的圆叫做这个三角形的内切圆，其圆心称为内心。

扇形：在圆上，由两条半径和一段弧围成的图形叫做扇形。

圆锥侧面展开图是一个扇形。

这个扇形的半径成为圆锥的母线。

〖圆和圆的相关量字母表示方法〗圆—⊙半径—r 弧—⌒直径—d 扇形弧长／圆锥母线—l 周长—C 面积—S〖圆和其他图形的位置关系〗圆和点的位置关系：以点P与圆O的为例（设P是一点，则PO是点到圆心的距离），P在⊙O外，PO＞r；P在⊙O上，PO＝r；P在⊙O内，PO＜r。

直线与圆有3种位置关系：无公共点为相离；有两个公共点为相交；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点。