贝叶斯决策的经典例题练习
贝叶斯决策例题(精选.)
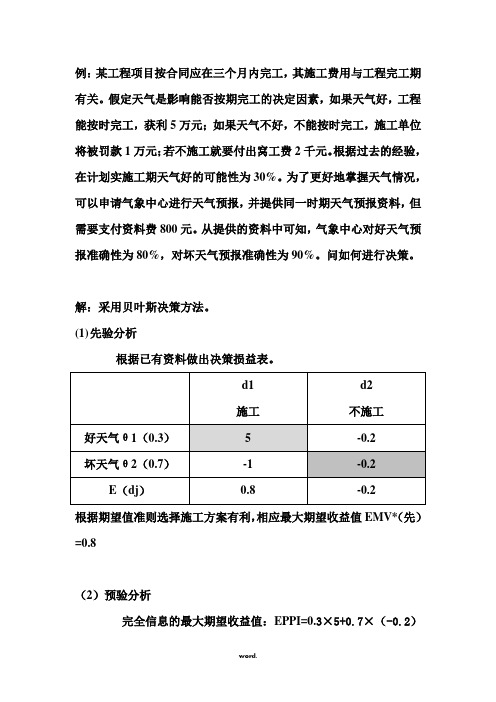
例：某工程项目按合同应在三个月内完工，其施工费用与工程完工期有关。
假定天气是影响能否按期完工的决定因素，如果天气好，工程能按时完工，获利5万元；如果天气不好，不能按时完工，施工单位将被罚款1万元；若不施工就要付出窝工费2千元。
根据过去的经验，在计划实施工期天气好的可能性为30%。
为了更好地掌握天气情况，可以申请气象中心进行天气预报，并提供同一时期天气预报资料，但需要支付资料费800元。
从提供的资料中可知，气象中心对好天气预报准确性为80%，对坏天气预报准确性为90%。
问如何进行决策。
解：采用贝叶斯决策方法。
(1)先验分析根据已有资料做出决策损益表。
根据期望值准则选择施工方案有利，相应最大期望收益值EMV*（先）=0.8（2）预验分析完全信息的最大期望收益值：EPPI=0.3×5+0.7×（-0.2）=1.36（万元）完全信息价值： EVPI=EPPI- EMV*（先）=1.36-0.8=0.56（万元）即，完全信息价值大于信息成本，请气象中心进行预报是合算的。
（3）后验分析①补充信息：气象中心将提供预报此时期内两种天气状态x 1(好天气)、x 2(坏天气)将会出现哪一种状态。
从气象中心提供的同期天气资料可得知条件概率： 天气好且预报天气也好的概率 P （x 1/θ1）=0.8 天气好而预报天气不好的概率 P （x 2/θ1）=0.2 天气坏而预报天气好的概率 P （x 1/θ2）=0.1 天气坏且预报天气也坏的概率 P （x 2/θ2）=0.9②计算后验概率分布：根据全概率公式和贝叶斯公式，计算后验概率。
预报天气好的概率1111212()()(/)()(/)P x P P x P P x θθθθ=+=0.31预报天气坏的概率2121222()()(/)()(/)P x P P x P P x θθθθ=+=0.69 预报天气好且天气实际也好的概率：111111()(/)(/)()P P x P x P x θθθ⋅==0.3×0.8/0.31=0.77预报天气好而天气坏的概率：212211()(/)(/)()P P x P x P x θθθ⋅==0.7×0.1/0.31=0.23预报天气坏而实际天气好的概率:121122()(/)(/)()P P x P x P x θθθ⋅==0.3×0.2/0.69=0.09预报天气坏且实际天气也坏的概率： 222222()(/)(/)()P P x P x P x θθθ⋅==0.7×0.9/0.69=0.91上述计算可以用表格表示：③ 后验决策：若气象中心预报天气好（x1）,则每个方案的最大期望收益值 E(d1/x1)=0.77×5+0.23×(-1)=3.62 E(d2/x1)=0.77×(-0.2)+0.23×(-0.2)=-0.2选择d1即施工的方案，相应在预报x1时的最大期望收益值E （X1）=3.62若气象中心预报天气不好（x2），各方案的最大期望收益值 E(d1/x2)=0.09×5+0.91×(-1)=-0.46 E(d2/x2)=0.09×(-0.2)+0.91×(-0.2)=-0.2选择d2即不施工的方案，相应在预报x2时的最大期望收益值E （X2）=-0.2④ 计算补充信息的价值：得到天气预报的情况下，后验决策的最大期望收益值：1122*()()()()()EMV P x E x P x E x =⋅+⋅后=0.31×3.62+0.69×（-0.2）=0.9842则补充的信息价值为：EMV*(后)-EMV*(先)=0.9842-0.8=0.1842补充信息价值大于信息费（800元），即这种费用是合算的。
贝叶斯公式典型例题
贝叶斯公式典型例题
贝叶斯公式是一种计算条件概率的公式，常用于根据已知条件更新某个事件发生的概率。
下面是一个贝叶斯公式的典型例题：
例：假设有两种类型的围棋棋手，分别是专业棋手和业余棋手。
专业棋手在比赛中获胜的概率为0.9，而业余棋手获胜的概率为0.3。
已知在所有棋手中，专业棋手占70%，业余棋手占30%。
现在有一场比赛，我们只知道其中一位棋手获胜了，那么这位棋手是专业棋手的概率是多少？
解：首先，我们定义以下事件：
•A：棋手是专业的
•B：棋手获胜
根据题意，我们知道：
•P(A) = 0.7（专业棋手占比）
•P(¬A) = 0.3（业余棋手占比）
•P(B|A) = 0.9（专业棋手获胜的概率）
•P(B|¬A) = 0.3（业余棋手获胜的概率）
我们要找的是P(A|B)，即在已知棋手获胜的条件下，棋手是专业的概率。
根据贝叶斯公式，我们有：
P(A|B) = \frac{P(A) \times P(B|A)}{P(A) \times P(B|A) + P(¬A) \times P(B|¬A)}将已知的概率值代入公式中，我们得到：
P(A|B) = \frac{0.7 \times 0.9}{0.7 \times 0.9 + 0.3 \times 0.3} = \frac{0.63}{0.63
+ 0.09} = \frac{0.63}{0.72} = 0.875
所以，在已知棋手获胜的条件下，这位棋手是专业棋手的概率为0.875。
这个例题展示了贝叶斯公式在更新条件概率方面的应用。
通过已知的概率值和贝叶斯公式，我们可以计算出在给定条件下的未知概率。
贝叶斯推理例子
贝叶斯推理例子
1. 嘿，你想想看啊，比如说你去买彩票，你觉得中奖的概率有多大呢？这就可以用贝叶斯推理呀！你先根据以往的开奖情况大概估计一个基础概率，然后每次开奖后根据新的结果来调整你的概率判断，这多有意思啊！
2. 来，咱说个生活中的例子。
你判断今天会不会下雨，你会先根据天气预报和以往的经验来有个初步想法吧，但如果突然天空变得阴沉沉的，你不得赶紧调整你觉得下雨的概率呀，这就是贝叶斯推理在起作用呀，你说是不是？
3. 你知道怎么猜别人手里的牌吗？这也能用贝叶斯推理呢！看他的表情动作，先有个初步判断，然后随着每一轮出牌，不断更新你对他手里牌的估计，哎呀，多带劲啊！
4. 你想想，你找工作的时候，对拿到某个 offer 的概率判断不也是这样嘛！开始根据公司的要求和自己的情况有个想法，然后面试过程中根据各种表现来调整，这可真是贝叶斯推理的活用呀！
5. 就像你猜你喜欢的人对你有没有意思，一开始你有个感觉，然后通过他跟你的每次互动，你不就会调整那个可能性嘛，这就是贝叶斯推理呀，神奇吧！
6. 好比你玩猜数字游戏，你先乱猜一个，然后根据提示不断缩小范围，调整你的猜测，这不就是活脱脱的贝叶斯推理嘛，多好玩呀！
7. 哎呀，你看医生诊断病情也是这样的呀！根据症状先有个初步判断，然后做各种检查，根据检查结果不断改变对病情的推测，贝叶斯推理真的无处不在呢！
8. 再比如你预测一场比赛的结果，先有个大概想法，比赛过程中根据双方的表现来不断调整胜败的概率，这不是贝叶斯推理在帮忙嘛，多有用啊！总之，贝叶斯推理在我们生活中可太常见啦，好多事情都能靠它来让我们的判断更准确呢！。
模式识别 第二章 贝叶斯决策论习题答案
t t −1
0 0 0.5 1 1 0 5 21 − 2 21 0 − 2 0 − 2 21 5 21 1 2
i =1 ωi ≠ωmax
∑ P (ω x ) p ( x ) d x
i
c
= ∫ 1 − P (ωmax x ) p ( x ) dx = 1 − ∫ P (ωmax x ) p ( x ) dx
d) 续上式：
(
)
P ( error ) = 1 − ∫ P (ωmax x ) p ( x ) dx ≤ 1− ∫ 1 1 c −1 p ( x ) dx = 1 − = c c c
n t
′ ′ ′ Σ′ = ∑ ( x′ k − μ )( x k − μ )
k =1 n
= ∑ Tt ( x 0 k − μ )( x 0 k − μ ) T
t k =1
n t = Tt ∑ ( x 0 k − μ )( x 0 k − μ ) T k =1 = T t ΣT
+∞ ai
1 1 ， p ( x ωi ) = exp ( − x − ai bi ) 2bi 2bi = x − a2 x − a1 b2 exp − b1 b1 b2 ；
b)
似然比 =
p ( x ω2 )
p ( x ω1 )
c)
x −1 a1 = 0, b1 = 1, a2 = 1, b2 = 2 ，则： 似然比 = 2exp −x 2
误差率的上界在 p ω1 x = p ω2 x = b) 如果我们令 p ω1 x = p ω2 x =
全概率公式和贝叶斯公式练习题
例题讲解:例题 1.市场上某产品由三家厂家提供，根据以往的记录，这三个厂家的次品率分别为，0.020.,0.01,0.03，三个厂家生产的产品所占的市场份额分别0.15,0.8,0.05.产品出厂后运到仓库，见面后再进入市场，设这三个厂家的产品在仓库是均匀混合（1）在仓库中随机的取一个产品，求它的次品的概率。
（2）在仓库中随机的取一个产品，发现为次品，如果你是管理者，该如何追究三个厂家的责任？例题2保险公司把被保险人分成三类”谨慎的”,”一般的”和”冒险的”，统计资料表明，上述三种人在一年内发生事故的概率依次为，0. 5. 0.15. 和0.30. 如果”谨慎的”被保险人占20%”一般的”，被保险人占50%，”冒失的”被保险人占30%，确认一个被保险人在一年内出事故的概率。
练习:1.设某工厂有两个车间生产同型号家用电器，第一车间的次品率为0.15，第二车间的次品率为0.12，两个车间的成品都混合堆放在一个仓库，假设第1,2车间生产的成品比例为2:3，今有一客户从成品仓库中随机提一台产品，求该产品合格的概率。
解：设B={从仓库中随机提出的一台是合格品}A i ={提出的一台是第i 车间生产的}，i=1,2则有分解B=A 1B ∪A 2B由题意P(A1)=2/5,P(A2)=3/5,P(B|A1)=0.85,P(B|A2)=0.88由全概率公式P(B)= P(A 1) P(B|A 1)+ P(A 2) P(B|A 2)=0.4*0.85+0.6*0.88=0.868.2. 盒中有a 个红球，b 个黑球，今随机地从中取出一个，观察其颜色后放回，并加上同色球c 个，再从盒中第二次抽取一球，求第二次抽出的是黑球的概率。
解：设A={第一次抽出的是黑球}，B={第二次抽出的是黑球}，则B AB AB =+， 由全概率公式()()()()()P B P A P B A P A P B A =+， 由题意(),(|),(),(|)b b c a b P A P B A P A P B A a b a b c a b a b c +====++++++ 所以()()()()()()b b c ab b P B a b a b c a b a b c a b+=+=+++++++ 3. 设某公路上经过的货车与客车的数量之比为2:1，货车中途停车修理的概率为0.02，客车为0.01，今有一辆汽车中途停车修理，求该汽车是货车的概率。
贝叶斯决策例子
贝叶斯决策练习某石油公司拟在一片估计含油的荒地上钻井。
如果钻井，费用为150万，若出油的概率为0.55，收入为800万元；若无油的概率为0.45，此时的收入为0。
该公司也可以转让开采权，转让费为160万元，但公司可以不担任何风险。
为了避免45％的无油风险，公司考虑通过地震试验来获取更多的信息，地震试验费用需要20万元。
已知有油的情况下，地震试验显示油气好的概率为0.8，显示油气不好的概率为0.2；在无油条件下，地震显示油气好的概率为0.15，而显示油气不好的概率为0.85。
又当试验表明油气好时，出让开采权的费用将增至400万元，试验表明油气不好时，出让开采权费用降至100万元，问该公司应该如何决策，使其期望收益值为最大。
解：该公司面临两个阶段的决策：第一阶段为要不要做地震试验，第二阶段为在做地震试验条件下，当油气显示分别为好与不好时，是采取钻井策略还是出让开采权。
若用A 1表示有油，A 2表示无油；用B 1表示地震试验显示油气好，B 2表示地震试验显示油气不好。
由题意可知：1211211222()0.55 ()0.45(|)0.8 (|)0.2(|)0.15 (|)0.85P A P A P B A P B A P B A P B A ======由贝叶斯公式计算得到：11111111212()(|)0.440.44(|)0.867()(|)()(|)0.440.06750.5075P A P B A P A B P A P B A P A P B A ====++ 同理，有： 2112220.0675(|)0.1330.50750.11(|)0.2230.49250.3825(|)0.7770.4925P A B P A B P A B ======该问题对应的决策树图采用逆序的方法，先计算事件点②③④的期望值：事件点 期望值② 800×0.867＋0×0.133＝693.6（万元）③ 800×0.223＋0×0.777＝178.4（万元）④ 800×0.55＋0×0.45＝440（万元） 在决策点2，按max[(693.6-150)，400]＝543.6万元，故选择钻井，删除出让开采权策略； 在决策点3，按max[(178.4-150)，100]＝100万元，故选择出让开采权，删除钻井策略； 在决策点4，按max[(440-150)，160]＝290万元，故选择钻井策略。
朴素贝叶斯公式例题
朴素贝叶斯公式例题朴素贝叶斯公式是一种基于贝叶斯定理的分类算法，它假设特征之间相互独立。
以下是一个朴素贝叶斯公式的例题：假设我们有一个数据集，其中包含了一些电子邮件的文本以及对应的标签（垃圾邮件或非垃圾邮件）。
我们想要使用朴素贝叶斯算法来对新的邮件进行分类。
现在，我们收到了一封新的邮件，内容如下："购买廉价药物，快速发货！"我们需要使用朴素贝叶斯公式来判断这封邮件是属于垃圾邮件还是非垃圾邮件。
为此，我们首先需要计算两个条件概率：P(垃圾邮件|文本)和P(非垃圾邮件|文本)。
根据朴素贝叶斯公式，我们可以将问题转化为计算以下两个概率：1. P(垃圾邮件|文本)：给定文本为"购买廉价药物，快速发货！"，我们需要计算该邮件为垃圾邮件的概率。
假设训练集中共有100封邮件，其中有30封垃圾邮件。
而在这30封垃圾邮件中，有10封包含了"购买廉价药物，快速发货！"这样的文本。
因此，P(文本|垃圾邮件) = 10 / 30 = 1/3。
另外，P(垃圾邮件)表示在数据集中出现垃圾邮件的概率，假设为0.3。
综合利用贝叶斯公式，可以计算P(垃圾邮件|文本)：P(垃圾邮件|文本) = (P(文本|垃圾邮件) * P(垃圾邮件)) / P(文本)2. P(非垃圾邮件|文本)：同样地，我们需要计算给定文本为"购买廉价药物，快速发货！"时，该邮件为非垃圾邮件的概率。
假设在100封邮件中，有70封是非垃圾邮件，其中有20封包含了"购买廉价药物，快速发货！"这样的文本。
因此，P(文本|非垃圾邮件) = 20 / 70 = 2/7。
同样地，假设P(非垃圾邮件) = 0.7。
综合利用贝叶斯公式，可以计算P(非垃圾邮件|文本)： P(非垃圾邮件|文本) = (P(文本|非垃圾邮件) * P(非垃圾邮件)) / P(文本)最后，比较P(垃圾邮件|文本)和P(非垃圾邮件|文本)的大小，即可确定这封邮件的分类。
最小风险贝叶斯例题
最小风险贝叶斯例题假设有两个袋子，袋子A中有3个红球和7个蓝球，袋子B中有6个红球和4个蓝球。
从这两个袋子中随机选择一个袋子，然后从该袋子中随机抽出一个球。
如果抽出的球是红色的，你需要根据最小风险贝叶斯准则来判断该球来自哪个袋子。
先定义一些符号：- 假设袋子A被选择的概率为P(A)，袋子B被选择的概率为P(B)。
由于只有2个袋子可供选择，因此P(A)+P(B)=1。
- 假设从袋子A中抽出红球的概率为P(红|A)，从袋子B中抽出红球的概率为P(红|B)。
根据上述数据，P(红|A)=3/10，P(红|B)=6/10。
- 我们需要计算的是P(A|红)，即在抽出红球的情况下，袋子A被选择的概率。
根据贝叶斯定理，我们有：P(A|红) = P(红|A) * P(A) / P(红)其中，P(红)表示从两个袋子中抽出红球的概率，可以用全概率公式计算：P(红) = P(红|A) * P(A) + P(红|B) * P(B)将上述数据代入公式，可得：P(红) = 3/10 * P(A) + 6/10 * P(B)因为P(A)+P(B)=1，所以可以将P(B)表示为1-P(A)，代入公式，得到：P(红) = 3/10 * P(A) + 6/10 * (1 - P(A)) = 6/10 - 3/10 * P(A)将P(红)代入P(A|红)的公式，得到：P(A|红) = P(红|A) * P(A) / (3/10 * P(A) + 6/10 - 3/10 * P(A)) 化简上式，得到：P(A|红) = 3/7因此，根据最小风险贝叶斯准则，我们应该选择袋子A，因为袋子A被选择的概率为3/7，大于袋子B的被选择概率2/7。
纯策略贝叶斯纳什均衡例题
纯策略贝叶斯纳什均衡例题引言：纯策略贝叶斯纳什均衡是博弈论中常用的概念之一，它可以用于分析多方参与的决策问题。
本文将通过一个例题来解释纯策略贝叶斯纳什均衡的概念及应用。
例题背景：假设有两家咖啡店，分别是A店和B店。
每天早晨，两家咖啡店都需要决定自己的咖啡价格。
同时，消费者也需要决定去哪家咖啡店购买。
假设消费者根据市场情况作出购买决策。
A店和B店的利润与消费者选择有关。
情景一：A店设置较高的价格，B店设置较低的价格。
这种情况下，消费者更愿意选择购买B店的咖啡。
B店的利润将最大化，而A店的利润将最小化。
情景二：A店和B店都设置较低的价格。
这种情况下，消费者会更加倾向于选择购买A店的咖啡。
A店的利润将最大化，而B店的利润将最小化。
情景三：A店和B店都设置较高的价格。
这种情况下，消费者没有购买的动力，两家咖啡店的利润都会很低。
分析与求解：我们可以将上述情景转化为一个博弈论的模型，其中A店和B店是两个决策者，他们需要根据对方的策略来决定自己的策略。
消费者的选择将影响两家咖啡店的利润。
根据纯策略贝叶斯纳什均衡的概念，我们需要确定每个决策者的策略组合，以获得最优的结果。
在这个例题中，我们需要确定A店和B店的咖啡价格。
假设A店有80%的机会成为消费者的首选，B店有20%的机会。
根据这个信息，我们可以得到以下策略组合：情景一：A店设置高价格，B店设置低价格。
情景二：A店设置低价格，B店设置低价格。
情景三：A店设置高价格，B店设置高价格。
然后我们可以计算每种策略组合下两家咖啡店的利润，并找出使两家咖啡店利润最大化的策略组合。
结论：通过计算，我们可以得到以下结果：情景一：A店设置高价格，B店设置低价格。
这种情况下，A店的利润最大化，B店的利润最小化。
因此，纯策略贝叶斯纳什均衡的结果是，A店设置高价格，B店设置低价格时，两家咖啡店的利润最优化。
扩展思考：本例题中我们假设了A店有80%的机会成为消费者的首选，B店有20%的机会。
贝叶斯博弈例题
贝叶斯博弈例题
贝叶斯博弈是一种非常具有挑战性的统计学原理，它主要关注一对对手之间的策略比较和定量比较，以挖掘优势和弊端，最终实现更优的博弈结果。
在游戏研究中，贝叶斯博弈是解决博弈结果的有效策略，它不仅可以挖掘双方的策略优势，还能提出强势的策略以实现获胜的可能性。
本文以一个实际的贝叶斯博弈例题为基础，分析其应用的原理及方法，力求指导解决类似例题的步骤及技巧。
例题：一位男子有一次机会抽取一样物品，可供抽取的物品有A、B、C，男子假设其中有一个物品比较珍贵，价值最高，请用贝叶斯博弈确定他要抽取哪一样？
- 1 -。
贝叶斯纳什均衡例题
贝叶斯纳什均衡例题
贝叶斯纳什均衡 (Bayesian Nash Equilibrium) 是一种非合作的博弈理论。
在贝叶斯纳什均衡中，每个参与者根据其他参与者的策略和历史数据，计算出自己在给定其他参与者的策略下的最大收益，并采取最优策略。
以下是一个贝叶斯纳什均衡的例题。
假设有三个人，分别是 A、B、C，他们玩一个猜拳游戏。
游戏规则如下:
1. A 和 B 随机猜拳，胜负概率均为 50%。
2. 如果 A 和 B 获胜，则 C 获胜的概率为 25%。
3. 如果 A 和 B 失败，则 C 获胜的概率为 75%。
现在问，谁是游戏的胜者，如果 A 和 B 采取随机策略，而 C 采取最优策略。
根据贝叶斯纳什均衡的定义，我们需要计算出每个参与者在给定其他参与者策略下的最优策略。
首先，对于 A 和 B，由于他们是随机的，所以可以采取任何策略，因此他们的最优策略是随机。
其次，对于 C，他需要计算出自己在 A 和 B 随机策略下的最大收益。
根据游戏规则，如果 A 和 B 随机，则 C 的最大收益为 25%。
因此，C 的最优策略是采取赢的概率为 25% 的拳法。
最后，由于 C 已经采取了最优策略，A 和 B 将不得不采取随机策略。
因此，游戏的胜者是 C。
需要注意的是，贝叶斯纳什均衡只适用于非合作的博弈理论。
在合作博弈中，参与者之间的策略选择需要基于信任和相互利益。
贝叶斯决策的例题练习
贝叶斯决策的例题练习公司内部档案编码：[OPPTR-OPPT28-OPPTL98-OPPNN08]一、贝叶斯决策(Bayes decision theory)【例】某企业设计出一种新产品，有两种方案可供选择：—是进行批量生产，二是出售专利。
这种新产品投放市场，估计有3种可能：畅销、中等、滞销，这3种情况发生的可能性依次估计为：，和。
方案在各种情况下的利润及期望利润如下表。
企业可以以1000元的成本委托专业市场调查机构调查该产品销售前景。
若实际市场状况为畅销，则调查结果为畅销、中等和滞销的概率分别为、和；若实际市场状况为中等，则调查结果为畅销、中等和滞销的概率分别为、和；若实际市场状况为滞销，则调查结果为畅销、中等和滞销的概率分别为、和。
问：企业是否委托专业市场调查机构进行调查解：1.验前分析：记方案d1为批量生产，方案d2为出售专利E(d1)=*80+*20+*(-5)=(万元)E(d2)=40*+7*+1*=(万元)记验前分析的最大期望收益为E1，则E1=max{E(d1),E(d2)}=(万元)因此验前分析后的决策为：批量生产E1不作市场调查的期望收益2.预验分析：（1）设调查机构调查的结果畅销、中等、滞销分别用H1、H2、H3表示由全概率公式P(H1)=*+*+*=P(H2)=*+*+*=P(H3)=*+*+*=（2）由贝叶斯公式有P(?1|H1)=*=P(?2|H1)=*=P(?3|H1)=*=P(?1|H2)=*=P(?2|H2)=*=P(?3|H2)=*=P(?1|H3)=*=P(?2|H3)=*=P(?3|H3)=*=（3）用后验分布代替先验分布，计算各方案的期望收益值a)当市场调查结果为畅销时E(d1|H1)=80* P(?1|H1)+20* P(?2|H1)+(-5)* P(?3|H1)=80*+20*+(-5)*=(万元)E(d2|H1)=40* P(?1|H1)+7* P(?2|H1)+1* P(?3|H1)=40*+7*+1*=(万元)因此，当市场调查畅销时，最优方案是d1，即批量生产b)当市场调查结果为中等时E(d1|H2)=80* P(?1|H2)+20* P(?2|H2)+(-5)* P(?3|H2)=(万元)E(d2|H2)=40* P(?1|H2)+7* P(?2|H2)+1* P(?3|H2)=40*+7*+1*=(万元)所以市场调查为中等时，最优方案是：d1，即批量生产c)当市场调查结果为滞销时E(d1|H3)=80* P(?1|H3)+20* P(?2|H3)+(-5)* P(?3|H3)=80*+20*+(-5)*=（万元）E(d2|H3)=40* P(?1|H3)+7* P(?2|H3)+1* P(?3|H3)=40*+7*+1*=（万元）因此市场调查为滞销时，最优方案是：d2，即出售专利（4）通过调查，该企业可获得的收益期望值为E2= E(d1|H1)* P(H1)+ E(d1|H2)* P(H2)+ E(d2|H3)* P(H3)=*+*+*=（万元）通过调查，该企业收益期望值能增加E2-E1=（万元）因此，在调查费用不超过万元的情况下，应进行市场调查3.验后分析（1）本题中调查费用1000<9600,所以应该进行市场调查（2）当市场调查结果为畅销时，选择方案1，即批量生产（3）当市场调查结果为中等时时，选择方案1，即批量生产（4）当市场调查结果为滞销时，选择方案2，即出售专利。
全概率与贝叶斯公式练习
全概率与贝叶斯公式
1.有三个箱子, 分别编号1, 2, 3. A号箱装有1红球, 4白球; B号箱装有2红球, 3白球;
C号箱装有3红球.某人从三箱中任取一箱, 再从箱中任取一球，则取到红球的概率为.
2.一盒中放12个乒乓球，其中有9个是新的，第一次比赛时，从中任取3个球来用于比赛，
赛后放回盒中，第二次比赛时再从盒中取3个球，问第二次取出的球全是新球的概率为.
3.某人赶赴高考有四种方式：家人接送、滴滴约车、骑自行车、步行，选择概率分别为0.4、
0.3、0.2、0.1，若家人接送则不会迟到，若选择滴滴约车、骑自行车、步行则迟到概率分
别为1
4、1
3
、1
12
，若此人考试迟到，则最大可能的赴考方式是.
4.甲乙两人同时对一敌机进行射击，甲乙击中的概率分别为0.5,0.6，若敌机被一人击中，则被
击落的概率为0.3；若被两人击中，则被击落的概率为0.8
（1）求敌机被击中的概率.
（2）求敌机被击落的概率.
5.在学习数学过程中，假设努力学习的学生有90%考试及格，不努力学习的学生有10%考试
及格。
经期末调查得知本学期有80%的同学努力学习。
（1）求期末考试的及格率.
（2）若某人考试及格，则其不努力学习的概率.
6.已知某人初始风评可信度为0.9，此人可信条件下说谎的概率为0.1，不可信的条件下说谎
的概率为0.5，
（1）此人第一次说谎后，求其可信度.（精确到0.01）
（2）此人第二次说谎后，求其可信度.（精确到0.01）
1。
贝叶斯准则例题
贝叶斯准则例题⼀、贝叶斯准则：例题1：设⼆元假设检验的观测信号模型为：H 0: x = -1+n H 1: x = 1+n其中n 是均值为0，⽅差为212nσ=的⾼斯观测噪声。
若两种假设是等先验概率的，⽽代价因⼦为000110111,8,4,2,c c c c ==== 试求贝叶斯（最佳）表达式和平均代价C:解：因为两种假设是等先验概率的所以 011()()2P H P H ==，这样，贝叶斯准备的似然⽐函数()x λ为：① 122110221(1)exp 1122(|)22()exp(4)(|)(1)1exp 112222x p x H x x p x H x πλπ--?==?=+ ?-??⽽似然⽐检测门限η为：010********(41)()()21()()(82)2P H c c P H c c η--=?=-- =1/2于是贝叶斯判决表达式为11exp(4)2H x H ><，两边取⾃然对数，并整理的最简判决表达式为10.1733H x H >-<②现在计算判决概率01(|)P H H 和00(|)P H H ，由于本例中检验统计量()l x x =，所以在两个假设下检验统计量的概率密度函数分别为：122012211(1)(|)exp 1122221(1)(|)exp 112222l p l H l p l H ππ+=-???-=-???这样，0.17330111220.1733(|)(|)1(1)exp 0.0486112222P H H p l H dll dl π--∞--∞=-=-=0.17330001220.1733(|)(|)1(1)exp 0.8790112222P H H p l H dll dl π--∞--∞=+=-=最后，利⽤贝叶斯平均代价表达式，01011110111010100000()()()()(|)()()(|)C P H c P H c P H c c P H H P H c c P H H =++---代⼊0000110(),(|),(|),P H P H H P H H c 等各数据，计算得： 1.8269C=总结：如果我们把判决表达式中的检测门限-0.1733稍作调整，例如调整为-0.1700极品-0.1800，则计算出的平均代价均⼤于检测门限为-0.1733的平均代价，这⼀结果从侧⾯验证了贝叶斯准则的确能使平均代价最⼩。
贝叶斯决策的经典例题练习
一、贝叶斯决策(Bayes decision theory)【例】某企业设计出一种新产品，有两种方案可供选择：—是进行批量生产，二是出售专利。
这种新产品投放市场，估计有3种可能：畅销、中等、滞销，这3种情况发生的可能性依次估计为：0.2，0.5和0.3。
方案在各种情况下的利润及期望利润如下表。
企业可以以1000元的成本委托专业市场调查机构调查该产品销售前景。
若实际市场状况为畅销，则调查结果为畅销、中等和滞销的概率分别为0.9、0.06和0.04；若实际市场状况为中等，则调查结果为畅销、中等和滞销的概率分别为0.05、0.9和0.05；若实际市场状况为滞销，则调查结果为畅销、中等和滞销的概率分别为0.04、0.06和0.9。
问：企业是否委托专业市场调查机构进行调查？解：1.验前分析：记方案d1为批量生产，方案d2为出售专利E(d1)=0.2*80+0.5*20+0.3*(-5)=24.5(万元)E(d2)=40*0.2+7*0.5+1*0.3=11.8(万元)记验前分析的最大期望收益为E1，则E1=max{E(d1),E(d2)}=24.5(万元)因此验前分析后的决策为：批量生产E1不作市场调查的期望收益2.预验分析：（1）设调查机构调查的结果畅销、中等、滞销分别用H1、H2、H3表示由全概率公式P(H1)=0.9*0.2+0.06*0.5+0.04*0.3=0.232P(H2)=0.05*0.2+0.9*0.5+0.05*0.3=0.475P(H3)=0.04*0.2+0.06*0.5+0.9*0.3=0.308（2）由贝叶斯公式有P(Ɵ1|H1)=0.9*0.2/0.232=0.776P(Ɵ2|H1)=0.06*0.5/0.232=0.129P(Ɵ3|H1)=0.04*0.3/0.232=0.052P(Ɵ1|H2)=0.05*0.2/0.475=0.021P(Ɵ2|H2)=0.9*0.5/0.475=0.947P(Ɵ3|H2)=0.05*0.3/0.475=0.032P(Ɵ1|H3)=0.04*0.2/0.308=0.026P(Ɵ2|H3)=0.06*0.5/0.308=0.097P(Ɵ3|H3)=0.9*0.3/0.308=0.877（3）用后验分布代替先验分布，计算各方案的期望收益值a)当市场调查结果为畅销时E(d1|H1)=80* P(Ɵ1|H1)+20* P(Ɵ2|H1)+(-5)* P(Ɵ3|H1)=80*0.776+20*0.129+(-5)*0.052=64.4(万元)E(d2|H1)=40* P(Ɵ1|H1)+7* P(Ɵ2|H1)+1* P(Ɵ3|H1)=40*0.776+7*0.129+1*0.052=31.995(万元)因此，当市场调查畅销时，最优方案是d1，即批量生产b)当市场调查结果为中等时E(d1|H2)=80* P(Ɵ1|H2)+20* P(Ɵ2|H2)+(-5)* P(Ɵ3|H2)=20.46(万元)E(d2|H2)=40* P(Ɵ1|H2)+7* P(Ɵ2|H2)+1* P(Ɵ3|H2)=40*0.021+7*0.947+1*0.032=7.501(万元)所以市场调查为中等时，最优方案是：d1，即批量生产c)当市场调查结果为滞销时E(d1|H3)=80* P(Ɵ1|H3)+20* P(Ɵ2|H3)+(-5)* P(Ɵ3|H3)=80*0.026+20*0.097+(-5)*0.877=-0.365（万元）E(d2|H3)=40* P(Ɵ1|H3)+7* P(Ɵ2|H3)+1* P(Ɵ3|H3)=40*0.026+7*0.097+1*0.877=2.596（万元）因此市场调查为滞销时，最优方案是：d2，即出售专利（4）通过调查，该企业可获得的收益期望值为E2= E(d1|H1)* P(H1)+ E(d1|H2)* P(H2)+ E(d2|H3)* P(H3)=64.4*0.232+20.46*0.475+2.596*0.308=25.46（万元）通过调查，该企业收益期望值能增加E2-E1=25.46-24.5=0.96（万元）因此，在调查费用不超过0.96万元的情况下，应进行市场调查3.验后分析（1）本题中调查费用1000<9600,所以应该进行市场调查（2）当市场调查结果为畅销时，选择方案1，即批量生产（3）当市场调查结果为中等时时，选择方案1，即批量生产（4）当市场调查结果为滞销时，选择方案2，即出售专利Welcome To Download !!!欢迎您的下载，资料仅供参考！。
贝叶斯纳什均衡例题假设有两家企业
贝叶斯纳什均衡例题假设有两家企业摘要：1.贝叶斯纳什均衡的概述2.贝叶斯纳什均衡的例题：两家企业的博弈3.贝叶斯纳什均衡的应用范围正文：一、贝叶斯纳什均衡的概述贝叶斯纳什均衡（Bayesian Nash Equilibrium）是一种博弈论中的概念，指的是在给定自己的特征和其他局中人特征的概率分布的情况下，每个局中人选择策略使自己的期望支付达到最大化，也就是说，没有人有积极性选择其他策略。
在这种均衡状态下，每个参与者都认为自己的选择是最佳的，因为其他参与者也作出了相同的选择。
二、贝叶斯纳什均衡的例题：两家企业的博弈假设有两家企业A 和B，它们分别面临市场进入与否的决策。
企业A 可以选择进入或不进入市场，企业B 也可以选择进入或不进入市场。
两个企业的收益取决于它们各自的决策以及对方企业的决策。
如果企业A 进入市场，企业B 选择阻挠的概率为x，此时企业A 的收益为-10；如果企业A 进入市场，企业B 不阻挠的概率为1-x，此时企业A 的收益为40。
同样，如果企业B 进入市场，企业A 选择阻挠的收益为-10，企业B 不阻挠的收益为40。
在这个博弈过程中，企业A 和企业B 都希望最大化自己的收益。
因此，它们需要根据对方的决策来选择自己的最优策略。
在贝叶斯纳什均衡状态下，企业A 和企业B 都选择了能使自己收益最大化的策略，此时没有人有积极性选择其他策略。
三、贝叶斯纳什均衡的应用范围贝叶斯纳什均衡是一种理论分析工具，它可以帮助我们在不确定性条件下，预测和分析各个参与者的决策行为。
在实际应用中，贝叶斯纳什均衡可以用于解决许多经济、社会和政治领域的问题，例如价格博弈、专利竞争、国际贸易等。
全概率公式和贝叶斯公式练习题
例题讲解:例题 1.市场上某产品由三家厂家提供，根据以往的记录，这三个厂家的次品率分别为，0.020.,0.01,0.03，三个厂家生产的产品所占的市场份额分别0.15,0.8,0.05.产品出厂后运到仓库，见面后再进入市场，设这三个厂家的产品在仓库是均匀混合（1）在仓库中随机的取一个产品，求它的次品的概率。
（2）在仓库中随机的取一个产品，发现为次品，如果你是管理者，该如何追究三个厂家的责任？例题2保险公司把被保险人分成三类”谨慎的”,”一般的”和”冒险的”，统计资料表明，上述三种人在一年内发生事故的概率依次为，0. 5. 0.15. 和0.30. 如果”谨慎的”被保险人占20%”一般的”，被保险人占50%，”冒失的”被保险人占30%，确认一个被保险人在一年内出事故的概率。
练习:1.设某工厂有两个车间生产同型号家用电器，第一车间的次品率为0.15，第二车间的次品率为0.12，两个车间的成品都混合堆放在一个仓库，假设第1,2车间生产的成品比例为2:3，今有一客户从成品仓库中随机提一台产品，求该产品合格的概率。
解：设B={从仓库中随机提出的一台是合格品}A i ={提出的一台是第i 车间生产的}，i=1,2则有分解B=A 1B ∪A 2B由题意P(A1)=2/5,P(A2)=3/5,P(B|A1)=0.85,P(B|A2)=0.88由全概率公式P(B)= P(A 1) P(B|A 1)+ P(A 2) P(B|A 2)=0.4*0.85+0.6*0.88=0.868.2. 盒中有a 个红球，b 个黑球，今随机地从中取出一个，观察其颜色后放回，并加上同色球c 个，再从盒中第二次抽取一球，求第二次抽出的是黑球的概率。
解：设A={第一次抽出的是黑球}，B={第二次抽出的是黑球}，则B AB AB =+， 由全概率公式()()()()()P B P A P B A P A P B A =+， 由题意(),(|),(),(|)b b c a b P A P B A P A P B A a b a b c a b a b c +====++++++ 所以()()()()()()b b c ab b P B a b a b c a b a b c a b+=+=+++++++ 3. 设某公路上经过的货车与客车的数量之比为2:1，货车中途停车修理的概率为0.02，客车为0.01，今有一辆汽车中途停车修理，求该汽车是货车的概率。
贝叶斯决策例题
解：采用贝叶斯决策方法。
根据期望值准则选择施工方案有利，相应最大期望收益值EMV*（先）=0.8（2）预验分析完全信息的最大期望收益值：EPPI=0.3×5+0.7×（-0.2）=1.36（万元）完全信息价值： EVPI=EPPI- EMV*（先）=1.36-0.8=0.56（万元） 即，完全信息价值大于信息成本，请气象中心进行预报是合算的。
（3）后验分析①补充信息：气象中心将提供预报此时期内两种天气状态x 1(好天气)、x 2(坏天气)将会出现哪一种状态。
从气象中心提供的同期天气资料可得知条件概率：天气好且预报天气也好的概率 P （x 1/θ1）=0.8天气好而预报天气不好的概率 P （x 2/θ1）=0.2天气坏而预报天气好的概率 P （x 1/θ2）=0.1天气坏且预报天气也坏的概率 P （x 2/θ2）=0.9②计算后验概率分布：根据全概率公式和贝叶斯公式，计算后验概率。
预报天气好的概率 1111212()()(/)()(/)P x P P x P P x θθθθ=+ =0.31预报天气坏的概率 2121222()()(/)()(/)P x P P x P P x θθθθ=+ =0.69预报天气好且天气实际也好的概率：111111()(/)(/)()P P x P x P x θθθ⋅==0.3×0.8/0.31=0.77 预报天气好而天气坏的概率：212211()(/)(/)()P P x P x P x θθθ⋅==0.7×0.1/0.31=0.23 预报天气坏而实际天气好的概率:121122()(/)(/)()P P x P x P x θθθ⋅==0.3×0.2/0.69=0.09 预报天气坏且实际天气也坏的概率：222222()(/)(/)()P P x P x P x θθθ⋅==0.7×0.9/0.69=0.91。
(贝叶斯决策例题)
Equation Chapter 1 Section 1例：某工程项目按合同应在三个月内完工，其施工费用与工程完工期有关。
假定天气是影响能否按期完工的决定因素，如果天气好，工程能按时完工，获利5万元；如果天气不好，不能按时完工，施工单位将被罚款1万元；若不施工就要付出窝工费2千元。
根据过去的经验，在计划实施工期天气好的可能性为30%。
为了更好地掌握天气情况，可以申请气象中心进行天气预报，并提供同一时期天气预报资料，但需要支付资料费800元。
从提供的资料中可知，气象中心对好天气预报准确性为80%，对坏天气预报准确性为90%。
问如何进行决策。
解：采用贝叶斯决策方法。
先验分析根据期望值准则选择施工方案有利，相应最大期望收益值EMV*（先）=0.8（2）预验分析完全信息的最大期望收益值：EPPI=0.3×5+0.7×（-0.2）=1.36（万元）完全信息价值： EVPI=EPPI- EMV*（先）=1.36-0.8=0.56（万元） 即，完全信息价值大于信息成本，请气象中心进行预报是合算的。
（3）后验分析①补充信息：气象中心将提供预报此时期内两种天气状态x1(好天气)、x2(坏天气)将会出现哪一种状态。
从气象中心提供的同期天气资料可得知条件概率： 天气好且预报天气也好的概率 P （x1/θ1）=0.8 天气好而预报天气不好的概率 P （x2/θ1）=0.2 天气坏而预报天气好的概率 P （x1/θ2）=0.1 天气坏且预报天气也坏的概率 P （x2/θ2）=0.9②计算后验概率分布：根据全概率公式和贝叶斯公式，计算后验概率。
预报天气好的概率1111212()()(/)()(/)P x P P x P P x θθθθ=+=0.31预报天气坏的概率2121222()()(/)()(/)P x P P x P P x θθθθ=+=0.69 预报天气好且天气实际也好的概率：111111()(/)(/)()P P x P x P x θθθ⋅==0.3×0.8/0.31=0.77预报天气好而天气坏的概率：212211()(/)(/)()P P x P x P x θθθ⋅==0.7×0.1/0.31=0.23预报天气坏而实际天气好的概率:121122()(/)(/)()P P x P x P x θθθ⋅==0.3×0.2/0.69=0.09预报天气坏且实际天气也坏的概率： 222222()(/)(/)()P P x P x P x θθθ⋅==0.7×0.9/0.69=0.91上述计算可以用表格表示：③ 后验决策：若气象中心预报天气好（x1）,则每个方案的最大期望收益值 E(d1/x1)=0.77×5+0.23×(-1)=3.62 E(d2/x1)=0.77×(-0.2)+0.23×(-0.2)=-0.2选择d1即施工的方案，相应在预报x1若气象中心预报天气不好（x2） E(d1/x2)=0.09×5+0.91×(-1)=-0.46 E(d2/x2)=0.09×(-0.2)+0.91×(-0.2)=-0.2选择d2即不施工的方案，相应在预报x2时的最大期望收益值E （X2）=-0.2④ 计算补充信息的价值：得到天气预报的情况下，后验决策的最大期望收益值：1122*()()()()()EMV P x E x P x E x =⋅+⋅后=0.31×3.62+0.69×（-0.2）=0.9842则补充的信息价值为：EMV*(后)- EMV*(先)=0.9842-0.8=0.1842补充信息价值大于信息费（800元），即这种费用是合算的。
Bayes补充例题及解答
关于Bayes 决策分析的补充例题：1、某公司经营某种商品，可以采取的经营方案有三种：1a （大批量），2a （中批量），3a （小批量）。
市场销售状态有三种：1θ（畅销），2θ（一般），3θ（滞已知市场销售状态概率2.0)(1=θP ，5.0)(2=θP ，3.0)(3=θP 。
该公司市场调研人员拟进行市场预测，其以往市场预测准确概率分布矩阵为：()()()321|||θθθj j j H P H P H P321H H H ⎪⎪⎪⎭⎫⎝⎛90.010.005.008.070.015.002.020.080.0 其中，1H ，2H ，3H 分别表示预测值畅销、一般、滞销。
市场预测费用为5万元。
通过决策分析回答以下问题：（1）如果不进行市场预测，应如何决策？如果有完全信息，计算EVPI ；（一）不进行市场预测时：⎪⎪⎪⎭⎫ ⎝⎛--==⨯69102040506030100)(33ij v V ,2.0)(1=θP ,5.0)(2=θP ,3.0)(3=θP ()173.0)60(5.0302.0100)(3111=⨯-+⨯+⨯==∑=i i i P v a E θ()243.0)20(5.0402.050)(3122=⨯-+⨯+⨯==∑=i i i P v a E θ()3.83.065.092.010)(3133=⨯+⨯+⨯==∑=i i i P v a E θ因此：312a a a ，先验最优方案2a a opt =，即经营中等批量的商品，且期望收益值为：()2421==a E E8.17248.4124)3.065.0402.0100()()()(max )(),(max ),(),(max 31=-=-⨯+⨯+⨯=-=-⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-=∑=opt i ij i j opt j j opt a E P v a E a V E a V a V E EVPI θθθθ（2）如果进行市场预测，应如何根据预测结果进行决策；计算EVAI ，并判断是否进行市场预测；（二）如果进行市场预测，并用它修正原先掌握的情况。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、贝叶斯决策(Bayes decision theory)
【例】某企业设计出一种新产品，有两种方案可供选择：—是进行批量生产，二是出售专利。
这种新产品投放市场，估计有3种可能：畅销、中等、滞销，这3种情况发生的可能性依次估计为：0.2，0.5和0.3。
方案在各种情况下的利润及期望利润如下表。
企业可以以1000元的成本委托专业市场调查机构调查该产品销售前景。
若实际市场状况为畅销，则调查结果为畅销、中等和滞销的概率分别为0.9、0.06和0.04；若实际市场状况为中等，则调查结果为畅销、中等和滞销的概率分别为0.05、0.9和0.05；若实际市场状况为滞销，则调查结果为畅销、中等和滞销的概率分别为0.04、0.06和0.9。
问：企业是否委托专业市场调查机构进行调查？
解：
1.验前分析：
记方案d1为批量生产，方案d2为出售专利
E(d1)=0.2*80+0.5*20+0.3*(-5)=24.5(万元)
E(d2)=40*0.2+7*0.5+1*0.3=11.8(万元)
记验前分析的最大期望收益为E1，则E1=max{E(d1),E(d2)}=24.5(万元)
因此验前分析后的决策为：批量生产
E1不作市场调查的期望收益
2.预验分析：
（1）设调查机构调查的结果畅销、中等、滞销分别用H1、H2、H3表示
由全概率公式
P(H1)=0.9*0.2+0.06*0.5+0.04*0.3=0.232
P(H2)=0.05*0.2+0.9*0.5+0.05*0.3=0.475
P(H3)=0.04*0.2+0.06*0.5+0.9*0.3=0.308
（2）由贝叶斯公式有
P(Ɵ1|H1)=0.9*0.2/0.232=0.776
P(Ɵ2|H1)=0.06*0.5/0.232=0.129
P(Ɵ3|H1)=0.04*0.3/0.232=0.052
P(Ɵ1|H2)=0.05*0.2/0.475=0.021
P(Ɵ2|H2)=0.9*0.5/0.475=0.947
P(Ɵ3|H2)=0.05*0.3/0.475=0.032
P(Ɵ1|H3)=0.04*0.2/0.308=0.026
P(Ɵ2|H3)=0.06*0.5/0.308=0.097
P(Ɵ3|H3)=0.9*0.3/0.308=0.877
（3）用后验分布代替先验分布，计算各方案的期望收益值
a)当市场调查结果为畅销时
E(d1|H1)=80* P(Ɵ1|H1)+20* P(Ɵ2|H1)+(-5)* P(Ɵ3|H1)
=80*0.776+20*0.129+(-5)*0.052=64.4(万元)
E(d2|H1)=40* P(Ɵ1|H1)+7* P(Ɵ2|H1)+1* P(Ɵ3|H1)
=40*0.776+7*0.129+1*0.052=31.995(万元)
因此，当市场调查畅销时，最优方案是d1，即批量生产
b)当市场调查结果为中等时
E(d1|H2)=80* P(Ɵ1|H2)+20* P(Ɵ2|H2)+(-5)* P(Ɵ3|H2)=20.46(万元)
E(d2|H2)=40* P(Ɵ1|H2)+7* P(Ɵ2|H2)+1* P(Ɵ3|H2)
=40*0.021+7*0.947+1*0.032=7.501(万元)
所以市场调查为中等时，最优方案是：d1，即批量生产
c)当市场调查结果为滞销时
E(d1|H3)=80* P(Ɵ1|H3)+20* P(Ɵ2|H3)+(-5)* P(Ɵ3|H3)
=80*0.026+20*0.097+(-5)*0.877=-0.365（万元）
E(d2|H3)=40* P(Ɵ1|H3)+7* P(Ɵ2|H3)+1* P(Ɵ3|H3)
=40*0.026+7*0.097+1*0.877=2.596（万元）
因此市场调查为滞销时，最优方案是：d2，即出售专利
（4）通过调查，该企业可获得的收益期望值为
E2= E(d1|H1)* P(H1)+ E(d1|H2)* P(H2)+ E(d2|H3)* P(H3)
=64.4*0.232+20.46*0.475+2.596*0.308=25.46（万元）通过调查，该企业收益期望值能增加
E2-E1=25.46-24.5=0.96（万元）
因此，在调查费用不超过0.96万元的情况下，应进行市场调查
3.验后分析
（1）本题中调查费用1000<9600,所以应该进行市场调查
（2）当市场调查结果为畅销时，选择方案1，即批量生产
（3）当市场调查结果为中等时时，选择方案1，即批量生产
（4）当市场调查结果为滞销时，选择方案2，即出售专利。