数学二次函数与三角形面积(周长最小与面积最大问题2)

合集下载

二次函数的最值问题——求线段，三角形周长及面积的最值

二次函数的最值问题——求线段，三角形周长及面积的最值摘要：二次函数作为初中最重要的函数，近几年来，中考拉分题常常利用二次函数求线段的最值、三角形周长的最小值及面积的最大值问题。

在解决二次函数的最值问题时，一般构建二次函数模型，通过数形结合把求三角形的周长、三角形面积的最值问题转化为求线段长度的问题。

关键词：二次函数；最值问题；轴对称；数形结合一、将军饮马“K”字形，两点之间线段最短问题1.二次函数与x轴交于点A（-1，0），B（3,0），与y轴交于点C（0,3）．在抛物线的对称轴上是否存在一点P，使得的分析：由已知，可求得二次函数的对称轴为，又因为二次函数图像关于对称轴对称可知：A、B两点关于对称，,连接BC与对称轴的交点为所求P点，则,所以CH＋EH的最小值为。

小结：利用二次函数求两线段和的最小值问题，我们通常是作其中一点关于对称轴的对称点，连接对称点与另一点得到的线段长度为我们所求的两线段和的最小值。

变式1.如问题1改为：的周长是否存在最小值？若存在，请求出的周长；若不存在，请说明理由。

分析：延伸1看起来跟问题1不一样，但实际上，万变不离其宗。

，已知A,C两点坐标，由勾股定理可得，,题目中要求周长的最小值可转化为求的最小值，也就转化为问题1，即：,问题2.如图，直线与抛物线交于点A（0,3），B(3,0) ,点F是线段AB上的动点，FE x轴，E在抛物线上，若点F的横坐标为m，请用含m的代数式表示EF的长并求EF的最大值。

分析：利用E、F分别在抛物线及一次函数上可得到，,因为,所以,可求得当时，EF的最大值为小结：利用二次函数求竖直线段的最大值，一般是通过设未知数表示出二次函数及一次函数图像上的两点，由横坐标相等，利用两点纵坐标相减可得到线段的长度，再利用二次函数求最值方法可求出线段的最大值。

变式1：问题2改为过E作,求的最大值是多少？分析：因为该一次函数，可知为等腰直角三角形，，要求的最大值只需求得的最大值，由此就转化为问题2，所以小结：求斜线段的最大值问题，一般转化为求平行于y轴线段的最值问题，再利用三角函数可求得斜线段的最大值。

二次函数与三角形的面积问题

二次函数与三角形的面积问题二次函数与三角形的面积问题教学目标：1.能够根据二次函数中不同图形的特点选择合适的方法解答图形的面积。

2.通过观察、分析、概括、总结等方法了解二次函数面积问题的基本类型，并掌握二次函数中面积问题的相关计算，从而体会数形结合思想和转化思想在二次函数中的应用。

3.掌握利用二次函数的解析式求出相关点的坐标，从而得出相关线段的长度，利用割补方法求图形的面积。

教学重点和难点：1.运用公式S=水平宽×铅垂高/2；2.运用二次函数解析式；3.将不规则的图形分割成规则图形，从而便于求出图形的总面积。

教学过程：类型一：三角形的某一条边在坐标轴上或者与坐标轴平行例1.已知：抛物线的顶点为D（1，-4），并经过点E（4，5），求：1）抛物线解析式；2）抛物线与x轴的交点A、B，与y轴交点C；3）求下列图形的面积△ABD、△ABC、△ABE、△OCD、△OCE。

解题思路：求出函数解析式y=ax²+bx+c；写出下列点的坐标：A(x1.0)；B(x2.0)；C(0.c)；求出下列线段的长：AO=BO=|c|；AB=|x1-x2|；OC=|c|。

求出下列图形的面积△ABD、△ABC、△ABE、△OCD、△OCE。

一般地，这类题目的做题步骤：1.求出二次函数的解析式；2.求出相关点的坐标；3.求出相关线段的长；4.选择合适方法求出图形的面积。

变式训练1.如图所示，已知抛物线y=ax²+bx+c（a≠0）与x轴相交于两点A(x1,0)，B(x2,0)(x1<x2)，与y轴负半轴相交于点C，若抛物线顶点P的横坐标是1，A、B两点间的距离为4，且△ABC的面积为6.1）求点A和B的坐标；2）求此抛物线的解析式；3）求四边形ACPB的面积。

类型二：三角形三边均不与坐标轴轴平行，做三角形的铅垂高。

（歪歪三角形拦腰来一刀）关于S=水平宽×铅垂高/2的知识点：如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”(a)，中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”。

二次函数中三角形问题(含问题详解)

二次函数中的三角形一．与三角形面积例1：如图，已知在同一坐标系中，直线22k y kx =+-与y 轴交于点P ，抛物线k x k x y 4)1(22++-=与x 轴交于)0,(),0,(21x B x A 两点。

C 是抛物线的顶点。

（1）求二次函数的最小值（用含k 的代数式表示）；（2）若点A 在点B 的左侧，且021<⋅x x 。

①当k 取何值时，直线通过点B ；②是否存在实数k ，使ABC ABP S S ∆∆=？如果存在，请求出此时抛物线的解析式；如果不存在，请说明理由。

例2：已知抛物线)1(3)4(2-+---=m x m x y 与x 轴交于A 、B 两点，与y 轴交于C 点，（1）求m 的取值范围；（2）若0<m ，直线1-=kx y 经过点A ，与y 轴交于点D ，且25=⋅BD AD ，求抛物线的解析式；（3）若A 点在B 点左边，在第一象限内，（2）中所得的抛物线上是否存在一点P ，使直线P A 平分ACD ∆的面积？若存在，求出P 点的坐标；若不存在，请说明理由。

例3．已知矩形ABCD 中，AB ＝2，AD ＝4，以AB 的垂直平分线为x 轴，AB 所在的直线为y 轴，建立平面直角坐标系(如图)。

(1)写出A 、B 、C 、D 及AD 的中点E 的坐标；(2)求以E 为顶点、对称轴平行于y 轴，并且经过点B 、C 的抛物线的解析式； (3)求对角线BD 与上述抛物线除点B 以外的另一交点P 的坐标；(4)△PEB 的面积S △PEB 与△PBC 的面积S △PBC 具有怎样的关系？证明你的结论。

A BC DO E x y(第25题图)例4.如图1，已知直线12y x =-与抛物线2164y x =-+交于AB ，两点．（1）求A B ，两点的坐标；（2）求线段AB 的垂直平分线的解析式；（3）如图2，取与线段AB 等长的一根橡皮筋，端点分别固定在A B ，两处．用铅笔拉着这根橡皮筋使笔尖P 在直线AB 上方的抛物线上移动，动点P 将与A B ，构成无数个三角形，这些三角形中是否存在一个面积最大的三角形？如果存在，求出最大面积，并指出此时P 点的坐标；如果不存在，请简要说明理由．二．与三角形形状例5. 如图，抛物线254y ax ax =-+经过ABC △的三个顶点，已知BC x ∥轴，点A 在x 轴上，点C 在y 轴上，且AC BC =．（1）求抛物线的对称轴；（2）写出A B C ，，三点的坐标并求抛物线的解析式；（3）探究：若点P 是抛物线对称轴上且在x 轴下方的动点，是否存在PAB △是等腰三角形．若存在，求出所有符合条件的点P 坐标；不存在，请说明理由．图2图1例 6.如图①，在平面直角坐标系中，点A 的坐标为(12)，，点B 的坐标为(31)，，二次函数2y x =的图象记为抛物线1l ．（1）平移抛物线1l ，使平移后的抛物线过点A ，但不过点B ，写出平移后的一个抛物线的函数表达式：（任写一个即可）．（2）平移抛物线1l ，使平移后的抛物线过A B ，两点，记为抛物线2l ，如图②，求抛物线2l 的函数表达式．（3）设抛物线2l 的顶点为C ，K 为y 轴上一点．若ABK ABC S S =△△，求点K 的坐标．（4）请在图③上用尺规作图的方式探究抛物线2l 上是否存在点P ，使ABP △为等腰三角形．若存在，请判断点P 共有几个可能的位置（保留作图痕迹）；若不存在，请说明师．x 图①x 图②x 图③例7. 已知：如图，抛物线2y ax bx c =++经过(1,0)A 、(5,0)B 、(0,5)C 三点．（1）求抛物线的函数关系式；（2）若过点C 的直线y kx b =+与抛物线相交于点E （4，m ），请求出△CBE 的面积S 的值；（3）在抛物线上求一点0P 使得△ABP 0为等腰三角形并写出0P 点的坐标；（4）除（3）中所求的0P 点外，在抛物线上是否还存在其它的点P 使得△ABP 为等腰三角形？若存在，请求出一共有几个满足条件的点P （要求简要说明理由，但不证明）；若不存在这样的点P ，请说明理由．例8.如图，在直角坐标系中，点A 的坐标为(－2，0)，连接OA ，将线段OA 绕原点O 顺时针旋转120°，得到线段OB ． (1)求点B 的坐标；(2)求经过A 、O 、B 三点的抛物线的解析式； (3)在(2)中抛物线的对称轴上是否存在点C ，使△BOC 的周长最小？若存在，求出点C 的坐标；若不存在，请说明理由；(4)如果点P 是(2)中的抛物线上的动点，且在x 轴的下方，那么△P AB 是否有最大面积？若有，求出此时P 点的坐标及△P AB 的最大面积；若没有，请说明理由．(注意：本题中的结果均保留根号)(第25题图)三．二次函数与三角形相似例9：已知一次函数1243--=x y 的图象分别交x 轴、y 轴于A 、C 两点，（1）求出A 、C 两点的坐标；（2）在x 轴上找出点B ，使ACB ∆∽AOC ∆，若抛物线过A 、B 、C 三点，求出此抛物线的解析式；（3）在（2）的条件下，设动点P 、Q 分别从A 、B 两点同时出发，以相同速度沿AC 、BA 向C 、A 运动，连结PQ ，使m AP =，是否存在m 的值，使以A 、P 、Q 为顶点的三角形与ABC ∆相似，若存在，求出所有m 的值；若不存在，请说明理由。

二次函数(面积、线段、特殊三角形问题)

xy DCBAOxy DCBAOxyEDCBAO一、三角形面积最值：求下列阴影面积对于左图，只需要用12S AB OC =⋅即可求出面积对于右图，由于3条边均不是坐标轴的平行线或垂线，不能采用最简单的方法求解对于不太“规则”的三角形，常采用以下方法去求面积：方法一：割补法（不唯一）如图，EDBECBS SS=-阴影，E 点坐标可通过直线CD 解析式求得方法二：水平宽，铅垂高过△CDB 的三个顶点分别作出与水平线垂直的三条直线外侧两条直线之间的距离叫△CDB 的“水平宽”，记为a 中间的这条直线在△CDB 内部线段的长度叫 △CDB 的“铅垂高”，记为h模块一面积最值问题二次函数的几种常考压轴题型我们可得出一种计算三角形面积的方法：12CDBSa h =⋅，即三角形面积等于水平宽与铅垂高乘积的一半．二、三角形面积数量问题：（1）三角形面积数量关系涉及有一个三角形的面积与一个已知三角形面积相等或有一定的倍数关系，一般通过构造两个三角形同底或等高；（2）有些类型也可以先求出已知三角形的面积，再设未知点的坐标，用未知点的坐标表示出未知三角形的面积，最后使之等于已知三角形的面积，列出等式，求解方程。

【例题】1．如图，抛物线经过A （4，0），B （1，0），C （0，﹣2）三点．（1）求出抛物线的解析式；（2）在直线AC上方的抛物线上有一点D ，使得△DCA 的面积最大，求出点D 的坐标．2．如图，抛物线y=﹣x 2+mx +n 与x 轴交于A 、B 两点，与y 轴交于点C ，抛物线的对称轴交x 轴于点D ，已知A （﹣1，0），C （0，2）．（1）求抛物线的表达式；（2）点E 是线段BC 上的一个动点，过点E 作x 轴的垂线与抛物线相交于点F ，当点E 运动到什么位置时，四边形CDBF 的面积最大？求出四边形CDBF 的最大面积及此时E 点的坐标．3.如图，抛物线223y x x =-++与直线1y x =+交于A ，C 两点，其中C 点坐标为（2，t ）．（1）若P 是抛物线上位于直线AC 上方的一个动点，求△APC 面积的最大值．（2）在直线AC 下方的抛物线上，是否存在点G ，使得6AGC S =△？如果存在，求出点G 的坐标；如果不存在，请说明理由．4.如图，抛物线343832+--=x x y 与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C 。

初中数学二次函数中三角形面积问题解析

∙∙∙∙初中数学二次函数中三角形面积问题解析一、命题意图二次函数中三角形面积相结合的题目是近年来中考数学中常见的问题,题型常考常新,体现了数形结合、化归转化、分类讨论数学思想等。

如果将三角形这一平面图形问题与二次函数相结合，就需要学生以逻辑思维和空间思维相结合的方式进行学习，以培养学生逻辑思维与空间思维能力相结合的基本数学思想，让学生学会自主思考问题的过程。

二、考点及对应的考纲要求初中数学课程教学中关于三角形面积问题的讨论一直是教学重点,这其中牵涉了二次函数与几何问题的融合,是初中数学课程中的一个难点。

求面积常用的方法：（1）直接法，若题已经给出或能由已知条件推出个边的长度并且通过坐标能找到对应的高，那么三角形的面积能直接用公式算出来。

（2）简单的组合，解决问题的途径常需要进行图形割补、等积变形等图形变换。

（3）面积不变同底等高或等底等高的转换，利用平行线得到三角形同底等高进行面积转化。

（4）如图，过△ABC 的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC 的“水平宽”(a )，中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h )”. 可得出一种计算三角形面积的新方法：ah S ABC 21=∆，即三角形面积等于水平宽与铅垂高乘积的一半。

三、试题讲解过程如图，在平面直角坐标系中，抛物线c bx ax y ++=2C （0，－4）三点.（1）求该抛物线的解析式；（2）若点D 是该抛物线上一动点，且在第四象限，当∆面积最大时，求点D 的坐标.解:（1）解法一: 由题意得，c=－4, ∴⎩⎨⎧=-+=--0441604b a b a ,解得：⎩⎨⎧-==31b a , ∴=x y 解法二: 由题意得，设y=a （x+1）（x-4）, ∴∴y=（x+1）（x-4）, ∴432--=x x y ,（2）解法一:由（1）可知，y=x 2－3x －4,设点D 为（x, x 2－3x －4）,过点D 作DE ∥OC 交BC 设直线BC 的解析式为y=kx ＋b,则∙∙∙⎩⎨⎧=+-=044b k b ，∴⎩⎨⎧-==41b k ，∴y=x －4, ∴E （x, x －4）∴DE=（x －4）－（x 2－3x －4）= －x 2＋4x,∵a=－1＜0, ∴当x=2时, DE 取最大值，S △BCD 解法二：由（1）可知，y=x 2－3x －4, 设点D 为（x,y ）,过点D 作DF ⊥OB 于点F,S △BCD =S 梯形OCDF ＋S △BDF －S △OBC=21x （4-y ）＋21（-y ）（4-x ）－8 =2x －2y －8=2x －2（x 2－3x －4）－8=－2x 2＋8x,∵a=－2＜0, ∴当x=2时, S △BCD 取最大值，∴D （2,－6解法三:由（1）可知，y=x 2－3x －4, 过点D 作DE ∥设直线BC 的解析式为y=kx ＋b, 则⎩⎨⎧=+-=044b k b ，∴⎩⎨⎧-==41b k ，∴y=x －4,∴设直线DE 的解析式为y=x ＋d,则x 2－3x －4=x ＋d, x 2∴当△=（-4）2-4（-4-d ）=0, d=-8, S △BCD 取最大值， ∴x 2－4x ＋4=0, ∴（x-2）2=0, ∴x 1=x 2=2, ∴D （2,－6）. 四、试题的拓展延伸及变式分析如图，在平面直角坐标系中，抛物线c bx ax y ++=2C （0，3）三点.（1）若点D 是抛物线的对称轴上一点，当ACD ∆求点D 的坐标；（2）在（1）的情况下，抛物线上是否存在除点A 得PCD ∆ 的面积与ACD ∆P 的坐标；若不存在，请说明理由.解：（1）∵抛物线c bx ax y ++=2经过A （1，0），B （3∴抛物线的对称轴l 是x=231+=2， ∵△ACD 的周长=AD+AC+CD, AC 是定值， ∴当AD+CD 最小时，△ACD 的周长最小，∵点A 、点B 关于对称轴l 对称，∴连接BC 交l 于点D ，即点D 为所求的点, 设直线BC 的解析式为n kx y +=，∴ ⎩⎨⎧=+=033n k n ，∴⎩⎨⎧=-=31n k ,∴直线BC 的解析式为3+-=x y ，∙∙当x=2时，y=-x+3=-2+3=1，∴点D 的坐标是（2，1）.（2）解：由（1）可知，∵抛物线c bx ax y ++=2经过A （1，0），B （3，0），C （0，3）三点，∴c=3, ∴⎩⎨⎧=++=++033903b a b a ,解得：⎩⎨⎧-==41b a ,∴342+-=x x y ,解法一：如图，①过点A 作AP 1∥CD 交抛物线于点P 1，∴设直线AP 1的解析式为d x y +-=， ∴∴d=1,∴直线AP 1的解析式为1+-=x y ，解方程1+-x =342+-x x ，（x-1）（x-2）∴x 1=1, x 2=2,当x 1=1时，11+-=x y =0当x 2=2时，12+-=x y =-1，∴点P 1②设直线AP 1交y 轴于点E （0，1）把直线BC 向上平移2个单位交抛物线于P 2得直线P 2P 3的解析式为5+-=x y ，解方程5+-x =342+-x x ， x 2－3x －2=0,∴x 3=2173+, x 4=2173-, 当x 3=2173+时，53+-=x y =2177-，当x 4=2173-时，54+-=x y =2177+， ∴点P 2的坐标是（2173+，2177-）,点P 3的坐标是（2173-，2177+）, 综上所述, 抛物线上存在点P 1（2，-1）,P 2（2173+，2177-）, P 3（2173-，2177+）, 使得△PCD 的面积与△ACD 的面积相等. 解法二：如图,过A 点作AE∥y 轴，交BC 于点E ．则E 点的纵坐标为231=+-．∴ AE＝2．设点P 为（n ，342+-n n ），过P 点作PF∥y 轴，交BC 于点F ，则点F 为（n ，n -3），PF∥AE．若PF ＝AE ，则△PCD 与△ACD 的面积相等．∙∙①若P 点在直线BC 的下方，则PF ＝（n -3）-（342+-n n ）=n 2-∴n n 32+-=2．解得21=n ，12=n ．当2=n 时，3-n-2∴P 1点坐标为（2，-1）．同理当1=n 时，P 点坐标为（1，0）（不合题意，舍去）．②若P 点在直线BC 的上方，则PF=（342+-n n ）-（n -3）=n n 32-∴232=-n n ．解得21733+=n ，4=n 当21733+=n 时，P 点的纵坐标为2177221733-=++-；当21734-=n 时，P 点的纵坐标为2177221733+=+--． ∴点P 2的坐标是（2173+，2177-）,点P 3的坐标是（2173-，2177+）, 综上所述, 抛物线上存在点P 1（2，-1）,P 2（2173+，2177-）, P 3（2173-，2177+）, 使得△PCD 的面积与△ACD 的面积相等. 在以上问题的分析中研究思路为：（1）分析图形的成因；（2）识别图形的形状；（3）找出图形的计算方法。

二次函数中的三角形面积问题教案

二次函数中的三角形面积问题教案《二次函数中的三角形面积问题教案》这是优秀的教学设计文章，希望可以对您的学习工作中带来帮助！作业内容二次函数中的三角形面积问题教案球溪高级中学郭燕教学目标知识与技能1.复习巩固二次函数的性质;2.通过观察分析，能够概括总结出二次函数中三角形面积问题的基本类型;3.能够用直接法和割补法求二次函数中的三角形面积;过程与方法在求面积的过程中，体会数形结合和转化思想在二次函数三角形面积问题中的应用。

情感态度与价值观5.进一步培养学生学习数学的兴趣和增强学生学习的自信心6.在转化，建模的过程中，体验解决问题的方法，培养学生合作交流意识和探索精神。

二、教学重难点重点：直接法和割补法(铅垂法)求二次函数中的三角形面积问题;难点：二次函数中三角形面积的最值问题。

三、教学过程【复习旧知】1.已知二次函数，请用五点法在方格纸上画出草图，并结合图像尽可能多地写出你认为正确的结论。

师生活动：学生作图，思考，发言;教师总结二次函数的性质可从开口方向，顶点，与坐标轴的交点，对称轴，最值，增减性，对称性等方面研究。

设计意图：复习巩固五点法作二次函数草图，同时简单回顾二次函数的性质。

【问题探究】若二次函数与x轴交于A，B两点(B在A的左边)，与y轴交于点C，顶点为点D。

【问题1】：任意连接ABCDO五点中的三个点，能组成哪些三角形?师生活动：学生思考后举手口答。

设计意图：引入今天的复习课内容——二次函数中的三角形面积问题。

【追问1】：在这四个三角形中，哪些三角形的面积比较好求，请写下来。

【追问2】：这些三角形面积为什么相对容易求解?——有一边在坐标轴上。

师生活动：学生思考求解，并积极发言，同时观察分析，总结规律。

设计意图：会利用公式直接计算至少有一边在坐标轴上的三角形面积。

【追问3】：若二次函数与y轴的交点关于对称轴的对称点为点E，你能求出和的面积吗?【追问4】：这两个三角形面积为什么也相对容易求解?——有一边平行于坐标轴。

二次函数与三角形面积(周长最小与面积最大问题2)

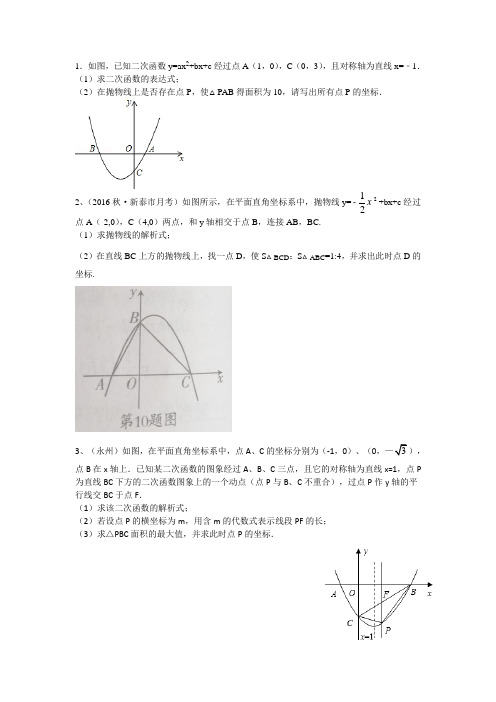
1．如图，已知二次函数y=ax 2+bx+c 经过点A （1，0），C （0，3），且对称轴为直线x=﹣1．（1）求二次函数的表达式；（2）在抛物线上是否存在点P ，使△PAB 得面积为10，请写出所有点P 的坐标．2、（2016秋·新泰市月考）如图所示，在平面直角坐标系中，抛物线y=212x -+bx+c 经过点A （-2,0），C （4,0）两点，和y 轴相交于点B ，连接AB ，BC.（1）求抛物线的解析式；（2）在直线BC 上方的抛物线上，找一点D ，使S △BCD ：S △ABC =1:4，并求出此时点D 的坐标.3、（永州）如图，在平面直角坐标系中，点A 、C 的坐标分别为（-1，0）、（0点B 在x 轴上．已知某二次函数的图象经过A 、B 、C 三点，且它的对称轴为直线x=1，点P 为直线BC 下方的二次函数图象上的一个动点（点P 与B 、C 不重合），过点P 作y 轴的平行线交BC 于点F ．（1）求该二次函数的解析式；（2）若设点P 的横坐标为m ，用含m 的代数式表示线段PF 的长；（3）求△PBC 面积的最大值，并求此时点P 的坐标．4．（2012•广西）已知抛物线y=ax2+2x+c的图象与x轴交于点A（3，0）和点C，与y轴交于点B（0，3）．（1）求抛物线的解析式；（2）在抛物线的对称轴上找一点D，使得点D到点B、C的距离之和最小，并求出点D的坐标；（3）在第一象限的抛物线上，是否存在一点P，使得△ABP的面积最大？若存在，求出点P的坐标；若不存在，请说明理由．5．（2011•茂名）如图，在平面直角坐标系xoy中，已知抛物线经过点A（0，4），B（1，0），C（5，0），抛物线对称轴l与x轴相交于点M．（1）求抛物线的解析式和对称轴；（3）连接AC．探索：在直线AC下方的抛物线上是否存在一点N，使△NAC的面积最大？若存在，请你求出点N的坐标；若不存在，请你说明理由．6．（2013•新疆）如图，已知抛物线y=ax2+bx+3与x轴交于A、B两点，过点A的直线l与抛物线交于点A、C，其中A点的坐标是（1，0），C点坐标是（4，3）．（1）求抛物线的解析式；（2）在（1）中抛物线的对称轴上是否存在点D，使△BCD的周长最小？若存在，求出点D的坐标，若不存在，请说明理由；（3）若点E是（1）中抛物线上的一个动点，且位于直线AC的下方，试求△ACE的最大面积及E点的坐标．7．（2009•江津区）如图，抛物线y=﹣x2+bx+c与x轴交于A（1，0），B（﹣3，0）两点．（1）求该抛物线的解析式；（2）设（1）中的抛物线交y轴与C点，在该抛物线的对称轴上是否存在点Q，使得△QAC 的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由；（3）在（1）中的抛物线上的第二象限上是否存在一点P，使△PBC的面积最大？若存在，求出点P的坐标及△PBC的面积最大值；若没有，请说明理由．8、如图，在直角坐标系中，抛物线经过点A（0,4），B（1,0），C（5,0）,对称轴与x轴相交于点M.（1）求抛物线的解析式和对称轴.（2）在抛物线的对称轴上是否存在一点P，使△PAB的周长最小？若存在，请求出P点坐标；若不存在，请说明理由.（3）连接AC，在直线AC的下方的抛物线上是否存在一点N，使△NAC的面积最大？若存在，求出点N坐标；若不存在，请说明理由.9、（广安）如图，已知抛物线y=x2+bx+c经过点（1，-5）和（-2，4）（1）求这条抛物线的解析式；（2）设此抛物线与直线y=x相交于点A，B（点B在点A的侧），平行于y轴的直线x=m（0＜m）与抛物线交于点M，与直线y=x交于点N，交x轴于点P，求线段MN的长（用含m的代数式表示）；（3）在条件（2）的情况下，连接OM、BM，是否存在m的值，使△BOM的面积S最大？若存在，请求出m的值；若不存在，请说明理由．10、（2017春·新泰市校级月考）如图所示，抛物线y=x2+bx+c与x轴交于A，B两点，B点坐标为（3，0），与y轴交于点C（0，-3）.（1）求抛物线的解析式；（2）点P在抛物线位于第四象限的部分上运动，当四边形ABPC的面积最大时，求点P的坐标和四边形ABPC的最大面积.11、（2016泰安）28．如图，在平面直角坐标系中，抛物线y=ax 2+bx+c 的顶点坐标为（2，9），与y 轴交于点A （0，5），与x 轴交于点E 、B ．（1）求二次函数y=ax 2+bx+c 的表达式；（2）过点A 作AC 平行于x 轴，交抛物线于点C ，点P 为抛物线上的一点（点P 在AC 上方），作PD 平行与y 轴交AB 于点D ，问当点P 在何位置时，四边形APCD 的面积最大？并求出最大面积；12、已知：抛物线2y ax bx c =++与x 轴交于A 、B 两点，与y 轴交于点C ．其中点A 在x轴的负半轴上，点C 在y 轴的负半轴上，线段OA 、OC 的长（OA<OC ）是方程2540x x -+=的两个根，且抛物线的对称轴是直线1x =．（1）求A 、B 、C 三点的坐标；（2）求此抛物线的解析式；（3）若点D 是线段AB 上的一个动点（与点A 、B 不重合），过点D 作DE ∥BC 交AC 于点E ，连结CD ，设BD 的长为m ，△CDE 的面积为S ，求S 与m 的函数关系式，并写出自变量m 的取值范围．S 是否存在最大值？若存在，求出最大值并求此时D 点坐标；若不存在，请说明理由．。

初中数学二次函数中三角形面积问题解析

（2）简单的组合，解决问题的途径常需要进行图形割补、等积变形等图形变换。

（3）面积不变同底等高或等底等高的转换，利用平行线得到三角形同底等高进行面积转化。

二次函数的周长与面积(含最值问题)

【知识梳理】一．二次函数之周长因为平面直角坐标系中点的坐标的几何意义为点到轴的距离，即横平竖直的线段长，所以处理二次函数压轴题的核心思想即为斜线段转化为横平竖直的线段（“斜转直”）．“斜转直”的几种处理思路：①斜线段转化为横平或竖直的线段；②计算有关周长或面积的问题其本质一般也可转化为计算线段，所以同样可利用“斜转直”来处理；③出现斜放的角时，一般也可根据该角构建直角三角形，来实现“斜转直”．二．二次函数之面积割补求面积——铅垂法：12APB B A S PM x x =⋅⋅- 12APB B A S PM x x =⋅⋅- Tips ：①过动点作铅垂线；②铅垂线平行于y 轴或垂直于x 轴．二次函数之周长与面积（含最值问题）【经典例题】【例一】1．如图，在平面直角坐标系中，抛物线y =（x ﹣2）2与x 轴交于点A ，与y 轴交于点B ．过点B 作BC ∥x 轴，交抛物线于点C ，过点A 作AD ∥y 轴，交BC 于点D ，点P 在BC 下方的抛物线上（P 不与B ，C 重合），连结PC ，PD ，则△PCD 面积的最大值是．2．已知直线经过点A （0，2），B （2，0），点C 在抛物线2y x 的图象上，则使得ABC S =2的点有（）个．A ．4B ．3C ．2D ．1【例二】1.如图，抛物线2(3)3(0)y ax a x a=+++≠与x轴交于点A（4，0），与y轴交于点B，在x轴上有一动点E（m，0）（0＜m＜4），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M．（1）求a的值和直线AB的函数表达式；（2）设△PMN的周长为C1，△AEN的周长为C2，若126 5CC=，求m的值；（3）求△PBA面积的最大值以及此时点E的坐标．2.如图，二次函数()2302y ax x c a =-+≠的图象与x 轴交于A 、B 两点，与y 轴交于C 点，已知点A （-1，0），点C （0，-2）．（1）求抛物线的函数解析式；（2）在抛物线的对称轴上，是否存在点Q ，使△ACQ 周长最短？若不存在，请说明理由；若存在，求出点Q 的坐标．（3）若点M 是线段BC 下方的抛物线上的一个动点，求△BCM 面积的最大值以及此时点M 的坐标．3.如图，在平面直角坐标系中，二次函数214y x bx c =-++的图象与坐标轴交于A 、B 、C 三点，其中点A 的坐标为（0，8），点B 的坐标为（-4，0）．（1）求该二次函数的表达式及点C 的坐标；（2）点D 的坐标为（0，4），点F 为该二次函数在第一象限内图象上的动点，连接CD 、CF ，以CD 、CF 为邻边作平行四边形CDEF ，设平行四边形CDEF 的面积为S ．求S 的最大值.4.如图，抛物线2=-++与x轴交于A（-1，0），B（3，0）两点，与y轴交于点C，对称轴与y x bx c抛物线交于点P，与直线BC交于点M，连接PB．（1）求抛物线的表达式；（2）抛物线上是否存在异于点P的一点Q，使△QMB与△PMB的面积相等？若存在，求出点Q的坐标；若不存在，请说明理由．（3）在第一象限对称轴右侧的抛物线上是否存在一点R，使△RMP与△RMB的面积相等？若存在，求出点R的坐标；若不存在，请说明理由．【能力训练】1．如图，在平面直角坐标系中，抛物线24y x x c =-++与y 轴交于点A ，过点A 作AB ∥x 轴交抛物线于点B ，则以AB 为边的等边三角形ABC 的周长为．2．如图所示，在平面直角坐标系中，点A 是x 轴上一动点，过A 作AC x ⊥轴交抛物线222y x x =++于点C ，以AC 为边作等边ABC ∆，高AD 的最小值为．3．如图，P 是抛物线22y x x =-++在第一象限上的点，过点P 分别向x 轴和y 轴引垂线，垂足分别为A ，B ，则四边形OAPB 周长的最大值为．4．如图，抛物线223y x x =-++与x 轴交于A ，B 两点，它的对称轴与x 轴交于点N ，过顶点M 作ME y ⊥轴于点E ，连结BE 交MN 于点F ．（1）求F 的坐标．（2）求EMF ∆与BNF ∆的面积之和．5.如图，在平面直角坐标系中，点A ，B 在x 轴上，点C ，D 在y 轴上且OB =OC =3，OA =OD =1，抛物线2(0)y ax bx c a =++≠经过A ，B ，C 三点，直线AD 与抛物线交于另一点E ．（1）求这条抛物线的解析式；（2）若M 是直线AD 上方抛物线上的一个动点，求△AME 面积的最大值．（3）在抛物线上是否存在点G ，使得AEG S =3？如果存在，求出点G 的坐标；如果不存在，请说明理由．。

「中考」二次函数与三角形面积问题.doc

「中考」二次函数与三角形面积问题【面积最大值】每年的中考题中都会出现大量与面积有关的压轴题，要学会三角形的面积求法，并推广到任意多边形面积的求法。

这是非常重要！【典型例题】如图，二次函数y=-x²+2x+3与y轴，x轴交于点A ，B，点C是直线AB上方抛物线上的一个动点（不与点A ，B重合），求△ABC面积的最大值．【分析】求面积的最值问题，通常设出点的动点的坐标，引入未知数来表示出面积，再利用二次函数的性质求解即可。

【方法一】分割——铅垂（高）法过点C作CD⊥x轴，垂足为D，交AB于点E，S△ABC＝S△ACE ＋S△BCE ＝1/2OB·CE【方法二】补全过点C作CD⊥y轴，垂足为D，过点B作BE⊥x轴，交CD于点E，S△ABC＝S矩形OBED －S△OAB －S△ACD －S△BCES△ABC＝S梯形ABED －S△ACD －S△BCE备注：本题此法繁琐，不建议用【方法三】补全连接OCS△ABC＝S△OAC ＋S△OBC －S△OAB备注：此法最容易掌握【方法四】平移过点C作CD∥AB，分别交y轴，x轴于点D，ES△ABC＝S△ABDS△ABC＝S△ABE【方法五】直接求过点C作CF⊥AB，垂足为FS△ABC＝1/2AB·CF ＝√2/4AB·CE备注：一般此类题目皆可直接求三角形面积，用相似或三角函数表示高。

【方法六】公式法拓展：如图，A（x1，y1），B（x2，y2），则S△ABC＝1/2 |x1y2−x2y1 |把△ABC向左平移3个单位长度，得到△OA′C′S△ABC＝S△OA′C′＝1/2 |xAyC-xCyA |备注：以上三角形面积公式可用于选择、填空题快速求得。

发现：当点C在OB的垂直平分线上时，S△ABC最大，即x=(0+3)/2=3/2时，S△ABC最大注意：点C的位置和点A、B关系密切，聪明的你，思考下，为什么会如此？【举一反三】如图，已知抛物线y＝ax2＋bx＋3与x轴交于A、B两点，过点A的直线l与抛物线交于点C，其中A点的坐标是（1，0），C点坐标是（4，3）．（1）求抛物线的解析式；（2）若点E是（1）中抛物线上的一个动点，且位于直线AC的下方，试求△ACE的最大面积及E点的坐标．。

“二次函数”面积最值问题的几种解法

“二次函数”面积最值问题的几种解法以微课堂公益课堂，奥数国家级教练与四位特级教师联手执教。

二次函数是初中数学的一个重点、难点，也是中考数学必考的一个知识点。

特别是在压轴题中，二次函数和几何综合出现的题型，才是最大的区分度。

而求三角形面积的最值问题，更是常见。

今天介绍二次函数考试题型种，面积最值问题的4种常用解法。

同学们只要熟练运用一两种解法，炉火纯青，在考试答题的时候，能够轻松答题，就好。

原题：在（1）中的抛物线上的第二象限是否存在一点P，使△PBC的面积最大？若存在，求出P点的坐标及△PBC的面积最大值，若没有，请说明理由。

考试题型，大多类似于此。

求面积最大值的动点坐标，并求出面积最大值。

一般解题思路和步骤是，设动点P的坐标，然后用代数式表达各线段的长。

通过公式计算，得出二次函数顶点式，则坐标和最值，即出。

解法一：补形，割形法。

方法要点是，把所求图像的面积适当的割补，转化成有利于面积表达的常规几何图形。

请看解题步骤。

解法二：铅锤定理，面积=铅锤高度×水平宽度÷2。

这是三角形面积表达方法的一种非常重要的定理。

铅锤定理，在教材上没有，但是大多数数学老师都会作为重点，在课堂上讲解。

因为，铅锤定理，在很多地方都用的到。

这里，也有铅锤定理的简单推导，建议大家认真体会。

解法二：铅锤定理，在求二次函数三角形面积最值问题，运用非常多。

设动点P的坐标，然后用代数式分别表达出铅锤高度和水平宽度，然后利用铅锤定理的计算公式，得出二次函数，必有最大值。

解法三：切线法。

这其实属于高中内容。

但是，基础好的同学也很容易理解，可以看看，提前了解一下。

解法四：三角函数法。

请大家认真看上面的解题步骤。

总之，从以上的四种解法可以得出一个规律。

过点P做辅助线，然后利用相关性质，找出各元素之间的关系。

设动点P的坐标，然后找出各线段的代数式，再通过面积计算公式，得出二次函数顶点式，求出三角形面积的最大值。

对于同学们中考数学来说，只要你熟练掌握解法一和解法二，那么二次函数几何综合题中，求三角形面积最大值问题，就非常简单了。

二次函数三角形最大值和最小值

二次函数是高中数学中的重要内容，在数学应用中有着广泛的应用。

本文将介绍二次函数在三角形中的最大值和最小值问题，通过对相关概念和定理的讲解，结合具体的数学实例，帮助读者深入理解二次函数与三角形的关系，从而掌握相关的解题方法和技巧。

二、二次函数与三角形1. 二次函数二次函数是形如y=ax^2+bx+c的函数，其中a、b、c为常数且a≠0。

二次函数的图像是一个开口向上或向下的抛物线，通过定点（0，c）。

2. 三角形三角形是平面几何中的基本图形之一，其具有三条边和三个角。

根据三角形的三个顶点的位置关系，可以分为等边三角形、等腰三角形、直角三角形等不同种类。

三、二次函数三角形最大值和最小值1. 最大值对于给定的二次函数y=ax^2+bx+c，在一定范围内求最大值，可以通过二次函数的顶点公式来求解。

顶点公式为x=-b/2a，y=f(-b/2a)。

结合数学实例，可以更加直观地理解最大值的求解方法。

与求最大值类似，对于给定的二次函数y=ax^2+bx+c，在一定范围内求最小值，也可以通过二次函数的顶点公式来求解。

在实际应用中，需要灵活运用二次函数图像的性质，加快最小值的求解过程。

四、应用举例通过具体的数学实例，可以更好地理解二次函数与三角形最大值和最小值的求解过程。

可以选择一个具体的三角形，确定对应的二次函数，通过求解二次函数的最大值和最小值来解决相关的数学问题。

五、总结通过本文的讲解，读者可以对二次函数与三角形最大值和最小值问题有一个较为全面的了解。

这一知识点不仅在高中数学学习中有重要意义，而且在各类数学竞赛和应用问题中都有广泛的应用。

加深对二次函数与三角形的理解，掌握相关的解题方法和技巧，对于提高数学水平具有重要意义。

六、二次函数与三角形面积的关系除了最大值和最小值问题外，二次函数与三角形还有一个重要的关系，那就是二次函数与三角形的面积。

在解决一些数学问题时，我们经常需要计算三角形的面积，而二次函数可以帮助我们更加方便地进行计算。

二次函数应用几何图形的最大面积问题课件

对未来学习的思考和展望
深入学习二次函数和几何图形的基础知识，掌握更多解决实际问题的技巧和方法。
拓展学习领域，了解更多与数学相关的学科知识，如线性代数、微积分等，为解决更复杂的问题提供支持。
关注数学在实际生活中的应用，了解数学与其他学科的交叉点，培养跨学科解决问题的能力。
THANKS
的最大面积。
03
几何图形面积的最大值问题
几何图形面积最大值的求解方法
03
代数法
几何法
参数法
通过代数运算和不等式性质，求出几何图形面积的最大值。
利用几何图形的性质和特点，通过作图和观察，求出面积最大值。
引入参数表示几何图形，通过参数的变化和约束条件，求出面积的最大值。
面积最大值在二次函数中的应用
二次函数应用几何图形的最大面积问题课件
目录
• 二次函数与几何图形的关系 • 二次函数的最值问题 • 几何图形面积的最大值问题 • 实际应用案例分析 • 总结与思考
01
二次函数与几何图形的关系
二次函数图像的几何意义
01
二次函数图像是抛物线，其顶点是函数的极值点。
02
二次函数图像的对称轴是x=h ，顶点的纵坐标是k。
二次函数与几何图形面积最大值问题紧密相关，通过合理设定函数参数，可以找到几何图形面积的最大值。
在解决实际问题时，需要综合考虑多种因素，如几何图形的形状、大小和位置等，以及二次函数的参数和约束条件。
二次函数开口方向和顶点位置对几何图形面积的影响是关键，需要根据实际情况调整函数表达式，以获得最佳效果。
01
总结词
02
详细描述
矩形面积最大化
在给定长和宽的条件下，利用二次函数求矩形的最大面积。通过设定长和宽为二次函数的形式，并利用求导数的方法找到面积的最大值。

二次函数图像中的三角形面积最大值的探讨

二次函数图像中的三角形面积最大值的探讨呕心写于2018.03.11晚二次函数图像中的三角形面积最值问题，有一个奇妙的结论，如图，当点E线段A B的中点时，△P A B 的面积取最大值。

为了探讨这个结论是否成立，我们给出一个一般情况下的二次函数。

如图，若二次函数（﹥0）与直线交与A、B两点，点P为抛物线上的一动点，且在直线A B的下方，，交A B于E，当△P A B的面积最大时，点E是A B的中点吗？探讨如下：（1）先求A B的中点的横坐标。

∴线段A B中点的横坐标为.（2）再求△P A B的面积取最大值时的点P的横坐标。

过点P作，交A B于E，则得：，求△P A B面积的最大值，就是求线段P E的最大值。

设点P的横坐标为m，则∴当时，P E取到最大值。

由（1）（2）得，当△P A B的面积取最大值时，点P的横坐标与线段A B的横坐标相同，即点E是线段A B 中点时，△P A B的面积取到最大值。

对于二次函数的系数﹤0时，结论同理可证。

例.如图，在直角坐标系中，点A的坐标为（6，8），连接O A，将线段O A绕原地O逆时针旋转至x轴负半轴上，得到线段O B.（1）求点B的坐标;（2）求经过AOB三点的抛物线的解析式;（3）如果点P是（2）中的抛物线上的动点，且在X轴的下方，△P A B是否有最大面积？若有，直接写出此时P点的坐标；若没有，请说明理由.解析：（1）易知B（-10，0）（2）（3）由点A（6,8）和点B（-10,0），可以得出线段A B中点的坐标为（-2,4）当利用上面的结论，对于这种问题直接求点的坐标可以迅速得解。

对于直接求点的坐标问题，或是直接求三角形面积最大值问题，可以使问题简单明了。

掌握了这个结论对于解题或检验自己解题是否正确有一定的作用。

练习：在平面直角坐标系中,已知抛物线经过A(−4,0),B(0,−4),C(2,0)三点。

(1)求抛物线的解析式；(2)若点M为第三象限内抛物线上一动点，点M的横坐标为m，△A M B的面积为S.求S关于m的函数关系式，并求出S的最大值。

二次函数中的三角形问题二

文档收集于互联网，已重新整理排版.word版本可编辑.欢迎下载支持.1文档来源为:从网络收集整理.word版本可编辑.文档收集于互联网，已重新整理排版.word版本可编辑.欢迎下载支持.1文档来源为:从网络收集整理.word版本可编辑.文档收集于互联网，已重新整理排版.word版本可编辑.欢迎下载支持.1文档来源为:从网络收集整理.word版本可编辑.文档收集于互联网，已重新整理排版.word版本可编辑.欢迎下载支持.1文档来源为:从网络收集整理.word版本可编辑.文档收集于互联网，已重新整理排版.word版本可编辑.欢迎下载支持.学习过程一、复习预习1文档来源为:从网络收集整理.word版本可编辑.文档收集于互联网，已重新整理排版.word版本可编辑.欢迎下载支持. （一）三角形的性质和判定：1、等腰三角形性质：两腰相等，两底角相等，三线合一（中线、高线、角平分线）。

判定：两腰相等，两底角相等，三线合一（中线、高线、角平分线）的三角形是等腰三角形。

2、直角三角形性质：满足勾股定理的三边关系，斜边上的中线等于斜边的一半。

1文档来源为:从网络收集整理.word版本可编辑.文档收集于互联网，已重新整理排版.word版本可编辑.欢迎下载支持. 判定：有一个角是直角的三角形是直角三角形。

3、等腰直角三角形性质：具有等腰三角形和等边三角形的所以性质，两底角相等且等于45°。

判定：具有等腰三角形和等边三角形的所以性质的三角形是等腰直角三角形4、等边三角形性质：三边相等，三个角相等且等于60°，三线合一，具有等腰三角形的一切性质。

1文档来源为:从网络收集整理.word版本可编辑.文档收集于互联网，已重新整理排版.word版本可编辑.欢迎下载支持. 判定：三边相等，三个角相等，有一个角是60°的等腰三角形是等边三角形。

（二）求作等腰三角形、直角三角形的方法：图一两圆一线图解图二两线一圆图解总结：（1）通过“两圆一线”可以找到所有满足条件的等腰三角形，要求的点（不与A、B点重合）即在两圆上以及两圆的公共弦上（2）通过“两线一圆”可以找到所有满足条件的直角三角形，要求的点（不与A、B点重合）即在圆上以及在两条与直径AB垂直的直线上。

二次函数中几何图形周长的最值问题题型及解法

2. 根据我市现目前考试题型来看，该部分是个重点，也是个难点，很大一部分学生对该部分望而生畏，几乎不敢动笔，分析了一下，其主要原因有两点：其一，因为此题涉及的解题过程比较繁杂，再加上思路不清晰，会花大量的时间思考，所以这部分学生就选择放弃了；另外的，还有部分学生是压根就不会做这类题，对解决该题没有思路，没有参考方向，所以根本不看这题。
C（0，﹣3）．如图，在直线BD和直线BC上是否分别存在点M、N，使得
△AMN的周长最小？若存在，请求出△AMN周长最小值以及M、N的坐标；
若不存在，请说明理由。
A1
做法：
E M
1.作A点关于直线BD的对称点对称点A1，与BD相交于点E 2.作A点关于直线BC的对称点对称点A2，与BD相交于点F
N F
做法：
1.作A点关于对称轴的对称点对称点B
2.链接CB与对称轴的交点就是我们做要求的G点的位置
G
3.连接AG
G 4.此时的△ACH的周长最小
（2）在直线BC上是否存在点H，使得△ACH的周长最小，若存在，
求出△GAC的周长最小值，并求出点G的坐标；若不存在，请说明
理由。
做法：
M
1.作A点关于直线BD的对
第二部分基本题型及解法
例题
1. 一个动点在抛物线上求三角形周长的最大值 45°角的直角三角形周长最大值的求法例1：（1）已知：抛物线y=ax2+bx+c（a≠0）经过点A（1，0），
B（3，0），C（0，﹣3）．如图，点P是直线BC上方抛物线上一动
点．过点P作PE平行y轴交BC于点E，作PF垂直BC交BC于点F，是否存在点P，使△PEF的周长最大？若存在，求出△PEF周长最大值，并

二次函数中几何图形周长的最值问题题型及解法

质，将几何图形周长转化为线段和差最值问题，连线与动点所在直线的交点既是所找之点 5. 运用相关知识和方法求出几何图形的最值
谢谢！
教育是行善的智慧无忧是无畏的行者
2. 根据我市现目前考试题型来看，该部分是个重点，也是个难点，很大一部分学生对该部分望而生畏，几乎不敢动笔，分析了一下，其主要原因有两点：其一，因为此题涉及的解题过程比较繁杂，再加上思路不清晰，会花大量的时间思考，所以这部分学生就选择放弃了；另外的，还有部分学生是压根就不会做这类题，对解决该题没有思路，没有参考方向，所以根本不看这题。
做法： 1.作A点关于直线OM的对称点对称点A1
A1
2.作A点关于直线OM的对称点对称点A2
3.链接A1A2与OM，ON相交于点P，Q，
P
此时的交点就是我们做要找的吃草和喝
水的位置
4.连接AP，AQ
Q A2
4.此时走的路程最短
例4：已知：抛物线y=ax2+bx+c（a≠0）经过点A（1，0），B（3，0），
C（0，﹣3）．如图，若点C关于点B的对称点为点E，是否存在x轴上的点
M，y轴上的点N，使得四边形DNME的周长最小？若存在，请求出M、N
点的坐标，并求出DNME的周长最小值；若不存在，请说明理由。
E
做法：
D’
1.作E点关于X轴的对称点对称点E’
2.作D点关于y轴的对称点对称点D’
NM
3.链接D’E’与x轴，y轴相交于点M，N，此时的交点就是我们做要找的点的位置
做法：
1.过D点作对称轴，与PQ相交于点F
2.C矩形 PQNM=2(PQ+PM)=2(2DF+PM)
3. 一个动点在一条直线上求三角形周长最小值

中考复习函数专题28 二次函数中的三角形问题(老师版)

专题28 二次函数中的三角形问题知识对接考点一、二次函数中的三角形问题考点分析：二次函数与三角形的综合解答题一般涉及到这样几个方面：1.三角形面积最值问题2.特殊三角形的存在问题包括等腰等边和直角三角形。

这类题目一般出现在压轴题最后两道上，对知识的综合运用要求比较高。

考点二、解决此类题目的基本步骤与思路1.抓住目标三角形，根据动点设点坐标2.根据所设未知数去表示三角形的底和高，一般常用割补法去求解三角形的面积从而得出面积的关系式3. 根据二次函数性质求出最大值.4.特殊三角形问题首先要画出三角形的大概形状，分类讨论的去研究。

例如等腰三角形要弄清楚以哪两条边为要，直角三角形需要搞清楚哪个角作为直角都需要我们去分类讨论。

要点补充：1.简单的直角三角形可以直接利用底乘高进行面积的表示2.复杂的利用“补”的方法构造矩形或者大三角形，整体减去部分的思想3.利用“割”的方法时，一般选用横割或者竖割，也就是做坐标轴的垂线。

4.利用点坐标表示线段长度时注意要用大的减去小的。

5.围绕不同的直角进行分类讨论，注意检验答案是否符合要求。

6.在勾股定理计算复杂的情况下，灵活的构造K字形相似去处理。

要点补充：专项训练一、单选题1．如图，直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上，三角形沿水平线从左向右匀速穿过正方形．设穿过时间为t，正方形与三角形不重合部分的面积为s（阴影部分），则s与t的大致图象为（）A ．B ．C ．D ．【答案】A 【分析】设三角形运动速度为1，分0≤t≤2时，2＜t≤2时，2＜时，时五种情况，可知等腰直角三角形与正方形的不重叠部分面积变化过程是变小--不变--变大，分别求出函数关系式，即可得出答案．【详解】∵等腰直角三角形的直角边长为1， ∵当s ＝12×1×1+2×2﹣212t ⨯＝92﹣12t 2；s ＝22-12+2×12t)2=t 2﹣112；t≤2时，s ＝2122-×1×1＝72；当2＜时，s ＝22-2×12(t -2)2=t 2﹣4t+152；当2+2＜s ＝22+12-2×12t+2）2=92t+2）2，∵等腰直角三角形与正方形的不重叠部分面积变化过程是变小--不变--变大，且变小、变大时的图象为抛物线，不变时的图象为直线， ∵A 符合要求，故选：A ．【点睛】考查了动点问题的函数图象，要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件，结合实际意义得到正确的结论，熟练掌握二次函数的图象是解题关键．2.定义：若抛物线的顶点与x 轴的两个交点构成的三角形是直角三角形，则这种抛物线就称为“美丽抛物线”．如图，直线l ：13y x b =+经过点10,4M ⎛⎫⎪⎝⎭一组抛物线的顶点()111B y ，，()222,B y ，()333,B y ，…(),n n B n y （n 为正整数），依次是直线l 上的点，这组抛物线与x 轴正半轴的交点依次是：()11,0A x ，()22,0A x ，()33,0A x ，…()11,0n n A x ++（n 为正整数）．若()101x d d =<<，当d 为（）时，这组抛物线中存在美丽抛物线A ．512或712B ．512或1112C ．712或1112D ．712【答案】B 【分析】由抛物线的对称性可知，所有构成的直角三角形必是以抛物线顶点为直角顶点的等腰三角形，所以此等腰三角形斜边上的高等于斜边的一半，又0＜d ＜1，所以等腰直角三角形斜边的长小于2，所以等腰直角三角形斜边的高一定小于1，即抛物线的顶点纵坐标必定小于1，据此对上一步结论分析可得满足美丽抛物线对应的顶点，再确定抛物线与x 轴的交点值与对称轴的距离，从而可求得d 的值【详解】解：直线l ：13y x b =+经过点M （0，14）则b=14，∵直线l ：1134y x =+由抛物线的对称性知：抛物线的顶点与x 轴的两个交点构成的直角三角形必为等腰直角三角形； ∵该等腰三角形的高等于斜边的一半 ∵0＜d ＜1∵该等腰直角三角形的斜边长小于2，斜边上的高小于1（即抛物线的顶点纵坐标小于1）∵当x=1时，11173412y =+=＜1；当x=2时，221113412y =+= ＜1；当x=3时，315144y =+=＞1； ∵美丽抛物线的顶点只有12,B B ∵若1B 为顶点，由17(1,)12B ，则7511212d =-= ， ∵若2B 为顶点，由211(2,)12B ，则11111(2)11212d ⎡⎤=---=⎢⎥⎣⎦综上所述，d 的值为512或1112时，存在美丽抛物线．故选B ．【点睛】此题主要考查抛物线与x 轴的交点，抛物线的对称性．3．如图，在10×10的网格中，每个小方格都是边长为1的小正方形，每个小正方形的顶点称为格点．若抛物线经过图中的三个格点，则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”．以O为坐标原点建立如图所示的平面直角坐标系，若抛物线与网格对角线OB的两个交点之间的距离为形的三个顶点，则满足上述条件且对称轴平行于y轴的抛物线条数是A．16B．15C．14D．13【答案】C【详解】根据在OB上的两个交点之间的距离为3，然后作出最左边开口向下的抛物线，再向右平移1个单位，向上平移1个单位得到开口向下的抛物线的条数，同理可得开口向上的抛物线的条数，然后相加即可得解：如图，开口向下，经过点（0，0），（1，3），（3，3）的抛物线的解析式为y=﹣x2+4x，然后向右平移1个单位，向上平移1个单位一次得到一条抛物线，可平移6次，∵一共有7条抛物线．同理可得开口向上的抛物线也有7条．∵满足上述条件且对称轴平行于y轴的抛物线条数是：7+7=14．故选C．4．如图，在10×10的网格中，每个小方格都是边长为1的小正方形，每个小正方形的顶点称为格点．如果抛物线经过图中的三个格点，那么以这三个格点为顶点的三角形称为该抛物线的“内接格点三角形”．设对称轴平行于y轴的抛物线与网格对角线OM的两个交点为A，B，其顶点为C，如果∵ABC是该抛物线的内接格点三角形，A，B，C的横坐标x A，x B，x C满足x A＜x C＜x B，那么符合上述条件的抛物线条数是（）。