南开结构化学分子晶体结构测定方法理论基础精品PPT课件
合集下载
南开大学结构化学精品课件-第2章

Nankai University
《结构化学》第二章 原子结构
Sir Joseph John Thomson
1897年发现电子(1906年物理奖) Cambridge Cavendish Lab.主任 学生中7 Nobel 获奖者
1911年建立原子模型 (1908年化学奖) Cavendish Lab. 主任(1919) 学生中超过11人 获Nobel奖
实数解 1 2(1 1 ) 1 cos
1 1 2 ei 1 2 cos i sin
sin 1 1 2 i (1 1 ) 1 sin
函数 m( )
m 0 1 1 2 2 3 3
Nankai University
2.1.4 方程的解及角量子数l
sin d d sin d d 2 2 sin m
Legendre)
化为联属勒让德(Associated 方程,具有已知解 有满足合格条 件的解
l (l 1)
l 0,1, 2,3... l | m |
对于给定的l m=0, ±1, …±l
( ) CPl m (cos )
|m|
与量子数 l, m 有关
|m| l |m| 1 d 2 2 l Pl (cos ) l (1 cos ) 2 (cos 1) 联属勒让德函数 2 l! d cos l |m|
l 为角量子数 (angular momentum quantum number)
2
1 2 1 1 2 2 Ze2 r 2 r r r r 2 sin θ θ sin θ θ r 2 sin 2 θ 2 r,θ, 2 E 4πε r r,θ, 0 0
《结构化学》课件

《结构化学》ppt课件
contents
目录
• 结构化学简介 • 原子结构与性质 • 分子的电子结构与性质 • 晶体结构与性质 • 结构化学实验结构化学的定义
总结词
结构化学是一门研究物质结构与 性质之间关系的科学。
详细描述
结构化学主要研究原子的排列方 式、电子分布和分子间的相互作 用,以揭示物质的基本性质和行 为。
晶体的电导率、热导率等性质取决于其内 部结构,不同晶体在这些方面表现出不同 的特性。
晶体的力学性质
晶体材料的应用
晶体的硬度、韧性等力学性质与其内部原 子排列密切相关,这些性质决定了晶体在 不同工程领域的应用价值。
晶体材料广泛应用于电子、光学、激光、 半导体等领域,如单晶硅、宝石等。了解 晶体的性质是实现这些应用的关键。
分子的选择性
分子的选择性是指分子在化学反应中对反应物的选择性和对产物的选择性。选择性强的分 子可以在特定条件下优先与某些反应物发生反应,产生特定的产物。
04
晶体结构与性质
晶体结构的基础知识
晶体定义与分类
晶体是由原子、分子或离子在空 间按一定规律重复排列形成的固 体物质。根据晶体内部原子、分 子或离子的排列方式,晶体可分 为七大晶系和14种空间点阵。
电子显微镜技术
• 总结词:分辨率和应用 • 电子显微镜技术是一种利用电子显微镜来观察样品的技术。相比光学显微镜,
电子显微镜具有更高的分辨率和更大的放大倍数,因此可以观察更细微的结构 和组分。 • 电子显微镜技术的分辨率一般在0.1~0.2nm左右,远高于光学显微镜的分辨 率(约200nm)。因此,电子显微镜可以观察到更小的晶体结构、病毒、蛋 白质等细微结构。 • 电子显微镜技术的应用范围很广,例如在生物学领域中,可以用于观察细胞、 病毒、蛋白质等生物样品的结构和形态;在环境科学领域中,可以用于观察污 染物的分布和形态;在材料科学领域中,可以用于观察金属、陶瓷、高分子等 材料的表面和断口形貌等。
contents
目录
• 结构化学简介 • 原子结构与性质 • 分子的电子结构与性质 • 晶体结构与性质 • 结构化学实验结构化学的定义
总结词
结构化学是一门研究物质结构与 性质之间关系的科学。
详细描述
结构化学主要研究原子的排列方 式、电子分布和分子间的相互作 用,以揭示物质的基本性质和行 为。
晶体的电导率、热导率等性质取决于其内 部结构,不同晶体在这些方面表现出不同 的特性。
晶体的力学性质
晶体材料的应用
晶体的硬度、韧性等力学性质与其内部原 子排列密切相关,这些性质决定了晶体在 不同工程领域的应用价值。
晶体材料广泛应用于电子、光学、激光、 半导体等领域,如单晶硅、宝石等。了解 晶体的性质是实现这些应用的关键。
分子的选择性
分子的选择性是指分子在化学反应中对反应物的选择性和对产物的选择性。选择性强的分 子可以在特定条件下优先与某些反应物发生反应,产生特定的产物。
04
晶体结构与性质
晶体结构的基础知识
晶体定义与分类
晶体是由原子、分子或离子在空 间按一定规律重复排列形成的固 体物质。根据晶体内部原子、分 子或离子的排列方式,晶体可分 为七大晶系和14种空间点阵。
电子显微镜技术
• 总结词:分辨率和应用 • 电子显微镜技术是一种利用电子显微镜来观察样品的技术。相比光学显微镜,
电子显微镜具有更高的分辨率和更大的放大倍数,因此可以观察更细微的结构 和组分。 • 电子显微镜技术的分辨率一般在0.1~0.2nm左右,远高于光学显微镜的分辨 率(约200nm)。因此,电子显微镜可以观察到更小的晶体结构、病毒、蛋 白质等细微结构。 • 电子显微镜技术的应用范围很广,例如在生物学领域中,可以用于观察细胞、 病毒、蛋白质等生物样品的结构和形态;在环境科学领域中,可以用于观察污 染物的分布和形态;在材料科学领域中,可以用于观察金属、陶瓷、高分子等 材料的表面和断口形貌等。
大学化学《结构化学-晶体结构》课件

3、各种晶体生长中会自发形成确定的多面体外形。 晶体在生长过程中自发形成晶面,晶面相交成
为晶棱,晶棱聚成顶点,使晶体具有某种多面体外 形的特点。
熔融的玻璃体冷却时,随着温度降低,粘度变 大,流动性变小,逐渐固化成表面光滑的无定形物, 工匠因此可将玻璃体制成各种形状的物品,它与晶 体有棱、有角、有晶面的情况完全不同。 4、晶体有确定的熔点而非晶态没有。
1.平移—点阵:
平移是晶体结构中最基本的对称操作, 可用T来表示
Tmnp=ma+nb+pc
m,n,p为任意整数 即一个平移矢量Tmnp作用在晶体三维点 阵上,使点阵点在a方向平移m单位,b方向 平移n单位,c方向平移p单位后,点阵结构 仍能复原。
⑵ 晶体的对称操作和对称元素受到点阵的制约: 其中旋转轴、螺旋轴和反轴的轴次只能为1、2、3、 4、6等几种;螺旋轴和滑移面中的滑移量也只能符 合点阵结构中平移量的几种数值。
晶体结构中可能存在的对称元素有:对称中心 ();镜面(m);轴次为1、2、3、4、6的旋转轴(1,2, 3,4,6)、螺旋轴(21,31,32,41,42,43,61,62,63,64,65)、反轴
学习要点
⑴晶体结构周期性与点阵。 ⑵ 7 个 晶 系 和 14 种 Bravias 空 间 格 子 。 ⑶晶胞、晶面间距。 ⑷ 晶体(X射线)衍射方向―Laue方程和Bragg方程。 ⑸ 晶体衍射强度与立方晶系的系统消光。
学时安排 学时----- 6学时
第八章.晶体的点阵结构和晶体的性质
晶体
远古时期,人类从宝石开始认识晶体。红 宝石、蓝宝石、祖母绿等晶体以其晶莹剔透 的外观,棱角分明的形状和艳丽的色彩,震 憾人们的感官。名贵的宝石镶嵌在帝王的王 冠上,成为权力与财富的象征,而现代人类 合成出来晶体,如超导晶体YBaCuO、光学 晶体BaB2O4、LiNbO3、磁学晶体NdFeB等 高科技产品,则推动着人类的现代化进程。
结构化学-晶体点阵结构PPT课件

按 a、b、c 之间的关系,以及 、、 之间的关系,晶体
可以分成 7 种不同的晶系,称为七大晶系,有十四种布拉维晶格。
.
59
分数坐标
由于取晶胞参数的三个素向量 a, b, c为单位,一个晶 胞内原子最大坐标为1,最小坐标为0,其余坐标在1~0之 间,因此,描述晶胞中原子的坐标为分数坐标。
立方面心晶胞净含4个原子,所以写出4组坐标即可:
20世纪80年代发现的以YBa2Cu3O7-x为 代表的氧化物超导体和球烯, 都震动了科 学界. 1991年以来又发现球烯与K、Rb 、 Cs等形成的离子化合物具有超导性,使人 们对分子超导体的前景充满希望。
现代科技中的晶体——超导材料
➢ 晶体的特性 ➢ 晶体的点阵结构理论 ➢ 晶体结构的密堆积原理 ➢ 金属晶体和离子晶体
• 金属晶体 • 离子晶体 • 分子晶体 • 共价键型晶体 • 混合键型晶体
密堆积原理是研究晶体结构的一项重要内容
晶体结构的密堆积原理
密堆积原理:是在无方向性和饱和性的金属键、离 子键和范德华力把晶体内部质点结合在一起的晶 体中,原子、离子或分子总是趋向于相互尽可能 配位数高,能充分利用空间的紧密堆积的结构方 式。
内容简介
介绍晶体物质的结构及其结构与性能的关 系,以及研究晶体结构的实验方法-X射线 晶体衍射法。
➢ 晶体的特性 ➢ 晶体的点阵结构理论 ➢ 晶体结构的密堆积原理 ➢ 金属晶体和离子晶体
➢ 晶体的特性 ➢ 晶体的点阵结构理论 ➢ 晶体结构的密堆积原理 ➢ 金属晶体和离子晶体
.
3
一、晶体的特性
固态物质:晶体和无定形体
3 晶体具有确定的熔点
晶体在熔化时必须吸收一定的熔融热才能转变为液态(同样在凝固 时放出同样大小的结晶热),见晶体加热曲线:随时间增加,温度 升高至T0时,晶体开始熔解,温度停止上升,此时所加的热量, 用于破坏晶体的格子构造,直到晶体完全熔解,温度才开始继续升 高
南开结构化学分子晶体结构测定方法理论基础精品PPT课件

H.A. Hauptman
J. Karle 发展了确定晶体分子结构的方法 1985年Nobel化学奖
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
9.1.1 晶体的X射线衍射效应
1. X射线的产生
热发射的自由电子高压加速金属 靶拦截白色X射线/特征X射线
Cooling Water
无消光
体心点阵(I)
h+k+l=奇
面心点阵(F)
h k l奇偶混杂
底心点阵(C)
h+k=奇
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
例:体心点阵型式的晶体(金属钠为立方体心)
晶胞内原子的分数坐标为:0,0,0; 1/2,1/2,1/2 其结构因子:
F f e f e i2 (h 0k 0l 0)
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
xh yk zl (xh* yk* zl*)n nN
平面点阵(h*l*k*)对于hkl( h=nh*, k=nk*, l=nl*)方向衍射 具有等程面的性质,该点阵面上任意两点的光程差为0
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
PQ (S S0 ) 0
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
9.1.2 衍射方向和晶胞参数
1. Laue方程
S
把空间点阵看成互不平行的三维直线点阵A
直线点阵的Laue方程:
O
P
a
=OA-BP= a(cos
6_分子结构和晶体结构 38页PPT文档

1 轨道杂化理论的基本要点
原子在形成分子时,为了增强成键能力,同 一原子中能量相近的不同类型的原子轨道重新 组合,形成能量、形状和方向与原轨道不同的 新的原子轨道。这种原子轨道重新组合的过程 称为原子轨道的杂化,所形成的新的原子轨道 称为杂化轨道。
杂化轨道理论的基本要点: (1) 在形成分子时,原子中能量相近的几个原子 轨道重新组合而形成一组新的原子轨道,这一过 程称为杂化,形成的新轨道称为杂化轨道。 (2) 轨道杂化可增大轨道重叠,增强原子轨道成 键能力; (3) 杂化轨道成键时,满足斥力最小原则,决定 了杂化轨道的夹角和键的方向。在不等性杂化时 ,键角会有偏离。 (4) 杂化轨道数目等于参与杂化的原子轨道数目
(1)键长 ( l ) 分子中城件的两原子核间的平衡距离(核间距
)
(2)键能(E) 化学键强弱的量度。
(3)键角 (α ) 在分子中键与键之间夹角称为键角。
价健理论局限性
无法解释分子的空间构型 健角 分子构型
H2O 104.50 V型 CH4 109.280 正四面体型
二 轨道杂化理论
1 轨道杂化理论的基本要点 2 轨道杂化的类型与分子的空间构型
4 共价键的类型
(一)σ键 原子轨道沿键轴(两原子核间联线)方向以
“头碰头” 方式重叠所形成的共价键称为σ键。 形成σ键时,原子轨道的重叠部分对于键轴呈 圆柱形对称,沿键轴方向旋转任意角度,轨道 的形状和符号均不改变。
(二)π键
原子轨道垂直于键轴以 “肩并肩” 方式重叠 所形成的共价化学键称为π键。形成π键时,原 子轨道的重叠部分对等地分布在包括键轴在内的 平面上、下两侧,形状相同,符号相反,呈镜面 反对称。
(三)配位键 按共用电子对提供的方式不同,共价键又可
南开大学结构化学精品课件-第3章

使用变分法可以在不解 Schrö dinger方程的情况下, 解得体系的基态能量及波函数。变分法是量子力学中最 常用的两种近似方法之一(另一种为微扰法)。
氢分子体系求解
1927年海特勒-伦敦 当时实验值: 1968年Kolos与Wolniewicz 1970年,G. Herzberg实验 MP2/6-31G MP2/6-311++G (3df,2pd) MP4(SDQ)/aug-cc-pvtz CID/aug-cc-pvqz CISD(T)/aug-cc-pv5z 解离能(eV) 3.14 4.74 4.7467 4.7467 4.018 4.4906 4.6810 4.7277 4.7416 键长(Å)
1 2
e
im
ra rb R
ra rb R
m=0, 1, 2, …
L()与M()为无穷级数,因此没有代数式。 电子能量只与m2有关,除m=0外,电子能级 都是双重简并的
Energy/hcRH
1.4 1.2 1.0
4
=|m|
符号
0
1
2
3
4
0.8 0.6 0.4 0.2 0 -0.2 0
W ˆ H d
*
d E 0
*
通常选择具有相同边界条件的一个适当的合格试探函 数,它包含若干个参数(c1,c2,…cn)。根据变分法原理,用数 学中极小值的求法, 通过求E/c1=0, E/c2=0, ..., E/cn=0, 确定c1,c2,…cn的取值, 使 所表示的体系状态为最佳。 线性变分法
A B d B A d S B A
W (cA 2 cA cB S cB ) cA H
结构化学 南开大学 张宏伟 课件

Nankai University
一、结构化学研究的主要内容
在原子、分子水平上讨论物质的性质与电子结构 和空间结构间的关系 • 绪论 • • • • • 第一章 量子力学基础 第二章 原子结构 第三章 共价键理论 第四章 HMO理论 第五章 计算化学 • • • • • 第六章 分子对称性 第七章 晶体学基础 第八章 金属和离子晶体 第九章 结构测定方法 模型实习
Compton
I. Langmuir, M. Planck, M. Curie, H.A. Lorentz, A. Einstein, P. Langevin, C.E. Guye, C.T.R. Wilson, O.W. Richardson. P. Debye, M. Knudsen, W.L. Bragg, H.A. Kramers, P.A.M. Dirac, A.H. Compton, L.V. de Broglie, M.Born, N. Bohr. A. Piccard, E. Henriot, P. Ehrenfest, E. Herzen, T. De Donder, E. Schroedinger, E. Verschaffelt, W. Pauli, W. Heisenberg, R. H. Fowler, L. Brillouin.
1. 量子力学(QM—Quantum Mechanics)
普朗克(1858-1947, Max Karl Ernst Ludwig Planck) 因发现能量子(量子理论)获1918年Nobel 物理奖 爱因斯坦(1879-1955, Albert Einstein) 因在数学物理方面的成就,特别是发现了光电 效应规律,获1921 年Nobel物理奖 尼尔斯·玻尔(1885-1962, Niels Henrik David Bohr) 因原子结构和原子辐射的研究 ,获 1922 年Nobel 物理奖 德布罗意(1892-1987, Louis Victor De Broglie) 因发现电子的波动性,获1929年Nobel物理奖
一、结构化学研究的主要内容
在原子、分子水平上讨论物质的性质与电子结构 和空间结构间的关系 • 绪论 • • • • • 第一章 量子力学基础 第二章 原子结构 第三章 共价键理论 第四章 HMO理论 第五章 计算化学 • • • • • 第六章 分子对称性 第七章 晶体学基础 第八章 金属和离子晶体 第九章 结构测定方法 模型实习
Compton
I. Langmuir, M. Planck, M. Curie, H.A. Lorentz, A. Einstein, P. Langevin, C.E. Guye, C.T.R. Wilson, O.W. Richardson. P. Debye, M. Knudsen, W.L. Bragg, H.A. Kramers, P.A.M. Dirac, A.H. Compton, L.V. de Broglie, M.Born, N. Bohr. A. Piccard, E. Henriot, P. Ehrenfest, E. Herzen, T. De Donder, E. Schroedinger, E. Verschaffelt, W. Pauli, W. Heisenberg, R. H. Fowler, L. Brillouin.
1. 量子力学(QM—Quantum Mechanics)
普朗克(1858-1947, Max Karl Ernst Ludwig Planck) 因发现能量子(量子理论)获1918年Nobel 物理奖 爱因斯坦(1879-1955, Albert Einstein) 因在数学物理方面的成就,特别是发现了光电 效应规律,获1921 年Nobel物理奖 尼尔斯·玻尔(1885-1962, Niels Henrik David Bohr) 因原子结构和原子辐射的研究 ,获 1922 年Nobel 物理奖 德布罗意(1892-1987, Louis Victor De Broglie) 因发现电子的波动性,获1929年Nobel物理奖
结构化学晶体的结构PPT课件

晶体的性质
同一性(或均匀性)。晶体中各部分的性质是 完全均匀一致、相同的。 各向异性。同一晶体在不同方向上具有不同的 性质。 自范性。晶体在适宜条件下,能自发地形成封 闭的几何多面体外形。 对称性。晶体的微观空间结构是对称的,宏观 外形也一般具有或多或少的对称性。 固定的熔点。
晶体的基本特征
在量子力学中,原子或分子等微观体系的能级是分离的, 当体系大到一定程度时,体系的某些能级间隔就非常小, 变成实际上连续的能带。
导带,满带,空带 禁带,重带
体系大小,N→∞
量子力学过渡到经典物理情形
(从微观到宏观)
导体,半导体,绝缘体
导体:导带,重带(满带与空带重叠)
半导体,绝缘体都有禁带,满带与空带不重叠,无导带 绝缘体的禁带大于5eV 半导体的禁带小于3eV
从微观上说,晶体最基本的特征就是原子、 分子或离子在空间周期性地有序排列。 晶体结构的周期性是晶体和非晶体最本质 的区别。 晶体:具有微观周期性结构的固体。
二 晶体的对称性
空间点阵与晶体结构 晶系
1 空间点阵与晶体结构
(1) 点阵结构
我们可以用一系列几何点在空间的排布来模拟晶体 中微粒的周期性排布规律。 点阵:由无数个没有大小、没有质量、不可分辨的 几何点,按照一定的重复规律排布得到的几何图形。 点阵理论:用点阵的性质来探讨晶体的几何结构的 理论。
原子、离子或分子按点阵排布的固体。
点阵 模型
晶体 结构
阵点
结构 基元
空间 点阵
晶体
平面 点阵
晶面
直线 点阵
素单位 复单位
晶棱 素晶胞 复晶胞
每个阵点代表晶体中基本的结构单元,可以是离子、 原子、分子或配合离子等。
几
结构化学晶体学基础ppt课件
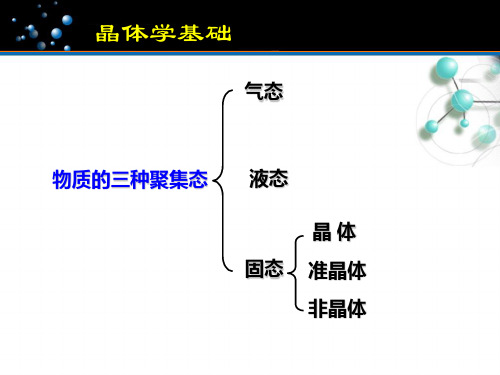
晶体学基础
气态
物质的三种聚集态 液态 晶体
固态 准晶体 非晶体
晶体学基础
• 非晶体
在它们内部原子或分子的排列没有周期性的结构 规律,像液体那样杂乱无章地分布,可以看作过冷 液体,称为玻璃体、无定形体或非晶态物质。
玻璃体的结构特点
晶体学基础
• 准晶体
准晶是一种介于晶体和非晶体之间的固体。准晶具有 完全有序的结构,然而又不具有晶体所应有的平移对称性, 因而可以具有晶体所不允许的宏观对称性。准晶体的发现, 是20世纪80年代晶体学研究中的一次突破。
金刚石中的滑移面
晶体的微观对称性
7.3.2 230个空间群 空间群符合一般用熊夫利和国际符号联合表示
晶体结构的周期性和点阵理论
3 晶体具有确定的熔点
晶体结构的周期性和点阵理论
4 晶体的对称性和对X射线的衍射
晶体的理想外形具有特定的对称性,这是内 部结构对称性的反映。晶体结构的周期大小和X 射线的波长相当,使它成为天然的三维光栅,能 够对X射线产生衍射。而晶体的X射线衍射,成 为了解晶体内部结构的重要实验方法。
晶胞
• 晶胞的两个基本要素:
晶胞
• 分数坐标
OP = xa + yb + zc
x, y, z为P原子的分数坐标。 x, y, z为三个晶轴方向单位 矢量的个数(是分数)(晶轴 不一定是相互垂直)。 x, y, z一定为分数
晶胞
• 凡不到一个周期的原子的坐标都必须标记,分 数坐标,即坐标都是分数,这样的晶胞并置形 成晶体。
点阵结构
2. 从晶体点阵结构中抽象出点阵 例1. 等径圆球排列形成的一密置列直线点阵
一个点阵点代表一个球 重复周期为a a = 2r
气态
物质的三种聚集态 液态 晶体
固态 准晶体 非晶体
晶体学基础
• 非晶体
在它们内部原子或分子的排列没有周期性的结构 规律,像液体那样杂乱无章地分布,可以看作过冷 液体,称为玻璃体、无定形体或非晶态物质。
玻璃体的结构特点
晶体学基础
• 准晶体
准晶是一种介于晶体和非晶体之间的固体。准晶具有 完全有序的结构,然而又不具有晶体所应有的平移对称性, 因而可以具有晶体所不允许的宏观对称性。准晶体的发现, 是20世纪80年代晶体学研究中的一次突破。
金刚石中的滑移面
晶体的微观对称性
7.3.2 230个空间群 空间群符合一般用熊夫利和国际符号联合表示
晶体结构的周期性和点阵理论
3 晶体具有确定的熔点
晶体结构的周期性和点阵理论
4 晶体的对称性和对X射线的衍射
晶体的理想外形具有特定的对称性,这是内 部结构对称性的反映。晶体结构的周期大小和X 射线的波长相当,使它成为天然的三维光栅,能 够对X射线产生衍射。而晶体的X射线衍射,成 为了解晶体内部结构的重要实验方法。
晶胞
• 晶胞的两个基本要素:
晶胞
• 分数坐标
OP = xa + yb + zc
x, y, z为P原子的分数坐标。 x, y, z为三个晶轴方向单位 矢量的个数(是分数)(晶轴 不一定是相互垂直)。 x, y, z一定为分数
晶胞
• 凡不到一个周期的原子的坐标都必须标记,分 数坐标,即坐标都是分数,这样的晶胞并置形 成晶体。
点阵结构
2. 从晶体点阵结构中抽象出点阵 例1. 等径圆球排列形成的一密置列直线点阵
一个点阵点代表一个球 重复周期为a a = 2r
第八章分子结构与晶体结构1-.ppt

The doubly charged small Ca2+ ions, and the triply charged PO43- ions attract one another very strongly and clamp together to form a rigid, insoluble solid. (not completely insoluble, osteoporosis,骨质疏松症)
序言:
• 原子怎样结合成为分子? - 化学键
– 离子键
Link
– 共价键
– 金属键
• 分子的形状? - 分子构型
–价电子对互斥理论
• 分子怎样组成物质材料?-分子间作用力
• 固体材料的结构?
-晶体结构
-无定型结构
一、化学键(Chemical Bonds)
1、离子键 (Ionic Bonds)
• Lewis结构式和八隅体规则 • 离子键及其特点 • 离子键强度与晶格能 • 离子化合物的性质
第八章 分子结构与晶体结构 (1)
序言 一、化学键
1 离子键 (本质、特征、强弱、离子半径) 2 共价键 (本质、特征、强弱、共价半径) 3 分子构型 (价电子对互斥理论) 4 杂化轨道理论 5 分子轨道理论 二、分子间力和氢键 1 分子间力 2 氢键 三、晶体结构 1 晶体的特征 2 晶格和晶胞 3 晶体的基本类型
Ca2+ (g) + 2Cl- (g) CaCl2 (s) – H = U = 2260.kJ/mol
离子键强度与晶格能:
Born-Lande 公式 U = -Ve ∝ Z1Z2/r
其中: Ve 为正负离子间吸引力和排斥力达平衡时,体系的 位距能。;Z1、Z2 分别为正负离子的电荷数; r为正负离子间
序言:
• 原子怎样结合成为分子? - 化学键
– 离子键
Link
– 共价键
– 金属键
• 分子的形状? - 分子构型
–价电子对互斥理论
• 分子怎样组成物质材料?-分子间作用力
• 固体材料的结构?
-晶体结构
-无定型结构
一、化学键(Chemical Bonds)
1、离子键 (Ionic Bonds)
• Lewis结构式和八隅体规则 • 离子键及其特点 • 离子键强度与晶格能 • 离子化合物的性质
第八章 分子结构与晶体结构 (1)
序言 一、化学键
1 离子键 (本质、特征、强弱、离子半径) 2 共价键 (本质、特征、强弱、共价半径) 3 分子构型 (价电子对互斥理论) 4 杂化轨道理论 5 分子轨道理论 二、分子间力和氢键 1 分子间力 2 氢键 三、晶体结构 1 晶体的特征 2 晶格和晶胞 3 晶体的基本类型
Ca2+ (g) + 2Cl- (g) CaCl2 (s) – H = U = 2260.kJ/mol
离子键强度与晶格能:
Born-Lande 公式 U = -Ve ∝ Z1Z2/r
其中: Ve 为正负离子间吸引力和排斥力达平衡时,体系的 位距能。;Z1、Z2 分别为正负离子的电荷数; r为正负离子间
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对某一固定晶体,dh*k*l*一定,X射线波长一定,当n取不
同值时,值不同
(110)
(220)
(330)
(110)
(110)面一级衍射
(110)面二级衍射
(110)面三级衍射
立方晶系Brag方程
sin 2
hkl
2 4a 2
(h2
k2
l2)
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
H.A. Hauptman
J. Karle 发展了确定晶体分子结构的方法 1985年Nobel化学奖
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
9.1.1 晶体的X射线衍射效应
1. X射线的产生
热发射的自由电子高压加速金属 靶拦截白色X射线/特征X射线
Cooling Water
mh nk pl (mh nk pl)
在满足Laue方程的衍射方向S,点阵中各点间的光程差一 定是波长的整数倍
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
2. Brag方程
将空间点阵视为一组平行且间距相等的平面点阵族,点 阵面指标(h*k*l*) xh*+yk*+zl*=N
9.1.3 衍射强度与晶胞中原子的分布
A1 B1 a
A2 B2 a 4
h=0
h
A1A2 光程差
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
9.1.2 衍射方向和晶胞参数
1. Laue方程
S
把空间点阵看成互不平行的三维直线点阵A
直线点阵的Laue方程:
O
P
a
=OA-BP= a(cos
= a(S S0) = h
cos0) h=0,
1,
2,
S0
... ...
S0
(S – S0)垂直于点阵面(h*l*k*)。 S与S0大小相等,(S–S0)与S和S0夹角相等
衍射与反射相仿(入射角=反射角) 衍射方向h = nh* k = nk* l = nl*
S0
S0
SS0
S
P
S
Q
相邻平面点阵面的光程差为波长的整数倍
P
M
N
Q
Nankai University
第九章 分子、晶体结构测 定方法理论基础
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
§9.1 X射线晶体结构分析原理
Max Von Laue 发现X射线在 晶体中的衍射
1914年Nobel
Henry Bragg
Lawrence Bragg 用X衍射研究晶 体结构 1915年Nobel
通过原点O的平面对应N=0,与O所在点阵面相邻的为N=1和N=1 有确定N值的平面点阵上任一点P(x, y, z) 在hkl( h = nh*,k = nk*,l = nl*)方向上与O点的光程差为
OP (S S0 ) (xa yb zc) (S S0 ) xa (S S0 ) yb (S S0 ) zc (S S0 )
K
n=1
(K层)
《结构化学》第九章 分子、晶体结构测定方法理论基础
2. 晶体对X射线的相干散射 原生X射线
X射线 晶体
热能 非散射能量转化 光电效应 透过(绝大部分)
不相干散射(反冲电子及波长 散射 和方向均改变的次生散射)
相干散射(次生衍射继承入射线的位相和波长)
3. 衍射效应
Nankai University
次生X射线干涉 迭加相互抵消
次生X射线干涉 迭加相互加强
《结构化学》第九章 分子、晶体结构测定方法理论基础
4:衍射方向和衍射强度
衍射方向:由于晶体中原子或电子的分布具有点阵式的周期 性规律,由周期性排列的原子散射次生X射线相互干涉 最大加强的方向。
衍射强度:不具有周期性排列的原子所散射的次生X射线相 互干涉,对各个衍射方向上的衍射强度产生影响
xh yk zl (xh* yk* zl*)n nN
平面点阵(h*l*k*)对于hkl( h=nh*, k=nk*, l=nl*)方向衍射 具有等程面的性质,该点阵面上任意两点的光程差为0
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
PQ (S S0 ) 0
衍射指标的整数性决定了衍射 方向的分立性
Laue方程把表示衍射方向的 hkl 和晶胞参数abc定量地 联系起来了。
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
O为点阵的原点 基本向量为a、b和c P为点阵中一点
OP ma nb pc
OP (S S0 ) (ma nb pc) (S S0 ) ma (S S0 ) nb (S S0 ) pc (S S0 )
B
空间点阵的Laue方程:
标量式
a(cos cos0) = h b(cos cos0) = k c(cos cos0) = l
矢量式
a ·(S S0) = h b ·(S S0) = k c ·(S S0) = l
h, k, l = 0, 1, 2, ...
Nankai University
2dh*k*l* sin n
Brag方程
dh*k*l*
n
相邻点阵面间距 衍射角,为入射(衍射)线与点阵面夹角 衍射级数, n=1, 2, 3,…
《结构化学》第九章 分子、晶体结构测定方法理论基础
h*k*l*晶面只能对满足衍射方向为 h = nh* k = nk* l = nl*的
角方向产生衍射,h k l为衍射指标。
《结构化学》第九章 分子、晶体结构测定方法理论基础
h k l为衍射指标 (与晶面指标不同,不一定是互质的)
S
-3
-2 -1 0 1 2
3
S
-3 -2 -1 0 1 2 3S0 NhomakorabeaS0
一组衍射指标规定一个衍射方向,这个衍射方向就是三
个直线点阵和三个衍射方向所规定的三个圆锥的相交线
方向(即同时满足三个方程解)
Metal Target
Beryllium Windows
Electron Beams
特征X射线强度大,波长确定. 常用的靶材:
I0
K
Cu (K1)=1.54056Å
K Mo (K)= 0.7010Å
n=3 (M层)
K
Fe (K)= 1.9373Å
n=2
(L层)
Nankai University
K1 K2
同值时,值不同
(110)
(220)
(330)
(110)
(110)面一级衍射
(110)面二级衍射
(110)面三级衍射
立方晶系Brag方程
sin 2
hkl
2 4a 2
(h2
k2
l2)
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
H.A. Hauptman
J. Karle 发展了确定晶体分子结构的方法 1985年Nobel化学奖
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
9.1.1 晶体的X射线衍射效应
1. X射线的产生
热发射的自由电子高压加速金属 靶拦截白色X射线/特征X射线
Cooling Water
mh nk pl (mh nk pl)
在满足Laue方程的衍射方向S,点阵中各点间的光程差一 定是波长的整数倍
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
2. Brag方程
将空间点阵视为一组平行且间距相等的平面点阵族,点 阵面指标(h*k*l*) xh*+yk*+zl*=N
9.1.3 衍射强度与晶胞中原子的分布
A1 B1 a
A2 B2 a 4
h=0
h
A1A2 光程差
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
9.1.2 衍射方向和晶胞参数
1. Laue方程
S
把空间点阵看成互不平行的三维直线点阵A
直线点阵的Laue方程:
O
P
a
=OA-BP= a(cos
= a(S S0) = h
cos0) h=0,
1,
2,
S0
... ...
S0
(S – S0)垂直于点阵面(h*l*k*)。 S与S0大小相等,(S–S0)与S和S0夹角相等
衍射与反射相仿(入射角=反射角) 衍射方向h = nh* k = nk* l = nl*
S0
S0
SS0
S
P
S
Q
相邻平面点阵面的光程差为波长的整数倍
P
M
N
Q
Nankai University
第九章 分子、晶体结构测 定方法理论基础
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
§9.1 X射线晶体结构分析原理
Max Von Laue 发现X射线在 晶体中的衍射
1914年Nobel
Henry Bragg
Lawrence Bragg 用X衍射研究晶 体结构 1915年Nobel
通过原点O的平面对应N=0,与O所在点阵面相邻的为N=1和N=1 有确定N值的平面点阵上任一点P(x, y, z) 在hkl( h = nh*,k = nk*,l = nl*)方向上与O点的光程差为
OP (S S0 ) (xa yb zc) (S S0 ) xa (S S0 ) yb (S S0 ) zc (S S0 )
K
n=1
(K层)
《结构化学》第九章 分子、晶体结构测定方法理论基础
2. 晶体对X射线的相干散射 原生X射线
X射线 晶体
热能 非散射能量转化 光电效应 透过(绝大部分)
不相干散射(反冲电子及波长 散射 和方向均改变的次生散射)
相干散射(次生衍射继承入射线的位相和波长)
3. 衍射效应
Nankai University
次生X射线干涉 迭加相互抵消
次生X射线干涉 迭加相互加强
《结构化学》第九章 分子、晶体结构测定方法理论基础
4:衍射方向和衍射强度
衍射方向:由于晶体中原子或电子的分布具有点阵式的周期 性规律,由周期性排列的原子散射次生X射线相互干涉 最大加强的方向。
衍射强度:不具有周期性排列的原子所散射的次生X射线相 互干涉,对各个衍射方向上的衍射强度产生影响
xh yk zl (xh* yk* zl*)n nN
平面点阵(h*l*k*)对于hkl( h=nh*, k=nk*, l=nl*)方向衍射 具有等程面的性质,该点阵面上任意两点的光程差为0
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
PQ (S S0 ) 0
衍射指标的整数性决定了衍射 方向的分立性
Laue方程把表示衍射方向的 hkl 和晶胞参数abc定量地 联系起来了。
Nankai University
《结构化学》第九章 分子、晶体结构测定方法理论基础
O为点阵的原点 基本向量为a、b和c P为点阵中一点
OP ma nb pc
OP (S S0 ) (ma nb pc) (S S0 ) ma (S S0 ) nb (S S0 ) pc (S S0 )
B
空间点阵的Laue方程:
标量式
a(cos cos0) = h b(cos cos0) = k c(cos cos0) = l
矢量式
a ·(S S0) = h b ·(S S0) = k c ·(S S0) = l
h, k, l = 0, 1, 2, ...
Nankai University
2dh*k*l* sin n
Brag方程
dh*k*l*
n
相邻点阵面间距 衍射角,为入射(衍射)线与点阵面夹角 衍射级数, n=1, 2, 3,…
《结构化学》第九章 分子、晶体结构测定方法理论基础
h*k*l*晶面只能对满足衍射方向为 h = nh* k = nk* l = nl*的
角方向产生衍射,h k l为衍射指标。
《结构化学》第九章 分子、晶体结构测定方法理论基础
h k l为衍射指标 (与晶面指标不同,不一定是互质的)
S
-3
-2 -1 0 1 2
3
S
-3 -2 -1 0 1 2 3S0 NhomakorabeaS0
一组衍射指标规定一个衍射方向,这个衍射方向就是三
个直线点阵和三个衍射方向所规定的三个圆锥的相交线
方向(即同时满足三个方程解)
Metal Target
Beryllium Windows
Electron Beams
特征X射线强度大,波长确定. 常用的靶材:
I0
K
Cu (K1)=1.54056Å
K Mo (K)= 0.7010Å
n=3 (M层)
K
Fe (K)= 1.9373Å
n=2
(L层)
Nankai University
K1 K2
