2019-2020学年度八年级10月月考卷(附答案)

合集下载

2019-2020年八年级数学10月调研试卷及答案

2019-2020年八年级数学10月调研试卷及答案亲爱的同学：坚定信心，相信自己，你一定会取得好成绩，祝你成功！一、细心选一选(本题有10小题，每小题3分，共30分，四选一） 1．在△ABC 中，已知∠B=40°，∠C=90°，则∠A 的度数为（ ▲ ） A ．40° B ．50° C ．60° D ．70° 2.以下列长度的三条线段能组成三角形的是( ▲ )A ．1cm ， 2cm ， 3.5cmB ．4cm ， 5cm ， 9cmC ．5cm ， 8cm ， 15cmD ．6cm ， 8cm ， 9cm 3.下列选项的图形中，不一定是轴对称图形的是(▲ )A ．线段B ．等腰三角形C ．直角三角形D ．圆 4.下列命题中，属于真命题的是( ▲ )A.同位角相等 B ．角平分线上的点到角两边的距离相等 C. 三角形的高线都在三角形内部 D.三个角对应相等的两个三角形全等 5.以下是四位同学在钝角三角形ABC 中画BC 边上的高，其中画法正确的是( ▲ )6.在△ABC 中，满足下列条件：①A=60C=30︒︒∠∠，；②A+B=C ∠∠∠③A:B:C=3:45∠∠∠：；④A=90C ︒∠-∠，能确定△ABC 是直角三角形的有（▲ ） A ．1个 B ．2个 C ．3个 D ．4个 7. 下列说法中，正确的是（ ▲ ）A. 每一个命题都有逆命题B. 假命题的逆命题一定是假命题C. 每一个定理都有逆定理D. 假命题没有逆命题8．如图△ABC 中，∠B=40°，∠C=80°，AD 平分∠BAC 交BC 于点D ，则∠ADC 的度数为( ▲ ) A ．110°B ．100°C ．70°D ．60°9．如图，△ABC 是等边三角形，DE ∥BC ，若AB=5，BD=3，则△ADE 的周长为(▲ ) A ．2 B ． 6 C ． 9 D ．1510.D,则图中是等腰三角形的个数共有( ▲ ) A.0个B. 1个C. 2个D.3个A B C D二、精心填一填（本题有6小题，每小题3分，共18分）11.若等腰三角形的两边长为3cm,5cm，则等腰三角形的周长为▲；12.如图，已知AC平分∠BAD，请添加一个条件后，使△ABC≌△ADC，你添加的条件是：▲；13.如图，∠ACB=Rt∠，D为AB的中点，已知CD=1cm，则AB的长为▲；14．如图，直线CD是线段AB的垂直平分线，P为直线CD上一点，若△PAB的周长为14，PA=4，则线段AB的长为▲；15.下面是一节数学课中的一个学习片段，阅读后回答.陈老师在执教《特殊三角形》一节复习课时，请同学们交流讨论这样一个问题:已知等腰△ABC 中,∠B=50°，求这个△ABC中∠A的度数。

2019-2020年八年级10月月考英语试卷

2019-2020年八年级10月月考英语试卷1.听力（每小题1分，共20分）第一部分听对话回答问题。

1.What does Bob do?A. B. C.2.How does Amy go to school every day?A. B. C.3.Where is the boy going this summer?A. B. C.4.What is Lucy’s?A. B. C.5.What does Mike like to do?A.Help sick people.B.Play computer games.C.Stay with children.6.What does the girl think of lions?A. Dangerous.B. Big.C. Cute7. Where does the boy’s father work?A. At a police station.B. At a bank.C. At a post office.8. Where is the bank?A. It’s north of the hotel.B. It’s south of the hotel.C. It’s east of the hotel.9. How much is the washing machine?A. 799 yuanB. 899 yuanC. 988 yuan10. What does Mr. Max help the woman do?A. Fix her computer.B. Clean her garden.C. Do the shopping.第二部分听对话和短文回答问题。

听对话，回答11——12小题。

11. When is the famous opera on?A. On TuesdayB. On Wednesday.C. On Thursday.12. When is the boy going to do that day?A. Watch the opera.B. Visit his grandmother.C. Have lessons.听第一篇短文，回答13——15小题。

2019-2020年八年级10月月考语文试题及答案

浙江省嘉兴市高新学校等七校2015-2016学年上学期10月联考八年级语文试卷2019-2020年八年级10月月考语文试题及答案温馨提示：本试卷共4页，四大题，21小题，总分100分，考试时间为120分钟，请你看清题目，认真答题，答案写在答题卷上。

一、语文知识积累与运用（20分）1.阅读下面这段文字，根据括号内的拼音写出相应的汉字。

（3分）阅读经典，咀jué（）经典，那些从容流淌的文字中，却常常涌动着令我们感动的爱的激流：阿长辛苦买来的粗zhuō ( )的《山海经》中蕴含着的浓浓关爱；父亲蹒跚的背影中流着的shì（）犊之情；老王在生命尽头的微薄的回馈所牵动的一个善良文人的愧怍……常常感动于生活中的细小的爱与关怀，我们才能更好的品味生活！2.根据提示默写。

（8分）（1）少壮不努力，_____________ 。

（《长歌行》）（2）树树皆秋色，_____________。

（王绩《野望》）（3）《桃花源记》中描写桃花源中人们安居乐业的句子是：，。

（4）《陋室铭》中与“时人莫小池中水，浅处无妨有卧龙”意思相近的句子是：_________，_____________。

（5）《陋室铭》中以“交往之雅”表明“陋室”不陋的语句是，。

3.文学学识与名著阅读。

（3分）（1）《桃花源记》的作者是东晋诗人陶渊明，又名潜，字，世称靖节先生。

（1分）（2）《朝花夕拾》是鲁迅回忆少年时期不同生活经历与体验的一部散文集。

请结合自己阅读的体验经历，说一说你最喜欢其中的哪一篇文章，谈一谈为什么？喜欢的文章《》喜欢的原因：_________________________________________________________________。

4.文言文重点词考查。

（6分）（1）解释下列语句中加点的词的意义。

（4分）欲穷．其林穷：便要．还家要：处处志．之志：有仙则名．名：（3）下列各组句子中加点词的意义和用法，相同的一组是（）（2分）A、武陵人以捕鱼为．业此人一一为．具言所闻B、何陋之．有有良田美池桑竹之．属C、其．中往来种作太守即遣人随其．往D.、便扶向．路寻向．所志二、现代文阅读（22分）请认真阅读下面的文章，完成5——12题（一）年轻时应该去远方（12分）肖复兴寒假的时候，儿子从美国发来一封电子邮件，告诉我利用这个假期，他要开车从他所在的北方出发到南方去，并画出了一共要穿越11个州的路线图。

2019-2020学年度人教版第一学期八年级语文10月月考卷

2019-2020学年度第一学期八年级语文10月月考卷一、积累与运用（35分）1．下列加点字的注音完全正确的一项是 ( ) （每个选择题2分）A.悠．闲(yōu) 溃．退(kuì) 星宿．(xiù)B.肃穆．(mù) 竹篙．(ɡāo) 赤裸．(luó)C.烧灼．(zhuó) 疟．疾(nuè) 要塞．(sài)D.寒噤．(jīn) 仄．歪(zè) 阻遏．(è)2．下列词语中无错别字的一项是 ( )A.眼花嘹乱晨曦血腥闪烁B.英勇善战荒谬憧憬珐琅C.响彻云宵杀戮箱箧揣摩D.锐不可挡纳粹惊骇铁锈3．选出理解错误的一项（）A．西蒙诺夫的《蜡烛》是一篇战地通讯，赞美了反法西斯同盟各国的友谊，讴歌了南斯拉夫人民对苏联红军的深厚友谊。

B．《芦花荡》中的主人公“老头子”老当益壮、智勇双全、爱憎分明，是个十全十美的人物形象。

C．《就英法联军远征中国给巴特勒上尉的信》中结尾一句“以上就是我对远征中国的全部赞誉”运用了反语的修辞手法。

课文中还有一些有些地方运用到了这种修辞手法，有辛辣的讽刺意味。

D．《长歌行》中“少壮不努力，老大徒伤悲”是主旨句，告诫人们要惜时向上。

4．下列句子中加线的词语使用正确的一项是（）A．游客沉湎．．在运河沿途迷人的风光中，真正领略到了杭州作为“水清、河畅、岸绿、景美”的亲水型宜居城市的风貌。

B．如果看了时下一些渲染情爱或暴力的小说、电影以后，就盲目地去模仿文学作品中某些人物的偏激行为，只能说明这些读者没有足够的鉴赏．．能力。

C．大家议论了好久，莫衷一是．．．．，想不出好办法。

D．广州亚运会期间，广州市实行了交通管制，交通拥堵的状况戛然而止．．．．。

5．下列各句中没有语病的一项是（）A．“神舟七号”飞船发射成功，谁能否认中国没有进入国际载人航天技术领域的能力？B．局长嘱咐几个考场的领导，新学期的工作一定要有新的起色。

2019-2020学年度第一学期初二数学月考八年级上册10月份月考数学试卷及答案解析

2019-2020学年度第一学期初二数学月考八年级上册10月份月考数学试卷及答案解析一、选择题（每题3分，共10题，满分30分）1．如图所示，图中不是轴对称图形的是（）A．B．C．D．2．下列各组线段中能围成三角形的是（）A．2cm，4cm，6cm B．8cm，4cm，6cmC．14cm，7cm，6cm D．2cm，3cm，6cm3．已知△ABC的三个内角∠A，∠B，∠C满足关系式∠B+∠C＝3∠A，则此三角形（）A．一定有一个内角为45°B．一定有一个内角为60°C．一定是直角三角形D．一定是钝角三角形4．工人师傅经常利用角尺平分一个任意角，如图所示，∠AOB是一个任意角，在边OA，OB上分别取OD＝OE，移动角尺，使角尺两边相同的刻度分别与D，E重合，这时过角尺顶点P的射线OP就是∠AOB的平分线．你认为工人师傅在此过程中用到的三角形全等的判定方法是这种作法的道理是（）A．SAS B．ASA C．AAS D．SSS（第4题）（第5题）（第6题）5．如图，点P是AB上任意一点，∠ABC＝∠ABD，还应补充一个条件，才能推出△APC≌△APD．从下列条件中补充一个条件，不一定能推出△APC≌△APD的是（）A．BC＝BD B．AC＝AD C．∠ACB＝∠ADB D．∠CAB＝∠DAB6．如图，在△PAB中，PA＝PB，M，N，K分别是PA，PB，AB上的点，且AM＝BK，BN＝AK，若∠MKN＝42°，则∠P的度数为（）A．44°B．66°C．96°D．92°7．一个正多边形的每一个外角都等于30°，则这个多边形的边数是（）A．6B．8C．9D．128．如图，直线l1，l2，l3表示三条公路．现要建造一个中转站P，使P到三条公路的距离都相等，则中转站P可选择的点有（）A．一处B．二处C．三处D．四处（第8题）（第9题）（第10题）9．△ABC中，AB＝AC＝12厘米，∠B＝∠C，BC＝9厘米，点D为AB的中点．如果点P在线段BC上以v厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．若点Q 的运动速度为3厘米/秒，则当△BPD与△CQP全等时，v的值为（）A．2.5B．3C．2.25或3D．1或510．如图，在△ABC中，AD、CF分别是∠BAC、∠ACB的角平分线，且AD、CF交于点I，IE⊥BC于E，下列结论：①∠BIE＝∠CID；②S＝IE（AB+BC+AC）；③BE＝（AB+BC﹣AC）；④AC＝AF+DC．其△ABC中正确的结论是（）A．①②③B．①②④C．②③④D．①②③④二、填空题（每题3分，共6题，满分18分）11．如图是两个全等三角形，图中的字母表示三角形的边长，则∠1等于多少度？．（第11题）（第12题）（第13题）12．如图，已知△ABC为直角三角形，∠C＝90°，若沿图中虚线剪去∠C，则∠1+∠2＝．13．如图，∠B＝∠DEF，AB＝DE，若要以“ASA”证明△ABC≌△DEF，则还缺条件．14．如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M、N，再分别以点M、N为圆心，大于MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD＝4，AB＝15，则△ABD的面积是．（第14题）（第15题）（第16题）15．如图，已知四边形ABCD中，对角线BD平分∠ABC，∠ADB＝32°，∠BCD+∠DCA＝180°，那么∠ACD为度．16．如图，在Rt△ABC和Rt△BCD中，∠BAC＝∠BDC＝90°，BC＝8，AB＝AC，∠CBD＝30°，BD＝4，M，N分别在BD，CD上，∠MAN＝45°，则△DMN的周长为．三、解答题（共8小题，共72分）17．（8分）在△ABC中，∠B＝∠A+10°，∠C＝∠B+10°，求△ABC各内角的度数．18．（8分）如图，已知AD＝AE，∠B＝∠C，求证：AB＝AC．19．（8分）已知等腰三角形的一边等于4，另一边等于9，求它的周长．20．（8分）如图，在平面直角坐标系中，A（﹣1，5），B（﹣1，0），C（﹣4，3）（1）在图中作出△ABC关于y轴的对称图形△A1B1C1；（2）求出△A1B1C1的面积；（3）将△ABC向左平移2个单位，再向上平移2个单位得△A2B2C2，请直接写出点A2，B2，C2的坐标．21．（8分）如图，AD平分∠EAC，DE⊥AB于E，DF⊥AC于F，BD＝CD，（1）求证：BE＝FC；（2）已知AC＝20，BE＝4，求AB的长．22．（10分）已知D、E分别为△ABC中AB、BC上的动点，直线DE与直线AC相交于F，∠ADE 的平分线与∠B的平分线相交于P，∠ACB的平分线与∠F的平分线相交于Q．（1）如图1，当F在AC的延长线上时，求∠P与∠Q之间的数量关系．（2）如图2，当F在AC的反向延长线上时，求∠P与∠Q之间的数量关系（用等式表示）．23．（10分）等腰Rt△ABC中，CA＝CB，∠ACB＝90°，点O是AB的中点．（1）如图1，求证：CO＝BO；（2）如图2，点M在边AC上，点N在边BC延长线上，MN﹣AM＝CN，求∠MON的度数；（3）如图3，AD∥BC，OD∥AC，AD与OD交于点D，Q是OB的中点，连接CQ、DQ，试判断线段CQ与DQ的关系，并给出证明．24．（12分）已知：在平面直角坐标系中A（0，a）、B（b，0），且满足4（a﹣2）2+（b﹣4）2＝0，点P（m，m）在线段AB上（1）求A、B的坐标；（2）如图1，若过P作PC⊥AB交x轴于C，交y轴交于点D，求的值；（3）如图2，以AB为斜边在AB下方作等腰直角△ABC，CG⊥OB于G，设I是∠OAB的角平分线与OP的交点，IH⊥AB于H．请探究的值是否发生改变，若不改变请求其值；若改变请说明理由．月考数学试卷参考答案与解析一、选择题（每题3分，共10题，满分30分）1．【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形．据此对图中的图形进行判断．【解答】解：A、有四条对称轴，是轴对称图形，故本选项错误；B、有三条对称轴，是轴对称图形，故本选项错误；C、不是轴对称图形，因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义，故本选项正确；D、有二条对称轴，是轴对称图形，故本选项错误．故选：C．2．【分析】根据三角形三边关系定理：三角形两边之和大于第三边进行分析即可．【解答】解：A、2+4＝6，不能组成三角形，故此选项错误；B、4+6＞10，能组成三角形，故此选项正确；C、6+7＜14，不能组成三角形，故此选项错误；D、2+3＜6，不能组成三角形，故此选项错误；故选：B．3．【分析】由三角形内角和定理知．【解答】解：∵∠B+∠C+∠A＝180°，∠B+∠C＝3∠A，∴∠B+∠C+∠A＝4∠A＝180°，∴∠A＝45°．故选：A．4．【分析】由三边对应相等得△DOF≌△EOF，即由SSS判定两个三角形全等．做题时要根据已知条件结合判定方法逐个验证．【解答】解：依题意知，在△DOF与△EOF中，，∴△DOF≌△EOF（SSS），∴∠AOF＝∠BOF，即OF即是∠AOB的平分线．故选：D．5．【分析】根据题意，∠ABC＝∠ABD，AB是公共边，结合选项，逐个验证得出正确结果．【解答】解：A、补充BC＝BD，先证出△BPC≌△BPD，后能推出△APC≌△APD，故正确；B、补充AC＝AD，不能推出△APC≌△APD，故错误；C、补充∠ACB＝∠ADB，先证出△ABC≌△ABD，后能推出△APC≌△APD，故正确；D、补充∠CAB＝∠DAB，先证出△ABC≌△ABD，后能推出△APC≌△APD，故正确．故选：B．6．【分析】根据等腰三角形的性质得到∠A＝∠B，证明△AMK≌△BKN，得到∠AMK＝∠BKN，根据三角形的外角的性质求出∠A＝∠MKN＝42°，根据三角形内角和定理计算即可．【解答】解：∵PA＝PB，∴∠A＝∠B，在△AMK和△BKN中，，∴△AMK≌△BKN，∴∠AMK＝∠BKN，∵∠MKB＝∠MKN+∠NKB＝∠A+∠AMK，∴∠A＝∠MKN＝42°，∴∠P＝180°﹣∠A﹣∠B＝96°，故选：C．7．【分析】任何一个多边形的外角都等于360°，用360除以每一个外角的度数就是这个多边形的边数．【解答】解：360÷30＝12（条）故选：D．8．【分析】到三条相互交叉的公路距离相等的地点应是三条角平分线的交点．把三条公路的中心部位看作三角形，那么这个三角形两个内角平分线的交点以及三个外角两两平分线的交点都满足要求．【解答】解：满足条件的有：（1）三角形两个内角平分线的交点，共一处；（2）三个外角两两平分线的交点，共三处．故选：D．9．【分析】分两种情况讨论：①若△BPD≌△CPQ，根据全等三角形的性质，则BD＝CQ＝6厘米，BP＝CP＝BC＝×9＝4.5（厘米），根据速度、路程、时间的关系即可求得；②若△BPD≌△CQP，则CP＝BD＝6厘米，BP＝CQ，得出，解得：v＝3．【解答】解：∵△ABC中，AB＝AC＝12厘米，点D为AB的中点，∴BD＝6厘米，若△BPD≌△CPQ，则需BD＝CQ＝6厘米，BP＝CP＝BC＝×9＝4.5（厘米），∵点Q的运动速度为3厘米/秒，∴点Q的运动时间为：6÷3＝2（s），∴v＝4.5÷2＝2.25（厘米/秒）；若△BPD≌△CQP，则需CP＝BD＝6厘米，BP＝CQ，∴，解得：v＝3；∴v的值为：2.25或3，故选：C．10．【分析】如图，作IM⊥AB于M，IN⊥AC于N．根据角平分线的性质定理以及全等三角形的判定和性质一一判断即可；【解答】解：如图，作IM⊥AB于M，IN⊥AC于N．∵AD 、CF 分别是∠BAC 、∠ACB 的角平分线，IM ⊥AB ，IN ⊥AC ，IE ⊥BC ，∴IE ＝IM ＝IN ，∴S △ABC ＝S △ABI +S △ACI +S △BCI ＝•AB •IM +•AC •IN +•BC •IE ＝•IE •（AB +BC +AC ），故②正确，∵∠ABC +∠ACB +∠BAC ＝180°，∠IBE ＝∠ABC ，∠IAC ＝∠BAC ，∠ICA ＝∠ACB ， ∴∠IBE +∠IAC +∠ICA ＝90°，∵∠CID ＝∠IAC +∠ICA ＝90°﹣∠IBE ＝∠BIE ，故①正确，∵BI ＝BI ，IM ＝IE ，∴Rt △BIM ≌Rt △BIE （HL ），∴BE ＝BM ，同法可证：AM ＝AN ，CN ＝CE ，∴BE ＝（AB +BC ﹣AC ），故③正确，④只有在∠ABC ＝60°的条件下，AC ＝AF +DC ，故④错误，故选：A ．二、填空题（每题3分，共6题，满分18分）11．【分析】根据图形和亲弟弟三角形的性质得出∠1＝∠C ，∠D ＝∠A ＝54°，∠E ＝∠B ＝60°，根据三角形内角和定理求出即可．【解答】解：∵△ABC ≌△DEF ，∴∠1＝∠C ，∠D ＝∠A ＝54°，∠E ＝∠B ＝60°，∴∠1＝180°﹣∠E ﹣∠F ＝66°，故答案为：66°．12．【分析】根据四边形内角和为360°可得∠1+∠2+∠A +∠B ＝360°，再根据直角三角形的性质可得∠A+∠B＝90°，进而可得∠1+∠2的和．【解答】解：∵四边形的内角和为360°，直角三角形中两个锐角和为90°∴∠1+∠2＝360°﹣（∠A+∠B）＝360°﹣90°＝270°．∴∠1+∠2＝270°．故答案为：270°．13．【分析】利用全等三角形的判定方法结合ASA得出即可．【解答】解：当添加∠A＝∠D时，可证明△ABC≌△DEF；理由：在△ABC和△DEF中，∴△ABC≌△DEF（ASA）．故答案为：∠A＝∠D．14．【分析】根据角平分线的性质得到DE＝DC＝4，根据三角形的面积公式计算即可．【解答】解：作DE⊥AB于E，由基本尺规作图可知，AD是△ABC的角平分线，∵∠C＝90°，DE⊥AB，∴DE＝DC＝4，∴△ABD的面积＝×AB×DE＝30，故答案为：30．15．【分析】延长BA和BC，过D点作DE⊥BA于E点，过D点作DF⊥BC于F点，根据BD是∠ABC的平分线可得出DE＝DF，过D点作DG⊥AC于G点，进而得出CD为∠ACF的平分线，设∠ABD＝x，则∠ABC＝2x，∠EAD＝∠ABD+∠ADB＝x+32，再根据∠BAE+∠BCF＝360°，即可得出结论．【解答】解：延长BA和BC，过D点作DE⊥BA于E点，过D点作DF⊥BC于F点，过D点作DG⊥AC于G点，∵BD是∠ABC的平分线，∴DE＝DF，又∵∠BCD+∠DCA＝180°，∠BCD+∠DCF＝180°，∴∠ACD＝∠DCF，∴DG＝DF＝DE∴AD为∠EAC的平分线，设∠ABD＝x，则∠ABC＝2x，∠EAD＝∠ABD+∠ADB＝x+32，∵∠BAE+∠BCF＝360°，∴2（x+32）+∠BAC+∠ACB+2∠ACD＝360，2x+64+180﹣2x+2∠ACD＝360，∠ACD＝58°．故答案为：58°．16．【分析】将△ACN绕点A逆时针旋转，得到△ABE，由旋转得出∠NAE＝90°，AN＝AE，∠ABE ＝∠ACD，∠EAB＝∠CAN，求出∠EAM＝∠MAN，根据SAS推出△AEM≌△ANM，根据全等得出MN＝ME，求出MN＝CN+BM，解直角三角形求出DC，即可求出△DMN的周长＝BD+DC，代入求出即可．【解答】解：将△ACN绕点A逆时针旋转，得到△ABE，如图：由旋转得：∠NAE＝90°，AN＝AE，∠ABE＝∠ACD，∠EAB＝∠CAN，∵∠BAC＝∠D＝90°，∴∠ABD+∠ACD＝360°﹣90°﹣90°＝180°，∴∠ABD+∠ABE＝180°，∴E，B，M三点共线，∵∠MAN＝45°，∠BAC＝90°，∴∠EAM＝∠EAB+∠BAM＝∠CAN+∠BAM＝∠BAC﹣∠MAN＝90°﹣45°＝45°，∴∠EAM＝∠MAN，在△AEM和△ANM中，，∴△AEM≌△ANM（SAS），∴MN＝ME，∴MN＝CN+BM，∵在Rt△BCD中，∠BDC＝90°，∠CBD＝30°，BD＝4，CD＝BD×tan∠CBD＝4，∴△DMN的周长为DM+DN+MN＝DM+DN+BM+CN＝BD+DC＝4+4，故答案为：4+4．三、解答题（共8小题，共72分）17．【分析】根据三角形的内角和定理，结合已知条件解方程即可．【解答】解：∵∠B＝∠A+10°，∠C＝∠B+10°，又∵∠A+∠B+∠C＝180°，∴∠A+（∠A+10°）+（∠A+10°+10°）＝180°，3∠A+30°＝180°，3∠A＝150°，∠A＝50°．∴∠B＝60°，∠C＝70°．18．【分析】根据AAS推出△ABE≌△ACD，根据全等三角形的性质得出即可．【解答】证明：在△ABE和△ACD中，∴△ABE≌△ACD（AAS），∴AB＝AC．19．【分析】此题先要分类讨论，已知等腰三角形的一边等于4，另一边等于9，先根据三角形的三边关系判定能否组成三角形，若能则求出其周长．【解答】解：当4为腰，9为底时，∵4+4＜9，∴不能构成三角形；当腰为9时，∵9+9＞4，∴能构成三角形，∴等腰三角形的周长为：9+9+4＝22．20．【分析】（1）分别作出点A，B，C关于y轴的对称点，再顺次连接即可得；（2）由图形得出A1B1＝5，这条边上的高为3，根据面积公式计算可得．（3）分别作出点A，B，C向左平移2个单位，再向上平移2个单位得到的对应点，再顺次连接即可得．【解答】解：（1）如图所示，△A1B1C1即为所求．（2）△A1B1C1的面积为×5×3＝；（3）如图所示，△A2B2C2即为所求，其中点A2的坐标为（﹣3，7），B2的坐标为（﹣3，2），C2的坐标为（﹣6，5）．21．【分析】（1）根据角平分线性质和全等三角形的性质即可解决问题；（2）由△ADE≌△ADF（AAS），推出AF＝AE，由BE＝CF＝4，AC＝20，推出AF＝AE＝20﹣4＝16即可解决问题；【解答】（1）证明：∵AD平分∠BAC，DE⊥AB于E，DF⊥AC于F，∴DE＝DF，∠DEB＝∠DFC＝90°，在Rt△BED和Rt△CFD中，∴Rt△BED≌Rt△CFD（HL），∴BE＝CF；（2）解：在△ADE和△ADF中，，∴△ADE≌△ADF（AAS），∴AF＝AE，∵BE＝CF＝4，AC＝20，∴AF＝AE＝20﹣4＝16，∴AB＝AE﹣BE＝16﹣4＝12．22．【分析】（1）先根据三角形内角和定理和三角形外角的性质求出2∠P＝∠DEB，2∠Q＝∠CEF，即可得出答案；（2）先根据三角形内角和定理和三角形外角的性质求出∠P＝∠BED，∠Q＝90°+∠FEC，根据邻补角互补求出即可．【解答】解：（1）∵DP是∠ADF的平分线，BP是∠ABC的平分线，∴∠ADF＝2∠ADP，∠ABC＝2∠ABP，∵∠ADF＝∠ABC+∠DEB，∠ADP＝∠P+∠ABP，∴2∠ADP＝2∠P+2∠ABP，∴∠DEB＝2∠P，同理∠CEF＝2∠Q，∵∠DEB＝∠CEF，∴2∠P＝2∠Q，∴∠P＝∠Q；（2）∠P+∠Q＝180°，理由是：∵由（1）知：2∠P＝∠BED，∴∠P＝∠BED，∵FQ是∠CFE的平分线，CQ是∠ACB的平分线，∴∠QFC＝∠EFC，∠QCF＝ACB，∵∠FEC+∠EFC+∠ECF＝180°，∴∠EFC+∠ECF＝180°﹣∠FEC，∴∠Q＝180°﹣（∠QFC+∠QCF）＝180°﹣（∠EFC+∠ECF）＝180°﹣（180°﹣∠FEC）＝90°+∠FEC，∴∠P+∠Q＝∠BED+90°+∠FEC＝90°+（∠BED+∠FEC）＝90°+＝180°．23．【分析】（1）根据等腰三角形的三线合一证明；（2）在线段BC上取点H，使CH＝AM，连接OH，分别证明△AOM≌△COH和△MON≌△HON，根据全等三角形的性质计算即可；（3）作DG⊥AO于G，证明△COQ≌△QGD，根据全等三角形的性质，垂直的定义证明．【解答】（1）证明：∵∠ACB＝90°，AO＝BO，∴CO＝AB＝BO；（2）解：在线段BC上取点H，使CH＝AM，连接OH，∵∠ACB＝90°，AO＝BO，∴∠A＝∠B＝45°，∠ACO＝∠BCO＝45°，在△AOM和△COH中，，∴△AOM≌△COH（SAS）∴OM＝OH，∵MN﹣AM＝CN，∴NM＝NH，在△MON和△HON中，，∴△MON≌△HON（SSS），∴∠MON＝∠HON，∴∠MON＝∠AOM+∠COH，∴∠MON＝∠AOC＝45°；（3）QC＝QD，QC⊥QD，理由如下：作DG⊥AO于G，∵AD∥BC，∴∠OAD＝∠B＝45°，∵OD∥AC，∴∠AOD＝∠OAC＝45°，∴DA＝DO，又DG⊥AO，∴DG＝AG＝AO＝OA，∵Q是OB的中点，∴OQ＝BQ＝OB，∴DG＝OQ，GQ＝OC，在△COQ和△QGD中，，∴△COQ≌△QGD（SAS），∴QC＝QD，∠GQD＝∠OCQ，∵∠OCQ+∠CQO＝90°，∴∠GQD+∠CQO＝90°，即∠CQD＝90°，∴QC⊥QD，则QC＝QD，QC⊥QD．24．【分析】（1）根据非负数的性质即可解决问题．（2）先求出直线AB的解析式，利用方程组求出点P坐标，再求出直线PC的解析式，求出点C 坐标即可解决问题．（3）如图2中，作IE⊥OA于E，CM⊥y轴于M，IF⊥OB于F．由△ACM≌△BCF，推出AM ＝BG，CM＝CG，推出BH﹣AH＝OB﹣OA＝2CG，即可解决问题．【解答】解：（1）∵4（a﹣2）2+（b﹣4）2＝0，又∵4（a﹣2）2≥0，（b﹣4）2≥0，∴a＝2，b＝4，∴A（0，2），B（4，0）．（2）如图1中，∵A（0，2），B（4，0），∴直线AB的解析式为y＝﹣x+2，∵P（m，m），∴点P在直线y＝x上，由解得，∴点P（，），∵PC⊥AB，∴直线PC的解析式为y＝2x﹣，∴点C坐标为（，0），∴OC＝，BC＝，∴＝＝5．（3）的值不变．理由如下：如图2中，作IE⊥OA于E，CM⊥y轴于M，IF⊥OB于F．∵设I是∠OAB的角平分线与OP的交点，OP平分∠AOB，∴I是内心，∵IH⊥AB，IE⊥OA，IF⊥OB，∴IE＝IH＝IF，易知AH＝AE，BF＝BH，∴BH﹣AH＝BF﹣AE＝OB﹣OA，∵∠MCG＝∠ACB＝90°，∴∠ACM＝∠BCG，在△ACM和△BCG中，，∴△ACM≌△BCF（AAS），∴AM＝BG，CM＝CG，∵∠OMC＝∠OGC＝∠MOG＝90°，∴四边形OMCG是矩形，∵CM＝CG，∴四边形OMCG是正方形，∴OM＝OG＝CG＝CM，∴BH﹣AH＝OB﹣AO＝（BG+OG）﹣（AM﹣OM）＝2CG，∴＝＝2．。

2019-2020学年度人教版八年级数学第一学期10月月考试题及答案

2019-2020学年度八年级数学第一学期10 月月考试卷（本检测题满分：120分，时间：100分钟）姓名:班别:分数:一、选择题（每题3分，共30分）1. 以下列各组长度的线段为边，能构成三角形的是( )A．7，3，4B．5，6，12C．3，4，5D．1，2，32. 等腰三角形的一个外角是80°，则其底角是（）A．100°B．100°或40°C．40°D．803．一个多边形的每一个外角都等于40°，那么这个多边形的内角和为（）A．1260°B．1080°C．1620°D．360°4．用一批完全相同的多边形地砖铺地面，不能进行镶嵌的是（）A.正三角形B.正方形C.正六边形D.正八边形5.下列说法正确的是()A.三角形的角平分线、中线及高都在三角形内B.直角三角形的高只有一条.C.三角形至少有一条高在形内D.钝角三角形的三条高都在形外.6．一个多边形的内角和比它的外角的和的2倍还大180°，这个多边形的边数是（）A．5B．6C．7D．87．在下图中，正确画出AC边上高的是（）．B BB BEA E C A C E A C E A C（A）（B）（C）（D）8．如图所示，∠A、∠1、∠2的大小关系是()A. ∠A ∠1∠2B.∠2∠1∠AC. ∠A ∠2∠1D.∠2∠A ∠19. 给出下列命题：⑴三角形的一个外角一定大于它的一个内角．⑵若一个三角形的三个内角之比为1：3：4，它肯定是直角三角形⑶三角形的最小内角不能大于60°⑷三角形的一个外角等于和它不相邻的两个内角的和其中真命题的个数是()（A）1个（B）2个（C）3个（D）4个10．如图1，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，则∠A与∠1+∠2之间有一种数量关系始终保持不变．请试着找一找这个规律，你发现的规律是（）A．∠A=∠1+∠2B．2∠A=∠1+∠2C ．3∠A=2∠1+∠2D ．3∠A=2（∠1+∠2）二、填空题（每题 4 分，共 24 分）11．为了使一扇旧木门不变形，木工师傅在木门的背面加钉了一根木条，这样做的道理是． 12．已知等腰三角形的两边长是 5cm 和 11cm ，则它的周长是_______13.一个等腰三角形的周长为 18,已知一边长为 5,则其他两边长为 ___. 14.已知一个三角形的三条边长为 2、7、 x ，则 x 的取值范围是 _______. 15．如图所示，AB∥CD，∠ABE＝66°，∠D＝54°，则∠E 的度数为．16.如图，∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F=.AEBFABCECDD15 题16 题三、解答题（共 66 分） ABC 17．已知△ABC 中，为钝角.请你按要求作图(不写作法，但要保留作图痕迹)：(1)过点 A 作 BC 的垂线 AD;AC(2)作的角平分线交 AC 于 E; B(3)取 AB 中点 F,连结 CF ．18.在△ABC 中，∠A-∠B=∠B-∠C =15°求∠A 、∠B 、∠C 的度数.19.如图，在△ABC 中，两条角平分线 BD 和 CE 相交于点 O ，若∠BOC=116°，求∠A 的度数AEODC 20.△ABC 中，AB=AC ，AC 上的中线 BD 把△ABC 的周长分为 24 ㎝和 30 ㎝两部分19，题求三角形的三边长.A BC B21．已知：如图，在△ABC中，∠BAC=900，AD⊥BC于D，AE平分∠DAC，∠B=500，求∠AEC的度数.AB D E C22.如图,ABC中,ABC=BAC,BAC的外角平分线交BC的延长线于点D,若ADC=12CAD,求ABC的度数。

湖北省武汉市2019-2020学年第一学期八年级数学10月月考试卷及答案解析

湖北省武汉市2019-2020学年第一学期八年级数学10月月考试卷及答案解析一、选择题1、小芳有两根长度分别为4cm 和9cm 的木条，他想钉一个三角形木框，桌子上有下列长度的几根木条，她应该选择的木条的长度只能是( ) A ．5cm B ．3cm C ．17cm D ．12cm2、下列四个图形中，线段BE 是△ABC 的高的是( )A ．B ．C ．D ．3、如图所示，两个三角形全等．其中已知某些边的长度和某些角的度数，则x 为( ) A ．65° B ．60° C ．55° D ．50°（第3题）（第5题）（第7题）4、一个多边形的内角和是外角和的3倍，这个多边形的边数是( ) A ．7 B ．8 C ．9 D ．105、如图所示，已知△ABC 为直角三角形，∠B ＝90°，若沿图中虚线剪去∠B ，则∠1＋∠2等于( )A ．90°B ．135°C ．270°D ．300°6、以下四个三角形分别满足以下条件：①∠A ＝∠B ＝∠C ；②∠A －∠B ＝∠C ；③∠A＝∠B ＝2∠C ；④∠A ＝∠B ＝∠C ，其中是直角三角形的个数为( )A ．1B ．2C ．3D ．47、如图，△ABC 中，∠A ＝40°，BD 、CE 是角平分线，则∠BEC ＋∠BDC ＝( ) A. 130° B. 140° C. 150° D. 160°8、如图，点E 、F 在AC 上，AD ＝BC ，DF ＝BE ，要使△ADF ≌△CBE ，还需要添加的一个条件是( )A ．∠A ＝∠CB ．∠D ＝∠BC ．AD ∥BC D ．DF ∥BE9、如图，方格中△ABC 的3个顶点分别在正方形的顶点（格点上），这样的三角形叫格点三角形，图中与△ABC 全等的格点三角形共有( )个(不含△ABC)． A. 3 B. 4 C. 7 D. 8（第8题）（第9题）（第10题）10、如图，△ABC 中，∠A ＝90°，角平分线BD 、CE 交于点I ，IF ⊥CE 交CA 于F ，下列结论：①∠DIF ＝45°；②CF ＋BE ＝BC ；③若AB ＝3，AC ＝4，BC ＝5，则AF ＝；其中正确结论的个数为( )A. 0个B. 1个C. 2个D. 3个二、填空题11、已知：如图，∠ABC ＝∠DEF ，AB ＝DE ，要说明△ABC ≌△DEF ，（1）若以“SAS ”为依据，还要添加的条件为___________；（2）若以“ASA ”为依据，还要添加的条件为______；（3）若以“AAS ”为依据，还要添加的条件为_____。

四川省成都市川大附中2019-2020学年八年级上册英语10月月考试卷含答案

四川省成都市川大附中2019-2020学年八年级上册英语10月月考试卷A卷（选择题：共100分）第一部分听力略（共30分）第二部分基础知识运用（共40分）六、选择填空。

（共15小题；计20分）A. 从以下各题的ABC三个选项中选择正确答案。

（共10小题，每小题1分；共计10分）31.--- Look! There is _______ ID card on the floor.---Who lost card? We'd better give it to our teacher.A. a, theB. the, aC. an, the.32.--- What do you think of your eating habits?---They are kind of _______, because I like junk food so much.A. healthyB. heavyC. unhealthy33. I have two friends. _______ of them could play the piano very well.A. BothB. AllC. None34. It seems that he has _______ to show us. Let’s go to bed.A. something interestingB. nothing interestingC. anything interesting35.--- _______ do you have a sports meeting?--- Once a year.A. How oftenB. How longC. How soon36. After they lost Basketball World Cup, Chinese basketball team should be hard-working _______ before.A. more; thanB. as...asC. less; than37. Mary was so excited at the good news that she could _______ say a word.A. sometimesB. alwaysC. hardly38.--- Lingling, did you go _______ last summer vacation?--- Yes. I went to Hangzhou.A. somewhere wonderfulB. anywhere wonderfulC. nowhere wonderful39. We can relax ourselves by _______ game shows on TV after a week's hard work.A. havingB. playingC. watching40. Many children use the Internet _______. It's not good for them.A. for studyB. for funC. for workB. 补全对话。

2019-2020年八年级10月月考数学试卷

2019-2020年八年级10月月考数学试卷一、选择题(每小题有四个选项, 其中只有一个是正确的，请把正确的答案填涂在答题卡上。

本大题共12个小题, 每小题3分, 共36分。

）1.在下列各数0，0.2，3π，，6.1010010001…，，中，无理数的个数是（）A.1B.2C.3D. 42.下列说法不正确的是（）A.27的立方根是B. 的立方根是C.-2的立方是-8D.-8的立方根是-23.下列四组数中不能构成直角三角形的一组是（）A. 1，2，B.3，5，4C. 5，12，13D.4，13 ,154.满足的整数x有（）个A.6个B.5个C.4个D.3个5.下列说法正确的是（）A．一个有理数的平方根有两个，它们互为相反数B．负数没有立方根C．无理数都是开不尽的方根数D．无理数都是无限小数6.下列运算中，正确的是（）A. B. C. D.=-37.已知一个数的两个平方根分别是a+3与2a-15，这个数的值为（）A.4 B．±7 C．-7 D．498.下列结论错误的是（）A．三个角度之比为1：2：3的三角形是直角三角形B．三个边长之比为3：4：5的三角形是直角三角形C．三个边长之比为8：16：17的三角形是直角三角形D．三个角度之比为1：1：2的三角形是直角三角形9.若代数式有意义，则x必须满足的条件是（）A. B. C. D.10.如图，△ABC中，∠B=90°，两直角边AB=7，BC=24，在三角形内有一点P到各边的距离相等，则这个距离是（）A.1B.3C.6 D．11.如图，小正方形边长为1，连接小正方形的三个顶点，可得△ABC ，则AC 边上的高是（）A . B. C. D.12.下列各组线段中的三个长度①9、12、15；②7、24、25；③32、42、52；④3a 、4a 、5a （a>0）；⑤m 2-n 2、2mn 、m 2+n 2（m 、n 为正整数，且m>n ）其中可以构成直角三角形的有（）A.5组B.4组C.3组D.2组第二部分（非选择题共84分）二、填空题( 本大题共5个小题, 每小题3分, 共15分)13.算术平方根和立方根都等于本身的数有______________。

部编版2019-2020学年度八年级上10月月考数学试卷(Word版)

2019-2020 学年度第一学期第一次月考八年级数学试卷一、选择题(共 10 小题，每题 3 分，计 30 分)1.下列各数：﹣2，0， 317，0.020020002…，π （）A ．4B ．3C ．2D ．12.在平面直角坐标系中，下列坐标所对应的点位于第三象限的是（）A ．（﹣1，2）B ．（1，2）C ．（2，﹣1）D ．（-1，-3）3.下列各组数中，互为相反数的是（）A ．2 与12B ．-2 ．2-与2 D ．-2 4.下列四个数中最小的数是（）A ．．-0.5 C ．05.下列运算正确的是（）A 5±B 2=-C =D ． 6.如图所示，长方形 ABCD 中，A （﹣4，1），B （0，1），BC=2，则点 D 的坐标是（） A ．（﹣4，3）B ．（﹣2，3）C ．（﹣3，3）D ．（4，-3）7.若 a 2 = 16= -2 ，则 a+b 的值是（）A ．12B ．12 或 4C ．14 或-2D ．14 8.已知点 A （﹣3，2m ﹣1）在 x 轴上，点 B （n +1，4）在 y 轴上，则点 C （m ，n ）在（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限9.已知点 P 1（a-1,5）和 P 2（2，b-1）关于 x 轴对称，则（a +b ）2019的值为（）A ．0B ．﹣1C ．1D ．（- 3）201910.如图，在正方形ABCD 中，AB＝9，点E 在CD 边上，且DE＝2CE，点P 是对角线AC 上的一个动点，则PE+PD 的最小值是（）A．．．9 D．9二、填空题（共计21 分）11.，的绝对值是。

12. ，=，13. 若点A（a，2）B（-3，b）在第二、第四象限的角平分线上，则a=，b=14. 已知M（-2,3），N（a，3）且MN=3，则点N 的坐标是。

15. 如图，数轴上点A 表示数﹣1，点B 表示数1，过数轴上的点B 作BC 垂直于数轴，若BC＝1，以A 为圆心，AC 为半径作圆弧交正半轴于点P，则点P 所表示的数是．16. 若x、y 都是实数，且y 2，那么x y 的值是17. 平面直角坐标系中，点A（﹣2，3），B（1，-4），经过点A 的直线l∥x 轴，点C 是直线l 上的一个动点，则线段BC 的长度最小时，点C 的坐标为．三、解答题（共计49 分）18. 计算（1（2）（2（4）22)+-01)（6-（54(19. 求下列各式中的 x 。

2019-2020学年八年级数学10月份月考试题(含解析) 新人教版

2019-2020学年八年级数学10月份月考试题（含解析) 新人教版一、细心选一选（每题3分共36分）1．如下书写的四个汉字，其中为轴对称图形的是( )A．B．C．D．2．如图，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在( )A．在AC，BC两边高线的交点处B．在AC，BC两边中线的交点处C．在AC，BC两边垂直平分线的交点处D．在∠A，∠B两内角平分线的交点处3．等腰三角形有两条边长为4cm和9cm，则该三角形的周长是( )A．17cm B．22cm C．17cm或22cm D．18cm4．等腰三角形的对称轴是( )A．顶角的平分线 B．底边上的高C．底边上的中线 D．底边上的高所在的直线5．和点P（﹣3，2）关于y轴对称的点是( )A．（3，2）B．（﹣3，2）C．（3，﹣2）D．（﹣3，﹣2）6．已知：如图，AC=AE，∠1=∠2，AB=AD，若∠D=25°，则∠B的度数为( )A．25° B．30° C．15° D．30°或15°7．如图，△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD和CE交于O，AO的延长线交BC 于F，则图中全等的直角三角形有( )A．3对B．4对C．5对D．6对8．如图，在△ABC中，AB的中垂线交BC于点E，若BE=2，则A、E两点的距离是( )A．4 B．2 C．3 D．9．正三角形ABC中，BD=CE，AD与BE交于点P，∠APE的度数为( )A．45° B．55° C．60° D．75°10．如图，已知△ABC，AB=AC，BD=CD，则下列结论中错误的是( )A．∠BAC=∠B B．∠1=∠2 C．AD⊥BC D．∠B=∠C11．如图，∠1=∠2，PD⊥OA，PE⊥OB，垂足分别为D，E，下列结论错误的是( )A．PD=PE B．OD=OE C．∠DPO=∠EPO D．PD=OD12．如图，已知AB=AC，AE=AF，BE与CF交于点D，则对于下列结论：①△ABE≌△ACF；②△BDF≌△CDE；③D在∠BAC的平分线上．其中正确的是( )A．①B．②C．①和②D．①②③二、专心填一填（每题4分共24分）13．如图，AD⊥BC，D为BC的中点，则△ABD≌△__________．14．如图，若AB=DE，BE=CF，要证△ABF≌△DEC，需补充条件__________或__________．15．已知：如图，△ABD≌△EBC，且∠1=∠2，AB=BE，则AD=__________，∠C=__________．16．如图，三角形ABC中，AB=AC，∠A=40度，AB的垂直平分线MN交AC于D，连接BD，∠DB C 等于__________度．17．如图，在△ABC中，AB=AC，AD是BC边上的高，点E、F是AD的三等分点，若△ABC的面积为12cm2，则图中阴影部分的面积是__________cm2．18．如图是一个轴对称图形，AD所在的直线是对称轴，仔细观察图形，回答下列问题：（1）线段BO、CF的对称线段是__________；（2）△ACE的对称三角形是__________．三、耐心做一做（本大题有6小题，共分60分）19．如图，∠1=∠2，∠3=∠4，求证：AC=AD．20．根据图中尺规作图的痕迹，先判断得出结论：__________，然后证明你的结论（不要求写已知、求证）21．在Rt△ABC中，∠BAC=90°，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．问△AEF与△DEB全等吗？说明理由．22．已知：如图，已知△ABC，（1）分别画出与△ABC关于x轴、y轴对称的图形△A1B1C1和△A2B2C2；（2）写出△A1B1C1和△A2B2C2各顶点坐标；（3）求△ABC的面积．23．如图：△ABC中，AB=AC=5，AB的垂直平分线DE交AB、AC于E、D，①若△BCD的周长为8，求BC的长；②若BC=4，求△BCD的周长．24．如图，∠B=∠C=90°，M是BC中点，DM平分∠ADC，求证：AM平分∠DAB．2015-2016学年山东省聊城市东昌府区郑家镇中学八年级（上）月考数学试卷（10月份）一、细心选一选（每题3分共36分）1．如下书写的四个汉字，其中为轴对称图形的是( )A．B．C．D．【考点】轴对称图形．【分析】根据轴对称图形与中心对称图形的概念求解．【解答】解：观察书写的四个汉字，只有“善”字是轴对称图形．故选B．【点评】掌握好轴对称的概念．轴对称的关键是寻找对称轴，两边图象折叠后可重合．2．如图，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在( )A．在AC，BC两边高线的交点处B．在AC，BC两边中线的交点处C．在A C，BC两边垂直平分线的交点处D．在∠A，∠B两内角平分线的交点处【考点】线段垂直平分线的性质．【专题】应用题．【分析】要求到三小区的距离相等，首先思考到A小区、B小区距离相等，根据线段垂直平分线定理的逆定理知满足条件的点在线段AB的垂直平分线上，同理到B小区、C小区的距离相等的点在线段BC的垂直平分线上，于是到三个小区的距离相等的点应是其交点，答案可得．【解答】解：根据线段的垂直平分线的性质：线段的垂直平分线上的点到线段的两个端点的距离相等．则超市应建在AC，BC两边垂直平分线的交点处．故选C．【点评】本题主要考查线段的垂直平分线的性质：线段的垂直平分线上的点到线段的两个端点的距离相等；此题是一道实际应用题，做题时，可分别考虑，先满足到两个小区的距离相等，再满足到另两个小区的距离相等，交点即可得到．3．等腰三角形有两条边长为4cm和9cm，则该三角形的周长是( )A．17cm B．22cm C．17cm或22cm D．18cm【考点】等腰三角形的性质；三角形三边关系．【分析】题目给出等腰三角形有两条边长为4cm和9cm，而没有明确腰是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．【解答】解：当腰是9cm时，底边是4cm，此时三角形的周长为9+9+4=22（cm）；当底边是9时，此时另两边是4，而4+4＜9，三者构不成三角形，此情况不成立；所以周长为22．故选B．【点评】本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．4．等腰三角形的对称轴是( )A．顶角的平分线 B．底边上的高C．底边上的中线 D．底边上的高所在的直线【考点】等腰三角形的性质；轴对称的性质．【分析】本题除了要根据等腰三角形的性质进行求解外，还要注意图形的对称轴是直线，而不是线段．【解答】解：根据等腰三角形的性质可知：顶角平分线、底边的中、底边的高所在的直线是等腰三角形的对称轴．故选D．【点评】本题考查了等腰三角形的性质和轴对称的性质；要注意的是图形的对称轴是直线，而等腰三角形的顶角平分线，底边上的高，底边上的中线都是线段．5．和点P（﹣3，2）关于y轴对称的点是( )A．（3，2）B．（﹣3，2）C．（3，﹣2）D．（﹣3，﹣2）【考点】关于x轴、y轴对称的点的坐标．【专题】计算题．【分析】平面直角坐标系中任意一点P（x，y），关于y轴的对称点的坐标是（﹣x，y），即关于纵轴的对称点，纵坐标不变，横坐标变成相反数．【解答】解：和点P（﹣3，2）关于y轴对称的点是（3，2），故选A．【点评】本题比较容易，考查平面直角坐标系关于坐标轴成轴对称的两点的坐标之间的关系．是需要识记的内容．6．已知：如图，AC=AE，∠1=∠2，AB=AD，若∠D=25°，则∠B的度数为( )A．25° B．30° C．15° D．30°或15°【考点】全等三角形的判定．【分析】由∠1=∠2可得∠BAC=∠DAE，再加AC=AE，AB=AD，即可得△ABC≌△ADE，从而∠B=∠D=30°．【解答】解：∵∠1=∠2，∴∠BAC=∠DAE，又∵AC=AE，AB=AD，∴△ABC≌△ADE，∴∠B=∠D=25°．故选A．【点评】本题考查三角形全等的判定及性质，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与．7．如图，△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD和CE交于O，AO的延长线交BC 于F，则图中全等的直角三角形有( )A．3对B．4对C．5对D．6对【考点】直角三角形全等的判定．【分析】△ADO≌△AEO，△DOC≌△EOB，△COF≌△BOF，△ACF≌△ABF，△ADB≌△AEC，△BCE≌△CBD．利用全等三角形的判定可证明，做题时，要结合已知条件与三角形全等的判定方法逐个验证．【解答】解：∵BD⊥AC，CE⊥AB，∴∠ADB=∠AEC=90°，∵AC=AB，∵∠CAE=∠BAD，∴△AEC≌△ADB；∴CE=BD，∵AC=AB，∴∠CBE=∠BCD，∵∠BEC=∠CDB=90°，∴△BCE≌△CBD；∴BE=CD，∴AD=AE，∵AO=AO，∴△AOD≌△AOE；∵∠DOC=∠EOB，∴△COD≌△BOE；∴OB=OC，∵AB=AC，∴CF=BF，AF⊥BC，∴△ACF≌△ABF，△COF≌△BOF．共6对，故选D．【点评】本题考查的是全等三角形的判定，判定两个三角形全等的一般方法有：SSS、SAS、HL．做题时要由易到难，不重不漏．8．如图，在△ABC中，AB的中垂线交BC于点E，若BE=2，则A、E两点的距离是( )A．4 B．2 C．3 D．【考点】线段垂直平分线的性质．【分析】连接AE，根据线段的垂直平分线的性质得到EA=EB，得到答案．【解答】解：连接AE，∵DE是AB的中垂线，∴EA=EB=2，故选：B．【点评】本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．9．正三角形ABC中，BD=CE，AD与BE交于点P，∠APE的度数为( )A．45° B．55° C．60° D．75°【考点】全等三角形的判定与性质；等边三角形的性质．【分析】根据条件三角形ABC是正三角形可得：AB=BC，BD=CE，∠ABD=∠C可以判定△ABD≌△BCE，即可得到∠BAD=∠CBE，又知∠APE=∠ABP+∠BAP，故知∠APE=∠ABP+∠CBE=∠B．【解答】解：∵△ABC是等边三角形，∴AB=BC，∠ABD=∠C=60°，在△ABD和△BCE中，∴△ABD≌△BCE（SAS），∴∠BAD=∠CBE，∵∠APE=∠ABP+∠BAP，∴∠APE=∠ABP+∠CBE=∠B=60°，故选C．【点评】本题主要考查等边三角形的性质和全等三角形的判定与性质的知识点，解答本题的关键是能看出∠APE=∠ABP+∠BAP，还要熟练掌握三角形全等的判定与性质定理．10．如图，已知△ABC，AB=AC，BD=CD，则下列结论中错误的是( )A．∠BAC=∠B B．∠1=∠2C．AD⊥BC D．∠B=∠C【考点】等腰三角形的性质．【分析】由在△ABC中，AB=AC，BD=CD，根据等边对等角与三线合一的性质，即可求得答案．【解答】解：∵AB=AC，BD=CD，∴∠1=∠2，AD⊥BC，∠B=∠C．故B、C、D正确，A错误．故选：A．【点评】此题考查了等腰三角形的性质．此题难度不大，注意掌握数形结合思想的应用．11．如图，∠1=∠2，PD⊥OA，PE⊥OB，垂足分别为D，E，下列结论错误的是( )A．PD=PE B．OD=OE C．∠DPO=∠EPO D．PD=OD【考点】角平分线的性质；全等三角形的判定与性质．【分析】由已知条件认真思考，首先可得△POE≌△POD，进而可得PD=PE，∠1=∠2，∠DPO=∠EPO；而OD，OP是无法证明是相等的，于是答案可得．【解答】解：A、∵∠POB=∠POA，PD⊥OA，PE⊥OB，∴PE=PD，正确，故本选项错误；B、∵PD⊥OA，PE⊥OB，∴∠PEO=∠PDO=90°，∵OP=OP，PE=PD，∴由勾股定理得：OE=OD，正确，故本选项错误；C、∵∠PEO=∠PDO=90°，∠POB=∠POA，∴由三角形的内角和定理得：∠DPO=∠EPO，正确，故本选项错误；D、根据已知不能推出PD=OD，错误，故本选项正确；故选D．【点评】本题考查了线段垂直平分线性质，角平分线性质，全等三角形的性质和判定的应用，注意：角平分线上的点到角两边的距离相等．12．如图，已知AB=AC，AE=AF，BE与CF交于点D，则对于下列结论：①△ABE≌△ACF；②△BDF≌△CDE；③D在∠BAC的平分线上．其中正确的是( )A．①B．②C．①和②D．①②③【考点】全等三角形的判定与性质．【分析】如图，证明△ABE≌△ACF，得到∠B=∠C；证明△CDE≌△BDF；证明△ADC≌△ADB，得到∠CAD=∠BAD；即可解决问题．【解答】解：如图，连接AD；在△ABE与△ACF中，，∴△ABE≌△ACF（SAS）；∴∠B=∠C；∵AB=AC，AE=AF，∴BF=CE；在△CDE与△BDF中，，∴△CDE≌△BDF（AAS），∴DC=DB；在△ADC与△ADB中，，∴△ADC≌△ADB（SAS），∴∠CAD=∠BAD；综上所述，①②③均正确，故选D【点评】该题主要考查了全等三角形的判定及其性质的应用问题；应牢固掌握全等三角形的判定及其性质定理，这是灵活运用解题的基础．二、专心填一填（每题4分共24分）13．如图，AD⊥BC，D为BC的中点，则△ABD≌△ACD．【考点】全等三角形的判定．【分析】三角形全等必须满足3个元素，垂直提供了两只角相等，中点提供了两边相等，加上一公共边，一对全等三角形就出来了，注意书写，对应点要在相应的位置．【解答】证明：∵AD⊥BC，D为BC的中点，∴∠ADB=∠ADC，BD=CD，在△ABD和△ACD中，∴△ABD≌△ACD（SAS）．故填ACD．【点评】本题考查三角形全等的判定方法；判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．本题书写时要注意对应点要在相应的位置，顺序要一致．14．如图，若AB=DE，BE=CF，要证△ABF≌△DEC，需补充条件AF=CD或∠B=∠DEC．【考点】全等三角形的判定．【专题】开放型．【分析】要使△ABF≌△DEC，已知AB=ED，EB=∠CF，具备了两组边对应相等，还缺少边或角对应相等的条件，结合判定方法及图形进行选择即可．【解答】解：可补充AF=CD或∠B=∠DEC；当AF=CD时，三条边对应相等，所以两三角形全等；当∠B=∠DEC时，两边夹一角，也全等．故填AF=CD或∠B=∠DEC．【点评】本题考查三角形全等的判定方法；判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．添加时注意：AAA、SSA不能判定两个三角形全等，不能添加，根据已知结合图形及判定方法选择条件是正确解答本题的关健．15．已知：如图，△ABD≌△EBC，且∠1=∠2，AB=BE，则AD=EC，∠C=∠D．【考点】全等三角形的性质．【专题】证明题．【分析】由△ABD≌△EBC，据两个三角形的对应边相等、对应角相等，即可得解．【解答】解：∵△ABD≌△EBC，且∠1=∠2，AB=BE，∴AD=EC，∠C=∠D．故答案各空分别填：EC、∠D．【点评】本题考查了全等三角形的性质，解题的关键是熟练找到两个全等三角形的对应边、对应角．16．如图，三角形ABC中，AB=AC，∠A=40度，AB的垂直平分线MN交AC于D，连接BD，∠DBC 等于30度．【考点】线段垂直平分线的性质；等腰三角形的性质．【分析】根据等腰三角形的性质和三角形内角和定理求出∠ABC和∠C的度数，根据线段的垂直平分线的性质得到DB=DA，求出∠DBA的度数，计算即可．【解答】解：∵AB=AC，∠A=40°，∴∠ABC=∠C=70°，∵MN是AB的垂直平分线，∴DB=DA，∴∠DBA=∠A=40°，∴∠DBC=∠ABC﹣∠DBA=30°，故答案为：30．【点评】本题考查的是线段的垂直平分线的性质和等腰三角形的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．17．如图，在△ABC中，AB=AC，AD是BC边上的高，点E、F是AD的三等分点，若△ABC的面积为12cm2，则图中阴影部分的面积是6cm2．【考点】轴对称的性质；等腰三角形的性质．【分析】由图，根据等腰三角形是轴对称图形知，△CEF和△BEF的面积相等，所以阴影部分的面积是三角形面积的一半．【解答】解：∵△ABC中，AB=AC，AD是BC边上的高，∴△ABC是轴对称图形，且直线AD是对称轴，∴△CEF和△BEF的面积相等，∴S阴影=S△ABD，∵AB=AC，AD是BC边上的高，∴BD=CD，∴S△ABD=S△ACD=S△ABC，∵S△ABC=12cm2，∴S阴影=12÷2=6cm2．故答案为：6．【点评】本题考查了等腰三角形的性质及轴对称性质；利用对称发现并利用△CEF和△BEF 的面积相等是正确解答本题的关键．18．如图是一个轴对称图形，AD所在的直线是对称轴，仔细观察图形，回答下列问题：（1）线段BO、CF的对称线段是CO，BE；（2）△ACE的对称三角形是△ABF．【考点】轴对称的性质．【分析】（1）结合图形，根据轴对称的性质得出即可；（2）结合图形，根据轴对称的性质得出即可．【解答】解：（1）线段BO的对称线段是CO，线段CF的对称线段是BE，故答案为：CO，BE；（2）△ACE的对称三角形是△ABF，故答案为：△ABF．【点评】本题考查了轴对称的性质的应用，主要考查学生观察图形的能力，注意：如果两个图形关于某一直线对称，那么这两个图形是全等形．三、耐心做一做（本大题有6小题，共分60分）19．如图，∠1=∠2，∠3=∠4，求证：AC=AD．【考点】全等三角形的判定与性质．【专题】证明题．【分析】先证出∠ABC=∠ABD，再由ASA证明△ABC≌△ABD，得出对应边相等即可．【解答】证明：∵∠3=∠4，∴∠ABC=∠ABD，在△ABC和△ABD中，，∴△ABC≌△ABD（ASA），∴AC=AD．【点评】本题考查了全等三角形的判定与性质；熟练掌握全等三角形的判定方法，证明三角形全等是解决问题的关键．20．根据图中尺规作图的痕迹，先判断得出结论：OM平分∠BOA，然后证明你的结论（不要求写已知、求证）【考点】作图—基本作图；全等三角形的判定与性质．【专题】作图题．【分析】根据图中尺规作图的痕迹可知，OC=OD，CM=DM，根据全等三角形的判定和性质得到答案．【解答】解：结论：OM平分∠BOA，证明：由作图的痕迹可知，OC=OD，CM=DM，在△COM和△DOM中，，∴△COM≌△DOM，∴∠COM=∠DOM，∴OM平分∠BOA．【点评】本题考查的是角平分线的作法和全等三角形的判定和性质，掌握基本尺规作图的步骤和全等三角形的判定定理和性质定理是解题的关键．21．在Rt△ABC中，∠BAC=90°，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．问△AEF与△DEB全等吗？说明理由．【考点】全等三角形的判定．【分析】由AF∥BC，根据两直线平行，内错角相等，可得∠AFE=∠DBE，又由E是AD的中点，可利用AAS，判定△AEF与△DEB全等．【解答】解：△AEF≌△DEB．理由如下：∵AF∥BC，∴∠AFE=∠DBE，∵E是AD的中点，∴AE=DE，在△AEF和△DEB中，，∴△AEF≌△（AAS）．【点评】此题考查了全等三角形的判定以及平行线的性质．注意判定全等三角形的方法有：SSS，SAS，ASA，AAS以及HL．22．已知：如图，已知△ABC，（1）分别画出与△ABC关于x轴、y轴对称的图形△A1B1C1和△A2B2C2；（2）写出△A1B1C1和△A2B2C2各顶点坐标；（3）求△ABC的面积．【考点】作图-轴对称变换．【分析】（1）根据关于x、y轴对称的点的坐标特点画出图形即可；（2）根据各点在坐标系内的位置写出各点坐标；（3）根据S△ABC=S四边形CDEF﹣S△ACD﹣S△ABE﹣S△BCF即可得出结论．【解答】解：（1）如图所示：（2）由图可知，△A1（0，2），B1（2，4），C1（4，1），A2（0，﹣2），B2（﹣2，﹣4），C2（﹣4，﹣1）．（3）S△ABC=S四边形CDEF﹣S△ACD﹣S△ABE﹣S△BCF=3×4﹣×1×4﹣×2×2﹣×2×3=12﹣2﹣3﹣2=5．【点评】本题考查的是轴对称变换，熟知关于坐标轴对称的点的坐标特点是解答此题的关键．23．如图：△ABC中，AB=AC=5，AB的垂直平分线DE交AB、AC于E、D，①若△BCD的周长为8，求BC的长；②若BC=4，求△BCD的周长．【考点】线段垂直平分线的性质；等腰三角形的性质．【分析】（1）利用线段垂直平分线的性质可知BD+CD=5，易求BC；（2）根据第一问中BD+CD=5，易求△BCD的周长．【解答】解：①AB=AC=5，DE垂直平分AB，故BD=AD．BD+CD=AD+CD=5．△BCD的周长为8⇒BC=3；②∵BC=4，BD+CD=5，∴△BCD=BD+CD+BC=9．【点评】本题考查的是线段垂直平分线的性质以及等腰三角形的性质；进行线段的有效转移是正确解答本题的关键．24．如图，∠B=∠C=90°，M是BC中点，DM平分∠ADC，求证：AM平分∠DAB．【考点】角平分线的性质．【专题】证明题．【分析】首先要作辅助线，ME⊥AD则利用角的平分线上的点到角的两边的距离相等可知ME=MC，再利用中点的条件可知ME=MB，再利用到角两边距离相等的点在角的平分线上的逆定理证明AM平分∠DAB．【解答】证明：作ME⊥AD，∵MC⊥DC，ME⊥DA，MD平分∠ADC，∴ME=MC，∵M为BC中点，∴MB=MC，又∵ME=MC，∴ME=MB，又∵ME⊥AD，MB⊥AB，∴AM平分∠DAB．【点评】本题考查了角平分线的性质；解题的关键是作出辅助线，然后利用角的平分线上的点到角的两边的距离相等的性质和到角两边距离相等的点在角的平分线上的定理进行证明即可．。

10月份月考答案

2019-2020学年度第一学期10月份考试八年级语文试卷说明： 1. 全卷共6页，满分为120分。

考试用时为120分钟。

2. 答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、考场号、座位号。

用2B铅笔把对应该号码的标号涂黑。

3. 答题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目的指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4. 本试卷设有附加题，共10分，考生可答可不答；该题得分作为补偿分计入总分，但全卷最后得分不得超过120分。

第一部分基础(24分)1.根据课文默写古诗文。

(10分)（1）东皋薄暮望，□□□□□。

（王绩《野望》）（1分）（2）妻子象禽兽，行止依林阻。

□□□□□，□□□□□。

(曹植《梁甫行》)（2分）（3）□□□□□，长河落日圆。

（王维《使至塞上》）（1分）（4）“□□□□□□□，□□□□□□□。

”由写虚幻的传说转为实写眼前的所见景物，描绘了一个空明、悠远的画面。

（崔颢《黄鹤楼》）(2分)（5）把李白《渡荆门送别》默写完整。

(4分)渡远荆门外，来从楚国游。

□□□□□，□□□□□。

仍怜故乡水，万里送行舟。

2根据拼音写出相应的词语。

(4分)(1)法国的普吕多姆(文学奖)，他在诗歌创作方面颇有jiàn shù( )。

（2）在两人时断时续、不急不缓的对话声中，舰、机配合得非常mò qì( ) （3）为了这一着，面对技术封锁，多少人dān jīng jié lǜ()，青丝变白发。

(4)1937年12月13日，侵华日军野蛮侵入南京，随后制造了cǎn jué rén huán ( )的南京大屠杀惨案.3. 下列句中加点成语使用不恰当的一项是( D )(3分)A．他因生理学方面的建树．．而被授予诺贝尔奖。

浙江省杭州市2019-2020学年八年级上(10月)月考数学试题(含答案)

浙江省杭州市2019-2020学年八年级上月考试题数学一、选择题：本题有10 小题，每小题3分，共30 分．在每小题给出的四个选项中，只有一项是符合要求的．1. 下列语句是命题的是(▲)A．作直线A B 的垂线B．在线段A B 上取点CC．同旁内角互补D．垂线段最短吗?2. 如图四个图形中，线段B E 是△ABC 的高线的是(▲)B C A B A EA．B．C．D．3. 具备下列条件的两个三角形中，一定全等的是(▲) A．有两边一角对应相等B．有两角一边分别相等C．三条边对应相等D．三个角对应相等4. 已知等腰三角形的两条边长分别是7和3，则第三条边长是(▲)A．8 B．7 C．4 D．35. 如图，等腰△ABC 的周长为21，底边B C=5，AB 的垂直平分线D E 交A B 于点D，交A C于点E，则△BEC 的周长为(▲)A．13 B．14 C．15 D．166. 一艘轮船由海平面上A地出发向南偏西40°的方向行驶40 海里到达B地，再由B地向北偏西20°的方向行驶40 海里到达C地，则A、C 两地相距(▲)A．30 海里B．40 海里C．50 海里D．60 海里第5题图第6题图第7题图第8题图第 10 题图7. 如图，N ，C ，A 三点在同一直线上，在△ ABC 中，∠A ：∠ABC ：∠ACB =3：5：10，又 △ MNC ≌△ABC ，则∠BCM ：∠BCN 等于(▲)A ．1：2B ．1：3C ．2：3D ．1：4 8. 如图，AB ∥CD ，AC ∥DB ，AD 与 B C 交于点 O ，AE ⊥BC 于点 E ，DF ⊥BC 于点 F ，那么图中全等的三角形有(▲)对 A ．5 B ．6 C ．7 D ．8 9. 一个等腰三角形的底边长为 5，一腰上中线把其周长分成的两部分的差为 3，则这个等腰三角形的腰长为(▲) A ．2 B ．8 C ．2 或 8 D ．10 10. 如图，在△ABC 中，AB =20cm ，AC =12cm ，点 P 从点 B 出发以每秒 3cm 的速度向点 A 运动，点 Q 从点 A 同时出发以每秒 2cm 的速度向点 C 运动，其中一个动点到达端点时，另一个动点也随之停止运动，当△APQ 是以 PQ 为底的等腰三角形时，运动的时间是(▲) A ．2.5 秒 B ．3 秒 C ．3.5 秒 D ．4 秒二、填空题：本题有 6 个小题，每小题 4 分，共 24 分． 11. 写出一个原命题是真命题，逆命题是假命题的命题： ▲ ． 12. 在“三角尺拼角”实验中，小明同学把一副三角尺按如图所示的方式放置，则 ∠1= ▲ °． 13. 如图，CE 平分∠ACB ，且 C E ⊥DB ，∠DAB =∠DBA ，又知 A C =18，△CDB 的周长为 28，则 B D 的长为 ▲ ． 14. 如图，在△ABC 中，AB =AC ，∠BAD =28°，AD =AE ，则∠EDC = ▲ ． 15. 已知△ABC 中，AB =BC ≠AC ，作与△ABC 只有一条公共边，且与△ABC 全等的三角形，这样的三角形一共能作出 ▲ 个． 16. 如图，C 为线段 A E 上一动点（不与 A 、E 重合），在 A E 同侧分别作等边△ABC 和等边△ CDE ，AD 与 B E 交于点 O ，AD 与 B C 交于点 P ，BE 与 C D 交于点 Q ，连接 P Q ，以下五个结论：①AD =BE ；②PQ ∥AE ；③AP =BQ ；④DE =DP ；⑤∠AOB =60°，其中正确的结论是 ▲ （把你认为正确的结论的序号都填上）．第 12 题图第 13 题图第 14 题图第 16 题图三、解答题：本题有 7 小题，共 66 分．解答应写出文字说明，证明过程或推演步骤． 17.（本题满分 6 分）指出下列命题的条件和结论，并改写成“如果……，那么……”的形式． (1)两直线平行，内错角相等；(2)三角形内角和等于 180°．18.（本题满分 8 分）一个零件的形状如图，按规定∠A = 90°，∠B 、∠C 分别是 32°和 21°．某检验工人量得∠BDC = 148°，就断定这个零件不合格，试用三角形的有关知识说明零件不合格的理由．19.（本题满分 8 分）第 18 题图如图，点 C ，F ，E ，B 在一条直线上， CFDBEA ， C E BF ，DFAE ．(1)求证：DF ∥AE ； (2)写出 C D 与 A B 之间的关系，并证明你的结论．第 19 题图20.（本题满分 10 分）如图，CD ∥AB ，∠ABC ，∠BCD 的角平分线交 A D 于 E 点，且 E 在 A D 上，CE 交 B A 的延长线于 F 点． (1)试问 B E 与 C F 互相垂直吗？若垂直，请说明理由； (2)若 C D =3，AB =4，求 B C 的长．第 20 题图21.（本题满分10 分）已知命题：“P 是等边△ABC 内的一点，若P到三边的距离相等，则P A=PB=PC．” (1)写出它的逆命题．判断其逆命题成立吗？若成立，请给出证明．(2)进一步证明：点P 到等边△ABC 各边的距离之和为定值．22.（本题满分12 分）如图，在R t△ABC 中，∠C90 ，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC 的其他边上，试画出所有不同的等腰三角形并说明画图方法．AC B第22 题图23.（本题满分12 分）如图(1)，等边△ABC 中，D 是A B 边上的动点，以C D 为一边，向上作等边△EDC，连接AE．(1)△DBC 和△EAC 会全等吗？请说说你的理由；(2)试说明A E∥BC 的理由；(3)如图(2)，将(1)动点D 运动到边BA 的延长线上，所作仍为等边三角形，请问是否仍有AE∥BC？证明你的猜想．第23 题图参考答案及评分建议一、选择题：本题有 10 小题，每小题 3 分，共 30 分．二、填空题：本题有 6 个小题，每小题 4 分，共 24 分． 11．不唯一，略 12．120° 13．8 14．14° 15．7 16．①②③⑤三、解答题：本题有 7 小题，共 66 分．解答应写出文字说明，证明过程或推演步骤．17．（1）如果两条直线平行，那么内错角相等（2）如果三个角是一个三角形的内角，那么这三个内角和等于 180°18．连接 A D 并延长至 E若是合格零件，则∠BDC=∠CDE+∠BDE =∠C+∠CAD+∠BAD+∠B=∠C+∠CAB+∠D =21°+90°+32°=143°而检验工人现测得∠BDC=148°，故两件不合格A 第 18 题图19．（1）证明： ∵CFD BEA ，点 C 、F 、E 、B 在一直线上∴∠DFE ＝∠AEF ∴DF ∥AE （2）CD 与 A B 之间的关系是：CD=AB ，且 C D ∥AB 证明：∵CE=BF ，∴CF=BE第 19 题图题号 1 2 3 4 5 6 7 8 9 10 答案CDCBABDCBD⎨ ⎩ ⎨ ⎩在 ΔCDF 和 ΔBAE 中CF BECFDBEADFAE∴ΔCDF≌ΔBAE ∴CD=BA ，∠C=∠B ∴CD ∥BA20．（1）垂直．理由：∵CD ∥AB ，∴∠ABC+∠BCD=180°，∵∠ABC ，∠BCD 的角平分线交于 E 点， ∴∠ABE=∠EBC ，∠DCE=∠ECB ，∴∠EBC+∠ECB= 1 ∠ABC+ 1 ∠BCD= 1（∠ABC+∠BCD ）=90°，2 2 2∴∠CEB =90°，∴BE 与 C F 互相垂直．（2）∵∠CEB=90°， ∴∠FEB=90°，在△FBE 和△CBE 中，∠CBE= ∠FBE ∵ BE BE，∠BEC = ∠BEF第 20 题图∴△FBE ≌△CBE （ASA ），∴BF=BC ，EF=EC ， ∵CD ∥AB ，∴∠DCE=∠AFE ， ∵∠FEA=∠CED ，∴△DCE≌△AFE，∴DC=AF，∵CD=3，AB=4，BF=AF+AB∴BF=BC=7．21．（1）逆命题：P 是等边三角形A BC 内的一点，若P A=PB=PC，则P到三边的距离相等．该逆命题成立．证明：∵PA=PB，∴P 在A B 的垂直平分线上，∵AC=BC，∴C 在A B 的垂直平分线上，∴CP 是A B 的垂直平分线，∴CP 平分∠ACB，同理，BP 平分∠ABC，AP 平分∠BAC，∴P 是△ABC 三个角的角平分线的交点，∴PD=PE=PF．（2）第21 题图∵AB=BC=AC 且S△ABC=S△ABP +S△PBC +S△APC,∴由面积法可得P点到各边的距离之和=任意边上的高线长，即为定值.22．图示及画法如下：①以B为圆心，BC 长为半径画弧，交A B 于点I，△BCD 就是等腰三角形；②以C为圆心，BC 长为半径画弧，交A B 于点D，△BCD 就是等腰三角形；③以A为圆心，AC 长为半径画弧，交A B 于点E，△ACE 就是等腰三角形；④以C为圆心，BC 长为半径画弧，交A C 于点F，△BCF 就是等腰三角形；⑤作A C 的垂直平分线交A B 于点H，△ACH 就是等腰三角形；⑥作A B 的垂直平分线交A C 于G，则△AGB 是等腰三角形；⎨ ⎩ ⑦作 B C 的垂直平分线交 A B 于 I ，则△BCI 是等腰三角形．图 1图 2 图 3 图 4 图 5 图 6 图 723．（1）△DBC 和△EAC 会全等证明：∵∠ACB=60°，∠DCE=60°，∴∠BCD=60°﹣∠ACD ，∠ACE=60°﹣∠ACD ∴∠BCD=∠ACE在△DBC 和△EAC 中，BC AC∵ ∠BCD=∠ACE ECDC∴△DBC ≌△EAC （SAS ），（2）∵△DBC ≌△EAC ， ∴∠EAC=∠B=60° 又∠ACB=60°， ∴∠EAC=∠ACB ，∴AE ∥BC（3）结论：AE ∥BC 理由：∵△ABC 、△EDC 为等边三角形∴BC=AC ，DC=CE ，∠BCA=∠DCE=60°∠BCA+∠ACD=∠DCE+∠ACD ，即∠BCD=∠ACE 在△DBC 和△EAC 中，⎨ ⎩B CA C∵∠BCD ∠ACEC D E C∴△DBC ≌△EAC （SAS ），∴∠EAC=∠B=60° 又∵∠ACB=60° ∴∠EAC=∠ACB ∴AE ∥BC ．第 23 题图。

2019-2020年八年级10月月考数学试卷

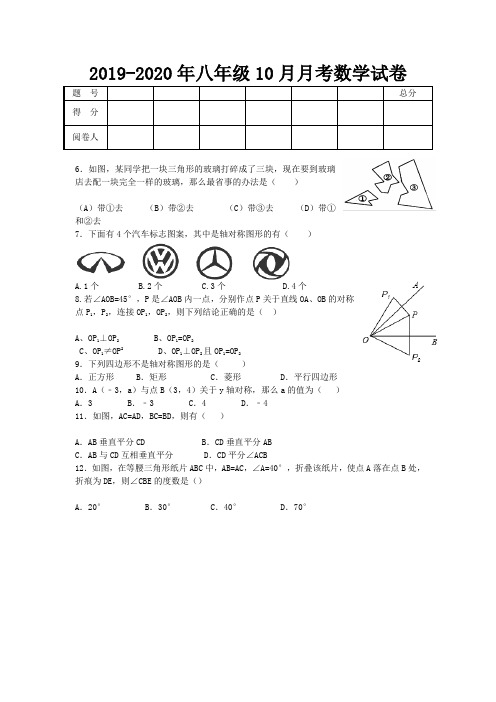
2019-2020年八年级10月月考数学试卷6．如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（）（A）带①去（B）带②去（C）带③去（D）带①和②去7．下面有4个汽车标志图案，其中是轴对称图形的有（）A.1个B.2个C.3个D.4个8.若∠AOB=45°，P是∠AOB内一点，分别作点P关于直线OA、OB的对称点P1，P2，连接OP1，OP2，则下列结论正确的是（）A、OP1⊥OP2B、OP1=OP2C、OP1≠OP2D、OP1⊥OP2且OP1=OP29．下列四边形不是轴对称图形的是（）A．正方形 B．矩形 C．菱形 D．平行四边形10．A（﹣3，a）与点B（3，4）关于y轴对称，那么a的值为（）A．3 B．﹣3 C．4 D．﹣411．如图，AC=AD，BC=BD，则有（）A．AB垂直平分CD B．CD垂直平分ABC．AB与CD互相垂直平分 D．CD平分∠ACB12．如图，在等腰三角形纸片ABC中，AB=AC，∠A=40°，折叠该纸片，使点A落在点B处，折痕为DE，则∠CBE的度数是（）A．20° B．30° C．40° D．70°二.填空题13．如图，△ABD ≌△ACE ，点B 和点C 是对应顶点，AB=9cm ，BD=7cm ，AD=4cm ，则DC=____________cm ．14．如图，若△ABC≌△ADE，且∠B=60°，∠C=30°则∠DAE= ．15．如图，OA=OD ，AD 、BC 相交于O ，要使DCO ABO ∆∆≌，应添加的条件是．（只填一个答案即可）16．如图，在Rt △ABC 中，∠A=90°，∠C=30°，D 为斜边上的一点且BD=AB ，过点D 作BC 的垂线，交AC 于点E ．若△CDE 的面积为a ，则四边形ABDE 的面积为．17．点P 在线段AB 的垂直平分线上，PA=7，则PB= ．18．如图，在△ABC 中，AB=AC ，∠A=20°，边AC 的垂直平分线交AC 于点D ，交AB 于点E ，则∠BCE 等于 °．19．如图，△ABC中，AB=AC，AB的垂直平分线交边AB于D点，交边AC于E点，若△ABC 与△EBC的周长分别是40cm，24cm，则AB= cm．20．点A（﹣2，3）关于x轴的对称点A′的坐标为 .21．已知，如图，AB=CD，AB∥CD，BE=FD，求证：△ABF≌△CDE22．尺规作图：画出线段AB的垂直平分线（不写作法，保留作图痕迹）23．已知，如图，在ABCD 中，E 、F 是对角线AC 上的两点，且AE=CF ，求证：DE=BF24．尺规作图：已知：∠α，线段a, b 求作：△ABC ，使∠A= , AB=a, AC=b 。

2019-2020年八年级10月月考数学试卷

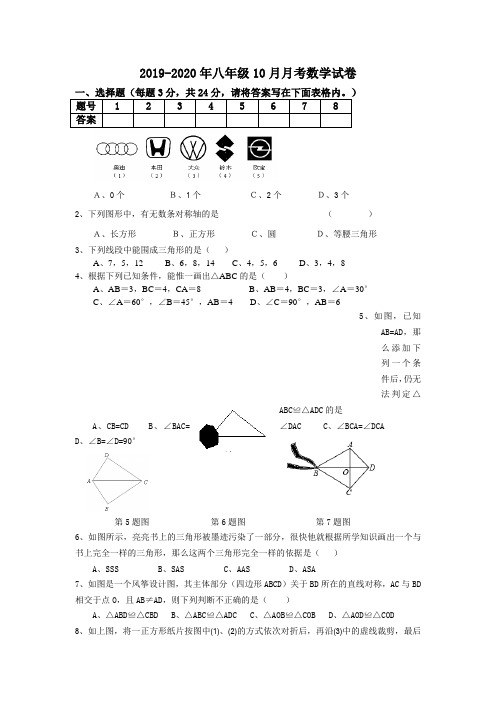
2019-2020年八年级10月月考数学试卷Ａ、0个Ｂ、1个Ｃ、2个Ｄ、3个2、下列图形中，有无数条对称轴的是（）Ａ、长方形Ｂ、正方形Ｃ、圆Ｄ、等腰三角形3、下列线段中能围成三角形的是（）A、7，5，12B、6，8，14C、4，5，6D、3，4，84、根据下列已知条件，能惟一画出△ABC的是（）A、AB＝3，BC＝4，CA＝8B、AB＝4，BC＝3，∠A＝30°C、∠A＝60°，∠B＝45°，AB＝4D、∠C＝90°，AB＝65、如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是A、CB=CDB、∠BAC=∠DACC、∠BCA=∠DCAD、∠B=∠D=90°第5题图第6题图第7题图6、如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（）A、SSSB、SASC、AASD、ASA7、如图是一个风筝设计图，其主体部分（四边形ABCD）关于BD所在的直线对称，AC与BD 相交于点O，且AB≠AD，则下列判断不正确的是（）A、△ABD≌△CBDB、△ABC≌△ADCC、△AOB≌△COBD、△AOD≌△COD8、如上图，将一正方形纸片按图中(1)、(2)的方式依次对折后，再沿(3)中的虚线裁剪，最后将(4)中的纸片打开铺平，所得图案应该是下面图案中的 ( )二、填空题（每题3分，共24分）9、如图，△ABC ≌△ADE ，∠B=100°，∠BAC=30°，那么∠AED=______．第12题图第9题图第10题图第11题图10、如图，∠1=∠2，要使△ABE ≌△ACE ，还需添加一个条件是（填上你认为适当的一个条件即可）.11、如图，AE=BF ，AD ∥BC ，AD=BC ，则有DF= .12、如图，△ABC 中，AD ⊥BC 于D ，要使△ABD ≌△ACD ，若根据“HL”判定，还需要加条件13、把两根钢条A B ，、B A ，的中点连在一起，可以做成一个测量工件内槽宽工具（卡钳），如图，若得AB=5厘米，则槽为厘米．第13题图第14题第15题图14、如图，AD=AE ，BE=CD ，∠1=∠2=100°，∠BAE=60°，那么∠CAE=________ 15、如图，∠A=∠E ， AC ⊥BE ，AB=EF ，BE=10，CF=4，则AC=________.关于直线l 对16、如图，∠A ＝30°，∠C'＝60°，△ABC 与△A'B'C'称，则∠B ＝_______．三、解答题（共72分）17、（本题满分8分）第16题图N第17题图如图，画出△ABC 关于直线MN 的轴对称图形△A'B'C'.18、（本题满分8分）如图，已知：点B 、F 、C 、E 在一条直线上，FB=CE ，AC=DF ．090=∠=∠D A ；求证：AB//DE19、（本题满分8分）如图， AC 与BD 交于点E ，且AC=DB ，AB=DC ．求证：D A ∠=∠；20、（本题满分8分）如图，已知AC⊥AB，DB⊥AB，AC ＝BE ，AE ＝BD ，试猜想线段CE 与DE 的大小与位置关系，并证明你的结论．21、(本题满分8分)如图，在△ABC 和△ABD 中，AC 与BD 相交于点E ，AD =BC ， ∠DAB =∠CBA ，求证：AC =B D ．22、（本题满分8分）如图，AC 和BD 相交于点O ，OA =OC ，OB =O D ．求证：DC ∥A B ．23、（本题满分12分）如图，已知点A、F、E、C在同一直线上，AB∥CD，∠ABE=∠CDF，AF=CE．（1）从图中任找两组全等三角形；（2）从（1）中任选一组进行证明．24、（本题满分12分）如图①A、E、F、C在一条直线上，AE=CF，过E、F分别作DE⊥AC，B F⊥AC，若AB=CD．（1）图①中有对全等三角形，并把它们写出来（2）求证：BD与EF互相平分于G；（3）若将△ABF的边AF沿GA方向移动变为图②时，其余条件不变，第（2）题中的结论是否成立，如果成立，请予证明．洪泽县新区中学2015—2016学年第一学期第一次月考八年级数学试卷答案 2015.10。