辽宁省高一数学下学期期末考试试题
辽宁省沈阳市重点联合体2024年高一下学期期末检测数学试题+答案

2023—2024学年度(下)联合体高一期末检测数学注意事项:1.答题时,考生务必将自己的姓名、准考证号填写在答题卡规定的位置上.2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦擦干净后,再选涂其他答案标号.3.答非选择题时,必须使用黑色墨水笔或黑色签字笔,将答案书写在答题卡规定的位置上,写在试题卷、草稿纸上无效.4.考试结束后,将试题卷和答题卡一并交回(满分:150分考试时间:120分钟).第I 卷(选择题,共58分)一、单选题(本大题共8小题,每小题5分,共40分.在每小题所给的四个选项中,有且只有一项是符合题目要求的)1.已知复数z 满足()2i 34i,i z −=−为虚数单位,则复数z 的共轭复数z =( ) A.12i + B.12i − C.2i − D.2i + 2.已知()9,8P −为角α终边上一点,则5sin 2cos 2sin 5cos αααα−=+( )A.6122−B.-2C.2261D.123.已知向量()()1,2,2,3ab ==−,若向量c 满足()c a + ∥,b c a ⊥ ,则向量c的坐标为( )A.77,24 −B.77,42 −−C.77,24−− D.77,42 −4.在ABC 中,已知角,,A B C 的对边分别为,,a b c ,若sin :sin :sin 4:7:9A B C =,则cos A =( ) A.1921−B.863C.1921D.16215.计算:πtan8=( ) A.1211+6.已知,m n 是空间中两条不同的直线,,αβ是两个不同的平面,则下列命题正确的是( ) A.若,,m n m αα⊂⊂∥,n β∥β,则α∥βB.若,n αβ⊥∥α,则n β⊥C.若α∥,m β∥α,则m ∥βD.若,,m n m αβ⊥⊂∥n ,则αβ⊥7.一个圆柱形容器内部的底面半径为4cm ,高为8cm ,将该容器注满水,然后将一个半径为4cm 的实心球缓慢放入该容器内,当球沉到容器底部时,留在圆柱形容器内的水的体积为( ) A.3320πcm 3 B.3128πcm 3 C.380πcm 3 D.364πcm 38.已知()π5cos 20243f x x=−的最大值为m ,若存在不同的实数12,x x ,使得对任意实数x 总有()()()12f x f x f x 成立,则12m x x −的最小值为( )A.5π2024 B.5π1012二、多选题(本大题共3小题,每小题6分,共18分.在每小题所给的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分)9.已知复数12,z z ,则下列结论正确的是( ) A.1212z z z z +=+ B.1212z z z z ⋅=⋅C.若12z z =,则2212z z =D.若12z z =,则1122z z z z ⋅=⋅10.已知ABC 的内角,,A B C 的对边分别为,,a b c ,下列四个结论中,正确的是( ) A.cos cos ca Bb A +B.若222a b c bc =++,则120A =C.若sin2sin2A B =,则ABC 为等腰直角三角形D.若222sin sin sin A B C +<,则ABC 是钝角三角形11.如图,在长方体1111ABCD A B C D −中,12,4,AB AA BC E ===为CD 的中点,M 是1A C 上一点,N 是平面1AED 内一点,则( )A.长方体1111ABCD A B C D −的外接球的表面积为24πB.1A C AE ⊥C.1A C ∥平面1AEDD.MN 第II 卷(非选择题,共92分)三、填空题(本大题共3小题,每小题5分,共15分)12.已知向量,a b满足3,12a a b =⋅=− ,则向量b 在向量a 的方向上的投影的数量为__________.13.已知πsin 12αα+=∈,则cos2α=__________. 14.如图,143,55P为锐角θ的终边与单位圆的交点,1OP 逆时针旋转π3得到22,OP OP 逆时针旋转π3得到31,,n OP OP − 逆时针旋转π3得到n OP ,则sin2θ=__________,点2024P 的横坐标为__________.四、解答题(本大题共5小题,共77分.解答时应写出必要的文字说明、证明过程或演算步骤)15.(13分)已知复数()()221118914i,z mm m m m =−++−+∈R ,其中i 为虚数单位.(1)若复数z 是纯虚数,求m 的值;(2)若复数z 在复平面内对应的点位于第二象限,求m 的取值范围.16.(15分)如图是函数()()sin (0,0,0π)f x A x A ωϕωϕ=+>>< 的部分图象.(1)求函数()f x 的解析式; (2)求函数ππ24y f x f x=+++的单调递增区间.17.(15分)在ABC 中,角,,A B C 所对的边分别是,,a b c ,已知向量(),(cos ,sin )m b n B C =,且m ∥n. (1)求B ;(2)若3b =,且ABC ,求ABC 的周长. 18.(17分)如图,在四棱锥P ABCD −中,PD ⊥底面ABCD ,且底面ABCD 为正方形,2PD CD ==,,,E F G 分别是,,AB PB CD 的中点.证明:(1)EF CD ⊥; (2)平面EFG ∥平面PAD .19.(17分)如图是一条“L ”,河道均足够长.现过点D修建一条栈道AB ,开辟出直角三角形区域(图中OAB )养殖观赏鱼,且π02OAB∠θθ=<<.点H 在线段AB 上,且OH AB ⊥.线段OH 将养殖区域分为两部分,其中OH 上方养殖金鱼,OH 下方养殖锦鲤.(1)当养殖区域的面积最小时,求θ的值,并求出此时的最小面积;(2)若游客可以在栈道AH上投喂金鱼,在河岸OB与栈道HB上投喂锦鲤,且希望投喂锦鲤的道路长度不小于投喂金鱼的道路长度,求θ的取值范围.2023—2024学年度(下)联合体高一期末检测数学参考答案及评分标准一、单选题(本大题共8小题,每小题5分,共40分)1.D 【解析】因为()()()()34i 2i 34i63i 8i 42i 2i2i 2i 5z −+−+−+====−−−+,所以2i z =+.2.B 【解析】因为()9,8P −为角α终边上一点,所以8tan 9α=−, 所以8525sin 2cos 5tan 29282sin 5cos 2tan 5259αααααα ×−− −− ===−++×−+. 3.A 【解析】设向量(),c m n = ,则()1,2c a m n +++.由()c a +∥,b c a ⊥,得()()31220,20,m n m n −+−+=+= 解得7,27,4m n=− =故向量c 的坐标为77,24 − . 4.C 【解析】因为sin :sin :sin 4:7:9A B C =,则由正弦定理可设4,7a k b k ==,9c k =.由余弦定理得22222249811619cos 227921b c a k k k A bc k k +−+−===⋅⋅. 5.C 【解析】因为2π2tanπππ8tan tan 1π4881tan 8 =+==−,所以2ππtan 2tan 1088+−=.易知πtan 8是方程2210x x +−=的根,且方程2210x x +−=的两根分别为11x=−,21x .因为当π0,2x∈时,tan 0x>,所以πtan 18=−.6.D 【解析】若,,m n m αα⊂⊂∥,n β∥β,则,αβ可能平行,也可能相交,故A 错误;若,n αβ⊥∥α,则n β⊥或n ∥β或n β⊂或n 与β相交(不垂直),故B 错误;若α∥,m β∥α,则m ∥β或m β⊂,故C 错误;因为,m m α⊥∥n ,所以n α⊥.又n β⊂,所以αβ⊥,故D正确.7.B 【解析】根据题意可知留在圆柱形容器内的水的体积等于圆柱形容器的体积减去实心球的体积,即()2334128π48π4πcm 33V =××−×=. 8.A 【解析】因为()π5cos 20243f x x=−,所以2ππ5,20241012m T ===. 由题意得()1f x 为最小值,()2f x 为最大值,所以12x x −的最小值为2T, 所以12m x x −的最小值为π5π55220242024T×=×=. 二、多选题(本大题共3小题,每小题6分,共18分.在每小题所给的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分)(评分标准:如果正确答案有2个,每个答案3分;如果正确答案有3个,每个答案2分)9.BD 【解析】对于A ,取121i,1i z z =+=−,则12122,z z z z +=+=, 故A 错误;对于B ,结合复数模的性质可知,1212z z z z ⋅=⋅,故B 正确;对于C ,令121,i z z ==,则12z z =,而22121,1z z ==−,故C 错误;对于D ,设1i z a b =+, 2i z c d =+,则12z z =时,2222a b c d +=+.又()()2211i i z z a b a b a b ⋅=+−=+,2222z z c d ⋅=+,所以112z z z ⋅=,故D 正确.故选:BD.10.ABD 【解析】由余弦定理得22222222222222cos cos 22222a c b b c a a c b b c a c a B b A a b c ac bc c c c +−+−+−+−+=⋅+⋅=+==,故A 正确;由余弦定理得2221cos 222b c a bc A bc bc +−−===−.而0180A << ,则120A = ,故B 正确;若sin2sin2A B =,即()()()()sin sin A B A B A B A B ++−=+−−,展开整理得()()cos sin 0A B A B +−=.因为0180,180180A B A B <+<−<−< ,所以90A B += 或0A B −= ,所以ABC 为直角三角形或等腰三角形或等腰直角三角形,故C 错误;若222sin sin sin A B C +<,由正弦定理得222a b c +<.由余弦定理得222cos 02a b c C ab+−=<,可得C 为钝角,则ABC 是钝角三角形,故D 正确.故选:ABD.11.ACD 【解析】在长方体1111ABCD A B C D −中,由12,4AB AA BC ===,可得长方体的体对角线长为.设长方体1111ABCD A B C D −的外接球的半径为R,则2R =R =,所以长方体的外接球的表面积为24π24πSR =,故A 正确;如图,连接AC .在长方体1111ABCD A B C D −中,易得1AA ⊥平面ABCD .因为AE ⊂平面ABCD ,所以1AA AE ⊥.假设1A C AE ⊥.因为11111,,AA AC A AA AC ∩=⊂平面1AA C ,所以AE ⊥平面1AA C .又因为AC ⊂平面1AA C ,所以AE AC ⊥.因为在矩形ABCD 中,AE 与AC 不垂直,所以假设不成立,所以1A C 与AE 不垂直,故B 错误;如图,连接1A D 交1AD 于点F ,连接EF .因为E 为CD 的中点,所以EF∥1A C .又因为1AC ⊄平面1AED ,且EF ⊂平面1AED ,所以1A C ∥平面1AED ,故C 正确;因为1A C ∥平面1AED ,且M 是1A C 上一点,N 是平面1AED内一点,所以点M 到平面1AED 的距离等于点1A 到平面1AED 的距离,即为MN 的最小值.设距离为d .因为在长方体1111ABCD A B C D −中,12,4AB AA BC ===,可得1AD =,1D E AE =.由余弦定理得222111112cos 25AD D E AE AD E AD D E ∠+−==⋅,所以1sin AD E ∠,所以112AD ES =× .由1111A AD E E AA D V V −−=,可得111421332h =××××,所以h =MN,故D 正确.故选:ACD.三、填空题(本大题共3小题,每小题5分,共15分)(评分标准:第14题第1个空2分,第2个空3分)12.-4 【解析】向量b 在向量a的方向上的投影的数量为12cos ,43a b b a b a ⋅−===−【解析】由π0,6α ∈ ,得πππ,12124α +∈ .因为πsin 12α +,所以πcos 12α +,所以2ππ3cos 212sin 6125αα +=−+= , πππ4sin 22sin cos 612125ααα+=++=,所以ππππππ341cos2cos 2cos 2cos sin 2sin 666666552αααα=+−=+++=+×=14.2425【解析】由题意得34sin ,cos 55θθ==,所以sin2θ=34242sin cos 25525θθ=××=.因为点2024P 所在角为2023π3θ+,则2023πππππcos cos 674πcos cos cos sin sin 33333θθθθθ+=++=+=−413525=×−=四、解答题(本大题共5小题,共77分)15.解:(1)因为复数z 是纯虚数,所以2211180,9140,m m m m −+= −+≠ 解得9m =.(2)因为复数z 在复平面内对应的点位于第二象限,所以2211180,9140,m m m m −+< −+>解得79m <<.16.(1)解:由图可知max ()2A f x ==,函数()f x 的最小正周期为7ππ4π123T=×−=, 则2π2π2πT ω===, 所以()()2sin 2f x x ϕ=+. 由7π7π2sin 2126f ϕ =+=,可得7πsin 16ϕ+=.因为0πϕ≤<,则π7π13π666ϕ<+<, 所以7ππ62ϕ+=,所以2π3ϕ=−,所以()2π2sin 23f x x=−. (2)ππ24y f x f x=+++π2ππ2π2sin 22sin 22343x x+−++−ππ2sin 22sin 236x x++−.令π23x θ=+,则ππ262x θ−=−,所以π2sin 2sin 2sin 2cos 2yθθθθ=+−=−π24x θ −=.令πππ2π22π,2122k x k k −≤+≤+∈Z , 解得7π5πππ,2424k x k k −≤≤+∈Z , 所以函数ππ24y f x f x=+++的单调递增区间为7π5ππ,π,2424k k k−+∈Z .17.解:(1)因为m ∥n,所以sin cos 0b C B =.由正弦定理得sin sin cos 0B C C B =.又sin 0C ≠,故tan B =.因为0πB <<,所以π3B =.(2)因为11sin 22S ac B ac === 所以163ac =. 由余弦定理得22222cos ()2b a c ac B a c ac ac =+−=+−−, 即2169()33a c +−×,解得5a c +=, 所以ABC 的周长为8abc ++=. 18.证明:(1)因为PD ⊥底面,ABCD CD ⊂平面ABCD , 所以CD PD ⊥.又因为底面ABCD 为正方形,所以CD AD ⊥,且,AD PD ⊂平面,PAD AD PD D ∩=, 所以CD ⊥平面PAD .因为PA ⊂平面PAD ,所以PA CD ⊥.又因为,E F 分别是,AB PB 的中点, 所以EF ∥PA ,所以EF CD ⊥.(2)因为,,E F G 分别是,,AB PB CD 的中点, 所以EF ∥,PA EG ∥AD . 又因为PA ⊂平面,PAD EF ⊄平面,PAD AD ⊂平面,PAD EG ⊄平面PAD , 所以EF ∥平面,PAD EG ∥平面PAD ,且,,EF EG E EF EG ∩=⊂平面EFG , 所以平面EFG ∥平面PAD . 19.解:(1)如图,过点D 分别作,DM OA DN OB ⊥⊥,垂足分别为,M N ,则DM ON DN OM ====tan DM AM θ==m ),tan BN DN θθ=⋅(m ). 养殖观赏鱼的面积为12OAB S OA OB =⋅)12θ= 13tan tan θθ=+ 由π0,2θ∈ 可得tan 0θ>,则13tan tan θθ+≥,当且仅当tan θ=,即π6θ=时取等号,此时OAB S = .故当π6θ=时,OAB S 的最小值为(2)由π2AOB OHA ∠∠==,可得BOH ∠θ=, 则m,tan m,m tan cos OHOH AH BH OH OB θθθ==⋅=. 由题意得BH OB AH +≥, 所以11tan cos tan θθθ+≥, 所以sin 1cos cos sin θθθθ+≥,所以()22sin 1sin cos 1sin θθθθ+≥=−, 则22sin sin 10θθ+−≥, 所以1sin 2θ≥或sin 1θ≤−(舍去). 又因为π02θ<<,所以ππ,62θ ∈ .。
辽宁省2021-2022高一数学下学期期末考试试题(含解析) (2)

辽宁省2021-2022高一数学下学期期末考试试题(含解析)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.在区间[]1,6上随机选取一个数a ,则3a ≤的概率为( ) A.45B.35C.25D.15【答案】C 【解析】 【分析】根据几何概型概率公式直接求解可得结果. 【详解】由几何概型概率公式可知,所求概率312615p -==- 本题正确选项:C【点睛】本题考查几何概型中的长度型概率问题的求解,属于基础题.2.为了从甲、乙两组中选一组参加“喜迎国庆共建小康”知识竞赛活动.班主任老师将两组最近的6次测试的成绩进行统计,得到如图所示的茎叶图.若甲、乙两组的平均成绩分别是x x 甲乙,.则下列说法正确的是( )A. x x >甲乙,乙组比甲组成绩稳定,应选乙组参加比赛B. x x >甲乙,甲组比乙组成绩稳定.应选甲组参加比赛C. x x <甲乙,甲组比乙组成绩稳定.应选甲组参加比赛D. x x <甲乙,乙组比甲组成绩稳定,应选乙组参加比赛 【答案】D 【解析】 【分析】由茎叶图数据分别计算两组的平均数;根据数据分布特点可知乙组成绩更稳定;由平均数和稳定性可知应选乙组参赛. 【详解】727879858692826x +++++==甲;788687879193876x +++++==乙x x ∴<甲乙乙组的数据集中在平均数附近∴乙组成绩更稳定∴应选乙组参加比赛本题正确选项:D【点睛】本题考查茎叶图的相关知识,涉及到平均数的计算、数据稳定性的估计等知识,属于基础题.3.已知随机事件A 和B 互斥,且()0.5P AUB =,()0.3P B =.则()P A =( ) A. 0.5 B. 0.2C. 0.7D. 0.8【答案】D 【解析】 【分析】根据互斥事件的概率公式可求得()P A ,利用对立事件概率公式求得结果. 【详解】A 与B 互斥()()()P A B P A P B ∴=+()0.50.30.2P A ∴=-=()()110.20.8P A P A ∴=-=-=本题正确选项:D【点睛】本题考查概率中的互斥事件、对立事件概率公式的应用,属于基础题.4.等差数列{}n a 的首项为1.公差不为0,若236,,a a a 成等比数列,则数列{}n a 的前10项和为( ) A. 80- B. 80 C. 24- D. 24【答案】A 【解析】 【分析】根据等比中项定义可得2326a a a =⋅;利用1a 和d 表示出等式,可构造方程求得d ;利用等差数列求和公式求得结果.【详解】由题意得:2326a a a =⋅设等差数列{}n a 公差为()0d d ≠,则()()()211125a d a d a d +=++即:()()()212115d d d +=++,解得:2d =-101109101090802S a d ⨯∴=+=-=- 本题正确选项:A【点睛】本题考查等差数列基本量的计算,涉及到等比中项、等差数列前n 项和公式的应用;关键是能够构造方程求出公差,属于常考题型.5.在ABC △中,内角,,A B C 所对的边分别为,,a b c .若cos cos sin b C c B a A +=,则角A 的值为( ) A.3πB.6π C.2π D.23π 【答案】C 【解析】 【分析】根据正弦定理将边化角,可得()2sin sin B C A +=,由()sin sin B C A +=可求得sin A ,根据A 的范围求得结果.【详解】由正弦定理得:()2sin cos sin cos sin sin B C C B B C A +=+=A B C π++=()()sin sin sin B C A A π∴+=-=()0,A π∈sin 0A ∴≠sin 1A ∴=2A π∴=本题正确选项:C【点睛】本题考查正弦定理边角互化的应用,涉及到两角和差正弦公式、三角形内角和、诱导公式的应用,属于基础题.6.已知等差数列{}n a 的前n 项和为n S .且1111S π=,则6tan 3a π⎛⎫-= ⎪⎝⎭( )3 B. 3 C. 33 【答案】C 【解析】 【分析】根据等差数列性质可知11611S a =,求得6a ,代入可求得结果. 【详解】()1111161111112a a S a π+===6a π∴=62tan tan 333a ππ⎛⎫∴-==- ⎪⎝⎭本题正确选项:C 【点睛】本题考查三角函数值的求解,关键是能够灵活应用等差数列下标和的性质,属于基础题. 7.已知0,2πα⎛⎫∈ ⎪⎝⎭,3sin 5α=,则tan2α=( )A.724B. 724-C.247D. 247-【答案】C 【解析】 【分析】根据同角三角函数关系可求得tan α;由二倍角的正切公式可求得结果.【详解】0,2πα⎛⎫∈ ⎪⎝⎭,3sin 5α=3tan 4α∴=232tan 242tan 291tan 7116ααα∴===--本题正确选项:C【点睛】本题考查二倍角的正切公式、同角三角函数关系的应用,属于基础题.8.袋子中有大小、形状完全相同的四个小球,分别写有和、“谐”、“校”“园”四个字,有放回地从中任意摸出一个小球,直到“和”、“谐”两个字都摸到就停止摸球,用随机模拟的方法估计恰好在第三次停止摸球的概率。
2024届辽宁沈阳市第31中学高一数学第二学期期末联考试题含解析

2024届辽宁沈阳市第31中学高一数学第二学期期末联考试题注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题:本大题共10小题,每小题5分,共50分。
在每个小题给出的四个选项中,恰有一项是符合题目要求的1.已知,,a b c 均为实数,则 “2b ac =”是“,,a b c 构成等比数列”的 ( )A .必要不充分条件B .充分不必要条件C .充要条件D .既不充分也不必要条件2.已知三角形ABC 为等边三角形,1AB =,设点P Q ,满足()1AP AB AQ AC R λλλ==-∈,,,若38BQ CP ⋅=-,则λ=( )A .12B .12C .12± D .123.已知圆C :()()2224x a y -+-=及直线l :30x y -+=,当直线l 被C 截得的弦长为a 等于( )A .B .2C .1D 14.若角α的终边经过点()1,2P --,则sin α=( )A .5-B .CD 5.已知变量x ,y 之间的线性回归方程为0.47.6ˆyx =-+,且变量x ,y 之间的一组相关数据如下表所示,则下列说法中错误的是( )A .变量x ,y 之间呈现负相关关系B .m 的值等于5C .变量x ,y 之间的相关系数0.4=-r6.在等比数列{}n a 中,1220a a +=,3440a a +=,则56a a +=() A .140B .120C .100D .807.已知直线1:310l mx y m --+=与2:310l x my m +--=相交于点P ,线段AB 是圆22:(1)(1)4C x y +++=的一条动弦,且23AB =,则PA PB +的最小值是( )A .22B .42C .222-D .422-8.若长方体三个面的面积分别为2,3,6,则此长方体的外接球的表面积等于( ) A .49πB .494πC .14πD .143π9.执行如图所示的程序框图,输出S 的值为( )A .-32B .32C .-12D .1210.已知{}n a 是等差数列,1010a =,其前10项和1070S =,则其公差d = A .23-B .13-C .13D .23二、填空题:本大题共6小题,每小题5分,共30分。
2021-2022学年辽宁省沈阳市高一下学期期末数学试题【含答案】

2021-2022学年辽宁省沈阳市高一下学期期末数学试题一、单选题1.若,则( )101i 1i z -=-z=A .1BC .2D .B【分析】先由复数的乘、除法公式化简,再由复数的模长公式即可求出答案.1i z =+【详解】由题得()()()21i 1i1i 1i z +==+-+=故选:B.2.已知向量,,.若,则( )()2,1a =-()1,1b =c a kb =+ a c ⊥ k =A .5B .3C .0D .-3A【分析】利用向量线性运算法则和垂直关系得到方程,求出5k =【详解】因为向量,,()2,1a =-()1,1b =所以,()2,1c a kb k k =+=-++因为,a c ⊥ 所以,4210k k -++=解得:,5k =故选:A.3.若,则( )()()2sin 2022πcos π23πcos 3cos 2αααα+-+=⎛⎫-- ⎪⎝⎭πtan 4α⎛⎫+=⎪⎝⎭A .B .C .D .113113-311311-D【分析】利用诱导公式、同角三角函数的基本关系式化简已知条件,求得,进而tan α求得.πtan 4α⎛⎫+ ⎪⎝⎭【详解】依题意:()()2sin 2022πcos π23πcos 3cos 2αααα+-+=⎛⎫-- ⎪⎝⎭即,解得,2sin cos 2tan 12sin 3cos tan 3αααααα++==----7tan 4α=-所以.πtan 13tan 41tan 11ααα+⎛⎫+==-⎪-⎝⎭故选:D4.已知,,,则( )cos1a =sin 2b =tan 3c =A .B .C .D .a b c <<c b a<<b c a<<c a b<<D【分析】依次判断出的范围,再比较大小即可.,,a b c【详解】由题意知,,tan 30c =<0cos1cos4a π<=<=2sin 2sin 3b π=>=故.c a b <<故选:D.5.在中,三内角A ,B ,C 对应的边分别为a ,b ,c ,且b =2,B =45°.若利ABC 用正弦定理解仅有唯一解,则( )ABCA .0<a ≤2B .2<aC .0<a ≤2或aD .0<a ≤2或a =D【分析】由正弦定理判断.【详解】解:由正弦定理得:sin sin a bA B ==所以,a A =因为,所以,45B =18045135A C +=-=因为仅有唯一解,ABC 所以A ,C 的值确定,当时,,仅有唯一解,此时45A ≤90C >ABC 0sin A <≤则0<a ≤2,当时,,仅有唯一解,此时90A = 45C =ABC a =当,且时,有两解,不符合题意,45135A <<90A ≠ ABC综上:0<a ≤2或a =故选:D .6.如图,一个底面半径为的圆锥,其内部有一个底面半径为a 的内接圆柱,且此2a,则该圆锥的体积为( ).3aA B C .D .3a 3a 3a 3aB【分析】作出该几何体的轴截面,求出内接圆柱的高,利用三角形相似求出圆锥的高,即可求的其体积.【详解】作出该几何体的轴截面如图示:AB 为圆锥的高,设内接圆柱的高为h ,而 ,2,BC a BD r a ===,即,3a 23πa h a =则,h =由于,故,则,AB ED ∥CAB CED △∽△h DCAB BC =即,故,22a a a -=AB =所以圆锥体积为 ,231π(2)3V a a=⨯⨯=故选:B7.圭表(如图甲)是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根直立的标竿(称为“表”)和一把呈南北方向水平固定摆放的与标竿垂直的长尺(称为“圭”).当太阳在正午时刻照射在表上时,日影便会投影在圭面上,圭面上日影长度最长的那一天定为冬至,日影长度最短的那一天定为夏至.图乙是一个根据某地的地理位置设计的圭表的示意图,已知某地冬至正午时太阳高度角(即)大ABC ∠约为15°,夏至正午时太阳高度角(即)大约为60°,圭面上冬至线与夏至线ADC ∠之间的距离(即DB 的长)为a ,则表高(即AC 的长)为()A .BCD(2aD【分析】根据图形,找到角度与边长之间的关系求解.【详解】.()tan tan15tan 45302ABC ∠=︒=︒-︒===在中,,在中,ABC (2tan ACBC ACABC ==∠ADC.tan tan 60AC AC CD ACADC ===∠︒由,得(22DBBC CD AC AC AC a ⎛=-=== ⎝,AC ==故选:D.8.已知正三棱锥P -ABC ,底面边长为3,高为1,四边形EFGH 为正三棱锥P -ABC 的一个截面,若截面为平行四边形,则四边形EFGH面积的最大值为( )A B C .D 32C【分析】又正三棱锥的性质求得三棱锥的侧棱长,结合平行四边形的面积公式及基本不等式求最值即可得解.【详解】设侧棱长为,则由底面边长为3,高为1可求得,a 1=2a =如图,设,则,且,于是AEAP λ=FG BF AE EH PC BP AP PC λ====1EF GH AB AB λ==-,()2,31EH EF λλ==-所以,()()21323161622EFGHS EH EF λλλλλλ+-⎛⎫=⋅=⋅-=-≤⋅= ⎪⎝⎭当且仅当即时取等号1λλ=-12λ=.故四边形的面积最大值为,EFGH 32故选:C.二、多选题9.已知的内角,,所对的边分别为,,,下列四个命题中正确的ABC A B C a b c 命题是( )A .若,则sin sin AB >a b>B .若是锐角三角形,则恒成立ABC sin cos A B >C .若,则一定是直角三角形cos cos b C c B a -=ABC D .若,则一定是锐角三角形222sin sin cos 1A C B +>+ABC ABC【分析】利用正弦定理边角互化可以判断出A 正确;由三角形内角和为,结合诱导π公式可推得B 正确;利用正弦定理及余弦定理即可判断出C 正确;利用同角三角函数的基本关系式及正弦定理及余弦定理结合三角形知识判断出D.【详解】对于A ,因为,所以由正弦定理得,所以,所以Asin sin A B >22a b R R >a b >正确;对于B ,若为锐角三角形,可得且,ABC 2A B π+>,(0,2A B π∈可得,且,2A Bπ>-(0,22B ππ-∈根据正弦函数的单调性,可得,所以,所以B 正确;sin sin()2A B π>-sin cos A B >对于C ,由正弦定理及,知,cos cos b C c B a -=sin cos sin cos sin B C C B A -=所以,因为,则或,又sin()sin B C A -=,0B C A πππ-<-<<<B C A -=B C A π-+=,则,三角形为直角三角形,故C 正确;A B C π++=2B π=对于D ,若,则,由正弦定理得222sin sin cos 1A C B +>+222sin sin sin 0A C B +>-,则角B 为锐角,但不一定是锐角三角形,故D 错误;2220a c b +->ABC 故选:ABC.10.已知函数的部分图象如图所示,下列说()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭法正确的是( )A .函数的图象关于点对称()y f x =π,06⎛⎫- ⎪⎝⎭B .函数的图象关于直线对称()y f x =5π12x =-C .函数在单调递减()y f x =2ππ,36⎡⎤--⎢⎣⎦D .该图象向右平移个单位可得的图象π62sin 2y x =ABD根据函数的图象,可求出的解析式,进而对选项逐个分析,可得出答案.()f x 【详解】由函数的图象可得,周期,所以,2A =ππ4π312T ⎛⎫=-= ⎪⎝⎭2π2π2πT ω===当时,函数取得最大值,即,所以π12x =ππ2sin 221212f ϕ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭,则,又,得,ππ22π122k ϕ⨯+=+()k ∈Z π2π3k ϕ=+π2ϕ<π3ϕ=故函数.()π2sin 23f x x ⎛⎫=+ ⎪⎝⎭对于A ,当时,,即点是函数π6x =-πππ2sin 22sin 00663f ⎛⎫⎛⎫-=-⨯+== ⎪ ⎪⎝⎭⎝⎭π,06⎛⎫- ⎪⎝⎭的一个对称中心,故A 正确;()f x 对于B ,当时,,即直线5π12x =-5π5πππ2sin 22sin 2121232f ⎛⎫⎛⎫⎛⎫-=-⨯+=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭是函数的一条对称轴,故B 正确;5π12x =-()f x 对于C ,令,解得,则函数ππ3π+2π2+2π232k x k ≤+≤()k ∈Z π7π+π+π1212k x k ≤≤的单调递减区间为,故C 错误;()f x π7π+π,+π1212k k ⎡⎤⎢⎥⎣⎦()k ∈Z 对于D ,将的图象向右平移个单位后,得到()f x π6的图象,即D 正确.ππ2sin 222sin 263y x x⎛⎫=-⨯+= ⎪⎝⎭故选:ABD.本题考查根据图象求三角函数解析式以及三角函数性质,考查推理能力与计算求解能力,属中档题.11.已知复数(其中为虚数单位,)则下列说法正确的有i z a b =+i ,a R b R ∈∈( )A .若,B .若,则z z =z R∈zR z ∈z R∈C .若,则D .若,则1z z =1z =2z z =0z =AC【分析】利用共轭复数的定义与复数的四则运算法则计算判断.【详解】当,即,得,z z =i i a b a b =+-0b =,A 正确;z R ∴∈,222222i 2i i z a b a b ab a b a b a b z +-==+-++当,则,z R z ∈22220200ab ab a b a b =⎧=⇒⎨+≠+⎩当时,,B 错误;0,0a b =≠z R ∉,即,得,1z z =()()i i 1a b a b +-=221a b +=,C 正确;1=,即,得,22z z=()()22i i a b a b +=-2i 2i ab ab =-,当时,,D 错误;0ab ∴=0,0a b ≠=0z≠故选:AC12.三棱锥中,平面平面ABC ,,S ABC -SAB ⊥390SAB ABC BAC ∠=∠=∠=︒,则( )2SA AC ==A .SA BC⊥B .三棱锥的外接球的表面积为S ABC -83πC .点A 到平面SBCD .二面角S BC A --AD【分析】根据平面ABC 可判断A 正误;求出直径SC ,再根据球的表面积公式课SA ⊥判断B 的正误;根据面面垂直的性质定理可知点A 到平面SBC 的距离为AG ,求出AG 可判断C 正误;根据题意可知∠SBA 为二面角的平面角,进而求出正切S BC A --值可判断D 正误.【详解】对于A ,因为平面平面ABC ,,即,SAB ⊥90SAB ∠=︒SA AB ⊥平面平面,平面SAB ,所以平面ABC ,SAB ABC AB =SA ⊂SA ⊥又因为平面ABC ,所以,故A 正确;BC ⊂SA BC ⊥对于B ,因为,,,SA BC ⊥AB BC ⊥SA AB A ⋂=所以平面SAB ,因为平面SAB ,BC ⊥SB ⊂所以.又平面ABC ,平面ABC ,BC SB ⊥SA ⊥AC ⊂所以,即,SA AC ⊥90SAC SBC ∠=∠=︒所以三棱锥外接球的直径为SC .因为,S ABC -2SA AC ==所以SC ==所以三棱锥的外接球的表面积,故B 错误;S ABC -224482SC S πππ⎛⎫=== ⎪⎝⎭对于C ,因为平面SAB ,平面SBC ,BC ⊥BC ⊂所以平面平面SBC ,过点A 作,交SB 于点G ,SAB ⊥AG SB ⊥根据面面垂直的性质定理,可得平面SBC ,AG ⊥故点A 到平面SBC 的距离为AG ,由,,390ABC BAC ∠=∠=︒2AC =得,则AB =SB ==则C 错误;AB SA AG SB ⨯===对于D ,,,所以∠SBA 为二面角的平面角,SB BC ⊥AB BC ⊥S BC A --在中,D 正确;Rt SAB tan SA SBA AB ∠===故选:AD.三、填空题13.若,,则___________.0,4πα⎛⎫∈ ⎪⎝⎭5sin 413πα⎛⎫-=-⎪⎝⎭cos 2=α120169【分析】由题设条件可解得,而5sin 413πα⎛⎫-=⎪⎝⎭,故由平方关系解得cos2sin 2sin 22sin cos 2444ππππααααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-=-=-- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,代入即得所求cos 4πα⎛⎫- ⎪⎝⎭【详解】55sin sin 413413ππαα⎛⎫⎛⎫-=-⇒-=⎪ ⎪⎝⎭⎝⎭又0,4πα⎛⎫∈ ⎪⎝⎭044ππα⇒<-<所以12cos 413πα⎛⎫-== ⎪⎝⎭cos2sin 2sin 22sin cos 2444ππππααααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-=-=-- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦120169=故12016914.已知函数在区间上是增函数,将函数的图像向()()sin 0f x x ωω=>π0,6⎛⎤ ⎝⎦()y f x =左平移个单位后得到的图像与将其向右平移个单位后所得到的图像重合.则的π32π3ω值为________.2【分析】根据增函数确定的范围,结合平移图像间的关系可得的值.ωω【详解】因为函数在区间上是增函数,所以,即()()sin 0f x x ωω=>π0,6⎛⎤⎥⎝⎦62ωππ≤;03ω<≤函数的图像向左平移个单位后得到的函数为()y f x =π3,sin sin 33y x x ωωωππ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭函数的图像向右平移个单位后所得到的函数为()y f x =2π3;2sin sin 33y x x ωωω2ππ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭因为二者的图像重合,所以,,即.2233k ωωππ⎛⎫--=π⎪⎝⎭Z k ∈2k ω=所以.2ω=故2.15.在三棱锥中,平面ABC ,,.以A 为球P ABC -PA ⊥AC CB ⊥4===PA AC BC 心,表面积为的球面与侧面PBC 的交线长为______.36ππ【分析】利用线面垂直的性质定理及判定定理证得平面PBC ,进而知球面与侧AH ⊥面PBC 的交线为以为圆心,半径为1的半圆弧,利用弧长公式求解.H 【详解】设以A 为球心的球的半径为,则,解得R 2436R ππ=3R =如图,取中点,由,PC H PA AC =AH PC ∴⊥又平面ABC ,平面ABC ,PA ⊥BC ⊂PA BC ∴⊥又,,所以平面PAC ,AC CB ⊥AC PA A ⋂=BC ⊥又平面PAC ,,又,平面PBC ,AH ⊂BC AH ∴⊥BC PC C ⋂=AH ∴⊥又,4===PA ACBC AH ∴=PB =又,1r ==作,则,,HE PB ⊥PEH PCB EH PH CB PB ∴=1PH CB EH PB ⋅∴===>所以球面与侧面PBC 的交线为以为圆心,半径为1的半圆弧,故所求长为H 1ππ⨯=故π四、双空题16.已知平面单位向量,,且,则在方向上的投影向量为a b |||a b a b +=- b a _________;()的最小值是_________.||a b λ-R λ∈12a2a【分析】分别根据投影向量的定义和单位向量的模化简即可求解.【详解】由,两边平方得,而在方向上的投影向量为|||a b a b +=- 1=2a b b a ,1=2||a b a ab(当时取得最小值)所以其最小值为||a b λ-≥ 12λ=故12a五、解答题17.已知向量,,.()0,6OA =-()8,0OB =(),OC x y =(1)若点A ,B ,C 三点共线,求实数x ,y 满足的关系;(2)若x =1且为钝角,求实数y 的取值范围.ACB ∠(1);34240x y --=(2)且.71y -<<214y ≠-【分析】(1)根据三点共线可得,结合共线向量的坐标表示可得答案;CA CB ∥(2)根据为钝角,可得且,不共线,利用坐标表示可得结果.ACB ∠0CA CB ⋅<CA CB 【详解】(1)因为A ,B ,C 三点共线,即,CA CB ∥ ,,所以,(),6CA x y =---()8,CB x y =--()()680xy y x ----=即;34240x y --=(2)因为为钝角,所以且,不共线,ACB ∠0CA CB ⋅<CA CB 由(1)得:当,且时,,1x =CA CB ∥ 214y =-因为,不共线,所以,CA CB 214y ≠-,,()1,6CA y =---()7,CB y =- ,2760CA CB y y ⋅=-++<解得:,71y -<<所以且.71y -<<214y ≠-18.如图,已知等腰梯形ABCD 的外接圆半径为2,,,点P 是AB CD ∥2AB CD =上半圆上的动点(不包含A ,B 两点),点Q 是线段PA 上的动点,将半圆APB 所在的平面沿直径AB 折起使得平面平面ABCD .PAB ⊥(1)求三棱锥P -ACD 体积的最大值;(2)当平面QBD 时,求的值.PC ∥PQQA(2)12【分析】(1)根据平面平面ABCD ,可知平面时,三棱锥P -ACD PAB ⊥PO ⊥ABCD 体积最大,利用锥体的体积公式可求答案;(2)根据平面QBD ,确定的位置,结合比例关系可得答案.PC ∥Q 【详解】(1)当时,PO AB ⊥平面,由平面平面,平面平面,PO ⊂PAB PAB ⊥ABCD PAB ⋂ABCD AB =知平面,PO ⊥ABCD 此时,到平面的距离最大,为,P ABCD 2PO =所以,的最大值为P ACD V -11122332ACDS PO ⨯⨯=⨯⨯=(2)连接交于点,连接,AC BD M QM 则平面平面,PAC QBD QM =依题意,平面,平面,所以,PC ∥QBD PC ⊂PAC PC QM ∥所以,,PQCM QAMA=等腰梯形中,,ABCD MAB MCD △△所以.12PQCM CD QAMAAB===19.已知函数为奇函数,且图()2()2sin 1(0,0 )2x f x x ωϕωϕωϕπ+⎛⎫=++-><< ⎪⎝⎭()f x 象的相邻两对称轴间的距离为.2π(1)求的解析式与单调递减区间;()f x (2)将函数的图象向右平移个单位长度,再把横坐标缩小为原来的(纵坐标()f x 6π12不变),得到函数的图象,当时,求方程的所有()y g x = 0,2x π⎡⎤∈⎢⎥⎣⎦()22()30g x x +-=根的和.(1),递减区间为,()2sin 2f x x =3,44k k ππππ⎡⎤++⎢⎥⎣⎦k ∈Z (2)43π【分析】(1)利用恒等变换化简后,结合三角函数的性质求解;(2)利用图象变换法则求得g (x )的函数表达式,解方程求得g (x )的值,利用换元思想,结合三角函数的图象和性质分析求得.【详解】(1)由题意,2())2sin 1)cos()2x f x x x x ωϕωϕωϕωϕ+⎛⎫=++-+-+ ⎪⎝⎭2sin 6x πωϕ⎛⎫=+- ⎪⎝⎭图象的相邻两对称轴间的距离为,()f x 2π的最小正周期为,即可得,∴()f x T π=2ω=又为奇函数,则,,()f x 6k πϕπ-=k ∈Z 又,,故,0ϕπ<<6πϕ∴=()2sin 2f x x =令,得3222,22k x k k ππππ++∈Z 3,44k x k k ππππ++∈Z函数的递减区间为,∴()f x 3,44k k ππππ⎡⎤++⎢⎥⎣⎦k ∈Z (2)将函数的图象向右平移个单位长度,可得的图象,()f x 6π2sin 23y x π⎛⎫=- ⎪⎝⎭再把横坐标缩小为原来的,得到函数的图象,12()2sin 43y g x x π⎛⎫==- ⎪⎝⎭又,则()22()30g x x -=()g x =()g x =即sin 43x π⎛⎫-= ⎪⎝⎭sin 43x π⎛⎫-=⎪⎝⎭令,当时,,43z x π=-0,2x π⎡⎤∈⎢⎥⎣⎦54,333z x πππ⎡⎤=-∈-⎢⎥⎣⎦画出的图象如图所示:sin y z =,关于对称,即,sin z =12,z z 2z π=12z z π+=有,sin z =345π45,,333z z z ππ=-==在上有两个不同的根,sin 43x π⎛⎫-= ⎪⎝⎭0,2π⎡⎤⎢⎥⎣⎦12,x x ,;124433x x πππ-+-=12512x x π∴+=又,sin 43x π⎛⎫-= ⎪⎝⎭50,,122ππ所以方程在内所有根的和为.()22()30g x x +-=0,2x π⎡⎤∈⎢⎥⎣⎦43π20.《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑.如图,已知PA ⊥平面ABC ,平面PAB ⊥平面PBC .(1)判断四面体P -ABC 是否为鳖臑,并给出证明;(2)若二面角B -AP -C 与二面角A -BC -P 的大小都是,求AC 与平面BCP 所成角4π的大小.(1)四面体P -ABC 为鳖臑,证明见解析(2)6π【分析】(1)作交于,根据面面垂直的性质可得平面,再AD PB ⊥PB D AD ⊥PBC 根据线面垂直的性质与判定证明平面,从而证明四面体P -ABC 四个面都BC ⊥PAB 为直角三角形即可;(2)由(1)连接,根据线面垂直的性质可得AC 与平面BCP 所成角为,CD ACD ∠再求解,从而得到即可sin ACD ∠ACD ∠【详解】(1)作交于,因为PA ⊥平面ABC ,平面ABC ,故AD PB ⊥PB D BC ⊂.又平面PAB ⊥平面PBC ,且平面PAB 平面PBC ,故平面,PA BC ⊥ PB =AD ⊥PBC 又平面,故,又,平面,故平面BC ⊂PBC AD BC ⊥AD PA A ⋂=,AD PA ⊂PAB BC ⊥,故.又PA ⊥平面ABC ,故,故四面体PAB ,BC BP BC BA ⊥⊥,PA AB PA AC ⊥⊥P-ABC 所有面都为直角三角形,故四面体P -ABC 为鳖臑(2)由(1),连接,二面角B -AP -C 的平面角为,二面角A -BC -P 的平面CD BAC ∠角为,故,故均为等腰直角三角形.设ABP ∠4BAC ABP π∠=∠=,BAC ABP ,则又平面,故AC 与平面BCP1AB BC AP ===AC BP ==CP =AD ⊥PBC 所成角为,又,且为锐角,故,即ACD ∠1sin 2AD ACD AC ∠===ACD ∠6π∠=ACD AC 与平面BCP 所成角的大小为6π21.请在①向量,,且;sin ,a c x B b c -⎛⎫= ⎪+⎝⎭ ,sin b c y A c a -⎛⎫= ⎪+⎝⎭ x y ⊥ ②这两个条件中任选一个填入横线上并解答.π2sin 3c A ⎛⎫=+ ⎪⎝⎭在锐角三角形ABC 中,已知角A ,B ,C 的对边分别为a ,b ,c ,且满足条件________.(1)求角C ;(2)若的面积为的取值范围.ABC 2a b +注.如果选择多个条件分别解答,按第一个解答计分.(1)π3C =(2)()8,10【分析】(1)选择①时,由向量垂直转化为向量的数量积为零,从而得到 之a b c 、、间的关系,用余弦定理求解即可.选择②时,由正弦定理及三角形内角和定理化简得到结果.(2)由三角形面积公式得到,再由余弦定理得到8ab =,利用锐角三角形列出不等式组,解出2228c a b =+-,构造函数,利用函数的单调性求出范围即可.24a <<()82f a a a =+【详解】(1)选择①:因为x y⊥所以,()()sin sin c a A b c Bb cc a --=++由正弦定理得,,()()c a a b c b cc a b--=++即,即,即,()()2222a c a b b c -=-2233ac bc a b +=+()()()222c a b a b a ab b +=+-+即.因为,222c a b ab =+-2221cos 22a b c C ab +-==又为锐角,所以.C π3C =选择②:因为,π2sin 3c A ⎛⎫=+ ⎪⎝⎭由正弦定理得,,π2sin sin 3B C A ⎛⎫=+ ⎪⎝⎭.sin sin cos B C A C A =又,()sin sin sin cos cos sin B A C AC A C=+=+.cos sin sin A C CA =因为,sin 0A >sin C C =又为锐角,所以.C tan C π3C =(2)因为1sin 2ABC S ab C === 所以,则.8ab =822a b a a +=+由余弦定理得,.①222222cos 8c a b ab C a b =+-=+-因为为锐角三角形,所以即ABC 0,0,cosA cosB >⎧⎨>⎩2222220,0.b c a a c b ⎧+->⎨+->⎩将①代入上式可得即解得.224,4,b a ⎧>⎨>⎩2284,4,a a ⎧⎛⎫>⎪ ⎪⎨⎝⎭⎪>⎩24a <<令,()82f a a a =+所以在上单调递增,所以,()f a ()24,()()()24f f a f <<即,即的取值范围为.()810f a <<2a b +()8,1022.如图,某公园改建一个三角形池塘,,百米,百米,现准90C =∠2AB =1BC =备养一批观赏鱼供游客观赏.(1)若在△ABC 内部取一点P ,建造连廊供游客观赏,方案一如图①,使得点P 是等腰三角形PBC 的顶点,且,求连廊的长(单位为百米);23CPB π∠=AP PC PB ++(2)若分别在AB ,BC ,CA 上取点D ,E ,F ,并建造连廊,使得△DEF 变成池中池,放养更名贵的鱼类供游客观赏:方案二如图②,使得△DEF 为正三角形,设为图②中2S △DEF 的面积,求的最小值;方案三如图③,使得DE 平行于AB ,且EF 垂直于2S DE ,设为图③中△DEF 的面积,求的取值范围.3S 3S(2)()2minS =3S ⎛∈ ⎝【分析】(1)先由中的余弦定理求出,再由中的余弦定理求出,PBC PC APC △AP 即可得到答案;(2)分别表示出方案②和方案③中的面积,利用三角函数的性质以及二次函数的性质求解最值即可.【详解】(1)解:因为点是等腰三角形的顶点,且,,P PBC 23CPB π∠=1BC =所以,6PCB π∠=由余弦定理可得,,解得222cos 2PB PC BC PCB PB PC +-∠=⋅PC =又因为,2ACB π∠=故,3ACP π∠=在中,,,所以Rt ACB △2AB =1BC =AC ==在中,由余弦定理可得,,ACP △2222cos3AP AC PC AC PC π=+-⋅⋅解得,AP =故,AP PC PB ++所以连廊AP PC PB ++(2)解:设图②中的正的边长为,,DEF a (0)CEF ααπ∠=<<则,,sin CF a α=sin AF a α=设,1EDB ∠=∠则,213B DEB DEB ππ∠=-∠-∠=-∠,233DEB DEBππαπ=--∠=-∠所以,2133ADF πππα∠=--∠=-在中,由正弦定理可得,,ADF sinsin DF AFA ADF =∠∠即,sin6aπ=即21sin()sin 32a a παα-=-即(其中为锐角,且,a ===θtanθ=所以,即222371sin 602a S =︒()2min S =图③中,设,,BE x =(0,1)x ∈因为,且,//DEAB EF DE ⊥所以,,,3DEC π∠=6FEB π∠=2EFB π∠=所以,cos6EF x π==,222cos3CE DE CExπ===-所以22111(22)))222DEF S EF DE x x x x=⋅⋅=⨯-=-+=-+ 所以当时,,12x =DEF S△DEF S ⎛∈ ⎝ 故3S ⎛∈ ⎝。
2019-2020学年辽宁省辽阳市高一下学期期末数学试卷 (解析版)

2019-2020学年辽宁省辽阳市高一第二学期期末数学试卷一、选择题(共12小题).1.sin(﹣480°)等于()A.﹣B.C.﹣D.2.一个几何体有6个顶点,则这个几何体可能是()A.三棱柱B.四棱锥C.四棱柱D.五棱台3.已知复数z满足z(1+i)=2i8,则z的虚部为()A.1B.i C.﹣1D.﹣i4.在△ABC中,角A,B,C所对的边分别为a,b,c.已知b═3,c=2,A=,则a=()A.5B.C.29D.5.平面向量=(1,m),=(﹣1,),且|﹣|=||,则||=()A.B.C.D.6.在△ABC中,角A,B,C所对的边分别为a,b,c.已知A=,B=,a=2,则△ABC的面积为()A.B.9﹣3C.D.3+97.如图,在直三棱柱ABC﹣A1B1C1中,四边形BCC1B1为正方形,BC=2AB=4,AB⊥BC,则异面直线AC1与BC所成角的余弦值为()A.B.C.D.8.下列函数中,周期为π的奇函数是()A.y=cos B.y=sin(2x+3π)C.y=cos(π+2x)D.y=|cos(x﹣)|9.如图,在△ABC中,=3,=3,则=()A.+B.+C.+D.+10.已知直线x=是函数f(x)=sin2+sinωx﹣(0<ω≤8)图象的一条对称轴,则ω=()A.2B.4C.6D.811.已知正方形ABCD的边长是4,将△ABC沿对角线AC折到△AB'C的位置,连接B'D.在翻折过程中,给出以下结论:①AB'⊥平面B'CD恒成立;②三棱锥B'﹣ACD的外接球的表面积始终是32π;③当二面角B'﹣AC﹣D为时,B'D=4;④三棱锥B'﹣ACD体积的最大值是.其中结论正确的个数是()A.1B.2C.3D.412.将函数y=sin x的图象向右平移个单位长度,再将横坐标缩短为原来的(ω>0)得到函数y=f(x)的图象,若y=f(x)在[0,]上的最大值为,则ω的取值个数为()A.1B.2C.3D.4二、填空题:本大题共4小题,每小题5分,共20分把答案填在答题卡中的横线上. 13.已知扇形的半径与面积都为2,则这个扇形的圆心角的弧度数是.14.在复平面内,复数z=2i对应的点为Z,将向量绕原点O按逆时针方向旋转,所得向量对应的复数是.15.已知点P(1,3)是角α终边上的一点,则tan(α+)=.16.已知O为△ABC内一点,且满足+3+5=,延长AO交BC于点D.若=λ,则λ=.三、解答题:本题共6小题,共70分要求写出必要的文字说明和解题过程.17.在△ABC中,角A,B,C的对边分别为a,b,c,在①b cos A cos C=a sin B sin C﹣b;②b sin B cos C+c sin2B=a cos B;③+a=2c这三个条件中任选一个,补充在下面问题中,并作答.已知D是BC上的一点,BC=2BD>AB,AD=2,AB=6,若____,求△ACD的面积.注:如果选择多个条件分别解答,按第一个解答计分.18.如图,在长方体ABCD﹣A1B1C1D1中,BC=CC1,E,F,G,H分别是棱AB,AA1,CC1,C1D1的中点.(1)证明:C1E⊥B1C.(2)证明:平面DEF∥平面B1GH.19.已知单位向量,的夹角为,向量=λ﹣,向量=2+3.(1)若∥,求λ的值;(2)若⊥,求||.20.已知向量=(cos(x﹣),sin(x﹣)),向量=(,﹣1),函数f(x)=•.(1)求f(x)的最大值;(2)若f(﹣α),f(﹣α)是关于x的方程25x2﹣10x+t=0的两根,且α∈(0,π),求+及t的值.21.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=2,AD=4,E是PB的中点,AF⊥PC,垂足为F.(1)证明:PD∥平面ACE.(2)求三棱锥A﹣CEF的体积.22.已知函数f(x)=A sin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示.(1)求A,ω和φ的值;(2)求函数y=f(x)在[1,2]上的单调递减区间;(3)若函数y=f(x)在区间[a,b]上恰有2020个零点,求b﹣a的取值范围.参考答案一、选择题:本大题共12小题,每小题5分,共60分在每小题给出的四个选项中,只有一项是符合题目要求的.1.sin(﹣480°)等于()A.﹣B.C.﹣D.【分析】所求式子中的角度变形后,利用诱导公式化简即可得到结果.解:sin(﹣480°)=﹣sin480°=﹣sin(360°+120°)=﹣sin120°=﹣.故选:C.2.一个几何体有6个顶点,则这个几何体可能是()A.三棱柱B.四棱锥C.四棱柱D.五棱台【分析】通过棱锥,棱柱,棱台的顶点个数,判断选项即可.解:三棱柱上下两个平面都是三角形,有6个顶点,满足题意,A正确;四棱锥5个顶点,B不正确;四棱柱,有8的顶点,C不正确;五棱台有10个顶点,D不正确;故选:A.3.已知复数z满足z(1+i)=2i8,则z的虚部为()A.1B.i C.﹣1D.﹣i【分析】把已知等式变形,再由复数代数形式的乘除运算化简得答案.解:由z(1+i)=2i8=2,得z=,∴z的虚部为﹣1.故选:C.4.在△ABC中,角A,B,C所对的边分别为a,b,c.已知b═3,c=2,A=,则a=()A.5B.C.29D.【分析】直接利用余弦定理求出结果.解:已知b═3,c=2,A=,利用余弦定理:a2=b2+c2﹣2bc cos A=9+8﹣,解得a=.故选:B.5.平面向量=(1,m),=(﹣1,),且|﹣|=||,则||=()A.B.C.D.【分析】本题先对|﹣|=||两边进行平方,转化成向量进行计算,化简整理可得,然后根据向量内积的坐标运算可解出m的值,即可计算出||的值.解:依题意,由|﹣|=||,可得|﹣|2=||2,即(﹣)2=()2,化简整理,得,∴1×(﹣1)+m×=0,解得m=,∴=(1,),∴||==.故选:A.6.在△ABC中,角A,B,C所对的边分别为a,b,c.已知A=,B=,a=2,则△ABC的面积为()A.B.9﹣3C.D.3+9【分析】由已知利用正弦定理可得b的值,根据两角和的正弦函数公式,三角形的面积公式即可计算得解.解:∵A=,B=,a=2,∴由正弦定理,可得b===3,∴S△ABC=ab sin C=ab sin(A+B)=ab(sin cos+cos sin)=()=.故选:C.7.如图,在直三棱柱ABC﹣A1B1C1中,四边形BCC1B1为正方形,BC=2AB=4,AB⊥BC,则异面直线AC1与BC所成角的余弦值为()A.B.C.D.【分析】由BC∥B1C1,得∠AC1B1是异面直线AC1与BC所成角(或所成角的补角),连结AB1,推导出B1C1⊥A1B1,B1C1⊥BB1,从而得到B1C1⊥平面ABB1A1,B1C1⊥AB1,由此能求出异面直线AC1与BC所成角的余弦值.解:在直三棱柱ABC﹣A1B1C1中,∵BC∥B1C1,∴∠AC1B1是异面直线AC1与BC所成角(或所成角的补角),如图,连结AB1,∵四边形BCC1B1为正方形,BC=2AB=4,AB⊥BC,∴B1C1⊥A1B1,B1C1⊥BB1,∵A1B1∩BB1=B1,∴B1C1⊥平面ABB1A1,∴B1C1⊥AB1,AB1==2,AC1==6,∴cos∠AC1B1=,∴异面直线AC1与BC所成角的余弦值为.故选:C.8.下列函数中,周期为π的奇函数是()A.y=cos B.y=sin(2x+3π)C.y=cos(π+2x)D.y=|cos(x﹣)|【分析】根据题意,依次分析选项中函数的奇偶性与周期性,综合即可得答案.解:根据题意,依次分析选项:对于A,y=cos=﹣sin,是奇函数,周期T==4π,不符合题意;对于B,y=sin(2x+3π)=﹣sin2x,是奇函数,周期T==π,符合题意;对于C,y=cos(π+2x)=cos x,是偶函数,不符合题意;对于D,y=|cos(x﹣)|=|sin x|,是偶函数,不符合题意;故选:B.9.如图,在△ABC中,=3,=3,则=()A.+B.+C.+D.+【分析】根据条件=,结合=3,代入化简可得=,再由向量加法法则可得答案解:因为=3,即有=,因为=3,所以=,则==()=,所以==,故选:A.10.已知直线x=是函数f(x)=sin2+sinωx﹣(0<ω≤8)图象的一条对称轴,则ω=()A.2B.4C.6D.8【分析】首先通过三角函数关系式的变换,把函数的关系式变形成正弦型函数,进一步利用函数的性质的应用求出结果.解:函数f(x)=sin2+sinωx﹣=ωx)+ωx﹣=sin (ωx﹣),令:ω﹣=(k∈Z),解得ω=4+(k∈Z),由于0<ω≤8,所以ω=4.故选:B.11.已知正方形ABCD的边长是4,将△ABC沿对角线AC折到△AB'C的位置,连接B'D.在翻折过程中,给出以下结论:①AB'⊥平面B'CD恒成立;②三棱锥B'﹣ACD的外接球的表面积始终是32π;③当二面角B'﹣AC﹣D为时,B'D=4;④三棱锥B'﹣ACD体积的最大值是.其中结论正确的个数是()A.1B.2C.3D.4【分析】对于①,若AB′⊥平面B′CD,则AB′⊥CD,推导出平面AB′D⊥平面ACD,在翻折过程中,B′始终在BD正上方,平面AB′D⊥平面ACD不成立;对于②,取AC中点O,推导出三棱锥B′﹣ACD的外接球半径R=2,其表面积S =32π;对于③,当二面角B′﹣AC﹣D为时,OB′⊥OD,从而B′D=4;对于④,当平面B′AC⊥平面ACD时,三棱锥B′﹣ACD的体积取最大值.解:对于①若AB′⊥平面B′CD,则AB′⊥CD,∵CD⊥AD,∴CD⊥平面AB′D,∵CD⊂平面ACD,∴平面AB′D⊥平面ACD,∵在翻折过程中,B′始终在BD正上方,不可能在AD正上方,∴平面AB′D⊥平面ACD不成立,故①错误;对于②,取AC中点O,∵ABCD是正方形,∴OA=OB=OB′=OC=OD=2,则三棱锥B′﹣ACD的外接球半径R=2,其表面积S=4πR2=32π,故②正确;对于③,当二面角B′﹣AC﹣D为时,OB′⊥OD,∴B′D=,故③正确;对于④,当平面B′AC⊥平面ACD时,三棱锥B′﹣ACD的体积取最大值,最大值为×42×=,故④正确.故选:C.12.将函数y=sin x的图象向右平移个单位长度,再将横坐标缩短为原来的(ω>0)得到函数y=f(x)的图象,若y=f(x)在[0,]上的最大值为,则ω的取值个数为()A.1B.2C.3D.4【分析】利用函数图象的平移与伸缩变换求得f(x)的解析式,再由x的范围求得ωx ﹣的范围,结合y=f(x)在[0,]上的最大值为,分类求解得答案.解:将函数y=sin x的图象向右平移个单位长度,可得y=sin(x﹣)的图象.再将横坐标缩短为原来的(ω>0)得到函数y=f(x)=sin(ωx﹣)的图象,∵x∈[0,]上,∴ωx﹣∈[﹣,π],当π≥,即ω≥4时,则=1,求得ω=5.当π<,即0<ω<4时,由题意可得sinπ=,作出函数y=sin[(x﹣1)]与y=的图象如图:由图可知,此时函数y=sin[(x﹣1)]与y=的图象有唯一交点,则sinπ=有唯一解.综上,ω的取值个数为2.故选:B.二、填空题:本大题共4小题,每小题5分,共20分把答案填在答题卡中的横线上. 13.已知扇形的半径与面积都为2,则这个扇形的圆心角的弧度数是1.【分析】设扇形的圆心角为α,由此求出弧长和面积,列方程求得α的值.解:设扇形的圆心角为α,则弧长l=2α,所以扇形的面积为:S=rl=×2×2α=2,解得α=1.故答案为:1.14.在复平面内,复数z=2i对应的点为Z,将向量绕原点O按逆时针方向旋转,所得向量对应的复数是.【分析】把复数2i直接乘以旋转复数cos+i sin得答案.解:复数z=2i对应的点为Z,将向量绕原点O按逆时针方向旋转,所得复数为2i(cos+i sin)=2i()=﹣+i.故答案为:+i.15.已知点P(1,3)是角α终边上的一点,则tan(α+)=﹣2.【分析】直接利用三角函数的定义和和角公式的运用求出结果.解:点P(1,3)是角α终边上的一点,所以tanα=3,则:=﹣2.故答案为:﹣216.已知O为△ABC内一点,且满足+3+5=,延长AO交BC于点D.若=λ,则λ=.【分析】条件可整理为=+,结合=λ,得到=+,设=k,列出关于λ,k的方程组,解之即可.解:因为+3+5=,所以+5()=,所以9=3+5,则=+,因为=λ,即﹣=λ(),所以=+,设=k=+,则,解得,故答案为:.三、解答题:本题共6小题,共70分要求写出必要的文字说明和解题过程.17.在△ABC中,角A,B,C的对边分别为a,b,c,在①b cos A cos C=a sin B sin C﹣b;②b sin B cos C+c sin2B=a cos B;③+a=2c这三个条件中任选一个,补充在下面问题中,并作答.已知D是BC上的一点,BC=2BD>AB,AD=2,AB=6,若____,求△ACD的面积.注:如果选择多个条件分别解答,按第一个解答计分.【分析】若选择①,利用正弦定理,两角差的余弦函数公式化简已知等式,结合sin B≠0,可求cos B=,结合范围B∈(0,π),可求B=;若选择②,利用三角函数恒等变换的应用化简已知等式,结合sin A≠0,可求tan B=,结合范围B∈(0,π),可求B=;若选择③,利用两角和的正弦函数公式化简已知等式,结合sin C≠0,可得cos B=,结合范围B∈(0,π),可求B=,在△ABD中,由余弦定理可得BD的值,进而根据三角形的面积公式即可计算求解.解:若选择①,则sin B cos A cos C=sin A sin B sin C﹣sin B,因为sin B≠0,所以cos A cos C﹣sin A sin C=﹣,即cos(A+C)=﹣,因为B=π﹣(A+C),所以cos(A+C)=﹣cos B=﹣,即cos B=,因为B∈(0,π),所以B=.若选择②,则sin2B cos C+sin C sin2B=sin A cos B,即sin2B cos C+sin C sin B cos B=sin A cos B,可得sin B sin(B+C)=sin A cos B,可得sin B sin A=sin A cos B,因为sin A≠0,可得sin B=cos B,可得tan B=,因为B∈(0,π),所以B=.若选择③,则sin B cos A+sin A cos B=2sin C cos B,即sin(B+A)=2sin C cos B,可得sin C =2sin C cos B,因为sin C≠0,可得cos B=,因为B∈(0,π),所以B=,在△ABD中,由余弦定理可得AD2=AB2+BD2﹣2AB•BD•cos B,可得28=36+BD2﹣2×,解得BD=4,或2,因为BC=2BD>AB=6,所以BD=4,所以BC=2BD=8,所以S△ACD=S△ABD=AB•BD•sin B==6.18.如图,在长方体ABCD﹣A1B1C1D1中,BC=CC1,E,F,G,H分别是棱AB,AA1,CC1,C1D1的中点.(1)证明:C1E⊥B1C.(2)证明:平面DEF∥平面B1GH.【分析】(1)连接BC1,可证四边形BCC1B1为正方形,得B1C⊥BC1,再由AB⊥平面BCC1B1,得AB⊥B1C,利用直线与平面垂直的判定可得B1C⊥平面BEC1,从而得C1E ⊥B1C;(2)由E,F,G,H分别是AB,AA1,CC1,C1D1的中点,可得EF∥GH,ED∥B1H,由直线与平面平行的判定可得EF∥平面B1GH,同理可证ED∥平面B1GH,由平面与平面平行的判定可得平面DEF∥平面B1GH.【解答】证明:(1)连接BC1,EC1,在长方体ABCD﹣A1B1C1D1中,∵BC=CC1,∴四边形BCC1B1为正方形,则B1C⊥BC1,又AB⊥平面BCC1B1,∴AB⊥B1C,∵AB∩BC1=B,AB,BC1⊂平面BEC1,∴B1C⊥平面BEC1,而C1E⊂平面BEC1,∴C1E⊥B1C;(2)∵E,F,G,H分别是AB,AA1,CC1,C1D1的中点,∴可得EF∥GH,ED∥B1H,∵EF⊄平面B1GH,GH⊂平面B1GH,∴EF∥平面B1GH,同理可证ED∥平面B1GH,∵ED∩EF=E,ED,EF⊂平面DEF,∴平面DEF∥平面B1GH.19.已知单位向量,的夹角为,向量=λ﹣,向量=2+3.(1)若∥,求λ的值;(2)若⊥,求||.【分析】(1)由题意利用两个向量共线的性质,求出λ的值.(2)由题意利用两个向量垂直的性质,求出λ的值,可得,从而求出||.解:(1)∵单位向量,的夹角为,∴与不共线.∵向量=λ﹣,向量=2+3,若∥,则=,∴λ=﹣.(2)若⊥,∵•=1×1×cos=﹣.∴•=(λ﹣)•(2+3)=2λ+(3λ﹣2)•﹣3=2λ+(3λ﹣2)•(﹣)﹣3=0,求得λ=4,∴=4﹣,∴||====.20.已知向量=(cos(x﹣),sin(x﹣)),向量=(,﹣1),函数f(x)=•.(1)求f(x)的最大值;(2)若f(﹣α),f(﹣α)是关于x的方程25x2﹣10x+t=0的两根,且α∈(0,π),求+及t的值.【分析】(1)通过向量的数量积以及两角和与差的三角函数化简函数的解析式,结合三角函数的最值求解即可.(2)利用方程的根,推出三角函数关系式,然后转化求解表达式的值即可.解:(1)向量=(cos(x﹣),sin(x﹣)),向量=(,﹣1),函数f(x)=•=cos(x﹣)﹣sin(x﹣)=2cos(x﹣+)=2cos x,所以函数f(x)的最大值为2.(2)f(﹣α),f(﹣α)是关于x的方程25x2﹣10x+t=0的两根,即2cosα与2sinα,α∈(0,π),是关于x的方程25x2﹣10x+t=0的两根,所以2cosα+2sinα=,4cosαsinα=,因为(cosα+sinα)2=1+2cosαsinα,所以,解得t=﹣48.所以+==sinα+cosα=.21.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=2,AD=4,E是PB的中点,AF⊥PC,垂足为F.(1)证明:PD∥平面ACE.(2)求三棱锥A﹣CEF的体积.【分析】(1)连结BD,交AC于H,连结EH,推导出EH∥PD,由此能证明PD∥平面ACE.(2)推导出PA⊥BC,BC⊥AB,BC⊥平面PAB,BC⊥AE,AE⊥PB,PC⊥平面AEF,由此能求出三棱锥A﹣CEF的体积.解:(1)证明:连结BD,交AC于H,连结EH,∵四边形ABCD是矩形,∴H是BD的中点,∵E是PB的中点,∴EH∥PD,∵EH⊂平面ACE,PD⊄平面ACE,∴PD∥平面ACE.(2)∵在四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,∴PA⊥BC,BC⊥AB,又PA∩AB=A,∴BC⊥平面PAB,∵AE⊂平面PAB,∴BC⊥AE,∵PA=AB=2,且E是PB的中点,∴AE⊥PB,且AE=,∵AF⊥PC,且AE∩AF=A,∴PC⊥平面AEF,在Rt△PAC中,PA=2,AC==2,则PC==2,∵AF⊥PC,∴AF===,则EF==,CF==,∴三棱锥A﹣CEF的体积:V===.22.已知函数f(x)=A sin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示.(1)求A,ω和φ的值;(2)求函数y=f(x)在[1,2]上的单调递减区间;(3)若函数y=f(x)在区间[a,b]上恰有2020个零点,求b﹣a的取值范围.【分析】(1)有图象可得A=1,T=2,进而求得ω=π,令x=,则π+φ=+2kπ(k∈Z),结合|φ|<,可求得φ;(2)由(1)求得f(x)解析式,令+2kπ≤πx﹣≤+2kπ,k∈Z,解之即可;(3)条件转化为f(x)在[)上有两个零点,即可得b﹣a取值范围.解:(1)由题可得A=1,T=2()=2,则=π,当x=时,f(x)取得最大值,则π+φ=+2kπ(k∈Z),所以φ=﹣+2kπ(k∈Z),又因为|φ|<,故φ=﹣;(2)由(1)可知f(x)=sin(πx﹣),令+2kπ≤πx﹣≤+2kπ,k∈Z,则≤x≤,k∈Z,故f(x)的单调递减区间为[,](k∈Z),则f(x)在[1,2]上的单调递减区间为[1,];(3)令f(x)=sin(πx﹣)=0,则πx﹣=kπ,解得x=k+,k∈Z,所以f(x)在[)上有两个零点,因为f(x)周期为2,若函数y=f(x)在区间[a,b]上恰有2020个零点,则1009×2+1≤b﹣a<1010×2,解得b﹣a的取值范围为[2019,2020).。
辽宁省高一数学下学期期末考试试题

辽宁省2021-2022高一数学下学期期末考试试题注意事项:1.本试卷分第Ⅰ卷、第Ⅱ卷两部分,共6页.满分150分;考试时间:120分钟.2.答题前,考生务必将自己的姓名、准考证号、考试科目、试卷类型用2B 铅笔涂在答题卡上.3.用铅笔把第Ⅰ卷的答案涂在答题卡上,用钢笔或圆珠笔把第Ⅱ卷的答案写在答题纸的相应位置上.4.考试结束,将答题卡和答题纸一并交回.第Ⅰ卷(选择题,共60分)一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.sin1110︒=A .23B .21C .3.12-2.=z (1+i)(2-i)的共轭复数z 为A .-3-iB .-3+iC .3+iD . 3-i3.若向量a =(6,m ),b =(2,-1),向量a 与b 垂直,则实数m 的值为A .-12B .12C .-3D .34.下列说法正确的是A .侧棱垂直于底面的棱柱一定是直棱柱B .棱柱中两个互相平行的平面一定是棱柱的底面C .棱柱中各条棱长都相等D .棱柱的侧面是平行四边形,但它的底面一定不是平行四边形 5.若51cos 2sin cos 5sin 3-=-+αααα,则tan α的值为A .23 B .-23 C .2316 D .-23166.已知函数f (x )=2sin(ωx +φ) 0,2⎛⎫>< ⎪⎝⎭πωϕ的部分图像如图所示,则ω,φ的值为A .2,3πωϕ==B .1,6πωϕ==C .2,3πωϕ==-D .1,3πωϕ==-7.求sin10sin 50sin 70︒︒︒的值A .21B .23 C .81D .833 8.自古以来,人们对于崇山峻岭都心存敬畏,同时感慨大自然的鬼斧神工,一代诗圣杜甫曾赋诗《望岳》:“岱宗夫如何?,一览众山小. ” 然而,随着技术手段的发展,山高路远便不再人们出行的阻碍,伟大领袖毛主席曾作词:“一桥飞架南北,天堑变通途”. 在科技腾飞的当下,路桥建设部门仍然潜心研究如何缩短空间距离方便出行,如港珠澳跨海大桥等. 如图为某工程队将A 到D 修建一条隧道,测量员测得一些数据如图所示(A ,B ,C ,D 在同一水平面内),则A ,D 间的距离为A .65123km -B .651213km -C .35123km -D .351213km -二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.) 9.在ABC ∆中,角A,B,C 所对边分别为a,b,c ,b =15,c =16,B =60°,则a 边为A .833+B .83161+C .833-D .83161-10.设m ,n 是两条不同的直线,α,β是两个不同的平面,则下列命题不正确的是A .若m ∥α,n ∥α,则m ∥nB .若m ∥α,m ∥β,则α∥βC .若m ∥n ,m ⊥α,则n ⊥αD .若m ∥α,α⊥β,则m ⊥β11.在ABC Rt ∆中,BD 为斜边AC 上的高,下列结论中正确的是A .2AB AB AC =⋅ B .2BC CB AC =⋅ C .2AC AB BD =⋅D .2BD BA BD BC BD =⋅=⋅12.如图,在边长为4的正三角形ABC 中,D ,E ,F 分别为各边的中点,G ,H 分别为DE ,AF 的中点,将ABC ∆沿DE ,EF ,DF 折成正四面体P DEF -,则在此正四面体中,下列说法正确的是 A .PG 与DH 所成的角的正弦值为23B .DF 与PE 成角2π C .GH 与PD 所成的角为4πD .PG 与EF 所成角余弦值为3第Ⅱ卷(非选择题,共90分)ADBC三、填空题(本大题共4小题,每小题5分,共20分.) 13.已知复数z =210(3i)+(i 为虚数单位),则|z |=________.14.化简:sin()tan()cos()2=cos()tan()++---παπαπααπα. 15.在三棱锥A BCD -中,ABC ∆是边长为3的正三角形,BD ⊥平面ABC 且BD =4,则该三棱锥的外接球的体积为 .16.已知向量a ,b 满足|a |=1,|b |=1,则|a +b |+|a -b |的最小值是______;最大值是_________.(本小题第一空2分,第二空3分)四、解答题(本题共6小题,共70分. 17题10分,18题—22题每题12分,解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分10分)已知:a =),cos ,sin 2(x x b =)cos 32,(cos x x - 设函数f (x )=a ⋅b +3+1.(1)求函数f (x )的最小正周期T 及单调递增区间; (2)当x ∈⎝ ⎛⎭⎪⎫π4,5π6时,求函数f (x )的值域.18.(本小题满分12分)已知ABC ∆的内角,,A B C 的对边分别为,,a b c ,若1cos 2b Ac a =-, (1)求B ;(2)若ABC ∆为锐角三角形,且1c =,求ABC ∆面积的取值范围.19. (本小题满分12分)如图,AB 是圆柱OO 1底面的直径,PA 是圆柱OO 1的母线,C 是圆O 上的点,Q 为PA 的中点,G 为AOC ∆的重心. (1)求证:BC PC ⊥; (2)求证:QG ∥平面PBC .20. (本小题满分12分)已知:1sin cos 2α+α=,2α∈ππ(,). (1)求sin cos α-α的值; (2)求tan ,tan 2αα的值.21.(本小题满分12分)如图,在边长为4的菱形ABCD 中,∠DAB =60°.点E ,F 分别在边CD ,CB 上,点E 与点C ,D 不重合,EF ⊥AC ,EF ∩AC =O .沿EF 将△CEF 翻折到△PEF 的位置,使平面PEF ⊥平面ABFED .(1)若AO :OC =5:3,求棱锥P -ABD 的体积; (2)当PB 取得最小值时,求二面角P -BF -D 的余弦值.22.(本小题满分12分)已知函数()()3sin 21(0)22f x x ππωϕωϕ++><<,-,函数()f x 的图像经过点112,π⎛⎫- ⎪⎝⎭且()f x 的最小正周期为2π. (1)求函数()f x 的解析式;(2)将函数)(x f y =图像上所有的点向下平移1个单位长度,再将函数图像上所有点的横坐标变为原来的2倍,纵坐标不变,再将图像上所有的点的横坐标不变,纵坐标变为原来23倍,得到函数()y h x =图像,令函数()()1g x h x =+,区间[,]a b (,a b R ∈且)a b <满足:()y g x =在[,]a b 上至少有30个零点,在所有满足上述条件的[,]a b 中,求b a -的最小值;(3)若1313(()1)cos 081222x m f x ⎡⎤+--++≤⎢⎥⎣⎦π对任意[]0,2x π∈恒成立,求实数m 的取值范围.2021年普通高中学业质量监测考试高一数学 参考答案及评分标准一、单项选择题 1-8 BDBA DCCA 二、多项选择题9.AC 10.ABD 11.AD 12.BCD 三、填空题13.1 14.αcos 15.2837π16. 2(2分);22(3分)四、解答题17.解:(1)f (x )=2sin ⎝⎛⎭⎪⎫2x -π3 π=T -----------------------------------4分由2k π-π2≤2x -π3≤2k π+π2,k ∈Z ,得k π-π12≤x ≤k π+5π12.则函数递增区间为⎣⎢⎡⎦⎥⎤k π-π12,k π+5π12,k ∈Z .-----------------5分(2)由π4<x <5π6,得π6<2x -π3<4π3,则-32<sin ⎝⎛⎭⎪⎫2x -π3≤ ∴1-3<y ≤3,即值域为(1-3,3].----------------------10分 18.(1)1cos 2b Ac a =-解:因为,1sin cos sin sin 2B AC A=-由正弦定理得11sin cos sin()sin sin cos sin cos cos sin sin 22B A A B A B A A B A B A=+-⇒=+- 110cos cos 22B B ⇒=-⇒=所以3B π=.------------------------------------------------------------------------------------------6分(2)因为ABC 是锐角三角形,由(1)知3B π=,A B C π++=得到23A C π+=, 故022032C C πππ⎧<<⎪⎪⎨⎪<-<⎪⎩,解得62C ππ<<.------------------------------------------------------8分又应用正弦定理sin sin a cA C=,1c =, 由三角形面积公式有:222sin()111sin 33sin sin sin 222sin sin ABCC a A Sac B c B c B c C Cπ-=⋅=⋅=⋅=22sin cos cos sin 333sin 3212313(sin cos )3tan 38tan C C C C C ππππ-==-=分又因3,tan 62C C ππ<<>331338tan C <+<故3382ABCS <<. 故ABCS的取值范围是33(------------------------------------------12分19.证:(1)由AB 是圆O 的直径,得AC ⊥BC .----------2分 由PA ⊥平面ABC ,BC ⊂平面ABC ,得PA ⊥BC ,-------4分 又PA ∩AC=A,PA ⊂平面PAC ,AC ⊂平面PAC , 所以BC ⊥平面PAC .又因为PC ⊂平面PAC所以BC PC ⊥;-----------------------------------6分 (2)连OG 并延长交AC 与M ,链接QM ,QO . --------8分 由G 为∆AOC 的重心,得M 为AC 中点, 由G 为PA 中点,得QM//PC .又O 为AB 中点,得OM//BC . --------------------10分 因为QM ∩MO=M, ,平面平面PBC OMQ //∴QG ⊂平面OMQ . 所以QG//平面PBC .------------------------------12分20.解:(1)因为,21cos sin =+αα平方得11+2sin cos 4αα=, 所以2sin cos -34αα=.----------2分由2απ<<π,2sin cos 0αα<,所以sin 0,cos 0αα<>.所以27(sin cos )12sin cos 4αααα-=-=.------------4分 所以7sin cos αα-=.--------------------6分 (2)由7sin cos 2αα-=-,结合1sin cos 2αα+= 可得7171sin αα-++==.------------8分所以sin7174tancos71ααα-+-===+-----------------------------10分1cossin sin sin1cos272222tan12sin3cos cos sin sin2222ααααααααααα---=====---------------------------------------------------------------12分21.解:(1)在边长为4菱形ABCD中,因为60DAB∠=︒,所以ABD∆,BDC∆为等边三角形,AC=34, 3:5:=OCAO,,233233=∴=∴POOC,--------3分∵菱形ABCD的对角线互相垂直,∴BD AC⊥,∴BD AO⊥,∵EF AC⊥,∴PO EF⊥.∵平面PEF⊥平面ABFED,平面PEF平面ABFED EF=,且PO⊂平面PEF,∴PO⊥平面ABFED,6233324213131ABD-=⨯⨯⨯⨯=⋅⋅=∴∆POSVABDP----------------6分(2)∵PO⊥平面ABFED, BO⊂平面ABFED,∴PO BO⊥设.AO BD H⋂=因为60DAB∠=︒,所以BDC∆为等边三角形,故4BD=,2,23HB HC==.又设PO x=,则23OH x=-,22OB OH+=HB 在POBRt∆中,所以2222(23)22(3)10PB x x x=-++=-+,当3x=时,min10PB=.------------8分由O做BF垂线,垂足为M,连接PM,BMPOABFEDABFED,BFPO⊥∴⊂⊥平面平面POMBMOPOOM平面,⊥∴=⋂PM BM POM PM ⊥∴⊂,平面所以二面角P-BF-D 的平面角为OMP ∠----------------------------10分 在POM Rt Δ中,21523==PM OM , 55PM OM OMP cos ==∠.----------------------------------------12分 22.解:(1)()()3sin 21f x x ωϕ=++,又函数()f x 的最小正周期为2π, 222ππω∴=,2ω∴=.-----------------------------1分 ()()3sin 41f x x ϕ∴++.又函数()f x 经过点-112π(,),所以(-)3sin -1=1123f ππϕ⎛⎫∴=++ ⎪⎝⎭,于是4(),12k k Z πϕπ⎛⎫⨯-+=∈ ⎪⎝⎭因为22πϕπ<<-,所以3πϕ=------------------------------------------2分()3413f x x π⎛⎫∴=++ ⎪⎝⎭.-------------------------------4分(2)由题意,h (x )=2sin (2x+π3 )()2sin 213g x x π⎛⎫=++ ⎪⎝⎭------------------------------------------6分令()0g x =得:1sin 232x π⎛⎫+=- ⎪⎝⎭ 72236x k πππ∴+=+或112236x k πππ+=+,k Z ∈解得:512x k π=π+或34x k ππ=+,k Z ∈∴相邻两个零点之间的距离为3π或23π-------------------------------------------7分若b a -最小,则,a b 均为()g x 的零点,此时在区间[],a a π+,[],2a a π+,…,[](),a m a m N π*+∈分别恰有3,5,,21m ⋅⋅⋅+个零点精品 Word 可修改 欢迎下载 ∴在区间[],14a a π+恰有214129⨯+=个零点(]14,a b π∴+至少有一个零点 ()143b a ππ∴-+≥,即431433b a πππ-≥+= 检验可知,在5543,12124πππ⎡⎤+⎢⎥⎣⎦恰有30个零点,满足题意(可有可无) b a ∴-的最小值为433π--------------------------8分。
辽宁省市高一数学下学期期末考试试题(含解析)

A. 若 ,则
B. 若 , , 分别表示 , 面积,则
C. 两个非零向量a,b,若 ,则a与b共线且反向
D. 若 ,则存在唯一实数 使得
【答案】AD
【解析】
【分析】
对每一个选项逐一分析判断得解.
【详解】A.若 ,则 ,如果 都是非零向量, ,显然满足已知条件,但是结论不一定成立,所以该选项是错误的;
辽宁省2021-2022高一数学下学期期末考试试题(含解析)
注意事项:
1.本试卷分第Ⅰ卷、第Ⅱ卷两部分,共4页。满分150分;考试时间:120分钟。
2.答题前,考生务必将自己的姓名、准考证号、考试科目、试卷类型用2B铅笔涂在答题卡上。
3.用铅笔把第Ⅰ卷的答案涂在答题卡上,用钢笔或圆珠把Ⅱ卷的答案写在答题纸的相应位置上。
(3)由两名运动员来自同一协会有 , , , ,共4种,利用古典概型,即可求解.
【详解】(1)由题意,从这6名运动员中随机抽取2名参加双打比赛,所有可能的结果为
, , , , , , , , ,
, , , , , ,共15种.
(2)因为丙协会至少有一名运动员参加双打比赛,所以编号为 , 的两名运动员至少有一人被抽到,其结果为:设“丙协会至少有一名运动员参加双打比赛”为事件 ,
分数段
[70,80)
[80,90)
[90,100)
[100,110)
[110,120)
x:y
1:2
2:1
6:5
1:2
1:1
【答案】(1) (2)平均分为 ,中位数为 (3)140人
【解析】
【分析】
(1)由题得 ,解方程即得解;(2)利用频率分布直方图中平均数和中位数的计算公式估计这200名学生的平均分和中位数;(3)分别计算每一段的人数即得解.
2021-2022学年辽宁省大连市高一下学期期末数学试题【含答案】

2021-2022学年辽宁省大连市高一下学期期末数学试题一、单选题1.已知复数,其中是虚数单位,则的共轭复数是( )()i 12i z =-i z A .B .C .D .2i -2i+12i+12i-A【分析】结合复数乘法、共轭复数等知识求得正确答案.【详解】.()2i 12i i,2iz z =+==--故选:A 2.若,且为第四象限角,则的值为( )12cos 13α=αtan αA .B .C .D .125125-512512-D【分析】结合同角三角函数的基本关系式求得正确答案.【详解】由于,且为第四象限角,12cos 13α=α所以,5sin 13α==-.sin 5tan cos 12ααα==-故选:D3.若、是空间中两条不同的直线,则的充分条件是( )a b a b ∥A .直线、都垂直于直线B .直线、都垂直于平面a b l a b αC .直线、都与直线成角D .直线、都与平面成角a b l 30°a b α60︒B【分析】根据线线平行、线线角等知识对选项进行分析,从而确定正确选项.【详解】A 选项,都与垂直,可能,A 选项错误.,a b l a b ⊥B 选项,都垂直于平面,则,B 选项正确.,a b αa b ∥C 选项,都与成角,可能相交,C 选项错误.,a b l 30°,a bD 选项,都与平面成角,可能异面,D 选项错误.,a b α60︒,a b 故选:B4.民间娱乐健身工具陀螺起源于我国,最早出土的石制陀螺是在山西夏县发现的新石器时代遗址.如图所示的是一个陀螺的立体结构图.已知底面圆的直径,16cm AB =圆柱体的高,圆锥体的高,则这个陀螺的表面积是( )8cm BC =6cm CD =A .B .C .D .2192πcm 2208πcm 2272πcm 2336πcm C【分析】结合组合体表面积的计算方法计算出正确答案.【详解】圆柱、圆锥的底面半径为,8cm,10cm =所以陀螺的表面积是.22π82π88π810272πcm ⨯+⨯⨯+⨯⨯=故选:C5.如图,小明同学为测量某建筑物的高度,在它的正东方向找到一座建筑物,CD AB 高为,在地面上的点(,,三点共线)测得楼顶、建筑物顶部的仰12m M B M D A C 角分别为和,在楼顶处测得建筑物顶部的仰角为,则小明测得建筑物15︒60︒A C 30°的高度为( )(精确到CD 1m 1.414≈ 1.732≈A .B .C .D .42m 45m 51m 57mD【分析】先求得,然后利用正弦定理求得,进而求得.AM CM CD 【详解】在直角三角形中,,ABM 1212sin15,sin15AM AM ︒==︒在三角形中,,ACM 301545,1806015105CAM CMA ∠=︒+︒=︒∠=︒-︒-︒=︒,1801054530ACM ∠=︒-︒-︒=︒由正弦定理得,sin 45sin 45sin 30sin 30CM AM AM CM ==⋅︒=︒︒︒在直角三角形中,CDM sin60,sin60CDCD CMCM︒==⋅︒======.363612 1.73257m=+=+⨯≈故选:D6.设是空间四个不同的点,在下列命题中,不正确的是A B C D,,,A.若与共面,则与共面AC BD AD BCB.若与是异面直线,则与是异面直线AC BD AD BCC.若==,则AB AC DB,DC AD BC⊥D.若==,则=AB AC DB,DC AD BCD【分析】由空间四点共面的判断可是A,B正确,;C,D画出图形,可以判定AD与BC不一定相等,证明BC与AD一定垂直.【详解】对于选项A,若与共面,则与共AC BD A B C D AD,,,是四点共面,则BC面,正确;对于选项B,若与是异面直线,则四点不共面,则与是异面AC BD,,,A B C D AD BC直线,正确;如图,空间四边形ABCD中,AB=AC,DB=DC,则AD与BC不一定相等,∴D错误;对于C,当四点共面时显然成立,A B C D,,,当四点不共面时,取BC的中点M,连接,,,A B C DAM、DM,AM⊥BC,DM⊥BC,∴BC⊥平面ADM,∴BC⊥AD,∴C正确;本题通过命题真假的判定,考查了空间中的直线共面与异面以及垂直问题,是综合题.7.将函数的图象向右平移个单位长度后,得到函数的图象,sin 2y x =ϕcos 26y x π⎛⎫=+ ⎪⎝⎭则的值可以是( )ϕA .B .C .D .12π6π3π23πD【分析】利用三角函数图象变换可得出变换后的函数解析式,由已知可得出关于的ϕ等式,即可得出结果.【详解】因为,2cos 2sin 2sin 26623y x x x ππππ⎛⎫⎛⎫⎛⎫=+=++=+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭将函数的图象向右平移个单位长度后,得到函数sin 2y x =ϕ的图象,()()sin 2sin 22y x x ϕϕ=-=-⎡⎤⎣⎦由题意可得,可得,当时,,()2223k k ππϕ=-∈Z ()3k k πϕπ=-∈Z 1k =23ϕπ=故选:D.8.已知圆台上下底面半径分别为3、4,圆台的母线与底面所成的角为.且该圆台45︒上下底面圆周都在某球面上,则该球的体积为( )A .B .C .D .100π5003π200π7003πB【分析】根据圆台轴截面及已知求圆台的高,再根据球体半径与圆台上下底面半径的几何关系列方程求出球体半径,进而求球体的体积.【详解】由题意,轴截面如下图示,1AE DE ==若球体半径为R ,则,可得.229(1R -=5R =所以该球体积为.3450033R ππ=故选:B 二、多选题9.设非零复数、所对应的向量分别为,,则下列选项能推出1z 2z 1OZ 2OZ的是( )12OZ OZ ⊥A .B .C .D .12i z z =122z z =12=z z 1212z z z z +=-AD【分析】A 根据的几何意义判断;B 由即可判断;C 由12i z z =122OZ OZ =即可判断;D 由并结合向量数量积的运算律即可12||||OZ OZ = 1212OZ OZ OZ OZ +=- 判断.【详解】A :等价于将绕原点逆时针旋转得到,即,符12i z z =2OZ 90︒1OZ 12OZ OZ ⊥合;B :等价于,即共线,不符合;122z z =122OZ OZ =12,OZ OZ C :等价于,但不一定有,不符合;12=z z 12||||OZ OZ =12OZ OZ ⊥ D :等价于,两边平方并应用数量积的运算律1212z z z z +=-1212OZ OZ OZ OZ +=-可得,即,符合.120OZ OZ ⋅=12OZ OZ ⊥ 故选:AD10.一个正方体内接于一个球,过球心作一个截面,则截面的图形可能是( )A.B.C.D.ABC【分析】根据正方体截面过外接球球心,讨论截面是否过顶点及所过顶点个数、是否与侧面平行,即可判断截面图形的元素.【详解】当过球心的截面不平行于侧面且不过顶点时,截面图形为A;当过球心的截面平行于一对侧面时,截面图形为C;当过球心的截面过其中4个顶点,则截面图形为圆中含一个长方形,B正确,D错误.故选:ABC11.下列各式正确的是()A.B.()()1tan11tan442+︒+︒=12sin10-=︒C.D.23sin7022cos10-=-︒︒)tan70cos102012︒⋅︒︒-=AC【分析】结合三角恒等变换对选项进行分析,从而确定正确答案.【详解】A选项,,()tan1tan44tan45tan144,11tan1tan44︒+︒︒=︒+︒=-︒⋅︒,tan1tan441tan1tan44︒+︒=-︒⋅︒所以()()1tan11tan441tan1tan44tan1tan44+︒+︒=+︒+︒+︒⋅︒,A选项正确.tan1tan44tan1t211an44︒⋅︒+︒⋅+-︒==B选项,1sin10=︒()()2cos60cos10sin60sin102cos601011sin20sin2022︒︒-︒︒︒+︒==︒︒,B选项错误.cos70sin20444sin20sin20︒︒=⋅=⋅=︒︒C 选项,,C 选项正确.23sin 703cos 203cos 2021cos 203cos 202cos 10222--︒-︒===+︒-︒-︒-︒D选项,)sin 70tan 70cos10201cos101cos 70⎫︒︒⋅︒⋅︒-=⋅︒⋅⎪⎪︒⎭cos 20cos10sin 20︒=⋅︒cos10︒,D 选项错误.()sin 20301sin10︒-︒===-︒故选:AC12.已知函数在区间上单调,且满足()()()sin 0,f x x ωϕωϕ=+>∈R 75,126ππ⎛⎫⎪⎝⎭有下列结论正确的有( )73124f f ππ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭A .203f π⎛⎫= ⎪⎝⎭B .若,则函数的最小正周期为;()56f x f x π⎛⎫-= ⎪⎝⎭()f x πC .关于x 的方程在区间上最多有4个不相等的实数解()1f x =[0,2)πD .若函数在区间上恰有5个零点,则的取值范围为()f x 213,36ππ⎡⎫⎪⎢⎣⎭ω8,33⎛⎤ ⎥⎝⎦ABD【分析】A :在上单调,,,故()f x 73,124ππ⎛⎫ ⎪⎝⎭73124f f ππ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭73212423πππ+=;203f π⎛⎫= ⎪⎝⎭B :求出区间右端点关于的对称点,由题可知在75,126ππ⎛⎫⎪⎝⎭56x π=23x π=2x π=()f x 上单调,据此可求出f (x )周期的范围,从而求出ω的范围.再根据5,26ππ⎛⎫ ⎪⎝⎭知是f (x )的对称轴,根据对称轴和对称中心距离为周期的()56f x f x π⎛⎫-= ⎪⎝⎭512x π=倍即可求出ω,从而求出其周期;()214k k +∈Z C :根据ω的范围求出周期的范围,根据正弦型函数一个完整周期只有一个最高点即可求解;D :由知,是函数在区间,上的第1个零点,而在203f π⎛⎫=⎪⎝⎭23π()f x 23π⎡⎢⎣136π⎫⎪⎭()f x 区间上恰有5个零点,则,据此即可求ω的范围.213,36ππ⎡⎫⎪⎢⎣⎭13252632T T ππ<- 【详解】A ,∵,∴在上单调,又7375,,124126ππππ⎛⎫⎛⎫⊆ ⎪ ⎪⎝⎭⎝⎭()f x 73,124ππ⎛⎫ ⎪⎝⎭,,∴,故A 正确;73124f f ππ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭73212423πππ+=203f π⎛⎫= ⎪⎝⎭B ,区间右端点关于的对称点为,∵,f (x )在75,126ππ⎛⎫⎪⎝⎭56x π=23x π=2x π=203f π⎛⎫= ⎪⎝⎭上单调,∴根据正弦函数图像特征可知在上单调,∴75,126ππ⎛⎫ ⎪⎝⎭()f x 5,26ππ⎛⎫⎪⎝⎭为的最小正周期,即3,又,∴.若512(62322T T ππππω-==⋅ ()f x )ω0>ω03ω< ,则的图象关于直线对称,结合,得()56f x f x π⎛⎫-= ⎪⎝⎭()f x 512x π=203f π⎛⎫= ⎪⎝⎭,即,故()252121312442k k T k ππππω++-===⋅∈Z ()42k k ω=+∈Z k =0,,故B 正确.2,T ωπ==C ,由,得,∴在区间上最多有3个完整的周期,而03ω< 23T π()f x [)0,2π在1个完整周期内只有1个解,故关于的方程在区间上最多()1f x =x ()1f x =[)0,2π有3个不相等的实数解,故C 错误.D ,由知,是函数在区间,上的第1个零点,而在203f π⎛⎫=⎪⎝⎭23π()f x 23π⎡⎢⎣136π⎫⎪⎭()f x 区间上恰有5个零点,则,结合,得,213,36ππ⎡⎫⎪⎢⎣⎭13252632T T ππ<- 2T πω=81033ω< 又,∴的取值范围为,故D 正确.03ω< ω8,33⎛⎤⎥⎝⎦故选:ABD.本题综合考察的周期、单调性、对称中心、对称轴等特性,()()()sin 0f x x ωϕω=+>解题的关键是熟练掌握正弦型函数对称轴,对称中心的位置特征,掌握正弦型函数单调性与周期的关系.常用结论:(1)单调区间的长度最长为半个周期;(2)一个完整周期内只有一个最值点;(3)对称轴和对称中心之间的距离为周期的倍.()214k k +∈Z 三、填空题13.函数的最小正周期为___________.()tan2xf x =2π直接由正切函数的周期公式可得答案.【详解】.212T ππ==故答案为.2π14.如图,在正四棱柱中,,是棱的中点,异面直1111ABCD A B C D-1AB =E BC 线与所成角的余弦值为,则______.1AB 1CE m m=127-【分析】作辅助线,根据异面直线的定义找到与所成角,解三角形即可求得1AB 1C E 答案.【详解】在正四棱柱中,连接 ,1111ABCD A B C D-1DC 则由于四边形是平行四边形,故 ,1111,AD B C AD B C =∥11AB C D 11AB DC ∥故异面直线与所成角即为与所成角,1AB 1C E 1DC 1C E 即即为异面直线与所成角或其补角,1DC E ∠1AB 1C E 设,则所以 ,12AA=1AB ==112,4CC DC ====1DE C E ===所以,1cos DC E ∠==故异面直线与所成角的余弦值为,则1AB 1C E m m =15.已知函数不是常数函数,且函数满足:定义域为,的图象关于()f x ()f x R ()f x 直线对称,的图象也关于点对称.写出一个满足条件的函数2x =()f x ()1,0______.(写出满足条件的一个即可)()f x (答案不唯一)()ππsin 22f x x ⎛⎫- ⎝=⎪⎭【分析】根据对称性确定正确答案.【详解】依题意,不是常数函数,定义域为,()f x R 图象关于直线对称,也关于点对称,2x =()1,0所以符合题意.()ππsin 22f x x ⎛⎫- ⎝=⎪⎭故(答案不唯一)()ππsin 22f x x ⎛⎫- ⎝=⎪⎭16.如图,四边形为正方形,平面,,若ABCD AG ⊥ABCD ////AG DF CE ,,,则______.3AG AB ==2DF =1CE =:B EGD G BEF V V --=22:1【分析】将几何体补全为正方体,由、G BEF ABCD GIHJ G HEBJ G HIFE B CDFE B DFGA V V V V V V ------=----求出体积,即可得结果.B EGD ABCD GIHJ G HEBJ G HIDE E BCD G ABD V V V V V V ------=----【详解】将几何体补全为正方体,如下图示,G BEF ABCD GIHJ G HEBJ G HIFE B CDFE B DFGAV V V V V V ------=----111111112735333333335332323232=-⨯⨯⨯⨯-⨯⨯⨯⨯-⨯⨯⨯⨯-⨯⨯⨯⨯.3=B EGD ABCD GIHJ G HEBJ G HIDE E BCD G ABDV V V V V V ------=----111111112735335313333332323232=-⨯⨯⨯⨯-⨯⨯⨯⨯-⨯⨯⨯⨯-⨯⨯⨯⨯.6=所以.:2:1B EGD G BEF V V --=故2:1四、解答题17.已知向量,.()1,2a =(),3b x =(1)若,求的值;()3a b b -⊥ x (2)若向量,夹角为锐角,求的取值范围.a b x(1);x =(2)或.362x -<<32x >【分析】(1)应用向量线性运算坐标表示可得,根据向量垂直的坐标3(3,3)a b x -=- 表示即可求参数值;(2)由题设有,注意排除,同向共线时对应x 值即可.60a b x ⋅=+> a b【详解】(1)由题设,,又,3(3,3)a b x -=- ()3a b b-⊥ 所以,即,(3)90x x -+=2390x x --=可得.x =(2)由题设,,即,60a b x ⋅=+>6x >-当,同向共线时,有且,此时,可得,不满足,夹角a b a b λ= 0λ>132x λλ=⎧⎨=⎩32x =a b 为锐角,综上,或.362x -<<32x >18.如图1,菱形中,,,垂足为点,将沿翻折ABCD 60A ∠=︒DE AB ⊥E AED DE 到,使,如图2.A ED ' A E BE '⊥(1)求证:平面;A E '⊥EBD (2)在线段上是否存在一点,使平面?若存在,求的值;若不存A D 'F EF ∥A BC 'DFFA '在,说明理由.(1)证明见解析;(2)存在,.1DFFA ='【分析】(1)推导出,由此能证明平面.,,DE AE A E DE A E BE ⊥⊥⊥''A E '⊥BCDE(2)分别取的中点,连接,推导出四边形是平行,A D A C '',F M ,,EF FM BM EBMF 四边形,,从而在线段上存在一点,使平面,且.//EF BM A D 'F //EF A BC '1DFFA ='【详解】(1)在菱形中,,ABCD ,DE AB DE AE ⊥∴⊥ ,,,A E DE A E BE DE BE E ''∴⊥⊥⋂= 平面.A E '∴⊥EBD (2)在线段上存在一点,使平面.A D 'F EF //A BC '理由如下:分别取的中点,连接,,A D A C '',F M ,,EF FM BM 为的中位线,,且,FM A DC 'FM DC ∴∥12FM DC =在菱形中,,且,ABCD EB DC ∥12EB DC=,且四边形是平行四边形,,FM EB ∴∥,FM EB =∴EBMF EF BM ∴∥平面平面,EF ⊄ ,A BC BM '⊂A BC '平面,EF ∴ A BC '为中点,F A D '.1DFFA ∴'=19.已知为坐标原点,对于函数,称向量为函数O ()sin cos f x a x b x =+(),a M b O =的相伴特征向量,同时称函数为向量的相伴函数.()f x ()f x OM (1)若向量为的相伴特征向量,求实数的值;()2,2m =()sin 4h x x πλ⎛⎫=+ ⎪⎝⎭λ(2)记向量的相伴函数是,求在的值域.()5,12m =()f x ()f x 20,3x π⎡⎤∈⎢⎥⎣⎦(1)(2)⎤⎥⎦【分析】(1)根据已知相伴特征向量的定义可得,即可求解;()2sin 2cos h x x x =+(2)根据相伴函数的定义结合三角恒等变换得到函数的解析式,利用正弦型函数()f x 的性质求解值域即可.【详解】(1)解:因为向量为的相伴特征向量,()2,2m =()sin 4h x x πλ⎛⎫=+ ⎪⎝⎭则,()sin 2sin 2cos 44h x x x x x ππλ⎛⎫⎛⎫=+=+=+ ⎪ ⎪⎝⎭⎝⎭解得.λ=(2)解:因为向量的相伴函数是()5,12m =,()5125sin 12cos 13sin cos 1313f x x x x x ⎛⎫=+=⨯+ ⎪⎝⎭设,则,512cos ,sin 1313θθ==sin 1θ<<32ππθ<<所以,()13sin()f x x θ=+当时,,20,3x π⎡⎤∈⎢⎥⎣⎦2,3x πϕϕϕ⎡⎤+∈+⎢⎥⎣⎦当时,函数有最大值为13,2x πϕ+=()f x 当时,即,函数有最小值为23x πϕϕ+=+23x π=()f x,222()5sin 12cos 333f πππ=⨯+⨯=故函数的值域为.()f x ⎤⎥⎦20.如图,在直三棱柱中,,且111ABC A B C -AC BC ⊥AC ==BC ,是棱的中点,是棱上的点,满足.12AA AB=D 1BB E 1CC 15CE EC =(1)证明:平面;AD ⊥1A DE (2)求直线与平面所成角的正弦值.AE 1ABB (1)证明见解析【分析】(1)先根据数量关系证明线线垂直,然后可得线面垂直;(2)先求解到平面的距离,然后根据线面角的定义求解正弦值.E 11ABB A【详解】(1)证明:因为,且;AC BC ⊥AC ==BC 3AB =因为,所以;12AA AB =16AA =因为是棱的中点,所以,D 1BB 1AD A D ==因为,所以;22211AD A D AA +=1AD A D ⊥因为,,所以;15CE EC =16AA =11,5C E CE ==在直角梯形中,,所以.11C B DE 11B C =13B D =DE =在直角三角形中,,所以ACE AC ==5CE AE 因为,所以.222AD DE AE +=AD DE ⊥由,,且,所以平面.1AD A D ⊥AD DE ⊥1=A D DE D ⋂AD ⊥1A DE (2)在直角三角形中,作于,如图,ACB CH AB ⊥H由等面积法可得;CH 由直棱柱的性质可得,所以平面;1AA CH ⊥CH ⊥11ABB A因为平面,所以到平面,1//CC 11ABB A E 11ABBA 设直线与平面所成角为,则AE 1ABB θsinθ==21.已知平面四边形中,,,.ABCD AB AD =AB AD ⊥AC =1BC =(1)若,求四边形的面积;56ACB π∠=ABCD (2)若记,.()0ACB θθπ∠=<<()CD f θ=①求的解析式;()f θ②求的最小值及此时角的值.CD θ(2)①②,此时.()f θ=CD 14πθ=【分析】(1)由余弦定理求得,,继而得,,根据三AB =cos CAB ∠sin DAC ∠AD 角形的面积公式可求得答案;(2)①由余弦定理求得,再由正弦定理求得,继而得,AB sin CAB ∠cos DAC ∠,根据余弦定理可求得;AD ()f θ②由角的范围和正弦函数的性质可求得的最小值及此时角的值.CD θ【详解】(1)在中,,,所 以ABCAC=1BC =56ACB π∠=,222+2cos AB AC CB AC BCACB =-⋅∠即,所以2225+11cos6AB π=-⨯AB =所以,222cos 2CA AB BCCABCA AB +-∠===⋅又,,所以AB AD =AB AD ⊥sin DAC ∠=AD AB ==所以,151sin 26ABC S π=⨯=19sin 24ADC S DAC =∠= 所以四边形ABCD (2)①在中,,,所 以ABC AC =1BC =ACB θ∠=,222+2cos AB AC CB AC BC θ=-⋅即,所以,222+11cos AB θ=-⨯24AB θ=-又,所以sin sin AB CB CAB θ=∠sinCAB ∠=又,,所以AB AD =AB AD⊥co s DAC ∠=,224A AB D θ=-=所以2222+cos AD AC CD AD AC DAC-⋅=∠4+3θ=--,7+4πθ⎛⎫=- ⎪⎝⎭所以;()CD f θ==②因为,所以,0θπ<<5444πππθ<<+所以当,即时,,42ππθ=+4πθ=min 14CD f π⎛⎫=== ⎪⎝⎭所以,此时.CD 14πθ=关键点睛:本题主要考查运用正弦定理、余弦定理解三角形,关键在于运用正弦定理 、余弦定理表示其边和角得的解析式.()f θ22.如图,在四棱锥中,,底面为正方形.记直线S ABCD -SAB SAD∠=∠π2≤ABCD 与平面所成的角为.SA ABCD θ(1)求证:平面平面;SAC ⊥SBD (2)若二面角的大小为,求的值;B SA D --2π3cos θ(3)当时,、中点为,,点为线段上的动点(包括端点),π2θ=SB BC M N P CD ,二面角的大小记为,求的取值范围.2SA AB =M NP A --αtan α(1)证明详见解析(3)2⎤⎦【分析】(1)通过证明平面来证得平面平面.BD ⊥SAC SAC ⊥SBD (2)判断出直线与平面所成的角,解直角三角形求得.SA ABCD θcos θ(3)作出二面角的平面角,结合三角函数值域的求法,求得的取值M NP A --tan α范围.【详解】(1)连接,交点设为,连接.,AC BD O SO 依题意可知,所以,SAB SAD ≅ AB SD =所以三角形中,,SBD SO BD ⊥由于,,BD AC AC SO O ⊥⋂=所以平面,BD ⊥SAC 由于平面,BD ⊂SBD 所以平面平面.SAC ⊥SBD (2)过作,垂足为,连接,B BK SA ⊥K DK 由已知,得,SAB SAD ≅ DK SA ⊥所以是二面角的平面角,BKD ∠B SA D --所以.2π3BKD ∠=设正方形的边长为,则,ABCD a BD =所以,,BK DK AK ===由于,,,DK SA BK SA DK BD K ⊥⊥⋂=所以平面,则.SA ⊥DKB SA KO ⊥过作,垂足为,S SE AC ⊥E 由于平面,所以,BD ⊥SAC BD SE ⊥由于,所以平面,AC BD O = SE ⊥ABCD 所以,即是直线与平面所成角.SAC θ∠=SAC ∠SA ABCD 在中,,Rt AKOAO =所以cos AK AO θ==(3)取中点,过作,垂足为,连接,AB Q Q QR NP ⊥R ,MQ MR 则为二面角的平面角,即,MRQ ∠M NP A --MRQ α∠=则,tan MQ QR α=由已知,设正方形的边长为,则,=MQ AB ABCD a MQ AB a ==在正方形中,设,ABCD PNC β∠=,当时,在三角形中,QN =π,arc tan 24PNC β⎡⎤∠=∈⎢⎥⎣⎦QNR ,3π3ππarc tan 2,442QNR β⎡⎤∠=-∈-⎢⎥⎣⎦()()3π3π3πsin arc tan 2sin cos arc tan 2cos sin arc tan 2444⎛⎫-=- ⎪⎝⎭==,3πsin 4β⎤⎛⎫-∈⎥ ⎪⎝⎭⎦.3πsin 4QR QN β⎛⎫=⋅- ⎪⎝⎭.tan MQ QRα==当时,在三角形中,,π0,4PNC β⎡⎤∠=∈⎢⎥⎣⎦QNR πππ,442QNR β⎡⎤∠=+∈⎢⎥⎣⎦,.πsin 4β⎤⎛⎫+∈⎥ ⎪⎝⎭⎦πsin 4QR QN β⎛⎫=⋅+ ⎪⎝⎭.tan 2MQQRα⎤==⎦综上所述,的取值范围是.tanα2⎤⎦。
辽宁省部分学校2022-2023学年高一下学期期末联考数学试题及参考答案

高一考试数学试卷注意事项:1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.4.本试卷主要考试内容:人教B 版必修第三册至必修第四册.一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.一个几何体的棱数是奇数,则这个几何体可能是( ) A .三棱锥 B .三棱柱C .四棱锥D .四棱柱2.31i2i −=+( ) A .31i 55−B .31i 55−+C .13i 55−D .13i 55−+ 3.若正五边形ABCDE 的中心为O ,以AO 所在的直线为轴,其余五边旋转半周形成的面围成一个几何体,则( ) A .该几何体为圆台B .该几何体是由圆台和圆锥组合而成的简单组合体C .该几何体为圆柱D .该几何体是由圆柱和圆锥组合而成的简单组合体4.已知向量(),1a m = ,()1,1b m =−,若()a ab ⊥+,则m =( )A .0或2B .2C .0或2−D .2−5.棣莫弗定理是由法国数学家棣莫弗发现的,由棣莫弗定理可以导出复数乘方公式:()()cos isin cos isin nnr r n n θθθθ + =+.根据复数乘方公式,复数20232cos isin 55ππ −+在复平面内对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限6.如图,在圆柱OO ′中,AB ,CD 分别为圆O ,O ′的直径,AB CD ∥,2AB BC ==,DE 为BC 的中点,则一只蚂蚁在圆柱表而从A 爬到E 的最短路径的长度为( )ABCD7.已知函数()2cos 3f x x πω=+(0ω>)在0,12π上恰有3个零点,则ω的取值范围为( ) A .(]40,48B .[)40,48C .(]42,46D .[)42,468.在直三棱柱111ABC A B C −中,23BAC π∠=,122AA AC AB ===,O 为四边形11AA C C 的中心,则异面直线1OB 与1A B 夹角的余弦值为( )ABCD二、选择题:本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.下列结论正确的是( )A .球心与球面上两个不同的点确定一个平面B .若直线l 上任意一点都不在平面α内,则l α∥C .若平面α∥平面β,直线l ⊥平面β,则l α⊥D .若直线l ∥平面α,直线l ⊥平面β,则αβ⊥ 10.已知()2,1A −,()3,2B ,()1,3C −,则( )A .()1,3AB =−−B .9AB AC ⋅=C.cos ,AB AC = D .AB 在AC 上的投影的数量为9511.若200450x x −+=(0x 为复数),则( ) A .02i x =±B .0054x x += C .2020258x x += D .4002455x x −=−12.在正三棱锥P ABC −中,PA 与底面ABC,AB = ) A .PC AB ⊥B .三棱锥P ABC −的体积为C .二面角P AB C −−的大小为3πD .三棱锥P ABC −的外接球的表面积为493π三、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.13.用斜二测画法画出的水平放置的ABC △的直观图如图所示,已知1A B ′′=,12A C ′′=,则BC =______.14.已知复数z 满足213i z z =++,则2z z +=______.15.在正四棱台1111ABCD A B C D −中,4AB =,112A B =,1AA =,则该棱台的体积为______.16.汾阳文峰塔建于明末清初,位于山西省汾阳市城区以东2公里的建昌村,该塔共十三层,雄伟挺拔,高度位于中国砖结构古塔之首.如图,某测绘小组为了测量汾阳文峰塔的实际高度AB ,选取了与塔底B 在同一水平面内的三个测量基点C ,D ,E ,现测得30BCD ∠=°,70BDC ∠=°,120BED °∠=,17.2m BE =,10.32m DE =,在点C 测得塔顶A 的仰角为62°,则塔高AB =______.(结果精确到1m ).参考数据:取tan62 1.88=°,sin700.94=°12.04=.四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)已知复数()216i z a a =+−,2223i z a a =−+,a ∈R .(1)若12z z +是纯虚数,求a ; (2)若120z z +>,求1z . 18.(12分)如图,正方体1111ABCD A B C D −被平面EFGH 截成两个几何体,其中E ,F ,G ,H 分别在棱11C D ,1CC ,1BB ,11A B 上.(1)证明:EF ∥平面DGH ;(2)若11122336AB A H BG EC FC =====,且直线HE 与GF 交于点O ,求三棱锥1O C EF −的体积.19.(12分)已知函数()()sin f x x ωϕ=+(0ω>,2πϕ<)在5,1818ππ−上单调递增,且直线18x π=−和518x π=为()f x 图象的两条对称轴. (1)求()f x 的解析式; (2)若函数()()6g x f x f x π=++,求()g x 的单调递增区间. 20.(12分)如图,在圆锥PO 中,AB 是圆O 的直径,C 为 AB 上更靠近A 的三等分点,D 为线段PO 的中点,且3PA =,圆锥PO 的侧面展开图是圆心角为43π的扇形.(1)求圆锥PO 的表面积; (2)求D 到平面PAC 的距离. 21.(12分)已知锐角ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,且()sin 1cos sin cos A B B A +=. (1)求A 的取值范围; (2)求2aa c+的取值范围.22.(12分)如图1,在等腰直角ABC △中,2C π∠=,D ,E 分别是AC ,AB 的中点,F 为线段CD 上一点(不含端点),将ADE △沿DE 翻折到1A DE △的位置,连接1A C ,1A B ,得到四棱锥1A BCDE −,如图2所示,且1A F CD ⊥.(1)证明:1A F ⊥平面BCDE ;(2)若直线1A E 与平面BCDE 1A BD C −−的平面角的正切值.高一考试数学试卷参考答案1.B 三棱锥有6条棱,三棱柱有9条棱,四棱锥有8条棱,四棱柱有12条棱.2.A31i 1i31i 2i 2i55−−==−+−. 3.B 由题意可知该几何体是由圆台和圆锥组合而成的简单组合体.4.C 由题意得()1,a b m m +=+,所以()10m m m ++=,得0m =或2−. 5.D 由题意得20232cos isin 55ππ−+()()2023202320232023332cos isin 2cos isin 5555ππππ=−+=−+, 因为()202320−<,3cos 05π<,3sin05π>,所以复数20232cos isin 55ππ −+在复平面内对应的点位于第四象限.6.A 如图,在半圆柱侧面的展开图上,AB π=,1BE =,则最短路径的长度为AE .7.D 因为0,12x π∈,所以,33123x πππωπω +∈+ .令2cos 03x πω +−= ,则cos 3x πω + .因为()2cos 3f x x πω =+在0,12π上有3个零点,所以232561236ππωππ≤+<,解得4246ω≤<. 8.C 如图,延长AB 至点D ,使AB BD =,延长11A B 至点E ,使111A B B E =,连接DE ,1B D ,易证11A B B D ∥,则异面直线1OB 与1A B 的夹角为1OB D ∠,过O 作FH AC ⊥,垂足为F ,交11A C 于H ,连接DF ,1B H ,OD ,由余弦定理得1B H =,DF =,所以12OB =,OD =,易得1B D =,所以1cos OB D ∠=.9.BCD 当球心与球面上两个不同的点在一条直线上时,不能确定一个平面,A 错误.易得B ,C ,D 正确.10.BCD 由题意得()1,3AB =,()3,4AC =− ,所以3129AB AC ⋅=−+=,cos ,AB AC AB ACAB AC⋅==,AB 在AC 上的投影的数量为95AB AC AC ⋅= . 11.ABD ()2200000450212i 2i x x x x x −+=⇒−=−⇒−=±⇒=±,A 正确.2000054504x x x x −+=⇒+=,B 正确. 22000200055254166x x x x x x +=⇒+=⇒+=,C 错误.22000045045x x x x −+=⇒=−,则()()()242200000000244524166425164251652555x x x x x x x x −=−−=−+=−+=×−+=−,D 正确. 12.ACD 由题意,作正三棱锥P ABC −,取AB 的中点D ,连接PD ,CD ,取等边ABC △的中心O ,连接PO ,AO ,如图所示.在正三棱锥P ABC −中,因为D 为AB 的中点,所以PD AB ⊥,在等边ABC △中,因为D 为AB 的中点,所以CD AB ⊥.又PD CD D = ,所以AB ⊥平面PDC ,则PC AB ⊥.易知PO ⊥平面ABC ,所以PAO ∠为PA 与底面ABC所成的角,则cos AO PAO AP∠=AB =2AO =,AP =,PO =,1DO =,所以三棱锥P ABC −的体积为(2133=.易知二面角P AB C −−的平面角为PDC ∠,又tan POPDC DO ∠=,所以3PDC π∠=.设正三棱锥P ABC −的外接球的半径为r ,则()222r PO CO r −+=,可得(224r r +=,解得r =,故正三棱锥P ABC −的外接球的表面积24943S r ππ==.故选ACD . 13由斜二测画法得,在ABC △中,2BAC π∠=,1AB AC ==,所以BC =14.3i −− 设i z a b =+(a ,b ∈R ),则()()i 2i 13i 2132i a b a b a b +=−++=++−, 所以21,32,a a b b =+ =− 得1,1.a b =− = 故()21i 21i 3i z z +=−++−−=−−.15.563如图,连接AC ,BD 交于点O ,连接11A C ,11B D 交于点1O ,连接1OO ,过1A 作1A M AC ⊥,垂足为M ,易得1A M 为四棱台1111ABCD A B C D −的高,则1111111122A O A C B ==1122AO AC ==, 所以)111(2AM AC A C =−=,12A M ==.故该棱台的体积为(156216433××++=.16.85m 由余弦定理得2222cos BD BE DE BE DE BED +−⋅⋅∠,则BD =212.0424.08m =×=.在BCD △中,由正弦定理得sin sin BD BCBCD BDC=∠∠, 则sin 24.080.9445.27m 1sin 2BD BDC BC BCD⋅∠×==≈∠.在ABC △中,62ACB ∠=°,所以tan 45.27 1.8885.107685m AB BC ACB =⋅∠≈×=≈. 17.解:(1)由题意得()2212236i z z a a a a ++−++−,因为12z z +是纯虚数,所以22230,60,a a a a +−= +−≠ ,得1a =.(2)因为120z z +>,所以22230,60,a a a a +−> +−=,得2a =.故144i z =−=.18.(1)证明:由正方体性质可得平面11ABB A ∥平面11DCC D ,∵平面11ABB A 平面EFGH GH =,平面11DCC D 平面EFGH EF =, ∴EF GH ∥.∵GH ⊂平面DGH ,EF ⊄平面DGH , ∴EF ∥平面DGH .(2)解:∵O HE ∈,HE ⊂平面1111A B C D ,∴O ∈平面1111A B C D .∵O GF ∈,GF ⊂平面11BCC B ,∴O ∈平面11BCC B . ∵平面1111A B C D 平面1111BCC B B C =,∴11O B C ∈.∵11OEC OHB △∽△,∴111123OC EC OB HB ==, 即()11263OC OC =+,则112OC =, ∴1111111118332O C EF C EF V S OC EC FC OC −=⋅=×⋅⋅=△.19.解:(1)设()f x 的最小正周期为T ,则5218183T ππππω ==−−=,得3ω=. 由题意得53182k ππϕπ×+=+(k ∈Z ), 得3k πϕπ=−+(k ∈Z ),因为2πϕ<,所以3πϕ=−.故()sin 33f x x π=−. (2)由题意得()sin 3sin 3sin 3cos 33233g x x x x x ππππ=−+−+=−+−333412x x πππ−+=−,由2322122k x k πππππ−+≤−≤+(k ∈Z ),得5272363363k k x ππππ−+≤≤+(k ∈Z ), 所以()g x 的单调递增区间为5272,363363k k ππππ−++ (k ∈Z ). 20.解:(1)由题意得4233AO ππ=×,得2AO =, 所以圆锥PO 的表面积为210AO AO PA πππ+⋅=.(2)由题意得D 到平面PAC 的距离等于O 到平面PAC 的距离的12. 因为C 为 AB 上更靠近A 的三等分点,所以AOC △为等边三角形,所以1sin 2AOC S AO CO AOC =⋅∠=△易得12PACS AC ==△,PO ==,设O 到平面PAC 的距离为h , 由1133O PAC PAC P AOC ADC V S h V S PO −−=⋅==⋅△△,得AOC PACS PO hS ⋅=△△ 故D 到平面PAC21.解:(1)由题意得()sin sin cos cos sin sin A B A B A B A =−=−, 所以A B A =−或A B A B π+−==(舍去),即2B A =.因为ABC △是锐角三角形,所以0,202,203,2A B A C A ππππ<<<<<=−<得,64A ππ∈ . (2)由正弦定理得()22sin 2sin sin sin sin sin cos cos sin aA A a cA AB A A B A B==+++++()2222sin 2sin 1sin sin cos2cos sin22cos sin sin 2cos 12sin cos A A A A A A A AA A A A A ==+++−+, 由,64A ππ ∈,得cos A ∈,232cos 1,2A ∈ , 所以2212,12cos 3aa cA =∈+ ,即2a a c +的取值范围为2,13. 22.(1)证明:∵2C π∠=,DE BC ∥,∴DE AD ⊥(1DE A D ⊥),DE CD ⊥. ∵1A D CD D = ,∴DE ⊥平面1A DC . ∵1A F ⊂平面1A DC ,∴1DE A F ⊥.又CD DE D = ,∴1A F ⊥平面BCDE .(2)解:在图2中,连接EF .由题意得1A D CD DE ==,∵1A F ⊥平面BCDE ,∴直线1A E 与平面BCDE 所成的角为1A EF ∠,则1tan A EF ∠=. 设DF x =,则1A F =,EF∴11tan A F A EF EF ∠=,得12A D x =,即F 为CD 的中点. 过F 作FO BD ⊥,垂足为O .∵1A F ⊥平面BCDE ,∴1A F BD ⊥, ∵1A F OF F = ,∴BD ⊥平面A OF ,∴1AO BD ⊥, ∴二面角1A BD C −−的平面角为1A OF ∠.由题意得4,2BC x CD x ==,则BD,∴12CD BC OF x BD ⋅=⋅,∵1A F =,∴11tan A F A OF OF ∠=.。
辽宁省沈阳市联合体2022-2023学年高一下学期期末数学试题(解析版)

2022—2023学年度(下)联合体高一期末检测数学(满分:150分 考试时间:120分钟)注意事项:1.答题时,考生务必将自己的姓名、准考证号填写在答题卡规定的位置上.2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦擦干净后,再选涂其他答案标号.3.答非选择题时,必须使用黑色墨水笔或黑色签字笔,将答案书写在答题卡规定的位置上,写在试题卷、草稿纸上无效.4.考试结束后,将试题卷和答题卡一并交回.第Ⅰ卷(选择题,共60分)一、单选题(本大题共8小题,每小题5分,共40分.在每小题所给的四个选项中,有且只有一项是符合题目要求的)1. cos1560°的值为( )A.12B. 12−C.D. 【答案】B 【解析】【分析】利用三角函数的诱导公式与特殊角的三角函数值求解即可. 【详解】()1cos1560cos 4360120cos1202°=×°+°=°=−. 故选:B.2. 已知i 为虚数单位,复数()2iR 2iz a −∈+,则它的共轭复数z 为( ) A.34i 55+ B. 34i 55−C. 41i 5+D. 41i 5−【答案】A 【解析】【分析】利用复数的四则运算与共轭复数的概念即可得解.【详解】因为2i (2i)(2i)34i 34i 2i (2i)(2i)555z−−−−====−++−,所以34i 55z =+. 故选:A.3. 如图,一个水平放置的四边形ABCD 的斜二测画法的直观图是矩形A B C D ′′′′,A B ′′=O ′是A D ′′的中点,则原四边形ABCD 的面积是( )A. B. C. D.【答案】A 【解析】【分析】首先求出O B ′′,A D ′′,即可得到平面图形中AD ,OB 的值,即可求出四边形ABCD 的面积.【详解】在直观图中O A B ′′′△为等腰直角三角形,所以O A A B ′′′′==所以O B ′′O ′是A D ′′的中点,所以2A D O A ′′′′==,所以在平面图形中AD =,2OB O B ′′==所以ABCD S AD OB =×==故选:A 4. 已知π02α<<,π2cos 65α+=−,则5πtan 6α −= ( )A.B. C.D. 【答案】C 【解析】【分析】利用三角函数的基本关系式与诱导公式即可得解.【详解】因为π02α<<,所以ππ2π663α<+<,则πsin 6α +所以πsin π6tan π6cos 6ααα+ += +,所以5πtan 6α−= ππtan πtan 66αα−+=−+.故选:C.5. 已知ABC 的外接圆半径为1,π3A =,则cos cos AC C AB B ⋅+⋅=() A. 12B. 1C.D.【答案】D 【解析】【分析】利用正弦定理化边为角,再利用两角和的正弦公式结合三角形内角和定理即可得解. 【详解】由正弦定理可得2sin sin sin AB AC BCC B A===, 所以2sin,2sinAB C AC B ==, 则()cos cos 2sin cos 2sin cos 2sin 2sin AC C AB B B C C B B C A ⋅+⋅=+=+==.故选:D6. 已知向量a 、b满足2= a ,b = 2a b ⋅=− ,设a 与a b + 的夹角为θ,则cos θ=( ) A.12B. 12−C.D. 【答案】C 【解析】【分析】由已知条件,求出a b + 及()a ab ⋅+,然后利用向量的夹角公式即可求解.【详解】解:因为2a = ,b = 2a b ⋅=−,所以a + ,.()22222a b a b a a ⋅++=⋅==− ,所以()cos a b ba a aθ⋅==++故选:C.7. 函数()1πtan 23f x x =− 在一个周期内的图像是( )A. B.C. D.【答案】A 【解析】【分析】利用正切函数的周期及单调区间排除错误选项,即可得到正确结果.【详解】函数()1πtan 23f x x =−的最小正周期π2π12T ==, ∵选项D 的最小正周期5πππ66T=−−=,D 错误; 令π1ππππ,2232k x k k −<−<+∈Z ,解得π5π2π2π,33k x k k −<<+∈Z ,故()1πtan 23f x x =− 的单调递增区间为()π5π2π,2π33k k k −+∈ Z , 取0k =,则()1πtan 23f x x =− 的单调递增区间为π5π,33 − ,故A 正确,B 、C 错误; 故选:A.8. 龙洗是我国著名的文物之一,因盆内有龙纹故称龙洗,为古代皇宫盥洗用具,其盆体可以近似看作一个圆台.如图,现有一龙洗盆高15cm,盆口直径为40cm,盆底直径为20cm .往盆内倒入水,当水深6cm时,盆内水的体积近似为( )A. 3581πcmB. 3872πcmC. 31152πcmD. 31436πcm【答案】B 【解析】【分析】结合题意,利用平行线分线段成比例求得EF ,从而利用圆台的体积公式即可得解. 【详解】如图所示,画出圆台的立体图形和轴截面平面图形,并延长EC 与FD 交于点G .根据题意,得20cm,10cm,15cm,6cm AB CD AC EC ====.设cm,cm CG x EF y ==,CG CD CGAG EF EG=,即1010,20156x x x y x ==++,解得15,14x y ==,所以盆内水的体积为(()2231π14106872πcm 3V =+×. 故选:B.二、多选题(本大题共4小题,每小题5分,共20分.在每小题所给的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)9. 已知i 为虚数单位,下列说法正确的是( ) A. 234i i i i 0+++=B. 2i 2+=C. 若()212i z =−,则z 的虚部为4D. 已知复数z 满足2z =,则复数z 在复平面内对应点的集合是以O 为圆心、以2为半径的圆【答案】AD 【解析】【分析】根据复数的乘方判断A ,根据复数的模判断B ,根据复数的乘法化简,再由复数的概念判断C ,根据复数的几何意义判断D.【详解】对于A :234i i i i i 1i 10+++=−−+=,故A 正确;对于B :2i +=,故B 错误;对于C :()()22i 12i 412i 34i z =−=−−−+=,所以z 的虚部为4−,故C 错误;对于D :令i z x y =+,,R x y ∈,因为2z =2=,则224x y +=, 所以复数z 在复平面内对应点的集合是以O 为圆心、以2为半径的圆,故D 正确; 故选:AD10. 已知,A B 为点,,,l m n 为直线,,αβ为平面,则下列命题成立的是( ) A. 若m l ⊥,n l ⊥,则//m nB. 若m α⊥,//m n ,//n β,则αβ⊥C. 若∈A l ,B l ∈,且A α∈,B α∈,则l ⊂αD. 若m n ⊥,m α⊂,n β⊂,则αβ⊥ 【答案】BC 【解析】【分析】对于AD ,利用线面的位置关系直观想象即可判断;对于B ,利用线面与面面平行与垂直的性质与判定定理判断即可;对于C ,利用平面的性质即可判断.【详解】对于A ,若,m l n l ⊥⊥,则直线,m n 可能平行、相交或异面,故A 错误; 对于B ,因为//,m n m α⊥,所以n α⊥.又因为//n β,所以β内存在一条直线//l n ,所以l α⊥.由l β⊂,从而得到αβ⊥,故B 正确;对于C ,如果一条直线上的两点在一个平面内,那么这条直线也在此平面内. 因为∈A l ,B l ∈,且,A B αα∈∈,则l ⊂α,故C 正确;对于D ,由m n ⊥,如下图示//,m m m β′′⊂,此时//αβ,故D 错误.故选:BC.11. 在ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,下列说法正确的是( ) A. 若A B >,则sin sin A B > B. 若cos sin +ba C c A ,则45A=° C. 若0AB AC BC AB AC+⋅=,则B C = D. 若4a =,π6B =,符合条件的ABC 只有一个,则24b << 【答案】ABC 【解析】【分析】根据正弦定理判断A 、D ,利用正弦定理将边化角,再结合诱导公式及两角和正弦公式即可判断B ,根据单位向量及向量加法的平行四边形法则判断C.【详解】对于A :在三角形中,由A B >可得a b >,根据正弦定理可得sin sin A B >,故A 正确; 对于B :因为cos sin +ba C c A ,由正弦定理可得sin sin cos sin sin sin()sin cos cos sin B A C C A A C A C A C =+=+=+, 所以sin sin cos sin C A A C =,由在三角形中sin 0C >, 所以tan 1A =,又0180A <<°°,所以45A=°,故B 正确; 对于C :由AB AB、AC AC分别为向量AB 、AC 方向上单位向量, 根据平行四边形法则向量AB AC AB AC+平分角BAC ∠, 又0AB AC BC AB AC+⋅=, 的的所以AB AC =,所以B C =,故C 正确;对于D :若24b <<,即sin a B b a <<,此时符合条件的ABC 有两个,故D 错误. 故选:ABC .12. 如图,正方体1111ABCD A B C D −的棱长为1,P 是正方形1111D C B A 的中心,E 是PC 的中点,则以下结论正确的是( )A. BD ⊥平面PACB. 平面1//PAD 平面BDEC. 三棱锥D BCE −的体积为112D. 异面直线PC 与AB 所成的角为45°【答案】ABC 【解析】【分析】对于A ,利用线面垂直的判定定理即可得解;对于B ,利用线面平行与面面平行的判定定理即可得解;对于C ,利用三棱锥的体积公式即可得解;对于D ,利用异面直线的定义与余弦定理即可得解.详解】对于A ,设AC 与BD 交于点O ,连接PO ,如图,则PO ⊥平面ABCD ,又BD ⊂平面ABCD ,所以PO BD ⊥,又,,,AC BD PO AC O PO AC ⊥=⊂ 平面PAC ,所以BD ⊥平面PAC ,故A 正确; 对于B ,连接OE ,因为,O E 分别是,AC PC 的中点,则//OE PA ,又OE ⊄平面1PAD ,PA ⊂平面1PAD ,故//OE 平面1PAD ,【易得1//D P BD ,又BD ⊄平面1PAD ,1D P ⊂平面1PAD ,故//BD 平面1PAD , 又OE BD O = ,,OE BD ⊂平面BDE ,所以平面1//PAD 平面BDE ,故B 正确; 对于C ,因为E 是PC 的中点,所以E 到底面ABCD 的距离为1122PO =, 则11111132212D BCE E BCD V V −−==××××=,故C 正确; 对于D ,因为//CD AB ,所以异面直线PC 与AB 所成的角为DCP ∠或其补角, 连接PD,则1,CD PC PD == PCD中,221cos DCP +−∠≠ 所以异面直线PC 与AB 所成的角不等于45°,故D 错误. 故选:ABC.【点睛】关键点睛:本题C 选项解决的关键是利用中点的性质得到E 到底面ABCD 的距离,从而利用等体积法即可得解.第Ⅱ卷(非选择题,共90分)三、填空题(本大题共45分,共20分)13. 若5sin cos 4αα+=,则sin 2α=______. 【答案】916【解析】【分析】根据二倍角的正弦公式及平方关系运算求解即可. 【详解】∵5sin cos 4αα+=, ∴()225sin cos 12sin cos 1sin 216ααααα+=+=+=,∴9sin 216α=, 故答案为:916.14. 已知复数13i z =+,213i z =−+(i 为虚数单位)在复平面上对应的点分别为1Z ,2Z ,则12OZ OZ ⋅=______. 在【答案】0 【解析】【分析】利用复数的几何意义得到12,Z Z 的坐标,从而得到12,OZ OZ,由此利用向量的数量积运算即可得解. 【详解】因为复数123i,13i z z =+=−+在复平面上对应的点分别为12,Z Z ,所以12(3,1),(1,3)Z Z −,则12(3,1),(1,3)OZ OZ −, 所以123(1)130OZ OZ ⋅=×−+×=.故答案为:0.15. 海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径A ,B 两点间的距离,现在珊瑚群岛上取两点C ,D ,测得80CD =,135ADB ∠=°,15BDC DCA ∠=∠=°,120ACB ∠=°,则A ,B 两点间的距离为______.【答案】 【解析】【分析】根据题意,求得各个角度,即可得AD 长,根据正弦定理,可得BD 长,根据余弦定理,即可得答案.【详解】因为135ADB ∠=°,15BDC DCA ∠=∠=°, 所以150ADC ∠=°,15DAC DCA ∠=∠=°, 所以80AD CD ==, 又因为120ACB ∠=°,所以135,30BCD CBD ∠=°∠=°,由正弦定理得:sin sin BD CDBCD CBD=∠∠8012=,解得BD = 在ABD △中,由余弦定理得2222cos AB AD BD AD BD ADB =+−⋅∠,所以22280280AB =+−×× ,解得AB =m .故答案为:16. 已知四棱锥P ABCD −的底面四边形ABCD且PA ⊥平面ABCD,PA =,点M 为线段PC 上的动点(不包含端点),则当三棱锥M BCD −的外接球的体积最小时,CM 的长为_________. 【答案】2 【解析】【分析】连接MA ,由题意知三棱锥M BCD −的外接球即四棱锥M ABCD −的外接球,然后设四棱锥M ABCD −外接球的球心为O ,半径为R ,连接AC 与BD 交于点1O ,利用几何体的结构特征分析出当O与1O 重合时,三棱锥M BCD −的外接球的体积最小,然后设CM 的中点为N ,连接1O N ,利用三角形相似求得CN ,即可求得CM 的长【详解】因为PA ⊥平面ABCD ,AC ⊂平面ABCD ,所以PA AC ⊥, 连接MA ,由题意可知三棱锥M BCD −的外接球即四棱锥M ABCD −的外接球, 则当三棱锥M BCD −外接球的体积最小时,四棱锥M ABCD −外接球的半径最小, 设四棱锥M ABCD −外接球的球心为O ,半径为R ,连接AC 与BD 交于点1O , 当O 与1O 不重合时,连接1OO ,易知1OO ⊥平面ABCD ,则11OO O C ⊥,连接OC ,在1Rt OO C △中,1R OC O C =>,当O 与1O 重合时,1R OC O C ==, 所以当三棱锥M BCD −的外接球的体积最小时,O 与1O 重合,1R O C =.设CM 的中点为N ,连接1O N ,易知1O N CM ⊥,则11cos CN ACO CN CO PC∠==,=1CN =,所以22CMCN ==,故答案为:2四、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17. 已知复数()()2220235i z mm m m =−−++−,m ∈R .(1)若复数z 为纯虚数,求实数m 的值; (2)当3m =时,求i z z +. 【答案】(1)4− (2)66i + 【解析】【分析】(1)根据实部为0,虚部不为0得到方程(不等式)组,解得即可; (2)首先求出z ,再根据复数代数形式的运算法则计算可得. 【小问1详解】因为复数()()2220235i z mm m m =−−++−为纯虚数,所以222002350m m m m −−= +−≠ ,解得4m =−【小问2详解】当3m =时1420i z =−−,所以()()2i i 1420i 1420i 14i 20i 1420i 66i z z +=−−+−+=−−−+=+. 18. 如图,AB 为半圆O 的直径,2AB =,C 为 AB 上一点(不含端点).(1)用向量的方法证明AC BC ⊥;(2)若C 是 AB 上更靠近点B 的三等分点,Q 为 AC 上的任意一点(不含端点),求QA CB ⋅的最大值. 【答案】(1)证明见解析 (2)12 【解析】【分析】(1)建立平面直角坐标系,利用向量垂直的坐标表示可证;(2)利用坐标表示出QA CB ⋅,然后由三角函数性质可得.【小问1详解】如图,建立平面直角坐标系.(方法一)由题意可知1OB =,设COB α∠=,则()0,απ∈, ()1,0A −,()10B ,,()cos ,sin C αα,得()cos 1,sin AC αα=+ ,()cos 1,sin BC αα=−,所以22cos 1sin 110AC BC αα⋅=−+=−=,故⊥AC BC ,即ACBC ⊥.(方法二)由题意可知1OB =,()1,0A −,()10B ,,设(),C a b ,则1OB OC ==,得221a b +=,得()1,ACa b =+ ,()1,BCa b =−,所以221110AC BC a b ⋅=−+=−=, 故⊥AC BC ,即AC BC ⊥.【小问2详解】由题意得3COB π∠=,则12C, 设QOB β∠=,则,3πβπ∈,()cos ,sin Q ββ, 由(1)得1,2CB OB OC =−= ,()1cos ,sin QA ββ=−−−,所以111cos sin 2262QA CB πβββ⋅=−−=−−,由,3πβπ∈,得5,666πππβ −∈ ,当62ππβ−=,即23πβ=时,()max12QA CB ⋅= . 故QA CB ⋅ 的最大值为12.19. 如图,在正六棱锥S ABCDEF −中,O 为底面中心,8SO =,4OB =.(1)若M ,N 分别是棱SB ,SC 的中点,证明://MN 平面SAD ; (2)若该正六棱锥的顶点都在球Q 的表面上,求球Q 的表面积和体积.【答案】(1)证明见解析 (2)100πS =,500π3V = 【解析】【分析】(1)依题意可得//MN BC ,再由正六边形的性质得到//AD BC ,即可得证;(2)依题意可知球心Q 一定在直线SO 上,设球Q 的半径为R ,利用勾股定理求出R ,在根据球的表面积与体积公式计算可得. 【小问1详解】因为M ,N 分别是棱SB ,SC 的中点,所以//MN BC ,在正六边形ABCDEF 中,60AOB OBC ∠=∠=°,所以//AD BC , 所以//MN AD ,又MN ⊄平面SAD ,AD ⊂平面SAD ,所以//MN 平面SAD 【小问2详解】依题意可知球心Q 一定在直线SO 上,设球Q 的半径为R ,则QSQB R ==, 又222QB OQ OB =+,所以()22284R R =−+,解得5R =,所以球Q 的表面积24π100πS R ==,体积34π500π33R V ==.20. 已知ABC 的内角A ,B ,C 所对的边分别是a ,b ,c ,且2sin tan b A a B =. (1)求角B ;(2)若4a c +=,求ABC 周长的最小值,并求出此时ABC 的面积. 【答案】(1)π3(2)ABC 的周长的最小值为6,ABC S = 【解析】【分析】(1)将切化弦,再由正弦定理将边化角,即可得解;(2)利用余弦定理及基本不等式求出b 的最小值,即可求出周长的最小值,与此时三角形的面积. 【小问1详解】因为sin 2sin tan cos BbA aB a B==,即2sin cos sin b A B a B =, 由正弦定理可得2sin sin cos sin sin B A B A B =, 因为sin 0A >,sin 0B >,所以2cos 1B =,所以1cos 2B =, 因为()0,πB ∈,所以π3B =. 【小问2详解】由余弦定理()22222cos 3163b a c ac B a c ac ac =+−=+−=−, 即2316ac b =−,所以223163122a c ac b + =−≤=,所以24b ≥,解得2b ≥或2b ≤−(舍去), 当且仅当2a c ==时取等号,所以min 2b =,即ABC 的周长的最小值为6,此时1sin 2ABC S ac B == 21. 已知向量()cos ,cos a x x =,()cos b x x = ,函数()2f x a b =⋅,x ∈R .(1)求函数()f x 的最小正周期、值域; (2)对任意实数1x ,2x ,定义{}11212212,max ,,x x x x x x x x ≥ =< ,设()}maxsin ,cos g x x a x =,x ∈R ,a 为大于0的常数,若对于任意1x ∈R ,总存在2x ∈R ,使得()()12g x f x =恒成立,求实数a的取值范围.【答案】(1)π;[1,3]−(2)【解析】【分析】(1)利用向量的数量积运算与辅助角公式化简()f x ,从而利用三角函数的性质即可得解; (2)将问题转化为{}{}()()y y g x y y f x =⊆=,从而结合{}12max ,x x 的定义,分类讨论求得()g x 的值域,由此利用数轴法即可得解.【小问1详解】因为()cos ,cos a x x =,()cos b x x = ,函数()2f x a b =⋅ ,所以2()2cos cos cos 2212 f x x x x x b x a =⋅=+=++π2sin 216x++,所以函数()f x 的最小正周期为2ππ2T ==, 因为x ∈R ,所以πsin 2[1,1]6x +∈−,所以π2sin 21[1,3]6x++∈−, 故函数()f x 的值域为[1,3]−. 【小问2详解】若对于任意1x ∈R ,总存在2x ∈R ,使得()()12g x f x =恒成立, 则{}{}()()y y g x y y f x =⊆=,因为}sin sin cos ()max sin ,cos cos sin cos x x a xg x x a x a x x a x≥< ,sin cos x a x ≥sin cos 0x a x −≥,即π2sin 06a x−≥, 因为0a >,则πsin 06x −≥,即π2π2ππ,6k x k k ≤−≤+∈Z ,解得π7π2π,2π,66x k k k∈++∈Z ,则()sin g x x =∈;sin cos x a x <时,则5ππ2π,2π,66x k k k∈−++∈ Z,()cos ,g x a x a =∈ , 综上:()g x的值域为, 又()f x 的值域为[1,3]−,所以013a >≥− ≤,解得a ∈ ,所以实数a 的取值范围是 .【点睛】关键点睛:本题解决的关键有二,一是将问题转化为()f x 与()g x 的值域之间的关系,二是理解新定义的含义,结合三角函数的性质,分类讨论求得()g x 的值域,从而得解.22. 如图,在四棱锥P ABCD −中,PA ⊥底面ABCD ,底面ABCD 是直角梯形,90ADC ∠= ,//AD BC ,AB AC ⊥,AB AC ==E 在AD 上,且2AE ED =.(1)已知点F 在BC 上,且2=CF FB ,证明:平面PEF ⊥平面PAC ; (2)求点D 到平面PAB 的距离. 【答案】(1)证明见解析(2 【解析】【分析】(1)证明出EF ⊥平面PAC ,再利用面面垂直的判定定理可证得结论成立;(2)取BC 的中点G ,连接DG ,取AB 的中点H ,连接GH ,分析可知点D 到平面PAB 的距离等于点C 到平面PAB 的距离,证明出GH ⊥平面PAB ,求出GH 的长,即为所求. 【小问1详解】由AB AC ⊥且AB AC ==ABC 是等腰直角三角形,且2BC ,又因为四边形ABCD 为直角梯形,且90ADC ∠= ,//AD BC ,则45CAD ACB ∠=∠= ,所以,cos 451AD DC AC === , 因为2BC =,2AE ED =,2=CF FB ,所以,2221333AE AD ==×=,1122333BF BC ==×=,又因为//AD BC ,即//AE BF ,且AE BF =, 所以,四边形AEFB 为平行四边形,即//EF AB , 又因为AB AC ⊥,故EFAC ⊥,因为PA ⊥底面ABCD ,EF ⊂底面ABCD ,所以,EF PA ⊥, 因为PA AC A = ,PA 、AC ⊂平面PAC ,所以,EF ⊥平面PAC , 因为EF ⊂平面PEF ,因此,平面PEF ⊥平面PAC . 【小问2详解】取BC 的中点G ,连接DG ,因为//AD BG ,12AD BC BG ==,则四边形ADGB 为平行四边形,所以,//AB DG , 因为AB ⊂平面PAB ,DG ⊄平面PAB ,所以,DG//平面PAB , 所以,点D 到平面PAB 的距离等于点G 到平面PAB 的距离, 因为PA ⊥平面ABCD ,AC ⊂平面ABCD ,所以,AC PA ⊥,又因为AC AB ⊥,AB PA A = ,AB 、PA ⊂平面PAB ,所以,AC ⊥平面PAB , 取AB 的中点H ,连接GH ,因为H 、G 分别为AB 、BC 的中点,所以,//GH AC ,所以,GH ⊥平面PAB ,又因为45ABC ∠= ,所以,点G 到平面PAB 的距离为12GHAC ==,所以,点D 到平面PAB .。
2022-2023学年辽宁省沈阳市高一下学期期末数学试题【含答案】

2022-2023学年辽宁省沈阳市高一下学期期末数学试题一、单选题1.若()i1iz a a =+∈-R 是纯虚数,则=a ()A .12-B .12C .1-D .1【答案】B【分析】化简复数z ,然后根据实部为0可得.【详解】因为i i(1+i)11i 1i (1i)(1+i)22z a a a =+=+=-+--是纯虚数,所以102a -=,得12a =.故选:B 2.设13cos6sin 622a =︒-︒,22tan131tan 13b ︒=-︒,1cos502c -︒=,则有()A .a b c >>B .a b c <<C .a c b<<D .b<c<a【答案】C【分析】利用辅助角公式化简a ,正切二倍角公式和放缩放化简b ,余弦二倍角公式化简c ,然后根据正弦函数的单调性比较可得.【详解】()13cos 6sin 6sin 30cos 6cos 30sin 6sin 306sin 2422a =︒-︒=︒︒-︒︒=︒-︒=︒,22tan13sin 26sin 26tan 26sin 261tan 13cos 261b ︒︒︒==︒=>=︒-︒︒,1cos50sin 252c -︒==︒,当090x ︒<<︒,sin y x =单调递增,所以sin 26sin 25sin 24︒>︒>︒,所以a c b <<.故选:C3.已知向量a ,b 满足||1a = ,||1b = ,a 与b 的夹角为π4,则a b - 在b 上的投影向量为()A .24b B .22b C .424b +rD .222b -+【答案】D【分析】根据数量积定义先计算()a b b -⋅,然后由投影向量定义可得.【详解】因为||1a = ,||1b = ,a 与b 的夹角为π4,所以()22π2cos 142a b b a b b a b b -⋅=⋅-=-=-,所以a b - 在b上的投影向量为()222122a b b b b b b b -⋅⎛⎫-+⋅=-= ⎪ ⎪⎝⎭.故选:D4.在ABC 中,120,BAC AD ∠=︒平分,3BAC AD ∠=,则2AC AB +的最小值为()A .632+B .632-C .962+D .962-【答案】C【分析】记,AB c AC b ==,在ABD △中,2293BD c c +=-,在ACD 中,2293CD b b =+-,由AD平分BAC ∠,得到c b =或3()b c bc +=,当c b =时,求得218AC AB +=;当3()b c bc +=时,得1113c b +=,再由1123(2)AC AB b c c b ⎛⎫+=++ ⎪⎝⎭,结合基本不等式求得结果.【详解】如图,记,AB cAC b ==,在ABD △中,3,60,AD BAD AB c =∠=︒=,则2221923932BD c c c c +-⨯⨯=-=+,在ACD 中,3,60,AD CAD AC b =∠=︒=,则2221923932CD b b b b =+-⨯⨯=+-,∵AD 平分BAC ∠,∴BD AB cCD AC b ==,∴2222229393BD c c c CD b b b+-==+-,∴()()22229393c b b b c c +-=+-,∴22229393c bc b b c -=-∴222233c bc b b c -=-,∴()()222230c b bc b c ---=∴3()()()0c b c b bc c b +---=,∴()[3()]0c b c b bc -+-=,∴c b =或3()b c bc +=,当c b =时,ABC 为等腰三角形,∴AD BC ⊥,6cos 60ADc b ===︒,∴2218AC AB b c +=+=;当3()b c bc +=时,13b c bc +=,即1113c b +=,∴11223(2)AC AB b c b c c b ⎛⎫+=+=++ ⎪⎝⎭233b c c b ⎛⎫=++ ⎪⎝⎭2323b c c b ⎛⎫≥⨯+ ⎪ ⎪⎝⎭962=+,当且仅当2b cc b=,即2c b =时,等号成立,∵96218+<,∴2AC AB +的最小值为962+.故选:C.5.正四棱锥S ABCD -的底面边长为2,高为2,E 是边BC 的中点,动点P 在表面上运动,并且总保持PE AC ⊥,则动点P 的轨迹的周长为()A .62+B .62-C .4D .51+【答案】A【分析】由题意,动点P 的轨迹为过E 且垂直AC 的平面与正四棱锥S ABCD -的交线,再根据线面垂直的性质求解即可.【详解】如图,设,AC BD 交于O ,连接SO ,由正四棱锥的性质可得,SO ⊥平面ABCD ,因为AC ⊂平面ABCD ,故SO AC ⊥.又BD AC ⊥,SO BD O ⋂=,SO BD ⊂,平面SBD ,故AC ⊥平面SBD .由题意,PE AC ⊥则动点P 的轨迹为过E 且垂直AC 的平面与正四棱锥S ABCD -的交线,即如图EFG ,则AC ⊥平面EFG .由线面垂直的性质可得平面//SBD 平面EFG ,又由面面平行的性质可得//EG SB ,//GF SD ,//EF BD ,又E 是边BC 的中点,故,,EG GF EF 分别为,,SBC SDC BCD 的中位线.由题意222,226BD SB SD ===+=,故()16622622EG EF GF ++=++=+.即动点P 的轨迹的周长为62+.故选:A6.已知底面半径为3的圆锥SO ,其轴截面为正三角形,若它的一个内接圆柱的底面半径为1,则此圆柱的侧面积为()A .3πB .23πC .43πD .83π【答案】C【分析】作出圆锥的轴截面SAB ,求出圆锥的高,利用三角形相似求出圆柱的高,再根据侧面积公式计算可得.【详解】如图作出圆锥的轴截面SAB ,依题意3OB OA ==,1OD OC ==,6SB =,所以2233SO SB OB =-=,易知BDF BOS ∽,则BD DFBO SO=,所以23DF =,即圆锥的内接圆柱的底面半径1r =,高23h =,所以圆柱的侧面积2π2123π43πS rh ==⨯⨯=.故选:C7.已知函数()2πcos (0)3f x x ωω⎛⎫=+> ⎪⎝⎭在ππ,2⎡⎤-⎢⎥⎣⎦上单调,且()y f x =的图象关于点π,03⎛⎫- ⎪⎝⎭对称,则()A .()f x 的周期为πB .若()()122f x f x -=,则12min 2πx x -=C .将()f x 的图像向右平移π3个单位长度后对应的函数为偶函数D .函数()22y f x =+在[]0,π上有2个零点【答案】B【分析】对于A ,根据题意确定周期范围,再根据图象关于点π,03⎛⎫- ⎪⎝⎭对称,结合正弦函数的对称中心求解即可;对于B ,由A 知()12πcos 23f x x ⎛⎫=+ ⎪⎝⎭,结合余弦函数的最值与周期性质判断即可;对于C ,根据三角函数平移性质判断即可;对于D ,根据余弦函数值直接求解即可.【详解】对于A ,因为函数2π()cos (0)3f x x ωω⎛⎫=+> ⎪⎝⎭在ππ,2⎡⎤-⎢⎥⎣⎦上单调,所以()f x 的最小正周期T 满足3π22T ≥,即π3π2ω≥,所以203ω<≤,因为()f x 的图象关于点π,03⎛⎫- ⎪⎝⎭对称,所以π2πππ,Z 332k k ω-+=+∈,得13,Z 2k k ω=-∈,所以当0k =时,12ω=,所以2π4π12T ==,故A 错误;对于B ,()12πcos 23f x x ⎛⎫=+ ⎪⎝⎭,()()122f x f x -=,则()()12,f x f x 为1,1-,则12min x x -为半周期,即2π,故B 正确;对于C ,将()f x 的图象向右平移π3个单位长度后得()1π2π1cos sin 2332g x x x ⎡⎤⎛⎫=-+=- ⎪⎢⎥⎝⎭⎣⎦的图象,()g x 为奇函数,故C 错误;对于D ,12π2cos 0232x ⎛⎫++= ⎪⎝⎭,即12π2cos 232x ⎛⎫+=- ⎪⎝⎭,令12π23t x =+,当[0,π]x ∈时,2π7π,36t ⎡⎤∈⎢⎥⎣⎦,故仅有3π4t =,故D 错误.故选:B.8.如图所示,在直三棱柱111ABC A B C -中,棱柱的侧面均为矩形,11AA =,3AB BC ==,1cos 3ABC ∠=,P 是线段1A B 上的一动点,则1AP PC +最小值为()A .6B .7C .13+D .25+【答案】B【分析】连接1BC ,得11A BC V ,以1A B 所在直线为轴,将11A BC V 所在平面旋转到平面11ABB A ,设点1C 的新位置为C ',连接AC ',再根据两点之间线段最短,结合勾股定理,余弦定理等求解AC '即可.【详解】连接1BC ,得11A BC V ,以1A B 所在直线为轴,将11A BC V 所在平面旋转到平面11ABB A ,设点1C 的新位置为C ',连接AC ',则有1C AP PC AP PC A '++'=≥,如图,当,,A P C '三点共线时,则AC '即为1AP PC +的最小值.在三角形ABC 中,3AB BC ==,1cos 3ABC ∠=,由余弦定理得:2212cos 332323AC AB BC AB BC B =+-⋅=+-⨯⨯=,所以112AC =,即12AC '=,在1A AB △中,11AA =,3AB =,由勾股定理可得:2211132A B AA AB =+=+=,且160AA B ∠=︒.同理可求:12C B =,因为11112A B BC A C ===,所以11A BC V 为等边三角形,所以1160BAC ∠=︒,所以在1AA C ' 中,111120AA C AA B BA C ''∠=∠+∠=︒,111,2AA A C '==,由余弦定理得:11421272AC ⎛⎫'=+-⨯⨯⨯-= ⎪⎝⎭.故选:B.二、多选题9.已知复数5iz 1i+=+,则下列说法正确的是()A .z 13=B .z 的虚部为-2C .z 在复平面内对应的点在第四象限D .z 的共轭复数为32i--【答案】BC【分析】根据复数的除法运算法则求出z ,再根据复数的模长公式、复数的概念、复数的几何表示以及共轭复数的概念可得答案.【详解】5i z 1i +=+(5i)(1i)(1i)(1i)+-=+-64i32i 2-==-,22||3(2)13z =+-=,故A 不正确;z 的虚部为-2,故B 正确;32i z =-在复平面内对应的点(3,2)-在第四象限,故C 正确;32i z =-的共轭复数为32i z =+,故D 错误.故选:BC10.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,下列命题是真命题的是()A .若cos cos aB b A =,则ABC 为等腰三角形B .若π4B =,2c =,65b =,则ABC 只有一解C .若()cos 2cos 0b A a c B +-=,则π3B =D .若ABC 为锐角三角形,则()()222222sin cos a b c A a b c B+->+-【答案】ACD【分析】对于A 、C :根据题意结合正弦定理运算分析即可;对于B :根据三角形解得个数的结论分析判断;对于D :根据题意结合正弦函数单调性分析判断.【详解】对于选项A :由cos cos a B b A =,由正弦定理可得sin cos sin cos A B B A =,则()sin 0A B -=,因为0,πA B <<,则ππA B -<-<,可得0A B -=,即A B =,所以ABC 为等腰三角形,故A 正确;对于选项B :若π4B =,2c =,65b =,则6sin 125c B c =<<=,所以ABC 有两解,故B 错误;对于选项C :若()cos 2cos 0b A a c B +-=,有正弦定理可得()sin cos sin 2sin cos 0B A A C B +-=,则()sin 2sin cos B A C B +=,即sin 2sin cos C C B =,因为(),0,πB C ∈,则sin 0C >,可得1cos 2B =,所以π3B =,故C 正确;对于选项D :若ABC 为锐角三角形,则π2A B π<+<,可得π2A B >-,且π0,2A ⎛⎫∈ ⎪⎝⎭,ππ0,22B ⎛⎫-∈ ⎪⎝⎭,则sin y x =在π0,2⎛⎫⎪⎝⎭上单调递增,所以πsin sin cos 2A B B ⎛⎫>-= ⎪⎝⎭,又因为π0,2A ⎛⎫∈ ⎪⎝⎭,则222cos 02a b cA ab+-=>,可得2220a b c +->,所以()()222222sin cos a b c A a b c B +->+-,故D 正确.故选:ACD.11.如图,四棱锥P ABCD -的底面为正方形,PD ⊥底面ABCD ,1PD AD ==,点E 是棱PB 的中点,过A ,D ,E 三点的平面α与平面PBC 的交线为l ,则()A .直线l 与平面PAD 有一个交点B .PC DE⊥C .直线PA 与l 所成角的余弦值为32D .平面α截四棱锥P ABCD -所得的上下两个几何体的体积之比为35【答案】BD【分析】根据所给图像,作PC 中点F ,连接EF ,则EF 为交线l ,然后根据线面平行的基本定理可判断A ;结和线面垂直的判定及性质可判断B ;结合异面直线所成角的定义可判断C ;结和棱锥的体积公式可判断D.【详解】如图,取棱PC 的中点F ,连接EF ,DF ,因为E 是棱PB 的中点,则//AD EF ,即A ,D ,E ,F 四点共面,则l 为直线EF ,又AD ⊂平面PAD ,EF ⊂/平面PAD ,所以//EF 平面PAD ,即//l 平面PAD ,故A 错误;由PD ⊥底面ABCD ,AD ⊂平面ABCD ,所以PD AD ⊥,由PD AD =,可得PDC △为等腰直角三角形,而斜边PC 的中点为F ,所以PC DF ⊥,再由底面ABCD 是正方形,易得AD CD ⊥,又PD CD D ⋂=,且,PD CD ⊂平面PDC ,所以AD ⊥平面PDC ,又PC ⊂平面PDC ,所以AD PC ⊥,又AD DF D ⋂=,且,AD DF ⊂平面ADFE ,所以PC ⊥平面ADFE ,又DE ⊂平面ADFE ,所以PC DE ⊥,故B 正确;由//AD EF ,则直线PA 与l 所成的角,即PA 与AD 所成的角,由PD AD ⊥,则2cos 2AD PAD AP ∠==,即PA 与AD 所成的角的余弦值为22,故C 错误;11111333P ABCD ABCD V PD S -=⋅=⨯⨯=,111122113322228P AEFD AEFD V PF S -⎛⎫=⋅=⨯⨯+⨯⨯= ⎪⎝⎭,所以1153824ABCDFE P ABCD P AEFD V V V --=-=-=,所以1385524P AEFD ABCDFEV V -==,故D 正确.故选:BD.12.在棱长为1的正方体1111ABCD A B C D -中,E ,F 分别为AB ,BC 的中点,则()A .异面直线1DD 与1B F 所成角的正切值为13B .点P 为正方形1111DC B A 内一点,当//DP 平面1B EF 时,DP 的最小值为324C .过点1D ,E ,F 的平面截正方体1111ABCD A B C D -所得的截面周长为2132+D .当三棱锥1B BEF -的所有顶点都在球O 的表面上时,球O 的表面积为3π【答案】BC【分析】根据11//DD BB 可得1∠BB F 即为异面直线1DD 与1B F 所成的角,即可判断A ,作出截面,找到P 的轨迹,即可求出DP 的最小值,从而判断B ,作出截面,再利用空间向量确定点的位置,从而求出线段的长度,即可得到截面周长,从而判断C ,确定球心及半径,即可求出外接球的表面积,从而判断D.【详解】对于A 选项,11//DD BB ,∴在1Rt BB F 中1∠BB F 即为异面直线1DD 与1B F 所成的角,11112tan 12BF BB F B B ∴∠===,∴异面直线1DD 与1B F 所成的角的正切值为12.故A 错误;对于B 选项,取11A D 的中点11,M D C 的中点N ,取AD 的中点S ,连接MN ,DM ,1,,DN A S SF ,1111//,,//SF AB A B SF AB A B ==∴11A B FS 为平行四边形,11//SA B F ∴,1//A S DM ,1//MD B F ∴,同理可得1//DN B E,又DM ⊄ 面1B EF ,1B F ⊂面1B EF ,DN ⊄面1B EF ,1B E ⊂面1B EF ,DM ∴//面1B EF ,//DN 面1B EF ,又DM DN D ⋂= ,DM DN ⊂,面DMN ,∴面//DMN 面1B EF ,又//DP 面1B EF ,P ∈面1111D C B A ,P ∴轨迹为线段MN ,∴在DMN 中,过D 作DP MN ⊥,此时DP 取得最小值,在1Rt DD M △中,112D M =,11=D D ,52DM ∴=,在1Rt DD N 中,112D N =,11=D D ,52DN ∴=,在1Rt MD N 中,112D N =,112D M =,22MN =∴,∴如图,在Rt DPN 中,223224MN DP DN ⎛⎫=-= ⎪⎝⎭.故B 项正确;对于C 选项,延长EF 交DA 的延长线于点G ,交DC 的延长线于点H ,连接1D H 交1CC 于点N ,连接1D G 交1AA 于点M ,再连接ME 、NF ,则过点1D ,E ,F 的平面截正方体1111ABCD A B C D -所得的截面图形为五边形1D MEFN ,平面11//AA D D 平面11BB C C ,截面1D MEFN 与平面11AA D D 和平面11BB C C 分别交于1D M 与FN ,1//D M NF ∴,同理可得1//D N ME ,如图以D 为原点,分别以DA 、DC 、1DD方向为x 轴、y 轴、z 轴正方向建立空间直角坐标系D xyz -,设AM m =,CN n =,则()1,0,M m ,()0,1,N n ,11,,02E ⎛⎫ ⎪⎝⎭,1,1,02F ⎛⎫⎪⎝⎭,()10,0,1D ,10,,2ME m ⎛⎫∴=- ⎪⎝⎭,()10,1,1D N n =-,()11,0,1D M m =- ,1,0,2NF n ⎛⎫=- ⎪⎝⎭ ,1//D M NF ,1//D N ME ,即1//D M NF 且1//D N ME,()()112112m n n m ⎧-=-⎪⎪∴⎨⎪-=-⎪⎩,解得1313m n ⎧=⎪⎪⎨⎪=⎪⎩,13AM ∴=,13CN =,123A M ∴=,123C N =,∴在11Rt D A M 中,111D A =,123A M =,1133D M ∴=,同理:1133D N =,在Rt MAE △中,13AM =,12AE =,136ME ∴=,同理:136FN =在Rt EBF △中,12BE BF ==,22EF ∴=,1113132222133622D M D N ME FN EF ∴++++=⨯+⨯+=+,即过点1D E F 、、的平面截正方体1111ABCD A B C D -所得的截面周长为2132+.故C 正确;对于D 选项,如图所示,取EF 的中点1O ,则111O E O F O B ==,过1O 作11//OO BB ,且使得111122OO BB ==,则O 为三棱锥1B BEF -的外接球的球心,所以OE 为外接球的半径,在Rt EBF △中,22EF =,22222211823224EF R OE OO ⎛⎫⎛⎫⎛⎫∴==+=+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭23π4π2S R ∴==球.故D 项错误,故选:BC .【点睛】关键点睛:解答本题的关键是结合空间中点、线、面的位置关系确定点的位置,从而求出线段最小值及截面周长.三、填空题13.已知2= a ,1= b ,3a b +=,则a b -= .【答案】7【分析】利用向量恒等式()2222||2a b a b a b ++-=+⨯ ,即可得到答案;【详解】()2222||2a b a b a b ++-=+⨯ ,22537a b ∴-=⨯-= ,7a b ∴-=,故答案为:714.在ABC 中,2π3A =,D 为BC 边上一点,且2BD DC =,则AD AB的最小值为.【答案】33【分析】将AD 用,AB AC 表示,再平方可求得2AD ,再由22AD AB 结合二次函数得性质即可得解.【详解】由2BD DC =,得()11213333AD AB BC AB AC AB AB AC =+=+-=+uuu r uuu r uuu r uuu r uuu r uuu r uuur uuu r ,则22222141433999AD AB AC AB AC AB AC ⎛⎫=+=++⋅ ⎪⎝⎭,所以222412999AD c b bc =+-,则222222224124121119991999933c b bc AD b b b AB c c c c +-⎛⎫==+⋅-⋅=-+≥ ⎪⎝⎭,当1bc=时,取等号,所以AD AB 的最小值为33.故答案为:33.【点睛】关键点点睛:将AD 用,AB AC表示,再平方是解决本题的关键.15.在ABC 中,D 、E 分别为AC 、BC 的中点,AE 交BD 于点M .若4AB =,6AC =,π3BAC ∠=,则ME MD ⋅=.【答案】29-【分析】分析可知M 为ABC 的重心,利用AB、AC 表示向量ME 、MD ,利用平面向量数量积的运算性质可求得ME MD ⋅的值.【详解】如下图所示:因为在ABC 中,D 、E 分别为AC 、BC 的中点,AE 交BD 于点M ,则M 为ABC 的重心,所以,()11113332ME AE AB BE AB BC ⎛⎫==+=+ ⎪⎝⎭()11113226AB AC AB AB AC ⎛⎫=+-=+ ⎪⎝⎭,()()11111233326MD BD AD AB AC AB AC AB ⎛⎫==-=-=- ⎪⎝⎭ ,因为4AB =,6AC =,π3BAC ∠=,由平面向量数量积的定义可得π1cos 641232AB AC AB AC ⋅=⋅=⨯⨯= ,所以,()()()2211223636ME MD AC AB AC AB AC AB AC AB ⋅=+⋅-=-⋅-()221261224369=--⨯=-.故答案为:29-.16.某园区有一块三角形空地ABC (如图),其中π103m,40m,2AB BC ABC ==∠=,现计划在该空地上划分三个区域种植不同的花卉,若要求23APB ∠=π,则CP 的最小值为m.【答案】102110-【分析】根据23APB ∠=π可知点P 的轨迹,再利用正弦定理以及圆周角和圆心角之间的关系,易知当P 为OC 与圆的交点时,CP 取最小值,再利用余弦定理即可求得结果.【详解】如图,因为23APB ∠=π,所以P 在如图所示的圆O 上,圆O 的半径为110310232⨯=,由圆周角的性质可得2πππ2πππ,2,33336ADB AOB OBA OAB ∠=-=∠=⨯=∠=∠=,连接OC ,可得OP CP OC +≥,所以当P 为OC 与圆的交点时,CP 取最小值,即CP OC OP =-,又10OB OP ==,在OBC △中,2π10,40,3OB BC OBC ==∠=,根据余弦定理可知22110402104010212OC ⎛⎫=+-⨯⨯⨯-= ⎪⎝⎭,所以CP 的最小值为()102110m -.故答案为:102110-四、解答题17.在ABC 中,角,,A B C 的对边分别是,,a b c ,且满足()sin sin sin c C a A b a B -=-.(1)求C ;(2)若4b =,ABC 的面积为63,求边长c 的值.【答案】(1)π3C =(2)27c =【分析】(1)根据题意,由正弦定理化简得到222a b c ab +-=,再由余弦定理求得1cos 2C =,即可求解;(2)由ABC 的面积为63,列出方程求得6a =,结合余弦定理,即可求解.【详解】(1)解:因为()sin sin sin c C a A b a B -=-,由正弦定理得()22c a b a b -=-,即222c a b ab =+-,即222a b c ab +-=,由余弦定理得2221cos 222a b c ab C ab ab +-===,又因为()0,πC ∈,所以π3C =.(2)解:由ABC 的面积为63,所以113sin 463222ABC S ab C a ==⨯⨯⨯= ,可得6a =,又由22212cos 3616264282c a b ab C =+-=+-⨯⨯⨯=,所以27c =.18.直三棱柱111ABC A B C -中,AB BC ⊥,D 为1CC 的中点,12BB BC =.(1)求证:平面1AB C ⊥平面ABD ;(2)若3AB BD ==,求三棱锥1B ABD -的体积.【答案】(1)证明见解析(2)63【分析】(1)先证AB ⊥平面11BB C C ,得到1B C AB ⊥①,再借助三角形相似证明1B C BD ⊥②,最后证出平面1AB C ⊥平面ABD ;(2)等体积法求1A BB D V -即可.【详解】(1) 111ABC A B C -为直三棱柱,∴1AB BB ⊥,又 AB BC ⊥,1BC BB B = ,∴AB ⊥平面11BB C C1B C ⊂平面11BB C C ,∴1B C AB ⊥①设BC t =,则12BB t =,12tan 2BB C ∠=,11222tCD CC ==,2tan 2CD CBD BC ∠==,∴1BB C CBD ∠=∠ 1190BB C B CB ︒∠+∠=,∴190CBD B CB ︒∠+∠=,故1B C BD ⊥②由①②,AB ABD ⊂平面,AD ABD ⊂平面,且AB BD B = ,知1B C ⊥平面ABD 又 1B C ⊂平面1AB C ,∴平面1AB C ⊥平面ABD(2)由222BC CD BD +=,得2232t t +=,解得2t =∴1BB D △的面积11122BB D S BB BC =⋅=△由(1)知AB ⊥平面11BB C C ,∴三棱锥1A BB D -的体积111633A BB D BB D V S AB -=⋅=△∴三棱锥1B ABD -的体积1163B ABD A BB D V V --==19.在长方体1111ABCD A B C D -中,11AD DD ==,3AB =,E 、F 、G 分别为AB 、BC 、11C D 的中点.(1)求三棱锥A GEF -的体积;(2)点P 在矩形ABCD 内,若直线1//D P 平面EFG ,求线段1D P 长度的最小值.【答案】(1)324(2)72【分析】(1)等体积由A GEF G AEF V V --=可得.(2)先证平面//EFG 平面1ACD ,则由直线1//D P 平面EFG 可得点P 在直线AC 上,进而可得线段1D P 长度的最小值【详解】(1)依题意有1131322228AEF S AE BF =⋅⋅=⋅⋅=,所以三棱锥A GEF -的体积11133133824A GEF G AEF AEF V V S DD --==⋅⋅=⋅⋅=;(2)如图,连结11,,AC D A D C ,∵,,E F G 分别为11,,AB BC C D 的中点,∴//,AC EF EF ⊄平面1ACD ,AC ⊂平面1ACD ,∴//EF 平面1,ACD∵1//,EG AD EG ⊄平面1ACD ,1AD ⊂平面1ACD ,∴//EG 平面1ACD ,∵EF EG E = ,∴平面//EFG 平面1ACD ,∵1//D P 平面EFG ,∴点P 在直线AC 上,在1ACD △中,112,2,2===AD AC CD ,12212722()222AD C S =⨯⨯-=,∴当1D P AC ⊥时,线段1D P 的长度最小,最小值为172=11222C AD S AC ⨯⨯△=72.20.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,22cos a c b C -=.(1)求B ;(2)若点D 为边BC 的中点,点E ,F 分别在边AB ,AC 上,π3EDF ∠=,2b c ==.设BDE α∠=,将DEF 的面积S 表示为α的函数,并求S 的取值范围.【答案】(1)π3;(2)33ππ,2π6216sin sin 3S ααα=≤≤⎛⎫- ⎪⎝⎭,333,48S ⎡⎤∈⎢⎥⎣⎦.【分析】(1)由余弦定理可得222a c b ac +-=,再根据余弦定理即可求解;(2)由题可得ABC 为等边三角形,ππ62α≤≤,在BDE 与CDF 中,分别由正弦定理求出DE ,DF ,根据三角形面积公式可得33ππ,2π6216sin sin 3S ααα=≤≤⎛⎫- ⎪⎝⎭,由三角恒等变换及正弦函数的图象与性质即可求解.【详解】(1)因为22cos a c b C -=,所以222222222a b c a b c a c b ab a +-+--=⋅=,即222a cb ac +-=,所以2221cos 222a cb ac B ac ac +-===.因为()0,πB ∈,所以π3B =.(2)由π3B =及2b c ==可知ABC 为等边三角形.又因为π3EDF∠=,BDEα∠=,所以ππ62α≤≤.在BDE中,2π3BEDα∠=-,由正弦定理可得,sin sinDE BDB BED=∠,即32π2sin3DEα=⎛⎫-⎪⎝⎭.在CDF中,CFDα∠=,由正弦定理可得,sin sinDF CDC CFD=∠,即32sinDFα=.所以31π33ππsin,2π2π8362sin sin16sin sin33Sααααα=⨯⨯=≤≤⎛⎫⎛⎫--⎪ ⎪⎝⎭⎝⎭.因为2π31sin sin cos sin sin322ααααα⎛⎫⎛⎫-=+⎪⎪ ⎪⎝⎭⎝⎭231311sin cos sin sin2cos222444ααααα=+=-+1π1sin2264α⎛⎫=-+⎪⎝⎭,因为ππ62α≤≤,所以ππ5π2,666α⎡⎤-∈⎢⎥⎣⎦,所以π1sin2,162α⎛⎫⎡⎤-∈⎪⎢⎥⎝⎭⎣⎦,所以1π113sin2,26424α⎛⎫⎡⎤-+∈⎪⎢⎥⎝⎭⎣⎦.所以[]2π16sin sin8,123αα⎛⎫-∈⎪⎝⎭,所以111,2π12816sin sin3αα⎡⎤∈⎢⎥⎛⎫⎣⎦-⎪⎝⎭,所以33333,2π4816sin sin3Sαα⎡⎤=∈⎢⎥⎛⎫⎣⎦-⎪⎝⎭.所以S 的取值范围为333,48⎡⎤⎢⎥⎣⎦.21.如图,在三棱锥-P ABC中,ABC是边长为62的等边三角形,且6PA PB PC===,PD⊥平面ABC,垂足为,D DE⊥平面PAB,垂足为E,连接PE并延长交AB于点G.(1)求二面角P AB C --的余弦值;(2)在平面PAC 内找一点F ,使得EF ⊥平面PAC ,说明作法及理由,并求四面体PDEF 的体积.【答案】(1)33;(2)答案见解析,43.【分析】(1)根据条件确定PGD ∠就是二面角P AB C --的平面角,构造三角形求解;(2)根据给定的条件知PB ⊥平面PAC ,过点E 作PB 的平行线与PA 交于F ,则EF ⊥平面PAC ,再求出三棱锥P EFD -的底面积和高即可.【详解】(1)PA PB PC == ,并且ABC 是等边三角形,∴三棱锥-P ABC 是正三棱锥,D 是ABC 的中心,点G 是AB 边的中点;由PD ⊥平面ABC ,DE ⊥平面PAB ,AB ⊂平面PAB ,可知,,AB PD AB DE PD DE D ⊥⊥⋂=,PD ⊂平面PDG ,DE ⊂平面PDG ,所以AB ⊥平面PDG ,进而得,AB PG AB DG ⊥⊥,所以PGD ∠就是二面角P AB C --的平面角,又ABC 是边长为62的等边三角形,且6PA PB PC ===,222PA PB AB +=,PAB ∴ 是等腰直角三角形,同理,PAC PBC △△都是等腰直角三角形;1322PG AB ∴==,113626332GD CG ==⨯⨯=,3cos 3GD PGD PG ∠==,即二面角P AB C --的余弦值为33;(2),,,PB PC PB PA PA PC P PA ⊥⊥=⊂ 平面PAC ,PC ⊂平面PAC ,PB ∴⊥平面PAC ,同理PC ⊥平面PAB ,又DE ⊥平面PAB ,//ED PC ∴,E ∴与点P ,D ,C 共面,即E 点在线段PG 上,又1,23EDG PGC ED PC ∴== ,2,223PE CD PE PG CG ===,π4APG ∠=,过E 点在平面PAB 内作PB 的平行线,与PA 交于F ,则EF ⊥平面PAC ,PEF !也是等腰直角三角形,22PEEF ==,又DE ⊥平面PAB ,EF ⊂平面PAB ,DE EF ∴⊥,将PEF !作为底面,则ED 是三棱锥D PEF -的高,11142223323P DEF D PEF PEF V V S DE --∴===⨯⨯⨯⨯= ,即四面体PDEF 的体积为43.22.已知点O 是锐角ABC 的外心,,,a b c 分别为角,,A B C 的对边,222a b c bc =+-,(1)求角A ;(2)若4a =,求ABC 面积的最大值;(3)若cos cos sin sin A C BA BC xOB C A+= ,求x 的取值范围.【答案】(1)π3A =(2)43(3)(2,1)--【分析】(1)利用余弦定理求出cos A 的值,结合角A 的取值范围可求得角A 的值;(2)利用余弦定理结合基本不等式求出bc 的最大值,结合三角形的面积公式可求得ABC 面积的最大值;(3)由题意画出图形,设ABC 的外接圆半径为R ,根据三角形外心的性质可得:,OD AB OE BC ⊥⊥,由向量的线性运算和向量数量积的运算,求出BA OB ⋅ 和BC OB ⋅ ,在已知的等式两边同时与OB 进行数量积运算,代入后由正弦定理化简,结合两角和的正弦公式和内角和定理求出x 的范围.【详解】(1)因为222a b c bc =+-,则222b c a bc +-=,由余弦定理可得2221cos 22b c a A bc +-==,因为()0,πA ∈,所以π3A =;(2)因为2222a b c bc bc bc bc =+-≥-=,则216bc a ≤=,当且仅当4b c ==时,等号成立,所以11πsin 16sin 43223ABC S bc A =≤⨯⨯=△,所以ABC 面积的最大值为43.(3)分别取AB ,BC 的中点D ,E ,连接OD ,OE ,可得211()||22BA OB BA OD DB BA DB BA BA BA ⎛⎫⋅=⋅+=⋅=⋅-=- ⎪⎝⎭ ,同理可得21||2BC OB BC ⋅=- ,由cos cos sin sin A C BA BC xOB C A += 得,2cos cos sin sin A C BA OB BC OB xOB C A ⋅+⋅= ,所以2221cos 1cos 2sin 2sin A C BA BC xOB C A -⋅-⋅= ,即2||||cos cos 2sin sin BA BC A BA C BC x OB C A ⋅⋅+⋅⋅=- ,在ABC 中,由正弦定理得:||||2sin sin BA BC R C A == ,(R 为ABC 的外接圆的半径)代入上式得2cos ||2cos ||22A BA R C BC R xR ⋅⋅+⋅⋅=- ,则cos ||cos ||A BA C BC xR ⋅+⋅=- ,由正弦定理得,||2sin ,||2sin BA R C BC R A == ,代入上式得,2sin cos 2cos sin R C A R C A xR +=-;所以2sin()C A x +=-,所以2sin B x =-,即2sin x B =-,因为π3A =,且ABC 为锐角三角形,2πππ0,0322B B <-<<<,所以ππ62B <<,所以1sin 12B <<,所以22sin 1B -<-<-,即x 的取值范围(2,1)--.。
2024年辽宁沈阳五校联考高一下学期期末数学试题答案

2023-2024学年度(下)沈阳市五校协作体期末考试高一年级数学试卷答案考试时间:120分钟 考试分数:150分一、单选题1-4. BACA 5-8. BDCC二、多选题9.ABD 10.BC. 11.BD .三、填空题12. . 13. 52π 14.(12+ 四、解答题15. (13分)【解】(1)因为cos cos a B b A a c −=−−,根据正弦定理,得()sin cos cos sin sin sin sin sin cos cos sin A B A B A C A A B A B −=−−=−−+,--- --- ---2分化简得2sin cos sin A B A =−,因为sin 0A >,所以1cos 2B =−, --- --- ---4分 因为()0,πB ∈,所以2π3B =. --- --- ---5分(2)在ABC 中,由余弦定理得2222π222cos3c c +−×,--- --- ---7分 所以22240c c +−=,解得4c =. --- --- ---9分因为BD 为ABC 的中线,所以2BD BA BC =+ ,所以2222π4||2cos 3BD c a ac =++⋅ , --- --- ---11分因为2,4a c ==,所以24||12BD = ,解得BD = 分(利用其它方法证明求解的按步骤给分)16. (15分)【解】(1)连接BD 交AC 于点O ,连接EO ,由底面ABCD 是正方形,故O 为BD 中点, 又点E 为线段PD 的中点,故//OE PB , --- --- ---3分 又OE ⊂平面AEC ,PB ⊄平面AEC ,故//PB 平面AEC ; --- --- ---4分(2)由点E 为线段PD 的中点,PA AD =,故AE PD ⊥,由PA ⊥平面ABCD ,CD ⊂平面ABCD ,故PA CD ⊥, --- --- ---6分 又底面ABCD 是正方形,故AD CD ⊥,又AD 、PA ⊂平面PAD ,AD PA A ∩=,故CD ⊥平面PAD ,又AE ⊂平面PAD ,故CD AE ⊥, --- --- ---8分 又CD 、PD ⊂平面PCD ,CD PD D = ,故⊥AE 平面PCD ;- -- --- ---10分 (3)由点E 为线段PD 的中点,故点P 与点D 到平面AEC 距离相等,--- --- ---12分 故1111222222323P BCE D BCE E BCD P BCD V V V V −−−−====×××××=.- -- --- ---15分 (利用其它方法证明求解的按步骤给分)17.(15分)【解】(1)对任意x ∈R 都有π()()3f x f x −=,则函数()f x 的图象关于直线π6x =对称, 于是ππ2π,Z 62k k ϕ+=+∈,而ππ(,)22ϕ∈−,则π0,3k ϕ==,所以π3ϕ=. --- --- ---4分 (2) ()2sin()3f x x π=+,当()0,πx ∈时,设ππ4π,333t x =+∈,y=2sin()t 在ππ,32t ∈ 为增函数,在π4π,23t ∈ 为减函数,所以方程()0f x m +=有唯一实根,等价于(()f t m m m +∈+ }{2m ∪+时有唯一实根,所以m 的范围.是m ∈ }{2∪− --- --- ---8分(3)由(1)知,()2sin()π6g x x =+,则()2sin()π6g x x −=−−, )ππ3o 6()2sin()2c s(f x x x =+=−,222)π[()]π4cos ()44sin 66(f x x x =−=−−, 当π[,π]6x ∈时,π5π[0,]66x −∈,πsin()[0,1]6x −∈,令πsin()[0,1]6x t −=∈, 显然22()2,[()]44g x t f x t −=−=−, --- --- ---12分 不等式22224()()2122(44)2121t ag x f x a at t a a t +−−>−⇔−−−>−⇔<+, 依题意,[0,1]t ∀∈,不等式2241t a t +<+恒成立, 显然1[1,2]t +∈,22242(1)6662(1)2(1)41111t t t t t t t t +−+−+++−++++44≥=,当且仅当62(1)1t t +=+,即1t =−时取等号,则4a <,所以实数a 的取值范围是4a <. --- --- ---15分18. (17分)【解】(1)证明:在正三棱柱111ABC A B C 中,因为点M 为11A B 的中点,则111C M A B ⊥,又1A A ⊥平面111A B C ,1C M ⊂平面111A B C ,则有11AA C M ⊥,而1111111,,AA A B A AA A B =⊂ 平面11AA B B ,于是1C M ⊥平面11AA B B ,1C M ⊂平面1BC M ,则平面1BC M ⊥平面11AA B B , --- --- ---5分(2)在平面11AA B B 内过点A 作AQ BM ⊥交1BB 于点Q ,平面1BC M 平面11AA B B BM =,因此AQ ⊥平面1BC M ,于是点Q 即为所要找的点,--- --- ---8分如下图所示,显然1ABQ BB M ,因此11BQ AB B M BB =, 即有214BQ =,于是12BQ =,1117422B Q B B BQ =−=−=,所以17B Q QB =.--- --- ---11分(3)在平面111A B C 上,过M 点作MN 垂直11B C 垂足为N ,因为点M 为11A B 的中点,所以N 为11B C 的四等分点,即111:3:4C N C B =, --- --- ---13分过N 点作1BC 的垂线NP 垂足为P ,连接MP,平面111A B C ⊥平面11CC B B ,平面111A B C 平面1111CC B B B C =,因此MN ⊥平面11CC B B ,所以有1MP BC ⊥,由二面角定义可得MPN ∠为二面角11M BC B −−的平面角, --- --- ---15分 11BC B 为直角三角形,1BC ∴边上的高为d =NP=34d =,所以tan MPN ∠ --- --- ---17分(利用其它方法证明求解的按步骤给分)19. (17分)【详解】(1)由4,AB AC =cos A--- --- ---2分取AB 的中点D ,连接OD ,则OD AB ⊥,所以18()=92AO AB AD DO AB AD AB ⋅=+⋅=⋅= ,同理可得85BO BC CO CA ⋅=⋅= ,,则AB AO BC BO CA CO ⋅+⋅+⋅ 的值为22; --- --- ---4分(2)不妨设||,||AB m AC n == ,因21()2AO AB AD DO AB AD AB m ⋅=+⋅=⋅= ,同理可得212AO AC n ⋅= , 则由AO xAB y AC =+ 可得2||AO x AB y AB AC ⋅=+⋅2221cos 2xm ymn A xm ymn m =+==,即得:2mx m +=① 又由AO xAB y AC =+ 可得2||AO AC x AB AC y AC ⋅⋅+2221cos 2xmn A yn yn n +=+=2ny n +=②---- --- ---6分 联立① ,②,解得:11x y = =则112()x y n m m n =++, --- --- --8分 因2n m m n+≥,当且仅当m n =时等号成立.即当m n =时,x y +取得最大值2 --- --- ---10分 (3)由cos A =π02A <<,则π4A =,由图知π22BOC A ∠=∠=,则0OB OC ⋅= , --- --- ---11分 设ABC 的外接圆半径为R ,则222222|sin 2cos2|sin 2||cos 2||B OB B OC B OB B OC R ⋅−⋅=⋅+⋅= ,即|sin 2cos2|B OB B OC R ⋅−⋅= , --- --- ---13分 又(sin 2cos 2)OA B OB B OC ⋅⋅−⋅ 2(sin 2cos cos 2cos )R B AOB B AOC ∠−∠, 而3π2π2AOB BOC AOC AOC ∠=−∠−∠=−∠, 则cos sin sin 2AOB AOC B ∠=−∠=−,而cos cos2AOC B ∠=, 故2222(sin 2cos2)(sin 2cos 2)OA B OB B OC R B B R ⋅⋅−⋅=−+=− ,--- --- ---15分不妨设OA 与sin 2cos2B OB B OC ⋅−⋅ 的夹角为θ, 则22cos 1||||(sin 2cos2)sin 2cos2OA B OB B OC OA B OB B C R R O θ⋅⋅−−===−⋅⋅⋅⋅− , 因[0,π]θ∈,故πθ=,即sin 2cos 2OA B OB B OC =−⋅+⋅ ,故sin 2cos20OA B OB B OC +⋅−⋅= ,得证. --- --- ---17分(利用其它方法证明求解的按步骤给分)。
2024届辽宁省重点中学数学高一第二学期期末教学质量检测试题含解析

2024届辽宁省重点中学数学高一第二学期期末教学质量检测试题注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共10小题,每小题5分,共50分。
在每个小题给出的四个选项中,恰有一项是符合题目要求的 1.若4sin()5πα-=,(,)2παπ∈,则cos α=( )A .35 B .35C .45-D .152.如图,长方体1111ABCD A B C D -中,6AB =,4=AD ,13AA =,分别过BC ,11A D 的两个平行截面将长方体分成三个部分,其体积分别记为111AEA DFD V V -=,11112EBE A FCF D V V -=,11113B E B C F C V V -=,.若123::1:4:1V V V =,则截面11A EFD 的面积为( )A .13B .13C .13D .8133.直线21y x =+在x 轴上的截距为( ) A .12-B .12C .1-D .14.设集合A ={x |x ≥–3},B ={x |–3<x <1},则A ∪B =( ) A .{x |x >–3} B .{x |x <1} C .{x |x ≥–3}D .{x |–3≤x <1}5.已知向量a 、b 满足||1,||2a b ==,且(4)a b b +⊥,则||a b +为( )A .3B . 6C .3D .66.设{}n a 是等比数列,则“12a a <”是“数列{}n a 是递增数列”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件7.中国古代的“礼”“乐”“射”“御”“书”“数”合称“六艺”.某校国学社团准备于周六上午9点分别在6个教室开展这六门课程讲座,每位同学只能选择一门课程,则甲乙两人至少有人选择“礼”的概率是( ) A .56B .2536C .13D .11368.在△ABC 中,a=3,b=5,sinA=,则sinB=( ) A .B .C .D .19.已知方程22112x y m m+=--表示焦点在y 轴上的椭圆,则m 的取值范围是( ) A .(1,2) B .31,2⎛⎫⎪⎝⎭C .(,1)(2,)-∞⋃+∞D .3(,1),2⎛⎫-∞⋃+∞⎪⎝⎭10.已知12F F ,是椭圆与双曲线的公共焦点,P 是它们的一个公共点,且12PF PF >,线段1PF 的垂直平分线过2F ,若椭圆的离心率为1e ,双曲线的离心率为2e ,则21e 2e 2+的最小值为() A 6B .3C .6D 3二、填空题:本大题共6小题,每小题5分,共30分。
2024届辽宁省四校高一数学第二学期期末学业质量监测试题含解析
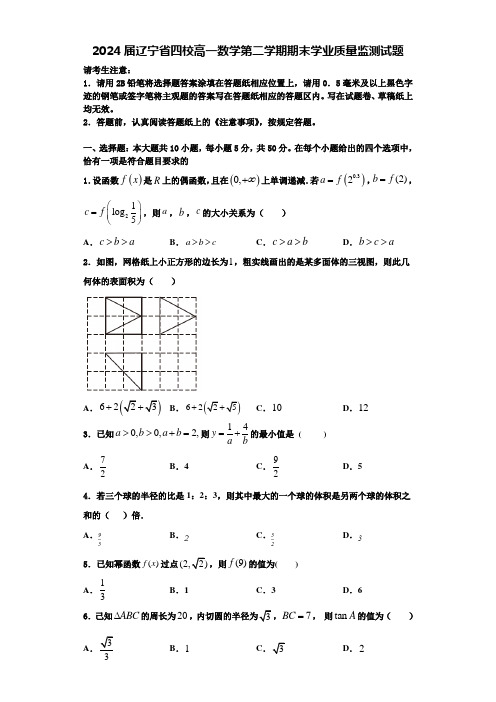
2024届辽宁省四校高一数学第二学期期末学业质量监测试题请考生注意:1.请用2B 铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。
写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题:本大题共10小题,每小题5分,共50分。
在每个小题给出的四个选项中,恰有一项是符合题目要求的1.设函数()f x 是R 上的偶函数,且在()0,∞+上单调递减.若()0.32a f =,(2)b f =,21log 5c f ⎛⎫= ⎪⎝⎭,则a ,b ,c 的大小关系为( )A .c b a >>B .a b c >>C .c a b >>D .b c a >>2.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则此几何体的表面积为( )A .()6223++ B .()6225++C .10D .123.已知0,0,2,a b a b >>+=则14y a b=+的最小值是 ( ) A .72B .4C .92D .54.若三个球的半径的比是1:2:3,则其中最大的一个球的体积是另两个球的体积之和的( )倍. A .B .C .D .5.已知幂函数()f x 过点2),则(9)f 的值为( ) A .13B .1C .3D .66.己知ABC ∆的周长为20,37BC =, 则tan A 的值为( )7.下列结论正确的是( ) A .若ac bc >则a b >; B .若ac bc =,则a b = C .若a b >,则11a b< D .若22ac bc >,则a b >;8.在2018年1月15日那天,某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查,5家商场的售价元和销售量件之间的一组数据如下表所示: 价格99.510.511销售量 118 6 5由散点图可知,销售量与价格之间有较强的线性相关关系,其线性回归方程是,且,则其中的( ) A .10B .11C .12D .10.59.设数列{}n a 是公差不为零的等差数列,它的前n 项和为n S ,且1S 、2S 、4S 成等比数列,则31a a 等于( ) A .5B .4C .3D .210.数列{}n a 的通项公式cos 2n n a n π=,其前n 项和为n S ,则2017S 等于( ) A .1006B .1008C .1006-D .1008-二、填空题:本大题共6小题,每小题5分,共30分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
辽宁省鞍山市第一中学、东北育才中学、辽宁省实验中学、大连市第八中学、大连市二十四中学2015-2016学年高一下学期期末考试数学试题
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.下列函数的最小正周期为的是()
A. B. C. D.
2.已知变量与正相关,且由观测数据算得样本平均数,则由该观测的数据算得的线性回归方程可能是()
A. B. C. D.
3.利用系统抽样从含有45个个体的总体中抽取一个容量为10的样本,则总体中每个个体被抽到的可能性是()
A. B. C. D.与第几次被抽取有关
4. 书架上有两本不同的数学书、一本语文书、一本英语书.从中选取2本,两本书中只有一本数学书的概率为()
A. B. C. D.
5.在中,角的对边分别为.已知,则角大小为()A. B. C.或 D.或
6.程序:;
for ;
end
print(%io(2),S)以上程序是用来计算()的值
A. B. C. D.
7.阅读如图所示的程序框图,运行相应的程序,输出的结果为()
A.4 B.5 C.6 D.7
8. 在上随机的取一个值,则使得关于的方程有实根的概率为()A. B. C. D.
9. 在中,点在直线上,且,点在直线上,且.若
,则()
A. B. C. D.
10.已知,,,,求()A. B. C. D.
11.将的图象向右平移个单位,再向下平移1个单位,得到函数的图象.若函数在区间上含有20个零点,则的最大值为()
A. B. C. D.
12.若锐角满足,则的取值范围是()
A. B. C. D.
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.求值: .
14. 某单位由老年教师27人,中年教师54人,青年教师81人,为了调查他们的身体状况,需从他们中
间抽取一个容量为36的样本,则青年教师被抽取的人数是 .
15.运行如图所示的框图,如果输出的,则输入的的取值范围为 .
16.将一副直角三角板拼成如图所示的四边形(其中,
),若,则 .
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.已知,.
(1)已知,求的值;
(2)求函数的单调递增区间.
18.高一数学期末考试试卷分值在,没有小数分值.从年级600名同学中随机抽取50名同学了解
期末数学考试成绩,他们成绩分布在分之间.以,,,,,分组的频率分布直方图如图所示:
(1)如规定分数在为优秀,根据样本的频率分布直方图估计年级期末数学考试中取得优秀的
学生人数;
(2)在分数为的所抽取的样本同学中,再随机选取两人,求此2人分数均在的概率.
19.今年的西部决赛勇士和雷霆共进行了七场比赛,经历了残酷的“抢七”比赛,两队的当家球星库里和杜兰特七场比赛的每场比赛的得分如下表:
第一场第二场第三场第四场第五场第六场第七场
库里26 28 24 22 31 29 36
杜兰特26 29 33 26 40 29 27
(1)绘制两人得分的茎叶图;
(2)右图是计算每位选手七场比赛的平均得分(图中用表示)的程序框图,请将框图中空缺的部分①②填充完整;
(3)分析并比较两位球星的七场比赛的平均得分及得分的稳定程度.
20.在中,角的对边分别为.满足.
(1)求角的大小;
(2)若的周长为20,面积为,求,.
21.已知,,,,
..
(1)若,求角;
(2)若,求.
22.已知函数.
(1)若对任意的,均有,求的取值范围;
(2)若对任意的,均有,求的取值范围.
高一数学试题答案
一、选择题:本大题共12小题,每小题5分,共60分.
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A B B D C D C A B B C C
二、填空题:本大题共4小题,每小题5分,共20分.
13.; 14.18; 15.; 16.
三、解答题:本大题共6个题,共70分.
17.解:(1)已知,
18.解:(1)年级期末数学考试中的取得优秀的学生人数大约为人.
(2)由频率分布直方图中可知样本的50人中为4人,记为,为3人,记为.
则所求事件的基本事件空间
共有21个基本事件
所求的事件包含6个基本事件
则2人分数均在的概率.
19.解:(1)如图
(2)①;②.
(3)库里的平均得分分
方差.
杜兰特的平均得分分
方差.
∴,则这七场比赛库里的平均得分低于杜兰特,但库里的得分更稳定一些.
20.解:(1),由正弦定理可得
,∴,则.
(2)∵,∴,又,∴,解得,∴,,解得.
21.解:(1)由向量夹角的余弦公式可得
,解得,又因为,∴.
(2)∵,,∴,∵,
,∴.
由,可得,∴.
22.解:(1),
由,得.
,当时,,要使恒成立,只需
,解得.
当时,,要使恒成立,只需,矛盾.
综上的取值范围是.
(2)
,
要使恒成立,只需,
则,因为,,
所以只需恒成立,则所求的的取值范围为.。
