正比例函数专项练习
正比例函数图像及性质竞品练习题由易到难

正比例函数第二课时正比例函数的图像及性质专项练习1.同一坐标系中,正比例函数,,,的图象如图所示,则下列式子成立的是()A. B. C. D.2.已知正比例函数,下列结论正确的是()A.图象是一条射线B.图象必经过点C.图象经过第一、三象限D.随的增大而减小3.下列关于正比例函数的结论中,正确的是()A.当时,函数值为2 B.随的增大而增大C.它的图象经过一、三象限D.它的图象一定不经过点4.一个乒乓球从光滑斜面自由滚下的路程y(米)与时间x(秒)的平方成正比例,当乒乓球滚下3米时,经过的时间为1.5秒,当时,该乒乓球所经过的路程为()A.5米B.米C.米D.米5.若点、都在函数的图象上,则与的大小关系是()A.B.C.D.无法确定6.已知点,均在正比例函数的图象上,且,则m的取值范围是()A.B.C.D.7.已知正比例函数的图象上两点,当时,有,那么的取值范围是()A.B.为任意实数C.D.8.七个边长为1的正方形如图摆放在平面直角坐标系中,直线将这七个正方形分成面积相等的两部分,则的值为()A.B.C.D.1二、填空题9.已知函数是正比例函数,且图象在第二、四象限内,则的值是______.10.在正比例函数中,y的值随着x值的增大而减小,则点在第_____象限.11.如图所示,将6×6的正方形网格放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形的顶点都在格点上,若直线()与正方形有公共点,则的取值范围是________.12.已知点都在正比例函数的图象上,则________(填“>”或“<”).13.点和点是一次函数图象上两点,当时,有,则______.(填“”或“”)14.正比例函数的图像经过,且,则k的范围是________.15.如图,在平面直角坐标系中,点在正比例函数的图象上,点和点都在轴上,当的面积是17.5时,则点的坐标是______.三、解答题16.已知正比例函数.(1)k为何值时,函数的图象经过第一、三象限;(2)k为何值时,函数值y随自变量x的增大而减小.17.已知正比例函数图象过点且点在这个函数的图象上,求a的值.18.一个正比例函数的图象经过点,求的值.19.已知:如图,正比例函数的图像经过点A,(1)请你求出该正比例函数的解析式;(2)若这个函数的图像还经过点,请你求出m的值.20.如图,某超市的消费卡售价(元)与面值(元)之间满足正比例函数关系,使用这张消费卡,在该超市可以购买任意商品.(1)求与之间的函数解析式:(2)小张购买了一张面值为元的消费卡,求小张购买这张消费卡时实际支付了多少元?21.如图,已知平面直角坐标系中,正比例函数的图象经过点.(1)求的值;(2)点是轴正半轴上一点,若,求线段的长.23.已知y是x的正比例函数,且当时,.(1)求这个正比例函数的解析式,并在平面直角坐标系中画出该函数的图象;(2)若点,在该函数图象上,试比较,的大小.24.已知关于x的正比例函数.(1)已知点在该正比例函数的图象上,求m的值;(2)在(1)的条件下,当时,求y的取值范围.25.已知是的正比例函数,当时,.(1)求与之间的函数关系式;(2)当时,求的最大值.。
中考数学《正比例函数图像和性质》专项练习题及答案

中考数学《正比例函数图像和性质》专项练习题及答案一、单选题1.若正比例函数的图象经过点(﹣1,2),则这个图象必经过点( )A .(1,2)B .(﹣1,﹣2)C .(2,﹣1)D .(1,﹣2)2.若正比例函数y=(1-2m )x 的图象经过点A (x 1,y 1)和点B (x 2,y 2),当x 1<x 2时,y 1>y 2,则m的取值范围是( ) A .m >0B .m <0C .m <12D .m >123.已知正比例函数 y =mx(m <0) 图象上有两点 P(x 1,y 1) , Q(x 2,y 2) 且 x 1<x 2 ,则 y 1与 y 2 的大小关系是( ) A .y 1>y 2B .y 1<y 2C .y 1=y 2D .不能确定4.正比例函数y =3x 的图象必经过点( )A .(﹣1,﹣3)B .(﹣1,3)C .(1,﹣3)D .(3,1)5.已知正比例函数y=(m-1)x ,若y 随x 增大而增大,则点(m ,1-m )所在的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限6.正比例函数y=kx (k ≠0)的函数值y 随着x 增大而减小,则一次函数y=x+k 的图象大致是( )A .B .C .D .7.若函数y=kx 的图象经过点(1,-2),那么该图象一定经过点( )A .(2,-1)B .( −12,1)C .(-2,1)D .(1, 12)8.若正比例函数y =(m ﹣2)x 的图象经过点A(x 1,y 1)和点B(x 2,y 2),当x 1<x 2时,y 1>y 2,则m 的取值范围是( ) A .m >0B .m <0C .m >2D .m <29.正比例函数y=2x与反比例函数y=2x的图象或性质的共有特征之一是()A.函数值y随x的增大而增大B.图象在第一、三象限都有分布C.图象与坐标轴有交点D.图象经过点(2,1)10.若一个正比例函数y=mx的图像经过P(4,-8),Q(m,n)两点,则n的值为()A.1B.8C.-2D.411.对于正比例函数y=kx,当自变量x的值增加3时,对应的函数值y减少6,则k的值为()A.2B.﹣2C.﹣3D.﹣0.512.如图,在平面直角坐标系中,点A的坐标为(0,6),沿x轴向右平移后得到A',A点的对应点A'在直线y=35x上,则点B与其对应点B'之间的距离为()A.4B.6C.8D.10二、填空题13.函数y= 1m−2 x中,如果y随x的增大而减小,那么m的取值范围是.(1)线段B1B2的长度为;(2)点A2022的坐标为;(3)线段B2021B2022的长度为.15.写出一个实数k的值,使得正比例函数y=kx的图象在二、四象限.16.正比例函数y=(m﹣2)x m的图象的经过第象限,y随着x的增大而.17.若正比例函数y=(m﹣2)x的图象经过一、三象限,则m的取值范围是.18.函数y=kx与y=6−x的图像如图所示,则k=.三、综合题19.已知正比例函数y=kx.(1)若函数图象经过第二、四象限,则k的范围是什么?(2)点(1,﹣2)在它的图象上,求它的表达式.20.已知正比例函数y=kx经过点A(−1,4) .(1)求正比例函数的表达式;(2)将(1)中正比例函数向下平移5个单位长度后得到的函数表达式是.21.已知正比例函数y=kx图象经过点(3,﹣6),求:(1)求这个函数解析式.(2)画出这个函数图象.(3)判断点A(4,﹣2)、点B(﹣1.5,3)是否在这个函数图象上(4)图象上的两点C(x1,y1)、D(x2,y2),如果x1>x2,比较y1、y2的大小.22.如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答:(1)甲是几点钟出发?(2)乙是几点钟出发,到十点时,他大约走了多少千米? (3)到十点为止,哪个人的速度快? (4)两人最终在几点钟相遇?23.已知函数y=(m+3)x m2+2m−2.(1)当m 为何值时,它是正比例函数? (2)当m 为何值时,它是反比例函数? (3)当m 为何值时,它是二次函数?24.一水果经销商购进了A ,B 两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:A 种水果/箱B 种水果/箱甲店11元 17元 乙店9元13元5箱,B 种水果两店各5箱,请你计算出经销商能盈利多少元?(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?参考答案1.【答案】D2.【答案】D3.【答案】A4.【答案】A5.【答案】D6.【答案】A7.【答案】B8.【答案】D9.【答案】B10.【答案】D11.【答案】B12.【答案】D13.【答案】m<214.【答案】(1)√3(2)A2021A2022=22020 (3)22020√315.【答案】-216.【答案】二、四;减小17.【答案】m>218.【答案】219.【答案】(1)解:∵函数图象经过第二、四象限∴k<0.(2)解:当x=1,y=﹣2时,则k=﹣2 即:y=﹣2x.20.【答案】(1)解:将点A(−1,4)代入y=kx,得4=−k,即k=−4.故函数解析式为:y=−4x(2)y=−4x−521.【答案】(1)解:将点(3,﹣6)代入y=kx得,﹣6=3k解得,k=﹣2函数解析式为y=﹣2x;(2)解:如图:函数过(0,0),(1,﹣2).(3)解:将点A(4,﹣2)、点B(﹣1.5,3)分别代入解析式得,﹣2≠﹣2×4;3=﹣2×(﹣1.5);故点A不在函数图象上,点B在函数图象上.(4)解:由于k=﹣2<0,故y随x的增大而减小,可得y1<y2.22.【答案】(1)解:甲8点出发(2)解:乙9点出发;到10时他大约走了13千米(3)解:到10时为止,乙的速度快(4)解:两人最终在12时相遇23.【答案】(1)解:当函数y=(m+3)x m2+2m−2是正比例函数∴m2+2m﹣2=1且m+3≠0解得:m1=﹣3(舍去),m2=1则m=1时,它是正比例函数;(2)解:当函数y=(m+3)x m2+2m−2是反比例函数∴m2+2m﹣2=﹣1且m+3≠0解得:m1=﹣1+√2,m2=﹣1﹣√2则m=﹣1±√2时,它是反比例函数;(3)解:当函数y=(m+3)x m 2+2m−2是二次函数 ∴m 2+2m ﹣2=2 且m+3≠0解得:m 1=﹣1+√5,m 2=﹣1﹣√5 则m=﹣1±√5时,它是二次函数.24.【答案】(1)解:经销商能盈利=5×11+5×17+5×9+5×13=5×50=250(2)解:设甲店配A 种水果x 箱,则甲店配B 种水果(10﹣x )箱 乙店配A 种水果(10﹣x )箱,乙店配B 种水果10﹣(10﹣x )=x 箱. ∵9×(10﹣x )+13x ≥100∴x ≥2 12经销商盈利为w=11x+17•(10﹣x )+9•(10﹣x )+13x=﹣2x+260. ∵﹣2<0∴w 随x 增大而减小 ∴当x=3时,w 值最大.甲店配A 种水果3箱,B 种水果7箱.乙店配A 种水果7箱,B 种水果3箱.最大盈利:﹣2×3+260=254(元).。
正比例函数习题

《正比例函数》习题(含答案)一、单选题1.下列函数中,正比例函数有( ).(1)2y x =-(2)y =3)1yx =-(4)v =5)213y x =-(6)2y r π=(7)22y x =A .1个B .2个C .3个D .4个 2.一个正比例函数的图象经过点(2,4)-,它的表达式为 ( )A .2y x =-B .2y x =C .12y x =-D .12y x = 3.若正比例函数y =(1-2m)x 的图象经过点A(x 1,y 1)和点B(x 2,y 2),当x 1<x 2时,y 1>y 2,则m 的取值范围是( )A .m <0B .m >0C .m <12D .m >12 4.若y 关于x 的函数(2)y a x b =-+是正比例函数,则a ,b 应满足的条件是( ) A .2a ≠ B .0b = C .2a =且0b = D .2a ≠且0b = 5.邮购一种图书,每册定价20元,另加书价的5%作邮资,购书x 册,需付款y (元)与x (册)的函数关系式为( )A .205%y x x =+B .20.5y x =C .20(15%)y x =+D .19.95y x = 6.对于正比例函数2y x =-,当自变量x 的值增加1时,函数y 的值增加( ) A .12 B .12- C .2 D .-2 7.下列四组点中,可以在同一个正比例函数图象上的一组点是( ). A .(2,3),(4,6)- B .(2,3),(4,6)- C .(2,3),(4,6)-- D .(2,3),(4,6)- 8.如果正比例函数y =(a ﹣1)x (a 是常数)的图象在第一、三象限,那么a 的取值范围是( )A .a <0B .a >0C .a <1D .a >1 9.若某正比例函数过(2,3)-,则关于此函数的叙述不.正确的是( ). A .函数值随自变量x 的增大而增大B .函数值随自变量x 的增大而减小C .函数图象关于原点对称D .函数图象过二、四象限 10.如图,三个正比例函数的图像分别对应的解析式是:①y ax =;②y bx =;③y cx =,则a 、b 、c 的大小关系是( ).A .a b c >>B .c b a <<C .b a c >>D .b c a >>二、填空题 11.形如_________的函数叫做正比例函数.其中_______叫做比例系数.12.下列正比例函数中,y 的值随着x 值的增大而减小的有______.(1)8y x =;(2)0.6y x =-;(3)y =;(4)y x =. 13.按下列要求写出解析式:(1)若正方形的周长为p ,边长为a ,那么边长a 与周长p 之间的关系式为_________; (2)一辆汽车的速度为60km/h ,则行使路程()km s 与行使时间()h t 之间的关系式为___________;(3)圆的半径为r ,则圆的周长c 与半径r 之间的关系式为__________.14.正比例函数的图像过A 点,A 点的横坐标为3.且A 点到x 轴的距离为2,则此函数解析式是___________________ .15.正比例函数()35y m x =+,当m ______时,y 随x 的增大而增大.16.放假了,小明和小丽去蔬菜加工厂社会实践,两人同时工作了一段时间后,休息时小明对小丽说:“我已加工了28kg ,你呢?”小丽思考了一会儿说:“我来考考你. 图(1)、图(2)分别表示你和我的工作量与工作时间的关系,你能算出我加工了多少千克吗?”小明思考后回答:“你难不倒我,你现在加工了______kg.”三、解答题17.已知y 是x 的正比例函数,当x=﹣3时,y=12.(1)求y 关于x 的函数解析式;(2)当12x =-时的函数值.18.如图所示,正比例函数图象经过点A ,求这个正比例函数的解析式.19.已知正比例函数()y k 2x =-. (1)若y 的值随着x 值的增大而减小,则k 的范围是什么?(2)点()23-,在它的图象上,求这个函数的表达式. (3)在()2的结论下,若x 的取值范围是2x 4-≤≤,求y 的取值范围.参考答案1.C2.A3.D4.D5.C6.D7.C8.D9.A10.C11.y kx =(k 是常数,0k ≠) k 12.(2)(4)13.4p a = 60s t = 2c r π= 14.23y x =或2-3y x = 15.53>- 16.2017.(1)由题意可设y=kx (k ≠0).则 12=﹣3k ,解得,k=﹣4,所以y 关于x 的函数解析式是y=﹣4x ; (2)由(1)知,y=﹣4x ,当x=﹣12时,y=﹣4×(﹣12)=2. 即当12x =-时的函数值是2.18.解:设该正比例函数的解析式为y =kx (k ≠0), 由图象可知,该函数图象过点A (1,3), ∴k =3,∴该正比例函数的解析式为y =3x . 19.解:()1y 的值随着x 的值增大而减小, ∴ k 20-<,解得2k <.()2将点()23-,代入函数解析式可得()32k 2-=-, 解得12k =, ∴这个函数的表达式为3y x 2=-. ()3当x 2=-时,()3y 232=-⨯-=, 当x 4=时,3y 462=-⨯=-, 302-<,∴ y 随x 的增大而减小, ∴ 当2x 4-≤≤时,6y 3-≤≤.。
人教版八年级数学下册正比例函数专项练习

正比例函数专项练习一、选择题1.一个正比例函数的图象经过点(2, -1),则它的解析式为()A. y=-2x B . y=2x C . y=- - x D . y=- x2212.关于函数y -x,下列结论中,正确的是()3A.函数图像经过点(1,3)B. 函数图像经过二、四象限C.y随x的增大而增大D. 不论x为何值,总有y>03.已知正比例函数y kx(k 0)的图像过第二、四象限,则()A.y随x的增大而增大B.y 随x的增大而减小C.当x 0时,y随x的增大而增大;当x 0时,y随x的增大而减少;D.不论x如何变化,y不变4.函数y (2 m 6)x2(1 m)x是正比例函数,则m的值是()A. m =-3B. m=1C. m =3 C. m>-35.已知(x1,y1)和d, y2)是直线y 3x上的两点,且x〔x2,则y1与y2的大小关系是()A. y1>y2B. y1<y2C. y〔二y2D. 以上都不可能X k6.正比例函数y= (k-3) x的图象经过一、三象限,那么k的取值范围是()A. k>0 B . k>3 C. k<0 D . k<37.关于函数y=-2x ,下列判断正确的是()A.图像必过点(0, 0)和(-1,-2)B.图像经过一、三象限C.y随x的增大而减小D. 不论x为何值,总有y<0二、填空题8.若正比例函数y=kx (k是常数,kw0)的图象经过第二、第四象限,则k的值可以是(写出一个即可).9.结合正比例函数y 4x的图像回答:当x 1时,y的取值范围是.210.若x, y是变量,且函数y (k 1)x k是正比例函数,则k ^11.正比例函数y kx (k为常数,k 0)的图像经过第象限,函数值随自变量的增大而.12.已知y与x成正比例,且x 2时y 6 ,贝U y 9时x .13.如果函数y 2mx 3 m是正比例函数,则m =三、解答题14.已知y (k 1)x k 1是正比例函数,求k的值.15.在函数y 3x的图像上取一点P ,过P点作PA± x轴A为垂足,己知P点的横坐标为-2 ,求A POA勺面积(O为坐标原点).16. 已知y+5 与3x+4 成正比例,当x=1 时,y=2.1)求y 与x 的函数关系式;2)求当x=-1 时的函数值;(3)设点(m,-2)在这个函数图象上,求m的值;(4)若x的取值范围是0&X&5,求y的取值范围。
正比例函数(六大类型)(题型专练)(原卷版)

专题12 正比例函数(六大类型)【题型一:正比例函数的定义】【题型二:判断正比例函数图像所在象限】【题型三:正比例函数的性质】【题型四:判断正比例函数的比例系数大小】【题型五:待定系数法求正比例函数解析式】【题型六:正比例函数的图像性质综合】【题型一:正比例函数的定义】1.下列函数中,是正比例函数的是()A.B.y=x2C.y=2x D.y=2x﹣1 2.下列函数中,表示y是x的正比例函数的是()A.y=﹣0.1x B.y=2x2C.y2=4x D.y=2x+1 3.下列关系中,属于成正比例函数关系的是()A.正方形的面积与边长B.三角形的周长与边长C.圆的面积与它的半径D.速度一定时,路程与时间4.若y=(m﹣2)x+(m2﹣4)是正比例函数,则m的取值是()A.2B.﹣2C.±2D.任意实数5.正比例函数的比例系数为()A.﹣2B.C.D.26.函数y=(m﹣n+1)x|n﹣1|+n﹣2是正比例函数,则m,n应满足的条件是()A.m≠﹣1,且n=0 B.m≠1,且n=0C.m≠﹣1,且n=2D.m≠1,且n=27.已知函数y=(m﹣1)x+m2﹣1是正比例函数,则m=﹣1.8.若y=2x+m2﹣1是正比例函数,则m=±1.【题型二:判断正比例函数图像所在象限】9.正比例函数y=的图象经过的象限是()A.第一、三象限B.第二、四象限C.第三、四象限D.第一、二象限10.正比例函数的图象经过的象限是()A.第一、三象限B.第一、二象限C.第二、四象限D.第三、四象限11.一次函数y=8x的图象经过的象限是()A.一、三B.二、四C.一、三、四D.二、三、四12.已知函数y=(m﹣2)是关于x的正比例函数,且其图象经过第二、四象限,则m的值是.13.请写出一个图象经过第一、三象限的正比例函数的解析式.【题型三:正比例函数的性质】14.下列函数中,函数值y随x的增大而增大的有()①y=x②y=﹣x③y=﹣5x﹣2④y=4x+1A.1个B.2个C.3个D.4个15.关于直线y=﹣2x,下列结论正确的是()A.图象必过点(1,2)B.图象经过第一、三象限C.与y=﹣2x+1平行D.y随x的增大而增大16.对于函数y=4x,下列说法正确的是()A.当x>0时,y随x的增大而减小B.当x<0时,y随x的增大而减小C.y随x的增大而减小D.y随x的增大而增大17.P1(﹣2,y1),P2(7,y2)是正比例函数y=kx(k>0)的图象上的两个点,则y1,y2的大小关系是()A.y1>y2B.y1<y2C.y1=y2D.不能确定18.点A(1,m)在函数y=2x的图象上,则m的值是()A.1B.2C.D.019.已知:函数y1=2x,y2=﹣x+3,若x<1,则y1y2(填“>”或“=”或“<”).【题型四:判断正比例函数的比例系数大小】20.如图,三个正比例函数的图象分别对应表达式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列为()A.a<b<c B.a<c<b C.b<a<c D.c<b<a 21.如图,三个正比例函数的图象对应的解析式为①y=ax,②y=bx,③y=cx,则a、b、c的大小关系是()A.a>b>c B.c>b>a C.b>a>c D.b>c>a 22.如图,三个正比例函数的图象分别对应的解析式是:①y=ax,②y=bx,③y=cx,请用“>”表示a,b,c的不等关系.23.如图,正比例函数y=kx,y=mx,y=nx在同一平面直角坐标系中的图象如图所示.则比例系数k,m,n的大小关系是.(按从大到小的顺序用“>”连接)24.如图,三个正比例函数的图象分别对应表达式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列并用“<”连接为.【题型五:待定系数法求正比例函数解析式】25.已知y=(2m﹣1)x是正比例函数,且y随x的增大而减小,那么这个函数的解析式为()A.y=﹣5x B.y=5x C.y=3x D.y=﹣3x26.已知y与x成正比例,当x=4时,y=3,则y与x之间的函数关系式为,将这个函数的图象向下平移3个单位长度,得到的新图象的函数关系式为.27.正比例函数的图象经过点(1,2),则函数的表达式为.28.已知y与x成正比例,且当x=2时,y=﹣3.则当x=﹣时,y=.29.已知y与x成正比例关系,当x=2时,y=4,求:当x=﹣3时y的值.30.若y=(m﹣2)x+m2﹣4是y关于x的正比例函数,求该正比例函数的解析式.31.已知y=y1+y2,y1与x成正比例,y2与x﹣3成正比例,当x=﹣1时,y=4;当x=1时,y=8,求y与x之间的函数关系式.【题型六:正比例函数的图像性质综合】32.在物理学中,重力的表达关系式是G=mg(G代表重力,g代表重力常数10,m代表物体的质量)(1)在这个正比例函数表达式中,是自变量,是因变量.(2)若一个物体的重力为100N,它的质量是kg(3)若甲乙两个物体总质量为9kg,乙的质量是甲的2倍,那么甲物体受到的重力是多少?33.分类讨论思想数学课上,老师要求同学们画函数y=|x|的图象,小红联想绝对值的性质得y=x(x≥0)或y=﹣x(x≤0),于是她很快作出了该函数的图象(如图).请回答:(1)小红所作的图对吗?如果不对,请你画出正确的函数图象.(2)根据上述的作图方法,请画出函数y=﹣3|x|的图象.。
正比例函数例题

正比例函数例题一.选择题(共16小题)1.已知函数y=xk+1是正比例函数,则k的值为()A.1 B.﹣1 C.0 D.12.下列问题中,是正比例函数的是()A.矩形面积固定,长和宽的关系B.正方形面积和边长之间的关系C.三角形的面积一定,底边和底边上的高之间的关系D.匀速运动中,速度固定时,路程和时间的关系3.已知函数y=(m1)x是正比例函数,且图象在第二、四象限内,则m 的值是()A.2 B.﹣2 C.2 D.﹣4.已知函数y=(1﹣3m)x是正比例函数,且y随x的增大而增大,那么m的取值范围是()A.m B.m C.m1 D.m15.下列式子中,表示y是x的正比例函数的是()A.y=x5 B.y=3x C.y=3x2 D.y2=3x6.正比例函数y=﹣2x的大致图象是()A.B.C.D.7.在下列各图象中,表示函数y=﹣kx(k0)的图象的是()A.B.C.D.8.一次函数y=﹣x的图象平分()A.第一、三象限B.第一、二象限C.第二、三象限D.第二、四象限9.如图所示,在同一直角坐标系中,一次函数y=k1x、y=k2x、y=k3x、y=k4x的图象分别为l1、l2、l3、l4,则下列关系中正确的是()A.k1k2<k3<k4 B.k2k1<k4<k3 C.k1k2<k4<k3 D.k2k1<k3<k410.已知正比例函数y=(m﹣1)x的图象上两点A(x1,y1),B(x2,y2),当x1x2时,有y1y2,那么m的取值范围是()A.m1 B.m1 C.m2 D.m011.已知正比例函数y=(m﹣3)x的图象过第二、四象限,则m的取值范围是()A.m3 B.m3 C.m3 D.m312.已知正比例函数y=(m1)x,y随x的增大而减小,则m的取值范围是()A.m﹣1 B.m﹣1 C.m﹣1 D.m﹣113.已知正比例函数y=kx(k0),点(2,﹣3)在函数上,则y随x的增大而()A.增大B.减小C.不变D.不能确定14.若点A(﹣5,y1)和点B(﹣2,y2)都在y=﹣x上,则y1与y2的大小关系为()A.y1y2 B.y1=y2 C.y1y2 D.y1y215.若正比例函数y=(1﹣2m)x的图象经过点A(x1,y1)和点B(x2,y2),当x1x2时,y1y2,则m的取值范围是()A.m0 B.m0 C.m D.m16.已知正比例函数y=(2t﹣1)x的图象上一点(x1,y1),且x1y10,x1y1>0,那么t的取值范围是()A.t0.5 B.t0.5 C.t0.5或t0.5 D.不确定。
完整版)正比例函数练习题及答案

完整版)正比例函数练习题及答案XXX正比例函数题姓名:____________________ 家长签字:____________________ 得分:____________________ 一.选择题(每小题3分,共30分。
)1.下列函数表达式中,y是x的正比例函数的是()A。
y=﹣2x2B。
y=1/xC。
y=x+2D。
y=x﹣22.若y=x+2b是正比例函数,则b的值是()A。
0B。
﹣2C。
2D。
1/23.若函数y=mx是关于x的正比例函数,则常数m的值等于()A。
±2B。
﹣2C。
0.5D。
24.下列说法正确的是()A。
圆面积公式S=πr2中,S与r成正比例关系B。
三角形面积公式S=ah中,当S是常量时,a与h成反比例关系C。
y=x2中,y与x成反比例关系D。
y=x+1中,y与x成正比例关系5.下列各选项中的y与x的关系为正比例函数的是()A。
正方形周长y(厘米)和它的边长x(厘米)的关系B。
圆的面积y(平方厘米)与半径x(厘米)的关系C。
如果直角三角形中一个锐角的度数为x,那么另一个锐角的度数y与x间的关系D。
一棵树的高度为60厘米,每个月长高3厘米,x月后这棵的树高度为y厘米6.若函数y=(m﹣3)|x|﹣2是正比例函数,则m值为()A。
3B。
﹣3C。
±3D。
不能确定7.已知正比例函数y=(k﹣2)x+k+2的k的取值正确的是()A。
k=2B。
k≠2C。
k=﹣2D。
k≠﹣28.已知正比例函数y=kx(k≠0)的图象如图所示,则在下列选项中k值可能是()A。
1B。
2C。
3D。
49.如图所示,在同一直角坐标系中,一次函数y=k1x、y=k2x、y=k3x、y=k4x的图象分别为l1、l2、l3、l4,则下列关系中正确的是()A。
k1<k2<k3<k4B。
k2<k1<k4<k3C。
k1<k2<k4<k3D。
k2<k1<k3<k410.在直角坐标系中,既是正比例函数y=kx,又是y的值随x的增大而减小的图象是()A。
正比例函数练习题(整理别人的)

正比例函数练习题一、判断题:下列函数中,哪些上正比例函数?如果是,指出它的比例系数.1、x y 2=2、1+=x y3、2x y =4、xy 3= 5、()x a y 12+= 6、31-=x y π 7、()212-+=x a y 8、x y 2= 二、填空题 1、已知正比例函数x y 2=,当3=x 时,函数值y =2、已知正比例函数x y 21-=,当3-=y ,自变量x 的值是 3、已知正比例函数kx y =,当自变量x 的值为—4 时,函数值y = 20,则比例系数k =三、选择题1、下列关系中的两个量成正比例的是( )A 、从甲地到乙地,所用的时间和速度;B 、正方形的面积与边长C 、买同样的作业本所要的钱数和作业本的数量;D 、人的体重与身高2、下列函数中,y 是x 的正比例函数的是( )A 、14+=x yB 、22x y =C 、x y 5-=D 、x y =3、下列说法中不成立的是( )A 、在y=3x -1中y+1与x 成正比例;B 、在2x y -=中y 与x 成正比例 C 、在y=2(x+1)中y 与x + 1成正比例; D 、在y = x + 3中y 与x 成正比例4、若函数()()x m x m y -++=1622是正比例函数,则m 的值是( )A .m= —3B .m=1C .m=3D .m> —35、已知(x 1,y 1)和(x 2,y 2)是直线y=-3x 上的两点,且x 1>x 2,则y 1与y 2的大小关系是( )A .y 1〉y 2B .y 1<y 2C .y 1=y 2D .以上都有可能 ☆巩固练习:写出下列各题中两变量之间的函数关系式,并判断是否为正比例函数。
(1)三角形的一边长5cm ,它的面积 s(cm)与这边上的高 h(cm)的函数关系式;(2)如果直角三角形中一个锐角的度数为α,那么另一个锐角的度数β与α间的函数关系式;(3)如果某种报纸的单价为1元,x 表示购买这种报纸的份数,那么购买报纸的总价y(元)与x 间的函数关系式.(4)电报收费标准是每个字0。
(完整word版)正比例函数专题

正比例函数专题◆ 知识归纳1.形如___________(k 是常数,k ≠0)的函数是正比例函数,其中k 叫 ,正比例函数都是常数与自变量的乘积的形式2.正比例函数y=kx (k 是常数,k ≠0)的图象是一条经过原点的直线,我们通常称之为直线y=kx . 当k>0时,图像位于第 象限,从左向右 ,y 随x 的增大而 ,也可以说成函数值随自变量的增大而_________;当k<0时,图像位于第 象限,从左向右 ,y 随x 的增大而 ,也可以说成函数值随自变量的增大而_________.3.正比例函数的图像是经过坐标 点和定点__ __两点的一条 。
根据两点确定一条直线,可以确定两个点(两点法)画正比例函数的图象.◆测试点----正比例函数的定义一、 根据正比例函数解析式的特点求值1. 若x 、y 是变量,且函数是正比例函数,则k 的值为多少?2. 如果y=x-2a+1是正比例函数,则a 的值为多少?3. 若y=(n-2)x ︳n ︳-1 ,是正比例函数,则n 的值为多少?4. 已知y=(k+2)x+k 2-4是正比例函数,求k 的值.5. 若函数y=(2m+6)x 2+(1-m )x 是正比例函数,求m 的值是多少?6.若函数是正比例函数,求m 的值是多少?)2(32-+=-m x y m 2)1(k x k y +=二、求正比例函数的解析式1.点A(2,4)在正比例函数图象上,求这个正比例函数的解析式2.根据下图正比例函数y=kx的图象,求得其解析式.3.已知y与x成正比例,且x=2时y=-6,(1)求y与x函数的解析式(2)当y=9时,求x的值是多少?.4.已知y与(x-1)成正比例,当x=4时,y=-12(1)写出y与x之间的函数关系式。
(2)当x=-2时,求函数值y。
(3)当y=20,求自变量x的值。
5.已知y-1与x+1成正比例,且当x=-2时,y=-1,(1)写出y与x之间的函数关系式(2)当x=-5时,y的值是多少?6.已知:y=y1+y2,y1与x成正比例,y2与x2成正比例,当x=1时,y=6,当x=3时,y=8,求y关于x的解析式。
正比例函数训练题

正比例函数训练题一、选择题。
1. 下列函数是正比例函数的是( ).A.y=-8xB.y=-8x+1C.y=82x +1D.y=- 8x2. 比例系数为 - 13 的正比例函数的图像必经过点( ).A.( -13, 19)B.(- 13,- 19 )C.(- 13,1)D.(-13,-1) 3. 已知A ()11,x y 、B (22,x y )在直线y=kx 上,且k <0, 1x >2x ,则( ).A. 1y >2yB.1y <2yC.1y =2yD.无法比较5. 关于函数y=-2x ,下列判断正确的是( ).A.图像必过点(0,0)和(-1,-2)B.图像经过一、三象限C.y 随x 的增大而减小D.不论x 为何值,总有y <06.下列说法不成立的是( )A 、在31y x =-中1y +与x 成正比例B 、在12y =-x 中y 与x 成正比例;C 、在y=2(x+1)中y 与1x +成正比例;D 、在3y x =+中y 与x 成正比例;7、若函数2(26)(1)y m x m x =++-是正比例函数,则m 的值是( )8、函数211x y x -=-中自变量x 的取值范围是 。
二、填空题。
1. 已知函数y=(k-1)x+2k -1是正比例函数,则K=________.2. 若y+3与x 成正比例,且x=2时,y=5,则x=5时,y=________.3. 当a=_________时,函数y=(a-2)x+2a -4是正比咧函数。
4. 某函数y=(2-m) 1m x +,是正比例函数,则此函数图象经过第__________象限。
5. 若正比例函数y=kx(k ≠0)经过点(-1,2),则该正比例函数的解析式为__________.6. 随着海拔高度的升高,大气压强下降,空气中的含氧量也随之下降,即含氧量y(g/3m)与大气压强x(KPa)成正比例函数关系。
当x=36(KPa)时,y=108(g/3m),请写出y与x的函数关系式________________.7已知正比例函数(12)=-如果y的值随x的值增大而减小,那么a的取值范圆是y a x三、解答题。
正比例函数图像性质专项练习题

正比例函数图像性质专项练习题1、.若y=(m-1)xm2是关于 x的正比例函数,则m=()2、已知正比例函数的比例系数是-5,则它的解析式为:()3、y=-3x 由于两点确定一条直线,画正比例函数图象时我们只需描点(0,0)和点 (1,k),连线即可,所以,可以取()和()点来画4、函数y =-4x的图象在第( ) 象限,经过点(0,)与点(1, ), y 随x的增大而;5、如果函数y =(m-2)x 的图象经过第一、三象限,那么m的取值范围是;6、正比例函数y=kx(1) 当k>0时,正比例函数的图像经过第一、三象限,自变量x 逐渐增大时,y的值也随着逐渐增大。
(2)当k<0时,正比例函数的图像经过第二、四象限,自变量x逐渐增大时,y 的值则随着逐渐减小。
7、函数 y=4x 经过象限,y 随 x 的减小而 .8、如果函数 y= - kx 的图像经过一、三象限,那么y = kx 的图像经过9、已知 ab<0,则函数 y=b/a 的图像经过第()象限。
10、下列图像哪个可能是函数y=-8x的图像()11、如果正比例函数y=(8-2a)x的图像经过二、四象限,求a的取值范围。
12、已知正比例函数y=(m+1)xm2 ,它的图像经过第几象限?13、.已知:正比例函数y= (2-k)x 的图像经过第二.四象限,则函数y=-kx的图像经过哪些象限?14、如果y= (1-m)x m2-2是正比例函数,且y随x的增大而减小,试求m的值15、如图是甲、乙两人的行程函数图,根据图像回答:⑴谁走得快?⑵求甲、乙两个函数解析式,并写出自变量的取值范围⑶当t = 4时,甲、乙两人行程相差多少?16、已知正比例函数 y=(m+√2 )x m2-1 它的图像除原点外在二、四象限内,求m值.17、若正比例函数图像又y=(3k-6)x的图像经过点A(x1,x2)和B(y1,y2),当x1<x2时, y1>y2,则k的取值范围是()A.k>2B.k<2C.k=2D.无法确定18、正比例函数y=(3m-1)x的图像经过点A(x1,x2)和B(y1,y2),且该图像经过第二、四象限. (1)求m的取值范围(2)当x1>x2时,比较 y1与y2的大小,并说明理由.19、已知某种小汽车的耗油量是每100km耗油15升.所使用的90#汽油今日涨价到5元/升.(1)写出汽车行驶途中所耗油费y(元)与行程x(km)之间的函数关系式;(2)在平面直角坐标系内描出大致的函数关系图;(3)计算娄底到长沙220 km所需油费是多少?.21、已知正比例函数图像经过点(2,-6),求出此函数解析式。
正比例函数专题练习
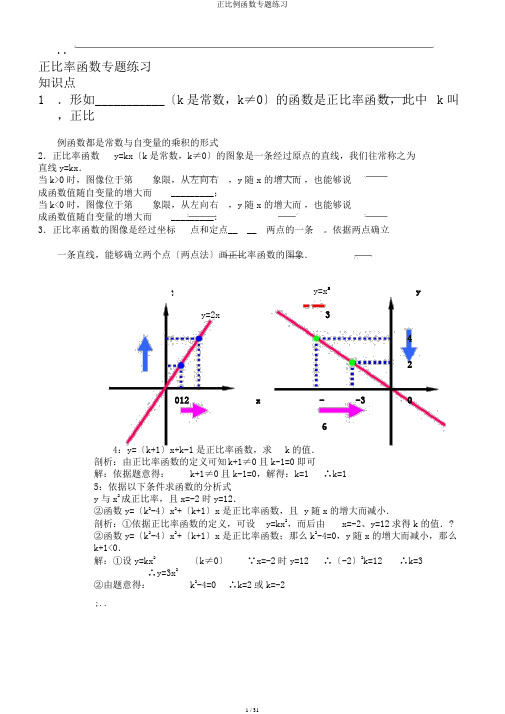
..正比率函数专题练习知识点1 .形如___________〔k是常数,k≠0〕的函数是正比率函数,此中k叫,正比例函数都是常数与自变量的乘积的形式2.正比率函数y=kx〔k是常数,k≠0〕的图象是一条经过原点的直线,我们往常称之为直线y=kx.当k>0时,图像位于第象限,从左向右,y随x的增大而,也能够说成函数值随自变量的增大而_________;当k<0时,图像位于第象限,从左向右,y随x的增大而,也能够说成函数值随自变量的增大而_________.3.正比率函数的图像是经过坐标点和定点__ __ 两点的一条。
依据两点确立一条直线,能够确立两个点〔两点法〕画正比率函数的图象.yy=2x y=x2y 34422012x--3064:y=〔k+1〕x+k-1是正比率函数,求k的值.剖析:由正比率函数的定义可知k+1≠0且k-1=0即可解:依据题意得:k+1≠0且k-1=0,解得:k=1 ∴k=15:依据以下条件求函数的分析式y与x2成正比率,且x=-2时y=12.②函数y=〔k2-4〕x2+〔k+1〕x是正比率函数,且y随x的增大而减小.剖析:①依据正比率函数的定义,可设y=kx2,而后由x=-2、y=12求得k的值.?②函数y=〔k2-4〕x2+〔k+1〕x是正比率函数;那么k2-4=0,y随x的增大而减小,那么k+1<0.解:①设y=kx2〔k≠0〕∵x=-2时y=12 ∴〔-2〕2k=12 ∴k=3∴y=3x2②由题意得:k2-4=0 ∴k=2或k=-2;..A..∵y随x的增大而减小,∴k+1<0∴k=-2 ∴y与x的函数关系式是:y=-x选择题1.以下关系中的两个量成正比率的是〔〕A .从甲地到乙地,所用的时间和速度;B.正方形的面积与边长C .买相同的作业本所要的钱数和作业本的数目;D.人的体重与身高2.以下函数中,y是x的正比率函数的是〔〕A .y=4x+1B .y=2x2C .y=- 5xD .y= x3.以下说法中不建立的是〔〕.在y=3x-1中y+1与x成正比率;B.在y=-x中y与x成正比率2C.在y=2〔x+1〕中y与x+1成正比率;D.在y=x+3中y与x成正比率解答题写出以下各题中x与y的关系式,并判断y是不是x的正比率函数?1〕电报收费标准是每个字元,电报费y〔元〕与字数x〔个〕之间的函数关系;2〕地面气温是28℃,假设每高升1km,气温降落5℃,那么气温x〔?℃〕?与高度y〔km〕的关系;3〕圆面积y〔cm2〕与半径x〔cm〕的关系.依据正比率函数分析式的特色求值假设x、y是变量,且函数 y=〔k+1〕x k2是正比率函数,那么的值为?假设y=x-2a+1是正比率函数,那么 a的值为?假设y=〔n-2〕x ︳-1,是正比率函数,那么n的值为?y=〔k+1〕x+k-5是正比率函数求k的值.假设函数y=〔2m+6〕x2+〔1-m〕x是正比率函数,那么m的值是〔〕函数y=(2m+1)x+m -3 假设函数图象经过原点,求m的值?二求正比率函数的分析式点A〔2,4〕在正比率函数图象上,那么这个正比率函数的分析式?正比率函数图象过〔-2,3〕,那么这个正比率函数的分析式?y与x成正比率,且x=2时y=-6,那么y=9时x的值是多少?.;....y与x成正比率,且x=-3时y=-9,那么y=-5时x的值是多少?三正比率函数图象的性质函数y=-7x的图象在第象限内,经过点(0, )与点(1, ),y随x的增大而.函数y=4x的图象在第象限内,经过点(0, )与点(1, ),y随x的增大而.正比率函数y=〔m-1〕x的图象经过一、三象限,那么m的取值范围是假设正比率函数图像又y=(3k-6)x 的图像经过点A〔x1,x2〕和B〔y1,y2〕,当x1<x2时,y1>y2,那么k的取值范围是点A〔-5,y1〕和点B〔-6,y2〕都在直线y=-9x的图像上那么y1与y2的大小关系是?〔x1,y1〕和〔x2,y2〕是直线y=-3x上的两点,且x1>x2,那么y1与y2?的大小关系是〔〕正比率函数y=(3m-1)x的图像经过点A〔x1,x2〕和B〔y1,y2〕,且该图像经过第二、四象限. 求m的取值范围当x1>x2时,比拟y1与y2的大小,并说明原因.研究题在函数y=-3x的图象上取一点P,过P点作PA⊥x轴,P点的横坐标为-?2,求△POA的面积〔O为坐标原点〕.如图,三个正比率函数的图像分别对应的分析式是①y=ax②y=bx③y=cx,那么a、b、c的大小关系是( )A.a>b>cB.c>b>aC.b>a>cD.b>c>a②③;..。
正比例函数练习题(整理别人的)

正比例函数练习题一、判断题:下列函数中,哪些上正比例函数?如果是,指出它的比例系数。
1、x y 2=2、1+=x y3、2x y =4、x y 3=5、()x a y 12+=6、31-=x y π 7、()212-+=x a y 8、x y 2=二、填空题1、已知正比例函数x y 2=,当3=x 时,函数值y =2、已知正比例函数x y 21-=,当3-=y ,自变量x 的值是 3、已知正比例函数kx y =,当自变量x 的值为—4 时,函数值y = 20,则比例系数k =三、选择题1、下列关系中的两个量成正比例的是( )A 、从甲地到乙地,所用的时间和速度;B 、正方形的面积与边长C 、买同样的作业本所要的钱数和作业本的数量;D 、人的体重与身高2、下列函数中,y 是x 的正比例函数的是( )A 、14+=x yB 、22x y =C 、x y 5-=D 、x y =3、下列说法中不成立的是( )A 、在y=3x -1中y+1与x 成正比例;B 、在2x y -=中y 与x 成正比例 C 、在y=2(x+1)中y 与x + 1成正比例; D 、在y = x + 3中y 与x 成正比例4、若函数()()x m x m y -++=1622是正比例函数,则m 的值是( ) A .m= —3 B .m=1 C .m=3 D .m> —35、已知(x 1,y 1)和(x 2,y 2)是直线y =-3x 上的两点,且x 1>x 2,则y 1与y 2的大小关系是( )A .y 1>y 2B .y 1<y 2C .y 1=y 2D .以上都有可能 ☆巩固练习:写出下列各题中两变量之间的函数关系式,并判断是否为正比例函数。
(1)三角形的一边长5cm,它的面积 s (cm)与这边上的高 h(cm)的函数关系式;(2)如果直角三角形中一个锐角的度数为α,那么另一个锐角的度数β与α间的函数关系式; (3)如果某种报纸的单价为1元,x 表示购买这种报纸的份数,那么购买报纸的总价y(元)与x 间的函数关系式.(4)电报收费标准是每个字0.1元,电报费y (元)与字数x (个)之间的函数关系; (5)地面气温是28℃,如果每升高1km ,气温下降5℃,则气温x (℃)与高度y (km )的关系;(6)圆面积y (cm 2)与半径x (cm )的关系☆直击中考1:1、当m 取什么数时,下列函数是正比例函数?(1)()x m y 2-=(2)x mx y += (3)()x m y 12+=2、若122-=m x y 是正比例函数,则m= ;若()322--=m x m y 是正比例函数,则m=4、已知y 与x 成正比例,当x=2时,y=8.(1)写出y 与x 之间的函数关系式。
正比例函数配套练习

正比例函数一.正比例函数的定义(共10小题)1.下列函数中是正比例函数的是()A.y=﹣8x B.y=C.y=5x2+6D.y=﹣0.5x﹣1 2.下列函数中,y是x的正比例函数的是()A.y=4x﹣1B.y=2x2C.D.3.下列关系式中,表示y是x的正比例函数的是()A.y=B.y=C.y=x+1D.y=2x24.下列变量之间关系中,一个变量是另一个变量的正比例函数的是()A.正方形的面积S随着边长x的变化而变化B.正方形的周长C随着边长x的变化而变化C.水箱有水10L,以0.5L/min的流量往外放水,水箱中的剩水量V(L)随着放水时间t(min)的变化而变化D.面积为20的三角形的一边a随着这边上的高h的变化而变化5.下列关系中,成正比例的是()A.圆的面积与半径B.矩形的面积一定时,长a和宽b之间的关系C.同种商品,购买的数量与金额D.正方形的面积与边长6.已知y=(k﹣2)x+(k2﹣4)是正比例函数,则k的值为.7.若y=(m﹣3)x|m|﹣2+m+n是正比例函数,则m=,n=.8.已知函数y=2x+m﹣1是正比例函数,则m=.9.已知是正比例函数,则m=.10.若x、y是变量,函数y=(k+1)是正比例函数,且经过第一、第三象限,则k=.二.正比例函数的图象(共6小题)11.函数y=的图象是()A.双曲线B.抛物线C.直线D.线段12.函数y=3x的图象经过()A.第一、三象限B.第二、四象限C.第一、二象限D.第三、四象限13.一次函数y=﹣x的图象平分()A.第一、三象限B.第一、二象限C.第二、三象限D.第二、四象限14.正比例函数y=﹣3x的大致图象是()A.B.C.D.15.在下列各图象中,表示函数y=﹣kx(k<0)的图象的是()A.B.C.D.16.正比例函数y=kx(k>0)的图象大致是()A.B.C.D.三.正比例函数的性质(共7小题)17.关于直线y=﹣2x,下列结论正确的是()A.图象必过点(1,2)B.图象经过第一、三象限C.与y=﹣2x+1平行D.y随x的增大而增大18.关于正比例函数y=﹣3x,下列结论正确的是()A.图象不经过原点B.y随x的增大而增大C.图象经过第二、四象限D.当x=时,y=119.已知正比例函数y=﹣2x,那么y的值随x的值增大而.(填“增大”或“减小”)20.函数y=(k﹣1)x+k+2是正比例函数.(1)求k的值;(2)当y=﹣3时,求x的值.21.如果正比例函数y=(k﹣3)x的图象经过第一、三象限,那么k的取值范围是.22.已知函数y=(m﹣2)是关于x的正比例函数,且其图象经过第二、四象限,则m的值是.23.结合函数y=﹣2x的图象回答,当x<﹣1时,y的取值范围.四.待定系数法求正比例函数解析式(共11小题)24.若一个正比例函数的图象经过点A(3,﹣6),则这个正比例函数的表达式为()A.y=﹣2x B.y=2x C.y=3x D.y=﹣6x25.已知y与x成正比,且当x=8时,y=16,求函数解析式.26.已知y与x成正比例,且x=3时,y=2,则y=3时,x的值为()A.B.C.2D.1227.已知:如图,正比例函数y=kx的图象经过点A,(1)请你求出该正比例函数的解析式;(2)若这个函数的图象还经过点B(m,m+3),请你求出m的值;(3)请你判断点P(﹣,1)是否在这个函数的图象上,为什么?28.正比例函数的图象经过点(2,﹣4)、(a,4),求这个函数的解析式和a的值.29.如图,在平面直角坐标系中,已知OA=4,则点A的坐标为,直线OA的解析式为.30.如图,△OPQ是边长为2的等边三角形,若正比例函数的图象过点P,则它的解析式是,若正比例函数图像过PQ中点,他的解释式为________31.下表中y是x的正比例函数,求出函数的表达式,并补全下表.x…12…y…﹣1﹣4…32.已知y﹣2与x成正比例,且x=2时,y=﹣6.求:(1)y与x的函数关系式;(2)当y=14时,x的值.33.若正比例函数图象上一点到y轴与到x轴距离之比是3:1,则此函数的解析式为.34.已知正比例函数y=kx的图象经过点(3,﹣6).(1)求这个函数的表达式.(2)在如图所示的直角坐标系中画出这个函数图象.(3)判断点A(4,﹣2)、点B(﹣1.5,3)是否在这个函数的图象上.。
正比例函数练习

正比例函数一、填空题(每小题4分,共40分)1、已知正比例函数y=2x,当x=3时,函数值y= 。
2、已知正比例函数,当y=-3时,自变量x 的值是 。
3、已知正比例函数y=kx ,当自变量x 的值为-4时,函数值y=20,则比例系数k= 。
4、大连市区与庄河两地之间的距离是160km ,若汽车以每小时80 km 的速度匀速从庄河开往大连,则汽车距庄河的路程s(km)与行驶的时间t(h)之间的函数关系式为 .5、已知一个正比例函数的图像经过点(-2,4),则这个正比例函数的表达式是 。
6、函数1y x =-中自变量x 的取值范围是 。
7如果函数23y mx m =+-是正比例函数,则m = 。
8、已知正比例函数(12)y a x =-如果y 的值随x 的值增大而减小,那么a 的取值范圆是 。
9、结合正比例函数4y x =的图像回答:当1x >时,y 的取值范围是 。
10、若x ,y 是变量,且函数2(1)k y k x =+是正比例函数,则k = 。
二、选择题(每小题3 分,共18分) 11、下列函数中,y 是x 的正比例函数的是( )A .y=4x+1B .y=2x 2C .y=-xD .y=12、已知函数y=-9x, 则下列说法错误的是( )A .函数图像经过第二,四象限。
B .y 的值随x 的增大而增大。
C .原点在函数的图像上。
D .y 的值随x 的增大而减小13、下列说法不成立的是( )A 、在31y x =-中1y +与x 成正比例B 、在12y =-x 中y 与x 成正比例; C 、在y=2(x+1)中y 与1x +成正比例;D 、在3y x =+中y 与x 成正比例;14、若函数2(26)(1)y m x m x =++-是正比例函数,则m 的值是( )A 、m =-3B 、m =1C 、m =3 C 、m >-315、已知11(,)x y 和22(,)x y 是直线3y x =-上的两点,且12x x >,则1y 与2y 的大小关系是( )A 、1y >2yB 、1y <2yC 、1y =2yD 、以上都不可能16、汽车开始行驶时,油箱内有油40 L ,如果每小时耗油5 L ,则油箱内的剩余油量Q (L )与 行驶时间t (h)之间的函数关系的图像应是( )A B C D三、解答题17、写出下列各题中x 与y 的关系式,并判断y 是否是x 的正比例函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正比例函数
一、概念
1、若y =x +2−b 是正比例函数,则b 的值是( )
A 、0
B 、−2
C 、2
D 、−0.5 2、下列说法中不成立的是( )
A 、在y =3x −1中y +1与x 成正比例
B 、在y =−x 2中y 与x 成正比例
C 、在y =2(x +1)中y 与x +1成正比例
D 、在y =x +3中y 与x 成正比例
二、图像
1、在下列四组点中可以在同一个正比例函数图像上的一组点是( )
A .(2,-3) (-4,6) B. (-2,3) (4,6)
C. (-2,-3) (4,-6)
D. (2,3) (-4,6)
2、如图,点B 、C 分别在两条直线 y =2x 和 y =kx 上,点A 、D 是x 轴上两点,已知ABCD 是正方形,求k 的值。
三、性质 1、 在正比例函数y=-3mx 中,函数y 的值随x 值的增大而增大,则p (m,5)在第
______ 象限。
2、(1)已知y=(2m-1)x m2-3是正比例函数,且y 随x 的增大而减小,求m 的值。
kx
(2)已知y=(2m-1)x m2-3是正比例函数,且函数图像经过第一、三象限,求m的值。
(3)已知y=(2m-1)x+m2-4是正比例函数,且y随x的增大而减小,求m的值。
(4)已知直线y=(a-2)x+a2-9经过原点,且y随x的增大而增大,求a的值。
四、
五、函数解析式
1、已知y与x2+1成正比例关系,且x=1时,y=4,求y与x之间的函数关系式。
2、
3、已知y-3与2x-1成正比例,且x=1时,y=6。
(1)
(2)求y与x之间的函数关系式;
(3)如果y的取值范围为0≤y≤5,求x的取值范围;
(4)若点A(x1 ,y1),B(x2 ,y2)都在函数的图像上,且y1>y2,试判断x1,x2的大小关系.。
