正比例函数及其性质练习题
正比例函数的图象与性质课件习题
在同一坐标系内画下列正比例函数的图像:
1 y 3x y x y x y 3
当k>0 时,它的图 像 经过第 一、三象 限
y 3x
3
yx
1 y x 3
1
3
1
o
x
在同一坐标系内画下列正比例函数的图像:
y 3x
y x
1 y x 3
y y 3x y x y 1 x
(1) 当k>0时,正比例函数的图像经过第一、三象 限,自变量x逐渐增大时,y的值也随着逐渐增大。 (2) 当k<0时,正比例函数的图像经过第二、四象限, 自变量x逐渐增大时,y的值则随着逐渐减小。
正 比 例 函 数
定义 图像
Y=kx(k≠0)
是经过原点和(1,k)点的一条直线 。
性 质
k>0
k<0
6.下列函数y=5x,y=-3x,y=1/2x,y=-1/3x中,y
随x的增大而减小的是———,y随x的增大而减小 且最先达到-10的是——。
能力提高:
想一想: 点燃蜡烛,蜡烛长度按照与时间成正比变短,长为21厘米 的蜡烛,已知点燃6分钟后,蜡烛变短3.6厘米,设蜡烛点 y 燃x分钟后变短y厘米,求 (1)用x表示函y数的解析式; (2)自变量x的取值范围; (3) 此蜡烛几分钟燃烧完?
能力提升!
m 2
1、已知函数 y (m 3) x , = 3 时,函数是正比例函数,图 减小 在 二、四 象限,y随x增大而
x 2、已知函数 y= 3 A(3,y1)
, 点
和点B (6,y2)在函数图象上, < 则 y1 y2(填“>”或“<”)。
x 3、已知函数 y 6
人教版八年级下册专项训练专题14 正比例函数图象和性质

专题14 正比例函数图象和性质一、知识点1、画正比例函数图象时,通常在坐标系中描出点________和________最为简单。
2、正比例函数y=kx(k是常数,k≠0)的图象是一条经过________的直线。
当k>0时,图象经过第________象限,y所x的增大而________。
当k<0时,图象经过第________象限,y所x的增大而________。
二、标准例题例1:若函数y=(2m+1)x2+(1﹣2m)x(m为常数)是正比例函数,则m的值为()A.m>12B.m=12C.m<12D.m=−12例2:若正比例函数y=(1+m)x 的图像经过点A(1,2m),则下列坐标对应的点也在该正比例函数的图像上的是()A.(2,1)B.(-1,2)C.(2,4)D.(-2,-1)例3:如图,在平面直角坐标系中,直线l:y=x+1与y轴交于点A1,如图所示依次作正方形A1B1C1O,正方形A2B2C2C1……正方形A n B n∁n C n﹣1(n为大于1的整数)使得点A1,A2,A3…A n在直线上,点C1,C2,C3,…∁n 在x轴正半轴上,请解决下列问题:(1)点A6的坐标是;点B6的坐标是;(2)点A n的坐标是,正方形A n B n∁n C n﹣1的面积是.例4:已知y与x﹣1成正比例,且当x=3时,y=4.(1)求y与x之间的函数表达式;(2)当x=﹣1时,求y的值;(3)当﹣3<y<5时,求x的取值范围.例5:已知正比例函数y=kx图象经过点(2,-4).(1)求这个函数的解析式;(2)图象上两点A(x1,y1)、B(x2,y2),如果x1<x2,比较y1,y2的大小.三、练习1.下列正比例函数中,y随x的值增大而增大的是()A.y=﹣2014x B.y=(√3﹣1)x C.y=(﹣π﹣3)x D.y=(1﹣π2)x2.已知点A(-5,y1)、B(-2,y2)都在直线y=-12x上,则y1与y2的关系是()A.y1≤y2B.y1=y2C.y1<y2D.y1>y23.若y关于x的函数y=(m–2)x+n是正比例函数,则m,n应满足的条件是()A.m≠2且n = 0B.m = 2且n ≠ 0C.m≠2D.n = 04.正比例函数y=2x的大致图象是()A.B.C.D.5.下列四组点中,可以在同一个正比例函数图象上的一组点是()A.(2 , −3),(−4 , 6)B.(−2 , 3),(4 , 6)C.(−2 , −3),(4 ,− 6)D.(2 , 3),(−4 , 6)6.直线y=kx过点A(m,n),B(m−3,n+4),则k的值是()A.43B.−43C.34D.−347.正比例函数y=kx(k>0)的图象大致是()A.B.C.D.8.已知正比例函数y=(2m﹣1)x的图象上两点A(x1,y1),B(x2,y2),当x1<x2时,有y1>y2,那么m 的取值范围是()A.m<12B.m>12C.m<0D.m>09.正比例函数y=kx的图像过点A(2,3),则此函数的图像还经过点()A.(-2,-3)B.(-2,3)C.(3,2)D.(-3,-2)10.已知y=(m+3)x m2−8是正比例函数,则m=______.11.点A(m,−3)向下平移3个单位后,恰好落在正比例函数y=−6x的图象上,则m的值为______.12.如图,直线y=√33x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A4的坐标为______,点A n______.13.函数y=(k-1)x2|k|-3是正比例函数,且y随x增大而减小,求(k+3)2019的值.14.如图,在边长为1个单位长度的小正方形组成的格点图中,点A、B、C都是格点.(1)点A坐标为;点B坐标为;点C坐标为;(2)画出△ABC关于原点对称的△A1B1C1;(3)已知M(1,4),在x轴上找一点P,使|PM﹣PB|的值最大(写出过程,保留作图痕迹),并写出点P 的坐标.15.一次函数y=kx+b.当x=-3时,y=0;当x=0时,y=-4(1)求k与b的值.(2)求该函数图象与x轴和y轴围成的图形面积.16.已知y与x+2成正比,当x=4时,y=4.(1)求y与x之间的函数关系式;(2)若点(a,3)在这个函数图象上,求a的值.17.请你用学习“一次函数”时积累的经验和方法研究函数y=|x|的图象和性质,并解决问题.(1)完成下列步骤,画出函数y=|x|的图象;①列表、填空;②描点:③连线(2)观察图象,当x______时,y随x的增大而增大;(3)结合图象,不等式|x|<x+2的解集为______.19.已知银行2006年9月的“半年期存款”年利率是2.25%,某人当年9月存入银行a元,经过半年到期时按规定缴纳20%利息税后,得到利息b元.问税后利息b(元)与本金a(元)成正比例吗?如果成正比例,那么求出这个比例系数.21.已知y与x成正比例,当x=4时,y=12.(1)写出y与x之间的函数解析式;(2)求当y=36时x的值;(3)判断点(-7,-10)是否是函数图象上的点.22.已知直线y=kx过点(−2,1),A是直线y=kx图像上的点,若过A向x轴作垂线,垂足为B,且SΔAB0=9,求点A的坐标.23.如图,点A(a,6)是第一象限内正比例函数y=3x的图象上的一点,AB⊥x轴,交直线OB于B点,三角形OAB的面积为5,求直线OB所对应的函数表达式.专题14 正比例函数图象和性质一、知识点1、画正比例函数图象时,通常在坐标系中描出点________和________最为简单。
正比例函数练习题及答案

正比例函数习题姓名:家长签字:得分:选择题(每小题3分,共30分。
)一.1.下列函数表达式中,y是x的正比例函数的是()A.y=-2x2B.y=xC.y=J^D.y=x-234x2.若y=x+2-b是正比例函数,则b的值是()A.0B.-2C.2D.-0.53.若函数广(2-m)是关于x的正比例函数,则常数m的值等于()A.±2B.-2C.±V3D.~V34.下列说法正确的是()A.圆面积公式S=nr2中,S与r成正比例关系B・三角形面积公式S=lah中,当S是常量时,a与h成反比例关系2°y皂+i中,y与x成反比例关系XD・中,y与x成正比例关系25.下列各选项中的y与x的关系为正比例函数的是()A.正方形周长y(厘米)和它的边长x(厘米)的关系B.圆的面积y(平方厘米)与半径x(厘米)的关系C.如果直角三角形中一个锐角的度数为x,那么另一个锐角的度数y与x间的关系D.一棵树的高度为60厘米,每个月长高3厘米,x月后这棵的树高度为y厘米6.若函数y=(m-3)x'®'*是正比例函数,则m值为()A.3B.-3C.±37.已知正比例函数y=(k-2)x+k+2的k的取值正确的是()A.k=2B.k^2C.k=-28.已知正比例函数)=1«(kOO)的图象如图所示,则在下列选项中k值可能是()A.1B.2C.39.如图所示,在同一直角坐标系中,一次函数y=Mx、y=k2x>y=k3x>y=k」x的图象分别为£、12>13>1」,则下列关系中正确的是()A.ki<k2<k3<k4B.k2<ki<k4<k3C.ki<k2<k4<k3D.k2<ki<k3<k410,在直角坐标系中,既是正比例函数尸=1«,又是y的值随X的增大而减小的图象是()A. B.J,/ C.J'| D.二.填空题(每小题3分,共27分。
正比例函数性质
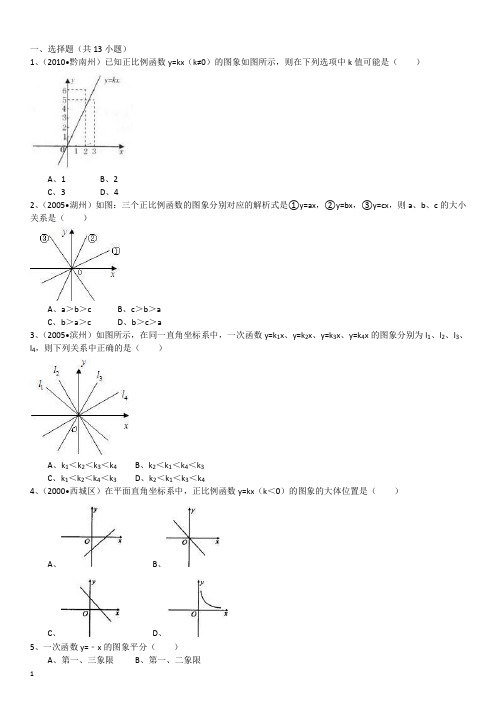
一、选择题(共13小题)1、(2010•黔南州)已知正比例函数y=kx(k≠0)的图象如图所示,则在下列选项中k值可能是()A、1B、2C、3D、42、(2005•湖州)如图:三个正比例函数的图象分别对应的解析式是①y=ax,②y=bx,③y=cx,则a、b、c的大小关系是()A、a>b>cB、c>b>aC、b>a>cD、b>c>a3、(2005•滨州)如图所示,在同一直角坐标系中,一次函数y=k1x、y=k2x、y=k3x、y=k4x的图象分别为l1、l2、l3、l4,则下列关系中正确的是()A、k1<k2<k3<k4B、k2<k1<k4<k3C、k1<k2<k4<k3D、k2<k1<k3<k44、(2000•西城区)在平面直角坐标系中,正比例函数y=kx(k<0)的图象的大体位置是()A、B、C、D、5、一次函数y=﹣x的图象平分()A、第一、三象限B、第一、二象限C、第二、三象限D、第二、四象限6、在平面直角坐标系中,一次函数y=2x+1的图象不经过()A、第一象限B、第二象限C、第三象限D、第四象限7、在直角坐标系中,既是正比例函数y=kx,又是y的值随x的增大而减小的图象是()A、B、C、D、8、(2011•湘西州)当k>0时,正比例函数y=kx的图象大致是()A、B、C、D、9、已知正比例函数y=kx+b的值随着x的增大而减小,则大致图象为()A、B、C、D、10、已知正比例函数y=kx (k≠0),当x=﹣1时,y=﹣2,则它的图象大致是()A、B、C、D、11、如图所示函数图象中,正比例函数的图象是()A、B、C、D、12、正比例函数y=kx的图象是经过原点的一条()A、射线B、双曲线C、线段D、直线13、结合函数y=﹣2x的图象回答,当x<﹣1时,y的取值范围()A、y<2B、y>2C、y≥D、y≤二、填空题(共1小题)14、正比例函数的图象是_________,当k>0时,直线y=kx过第_________象限,y随x的增大而_________.答案与评分标准一、选择题(共13小题)1、(2010•黔南州)已知正比例函数y=kx(k≠0)的图象如图所示,则在下列选项中k值可能是()A、1B、2C、3D、4考点:正比例函数的图象。
4.3 正比例函数的图像与性质 同步作业(含答案)

正比例函数的图像与性质1.[2018·陕西]如图,在矩形AOBC 中,A (-2,0),B (0,1).若正比例函数y =kx 的图象经过点C ,则k 的值为( )A .-12 B.12 C .-2 D .22.关于正比例函数y =-2x ,下列说法正确的是( )A .图象必经过点(-1,-2)B .图象经过第一、三象限C .y 随x 的增大而减小D .不论x 取何值,总有y <03.已知正比例函数y =kx (k <0)的图象上两点A (x 1,y 1),B (x 1,y 2),且x 1<x 2,则下列不等式中恒成立的是( )A .y 1+y 2>0B .y 1+y 2<0C .y 1-y 2>0D .y 1-y 2<04.如图,三个正比例函数的图象分别对应表达式:①y =ax ;②y =bx ;③y =cx .将a ,b ,c 从小到大排列并用“<”连接为_________.5.在正比例函数y =-3mx 中,函数y 的值随x 值的增大而增大,则P (m ,5)在第____象限. 6.已知正比例函数的图象经过点(-1,2). (1)求此正比例函数的表达式; (2)点(2,-5)是否在此函数的图象上?7.在同一直角坐标系上画出函数y =2x ,y =-13x ,y =-0.6x 的图象.8.在如图所示的平面直角坐标系中,点P 是直线y =x 上的动点,A (1,0),B (2,0)是x 轴上的两点,则P A +PB 的最小值为________.9.已知正比例函数y =(m +2)x 中,y 的值随x 的增大而增大,而正比例函数y =(2m -3)x 中,y 的值随x 的增大而减小,且m 为整数,你能求出m 的可能值吗?为什么?10.[2018·贵港]如图,直线l 为y =3x ,过点A 1(1,0)作A 1B 1⊥x 轴,与直线l 交于点B 1,以原点O 为圆心,OB 1长为半径画弧交x 轴于点A 2;再作A 2B 2⊥x 轴,交直线l 于点B 2,以原点O 为圆心,OB 2的长为半径画弧交x 轴于点A 3;…,按此作法进行下去,则点An 的坐标为__________.参考答案1.A2.C3.C4.a<c<b5.二6.解:(1)y=-2x;(2)点(2,-5)不在此函数的图象上.7.解:列表如下:画出图象如下:答图8. 5答图【解析】如答图,作A点关于直线y=x的对称点A′,连接A′B,交直线y=x于点P,此时P A+PB最小,由题意可得OA′=1,BO=2,P A′=P A,此时,P A+PB=A′B=12+22= 5.9.解:m 的可能值为-1,0,1.理由如下:∵正比例函数y =(m +2)x 中,y 的值随x 的增大而增大, ∴m +2>0,解得m >-2.∵正比例函数y =(2m -3)x 中,y 的值随x 的增大而减小, ∴2m -3<0,解得m <32,∴-2<m <32.∵m 为整数,∴m 的可能值为-1,0,1. 10. (2n -1,0)【解析】 直线y =3x ,点A 1坐标为(1,0),过点A 1作x 轴的垂线交直线l 于点B 1,可知B 1点的坐标为(1,3),以原点O 为圆心,OB 1长为半径画弧交x 轴于点A 2,OA 2=OB 1,所以OA 2=12+(3)2=2,因此点A 2的坐标为(2,0),同理,可求得点B 2的坐标为(2,23),故点A 3的坐标为(4,0),B 3(4,43),…,所以An 的坐标为(2n -1,0)。
4.3.1 正比例函数的图象和性质 湘教版数学八年级下册同步练习(含答案)

4.3 一次函数的图象1 正比例函数的图象和性质要点感知1画函数图象的步骤:(1)__________;(2)__________:建立直角坐标系,以__________为横坐标,__________为纵坐标,确定点的坐标;(3)__________.预习练习1-1下面所给点的坐标满足y=-2x的是( )A.(2,-1)B.(-1,2)C.(1,2)D.(2,1)要点感知2 正比例函数y=kx(k为常数,k≠0)的图象是一条__________,因此画正比例函数图象时,只要描出图象上的__________,然后过两点作一条直线即可,这条直线叫作“直线__________”.预习练习2-1 如图,某正比例函数的图象过点M(-2,1),则此正比例函数表达式为( )A.y=-xB.y=xC.y=-2xD.y=2x要点感知3 正比例函数图象的性质:直线y=kx(k≠0)是一条经过________的直线.当k>0时,直线y=kx经过第_______象限,从左到右,y随x的增大而________;当k<0时,直线y=kx经过第_____象限,从左到右,y随x的增大而________.知识点1 画正比例函数的图象1.正比例函数y=3x的大致图像是( )2.已知正比例函数y=x,请在平面直角坐标系中画出这个函数的图象.知识点2 正比例函数的图象与性质3.已知函数y=kx的函数值随x的增大而增大,则函数的图象经过( )A.第一、二象限B.第一、三象限C.第二、三象限D.第二、四象限4.对于函数y=-k2x(k是常数,k≠0)的图象,下列说法不正确的是( )A.其函数图象是一条直线B.其函数图象过点(,-k)C.其函数图象经过一、三象限D.y随着x增大而减小5.正比例函数y=-x的图象平分( )A.第一、三象限B.第一、二象限C.第二、三象限D.第二、四象限6.函数y=-5x的图象在第__________象限内,y随x的增大而__________.知识点3 实际问题中的正比例函数7.一根蜡烛长20 cm,点燃后每小时燃烧5 cm,则蜡烛燃烧的长度y(cm)与燃烧时间x(h)的函数关系用图象表示为下图中的( )8.小明用16元零花钱购买水果,已知水果单价是每千克4元,设买水果x千克用去的钱为y元,(1)求买水果用去的钱y(元)随买水果的数量x(千克)而变化的函数表达式;(2)画出这个函数的图象.9.已知正比例函数y=kx(k≠0),当x=1时,y=-2,则它的图象大致是( )10.已知正比例函数y=(3k-1)x,若y随x的增大而增大,则k的取值范围是( )A.k<0B.k>0C.k<D.k>11.若点A(-2,m)在正比例函数y=-x的图象上,则m的值是( )A. B.- C.1 D.-112.已知正比例函数y=kx(k<0)的图象上两点A(x1,y1)、B(x2,y2),且x1<x2,则下列不等式中恒成立的是( )A.y1+y2>0B.y1+y2<0C.y1-y2>0D.y1-y2<013.甲、乙两人在一次百米赛跑中,路程s(米)与赛跑时间t(秒)的关系如图所示,则下列说法正确的是( )A.甲、乙两人的速度相同B.甲先到达终点C.乙用的时间短D.乙比甲跑的路程多14.写出一个图像经过一、三象限的正比例函数y=kx(k≠0)的解析式(关系式):_______________.15.当m=__________时,函数y=mx3m+4是正比例函数,此函数y随x的增大而__________.16.如图,正比例函数y=kx,y=mx,y=nx在同一平面直角坐标系中的图象如图所示.则系数k,m,n的大小关系是__________.17.已知正比例函数y=(k-2)x.(1)若函数图象经过第二、四象限,则k的范围是什么?(2)若函数图象经过第一、三象限,则k的范围是什么?18.已知正比例函数图象经过点(-1,2).(1)求此正比例函数的表达式;(2)画出这个函数图象;(3)点(2,-5)是否在此函数图象上?(4)若这个图象还经过点A(a,8),求点A的坐标.19.已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.(1)求正比例函数的表达式;(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.参考答案要点感知1(1)列表(2)描点自变量值相应的函数值(3)连线预习练习1-1B要点感知2 直线两点y=kx预习练习2-1A要点感知3 原点一、三上升增大二、四下降减少1.B2.图略.3.B4.C5.D6.二、四减小7.A8.(1)根据题意可得y=4x(0≤x≤4).(2)当x=0时,y=0;当x=4时,y=16.在平面直角坐标系中画出两点O(0,0),A(4,16),过这两点作线段OA,线段OA即函数y=4x(0≤x≤4)的图象,如图.9.A 10.D 11.C 12.C 13.B 14.y=3x(答案不唯一) 15.-1减小16.k>m>n 17.(1)k-2<0,∴k<2;(2)k-2>0,∴k>2.18.(1)设函数的表达式为:y=kx,则-k=2,即k=-2.故正比例函数的表达式为:y=-2x.(2)图象图略.(3)将点(2,-5)代入,左边=-5,右边=-4,左边≠右边,故点(2,-5)不在此函数图象上.(4)把(a,8)代入y=-2x,得8=-2a.解得a=-4.故点A的坐标是(-4,8).19.(1)∵点A的横坐标为3,且△AOH的面积为3,∴点A的纵坐标为-2,点A的坐标为(3,-2).∵正比例函数y=kx经过点A,∴3k=-2.解得k=-.∴正比例函数的表达式是y=-x.(2)∵△AOP的面积为5,点A的坐标为(3,-2),∴OP=5.∴点P的坐标为(5,0)或(-5,0).。
中考数学《正比例函数图像和性质》专项练习题及答案

中考数学《正比例函数图像和性质》专项练习题及答案一、单选题1.若正比例函数的图象经过点(﹣1,2),则这个图象必经过点( )A .(1,2)B .(﹣1,﹣2)C .(2,﹣1)D .(1,﹣2)2.若正比例函数y=(1-2m )x 的图象经过点A (x 1,y 1)和点B (x 2,y 2),当x 1<x 2时,y 1>y 2,则m的取值范围是( ) A .m >0B .m <0C .m <12D .m >123.已知正比例函数 y =mx(m <0) 图象上有两点 P(x 1,y 1) , Q(x 2,y 2) 且 x 1<x 2 ,则 y 1与 y 2 的大小关系是( ) A .y 1>y 2B .y 1<y 2C .y 1=y 2D .不能确定4.正比例函数y =3x 的图象必经过点( )A .(﹣1,﹣3)B .(﹣1,3)C .(1,﹣3)D .(3,1)5.已知正比例函数y=(m-1)x ,若y 随x 增大而增大,则点(m ,1-m )所在的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限6.正比例函数y=kx (k ≠0)的函数值y 随着x 增大而减小,则一次函数y=x+k 的图象大致是( )A .B .C .D .7.若函数y=kx 的图象经过点(1,-2),那么该图象一定经过点( )A .(2,-1)B .( −12,1)C .(-2,1)D .(1, 12)8.若正比例函数y =(m ﹣2)x 的图象经过点A(x 1,y 1)和点B(x 2,y 2),当x 1<x 2时,y 1>y 2,则m 的取值范围是( ) A .m >0B .m <0C .m >2D .m <29.正比例函数y=2x与反比例函数y=2x的图象或性质的共有特征之一是()A.函数值y随x的增大而增大B.图象在第一、三象限都有分布C.图象与坐标轴有交点D.图象经过点(2,1)10.若一个正比例函数y=mx的图像经过P(4,-8),Q(m,n)两点,则n的值为()A.1B.8C.-2D.411.对于正比例函数y=kx,当自变量x的值增加3时,对应的函数值y减少6,则k的值为()A.2B.﹣2C.﹣3D.﹣0.512.如图,在平面直角坐标系中,点A的坐标为(0,6),沿x轴向右平移后得到A',A点的对应点A'在直线y=35x上,则点B与其对应点B'之间的距离为()A.4B.6C.8D.10二、填空题13.函数y= 1m−2 x中,如果y随x的增大而减小,那么m的取值范围是.(1)线段B1B2的长度为;(2)点A2022的坐标为;(3)线段B2021B2022的长度为.15.写出一个实数k的值,使得正比例函数y=kx的图象在二、四象限.16.正比例函数y=(m﹣2)x m的图象的经过第象限,y随着x的增大而.17.若正比例函数y=(m﹣2)x的图象经过一、三象限,则m的取值范围是.18.函数y=kx与y=6−x的图像如图所示,则k=.三、综合题19.已知正比例函数y=kx.(1)若函数图象经过第二、四象限,则k的范围是什么?(2)点(1,﹣2)在它的图象上,求它的表达式.20.已知正比例函数y=kx经过点A(−1,4) .(1)求正比例函数的表达式;(2)将(1)中正比例函数向下平移5个单位长度后得到的函数表达式是.21.已知正比例函数y=kx图象经过点(3,﹣6),求:(1)求这个函数解析式.(2)画出这个函数图象.(3)判断点A(4,﹣2)、点B(﹣1.5,3)是否在这个函数图象上(4)图象上的两点C(x1,y1)、D(x2,y2),如果x1>x2,比较y1、y2的大小.22.如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答:(1)甲是几点钟出发?(2)乙是几点钟出发,到十点时,他大约走了多少千米? (3)到十点为止,哪个人的速度快? (4)两人最终在几点钟相遇?23.已知函数y=(m+3)x m2+2m−2.(1)当m 为何值时,它是正比例函数? (2)当m 为何值时,它是反比例函数? (3)当m 为何值时,它是二次函数?24.一水果经销商购进了A ,B 两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:A 种水果/箱B 种水果/箱甲店11元 17元 乙店9元13元5箱,B 种水果两店各5箱,请你计算出经销商能盈利多少元?(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?参考答案1.【答案】D2.【答案】D3.【答案】A4.【答案】A5.【答案】D6.【答案】A7.【答案】B8.【答案】D9.【答案】B10.【答案】D11.【答案】B12.【答案】D13.【答案】m<214.【答案】(1)√3(2)A2021A2022=22020 (3)22020√315.【答案】-216.【答案】二、四;减小17.【答案】m>218.【答案】219.【答案】(1)解:∵函数图象经过第二、四象限∴k<0.(2)解:当x=1,y=﹣2时,则k=﹣2 即:y=﹣2x.20.【答案】(1)解:将点A(−1,4)代入y=kx,得4=−k,即k=−4.故函数解析式为:y=−4x(2)y=−4x−521.【答案】(1)解:将点(3,﹣6)代入y=kx得,﹣6=3k解得,k=﹣2函数解析式为y=﹣2x;(2)解:如图:函数过(0,0),(1,﹣2).(3)解:将点A(4,﹣2)、点B(﹣1.5,3)分别代入解析式得,﹣2≠﹣2×4;3=﹣2×(﹣1.5);故点A不在函数图象上,点B在函数图象上.(4)解:由于k=﹣2<0,故y随x的增大而减小,可得y1<y2.22.【答案】(1)解:甲8点出发(2)解:乙9点出发;到10时他大约走了13千米(3)解:到10时为止,乙的速度快(4)解:两人最终在12时相遇23.【答案】(1)解:当函数y=(m+3)x m2+2m−2是正比例函数∴m2+2m﹣2=1且m+3≠0解得:m1=﹣3(舍去),m2=1则m=1时,它是正比例函数;(2)解:当函数y=(m+3)x m2+2m−2是反比例函数∴m2+2m﹣2=﹣1且m+3≠0解得:m1=﹣1+√2,m2=﹣1﹣√2则m=﹣1±√2时,它是反比例函数;(3)解:当函数y=(m+3)x m 2+2m−2是二次函数 ∴m 2+2m ﹣2=2 且m+3≠0解得:m 1=﹣1+√5,m 2=﹣1﹣√5 则m=﹣1±√5时,它是二次函数.24.【答案】(1)解:经销商能盈利=5×11+5×17+5×9+5×13=5×50=250(2)解:设甲店配A 种水果x 箱,则甲店配B 种水果(10﹣x )箱 乙店配A 种水果(10﹣x )箱,乙店配B 种水果10﹣(10﹣x )=x 箱. ∵9×(10﹣x )+13x ≥100∴x ≥2 12经销商盈利为w=11x+17•(10﹣x )+9•(10﹣x )+13x=﹣2x+260. ∵﹣2<0∴w 随x 增大而减小 ∴当x=3时,w 值最大.甲店配A 种水果3箱,B 种水果7箱.乙店配A 种水果7箱,B 种水果3箱.最大盈利:﹣2×3+260=254(元).。
第1课时正比例函数的图象及性质练习试题(含答案解析)

WORD格式.整理版第1课时正比例函数的图象和性质一.选择题(共10小题)y=3.若函数是关于x的正比例函数,则常数m的值等于()Dah中,中,8题图 9题图9.如图所示,在同一直角坐标系中,一次函数y=k1x、y=k2x、y=k3x、y=k4x的图象分别为l1、l2、l3、l4,则下列B C D11.若函数y﹦(m+1)x+m2﹣1是正比例函数,则m的值为_________ .14.请写出直线y=6x 上的一个点的坐标: _________ .15.已知正比例函数y=kx (k≠0),且y 随x 的增大而增大,请写出符合上述条件的k 的一个值: _________ .16.已知正比例函数y=(m ﹣1)的图象在第二、第四象限,则m 的值为 _________ .17.若p 1(x 1,y 1) p 2(x 2,y 2)是正比例函数y=﹣6x 的图象上的两点,且x 1<x 2,则y 1,y 2的大小关系是:y 1 _________ y 2.点A (-5,y 1)和点B (-6,y 2)都在直线y= -9x 的图像上则y 1__________ y 218.正比例函数y=(m ﹣2)x m 的图象的经过第 _________ 象限,y 随着x 的增大而 _________ .19.函数y=﹣7x 的图象在第 _________ 象限内,经过点(1, _________ ),y 随x 的增大而 _________ .三.解答题(共3小题)20.已知:如图,正比例函数的图象经过点P 和点Q (﹣m ,m+3),求m 的值.21.已知y+2与x ﹣1成正比例,且x=3时y=4.(1)求y 与x 之间的函数关系式;(2)当y=1时,求x 的值.22.已知y=y 1+y 2,y 1与x 2成正比例,y 2与x ﹣2成正比例,当x=1时,y=5;当x=﹣1时,y=11,求y 与x 之间的函数表达式,并求当x=2时y 的值.23. 为缓解用电紧张矛盾,某电力公司特制定了新的用电收费标准,每月用电量()x kW h 与应付饱费y (元)的关系如图所示。
正比例函数图像及性质

WORD 格式整理版正比例函数的图像和性质知识精要1.正比例函数的图像一般地,正比例函数 y=kx(k 是常数, k 0)的图像是经过原点 O(0,0) 和点 M(1,k)的一条直线。
我们把正比例函数 y=kx 的图像叫做直线 y=kx。
2.正比例函数性质精讲名题x m 3例 1. 若函数 y=(m-1)是正比例函数,则m=,函数的图像经过象限。
解:m=4, 图像经过第一、三象限。
例 2. 已知 y-1 与 2x 成正比例,当 x=-1 时, y=5, 求 y 与 x 的函数解析式。
解:∵ y-1 与 2x 成正比例∴设y-1=k ·2x (k0 )把x=-1,y=5代入,得k=-2,∴ y-1=-2·2x∴y=-4x+1例 3. 已知 y 与 x 的正比例函数,且当x=6 时 y=-2WORD 格式整理版(1)求出这个函数的解析式;(2)在直角坐标平面内画出这个函数的图像;(3)如果点 P(a, 4)在这个函数的图像上,求 a 的值;(4)试问,点 A(-6 , 2)关于原点对称的点 B 是否也在这个图像上?解: (1)设 y=k·x ( k 0)当 x=6 时, y=-2 ∴-2=6k ∴k 1∴这个函数的解析式为 y1x 33(2)y 1x 的定义域是一切实数,图像如图所示:3(3)如果点 P(a, 4)在这个函数的图像上,∴41a ,∴a=-12 3(4)点 A(-6 ,2)关于原点对称的点 B 的坐标( 6,-2 ),当 x=6 时, y=162因此,点 B 也在直线y 1x 上33例 4. 已知点 ( x1, y1 ) ,( x2, y2 ) 在正比例函数 y=(k-2)x的图像上,当x1x2时, y1y2,那么k 的取值范围是多少?解:由题意,得函数y 随 x 的值增大而减小,∴k-2<0, ∴k<2例 5. (1)已知 y=ax 是经过第二、四象限的直线,且 a 3 在实数范围内有意义,求 a 的取值范围。
中考数学-一次函数正比例函数的图像及性质(含答案)专题练习

中考数学-一次函数正比例函数的图像及性质(含答案)专题练习一、单选题1.已知正比例函数y=kx(k≠0),点(2,-3)在函数上,则y随x的增大而()A. 增大B. 减小C. 不变D. 不能确定2.已知函数y=x+k+1是正比例函数,则k的值为()A.1B.﹣1C.0D.±13.正比例函数y=(2k+1)x,若y随x增大而减小,则k的取值范围是()A. k>﹣B. k<﹣C. k=D. k=04.若正比例函数y=kx的图象经过点A(k,9),且经过第一、三象限,则k的值是()A. ﹣9B. ﹣3C. 3D. ﹣3或35.若正比例函数y=(1-2m)x的图象经过点A(x1,y1)和点B(x2,y2),当x1< x2时,y1>y2,则m的取值范围是()A. m<0B. m>0C.D.6.在下列四组点中,可以在同一个正比例函数图象上的一组点是()A. (2,﹣3),(﹣4,6)B. (﹣2,3),(4,6)C. (﹣2,﹣3),(4,﹣6)D. (2,3),(﹣4,6)7.正比例函数y=kx(k≠0)的图像在第二、四象限,则一次函数y=x+k的图像大致是()A. B. C. D.8.下列点不在正比例函数y=﹣2x的图象上的是()A. (5,﹣10)B. (0,0)C. (2,﹣1)D. (1,﹣2)9.正比例函数y=(2k+1)x,若y随x增大而减小,则k的取值范围是()A. k>﹣B. k<﹣C. k=D. k=010.关于函数y=﹣x,下列结论正确的是()A. 函数图象必过点(﹣2,﹣1)B. 函数图象经过第1、3象限C. y随x的增大而减小D. y随x的增大而增大11.下列式子中,表示y是x的正比例函数的是()A.y=x﹣1B.y=2xC.y=2x2D.y2=2x12.下列变量之间关系中,一个变量是另一个变量的正比例函数的是()A. 正方形的面积S随着边长x的变化而变化B. 正方形的周长C随着边长x的变化而变化C. 水箱有水10L,以0.5L/min的流量往外放水,水箱中的剩水量V(L)随着放水时间t(min)的变化而变化D. 面积为20的三角形的一边a随着这边上的高h的变化而变化13.P1(x1,y1),P2(x2,y2)是正比例函数图象上的两点,下列判断中,正确的是A. y1>y2B. y1<y2C. 当x1<x2时,y1<y2D. 当x1<x2时,y1>y214.下列四个点中,在正比例函数的图象上的点是()A. (2,5)B. (5,2)C. (2,—5)D. (5,—2)15.若正比例函数的图象经过点(2,﹣3),则这个图象必经过点()A. (﹣3,﹣2)B. (2,3)C. (3,﹣2)D. (﹣2,3)16.下列关系中,是正比例关系的是()A. 当路程s一定时,速度v与时间tB. 圆的面积S与圆的半径RC. 正方体的体积V与棱长aD. 正方形的周长C与它的一边长a17.下列问题中,两个变量成正比例关系的是()A. 等腰三角形的面积一定,它的底边和底边上的高B. 等边三角形的面积与它的边长C. 长方形的长确定,它的周长与宽D. 长方形的长确定,它的面积与宽18.下列各点中,在正比例函数y=-2x图象上的是()A. (-2,-1)B. (1,2)C. (2,-1)D. (1,-2)19.一次函数y=4x,y=﹣7x,y=的共同特点是()A. 图象位于同样的象限B. y随x增大而减小C. y随x增大而增大D. 图象都过原点二、填空题20.已知正比例函数y=kx(k是常数,k≠0),y随x的增大而减小,写出一个符合条件的k的值为________.21.写出一个正比例函数,使其图象经过第二、四象限:________.22.若函数y=(2m+6)x+(1﹣m)是正比例函数,则m的值是________.23.写一个图象经过第二、四象限的正比例函数:________24.将正比例函数y=2x的图象向上平移3个单位,所得的直线不经过第________象限.答案解析部分一、单选题1.已知正比例函数y=kx(k≠0),点(2,-3)在函数上,则y随x的增大而()A. 增大B. 减小C. 不变D. 不能确定【答案】B【考点】正比例函数的图象和性质【解析】【解答】∵点(2,-3)在正比例函数y=kx(k≠0)上,∴函数图象经过二四象限,∴y随着x的增大而减小,故选B【分析】首先根据函数的图象经过的点的坐标确定函数的图象经过的象限,然后确定其增减性即可2.已知函数y=x+k+1是正比例函数,则k的值为()A.1B.﹣1C.0D.±1【答案】B【考点】正比例函数的图象和性质【解析】【解答】解:由题意,得k+1=0,解得k=﹣1,故选:B.【分析】根据正比例函数的定义,可得答案.3.正比例函数y=(2k+1)x,若y随x增大而减小,则k的取值范围是()A. k>﹣B. k<﹣C. k=D. k=0 【答案】B【考点】正比例函数的图象和性质【解析】【解答】解:∵正比例函数y=(2k+1)x中,y的值随自变量x的值增大而减小,∴2k+1<0,解得,k<﹣;故选B.【分析】根据正比例函数图象与系数的关系列出关于k的不等式2k+1<0,然后解不等式即可.4.若正比例函数y=kx的图象经过点A(k,9),且经过第一、三象限,则k的值是()A. ﹣9B. ﹣3C. 3D. ﹣3或3 【答案】C【考点】正比例函数的图象和性质【解析】【解答】解:∵正比例函数y=kx(k≠0)的图象经过第一、三象限∴k>0,把(k,9)代入y=kx得k2=9,解得k1=﹣3,k2=3,∴k=3,故选C.【分析】根据正比例函数的性质得k>0,再把(k,9)代入y=kx得到关于k的一元二次方程,解此方程确定满足条件的k的值.5.若正比例函数y=(1-2m)x的图象经过点A(x1,y1)和点B(x2,y2),当x1< x2时,y1>y2,则m的取值范围是()A. m<0B. m>0C.D.【答案】D【考点】正比例函数的图象和性质【解析】【分析】由题目所给信息“当x1<x2时,y1>y2”可以知道,y随x的增大而减小,则由一次函数性质可以知道应有:1-2m<0,进而可得出m的取值范围.【解答】由题目分析可知:在正比例函数y=(1-2m)x中,y随x的增大而减小由一次函数性质可知应有:1-2m<0,即-2m<-1,解得:m>.【点评】此题主要考查了一次函数的图象性质,只有掌握它的性质才能灵活运用.6.在下列四组点中,可以在同一个正比例函数图象上的一组点是()A. (2,﹣3),(﹣4,6)B. (﹣2,3),(4,6)C. (﹣2,﹣3),(4,﹣6)D. (2,3),(﹣4,6)【答案】A【考点】正比例函数的图象和性质【解析】【分析】根据正比例函数关系式y=kx,可得k=,再依次分析各选项即可判断。
正比例函数(六大类型)(题型专练)(原卷版)

专题12 正比例函数(六大类型)【题型一:正比例函数的定义】【题型二:判断正比例函数图像所在象限】【题型三:正比例函数的性质】【题型四:判断正比例函数的比例系数大小】【题型五:待定系数法求正比例函数解析式】【题型六:正比例函数的图像性质综合】【题型一:正比例函数的定义】1.下列函数中,是正比例函数的是()A.B.y=x2C.y=2x D.y=2x﹣1 2.下列函数中,表示y是x的正比例函数的是()A.y=﹣0.1x B.y=2x2C.y2=4x D.y=2x+1 3.下列关系中,属于成正比例函数关系的是()A.正方形的面积与边长B.三角形的周长与边长C.圆的面积与它的半径D.速度一定时,路程与时间4.若y=(m﹣2)x+(m2﹣4)是正比例函数,则m的取值是()A.2B.﹣2C.±2D.任意实数5.正比例函数的比例系数为()A.﹣2B.C.D.26.函数y=(m﹣n+1)x|n﹣1|+n﹣2是正比例函数,则m,n应满足的条件是()A.m≠﹣1,且n=0 B.m≠1,且n=0C.m≠﹣1,且n=2D.m≠1,且n=27.已知函数y=(m﹣1)x+m2﹣1是正比例函数,则m=﹣1.8.若y=2x+m2﹣1是正比例函数,则m=±1.【题型二:判断正比例函数图像所在象限】9.正比例函数y=的图象经过的象限是()A.第一、三象限B.第二、四象限C.第三、四象限D.第一、二象限10.正比例函数的图象经过的象限是()A.第一、三象限B.第一、二象限C.第二、四象限D.第三、四象限11.一次函数y=8x的图象经过的象限是()A.一、三B.二、四C.一、三、四D.二、三、四12.已知函数y=(m﹣2)是关于x的正比例函数,且其图象经过第二、四象限,则m的值是.13.请写出一个图象经过第一、三象限的正比例函数的解析式.【题型三:正比例函数的性质】14.下列函数中,函数值y随x的增大而增大的有()①y=x②y=﹣x③y=﹣5x﹣2④y=4x+1A.1个B.2个C.3个D.4个15.关于直线y=﹣2x,下列结论正确的是()A.图象必过点(1,2)B.图象经过第一、三象限C.与y=﹣2x+1平行D.y随x的增大而增大16.对于函数y=4x,下列说法正确的是()A.当x>0时,y随x的增大而减小B.当x<0时,y随x的增大而减小C.y随x的增大而减小D.y随x的增大而增大17.P1(﹣2,y1),P2(7,y2)是正比例函数y=kx(k>0)的图象上的两个点,则y1,y2的大小关系是()A.y1>y2B.y1<y2C.y1=y2D.不能确定18.点A(1,m)在函数y=2x的图象上,则m的值是()A.1B.2C.D.019.已知:函数y1=2x,y2=﹣x+3,若x<1,则y1y2(填“>”或“=”或“<”).【题型四:判断正比例函数的比例系数大小】20.如图,三个正比例函数的图象分别对应表达式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列为()A.a<b<c B.a<c<b C.b<a<c D.c<b<a 21.如图,三个正比例函数的图象对应的解析式为①y=ax,②y=bx,③y=cx,则a、b、c的大小关系是()A.a>b>c B.c>b>a C.b>a>c D.b>c>a 22.如图,三个正比例函数的图象分别对应的解析式是:①y=ax,②y=bx,③y=cx,请用“>”表示a,b,c的不等关系.23.如图,正比例函数y=kx,y=mx,y=nx在同一平面直角坐标系中的图象如图所示.则比例系数k,m,n的大小关系是.(按从大到小的顺序用“>”连接)24.如图,三个正比例函数的图象分别对应表达式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列并用“<”连接为.【题型五:待定系数法求正比例函数解析式】25.已知y=(2m﹣1)x是正比例函数,且y随x的增大而减小,那么这个函数的解析式为()A.y=﹣5x B.y=5x C.y=3x D.y=﹣3x26.已知y与x成正比例,当x=4时,y=3,则y与x之间的函数关系式为,将这个函数的图象向下平移3个单位长度,得到的新图象的函数关系式为.27.正比例函数的图象经过点(1,2),则函数的表达式为.28.已知y与x成正比例,且当x=2时,y=﹣3.则当x=﹣时,y=.29.已知y与x成正比例关系,当x=2时,y=4,求:当x=﹣3时y的值.30.若y=(m﹣2)x+m2﹣4是y关于x的正比例函数,求该正比例函数的解析式.31.已知y=y1+y2,y1与x成正比例,y2与x﹣3成正比例,当x=﹣1时,y=4;当x=1时,y=8,求y与x之间的函数关系式.【题型六:正比例函数的图像性质综合】32.在物理学中,重力的表达关系式是G=mg(G代表重力,g代表重力常数10,m代表物体的质量)(1)在这个正比例函数表达式中,是自变量,是因变量.(2)若一个物体的重力为100N,它的质量是kg(3)若甲乙两个物体总质量为9kg,乙的质量是甲的2倍,那么甲物体受到的重力是多少?33.分类讨论思想数学课上,老师要求同学们画函数y=|x|的图象,小红联想绝对值的性质得y=x(x≥0)或y=﹣x(x≤0),于是她很快作出了该函数的图象(如图).请回答:(1)小红所作的图对吗?如果不对,请你画出正确的函数图象.(2)根据上述的作图方法,请画出函数y=﹣3|x|的图象.。
正比例函数图像及性质

正比例函数的图像和性质知识精要1.正比例函数的图像一般地,正比例函数y=kx(k是常数,k0≠)的图像是经过原点O(0,0)和点M(1,k)的一条直线。
我们把正比例函数y=kx的图像叫做直线y=kx。
2.正比例函数性质精讲名题例1.若函数y=(m-1)3-mx是正比例函数,则m= ,函数的图像经过象限。
解:m=4,图像经过第一、三象限。
例2.已知y-1与2x成正比例,当x=-1时,y=5,求y与x的函数解析式。
解:∵y-1与2x成正比例∴设y-1=k·2x (k0≠)把x=-1,y=5代入,得k=-2,∴y-1=-2·2x∴y=-4x+1例3.已知y与x的正比例函数,且当x=6时y=-2(1)求出这个函数的解析式;(2)在直角坐标平面内画出这个函数的图像;(3)如果点P (a ,4)在这个函数的图像上,求a 的值;(4)试问,点A (-6,2)关于原点对称的点B 是否也在这个图像上?解:(1) 设y=k ·x (k 0≠)当x=6时,y=-2∴-2=6k ∴31-=k ∴这个函数的解析式为x y 31-=(2) x y 31-=的定义域是一切实数,图像如图所示:(3)如果点P (a ,4)在这个函数的图像上,∴a 314-=,∴a=-12(4)点A (-6,2)关于原点对称的点B 的坐标(6,-2),当x=6时,y=2631-=⨯- 因此,点B 也在直线x y 31-=上例4.已知点(11,y x ),(22,y x )在正比例函数y=(k-2)x 的图像上,当21x x >时,21y y <,那么k 的取值范围是多少?解:由题意,得函数y 随x 的值增大而减小,∴k-2<0,∴k<2例5.(1)已知y=ax 是经过第二、四象限的直线,且3+a 在实数范围内有意义,求a 的取值范围。
(2)已知函数y=(2m+1)x 的值随自变量x 的值增大而增大,且函数y=(3m+1)x 的值随自变量x 的增大而减小,求m 的取值范围。
正比例函数的图象与性质

的图象从左向右下降.
(3)当m <2 时,正比例函数 y=(2小.
(4) 正比例函数 y (2m 1) x 的图象上 的两点 A( x1, y1 ), B( x2 , y2 ) ,当 x1 x2 时, 有 y1 y2 ,求 m 的取值范围.
1、巩固练习:
(1)正比例函数 y 2 x 是一条经
过原点的直线,位于第 一、三 象 限,从左向右上升 ,即随着x 的增 大y也增大 .
(2)正比例函数y=-5x 是一条经 过 原点 直线,位于第 二、四 象
限,从左向右 下降 ,即随着x的
增大y 减小 .
2、进阶练习: (1)正比例函数y=(m-4)x , 当m >4 时,图象过第一、三象限.
比较 y1 、y2 、y3 的大小.
(2)当m
时,正比例函数 y=(2m-4)x
的图象从左向右下降.
(3)当m 时,正比例函数 y=(2m-4)x
中,y 的值随x 的增大而减小.
(4) 正比例函数
y (2m 1) x 的图象上的 两点 A( x1, y1 ), B( x2 , y2 ) ,当 x1 x2 时, 有 y1 y2 ,求 m 的取值范围.
3、拓展练习:
5 已知 A(11, y1 ), B ( , y2 ), C (5, y3 ) 2 在正比例函数 y 6 x 的图象上,试
比较
y3 的大小. y1 、y2 、
思考:
5 已知 A(11, y1 ), B ( , y2 ), C (5, y3 ) 2 在正比例函数 y mx 的图象上,试
4.3 正比例函数的图象及性质 练习题 2021——2022学年北师大版八年级数学上册

3 第1课时 正比例函数的图象及性质【基础练习】知识点 1 正比例函数的图象1.正比例函数y=3x 的大致图象是( )图12.(1)函数y=5x 的图象经过的象限是第 象限;(2)写出一个实数k 的值: ,使得正比例函数y=kx 的图象经过第二、四象限.3.在同一平面直角坐标系中画出下列函数的图象:(1)y=-23x ; (2)y=3x ; (3)y=23x.图2知识点 2 正比例函数图象上点的坐标4.已知正比例函数y=3x 的图象经过点(1,m ),则m 的值为( )A .13B .3C .-13D .-35.点(-2,6)在正比例函数y=kx 的图象上,下列各点在此函数图象上的为( )A .(3,1)B .(-3,1)C .(1,3)D .(-1,3)6.(1)函数y=6x 的图象是经过点(0, )和点( ,6)的一条直线;(2)若正比例函数的图象经过点(-1,4)和(m ,3),则m 的值为 .7.[教材习题4.3第4题变式]已知:如图3,正比例函数的图象经过点P(-1,2)和点Q(-m,m+3).(1)求该函数的表达式;(2)求m的值;(3)判定这个函数的图象必经过(1,-2),(-1,-2),(2,-1),(1,2)中的哪个点.图3知识点3正比例函数的性质8.关于正比例函数y=-3x,下列结论正确的是()A.图象不经过原点B.y随x的增大而增大C.图象经过第二、四象限D.当x=1时,y=139.已知函数y=(a-1)x,且y的值随着x值的增大而增大,那么a的取值范围是()A.a>1B.a<1C.a>0D.a<010.已知(x1,y1)和(x2,y2)是直线y=-3x上的两点,若x1>x2,则y1与y2的大小关系是()A.y1>y2B.y1<y2C.y1=y2D.以上都有可能11.设正比例函数y=mx的图象经过点A(m,4),且y的值随x值的增大而减小,则m的值为()A.2B.-2C.4D.-412.对于关于x的正比例函数y=mx|m|-1,若其图象经过第一、三象限,则m的值为,且y 的值随x值的增大而.13.已知关于x的正比例函数y=(m+2)x.(1)m为何值时,函数图象经过第一、三象限?(2)m 为何值时,y 随x 的增大而减小?(3)m 为何值时,点(1,3)在该函数的图象上?【能力提升】14.设点A (a ,b )是正比例函数y=-32x 图象上的任意一点,则下列等式一定成立的是( )A .2a+3b=0B .2a -3b=0C .3a -2b=0D .3a+2b=0 15.如果一个正比例函数的图象经过不同..象限的两点A (2,m ),B (n ,3),那么一定有( ) A .m>0,n>0 B .m>0,n<0C .m<0,n>0D .m<0,n<016.若关于x 的正比例函数y=(1-m )x 的图象经过点A (x 1,y 1)和点B (x 2,y 2),当x 1<x 2时,y 1>y 2,则m 的取值范围是( )A .m<0B .m>0C .m<1D .m>117.正比例函数y=kx ,当x 每增加3时,y 就减小2,则k 的值为( )A .32B .-32C .23D .-23 18.如图4,在同一直角坐标系中,正比例函数y=k 1x ,y=k 2x ,y=k 3x ,y=k 4x 的图象分别是l 1,l 2,l 3,l 4,则下列关系正确的是( )图4A .k 1<k 2<k 3<k 4B .k 2<k 1<k 4<k 3C .k 1<k 2<k 4<k 3D .k 2<k 1<k 3<k 419.定义运算“※”为a ※b={ab (b ≥0),-ab (b <0),则函数y=2※x 的图象大致是( )图520.已知正比例函数图象上一点A 到x 轴的距离为4,点A 的横坐标为-2,则这个函数的表达式为 .21.已知正比例函数y=kx (k ≠0),当-3≤x ≤1时,对应的y 的取值范围是-1≤y ≤13,且y 随x 的增大而增大,则k 的值为 .22.已知y 与x 成正比例,当x=1时,y=2.(1)求y 与x 之间的函数关系式;(2)求当x=-1时的函数值;(3)若点(-1,m ),(5,n )在此函数的图象上,比较m ,n 的大小.23.(1)在同一坐标系内画出正比例函数y 1=-2x 与y 2=12x 的图象;(2)请你用量角器度量一下(1)中这两条直线的夹角,你发现这两条直线的位置关系是 ;(3)在平面直角坐标系中,直线y=23x 与直线y=-32x 的位置关系是 ;(4)若直线y=(m -1)x (m 为常数)与直线y=-3x 互相垂直,求m 的值.答案1.B [解析] 因为在y=3x 中,k=3>0,所以图象过原点且经过第一、三象限.故选B .2.(1)一、三 (2)答案不唯一,如-23.解:如图所示.4.B5.D6.(1)0 1 (2)-347.解:(1)设正比例函数的表达式为y=kx.因为它的图象经过点P (-1,2),所以2=-k ,即k=-2.所以正比例函数的表达式为y=-2x.(2)因为正比例函数的图象经过点Q (-m ,m+3),所以m+3=2m.所以m=3.(3)把点(1,-2),(-1,-2),(2,-1),(1,2)的坐标分别代入y=-2x 中,等号成立的点就在正比例函数y=-2x 的图象上,所以这个函数的图象必经过点(1,-2).8.C 9.A 10.B 11.B12.2 增大13.解:(1)因为函数图象经过第一、三象限,所以m+2>0,解得m>-2.(2)因为y 随x 的增大而减小,所以m+2<0,解得m<-2.(3)因为点(1,3)在该函数的图象上,所以m+2=3,解得m=1.14.D [解析] 把点A (a ,b )的坐标代入正比例函数y=-32x 中,可得-32a=b ,即3a+2b=0. 15.D 16.D17.D [解析] 根据题意得y -2=k (x+3),y -2=kx+3k ,而y=kx ,所以3k=-2,解得k=-23.18.B [解析] 对正比例函数的图象来说,当k>0时,k 的值越大,直线与x 轴正半轴所夹的锐角越大,所以k3>k4;当k<0时,k的值越大,直线与x轴负半轴所夹的锐角越小,所以k2<k1.因为正数大于一切负数,所以k2<k1<k4<k3.19.C20.y=2x或y=-2x21.1322.解:(1)设y与x之间的函数关系式为y=kx.将x=1,y=2代入,得k=2,故y与x之间的函数关系式为y=2x.(2)当x=-1时,y=2×(-1)=-2.(3)因为k=2>0,所以y的值随着x值的增大而增大.因为-1<5,所以m<n.23.解:(1)如图.(2)互相垂直(3)互相垂直.(4)由题意可得-3(m-1)=-1,解得m=43。
2020学年八年级数学下册 第十九章19.2.1 正比例函数 第2课时 正比例函数的图象与性质练习

第2课时 正比例函数的图象与性质知识点 1 正比例函数的图象1.正比例函数y =2x 的大致图象是( )图19-2-12.经过以下一组点可以画出函数y =-3x 的图象的是( ) A .(0,0)和(3,-1) B .(1,-3)和(-1,3) C .(1,3)和(-3,1) D .(-1,-3)和(1,3)3.若正比例函数y =kx 的图象在第二、四象限,则k 的取值可以是( ) A .1 B .0或1 C .±1 D .-14.[2018·常州]一个正比例函数的图象经过点(2,-1),则它的解析式为( ) A .y =-2x B .y =2x C .y =-12x D .y =12x5.已知正比例函数y =(k +1)x 的图象经过第一、三象限,则k 的取值范围是________. 6.已知函数:①y =12x ,②y =x ,③y =2x ,④y =-2x .(1)在同一平面直角坐标系中画出各函数的图象;(2)观察这些函数的图象可以发现,随着|k |的增大,直线与y 轴的位置关系有何变化?(k 指比例系数) (3)猜想函数①和④的图象的位置关系.知识点 2 正比例函数的性质7.对于函数y =-2x ,下列说法不正确的是( ) A .它的图象是一条直线 B .y 随着x 的增大而增大 C .它的图象过点(-1,2) D .它的图象经过第二、四象限8.在关于x 的正比例函数y =(k -1)x 中,y 随x 的增大而减小,则k 的取值范围是( ) A .k <1 B .k >1 C .k ≤1 D .k ≥19.已知正比例函数y =kx (k <0)的图象上有两点A (x 1,y 1),B (x 2,y 2),且x 1<x 2,则下列不等式中恒成立的是( )A .y 1+y 2>0B .y 1+y 2<0C .y 1-y 2>0D .y 1-y 2<010.若正比例函数y =(1-4m )x 的图象经过点A (x 1,y 1)和点B (x 2,y 2),当x 1<x 2时, y 1>y 2,则m 的取值范围是( )A .m <0B .m >0C .m <14D .m >1411.[2018·陕西]如图19-2-2,在矩形AOBC 中,A (-2,0),B (0,1).若正比例函数y =kx 的图象经过点C ,则k 的值为( )图19-2-2A .-12 B.12C .-2D .212.已知正比例函数y =3x 的图象经过点A (-1,y 1),B (-2,y 2),则y 1________y 2(填“>”“<”或“=”).13.写出一个图象经过第一、三象限的正比例函数y =kx (k ≠0)的解析式:________.14.如图19-2-3,三个正比例函数的图象对应的解析式为:①y =ax ,②y =bx ,③y =cx ,则a ,b ,c 的大小关系是( )A .a >b >cB .c >b >aC .b >a >cD .b >c >a图19-2-3 图19-2-415.放学后,小明骑车回家,他经过的路程s (千米)与所用时间t (分)的函数关系如图19-2-4所示,则小明的骑车速度是________千米/分.16.已知正比例函数y =kx (k 是常数,k ≠0),当-3≤x ≤1时,对应的y 的取值范围是-1≤y ≤13,且y 随x 的增大而增大,则k 的值为________.17.已知正比例函数y =kx ,当x =1时,y =2.(1)求正比例函数的解析式; (2)求当x =-1时的函数值;(3)当y 的取值范围是0≤y ≤5时,求x 的取值范围.18.2[018·昆明改编]如图19-2-5,点A 的坐标为(4,2),将点A 绕坐标原点O 旋转90°后,再向左平移1个单位长度得到点A ′,求过点A ′的正比例函数图象的解析式.图19-2-519.如图19-2-6,已知正比例函数y=kx的图象经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为H,点A的横坐标为3,且△AOH的面积为3.(1)求正比例函数的解析式.(2)在x轴上是否存在一点P,使△AOP的面积为5?若存在,求出点P的坐标;若不存在,请说明理由.图19-2-6拓广探究创新练冲刺满分20.[2018·贵港]如图19-2-7,直线l的解析式为y=3x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3;…;按此作法进行下去,则点A n的坐标为________.图19-2-7教师详解详析1.B 2.B3.D [解析] ∵正比例函数y =kx 的图象在第二、四象限,∴k <0.故选D. 4.C5.k >-1 [解析] ∵正比例函数y =(k +1)x 的图象经过第一、三象限,∴k +1>0,∴k >-1. 6.解:(1)如图:(2)观察这些函数的图象可以发现,随着|k |的增大,直线与y 轴的夹角越来越小. (3)函数①和④的图象互相垂直. 7.B8.A [解析] 由正比例函数的性质可知:当y 随x 的增大而减小时,k -1<0,即k <1.故选A. 9.C10.D [解析] 因为当x 增大时,y 减小,说明函数y 随着x 的增大而减小,则有1-4m <0,解得m >14.故选D.11.A [解析] 由A (-2,0),B (0,1)可得C (-2,1).把点C 的坐标代入y =kx ,得-2k =1,解得k =-12.故选A. 12.>13.y =2x (答案不唯一) [解析] ∵正比例函数y =kx 的图象经过第一、三象限, ∴k >0,当k 取2时可得函数解析式为y =2x .14.B [解析] ∵y =ax ,y =bx ,y =cx 的图象都在第一、三象限,∴a >0,b >0,c >0.∵直线越陡,则|k |越大,∴c >b >a .15.0.2 16.1317.解:(1)将x =1,y =2代入y =kx ,得k =2, 故正比例函数的解析式为y =2x .(2)当x =-1时,y =2×(-1)=-2. (3)∵0≤y ≤5,∴0≤2x ≤5, 解得0≤x ≤52.18.解:当点A 绕坐标原点O 逆时针旋转90°后,再向左平移1个单位长度得到点A ′, 则A ′(-3,4).设过点A ′的正比例函数图象的解析式为y =k 1x , 则4=-3k 1, 解得k 1=-43,则过点A ′的正比例函数图象的解析式为y =-43x .同理可得:当点A 绕坐标原点O 顺时针旋转90°后,再向左平移1个单位长度得到点A ″,则A ″(1,-4). 设过点A ″的正比例函数图象的解析式为y =k 2x , 则k 2=-4,则过点A ″的正比例函数图象的解析式为y =-4x .综上所述,过点A ′的正比例函数图象的解析式为y =-43x 或y =-4x .19.解:(1)∵点A 的横坐标为3,且△AOH 的面积为3, ∴点A 的纵坐标为-2,∴点A 的坐标为(3,-2). ∵正比例函数y =kx 的图象经过点A , ∴3k =-2,∴k =-23,∴正比例函数的解析式是y =-23x .(2)存在.∵△AOP 的面积为5,点A 的坐标为(3,-2), ∴OP =5,∴点P 的坐标为(5,0)或(-5,0).20.(2n -1,0) [解析] 直线l 的解析式为y =3x ,点A 1的坐标为(1,0),过点A 1作x 轴的垂线交直线l 于点B 1,可知点B 1的坐标为(1,3),以原点O 为圆心,OB 1长为半径画弧交x 轴于点A 2,则OA 2=OB 1,所以OA 2=12+(3)2=2,所以点A 2的坐标为(2,0).同理,可求得点B 2的坐标为(2,2 3),故OA 3=22+(2 3)2=4,则点A 3的坐标为(4,0),所以点B 3的坐标为(4,4 3).…所以点A n 的坐标为(2n -1,0).。
【初中数学】人教版八年级下册第2课时 正比例函数的图象与性质(练习题)

人教版八年级下册第2课时正比例函数的图象与性质(356)1.已知正比例函数y=(m−1)x的图象上有两点A(x1,y1),B(x2,y2),当x1<x2时,有y1>y2.(1)求m的取值范围;(2)当m取最大整数时,画出该函数图象2.已知正比例函数y=(1−2a)x.(1)若函数的图象经过第一、三象限,试求a的取值范围(2)若点A(x1,y1)和点B(x2,y2)为函数图象上的两点,且x1<x2,y1>y2,试求a的取值范围.(3)若函数的图象经过点(−1,2).①求此函数的解析式并作出其图象;②如果x的取值范围是−1<x<5,求y的取值范围3.对于正比例函数y=kx(k≠0),当自变量x的值减小2时,函数y的值减小−6,则k的值为()A.13B.−13C.3D.−34.已知正比例函数y=(2m+4)x.求:(1)m为何值时,函数图象经过第一、三象限;(2)m为何值时,y随x的增大而减小?(3)m为何值时,点(1,3)在该函数图象上?5.已知正比例函数y=kx(k≠0)的图象如图所示,则k的值可能是()A.1B.2C.3D.46.已知函数y=x,y=−2x,y=12x,y=3x.(1)在同一直角坐标系内画出它们的图象;(2)探索发现:观察这些函数的图象可以发现,随着|k|的增大,直线与y轴的位置关系有何变化?(3)灵活运用:已知正比例函数y1=k1x,y2=k2x在同一坐标系中的图象如图所示,则k1与k2的大小关系为.7.正比例函数y=kx的图象如图所示,则k的取值范围是()A.k>0B.k<0C.k>1D.k<18.一次函数y=4x,y=−7x,y=−45x的共同特点是()A.图象位于同样的象限B.y随x的增大而减小C.y随x的增大而增大D.图象都过原点9.已知正比例函数y=(2k+1)x,若y随x的增大而减小,则k的取值范围是().A.k>−12B.k<−12C.k=12D.k=010.已知一次函数y1=2x与y2=5x.(1)在同一直角坐标系中画出这两个函数的图象;(2)预测哪一个函数的函数值先达到10011.函数y=|2x|的图象是()A. B. C. D.12.定义运算“∗”为:a∗b={ab(b>0),−ab(b≤0),如:1∗(−2)=−1×(−2)=2,则函数y=2∗x的图象大致是()A. B. C. D.13.如图,三个正比例函数的图象分别对应的解析式是:①y=ax,②y=bx,③y=cx,则a,b,c的大小关系是()A.a>b>cB.c>b>aC.b>a>cD.b>c>a14.下列关于正比例函数y=3x的说法中,正确的是()A.当x=3时,y=1B.它的图象是一条过原点的直线C.y随x的增大而减小D.它的图象经过第二、四象限15.经过以下一组点可以画出函数y=2x的图象的是()A.(0,0)和(2,1)B.(1,2)和(−1,−2)C.(1,2)和(2,1)D.(−1,2)和(1,2)16.正比例函数y=−2x的大致图象是()A. B. C. D.参考答案1(1)【答案】解:依题意,得m−1<0,∴m<1,∴m的取值范围是m<1.(2)【答案】∵m<1,∴m取最大整数0,∴解析式为y=−x,图象如图所示:2(1)【答案】解:由正比例函数y=(1−2a)x的图象经过第一、三象限,可得1−2a>0,则a<12(2)【答案】∵正比例函数y=(1−2a)x的图象上两点A(x1,y1)和B(x2,y2),且x1<x2时,y1>y2,∴y随x的增大而减小,∴1−2a<0,.解得a>12(3)【答案】①∵正比例函数y=(1−2a)x的图象经过点(−1,2),∴2=−(1−2a),,解得a=32∴正比例函数的解析式是y=−2x;画出函数图象如图:②把x=−1代入y=−2x得y=2,把x=5代入y=−2x得y=−10,∴y的取值范围为−10<y<2.3.【答案】:D【解析】:根据题意得y+6=k(x−2),即y+6=kx−2k,而y=kx,所以−2k=6,解得k=−3.4(1)【答案】解:∵函数图象经过第一、三象限,∴2m+4>0,解得m>−2(2)【答案】∵y随x的增大而减小,∴2m+4<0,解得m<−2(3)【答案】∵点(1,3)在该函数图象上,∴2m+4=3,解得m=−125.【答案】:B<k<3【解析】:由图象知536(1)【答案】如图:(2)【答案】观察这些函数的图象可以发现,随着|k|的增大,直线与y轴的夹角越来越小(3)【答案】由(2)得到的规律可知,k1>k27.【答案】:A【解析】:∵函数y=kx的图象经过第一、三象限,∴k>0.8.【答案】:D9.【答案】:B【解析】:∵正比例函数y=(2k+1)x中,y随自变量x的增大而减小,∴2k+1<0,.解得k<−1210(1)【答案】解:在同一直角坐标系中画出这两个函数的图象如图:(2)【答案】预测函数y2=5x的函数值先达到10011.【答案】:C【解析】:函数y=|2x|,当x≥0时,y=2x;当x<0时,y=−2x.12.【答案】:C【解析】:y=2∗x={2x(x>0)−2x(x⩽0),x>0时,图象是y=2x的正比例函数中y轴右侧的部分;x≤0时,图象是y=﹣2x的正比例函数中y左侧的部分.故选:C.13.【答案】:C【解析】:首先根据图象经过的象限,得a>0,b>0,c<0,对于直线②①,过点(1,0)作垂直于x轴的直线,直线与②的交点高于直线与①的交点,即b>a.15.【答案】:B【解析】:A项,∵当x=2时,y=4≠1,∴点(2,1)不符合,故本选项错误;B项,∵当x=1时,y=2;当x=−1时,y=−2,∴两点均符合,故本选项正确;C项,∵当x=2时,y=4≠1,∴点(2,1)不符合,故本选项错误;D项,∵当x=−1时,y=−2≠2,∴点(−1,2)不符合,故本选项错误.16.【答案】:C。
上海初中数学八年级上---18.2(3)正比例函数的性质(含答案)

18.2(3)正比例函数的性质一、填空题1. 正比例函数y =2x 的图像经过第______象限,并且y 随x 的增大而__________.2. 正比例函数y =-2x 的图像经过第________象限,并且y 随x 的增大而________.3. 如果正比例函数y =kx (k ≠0)的图像经过第二、四象限,那么y 随x 的增大而________.4. 如果正比例函数y =kx (k ≠0)的图像经过第一、三象限,那么y 随x 的增大而________.5. 如果点P (a ,b )在第二象限,则函数y =b ax 的图像经过第________象限,那么y 随x 的增大而________.6. 已知正比例函数y =(1-k )x 的图像经过第一、三象限,则k 的取值范围为________.7. 已知正比例函数y =⎝ ⎛⎭⎪⎫1-23a x 中,y 随x 的增大而减小,则a 的取值范围为________. 8. 正比例函数y =kx (k ≠0)的图像与直线y =-2x 关于y 轴对称,则k =________.9.正比例函数y =kx 的图像经过第二、四象限,点A (a ,1)、B (-1,b )都在这个函数图像上,则a -b ________0.10. 已知点P 在直线y =-3x 上,若点P 的纵坐标大于3,则点P 的横坐标x 的取值范围为________.11.已知(x 1,y 1)和(x 2,y 2)是直线y = -3 x 上的两点,且x 1> x 2,则y 1与y 2•的大小关系是二、简答题12.正比例函数()x a y 15-=的图像经过点(1,4),求a 的值13.正比例函数1212-+⎪⎭⎫ ⎝⎛+=k x k y 的图像经过第一、第三象限,求函数的解析式14.在函数y = -3x 的图象上取一点P ,过P 点作PA ⊥x 轴,已知P 点的横坐标为-2,求△POA 的面积(O 为坐标原点).15. 已知:正比例函数图像经过点(-2,4).(1)如果点(a,1)和(-1,b)在函数图像上,求:a、b的值;(2)过图像上一点P作y轴的垂线,垂足为Q(0,-8),求:△OPQ的面积.16. 在正比例函数y=kx(k≠0)的图像上有一点P(2,a),过P作PA⊥x轴,PB⊥y轴,垂足分别为A、B,若S四边形OAPB=6,求:此正比例函数的解析式.三、提高题17. 如图,长方形OABC边BC=4,AB=2.(1)直线y=kx(k≠0),交边AB于点P,求k的取值范围;(2)直线y=kx(k≠0),将长方形OABC的面积分成两部分,靠近y轴的一部分记作S,试写出S关于k的解析式;(3)直线y=kx(k≠0),是否可能将长方形OABC的面积分成两部分的面积比为2∶3?若能,求出k的值;若不能,说明理由.18.2(3)正比例函数的性质一.1.一、三 增大 2.二、四 减小 3.减小 4.增大 5.二、四 减小6.k <17.a >23 8.2 9. < 10.x <-3 11. 12y y < 二.12. a=1 13.y=23x 14.6 15.(1)a=-21 b=2 (2)16 16.y=23x 或y=-23x 三. 17.⑴(0<k ≤21) ⑵ ①当点P 在BC 边上时21()2s k k => ②当点P 在AB 边上时188(0)2s k k =-<≤(3)①当点P 在BC 边上时58k = ② 当点P 在AB 边上时25k =。
人教版八年级下册知识点试题精选-正比例函数的性质

关于正比例函数的性质一.选择题(共20小题)1.正比例函数的图象经过第二、四象限,那么k为()A.k=﹣1 B.k=2 C.k=﹣1或k=2 D.不能确定2.函数y=﹣3x中,y随x的变化正确的是()A.增大而增大B.不变C.减小而减小D.增大而减小3.若正比例函数y=kx的图象经过点(1,3),则此正比例函数的图象经过()A.第一、二象限B.第一、三象限C.第二、四象限D.第三、四象限4.已知正比例函数y=kx(k≠0),点(2,﹣3)在函数上,则y随x的增大而()A.增大B.减小C.不变D.不能确定5.对于正比例函数y=mx,当x增大时,y随x增大而增大,则m的取值范围是()A.m<0 B.m≤0 C.m>0 D.m≥06.若点A(﹣5,y1)和点B(﹣2,y2)都在y=﹣x上,则y1与y2的大小关系为()A.y1>y2B.y1=y2C.y1<y2D.y1≤y27.正比例函数y=kx的y值随x的增大而减小,则此函数的图象经过()A.一、二象限B.一、三象限C.二、三象限D.二、四象限8.关于函数y=﹣x,下列结论正确的是()A.函数图象必过点(﹣2,﹣1)B.函数图象经过第1、3象限C.y随x的增大而减小 D.y随x的增大而增大9.对于正比例函数y=k2x(k是常数,k≠0)的图象,下列说法正确的是()A.是一条抛物线B.过点(,k)C.经过一、二象限 D.y随着x增大而减小10.关于正比例函数y=﹣2x,下列结论正确的是()A.图象必经过点(﹣1,﹣2)B.图象经过第一、三象限C.y随x的增大而减小 D.不论x取何值,总有y<011.关于函数y=,下列结论正确的是()A.函数图象必经过点(1,2)B.函数图象经过二、四象限C.y随x的增大而减小 D.y随x的增大而增大12.下面所给点的坐标满足y=﹣2x的是()A.(2,﹣1)B.(﹣1,2)C.(1,2) D.(2,1)13.关于正比例函数y=﹣3x,下列结论正确的是()A.图象经过点(﹣3,1)B.图象经过第一、三象限C.函数值y随x的增大而增大D.图象与直线y=1﹣3x的倾斜程度相同14.正比例函数y=2x的图象所过的象限是()A.一、三象限B.二、四象限C.一、二象限D.三、四象限15.下列一次函数中,y的值随着x值的增大而减小的有()①y=10x﹣9;②y=﹣0.3x+2;③y=x+4;④y=(﹣)x;⑤y=7﹣x;⑥y=8+(﹣2)x.A.①③⑥B.②⑤⑥C.④⑤⑥D.②④⑤16.若正比例函数的图象经过点(2,﹣3),则这个图象必经过点()A.(﹣3,﹣2)B.(2,3) C.(3,﹣2)D.(﹣2,3)17.对于y=k2x(k≠0)的图象下列说法不正确的是()A.是一条直线B.过点(,k)C.经过一、三象限或二、四象限D.y随x增大而增大18.已知函数y=(k﹣3)x,y随x的增大而减小,则常数k的取值范围是()A.k>3 B.k<3 C.k<﹣3 D.k<019.已知正比例函数y=(m﹣3)x的图象过第二、四象限,则m的取值范围是()A.m≥3 B.m>3 C.m≤3 D.m<320.下列函数中,y随x的增大而增大的函数是()A.y=3﹣x B.y=﹣0.5x C.y=﹣2x+1 D.y=x二.填空题(共20小题)21.正比例函数y=x的图象与x轴所成的锐角的度数是.22.如果正比例函数y=(k﹣1)x的图象经过第二、四象限,那么k的取值范围是.23.若直线y=kx(k≠0)经过点(﹣2,6),则y随x的增大而.24.正比例函数y=kx的图象是经过点和的.25.已知正比例函数y=(k+3)x,若y随x的增大而减小,则k的取值范围是.26.正比例函数y=﹣x的图象经过第象限.27.正比例函数y=3x的图象经过第象限.28.函数y=5x的图象经过象限,函数图象从左往右呈趋势,y 随x的增大而;函数y=﹣5x的图象经过第象限,函数图象从左往右呈趋势,y 随x的增大而.29.正比例函数的图象一定经过的点的坐标为.30.正比例函数y=x的图象是经过点(0,)和点(1,)的一条直线.31.已知函数y=(2m﹣9)x|m|﹣5是正比例函数,且图象经过第二,四象限,则m的值为.32.在同一坐标系中,如图所示,一次函数y=k1x,y=k2x,y=k3x,y=k4x的图象分别为l1,l2,l3,l4,则k1,k2,k3,k4的大小关系是.33.正比例函数y=kx(k≠0)的图象是一条经过点的直线.34.已知点P1(x1,y1)和点P2(x2,y2)是正比例函数y=kx(k≠0)图象上的两点,且当x1<x2时,y1<y2,则k的取值范围是.35.A(﹣1,3)在正比例函数y=kx图象上,则y随着x的增大而.36.已知正比例函数y=kx(k≠0)的图象经过原点、第二象限与第四象限,请写出符合上述条件的k的一个值:.37.函数的图象经过第象限.38.正比例函数y=﹣5x中,y随着x的增大而.39.函数y=(m﹣3)是正比例函数,则m=,y随x的增大而.40.若函数y=(1﹣k)x2|k|﹣3是正比例函数,且y随x的增大而减小,则(k﹣3)2017=.三.解答题(共10小题)41.已知正比例函数图象上一个点A到x轴的距离为4,这个点A的横坐标为﹣2,请回答下列问题:(1)求这个正比例函数;(2)这个正比例函数经过哪几个象限?(3)这个正比例函数的函数值y是随着x增大而增大?还是随着x增大而减小?42.已知正比例函数y=(2m+4)x.求:(1)m为何值时,函数图象经过一、三象限;(2)m为何值时,y随x的增大而减小;(3)m为何值时,点(1,3)在该函数图象上.43.在物理学中,重力的表达关系式是G=mg(G代表重力,g代表重力常数10,m代表物体的质量)(1)在这个正比例函数表达式中,是自变量,是因变量.(2)若一个物体的重力为100N,它的质量是kg(3)若甲乙两个物体总质量为9kg,乙的质量是甲的2倍,那么甲物体受到的重力是多少?44.已知正比例函数y=(2﹣k)x的图象经过第二、四象限,求函数y=﹣kx的图象经过哪些象限?45.已知y﹣2与3x﹣4成正比例函数关系,且当x=2时,y=3.(1)写出y与x之间的函数解析式;(2)若点P(a,﹣3)在这个函数的图象上,求a的值;(3)若y的取值范围为﹣1≤y≤1,求x的取值范围.46.已知y与x成正比例函数,当x=1时,y=2.求:(1)求y与x之间的函数关系式;(2)求当x=﹣1时的函数值;(3)如果当y的取值范围是0≤y≤5,求x的取值范围.47.在学习一次函数时,通过描点画图,直观的得出正比例函数y=kx(k>0)的图象是一条直线.现在你能对这个结论给出证明吗?48.当m为何值时,正比例函数y=(m﹣1)x的图象在哪几个象限y随x的增大而减小?49.已知正比例函数y=(3k﹣1)x,若y随x的增大而增大,求k的取值范围.50.已知正比例函数y1=﹣2x的图象如图.(1)在平面直角坐标系中,画出一次函数y2=2x﹣4的图象;(2)若y2<y1,则x的取值范围是.关于正比例函数的性质参考答案与试题解析一.选择题(共20小题)1.正比例函数的图象经过第二、四象限,那么k为()A.k=﹣1 B.k=2 C.k=﹣1或k=2 D.不能确定【分析】根据正比例函数所经过的象限确定(k﹣1)的符号,且k2﹣k﹣1=1.【解答】解:∵正比例函数的图象经过第二、四象限,∴k2﹣k﹣1=1,且k﹣1<0,解得,k=2(不会题意,舍去),k=﹣1.故选A.【点评】本题考查了正比例函数的定义、正比例函数图象的性质.正比例函数y=﹣kx(k≠0)的图象是经过原点的一条直线.当k>0时,图象经过一、三象限,y随x的增大而增大;当k<0时,图象经过二、四象限,y随x的增大而减小.2.函数y=﹣3x中,y随x的变化正确的是()A.增大而增大B.不变C.减小而减小D.增大而减小【分析】根据正比例函数的性质当k<0时,图象经过二、四象限,y随x的增大而减小.可直接得到答案.【解答】解:∵k=﹣3<0,∴y随x的增大而减小,故选:D.【点评】此题主要考查了正比例函数的性质,关键是掌握正比例函数图象的性质:它是经过原点的一条直线.当k>0时,图象经过一、三象限,y随x的增大而增大;当k<0时,图象经过二、四象限,y随x的增大而减小.3.若正比例函数y=kx的图象经过点(1,3),则此正比例函数的图象经过()A.第一、二象限B.第一、三象限C.第二、四象限D.第三、四象限【分析】把点A(1,3)代入函数解析式求出k值即可得解,根据k的符号确定其图象所经过的象限.【解答】解:∵正比例函数y=kx的图象经过点(1,3),∴3=k,即k=3>0,∴此正比例函数的图象经过第一、三象限.故选:B.【点评】考查了正比例函数图象的性质:它是经过原点的一条直线.当k>0时,图象经过一、三象限;当k<0时,图象经过二、四象限.4.已知正比例函数y=kx(k≠0),点(2,﹣3)在函数上,则y随x的增大而()A.增大B.减小C.不变D.不能确定【分析】首先根据函数的图象经过的点的坐标确定函数的图象经过的象限,然后确定其增减性即可.【解答】解:∵点(2,﹣3)在正比例函数y=kx(k≠0)上,∴函数图象经过二四象限,∴y随着x的增大而减小,故选B.【点评】本题考查了正比例函数的性质,解题的关键是牢记正比例函数的比例系数对函数图象的影响.5.对于正比例函数y=mx,当x增大时,y随x增大而增大,则m的取值范围是()A.m<0 B.m≤0 C.m>0 D.m≥0【分析】根据正比例函数的性质解答即可.【解答】解:∵对于正比例函数y=mx,当x增大时,y随x增大而增大,∴m>0.故选C.【点评】此题利用的规律:在直线y=kx中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.6.若点A(﹣5,y1)和点B(﹣2,y2)都在y=﹣x上,则y1与y2的大小关系为()A.y1>y2B.y1=y2C.y1<y2D.y1≤y2【分析】把点A和点B的横坐标分别代入y=﹣x,分别求出y1与y2的值,然后比较即可.【解答】解:把点A(﹣5,y1)和点B(﹣2,y2)分别代入y=﹣x,得y1=﹣×(﹣5)=;y2=﹣×(﹣2)=1,∵>1,∴y1>y2.故选A.【点评】本题较简单,可把点A(﹣5,y1)和点B(﹣2,y2)分别代入函数解析式进行比较,也可直接根据正比例函数的增减性进行比较.7.正比例函数y=kx的y值随x的增大而减小,则此函数的图象经过()A.一、二象限B.一、三象限C.二、三象限D.二、四象限【分析】直接根据正比例函数的性质求解.【解答】解:∵正比例函数y=kx的y值随x的增大而减小,∴图象经过第二、四象限.故选D.【点评】本题考查了正比例函数的性质:正比例函数y=kx(k≠0)的图象为直线,当k>0,图象经过第一、三象限,y值随x的增大而增大;当k<0,图象经过第二、四象限,y值随x的增大而减小.8.关于函数y=﹣x,下列结论正确的是()A.函数图象必过点(﹣2,﹣1)B.函数图象经过第1、3象限C.y随x的增大而减小 D.y随x的增大而增大【分析】根据正比例函数图象的性质确定正确的选项即可.【解答】解:A、当x=﹣2时,y=1,错误;B、根据k<0,得图象经过二、四象限,故错误;C、根据k<0,得图象经过二、四象限,y随x的增大而减小,正确;D、不对;故选C.【点评】考查了正比例函数图象的性质:它是经过原点的一条直线.当k>0时,图象经过一、三象限,y随x的增大而增大;当k<0时,图象经过二、四象限,y随x的增大而减小.要判断一点是否在直线上,只需把点的坐标代入,看是否满足解析式.9.对于正比例函数y=k2x(k是常数,k≠0)的图象,下列说法正确的是()A.是一条抛物线B.过点(,k)C.经过一、二象限 D.y随着x增大而减小【分析】先判断出函数y=k2x(k是常数,k≠0)图象的形状,再根据函数图象的性质进行逐一分析解答,解答.【解答】解:函数y=k2x(k是常数,k≠0)符合正比例函数的形式.A、错误,函数的图象是一条直线;B、正确,函数的图象过点(,k);C、错误,∵k是常数,k≠0,∴k2>0,∴函数的图象经过1,3象限;D、错误,是增函数,故y随着x的增大而增大.故选B.【点评】本题考查的是正比例函数的性质,在直线y=kx(k≠0)中:当k>0时,函数图象过一、三象限,y随x的增大而增大;当k<0时,函数图象过二、四象限,y随x的增大而减小.10.关于正比例函数y=﹣2x,下列结论正确的是()A.图象必经过点(﹣1,﹣2)B.图象经过第一、三象限C.y随x的增大而减小 D.不论x取何值,总有y<0【分析】根据正比例函数图象的性质可知.【解答】解:A、当x=﹣1时,y=2,错误;B、不对;C、根据k<0,得图象经过二、四象限,y随x的增大而减小,正确;D、不对;故选C.【点评】了解正比例函数图象的性质:它是经过原点的一条直线.当k>0时,图象经过一、三象限,y随x的增大而增大;当k<0时,图象经过二、四象限,y随x的增大而减小.要判断一点是否在直线上,只需把点的坐标代入,看是否满足解析式.11.关于函数y=,下列结论正确的是()A.函数图象必经过点(1,2)B.函数图象经过二、四象限C.y随x的增大而减小 D.y随x的增大而增大【分析】根据正比例函数图象的性质分析.【解答】解:A、当x=1时,y=,错误;B、因为k>0,所以图象经过第一、三象限,错误;C、因为k>0,所以y随x的增大而增大,C错误;D、正确.故选D.【点评】了解正比例函数图象的性质:它是经过原点的一条直线.当k>0时,图象经过一、三象限,y随x的增大而增大.当k<0时,图象经过二、四象限,y随x的增大而减小.12.下面所给点的坐标满足y=﹣2x的是()A.(2,﹣1)B.(﹣1,2)C.(1,2) D.(2,1)【分析】用代入法即可.【解答】解:A、当x=2时,y=﹣4,错误;B、当x=﹣1时,y=2,正确;C、当x=1时,y=﹣2,错误;D、错误.故选B.【点评】能够正确把点的横坐标代入解析式,计算它的纵坐标的值,看是否一致,即可判断.13.关于正比例函数y=﹣3x,下列结论正确的是()A.图象经过点(﹣3,1)B.图象经过第一、三象限C.函数值y随x的增大而增大D.图象与直线y=1﹣3x的倾斜程度相同【分析】根据正比例函数的性质直接解答即可.【解答】解:A、将(﹣3,1)代入解析式,得,1≠﹣9,故本选项错误;B、由于﹣3<0,则函数图象过二、四象限,故本选项错误;C、由于函数图象过二、四象限,则函数值y随x的增大而减小,故本选项错误;D、由于两函数比例系数相同,则其倾斜程度相同,故本选项正确.故选D.【点评】本题考查了正比例函数的性质,熟悉函数的图象及系数与图象的关系是解题的关键.14.正比例函数y=2x的图象所过的象限是()A.一、三象限B.二、四象限C.一、二象限D.三、四象限【分析】根据正比例函数的性质进行解答即可.【解答】解:∵正比例函数y=2x中,k=2>0,∴此函数的图象经过一、三象限.故选A.【点评】本题考查的是正比例函数的性质,即正比例函数y=kx(k≠0)中,当k >0时,函数的图象经过一、三象限.15.下列一次函数中,y的值随着x值的增大而减小的有()①y=10x﹣9;②y=﹣0.3x+2;③y=x+4;④y=(﹣)x;⑤y=7﹣x;⑥y=8+(﹣2)x.A.①③⑥B.②⑤⑥C.④⑤⑥D.②④⑤【分析】根据一次函数的性质对各题进行逐一分析即可.【解答】解:当k<0时y随着x的增大而减小,①y=10x﹣9;②y=﹣0.3x+2;③y=x+4;④y=(﹣)x;⑤y=7﹣x;⑥y=8+(﹣2)x中,比例系数小于0的有②④⑤,故y的值随着x值的增大而减小的有②④⑤,故选:D.【点评】本题考查的是一次函数的性质,即一次函数y=kx+b(k≠0)中,k>0,y随x的增大而增大;k<0,y随x的增大而减小.16.若正比例函数的图象经过点(2,﹣3),则这个图象必经过点()A.(﹣3,﹣2)B.(2,3) C.(3,﹣2)D.(﹣2,3)【分析】求出函数解析式,然后根据正比例函数的定义用代入法计算.【解答】解:设正比例函数的解析式为y=kx(k≠0),因为正比例函数y=kx的图象经过点(2,﹣3),所以﹣3=2k,解得:k=﹣,所以y=﹣x,把这四个选项中的点的坐标分别代入y=﹣x中,等号成立的点就在正比例函数y=﹣x的图象上,所以这个图象必经过点(﹣2,3).故选D.【点评】本题考查正比例函数的知识.关键是先求出函数的解析式,然后代值验证答案.17.对于y=k2x(k≠0)的图象下列说法不正确的是()A.是一条直线B.过点(,k)C.经过一、三象限或二、四象限D.y随x增大而增大【分析】根据y=k2x(k≠0),可知k2>0,从而可知y=k2x(k≠0)的图象的情况,从而可以解答本题.【解答】解:∵y=k2x(k≠0),∴k2>0.∴y=k2x(k≠0)的图象是正比例函数的图象,图象在第一、三象限,y随x的增大而增大,图象是一条直线.当x=时,y=k2x=.即y=k2x(k≠0)的图象过点().由上可得,选项A的说法正确,选项B的说法正确,选项C的说法不正确,选项D的说法正确.故选C.【点评】本题考查的是正比例函数的性质,解题的关键是明确在正比例函数y=kx (k≠0)中:当k>0时,函数图象过一、三象限,y随x的增大而增大;当k<0时,函数图象过二、四象限,y随x的增大而减小.18.已知函数y=(k﹣3)x,y随x的增大而减小,则常数k的取值范围是()A.k>3 B.k<3 C.k<﹣3 D.k<0【分析】先根据正比例函数的性质列出关于k的不等式,求出k的取值范围即可.【解答】解:∵函数y=(k﹣3)x,y随x的增大而减小,∴k﹣3<0,解得k<3.故选B.【点评】本题考查的是正比例函数的性质,熟知正比例函数的增减性是解答此题的关键.19.已知正比例函数y=(m﹣3)x的图象过第二、四象限,则m的取值范围是()A.m≥3 B.m>3 C.m≤3 D.m<3【分析】直接利用正比例函数的定义得出m的取值范围即可.【解答】解:∵正比例函数y=(m﹣3)x的图象过第二、四象限,∴m﹣3<0,解得:m<3.故选:D.【点评】此题主要考查了正比例函数的性质,正确把握正比例函数的性质是解题关键.20.下列函数中,y随x的增大而增大的函数是()A.y=3﹣x B.y=﹣0.5x C.y=﹣2x+1 D.y=x【分析】根据一次函数的性质对各选项进行逐一分析即可.【解答】解:A、∵y=3﹣x中k=﹣1<0,∴y随x的增大而减小,故本选项错误;B、∵y=﹣0.5x中k=﹣0.5<0,∴y随x的增大而减小,故本选项错误;C、∵y=﹣2x+1中k=﹣2<0,∴y随x的增大而减小,故本选项错误.D、∵y=x中k=>0,∴y随x的增大而增大,故本选项正确;故选D.【点评】本题考查的是一次函数的性质,熟知一次函数y=kx+b(k≠0)中,当k >0时y随x的增大而增大是解答此题的关键.二.填空题(共20小题)21.正比例函数y=x的图象与x轴所成的锐角的度数是45.【分析】根据正比例函数y=x图象上的点到两坐标轴的距离相等可以得到答案.【解答】解:∵正比例函数y=x图象上的点到两坐标轴的距离相等,∴其图象是一、三象限的角平分线,∴与x轴所成的锐角的度数是45°,故答案为:45.【点评】本题考查了正比例函数的性质,牢记其性质是解决本题的关键.22.如果正比例函数y=(k﹣1)x的图象经过第二、四象限,那么k的取值范围是k<1.【分析】根据正比例函数的性质(正比例函数y=kx(k≠0),当k<0时,该函数的图象经过第二、四象限)解答.【解答】解:正比例函数y=(k﹣1)x的图象经过第二、四象限,∴k﹣1<0,解得,k<1.故答案是:k<1.【点评】本题主要考查了正比例函数的性质.正比例函数y=kx(k≠0),当k<0时,该函数的图象经过第二、四象限;当k>0时,该函数的图象经过第一、三象限.23.若直线y=kx(k≠0)经过点(﹣2,6),则y随x的增大而减小.【分析】先把(﹣2,6)代入直线y=kx,求出k,然后根据正比例函数的性质即可得到y随x的增大而怎样变化.【解答】解:∵直线y=kx(k≠0)经过点(﹣2,6),∴6=﹣2•k,∴k=﹣3<0,∴y随x的增大而减小.故答案为:减小.【点评】本题考查了正比例函数y=kx(k≠0)的性质:当k>0,图象经过第一、三象限,y随x的增大而增大;当k<0,图象经过第二、四象限,y随x的增大而减小.24.正比例函数y=kx的图象是经过点(0,0)和(1,k)的一条直线.【分析】正比例函数的图象是一条过原点的直线,当x=1时,y=k,由此可得出答案.【解答】解:由正比例函数图象的特点可得:正比例函数的图象是一条过原点的直线,当x=1时,y=k,∴图象还过(1,k)点,∴正比例函数y=kx的图象是经过点(0,0)和(1,k)的一条直线.故答案为:(0,0),(1,k),一条直线.【点评】此题主要考查了正比例函数的性质,同学们应熟练掌握根据函数式判断出函数图象的位置,这是考查重点内容之一.25.已知正比例函数y=(k+3)x,若y随x的增大而减小,则k的取值范围是k <﹣3.【分析】根据正比例函数图象与系数的关系列出关于k的不等式k+3<0,然后解不等式即可.【解答】解:∵正比例函数y=(k+3)x中,y的值随自变量x的值增大而减小,∴k+3<0,解得,k<﹣3;故答案为:k<﹣3.【点评】本题主要考查正比例函数图象在坐标平面内的位置与k的关系.解答本题注意理解:直线y=kx所在的位置与k的符号有直接的关系.k>0时,直线必经过一、三象限,y随x的增大而增大;k<0时,直线必经过二、四象限,y随x的增大而减小.26.正比例函数y=﹣x的图象经过第二、四象限.【分析】直接根据正比例函数的性质进行解答即可.【解答】解:∵正比例函数y=﹣x中,k=﹣<0,∴此函数的图象经过第二、四象限.故答案为:二、四.【点评】本题考查的是正比例函数的性质,熟知正比例函数y=kx(k≠0)中,当k<0时,函数图象经过第二、第四象限是解答此题的关键.27.正比例函数y=3x的图象经过第一、三象限.【分析】根据k=3>0和正比例函数的性质即可得到答案.【解答】解:∵k=3>0,∴正比例函数y=3x的图象经过一、三象限.故答案为:一、三.【点评】本题主要考查对正比例函数的性质的理解和掌握,能熟练地运用正比例函数的性质进行说理是解此题的关键.28.函数y=5x的图象经过一三象限,函数图象从左往右呈上升趋势,y 随x的增大而增大;函数y=﹣5x的图象经过第二四象限,函数图象从左往右呈下降趋势,y 随x的增大而减小.【分析】利用这个比例函数的性质结合比例系数的符号直接回答即可.【解答】解:函数y=5x的图象经过一三象限,函数图象从左往右呈上升趋势,y随x的增大而增大;函数y=﹣5x的图象经过第二四象限,函数图象从左往右呈下降趋势,y随x的增大而减小,故答案为:一三,上升,增大;二四,下降,减小.【点评】本题考查了正比例函数的性质,正比例函数y=kx(k≠0),k>0时,图象在一三象限,呈上升趋势,当k<0时,图象在二四象限,呈下降趋势.29.正比例函数的图象一定经过的点的坐标为(0,0).【分析】由于正比例函数的一般形式为y=kx,所以当x=0时,y=0,由此即可确定正比例函数的图象一定经过什么点.【解答】解:∵正比例函数的一般形式为y=kx,∴当x=0时,y=0,∴正比例函数的图象一定经过原点.故答案为:(0,0).【点评】此题比较简单,主要考查了正比例函数图象的性质:正比例函数的图象一定经过原点.30.正比例函数y=x的图象是经过点(0,0)和点(1,)的一条直线.【分析】分别将两点的横坐标代入正比例函数的解析式即可求得其纵坐标.【解答】解:当x=0时,y=×0=0,当x=1时,y=×1=,故答案为:0,.【点评】本题考查了正比例函数的性质,正比例函数的图象是过原点的一条直线,难度不大.31.已知函数y=(2m﹣9)x|m|﹣5是正比例函数,且图象经过第二,四象限,则m的值为﹣6.【分析】根据正比例函数的定义可得出关于m的方程,解出即可.【解答】解:由题意可得:2m﹣9<0,|m|﹣5=1,∴m=﹣6.故填﹣6.【点评】解题关键是掌握正比例函数的定义条件以及题意:正比例函数y=kx的定义条件是:k为常数且k≠0,自变量次数为1.且图象经过第二,四象限,则k<0.32.在同一坐标系中,如图所示,一次函数y=k1x,y=k2x,y=k3x,y=k4x的图象分别为l1,l2,l3,l4,则k1,k2,k3,k4的大小关系是k3>k4>k1>k2.【分析】想知道k之间的大小关系,图中又无其他信息,对此我们可以自己找点来近似的估计k值,如可近似估计四条线上的各一个异于(0,0)的点,然后代入求出k1、k2、k3、k4.再比较即可.【解答】解:把x=1代入y=k1x,y=k2x,y=k3x,y=k4x中,可得:k3>k4>k1>k2.故答案为:k3>k4>k1>k2.【点评】本题考察学生对直线y=kx+b这个基本解析式的理解,尤其是对其中两个系数k,b的掌握和理解是关键.33.正比例函数y=kx(k≠0)的图象是一条经过点(0,0)的直线.【分析】正比例函数的图象是一条过原点的直线,由此可得出答案.【解答】解:由正比例函数图象的特点可得:正比例函数的图象是一条过原点的直线.故答案为(0,0).【点评】本题考查正比例函数的图象的特点,属于基础题,注意掌握正比例函数的图象是一条过原点的直线.34.已知点P1(x1,y1)和点P2(x2,y2)是正比例函数y=kx(k≠0)图象上的两点,且当x1<x2时,y1<y2,则k的取值范围是k>0.【分析】根据正比例函数的变化规律计算.【解答】解:由于x1<x2,y1<y2,说明y随x的减小而减小,∴k>0;也可计算:y1=kx1,y2=kx2,y1<y2,即kx1<kx2k(x1﹣x2)<0,∵x1<x2,∴x1﹣x2<0,∴k>0.【点评】此题主要考查了正比例函数的变化规律:当k>0时,图象经过一、三象限,y随x的增大而增大;当k<0时,图象经过二、四象限,y随x的增大而减小.35.A(﹣1,3)在正比例函数y=kx图象上,则y随着x的增大而减小.【分析】把A(﹣1,3)代入y=kx求出k,根据议程函数的性质即可求出答案.【解答】解:把A(﹣1,3)代入y=kx得:3=﹣k,∴k=﹣3<0,∴y随x的增大而减小.故答案为:减小.【点评】本题主要考查对解一元一次方程,一次函数的性质等知识点的理解和掌握,能根据一次函数的性质进行说理是解此题的关键.36.已知正比例函数y=kx(k≠0)的图象经过原点、第二象限与第四象限,请写出符合上述条件的k的一个值:﹣2(只要是负数即可,答案不唯一.).【分析】根据正比例函数的性质:它是经过原点的一条直线,当k<0时,图象经过二、四象限即可求解.【解答】解:根据题意,知k<0.故填﹣2.(只要k<0均可)【点评】考查了正比例函数图象的性质:它是经过原点的一条直线.当k>0时,图象经过一、三象限,y随x的增大而增大;当k<0时,图象经过二、四象限,y随x的增大而减小.37.函数的图象经过第二、四象限.【分析】根据正比例函数中k=﹣进行判断即可.【解答】解:∵函数中k=﹣<0,∴此函数的图象经过二、四象限.故答案为:二、四.【点评】本题考查的是正比例函数的性质,即正比例函数y=kx中,当k<0时,函数图象经过二、四象限.38.正比例函数y=﹣5x中,y随着x的增大而减小.【分析】直接根据正比例函数的图象与系数的关系进行解答即可.【解答】解:∵正比例函数y=﹣5x中k=﹣5<0,∴y随着x的增大而减小.故答案为:减小.【点评】本题考查的是正比例函数的性质,熟知正比例函数y=kx中,当k<0时,y随着x的增大而减小是解答此题的关键.39.函数y=(m﹣3)是正比例函数,则m=﹣3,y随x的增大而减小.【分析】根据正比例函数的定义可得出关于m的方程,继而可得出m的值.【解答】解:m﹣3≠0,m2﹣8=1,则m=﹣3,y=﹣6x,∴y随x的增大而减小.【点评】解题关键是掌握正比例函数的定义条件:正比例函数y=kx的定义条件是:k为常数且k≠0,自变量次数为1.40.若函数y=(1﹣k)x2|k|﹣3是正比例函数,且y随x的增大而减小,则(k﹣3)2017=﹣1.【分析】由正比例函数的定义可求得k的取值,再再利用其增减性进行取舍,代入代数式求值即可.【解答】解:∵y=(1﹣k)x2|k|﹣3是正比例函数,∴2|k|﹣3=1,解得k=2或k=﹣2,∵y随x的增大而减小,∴1﹣k<0,即k>1,∴k=2,∴(k﹣3)2017=(2﹣3)2017=﹣1,故答案为:﹣1.【点评】本题主要考查正比例函数性质,掌握正比例函数的增减性是解题的关键,即在y=kx中,当k>0时,y随x的增大而增大,当k<0时,y随x的增大而减小.三.解答题(共10小题)41.已知正比例函数图象上一个点A到x轴的距离为4,这个点A的横坐标为﹣2,请回答下列问题:(1)求这个正比例函数;(2)这个正比例函数经过哪几个象限?(3)这个正比例函数的函数值y是随着x增大而增大?还是随着x增大而减小?【分析】(1)根据题意得出A点坐标,进而求出函数解析式;(2)利用(1)中所求得出经过的象限;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正比例函数专题练习
知识点
1.形如___________(k是常数,k≠0)的函数是正比例函数,其中k 叫,正比例函数都是常数与自变量的乘积的形式
2.正比例函数y=kx(k是常数,k≠0)的图象是一条经过________的_______,我们通常称之为直线y=kx.当k>0时,图像位于第象限,从左向右,y随x的增大而,也可以说成函数值随自变量的增大而_________;当k<0时,图像位于第象限,从左向右,y随x的增大而,也可以说成函数值随自变量的增大而_________.
3.正比例函数的图像是经过坐标点和定点__ __两点的一条。
根据两点确定一条直线,可以确定两个点(两点法)画正比例函数的图象.
一、填空题(每小题3分,共30·分)
1、形如的函数是正比例函数。
2、大连市区与庄河两地之间的距离是160km,若汽车以每小时80 km 的速度匀速从庄河开往大连,则汽车距庄河的路程s (km)与行驶的时间t(h)之间的函数关系式为.
3、正比例函数y kx
=(k为常数,0
k<)的图像经过第象限,函数值随自变量的增大而。
4、已知一个正比例函数的图像经过点(-2,4),则这个正比例函数的表达式是。
5、已知y与x成正比例,且2
x=时6
y=-,则9
y=时x=。
6如果函数23
y mx m
=+-是正比例函数,则m= 。
7.若x、y是变量,且函数2
)1
(k x
k
y+
=是正比例函数,则k的值为_____________。
8.已知y=(k+1)x+k-5是正比例函数求k的值是______________.
9.若函数y=(2m+6)x2+(1-m)x是正比例函数,则m的值是______________.
10.已知函数y=(2m+1)x+m-3若此函数图象经过原点,则m=____________. 8、已知正比例函数(12)
y a x
=-如果y的值随x的值增大而减小,那么a的取值范圆是
9、结合正比例函数4
y x
=的图像回答:当1
x>时,y的取值范围是。
10.函数y=-7x的图象在第象限内,经过点(0, )与点(1, ),y随x的增大而 .函数y=4x的图象在第
象限内,经过点(0, )与点(1, ),y随x的增而 .
11.正比例函数x
m
y)1
(-
=的图象经过一、三象限,则m的取值范围是
12.若正比例函数图像又x
k)6
3(
y-
=的图像经过点)
,
(
1
1
y
x
A和B)
,
(
2
2
y
x
B,当2
1
x
x<
时,
2
1
y
y>则k的取值范围是
13、已知正比例函数y=kx(k≠0)的图象如图所示,则在下列选项中k值可能是()
A、1
B、2
C、3
D、4
14、(2000•西城区)在平面直角坐标系中,正比例函数y=kx(k<0)的图象
的大体位置是()
15、一次函数y=﹣x的图象平分()
A、第一、三象限
B、第一、二象限
C、第二、三象限
D、第二、四象限
16、在直角坐标系中,既是正比例函数y=kx,又是y的值随x的增大而减小的图象是()
17、当k>0时,正比例函数y=kx的图象大致是()
18、已知正比例函数y=kx (k≠0),当x=﹣1时,y=﹣2,则它的图象大致是()
19、如图所示函数图象中,正比例函数的图象是()20、正比例函数y=kx的图象是经过原点的一条()
A、射线
B、双曲线
C、线段
D、直线
21、结合函数y=﹣2x的图象回答,当x<﹣1时,y的取值范围()
A、y<2
B、y>2
C、y≥错误!未找到引用源。
D、y≤错误!未找到引用源。
22.正比例函数x
m
y)1
3(-
=的图像经过点)
,
(
)
,
(
2
2
1
1
y
x
B
y
x
A和且该图像经过第二、四象限.
(1)求m的取值范围
(2)当x1>x2时,比较y1与y2的大小,并说明理由.。
