数学建模实验 ——曲线拟合与回归分析
spss曲线拟合与回归分析
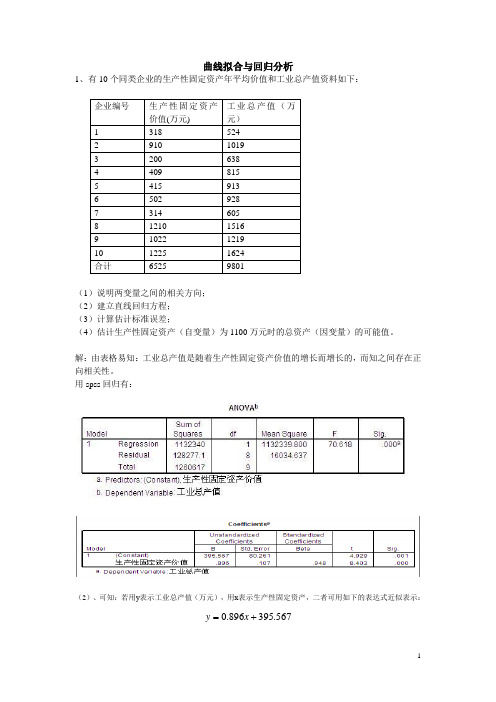
曲线拟合与回归分析1、有10个同类企业的生产性固定资产年平均价值和工业总产值资料如下:(1)说明两变量之间的相关方向;(2)建立直线回归方程;(3)计算估计标准误差;(4)估计生产性固定资产(自变量)为1100万元时的总资产(因变量)的可能值。
解:由表格易知:工业总产值是随着生产性固定资产价值的增长而增长的,而知之间存在正向相关性。
用spss回归有:(2)、可知:若用y表示工业总产值(万元),用x表示生产性固定资产,二者可用如下的表达式近似表示:=x.0+y.567395896(3)、用spss回归知标准误差为80.216(万元)。
(4)、当固定资产为1100时,总产值可能是(0.896*1100+395.567-80.216~0.896*1100+395.567+80.216)即(1301.0~146.4)这个范围内的某个值。
另外,用MATLAP也可以得到相同的结果:程序如下所示:function [b,bint,r,rint,stats] = regression1x = [318 910 200 409 415 502 314 1210 1022 1225];y = [524 1019 638 815 913 928 605 1516 1219 1624];X = [ones(size(x))', x'];[b,bint,r,rint,stats] = regress(y',X,0.05);display(b);display(stats);x1 = [300:10:1250];y1 = b(1) + b(2)*x1;figure;plot(x,y,'ro',x1,y1,'g-');industry = ones(6,1);construction = ones(6,1);industry(1) =1022;construction(1) = 1219;for i = 1:5industry(i+1) =industry(i) * 1.045;construction(i+1) = b(1) + b(2)* construction(i+1);enddisplay(industry);display( construction);end运行结果如下所示:b =395.56700.8958stats =1.0e+004 *0.0001 0.0071 0.0000 1.6035industry =1.0e+003 *1.02201.06801.11601.16631.21881.2736construction =1.0e+003 *1.2190 0.3965 0.3965 0.3965 0.3965 0.3965200400600800100012001400生产性固定资产价值(万元)工业总价值(万元)2、设某公司下属10个门市部有关资料如下:(1)、确定适宜的 回归模型; (2)、计算有关指标,判断这三种经济现象之间的紧密程度。
回归分析(曲线拟合)算法探究

yi )
0
Q(a, b)
b
m
2 (a bxi
i 1
yi )xi
0
整理得到拟合曲线满足的方程:
ma
(
m i 1
xi )b
m i 1
yi
m
m
m
(
i 1
xi )a
(
i 1
xi2 )b
xi yi
i 1
最小二乘算法介绍
上式称为拟合曲线的法方程,可用消元法或者克莱姆方法解得:
m
yi
a i1 m xi yi i1
属性
text text text text Caption Caption Caption Caption Caption Caption Caption Caption Caption Scale Caption Caption Caption
值
自变量的观测值 因变量的观测值
X坐标名称 Y坐标名称 拟合类型 三次样条函数插值 最小二乘法 对数拟合 双曲线拟合 指数拟合
m
xi
i1
m
xi2
i1
m
m
xi
mm
mm
m
m
m
i1 m
( yi xi2 xi xi yi ) (m xi2 ( xi )2
xi
xi2
i1 i1
i1 i1
i1
i1
i1
i1
m
m
m
m
mHale Waihona Puke b (m xi yi xi yi ) (m xi2 ( xi )2 )
i 1
i1 i1
CH3COOC2H5 +Na+ +OH- = CH3 COO- +Na++C2H5OH 设NaOH和CH3COOC2H5 的初始浓度分别为a和b. 当a = b时, 有线性方程
回归分析曲线拟合通用课件

研究生物标志物与疾病之间的 关系,预测疾病的发生风险。
金融市场分析
分析股票价格、利率等金融变 量的相关性,进行市场预测和 风险管理。
社会科学研究
研究社会现象之间的相关关系 ,如教育程度与收入的关系、 人口增长与经济发展的线性回归模型
线性回归模型是一种预测模型,用于描 述因变量和自变量之间的线性关系。
SPSS实现
SPSS实现步骤 1. 打开SPSS软件; 2. 导入数据;
SPSS实现
01
3. 选择回归分析命令;
02
4. 设置回归分析的变量和选项;
03
5. 运行回归分析;
04
6. 查看并解释结果。
THANKS
感谢观看
回归分析曲线拟合通用课件
• 回归分析概述 • 线性回归分析 • 非线性回归分析 • 曲线拟合方法 • 回归分析的实践应用 • 回归分析的软件实现
01
回归分析概述
回归分析的定义
01
回归分析是一种统计学方法,用 于研究自变量和因变量之间的相 关关系,并建立数学模型来预测 因变量的值。
02
它通过分析数据中的变异关系, 找出影响因变量的主要因素,并 建立回归方程,用于预测和控制 因变量的取值。
线性回归模型的假设包括:误差项的独立性、误差项的同方差性、误差 项的无偏性和误差项的正态性。
对假设的检验可以通过一些统计量进行,如残差图、Q-Q图、Durbin Watson检验等。如果模型的假设不满足,可能需要重新考虑模型的建立 或对数据进行适当的变换。
03
非线性回归分析
非线性回归模型
线性回归模型的局限性
回归分析的分类
01
02
03
一元线性回归
数学建模之曲线拟合

14 0.687 0.691
17 0.64 0.638
27 0.493 0.488
31 0.44 0.439
c=1.003819exp(-0.02669t)
c,t 关系图 1 0.8 0.6 0.4 0.2 0 0 10 20 t 30 40 系列1 系列2
c
c, t¹ Ø Ï µ Í ¼ 1
© ¨mol/L£ c£
0.8 0.6 0.4 0.2 0 0 10 20 t£ ¨min£ ©
3
µ Á Ï Ð 1
30
40
Ⅱ、选 y
1 型试探,将曲线变直,这时 ax b
y=1/cA x=t 算得 1/cA 为:
T 1/cA 2 1.005 5 1.018 8 1.28 1/cA~ t 数表 11 14 1.335 1.445 17 1.568 27 2.028 31 2.273 35 2.507
1
在某液相反应中,不同时间下测的某组成的浓度见下表, 试作出其经验方程。 浓度随时间的变化关系 2 5 8 11 14 17 27 31 时间 t(min) 浓度 cA 0.948 0.879 0.813 0.749 0.687 0.640 0.493 0.440 (mol/L)
35 0.391
Ⅰ、首先将实验数据 t~cA 作图,图像表明,这是一条曲线,不是 y=a+bx 型直线,因此,对照样板曲线重新选型。
lnc, lnt 关系图 0 -0.2 0 1 2 3 4
lnc
-0.4 -0.6 -0.8 -1 lnt 系列1
作 lnc ~lnt 的图,发现原来的曲线不但没变直,反而更加弯曲了。说明这 个类型的经验公式更不适合了。
Ⅳ、又重新选型,选用 y=aebx 型,再试探 y=lncA x=t
数学建模回归分析实验报告[1]
![数学建模回归分析实验报告[1]](https://img.taocdn.com/s3/m/039578ef9e314332396893fb.png)
beta = 21.0058 19.5285
所以:养护日期 x(日)及抗压强度 y(kg/cm2)的回归方程:y=21.0050+19.5288ln(x)
(2)、主程序如下: x=[2 3 4 5 7 9 12 14 17 21 28 56]; y=[35 42 47 53 59 65 68 73 76 82 86 99]; beta0=[1 1]'; [beta,r,J]=nlinfit(x',y','volum',beta0); beta
(3)、输出结果:
实验目的 1、直观了解回归分析基本内容。 2、掌握用数学软件求解回归分析问题。 实验内容 1、回归分析的基本理论。 2、用数学软件求解回归分析问题。
程序设计
1、考察温度 x 对产量 y 的影响,测得下列 10 组数据:
温度(℃) 20 25 30
35
40
45
50
55
60
65
产量(kg) 13.2 15.1 16.4 17.1 17.9 18.7 19.6 21.2 22.5 24.3
差的置信区间均包含零点,这说明回归模型 y=9.1212+0.2230x 能较好的符合原 始数据,没有异常点.
(5)、预测及作图: z=b(1)+b(2)*x plot(x,Y,'k+',x,z,'r')
预测 x=42℃时产量的估值.y=18.4872
2、某零件上有一段曲线,为了在程序控制机床上加工这一零件,需要求这段曲 线的解析表达式,在曲线横坐标 xi 处测得纵坐标 yi 共 11 对数据如下:
s=[0.6 2.0 4.4 7.5 11.8 17.1 23.3 31.2 39.6 49.7 61.7];
数学建模曲线拟合

曲线拟合摘要根究已有数据研究y关于x的关系,对于不同的要求得到不同的结果。
问题一中目标为使的各个观察值同按直线关系所预期的值的偏差平方和为最小,利用MATLAB中tlsqcurvefi函数在最小二乘法原理下拟合出所求直线。
问题二目标为使绝对偏差总和为最小,使用MATLAB中的fminsearch函数,在题目约束条件内求的最优答案,以此方法同样求得问题三中最大偏差为最小时的直线。
问题四拟合的曲线为二阶多项式,方法同前三问类似。
问题五为求得最佳的曲线,将之前的一次曲线换成多次曲线进行拟合得到新的结果。
经试验发现高阶多项式的阶数越高拟和效果最好。
)关键词:函数拟合最小二乘法线性规划|<¥一、问题的重述已知一个量y 依赖于另一个量x ,现收集有数据如下:(1)求拟合以上数据的直线a bx y +=。
目标为使y 的各个观察值同按直线关系所预期的值的偏差平方和为最小。
(2)求拟合以上数据的直线a bx y +=,目标为使y 的各个观察值同按直线关系所预期的值的绝对偏差总和为最小。
(3)求拟合以上数据的直线,目标为使y 的各个观察值同按直线关系所预期的值的最大偏差为最小。
(4)求拟合以上数据的曲线a bx cx y ++=2,实现(1)(2)(3)三种目标。
}(5)试一试其它的曲线,可否找出最好的?二、问题的分析对于问题一,利用MATLAB 中的最小二乘法对数据进行拟合得到直线,目标为使各个观察值同按直线关系所预期的值的偏差平方和为最小。
对于问题二、三、四均利用MATLAB 中的fminsearch 函数,在题目要求的约束条件下找到最佳答案。
对于问题五,改变多项式最高次次数,拟合后计算残差,和二次多项式比较,再增加次数后拟合,和原多项式比较残差,进而找到最好的曲线。
~三、基本假设1.表中数据真实可信,每个点都具有意义。
四、模型的建立与求解1.问题一 :对给定数据点(){}),,1,0(,m i Y X i i =,在取定的函数类Φ 中,求()Φ∈x p ,使误差的平方和2E 最小,()[]22∑-=i i Y X p E 。
数学建模-回归分析

一、变量之间的两种关系 1、函数关系:y = f (x) 。
2、相关关系:X ,Y 之间有联系,但由 其中一个不能唯一的确定另一个的值。 如: 年龄 X ,血压 Y ; 单位成本 X ,产量 Y ; 高考成绩 X ,大学成绩 Y ; 身高 X ,体重 Y 等等。
二、研究相关关系的内容有
1、相关分析——相关方向及程度(第九章)。 增大而增大——正相关; 增大而减小——负相关。 2、回归分析——模拟相关变量之间的内在 联系,建立相关变量间的近似表达式 (经验 公式)(第八章)。 相关程度强,经验公式的有效性就强, 反之就弱。
三、一般曲线性模型 1、一般一元曲线模型
y = f ( x) + ε
对于此类模型的转换,可用泰勒展开 公式,把 在零点展开,再做简单的变 f ( x) 换可以得到多元线性回归模型。 2、一般多元曲线模型
y = f ( x1 , x2源自,⋯ , xm ) + ε
对于此类模型也要尽量转化为线性模 型,具体可参考其他统计软件书,这里不 做介绍。
ˆ ˆ ˆ ˆ y = b0 + b1 x1 + ⋯ + bm x m
2、利用平方和分解得到 ST , S回 , S剩。 3、计算模型拟合度 S ,R ,R 。 (1)标准误差(或标准残差)
S =
S剩 ( n − m − 1)
当 S 越大,拟合越差,反之,S 越小, 拟合越好。 (2)复相关函数
R =
2
仍是 R 越大拟合越好。 注: a、修正的原因:R 的大小与变量的个数以及样本 个数有关; 比 R 要常用。 R b、S 和 R 是对拟合程度进行评价,但S与 R 的分 布没有给出,故不能用于检验。 用处:在多种回归模型(线性,非线性)时, 用来比较那种最好;如:通过回归方程显著性检验 得到:
数学建模与数学实验 回归分析

2、多项式回归
设变量 x、Y 的回归模型为 Y 0 1x 2 x2 ... p x p
其中 p 是已知的,i (i 1,2,, p) 是未知参数, 服从正态分布 N (0, 2 ) .
Y 0 1x 2 x2 ... k xk
腿长
88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102
以身高x为横坐标,以腿长y为纵坐标将这些数据点(xI,yi) 在平面直角坐标系上标出.
解答
102
100
98
y 0 1x
96
949290 Nhomakorabea88
86
84
140
145
150
155
160
165
2019/7/8
17
二、模型参数估计
1、对 i 和 2 作估计
用最小二乘法求0 ,..., k 的估计量:作离差平方和
n
Q yi 0 1xi1 ... k xik 2 i 1
选择 0 ,..., k 使 Q 达到最小。
解得估计值 ˆ
进行检验.
假设 H 0 : 1 0 被拒绝,则回归显著,认为 y 与 x 存在线性关 系,所求的线性回归方程有意义;否则回归不显著,y 与 x 的关系 不能用一元线性回归模型来描述,所得的回归方程也无意义.
2019/7/8
8
(Ⅰ)F检验法
当 H 0 成立时,
F
U
~F(1,n-2)
Qe /(n 2)
变量的值 x1* ,..., xk ,用 yˆ * ˆ0 ˆ1 x1* ... ˆk xk * 来预测
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
曲线拟合与回归分析
1、有10个同类企业的生产性固定资产年平均价值和工业总产值资料如下:
(1)说明两变量之间的相关方向;
(2)建立直线回归方程;
(3)计算估计标准误差;
(4)估计生产性固定资产(自变量)为1100万元时的总资产
(因变量)的可能值。
解:
(1)工业总产值是随着生产性固定资产价值的增长而增长的,存
在正向相关性。
用spss回归
(2)spss回归可知:若用y表示工业总产值(万元),用x表示生产性固定资产,二者可用如下的表达式近似表示:
.0+
y
=x
896
.
395
567
(3)spss回归知标准误差为80.216(万元)。
(4)当固定资产为1100时,总产值为:
(0.896*1100+395.567-80.216~0.896*1100+395.567+80.216)
即(1301.0~146.4)这个范围内的某个值。
MATLAB程序如下所示:
function [b,bint,r,rint,stats] = regression1
x = [318 910 200 409 415 502 314 1210 1022 1225];
y = [524 1019 638 815 913 928 605 1516 1219 1624];
X = [ones(size(x))', x'];
[b,bint,r,rint,stats] = regress(y',X,0.05);
display(b);
display(stats);
x1 = [300:10:1250];
y1 = b(1) + b(2)*x1;
figure;plot(x,y,'ro',x1,y1,'g-');
生产性固定资产价值(万元)
工业总价值(万元)
industry = ones(6,1); construction = ones(6,1); industry(1) =1022; construction(1) = 1219; for i = 1:5
industry(i+1) =industry(i) * 1.045;
construction(i+1) = b(1) + b(2)* construction(i+1); end
display(industry); display( construction); end
运行结果:b = 395.5670 0.8958 stats = 1.0e+004 *
0.0001 0.0071 0.0000 1.6035 industry = 1.0e+003 * 1.0220 1.0680 1.1160 1.1663 1.2188 1.2736 construction = 1.0e+003 * 1.2190 0.3965 0.3965 0.3965 0.3965 0.3965。
