2018考研数学冲刺模拟卷
考研数学三模拟题2018年(33)_真题(含答案与解析)-交互
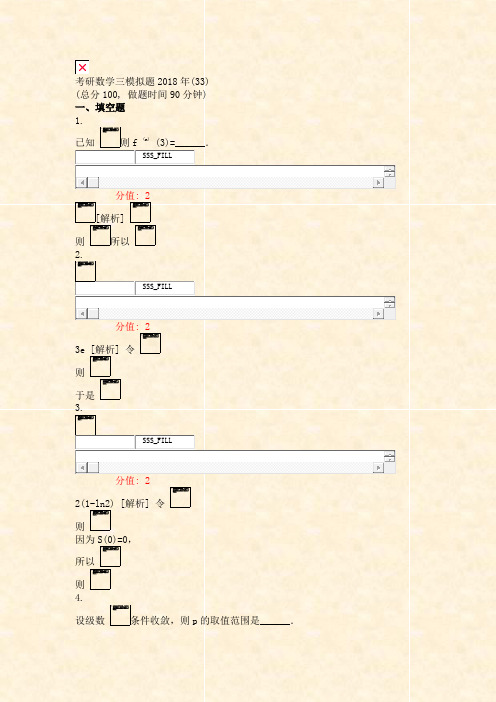
考研数学三模拟题2018年(33)(总分100, 做题时间90分钟)一、填空题1.已知则f (n) (3)=______.SSS_FILL分值: 2[解析]则所以2.SSS_FILL分值: 23e [解析] 令则于是3.SSS_FILL分值: 22(1-ln2) [解析] 令则因为S(0)=0,所以则4.设级数条件收敛,则p的取值范围是______.SSS_FILL分值: 2[解析]因为条件收敛,所以即p的范围是5.设y=y(x)满足,且有y(1)=1,则.SSS_TEXT_QUSTI分值: 2[解析] 由得函数y=y(x)可微且,积分得,因为y(1)=1,所以C=0,于是,故6.微分方程的通解为______.SSS_TEXT_QUSTI分值: 2[解析] 由,得,即,令z=e y,则,解得,所以原方程的通解为.7.微分方程yy"-2(y") 2 =0的通解为______.SSS_TEXT_QUSTI分值: 2y=C或者[解析] 令y"=p,得,代入原方程得则p=0,或.当p=0时,y=C;当时,,即.由,得,从而,所以原方程的通解为y=C或者.8.微分方程的通解为______.SSS_TEXT_QUSTI分值: 2lnx+C [解析] 令,所以9.以y=C1 e x +e x (C2cosx+C3sinx)为特解的三阶常系数齐次线性微分方程为______.SSS_TEXT_QUSTI分值: 2y""-3y"+4y"-2y=0 [解析] 特征值为λ1 =1,λ2,3=1±i,特征方程为(λ-1)(λ-1+i)(λ-1-i)=0,即λ 3 -3λ 2+4λ-2=0,所求方程为y""-3y"+4y"-2y=0.10.设y(x)为微分方程y"-4y"+4y=0满足初始条件y(0)=1,y"(0)=2的特解,则SSS_TEXT_QUSTI分值: 2[解析] y"-4y"+4y=0的通解为y=(C1 +C2x)e 2x,由初始条件y(0)=1,y"(0)=2得C1 =1,C2=0,则y=e 2x,于是11.差分方程yt+1 -2yt=3×2 t的通解为y(t)=______.SSS_TEXT_QUSTI分值: 2[解析] yt+1 -2yt=0的通解为y(t)=C×2 t,f(t)=3×2 t,因为2为特征值,所以设特解为yt*=at×2 t,代入原方程得,故原方程的通解.二、选择题1.设条件收敛,且,则______.SSS_SINGLE_SELA |r|<1B |r|>1C r=-1D r=1分值: 2答案:C[解析] 因为条件收敛,所以级数一定不是正项或负项级数,故r≤0.若|r|<1,则,级数绝对收敛,矛盾;若|r|>1,则,存在充分大的N,当n>N时,{|un|}单调增加,,于是发散,矛盾,故|r|=1,再由r≤0得r=-1,选C.2.设,则______.A.B.C.D.SSS_SIMPLE_SINA B C D分值: 2答案:B[解析] 显然条件收敛,,因为,而收敛,所以收敛,选B.3.设幂级数在x=6处条件收敛,则幂级数的收敛半径为______.A.2B.4C.D.无法确定SSS_SIMPLE_SINA B C D分值: 2答案:A[解析] 因为在x=6处条件收敛,所以级数的收敛半径为R=4,又因为级数有相同的收敛半径,所以的收敛半径为R=4,于是的收敛半径为R=2,选A.4.设y(x)是微分方程y"+(x-1)y"+x 2 y=e x满足初始条件y(0)=0,y"(0)=1的解,则______.SSS_SINGLE_SELA 等于1B 等于2C 等于0D 不存在分值: 2答案:A[解析] 微分方程y"+(x-1)y"+x 2 y=e x中,令x=0,则y"(0)=2,于是,选A.5.二阶常系数非齐次线性微分方程y"-2y"-3y=(2x+1)e -x的特解形式为______.• A.(ax+b)e-x•**•**(ax+b)e-x**(ax+b)e-xSSS_SIMPLE_SINA B C D分值: 2答案:D[解析] 方程y"-2y"-3y=(2x+1)e -x的特征方程为λ 2 -2λ-3=0,特征值为λ1 =-1,λ2=3,故方程y"-2y"-3y=(2x+1)e -x的特解形式为x(ax+b)e -x,选D.6.设φ1 (x),φ2(x),φ3(x)为二阶非齐次线性方程y"+a1(x)y"+a2(x)y=f(x)的三个线性无关解,则该方程的通解为______.SSS_SINGLE_SELA C1[φ1(x)+φ2(x)]+C2φ3(x)B C1[φ1(x)-φ2(x)]+C2φ3(x)C C1[φ1(x)+φ2(x)]+C2[φ1(x)-φ3(x)]D C1φ1(x)+C2φ2(x)+C3φ3(x),其中C1+C2+C3=1分值: 2答案:D[解析] 因为φ1 (x),φ2(x),φ3(x)为方程y"+a1(x)y"+a2(x)y=f(x)的三个线性无关解,所以φ1 (x)-φ3(x),φ2(x)-φ3(x)为方程y"+a1(x)y"+a2(x)y=0的两个线性无关解,于是方程y"+a1 (x)y"+a2(x)y=f(x)的通解为C1[φ1(x)-φ3(x)]+C2[φ2(x)-φ3(x)]+φ3(x)即C1φ1(x)+C2φ2(x)+C3φ3(x),其中C3=1-C1-C2或C1+C2+C3=1,选D.三、解答题1.讨论级数的敛散性.SSS_TEXT_QUSTI分值: 5解令则因为而收敛,所以收敛,由正项级数的比较审敛法得收敛.2.设收敛,举例说明级数不一定收敛;若是正项收敛级数,证明一定收敛.SSS_TEXT_QUSTI分值: 5解令,由交错级数的Leibniz审敛法,级数收敛,而发散.设是正项收敛级数,则,取ε0 =1,存在自然数N,当n>N时,|an-0|<1,从而0≤an<1,当n>N时,有.由收敛得收敛,再由比较审敛法得收敛,所以收敛.3.设,级数中,哪个级数一定收敛?SSS_TEXT_QUSTI分值: 5解不一定收敛,如,显然,而,因为收敛,而发散,所以发散;不一定收敛,如,显然发散;不一定收敛,如,显然发散;一定收敛.由,得,又收敛,所以收敛,即绝对收敛,所以一定收敛.4.若正项级数收敛,证明:收敛.SSS_TEXT_QUSTI分值: 5证明因为收敛,所以,当x>0时,ln(1+x)<x,于是为正项级数,而,所以再由收敛,故收敛.设.SSS_TEXT_QUSTI5.求的值;分值: 2.5解,则,,因为,所以.SSS_TEXT_QUSTI6.证明:对任意常数λ>0,收敛.分值: 2.5证明因为,所以,而收敛(λ>0),所以收敛.7.设,讨论级数的敛散性,若收敛求其和.SSS_TEXT_QUSTI分值: 5解因为收敛,所以收敛.因为所以于是的和为8.设{nan}收敛,且收敛,证明:级数收敛.SSS_TEXT_QUSTI分值: 6证明令Sn =a1+a2+…+an,S"n+1=(a1-a)+2(a2-a1)+…+(n+1)(an+1 -an),则S"n+1 =(n+1)an+1-Sn-a,因为收敛且数列{nan}收敛,所以都存在,于是存在,根据级数收敛的定义,收敛.9.设an>0(n=1,2,…)且单调减少,又级数发散,判断的敛散性.SSS_TEXT_QUSTI分值: 6解因为单调减少且an>0(n=1,2,…),所以存在,令,由发散,得A>0.根据正项级数的根值审敛法,由,得级数收敛.证明:SSS_TEXT_QUSTI10.设an >0,且{nan}有界,则级数收敛;分值: 3证明因为{nan }有界,所以存在M>0,使得0<nan≤M,即,而级数收敛,所以级数收敛.SSS_TEXT_QUSTI11.若,则级数收敛.分值: 3证明取,因为,所以存在N>0,当n>N时,,即,或者,而收敛,所以收敛.设(n=1,2,…;an >0,bn>0),证明:SSS_TEXT_QUSTI12.若级数收敛,则级数收敛;分值: 3证明由,则数列单调递减有下界,根据极限存在准则,存在,令.无论A=0还是A>0,若级数收敛,则级数收敛.SSS_TEXT_QUSTI13.若级数发散,则级数发散.分值: 3证明若A=0,由级数发散,得级数发散;若A>0,级数敛散性相同,故若级数发散,则级数发散.14.设{un },{cn}为正项数列,证明:(1)若对一切正整数n满足cn un-cn+1un+1≤0,且发散,则也发散;(2)若对一切正整数n满足,且收敛,则也收敛.SSS_TEXT_QUSTI分值: 6证明显然为正项级数.(1)因为对所有n满足cn un-cn+1un+1≤0,于是cn un≤cn+1un+1cnun≥…≥c1u1>0,从而.因为发散,所以也发散.(2)因为对所有n满足,则cn un-cn+1un+1≥aun+1,即cn un≥(cn+1+a)an+1,所以,于是因为收敛,所以也收敛.15.对常数p,讨论幂级数的收敛区间.SSS_TEXT_QUSTI分值: 6解由,得幂级数的收敛半径为R=1.(1)当p<0时,记q=-p,则有,因而当x=±1时,发散,此时幂级数的收敛区间为(-1,1),(2)当0<p<1时,对,因为,所以x=1时,级数发散,当x=-1时,显然收敛,此时幂级数的收敛区间为[-1,1);(3)当p>1时,对,因为,而收敛,所以级数收敛,当x=-1时,显然绝对收敛,此时幂级数的收敛区间为[-1,1].1。
2018考研数学冲刺模拟卷答案与解析(数学一)

2018考研数学冲刺模拟卷(数学一)答案与解析一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求的,请将所选项前的字母填在答题纸...指定位置上. (1)若函数210(),0x f x axb x ⎧>⎪=⎨⎪≤⎩在0x =处连续,则( ) (A)14ab =(B)12ab =-(C)0ab =(D)2ab =【答案】A.【解析】222001114lim lim ,()4x x xf x ax ax a++→→==在0x =处连续11.44b ab a ∴=⇒=选A.(2)设函数()f x 可导,且2'()()0f x f x >,则( )(A )(1)(1)f f >- (B )(1)(1)f f <- (C )(1)(1)f f >- (D )(1)(1)f f <- 【答案】A.【解析】3332()(1)(1)()()0,(1)(1)333f x f f f x f x f f '⎛⎫-'=>>⇒>- ⎪⎝⎭,所以选A 。
(3)设函数22(,,)f x y z x y z =+,单位向量1{1,2,2}3n =,则(1,2,0)f n∂=∂________.(A )12(B )6(C )4(D )2【答案】D. 【解析】(1,2,0)(1,2,0)122{4,1,0}{4,1,0}{,,} 2.333f gradfgradf n n∂=⇒=⋅=⋅=∂选D.(4)甲乙两人赛跑,计时开始时,甲在乙前方10(单位:m )处,图中实线表示甲的速度曲线1()v v t =(单位:/m s ),虚线表示乙的速度曲线2()v v t =,三块阴影部分面积的数值依次为10,20,3,计时开始后乙超过上甲的时刻记为0t (单位:s ),则( )(A )010t =(B )01520t <<(C )025t =(D )025t >【答案】D.【解析】从0到0t 这段时间内甲乙的位移分别为120(t),(t),t t v dt v dt ⎰⎰则乙要超过甲,则210(t)v (t)10t v dt ->⎰,当025t >时满足,故选D.(5)设A 为m n 阶矩阵,且r Am n ,则下列结论正确的是(A )A 的任意m 阶子式都不等于零 (B )A 的任意m 个列向量线性无关 (C )方程组AX b 一定有无穷多解 (D )矩阵A 经过初等行变换可化为m E O【答案】C.【解析】对于选项C ,=min ,m r Ar A m n m r A m n 所以选项C 正确,对于选项A 和B ,r(A)=m ,由秩的定义可得,存在一个m 阶行列式不为零,从而m 阶行列式所在的列向量组线性无关,所以选项A 和B 不正确对于选项D ,矩阵A 经过初等行变换和列变换才可化为m E O ,所以选项D 不正确 (6)设1122331,0,2,,0,2,1,,1,2,3,TTTc c c ,41,0,1,0T,其中1,2,3i c i为任意实数,则(A )1234,,,必线性相关 (B )1234,,,必线性无关(C )123,,必线性相关(D )234,,必线性无关【答案】D.【解析】1234312101101100000001c cc 经初等行变换所以12344r,从而选项A 和B 均不正确1233r,从而选项C 不正确利用排除法可得正确答案为D对于选项D ,23411001100100经初等行变换,从而可得2343r向量的个数,所以234,,必线性无关(7)设二维随机变量,X Y 的联合分布函数为,F x y ,边缘分布函数分别为X F x 和Y F y ,则,P Xx Y y(A ) 1X Y F x F y (B ) 11X Y F x F y(C )2,X Y F x F y F x y (D ) 1,X Y F x F yF x y【答案】D. 【解析】设,AX x B Y y ,则,,X Y F xP X x F y P Yy ,,F x y P X x Y y所以, 1 1 1,X Y P X x YyP ABP A B P A B P A P B P AB F xF yF x y所以正确答案为D(8)设总体X 服从正态分布2(0,)N ,1X ,…,n X 是取自总体X 的简单随机样本,其均值、方差分别为X ,2S .则(A ))11(22-n F S X,~ (B ))11()1(22--n F S X n ,~(C ))11(22-n F S X n ,~ (D ))11()1(22-+n F SXn ,~ 【答案】C.【解析】2222200,0,11X n XX N N nnn XnX~~~而22211n S n ~,且X 与2S 相互独立所以2222222221111,111nXn S nXn F n n SSn ~~所以正确答案为C.二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸...指定位置上. (9) 函数()ln(12)f x x =-的麦克劳林公式中nx 项的系数为__________【答案】2(1)!!n n n --.【解析】因为()()2(1)!()(0)2(1)!(12)n n n n nn fx f n x -=-⇒=---,故n x 项的系数为2(1)!!n n n --。
2018考研数学模拟题完整版及参考答案(数二)

2018考研数学模拟题完整版及参考答案(数二)一、选择题:1-8小题,每小题4分,共32分. 每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.(1)设函数()y f x =具有二阶导数,且()0,()0f x f x '''>>,x ∆为自变量x 在点0x 处的增量,d y y ∆与分别为()f x 在点0x 处对应的增量与微分,若0x ∆>,则( )(A) 0d y y <<∆. (B) 0d y y <∆<.(C) d 0y y ∆<<. (D) d 0y y <∆< .(2)设()f x 是奇函数,除0x =外处处连续,0x =是其第一类间断点,则()d x f t t ⎰是(A )连续的奇函数.(B )连续的偶函数(C )在0x =间断的奇函数(D )在0x =间断的偶函数. ( )(3)设函数()g x 可微,1()()e ,(1)1,(1)2g x h x h g +''===,则(1)g 等于( ) (A )ln 31-. (B )ln 3 1.--(C )ln 2 1.--(D )ln 2 1.-(4)函数212e e e x x x y C C x -=++满足的一个微分方程是 [ ] (A )23e .x y y y x '''--= (B )23e .x y y y '''--=(C )23e .x y y y x '''+-=(D )23e .x y y y '''+-=(5)设(,)f x y 为连续函数,则140d (cos ,sin )d f r r r r πθθθ⎰⎰等于()(A)(,)d xx f x y y . (B )0(,)d x f x y y .(C)(,)d yy f x y x . (D)(,)d y f x y x .(6)设(,)(,)f x y x y ϕ与均为可微函数,且(,)0y x y ϕ'≠,已知00(,)x y 是(,)f x y 在约束条件(,)0x y ϕ=下的一个极值点,下列选项正确的是()(A) 若00(,)0x f x y '=,则00(,)0y f x y '=. (B) 若00(,)0x f x y '=,则00(,)0y f x y '≠.(C) 若00(,)0x f x y '≠,则00(,)0y f x y '=.(D) 若00(,)0x f x y '≠,则00(,)0y f x y '≠. (7)设12,,,s ααα 均为n 维列向量,A 为m n ⨯矩阵,下列选项正确的是 [ ](A) 若12,,,s ααα 线性相关,则12,,,s A A A ααα 线性相关. (B) 若12,,,s ααα 线性相关,则12,,,s A A A ααα 线性无关. (C) 若12,,,s ααα 线性无关,则12,,,s A A A ααα 线性相关.(D) 若12,,,s ααα 线性无关,则12,,,s A A A ααα 线性无关.(8)设A 为3阶矩阵,将A 的第2行加到第1行得B ,再将B 的第1列的1-倍加到第2列得C ,记110010001P ⎛⎫ ⎪= ⎪ ⎪⎝⎭,则()(A)1C P AP -=. (B)1C PAP -=. (C)T C P AP =. (D)T C PAP =.一.填空题 (9)曲线4sin 52cos x xy x x+=- 的水平渐近线方程为(10)设函数2301sin d ,0(),0x t t x f x x a x ⎧≠⎪=⎨⎪=⎩⎰ 在0x =处连续,则a =(11)广义积分22d (1)x xx +∞=+⎰. (12) 微分方程(1)y x y x-'=的通解是 (13)设函数()y y x =由方程1e yy x =-确定,则d d x y x==(14)设矩阵2112A ⎛⎫= ⎪-⎝⎭,E 为2阶单位矩阵,矩阵B 满足2BA B E =+,则=B .三 、解答题:15-23小题,共94分.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分10分) 试确定,,A B C 的值,使得23e (1)1()x Bx Cx Ax o x ++=++,其中3()o x 是当0x →时比3x 高阶的无穷小. (16)(本题满分10分)求 arcsin e d e xxx ⎰. (17)(本题满分10分)设区域{}22(,)1,0D x y x y x =+≤≥, 计算二重积分221d d .1Dxyx y x y +++⎰⎰ (18)(本题满分12分)设数列{}n x 满足110,sin (1,2,)n n x x x n π+<<== (Ⅰ)证明lim n n x →∞存在,并求该极限;(Ⅱ)计算11lim n x n n n x x +→∞⎛⎫ ⎪⎝⎭. (19)(本题满分10分) 证明:当0a b π<<<时,sin 2cos sin 2cos b b b b a a a a ππ++>++.(20)(本题满分12分)设函数()f u 在(0,)+∞内具有二阶导数,且z f=满足等式22220z zx y∂∂+=∂∂. (I )验证()()0f u f u u'''+=; (II )若(1)0,(1)1f f '==,求函数()f u 的表达式. (21)(本题满分12分)已知曲线L 的方程221,(0)4x t t y t t⎧=+≥⎨=-⎩(I )讨论L 的凹凸性;(II )过点(1,0)-引L 的切线,求切点00(,)x y ,并写出切线的方程;(III )求此切线与L (对应于0x x ≤的部分)及x 轴所围成的平面图形的面积. (22)(本题满分9分) 已知非齐次线性方程组1234123412341435131x x x x x x x x ax x x bx +++=-⎧⎪++-=-⎨⎪+++=⎩ 有3个线性无关的解.(Ⅰ)证明方程组系数矩阵A 的秩()2r A =; (Ⅱ)求,a b 的值及方程组的通解. (23)(本题满分9分)设3阶实对称矩阵A 的各行元素之和均为3,向量()()TT121,2,1,0,1,1αα=--=-是线性方程组0Ax =的两个解.(Ⅰ) 求A 的特征值与特征向量;(Ⅱ) 求正交矩阵Q 和对角矩阵Λ,使得T Q AQ =Λ.2018可锐考研数学答案(四)1. A 【分析】 题设条件有明显的几何意义,用图示法求解. 【详解】 由()0,()0f x f x '''>>知,函数()f x 单调增加,曲线()y f x =凹向,作函数()y f x =的图形如右图所示,显然当0x ∆>时,00d ()d ()0y y f x x f x x ''∆>==∆>,故应选(A).【评注】 对于题设条件有明显的几何意义或所给函数图形容易绘出时,图示法是求解此题的首选方法.本题还可用拉格朗日定理求解:0000()()(),y f x x f x f x x x x ξξ'∆=+∆-=∆<<+∆因为()0f x ''>,所以()f x '单调增加,即0()()f f x ξ''>,又0x ∆>, 则 0()()d 0y f x f x x y ξ''∆=∆>∆=>,即0d y y <<∆.定义一般教科书均有,类似例题见《数学复习指南》(理工类)P .165【例6.1】,P .193【1(3)】.2. B 【分析】由于题设条件含有抽象函数,本题最简便的方法是用赋值法求解,即取符合题设条件的特殊函数()f x 去计算0()()d x F x f t t =⎰,然后选择正确选项.【详解】取,0()1,0x x f x x ≠⎧=⎨=⎩. 则当0x ≠时,()2220011()()d lim d lim 22x xF x f t t t t x x εεεε++→→===-=⎰⎰, 而0(0)0lim ()x F F x →==,所以()F x 为连续的偶函数,则选项(B)正确,故选(B).【评注】对于题设条件含抽象函数或备选项为抽象函数形式结果以及数值型结果的选择题,用赋值法求解往往能收到奇效.符合题设条件的函数在多教科书上均可见到,完全类似例题见2006文登最新模拟试卷(数学三)(8).3. C 【分析】题设条件1()()e g x h x +=两边对x 求导,再令1x =即可. 【详解】1()()e g x h x +=两边对x 求导,得1()()e ()g x h x g x +''=.上式中令1x =,又(1)1,(1)2h g ''==,可得1(1)1(1)1(1)e (1)2e (1)ln 21g g h g g ++''===⇒=--,故选(C ).【评注】本题考查复合函数求导,属基本题型. 完全类似例题见文登暑期辅导班《高等数学》第2讲第2节【例12】,《数学复习指南》理工类P.47【例2.4】,《数学题型集粹与练习题集》理工类P.1【典例精析】.4. D 【分析】本题考查二阶常系数线性非齐次微分方程解的结构及非齐次方程的特解与对应齐次微分方程特征根的关系.故先从所给解分析出对应齐次微分方程的特征方程的根,然后由特解形式判定非齐次项形式.【详解】由所给解的形式,可知原微分方程对应的齐次微分方程的特征根为121,2λλ==-.则对应的齐次微分方程的特征方程为2(1)(2)0,20λλλλ-+=+-=即. 故对应的齐次微分方程为 20y y y '''+-=.又*e xy x =为原微分方程的一个特解,而1λ=为特征单根,故原非齐次线性微分方程右端的非齐次项应具有形式()e x f x C =(C 为常数).所以综合比较四个选项,应选(D ). 【评注】对于由常系数非齐次线性微分方程的通解反求微分方程的问题,关键是要掌握对应齐次微分方程的特征根和对应特解的关系以及非齐次方程的特解形式..完全类似例题见文登暑期辅导班《高等数学》第7讲第2节【例9】和【例10】,《数学复习指南》P .156【例 5.16】,《数学题型集粹与练习题集》(理工类)P .195(题型演练3),《考研数学过关基本题型》(理工类)P.126【例14】及练习.5. C 【分析】 本题考查将坐标系下的累次积分转换为直角坐标系下的累次积分,首先由题设画出积分区域的图形,然后化为直角坐标系下累次积分即可.【详解】 由题设可知积分区域D 如右图所示,显然是Y 型域,则原式0(,)d yy f x y x =.故选(C).【评注】 本题为基本题型,关键是首先画出积分区域的图形.完全类似例题见文登暑期辅导班《高等数学》第10讲第2节例4,《数学复习指南》(理工类)P.286【例10.6】,《考研数学过关基本题型》(理工类)P .93【例6】及练习.6. D 【分析】 利用拉格朗日函数(,,)(,)(,)F x y f x y x y λλϕ=+在000(,,)x y λ(0λ是对应00,x y 的参数λ的值)取到极值的必要条件即可.【详解】 作拉格朗日函数(,,)(,)(,)F x y f x y x y λλϕ=+,并记对应00,x y 的参数λ的值为0λ,则000000(,,)0(,,)0x y F x y F x y λλ⎧'=⎪⎨'=⎪⎩, 即0000000000(,)(,)0(,)(,)0x x y y f x y x y f x y x y λϕλϕ⎧''+=⎪⎨''+=⎪⎩ .消去0λ,得00000000(,)(,)(,)(,)0x y y x f x y x y f x y x y ϕϕ''''-=, 整理得 000000001(,)(,)(,)(,)x y x y f x y f x y x y x y ϕϕ'''='.(因为(,)0y x y ϕ'≠),若00(,)0x f x y '≠,则00(,)0y f x y '≠.故选(D).【评注】 本题考查了二元函数极值的必要条件和拉格朗日乘数法.相关定理见《数学复习指南》(理工类)P.251定理1及P.253条件极值的求法.7. A 【分析】 本题考查向量组的线性相关性问题,利用定义或性质进行判定.【详解】 记12(,,,)s B ααα= ,则12(,,,)s A A A AB ααα= .所以,若向量组12,,,s ααα 线性相关,则()r B s <,从而()()r AB r B s ≤<,向量组12,,,s A A A ααα 也线性相关,故应选(A).【评注】 对于向量组的线性相关问题,可用定义,秩,也可转化为齐次线性方程组有无非零解进行讨论.8. B 【分析】利用矩阵的初等变换与初等矩阵的关系以及初等矩阵的性质可得.【详解】由题设可得110110110110,010********1001001001B AC B A --⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ , 而 1110010001P --⎛⎫⎪= ⎪ ⎪⎝⎭,则有1C PAP -=.故应选(B).【评注】(1)每一个初等变换都对应一个初等矩阵,并且对矩阵A 施行一个初等行(列)变换,相当于左(右)乘相应的初等矩阵.(2)牢记三种初等矩阵的转置和逆矩阵与初等矩阵的关系. 完全类似例题及性质见《数学复习指南》(理工类)P.381【例2.19】,文登暑期辅导班《线性代数》第2讲例12.9. 【分析】 直接利用曲线的水平渐近线的定义求解即可.【详解】 4s i n 14s i n1l i m l i m 2c o s 52c o s 55x x x x x x xx x x →∞→∞++==--.故曲线的水平渐近线方程为 15y =.【评注】本题为基本题型,应熟练掌握曲线的水平渐近线,垂直渐近线和斜渐近线的求法.注意当曲线存在水平渐近线时,斜渐近线不存在,为什么?完全类似例题见文登暑期辅导班《高等数学》第6讲第4节【例12】,《数学复习指南》(理工类)P.180【例6.30】,【例6.31】.10. 【分析】本题为已知分段函数连续反求参数的问题.直接利用函数的连续性定义即可.【详解】 由题设知,函数()f x 在 0x =处连续,则 0lim ()(0)x f x f a →==,又因为 2203200sin d sin 1lim ()limlim 33xx x x t t x f x x x →→→===⎰. 所以 13a =. 【评注】遇到求分段函数在分段点的连续性问题,一般从定义入手.本题还考查了积分上限函数的求导,洛必达法则和等价无穷小代换等多个基本知识点,属基本题型.完全类似例题见文登暑期辅导班《高等数学》第1讲第1节【例13】,《数学复习指南》(理工类)P.35【例1.51】.88年,89年,94年和03年均考过该类型的试题,本题属重点题型.11. 【分析】利用凑微分法和牛顿-莱布尼兹公式求解.【详解】2022222200d 1d(1+)111111lim lim lim (1)2(1)21+21+22b bb b b x x x x x xb +∞→∞→∞→∞==-=-+=++⎰⎰.【评注】 本题属基本题型,对广义积分,若奇点在积分域的边界,则可用牛顿-莱布尼兹公式求解,注意取极限.完全类似例题见文登暑期辅导班《高等数学》第5讲第6节【例1】,《数学复习指南》(理工类)P.119【例3.74】.12 .【分析】本方程为可分离变量型,先分离变量,然后两边积分即可【详解】 原方程等价为d 11d y x y x ⎛⎫=- ⎪⎝⎭, 两边积分得 1ln ln y x x C =-+,整理得e xy Cx -=.(1e CC =)【评注】 本题属基本题型.完全类似公式见《数学复习指南》(理工类)P .139.13. 【分析】本题为隐函数求导,可通过方程两边对x 求导(注意y 是x 的函数),一阶微分形式不变性和隐函数存在定理求解.【详解】 方法一:方程两边对x 求导,得e e y y y xy ''=--.又由原方程知,0,1x y ==时.代入上式得d e d x x y y x=='==-.方法二:方程两边微分,得d e d e d yyy x x y =--,代入0,1x y ==,得0d e d x y x==-.方法三:令(,)1e yF x y y x =-+,则()0,10,10,10,1ee,1e 1yy x y x y x y x y F F x xy========∂∂===+=∂∂,故0,10,1d e d x y x x y F y xF xy=====∂∂=-=-∂∂.【评注】 本题属基本题型.求方程确定的隐函数在某点处的导数或微分时,不必写出其导数或微分的一般式完全类似例题见文登暑期辅导班《高等数学》第2讲第2节【例14】,《数学复习指南》(理工类)P.50【例2.12】.14. 【分析】 将矩阵方程改写为AX B XA B AXB C ===或或的形式,再用方阵相乘的行列式性质进行计算即可.【详解】 由题设,有()2B A E E -= 于是有 4B A E -=,而11211A E -==-,所以2B =. 【评注】 本题关键是将其转化为用矩阵乘积形式表示.类似题2005年考过.完全类似例题见文登暑期辅导班线性代数第1讲例6,《数学复习指南》(理工类)P .378【例2.12】15.【分析】题设方程右边为关于x 的多项式,要联想到e x 的泰勒级数展开式,比较x 的同次项系数,可得,,A B C 的值.【详解】将e x的泰勒级数展开式233e 1()26xx x x o x =++++代入题设等式得 233231()[1]1()26x x x o x Bx Cx Ax o x ⎡⎤++++++=++⎢⎥⎣⎦整理得233111(1)()1()226B B x B C x C o x Ax o x ⎛⎫⎛⎫+++++++++=++ ⎪ ⎪⎝⎭⎝⎭比较两边同次幂系数得11021026B A B C B C ⎧⎪+=⎪⎪++=⎨⎪⎪++=⎪⎩,解得132316A B C ⎧=⎪⎪⎪=-⎨⎪⎪=⎪⎩. 【评注】题设条件中含有高阶无穷小形式的条件时,要想到用麦克劳林公式或泰勒公式求解.要熟练掌握常用函数的泰勒公式.相应公式见《数学复习指南》理工类P .124表格.16.【分析】题设积分中含反三角函数,利用分部积分法.【详解】arcsin e d arcsin e de e arcsin e e e x x x x x x xx x x --=-=-+⎰⎰⎰-e arcsin e x x x -=-+.令t =221ln(1),d d 21tx t x t t =-=--, 所以21111d d 1211x t t t t t ⎛⎫==- ⎪--+⎝⎭⎰⎰111ln ln 212t C t -=+=+.【评注】被积函数中为两种不同类型函数乘积且无法用凑微分法求解时,要想到用分部积分法计算;对含根式的积分,要想到分式有理化及根式代换.本题为基本题型,完全相似例题见文登暑期辅导班《高等数学》第3讲第3节【例6】,《数学复习指南》理工类P.79【例3.21】.17. 【分析】 由于积分区域D 关于x 轴对称,故可先利用二重积分的对称性结论简化所求积分,又积分区域为圆域的一部分,则将其化为极坐标系下累次积分即可.【详解】 积分区域D 如右图所示.因为区域D 关于x 轴对称,函数221(,)1f x y x y=++是变量y 的偶函数,函数22(,)1xyg x y x y =++是变量y 的奇函数.则112222220011ln 2d d 2d d 2d d 1112DD r x y x y r xy x y r ππθ===+++++⎰⎰⎰⎰⎰⎰22d d 01Dxyx y x y =++⎰⎰, 故22222211ln 2d d d d d d 1112D D Dxy xy x y x y x y x y x y x y π+=+=++++++⎰⎰⎰⎰⎰⎰. 【评注】只要见到积分区域具有对称性的二重积分计算问题,就要想到考查被积函数或其代数和的每一部分是否具有奇偶性,以便简化计算.完全类似例题见文登暑期辅导班《高等数学》第10讲第1节例1和例2,《数学复习指南》(理工类)P .284【例10.1】18. 【分析】 一般利用单调增加有上界或单调减少有下界数列必有极限的准则来证明数列极限的存在. (Ⅱ)的计算需利用(Ⅰ)的结果.【详解】 (Ⅰ)因为10x π<<,则210sin 1x x π<=≤<. 可推得 10sin 1,1,2,n n x x n π+<=≤<= ,则数列{}n x 有界. 于是1sin 1n nn nx x x x +=<,(因当0sin x x x ><时,), 则有1n n x x +<,可见数列{}n x 单调减少,故由单调减少有下界数列必有极限知极限lim n n x →∞存在.设lim n n x l →∞=,在1s i n n n x x +=两边令n →∞,得 sin l l =,解得0l =,即l i m 0n n x →∞=.(Ⅱ) 因 22111sin lim lim nn x x n n n n n n x x x x +→∞→∞⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭,由(Ⅰ)知该极限为1∞型, 令n t x =,则,0n t →∞→,而222sin 111111sin 1000sin sin sin lim lim 11lim 11tt t t t t t t t t t t t t t t -⋅-→→→⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥=+-=+- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,又 33233000()1sin sin 13!lim 1lim lim 6t t t t t o t tt t t t t t t →→→-+--⎛⎫-===- ⎪⎝⎭. (利用了sin x 的麦克劳林展开式)故 2211116sin lim lim e nn x x n n n n n n x x x x -+→∞→∞⎛⎫⎛⎫== ⎪⎪⎝⎭⎝⎭.19. 【详解】 令()sin 2cos sin 2cos ,0f x x x x x a a a a a x b πππ=++---<≤≤<,则 ()sin cos 2sin cos sin f x x x x x x x x ππ'=+-+=-+,且()0f π'=. 又 ()cos sin cos sin 0f x x x x x x x ''=--=-<,(0,s i n 0x x x π<<>时),故当0a x b π<≤≤<时,()f x '单调减少,即()()0f x f π''>=,则()f x 单调增加,于是()()0f b f a >=,即sin 2cos sin 2cos b b b b a a a a ππ++>++.20利用复合函数偏导数计算方法求出2222,z z x y ∂∂∂∂代入22220z zx y∂∂+=∂∂即可得(I ).按常规方法解(II )即可.【详解】 (I )设u =((z z f u f u x y ∂∂''==∂∂. 22()()z f u f u x ∂'''=+∂()22322222()()x y f u f u x y x y '''=⋅+⋅++,()2223222222()()z y x f u f u y x yxy∂'''=⋅+⋅∂++.将2222,z z x y ∂∂∂∂代入22220z zx y∂∂+=∂∂得 ()()0f u f u u'''+=. (II ) 令()f u p '=,则d d 0p p u p u p u'+=⇒=-,两边积分得1ln ln ln p u C =-+,即1C p u =,亦即 1()C f u u'=. 由(1)1f '=可得 11C =.所以有 1()f u u'=,两边积分得 2()ln f u u C =+, 由(1)0f =可得 20C =,故 ()ln f u u =.【评注】 本题为基础题型,着重考查多元复合函数的偏导数的计算及可降阶方程的求解.完全类似例题见文登暑期辅导班《高等数学》第8讲第1节【例8】,《数学复习指南》(理工类)P.336【例12.14】,P .337【例12.15】21. 【分析】 (I )利用曲线凹凸的定义来判定;(II )先写出切线方程,然后利用 (1,0)-在切线上 ; (III )利用定积分计算平面图形的面积.【详解】 (I )因为d d d d 422d 2,421d d d d 2d yx y y t t t t x t t x t tt-==-⇒===-2223d d d 12110,(0)d d d d 2d y y t x x t x t tt t⎛⎫⎛⎫=⋅=-⋅=-<> ⎪ ⎪⎝⎭⎝⎭故曲线L 当0t ≥时是凸的.(II )由(I )知,切线方程为201(1)y x t ⎛⎫-=-+⎪⎝⎭,设2001x t =+,20004y t t =-,则220000241(2)t t t t ⎛⎫-=-+⎪⎝⎭,即23200004(2)(2)t t t t -=-+ 整理得 20000020(1)(2)01,2(t t t t t +-=⇒-+=⇒=-舍去).将01t =代入参数方程,得切点为(2,3),故切线方程为231(2)1y x ⎛⎫-=-- ⎪⎝⎭,即1y x =+.(III )由题设可知,所求平面图形如下图所示,其中各点坐标为(1,0),(2,0),(2,3),(1,0)A B C D -,设L 的方程()x g y =,则()3()(1)d S g y y y =--⎡⎤⎣⎦⎰ 由参数方程可得2t =,即(221x =+.由于(2,3)在L 上,则(2()219x g y y ==+=--.于是(309(1)d S y y y ⎡⎤=----⎣⎦⎰3(102)d 4y y y =--⎰⎰()()3233208710433y yy =-+-=. 【评注】 本题为基本题型,第3问求平面图形的面积时,要将参数方程转化为直角坐标方程求解.完全类似例题和公式见《数学复习指南》(理工类)P.187【例6.40】.22. 【分析】 (I )根据系数矩阵的秩与基础解系的关系证明;(II )利用初等变换求矩阵A 的秩确定参数,a b ,然后解方程组.【详解】 (I ) 设123,,ααα是方程组Ax β=的3个线性无关的解,其中111114351,1131A a b β-⎛⎫⎛⎫⎪ ⎪=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭.则有 1213()0,()0A A αααα-=-=. 则1213,αααα--是对应齐次线性方程组0Ax =的解,且线性无关.(否则,易推出123,,ααα线性相关,矛盾).所以 ()2n r A -≥,即4()2()2r A r A -≥⇒≤.又矩阵A 中有一个2阶子式111043=-≠,所以()2r A ≤. 因此 ()2r A =. (II ) 因为11111111111143510115011513013004245A a b a a b a a b a ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-→--→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪----+-⎝⎭⎝⎭⎝⎭.又()2r A =,则42024503a a b a b -==⎧⎧⇒⎨⎨+-==-⎩⎩. 对原方程组的增广矩阵A 施行初等行变换,111111024243511011532133100000A --⎛⎫⎛⎫ ⎪ ⎪=--→-- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭,故原方程组与下面的方程组同解.13423424253x x x x x x =-++⎧⎨=--⎩.选34,x x 为自由变量,则134234334424253x x x x x x x x x x =-++⎧⎪=--⎪⎨=⎪⎪=⎩. 故所求通解为12242153100010x k k -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪=++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,12,k k 为任意常数.【评注】 本题综合考查矩阵的秩,初等变换,方程组系数矩阵的秩和基础解系的关系以及方程组求解等多个知识点,特别是第一部分比较新颖. 这是考查综合思维能力的一种重要表现形式,今后类似问题将会越来越多.完全类似例题见《数学复习指南》(理工类)P .427【例4.5】,P.431【例4.11】.23. 解: 由矩阵A 的各行元素之和均为3及矩阵乘法可得矩阵A 的一个特征值和对应的特征向量;由齐次线性方程组0Ax =有非零解可知A 必有零特征值,其非零解是0特征值所对应的特征向量.将A 的线性无关的特征向量正交化可得正交矩阵Q .【详解】 (Ⅰ) 因为矩阵A 的各行元素之和均为3,所以1311331131A ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则由特征值和特征向量的定义知,3λ=是矩阵A 的特征值,T (1,1,1)α=是对应的特征向量.对应3λ=的全部特征向量为k α,其中k 为不为零的常数.又由题设知 120,0A A αα==,即11220,0A A αααα=⋅=⋅,而且12,αα线性无关,所以0λ=是矩阵A 的二重特征值,12,αα是其对应的特征向量,对应0λ=的全部特征向量为 1122k k αα+,其中12,k k 为不全为零的常数.(Ⅱ) 因为A 是实对称矩阵,所以α与12,αα正交,所以只需将12,αα正交. 取11βα=,()()21221111012,3120,61112αββαβββ⎛⎫-⎪-⎛⎫⎛⎫⎪- ⎪ ⎪=-=--= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ ⎪⎝⎭. 再将12,,αββ单位化,得1212312,,0ββαηηηαββ⎛⎛ ⎪====== ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭ ⎪⎝⎭, 令 []123,,Q ηηη=,则1T Q Q -=,由A 是实对称矩阵必可相似对角化,得T300Q AQ ⎡⎤⎢⎥==Λ⎢⎥⎢⎥⎣⎦.。
2018年考研数学模拟试题(数学一)

本试卷满分150,考试时间180分钟一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求的,请将所选项前的字母填在答题纸...指定位置上. (1)下列结论中正确的是( )(A )若)(x f 在a x =点处连续,则)(x f 在a x =点处也必连续; (B )若)(2x f 在a x =点处连续,则)(x f 在a x =点处也必连续; (C )若)(1x f 在a x =点处连续,则)(x f 在a x =点处也必连续; (D )若)(x f 在a x =点处连续,则)(1x f 在a x =点处也必连续. (2)设a 为常数,则级数21sin()[n na n n∞=∑( ) (A )绝对收敛 (B )条件收敛 (C )发散 (D )收敛性与a 的取值有关 (3)设曲线积分[()]sin ()cos xLf x e ydx f x ydy --⎰与路径无关,其中()f x 具有一阶连续导数,且(0)0,f =则()f x 等于( )(A )1()2x x e e -- (B )1()2x x e e -- (C )1()12x x e e -+- (D )11()2x x e e --+ (4)设()f x 为微分方程'()y xy g x -=满足(0)1y =的解,而20()sin()xg x x t dt =-⎰,则(A )在点0x =处()f x 取极大值 (B )在点0x =处()f x 取极小值 (C )点(0,(0))f 为曲线()y f x =的拐点 (D )0x =不是()f x 极值点,也不是拐点(5)假设A 是n 阶方阵,其秩r n <,那么在A 的n 个行向量中( ) (A) 必有r 个行向量线性无关. (B) 任意r 个行向量线性无关.版权所有 翻印必究(C) 任意r 个行向量都构成最大线性无关向量组.(D) 任何一个行向量都可以由其他r 个行向量线性表出. (6)二次型T f x Ax =正定的充要条件是( )(A)||0A > (B)A 的负惯性指数为0(C)存在n 阶矩阵,TC A C C =使 (D)A 合同于E(7)设A B 、为两随机事件,且B A ⊂,则下列式子正确的是( ) (A)()()P A B P A += (B)()()P AB P A =(C)(|)()P B A P B = (D)()()()P B A P B P A -=-(8)设随机变量X 和Y 相互独立且均服从正态分布()2,N μσ,若概率{}12P aX bY μ-<=,则( )(A )11,22a b == (B )11,22a b ==-(C )11,22a b =-= (D )11,22a b =-=-二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸...指定位置上. (9)具有特解123,2,3x x xy e y xe y e --===的三阶常系数齐次线性微分方程是_______。
考研数学三模拟题2018年(13)_真题(含答案与解析)-交互

考研数学三模拟题2018年(13)(总分100, 做题时间90分钟)一、填空题1.设且存在三阶非零矩阵B,使得AB=O,则a=______,b=______.SSS_FILL分值: 12 1[解析] 因为AB=O,所以r(A)+r(B)≤3,又B≠O,于是r(B)≥1,故r(A)≤2,从而a=2,b=1.2.设η为非零向量,η为方程组AX=0的解,则a=______,方程组的通解为______.SSS_FILL分值: 13 k(-3,1,2) T [解析] AX=0有非零解,所以|A|=0,解得a=3,于是方程组AX=0的通解为k(-3,1,2) T.二、选择题1.设A是m×s矩阵,B为s×n矩阵,则方程组BX=0与ABX=0同解的充分条件是______.SSS_SINGLE_SELA r(A)=sB r(A)=mC r(B)=sD r(B)=n分值: 1答案:A[解析] 设r(A)=s,显然方程组BX=0的解一定为方程组ABX=0的解,反之,若ABX=0。
因为r(A)=s,所以方程组AY=0只有零解,故BX=0,即方程组BX=0与方程组ABX=0同解,选A.2.设n阶矩阵A的伴随矩阵A *≠O,且非齐次线性方程组AX=b有两个不同解η1,η2,则下列命题正确的是______.A.AX=b的通解为k1η1+k2η2B.η1+η2为AX=b的解C.方程组AX=0的通解为k(η1 -η2)D.AX=b的通解为SSS_SIMPLE_SINA B C D分值: 1答案:C[解析] 因为非齐次线性方程组AX=b的解不唯一,所以r(A)<n,又因为A *≠O,所以r(A)=n-1,η2 -η1为齐次线性方程组AX=0的基础解系,选C.3.设有方程组AX=0与BX=0,其中A,B都是m×n矩阵,下列四个命题:(1)若AX=0的解都是BX=0的解,则r(A)≥r(B)(2)若r(A)≥r(B),则AX=0的解都是BX=0的解(3)若AX=0与BX=0同解,则r(A)=r(B)(4)若r(A)=r(B),则AX=0与BX=0同解以上命题正确的是______.SSS_SINGLE_SELA (1)(2)B (1)(3)C (2)(4)D (3)(4)分值: 1答案:B[解析] 若方程组AX=0的解都是方程组BX=0的解,则n-r(A)≤n-r(B),从而r(A)≥r(B),(1)为正确的命题;显然(2)不正确;因为同解方程组系数矩阵的秩相等,但反之不对,所以(3)是正确的,(4)是错误的,选B.4.设A是m×n矩阵,B是n×m矩阵,则______.SSS_SINGLE_SELA 当m>n时,线性齐次方程组ABX=0有非零解B 当m>n时,线性齐次方程组ABX=0只有零解C 当n>m时,线性齐次方程组ABX=0有非零解D 当n>m时,线性齐次方程组ABX=0只有零解分值: 1答案:A[解析] AB为m阶方阵,当m>n时,因为r(A)≤n,r(B)≤n且r(AB)≤min{r(A),r(B)},所以r(AB)<m,于是方程组ABX=0有非零解,选A.5.设A为m×n阶矩阵,则方程组AX=b有唯一解的充分必要条件是______.SSS_SINGLE_SELA r(A)=mB r(A)=nC A为可逆矩阵D r(A)=n且b可由A的列向量组线性表示分值: 1答案:D[解析] 方程组AX=b有解的充分必要条件是b可由矩阵A的列向量组线性表示,在方程组AX=b有解的情形下,其有唯一解的充分必要条件是r(A)=n,故选D.三、解答题1.设向量组α1,α2,…,αn-1为n维线性无关的列向量组,且与非零向量β1,β2正交.证明:β1,β2线性相关.SSS_TEXT_QUSTI分值: 5[证明] 令因为α1,α2,…,αn-1与β1,β2正交,所以Aβ1 =0,Aβ2=0,即β1,β2为方程组AX=0的两个非零解,因为r(A)=n-1,所以方程组AX=0的基础解系含有一个线性无关的解向量,所以β1,β2线性相关.2.设齐次线性方程组其中ab≠0,n≥2.讨论a,b取何值时,方程组只有零解、有无穷多个解?在有无穷多个解时求出其通解.SSS_TEXT_QUSTI分值: 5[解](1)当a≠b,a≠(1-n)b时,方程组只有零解;(2)当a=b时,方程组的同解方程组为x1 +x2+…+xn=0,其通解为X=k1(-1,1,0,…,0) T +k2 (-1,0,1,…,0) T+…+kn-1(-1,0,…,0,1) T(k1,k2,…,kn-1为任意常数);(3)令当a=(1-n)b时,r(A)=n-1,显然(1,1,…,1) T为方程组的一个解,故方程组的通解为k(1,1,…,1) T (k为任意常数).3.设A为三阶矩阵,A的第一行元素为a,b,c且不全为零,又且AB=O,求方程组AX=0的通解.SSS_TEXT_QUSTI分值: 5[解] 由AB=O得r(A)+r(B)≤3且r(A)≥1.(1)当k≠9时,因为r(B)=2,所以r(A)=1,方程组AX=0的基础解系含有两个线性无关的解向量,显然基础解系可取B的第1、3两列,故通解为(2)当k=9时,r(B)=1,1≤r(A)≤2,当r(A)=2时,方程组AX=0的通解为当r(A)=1时,A的任意两行都成比例,不妨设a≠0,由得通解为4.a,b取何值时,方程组有解?SSS_TEXT_QUSTI分值: 5[解](1)a≠1时,唯一解为(2)a=1,b≠-1时,r(A)≠ ,因此方程组无解;(3)a=1,b=-1时,通解为X=k1 (1,-2,1,0) T +k2(1,-2,0,1) T +(-1,1,0,0) T (k1,k2为任意常数).5.A,B为n阶矩阵且r(A)+r(B)<n.证明:方程组AX=0与BX=0有公共的非零解.SSS_TEXT_QUSTI分值: 5[证明] 方程组的解即为方程组AX=0与BX=0的公共解.因为所以方程组有非零解,故方程组AX=0与BX=0有公共的非零解.设(Ⅰ) α1,α2,α3,α4为四元非齐次线性方程组BX=b的四个解,其中α1=SSS_TEXT_QUSTI 6.求方程组(Ⅰ)的基础解系;分值: 2[解] 方程组(Ⅰ)的基础解系为SSS_TEXT_QUSTI7.求方程组(Ⅱ)BX=0的基础解系;分值: 2[解] 因为r(B)=2,所以方程组(Ⅱ)的基础解系含有两个线性无关的解向量,为方程组(Ⅱ)的基础解系;SSS_TEXT_QUSTI8.(Ⅰ)与(Ⅱ)是否有公共的非零解?若有公共解求出其公共解.分值: 2[解] 方程组(Ⅰ)的通解为方程组(Ⅱ)的通解为=k,则方程组(Ⅰ)与方程组(Ⅱ)的公共解为k(-1,令,则有取k21,1,1) T (其中k为任意常数).设(Ⅰ)(Ⅱ)SSS_TEXT_QUSTI9.求(Ⅰ),(Ⅱ)的基础解系;分值: 3[解] 的基础解系为的基础解系为SSS_TEXT_QUSTI10.求(Ⅰ),(Ⅱ)的公共解.分值: 3[解] 方法一(Ⅰ),(Ⅱ)公共解即为的解,(Ⅰ),(Ⅱ)的公共解为方法二(Ⅰ)的通解代入(Ⅱ) =2k2,故(Ⅰ),(Ⅱ)的公共解为(-k,k,2k,k) T =k(-1,1,2,1) T (k为任意常数).方法三(Ⅰ)的通解为(Ⅱ)的通解为令∴(Ⅰ),(Ⅱ)的公共解为11.问a,b,c取何值时,(Ⅰ),(Ⅱ)为同解方程组?SSS_TEXT_QUSTI分值: 5[解] 方法一的通解为把(Ⅱ)的通解代入(Ⅰ),得方法二因为(Ⅰ),(Ⅱ)同解,所以它们的增广矩阵有等价的行向量组,(Ⅱ)的增广矩阵为阶梯阵,其行向量组线性无关.α1可由β1,β2,β3唯一线性表出,α1=-2β1+β2+aβ2a=-1,α2可由β1,β2,β3唯一线性表出,α2=β1+β2-β3b=-2,α3可由β1,β2,β3唯一线性表出,α3=3β1+β2+β3c=4.12.证明线性方程组(Ⅰ)有解的充分必要条件是方程组(Ⅲ)是同解方程组.SSS_TEXT_QUSTI分值: 5[证明] 令方程组(Ⅰ)可写为AX=b,方程组(Ⅱ)、(Ⅲ)可分别写为A TY=0及若方程组(Ⅰ)有解,则r(A)=r( ),从而又因为(Ⅲ)的解一定为(Ⅱ)的解,所以(Ⅱ)与(Ⅲ)同解;反之,若(Ⅱ)与(Ⅲ)同解,则从而r(A)=r( ),故方程组(Ⅰ)有解.13.设的一个基础解系为写出的通解并说明理由.SSS_TEXT_QUSTI分值: 5[解] 令则(Ⅰ)可写为AX=0,令其中则(Ⅱ)可写为BY=0,因为β1,β2,…,βn为(Ⅰ)的基础解系,因此r(A)=n,β1,β2,…,βn线性无关,.α1T,α2T,…,αn T为BY=0的一组解,而r(B)=n,α1T,α2T,…,αnT线性无关,因此α1T,α2T,…,αnT为BY=0的一个基础解系.14.设A是m×s矩阵,B是s×n矩阵,且r(B)=r(AB).证明:方程组BX=0与ABX=0是同解方程组.SSS_TEXT_QUSTI分值: 5[证明] 首先,方程组BX=0的解一定是方程组ABX=0的解.令r(B)=r且ξ1,ξ2,…,ξn-r是方程组BX=0的基础解系,现设方程组ABX=0有一个解η0不是方程组BX=0的解,即Bη≠0,显然ξ1,ξ2,…,ξn-r,η0线性无关,若ξ1,ξ2,…,ξn-r,η线性相关,则存在不全为零的常数k1,k2,…,kn-r,k,使得k1ξ1+k2ξ2+…+kn-rξn-r +kη=0,若k=0,则k1ξ1+k2ξ2+…+kn-rξn-r+kη=0,因为ξ1,ξ2,…,ξn-r线性无关,所以k1=k2=…=kn-r=0,从而ξ1,ξ2,…,ξn-r,η线性无关,所以k≠0,故η可由ξ1,ξ2,…,ξn-r线性表示,由齐次线性方程组解的结构,有Bη=0,矛盾,所以ξ1,ξ2,…,ξn-r,η线性无关,且为方程组ABX=0的解,从而n-r(AB)≥n-r+1,r(AB)≤r-1,这与r(B)=r(AB)矛盾,故方程组BX=0与ABX=0同解.设A,B,C,D都是n阶矩阵,r(CA+DB)=n.SSS_TEXT_QUSTI15.证明分值: 3[证明] 因为n=r(CA+DB)=所以SSS_TEXT_QUSTI16.设ξ1,ξ2,…,ξr与η1,η2,…,ηs分别为方程组Ax=0与BX=0的基础解系,证明:ξ1,ξ2,…,ξr,η1,η2,…,ηs线性无关.分值: 3[证明] 因为所以方程组只有零解,从而方程组AX=0与BX=0没有非零的公共解,故ξ1,ξ2,…,ξr与η1,η2,…,ηs线性无关.17.设A为n阶矩阵,A11≠0.证明:非齐次线性方程组AX=b有无穷多个解的充分必要条件是A * b=0.SSS_TEXT_QUSTI分值: 5[证明] 设非齐次线性方程组AX=b有无穷多个解,则r(A)<n,从而|A|=0,于是A * b=A * AX=|A|X=0.反之,设A * b=0,因为b≠0,所以方程组A * X=0有非零解,从而r(A * )<n,又A11≠0,所以r(A * )=1,且r(A)=n-1.因为r(A * )=1,所以方程组A * X=0的基础解系含有n-1个线性无关的解向量,而A * A=0,所以A的列向量组α1,α2,…,αn为方程组A * X=0的一组解向量.由A11≠0,得α2,…,αn线性无关,所以α2,…,αn是方程组A* X=0的基础解系.因为A * b=0,所以b可由α2,…,αn线性表示,也可由α1,α2,…,αn线性表示,故r(A)= =n-1<n,即方程组AX=b有无穷多个解.18.证明:r(AB)≤min{r(A),r(B)}.SSS_TEXT_QUSTI分值: 5[证明] 令r(B)=r,BX=0的基础解系含有n-r个线性无关的解向量,因为BX=0的解一定是ABX=0的解,所以ABX=0的基础解系所含的线性无关的解向量的个数不少于BX=0的基础解系所含的线性无关的解向量的个数,即n-r(AB)≥n-r(B),r(AB)≤r(B);又因为r[(AB) T ]=r(AB)=r(B T A T)≤r(A T )=r(A),所以r(AB)≤min{r(A),r(B)}.19.证明:r(A)=r(A T A).SSS_TEXT_QUSTI分值: 5[证明] 只需证明AX=0与A T AX=0为同解方程组即可.若AX0 =0,则A T AX=0.反之,若A T AX0 =0,则XT A T AX=0 (AX) T (AX)=0 AX=0,所以AX=0与A T AX=0为同解方程组,从而r(A)=r(A T A).20.设A是m×n矩阵,且非齐次线性方程组AX=b满足.证明:方程组AX=b 的线性无关的解向量的个数最多是n-r+1个.SSS_TEXT_QUSTI分值: 5[证明] 因为r(A)=r<n,所以齐次线性方程组AX=0的基础解系含有n-r个线性无关的解向量,设为ξ1,ξ2,…,ξn-r.设η为方程组AX=b的一个特解,令β0=η,β1=ξ1+η,β2=ξ2+η…,βn-r=ξn-r+η0,显然β,β1,β2,…,βn-r为方程组AX=b的一组解.令k0β+k1β1+…+kn-rβn-r=0,即(k0 +k1+…+kn-r)η+k1β1+k2β2+…+kn-rβn-r=0,上式两边左乘A得(k0 +k1+…+kn-r)b=0,因为b为非零列向量,所以k0 +k1+…+kn-r=0,于是k1ξ1+k2ξ2+…+kn-rξn-r=0,注意到ξ1,ξ2,…,ξn-r线性无关,所以k1=k2=…=kn-r=0,故β0,ξ1,ξ2,…,ξn-r线性无关,即方程组AX=b存在由n-r+1个线性无关的解向量构成的向量组.设ξ1,ξ2,…,ξn-r+2为方程组AX=b的一组线性无关解,令γ1=β2-β1,γ2=β3-β1,…,γn-r+1=βn-r+2-β1,根据定义,易证γ1,γ2,…,γn-r+1线性无关,又γ1,γ2,…,γn-r+1为齐次线性方程组AX=0的一组解,即方程组AX=0含有n-r+1个线性无关的解,矛盾,所以AX=b的任意n-r+2个解向量都是线性相关的,所以AX=b的线性无关的解向量的个数最多为n-r+1个.21.讨论方程组的解的情况,在方程组有解时求出其解,其中a,b为常数.SSS_TEXT_QUSTI分值: 5[解](1)当a≠-1,b≠-2时.因为D≠0,所以方程组有唯一解,由克拉默法则得(2)当a=-1,b≠-2时,当b≠-1时,方程组无解当b=-1时,方程组的通解为(3)当a≠-1,b=-2时,当a=1时,方程组的通解为当a≠1时,显然r(A)=2≠ =3,方程组元解.22.设问a,b,c为何值时,矩阵方程AX=B有解?有解时求出全部解.SSS_TEXT_QUSTI分值: 5[解] 令X=(X1,X2,X3),B=(β1,β2,β3),方程组AX=B等价于则AX=B有解的充分必要条件是r(A)=r( ),由r(A)=r( )得a=1,b=2,c=-2,此时AX1=β1的通解为AX2=β2的通解为AX 3 =β 3 的通解为 则 其中k 1 ,k 2 ,k 3 为任意常数. 1。
考研数学二模拟题2018年(23)_真题(含答案与解析)-交互

考研数学二模拟题2018年(23)(总分150, 做题时间90分钟)一、选择题每小题给出的四个选项中,只有一项符合题目要求.1.已知当x→0时,函数f(x)=3sinx-sin3x与cx k是等价无穷小,则SSS_SINGLE_SELA k=1,c=4.B k=1,c=-4.C k=3,c=4.D k=3,c=-4.该问题分值: 4答案:C[解析一] 用泰勒公式由题意即所以k=3,c=4.因此应选C.[解析二] 欲使由洛必达法则可得,只需和差化积得亦是所以k=3,c=4.因此应选C.2.设函数y=f(x)由方程cos(xy)+lny-x=1确定,则=SSS_SINGLE_SELA 2.B 1.C -1.D -2.该问题分值: 4答案:A[解析] 在方程cos(xy)+lny-x=1中,令x=0,得y=1,等式两端对x求导得将x=0,y=1代入上式,得y"(0)=1.于是选A.本题利用隐函数求导方法与导数定义,属基本题型.3.设函数f(x)在(-∞,+∞)内连续,其导函数的图形如图所示,则SSS_SINGLE_SELA 函数f(x)有2个极值点,曲线y=f(x)有2个拐点.B 函数f(x)有2个极值点,曲线y=f(x)有3个拐点.C 函数f(x)有3个极值点,曲线y=f(x)有1个拐点.D 函数f(x)有3个极值点,曲线y=f(x)有2个拐点.该问题分值: 4答案:B[解析] 从图可看出,函数f(x)有3个驻点及1个不可导点,前两个驻点两侧f"(x)符号相反,而后一个驻点及不可导点两侧f"(x)符号相同,故函数f(x)有2个极值点.函数f(x)有两个二阶导数等于零的点及一个二阶导数不存在的点,在这些的点两侧曲线y=f"(x)的单调性相反,因而曲线y=f(x)有3个拐点.应选B.4.设函数y=y(x)由参数方程确定,则曲线y=y(x)在x=3处的法线与x轴交点的横坐标是A.B.C.-8ln2+3.D.8ln2+3.SSS_SIMPLE_SINA B C D该问题分值: 4答案:A[解析] 先由x=3确定t的取值,进而求出在此点的导数及相应的法线方程,从而可得所需的横坐标.当x=3时,有t 2 +2t=3,得t=1,t=-3(舍去,此时y 无意义),于是可见过点x=3(此时y=ln2)的法线方程为:y-ln2=-8(x-3),令y=0,得其与x轴交点的横坐标为:故应A.注意本题法线的斜率应为-8.此类问题没有本质困难,但在计算过程中应特别小心,稍不注意答案就可能出错.5.设f(x,y)为连续函数,则等于A.B.C.D.SSS_SIMPLE_SINA B C D该问题分值: 4答案:C[解析] 本题考查将极坐标系下的累次积分转换为直角坐标系下的累次积分,首先由题设画出积分区域的图形,然后化为直角坐标系下累次积分即可.由题设可知积分区域D如图所示,显然是Y型域,则故选C.本题为基本题型,关键是首先画出积分区域的图形.6.设函数f(u,v)满足则依次是A.B.C.D.SSS_SIMPLE_SINA B C D该问题分值: 4答案:D[解析一] 先求出f(u,v),直接求偏导数即可.令则故所以选D.[解析二] 令时,方程两边分别对x,y求偏导数得把代入上两式解方程组有应选D.7.n阶矩阵A具有,n个不同的特征值是A与对角矩阵相似的SSS_SINGLE_SELA 充分必要条件.B 充分而非必要条件.C 必要而非充分条件.D 既非充分也非必要条件.该问题分值: 4答案:B[解析] A~Λ A有n个线性无关的特征向量.当λ1≠λ2时,λ1与λ2的特征向量必线性无关.因此,若A有n个不同的特征值,则矩阵A必有n个线性无关的特征向量.那么矩阵A必可相似对角化.由于矩阵A的特征值有重根时,矩阵A仍有可能相似对角化,所以特征值不同是A能相似对角化的充分条件,并不必要.故应选B.8.设A是n阶矩阵,α是n维列向量,若秩则线性方程组A.Ax=α必有无穷多解.B.Ax=α必有惟一解.C.D.SSS_SIMPLE_SINA B C D该问题分值: 4答案:D[解析] 因A是n阶矩阵,是n+1阶矩阵,有所以必有非零解.二、填空题1.曲线的斜渐近线方程为______.该问题分值: 4[解析] 本题属基本题型,直接用斜渐近线方程公式进行计算即可.因为于是所求斜渐近线方程为如何求垂直渐近线、水平渐近线和斜渐近线,是基本要求,应熟练掌握.这里应注意两点:1.当存在水平渐近线时,不需要再求斜渐近线;2.若当x→∞时,极限不存在,则应进一步讨论x→+∞或x→-∞的情形,即在右或左侧是否存在斜渐近线,本题定义域为x>0,所以只考虑x→+∞的情形。
2018考研数学冲刺模拟卷(数学二).doc

2018考研数学冲刺模拟卷(数学二)一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求的,请将所选项前的字母填在答题纸...指定位置上. (1)若函数0(),0x f x b x >=⎪≤⎩在0x =处连续,则( ) (A)14ab =(B)12ab =-(C)0ab =(D)2ab =(2)设二阶可导函数()f x 满足(1)(1)1,(0)1f f f =-=-=且''()0f x <,则( )(A)11()0f x dx ->⎰(B )11()0f x dx -<⎰(C )11()()f x dx f x dx ->⎰⎰ (D )11()()f x dx f x dx -<⎰⎰(3)设数列{}n x 收敛,则( )(A )当lim tan 0n n x →∞=时,lim 0n n x →∞= (B)当lim(0n n x →∞=时,lim 0n n x →∞=(C )当2lim()0n n n x x →∞-=时,lim 0n n x →∞= (D )当lim(sin )0n n n x x →∞+=时,lim 0n n x →∞=(4)微分方程244(1sin 2)xy y y e x '''-+=+的特解可设为*y =( )(A )22(cos 2sin 2)xx Aee B x C x ++ (B )22(cos 2sin 2)x x Axe e B x C x ++ (C )222(cos 2sin 2)xx Ax ee B x C x ++ (D )22(cos 2sin 2)x x Axe e B x C x ++(5)设(,)f x y 具有一阶偏导数,且对任意的(,)x y ,都有(,)(,)0,0f x y f x y x y∂∂<>∂∂,则( )(A )(0,0)(1,1)f f > (B )(0,0)(1,1)f f < (C )(0,1)(1,0)f f > (D )(0,1)(1,0)f f < (6)甲乙两人赛跑,计时开始时,甲在乙前方10(单位:m )处,图中实线表示甲的速度曲线1()v v t =(单位:/m s ),虚线表示乙的速度曲线2()v v t =,三块阴影部分面积的数值依次为10,20,3,计时开始后乙超过上甲的时刻记为0t (单位:s ),则( )(A )010t =(B )01520t <<(C )025t =(D )025t >(7)设A 为m n ´阶矩阵,且()r A m n =<,则下列结论正确的是( ) (A )A 的任意m 阶子式都不等于零 (B )A 的任意m 个列向量线性无关(C )方程组AX b =一定有无穷多解 (D )矩阵A 经过初等行变换可化为()m E O (8)设()111,0,2,T c a =,()220,2,1,T c a =,()331,2,3,Tc a =,()41,0,1,0Ta =,其中()1,2,3i c i =为任意实数,则( )(A )1234,,,a a a a 必线性相关 (B )1234,,,a a a a 必线性无关 (C )123,,a a a 必线性相关 (D )234,,a a a 必线性无关二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸...指定位置上. (9) 曲线21ln(1)x y x e x=++的斜渐近线方程为_______ (10) 设函数()y y x =由参数方程()0sin ttux t e y u e du ⎧=+⎪⎨=+⎪⎩⎰确定,则220t d y dx ==______ (11)21ln xdx x+∞=⎰_______ (12) 设函数(,)f x y 具有一阶连续偏导数,且,(1)y y f fye x y e x y∂∂==+∂∂,(0,0)0f =, 则(,)_______f x y =.(13)已知1tan ()x tf x dt t=⎰,则10()______f x dx =⎰.(14)设,a b 为四维非零的正交向量,且TA ab =,则A 的所有特征值为 .三、解答题:15—23小题,共94分.请将解答写在答题纸...指定位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分10分)求极限0limx t x dt du+→⎰⎰设函数()f u 在()0,+∞内具有二阶导数,且z f=满足等式22222212z z z z x y z x y x y x y ⎛⎫⎛⎫∂∂∂∂ +=++ ⎪ ∂∂+∂∂⎝⎭⎝,若()()00,01,f f '==求函数()f u 的表达式.(17)求()()21ln ln limnn k k n k n n →∞=+-∑(18)(本题满分10分)设函数()f x 连续,且()2013arccot 2xtf x t dt x -=⎰.已知()21f =,求()32f x dx ⎰的值.(19)(本题满分10分)设()y f x =是区间[0,1]上的任一非负连续函数,()f x 在区间(0,1)内可导,且2()(),f x f x x'>-试证明在(0,1)内,1()()0x xf x f t dt -=⎰存在唯一实根.(20)(本题满分11分)已知平面区域(){}22,|2,D x y xy x =+≤计算二重积分()21Dy dxdy +⎰⎰。
★试卷3套精选★陕西省名校2018年考前冲刺必刷卷数学试题二

中考数学模拟试卷一、选择题(本题包括10个小题,每小题只有一个选项符合题意)1.如图,数轴上有A ,B ,C ,D 四个点,其中表示互为相反数的点是A .点A 和点CB .点B 和点DC .点A 和点DD .点B 和点C【答案】C【解析】根据相反数的定义进行解答即可.【详解】解:由A 表示-2,B 表示-1,C 表示0.75,D 表示2.根据相反数和为0的特点,可确定点A 和点D 表示互为相反数的点.故答案为C.【点睛】本题考查了相反数的定义,掌握相反数和为0是解答本题的关键.2.甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图,则符合这一结果的实验可能是( )A .掷一枚正六面体的骰子,出现1点的概率B .抛一枚硬币,出现正面的概率C .从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率D .任意写一个整数,它能被2整除的概率【答案】C【解析】解:A .掷一枚正六面体的骰子,出现1点的概率为16,故此选项错误; B .掷一枚硬币,出现正面朝上的概率为12,故此选项错误; C .从一装有2个白球和1个红球的袋子中任取一球,取到红球的概率是:11123=+≈0.33;故此选项正确; D .任意写出一个整数,能被2整除的概率为12,故此选项错误. 故选C . 3.如图,二次函数y =ax 2+bx +c(a≠0)的图象经过点A ,B ,C .现有下面四个推断:①抛物线开口向下;②当x=-2时,y 取最大值;③当m<4时,关于x 的一元二次方程ax 2+bx +c=m 必有两个不相等的实数根;④直线y=kx+c(k≠0)经过点A,C,当kx+c> ax2+bx+c时,x的取值范围是-4<x<0;其中推断正确的是()A.①②B.①③C.①③④D.②③④【答案】B【解析】结合函数图象,利用二次函数的对称性,恰当使用排除法,以及根据函数图象与不等式的关系可以得出正确答案.【详解】解:①由图象可知,抛物线开口向下,所以①正确;②若当x=-2时,y取最大值,则由于点A和点B到x=-2的距离相等,这两点的纵坐标应该相等,但是图中点A和点B的纵坐标显然不相等,所以②错误,从而排除掉A和D;剩下的选项中都有③,所以③是正确的;易知直线y=kx+c(k≠0)经过点A,C,当kx+c>ax2+bx+c时,x的取值范围是x<-4或x>0,从而④错误.故选:B.【点睛】本题考查二次函数的图象,二次函数的对称性,以及二次函数与一元二次方程,二次函数与不等式的关系,属于较复杂的二次函数综合选择题.4.二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②3b+2c<0;③4a+c <2b;④m(am+b)+b<a(m≠﹣1),其中结论正确的个数是()A.1 B.2 C.3 D.4【答案】C【解析】试题解析:∵图象与x轴有两个交点,∴方程ax2+bx+c=0有两个不相等的实数根,∴b2﹣4ac>0,∴4ac﹣b2<0,①正确;∵﹣=﹣1,∴b=2a,∵a+b+c<0,∴b+b+c<0,3b+2c<0,∴②是正确;∵当x=﹣2时,y>0,∴4a﹣2b+c>0,∴4a+c>2b,③错误;∵由图象可知x=﹣1时该二次函数取得最大值,∴a﹣b+c>am2+bm+c(m≠﹣1).∴m(am+b)<a﹣b.故④正确∴正确的有①②④三个,故选C.考点:二次函数图象与系数的关系.【详解】请在此输入详解!5.下列计算正确的是()A.2a2﹣a2=1 B.(ab)2=ab2C.a2+a3=a5D.(a2)3=a6【答案】D【解析】根据合并同类项法则判断A、C;根据积的乘方法则判断B;根据幂的乘方法判断D,由此即可得答案.【详解】A、2a2﹣a2=a2,故A错误;B、(ab)2=a2b2,故B错误;C、a2与a3不是同类项,不能合并,故C错误;D、(a2)3=a6,故D正确,故选D.【点睛】本题考查幂的乘方与积的乘方,合并同类项,熟练掌握各运算的运算性质和运算法则是解题的关键.6.如图,AD是半圆O的直径,AD=12,B,C是半圆O上两点.若AB BC CD==,则图中阴影部分的面积是()A .6πB .12πC .18πD .24π【答案】A 【解析】根据圆心角与弧的关系得到∠AOB=∠BOC=∠COD=60°,根据扇形面积公式计算即可.【详解】∵AB BC CD ==,∴∠AOB=∠BOC=∠COD=60°.∴阴影部分面积=2606=6360⨯ππ. 故答案为:A.【点睛】本题考查的知识点是扇形面积的计算,解题关键是利用圆心角与弧的关系得到∠AOB=∠BOC=∠COD=60°. 7.如图,数轴上有A ,B ,C ,D 四个点,其中表示互为倒数的点是( )A .点A 与点BB .点A 与点DC .点B 与点D D .点B 与点C 【答案】A【解析】试题分析:主要考查倒数的定义和数轴,要求熟练掌握.需要注意的是:倒数的性质:负数的倒数还是负数,正数的倒数是正数,0没有倒数.倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.根据倒数定义可知,-2的倒数是-12,有数轴可知A 对应的数为-2,B 对应的数为-12,所以A 与B 是互为倒数.故选A .考点:1.倒数的定义;2.数轴.8.如图是由若干个相同的小正方体搭成的一个几何体的主视图和俯视图,则所需的小正方体的个数最少是( )A .6B .5C .4D .3【答案】B 【解析】主视图、俯视图是分别从物体正面、上面看,所得到的图形.【详解】综合主视图和俯视图,底层最少有4个小立方体,第二层最少有1个小立方体,因此搭成这个几何体的小正方体的个数最少是5个.故选:B.【点睛】此题考查由三视图判断几何体,解题关键在于识别图形9.不等式5+2x <1的解集在数轴上表示正确的是( ).A.B.C.D.【答案】C【解析】先解不等式得到x<-1,根据数轴表示数的方法得到解集在-1的左边.【详解】5+1x<1,移项得1x<-4,系数化为1得x<-1.故选C.【点睛】本题考查了在数轴上表示不等式的解集:先求出不等式组的解集,然后根据数轴表示数的方法把对应的未知数的取值范围通过画区间的方法表示出来,等号时用实心,不等时用空心.10.利用运算律简便计算52×(–999)+49×(–999)+999正确的是A.–999×(52+49)=–999×101=–100899B.–999×(52+49–1)=–999×100=–99900C.–999×(52+49+1)=–999×102=–101898D.–999×(52+49–99)=–999×2=–1998【答案】B【解析】根据乘法分配律和有理数的混合运算法则可以解答本题.【详解】原式=-999×(52+49-1)=-999×100=-1.故选B.【点睛】本题考查了有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.二、填空题(本题包括8个小题)11.如图,等边三角形AOB的顶点A的坐标为(﹣4,0),顶点B在反比例函数kyx(x<0)的图象上,则k= .【答案】-43.【解析】过点B作BD⊥x轴于点D,因为△AOB是等边三角形,点A的坐标为(-4,0)所∠AOB=60°,根据锐角三角函数的定义求出BD及OD的长,可得出B点坐标,进而得出反比例函数的解析式.【详解】过点B作BD⊥x轴于点D,∵△AOB是等边三角形,点A的坐标为(﹣4,0),∴∠AOB=60°,OB=OA=AB=4,∴OD= OB=2,BD=OB•sin60°=4×3=23,2∴B(﹣2,23),∴k=﹣2×23=﹣43.【点睛】本题考查了反比例函数图象上点的坐标特点、等边三角形的性质、解直角三角函数等知识,难度适中.12.如图是一个几何体的三视图(图中尺寸单位:cm),根据图中数据计算,这个几何体的表面积为cm.__________2【答案】16【解析】分析:由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状,确定圆锥的母线长和底面半径,从而确定其表面积.详解:由主视图和左视图为三角形判断出是锥体,由俯视图是圆形可判断出这个几何体应该是圆锥;根据三视图知:该圆锥的母线长为6cm,底面半径为2cm,故表面积=πrl+πr2=π×2×6+π×22=16π(cm2).故答案为:16π.点睛:考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.13.将两张三角形纸片如图摆放,量得∠1+∠2+∠3+∠4=220°,则∠5=__.【答案】40°【解析】直接利用三角形内角和定理得出∠6+∠7的度数,进而得出答案.【详解】如图所示:∠1+∠2+∠6=180°,∠3+∠4+∠7=180°,∵∠1+∠2+∠3+∠4=220°,∴∠1+∠2+∠6+∠3+∠4+∠7=360°,∴∠6+∠7=140°,∴∠5=180°-(∠6+∠7)=40°.故答案为40°.【点睛】主要考查了三角形内角和定理,正确应用三角形内角和定理是解题关键.14.如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m.水面下降2.5m,水面宽度增加_____m.【答案】1.【解析】根据已知建立平面直角坐标系,进而求出二次函数解析式,再通过把y=-1.5代入抛物线解析式得出水面宽度,即可得出答案【详解】解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半1米,抛物线顶点C坐标为(0,1),设顶点式y=ax1+1,把A点坐标(-1,0)代入得a=-0.5,∴抛物线解析式为y=-0.5x1+1,当水面下降1.5米,通过抛物线在图上的观察可转化为:当y=-1.5时,对应的抛物线上两点之间的距离,也就是直线y=-1与抛物线相交的两点之间的距离,可以通过把y=-1.5代入抛物线解析式得出:-1.5=-0.5x1+1,解得:x=±3,1×3-4=1,所以水面下降1.5m,水面宽度增加1米.故答案为1.【点睛】本题考查了二次函数的应用,根据已知建立坐标系从而得出二次函数解析式是解决问题的关键,学会把实际问题转化为二次函数,利用二次函数的性质解决问题,属于中考常考题型.15.在平面直角坐标系中,如果点P坐标为(m,n),向量OP可以用点P的坐标表示为OP=(m,n),已知:OA=(x1,y1),OB=(x2,y2),如果x1•x2+y1•y2=0,那么OA与OB互相垂直,下列四组向量:①OC=(2,1),OD=(﹣1,2);②OE=(cos30°,tan45°),OF=(﹣1,sin60°);③OG=3﹣2,﹣2),OH=32,12);④OC=(π0,2),ON=(2,﹣1).其中互相垂直的是______(填上所有正确答案的符号).【答案】①③④【解析】分析:根据两个向量垂直的判定方法一一判断即可;详解:①∵2×(−1)+1×2=0,∴OC 与OD 垂直;②∵33cos301tan45sin60322⨯+⋅=+=, ∴OE 与OF 不垂直.③∵()()()13232202-++-⨯=, ∴OG 与OH 垂直.④∵()02210π⨯+⨯-=,∴OM 与ON 垂直.故答案为:①③④.点睛:考查平面向量,解题的关键是掌握向量垂直的定义.16.如图,这是一幅长为3m ,宽为1m 的长方形世界杯宣传画,为测量宣传画上世界杯图案的面积,现将宣传画平铺在地上,向长方形宣传画内随机投掷骰子(假设骰子落在长方形内的每一点都是等可能的),经过大量重复投掷试验,发现骰子落在世界杯图案中的频率稳定在常数0.4附近,由此可估计宣传画上世界杯图案的面积约为___________________m 1.【答案】1.4【解析】由概率估计图案在整副画中所占比例,再求出图案的面积.【详解】估计宣传画上世界杯图案的面积约为3×1×0.4=1.4m 1.故答案为1.4【点睛】本题考核知识点:几何概率. 解题关键点:由几何概率估计图案在整副画中所占比例.17.如图,△ABC 中,AD 是中线,BC=8,∠B=∠DAC ,则线段 AC 的长为________.【答案】2【解析】已知BC=8, AD 是中线,可得CD=4, 在△CBA 和△CAD 中, 由∠B=∠DAC ,∠C=∠C , 可判定△CBA ∽△CAD ,根据相似三角形的性质可得 AC CD BC AC= , 即可得AC 2=CD•BC=4×8=32,解得2.18.一元二次方程()21210k x x ---=有两个不相等的实数根,则k 的取值范围是________. 【答案】2k <且1k ≠【解析】根据一元二次方程的根与判别式△的关系,结合一元二次方程的定义解答即可.【详解】由题意可得,1−k≠0,△=4+4(1−k)>0,∴k <2且k≠1.故答案为k <2且k≠1.【点睛】本题主要考查了一元二次方程的根的判别式的应用,解题中要注意不要漏掉对二次项系数1-k≠0的考虑.三、解答题(本题包括8个小题)19.已知:如图,E 、F 是四边形ABCD 的对角线AC 上的两点,AF=CE ,DF=BE ,DF ∥BE .求证:(1)△AFD ≌△CEB .(2)四边形ABCD 是平行四边形.【答案】证明见解析【解析】证明:(1)∵DF ∥BE ,∴∠DFE=∠BEF .又∵AF=CE ,DF=BE ,∴△AFD ≌△CEB (SAS ).(2)由(1)知△AFD ≌△CEB ,∴∠DAC=∠BCA ,AD=BC ,∴AD ∥BC .∴四边形ABCD 是平行四边形(一组对边平行且相等的四边形是平行四边形).(1)利用两边和它们的夹角对应相等的两三角形全等(SAS ),这一判定定理容易证明△AFD ≌△CEB .(2)由△AFD ≌△CEB ,容易证明AD=BC 且AD ∥BC ,可根据一组对边平行且相等的四边形是平行四边形.20.已知:正方形ABCD 绕点A 顺时针旋转至正方形AEFG ,连接CE DF 、.如图,求证:CE DF =;如图,延长CB 交EF 于M ,延长FG 交CD 于N ,在不添加任何辅助线的情况下,请直接写出如图中的四个角,使写出的每一个角的大小都等于旋转角.【答案】(1)证明见解析;(2),,,DAG BAE CNF FMC ∠∠∠∠.【解析】(1)连接AF 、AC ,易证∠EAC=∠DAF ,再证明ΔEAC ≅ΔDAF ,根据全等三角形的性质即可得CE=DF ;(2)由旋转的性质可得∠DAG 、∠BAE 都是旋转角,在四边形AEMB 中,∠BAE+∠EMB=180°,∠FMC+∠EMB=180°,可得∠FMC=∠BAE ,同理可得∠DAG=∠CNF ,由此即可解答.【详解】(1)证明:连接,AF AC ,∵正方形ABCD 旋转至正方形AEFG∴DAG BAE ∠∠=,45BAC GAF ∠=∠=︒∴BAE BAC DAG GAF ∠+∠=∠+∠∴EAC DAF ∠=∠在EAC ∆和DAF ∆中,AE AD EAC FAD AC AF =⎧⎪∠=∠⎨⎪=⎩, ∴EAC DAF ∆≅∆∴CE DF =(2).∠DAG 、∠BAE 、∠FMC 、∠CNF ;由旋转的性质可得∠DAG 、∠BAE 都是旋转角,在四边形AEMB 中,∠BAE+∠EMB=180°,∠FMC+∠EMB=180°,可得∠FMC=∠BAE ,同理可得∠DAG=∠CNF ,【点睛】本题考查了正方形的性质、旋转的性质及全等三角形的判定与性质,证明ΔEAC ≅ΔDAF 是解决问题的关键. 21.某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完,商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,每台的售价也上调了200元.商场第一次购入的空调每台进价是多少元?商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?【答案】(1)2400元;(2)8台.【解析】试题分析:(1)设商场第一次购入的空调每台进价是x 元,根据题目条件“商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,每台的售价也上调了200元”列出分式方程解答即可;(2)设最多将y 台空调打折出售,根据题目条件“在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售”列出不等式并解答即可.试题解析:(1)设第一次购入的空调每台进价是x 元,依题意,得 52000240002,200x x=⨯+ 解得2400.x = 经检验,2400x =是原方程的解.答:第一次购入的空调每台进价是2 400元.(2)由(1)知第一次购入空调的台数为24 000÷2 400=10(台),第二次购入空调的台数为10×2=20(台).设第二次将y 台空调打折出售,由题意,得()()()()30001030002000.95300020020122%2400052000y y ⨯++⨯⋅+⋅-≥+⨯+(),解得8y ≤. 答:最多可将8台空调打折出售.22.如图,已知,等腰Rt △OAB 中,∠AOB=90°,等腰Rt △EOF 中,∠EOF=90°,连结AE 、BF .求证:(1)AE=BF ;(2)AE ⊥BF .【答案】见解析【解析】(1)可以把要证明相等的线段AE ,CF 放到△AEO ,△BFO 中考虑全等的条件,由两个等腰直角三角形得AO=BO ,OE=OF ,再找夹角相等,这两个夹角都是直角减去∠BOE 的结果,所以相等,由此可以证明△AEO ≌△BFO ;(2)由(1)知:∠OAC=∠OBF ,∴∠BDA=∠AOB=90°,由此可以证明AE ⊥BF【详解】解:(1)证明:在△AEO 与△BFO 中,∵Rt △OAB 与Rt △EOF 等腰直角三角形,∴AO=OB ,OE=OF ,∠AOE=90°-∠BOE=∠BOF ,∴△AEO ≌△BFO ,∴AE=BF;(2)延长AE交BF于D,交OB于C,则∠BCD=∠ACO由(1)知:∠OAC=∠OBF,∴∠BDA=∠AOB=90°,∴AE⊥BF.23.已知Rt△ABC中,∠ACB=90°,CA=CB=4,另有一块等腰直角三角板的直角顶点放在C处,CP=CQ =2,将三角板CPQ绕点C旋转(保持点P在△ABC内部),连接AP、BP、BQ.如图1求证:AP=BQ;如图2当三角板CPQ绕点C旋转到点A、P、Q在同一直线时,求AP的长;设射线AP与射线BQ相交于点E,连接EC,写出旋转过程中EP、EQ、EC之间的数量关系.【答案】(1)证明见解析(2142(3)EP+EQ= 2EC【解析】(1)由题意可得:∠ACP=∠BCQ,即可证△ACP≌△BCQ,可得AP=CQ;作CH⊥PQ 于H,由题意可求2,可得2,根据勾股定理可求14,即可求AP 的长;作CM⊥BQ 于M,CN⊥EP 于N,设BC 交AE 于O,由题意可证△CNP≌△ CMQ,可得CN=CM,QM=PN,即可证Rt△CEM≌Rt△CEN,EN=EM,∠CEM=∠CEN=45°,则可求得EP、EQ、EC 之间的数量关系.【详解】解:(1)如图1 中,∵∠ACB=∠PCQ=90°,∴∠ACP=∠BCQ 且AC=BC,CP=CQ∴△ACP≌△BCQ(SAS)∴PA=BQ如图 2 中,作CH⊥PQ 于H∵A、P、Q 共线,PC=2,∴PQ=22,∵PC=CQ,CH⊥PQ∴CH=PH= 2在Rt△ACH 中,AH=22= 14AC CH∴PA=AH﹣PH= 14-2解:结论:EP+EQ=2EC理由:如图 3 中,作CM⊥BQ 于M,CN⊥EP 于N,设BC 交AE 于O.∵△ACP≌△BCQ,∴∠CAO=∠OBE,∵∠AOC=∠BOE,∴∠OEB=∠ACO=90°,∵∠M=∠CNE=∠MEN=90°,∴∠MCN=∠PCQ=90°,∴∠PCN=∠QCM,∵PC=CQ,∠CNP=∠M=90°,∴△CNP≌△CMQ(AAS),∴CN=CM ,QM=PN ,∴CE=CE ,∴Rt △CEM ≌Rt △CEN (HL ),∴EN=EM ,∠CEM=∠CEN=45°∴EP+EQ=EN+PN+EM ﹣MQ=2EN ,,∴EC【点睛】本题考查几何变换综合题,解答关键是等腰直角三角形的性质,全等三角形的性质和判定,添加恰当辅助线构造全等三角形.24.先化简:2222421121x x x x x x x ---÷+--+,然后在不等式2x ≤的非负整数解中选择一个适当的数代入求值. 【答案】21x +;2. 【解析】先将后面的两个式子进行因式分解并约分,然后计算减法,根据题意选择x=0代入化简后的式子即可得出答案.【详解】解:原式=()()()()222121112x x x x x x x ---⋅++-- =()21211x x x x --++ =21x + 2x ≤的非负整数解有:2,1,0,其中当x 取2或1时分母等于0,不符合条件,故x 只能取0∴将x=0代入得:原式=2【点睛】本题考查的是分式的化简求值,注意选择数时一定要考虑化简前的式子是否有意义.25.在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC 的顶点A 、C 的坐标分别为()4,5-,(1,3)-.请在如图所示的网格平面内作出平面直角坐标系;请作出ABC ∆关于y 轴对称的'''A B C ∆;点'B 的坐标为 .ABC ∆的面积为 .【答案】(1)见解析;(2)见解析;(3)'(2,1)B ;(4)4.【解析】(1)根据C 点坐标确定原点位置,然后作出坐标系即可;(2)首先确定A 、B 、C 三点关于y 轴对称的点的位置,再连接即可;(3)根据点B'在坐标系中的位置写出其坐标即可(4)利用长方形的面积剪去周围多余三角形的面积即可.【详解】解:(1)如图所示:(2)如图所示:(3)结合图形可得:()B'2,1;(4)ΔABC 111S 34231224222=⨯-⨯⨯-⨯⨯-⨯⨯ 123144=---=.【点睛】此题主要考查了作图−−轴对称变换,关键是确定组成图形的关键点的对称点位置.26.如图,点B 、E 、C 、F 在同一条直线上,AB =DE ,AC =DF ,BE =CF ,求证:AB ∥DE .【答案】详见解析.【解析】试题分析:利用SSS 证明△ABC ≌△DEF ,根据全等三角形的性质可得∠B=∠DEF ,再由平行线的判定即可得AB ∥DE .试题解析:证明:由BE =CF 可得BC =EF ,又AB =DE ,AC =DF ,故△ABC≌△DEF(SSS),则∠B=∠DEF,∴AB∥DE.考点:全等三角形的判定与性质.中考数学模拟试卷一、选择题(本题包括10个小题,每小题只有一个选项符合题意)1.下列各式计算正确的是( )A.633-=B.1236⨯=C.3535+=D.1025÷=【答案】B【解析】A选项中,∵63、不是同类二次根式,不能合并,∴本选项错误;B选项中,∵123=36=6⨯,∴本选项正确;C选项中,∵35=35⨯,而不是等于3+5,∴本选项错误;D选项中,∵10102=5÷≠,∴本选项错误;故选B.2.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是()A.小明中途休息用了20分钟B.小明休息前爬山的平均速度为每分钟70米C.小明在上述过程中所走的路程为6600米D.小明休息前爬山的平均速度大于休息后爬山的平均速度【答案】C【解析】根据图像,结合行程问题的数量关系逐项分析可得出答案.【详解】从图象来看,小明在第40分钟时开始休息,第60分钟时结束休息,故休息用了20分钟,A正确;小明休息前爬山的平均速度为:28007040=(米/分),B正确;小明在上述过程中所走的路程为3800米,C错误;小明休息前爬山的平均速度为:70米/分,大于休息后爬山的平均速度:380028002510060-=-米/分,D正确.故选C.考点:函数的图象、行程问题.3.把不等式组24030xx-≥⎧⎨->⎩的解集表示在数轴上,正确的是()A .B .C .D .【答案】A【解析】分别求出各个不等式的解集,再求出这些解集的公共部分并在数轴上表示出来即可.【详解】2x40 30x-≥⎧⎨-⎩①>②由①,得x≥2,由②,得x<1,所以不等式组的解集是:2≤x<1.不等式组的解集在数轴上表示为:.故选A.【点睛】本题考查的是解一元一次不等式组.熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.4.如图,下列条件不能判定△ADB∽△ABC的是()A.∠ABD=∠ACB B.∠ADB=∠ABCC.AB2=AD•AC D.AD AB AB BC=【答案】D【解析】根据有两个角对应相等的三角形相似,以及根据两边对应成比例且夹角相等的两个三角形相似,分别判断得出即可.【详解】解:A、∵∠ABD=∠ACB,∠A=∠A,∴△ABC∽△ADB,故此选项不合题意;B、∵∠ADB=∠ABC,∠A=∠A,∴△ABC∽△ADB,故此选项不合题意;C、∵AB2=AD•AC,∴AC ABAB AD=,∠A=∠A,△ABC∽△ADB,故此选项不合题意;D、ADAB=ABBC不能判定△ADB∽△ABC,故此选项符合题意.故选D.【点睛】点评:本题考查了相似三角形的判定,利用了有两个角对应相等的三角形相似,两边对应成比例且夹角相等的两个三角形相似.5.如图,甲圆柱型容器的底面积为30cm2,高为8cm,乙圆柱型容器底面积为xcm2,若将甲容器装满水,然后再将甲容器里的水全部倒入乙容器中(乙容器无水溢出),则乙容器水面高度y(cm)与x(cm2)之间的大致图象是()A.B.C.D.【答案】C【解析】根据题意可以写出y关于x的函数关系式,然后令x=40求出相应的y值,即可解答本题.【详解】解:由题意可得,y=308x⨯=240x,当x=40时,y=6,故选C.【点睛】本题考查了反比例函数的图象,根据题意列出函数解析式是解决此题的关键.6.如图分别是某班全体学生上学时乘车、步行、骑车人数的分布直方图和扇形统计图(两图都不完整),下列结论错误的是( )A.该班总人数为50 B.步行人数为30C.乘车人数是骑车人数的2.5倍D.骑车人数占20%【答案】B【解析】根据乘车人数是25人,而乘车人数所占的比例是50%,即可求得总人数,然后根据百分比的含义即可求得步行的人数,以及骑车人数所占的比例.【详解】A 、总人数是:25÷50%=50(人),故A 正确;B 、步行的人数是:50×30%=15(人),故B 错误;C 、乘车人数是骑车人数倍数是:50%÷20%=2.5,故C 正确;D 、骑车人数所占的比例是:1-50%-30%=20%,故D 正确.由于该题选择错误的,故选B .【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.7.二次函数y=ax 2+bx+c 的图象在平面直角坐标系中的位置如图所示,则一次函数y=ax+b 与反比例函数y=c x在同一平面直角坐标系中的图象可能是( )A .B .C .D .【答案】C【解析】试题分析:∵二次函数图象开口方向向下,∴a <0,∵对称轴为直线2b x a=->0,∴b >0,∵与y 轴的正半轴相交,∴c >0,∴y ax b =+的图象经过第一、二、四象限,反比例函数c y x=图象在第一三象限,只有C 选项图象符合.故选C .考点:1.二次函数的图象;2.一次函数的图象;3.反比例函数的图象.8.将一副三角板按如图方式摆放,∠1与∠2不一定互补的是( )A.B. C. D.【答案】D【解析】A选项:∠1+∠2=360°-90°×2=180°;B选项:∵∠2+∠3=90°,∠3+∠4=90°,∴∠2=∠4,∵∠1+∠4=180°,∴∠1+∠2=180°;C选项:∵∠ABC=∠DEC=90°,∴AB∥DE,∴∠2=∠EFC,∵∠1+∠EFC=180°,∴∠1+∠2=180°;D选项:∠1和∠2不一定互补.故选D.点睛:本题主要掌握平行线的性质与判定定理,关键在于通过角度之间的转化得出∠1和∠2的互补关系. 9.如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为()A .(2,23)B .(﹣2,4)C .(﹣2,22)D .(﹣2,23)【答案】D 【解析】分析:作BC ⊥x 轴于C ,如图,根据等边三角形的性质得4,2,60OA OB AC OC BOA ====∠=,则易得A 点坐标和O 点坐标,再利用勾股定理计算出224223BC =-=,然后根据第二象限点的坐标特征可写出B 点坐标;由旋转的性质得60,AOA BOB OA OB OA OB ∠'=∠'==='=',则点A′与点B 重合,于是可得点A′的坐标.详解:作BC ⊥x 轴于C ,如图,∵△OAB 是边长为4的等边三角形∴4,2,60OA OB AC OC BOA ====∠=,∴A 点坐标为(−4,0),O 点坐标为(0,0),在Rt △BOC 中,224223BC =-=,∴B 点坐标为(2,23)-;∵△OAB 按顺时针方向旋转60,得到△OA′B′,∴60,AOA BOB OA OB OA OB ∠'=∠'==='=',∴点A′与点B 重合,即点A′的坐标为(2,3)-,故选D.点睛:考查图形的旋转,等边三角形的性质.求解时,注意等边三角形三线合一的性质.10.为确保信息安全,信息需加密传输,发送方将明文加密后传输给接收方,接收方收到密文后解密还原为明文,已知某种加密规则为,明文a ,b 对应的密文为a +2b ,2a -b ,例如:明文1,2对应的密文是5,0,当接收方收到的密文是1,7时,解密得到的明文是( )A .3,-1B .1,-3C .-3,1D .-1,3【答案】A【解析】根据题意可得方程组2127a b a b +=⎧⎨-=⎩,再解方程组即可. 【详解】由题意得:2127a b a b +=⎧⎨-=⎩, 解得:31a b =⎧⎨=-⎩, 故选A .二、填空题(本题包括8个小题)11.不等式组20262x x ->⎧⎨->⎩①②的解是________. 【答案】x >4【解析】分别解出不等式组中的每一个不等式,然后根据同大取大得出不等式组的解集.【详解】由①得:x >2;由②得 :x >4;∴此不等式组的解集为x >4;故答案为x >4.【点睛】考查了解一元一次不等式组,一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.12.如图,在平面直角坐标系xOy 中,点A 的坐标为A(1,0),等腰直角三角形ABC 的边AB 在x 轴的正半轴上,∠ABC=90°,点B 在点A 的右侧,点C 在第一象限。
考研数学二模拟题2018年(2)_真题(含答案与解析)-交互

考研数学二模拟题2018年(2)(总分100, 做题时间90分钟)一、填空题1.曲线y=x 2 e -x2的渐近线方程为______.SSS_FILL分值: 1y=0.[解析] 由于,原曲线仅有一条水平渐近线y=0.2.曲线的渐近线方程为______.SSS_FILL分值: 1. [解析] 计算可得曲线不存在水平渐近线和铅直渐近线.故此曲线的渐近线方程为.3.曲线的斜渐近线方程为______.SSS_FILL分值: 1y=2x+1. [解析]所以斜渐近线方程为y=2x+1.4.曲线的斜渐近线方程为______.SSS_FILL分值: 1. [解析] 因为故斜渐近线方程为.5.曲线的水平渐近线方程为______.SSS_FILL分值: 1. [解析] 因为故曲线的水平渐近线方程为.6.曲线的渐近线方程为______.SSS_FILL分值: 1y=2x. [解析] 由于函数连续,所以曲线无铅直渐近线;又因为都不存在,所以曲线无水平渐近线.考虑到所以曲线有斜渐近线y=2x.7.曲线y=x 2 +x(x<0)上曲率为的点的坐标是______.SSS_FILL分值: 1(-1,0). [解析] 将y"=2x+1,y"=2代入曲率公式,得整理后有x 2 +x=0,由于x<0,故取x=-1,从而y| x=-1 =0,故所求点的坐标为(-1,0).8.曲线的斜渐近线方程为______.SSS_FILL分值: 1. [解析]则斜渐近线方程为.二、选择题1.当x>0时,曲线SSS_SINGLE_SELA 有且仅有水平渐近线.B 有且仅有铅直渐近线.C 既有水平渐近线,也有铅直渐近线.D 既无水平渐近线,也无铅直渐近线.分值: 1答案:A[解析] 由于,又,则原曲线在(0,+∞)有且仅有水平渐近线y=1.2.曲线的渐近线有SSS_SINGLE_SELA 1条.B 2条.C 3条.D 4条.分值: 1答案:B[解析] 由可知原曲线有水平渐近线.又,则原曲线有铅直渐近线x=0,虽然原题中当x=1,x=-2时分母为零,但都不是∞,故原曲线的渐近线有两条.3.曲线渐近线的条数为SSS_SINGLE_SELA 0.B 1.C 2.D 3.分值: 1答案:D[解析]所以x=0是一条铅直渐近线.又所以沿x→+∞方向没有水平渐近线.又所以沿x→+∞方向有斜渐近线y=x.再看沿x→-∞方向:所以沿x→-∞方向该曲线有水平渐近线y=0.即然沿x→-∞方向已有水平渐近线,此曲线当然不可能再有斜渐近线.故共有3条渐近线,应选D.对于(*)式中极限还有如下处理:,或者令e x =t,然后再处理.4.曲线的渐近线的条数为SSS_SINGLE_SELA 0.B 1.C 2.D 3.分值: 1答案:C[解析] 因为所以故x=1是曲线的铅直渐近线,且是唯一的一条铅直渐近线.因为所以y=1是曲线的水平渐近线.综上可知,曲线有两条渐近线.5.下列曲线中有渐近线的是A.y=x+sinx.B.y=x 2 +sinx.C.D.SSS_SIMPLE_SINA B C D分值: 1答案:C[解析] 对于,可知.又,所以有斜渐近线y=x,因此应选C.6.曲线上对应于t=1的点处的曲率半径是A.B.C.D.SSS_SIMPLE_SINA B C D分值: 1答案:C[解析] 曲线在点(x,f(x))处的曲率公式,曲率半径.本题中,所以,对应于t=1的点处有y"=3,y"=-1,所以,曲率半径.应选C.7.设函数f(x)在[0,1]上f"(x)>0,则f"(1),f"(0),f(1)-f(0)或f(0)-f(1)的大小顺序是SSS_SINGLE_SELA f"(1)>f"(0)>f(1)-f(0).B f"(1)>f(1)-f(0)>f"(0).C f(1)-f(0)>f"(1)>f"(0).D f"(1)>f(0)-f(1)>f"(0).分值: 1答案:B[解析] 由于f"(x)>0,x∈[0,1],则f"(x)单调增加,又f(1)-f(0)=f"(c),c∈(0,1),从而f"(1)>f"(c)>f"(0),即f"(1)>f(1)-f(0)>f"(0).8.设函数f(x),g(x)是大于零的可导函数,且f"(x)g(x)-f(x)g"(x)<0,则当a <x<b时,有SSS_SINGLE_SELA f(x)g(b)>f(b)g(x).B f(x)g(a)>f(a)g(x).C f(x)g(x)>f(b)g(b).D f(x)g(x)>f(a)g(a).分值: 1答案:A[解析] 看起来,选项眼花缭乱,其实仔细审题发现,A,B两项是在区间(a,b)内的值与两端点处的值比大小,C,D两项是f(x)g(x)在区间(a,b)内的值与两端点处的值比大小.题干中含有某种形式的导数的不等式,就想到用单调性.题干中表述的是谁的导数呢?经验算,故应选A.9.已知函数f(x)在区间(1-δ,1+δ)内具有二阶导数,f"(x)严格单调减少,且f(1)=f"(1)=1,则SSS_SINGLE_SELA 在(1-δ,1)和(1,1+δ)内均有f(x)<x.B 在(1-δ,1)和(1,1+δ)内均有f(x)>x.C 在(1-δ,1)内,f(x)<x,在(1,1+δ)内,f(x)>x.D 在(1-δ,1)内,f(x)>x,在(1,1+δ)内,f(x)<x.分值: 1答案:A[解析] 由选项看出,题目是要确定x与f(x)在所讨论区间内的大小关系,因此,构造辅助函数F(x)=f(x)-x.由题目的条件知F(1)=0,F"(1)=0,f"(x)=f"(x)<0,∈(1-δ,1+δ),故F(x)在x=1处取得极大值,即F(1)=0在区间(1-δ,1+δ)内为极大值,从而f(x)-x<0,x∈(1-δ,1)∪(1,1+δ),即A正确.三、解答题1.对函数填写下表.单调减区间单调增区间极值点极值凹区间凸区间拐点渐近线SSS_TEXT_QUSTI分值: 6解单调减区间(-∞,-2),(0,+∞) 凹区间(-3,0),(0,+∞) 单调增区间(-2,0) 凸区间(-∞,-3)极值点-2 拐点极值渐近线x=0和y=0 2.设,求(1)函数的增减区间及极值;(2)函数图像的凹凸区间及拐点;(3)渐近线;(4)作出其图形.SSS_TEXT_QUSTI分值: 7解定义域(-∞,0)∪(0,+∞).当时,y=0.(1) ,故驻点为x=2.又x (-∞,0) (0,2) 2 (2,+∞)y" + - 0 +y ↗ ↘ 3 ↗所以,(-∞,0)及(2,+∞)为增区间,(0,2)为减区间,x=2为极小值点,极小值为y=3.(2) ,故(-∞,0),(0,+∞)均为凹区间,无拐点.(3)因所以,x=0为铅直渐近线,y=x为斜渐近线.(4)函数的图形如图所示.3.如图所示,设曲线L的方程y=f(x),且y">0,又MT,MP分别为该曲线在点M(x0,y)处的切线和法线.已知线段MP的长度为(其中y"=y"(x0 ),y"=y"(x)),试推导出点P(ξ,η)的坐标表达式.SSS_TEXT_QUSTI分值: 7解由题设①又PM⊥MT,所以②由①,②式得.由于y">0,曲线L是凹的,故y-η<0,从而.又,于是得因此P点坐标为4.已知函数,求(Ⅰ)函数的增减区间及极值;(Ⅱ)函数图形的凹凸区间及拐点;(Ⅲ)函数图形的渐近线.SSS_TEXT_QUSTI分值: 7解所给函数的定义域为(-∞,1)∪(1,+∞).,令y"=0,得驻点x=0及x=3.,令y"=0,得x=0.列表讨论如下:x (-∞,0) 0 (0,1) (1,3) 3 (3,+∞)y" + 0 + - 0 +y" - 0 + + + +y ↗ 拐点↗ ↘ 极小值↗由此可知:(Ⅰ)函数的单调增加区间为(-∞,1)和(3,+∞),单调减少区间为(1,3);极小值为(Ⅱ)函数图形在区间(-∞,0)内是凸的.在区间(0,1),(1,+∞)内是凹的,拐点为点(0,0).(Ⅲ)由知,x=1是函数图形的铅直渐近线.又故y=x+2是函数图形的斜渐近线.5.证明:当x>0时,有不等式.SSS_TEXT_QUSTI分值: 7证考虑函数x>0,有所以f(x)在(0,+∞)上是单调减少的.又,知当x>0时,,即.6.利用导数证明:当x>1时,SSS_TEXT_QUSTI分值: 7证令f(x)=(1+x)ln(1+x)-xlnx,则,故在[1,+∞)内f(x)为严格增函数.又f(1)=2ln2>0,所以有f(x)>0,x>1.从而得7.设f"(x)<0,f(0)=0,证明对任何x1>0,x2>0,有f(x1+x2)<f(x1 )+f(x2).SSS_TEXT_QUSTI分值: 7证法1 令F(x)=f(x)+f(x2 )-f(x+x2),F(0)=0,又F"(x)=f"(x)-f"(x+x2)=f"(ξ)(-x2)>0.ξ∈(x,x+x2)(拉格朗日中值定理),故F(x1)>F(0)=0,x1>0,即f(x1)+f(x2)-f(x1+x2)>0.证法2 不妨设x1≤x2(x2≤x1时类似可证),则由拉格朗日中值定理可得f(x1 )-f(0)=x1f"(ξ1),0<ξ1<x1,f(x1 +x2)-f(x2)=x1f"(ξ2),x2<ξ2<x1+x2.又已知f"(x)<0,故f"(ξ2 )<f"(ξ1).比较以上两式即得f(x1 +x2)<f(x1)+f(x2).证法1采用把其中一个常量字母x1改为变量x(常数变量化)转化为函数不等式,再利用单调性的手段加以证明,这种方法是证明这类常数不等式常用的一种方法.8.设x>0,常数a>e.证明:(a+x) a<a a+x.SSS_TEXT_QUSTI分值: 7证由函数y=lnx的单调性,只需证aln(a+x)<(a+x)lna.设f(x)=(a+x)lna-aln(a+x),则f(x)在[0,+∞)内连续、可导,且所以f(x)在[0,+∞)内单增.又f(0)=0.从而得f(x)>0,x>0,即aln(a+x)<(a+x)lna,x>0.所以(a+x) a<a a+x,x>0.9.设,且f"(x)>0,证明:f(x)≥x.SSS_TEXT_QUSTI分值: 7证法1 因f(x)连续且具有一阶导数,故由知f(0)=0..由f(x)的泰勒公式得,ξ在0与x之间.因f"(ξ)>0,所以f(x)≥x.证法2 易推知f(0)=0,f"(0)=1,令F(x)=f(x)-x,则F"(x)=f"(x)-1,f"(x)=f"(x)>0,有F"(0)=f"(0)-1=0,则x=0是唯一的极小值点,也是最小值点,于是F(x)=f(x)-x≥F(0)=0.证毕.设x∈(0,1),证明:SSS_TEXT_QUSTI10.(1+x)ln 2 (1+x)<x 2;分值: 3.5证令φ(x)=(1+x)ln 2 (1+x)-x 2,有φ(0)=0,φ"(x)=ln 2 (1+x)+2ln(1+x)-2x,还看不出在(0,1)内φ"(x)是否定号.为此,再计算φ"(0)=0.再计算φ"(0)=0,于是φ"(x)在(0,1)内严格单调减少,又φ"(0)=0,所以在(0,1)内φ"(x)<o.于是φ"(x)在(0,1)内严格单调减少,又φ"(0)=0,故在(0,1)内φ"(x)<0.因此φ(x)在(0,1)内严格单调减少,又φ(0)=0,故在(0,1)内φ(x)<0.证毕.SSS_TEXT_QUSTI11.分值: 3.5证令有由上一小题知,当x∈(0,1)时f"(x)<0,于是在(0,1)内f(x)严格单调减少,,故当x∈(0,1)时,不等式左边证毕.又故当x∈(0,1)时,.不等式右边证毕.函数f(x)在[0,+∞)上可导,f(0)=1,且满足等式.SSS_TEXT_QUSTI12.求导数f"(x);分值: 3.5解由题设知上式两边对x求导,得(x+1)f"(x)=-(x+2)f"(x).设u=f"(x)则有解之得由f(0)=1及f"(0)+f(0)=0,知f"(0)=-1,从而C=-1.因此SSS_TEXT_QUSTI13.证明:当x≥0时,成立不等式:e -x≤f(x)≤1.分值: 3.5证当x≥0时,f"(x)<0,即f(x)单调减少,又f(0)=1,所以f(x)≤f(0)=1.设φ(x)=f(x)-e -x,则当x≥0时,φ"(x)≥0,即φ(x)单调增加,因而φ(x)≥φ(0)=0,即有f(x)≥e -x.综上所述,当x≥0时,不等式e -x≤f(x)≤1成立.14.设0<a<b,证明不等式SSS_TEXT_QUSTI分值: 7证先证右边的不等式.设因为故当x>a时φ(x)单调减少,又φ(a)=0,所以,当x>a时,φ(x)<φ(a)=0,即特别地,当x=b>a时,便有即其次证明左边的不等式.设f(x)=lnx(x>a>0),由拉格朗日中值定理知,至少存在一点ξ∈(a,b),使由于0<a<ξ<b,故又由于a 2 +b 2>2ab,所以,从而有1。
考研数学二模拟题2018年(20)_真题-无答案

考研数学二模拟题2018年(20)(总分150,考试时间90分钟)一、选择题每小题给出的四个选项中,只有一项符合题目要求.1. 设f(x)在[0,1]连续且非负但不恒等于零,记则它们的大小关系为A. I1<I2<I3.B. I3<I1<I2.C. I2<I1<I3.D. I3<I2<I1.2. 设f(x)在[a,b]上连续,在(a,b)内二阶可导,且f"(x)>0(x∈(a,b)),又则下列不等式成立的是A. L>M>N.B. L>N>M.C. M>L>N.D. N>L>M.3. 设其中1<λ≤2,则f(x)在x=0处A. 不连续.B. 连续但不可导.C. 可导但f"(x)在x=0不连续.D. 可导且f"(x)在x=0连续.4. 设f(x)是arcsin(1-x)的原函数且f(0)=0,则A.B.C.D.5. 设f(x)在[0,+∞)连续,又f(x)是的解,则A.0.B.a.C.∞.D.6. 设区域D:x2+y2≤1,则可以化成的累次积分为A.B.C.D.7. 已知α1,α2,α3,α4是齐次方程组Ax=0的基础解系,则Ax=0的基础解系还可以是A. α1-α2,α2-α3,α3-α4,α4-α1.B. α1+α2,α2+α3,α3+α4,α4+α1.C. α1,α2+α3,α3+α4,α4.D. α1+α2,α2-α3,α3-α4,α4+α1.8. 设矩阵,则A和BA. 合同,但不相似.B. 合同,且相似.C. 相似,但不合同.D. 既不合同,也不相似.二、填空题1. 数列极限2. 设周期函数f(x)在(-∞,+∞)内可导,周期为4,又则曲线y=f(x)在点(5,f(5))处的切线的斜率为______.3. 函数的值域区间是______.4. 设有摆线则L绕x轴旋转一周所成的旋转面的面积A=______.5. 设u=u(x,y),则u(x,y)=______.6. 三元二次型xTAx经正交变换x=Qy化为标准型如果矩阵A属于特征值λ=1的特征向量是α=(1,1,-2)T,那么Q=______.三、解答题15~23小题,共94分.解答应写出文字说明、证明过程或演算步骤.1. 设f(x)在[0,+∞)连续且则在(0,+∞)为常数;2. 设f(x)在(a,b)二阶可导且x∈(a,b)时则lnf(x)在(a,b)为凹函数.已知函数y=y(x)由方程ey+6xy+x2-1=0确定.3. 求证:y(x)在x=0取极值,并判断是极大值还是极小值,又判断曲线y=y(x)在x=0附近的凹凸性;4. 求证:g(y)=ey+6y在(-∞,+∞)有唯一零点,该零点取负值.5. 求证:y(x)在x=1某邻域是单调下降的.已知通过x轴上的两点A(1,0),B(3,0)的抛物线y=a(x-1)(x-3),a为参数.6. 求证:两坐标轴与该抛物线所围成的面积等于x轴与该抛物线所围成的面积;7. 计算上述两个平面图形绕x轴旋转一周所产生的两个旋转体体积之比.8. 设曲线Γ的方程为φ(x,y)=0,其中φ(x,y)有一阶连续偏导数且在Γ上任意点处φ"x(x,y)与φ"y(x,y)不同时为零.设点P(x*,y*)为Γ外一点,(Q在Γ上,坐标为(x0,y0))为点P 到曲线Γ的最短距离.求证:必位于曲线Γ在点Q处的法线.9. 计算10. 有一弹性轻绳(即本身的重量可忽略不计)上端固定,下端悬挂一重量为3克的物体,且已知此绳受一克重量的外力作用时伸长厘米.如果物体在绳子拉直并未伸长时放下,问物体向下运动到什么地方又开始上升?设x∈(-∞,+∞)时f(x)有连续的导数,且又数列{xn}如下定义:x1任意给定,xn+1=f(xn)(n=1,2,3,…),求证:11. 存在;12. 方程x=f(x)有唯一根.已知齐次方程组Ax=0为又矩阵B是2×4矩阵,Bx=0的基础解系为α1=(1,-2,3,-1)T,α2=(0,1,-2,1)T13. 求矩阵B;14. 若Ax=0与Bx=0同解,求a1,a2,a3,a4的值;15. 求方程组Ax=0满足x3=-x4的所有解.16. 已知矩阵只有2个线性无关的特征向量,求a的值并求A的特征值和特征向量.。
考研数学二模拟题2018年(1)_真题(含答案与解析)-交互
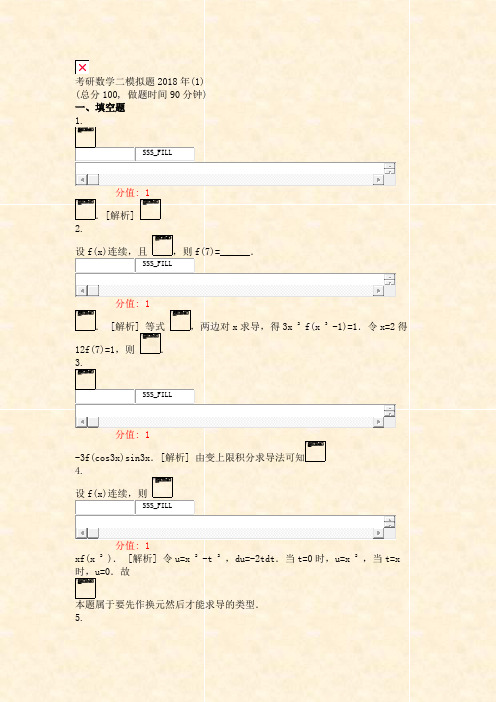
考研数学二模拟题2018年(1)(总分100, 做题时间90分钟)一、填空题1.SSS_FILL分值: 1.[解析]2.设f(x)连续,且,则f(7)=______.SSS_FILL分值: 1. [解析] 等式,两边对x求导,得3x 2 f(x 3 -1)=1.令x=2得12f(7)=1,则.3.SSS_FILL分值: 1-3f(cos3x)sin3x.[解析] 由变上限积分求导法可知4.设f(x)连续,则SSS_FILL分值: 1xf(x 2 ). [解析] 令u=x 2 -t 2,du=-2tdt.当t=0时,u=x 2,当t=x 时,u=0.故本题属于要先作换元然后才能求导的类型.5.设函数f(x)连续,.若φ(1)=1,φ"(1)=5,则f(1)=______.SSS_FILL分值: 12. [解析] 改写,由变限积分求导法得由得f(1)=2.6.由曲线y=xe x与直线y=ex所围成图形的面积S=______.SSS_FILL分值: 1. [解析] 由xe x =ex可知x(e x -e)=0.则x=0或x=1.故二、选择题1.设,其中f(x)连续,s>0,t>0,则I的值SSS_SINGLE_SELA 依赖于s,t.B 依赖于s,t,x.C 依赖于t,x,不依赖于s.D 依赖于s,不依赖于t.分值: 1答案:D[解析] ,由此可见,I的值只与s有关,所以应选D.2.设函数记,0≤x≤2,则A.B.C.D.SSS_SIMPLE_SINA B C D分值: 1答案:B[解析] 当0≤x≤1时,;当1<x≤2时,.由此可见应选B.f(x)在[0,2]上可积,则在[0,2]上连续,于是排除A,C,D.3.设f(x)连续,,则F"(x)等于•**(x4).•**(x4).•**(x4).**(x2).SSS_SIMPLE_SINA B C D分值: 1答案:C[解析] 由知F"(x)=2xf(x 4 ).故应选C.4.已知设,则F(x)为A.B.C.D.SSS_SIMPLE_SINA B C D分值: 1答案:D[解析]所以应选D.f(x)在[0,2]上可积,则在[0,2]上连续,于是排除A,B,C.5.设函数f(x)连续,则下列函数中,必为偶函数的是A.B.C.D.SSS_SIMPLE_SINA B C D分值: 1答案:D[解析] 设,则即F(x)是偶函数,D是正确的.类似方法可以证明A,C均为奇函数.而对B中的函数,因为由所给条件不能推出为偶函数.6.设f(x)是奇函数,除x=0外处处连续,x=0是其第一类间断点,则是SSS_SINGLE_SELA 连续的奇函数.B 连续的偶函数.C 在x=0间断的奇函数.D 在x=0间断的偶函数.分值: 1答案:B[解析] 解法1 取函数它满足题设条件,则是一个连续的偶函数,从而排除了选项A,C,D,故选B.解法2 显然f(x)在任何有限区间[a,b]上都可积,于是连续;又因f(x)是奇函数,则是偶函数,故选B.7.设函数y=f(x)在区间[-1,3]上的图形如图所示.则函数的图形为A.B.C.D.SSS_SIMPLE_SINA B C D分值: 1答案:D[解析] 根据题中函数y=f(x)的图形,可知函数在除了x=0,x=2两点外可导,且F"(x)=f(x).由此可知:函数F(x)在(-1,0)内单调递增,在(0,1)内单调递减,在(1,2)内单调递增,在(2,3)内恒为常数.由于函数F(x)连续,且F(0)=0,所以正确选项只能是D.8.设函数,则SSS_SINGLE_SELA x=π是函数F(x)的跳跃间断点.B x=π是函数F(x)的可去间断点.C F(x)在x=π处连续但不可导.D F(x)在x=π处可导.分值: 1答案:C9.曲线y=x(x-1)(2-x)与x轴所围图形面积可表示为A.B.C.D.SSS_SIMPLE_SINA B C D分值: 1答案:C[解析] y=x(x-1)(2-x)与x轴的交点为x=0,x=1,x=2,因此该曲线与x轴围成的面积为所以应选C.10.由曲线与x轴围成的平面图形绕x轴旋转而成的旋转体的体积为A.B.C.D.SSS_SIMPLE_SINA B C D分值: 1答案:B[解析]11.曲线与x轴所围成的图形,绕x轴旋转一周所成旋转体的体积为A.B.π.C.D.π 2.SSS_SIMPLE_SINA B C D分值: 1答案:C[解析]12.设f(x),g(x)在区间[a,b]上连续,且g(x)<f(x)<m(m为常数),由曲线y=g(x),y=f(x),x=a及x=b所围平面图形绕直线y=m旋转而成的旋转体体积为A.B.C.D.SSS_SIMPLE_SINA B C D分值: 1答案:B[解析] 先画草图如图所示,对x积分。
考研数学一模拟题2018年(33)_真题-无答案

考研数学一模拟题2018年(33)(总分150,考试时间90分钟)一、选择题(下列每题给出的四个选项中,只有一个选项是符合题目要求的.) 1. 设则f(x)在x=0处______A. 间断B. 连续,但不可导C. 可导,且f"(0)=0D. 导数连续2. 下列选项正确的是______A.B.C.D.3. 设区域D:1≤x2+y2≤22,f是区域D上的连续函数,则等于______ A.B.C.D.4. 设等于______ A.0B.1C.D.-15. n阶实对称矩阵A正定的充要条件是______A.A的所有特征值非负**(A)=n**的所有k阶子式为正(1≤k≤n)**为正定矩阵6. 已知α1,α2,β1,β2均是n维(n≥2)向量,则______A. α1,α2线性无关,β1,β2线性无关,必有α1+β1,α2+β2线性无关B. α1,α2线性相关,β1,β2线性相关,必有α1+β1,α2+β2线性相关C. α1,α2线性无关,β1,β2线性相关,必有α1+β1,α2+β2线性无关D. α1,α2线性相关,β1,β2线性无关,则α1+β1,α2+β2可能线性相关,可能线性无关7. 已知随机变量X的密度函数则概率P{λ<X<λ+a}(a>0)的值A. 与a无关,随λ的增大而增大B. 与a无关,随λ的增大而减小C. 与λ无关,随a的增大而增大D. 与λ无关,随a的增大而减小8. 设随机变量X与Y分别服从正态分布N(-1,2)与N(1,2),且X与Y不相关,aX+Y与X+bY亦不相关,则一定有______A. a=b=0B. a=b≠0C. ab=0D. a+b=0二、填空题(每小题4分,共24分.)1. =______.2. 若则=______.3. 设g(x)处处连续,且则f"(0)=______.4. y"+y"=xe-x的通解是______.5. 已知,B是三阶非零矩阵,且AB=0,则ab=______.6. 设X,Y为相互独立的随机变量,且X~N(1,2),Y服从参数λ=3的泊松分布,则D(XY)=______.三、解答题(共94分.解答应写出文字说明、证明过程或演算步骤.)1.2. 设可微函数f(x),g(x)满足f"(x)=g(x),g"(x)=f(x),且f(0)=0,g(x)≠0,又设试导出φ(x)所满足的微分方程,并求φ(x).3. 设x>-1,证明:当0<a<1时,(1+x)a≤1+ax;而当a<0或a>1时,(1+x)a≥1+ax.4. 已知a0=3,a1=5,且对任何自然数证明当|x|<1时,幂级数收敛,并求其和函数.5. 计算曲面积分其中Σ为上半球体的表面外侧.设A是三阶矩阵,α1,α2,α3是线性无关的三维向量组,且Aα1=α2,A2α1=α3,A3α1=α1.6. 证明:A3=E;7. 若α1=(2,-2,1)T,α2=(1,1,-1)T,α3=(1,2,-2)T,求A.8. 设A,B都是三阶矩阵,满足AB=A-B.若λ1,λ2,λ3是A的三个不同的特征值,证明:(1)λi≠-1(i=1,2,3);(2)存在可逆矩阵C,使C-1AC,C-1BC同时为对角矩阵.已知X,Y服从相同的分布若P(|X|=|Y|=0.9. 求出(X,Y)的联合分布律;10. 求出X,Y的相关系数;11. 讨论X,Y的相关性,独立性.设总体X的概率密度函数为X1,X2,…,Xn为简单随机样本.12. 确定常数a;13. 求λ的极大似然估计量;14. (2)中求出的估计量是否为λ的无偏估计量?。
考研数学三模拟题2018年(45)_真题(含答案与解析)-交互
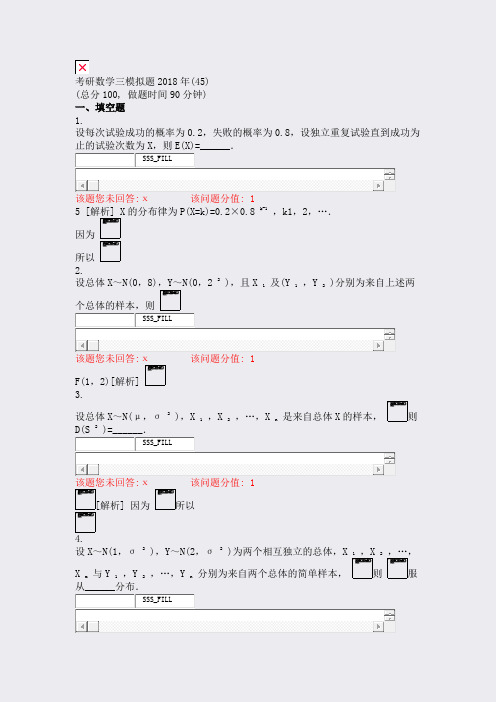
考研数学三模拟题2018年(45)(总分100, 做题时间90分钟)一、填空题1.设每次试验成功的概率为0.2,失败的概率为0.8,设独立重复试验直到成功为止的试验次数为X,则E(X)=______.SSS_FILL该题您未回答:х该问题分值: 15 [解析] X的分布律为P(X=k)=0.2×0.8 k-1,k1,2,….因为所以2.设总体X~N(0,8),Y~N(0,2 2 ),且X1及(Y1,Y2)分别为来自上述两个总体的样本,则SSS_FILL该题您未回答:х该问题分值: 1F(1,2)[解析]3.设总体X~N(μ,σ 2 ),X1,X2,…,Xn是来自总体X的样本,则D(S 2 )=______.SSS_FILL该题您未回答:х该问题分值: 1 [解析] 因为所以4.设X~N(1,σ 2 ),Y~N(2,σ 2 )为两个相互独立的总体,X1,X2,…,Xm 与Y1,Y2,…,Yn分别为来自两个总体的简单样本,则服从______分布.SSS_FILL该题您未回答:х该问题分值: 1[解析]且相互独立,则5.设X~N(μ,σ 2 ),其中σ 2已知,μ为未知参数.从总体X中抽取容量为16的简单随机样本.且μ的置信度为0.95的置信区间中的最小长度为0.588,则σ 2 =______.SSS_FILL该题您未回答:х该问题分值: 1** [解析] 在σ 2 已知的情况下,μ的置信区间为 /其中 /于是有 /二、选择题1.对于随机变量X1,X2,…,Xn,下列说法不正确的是______.A.若X1,X2,…,Xn两两不相关,则B.若X1,X2,…,Xn相互独立,则D(X1+X2+…+Xn)=D(X1)+D(X2)+…+D(Xn)C.若X1,X2,…,Xn相互独立同分布,服从N(0,σ 2 ),则D.若D(X1 +X2+…+Xn)=D(X1)+D(X2)+…+D(Xn),则X1+X2+…+Xn两两不相关SSS_SIMPLE_SINA B C D该题您未回答:х该问题分值: 1答案:D[解析] 若X1 +X2+…+Xn相互独立,则B,C是正确的,若X1+X2+…+Xn两两不相关,则A是正确的,选.2.设(X,Y)服从二维正态分布,其边缘分布为X~N(1,1),Y~N(2,4),X,Y的相关系数为ρXY=-0.5,且P(aX+by≤1)=0.5,则______.A.B.C.D.SSS_SIMPLE_SINA B C D该题您未回答:х该问题分值: 1答案:D[解析] 因为(X,Y)服从二维正态分布,所以aX+bY服从正态分布,E(aX+bY)=a+2b,D(aX+by)=a 2 +4b 2 +2abCov(X,Y)=a 2 +4b 2 -2ab,即aX+bY~N(a+2b,a 2 +4b 2 -2ab),由P(aX+by≤1)=0.5得a+2b=1,所以选D.3.设X1,X2,…,Xn是来自正态总体X~N(μ,σ 2 )的简单随机样本,记则服从t(n-1)分布的随机变量是______.A.B.C.D.SSS_SIMPLE_SINA B C D该题您未回答:х该问题分值: 1答案:D[解析] 即选D.4.设X~t(n),则下列结论正确的是______.A.X 2~F(1,n)B.C.X 2~χ 2 (n)D.X 2~χ 2 (n-1)SSS_SIMPLE_SINA B C D该题您未回答:х该问题分值: 1答案:A[解析] 由X~t(n),得其中U~N(0,1),V~χ 2 (n),且U,V相互独立,于是选A.5.从正态总体X~N(0,σ 2 )中抽取简单随机样本X1,X2,…,Xn,则可作为参数σ 2的无偏估计量的是______.A.B.C.D.SSS_SIMPLE_SINA B C D该题您未回答:х该问题分值: 1答案:A[解析] 因为所以为σ 2的无偏估计量,选A.三、解答题1.设总体X~N(0,σ 2 ),X1,X2,…,Xn为来自总体X的简单随机样本,S 2 = 求所服从的分布.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 6 [解] 又且相互独立,则即设X1,X2,…,Xn(n>2)是来自总体X~N(0,1)的简单随机样本,记Yi=Xi- (i=1,2,…,n).求:SSS_TEXT_QUSTI2.D(Yi);该题您未回答:х该问题分值: 3[解] 由得SSS_TEXT_QUSTI3.Cov(Y1,Yn).该题您未回答:х该问题分值: 3[解] 因为X 1 ,X 2 ,…,X n (n >2)相互独立, 所以 由 得4.设总体X ~N(μ,σ 2 ),X 1 ,X 2 ,…,X n 是来自总体X 的样本,令 求E(X 1 T).SSS_TEXT_QUSTI该题您未回答:х 该问题分值: 6[解] 因为X 1 ,X 2 ,…,X n 独立同分布,所以有E(X 1 T)=E(X 2 T)=…=E(X n T)5.设总体X 服从正态分布N(μ,σ 2 )(σ>0),X 1 ,X 2 ,…,X n 为来自总体X 的简单随机样本,令求Y 的数学期望与方差.SSS_TEXT_QUSTI该题您未回答:х 该问题分值: 6 [解]而于是 6.设总体X 服从正态分布N(μ,σ 2 )(σ>0).从该总体中抽取简单随机样本X1,X 2 ,…,X 2n (n >2).令求统计量 的数学期望.SSS_TEXT_QUSTI该题您未回答:х 该问题分值: 6[解] 令Y i =X i +X n+i (i=1,2,…,n),则Y 1 ,Y 2 ,…,Y n 为正态总体N(2μ,2σ 2 )的简单随机样本,=(n-1)S 2 ,其中S 2 为样本Y 1 ,Y2,…,Y n 的方差,而E(S 2 )=2σ 2 ,所以统计量U= 的数学期望为E(U)=E[(n-1)S 2 ]=2(n-1)σ 2 . 7.设总体且X,Y相互独立,来自总体X,Y的样本均值为,样本方差为记求统计量的数学期望.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 6[解] 由相互独立,可知a,b与相互独立,显然a+b=1.E(U)=μ[E(a)+E(b)]=μE(a+b)=μE(1)=μ.8.设总体X~N(μ,σ 2 ),X1,X2,…,Xn+1为总体X的简单随机样本,记求统计量服从的分布.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 6[解] 因为Xn+1~N(μ,σ 2 ),且它们相互独立,所以又相互独立,所以由t分布的定义,有9.设总体X的概率分布为X 0 1 2 3p θ 2 2θ(1-θ) θ 2 1-2θ是未知参数.用样本值3,1,3,0,3,1,2,3求θ的矩估计值和最大似然估计值.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 6[解] E(X)=0×θ 2+1×2θ(1-θ)+2×θ 2+3×(1-2θ)=3-4θ,令得参数θ的矩估计值为L(θ)=θ 2×[2θ(1-θ)] 2×θ 2×(1-2θ) 4=4θ 6 (1-θ) 2 (1-2θ) 4,lnL(θ)=ln4+6lnθ+2ln(1-θ)+4ln(1-2θ),令得参数θ的最大似然估计值为10.设总体样本值为1,1,3,2,1,2,3,3,求θ的矩估计和最大似然估计.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 7[解] (1)X为离散型随机变量,其分布律为E(X)=3-3θ.今3-3θ=2得θ的矩估计值为(2)L(1,1,3,2,1,2,3,3;θ)=P(X=1)P(X=1)…P(X=3)=θ 3×θ 2×(1-2θ) 3,lnL(θ)=5lnθ+3ln(1-2θ),令得θ的最大似然估计值为11.设总体X~U[0,θ],其中θ>0,求θ的极大似然估计量,判断其是否是θ的无偏估计量.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 7[解] 总体X的密度函数和分布函数分别为设x1,x2,…,xθ为总体X的样本观察值,似然函数为(i=1,2,…,n).当0<xi<θ(i=1,2,…,n)时,且当θ越小时L(θ)越大,所以θ的最大似然估计值为=max{x1,x2,…,xn},θ的最大似然估计量为=max{X1,X2,…,Xn}.因为=max{X1,X2,…,Xn}的分布函数为则的概率密度为所以=max{X1,X2,…,Xn}不是θ的无偏估计量.12.设总体X的密度函数为θ>0为未知参数,a>0为已知参数,求θ的极大似然估计量.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 7[解]令得参数θ的极大似然估计量为13.设总体X~U(θ1,θ2),X1,X2,…,Xn是来自总体X的样本,求θ1,θ2的矩估计和最大似然估计.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 7 [解] (1)令(2)lnL(θ1,θ2)=-nln(θ2-θ1),而因为lnL(θ1,θ2)是θ1的单调增函数,是θ2的单调减函数,所以14.设总体X在区间(0,θ)内服从均匀分布,X1,X2,X3是来自总体的简单随机样本.证明:都是参数θ的无偏估计量,试比较其有效性.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 7[解] 因为总体X在区间(0,θ)内服从均匀分布,所以分布函数为令则则U,V的密度函数分别为因为所以都是参数θ的无偏估计量.因为所以更有效.15.设总体X,Y相互独立且都服从N(μ,σ 2 )分布,(X1,X2,…,Xm)与(Y1,Y2,…,Yn)分别为来自总体X,Y的简单随机样本.证明:为参数σ 2的无偏估计量.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 7[证明] 令因为所以于是即为参数σ 2的无偏估计量.1。
考研数学三模拟题2018年(4)_真题(含答案与解析)-交互

考研数学三模拟题2018年(4) (总分100, 做题时间90分钟) 解答题 1.若随机变量序列X 1 ,X 2 ,…,X n ,…满足条件 证明:{X n }服从大数定律.SSS_TEXT_QUSTI该题您未回答:х 该问题分值: 1.5 【证】由切比雪夫不等式,对任意的ε>0有所以对任意的ε>0,故{X n }服从大数定律. 2.某计算机系统有100个终端,每个终端有20%的时间在使用,若各个终端使用与否相互独立,试求有10个或更多个终端在使用的概率.SSS_TEXT_QUSTI该题您未回答:х 该问题分值: 1.5【解】设则同时使用的终端数所求概率为3.设X 1 ,X 2 ,…,X n 为总体X 的一个样本,EX=μ,DX=σ 2 <∞,求SSS_TEXT_QUSTI该题您未回答:х 该问题分值: 1.5【解】 进而有从装有1个白球,2个黑球的罐子里有放回地取球,记 这样连续取5次得样本X 1 ,X 2 ,X 3 ,X 4 ,X 5 .记Y=X 1 +X 2 +…+X 5 ,求:SSS_TEXT_QUSTI4.Y的分布律,EY,E(Y 2 );该题您未回答:х该问题分值: 1.75【解】Y是连续5次取球中取得黑球的个数,所以从而SSS_TEXT_QUSTI5.,E(S 2 )(其中,S 2分别为样本X1,X2,…,X5的均值与方差).该题您未回答:х该问题分值: 1.75【解】由于X的分布律为所以6.若X~χ 2 (n),证明:EX=n,DX=2n.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】因X~χ 2 (n),所以X可表示为其中X1,X2,…,Xn相互独立,且均服从N(0,1),于是7.已知X~t(n),求证:X 2~F(1,n).SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】X~t(n),则X可表示为其中Z~N(0,1),Y~χ 2 (n)且Z,Y相互独立,又Z 2~χ 2 (1),于是8.设X1,X2,…,Xm,Y1,Y2,…,Yn独立.Xi~N(a,σ 2 ),i=1,2,…,m,Yi~N(b,σ 2 ),i=1,2,…,n,而α,β为常数.试求的分布.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】由于Xi ~N(a,σ 2 ),i=1,2,…,m,Yi~N(b,σ 2 ),i=1,2,…,n,且X1,X2,…,Xm,Y1,Y2,…,Yn相互独立,则也服从正态分布.所以9.一个罐子里装有黑球和白球,黑、白球数之比为a:1.现有放回的一个接一个地抽球,直至抽到黑球为止,记X为所抽到的白球个数.这样做了n次以后,获得一组样本:X1,X2,…,Xn基于此,求未知参数a的矩估计和最大似然估计.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】由题意知,随机变量X的分布律为令解得对于给定的样本X1,X2,…,Xn,似然函数为取对数,得令得解得10.罐中有N个硬币,其中有θ个是普通硬币(掷出正面与反面的概率各为0.5),其余N-θ个硬币两面都是正面,从罐中随机取出一个硬币,把它连掷两次,记下结果,但不去查看它属于哪种硬币,如此重复n次,若掷出0次、1次、2次正面的次数分别为n0,n1,n2,利用(1)矩法;(2)最大似然法,求参数θ的估计量.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】设X为“连掷两次正面出现的次数”,A={取出的硬币为普通硬币},则即X的分布为(1) 解得θ=N(2-μ1),θ的矩估计为(2)解得θ的最大似然估计11.设总体X的概率密度为又设X1,X2,…,Xn是来自X的一个简单随机样本,求未知参数θ的矩估计量SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】X的数学期望为用样本均值代替①中的EX得此方程的解即为θ的矩估计量12.设总体X的概率密度为试用样本X1,X2,…,Xn求参数α的矩估计和最大似然估计.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】先求矩估计:解得所以α的矩估计为再求极大似然估计:解得α的极大似然估计:13.设X1,X2,…,Xn是来自对数级数分布的一个样本,求p的矩估计.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】因为p很难解出来,所以再求总体的二阶原点矩①÷②得所以所以得p的矩估计14.设总体X服从参数为N和p的二项分布,X1,X2,Xn为取自X的样本,试求参数N和p的矩估计.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】解之得N=μ1/p,即所以N和p的矩估计为15.设总体X的分布列为截尾几何分布P{X=k}=θk-1(1-θ), k=1,2,…,r,P{X=r+1}=θr,从中抽得样本X1,X2,…,Xn,其中有m个取值为r+1,求θ的极大似然估计.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】解似然方程得θ的极大似然估计设总体X服从正态分布N(μ,σ 2 ),X1,X2,…,Xn是其样本.SSS_TEXT_QUSTI16.求C使得是σ 2的无偏估计量;该题您未回答:х该问题分值: 2【解】可见当是σ 2的无偏估计量.SSS_TEXT_QUSTI17.求k使得为σ的无偏估计量.该题您未回答:х该问题分值: 2【解】18.设X1,X2,…,Xn是来自总体X的一个样本,是θ的一个估计量,若θ+kn,试证:是θ的相合(一致)估计量.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】由切比雪夫不等式,对任意的ε>0有于是即依概率收敛于θ,故是θ的相合(一致)估计量.19.设X1,X2,…,Xn是取自均匀分布在[0,θ]上的一个样本,试证:Tn=max{X1,X2,…,Xn}是θ的相合估计.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】Tn =X(n)的分布函数为Tn的密度为所以由切比雪夫不等式有当n→∞时,故Tn是θ的相合估计.20.已知X具有概率密度X1,X2,…,Xn为X的简单随机样本.求未知参数α的矩估计和最大似然估计.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】先求矩估计.故再求最大似然估计得α的最大似然估计21.设总体X~N(μ,σ 2 ),X1,X2,X3是来自X的样本,证明:估计量都是μ的无偏估计,并指出它们中哪一个最有效.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】故都是μ的无偏估计.所以最有效.22.设X1,X2,…,Xn为总体X的一个样本,设EX=μ,DX=σ 2,试确定常数C,使为μ 2的无偏估计.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】由题意知:23.设总体服从U[0,θ],X1,X2,…,Xn为总体的样本,证明:为θ的一致估计.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】由切比雪夫不等式有:因此得为θ的一致估计.24.设从均值为μ,方差为σ 2>0的总体中分别抽取容量为n1,n2的两个独立样本,样本均值分别为证明:对于任何满足条件a+b=1的常数a,b,是μ的无偏估计量,并确定常数a,b,使得方差DT达到最小.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】由题意得:所以故T是μ的无偏估计量.又令对a求导并解方程如下:得到所以处取得极小值,此时方差DT达到最小.25.设X1,X2,…,Xn独立同分布,X2的取值有四种可能,其概率分布分别为:p1 =1-θ,p2=θ-θ 2,p3=θ 2 -θ 3,p4=θ 3,记N,为X1,X2,…,Xn中出现各种可能的结果的次数,N1+N2+N3+N4=n.确定a1,a2,a3,a4使为θ的无偏估计.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】由于Ni ~B(n,pi),i=1,2,3,4,所以E(Ni)=npi,从而有:若使T是θ的无偏估计,即要求解之得:即是θ的无偏估计.设总体X~N(μ1,σ 2 ),Y~N(μ2,σ 2 ).从总体X,Y中独立地抽取两个容量为m,n的样本X1,…,Xm和Y1,…,Yn.记样本均值分别为若是σ 2的无偏估计.求:SSS_TEXT_QUSTI26.C;该题您未回答:х该问题分值: 2【解】 同理故则SSS_TEXT_QUSTI27.Z 的方差DZ .该题您未回答:х 该问题分值: 2 【解】因故 则有28.设有k 台仪器,已知用第i 台仪器测量时,测定值总体的标准差为σ i ,i=1,2,…,k ,用这些仪器独立地对某一物理量θ各观察一次,分别得到X 1 ,X 2 ,…,X k ,设仪器都没有系统误差,即E(X i )=θ,i=1,2,…,k ,试求:a 1 ,a 2 ,…,a k 应取何值,使用 估计θ时, 是无偏的,并且最小?SSS_TEXT_QUSTI该题您未回答:х 该问题分值: 2 【解】(1)即当 是无偏的.(2)令函数 问题归结为求多元函数g(a 1 ,a 2 ,…,a k )在条件 之下的最小值.作拉格朗日函数:G(a 1 ,a 2 ,…,a k ,λ)=g(a 1 ,a 2 ,…,a k )+λ(a 1 +a 2 +…+a k -1).29.设{X n }是一随机变量序列,X n 的密度函数为:试证:SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】对任意给定的ε>0,由于30.设X1,X2, (X)n,…是独立同分布的随机变量序列,EXi=μ,DXi=σ2,i=1,2,…,令证明:随机变量序列{Yn}依概率收敛于μ.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】由切比雪夫不等式得:所以31.一生产线生产的产品成箱包装,每箱的重量是随机的,假设每箱平均重量50千克,标准差为5千克,若用最大载重为5吨的汽车承运,试用中心极限定理说明每辆车最多可装多少箱,才能保障不超载的概率大于0.977(Φ(2)=0.977).SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】设Xi是“装运的第i箱的重量”,n表示装运箱数.则EXi =50,DXi=5 2 =25,且装运的总重量Y=X1 +X2+…+Xn,{Xn}独立同分布,EY=50n,DY=25n.由列维—林德伯格中心极限定理知Y~N(50n,25n).于是故也就是最多可以装98箱.32.用概率论方法证明:SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】设{Xn }为一独立同分布随机变量序列,每个Xk服从参数为1的泊松分布,则EXk =1,DXk=1,服从参数为n的泊松分布.故有由列维—林德伯格中心极限定理知:33.截至2010年10月25日,上海世博会参观人数超过了7000万人.游园最大的痛苦就是人太多.假设游客到达中国馆有三条路径,沿第一条路径走3个小时可到达;沿第二条路径走5个小时又回到原处;沿第三条路径走7个小时也回到原处.假定游客总是等可能地在三条路径中选择一个,试求他平均要用多少时间才能到达中国馆.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】设游客需要X小时到达中国馆,则X的可能取值为3,5+3,7+3,5+5+3,5+7+3,7+7+3,…要写出X的分布律很困难,所以无法直接求EX.为此令Y={第一次所选的路径},即{Y=i}表示“选择第i条路径”.则因为E(X|Y=1)=3,E(X|Y=2)=5+EX,E(X|Y=3)=7+EX,所以故EX=15,即该游客平均要15个小时才能到达中国馆.34.设X1,X2, (X)n为一列独立同分布的随机变量,随机变量N只取正整数且N与{Xn}独立,求证:SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】35.假设你是参加某卫视“相亲节目”的男嘉宾,现有n位女嘉宾在你面前自左到右排在一条直线上,每两位相邻的女嘉宾的距离为a(米).假设每位女嘉宾举手时你必须和她去握手,每位女嘉宾举手的概率均为,且相互独立,若Z 表示你和一位女嘉宾握手后到另一位举手的女嘉宾处所走的路程,求EZ.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】设按从左到右的顺序将女嘉宾编号为1,2,…,n.X为“已经握手的女嘉宾的编号”,Y表示“将要去握手的女嘉宾的编号”,则于是36.对于任意二事件A1,A2,考虑二随机变量试证明:随机变量X1和X2独立的充分必要条件是事件A1和A2相互独立.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】记pi =P(Ai)(i=1,2),p12=P(A1A2),而ρ是X1和X2的相关系数.易见,随机变量X1和X2都服从0—1分布,并且(1)必要性.设随机变量X1和X2独立,则P(A1 A2)=P{X1=1,X2=1}=P{X1=1}P{X2=1}=P(A1)P(A2).从而,事件A1和A2相互独立.(2)充分性.设事件A1和A2相互独立,则也都独立,故从而,随机变量X1和X2相互独立.37.假设有四张同样卡片,其中三张上分别只印有a1,a2,a3,而另一张上同时印有a1,a2,a3.现在随意抽取一张卡片,令Ak={卡片上印有ak }.证明:事件A1,A2,A3两两独立但不相互独立.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】由于对任意k,j=1,2,3且k≠j,有可见事件A1,A2,A3两两独立.但是,由于可见事件A1,A2,A3不相互独立.38.某商品一周的需求量X是随机变量,已知其概率密度为假设各周的需求量相互独立,以Uk表示k周的总需求量,试求:(1)U2和U3的概率密度fk(x)(k=2,3);(2)接连三周中的周最大需求量的概率密度f(3)(x).SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】以Xi (i=1,2,3)表示“第i周的需求量”,则Xi的概率密度均为而U2 =X1+X2,U3=U2+X3.三周中周最大需求量为X(3)=max{X1,X2,X3}.(1)当x≤0时,显然f2 (x)=f3(x)=0;对于x>0,有于是,两周和三周的总需求量U2和U3的概率密度(2)设F(x)是随机变量X的分布函数.由题意知连续三周中的周最大需求量X(3)的分布函数为G(x)=[F(x)] 3.于是,有39.设X和Y相互独立都服从0-1分布:P{X=1}=P{Y=1}=0.6,试证明:U=X+Y,V=X-Y不相关,但是不独立.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2由协方差的定义和性质,以及X和Y相互独立,可见Cov(U,V)=E(UV)-EUEV=E(X 2 -Y 2 )-E(X+Y)E(X-Y)=E(X 2 )-E(Y 2 )=0.于是,U=X+Y,V=X-Y不相关.(2)现在证明U=X+Y,V=X-Y不独立.事实上,由P{U=0}=P{X=0,Y=0}=P{X=0}P{Y=0}=0.16,P{V=0}=P{X=0,Y=0}+P{X=1,Y=1}=P{X=0}P{Y=0}+P{X=1}P{Y=1}=0.52,P{U=0,V=0}=P{X=0,Y=0}=P{X=0}P{Y=0}=0.16≠0.16×0.52=P{U=0}P{V=0},可见U和V不独立.40.假设G={(x,y)|x 2 +y 2≤r 2 }是以原点为圆心,半径为r的圆形区域,而随机变量X和Y的联合分布是在网G上的均匀分布.试确定随机变量X和Y的独立性和相关性.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】(1)X和Y的联合密度为那么,X的密度函数f1 (x)和Y的密度函数f2(y)相应为由于f(x,y)≠f1 (x)f2(y),可见随机变量X和Y不独立.(2)证明X和Y不相关,即X和Y的相关系数ρ=0.因此,有于是,X和Y的相关系数ρ=0.这样,X和Y虽然不相关,但是不独立.41.假设某季节性商品,适时地售出1千克可以获利s元,季后销售每千克净亏损t元.假设一家商店在季节内该商品的销售量X(千克)是一随机变量,并且在区间(a,b)内均匀分布.问季初应安排多少这种商品,可以使期望销售利润最大?SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】根据条件随机变量X的概率密度为以Y=P(h)表示“销售利润”,它与季初应安排商品的数量h有关.由条件知为求使期望利润最大的h,我们计算销售利润Y=P(h)的数学期望.为此,首先注意到:a<h<b,销售利润Y=P(h)的数学期望为对h求导并令其等于0,得于是,季初安排h千克商品,可以使期望销售利润最大.42.独立地重复进行某项试验,直到成功为止,每次试验成功的概率为p.假设前5次试验每次的试验费用为10元,从第6次起每次的试验费用为5元.试求这项试验的总费用的期望值a.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】以X表示“试验的总次数”,首先求X的概率分布.设Ak={第k次试验成功}(k=1,2,…),则P(Ak)=p,X的概率分布为其中q=1-p.于是试验的总次数X服从参数为p的几何分布.现在求试验的总费用的期望值a.由条件知,试验的总费用为该项试验的总费用Y是一随机变量,其期望值为例如,设p=0.8,q=0.2,得a=12.498元;设p=q=0.5,得a=19.6875元;设p=0.2,q=0.8,得a=41.808元;设p=0.1,q=0.9,得a=70.4755元.43.利用列维—林德伯格定理,证明:棣莫弗—拉普拉斯定理.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】设随机变量X1,X2,…,Xn相互独立,同服从0—1分布;EXi =p,DXi=pq (i=1,2,…,n),Sn =X1+X2+…+Xn,ESn=np,DSn=npq,其中q=1-p.X1,X2,…,Xn满足列维—林德伯格定理的条件:X1,X2,…,Xn独立同分布且数学期望和方差存在,当n充分大时近似地Sn~N(np,npq).44.某保险公司接受了10000辆电动自行车的保险,每辆车每年的保费为12元.若车丢失,则赔偿车主1000元.假设车的丢失率为0.006,对于此项业务,试利用中心极限定理,求保险公司:(1)亏损的概率α;(2)一年获利润不少于40000元的概率β;(3)一年获利润不少于60000元的概率γ.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】设X为“需要赔偿的车主人数”,则需要赔偿的金额为Y=0.1X(万元);保费总收入C=12万元.易见,随机变量X服从参数为n,p的二项分布,其中n=10000,p=0.006;EX=np=60,DX=np(1-p)=59.64.由棣莫弗—拉普拉斯定理知,随机变量X近似服从正态分布N(60,59,64),随机变量Y近似服从正态分布N(6,0.5964).(1)保险公司亏损的概率(2)保险公司一年获利润不少于4万元的概率(3)保险公司一年获利润不少于6万元的概率45.将n个观测数据相加时,首先对小数部分按“四舍五入”舍去小数位后化为整数.试利用中心极限定理估计:(1)试当n=1500时求舍位误差之和的绝对值大于15的概率;(2)估计数据个数n满足何条件时,以不小于90%的概率,使舍位误差之和的绝对值小于10的数据个数n.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】设Xi 是“第i个数据的舍位误差”,由条件可以认为Xi独立且都在区间[-0.5,0.5]上服从均匀分布,从而EXi =0,DXi=1/12.记Sn =X1+X2+…+Xn,为n个数据的舍位误差之和,则ESn =0,DSn=n/12.根据列维—林德伯格中心极限定理,当n充分大时Sn近似服从N(0,n/12).记Φ(x)为N(0,1)的分布函数.(1)由于近似服从标准正态分布,且n=1500,可见(2)数据个数n应满足条件:由于近似服从N(0,1),可见于是,当n>721时,才能使误差之和的绝对值小于10的概率不小于90%.46.设X是任一非负(离散型或连续型)随机变量,已知的数学期望存在,而ε>0是任意实数.证明:不等式SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】(1)设X是离散型随机变量,其一切可能值为{xi},则(2)设X是连续型随机变量,其概率密度为f(x),则47.设事件A出现的概率为p=0.5,试利用切比雪夫不等式,估计在1000次独立重复试验中事件A出现的次数在450到550次之间的概率α.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】设vn是“1000次独立重复试验中事件A出现的次数”,则vn~B(1000,0.5),EX=1000×0.5=500,DX=1000×0.5 2 =250.利用切比雪夫不等式,知设来自总体X的简单随机样本X1,X2,…,Xn,总体X的概率分布为其中0<θ<1.分别以v1,v2表示X1,X2,…,Xn中1,2出现的次数,试求SSS_TEXT_QUSTI48.未知参数θ的最大似然估计量;该题您未回答:х该问题分值: 2【解】求参数θ的最大似然估计量.样本X1,X2,…,Xn中1,2和3出现的次数分别为v1,v2和n-v1-v2,则似然函数和似然方程为似然方程的唯一解就是参数θ的最大似然估计量SSS_TEXT_QUSTI49.未知参数θ的矩估计量;该题您未回答:х该问题分值: 2【解】求参数θ的矩估计量.总体X的数学期望为EX=θ 2+4θ(1-θ)+3(1-θ) 2.在上式中用样本均值估计数学期望EX,可得θ的矩估计量SSS_TEXT_QUSTI50.当样本值为1,1,2,1,3,2时的最大似然估计值和矩估计值.该题您未回答:х该问题分值: 2【解】对于样本值1,1,2,1,3,2,由上面得到的一般公式,可得最大似然估计值矩估计值51.假设一批产品的不合格品数与合格品数之比为R(未知常数).现在按还原抽样方式随意抽取的n件中发现k件不合格品.试求R的最大似然估计值.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】设a是这批产品中不合格品的件数,b是合格品的件数.从而,a=Rb,合格品率为设X是“随意抽取的一件产品中不合格品的件数”,则X服从参数为p的0-1分布.对于来自总体X的简单随机样本X1,X2,…,Xn,记vn=X1+X2+…+Xn,则似然函数和似然方程为由条件知vn =X1+X2+…+Xn=k,于是似然方程的唯一解即是R的最大似然估计值.1。
2018考研数学三模拟1试卷与解答

(B) 必要非充分
(C) 充分必要
1 1 x 2
(D) 非充分且非必要
(4)设 f ( x, y ) 为连续函数,则使 ( ) (A) f ( x, y) f ( x, y)
x 2 y 2 1
f ( x, y )dxdy 4 dx
0
0
f ( x, y )dy 成立的一个充分条件是
n x
x
(C)若 lim f ( x) , lim g ( x) 均不存在,则 lim f ( x) g ( x) 不存在
x x0 x x0 x x0
(D) lim[ f ( x) g ( x)] 不存在,但 lim g ( x) 存在,则 lim f ( x) 不存在
第 4 页 共 9 页
需要论文查重、建立模板请联系群主371991061
2018 数学考研模拟试卷
合肥工业大学 (共创) 考研辅导中心
Tel: 0551-62905018
数学三(模拟 1)参考答案
一、选择题: (1)~(8)小题,每小题 4 分,共 32 分.
(1)【解】当 f ( x)
0, x 0, 1, x 0, g ( x) ,则 lim f ( x) g ( x) 0 是存在的,故【答案】C. x 0 1, x 0. 0, x 0.
2
, X n 是 X ~ P( ) (Poisson 分布)的简单随机样本, X 与S 2 分别是样本 X1 ,
). (C) n、 (D) (B)
, X n 的样本
、
n
、
、
n
二、填空题:9~14 小题,每小题 4 分,共 24 分.请将答案写在答题纸指点位置上.
考研数学三模拟题2018年(27)_真题(含答案与解析)-交互

考研数学三模拟题2018年(27) (总分100, 做题时间90分钟)一、填空题1.设A为三阶实对称矩阵,α1 =(a,-a,1) T是方程组AX=0的解,α2=(a,1,1-a) T是方程组(A+E)X=0的解,则a=______.SSS_FILL该题您未回答:х该问题分值: 11 [解析] 因为A为实对称矩阵,所以不同特征值对应的特征向量正交,因为AX=0及(A+E)X=0有非零解,所以λ1 =0,λ2=-1为矩阵A的特征值,α1=(a,-a,1) T,α2=(a,1,1-a) T是它们对应的特征向量,所以有=a 2 -a+1-a=0,解得a=1.2.设有三个线性无关的特征向量,则a=______.SSS_FILL该题您未回答:х该问题分值: 14 [解析] 由得λ1 =-1,λ2=λ3=1.因为A有三个线性无关的特征向量,所以r(E-A)=1,解得a=4.3.设有三个线性无关的特征向量,则a=______.SSS_FILL该题您未回答:х该问题分值: 10 [解析] 由|λE-A|=0得A的特征值为λ1 =-2,λ2=λ3=6.因为A有三个线性无关的特征向量,所以A可以对角化,从而r(6E-A)=1,解得a=0.4.f(x1,x2,x3,x4)=X T AX的正惯性指数是2,且A 2 -2A=O,该二次型的规范形为______.SSS_FILL该题您未回答:х该问题分值: 1[解析] A 2 -2A=0 r(A)+r(2E-A)=4 A可以对角化,λ1 =2,λ2=0,又二次型的正惯性指数为2,所以λ1 =2,λ2=0分别都是二重,所以该二次型的规范形为.二、选择题1.设A为n阶矩阵,下列结论正确的是______.A.矩阵A的秩与矩阵A的非零特征值的个数相等B.若A~B,则矩阵A与矩阵B相似于同一对角阵C.若r(A)=r<n,则A经过有限次初等行变换可化为D.若矩阵A可对角化,则A的秩与其非零特征值的个数相等SSS_SIMPLE_SINA B C D该题您未回答:х该问题分值: 1答案:D[解析] A不对,如A的两个特征值都是0,但r(A)=1;B不对,因为A~B不一定保证A,B可以对角化;C不对,如A经过有限次行变换化为经过行变换不能化为因为A可以对角化,所以存在可逆矩阵P,使得于是r(A)= 故选D.2.设A,B为n阶可逆矩阵,则______.• A.存在可逆矩阵P,使得P-1AP=B• B.存在正交矩阵Q,使得Q T AQ=B•**,B与同一个对角矩阵相似D.存在可逆矩阵P,Q,使得PAQ=BSSS_SIMPLE_SINA B C D该题您未回答:х该问题分值: 1答案:D[解析] 因为A,B都是可逆矩阵.所以A,B等价,即存在可逆矩阵P,Q,使得PAQ=B,选D.3.设则A与B______.SSS_SINGLE_SELA 合同且相似B 相似但不合同C 合同但不相似D 既不相似又不合同该题您未回答:х该问题分值: 1答案:C[解析] 显然A,B都是实对称矩阵,由|λE-A|=0,得A的特征值为λ1=1,λ2 =2,λ3=9,由|λE-B|=0,得B的特征值为λ1=1,λ2=λ3=3,因为A,B惯性指数相等,但特征值不相同,所以A,B合同但不相似,选C.4.设A是三阶实对称矩阵,若对任意的三维列向量X,有X T AX=0,则______.SSS_SINGLE_SELA |A|=0B |A|>0C |A|<0D 以上都不对该题您未回答:х该问题分值: 1答案:A[解析] 设二次型其中Q为正交矩阵.取则f=X T AX=λ1=0,同理可得λ2=λ3=0,由于A是实对称矩阵,所以r(A)=0,从而A=O,选A.三、解答题1.设有三个线性无关的特征向量,求a及A n.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 5[解] 由得λ1=λ2,λ3=2.因为矩阵A有三个线性无关的特征向量,所以A一定可对角化,从而r(E-A)=1,即a=1,故由λ=1时,由(E-A)X=0,得由λ=2时,由(2E-A)X=0,得令则两边n次幂得从而设方程组有无穷多个解,为矩阵A的分别属于特征值λ1=1,λ2 =-2,λ3=-1的特征向量.SSS_TEXT_QUSTI2.求A;该题您未回答:х该问题分值: 3[解] 因为方程组有无穷多个解,所以解得a=1.令则从SSS_TEXT_QUSTI3.求|A * +3E|.该题您未回答:х该问题分值: 3[解] |A|=2,A *对应的特征值为即2,-1,-2,A * +3E对应的特征值为5,2,1,所以|A * +3E|=10.=2是A 设A为三阶实对称矩阵,A的每行元素之和为5,AX=0有非零解且λ1的特征值,对应特征向量为(-1,0,1) T.SSS_TEXT_QUSTI4.求A的其他特征值与特征向量;该题您未回答:х该问题分值: 3[解] 因为A的每行元素之和为5,所以有=5,对应的特征向量为即A有特征值λ2又因为AX=0有非零解,所以r(A)<3,从而A有特征值0,设特征值0对应的特征向量为,根据不同特征值对应的特征向量正交得解得特征值0对应的特征向量为SSS_TEXT_QUSTI5.求A.该题您未回答:х该问题分值: 3[解] 令由得6.设求a,b及正交矩阵P,使得P T AP=B.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 5[解] 因为A~B,所以tr(A)=tr(B),|A|=|B|,即解得a=1,b=0,则因为A~B,所以矩阵A,B的特征值都为λ1 =1,λ2=0,λ3=6.当λ=1时,由(E-A)X=0,得当λ=0时,由(0E-A)X=0,得当λ=6时,由(6E-A)X=0,得令再令则有P T AP=B.7.设A,B为n阶矩阵,且r(A)+r(B)<n.证明:A,B有公共的特征向量.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 5[证明] 因为r(A)+r(B)<n,所以r(A)<n,r(B)<n,于是λ=0为A,B公共的特征值,A的属于特征值λ=0的特征向量即为方程组AX=0的非零解;B的属于特征值λ=0的特征向量即为方程组BX=0的非零解,因为所以方程组有非零解,即A,B有公共的特征向量.设A是b阶矩阵,α1,α2,…,αn是n维列向量,且αn≠0,若Aα1=α2,Aα2=α3,…,Aαn-1=αn,Aαn=0.SSS_TEXT_QUSTI8.证明:α1,α2,…,αn线性无关;该题您未回答:х该问题分值: 2.5[证明] 令x1α1+x2α2+…+rnαn=0,则x1Aα1+x2Aα2+…+xnAαn=0 x1α2+x2α3+…+xn-1αn=0x1Aα2+x2Aα3+…+xn-1Aαn=0 x1α3+x2α4+…+xn-22αn-2=0 …x1αn=0因为αn ≠0,所以x1=0,反推可得x2=…=xn=0,所以α1,α2,…,αn线性无关.SSS_TEXT_QUSTI9.求A的特征值与特征向量.该题您未回答:х该问题分值: 2.5[解] 令P=(α1,α2,…,αn),则则A与B相似,由|λE=B|=0 λ1=…=λn=0,即A的特征值全为零,又r(A)=n-1,所以AX=0的基础解系只含有一个线性无关的解向量,而Aαn =0αn(αn≠0),所以A的全部特征向量为kαn(k≠0).10.设A为三阶方阵,A的每行元素之和为5,AX=0的通解为设β= 求Aβ.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 5[解] 因为A的每行元素之和为5,所以有即A有一个特征值为λ1=5,其对应的特征向量为又AX=0的通解为则r(A)=1 λ2=λ3=0,其对应的特征向量为Aξ2 =0,Aξ3=0.令x1ξ1,x2ξ2,x3ξ3=β,解得x1=8,x2=-1,x3=-2,则Aβ=8Aξ1 -Aξ2-2Aξ3=8Aξ1=11.求a,b及可逆矩阵P,使得P -1 AP=B.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 5[解] 由|λE-B|=0,得λ1 =-1,λ2=1,λ3=2,因为A~B,所以A的特征值为λ1 =-1,λ2=1,λ3=2.由tr(A)=λ1+λ2+λ3,得a=1,再由|A|=b=λ1λ2λ3=-2,得b=-2,即A=由(-E-A)X=0,得ξ1=(1,1,0) T;由(E-A)X=0,得ξ2=(-2,1,1) T;由(2E-A)X=0,得ξ3=(-2,1,0) T,令则由(-E-B)X=0,得η1=(-1,0,1) T;由(E-B)X=0,得η2=(1,0,0) T;由(2E-B)X=0,得η3=(8,3,4) T,令则由得令则P -1 AP=B.12.设求A的特征值与特征向量,判断矩阵A是否可对角化,若可对角化,求出可逆矩阵P及对角阵.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 5[解] |λE-A|= =(λ+a-1)(λ-a)(λ-a-1)=0,得矩阵A的特征值为λ1=1-a,λ2 =a,λ3=1+a.(1)当1-a≠a,1-a≠1+a,a≠1+a,即a≠0且时,因为矩阵A有三个不同的特征值,所以A一定可以对角化.λ1 =1-a时,由[(1-a)E-A]X=0得λ2=a时,由(aE-A)X=0得ξ2=λ3=1+a时,由[(1+a)E-A]X=0得(2)当a=0时,λ1=λ3=1,因为r(E-A)=2,所以方程组(E-A)X=0的基础解系只含有一个线性无关的解向量,故矩阵A不可以对角化.(3)当时,,因为,所以方程组的基础解系只含有一个线性无关的解向量,故A不可以对角化.13.设A为m×n实矩阵,且r(A)=n.证明:A T A的特征值全大于零.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 5[证明] 首先A T A为实对称矩阵,r(A T A)=n,对任意的X>0,X T (A TA)X=(AX) T (AX),令AX=α,因为r(A)=n,所以α≠0,所以(AX) T(AX)=α T α=|α| 2>0,即二次型X T (A T A)X是正定二次型,A T A为正定矩阵,所以A T A的特征值全大于零.14.设A为n阶正定矩阵.证明:对任意的可逆矩阵P,P T AP为正定矩阵.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 5[证明] 首先A T =A,因为(p T AP) T =P T A T (P T ) T =P T AP,所以P T AP为对称矩阵,对任意的X≠0,X T (P T AP)X=(PX) T A(PX),令PX=α,因为P 可逆且X≠0,所以α≠0,又因为A为正定矩阵,所以α T Aα>0,即X T (P T AP)X>0,故X T (P T AP)X为正定二次型,于是P T AP为正定矩阵.15.设P为可逆矩阵,A=P T P.证明:A是正定矩阵.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 5[证明] 显然A T =A,对任意的X≠0,X T AX=(PX) T (PX),因为X≠0且P可逆,所以PX≠0,于是X T AX=(PX) T (PX)=|PX| 2>0,即X T AX为正定二次型,故A为正定矩阵.16.设A,B为n阶正定矩阵.证明:A+B为正定矩阵.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 5[证明] 因为A,B正定,所以A T =A,B T =B,从而(A+B) T =A+B,即A+B为对称矩阵.对任意的X≠0,X T (A+B)X=X T AX+X T BX,因为A,B为正定矩阵,所以X T AX>0,X T BX>0,因此X T (A+B)X>0,于是A+B为正定矩阵.17.三元二次型f=X T AX经过正交变换化为标准形,且A * +2E的非零特征值对应的特征向量为求此二次型.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 5[解] 因为f=X T AX经过正交变换后的标准形为,所以矩阵A的特征值为λ1=λ2=1,λ3=-2.由|A|=λ1λ2λ3=-2得A *的特征值为μ1=μ2 =-2,μ3=1,从而A * +2E的特征值为0,0,3,即α1为A * +2E的属于特征值3的特征向量,故也为A的属于特征值λ3=-2的特征向量.令A的属于特征值λ1=λ2=1的特征向量为因为A为实对称矩阵,所以有=0,即x1 +x3=0故矩阵A的属于λ1=λ2=1的特征向量为令由得所求的二次型为18.设二次型经过正交变换X=QY化为标准形,求参数a,b及正交矩阵Q.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 5[解] 二次型的矩阵形式为f=X T AX其中因为所以A~B(因为正交矩阵的转置矩阵即为其逆矩阵),于是A的特征值为1,1,4.而|λE-A|=λ 3 -(a+4)λ 2 +(4a-b 2+2)λ+(-3a-2b+2b 2 +2),所以有λ 3 -(a+4)λ 2 +(4a-b 2+2)λ+(-3a-2b+2b 2+2)=(λ-1) 2(λ-4),解得a=2,b=1.当λ1=λ2=1时,由(E-A)X=0得由λ3=4时,由(4E-A)X=0得显然ξ1,ξ2,ξ3两两正交,单位化为则19.设齐次线性方程组有非零解,且为正定矩阵,求a,并求当|A|= 时X T AX的最大值.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 5[解] 因为方程组有非零解,所以=a(a+1)(a-3)=0,即a=-1或a=0或a=3.因为A是正定矩阵,所以aii>0(i=1,2,3),所以a=3.当a=3时,由得A的特征值为1,4,10.因为A为实对称矩阵,所以存在正交矩阵Q,使得而当时,=Y T Y=Y T Q T QY=(QY) T (QY)=X T X=|X| 2 =2所以当时,X T AX的最大值为20(最大值20可以取到,如y1 =y2=0,y3= ).20.设A为实对称矩阵,且A的特征值都大于零.证明:A为正定矩阵.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 5[证明] A所对应的二次型为f=X T AX,因为A是实对称矩阵,所以存在正交变换X=QY,使得对任意的X≠0,因为X=QY,所以Y=Q T X≠0,于是,即对任意的X≠0有X T AX>0,所以X T AX为正定二次型,故A 为正定矩阵.21.设A为m阶正定矩阵,B为m×n实矩阵.证明:B T AB正定的充分必要条件是r(B)=n.SSS_TEXT_QUSTI该题您未回答:х该问题分值: 5[证明] 因为(B T AB) T =B T A T (B T ) T =B T AB,所以B T AB为对称矩阵,设B T AB是正定矩阵,则对任意的X≠0,X T B T ABX=(BX) T A(BX)>0,所以BX≠0,即对任意的X≠0有BX≠0,或方程组BX=0只有零解,所以r(B)=n.反之,设r(B)=n,则对任意的X≠0,有BX≠0,因为A为正定矩阵,所以X T (B T AB)X=(BX) T A(BX)>0,所以B T AB为正定矩阵.1。
考研数学三模拟题2018年(29)_真题-无答案

考研数学三模拟题2018年(29)(总分100,考试时间90分钟)解答题1. 证明:方阵A是正交矩阵,即AA T=E的充分必要条件是:(1)A的列向量组组成标准正交向量组,即或(2)A的行向量组组成标准正交向量组,即2. 证明:n>3的非零实方阵A,若它的每个元素等于自己的代数余子式,则A是正交矩阵.3. 证明:方阵A是正交矩阵的充分必要条件是|A|=±1,且若|A|=1,则它的每一个元素等于自己的代数余子式;若|A|=-1,则它的每个元素等于自己的代数余子式乘-1.设α=[a1,a2,…,an]T≠0,β=[b1,b2,…,bn]T≠0,且αTβ=0,A=E+αβT,试计算:4. |A|;5. An;6. A-1.7. 设A是主对角元为0的四阶实对称阵,E是4阶单位阵,且E+AB是不可逆的对称阵,求A.8. 设证明:A=E+B可逆,并求A-1.9. A,B均是n阶矩阵,且AB=A+B.证明:A-E可逆,并求(A-E)-1.10. 设B是可逆阵,A和B同阶,且满足A2+AB+B2=O证明:A和A+B都是可逆阵,并求A-1和(A+B)-1.11. 已知A,B是三阶方阵,A≠O,AB=O.证明:B不可逆.12. 设A=(aij)n×n,且求r(A*)及A*.13. 已知n阶矩阵求|A|中元素的代数余子式之和,第i行元素的代数余子式之和及主对角元的代数余子式之和14. 设矩阵A的伴随矩阵且ABA-1=BA-1+3E,求B.15. 设A是n阶可逆阵,将A的第i行和第j行对换得到的矩阵记为B.证明:B可逆,并推导A-1和B-1的关系.16. 设A是n阶可逆阵,其每行元素之和都等于常数a.证明:(1)a≠0;(2)A-1的每行元素之和均为.17. A,B为n阶方阵.证明:18. 计算19. 设有矩阵Am×n,Bn×m,Em+AB可逆.(1)验证:En+BA也可逆,且(En+BA)-1=En-B(Em+AB)-1A;(2)设其中利用(1)证明:P可逆,并求P-1.20. 已知α1=[1,-1,1]T,α2=[1,t,-1]T,α3=[t,1,2]T,β=[4,t2,-1]T,若β可由α1,α2,α3线性表示,且表示法不唯一,求t及β的表达式.21. 设向量组α1,α2,…,αs(s≥2)线性无关,且β1=α1+α2,β2=α2+α3,…,βs-1=αs-1+αs,βs=αs+α1.讨论向量组β1,β2,…,βs的线性相关性.22. 设向量组α1,α2,…,αt是齐次线性方程组Ax=0的一个基础解系,向量β不是方程组Ax=0的解,即Aβ≠0.证明:向量组β,β+α1,β+α2,…,β+αt线性无关.23. 设向量组(Ⅰ)与向量组(Ⅱ),若(Ⅰ)可由(Ⅱ)线性表示,且r(Ⅰ)=r(Ⅱ)=r.证明:(Ⅰ)与(Ⅱ)等价.24. 求齐次线性方程组的基础解系.25. 问λ为何值时,线性方程组有解,并求出解的一般形式.26. λ为何值时,方程组无解,有唯一解或有无穷多解?并在有无穷多解时写出方程组的通解.设四元齐次线性方程组(Ⅰ)为又已知某齐次线性方程组(Ⅱ)的通解为k1[0,1,1,0]T+k2[-1,2,2,1]T.27. 求线性方程组(Ⅰ)的基础解系;28. 问线性方程组(Ⅰ)和(Ⅱ)是否有非零公共解?若有,则求出所有的非零公共解.若没有,则说明理由.29. 设γ1,γ2,…,γt和η1,η2,…,ηs分别是AX=0和BX=0的基础解系.证明:AX=0和BX=0有非零公共解的充要条件是γ1,γ2,…,γt和η1,η2,…,ηs线性相关.30. 已知α1=[1,2,-3,1]T,α2=[5,-5,a,11]T,α3=[1,-3,6,3]T,α4=[2,-1,3,a]T.问:(1)a为何值时,向量组α1,α2,α3,α4线性相关;(2)a为何值时,向量组α1,α2,α3,α4线性无关;(3)a为何值时,α4能由α1,α2,α3线性表出,并写出它的表出式.31. 已知问λ取何值时,(1)β可由α1,α2,α3线性表出,且表达式唯一;(2)β可由α1,α2,α3线性表出,但表达式不唯一;(3)β不能由α1,α2,α3线性表出.32. 设向量组α1=[a11,a21,…,an1]T,α2=[a12,a22,…,an2]T,…,αs=[a1s,a2s,…,ans]T.证明:向量组α1,α2,…,αs线性相关(线性无关)的充要条件是齐次线性方程组有非零解(有唯一零解).33. 已知α1,α2,…,αs线性无关,β可由α1,α2,…,αs线性表出,且表示式的系数全不为零.证明:α1,α2,…,αs,β中任意s个向量线性无关.34. 已知向量组α1,α2,…,αs+1(s>1)线性无关,βi=αi+tαi+1,i=1,2,…,s.证明:向量组β1,β2,…,βs线性无关.设A是3×3矩阵,α1,α2,α3是三维列向量,且线性无关,已知Aα1=α2+α3,Aα2=α1+α3,Aα3=α1+α2.35. 证明:Aα1,Aα2,Aα3线性无关;36. 求|A|.37. 已知A是n阶矩阵,α1,α2,…,αs是n维线性无关向量组,若Aα1,Aα2,…,Aαs 线性相关.证明:A不可逆.38. 设A是n×m阶矩阵,B是m×n矩阵,E是n阶单位阵.若AB=E,证明:B的列向量组线性无关.。
考研数学一模拟题2018年(68)_真题-无答案

考研数学一模拟题2018年(68)(总分150,考试时间90分钟)一、选择题(下列每题给出的四个选项中,只有一个选项是符合题目要求的.)1. 设函数f(x)在[1,2]上有二阶导数,f(1)=f(2)=0,F(x)=(x-1)2f(x),则F"(x)在(1,2)内______A. 没有零点B. 至少有一个零点C. 有两个零点D. 有且仅有一个零点2. 设f"x(a,b)存在,则等于______A.f"x(a,b)B.0C.2f"x(a,b)D.3. 设其中a≠0为常数,h(x)为连续函数且h(0)≠0,当x→0时,则______A. f(x)与g(x)是同阶无穷小,但不是等价无穷小B. f(x)与g(x)是等价无穷小C. f(x)是g(x)的高阶无穷小D. g(x)是f(x)的高阶无穷小4. 设y(x)是方程y"+a1y"+a2y=ex满足初始条件y(0)=1,y"(0)=0的特解(a1,a2均为常数),则______A. 对于a2<1时,x=0是y(x)的极大值点B. 对于a2<1时,x=0是y(x)的极小值点C. 对于a2>1时,x=0不是y(x)的极大值点D. 对于a2>1时,x=0是y(x)的极小值点5. 若向量β可由向量组α1,α2,…,αt线性表示,则下列结论中正确的是______A. 存在一组不全为零的数k1,k2,…,kt使等式β=k1α1+k2α2+…+ktαt成立B. 存在一组全为零的数k1,k2,…,kt使等式β=k1α1+k2α2+…+ktαt成立C. 存在一组数k1,k2,…,kt使等式β=k1α1+k2α2+…+ktαt成立D. 对β的线性表示式唯一6. 已知矩阵,那么与A既相似又合同的矩阵是______A.B.C.D.7. 设随机变量X与Y均服从正态分布,X~N(μ,62),Y~N(μ,82),记P1=P{X≤μ-6},P2={Y≥μ+8},则______A. 对任何实数μ,都有P1=P2B. 对任何实数μ,都有P1<P2C. 只对μ的个别值,才有P1=P2D. 对任何实数μ,都有P1>P28. 设总体X服从正态分布N(0,σ2)(σ2已知),X1,X2,…,Xn是取自总体X的简单随机样本,S2为样本方差,则______A.B.C.D.二、填空题(每小题4分,共24分.)1. =______.2. 数列的最小项的项数n=______,且该项的数值为______.3. 设u=f(x,xy,xyz),则=______.4. 幂级数的收敛域为______.5. 设,B为三阶方阵,且秩(B)=2,若秩(AB)=1,则t=______.6. 设X,Y服从二维正态分布,则D(3X-2Y)=______.三、解答题(共94分.解答应写出文字说明、证明过程或演算步骤.)1. 设n是曲面2x2+3y2+z2=6在点P(1,1,1)处的指向外侧的法向量,求函数在点P处沿方向n的方向导数;2. 求微分方程3y"-2y"=4x的一般解.3. 计算其中D:x2+y2≤1.4. 试确定A,B,C的值,使得ex(1+Bx+Cx2)=1+Ax+o(x3),其中o(x3)是当x→0时比x3高阶的无穷小.5. 设f(x)在(a,b)内可微,且证明对于在f"(0)与g(x1)之间的任何值μ,在0与x1之间至少存在一点ξ使f"(ξ)=μ.6. 设求证:对任意的c>0,方程f(x)=c在[1,+∞)上有唯一解.7. 设三阶矩阵,试求r(A).8. 设λ1,λ2为n阶方阵A的特征值,且λ1≠λ2,而x1,x2分别为对应的特征向量,试证明ax1+bx2不是A的特征向量,ab≠0.先将2封信投入编号为1,2,3的3个邮筒,设X,Y分别表示投入第1号和第2号邮筒的信的数目.试求:9. (X,Y)的联合分布;10. X与Y是否相互独立?11. Y=0时X的条件分布;12. 随机变量函数Z=2X+Y与U=XY的分布;13. 随机变量M=max(X,Y)与m=min(X,Y)的分布.14. 假设二维随机变量(X,y)在矩形G={(x,y)|0≤x≤2,0≤y≤1}上服从均匀分布,记求:(1)U与V的联合分布;(2)U与V的相关系数ρ.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考研数学冲刺模拟卷(数学二)
一、选择题:~小题,每小题分,共分,下列每小题给出的四个选项中,只有一项符合题目要求的,请将所选项前的字母填在答题纸...
指定位置上.
()若函数0(),0x f x b x >=⎪≤⎩
在0x =处连续,则( ) ()14
ab =
()12
ab =-
()0ab =
()2ab =
()设二阶可导函数()f x 满足(1)(1)1,(0)1f f f =-=-=且''
()0f x <,则( )
()
1
1
()0f x dx ->⎰
()11
()0f x dx -<⎰ ()011
()()f x dx f x dx ->⎰⎰ ()01
1
()()f x dx f x dx -<⎰⎰
()设数列{}n x 收敛,则( )
()当lim tan 0n n x →∞
=时,lim 0n n x →∞
=
()当lim(0n n x →∞
=时,lim 0n n x →∞=
()当2lim()0n n n x x →∞
-=时,lim 0n n x →∞= ()当lim(sin )0n n n x x →∞
+=时,lim 0n n x →∞
=
()微分方程244(1sin 2)x
y y y e x '''-+=+的特解可设为*
y =( ) ()22(cos 2sin 2)x
x Ae
e B x C x ++ ()22(cos 2sin 2)x x Axe e B x C x ++ ()222(cos 2sin 2)x
x Ax e
e B x C x ++ ()22(cos 2sin 2)x x Axe e B x C x ++
()设(,)f x y 具有一阶偏导数,且对任意的(,)x y ,都有(,)(,)
0,0f x y f x y x y
∂∂<>∂∂,则( )
()(0,0)(1,1)f f > ()(0,0)(1,1)f f < ()(0,1)(1,0)f f > ()(0,1)(1,0)f f < ()甲乙两人赛跑,计时开始时,甲在乙前方(单位:)处,图中实线表示甲的速度曲线1()v v t =(单位:/m s ),虚线表示乙的速度曲线2()v v t =,三块阴影部分面积的数值依次为,计时开始后乙超过上甲的时刻记为0t (单位:),则( )
()010t =
()01520t <<
()025t = ()025t >
()设A 为m n ´阶矩阵,且()
r A m n =<,则下列结论正确的是( ) ()A 的任意m 阶子式都不等于零 ()A 的任意m 个列向量线性无关
()方程组AX b =一定有无穷多解 ()矩阵A 经过初等行变换可化为()
m E O ()设()111,
0,2,T c a =,()220,2,1,T c a =,()
331,2,3,T
c a =,
()41,0,1,0T
a =,
其中()
1,2,3i c i =为任意实数,则( )
()1234,,,a a a a 必线性相关 ()1234,,,a a a a 必线性无关 ()123,,a a a 必线性相关 ()234,,a a a 必线性无关
二、填空题:-小题,每小题分,共分,请将答案写在答题纸...指定位置上. () 曲线21
ln(1)x y x e x
=+
+的斜渐近线方程为 () 设函数()y y x =由参数方程()0sin t
t
u
x t e y u e du ⎧=+⎪
⎨=+⎪⎩
⎰确定,则220t d y dx == ()
21
ln x
dx x
+∞
=⎰
() 设函数(,)f x y 具有一阶连续偏导数,且,(1)y y f f
ye x y e x y
∂∂==+∂∂,(0,0)0f =, 则(,)_______f x y =. ()已知1
tan ()x t
f x dt t
=
⎰,则10()______f x dx =⎰.
()设,a b 为四维非零的正交向量,且T
A ab =,则A 的所有特征值为 .
三、解答题:—小题,共分.请将解答写在答题纸...指定位置上.解答应写出文字说明、证明过程或演算步骤.
()
(本题满分分)求极限
lim x t x dt du
+
→⎰⎰
()(本题满分分)设函数()f u 在()0,
+∞内具有二阶导数,且z f
=
满足等式
22222212z z z z x y z x y x y x y ⎛⎫⎛⎫
∂∂∂∂ +=++ ⎪ ∂∂+∂∂⎝⎭⎝,若()()00,01,f f '==求函数()f u 的表达式.
()求()()
2
1
ln ln lim
n
n k k n k n n →∞
=+-∑
()(本题满分分)设函数()f x 连续,且
()2
13arccot 2
x
tf x t dt x -=⎰.已知()21f =,求()3
2
f x dx ⎰的值.
()(本题满分分)设()y f x =是区间[0,1]上的任一非负连续函数,()f x 在区间(0,1)内可导,且2()
(),f x f x x
'>-
试证明在(0,1)内,1()()0x xf x f t dt -=⎰存在唯一实根.
()(本题满分分)已知平面区域(){}2
2
,|2,D x y x
y x =
+≤计算二重积分()2
1D
y dxdy +⎰⎰。
()(本题满分分)设()y x 是区间30,2⎛
⎫
⎪⎝
⎭
内的可导函数,且(1)1y =,点P 是曲线: ()y y x =上任意一点,在点处的切线与轴相交于点()
,0p X ,法线与轴相交于点()
0,p Y ,若p p X Y =,求上点的坐标(),x y 满足的方程。
()(本题满分分)设1234,,,,a a a a b 均为四维列向量,()
1234,,,A a a a a =,非齐次线性方程组AX b =的通解为()()1,
2,0,32,3,1,5T T
k -+-
(Ⅰ)求方程组()
234,,X a a a b =的通解;
(Ⅱ)求方程组()
12344,,,,X a a a a a b b +=的通解.
()设二次型()
222
123123121323,,,53266f x x x x ax x x x x x x x =++-+-的矩阵合同于
100010000骣琪琪琪琪桫
. (Ⅰ)求常数a ;(Ⅱ)用正交变换法化二次型()123,,f x x x 为标准形.。
