传热学热对流计算 (1)

合集下载

传热学计算总结

《传热学》计算题总结一、题型导热换热、对流换热、辐射换热、换热器二、公式小结1、平壁稳态导热第一类边界条件： 1）单层：xt t t t w w w δ121--=221/)(m W t t q w w -=δλ多层∑∑=+=+-=-=ni in n i i in R t t t t q 1,11111λλδ第三类边界条件：传热问题2112111h h t t q n i i f f ++-=∑=λδ单位W/m 22、圆筒壁稳态导热第一类边界条件单层：121121r r n r r nt t t t w w w =--()12212112212r r n l t t t t r r n lw w w w πλπλ-=-=Φ多层：∑=++-=Φn i ii i n w w r r n l t t 111,1121 λπ第三类边界条件：1211112121ln 2121+=+++-=∑n n i i if f l r h ri r r h t t q ππλπ单位：W/m3、对流换热牛顿冷却公式：[]W )(f w t t hA Φ-=吸放热热量（热对流）：tvc t t mc p f f p ∆=-=Φρ)(21平板对流换热表面换热系数h管内对流换热表面换热系数h ：n Nu Pr Re023.08.0=（紊流，流体被加热n=0.4,流体被冷却 n=0.3）对流换热解题步骤1）定性温度→查物性，下标f 由t f 确定，下标w 由t w 确定； 2）由Re 判断流态；3）据Re 选择准则关联式计算Nu f ； 4）计算h 。

注意：1）外掠平板定性温度tm=1/2(tw+tf);管内定性温度tf 2）外掠平板临界Re=5×105；管内临界Re=104 3）换热量据牛顿冷却公式计算。

4、辐射换热斯蒂芬－玻尔兹曼定律（四次方定律）: （黑体）两表面封闭体系的辐射换热量：（实际表面）几种特殊情况的简化式：（a ） X 1-2=1时：（其中一个表面为平面或凸表面）（b ）A 1=A 2 时：（两无限大平壁之间）(c) A 1/A 2≈0 时（空腔与内包壁）遮热板：111)T T (21214241b 2,1-+-=εεσq5、换热器设计计算传热过程方程式m t kA ∆=Φ；minmax minmax t lnt t t t m ∆∆∆-∆=∆热平衡式)()(22221111t t c M t t c M '-''=''-'=Φ，其中M 为质量流量kg/s,c 为定压比热，由对应算术平均温度确定。

热传递热量计算公式

热传递热量计算公式
热传递是指热量从一个物体传递到另一个物体的过程。

热传递的计算可以通过多种公式来实现，具体取决于热传递的方式。

以下是一些常见的热传递计算公式：
1. 热传导（导热）的计算公式：
热传导是指热量通过物质内部传递的过程。

其计算公式可以用傅立叶定律来表示：
Q = -kAΔT/Δx.
其中，Q表示传导热量，k表示热导率，A表示传热面积，ΔT表示温度差，Δx表示传热距离。

2. 热对流的计算公式：
热对流是指热量通过流体（气体或液体）对流传递的过程。

其计算公式可以用牛顿冷却定律来表示：
Q = hAΔT.
其中，Q表示对流热量，h表示对流换热系数，A表示传热面积，ΔT表示温度差。

3. 热辐射的计算公式：
热辐射是指热量通过辐射传递的过程。

其计算公式可以用斯特藩-玻尔兹曼定律来表示：
Q = εσA(T₁^4 T₂^4)。

其中，Q表示辐射热量，ε表示发射率，σ表示斯特藩-玻尔兹曼常数，A表示辐射面积，T₁和T₂分别表示两个物体的绝对温度。

以上是一些常见的热传递计算公式，它们分别适用于不同的热传递方式。

在实际问题中，需要根据具体情况选择合适的公式进行计算。

传热学(第9章--对流换热)

— —
横向节距纵向节距
23
9-3 流体有相变时的对流换热
一、凝结换热
1.特点：
——蒸汽和低于饱和温度的冷壁面相接触时会发生凝结换热，放出凝结潜热。（如电厂中：凝汽器和回热加热器内，管外蒸汽与管外壁的换热）
➢两种凝结方式：根据凝结液体依附在壁面上的形
态不同分.
tw ts
1）膜状凝结：凝结液体能润湿壁面，
腾换热设备安全经济的工作区为泡态沸腾区。
34
炉内高热负荷区水冷壁沸腾换热的强化
35
各种对流换热比较
液体对流换热比气体强；
对同一种流体，强制对流换热比自然对流换热强；
紊流换热比层流换热强；横向冲刷比纵向冲刷强；
有相变的对流换热比无相变换热强。
表9-5 各种对流换热平均换热系数的大致范围
换热系数 α[w/(m2.K)]
二是在蒸汽中混入油类或脂类物质。对紫铜管进行表面改性处理，能在实验室条件下实现连续的珠状凝结，但在工业换热器上应用，尚待时日。
26
2.影响蒸汽膜状凝结换热的因素：
（1）蒸汽中含有不凝结气体的影响 ➢ 蒸汽中含有不凝结气体（如空气）时，即使含量极微，
也会对凝结换热产生十分有害的影响。不凝结气体将会在液膜外侧聚集而形成一层气膜，使热阻大大增加，从而恶化传热。
21
（1）管束排列方式的影响
s1
s1
s2
顺排
s2
叉排
叉排：换热系数大，但流动阻力大. 顺排：换热系数小，但流动阻力小.
22
s1
s1
s2
s2
顺排
叉排
（2）流动方向上管排数的影响
后排管受前排管尾流的扰动作用对平均换热系数的影响直到20排以上的管子才能消失。

计算重点公式传热学

计算重点公式传热学传热学是研究热能在物质之间传递的学科，涵盖了热传导、热对流和热辐射三种传热方式。

在工程和科学领域中，计算传热是非常重要的，可以用来优化和设计各种热能设备和系统。

下面将介绍一些重要的传热计算公式。

1.热传导计算公式热传导是通过分子间的相互作用传递热能的方式。

对于常见的一维热传导问题，可以使用傅里叶热传导定律进行计算：q = -kA(dT/dx)其中，q是单位时间内通过物体的热量流率，k是物质的热导率，A 是传热截面积，dT/dx是温度梯度。

如果传热是在不同的材料之间进行，还需要考虑热传导的界面热阻。

界面热阻的计算公式为：R=1/(hA)其中，R是界面热阻，h是对流传热系数。

2.热对流计算公式热对流是通过流体的对流传递热能的方式。

对于流体中的对流传热，可以使用牛顿冷却定律进行计算：q=hAΔT其中，q是单位时间内通过物体的热量流率，h是对流传热系数，A 是传热表面积，ΔT是流体和物体之间的温度差。

对流传热系数h可以通过实验测量或者经验公式进行估算，常用的计算公式有Nusselt数和普朗特数。

3.热辐射计算公式热辐射是通过物体表面的电磁辐射传递热能的方式。

对于黑体辐射，可以使用斯特藩—玻尔兹曼定律进行计算：q=σAε(T^4)其中，q是单位时间内通过物体的热量流率，σ是斯特藩—玻尔兹曼常数，A是物体的表面积，ε是物体的辐射率，T是物体的温度。

对于非黑体的辐射传热，还需要考虑辐射率和视觉系数等因素。

4.综合传热计算在实际问题中，常常会有多种传热方式同时存在。

此时，需要将不同传热方式的热流量进行累加，得到总的传热量。

根据能量守恒定律，可以得到以下综合传热公式：q_total = q_conduction + q_convection + q_radiation其中，q_total是总的热量流率，q_conduction是热传导的热量流率，q_convection是热对流的热量流率，q_radiation是热辐射的热量流率。

对流传热

对流传热第一题：知识点总结（一）对流传热概述1、对流传热：流体流过固体壁时的热量传递。

传热机理：热对流和热传导的联合作用热流量用牛顿冷却公式表示：Φ=hA△t其中对流传热面积A，温差△t，对流传热系数h2、影响对流传热系数的因素（1）流动的起因：>由于流动起因的不同，对流换热分为强迫对流传热与自然对流传热两大类。

（2）流动速度：>根据粘性流体流动存在着层流和湍流两种状态，对流传热分为层流对流传热与湍流对流传热两大类。

（3）流体有无相变：同种流体发生相变的换热强度比无相变时大得多。

（4）壁面的几何形状、大小和位置：对流体在壁面上的运动状态、速度分布和温度分布有很大影响。

（5）流体的热物理性质：影响对流传热系数有热导率λ，密度，比定压热容，流体粘度，体积膨胀系数。

综上所述，影响对流传热系数h的主要因素，可定性地用函数形式表示为h=f（v，l，λ，，，或，，）（二）流动边界层和热边界层1、流动边界层特性：（1）流体雷诺数较大时，流动边界层厚度与物体的几何尺寸相比很小；（2）流体流速变化几乎完全在流动边界层内，而边界层外的主流区流速几乎不变化；（3）在边界层内，粘性力和惯性力具有相同的量级，他们均不可忽略；（4）在垂直于壁面方向上，流体压力实际上可视为不变，即=0；（5）当雷诺数大到一定数值时，边界层内的流动状态可分为层流和湍流。

2、热边界层定义：当流体流过物体，而平物体表面的温度与来流流体的温度不相等时，在壁面上方形成的温度发生显著变化的薄层，称为热边界层。

热边界层厚度：当壁面与流体之间的温差达到壁面与来流流体之间的温差的0.99倍时，即=0.99，此位置就是边界层的外边缘，而该点到壁面之间的距离则是热边界层的厚度记为。

与δ一般不相等。

3、普朗特数流动边界层厚度δ反应流体分子动量扩散能力，与运动粘度有关；而热边界层厚度反应流体分子热量扩散的能力，与热扩散率a有关。

==它的大小表征流体动量扩散率与热量扩散率之比（三）边界层对流传热微分方程组1、连续性方程+=02、动量微分方程根据动量定理可导出流体边界层动量微分方程流体纵掠平壁时3、能量微分方程热扩散率a=边界层能量微分方程式：+=4、对流传热微分方程-------x处的对流传热温差------流体的热导率-------x处壁面上流体的温度变化率（四）、管内强迫对流传热1、全管长平均温度可取管的进、出口断面平均温度的算术平均值作为全管长温度的平均，即=（）2、层流和湍流的判别由雷诺数Re大小来判别针对管内流动，当Re<2200时为层流；Re>1×时为湍流；2200<Re<1×时则为不稳定的过渡段（1）管内流动：（2）板内流动：湍流强迫对流传热管内强迫对流平均对流传热系数特征数关联式为：=0.023R P:考虑边界层内温度分布对对流传热系数影响的温度修正系数；:考虑短管管长对对流传热系数影响的短管修正系数；:考虑管道弯曲对对流传热系数影响的弯管修正系数。

传热学第五章对流换热

第五章
§5-1 §5-2 §5-3 §5-4 §5-5 §5-6 §5-7 §5-8
对流换热
Convective heat transfer
对流换热概说对流换热的数学描写对流换热边界层微分方程组对流换热边界层积分方程组相似理论与量纲分析管内受迫流动横向外掠圆管的对流换热自然对流换热及实验关联式
λ ∂t 换热微分方程（描写h的本质，hx = − ∆t ( ∂y ) y =0 dA）连续性方程（描写流体流动状态，即质量守恒）动量微分方程（描写流动状态，即动量守恒）能量微分方程（描写流体中温度场分布）
对流换热微分方程组先作假设：（1）仅考虑二维问题；（2）流体为不可压缩的牛顿流体，稳定流动；（3）常物性，无内热源；（4）忽略由粘性摩擦而产生的耗散热。以二维坐标系中的微元体为分析对象，根据热力学第一定律，对于这样一个开口系统，有：
同理：（） dτ qm hout − qm hin ≈ ρcp (
y
H y + dy − H y =
∂t ∂v ⋅ v + ⋅ t )dxdydτ ∂y ∂y
（qm h)out − (qm h)in ∴ ∂t ∂t ∂u ∂v = ρ c p (u + v )dxdy + ρ c p t ( + )dxdy ∂x ∂y ∂x ∂y ∂t ∂t = ρ c p (u + v )dxdy (d ) ∂x ∂y
1.流动边界层（Velocity boundary layer ）
如果流体为没有粘性流体，流体流过平板时，流速在截面上一直保持不变。如果流体为粘性流体，情况会如何呢？我们用一测速仪来测量壁面附近的速度分布。测量发现在法向方向上，即y方向上，壁面上速度为零，随着y方向的增加，流速急剧增加，到达一薄层后，流速接近或等于来流速度，德国科学家普朗特L.Prandtl研究了这一现象，并且在 1904年第一次提出了边界层的概念。

传热学第五章对流原理.

层流边界层紊流核心区
过渡区紊流边界层层流底层主流区速度边界层厚度临界距离
层流
过渡流
湍流
u
y
x

xc

层流底层缓冲层
根据流体力学知识，层流边界层厚度 xv 5x 5x 5 vf vf x Re x

在层流边界层内的速度分布线为抛物线型；在紊流边界层内，层流底层部分的速度分布较陡，接近于直线，而在底层以外的区域，由于流体微团的紊流运动，动量传递被强化了，速度变化趋于平缓。

如果流体的流动是由于流体冷热部分的密度不同引起的浮升力造成的，则称为自然对流。暖气片的散热，蒸汽或其他热流体输送管道的热量损失，都与这类换热有关。一般来讲：强迫对流换热优于自然对流。
二、在分析对流换热时，还应分清流体的流态。流体力学告诉我们，流体受迫在流道内流动时可以有两种不同性质的流态。流体分层地平行于流道的壁面流动，呈现层流状态。但当流动状态到超过某一临界值时，流体的流动出现了旋涡，而且在不断地发展和扩散，引起不规则的脉动，使流动呈现紊流状态。
α ＝q/（tf－tw） W
对流换热系数 α表征着对流换热的强弱。
在数值上，它等于流体和壁面之间的温度差为 1℃时，通过对流换热交换的热流密度。单位为W/(m２·℃)。对流换热量以及相应的换热系数的大小，将更多地取决于流体的运动性质和情况。
一、速度边界层
流体力学指出，具有粘性且能湿润固体壁面的流体，流过壁面会产生粘性力。根据牛顿粘性（内摩擦）定律，流体粘性力 τ 与垂直于运动方程速度梯度 (dv/dy ）成正比，即: τ＝μ（dv/dy）Ｎ／m２（5-2）式中，μ 称为流体的动力粘度，单位为Pa· s 或kg/(m· s）。

传热学第五章_对流换热原理-1

Velocity = v Velocity = 0
Velocity Temperature
Boundary Boundary
Layer
Layer
HOT SURFACE, TEMP = TH
3. 热边界层厚度δt和流动边界层厚度δ的区别与联系
(2) 边界层产生原因：
由于粘性的作用，流体与壁面之间产生一粘滞力，粘滞力使得靠近壁面处的速度逐渐下降，最后使壁面上的流体速度降为零，流体质点在壁面上产生一薄层。随着流体的流动，粘滞力向内传递，形成的薄层又阻碍邻近流体层中微粒运动的作用，依此类推，形成的薄层又阻碍邻近流体层微粒运动，到一定程度，粘滞力不再起作用。
➢ 如果流体为粘性流体，情况会如何呢？我们用一测速仪来测量壁面附近的速度分布。测量发现在法向方向上，即y 方向上，壁面上速度为零，随着y方向的增加，流速急剧增加，到达一薄层后，流速接近或等于来流速度，普朗特研究了这一现象，并且在1904年第一次提出了边界层的概念。
普朗特在仔细观察了粘性流体流过固体表面的特性后提出了突破性的见解。他认为，粘滞性起作用的区域仅仅局限在靠近壁面的薄层内。在此薄层以外，由于速度梯度很小粘滞性所造成的切应力可以略而不计，于是该区域中的流动可以作为理想流体的无旋流动。这种在固体表面附近流体速度发生剧烈变化的薄层称为流动边界层(又称速度边界层)．图5—5示出了产生流动边界层的两种常见情形。如图5—5a所示，从y＝o处u＝0开始，流体的速度随着离开壁面距离y的增加而急剧增大，经过一个薄层后u增长到接近主流速度。这个薄层即为流动边界层，其厚度视规定的接近主流速度程度的不同而不同。通常规定达到主流速度的99％处的距离y为流动边界层的厚度，记为δ 。

工程热力学和传热学16对流换热计算

解： t 200 30 q裸管＝ 1700W m 2 1 1 10 q绝缘 t 50 30 200W m 2 1 1 10
4、尺寸为 100cm 80cm的大玻璃窗，玻璃厚 104cm, 0.762W (m K )。室内空气与玻璃板的换热系数 1＝10W (m 2 K )，室外空气与玻璃板的换热系数 2 ＝20W (m 2 K )。室内空气温度为 20C，室外大气温度为－ 20C。试求通过该玻璃窗的热流量Q和热流密度q。
tf1＝20°C q
α1 tt
w1
α2 tf2＝－20°C
tw2
1
1 2
1
教材P155 中（ 13 - 8式）：k
1

1 是错误的。 2
1．火管锅炉炉胆的热流密度为48000Ｗ／ｍ２，钢板制成的炉胆厚度为２０ｍｍ，试求其内外壁面的温差, 设:(1)炉胆两侧没有污垢；(2)在水的一侧积有1.5㎜厚的水垢；(3)在水的一侧积有1.5㎜，另一侧积有２㎜厚的烟灰。
2．蒸汽管的外径为108ｍｍ,管外包以λ＝0.1Ｗ/(m·K)的绝热材料,蒸汽温度为 330℃(由于蒸汽与管壁间的对流热阻和管壁的导热热阻要比绝热材料的热阻小得多, 可略去不计,所以可近似地认为绝热层内壁的温度等于蒸汽的温度)。若要使绝热层外壁面的温度不超过40℃,每米管长的热损失不超过ql＝150Ｗ/m,试求绝热层的最小厚度应为多少。 d 330 40 d （330 40） 2 0.1 1.215 解：qmin ln 2 ＝1.215 2 e d d1 150 d1 ln 2 d1 2 d2 1 d 2 d1 d1 e1.215 1 min＝ d1 0.108 ＝0.128m 2 2 2 解说：

对流换热公式汇总与分析精品

对流换热公式汇总与分析【摘要】流体与固体壁直接接触时所发生的热量传递过程，称为对流换热，它已不是基本传热方式。

本文尝试对对流换热进行简单分类并对无相变对流换热公式简单汇总与分析。

【关键词】对流换热类型公式适用范围对流换热的基本计算形式一一牛顿冷却公式：q=h(t w-t f) (W/m2)或Am2上热流量门二h(t w -t f) (W)上式中表面传热系数h最为关键，表面传热系数是众多因素的函数，即h = f(u,t w，t f, ■ ,C p,匚:，fl)综上所述，由于影响对流换热的因素很多，因此对流换热的分析与计算将分类进行，本文所涉及的典型换热类型如表 1所示。

表1典型换热类型1.1内部流动1.1.1圆管内受迫对流换热(1)层流换热公式西德和塔特提出的常壁温层流换热关联式为Nu =1.86Re73 Pr；/3(g)1/3( -)0.14f f f Iw或写成NU f =1.86(Pe f d)1/3(>)0.14f I (J.w式中引用了几何参数准则d，以考虑进口段的影响。

[1适用范围：0.48 ::: Pr <16700，0.0044 ：：(」厂：9.75。

—w定性温度取全管长流体的平均温度，定性尺寸为管内径d。

如果管子较长，以致[(Re 卩芒)1/3(土)0.14]乞 2lw则NU f可作为常数处理，采用下式计算表面传热系数。

常物性流体在热充分发展段的 Nu是NU f =4.36(q=co nsl)NU f =3.66(t w =c onst)(2)过渡流换热公式对于气体，0.6 ::: Pr f :: 1.5， 0.5 ：：匚：:1.5，2300 :: Re f :: 104。

0.8 0.4 d、2/3 Tf、0.45NU f =0.0214(Re f -100)Pr f [1 (一)]()l T wPr对于液体，1.5 ：： Pr f ::: 500，0.05 —：： 20，2300 :: Re f :: 104。

传热学对流换热

传热学 / 对流换热
二、连续性微分方程（质量守恒方程）
依据质量守恒定律，在单位时间内，净流入微元体的质量等于微元体内的质量增量。
（2）层流状态时，以导热为主， dt/dy较大，对流换热较弱；
（有热边界层和层流速度边界层）（3）湍流状态时，对流很强，导热可忽略， dt/dy很小；在壁面附近的层流底层，此处主要依靠导热， dt/dy 较大。（有热边界层、湍流速度边界层及层流底层）
传热学 / 对流换热
（四）热边界层厚度与热阻的关系
自然界中的种种对流现象电子器件冷却
强制对流与自然对流
沸腾换热原理
空调蒸发器、冷凝器动物的身体散热
传热学 / 对流换热
热对流（Convection）
流体中（气体或液体）温度不同的各部分之间，由于发生相对的宏观运动而把热量由一处传递到另一处的现象。自然界不存在单一的热对流，必然同时伴随着热传导。
二、边界层
（一）速度(流动)边界层
1、速度边界层的形成原因粘性流体流过固体壁面时，由于流体与壁面之间摩擦阻力的影响，壁面附近的流体速度会减小，即从来流速度减小到壁面的零速度。 2、速度边界层图，见右图。
u 0.99u
传热学 / 对流换热 3、速度边界层定义把紧靠壁面、速度变化比较剧烈的流体层叫做速度（流动）边界层。
由于各层流体之间的速度不同，相互间就存在着相对滑动，即流体发生了剪切变形，于是各层之间产生出一种抵抗变形的力，称为内摩擦力或粘性力。
传热学 / 对流换热
2、牛顿内摩擦定律
流体运动所产生的内摩擦力与沿接触面法线方向的速度梯度成正比，与接触面的面积成正比，并与流体的物理性质有关。 du du f A dy dy

对流换热基本方程

(M n )c v v F n(m v n )(m v n )
in
out
对流换热基本方程
(M n )c v v F n(m v n )(m v n )
in
out
应用在x方向, 得到:来自( uxy)u 2 y
u
2
x
(u2 )xy
uvx
uv
y
(
uv)yx
xy ( x
x x
x (uxyv) 得到x方向纳维尔-斯托克斯方程
D DuPxx2ux32(uxyv) y(uxyv)Fx
对流换热基本方程
流体是常物性和不可压缩的，上式简化为
( u u u x v u y) P x ( x 2 u 2 y 2 u 2) F x
对直流角换热坐基标本系方下程的三维的常物性、不可压缩流体的纳维尔-斯托克斯方程
对流换热微分方程组的求解途径主要有：数学分析方法，数值求解方法和实验求解方法
对流换热基本方程
6-6 数量级分析
数量级分析的目的是，应用传热学的基本原理对所研究的物理量的数量级进行估算，即确定其数量级范围
cp tx22t
c p
t
～
c p
t
2t 2
x(xt)
～
t
t 2
对流换热基本方程
得到
～ 2 a
常物性的不可压缩流体，速度场与温度场无关，可以单独求解，因N-S方程和连续性方程构成了关于压力P和速度u、v、w的封闭方程组。
对于可压缩流体，密度不是常数，即使其它物性参数保持常量，动量方程也不能单独求解，因为密度与温度相关，动量方程与能量方程是耦合的，通过补充密度与温度的关系式，同时求解动量方程和能量方程，或已知温度分布，才能获得速度分布

传热学第二章对流换热

δtt
tw
第一节对流换热分析及牛顿冷却定律一、边界层概念
在层流边界层中，在层流边界层中，热量的传递只能依靠流体层与层间的导热作用，此时对流换热较弱。在紊流边界层中，导热作用，此时对流换热较弱。在紊流边界层中，层流底层的热量传递方式仍是导热，层的热量传递方式仍是导热，但在层流底层以外存在着对因而对流换热较强。流，因而对流换热较强。所以对流换热实际上是包括流体层流的导热和层流以外的对流共同作用的综合传热过程。层流的导热和层流以外的对流共同作用的综合传热过程。若同一流体在相同的温度下流过同一壁面时，若同一流体在相同的温度下流过同一壁面时，则层流底层越薄，对流换热越强烈。越薄，对流换热越强烈。
第一节对流换热分析及牛顿冷却定律一、边界层概念
（一）速度边界层当粘性流体流过固体壁面时，当粘性流体流过固体壁面时，若用仪器测出沿壁面法线方方向不同点的速度u，将得到如图所示的速度分布图。向Y方向不同点的速度，将得到如图所示的速度分布图。方向不同点的速度它表明从y=0处u=0开始，速度u随着方向离壁面的距离它表明从处开始，速度随着y方向离壁面的距离开始随着的增加而迅速增大，经过厚度为δ的薄层的薄层，接近达到主流的增加而迅速增大，经过厚度为的薄层，u接近达到主流速度u ，这个y= 的薄层即为速度边界层的薄层即为速度边界层，为边界层厚速度 ∞，这个 δ的薄层即为速度边界层， δ为边界层厚度。边界层厚度理论上应等于由壁面到流体达到主流速度点之间的距离，但这个点的位置难于准确确定，点之间的距离，但这个点的位置难于准确确定，故通常把 u/ u∞=0.99处离壁面的垂直距离定义为边界层厚度。实验处离壁面的垂直距离定义为边界层厚度。处离壁面的垂直距离定义为边界层厚度表明δ与壁面尺寸相比是一个极小的量。与壁面尺寸L相比是一个极小的量表明与壁面尺寸相比是一个极小的量。

传热学第五章对流换热计算

R 2 e3 1 00 0 ， P 0 1 r0 .5 0 5， 0 Pf0 r0 .0 5 20 P wr
2019/11/19
23
华中科技大学热科学与工程实验室
HUST Lab of Thermal Science & Engineering
例1 空气以2m/s的速度在内径为10 mm的管内流动，入口处空气的温度为20℃，管壁温度为120℃，试确定将空气加热至60℃所需管子的长度。
2019/11/19
20
华中科技大学热科学与工程实验室
HUST Lab of Thermal Science & Engineering
③短管当管子的长径比l/d<60时，属于短管内流动换热，进口段的影响不能忽视。此时亦应在按照长管计算出结果的基础上乘以相应的修正
系数Cl。 cl 1dl0.7
充分发展区：边界层汇合于管子中心线以后的区域，即进入定型流动的区域。
2019/11/19
3
华中科技大学热科学与工程实验室
HUST Lab of Thermal Science & Engineering
充分发展段为层流流动
为什么平均换热系数比局部换热系数高？
入口段的边界层厚度较薄，传热阻力小，表面传热系数大（即，对流换热强）
为什么气体和液体的修正方式不一样？
2019/11/19
18
华中科技大学热科学与工程实验室
HUST Lab of Thermal Science & Engineering
② 螺旋管或弯管弯曲的管道中流动的流体，在弯曲处由于离心力的作用会形成垂直于流动方向的二次流动，从而加强流体的扰动，带来换热的增强。

传热学-相变对流换热

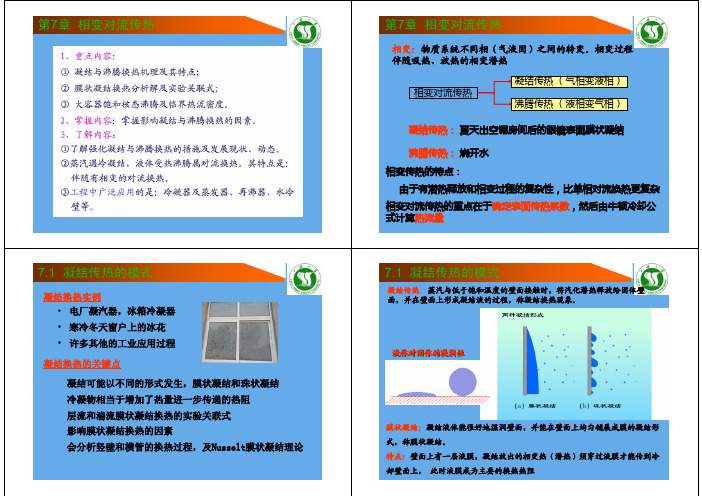
实验结果修正
实验关联式
膜状凝结实验关联式：
竖壁（层流）
hV
=
1.13
⎡ grρ
⎢ ⎣
η
l
l(
t
s
λ2 3
ll
− tw
⎤1/ 4
)
⎥ ⎦
Rec<1600
竖壁（湍流） Rec>1600
Nu
=
Ga1/ 3
58
P rs− 1 / 2
⎛ ⎜ ⎝
P rw P rs
Re
⎞1 ⎟
/
4
(R e 3
/
4
−
⎠
253
)+
9200
7.2 膜状凝结分析解及计算关联式
努塞尔纯净饱和蒸汽层流膜状凝结理论分析解
以竖壁、稳态、膜状凝结为例：
y
连续性方程：
∂u + ∂v = 0 ∂x ∂y
g
动量方程：
ρ（l u
∂u ∂x
+
v
∂u ) ∂y
=
ρl g
−
dp dx
+ηl
∂2u ∂y 2
tw
tδ ts
能量方程：
u
∂t ∂x
+
v
∂t ∂y
=
al
∂ 2t ∂y 2
x
假设3：液膜速度很低，忽略其惯性力
dp/dx为液膜在x方向压力梯度，等于y＝δ处蒸汽侧压力梯度(dp/dx)v
假设2：蒸汽静止。 dp dx
=
⎜⎛ ⎝
dp dx
⎟⎞ ⎠v
=
ρv g
7.2 膜状凝结分析解及计算关联式
努塞尔纯净饱和蒸汽层流膜状凝结理论分析解

传热学讲义对流换热——第六章

第六章单相流体对流换热及准则关联式第一节管内受迫对流换热本章重点：准确掌握准则方程式的适用条件和定性温度、定型尺寸的确定。

1-1 一般分析),,,,,,,,(l c t t u f h p f w μαρλ=流体受迫在管内对流换热时，还应考虑以下因素的影响：① 进口段与充分发展段，② 平均流速与平均温度，③ 物性场的不均匀性，④ 管子的几何特征。

一、进口段与充分发展段1．流体在管内流动的主要特征是，流动存在着两个明显的流动区段，即流动进口（或发展）段和流动充分发展段，如图所示。

（1）从管子进口到边界层汇合处的这段管长内的流动称为管内流动进口段。

（2）进入定型流动的区域称为流动充分发展段。

在流动充分发展段，流体的径向速度分量v 为零，且轴向速度u 不再沿轴向变化，即：0=∂∂xu， 0=v 2．管内的流态（1）如果边界层在管中心处汇合时流体流动仍然保持层流，那么进入充分发展区后也就继续保持层流流动状态，从而构成流体管内层流流动过程。

2300Re <用νdu m =Re 判断流态, 式中 m u 为管内流体的截面平均流速， d 为管子的内直径，ν为流体的运动黏度。

（2）如果边界层在管中心处汇合时流体已经从层流流动完全转变为紊流流动，那么进入充分发展区后就会维持紊流流动状态，从而构成流体管内紊流流动过程。

410Re >（3）如果边界层汇合时正处于流动从层流向紊流过渡的区域，那么其后的流动就会是过渡性的不稳定的流动，称为流体管内过渡流动过程。

410Re 2300<<3．热进口段和热充分发展段当流体温度和管壁温度不同时，在管子的进口区域同时也有热边界层在发展，随着流体向管内深入，热边界层最后也会在管中心汇合，从而进入热充分发展的流动换热区域，在热边界层汇合之前也就必然存在热进口区段。

随着流动从层流变为紊流，热边界层亦有层流和紊流热边界层之分。

热充分发展段的特征对常物性流体，在常热流和常壁温边界条件下，热充分发展段的特征是：)(1x f t f =及)(2x f t w =与管内任意点的温度),(r x f t =组成的无量纲温度⎪⎪⎭⎫⎝⎛--x f x w w t t t t ,,x ,随管长保持不变，即： 0,,x ,=⎪⎪⎭⎫ ⎝⎛--∂∂x f x w w t t t t x 式中，t —管内任意点的温度，),(r x f t = ⇒xf x w w t t tt ,,x ,--仅是r 的函数。

初中物理热学公式大全(热学)

初中物理热学公式大全(热学)一、热量和热传递热传递通过传导、对流和辐射三种方式进行。

对于任意物体，热量的传递可以表示为：热量传递公式：Q = mcΔT其中，Q代表热量，m代表物体的质量，c代表物体的比热容，ΔT代表温度的变化。

对于热传导，我们可以使用如下公式计算传导热流量：热传导公式：Q = K * A * (ΔT / d)其中，Q代表传导热流量，K代表物体的导热系数，A代表传热面的面积，ΔT代表温度的差异，d代表传热面的厚度。

热传递还可以通过对流进行，我们可以使用以下公式计算对流热流量：对流热流量公式：Q = h * A * ΔT其中，Q代表对流热流量，h代表对流热传导系数，A代表传热面的面积，ΔT代表温度的差异。

另外，对于辐射的热传递，我们可以使用以下公式计算辐射热流量：辐射热流量公式：Q = ε * σ * A * (T₁⁴ - T₂⁴)其中，Q代表辐射热流量，ε代表物体的辐射率，σ代表斯特藩—玻尔兹曼常数，A代表辐射面的面积，T₁和T₂分别代表两个物体的温度。

二、热膨胀物体在温度变化下会发生热膨胀，我们可以使用以下公式计算热膨胀量：线膨胀公式：ΔL = α * L * ΔT其中，ΔL代表长度的变化，α代表线膨胀系数，L代表初始长度，ΔT代表温度的变化。

体膨胀公式：ΔV = β * V * ΔT其中，ΔV代表体积的变化，β代表体膨胀系数，V代表初始体积，ΔT代表温度的变化。

三、热效应热量对物体的影响可以通过以下公式计算：物体的温度变化公式：Q = mcΔT其中，Q代表热量，m代表物体的质量，c代表物体的比热容，ΔT代表温度的变化。

相变时热量变化公式：Q = mL其中，Q代表热量，m代表物体的质量，L代表物质的相变潜热。

以上是初中物理热学中常用的公式，希望对你的学习有所帮助！。

工程热力学与传热学第十六章各种对流换热过程的特征及其计算公式

1/ 3
f w
0.14
定性温度为流体平均温度 t f （ w 按壁温 t w 确定），管内径为特征长度，管子处于均匀壁温。实验验证范围为： Pr f 0.48 ~ 16700,
f 0.0044 ~ 9.75， w
Re f Pr f f l / d w
下脚标 l 表示液相
考虑假定（3）液膜的惯性力忽略
u u l (u v ) 0 x y
考虑假定（7）忽略蒸汽密度
dp 0 dx
u v x y 0 u u dp 2u l (u x v y ) dx l g l 2 y t t 2t u x v y al 2 y
1 t m (t f t w ) 2
定形尺寸为沿流动方向平壁的长度L
二、流体在管道内换热
入口段的热边界层较薄，局部换热系数比充分发展段的高，且沿着主流方向逐渐降低，逐渐靠近充分发展段，局部换热系数逐渐趋于稳定。工程技术中常常利用入口段换热效果好这一特点来强化设备的换热。
管内受迫对流换热实验关联式管内受迫对流流动和换热的特征
第十六章各种对流换热过程的特征及其计算公式
本章要点： 1。着重掌握受迫、自然对流换热的基本原理和基本计算 2。着重掌握凝结、沸腾换热的基本概念及影响因素本章难点：受迫、自然对流换热的分析计算凝结、沸腾换热的分析解本章主要内容：
第一节受迫对流换热
第二节自然对流换热
第三节蒸汽凝结换热第四节液体沸腾换热
状凝结理论
1 、凝结换热现象
蒸汽与低于饱和温度的壁面接触时，将汽化
潜热释放给固体壁面，并在壁面上形成凝结液的

第五章对流传热理论基础

动量方程中的惯性力项和能量方程中的对流项均为非线性项，难以直接求解
简化
流动
普朗特速度边界层
类比
对流换热
波尔豪森热边界层
38
传热学
一、流动边界层
1、流动边界层及其厚度定义：当流体流过固体壁面时,由于流体粘性的作用,使得在固体壁面附近存在速度发生剧烈变化的薄层称为流动边界层或速度边界层。
实际流动 ≈ 边界层区粘性流动+主流区无粘性理想流动
大空间自然对流有限空间自然对流
沸腾换热有相变
凝结换热
大容器沸腾管内沸腾
管外凝结管内凝结
14
传热学
六、研究对流传热的方法（确定h的方法）
四种：1）分析法；2）实验法；3）比拟法；4）数值法
适当介绍
重点介绍一定介绍
不作介绍
1）分析法
解析：二维、楔形流、平板边界层积分方程（近似解析）
2）实验法
u∞
y δ
0x xc
粘性底层
掠过平板时边界层的形成与发展
湍流核心缓冲层
41
传热学
层流：流体做有秩序的分层流动，各层互不干扰，只有分子扩散，
无大微团掺混
湍流：流体微团掺混，紊乱的不规则脉动
粘性底层 :速度梯度较大、分子扩散—导热
湍流边界层
缓冲层 :导热+对流湍流核心 :质点脉动强化动量传递，速度变化
换热表面的形状、大小、换热表面与流体运动方向的相对位置及换热表面的状态（光滑或粗糙）
内部流动对流传热：管内或槽内外部流动对流传热：外掠平板、圆管、管束
10
传热学
11
传热学
(5) 流体的热物理性质：
热导率 [W (m C)] 比热容 c [J (kg C)]

传热学5-对流换热分析

Mx
M x dx x
M y vdx
单位时间内、沿x轴方向、经x表面流入微元体的质量单位时间内、沿x轴方向、经 x+dx表面流出微元体的质量
M x udy
M x M x dx M x dx x
单位时间内、沿x轴方向流入微元体的净质量：
M x M x dx

无论流体流动与否， p 都存在；而 ii只存在于流动时

同一点处各方向的 p 都相同；而 ii与表面方向有关
推导过程见P110 动量微分方程 — Navier-Stokes方程（N-S方程）
u u u p u u （ u v ) Fx ( 2 2 ) x y x x y
M x ( u ) dx dxdy x x
单位时间内、沿 y 轴方向流入微元体的净质量：
M y M y dy
单位时间内微元体内流体质量的变化:
( v) dy dxdy y y
M y
( dxdy) dxdy
Mx
速度场和温度场由对流换热微分方程组确定：质量守恒方程、动量守恒方程、能量守恒方程
2 质量守恒方程(连续性方程) 流体的连续流动遵循质量守恒规律
(x, y) 处取出边长为 dx、dy 的微元体（z方向为单位长度），M 为质量流量 [kg/s]
从流场中
Mx
M x dx x
M y vdx
热的核心问题

研究对流换热的方法：
（1）分析法（2）实验法（3）比拟法（4）数值法
传热系数大致范围
5 对流换热的影响因素
对流换热是流体的导热和对流两种基本传热方式共同作用的结果。其影响因素主要有以下五个方面： (1)流动起因 (2)流动状态 (3)流体有无相变