加减法(奥数)的巧算

合集下载

小学三年级奥数讲解：加减巧算

小学三年级奥数讲解：加减巧算（经典版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的经典范文，如职场文书、合同协议、策划方案、规章制度、演讲致辞、应急预案、心得体会、教学资料、作文大全、其他范文等等，想了解不同范文格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays, such as workplace documents, contract agreements, planning plans, rules and regulations, speeches, emergency plans, experiences, teaching materials, essay summaries, and other sample essays. If you want to learn about different sample formats and writing methods, please stay tuned!小学三年级奥数讲解：加减巧算小学三年级奥数讲解：加减巧算在日常学习、工作或生活中，许多人都知道奥数吧，下面是本店铺为大家收集的小学三年级奥数讲解：加减巧算，供大家参考借鉴，希望可以帮助到有需要的朋友。

三年级奥数加减法的速算与巧算.

如：1+9=10，3+7=10，2+8=10， 4+6=10，5+5=10。
又如：11+89=100，33＋67=100， 22+78=100，44+56=100， 55+45=100，在上面算式中，
1叫9的“补数”；89叫11的“补数”，11
凑整法〔补数法〕
例1 计算： (1) 1+2+3+4+5+6+7+8+9+10
= ( 1+9)+ ( 2+8)+ ( 3+7)+ ( 4+6)+5+10 =10+10+10+10+10+5 =55
(2) 1+3+5+7+9+11+13+15+17+19 =(1+19)+(3+17)+(5+15)+(7+13)+(9+11) =20+20+20+20+20 =100
凑整法〔补数法〕
如：43+(38＋45)＋(55＋62＋57) =43+38+45+55+62+57 =〔43+57〕+〔38+62〕 +〔45+55〕 =100+100+100 =300
去括号添括号法则
2.在加、减法混合运算中，添括号时：假设添加的括号前面是“＋”号，那么括号内的数的原运算符号不变；假设添加的括号前面是“-”号，那么括号内的数的原运算符号“＋”变为“－”，“-”变为“＋”。

二年级奥数加减法的巧算完美

米尺
钢尺
游标卡尺
卷尺
学生用尺
下面的几种测量方法哪种正确？哪种不正确？为什么？
1、（
）
0厘米 1
2
3
4
5
6
0厘米 1
2
3
4
5
6
2、（
）
3、（
）
这是一把断尺。
没有零刻度，怎么量呢？
1cm
2
3
4
5
6
7
8
直尺上1厘米中间每一小格的长度是1毫米。
数一数，1厘米有多少毫米。
1厘米=10毫米
1分硬币的厚度大约是1毫米。
（2）624-96 =624-100+4 =524+4 =528
课堂总结：凑整法是在加减法简便运算中最为常见的一种方法。在运用凑整法时要记住16个字——多加要减、少加再加。少减再减、多减要加。
你学会了吗？
1、复习上节课的知识。
2、进行一个小游戏。
游戏名称：碰球。
游戏过程：老师出示数字，例如数字8，对学生说：嗨、嗨，我的3球碰几球？学生可以说：嗨、嗨，你的3 球碰5球。学生说出的数必须与老师说的数合起来是8。
加减法的巧算
1、凑整法
【例1】用简便方法计算（1）64+97 (2)999+99+9 =64+100-3 =1000+100+10-3 =164-3 =1110-3 =161 =1107
小结：在加法中运用凑整的方法时，根据和不变的规律——多加要减、少加再减
（1）98+113 （2）109+98+3 =100+1132 =213-2 =211 =109+100-2+3 =209-2+3 =210

三年级奥数第3专题-加减法的巧算

加减法的巧算（要求： 1.掌握用“凑整”的方法进行简单的计算2. 根据减法的性质，简化运算。

几个数相加，利用移位凑整的方法，将加数中能凑成整十，整百，整千等的数交换顺序，先进行凑整，然后再与其他一些加数相加，得出结果。

在加减混合算式与连减算式中，将减数先结合起来，集中一次相减，可简化运算。

几个相近的数相加，可以选择其中一个数，最好是整十，整百等的数为“基准数” 。

再把大于基准数的数写成基准数与一个数的和，小于基准数的数写成基准数与一个数的差，将加法改为乘法计算。

几个数相加减时，如果不能直接“凑整” ，就可以利用加整减零，减整加零或变更被减数。

）例题 1 计算（1）3326+303 （2）574+498方法一：先看做整十，整百，整千的数进行计算。

方法二：根据“和”的变化规律：一个加数增加多少，另一个加数就减少多少，那么和不变，来进行简算。

1) 3326+303 =3326+300+3 =3626+3 =36292)574+498 =574+500-2 =1074-2=1072=(3326+3) + (303-3 ) = (574-2) + (498+2)=3329+300 =572+500=3629 =1072特别注意：在计算时，将接近整十，整百，整千的数看成整十，整百, 整千的数进行计算，然后根据和不变的规律，多加的要减掉，少加的要补上。

例题 2 计算487+321+113+479方法：487和113, 321和479分别可以凑成整百数。

我们可以通过交换位置的方法，487+113得600, 321+479得800.487+321+113+479=(487+113) + (321+479)=600+800=1400特别注意：这道题要运用凑整的思路，将487和113, 321和479分别凑成整百数，便于计算。

注意：先算的要加括号。

例题 3 计算9998+998+98+8方法：本题可釆用凑整的方法，将9998, 998, 98分别凑成10000, 1000, 100.而凑成这些数可从8里面借用。

小学生奥数加减法的巧算知识点及练习题

小学生奥数加减法的巧算知识点及练习题一、进位法：进位法是指在加法中，当相加的两个数相加而达到或超过10时，我们将其进位到更高的一位上。

例如，8+6=14，我们将4保留在个位上，并将1进位到十位上，所以答案是14练习题：1.5+7=?2.8+9=?3.3+6=?4.4+8=?5.9+9=?二、借位法：借位法是指在减法中，当我们无法从被减数的位数中进行减法运算时，我们需要向高位借位，以便能够继续进行减法运算。

例如，11-8=3，我们从个位上的数字1借1个十位，然后我们将它和原本的11相减，得到3练习题：1.7-3=?2.10-5=?3.9-6=?4.8-4=?5.11-9=?三、进位与借位相结合：在复杂一点的加减法问题中，我们可能需要同时使用进位法和借位法来解决问题。

首先我们通过进位法解决进位问题，然后再使用借位法解决借位问题。

练习题：1.23+16=?2.74-38=?3.64+38=?4.52-19=?5.87+45=?四、左对齐法：左对齐法是指在进行列竖式加减法时，我们将数对齐在同一列进行计算。

借位时，将借位数字与原位的数字对齐并进行运算。

这种方法可以减少出错的概率，也可以更方便地进行计算。

练习题：1.347+26=?2.870-36=?3.528+91=?4.742-281=?5.965+47=?以上就是一些小学生奥数加减法的巧算知识点及练习题。

通过掌握这些知识点和技巧，可以帮助小学生更快、更准确地进行加减法运算。

同时，在练习过程中，要注重培养孩子的思维能力和逻辑思维能力，通过不断的练习提高解题的速度和准确性。

奥数加减法巧算

奥数加减法巧算在数学的学习中，加减法的巧算方法能够帮助我们快速、准确地得出计算结果，尤其是在奥数的学习中，掌握这些巧算技巧更是如虎添翼。

接下来，就让我们一起来探索加减法巧算的奇妙世界吧！一、凑整法凑整法是加减法巧算中最常用的方法之一。

所谓凑整，就是把一些数凑成整十、整百、整千的数，这样可以使计算变得更加简便。

例如：23 ＋ 48 ＋ 77 ＝（23 ＋ 77）＋ 48 ＝ 100 ＋ 48 ＝ 148 ，在这个式子中，我们将 23 和 77 先相加凑成 100，再与 48 相加，计算就变得简单多了。

再比如：187 56 44 ＝ 187 （56 ＋ 44）＝ 187 100 ＝ 87 ，这里把56 和 44 相加凑成 100，然后用 187 减去它们的和，大大简化了计算。

二、带符号搬家法在加减法运算中，我们可以带着数字前面的符号一起“搬家”，这样可以改变运算顺序，使计算更加简便。

比如：154 ＋ 78 54 ＝ 154 54 ＋ 78 ＝ 100 ＋ 78 ＝ 178 ，通过将＋ 78 和 54 的位置交换，先计算 154 54 ，再加上 78 ，计算轻松了不少。

三、基准数法当遇到多个相近的数相加时，可以选择一个基准数，先计算出每个数与基准数的差，再将这些差相加，最后加上基准数与个数的乘积。

例如：计算 98 ＋ 102 ＋ 97 ＋ 101 ＋ 99 ，我们可以选择 100 作为基准数，那么原式就可以转化为：（100 2）＋（100 ＋ 2）＋（100 3）＋（100 ＋ 1）＋（100 1）＝ 100×5 ＋（ 2 ＋ 2 3 ＋ 1 1）＝500 3 ＝ 497 。

四、拆数法把一个数拆分成两个或多个数，然后再进行计算，有时会使计算变得简单。

比如：28 ＋ 99 ＝ 28 ＋ 100 1 ＝ 128 1 ＝ 127 ，把 99 拆分成 1001 。

再比如：167 98 ＝ 167 100 ＋ 2 ＝ 67 ＋ 2 ＝ 69 ，把 98 拆分成100 2 。

小学三年级(奥数)专项训练加减法巧算

三年级专项训练加减法的巧算[知识概述]：1.巧算主要是运用“凑整”的方法，把接近整十、整百、整千的数看做所接近的数进行简算。

凑整之后，对于原数与整十、整百、整千……相差的数，要根据“多加要减去，少加要加上，多减要加上，少减要减去”的原则进行处理。

另外，可结合加法交换律、结合律及减法性质凑整，从而达到简算目的。

2. A-B-C=A-(B+C) A-(B-C)=A-B+C[典例精讲]例1：你有好办法迅速计算出结果吗？（1）502+799-298-97 （2）9999+999+99+9=500+2+800-1-300+2-100+3 =10000+1000+100+10-4=906 =11106变式练习1:（1）75＋26＋25；（2）72＋67＋28；（3）1272—998；（4）9997＋2598＋7401；（5）536+541+464+459；例2：计算下面各题。

（1）487+321+113+479 （2）723-251+177 =（487+113）+（321+479） =723+177）-250-1（3）872+284-272 （4）537-142-58=872-272+284 =537-（142+58）变式练习2:⑴ 464－350＋136；⑵ 997＋102＋999＋104＋998；⑶ 967+385-167；⑷ 947-126－574；例3：计算下面各题。

（1）321+（279-155）（2）327-（54+72）☆（3）432-（154-68）=321+279-155 =327-72-54 =432+68-154变式练习3：（1）467+（233-550）（2）964-84-16；（3）563-（128+63）（4）8457＋（900－457）；☆（5）7923－（923－725）；（6）832－（454＋332）＋654；☆ (7) 568－（128－332）－72；作业：家长签字：时间：月日A组基础训练1、计算下面各题。

小学生奥数加减法的巧算知识点及练习题

小学生奥数加减法的巧算知识点及练习题1.小学生奥数加减法的巧算知识点第一，在连减或加、减混合运算中，如果算式中没有括号，计算时可以“抱”着前面的符号“搬家”。

一般的，有a-b-c=a-c-ba-b+c=a+c-b第二，在加、减混合运算中，如果括号的前面是“-”号，那么，去掉括号时，括号内的减号变加号，加号变减号；如果括号的前面是“+”号，那么，去掉括号时，括号内的符号不变，一般把这种做法叫做同级运算去括号的性质。

一般的有a-（b+c）=a-b-ca-（b-c）=a-b+ca+（b+c）=a+b+ca+（b-c）=a+b-c2.小学生奥数加减法的巧算知识点我们如果在计算时，想要又快又对，方法很重要。

第一，要掌握计算法则和运算顺序。

第二，要了解题目的特点，发现题中的特点或规律，才能选用合理的计算方法。

第三，要巧算加减法，首先要掌握加减法中的运算定律和性质。

加法中的运算定律主要有：加法交换律和加法结合律。

1、加法交换律：两个数相加，交换加数的位置，它们的和不变。

一般有a+b=b+a2、加法结合律：三个数相加，先把前两个数相加，再加上第三个数；或者先把后两个数相加，再同第一个数相加，它们的和不变。

一般有（a+b）+c=a+（b+c）3.小学生奥数加减法的巧算知识点减法的性质（1）一个数减去几个数的和，等于从这个数里依次减去和中的每个加数。

一般有a-（b+c）=a-b-c反之，一个数连续减去几个数，等于从这个数里减去这几个数的和。

即：a-b-c=a-（b+c）（2）一个数减去两个数的差，等于从这个数中减去差里的被减数（在能减的情况下），再加上差里的减数。

一般的，有：a-（b-c）=a-b+c（3）几个数的和减去一个数，等于从任何一个加数里减去这个数（在能减的情况下），再同其余的加数相加。

一般的有：（a+b+c）-d=（a-d）+b+c=a+（b-d）+c=a+b+（c-d）4.小学生奥数加减法的巧算练习题175－75÷2568＋35×13725－（125＋237）（114＋166）÷35432÷（9×8）1*0＋40216＋30525×3247＋236＋646×（15×9）402＋35943＋78＋122＋25725×（26×4）25×44354＋（229＋46）9.26-4.38-2.629.26-(4.38+2.26)9.26-(4.38-2.744.75-9.64+8.25-1.3614.529+(2.471-3)38.68-(4.7-2.32)415－176－248.29＋3.7＋0.71＋6.3125×89×8428×78＋572×785.小学生奥数加减法的巧算练习题1、计算：9998+998+99+9+69998+998+99+9+6=（10000-2）+（1000-2）+（100-1）+（10-1）+6=10000+1000+100+10+（6-2-2-1-1）=111102、计算：1966+1976+1986+1996+20061966+1976+1986+1996+2006=（1986-21）+（1986-10）+1986+（1986+10）+（1986+20）=1986×5-（20+10-10-20）=99303、计算：1234+2341+3412+41231234+2341+3412+4123=（1000+200+30+4）+（2000+300+40+1）+（3000+400+10+2）+（4000+100+20+3）=（1000+2000+3000+4000）+（200+300+400+100）+（30+40+10+20）+（4+1+2+3）=10000+1000+100+10=111106.小学生奥数加减法的巧算练习题1、计算：123+234+345-456+567-678+789-890123+234+345-456+567-678+789-890=123+234+345+（567-456）+（7*78）-890=123+234+345+111+111-890=234+（123+567）-890=234+690-890=34+890-890=342、569+384+147-328-167-529569+384+147-328-167-529=（569-529）+147-（147+20）+388-4-328=40-20+56=763、计算：6472-（4476-2480）+5319-（3323-1327）+9354-（7358-5362）+6839-（4843-2847）6472-（4476-2480）+5319-（3323-1327）+9354-（7358-5362）+6839-（4843-2847）=（6480-8）+（5320-1）+（9360-6）+（6840-1）-（4476-2476-4）-（3323-1323-4）-（7358-5358-4）-（4843-2843-4）=（6480+5320）+（9360+6840）-8-1-6-1-2000+4-2000+4-2000+4-2000+4=11800+16200-8000-16+16=28000-8000=20000小学生奥数加减法的巧算知识点及练习题。

二年级奥数第一讲加减法中的简便运算

二年级奥数第一讲加减法中的简便运算二年级奥数第一讲：加减法中的简便运算在加减法中，我们可以使用简便运算来简化计算。

需要注意的是：同级运算，括号外面是减号的，可以添上或去掉括号，括号里的符号需要改变，加号变成减号，减号变成加号。

当所有括号都去掉后，我们可以将数与前面的符号一起移动，第一个数前面为加号。

以下是常用的简便运算方法：加法：1) A + B = B + A；2) (A + B) + C = A + (B + C)。

减法：1) A - B - C - A + (B + C)；2) A - B + C - A - (B - C)。

例一：使用加法中的凑整，计算：1) 98 + 37；2) 999 + 99 + 9.解：1) 98接近于100，所以98 + 37可以看成100 + 37，多加了2，因此最后要减去2；2) 3个加数都分别接近整干、整百、整十数，我们可以把999看作1000，99看作100，9看作10，这样每个数都多加了1，最后再从它们的和中减去3，就可以得到答案。

计算：1) 68 + 103；2) 109 + 98 + 8.例二：使用加法的交换律与结合律，计算：345 + 27 + 655 + 373.解：345与655、27与373分别能凑成整千、整百的数，所以可以利用加法的交换律和结合律，先交换加数的位置，再凑整。

计算：329 + 67 + 233 + 271.例三：使用减法中的凑整，计算：1) 375 - 98；2) 534 - 109.解：1) 98接近100，可以把原式看作375 - 100，多减了2，因此还要加上2；2) 109接近100，可以把原式看作534 - 100，少减了9，因此还要减去9.计算练：1) 562-205 = 3572) 624-96 = 528利用减法性质计算：1) 869-(69+34) = 7662) 500-56-44 = 400找基准数巧算：93+92+88+89+90+86+91+87 = 706观察这8个数的大小接近，都与90接近，将这些数看成90，即8个90，再将每个数与90相比，大的加几，小的减几，得到706.。

(小学奥数)分数加减法速算与巧算

分數加減法速算與巧算教學目標本講知識點屬於計算板塊的部分，難度並不大。

要求學生熟記加減法運算規則和運算律，並在計算中運用湊整的技巧。

知識點撥一、基本運算律及公式一、加法加法交換律：兩個數相加，交換加數的位置，他們的和不變。

即：a＋b＝b ＋a其中a，b各表示任意一數．例如，7＋8＝8＋7＝15.總結：多個數相加，任意交換相加的次序，其和不變．加法結合律：三個數相加，先把前兩個數相加，再加上第三個數；或者先把後兩個數相加，再與第一個數相加，他們的和不變。

即：a＋b＋c＝（a＋b）＋c＝a＋（b＋c）其中a，b，c各表示任意一數．例如，5＋6＋8＝（5＋6）＋8＝5＋(6＋8).總結：多個數相加，也可以把其中的任意兩個數或者多個數相加，其和不變。

二、減法在連減或者加減混合運算中，如果算式中沒有括弧，那麼計算時要帶數字前面的運算符號“搬家”．例如：a－b－c＝a－c－b，a－b＋c＝a＋c－b，其中a，b，c各表示一個數．在加減法混合運算中，去括弧時：如果括弧前面是“＋”號，那麼去掉括弧後，括弧內的數的運算符號不變；如果括弧前面是“－”號，那麼去掉括弧後，括弧內的數的運算符號“＋”變為“－”，“－”變為“＋”．如：a＋（b－c）＝a＋b－ca－（b＋c）＝a－b－ca－（b－c）＝a－b＋c在加、減法混合運算中，添括弧時：如果添加的括弧前面是“＋”，那麼括弧內的數的原運算符號不變；如果添加的括弧前面是“－”，那麼括弧內的數的原運算符號“＋”變為“－”，“－”變為“＋”。

如：a＋b－c＝a＋（b－c）a－b＋c＝a－（b－c）a－b－c＝a－（b＋c）二、加減法中的速算與巧算速算巧算的核心思想和本質：湊整常用的思想方法：1、分組湊整法．把幾個互為“補數”的減數先加起來，再從被減數中減去，或先減去那些與被減數有相同尾數的減數．“補數”就是兩個數相加，如果恰好湊成整十、整百、整千……，就把其中的一個數叫做另一個數的“補數”．2、加補湊整法．有些算式中直接湊整不明顯，這時可“借數”或“拆數”湊整．3、數值原理法．先把加在一起為整十、整百、整千……的數相加，然後再與其它的數相加．4、“基準數”法，基準當幾個數比較接近於某一整數的數相加時，選這個整數為“基準數”（要注意把多加的數減去，把少加的數加上）【例 1】1141041004 2282082008+++=_____【考點】分數約分【難度】1星【題型】計算【關鍵字】希望杯，五年級，一試【解析】原式=1111=22222+++【答案】2【例 2】如果111207265009A+=，則A=________（4級）【考點】分數約分【難度】2星【題型】計算【關鍵字】希望杯，六年級，一試【解析】111112591 207265009873773725125920082008+=+=⨯=⨯⨯⨯⨯，所以A=2008.【答案】2008模組一：分組湊整思想【例 3】1121123211219951 1222333331995199519951995 +++++++++++++++【考點】分組湊整【難度】3星【題型】計算【解析】觀察可知分母是1的和為1；分母是2的和為2；分母是3的和為3；……依次類推；分母是1995的和為1995.這樣，此題簡化成求1231995++++例題精講的和.11211232112199511222333331995199519951995+++++++++++++++ 12341995119951995299819951991010=+++++=+⨯÷=⨯=() 【答案】1991010【例 4】 1111222233318181923420345204520192020⎛⎫⎛⎫⎛⎫⎛⎫+++++++++++++++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ 【考點】分組湊整【難度】3星【題型】計算【解析】觀察可知分母是2分子和為1分母是3分子和為12+；分母是4分子和為123++；……依次類推；分母是20子和為12319++++. 原式()1111(12)(123)1231923420=+⨯++⨯++++⨯++++ ()1111(12)22(13)3211919223420=+⨯+⨯÷+⨯+⨯÷++⨯+⨯÷ 12319952222=++++= 【例 1】分母為1996的所有最簡分數之和是_________【考點】分組湊整【難度】2星【題型】計算【解析】因為1996=2×2×499。

小学三年级奥数第4讲加减巧算附答案解析

第4讲加减巧算一、知识要点在进行加减运算时，为了又快又好，除了要熟练地掌握计算法则外，还需要掌握一些巧算的方法。

加减法的巧算主要是运用“凑整”的方法，把接近整十、整百、整千的数看做所接近的数进行简算。

进行加减巧算时，凑整之后，对于原数与整十、整百、整千……相差的数，要根据“多加要减去，少加要再加，多减要加上，少减要再减”的原则进行处理。

另外，可以结合加法交换律、结合律以及减法的性质进行凑整，从而达到简算的目的。

二、精讲精练【例题1】你有好办法迅速算出结果吗？(1) 502+799-298-98 (2) 9999+999+99+9练习1：计算。

(1) 308+203-399-97 (2) 99999+9999+999+99+9(3) 1999+199+19 (4) 375+483+525+617【例题2】计算。

(1) 487+321+113+279 (2) 736-567+264(3) 877+345-677 (4) 528-248-152练习2：计算。

(1) 321+127+73+279 (2) 235-125+365 (3) 987-733-167 (4) 487+(413-89)【例题3】计算下面各题。

(1) 962-(284+262) (2) 432-(154-168)练习3：计算。

(1) 421+(279-125) (2) 812+(168-112)(3) 823-(175+323) (4) 538-(283-162) 【例题4】2000-111-89-112-88-113-87-114-86-115-85-116-84练习4：计算。

(1)800-99-1-98-2-97-3-96-4-95-5(2) 1000-10-20-30-40-50-60-70-80-90【例题5】计算: 98+97-96-95+94+93-92-91+90+89-88-87……-4-3+2+1练习5：计算。

(1) 2009+1+2-3-4+5+6-7-8+9+10-11-12+13+14……+2006(2) 1+2-3+4+5-6+7+8-9……+97+98-99三、课后作业1、计算下列各题。

小学2年级奥数加减法的巧算(精品)

（1）375-98
=375-100+2 =275+2 =277
（2）534-109
=534-100-9 =434-9 =425
（1）562-205
=562-200-5 =362-5 =357
（2）624-96
=624-100+4 =524+4 =528
课堂总结：凑整法是在加减法简便运算中最为常见的一种方法。在运用凑整法时要记住16个字— —多加要减、少加再加。少减再减、多减要加。
练一练
1000-76-24-64-36-55-45
=1000-【（76+24）+（64+36）+（55+45）】 =1000-【100+100+100】 =1000-300 =700
总结：本节课主要学习了加减法简便运算常见的两种方法。1、加法的交换律和结合律（运用加法的交换律和结合律将两数凑成整十、整百、整千的数，再计算）。 2、找准基数（在几个大小相差不多的数中，找一个与每个数都近似的数，把它看作基准数，然后每个数与基准数比较，比基准数大的，多几就再加几；比基准数小的，少几就再减几）。
=（329+271）+（67+233） =600+300 =900
例题精讲
【例5】用简便方法计算
93+92+88+89+90+86+91+87
=（90+3）+（90+2）+（90-2）+（90-1）+90+（90-4）+（90+1）+（90-3） =90×8+（3+2-2-1-4+1-3）

小学奥数简单的整数加减中的巧算

【例4】
（1）（2）（3）
（3）（5）
【例5】
（1）（2）
4.抵消的概念
在有加有减的运算中，如果加上某个数，又减去这个数，那么就可以将这个出现两次的数划去，不参加运算，这称为“抵消”。
实际应用：
在做多个数的加减运算时，可以利用草稿，将加的放在一边，减的放在另一边，然后将两边相同的数互相抵消。
【例6】
（1）（2）
（2）
（3）
5.在做加减法时，如果所有相加的数都相等，那么只需要将一个相加的数乘以相加数的个数就可以了。如果相加的数不全相等，但相差不多，我们可以取一个数作为标准数，利用乘法，再略加调整。
【例7】
6.几个相近的数相加，选择其中一个作为“标准数”，其他数表示为“标准数”加或减去一个较小数，这样原来较大数的加减可转化为几个较小数的加减。
【例8】
【例2】
（1）（2）299999+29999+2999+299+29
2.一个数连续减去几个数，等于从这个数中减去这几个数的和。【例3】Fra bibliotek（1）（2）
3.添括号和去括号
（1）如果去（或添）的括号前面是“＋”号，那么去（或添）括号后，里面的运算符号不变
（2）如果去（或添）的括号前面是“-”号，那么去（或添）括号后，里面的运算符号都要变号：“＋”号变为“-”号，“-”号变为“＋”号
三年级
1.补数和互补的定义：两个自然数相加，如果它们的和恰好是整十、整百、整千......那么就称其中一个数为另一个数的“补数”，这两个数称为互补。
实际应用：
（1）在做加减法运算中，如果有两个数互为补数，那么可以先求他们的和；
（2）如果没有互补的加数，那么可以设法分出互补的加数。

二年级奥数：加减法巧算

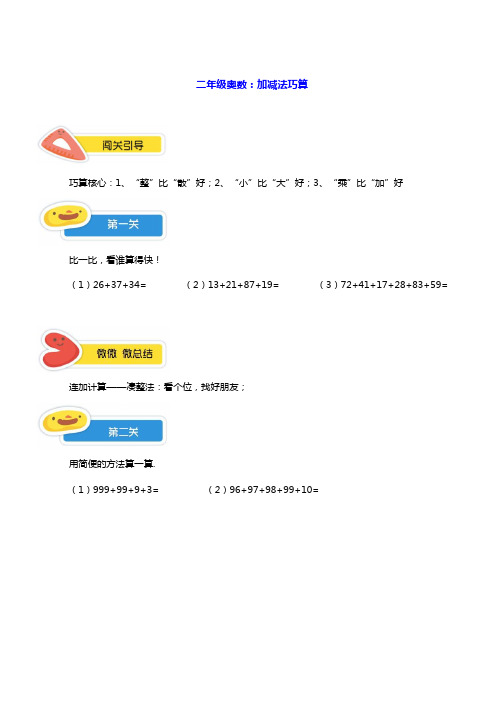
二年级奥数：加减法巧算巧算核心：1、“整”比“散”好；2、“小”比“大”好；3、“乘”比“加”好比一比，看谁算得快！（1）26+37+34= （2）13+21+87+19= （3）72+41+17+28+83+59=连加计算——凑整法：看个位，找好朋友；用简便的方法算一算.（1）999+99+9+3= （2）96+97+98+99+10=连加计算——加补凑整法：拆小数，补大数；小朋友，快来挑战加减混合计算题吧！（1）43-25+57= （2）87+49-67= （3）74+58-34-28=加减混合——带符号搬家：加法个位找朋友，减法个位找相同；渣渣兔带了 100 块去超市买东西，先买了一个笔袋 24 元，又买了一个书包 56 元，还剩下多少钱呢?【拓展】：354-128-72=连减——添括号法（购物车法）：变减为加，先加再减.以下算式你会怎么算呢?（1）95-（28+35）= （2）132-（32+49）= （3）48+（73-28）=有括号的计算——括号内不好算，尝试去括号：（1）括号前是“＋”，直接去括号；（2）括号前是“-”，括号内所有符号都变号；一、连加计算：看个位凑整；加补凑整；二、加减混合：带符号搬家；三、连减计算：添括号，变减为加；四、有括号的算式：去括号计算.cc 猫去商店买东西，它买了一个杯子 15 元，买了一条毛巾 12 元，买了一个文具盒 23 元，它付给售货员 100 元，应找回多少钱?【练习 1】快速计算下列算式.（1）18+26+24+32= （2）4+4+4+4+6+6=【练习 2】快速计算下列算式.（1）53+14+37-14= （2）9998+998+98+8=【练习 3】计算下面各题.（1）73-32-18= （2）87-15-4-1=【练习 4】下面的题怎么算比较简便?（1）76-（32+16）= （2）85-（15+29）=【练习 5】算一算下面的算式.84-3-3-3-3-3-3-3-3=。

奥数第一讲-三年级-加减法巧算

减法中的巧算
5、先减去那些与被减数有一样尾
数的减数
例5：巧算下面各题：
〔1〕4723-〔723＋189〕〔2〕2356-159-256
= 4723-723-189 = 4000-189 = 3811
= 2356-256-159 = 2100-159 = 1941
一起来找找好朋友吧？
〔1〕3863-〔145＋263〕〔2〕175-89-75 〔3〕2543-410-43
= 187
〔2〕99 ＋ 136＋101
= 99＋101＋136 = 200 ＋ 136 = 336
〔3〕972＋639＋28
= 972＋28 ＋639 = 1000 ＋ 639 = 1639
一起来找找好朋友吧？
森林动物园里，有4个班级，每个班级的学生数量分别是38人，47人， 52人和33人，请问学校里共有多少名学生？
我们也来比一比吧！
2、两个数的和为100，这两个数可能是多少？ 11+89=100 33＋67=100
63+37=100 45+55=100……
速算巧算方法一：补数凑整
什么叫“补数”
两个数相加，假设能恰好凑成整十、整百、整千、整万…，就把其中的一个数叫做另
一个数的“补数”
你能说说下面式子中的补数吗
O(∩_∩)O
下课啦！
125+46+54
1、用简便方法求和：
①536+〔541+464〕+459
② 588＋264＋148
③ 8996＋3458＋7542 ④567+538+562＋555＋533
2、用简便方法求差： ① 1870-280-520 ② 4995-〔995-480〕 ③ 4250-294＋94 ④ 1272-995

小学奥数整数加减法速算及巧算

整数加减法速算与巧算一、基本运算律及公式一、加法加法交换律：两个数相加，交换加数的位置，他们的和不变。

即：a＋b＝b＋a其中a，b各表示任意一数．例如，7＋8＝8＋7＝15.总结：多个数相加，任意交换相加的次序，其和不变．加法结合律：三个数相加，先把前两个数相加，再加上第三个数；或者先把后两个数相加，再与第一个数相加，他们的和不变。

即：a＋b＋c＝（a＋b）＋c＝a＋（b＋c）其中a，b，c各表示任意一数．例如，5＋6＋8＝（5＋6）＋8＝5＋(6＋8).总结：多个数相加，也可以把其中的任意两个数或者多个数相加，其和不变。

二、减法在连减或者加减混合运算中，如果算式中没有括号，那么计算时要带数字前面的运算符号“搬家”．例如：a－b－c＝a－c－b，a－b＋c＝a＋c－b，其中a，b，c各表示一个数．在加减法混合运算中，去括号时：如果括号前面是“＋”号，那么去掉括号后，括号内的数的运算符号不变；如果括号前面是“－”号，那么去掉括号后，括号内的数的运算符号“＋”变为“－”，“－”变为“＋”．如：a＋（b－c）＝a＋b－ca－（b＋c）＝a－b－ca－（b－c）＝a－b＋c在加、减法混合运算中，添括号时：如果添加的括号前面是“＋”，那么括号内的数的原运算符号不变；如果添加的括号前面是“－”，那么括号内的数的原运算符号“＋”变为“－”，“－”变为“＋”。

如：a＋b－c＝a＋（b－c）a－b＋c＝a－（b－c）a－b－c＝a－（b＋c）二、加减法中的速算与巧算速算巧算的核心思想和本质：凑整常用的思想方法：1、分组凑整法．把几个互为“补数”的减数先加起来，再从被减数中减去，或先减去那些与被减数有相同尾数的减数．“补数”就是两个数相加，如果恰好凑成整十、整百、整千……，就把其中的一个数叫做另一个数的“补数”．2、加补凑整法．有些算式中直接凑整不明显，这时可“借数”或“拆数”凑整．3、数值原理法．先把加在一起为整十、整百、整千……的数相加，然后再与其它的数相加．4、“基准数”法，基准当几个数比较接近于某一整数的数相加时，选这个整数为“基准数”（要注意把多加的数减去，把少加的数加上）例题精讲模块一：分组凑整【例 1】计算：（1）117＋229＋333＋471＋528＋622（2）（1350＋249＋468）＋（251＋332＋1650）（3）756－248－352（4）894－89－111－95－105－94【巩固】计算57911131517192123+++++++++=．【巩固】同学们，你们有什么好办法又快又准的算出下面各题的答案？把你的好方法讲一讲！也当一次小老师！⑴1847192862813664++++-+--⑵1234567887661594322⑶200077415923----⑷617271438315771+-+--【巩固】计算12233344445555666778+++++++【例 2】看谁的方法最巧呢？⑴123181920+++⋅⋅⋅+++⑵46810323436++++⋅⋅⋅+++【例 3】计算：20052004200320022001200019991998199719967654321+--++--++-⋅⋅⋅--++--+【巩固】计算：123456789949596979899100101+--++--+++--++--+=。

加减法(奥数)的巧算

小学三年级奥数讲解：加减巧算

三年级奥数加减法的速算与巧算.

二年级奥数加减法的巧算完美

三年级奥数第3专题-加减法的巧算

小学生奥数加减法的巧算知识点及练习题

奥数加减法巧算

小学三年级(奥数)专项训练 加减法巧算

小学生奥数加减法的巧算知识点及练习题

二年级奥数第一讲加减法中的简便运算

(小学奥数)分数加减法速算与巧算

小学三年级奥数第4讲 加减巧算附答案解析

小学2年级奥数加减法的巧算(精品)

小学奥数简单的整数加减中的巧算

二年级奥数：加减法巧算

奥数第一讲-三年级-加减法巧算

小学奥数整数加减法速算及巧算

小学三年级(奥数)专项训练加减法巧算

小学三年级奥数第4讲加减巧算附答案解析