量子粒子群算法
一种具有自我更新机制的量子粒子群优化算法

一种具有自我更新机制的量子粒子群优化算法奚茂龙;吴小俊;方伟;孙俊【摘要】Life body has limited life in nature;it will be aging and die with time. The aging mechanism is very important to keep swarm diversity during evolutionary process. For the phenomenon that Quantum-behaved Particle Swarm Optimi-zation(QPSO)is often premature convergence, self-renewal mechanism is proposed into QPSO, and a leading particle and challengers are introduced. When the leading power of leading particle is exhausted, one challenger will select to be the new leading particle and continues keeping the diversity of swarm with a certain renewal mechanism. Furthermore, global convergence of the proposed algorithm is proved. Finally, the comparison and analysis of results with the proposed method and classical improved QPSO algorithm based on twelve CEC2005 benchmark function is given, the simulation results show stronger global searching ability of the modified algorithm. Especially in the seven multi-model test func-tions, the comprehensive performance is optimal.%自然界中生命体都存在着有限的生命周期,随着时间的推移生命体会出现老化并死亡的现象,这种老化机制对于生命群体进化并保持多样性有重要影响。
量子行为粒子群优化算法-中文版

量子行为粒子群优化
02
算法的实现过程
初始化阶段
01
02
03
初始化粒子群
在解空间中随机初始化一 组粒子,每个粒子代表一 个潜在的解。
初始化粒子速度
为每个粒子随机分配一个 速度,用于控制其位置的 变化。
初始化粒子位置
根据问题的约束条件和目 标函数,为每个粒子随机 分配一个初始位置。
更新阶段
计算适应度值
量子行为粒子群优化算法的基本原理
• 量子行为粒子群优化算法的基本原理是:每个粒子被视为一 个量子比特,其状态由波函数表示。粒子通过不断更新自己 的位置和速度来搜索解空间,同时通过与其它粒子的信息共 享和协作来不断逼近最优解。在更新过程中,粒子不仅受到 自身经验和群体最佳位置的影响,还受到量子旋转门和量子 测量等量子操作的作用,从而在解空间中实现全局搜索和局 部搜索的平衡。
THANKS.
组合优化问题
组合优化问题是指在一组可行解中寻 找最优解的问题,如旅行商问题、背 包问题、图着色问题等。
量子行为粒子群优化算法能够处理这 类问题,通过粒子间的信息共享和协 作,寻找最优解或近似最优解。
机器学习与数据挖掘
在机器学习和数据挖掘领域,量子行为粒子群优化算法可用 于特征选择、模型参数优化和超参数调整等方面。
算法在实际问题中的应用前景
组合优化问题
量子行为粒子群优化算法在求解组合优化问题方面具有优 势,如旅行商问题、背包问题等,有望在实际生产、物流 等领域得到广泛应用。
机器学习与数据挖掘
量子行为粒子群优化算法可用于特征选择、模型参数优化 等方面,为机器学习和数据挖掘提供新的思路和方法。
控制系统优化
在控制系统的参数优化和控制器设计中,量子行为粒子群 优化算法具有潜在的应用价值,有助于提高控制系统的性 能和稳定性。
量子粒子群算法的MPPT技术

• 160•由于可再生能源深受环境、气候等外部因素影响,作为光伏转换的重要组成部分,当光伏电池发生局部遮挡时,就会伴随出现其特性曲线的多峰值现象。
对于该类情况,传统的电导增量法(incremental conductance,IC )、扰动与观察算法(perturb and observe,P&O )容易误追踪到局部最大功率点(local peak,LP ),导致效率降低。
所以,为了能够准确追踪到全局最大功率点(global peak,GP ),从而保证转换效率,本文提出一种基于量子粒子群算法的最大功率点跟踪技术(maximum power point tracking technique,MPPT )。
通过搭建Matlab 仿真,其结果表明该算法不仅能跟踪到GP ,而且能有效地减小稳态振荡。
在太阳能阵列中,如果出现至少一个光伏电池被遮挡的情况,即属于遮阴现象,若光伏阵列对此没有一些有效的应对保护措施,就会导致光伏系统整体功率的下降,并且受遮挡电池所在的光伏组件会成为负载而消耗功率。
当因此消耗的功率过多时,会造成该组件局部温度过高,甚至导致组件毁坏。
为了尽可能地避免上述问题,可通过给太阳能阵列外接旁路二极管的方法进行解决。
旁路二极管的工作逻辑设计如下:当太阳能阵列的电流未超过被遮挡电池的短路电流I sc 时,受遮挡电池所在支路的旁路二极管不导通;否则,旁路二极管导通,使得电流不从受遮挡的组件上流过,从而降低由此引起的功率消耗。
上述外接旁路二极管,在光照强度均匀照射下不起作用,但是,在受到不均匀光照强度照射时,由于旁路二极管的导通,便会造成太阳能阵列的特性曲线出现多峰值现象。
由此可知,当特性曲线出现多峰值时,传统MPPT 方法不再奏效,且容易陷入局部最大功率点LP 。
针对该问题,本文提出了一种基于量子粒子群算法的MPPT 技术,利用粒子群的全局搜索能力,达到精准追踪全局最大功率点GP 的目的。
QPSO算法简介

QPSO 算法简介对标准的PSO 算法而言,算法收敛速度很快,但极易陷入局部最优。
为了解决之一不足,2004年,孙俊[46]从量子力学角度出发提出了量子粒子群(QPSO )算法,QPSO 算法的全局搜索能力要远远优于一般的PSO 算法。
QPSO 算法与PSO 算法是两种不同的运动方式,并不是在PSO 算法的位置与速度更新公式上添加算子,因在理论上QPSO 算法与PSO 算法的复杂度是相当的。
在QPSO 算法中,粒子被认为具有量子行为并参考了量子力学中量子的不确定性原理,故无法同时确定粒子的位置与速度的精确值。
QPSO 算法中粒子的更新是通过观测得到新个体,即给定一个概率去观测粒子,那么就会得到它得一个位置,对于每个粒子来说,会随机产生多个概率,利用蒙特卡罗思想进行观测,得到多个个体,然后选取个体最优,并依次评价其余个体,最终得到下代个体,如此进行搜索[47]。
QPSO 算法中粒子没有速度矢量,其位置迭代公式为:()()()1ln 1/id id id id X t p p X t u β+=±⋅-⋅式中,β——压缩-扩张系数,控制算法的收敛速度;u ——(0,1)之间的随机数。
上式中id p 称为局部吸引因子,由个体最优位置和全局最优位置共同决定,为了保证算法收敛,其表达式为:()1id i i p pBest gBest ϕϕ=⨯+-⨯式中:ϕ——(0,1)之间的随机数。
粒子i 的个体最优位置由式(2-14)确定:()()()()()()(),1=1,1i i i i i i i X t if f X t f pBest t pBest t pBest t iff X t f pBest t ⎧<-⎡⎤⎡⎤⎪⎣⎦⎣⎦⎨-≥-⎡⎤⎡⎤⎪⎣⎦⎣⎦⎩2.3.2 基于平均最优位置的QPSO 算法对于QPSO ,在迭代过程中通过个体极值与全局极值的相关信息进行下一步搜索,迭代末期,群体多样性会急剧恶化,个体容易陷入局部最优,故而孙俊等在算法中引入了平均最优位置(mean best position ,mbest )。
优化算法-粒子群优化算法

步骤四:对于粒子的每一维,根据式(1)计算得到一个随机点 的位置。
步骤五:根据式(2)计算粒子的新的位置。
步骤六:判断是否满足终止条件。
粒子群优化算法
PSO算法在组合优化问题中的应用
典型的组合优化问题:TSP
粒子群优化算法
量子行为粒子群优化算法的基本模型
群智能中个体的差异是有限的,不是趋向于无穷大的。群体的聚 集性是由相互学习的特点决定的。
个体的学习有以下特点: 追随性:学习群体中最优的知识
记忆性:受自身经验知识的束缚
创造性:使个体远离现有知识
粒子群优化算法
聚集性在力学中,用粒子的束缚态来描述。产生束缚态的原因是 在粒子运动的中心存在某种吸引势场,为此可以建立一个量子化 的吸引势场来束缚粒子(个体)以使群体具有聚集态。
描述为: 给定n 个城市和两两城市之间的距离, 求一条访问各城市
一次且仅一次的最短路线. TSP 是著名的组合优化问题, 是NP难题, 常被用来验证智能启发式算法的有效性。
vid (t 1) wvid (t) c1r1 pid (t) xid (t) c2r2( pgd (t) xid (t))
xid (t 1) xid (t) vid (t 1)
粒子群优化算法
w 惯性权重 可以是正常数,也可以是以时间为变量的线性或非线性
正数。
粒子群优化算法
通常动态权重可以获得比固定值更好的寻优结果,动态权重可以在 pso搜索过程中呈线性变化,也可以根据pso性能的某个测度函数 而动态改变,目前采用的是shi建议的随时间线性递减权值策略。
粒子群优化算法
带自适应变异的量子粒子群优化算法

带 自适应变异 的量子粒子 群优化算 法
刘 俊芳 高岳林 ,
LI U J nfng , u a GA O Yuei ln
1 . 宁夏大学 数学计算机学 院 , 川 7 0 2 银 5 0 1
关键 词 : 局 最优 化 ; 子 群 优 化 ; 子 粒 子 群 优 化 ; 全 粒 量 自适 应 变 异 DO :0 7 8 .s.028 3 . 1. .1 文 章 编 号 :0 28 3 ( 0 1 0 —0 10 文 献 标 识 码 : 中 图 分 类 号 :P1 I 1. 7 /i n10 -3 1 0 1 30 2 3 js 2 0 10 -3 12 1 )30 4 -3 A T 8
1 引言
粒子群优化( at l S r pi zt n P O) 由Ke . P rce wam O t ai ,S 是 i mi o n
量子粒子群优化 ( AMQ S 算法 , P O) 即在群体的适应度方差和空 间位置的聚集度 的基础上对群体 中每代粒子的个体极值位置进 行 自适应变异来增加种群的多样 陛, 从而实现全局寻优的 目的。
ig a d Ap l ain ,01 , 7 3 : 1 4 . n n p i t s 2 1 4 ( ) 4 — 3 c o
A sr c : A Q a tm at l w r O t z t n Alo i m i a t e Muain AMQ S b ta t u nu P r ce i S am p i a o g r h w t Ad p i t o ( mi i t h v t P O) i gv nWh n te po s ie . e h r —
量子粒子群算法的公式

量子粒子群算法的公式量子粒子群算法(Quantum Particle Swarm Optimization,QPSO)是一种元启发式优化算法,它结合了粒子群优化算法和量子计算的概念。
其公式可以用以下方式表示:1. 初始化量子粒子的位置和速度:\( x_i^0 = rand(x_{\text{min}}, x_{\text{max}}) \)。
\( v_i^0 = rand(-|x_{\text{max}}-x_{\text{min}}|, |x_{\text{max}}-x_{\text{min}}|) \)。
2. 计算适应度:\( f_i^0 = f(x_i^0) \)。
3. 更新量子粒子的位置和速度:\( x_i^{t+1} = x_i^t + v_i^t \)。
\( v_i^{t+1} = \frac{1}{2} \left( \frac{1}{N}\sum_{j=1}^{N} \frac{1}{\sqrt{1 + \frac{(x_i^tx_j^t)^2}{\lambda^2}}} \right)^2 v_i^t \)。
其中,\( x_i^t \) 表示第 \( i \) 个粒子在第 \( t \) 代的位置,\( v_i^t \) 表示第 \( i \) 个粒子在第 \( t \) 代的速度,\( f(x_i^t) \) 表示第 \( i \) 个粒子在位置 \( x_i^t \) 的适应度,\( x_{\text{min}} \) 和 \( x_{\text{max}} \) 分别表示搜索空间的最小值和最大值,\( N \) 表示粒子群中粒子的数量,\( \lambda \) 是一个常数。
以上公式描述了量子粒子群算法的基本过程,通过不断迭代更新粒子的位置和速度,以及根据适应度函数进行优化,最终寻找到最优解。
这种算法结合了经典粒子群优化算法和量子力学的概念,具有较强的全局搜索能力和收敛速度。
粒子群算法步骤

粒子群算法(Particle Swarm Optimization,PSO)是一种基于群体智能的优化算法,用于解决优化问题。
下面是粒子群算法的一般步骤:1. 初始化参数:- 定义问题的适应度函数。
- 设置群体规模(粒子数量)和迭代次数。
- 随机初始化每个粒子的位置和速度。
- 设置每个粒子的个体最佳位置和整个群体的全局最佳位置。
2. 迭代优化:- 对于每个粒子:- 根据当前位置和速度更新粒子的新速度。
- 根据新速度更新粒子的新位置。
- 根据新位置计算适应度函数值。
- 更新粒子的个体最佳位置和整个群体的全局最佳位置。
- 结束条件判断:达到预设的迭代次数或满足特定的停止条件。
3. 输出结果:- 输出全局最佳位置对应的解作为优化问题的最优解。
在更新粒子的速度和位置时,通常使用以下公式:速度更新:v(t+1) = w * v(t) + c1 * r1 * (pbest - x(t)) + c2 * r2 * (gbest - x(t))位置更新:x(t+1) = x(t) + v(t+1)其中:- v(t) 是粒子在时间t 的速度。
- x(t) 是粒子在时间t 的位置。
- w 是惯性权重,用于平衡粒子的历史速度和当前速度的影响。
- c1 和c2 是加速因子,控制个体和全局最佳位置对粒子速度的影响。
- r1 和r2 是随机数,用于引入随机性。
- pbest 是粒子的个体最佳位置。
- gbest 是整个群体的全局最佳位置。
以上是粒子群算法的基本步骤,您可以根据具体的优化问题进行调整和扩展。
粒子群算法粒子群算法简介
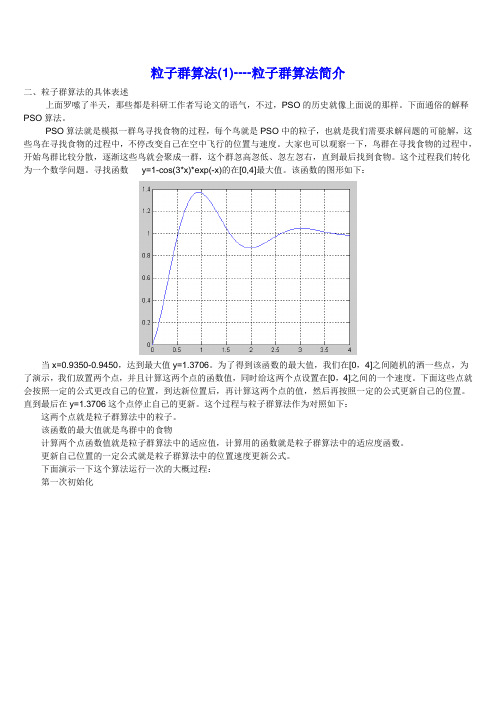
粒子群算法(1)----粒子群算法简介二、粒子群算法的具体表述上面罗嗦了半天,那些都是科研工作者写论文的语气,不过,PSO的历史就像上面说的那样。
下面通俗的解释PSO算法。
PSO算法就是模拟一群鸟寻找食物的过程,每个鸟就是PSO中的粒子,也就是我们需要求解问题的可能解,这些鸟在寻找食物的过程中,不停改变自己在空中飞行的位置与速度。
大家也可以观察一下,鸟群在寻找食物的过程中,开始鸟群比较分散,逐渐这些鸟就会聚成一群,这个群忽高忽低、忽左忽右,直到最后找到食物。
这个过程我们转化为一个数学问题。
寻找函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
该函数的图形如下:当x=0.9350-0.9450,达到最大值y=1.3706。
为了得到该函数的最大值,我们在[0,4]之间随机的洒一些点,为了演示,我们放置两个点,并且计算这两个点的函数值,同时给这两个点设置在[0,4]之间的一个速度。
下面这些点就会按照一定的公式更改自己的位置,到达新位置后,再计算这两个点的值,然后再按照一定的公式更新自己的位置。
直到最后在y=1.3706这个点停止自己的更新。
这个过程与粒子群算法作为对照如下:这两个点就是粒子群算法中的粒子。
该函数的最大值就是鸟群中的食物计算两个点函数值就是粒子群算法中的适应值,计算用的函数就是粒子群算法中的适应度函数。
更新自己位置的一定公式就是粒子群算法中的位置速度更新公式。
下面演示一下这个算法运行一次的大概过程:第一次初始化第一次更新位置第二次更新位置第21次更新最后的结果(30次迭代)最后所有的点都集中在最大值的地方。
粒子群算法(2)----标准的粒子群算法在上一节的叙述中,唯一没有给大家介绍的就是函数的这些随机的点(粒子)是如何运动的,只是说按照一定的公式更新。
这个公式就是粒子群算法中的位置速度更新公式。
下面就介绍这个公式是什么。
在上一节中我们求取函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
自适应免疫量子粒子群优化并行算法

n e i g a d A p i t n , 0 0 4 ( 1 : 43 。 e rn n p l a i s 2 1 ,6 2 ) 3 — 6 c o
Abtat T e A at e I s c: h dp v mmu e Qunu bh v d P rc wa O t zt n P rl la o tm ( Q S ) i peet . r i n a t m-eaБайду номын сангаас at l S r ie m pi ao aal l rh AI P OP s rsne I mi i e gi dn
g a d mmu o o i e h im a e mp o e , n a a a t e mmu e u n u — e a e p ril s r o t z t n lo Y n i n l g c m c a s r e l y d a d n n d p i i v n q a tm b h v d a t e wa c m p mi ai ag — i o
3 4
2 1 ,62 ) 0 0 4 ( 1
C m ue E gneiga d p l ain 计算机工程与应用 o p t n i r n A pi t s r e n c o
@研 究、 讨@ 探
自适应免疫量子粒子群优化并 行算法
成 新文
CHENG n we Xi . n
四川理工学院 计算机学院 , 四川 自贡 63 0 400
Ke r s y wo d :p r c e s I Io t z t n; a t m e h o o y;mm u o o i e h n s ; a all c mp tt n a t l wa1 p i a o q n u tc n l g i i T mi i u n lgc m c a i m p l o ua o r e i
粒子群算法原理

粒子群算法原理
粒子群算法(Particle Swarm Optimization,PSO)是一种基于群体智能的优化算法。
其原理受到鸟群觅食行为的启发,通过模拟鸟群中的协同学习和合作行为来寻求最优解。
PSO算法中,解空间被划分为一定数量的“粒子”。
每个粒子代表一个解,并具有自己的位置和速度。
粒子通过在解空间中移动来逐步搜索最优解。
粒子的速度是算法的核心,它决定了粒子下一步的移动方向和距离。
每个粒子的速度包括两个部分:当前速度和历史最优速度。
当前速度代表了粒子当前的移动方向和距离,历史最优速度代表了粒子在过去的搜索过程中达到的最优速度。
在每一次迭代中,粒子会根据当前速度和历史最优速度进行位置更新。
位置更新的方法是通过加速度来实现的。
加速度由两个部分组成:自身速度和与最优解的距离。
粒子倾向于保持自身速度的一部分,同时也受到距离最优解的吸引力影响。
通过不断迭代,粒子群逐渐向最优解靠近。
在搜索过程中,粒子会根据当前解的适应度评估情况来确定自己的历史最优解,并且会与群体中其他粒子进行信息共享,以便更好地利用群体智慧。
PSO算法的优点是简单、易于理解和实现。
然而,它也存在一些缺点,例如易陷入局部最优解、收敛速度较慢等。
因此,
在具体应用中需要根据问题的特点选择适当的参数和改进方法,以获得更好的优化效果。
量子粒子群算法 进度管理

量子粒子群算法进度管理嘿,朋友!你知道吗?当咱们谈到量子粒子群算法和进度管理,就好像是在驾驭一辆超级酷炫但又有点复杂的未来跑车。
先来说说量子粒子群算法,这可真是个神奇的玩意儿!它就像是一群充满智慧和活力的小精灵,在数据的世界里快速穿梭,寻找着最优的解决方案。
你想想看,这些小精灵们可不满足于常规的路径,它们会以一种超乎想象的方式跳跃、融合,不断尝试新的可能。
这是不是有点像咱们小时候玩的寻宝游戏,只不过这个宝藏是解决问题的最佳答案。
再讲讲进度管理,这可太重要啦!如果把一个项目比作一场马拉松比赛,那进度管理就是那个拿着秒表和路线图的教练。
它得时刻盯着运动员们的步伐,调整节奏,避免有人跑太快耗尽体力,也不能让有人掉队。
要是没有良好的进度管理,就好像你做饭的时候,一会儿忘了放盐,一会儿又把火开得太大,最后这顿饭能好吃吗?在运用量子粒子群算法进行进度管理时,咱们得有一双敏锐的眼睛。
要能从那些看似无序的数据中找到规律,就像在一堆乱麻中迅速找到线头一样。
而且还得有耐心,不能因为一时半会儿没看到效果就着急上火。
这就好比你种了一颗种子,不能天天把它挖出来看看有没有发芽呀!还有啊,要灵活调整策略。
就像开车在路上,遇到堵车就得换条路走。
如果一味地死磕,那可就容易陷入僵局。
比如说,当算法给出的方案在实际操作中遇到了困难,难道咱们还能硬着头皮往前冲?当然不能啦!而且,团队的沟通也至关重要。
大家得像一个紧密合作的乐队,每个成员都清楚自己的节奏和任务。
要是有人乱了节拍,那整个演出不就砸了?总之,量子粒子群算法和进度管理的结合,是一门高深但又有趣的学问。
只要咱们用心去琢磨,就一定能让项目像火箭一样顺利升空!朋友,让咱们一起加油,把这事儿干得漂漂亮亮的!。
基于量子粒子群算法的测试数据自动生成算法

Al o ihm o g rt f rAut m a cGe r to fTe t a aBa e n o i t ne a n o s t s d o i D O a t ri wa m im ia o  ̄ n um Pa t deS r Opt z t n i
种 应用 于软件 测试 中的基 于量子粒子群 算法 ( S QP O)的测试 数据 自动 生成 算法。该算 法是在 粒子群 ( S P O)算 法基础
上 引入量子理论的思想 。解 决了P O算法搜 索空 间有 限,容 易陷入 局部 最优 解的 问题 。通过具体 实验证 明,该 方法是 有效 S 可行 的 ,其效率也 明显高于 G A算法和 P O算法。 S 关键词 :软件 测试 ;测试数 据生成 ;粒子群算法 ;量子粒子群算法 中图分类 号 :TP 1 31 文献标识 码 :A 文章编 号 :17 9 7 (0 2 2 0 7 3 6 2 8 0 2 1 )0 13 0
YU h n a g Z ey n
( l g f mp tr gn eig,Hu ii n t ueo c n lg Col eo e Co ue ie r En n aynI si t f t Teh oo y,Hu i n2 3 0 a’ 2 0 3) a
A sr c :I h a e ot r e t g a p i o t e q a t m— a e at l s r o t zt n ( S b t t n ti p p r a s f e tsi p l d t h u nu b s d p r c wa a s wa n e ie m pi ai mi o QP O) o u fa —
混沌量子粒子群算法在模型修正中的应用

1Re e rh C n e f S tl t e h oo y, r i n t u e o e h o o , r i 1 0 0 , h n . s a c e t r o ae l e T c n lg Hab n I si t f T c n l g Ha b n 5 0 1 C i a i t y
2C i cdm fS aeT cn l yB in 0 0 6 C ia .hn A ae y o pc eh o g , e i 10 8 , hn a o jg
E— i: r a 0 4 e @1 3c r mal e i 2 0 rn 6 .o c n
QI u l g KO in r n L O e - o o e u d t g b s d Ol c a s q a U n— e a e a t l s a m p i N Y -i , NG X a - e , U W n b . d l p ai a e i h o u n u b h v d p ri e w r o t n M n c —
2 0 2 1 ,6 2 4 004 ()
C m u rE gnei n p l ao s o p t nier g ad A pi t n 计算机工程 与应用 e n ci
混沌量子粒子群算法在模型修正 中的应用
秦 玉 灵 ・孔宪 仁 t罗文波 2 , ,
Q N Y -ig, O G X a —e L O We— o I u l K N in Fn,U n b n
摘
要: 混沌粒子群 算法和量子粒子群算法在 一定程度上 改进 了标 准粒子群算法的搜 索质量 , 两者仍存在收敛速度慢 、 但 易陷入
具有分工策略的量子粒子群优化算法

Q atm_ e ae at l s r o t z t nwi ii o f r rtg u nu b h v dp r ce wam pi ai t dvs no ks aey i mi o h i wo t
J ANG e , F I L i ENG n S Bi , UN u Jn
_
0 引 言
微 粒 群 优 化 算法 (atls amot i t n P o 属 于智 能 prcew r i z i ,S ) i pm ao
群 方 法 的 一个 分 类 , 1 9 年 首次 由 K n e y与 E e at 首 是 95 en d b r r等 h
单 社会 的模拟 , 最初 设想是 模拟对 鸟群 觅食 的过程 , 来发 后
现 P O 是 一 种 很 好 的优 化 工 具 。 S P O优 化 算 法 与 其 它 进 化 算 法 相 类 似 , 是 将 寻优 的 参 S 也
数组合 成群体 , 通过 对环境 的适 应度来将群 体 中的个体 向好
的 区 域 移 动 。 与 其 它 进 化 算 法 不 同 , 描 述 个 体 时 , 其 看 在 将 成 是 D 维 寻 优 搜 索 空 间 的 一 个 没 有 体 积 的 微 粒 ( )结 合 微 点 ,
维普资讯
第 2 卷 第 2 期 Hale Waihona Puke 8 2VO . 8 12
N O 22 .
计 算 机 工 程 与 设 计
Co u e n i e r g a d De i n mp t rE g n e i n s n g
20 年 1 月 07 1
次 提 出 的 , 一 种 新 的 进 化 算 法 。与遗 传算 法 ( A 、 化 规划 是 G )进 (P等相 比 , E) 其具 有实 现简 单 、 优化 效 果和 速 率快 等优 点 。 目前 已 有 的研 究表 明 P O 算 法在 优化 问题 中取得 了 比较 好 的效 果 。但 S 当面 临 复杂 的优 化 问题 ,由于 目标 等 问题 存在 很 多 的局 部极 值 , 也 不可避 免 地存 在着 早 熟 、 收敛 速度 慢 等一 些缺 陷。
关于量子粒子群算法(QPSO)

关于量子粒子群算法的杂七杂八1 关于PSO说到GPSO,必须要说到它的源头,也就是PSO,也就是粒子群算法按照北京航空航天大学的王小川老师说法,粒子群优化算法(Particle swarm optimization,PSO)是模拟鸟群捕食行为的优化算法。
不同于遗传算法(Genetic Alogrithm,GA),粒子群算法是有记忆的,之前迭代过程中的最优位置和最优方向都会保留下来并作用于粒子群的更新。
这个算法的应用太广了,如果学习了一段时间的机器学习,即将迈入深度学习的阶段,一定要迈过去的两个坎,一个是RBM,就是受限玻尔兹曼机,另一个就是PSO1.1相关的名词解释粒子群长度:粒子群长度等于每一个参数取值范围的大小。
粒子群维度:粒子群维度等于待寻优参数的数量。
这个根据项目的具体要求可以十分容易的敲定粒子群位置:粒子群位置包含参数取值的具体数值。
粒子群方向:粒子群方向表示参数取值的变化方向。
个人感觉这里也可以理解成想原本的粒子(或者是cluster中的拥有实际含义的矩阵)的方向向量进行进一步的分解,从某种意义上说,其实它加大了分解出来的向量之间的联系,算是在某种程度上对于数据的维度进行了一定的扩充。
适应度函数:表征粒子对应的模型评价指标。
关于适应度函数的取值其实不止一个算法或者是模型中提到了关于适应度函数的具体含义与在具有特定条件与背景之下可能有效的适应度函数的取法,经典的如北京航空航天大学的王小川老师在他的著作中认为可以将适应度函数的取值设定为cluster中的单个样本的值对应的总的cluster的mean值的均方差的倒数,当然这个说法并不唯一,而且是在不同的条件下取值并不完全相同。
《43个案例分析》中单只要是涉及到函数的拟合的,适应度函数的取值都为待拟合的函数的取值的倒数。
目前尚无较为肯定的经验公式或者是对应的参照物图表可以归纳所有情况。
pbest:(局部最优)pbest的长度等于粒子群长度,表示每一个参数取值的变化过程中,到目前为止最优适应度函数值对应的取值。
量子粒子群算法

量子粒子群算法
量子粒子群算法(QPSO)是一种基于量子力学的进化算法,它是对粒子群算法(PSO)的改进。
QPSO使用了量子比特作为代替二进制比特的信息储存方式。
这种算法的主要优势在于其能够快速收敛并且易于实现。
QPSO的基本思想是,将优化问题中的每个解表示为量子态。
通过对这些量子态的测量和演化,可以找到全局最优解。
在QPSO中,每个量子态都表示一个解并且有一个对应的能量值。
量子态之间的转化和演化通过量子门来实现。
与PSO相比,QPSO具有更好的全局搜索能力和更快的收敛速度。
此外,QPSO还可以通过改变初始量子态来进行优化问题的不同运算。
因此,QPSO在多种优化问题中都有广泛的应用,包括函数优化、组合优化和机器学习等。
总的来说,QPSO是一种非常有前途的优化算法,它的研究和应用前景非常广阔。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
glofit=fitness(maxfitindex,bestchain); %获得全局最大适应度
%---------程序主循环开始----------------------------
for gen=1:1:maxgen
end
end
%---------初始化全局最优解--------------------------
gloangle(1,:)=angle(maxfitindex,:); %获得全局最优相位
glochrom(1,:,:)=chrom(maxfitindex,:,:); %初始化全局最优位置
hromx(i,j,1)))^0.5)
-(chromx(i,j,2)+1)*cos((abs(chromx(i,j,2)+1-chromx(i,j,1)))^0.5)*sin((abs(chromx(i,j,2)+1+chromx(i
,j,1)))^0.5);
selffitness(i,j)=-selfchromx(i,j,1)*sin((abs(selfchromx(i,j,2)+1-selfchromx(i,j,1)))^0.5)*cos((abs(self
for i=2:1:popsize
for j=1:1:2
if minfit>fitness(i,j)
minfit=fitness(i,j);minfitindex=i;
end
if maxfit<fitness(i,j)
maxfit=fitness(i,j);maxfitindex=i;bestchain=j;
end
end
end
1%
---------计算适应度----------------------------
for i=1:1:popsize
for j=1:1:2
fitness(i,j)=-chromx(i,j,1)*sin((abs(chromx(i,j,2)+1-chromx(i,j,1)))^0.5)*cos((abs(chromx(i,j,2)+1+c
end
avgfit=avgfit+fitness(i,j)/(2*popsize);
end
end
%---------更新自身最优位置---------------------
for i=1:1:popsize
t1=fitness(i,1);
if t1<fitness(i,2)
chromx(i,j,2)+1+selfchromx(i,j,1)))^0.5)
-(selfchromx(i,j,2)+1)*cos((abs(selfchromx(i,j,2)+1-selfchromx(i,j,1)))^0.5)*sin((abs(selfchromx(i,j,
2)+1+selfchromx(i,j,1)))^0.5);
chromx(i,j,k)=0.5*(varrange(k,2)*(1+chrom(i,j,k))+varrange(k,1)*(1-chrom(i,j,k)));
selfchromx(i,j,k)=0.5*(varrange(k,2)*(1+selfchrom(i,j,k))+varrange(k,1)*(1-selfchrom(i,j,k)));
t1=t1-2*pi;
end
t2=gloangle(1,j)-angle(i,j);
if t2<-pi
t2=t2+2*pi;
end
if t2>pi
t2=t2-2*pi;
end
dangle(i,j)=inertia*dangle(i,j)+selfw*rand*t1+globalw*rand*t2;
for i=1:1:popsize
for j=1:1:vartotal
if rand<mutatep
angle(i,j)=pi/2-angle(i,j); %变异后的相位
chrom(i,1,j)=cos(angle(i,j)); %变异后的位置
chrom(i,2,j)=sin(angle(i,j)); %变异后的位置
angle(i,j)=angle(i,j)+dangle(i,j); %移动后的相位
chrom(i,1,j)=cos(angle(i,j)); %移动后的位置
chrom(i,2,j)=sin(angle(i,j)); %移动后的位置
%解空间变换
chromx(i,1,j)=0.5*(varrange(j,2)*(1+chrom(i,1,j))+varrange(j,1)*(1-chrom(i,1,j)));
,j,1)))^0.5);%计算适应度
end
end
%---------统计适应度----------------------------
minfit=fitness(1,1);
if fitness(1,1)>fitness(1,2)
minfit=fitness(1,2);
end
end
end
for j=1:1:2
fitness(i,j)=-chromx(i,j,1)*sin((abs(chromx(i,j,2)+1-chromx(i,j,1)))^0.5)*cos((abs(chromx(i,j,2)+1+c
hromx(i,j,1)))^0.5)
-(chromx(i,j,2)+1)*cos((abs(chromx(i,j,2)+1-chromx(i,j,1)))^0.5)*sin((abs(chromx(i,j,2)+1+chromx(i
%---------粒子位置移动------------------------------
for i=1:1:popsize
for j=1:1:vartotal
t1=selfangle(i,j)-angle(i,j);
if t1<-pi
t1=t1+2*pi;
end
if t1>pi
maxfit=fitness(1,2);bestchain=2;
if fitness(1,1)>fitness(1,2)
maxfit=fitness(1,1);bestchain=1;
end
minfitindex=1;maxfitindex=1;
avgfit=(fitness(1,1)+fitness(1,2))/(2*popsize);
chrom(i,1,j)=cos(angle(i,j)); %第 i 个粒子(量子染色体)的幅角余弦
chrom(i,2,j)=sin(angle(i,j)); %第 i 个粒子(量子染色体)的幅角正弦
selfangle(i,j)=2*pi*rand;
selfchrom(i,1,j)=cos(angle(i,j));%第 i 个粒子自身最优位置的幅角余弦
hromx(i,j,1)))^0.5)
-(chromx(i,j,2)+1)*cos((abs(chromx(i,j,2)+1-chromx(i,j,1)))^0.5)*sin((abs(chromx(i,j,2)+1+chromx(i
,j,1)))^0.5);%计算适应度
end
end
%---------粒子位置变异------------------------
selfchromx(i,:,:)=chromx(i,:,:);
selffitness(i,:)=fitness(i,:);
end
end
%---------更新全局最优位置--------------------
if glofit<fitness(maxfitindex,bestchain)
end
end
%---------适应度统计------------------------------
minfit=fitness(1,1);
if fitness(1,1)>fitness(1,2)
minfit=fitness(1,2);
end
maxfit=fitness(1,2);bestchain=2;
for j=1:1:2
if minfit>fitness(i,j)
minfit=fitness(i,j);minfitindex=i;
end
if maxfit<fitness(i,j)
maxfit=fitness(i,j);maxfitindex=i;bestchain=j;
end
avgfit=avgfit+fitness(i,j)/(2*popsize);
if fitness(1,1)>fitness(1,2);
maxfit=fitness(1,1);bestchain=1;
end
minfitindex=1;maxfitindex=1;
avgfit=(fitness(1,1)+fitness(1,2))/(2*popsize);
