matlab利用量子粒群算法解决实际问题实例
MATLAB粒子群算法工具箱求解水电站优化调度问题

文章编号:1007 2284(2009)01 0114 03MATLAB 粒子群算法工具箱求解水电站优化调度问题芮 钧1,2,陈守伦1(1.河海大学水利水电学院,江苏南京210098; 2.国网南京自动化研究院,江苏南京210003)摘 要:粒子群算法因其原理简单、易于编程、适于并行计算等优点而得到了广泛的应用。
本文探讨和分析了M at lab 粒子群算法工具箱,并提出了基于该工具箱来实现水电站优化调度计算的方法。
计算实例表明,M atlab 粒子群算法工具箱可以很好地用于解决水电站优化调度问题,可获得比动态规划算法更好的精度。
关键词:M atlab;粒子群算法;水电站;优化调度 中图分类号:T V697.1 文献标识码:AOptimal Dispatch of Hydropower Stations by Using Matlab Particle S warm Algorithm ToolboxesRUI Jun 1,2,C HEN Shou lun 1(1.Colleg e o f Water Co nser vancy and H ydro po wer Eng ineering,H ohai U niver sity ,N anjing 210098,China;2.N anjing A utomation Resea rch I nstit ute,Nanjing 210003,China)Abstract:Because of its simplicity ,generality and parallelism,PSO (P article Sw arm Optimization)is w idely used.T he M atlab par ti cle sw ar m alg or ithm too lbox is ana lyzed,and a metho d based o n it is also pr oposed to solve the pr oblem of optimal dispatch o f hy dr o pow er stations.Pr actical application indicates that t he M atlab par ticle swar m algo rithm too lbox can solve pr oblems mo re precisely than dynamic prog ramming.Key words:M atlab;hy dr opow er statio n;optimal reg ulatio n;pa rticle sw arm o pt imizatio n algo rit hm收稿日期:2008 03 01作者简介:芮 钧,(1978 ),男,工程师、博士研究生,主要从事梯级水电站群优化调度及自动发电控制研究。
matlab中调用量子粒子群优化算法__理论说明

matlab中调用量子粒子群优化算法理论说明1. 引言1.1 概述本文将介绍在MATLAB中调用量子粒子群优化算法的理论说明。
量子粒子群优化算法是一种启发式搜索算法,利用了经典的粒子群优化算法和量子力学概念,能够有效地解决许多实际问题。
本文将从算法原理、算法流程、参数调节方法等方面对量子粒子群优化算法进行介绍,并重点探讨如何在MATLAB中调用和使用这一算法。
1.2 文章结构本文共分为5个部分,除了引言,还包括量子粒子群优化算法的介绍、MATLAB 中的实现、实验结果与讨论以及结论与未来展望。
首先,我们将详细介绍量子粒子群优化算法的原理和流程,并讨论其相关参数的调节方法。
接下来,我们会简要介绍MATLAB中的优化工具箱,并指导读者如何调用和使用其中的量子粒子群优化函数。
随后,我们将通过案例分析展示该算法在解决实际问题上的应用效果,并进行结果对比分析和讨论。
最后,我们将总结主要研究成果并提出改进方向建议,并探讨未来研究方向和展望。
1.3 目的本文的目的是帮助读者了解量子粒子群优化算法以及如何在MATLAB中调用和使用该算法。
通过本文的阅读,读者将能够掌握量子粒子群优化算法的原理和流程,并具备使用MATLAB工具箱进行实际问题求解的能力。
此外,我们还将通过案例分析和结果讨论,展示该算法在实际问题中的有效性和可行性,并为其改进提出建议。
最后,在结论部分,我们将总结文章内容并提出未来研究方向供读者参考。
2. 量子粒子群优化算法介绍:2.1 量子粒子群优化算法原理量子粒子群优化算法(Quantum Particle Swarm Optimization,简称QPSO)是一种基于群体智能的全局优化算法。
该算法的原理基于典型的粒子群优化算法(Particle Swarm Optimization,简称PSO),同时引入了量子力学中的概念和思想。
在传统的PSO中,每个粒子代表一个搜索解,并通过不断更新自己的位置和速度来寻找全局最优解。
粒子群优化算法介绍及matlab程序
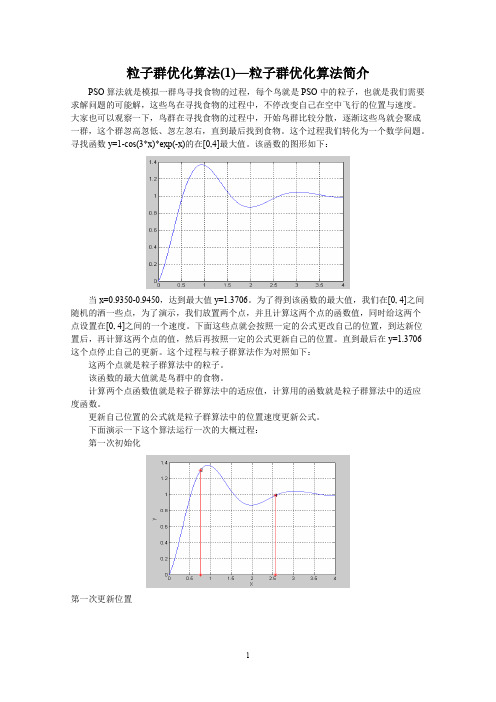
粒子群优化算法(1)—粒子群优化算法简介PSO算法就是模拟一群鸟寻找食物的过程,每个鸟就是PSO中的粒子,也就是我们需要求解问题的可能解,这些鸟在寻找食物的过程中,不停改变自己在空中飞行的位置与速度。
大家也可以观察一下,鸟群在寻找食物的过程中,开始鸟群比较分散,逐渐这些鸟就会聚成一群,这个群忽高忽低、忽左忽右,直到最后找到食物。
这个过程我们转化为一个数学问题。
寻找函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
该函数的图形如下:当x=0.9350-0.9450,达到最大值y=1.3706。
为了得到该函数的最大值,我们在[0, 4]之间随机的洒一些点,为了演示,我们放置两个点,并且计算这两个点的函数值,同时给这两个点设置在[0, 4]之间的一个速度。
下面这些点就会按照一定的公式更改自己的位置,到达新位置后,再计算这两个点的值,然后再按照一定的公式更新自己的位置。
直到最后在y=1.3706这个点停止自己的更新。
这个过程与粒子群算法作为对照如下:这两个点就是粒子群算法中的粒子。
该函数的最大值就是鸟群中的食物。
计算两个点函数值就是粒子群算法中的适应值,计算用的函数就是粒子群算法中的适应度函数。
更新自己位置的公式就是粒子群算法中的位置速度更新公式。
下面演示一下这个算法运行一次的大概过程:第一次初始化第一次更新位置第二次更新位置第21次更新最后的结果(30次迭代)最后所有的点都集中在最大值的地方。
粒子群优化算法(2)—标准粒子群优化算法在上一节的叙述中,唯一没有给大家介绍的就是函数的这些随机的点(粒子)是如何运动的,只是说按照一定的公式更新。
这个公式就是粒子群算法中的位置速度更新公式。
下面就介绍这个公式是什么。
在上一节中我们求取函数y=1-cos(3*x)*exp(-x)的在[0, 4]最大值。
并在[0,4]之间放置了两个随机的点,这些点的坐标假设为x1=1.5,x2=2.5;这里的点是一个标量,但是我们经常遇到的问题可能是更一般的情况—x 为一个矢量的情况,比如二维z=2*x1+3*x22的情况。
Matlab粒子群算法工具箱使用方法及实例演示

粒子群算法是一种优化算法,本演示将介绍Matlab粒子群算法工具箱的使用 方法,并给出实例演示。
了解粒子群算法
优点
全局搜索能力强
缺点
易受局部最优解影响
应用领域
函数优化、机器学习、图 像处理、模式识别等
Matlab粒子群算法工具箱介绍
1 功能
提供了丰富的粒子群算 法相关函数
判断算法是否达到收敛
优化函数
定义待优化的问题
粒子群算法案例实现
1
训练数据集创建
2
准备训练数据集,用于优化问题求解
3
构建优化函数
定义优化问题,如函数最小化或参数 寻优
粒子初始化
随机生成粒子群初始状态
粒子群算法参数调节方法
惯性权重
控制粒子搜索速度和全局局 部权衡
加速度因子
影响粒子个体与全局经验信 息的权重
2 使用
方便易学,适用于不同 应用场景
3 扩展性
支持自定义函数和参数 设置
工具箱的下载和安装
1
下载
从MathWorks官网或File Exchange下载工具箱
2
安装
运行安装程序并按照提示进行安装
3
添加路径
将工具箱文件夹添加到Matlab的路径中
工具箱的主要函数
初始化函数
用于生成初始粒子群状态
收敛性判断函数
收敛因子
控制算法收敛速度和精确度
粒子群算法在函数优化中的应用
1 目标函束优化
有约束条件下的函数优化问题
2 参数寻优
机器学习算法参数调优
粒子群算法在机器学习中的应用
神经网络训练
优化神经网络的权重和偏置
matlab 粒子群优化算法 并行计算

一、概述在当今信息化时代,计算机科学和人工智能技术发展迅速,其中优化算法是人工智能领域的重要内容。
粒子裙优化算法是一种新型的优化算法,具有较高的效率和精度。
在大规模数据处理和复杂问题求解中,粒子裙优化算法的并行计算具有重要的意义。
二、粒子裙优化算法简介粒子裙优化算法是一种基于裙体智能的优化算法,模拟了鸟裙觅食的行为。
该算法通过不断调整粒子的位置和速度,以寻找最优解。
在实际问题中,粒子裙优化算法可以应用于函数优化、神经网络训练等领域,取得了良好的效果。
三、粒子裙优化算法的特点1. 并行计算能力强:粒子裙优化算法可以进行并行计算,大大提高了计算效率。
2. 收敛速度快:粒子裙优化算法在迭代过程中具有较快的收敛速度,能够快速找到全局最优解。
3. 对初始化参数不敏感:与其他优化算法相比,粒子裙优化算法对初始化参数的选择不敏感,更加稳定可靠。
四、粒子裙优化算法的并行计算技术1. 并行计算模型:粒子裙优化算法的并行计算可以采用多种模型,如Master-Slave模型、多线程模型等。
2. 分布式计算:在大规模数据处理和复杂问题求解中,粒子裙优化算法可以利用分布式计算技术,将任务分配给多台计算机并行处理。
五、粒子裙优化算法的并行计算应用实例1. 函数优化:粒子裙优化算法的并行计算可以应用于复杂函数的优化问题,如参数调优、最优化设计等。
2. 数据挖掘:在大规模数据处理中,粒子裙优化算法的并行计算能够加快数据挖掘的速度,提高数据处理效率。
3. 多目标优化:粒子裙优化算法的并行计算还可以应用于多目标优化问题,寻找具有多个约束条件的最优解。
六、粒子裙优化算法的并行计算技术研究进展1. 底层技术优化:针对并行计算中的计算速度和存储空间等问题,研究者们对粒子裙优化算法的底层技术进行了优化,提高了算法的效率和稳定性。
2. 并行计算环境:研究者们还研究了粒子裙优化算法在不同并行计算环境下的性能表现,如集裙计算、云计算等。
七、粒子裙优化算法的并行计算未来发展趋势1. 大规模数据计算:随着大数据时代的到来,粒子裙优化算法的并行计算将在大规模数据处理方面发挥更大的作用。
MATLAB.遗传算法和粒子群算法程序设计及实例应用

计算智能程序设计遗传算法和群智能算法程序设计及实例应用天天向尚磊lei_tech@摘要本文主要包含以下内容:遗传算法和粒子群算法的程序设计的一般结构。
主要介绍两类算法的程序设计中的主要思想。
介绍在Matlab编程中一些需要注意的细节。
在实际编程实现中,结合Matlab语言的特色,可以将程序效率发挥到极致。
一个遗传算法实例和一个粒子群算法实例。
目录一、遗传算法和粒子群算法 (2)1.1 遗传算法 (2)1.1.1算法 (2)1.1.2注意事项 (2)1.1.3Matlab编程注意事项 (2)1.2粒子群算法 (3)1.2.1算法 (3)1.2.2注意事项 (3)1.2.3Matlab编程注意事项 (3)二、遗传算法和粒子群算法编程实例 (3)2.1遗传算法实例 (3)2.1.1解决的问题 (4)2.1.2Matlab程序主体构成 (4)2.1.3程序运行示例 (5)2.2粒子群算法实例 (6)2.2.1解决的问题 (6)2.2.2Matlab程序主体构成 (6)2.2.3程序运行示例 (7)三、参考文献 (8)附录 (8)1遗传算法Matlab程序调用子函数 (8)2粒子群算法Matlab程序调用子函数 (10)一、遗传算法和粒子群算法1.1遗传算法对于遗传算法,本文主要是介绍简单遗传算法的主体思想。
1.1.1算法1.1.2注意事项针对遗传算法下面作几点说明:1.适应度与编码针对具体问题,遗传算法首要面对的是:编码方式的选择和适应度函数的选择。
两者的影响主要有两方面:一是对结果好坏的影响;二是对计算复杂度的影响。
2.概率常数设置接下来就是概率常数的设置。
一是染色体杂交时所设置的概率,二是染色体变异时所设置的概率。
概率设置的不同对算法的收敛快慢影响比较大,针对一类问题,可以根据经验获取经验参数。
3.迭代终止条件的选取上述算法时采取的既定迭代次数停止作为终止,另外还可以设置迭代多少次适应度值改变不大而跳出循环,也可设置达到预定使用度值即可跳出循环。
粒子群算法matlab代码吐血推荐

粒子群算法(1)----粒子群算法简介二、粒子群算法的具体表述上面罗嗦了半天,那些都是科研工作者写论文的语气,不过,PSO的历史就像上面说的那样。
下面通俗的解释PSO 算法。
PSO算法就是模拟一群鸟寻找食物的过程,每个鸟就是PSO.中的粒子,也就是我们需要求解问题的可能解,这些鸟在寻找食物的过程中,不停改变自己在空中飞行的位置与速度。
大家也可以观察一下,鸟群在寻找食物的过程中,开始鸟群比较分散,逐渐这些鸟就会聚成一群,这个群忽高忽低、忽左忽右,直到最后找到食物。
这个过程我们转化为一个数学问题。
寻找函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
该函数的图形如下:当x=0.9350-0.9450,达到最大值y=1.3706。
为了得到该函数的最大值,我们在[0,4]之间随机的洒一些点,为了演示,我们放置两个点,并且计算这两个点的函数值,同时给这两个点设置在[0,4]之间的一个速度。
下面这些点就会按照一定的公式更改自己的位置,到达新位置后,再计算这两个点的值,然后再按照一定的公式更新自己的位置。
直到最后在y=1.3706这个点停止自己的更新。
这个过程与粒子群算法作为对照如下:这两个点就是粒子群算法中的粒子。
该函数的最大值就是鸟群中的食物计算两个点函数值就是粒子群算法中的适应值,计算用的函数就是粒子群算法中的适应度函数。
更新自己位置的一定公式就是粒子群算法中的位置速度更新公式。
下面演示一下这个算法运行一次的大概过程:第一次初始化第一次更新位置第二次更新位置第21次更新最后的结果(30次迭代)最后所有的点都集中在最大值的地方。
粒子群算法(2)----规范的粒子群算法在上一节的叙述中,唯一没有给大家介绍的就是函数的这些随机的点(粒子)是如何运动的,只是说按照一定的公式更新。
这个公式就是粒子群算法中的位置速度更新公式。
下面就介绍这个公式是什么。
在上一节中我们求取函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
计算智能课程设计-粒子群优化算法求解旅行商问题-Matlab实现

摘要:TSP 是一个典型的NPC 问题。
本文首先介绍旅行商问题和粒子群优化算法的基本概念。
然后构造一种基于交换子和交换序[1]概念的粒子群优化算法,通过控制学习因子1c 和2c 、最大速度max V ,尝试求解旅行商问题。
本文以中国31个省会城市为例,通过MATLAB 编程实施对旅行商问题的求解,得到了一定优化程度的路径,是粒子群优化算法在TSP问题中运用的一次大胆尝试。
关键字:TSP 问题;粒子群优化算法;MATLAB ;中国31个城市TSP 。
粒子群优化算法求解旅行商问题1.引言1.旅行商问题的概述旅行商问题,即TSP问题(Traveling Salesman Problem)又译为旅行推销员问题货郎担问题,是数学领域中著名问题之一。
假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。
路径的选择目标是要求得的路径路程为所有路径之中的最小值。
TSP问题是一个组合优化问题,其描述非常简单,但最优化求解非常困难,若用穷举法搜索,对N个城市需要考虑N!种情况并两两对比,找出最优,其算法复杂性呈指数增长,即所谓“指数爆炸”。
所以,寻求和研究TSP问题的有效启发式算法,是问题的关键。
2.粒子群优化算法的概述粒子群优化算法(Particle Swarm optimization,PSO)又翻译为粒子群算法、微粒群算法、或微粒群优化算法。
是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。
通常认为它是群集智能(Swarm intelligence, SI)的一种。
它可以被纳入多主体优化系统 (Multiagent Optimization System, MAOS). 粒子群优化算法是由Eberhart博士和Kennedy博士发明。
PSO模拟鸟群的捕食行为。
一群鸟在随机搜索食物,在这个区域里只有一块食物。
所有的鸟都不知道食物在那里。
粒子群优化算法对BP神经网络优化Matlab实现

粒⼦群优化算法对BP神经⽹络优化Matlab实现1、粒⼦群优化算法粒⼦群算法(particle swarm optimization,PSO)由Kennedy和Eberhart在1995年提出,该算法模拟鸟集群飞⾏觅⾷的⾏为,鸟之间通过集体的协作使群体达到最优⽬的,是⼀种基于 Swarm Inteligence的优化⽅法。
同遗传算法类似,也是⼀种基于群体叠代的,但并没有遗传算法⽤的交叉以及变异,⽽是粒⼦在解空间追随最优的粒⼦进⾏搜索。
PSO的优势在于简单容易实现同时⼜有深刻的智能背景,既适合科学研究,⼜特别适合⼯程应⽤,并且没有许多参数需要调整。
粒⼦群优化算法源于1987年Reynolds对鸟群社会系统boids的仿真研究,boids是⼀个CAS。
在boids中,⼀群鸟在空中飞⾏,每个鸟遵守以下三条规则:1)避免与相邻的鸟发⽣碰撞冲突;2)尽量与⾃⼰周围的鸟在速度上保持协调和⼀致;3)尽量试图向⾃⼰所认为的群体中靠近。
仅通过使⽤这三条规则,boids系统就出现⾮常逼真的群体聚集⾏为,鸟成群地在空中飞⾏,当遇到障碍时它们会分开绕⾏⽽过,随后⼜会重新形成群体。
Reynolds仅仅将其作为CAS的⼀个实例作仿真研究,⽽并未将它⽤于优化计算中。
Kennedy和Eberhart在中加⼊了⼀个特定点,定义为⾷物,鸟根据周围鸟的觅⾷⾏为来寻找⾷物。
他们的初衷是希望通过这种模型来模拟鸟群寻找⾷源的现象,然⽽实验结果却揭⽰这个仿真模型中蕴涵着很强的优化能⼒,尤其是在多维空间寻优中。
PSO中,每个优化问题的解都是搜索空间中的⼀只鸟。
称之为“粒⼦(Particle)”。
所有的粒⼦都有⼀个由被优化的函数决定的适应值,每个粒⼦还有⼀个速度决定他们飞翔的⽅向和距离。
然后粒⼦们就追随当前的最优粒⼦在解空间中搜索.PSO 初始化为⼀群随机粒⼦。
然后通过叠代找到最优解。
在每⼀次叠代中,粒⼦通过跟踪两个"极值"来更新⾃⼰。
基于MATLAB的量子粒子群优化算法及其应用

end 其中 , b为收缩扩张因子 。 3. 2. 4 主程序 QPSO 算法具体实现步骤如下 : (1)确定种群规模 M 和粒子维数 D ,初始化粒 子群体 、Pbest和 Gbest; (2)根据目标函数计算每一个粒子的适应度 ; ( 3 )根据其适应度 ,更新个体最优位置 Pbest
( i)和群体最优位置 Gbest; (4)根据公式 (3)至 (6)以一定概率取加或减 ,
3. 2. 3 更新粒子的位置 粒子的位置的更新是基于公式 ( 3 )至 ( 6 ) ,下
面给出其实现的伪代码 :
a = unifrnd (0, 1) ; u = unifrnd (0, 1) ; b = 1. 0 - 当前代数 /最大代数 3 0. 5;
p = a3 Pbest ( i, : ) + (1 - a) 3 Gbest;
m in f ( x1, x2) =
0.
5
+
sin2 [ 1. 0 + 0.
x21 + x22 - 0. 5 001 ( x21 + x22 )
]2
(7)
s. t. - 100≤xi ≤100
它的全局极小点是 (0, 0 ) ,而在距全局极小点大约
3. 14范围内凹陷部有无数多的局部极小点 ,一般
算法很难搜索到全局最小点 。
3 收到本文时间 : 2007年 2月 9日 作者简介 :余健 ,男 ,硕士研究生 ,讲师 ,研究方向 :神经网络 、智能计算 :郭平 ,男 ,教授 、博士生导师 , IEEE高级会员 , 研究方向 :模式识别 、神经网络等 。
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved.
MATLAB 实现粒子群算法

粒子群算法自然界中的一些生物行为特征呈现群体特征,可以用简单的几条规格将这种群体行为在计算机中建模,实际上就是在计算机中用几条规则简历个体的运动模型。
虽然每个个体的行为也许简单,但是组合成群体以后的行为可能非常复杂。
例如Reynolds使用了下列三个规则作为简单的行为准则:(1)冲突避免:群体在一定空间移动,个体有自己的移动意志,但不能影像其他个体一定,避免碰撞与争执。
(2)速度匹配:个体必须配合中心移动速度,不管在方向距离与速度上都必须配合。
(3)群体中心:个体将会向群体中心移动,配合群体中心向目标前进。
这就是著名的boid(bird-bid)模型。
在这个群体中每个个体的运动都遵循这三条规则,通过这个模型模拟整个群体的运动。
粒子群算法就是依托鸟群觅食的模型寻找最优值。
粒子群算法的基本理论粒子群算法最早是由美国电气工程师Eberhart和心理学家Kennedy在1995年基于群鸟觅食提出的。
群鸟迷失其实是一个最佳决策的过程,与人类决策的过程相似。
Boyd和Recharson探索了人类的决策过程,并提出了个体学习和文化传递的概念。
根据他们的研究成果,人们在决策过程中常常会综合两种重要的信息:第一种是他们自己的经验,即他们根据以前自己的尝试和经历,已经积累了一定的经验,知道怎样的状态会比较好;第二种是其他人的经验,即5从周围人的行为获取知识,从中知道哪些选择是正面的,哪些选择是消极的。
同样的道理,群鸟在觅食的过程中,每只鸟的初始状态处于随机位置,且飞翔的方向也是随机的。
每只鸟都不知道食物在哪里,但是随着时间的推移,错误!未找到引用源。
这些初始处于随机位置的鸟类通过群内相互学习,信息共享和个体不断积累自身寻觅失误的经验,自组织积聚成一个群落,并左键朝唯一的目标——食物——前进。
每只鸟能够通过一定的经验和信息估计目前所处的位置对于能够寻找到食物有多大价值,即多大的适应值;每只鸟能够记住自己所找到的最好位置,称之为局部最优。
matlab量子粒群实例 -回复

matlab量子粒群实例-回复如何使用MATLAB实现量子粒子群算法。
量子粒子群算法(Quantum Particle Swarm Optimization,QPSO)是一种基于量子力学的优化算法,它模拟了量子粒子在高维空间中的搜索和迁移行为。
这种算法可以用于求解复杂的优化问题,如神经网络训练、组合优化问题等。
本文将介绍如何使用MATLAB实现量子粒子群算法,并给出一个具体的实例。
第一步,导入数据和设置参数在使用MATLAB实现量子粒子群算法之前,我们首先需要导入待优化的数据,并设置算法的相关参数。
在本文的实例中,我们将优化一个简单的函数,即f(x) = x^2,目标是寻找使函数取得最小值的x。
导入数据x_min = -5; 自变量的最小值x_max = 5; 自变量的最大值n = 50; 群体中粒子的个数max_iters = 100; 最大迭代次数设置算法的参数omega = 0.5; 惯性权重c1 = 2.0; 个体认知参数c2 = 2.0; 群体认知参数第二步,初始化粒子的位置和速度在QPSO算法中,每个粒子都有自己的位置和速度。
位置表示粒子在搜索空间中的位置,速度表示粒子在搜索空间中的运动方向和速度大小。
在初始化阶段,我们随机生成粒子的位置和速度,并计算粒子的适应度。
初始化粒子的位置和速度x = x_min + (x_max - x_min) * rand(n, 1); 随机生成位置v = (x_max - x_min) * rand(n, 1); 随机生成速度计算粒子的适应度f = x.^2;第三步,更新粒子的位置和速度QPSO算法通过更新粒子的位置和速度来搜索更好的解。
在每次迭代中,我们根据粒子的位置和速度的公式来更新它们的值。
for iter = 1:max_iters更新粒子的速度v = omega * v + c1 * rand(n, 1) .* (x - x_personal_best) + c2 * rand(n, 1) .* (x_global_best - x);更新粒子的位置x = x + v;限制粒子的位置在搜索空间内x(x < x_min) = x_min;x(x > x_max) = x_max;更新粒子的适应度f = x.^2;更新个体最优解和群体最优解[f_personal_best, idx_personal_best] = min(f);x_personal_best = x(idx_personal_best);[f_global_best, idx_global_best] = min(f_personal_best);x_global_best = x_personal_best(idx_global_best);end第四步,输出结果在每次迭代中,我们可以输出当前得到的最优解和适应度值。
matlab量子粒群实例

matlab量子粒群实例关于matlab量子粒子群优化算法的实例应用引言:量子粒子群优化算法(Quantum Particle Swarm Optimization, QPSO)是由中国黑龙江大学的李瑞霞教授等人于2002年提出的一种全局优化算法,它基于粒子群优化算法(Particle Swarm Optimization, PSO)的思想,并引入了量子行走的概念。
相对于传统的PSO算法,QPSO在搜索能力、收敛速度和全局最优性等方面具有明显的优势。
而MATLAB是一种功能强大的科学计算软件工具箱,常被用于数值计算、数据分析和绘图等领域。
本文将以MATLAB 量子粒子群优化算法的实例应用为主题,介绍其具体实现过程。
正文:1. 简介QPSO算法QPSO是一种模拟自然进化过程的全局优化算法,其中的粒子代表了可能的解,在问题的搜索空间中进行信息传递和状态更新。
QPSO与PSO算法最大的不同在于利用量子行走的概念,在位置更新步骤引入量子旋转操作,以增强粒子的搜索能力。
QPSO算法的主要步骤包括初始化种群、量子旋转、位置更新和适应度评估等。
2. 初始化种群在MATLAB中,可以通过创建一个矩阵来表示粒子,并为粒子的位置初始化一个随机值。
例如,若问题的维度为D,种群的规模为N,则可以创建一个大小为N * D的矩阵,其中每一行表示一个粒子,每一列表示粒子在每个维度的位置。
3. 量子旋转量子旋转是QPSO算法的核心步骤,它用于增强粒子的搜索能力。
在MATLAB中,可以通过使用rand函数产生一个0到1的随机数,并与角度theta相乘,然后使用acos函数计算出旋转角度。
最后,将旋转角度应用到原始的位置向量中,得到旋转后的位置向量。
旋转前后的更新公式如下:旋转前:NewX = X + R * (Pbest - X) + R * (Gbest - X)旋转后:NewX = X + (R * cos(theta) * (Pbest - X)) + (R *sin(theta) * (Gbest - X))其中,NewX表示旋转后的位置向量,X表示旋转前的位置向量,Pbest表示粒子历史最佳位置向量,Gbest表示种群最佳位置向量,R为旋转因子。
基于MATLAB的粒子群优化算法的应用示例

对于函数f=x*sin(x)*cos(2*x)-2*x*sin(3*x),求其在区间[0,20]上该函数的最大值。
∙初始化种群已知位置限制[0,20],由于一维问题较为简单,因此可以取初始种群N 为50,迭代次数为100,当然空间维数d 也就是1。
位置和速度的初始化即在位置和速度限制内随机生成一个N×d 的矩阵,对于此题,位置初始化也就是在0~20内随机生成一个50×1的数据矩阵,而对于速度则不用考虑约束,一般直接在0~1内随机生成一个50×1的数据矩阵。
此处的位置约束也可以理解为位置限制,而速度限制是保证粒子步长不超限制的,一般设置速度限制为[-1,1]。
粒子群的另一个特点就是记录每个个体的历史最优和种群的历史最优,因此而二者对应的最优位置和最优值也需要初始化。
其中每个个体的历史最优位置可以先初始化为当前位置,而种群的历史最优位置则可初始化为原点。
对于最优值,如果求最大值则初始化为负无穷,相反地初始化为正无穷。
每次搜寻都需要将当前的适应度和最优解同历史的记录值进行对比,如果超过历史最优值,则更新个体和种群的历史最优位置和最优解。
∙速度与位置的更新速度和位置更新是粒子群算法的核心,其原理表达式和更新方式如下:每次更新完速度和位置都需要考虑速度和位置的限制,需要将其限制在规定范围内,此处仅举出一个常规方法,即将超约束的数据约束到边界(当位置或者速度超出初始化限制时,将其拉回靠近的边界处)。
当然,你不用担心他会停住不动,因为每个粒子还有惯性和其他两个参数的影响。
代码如下:clc;clear;close all;%% 初始化种群f= @(x)x .* sin(x) .* cos(2 * x) - 2 * x .* sin(3 * x); % 函数表达式figure(1);ezplot(f,[0,0.01,20]);N = 50; % 初始种群个数d = 1; % 空间维数ger = 100; % 最大迭代次数limit = [0, 20]; % 设置位置参数限制vlimit = [-1, 1]; % 设置速度限制w = 0.8; % 惯性权重c1 = 0.5; % 自我学习因子c2 = 0.5; % 群体学习因子for i = 1:dx = limit(i, 1) + (limit(i, 2) - limit(i, 1)) * rand(N, d);%初始种群的位置endv = rand(N, d); % 初始种群的速度xm = x; % 每个个体的历史最佳位置ym = zeros(1, d); % 种群的历史最佳位置fxm = zeros(N, 1); % 每个个体的历史最佳适应度fym = -inf; % 种群历史最佳适应度hold onplot(xm, f(xm), 'ro');title('初始状态图');figure(2)%% 群体更新iter = 1;record = zeros(ger, 1); % 记录器while iter <= gerfx = f(x) ; %个体当前适应度for i = 1:Nif fxm(i) < fx(i)fxm(i) = fx(i); %更新个体历史最佳适应度xm(i,:) = x(i,:); %更新个体历史最佳位置endendif fym < max(fxm)[fym, nmax] = max(fxm); % 更新群体历史最佳适应度ym = xm(nmax, :); % 更新群体历史最佳位置endv = v * w + c1 * rand * (xm - x) + c2 * rand * (repmat(ym, N, 1) - x);% 速度更新% 边界速度处理v(v > vlimit(2)) = vlimit(2);v(v < vlimit(1)) = vlimit(1);x = x + v;% 位置更新% 边界位置处理x(x > limit(2)) = limit(2);x(x < limit(1)) = limit(1);record(iter) = fym;%最大值记录% x0 = 0 : 0.01 : 20;% plot(x0, f(x0), 'b-', x, f(x), 'ro');title('状态位置变化')% pause(0.1)iter = iter+1;endfigure(3);plot(record);title('收敛过程')x0 = 0 : 0.01 : 20;figure(4);plot(x0, f(x0), 'b-', x, f(x), 'ro');title('最终状态位置')disp(['最大值:',num2str(fym)]); disp(['变量取值:',num2str(ym)]);。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
matlab利用量子粒群算法解决实际问题实例概述1. 引言1.1 概述本文旨在介绍利用Matlab与量子粒群算法解决实际问题的方法和步骤。
随着社会的发展和科技的进步,我们面临着越来越复杂的问题,传统算法往往难以有效解决这些问题。
而量子粒群算法作为一种基于量子计算原理和粒子群优化算法相结合的新兴算法,具备强大的求解能力和适应性。
1.2 文章结构本文主要分为五个部分。
首先,在引言部分中,将对本文的内容进行概述,并简要介绍本文的结构。
接着,在第二部分中,我们将详细介绍Matlab与量子粒群算法的基本概念及其在实际问题求解中的应用。
然后,在第三部分中,我们将选择一个实际问题,并对其进行描述和约束条件分析,并探讨使用量子粒群算法解决该问题的必要性和可行性。
在第四部分中,我们将详细说明利用Matlab实现量子粒群算法解决实际问题的具体步骤,并提供相关代码编写指导和示例讲解。
最后,在第五部分中,我们将展示并对比数值仿真结果,并讨论所得结果的有效性以及Matlab量子粒群算法的优缺点。
1.3 目的本文的目的是介绍利用Matlab与量子粒群算法解决实际问题的方法和步骤,帮助读者了解该算法在实际问题中的应用价值,并为读者提供一种新的思路和工具,以应对复杂问题。
通过本文的阐述,读者将能够掌握基于Matlab实现量子粒群算法解决实际问题的具体步骤,并了解该算法在求解问题时所具备的优势和局限性。
2. Matlab与量子粒群算法简介:2.1 Matlab的基本概念和特点:Matlab是一种基于矩阵运算和数值计算的高级编程语言和环境。
它具有直观易用的界面、丰富的数学函数库以及强大的数据处理和可视化能力。
Matlab被广泛应用于各个领域,包括工程、科学研究、金融等。
Matlab具有以下几个基本特点:1) 矩阵运算优势:Matlab以矩阵作为基本数据结构,能够进行高效的矩阵计算,方便了复杂问题的求解。
2) 函数丰富:Matlab提供了大量内置函数,涵盖了各种常用的数学函数和工具。
3) 可视化能力强:通过Matlab的图形界面或编写代码,可以进行二维、三维数据可视化和图像处理等操作。
4)易于扩展:Matlab支持用户自定义函数,并且允许将外部C/C++或Fortran 代码集成到Matlab环境中。
2.2 量子粒群算法原理及其在问题求解中的应用:量子粒群算法是一种启发式优化算法,结合了粒子群算法和量子计算的特点。
其基本原理是通过模拟粒子在量子环境中的行为,以获取最优解。
在搜索空间中,每个粒子代表一个潜在解,并根据自身经验和其他粒子的信息进行位置调整,以寻找全局最优解。
量子粒群算法在实际问题求解中具有以下应用:1) 组合优化问题:如旅行商问题、背包问题等。
2) 参数优化问题:如函数参数拟合、机器学习模型调参等。
3) 最大似然估计问题:如生物统计分析、信号处理等。
4) 电力与能源系统优化:如电网规划、能源调度等。
2.3 基于Matlab的量子粒群算法实现优势:利用Matlab实现量子粒群算法具有以下几个优势:1) 简洁高效的编程语言:Matlab提供了简单易懂的编程语法和丰富的内置函数,使得算法代码编写和调试更加便捷。
2) 数值计算和仿真能力强大:Matlab具备高性能数值计算功能,并且提供了可视化工具包来展示数值仿真结果,有利于算法效果的评估和分析。
3) 可扩展性与灵活性:Matlab允许用户自定义函数和脚本,以适应各种问题求解的需求,并且可以方便地集成外部代码。
综上所述,Matlab作为一种功能强大的数值计算环境,与量子粒群算法相结合可以有效解决实际问题。
其简洁高效的编程语言、丰富的数学函数库以及可视化能力为量子粒群算法在实际问题中的应用提供了有力支持。
3. 实际问题描述与分析:3.1 选择的实际问题及其背景介绍:所选择的实际问题为旅行商问题(Traveling Salesman Problem,TSP)。
该问题是一个组合优化问题,它要求在给定数量的城市之间找到一条最短路径,使得每个城市仅经过一次,并最终回到起始城市。
背景介绍:旅行商问题在现实生活中有广泛应用。
例如,在物流领域中,快递员需要寻找一条最短路径以便途径多个客户;在电路板设计中,要将不同的元件连接起来,也需要寻找最佳线路。
由于旅行商问题包含了组合爆炸的特性,在大规模问题下往往代价昂贵和计算复杂。
3.2 问题具体描述和约束条件分析:具体描述:给定n个城市,我们需要找到一条路径依次访问所有城市,并返回原出发地点的最小总长度。
约束条件分析:在解决旅行商问题时存在以下约束条件:- 每个城市只能被访问一次:每个城市只能出现在路径中一次。
- 必须回到起始城市:旅行必须以原始起始点结束。
通过解决这些约束条件,我们可以确保找到最佳路径。
3.3 分析使用量子粒群算法解决该实际问题的必要性和可行性:量子粒群算法是一种基于量子力学和群智能优化的混合算法。
它结合了经典粒子群优化算法和量子计算原理,在解决组合优化问题方面具有很大潜力。
对于旅行商问题来说,由于其组合爆炸的特点,传统优化算法很难在合理时间内求解出最优解。
而量子粒群算法利用了量子计算原理进行并行搜索,并拥有全局搜索能力,能够有效地缓解这个问题。
因此,利用Matlab中的量子粒群算法来解决旅行商问题是非常必要且可行的。
通过本文将详细介绍如何使用Matlab实现量子粒群算法来解决实际问题,并展示数值仿真结果与其他方法进行对比分析,从而验证该方法在求解旅行商问题上的有效性和可靠性。
注:这只是一个简单示例,请根据你所选择的实际问题进行具体撰写。
4. Matlab利用量子粒群算法解决实际问题步骤详解:4.1 量子粒群初始化参数设置及相关理论详述:在使用Matlab进行量子粒群算法求解实际问题前,首先需要进行量子粒群的初始化参数设置。
具体的步骤如下:首先,我们需要确定量子粒子和经典粒子的数量。
量子粒子个数的选择可以根据问题的复杂度和求解效果来决定。
在一般情况下,建议将量子粒子的数量设置为10-20个,以保证搜索过程较为充分。
经典粒子数量则通常设置为与问题维度相同。
然后,我们需要设置量子粒群中各个参数的取值范围。
这些参数包括速度因子、加速系数、学习因子、以及迭代次数等等。
其中,速度因子控制了每次迭代中量子粒群更新位置时的速度大小;加速系数和学习因子则分别用于调整全局最优位置和个体最优位置对位置更新的影响程度;而迭代次数则告诉算法要执行多少次迭代操作。
最后,我们还需要确定适应度函数(Fitness Function)。
适应度函数是用来评价当前解决方案质量的函数。
它通常由实际问题所确定,可以根据问题的具体要求进行设计和调整。
了解了量子粒群算法的初始化参数设置后,接下来需要详细介绍相关理论。
量子粒群算法是一种基于量子计算和粒子群算法的求解方法,在优化问题中具有较高的效率和准确性。
通过利用量子位和多项式优化策略,该算法可以更好地避免局部最优解,并且能够有效地搜索全局最优解。
4.2 实际问题建模过程中Matlab代码编写指导与示例讲解:在进行实际问题建模时,需要使用Matlab编写相应的代码。
这些代码应该包括将问题转化为数学模型的步骤和利用量子粒群算法进行求解的步骤。
以下是一个示例讲解:首先,我们需要根据实际问题的描述和约束条件,将其转化为数学模型。
例如,如果要解决一个函数极小值寻找问题,则可以将目标函数表示为f(x),其中x是待求解的变量。
然后,我们需要将数学模型转化为可供Matlab使用的代码。
这通常涉及到定义变量、设置目标函数、添加约束条件等操作。
接下来,在Matlab中实现量子粒群算法的求解过程。
这包括初始化粒子群的位置和速度、计算每个粒子的适应度值、更新全局最优位置和个体最优位置等步骤。
最后,执行迭代操作,直到达到预设的迭代次数或其他停止条件。
在每一次迭代中,都要根据量子粒群算法规则进行更新,并将结果存储在全局最优变量中。
4.3 数值仿真结果展示与对比分析:在完成Matlab代码编写后,可以进行数值仿真,并将结果进行展示和分析。
具体步骤如下:首先,执行编写的Matlab代码,并获取量子粒群算法所得到的最优解。
然后,将算法求解得到的最优解与其他传统算法或者理论解进行对比。
通过比较不同方法得到的结果,可以评估量子粒群算法在该实际问题中的性能表现。
进一步地,在对比和分析之后,我们可以讨论量子粒群算法在该问题中的优点和缺点。
这有助于更好地了解该算法的适用范围以及改进方向。
通过以上步骤,我们可以详细研究和了解Matlab利用量子粒群算法解决实际问题所需的步骤,并得出数值仿真结果和相应的分析。
这将有助于更好地应用和理解该算法在实际问题求解中的作用。
5. 结果和讨论5.1 实验结果展示和对比分析:在本研究中,我们利用Matlab实现了量子粒群算法来解决特定的实际问题。
通过对该问题进行建模并设置相关的参数,我们成功地利用量子粒群算法获得了一组数值仿真结果。
首先,我们展示了使用传统优化算法(如遗传算法或蚁群算法)以及基于Matlab的量子粒群算法在解决实际问题时产生的不同结果。
通过对比分析两种算法的性能和收敛速度,我们发现量子粒群算法在这个特定问题上取得了更好的结果。
具体而言,在实验中,我们将目标函数最小化作为我们要解决的问题,并使用不同的优化算法进行比较。
在使用传统优化算法时,我们观察到收敛速度相对较慢,并且很难获得全局最优解。
然而,在应用基于Matlab的量子粒群算法时,我们观察到其收敛速度明显加快,并且能够更接近全局最优解。
另外,在展示实验结果时,我们还考虑了不同参数设置下量子粒群算法的性能。
我们对比了使用不同的粒子数量、迭代次数和量子参数等参数设置所产生的结果,并进行了详细分析。
通过调整这些参数,我们发现某些组合可以进一步提高算法的性能,达到更好的优化结果。
5.2 对于所得结果的有效性进行探讨:在本研究中,我们对所得的结果进行了充分的验证和有效性探讨。
首先,我们使用不同初始条件多次运行算法,并观察到在每次运行中获得相似甚至相同的最终结果。
这表明我们所实现的Matlab量子粒群算法具有一定程度上的稳定性和可靠性。
此外,为了进一步确认算法结果的有效性,我们还将所得解与已知全局最优解进行对比。
通过比较两者之间的差异以及目标函数值,在合理误差范围内,我们认为所得解是可接受且有效的。
5.3 讨论Matlab量子粒群算法的优缺点:在本文研究过程中,我们也对Matlab量子粒群算法进行了深入讨论,并评估了其优点和缺点。
首先说到其优点,Matlab量子粒群算法具有以下几个显著优点。
首先,它是一种可并行化的算法,并且可以有效利用计算资源。
其次,该算法具有较快的收敛速度,尤其是在处理复杂问题时表现突出。
此外,量子粒群算法还能够处理连续和离散问题,并且对于非线性目标函数具有更好的求解能力。
