两条直线的位置关系1(1)
两条直线的位置关系(1)

父亲上学时,按照当时来讲,是有钱家的孩子才能上得了学的,大冬天的能提着暖手的火炉子上学,相当得气派,穿着得自然要好点。父亲的婆婆赵氏很支持我父亲的学业,因此,父亲能顺利地从 陕西泾干中学高中毕业。听父亲讲过,家里人把一头毛驴卖掉了供我父亲上学。父亲的勤奋也证明了这头毛驴卖掉是正确的。在我爷爷的八个孩子当中,父亲排行老二,也就只有父亲一个人跳出了农门, 到了外面做事,当了国家干部。也有人说,父亲是赵氏一手养大看大的娃娃,性格和脾气很像赵氏,而赵氏出自泾阳县里的一个大家族。在历史上,从赵氏的娘家大户焦家的确走出了几位泾阳名人, 《泾阳县志》2001年版上都有记载。
父亲的家境是一个殷实的家庭,有着好地百亩,有着好多长工,比如叫什么王相、什么张相。回想当年定成分时,我们家被什么的小组划定成为了富农。而事实上,有人也说了是我爷爷得罪了村里 的人,我们家顶多是一个中农。父亲的父亲,也就是我爷爷是过继给了同村的另一户杨家。因此,我爷爷的名字从原本的德理改成了长德,在家排行老四。我祖爷,按照血统上讲的是应该是杨居耀,过 继给了另一户杨家,我祖爷名字改叫成了杨天佑,有着一大家子的人,还有要经营的生意,听我父亲讲是在甘肃张掖一带。杨天佑有三个女儿,没有儿子,我爷爷到了杨天佑家,延续了香火。而杨天佑 家里的生意都是由我父亲的婆婆赵氏,也就是杨天佑的内人来经营着的。电游网 Leabharlann
11.3.1两条直线的位置关系(1)

联立方程组,行列式法判断方程组解的情况.
二、两条直线位置关系
已知两条直线方程为
l1 : a1 x b1 y c1 0 l2 : a2 x b2 y c2 0
c1 b1 c2 b2 , Dy a1 a2 c1 c2
记D
a1
b1
a2 b2
, Dx
Dx Dy 当 D 0 时,两直线相交于点 ( , ) ; D D
x m 2 y 6 解:联立方程组,整理得: (m 2) x 3my 2m 1 m2 D m(m 1)(m 3) m 2 3m
Dx 6 m2 2m 3m 1 6 2m(m 3)(m 3)
l1 : x m y 6 0, l2 : (m 2) x 3my 2m 0
三、典型例题
例1.判定下列各组直线的位置关系,如果相交, 那么求出交点坐标:
2 l1 : 3x 4 y 12 0, l2 : y 0
3 4 解: D 4 两直线相交. 1 0
即两直线相交, 交点坐标为(4,0)
三、典型例题
例1.判定下列各组直线的位置关系,如果相交, 那么求出交点坐标:
当 D Dx Dy 0 时,两直线重合;
当 D 0, Dx 0 或 Dy 0 时,两直线平行.
三、典型例题
例1.判定下列各组直线的位置关系,如果相交, 那么求出交点坐标:
1 l1 : 3x 4 y 12 0, l2 : 7 x 12 y 1 0 2 l1 : 3x 4 y 12 0, l2 : y 0 3 l1 : 3x 4 y 12 0, l2 : 6 x 8 y 5 0
两条直线的位置关系(相交平行重合)

或 A1 B1 C1 A2 B2 C2
( A2、B2、C2 0)
(2)求过点A(1,-4)且与直线2x+3y+5=0平 行的直线的方程
解:设∵直所线求方直程线为与2已x知+直3y线+平C=行0 ∴代所入求点直(线1,k=-4-)32 。得 2-12+C=0 ∴C=所1求0 直线的方程是y+4=- 32(x-1) 所即求直2x线+3的y+方10程=0是 2x+3y+10=0
例2.已知直线方程l1:x+mБайду номын сангаас+6=0, l2:(m-2) x+3y+2m=0 , 当m为何值时 l1、 l2(1)相交 (2)平行 (3)重合
例3.已知三条直线ax+y+1=0, x+y+a=0 x+ay+1=0 可构成三角形,求a的取值条件。
两条直线的位置关系(1)
---------相交、平行、重合
问1.两条不重合直线l1与l2的倾斜角相等, 这两条直线的位置关系如何?
两直线平行或重合 问2.两条直线l1与l2平行, 1)这两条直线的倾斜角大小有何关系?
2)这两条直线的纵截距相等吗?
3)斜率相等吗? 1)两直线平行倾斜角相等;
2)如果纵截距存在,则纵截距不相等; 3) 倾斜角不为900时斜率相等,为900时斜率不存在
已知直线l1与l2的斜截式方程为
l1:y=k1x+b1 l2:y=k2x+b2,
直线l1∥ l2
k1=k2且b1 ≠ b2
直线l1、 l2重合
k1=k2且b1 = b2
直线l1、 l2相交
人教版高中数学必修一 两条直线的位置关系(1)-课件

x
2
y
5
0,
可得 x 3, y 1.
因此 l1与 l2相交,而且交点的坐标为(-3,-1).
例题2.已知直线 l 过点(1,-4)且与直线2x+3y+5=0平行, 求直线 l 的方程. 解:设直线 l 的方程为2x+3y+C=0.由于 l 过点(1,-4),
因此 2 1+3(-4)+C=0
解得C=10. 因此直线 l 的方程为2x+3y+10=0.
北京市中小学空中课堂
两条直线的位置关系(1)
高二年级 数学
主讲人 李娜 北京市第八中学
判断两条直线的位置关系
若两条直线 l1 : y=k1x b1,l2 : y k2 x b2
y l2
y l2
b2
l1 b2
O
x
x
O
b1
b1
l1
k1 k2
bk11
=k2 b2
y l2 (l1)
b2(b1 )
(1)l1 : x y 1 0,l2 : 2x 2 y 1 0
1
另解:两条直线的一般式方程满足:2
=
1 2
1 1
所以两直线平行.
例题1.判断下列各对直线的位置关系,如果相交, 求出交点坐标:
(2)l1 : x 2 y 1 0,l2 : x 2 y 5 0
解方程组 x 2 y 1 0,
课堂小结
1.通过斜截式方程判断两条直线的位置关系; 2.通过一般式方程判断两条直线的位置关系; 3.求两条直线的交点坐标.
人教社作B版业课本
P91练习A第1、2、3题;
谢谢
在 v1 与 v2 共线时,存在实常数 ,使得 v1 v2 因为 v1 与 v2 都不是零向量,所以 0,且
第讲两直线的位置关系

从而得两条直线的交点为(9,-4), 又当 x=9,y=-4 时,有 9(m-1)+(-4)(2m-1)=m-5, 即点(9,-4)在直线(m-1)x+(2m-1)y=m-5 上, 故直线(m-1)x+(2m-1)y=m-5 都通过定点(9,-4).
证法二:∵(m-1)x+(2m-1)y=m-5, ∴m(x+2y-1)-(x+y-5)=0. 则直线(m-1)x+(2m-1)y=m-5 都通过直线 x+2y-1=0 与 x+y-5=0 的交点. 由方程组xx+ +2y-y-51==00. , 解得 x=9,y=-4,即过点(9,-4). 所以直线(m-1)x+(2m-1)y=m-5 经过定点(9,-4).
(1)l1与l2相交;(2)l1⊥l2;(3)l1∥l2;(4)l1,l2重合. 解题思路:根据两直线的位置关系列式再求解.
解析:(1)由已知1×3≠m(m-2), 即m2-2m-3≠0,解得m≠-1且m≠3. 故当m≠-1且m≠3时,l1与l2相交. (2)当 1·(m-2)+m·3=0,即 m=12时,l1⊥l2. (3)当m-1 2=m3 且26m≠m3 ,即 m=-1 时,l1∥l2.
等于( D )
A.2
B.1
C.0
D.-1
4.(2010年上海)圆C:x2+y2-2x-4y+4=0的圆心到直线 3x+4y+4=0 的距离 d=__3__.
5.原点在直线l上的射影是P(-2,1),则l的斜率为__2_. 解析:kOP=-12=-12,则 kl=2.
考点1 两直线的平行与垂直关系
例1:已知直线l1:x+my+6=0,l2:(m-2)x+3y+2m=0, 求m的值,使得:
证法三:∵(m-1)x+(2m-1)y=m-5, ∴m(x+2y-1)=x+y-5. 由 m 为任意实数,知关于 m 的一元一次方程 m(x+2y-1)= x+y-5 的解集为 R, ∴xx+ +2y-y-51==00. , 解得 x=9,y=-4. 所以直线(m-1)x+(2m-1)y=m-5 都通过定点(9,-4).
2.1两条直线的位置关系(1)
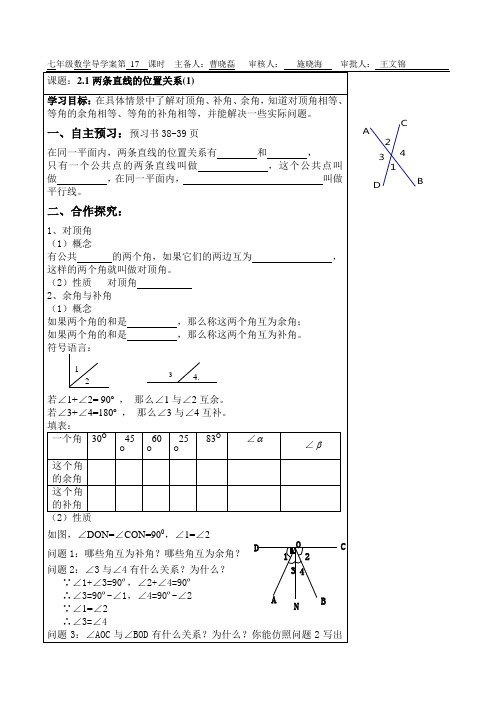
4、填空: ∵∠A+∠B=90º,∠B+∠C=90º ∴∠A ∠C( ) ∵∠1+∠3=90º,∠2+∠4=90º且∠1=∠2 ∴∠3 ∠4( ) 5、一个角的补角与这个角的余角的和比平角少 10°,求这个角.
课后反思:
七年级数学导学案第 17 课时 主备人:曹晓磊
审核人:
施晓海
审批人: 王文锦
课题:2.1 两条直线的位置关系(1) 学习目标: 在具体情景中了解对顶角、 补角、 余角, 知道对顶角相等、 等角的余角相等、等角的补角相等,并能解决一些实际问题。
一、自主预习:预习书 38-39 页
在同一平面内,两条直线的位置关系有 只有一个公共点的两条直线叫做 做 , 在同一平面内, 平行线。 和 , ,这个公共点叫 叫做
1
三、当堂检测:1、判断题:对的打“√”, 错的打“×” 。
① 一个角的余角一定是锐角。 ( ② 一个角的补角一定是钝角。 ( ) ) 互为余角。 ( )
③ 若∠1+∠2+∠3=90°, 那么∠1、 ∠2、 ∠3 2、下列说法正确的是( )
A. 相 等 的 角 是 对 顶 角 C.两条直线相交所成的角是对顶角 角是对顶角
,
一个角 30
45
60
25
83
∠
O
O
O
∠
这个角 的余角 这个角 的补角 (2)性质 如图,∠DON=∠CON=900,∠1=∠2 问题 1:哪些角互为补角?哪些角互为余角有什么关系?为什么? 3 4 ∵∠1+∠3=90º,∠2+∠4=90º ∴∠3=90º-∠1,∠4=90º-∠2 A B N ∵∠1=∠2 ∴∠3=∠4 问题 3:∠AOC 与∠BOD 有什么关系?为什么?你能仿照问题 2 写出
高中数学优秀教案第二册上.两条直线的位置关系(一)

两条直线的平行与垂直一、教学目标(一)知识教学点掌握两条直线平行与垂直的条件,会运用条件判断两直线是否平行或垂直,能运用条件确定两平行或垂直直线的方程系数.一条直线与另一条直线所成角的概念及其公式,两直线的夹角公式,能熟练运用公式解题.(二)能力训练点通过研究两直线平行或垂直的条件的讨论,培养学生运用已有知识解决新问题的能力以及学生的数形结合能力.通过课题的引入,训练学生由特殊到一般,定性、定量逐层深入研究问题的思想方法;通过公式的推导,培养学生综合运用知识解决问题的能力.(三)学科渗透点通过对两直线平行与垂直的位置关系的研究,培养学生的成功意识,激发学生学习的兴趣.训练学生由特殊到一般,定性、定量逐步深入地研究问题的习惯.二、教材分析1.重点:两条直线平行和垂直的条件是解析几何中的一个重点,要求学生能熟练掌握,灵活运用.2.难点:启发学生把研究两直线的平行与垂直问题转化为考查两直线的斜率的关系问题.公式的记忆与应用.3.疑点:对于两直线中有一条直线斜率不存在的情况课本上没有考虑,上课时要注意解决好这个问题.推导l1、l2的角公式时的构图的分类依据.三、活动设计提问、讨论、解答.四、教学过程(一)特殊情况下的两直线平行与垂直这一节课,我们研究怎样通过两直线的方程来判断两直线的平行与垂直.当两条直线中有一条直线没有斜率时:(1)当另一条直线的斜率也不存在时,两直线的倾斜角为90°,互相平行;(2)当另一条直线的斜率为0时,一条直线的倾斜角为90°,另一条直线的倾斜角为0°,两直线互相垂直.(二)斜率存在时两直线的平行与垂直设直线l1和l2的斜率为k1和k2,它们的方程分别是l1: y=k1x+b1; l2: y=k2x+b2.两直线的平行与垂直是由两直线的方向来决定的,两直线的方向又是由直线的倾斜角与斜率决定的,所以我们下面要解决的问题是两平行与垂直的直线它们的斜率有什么特征.我们首先研究两条直线平行(不重合)的情形.如果l1∥l2(图1—29),那么它们的倾斜角相等:α1=α2.∴tgα1=tgα2.即k1=k2.反过来,如果两条直线的斜率相等,k1=k2,那么tgα1=tgα2.由于0°≤α1<180°,0°≤α<180°,∴α1=α2.∵两直线不重合,∴l1∥l2.两条直线有斜率且不重合,如果它们平行,那么它们的斜率相等;反之,如果它们的斜率相等,则它们平行,即eq \x( )要注意,上面的等价是在两直线不重合且斜率存在的前提下才成立的,缺少这个前提,结论并不存立.现在研究两条直线垂直的情形.如果l1⊥l2,这时α1≠α2,否则两直线平行.设α2<α1(图1—30),甲图的特征是l1与l2的交点在x轴上方;乙图的特征是l1与l2的交点在x轴下方;丙图的特征是l1与l2的交点在x轴上,无论哪种情况下都有α1=90°+α2.因为l1、l2的斜率是k1、k2,即α1≠90°,所以α2≠0°.可以推出α1=90°+α2.l1⊥l2.两条直线都有斜率,如果它们互相垂直,则它们的斜率互为负倒数;反之,如果它们的斜率互为负倒数,则它们互相垂直,即(三)例题例1 已知两条直线l1:2x—4y+7=0,L2:x—2y+5=0.求证:l1∥l2.证明两直线平行,需说明两个要点:(1)两直线斜率相等;(2)两直线不重合.证明:把l1、l2的方程写成斜截式:∴两直线不相交.∵两直线不重合,∴l1∥l2.例2求过点A(1,-4),且与直线2x+3y+5=0平等的直线方程.即2x+3y+10= 0.解法2 因所求直线与2x+3y+5=0平行,可设所求直线方程为2x+3y+m=0,将A(1,-4)代入有m=10,故所求直线方程为2x+3y+10=0.例3 已知两条直线l1:2x—4y+7=0,l2:2x+y—5=0.求证:l1⊥l2.∴l1⊥l2.例4 求过点A(2,1),且与直线2x+y—10=0垂直的直线方程.解法1 已知直线的斜率k1=-2.∵所求直线与已知直线垂直,根据点斜式得所求直线的方程是就是x—2y=0.解法2 因所求直线与已知直线垂直,所以可设所求直线方程是x-2y+m=0,将点A(2,1)代入方程得m=0,所求直线的方程是x—2y=0.(四)两条直线的夹角两条直线l1和l2相交构成四个角,它们是两对对顶角.为了区别这些角,我们把直线l1依逆时针方向旋转到与l2重合时所转的角,叫做l1到l2的角.图1-27中,直线l1到l2的角是θ1,l2到l1的角是θ2(θ1+θ2=180°).l1到l2的角有三个要点:始边、终边和旋转方向.现在我们来求斜率分别为k1、k2的两条直线l1到l2的角,设已知直线的方程分别是l1∶y=k1x+b1 l2∶y=k2x+b2如果1+k1k2=0,那么θ=90°,下面研究1+k1k2≠0的情形.由于直线的方向是由直线的倾角决定的,所以我们从研究θ与l1和l2的倾角的关系入手考虑问题.设l1、l2的倾斜角分别是α1和α2(图1—32),甲图的特征是l1到l2的角是l1、l2和x轴围成的三角形的内角;乙图的特征是l1到l2的角是l1、l2与x轴围成的三角形的外角.tgα1=k1,tgα2=k2.∵θ=α2—α1(图1-32),或θ=π-(α1—α2)=π+(α2-α1),∴tgθ=tg(α2-α1).或tgθ=tg[π(α2—α1)]=tg(α2-α1).可得即eq \x( )上面的关系记忆时,可抓住分子是终边斜率减始边斜率的特征进行记忆.(五)夹角公式从一条直线到另一条直线的角,可能不大于直角,也可能大于直角,但我们常常只需要考虑不大于直角的角(就是两条直线所成的角,简称夹角)就可以了,这时可以用下面的公式(六)例题解:k1=—2,k2=1.∴θ=arctg3≈71°34′.本例题用来熟悉夹角公式.例2 已知直线l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0(B1≠0、B2≠0、A1A2+B1B2≠0),l1到l2的角是θ,求证:证明:设两条直线l1、l2的斜率分别为k1、k2,则这个例题用来熟悉直线l1到l2的角.例3等腰三角形一腰所在的直线l1的方程是x-2y-2=0,底边所在的直线l2的方程是x+y-1=0,点(—2,0)在另一腰上,求这腰所在直线l3的方程.解:先作图演示一腰到底的角与底到另一腰的角相等,并且与两腰到底的角与底到另一腰的角相等,并且与两腰的顺序无关.设l1、l2、l3的斜率分别是k1、k2、k3,l1到l2的角是θ1,l2到l3的角是θ2,则.因为l1、l2、l3所围成的三角形是等腰三角形,所以θ1=θ2.tgθ2=tgθ1=-3.解得k3=2.因为l3经过点(—2,0),斜率为2,写出点斜式为y=2[x-(-2)],即2x—y+4=0.这就是直线l3的方程.讲此例题时,一定要说明:无须作图,任一腰到底的角与底到另一腰的角都相等,要为锐角都为锐角,要为钝角都为钝角.(四)课后小结(1)斜率存在的不重合的两直线平行的等价条件;(2)两斜率存在的直线垂直的等价条件;(3)与已知直线平行的直线的设法;(4)与已知直线垂直的直线的设法.(5)l1到l2的角的概念及l1与l2夹角的概念;(6)l1到l2的角的正切公式;(7)l1与l2的夹角的正切公式;(8)等腰三角形中,一腰所在直线到底面所在直线的角,等于底边所在直线到另一腰所在直线的角.五、布置作业1.7练习第1,2,3题习题三第3,10题。
11.3两条直线的位置关系(1)

例2:求经过原点且过直线 l1 : x 2 y 2 0与 l2 : 2 x y 2 0 的交点的直线l的方程。
例题
例3、讨论下列各组直线之间的位置关系: (1)l1 : x m y 6 0,
2
(2)l1 : y 1 k1 x 3,
l2 : m 2x 3my 2m 0; l2 : y 1 k 2 x 3 。
Dx D y 此时直线l1、l2相交于一点 , D D 此时直线l1与直线l2相交
2 当D 0时,
(i)若Dx 0 或D y 0
方程组无解,两直线l1、l2没有公共 点,即两直线平行。
(ii)若Dx D y 0
方程组有无数解,两直线l1、l2重合。
例题
例 1、判断下列各组直线的 位置关系, 若相交,求出交点坐标 :
例题
例4、是否存在实数k,使直线 l1 : 3x k 2 y 6 0, l2 : kx 2k 3 y 2 0 平行?若存在,求k的值; 若不存在,请说明理由。
a1 x b1 y c1 0 a 2 x b2 y c 2 0
的解取决于系数构成的 行列式的值:
D a 1 b1 a 2 b2
Dx c1 b1 c 2 b2
Dy
a 1 c1 a2 c2
1当D 0, 即a1b2 a2b1时,
x 方程组有唯一解 y Dx D Dy D 。
11.3两条直线的位置关系
两条直线的相交、平行ቤተ መጻሕፍቲ ባይዱ重合
提问:在同一平面内两条直线的位置关 系有哪几种?这些位置关系在直线方程 上是怎样体现的呢?
设直角坐标平面上两条 直线的方程分别为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小结:(两种形式使用条件) 斜截式要求斜率存在 一般式的等价条件转化为整式 特殊形式如何判断?
二.两条直线垂直的条件(特殊的相交)
1.已知两条直线的方程为:
l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0,
y=k1x+b1
;
y=k2x+b2;
斜截式:
k1k2=-1
一般式:
20=0.
3x-4y+1=0
则过P与l平行的直线方程 4x+3y-7=0
是
.
过P与l垂直的直线方程
2.设直线l1:(m-2)x+3y+2m=0与 l2:x+my+6=0,
当m∈ {m|m≠3且m≠-1 }
时,l1与-l21相交;
当m= 1
2
当m=
时,l1与l2平行; 时,l1⊥l2.
感谢下 载
A1A2+B1B2=0.
两直线垂直位置关系的应用
1.判断下列各组中的两条直线是否垂直
(1)2x-4y-7=0与2x+y-5=0; (2)y=3x+1与y=- 1 x+5; (3)2x=7与3y-5=03.
一般地,我们可以把与直线Ax+By+C=0 垂直的直线方程表示为Bx-Ay+D=0.
2.求通过下列各点且与已知直线垂直的 直线方程。
2.2.3两条直线的位置关系(一)
平面内两条直线的交点个数分类:
没有交点 只有一个交点
三种位置关系
平行 相交
有无数个交点
重合
问题1.已知两条直线的方程为:
l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0,
y=k1x+b1
;
y=k2x+b2;
当它们斜平截式行: 、பைடு நூலகம்合k1=k2、,b1≠相b2 交时,应满足什么条
件平行?
一般式: 相交
A1 B1 C1 A2 B2 C2
重合
两直线平行、相交、重合位置关系的应用
1.下列直线中与直线x-y-1=0平行的是( )
A. x+y-1=0
B. x-y+1=0
C. ax-ay-a=0
D. x-y+1=0或ax-ay-a=0
2、若直线l1:2x+my+1=0与l2:y=3x-1平行, 求m.
x-2y+C=0,
因为直线过点(1,2),代入方程,
解得C=3, 所以所求的直线方程为x-2y+3=0.
3.若直线(2a+5)x+(a-2)y+4=0与直线(2
-a)x+(a+3)y-1=0互相垂直,则 C
(
)
(A)a=2
(B)a=-2
(C)a=2或a=-2
(D)a=2,0,-2
课后检测
1.已知点P(1,1)和直线l:3x-4y-
(1)(-1,3),y=2x-3; (2)(1,2),2x+y-10=0.
解:(1)设所求的直线方程为y=- 1 x+b
2
因为直线过点(-1,3),代入方程,得b=
15
所以所求的直线方程为y=- 2 x+ 2,
5 2
即x+2y-5=0.
(2)(1,2),2x+y-10=0.
解:(2)设所求的直线方程为
3.求通过下列各点且与已知直线平行的 直线方程:
(1)(-1,2),y=1 x+1;
2
(2)(1,-4) , 2x+3y+5=0.
答案: (1)x-2y+5=0.
(2)2x+3y+10=0.
4.给出下列几种说法: ①若直线l1与l2都无斜率,则l1与l2一定不垂直; ②l1⊥l2,则k1·k2=-1; ③若直线l1与l2的斜率相等,则l1∥l2; ④若直线l1∥l2,则两直线的斜率相等; ⑤若两直线的斜率不相等,则两直线不平行. 你认为正确的说法有_________. (把正确说法的序号都写上)
