全国大学生数学建模竞赛A题
全国大学生数学建模大赛国家一等奖论文A题

=
− − ( − 1)′
, = 1, 2, · · ·, 210
当逐渐增大,锚链受到的竖直向下方向的合力与支持力之差先逐渐接近于0,
再等于0,直至小于0。当合力小于0时,锚链以海床接触,此时海床提供向上的支持
力,其大小与′ 相等。因此可将小于0 的值都作零处理,故锚链接触海床时,
对于问题二,首先考虑第一个子问题,将风速36/直接代入问题一的模型中,
得出此条件下的吃水深度为0.723,各钢管倾斜角度(度)依次为8.960、9.014、9.068
、9.123,钢桶倾斜角(度)为9.179,锚链链接处的切线方向与海床的夹角(度)为18.414,
游动区域半径为18.80。发现此条件下,水声通讯系统设备的工作效果较差,且锚被
计与应用对海上科学发展有重要意义。
1.2 问题的提出
已知某近浅海传输节点(如图1所示),将浮标视作底面直径2为、高为2、质量
为1000的圆柱体,锚的质量为600,钢管共4节,每节长度为1,直径为50,
每节钢管的质量为10。水声通讯系统安装在一个长为1、外径为30的密封圆
柱形钢桶内,设备和钢桶总质量为100。
Step1: 遍历求解
令吃水深度ℎ的初始值为0.1,以0.0005为单位逐步增加至2。( 浮标高度为2,
完全浸没时吃水深度ℎ则为2 ),记录对应的数据,选取水下物体竖直方向高度和
与海域水深最接近的组别,进一步进行计算,结果如下表所示(具体程序见附录):
表 1: 不同风速的相关结果表
以风速24/的情况为例,绘制游动区域图:
题意的变量临界值。以水深16、系统各部分递推关系式和钢桶与竖直方向夹角小
于5°为约束条件,将多目标优化转化为单目标优化。通过调节决策变量中锚链的型
全国大学生数学建模竞赛a题(2255)

优秀论文选编A题之一(全国一等奖)奥运会临时超市网点设计广西师范大学,吴宗显、单俊辉、谭春亮;指导教师:数学建模组摘要:本文首先根据问卷调查数据计算观众出行、用餐和购物等方面的分布,分析各种分布的特点。
然后,根据观众出行、用餐分布,场馆分布情况和最短距离原则,测算出测算20个商区的人流量及其分布。
最后,根据商圈分析中零售引力法则(即里利法则)、哈夫概率模型、饱和理论,建立设计MS网点大小规模类型的数学模型。
在约定大规模MS网点的面积为1个单位的基础上,经过计算求解,得到小规模MS网点的面积为0.6个单位,并得出20个MS网点的设计方案,具体设计方案是:A区有2个大规模MS网点,分别设在A6小区和A1小区,其余8个小区均为小规模MS网点;B区有2个大规模MS网点,分别设在B6小区和B3小区,其余4个小区均为小规模MS网点;C区有1个大规模MS网点,设在C4小区,其余3个小区均为小规模MS网点。
奥运会临时超市网点设计一、问题的分析与基本假设(一)问题的分析题目要求完成如下工作:1、根据附录中给出的问卷调查数据,找出了观众在出行、用餐和购物等方面所反映的规律2、在一天内每位观众平均出行两次,一次为进出场馆,一次为餐饮,并且出行均采取最短路径前提下。
依据1的结果,测算图2中20个商区的人流量分布。
3、按照满足奥运会期间的购物需求、分布基本均衡和商业上赢利的要求,根据流量分布规律,在有两种大小不同规模的MS类型供选择情况下,给出图2中20个商区内MS网点的设计方案(即每个商区内不同类型MS的个数)。
(二)基本假设1、假定A区(国家体育场)容量为10万人,B区(国家体育馆)容量为6万人,C区(国家游泳中心)容量为4万人。
三个场馆的每个看台容量均为1万人,出口对准一个商区,各商区面积相同。
2、无论乘坐何种交通工具的观众所持的票号是随机的。
二、问卷调查数据的统计与分布规律我们把附录中三次调查的数据综合起来并进行的统计和分析得出的观众在出行、用餐和购物等方面的规律如下:1、整个人群的各种行为的分布规律(1)用不同的交通方式的人数及其分别所占总人数的比例除私车方式偏少一些(仅有9.0377%)外,其余方式分布都比较均匀,均为16%-20%,这说明场馆周围布局的交通车站是比较合理的。
2023国赛数学建模a题

2023国赛数学建模a题一、选择题(每题4分,共20分)下列函数中,是奇函数的是()A. y = x^2B. y = |x|C. y = 1/xD. y = x^3已知直线l 过点P(1, 2),且与直线y = 3x 平行,则直线l 的方程是()A. y = 3x - 1B. y = 3x + 1C. y = 3x - 5D. y = 3x + 5下列等式中正确的是()A. sin(π/2 + α) = cosαB. cos(π/2 + α) = sinαC. tan(π/2 + α) = -cotαD. sin(π - α) = -sinα设随机变量X 服从正态分布N(2, σ^2),若P(X < 4) = 0.9,则P(0 < X < 2) = ()A. 0.4B. 0.3C. 0.2D. 0.1在△ABC中,若 A = 60°,b = 1,S△ABC = √3,则 a = ()A. 1B. 2C. √3D. √2二、填空题(每题4分,共16分)函数y = √(x - 1) 的定义域是_______。
若直线x + y + k = 0 与圆x^2 + y^2 = 1 相切,则k = _______。
已知等差数列{an} 的前n 项和为Sn,若a1 = 1,S3 = 9,则a2 + a4 = _______。
若x, y 满足约束条件{ x + y ≤ 1, x - y ≥ -1, y ≥ 0 },则z = 2x + y 的最大值为_______。
三、解答题(共64分)10.(12分)求函数y = 2sin(2x - π/6) 的单调递增区间。
11.(12分)在△ABC中,已知a = 5,b = 8,cosC = 11/16,求sinA 的值。
12.(12分)已知函数f(x) = x^3 + ax^2 + bx + c 在x = 1 与x = -1 时取得极值。
(1)求a,b 的值;(2)若对于任意x ∈ [-2, 2],都有f(x) < c^2 成立,求 c 的取值范围。
2023数学建模国赛a题详解

2023数学建模国赛a题详解2023数学建模国赛A题要求我们通过研究某公司的数据集,分析并预测销售额的变化规律。
本文将详细解析解题思路和方法,并进行具体的数据分析和预测。
1. 问题描述与分析我们首先需要详细了解题目描述和所给的数据集。
根据题目要求,我们已经得知某公司的销售数据集包括了过去几年的销售额数据,每个季度为一个数据点。
我们的目标是利用这些数据进行分析和预测,找出销售额的变化规律,并给出未来一段时间内的销售额预测。
2. 数据处理与可视化在进行数据分析之前,我们首先需要对所给的数据进行处理和可视化。
我们可以借助Python编程语言中的数据分析库,如NumPy和Pandas,对数据进行导入和处理。
然后,我们可以使用Matplotlib或Seaborn等库来绘制可视化图表,以更好地理解数据的分布和趋势。
3. 数据分析与模型建立在对数据进行可视化之后,我们可以开始进行数据分析和模型建立。
根据经验,销售额的变化往往受多个因素的影响,比如季节性变化、市场需求、竞争压力等等。
我们可以通过构建适当的数学模型来描述这些因素与销售额之间的关系,并进行参数估计和模型验证。
以季节性变化为例,我们可以使用时间序列分析方法,如ARIMA模型或季节性指数平滑方法,来捕捉销售额随季节变化的规律。
此外,我们还可以考虑使用回归分析或神经网络等方法,以探索销售额与其他因素之间的复杂关系。
4. 模型评估与预测在模型建立之后,我们需要对模型进行评估和预测。
我们可以使用历史数据的一部分来验证模型的拟合效果,比较模型预测值与真实值的差异。
如果模型表现良好,则可以将其应用于未来一段时间内的销售额预测。
在进行预测时,我们应该注意模型的置信区间和误差范围。
销售额的预测结果往往是一个区间范围,而不是一个确定的数值。
这是由于预测中存在不确定性和随机性因素的影响。
我们可以使用Bootstrap方法或蒙特卡洛模拟等方法,来估计销售额的置信区间和误差范围。
2023数学建模国赛a题思路

2023数学建模国赛a题思路
2023数学建模国赛A题是关于水电站优化选址和建设的题目,可以按照以下步骤进行思路分析:
1. 问题一:水电站的最优选址
首先,需要考虑投入和收入、地质和水文条件、环境成本等各个因素,这些因素可以被看作优化模型中的约束条件。
目标函数可以是最优水电站的位置。
由于这是一个优化问题,需要定义目标函数并确定最大化或最小化的目标,同时定义约束条件,例如线性约束、非线性约束等。
2. 问题二:建设多个水电站
目标是使得能源最大,约束条件与问题一相同。
这需要对问题一的优化模型进行延申,对建设水电站的个数以及发电能力进行求解。
3. 问题三:红旗河项目
这是一个引水工程项目,目的是将雅鲁藏布江的水输送到西北地区,改善西北地区的缺水状况和自然环境。
这个问题需要结合地理知识和工程知识进行建模和求解。
以上是对2023数学建模国赛A题思路的分析,具体解题过程还需要根据实际问题进行建模和求解。
全国大学生数学建模竞赛题目A题
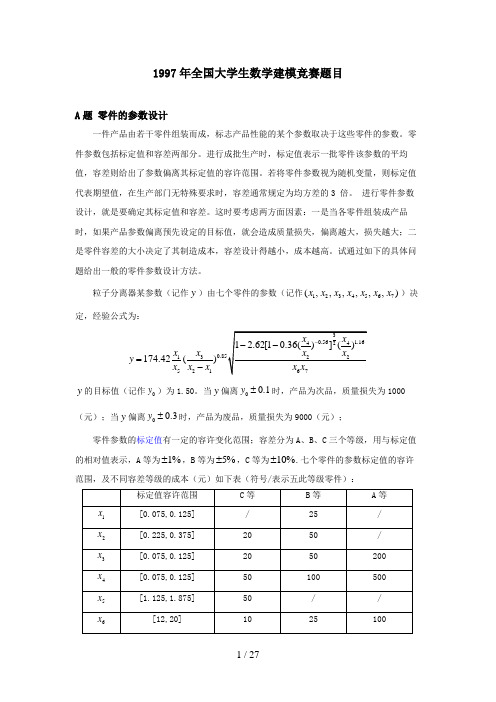
1997年全国大学生数学建模竞赛题目A 题 零件的参数设计一件产品由若干零件组装而成,标志产品性能的某个参数取决于这些零件的参数。
零件参数包括标定值和容差两部分。
进行成批生产时,标定值表示一批零件该参数的平均值,容差则给出了参数偏离其标定值的容许范围。
若将零件参数视为随机变量,则标定值代表期望值,在生产部门无特殊要求时,容差通常规定为均方差的3 倍。
进行零件参数设计,就是要确定其标定值和容差。
这时要考虑两方面因素:一是当各零件组装成产品时,如果产品参数偏离预先设定的目标值,就会造成质量损失,偏离越大,损失越大;二是零件容差的大小决定了其制造成本,容差设计得越小,成本越高。
试通过如下的具体问题给出一般的零件参数设计方法。
粒子分离器某参数(记作y )由七个零件的参数(记作1234567(,,,,,,)x x x x x x x )决定,经验公式为:31521174.42()x x y x x x =-y 的目标值(记作0y )为1.50。
当y 偏离00.1y ±时,产品为次品,质量损失为1000(元);当y 偏离00.3y ±时,产品为废品,质量损失为9000(元);零件参数的标定值有一定的容许变化范围;容差分为A 、B 、C 三个等级,用与标定值的相对值表示,A 等为1%±,B 等为5%±,C 等为10%±.七个零件的参数标定值的容许范围,及不同容差等级的成本(元)如下表(符号/表示五此等级零件):现进行成批生产,每批产量1000个。
在原设计中,七个零件参数标定值为10.1x=,20.3x=,30.1x=,40.1x=,51.5x=,616x=,70.75x=;容差均取最便宜的等级。
请你综合考虑y偏离0y造成的损失和零件成本,重新设计零件参数(包括标定值和容差),并与原设计比较,总费用降低了多少?B题截断切割某些工业部门(如贵重石材加工等)采用截断切割的加工方式。
2022年全国大学生数学建模竞赛A题

2022年全国大学生数学建模竞赛A题(请先阅读“全国大学生数学建模竞赛论文格式规范”)A题系泊系统的设计近浅海观测网的传输节点由浮标系统、系泊系统和水声通讯系统组成(如图1所示)。
某型传输节点的浮标系统可简化为底面直径2m、高2m的圆柱体,浮标的质量为1000kg。
系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成。
锚的质量为600kg,锚链选用无档普通链环,近浅海观测网的常用型号及其参数在附表中列出。
钢管共4节,每节长度1m,直径为50mm,每节钢管的质量为10kg。
要求锚链末端与锚的链接处的切线方向与海床的夹角不超过16度错误!未找到引用源。
,否则锚会被拖行,致使节点移位丢失。
水声通讯系统安装在一个长1m、外径30cm的密封圆柱形钢桶内,设备和钢桶总质量为100kg。
钢桶上接第4节钢管,下接电焊锚链。
钢桶竖直时,水声通讯设备的工作效果最佳。
若钢桶倾斜,则影响设备的工作效果。
钢桶的倾斜角度(钢桶与竖直线的夹角)超过5度时,设备的工作效果较差。
为了控制钢桶的倾斜角度,钢桶与电焊锚链链接处可悬挂重物球。
图1传输节点示意图(仅为结构模块示意图,未考虑尺寸比例)系泊系统的设计问题就是确定锚链的型号、长度和重物球的质量,使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。
问题1某型传输节点选用II型电焊锚链22.05m,选用的重物球的质量为1200kg。
现将该型传输节点布放在水深18m、海床平坦、海水密度为1.025某103kg/m3的海域。
若海水静止,分别计算海面风速为12m/和24m/时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
问题2在问题1的假设下,计算海面风速为36m/时钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域。
请调节重物球的质量,使得钢桶的倾斜角度不超过5度,锚链在锚点与海床的夹角不超过16度。
问题3由于潮汐等因素的影响,布放海域的实测水深介于16m~20m之间。
全国大学生数学建模竞赛A题解析

三、解题思路(续)
(4)对于实际储油罐,建立罐体变位后罐内储油量
V与油位高度h及纵向倾斜角度 和 横向偏转角度 之间 的关系模型,即 V。F(,,h)
由于本问较复杂,需要分情况建立模型,可以先考 虑只发生纵向变位的情况。
三、解题思路(续)
球冠Ⅰ的体积表达式为:
其中
三、解题思路(续)
球冠III的体积表达式为:
atabnhaaltanz a2z2a2arcsinaz2a2dz, 0hLltan
V( ,h) atabn
haltan haLltanz
a2z2a2arcsinaz2a2dz,
(Ll)tanh2altan
LabaahLltanz a2z2a2arcsinaz2a2dz, 0hLltan
180
190
200
L 19265.60 21941.18 24674.88 27450.77 30253.25 33066.99 35876.76 38667.27 41423.11 44128.48
h 210
220
230
240
250
260
270
280
290
3400
L 46767.21 49322.44 51776.40 54109.93 56302.12 58329.27 60163.39 61768.90 63093.63 64026.17
ax
h
三、解题思路(续)
利用积分可以计算出油位高度为h时实验罐的截面 面积,于是得到油位高度与储油量的计算公式:
V (H ) 2 a b b a (h b )2 b h h 2 a b a rc s in h b b L
其中a,b,L分别是实验罐截面椭圆的长半轴、短半轴 和罐体长度,h为油位高度。
全国大学生数学建模竞赛A题葡萄酒评价分析

全国大学生数学建模竞赛A题葡萄酒评价分析葡萄酒是一种古老而美妙的饮品,其种类繁多,风味各异。
如何对葡萄酒进行准确的评价和分析成为了葡萄酒爱好者和生产商们共同关注的问题。
在此次全国大学生数学建模竞赛A题中,我们将围绕葡萄酒的评价和分析展开讨论。
1. 引言葡萄酒是一种由葡萄经过发酵而成的酒类饮品。
葡萄酒的风味和品质受到许多因素的影响,如产地、葡萄品种、酿造工艺等。
为了准确评价葡萄酒的质量和特点,我们需要建立相应的评价指标和模型。
2. 数据分析为了进行葡萄酒评价,我们首先需要收集相关的数据。
通过对不同品牌、不同种类的葡萄酒进行采样和测试,我们可以获得葡萄酒的关键指标,如酒精含量、酸度、甜度、单宁含量等。
在数据分析中,我们可以运用统计学方法和数学建模技术,对数据进行整理和处理。
通过计算均值、方差、相关系数等指标,我们可以得到葡萄酒的基本特征和相互之间的关系。
3. 葡萄酒评价指标体系建立基于数据分析的结果,我们可以建立葡萄酒评价指标体系。
这一体系应该包含对葡萄酒各项指标的评价方法和权重。
常见的评价指标包括酒精含量、色泽、香气、口感等。
在指标体系中,我们可以采用层次分析法,通过对各个指标的重要性进行排序和评估。
同时,还可以利用数学模型,将各项指标综合起来,得到最终的评价结果。
4. 葡萄酒评价模型构建在对葡萄酒进行评价时,我们可以利用数学建模方法构建评价模型。
常用的模型包括多元回归模型、灰色关联度模型等。
多元回归模型可以用来分析葡萄酒各项指标之间的关系,进而预测葡萄酒的品质。
灰色关联度模型则可以用来度量葡萄酒各个指标对品质的影响程度。
通过不断地调整模型和参数,我们可以得到更准确的葡萄酒评价结果,并为葡萄酒生产商提供有针对性的改进建议。
5. 葡萄酒评价系统设计为了方便葡萄酒评价和分析的实施,我们可以设计一个葡萄酒评价系统。
该系统可以包括数据输入、数据处理、指标评价、模型计算等功能模块。
数据输入模块用于将葡萄酒相关数据录入系统。
2020 华数杯全国大学生数学建模竞赛题目A题

2020 华数杯全国大学生数学建模竞赛题目(请先阅读“华数杯数学建模竞赛论文格式规范与提交说明”)A 题带相变材料的低温防护服御寒仿真模拟在一些特定的场合,人们往往需要在极寒天气下作业,如高山高原工作、潜水员水下工作、现代化工厂的低温车间以及寒冷气候下的野外作业等。
为了能使工作顺利进行,科学家们一直在研究低温防护复合材料,试图做成防护服用以保护在超低温环境下的工作者。
某研究所研制的低温防护复合材料:三层结构,包括内层织物层、中间层功能层、外层隔热层。
内层织物层主要用于舒适性。
中间层是一种特殊的材料,可以产生并释放热量,用以延缓人体温度过快降低,称为相变材料。
外层隔热层主要是延缓热量对外过快传递。
低温防护材料主要用于短时间的低温防护,有效降低外界环境对人体的伤害。
为了延缓人体温度过快降低,研制的复合材料的中间层要具有良好的保温性能。
中间层有两个特性,特性一是厚度不能大于0.45mm,因为中间层的硬度与厚度成正比,一旦超过0.45mm,人体将无法伸展,也就无法工作。
特性二是在高于25℃左右(根据材料不同这个临界点会有小的变化)为液态,低于25℃开始固化,固化时就开始放热,一直到14.7℃左右固化完毕,将不再放热。
具体数据详见附件1。
注意:附件1 中的数据放热温度范围与上面表述温度范围有差异,以附件数据为准。
热量传递方式有对流、辐射和传导三种。
但在超低温下,对外辐射微不足道,因此一般不予考虑。
内层织物与人体表面之间有空气流动,外层隔热层与外部环境之间也有空气流动。
空气流速不一样,所计算出来的表面换热系数也会不一样。
至于热传导能力(热导率),是材料的物理属性。
附件2 给出了三层材料的物理属性值。
为检验这种复合材料的耐低温效果,科研者按照附件 2 提供的厚度为一名身高 1.70m,体重为60kg 的中国实验者(消耗的衣料面积一般不超过人体表面积的 1.25 倍)制作了一套耐低温服装。
实验者将前往南极洲长城站在-40℃的低温下进行工作实验。
2022华数杯全国大学生数学建模竞赛A、B、C题

2022华数杯全国大学生数学建模竞赛题目(请先阅读“华数杯数学建模竞赛论文格式规范与提交说明”)A 题环形振荡器的优化设计芯片是指内含集成电路的硅片,在我们日常生活中的手机、电脑、电视、家用电器等领域都会使用到,是高端制造业的核心基石。
芯片的制造工艺非常复杂,要经历上千道工序经过复杂工艺加工制造。
尤其是数字芯片,随着工艺尺寸的不断缩小,数字芯片的优化设计变得尤为重要。
而环形振荡器是数字时钟芯片中的一种重要的结构,其设计中有三个重要的指标需要考虑:速度、面积和功耗。
速度是指电路运行的时钟频率,一般来说,速度越快,能处理的数据量就越多,性能越好。
面积是指电路的物理实现需要占用硅片的面积,占用的面积越小,芯片成本越低。
功耗是指电路工作所消耗的能量,功耗越低,发热量也越低,设备工作的时间更长,使用寿命越久。
速度、面积、功耗是互相牵制的,在相同的制造工艺(制程)以及相同的电路条件下,一般来说,速度越快,晶体管尺寸越小,功耗也越高,反之亦然。
相关概念与参数介绍见附录1。
请阅读相关文档说明,回答下列问题。
1.环形振荡器的频率公式为1/(2)pd f n t =⨯,其中n 为反相器的个数,pd t 为单级反相器的延迟时间。
反相器的负载电容与下一级的反相器的栅极面积成正比,为2nF/μm 2。
反相器工作时的电流公式可以分为以下两个阶段:饱和区和线性区。
两个阶段的公式为:221[()]21()2gs th ds ds ds gs th d gs th ds gs thWK V V V V V V V L I W K V V V V V L⎧--<-⎪⎪=⎨⎪->-⎪⎩,,式中,V gs 表示栅源之间的电压,V ds 表示漏源之间电压,V th 表示阈值电压。
请根据以上内容,计算表1中不同设计方案的环形振荡器的输出频率。
表1环形振荡器输出频率计算表序号反相器个数PMOS 宽长比NMOS 宽长比电源电压/V输出频率111400n/100n 200n/100n 1.2211800n/200n 400n/200n 1.23111.6u/0.4u 0.8u/0.4u 1.2431200n/100n400n/100n 1.2531400n/200n800n/200n 1.26310.8u/0.4u 1.6u/0.4u 1.2751500n/100n500n/100n 1.28511000n/200n1000n/200n 1.2951 1.8u/0.3u 1.8u/0.3u 1.210992u/0.5u1u/0.5u 1.22.环形振荡器的版图见附录1。
2021高教社杯全国大学生数学建模竞赛A题

2021高教社杯全国大学生数学建模竞赛A题2021高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》(以下简称为“竞赛章程和参赛规则”,可从全国大学生数学建模竞赛网站下载)。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A 我们的参赛报名号为(如果赛区设置报名号的话): 11012 所属学校(请填写完整的全名):哈尔滨理工大学参赛队员 (打印并签名) :1. 鲍国龙 2. 秦曦 3. 耿海龙指导教师或指导教师组负责人 (打印并签名):陈东彦(论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名。
以上内容请仔细核对,提交后将不再允许做任何修改。
如填写错误,论文可能被取消评奖资格。
)日期: 2021 年 9 月 13 日赛区评阅编号(由赛区组委会评阅前进行编号): 2021高教社杯全国大学生数学建模竞赛编号专用页评阅人评分备注赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):车道被占用对城市道路通行能力的影响摘要本文以通过对事故横断面车流量统计分析,从车道的实际通行能力入手,研究发生事故后车道的实际通行能力的变化情况及影响因素。
2023数学建模国赛a题评分标准

2023数学建模国赛a题评分标准近年来,数学建模竞赛在我国高校中越来越受到重视。
其中,数学建模国赛a题一直是备受关注的焦点,其评分标准更是备受关注。
在这篇文章中,我们将对2023数学建模国赛a题的评分标准进行全面评估和探讨,以便更深入地了解这一重要主题。
一、评分标准的深度2023数学建模国赛a题的评分标准需要考虑到多方面的因素。
需要考虑模型的建立是否符合实际问题的要求,包括问题的抽象程度、建模方法的合理性等。
需要评价模型的求解方法是否正确、有效,并探讨对求解方法的合理性和实用性。
需要考虑结果的分析和讨论是否充分、深入,是否对模型的局限性和改进空间进行了全面的思考。
这些深度的评分标准要求选手在整个建模过程中都要有深入的思考和全面的考量,同时也要求评委能够全面客观地评价选手的模型,确保公平公正。
二、评分标准的广度在评分标准的广度方面,2023数学建模国赛a题的评分标准也需要包含多方面的内容。
需要全面考虑数学建模的基本要求,包括建模的数学理论基础、数学建模的一般流程和方法等。
需要对选手的团队合作能力、创新能力、解决问题的能力等进行全面的考量。
还要考虑到选手对于实际问题的理解和对于建模过程的反思与总结,确保评分标准的广度能够全面覆盖选手的能力和水平。
总结和回顾2023数学建模国赛a题的评分标准涵盖了深度和广度两个方面,要求选手在整个建模过程中都要有深入的思考和全面的考量。
评委也需要能全面客观地评价选手的模型,确保公平公正。
对于选手来说,除了要具备扎实的数学基础和建模能力外,还需要具备团队合作能力、创新能力和解决问题的能力,以及对实际问题的深刻理解和对建模过程的深入反思与总结。
个人观点和理解在我看来,2023数学建模国赛a题的评分标准是非常全面和严谨的。
它不仅要求选手具备扎实的数学基础和建模能力,还要求选手具备团队合作能力、创新能力和解决问题的能力,以及对实际问题的深刻理解和对建模过程的深入反思与总结。
这些要求都是非常重要的,它们不仅能够培养学生的综合能力,还能够培养学生的创新精神和团队合作精神,为他们未来的发展打下良好的基础。
高教社杯全国大学生数学建模竞赛A题太阳影子定位

高教社杯全国大学生数学建模竞赛A题太阳影子定位IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】摘要通过太阳影子定位技术可以确定视频的拍摄地点和时间,为拍摄出更好的视频,掌握太阳影子的变化规律就变得尤为重要。
本文主要综合运用了地理学、几何学、统计学、数学分析和高等代数等知识,并利用MATLAB,SPSS和mathematica等计算机软件,通过建立数学模型来研究影子长度的变化特征,进一步确定视频的拍摄地点和时间。
针对问题一,首先我们通过分析影子长度的影响因素得到与影子长度的关系(见表达式六)整理计算之后,就得到了影子长度的数学模型。
然后我们通过分析他们之间的关系,再利用MATLAB编程,得到了影子长度关于各个参数的变化规律(见图3到图7)。
其次根据我们建立的模型,利用MATLAB编程画出了给定时间天安门广场3米高的直杆的太阳影子长度的变化曲线(见图8),然后在考虑折射率的情况下又画了一条变化曲线(见图9),最后进行了误差分析(见图10)。
针对问题二,我们采用了测试分析法(数据分析法和计算机仿真相结合),通过分析各个参量之间的关系,先以影长l为目标做回归,用模型一的模型,通过SPSS进行拟合得到多组数据,再用MATLAB进行检验得到符合的两组经纬度。
然后我们又以太阳方位角K为目标做回归,得到模型(见表达式12),其计算方法与影长l做回归目标时一样。
我们分步做了两次拟合,先用MATLAB拟合出经度,再N E和杆长做回归模型(见表达式14)最后得到经纬度(18.74,109.35)=。
综上可知,肯定有一地点是在海南,还有一个地点可能在云南。
1.993L m针对问题三,我们用问题二中的多项式回归,得到回归模型(见表达式17和20)=,得到天数利用附件二得到的经纬度为(32.83N,110.25E)和杆长L 3.03m=,得到天n=。
利用附件三得到的经纬度为(39.19N,79.5E)和杆长L 1.962m 307n数=140针对问题四,首先运用MATLAB软件,根据画面灰度,运用MATLAB软件,把视频转化成二值图,求得影子端点的像素坐标,然后根据相似原理,把像素坐标转化成水平面上的坐标(消去了视角的影响),进而求得影子的长度。
数学建模竞赛a题

数学建模竞赛A题的题目可能涉及各种主题,例如经济、金融、人口、环境、医疗等等。
由于题目未提供具体细节,我将提供一个通用的回答框架和示例来帮助你回答这个问题。
请注意,这只是一个示例,你可能需要根据你的具体问题和数据来调整答案。
一、回答框架1. 介绍:简要说明题目背景和目的。
2. 建模思路:阐述你的建模思路和方法,包括假设、变量、模型类型等。
3. 求解过程:详细描述求解过程,包括数据收集、处理、模型拟合、参数估计等步骤。
4. 结果分析:对模型结果进行分析,讨论误差来源、预测精度等。
5. 结论和建议:总结你的结论,提出可能的改进和建议。
二、示例答案1. 介绍:数学建模竞赛A题可能涉及各种主题,例如经济、金融、人口、环境、医疗等等。
本次回答将基于一个假设的主题进行建模,旨在说明建模的一般思路和方法。
2. 建模思路:* 假设:假设数据符合某种分布(例如正态分布),并考虑随机误差的影响。
* 变量:建立变量之间的关系,包括因变量和自变量。
根据题目要求,可能需要考虑多个自变量。
* 模型类型:选择合适的模型类型(例如线性回归模型),并考虑模型的适用性。
* 求解方法:使用适当的求解方法(例如最小二乘法)进行参数估计和拟合。
3. 求解过程:* 数据收集:收集相关数据,包括自变量和因变量的观测值。
* 数据处理:对数据进行清洗和预处理,包括缺失值填充、异常值处理等。
* 模型拟合:使用最小二乘法等方法进行参数估计和拟合,得到模型的系数和标准误差等参数。
* 模型验证:通过与其他数据和方法进行比较和验证,评估模型的预测精度和适用性。
4. 结果分析:* 模型检验:对模型的拟合程度进行检验,如决定系数R-squared等指标。
* 结果解释:解释模型的结果,包括各自变量的影响程度和趋势。
对于本题,可以分析自变量对因变量的影响程度和方向,并解释模型的预测精度和适用性。
5. 结论和建议:* 结论:总结模型的结论,包括自变量对因变量的影响程度和趋势,以及模型的预测精度和适用性。
2023数学建模国赛a题详解

2023数学建模国赛A题详解一、引言2023年数学建模国赛A题是一个涉及多个学科知识的综合性问题,需要学生在有限的时间内分析问题、建立数学模型并进行求解。
本文将对2023年数学建模国赛A题进行详细解析,帮助读者更好地理解这个问题,为参加比赛的同学提供一定的参考。
二、题目分析2023年数学建模国赛A题是关于XXX的问题。
题目要求参赛者通过建立数学模型,分析XXX的变化规律,解决XXX问题。
该问题涉及到多个学科领域的知识,如数学、物理、经济等,需要参赛者进行全面的分析和研究。
三、问题分析针对题目中提出的问题,首先需要分析问题背景和相关信息,明确问题的要求和目标。
根据题目提示,我们可以得出问题的具体内容和需要解决的核心问题,进而确定建模的思路和方法。
四、建模过程1. 确定问题的数学模型针对题目中的具体问题,需要先建立相应的数学模型。
根据问题的特点和要求,可以选择合适的数学方法进行建模,如微分方程、概率统计等。
2. 数据处理与分析在建立数学模型的过程中,可能需要对现有数据进行处理和分析,以获取问题所需的相关信息。
数据的准确性和完整性对建模的结果影响巨大,因此需要对数据进行严格的处理和分析。
3. 模型求解与验证完成数学模型建立后,需要进行模型求解并验证。
通过数学工具和计算机软件,对模型进行求解,并与实际数据进行对比,验证模型的准确性和可靠性。
五、结果分析1. 结果的合理性分析完成模型求解后,需要对结果进行合理性分析。
根据题目要求和实际情况,分析模型的结果是否符合实际,是否具有合理性和可行性。
2. 结果的意义和推广模型求解得到的结果需要具有一定的意义和推广价值,需要对结果进行深入的分析和讨论,探讨模型结果在实际应用中的意义和价值。
六、总结与展望本文对2023年数学建模国赛A题进行了详细解析,并进行了建模过程和结果分析。
在参赛过程中,需要结合题目要求和实际情况,进行全面、深入的分析和研究,不断完善数学模型和求解方法,以获得更好的比赛成绩。
2021年数学建模国赛a题

2021年数学建模国赛a题
2021年数学建模国赛A题是关于仓储管理和物流优化的问题。
该题目要求参赛者基于实际数据和情景,运用数学建模的方法,针
对仓储管理和物流优化提出合理的方案和算法。
首先,这个题目涉及到仓储管理和物流优化,需要从多个角度
来考虑。
在仓储管理方面,可以讨论如何最大限度地利用仓库空间,如何设计合理的仓储布局以提高工作效率,以及如何减少库存成本。
在物流优化方面,可以探讨如何优化配送路线,如何降低运输成本,以及如何提高配送效率。
其次,针对这个题目,可以从数学建模的角度进行分析。
可以
运用线性规划、整数规划、动态规划等数学建模方法,建立相应的
数学模型,以解决仓储管理和物流优化中的实际问题。
通过数学建模,可以量化问题,找到最优解,为实际问题提供科学的决策依据。
此外,还可以从实际案例和经验角度来回答这个问题。
可以结
合实际的仓储管理和物流优化案例,分析成功的经验和教训,探讨
如何借鉴先进的管理经验和技术手段,提高仓储管理和物流优化的
水平。
综上所述,针对2021年数学建模国赛A题,需要从仓储管理和
物流优化的多个角度进行全面的分析和讨论,结合数学建模的方法,实际案例和经验,提出合理的方案和算法。
这样才能全面、准确地
回答这个问题。
全国数学建模竞赛2023a题

全国数学建模竞赛2023年的A题是关于"气候变化与可持续发展"的议题。
这个题目涉及到环境科学、经济学、社会学等多个领域,需要我们从多个角度来分析和解决。
下面我将尝试用500-800字回答这个问题。
题目背景:气候变化是当前全球面临的重要环境问题,它对人类社会和经济造成了巨大的影响。
为了应对气候变化,实现可持续发展,我们需要从多个角度来考虑解决方案。
本次竞赛要求我们从气候变化的背景和影响、可持续发展的重要性、以及如何将两者结合起来三个方面进行建模和解答。
问题分析:1. 气候变化的影响:气候变化会导致极端天气事件增多、海平面上升、生态系统退化等问题。
我们需要考虑这些影响对人类社会和经济的影响,如农业产量下降、疾病传播、财产损失等。
2. 可持续发展的重要性:可持续发展是指在满足当代人需求的同时,不损害后代人满足其需求的能力。
我们需要考虑如何在经济发展、环境保护和社会公平之间找到平衡点。
3. 气候变化与可持续发展的结合:如何将气候变化和可持续发展结合起来,实现双赢是本次竞赛的核心问题。
我们需要提出一种综合性的解决方案,既能应对气候变化,又能实现可持续发展。
模型建立:1. 建立数学模型:根据问题分析,我们可以建立数学模型来描述气候变化的影响、可持续发展的目标以及两者之间的相互作用。
可以使用统计学、环境科学、经济学等领域的理论和方法来建立模型。
2. 建立系统模型:为了更全面地描述问题,我们可以建立包含人类社会、经济、环境等多个子系统的系统模型。
通过系统分析,我们可以更好地理解各个因素之间的相互作用和影响。
3. 建立优化模型:为了找到最佳的解决方案,我们可以建立优化模型,将气候变化、可持续发展等目标转化为数学优化问题,通过求解最优解来找到最佳的解决方案。
模型验证:1. 案例分析:我们可以收集相关案例进行分析,了解其他国家和地区在应对气候变化和实现可持续发展方面的经验和教训,为我们的模型验证提供参考。
2022 年高教社杯全国大学生数学建模竞赛题目 A题

2022年高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A题波浪能最大输出功率设计随着经济和社会的发展,人类面临能源需求和环境污染的双重挑战,发展可再生能源产业已成为世界各国的共识。
波浪能作为一种重要的海洋可再生能源,分布广泛,储量丰富,具有可观的应用前景。
波浪能装置的能量转换效率是波浪能规模化利用的关键问题之一。
图1为一种波浪能装置示意图,由浮子、振子、中轴以及能量输出系统(PTO,包括弹簧和阻尼器)构成,其中振子、中轴及PTO被密封在浮子内部;浮子由质量均匀分布的圆柱壳体和圆锥壳体组成;两壳体连接部分有一个隔层,作为安装中轴的支撑面;振子是穿在中轴上的圆柱体,通过PTO系统与中轴底座连接。
在波浪的作用下,浮子运动并带动振子运动(参见附件1和附件2),通过两者的相对运动驱动阻尼器做功,并将所做的功作为能量输出。
考虑海水是无粘及无旋的,浮子在线性周期微幅波作用下会受到波浪激励力(矩)、附加惯性力(矩)、兴波阻尼力(矩)和静水恢复力(矩)。
在分析下面问题时,忽略中轴、底座、隔层及PTO的质量和各种摩擦。
图1 波浪能装置示意图请建立数学模型解决以下问题:问题1如图1所示,中轴底座固定于隔层的中心位置,弹簧和直线阻尼器一端固定在振子上,一端固定在中轴底座上,振子沿中轴做往复运动。
直线阻尼器的阻尼力与浮子和振子的相对速度成正比,比例系数为直线阻尼器的阻尼系数。
考虑浮子在波浪中只做垂荡运动(参见附件1),建立浮子与振子的运动模型。
初始时刻浮子和振子平衡于静水中,利用附件3和附件4提供的参数值(其中波浪频率取1.4005 s−1,这里及以下出现的频率均指圆频率,角度均采用弧度制),分别对以下两种情况计算浮子和振子在波浪激励力f cosωt(f为波浪激励力振幅,ω为波浪频率)作用下前40个波浪周期内时间间隔为0.2 s的垂荡位移和速度:(1) 直线阻尼器的阻尼系数为10000 N·s/m;(2) 直线阻尼器的阻尼系数与浮子和振子的相对速度的绝对值的幂成正比,其中比例系数取10000,幂指数取0.5。
