积分法求梁的位移资料
合集下载
工程力学第2节 确定梁位移的积分法

例10-3 如图图示简支梁, l 4m ,弯曲刚度EI 1640N m2。在无限接近右支座 B 处受到矩为的集中 力偶 M e 120 N m 作用,试求 (1)转角方程和位移方 程;(2)梁的最大挠度。
解:(1)转角方程和 位移方程 x
Me FA FB l
梁的弯矩方程为
5
3
4
令 x 0,得B截面的挠度为
ql yB ( ) 30 EI
Me 2 x C (1) 将上式一次积分得转角 y' 2EIl
Me M ( x) x l
转角方程
Me 2 y' x C 2EIl
(1)
再次积分,可得挠度方程:
Me 3 y x Cx D (2) 6EIl 边界条件: x 0 时,y0 0 ; x l 时,yl 0 M el D0 C 6EI M e 2 M el 2 0 . 00915 x 0.0488 x 2EIl 6EI M e 3 M el 3 x 0.0488x y x x 0.00305 6EIl 6EI
再次积分,可得挠度方程:
1 1 1 3 4 y ( qlx qx ) Cx D EI 12 24
1 1 1 3 2 ( qlx qx ) C EI 4 6 1 1 1 3 4 y ( qlx qx ) Cx D EI 12 24 边界条件: x 0 时,y0 0 ; x l 时,yl 0
补充例 悬臂梁AB在三角形分布载荷作用下,跨 度为l,抗弯刚度为EI,如图所示。试求B截面的挠度。 解:与B截面距离为 x 的任一截面的载荷集度为
x q( x) q l
(0 x l )
用积分法求梁的变形
3
M ( x) EI Z
d 2 M ( x) 2 dx EI Z
d 2 M ( x) 2 dx EI Z
o
M
M
x
o
x
d2y 0 2 dx
y y
M
d2y 0 2 dx
M
d 2 M ( x) 2 dx EI Z
梁挠曲线近似微分方程
d 2 M ( x) 2 dx EI Z
x0
x0
L b 3
1 L 2
一般认为梁的最大挠度就发生在跨中
b0
3 L 0.577 L 3
例题 5.4
画出挠曲线大致形状。图中C为中间铰。
F
A
两根梁由中间铰连接,挠曲线在 中间铰处,挠度连续,但转角不 连续。
1 2
1 2
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
y
A
C
B
x
C
B
tan
d dx
d dx
M ( x) EI Z dx C1
M ( x ) 在小变形情况下,任一截面的转角等于挠曲线 在该截面处的切线斜率。 dx dx C1 x C2 EI Z
通过积分求弯曲位移的特征: 1、适用于细长梁在线弹性范围内、小变形情况下的对称弯曲。
B
2M ( x ) d d Fx dx C C EI Fxdx EI C z 11 z 1 dx dx 2 EI Z
x
y
边界条件
2 3 Fx C xC Fx EI dx z 2 EI z 1 x C2 26 C1
M ( x) EI Z
d 2 M ( x) 2 dx EI Z
d 2 M ( x) 2 dx EI Z
o
M
M
x
o
x
d2y 0 2 dx
y y
M
d2y 0 2 dx
M
d 2 M ( x) 2 dx EI Z
梁挠曲线近似微分方程
d 2 M ( x) 2 dx EI Z
x0
x0
L b 3
1 L 2
一般认为梁的最大挠度就发生在跨中
b0
3 L 0.577 L 3
例题 5.4
画出挠曲线大致形状。图中C为中间铰。
F
A
两根梁由中间铰连接,挠曲线在 中间铰处,挠度连续,但转角不 连续。
1 2
1 2
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
y
A
C
B
x
C
B
tan
d dx
d dx
M ( x) EI Z dx C1
M ( x ) 在小变形情况下,任一截面的转角等于挠曲线 在该截面处的切线斜率。 dx dx C1 x C2 EI Z
通过积分求弯曲位移的特征: 1、适用于细长梁在线弹性范围内、小变形情况下的对称弯曲。
B
2M ( x ) d d Fx dx C C EI Fxdx EI C z 11 z 1 dx dx 2 EI Z
x
y
边界条件
2 3 Fx C xC Fx EI dx z 2 EI z 1 x C2 26 C1
材料力学 梁 弯曲位移

D点的连续条件: x = a, 1' 2 ' 1 2
1 ( 0 x a)
2 (axl )
挠曲线方程
EI
1"
M1
F
b l
x
EI
2"
M
2
F
b l
x
F
(
x
a)
转角方程
EI
'
1
F b l
x2 2
C1
EI
2'
F
b l
x2 2
F
(
xa)2 2
D1
挠度方程
EI
1
F
b l
x3 6
C1 x
C2
EI
2
F
b l
式中:积分常数 C1 、C2 可通过梁挠曲线的 边界条件 和 变形 连续性条件 来确定。
1、边界条件
A
l A= 0
B
B= 0
A
A= 0
B
B= 0
在简支梁或外伸梁中, 铰支座处的挠度 都应等于零。
A 0 B 0
A
B
l A= 0 A= 0
在悬臂梁 中,固定端处的挠度 和转角 都应等于零。
A 0, A 0
F
(
xa)2 2
D1
挠度方程
EI
1
F
b l
x3 6
C1 x
C2
EI
2
F
b l
x3 6
F
(x 6
a)3
D1
x
D2
x = 0 , 1 = 0
x = l , 2= 0
再将边界条件代入方程可解得:
结构位移和刚度—梁的刚度计算(建筑力学)

二、用积分法求梁的变形
1.挠曲线近似微分方程
y( x)
M (x) EI
2.用积分法求变形 EI (x) M (x)dx C1
三、用叠加法求梁的变形
EIy(x) [ M (x)dx C1]dx C2
叠加法—梁截面的总变形,就等于各个荷载单独作用时产生变形的代数和。
四、梁的刚度计算 ymax [ f ]
梁的刚度计算
主要内容
梁的刚度条件和设计准则 梁的刚度计算 梁的刚度计算工程实例
梁的刚度计算
➢ 如果梁的弯曲变形过大,即使强度满足要求,也不能正常工作。例如:房 屋的楼面板或者梁长时间受较大荷载作用,导致变形过大,会造成抹灰面 出现裂缝,工业厂房的吊车梁变形过大,会影响吊车梁的正常使用等。设 计梁时,除了进行强度计算外,还应考虑进行刚度计算,需要把梁的最大 挠度和最大转角限制在一定的允许范围内。
l
l
课后作业:《建筑力学练习册》 练习二十五
3.6 4 4
3.6kN m
2、按正应力强度设计。查强度准则
3.6kNm
max
M max Wz
M max 0.1d 3
[ ]
得:
d3
M max
3
3.6 106 mm 153.3mm
0.1[ ] 0.110
取d=160mm
梁的刚度计算
3、按梁的刚度准则校核。
查变形表得
ymax
Fl 3 48EI
为:
ymax [ f ]
l
l
式中 ymax 为最大相对挠度,[ f ] 为许用相对挠度,其值可
l
l
根据梁的工作情况及要求查阅有关设计手册。土建工程中的许
用相对挠度值 [ f ] 常限制在
材料力学 梁位移

1.梁在荷载作用下产生的变形是微小的; 2.材料在线弹性范围内工作,梁的位移与荷载呈
线性关系;
3.梁上每个荷载引起的位移,不受其他荷载的影响。
简单载荷下梁的挠度和转角见附录IV,必须记住!
例5-5 试用叠加原理求图示弯曲刚度为EIz的简支梁的跨中截面挠 度ωc和梁端截面的转角θA,θB.
F A
wC 2 0
q 2l 2 A2 B 2
24EI
3
ql 384EI
3
wC wC1 wC 2
5ql 5ql 0 768EI 768EI
4
4
(向下)
A A1 A2
ql3 ql3 3ql3 (顺时针) 48EI 384EI 128EI
应选22a工字钢,Wz=309cm3, Iz=3400cm4
(2)校核刚度
wmax Fl 3 40 103 45003 l 11.2mm [ w] 11.25mm 3 4 48EI 48 200 10 3400 10 400
选择22a工字钢。
2、提高刚度措施
T 2L V 2GI P
作业:5-11,5-15(a)
练习题1 用叠加原理求图示弯曲刚度为EI的悬臂梁B 截面的挠度和转角。
q0 q(x) A B x
dx l
x
y
q(x)dx
(a)
A x l
B
x
dwB
解:在任意截面x处取微段dx,则作用在微段上的微 集中荷载为:
q0 x q ( x )d x dx l
w 其中, 与 l
max
为许可值,可查设计手册。
例5-9 图示简支梁,F=40kN, l=4.5m, [σ]=150MPa, [w/l]=1/400, E=200GPa, 选择工字钢型号。 A F l
线性关系;
3.梁上每个荷载引起的位移,不受其他荷载的影响。
简单载荷下梁的挠度和转角见附录IV,必须记住!
例5-5 试用叠加原理求图示弯曲刚度为EIz的简支梁的跨中截面挠 度ωc和梁端截面的转角θA,θB.
F A
wC 2 0
q 2l 2 A2 B 2
24EI
3
ql 384EI
3
wC wC1 wC 2
5ql 5ql 0 768EI 768EI
4
4
(向下)
A A1 A2
ql3 ql3 3ql3 (顺时针) 48EI 384EI 128EI
应选22a工字钢,Wz=309cm3, Iz=3400cm4
(2)校核刚度
wmax Fl 3 40 103 45003 l 11.2mm [ w] 11.25mm 3 4 48EI 48 200 10 3400 10 400
选择22a工字钢。
2、提高刚度措施
T 2L V 2GI P
作业:5-11,5-15(a)
练习题1 用叠加原理求图示弯曲刚度为EI的悬臂梁B 截面的挠度和转角。
q0 q(x) A B x
dx l
x
y
q(x)dx
(a)
A x l
B
x
dwB
解:在任意截面x处取微段dx,则作用在微段上的微 集中荷载为:
q0 x q ( x )d x dx l
w 其中, 与 l
max
为许可值,可查设计手册。
例5-9 图示简支梁,F=40kN, l=4.5m, [σ]=150MPa, [w/l]=1/400, E=200GPa, 选择工字钢型号。 A F l
梁位移

看书讲解 P235。
17
§9-5
1、刚度条件
梁的刚度条件、提高梁刚度的主要措施
最大挠度 : ymax [ y], 最大转角: max [ ],
[y]=(0.0003~0.0005)l
梁的许用挠度值 梁的许用转角值
l为轴承间距。
对于一般轴,取
[]=(0.001~0.005)rad
EI z
不定积分中,出现两个积分常数C、D。这由支承条件和边界 条件确定,即x=0处 y A 0, A 0 而且对于分段的M z (x) 、或有集中力、集中力偶、间断的 分布力等时, 应该分段积分。每一个分段中都有两个积分常数, 它们要满足连续变形条件。
7
例1:9.1 求挠度方程和转角方程,并确定最大值。 解:确定支座反力:
Pb x P( x a) l
( a x b)
Pb 2 1 2 EI z 2 ( x) x Px Pax C2 2l 2 ( a x b) Pb 3 1 3 1 2 EI z y2 ( x) x Px Pax C2 x D2 6l 6 2
2
线位移 梁轴线上的任一点C(即截面的形心) 在梁变形后将移到 c ,因而有线位移 cc 。 由于梁的变形小,C点沿变形前梁轴方向(x方向)的位移可以 忽略,因此可以认为 cc 垂直于梁变形前轴线AB。 挠度: AB 梁上的一点(横截面上的形心)在垂直于梁变形前 轴线方向的线位移,称为挠度y。 角位移: 梁变形时,其横截面形心不仅有线位移。而且整个横截面 绕其中性轴转动一个角度,因而有角位移 。 转角:梁一横截面绕其中性轴转动的角度。 在工程实际中,挠度和转角是度量弯曲变形的两个基本量。
19
17
§9-5
1、刚度条件
梁的刚度条件、提高梁刚度的主要措施
最大挠度 : ymax [ y], 最大转角: max [ ],
[y]=(0.0003~0.0005)l
梁的许用挠度值 梁的许用转角值
l为轴承间距。
对于一般轴,取
[]=(0.001~0.005)rad
EI z
不定积分中,出现两个积分常数C、D。这由支承条件和边界 条件确定,即x=0处 y A 0, A 0 而且对于分段的M z (x) 、或有集中力、集中力偶、间断的 分布力等时, 应该分段积分。每一个分段中都有两个积分常数, 它们要满足连续变形条件。
7
例1:9.1 求挠度方程和转角方程,并确定最大值。 解:确定支座反力:
Pb x P( x a) l
( a x b)
Pb 2 1 2 EI z 2 ( x) x Px Pax C2 2l 2 ( a x b) Pb 3 1 3 1 2 EI z y2 ( x) x Px Pax C2 x D2 6l 6 2
2
线位移 梁轴线上的任一点C(即截面的形心) 在梁变形后将移到 c ,因而有线位移 cc 。 由于梁的变形小,C点沿变形前梁轴方向(x方向)的位移可以 忽略,因此可以认为 cc 垂直于梁变形前轴线AB。 挠度: AB 梁上的一点(横截面上的形心)在垂直于梁变形前 轴线方向的线位移,称为挠度y。 角位移: 梁变形时,其横截面形心不仅有线位移。而且整个横截面 绕其中性轴转动一个角度,因而有角位移 。 转角:梁一横截面绕其中性轴转动的角度。 在工程实际中,挠度和转角是度量弯曲变形的两个基本量。
19
材料力学 积分法求梁的变形

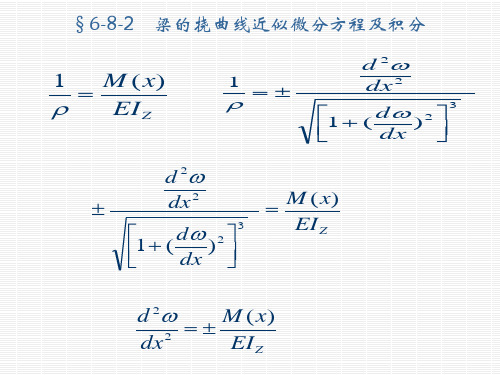
一、挠曲线近似微分方程
M ( x ) = r EI Z 1
1 = ± r d 2 w dx 2 d w é 2 ù 1 + ( ) ê ú dx ë û
3
±
d 2 w dx 2 d w 2 ù é 1 + ( ) ú ê dx û ë
3
M ( x ) = EI Z
边界条件、连续条件应用举例
弯矩图分三段,共6 个积分常数需6个边界条 件和连续条件 A B
P C D
w
铰连接
ω A点: A = 0, q A = 0
B 点 : w B 左 = w B 右
C点 : w C左 = w C右
D点:w D = 0
q C 左 = q C 右
边界条件、连续条件应用举例
y
边界条件
3 qL C1 = 6 EI z
EI zw =
1 (L - x )4 + C q 1 x + C 2 24
x = 0 x = 0 x = L
q = 0 w = 0
qL3 q B = 6 EI z
q =-
3 qL C2 =24 EI z
挠曲线方程应分两段AB,BC.
F A
a
q
B
EI z
L
共有四个积分常数
C
x
边界条件
x = a x = a + L
连续条件
w B = 0 wC = 0
y
x = a
w B1 = w B 2 q B1 = q B 2
例题 5.4 &
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
M ( x ) = r EI Z 1
1 = ± r d 2 w dx 2 d w é 2 ù 1 + ( ) ê ú dx ë û
3
±
d 2 w dx 2 d w 2 ù é 1 + ( ) ú ê dx û ë
3
M ( x ) = EI Z
边界条件、连续条件应用举例
弯矩图分三段,共6 个积分常数需6个边界条 件和连续条件 A B
P C D
w
铰连接
ω A点: A = 0, q A = 0
B 点 : w B 左 = w B 右
C点 : w C左 = w C右
D点:w D = 0
q C 左 = q C 右
边界条件、连续条件应用举例
y
边界条件
3 qL C1 = 6 EI z
EI zw =
1 (L - x )4 + C q 1 x + C 2 24
x = 0 x = 0 x = L
q = 0 w = 0
qL3 q B = 6 EI z
q =-
3 qL C2 =24 EI z
挠曲线方程应分两段AB,BC.
F A
a
q
B
EI z
L
共有四个积分常数
C
x
边界条件
x = a x = a + L
连续条件
w B = 0 wC = 0
y
x = a
w B1 = w B 2 q B1 = q B 2
例题 5.4 &
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
第六章 梁的位移

可解出
Fa 2 c2 , 2
1 1 1 EI z v ql 2 x 2 qlx3 qx 4 c1 x c2 4 6 24
(2)
2.16
第6章
梁的位移
6.2 用积分法求梁的位移
考虑边界条件,对于悬臂梁来说,悬臂端的转角和挠度为0,即
x0 x0
v 0
v0
将上述2个边界条件代入式(1)和式(2),可解出积分常数为
1 1 EI z v qlx 2 qx3 c1 4 6
(2)
2.20
第6章
该梁的边界条件为
梁的位移
6.2 用积分法求梁的位移
x0 x 1
v0 v0
先将第1个边界条件代入式(2),解出积分常数c2:
c2 0
再将第2个边界条件代入式(2),可解出积分常数c1:
ql 3 c1 24
tan v f ( x)
即有
f ( x)
(c)
2.6
Qm
第6章
梁的位移
6.1 梁的挠曲线微分方程
式(c)称为转角方程,它表达了梁各横截面转角与挠度的关系。 在第5章,我们曾建立了挠曲线曲率(curvature)与弯矩的关系,即式 (5.1)所示 1 M EI z 在高等数学中,我们有曲率公式如下:
2.9
第6章
梁的位移
6.1 梁的挠曲线微分方程
x M (a) M (b) M M
x
M<0
vⅱ >0
y y
M>0
vⅱ <0
图6.2 曲率正负号的规定 (a) 梁受负弯矩作用;(b)梁受正弯矩作用
2.10
第6章
梁的位移
6.2 用积分法求梁的位移
梁的位移
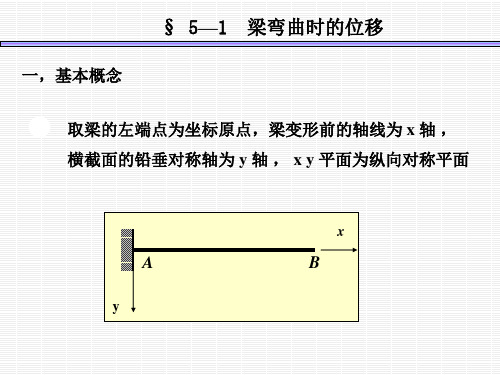
移,称为该截面的挠度.用w表示.
A
C
B
x
w挠度
C'
B'
衡量梁弯曲变形程度的曲线是曲率,我们为什么用挠度和转
角?
2、转角 (slope)
横截面对其原来位置的角位移,称为该截面的转角. 用 表示
横截面的转角也就是曲线在该点处的切线与X轴之间的夹角
A
C
B
x
C'
w挠度(
B 转角
3、挠曲线 (Deflection curve) 梁变形后的轴线称为挠曲线 . 也称弹性曲线
EIz2
Fb 6L
x3
1 6
Fx
a3
Fb
L2 b2 6L
x
EIz1
Fb 2L
x2
Fb
L2 6L
b2
EIz1
Fb 6L
x3
Fb
L2 6L
b2
x
例题 5.3 求图示简支梁在集中荷载F的作用下(F力在右半跨)的最大挠度。
a A
Fb L
6EIz 2EIz 3EIz
例题 5.2
求图所示悬臂梁B端的挠度与转角。
A
x
l
y
边界条件
x0 0 x0 0
xL
B
qL3 6EI z
M x 1 qL x2
B
2
x
EI z
M
x
1 2
q
L
x
2
EI z
EI z
A
C
B
x
w挠度
C'
B'
衡量梁弯曲变形程度的曲线是曲率,我们为什么用挠度和转
角?
2、转角 (slope)
横截面对其原来位置的角位移,称为该截面的转角. 用 表示
横截面的转角也就是曲线在该点处的切线与X轴之间的夹角
A
C
B
x
C'
w挠度(
B 转角
3、挠曲线 (Deflection curve) 梁变形后的轴线称为挠曲线 . 也称弹性曲线
EIz2
Fb 6L
x3
1 6
Fx
a3
Fb
L2 b2 6L
x
EIz1
Fb 2L
x2
Fb
L2 6L
b2
EIz1
Fb 6L
x3
Fb
L2 6L
b2
x
例题 5.3 求图示简支梁在集中荷载F的作用下(F力在右半跨)的最大挠度。
a A
Fb L
6EIz 2EIz 3EIz
例题 5.2
求图所示悬臂梁B端的挠度与转角。
A
x
l
y
边界条件
x0 0 x0 0
xL
B
qL3 6EI z
M x 1 qL x2
B
2
x
EI z
M
x
1 2
q
L
x
2
EI z
EI z
梁位移

EI z
2
y(x) 1 (1 Plx2 1 Plx3)
EI z 2
6
ymax
y(l)
1 EIz
(1 2
Pl3
1 6
Pl3)
Pl3 3EIz
()
max
(l)
1 EIz
(Pl2
1 2
Pl2)
Pl2(逆时针) 2EIz
9
例2:求此梁的转角方程和挠度方程,确定最大转角,挠度。
由于梁变形后横截面仍垂直于轴线,因此任一截面的转角,
也可用截面形心处挠曲线的切线与x轴的夹角来表示。
则有: (切线) dy(x) tg
dx
因很小,可写成 tg
(x) dy(x) y
dx
即:任一横截面的转角 等于该截面处挠度y 对x的一阶导数,只
要知道梁的挠曲线方程,则可确定任一点的挠度和截面的转角。
分布力等时, 应该分段积分。每一个分段中都有两个积分常数,
它们要满足连续变形条件。
7
例1:9.1 求挠度方程和转角方程,并确定最大值。
解:确定支座反力:
RA P MA Pl
弯矩方程:
M (x) Pl Px
挠度、转角方程:
EIz (x) (Pl Px)dx C
因分段(x=a)处曲线连续变形,
y11
(a) (a)
y2
2
(a) (a)
C1
C2
Pb 6l
(b2
l2)
y1
y2 (x)
(x)
工程力学08-梁的位移分析和刚度条件

8.1 基本概念
8.1.2 梁的挠度与转角
现研究梁上一截面C的位移 ,它由C移动到C1位置
w—截面形心的垂直位移,称“挠度” q—截面相对变形前绕中性轴转过的角度,称 “转角” y θ 挠度与转角的关系 A C dw θ = tanq (8-2) dx C1 x 或: dw = q (8-3) dx w=w(x)—挠度是截面的函数,称“挠度方程”
(0≤x1≤a)
Fb x12 AC段: EIq1=EIw1’= + C1 2 l Fb x13 EIw1= + C1x1+ D1 l 6
(a)
(b)
《工程力学》
Bengbu college . The Department of Mechanical and Electronical Engineering .w.p_chen
(a≤x≤l)
应用举例a xຫໍສະໝຸດ C x2 lFb
FRB B
x
Fb 2 – b2 – 3x2)+ 3l (x – a)2] q=+ [(l b 6EIl
Fb 2 2 –x2)x+ l (x – a)3] w= + [(l – b 6EIl b
《工程力学》
Bengbu college . The Department of Mechanical and Electronical Engineering .w.p_chen
8.2 小挠度微分方程及其积分
8.2.2 积分常数的确定 约束条件与连续条件 常见约束、连续条件 载荷作用处: y
F
a b x
x=a, w1=w2,q1=q2
中间支座处:
y x l a
连 续 条 件
11梁的位移计算

q(l / 2) ql =− vC = − 8EI 128EI q (l / 2)3 ql 3 θC = − =− 6 EI 48 EI
4 4
q
梁变形后CB段必保持为直线
A
l/2
C θC
θC
l
B
v B1
vB2
v B1
ql 4 = vC = − 128 EI
vB 2
l l ql 4 = tan θ C = θ C = − 2 2 96 EI
31
例
7
机床主轴的支撑和受力可简化为如图所示的外伸梁, 其中 P 为由于切削而施加于卡盘上的力,P2 为齿轮间 1 的相互作用力。主轴为空心圆截面,外径 D = 80mm , l a 内径 d = 40mm , = 400mm, = 100mm , P = 2kN , 1 P2 = 1kN ,材料的弹性模量为 E = 200GPa 。规定 主轴的许用转角和许用挠度为:卡盘D处的挠度不超过 两轴承间距的 1 / 10 4 ,轴承B处的转角不超过 1 / 103 rad 。 试校核主轴的刚度。
(a ≤ x2 ≤ l )
d 2v b EI 2 = Fx1 dx l
(0 ≤ x1 ≤ a )
d 2v b EI 2 = Fx2 − F ( x2 − a ) dx l
(a ≤ x2 ≤ l )
17
例
3
2、分两段积分
b EIθ 1 = Fx12 + C1 2l
b EIv1 = Fx13 + C1 x1 + D1 6l
v1 = v2
12
例
1
如图所示悬臂梁,在自由端受集中力P作用,设EI为 常量,试求梁的最大挠度和最大转角。
4 4
q
梁变形后CB段必保持为直线
A
l/2
C θC
θC
l
B
v B1
vB2
v B1
ql 4 = vC = − 128 EI
vB 2
l l ql 4 = tan θ C = θ C = − 2 2 96 EI
31
例
7
机床主轴的支撑和受力可简化为如图所示的外伸梁, 其中 P 为由于切削而施加于卡盘上的力,P2 为齿轮间 1 的相互作用力。主轴为空心圆截面,外径 D = 80mm , l a 内径 d = 40mm , = 400mm, = 100mm , P = 2kN , 1 P2 = 1kN ,材料的弹性模量为 E = 200GPa 。规定 主轴的许用转角和许用挠度为:卡盘D处的挠度不超过 两轴承间距的 1 / 10 4 ,轴承B处的转角不超过 1 / 103 rad 。 试校核主轴的刚度。
(a ≤ x2 ≤ l )
d 2v b EI 2 = Fx1 dx l
(0 ≤ x1 ≤ a )
d 2v b EI 2 = Fx2 − F ( x2 − a ) dx l
(a ≤ x2 ≤ l )
17
例
3
2、分两段积分
b EIθ 1 = Fx12 + C1 2l
b EIv1 = Fx13 + C1 x1 + D1 6l
v1 = v2
12
例
1
如图所示悬臂梁,在自由端受集中力P作用,设EI为 常量,试求梁的最大挠度和最大转角。
材料力学第五章梁弯曲时的位移分析

a)2
C2 x2 D2
C2
B B x
FBy
目录
5.2 积分法求梁的挠度和转角
4)由边界条件确定积分常数
位移边界条件
x1 0, w1(0) 0 x2 l, w2 (l) 0
光滑连续条件
x1 x2 a, 1(a) 2 (a)
x1 x2 a, w1(a) y2 (a) 代入求解,得
x1 ,0
x1
a
y
CB 段:
M x2
FAy
x2
F ( x2
a)
Fb l
x2
F ( x2
a),
a x2 l
目录
5.2 积分法求梁的挠度和转角
3)列挠曲线近似微分方程并积分
F
AC 段: 0 x1 a
EI
d 2w1 dx12
M (x1)
Fb l
x1
EI
dw1 dx1
EI (x1)
Fb 2l
x2 1
EI dw EI 1 F (l x)2 C
dx
2
EIw 1 F (l x)3 Cx D 6
代入求解
C 1 Fl2, D 1 Fl3
2
6
5)确定转角方程和挠度方程
EI 1 F (l x)2 1 Fl2
2
2
Ax
y
yB
l
F Bx
B
EIw 1 F (l x)3 1 Fl2x 1 Fl3
目录
5.2 积分法求梁的挠度和转角
例2 求梁的转角方程和挠度方程,并求最大转角和最大挠度,
梁的EI已知,l=a+b,a>b。
F
解 1)由梁整体平衡分析得:
工程力学 梁的位移计算(41)
41-10
梁的位移计算
思考: 思考:
用积分法计算图示梁的挠度和转角, 用积分法计算图示梁的挠度和转角,其边界条件和 连续条件是什么? 连续条件是什么?
y
q
x
l
a
x = a+l v = 0 θ = 0
答:边界条件 x = 0 v = 0 连续性条件 x = l
v1 = v2
41-11
例
1
如图所示悬臂梁, 作用, 如图所示悬臂梁,在自由端受集中力P作用,设EI为 常量,试求梁的最大挠度和最大转角。 常量,试求梁的最大挠度和最大转角。
41-33
梁的位移计算
增加支撑
41-34
梁的位移计算
改善受力情况 改善受力情况可以减小弯矩,从而减小梁的挠度和转角。 改善受力情况可以减小弯矩,从而减小梁的挠度和转角。
P
y
l
x
ql v= 3EI z
4
y
q
x
l
ql v= 8 EI z
41-35
4
梁的位移计算
§11-6 11-
简单静不定梁
梁支座约束力的数目超出了独立的平衡方程数目, 梁支座约束力的数目超出了独立的平衡方程数目, 因而仅靠平衡方程不能求解--静不定梁。 --静不定梁 因而仅靠平衡方程不能求解--静不定梁。
解 1、建立挠曲线近似微分方程
取坐标系如图所示, 取坐标系如图所示,弯矩方程
P
y
l
x
M ( x) = − P(l − x) = P ( x − l )
d v P( x − l ) = 2 dx EI z
2
x
2、积分求通解
P P x2 θ =∫ ( x − l )dx = ( − lx ) + C EI z EI z 2
梁的位移计算
思考: 思考:
用积分法计算图示梁的挠度和转角, 用积分法计算图示梁的挠度和转角,其边界条件和 连续条件是什么? 连续条件是什么?
y
q
x
l
a
x = a+l v = 0 θ = 0
答:边界条件 x = 0 v = 0 连续性条件 x = l
v1 = v2
41-11
例
1
如图所示悬臂梁, 作用, 如图所示悬臂梁,在自由端受集中力P作用,设EI为 常量,试求梁的最大挠度和最大转角。 常量,试求梁的最大挠度和最大转角。
41-33
梁的位移计算
增加支撑
41-34
梁的位移计算
改善受力情况 改善受力情况可以减小弯矩,从而减小梁的挠度和转角。 改善受力情况可以减小弯矩,从而减小梁的挠度和转角。
P
y
l
x
ql v= 3EI z
4
y
q
x
l
ql v= 8 EI z
41-35
4
梁的位移计算
§11-6 11-
简单静不定梁
梁支座约束力的数目超出了独立的平衡方程数目, 梁支座约束力的数目超出了独立的平衡方程数目, 因而仅靠平衡方程不能求解--静不定梁。 --静不定梁 因而仅靠平衡方程不能求解--静不定梁。
解 1、建立挠曲线近似微分方程
取坐标系如图所示, 取坐标系如图所示,弯矩方程
P
y
l
x
M ( x) = − P(l − x) = P ( x − l )
d v P( x − l ) = 2 dx EI z
2
x
2、积分求通解
P P x2 θ =∫ ( x − l )dx = ( − lx ) + C EI z EI z 2
第7章_梁的位移

第7章梁的位移
本章导读
基本要求:掌握挠曲线、挠度和转角的概念;熟练建立弯曲 变形的挠曲线近似微分方程;熟练掌握利用积分法、叠加法 计算梁的位移;能够进行梁的刚度校核;了解提高梁刚度的
一些措施;了解超静定梁的一般概念和分析方法。
重点:挠曲线近似微分方程,叠加法求梁变形。 难点:积分法中利用边界条件和连续条件确定积分常数;叠 加法中用逐段刚化法求梁的撕裂度和转角。
④优点:使用范围广,直接求出较精确; 缺点:计算较繁。
7.2梁的挠曲线的近视微分方程及其积分
例 求下列各等截面直梁的弹性曲线、最大挠度及最大转角。 P 解: L 建立坐标系并写出弯矩方程
M ( x) P( x L)
x
f
写出微分方程的积分并积分 应用位移边界条件求积分常数
EIw" M ( x) P( L x)
7.5 超静定梁
例9-4。图示杆系中,AB和CD梁的抗弯为EI,BD杆的拉压刚度是EA,不计剪切变形的影响,求BD
杆的内力。
A
B l/2
解(a) 确定静不定梁的基本结构 取D为多余约束
A
B
F y 'D
C
l
D
D (1)
FyD
C
(2)
D
(b) 求变形几何关系
wD1 wD 2
7.5 超静定梁
(c) 求物理关系
7.2梁的挠曲线的近视微分方程及其积分
P
L
x f 写出弹性曲线方程并画出曲线
w( x)
P ( L x)3 3L2 x L3 6 EI
最大挠度及最大转角
PL2 max ( L) 2 EI
wmax
本章导读
基本要求:掌握挠曲线、挠度和转角的概念;熟练建立弯曲 变形的挠曲线近似微分方程;熟练掌握利用积分法、叠加法 计算梁的位移;能够进行梁的刚度校核;了解提高梁刚度的
一些措施;了解超静定梁的一般概念和分析方法。
重点:挠曲线近似微分方程,叠加法求梁变形。 难点:积分法中利用边界条件和连续条件确定积分常数;叠 加法中用逐段刚化法求梁的撕裂度和转角。
④优点:使用范围广,直接求出较精确; 缺点:计算较繁。
7.2梁的挠曲线的近视微分方程及其积分
例 求下列各等截面直梁的弹性曲线、最大挠度及最大转角。 P 解: L 建立坐标系并写出弯矩方程
M ( x) P( x L)
x
f
写出微分方程的积分并积分 应用位移边界条件求积分常数
EIw" M ( x) P( L x)
7.5 超静定梁
例9-4。图示杆系中,AB和CD梁的抗弯为EI,BD杆的拉压刚度是EA,不计剪切变形的影响,求BD
杆的内力。
A
B l/2
解(a) 确定静不定梁的基本结构 取D为多余约束
A
B
F y 'D
C
l
D
D (1)
FyD
C
(2)
D
(b) 求变形几何关系
wD1 wD 2
7.5 超静定梁
(c) 求物理关系
7.2梁的挠曲线的近视微分方程及其积分
P
L
x f 写出弹性曲线方程并画出曲线
w( x)
P ( L x)3 3L2 x L3 6 EI
最大挠度及最大转角
PL2 max ( L) 2 EI
wmax
