北大版高等数学第4章习题集解答
北大版高等数学课后习题答案_完整版

习题1.1222222222222222222.,,.3,3.3,,313 2.961,9124,31.3,93,3,3.,,.,,,,p p p q p q p q q p p k p k p k k p k k p p k k q q k q p q p a a a b p a pb b b====+=+=++=++======为互素自然数除尽必除尽否则或除将余故类似得除尽与互素矛盾.设是正的素数为互素自然数,则素证 2.证 1.2222222,,.,..,:(1)|||1| 3.\;(2)|3| 2.0,13,22,1,(1,0);01,13,13,(0,1);1,13,3/2,(1,3/2).(1,0)(0,1)p a p a a pk p k pb pk b p b a b x x x x x x x x x x x x x x x X ===+-<-<<-+-<>->--<<+-<<>+-<<=-⋃数除尽故除尽类似得除尽此与为互素自然数矛盾.解下列不等式若则若则若则3.解(1)222(1,3/2).(2)232,15,1||5,1||(1).,(1)||||||;(2)||1,|||| 1.(1)|||()|||||||||,||||||.(2)|||()||||||x x x x x a b a b a b a b a b a a b b a b b a b b a b a b a b a b b a b b ⋃-<-<<<<<<<=⋃-+≥--<<+=++-≤++-=+++≥-=+-≤+-<设为任意实数证明设证明证4.,| 1.(1)|6|0.1;(2)||.60.160.1. 5.9 6.1.(, 6.1)( 5.9,).(2)0,(,)(,);0,;0,(,).11,01,.1, 1.11x x a l x x x x X l X a l a l l x a l X a a n n a b a ++>->+>+<->-<-=-∞-⋃-+∞>=++∞⋃-∞-=≠<=-∞+∞-><<>=>-=-=解下列不等式或或若若若若证明其中为自然数若解(1)证5.:6.1200001)(1)1).(,),(,).1/10.{|}.(,),,{|},10{|}./10,(1)/10,/10(1)/101/10n n n n n n n n n n n b b n a b a b n b a mA A m A a b ABC B A x x b C A x x a B m m C b a m m --+++><-=∈⋂=∅=⋃=⋂≥=⋂≤-∈-≤-Z 设为任意一个开区间证明中必有有理数取自然数 满足考虑有理数集合= 若则中有最小数-=证7.(,),(,).1/10.|}.10n n n n a b a b mn b a A m <-=∈Z ,此与的选取矛盾. 设为任意一个开区间证明中必有无理数取自然数 满足考虑无理数集合 以下仿8题.8.证习题1.26426642642666613.(1,)1).13.(,).13||13,||1,3,11||3,(,).yy xx x xyxx x x x x x xx xx x xy y x=+∞===<>++=-∞+∞+++++≤≤>≤=++=≤∈-∞+∞证明函数内是有界函数.研究函数在内是否有界时,时证解习题1.4221.-(1)0);(2)lim;(3)lim;(4)lim cos cos.1)0,,,||.,||,|,(2)0x ax x a x a x axa x a e e x ax a x aεδεεεδδεε→→→→→>===∀>=<<<-<=-<<∀>直接用说法证明下列各极限等式:要使取则当时故证(222222,|| 1.||||||,|||||2|1|2|,1|2|)||,||.min{,1},||,1|2|1|2|||,lim(3)0,.||(1),01),1x ax a a x a x aax a x a x a x ax a x a a aa x a x a x aa ax a x ax a e e e e eeεεεεδδεεεε→---<-=+-<+≤-+<++-<-<=-<++-<=∀>>-=-<<-<<不妨设要使由于只需(取则当时故设要使即(.1,0ln1,min{,1},0,||,1|2|lim lim lim0,|cos cos|2sin sin2sin sin||,2222,|,|cos cosx aax aax a x a x ax a x a x aeex a x a e ee ae e e e e ex a x a x a x ax a x a x a x aεεεδδεεδεδ-→+→-→<+⎛⎫<-<+=<-<-<⎪+⎝⎭===+-+-∀>-==≤-=-<-取则当时故类似证故要使取则当|时...(4)2|,lim cos cos.2.lim(),(,)(,),().1,0,0|-|,|()|1,|()||()||()|||1||.(1)1(1)lim lim2x ax ax xx af x l a a a a a u f xx a f x lf x f x l l f x l l l Mxxεδδεδδ→→→→<==-⋃+==><<-<=-+≤-+<+=+-=故设证明存在的一个空心邻域使得函数在该邻域内使有界函数对于存在使得当 时从而求下列极限证3.:2002222200000221222lim(1) 1.222sin sin1cos11122(2)lim lim lim1.2222(3)0).22(4)lim.22332(5)lim22xx x xx xxxx x xxx xxxx xax xx xx xx x→→→→→→→→+=+=⎛⎫⎛⎫⎛⎫⎪ ⎪⎪-⎝⎭⎝⎭⎪====⎪⎪⎝⎭==>---=-------2.33-=-20103030300022********(23)(22)2(6)lim 1.(21)2 1.13132(8)lim lim lim 11(1)(1)(1)(1)(1)(2)lim lim (1)(1)x x x x x x x x x x x x x x x x x x x x x x x x x x x x →∞→→→-→-→-→--+==+==-+---⎛⎫-== ⎪+++-++-+⎝⎭+-==+-+214442100(2)31.(1)3244.63(1)1(1)12(10)lim lim lim .1(11)lim x x x nnnx y y x x x x n n ny y y x y n x y y→-→→→→→→→∞--==--+====-+++-+-===- 101100100101001010.(12)lim (0)./,(13)lim (0)0, , .(14)x m m m mnn n x n nmm m n nx n x x a x a x a a b b x b x b b a b m n a x a x a a b n mb xb x b m n--→--→∞→∞→∞==+++≠=+++=⎧+++⎪≠=>⎨+++⎪∞>⎩= 1.=00222220(15)()5lim(1)55lim .3(1)(16)0,l xx x x x x xx x x a →→→→=++=++==++>00imlim lim x a x a x a →+→+→+⎫=⎫=+00lim lim x a x a →+→+⎛⎫=⎛⎫==000222200000sin 14.lim 1lim 1sin sin (1)lim lim lim cos .tan sin sin(2)sin(2)2(2)lim lim lim 100323tan 3sin 2tan 3sin 2(3)lim lim lim sin 5sin 5xx x x x x x x x x x x x e x x x x x x x x x x x x xx x x x x αααββββ→→∞→→→→→→→→→⎛⎫=+= ⎪⎝⎭=====-=- 利用及求下列极限:00()1/0321.sin 5555(4)lim lim 2cos sinsin sin 22(5)lim lim cos .2(6)lim 1lim 1lim 1.(7)lim(15)x x x a x a kxxxk kk k x x x yy x x xxx a x a x a a x a x ak k k e x x x y →→+→→----→∞→∞→∞→=-===+--==--⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥+=+=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦-=51/(5)50100100lim(15).111(8)lim 1lim 1lim 1.5.lim ()lim ().lim ():0,0,0|-|().lim (y y x xx x x x ax x a x y e e x x x f x f x f x A x a f x A f x δδ--→+→∞→∞→∞→→-∞→→-∞⎡⎤-=⎢⎥⎣⎦⎡⎤⎛⎫⎛⎫⎛⎫+=++= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦=+∞=-∞=+∞>><<>给出及的严格定义对于任意给定的存在使得当时):0,0,().A x f x A =-∞>∆><-∆<-对于任意给定的存在使得当时习题1.5222 21.(2)sin5.(1)0,|.,,|||||,0555()(2)(1)0,|sin5sin5|2|cos||sin|.22xx x axx x x xx a x ax aεδεεεδδεεε-==∀>=<≤<<=<<=+-∀>-=<试用说法证明连续在任意一点连续要使只需取则当时有连续.要使由于证000000555()2|cos||sin|5||,5||,||,225,|||sin5sin5|,sin55()()0,0||()0.(),()/2,0||(x a x ax a x a x ax a x a x x a y f x x f x x x f xf x x f x x xf xεεεδδεδδεδδ+-≤--<-<=-<-<==>>-<>=>-<只需取则当时有故在任意一点连续.2.设在处连续且证明存在使得当时由于在处连续对于存在存在使得当时证000000000000 )()|()/2,()()()/2()/20.3.()(,),|()|(,),?(,),.0,0|||()()|,||()||()|||()()|,||.f x f x f x f x f x f xf x a b f x a bx a b f x x xf x f x f x f x f x f x f xεδδεε-<>-=>∈>>-<-<-≤-<于是设在上连续证明在上也连续并且问其逆命题是否成立任取在连续任给存在使得当时此时故在连续其证0001,,(),()|11,ln(1),1,0,(1)()(2)()arccos, 1.0;lim()lim1(0),lim()(0)x x xxf x f xxax xxf x f xa x xa x xf x f f x fπ→-→→+⎧=≡⎨-⎩+≥⎧<==⎨<+≥⎩⎪⎩=====逆命题是有理数不真例如处处不连续但是|处处连续.是无理数4.适当地选取,使下列函数处处连续:解(1)11112sin2limsin31.(2)lim()lim ln(1)ln2(1),lim()lim arccos(1)ln2,ln2.5.3:(1)lim cos cos lim cos0 1.(2)lim(3)lim xx x x xx xxxxxaf x x f f x a x a fax xe eπ→→+→+→-→-→+∞→+∞→→==+====-===-=====利用初等函数的连续性及定理求下列极限sin22sin3322.(4)lim arctan arctan lim arctan1.114xxx xex xπ→∞→∞====++()()(ln ())()(5)6.lim ()0,lim (),lim)().lim)()lim)x g x b x x x x x x g x f x g x x x x x f x a g x b f x a f x e →→→→→====>====设证明证0lim [(ln ())()]ln 22.7.,,(1)()cos ([]),,(2)()sgn(sin ),,,,1,(3)()1,1/2, 1.1(4)()x x f x g x b a b e e a f x x x n f x x n n x x f x x x x f x ππ→===-∈=∈⎧≠==⎨=⎩+=Z Z 指出下列函数的间断点及其类型若是可去间断点请修改函数在该点的函数值,使之称为连续函数:间断点第一类间断点.间断点第一类间断点.间断点第一类间断点.,011,sin,12,11,01,2(5)(),12,2,1,2 3.1x x x x x x f x x x x x xπ⎧≤≤⎪=⎨<≤⎪-⎩⎧≤≤⎪-⎪=<≤=⎨⎪⎪<≤-⎩间断点第二类间断点.间断点第一类间断点.0000008.(),(),()()()()()()()()()()(()())()()()()()0,()().y f x y g x x h x f x g x x f x g x x h x f x g x x x g x f x g x f x x x f x g x x f x g x D x ϕϕ===+==+=+-=≡=R R 设在上是连续函数而在上有定义但在一点处间断.问函数及在点是否一定间断?在点一定间断.因为如果它在点连续,将在点连续,矛盾.而在点未必间断.例如解习题1.600001.:()lim (),lim (),,,,()0,()0,[,],,(,),()0.2.01,,sin ,.(x x P x P x P x A B A B P A P B P A B x A B P x y y x x f x εε→+∞→-∞=+∞=-∞<<>∈=<<∈=-R 证明任一奇数次实系数多项式至少有一实根.设是一奇数次实系数多项式,不妨设首项系数是正数,则存在在连续根据连续函数的中间值定理存在使得设证明对于任意一个方程有解且解是唯一的令证证000000000000000212121212121)sin ,(||1)||1||,(||1)||1||,[||1,||1],,[||1,||1],().,()()(sin sin )||0,.3.()(,x x f y y y y f y y y y f y y x y y f x y x x f x f x x x x x x x x x f x a b εεεεε=---=--+<-≤+≥+->≥--+∈--+=>-=---≥--->在连续由中间值定理存在设故解唯一设在1212112212121121121112212221212121212),,(,),0,0,(,)()()().()(),.()(),()()()()()()()(),[,]x x a b m m a b m f x m f x f m m f x f x x f x f x m f x m f x m f x m f x m f x m f x f x f x m m m m m m x x ξξξ∈>>∈+=+==<+++=≤≤=+++连续又设证明存在使得如果取即可设则在上利用连续函数的中间值定理证.4.()[0,1]0()1,[0,1].[0,1]().()(),(0)(0)0,(1)(1)10.,01.,,(0,1),()0,().5.()[0,2],(0)(2).y f x f x x t f t t g t f t t g f g f t t g t f t t y f x f f =≤≤∀∈∈==-=≥=-≤∈====即可设在上连续且证明在存在一点使得如果有一个等号成立取为或如果等号都不成立则由连续函数的中间值定理存在使得即设在上连续且证明证12121212[0,2],||1,()().()(1)(),[0,1].(0)(1)(0),(1)(2)(1)(0)(1)(0).(0)0,(1)(0),0, 1.(0)0,(0),(1),,(0,1)()(1x x x x f x f x g x f x f x x g f f g f f f f g g f f x x g g g g f ξξξ-===+-∈=-=-=-=-====≠∈=+在存在两点与使得且令如果则取如果则异号由连续函数的中间值定理存在使得证12)()0,, 1.f x x ξξξ-===+取第一章总练习题221.:581 2.3|58|1422.|58|6,586586,.3552(2)33,52333,015.5(3)|1||2|1(1)(2),2144,.22|2|,.2,2,4,2;2,3x x x x x x x x x x x x x x x x x y x x x y x y x y x y x y x -≥-≥-≥-≥-≤-≥≤-≤-≤-≤≤≤+≥-+≥-+≥-+≥=+-≤=+≤=->=求解下列不等式()或或设试将表示成的函数当时当时解解解2.解222312312,4,(2).32,41(2), 4.313.1.22,4(1)44,0.1,0.4.:1232(1)2.222221211,.22123222n n y x y y y x y y x x x x x x x x x x n n n n ->=--≤⎧⎪=⎨->⎪⎩<+≥-<++<++>≥-≠+++++=-+==++ 的全部用数学归纳法证明下列等式当时,2-等式成立设等式对于成立,则解证1231111121211222112312222222124(1)(1)3222,22221..1(1)(2)123(1).(1)1(11)1(1)1,(1)(1)n n n n n n n n n n n n n n n n n n n n n x nx x x nxx x x x x n x x ++++++-+++++=++++++++-+++=-+=-=-+-++++++=≠--++-===-- 即等式对于也成立故等式对于任意正整数皆成立当时证1,1212.1(1)123(1)(1)(1)n n n nnn n x nx x x nxn x n xx +--++++++++=++- 等式成立设等式对于成立,则122122112211221221(1)(1)(1)(1)1(1)(12)(1)(1)1(1)(2)(1)(1)1(1)(2)(1)(1)1(2)(1),(1)1n n n n n n n n n n n n n n n n n n n x nx x n x x n x nx x x n x x n x nx x x x n x n x nx x x x n x n x n x x n ++++++++++-+++-+=--+++-++=--+++-++=--+++-++=--+++=-+即等式对于成立.,.|2|||25.()(1)(4),(1),(2),(2);(2)();(3)0()(4)224211222422(1)(4)1,(1)2,(2)2,(2)0.41224/,2(2)()x x f x xf f f f f x x f x x f f f f x x f x +--=---→→----------==--==-====----≤-=由归纳原理等式对于所有正整数都成立设求的值将表成分段函数当时是否有极限:当时是否有极限?解00022222222;2,20;0,0.(3).lim ()2,lim ()0lim ().(4).lim ()lim (4/)2,lim ()lim 22lim (),lim () 2.6.()[14],()14(1)(0),x x x x x x x x x x x f x f x f x f x x f x f x f x f x x f x x f →-→+→-→--→--→-+→-+→--→-⎧⎪-<≤⎨⎪>⎩==≠=-======--无因为有设即是不超过的最大整数.求003,;2(2)()0?(3)()?391(1)(0)[14]14,1467.[12]12.244(2).lim ()lim[14]14(0).(3).()12,()x y x x f f f x x f x x f f f f x y f f x f x →→+⎛⎫⎪⎝⎭==⎛⎫⎡⎤⎡⎤=-=-=-=-+=-=-=- ⎪⎢⎥⎢⎥⎝⎭⎣⎦⎣⎦=-=-==-的值在处是否连续在连续因为不连续因为解111111.7.,0,,:(1)(1);(2)(1).n n n n n n a b a b n b a b a n b n a b a b a++++=-≤<--<++<--设两常数满足对一切自然数证明1111111()()(1),(1).118.1,2,3,,1,1.:{},{}..111,1,7,111n n n n n n n n n n n n nn n n n n n n b a b a b b a a b b b b n b b a b a b a n a b a n a b n n a b a b a b n nn ++--+++--+++=<+++=+--->+-⎛⎫⎛⎫==+=+ ⎪ ⎪⎝⎭⎝⎭<+=++⎛+ ⎝ 类似有对令证明序列单调上升而序列单调下降,并且令则由题中的不等式证证=11111111111(1)1,111111111(1)11(1)1111111,11111.1111(1)11n n nn n nn nn nn n n n n n n n n n n n n n n n n n n n n n +++++++⎫⎛⎫-+⎪ ⎪+⎛⎫⎭⎝⎭<++ ⎪⎝⎭-+⎛⎫⎛⎫⎛⎫+-+<++ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫+-+<+ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫+<+ ⎪ ⎪+⎝⎭⎝⎭⎛⎫+ ⎛⎫⎝⎭++< ⎪+⎝⎭111111121111111111(1)1111(1)11111111111111111.1111111.111n n nn n nn n n n n n n n n n n n n n n n n n nn n n n n +++++++⎛⎫-+⎪ ⎪+⎝⎭-+⎛⎫⎛⎫⎛⎫++<+-+ ⎪ ⎪⎪+++⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫+<+-+ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫+++<+ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎛⎫++>+ ⎪++⎝⎭⇔我们证明22111211111(1)11..(1)(1)1111,1,1,11.nn n n n n n n n n n n e e e n n n n ++++>+++++⇔>++⎛⎫⎛⎫⎛⎫⎛⎫→∞+→+→+<<+ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭最后不等式显然成立当时故9.求极限22222222221111lim 1111234111111112341324351111().2233442210.()lim (00, ()lim n n n n n n n n n n n n nxf x a nx ax nxf x nx a →∞→∞→∞⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭++==→→∞=≠+===+ 作函数)的图形.解解0;1/,0.x x ⎧⎨≠⎩1111.?,()[,]|()|,[,].,(),[,],max{||,||}1,|()|,[,].,|()|,[,],(),[,].12.f x a b M f x M x a b M N f x N x a b M M N f x M x a b M f x M x a b M f x M x a b <∀∈≤≤∀∈=+<∀∈<∀∈-<<∀∈1在关于有界函数的定义下证明函数在区间上为有界函数的充要条件为存在一个正的常数使得设存在常数使得M 取则有反之若存在一个正的常数使得则证12121212:()()[,],()()()()[,].,,|()|,|()|,[,].|()()||()||()|,|()()||()||()|,[,].113.:()cos 0y f x y g x a b f x g x f x g x a b M M f x M g x M x a b f x g x f x g x M M f x g x f x g x M M x a b f x x x xπ==+<<∀∈+≤+<+=<∀∈==证明若函数及在上均为有界函数则及也都是上的有界函数存在证明在的任一证,0().11(,),00,,,(),1()(,)0,()(21/2)cos(21/2)0,21/20().n x f x M n n M f n M n nf x f x n n n x f x δδδδδδπ→->><>=>-=→=++=→∞+→n 邻域内都是无界的但当时不是无穷大量任取一个邻域和取正整数满足和则故在无界.但是x 故当时不是无穷大量证11111000114.lim (1)ln (0).1ln 1,ln ln(1),.lim lim 10.ln(1)ln(1)lim lim ln(1)ln lim(1)ln 1,ln (1)ln ().ln(1)15.()()nn nn n n n n y y y y y n nn n x x x xx y x y n y x n y y y y e y y xn x x n y f x g x →∞→∞→∞→→→-=>-==+==-=++=+=+==-=→→∞+证明令则注意到我们有设及在实轴上有证00002022222220000.:()(),,()lim ()lim ()().1cos 116.lim.22sin 1cos 2sin 1sin 12lim lim lim lim 1422n n n n n x x x y y f x g x x x x f x f x g x g x x x x x y y x x y y →∞→∞→→→→→→===-=⎛⎫-==== ⎪⎝⎭ 定义且连续证明若与在有理数集合处处相等,则它们在整个实轴上处处相等.任取一个无理数取有理数序列证明证证0011000000001.2ln(1)17.:(1)lim 1;(2)lim .ln(1)(1)lim lim ln(1)ln lim(1)ln 1.(1)11(2)lim lim lim lim ln(1)ln(1)lim1.1x a xa y x y y y y y x a a a x x aa ax x x y y a a y e e e y x y y y e ye e e e e y e e e y x x x y ye e +→→→→→+→→→→→=+-==+=+=+==---====++== 证明证0111018.()lim ()0,()lim ()()0.|()|,0||.0,0,0|||()|/.min{,},0||,|()()||()||()|,li x ax ay f x a f x y g x a f x g x g x M x a x a f x M x a f x g x f x g x M Mδεδδεδδδδεε→→====<<-<>><-<<=<-<=<= 设在点附近有定义且有极限又设在点附近有定义,且是有界函数.证明设对于任意存在使得当时令则时故证m ()()0.x af xg x →=19.()(,),,()()|()|() () ()(),()(,).y f x c g x f x f x c g x c f x cc f x c g x g x =-∞+∞≤⎧⎪=>⎨⎪-<-⎩-∞+∞设在中连续又设为正的常数定义如下 当当当试画出的略图并证明在上连续0000000000000|()|,0,||lim ()lim ()()().(),0,||()lim ()lim ().(),().0,,0,x x x x x x x x f x c x x g x f x f x g x f x c x x f x c g x c c g x f x c g x c c δδδδεεδ→→→→<>-<===>>-<>=====><>一若则存在当时|f(x)|<c,g(x)=f(x),若则存在当时,g(x)=c,若则对于任意不妨设存在使证()0000121212|||()|.||.(),()(),|()()||()|,(),(),|()-()|0.()()min{(),}max{(),}().max{(),()}(|()()|()())/2.min x x f x c x x f x c g x f x g x g x f x c f x c g x c g x g x g x f x c f x c f x f x f x f x f x f x f x δεδεε-<-<-<≤=-=-<>==<=+--=-++得当时设若则若 则二利用证121212123123123111123{(),()}(|()()|(()())/2.120.()[,],[()()()],3,,[,].[,],().()()(),(),.()min{(),(),()},f x f x f x f x f x f x f x a b f x f x f x x x x a b c a b f c f x f x f x f x c x f x f x f x f x f ηηη=--++=++∈∈======设在上连续又设其中证明存在一点使得若则取即可否则设证31231313000000()min{(),(),()},()(),[,],,[,],().21.()(),()g(),,.0()g()()g()x f x f x f x f x f x f x x c a b f c y f x x g x x x kf x l x x k l l kf x l x x kf x l x x ηη=<<∈==+=+≠+在连续根据连续函数的中间值定理存在一点使得设 在点连续而在点附近有定义但在不连续问是否在连续其中为常数如果在连续;如果在解,l 0,000000||()[[()lg()]()]/.22.Dirichlet ..,()1;,()0;lim (),()11(1)lim 0;(2)lim (arctan )sin 12n n n n x x x x x g x kf x x kf x l x x x x D x x x D x D x D x x x x x →→∞→+∞=+-''→→→→+⎛⎫= ⎪+⎝⎭不连续,因否则将在连续证明函数处处不连续任意取取有理数列则取无理数列则故不存在在不连续.23.求下列极限:证222001/112132100;2tan 5tan 5/5(3)lim lim 5.ln(1)sin [[ln(1)]/]sin /1lim(1).24.()[0,),0().0,(),(),,().{x x y x y n n x x x x x x x x x x x y e y f x f x x a a f a a f a a f a π→→→→+=====++++=+==+∞≤≤≥=== 设函数在内连续且满足设是一任意数并假定一般地试证明11},lim .lim ,(),().(),{}()0(1,2,),{}n n n n n n n n n n n n a a l a l f x x f l l a f a a a a f a n a →∞→∞++====≤=≥=单调递减且极限存在若则是方程的根即单调递减.又单调递减有下界,证111lim ,lim lim ()(lim )().25.()(,),:(0)1,(1),()()().()((,)).()()().()()n n n n n n n n n x n n a l a l a f a f a f l y E x E E e E x y E x E y E x e x E x x E x E x E nx E x +→∞→∞→∞→∞======-∞+∞==+==∀∈-∞+∞++== 故有极限.设则设函数在内有定义且处处连续并且满足下列条件证明用数学归纳法易得于是证11.,()(11)(1).1(0)(())()()(),().().1111,(1)()()()(),().11()()().,n n n n n n nn mmm n n n E n E E e E E n n E n E n e E n E n e E n e n E E n E n E e E E e n n n n m E E m E e e r E n n n -=++====+-=-=--======⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭设是正整数则于对于任意整数对于任意整数即对于所有有理数lim ().,,(),()lim ()lim ().nn n r x x x x n n n r e x x E x E x E x e e e e →∞→∞→∞=→====n 对于无理数取有理数列x 由的连续性的连续性习题2.1201.,.,.()2(0)(1),;(2),?(3)lim ,?x l O x x m x x x l x x m mx mx ∆→=≤≤∆∆∆∆∆∆设一物质细杆的长为其质量在横截面的分布上可以看作均匀的现取杆的左端点为坐标原点杆所在直线为轴设从左端点到细杆上任一点之间那一段的质量为给自变量一个增量求的相应增量求比值问它的物理意义是什么求极限问它的物理意义是什么2222222000(1)2()22(2)22(2).2(2)(2)2(2).(3)lim lim 2(2)4.lim x x x m x x x x x x x x x x x m x x x m x x x x x x x x m mx x x x x x∆→∆→∆→∆=+∆-=+∆+∆-=∆+∆∆∆+∆∆==+∆+∆∆∆∆∆∆=+∆=∆∆是到那段细杆的平均线密度.是细杆在点的线密度.解3330322332220002.,:(1);(2)0;(3)sin 5.()(1)lim(33)limlim (33)3.(2)lim limlim x x x xx x y ax y p y x a x x ax y xx x x x x x x a a x x x x ax x y ∆→∆→∆→∆→→→==>=+∆-'=∆+∆+∆+∆-==+∆+∆=∆'===根据定义求下列函数的导函数解00000limlim5(2)52cossin sin 5()sin 522(3)limlim55(2)552cos sin sin5(2)2222lim 5lim cos lim 5522x x x x x x x x x xx x xy xxx x x x x x x →→∆→∆→∆→∆→∆→===+∆∆+∆-'==∆∆+∆∆∆+∆==∆∆ 5cos5.2x x =00223.()(,()):(1)2,(0,1); (2)2,(3,11).(1)2ln 2,(0)ln 2,1ln 2(-0),(ln 2) 1.(2)2,(3)6,:116(3).4.2(0)(,)(0,0)x x y f x M x f x y M y x B y y y x y x y x y y x y px p M x y x y ===+''==-==+''==-=-=>>>求下列曲线在指定点处的切线方程切线方程切线方程试求抛物线上任一点处的切线斜率解,0,.2p F x ⎛⎫⎪⎝⎭,并证明:从抛物线的焦点发射光线时其反射线一定平行于轴2000,().(),.,2,.2,.p py y M PMN Y y X x yy p y x N X y X x X x x y p p FN x FM p x FN FNM FMN M PQ x PMQ FNM FMN '===-=--=-=-=-=+=====+=∠=∠∠=∠=∠过点的切线方程:切线与轴交点(,0),故过作平行于轴则证2005.2341,.224,1,6,4112564(1),4 2.:6(1),.444y x x y x y x x y k y x y x y x y x =++=-'=+====⎛⎫-=-=+-=--=-+ ⎪⎝⎭曲线上哪一点的切线与直线平行并求曲线在该点的切线和法线方程切线方程:法线方程解323226.,,;(),,, (1)():(2)();(3)().()lim ()lim,lim ()limr R r R r R r R r g r GMrr R Rg r R M G GM r R r g r r g r g r r GMr GMr R g r g r R RGM g r r →-→-→+→+⎧<⎪⎪=⎨⎪≥⎪⎩≠====离地球中心处的重力加速度是的函数其表达式为其中是地球的半径是地球的质量是引力常数.问是否为的连续函数作的草图是否是的可导函数明显地时连续.解,2lim (),()r R GMg r g r r R R→-==在连续.(2)33(3)()2(),()(),().r R g r GM GMg R g R g R g r r R R R-+-≠'''==-≠=时可导.在不可导227.(),:(1,3)(),(0)3,(2) 1.3(),()2.34111113,,3(),()3.2222P x y P x P P a b c P x ax bx c P x ax b b a b b a c a b P x x x ''===++=⎧⎪'=++=+=⎨⎪+=⎩==-=-+==-++求二次函数已知点在曲线上且解3222222222228.:(1)87,24 1.(2)(53)(62),5(62)12(53)903610.(3)(1)(1)tan (1)tan ,(2)tan (1)sec .9(92)(56)5(9)51254(4),56(56)y x x y x y x x y x x x x x y x x x x x y x x x x x x x x x x x x y y x x '=++=+'=+-=-++=+-'=+-=-=+-+++-+++'===++求下列函数的导函数22.(56)122(5)1(1),.11(1)x x y x y x x x ++'==-+≠=---23322222226(6)(1),.1(1)1(21)(1)1(7),.(8)10,1010ln1010(1ln10).sin cos sin (9)cos ,cos sin .(10)sin ,sin cos (s x x x x xx x x x x x x x x y x y x x x x x e e x x x x y y e e ey x y x x x x x xy x x y x x x x xy e x y e x e x e -'=≠=--+++-++-+-'==='==+=+-'=+=-+'==+= in cos ).x x + 00000001001100009.:()()()(),()0().()()(1)(2).()()(),()0()()()()()()(()()())()(),(m k k k k k P x P x x x g x g x x P x m x P x k x P x k k P x x x g x g x P x k x x g x x x g x x x kg x x x g x x x h x h x ---=-≠'->=-≠''=-+-'=-+-=-定义若多项式可表为则称是的重根今若已知是的重根,证明是的重根证00)()0,()(1)kg x x P x k '=≠-由定义是的重根.000000010.()(,),()(),().()(0),(0)0.()(0)()(0)()(0)(0)lim lim lim (0),(0)0.()()11.(),lim 22x x x x f x a a f x f x f x f x f f f x f f x f f x f f f f x x xf x x f x x f x x f x→→→∆→--=''=-----'''==-=-=-+∆--∆'=∆若在中有定义且满足则称为偶函数设是偶函数,且存在试证明设在处可导证明证=000000000000000000000().()()()()()()1lim lim 22()()()()1lim 2()()()()11lim lim [()22x x x x x x f x x f x x f x x f x f x x f x x x x f x x f x f x x f x x x f x x f x f x x f x f x x x ∆→∆→∆→∆→∆→+∆--∆+∆--∆-⎡⎤=-⎢⎥∆∆∆⎣⎦+∆--∆-⎡⎤=+⎢⎥∆-∆⎣⎦+∆--∆-⎡⎤'=+=+⎢⎥∆-∆⎣⎦证002()]().12.,(0/2)()((),()):.f x f x y x t t P t x t y t OP x t t π''==<<=一质点沿曲线运动且已知时刻时质点所在位置满足直线与轴的夹角恰为求时刻时质点的位置速度及加速度.222222422222()()()tan ,()tan ,()()(tan ,tan ),()(sec ,2tan sec ),()(2sec tan ,2sec 4tan sec )2sec (sec ,2tan ).y t x t x t t y t t x t x t t t v t t t t v t t t t t t t t t ===='=''=+=位置解1/1/1/1/1/000013.,0()10, 00.1111(0)lim lim 1,(0)lim lim 0.1114.()||(),()()0.().()lim xx x x x x x x x x xx f x e x x x x e e f f x e xe f x x a x x x a a f x x a f a ϕϕϕ→-→-→+→+-→⎧≠⎪=+⎨⎪=⎩=++''======++=-=≠='=求函数在的左右导数设其中在处连续且证明在不可导-+解证()()()()(),()lim ()().a x a a x x x a x a a a f a x a x aϕϕϕϕ-→---''=-==≠--+-f习题2.2()()()22221.,:sin111(2)[ln(1)],.[ln(1)](1).111(3)2.22x x xx x xx x xx x x x''=-=-='''-=-=-=---'''⎡==⎣'''⎡=+=⎣=下列各题的计算是否正确指出错误并加以改正错错错3322222()221(4)ln|2sin|(14sin)cos,.2sin1ln|2sin|(14sin cos).2sin2.(())()|.() 1.(1)(),(0),(),(sin);(2)(),(sin);(3)u g xx x x xx xx x x xx xf g x f u f x xf x f f x f xd df x f xdx dx=='⎡⎤+=+⎣⎦+'⎡⎤+=+⎣⎦+''==+''''错记现设求求[]()[][]2222223(())(())?.(1)()2,(0)0,()2,(sin)2sin.(2)()()224.(sin)(sin)(sin)2sin cos sin2.(3)(())(()),(())(())().f g x f g xf x x f f x x f x xdf x f x x x x xdxdf x f x x x x xdxf g x f g x f g x f g x g x''''''====''===''==='''''=与是否相同指出两者的关系与不同解()()()222233312232323.2236(1),.111(2)sec,(cos)(cos)(cos)(cos)(sin)tan sec.(3)sin3cos5,3cos35sin5.(4)sin cos3,3sin cos cos33sin sin33sinx xy yx x xy x y x x x x x x x y x x y x xy x x y x x x x x---'==-=----'''===-=--='=+=-'==-=求下列函数的导函数:2(cos cos3sin sin3)3sin cos4.x x x x x x x-=22222222222232222222241sin 2sin cos cos (1sin )(sin )2(5),cos cos sin 2cos 2(1sin )(sin ).cos 1(6)tan tan ,tan sec sec 13tan sec tan tan (sec 1)tan .(7)sin ,s ax ax x x x x x x x y y x x x x x x x xy x x x y x x x x x x x x x y e bx y ae +-+-'==++='=-+=-+=-=-='==5422in cos (sin cos ).(8)cos 5cos 11(9)ln tan ,sec 24224tan 2411112tan cos 2sin 24242ax ax bx be bx e a bx b bx y y x x y y x x x x ππππππ+=+'==-=⎛⎫⎛⎫'=+=+ ⎪ ⎪⎛⎫⎝⎭⎝⎭+ ⎪⎝⎭==⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭222cos 42411sec .cos sin()211()()1(10)ln (0,),.22()x x xx x a x a x a x a y a x a y a x a a x a x a x aππ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭===+-++--'=>≠±==+-+-2222222224.:1(1)arcsin (0),11111(2)arctan (0),.1(3)arccos (||1),2arccos 1111(4)arctan ,.111(5)ar 2xy a y aa x y a y a a a a a xx a y x x x y x x y y x x x xa y '=>=='=>==+⎛⎫+ ⎪⎝⎭'=<=--'===-++= 求下列函数的导函数csin (0),x a a>22222222(6)ln0)212(7)arcsin,1ya xy aayxy xx'=+==+=>⎛⎫'=+===≠±+22222222221.112sgn(1)2.111(8)(0).212211sec2()tan()cos()s22x xyx xxxy a bxyxx xa b a b a b a b--'===++-⎫=>≥⎪⎪⎭⎛⎫'= ⎪⎝⎭==++-++-2in21.cos(9)(1ln(1ln(1ln(1 /.(10)(11)(12)xa b xy yy yy yy yy y=+=+=+++++ '=⎡⎤'='=='==y y'==(13)ln(121(14)(ln(1)ln(31)ln(2),331211131321211.13132(15),(1).(16)xxxx e x e x x e y x y y x y x x x y y x x x y y x x x y e e y e e e e e ⎛⎫'=+===-=-+++-'-=++-+--⎡⎤'=++⎢⎥-+-⎣⎦'=+=+=+ 11112(0).ln ()ln ln ln ln .aaxa a xaaxa x a a a x a a x a ax a a x y x a a a y a x a a ax a aa aa x a aa x a a a ----=++>'=++=++222225.()1()()84,tan (),24001001()arctan ,()100110t x t t x t t t t t t t t θθθθ===='==+ 2一雷达的探测器瞄准着一枚安装在发射台上的火箭,它与发射台之间的距离是400m.设t=0时向上垂直地发射火箭,初速度为0,火箭以的匀加速度8m/s 垂直地向上运动;若雷达探测器始终瞄准着火箭.问:自火箭发射后10秒钟时,探测器的仰角的变化速率是多少?解222110,(10)0.1(/).505010101006.,2m t s θπθ'==⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭弧度在图示的装置中飞轮的半径为且以每秒旋转4圈的匀角速度按顺时针方向旋转.问:当飞轮的旋转角为=时,活塞向右移动的速率是多少?20()2cos8()16sin 811()8,,,()16.2161616m/s.x t t x t t t t t x ππππαπππ=+'=-'====-活塞向右移动的速率是解习题2.323222(1)(1).1.0,?(1)10100.1(2)2(3)(1cos )2sin ,222.:0,()().()().()()3.()()(0),()()(0).o o o x o o o x x y x x x y x xy x x x x x x x x x x x x xx x x x x x αααααβ=→=++===-=→=====→=→ 当时下列各函数是的几阶无穷小量阶.阶.阶.已知当时试证明设试证明证00(1)(1)(1)()()()(0).()()()().()()().4.(1)sin ,/4.sin cos ,1,1.444(2)(1)(0).o o o o o o o x x x x x x x x x x xx x x x y x x x y x x x y dy dx y x y ααβαβαβππππα+=→+=+=+=+=⎛⎫⎫⎫''===+=+=+ ⎪⎪⎪⎝⎭⎭⎭=+>':上述结果有时可以写成计算下列函数在指定点处的微分:是常数证122(1),(0),.5.1222(1)1,,.11(1)(1)(2),(1).(1).26.(1),3 3.001,11,(3).222.001x x x x x x y dy dx x dxy y dy x x x x y xe y e xe e x dy e x dx y x x x y y αααα-'=+==-'==-+=-=-++++'==+=+=+=≠-''=-∆=求下列各函数的微分:设计算当由变到时函数的增量和向相应的微分.22解 y =-(x-1)1222113333332220.0010.0011,.2.00127..1.162(1) 2.002.5328.:11(1)(0).0,.33(2)()()(,,).2()2()dy y x y a a xy y y x x a y b c a b c x a y b y ---=-=-==+=⎛⎫''+=>+==- ⎪⎝⎭-+-='-+-= 求下列方程所确定的隐函数的导函数为常数0,.x ay y b-'=--。
北大版高等数学第四章 微分中值定理与泰勒公式答案 第四章总练习题

第四章总练习题000000001..()()[()()].()(),[0,].()()(),(0)0.L ag ran g e ,(0,1)()(0)(),f x h f x h f x h f x h h f x x f x x x h g g x f x x f x x g g h g g h h θθθθθθ''+--=++-+--∈'''=++-=∈'-=00设y =f (x )在[x -h ,x +h ](h >0)内可导证明存在,0<<1使得令g (x )=(x )在[0,h ]内可导,根据公式存在使得证00000()()[()()].2.:0,()1/4()1/2lim ()1/4,lim ()1/2.4(())211()(124x x f x h f x h f x h f x h h x x x x x x x x x x θθθθθθθθ→→+∞''+--=++-≥=≤≤=====+=++=+-即证明当时等式中的满足且证).11()(12),44111()(12)(1(1)2).44211lim ()lim(12).441lim ()lim(12)41lim4x x x x x xx x x x x x x x x x θθθθ→→→+∞→+∞→+∞≥+=-=+-≤+++-==+==+=由算术几何平均不等式得22111limlim.4423,0123.()()[0,2]1, 1,01(2)(0)1().120, 1x xxx f x f x x x x x f f f x x x →+∞→+∞====⎧-≤≤⎪⎪=⎨⎪<<+∞⎪⎩-≤≤⎧-⎪'==⎨--<<+∞⎪⎩设求在闭区间上的微分中值定理的中间值.解2/23/21.221111,;,()[0,2]222x x x f x x-=--=-=-=-=1在闭区间上的微分中值定理的中间值为或22324.[1,1]C au ch y ()()()30(1,1),C au ch y (1)(1)()()0,()200,(0)0,.(1)(1)()()5.()[,],(,f x x g x x g x x f f f c f c f c c c g g g g c g c f x a b a -=='=∈-''--''======''--在闭区间上中值定理对于函数与是否成立?并说明理由.由于有零点中值定理的条件不满足.其实其结论也不成立.因为若,但无意义设在上连续在解2121212),()0,(,)()()0,(,)()0.(,),()0,R o lle (,),(,)()()0.()[,](,),()0,()0,(,).(b f x x a b f a f b x a b f x c a b f c a c c c b f c f c f x c c c c f f x x a b f ξξ''≠∈==∈≠∈=∈∈''=='''''∈=≠∈''上有二阶导数且又证明当时若存在则由定理存在使得对于在应用定理,存在使得此与条件矛盾由假设1证一,c 证二,00)0,(,),,().()(,())(,0)(,())(,0),()0,(,).6.()[,],()()0,(,)()0.:(,)()0.x x a b D a rb o u x f x f x a f a a b f b b f x x a b f x a b f a f b c a b f c a b x f x ''''≠∈==<∈==∈>''<根据定理恒正或恒负不妨设恒正,于是f 下凸,曲线严格在连结的弦下方故设在上有二阶导数且又存在使证明在内至少存在一点使由公式存在证一,c 12121221021()()()(,),()0,()()()(,),()0.()[,]L ag ran g e (,),()()()0.,()0,(,),[,],(,(f c f a f c a c f c c a c af b f c f c c b f c b cc af x c c c c f c f c f x c c f x x a b f a b a f a -'∈==>----'∈==<--'∈''-''=<-''≥∈0满足存在满足对于在应用公式,存在x 使得若不然在下凸曲线在连结12c 证二))(,0)(,())(,0),()0,(,).a b f b b f x x a b ==≤∈的弦下方故1201120121100112121201120127.1-12101.(),1111-121()1-12n n n n n n n nn n n n n n n n n a a a a a a x a xa xa n nn a xa xa a a a x a xa a f x x n nn n n n a a a a f x a x a x a x a n n n ---+-----++++=++++++⎛⎫=++++-+++++ ⎪+-+⎝⎭'=++++-++++++ 证明方程在与之间有一个根考虑函数证1201120121(0)(1)0.,(0,1),()0,1-12101.n nn n n n n a f f R o lle c f c c a a a a a a x a xa xa n nn ---⎛⎫ ⎪⎝⎭'==∈=++++=++++++ 由定理存在即是在与之间的一个根00000008.()(,),,().?L ag ran g e ,()()()(),|()||()()()||()||()||()||(f x a b f x f x f x f c x x f x f x f c x x f x f c x x f x ''∈∈'-=-''=+-≤+-≤0设函数在有限区间内可导但无界证明在(a ,b )内也无界逆命题是否成立试举例说明.若不然设f (x )在(a ,b )内有界M ,取定x (a ,b ),则对于任意 x (a ,b ),根据 公式证,)|||().(0,1),01,(0,1)M b a +-<<=逆命题不成立.例内有界但是内无界.(1)(1)00002009.()[,](),(),()[,].(:()()()()()0,()).()[,]2,()()()()0,()n n kf x a b n k k f x fx a b f x f x x x g x g x x f x k n f x a b x f x x x g x g x f x --=-≠'=-≠若函数在区间上有个根一个重根算作个根且存在证明在至少有一个根注意若可以表示成且则称为的重根我们对于作归纳法证明函数在区间上有2个根.如果是重根则且则证.2000121212012001002()()()(),().()[,],,,[,]R o lle ,(,),()0..()[,]11,()()()()0,()(n x x g x x x g x f x x f x a b x x x x x x x x x f x n f x a b n f n x f x x x g x g x f x +''=-+-<'∈=++=-≠'=有根如果在区间上有2个不同的根在应用定理存在使得设结论对于个根的情况成立现在假定在区间上有个根.如果有重根重根则且则10000011000111211121)()()()()()((1)()()()),(1)()()()(),()(1)()0,().1,,[,],,[,]R o lle ,(,),,(n n nn n n n n n n x x g x x x g x x x n g x x x g x n g x x x g x g x g x n g x f x x f n x x x x x x c x x c x x ++++'+-+-=-++-'++-==+≠+∈∈ 有n 重根如果如果有个单重根在区间上应用定理存在,11112111121111])()()0,().,,,,,,11, 1.[,],,[,]R o lle ,(,),,()()()0.()1(1)n kk k i i k k k kk ii f c f c f x n f x n n n k n n x x x x c x x c f c f c f x k nn =---='''===+>>=+∈∈''''===-+-=∑∑ 1k -1k 使得至少有个根如果有不同的根x 重数分别为在上应用定理存在x ,x 使得至少有根个.对f (x )()(1)(())().n n f x fx +'=用归纳假设,至少有一个根22111111112111110.:L eren d re ()[(1)](1,1).2!1()(1)],(1)(1)0,[ 1.1]R o lle 2!(1,1),()0.(1)(1)0(1),1)(,1)R o lle 1),n nn nnnndP x x n n d xf x x f f f n c f c f f n f c c c c =---=-=-''''∈-=-==>-∈-证明多项式在内有个根对于在应用定理,存在使得当时对于在(,应用定理,存在(,证=2122211211(-1)(-1)111111121()12,1)()()0.()(1,1),,(1)(1)0R o lle ,,,(1,1)()()0.()n n n n n n n n n n n n n n c c f c f c x c c ffc c c c x x f x P x P x --------''∈==--==∈-== (n -1)1(使得如此下去,f 在有零点,,在(-1,),(,),,(,1)应用定理, 得到x 使得是n 次多项式,至多有n 个零点()n P x n ,故恰有个零点.00011.(,),lim ()lim ().:(,),()0.()lim ()lim ().(,),(,),()0.(),().,,(,),()(x x x x f f x f x c f c f x f x f x A x c f c f x A f x A a b x a b f a f x →-∞→+∞→-∞→+∞-∞+∞='∈-∞+∞=≡==∈-∞+∞∈-∞+∞'=≠><∈<设函数在内可导且证明必存在一点使得证若取任意一点都有设存在不妨设根据极限不等式存在a ,b ,满足:000000),()().[,],[,]()()(),()()(),(,),,F erm at ,()0.()()lim ()0lim0.lim ()0x x x f b f x f a b c a b f c f x f a f c f x f b x a b x f c f x f x f x xf x x →+∞→+∞→+∞<∈≥>≥>∈'='∞=='=0在连续必在一点取最大值. 故为极大值点根据引理12.设函数在无穷区间(x ,+)可导,且,证明证由于,根据极限定义,存在正数101111111111,|()|()()()()()())|()|()|()||()||()||()|.,.m ax {,},()(),2,lim0.x x f x f x f x f x f c x x f x f x f x x x x x f x f x f x f x x X x xx f x f x x X xxεεεεεεε→+∞'>'-+-++==≤<+<>=><=11使得x >x 时<.(x -x 为使只需令当时必有故13.()[,),()0,()()0,,()0.()0,()()()()()()0,(),,,,f x a f x l f a f a a a l f x f a f a f a f a a f a f c f a l l l l f a f a a l a a '+∞>>⎛⎫<-⎪⎝⎭=<⎛⎫⎛⎫⎛⎫'-=+->+-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎡⎤-⎢⎥⎣⎦设函数在无穷区间内连续且当x >a 时其中l 为常数.证明:若则在区间内方程有唯一实根证在连续由连续怀念书函数的中间值定理在区间()()0.,()R o lle ,(),,()0.14.()(,)lim ()0.()(1)(),lim ()0.lim ()lim ((1)())lim (x x x x x f a f x l f a f x a a f x l l f x f x g x f x f x g x g x f x f x f →∞→∞→∞→∞→∞⎛⎫-= ⎪⎝⎭⎛⎫''->> ⎪⎝⎭'-∞+∞==+-='=+-=内方程至少有一实根若有两个实根根据定理将在有一零点这与条件矛盾设函数在上可导,且现令证明证)(01)0.x θθ+<<=12121215.()[,]L ip sch iz ,0,,[,],|()()|||.(1)()[,],()[,]L ip sch iz (2)(1)?(3)[,]L ip sch iz (1)()[,]0,f x a b L x x a b f x f x L x x f x a b f x a b a b f x a b L >∈-≤-''>称函数在满足条件若存在常数使对于任意都有若在连续则在满足条件中所述事实的逆命题是否成立举一个在上连续但不满足条件的函数.解在连续,存在常数12121212122121|()|.[,].,[,],,[,],|()()||()()||()|()().(2).()[,]L ip sch iz ()[,]()||[1,1]L ip sch iz f x L x a b x x a b x x c x x f x f x f c x x f c x x L x x f x a b f x a b f x x '≤∈∈<∈''-=-=-≤-'=-使得根据中值公式,对于任意存在使得否在满足条件,未必处处可导,更谈不到在连续.例如,在 满足条件111111(3)()[0,1],L ip sch iz ()(0,1].16.()[,],()()[,],()()().()()(()())()()()()b annii i i i i i ni i i i f x f x F x a b F x f x a b f x d x F b F a F b F a F x F xF x x f x x ξξ--==-=='='==-'-=-=--→⎰∑∑∑,但在0不可导.连续但不满足条件,因其导函数无界设在可导且其导函数在上可积证明证1()(()0).{}[,].17.()(),(,),()()(),1,,b ai n f x d x x a b P x a P x b c a b P x c P x n P x x x n λ∆→--∈-∈<<+⎰为的分割设多项式与的全部根都是单实根证明对于任意实数多项式的根也全都是单实根.证不妨设a =0,b >0,c (0,b ),是次多项式,且首项系数为正.有单实根则这些根把实轴分为个区间每个区间保持固定正负号且正负相间.否则某个根将为极值点,导数为111232322212221222lim ().0(),,(,),,,(,),(,),().nx k k k k k k i n k P x b P x b x x x x x x x x x x x x x x P x b →∞----=''∞>=<<'''''''<∈∈∈+∞= 零,此与单实根矛盾.在两个无穷区间保持正号,且严格单调递增或递减,在每个有穷区间有一个最值点,且在其两侧分别递增和递减,设为偶数,则=+设且有n 个单实根.必有根据连续函数的中间值定1122233322222*********,(0,),(,),(,),(,),(,),(,),(,),().,k k k k k k k k i i c b c x c x x c x x c x x c x x c x P c c P n c ------'∈∈-∞∈'''∈∈∈+∞∈+∞=理对于存在使得为次多项式是P (x )=c 的所有单实根.。
北师大数学选修作业:第4章 导数应用4 含解析

第四章 4.1.2A级基础巩固一、选择题1.已知函数y=x3-3x+c的图像与x轴恰有两个公共点,则c=(A)A.-2或2B.-9或3C.-1或1D.-3或1[解析]∵y′=3x2-3,∴当y′=0时,x=±1,则x,y′,y的变化情况如下表:x (-∞,-1)-1(-1,1)1(1,+∞)y′+-+y c+2c-2或c=2.2.已知a为函数f(x)=x3-12x的极小值点,则a=(D)A.-4 B.-2C.4 D.2[解析]f′(x)=3x2-12,令f′(x)>0得x<-2或x>2,令f′(x)<0得-2<x<2,∴f(x)在(-∞,-2),(2,+∞)上单调递增,在(-2,2)上单调递减,∴当x=2时,f(x)取极小值,即2是函数f(x)的极小值点,故a=2.3.下图是函数y=f(x)的导函数y=f′(x)的图像,给出下列命题:①x=-3是函数y=f(x)的极值点;②x=-1是函数y=f(x)的最小值点;③曲线y=f(x)在x=0处的切线斜率小于零;④函数y=f(x)在区间(-3,1)上单调递增.其中,正确命题的序号是( B ) A .①② B .①④ C .②③D .③④[解析] f ′(-3)=0,且在x =-3的两侧,导函数由负到正,所以x =-3为f (x )的极小值点.当x ∈(-3,-1)时,f ′(x )>0,f (x )单调递增,所以①④正确.4.设函数f (x )=2x +ln x ,则( D )A .x =12为f (x )的极大值点B .x =12为f (x )的极小值点C .x =2为f (x )的极大值点D .x =2为f (x )的极小值点[解析] 本节考查了利用导数工具来探索其极值点问题. f ′(x )=-2x 2+1x =1x (1-2x ),由f ′(x )=0可得x =2.当0<x <2时,f ′(x )<0,f (x )递减,当x >2时, f ′(x )>0,∴f (x )单调递增.所以x =2为极小值点. 对于含有对数形式的函数在求导时,不要忽视定义域.5.若a >0,b >0,且函数f (x )=4x 3-ax 2-2bx +2在x =1处有极值,则ab 的最大值等于( D )A .2B .3C .6D .9[解析] f ′(x )=12x 2-2ax -2b ,由条件知f ′(1)=0,∴a +b =6,∴ab ≤(a +b2)2=9,等号在a =b =3时成立,故选D .6.已知函数f (x )=x 3+mx 2+(m +6)x +1既存在极大值又存在极小值,则实数m 的取值范围是( D )A .[-3,6]B .(-3,6)C .(-∞,-3]∪[6,+∞)D .(-∞,-3)∪(6,+∞)[解析] 函数的导数为f ′(x )=3x 2+2mx +(m +6),要使函数f (x )既存在极大值又存在极小值,则f ′(x )=0有两个不同的根,所以判别式Δ>0,即Δ=4m 2-12(m +6)>0,所以m 2-3m -18>0,解得m >6或m <-3.二、填空题7.函数f (x )=-13x 3+12x 2+2x 取得极小值时,x 的值是__-1__.[解析] f ′(x )=-x 2+x +2=-(x -2)(x +1),令f ′(x )>0得-1<x <2,令f ′(x )<0,得x <-1或x >2,∴函数f (x )在(-∞,-1),(2,+∞)上递减,在(-1,2)上递增,∴当x =-1时,函数f (x )取得极小值.8.函数y =x e x 在其极值点处的切线方程为 y =-1e.[解析] ∵y =x e x ,∴y ′=e x +x e x =e x (x +1),当x =-1时y 有极小值,此时y |x =-1=-1e ,而y ′|x =-1=0,∴切线方程为y =-1e.三、解答题9.设函数y =x 3+ax 2+bx +c 的图像如图所示,且与y =0在原点相切,若函数的极小值为-4.(1)求a 、b 、c 的值; (2)求函数的递减区间.[解析] (1)因为函数的图像经过点(0,0), 易得c =0.又图像与x 轴相切于点(0,0),且y ′=3x 2+2ax +b , 故0=3×02+2a ×0+b ,解得b =0. 所以y =x 3+ax 2,则y ′=3x 2+2ax . 令y ′=0,解得x =0或x =-23a ,即x =0和x =-23a 是极值点.由图像知函数在x =0处取极大值,故在x=-23a时取极小值.当x=-23a时,函数有极小值-4,所以(-23+a(-2a3)2=-4,3a)整理得a3=-27,解得a=-3.故a=-3、b=0、c=0.(2)由(1)得y=x3-3x2,则y′=3x2-6x,令y′<0,即y′=3x2-6x<0,解得0<x<2,所以,函数的递减区间是(0,2).B级素养提升一、选择题1.函数y=x3-3x2-9x(-2<x<2)有(C)A.极大值5,极小值-27B.极大值5,极小值-11C.极大值5,无极小值D.极小值-27,无极大值[解析]y′=3x2-6x-9=3(x-3)(x+1),∵-2<x<2,∴令y′>0得-2<x<-1,令y′<0得-1<x<2,∴函数在(-2,-1)上递增,在(-1,2)上递减,∴当x=-1时,f(x)取极大值f(-1)=-1-3+9=5,f(x)无极小值.2.已知函数y=2x3+ax2+36x-24在x=2处有极值,则该函数的一个递增区间是(B) A.(2,3) B.(3,+∞)C.(2,+∞) D.(-∞,3)[解析]y′=6x2+2ax+36,由已知得24+4a+36=0,∴a=-15.∴y′=6x2-30x+36=6(x2-5x+6)=6(x-2)(x-3),令y ′>0,得x <2或x >3,故选B .3.已知函数f (x )=x 3-px 2-qx 的图像与x 轴切于(1,0)点,则f (x )的极大值、极小值分别为( A )A .427,0B .0,427C .-427,0D .0,-427[解析] f ′(x )=3x 2-2px -q , 由f ′(1)=0,f (1)=0得,⎩⎪⎨⎪⎧ 3-2p -q =01-p -q =0,解得⎩⎪⎨⎪⎧p =2q =-1,∴f (x )=x 3-2x 2+x . 由f ′(x )=3x 2-4x +1=0得x =13或x =1,易得当x =13时f (x )取极大值427.当x =1时f (x )取极小值0.4.若函数f (x )=13x 3+x 2-23在区间(a ,a +5)上存在最小值,则实数a 的取值范围是( C )A .[-5,0)B .(-5,0)C .[-3,0)D .(-3,0)[解析] 由题意,f ′(x )=x 2+2x =x (x +2),故f (x )在(-∞,-2),(0,+∞)上是增函数,在(-2,0)上是减函数,作出其图像如图所示,令13x 3+x 2-23=-23得,x =0或x =-3,则结合图像可知,⎩⎪⎨⎪⎧-3≤a <0,a +5>0,解得a ∈[-3,0),故选C .二、填空题5.设x =1与x =2是函数f (x )=a ln x +bx 2+x 的两个极值点,则常数a = -23 .[解析] f ′(x )=ax+2bx +1,由题意得⎩⎪⎨⎪⎧a +2b +1=0a 2+4b +1=0,∴a =-23.6.直线y =a 与函数f (x )=x 3-3x 的图像有相异的三个公共点,则a 的取值范围是__(-2,2)__.[解析] f ′(x )=3x 2-3,由3x 2-3=0得x =1或-1, 当x <-1,或x >1时,f ′(x )>0,f (x )单调增; 当-1<x <1时,f ′(x )<0,f (x )单调减.∴x =-1时,f (x )取到极大值f (-1)=2,x =1时,f (x )取到极小值f (1)=-2,∴欲使直线y =a 与函数f (x )的图像有相异的三个公共点,应有-2<a <2.三、解答题7.设x =-2,x =4是函数f (x )=x 3+ax 2+bx 的两个极值点. (1)求常数a 、b 的值;(2)判断x =-2,x =4是函数f (x )的极大值点还是极小值点,并说明理由. [解析] (1)f ′(x )=3x 2+2ax +b ,由题意得⎩⎪⎨⎪⎧12-4a +b =048+8a +b =0,解得⎩⎪⎨⎪⎧a =-3b =-24.(2)由(1)知f ′(x )=3x 2-6x -24 =3(x 2-2x -8) =3(x -4)(x +2),令f ′(x )>0,得x <-2或x >4, 令f ′(x )<0,得-2<x <4.∴f (x )在(-∞,-2),(4,+∞)上单调递增,在(-2,4)上单调递减,∴当x =-2时, f (x )取极大值,当x =4时, f (x )取极小值,故x =-2是极大值点,x =4是极小值点.8.(2018·北京文,19)设函数f (x )=[ax 2-(3a +1)x +3a +2]e x .(1)若曲线y =f (x )在点(2,f (2))处的切线斜率为0,求a ; (2)若f (x )在x =1处取得极小值,求a 的取值范围. [解析] (1)因为f (x )=[ax 2-(3a +1)x +3a +2]e x , 所以f ′(x )=[ax 2-(a +1)x +1]e x , f ′(2)=(2a -1)e 2.由题设知f ′(2)=0,即(2a -1)e 2=0,解得a =12.(2)由(1)得f ′(x )=[ax 2-(a +1)x +1]e x =(ax -1)(x -1)e x .若a >1,则当x ∈⎝⎛⎭⎫1a ,1时,f ′(x )<0; 当x ∈(1,+∞)时,f ′(x )>0. 所以f (x )在x =1处取得极小值.若a ≤1,则当x ∈(0,1)时,ax -1≤x -1<0, 所以f ′(x )>0.所以1不是f (x )的极小值点.综上可知,a 的取值范围是(1,+∞).。
2018版高考数学文北师大版大一轮复习讲义教师版文档 第四章 三角函数、解三角形 4.5 第2课时 含答案 精品

第2课时 简单的三角恒等变形题型一 三角函数式的化简例1 (1)化简:2cos 4x -2cos 2x +122tan ⎝⎛⎭⎫π4-x sin 2⎝⎛⎭⎫π4+x =________.(2)已知cos(θ+π4)=1010,θ∈(0,π2),则sin(2θ-π3)=________.答案 (1)12cos 2x (2)4-3310解析 (1)原式=12(4cos 4x -4cos 2x +1)2×sin ⎝⎛⎭⎫π4-x cos ⎝⎛⎭⎫π4-x ·cos 2⎝⎛⎭⎫π4-x=(2cos 2x -1)24sin ⎝⎛⎭⎫π4-x cos ⎝⎛⎭⎫π4-x=cos 22x2sin ⎝⎛⎭⎫π2-2x=cos 22x 2cos 2x =12cos 2x . (2)由题意可得,cos 2⎝⎛⎭⎫θ+π4=1+cos ⎝⎛⎭⎫2θ+π22=110,cos ⎝⎛⎭⎫2θ+π2=-sin 2θ=-45,即sin 2θ=45. 因为cos ⎝⎛⎭⎫θ+π4=1010>0,θ∈⎝⎛⎭⎫0,π2, 所以0<θ<π4,2θ∈⎝⎛⎭⎫0,π2, 根据同角三角函数基本关系式可得cos 2θ=35,由两角差的正弦公式可得sin ⎝⎛⎭⎫2θ-π3=sin 2θcos π3-cos 2θsin π3=4-3310. 思维升华 (1)三角函数式的化简要遵循“三看”原则,一看角,二看名,三看式子结构与特征.(2)三角函数式化简要注意观察条件中角之间的联系(和、差、倍、互余、互补等),寻找式子和三角函数公式之间的共同点.(1)已知cos(x -π6)=-33,则cos x +cos(x -π3)=________.(2)若α∈⎝⎛⎭⎫π2,π,且3cos 2α=sin ⎝⎛⎭⎫π4-α,则sin 2α的值为( ) A.118 B .-118 C.1718 D .-1718 答案 (1)-1 (2)D 解析 (1)cos x +cos(x -π3)=cos x +12cos x +32sin x=32cos x +32sin x =3cos(x -π6) =3×(-33)=-1. (2)cos 2α=sin ⎝⎛⎭⎫π2-2α =sin ⎣⎡⎦⎤2⎝⎛⎭⎫π4-α =2sin ⎝⎛⎭⎫π4-αcos ⎝⎛⎭⎫π4-α 代入原式,得6sin ⎝⎛⎭⎫π4-αcos ⎝⎛⎭⎫π4-α=sin ⎝⎛⎭⎫π4-α, ∵α∈⎝⎛⎭⎫π2,π,∴cos ⎝⎛⎭⎫π4-α=16, ∴sin 2α=cos ⎝⎛⎭⎫π2-2α =2cos 2⎝⎛⎭⎫π4-α-1=-1718. 题型二 三角函数的求值 命题点1 给值求值问题例2 (1)(2016·合肥联考)已知α,β为锐角,cos α=17,sin(α+β)=5314,则cos β=________.答案 12解析 ∵α为锐角, ∴sin α=1-(17)2=437.∵α,β∈(0,π2),∴0<α+β<π.又∵sin(α+β)<sin α,∴α+β>π2,∴cos(α+β)=-1114.cos β=cos [(α+β)-α]=cos(α+β)cos α+sin(α+β)sin α =-1114×17+5314×437=4998=12.(2)(2015·广东)已知tan α=2. ①求tan(α+π4)的值;②求sin 2αsin 2α+sin αcos α-cos 2α-1的值.解 ①tan(α+π4)=tan α+tanπ41-tan αtanπ4=2+11-2×1=-3.②sin 2αsin 2α+sin αcos α-cos 2α-1=2sin αcos αsin 2α+sin αcos α-2cos 2α=2tan αtan 2α+tan α-2=2×24+2-2=1.命题点2 给值求角问题例3 (1)设α,β为钝角,且sin α=55,cos β=-31010,则α+β的值为( ) A.3π4 B.5π4 C.7π4D.5π4或7π4(2)已知α,β∈(0,π),且tan(α-β)=12,tan β=-17,则2α-β的值为________.答案 (1)C (2)-3π4解析 (1)∵α,β为钝角,sin α=55,cos β=-31010, ∴cos α=-255,sin β=1010,∴cos(α+β)=cos αcos β-sin αsin β=22>0.又α+β∈(π,2π),∴α+β∈(3π2,2π),∴α+β=7π4.(2)∵tan α=tan [(α-β)+β] =tan (α-β)+tan β1-tan (α-β)tan β=12-171+12×17=13>0,∴0<α<π2.又∵tan 2α=2tan α1-tan 2α=2×131-(13)2=34>0, ∴0<2α<π2,∴tan(2α-β)=tan 2α-tan β1+tan 2αtan β=34+171-34×17=1.∵tan β=-17<0,∴π2<β<π,-π<2α-β<0, ∴2α-β=-3π4.引申探究本例(1)中,若α,β为锐角,sin α=55,cos β=31010,则α+β=________. 答案 π4解析 ∵α,β为锐角,∴cos α=255,sin β=1010,∴cos(α+β)=cos αcos β-sin αsin β =255×31010-55×1010=22. 又0<α+β<π,∴α+β=π4.思维升华 (1)给值求值问题的关键在“变角”,通过角之间的联系寻找转化方法; (2)给值求角问题:先求角的某一三角函数值,再求角的范围确定角.(1)已知α∈⎝⎛⎭⎫0,π2,且2sin 2α-sin α·cos α-3cos 2α=0,则sin ⎝⎛⎭⎫α+π4sin 2α+cos 2α+1=________. (2)已知sin α=55,sin(α-β)=-1010,α,β均为锐角,则角β等于( ) A.5π12 B.π3 C.π4 D.π6 答案 (1)268(2)C 解析 (1)∵α∈⎝⎛⎭⎫0,π2,且2sin 2α-sin α·cos α-3cos 2α=0,则(2sin α-3cos α)·(sin α+cos α)=0,∴2sin α=3cos α, 又sin 2α+cos 2α=1, ∴cos α=213,sin α=313, ∴sin ⎝⎛⎭⎫α+π4sin 2α+cos 2α+1=22(sin α+cos α)(sin α+cos α)2+(cos 2α-sin 2α)=268. (2)∵α、β均为锐角,∴-π2<α-β<π2.又sin(α-β)=-1010,∴cos(α-β)=31010. 又sin α=55,∴cos α=255, ∴sin β=sin [α-(α-β)]=sin αcos(α-β)-cos αsin(α-β) =55×31010-255×(-1010)=22. ∴β=π4.题型三 三角恒等变形的应用例4 (2016·天津)已知函数f (x )=4tan x sin ⎝⎛⎭⎫π2-x ·cos ⎝⎛⎭⎫x -π3- 3.(1)求f (x )的定义域与最小正周期; (2)讨论f (x )在区间⎣⎡⎦⎤-π4,π4上的单调性. 解 (1)f (x )的定义域为{x |x ≠π2+k π,k ∈Z }.f (x )=4tan x cos x cos ⎝⎛⎭⎫x -π3- 3 =4sin x cos ⎝⎛⎭⎫x -π3- 3 =4sin x ⎝⎛⎭⎫12cos x +32sin x - 3=2sin x cos x +23sin 2x - 3 =sin 2x +3(1-cos 2x )- 3 =sin 2x -3cos 2x =2sin ⎝⎛⎭⎫2x -π3. 所以f (x )的最小正周期T =2π2=π.(2)令z =2x -π3,则函数y =2sin z 的单调递增区间是⎣⎡⎦⎤-π2+2k π,π2+2k π,k ∈Z .由-π2+2k π≤2x -π3≤π2+2k π,k ∈Z ,得-π12+k π≤x ≤5π12+k π,k ∈Z .设A =⎣⎡⎦⎤-π4,π4,B ={x |-π12+k π≤x ≤5π12+k π,k ∈Z },易知A ∩B =⎣⎡⎦⎤-π12,π4. 所以当x ∈⎣⎡⎦⎤-π4,π4时,f (x )在区间⎣⎡⎦⎤-π12,π4上是增加的,在区间⎣⎡⎦⎤-π4,-π12上是减少的. 思维升华 三角恒等变形的应用策略(1)进行三角恒等变形要抓住:变角、变函数名称、变结构,尤其是角之间的关系;注意公式的逆用和变形使用.(2)把形如y =a sin x +b cos x 化为y =a 2+b 2sin(x +φ),可进一步研究函数的周期、单调性、最值与对称性.(1)函数f (x )=sin(x +φ)-2sin φcos x 的最大值为________.(2)函数f (x )=sin(2x -π4)-22sin 2x 的最小正周期是________.答案 (1)1 (2)π解析 (1)因为f (x )=sin(x +φ)-2sin φcos x=sin x cos φ-cos x sin φ=sin(x -φ), -1≤sin(x -φ)≤1,所以f (x )的最大值为1. (2)f (x )=22sin 2x -22cos 2x -2(1-cos 2x ) =22sin 2x +22cos 2x -2=sin(2x +π4)-2, ∴T =2π2=π.9.化归思想和整体代换思想在三角函数中的应用典例 (12分)(2015·重庆)已知函数f (x )=sin ⎝⎛⎭⎫π2-x sin x -3cos 2x . (1)求f (x )的最小正周期和最大值; (2)讨论f (x )在⎣⎡⎦⎤π6,2π3上的单调性.思想方法指导 (1)讨论形如y =a sin ωx +b cos ωx 型函数的性质,一律化成y =a 2+b 2sin(ωx +φ)型的函数.(2)研究y =A sin(ωx +φ)型函数的最值、单调性,可将ωx +φ视为一个整体,换元后结合y =sin x 的图像解决. 规范解答解 (1)f (x )=sin ⎝⎛⎭⎫π2-x sin x -3cos 2x =cos x sin x -32(1+cos 2x )=12sin 2x -32cos 2x -32=sin ⎝⎛⎭⎫2x -π3-32,[4分] 因此f (x )的最小正周期为π,最大值为2-32.[6分](2)当x ∈⎣⎡⎦⎤π6,2π3时,0≤2x -π3≤π,[7分] 从而当0≤2x -π3≤π2,即π6≤x ≤5π12时,f (x )是增加的,[9分] 当π2≤2x -π3≤π, 即5π12≤x ≤2π3时,f (x )是减少的.[11分]综上可知,f (x )在⎣⎡⎦⎤π6,5π12上是增加的;在⎣⎡⎦⎤5π12,2π3上是减少的.[12分]1.(2016·青岛模拟)设tan(α-π4)=14,则tan(α+π4)等于( )A .-2B .2C .-4D .4 答案 C解析 因为tan(α-π4)=tan α-11+tan α=14,所以tan α=53,故tan(α+π4)=tan α+11-tan α=-4,故选C.2.(2016·全国甲卷)若cos ⎝⎛⎭⎫π4-α=35,则sin 2α等于( ) A.725 B.15 C .-15 D .-725 答案 D解析 因为sin 2α=cos ⎝⎛⎭⎫π2-2α=2cos 2⎝⎛⎭⎫π4-α-1,又因为cos ⎝⎛⎭⎫π4-α=35,所以sin 2α=2×925-1=-725,故选D.3.(2016·福州模拟)已知tan α=3,则sin 2αcos 2α的值等于( )A .2B .3C .4D .6 答案 D 解析sin 2αcos 2α=2sin αcos αcos 2α=2tan α=2×3=6. 4.已知tan(α+π4)=12,且-π2<α<0,则2sin 2α+sin 2αcos (α-π4)等于( )A .-255B .-3510C .-31010D.255答案 A解析 由tan(α+π4)=tan α+11-tan α=12,得tan α=-13.又-π2<α<0,所以sin α=-1010.故2sin 2α+sin 2αcos (α-π4)=2sin α(sin α+cos α)22(sin α+cos α)=22sin α=-255.5.设α∈(0,π2),β∈(0,π2),且tan α=1+sin βcos β,则( )A .3α-β=π2B .2α-β=π2C .3α+β=π2D .2α+β=π2答案 B解析 由tan α=1+sin βcos β,得sin αcos α=1+sin βcos β,即sin αcos β=cos α+cos αsin β, ∴sin(α-β)=cos α=sin(π2-α).∵α∈(0,π2),β∈(0,π2),∴α-β∈(-π2,π2),π2-α∈(0,π2),由sin(α-β)=sin(π2-α),得α-β=π2-α,∴2α-β=π2.6.函数f (x )=sin(2x +θ)+3cos(2x +θ)⎝⎛⎭⎫|θ|<π2的图像关于点⎝⎛⎭⎫π6,0对称,则f (x )的单调递增区间为( )A.⎣⎡⎦⎤π3+k π,5π6+k π,k ∈Z B.⎣⎡⎦⎤-π6+k π,π3+k π,k ∈Z C.⎣⎡⎦⎤-7π12+k π,-π12+k π,k ∈Z D.⎣⎡⎦⎤-π12+k π,5π12+k π,k ∈Z 答案 C解析 ∵f (x )=sin(2x +θ)+3cos(2x +θ)=2sin ⎝⎛⎭⎫2x +θ+π3, 由题意知2×π6+θ+π3=k π(k ∈Z ),∴θ=k π-23π(k ∈Z ).∵|θ|<π2,∴θ=π3.∴f (x )=2sin ⎝⎛⎭⎫2x +23π. 由2k π-π2≤2x +23π≤2k π+π2(k ∈Z ),得k π-712π≤x ≤k π-π12(k ∈Z ).故选C.7.若f (x )=2tan x -2sin 2 x2-1sin x 2cosx2,则f ⎝⎛⎭⎫π12的值为______. 答案 8解析 ∵f (x )=2tan x +1-2sin 2x 212sin x =2tan x +2cos x sin x =2sin x cos x =4sin 2x ,∴f ⎝⎛⎭⎫π12=4sinπ6=8. 8.若锐角α、β满足(1+3tan α)(1+3tan β)=4,则α+β=________. 答案 π3解析 由(1+3tan α)(1+3tan β)=4, 可得tan α+tan β1-tan αtan β=3,即tan(α+β)= 3.又α+β∈(0,π),∴α+β=π3.9.化简:3tan 12°-3(4cos 212°-2)sin 12°=________. 答案 -4 3解析 原式=3·sin 12°cos 12°-32(2cos 212°-1)sin 12°=23(12sin 12°-32cos 12°)cos 12°2cos 24°sin 12°=23sin (-48°)2cos 24°sin 12°cos 12°=-23sin 48°sin 24°cos 24°=-23sin 48°12sin 48°=-4 3. 10.函数f (x )=3sin 23x -2sin 213x (π2≤x ≤3π4)的最小值是________. 答案 3-1解析 f (x )=3sin 23x -(1-cos 23x ) =2sin(23x +π6)-1, 又π2≤x ≤3π4,∴π2≤23x +π6≤23π, ∴f (x )min =2sin 23π-1=3-1. 11.已知函数f (x )=cos 2x +sin x cos x ,x ∈R .(1)求f (π6)的值; (2)若sin α=35,且α∈(π2,π),求f (α2+π24). 解 (1)f (π6)=cos 2π6+sin π6cos π6=(32)2+12×32=3+34. (2)因为f (x )=cos 2x +sin x cos x =1+cos 2x 2+12sin 2x =12+12(sin 2x +cos 2x )=12+22sin(2x +π4), 所以f (α2+π24)=12+22sin(α+π12+π4) =12+22sin(α+π3)=12+22(12sin α+32cos α). 又因为sin α=35,且α∈(π2,π), 所以cos α=-45, 所以f (α2+π24)=12+22(12×35-32×45) =10+32-4620. 12.(2017·西安一中月考)已知函数f (x )=4cos ωx cos(ωx +π3),ω>0的最小正周期为π. (1)求ω的值;(2)讨论f (x )在区间[0,5π6]上的单调性. 解 f (x )=4cos ωx cos(ωx +π3) =4cos ωx ·(12cos ωx -32sin ωx ) =2cos 2ωx -23sin ωx cos ωx=1+cos 2ωx -3sin 2ωx=1+2cos(2ωx +π3). (1)因为函数f (x )=4cos ωx cos(ωx +π3)(ω>0)的最小正周期为π, 故2π2ω=π,所以ω=1. (2)由(1)知f (x )=1+2cos(2x +π3),x ∈[0,5π6], 故π3≤2x +π3≤2π, 当π3≤2x +π3≤π时,即0≤x ≤π3时, f (x )=1+2cos(2x +π3)为减函数; 当π<2x +π3≤2π,即π3<x ≤5π6时, f (x )=1+2cos(2x +π3)为增函数, 所以f (x )=1+2cos(2x +π3)的减区间为[0,π3],增区间为(π3,5π6]. 13.已知函数f (x )=sin x2sin(π2+x 2). (1)求函数f (x )在[-π,0]上的单调区间.(2)已知角α满足α∈(0,π2),2f (2α)+4f (π2-2α)=1,求f (α)的值. 解 f (x )=sin x 2sin(π2+x 2) =sin x 2cos x 2=12sin x . (1)函数f (x )的单调递减区间为[-π,-π2],单调递增区间为[-π2,0]. (2)2f (2α)+4f (π2-2α)=1 ⇒sin 2α+2sin(π2-2α)=1⇒2sin αcos α+2(cos 2α-sin 2α)=1 ⇒cos 2α+2sin αcos α-3sin 2α=0 ⇒(cos α+3sin α)(cos α-sin α)=0.∵α∈(0,π2), ∴cos α-sin α=0⇒tan α=1得α=π4, ∴f (α)=12sin π4=24.。
北大版高等数学课后习题答案_完整版

习题 1.12222222222222222223.33,,.3,3.3,,313 2.961,9124,31.3,93,3,3.,,.,,,,p p p q p q p q q p p k p k p k k p k k p p k k q q k q p q p p a a p a b p a pb b b====+=+=++=++======证明为无理数若不是无理数,则为互素自然数除尽必除尽否则或除将余故类似得除尽与互素矛盾.设是正的素数证明是无理数设为互素自然数,则素证 2.证 1.2222222,,.,..,:(1)|||1| 3.\;(2)|3| 2.0,13,22,1,(1,0);01,13,13,(0,1);1,13,3/2,(1,3/2).(1,0)(0,1)p a p a a pk p k pb pk b p b a b x x x x x x x x x x x x x x x X ===+-<-<<-+-<>->--<<+-<<>+-<<=-⋃数除尽故除尽类似得除尽此与为互素自然数矛盾.解下列不等式若则若则若则3.解 (1)222(1,3/2).(2)232,15,1||5,1||5,(1,5)(5,1).,(1)||||||;(2)||1,|||| 1.(1)|||()|||||||||,||||||.(2)|||()||||||x x x x x a b a b a b a b a b a a b b a b b a b b a b a b a b a b b a b b ⋃-<-<<<<<<<=⋃--+≥--<<+=++-≤++-=+++≥-=+-≤+-<设为任意实数证明设证明证4.,| 1.(1)|6|0.1;(2)||.60.160.1. 5.9 6.1.(, 6.1)( 5.9,).(2)0,(,)(,);0,;0,(,).11,01,.1, 1.11n nn n x x a l x x x x X l X a l a l l x a l X a a a n n a a b a a ++>->+>+<->-<-=-∞-⋃-+∞>=++∞⋃-∞-=≠<=-∞+∞-><-<>=>-=-=解下列不等式或或若若若若证明其中为自然数若显然解(1)证5.:6.120000(1)(1)(1).(,),(,).1/10.{|}.(,),,{|},10{|}./10,(1)/10,/10(1)/101/10n n n n n n n n n n n n n a b b n a a b a b n b a mA A m A a b ABC B A x x b C A x x a B m m C b a m m ---+++>-<-=∈⋂=∅=⋃=⋂≥=⋂≤-∈-≤-Z 设为任意一个开区间证明中必有有理数取自然数 满足考虑有理数集合= 若则中有最小数-=证7.(,),(,).1/10.{2|}.10n n nn a b a b mn b a A m <-=+∈Z ,此与的选取矛盾. 设为任意一个开区间证明中必有无理数取自然数 满足考虑无理数集合 以下仿8题.8.证习题1.26426642642666613.1(1,)(1)(1)111(1).112113.(,).13||13,||1,3,11||3,(,).y x x x x x x y x x x x x x x x x x y x x x x x x x x x x x x xy y x =+-+∞+-++=+-==<>+++++++=-∞+∞+++++≤≤>≤=++=≤∈-∞+∞证明函数在内是有界函数.研究函数在内是否有界时,时证解习题 1.4221.-(1)lim(0);(2)lim ;(3)lim ;(4)lim cos cos .|-||-||-|1)0,||,,||,||.,||,||,lim.(2)0x a x ax ax ax ax ax a a x a e e x a x a x a x a x a x a x a ax a x a a a x a x a x a aεδεεεεδεδεε→→→→→=>===∀>-=<<-+-<-<=-<-<=∀>直接用说法证明下列各极限等式:要使由于只需取则当时故证(222222,|| 1.||||||,|||||2|1|2|,1|2|)||,||.m in{,1},||,1|2|1|2|||,lim (3)0,.||(1),01),1x ax a a x a x a ax a x a x a x a x a x a a a a x a x a x a a a x a x a x a e e e e e eεεεεδδεεεε→---<-=+-<+≤-+<++-<-<=-<++-<=∀>>-=-<<-<<不妨设要使由于只需(取则当时故设要使即(.1,0ln 1,m in{,1},0,||,1|2|lim lim lim 0,|cos cos |2sinsin 2sin sin ||,2222,|,|cos cos x a ax a a x a x a x a x a x a x ae e x a x a e e e a e e e e e e x a x a x a x ax a x a x a x a εεεδδεεδεδ-→+→-→<+⎛⎫<-<+=<-<-< ⎪+⎝⎭===+-+-∀>-==≤-=-<-取则当时故类似证故要使取则当|时. ..(4)20|,lim cos cos .2.lim (),(,)(,),().1,0,0|-|,|()|1,|()||()||()|||1||.(1)1(1)limlim 2x ax ax x x a f x l a a a a a u f x x a f x l f x f x l l f x l l l M x x εδδεδδ→→→→<==-⋃+==><<-<=-+≤-+<+=+-=故设证明存在的一个空心邻域使得函数在该邻域内使有界函数对于存在使得当 时从而求下列极限证 3.:2002222200002212202lim (1) 1.222sin sin 1cos 11122(2)lim lim lim 1.22221(3)limlim(0).()222(4)lim.22332(5)lim 22x x x x x x x x x x xx x x x x x x x a axa xx x a a ax x x x x x x x →→→→→→→→+=+=⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪-⎝⎭⎝⎭ ⎪==== ⎪⎪⎝⎭+-==>++---=------- 2.33-=-20103030300022********(23)(22)2(6)lim 1.(21)2112(7)limlim 1.(11)13132(8)lim lim lim 11(1)(1)(1)(1)(1)(2)lim lim (1)(1)x x x x x x x x x x x x x xxx x x x x x x x x x x x x x x x x x x x →∞→→→-→-→-→--+==++--==++--+---⎛⎫-== ⎪+++-++-+⎝⎭+-==+-+214442100(2)31.(1)3123(123)(2)(123)(9)limlim 2(2)(2)(123)(28)(2)244lim.63(4)(123)(1)1(1)12(10)lim lim lim .1(11)lim x x x n n nx y y x x x x x x x x x x x x x x x x n n ny y y x y n x y yx →-→→→→→→→∞--==--++-+-+++=--+++-+===-++-+++-+-===- ()22221011001001010*******11lim 0.11(12)lim (0)./,(13)lim (0)0, , .818(14)lim lim 1x m m m mnn n x nn mm m n n x n x x x x x a x a x a a b b x b x b b a b m n a x a x a a b n mb x b x b m n x x →∞--→--→∞→∞→∞+--==++-+++≠=+++=⎧+++⎪≠=>⎨+++⎪∞>⎩++=+ 42/ 1.11/x x =+332022333333222333322333322033331312(15)lim(1312)(13131212)lim()(13131212)5lim(1)(13131212)55lim .3(1)(13131212)(16)0,l x x x x x xx x x x x x x x x x x x x x xx x x x x x x x x x x a →→→→+--++--+++-+-=++++-+-=++++-+-==++++-+-> 22220001im lim ()()1lim ()x a x a x a x a x ax a x a x a x a x a x a x a x a x a x a →+→+→+⎛⎫-+--=+ ⎪ ⎪+--⎝⎭⎛⎫-+=+ ⎪ ⎪+-++⎝⎭00()1lim ()11lim .()2x a x a x a x a x a x a x a x a x a x a x a a →+→+⎛⎫-=+ ⎪+-++⎝⎭⎛⎫-=+= ⎪ ⎪+++⎝⎭000222200000sin 14.lim 1lim 1sin sin (1)lim lim lim cos .tan sin sin(2)sin(2)2(2)lim lim lim 100323tan 3sin 2tan 3sin 2(3)lim lim lim sin 5sin 5xx x x x x x x x x x x x e x x x x x x x x x x x x xx x x x x αααββββ→→∞→→→→→→→→→⎛⎫=+= ⎪⎝⎭=====-=- 利用及求下列极限:00()1/0321.sin 5555(4)lim lim 2.1cos 2sin2cos sinsin sin 22(5)lim lim cos .2(6)lim 1lim 1lim 1.(7)lim(15)x x x a x a kxxxk kk k x x x yy x x x xxx x a x a x a a x a x ak k k e x x x y →+→+→→----→∞→∞→∞→=-===-+--==--⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥+=+=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦-=51/(5)50100100lim(15).111(8)lim 1lim 1lim 1.5.lim ()lim ().lim ():0,0,0|-|().lim (y y x xx x x x ax x a x y e e x x x f x f x f x A x a f x A f x δδ--→+→∞→∞→∞→→-∞→→-∞⎡⎤-=⎢⎥⎣⎦⎡⎤⎛⎫⎛⎫⎛⎫+=++= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦=+∞=-∞=+∞>><<>给出及的严格定义对于任意给定的存在使得当时):0,0,().A x f x A =-∞>∆><-∆<-对于任意给定的存在使得当时习题1.52222222222221.(1)10(2)sin 5.(1)0,|110|.,1111,||,,|||110|,10555()(2)(1)0,|sin 5sin 5|2|cos ||sin |.22x x x x a x x x x x x x x x x x x x a x a x a εδεεεεδεδεεε-+==∀>+-+=<≤++++<<=<+-+<+=+-∀>-=<试用说法证明在连续在任意一点连续要使由于只需取则当时有故在连续.要使由于证000000555()2|cos ||sin |5||,5||,||,225,|||sin 5sin 5|,sin 55()()0,0||()0.(),()/2,0||(x a x a x a x a x a x a x a x x a y f x x f x x x f x f x x f x x x f x εεεδδεδδεδδ+-≤--<-<=-<-<==>>-<>=>-<只需取则当时有故在任意一点连续.2.设在处连续且证明存在使得当时由于在处连续对于存在存在使得当时证000000000000)()|()/2,()()()/2()/20.3.()(,),|()|(,),?(,),.0,0|||()()|,||()||()|||()()|,||.f x f x f x f x f x f x f x a b f x a b x a b f x x x f x f x f x f x f x f x f x εδδεε-<>-=>∈>>-<-<-≤-< 于是设在上连续证明在上也连续并且问其逆命题是否成立任取在连续任给存在使得当时此时故在连续其证 220001,,(),()|11,ln(1), 1,1,0,(1)()(2)()arccos , 1. 0;lim ()lim 11(0),lim ()(0)x x x x f x f x x a x x x x f x f x a x x a x x f x x f f x f π→-→-→+⎧=≡⎨-⎩⎧+≥⎧⎪+<==⎨⎨<+≥⎩⎪⎩=+====逆命题是有理数不真例如处处不连续但是|处处连续.是无理数4.适当地选取,使下列函数处处连续:解(1)0111122sin 2limsin301.(2)lim ()lim ln(1)ln 2(1),lim ()lim arccos (1)ln 2,ln 2.5.3:11(1)lim coscos lim cos 0 1.(2)lim 2.(3)lim x x x x x x x xx x xx a f x x f f x a x a f a x x x xx x xeeπ→→+→+→-→-→+∞→+∞→→==+====-===-+-+-=====利用初等函数的连续性及定理求下列极限sin 22sin334422.88(4)lim arctan arctan lim arctan1.114xx x x e x x x x π→∞→∞=++===++22222222()()(ln ())()(5)lim (12)||lim (12)||3||33lim lim .21211/12/6.lim ()0,lim (),lim)().lim)()lim)x x x x g x b x x x x x x g x f x g x x x x x x x x x x x x x x x x f x a g x b f x a f x e →∞→∞→∞→∞→→→→→⎡⎤+--=+--⎣⎦⎡⎤⎡⎤===⎢⎥⎢⎥++-++-⎣⎦⎣⎦=>====设证明证0lim [(ln ())()]ln 22.7.,,(1)()cos ([]),,(2)()sgn(sin ),,,,1,(3)()1,1/2, 1.1(4)()x x f x g x b a b e e a f x x x n f x x n n x x f x x x x f x ππ→===-∈=∈⎧≠==⎨=⎩+=Z Z 指出下列函数的间断点及其类型若是可去间断点请修改函数在该点的函数值,使之称为连续函数:间断点第一类间断点.间断点第一类间断点.间断点第一类间断点.,011,sin,12,11,01,2(5)(),12,2,1,2 3.1x x x x x x f x x x x x xπ⎧≤≤⎪=⎨<≤⎪-⎩⎧≤≤⎪-⎪=<≤=⎨⎪⎪<≤-⎩间断点第二类间断点.间断点第一类间断点.0000008.(),(),()()()()()()()()()()(()())()()()()()0,()().y f x y g x x h x f x g x x f x g x x h x f x g x x x g x f x g x f x x x f x g x x f x g x D x ϕϕ===+==+=+-=≡=R R 设在上是连续函数而在上有定义但在一点处间断.问函数及在点是否一定间断?在点一定间断.因为如果它在点连续,将在点连续,矛盾.而在点未必间断.例如解习题1.600001.:()lim (),lim (),,,,()0,()0,[,],,(,),()0.2.01,,sin ,.(x x P x P x P x A B A B P A P B P A B x A B P x y y x x f x εε→+∞→-∞=+∞=-∞<<>∈=<<∈=-R 证明任一奇数次实系数多项式至少有一实根.设是一奇数次实系数多项式,不妨设首项系数是正数,则存在在连续根据连续函数的中间值定理存在使得设证明对于任意一个方程有解且解是唯一的令证证000000000000000212121212121)sin ,(||1)||1||,(||1)||1||,[||1,||1],,[||1,||1],().,()()(sin sin )||0,.3.()(,x x f y y y y f y y y y f y y x y y f x y x x f x f x x x x x x x x x f x a b εεεεε=---=--+<-≤+≥+->≥--+∈--+=>-=---≥--->在连续由中间值定理存在设故解唯一设在1212112212121121121112212221212121212),,(,),0,0,(,)()()().()(),.()(),()()()()()()()(),[,]x x a b m m a b m f x m f x f m m f x f x x f x f x m f x m f x m f x m f x m f x m f x f x f x m m m m m m x x ξξξ∈>>∈+=+==<+++=≤≤=+++连续又设证明存在使得如果取即可设则在上利用连续函数的中间值定理证.4.()[0,1]0()1,[0,1].[0,1]().()(),(0)(0)0,(1)(1)10.,01.,,(0,1),()0,().5.()[0,2],(0)(2).y f x f x x t f t t g t f t t g f g f t t g t f t t y f x f f =≤≤∀∈∈==-=≥=-≤∈====即可设在上连续且证明在存在一点使得如果有一个等号成立取为或如果等号都不成立则由连续函数的中间值定理存在使得即设在上连续且证明证12121212[0,2],||1,()().()(1)(),[0,1].(0)(1)(0),(1)(2)(1)(0)(1)(0).(0)0,(1)(0),0, 1.(0)0,(0),(1),,(0,1)()(1x x x x f x f x g x f x f x x g f f g f f f f g g f f x x g g g g f ξξξ-===+-∈=-=-=-=-====≠∈=+在存在两点与使得且令如果则取如果则异号由连续函数的中间值定理存在使得证12)()0,, 1.f x x ξξξ-===+取第一章总练习题221.:581 2.3|58|1422.|58|6,586586,.3552(2)33,52333,015.5(3)|1||2|1(1)(2),2144,.22|2|,.2,2,4,2;2,3x x x x x x x x x x x x x x x x x y x x x y x y x y x y x y x -≥-≥-≥-≥-≤-≥≤-≤-≤-≤≤≤+≥-+≥-+≥-+≥=+-≤=+≤=->=求解下列不等式()或或设试将表示成的函数当时当时解解解2.解222312312,4,(2).32,41(2), 4.313.11.21. 212,4(1)44,0.1,0.4.:1232(1)2.222221211,.22123222n n y x y y y x y y x x x x x x x x x x x x n n n n ->=--≤⎧⎪=⎨->⎪⎩+<+≥-+<++<++>≥-≠+++++=-+==++ 求出满足不等式的全部用数学归纳法证明下列等式当时,2-等式成立设等式对于成立,则解证1231111121211222112312222222124(1)(1)3222,22221..1(1)(2)123(1).(1)1(11)1(1)1,(1)(1)n n n n n n n n n n n n n n n n n n n n n x nx x x nxx x x x x n x x ++++++-+++++=++++++++-+++=-+=-=-+-++++++=≠--++-===-- 即等式对于也成立故等式对于任意正整数皆成立当时证1,1212.1(1)123(1)(1)(1)n n n nnn n x nx x x nxn x n xx +--++++++++=++- 等式成立设等式对于成立,则122122112211221221(1)(1)(1)(1)1(1)(12)(1)(1)1(1)(2)(1)(1)1(1)(2)(1)(1)1(2)(1),(1)1n n n n n n n n n n n n n n n n n n n x nx x n x x n x nx x x n x x n x nx x x x n x n x nx x x x n x n x n x x n ++++++++++-+++-+=--+++-++=--+++-++=--+++-++=--+++=-+即等式对于成立.,.|2|||25.()(1)(4),(1),(2),(2);(2)();(3)0()(4)224211222422(1)(4)1,(1)2,(2)2,(2)0.41224/,2(2)()x x f x xf f f f f x x f x x f f f f x x f x +--=---→→----------==--==-====----≤-=由归纳原理等式对于所有正整数都成立设求的值将表成分段函数当时是否有极限:当时是否有极限?解00022222222;2,20;0,0.(3).lim ()2,lim ()0lim ().(4).lim ()lim (4/)2,lim ()lim 22lim (),lim () 2.6.()[14],()14(1)(0),x x x x x x x x x x x f x f x f x f x x f x f x f x f x x f x x f →-→+→-→--→--→-+→-+→--→-⎧⎪-<≤⎨⎪>⎩==≠=-======--无因为有设即是不超过的最大整数.求00223,(2);2(2)()0?(3)()2?391(1)(0)[14]14,1467.(2)[12]12.244(2).lim ()lim[14]14(0).(3).lim ()12,lim ()x y x x f f f x x f x x f f f f x y f f x f x →→+→+→-⎛⎫⎪⎝⎭==⎛⎫⎡⎤⎡⎤=-=-=-=-+=-=-=- ⎪⎢⎥⎢⎥⎝⎭⎣⎦⎣⎦=-=-==-的值在处是否连续在处是否连续连续因为不连续因为解111111.7.,0,,:(1)(1);(2)(1).n n n n n n a b a b n b a b a n b n a b a b a++++=-≤<--<++<--设两常数满足对一切自然数证明1111111()()(1),(1).118.1,2,3,,1,1.:{},{}..111,1,7,111n n n n n n n n n n n n nn n n n n n n b a b a b b a a b b b b n b b a b a b a n a b a n a b n n a b a b a b n nn ++--+++--+++=<+++=+--->+-⎛⎫⎛⎫==+=+ ⎪ ⎪⎝⎭⎝⎭<+=++⎛+ ⎝ 类似有对令证明序列单调上升而序列单调下降,并且令则由题中的不等式证证=11111111111(1)1,111111111(1)11(1)1111111,11111.1111(1)11n n nn n nn nn nn n n n n n n n n n n n n n n n n n n n n n +++++++⎫⎛⎫-+⎪ ⎪+⎛⎫⎭⎝⎭<++ ⎪⎝⎭-+⎛⎫⎛⎫⎛⎫+-+<++ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫+-+<+ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫+<+ ⎪ ⎪+⎝⎭⎝⎭⎛⎫+ ⎛⎫⎝⎭++< ⎪+⎝⎭111111121111111111(1)1111(1)11111111111111111.1111111.111n n nn n nn n n n n n n n n n n n n n n n n n nn n n n n +++++++⎛⎫-+⎪ ⎪+⎝⎭-+⎛⎫⎛⎫⎛⎫++<+-+ ⎪ ⎪⎪+++⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫+<+-+ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫+++<+ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎛⎫++>+ ⎪++⎝⎭⇔我们证明22111211111(1)11..(1)(1)1111,1,1,11.nn n n n n n n n n n n e e e n n n n ++++>+++++⇔>++⎛⎫⎛⎫⎛⎫⎛⎫→∞+→+→+<<+ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭最后不等式显然成立当时故9.求极限22222222221111lim 1111234111111112341324351111().2233442210.()lim (00, ()lim n n n n n n n n n n n n nxf x a nx ax nxf x nx a →∞→∞→∞⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭++==→→∞=≠+===+ 作函数)的图形.解解0;1/,0.x x ⎧⎨≠⎩1111.§2,()[,]|()|,[,].,(),[,],max{||,||}1,|()|,[,].,|()|,[,],(),[,].12.f x a b M f x M x a b M N f x N x a b M M N f x M x a b M f x M x a b M f x M x a b <∀∈≤≤∀∈=+<∀∈<∀∈-<<∀∈1在关于有界函数的定义下证明函数在区间上为有界函数的充要条件为存在一个正的常数使得设存在常数使得M 取则有反之若存在一个正的常数使得则证12121212:()()[,],()()()()[,].,,|()|,|()|,[,].|()()||()||()|,|()()||()||()|,[,].113.:()cos 0y f x y g x a b f x g x f x g x a b M M f x M g x M x a b f x g x f x g x M M f x g x f x g x M M x a b f x x x xπ==+<<∀∈+≤+<+=<∀∈==证明若函数及在上均为有界函数则及也都是上的有界函数存在证明在的任一证,0().11(,),00,,,(),1()(,)0,()(21/2)cos(21/2)0,21/20().n x f x M n n M f n M n nf x f x n n n x f x δδδδδδπ→->><>=>-=→=++=→∞+→n 邻域内都是无界的但当时不是无穷大量任取一个邻域和取正整数满足和则故在无界.但是x 故当时不是无穷大量证11111000114.lim (1)ln (0).1ln 1,ln ln(1),.lim lim 10.ln(1)ln(1)lim lim ln(1)ln lim(1)ln 1,ln (1)ln ().ln(1)15.()()nn nn n n n n y y y y y n nn n x x x xx y x y n y x n y y y y e y y xn x x n y f x g x →∞→∞→∞→→→-=>-==+==-=++=+=+==-=→→∞+证明令则注意到我们有设及在实轴上有证00002022222220000.:()(),,()lim ()lim ()().1cos 116.lim.22sin 1cos 2sin 1sin 12lim lim lim lim 1422n n n n n x x x y y f x g x x x x f x f x g x g x x x x x y y x x y y →∞→∞→→→→→→===-=⎛⎫-==== ⎪⎝⎭ 定义且连续证明若与在有理数集合处处相等,则它们在整个实轴上处处相等.任取一个无理数取有理数序列证明证证0011000000001.2ln(1)17.:(1)lim 1;(2)lim .ln(1)(1)lim lim ln(1)ln lim(1)ln 1.(1)11(2)lim lim lim lim ln(1)ln(1)lim1.1x a xa y x y y y y y x a a a x x aa ax x x y y a a y e e e y x y y y e ye e e e e y e e e y x x x y ye e +→→→→→+→→→→→=+-==+=+=+==---====++== 证明证0111018.()lim ()0,()lim ()()0.|()|,0||.0,0,0|||()|/.min{,},0||,|()()||()||()|,li x ax ay f x a f x y g x a f x g x g x M x a x a f x M x a f x g x f x g x M Mδεδδεδδδδεε→→====<<-<>><-<<=<-<=<= 设在点附近有定义且有极限又设在点附近有定义,且是有界函数.证明设对于任意存在使得当时令则时故证m ()()0.x af xg x →=19.()(,),,()()|()|() () ()(),()(,).y f x c g x f x f x c g x c f x cc f x c g x g x =-∞+∞≤⎧⎪=>⎨⎪-<-⎩-∞+∞设在中连续又设为正的常数定义如下 当当当试画出的略图并证明在上连续0000000000000|()|,0,||lim ()lim ()()().(),0,||()lim ()lim ().(),().0,,0,x x x x x x x x f x c x x g x f x f x g x f x c x x f x c g x c c g x f x c g x c c δδδδεεδ→→→→<>-<===>>-<>=====><>一若则存在当时|f(x)|<c,g(x)=f(x),若则存在当时,g(x)=c,若则对于任意不妨设存在使证()0000121212|||()|.||.(),()(),|()()||()|,(),(),|()-()|0.()()min{(),}max{(),}().max{(),()}(|()()|()())/2.min x x f x c x x f x c g x f x g x g x f x c f x c g x c g x g x g x f x c f x c f x f x f x f x f x f x f x δεδεε-<-<-<≤=-=-<>==<=+--=-++得当时设若则若 则二利用证121212123123123111123{(),()}(|()()|(()())/2.120.()[,],[()()()],3,,[,].[,],().()()(),(),.()min{(),(),()},f x f x f x f x f x f x f x a b f x f x f x x x x a b c a b f c f x f x f x f x c x f x f x f x f x f ηηη=--++=++∈∈======设在上连续又设其中证明存在一点使得若则取即可否则设证31231313000000()min{(),(),()},()(),[,],,[,],().21.()(),()g(),,.0()g()()g()x f x f x f x f x f x f x x c a b f c y f x x g x x x kf x l x x k l l kf x l x x kf x l x x ηη=<<∈==+=+≠+在连续根据连续函数的中间值定理存在一点使得设 在点连续而在点附近有定义但在不连续问是否在连续其中为常数如果在连续;如果在解,l 0,000000||()[[()lg()]()]/.22.Dirichlet ..,()1;,()0;lim (),()11(1)lim 0;(2)lim (arctan )sin 12n n n n x x x x x g x kf x x kf x l x x x x D x x x D x D x D x x x x x →→∞→+∞=+-''→→→→+⎛⎫= ⎪+⎝⎭不连续,因否则将在连续证明函数处处不连续任意取取有理数列则取无理数列则故不存在在不连续.23.求下列极限:证2220011/1112132100;2tan 5tan 5/5(3)lim lim 5.ln(1)sin [[ln(1)]/]sin /1(4)lim()lim(1).24.()[0,),0().0,(),(),,().{x x y x x y n n x x x x x x x x x x x x y e y f x f x x a a f a a f a a f a π→→-→→+=====++++=+==+∞≤≤≥=== 设函数在内连续且满足设是一任意数并假定一般地试证明11},lim .lim ,(),().(),{}()0(1,2,),{}n n n n n n n n n n n n a a l a l f x x f l l a f a a a a f a n a →∞→∞++====≤=≥=单调递减且极限存在若则是方程的根即单调递减.又单调递减有下界,证111lim ,lim lim ()(lim )().25.()(,),:(0)1,(1),()()().()((,)).()()().()()n n n n n n n n n x n n a l a l a f a f a f l y E x E E e E x y E x E y E x e x E x x E x E x E nx E x +→∞→∞→∞→∞======-∞+∞==+==∀∈-∞+∞++== 故有极限.设则设函数在内有定义且处处连续并且满足下列条件证明用数学归纳法易得于是证11.,()(11)(1).1(0)(())()()(),().().1111,(1)()()()(),().11()()().,n n n n n n nn mmm n n n E n E E e E E n n E n E n e E n E n e E n e n E E n E n E e E E e n n n n m E E m E e e r E n n n -=++====+-=-=--======⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭设是正整数则于对于任意整数对于任意整数即对于所有有理数lim ().,,(),()lim ()lim ().nnn r x x x x n n n r e x x E x E x E x e ee e →∞→∞→∞=→====n 对于无理数取有理数列x 由的连续性的连续性习题2.1201.,.,.()2(0)(1),;(2),?(3)lim ,?x l O x x m x x x l x x m mx mx ∆→=≤≤∆∆∆∆∆∆设一物质细杆的长为其质量在横截面的分布上可以看作均匀的现取杆的左端点为坐标原点杆所在直线为轴设从左端点到细杆上任一点之间那一段的质量为给自变量一个增量求的相应增量求比值问它的物理意义是什么求极限问它的物理意义是什么2222222000(1)2()22(2)22(2).2(2)(2)2(2).(3)lim lim 2(2)4.lim x x x m x x x x x x x x x x x m x x x m x x x x x x x x m mx x x x x x∆→∆→∆→∆=+∆-=+∆+∆-=∆+∆∆∆+∆∆==+∆+∆∆∆∆∆∆=+∆=∆∆是到那段细杆的平均线密度.是细杆在点的线密度.解333032233222000002.,:(1);(2)2,0;(3)sin 5.()(1)lim(33)lim lim (33)3.2()2(2)lim 2lim(2lim x x x x x x y ax y px p y x a x x ax y xx x x x x x x a a x x x x ax xp x x px x x xy p x xx p ∆→∆→∆→∆→∆→∆→==>=+∆-'=∆+∆+∆+∆-==+∆+∆=∆+∆-+∆-'==∆∆+∆=根据定义求下列函数的导函数解0000000)()2lim()()212lim.25(2)52cossin sin 5()sin 522(3)limlim55(2)552cos sin sin5(2)2222lim 5lim cos lim 5522x x x x x x x x x x x x xp x x x x x x x x p p x x x xx x xx x xy x xx x x x x x x ∆→∆→∆→∆→∆→∆→∆→-+∆+∆=∆+∆+∆+∆+==+∆++∆∆+∆-'==∆∆+∆∆∆+∆==∆∆ 5cos5.2x x =00223.()(,()):(1)2,(0,1); (2)2,(3,11).(1)2ln 2,(0)ln 2,1ln 2(-0),(ln 2) 1.(2)2,(3)6,:116(3).4.2(0)(,)(0,0)x x y f x M x f x y M y x B y y y x y x y x y y x y px p M x y x y ===+''==-==+''==-=-=>>>求下列曲线在指定点处的切线方程切线方程切线方程试求抛物线上任一点处的切线斜率解,0,.2p F x ⎛⎫⎪⎝⎭,并证明:从抛物线的焦点发射光线时其反射线一定平行于轴200022222222,,().22(),.,2222,.222,.p p py px y M PMN Y y X x yy px p y x N X y X x X x x y p p p p FN x FM x y x pxp p p x px x x FN FNM FMN M PQ x PMQ FNM FMN '===-=--=-=-=-⎛⎫⎛⎫=+=-+=-+ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫=++=+=+=∠=∠ ⎪ ⎪⎝⎭⎝⎭∠=∠=∠过点的切线方程:切线与轴交点(,0),故过作平行于轴则证2005.2341,.224,1,6,4112564(1),4 2.:6(1),.444y x x y x y x x y k y x y x y x y x =++=-'=+====⎛⎫-=-=+-=--=-+ ⎪⎝⎭曲线上哪一点的切线与直线平行并求曲线在该点的切线和法线方程切线方程:法线方程解 323226.,,;(),,, (1)():(2)();(3)().()lim ()lim,lim ()limr R r R r R r R r g r GMrr R R g r R M G GM r R rg r r g r g r r GMr GMr R g r g r R RGM g r r →-→-→+→+⎧<⎪⎪=⎨⎪≥⎪⎩≠====离地球中心处的重力加速度是的函数其表达式为其中是地球的半径是地球的质量是引力常数.问是否为的连续函数作的草图是否是的可导函数明显地时连续.解,2lim (),()r R GMg r g r r R R→-==在连续.(2)33(3)()2(),()(),().r R g r GM GM g R g R g R g r r R R R-+-≠'''==-≠=时可导.在不可导227.(),:(1,3)(),(0)3,(2) 1.3(),()2.34111113,,3(),()3.2222P x y P x P P a b c P x ax bx c P x ax b b a b b a c a b P x x x ''===++=⎧⎪'=++=+=⎨⎪+=⎩==-=-+==-++求二次函数已知点在曲线上且解3222222222228.:(1)87,24 1.(2)(53)(62),5(62)12(53)903610.(3)(1)(1)tan (1)tan ,(2)tan (1)sec .9(92)(56)5(9)51254(4),56(56)y x x y x y x x y x x x x x y x x x x x y x x x x x x x x x x x x y y x x '=++=+'=+-=-++=+-'=+-=-=+-+++-+++'===++求下列函数的导函数22.(56)122(5)1(1),.11(1)x x y x y x x x ++'==-+≠=---23322222226(6)(1),.1(1)1(21)(1)1(7),.(8)10,1010ln1010(1ln10).sin cos sin (9)cos ,cos sin .(10)sin ,sin cos (s x x x x xx x x x x x x x x y x y x x x x x e e x x x x y y e e ey x y x x x x x xy x x y x x x x x y e x y e x e x e -'=≠=--+++-++-+-'==='==+=+-'=+=-+'==+= in cos ).x x +00000001001100009.:()()()(),()0().()()(1)(2).()()(),()0()()()()()()(()()())()(),(m k k k k k P x P x x x g x g x x P x m x P x k x P x k k P x x x g x g x P x k x x g x x x g x x x kg x x x g x x x h x h x ---=-≠'->=-≠''=-+-'=-+-=-定义若多项式可表为则称是的重根今若已知是的重根,证明是的重根证00)()0,()(1)kg x x P x k '=≠-由定义是的重根.000000010.()(,),()(),().()(0),(0)0.()(0)()(0)()(0)(0)lim lim lim (0),(0)0.()()11.(),lim 22x x x x f x a a f x f x f x f x f f f x f f x f f x f f f f x x xf x x f x x f x x f x→→→∆→--=''=-----'''==-=-=-+∆--∆'=∆若在中有定义且满足则称为偶函数设是偶函数,且存在试证明设在处可导证明证=000000000000000000000().()()()()()()1lim lim 22()()()()1lim 2()()()()11lim lim [()22x x x x x x f x x f x x f x x f x f x x f x x x x f x x f x f x x f x x x f x x f x f x x f x f x x x ∆→∆→∆→∆→∆→+∆--∆+∆--∆-⎡⎤=-⎢⎥∆∆∆⎣⎦+∆--∆-⎡⎤=+⎢⎥∆-∆⎣⎦+∆--∆-⎡⎤'=+=+⎢⎥∆-∆⎣⎦证002()]().12.,(0/2)()((),()):.f x f x y x t t P t x t y t OP x t t π''==<<=一质点沿曲线运动且已知时刻时质点所在位置满足直线与轴的夹角恰为求时刻时质点的位置速度及加速度.222222422222()()()tan ,()tan ,()()(tan ,tan ),()(sec ,2tan sec ),()(2sec tan ,2sec 4tan sec )2sec (sec ,2tan ).y t x t x t t y t t x t x t t t v t t t t v t t t t t t t t t ===='=''=+=位置解y =x 21/1/1/1/1/000013.,0()10, 00.1111(0)lim lim 1,(0)lim lim 0.1114.()||(),()()0.().()lim xx x x x x x x x x xx f x ex x x x e e f f x e xe f x x a x x x a a f x x a f a ϕϕϕ→-→-→+→+-→⎧≠⎪=+⎨⎪=⎩=++''======++=-=≠='=求函数在的左右导数设其中在处连续且证明在不可导-+解证()()()()(),()lim ()().a x a a x x x a x a a a f a x a x aϕϕϕϕ-→---''=-==≠--+-f 习题2.2()()()()()()2222222222222221.,:sin (1)(cos )sin ,.(cos )sin .2111(2)[ln(1)],.[ln(1)](1).111(3)112,.111121121xx x x x x xx x x x x x x x x x x x xx x x x x x x x x x x x x x '''=-=-=-'''-=-=-=---'''⎡⎤+=+=⎣⎦+'''⎡⎤+=+++=++⎣⎦+=++下列各题的计算是否正确指出错误并加以改正错错错332222222()2223.111(4)ln |2sin |(14sin )cos ,.2sin 1ln |2sin |(14sin cos ).2sin 2.(())()|.() 1.(1)(),(0),(),(sin );(2)(),(sin );(3)u g x x x xxx x x x x x x x x x x x f g x f u f x x f x f f x f x d d f x f x dx dx=+=++'⎡⎤+=+⎣⎦+'⎡⎤+=+⎣⎦+''==+''''错记现设求求[]()[][]2222223(())(())?.(1)()2,(0)0,()2,(sin )2sin .(2)()()224.(sin )(sin )(sin )2sin cos sin 2.(3)(())(()),(())(())().f g x f g x f x x f f x x f x x df x f x x x x x dxdf x f x x x x x dxf g x f g x f g x f g x g x ''''''====''===''==='''''= 与是否相同指出两者的关系与不同解()()()222233312232323.2236(1),.111(2)sec ,(cos )(cos )(cos )(cos )(sin )tan sec .(3)sin 3cos5,3cos35sin 5.(4)sin cos3,3sin cos cos33sin sin 33sin x x y y x x x y x y x x x x x x x y x x y x x y x x y x x x x x ---'==-=----'''===-=--='=+=-'==-= 求下列函数的导函数:2(cos cos3sin sin 3)3sin cos 4.x x x x x x x -=22222222222232222222241sin 2sin cos cos (1sin )(sin )2(5),cos cos sin 2cos 2(1sin )(sin ).cos 1(6)tan tan ,tan sec sec 13tan sec tan tan (sec 1)tan .(7)sin ,s ax ax x x x x x x x y y x x x x x x x xy x x x y x x x x x x x x x y e bx y ae +-+-'==++='=-+=-+=-=-='==524222422222in cos (sin cos ).(8)cos 1,5cos 1(sin 1)15cos 1sin 1.111(9)ln tan ,sec 24224tan 2411112tan cos 2sin 24242ax ax bx be bx e a bx b bx xy x y x x x x x x xx x y y x x x x ππππππ+=+'=+=+-++++=-+⎛⎫⎛⎫'=+=+ ⎪ ⎪⎛⎫⎝⎭⎝⎭+ ⎪⎝⎭==⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭222cos 42411sec .cos sin()211()()1(10)ln (0,),.22()x x x x x a x a x a x a y a x a y a x a a x a x a x a ππ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭===+-++--'=>≠±==+-+-2222222222222224.:111(1)arcsin (0),.111111(2)arctan (0),.1(3)arccos (||1),2arccos .11111(4)arctan ,.111(5)ar 22xy a y aa a x x a x y a y a a a a a x x a x y x x x y x x xy y x x x xx a y a x '=>==-⎛⎫- ⎪⎝⎭'=>==+⎛⎫+ ⎪⎝⎭'=<=---'===-++=-+ 求下列函数的导函数csin (0),x a a>22222222222222222222222222222222222222222121122211.2(6)ln (0)221112221.2222(7)arcsin ,1x x a y a x a a x x a x a a x a x a x a x x a x x a y x a a a x x a xy x a x a x x a x a x a x a x a x a x a xy x x -'=-++-⎛⎫- ⎪⎝⎭=--+=---++=++>⎛⎫'=++++ ⎪++++⎝⎭=+++=+++=≠±+222222222222222222221.12(1)22112sgn(1)2.(1)11141(1)2(8)arctan tan (0).2211sec 221tan 211sec 2()tan ()cos ()s 22x x x x x y x x x x xx a b x y a b a b a b a b x y a b x a ba b a b x x x a b a b a b a b +---'===+++--+⎛⎫-=>≥ ⎪ ⎪+-⎝⎭-⎛⎫'=⎪-+⎝⎭-++==++-++- 2222222in 21.cos (9)(1)(12)(13),ln ln(1)ln(12)ln(13)123/,2(1)2(12)22(13)3123.2(1)2(12)22(13)314(10)12,.212(11),.(12)x a b x y x x x y x x x y y x x x x x x y y x x x x x x xy x x y x x xy x a y x a =+=+++=+++++'=+++++⎡⎤'=++⎢⎥+++⎣⎦+'=++=++'=+=+2222,.xy a x y a x-'=-=-222222222311(13)ln(),1.21(14)(1)(31)(2).ln ln(1)ln(31)ln(2),331211131321211.13132(15),(1).(16)xxxx e x e x x e x y x x a y x x a x a x ay x x x y x x x y y x x x y y x x x y e e y e e e e e ⎛⎫'=++=+= ⎪++++⎝⎭=-+-=-+++-'-=++-+--⎡⎤'=++⎢⎥-+-⎣⎦'=+=+=+ 11112(0).ln ()ln ln ln ln .aaxa a xaaxa x a a a x a a x a ax a a x y x a a a y a x a a ax a aa aa x a aa x a a a ----=++>'=++=++222225.()1()()84,tan (),24001001()arctan ,()100110t x t t x t t t t t t t t θθθθ===='==+ 2一雷达的探测器瞄准着一枚安装在发射台上的火箭,它与发射台之间的距离是400m.设t=0时向上垂直地发射火箭,初速度为0,火箭以的匀加速度8m/s 垂直地向上运动;若雷达探测器始终瞄准着火箭.问:自火箭发射后10秒钟时,探测器的仰角的变化速率是多少?解222110,(10)0.1(/).505010101006.,2m t s θπθ'==⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭弧度在图示的装置中飞轮的半径为且以每秒旋转4圈的匀角速度按顺时针方向旋转.问:当飞轮的旋转角为=时,活塞向右移动的速率是多少?2220()2cos8364sin 8,8sin 8cos8(8)()16sin 8,2364sin 811()8,,,()16.2161616m/s.x t t t t t x t t tt t t x πππππππππαπππ=+--'=-+-'====- 活塞向右移动的速率是解习题2.323222(1)(1).1.0,?(1)10100.1sin (2)(22)sin ,222(3)(1cos )2sin ,222.:0,()().()().()()3.()()(0),()()(0).o o o x o o o x x y x x x x xy x x x xy x x x x x x x x x x x x xx x x x x x αααααβ=→=++=+-=++=-=→=====→=→ 当时下列各函数是的几阶无穷小量阶.阶.阶.已知当时试证明设试证明证00(1)(1)(1)()()()(0).()()()().()()().4.11(1)sin ,/4.sin cos ,1,1.44422(2)(1)(0).o o o o o o o x x x x x x x x x x xx x x x y x x x y x x x y dy dx y x y ααβαβαβππππα+=→+=+=+=+=⎛⎫⎛⎫⎛⎫''===+=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=+>':上述结果有时可以写成计算下列函数在指定点处的微分:是常数证122(1),(0),.5.1222(1)1,,.11(1)(1)(2),(1).(1).26.(1),3 3.001,11,(3).222.001x x x x x x y dy dx x dx y y dy x x x x y xe y e xe e x dy e x dx y x x x y y αααα-'=+==-'==-+=-=-++++'==+=+=+=≠-''=-∆=求下列各函数的微分:设计算当由变到时函数的增量和向相应的微分.22解 y =-(x -1)5551222113333332220.0010.0011,.2.00127.32.16.1.1632.1621.16/322(1) 2.002.5328.:11(1)(0).0,.33(2)()()(,,).2()2()dy y x y a a xy y y x x a y b c a b c x a y b y ---=-=-=+=+=⎛⎫''+=>+==- ⎪⎝⎭-+-='-+-= 试计算的近似值求下列方程所确定的隐函数的导函数为常数解0,.x ay y b-'=--。
2018版高考数学文北师大版大一轮复习讲义教师版文档
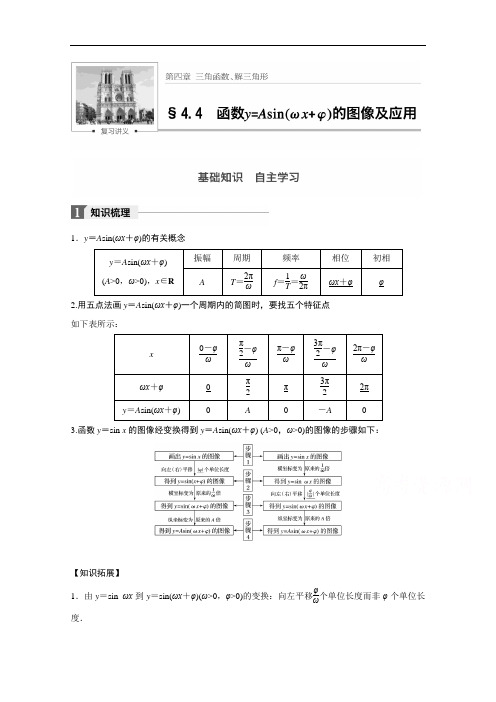
1.y =A sin(ωx +φ)的有关概念2.用五点法画y =A sin(ωx +φ)一个周期内的简图时,要找五个特征点 如下表所示:3.函数y =sin x 的图像经变换得到y =A sin(ωx +φ) (A >0,ω>0)的图像的步骤如下:【知识拓展】1.由y =sin ωx 到y =sin(ωx +φ)(ω>0,φ>0)的变换:向左平移φω个单位长度而非φ个单位长度.2.函数y =A sin(ωx +φ)的对称轴由ωx +φ=k π+π2,k ∈Z 确定;对称中心由ωx +φ=k π,k ∈Z确定其横坐标. 【思考辨析】判断下列结论是否正确(请在括号中打“√”或“×”)(1)y =sin ⎝⎛⎭⎫x -π4的图像是由y =sin ⎝⎛⎭⎫x +π4的图像向右平移π2个单位得到的.( √ ) (2)将函数y =sin ωx 的图像向右平移φ(φ>0)个单位长度,得到函数y =sin(ωx -φ)的图像.( × )(3)利用图像变换作图时“先平移,后伸缩”与“先伸缩,后平移”中平移的长度一致.( × ) (4)函数y =A sin(ωx +φ)的最小正周期为T =2πω.( × )(5)把y =sin x 的图像上各点纵坐标不变,横坐标缩短为原来的12,所得图像对应的函数解析式为y =sin 12x .( × )(6)若函数y =A cos(ωx +φ)的最小正周期为T ,则函数图像的两个相邻对称中心之间的距离为T2.( √ )1.(教材改编)y =2sin(12x -π3)的振幅,频率和初相分别为( )A .2,4π,π3B .2,14π,π3C .2,14π,-π3D .2,4π,-π3答案 C解析 由题意知A =2,f =1T =ω=1,初相为-π3.2.(2015·山东)要得到函数y =sin ⎝⎛⎭⎫4x -π3的图像,只需将函数y =sin 4x 的图像( ) A .向左平移π12个单位B .向右平移π12个单位C .向左平移π3个单位D .向右平移π3个单位答案 B解析 ∵y =sin ⎝⎛⎭⎫4x -π3=sin ⎣⎡⎦⎤4⎝⎛⎭⎫x -π12,∴要得到y =sin ⎝⎛⎭⎫4x -π3的图像,只需将函数y =sin 4x 的图像向右平移π12个单位. 3.(2016·青岛模拟)将函数y =sin x 的图像上所有的点向右平行移动π10个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是( ) A .y =sin(2x -π10)B .y =sin(2x -π5)C .y =sin(12x -π10)D .y =sin(12x -π20)答案 C解析 y =sin x π10−−−−−→右移个单位y =sin(x -π10)―――――→横坐标伸长到原来的2倍y =sin(12x -π10). 4.(2016·陕西千阳中学模拟)函数f (x )=2sin(ωx +φ)(ω>0,-π2<φ<π2)的部分图像如图所示,则ω,φ的值分别是( )A .2,-π3B .2,-π6C .4,-π6D .4,π3答案 A解析 由图像可知,34T =5π12-(-π3)=9π12,∴T =π,∴ω=2πT=2.∵(5π12,2)在图像上,∴2×5π12+φ=2k π+π2, φ=2k π-π3(k ∈Z ),∵-π2<φ<π2,∴φ=-π3.5.若将函数f (x )=sin(2x +π4)的图像向右平移φ个单位,所得图像关于y 轴对称,则φ的最小正值是________. 答案3π8解析 ∵函数f (x )=sin(2x +π4)的图像向右平移φ个单位得到g (x )=sin[2(x -φ)+π4]=sin(2x +π4-2φ),又∵g (x )是偶函数,∴π4-2φ=k π+π2(k ∈Z ),∴φ=-k π2-π8(k ∈Z ).当k =-1时,φ取得最小正值3π8.题型一 函数y =A sin(ωx +φ)的图像及变换例1 (2015·湖北)某同学用“五点法”画函数f (x )=A sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|<π2在某一个周期内的图像时,列表并填入了部分数据,如下表:(1) 请将上表数据补充完整,并直接写出函数f (x )的解析式;(2) 将y =f (x )图像上所有点向左平移θ(θ>0)个单位长度,得到y =g (x )的图像.若y =g (x )图像的一个对称中心为⎝⎛⎭⎫5π12,0,求θ的最小值.解 (1)根据表中已知数据,解得A =5,ω=2,φ=-π6.数据补全如下表:且函数解析式为f (x )=5sin ⎝⎛⎭⎫2x -π6. (2)由(1)知f (x )=5sin ⎝⎛⎭⎫2x -π6, 得g (x )=5sin ⎝⎛⎭⎫2x +2θ-π6. 因为函数y =sin x 图像的对称中心为(k π,0),k ∈Z .令2x +2θ-π6=k π,解得x =k π2+π12-θ,k ∈Z .由于函数y =g (x )的图像关于点⎝⎛⎭⎫5π12,0成中心对称, 所以令k π2+π12-θ=5π12,解得θ=k π2-π3,k ∈Z .由θ>0可知,当k =1时,θ取得最小值π6.引申探究在本例(2)中,将f (x )图像上所有点向左平移π6个单位长度,得到g (x )的图像,求g (x )的解析式,并写出g (x )图像的对称中心. 解 由(1)知f (x )=5sin(2x -π6),因此g (x )=5sin[2(x +π6)-π6]=5sin(2x +π6).因为y =sin x 的对称中心为(k π,0),k ∈Z . 令2x +π6=k π,k ∈Z ,解得x =k π2-π12,k ∈Z .即y =g (x )图像的对称中心为(k π2-π12,0),k ∈Z .思维升华 (1)五点法作简图:用“五点法”作y =A sin(ωx +φ)的简图,主要是通过变量代换,设z =ωx +φ,由z 取0,π2,π,32π,2π来求出相应的x ,通过列表,计算得出五点坐标,描点后得出图像.(2)图像变换:由函数y =sin x 的图像通过变换得到y =A sin(ωx +φ)的图像,有两种主要途径:“先平移后伸缩”与“先伸缩后平移”.把函数y =sin x 的图像上所有点的横坐标缩小到原来的一半,纵坐标保持不变,再把所得函数图像向左平移π4个单位,得到的函数图像的解析式是( )A .y =cos 2xB .y =-sin 2xC .y =sin(2x -π4)D .y =sin(2x +π4)答案 A解析 由y =sin x 图像上所有点的横坐标缩小到原来的一半,纵坐标保持不变,所得图像的解析式为y =sin 2x ,再向左平移π4个单位得y =sin 2(x +π4),即y =cos 2x .题型二 由图像确定y =A sin(ωx +φ)的解析式例2 已知函数f (x )=A sin(ωx +φ) (A >0,|φ|<π2,ω>0)的图像的一部分如图所示.(1)求f (x )的表达式; (2)试写出f (x )的对称轴方程.解 (1)观察图像可知A =2且点(0,1)在图像上, ∴1=2sin(ω·0+φ),即sin φ=12.∵|φ|<π2,∴φ=π6,又∵1112π是函数的一个零点且是图像递增穿过x 轴形成的零点,∴11π12ω+π6=2π,∴ω=2. ∴f (x )=2sin(2x +π6).(2)设2x +π6=B ,则函数y =2sin B 的对称轴方程为B =π2+k π,k ∈Z ,即2x +π6=π2+k π(k ∈Z ),解得x =k π2+π6(k ∈Z ),∴f (x )=2sin(2x +π6)的对称轴方程为x =k π2+π6(k ∈Z ).思维升华 求y =A sin(ωx +φ)+B (A >0,ω>0)解析式的步骤 (1)求A ,B ,确定函数的最大值M 和最小值m ,则A =M -m 2,B =M +m2. (2)求ω,确定函数的周期T ,则ω=2πT .(3)求φ,常用方法如下:①代入法:把图像上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)或把图像的最高点或最低点代入.②五点法:确定φ值时,往往以寻找“五点法”中的特殊点作为突破口.具体如下:“第一点”(即图像上升时与x 轴的交点)为ωx +φ=0;“第二点”(即图像的最高点)为ωx +φ=π2;“第三点”(即图像下降时与x 轴的交点)为ωx +φ=π;“第四点”(即图像的最低点)为ωx +φ=3π2;“第五点”为ωx +φ=2π.(2016·太原模拟)已知函数f (x )=sin(ωx +φ)(ω>0,|φ|<π2)的部分图像如图所示,则y =f (x +π6)取得最小值时x 的集合为( )A .{x |x =k π-π6,k ∈Z }B .{x |x =k π-π3,k ∈Z }C .{x |x =2k π-π6,k ∈Z }D .{x |x =2k π-π3,k ∈Z }答案 B解析 根据所给图像,周期T =4×(7π12-π3)=π,故π=2πω,∴ω=2,因此f (x )=sin(2x +φ),另外图像经过点(7π12,0),代入有2×7π12+φ=k π(k ∈Z ),再由|φ|<π2,得φ=-π6,∴f (x +π6)=sin(2x+π6),当2x +π6=-π2+2k π (k ∈Z ),即x =-π3+k π(k ∈Z )时,y =f (x +π6)取得最小值.题型三 三角函数图像性质的应用命题点1 三角函数模型的应用例3 (2015·陕西)如图,某港口一天6时到18时的水深变化曲线近似满足函数y =3sin ⎝⎛⎭⎫π6x +φ+k ,据此函数可知,这段时间水深(单位:m)的最大值为( )A .5B .6C .8D .10答案 C解析 由题干图易得y min =k -3=2,则k =5. ∴y max =k +3=8.命题点2 函数零点(方程根)问题例4 已知关于x 的方程2sin 2x -3sin 2x +m -1=0在⎝⎛⎭⎫π2,π上有两个不同的实数根,则m 的取值范围是________. 答案 (-2,-1)解析 方程2sin 2x -3sin 2x +m -1=0可转化为 m =1-2sin 2x +3sin 2x =cos 2x +3sin 2x =2sin ⎝⎛⎭⎫2x +π6,x ∈⎝⎛⎭⎫π2,π. 设2x +π6=t ,则t ∈⎝⎛⎭⎫76π,136π, ∴题目条件可转化为m2=sin t ,t ∈⎝⎛⎭⎫76π,136π有两个不同的实数根. ∴y =m2和y =sin t ,t ∈⎝⎛⎭⎫76π,136π的图像有两个不同交点,如图:由图像观察知,m 2的范围为(-1,-12),故m 的取值范围是(-2,-1). 引申探究例4中,若将“有两个不同的实数根”改成“有实根”,则m 的取值范围是__________. 答案 [-2,1)解析 由例4知,m2的范围是⎣⎡⎭⎫-1,12, ∴-2≤m <1,∴m 的取值范围是[-2,1). 命题点3 图像与性质的综合应用例5 已知函数f (x )=3sin(ωx +φ)(ω>0,-π2≤φ<π2)的图像关于直线x =π3对称,且图像上相邻两个最高点的距离为π. (1)求ω和φ的值;(2)当x ∈[0,π2]时,求函数y =f (x )的最大值和最小值.解 (1)因为f (x )的图像上相邻两个最高点的距离为π,所以f (x )的最小正周期T =π,从而ω=2πT =2.又因为f (x )的图像关于直线x =π3对称,所以2·π3+φ=k π+π2,k ∈Z ,由-π2≤φ<π2,得k =0,所以φ=π2-2π3=-π6.综上,ω=2,φ=-π6.(2)由(1)知f (x )=3sin(2x -π6),当x ∈[0,π2]时,-π6≤2x -π6≤5π6,∴当2x -π6=π2,即x =π3时,f (x )最大值=3;当2x -π6=-π6,即x =0时,f (x )最小值=-32.思维升华 (1)三角函数模型的应用体现在两方面:一是已知函数模型求解数学问题;二是把实际问题抽象转化成数学问题,建立数学模型,再利用三角函数的有关知识解决问题. (2)方程根的个数可转化为两个函数图像的交点个数.(3)研究y =A sin(ωx +φ)的性质时可将ωx +φ视为一个整体,利用换元法和数形结合思想进行解题.已知函数f (x )=cos(3x +π3),其中x ∈[π6,m ],若f (x )的值域是[-1,-32],则m的取值范围是__________. 答案 [2π9,5π18]解析 画出函数的图像.由x ∈[π6,m ],可知5π6≤3x +π3≤3m +π3,因为f (π6)=cos 5π6=-32且f (2π9)=cos π=-1,要使f (x )的值域是[-1,-32], 只要2π9≤m ≤5π18,即m ∈[2π9,5π18].4.三角函数图像与性质的综合问题典例 (12分)已知函数f (x )=23sin(x 2+π4)·cos(x 2+π4)-sin(x +π).(1)求f (x )的最小正周期;(2)若将f (x )的图像向右平移π6个单位长度,得到函数g (x )的图像,求函数g (x )在区间[0,π]上的最大值和最小值.思维点拨 (1)先将f (x )化成y =A sin(ωx +φ)的形式再求周期;(2)将f (x )解析式中的x 换成x -π6,得g (x ),然后利用整体思想求最值.规范解答解 (1)f (x )=23sin(x 2+π4)·cos(x 2+π4)-sin(x +π)=3cos x +sin x [3分]=2sin(x +π3),[5分]于是T =2π1=2π.[6分](2)由已知得g (x )=f (x -π6)=2sin(x +π6),[8分]∵x ∈[0,π],∴x +π6∈[π6,7π6],∴sin(x +π6)∈[-12,1],[10分]∴g (x )=2sin(x +π6)∈[-1,2].[11分]故函数g (x )在区间[0,π]上的最大值为2,最小值为-1.[12分]解决三角函数图像与性质的综合问题的一般步骤: 第一步:(化简)将f (x )化为a sin x +b cos x 的形式; 第二步:(用辅助角公式)构造f (x )=a 2+b 2· (sin x ·a a 2+b 2+cos x ·ba 2+b2); 第三步:(求性质)利用f (x )=a 2+b 2sin(x +φ)研究三角函数的性质; 第四步:(反思)反思回顾,查看关键点、易错点和答题规范.1.为了得到函数y =cos(2x +π3)的图像,可将函数y =sin 2x 的图像( )A .向左平移5π6个单位长度B .向右平移5π6个单位长度C .向左平移5π12个单位长度D .向右平移5π12个单位长度答案 C解析 由题意,得y =cos(2x +π3)=sin(2x +π3+π2)=sin 2(x +5π12),则它是由y =sin 2x 向左平移5π12个单位得到的,故选C.2.若f (x )=sin(2x +φ)+b ,对任意实数x 都有f ⎝⎛⎭⎫x +π3=f (-x ),f ⎝⎛⎭⎫2π3=-1,则实数b 的值为( ) A .-2或0 B .0或1 C .±1 D .±2答案 A解析 由f ⎝⎛⎭⎫x +π3=f (-x )可得f (x )的图像关于直线x =π6对称,∴2×π6+φ=π2+k π,k ∈Z .当直线x =π6经过最高点时,φ=π6;当直线x =π6经过最低点时,φ=-56π.若f (x )=sin ⎝⎛⎭⎫2x +π6+b ,由f ⎝⎛⎭⎫23π=-1,得b =0;若f (x )=sin ⎝⎛⎭⎫2x -56π+b ,由f ⎝⎛⎭⎫23π=-1,得b =-2.所以b =-2或b =0. 3.已知函数f (x )=3sin ωx +cos ωx (ω>0),x ∈R .在曲线y =f (x )与直线y =1的交点中,若相邻交点距离的最小值为π3,则f (x )的最小正周期为( )A.π2B.2π3 C .π D .2π 答案 C解析 f (x )=3sin ωx +cos ωx =2sin(ωx +π6)(ω>0).由2sin(ωx +π6)=1,得sin(ωx +π6)=12,∴ωx +π6=2k π+π6或ωx +π6=2k π+56π(k ∈Z ).令k =0,得ωx 1+π6=π6,ωx 2+π6=56π,∴x 1=0,x 2=2π3ω.由|x 1-x 2|=π3,得2π3ω=π3,∴ω=2.故f (x )的最小正周期T =2π2=π.4.函数f (x )=sin(ωx +φ) (x ∈R ,ω>0,|φ|<π2)的部分图像如图所示,如果x 1,x 2∈(-π6,π3)且f (x 1)=f (x 2),则f (x 1+x 2)等于( )A.12B.32C.22 D .1 答案 B解析 观察图像可知,A =1,T =π, ∴ω=2,f (x )=sin(2x +φ).将(-π6,0)代入上式得sin(-π3+φ)=0,由|φ|<π2,得φ=π3,则f (x )=sin(2x +π3).函数图像的对称轴为x =-π6+π32=π12.又x 1,x 2∈(-π6,π3),且f (x 1)=f (x 2),∴x 1+x 22=π12,∴x 1+x 2=π6,∴f (x 1+x 2)=sin(2×π6+π3)=32.故选B.5.函数f (x )=sin(2x +φ)⎝⎛⎭⎫|φ|<π2的图像向左平移π6个单位后所得函数图像的解析式是奇函数,则函数f (x )在⎣⎡⎦⎤0,π2上的最小值为( ) A .-32 B .-12 C.12 D.32答案 A解析 由函数f (x )的图像向左平移π6个单位得g (x )=sin ⎝⎛⎭⎫2x +φ+π3的图像, 因为是奇函数,所以φ+π3=k π,k ∈Z ,又因为|φ|<π2,所以φ=-π3,所以f (x )=sin ⎝⎛⎭⎫2x -π3. 又x ∈⎣⎡⎦⎤0,π2,所以2x -π3∈⎣⎡⎦⎤-π3,2π3, 所以当x =0时,f (x )取得最小值为-32. 6.(2016·太原模拟)已知函数f (x )=sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|<π2的最小正周期是π,若将f (x )的图像向右平移π3个单位后得到的图像关于原点对称,则函数f (x )的图像( )A .关于直线x =π12对称B .关于直线x =5π12对称C .关于点⎝⎛⎭⎫π12,0对称 D .关于点⎝⎛⎭⎫5π12,0对称答案 B解析 由题意知2πω=π,∴ω=2;又由f (x )的图像向右平移π3个单位后得到y =sin[2⎝⎛⎭⎫x -π3+φ]=sin ⎝⎛⎭⎫2x +φ-23π,此时关于原点对称,∴-2π3+φ=k π,k ∈Z ,∴φ=2π3+k π,k ∈Z ,又|φ|<π2,∴φ=-π3,∴f (x )=sin ⎝⎛⎭⎫2x -π3. 当x =π12时,2x -π3=-π6,∴A 、C 错误;当x =5π12时,2x -π3=π2,∴B 正确,D 错误.7.(2016·全国丙卷)函数y =sin x -3cos x 的图像可由函数y =sin x +3cos x 的图像至少向右平移________个单位长度得到. 答案2π3解析 y =sin x -3cos x =2sin ⎝⎛⎭⎫x -π3,y =sin x +3cos x =2sin ⎝⎛⎭⎫x +π3,因此至少向右平移2π3个单位长度得到.8.(2016·长春模拟)设偶函数f (x )=A sin(ωx +φ) (A >0,ω>0,0<φ<π)的部分图像如图所示,△KLM 为等腰直角三角形,∠KML =90°,KL =1,则f (16)的值为________.答案34解析 由题意知,点M 到x 轴的距离是12,根据题意可设f (x )=12cos ωx ,又由题图知12·2πω=1,所以ω=π,所以f (x )=12cos πx ,故f (16)=12cos π6=34.9.(2015·天津)已知函数f (x )=sin ωx +cos ωx (ω>0),x ∈R .若函数f (x )在区间(-ω,ω)内单调递增,且函数y =f (x )的图像关于直线x =ω对称,则ω的值为________. 答案π2解析 f (x )=sin ωx +cos ωx =2sin ⎝⎛⎭⎫ωx +π4, 因为f (x )在区间(-ω,ω)内单调递增,且函数图像关于直线x =ω对称,所以f (ω)必为一个周期上的最大值,所以有ω·ω+π4=2k π+π2,k ∈Z ,所以ω2=π4+2k π,k ∈Z .又ω-(-ω)≤2πω2,即ω2≤π2,即ω2=π4,所以ω=π2.10.(2016·邢台模拟)先把函数f (x )=sin(x -π6)的图像上各点的横坐标变为原来的12(纵坐标不变),再把新得到的图像向右平移π3个单位,得到y =g (x )的图像.当x ∈(π4,3π4)时,函数g (x )的值域为________. 答案 (-32,1] 解析 依题意得 g (x )=sin[2(x -π3)-π6]=sin(2x -5π6),当x ∈(π4,3π4)时,2x -5π6∈(-π3,2π3),此时sin(2x -5π6)∈(-32,1],故g (x )的值域是(-32,1]. 11.已知函数y =A sin(ωx +φ) (A >0,ω>0)的图像过点P (π12,0),图像上与点P 最近的一个最高点是Q (π3,5).(1)求函数的解析式; (2)求函数f (x )的递增区间.解 (1)依题意得A =5,周期T =4(π3-π12)=π,∴ω=2ππ=2.故y =5sin(2x +φ),又图像过点P (π12,0),∴5sin(π6+φ)=0,由已知可得π6+φ=0,∴φ=-π6,∴y =5sin(2x -π6).(2)由-π2+2k π≤2x -π6≤π2+2k π,k ∈Z ,得-π6+k π≤x ≤π3+k π,k ∈Z ,故函数f (x )的递增区间为[k π-π6,k π+π3] (k ∈Z ).12.已知函数f (x )=3cos 2x +sin x ·cos x -32. (1)求函数f (x )的最小正周期T 和函数f (x )的单调递增区间; (2)若函数f (x )的对称中心为(x,0),求x ∈[0,2π)的所有x 的和. 解 (1)由题意得f (x )=sin(2x +π3),∴T =2π2=π,令-π2+2k π≤2x +π3≤π2+2k π,k ∈Z .可得函数f (x )的单调递增区间为[-5π12+k π,π12+k π],k ∈Z .(2)令2x +π3=k π,k ∈Z ,可得x =-π6+k π2,k ∈Z .∵x ∈[0,2π),∴k 可取1,2,3,4. ∴所有满足条件的x 的和为2π6+5π6+8π6+11π6=13π3. 13.(2016·潍坊模拟)函数f (x )=A sin(ωx +φ)(A >0,ω>0,0<φ<π2)的部分图像如图所示.(1)求f (x )的解析式;(2)设g (x )=[f (x -π12)]2,求函数g (x )在x ∈[-π6,π3]上的最大值,并确定此时x 的值.解 (1)由题图知A =2,T 4=π3,则2πω=4×π3,∴ω=32. 又f (-π6)=2sin[32×(-π6)+φ]=2sin(-π4+φ)=0,∴sin(φ-π4)=0,∵0<φ<π2,∴-π4<φ-π4<π4,∴φ-π4=0,即φ=π4,∴f (x )的解析式为f (x )=2sin(32x +π4).(2)由(1)可得f (x -π12)=2sin[32(x -π12)+π4]=2sin(32x +π8),∴g (x )=[f (x -π12)]2=4×1-cos (3x +π4)2=2-2cos(3x +π4),∵x ∈[-π6,π3],∴-π4≤3x +π4≤5π4,∴当3x +π4=π,即x =π4时,g (x )max =4.。
北师大版数学选修4-2练习:(第4章)逆变换与逆矩阵(2)(含答案)

第四章 逆变换与逆矩阵 同步练习(二)1、下列矩阵中,不存在逆矩阵的是( )A 、⎪⎪⎭⎫ ⎝⎛-2032B 、⎪⎪⎪⎪⎭⎫ ⎝⎛-221431 C 、⎪⎪⎭⎫ ⎝⎛23231 D 、⎪⎪⎭⎫ ⎝⎛-011302、=-2410152( )A 、198B 、-198C 、-270D 、2703、⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-13913214M ,则=M ( )A 、⎪⎪⎭⎫ ⎝⎛1102 B 、⎪⎪⎭⎫ ⎝⎛-227357 C 、⎪⎪⎭⎫ ⎝⎛-0142814 D 、⎪⎪⎭⎫⎝⎛11204、对于任意的矩阵A 、M 、N ,下列结论正确的是( )A 、NM MN =B 、11--=NM M NC 、N NM M =-1D 、N MN M =-15、(1)若⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-21041110211M ,则_______=M ;(2)⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛-210y x5312所表示的二元一次方程组为___________。
6、⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫⎝⎛-=0110,1001B A ,则_________)(1=-AB 。
7、⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛1002022002110M ,则___________=M 。
8、(1)______=-818781-83;(2)_______=3cos 3sin 3sin -3cos ππππ。
9、计算下列矩阵的逆矩阵:(1)⎪⎪⎭⎫ ⎝⎛--=3523M ; (2)⎪⎪⎭⎫ ⎝⎛=1143M 。
10、判断下列矩阵是否存在逆矩阵,若存在,则求出逆矩阵,若不存在,说明理由。
(1)⎪⎪⎪⎪⎭⎫⎝⎛=21212323M ; (2)⎪⎪⎭⎫ ⎝⎛=1021M11、利用逆矩阵解二元一次方程组:⎩⎨⎧=+=-7y 3x 42y 3x12、已知)(,cos sin sin cos R x ∈=ααααα,求62+-=x x y 的最大值与最小值。
最新北大版高等数学课后习题答案+完整版优秀名师资料

北大版高等数学课后习题答案完整版习题 1.11. 证明 3为无理数. 证若 3不是无理数,则 3 p p2 , p, q为互素自然数.32 , p 2 3q 2 .3除尽p 2 , q q必除尽p, 否则p 3k , 1或p 3k , 2. p 2 9k 2 , 6k , 1, p 2 9k 2 ,12k , 4,3除 p 2 将余1.故p 3k ,9k 2 3q 2 , q 2 3k 2 , 类似得3除尽q.与p, q互素矛盾. 2. p是正的素数, 证明p是无理数. 设证设 p a a2 , a, b为互素自然数,则p 2 , a 2 pb 2 , 素数p除尽a 2 , 故p除尽a, b b 2 2 2 2 2 a pk . p k pb , pk b .类似得p除尽b.此与a, b为互素自然数矛盾.(1)若x 0, 则 , x , 1 , x 3, 2 x 3. 解下列不等式 : (1) | x | , | x ,1| 3.\;(2) | x 2 , 3 | 2. 解,2, x ,1, (,1, 0); 若0 x 1, 则x , 1 , x 3,1 3, (0,1); 若x 1, 则x , x , 1 3, x 3 / 2, (1,3 / 2). X (,1, 0) (0,1) (1,3 / 2). (2) , 2 x 2 , 3 2,1 x 2 5,1 | x |2 5,1| x | 5, x (1, 5) ( , 5, ,1). 4. a, b为任意实数,(1)证明 | a , b | |a | , |b |;(2)设 | a , b | 1, 证明 | a | | b | ,1. 设证(1) | a | | a ,b , (,b) | | a , b | , | ,b | | a , b | , | b |,| a , b | | a | , | b | .(2) | a| | b , (a , b) | | b | , | a , b | | b | ,1. 5. 解下列不等式: (1) | x , 6 | 0.1;(2) | x , a | l. 解(1)x , 6 0.1或x , 6 ,0.1.x ,5.9或x ,6.1.X (, , ,6.1) (,5.9, , ). (2)若l 0, X (a , l , , ) (, , a , l ); 若l 0, x a; 若l 0, X (, , , ). a ,1 6. a 1, 证明0 n a , 1 若 , 其中n a b 1.a , 1 n a , 1 ( n a , 1)(b n ,1 , b n , 2 , , 1) n为自然数. n 证若a 1, 显然n( n a , 1). 7. (a, b)为任意一个开区间, 证明(a, b)中必有有理数. 设证取自然数n 满足1/10nb , a.考虑有理数集合 m A=An { n | m Z}. 若An (a, b) , 则A B C , B A {x | x b}, 10 C A {x | x a}.B中有最小数m0 /10n , (m0 , 1) /10 n C , b , a m0 /10n -(m0 , 1) /10n =1/10 n ,此与n的选取矛盾. 8. (a, b)为任意一个开区间, 证明(a, b)中必有无理数. 设证取自然数n 满足1/10n b , a.考虑无理数集合An { 2 , m | m Z}. 以下仿8题. 10nn习题 1.2-1-13.证明函数y 1 , x , x在(1, , )内是有界函数. ( 1 , x , x )( 1 , x , x ) 1 1 ( x 1). 1, x , x 1,x , x 2 ,1 x6 , x4 , x2 13.研究函数y 在(, , , )内是否有界. 1 , x6x6 , x4 , x2 x 6 , x 4 , x 2 3x 6 解 | x | 1时, 3,| x | 1时, 6 3, 1 , x6 1 , x6 x | y | y 3, x (, , , ). 证y 1 , x , x习题 1.41.直接用 - 说法证明下列各极限等式: (1) limx axa ( a 0); (2) lim x 2 a 2 ; (3) lim e x e a ; (4) lim cos x cos a.x a x a x a证(1), 0, 要使 | 只需x,| x-a| | x-a| | x-a| a | ,由于 , x, a x, a a x a.| x,a| ,| x , a | a .取 a , 则当 | x , a | 时,| x , a | , 故 lim x a a 2 2 (2), 0, 不妨设 | x , a | 1.要使 | x , a | | x , a || x , a | ,由于| x , a | | x , a | , | 2a | 1, |2a |, 只需(1, | 2a |) | x , a | ,| x , a | | x 2 , a 2 | , 故 lim x2 a 2 .x a1, | 2a |.取 min{ ,1}, 则当 | x , a | 时, 1, | 2a |(3) , 0, 设x a.要使 | e x , e a | e a (e x , a , 1) , 即0 (e x , a , 1)ea,1 e x , a 1 ,ea,0 x , a ln 1 , a , 取 min{ ,1}, 则当0 x , a 时,| e x , e a |, e 1, | 2a | 故 lim e x e a . 类似证 lim e x e a . lim e x e a . 故x a , x a , x ax,a x,a x,a x,a (4) 0, 要使 | cos x , cos a | 2 sin , sin 2 sin sin | x , a |, 2 2 2 2 取, 则当|x , a | 时,| cos x , cos a | , 故 lim cos x cos a.x a2.设 lim f ( x) l , 证明存在a的一个空心邻域( a , , a) ( a, a , ),使得函数u f ( x)在x a该邻域内使有界函数. 证对于 1, 存在 0, 使得当 0 | x - a | 时,| f( x ) , l | 1, 从而 | f ( x) | | f ( x) , l , l | | f ( x) , l | , | l | 1, | l | M . 3. 求下列极限 : (1) limx 0(1 , x ) 2 , 1 2x , x2 x lim lim(1 , ) 1. x 0 x 0 2x 2x 22x x 2 sin 2 sin 2 1 , cos x 2 1 lim 12 1 . (2) lim lim 1 x 0 x 0 x x2 x2 2 x 0 2 2 2 (3) limx 0x,a , xalimx 0x x( x , a ,a)1 ( a 0).2 ax2 , x , 2 2 x2 , 2 x , 3 x2 , x , 2 (5) lim x 0 2 x 2 , 2 x , 3 (4) limx 1,2 . ,3 ,2 . ,3-2-(6) lim(2 x , 3) 20 (2 x , 2)10 230 30 1. x (2 x , 1)30 2x 0(7) lim1, x , 1, x 2x lim 1. x 0 x ( 1 , x , 1 , x ) x3 x2 , x , 1 , 3 x2 , x , 2 1 (8) lim , 3 lim lim x ,1 x , 1 x , 1x ,1 ( x , 1)( x 2 , x , 1) x ,1 ( x , 1)( x 2 , x , 1) ( x , 1)( x , 2) ( x , 2) ,3 lim lim 2 ,1. 2 x ,1 ( x , 1)( x , x ,1) x ,1 ( x , x , 1) 3 (9) limx 41, 2x , 3 ( 1 , 2 x , 3)( x , 2)( 1 , 2 x , 3) lim x 4 x ,2 ( x ,2)( x , 2)( 1 , 2 x , 3)lim(2 x , 8)( x , 2) 2 4 4 . x 4 ( x , 4)( 1 , 2 x , 3) 6 3n nn(n , 1) 2 y , , yn x,1 (1 , y ) , 1 2 (10) lim lim lim n. x 1 x , 1 y 0 y 0 y y 2 (11) lim x 2 , 1 , x 2 , 1 lim 0. x x x2 , 1 , x2 ,1 a x m , a x m ,1 , , am a (12) lim 0 n 1 n ,1 (bn 0) m . x0 b x , b x , , bn bn 0 1 ny ,,,a0 / b0 , m n a0 x m , a1 x m ,1 , , am (13) lim (a0 0 0) 0, b n m x b x n , b x n ,1 , , b 0 1 n , m n. x4 , 8 1 , 8 / x4 (14) lim 2 lim 1. x x , 1 x 1 , 1/ x 23(15) limx 01 , 3x , 3 1 ,2 x x , x22 2limx 0( 3 1 , 3 x , 3 1 , 2 x )( 3 1 , 3 x , 3 1 , 3 x 3 1 , 2 x , 3 1 , 2 x ) ( x , x 2 )( 3 1 , 3 x , 3 1 , 3 x 3 1 , 2 x ,3 1 , 2 x ) 5x2 2 2 2limx 0x(1 , x)( 3 1 , 3 x , 3 1 , 3 x 3 1 , 2 x , 3 1 , 2 x ) 5 5 lim . 22 x 0 (1 , x)(3 1 , 3 x , 3 1 , 3 x3 1 , 2 x , 3 1 , 2 x ) 3 (16) a 0, lim x , a , x,a x2 , a2x a , 0x, a 1 lim , 2 2 x a , 0 x,a x ,a( x , a )( x , a ) 1 lim x , a x , a( x , a) , x , a x a ,0-3-( x , a) 1 lim , x a , 0 x,a x , a x , a( x , a) x,a 1 1 lim x , a( x , a ) ,x , a 2a . x a , 0sin x 1 4.利用lim 1及 lim 1 , e求下列极限: x x x x sin x sinx (1) lim lim lim cos x . x 0 tan x x 0 sin x x 0 sin(2 x 2 ) sin(2x 2 ) 2x2 lim lim 1 0 0 x x 0 x 0 3 x 3x 2x2 tan 3 x , sin 2 x tan 3 xsin 2 x 3 2 1 (3) lim lim , lim , . x 0 x 0 sin 5 x x 0 sin 5 x sin 5 x5 5 5 x x (4) lim lim 2.x 0 , 1 , cos x x 0 , x 2 sin 2 x,a x,a cos sin sin x , sin a 2 2cos a. (5) lim lim x a x a x,ax,a 2 (2) lim k (6) lim 1 , x x,x xk lim 1 , x xx (,k ) kx k k lim 1 , x x ,5,ke, k .(7) lim(1 , 5 y )1/ y lim(1 , 5 y )1/(5 y ) e ,5 . y 0 y 0 1 11 (8) lim 1 , lim 1 , lim 1 , e. x x x xx x 5.给出lim f ( x) , 及 lim f ( x) , 的严格定义.x x a x , x ,100 100lim f ( x) , : 对于任意给定的A 0, 存在 0, 使得当0 | x - a | 时f ( x)A.x a x ,lim f ( x) , : 对于任意给定的A 0, 存在 0, 使得当x , 时f ( x) , A.习题 1.5-4-1.试用 , 说法证明 (1) 1 , x 2 在x 0连续 (2) sin 5 x在任意一点x a连续. 证(1), 0, 要使 | 1 , x 2 , 1 , 02 | x2 1, x ,12.由于x2 1, x ,12x 2 , 只需x 2 ,| x | , 取 , 则当 | x | 时有 | 1 , x 2 , 1 , 0 2 | , 故 1 , x 2 在x0连续. (2)(1), 0, 要使 | sin 5 x , sin 5a | 2 | cos 由于2 | cos 5x , 5a 5( x , a ) || sin |. 2 25 x , 5a 5( x , a) || sin | 5 | x , a |, 只需5 | x , a | ,| x , a | , 2 2 5取 , 则当 | x , a | 时有 | sin 5 x , sin 5a | , 故 sin 5 x在任意一点x a连续. 5 2.设y f ( x)在x0处连续且f ( x0 ) 0, 证明存在 0使得当 | x , x0 | 时f ( x) 0. 证由于f ( x)在x0处连续, 对于 f ( x0 ) / 2, 存在存在 0使得当 | x , x0 | 时 f ( x) , f ( x0 ) | f ( x0 ) / 2, 于是f ( x) f( x0 ) , f ( x0 ) / 2 f ( x0 ) / 2 0. 3.设f ( x)在(a, b)上连续, 证明 |f ( x) | 在( a, b)上也连续, 并且问其逆命题是否成立 ? 证任取 x0 (a, b), f 在x0连续.任给 0, 存在 0使得当 | x , x0 | 时 | f ( x) , f ( x0 ) | , 此时 || f ( x) | , | f ( x0 ) || | f ( x) , f ( x0 ) | , 故 | f | 在x0连续.其逆命题 1, x是有理数不真, 例如f ( x) 处处不连续, 但是|f ( x) | 1处处连续. ,1, x是无理数 4.适当地选取a,使下列函数处处连续: 1 , x 2 , x 0, ln(1 , x), x 1, (1) f ( x) (2) f ( x) x 0;a arccos x, x 1. a , x 解(1) lim f ( x) lim 1 , x 2 1 f (0), lim f ( x) f (0)a 1.x 0 , x 0, x 0,(2) lim f ( x) lim ln(1 , x) ln 2 f (1), lim f ( x) lim a arccosx ,a f (1) ln 2,x 1, x 1, x 1, x 1,a , ln 2. 5.利用初等函数的连续性及定理3求下列极限 : (1) lim cosx ,1, x , x 1, x , x cos lim cos 0 1. x , x x 2 2.lim sin 2 x 2(2) lim xx 2 x 0x(3) lim e sin 3 x e x 0 sin 3 x e 3 . (4) lim arctanxsin 2 xx4 , 8 x4 , 8 arctan lim 2 arctan1 . 2 x x , 1 x ,1 4-5-(5) lim ( x 2 , 1 , x 2 , 2) | x | lim ( x 2 , 1 , x 2 , 2) | x | xx 3| x |3 3 lim . lim 2 2 2 2 x x 2 x ,1 , x , 2 1 , 1/ x , 1 , 2 / x 6.设 lim f ( x) a 0, lim g ( x) b, 证明 lim) f ( x) g ( x ) a b .x x0 x x0 x x0证 lim) f ( x) g ( x ) lim)e(ln f ( x )) g ( x ) e x x0x x0 x x0lim [(ln f ( x )) g ( x )]eb ln a a b .7.指出下列函数的间断点及其类型, 若是可去间断点, 请修改函数在该点的函数值, 使之称为连续函数: (1) f ( x) cos ( x , [ x]), 间断点n Z,第一类间断点. (2) f ( x) sgn(sin x), 间断点n , n Z, 第一类间断点. x 2 , x 1, (3) f ( x) 间断点x 1, 第一类间断点. 1/ 2, x 1. x 2 , 1, 0 x 1 (4)f ( x) 间断点x 1, 第二类间断点. ,1 x 2, sin x ,1 1 2 , x , 0 x 1, (5) f ( x) x,1 x2, 间断点x 2, 第一类间断点. 1 , 2 x 3. 1 , x8.设y f ( x)在R上是连续函数, 而y g ( x)在R上有定义, 但在一点x0处间断. 问函数h( x) f ( x) , g ( x)及 ( x) f ( x) g ( x)在x0点是否一定间断? 解h( x) f ( x) , g ( x)在x0点一定间断.因为如果它在x0点连续, g ( x) ( f ( x) , g ( x)) , f ( x)将在x0点连续,矛盾.而( x) f ( x) g ( x)在x0点未必间断.例如f ( x) 0, g ( x) D( x).习题 1.6-6-1.证明 : 任一奇数次实系数多项式至少有一实根. 证设P ( x)是一奇数次实系数多项式,不妨设首项系数是正数,则 lim P ( x) , ,x , x ,lim P ( x) , , 存在A, B, A B, P ( A) 0, P ( B ) 0, P在[ A, B]连续,根据连续函数的中间值定理, 存在x0 ( A, B), 使得P ( x0 ) 0. 2.设0 1, 证明对于任意一个y0 R, 方程y0 x , sin x有解, 且解是唯一的. 证令f ( x) x , sin x, f ( , | y0 | ,1) , | y0 | ,1 , , | y0 | y0 , f (| y0 | ,1) | y0 | ,1 , |y0 | y0 , f 在[, | y0 | ,1,| y0 | ,1]连续,由中间值定理, 存在 x0 [, | y0 | ,1,| y0 | ,1], f ( x0 ) y0 .设x2 x1 , f( x2 ) , f ( x1 ) x2 , x1 , (sin x2 , sin x1 ) x2 , x1 , | x2 , x1 | 0, 故解唯一. 3.设f ( x)在(a, b)连续, 又设x1 , x2 (a,b), m1 0, m2 0, 证明存在 (a, b)使得 f ( ) m1 f ( x1 ) , m2 f ( x2 ) . m1 , m2 m1 f ( x1 ) , m2 f ( x1 ) m1 f ( x1 ) , m2 f ( x2 ) m1 f ( x2 ) , m2 f ( x2 ) f ( x2 ), m1 , m2 m1 , m2m1 , m2证如果f ( x1 ) f ( x2 ), 取 x1即可.设f ( x1 ) f ( x2 ), 则 f ( x1 ) 在[ x1 , x2 ]上利用连续函数的中间值定理即可. 4.设y f ( x)在[0,1]上连续且0 f ( x)1, ,x [0,1].证明在存在一点t [0,1]使得 f (t ) t. 证g (t ) f (t ) ,t , g (0) f (0) 0, g (1) f (1) , 1 0.如果有一个等号成立, 取t为0 或1.如果等号都不成立, 则由连续函数的中间值定理, 存在t (0,1), 使得g (t ) 0, 即f (t ) t. 5.设y f ( x)在[0, 2]上连续, 且f(0) f (2).证明在[0, 2]存在两点x1与x2 , 使得 | x1 , x2 | 1, 且f( x1 ) f ( x2 ). 证令g ( x)f ( x , 1) , f ( x), x [0,1].g (0) f (1) , f (0), g (1) f (2) , f(1) f (0), f (1) , g (0).如果g (0) 0, 则 f (1) f (0), 取x1 0, x2 1.如果g (0) 0, 则g (0), g(1)异号,由连续函数的中间值定理, 存在 (0,1)使得g ( ) f ( , 1) , f ( ) 0, 取x1, x2 , 1.第一章总练习题-7-1.求解下列不等式 : 5x , 8 () 12. 3 | 5x , 8 | 14 2 解 2. | 5 x , 8| 6,5 x , 8 6或5 x , 8,6, x 或x . 3 5 5 2 (2) x , 3 3, 5 2 解 , 3 x , 3 3, 0 x 15. 5 (3) | x , 1| | x , 2 | 1 解( x , 1) 2 ( x , 2) 2 , 2 x , 1 ,4 x , 4, x . 2 2.y 2 x , | 2 , x |, 试将x表示成y的函数. 设1 解当x 2时, y x , 2, y 4, x y , 2;当x 2时, y 3x , 2, y 4, x ( y ,2). 3 y , 2, y 4 x 1 3 ( y , 2), y 4. 1 3.求出满足不等式 1 , x 1 , x的全部x. 2 解x ,1.2 1 , x x , 2, 4(1 , x) x 2 , 4 x , 4, x 2 0.x ,1, x 0. 4.用数学归纳法证明下列等式 : 1 23 n n,2 (1) , 2 , 3 , , n 2 , n . 2 2 2 2 2 1, 2 1 证当n 1时,2- 1 , 等式成立.设等式对于n成立,则 2 2 1 2 3 n ,1 1 2 3 n n ,1 , 2 , 3 , , n ,1 , 2 , 3 , , n ,n ,1 2 2 2 2 2 2 2 2 2 n , 2 n ,1 2n , 4 , (n ,1) (n , 1) , 3 2 , n , n ,1 2 , 2, , n ,1 2 2 2 2n ,1 即等式对于n , 1也成立.故等式对于任意正整数皆成立. (2)1 , 2 x , 3 x , , nx2 n ,11 , (n , 1) x n , nx n ,1 ( x 1). (1 , x) 21 , (1 , 1) x n , 1x1,1 (1 , x)2 证当n 1时, 1, 等式成立. (1 , x) 2 (1 , x) 2 设等式对于n成立,则 1 , 2 x , 3 x 2 , , nx n ,1 , (n , 1) x n 1 , (n , 1) x n , nx n ,1 , (n , 1) x n 2 (1 , x)-8-1 , (n , 1) x n , nx n ,1 , (1 , x)2 (n , 1) x n (1 , x) 2 1 , (n , 1) x n , nx n ,1 , (1 , 2 x , x 2 )( n , 1) x n (1 , x) 21 , (n , 1) x n , nx n ,1 , ( x n ,2 x n ,1 , x n , 2 )(n , 1) (1 , x) 2 1 , (n , 1) x n , nx n ,1 , ( x n , 2 x n ,1 , x n ,2 )(n , 1) (1 , x) 2 1 , (n , 2) x n ,1 , (n , 1) x n , 2 , (1 , x) 2即等式对于n , 1成立.由归纳原理, 等式对于所有正整数都成立. 5.设f ( x) | 2 , x | , | x | ,2 x (1)求f (,4), f (,1), f (,2), f (2)的值; (2)将f ( x)表成分段函数; (3)当x 0时f ( x)是否有极限: (4)当x ,2时是否有极限? 解(1) f (,4) 2,4,2 1 ,1 , 2 ,2 , 2 4,2,2 ,1, f (,1) 2, f (,2) 2, f (2)0. ,4 ,1 ,2 2 ,4 / x, x ,2; (2) f ( x) 2, ,2 x 0; 0, x 0. (3)无因为lim f( x) 2, lim f ( x) 0 lim f ( x). .x 0 , x 0, x 0,(4)有. lim f ( x)lim ( ,4 / x) 2, lim f ( x) lim 2 2 lim f ( x), lim f ( x) 2.x ,2 , x ,2 , x ,2 , 2 x ,2 , x ,2 , x ,26.设f ( x) [ x , 14], 即f ( x)是不超过x , 14的最大整数.23 (1)求f (0), f , f ( 2)的值; 2 (2) f ( x)在x 0处是否连续 ? (3) f ( x)在x2处是否连续 ? 1 3 9 解(1) f (0) [ ,14] ,14, f , 14 ,6 ,,7. f ( 2) [ ,12] ,12. 4 2 4 (2)连续因为 lim f ( x) lim[ y , 14] ,14f (0). .x 0 y 0 ,(3)不连续因为 lim f ( x) ,12, lim f ( x) ,11. .x 2 , x 2 ,7.设两常数a, b满足0 a b, 对一切自然数n, 证明 : (1) b n ,1 , a n ,1b n ,1 , a n ,1 (n , 1)b n ;(2)( n , 1) a n . b,a b,a-9-证b n ,1 , a n ,1 (b , a )(b n , b n ,1a , , a n ) b n , b n ,1b , , b n (n , 1)b n , b,a b,a b n ,1 , a n ,1类似有 (n , 1)a n . b,an n ,11 1 8.对n 1, 2,3, , 令an 1 , , bn 1 , . n n 证明 : 序列{an }单调上升, 而序列{bn }单调下降,并且.an bn . 证令a = 1 , 1 1 , n n ,11 1 , b 1 , , 则由7题中的不等式, n ,1 nn ,11 , 1 , n ,1 1 1 , n n ,1 1 , 1 , n ,1n1 (n , 1) 1 , , n 1 1 (n , 1) 1 , n n(n , 1)n ,1 nn1 1 , n 1 1 , nn ,1n ,1n ,11 1 1 , 1 , 1 , n n n ,1n ,1,1 1 1 , 1 , n n ,1n.n ,1 n ,11 1 n 1 , , 1 , 1 n n ,1 (n , 1) 1 , 1 1 n ,1 , n n ,11 1 1 (n , 1) 1 , 1 , n , 1 n(n , 1) n 1 1 1 1 ,1 , n ,1 n nn n n ,1 n n ,11 , 1 , n ,1n ,1n ,11 , 1 , n ,1n ,11 1 1 1 1 , ,1, 1 , n ,1 n n ,1 n2.1 1 1 我们证明 , 1 , 1 , . n n ,1 n ,1 1 12 1 ,1, 1, , n n ,1 n , 1 (n , 1) 2 1 1.最后不等式显然成立. n(n , 1) (n , 1) 2 1 1 当n 时, 1 , e, 1 ,n n9.求极限- 10 n n ,11 1 e, 故 1 , e 1 , n nnn ,1.1 1 1 1 lim 1 ,2 1 , 2 1 , 21 ,2 n 234 n 1 1 1 1 解 1 , 21 ,2 1 , 2 1 , 2 234 n 1 3 2 4 35 n n ,1 1 n ,1 1(n ). 2 2 3 34 4 n n n 2 2 nx 10.作函数f ( x) lim 2 ( a 0)的图形.n nx , a 0, x 0; nx 解f ( x) lim 2 n nx , a 1/ x, x 0.11.在 ? 关于有界函数的定义下, 证明函数f ( x)在区间[ a, b]上为有界函数的充要条件为存在一个正的常数M 使得 | f ( x) | M , ,x [a, b]. 证设存在常数M 1 , N 使得M1 f ( x)N , ,x [a, b], 取M max{| M 1 |,| N |} , 1, 则有 | f ( x) | M , ,x [ a, b]. 反之, 若存在一个正的常数M 使得 | f ( x) | M , ,x [ a, b], 则 , M f ( x) M , ,x [a, b]. 12.证明 :若函数y f ( x)及y g ( x)在[a, b]上均为有界函数, 则f ( x) , g ( x )及f ( x ) g ( x ) 也都是[a, b]上的有界函数. 证存在M 1 , M 2 ,| f ( x) | M 1 ,| g ( x) | M 2 , ,x [ a, b]. | f ( x) , g ( x)| | f ( x) | , | g ( x) | M 1 , M 2 , | f ( x) g ( x) | | f ( x) || g ( x) | M 1M 2 , ,x [ a, b]. 13.证明 : f ( x) 1 cos 在x 0的任一邻域内都是无界的, 但当x 0时f ( x )不是无穷大量.x x 1 1 证任取一个邻域(, , ), 0和M 0, 取正整数n, 满足和n M , 则f ( ) n M , n n 1 故f ( x)在(, , )无界.但是xn 0, f ( xn ) (2n , 1/2) cos(2n , 1/ 2) 0 , 2n , 1/ 2 故当x 0时f ( x )不是无穷大量.- 11 -14.证明 lim n( x n , 1) ln x( x 0).n 1 1 ln x 证令x , 1 yn , 则 ln x ln(1 , y ), n .lim yn lim x n , 1 0. n nln(1 , y ) n 1 n1ln(1 , y ) 注意到 lim lim ln(1 , y ) y ln lim(1 , y ) y ln e 1, y 0 y 0 y 0 y1 1我们有n( x n , 1)1yn ln x ln x(n ). ln(1 , yn )15.设f ( x)及g ( x)在实轴上有定义且连续.证明 : 若f ( x)与g ( x)在有理数集合处处相等,则它们在整个实轴上处处相等. 证任取一个无理数x0 , 取有理数序列xn x0 , f ( x0 ) lim f ( xn ) lim g ( xn ) g ( x0 ).n n16.证明 lim1 , cos x 1 . x 0 x2 2 2sin 2x 2 2 2 lim 2sin y 1 lim sin y 1 2 1 . 1 y 0 x2 4 y2 2 y 0 y2 2 x,a x ln(1 , y ) e ,e 17.证明 : (1) lim 1;(2) lim ea . y 0 x 0 y x 1 , cos x 证 lim lim x 0 x 0 x2 ln(1 , y ) 证(1) lim lim ln(1 , y ) y ln lim(1 , y ) y ln e 1. y 0 y 0 y0 y1 1e x , a , ea e a (e x , 1) ex ,1 a y 1 lim e a lim e lim ea x 0 x 0 x 0 y 0 ln(1 , y ) ln(1 , y ) x x x lim y 0 y 1 ea ea . 1 18.设y f ( x)在a点附近有定义且有极限 lim f ( x) 0, 又设y g ( x)在a点附近有 (2) limx a定义,且是有界函数.证明 lim f ( x) g ( x) 0.x a证设 | g ( x) | M , 0 | x , a | 0 .对于任意 0, 存在 1 0, 使得当0 | x , a |1时 | f ( x) | / M .令 min{ 1 , 0 }, 则0 | x , a | 时,| f ( x) g ( x) | | f ( x) || g ( x) |MM , 故 lim f ( x) g ( x) 0.x a19.设y f ( x)在(, , , )中连续, 又设c为正的常数, 定义g ( x)如下 f ( x) 当 | f ( x) | c g ( x ) c 当f ( x) c ,c 当f ( x) ,c 试画出g ( x)的略图, 并证明 g ( x)在(, , , )上连续.- 12 -证(一)若 | f ( x0 ) | c, 则存在 0 0, 当 | x , x0 | 0时|f(x)|<c,g(x)=f(x),x x0lim g ( x) lim f ( x) f ( x0 ) g ( x0 ).x x0若f ( x0 ) c, 则存在 0 0,当 | x , x0 | 0时f ( x) c,g(x)=c,x x0lim g ( x) lim c c g ( x0 ).x x0若f ( x0 ) c, 则g ( x0 ) c.对于任意 0, 不妨设 c, 存在 0, 使得当 |x , x0 | 时 | f ( x) , c | .设 | x , x0 | .若f ( x) c, 则g ( x) f( x),| g ( x) , g ( x0 ) | | f ( x) , c | , 若f ( x) c, 则g ( x) c,| g ( x) - g ( x0 ) | 0 . 证(二)利用g ( x)min{ f ( x), c} , max{ f ( x), ,c} , f ( x). max{ f1 ( x), f 2 ( x)} (| f1 ( x) , f 2 ( x) | , f1 ( x) , f 2( x)) / 2. min{ f1 ( x), f 2 ( x)} (, | f1 ( x) , f 2 ( x) | ,( f1 ( x) , f 2 ( x)) / 2. 1 20.设f ( x)在[a, b]上连续, 又设 [ f ( x1 ) , f ( x2 ) , f ( x3 )], 3 其中x1 , x2 , x3 [a, b].证明存在一点c [a, b], 使得f (c) . 证若f ( x1 ) f ( x2 ) f ( x3 ), 则 f ( x1 ), 取c x1即可. 否则设f ( x1 ) min{ f ( x1 ), f ( x2 ), f ( x3 )}, f ( x3 ) min{ f( x1 ), f ( x2 ), f ( x3 )}, f ( x1 )f ( x3 ), f 在[ x1 , x3 ]连续, 根据连续函数的中间值定理, 存在一点c [a, b], 使得f (c). 21.设 y f ( x)在点x0连续而g ( x)在点x0附近有定义, 但在x0不连续问kf ( x) , l g( x ) 是否在x0连续, 其中k , l为常数. 解如果l 0,kf( x) , l g( x)在x0连续;如果l 0,kf ( x) , l g( x )在x0不连续,因否则 g ( x) [[kf ( x) , lg( x)] , kf ( x)] / l 将在x0连续. 22.证明Dirichlet函数处处不连续. 证任意取x0 .取有理数列xn x0 , 则D( xn ) 1; 取无理数列xn x0 , 则D( xn ) 0; 故 lim D( x)不存在, D( x)在x0不连续.x x023.求下列极限: 1 1, x (1) lim 0;(2) xlim (arctan x) sin 0 0; x 1 ,2 x , x 2 tan 5 x tan 5 x / x 5 (3) lim lim 5. 2 2 2 x 0 ln(1 , x ) , sin x x 0x[[ln(1 , x )] / x ] , sinx / x 1| x|(4) lim( x )x 11 x ,1lim(1 , y )1/ y e.y 024.设函数y f ( x)在[0, , )内连续, 且满足0 f ( x) x.设a1 0是一任意数, 并假定 a2 f (a1 ), a3 f (a2 ), , 一般地an ,1 f (an ).试证明{an }单调递减, 且极限 lim an 存在.n若l lim an , 则l是方程f ( x) x的根,即f (l ) l.n证an ,1 f (an ) an ,{an }单调递减.又an ,1 f (an ) 0(n 1, 2, ),{an }单调递减有下界,- 13 -故an有极限.设l lim an , 则l lim an ,1 lim f (an ) f (lim an ) f(l ).n n n n25.设函数y E ( x)在(, , , )内有定义且处处连续, 并且满足下列条件 : E (0) 1, E (1)e, E ( x , y ) E ( x) E ( y ). 证明E ( x) e x (,x (, , , )). 证用数学归纳法易得E ( x1 ,, xn ) E ( x1 ) E ( xn ).于是E (nx) E ( x) n . 设n是正整数, 则E (n) E (1 , , 1) E (1) n e n . 1 E (0) E (n , (, n)) E ( n) E ( , n) e n E ( , n), E ( ,n) e , n .于对于任意整数 E ( n) e n .1 1 1 1 1 对于任意整数n, E (1) E (n ) E (n) E ( ) e n E ( ), E ( ) e n . n n nn m 1 m 1 1 n E ( ) E (m ) E ( ) e e n .即对于所有有理数r , E (r ) e r . n n n 对于无理数x, 取有理数列xn x,由E ( x)的连续性, m mE ( x) lim E ( xn ) lim e xn e n (e x的连续性) e x .n nlim xn习题 2.11.设一物质细杆的长为l , 其质量在横截面的分布上可以看作均匀的现取杆的左端点为坐标原点O, 杆所在直线为x轴设从左端点到 . . 细杆上任一点x之间那一段的质量为m( x) 2 x 2 (0 x l ) (1)给自变量x一个增量 x, 求的相应增量 m; m ,问它的物理意义是什么? x m (3)求极限 lim ,问它的物理意义是什么? x 0 x (2)求比值解(1) m 2( x , x) 2 , 2 x 2 2( x 2 , 2 x x , x 2 ) , 2 x 2 2(2 x x , x 2 ). m 2(2x x , x 2 ) m 2(2 x , x). 是x到x , x那段细杆的平均线密度. x x x m m (3) lim lim 2(2 x , x) 4 x. lim 是细杆在点x的线密度. x 0 x x 0 x0 x (2)- 14 -2.根据定义, 求下列函数的导函数 : (1) y ax3 ;(2) y 2 px , p 0;(3) y sin 5 x. 解(1) y lim a( x , x)3 , ax3 x 0 x 3 2 ( x , 3x x , 3x x 2 , x 3 ) , x 3 a lim a lim(3x 2 , 3x x , x 2 ) 3ax 2 . x 0 x 0 xx 0(2) y lim 2 p lim 2 p lim2 p( x , x) , 2 px x , x , x 2 p lim x 0 x x( x , x , x )( x , x , x ) x 2 p lim x 0 x 0 x ( x, x , x( x , x , x ) x)x 02p 1 . x , x , x 2 x5(2 x , x) 5 x 2 cos sin sin 5( x , x) , sin 5 x 2 2 (3) y lim lim x 0 x 0 xx 5 5(2 x , x) 5 x 5 x 2 cos sin sin 5(2 x , x) 2 2 5 lim cos 2 5cos 5 x. lim 2lim x 0 x 0 x 0 5 x 5 x 2 2 23.求下列曲线y f ( x)在指定点M ( x0 , f ( x0 ))处的切线方程 : (1) y 2 x , M (0,1); (2) yx 2 , 2, B(3,11). 解(1) y 2 x ln 2, y (0) ln 2, 切线方程y , 1 ln2( x - 0), y (ln 2) x , 1. (2) y 2 x, y (3) 6, 切线方程 : y , 11 6( x , 3). 4.试求抛物线y 2 2 px( p 0)上任一点M ( x, y )( x 0, y 0)处的切线斜率, p 并证明:从抛物线的焦点F , 0 发射光线时, 其反射线一定平行于x轴. 2 - 15 -证y 2 px , y2p p p , 过点M 的切线PMN 方程:Y , y ( X , x). y 2 2 px yp y2 切线与x轴交点N(X 0 ,0),, y ( X 0 , x), X 0 x , , x. y p p p p FN , x,FM x , , y 2 x , , 2 px 2 2 2 p p p x 2 , px , x ,x , FN , 故 FNM FMN . 2 2 2 过M 作PQ平行于x轴, 则 PMQFNM FMN .5.曲线y x 2 , 2 x , 3上哪一点的切线与直线y 4 x , 1平行, 并求曲线在该点的切线和法线方程. 解 y 2 x , 2 4, x0 1, y0 6, k 4 1 25 1 切线方程:y , 6 4( x , 1), y4 x , 2.法线方程 : y , 6 , ( x , 1), y , x , . 4 4 46.离地球中心r处的重力加速度g是r的函数, 其表达式为 GMr R 3 , r R;g (r )其中R是地球的半径, M 是地球的质量, G是引力常数. GM , r R r2 (1)问g (r )是否为r的连续函数 : (2)作g (r )的草图; (3) g (r )是否是r的可导函数. 解明显地,r R时g (r )连续.lim g (r ) limr R, r R, r R,2222GMr GM 2 , R3 Rlim g (r ) limr R,GM GM 2 lim g (r ), g (r )在r R连续. r R, r2 R(2)(3)r R时g (r )可导. g , ( R) GM 2GM , g , ( R) , 3 g , ( R), g (r )在r R不可导. 3 R R- 16 -7.求二次函数P( x),已知 : 点(1,3)在曲线y P ( x)上, 且P (0) 3, P (2) 1. a , b , c3 解P ( x) ax , bx , c, P ( x) 2ax , b. b 3 4a , b 121 1 1 1 b 3, a , , c 3 , (a , b) , P( x) , x2 ,3 x , . 2 2 2 28.求下列函数的导函数 : (1) y 8 x3 , x , 7, y 24 x 2 , 1. (2) y (5 x , 3)(6 x 2 , 2), y5(6 x 2 , 2) , 12 x(5 x , 3) 90 x 2 , 36 x , 10. (3) y ( x , 1)( x , 1) tan x ( x 2 , 1) tan x, y (2x) tan x, ( x 2 , 1) sec 2 x. 9 x , x2 (9 , 2 x)(5 x , 6) , 5(9 x , x 2 ) 5x 2 , 12 x , 54 , y . 5x , 6 (5 x , 6) 2(5 x , 6) 2 1, x 2 2 (5) y ,1 , ( x 1), y . 1, x 1, x (1 , x) 2 (4)y2 ,6 x 2 ( x 1), y3 . x3 , 1 ( x , 1) 2(6) y (7) yx2 , x , 1 (2 x , 1)e x , e x ( x 2 , x , 1) , x 2 , x , 1 , y . exe2 x ex (8) y x x , y 10 x ,x x ln10 10 x (1 , x ln10). 10 10 sin x x cos x , sin x , y cos x ,x sin x , . x x2 (10) y e xsin x, y e x sin x , e x cos x e x (sin x , cos x). (9) y x cos x ,9.定义 : 若多项式P( x)可表为P( x) ( x , x0 ) m g ( x), g ( x0 ) 0则称x0是P ( x)的m重根.今若已知x0是P ( x)的k重根,证明x0是P ( x)的(k , 1)重根 (k 2). 证P ( x) ( x , x0 )k g ( x), g ( x0 ) 0 P ( x) k ( x , x0 ) k ,1 g ( x) , ( x , x0 ) kg ( x) ( x , x0 ) k ,1 (kg ( x) ,( x , x0 ) g ( x)) ( x , x0 ) k ,1 h( x), h( x0 ) kg (0 x) 0,由定义x0是P ( x)的(k , 1)重根.- 17 -10.若f ( x)在( ,a, a)中有定义, 且满足f ( , x) f ( x), 则称f ( x)为偶函数.设f ( x) 是偶函数,且f (0)存在, 试证明f (0) 0. f ( x) , f (0) f (, x) , f (0) f ( ,x) , f (0) lim , lim , f (0), f (0) 0. x 0 x 0 x x ,x f ( x0 , x) , f ( x0 , x) 11.设f ( x)在x0处可导, 证明 lim 2 f( x0 ). x 0 2 x f ( x0 , x) , f ( x0 , x) 1 f ( x0 , x) , f ( x0 ) f ( x0 , x) , f ( x0 ) 证 lim lim , x 0 2 x 2 x 0 x x 证f (0) = lim x 01 f ( x0 , x) , f ( x0 ) f ( x0 , x) , f ( x0 ) lim ,2 x 0 x , x f ( x0 , x) , f ( x0 ) f ( x0 , x) , f ( x0 ) 1 1 lim , lim x 0 2 [ f( x0 ) , f ( x0 )] f( x0 ). x 0 2 x , x12.一质点沿曲线y x 2 运动, 且已知时刻t (0 t / 2)时质点所在位置 P(t )( x(t ), y (t ))满足 : 直线OP与x轴的夹角恰为t.求时刻t时质点的位置速度及加速度.y (t ) x 2 (t ) 解 x(t ) tan t , y (t ) tan 2 t , x(t ) x(t ) 位置(tan t , tan 2 t ), v (t )(sec2 t , 2 tan t sec 2 t ), v (t ) (2sec2 t tan t , 2sec 4 t , 4tan 2 t sec 2 t ) 2sec2 t (sec2 t , 2tan 2 t ).y=x2- 18 -13.求函数 x ,x 0 f ( x) 1 , e1/ x 0, x 0 在x 0的左右导数. x x 1/ x1/ x 1 1 解f - (0) lim 1 , e lim 1, f + (0) lim 1 , e lim 0. 1/ x x 0 ,x 0 , 1 , e x0 , x 0 , 1 , e1/ x x x 14.设f ( x) | x , a | ( x), 其中 ( x)在x a处连续且 (a) 0.证明f ( x)在x a不可导. (a , x) (x) ( x , a) ( x) 证f , (a) lim , (a), f+ (a) lim ( a) f - ( a). x a , x a , x,a x,a习题 2.2- 19 -1.下列各题的计算是否正确, 指出错误并加以改正 : (1)(cos x ) , sin x , 错.(cos x ) , sin x x , (2)[ln(1 , x)] (3) x 2 sin x . 2 x1 1 1 , 错.[ln(1 , x)] (1 , x) . 1, x 1, x x ,1 x 1 , x2 , x 2 , 1 , x 2 2 x , 错.1 , x2,,x 2 1 , x 2 , x 2 , 2x 1 , x2 , x3,1 , x2 , , x2 , 2 x , 3x3,,1 , x2, 2 x 1 , x2, x2x 1 , x2. 1 , x2 1 (4) ln | x , 2sin 2 x | x , 2sin 2 x (1 , 4sin x) cos x, 错. 1 ln | x , 2sin 2 x | x , 2sin 2 x (1 , 4sin x cos x). 2.记f ( g( x)) f (u ) |u g ( x ) .现设f ( x)x 2 , 1. 1 , x2 (1)求f ( x), f (0), f ( x 2 ), f (sin x); d d (2)求f ( x 2 ), f (sin x); dx dx (3) f( g ( x))与 f ( g ( x)) 是否相同 ? 指出两者的关系. 解(1) f ( x) 2 x, f (0) 0, f ( x 2 ) 2 x 2 , f (sin x) 2sin x. (2) d f ( x 2 ) f ( x 2 ) , x 2 , 2 x 2 2 x 4x 3 . dxd f (sin x) f (sin x)(sin x) 2sin x cos x sin 2 x. dx (3) f ( g ( x))与 f ( g ( x))不同, f ( g ( x)) f ( g ( x)) g ( x).3.求下列函数的导函数: (1) y 2 2 x 2 3 6 x2 , y , , . 2 2 3 3 x3 , 1 , x , 1, , x , 1,(2) y sec x, y , (cos x) ,1 , ,(cos x) ,2 (cos x) ,(cos x) ,2 ( ,sin x) tan x sec x. (3)y sin 3 x , cos 5 x, y 3cos 3 x , 5sin 5 x. (4) y sin 3 x cos 3x, y3sin 2 x cos x cos3x , 3sin 3 x sin 3 x 3sin 2 x(cos x cos 3x , sin x sin 3x) 3sin 2 x cos 4 x.- 20 -1 , sin2 x 2sin x cos x cos x 2 , (1 , sin 2 x)( , sin x 2 )2 x (5) y ,y cos x 2 cos 2 x 2 sin 2 x cos x 2 , 2 x(1 , sin 2 x)(sin x 2 ) .cos 2 x 2 1 (6) y tan 3 x , tan x , x, y tan 2 x sec 2 x , sec 2 x , 1 3 2 tan x sec 2 x , tan 2 x tan 2 x(sec 2 x , 1) tan 4 x.(7) y e ax sin bx, y ae ax sin bx , be ax cos bx e ax (a sin bx , b cos bx). x (8) y cos5 1 , x 2 , y 5cos 4 1 , x 2 ( , sin 1 , x 2 ) 1 , x2 , 5 x cos 4 1 , x 2 sin 1 , x 2 1 , x2 .1 1 x x (9) y ln tan , , y sec2 , 2 x 2 4 2 4tan , 2 4 1 1 1 1 2 x x x x tan , cos 2 ,2sin , cos , 2 4 2 4 2 4 2 4 1 1 sec x. cos x sin( x , ) 2 1x,a 1 x , a ( x , a) , ( x , a) 1 (10) y ln (a 0, xa ), y 2 . 2 2a x , a 2a x , a ( x , a) x , a24.求下列函数的导函数 : x (1) y arcsin (a 0), y a 1 1 . 2 a2 , x2 x a 1,a 1 x 1 1 1 1 (2) y arctan (a 0), y 2 . 2 a a a x a a , x2 1, ax2 2 2 x arccos x , (3) y x arccos x(| x | 1), y . 1 , x2 1 1 ,1 1 (4) y arctan , y , . 1 x2 x 1 , x2 1, 2 x 2 x 2 a x (5) y a , x 2 , arcsin ( a 0), 2 2 a 1- 21 -y1 2 x ,2 x a2 a , x2 , , 2 2 a2 , x2 21 2 x a 1, a11 2 x2 a2 2 a ,x , , a2 , x2 . 2 2 2 2 2 a ,x a ,x x 2 a2 x , x2 ,a2 2 (6) y x , a , ln (a 0) 2 2 aa2 1 x , 1 , 2 x2 , a2 2 x , x2 , a2 x , a2 1 2 x2 a2 x , a2 , , x2 , a2 . 2 2 2 2 2 2 x ,a2 x ,a 2x (7) y arcsin 2 , x 1. x ,1 1 2( x 2 , 1) , 2 x 2 x 1 1 , x 2 2sgn(1 , x 2 ) y 2 2. 2 ( x 2 , 1) 2 x2 , 1 x ,1 x ,1 4x2 1, 2 ( x , 1) 2 y 1 2 x x ,a2 , 2 2 x (8) y y a ,b x arctan tan ( a b 0). a,b 2 a 2 , b2 2 22 21 a ,b x 1 sec2 2 2 a , b 1 , a , b tan 2 x a , b a,b 2 1 x 1 sec 2 x 2 ( a , b) cos 2 x , ( a , b) sin 2 x a , b , (a , b) tan 2 2 2 2 1 .a ,b cos x (9) y (1 , x )(1 , 2 x )(1 , 3 x ), ln y ln(1 ,x ) , ln(1 , 2 x ) , ln(1 , 3 x ) y / y 1 2(1 , x ) x , 2 3 , , 2(1 , 2 x ) 2 x 2(1 , 3 x ) 3 x1 2 3 y y , , . 2(1 , x ) x 2(1 , 2 x ) 2 x 2(1 , 3 x ) 3 x 1, 4x (10) y 1 , x , 2 x 2 , y . 2 1 , x , 2 x2 x (11) y x 2 , a 2 , y . x2 , a2 ,x (12) y a 2 , x 2 , y . a2 , x2- 22 -x 1 . 1 , 2 x , x2 , a2 x , a2 x2 , a2 2 1 (14) y ( x , 1) 3 (3 x , 1) 2 (2 , x).ln yln( x , 1) , ln(3 x , 1) , ln(2 , x), 3 3 y 1 2 1 ,1 , , y x , 1 3x , 1 3 2 , x (13) y ln( x , x 2 , a 2 ), y1 2 1 ,1 1 y y , , . x , 1 3x , 1 3 2 , x (15) y e x , ee , y e x ,ee e xe x (1 , e e ).x x x(16) y x a , a x , a a (a 0).a a xy a a x a aa xaaa,1, a x ln a (ax a ,1 ) , a a ln aa x ln aa x a x,1, a ln aa x x a ,1 , a a a x ln 2 a.5.一雷达的探测器瞄准着一枚安装在发射台上的火箭,它与发射台之间的距离是400m.设t=0时向上垂直地发射火箭,初速度为0,火箭以的匀加速度8m/s2垂直地向上运动;若雷达探测器始终瞄准着火箭.问:自火箭发射后10秒钟时,探测器的仰角 (t )的变化速率是多少? 1 x(t ) t 2 解x(t ) 2 4t 2 , tan (t ) 8t , 2 400 100t2 1 t 1 10 (t ) arctan , (t ) , (10) 0.1(弧度 / s). 2 2 2 2 50 100 t 50 10 1, 1, 100 100 6.在图示的装置中, 飞轮的半径为2m且以每秒旋转4圈的匀角速度按顺时针方向旋转.问:当飞轮的旋转角为 = 时,活塞向右移动的速率是多少? 2- 23 -解x(t ) 2 cos8 t , 36 , 4sin 2 8 t , ,8sin 8 t cos8 t (8 ) x(t ) ,16 sin 8 t , , 236 , 4sin 2 8 t 1 1 (t ) 8 t ,, t0 , x ( ) ,16 . 2 16 16 活塞向右移动的速率是16 m/s.习题 2.3- 24 -1.当x 0时, 下列各函数是x的几阶无穷小量 ? (1) y x , 10 x 2 , 100 x 3 .1阶. (2) y ( x , 2 , 2) sin x x sin x , 2阶. x,2, 2x (3) y x(1 , cos x) x 2sin 2 , 2阶. 2 2.已知 : 当x 0时, ( x) o( x 2 ).试证明( x) o( x). ( x) ( x) 证 2 x o(1) x o(1). x x 3.设 ( x) o( x)( x 0), ( x)o( x)( x 0).试证明: ( x) , ( x) o( x)( x 0). o(1) , o(1) o(1). x x x 上述结果有时可以写成o( x) , o( x) o( x). 证 4.计算下列函数在指定点x0处的微分: 11 (1) y x sin x, x0 / 4. y sin x , x cos x, y 1 , , dy 1 ,dx. 2 4 2 4 4 (2) y (1 , x) ( 0是常数). y (1 , x) ,1 , y (0), dy dx. 5.求下列各函数的微分: (1) y 1, x 2 2 2dx ,1 , , y , , dy , .2 1, x 1, x(1 , x) (1 , x) 2( x) , ( x)( x),( x)(2) y xe x , y e x , xe x e x (1 , x ).dy e x (1 , x )dx. 2 6.设y( x 1), 计算当x由3变到3.001时, 函数的增量和向相应的微分. x ,1 2 1 解 y = , y(3) , . 2 (x -1) 2 2 0.001 0.001 y ,1 , , dy , . 2.001 2.001 2 7.试计算5 32.16的近似值. 1 .16 解 5 32.162 5 1 , .16 / 32 2 (1 , ) 2.002. 5 32 8.求下列方程所确定的隐函数的导函数 : 1 ,1 1 ,1y 3 (1) x , y a ( a 0). x 3 , y 3 y 0, y , . 3 3 x2 3 2 3 2 3 1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题4.13212121.()32[0,1][1,2]Rolle 0,(0)(1)(2)0,()[0,1][1,2]Rolle 620,33(0,1),(1,2),()()0.332.f x x x x f f f f f x x x xx x f x f x =-+==='-+===+''=∈===2验证函数在区间及上满足定理的条件并分别求出导数为的点.处处可导故在区间及上满足定理的条件.f (x)=3x 讨论下列解1111()[1,1]Rolle ,,(1,1),()0.(1)()(1)(1),,;(2)()1(1)()(1)(1)(1)(1)(1)(1)()0,(1,1),()0.1(2)(m n m n m n m n f x c f c f x x x m n f x f x m x x n x x m nx x m mx n nx c f c m f x -----∈-'==+-='=+--+--'=+----==∈-=+'函数在区间上是否满足定理的条件若满足求使为正整数解1/32),(0).33.()ln [1,],?11(),()(1)ln ln11(1), 1.grange (1)|sin sin |||;(2)|tan tan |||,,(/2,/2);(3)ln x f f x x e c f x f e f e e c e x cy x x y x y y x x y b a b b b a ππ-'=-=='=-=-==-=--≤--≥-∈--<<不存在写出函数在区间上的微分中值公式并求出其中的应用中值定理,证明下列不等式:解222(0).(1)|sin sin ||(sin )|()||cos |||||.(2)|tan tan ||(tan )|()|sec ||||.(3)ln ln ln (ln )|()((,)).5.()(1)(4)x c x c x c aa b ax y x x y c x y x y y x x y x c y x y x b a b b a b ab a x b ac a b a a c aP x x x ===-<<'-=-=-≤-'-=-=-≥----'<=-=-=∈<=--证明多项式的导函数的证1,212,.()1,2,Rolle ,,,()(2,1),(1,1),(1,2).6.,,,:()cos cos 2cos (0,).n n P x P x c c c f x c x c x c nx π±±---=+++L L 三个根都是实根并指出它们的范围有四个实根根根据定理它的导函数有三个实根又作为四次多项式的导函数是三次多项式,最多三个实根,故的导函数的三个根都是实根,分别在区间设为任意实数证明函数在内必有根证1211()sin sin 2sin [0,]2((0)()0),()(0,).n g x c x c x c nx ng g f x πππ=+++==L 在满足定理的条件故其导函数在内必有根证22(()()7.()()(,),()0,0,(,).()():,()(),(,).(()()()()()()()()()0,()()()(),,,()(),()f xg x f x g x a b g x x a b f x g x k f x kg x x a b f x g x f x g x f x f x g x f x g x g x g x g x f x k k f x kg x g x ≠=∈''=∈'''''⎛⎫-=== ⎪⎝⎭==设函数与在内可微且证明存在常数使根据公式的一个推论存在常数使即证(,).8.()(-,)(),.:(),,,.(())()0,.,(),.9.(1)arcsin arccos /2,-11;(2)arctan .x a b f x f x k x f x kx b x k b f x kx f x k k k x f x kx b x x x x x x π∈'∞+∞=-∞<<+∞=+-∞<<+∞''-=-=-=-∞<<+∞-=-∞<<+∞+=≤≤=-∞<<+∞设在上可微且证明其中为常数证明下列等式:证证(1)2arcsin arccos arcsin arccos 0,(1,1),arcsin arccos [1,1],arcsinarccos ,arcsin 0arccos 0,arcsinarccos .22(2)arctan11x x x x x x x x x C C x x x x ππ'''+⎛⎫=+=∈-+- ⎝+==+=+='⎛⎫- ⎝=-+在连续故()=()+()210,1arctan ,00,arctan 0,(,).x x C x C x x =-=+-===-=∈-∞+∞以代入得故220210.:sin ,0/2.sin ()(0/2),(0)1,[0,/2],cos sin cos (tan )(0,/2),()0.2[0,/2],()()(0)1,0/2.211.()(,),(,),li x x x x xf x x f f xx x x x x x f f x x x f f f x f x f x a b x a b πππππππππ<<<<=<≤=--'==<=<<=<<∈证明不等式在连续在可导在严格单调递减设函数在内可微对于任意一点若证 00000000m (),lim ()().()()limlim (01)lim ()lim ().12.(Darboux )()(,),[,](,),()().::x x x x x x x x x f x f x f x f x x x f x xf x x f x y f x A B a b A B f a f b θθθη→→∆→∆→∆→→'''='+∆∆∆'==<<∆∆''=+∆==⊂''<存在则中值定理设在区间中可导又设且证明对于任意给定的00f(x +x)-f(x )证x 1011222()(),(,)().()()()0().()lim 0,)/20,()()00,()()0.()().:0()/2,()().[,]x f a f b c a b f c f a x f a f a f b f a b a xf a x f a x f a x f a f a f a x b a f b f b f a b c ηηδδδδδδ∆→+''<<∈'=+∆-'''<<=<->>∆+∆-<∆≤<+∆-<+<∆<<--<都存在使得先设存在(使得时即特别类似存在某点取最小证1,()()(),,,.(,),Fermat ()0.:()().()().()(),()()0,()()0,,(,)()()0,().f c f a f a c a c b c a b c f c f a f bg x f x x g x f x g a f a g b f b c a b g c f c f c δηηηηηηηη≤+<≠≠∈'''''=<<=-=-''''=-<=->∈'''=-==值f(c)同理是极小值点, 由引理,再设考虑由前面的结果存在使得即习题4.20000000L Hospital :212ln 2ln 21.lim lim .313ln 3ln 3cos 1sin sin 2.lim lim lim 1.ln(1)11/(1)13.lim ln(1)lim x x x x x x x x x x x x x xx x x xx →→→→→→→'-==---==-=--+-+⎛⎫-⎪⎪+⎭⎛=用法则求下列极限000/2lim lim 1lim .2tan 34.lim lim tan x x x x x x x π→→→→⎫⎛⎫==⎛⎫==-=222/222001000000001/5010003sec 3 3.sec ln(cos )(1/(cos ))(sin )5lim lim .ln(cos )(1/(cos ))(sin )ln 1/16.lim ln (0)lim lim lim 0.()7.lim lim x x a x x x x x x y x x ax ax ax a a bx bx bx b bx x x x x x x e y x e παααααα→→→---→+→+→+→+-→→+∞=-==->===-=-=505050/50/50/50220222200022250lim lim lim 0.8.lim (tan ).(tan ),lim ln lim (2)ln tan ln tan sec /tan lim lim 2lim 122(2)y y y y y y y x x x x x z x x y y e e e x y x y x xx x x x x ππππππππππ→+∞→+∞→+∞--→-→-→-→-→-→-⎛⎫⎛⎫⎛⎫==== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭==-===----()022ln 200022lim ln 01/0033000tan 0,lim lim sin 1.1ln 9.lim 1(0)lim lim ln .1arcsin arcsin 10.lim lim sin x yx x yy y xx y y y y y z z y ez ee a a aa x a a y y y y yy y πππ→-→-→-→∞→→→→→=====-->===--==20011111230111.3361ln 111.lim lim 1ln (1)ln ln 11ln lim lim ln (1)/ln (1)1/1lim .ln 22112.lim l sin y y y y y y y x x y y y y y y y y y y y y y y y y y y x e x x →→→→→→→-→==-=-⎛⎫⎛⎫-+-= ⎪ ⎪--⎝⎭⎝⎭⎛⎫⎛⎫+-== ⎪ ⎪+-+-⎝⎭⎝⎭⎛⎫== ⎪+⎝⎭--=22224200001/1/02220002011im lim 11lim lim .222arctan arctan 13.lim ,,arctan arctan 1ln (/arctan )lim ln lim lim 2(1)arctan lim 2x y x y y y y y x x x x x x x x e y e x y e e y x x y x x xx xx x x x x y x xx x x --→→--→→→→→→→----=-+-===-⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭-+⨯==-+=232001/1/3011ln ln 112arctan 1arctan 1lim lim ,633arctan lim .14.lim arctan .arctan .22ln arctan 2lim ln lim lim ln arctan (12x x x x xxx x x x x x x x x x x e x x y x x x y x x ππππ→→-→→+∞→+∞→+∞→+∞--==-=-⎛⎫= ⎪⎝⎭⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭⎛⎫- ⎪⎝⎭==-⎛⎫- ⎪⎝⎭21ln 12222200000)limlim 1,lim arctan .112arctan (1)(1)tan sec 1tan 215.lim lim lim lim lim 2.sin 1cos 1cos 1cos sin xx x x x x x x x x x x x e x x x x x x x x x x x x x x x x π-→+∞→+∞→+∞→→→→→+⎛⎫=-=-=--= ⎪⎛⎫⎛⎫⎝⎭++ ⎪ ⎪⎝⎭⎝⎭--=====---- 2000111cosh cos sinh sin cosh cos 16.limlim lim 1.22(ln 1)1(ln 1)117.lim lim lim ln 11/11x x x x x xx x x x x x x x xx x x x x x x x x x x x →→→→→→-++===-+-+-==-+--211222/(ln 1)lim 2.12218.lim arctan .arctan .21ln(arctan )(1/arctan )21lim ln lim lim,112lim arctan .x x x xxx x x x xx x x x x y x x x x y x x x e ππππππ-→→+∞→+∞→+∞→+∞-→+∞++==--⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭⨯+===--⎛⎫= ⎪⎝⎭习题4.3221221223212222211.0Taylor :(1)sinh 2111()22!(21)!2!(21)!().3!(21)!111(2)ln 2122221x xn n n n n n n o o x e e x x x x x x x x n n x x x x n x x x x x x x n n -+++++-=-=⎛⎫⎛⎫⎛⎫=++++--++-+ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭=++++++⎛⎫-=--+---- ⎪+-⎝⎭L L L L 求下列函数再点的的局部公式22212321224221212223()2221().32111(2)(2)(2)(3)sin (1cos 2)(1)().222!4!(2)!21(4)(21)(1())1(n n nn n nn n n n o o o o x x x x n n x x x x n x x x x x x n x x x x x x x x x x x ---+⎛⎫⎛⎫+-++ ⎪ ⎪-⎝⎭⎝⎭⎛⎫=-++++ ⎪-⎝⎭⎛⎫=-=-++-+ ⎪⎝⎭+-=-+-++++-=-+++L L L L L 22211236636342333())2(())(1())1222().(5)cos 1(1)().2!(2)!2.0Taylor :(1)sin ()sin 1()266n n n n n n n n nn n x xo o o o o o x x x x x x x x x x x x x x x x x n x e x x x x x e x x x x ++++++-+++++++++=-----+=-++-+=⎛⎫=++++-+ ⎪⎝⎭L L L L 求下列函数再点的的局部公式至所指定的阶数解3424424234452344333()().3()11151()1()2816128224153251().2816384)111(2)(228o o o o o x x x x x x x x x x x x x x x x x x x x x x x x x x ⎛⎫=+++ ⎪⎝⎭⎛⎫⎛⎫=+-+-+-++ ⎪⎪⎝⎭⎝⎭=+--++=+-+--+233222231)(2)161111(3)(3)(3)2816x x x x x x x x ⎛⎫+-+ ⎪⎝⎭⎛⎫-+-+--++-+ ⎪⎝⎭323223332331111(2)(4)(8)28161111(3)(96)(27)()28161115().2816o o x x x x x x x x x x x x x x ⎛⎫=+-+-+- ⎪⎝⎭⎛⎫-+-+--+-+ ⎪⎝⎭=+++222221212003521211/23.0Taylor (1)arctan .11(1)()11(1)(2)arcsin ()121(1)().352111111222(1)n n n k n x k n k n n n o o o x x x x x xx dt x x t k x x x x x n k x ++=++-==-++-++-==+++=-+++-++⎛⎫⎛⎫⎛⎫-----+ ⎪⎪ ⎝⎭⎝⎭⎝⎭=+=∑⎰L L L 求下列函数在点的局部公式:解202000212100()!(21)!!(1)()(2)!!(21)!!(),(2)!!(21)!!arcsin ()(2)!!(21)!!().(2)!!(21)4.Taylor :1(1)lim n k n k nk kn k nkn k nx x k nk nk n k x o o o o o x x k k x x k k x x k k x t dx t dt k k x t k k ====++=→⎪+-=-+-=+-=+-=++-∑∑∑∑⎰⎰∑利用公式求下列极限2422423402200000011()21lim.sin 2816()111112(2)lim lim lim lim .1(1)(1)(())21cos 1sin cos (3)lim lim sin sin sin x x x xx x x x x x x x x o o o x x x x x e x x x x x e x e x x e x e x e x x x x x x x x x x x x -→→→→→→→⎛⎫---++ ⎪-⎝⎭==-+----⎛⎫-==== ⎪---+⎝⎭-⎛⎫-= ⎪⎝⎭32333001sin ()1()62sin cos 1lim lim .3x x o xx x x x x x x x x x →→⎛⎫ ⎪⎝⎭⎛⎫---+ ⎪-⎝⎭===习题4.4532222221221.:(1)35.1515(1),15(1)15(1)(1)0,1,0, 1.y x xx x xy x x x x x x x x=-'-=-'=-=-+==-==求下列函数的单调性区间与极值点4解y=15x2132311(2).0.2110, 1.y xx xxy xx x x=-≠-'=-+=== x (-∞,0) (0,1) 1 (1,+ ∞)x (-∞,-1) -1 (-1,0) 0 (0,1) 1 (1,+ ∞) y'+ 0 -0 -0 +y 极大值❍无极值❍极小值22225.,sin cos sin(),,||/2.()sin()(sin cos)(0)0,()cos()cos,()sin().()sin()()(0)(0),22|()||sin()(sin cos)|2x a x a a x axf x a x a x af f x a x af x a xf c a cf x f f x x xxf x a x a x a++=+-+'==+-''=-+''-+'=++==+-+≤当较小时可用近似代替其中为常数试证其误差不超过证23441/32342344.116.01/3,1,26810.11111 1,126242624243.000717810.x xx xx xx e x x x ee e ee x x x x e x x x xθθ--<≤=+++⨯⎛⎫⎛⎫=++++-+++=≤⨯⎪ ⎪⎝⎭⎝⎭=<⨯L设按公式计算的近似值试证公式误差不超过证y'+ -0+y ❍极小值222222222(3),(,).1121220, 1.(1)(1)xy xxx x xy xx x=∈-∞+∞++--'=⨯=⨯==±++x (-∞,-1) -1 (-1,1) 1 (1,+∞) y'-0 + 0 -y ❍极小值-1 极大值1 ❍22222221(4)ln,0.2(ln)(1/)ln2(ln)ln ln[2ln]0,1,.y x xxx x x x x x x xy x x ex x x=>---'====== x (0,1) 1 (1,e2) e2(e2,+ ∞) y'-0 + 0 -y ❍极小值 极大值❍32222.()29122[1,3],.()618126(32)6(1)(2)0,1,2.(1)21,(1)7,(2)6,(3)11.(1)21,(3)11f x x x x f x x x x x x x x f f f f f f =-++-'=-+=-+=--==-=-===-=-=求函数在区间上的最大值与最小值并指明最大值点与最小值点是最小值是最大值.解()()()()2222203.22()()2(),/2.3222()(2)430,3333,(/2)()0.().44312.22p x V x p x p x px p p x p x p V p p x px p px p x p V p V p V p p p p ππππ=---=--≤≤'=---=-+=====-=将周长为的等腰三角形绕其底边旋转一周,求使所得旋转体体积最大的等腰三角形的底边长度.设腰长为则是最大值等腰三角形的底边长度 解,23x322324.,()12,(),[0,3].()32,320,1 2.3,0.()3.()333(1)(1)0,1,()6,(1)6,(1),(l k f x x lx kx x l k f x f x x lx k l k l k k l f x x x f x x x x x f x x f f f =++=-'=++-+=-+-==-='=-=-=-+=''''=±=±=±求出常数与的值使函数在处有极值并求出在这样的与之下的所有极值点以及在上的最小值和最大值是极小值解 1).(0)0,(1)2,(3)18.(1)2,(3)18.f f f f f -==-==-=是极大值是最小值是最大值5.,,,.sin OB OA a O A Kϕπ设一电灯可以沿垂直线移动是一条水平线长度为.问灯距离点多高时点有最大的照度6.,,?a b 若两条宽分别为及的河垂直相交若一船从一河转入另一河问其最大的长度是多少3000/2csc sec ,0.2sec tan csc cotsec tan 0,,csc cot tan ,tan arctan lim (),lim (),02l a b al a b ba b l l l θθπθπνθθθθθθθθθθθθπθθθ→→=+<<'=-+=====⎛⎫=+∞=+∞ ⎪⎝⎭设船与一岸夹角为则船长为在,有最小值,是最小值点.解,()()()()222222220.7.()(),0.32()3233323()0,.333a a a x V a x a x x a V x a x a x x ax a ax ax a x a x a x πππππ==-+≤≤'=-++-=--+=-+-=--+==在半径为问其高及底半径应是多少?设球心到内接圆锥体底的距离为,则锥体体积=解3332(0),()0,().()333273a aV a V a V a V ππ===⨯为最大值.ab20222222224,0,4,0,(4)2.89.4(18,0)()1818(),0().44lim (),()[0118180,448z h a V h a V V a r a ay x y z d f y y z g z z z y g z g z z z z →+∞''<<>>===⎛⎫⎛⎫==-+=-+=≤<+∞= ⎪ ⎪⎝⎭⎝⎭=+∞+∞⎛⎫'-+=-= ⎪⎝⎭当时当时为最小值,此时在曲线上求出到点的距离最短的点. 在,)有最小值.g (z)=2解()()2222264,(0)324,(64)68(0),(64)8,16.44(18,0)(16,8),(16,8)10.,.,(),0.2()232g g g y g y z x y x H H x HV x R x x R RV x R x x Rx x x R ππππ===<==±===-=-≤≤'=--=-=为最小值.曲线上到点的距离最短的点.试求内接于已知圆锥且有最大体积的正圆柱的高度.设已知圆锥的高度为底半径为设内接正圆柱的底半径为则其体积为解()2222230,0,.322(0)()0..().33311.1.cos ,02.sin (,0),cos (1sin ),0.2x x R H H V V R V R h R R R x y x a bx a t t y b t b S ab t t t S ππ-==⎛⎫==-= ⎪⎝⎭+==⎧≤≤⎨=⎩-=+≤≤'为最大值此时内接正圆柱的高度=试求内接于椭圆且其底平行于轴的最大等腰三角形的面积设内接等腰三角形的顶点在而底边上的一个顶点在第一象限.内接三角形面积解22200[sin (1sin )cos ][1sin 2sin ](sin )1(21)(21)(1)0,sin .21133(0),()0,()11.242ab t t t ab t t t z ab z z ab z z z t S ab S S t ab ab π=-++=--==-+-=--+===⎛⎫===-+= ⎪⎝⎭为最大值222012.8m/min ,50m ,,6m/min.??.()(8)(506),0.lim (),()0.()12812(506)2006000, 3.(0)50,t A O B x x A B s f t t t t f t f t t f t t t t t f f →+∞==+-≥=+∞≥'=--=-===设动点自平面坐标的原点开始以速度沿y轴正向前进而点在轴的正向距离原点处同时沿轴向原点作匀速运动速度为问何时与距离最近最近的距离是多少在取最小值解222(3)24321600,40.340m.d d =+===开始后分钟达到最近距离习题4.5()()()()22222222222321.()()212,()12(2)4642320,0,x x x x x xx x f x xe f x e x e e x f x e x x xe e x x xe x x --------='''-=-=---=-+=-+==求函数 的凸凹性区间及拐点.解=x(-∞,-32)-32(-32,0) 0(0, -32) 32(32,+∞)f " - 0 + 0 - 0 + f⋂拐点⋃拐点⋂拐点⋃x(,0)-∞0 (0,1)1 (1,2)2 (2,)+∞y '- 0 + + 0 - y ''+ + - - y☎⋃极小值⋃拐点⋂极大值☎⋂2321,(,).32(2)0,0,2.220, 1.y x x x y x x x x x y x x =-∈-∞∞'=-=-==''=-==作下列函数的图形:2.222223.,(,).2(2)(2)0,0,2;(2)(22)(42)0,2 2.x x x x x x x x y x e x y xe x e e x x e x x x y e x x e x e x x x --------'=∈-∞+∞=-=-=-==''=--+-=-+==±x(,0)-∞(0,22)-22-(22,2)-2(2,22)+22+ (22,)++∞y '-+ +--y ''++--+y]⋃ 极小值 Z ⋃ 拐点 Z ⋂极大值 ]⋂ 拐点 ]⋃x(,1)-∞-1-(1,0)- (0,1)1(1,)+∞y ' + 0 - -0 + y ''- -+ + y⋂极大值☎⋂☎⋃极小值⋃222314.,0.1110,21;.y x x xx y x x xy x =+≠-'=-==''=±=x(,1)-∞- -1(1,1)- (1,5)5(5,)+∞y ' + 0 + - 0 + y ''-+++yZ ⋂拐点 Z ⋃ ]⋃ 极小值 Z ⋃32223422244323226(1)5., 1.(1)3(1)(1)2(1)(1)(1)(1)(1)(3322)(1)(1)(5)(1)(5),(1)(1)(1)0,1,5.[2(1)(5)(1)](1)3(1)(5)(1)(1)[2(x y x x x x x x y x x x x x x x x x x x x x y x x x x x x x x y x x +=≠-+--+-'=-+----+--+-===---'==-+-++--+--''=-+=22442422441)(5)(1)](1)3(1)(5)(1)(1){[2(5)(1)](1)3(1)(5)}(1)(1){(39)(1)3(45)}(1)(1){(3129)3(45)}24(1)0 1.(1)(1)x x x x x x x x x x x x x x x x x x x x x x x x x x x x -++--+--+-++--+-=-+-----=-+-+---+====---,224333/2ln6.,0.1ln0,.12(1ln)12(1ln)32ln),0,.xy xxxy x exx x x x xxyx x xy x e=>-'===-⨯--+--''==-=-''==x (,)e-∞ e 3/2(,)e e3/2e3/2(,)e+∞y'-0 + +y''+ + 0 -y ]⋃极小值Z⋃拐点Z⋂221221221121122121()(,)()(,).()0,(,).()(,)(,),,(,),,()()()(),()()()().0(()())(),y f x a b f x a b f x x a b y f x a b a b x a b xf x f x f x x x f x f x f x x xf x f x x xx x''''=≤∈=∈<''≤+-≤+-''≤--->117.设函数在内有二阶导数且在内向上凸证明在在内向上凸故对于任意x x两式相加得消去得证12210()(),()(),(),()0, (,).f x f x f x f x f x f xx a b'''''''≤-≤≤∈即是单调递减函数故习题4.632223/223/221.:111(1)31,;399(2)3,12(3)()(sin ),()(1cos ),,|6|(1)91,18, 6.(1)(10)112(2)1,1,1(1)(y x x x y x x t a t t y t a t a t y y x y x K y y x y y x x π⎛⎫=-+- ⎪⎝⎭⎛⎫=⎪-⎝⎭=-=-''-'''=-===='++'''=++=-=--求下列曲线在指定点的曲率在处在处;其中为常数在=/2处.解33/22223/222223/21164..91)125(1)16(3)(1cos ),sin ,sin ,cos ,()2.21(0,1)(1)(1)154,40,1,44||14,(1)4K x a x a t x a t y a t y a t K a a y x y y y y x y y y y y K R y αβ==-+''''''=-=====+=+'''++'''==-==+=+=''''''==='+求曲线在点处的曲率圆方程.00解.=x 222223/223/251,:().443.243?.44-4, 4.1,(1,1)(1)(1(44)).x y y x x y y x y K x y x ⎛⎫+-= ⎪⎝⎭=-+'''''====='++-曲率圆方程问曲线上哪一点处曲率最大并对其作几何解释当时最大对应点恰是抛物线的顶点解第四章总练习题000000001..()()[()()].()(),[0,].()()(),(0)0.Lagrange ,(0,1)()(0)(),f x h f x h f x h f x h h f x x f x x x h g g x f x x f x x g g h g g h h θθθθθθ''+--=++-+--∈'''=++-=∈'-=00设y=f(x)在[x -h,x +h](h>0)内可导证明存在,0<<1使得令g(x)=(x)在[0,h]内可导,根据公式存在使得证00000()()[()()].2.:0,()1/4()1/2lim ()1/4,lim ()1/2.4(())211()(124x x f x h f x h f x h f x h h x x x x x x x x x x θθθθθθθθ→→+∞''+--=++-≥=≤≤=====+=++=+即证明当时中的满足且00).11()(12),44111()(12)(1(1)2).44211lim ()lim (12).441lim ()lim (12)41lim 4x x x x xx x x x x x x x x x x θθθθ→→→+∞→+∞≥+=-=+≤+++-==+==+=由算术几何平均不等式得22111lim lim .4423,0123.()()[0,2]1, 1,01(2)(0)1().120, 1x xx x f x f x x xx x f f f x x x====⎧-≤≤⎪⎪=⎨⎪<<+∞⎪⎩-≤≤⎧-⎪'==⎨--<<+∞⎪⎩设求在闭区间上的微分中值定理的中间值.解2/23/21.221111,;,()[0,2]222x x x f x x -=--=-=-=-=1在闭区间上的微分中值定理的中间值为22324.[1,1]Cauchy ()()()30(1,1),Cauchy (1)(1)()()0,()200,(0)0,.(1)(1)()()5.()[,],(,f x x g x x g x x f f f c f c f c c c g g g g c g c f x a b a -=='=∈-''--''======''--在闭区间上中值定理对于函数与是否成立?并说明理由.由于有零点中值定理的条件不满足.其实其结论也不成立.因为若,但无意义设在上连续在解2121212),()0,(,)()()0,(,)()0.(,),()0,Rolle (,),(,)()()0.()[,](,),()0,()0,(,).(b f x x a b f a f b x a b f x c a b f c a c c c b f c f c f x c c c c f f x x a b f ξξ''≠∈==∈≠∈=∈∈''=='''''∈=≠∈''上有二阶导数且又证明当时若存在则由定理存在使得对于在应用定理,存在使得此与条件矛盾由假设1证一,c 证二,00)0,(,),,().()(,())(,0)(,())(,0),()0,(,).6.()[,],()()0,(,)()0.:(,)()0.x x a b Darboux f x f x a f a a b f b b f x x a b f x a b f a f b c a b f c a b x f x ''''≠∈==<∈==∈>''<根据定理恒正或恒负不妨设恒正,于是f下凸,曲线严格在连结的弦下方故设在上有二阶导数且又存在使证明在内至少存在一点使由公式存在证一,c 12121221021()()()(,),()0,()()()(,),()0.()[,]Lagrange (,),()()()0.,()0,(,),[,],(,(f c f a f c a c f c c a c af b f c f c c b f c b c c af x c c c c f c f c f x c c f x x a b f a b a f a -'∈==>----'∈==<--'∈''-''=<-''≥∈0满足存在满足对于在应用公式,存在x 使得若不然在下凸曲线在连结12c 证二))(,0)(,())(,0),()0,(,).a b f b b f x x a b ==≤∈的弦下方故1201120121100112121201120127.1-12101.(),1111-121()1-12n n n n nn n n n n n n n n n n n a a a a aa x a x a x a n n n a x a x a a a a x a x a af x x n n n n n n aa a a f x a x a x a x a n n n ---+-----++++=++++++⎛⎫=++++-+++++ ⎪+-+⎝⎭'=++++-++++++L L L L L L 证明方程在与之间有一个根考虑函数证1201120121(0)(1)0.,(0,1),()0,1-12101.n n n n n nn a f f Rolle c f c c a a a a aa x a x a x a n n n ---⎛⎫ ⎪⎝⎭'==∈=++++=++++++L L 由定理存在即是在与之间的一个根00000008.()(,),,().?Lagrange ,()()()(),|()||()()()||()||()||()||(f x a b f x f x f x f c x x f x f x f c x x f x f c x x f x ''∈∈'-=-''=+-≤+-≤0设函数在有限区间内可导但无界证明在(a,b)内也无界逆命题是否成立试举例说明.若不然设f (x)在(a,b)内有界M,取定x (a,b),则对于任意 x (a,b),根据 公式证,)|||().(0,1),01,(0,1)M b a +-<<=内有界内无界.(1)(1)00002009.()[,](),(),()[,].(:()()()()()0,()).()[,]2,()()()()0,()n n k f x a b n k k f x f x a b f x f x x x g x g x x f x k n f x a b x f x x x g x g x f x --=-≠'=-≠若函数在区间上有个根一个重根算作个根且存在证明在至少有一个根注意若可以表示成且则称为的重根我们对于作归纳法证明函数在区间上有2个根.如果是重根则且则证.2000121212012001002()()()(),().()[,],,,[,]Rolle ,(,),()0..()[,]11,()()()()0,()(n x x g x x x g x f x x f x a b x x x x x x x x x f x n f x a b n f n x f x x x g x g x f x +''=-+-<'∈=++=-≠'=有根如果在区间上有2个不同的根在应用定理存在使得设结论对于个根的情况成立现在假定在区间上有个根.如果有重根重根则且则10000011000111211121)()()()()()((1)()()()),(1)()()()(),()(1)()0,().1,,[,],,[,]Rolle ,(,),,(n n n n n n n n n n x x g x x x g x x x n g x x x g x n g x x x g x g x g x n g x f x x f n x x x x x x c x x c x x ++++'+-+-=-++-'++-==+≠+∈∈L L L 有n重根如果如果有个单重根在区间上应用定理存在,11112111121111])()()0,().,,,,,,11,1.[,],,[,]Rolle ,(,),,()()()0.()1(1)n kk k i i k k k kk i i f c f c f x n f x n n n k n n x x x x c x x c f c f c f x k n n =---='''===+>>=+∈∈''''===-+-=∑∑L L L L L L 1k-1k 使得至少有个根如果有不同的根x 重数分别为在上应用定理存在x ,x 使得至少有根个.对f (x)()(1)(())().n n f x f x +'=用归纳假设,至少有一个根22111111112111110.:Lerendre ()[(1)](1,1).2!1()(1)],(1)(1)0,[ 1.1]Rolle 2!(1,1),()0.(1)(1)0(1),1)(,1)Rolle 1),n n n n nn n d P x x n n dxf x x f f f n c f c f f n f c c c c =---=-=-''''∈-=-==>-∈-证明多项式在内有个根对于在应用定理,存在使得当时对于在(,应用定理,存在(,证=2122211211(-1)(-1)111111121()12,1)()()0.()(1,1),,(1)(1)0Rolle ,,,(1,1)()()0.()n n n n n n n n n n n n n n c c f c f c x c c f f c c c c x x fx P x P x --------''∈==--==∈-==L L L (n-1)1(使得如此下去,f 在有零点,,在(-1,),(,),,(,1)应用定理, 得到x 使得是n 次多项式,至多有n 个零点()n P x n ,故恰有个零点.00011.(,),lim ()lim ().:(,),()0.()lim ()lim ().(,),(,),()0.(),().,,(,),()(x x x x f f x f x c f c f x f x f x A x c f c f x A f x A a b x a b f a f x →-∞→+∞→-∞→+∞-∞+∞='∈-∞+∞=≡==∈-∞+∞∈-∞+∞'=≠><∈<设函数在内可导且证明必存在一点使得证若取任意一点都有设存在不妨设根据极限不等式存在a,b,满足:000000),()().[,],[,]()()(),()()(),(,),,Fermat ,()0.()()lim ()0lim0.lim ()0x x x f b f x f a b c a b f c f x f a f c f x f b x a b x f c f x f x f x xf x x →+∞→+∞→+∞<∈≥>≥>∈'='∞=='=0在连续必在一点取最大值. 故为极大值点根据引理12.设函数在无穷区间(x ,+)可导,且,证明证由于,根据极限定义,存在正数101111111111,|()|()()()()()())|()|()|()||()||()||()|.,.max{,},()(),2,lim 0.x x f x f x f x f x f c x x f x f x f x x x x x f x f x f x f x x X x x x f x f x x X x x εεεεεεε→+∞'>'-+-++==≤<+<>=><=11使得x>x 时<.(x-x 为使只需令当时必有故13.()[,),()0,()()0,,()0.()0,()()()()()()0,(),,,,f x a f x l f a f a a a l f x f a f a f a f a a f a f c f a l l l l f a f a a l a a '+∞>>⎛⎫<- ⎪⎝⎭=<⎛⎫⎛⎫⎛⎫'-=+->+-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎡⎤-⎢⎥⎣⎦设函数在无穷区间内连续且当x>a 时其中l 为常数.证明:若则在区间内方程有唯一实根证在连续由连续怀念书函数的中间值定理在区间()()0.,()Rolle ,(),,()0.14.()(,)lim ()0.()(1)(),lim ()0.lim ()lim((1)())lim (x x x x x f a f x l f a f x a a f x l l f x f x g x f x f x g x g x f x f x f →∞→∞→∞→∞→∞⎛⎫-= ⎪⎝⎭⎛⎫''->> ⎪⎝⎭'-∞+∞==+-='=+-=内方程至少有一实根若有两个实根根据定理将在有一零点这与条件矛盾设函数在上可导,且现令证明证)(01)0.x θθ+<<=12121215.()[,]Lipschiz ,0,,[,],|()()|||.(1)()[,],()[,]Lipschiz (2)(1)?(3)[,]Lipschiz (1)()[,]0,f x a b L x x a b f x f x L x x f x a b f x a b a b f x a b L >∈-≤-''>称函数在满足条件若存在常数使对于任意都有若在连续则在满足条件中所述事实的逆命题是否成立举一个在上连续但不满足条件的函数.解在连续,存在常数12121212122121|()|.[,].,[,],,[,],|()()||()()||()|()().(2).()[,]Lipschiz ()[,]()||[1,1]Lipschiz f x L x a b x x a b x x c x x f x f x f c x x f c x x L x x f x a b f x a b f x x '≤∈∈<∈''-=-=-≤-'=-使得根据中值公式,对于任意存在使得否在满足条件,未必处处可导,更谈不到在连续.例如,在 满足条件111111(3)()[0,1],Lipschiz ()(0,1].16.()[,],()()[,],()()().()()(()())()()()()banni i i i i i i ni i i i f x f x F x a b F x f x a b f x dx F b F a F b F a F x F x F x x f x x ξξ--==-=='='==-'-=-=--→⎰∑∑∑,但在0不可导.连续但不满足条件,因其导函数无界设在可导且其导函数在上可积证明证1()(()0).{}[,].17.()(),(,),()()(),1,,bai n f x dx x a b P x a P x b c a b P x c P x n P x x x n λ∆→--∈-∈<<+⎰L 为的分割设多项式与的全部根都是单实根证明对于任意实数多项式的根也全都是单实根.证不妨设a=0,b>0,c (0,b),是次多项式,且首项系数为正.有单实根则这些根把实轴分为个区间每个区间保持固定正负号且正负相间.否则某个根将为极值点,导数为111232322212221222lim ().0(),,(,),,,(,),(,),().n x k k k k k k i n k P x b P x b x x x x x x x x x x x x x x P x b →∞----=''∞>=<<'''''''<∈∈∈+∞=L L 零,此与单实根矛盾.在两个无穷区间保持正号,且严格单调递增或递减,在每个有穷区间有一个最值点,且在其两侧分别递增和递减,设为偶数,则=+设且有n 个单实根.必有根据连续函数的中间值定1122233322222*********,(0,),(,),(,),(,),(,),(,),(,),().,k k k k k k k k i i c b c x c x x c x x c x x c x x c x P c c P n c ------'∈∈-∞∈'''∈∈∈+∞∈+∞=理对于存在使得为次多项式是P(x)=c 的所有单实根.18.()(,),,()0.()()0(,)(),()()0,[,](,)),.Rolle ()(()())0,()()0.19.3x f x a b f x f x f x a b f x g a g b g a b a b g x e f x f x f x f x A x -∞+∞='+==='''∈=+=+=设函数在内可导且是方程的两个实根证明方程在内至少有一个实根.设在 连续, 在可导根据定理, 存在 c (a,b),使得即决定常数的范围,使方程x 证 g(x)=e 43243232322212318624.()38624,()1224122412(22)12[(2)(2)]12(2)(1)12(2)(1)(1)0,.1,1, 2.()19,(1)13,(2)8.((x x x A P x x x x x P x x x x x x x x x x x x x x x x x x P x P P P --++'=--+=--+=--+=---=--=--+==-===-==-有四个不相等的实根根据这些数据画图,由图易知当在区间解4321),(2))(13,8)38624P x x x x A -=----++时有四个不相等的实根.2300220.()1(1).:()023,.0()0,21lim (),lim (),,,,()0,()0.(,),()0.()1nn x x x x x f x x f x n nn x f x f n k f x f x a b a b f a f b x a b f x f x x x →-∞→+∞=-+-++-=≤>=-=+∞=-∞<><∈='=-+-L 设证明方程当为奇数时有一个实根当为偶数时无实根当时故只有正根当为奇数时,存在根据连续函数的中间值定理,存在使得 证 ,2122222110(0),0,,1.1210, 1.101,()0,1,()0,(1)0,(1)0,().21.()()()()[,k k k k x x x x f x x n k x x x x x x f x x f x f x f n f x u x v x u x v x a ---++-=<>>---+'=-+-++===--''<<<>>>>''L L 当时严格单调递减故实根唯一当为偶数时,f (x)=是时的最小值故当为偶数时无实根设函数与以及它们的导函数与在区间],[,].()(),.()().()().b uv u v a b u x v x u x v x u x v x ''-上都连续且在上恒不等于零证明在的相邻根之间必有一根反之也对即有与的根互相交错地出现试句举处满足上述条件的与121212121212212,()[,].0,()0,()0.()[,],[,],()()0,Rolle ,[,],()()0,)()0,[,]x x u x a b x x u v uv v x v x v x ux x w a b w x w x c x x vu v uv w c c u v uv c u v uv v x x ''<-≠≠≠==∈''-'''''==-=-设是的在的两个根,由于如果在上没有根则=在连续由定理存在使得即(此与恒不等于零的假设矛盾.故v(x)在上有证cos(),sin ,--10,sin cos .u x v x u v uv x x ''===≠根.例如的根交错出现22222222222arctan 22.:0(),arctan (tanh ).tanh 2tanh arctan arctan sinh cosh (1)arctan 1cosh ()tanh tanh (1)tanh cosh 1sinh 2(1)arctan ()2(1)tanh cosh x x f x x x x x xx x x x x x x f x x x x x x x x xg x x x x π'>=<-'-+⎛⎫+'=== ⎪+⎝⎭-+==+证明当时函数单调递增且证22222222222222.(1)tanh cosh (0)0.()cosh 212arctan ,(0)0,2()2sinh 22arctan ,(0)0,12(1)222(1)()4cosh 224cosh 21(1)11444cosh 20(0cosh 11x x x g g x x x x g xg x x x g xx x x g x x x x x x x x x x x x x +=''=--=''''=--=++--'''=--⨯=--++++=-+>>++当时31),Taylor 0()()0,()0,.3!arctan arctan lim ()lim ,0.tanh 2tanh 2x x x g x g x x f x f x x f x x x x θππ→+∞→+∞>>'=>>==><由公式,对于有严格单调递增故对于有22222tan 23.:0.2sin ()sin tan ,()cos tan sin sec 2sin sin sec 2,()cos sec 2sin sec tan 2(cos sec 2)2sin sec 201(cos sec cos 2,(0,/2)).cos (0)(0)0x x x x xf x x x x f x x x x x x x x x x f x x x x x x x x x x x x x x xf f ππ<<<=-'=+-=+-''=++-=+-+->+=+≥∈'==证明当时有证2223222,Taylor ()tan ()0,sin tan 0,((0,/2)).2sin 24.:(1)1,0.(2)ln(1),0.2(3)sin ,0.611,0.21(2)ln(1),0.(1)ln(1)x x xf x x x f x x x x x x x xe x x x x x x x x x x x e e x x x x x x x x x x x x x θθπθ''=>-><∈>+≠-<+>-<<>=++>+≠+=-<>++=-根据公式,证明下列不等式证(1)2233321,0.23(1)2(3)()sin ,(0)0,()1cos 0,2()0,0,()(0)0,0.()sin ,6()cos 1,()sin 0,0.02,()(0)0,x x x x x f x x x f f x x x n f x x f f x f x x g x x x x g x x g x x x x g x g x g x θπ+>->+''=-==-≥==>>=>⎛⎫=-- ⎪⎝⎭⎛⎫'''=--=-+>>> ⎪⎝⎭>=仅当时故当时严格单调递增当时严格单调递增2111ln 120.25.(1)(1)(1),[0,1)...ln ln(1),11...26.()tan /4Taylor tan(50)()sec ,()nn n n n nniin n i i qx qn n n x q q q q x q q qx x q q q q x eex x f x x x f x x f x π+==-︒>=+++∈-=+<=<--=<=='''==∑∑L 设其中常数证明序列有极限单调递增有上界故有极限求函数在处的三阶多项式,并由此估计的值.证解22242sec tan ,()4sec tan 2sec .x x f x x x x '''=+()1,()2,()4,()16.4444f f f f ππππ''''''====。
