用代入消元法解二元一次方程练习题
人教版七年级下数学8.2解二元一次方程组基础练习题(无答案)

(1) ⎨ ⎧7x +5y = 3(2) ⎨= y (3) ⎨ 2 3解二元一次方程组基础练习肖老师知识点一:代入消元法解方程组:⎧ y = 2x - 3 ⎩3x + 2y =1⎩2x - y = -4⎧ x ⎪⎪⎩3x + 4y =18⎧ x + 5y = 6(4) ⎨⎩3x - 6y - 4 = 0知识点二:用加减法解方程组:⎧x - y = 3(1) ⎨⎩x + y =1⎧ 4x -3y = 0(2) ⎨⎩12x +3y = 8⎧ 4x -3y = 5(3) ⎨⎩4x + 6y =14 ⎧4x + y = 5(4) ⎨⎩3x - 2y =1(5) ⎨ ⎧ 3x - 2y = 7(6) ⎨⎧ x y (2)(化简后整体法) ⎨ ⎪2 + 3 = 2(4)(先化简) ⎨ ⎧ y +1 x + 2(5)(化简后整体法) ⎨ 4⎩ ⎩⎧5x + 4y = 6 ⎩2x +3y =1⎩2x +3y =17拓展训练:解下列方程:⎧ 3(y - 2) = x +1 (1)(先化简) ⎨⎩2(x -1) = 5y -8⎧4x -15y -17= 0 (3)(整体法) ⎨⎩6x - 25y - 23= 0⎪ = 3⎪ 2x -3y =1⎪ =2 3 ⎪3x + 4y =18⎧x y 13x y 3 ⎪ - = ⎩ 3 4 2⎧21x + 23y = 243 (6)(整体法) ⎨⎩23x + 21y = 241⎪5+4=2(7)先化简)6+7=1(8)可化简或整体法)((⎩y=1是方程2x+a y=5的解,则a=⎧2x-13y-23x+13y+2⎪-=0⎩54⎧3x-2y2x+3y⎪3x-2y2x+3y⎪-=5⎩67(9)(你懂的)(10)(先化简)(11)先化简)(12)整体法)综合训练:一.填空题1.在方程y=-3x-2中,若x=2,则y=_____.若y=2,则x=______;2.若方程2x-y=3写成用含x的式子表示y的形式:_________________;写成用含y的式子表示x的形式:___________________________;⎧x=23.已知⎨.⎧x=14.二元一次方程3x-my=4和mx+ny=3有一个公共解⎨,则⎩y=-11. 对于方程组 (1) ⎨ ,( 2) ⎨ ,( 3) ⎨1 ,( 4) ⎨ xy = -10 x + y = -2 x - y = 1 y 5B. 3.方程组 ⎨ 1 1 1 的解为()⎩B. ⎨ 3⎪⎩ 2⎪⎪ 2 ⎩ 4.已知 a , b 满足方程组 ⎨,则 a - b 的值为( )2a + b = 7 ⎩ ax + by = c⎧m=______,n=_____;5.已知 | a - b + 2 | + (b - 3)2 = 0 ,那么 ab = ______6.方程 3x+y=7 的正整数解为_____________二、选择题⎧ x + y = 3 ⎧ x = 2 ⎪ ⎧ x = 2 y ⎩ ⎩ ⎪ ⎩⎧ x + y = 5⎩, 是二元一次方程组的为()A.(1)和(2)B.(3)和(4)C.(1)和(3)D.(2)和(4)⎧ x = 22.若 ⎨是方程 kx - 2 y = 2 的一个解,则 k 等于( )⎩ y = 5A. 85 3 C .6D. -83⎧3x = 4 y ⎪⎪ 2 x - 3 y = 8⎧ x = 4 A. ⎨⎩ y = 3⎧ x = 2 ⎪ y = ⎧ 1 x = C . ⎨⎪ y = 3 ⎪ 8⎧ 1⎪ x = D. ⎨ 4⎪⎩ y = 0⎧a + 2b = 8⎩A.-1B.0C.1D.2 ⎧ x + y = 15.如果方程组 ⎨有唯一的一组解,那么 a ,b ,c 的值应当满足( ) A .a=1,c=1B .a ≠bC .a=b=1,c ≠1D .a=1,c ≠16.已知 x ,y 满足方程组 ⎨ x + m = 4⎩ y - 5 = m,则无论 m 取何值,x ,y 恒有关系式是( )A .x+y=1B .x+y=-1C .x+y=9D .x+y=9⎩y=2m-2,是方程组4x-3y=10的一组解,求m的值。
人教版七年级数学下册第八章二元一次方程组课时分层练习题及答案(每课时2-3套)

8.1 二元一次方程组基础题知识点1 认识二元一次方程(组)1.下列方程中,是二元一次方程的是(D )A .3x -2y =4zB .6xy +9=0C .1x +4y =6D .4x =y -242.下列方程组中,是二元一次方程组的是(A )A .⎩⎪⎨⎪⎧x +y =42x +3y =7 B .⎩⎪⎨⎪⎧2a -3b =115b -4c =6C .⎩⎪⎨⎪⎧x 2=9y =2x D .⎩⎪⎨⎪⎧x +y =8x 2-y =4 3.(龙口市期中)在方程(k -2)x 2+(2-3k)x +(k +1)y +3k =0中,若此方程为关于x ,y 的二元一次方程,则k 值为(C )A .-2B .2或-2C .2D .以上答案都不对4.写出一个未知数为a ,b 的二元一次方程组:答案不唯一,如⎩⎪⎨⎪⎧2a +b =1,a -b =2等.5.已知方程x m -3+y2-n=6是二元一次方程,则m -n =3.6.已知xm +n y 2与xym -n的和是单项式,则可列得二元一次方程组⎩⎪⎨⎪⎧m +n =1m -n =2.知识点2 二元一次方程(组)的解7.二元一次方程x -2y =1有无数多个解,下列四组值中不是该方程的解的是(B )A .⎩⎪⎨⎪⎧x =0y =-12 B .⎩⎪⎨⎪⎧x =1y =1 C .⎩⎪⎨⎪⎧x =1y =0 D .⎩⎪⎨⎪⎧x =-1y =-1 8.(丹东中考)二元一次方程组⎩⎪⎨⎪⎧x +y =5,2x -y =4的解为(C )A .⎩⎪⎨⎪⎧x =1y =4B .⎩⎪⎨⎪⎧x =2y =3C .⎩⎪⎨⎪⎧x =3y =2D .⎩⎪⎨⎪⎧x =4y =1 9.若⎩⎪⎨⎪⎧x =1,y =2是关于x ,y 的二元一次方程ax ―3y =1的解,则a 的值为(D )A .-5B .-1C .2D .7知识点3 建立方程组模型解实际问题10.(温州中考)已知甲、乙两数的和是7,甲数是乙数的2倍.设甲数为x ,乙数为y ,根据题意,列方程组正确的是(A )A .⎩⎪⎨⎪⎧x +y =7x =2y B .⎩⎪⎨⎪⎧x +y =7y =2xC .⎩⎪⎨⎪⎧x +2y =7x =2yD .⎩⎪⎨⎪⎧2x +y =7y =2x 11.(盘锦中考)有大小两种货车,2辆大货车与3辆小货车一次可以运货15.5吨,5辆大货车与6辆小货车一次可以运货35吨,设一辆大货车一次可以运货x 吨,一辆小货车一次可以运货y 吨,根据题意所列方程组正确的是(A )A .⎩⎪⎨⎪⎧2x +3y =15.55x +6y =35B .⎩⎪⎨⎪⎧2x +3y =355x +6y =15.5C .⎩⎪⎨⎪⎧3x +2y =15.55x +6y =35D .⎩⎪⎨⎪⎧2x +3y =15.56x +5y =35 中档题12.(大名县期末)若方程x |a|-1+(a -2)y =3是二元一次方程,则a 的取值范围是(C ) A .a >2 B .a =2 C .a =-2 D .a <-213.(萧山区期中)方程y =1-x 与3x +2y =5的公共解是(B )A .⎩⎪⎨⎪⎧x =-3y =-2B .⎩⎪⎨⎪⎧x =3y =-2C .⎩⎪⎨⎪⎧x =-3y =4D .⎩⎪⎨⎪⎧x =3y =2 14.(内江中考)植树节这天有20名同学种了52棵树苗,其中男生每人种树3棵,女生每人种树2棵.设男生有x 人,女生有y 人,根据题意,下列方程组正确的是(D )A .⎩⎪⎨⎪⎧x +y =523x +2y =20B .⎩⎪⎨⎪⎧x +y =522x +3y =20C .⎩⎪⎨⎪⎧x +y =202x +3y =52D .⎩⎪⎨⎪⎧x +y =203x +2y =52 15.(齐齐哈尔中考)为了开展阳光体育活动,某班计划购买毽子和跳绳两种体育用品,共花费35元,毽子单价3元,跳绳单价5元,购买方案有(B )A .1种B .2种C .3种D .4种16.(滨州模拟)若⎩⎪⎨⎪⎧x =a ,y =b 是方程2x +y =0的解,则6a +3b +2=2.17.已知两个二元一次方程:①3x -y =0,②7x -2y =2.(1)对于给出x 的值,在下表中分别写出对应的y 的值; x -2 -1 0 1 2 3 4 y ① -6 -3 0 3 6 9 12 y ②-8-4.5-12.569.513(2)请你写出方程组⎩⎪⎨⎪⎧3x -y =0,7x -2y =2的解.解:⎩⎪⎨⎪⎧x =2,y =6.18.已知甲种物品每个重4 kg ,乙种物品每个重7 kg ,现有甲种物品x 个,乙种物品y 个,共重76 kg .(1)列出关于x ,y 的二元一次方程; (2)若x =12,则y =4;(3)若乙种物品有8个,则甲种物品有5个; (4)写出满足条件的x ,y 的全部整数解. 解:(1)4x +7y =76.(4)由4x +7y =76,得x =76-7y4.又由题意得y 为正整数,当y =0时,x =19; 当y =1时,x =76-74=694,不合题意;当y =2时,x =76-2×74=312,不合题意;当y =3时,x =76-3×74=554,不合题意;当y =4时,x =76-4×74=12;当y =5时,x =76-5×74=414,不合题意;当y =6时,x =76-6×74=172,不合题意;当y =7时,x =76-7×74=274,不合题意;当y =8时,x =76-8×74=5;当y =9时,x =76-9×74=134,不合题意;当y =10时,x =76-10×74=32,不合题意;当y =11时,x =76-11×74<0,不合题意.∴满足x ,y 的全部整数解是⎩⎪⎨⎪⎧x =5,y =8,⎩⎪⎨⎪⎧x =12,y =4,⎩⎪⎨⎪⎧x =19,y =0.19.根据题意列出方程组:(1)明明到邮局买0.8元与2元的邮票共13枚,共花去20元钱,问明明两种邮票各买了多少枚?(2)将若干只鸡放入若干笼中,若每个笼中放4只,则有一鸡无笼可放;若每个笼中放5只,则有一笼无鸡可放,问有多少只鸡,多少个笼?解:(1)设0.8元的邮票买了x 枚,2元的邮票买了y 枚,根据题意得⎩⎪⎨⎪⎧x +y =13,0.8x +2y =20.(2)设有x 只鸡,y 个笼,根据题意得⎩⎪⎨⎪⎧4y +1=x ,5(y -1)=x.综合题20.甲、乙两人共同解方程组⎩⎪⎨⎪⎧ax +5y =15,①4x -by =-2,②由于甲看错了方程①中的a ,得到方程组的解为⎩⎪⎨⎪⎧x =-3,y =-1;乙看错了方程②中的b ,得到方程组的解为⎩⎪⎨⎪⎧x =5,y =4.试计算a 2 016+(-110b)2 017.解:把⎩⎪⎨⎪⎧x =-3,y =-1代入方程②中,得4×(-3)-b ×(-1)=-2,解得b =10.把⎩⎪⎨⎪⎧x =5,y =4代入方程①中,得5a+5×4=15,解得a=-1.∴a2 016+(-110b)2 017=(-1)2 016+(-110×10)2 017=1+(-1)=0. 不用注册,免费下载!【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
用代入消元法解二元一次方程组练习题

用代入消元法解二元一次方程组练习题IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】消元(一)一、填空题 1.已知-=1x y ,用含有x 的代数式表示y 为:=y ; 用含有y 的代数式表示x 为:x = . 2.已知4+5=3x y ,用含有x 的代数式表示y 为:=y ; 用含有y 的代数式表示x 为:x =. 3..若⎩⎨⎧-==1,1y x 和⎩⎨⎧==3,2y x 是关于x ,y 的方程y =kx +b 的两个解,则k =_____,b =______.4.在方程3x +5y =10中,若3x =6,则x =______,y =______.二、选择题5..以方程组⎩⎨⎧-=+-=1,2x y x y 的解为坐标的点(x ,y )在平面直角坐标系中的位置是(). (A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限三、用代入消元法解下列方程7.⎩⎨⎧=+=+.53,1y x y x 8.⎩⎨⎧==-.3:4:,52y x y x . 9.326431m n m n +=⎧⎨-=⎩ ① ②10.用代入消元法解方程组⎩⎨⎧=-=+②①52,243y x y x 使得代入后化简比较容易的变形是(). (A)由①得342y x -=(B)由①得432x y -= (C)由②得25+=y x (D)由②得y =2x -511.把x =1和x =-1分别代入式子x 2+bx +c 中,值分别为2和8,则b 、c 的值是().(A)⎩⎨⎧==4,3c b (B)⎩⎨⎧-==4,3c b (C)⎩⎨⎧-=-=4,3c b (D)⎩⎨⎧=-=4,3c b 12如果关于x ,y 的方程组⎪⎩⎪⎨⎧-=-+=-321,734k y x k y x 的解中,x 与y 互为相反数,求k 的值.13.若|x -y -1|+(2x -3y +4)2=0,则x,y 各是多少?。
8.2《消元——解二元一次方程组》同步练习题(2)及答案

。
二. 选择题 10. 若 y=kx+b中,当 x=-1 时,y=1;当 x=2 时,y=-2,则 k 与 b 为( )
k 1 A. b 1
k 1 B. b 0
k 1 C. b 2
k 1 D. b 4
x 1
ax by 0
8.2《消元——解二元一次方程组》同步练习题(2)
知识点:
1、代入法:用代入消元法解二元一次方程组的步骤: (1)从方程组中选取一个系数比较简单的方程,把其中的某一个未知数用 含另一个未知数的式子表示出来. (2)把(1)中所得的方程代入另一个方程,消去一个未知数.
(3)解所得到的一元一次方程,求得一个未知数的值.
13. 对于方程组 4x 5y 17 ,用加减法消去 x,得到的方程是(
)
A. 2y=-2
B. 2y=-36 C. 12y=-2 D. 12y=- 36
14.
将方程-
1 2
x+y=1中
x
的系数变为
5,则以下正确的是(
)
A. 5x+y=7
B. 5x+10y=10 C. 5x-10y=10 D. 5x-10y=-10
∴原方程组解为 x 2 y 2
(4)解:由②得:x=3y-7……③ ③代入① :2(3y-7)+5y=8 11y=22 y=2
把 y=2代入③得 x=-1 ∴原方程组解为
x 1 y 2
16. (1)解:②×4-①×3 得:11y=-33 ∴y=-3 把 y=-3 代入①得:4x-9=3 x=3
7. 二元一次方程组 kx 2 y 5 的解是方程 x-y=1的解,则 k=
。
专题 解二元一次方程组(计算题50题)(原卷版)
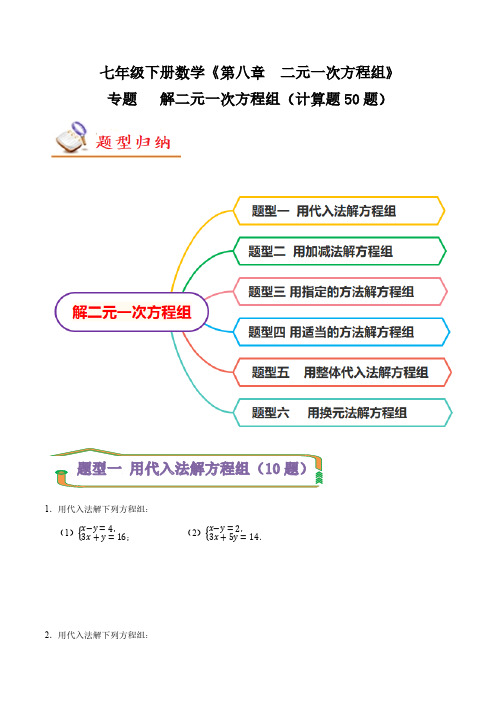
七年级下册数学《第八章二元一次方程组》专题解二元一次方程组(计算题50题)1.用代入法解下列方程组:(1)x−y=4,3x+y=16;(2)x−y=2,3x+5y=14.2.用代入法解下列方程组:(1)2x−y=33x+2y=8;(2)u+v=103u−2v=5.3.用代入法解下列方程组:(1)3x−y=2,9x+8y=17;(2)3x−4y=10x+3y=12.4.用代入法解下列方程组.(1)x+2y=4y=2x−3;(2)x−y=44x+2y=−2.5.用代入法解下列方程组:(1)5x+4y=−1.52x−3y=4(2)4x−3y−10=03x−2y=06.用代入法解下列方程组:(1)x−y=42x+y=5;(2)3x−y=29x+8y=17;(3)3x+2y=−8 6x−3y=−9.7.用代入法解下列方程组:(1)3x+2y=11,①x=y+3,②(2)4x−3y=36,①y+5x=7,②(3)2x−3y=1,①3x+2y=8,②8.用代入法解下列方程组:(1)5x+2y=15①8x+3y=−1②;(2)3(y−2)=x−172(x−1)=5y−8.9.用代入法解下列方程组:(1)x=6−5y3x−6y=4(2)5x+2y=15x+y=6(3)3x+4y=22x−y=5(4)2x+3y=73x−5y=110.用代入法解下列方程组:(1)2x+y=3x+2y=−6;(2)x+5y=43x−6y=5;(3)2x−y=63x+2y=2;(4)5x+2y=113y−x=−9;1.用加减法解下列方程组:(1)4x−y =143x +y =7 (2x−2y =7x−3y =−82.用加减法解下列方程组:(1)2m +7n =53m +n =−2(2)2u−5v =124u +3v =−2(3y 7=12+y 7=133.用加减法解下列方程组:(1)x−y =52x +y =4;(2)x−2y =33x +4y =−1.4.用加减法解下列方程组:(1)4x−3y =11,2x +y =13;(2)x−y =3,2y +3(x−y)=115.用加减法解下列方程组:(1)3μ+2t =76μ−2t =11 (2)2a +b =33a +b =4.6.(2023•市北区校级开学)用加减法解下列方程组:(1)3y−4x =04x +y =8; (2+y =3x−32y =−1.7.(2022秋•陕西期末)用加减法解下列方程组:(1)x−y =33x−8y =14; (2+2y =10=1+y 13.8.用加减法解下列方程组:(1)x +3=y ,2(x +1)−y =6; (2)x +y =2800,96%x +64%y =2800×92%.9.用加减法解下列方程组:(1)x−y =5,①2x +y =4;②(2)x−2y =1,①x +3y =6;②(3)2x−y =5,①x−1=12(2y−1).②10.用加减法解下列方程组:(1)x +3y =62x−3y =3 (2)7x +8y =−57x−y =4(3)y−1=3(x−2)y+4=2(x+1)(4+y4=1−y3=−1.1.(2022春•新田县期中)用指定的方法解下列方程组:(1)2x−5y=14①y=−x②(代入法);(2)2x+3y=9①3x+5y=16②(加减法).2.(2022春•安岳县校级月考)解下列方程组:(1)3x−y=75x+2y=8(用代入法);(2+n3=10−n4=5(用加减法).3.(2022春•大连期中)用指定的方法解下列方程组:(1)x−3y=42x+y=13(代入法);(2)5x+2y=4x+4y=−6(加减法).4.(2022春•宁远县月考)请用指定的方法解下列方程组(1)5a−b=113a+b=7(代入消元法);(2)2x−5y=245x+2y=31(加减消元法).5.(2021秋•蒲城县期末)请用指定的方法解下列方程组:(1)2x+3y=11①x=y+3②(代入消元法);(2)3x−2y=2①4x+y=10②(加减消元法).6.(2022秋•历下区期中)请用指定的方法解下列方程组:(1)m−n2=22m+3n=12(代入法);(2)6s−5t=36s+t=−15(加减法).7.(2022春•泰安期中)用指定的方法解下列方程组(1)3x+4y=19x−y=4(代入消元法);(2)2x+3y=−53x−2y=12(加减消元法);(35(x−9)=6(y−2)−y13=2.8.(2021秋•历下区期中)请用指定的方法解下列方程组:(1)3x+2y=14x=y+3;(代入法)(2)2x+3y=123x+4y=17.(加减法)9.(2021春•沙河口区期末)用指定的方法解下列方程组:(1)y=2x−33x+2y=8(代入法);(2)3x+4y=165x−6y=33(加减法).10.用指定的方法解下列方程组:(1)3x+4y=19x−y=4(代入法);(2)2x+3y=−53x−2y=12(加减法).1.(2022•苏州模拟)用适当的方法解下列方程组.(1)x+2y=9y−3x=1;(2x−34y=1=4.2.(2022秋•锦江区校级期末)用适当的方法解下列方程组.(1)x=2y−14x+3y=7;(2)3x+2y=22x+3y=28,.3.用适当的方法解下列方程组:(1)x+2y=0,3x+4y=6;(2=2y1)−y=11(3)x+0.4y=40,0.5x+0.7y=35;(4+n−m4=−14,5(n1)12=2.4.(2022•天津模拟)用适当的方法解下列方程组:(1)x +y =52x−y =4; (2=y 24−y−33=112.5.(2021•越城区校级开学)用适当的方法解下列方程组:(1)2x−3y =7x−3y =7. (2)0.3p +0.4q =40.2p +2=0.9q .6.(2022春•东城区校级月考)用适当的方法解下列方程组(1)x +y =52x +y =8; (2)2x +3y =73x−2y =4.7.(2021春•哈尔滨期末)用适当的方法解下列方程组(1)x +2y =93x−2y =−1 (2)2x−y =53x +4y =28.(2022春•椒江区校级期中)用适当的方法解下列方程组:(1)2x +3y =16①x +4y =13②; (2)2s t 3=3s−2t 8=3.9.(2022春•诸暨市期中)用适当的方法解下列方程组:(1)y=2x−1x+2y=−7(2+y3=7+y2=810.(2021春•南湖区校级期中)用适当的方法解下列方程组:(1)3x+2y=9x−y=8;(2=x y2=7.1.先阅读材料,然后解方程组:材料:解方程组x+y=4①3(x+y)+y=14②在本题中,先将x+y看作一个整体,将①整体代入②,得3×4+y=14,解得y=2.把y=2代入①得x=2,所以x=2 y=2这种解法称为“整体代入法”,你若留心观察,有很多方程组可采用此法解答,请用这种方法解方程组x−y−1=0①4(x−y)−y=5②.2.(2021秋•乐平市期末)解方程组3x−2y=8⋯⋯⋯①3(3x−2y)+4y=20⋯.②时,可把①代入②得:3×8+4y=20,求得y=﹣1,从而进一步求得x=2y=−1这种解法为“整体代入法“,请用这样的方法解下列方程组2x−3y=123(2x−3y)+5y=26.3.先阅读,然后解方程组.解方程组x−y−1=0①4(x−y)−y=5②时,可由①得x﹣y=1.③,然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得x=0y=−1这种方法被称为“整体代入法”,请用这样的方法解下列方程组:=0=2y+1.4.(2022春•太和县期末)先阅读,然后解方程组.解方程组x−y−1=0①4(x−y)−y=5②时,可由①得x﹣y=1,③然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得x=0①y=−1②这种方法被称为“整体代入法”,+2y=9.5.先阅读,然后解方程组.解方程组x−y−1=0①4(x−y)−y=5②时,可由①得x﹣y=1③,然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得x这种方法被称为“整体代入法”,请用这样的方法解下列方程组:2x−3y−2=03(2x−3y)+y=7.1.用换元法解下列方程组+2y=12−1y=342.用换元法解下列方程组:(1)3(x+y)+2(x−y)=36(x+y)−4(x−y)=−16(2+x5y3=2−(x+5y)=5.3.(2022春•云阳县期中)阅读探索:解方程组(a−1)+2(b+2)=62(a−1)+(b+2)=6解:设a﹣1=x,b+2=y原方程组可以化为x+2y=62x+y=6,解得x=2y=2,即:a−1=2b+2=2∴a=3b=0,此种解方程组的方法叫换元法.(1)拓展提高运用上述方法解下列方程组(a4−1)+2(b5+2)=102(a4−1)+(b5+2)=11;(2)能力运用已知关于x,y的方程组a1x+b1y=c1a2x+b2y=c2的解为x=6y=7,求关于m、n的方程组a1(m−2)+b1(n+3)=c1a2(m−2)+b2(n+3)=c2的解.4+x−y10=3①−x−y10=−1②,你会解这个方程组吗?小明、小刚、小芳争论了一会儿,他们分别写出了一种方法:小明:把原方程组整理得8x+2y=90③2x+8y=−30④④×4﹣③得30y=﹣210,所以y=﹣7把y=﹣7代入③得8x=104,所以x=13,即x=13y=−7小刚:设x y6=m,x−y10=n,则m+n=3③m−n=−1④③+④得m=1,③﹣④得m=2,=1=2,所以x+y=6x−y=20,所以x=13y=−7.小芳:①+②得2(x y)6=2,即x+y=6.③①﹣②得2(x−y)10=4,即x﹣y=20.④③④组成方程组得x=13③﹣④得y =﹣7,即x =13y =−7.老师看过后,非常高兴,特别是小刚的方法独特,像小刚的这种方法叫做换元法,你能用换元法解下列方程组吗?+2x 3y 7=1−2x 3y 7=5.5.(2022春•卧龙区校级月考)阅读探索(1)知识积累解方程组(a−1)+2(b +2)=62(a−1)+(b +2)=6.解:设a ﹣1=x ,b +2=y .原方程组可变为x +2y =62x +y =6,解这个方程组得x =2y =2,即a−1=2b +2=2,所以a =3b =0,这种解方程组的方法叫换元法.(2)拓展提高运用上述方法解下列方程组:(m 3−1)+2(n 5+2)=43(m 3−1)−(n 5+2)=5.(3)能力运用已知关于x ,y 的方程组a 1x +b 1y =c 1a 2x +b 2y =c 2的解为x =3y =4,请直接写出关于m 、n 的方程组a 1(m +2)−b 1n =c 1a 2(m +2)−b 2n =c 2的解是 .。
消元解二元一次方程组练习题(含答案)

《8.2消元解二元一次方程组》同步练习题一、选择题(每小题只有一个正确答案)1.已知二元一次方程组 ,如果用加减法消去n ,则下列方法可行的是( )A. ①×4+②×5B. ①×5+②×4C. ①×5-②×4D. ①×4-②×52.把方程2x+3y ﹣1=0改写成含x 的式子表示y 的形式为( ) A. y=(2x ﹣1) B. y=(1﹣2x ) C. y=3(2x ﹣1) D. y=3(1﹣2x )3.方程组1{ 25x y x y -=+=的解是( )A. 1{ 2x y =-=B. 2{ 1x y ==-C. 1{ 2x y ==D. 2{ 1x y ==4.已知方程组:的解是:,则方程组: 的解是( ) A. B. C. D. 5.用加减消元法解方程组358{ 752x y x y -=+= 将两个方程相加,得( )A. 3x=8B. 7x=2C. 10x=8D. 10x=106.已知二元一次方程2x +3y -2=0,当x ,y 互为相反数时,x ,y 的值分别为( )A. 2,-2B. -2,2C. 3,-3D. -3,37.已知23x y --+(2x +y +11)2=0,则( )A. 2,{ 1x y ==B. 0,{ 3x y ==-C. 1,{ 5x y =-=-D. 2,{ 7x y =-=-二、填空题8.如果方程组的解是方程的一个解,则的值为____________.9.若方程组与有相同的解,则a= ________,b= ________. 10.方程组313{ 3131x y x y +=-=-的两个方程只要两边_______,就可以消去未知数_______. 11.若6{ 20x y x y -=+=,则 32x y +=__________________. 12.如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍.如果搭建正三角形和正六边形共用了2016根火柴棍,并且正三角形的个数比正六边形的个数多6个,那么能连续搭建正三角形的个数是__________三、解答题13.解方程组:(1);(2).14.()() 344 {126x y x yx y x y+--=+-+=15.用合适的方法解下列方程组:(1)402{3222y xx y=-+=(2)235{421x yx y+=-=(3)6515{33x yx y+=-=-16.甲、乙两人解关于x, y的方程组,甲因看错a,解得,乙将其中一个方程的b写成了它的相反数,解得,求a、b 的值.。
二元一次方程组解法练习题精选(含答案)
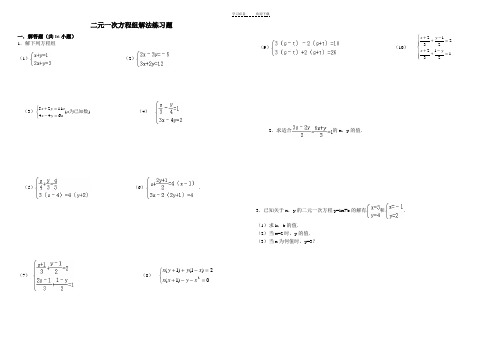
二元一次方程组解法练习题一.解答题(共16小题) 1.解下列方程组 (1)(2)(3))(6441125为已知数a a y x a y x ⎩⎨⎧=-=+ (4)(5)(6).(7)(8)⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x(9)(10) ⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x2.求适合的x ,y 的值.3.已知关于x ,y 的二元一次方程y=kx+b 的解有和.(1)求k ,b 的值.(2)当x=2时,y 的值. (3)当x 为何值时,y=3?1.解下列方程组(1)(2);(3);(4)(5).(6)(7)(8)(9)(10);2.在解方程组时,由于粗心,甲看错了方程组中的a ,而得解为,乙看错了方程组中的b ,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解..求适合得到一组新的方程解:由题意得:﹣,((()故原方程组的解为.故原方程组的解为.)原方程组可化为.所以原方程组的解为)原方程组可化为:x=x=代入×所以原方程组的解为:原方程组可化为,所以方程组的解为4.解方程组:)原方程组化为y=所以原方程组的解为5.解方程组:解:即解得所以方程组的解为.6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?的二元一次方程组,再运用加减消元)依题意得:,.y=,.x+7.解方程组:(1);(2).)原方程组可化为∴方程组的解为)原方程可化为,,∴方程组的解为解:原方程组可化为则原方程组的解为.9.解方程组:解:原方程变形为:y=解之得10.解下列方程组: (1)(2),,代入=.所以原方程组的解为)原方程组整理为所以原方程组的解为.(2),解得∴原方程组可化为,解得∴∴原方程组的解为.12.解二元一次方程组: (1);.则方程组的解是)此方程组通过化简可得:则方程组的解是13.在解方程组时,由于粗心,甲看错了方程组中的a ,而得解为,乙看错了方程组中的b ,而得解为.(1)甲把a 看成了什么,乙把b 看成了什么? (2)求出原方程组的正确解. 代入方程组,得解得:把,得解得:∴方程组为则原方程组的解是.,x=y=∴原方程组的解为;.,故原方程组的解为.)化简整理为,故原方程组的解为.(∴原方程组的解为;)原方程组可化为∴原方程组的解为.。
代入消元法解二元一次方程组专题习题

代入消元法解二元一次方程组专题习题1.已知$x-y=1$,用含有$x$的代数式表示$y$为:$y=x-1$;用含有$y$的代数式表示$x$为:$x=y+1$。
2.已知$x-2y=1$,用含有$x$的代数式表示$y$为:$y=\frac{x-1}{2}$;用含有$y$的代数式表示$x$为:$x=2y+1$。
3.已知$4x+5y=3$,用含有$x$的代数式表示$y$为:$y=\frac{3-4x}{5}$;用含有$y$的代数式表示$x$为:$x=\frac{3-5y}{4}$。
4.用代入法解下列方程组:1)$\begin{cases}y=4x\\2x+y=5\end{cases}$解:将$y=4x$代入$2x+y=5$得:2x+4x=5$,解方程得:$x=\frac{5}{6}$,将$x=\frac{5}{6}$代入$y=4x$得:$y=2\frac{2}{3}$,所以,原方程组的解为:$(x,y)=(\frac{5}{6},2\frac{2}{3})$。
2)$\begin{cases}x-y=4\\2x+y=5\end{cases}$解:将$x-y=4$解出$y$得:$y=x-4$,将$y=x-4$代入$2x+y=5$得:2x+x-4=5$,解方程得:$x=3$,将$x=3$代入$y=x-4$得:$y=-1$,所以,原方程组的解为:$(x,y)=(3,-1)$。
3)$\begin{cases}3m+2n=6\\4m-3n=1\end{cases}$解:将$3m+2n=6$解出$3m$得:$3m=6-2n$,即$m=2-\frac{2}{3}n$,将$m=2-\frac{2}{3}n$代入$4m-3n=1$得:4(2-\frac{2}{3}n)-3n=1$,解方程得:$n=-\frac{5}{2}$,将$n=-\frac{5}{2}$代入$m=2-\frac{2}{3}n$得:$m=4$,所以,原方程组的解为:$(m,n)=(4,-\frac{5}{2})$。
2.3.1 代入消元法 浙教版七年级数学下册同步练习(含解析)

2.3 解二元一次方程组第1课时 代入消元法基础过关全练知识点 代入消元法1.(2022湖南株洲中考)对于二元一次方程组{y =x −1,①x +2y =7,②将①式代入②式,消去y 可以得到( ) A.x+2x-1=7 B.x+2x-2=7C.x+x-1=7D.x+2x+2=72.四名学生利用代入法解二元一次方程组{3x −4y =5,①x −2y =3②时,提出四种不同的解法,其中解法不正确的是( ) A.由①得x=5+4y 3③,将③代入② B.由①得y=3x−54③,将③代入② C.由②得y=-x−32③,将③代入①D.由②得x=3+2y ③,将③代入①3.(2022江苏无锡中考)二元一次方程组{3x +2y =12,2x −y =1的解为 .4.【新独家原创】 已知关于a,b 的二元一次方程组{a +m =3,b −3=m,则-a-b 的值为 .5.(2021浙江丽水中考)解方程组:{x =2y,x −y =6.6.【易错题】下面是老师在铭铭的数学作业本上截取的部分内容:解方程组{2x −y =3,①x +y =−12.②解:方程①变形,得y=2x-3③, 第一步把方程③代入方程①,得2x-(2x-3)=3, 第二步整理,得3=3, 第三步因为x 可以取任意实数,所以原方程组有无数个解.问题:这种解方程组的方法叫 ;铭铭的解法正确吗?如果不正确,错在哪一步?并求出正确的解.能力提升全练7.已知单项式-3x m-1y 3与52x n y m+n 是同类项,那么m,n 的值分别是 ( )A.2,1B.1,2C.0,-1D.-1,28.小明说{x =−1,y =2为方程ax+by=10的解,小惠说{x =2,y =−1为方程ax+by=10的解,两人谁也不能说服对方.若他们的说法都正确,则a,b 的值分别为 ( )A.12,10B.9,10C.10,11D.10,109.(2022浙江杭州西湖期中,9,)在解关于x,y 的方程组{ax −2by =8①,2x =by +2②时,小明将方程①中的“-”看成了“+”,得到的解为{x =2,y =1,则原方程组的解为 ( ) A.{a =2b =2 B.{x =2y =2 C.{x =−2y =−3 D.{x =2y =−110.如果|x-2y+1|+|x+y-5|=0,那么x= .11.(2022浙江杭州期中改编,15,)若 1 314x+17y=2y+x-5=2x-3,则2(x-2y)= .12.(2022浙江杭州萧山期中,14,)对于有理数x,y,定义一种新运算:x ⊕y=ax+by-5,其中a,b 为常数.已知1⊕2=9,(-3)⊕3=-2,则2a+b= .13.(2022浙江杭州余杭月考,15,)已知关于x,y 的二元一次方程(3x-2y+9)+m(2x+y-1)=0,无论m 取何值,方程总有一个固定不变的解,这个解是 .14.【一题多解】当关于x,y 的二元一次方程组{2x −y −4m =0,14x −3y −20=0中y 的值是x 值的3倍时,求x,y 的值.15.已知关于x,y 的二元一次方程组{ax +5y =4,5x +y =3与{x −2y =5,5x +by =1的解相同,求a,b 的值.素养探究全练16.【运算能力】材料:解方程组{x −y −1=0①,4(x −y)−y =5②时,可由①得x-y=1③,然后将③代入②得4×1-y=5,解得y=-1,将y=-1代入③,得x-(-1)=1,解得x=0,∴方程组的解为{x =0,y =−1,这种方法被称为“整体代入法”.请用这样的方法解方程组{2x −y −2=0,6x−3y+45+2y =12.17.【运算能力】三个同学对问题“若关于x,y 的二元一次方程组{a 1x +b 1y =c 1,a 2x +b 2y =c 2的解是{x =3,y =4,求关于x,y 的二元一次方程组{3a 1x +2b 1y =5c 1,3a 2x +2b 2y =5c 2的解”提出各自的想法.甲说:“这个题目条件不够,不能求解.”乙说:“它们的系数有一定的规律,可以试试.”丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元的方法来解决?”参考他们的讨论,解决上述问题.答案全解全析基础过关全练1.B 将①式代入②式,得x+2(x-1)=7,∴x+2x-2=7,故选B.2.C C 中,应该由②得y=x−32,故选项C 解法错误,符合题意,故选C.3.答案 {x =2y =3 解析 {3x +2y =12,①2x −y =1②,由②得y=2x-1③,将③代入①得3x+2(2x-1)=12,解得x=2,将x=2代入③得y=3,∴原方程组的解为{x =2,y =3. 4.答案 -6解析 {a +m =3①,b −3=m②,把②代入①,得a+b-3=3, ∴a+b=6,∴-a-b=-6.5.解析 {x =2y①,x −y =6②,把①代入②得,2y-y=6,解得y=6, 把y=6代入①得,x=12, 则原方程组的解为{x =12,y =6. 6.解析 代入消元法.铭铭的解法不正确,错在第二步,正确解法:将方程①变形,得y=2x-3③,把③代入②,得x+2x-3=-12,解得x=-3,把x=-3代入③,得y=-9,所以原方程组的解为{x =−3,y =−9.能力提升全练7.A 根据题意得{m −1=n,m +n =3,解得{m =2,n =1.故选A. 8.D 由{x =−1,y =2为方程ax+by=10的解,{x =2,y =−1为方程ax+by=10的解,得{−a +2b =10,2a −b =10,解得{a =10,b =10.故选D. 9.C 把{x =2,y =1代入{ax +2by =8,2x =by +2,得{2a +2b =8,4=b +2,解得{a =2,b =2, ∴原方程组为{2x −4y =8,2x =2y +2,解得{x =−2,y =−3.故选C. 10.答案 3解析 ∵|x-2y+1|+|x+y-5|=0,∴{x −2y +1=0,①x +y −5=0,②由①得x=2y-1③,把③代入②,得2y-1+y-5=0,解得y=2,把y=2代入③,得x=2×2-1=3,∴原方程组的解为{x =3,y =2.11.答案 -4解析 由2y+x-5=2x-3得2y+x-2x=-3+5,∴2y-x=2,∴x-2y=-2.∴2(x-2y)=2×(-2)=-4.12.答案 13解析 根据题中的新定义得{a +2b −5=9,−3a +3b −5=−2,整理得{a +2b =14,①−a +b =1,②由②得b=1+a ③,把③代入①,得a+2(1+a)=14,解得a=4,把a=4代入③,得b=1+4=5.则原方程组的解为{a =4,b =5,则2a+b=8+5=13.13.答案 {x =−1y =3解析 ∵无论m 取何值,方程总有一个固定不变的解,∴{2x +y −1=0,3x −2y +9=0,解得{x =−1,y =3. 14.解析 解法一:∵y 的值是x 值的3倍,∴y=3x,∴{2x −3x −4m =0,14x −9x −20=0,解得{x =4,m =−1, ∴y=3×4=12.故x 的值为4,y 的值为12.解法二:{2x −y −4m =0,①14x −3y −20=0,② 由①得,y=2x-4m,③把③代入②,得14x-3(2x-4m)-20=0,∴x=−3m+52,∴y=-7m+5,∵y 的值是x 值的3倍,∴y=3x,∴-7m+5=3×−3m+52,解得m=-1.∴x=4,y=12.故x 的值为4,y 的值为12.15.解析 ∵两个方程组的解相同,∴可用方程5x+y=3,x-2y=5组成新方程组,得{5x +y =3,①x −2y =5,②由①得,y=3-5x ③,把③代入②,得x-2(3-5x)=5,解得x=1,把x=1代入③得y=-2,∴此方程组的解为{x =1,y =−2,把{x =1,y =−2代入{ax +5y =4,5x +by =1,得{a −10=4,5−2b =1,解得{a =14,b =2.素养探究全练16.解析 {2x −y −2=0,①6x−3y+45+2y =12,② 由①得2x-y=2③,将③代入②得3×2+45+2y=12,解得y=5,把y=5代入③得2x-5=2,解得x=3.5.所以原方程组的解为{x =3.5,y =5.17.解析 方程组{3a 1x +2b 1y =5c 1,3a 2x +2b 2y =5c 2中的两个方程的两边都除以5,得{a 1(35x)+b 1(25y)=c 1,a 2(35x)+b 2(25y)=c 2, 因为方程组{a 1x +b 1y =c 1,a 2x +b 2y =c 2的解是{x =3,y =4,所以{35x =3,25y =4,解得{x =5,y =10.所以方程组{3a 1x +2b 1y =5c 1,3a 2x +2b 2y =5c 2的解是{x =5,y =10.。
二元一次方程组计算题及过程答案代入消元法

二元一次方程组计算题及过程答案代入消元法在数学中,我们常常会遇到二元一次方程组,它们可以表示为如下形式:ax + by = cdx + ey = f其中a、b、c、d、e、f是已知的常数,而x和y则是我们需要求解的变量。
解二元一次方程组的方法有很多种,其中代入消元法是一种比较常用且易于理解的方法。
下面我们就来看一个具体的例子,来解释如何使用代入消元法来解决二元一次方程组。
计算题:给定以下的二元一次方程组:1.2x + 3y = 102.4x - y = 5请根据代入消元法,计算出x和y的值。
解题过程:第一步:用第一个方程求解出一个未知数的表达式。
从第一个方程中解出x的表达式:2x + 3y = 102x = 10 - 3yx = (10 - 3y) / 2第二步:将x的表达式代入第二个方程中。
将x的表达式代入第二个方程中得到:4((10 - 3y) / 2) - y = 58 - 6y - y = 5-7y = -3y = 3/7第三步:将得到的y的值代入x的表达式中。
将y的值代入x的表达式中得到:x = (10 - 3*(3/7)) / 2x = (10 - 9/7) / 2x = 65/14答案:根据代入消元法的计算,我们得到x=65/14,y=3/7。
通过以上计算过程,我们成功使用代入消元法解决了给定的二元一次方程组,得到了未知数x和y的值。
这种方法虽然繁琐,但是确实是一种有效且可靠的解题方法。
希望这个例子能帮助你更好地理解代入消元法的应用。
总结:二元一次方程组的解题方法有很多种,代入消元法是其中一种常用且易于理解的方法。
在解题过程中,我们首先通过一个已知方程解出其中一个未知数的表达式,然后将其代入另一个方程中得到另一个未知数的值,最后将得到的值代回原表达式中求解出另一个未知数的值。
这种方法虽然繁琐,但是在解决一些复杂的问题时非常实用。
代入法解二元一次方程组(二)专题训练

目录代入法解二元一次方程组(二)专题训练 (2)(一)导入新课 (3)(二)讲解新知 (3)(三)课堂练习 (4)(四)小结作业 (4)解二元一次方程组(专题练习二) (23)代入法解二元一次方程组(二)专题训练真题示例:《代入法解二元一次方程组》【考题回顾】1.题目:代入法解二元一次方程组2.内容:3.基本要求:(1)试讲时间10分钟以内;(2)讲解要目的明确、条理清楚、重点突出;【考题解析】【教案设计】(一)导入新课创设两名同学去文具店买文具的情境,引导学生列出方程组,点明这是前面所学的二元一次方程组,这节课学习如何解二一次方程组。
引入课题。
(或者复习导入:回顾一元一次方程及其求解方法。
)(二)讲解新知请学生同桌两人为一组,尝试解方程组:,教师巡视并提示:学过解什么样的方程?可否将二元一次方程组转化为会求解的方程?请学生上黑板板演计算过程,结合板书教师讲解,由②知x=13-4y③,将③代入①,则:2(13-4y)+3y=16,化简求得:y=2。
将y=2代入③中,求得:x=5。
所以原方程组的解是。
教师肯定学生作答,并请学生尝试用x表示y进行求解,比较求得的结果是否一样。
请学生比较两次求解过程,思考上面解方程组的基本思路是什么,主要步骤又有哪些。
预设学生能够回答出。
上题是将二元一次方程组转化为一元一次方程来进行求解。
师生共同总结步骤:(1)将其中一个方程中的某个未知数用含有另一个未知数的代数式表示出来,(2)把得到的式子代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程,并求解;(3)把求得的解代入方程,求得另一个未知数的解。
教师总结:这种解方程组的方法称为代入消元法。
简称代入法。
(三)课堂练习练习:用代入法解下列方程组:(1)(2)(四)小结作业小结:重点回顾代入法解二元一次方程组的基本思路及步骤。
作业:思考练习题中的两个方程组是否有其他的求解方法。
【板书设计】【答辩解析】1.二元一次方程组有哪些解法?答:初中所学解二元一次方程组主要有以下两种解法:①代入消元法:将方程组中的一个方程的某个未知数用含有另一个未知数的代数式表示出来,代入到另一个方程中,消去一个未知数,得到一个一元一次方程,最后求得方程的解。
代入消元法解二元一次方程组

5 用 x代替y, 2 消未知数y
解这个方程组,可以先消 x吗?
• 这节课你有哪些收获?
解这个方程,得 x=18
归纳
上面的解方程组的基本思路是什么? 基本步骤有哪些?
上面解方程组的基本思路是“消元”— —把“二元”变为“一元”。 主要步骤是:将其中的一个方程中的某个 未知数用含有另一个未知数的代数式表现 出来,并代入另一个方程中,从而消去一 个未知数,化二元一次方程组为一元一次 方程。这种解方程组的方法称为代入消元 法,简称代入法。
3x – 2(1 – 2x)= 19 3x – 2 + 4x = 19 3x + 4x = 19 + 2 7x = 21 x=3 把x = 3代入③,得 y = 1 – 2x = 1 - 2×3= - 5 x=3 ∴ y=-5
试一试: 用代入法解二元一次方程组
x+5y 6 3x 6 y 4
2x+ (22-x) =40 解得 x=18 22-18=4
答:这个队胜18场,只负4场.
设篮球队胜了x场,负了y场. 根据题意得方程组
x+y = 22
2x+y = 40 由①得, y = 22-x 把③ 代入② ,得 2x+ (22-x) = 40
①
②
③
把 x=18 代入③ ,得 y=4 这样的形式 叫做“用 x 所以这个方程组的解是 表示 y”. 记 住啦! x=18 y = 4.
① ②
① 最为简单的方法是将________式中的
X=6-5y _________表示为__________, x
② 再代入__________
1、解二元一次方程组 x+y=5 ① ⑵ ⑴ x-y=1 ②
二元一次方程专项练习60题+解析答案

一元二次方程专练60题一.解答题(共60小题)1.解二元一次方程组.(1);(2).2.解下列方程组:(1);(2).3.解方程组:(1);(2).4.解方程组.(1);(2).5.解方程组:(1);(2).6.解下列方程组:(1);(2).7.解方程组:(1);(2).8.解二元一次方程组:(1);(2).9.按要求解下列方程组:(1)(用代入消元法);(2)(用加减消元法).10.解方程组:(1);(2).11.解下列方程组:(1)(代入消元法);(2)(加减消元法).12.解下列方程组:(1);(2).13.用指定的方法解下列方程组:(1)(代入法);(2)(加减法).14.解下列方程组.(1);(2).15.解方程组:(1);(2).16.解下列方程组:(1);(2).17.解二元一次方程组:(1).(2).18.解方程组:(1);(2).19.解方程组:(1);(2).20.用适当的方法解下列方程组:(1)(2).21.解方程组:(1);(2).22.解二元一次方程组:(1);(2).23.解二元一次方程组:(1);(2).24.解方程组:(1);(2).25.解方程组:(1);(2).26.解方程组:(1);(2).27.解方程组:(1);(2).28.解方程组:(1);(2).29.解方程组:(1);(2).30.解方程组:(1);(2).31.解方程组:(1);(2).32.解方程组:(1);(2).33.用适当的方法解方程组:(1);(2).34.解下列方程组:(1);(2).35.解方程组:(1);(2).36.解方程组:(1);(2).37.解方程组:(1);38.解方程组:(1);(2).39.解方程组:(1);(2).40.解下列方程组:(1);41.解下列方程组:(1);(2).42.用加减消元法解方程:(1);(2).43.解二元一次方程组:(1);44.解方程组:(1);(2).45.解方程:(1);(2).46.用适当的方法解下列方程组:(1);47.解方程组:(1);(2).48.解方程组:(1);(2).49.解方程组:(1);(2).50.解方程组:(1);(2).51.阅读以下材料:解方程组:;小亮在解决这个问题时,发现了一种新的方法,他把这种方法叫做“整体代入法”,解题过程如下:解:由①得x﹣y=1③,将③代入②得:(1)请你替小亮补全完整的解题过程;(2)请你用这种方法解方程组:.52.已知关于x、y的方程组的解满足x+y =﹣10,求代数式m2﹣2m+1的值.53.在解方程组时,由于粗心,甲看错了方程组中的a,得解为;乙看错了方程组中的b,得解为.(1)甲把a错看成了什么?乙把b错看成了什么?(2)求出原方程组的正确解.54.已知方程组和方程组的解相同求a、b的值.55.甲和乙两人同解方程组甲因抄错了a,解得,乙因抄错了b,解得,求5a﹣2b 的值.56.对于实数x、y,定义新运算:x*y=ax+by;其中a、b是常数,等式右边是通常的加法和乘法运算,已知1*2=1,(﹣3)*3=6.(1)分别求出a、b的值;(2)根据上述定义新运算,试求2*(﹣4)的值.57.甲、乙两位同学在解方程组时,甲把字母a看错了得到方程组的解为;乙把字母b看错了得到方程组的解为.(1)求a,b的正确值;(2)求原方程组的解.58.定义一种新运算“※”:规定m※n=am+bn﹣mn,其中a,b为常数,且6※15=270,8※10=360,求﹣2※1的值.59.若关于x,y的方程组与方程组的解相同.(1)求两个方程组的相同解;(2)求(3a﹣b)2023的值.60.已知方程组和有相同的解,求a﹣2b的值.一元二次方程专练60题参考答案与试题解析一.解答题(共60小题)1.解二元一次方程组.(1);(2).【解答】解:(1)①+②,得4x=12,∴x=3.把x=3代入②,得3+2y=3,解得y=0所以原方程组的解为;(2),②化简得:2(x﹣2)﹣3(y﹣2)=6,即2x﹣3y=4③,①+③得:3x=18,解得:x=6,将x=6代入①得:6+3y=14,解得:y=,∴原方程组的解为:.2.解下列方程组:(1);(2).【解答】解:(1),由①得,3x+2y=12③,②×③﹣③×2,得5y=60,解得y=12,将y=12代入③,得3x+24=12,解得x=﹣4,∴原方程组的解为;(2),由①得x+1=5y+10,∴x=5y+9③,由②得6x﹣15﹣12y﹣16=5,整理,得6x﹣12y=36,∴x﹣2y=6④,将③代入④,得5y+9﹣2y=6,解得y=﹣1,将y=﹣1代入③,得x=﹣5+9=4,∴原方程组的解为.3.解方程组:(1);(2).【解答】解:(1),把①代入②,得3x+4x=7,解得x=1,把x=1代入①,得y=2,故原方程组的解为;(2),①+②,得6x=24,解得x=4,把x=4代入②,得y=5,故原方程组的解为.4.解方程组.(1);(2).【解答】解:(1),①﹣②得:9y=18,解得:y=2,把y=2代入①中得:3x+10=5,解得:x=﹣,∴原方程组的解为:;(2)将原方程组化简整理得:,①×3得:24u+27v=36③,③﹣②得:2v=22,解得:v=11,把v=11代入①中得:8u+99=12,解得:u=﹣,∴原方程组的解为:.5.解方程组:(1);(2).【解答】解:(1),①×2﹣②得:5x=﹣5,解得:x=﹣1,将x=﹣1代入①得:﹣3﹣y=﹣4,解得:y=1,故原方程组的解为;(2),①×5+②×3得:19x=19,解得:x=1,将x=1代入①得:2+3y=8,解得:y=2,故原方程组的解为.6.解下列方程组:(1);(2).【解答】解:(1),把②代入①得,6y﹣7﹣y=13,解得y=4;把y=4代入②得,x=6×4﹣7=17,故方程组的解为;(2),①×3﹣②×2得,6x+15y﹣6x﹣4y=24﹣10,解得y=,把y=代入②得,3x+2×=5,解得x=,故方程组的解为.7.解方程组:(1);(2).【解答】解:(1),①+②×2,得11x=33,解得:x=3,把x=3代入①,得9+2y=7,解得:y=﹣1,所以方程组的解是;(2)整理得:,①×2+②,得5x=15,解得:x=3,把x=3代入①,得3+2y=7,解得:y=2,所以方程组的解是.8.解二元一次方程组:(1);(2).【解答】解:(1),①﹣②×2,得7y=﹣14,解得y=﹣2,将y=﹣2代入①,得2x﹣2=2,解得x=2,∴原方程组的解为;(2),由①得,3x+4y=36③,由②得3x﹣2y=9④,③﹣④,得6y=27,解得y=,将y=代入④,得3x﹣9=9,解得x=6,∴原方程组的解为.9.按要求解下列方程组:(1)(用代入消元法);(2)(用加减消元法).【解答】解:(1),由②,得y=5﹣3x③,把③代入①,得3x+2(5﹣3x)=7,解得x=1,把x=1代入①,得y=2,故原方程组的解为;(2),①+②×2,得7x=21,解得x=3,把x=3代入②,得y=5,故原方程组的解为.10.解方程组:(1);(2).【解答】解:(1),①×4得:8x﹣4y=20③,②+③得:11x=22,解得:x=2,把x=2代入①得:4﹣y=5,解得:y=﹣1,故原方程组的解是:;(2),整理得:,①+②得:8y=24,解得:y=3,把y=3代入②得:x+15=10,解得:x=﹣5,故原方程组的解是:.11.解下列方程组:(1)(代入消元法);(2)(加减消元法).【解答】解:(1),由①得:x=1+2y③,把③代入②,得4(1+2 y)+3y=26,解得:y=2,把y=2代入③,得x=1+2×2=5,所以;(2),由①+②,得7x=21,解得:x=3,把x=3代入①,得2×3+3y=3,解得:y=﹣1,所以.12.解下列方程组:(1);(2).【解答】解:(1)将原方程组化简整理得:,②×4得:8x+20y=28③,③﹣①得:27y=27,解得:y=1,把y=1代入②中得:2x+5=7,解得:x=1,∴原方程组的解为:;(2)将原方程组化简整理得:,①×3得:9x﹣12y=﹣21③,②×4得:8x+12y=4④,③+④得:17x=﹣17,解得:x=﹣1,把x=﹣1代入②中得:﹣2+3y=1,解得:y=1,∴原方程组的解为:.13.用指定的方法解下列方程组:(1)(代入法);(2)(加减法).【解答】解:(1),把①代入②得:4x+3(2x﹣2)=5,解得x=,把x=代入①得:y=2×﹣2=,∴方程组的解为;(2),①×3得:3x+9y=﹣3③,③﹣②得:11y=﹣11,解得:y=﹣1,把y=﹣1代入①得:x﹣3=﹣1,解得:x=2,∴方程组的解为.14.解下列方程组.(1);(2).【解答】解:(1),由①+②得,5x=﹣5,解得x=﹣1,将x=﹣1代入①,得﹣2+5y=8,解得y=2,∴方程组的解为;(2),由①×3,②×2得:,由③+④得,13x=26,解得:x=2,把x=2代入①,得y=4,所以方程组的解为:.15.解方程组:(1);(2).【解答】解:(1),由①得,x=1+2y③,把③代入②,得3(1+2y)﹣y=3,解得y=0,把y=0代入③,得x=1,所以原方程组的解为:;(2)原方程组可化为,①+②得,4x=24,解得x=6,①﹣②得,6y=﹣6,解得y=﹣1,所以原方程组的解为:.16.解下列方程组:(1);(2).【解答】解:(1),①+②,得2x=12,解得x=6,将x=6代入①,得6﹣y=5,解得y=1,∴原方程组的解为;(2)原方程组化为,①﹣②,得25y=10,解得y=,将y=代入①,得5x+6=6,解得x=0,∴原方程组的解为.17.解二元一次方程组:(1).(2).【解答】解:(1),②﹣①×2得:x=6,把x=6代入①得:6+2y=0,解得y=﹣3.∴方程组的解是.(2),①×2+②×3得:13x=65,解得x=5.把x=5代入①得:10+3y=16,解得y=2.∴方程组的解是.18.解方程组:(1);(2).【解答】解:(1)对于方程组,①×2得:4x﹣10y=24③,②﹣③得:﹣13y=26,∴y=﹣2,将y=﹣2代入①得:x=1,∴原方程组的解为:.(2)对于方程组,将①代入②得:2×2y+y=5,∴y=1,将y=1代入①得:x=2,∴原方程组的解为:.19.解方程组:(1);(2).【解答】解:(1),①+②得4x=8,∴x=2,把x=2代入①得2+2y=3,,∴原方程组的解是.(2),整理得:,由①得:s=﹣2t③,把③代入②得:t=﹣2;把t=﹣2 代入③得:s=4,∴原方程组的解是.20.用适当的方法解下列方程组:(1)(2).【解答】解:(1),①+②得:6x=18,解得:x=3,把x=3代入①得:y=﹣4,则方程组的解为;(2),把①代入②得:4x﹣14=2,解得:x=4,把x=4代入①得:y=3,则方程组的解为.21.解方程组:(1);(2).【解答】解:(1),原方程可化为:,①+②×5得:46y=46,∴y=1,将y=1代入①得:x=7,∴原方程组得解为:;(2),原方程可化为:,①×4+②得:19x=57,∴x=3,将x=3代入①得:y=0,∴原方程组得解为:.22.解二元一次方程组:(1);(2).【解答】解:(1),②﹣①,得y=1,把y=1代入①,得x=2,故原方程组的解为;(2)原方程组整理,得,②﹣①×2,得7y=7,解得y=1,把y=1代入①,得x=5.故原方程组的解为.23.解二元一次方程组:(1);(2).【解答】解:(1),由②得y=13﹣2x③,把③代入①,得4x﹣3(13﹣2x)=11,解得x=5,把x=5代入③,得y=3,∴这个方程组的解是;(2),①×2﹣②×3,得﹣19y=19,解得y=﹣1.把y=﹣1代入①,得3x+2=5,解得x=1,∴这个方程组的解为.24.解方程组:(1);(2).【解答】解:(1),把①代入②,得3x﹣8(x﹣3)=14,解得x=2,把x=2代入①,得y=﹣1,故原方程组的解为;(2),①×2﹣②,得7x=35,解得x=5,把x=5代入①,得y=0,故原方程组的解为.25.解方程组:(1);(2).【解答】解:(1),由①+②得:4x=8,解得:x=2,将x=2代入①得:2﹣2y=1,解得:y=,∴方程组的解为:;(2),由①可得:x=3﹣2y③,将③代入②得:3(3﹣2y)﹣4y=4,解得:y=,将y=代入③得:x=3﹣2×,解得:x=2,∴原方程组的解为:.26.解方程组:(1);(2).【解答】解:(1),①×2得:4x﹣2y=0③,②+③得:5x=5,解得:x=1,把x=1代入①中得:y=2,∴原方程组的解为:.(2),②×2,8x﹣2y=6③,①+③得:11x=11,解得:x=1,把x=1代入②,得4﹣y=3,解得:y=1,∴原方程组的解为:.27.解方程组:(1);(2).【解答】解:(1),①+②,得7x=35,解得:x=5,把x=5代入①,得10﹣3y=﹣2,解得:y=4,所以方程组的解是;(2),①+②×2,得11x=11,解得:x=1,把x=1代入②,得4﹣y=3,解得:y=1,所以方程组的解是.28.解方程组:(1);(2).【解答】解:(1),把②代入①得y﹣9+3y=7,解得y=4,把y=4代入②得x=4﹣9=﹣5,所以方程组的解为;(2),①×2+②得10x+3x=34+5,解得x=3,把x=3代入②得9+4y=5,解得y=﹣1,所以方程组的解为.29.解方程组:(1);(2).【解答】解:(1),①+②得:4x=8,解得:x=2,把x=2代入①得:2+2y=﹣1,解得:,∴方程组的解为;(2),由②得:y=2x﹣2,把y=2x﹣2代入①得:4x﹣3(2x﹣2)=5,解得:,把代入y=2x﹣2得:,∴方程组的解为.30.解方程组:(1);(2).【解答】解:(1),将①代入②,可得:3x+2x+3=18,解得x=3,把x=3代入①,可得:y=9,∴原方程组的解是.(2),①×2﹣②,可得7y=35,解得y=5,把y=5代入①,可得:x=0,∴原方程组的解是.31.解方程组:(1);(2).【解答】解:(1),把①代入②得:3x+2(2x﹣1)=5,解得:x=1,把x=1代入①得:y=2﹣1=1,故原方程组的解是:;(2),①+②得:3m=6,解得:m=2,把m=2代入①得:2+3n=5,解得:n=1,故原方程组的解是:.32.解方程组:(1);(2).【解答】解:(1)把②代入①中,得3x+2(2x﹣8)=5.解得x=3.把x=3代入②中,得y=2×3﹣8解得y=﹣2.∴这个方程组的解为;(2)①﹣②,得﹣4y=8.解得y=﹣2.把y=﹣2代入①中,得2x+2=10.解得x=4.∴这个方程组的解为.33.用适当的方法解方程组:(1);(2).【解答】解:(1),②﹣①×3得:x=1,把x=1代入①中,解得:y=1,∴这个方程组的解为;(2)方程组整理为:,②×2+①得:5x=30,解得:x=6,把x=6代入②中,解得:y=9,∴这个方程组的解为.34.解下列方程组:(1);(2).【解答】解:(1),将①代入②,得:3x﹣2(2x+1)=2,解得:x=﹣4,把x=﹣4代入①得:y=﹣7,∴方程组的解为:;(2)①×2+②,得:5x=10,解得:x=2,把x=2代入①,得:4+y=1,解得:y=﹣3,∴方程组的解为:.35.解方程组:(1);(2).【解答】解:(1),①+②得,7x=14,解得x=2,把x=2代入①得,3×2+7y=9,解得y=,∴方程组的解是;(2),①×3得,15x+6y=12③,②×2得,16x+6y=14④,④﹣③得,x=2,把x=2代入①得,y=﹣3,∴方程组的解是.36.解方程组:(1);(2).【解答】解:(1),②﹣①得:y=2,把y=2代入①得:,∴方程组的解为:;(2),由③得:y=3﹣2x,把y=3﹣2x代入④得:3x﹣5(3﹣2x)=11,3x﹣15+10x=11,13x=26,x=2,把x=2代入y=3﹣2x得:y=﹣1,∴方程组的解为:.37.解方程组:(1);(2).【解答】解:(1),①×3得:3x﹣15y=0③,②﹣③得:17y=17,解得:y=1,把y=1代入①得:x﹣5=0,解得:x=5,∴原方程组的解为:;(2),把①代入②得:y﹣13﹣6y=7,解得:y=﹣4,把y=﹣4代入①得:x=﹣4﹣13=﹣17,∴原方程组的解为:.38.解方程组:(1);(2).【解答】解:(1),①+②得:5x=25,解得:x=5,把x=5代入①得:5﹣3y=10,解得:y=﹣,故原方程组的解是:;(2),由①得:3x﹣2y=8③,②+③得:6x=12,解得:x=2,把x=2代入②得:6+2y=4,解得:y=﹣1,故原方程组的解是:.39.解方程组:(1);(2).【解答】解:(1),①+②得:3x=12,解得:x=4,把x=4代入①得:4﹣y=2,解得:y=2,则方程组的解为;(2)方程组整理得:,①×4﹣②×3得:﹣7x=﹣14,解得:x=2,把x=2代入①得:4﹣3y=1,解得:y=1,则方程组的解为.40.解下列方程组:(1);(2).【解答】解:(1),由①,得x=y+3③,把③代入②,得3y+9﹣8y=14,解得y=﹣1,把y=﹣1代入①,得x=2,故原方程组的解为;(2),①×2+②,得11x=11,解得x=1,把x=1代入①,得x=﹣2,故原方程组的解为.41.解下列方程组:(1);(2).【解答】解:(1),②代入①,可得x+2x﹣1=2,解得,x=1,将x=1代入②,可得y=1,故方程组的解为.(2),②﹣①,可得,解得,x=3,将x=3代入①,可得y=2,故方程组的解为.42.用加减消元法解方程:(1);(2).【解答】解:(1),①﹣②得:12y=﹣36,即y=﹣3,把y=﹣3代入①得:x=,则方程组的解为;(2)方程组整理得:,①﹣②得:4y=28,即y=7,把y=7代入①得:x=5,则方程组的解为.43.解二元一次方程组:(1);(2).【解答】解:(1)方程整理得,由①+②得:5a+5b=﹣5,即a+b=﹣1③,由①﹣③×2得:b=1,把b=1代入③得:a+1=﹣1,解得a=﹣2,∴方程组的解是.(2),由②得:x=3y﹣2③,把③代入①得:9(3y﹣2)﹣7y﹣12=0,解得y=,把y=代入③得x=﹣2=,∴方程组的解是.44.解方程组:(1);(2).【解答】解:(1),解:①+②得3x=33,解得x=11,把x=11代入①得y=14,∴方程组的解是;(2),解:原方程组可化为,①﹣②得6x=6,解得x=1,把x=1代入①得,∴方程组的解是.45.解方程:(1);(2).【解答】解:(1),①代入②得,2x+(3x+1)=﹣9,解得:x=﹣2,将x=﹣2代入①得,y=﹣5,∴方程组的解为:;(2),①×2+②得,6x+x=14,解得:x=2,将x=2代入①得6﹣2y=5,解得:,∴方程组的解为:.46.用适当的方法解下列方程组:(1);(2).【解答】解:(1),由①﹣②×2得:3y﹣(﹣2y)=1﹣5×2,解得:,将代入②得:,解得:,∴原方程组的解为;(2),由①×2+②得:7x=14,解得:x=2,把x=2代入①得:2×2+y=2,解得:y=﹣2,∴原方程组的解为.47.解方程组:(1);(2).【解答】解:(1),①×3+②得:7y=28,解得:y=4,将y=4代入①得:x=1,∴方程组的解为:;(2)整理得:,①+②×5得:23y=23,解得y=1,把y=1代入①得:5x﹣2=﹣12,解得x=﹣2,∴方程组的解为.48.解方程组:(1);(2).【解答】解:(1),①+②得,2x=6,解得:x=3,把x=3代入①得y=﹣1,∴方程组的解为;(2),①×2,得10x+4y=50③,③﹣②,得7x=35,解得:x=5,把x=5代入①得,25+2y=25,解得:y=0,所以方程组的解为.49.解方程组:(1);(2).【解答】解:(1),整理得:,由①﹣②得:4y=28,解得:y=7,把y=7代入①得:3x﹣7=8,解得:x=5,∴原方程组的解为:;(2),由②﹣①得:5x=15,解得:x=3,把x=3代入①得:y﹣2×3=0,解得:y=6,∴原方程组的解为.50.解方程组:(1);(2).【解答】解:(1),②×3得:15x+3y=21③,①+③得:19x=38,解得:x=2,把x=2代入②得:10+y=7,解得:y=﹣3,故原方程组的解是:;(2),①×2得:2x﹣4y=16③,②+③得:5x=10,解得:x=2,把x=2代入①得:2﹣2y=8,解得:y=﹣3,故原方程组的解是:.51.阅读以下材料:解方程组:;小亮在解决这个问题时,发现了一种新的方法,他把这种方法叫做“整体代入法”,解题过程如下:解:由①得x﹣y=1③,将③代入②得:(1)请你替小亮补全完整的解题过程;(2)请你用这种方法解方程组:.【解答】解:(1)由①得x﹣y=1③,将③代入②得:4×1﹣y=0,解得y=4,把y=4代入①得:x﹣4﹣1=0,解得x=5,故原方程组的解是:;(2),整理得:,把③代入④得:2×2+1+15y=50,解得y=3,把y=3代入①得:3x﹣3﹣2=0,解得x=,故原方程组的解是:.52.已知关于x、y的方程组的解满足x+y =﹣10,求代数式m2﹣2m+1的值.【解答】解:,①×2﹣②×3得:y=4﹣m,把y=4﹣m代入②得:x=2m﹣6,代入x+y=﹣10得:4﹣m+2m﹣6=﹣10,解得:m=﹣8,则原式=(m﹣1)2=81.53.在解方程组时,由于粗心,甲看错了方程组中的a,得解为;乙看错了方程组中的b,得解为.(1)甲把a错看成了什么?乙把b错看成了什么?(2)求出原方程组的正确解.【解答】解:(1)将x=,y=﹣2代入方程组得:,解得:,将x=3,y=﹣7代入方程组得:,解得:,则甲把a错看成了1;乙把b错看成了1;(2)根据(1)得正确的a=2,b=3,则方程组为,解得:.54.已知方程组和方程组的解相同求a、b的值.【解答】解:方程组的解为,由于方程组和方程组的解相同,所以,解得.55.甲和乙两人同解方程组甲因抄错了a,解得,乙因抄错了b,解得,求5a﹣2b的值.【解答】解:由题意,是bx+y=12的解得5b+2=12,解得b=2.又是x+ay=5的解得3+2a=5,解得a=1,∴5a﹣2b=5×1﹣2×2=1.56.对于实数x、y,定义新运算:x*y=ax+by;其中a、b是常数,等式右边是通常的加法和乘法运算,已知1*2=1,(﹣3)*3=6.(1)分别求出a、b的值;(2)根据上述定义新运算,试求2*(﹣4)的值.【解答】解:(1)根据题中的新定义化简得:,解得:;(2)根据题中的新定义得:原式=2×(﹣1)+(﹣4)×1=﹣2﹣4=﹣6.57.甲、乙两位同学在解方程组时,甲把字母a看错了得到方程组的解为;乙把字母b看错了得到方程组的解为.(1)求a,b的正确值;(2)求原方程组的解.【解答】解:(1)由题意,将代入bx﹣4y=4,得4b﹣4=4,∴b=2,将代入ax+3y=9,得3a+6=9,∴a=1;(2),①×2﹣②,得y=1.4,将y=1.4代入①得,x=4.8,∴方程组的解为.58.定义一种新运算“※”:规定m※n=am+bn﹣mn,其中a,b为常数,且6※15=270,8※10=360,求﹣2※1的值.【解答】解:∵6※15=270,8※10=360,∴,解得:,∴﹣2※1=﹣100+4﹣(﹣2)×1=﹣94.59.若关于x,y的方程组与方程组的解相同.(1)求两个方程组的相同解;(2)求(3a﹣b)2023的值.【解答】解:(1)两方程组化简可得,,∵两方程组同解,∴①×2+②得:7x=21,解得:x=3,把x=3代入①式得:y=1,∴两个方程组的相同解为;(2)把代入方程组可得:①﹣②式得:2a=﹣4,解得:a=﹣2,把a=﹣2代入②式得:b=﹣5,∴(3a﹣b)2023=(﹣6+5)2023=﹣1.60.已知方程组和有相同的解,求a﹣2b的值.【解答】解:联立得:,①×2+②得:11x=11,解得:x=1,把x=1代入②得:y=﹣2,把代入,得,解得:,则a﹣2b=14﹣4=10.。
8.2.1消元-代入法解二元一次方程组复习

变
4x + 5y = 4
用含x 的一次式表示y:
y=
4 4x 5 4 5y 4
代
用含y 的一次式表示x:
x=
求 写
4、写出方程组的解
例1 解方程组 2s = 3t 3s – 2t = 5
解: 2s = 3t 3s – 2t = 5 s 由①得: =
3 t 2
① ② ③
练习: 2x – 7y = 8 3x–8y–10 = 0 ① 解: 2x – 7y = 8 3x -8y- 10= 0 ② 由①得:2x =8 + 7y 把③代入②得:
8 7y x= 2
3(8 7 y) 8 y 10 0 2
∴
x = 6/5 y = -4/5
4 8 7 ( ) 5 2
=6/5
例2、用代入法解方程组:
y x 2 3 1 6 ( 2 x 1) 3 y 2 5 2 3
a 由②得: = -2b - 1 ③ 把③代入①得:
2x + ay = 3b ax - by = 1 的解,
②
把b = -4/7 代入③,得: a = -2b - 1 = -2×(-4/7)-1 a = 1/7 ∴ a = 1/7
-2 + 2(-2b – 1)= 3b -2 – 4b – 2 = 3b -4b – 3b = + 2 + 2 -7b = 4 b = -4/7
4(x + y)- 5(x – y)= 2
能 力 检 验
x = -1, x = 2, 2,若 和 是方程 mx + ny = 10 的两个解, y = 2, y = -2, 求 m 、n 的值.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
消元(一)
学习要求
会用代入消元法解二元一次方程组.
课堂学习检测
一、填空题
1.已知方程6x -3y =5,用含x 的式子表示y ,则y =______.
2.若⎩⎨⎧-==1,1y x 和⎩
⎨⎧==3,2y x 是关于x ,y 的方程y =kx +b 的两个解,则k =______,b =______. 3.在方程3x +5y =10中,若3x =6,则x =______,y =______.
二、选择题
4.方程组⎩
⎨⎧=++=143,5y x y x 的解是( ). (A)无解 (B)无数解 (C)⎩⎨⎧=-=.3,2y x (D)⎩⎨⎧-==.
2,3y x 5.以方程组⎩
⎨⎧-=+-=1,2x y x y 的解为坐标的点(x ,y )在平面直角坐标系中的位置是( ). (A)第一象限
(B)第二象限 (C)第三象限 (D)第四象限 6.下列方程组中和方程组⎩⎨
⎧=+-=732,43y x y x 同解的是( ). (A)⎩
⎨⎧=+=.732,11y x x (B)⎩⎨⎧=+=.732,5y x y (C)⎩⎨⎧=+--=.7386,43y x y x (D)⎩
⎨⎧-==.43,1y x x 三、用代入消元法解下列方程
7.⎩⎨⎧=+=+.53,1y x y x 8.⎩
⎨⎧=+=+.643,02b a b a
综合、运用、诊断
一、填空题
9.小明用36元买了两种邮票共40枚,其中一种面值1元,一种面值0.8元,则小明买了
面值1元的邮票______张,面值0.8元的邮票______张.
10.已知⎩⎨⎧-==.2,1y x 和⎩
⎨⎧==.0,2.y x 都是方程ax -by =1的解,则a =______,b =______.
11.若|x -y -1|+(2x -3y +4)2=0,则x =______,y =______.
二、选择题
12.用代入消元法解方程组⎩
⎨⎧=-=+②①52,243y x y x 使得代入后化简比较容易的变形是( ). (A)由①得342y x -=
(B)由①得432x y -= (C)由②得2
5+=y x (D)由②得y =2x -5 13.已知x =3t +1,y =2t -1,用含x 的式子表示y ,其结果是( ). (A)3
1-=x y (B)21+=
y x (C)352-=x y (D)312--=x y 14.把x =1和x =-1分别代入式子x 2+bx +c 中,值分别为2和8,则b 、c 的值是( ).
(A)⎩⎨⎧==4,3c b (B)⎩⎨⎧-==4,3c b (C)⎩⎨⎧-=-=4,3c b (D)⎩⎨⎧=-=4
,3c b 三、用代入消元法解下列方程组
15.⎩
⎨⎧-=-=-.234,423x y y x 16.⎩
⎨⎧==-.3:4:,52y x y x
拓展、探究、思考
17.如果关于x ,y 的方程组⎪⎩⎪⎨⎧-=-+=-32
1,734k y x k y x 的解中,x 与y 互为相反数,求k 的值.
18.研究下列方程组的解的个数:
(1)⎩⎨⎧=-=-.342,12y x y x (2)⎩⎨⎧=-=-.32,12y x y x (3)⎩
⎨⎧=-=-.242,12y x y x
你发现了什么规律?
19.对于有理数x ,y 定义新运算:x *y =ax +by +5,其中a ,b 为常数.
已知1*2=9,(-3)*3=2,求a ,b 的值.。
