基础物理常数全表PDF
普朗克常数和普朗克质量

$ # + ’/"010 . "# $% 23 !
&" 卷(’##’ 年)) 期
值代入 ("#) 式, 计算结果得 ・ &#& ・
*+ ((() ! ! "#$%"& ’ () , 这表明, 两个带电粒子之间的相互作用, 如以 "! 来
量度, 只是这一自然尺度的 ()+ 分之一 , 用 (()) 式除 即得 !以!) ! "# $ $ $ - "# $ "! , !) !( (-& # $ ))) ) , 因为 所以 !) ! (, (($) $ - "# ) , ! !((-& # $ )) 这就是电磁相互作用与强相互作用的强度比, 即前
!" #$%"&’() *%))
)*+, -./01/23
( "#$%& ’&($)%&* +%,($(-(. /)0 12-3&($)%&* 4.,.&03# ,5.$6$%7 !"""##,"#$%& )
%+,-./0-
* 45/67 568/69 /: ;56:62<6= >7 <.566 7?2=@A62<@B ;.C:/D@B E?@2</</6: =65/86= 4C F@G HB@2DI /2 !$!%,560
$’1 (5) "" + & ! "1") . "# 4*! 在原子核内, 核子具有的势能随作用距离而变化 ! 作
乙醇物理常数表

乙醇物理常数表
乙醇是一种常见的有机化合物,也称作乙醇酒精。
其化学式为
C2H5OH,是一种无色、可燃的液体,有着独特的香味。
作为一种重要的工业化学品和生物燃料原料,乙醇物理常数是我们需要了解和掌握的基础知识。
乙醇具有许多重要的物理常数,其中比较常见的包括密度、沸点、熔点、折射率等。
乙醇的密度为0.79 g/cm3,沸点为78.4℃,熔点为-114.1℃。
乙醇在常温下呈现出无色透明的状态,也是一种弱酸性物质,在水中可以呈现出亲水性溶解性。
此外,乙醇还有着很强的折射性能。
它的折射率随着波长的变化而发生变化,且变化量比较大。
例如,当波长为589.3 nm时,其折射率为1.361。
这种折射性能对于科研研究和晶体制备等方面都有着重要的应用价值。
总之,乙醇是一种重要的有机化合物,在生产和科研领域都有着广泛的应用。
了解乙醇的物理常数对于科研实验的设计以及工业制造过程的控制都有着重要的价值。
Iupilon-基础物理性能表-
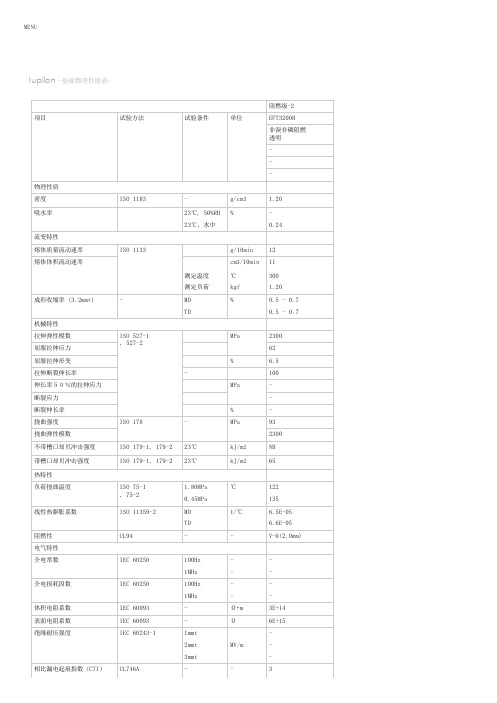
阻燃级-2项目试验方法试验条件单位EFT3200H 非溴非磷阻燃 透明---物理性质 密度ISO 1183-g/cm 3 1.20吸水率23℃, 50%RH %-23℃、水中0.24流变特性 熔体质量流动速率ISO 1133g/10min 12熔体体积流动速率cm 3/10min 11测定温度℃300测定负荷kgf 1.20成形收缩率 (3.2mmt)-MD %0.5 - 0.7TD0.5 - 0.7机械特性 拉伸弹性模数ISO 527-1 , 527-2MPa 2300屈服拉伸应力 62屈服拉伸形变 % 6.5拉伸断裂伸长率- 100伸长率50%的拉伸应力 MPa -断裂应力 -断裂伸长率 %-挠曲强度ISO 178-MPa 93挠曲弹性模数2300不带槽口却贝冲击强度ISO 179-1, 179-223℃kJ/m 2NB 带槽口却贝冲击强度ISO 179-1, 179-223℃kJ/m 265热特性 负荷挠曲温度ISO 75-1 , 75-2 1.80MPa ℃1220.45MPa 135线性热膨胀系数ISO 11359-2MD 1/℃ 6.5E-05TD6.6E-05阻燃性UL94--V-0(2.0mm)电气特性 介电常数IEC 60250100Hz --1MHz--介电损耗因数IEC 60250100Hz --1MHz--体积电阻系数IEC 60093-Ω・m 3E+14表面电阻系数IEC 60093-Ω6E+15绝缘耐压强度IEC 60243-11mmt -2mmt MV/m -3mmt-相比漏电起痕指数(CTI)UL746A--3MENUIupilon -基础物理性能表-备考EFT3200HU(耐候性改良)标准成型条件 -以下是具有代表性的成型条件-预备干燥热风干燥120℃---約4-8小时料管温度(后部)℃270-290料管温度 (中央部)℃280-300料管温度 (前部)℃280-310喷嘴温度℃280-310模具温度℃70-100射出圧力MPa50-150螺杆回转数rpm50-100注意记载数据仅为代表值。
光电子物理基础第一章-物质中光的吸收和发射

• 有限范围内成立;需修正
2)禁戒的直接跃迁 • 在某些材料中,k=0的直接跃迁是禁止 的,k≠0的直接跃迁是允许的, Wif正比于k2, 正比于(hν-Eg),则αd=α(hν-Eg)3/2,其中
α = 2 / 3 ⋅ B(2mr / m) f if' / hνf if
直接跃迁的吸收系数随频率的 变化
1.3.2 激子吸收
基本吸收中,认为被激发电子变成了导带中自 由粒子,价带中产生的空穴也是自由的。但是 受激电子与空穴会彼此吸引(库仑场),有可能 形成束缚态,称为激子。电中性 能在晶体中自由运动的激子称自由激子,又称 瓦尼尔(Wannier)激子。不能自由运动的激子 称束缚激子,又称弗伦克尔(Frankel)激子。
1/ 2
1.3.3 杂质吸收
三个方面 1)从杂质中心的基态到激发 态的激发,可引起线状吸收 谱。 2)电子从施主能级到导带或 从价带到受主能级的吸收跃 迁 红外区
3)从价带到施主能级或从被 电子占据的受主能级到导 带的吸收跃迁。 几率小。 浅受主能级到导带的跃迁 吸收跃迁系数
α = AA N A (hν − E g + E A )1/ 2
中红外范围内,自由载流子吸收按λ2规 律变化。近红外区不再适用。 电子在导带中跃迁,不同能量状态间跃 迁,则必须改变波矢量,为了动量守恒, 电子动量的改变可由声子或电离杂质的 散射来获得补偿。 近红外区域,M.Becker等人指出①电子 受到声学声子散射, α ∝λ1.5②电子受到 光学声子散射, α ∝λ2.5 ③受杂质散射, α ∝λ3∼3.5
(1)允许的跃迁 (2)禁止的跃迁
3)布尔斯坦-莫斯移动 重掺杂半导体的本 征吸收限向高频方 向移动,布尔斯坦 -莫斯移动 4)带尾效应 • 直接跃迁吸收系数 的光谱曲线,吸收 系数随光子能量减 小呈指数衰减
《大学基础物理学》农科用教材自作pdf课件-05稳恒电流

V2 dV = RT ln RT V1 V
V2 C 1 (∴ = ) V1 C 2
A RT C 1 ln 得电动势 ε = = q ZF C 2
Z为价电荷数 F为法拉第常数,F=96485C/mol
海 南 大 学
第五章 恒定电流( steady current )
三、细胞内外的扩散电动势
海 纳 百 川
第五章 恒定电流( steady current )
具有相同温度T的两金属A、B的接触电势差
U AB = U
海 纳
' AB
+U
" AB
kT n A ln = VB − V A + e nB
A
B
大 道
若有三种相同温度T的两金属A、B、C的接触电势差
kT n A U AB = U + U = VB − V A + ln e nB 百 kT nB ' " U BC = U BC + U BC = VC − V A + ln e nC 川 kT n A U AC = U AB + U BC = VC − V A + ln e nC
细胞内的主要是K+、Na+和Cl-三种 离子,扩散电动势为
ε=
RT ln ZF PK K + PK K +
o i
大 K+ 道 致 远 Na+
+ PNa Na + + PNa Na
+
o i
+ PCl Cl − + PCl Cl
−
i o
(V )
Cl-
i、o分别表示膜内、外; PK、 PNa、 PCl是细胞膜对K+、 Na+和Cl-的通透系数;
基础物理实验课件 光电效应法测定普朗克常数

北京航空航天大学物理实验中心
XXX
将实验仪及汞灯电源接通(汞 灯及光电管暗盒遮光盖盖上),
预热20分钟。
预习思考题
▪ ① 经典的光波动理论在哪些方面不能解释光电 效应的实验结果?
▪ ② 光电效应有哪些规律,爱因斯坦方程的物理 意义是什么?
▪ ③ 光电流与光通量有直线关系的前提是什么? 掌握光电特性有什么意义?
▪ ⑥ 光电流是否随光源的强度变化而变化? 截止电压是否因光强不同而变化?
▪ ⑦ 测量普朗克常量实验中有哪些误差来 源?如何减小这些误差?
谢谢!
▪ 2、用作图法求出Uo -ν直线的斜率k,利用h = ek求出普朗克常数,并算出所测值与公认值之间 的相对误差。
▪ 3、利用线性回归法计算普朗克常数h,将结果与 作图法求出结果进行比较。
▪ 4、利用表2中的数据,作出对应于不同频率及光 强的伏安特性曲线。
实验后思考题
▪ ⑤ 定性解释I- U特性曲线和U0 -ν曲线 及其截距的意义。
实验仪器介绍
图5 仪器结构图
实验仪
1
2
3
4ቤተ መጻሕፍቲ ባይዱ
5
6
1汞灯电源 2汞灯 3滤色片 4光阑 5光电管 6基座
实验内容和操作提示
▪ 调整光电管与汞灯距离为约40cm并保持不变。用 专用连接线将光电管暗箱电压输入端与实验仪电 压输出端(后面板上)连接起来(红—红,蓝— 蓝)。务必反复检查,切勿连错!
测普朗克常数h
▪ 3、进一步练习利用线性回归和作图法处 理实验数据。
实验原理
爱因斯坦光电效应方程
h 1 m 2 W
2
U0
h (
e
0 )
物理学常量

物理学常量1. 光速(c):在真空中,光速的值约为299,792,458米/秒。
这是一个不可超越的极限速度,也是狭义相对论的基石。
2. 普朗克常数(h):普朗克常数的值约为6.62607015×10^-34 J·s,是量子力学的基础。
它描述了能量的最小单位,即量子。
3. 玻尔兹曼常数(k):玻尔兹曼常数的值约为1.380649×10^-23 J/K,是统计力学中的关键常数,用于描述热运动。
4. 电子电荷(e):电子的电荷大约为1.602176634×10^-19 C,是电磁学的基本单位。
5. 质子质量(m_p):质子的静止质量约为1.672621898×10^-27 kg,是原子物理学和核物理学中的重要参数。
6. 牛顿常数(G):牛顿引力常数的值约为 6.67430×10^-11 N·m^2/kg^2,是描述万有引力的基础。
7. 约化普朗克常数(ħ):约化普朗克常数的值约为1.054571817×10^-34 J·s,是量子力学中的重要常数。
8. 真空介电常数(ε_0):真空介电常数的值约为8.854187817×10^-12 F/m,是电磁学中的基本常数。
9. 微分电荷(e):电子的电荷约为1.602176634×10^-19 C,是电磁学的基本单位。
10. 阿伏伽德罗常数(N_A):阿伏伽德罗常数的值约为6.02214076×10^23 mol^-1,描述了一摩尔物质中分子或原子的数量。
这些常量在物理学各个领域中扮演着关键作用,是构建理论和进行计算的基础。
它们反映了自然界的基本规律和特性。
物理常数单位制

黄晨 * 2004 年 9 月 (* 联系地址 复旦大学化学系表面化学实验室 eMail morning_yellow@)
一 国际单位制(SI)和高斯单位制(CGS)的力学量纲和单位
力学物理定律在国际单位制(简称国际制 记作 SI)和高斯单位制(简称高斯制 又称为厘 米克秒制 记作 CGS)中具有相同的形式 并且它们都以长度 质量和时间作为基本量纲 所以所有的力学量都具有相同的量纲 另外 这两个单位之间的换算也相当方便 都是 10 的次方数
它是电动力学中最常用的单位制 另一套以安培定律为基础 称为电磁制 记作 CGSM 它
是国际单位制的理论基础
静电学中最基本的定律是库仑定律 而该定律在国际制和静电制中有着不同的形式 国
际制的形式是
这里 ε0 是真空中的介电常数 而电磁制则是
F
=
q1q2 4πε0r 2
其数值为 8.8541878×10−12C2/Nm2
如果静电制单位和电磁制单位的量纲之比为 L−nTn 那么两者的换算关系就是
1 静电制单位 = (2.99792458×1010)n 电磁制单位
(4-3)
例如 国际制中电容单位 F 的量纲为 L−2M−1T4I2 要把它转化为静电制单位 cm 首先要
经过电磁制单位 cm/s2 关系是 1F(SI) = 10−9(cm/s2)−1(CGSM) 由于电容在电磁制中的量纲
制和高斯制之间并不存在 但是在某些单位之间 例如能量单位 J 和 eV 就相差一个基本
电荷 e/C 该常数的不确定度就是这两个单位比值的不确定度 根据这个道理 同一物理常
数在不同单位下具有不一样的不确定度 例如基本电荷 用 C(库仑)时不确定度为 0.09ppm
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Fundamental Physical Constants—Complete ListingRelative std.Quantity Symbol Value Unit uncert.u rUNIVERSALspeed of light in vacuum c,c029*******m s−1(exact) magnetic constantµ04π×10−7N A−2=12.566370614...×10−7N A−2(exact) electric constant1/µ0c2ε08.854187817...×10−12F m−1(exact) characteristic impedanceof vacuum µ0/ 0=µ0c Z0376.730313461...Ω(exact) Newtonian constantof gravitation G6.673(10)×10−11m3kg−1s−21.5×10−3G/¯h c6.707(10)×10−39(GeV/c2)−21.5×10−3 Planck constant h6.62606876(52)×10−34J s7.8×10−8 in eV s4.13566727(16)×10−15eV s3.9×10−8 h/2π¯h1.054571596(82)×10−34J s7.8×10−8 in eV s6.58211889(26)×10−16eV s3.9×10−8Planck mass(¯h c/G)1/2m P2.1767(16)×10−8kg7.5×10−4 Planck length¯h/m P c=(¯h G/c3)1/2l P1.6160(12)×10−35m7.5×10−4 Planck time l P/c=(¯h G/c5)1/2t P5.3906(40)×10−44s7.5×10−4ELECTROMAGNETICelementary charge e1.602176462(63)×10−19C3.9×10−8e/h2.417989491(95)×1014A J−13.9×10−8magneticflux quantum h/2eΦ02.067833636(81)×10−15Wb3.9×10−8 conductance quantum2e2/h G07.748091696(28)×10−5S3.7×10−9 inverse of conductance quantum G−1012906.403786(47)Ω3.7×10−9 Josephson constant a2e/h K J483597.898(19)×109Hz V−13.9×10−8 von Klitzing constant bh/e2=µ0c/2αR K25812.807572(95)Ω3.7×10−9Bohr magneton e¯h/2m eµB927.400899(37)×10−26J T−14.0×10−8 in eV T−15.788381749(43)×10−5eV T−17.3×10−9µB/h13.99624624(56)×109Hz T−14.0×10−8µB/hc46.6864521(19)m−1T−14.0×10−8µB/k0.6717131(12)K T−11.7×10−6nuclear magneton e¯h/2m pµN5.05078317(20)×10−27J T−14.0×10−8 in eV T−13.152451238(24)×10−8eV T−17.6×10−9µN/h7.62259396(31)MHz T−14.0×10−8µN/hc2.54262366(10)×10−2m−1T−14.0×10−8µN/k3.6582638(64)×10−4K T−11.7×10−6ATOMIC AND NUCLEARGeneralfine-structure constant e2/4π 0¯h cα7.297352533(27)×10−33.7×10−9 inversefine-structure constantα−1137.03599976(50)3.7×10−9Fundamental Physical Constants—Complete ListingRelative std.Quantity Symbol Value Unit uncert.u r Rydberg constantα2m e c/2h R∞10973731.568549(83)m−17.6×10−12R∞c3.289841960368(25)×1015Hz7.6×10−12R∞hc2.17987190(17)×10−18J7.8×10−8 R∞hc in eV13.60569172(53)eV3.9×10−8Bohr radiusα/4πR∞=4π 0¯h2/m e e2a00.5291772083(19)×10−10m3.7×10−9 Hartree energy e2/4πε0a0=2R∞hc=α2m e c2E h4.35974381(34)×10−18J7.8×10−8 in eV27.2113834(11)eV3.9×10−8 quantum of circulation h/2m e3.636947516(27)×10−4m2s−17.3×10−9h/m e7.273895032(53)×10−4m2s−17.3×10−9ElectroweakFermi coupling constant c G F/(¯h c)31.16639(1)×10−5GeV−28.6×10−6 weak mixing angle dθW(on-shell scheme)≡1−(m W/m Z)2sin2θW0.2224(19)8.7×10−3 sin2θW=s2WElectron,e−electron mass m e9.10938188(72)×10−31kg7.9×10−8 in u,m e=A r(e)u(electronrelative atomic mass times u)5.485799110(12)×10−4u2.1×10−9 energy equivalent m e c28.18710414(64)×10−14J7.9×10−8 in MeV0.510998902(21)MeV4.0×10−8electron-muon mass ratio m e/mµ4.83633210(15)×10−33.0×10−8 electron-tau mass ratio m e/mτ2.87555(47)×10−41.6×10−4 electron-proton mass ratio m e/m p5.446170232(12)×10−42.1×10−9 electron-neutron mass ratio m e/m n5.438673462(12)×10−42.2×10−9 electron-deuteron mass ratio m e/m d2.7244371170(58)×10−42.1×10−9 electron to alpha particle mass ratio m e/mα1.3709335611(29)×10−42.1×10−9electron charge to mass quotient−e/m e−1.758820174(71)×1011C kg−14.0×10−8 electron molar mass N A m e M(e),M e5.485799110(12)×10−7kg mol−12.1×10−9 Compton wavelength h/m e cλC2.426310215(18)×10−12m7.3×10−9λC/2π=αa0=α2/4πR∞λC386.1592642(28)×10−15m7.3×10−9 classical electron radiusα2a0r e2.817940285(31)×10−15m1.1×10−8 Thomson cross section(8π/3)r2eσe0.665245854(15)×10−28m22.2×10−8electron magnetic momentµe−928.476362(37)×10−26J T−14.0×10−8 to Bohr magneton ratioµe/µB−1.0011596521869(41)4.1×10−12 to nuclear magneton ratioµe/µN−1838.2819660(39)2.1×10−9 electron magnetic momentanomaly|µe|/µB−1a e1.1596521869(41)×10−33.5×10−9 electron g-factor−2(1+a e)g e−2.0023193043737(82)4.1×10−12electron-muonmagnetic moment ratioµe/µµ206.7669720(63)3.0×10−8Fundamental Physical Constants—Complete ListingRelative std.Quantity Symbol Value Unit uncert.u r electron-protonmagnetic moment ratioµe/µp−658.2106875(66)1.0×10−8 electron to shielded protonmagnetic moment ratioµe/µ p−658.2275954(71)1.1×10−8 (H2O,sphere,25◦C)electron-neutronmagnetic moment ratioµe/µn960.92050(23)2.4×10−7 electron-deuteronmagnetic moment ratioµe/µd−2143.923498(23)1.1×10−8 electron to shielded helion emagnetic moment ratioµe/µh 864.058255(10)1.2×10−8(gas,sphere,25◦C)electron gyromagnetic ratio2|µe|/¯hγe1.760859794(71)×1011s−1T−14.0×10−8γe/2π28024.9540(11)MHz T−14.0×10−8Muon,µ−muon mass mµ1.88353109(16)×10−28kg8.4×10−8 in u,mµ=A r(µ)u(muonrelative atomic mass times u)0.1134289168(34)u3.0×10−8 energy equivalent mµc21.69283332(14)×10−11J8.4×10−8 in MeV105.6583568(52)MeV4.9×10−8 muon-electron mass ratio mµ/m e206.7682657(63)3.0×10−8 muon-tau mass ratio mµ/mτ5.94572(97)×10−21.6×10−4 muon-proton mass ratio mµ/m p0.1126095173(34)3.0×10−8 muon-neutron mass ratio mµ/m n0.1124545079(34)3.0×10−8 muon molar mass N A mµM(µ),Mµ0.1134289168(34)×10−3kg mol−13.0×10−8 muon Compton wavelength h/mµcλC,µ11.73444197(35)×10−15m2.9×10−8λC,µ/2πλC,µ1.867594444(55)×10−15m2.9×10−8 muon magnetic momentµµ−4.49044813(22)×10−26J T−14.9×10−8 to Bohr magneton ratioµµ/µB−4.84197085(15)×10−33.0×10−8 to nuclear magneton ratioµµ/µN−8.89059770(27)3.0×10−8 muon magnetic moment anomaly|µµ|/(e¯h/2mµ)−1aµ1.16591602(64)×10−35.5×10−7 muon g-factor−2(1+aµ)gµ−2.0023318320(13)6.4×10−10 muon-protonmagnetic moment ratioµµ/µp−3.18334539(10)3.2×10−8Tau,τ−tau mass f mτ3.16788(52)×10−27kg1.6×10−4 in u,mτ=A r(τ)u(taurelative atomic mass times u)1.90774(31)u1.6×10−4 energy equivalent mτc22.84715(46)×10−10J1.6×10−4 in MeV1777.05(29)MeV1.6×10−4Fundamental Physical Constants—Complete ListingRelative std.Quantity Symbol Value Unit uncert.u r tau-electron mass ratio mτ/m e3477.60(57)1.6×10−4 tau-muon mass ratio mτ/mµ16.8188(27)1.6×10−4 tau-proton mass ratio mτ/m p1.89396(31)1.6×10−4 tau-neutron mass ratio mτ/m n1.89135(31)1.6×10−4 tau molar mass N A mτM(τ),Mτ1.90774(31)×10−3kg mol−11.6×10−4tau Compton wavelength h/mτcλC,τ0.69770(11)×10−15m1.6×10−4λC,τ/2πλ,τ0.111042(18)×10−15m1.6×10−4Proton,pproton mass m p1.67262158(13)×10−27kg7.9×10−8 in u,m p=A r(p)u(protonrelative atomic mass times u)1.00727646688(13)u1.3×10−10 energy equivalent m p c21.50327731(12)×10−10J7.9×10−8 in MeV938.271998(38)MeV4.0×10−8 proton-electron mass ratio m p/m e1836.1526675(39)2.1×10−9 proton-muon mass ratio m p/mµ8.88024408(27)3.0×10−8 proton-tau mass ratio m p/mτ0.527994(86)1.6×10−4 proton-neutron mass ratio m p/m n0.99862347855(58)5.8×10−10 proton charge to mass quotient e/m p9.57883408(38)×107C kg−14.0×10−8 proton molar mass N A m p M(p),M p1.00727646688(13)×10−3kg mol−11.3×10−10proton Compton wavelength h/m p cλC,p1.321409847(10)×10−15m7.6×10−9λC,p/2πλC,p0.2103089089(16)×10−15m7.6×10−9 proton magnetic momentµp1.410606633(58)×10−26J T−14.1×10−8 to Bohr magneton ratioµp/µB1.521032203(15)×10−31.0×10−8 to nuclear magneton ratioµp/µN2.792847337(29)1.0×10−8 proton g-factor2µp/µN g p5.585694675(57)1.0×10−8 proton-neutronmagnetic moment ratioµp/µn−1.45989805(34)2.4×10−7 shielded proton magnetic momentµ p1.410570399(59)×10−26J T−14.2×10−8 (H2O,sphere,25◦C)to Bohr magneton ratioµ p/µB1.520993132(16)×10−31.1×10−8 to nuclear magneton ratioµ p/µN2.792775597(31)1.1×10−8 proton magnetic shieldingcorrection1−µ p/µpσ p25.687(15)×10−65.7×10−4 (H2O,sphere,25◦C)proton gyromagnetic ratio2µp/¯hγp2.67522212(11)×108s−1T−14.1×10−8γp/2π42.5774825(18)MHz T−14.1×10−8 shielded proton gyromagneticratio2µ p/¯hγ p2.67515341(11)×108s−1T−14.2×10−8 (H2O,sphere,25◦C)γ p/2π42.5763888(18)MHz T−14.2×10−8Neutron,nFundamental Physical Constants—Complete ListingRelative std.Quantity Symbol Value Unit uncert.u r neutron mass m n1.67492716(13)×10−27kg7.9×10−8 in u,m n=A r(n)u(neutronrelative atomic mass times u)1.00866491578(55)u5.4×10−10 energy equivalent m n c21.50534946(12)×10−10J7.9×10−8 in MeV939.565330(38)MeV4.0×10−8neutron-electron mass ratio m n/m e1838.6836550(40)2.2×10−9 neutron-muon mass ratio m n/mµ8.89248478(27)3.0×10−8 neutron-tau mass ratio m n/mτ0.528722(86)1.6×10−4 neutron-proton mass ratio m n/m p1.00137841887(58)5.8×10−10 neutron molar mass N A m n M(n),M n1.00866491578(55)×10−3kg mol−15.4×10−10neutron Compton wavelength h/m n cλC,n1.319590898(10)×10−15m7.6×10−9λC,n/2πλC,n0.2100194142(16)×10−15m7.6×10−9 neutron magnetic momentµn−0.96623640(23)×10−26J T−12.4×10−7 to Bohr magneton ratioµn/µB−1.04187563(25)×10−32.4×10−7to nuclear magneton ratioµn/µN−1.91304272(45)2.4×10−7neutron g-factor2µn/µN g n−3.82608545(90)2.4×10−7 neutron-electronmagnetic moment ratioµn/µe1.04066882(25)×10−32.4×10−7 neutron-protonmagnetic moment ratioµn/µp−0.68497934(16)2.4×10−7 neutron to shielded protonmagnetic moment ratioµn/µ p−0.68499694(16)2.4×10−7 (H2O,sphere,25◦C)neutron gyromagnetic ratio2|µn|/¯hγn1.83247188(44)×108s−1T−12.4×10−7γn/2π29.1646958(70)MHz T−12.4×10−7Deuteron,ddeuteron mass m d3.34358309(26)×10−27kg7.9×10−8 in u,m d=A r(d)u(deuteronrelative atomic mass times u)2.01355321271(35)u1.7×10−10 energy equivalent m d c23.00506262(24)×10−10J7.9×10−8 in MeV1875.612762(75)MeV4.0×10−8deuteron-electron mass ratio m d/m e3670.4829550(78)2.1×10−9 deuteron-proton mass ratio m d/m p1.99900750083(41)2.0×10−10 deuteron molar mass N A m d M(d),M d2.01355321271(35)×10−3kg mol−11.7×10−10 deuteron magnetic momentµd0.433073457(18)×10−26J T−14.2×10−8 to Bohr magneton ratioµd/µB0.4669754556(50)×10−31.1×10−8 to nuclear magneton ratioµd/µN0.8574382284(94)1.1×10−8 deuteron-electronmagnetic moment ratioµd/µe−4.664345537(50)×10−41.1×10−8 deuteron-protonmagnetic moment ratioµd/µp0.3070122083(45)1.5×10−8Fundamental Physical Constants—Complete ListingRelative std.Quantity Symbol Value Unit uncert.u r deuteron-neutronmagnetic moment ratioµd/µn−0.44820652(11)2.4×10−7Helion,hhelion mass e m h5.00641174(39)×10−27kg7.9×10−8 in u,m h=A r(h)u(helionrelative atomic mass times u)3.01493223469(86)u2.8×10−10 energy equivalent m h c24.49953848(35)×10−10J7.9×10−8 in MeV2808.39132(11)MeV4.0×10−8 helion-electron mass ratio m h/m e5495.885238(12)2.1×10−9 helion-proton mass ratio m h/m p2.99315265850(93)3.1×10−10 helion molar mass N A m h M(h),M h3.01493223469(86)×10−3kg mol−12.8×10−10shielded helion magnetic momentµh −1.074552967(45)×10−26J T−14.2×10−8(gas,sphere,25◦C)to Bohr magneton ratioµh /µB−1.158671474(14)×10−31.2×10−8to nuclear magneton ratioµh /µN−2.127497718(25)1.2×10−8shielded helion to protonmagnetic moment ratioµh /µp−0.761766563(12)1.5×10−8(gas,sphere,25◦C)shielded helion to shielded protonmagnetic moment ratioµh /µ p−0.7617861313(33)4.3×10−9(gas/H2O,spheres,25◦C) shielded helion gyromagneticratio2|µh |/¯hγ h2.037894764(85)×108s−1T−14.2×10−8(gas,sphere,25◦C)γh/2π32.4341025(14)MHz T−14.2×10−8Alpha particle,αalpha particle mass mα6.64465598(52)×10−27kg7.9×10−8 in u,mα=A r(α)u(alpha particlerelative atomic mass times u)4.0015061747(10)u2.5×10−10 energy equivalent mαc25.97191897(47)×10−10J7.9×10−8 in MeV3727.37904(15)MeV4.0×10−8 alpha particle to electron mass ratio mα/m e7294.299508(16)2.1×10−9 alpha particle to proton mass ratio mα/m p3.9725996846(11)2.8×10−10 alpha particle molar mass N A mαM(α),Mα4.0015061747(10)×10−3kg mol−12.5×10−10PHYSICO-CHEMICALAvogadro constant N A,L6.02214199(47)×1023mol−17.9×10−8 atomic mass constantm u=1m(12C)=1u m u1.66053873(13)×10−27kg7.9×10−8 =10−3kg mol−1/N Aenergy equivalent m u c21.49241778(12)×10−10J7.9×10−8 in MeV931.494013(37)MeV4.0×10−8 Faraday constant g N A e F96485.3415(39)C mol−14.0×10−8Fundamental Physical Constants—Complete ListingRelative std.Quantity Symbol Value Unit uncert.u r molar Planck constant N A h3.990312689(30)×10−10J s mol−17.6×10−9N A hc0.11962656492(91)J m mol−17.6×10−9 molar gas constant R8.314472(15)J mol−1K−11.7×10−6 Boltzmann constant R/N A k1.3806503(24)×10−23J K−11.7×10−6 in eV K−18.617342(15)×10−5eV K−11.7×10−6k/h2.0836644(36)×1010Hz K−11.7×10−6k/hc69.50356(12)m−1K−11.7×10−6 molar volume of ideal gas RT/pT=273.15K,p=101.325kPa V m22.413996(39)×10−3m3mol−11.7×10−6 Loschmidt constant N A/V m n02.6867775(47)×1025m−31.7×10−6 T=273.15K,p=100kPa V m22.710981(40)×10−3m3mol−11.7×10−6 Sackur-Tetrode constant(absolute entropy constant)h5 2+ln[(2πm u kT1/h2)3/2kT1/p0]T1=1K,p0=100kPa S0/R−1.1517048(44)3.8×10−6 T1=1K,p0=101.325kPa−1.1648678(44)3.7×10−6Stefan-Boltzmann constant(π2/60)k4/¯h3c2σ5.670400(40)×10−8W m−2K−47.0×10−6first radiation constant2πhc2c13.74177107(29)×10−16W m27.8×10−8first radiation constant for spectral radiance2hc2c1L1.191042722(93)×10−16W m2sr−17.8×10−8 second radiation constant hc/k c21.4387752(25)×10−2m K1.7×10−6Wien displacement law constantb=λmax T=c2/4.965114231...b2.8977686(51)×10−3m K1.7×10−6a See the“Adopted values”table for the conventional value adopted internationally for realizing representations of the volt using the Joseph-son effect.b See the“Adopted values”table for the conventional value adopted internationally for realizing representations of the ohm using the quantum Hall effect.c Value recommended by the Particle Data Group,Caso et al.,Eur.Phys.J.C3(1-4),1-794(1998).d Based on the ratio of the masses of the W and Z bosons m W/m Z recommended by the Particle Data Group(Caso et al.,1998).The value for sin2θW they recommend,which is based on a particular variant of the modified minimal subtraction(MS)scheme,is sin2ˆθW(M Z)=0.23124(24).e The helion,symbol h,is the nucleus of the3He atom.f This and all other values involving mτare based on the value of mτc2in MeV recommended by the Particle Data Group,Caso et al.,Eur.Phys. J.C3(1-4),1-794(1998),but with a standard uncertainty of0.29MeV rather than the quoted uncertainty of−0.26MeV,+0.29MeV.g The numerical value of F to be used in coulometric chemical measurements is96485.3432(76)[7.9×10−8]when the relevant current is mea-sured in terms of representations of the volt and ohm based on the Josephson and quantum Hall effects and the internationally adopted conventional values of the Josephson and von Klitzing constants K J−90and R K−90given in the“Adopted values”table.h The entropy of an ideal monoatomic gas of relative atomic mass A r is given by S=S0+3R ln A r−R ln(p/p0)+5R ln(T/K).i The relative atomic mass A r(X)of particle X with mass m(X)is defined by A r(X)=m(X)/m u,where m u=m(12C)/12=M u/N A=1u is the atomic mass constant,N A is the Avogadro constant,and u is the atomic mass unit.Thus the mass of particle X in u is m(X)=A r(X)u and the molar mass of X is M(X)=A r(X)M u.j This is the value adopted internationally for realizing representations of the volt using the Josephson effect.k This is the value adopted internationally for realizing representations of the ohm using the quantum Hall effect.a This is the lattice parameter (unit cell edge length)of an ideal single crystal of naturally occurring Si free of impurities and imperfections,and is deduced from lattice spacing measurements on extremely pure and nearly perfect single crystals of Si by correcting for the effects of impurities.。
