(表13-23)水平地震作用下弯矩和剪力计算表
各类梁的弯矩剪力计算汇总表
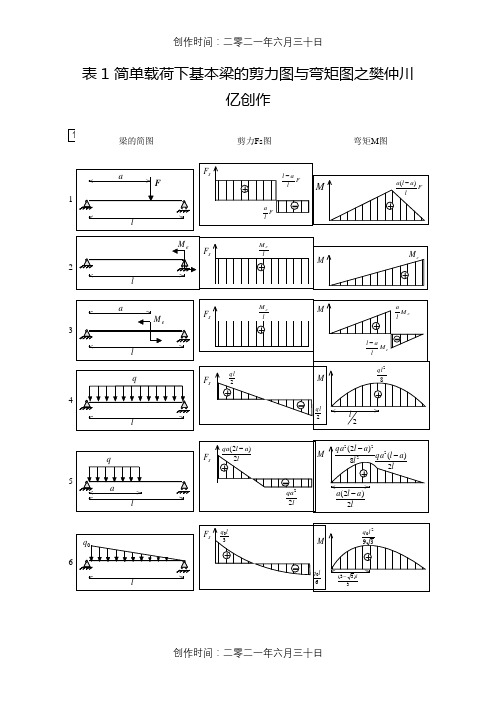
表1 简单载荷下基本梁的剪力图与弯矩图之樊仲川亿创作1注:外伸梁 = 悬臂梁 + 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征某一段梁上的外力情况剪力图的特征无载荷突变转折无变动突变斜直线零点极值表3 各种约束类型对应的鸿沟条件约束类型位移鸿沟条件力鸿沟条件(约束端无集中载荷)—自由端—注:力鸿沟条件即剪力图、弯矩图在该约束处的特征.经常使用截面几何与力学特征表表2-5 创作时间:二零二一年六月三十日创作时间:二零二一年六月三十日创作时间:二零二一年六月三十日创作时间:二零二一年六月三十日创作时间:二零二一年六月三十日创作时间:二零二一年六月三十日创作时间:二零二一年六月三十日创作时间:二零二一年六月三十日注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4).基本计算公式如下:⎰•=AdAy I 22.W 称为截面抵当矩(mm 3), 它暗示截面抵当弯曲变形能力的年夜小, 基本计算公式如下:max y I W =3.i 称截面回转半径(mm ), 其基本计算公式如下:A I i =4.上列各式中, A为截面面积(mm2), y为截面边缘到主轴(形心轴)的距离(mm), I为对主轴(形心轴)的惯性矩.5.上列各项几何及力学特征, 主要用于验算构件截面的承载力和刚度.创作时间:二零二一年六月三十日2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=. 2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EI w 100Fl 表中系数3⨯=. [例1] 已知二跨等跨梁l =5m, 均布荷载q =11.76kN/m, 每跨各有一集中荷载F =29.4kN, 求中间支座的最年夜弯矩和剪力.[解] M B 支××52××5)·mV B 左×××29.4)[例2] 已知三跨等跨梁l =6m, 均布荷载q =11.76kN/m, 求边跨最年夜跨中弯矩.××62·m.2)三跨等跨梁的内力和挠度系数 表2-12注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql表中系数4⨯=. 2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EI w 100Fl 表中系数3⨯=.3)四跨等跨连续梁内力和挠度系数表2-13注:同三跨等跨连续梁.4)五跨等跨连续梁内力和挠度系数表2-14注:同三跨等跨连续梁.创作时间:二零二一年六月三十日(2)不等跨连续梁的内力系数(表2-15、表2-16)1)二不等跨梁的内力系数表2-15创作时间:二零二一年六月三十日注:1.M=表中系数×ql21;V=表中系数×ql1;2.(M max)、(V max)暗示它为相应跨内的最年夜内力.2)三不等跨梁内力系数表2-16创作时间:二零二一年六月三十日创作时间:二零二一年六月三十日注:1.M=表中系数×ql21;V=表中系数×ql1;2.(M max)、(V max)为荷载在最晦气安插时的最年夜内力.创作时间:二零二一年六月三十日4.双向板在均布荷载作用下的内力及变形系数表(表2-17~表2-22) 符号说明如下:刚度 )1(1223υ-=Eh K 式中 E ——弹性模量;h ——板厚; ν——泊松比;ω、ωmax ——分别为板中心点的挠度和最年夜挠度;M x ——为平行于l x 方向板中心点的弯矩; M y ——为平行于l y 方向板中心点的弯矩; M x 0——固定边中点沿l x 方向的弯矩; M y 0——固定边中点沿l y 方向的弯矩. 正负号的规定:弯矩——使板的受荷面受压者为正; 挠度——变位方向与荷载方向相同者为正.四边简支 表2-17三边简支, 一边固定 表2-18两边简支, 两边固定表2-19 一边简支, 三边固定表2-20四边固定表2-21两边简支, 两边固定表2-22 5.拱的内力计算表(表2-23)各种荷载作用下双铰抛物线拱计算公式表2-23注:表中的K为轴向力变形影响的修正系数.(1)无拉杆双铰拱1)在竖向荷载作用下的轴向力变形修正系数式中 I c——拱顶截面惯性矩;A c——拱顶截面面积;A——拱上任意点截面面积.当为矩形等宽度实腹式变截面拱时,公式I=I c/cosθ所代表的截面惯性矩变动规律相当于下列的截面面积变动公式:此时, 上式中的n可表告竣如下形式:下表中列出了矩形等宽度实腹式变截面拱的n值.f/ln2)在水平荷载作用下的轴向力变形修正系数, 近似取K=1(2)带拉杆双铰拱1)在竖向荷载作用下的轴向力变形修正系数式中 E——拱圈资料的弹性模量;E1——拉杆资料的弹性模量;A1——拉杆的截面积.2)在水平荷载作用下的轴向力变形修正系数(略去拱圈轴向力变形影响)式中 f——为矢高;l——为拱的跨度.6.刚架内力计算表内力的正负号规定如下:V——向上者为正;H——向内者为正;M——刚架中虚线的一面受拉为正.(1)“┌┐”形刚架内力计算(表2-24、表2-25)“┌┐”形刚架内力计算表(一)表2-34“┌┐”形刚架内力计算表(二)表2-35(2)“”形刚架的内力计算(表2-26)“”形刚架的内力计算表表2-26。
计算水平地震作用的底部剪力法

—高振型影响系数 (规范取0.85)
FEK 1Geq
Geq—结构等效总重力荷载代表值,0.85G
二、各质点的水平地震作用标准值的计算
Fi F 1i 1 1 x1i Gi
Fn Fk
Gk
1 1H i Gi
FEK F1k 1 1H k Gk
k 1 k 1 n n
(4)顶部附加水平地震作用
Fn n FEK 1.4Tg 0.56
顶部附加地震作用系数
Tg ( s)
0.35
T1 1.4Tg
T1 1.4Tg
0 0 0
T1 1.4Tg
n 0
0.08T1 0.07 0.35 ~ 0.55 0.08T1 0.01
0.55
(5)计算各层的水平地震作 用标准值 HG
地震影响
地震影响系数最大值(阻尼比为0.05)
烈度 6 7 8 9
多遇地震
罕遇地震
0.04
-----
0.08(0.12)
0.50(0.72)
0.16(0.24)
0.90(1.20)
0.32
1.40
例1:试用底部剪力法计算图示框 架多遇地震时的层间剪力。已知 结构的基本周期T1=0.467s ,抗震 设防烈度为8度,Ⅱ类场地,设计地 震分组为第二组。
各层水平地震作用
Fi H i Gi
H
k 1
n
FEK
层 6 Gi (kN) 3856.9 Hi (m) 17.45 Gi Hi (kN.m) 67320.9 75003.75 61274.25 47544.75 33815.25 Fi (kN) 884.5 Vi (kN) 884.5 1870.2 2675.5 3300.3 3744.7 4025.1
各类梁的弯矩剪力计算汇总表

表1 简单载荷下基本梁的剪力图与弯矩图表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =m ,每跨各有一集中荷载F =,求中间支座的最大弯矩和剪力。
[解] M B 支=(-××52)+(-××5)=(-)+()=-·m V B 左=(-××5)+(-×)=(-)+(-)=-[例2] 已知三跨等跨梁l =6m ,均布荷载q =m ,求边跨最大跨中弯矩。
水平地震作用计算

⽔平地震作⽤计算⽔平地震作⽤计算5.2 ⽔平地震作⽤计算5.2.1 采⽤底部剪⼒法时,各楼层可仅取⼀个⾃由度,结构的⽔平地震作⽤标准值,应按下列公式确定(图5.2.1):式中F Ek——结构总⽔平地震作⽤标准值;α1——相应于结构基本⾃振周期的⽔平地震影响系数值,应按本规范第5.1.4、5.1.5 条确定,多层砌体房屋、底部框架砌体房屋,宜取⽔平地震影响系数最⼤值;G eq——结构等效总重⼒荷载,单质点应取总重⼒荷载代表值,多质点可取总重⼒荷载代表值的85%;F i——质点i的⽔平地震作⽤标准值;G i,G j——分别为集中于质点i、j的重⼒荷载代表值,应按本规范第5.1.3 条确定;H i,H j——分别为质点i、j的计算⾼度;δn——顶部附加地震作⽤系数,多层钢筋混凝⼟和钢结构房屋可按表5.2.1采⽤,其他房屋可采⽤0.0;△F n——顶部附加⽔平地震作⽤。
5.2.2 采⽤振型分解反应谱法时,不进⾏扭转耦联计算的结构,应按下列规定计算其地震作⽤和作⽤效应:1 结构j振型i 质点的⽔平地震作⽤标准值,应按下列公式确定:2 ⽔平地震作⽤效应(弯矩、剪⼒、轴向⼒和变形),当相邻振型的周期⽐⼩于0.85 时,可按下式确定:5.2.3 ⽔平地震作⽤下,建筑结构的扭转耦联地震效应应符合下列要求:1 规则结构不进⾏扭转耦联计算时,平⾏于地震作⽤⽅向的两个边榀各构件,其地震作⽤效应应乘以增⼤系数。
⼀般情况下,短边可按1.15 采⽤,长边可按1.05采⽤;当扭转刚度较⼩时,周边各构件宜按不⼩于1.3采⽤。
⾓部构件宜同时乘以两个⽅向各⾃的增⼤系数。
2 按扭转耦联振型分解法计算时,各楼层可取两个正交的⽔平位移和⼀个转⾓共三个⾃由度,并应按下列公式计算结构的地震作⽤和作⽤效应。
确有依据时,尚可采⽤简化计算⽅法确定地震作⽤效应。
2)单向⽔平地震作⽤下的扭转耦联效应,可按下列公式确定:3)双向⽔平地震作⽤下的扭转耦联效应,可按下列公式中的较⼤值确定:5.2.4 采⽤底部剪⼒法时,突出屋⾯的屋顶间、⼥⼉墙、烟囱等的地震作⽤效应,宜乘以增⼤系数3,此增⼤部分不应往下传递,但与该突出部分相连的构件应予计⼊;采⽤振型分解法时,突出屋⾯部分可作为⼀个质点;单层⼚房突出屋⾯天窗架的地震作⽤效应的增⼤系数,应按本规范第9章的有关规定采⽤。
各类梁的弯矩剪力计算汇总表
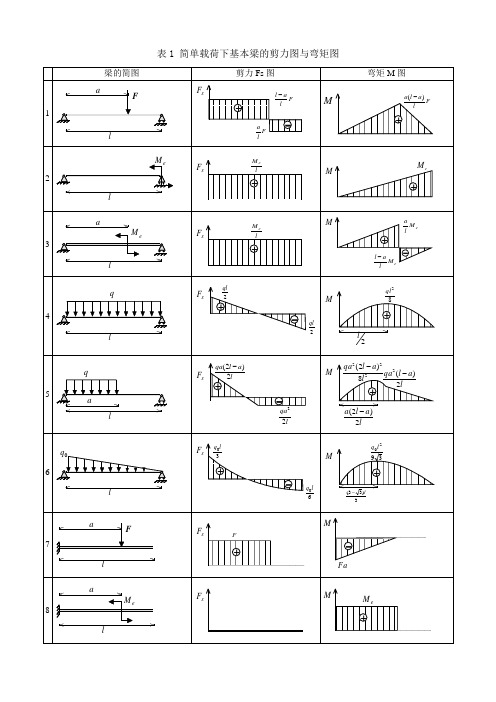
表1 简单载荷下基本梁的剪力图与弯矩图表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·m V B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
各类梁的弯矩剪力计算汇总表
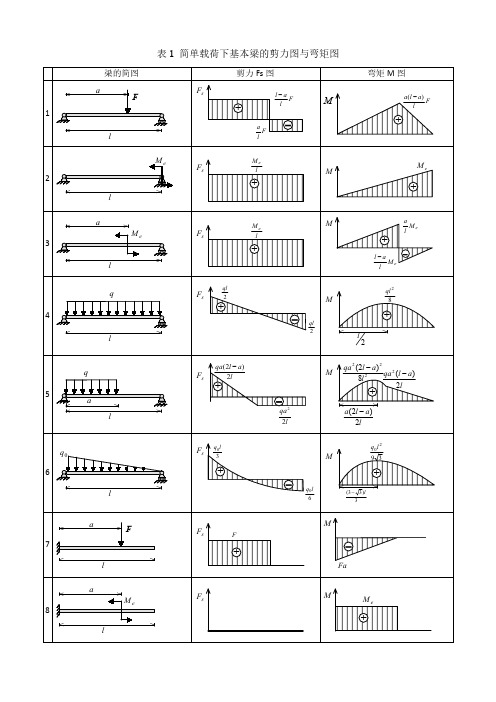
表1简单载荷下基本梁的剪力图与弯矩图注:外伸梁=悬臂梁+端部作用集中力偶的简支梁表2各种载荷下剪力图与弯矩图的特征表3各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰∙=A dAyI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:max y IW =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1]已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解]M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·mV B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2]已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
各类梁弯矩剪力计算汇总表
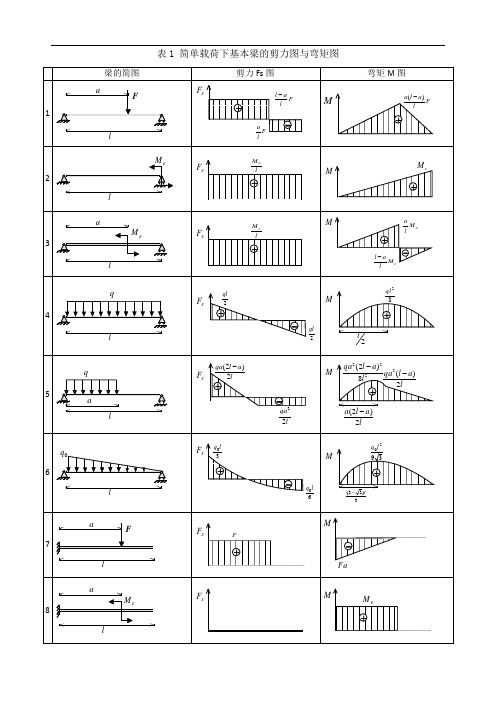
表1 简单载荷下基本梁的剪力图与弯矩图表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =m ,每跨各有一集中荷载F =,求中间支座的最大弯矩和剪力。
[解] M B 支=(-××52)+(-××5)=(-)+()=-·m V B 左=(-××5)+(-×)=(-)+(-)=-[例2] 已知三跨等跨梁l =6m ,均布荷载q =m ,求边跨最大跨中弯矩。
各类梁的弯矩剪力计算汇总表-剪力计算公式一览表

表 1 简单载荷下基本梁的剪力图与弯矩图注:外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁2.单跨梁的内力及变形表(表2-6~表2-10)1)简支梁的反力、剪力、弯矩、挠度表2-62)悬臂梁的反力、剪力、弯矩和挠度表2-73)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-84)两端固定梁的反力、剪力、弯矩和挠度表2-95 )外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14 )1)二跨等跨梁的内力和挠度系数表2-11均布荷载 q =11.76kN/m ,每跨各有一集中荷载 F =29.4kN ,求中间支座的最大弯矩和剪力。
M B 支=(-0.125×11.76×52)+(- 0.188×29.4×5)=(- 36.75)+( -27.64)=- 64.39kN ·mV B 左=(-0.625×11.76×5)+(- 0.688×29.4)=(- 36.75)+(- 20.23)=- 56.98kN[例 2] 已知三跨等跨梁 l = 6m ,均布荷载 q =11.76kN/m ,求边跨最大跨中弯矩 [解 ] M1 = 0.080×11.76×62=33.87kN ·m 。
2)三跨等跨梁的内力和挠度系数 表 2-12注: 1.在均布荷载作用下: M =表中系数×4ql 2;V =表中系数× ql ; w 表中系数ql。
100EI Fl 3Fl ;V =表中系数× F ; w 表中系数 Fl。
100EI2.在集中荷载作用下: M =表中系数×[例 1] 已知二跨等跨梁 l =5m ,[解]f ⅜ 跨内帰大 支座弯矩 弯矩荷載图VCXAflM 2-0.5500 -O I OSo-O (O 5Q0.4500.550(Jf≡¾-0,050 -0.500 D.0751-0.050 -0.050 -0,0500,5000.050UHiD跨度中点挠度-0.45(J 0,990 -0.625 0.990L A 4-L073L054-0÷117-0.033 0.383D-0.C67 0.0170.433f t J÷175 -0.150一(L 1500.350-0,075 -0.0750.425ΓJ⅛3.175 -0.075-0.075-0,07S0.050-0.3131 0,677 -0.313λ1620.1370 + 175-o r osα 0,325-0.617-0.4170*033 0.5β3 0.033-0.5670.0830.5730.365 -0.208-O.on-0,017 0.885 -0.313 0.104-0.650 0.500"-W0.650-0,5750 0.575-0.425E146 1.6150.208 1.146- 0,075- 0,50C 0.5000.0750.075-0Λ69-0.9371U46L 615-0.469-0,675-0.375 0,6250.0500.0500.9900.677 L 0.3124 注:1.在均布荷载作用下:M =表中系数× ql2;V=表中系数× ql;w表中系数ql 100EI2.在集中荷载作用下:M =表中系数× Fl;V=表中系数× F;w 表中系数Fl。
各类梁的弯矩剪力计算汇总表-剪力计算公式一览表之令狐文艳创作
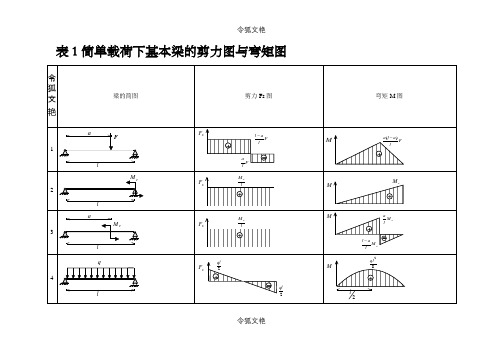
表1 简单载荷下基本梁的剪力图与弯矩图令狐文艳令狐文艳注:外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁令狐文艳2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;EI w 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EI w 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·mV B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN ·m 。
2)三跨等跨梁的内力和挠度系数 表2-12注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=。
地震内力计算表
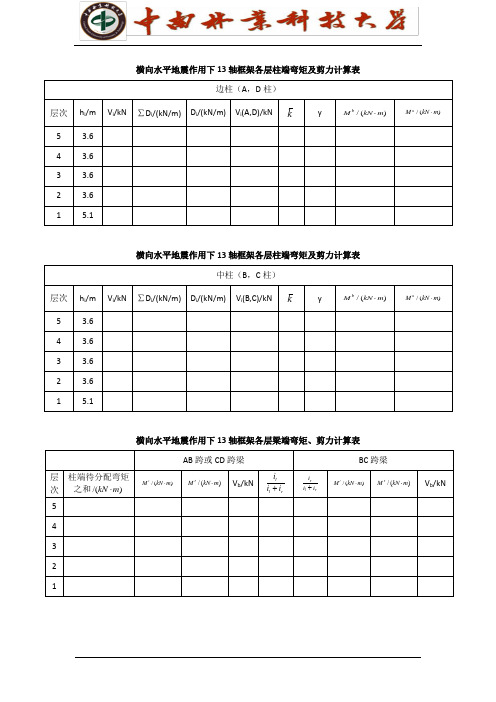
k
y
M
b
/ ( kN ⋅ m )
M u / ( kN ⋅ m )
轴框架各层梁端弯矩、 横向水平地震作用下 13 轴框架各层梁端弯矩、剪力计算表 AB 跨或 CD 跨梁 层 次 5 4 3 2 1 柱端待分配弯矩 之和 /(kN ⋅ m)
M l / ( kN ⋅ m)
BC 跨梁
il il + ir
ir il + ir
边柱轴力 N/kN
中柱轴力 N/kN
Vb/kN
横向水平地震作用下 13 轴框架各层柱端弯矩及剪力计算表 边柱(A,D 柱) 层次 5 4 3 2 1 hi/m 3.6 3.6 3.6 3.6 5.1 Vi/kN ∑Di/(kN/m) Di/(kN/m) Vi(A,D)/kN
k
y
M
b
/ ( kN ⋅ m )
M u / ( kN ⋅ m )
横向水平地震作用下 13 轴框架各层柱端弯矩及剪力计算表 中柱(B,C 柱) 层次 5 4 3 2 1 hi/m 3.6 3.6 3.6 3.6 5.1 Vi/kN ∑Di/(kN/m) Di/(kN/m) Vi(B,C)/kN
M l / ( kN ⋅ m)
M r / (kN ⋅ m)
Vb/kN
M r / (kN ⋅ m)
Vb/kN
横向水平地震作用下 13 轴框架各层柱轴力计算表 AB,CD 跨梁端剪力 层次 5 4 3 2 1
注:表中柱轴力中的负号表示拉力,当为左震作用时,左侧两根柱为拉力,对应的右侧两根柱为压力
BC 跨梁端剪力 Vb/kN
水平地震作用下的内力和位移计算

第8章水平地震作用下的内力和位移计算重力荷载代表值计算顶层重力荷载代表值包括:屋面恒载:纵、横梁自重,半层柱自重,女儿墙自重,半层墙体自重。
其他层重力荷载代表值包括:楼面恒载,50%楼面活荷载,纵、横梁自重,楼面上、下各半层柱及纵、横墙体自重。
第五层重力荷载代表值计算层高H=,屋面板厚h=120mm半层柱自重(b×h=500mm×500mm):4×25×××2=柱自重:屋面梁自重()() kNmmmkNmmmkNmmm kN16. 1472)25.06.6(/495.145.06.616 .3)3.03(/495.123.06.7/16 .3=⨯-⨯+⨯-⨯++⨯+⨯-⨯屋面梁自重:半层墙自重顶层无窗墙(190厚):()KN25.316.66.029.3202.02019.025.14=⨯⎪⎭⎫⎝⎛-⨯⨯⨯+⨯带窗墙(190厚):()()KN98.82345.002.02019.025.1428.15.16.66.029.3202.02019.025.14=⨯⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⨯+⨯⨯⨯-⨯⎪⎭⎫⎝⎛-⨯⨯⨯+⨯墙自重: KN女儿墙:()KN04.376.66.1202.02019.025.14=⨯⨯⨯⨯+⨯屋面板自重kNmmmmkN78.780)326.7(6.6/5.62=+⨯⨯⨯第五层重量 ++++= KN 顶层重力荷载代表值 G 5 = KN第二至四层重力荷载代表值计算层高H=,楼面板厚h=100mm半层柱自重:同第五层,为 KN 则整层为×2= KN 楼面梁自重:()()kN m m m kN m m m kN m m m kN 3.1542)25.06.6(/6.145.06.63.3)3.03(/6.123.06.7/3.3=⨯-⨯+⨯-⨯++⨯+⨯-⨯半墙自重:同第五层,为则整层为2××4= KN 楼面板自重:4××(+3+)= KN 第二至四层各层重量=+++= KN 第二至四层各层重力荷载代表值为:()KN G 61.111336.65.326.76.65.2%5056.9534-2=⨯⨯+⨯⨯⨯⨯+= 活载:Q 2-4=KN 05.160%5036.65.326.76.65.2=⨯⨯⨯+⨯⨯⨯)(第一层重力荷载代表值计算层高H=,柱高H 2=++=,楼面板厚h=100mm 半层柱自重:(b ×h=500mm ×500mm ):4×25×××2=65 KN 则柱自重:65+= KN 楼面梁自重:同第2层,为 KN 半层墙自重(190mm ):()()KN 14.3145.002.02019.025.1428.15.16.66.022.4202.02019.025.14=-⨯+⨯⨯⨯-⨯⎪⎭⎫⎝⎛-⨯⨯⨯+⨯二层半墙自重(190mm ): KN则墙自重为:(+)×4= KN 楼面板自重:同第2层,为 第1层重量=+++=第1层重力荷载代表值为:G 1=+50%×(×××2+××3)= KN 活载:Q=50%×(×××2+××3)= KN 综上所述,结构等效总重力荷载代表值为:()()123450.850.850.851013.46917.3731106.654141.39eq E G G G G G G G KN==⨯++++=⨯+⨯+=G eq ==×(G 1+G 2+G 3+G 4+G 5)=×+×3+ =水平地震作用计算和位移计算结构基本自振周期的计算框架梁柱的抗侧刚度计算见表6-1、表6-2、表6-3. 表6-1 横梁、框架柱线刚度计算考虑梁柱线刚度比,用D 值法计算各楼层框架柱的侧向刚度。
(完整版)各类梁的弯矩剪力计算汇总表
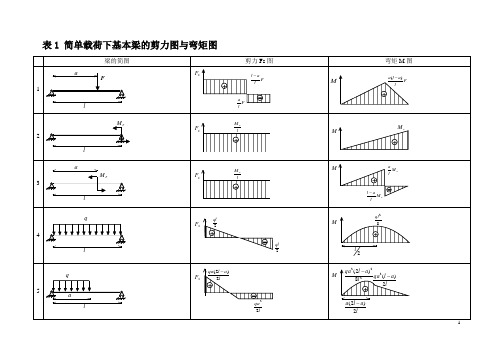
表1 简单载荷下基本梁的剪力图与弯矩图注:外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·mV B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN ·m 。
2)三跨等跨梁的内力和挠度系数 表2-12注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
各类梁的弯矩剪力计算汇总表-剪力计算公式一览表

表 1 简单载荷下基本梁的剪力图与弯矩图注:外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁2.单跨梁的内力及变形表(表2-6~表2-10)1)简支梁的反力、剪力、弯矩、挠度表2-62)悬臂梁的反力、剪力、弯矩和挠度表2-73)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-84)两端固定梁的反力、剪力、弯矩和挠度表2-95 )外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14 )1)二跨等跨梁的内力和挠度系数表2-11均布荷载 q =11.76kN/m ,每跨各有一集中荷载 F =29.4kN ,求中间支座的最大弯矩和剪力。
M B 支=(-0.125×11.76×52)+(- 0.188×29.4×5)=(- 36.75)+( -27.64)=- 64.39kN ·mV B 左=(-0.625×11.76×5)+(- 0.688×29.4)=(- 36.75)+(- 20.23)=- 56.98kN[例 2] 已知三跨等跨梁 l = 6m ,均布荷载 q =11.76kN/m ,求边跨最大跨中弯矩 [解 ] M1 = 0.080×11.76×62=33.87kN ·m 。
2)三跨等跨梁的内力和挠度系数 表 2-12注: 1.在均布荷载作用下: M =表中系数×4ql 2;V =表中系数× ql ; w 表中系数ql。
100EI Fl 3Fl ;V =表中系数× F ; w 表中系数 Fl。
100EI2.在集中荷载作用下: M =表中系数×[例 1] 已知二跨等跨梁 l =5m ,[解]f ⅜ 跨内帰大 支座弯矩 弯矩荷載图VCXAflM 2-0.5500 -O I OSo-O (O 5Q0.4500.550(Jf≡¾-0,050 -0.500 D.0751-0.050 -0.050 -0,0500,5000.050UHiD跨度中点挠度-0.45(J 0,990 -0.625 0.990L A 4-L073L054-0÷117-0.033 0.383D-0.C67 0.0170.433f t J÷175 -0.150一(L 1500.350-0,075 -0.0750.425ΓJ⅛3.175 -0.075-0.075-0,07S0.050-0.3131 0,677 -0.313λ1620.1370 + 175-o r osα 0,325-0.617-0.4170*033 0.5β3 0.033-0.5670.0830.5730.365 -0.208-O.on-0,017 0.885 -0.313 0.104-0.650 0.500"-W0.650-0,5750 0.575-0.425E146 1.6150.208 1.146- 0,075- 0,50C 0.5000.0750.075-0Λ69-0.9371U46L 615-0.469-0,675-0.375 0,6250.0500.0500.9900.677 L 0.3124 注:1.在均布荷载作用下:M =表中系数× ql2;V=表中系数× ql;w表中系数ql 100EI2.在集中荷载作用下:M =表中系数× Fl;V=表中系数× F;w 表中系数Fl。
5.2 水平地震作用计算

5.2 水平地震作用计算5.2.1采用底部剪力法时,各楼层可仅取一个自由度,结构的水平地震作用标准值,应按下列公式确定(图5.2.1):式中FEk-结构总水平地震作用标准值;α1-相应于结构基本自振周期的水平地震影响系数值,应按本章第5.1.4条确定,多层砌体房屋、底部框架和多层内框架砖房,宜取水平地震影响系数最大值;Geq-结构等效总重力荷载,单质点应取总重力荷载代表值,多质点可取总重力荷载代表值的85%;Fi-质点i的水平地震作用标准值;Gi,Gj-分别为集中于质点i、j的重力荷载代表值,应按本章第5.1.3条确定;Hi,Hj-分别为质点i、j的计算高度;δn顶部附加地震作用系数,多层钢筋混凝土和钢结构房屋可按表5.2.1采用,多层内框架砖房可采用0.2;其他房屋可采用0.0;ΔFn-顶部附加水平地震作用。
注:T1为结构基本自振周期。
5.2.2采用振型分解反应谱法时,不进行扭转耦联计算的结构,应按下列规定计算其地震作用和作用效应:1 结构j振型i质点的水平地震作用标准值,应按下列公式确定:d式中Fji-j振型i质点的水平地震作用标准值;αj-相应于j振型自振周期的地震影响系数,应按本章第5.1.4条确定;Xji-j振型i质点的水平相对位移;rj-j振型的参与系数。
2 水平地震作用效应(弯矩、剪力、轴向力和变形),应按下式确定:式中SEk-水平地震作用标准值的效应;Sj-j振型水平地震作用标准值的效应,可只取前2~3个振型,当基本自振周期大于1.5s或房屋高宽比大于5时,振型个数应适当增加。
5.2.3 建筑结构估计水平地震作用扭转影响时,应按下列规定计算其地震作用和作用效应:1 规则结构不进行扭转耦联计算时,平行于地震作用方向的两个边榀,其地震作用效应应乘以增大系数。
一般情况下,短边可按1.15采用,长边可按1.05采用;当扭转刚度较小时宜按不小于1.3采用2扭转耦联振型分解法计算时各楼层可取两个正交的水平位移和一个转角共三个自由度并应按下列公式计算结构的地震作用和作用效应确有依据时尚可采用简化计算方法确定地震作用效应。
