固体物理第10次课
固体物理基础课后1到10题答案

一.本章习题P272习题1.试证理想六方密堆结构中c/a=.一. 说明:C 是上下底面距离,a 是六边形边长。
二. 分析:首先看是怎样密堆的。
如图(书图(a),P8),六方密堆结构每个格点有12个近邻。
(同一面上有6个,上下各有3个)上下底面中间各有一个球,共有六个球与之相切,每个球直径为a 。
中间层的三个球相切,又分别与上下底面的各七个球相切。
球心之间距离为a 。
所以球心之间即格点之间距离均为a (不管是同层还是上下层之间)。
三. 证明:如图OA=a ,OO ’=C/2(中间层是上下面层的一半),AB=a O ’是ΔABC 的三垂线交点33'a AB AO ==∴(由余弦定理)330cos 2,30cos 230cos 2222a a x x a ax x a x ===-+=οοο633.1322384132)2()2()3()2(2222222222''≈===∴+=+=+=a c c a ac a ac OA AO OO2.若晶胞基矢c b a ρρρ,,互相垂直,试求晶面族(hkl )的面间距。
一、分析:我们想到倒格矢与面间距的关系G d ρπ2=。
倒格矢与晶面族 (hkl )的关系321b l b k b h G ρρρρ++=写出)(321b b b ρρρ与正格子基矢 )(c b a ρρρ的关系。
即可得与晶面族(hkl ) 垂直的倒格矢G ρ。
进而求得此面间距d 。
二、解:c b a ρρρΘ,,互相垂直,可令k c c j b b i a a ρρρρρρ===,,晶胞体积abc c b a v =⨯⋅=)(ρρρ倒格子基矢:kcj b i a abc b a v b j b i a k c abc a c v b ia k c jb abc c b v b ρρρρρρρρρρρρρρρρρρπππππππππ2)(2)(22)(2)(22)(2)(2321=⨯=⨯==⨯=⨯==⨯=⨯=而与 (hkl )晶面族垂直的倒格矢 222321)()()(2)(2cl b k a h G k cl j b k i a h b l b k b h G ++=∴++=++=ππρρρρρρρρ故(hkl ) 晶面族的面间距222222)()()(1)()()(222cl b k a h cl b k a h G d ++=++==πππρ3.若在体心立方晶胞的每个面中心处加一个同类原子,试说明这种晶体的原胞应如何选择?每个原胞含有几个原子?1.分析:考虑选取原胞的条件:(即布拉菲晶格的最小单元)(1)体积最小的重复结构单元(2)只包含一个格点(3)能反映晶格的周期性应将几个原子组合成一个格点,然后构成原胞。
固体物理学-宏观对称性和晶格分类

ε xy ε yy
ε ε
xz yz
⎤ ⎥ ⎥
⎣⎢ε zx ε zy ε zz ⎥⎦
立方对称晶体:
⎡ε0 0 0 ⎤
ε
=
⎢ ⎢
0
ε0
0
⎥ ⎥
⎣⎢ 0 0 ε0 ⎥⎦
六方对称晶体:
⎡ε ⊥ 0 0 ⎤
ε
=
⎢ ⎢
0
ε⊥
0
⎥ ⎥
⎣⎢ 0 0 ε // ⎥⎦
11
晶体宏观对称性及其分类
• 宏观对称性 • 点群 • 空间群 • 晶体结构分类
群为一组“元素”的集合,G≡(E, A, B, C, …),且这些“元素”在定义 一定的“乘法法则”下(不等价于数学乘法),满足下列性质: 1. 闭合性--- 集合内任意两元素“乘积”仍为集合元素
A, B ∈ G, 则AB=C ∈ G 2. 单元性---存在单位元素E,使得所有元素A:
AE= A 3. 可逆性---任意元素A存在逆元素A-1 满足
4
立方对称(sc、bcc、fcc)操作
(a)
(b)
(c)
•沿图(a)立方轴转动π/2、 π、 3π/2,有3个立方轴,共9个对称操作。 •沿图(b)面对角线转动π,有6条面对角线,共6个对称操作。 •沿图(c)体对角线转动2π/3、 4π/3,有4个体对角线,共8个对称操作。 •不动为一个对称操作。 •以上共24个对称操作,以上操作再加上反演为新的对称操作。 •共48个对称操作。
5
正四面体对称操作
•沿立方轴转动 π,有3个立方轴,共3个对称操作。 •沿图(c)体对角线转动2π/3、 4π/3,有4个体对角线,共8个对称操作。 •不动为一个对称操作。以上共12个对称操作。 •相对立方对称,少去的12个对称操作,即绕立方轴转π/2、3π/2以及绕 面对角线转动π,再加上中心反演为正四面体的对称操作。 •共24个对称操作。
固体物理习题解答

,在 时为
.(课本数据有误)
试计算
(1) 费米能和费米温度;
(2) 费米球的半径;
(3) 费米速度;
(4) 费米球的最大横截面积;
(5) 室温下和绝对零度附近电子的平均自由程.
解:电子数密度
.
费米波矢
(1) 费米能
费米温度
(2) 费米球的半径 (3) 费米速度
(4) 费米球的最大横截面
(5) 平均自由时间
证:比热
高温时,
,即
按 Maclaurin 公式展开 取前三项有
,其中
,
.
, 很小,于是
, ,于是
4.(3.12)设某离子晶体中相邻两离子的相互作用势能为
为待定常数,平衡间距 解:平衡时,有
,求线膨胀系数 .
线膨胀系数
,
其中
,
.
即
10 / 15
1.(4.3)如果已知空位形成能为 是多少?
解:
作业 5
应满足布洛赫定理,若晶格常数为 ,电子的波函数为
(2)
.
(3)
( 是某个确定的函数)
试求电子在这些状态的波矢.
解:一维布洛赫定理为
.
(1)
(2) (3) 2(6.2)设一维电子能带可以写成
其中 为晶格常数,试求 (1) 能带的宽度; (2) 电子的平均速度; (3) 能带底部和顶部的电子有效质量.
解:(1)
马德隆常数
,对于一维晶格,选取一个正离子作为参考离子,在求和中对负离子取正号,
对正离子取负号,参考离子两边的离子是对称分布的,则有
时,由
两边积分,有
取 ,得
故由两种离子组成、间距为 的一维晶格的马德隆常数
固体物理习题与答案汇总整理终极版

11级第一次(作业)请充分利用网络、本校及外校图书馆的相关资料,同时联系相关专业的老师,调查关于固体物理的简史、发展趋势以及当代的热门前沿课题(针对自己感兴趣的某个方面),形成一份报告,阐述自己的看法,要求2000字以上。
(已经在第一次课布置,11月1日前后上交)11级固体物理第2次习题和思考题1.在结晶学中,我们课堂上讲的单胞,也叫元胞,或者叫结晶学原胞,也叫晶胞,试回忆一下晶胞是按晶体的什么特性选取的?答:在结晶学中,晶胞选取的原则是既要考虑晶体结构的周期性又要考虑晶体的宏观对称性。
2.解释Bravais 点阵并画出氯化钠晶体的结点所构成的Bravais 点阵。
答:晶体的部结构可以概括为由一些相同的结点构成的基元在空间有规则的作周期性的无限分布,这些结点构成点阵,如果基元只由一个结点构成,这种点阵称为Bravais 点阵。
氯化钠晶体的Bravais 点阵可参照书p8的图1-13,点阵的结点由钠离子和氯离子组成。
3.说明金刚石结构是复式点阵的原因。
答:金刚石结构可这样描述:面心立方的体心向顶角引8条对角线,在互不相邻的四条对角线中点,各有一个原子。
以金刚石为例,顶角和面心处的原子周围情况和对角线上的原子周围情况不相同,因而金刚石结构是复式晶格,可看作两套面心立方子晶格沿体对角线移开1/4体对角线长度而成。
Bravais 点阵包含两个原子。
4.体心立方点阵和面心立方点阵互为正、倒格子,试证明之。
答:面心立方的三个基矢为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=)(2)(2)(2321i k a a k j a a j i a a ρρρρρρρρρ其体积为43a ,根据倒格矢的定义得:⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=⨯⋅⨯=++-=⨯⋅⨯=+-=⨯⋅⨯=)(2)(2)(2)(2)(2)(2321213321132321321k j i a a a a a a b k j i a a a a a a b k j i a a a a a a b ρρρρρρρρρρρρρρρρρρρρρρρρρρρππππππ 可见,除了系数不同之外,方向正好是体心立方的晶格基矢。
固体物理基础(吴代鸣之高教版)课后1到31题答案

一. 本章习题P272习题1.试证理想六方密堆结构中c/a=1.633.一. 说明:C 是上下底面距离,a 是六边形边长。
二. 分析:首先看是怎样密堆的。
如图(书图1.10(a),P8),六方密堆结构每个格点有12个近邻。
(同一面上有6个,上下各有3个)上下底面中间各有一个球,共有六个球与之相切,每个球直径为a 。
中间层的三个球相切,又分别与上下底面的各七个球相切。
球心之间距离为a 。
所以球心之间即格点之间距离均为a (不管是同层还是上下层之间)。
三. 证明:如图OA=a ,OO ’=C/2(中间层是上下面层的一半),AB=a O ’是ΔABC 的三垂线交点33'a AB AO ==∴(由余弦定理)330cos 2,30cos 230cos 2222a a x x a ax x a x ===-+=633.1322384132)2()2()3()2(2222222222''≈===∴+=+=+=a c c a ac a a c OA AO OO2.若晶胞基矢c b a,,互相垂直,试求晶面族(hkl )的面间距。
一、分析:我们想到倒格矢与面间距的关系G d π2=。
倒格矢与晶面族 (hkl )的关系321b l b k b h G++=写出)(321b b b 与正格子基矢 )(c b a的关系。
即可得与晶面族(hkl ) 垂直的倒格矢G。
进而求得此面间距d 。
二、解:c b a ,,互相垂直,可令k c c j b b i a a===,,晶胞体积abc c b a v =⨯⋅=)(倒格子基矢:kcj b i a abc b a v b j b i a k c abc a c v b ia k c jb abc c b v b πππππππππ2)(2)(22)(2)(22)(2)(2321=⨯=⨯==⨯=⨯==⨯=⨯=而与 (hkl )晶面族垂直的倒格矢 222321)()()(2)(2clb k a h G k cl j b k i a h b l b k b h G ++=∴++=++=ππ故(hkl ) 晶面族的面间距222222)()()(1)()()(222cl b k a h cl b k a h G d ++=++==πππ3.若在体心立方晶胞的每个面中心处加一个同类原子,试说明这种晶体的原胞应如何选择?每个原胞含有几个原子?1. 分析:考虑选取原胞的条件:(即布拉菲晶格的最小单元) (1) 体积最小的重复结构单元 (2) 只包含一个格点(3)能反映晶格的周期性应将几个原子组合成一个格点,然后构成原胞。
固体物理教学设计

固体物理教学设计一、教学目标本次固体物理教学旨在让学生了解固体物理的基本知识,掌握固体的性质和特点。
学生应该能够:1.掌握固体物理的基本概念;2.了解固体物理的基本性质;3.能够运用所学知识分析解决实际问题;4.加深对物质性质和物态变化的理解。
二、教学内容2.1 固体物理的概念1.物质的构成;2.固体的定义;3.固体的分类。
2.2 固体物理的性质1.固体物质的密度;2.固体物质的硬度;3.固体物质的弹性;4.固体物质的导电性;5.固体物质的热传导性。
2.3 固体物理的实际应用1.固体材料的力学性能;2.固体材料的热学性能;3.固体材料的电学性能;4.固体材料的磁学性能。
三、教学方法本次课程采用讲授与实验相结合的教学方法,课堂分为两个部分:3.1 理论讲解首先讲解固体物理的概念和性质,介绍固体材料在生活中的应用。
教师需要举例说明,让学生了解如何从现实生活中发现物理学知识。
3.2 实验操作带领学生进行实验操作,让学生亲身体验固体物理的性质。
可以安排以下实验:1.用一块铁板在两字夹板中制成贝壳形;2.用钛合金板弯曲后,恢复到原来的形状;3.用与红外线相同波长的激光穿过水晶管;4.反复将弹簧挤压,测量弹簧周围的磁场强度。
四、教学反思在教学过程中,我发现学生对固体物理的初步认识还很浅显,需要在讲解中加入更多例子。
学生在实验中感受到了固体物理的性质,但是部分实验需要深入解释,让学生更好地理解,并加强实验记录和分析总结。
下一步需要更有针对性地准备课前预习材料,增加对固体物理的理解和掌握。
同时,教师还需要不断更新教学内容,加强实战性案例,让学生更好地掌握固体物理的知识,拓宽应用领域。
固体物理学答案(朱建国版)

固体物理学·习题指导配合《固体物理学(朱建国等编著)》使用2019年11月20日第1章晶体结构 (1)第2章晶体的结合 (12)第3章晶格振动和晶体的热学性质 (20)第4章晶体缺陷 (33)第5章金属电子论 (37)第1章 晶体结构1.1 有许多金属即可形成体心立方结构,也可以形成面心立方结构。
从一种结构转变为另一种结构时体积变化很小.设体积的变化可以忽略,并以R f 和R b 代表面心立方和体心立方结构中最近邻原子间的距离,试问R f /R b 等于 多少?答:由题意已知,面心、体心立方结构同一棱边相邻原子的距离相等,都设为a : 对于面心立方,处于 面心的原子与顶角原子的距离为:R f =22a 对于体心立方,处于体心的原子与顶角原子的距离为:Rb =32a 那么,Rf Rb =23aa=631.2 晶面指数为(123)的晶面ABC 是离原点O 最近的晶面,OA 、OB 和OC 分别与基失a 1,a 2和a 3重合,除O 点外,OA ,OB 和OC 上是否有格点?若ABC 面的指数为(234),情况又如何?答:晶面族(123)截a 1,a 2,a 3分别为1,2,3等份,ABC 面是离原点O 最近的晶面,OA 的长度等于a 1的长度,OB 的长度等于a 2长度的1/2,OC 的长度等于a 3长度的1/3,所以只有A 点是格点。
若ABC 面的指数为(234)的晶面族,则A 、B 和C 都不是格点。
1.3 二维布拉维点阵只有5种,试列举并画图表示之。
答:二维布拉维点阵只有五种类型,两晶轴b a 、,夹角ϕ,如下表所示。
序号 晶系 基矢长度与夹角关系 布拉维晶胞类型 所属点群 1 斜方 任意2,πϕ≠b a 、简单斜方(图中1所示) 1,2 2 正方 2,πϕ==b a简单正方(图中2所示) 4,4mm 3 六角 32,πϕ==b a简单六角(图中3所示) 3,3m ,6,6mm 4长方2,πϕ=≠b a简单长方(图中4所示) 有心长方(图中5所示)1mm ,2mm1 简单斜方2 简单正方3 简单六角4 简单长方5 有心长方二维布拉维点阵1.4 在六方晶系中,晶面常用4个指数(hkil )来表示,如图所示,前3个指数表示晶面族中最靠近原点的晶面在互成120°的共平面轴a 1,a 2,a 3上的截距a 1/h ,a 2/k ,a 3/i ,第四个指数表示该晶面的六重轴c 上的截距c/l.证明:i=-(h+k ) 并将下列用(hkl )表示的晶面改用(hkil )表示:(001)(133)(110)(323)(100)(010)(213)答:证明设晶面族(hkil )的晶面间距为d ,晶面法线方向的单位矢量为n °。
固体物理习题参考答案

固体物理第一次习题参考答案1.如果将等体积球分别排成下列结构,设x 表示刚球所占体积与总体积之比,证明结构 x简单立方 0.526x π=≈体心立方 30.688x π=≈ 面心立方 20.746x π=≈ 六角密排 20.746x π=≈ 金刚石 30.3416x π=≈解:设钢球半径为r ,立方晶系晶格常数为a ,六角密排晶格常数为a,c 钢球体积为V 1,总体积为V 2(1)简单立方单胞含一个原子,a r =2 52.06343321≈==ππa r V V(2)体心立方取惯用单胞,含两个原子,r a 43= 68.0833423321≈=⋅=ππar V V (3)面心立方取惯用单胞,含4个原子,r a =2 74.0623443321≈=⋅=ππar V V (4)六角密排与面心立方同为密堆积结构,可预期二者具有相同的空间占有率 取图示单胞,含两个原子,a r =2 单胞高度a c 38=(见第2题) 74.062233422321≈=⋅⋅=ππc a r V V (5)金刚石取惯用单胞,含8个原子,r a 2341= 34.01633483321≈=⋅=ππar V V2.试证六方密排密堆积结构中128() 1.6333c a =≈解: 六角密排,如图示,4个原子构成正四面体222)2332(2a a c =⋅+⎪⎭⎫⎝⎛ ⇒ a c 38=3.证明:体心立方晶格的倒格子是面心立方,面心立方的倒格子是体心立方。
证:体心立方基矢取为⎪⎪⎪⎩⎪⎪⎪⎨⎧+-=++-=-+=)(2)(2)(2321k j i a a k j i a a k j i a a其中a 为晶格常数其倒格子基矢,按定义)(2)(21111114212)(223321j i b j i a kj ia a a a b+=+=--⋅=⨯Ω=πππ)(2)(2132k j b a a b +=⨯Ω=π)(2)(2213k i b a a b +=⨯Ω=π可见,体心立方的倒格子是晶格常数为a b π4=的面心立方。
固体物理实验方法简单题

1.说明X射线谱的分类及产生物理机制?一种是连续X射线谱,与靶材料无关,是高速电子受到靶的抑制作用,速度骤减,小于1%的电子动能转化为X射线光能,电子所减少的能量ε∆就作为一个X射线光量子辐射出来,其频率υ由爱因斯坦方程给出:=∆hυε数量极大的电子射向阳极靶受到减速的条件不可能相同,电子损失的能量也不同,因而出现了不同波长及不同数量的光量子,形成了连续分布的X射线谱。
另一种是特征X射线线标识谱,与加速电压无关,而与靶材料有关。
不同靶元素的X射线标识谱具有相似的结构,随着靶原子的原子序数Z的增加,只是单调变化,而不是周期性变化。
标识谱的这一特征表明它是原子内层电子跃迁所产生的。
当高速电子轰击靶原子,将原子内层电子电离,内层产生一个电子的空位,外层电子跃迁到内层空位所发出的辐射谱线就是标识谱。
当管电压比较小时,只有连续X射线产生。
当管电压上升到超过某一临界激发电压时,在某一特定的波长处,将会有强度极强的特征X射线叠加在连续X射线谱上,此即为特征X射线,又名标识X 射线。
特征X射线谱的产生机理起源于电子的跃迁。
某些高速射向阳极靶的电子能量足够大,可能将靶元素原子的内层电子击出,电子从能量较高的态迁到能量较低的态时发出辐射。
2.什么是俄歇效应,什么是厄瓦尔德球?俄歇效应是原子发射的一个电子导致另一个或多个电子(俄歇电子)被发射出来而非辐射X射线(不能用光电效应解释),使原子、分子成为高阶离子的物理现象,是伴随一个电子能量降低的同时,另一个(或多个)电子能量增高的跃迁过程。
当X射线或γ射线辐射到物体上时,由于光子能量很高,能穿入物体,使原子内壳层上的束缚电子发射出来。
当一个处于内层电子被移除后,在内壳层上出现空位,而原子外壳层上高能级的电子可能跃迁到这空位上,同时释放能量。
一定的内原子壳空位可以引起一个或多个俄歇电子跃迁。
跃迁时释放的能量将以辐射的形式向外发射。
通常能量以发射光子的形式释放,但也可以通过发射原子中的一个电子来释放,被发射的电子叫做俄歇电子。
2009~2010学年第一学期信息学院电子、通信工程专业2006级本科生课程表(校本部)

2009~2010学年第一学期信息学院电子、通信工程专业2006级
本科生课程表(校本部)
学生人数:51人内招39人外招12人
2、06级毕业实习一周(1学分),具体时间、地点由系通知,指导教师:杨恢东等现代电子教研室教师
2009~2010学年第一学期信息学院电子、通信工程专业2007级
本科生课程表(校本部)
学生人数:74人内招63人外招11人
注:课室编号第一个数字“A”是新教学大楼,“B”是成教楼,“C”是科学馆,“南”是南海楼。
2009~2010学年第一学期信息学院电子技术与科学专业2007级
本科生课程表(校本部)
学生人数:20人内招20人
2009~2010学年第一学期信息学院电子、通信工程专业2008级
本科生课程表(校本部)
2009~2010学年第一学期信息学院电子技术与科学专业2008级
本科生课程表(校本部)
注:2009级本科生从第二周周三(9月16日)开始上课。
2009~2010学年第一学期信息学院电子、通信、电科专业2009级本科生课程表 (珠海校区) 2009年7月20日第二版
预计学生人数:108人内招93人外招15人。
固体物理学答案(朱建国版)

固体物理学·习题指导配合《固体物理学(朱建国等编著)》使用2020年6月21日第1章晶体结构 0第2章晶体的结合 (13)第3章晶格振动和晶体的热学性质 (22)第4章晶体缺陷 (35)第5章金属电子论 (39)第1章晶体结构有许多金属即可形成体心立方结构,也可以形成面心立方结构。
从一种结构转变为另一种结构时体积变化很小.设体积的变化可以忽略,并以R f和R b代表面心立方和体心立方结构中最近邻原子间的距离,试问R f/R b等于多少答:由题意已知,面心、体心立方结构同一棱边相邻原子的距离相等,都设为a:对于面心立方,处于面心的原子与顶角原子的距离为:R f=2a对于体心立方,处于体心的原子与顶角原子的距离为:R b=2a那么,Rf Rb晶面指数为(123)的晶面ABC是离原点O最近的晶面,OA、OB和OC分别与基失a1,a2和a3重合,除O点外,OA,OB和OC上是否有格点若ABC面的指数为(234),情况又如何答:晶面族(123)截a1,a2,a3分别为1,2,3等份,ABC面是离原点O最近的晶面,OA的长度等于a1的长度,OB的长度等于a2长度的1/2,OC的长度等于a3长度的1/3,所以只有A 点是格点。
若ABC面的指数为(234)的晶面族,则A、B和C都不是格点。
二维布拉维点阵只有5种,试列举并画图表示之。
答:二维布拉维点阵只有五种类型,两晶轴ba、,夹角ϕ,如下表所示。
4长方2,πϕ=≠ba简单长方(图中4所示)有心长方(图中5所示)1mm,2mm1 简单斜方2 简单正方3 简单六角4 简单长方5 有心长方二维布拉维点阵在六方晶系中,晶面常用4个指数(hkil)来表示,如图所示,前3个指数表示晶面族中最靠近原点的晶面在互成120°的共平面轴a1,a2,a3上的截距a1/h,a2/k,a3/i,第四个指数表示该晶面的六重轴c上的截距c/l.证明:i=-(h+k)并将下列用(hkl)表示的晶面改用(hkil)表示:(001)(133)(110)(323)(100)(010)(213)答:证明设晶面族(hkil)的晶面间距为d,晶面法线方向的单位矢量为n°。
黄昆固体物理习题解答

π
同理
2π (k + i ) a 2π (i + j) b3 = a b2 =
说明体心立方晶格的 与面心立方晶格基矢对比,正是晶格常数为 4π / a 的面心立方的基矢, 倒格子确实是面心立方。注意,倒格子不是真实空间的几何分布,因此该面心立方只是形式 上的,或者说是倒格子空间中的布拉菲格子。 根据定义,面心立方的倒格子基矢为
α = 2[1 − + − + ]
因为
1 1 1 2 3 4
∵ ln(1 + x ) =
x x 2 x3 x 4 − + − + 1 2 3 4
当 x = 1 时,有
1 12 13 14 ∵ ln(1 + 1) = − + − + 1 2 3 4
α = 2 ln 2 所以 (排斥势看作不变) 2.2 讨论使离子电荷加倍引起的对 NaCl 晶格常数及结合能的影响。 解:按照与书中同样的思路,系统内能为
⎡ ε11 ε12 ε =⎢ ⎢ε 21 ε 22 ⎢ ⎣ε 31 ε 32
如果介电常数张量为
ε13 ⎤ ε 23 ⎥ ⎥ ε 33 ⎥ ⎦
将 Ax −π 代入变换关系,而且该变换为对称变换,得
⎡ ε11 ε12 ⎢ε ⎢ 21 ε 22 ⎢ ⎣ε 31 ε 32
所以
ε13 ⎤ ⎡ ε11 −ε12 −ε13 ⎤ ⎢ ε 23 ⎥ ε 23 ⎥ ⎥ = ⎢ −ε 21 ε 22 ⎥ ⎢ ⎥ ε 33 ⎥ − ε ε ε 32 33 ⎦ ⎦ ⎣ 31
= (2π )3
υc
1.5 证明:倒格子矢量 G = h1b1 + h2b2 + h3b3 垂直于密勒指数为 ( h1h2 h3 ) 的晶面系。 证明:根据定义,密勒指数为 ( h1h2 h3 ) 的晶面系中距离原点最近的平面 ABC 交于基矢的截 距分别为
固体物理第二章答案

第21. 有一晶体,平衡时体积为 0V , 原子间相互作用势为0.如果相距为 r 的两原子互作用势为 ()n m r r a r u β+-= 证明(1) 体积弹性模量为 K=.90V mnU (2) 求出体心立方结构惰性分子的体积弹性模量.[解答]设晶体共含有 N 个原子,则总能量为U(r)=()∑∑i jij r u '21. 由于晶体表面层的原子数目与晶体内原子数目相比小得多,因此可忽略它们之间的基异,于是上式简化为 U=().2'∑jijr u N设最近邻原子间的距离为R 则有j ij a r =R再令 A ,1'∑=j m j m a A ,1'∑=jn j n a 得到 U=.200⎪⎪⎭⎫ ⎝⎛+-n n m m R A R A N βα 平衡时R=R 0,则由已知条件U(R 0) = 0U 得0002U R A R A N n n m m =⎪⎪⎭⎫⎝⎛+-βα 由平衡条件 0)(0=R dRR dU得021010=⎪⎪⎭⎫⎝⎛-++n nm m R A n R A m N βα. 由(1),(2)两式可解得.)(2,)(20000n n m m nR n m N U A nR n m N U A -=-=βα利用体积弹性模量公式[参见《固体物理教程》(2.14)式]K=0220209R R U V R ⎪⎪⎭⎫ ⎝⎛∂∂得K= ⎥⎦⎤⎢⎣⎡+++-n n m m R A n n R A m m N V 000)1()1(291βα = ⎥⎦⎤⎢⎣⎡-++-+-)(2)1()(2)1(2910000000n m N mR U R n n n m N nR U R m m N V nnm m = .900V mn U - 由于,00<U 因此,00U U -= 于是 K= .90V mnU (1) 由《固体物理教程》(2.18)式可知,一对惰性气体分子的互作用能为.)(126r B r A r u +-=若令 61,42⎪⎭⎫⎝⎛==A B B A σε,则N 个惰性气体分子的互作用势能可表示为⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=6612122)(R A R A N r U σσε.由平衡条件0)(0=R dRR dU 可得 R .2616120⎪⎪⎭⎫ ⎝⎛=A A σ进一步得 .2)(122600A A N R U U ε-==代入K=.900V mn U 并取 m =6,n =12,V 300334R N =得 K=5126123233⎪⎪⎭⎫⎝⎛A A A σε.对体心立方晶体有 A .11.9,25.12126==A 于是.1.703σε=K 2. 一维原子链,正负离子间距为a ,试证:马德隆常数为2=μ1n2. [解答] 相距ij r 的两个离子间的互作用势能可表示成.4)(2n ijij ij r br q r u +=πμ设最近邻原子间的距离为R 则有 R a r j ij =, 则总的离子间的互作用势能 U=()∑∑∑-⎪⎪⎭⎫ ⎝⎛±-=jn jn j j j ij a bRa R q N r u N ''0'114[22πε. 基中 jja 1'±=∑μ 为离子晶格的马德隆常数,式中+;- 号分别对应于与参考离子相异和相同的离子.任选一正离子作为参考离子,在求和中对负离子到正号,对正离子取负号,考虑到对一维离子两边的离子是正负对称分布的,则有.413121112)1('⎥⎦⎤⎢⎣⎡+-+-=±=∑Λj ja μ利用正面的展开式 1n(1+x ),432432Λ+-+-x x x x 并令 1=x 得Λ+-+-41312111=1n(1+1)=1n2.于是,一维离子链的马德常数为2=μ1n23. 计算面心立方面简单格子的6A 和12A(1) 只计最近邻; (2) 计算到次近邻; (3) 计算到次近邻.[解答]图2.26示出了面心立方简单格子的一个晶胞.角顶O 原子周围有8个这样的晶胞,标号为1的原子是原子O 的最近邻标号为2的原子是O 原子的最近邻,标号为3的原子是O 原子的次次近邻.由此得到,面心立方简单格子任一原子有12个最近邻,6个次近邻及24个次次近邻.以最近邻距离度量,其距离分别为:.3,2,1===j j j a a a 由 .1,112'126'6⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=∑∑jj j j a A a A图2.6 面心立方晶胞得(1) 只计最近邻时1211*12)1(66=⎪⎭⎫⎝⎛=A , 1211*12)1(1212\=⎪⎭⎫⎝⎛=A .(2) 计算到次近邻时.094.1221*611*12)2(,750.1221*611*12)2(121212666=⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛==⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛=A A(3) 计算到次次近邻时.127.12033.0094.1231*2421*611*12)3(,639.13899.0750.1231*2421*611*12)3(121212126666=+=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛==+=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛=A A 由以上可以看出,由于12A中的幂指数较大,12A 收敛得很快,而6A 中的幂指数较小,因此 6A 收敛得较慢,通常所采用的面心立方简单格子的 6A 和 12A 的数值分别是14.45与12.13.4. 用埃夫琴方法计算二维正方离子(正负两种)格子的马德隆常数. [解答]马德隆常数的定义式为 jja 1'±=∑μ,式中+、-号分别对应于与参考离子相异和相同的离子,二维正方离子(正负两种)格子,实际是一个面心正方格子,图 2.7示出了一个埃夫琴晶胞.设参考离子O 为正离子,位于边棱中点的离子为负离子,它们对晶胞的贡献为4*(1/2).对参考离子库仑能的贡献为图2.7二维正方离子晶格.121*4顶角上的离子为正离子,它们对晶胞的贡献为4*(1/4), 对参考离子库仑能的贡献为 .241*4-因此通过一个埃夫琴晶胞算出的马德隆常数为 .293.1241*4121*4=-=ν再选取422=个埃夫琴晶胞作为考虑对象,这时离子O 的最的邻,次近邻均在所考虑的范围内,它们对库仑能的贡献为,2414-而边棱上的离子对库仑能的贡献为 ,521*8221*4+- 顶角上的离子对为库仑能的贡献为 ,841*4-这时算出的马德隆常数为图 2.8 4个埃夫琴晶胞同理对932=个埃夫琴晶胞进行计算,所得结果为611.11841*41321*81021*8321*48458242414=⎪⎪⎪⎪⎭⎫ ⎝⎛-+-+⎪⎪⎭⎫ ⎝⎛-+-+⎪⎭⎫ ⎝⎛-=μ 对 1642=个埃夫琴晶胞进行计算,所得结果为614.13241*42521*81721*81021*8421*4184138108348458242414=⎪⎪⎪⎪⎭⎫ ⎝⎛-+-+-+⎪⎪⎭⎫ ⎝⎛-+-+⎪⎪⎭⎫ ⎝⎛-+-+⎪⎭⎫ ⎝⎛-=μ当选取 n 2个埃夫琴晶胞来计算二维正方离子(正负两种)格子的马德隆常数,其计算公式(参见刘策军,二维NaC1 晶体马德隆常数计算,《大学物理》,Vo1.14,No.12,1995.)为 [][].1,8411>+++=--n D C B A n n n n μ其中 ,21)1(,1)1(11111nB t A n n n t t n +-=+--=-=∑,1)1(1)1()2()1(1)1()1(2112212221112122122222222221⎪⎪⎪⎪⎪⎭⎫⎝⎛+--+--+-+-+--++⎪⎪⎭⎫⎝⎛+++-+⎪⎪⎭⎫ ⎝⎛+---n n n n n C n n ΛΛ.121)1()1(2181222222+-+-++++-=n n n n n D n n Λ5. 用埃夫琴方法计算CsCl 型离子晶体的马德隆常数(1) 只计最近邻 (2) 取八个晶胞 [解答](1) 图2.29是CsCl 晶胸结构,即只计及最近邻的最小埃夫琴晶胞,图2.29()a 是将Cs +双在体心位置的结构,图2.9(a)是将 Cl -取在体心位置的结构,容易求得在只计及最近邻情况下,马德隆常数为1.图2.29 (a )Cs 取为体心的CsC1晶胞,(b) C1取为体心的CsC1晶胞(2)图2.10是由8个CsCl 晶胞构成的埃夫琴晶胞,8个最近邻在埃夫琴晶胞内,每个离子对晶胞的贡献为1,它们与参考离子异号,所以这8个离子对马德隆常数的贡献为8埃夫琴晶胞6个面上的离子与参考离子同号,它们对埃夫琴晶胞的贡献是21,它们与参考离子的距离为32R 它们对马德隆常数的贡献为-()3/2*621图 2.10 8个CsCl 晶胞构成的一个埃夫琴晶胞埃夫琴晶胞楞上的12个离子,与参考离子同号,它们对埃夫琴晶胞的贡献是41它们与参考离子的距离为322R 它们对马德隆常数的贡献为-()3224/1*12埃夫琴晶胞角顶上的 8个离子,与参考离子同号,它们对埃夫琴晶胞的贡献是81它们与参考离子的距离为2R 它们对马德隆常数的贡献为 -()281*8,由8个CsCl 晶胞构成的埃夫琴晶胞计算的马德隆常数.064806.32)8/1(*8322)4/1(*123/2)2/1(*68=---=μ 为了进一步找到马德常数的规律,我们以计算了由27个CsCl 晶胞构成的埃夫琴晶胞的马德隆常数,结果发现,由27个CsCl 晶胞构成的埃夫琴晶胞的马德隆常数是0.439665.马德隆常数的不收敛,说明CsCl 晶胞的结构的马德隆常数不能用传统的埃夫琴方法计算.为了找出合理的计算方法,必须首先找出采用单个埃夫琴晶胞时马德隆常数不收敛的原因.为了便于计算,通常取参考离子处于埃夫琴晶胞的中心.如果以Cs +作参考离子,由于埃夫琴晶胞是电中性的要求,则边长为pa 2(p 是大于或等于1的整数)的埃夫琴晶胞是由(2p )3个CsCl 晶胞所构成,埃夫琴晶胞最外层的离子与参考离子同号,而边长为(2p +1)的埃夫琴晶胞是由(2p +1)3 个 CsCl 晶胞所构成,但埃夫琴晶胞的最外层离子与参考离子异号,如果以C1-作参考离子也有同样的规律,设参考离子处于坐标原点O ,沿与晶胞垂直的方向(分别取为x,y,z 图2.11示出了z 轴)看去,与参考郭同号的离子都分布在距O 点ia 的层面上,其中i 是大于等于 1的整数,与 O 点离子异号的离子都分布在距O 点(i -0.5)a 的层面上,图 2.11(a) 示出了同号离子层,图2.11(b)示出了异号离子层.图2.11 离子层示意图(a)表示同号离子层, O 离子所在层与 O '离子所在层相距ia(b)表示异号离子层, O 离子所在层和O ' 离子所在层相距(i -0.5)a当 CsCl 埃夫琴晶胞边长很大时,晶胞最外层的任一个离子对参考离子的库仑能都变得很小,但它们对参考离子总的库仑能不能忽略.对于由(2p )3个CsCl 晶胞所构成的埃夫琴晶胞来说,最外层有6*(2p )2个与参考离子同号的离子,它们与参考离子的距离为(1/2)pa ~(23)pa ,它们与参考离子的库仑能为a pe 024πε量级,这是一个相对大的正值.对于由(2p +1)3个CsCl 晶胞所构成的埃夫琴晶胞来说,离外层有6*(2p +1)2个与参考离子异号的离子,它们与参考离子的库仑能为a pe 024πε-量级,这是一个绝对值相对大的负值,因此,由(2p )3个CsCl 晶胞构成的埃夫琴晶胞所计算的库仑能,与由(2p +1)3个CsCl 晶胞构成的埃夫琴晶胞所计算的库仑能会有较大的差异.即每一情况计算的库仑能都不能代表CsCl 晶体离子间相互作用的库仑能.因此这两种情况所计算的马德隆常数也必定有较大的差异,由1个CsCl 晶胞、8个CsCl 晶胞和27个CsCl 晶胞构成的埃夫琴晶胞的计算可知, CsCl 埃夫琴晶胞体积不大时,这种现象已经存在.为了克服埃夫琴方法在计算马德隆常数时的局限性,可采取以下方法,令由 (2p )3个CsCl 晶胞构成的埃夫琴晶胞计算的库仑能为1U ,由(2p +1)3个CsCl 晶胞构成的埃夫琴晶胞所计算的库仑能为1U ,则CsCl 晶体离子间相互作用的库仑能可近似取作 )(2121U U U +=(1) 因子1/2 的引入是考虑除了(2p +1)3个CsCl 晶胞构成的埃夫琴晶胞最外层离子外,其他离子间的库仑能都累计了两偏,计算1U 和2U 时要选取体积足够大的埃夫琴晶胞,此时埃夫琴晶胞最外层离子数与晶胞内的离子数相比是个很小的数,相应的马德隆常数应为 )(2121μμμ+=(2) 其中:=1μ⎪⎪⎭⎫ ⎝⎛±∑i ja 1'是由(2p )3个CsC1晶胞构成的埃夫琴晶胞计算的值; =1μ⎪⎪⎭⎫ ⎝⎛±∑i ja 1'由 (2p +1)3 个CsC1晶胞构成的埃夫琴晶胞所计算成本的值.为简化计算,特选取晶胞边长a 为计算单位,由于,32a R =所以,23'μμ= ⎪⎪⎭⎫ ⎝⎛±=∑'''1i i a μ (3) 其中'i a 是某一离子到参点的距离与a 的比值.考虑到对称性,对选定的埃夫琴晶胞,把晶胞的离子看成分布在一个个以参考离子为对称心的正六面体的六个面上,体积不同的正六面六个面上的离子分别计算.由(2p )3个CsC1晶胞构成埃夫琴晶胞时,由分析整理可得,231111⎪⎪⎭⎫ ⎝⎛++=∑∑=-=p pi i p i i C B A μ (4) 由(2p +1)3个 CsC1 晶胸构成埃夫琴晶胞时,,231112⎪⎪⎭⎫ ⎝⎛++=∑∑=-=p pi i p i i D B A μ (5)其中:),1(''''22'2'p i i y x k A i x iy y x i <≤++-=∑∑(6)i A 表示与 O 点距离为ia 的6个面上所有的离子对马德隆常数的面贡献,因为这些离子与参考离子同号,故到负号.'x 、'y 是离子在平面 '''y x o 上的坐标, ''y x k 代表 6个面上等价离子的个数,其取值规则为:(1) 在角上(如E 点),即'x =i 且 'y = i. 时, ''y x k =8;(2) 在棱与坐标轴的交点(如 F 点),'x =i 且'y = 0或 'x =0且'y = 0时, ''y x k =6 (3) 在棱上的其他点(如H 、I 点)即不满足上述条件,且'x =i 或'y = i.时, ''y x k =12 (4) 在'O 点,即'x =0且'y = 0时, ''y x k =6(5) 在除'O 点外的面上的点(如J 点),即不满足上述条件时,''y x k =24.),1()5.0(5.05.05.05.022'2''''''p i i y x k B i x i y yx i ≤≤-++=∑∑-=-=(7)i B 代表距O 点距离为(i -0.5)a 的6个面上的离子对马德隆常数的贡献,因为这种些离子与参考离子异号,故取正号. 'x ,'y 是离子在平面'''y x o 上的坐标, '''y x k 代表这6个面上等价离子的个数,其取值规则为:(1) 在角上(如K 点),即'x =i 且 'y = i.时, '''y x k =8;(2) 在棱下(如L 、M 点),即不满足不述条件,且'x =i 或'y = i 时,'''y x k =12; (3) 在面上(如N 点)好不满足上述条件时, '''y x k =24.),(0022'2'"''''p i i y x k C i x iy i yx =++-=∑∑==i C 表示在边长为2pa 的晶胞最外层,即与参考离子相距pa 的6个面上的离子对马德隆常数的贡献,应取负号,与iA 的不同在于"''y x k的取值: (1) 在角上, "''y x k =''y x k /8; (2) 在棱上, "''y x k =''y x k /4; (3) 在面上, "''y x k=''y x k /2.),()5.0(5.05.05.05.022'2''''''''p i i y x k D i x i y yx i =-++=∑∑-=-=i D 表示在边长为2a p )1(+的晶胞最外层,即与参考离子相距(p +0.5)a 的离子层对马德隆常数的贡献,应取正号,与i B 的不同在于'''''yx k 的取值: (1) 在角上, '''''y x k ='''y x k /8; (2) 在棱上, '''''y x k ='''y x k /4; (3) 在面上, '''''y x k ='''y x k /2.表2.1给出了计算结果,给出的μ是由分别对应2p 和2p+1的1μ和2μ求得的,实际上, 1μ和2μ只需对应边长相近的埃夫琴晶胞即可,如取对应2p 和2p-1的埃夫琴晶胞也可得到一样的收敛结果,由以上数据可见,马德隆常数μ随晶胞边长的增大而迅速收敛.该方法适用于NaC1结构以外离子晶体马德隆常数的计算.6.只计及最近邻间的排斥作用时,一离子晶体离子间的互作用势为⎪⎪⎩⎪⎪⎨⎧±-=-)2(,)1(,)(22r e R e e r u R ρλ(1)最近邻(2)最近邻以外 式中ρλ,是常数,R 是最近邻距离,求晶体平衡时,原子间总的互作用势.[解 答]设离子数目为2N,以j ij a r =R 表示第j 个离子到参考离子i 的距离,忽略表面效应,则总的相互作用能可表示为U =N ⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛±-∑∑-ρλR j j e R a e 2' (∑表示最近邻)=N ,2⎥⎦⎤⎢⎣⎡+--ρλμR e Z R e其中⎪⎪⎭⎫⎝⎛±=∑j ia 1'μ 为马德隆常数,+号对应于异号离子,-号对应于同号离子;Z 为任一离子的最近邻数目,设平衡时R=R 0 ,由平衡条件,02020=⎥⎦⎤⎢⎣⎡+=-ρρλμR R e Z R e N dRdU 得.0202ρλμρR e Z R e -=平衡时的总相互作用为.1)(0020200⎪⎪⎭⎫⎝⎛-=⎥⎦⎤⎢⎣⎡+-=-R R e N e Z R e N R U R ρμλμρ 7. 设离子晶体中,离子间的互作用势为⎪⎪⎩⎪⎪⎨⎧±+-=最近邻以外最近邻,,)(22re R b R e r u m(1) 求晶体平衡时,离子间总的相互作用势能)(0R U (2) 证明: )(0R U 11-⎪⎪⎭⎫⎝⎛∝m mZ μ其中μ是马德隆常数,Z 是晶体配位数 [解答](1)设离子数目为2N , 以j ij a r =R 表示第j 个离子到参考离子i 的距离,忽略表面效应,则总的相互作用能可表示U =N ⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛±-∑∑m j j R b R a e 2'(∑表示最近邻) =N ,2⎥⎦⎤⎢⎣⎡+-m R b Z Re μ其中⎪⎪⎭⎫ ⎝⎛±=∑j i a 1'μ,为马德隆常数,+号对应于异号离子,-号对应于同号离子.Z 为任一离子的最近邻数目,设平衡时R=R 0由平衡条件,0102020=⎥⎦⎤⎢⎣⎡-=+m R R Zmb R e N drdUμ得10-m R Zmb=2e μ即1120-⎪⎪⎭⎫ ⎝⎛=m e Zmb R μ.于是,晶体平衡时离子间总的相互作用势能0U =).1(000--=⎥⎦⎤⎢⎣⎡+-m R NZbR b Z R Zmb N m m m(2)晶体平衡时离子间的相互作用势能可进一步化为0U =.)()()1()1(1111121211--------=⎪⎪⎭⎫ ⎝⎛--m m m m mm m m m m mb Ze Nbm e Zmb ZNbm μμ由上式可知 .110-⎪⎪⎭⎫⎝⎛∝m mZ U μ8.一维离子链,其上等间距载有正负2N 个离子,设离子间的泡利排斥只出现在最近邻离子之间,且为b/R n,b,n 是常R 是两最近邻离子的间距,设离子电荷为q ,(1) 试证明平衡间距下 )(0R U =;114212002⎪⎭⎫⎝⎛--n R n Nq πε(2) 令晶体被压缩,使0R )1(0δ-→R , 试证明在晶体被压缩单位长度的过程中外力作功的主项为c 2δ其中c=;21)1(02R n q n -(3) 求原子链被压缩了2)1(0<<e e NR δδ时的外力[解答](1) 因为离子间是等间距的,且都等于R ,所以认定离子与第j 个离子的距离j r 总可表示成为R a r j j =ja 是一整数,于是离子间总的互作用势能⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛±-=⎥⎥⎦⎤⎢⎢⎣⎡+=∑∑n i in j j j R b a R q N r b r q N R U 214242)('202'0πεπεμ,其中+、-分别对应相异离子和相同离子的相互作用.一维离子晶格的马德隆常数(参见本章习题2)为=⎪⎪⎭⎫ ⎝⎛±∑i ia 1'21n2. 利用平衡条件0)(0=R dRR dU得到b=nq 01-n 0241n2R πε,)(R U =⎪⎪⎭⎫ ⎝⎛---n n nR R R Nq 102141n22πε. 在平衡间距下⎪⎭⎫⎝⎛--n R Nq R U 1141n22)(0020πε.(2) 将互作用势能在平衡间距附近展成级数Λ+-⎪⎪⎭⎫ ⎝⎛+-⎪⎭⎫⎝⎛+=202200)(21)()()(0R R dR U d R R dR dU R U R U R R 由外力作的功等于晶体内能的增量,可得外力作功的主项为W=20220)(21)()(0R R dR U d R U R U R-⎪⎪⎭⎫ ⎝⎛=-, 其中利用平衡条件,将R=R )1(0δ- ,代入上式,得到W=δδπε)2(421)1(2102002NR R n q n ⎥⎥⎦⎤⎢⎢⎣⎡-. 晶体被压缩单位长度的过程中,外力作的功的主项δ02W NR =δπε⎥⎥⎦⎤⎢⎢⎣⎡-2002421)1(21R n q n 令c=202421)1(R n q n πε-(CGS)得到在晶体被压缩单位长度的过程中,外力作的功的主项为2δc . (3)设e δδ=时外力为F e ,由于在弹性范围内,外力与晶格的形变成正比,所以 F= )2(0δαNR , F e = )2(0e NR δα,其中α为比例系数离子链被压缩e NR δ02过程中外力作的功W e =δδαδδd NR NR Fdx e eNR e 020002)]2([0⎰⎰== e e e F NR NR δδα022022121)2(=.由于 W e =)2(20e eNR c δδ,所以离子链被压缩了e NR δ02时的外力为F e =202)1(21R n n q c ee δδ-=.9.设泡利排斥项的形式不变,讨论电荷加倍对NaC1晶格常数,体积弹性模量以及结合能的影响。
物理系本科、研究生课程表
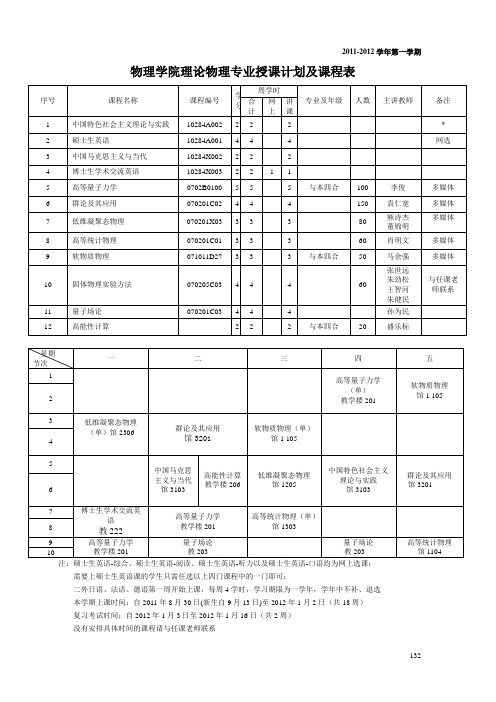
2011-2012学年第一学期物理学院理论物理专业授课计划及课程表注:硕士生英语-综合、硕士生英语-阅读、硕士生英语-听力以及硕士生英语-口语均为网上选课;需要上硕士生英语课的学生只需任选以上四门课程中的一门即可;二外日语、法语、德语第一周开始上课,每周4学时,学习期限为一学年,学年中不补、退选本学期上课时间:自2011年8月30日(新生自9月13日)至2012年1月2日(共18周)复习考试时间:自2012年1月3日至2012年1月16日(共2周)没有安排具体时间的课程请与任课老师联系1322011-2012学年第一学期物理学院凝聚态物理专业授课计划及课程表注:硕士生英语-综合、硕士生英语-阅读、硕士生英语-听力以及硕士生英语-口语均为网上选课;需要上硕士生英语课的学生只需任选以上四门课程中的一门即可;二外日语、法语、德语第一周开始上课,每周4学时,学习期限为一学年,学年中不补、退选本学期上课时间:自2011年8月30日(新生自9月13日)至2012年1月2日(共18周)复习考试时间:自2012年1月3日至2012年1月16日(共2周)没有安排具体时间的课程请与任课老师联系1332011-2012学年第一学期物理学院光学专业授课计划及课程表注:硕士生英语-综合、硕士生英语-阅读、硕士生英语-听力以及硕士生英语-口语均为网上选课;需要上硕士生英语课的学生只需任选以上四门课程中的一门即可;二外日语、法语、德语第一周开始上课,每周4学时,学习期限为一学年,学年中不补、退选本学期上课时间:自2011年8月30日(新生自9月13日)至2012年1月2日(共18周)复习考试时间:自2012年1月3日至2012年1月16日(共2周)没有安排具体时间的课程请与任课老师联系1342011-2012学年第一学期物理学院生物物理专业授课计划及课程表注:硕士生英语-综合、硕士生英语-阅读、硕士生英语-听力以及硕士生英语-口语均为网上选课;需要上硕士生英语课的学生只需任选以上四门课程中的一门即可;二外日语、法语、德语第一周开始上课,每周4学时,学习期限为一学年,学年中不补、退选本学期上课时间:自2011年8月30日(新生自9月13日)至2012年1月2日(共18周)复习考试时间:自2012年1月3日至2012年1月16日(共2周)没有安排具体时间的课程请与任课老师联系1352011-2012学年第一学期物理学院粒子物理与原子核物理专业授课计划及课程表注:硕士生英语-综合、硕士生英语-阅读、硕士生英语-听力以及硕士生英语-口语均为网上选课;需要上硕士生英语课的学生只需任选以上四门课程中的一门即可;二外日语、法语、德语第一周开始上课,每周4学时,学习期限为一学年,学年中不补、退选本学期上课时间:自2011年8月30日(新生自9月13日)至2012年1月2日(共18周)复习考试时间:自2012年1月3日至2012年1月16日(共2周)没有安排具体时间的课程请与任课老师联系1362011-2012学年第一学期物理学院制冷及低温工程专业授课计划及课程表注:硕士生英语-综合、硕士生英语-阅读、硕士生英语-听力以及硕士生英语-口语均为网上选课;需要上硕士生英语课的学生只需任选以上四门课程中的一门即可;二外日语、法语、德语第一周开始上课,每周4学时,学习期限为一学年,学年中不补、退选本学期上课时间:自2011年8月30日(新生自9月13日)至2012年1月2日(共18周)复习考试时间:自2012年1月3日至2012年1月16日(共2周)没有安排具体时间的课程请与任课老师联系1372011-2012学年第一学期物理学院声学专业授课计划及课程表注:硕士生英语-综合、硕士生英语-阅读、硕士生英语-听力以及硕士生英语-口语均为网上选课;需要上硕士生英语课的学生只需任选以上四门课程中的一门即可;二外日语、法语、德语第一周开始上课,每周4学时,学习期限为一学年,学年中不补、退选本学期上课时间:自2011年8月30日(新生自9月13日)至2012年1月2日(共18周)复习考试时间:自2012年1月3日至2012年1月16日(共2周)没有安排具体时间的课程请与任课老师联系138大学物理题典(第二版),胡盘新主编,上海交通大学出版社,200713938 粒子物理与核物理实验中的数据分析 339 现代辐射探测与测量 240 宇宙线粒子探测与物理实验 141 粒子物理专题II 242 非线性动力学与混沌 443 宇宙学 244 恒星物理学 345 星系物理学 346 有限温度量子场论 447 波尔兹曼方程及其应用140141142143。
黄昆固体物理习题解答-完整版

⎜⎝ε31 ε32 ε33 ⎟⎠ ⎜⎝ − ε31 ε32 ε33 ⎟⎠
⎜⎝ 0 ε32 ε33 ⎟⎠
⎜⎛ ε11 + 3ε 22
− 3ε11 + 3ε 22 − 3ε 23 ⎟⎞
得
⎜⎛ ε11 ⎜0 ⎜⎝ 0
0 ε 22 ε 32
0 ⎟⎞
⎜ ⎜
ε 23 ⎟ = ⎜ −
ε33 ⎟⎠
⎜ ⎜
⎜⎝
44
3ε11 + 3ε 22
《固体物理》习题解答
第一章 习 题
1.1 如果将等体积球分别排列下列结构,设x表示刚球所占体积与总体积之比,证明
结构 简单立方(书P2, 图1-2) 体心立方(书P3, 图1-3)
面心立方(书P3, 图1-7)
六方密排(书P4, 图1-6)
金刚石(书P5, 图1-8)
x
π / 6 ≈ 0.52 3π / 8 ≈ 0.68
最后,感谢各位虫友一直以来对小木虫物理版的支持!同时也希望,今后能 后更多的虫友来加入物理版,把这里建成大家交流的乐园!
zt978031 2010 年 4 月 7 日
目录
第一章 习 题··························· 1 第二章 习 题··························· 6 第三章 习 题···························10 第五章 习 题···························31 第六章 习 题···························36 第七章 习 题···························42
倒格子基矢 b1
=
2π
a2 × a3 a1 ⋅ a2 × a3
大2第一学期课表

班级
班级
班级
班级
凡遇法定节假日及重大活动课程依次顺延一周或调课;
班级
班级
班级
班级
班级
班级
班级
班级
凡遇法定节假日及重大活动课程依次顺延一周或调课;
班级
班级
班级
班级
班级
班级
班级
班级
班级
凡遇法定节假日及重大活动课程依次顺延一周或调课;
班级
班级
班级
班级
班级
班级
班级
班级
班级
班级
班级
班级
班级课程表
技活动(01-01);系统仿真设计(01-02);职前培训(01-01)班级课程表
技术课程设计(01-02);教育或生产实习(01-01);课外科技活动(01-01);系统仿班级课程表
8);教育或生产实习(01-02);可编程序控制器原理及应用课程设计(15-16);课
班级课程表
2);教育或生产实习(01-01);可编程序控制器原理及应用课程设计(15-16);课
,从第7周开始上理论课。
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表
班级课程表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 10 次 课
教学目的:掌握一维双原子链运动方程的建立和求解;理解晶格振动的色散关系;掌握声学波和光学波的特点;
教学内容: §3.2 一维双原子链
重点难点:一维双原子链运动方程的建立和求解;晶格振动的色散关系;声
学波和光学波的特点;色散关系;
§3.2 一维双原子链
除了少数元素晶体外,大多数晶体的原胞中都含有不止一个原子,就是复式格
子。
一维双原子链就是最简单的复式格子。
1. 一维复式格子的情形——一维无限长链
—— P 和Q 两种不同原子:m 、M (M>m )构成的一维复式格子 —— 相邻同种原子间的距离为2a —— 复式格子的晶格常数 —— 如图XCH003_005所示
质量为m 的原子位于2n , 2n+2, 2n+4 ……。
质量为M 的原子位于2n-1, 2n+1, 2n+3 ……。
2. 牛顿运动方程
原子间的力常数均为β,类似于一维单原子链的运动方程。
第2n 个m 原子的方程:)2(121222-+---=n n n n m μμμβμ
第2n+1个M 原子的方程:)2(222122n n n n M μμμβμ
---=++ —— 体系N 个原胞,有2N 个独立的方程 3. 方程的解:
]
)12([12])2([2aq n t i n q na t i n Be
Ae +-+-==ωωμμ —— A 和B 分别是m 原子和M 原子振动的振幅
—— 因为m M >,复式格子中不同原子振动的振幅一般来说是不同的 将试探解
]
)12([12])2([2aq n t i n q na t i n Be
Ae +-+-==ωωμμ带回到运动方程得到:
B
A e
e
B M A B e e A m iaq
iaq
iaq iaq ββωββω2)(2)(2
2-+=--+=---,
移项,整理得:
)2()cos 2(0)cos 2()2(2
2=-+-=--B M A aq B aq A m ωβββωβ
若A 、B 有非零的解,系数行列式满足:
02cos 2cos 2222=----ωβββωβM aq aq
m
由此解出两个2ω的值:
}]sin )
(41[1{)(21
2
2
2
aq M m mM mM M m +--+=-
βω }]sin )
(41[1{)(21
22
2
aq M m mM
mM M m +-++=+
βω 由解,我们可以画出两只格波的色散关系曲线,如图XCH003_006_01所示 。
4. 格波的振幅 将2
+ω和2
-ω分别代入
)2()cos 2(0)cos 2()2(2
2=-+-=--B M A aq B aq A m ωβββωβ
得到aq m A B cos 22)(2ββω--=++和aq
m A B
cos 22)(2ββω--=--
—— 从
]
)12([12])2([2aq n t i n q na t i n Be
Ae +-+-==ωωμμ得到相邻原胞之间的相位差是aq 2
—— 为保证波函数的单值性,一维复式格子q 的值限制在:ππ≤<-aq 2 —— 第一布里渊区 a
q a
22π
π
≤
<-
—— 第一布里渊区大小:
a
π
采用周期性边界条件:n n N μμ=+,h aq N π2)2(=
π22aN
h
q =
—— h 为整数 —— 每个波矢在第一布里渊区占的线度:Na
q π
=
—— 第一布里渊区允许q 的数目:
N Na
a =π
π
/
—— 晶格中的原胞数目
对应一个q 有两支格波:一支声学波和一支光学波 —— 总的格波数目为2N ,为原子的数目2N 5. 色散关系的特点 当a
q 2π
±
→(布里渊边界) —— 短波极限情况
两种格波的频率:2
1
2121min 2
1
2
121
max )2()}(){()()()2()}(){()()(m
m M M m mM M
m M M m mM β
βωβ
β
ω=-++==--+=+- 因为M >m ,所以:max min )()(-+>ωω,可见在max min )()(-+>>ωωω时没有格波。
max min )(~)(-+ωω之间的频率范围叫频率间隙 —— 一维双原子晶格叫做带通滤波器。
如图XCH003_006_01所示。
6.两种格波中m 和M 原子振动振幅之比:
aq m A B cos 22)(2ββω--
=++和 aq
m A B
cos 22)(2ββω--=-- —— 如图XCH003_007所示 1)a
q 2π
±
→时m 和M 原子振动的振幅
声学波:aq
m A B
cos 22)(2
ββω--=--
0)2(cos →±
a a π
——∞→-)(A
B
B>>A (红线表示) —— 可以认为A =0
,
即m 原子静止不动,相邻原子振动的相位相反 原子的振动如图XCH003_007_01所示
光学波:aq
m A B
cos 22)(2ββω--=++
0)2(cos →±
a a π
——0)(→+A
B
B<<A (蓝色线表示)—— 可以认为B=0,即M 原子静止不动,相邻原子振动的相位相
反
—— 原子振动如图XCH003_007_02所示
2) 0→q —— 长波极限情况 声学波 —— 长声学波
}]sin )
(41[1{)(21
22
2
aq M m mM mM M m +--+=-
βω——1)(sin )(422<<+aq M m mM 利用 1<<x —— 2
11x x -=- 整理后得到:)sin(2qa M
m +=
-β
ω—— qa qa ≈)sin( ——q M
m a
+=-β
ω2 ——-ω的色散关系与一维布拉伐格子的情形形式上是相同的,由完全相同原子所组成的布拉伐格子只有声学波。
将0,01==ωq 代入aq
m A B
cos 22)(2ββω--=--
得到:1)(=-A
B
—— 原胞中两个原子振动振幅相同,如图XCH003_008_01所示
—— 在长声学波中相邻原子振动方向相同,并且振幅相同,代表的是原胞质心的振动。
光学波 —— 长光学波
}]sin )
(41[1{)(21
2
2
2
aq M m mM mM M m +-++=+
βω ——
1sin )
(422
<<+aq M m mM
——0→q 当0→q (波长λ很大)时:μ
β
ω2=+,m
M Mm
+=
μ(有效质量) 将μ
β
ω2=
+和1cos →aq 代入aq m A B
cos 22)(2ββω--=++
得到:M
m
A B -=+)(—— 长光学波中同种原子振动相位一致,相邻原子振动方向相
反
—— 原胞质心保持不变的振动,原胞中原子之间的相对运动。
如图XCH003_008_02所示
7.长光学波与电磁波的作用
—— 在长波极限下,对于典型的βμ和值,可以得到s /10~102)(14130==+μ
β
ω,
对应于远红外的光波。
—— 用远红外的光波激发离子晶体时,可以引起晶体中长光学波的共振吸收 光波的频率q c 0=ω—— c 0为光速 —— 如图XCH003_006_04中的直线
波矢约~1014cm-1——远远小于一般格波的波矢 1
——只有的0
q长光学波可以与远红外的光波发生共振吸收
——将可以与光波作用的长光学波声子称为电磁声子
作业:3.2, 3.3。
