九年级数学下册第三章圆8圆内接正多边形作业课件新版北师大版.ppt
2021年北师大版九年级数学下册第三章《8 圆内接正多边形(1)》公开课课件

•
THE END 17、一个人如果不到最高峰,他就没有片刻的安宁,他也就不会感到生命的恬静和光荣。2021/2/52021/2/52021/2/52021/2/5
谢谢观看
倍 速 课 时 学 练
=弧பைடு நூலகம்nA1,
A1
∴弧A2A3An=弧A3A4A1= 弧A4A5A2=…=弧A1A2An-1,
A6 · O A2
A5 A
A3
A1 A2 A3 An.
∴ 多边形A1A2A3A4…An是正多边形.
3.分别求出半径为R的圆内接正三角形,正方形的边长,边心距和面积.
解:作等边△ABC的边BC上的高AD,垂足为D.
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
。2021年2月5日星期五2021/2/52021/2/52021/2/5
• 15、会当凌绝顶,一览众山小。2021年2月2021/2/52021/2/52021/2/52/5/2021
• 16、如果一个人不知道他要驶向哪头,那么任何风都不是顺风。2021/2/52021/2/5February 5, 2021
8 圆内接正多边形(1)(第1课时)
九年级数学下册 3.8 圆内接正多边形课件1 (新版)北师大版.ppt

3
圆内接正多边形的概念
定义:顶点都在同一个圆上的正多边形叫做圆内接 正多边形.这个圆叫做该正多边形的外接圆.
如图,说出正五边形的中心 、半径、中心角、边心距.
E
A
D
·O
BM C
4
圆内接正多边形的有关计算
例 如图,在圆内接正六边形ABCDEF中,半径OC=4, OM垂直于BC,垂足为M.
求这个正六边形的中心角、边长和边心距.
F
E
A
O.
D
G
B
C
5
用尺规作圆内接正六、四边形 1.用尺规作一个已知圆的内接正六边形. 2.用尺规作一个已知圆的内接正四边形. 3.思考:作正多边形有哪些方法?
9
基础作业:课本P99 习题3.10,第4题. 拓展作业:课本P99 问题解决.
10
6
1.把边长为6的正三角形剪去三个三角形得到一个 正六边形DFKKGE,求这个正六边形的面积.
2.分别求出半径为6cm的圆内接正三角形的边长和 边心距.
7
通过本节课的学习,你有哪些收获?有 何感想?学会了哪些方法?先想一想,再 分享给大家.
8
1.正三角形的边心距、半径和高的比是
.
2.求出半径为6cm的圆内接正四边形的边长、边心距 和面积.
北师大版九年级数学下册第三章3.8_圆内接正多边形(共28张PPT)

⌒ ⌒ ⌒⌒ ⌒ 证明:(1〕∵AB=BC=CD=DE=EA,
A
∴AB=BC=CD=DE=EA,
∵B⌒CE=⌒CDA⌒=3AB,
1
B2
5E
∴∠1=∠2, 同理∠2=∠3=∠4=∠5,
3
4
C
D
又∵顶点A,B,C,D,E都在⊙O上,
∴五边形ABCDE是⊙O的内接正五边形.
〔2〕连接OA,OB,OC,那么 ∠OAB=∠OBA=∠OBC=∠OCB. ∵TP,PQ,QR分别是以A,B,C 为切点的⊙O的切线, ∴∠OAP=∠OBP=∠OBQ=∠OCQ. ∴∠PAB=∠PBA=∠QBC=∠QCB.
P B Q
C
A
T
E O
S
D R
又∵A⌒B=⌒BC, ∴AB=BC, ∴△PAB与△QBC是全等的等腰三角形. ∴∠P=∠Q,PQ=2PA. 同理∠Q=∠R=∠S=∠T,
A
求证:正五边形的对角线相等
B
E
C
D
怎样找圆的内接正三角形? A
D
怎样找圆的外切正三角形?
H
B
C
A
D
怎样找圆的内接正方形?
E
0
G 怎样找圆的外切正方形?
B
C
怎样找圆的内接正n边形?
F
怎样找圆的外切正n边形?
【例题】
【例1】把圆分成5等份,求证:
⑴依次连接各分点所得的五边形是这个圆的内接 正五边形;
在Rt△OBD中,∠OBD=30°,
边心距OD=1 R.
A
2
在Rt△ABD中,∠BAD=30°,
九年级数学下册 第三章 圆 3.8 圆内接正多边形课件 北师大下册数学课件

Image
12/10/2021
第四十五页,共四十五页。
第四十页,共四十五页。
当圆周角的顶点(dǐngdiǎn)在优A B弧 18°.
上时,AB所对的圆周角为
当圆周角的顶点在劣弧 A B上时,AB所对的圆周角为 180°-18°=162°,
∴综上所述答案为:18°或162°.
答案:18°或162°
第四十一页,共四十五页。
【一题多变】
已已知知圆圆内内接接正正三三角角形形(zhè(nzɡhèsnāɡn sjāinǎojixǎíonɡx)í的n3ɡ)面的积面为积为,则,该则圆的该内圆接的正内 边边形形的的边边心心距距是是 (( B ))
径,外接圆半径和高的比是(
)D
A.1∶2∶ B.2∶3∶4 3
C.1∶ ∶2 D.1∶2∶3
3
第四十四页,共四十五页。
内容(nèiróng)总结
8 圆内接正多边形。正多边形:_______________,_______________的多边。这个圆叫做这
No 个正多边形的___________.这个多边形叫。2.尺规作图:(1)因为与半径相等的弦长所对的圆心角。
第三页,共四十五页。
第四页,共四十五页。
这个(zhè ge)圆叫做这个(zhè ge)正多边外形接的圆___________.这个多边形
做圆内接正多边形.
第五页,共四十五页。
【探究二】应用(yìngyòng)等分圆周的方法作正多边形: 1.应用量角器,根据相等的圆心角所对的弧____相__等__(_xi,āngděng) 把360°的圆心角n等分,依次连接各个分点,得到圆内 接正n边形.
2019年北师大版九年级数学下册课件:3.8 圆内接正多边形(共21张PPT)

3.8 圆内接正多边形
县 委 书 记 在 县委全 体(扩大 )会议 上的报 告 文 章 标 题 :县 委书记 在20xx年 县委 全体(扩 大)会 议上的 报告
提 高 发 展 质 量加快 发展速 度
努 力 推 动 ___经 济社 会又好 又快发 展 ──在 共 ___县 委 十 一 届二 次全体 (扩大)会 议上 的报告
的内接多边形周长为3,⊙O的外切多边形周长为3.4,则下列各数中与此
圆的周长最接近的是(
)
C
A. 6 B. 8 C. 10 D. 17
8.如图,由7个形状、大小完全相同的正六边形组成网格,正六边形 的顶点称为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点
上,则△ABC的面积是_______2__3_______.
A.30° B.35° C.45° D.60°
3.正六边形边心距为 3,则该正六边形的边长是( B ) A. 3 B.2 C.3 D.2 3 4.将一个边长为 1 的正八边形补成如图所示的正方形,这个正方形的 边长等于______1_+____2______.(结果保留根号)
5.点M,N分别是正八边形相邻的边AB,BC上的点,且AM=BN, 点O是正八边形中心,则∠MON=____4_5_°____.
9.用直尺和圆规作一个圆的内接正三角形. 解:作图略
10.已知正多边形的一个外角为 90°,则它的边长、边心距、外接圆
半径之比为( B )
A.6∶ 3∶2 3 B.2∶1∶ 2
C.2∶2∶ 3
D.1∶1∶ 3
11.(泸州中考)以半径为 1 的圆的内接正三角形、正方形、正六边形的
边心距为三边作三角形,则该三角形的面积是( D )
3.8 圆内接正多边形 课件 (29张PPT) 2023-2024学年北师大版数学九年级下册

归纳
圆内接正多边形的辅助线
F
E
A
O·
D
rR
BMC
1.连半径,得中心角; 2.作边心距,构造直角三角形.
半径R
O 中心角一半 边心距r
C
M
边长一半
例2 如图2,正六边形的边长为2,分别以正六边形的六条边为直径向外
作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分
面积)是( A ) A.6 3-π
.O
分析:因为正六边形每条边所对的圆心角为 60º ,所以正六边形的边长 与圆的半径 相等 .因此, 在半径为r的圆上依次截取等于 r 的弦, 即可将圆六等分.
作法:(1)作⊙O的任意一条直径FC;
(2)分别以F,C 为圆心,以 r 为半径作弧,与⊙O 交于点E,A和D,B;
(3)依次连接AB、BC、CD、DE、EF、FA,便得到正六边形ABCDEF
2
2
F
E
A
O
D
4m
r
B PC
5.(2023武汉)如图,在圆内接四边形ABCD中,AB=AD,
即为所求.
E
D
F
.O C
A
B
针对训练
1.下列说法中,不正确的是( D ) A.正多边形一定有一个外接圆和一个内切圆 B.各边相等且各角相等的多边形是正多边形 C.正多边形的内切圆和外接圆是同心圆 D.正多边形既是轴对称图形,又是中心对称图形
二 圆内接正多边形的有关计算
正n边形的一个内角的度数是多少? 中心角呢?正多边形的中心角与外角 的大小有什么关系?
A. 2
B. 4
C. 2 2
D. 4 2
A
D
O
新北师大版九年级数学下册第三章《车轮为什么是圆的》公开课课件(共24张PPT)

一石激起千层浪 乐在其中
奥运五环
小憩片刻 祥子
仔细观察,同学们发现了什么?
议一议、说一说
O
B
1、车轮为什么做成圆形的?
A C
2、如果车轮做成三角形或正方
形的,坐车的人会是什么感觉?
把于车轮的半 径,当车轮在平面上滚动时,车轮中 心与平面的距离保持不变,因此,当 车辆在平坦的路上行驶时,坐车的人 会感到非常平稳,这就是车轮都做成 圆形的数学道路。圆上的点到圆心的 距离是一个定值
B
A
(答:点A在圆上、点B在圆内、点C在圆外)
(2)在以上三种关系中,点到圆心的距离与圆 的半径在数量上有什么关系?
如果⊙O的半径为r,点P 到圆心O的距离为d,那么 ①点P在圆外 d>r ②点P在圆上 d=r; ③点P在圆内 d<r.
O P r
P
做一做
已知⊙O 的面积 为 9π ,判断 点 P 与 ⊙O的位置关系. (1) 若PO=4.5 则点P在 圆外 ; (2)若PO=2,点P在 圆内 ; 3 (3)若PO= ,则点P在圆上.
设⊙O的半径为r,则点P与⊙O的位置关系有:
(1)点P在⊙O上 (2)点P在⊙O内 (3)点P在⊙O外 OP=r OP<r OP>r
想一想:
C
1、图:已知Rt△ABC,AB<BC ∠B=90°,试以点B为圆心,BA为半 径画圆。 2、根据图形回答下列问题: (1)看图想一想, Rt△ABC的各个 顶点与⊙B在位置上有什么关系?
y
B(0,4)
0
A(3,0)
x
4.在半径为5cm的⊙O上有一点P,则OP的长为 5cm _______. 5. 已知⊙O的半径为6cm,P为线段OA的中点,若点 P在⊙O上,则OA的长( B ) A.等于6cm B.等于12cm; C.小于6cm D.大于12cm 6.⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标 为(4,2),则点P与⊙O 的位置关系是( A ) A.点P在⊙O内; B.点P的⊙O上; C.点P在⊙O外; D.点P在⊙O上或⊙O外
北师大版九年级数学下册第三章8圆内接正多边形

n
其中正确的命题有 ( ) A.2个 B.3个 C.4个 D.5个
答案 A ①正多边形都有一个内切圆和一个外接圆,这两个圆是同心圆, 圆心是正多边形的中心,故①正确;②各边相等的圆外切多边形的各内角不 一定相等,故不一定是正多边形,如菱形,故②错误;③圆内接矩形的各内角 相等,但不是正多边形,故③错误;④边数是偶数的正多边形既是轴对称图 形又是中心对称图形,而边数是奇数的正多边形只是轴对称图形,不是中心
2.如图,在正八边形ABCDEFGH中,四边形BCFG的面积为20 cm2,则正八边
形的面积为
cm2.
答案 40 解析 如图,连接AD、HE,分别交BG、CF于点O、P、M、N, 则△ABO,△CDP,△EFN,△HGM均为全等的等腰直角三角形,四边形 BCPO、四边形GFNM为全等的矩形. 设正八边形的边长为a cm,
初中数学(北师大版)
九年级 下册
第三章 圆
知识点一 圆内接正多边形 顶点都在同一圆上的正多边形叫做圆内接正多边形.这个圆叫做该正
多边形的外接圆. 把一个圆n(n≥3)等分,依次连接各分点,我们就可以作出一个圆内接正n边 形. (1)相关定义:
名称 中心
半径 中心角 边心距
概念
图形
ห้องสมุดไป่ตู้
一个正多边形的外接圆的圆心 叫做这个正多边形的中心
1.正六边形的边心距与边长之比为 ( ) A. 3 ∶3 B. 3 ∶2 C.1∶2 D. 2 ∶2
答案 B 如图,设正六边形ABCDEF的边长为2a,O为正六边形的中心,连 接OA、OB,作OM⊥AB于M, ∴△OAB是等边三角形, ∴OA=OB=AB=2a,AM=BM=a. 在Rt△OAM中,由勾股定理可得OM= 3 a, 则正六边形的边心距与边长之比为OM∶AB= 3 a∶2a= 3 ∶2,故选B.
北师大版九年级数学下册第三章《第三章 第1节 圆》优质课件

当OA=1cm时,点A在 ⊙O内 ; 点在圆上,点在圆 内.
当OB=4cm时,点B在 ⊙O外 .
例2.已知:如图,矩形ABCD的对角 线相交于点O, 试猜想:矩形的四个顶点能在同一 个圆上吗?
AA
DD
OO
BB
CC
答:在矩形ABCD中,有OA=OB=OC=OD,四个顶点 在同一个圆上,故矩形四个顶点能在同一个圆上.
2.(新疆建设兵团·中考)如图,王大爷家屋后有一块
长12m,宽8m的矩形空地,他在以BC为直径的半圆内种
菜,他家养的一只羊平时拴在A处,为了不让羊吃到菜,
拴羊的绳子可以选用( )
A.3m
B.5m
C.7m
D.9m
答案:A
3.(泉州·中考) 已知三角形的三边长分别为3,4,5, 则它的边与半径为1的圆的公共点个数所有可能的情况是 ________.(写出符合的一种情况即可) 【解析】∵圆心的位置不确定,∴交点个数共有5种情况即 0、1、2、3、4.故答案为0或1或2或3、4. 答案:2(符合答案即可)
善性是难能可贵的,也是高尚和值得称赞 的。
——亚里士多德
You made my day!
这一 样个 的人 人所 才受 有的 学教 问育 。超
过 了 自 己 的 智 力 ,
我们,还在路上……
【规律方法】1.判断点与圆的位置关系的方法:
设⊙O的半径为r,则点P与⊙O的位置关系有
(1)点P在⊙O上
OP=r
(2)点P在⊙O内
OP<r
(3)点P在⊙O外
OP>r
2.要证明几个点在同一个圆上,只要证明这几个点到同一
个定点的距离相等.
通过本课时的学习,需要我们掌握:
1.从运动和集合的观点理解圆的定义. 2.点与圆的位置关系. 3.证明几个点在同一个圆上的方法.
北师大数学九年级下册第三章-圆内接正多边形(含解析)
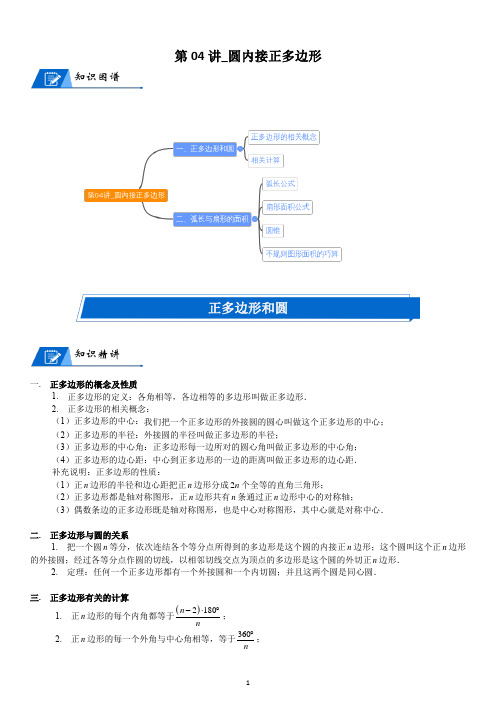
第04讲_圆内接正多边形知识图谱正多边形和圆知识精讲一. 正多边形的概念及性质1. 正多边形的定义:各角相等,各边相等的多边形叫做正多边形.2. 正多边形的相关概念:(1)正多边形的中心:我们把一个正多边形的外接圆的圆心叫做这个正多边形的中心;(2)正多边形的半径:外接圆的半径叫做正多边形的半径;(3)正多边形的中心角:正多边形每一边所对的圆心角叫做正多边形的中心角;(4)正多边形的边心距:中心到正多边形的一边的距离叫做正多边形的边心距.补充说明:正多边形的性质:(1)正n边形的半径和边心距把正n边形分成2n个全等的直角三角形;(2)正多边形都是轴对称图形,正n边形共有n条通过正n边形中心的对称轴;(3)偶数条边的正多边形既是轴对称图形,也是中心对称图形,其中心就是对称中心.二. 正多边形与圆的关系1. 把一个圆n等分,依次连结各个等分点所得到的多边形是这个圆的内接正n边形;这个圆叫这个正n边形的外接圆;经过各等分点作圆的切线,以相邻切线交点为顶点的多边形是这个圆的外切正n边形.2. 定理:任何一个正多边形都有一个外接圆和一个内切圆;并且这两个圆是同心圆.三. 正多边形有关的计算1. 正n边形的每个内角都等于()2180nn-⋅︒;2. 正n边形的每一个外角与中心角相等,等于360n︒;3. 设正n 边形的边长为n a ,半径为R ,边心距为n d ,周长为n C ,面积为n S ;则:222111422n n n n n n n n n R d a C na S n d a d C =+==⋅⋅=⋅,,三点剖析考点:正多边形的概念、性质及相关计算重难点:正多边形相关计算.易错点:对正多边形相关的概念混淆不清.正多边形的相关概念例题1、 下面给出六个命题:①各角相等的圆内接多边形是正多边形;②各边相等的圆内接多边形是正多边形;③正多边形是中心对称图形;④各角均为120︒的六边形是正六边形;⑤边数相同的正n 边形的面积之比等于它们边长的平方比;⑥各边相等的圆外切多边形是正多边形.其中,正确的命题是_____________. 【答案】 ②⑤【解析】 ①错误,反例:矩形各角相等但不是正四边形;②正确,边相等则各边所对的圆心角相等,由半径和圆心角可构成 个全等的等腰三角形,则多边形的各内角也相等;③错误,正奇数边形不是中心对称图形;④错误,在正六边形的基础上作任意一组对边的平行线,仍然截出一个六边形,各内角均为,但不是正六边形;⑤正确,相似的性质;⑥错误,只要使切点与圆心的连线不平分多边形的边长即可.例题2、 若正多边形的一个外角为60º,则这个正多边形的中心角的度数是( ) A.30° B.60° C.90° D.120° 【答案】 B【解析】 由于任意多边形的外角和均为360°,所以这个正多边形的边数为360660=,所以正六边形的中心角的度数为360606︒=︒.例题3、 正六边形的边心距与边长之比为( )A.3:3B.3:2C.1:2D.2:2【答案】 B【解析】 此题考查了正多边形和圆的关系.此题难度不大,注意掌握数形结合思想的应用.首先根据题意画出图形,然后设六边形的边长是a ,由勾股定理即可求得OC 的长,继而求得答案.如图:设六边形的边长是a , 则半径长也是a ;经过正六边形的中心O 作边AB 的垂线OC ,则AC=12AB=12a ,∴OC=22OA AC -=32a ,a n d nR O CBA∴正六边形的边心距与边长之比为:32a:a=3:2.故选B.例题4、已知:线段a(如图)(1)求作:正六边形ABCDEF,使边长为a(用尺规作图,要保留作图痕迹,不写作法及证明)(2)若a=2cm,则半径R=______cm,边心距r=______cm,周长p=______cm,面积S=______cm2.【答案】(1)(2)2,3,12,63【解析】(1)如图,正六边形ABCDEF即为所求;(2)∵a=2cm,∴半径R=2cm.∵OA=OB=AB=a,∴∠OAB=60°,∴r=OG=OA•sin60°=2×332cm.∵a=2cm,∴周长p=6a=12cm,∴S正六边形ABCDEF=6S△OAB=6×12×2×3=63(cm2).相关计算例题1、如图,⊙O是△ABC的内切圆,若∠ABC=70°,∠ACB=40°,则∠BOC=__________________°.【答案】125【解析】∵⊙O是△ABC的内切圆,∴OB平分∠ABC,OC平分∠ACB,∴∠OBC=∠ABC=35°,∠OCB=∠ACB=20°,∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣35°﹣20°=125°.例题2、已知正六边形的边长为2,则它的内切圆的半径为()A.1B.3C.2D.23【答案】B【解析】如图,连接OA、OB,OG;∵六边形ABCDEF是边长为2的正六边形,∴△OAB是等边三角形,∴OA=AB=2,∴OG=OA•sin60°=2×32=3,∴边长为2的正六边形的内切圆的半径为3.例题3、如图1、2、3、…..、n,M、N分别是O的内接正三角形ABC、正方形ABCD、五边形ABCDE、…..、正n边形ABCDE…..的边AB、BC上的点,且BM CN=,连接OM、ON.(1)求图1中MON∠的度数;(2)图2中MON∠的度数是____________,图3中MON∠的度数是____________;(3)试探究MON∠的度数与正n边形边数n的关系(直接写出答案).【答案】(1)120︒;(2)90︒,72︒;(3)360 n︒【解析】解:分别连接OB、OC,(1)AB AC=ABC ACB∴∠=∠OC OB=,O是外接圆的圆心,CO ACB∴∠平分30OBC OCB∴∠=∠=︒30OBM OCN∴∠=∠=︒BM CN=,OC OB=OMB ONC∴∆∆≌BOM NOC∴∠=∠60BAC∠=︒120BOC∴∠=︒120MON BOC∴∠=∠=︒(2)同(1)可得MON∠的度数是90︒;图3中MON∠的度数是72︒(3)由(1)可知,360==1203MON︒∠︒;在(2)中,360==904MON︒∠︒;在(3)中360==725MON︒∠︒…..,故当n时,360 MONn︒∠=.随练1、如图,正五边形ABCDE内接于⊙O,则∠CAD=___________度.【答案】 36【解析】 ∵五边形ABCDE 是正五边形,∴AB =BC =CD =DE =EA =72°,∴∠CAD=12×72°=36°.随练2、 已知正多边形的半径与边长相等,那么正多边形的边数是( ) A.4 B.5 C.6 D.8 【答案】 C【解析】 ∵正多边形的半径与边长相等,∴正多边形的相邻的两条半径与一条边围成一个正三角形, ∴正多边形的中心角为60°∵正多边形所有中心角的和为360°, ∴360606︒÷︒=,∴正多边形的边数为6,随练3、 若等边三角形的边长是12厘米,则其内切圆的面积为 . 【答案】 12π平方厘米. 【解析】 如图,作OD ⊥AB , ∵等边三角形的边长为12厘米, ∴AD=6厘米.又∵∠DAO=12∠BAC=12×60°=30°,∴tan30°=6DO DOAD ==33, ∴DO=23厘米,∴其内切圆的面积=π(23)2=12π. 故答案为:12π平方厘米.随练4、 如图,ABCD 是O ⊙的内接正方形,PQRS 是半圆的内接正方形,那么正方形PQRS 与正方形ABCD 的面积之比为____________.【答案】 2:5 【解析】随练5、 已知圆内接正方形的面积为2,求该圆的外切正三角形的外接圆的外切正六边形的面积.SOR Q P D CBA【答案】 3【解析】 如图,设AB 是圆内接正方形的边长,CD 是外切正三角形的边长,EF 是外切正六边形的边长,连结OA OB OC OE 、、、.∵AB 是内接正方形的边长,内接正方形面积为2,∴290AB OA OB AOB ==∠=︒,,∴1OA OB ==.∵CD 是外切正三角形的边长,∴60OA CD AOC ⊥∠=︒,,∴22OC OA ==. ∵EF 是外切正六边形的边长,∴602OC EF OEF OE EF CE ⊥∠=︒==,,,∴323CE ==, ∴43EF ,∴263436683EOF S S ∆===⎝⎭随练6、 已知直角三角形的外接圆半径为6,内切圆半径为2,那么这个三角形的面积是( ) A.32 B.34 C.27 D.28 【答案】 D【解析】 暂无解析弧长与扇形的面积知识精讲一.弧长公式1.圆的周长:2πR C =2.弧长公式:π180nl R =(其中,l 表示弧长,n 表示这段弧所对圆心角度数值;R 表示该弧所在圆的半径).二.扇形面积公式1.圆的面积公式:2πS R =2.扇形面积公式:21π3602n S R lR ==扇形(n 表示扇形圆心角度数值;R 表示半径).三.圆锥、圆柱的侧面积与全面积1.圆锥(1)圆锥的侧面积:1=22S r l rl ππ=侧(以下公式中的l 均指扇形母线长);(2)圆锥的全面积:221=+=+22S S S r r l r rl ππππ=+全底侧;(3)圆锥的体积:213V r h π=;(4)圆锥的高、底面半径、母线之间的关系:222r h l +=;(5)设圆锥的底面半径为r ,母线长为l ,侧面展开图的圆心角为n ︒;则有:360S r n l S ==底侧O BADC2.圆柱(1)圆柱的侧面积:=2S r h π侧(2)圆柱的全面积:2=2πr 2πS S S rh=++侧全底四.不规则图形面积的巧算一般利用拼凑法,割补法,把不规则图形切割拼接成面积容易计算的图形再进行计算,例如:弓形面积:=S S S -弓形三角形扇形.三点剖析一.考点:弧长、扇形面积公式,圆锥的侧面积、全面积计算 二.重难点:1.计算扇形面积,计算圆锥的侧面积;2.计算扇形面积的时候,除了用圆心角求面积,也可以用弧长求面积; 三.易错点:1.圆锥相关面积计算时,注意每个量对应关系; 2.计算圆锥侧面积时,注意母线和圆锥的高是不相等的.弧长公式例题1、 一个扇形的半径为8cm ,弧长为163cm π,则扇形的圆心角为__________. 【答案】 120︒【解析】 设扇形圆心角为n ︒,根据弧长公式可得:8161803n ππ=,解得:120n =︒.例题2、 如图,在Rt ∴ABC 中,∴C=90°,∴A=20°,BC=3,以点C 为圆心,BC 的长为半径的∴C 交AB 于点D ,交AC 于点E ,则(劣弧)的长为( )A.πB.πC.πD.π【答案】 A【解析】 连接CD ,如图所示, ∴∴C=90°,∴A=20°, ∴∴B=70°.l2πrrOh 2πrh O r∴CB=CD,∴∴BDC=∴B=70°,∴∴BCD=40°,∴的长为=.故选A.例题3、如图,半径为2cm的圆O与地面相切于点B,圆周上一点A距地面高为(2+3)cm,圆O沿地面BC 方向滚动,当点A第一次接触地面时,圆O在地面上滚动的距离为.【答案】53πcm.【解析】作AD⊥BC于D,OE⊥AD于E,则AE=2+3﹣2=3,又OA=2,∴sin∠AOE=32 AEOA=,∴∠AOE=60°,则AB的长为()6090251803ππ+⨯⨯=,则圆O在地面上滚动的距离为53πcm,故答案为:53πcm.例题4、如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.(1)求证:AE平分∠DAC;(2)若AB=4,∠ABE=60°.①求AD的长;②求出图中阴影部分的面积.【答案】(1)AE平分∠DAC(2)①3;②43π﹣3【解析】(1)证明:连接OE,如图,∵CD与⊙O相切于点E,∴OE⊥CD,∵AD⊥CD,∴OE∥AD,∴∠DAE=∠AEO,∵AO=OE,∴∠AEO=∠OAE,∴∠OAE=∠DAE,∴AE平分∠DAC;(2)解:①∵AB是直径,∴∠AEB=90°,∠ABE=60°.∴∠EAB=30°,在Rt△ABE中,BE=12AB=12×4=2,AE=3BE=23,在Rt△ADE中,∠DAE=∠BAE=30°,∴DE=12AE=3,∴AD=3DE=3×3=3;②∵OA=OB,∴∠AEO=∠OAE=30°,∴∠AOE=120°,∴阴影部分的面积=S扇形AOE﹣S△AOE=S扇形AOE﹣12S△ABE=21202360π﹣12•12•23•2=43π﹣3.例题5、【答案】5π【解析】暂无解析随练1、 如图,以AB 为直径的⊙O 与弦CD 相交于点E ,且AC=2,AE=3,CE=1.则BD 的长是( )A.39π B.239πC.33π D.233π【答案】 B【解析】 连接OC ,∵△ACE 中,AC=2,AE=3,CE=1, ∴AE 2+CE 2=AC 2,∴△ACE 是直角三角形,即AE ⊥CD ,∵sinA=CE AC =12,∴∠A=30°, ∴∠COE=60°,∴CE OC =sin ∠COE ,即1OC =32,解得OC=233,∵AE ⊥CD , ∴BC =BD ,∴BD =BC =23603180π⨯=239π.随练2、 如图,等边三角形MNP 的边长为1,线段AB 的长为4,点M 与A 重合,点N 在线段AB 上.MNP △沿线段AB 按A B −−→的方向滚动,直至MNP △中有一个点与点B 重合为止,则点P 经过的路程为__________.【答案】43π 【解析】 该题考查的是弧长的计算.点P 经过的路程是两段弧,半径为1,圆心角为120︒,根据1=180n Rπ进行计算即可.故点P 经过的路程为:1201421803ππ⨯⨯⨯=.故答案为:43π.A (M )PNB扇形面积公式例题1、如图,一扇形纸扇完全打开后,外侧两竹条和AC的夹角为120°,长为25cm,贴纸部分的宽BD 为15cm,若纸扇两面贴纸,则贴纸的面积为()A.175πcm2B.350πcm2C.πcm2D.150πcm2【答案】B【解析】∴AB=25,BD=15,∴AD=25-15=10,∴S贴纸=(﹣)×2=350πcm2,例题2、如图,AB是⊙O的直径,弦CD⊥AB于点E,⊙O的半径为3,弦CD的长为3cm,则图中阴影部分面积是_____.【答案】π﹣33 4【解析】∵弦CD⊥AB于点E,∴CE=32,∵OC=3,∴OE=32,∴∠OCE=30°,∴∠COD=120°,∴图中阴影部分面积=()21203360π⋅⨯﹣12×3×32=π﹣334,例题3、如图(a),有一张矩形纸片ABCD,其中AD=6cm,以AD为直径的半圆,正好与对边BC相切,将矩形纸片ABCD沿DE折叠,使点A落在BC上,如图(b).则半圆还露在外面的部分(阴影部分)的面积为.【答案】(3π﹣)cm2.【解析】作OH∴DK于H,连接OK,∴以AD为直径的半圆,正好与对边BC相切,∴AD=2CD,∴A'D=2CD,∴∴C=90°,∴∴DA'C=30°,∴∴ODH=30°,∴∴DOH=60°,∴∴DOK=120°,∴扇形ODK的面积为=3πcm2,∴∴ODH=∴OKH=30°,OD=3cm,∴OH=cm,DH=cm;∴DK=3cm,∴∴ODK的面积为cm2,∴半圆还露在外面的部分(阴影部分)的面积是:(3π﹣)cm2.随练1、如图,正方形ABCD的边长为2,连接BD,先以D为圆心,DA为半径作弧AC,再以D为圆心,DB 为半径作弧BE,且D、C、E三点共线,则图中两个阴影部分的面积之和是()A.12π B.12π+1 C.π D.π+1【答案】A【解析】∵AB=2,∴BD=22,S阴影=S扇形BDE﹣12S扇形ACD=()24522360π﹣12×904360π⨯=π﹣12π=12π,故选A.随练2、如图,三个小正方形的边长都为1,则图中阴影部分面积的和是(结果保留π).【答案】.【解析】根据图示知,∴1+∴2=180°﹣90°﹣45°=45°,∴∴ABC+∴ADC=180°,∴图中阴影部分的圆心角的和是90°+90°﹣∴1﹣∴2=135°,∴阴影部分的面积应为:S==.故答案是:.圆锥例题1、如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为()A.30πcm2B.48πcm2C.60πcm2D.80πcm2【答案】C【解析】∴h=8,r=6,可设圆锥母线长为l,由勾股定理,l==10,=×2×6π×10=60π,圆锥侧面展开图的面积为:S侧所以圆锥的侧面积为60πcm2.h=23cm,底面半径r=2cm,则圆锥体的全面积为____cm2.A.43πB.8πC.12πD.(43+4)π【答案】C【解析】本题利用了圆的周长公式和扇形面积公式求解,牢记公式是解答本题的关键.表面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2.底面圆的半径为2,则底面周长=4π,∵底面半径为2cm、高为23cm,∵圆锥的母线长为4cm,∵侧面面积=12×4π×4=8π; 底面积为=4π,全面积为:8π+4π=12πcm 2. 故选:C .例题3、 将半径为3cm 的圆形纸片沿AB 折叠后,圆弧恰好能经过圆心O ,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为__________.【答案】22.【解析】 过O 点作OC AB ⊥,垂足为D ,交O 于点C ,由折叠的性质可知,1122OD OC OA ==,由此可得,在Rt AOD ∆中,30A ∠=︒,同理可得30B ∠=︒,在AOB ∆中,由内角和定理,得180120AOB A B ∠=︒-∠-∠=︒AB ∴的长为12032180ππ⨯=设围成的圆锥的底面半径为r ,则22r ππ=1r cm ∴=∴圆锥的高为223122-=随练1、 圆锥的底面半径为4cm ,高为3cm ,则它的表面积为( ) A.12πcm 2 B.20πcm 2 C.26πcm 2 D.36πcm 2【答案】 D【解析】 底面周长是2×4π=8πcm ,底面积是:42π=16πcm 2. 母线长是:22345+=,则圆锥的侧面积是:218π520πcm 2⨯⨯=,则圆锥的表面积为16π+20π=36πcm 2.随练2、 已知扇形的圆心角为120°,所对的弧长为83π,则此扇形的面积是______. 【答案】163π【解析】 ∵扇形的圆心角为120°,所对的弧长为83π, ∴l=120R 81803⨯=ππ, 解得:R=4,则扇形面积为12Rl=163π随练3、 如图,在菱形ABCD 中,AB=2,∠C=120°,以点C 为圆心的与AB ,AD 分别相切于点G ,H ,与BC ,CD 分别相交于点E ,F .若用扇形CEF 作一个圆锥的侧面,则这个圆锥的高是__________.【答案】 2【解析】 如图:连接CG , ∵∠C=120°, ∴∠B=60°,∵AB 与相切,∴CG ⊥AB ,在直角△CBG 中,CG=BC•sin60°=2×=3,即圆锥的母线长是3, 设圆锥底面的半径为r ,则:2πr=,∴r=1.则圆锥的高是:=2.不规则图形面积的巧算例题1、 如图,AB 是∴O 的直径,弦CD ∴AB ,∴CDB=30°,CD=2,则S 阴影=( )A.πB.2πC.D.π【答案】 D【解析】 如图,CD ∴AB ,交AB 于点E , ∴AB 是直径,∴CE=DE=CD=, 又∴∴CDB=30° ∴∴COE=60°, ∴OE=1,OC=2, ∴BE=1,∴S ∴BED =S ∴OEC , ∴S 阴影=S 扇形BOC ==.故选:D .例题2、如图,半圆O的直径AB=2,弦CD∴AB,∴COD=90°,则图中阴影部分的面积为.【答案】.【解析】∴弦CD∴AB,∴S∴ACD=S∴OCD,∴S阴影=S扇形COD=•π•=×π×=.例题3、如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是4cm(1)请判断DE与⊙O的位置关系,并说明理由;(2)求图中阴影部分的面积(结果用π表示).【答案】(1)DE为⊙O的切线(2)(24﹣4π)cm2【解析】(1)DE与⊙O相切.理由如下:连结OD,BD,则∠ABD=∠ACD=45°,∵AB是直径,∴∠ADB=90°,∴△ADB为等腰直角三角形,∵点O为AB的中点,∴OD⊥AB,∵DE∥AB,∴OD⊥DE,∵OD是半径,∴DE为⊙O的切线;(2)∵BE∥AD,DE∥AB,∴四边形ABED为平行四边形,∴DE=AB=8cm,∴S阴影部分=S梯形BODE﹣S扇形OBD=12(4+8)×4﹣2904360π••=(24﹣4π)cm2.随练1、 如图,四边形ABCD 是菱形,∠A=60°,AB=2,扇形EBF 的半径为2,圆心角为60°,则图中阴影部分的面积是____________.【答案】23π﹣3 【解析】 如图,连接BD .∵四边形ABCD 是菱形,∠A=60°, ∴∠ADC=120°, ∴∠1=∠2=60°,∴△DAB 是等边三角形, ∵AB=2,∴△ABD 的高为3,∵扇形BEF 的半径为2,圆心角为60°, ∴∠4+∠5=60°,∠3+∠5=60°, ∴∠3=∠4,设AD 、BE 相交于点G ,设BF 、DC 相交于点H ,在△ABG 和△DBH 中,234A AB BD ⎧∠=∠⎪=⎨⎪∠=∠⎩,∴△ABG ≌△DBH (ASA ),∴四边形GBHD 的面积等于△ABD 的面积,∴图中阴影部分的面积是:S 扇形EBF ﹣S △ABD =260213602π⨯-×2×3=23π﹣3.随练2、 如图,在∴BCE 中,点A 时边BE 上一点,以AB 为直径的∴O 与CE 相切于点D ,AD ∴OC ,点F为OC 与∴O 的交点,连接AF . (1)求证:CB 是∴O 的切线;(2)若∴ECB=60°,AB=6,求图中阴影部分的面积.【答案】(1)证明见解析;(2)π.【解析】(1)证明:连接OD,与AF相交于点G,∴CE与∴O相切于点D,∴OD∴CE,∴∴CDO=90°,∴AD∴OC,∴∴ADO=∴1,∴DAO=∴2,∴OA=OD,∴∴ADO=∴DAO,∴∴1=∴2,在∴CDO和∴CBO中,,∴∴CDO∴∴CBO,∴∴CBO=∴CDO=90°,∴CB是∴O的切线.(2)由(1)可知∴3=∴BCO,∴1=∴2,∴∴ECB=60°,∴∴3=∴ECB=30°,∴∴1=∴2=60°,∴∴4=60°,∴OA=OD,∴∴OAD是等边三角形,∴AD=OD=OF,∴∴1=∴ADO,在∴ADG和∴FOG中,,∴∴ADG∴∴FOG,∴S∴ADG=S∴FOG,∴AB=6,∴∴O的半径r=3,∴S阴=S扇形ODF==π.随练3、如图,直径AB为10的半圆,绕A点逆时针旋转60°,此时点B旋转到点B′,则图中阴影部分的面积是.【答案】 .【解析】 如图,∴AB=AB ′=8,∴BAB ′=60° ∴图中阴影部分的面积是: S=S 扇形B ′AB +S 半圆O ′﹣S 半圆O =+π×52﹣π×52 =π.拓展1、 若正六边形的边长为4,则它的内切圆面积为( ) A.9π B.10π C.12π D.15π【答案】 C【解析】 连接OD 、OE ,作OM ⊥DE 于M , ∵六边形ABCDEF 是边长为4的正六边形, ∴△ODE 是等边三角形, ∴OD =DE =4,∴3sin 604232OM OD =•︒=⨯=,∴它的内切圆面积2(23)12=π⨯=π.2、 边长为4的正六边形的边心距________,中心角等于________度,边长为________. 【答案】 23;60;4【解析】 六边形每个中心角度数为360÷6=60°,根据每个中心角都分六边形为等边三角形,∵正六边形的边长为4, 则每个等边三角形的高即圆心距为:sin 6023CO BO =⋅︒=.3、正六边形的外接圆的半径与内切圆的半径之比为________.【答案】 2:3 【解析】 暂无解析4、 如图,正十二边形A 1A 2…A 12,连接A 3A 7,A 7A 10,则∠A 3A 7A 10=________________.【答案】 75°【解析】 设该正十二边形的圆心为O ,如图,连接A 10O 和A 3O ,由题意知,∧3110A A A =512⊙O 的周长,∴∠A3OA10=536012⨯=150°,∴∠A 3A 7A 10=75°,5、 (1)已知:如图1,ABC ∆是O ⊙的内接正三角形,点P 为弧BC 上一动点,求证:PA PB PC =+ (2)如图2,四边形ABCD 是O ⊙的内接正方形,点P 为弧BC 上一动点,求证:2PA PC PB =+(3)如图3,六边形ABCDEF 是O ⊙的内接正六边形,点P 为弧BC 上一动点,请探究PA PB PC 、、三者之间有何数量关系,并给予证明.【答案】 见解析【解析】 (1)证明:延长BP 至E ,使PE PC =,连结CE .OCABPPODAB COPFDCA1260,3460∠=∠=︒∠=∠=︒60,CPE PCE ∴∠=︒∴∆是等边三角形.,,360,CE PC E ∴=∠=∠=︒又EBC PAC ∠=∠, BEC APC ∴∆∆≌ PA BE PB PC ∴==+.(2)证明:过点B 作BE PB ⊥交PA 于E ,122390,13∠+∠=∠+∠=︒∴∠=∠,又45APB ∠=︒,,2,BP BE PE PB ∴=∴=,,AB BC ABE CBP PC AE =∴∆∆∴=≌.2PA AE PE PC PB ∴=+=+(3)答:3PA PC PB =+证明:在AP 上截取AQ PC =,连结BQ ,,BAP BCP AB BC ∠=∠=,,ABQ CBP ∴∆≅∆BQ BP ∴=.又30,APB ∠=︒3PQ PB ∴=,3PA PQ AQ PB PC ∴=+=+6、 如图,四边形ABCD 内接于⊙O ,点E 在对角线AC 上,EC =BC =DC .(1)若∠CBD =39°,求∠BAD 的度数;(2)求证:∠1=∠2.【答案】 (1)78°(2)见解析【解析】 (1)∵BC =DC ,∴∠CBD =∠CDB =39°,∵∠BAC =∠CDB =39°,∠CAD =∠CBD =39°,∴∠BAD =∠BAC +∠CAD =39°+39°=78°;(2)∵EC =BC ,∴∠CEB =∠CBE ,而∠CEB =∠2+∠BAE ,∠CBE =∠1+∠CBD ,∴∠2+∠BAE =∠1+∠CBD ,∵∠BAE =∠BDC =∠CBD ,∴∠1=∠2.7、 如图,在等腰Rt △ABC 中,AC=BC=22,点P 在以斜边AB 为直径的半圆上,M 为PC 的中点.当点P 沿半圆从点A 运动至点B 时,点M 运动的路径长是( )321E C B ADO PO Q AB C D E F PA.2πB.πC.22D.2 【答案】 B 【解析】 取AB 的中点O 、AE 的中点E 、BC 的中点F ,连结OC 、OP 、OM 、OE 、OF 、EF ,如图, ∵在等腰Rt △ABC 中,AC=BC=22,∴AB=2BC=4,∴OC=12AB=2,OP=12AB=2, ∵M 为PC 的中点,∴OM ⊥PC ,∴∠CMO=90°,∴点M 在以OC 为直径的圆上,点P 点在A 点时,M 点在E 点;点P 点在B 点时,M 点在F 点,易得四边形CEOF 为正方形,EF=OC=2, ∴M 点的路径为以EF 为直径的半圆,∴点M 运动的路径长=12•2π•1=π.8、 在Rt △ABC 中,∠C =90°,AC =BC =1,将其放入平面直角坐标系,使A 点与原点重合,AB 在x 轴上,△ABC沿x 轴顺时针无滑动的滚动,点A 再次落在x 轴时停止滚动,则点A 经过的路线与x 轴围成图形的面积为________.【答案】 12π+【解析】 ∵∠C =90°,AC =BC =1, ∴22112AB =+=;根据题意得:2△ABC 绕点B 顺时针旋转135°,BC 落在x 轴上;△ABC 再绕点C 顺时针旋转90°,AC 落在x 轴上,停止滚动;∴点A 的运动轨迹是:先绕点B 旋转135°,再绕点C 旋转90°;如图所示:∴点A 经过的路线与x 轴围成的图形是:一个圆心角为135°,半径为2的扇形,加上△ABC ,再加上圆心角是90°,半径是1的扇形;∴点A 经过的路线与x 轴围成图形的面积22135(2)190111136023602⨯π⨯⨯π⨯=+⨯⨯+=π+.9、如图,在正方形ABCD中,AB=2,连接AC,以点C为圆心、AC长为半径画弧,与BC的延长线交于点E,则图中AE的长为________.【答案】32 2π【解析】∵四边形ABCD为正方形,∴222CA AB==,∠ACB=45°,∴∠ACE=135°,∴AE的长度13522321802π==π.10、如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为()A.10cmB.15cmC.10cmD.20cm【答案】D【解析】过O作OE⊥AB于E,∵OA=OD=60cm,∠AOB=120°,∴∠A=∠B=30°,∴OE=OA=30cm,∴弧CD的长==20π,设圆锥的底面圆的半径为r,则2πr=20π,解得r=10,∴圆锥的高==20.11、用一个圆心角为120°,半径为3的扇形做一个圆锥的侧面,这个圆锥的底面圆的半径为________.【答案】1【解析】 暂无解析12、 若扇形的半径为30cm ,圆心角为60°,则此扇形围成圆锥的底面半径为 cm . 【答案】 5 【解析】 设圆锥的底面半径为r ,根据题意得2π•r=6030180π⨯,解得r=5, 即圆锥的底面半径为5cm .故答案为5.13、 将△ABC 绕点B 逆时针旋转到△A′BC′,使A 、B 、C′在同一直线上,若∠BCA =90°,∠BAC =30°,AB =4cm ,则图中阴影部分面积为________cm 2.【答案】 4π【解析】 ∵∠BCA =90°,∠BAC =30°,AB =4cm ,∴BC =2,23AC =,∠A′BA =120°,∠CBC′=120°,∴阴影部分面积=(S △A′BC′+S 扇形BAA ′)-S 扇形BCC′-S △ABC 222120π(42)4πcm 360=⨯-=. 14、 一张圆心角为45°的扇形纸板和圆形纸板按如图方式剪得一个正方形,边长都为1,则扇形纸板和圆形纸板的面积比是__________.【答案】 5:4【解析】 如图1,连接OD ,∵四边形ABCD 是正方形,∴∠DCB=∠ABO=90°,AB=BC=CD=1,∵∠AOB=45°,∴OB=AB=1,由勾股定理得:OD=222+1=5,∴扇形的面积24555=3608ππ⨯(); 如图2,连接MB 、MC ,∵四边形ABCD 是⊙M 的内接四边形,四边形ABCD 是正方形,∴∠BMC=90°,MB=MC ,∴∠MCB=∠MBC=45°,∵BC=1,∴MC=MB=22, ∴⊙M 的面积是π×(22)2=12π, ∴扇形和圆形纸板的面积比是515=824ππ÷().15、 如图,△ABC 中,AC =BC ,AB =4,∠ACB =90°,以AB 的中点D 为圆心DC 长为半径作14圆DEF ,设∠BDF =α(0°<α<90°),当α变化时图中阴影部分的面积为________(14圆:∠EDF =90°,14圆的面积21π4r =⋅)【答案】 π-2【解析】 作DM ⊥AC 于M ,DN ⊥BC 于N ,连接DC ,如图所示:∵CA =CB ,∠ACB =90°,∴∠A =∠B =45°,DM AD =,DN =, ∴DM =DN ,∴四边形DMCN 是正方形,∴∠MDN =90°,∴∠MDG =90°-∠GDN ,∵∠EDF =90°,∴∠NDH =90°-∠GDN ,∴∠MDG =∠NDH ,在△DMG 和△DNH 中,MDG NDH DMG DNH DM DN ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△DMG ≌△DNH (AAS ),∴四边形DGCH 的面积=正方形DMCN 的面积,∵正方形DMCN 的面积2218DM AB ==21428=⨯=, ∴四边形DGCH 的面积218AB =, ∵扇形FDE 的面积22290πππ4π3601616CD AB ⋅⨯===, ∴阴影部分的面积=扇形面积-四边形DGCH 的面积=π-2.16、 如图,ABCD 是平行四边形,AB 是O 的直径,点D 在O 上1AD OA ==,则图中阴影部分的面积为__________.【答案】 34 【解析】 连接DO EO BE ,,,过点D DF AB F ⊥作于点,1AD OA AD AO DO ==∴==,,AOD ∴∆是等边三角形,ABCD 四边形是平行四边形,//60DC AB CDO DOA ∴∴∠=∠=︒,, ODE ∴∆是等边三角形,同理可得出OBE ∆是等边三角形且3个等边三角形全等, ∴阴影部分面积等于BCE ∆面积,36012DF ADsin DE EC =︒===,, ∴图中阴影部分的面积为:34.。
3.8 圆内接正多边形 精品作业课件(课程配套练习) 公开课一等奖课件

︵ 14.已知 PA,PB 分别切⊙O 于点 A,B,E 是AB 上动点 ( 不与 A , B 重合 ) ,∠ P = 50 °,则∠COD = __65°__.
三、解答题(共 36 分) 15.(10 分)如图,AC⊥BC 于点 C,BC=4,AC=3,⊙ O 与直线 AB,BC,CA 均相切,求⊙O 的半径.
10.如图,Rt△ABC 的内切圆⊙O 与两直角边 AB,BC ︵ 分别相切于点 D,E,过劣弧DE(不包括端点 D,E)上任一点 P 作⊙O 的切线 MN 与 AB,BC 分别交于点 M,N,若⊙O 的 半径为 r,则 Rt△MBN 的周长为( C ) A.r 3 B. r C.2r 2 5 D. r 2
1 .顶点都在__ 同一个圆 __ 上的正多边形叫做圆的内接 正多边形,这个圆叫做正多边形的__外接圆__. 2.将一个圆 n 等分(n≥3),顺次连接各分点得到该圆的 __内接正 n 边形__. 3 .正多边形__ 外接圆的圆心 __ 叫做正多边形的中心, __外接圆的半径__叫做正多边形的半径,正多边形的中心到 一边的距离是它的__边心距__. 4.以圆的__半径__为弦长等分圆可得到内接正六边形.
3.(4 分)如图,PA,PB 是⊙O 的切线,A,B 为 切点,PO 交 AB 于点 D,AO 交⊙O 于点 C,连接 BC, 则下列结论不一定成立的是( D ) A.PO⊥AB C.PD∥BC B.AD=DB 1 D.OD=4PD
4.(4 分)如图,PA,PB 是⊙O 的切线,A,B 为切点, AC 是⊙O 的直径,∠P=40°,则∠BAC=__20°__. 5.(4 分)如图,PA,PB 是⊙O 的两条切线,切点分别是 A,B,如果 OP=4,OA=2,则 PB=__2 3__.
3.8 圆内接正多边形课件(共18张PPT) 北师大版九年级下册数学

°
(3)∠MON=
.
合作探究
有一个亭子(如图),它的地基是半径为8 m的正六边形,
求地基的周长和面积.(结果保留根号)
合作探究
解:如图,连接OB、OC,
∵六边形ABCDEF是正六边形,
°
∴∠BOC= =60°,
∴△OBC是等边三角形,
∴BC=OB=8 m,
于另一点,依次下去,在圆周上得到六个点;
合作探究
(3)依次每隔一点相连接,就得到了这个圆的一个内接正三
角形.
合作探究
已知正方形ABCD的边心距OE= cm,求这个正方
形外接圆☉O的面积.
合作探究
解:如图,连接OC、OD,
∵☉O是正方形ABCD的外接圆,∴O是对角线AC、BD的交
点,
∴∠ODE=∠ADC=45°.
∴正六边形ABCDEF的周长=6×8=48 m.
合作探究
过O作OG⊥BC于G,
∵△OBC是等边三角形,OB=8 m,
∴∠OBC=60°,
∴OG=OB·sin∠OBC=8×
=4
∴S△OBC=BC·OG=×8×4
m,
=16 (m2),
∴S正六边形ABCDEF=6S△OBC=6×16 =96 m2.
.
2.如图,四边形ABCD是☉O的内接正方形,P是上不同
于点C的任意一点,则∠BPC的大小是(B
A.22.5°
B.45°
C.30°
D.50°
)
合作探究
用尺规作一个已知圆的内接正三角形.
解:作法为(1)以圆周上任意一点为圆心,以圆的半径为半
九年级数学下册3.8圆内接正多边形正多边形和圆课标解读素材北师大版(new)

正多边形和圆课标解读一、课标要求正多边形和圆一节包括一个例题、一个画图,都是正多边形和圆之间的关系.《义务教育数学课程标准(2011年版)》对正多边形和圆一节提出了具体的教学要求,本小节的教学要求是:1.了解正多边形的概念及正多边形与圆的关系.2.能用尺规完成作三角形的外接圆、内切圆;作圆的内接正方形和正六边形.二、课标解读正多边形是生活中常见的图形,因此正多边形的有关计算在生活中经常用到.圆的许多性质,比较集中地反映了事物内部量变与质变、一般与特殊、矛盾的对立统一等关系.由于正多边形与圆有着密切的联系,所以可以应用圆的有关知识来研究正多边形的问题.正多边形是一种特殊的多边形,在生产和生活中有着广泛的应用,它有一些类似于圆的性质.例如正多边形的边数越多,它的周长就越接近圆的周长,它的面积就越接近圆的面积.又如,圆有独特的对称性,它不仅是轴对称图形、中心对称图形,而且它的任意一条直径所在直线都是它的对称轴,绕圆心旋转任意一个角度都能和原来的图形重合.而正多边形也是轴对称图形,正n边形有n条对称轴;而且绕中心每旋转一个中心角,都能和原来的图形重合,这是正n边形的旋转对称性;当n为偶数时,它也是中心对称图形.本小节需要学习的内容是:1.了解正多边形的对称性,正多边形都是轴对称图形,对称轴的条数等于正多边形的边数;正多边形都是旋转对称图形,旋转中心是圆心,旋转的最小角度等于正多边形的中心角;正偶数边形是中心对称图形.由于学生对轴对称图形、中心对称图形的概念比较熟悉,通过操作、思考来解答课本中提出的问题一般不会感到困难,所以,教学中要发挥学生的主体作用,通过学生的独立思考、实践自主解决.2.学生应该掌握正多边形的中心、中心角、半径、边心距等有关概念,如图,会计算正多边形的中心角、边长、边心距、半径、周长和面积.这些概念与正多边形的外接圆关系密切,是进行与正多边形有关计算的基础.3.由于正多边形在生产和生活中有着广泛的应用,因此很多时候需要画正多边形.会利用等分圆周法画正多边形,利用量角器或直尺和圆规画图,把圆分成相等的一些弧,就可以得到这个圆的内接正多边形.利用量角器可以画任意正多边形,而利用直尺和圆规只能作特殊的正多边形.等分圆周方法画正多边形体现了正多边形与圆的关系;尺规作图画正多边形体现了一些特殊的正多边形的性质.例如,在⊙O中用不同的方法画圆的内接正三角形.如图:图 1 图 2 图3作法:度量法①:如图1,作半径OA,用量角器或30°角的三角板度量,使∠1=∠2=30°.度量法②:如图2,用量角器度量,使圆心角∠AOB=∠BOC=∠COA=120°.尺规作图法:用圆规在⊙O上顺次截取6条长度等于半径的弦,间隔顺次连接其中的AB、BC、CA即可.利用直尺和圆规只能作特殊的正多边形,如正方形、正三角形、正六边形,如图.用尺规作图的方法画圆的内接正方形,只要作出已知⊙O的互相垂直的直径,就可以把圆四等分,从而作出圆内接正方形,再过圆心作各边的垂线与⊙O相交,或作各中心角的角平分线与⊙O相交,即可以作出圆内接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形、…….4.正多边形的有关计算是本节的重点内容,这些计算都是几何中的基础知识,正确掌握它们要综合运用以前所学的知识,这些知识在生产和生活中也常用到.本节教学难点在学生对正n边形中“n"的接受和理解上.学生对三角形、四边形、圆等具体图形比较习惯,对于泛指的n边形并不习惯.为了降低难度,涉及的证明、计算等问题都结合具体的多边形为例,教学时要注意把这种针对具体图形的结论和方法推广,使学生实现由具体到抽象、特殊到一般的认识上的飞跃,提高学生的思维能力.尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
北师大版九年级数学下册《圆——圆周角和圆心角的关系》教学PPT课件(6篇)

D
O2
O1
E
B
F
新知探究
【跟踪训练】
1.圆内接四边形ABCD中,∠A, ∠B, ∠C的度数之比是
135°
1:2:3,则这个四边形最大角的度数是_________.
D
A
2.四边形ABCD内接于圆,AD∥BC,AB+CD=AD+BC ,
25
若AD=4,BC=6,则四边形ABCD的面积为_______.
A
A
O
O
BB
C
C
课堂小测
3. 如图,点B,C在⊙O上,且BO=BC,则圆周角∠BAC等于( D )
A
A.60°
B.50°
C.40°
D.30°
O
B
C
课堂小测
4 . 如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E.若
∠AOD=60°,则∠DBC的度数为( A)
A.30°
B.40°
C.50°
B
D.60°
D
C
OC垂直平分AD
(1)OC与AD的位置关系是__________________;
A
平行
(2)OC与BD的位置关系是___________;
4
(3)若OC=2cm,则BD=______cm.
O1
O
B
新知探究
4.如图,△ABC的顶点均在⊙O上, AB=4, ∠C=30°,求⊙O的直径.
解:连接AO并延长交⊙O于点E,
3 . 当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆
心角∠AOC的大小关系会怎样?
提示:能否也转化为1的情况?
A
C
过点B作直径BD.由1可得:
北师大版九年级下册 第三章3.4 圆周角(共21张PPT)-专业PPT文档

再分别量出图中AB所对的圆周角和圆心角的度数, 比较一下,你有什么发现?
圆周角的度数恰好等于这条弧所对的圆心角度数的一半
目标:理解圆周角的概念;理解并掌握圆周角定理及推论; 会应用定理及推论解决有关证明、计算问题
观察与思考
观察下图中,圆周角与圆心之间存在什么位置关系?
A
A
A
O
C
O
O C
B
C
B
D
D
B
已知,如图,∠BAC是圆O中弧BC所对的圆周角, ∠BOC是弧BC所对的圆心角。
1 求证: ∠BAC= 2 ∠BOC
目标:理解圆周角的概念;理解并掌握圆周角定理及推论; 会应用定理及推论解决有关证明、计算问题
圆周角定理
在同圆或等圆中,同弧或等弧所对的圆
周角相等,都等于这条弧所对的圆心角
练习:
判别下列各图形中的角是不是圆周角,并说明理 由
不是
不是
不是
不是
是
不是
目标:理解圆周角的概念;理解并掌握圆周角定理及推论; 会应用定理及推论解决有关证明、计算问题
(
(
探究1
分别度量一下教材84页探究中AB所对的两 个圆周角的度数,比较一下,再变动点C在 圆周上的位置,圆周角的度数有没有变化? 你能发现什么规律?
过其中的圆弧形玻璃AB观看窗内的海洋动物,同学甲站在圆
心的O位置,同学乙站在正对着玻璃窗的靠墙的位置C,他
们的视角(∠AOB和∠ACB)有什么关系?如果同学丙丁分
别站在其他靠墙的位置D和E,他们的视角( ∠ADB和
∠AEB )和同学乙的视角相同吗?
丙(D) A
由圆周角定理可知:
北师大版九年级数学下册:3.8《圆内接正多边形》教学设计

北师大版九年级数学下册:3.8《圆内接正多边形》教学设计一. 教材分析《圆内接正多边形》是北师大版九年级数学下册第3.8节的内容,本节主要让学生了解圆内接正多边形的概念及其性质,学会用数学方法证明圆内接正多边形的性质,并能够运用这些性质解决一些实际问题。
教材通过引导学生在探究圆内接正多边形的过程中,培养学生的逻辑思维能力和空间想象能力。
二. 学情分析九年级的学生已经掌握了多边形的性质,对圆的相关知识也有所了解。
但学生对圆内接正多边形的概念和性质认识尚浅,需要通过实例和证明来加深理解。
此外,学生可能对证明圆内接正多边形性质的方法感到困惑,需要教师引导和启发。
三. 教学目标1.了解圆内接正多边形的概念及其性质。
2.学会用数学方法证明圆内接正多边形的性质。
3.培养学生的逻辑思维能力和空间想象能力。
4.能够运用圆内接正多边形的性质解决实际问题。
四. 教学重难点1.圆内接正多边形的概念及其性质。
2.如何证明圆内接正多边形的性质。
3.圆内接正多边形性质在实际问题中的应用。
五. 教学方法1.引导法:教师通过提问、启发引导学生思考和探究圆内接正多边形的性质。
2.示例法:教师通过展示实例,让学生理解圆内接正多边形的性质。
3.证明法:教师引导学生运用已学知识证明圆内接正多边形的性质。
4.练习法:学生通过做练习题,巩固对圆内接正多边形性质的理解。
六. 教学准备1.教学PPT:包含圆内接正多边形的概念、性质、证明方法及实际应用。
2.练习题:针对圆内接正多边形性质的习题,包括选择题、填空题和解答题。
3.教学黑板:用于板书关键点和证明过程。
七. 教学过程1.导入(5分钟)教师通过提问方式引导学生回顾多边形的性质,为新课的学习做好铺垫。
例如:“我们已经学习了多边形的哪些性质?这些性质如何应用到实际问题中?”2.呈现(10分钟)教师利用PPT呈现圆内接正多边形的概念和性质,让学生初步了解。
同时,通过示例法,展示圆内接正多边形的性质在实际问题中的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9.已知⊙O 和⊙O 上的一点 A. (1)作⊙O 的内接正方形 ABCD 和内接正六边形 AEFCGH; (2)在(1)题的作图中,如果点 E 在A︵D上,求证:DE 是⊙O 内接 正十二边形的一边.
(1)作法:①作直径AC;②作直径BD⊥AC;③依次连接A,B,C,D 四点,∴四边形ABCD即为⊙O的内接正方形.(图略)①分别以A,C 为圆心,OA的长为半径作弧,交⊙O于E,F,G,H;②顺次连接A, E,F,C,G,H各点,∴六边形AEFCGH为⊙O的内接正六边形(图 略)
(2)连接 OE,DE,图略.∵∠AOD=3604°=90°,∠AOE=3660° =60°,∴∠DOE=90°-60°=30°,∴DE 为⊙O 的内接正十二 边形的一边 .
ห้องสมุดไป่ตู้
10.如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一 边,CD=5 cm,求⊙O的半径R. 连接 OB,OC,OD,图略.∵等边△ABC 内接于⊙O, BD 为内接正十二边形的一边,∴∠BOC=13×360°=120
18.(导学号:37554069)如图,有一圆内接正八边形ABCDEFGH, 若△ADE的面积为10,则这个正八边形的面积为__4_0___.
19.如图,有一个圆O和两个正六边形T1,T2,T1的6个顶点都在圆 周上,T2的6条边都和圆O相切(我们称T1,T2分别为圆O的内接正六边 形和外切正六边形).
第三章 圆
3.8 圆内接正多边形
知识点:圆内接正多边形
1.(2017·滨州)若正方形的外接圆半径为 2,则其内切圆半径为( A )
A. 2
B.2 2
2 C. 2
D.1
2.(2017·沈阳)如图,正六边形 ABCDEF 内接于⊙O,正六边形的 周长是 12,则⊙O 的半径是( B )
A. 3 B.2 C.2 2 D.2 3
°,∠BOD=112×360°=30°,∴∠COD=∠BOC-∠ BOD=90°,∵OC=OD,∴∠OCD=45°,∴OC= CD×cos 45°=5 2× 22=5(cm),即⊙O 的半径 R=5 cm
易错点:混淆正多边形的边心距和半径而出错 11.正六边形的边心距为 3,则该正六边形的边长是( B ) A. 3 B.2 C.3 D.2 3
6.一个正方形的边长为4 cm,则它的中心角是__9_0_____°,半 径是___2__2___cm,边心距是___2_____cm.
7.在半径为R的圆中,内接正方形与内接正六边形的边长之比为 ___2_∶__1__.
8.如图,AB,AC分别是⊙O的内接正六边形和内接正十边形的一 边,则BC是⊙O的内接正__十__五____边形的边.
A.( 22)n B.(12)n C.( 23)n D.(34)n
15.(2016·威海)如图,正方形ABCD内接于⊙O,其边长为4,则 ⊙O的内接正三角形EFG的边长为__2___6___.
16.如图,正五边形ABCDE的对角线AC和BE相交于点M,求证: (1)AC∥DE; (2)ME=AE.
12.如图,以正六边形ADHGFE的一边AD为边向外作正方形ABCD, 则∠BED的度数为( ) B
A.30° B.45° C.50° D.60°
13.(导学号:37554068)如图,由 7 个形状、大小完全相同的正 六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的 边长为 1,△ABC 的顶点都在格点上,则△ABC 的面积是( D )
3.(2017·达州)以半径为 2 的圆的内接正三角形、正方形、正六边 形的边心距为三边作三角形,则该三角形的面积是( A )
23 A. 2 B. 2 C. 2 D. 3
4.一个正n边形的面积是240 cm2,周长是60 cm,则边心距是 __8__c_m___.
5.如图,要拧开一个边长为a=6 cm的正六边形螺帽,扳手张开的 开口b至少为__6___3___cm.
17.如图,正方形ABCD的边长为a cm,剪去4个角后成为正八边形, 求正八边形的边长和面积. 由题意,设 LE=LK=x cm.∵△AEL 是等腰直角 三角形,∴AL= 22x=DK.又∵AD=a,∴ 22x+ 22x+x=a,解得 x= 2a+1=( 2-1)a,∴S 正八边 形=S 正方形 ABCD-4×S△AEL=a2-4×12×[ 22×( 2 -1)a]2=(2 2-2)a2(cm2)
(1)由题意,得∠EDC=(5-2)5 ·180°=108°. ∠DCA=21×2×3650°=72°.∴∠EDC+∠DCA =108°+72°=180°,∴AC∥DE
(2)由题意,得∠DEB=∠EAC=12×2×3605°=72°.∵AC∥DE, ∴∠AME=∠DEB=72°.∴∠AME=∠EAC,∴ME=AE
(1)设T1,T2的边长分别为a,b,圆O的半径为r,求r∶a及r∶b的值; (2)求正六边形T1,T2的面积比S1∶S2的值.
(1)连接圆心 O 和 T1 的 6 个顶点可得 6 个全等的正三角形,所以 r∶a =1∶1;连接圆心 O 和 T2 相邻的两个顶点,得以圆 O 半径为高的正 三角形,所以 r∶b= 3∶2 (2)T1∶T2 的边长比是 3∶2,所以 S1∶ S2=(a∶b)2=3∶4
A. 2 B.2 3 C.3 2 D.3 3
14.如图,先作正方形 ABCD 的内切圆,再作这个内切圆的内接正 方形 A1B1C1D1,把这一过程称为第一次数学操作.接下来,作正方形 A1B1C1D1 的内切圆,再作这个内切圆的内接正方形 A2B2C2D2,称为第二 次数学操作……按此规律如此下去,当完成第 n 次数学操作后,得到正 方形 AnBnCnDn,则AAnBBn的值为( A )
