高中抛物线知识点归纳总结与练习题及答案
抛物线知识点总结及练习
抛物线知识点总结及练习一、抛物线的定义：平面上给予一直线L 及L 外一定点F ，则平面上所有到直线L 的距离恰等于到定点F 的距离之所有动点P 所形成的图形就称为抛物线，其中L 称为准线，F 称为焦点。
二、名词的认识：(一)对称轴﹕通过焦点F 且与准线L 垂直之直线M ，又简称为轴。
(二)顶 点﹕抛物线与对称轴的交点V 。
(三)焦 距﹕焦点F 与顶点V 的距离VF 。
(四)弦﹕抛物线上任取相异两点A 、B 的连线段。
(五)焦弦﹕过焦点F 的弦AC 。
(六)正焦弦﹕垂直于对称轴的焦弦MN 。
(注) 正焦弦长 MN 是焦距 FV 的 4 倍.三、抛物线的标准式：2y ax bx c =++ 配方 2()y a x h k =-+四、抛物线方程式：标准式焦点准线图形24y cx = F (,0)c :L x c =-0c >0c <24x cy = F (0,)c:L y c =-0c >0c <观念延伸：平移后的抛物线之方程式与其图形则会变成？标准式图形2y k c x h-=-()4()c<c>02-=-x h c y k()4()c<c>0例1：右图是一张科学家所记录的草图。
草图描绘着一颗绕着太阳运行之彗星的轨迹，其中的A、B、C、D、E 五点是科学家观察到彗星所在的位置。
经过仔细的计算，这颗彗星所运行的轨迹是一条抛物线，太阳位于其焦点且其准线是一条水平线。
则根据这张草图，彗星在被观察到的五点A、B、C、D、E与太阳之距离的大小顺序为何？【练习题】右图为一抛物线的部分图形， A、B、C、D、E个点中有一为其焦点。
试判断何点是其焦点？例2：求满足下列各条件的抛物线方程式：(1)焦点 F (2,0)，准线:2L x =- (2)焦点 F (0,3)-，准线:3L y =.【练习题】求满足下列各条件的抛物线方程式：(1) 焦点 F (1,0)-，准线:1L x = (2) 焦点 F (0,4)，准线:4L y =-例3：求抛物线216y x =-的顶点、焦点、准线与正焦弦长。
抛物线知识点全面总结及经典例题
x（p>0）
2
y p 2
y≤0 x∈R
y轴
例１：已知抛物线关于x轴对称，它的顶点 在坐标原点，并且经过点M2（2２， ），求
它的标准方程。
变式:顶点在坐标原点，对称轴为坐标 轴，并且经过点M（２，2 2 ），抛物 线的标准方程。
例2：已知抛物线的方程为y2=4x,直线 l 经过点P(-2,1),斜率为k.当k为何值 时,直线与抛物线:只有一个公共点;有
1 FA
|
|
1 FB
|
是否为定值？
y
A ( x1, y1 )
这一结论非常奇妙, 变中有不变,动中有不动.
F
O
x
B ( x2, y2 )
例9、正三角形的一个顶点位于坐标原点，另外两个
顶点在抛物线 y2 2 px( p 0)上，求这个三角形的边长。
解：如图，设正三角形OAB的顶点A、
y
A (x1,y1)
（2）已知抛物线的方程是 y 6x2，求它的焦点坐标和准
线方程；
(3)已知抛物线的焦点坐标是F(0,-2)，求它的标准方程．
解：（1）因为焦点在x轴的正半轴上，p=3，所以焦点坐
标是
(3 2
,
0)
，准线方程是
x
3 2
.
（2）因为抛物线的标准方程 x2 1 y，焦点在y轴的正
半轴上，p 是y 1
X1=X2. 由此可得|y1|=|y2|,，即线段AB关于x轴对称。
(x2,y2)
B
因为x轴垂直于AB，且 AOX 30，所以 y1 tan 30 3
x1
y12 2p
,
x1
抛物线知识点归纳总结与经典习题
抛物线一、抛物线的定义及其应用例1、设P是抛物线y2＝4x上的一个动点．(1)求点P到点A(－1,1)的距离与点P到直线x＝－1的距离之和的最小值；(2)若B(3,2)，求|PB|＋|PF|的最小值．例2、设M(x0，y0)为抛物线C：x2＝8y上一点，F为抛物线C的焦点，以F为圆心、|FM|为半径的圆和抛物线C的准线相交，则y0的取值范围是( )A．(0,2) B．[0,2] C．(2，＋∞) D．[2，＋∞)二、抛物线的标准方程和几何性质例3、抛物线y2＝2px(p>0)的焦点为F，准线为l，经过F的直线与抛物线交于A、B两点，交准线于C点，点A在x轴上方，AK⊥l，垂足为K，若|BC|＝2|BF|，且|AF|＝4，则△AKF的面积是 ( )A．4 B．3 3 C．4 3 D．8例4、过抛物线y2＝2px(p>0)的焦点F的直线交抛物线于点A、B，交其准线l于点C，若|BC|＝2|BF|，且|AF|＝3则此抛物线的方程为 ( )A．y2＝32x B．y2＝9x C．y2＝92x D．y2＝3x三、抛物线的综合问题例5、已知平面内一动点P到点F(1,0)的距离与点P到y轴的距离的差等于1.(1)求动点P的轨迹C的方程；(2)过点F作两条斜率存在且互相垂直的直线l1，l2，设l1与轨迹C相交于点A，B，l2与轨迹C相交于点D，E，求AD·EB的最小值练习题1．已知抛物线x2＝ay的焦点恰好为双曲线y2－x2＝2的上焦点，则a等于( ）A．1 B．4 C．8 D．162．抛物线y＝－4x2上的一点M到焦点的距离为1，则点M的纵坐标是 ( )A．－1716B．－1516C.716D.15163．已知F是拋物线y2＝x的焦点，A，B是该拋物线上的两点，|AF|＋|BF|＝3，则线段AB的中点到y轴的距离为 ( )A.34B．1 C.54D.744．已知抛物线y2＝2px，以过焦点的弦为直径的圆与抛物线准线的位置关系是( ) A．相离B．相交 C．相切D．不确定5．已知F为抛物线y2＝8x的焦点，过F且斜率为1的直线交抛物线于A、B两点，则||FA|－|FB||的值等于 ( ) A．4 2 B．8C． 8 2 D．166．在y＝2x2上有一点P，它到A(1,3)的距离与它到焦点的距离之和最小，则点P的坐标是 ( ) A．(－2,1) B．(1,2) C．(2,1) D．(－1,2)7．设抛物线y2＝8x的焦点为F，准线为l，P为抛物线上一点，PA⊥l，A为垂足．如果直线AF的斜率为－3，那么|PF|＝ ( )A．4 3 B．8 C．8 3 D．168．抛物线的顶点在原点，准线方程为x＝－2，抛物线的方程（）A．y2＝－8x B．y2＝8x C．y2＝－4x D．y2＝4x9以抛物线x2＝16y的焦点为圆心，且与抛物线的准线相切的圆的方程为______．10．已知抛物线的顶点在原点，对称轴为y轴，抛物线上一点Q(－3，m)到焦点的距离是5，则抛物线的方程为________．11．已知抛物线y2＝4x与直线2x＋y－4＝0相交于A、B两点，抛物线的焦点为F，那么|FA| ＋|FB| ＝________.12．过抛物线y2＝4x的焦点作直线交抛物线于A(x1，y1)，B(x2， y2)两点，若x1＋x2＝6，那么 |AB|等于________13．根据下列条件求抛物线的标准方程：(1)抛物线的焦点是双曲线 16x2－9y2＝144的左顶点；(2)过点P(2，－4)．14已知点M(1，y)在抛物线C：y2＝2px(p>0)上，M点到抛物线C的焦点F的距离为2，直线l：y＝－12x＋b与抛物线C交于A，B两点．(1)求抛物线C的方程；(2)若以AB为直径的圆与x轴相切，求该圆的方程．一、抛物线的定义及其应用例1、(1)如图，易知抛物线的焦点为F (1,0)，准线是x ＝－1.由抛物线的定义知：点P 到直线x ＝－1的距离等于点P 到焦点F 的距离． 于是，问题转化为：在曲线上求一点P ，使点P 到点A (－1,1)的距离与点P 到F (1,0)的距离之和最小．显然，连结AF 交曲线于P 点，则所求的最小值为|AF |，即为 5.(2)如图，自点B 作BQ 垂直准线于Q ，交抛物线于点P 1，则|P 1Q |＝|P 1F |.则有|PB |＋|PF |≥|P 1B |＋|P 1Q |＝|BQ |＝4.即|PB |＋|PF |的最小值为4.例2、解析：圆心到抛物线准线的距离为p ，即p ＝4，根据已 知只要|FM |>4即可．根据抛物线定|FM |＝y 0＋2由y 0＋2>4，解得y 0>2，故y 0的取值范围是(2，＋∞)．二、抛物线的标准方程和几何性质例3、设点A (x 1，y 1)，其中y 1>0.由点B 作抛物线的准线的垂线，垂足为B 1.则有 |BF |＝|BB 1|；又|CB |＝2|FB |，因此有|CB |＝2|BB 1|，cos ∠CBB 1＝|BB 1||BC |＝12，∠CBB 1＝π3.即直线AB 与x 轴的夹角为π3.又|AF |＝|AK |＝x 1＋p2＝4，因此y 1＝4sin π3＝23，因此△AKF 的面积等于12|AK |·y 1＝12×4×23＝4 3.例4．分别过点A 、B 作AA 1、BB 1垂直于l ，且垂足分别为A 1、B 1，由已知条件|BC |＝2|BF |得|BC |＝2|BB 1|，∴∠BCB 1＝30°，又|AA 1|＝|AF |＝3，∴|AC |＝2|AA 1|＝6，∴|CF |＝|AC |－|AF |＝6－3＝3，∴F 为线段AC 的中点．故点F 到准线的距离为p ＝12|AA 1|＝32，故抛物线的方程为y 2＝3x .三、抛物线的综合问题例5、 (1)设动点P 的坐标为(x ，y )，由题意有x －12＋y 2－|x |＝1.化简得y 2＝2x ＋2|x |. 当x ≥0时，y 2＝4x ；当x <0时，y ＝0.所以，动点P 的轨迹C 的方程为y 2＝4x (x ≥0)和y ＝0(x <0)． (2)由题意知，直线l 1的斜率存在且不为0，设为k ，则l 1的方程为y ＝k (x －1)．由⎩⎨⎧y ＝k x －1y 2＝4x，得k 2x 2－(2k 2＋4)x ＋k 2＝0. (7分)设A (x 1，y 1)，B (x 2，y 2)，则x 1，x 2是上述方程的两个实根，于是x 1＋x 2＝2＋4k2，x 1x 2＝1. (8分)因为l 1⊥l 2，所以l 2的斜率为－1k. 设D (x 3，y 3)，E (x 4，y 4)，则同理可得x 3＋x 4＝2＋4k 2，x 3x 4＝1. ＝(x 1＋1)(x 2＋1)＋(x 3＋1)·(x 4＋1)＝ x 1x 2＋(x 1＋x 2)＋1＋x 3x 4＋(x 3＋x 4)＋1 (11分) ＝1＋(2＋4k 2)＋1＋1＋(2＋4k 2)＋1＝8＋4(k 2＋1k2)≥8＋4×2k 2·1k2＝16.当且仅当k 2＝1k2，即k ＝±1时， AD ·EB 取最小值16.练习题：1．解析：根据抛物线方程可得其焦点坐标为(0，a4)，双曲线的上焦点为(0,2)，依题意则有a4＝2解得a ＝8.2．解析：抛物线方程可化为x 2＝－y 4，其准线方程为y ＝116.设M (x 0，y 0)，则由抛物线的定义，可知116－y 0＝1⇒y 0＝－1516.3．解析：根据拋物线定义与梯形中位线定理，得线段AB 中点到y 轴的距离为：12(|AF |＋|BF |)－14＝32－14＝54. 4．解析：设抛物线焦点弦为AB ，中点为M ，准线l ，A 1、B 1分别为A 、B 在直线l 上的射影，则|AA 1|＝|AF |，|BB 1|＝|BF |，于是M 到l 的距离d ＝12(|AA 1|＋|BB 1|)＝12(|AF |＋|BF |)＝12|AB |＝半径，故相切． 5．解析：依题意F (2,0)，所以直线方程为y ＝x －2由⎩⎨⎧y ＝x －2，y 2＝8x ，消去y得x 2－12x ＋4＝0.设A (x 1，y 1)，B (x 2，y 2)，则||FA |－|FB ||＝|(x 1＋2)－(x 2＋2)|＝|x 1－x 2|＝(x 1＋x 2)2－4x 1x 2＝144－16＝8 2.6．解析：如图所示，直线l 为抛物线y ＝2x 2的准线，F 为其焦点，PN ⊥l ，AN 1⊥l ，由抛物线的定义知，|PF |＝|PN |，∴|AP |＋|PF |＝|AP |＋|PN |≥|AN 1|，当且仅当A 、P 、N 三点共线时取等号．∴P 点的横坐标与A 点的横坐标相同即为1，则可排除A 、C 、D.答案：B7．解析：设抛物线y 2＝8x 的焦点为F ，准线为l ，P 为抛物线上一点，PA ⊥l ，A 为垂足．如果直线AF 的斜率为－3，那么|PF |＝ ( ) A ．4 3 B ．8 C ．8 3 D ．168．解析：由准线方程x ＝－2，可知抛物线为焦点在x 轴正 ，半轴上的标准方程，同时得p ＝4，所以标准方程为 y 2＝2px ＝8x9．解析：抛物线的焦点为F (0,4)，准线为y ＝－4，则圆心为(0,4)，半径r ＝8. 所以，圆的方程为x 2＋(y －4)2＝64.10．解析：设抛物线方程为x 2＝ay (a ≠0)，则准线为y ＝－a4.∵Q (－3，m )在抛物线上，∴9＝am .而点Q 到焦点的距离等于点Q 到准线的距离，∴|m －(－a4)|＝5.将m ＝9a 代入，得|9a ＋a4|＝5，解得，a ＝±2，或a ＝±18，∴所求抛物线的方程为x 2＝±2y ，或x 2＝±18y .11．解析：由⎩⎨⎧y 2＝4x 2x ＋y －4＝0，消去y ，得x 2－5x ＋4＝0(*)，方程(*)的两根为A 、B 两点的横坐标，故x 1＋x 2＝5，因为抛物线y 2＝4x 的焦点为F (1,0)，所以| FA | ＋| FB | ＝(x 1＋1)＋(x 2＋1)＝712．解析：因线段AB 过焦点F ，则|AB |＝|AF |＋|BF |.又由抛物线的定义知|AF |＝x 1＋1，|BF |＝x 2＋1，故|AB |＝x 1＋x 2＋2＝8.13．解析：双曲线方程化为x 29－y 216＝1，左顶点为(－3,0)，由题设抛物线方程为y 2＝－2px (p >0)，则－p2＝－3，∴p ＝6，∴抛物线方程为y 2＝－12x .(2)由于P (2，－4)在第四象限且抛物线对称轴为坐标轴，可设抛物线方程为y 2＝mx 或x 2＝ny ，代入P 点坐标求得m ＝8，n ＝－1， ∴所求抛物线方程为y 2＝8x 或x 2＝－y .14． (1)抛物线y 2＝2px (p >0)的准线为x ＝－p2，由抛物线定义和已知条件可知|MF |＝1－(－p 2)＝1＋p2＝2，解得p ＝2, 故所求抛物线C 的方程为y 2＝4x .(2)联立⎩⎨⎧y ＝－12x ＋b ，y 2＝4x消去x 并化简整理得y 2＋8y －8b ＝0.依题意应有Δ＝64＋32b >0，解得b >－2.设A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 2＝－8，y 1y 2＝－8b ，设圆心Q (x 0，y 0)，则应用x 0＝x 1＋x 22，y 0＝y 1＋y 22＝－4.因为以AB 为直径的圆与x 轴相切，所以圆的半径为r ＝|y 0|＝4. 又|AB |＝x 1－x 22y 1－y 22＝1＋4y 1－y 22＝ 5[y 1＋y 22－4y 1y 2]＝564＋32b所以|AB|＝2r＝564＋32b＝8，解得b＝－8 5 .所以x1＋x2＝2b－2y1＋2b－2y2＝4b＋16＝485，则圆心Q的坐标为(245，－4)．故所求圆的方程为(x－245)2＋(y＋4)2＝16.。
高中抛物线知识点归纳总结与练习题及答案
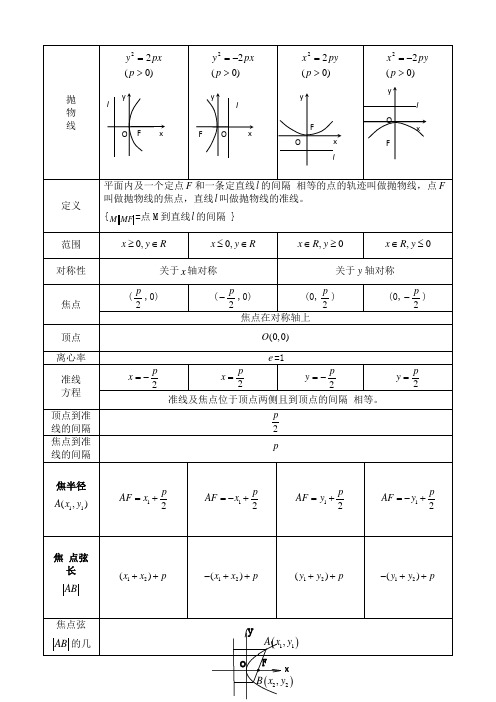
条性质11(,)A x y 22(,)B x y以AB 为直径的圆必及准线l 相切假设AB 的倾斜角为α，那么22sin pAB α=假设AB 的倾斜角为α，那么22cos pAB α=2124p x x = 212y y p =-112AF BF AB AF BF AF BF AF BF p++===•• 切线 方程00()y y p x x =+ 00()y y p x x =-+ 00()x x p y y =+ 00()x x p y y =-+一． 直线及抛物线的位置关系 直线，抛物线，，消y 得：〔1〕当0时，直线l 及抛物线的对称轴平行，有一个交点； 〔2〕当k ≠0时，Δ＞0，直线l 及抛物线相交，两个不同交点； Δ=0， 直线l 及抛物线相切，一个切点； Δ＜0，直线l 及抛物线相离，无公共点。
（3）假设直线及抛物线只有一个公共点,那么直线及抛物线必相切吗〔不肯定〕 二． 关于直线及抛物线的位置关系问题常用途理方法 直线l ：b kx y += 抛物线，)0( p① 联立方程法：⎩⎨⎧=+=pxy bkx y 22⇒0)(2222=+-+b x p kb x k 设交点坐标为),(11y x A ,),(22y x B ，那么有0 ∆,以及2121,x x x x +，还可进一步求出bx x k b kx b kx y y 2)(212121++=+++=+，2212122121)())((b x x kb x x k b kx b kx y y +++=++=在涉及弦长，中点，对称，面积等问题时，常用此法，比方 1. 相交弦的弦长2122122124)(11x x x x k x x k AB -++=-+=ak ∆+=21 或 2122122124)(1111y y y y k y y k AB -++=-+=ak ∆+=21b. 中点),(00y x M , 2210x x x +=， 2210y y y +=② 点差法：设交点坐标为),(11y x A ，),(22y x B ，代入抛物线方程，得1212px y = 2222px y =将两式相减，可得)(2))((212121x x p y y y y -=+-2121212y y px x y y +=--a. 在涉及斜率问题时，212y y pk AB +=b. 在涉及中点轨迹问题时，设线段AB 的中点为),(00y x M ，021*******y py p y y p x x y y ==+=--， 即0y pk AB =， 同理，对于抛物线)0(22≠=p py x ，假设直线l 及抛物线相交于B A 、两点，点),(00y x M 是弦AB 的中点，那么有px p x p x x k AB 0021222==+=〔留意能用这个公式的条件：1〕直线及抛物线有两个不同的交点，2〕直线的斜率存在，且不等于零〕抛物线练习及答案1、点P 在抛物线y 2 = 4x 上，那么点P 到点Q 〔2，－1〕的间隔 及点P 到抛物线焦点间隔 之和获得最小值时，点P 的坐标为 。
高中抛物线知识点归纳总结与练习题(含答案)
则 AFK 的面积为
。
7、已知双曲线 x2 y2 1，则以双曲线中心为焦点，以双曲线左焦点为顶点的抛物线方程 45
为
。
8、在平面直角坐标系 xoy 中，有一定点 A(2,1) ,若线段 OA 的垂直平分线过抛物线
y2 2 px( p 0) 焦点，则该抛物线的方程是
高中抛物线知识点归纳总结与练习题
y 2 2 px ( p 0)
抛
y l
物
线
OF x
y 2 2 px ( p 0)
y l
FO x
x 2 2 py ( p 0)
y
F
O
x
l
x 2 2 py ( p 0)
y l
O x
F
定义 范围
平面内与一个定点 F 和一条定直线 l 的距离相等的点的轨迹叫做抛物线，点 F 叫 做抛物线的焦点，直线 l 叫做抛物线的准线。
二． 关于直线与抛物线的位置关系问题常用处理方法
直线 l ： y kx b 抛物线
1 联立方程法：
y kx b
y
2
2
px
k 2x22源自kbp)x
b2
0
， ( p 0)
设交点坐标为 A(x1, y1) , B(x2, y2 ) ，则有 0 ,以及 x1 x2, x1x2 ，还可进一步求出
距离之和的最小值为
。
3、直线 y x 3 与抛物线 y2 4x 交于 A, B 两点，过 A, B 两点向抛物线的准线作垂线，垂足分
别为 P,Q ，则梯形 APQB 的面积为
。
4、设 O 是坐标原点， F 是抛物线 y2 2 px( p 0) 的焦点， A 是抛物线上的一点， FA 与 x 轴正
抛物线及其性质知识点大全与经典例题及解析
抛物线及其性质【考纲说明】1、掌握抛物线的简单几何性质，能运用性质解决与抛物线有关问题。
2、通过类比，找出抛物线与椭圆，双曲线的性质之间的区别与联系。
【知识梳理】1．抛物线定义：平面内到一定点F 和一条定直线l 的距离相等的点的轨迹称为抛物线． 2．抛物线四种标准方程的几何性质：图形参数p 几何意义 参数p 表示焦点到准线的距离，p 越大，开口越阔.开口方向 右左上下 标 准方 程 22(0)y px p => 22(0)y px p =-> 22(0)x py p =>22(0)x py p =->焦 点位 置 X 正X 负Y 正Y 负焦 点坐 标 (,0)2p (,0)2p -(0,)2p(0,)2p -准 线方 程2p x =-2p x =2p y =-2p y =围 0,x y R ≥∈0,x y R ≤∈0,y x R ≥∈0,y x R ≤∈对 称轴 X 轴X 轴Y 轴Y 轴顶 点坐 标 （0,0）离心率 1e =通 径 2p焦半径11(,)A x y 12p AF x =+12p AF x =-+12p AF y =+12p AF y =-+焦点弦长AB12()x x p ++ 12()x x p -++ 12()y y p ++ 12()y y p -++焦点弦长AB以AB 为直径的圆必与准线l 相切3．抛物线)0(22>=p px y 的几何性质：(1)范围 因为p>0，由方程可知x ≥0，所以抛物线在y 轴的右侧，当x 的值增大时，|y |也增大，说明抛物线向右上方和右下方无限延伸． (2)对称性：对称轴要看一次项，符号决定开口方向． (3)顶点（0，0），离心率：1=e ，焦点(,0)2p F ，准线2px -=，焦准距p ． (4) 焦点弦：抛物线)0(22>=p px y 的焦点弦AB ，),(11y x A ,),(22y x B ,则p x x AB ++=21||． 弦长|AB|=x 1+x 2+p,当x 1=x 2时，通径最短为2p 。
高中抛物线知识点归纳总结与练习题及标准答案
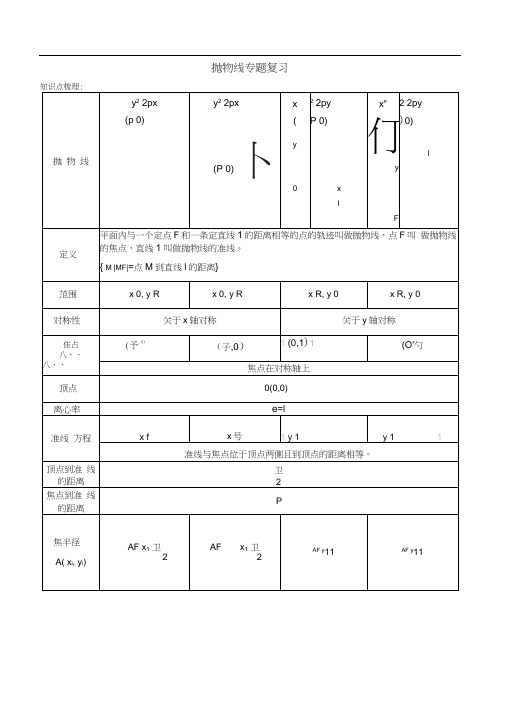
抛物线专题复习•直线与抛物线的位置关系，消y得：1）当k=0 时，直线l 与抛物线的对称轴平行，有一个交点；（2）当k丰0时，△>0,直线l与抛物线相交，两个不同交点；△=0,直线I与抛物线相切，一个切点；△v0，直线I与抛物线相离，无公共点。
3）若直线与抛物线只有一个公共点, 则直线与抛物线必相切吗?（不一定）．关于直线与抛物线的位置关系问题常用处理方法直线I : y kx b 抛物线，(p 0)联立方程法：y kx b 2 2 22k x 2(kb p)x b 0y 2px设交点坐标为A(x「y i) , B(x2,y2),则有0 ,以及为X2,%X2 ,还可进一步求出2 2y y2kx.( b kx2 b k(x1x2) 2b，y1 y2(kx1b)(kx2b) k X j X2kb(X j x2) b在涉及弦长，中点，对称，面积等问题时，常用此法，比如 相交弦AB 的弦长AB v 1 k 2|% x 2| 』k 2x 2)2 4x 1x 2 4l __k 2或 AB y 1 召 y i y 2抛物线练习1、 已知点P 在抛物线y 2 = 4x 上，那么点P 到点Q (2，— 1)的距离与点P 到抛物线焦点距离之和取得最小值时，点P 的坐标为 ___________2、 已知点P 是抛物线y 2 2x 上的一个动点，则点 P 到点(0，2)的距离与P 到该抛物线准线的距离之和的 最小值为 ___________23、 直线y x 3与抛物线y 4x 交于A, B 两点，过代B 两点向抛物线的准线作垂线，垂足分别为 P,Q ，则梯形APQB 的面积为 __________2 ULWo4、 设O 是坐标原点，F 是抛物线y 2 2px(p 0)的焦点，A 是抛物线上的一点，FA 与x 轴正向的夹角为60°， uuu 则OA 为 ___________5、 抛物线y 2 4x 的焦点为F ,准线为I ,经过F 且斜率为 3的直线与抛物线在 x 轴上方的部分相交于点 A ，1「2心1 y 2)2 4y 』2ki 2 a.5AK 丄l ，垂足为K ,则△ AKF 的面积是 ______________6、 已知抛物线C: y 2 8x 的焦点为F ,准线与x 轴的交点为K ,点A 在C 上且AK| J 2|AF |，贝U AFK的面积为 ___________2 27、 已知双曲线 —1，则以双曲线中心为焦点，以双曲线左焦点为顶点的抛物线方程为4 52&在平面直角坐标系 xoy 中，有一定点 A(2,1)，若线段0A 的垂直平分线过抛物线 y 2 px( p 0)则该抛物线的方程是 ___________ 。
抛物线知识点总结及例题讲解
当 a0 时，对称轴左边 y 随 x 的增大而减小，对称轴右边 y 随 x 的增大而增大，当 a0 时，
情况相反. ② ③ ④ 抛物线的最高点或最低点都是指抛物线的顶点. 只要解析式的二次项系数的绝对值相同，两条抛物线的形状就相同. 一元二次方程 ax bx c 0 （a≠0）的根，就是抛物线 y ax bx c 与 x 轴 交点的
2 2 2
.
5.二次函数 y ax c （c 不为零） ，当 x 取 x1，x2（x1≠x2）时，函数值相等，则 x1 与 x2 的关系 是 .
2
6.抛物线 y ax bx c 当 b=0 时，对称轴是 侧，当 a，b 异号时，对称轴在 y 轴 7.抛物线 y 2( x 1) 3 开口
B. ,0
1 2
C.（-1，5）
D.（3，4）
5
杭州龙文教育科技有限公司
个性化辅导讲义
17.直线 y A.0 个
5 1 x 2 与抛物线 y x 2 x 的交点个数是（ 2 2
B.1 个
2
）
C.2 个
D.互相重合的两个 ）
18.关于抛物线 y ax bx c （a≠0） ，下面几点结论中，正确的有（ ①
2
b 2 4ac b 2 ， ) 2a 4a
∴顶点是 (
b 4ac b 2 b , ) ，对称轴是直线 x . 2a 4a 2a
2
（2） 配方法： 运用配方的方法， 将抛物线的解析式化为 y a( x h) k 的形式， 得到顶点为 (h, k ) ， 对称轴是直线 .
y
b ＜1 2a ∴ 2a b ＞0
-1
O
高中抛物线知识点归纳总结与练习题与答案
一． 直线与抛物线的位置关系 直线，抛物线，，消y 得：（1）当k=0时，直线l 与抛物线的对称轴平行，有一个交点； （2）当k ≠0时，Δ＞0，直线l 与抛物线相交，两个不同交点； Δ=0， 直线l 与抛物线相切，一个切点； Δ＜0，直线l 与抛物线相离，无公共点。
（3）若直线与抛物线只有一个公共点,则直线与抛物线必相切吗?（不一定）二． 关于直线与抛物线的位置关系问题常用处理方法 直线l ：b kx y += 抛物线，)0( p① 联立方程法：⎩⎨⎧=+=pxy bkx y 22⇒0)(2222=+-+b x p kb x k 设交点坐标为),(11y x A ,),(22y x B ，则有0 ∆,以及2121,x x x x +，还可进一步求出bx x k b kx b kx y y 2)(212121++=+++=+，2212122121)())((b x x kb x x k b kx b kx y y +++=++=在涉及弦长，中点，对称，面积等问题时，常用此法，比如 1. 相交弦AB 的弦长2122122124)(11x x x x k x x k AB -++=-+=ak ∆+=21 或 2122122124)(1111y y y y k y y k AB -++=-+=ak ∆+=21 b. 中点),(00y x M , 2210x x x +=， 2210y y y += ② 点差法：设交点坐标为),(11y x A ，),(22y x B ，代入抛物线方程，得1212px y = 2222px y =将两式相减，可得)(2))((212121x x p y y y y -=+-2121212y y px x y y +=--a. 在涉及斜率问题时，212y y pk AB +=b. 在涉及中点轨迹问题时，设线段AB 的中点为),(00y x M ，021*******y py p y y p x x y y ==+=--， 即0y p k AB =， 同理，对于抛物线)0(22≠=p py x ，若直线l 与抛物线相交于B A 、两点，点),(00y x M 是弦AB 的中点，则有px p x p x x k AB 0021222==+=（注意能用这个公式的条件：1）直线与抛物线有两个不同的交点，2）直线的斜率存在，且不等于零）抛物线练习及答案1、已知点P 在抛物线y 2 = 4x 上，那么点P 到点Q （2，－1）的距离与点P 到抛物线焦点距离之和取得最小值时，点P 的坐标为 。
抛物线练习题带答案,知识点总结(基础版)
抛物线重难点复习一．知识点总结2.,,C F p M C 焦抛物线的焦点为为是准距上的点min ;.2pMF OF MF MF p ===(1)(2)若与对称轴垂直，则2000(,)2(0)23p M x y y px p MF x =>=±+±若是抛物线上的点则() 2000(,)224p P x y x py PF y =±=±+若是抛物线上的(点，则) (5).()(90)1cos s ()1co p MF MF pp or MF p MF MF θθθθ≥≤-+==≤ 若与抛物线的为则夹角，对称轴1)2MF MF MF 以为直径的圆与坐标轴相切(的中点到坐标轴的距离为(6)1122(,)(,),.F l A x y B x y l k θ3.过焦点的直线交抛物线于点、，记直线的斜率为倾斜角为221222:2,(),sin 2sin AOB p p C y px AB x x p S θθ∆==++==（1）若抛物线则221222:2,()cos 2cos AOB p p C x py AB y y p S θθ∆==++==（2）若抛物线则， 222222121212124:2,,;:2,,44p p C y px y y p x x C x py x x p y y ==-===-=（）若抛物线则若抛物线则112(3)2();p AF BF p+=通焦点弦的最径小值为 (5)以AB 为直径的圆与准线相切12MN AB ⎛⎫=⎪⎝⎭（6）以CD 为直径的圆与AB 相切与焦点F1．已知抛物线22(0)y px p =>上横坐标为 3 的点到其焦点的距离为 4，则p =________. 【答案】2【解析】抛物线y 2=2px （p ＞0， ∵抛物线y 2=2px （p ＞04，∴p=2.故答案为2.2．已知F 是抛物线y 2=2x 的焦点，A ,B 是该抛物线上的两点，|AF |+|BF |=11，则线段AB 的中点到y 轴的距离为（ ） A. 3 B. 4 C. 5 D. 7 【答案】C 【解析】∵F 是抛物线y 2=2x 的焦点∴F (12,0) ,准线方程x =−12， 设A (x 1,y 1),B (x 2,y 2)∴|AF |+|BF |=x 1+1+x 2+1=11x 1+x 2=10,∴线段AB 的中点横坐标为5∴线段AB 5，所以B 选项是正确的.3．已知抛物线C ：的焦点为F ，()00A x y ，是C 上一点，则0x =（ ）A. 2B. 2±C. 4D. 4± 【答案】D【解析】28x y =，如图，由抛物线的几何意义，可知0022AF Al y y ===+，所以02y =， 所以04x =±，故选D 。
抛物线练习题带答案,知识点总结(提高版)
抛物线重难点复习一．知识点总结2.,,C F p M C 焦抛物线的焦点为为是准距上的点min ;.2pMF OF MF MF p ===(1)(2)若与对称轴垂直，则2000(,)2(0)23p M x y y px p MF x =>=±+±若是抛物线上的点则() 2000(,)224p P x y x py PF y =±=±+若是抛物线上的(点，则) (5).()(90)1cos s ()1co p MF MF pp or MF p MF MF θθθθ≥≤-+==≤若与抛物线的为则夹角，对称轴1)2MF MF MF 以为直径的圆与坐标轴相切(的中点到坐标轴的距离为(6)1122(,)(,),.F l A x y B x y l k θ3.过焦点的直线交抛物线于点、，记直线的斜率为倾斜角为221222:2,(),sin 2sin AOB p p C y px AB x x p S θθ∆==++==（1）若抛物线则 221222:2,()cos 2cos AOB p p C x py AB y y p S θθ∆==++==（2）若抛物线则，112(3)2();p AF BF p+=通焦点弦的最径小值为222222121212124:2,,;:2,,44p p C y px y y p x x C x py x x p y y ==-===-=（）若抛物线则若抛物线则 (5)以AB 为直径的圆与准线相切12MN AB ⎛⎫=⎪⎝⎭标准方程22(0)y px p => 22(0)y px p =-> 22(0)x py p => 22(0)x py p =>图形焦点坐标 (,0)2p (,0)2p -(0,)2p(0,)2p -准线方程 2p x =-2p x =2p y =-2p y =范围 0x ≥ 0x ≤ 0y ≥0y ≤对称性 x 轴x 轴y 轴 y 轴 顶点 (0,0)(0,0)(0,0)(0,0)离心率 1e =1e =1e =1e =通径2p（6）以CD 为直径的圆与AB 相切与焦点F1．已知抛物线C ： 2x的焦点为F ， ()00A x y ，是C 上一点，则0x =（ ）A. 2B. 2±C. 4D. 4± 【答案】D【解析】28x y =，如图，由抛物线的几何意义，可知0022AF Al y y ===+，所以02y =， 。
高中抛物线知识点归纳总结与练习题与答案
直线与抛物线的位置关系直线■:、•二，抛物线「占八y =hr+J<，=2丹消y得.+2(肪-p)x+护二0(1) 当k=0时，直线I与抛物线的对称轴平行，有一个交点；(2) 当k M 0 时，△>0,直线I与抛物线相交，两个不同交点；△=0,直线I与抛物线相切，一个切点；△v0，直线I与抛物线相离，无公共点。
(3) 若直线与抛物线只有一个公共点，则直线与抛物线必相切吗？(不一定)-------- •- •关于直线与抛物线的位置关系问题常用处理方法直线1:kx b 抛物线- 丁芒八，(p ' 0)①联立方程法：y =kx +b 2 2 2:2二k2x2+2(kb — p)x+b2 =0y =2px设交点坐标为Ad-yJ, BX M)，则有:'0 ,以及x「，还可进一步求出y 1 y 2 二 kx i b kx 2 b = k(x 1 x 2) 2b2 2y 1y 2 =(kx b)(kx 2 b) = k X j X 2 kb(x-i x 2) b在涉及弦长，中点，对称，面积等问题时，常用此法，比如 1. 相交弦AB 的弦长AB| = J i +冏为—x 2| = J l + k 2 J% +x 2)2 —4X J X 2 = J l + k 2-p I 9!1 2 - 2+■^2^ (y i + y 2)—4y i y 2 =H 1 + kb. 中点 M （X 0,yo ）, X 0 二宁②点差法： 设交点坐标为A （X 1，yJ ，B （X 2,y 2），代入抛物线方程，得2 2 y 12px 1y 2 2px 2将两式相减，可得（% -丫2）（% y 2）=2卩（％ -X 2）y 1 -y 2 _ 2p X 1 -X 2 y 1 y 2屮-七 _ 2p _ 2p _ p 捲 一X 2y 1 y 22 y y °同理，对于抛物线X 2 =2py （p=0），若直线l 与抛物线相交于A 、 是弦AB 的中点，则有k AB 二凶」二空0 =些2p 2p p（注意能用这个公式的条件：1）直线与抛物线有两个不同的交点, 在，且不等于零）a.在涉及斜率问题时,k AB2p y 1 y 2b.在涉及中点轨迹问题时，设线段AB 的中点为 M （x o ，y o ），B 两点，点 M (X o , y o ) 2）直线的斜率存AB =、：i +^卜1 _y2 =抛物线练习及答案21已知点P 在抛物线y = 4x 上，那么点P 到点Q (2, - 1)的距离与点 P 到抛物线焦点距离之1和取得最小值时，点 P 的坐标为。
(2021年整理)(完整)高中抛物线知识点归纳总结与练习题及答案
（完整）高中抛物线知识点归纳总结与练习题及答案编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（完整）高中抛物线知识点归纳总结与练习题及答案）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（完整）高中抛物线知识点归纳总结与练习题及答案的全部内容。
焦 点弦 长AB12()x x p ++12()x x p -++ 12()y y p ++ 12()y y p -++焦点弦AB 的几条性质11(,)A x y 22(,)B x y以AB 为直径的圆必与准线l 相切若AB 的倾斜角为α，则22sin pAB α=若AB 的倾斜角为α，则22cos pAB α=2124p x x = 212y y p =-112AF BF AB AF BF AF BF AF BF p++===•• 切线方程00()y y p x x =+00()y y p x x =-+ 00()x x p y y =+ 00()x x p y y =-+一．直线与抛物线的位置关系直线,抛物线,，消y 得：(1）当k=0时,直线l 与抛物线的对称轴平行，有一个交点； （2)当k ≠0时，Δ＞0，直线l 与抛物线相交，两个不同交点； Δ=0， 直线l 与抛物线相切，一个切点;ox ()22,B x yFy ()11,A x yΔ＜0，直线l 与抛物线相离，无公共点。
（3）若直线与抛物线只有一个公共点,则直线与抛物线必相切吗?(不一定)二． 关于直线与抛物线的位置关系问题常用处理方法直线l ：b kx y += 抛物线,)0( p① 联立方程法:⎩⎨⎧=+=pxy bkx y 22⇒0)(2222=+-+b x p kb x k 设交点坐标为),(11y x A ,),(22y x B ，则有0 ∆,以及2121,x x x x +，还可进一步求出b x x k b kx b kx y y 2)(212121++=+++=+，2212122121)())((b x x kb x x k b kx b kx y y +++=++=在涉及弦长，中点，对称，面积等问题时，常用此法，比如1. 相交弦AB 的弦长2122122124)(11x x x x k x x k AB -++=-+=ak ∆+=21 或 2122122124)(1111y y y y k y y k AB -++=-+=ak ∆+=21 b. 中点),(00y x M ， 2210x x x +=, 2210yy y +=② 点差法：设交点坐标为),(11y x A ，),(22y x B ，代入抛物线方程,得1212px y = 2222px y =将两式相减，可得)(2))((212121x x p y y y y -=+-2121212y y px x y y +=--a. 在涉及斜率问题时，212y y pk AB +=b. 在涉及中点轨迹问题时，设线段AB 的中点为),(00y x M ,021*******y py p y y p x x y y ==+=--， 即0y p k AB =, 同理，对于抛物线)0(22≠=p py x ，若直线l 与抛物线相交于B A 、两点，点),(00y x M 是弦AB 的中点，则有px p x p x x k AB 0021222==+=(注意能用这个公式的条件：1)直线与抛物线有两个不同的交点，2)直线的斜率存在，且不等于零）抛物线练习及答案1、已知点P 在抛物线y 2= 4x 上，那么点P 到点Q （2,－1）的距离与点P 到抛物线焦点距离之和取得最小值时，点P 的坐标为 。
高考一轮复习 抛物线 知识点+例题+练习
自主梳理1．抛物线的概念平面内到一个定点F 和一条定直线l (F 不在l 上)的距离________的点的轨迹叫做抛物线．点F 叫做抛物线的________，直线l 叫做抛物线的________．2．抛物线的标准方程与几何性质标准方程y 2＝2px (p >0) y 2＝－2px (p >0) x 2＝2py (p >0) x 2＝－2py (p >0) p 的几何意义：焦点F 到准线l 的距离图形顶点 O (0,0)对称轴 y ＝0x ＝0焦点 F (p2，0) F (－p2，0)F (0，p 2)F (0，－p2)离心率 e ＝1准线 方程 x ＝－p 2x ＝p 2 y ＝－p 2y ＝p 2 范围 x ≥0， y ∈R x ≤0， y ∈R y ≥0， x ∈R y ≤0， x ∈R 开口 方向向右向左向上向下自我检测1．抛物线y 2＝8x 的焦点到准线的距离是________．2．若抛物线y 2＝2px 的焦点与椭圆x 26＋y 22＝1的右焦点重合，则p 的值为________．3．设抛物线的顶点在原点，准线方程为x ＝－2，则抛物线的方程是________．4．设F 为抛物线y 2＝4x 的焦点，A 、B 、C 为该抛物线上三点，若F A →＋FB →＋FC →＝0，则|F A →|＋|FB →|＋|FC →|＝________.5．已知抛物线方程为y 2＝2px (p >0)，过该抛物线焦点F 且不与x 轴垂直的直线AB 交抛物线于A 、B 两点，过点A 、点B 分别作AM 、BN 垂直于抛物线的准线，分别交准线于M 、N 两点，那么∠MFN ＝________.学生姓名 教师姓名班主任 日期时间段年级课时教学内容 抛物线复习教学目标 1.掌握抛物线的定义、几何图形和标准方程，知道它们的简单几何性质. 2.理解数形结合的思想． 重点 同上 难点同上探究点一抛物线的定义及应用例1已知抛物线y2＝2x的焦点是F，点P是抛物线上的动点，又有点A(3,2)，求P A ＋PF的最小值，并求出取最小值时P点的坐标．变式迁移1已知点P在抛物线y2＝4x上，那么点P到点Q(2，－1)的距离与点P到抛物线焦点距离之和取得最小值时，点P的坐标为________．探究点二求抛物线的标准方程例2已知抛物线的顶点在原点，焦点在y轴上，抛物线上一点M(m，－3)到焦点的距离为5，求m的值、抛物线方程和准线方程．变式迁移2 根据下列条件求抛物线的标准方程：(1)抛物线的焦点F 是双曲线16x 2－9y 2＝144的左顶点； (2)过点P (2，－4)．探究点三 抛物线的几何性质例3 过抛物线y 2＝2px 的焦点F 的直线和抛物线相交于A ，B 两点，如图所示．(1)若A ，B 的纵坐标分别为y 1，y 2，求证：y 1y 2＝－p 2；(2)若直线AO 与抛物线的准线相交于点C ，求证：BC ∥x 轴．变式迁移3 已知AB 是抛物线y 2＝2px (p >0)的焦点弦，F 为抛物线的焦点，A (x 1，y 1)，B (x 2，y 2)．求证：(1)x 1x 2＝p 24；(2)1AF ＋1BF为定值．一、填空题1．已知抛物线C ：y 2＝4x 的焦点为F ，直线y ＝2x －4与C 交于A ，B 两点，则cos ∠AFB 等于________．2．将两个顶点在抛物线y 2＝2px (p >0)上，另一个顶点是此抛物线焦点的正三角形个数记为n ，则n ＝________.3．已知抛物线y 2＝2px ，以过焦点的弦为直径的圆与抛物线准线的位置关系是________．4．抛物线y 2＝x 上到其准线和顶点距离相等的点的坐标为________．5．设O 为坐标原点，F 为抛物线y 2＝4x 的焦点，A 为抛物线上一点，若OA →·AF →＝－4，则点A 的坐标为________．6．设圆C 位于抛物线y 2＝2x 与直线x ＝3所围成的封闭区域(包含边界)内，则圆C 的半径能取到的最大值为________．7．已知A 、B 是抛物线x 2＝4y 上的两点，线段AB 的中点为M (2,2)，则AB ＝________.8．设抛物线y 2＝2px (p >0)的焦点为F ，点A (0，2)．若线段F A 的中点B 在抛物线上，则B 到该抛物线准线的距离为________．二、解答题9．已知顶点在原点，焦点在x 轴上的抛物线截直线y ＝2x ＋1所得的弦长为15，求抛物线方程．10．已知抛物线C：x2＝8y.AB是抛物线C的动弦，且AB过F(0,2)，分别以A、B为切点作轨迹C的切线，设两切线交点为Q，证明：AQ⊥BQ.轨迹方程自主梳理1．曲线的方程与方程的曲线如果曲线C 上点的坐标(x ，y )都是方程f (x ，y )＝0的解，且以方程f (x ，y )＝0的解(x ，y )为坐标的点都在曲线C 上，那么，方程f (x ，y )＝0叫做曲线C 的方程．曲线C 叫做方程f (x ，y )＝0的曲线．2．求曲线方程的一般方法(五步法)求曲线(图形)的方程，一般有下面几个步骤：(1)建立适当的坐标系，用有序实数对(x ，y )表示曲线上任意一点M 的坐标； (2)写出适合条件p 的点M 的集合P ＝{M |p (M )}； (3)用坐标表示条件p (M )，列出方程f (x ，y )＝0； (4)化方程f (x ，y )＝0为最简形式；(5)说明以化简后的方程的解为坐标的点都在曲线上．3．求曲线方程的常用方法：(1)直接法；(2)定义法；(3)代入法；(4)参数法．自我检测1．已知动点P 在曲线2x 2－y ＝0上移动，则点A (0，－1)与点P 连线中点的轨迹方程为______________．2．一动圆与圆O ：x 2＋y 2＝1外切，而与圆C ：x 2＋y 2－6x ＋8＝0内切，那么动圆的圆心P 的轨迹是__________________________________________________________________．3．已知A (0,7)、B (0，－7)、C (12,2)，以C 为一个焦点作过A 、B 的椭圆，椭圆的另一个焦点F 的轨迹方程是______________________．4．若M 、N 为两个定点且MN ＝6，动点P 满足PM →·PN →＝0，则P 点的轨迹方程为________．5．若曲线C 1：x 2＋y 2－2x ＝0与曲线C 2：y (y －mx －m )＝0有四个不同的交点，则实数m 的取值范围是__________________．探究点一 直接法求轨迹方程例1 动点P 与两定点A (a,0)，B (－a,0)连线的斜率的乘积为k ，试求点P 的轨迹方程，并讨论轨迹是什么曲线．变式迁移1 已知两点M (－2,0)、N (2,0)，点P 为坐标平面内的动点，满足|MN →||MP →|＋MN →·NP →＝0，则动点P (x ，y )的轨迹方程为______________．探究点二 定义法求轨迹方程例2 已知两个定圆O 1和O 2，它们的半径分别是1和2，且O 1O 2＝4.动圆M 与圆O 1内切，又与圆O 2外切，建立适当的坐标系，求动圆圆心M 的轨迹方程，并说明轨迹是何种曲线．变式迁移2 在△ABC 中，A 为动点，B 、C 为定点，B ⎝⎛⎭⎫－a 2，0，C ⎝⎛⎭⎫a2，0，且满足条件sin C －sin B ＝12sin A ，则动点A 的轨迹方程为____________________________________．探究点三 相关点法(代入法)求轨迹方程例3 如图所示，从双曲线x 2－y 2＝1上一点Q 引直线x ＋y ＝2的垂线，垂足为N . 求线段QN 的中点P 的轨迹方程．变式迁移3 已知长为1＋2的线段AB 的两个端点A 、B 分别在x 轴、y 轴上滑动，P是AB 上一点，且AP →＝22PB →.求点P 的轨迹C 的方程．一、填空题1．已知椭圆的焦点是F 1、F 2，P 是椭圆的一个动点，如果M 是线段F 1P 的中点，则动点M 的轨迹是_________________________________________________________________．2．已知A 、B 是两个定点，且AB ＝3，CB －CA ＝2，则点C 的轨迹方程为______________．3．长为3的线段AB 的端点A 、B 分别在x 轴、y 轴上移动，AC →＝2CB →，则点C 的轨迹方程为____________．4．如图，圆O ：x 2＋y 2＝16，A (－2，0)，B (2,0)为两个定点．直线l 是圆O 的一条切线，若经过A 、B 两点的抛物线以直线l 为准线，则抛物线焦点所在的轨迹是________．5．P 是椭圆x 216＋y 29＝1上的动点，作PD ⊥y 轴，D 为垂足，则PD 中点的轨迹方程为____________．6．已知两定点A (－2,0)，B (1,0)，如果动点P 满足P A ＝2PB ，则点P 的轨迹所包围的图形的面积等于______．7．已知△ABC 的顶点B (0,0)，C (5,0)，AB 边上的中线长CD ＝3，则顶点A 的轨迹方程为______________．8．平面上有三点A (－2，y )，B ⎝⎛⎭⎫0，y 2，C (x ，y )，若AB →⊥BC →，则动点C 的轨迹方程为__________．二、解答题9．已知抛物线y2＝4px (p>0)，O为顶点，A，B为抛物线上的两动点，且满足OA⊥OB，如果OM⊥AB于点M，求点M的轨迹方程．10．已知椭圆C的中心为平面直角坐标系xOy的原点，焦点在x轴上，它的一个顶点到两个焦点的距离分别是7和1.(1)求椭圆C的方程；(2)若P为椭圆C上的动点，M为过P且垂直于x轴的直线上的一点，OPOM＝λ，求点M 的轨迹方程，并说明轨迹是什么曲线．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
焦半径11(,)A x y12p AF x =+12p AF x =-+12p AF y =+12p AF y =-+焦 点弦 长AB12()x x p ++12()x x p -++ 12()y y p ++ 12()y y p -++焦点弦AB 的几条性质11(,)A x y 22(,)B x y以AB 为直径的圆必及准线l 相切若AB 的倾斜角为α，则22sin pAB α=若AB 的倾斜角为α，则22cos pAB α=2124p x x = 212y y p =-112AF BF AB AF BF AF BF AF BF p++===•• 切线方程00()y y p x x =+00()y y p x x =-+ 00()x x p y y =+ 00()x x p y y =-+一． 直线及抛物线的位置关系直线，抛物线，，消y 得：ox ()22,B x yFy ()11,A x y（1）当k=0时，直线l 及抛物线的对称轴平行，有一个交点； （2）当k ≠0时，Δ＞0，直线l 及抛物线相交，两个不同交点； Δ=0， 直线l 及抛物线相切，一个切点； Δ＜0，直线l 及抛物线相离，无公共点。
（3）若直线及抛物线只有一个公共点,则直线及抛物线必相切吗?（不一定）二． 关于直线及抛物线的位置关系问题常用处理方法直线l ：b kx y += 抛物线，)0( p① 联立方程法：⎩⎨⎧=+=pxy bkx y 22⇒0)(2222=+-+b x p kb x k 设交点坐标为),(11y x A ,),(22y x B ，则有0 ∆,以及2121,x x x x +，还可进一步求出bx x k b kx b kx y y 2)(212121++=+++=+，2212122121)())((b x x kb x x k b kx b kx y y +++=++=在涉及弦长，中点，对称，面积等问题时，常用此法，比如1. 相交弦AB 的弦长2122122124)(11x x x x k x x k AB -++=-+=ak ∆+=21 或 2122122124)(1111y y y y k y y k AB -++=-+=ak ∆+=21 b. 中点),(00y x M , 2210x x x +=， 2210yy y +=② 点差法：设交点坐标为),(11y x A ，),(22y x B ，代入抛物线方程，得1212px y = 2222px y =将两式相减，可得)(2))((212121x x p y y y y -=+-2121212y y px x y y +=--a. 在涉及斜率问题时，212y y pk AB +=b. 在涉及中点轨迹问题时，设线段AB 的中点为),(00y x M ，021*******y py p y y p x x y y ==+=--， 即0y pk AB =， 同理，对于抛物线)0(22≠=p py x ，若直线l 及抛物线相交于B A 、两点，点),(00y x M 是弦AB 的中点，则有px p x p x x k AB 0021222==+=（注意能用这个公式的条件：1）直线及抛物线有两个不同的交点，2）直线的斜率存在，且不等于零）抛物线练习及答案1、已知点P 在抛物线y 2 = 4x 上，那么点P 到点Q （2，－1）的距离及点P 到抛物线焦点距离之和取得最小值时，点P 的坐标为 。
（41,－1）2、已知点P 是抛物线22y x =上的一个动点，则点P 到点（0，2）的距离及P 到该抛物线准线的距离之和的最小值为。
3、直线3y x =-及抛物线24y x =交于,A B 两点，过,A B 两点向抛物线的准线作垂线，垂足分别为,P Q ，则梯形APQB 的面积为 。
484、设O 是坐标原点，F 是抛物线22(0)y px p =>的焦点，A 是抛物线上的一点，FA 及x 轴正向的夹角为60，则OA 为 。
5、抛物线24y x =的焦点为F ，准线为l ，经过F 线在x 轴上方的部分相交于点A ，AK l ⊥，垂足为K ，则AKF △的面积是 。
6、已知抛物线2:8C y x =的焦点为F ，准线及x 轴的交点为K ，点A 在C 上且AK =，则AFK ∆的面积为 。
87、已知双曲线22145x y -=，则以双曲线中心为焦点，以双曲线左焦点为顶点的抛物线方程为 。
8、在平面直角坐标系xoy 中，有一定点(2,1)A ,若线段OA 的垂直平分线过抛物线22(0)y px p =>则该抛物线的方程是 。
9、在平面直角坐标系xoy 中，已知抛物线关于x 轴对称，顶点在原点O ，且过点P(2，4)，则该抛物线的方程是 。
28y x =10、抛物线2y x =-上的点到直线4380x y +-=距离的最小值是 。
4311、已知抛物线y 2=4x,过点P(4,0)的直线及抛物线相交于A(x 1,y 1),B(x 2,y 2)两点，则y 12+y 22的最小值是 。
3212、若曲线2y ＝|x |＋1及直线y ＝kx ＋b 没有公共点，则k 、b 分别应满足的条件是 。
k =0,-1<b <113、已知抛物线y-x 2+3上存在关于直线x+y=0对称的相异两点A 、B ，则|AB|等于（ ）CA.3B.4C.32D.4214、已知抛物线22(0)y px p =>的焦点为F ，点111222()()P x y P x y ，，，，333()P x y ，在抛物线上，且2132x x x =+， 则有（ ）ＣＡ．123FP FP FP += Ｂ．222123FP FP FP += Ｃ．2132FP FP FP =+Ｄ．2213FP FP FP =·15、已知点11(,)A x y ,22(,)B x y 12(0)x x ≠是抛物线22(0)y px p =>上的两个动点,O 是坐标原点,向量OA ,OB 满足OA OB OA OB +=-.设圆C 的方程为221212()()0x y x x x y y y +-+-+=。
(1) 证明线段AB 是圆C 的直径;(2)当圆C 的圆心到直线x-2y=0的距离的最小值为5时，求p 的值。
解： (1)证明1: 22,()()OA OB OA OB OA OB OA OB +=-∴+=-，222222OA OA OB OB OA OA OB OB +⋅+=-⋅+，整理得: 0OA OB ⋅=，12120x x y y ∴⋅+⋅=，设M(x,y)是以线段AB 为直径的圆上的任意一点,则0MA MB ⋅=，即1212()()()()0x x x x y y y y --+--=，整理得:221212()()0x y x x x y y y +-+-+=， 故线段AB 是圆C 的直径。
证明2: 22,()()OA OB OA OB OA OB OA OB +=-∴+=-，222222OA OA OB OB OA OA OB OB +⋅+=-⋅+，整理得: 0OA OB ⋅=，12120x x y y ∴⋅+⋅= (1)设(x,y)是以线段AB 为直径的圆上则即2112211(,)y y y y x x x x x x x x --⋅=-≠≠--， 去分母得: 1212()()()()0x x x x y y y y --+--=，点11122122(,),(,),(,)(,)x y x y x y x y 满足上方程,展开并将(1)代入得:221212()()0x y x x x y y y +-+-+=，故线段AB 是圆C 的直径。
证明3: 22,()()OA OB OA OB OA OB OA OB +=-∴+=-，222222OA OA OB OB OA OA OB OB +⋅+=-⋅+，整理得: 0OA OB ⋅=，12120x x y y ∴⋅+⋅=……(1) 以线段AB 为直径的圆的方程为2222121212121()()[()()]224x x y y x y x x y y ++-+-=-+-， 展开并将(1)代入得:221212()()0x y x x x y y y +-+-+=， 故线段AB 是圆C 的直径(2)解法1:设圆C 的圆心为C(x,y),则121222x x x y y y +⎧=⎪⎪⎨+⎪=⎪⎩ 2211222,2(0)y px y px p ==>，22121224y y x x p∴=，又因12120x x y y ⋅+⋅=， 1212x x y y ∴⋅=-⋅，22121224y y y y p∴-⋅=，12120,0x x y y ⋅≠∴⋅≠，2124y y p ∴⋅=-， 2222121212121211()(2)2444x x y y x y y y y y y p p p +==+=++-221(2)y p p=+， 所以圆心的轨迹方程为222y px p =-， 设圆心C 到直线x-2y=0的距离为d,则22221|(2)2|y py d +-===22=当y=p 时,d=，2p ∴=.解法2: 设圆C 的圆心为C(x,y),则121222x x x y y y +⎧=⎪⎪⎨+⎪=⎪⎩ 2211222,2(0)y px y px p ==>，22121224y y x x p ∴=，又因12120x x y y ⋅+⋅=，1212x x y y ∴⋅=-⋅，22121224y y y y p∴-⋅=，12120,0x x y y ⋅≠∴⋅≠，2124y y p ∴⋅=-，2222121212121211()(2)2444x x y y x y y y y y y p p p +==+=++-221(2)y p p=+， 所以圆心的轨迹方程为222y px p =-， 设直线x-2y+m=0到直线x-2y=0的距离为5,则2m =±，因为x-2y+2=0及222y px p =-无公共点,所以当x-2y-2=0及222y px p =-仅有一个公共点时,该点到直线x-2y=0的距离最小值为522220(2)2(3)x y y px p--=⎧⎨=-⎩ 将(2)代入(3)得222220y py p p -+-=，2244(22)0p p p ∴∆=--=，02.p p >∴=解法3: 设圆C 的圆心为C(x,y),则121222x x x y y y +⎧=⎪⎪⎨+⎪=⎪⎩圆心C 到直线x-2y=0的距离为d,则1212|()|x x y y d +-+=2211222,2(0)y px y px p ==>，22121224y y x x p∴=，又因12120x x y y ⋅+⋅=，1212x x y y ∴⋅=-⋅，22121224y y y y p ∴-⋅=，12120,0x x y y ⋅≠∴⋅≠，2124y y p ∴⋅=-，2212122221|()()|y y y y d +-+∴==22=， 当122y y p +=时,d5=，2p ∴=.16、已知椭圆C 1:22143x y +=,抛物线C 2:2()2(0)y m px p -=>,且C 1、C 2的公共弦AB 过椭圆C 1的右焦点.(1)当AB⊥x 轴时,求m 、p 的值，并判断抛物线C 2的焦点是否在直线AB 上；(2)是否存在m 、p 的值，使抛物线C 2的焦点恰在直线AB 上？若存在，求出符合条件的m 、p 的值；若不存在，请说明理由.解：（1）当AB⊥x 轴时，点A 、B 关于x 轴对称，所以m ＝0，直线AB 的方程为x=1，从而点A 的坐标为（1，23）或（1，－23）. 因为点A 在抛物线上，所以p 249=，即89=p . 此时C 2的焦点坐标为（169，0），该焦点不在直线AB 上.（2）解法一 当C 2的焦点在AB 时，由（Ⅰ）知直线AB 的斜率存在，设直线AB 的方程为)1(-=x k y .由⎪⎩⎪⎨⎧=+-=134)1(22y x x k y 消去y 得01248)43(2222=-+-+k x k x k . ……①设A 、B 的坐标分别为（x 1,y 1）, （x 2,y 2）, 则x 1,x 2是方程①的两根，x 1＋x 2＝22438k k +.因为AB 既是过C 1的右焦点的弦，又是过C 2所以)(214)212()212(2121x x x x AB +-=-+-=，且1212()()22p pAB x x x x p =+++=++.从而121214()2x x p x x ++=-+.所以12463px x -+=，即22846343k p k -=+.解得6,62±==k k 即.因为C 2的焦点),32(m F '在直线)1(-=x k y 上，所以k m 31-=.即3636-==m m 或.当36=m 时，直线AB 的方程为)1(6--=x y ； 当36-=m 时，直线AB 的方程为)1(6-=x y .解法二 当C 2的焦点在AB 时，由（Ⅰ）知直线AB 的斜率存在，设直线AB 的方程为)1(-=x k y .由⎪⎩⎪⎨⎧-==-)1(38)(2x k y x m y 消去y 得x m k kx 38)(2=--. ……①因为C 2的焦点),32(m F '在直线)1(-=x k y 上，所以)132(-=k m ，即k m 31-=.代入①有x k kx 38)32(2=-.即094)2(342222=++-k x k x k . ……②设A 、B 的坐标分别为（x 1,y 1）, （x 2,y 2）, 则x 1,x 2是方程②的两根，x 1＋x 2＝223)2(4k k +.由⎪⎩⎪⎨⎧=+-=134)1(22y x x k y 消去y 得01248)43(2222=-+-+k x k x k . ……③由于x 1,x 2也是方程③的两根，所以x 1＋x 2＝22438k k +.从而223)2(4kk +＝22438kk +. 解得6,62±==k k 即.因为C 2的焦点),32(m F '在直线)1(-=x k y 上，所以k m 31-=.即3636-==m m 或.当36=m 时，直线AB 的方程为)1(6--=x y ； 当36-=m 时，直线AB 的方程为)1(6-=x y .解法三 设A 、B 的坐标分别为（x 1,y 1）, （x 2,y 2）, 因为AB 既过C 1的右焦点)0,1(F ，又是过C 2的焦点),32(m F '，所以)212()212()2()2(212121x x p x x p x p x AB -+-=++=+++=.即916)4(3221=-=+p x x . ……① 由（Ⅰ）知21x x ≠，于是直线AB 的斜率m m x x y y k 313201212=--=--=， ……②且直线AB 的方程是)1(3--=x m y ,所以32)2(32121m x x m y y =-+-=+. ……③又因为⎪⎩⎪⎨⎧=+=+1243124322222121y x y x ，所以0)(4)(312122121=--⋅+++x x y y y y x x . ……④ 将①、②、③代入④得322=m ，即3636-==m m 或.当36=m 时，直线AB 的方程为)1(6--=x y ； 当36-=m 时，直线AB 的方程为)1(6-=x y .17、如图，倾斜角为a 的直线经过抛物线x y 82=的焦点F ，且及抛物线交于A 、B 两点。