第六章 有限元三角形单元程序设计
有限元单元法程序设计

有限元单元法程序设计是有限元分析(FEA)中的重要环节,它通过将连续的物理问题离散化为大量的、相互之间仅按特定方式相互联系的有限个单元的组合,从而进行求解。
以下是一个简单的有限元单元法程序设计的例子:
1.定义节点和单元:首先,我们需要定义模型的节点(nodes)和单元(elements)。
节点是空间中的点,而单元是由节点连接而成的物理实体。
2.建立网格:然后,我们需要根据模型的形状和大小,建立起一个合适的网格。
这个网格应该能够捕捉到模型的主要特征,并且足够细以捕捉到细节。
3.定义材料属性:接下来,我们需要为每个单元定义材料属性,比如弹性模量、泊松比、密度等。
4.施加载荷和约束:然后,我们需要根据问题的要求,对模型施加载荷和约束。
例如,我们可能需要施加压力、重力等载荷,以及位移、转动等约束。
5.进行有限元分析:最后,我们使用有限元方法进行求解。
这包括计算每个节点的位移和应力,以及根据这些结果进行后处理,比如生成报告、生成可视化图像等。
以上就是一个简单的有限元单元法程序设计的过程。
在实际应用
中,还需要考虑很多其他的因素,比如模型的复杂性、计算资源的限制等。
因此,编写一个有效的有限元程序需要深入理解有限元方法、计算机科学和工程知识。
有限元中三角形单元源程序

附录:平面问题三角形单元源程序******************************************************************* * ANALYSIS PROGTAM OF FINITE ELEMENT METHOD * * FOR PLANE STRESS/STRAIN OF TRIANGULAR ELEMENT * * ----- FEMT3.FOR ----- * *------------------------------------------------------------- * * Subroutines: 1-SDATA, 2-STE, 3-ATE, 4-DTE, 5-BTE, 6-STIFF * * 7-EQUPE, 8-INSCD, 9-BGSMT, 10-SIGME * ******************************************************************* DIMENSION LND(50,3),X(100),Y(100),JR(20,3),PJ(20,3),P(200) REAL KS(200,100)OPEN(5,FILE='FEMT3.DAT')OPEN(6,FILE='FEMT3.OUT',STATUS='NEW')READ(5,*) NJ,NE,NS,NPJ,IPS(结点、单元、支承、荷载、类型)WRITE(6,*)' FINITE ELEMENT ANALYSIS IN PLANE PROBLEM'WRITE(6,*)' SOURCE DATA OUTPUT'WRITE(6,20) NJ,NE,NS,NPJ,IPS20 FORMAT(4X,'NJ',3X,'NE',3X,'NS',3X,'NPJ',2X,'IPS'/1X,5I5)IF(IPS.EQ.0) WRITE(6,*)' PLANE STRESS PROBLEM'IF(IPS.EQ.1) WRITE(6,*)' PLANE STRAIN PROBLEM'CALL SDATA(NJ,NE,NS,NW,NPJ,IPS,E,PR,T,V,LND,X,Y,JR,PJ)NJ2=2*NJWRITE(6,50) NJ250 FORMAT(/1X,'DEGREES OF FREEDOM=',I5)WRITE(6,60) NW60 FORMAT(1X,'BAND WIDTH=',I5)CALL STIFF(NJ,NE,NJ2,NW,LND,X,Y,E,PR,T,KS)(总刚6)CALL EQUPE(NJ,NE,NPJ,NJ2,T,V,LND,X,Y,PJ,P)({P}7)CALL INSCD(NS,NW,NJ2,JR,KS,P)(引入支承条件8)CALL BGSMT(NJ,NJ2,NW,KS,P)(解方程9)CALL SIGME(NE,NJ,NJ2,E,PR,LND,X,Y,P)(求应力10)CLOSE(5)CLOSE(6)END*--------------------------------------------------------C SUBPROGRAM-1C INPUT STRUCTURAL DATASUBROUTINE SDATA(NJ,NE,NS,NW,NPJ,IPS,E,PR,* T,V,LND,X,Y,JR,PJ)DIMENSION LND(NE,3),X(NJ),Y(NJ),JR(NS,3),PJ(NPJ,3)READ(5,*) E,PR,T,V(弹性模量、泊松比、厚度、容重)WRITE(6,10) E,PR,T,V10 FORMAT(/6X,'E',10X,'PR',9X,'T',9X,'V'/,4F10.2)READ(5,*)((LND(I,J),J=1,3),I=1,NE)(结点编码)WRITE(6,20)20 FORMAT(/1X,'ELEMENT INFORMATION'/3X,'ELEM',3X,* 'I J K'/)WRITE(6,30)(I,(LND(I,J),J=1,3),I=1,NE)30 FORMAT(1X,4I5)READ(5,*)(X(I),Y(I),I=1,NJ)(结点坐标)WRITE(6,40)40 FORMAT(/1X,'COORDINATES OF NODES'/3X,'NODES',* 8X,'X',13X,'Y')WRITE(6,50)(I,X(I),Y(I),I=1,NJ)50 FORMAT(1X,I5,2E15.6)READ(5,*)((JR(I,J),J=1,3),I=1,NS)(约束信息)WRITE(6,60)60 FORMAT(/1X,'CONSTRAINED NODES'/3X,'NODE',3X,'X',4X,'Y') WRITE(6,70)((JR(I,J),J=1,3),I=1,NS)70 FORMAT(1X,3I5)READ(5,*)((PJ(I,J),J=1,3),I=1,NPJ)(荷载信息)WRITE(6,80)80 FORMAT(/1X,'LOAD CASES'/3X,'NODE',8X,'X',13X,'Y')WRITE(6,90)((PJ(I,J),J=1,3),I=1,NPJ)90 FORMAT(1X,F5.0,2E15.6)100 NW=0(半带宽)DO 110 IE=1,NEDO 110 I=1,3DO 110 J=1,3IW=IABS(LND(IE,I)-LND(IE,J))IF(NW.LT.IW) THENNW=IWENDIF110 CONTINUENW=(NW+1)*2IF(IPS.NE.0) THENE=E/(1.0-PR*PR)PR=PR/(1.0-PR)ENDIFEND*---------------------------------------------------------C SUBPROGRAM-2C CALCULATE ELEMENT STIFFNESS MATRIXSUBROUTINE STE(IE,NJ,NE,LND,X,Y,E,PR,T,KE)DIMENSION LND(NE,3),X(NJ),Y(NJ),B(3,6),D(3,3)REAL KE(6,6)CALL ATE(IE,NJ,NE,LND,X,Y,AE)CALL DTE(E,PR,D)CALL BTE(IE,NJ,NE,LND,X,Y,AE,B)DO 10 I=1,6DO 10 J=1,6KE(I,J)=0.DO 10 K=1,3DO 10 K1=1,310 KE(I,J)=KE(I,J)+B(K,I)*D(K,K1)*B(K1,J)C=AE*TDO 30 I=1,6DO 30 J=1,630 KE(I,J)=KE(I,J)*CEND*------------------------------------------------ C SUBPROGRAM-3C CALCULATE ELEMENT AREASUBROUTINE ATE(IE,NJ,NE,LND,X,Y,AE)DIMENSION LND(NE,3),X(NJ),Y(NJ)I=LND(IE,1)J=LND(IE,2)K=LND(IE,3)XIJ=X(J)-X(I)YIJ=Y(J)-Y(I)XIK=X(K)-X(I)YIK=Y(K)-Y(I)AE=.5*(XIJ*YIK-XIK*YIJ)END*----------------------------------------------C SUBPROGRAM-4C CALCULATE ELASTICITY MATRIXSUBROUTINE DTE(E,PR,D)DIMENSION D(3,3)DO 10 I=1,3DO 10 J=1,310 D(I,J)=0.D(1,1)=E/(1.-PR*PR)D(1,2)=E*PR/(1.-PR*PR)D(2,1)=D(1,2)D(2,2)=D(1,1)D(3,3)=.5*E/(1.+PR)END*------------------------------------------------ C SUBPROGRAM-5C CALCULATE MATRIX [B]SUBROUTINE BTE(IE,NJ,NE,LND,X,Y,AE,B)DIMENSION LND(NE,3),X(NJ),Y(NJ),B(3,6)I=LND(IE,1)J=LND(IE,2)K=LND(IE,3)DO 10 II=1,3DO 10 JJ=1,610 B(II,JJ)=0.B(1,1)=Y(J)-Y(K)B(1,3)=Y(K)-Y(I)B(1,5)=Y(I)-Y(J)B(2,2)=X(K)-X(J)B(2,4)=X(I)-X(K)B(2,6)=X(J)-X(I)B(3,1)=B(2,2)B(3,2)=B(1,1)B(3,3)=B(2,4)B(3,4)=B(1,3)B(3,5)=B(2,6)B(3,6)=B(1,5)DO 20 I1=1,3DO 20 J1=1,620 B(I1,J1)=.5/AE*B(I1,J1)END*------------------------------------------------------- C SUBPROGRAM-6C CALCULATE GLOBAL STIFFNESS MATRIXSUBROUTINE STIFF(NJ,NE,NJ2,NW,LND,X,Y,E,PR,T,KS) DIMENSION LND(NE,3),X(NJ),Y(NJ)REAL KS(NJ2,NW),KE(6,6)DO 5 I=1,NJ2DO 5 J=1,NW5 KS(I,J)=0.DO 10 IE=1,NECALL STE(IE,NJ,NE,LND,X,Y,E,PR,T,KE)DO 10 I=1,3IZ=LND(IE,I)DO 10 II=1,2IH =2*(I -1)+IIIDH=2*(IZ-1)+IIDO 10 J=1,3JZ=LND(IE,J)DO 10 JJ=1,2L =2*(J -1)+JJIL=2*(JZ-1)+JJIF(IL.GE.IDH) THENIDL=IL-IDH+1KS(IDH,IDL)=KS(IDH,IDL)+KE(IH,L)ENDIF10 CONTINUEEND*-------------------------------------------------------- C SUBPROGRAM-7C CALCULATE NODAL LOAD VECTORSUBROUTINE EQUPE(NJ,NE,NPJ,NJ2,T,V,LND,X,Y,PJ,P) DIMENSION LND(NE,3),X(NJ),Y(NJ),PJ(NPJ,3),P(NJ2) DO 10 I=1,NJ210 P(I)=0.DO 20 I=1,NPJII=PJ(I,1)P(2*II-1)=PJ(I,2)20 P(2*II)=PJ(I,3)30 IF(V.EQ.0.) GOTO 50DO 40 IE=1,NECALL ATE(IE,NJ,NE,LND,X,Y,AE)PE=-V*AE*T/3.DO 40 I=1,3II=LND(IE,I)40 P(2*II)=P(2*II)+PE50 RETURNEND*---------------------------------------------C SUBPROGRAM-8C INTRODUCE BOUNDARY CONDITIONSUBROUTINE INSCD(NS,NW,NJ2,JR,KS,P)DIMENSION P(NJ2),JR(NS,3)REAL KS(NJ2,NW)DO 30 I=1,NSIR=JR(I,1)DO 30 J=2,3IF(JR(I,J).EQ.0) GOTO 30II=2*IR+J-3KS(II,1)=1.DO 10 JJ=2,NW10 KS(II,JJ)=0.IF(II.GT.NW) JO=NWIF(II.LE.NW) JO=IIDO 20 JJ=2,JO20 KS(II-JJ+1,JJ)=0.P(II)=0.30 CONTINUEEND*-------------------------------------------C SUBPROGRAM-9C SOLVE EQUATIONS BY GS METHODSUBROUTINE BGSMT(NJ,NJ2,NW,KS,P)DIMENSION P(NJ2)REAL KS(NJ2,NW)NJ1=NJ2-1DO 20 K=1,NJ1IF(NJ2.GT.K+NW-1) IM=K+NW-1IF(NJ2.LE.K+NW-1) IM=NJ2K1=K+1DO 20 I=K1,IML=I-K+1C=KS(K,L)/KS(K,1)IW=NW-L+1DO 10 J=1,IWM=J+I-K10 KS(I,J)=KS(I,J)-C*KS(K,M)20 P(I)=P(I)-C*P(K)P(NJ2)=P(NJ2)/KS(NJ2,1)DO 40 I1=1,NJ1I=NJ2-I1IF(NW.GT.NJ2-I+1) JO=NJ2-I+1IF(NW.LE.NJ2-I+1) JO=NWDO 30 J=2,JOK=J+I-130 P(I)=P(I)-KS(I,J)*P(K)40 P(I)=P(I)/KS(I,1)WRITE(6,50)50 FORMAT(/1X,'NODAL DISPLACEMENTS'/3X,* 'NODE',5X,'X-DISP.',8X,'Y-DISP.')DO 60 I=1,NJ60 WRITE(6,70) I,P(2*I-1),P(2*I)70 FORMAT(1X,I5,2E15.6)END*---------------------------------------------------C SUBPROGRAM-10C CALCULATE ELEMENT STRESS MATRIXSUBROUTINE SIGME(NE,NJ,NJ2,E,PR,LND,X,Y,P)DIMENSION LND(NE,3),X(NJ),Y(NJ),D(3,3),B(3,6), * S(3,6),ST(3),P(NJ2),DE(6)WRITE(6,*)WRITE(6,*)' ELEMENT STRESSES'CALL DTE(E,PR,D)DO 50 IE=1,NECALL ATE(IE,NJ,NE,LND,X,Y,AE)CALL BTE(IE,NJ,NE,LND,X,Y,AE,B)DO 10 I=1,3DO 10 J=1,6S(I,J)=0.DO 10 K=1,310 S(I,J)=S(I,J)+D(I,K)*B(K,J)DO 20 I=1,3DO 20 J=1,2IH=2*(I-1)+JIW=2*(LND(IE,I)-1)+J20 DE(IH)=P(IW)DO 30 I=1,3ST(I)=0.DO 30 J=1,630 ST(I)=ST(I)+S(I,J)*DE(J)SGX=ST(1)SGY=ST(2)TXY=ST(3)ASG=(SGX+SGY)*.5RSG=SQRT(.25*(SGX-SGY)**2+TXY*TXY)SGMA=ASG+RSGSGMI=ASG-RSGIF(SGY.EQ.SGMI) CETA=0.IF(SGY.NE.SGMI) CETA=90.-57.29578*ATAN* (TXY/(SGY-SGMI))50 WRITE(6,60) IE,SGX,SGY,TXY,SGMA,SGMI,CETA60 FORMAT(1X,'ELEMENT NO.=',I4/2X,'SIGX=',E10.4, * 2X,'SIGY=',E10.4,2X,'TXY =',E10.4/2X,'SGMA=', * E10.4,2X,'SGMI=',E10.4,2X,'CETA=',E10.4)END。
matlab有限元三角形单元编程

matlab有限元三角形单元编程
在MATLAB中进行有限元分析,可以使用其自带的有限元分析工具箱(FEATool)进行编程。
以下是一个简单的例子,演示如何使用三角形单元进行有限元分析:
1. 打开MATLAB,进入FEATool环境。
2. 创建新的有限元模型。
选择“Model”菜单下的“New Model”选项,进入“Model Builder”界面。
3. 在“Model Builder”界面中,选择“2D Triangle”单元类型,并在绘图区域中绘制出三角形网格。
4. 在“Model Builder”界面中,设置材料属性、边界条件和载荷等参数。
5. 运行有限元分析。
选择“Model”菜单下的“Solve”选项,进行有限元求解。
6. 查看结果。
选择“Model”菜单下的“Results”选项,可以查看位移、应力、应变等结果。
以上是一个简单的例子,演示了如何使用三角形单元进行有限元分析。
在实际应用中,还需要根据具体问题进行详细的建模和计算。
第6章——常应变三角形单元

[S1
S 2 S3 ]
ci 1-µ bi 2
bi E µb = Si DB = i i 2 A(1 − µ 2 ) 1-µ ci 2
µ ci
平面应变:用平面应变弹性矩阵代入得到类似结果。
22:42
有限单元法
崔向阳
16
单元应变和应力矩阵
由于同一单元中的D、B矩阵都是常数矩阵,所以S矩阵也是常 数矩阵。也就是说,三角形三节点单元内的应力分量也是常 量。 当然,相邻单元的E, µ, A和bi、ci(i,j,m)一般不完全相同, 因而具有不同的应力,这就造成在相邻单元的公共边上存在 着应力突变现象。但是随着网格的细分,这种突变将会迅速 减小。
m j
h
1 i U = ∫∫ (σ xε x + σ yε y + τ xyγ xy )hdxdy x 2 A 1 T T T T = ∫∫ σ T εhdxdy σ = ( D ε ) = ε D 2 A
−1
u1 u2 u 3
u ( x, y ) = {1 x
1 x1 y} 1 x2 1 x3
y1 y2 y3
−1
u1 u2 u 3
4
22:42
有限单元法
崔向阳
平面三角形单元
假设
{ N1
N2
N 3 } = {1 x
m 相邻单元的位移在公共边上是连续的 形函数在单元上的面积分和边界上的线积分公式为 i
j p
A ∫ ∫A Ni dxdy = 3
式中 lij 为 ij 边的长度。
Ni =1 i m j
22:42
1 ∫ij Ni dl = 2 lij
有限元单元法程序设计

有限元单元法程序设计有限元单元法是一种用于工程结构分析和设计的计算方法,它将大型结构分解为许多小的离散单元,通过分析单元之间的相互作用来预测结构的力学行为。
有限元单元法程序设计是指针对特定工程问题,编写计算机程序来实现有限元分析的过程。
下面将介绍有限元单元法程序设计的基本流程和关键要点。
一、问题建模和网格划分有限元单元法程序设计的第一步是对工程结构进行合理的建模和网格划分。
建模的目的是将实际结构抽象为适用于有限元分析的数学模型,包括定义结构的几何特征、材料属性、边界条件等。
网格划分是将结构分解为许多小的单元,每个单元具有一定的形状和尺寸,以便于数值计算。
常用的单元形状包括三角形、四边形、四面体、六面体等,根据结构的特点选择合适的单元形状和尺寸。
二、单元刚度矩阵和载荷矩阵的求解在有限元单元法程序设计中,需要编写算法来求解每个单元的刚度矩阵和载荷矩阵。
单元刚度矩阵描述了单元内部的力学性能,包括刚度、弹性模量、泊松比等,它们通常通过数学公式或有限元理论推导得到。
载荷矩阵描述了单元受到的外部荷载,可以是均匀分布载荷、集中载荷或者边界条件引起的约束力。
通过合适的数值积分方法,可以计算得到每个单元的刚度矩阵和载荷矩阵。
三、组装全局刚度矩阵和载荷向量在有限元单元法程序设计中,需要将所有单元的刚度矩阵和载荷向量组装成整个结构的全局刚度矩阵和载荷向量。
这涉及到单元之间的连接关系以及边界条件的处理。
采用适当的组装算法,可以将各个单元的刚度矩阵和载荷向量叠加在一起,形成整个结构的刚度矩阵和载荷向量。
四、求解位移和应力有限元单元法程序设计的最后一步是求解结构的位移和应力。
通过斯蒂芬-泰勒算法或者其他迭代算法,可以得到整个结构的位移分布,然后根据位移场计算各个点的应变和应力。
这一过程涉及到对整个结构刚度矩阵的求解和对位移的后处理。
有限元单元法程序设计是一个复杂而又精密的工作,需要深入理解有限元原理、结构力学知识和数学方法。
matlab有限元三角形单元程序

matlab有限元三角形单元程序以下是一个简单的 MATLAB 有限元三角形单元程序的示例:```matlab% 定义模型参数E = 1000; % 弹性模量nu = 0.3; % 泊松比thickness = 1; % 板的厚度% 定义节点坐标nodes = [0, 0; 1, 0; 1, 1; 0, 1; 0.5, 0.5];% 定义单元连接关系connectivity = [1, 2, 5; 2, 3, 5; 3, 4, 5; 4, 1, 5];% 计算总节点数和总单元数numNodes = size(nodes, 1);numElements = size(connectivity, 1);% 初始化全局刚度矩阵和载荷向量K = zeros(numNodes);F = zeros(numNodes, 1);% 循环遍历每个单元for i = 1:numElements% 查找当前单元的节点编号nodesIndex = connectivity(i, :);% 根据节点编号从全局坐标矩阵中取出节点坐标coordinates = nodes(nodesIndex, :);% 计算当前单元的局部刚度矩阵localK = calculateLocalStiffness(E, nu, thickness, coordinates);% 组装局部刚度矩阵到全局刚度矩阵中K(nodesIndex, nodesIndex) = K(nodesIndex, nodesIndex) + localK;% 计算当前单元的局部载荷向量localF = calculateLocalLoad(thickness, coordinates);% 组装局部载荷向量到全局载荷向量中F(nodesIndex) = F(nodesIndex) + localF;end% 边界条件:节点1固定K(1, :) = 0;K(1, 1) = 1;F(1) = 0;% 解线性方程组U = K \ F;% 输出位移结果disp('节点位移:');disp(U);% 计算应力结果stress = calculateStress(E, nu, thickness, nodes, connectivity, U);% 输出应力结果disp('节点应力:');disp(stress);% 计算局部刚度矩阵的函数function localK = calculateLocalStiffness(E, nu, thickness, coordinates)% 计算单元的雅可比矩阵J = (1/2) * [coordinates(2,1)-coordinates(1,1), coordinates(3,1)-coordinates(1,1);coordinates(2,2)-coordinates(1,2), coordinates(3,2)-coordinates(1,2)];% 计算雅可比矩阵的逆矩阵invJ = inv(J);% 计算单元刚度矩阵B = invJ * [-1, 1, 0; -1, 0, 1];D = (E/(1-nu^2)) * [1, nu, 0; nu, 1, 0; 0, 0, (1-nu)/2]; localK = thickness * abs(det(J)) * (B' * D * B);end% 计算局部载荷向量的函数function localF = calculateLocalLoad(thickness, coordinates) localF = zeros(3, 1);midPoint = [sum(coordinates(:,1))/3,sum(coordinates(:,2))/3];localF(3) = thickness * 1 * det([coordinates(1,:); coordinates(2,:); midPoint]);end% 计算各节点应力的函数function stress = calculateStress(E, nu, thickness, nodes, connectivity, U)stress = zeros(size(nodes, 1), 3);for i = 1:size(connectivity, 1)nodesIndex = connectivity(i, :);coordinates = nodes(nodesIndex, :);Ke = calculateLocalStiffness(E, nu, thickness, coordinates);Ue = U(nodesIndex);stress(nodesIndex, :) = stress(nodesIndex, :) + (Ke * Ue)';endstress = stress / thickness;end```这个程序实现了一个简单的平面三角形单元有限元分析,包括定义节点坐标和单元连接关系、计算全局刚度矩阵和载荷向量、施加边界条件、解线性方程组、计算节点位移和应力等。
三角形单元有限元程序设计

三角形单元有限元程序设计一、引言
⑴文档背景
⑵文档目的
⑶读者对象
⑷名词解释
二、程序结构设计
⑴程序流程图
⑵程序组成模块描述
⑶主要数据结构设计
⑷代码逻辑设计
三、数据预处理
⑴数据输入格式与读取
⑵数据清洗与去噪
⑶数据预处理方法
⑷数据分割与划分
四、网格
⑴网格算法介绍
⑵网格质量评估与改善
⑶网格的实现方法
五、有限元方法
⑴有限元离散的原理
⑵有限元单元的选择
⑶有限元离散的网格节点选取
⑷有限元插值函数的计算六、模型求解
⑴线性方程组的求解方法
⑵模型参数的设置与调整
⑶迭代算法的选择与实现七、模型评估与验证
⑴结果评估指标的选择
⑵模型验证方法
⑶结果可视化与分析
八、性能优化
⑴程序性能分析与评估
⑵程序高效化的方法与技巧
⑶并行计算与优化
九、实例与案例
⑴实例介绍与问题描述
⑵实例数据处理过程
⑶实例模型求解与结果分析十、总结与展望
⑴工作总结
⑵程序改进与优化展望
⑶研究方向与发展趋势
十一、附件
●附件1、程序源代码
●附件2、输入数据样例文件
●附件3、网格结果数据文件附录:法律名词及注释
●法律名词1、注释1
●法律名词2、注释2
●法律名词3、注释3
请注意,附件的具体文件名和数据内容将根据你的实际情况进行调整。
法律名词及注释部分需要根据实际需要进行扩充和修改。
请合理对文档结构和章节内容进行调整,以符合你的具体要求。
第六章三角形单元的有限元法程序设计

从第j列的主对角线元素起到该列上方第一个非零 元素为止,所含元素的个数称为第j列的列高,记为hj ; 如果把第j列上方第1个非零元素的行号记为mj,则第j 列的列高为 hj = j - mj + 1 其实,hj就是第j行的左带宽,因而必有 UBW= max(hj)
j=1,2, …,N
利用节点位移信息数组 ID (去约束后节点位移自 由度编码),可容易地确定刚度矩阵 [K] 任何一列的 列高。
{ } [S ]{ }
例1:对角受压的正方形薄板,载 荷沿厚度均匀分布,为2N/m。由 于对称性,取1/4部分作为计算对
2N/m y x
象,试用有限元程序进行计算。
2N/m 2m 2m
h 1.0m, E 1.0, 0.0
例2:简支梁,梁高3m,跨度18m,厚度1m,承 受均布荷载10N/m2。已知 E 2 1010 N / m2 , 0.167
y为挤压应力,属次要应 力。材料力学不考虑 , FEM与弹性力学误差较大。
6.2 提高计算精度的方法
(1) 计算结果的整理 计算结果包括位移和应力两个方面。在位移方 面,一般无须进行整理工作。应力结果则需要 整理。通常认为计算出的应力是三角形单元形 心处的应力。而相邻单元之间的应力存在突变, 甚至正、负符号都不相同。为了由计算结果推 算出结构内某一点的接接实际的应力,必须通 过某种平均计算。通常可采用两单元平均法或 绕结点平均法。
平均法整理单元应力
两单元平均法:把两个相邻单元中的常应力加 以平均,用来表示公共边界中点处的应力。 绕结点平均法:把环绕某一结点的各单元常应 力加以平均,用以表示该结点的应力。在内结 点效果较好,而在边界结点可能很差,一般改 为应由内结点的应力外推计算出来。 (2)网格的细分 通过网格的细分,使每个单元的面积缩小,那 么尽管每个单元是应变、常应力单元,仍可较 好地反映结构中的应力变化,使得到的解答收 敛于问题的精确解。
有限元三角形单元求解方法
假设整体结构被划分为ne个单元和n个节点,在整体坐标系下,对于每个
单元均有:
(12)
将上述这些方程集合起来(整体坐标下叠加),便可得到整个结构的平衡方程。为此,需要将 、 、 体积膨胀,分别扩大为 , , 的矩阵才能相加。膨胀后,原有节点号对应位置的元素不变,而其它元素均为零。
对于整体结构有
将四个节点的坐标值带入上式
其中
(13)
总刚度矩阵处理
为了方便计算可以采用划零置一法对自由状态的刚度矩阵进行修正,将零位移对应的刚度矩阵的行和列置零,对角线上的主元素置一,其他元素不变,与此同时还要对 修正,将与位移项对应的各项置零。
具体参照论《总刚度矩阵的奇异性与非奇异性_边界条件处理方法的讨论》
四边形共四个节点,每个节点有x,y两个自由度,共8个自由度。因此x和y方向的位移场可以各有4个待定系数,即取以下多项式作为单元的位移场模式
(3)
求得
(4)
由此得到
(5)
式中: ;A为三角形单元的面积,为使面积的值为正,本单元节点号的次序必须是逆时针转向。
将式(5)带入式(2)得:
(6)
式中 ; ;
写成矩阵的形式 单元应变
(7)
将式(6)带入式(7)得
(8)
对于弹性力学的平面应力问题,应力应变关系可表示为:
(9)
(10)
单元刚度矩阵
(11)
三角形单元刚度矩阵
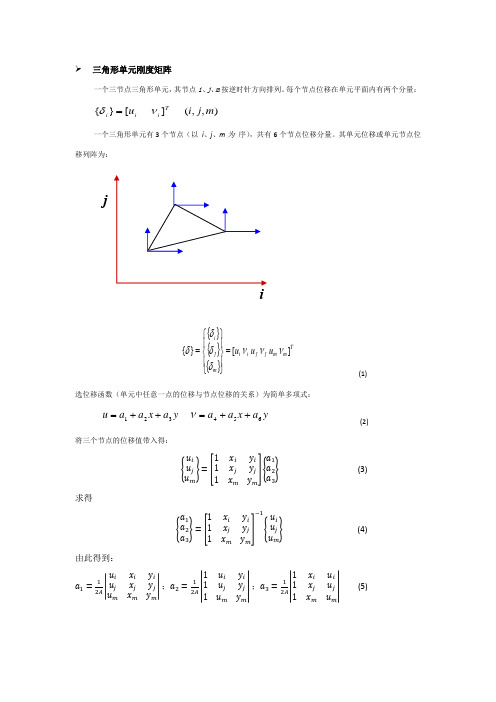
一个三节点三角形单元,其节点i、j、m按逆时针方向排列。每个有3个节点(以i、j、m为序),共有6个节点位移分量。其单元位移或单元节点位移列阵为:
(1)
选位移函数(单元中任意一点的位移与节点位移的关系)为简单多项式:
(2)
将三个节点的位移值带入得:
有限元三角形划分程序

J0=z;
for(j=2;j<=J0;j++)
KZ[z-j+1][j]=0.0;
}
P[z]=0.0;
}
NJ1=NJ2-1;
for(k=1;k<=NJ1;k++)
{
if(NJ2>k+DD-1)
IM=k+DD-1;
{
printf("%2d %-21.6f %-21.6f\n",i,P[2*i-1],P[2*i]);
}
for(E=1;E<=NE;E++)
{
DUGD(E,2);
for(i=1;i<=3;i++)
{
for(j=1;j<=2;j++)
dh=2*(JM[E][i]-1)+ii;
for(j=1;j<=3;j++)
{
for(jj=1;jj<=2;jj++)
{
)+jj;
dl=zl-dh+1;
{
S[i][j]=0.0;
for(k=1;k<=3;k++)
S[i][j]=S[i][j]+D[i][k]*B[k][j];
}
}
if(ASK>2)
{
for(i=1;i<=6;i++)
P[2*ME]=P[2*ME]+PE;
}
}
for(i=1;i<=NZ;i++)
弹性力学有限元-06-三角形单元

第6章 有限元法
6.1 概述 The finite element method
在17世纪, 牛顿和莱布尼茨发明了积分法,证明了该运算具有 整体对局部的可加性。
在18世纪,著名数学家高斯提出了加权余值法及线性代数方程组 的解法。另一位数学家Lagrange提出泛函分析。泛函分析是将 偏微分方程改写为积分表达式的另一途经。
1960年,美国加州大学伯克利分校的R.W.Clough教授在论文 中提出了“有限单元”,这样的名词。 值得骄傲的是我国南京 大学冯康教授在此前后独立地在论文中提出了“有限单元”
第6章 有限元法
The finite element method
有限元计算方法作为一种技术更多的与FEM软件的发展紧密的 结合起来。方法不断更新,优胜劣汰,传承和发展.有限元算法 (FFE)。在传统有限元分析的数值计算方法之中,有直接计算 法(DirectSolver)与迭代法(Iterative 所谓快速解法)两种。
3、单元内任意点的位移列阵f
{ f } [u ]T
(6-3)
y
m
v
·
u
j
i
y
m
· j
i
x
x
图6-1
4、单元内任意点的应变列阵
{} [ x y xy ]T
(6-4)
5、单元内任意点的应力列阵
{} [ x y xy ]T
y
m
· j
i
(6-5)
6、几何方程(Geometric equax tions)
3
1
3
5
7
9
66 6
④
⑤
555
单元、节点需编号
8
有限元三角形单元

有限元三角形单元
有限元三角形单元是有限元分析中常用的基本构件,用于建立复杂结构的数学模型,以进行工程分析。
这些三角形单元是用来离散化连续问题的,将其转换为有限元模型,以便计算机可以进行数值求解。
在有限元分析中,三角形单元有不同类型,其中常见的包括:
1. 线性三角形单元:
- 由三个节点组成的简单三角形单元。
- 三角形的三条边都是直线。
- 这种单元的形状函数是线性的,适用于简单的结构和问题。
2. 二阶和高阶三角形单元:
- 包括更多节点以提高精度的三角形单元。
- 二阶三角形单元具有额外的中间节点,使得形状函数更复杂,从而提高了精度。
- 高阶三角形单元同样通过增加节点来提高精度,但也增加了计算复杂度。
这些三角形单元被用于建立有限元模型,将结构或物体分割成小的几何形状,每个形状都有对应的节点和单元连接关系。
通过这些节点之间的位移和边界条件来建立结构的数学模型,从而进行力学、热力学等各种工程分析。
选择适当类型和精度的三角形单元对于准确地模拟实际问题非常重要,因为它们直接影响到模型的计算精度和效率。
有限元平面问题三角形实例

有限元平面问题三角形实例有限元法是一种常用的计算方法,可以用来解决各种工程问题。
其中,有限元平面问题是有限元法的一种应用,常用于分析三角形结构。
在有限元平面问题中,我们通常会将结构划分成许多小的单元,每个单元由节点和单元刚度矩阵组成。
而三角形结构则是有限元平面问题中常用的一种单元形状。
三角形结构的特点是简单而且易于处理,因此广泛应用于各种领域,如土木工程、机械工程、航空航天等。
下面我们就以一个实际的例子来说明如何应用有限元平面问题分析三角形结构。
假设我们要分析一个三角形钢板在受力作用下的变形情况。
首先,我们需要将钢板划分为许多小的三角形单元。
每个单元由三个节点组成,节点之间通过边连接。
在有限元分析中,我们需要对每个单元进行网格划分,并确定节点的坐标和边的长度。
然后,通过求解节点的位移和应力分布,可以得到钢板在受力作用下的变形情况。
具体来说,我们可以通过求解线性方程组来得到节点的位移。
而节点的应力则可以通过应变-位移关系来计算。
通过这种方式,我们可以得到钢板在受力作用下各个节点的位移和应力分布情况。
有限元平面问题的分析结果可以帮助我们了解结构的强度和刚度情况,为设计和优化提供依据。
例如,在钢板的设计中,我们可以通过有限元分析来确定合适的材料和尺寸,以满足结构的强度和刚度要求。
除了钢板,有限元平面问题还可以应用于其他类型的三角形结构。
例如,在土木工程中,我们可以使用有限元分析来分析三角形桥梁或者三角形支撑结构的变形和应力分布情况。
有限元平面问题是一种常用的分析方法,可以应用于各种三角形结构的分析。
通过对节点的位移和应力分布的求解,我们可以得到结构在受力作用下的变形情况。
这对于工程设计和优化至关重要,可以帮助我们提高结构的强度和刚度,确保其安全可靠。
有限元作业:三角形单元求解

《有限元作业》年级2015级学院机电工程学院专业名称班级学号学生2016年05月如下图所示为一受集中力P作用的结构,弹性模量E为常量,泊松比V=1/6,厚度为I=1。
按平面应力问题计算,运用有限元方法,分别采用三角形及四边形单元求解,求节点位移及单元应力(要求三角形单元数量不少于4个,四边形单元不少于2个)图(一)图(二)三角形单元求解图(三)四边形单元求解(1)如图划分三角形单元,工分成四个分别为④(2)如图分别进行编号1、2、3、4、5、6,并建立坐标系(3)编程进行求解,得出结果,其中假设力P=2000N调用Triangle2D3Node_Stiffness函数,求出单元刚度矩阵k1 =1.0e+06 *7.2857 -3.0000 -2.1429 0.8571 -5.1429 2.1429-3.0000 7.2857 2.1429 -5.1429 0.8571 -2.1429 -2.1429 2.1429 2.1429 0 0 -2.14290.8571 -5.1429 0 5.1429 -0.8571 0-5.1429 0.8571 0 -0.8571 5.1429 02.1429 -2.1429 -2.1429 0 0 2.1429k2 =1.0e+06 *5.1429 0 -5.1429 0.8571 0 -0.85710 2.1429 2.1429 -2.1429 -2.1429 0-5.1429 2.1429 7.2857 -3.0000 -2.1429 0.85710.8571 -2.1429 -3.0000 7.2857 2.1429 -5.14290 -2.1429 -2.1429 2.1429 2.1429 0-0.8571 0 0.8571 -5.1429 0 5.1429 k3 =1.0e+06 *2.1429 0 -2.1429 -2.1429 0 2.14290 5.1429 -0.8571 -5.1429 0.8571 0-2.1429 -0.8571 7.2857 3.0000 -5.1429 -2.1429 -2.1429 -5.1429 3.0000 7.2857 -0.8571 -2.14290 0.8571 -5.1429 -0.8571 5.1429 02.1429 0 -2.1429 -2.1429 0 2.1429 k4 =1.0e+06 *2.1429 0 -2.1429 -2.1429 0 2.14290 5.1429 -0.8571 -5.1429 0.8571 0-2.1429 -0.8571 7.2857 3.0000 -5.1429 -2.1429 -2.1429 -5.1429 3.0000 7.2857 -0.8571 -2.14290 0.8571 -5.1429 -0.8571 5.1429 02.1429 0 -2.1429 -2.1429 0 2.1429 调用Triangle2D3Node_Assembly函数,求出总体刚度矩阵求出的节点位移U =-0.00040.00080.00050.00100.00070.0023-0.00070.0026调用Triangle2D3Node_Stress函数,求出应力,S1、S2、S3、中求出的分别为Sx,Sy,SxyS1 =1.0e+03 *-4.4086-0.73483.5914S2 =1.0e+03 *4.4086-0.64050.4086S3 =1.0e+03 *1.8907-1.06012.1093S4 =1.0e+03 *-1.89072.10931.8907二、(1)如图划分四边形单元,工分成四个分别为(2)如图分别进行编号1、2、3、4、5、6,并建立坐标系(3)编程进行求解,得出结果,其中假设力P=2000N调用Quad2D4Node_Stiffness函数,求出单元刚度矩阵调用Quad2D4Node_Assembly函数,求出求出总体刚度矩阵求出节点位移U =0.00120.0017-0.00120.00170.00160.0049-0.00170.0052调用Quad2D4Node_Stress函数,求出单元应力中的的S1、S2、S3分别为Sx,Sy,Sxy应力分量S1 =1.0e+03 *0.0000-0.24782.0000S2 =1.0e+07 *0.68564.1135-1.7137程序附录一、1、三角形单元总程序:E=1e7;NU=1/6;t=1;ID=1;%调用Triangle2D3Node_Stiffness函数,求出单元刚度矩阵k1=Triangle2D3Node_Stiffness(E,NU,t,0,1,0,0,1,1,ID)k2=Triangle2D3Node_Stiffness(E,NU,t,0,0,1,0,1,1,ID)k3=Triangle2D3Node_Stiffness(E,NU,t,1,1,1,0,2,0,ID)k4=Triangle2D3Node_Stiffness(E,NU,t,2,0,2,1,1,1,ID)%调用Triangle2D3Node_Assembly函数,求出总体刚度矩阵KK = zeros(12,12);KK=Triangle2D3Node_Assembly(KK,k1,1,2,3);KK=Triangle2D3Node_Assembly(KK,k2,2,4,3);KK=Triangle2D3Node_Assembly(KK,k3,3,4,5);KK=Triangle2D3Node_Assembly(KK,k4,5,6,3)% 边界条件的处理及刚度方程求解k=KK(5:12,5:12)p=[0;0;0;0;0;0;0;2000]u=k\p%支反力的计算U=[0;0;0;0;u] %为节点位移P=KK*U%调用Triangle2D3Node_Strain函数,求出应变SN1、SN2、SN3中求出的分别为SNx,SNy,SNxyu1=[U(1);U(2);U(3);U(4);U(5);U(6)];u2=[U(3);U(4);U(7);U(8);U(5);U(6)];u3=[U(5);U(6);U(7);U(8);U(9);U(10)];u4=[U(9);U(10);U(11);U(12);U(5);U(6)];SN1=Triangle2D3Node_Strain(0,1,0,0,1,1,u1)SN2=Triangle2D3Node_Strain(0,0,1,0,1,1,u2)SN3=Triangle2D3Node_Strain(1,1,1,0,2,0,u3)SN4=Triangle2D3Node_Strain(2,0,2,1,1,1,u4)%调用Triangle2D3Node_Stress函数,求出应力,S1、S2、S3、中求出的分别为Sx,Sy,Sxyu1=[U(1);U(2);U(3);U(4);U(5);U(6)];u2=[U(3);U(4);U(7);U(8);U(5);U(6)];u3=[U(5);U(6);U(7);U(8);U(9);U(10)];u4=[U(9);U(10);U(11);U(12);U(5);U(6)];S1=Triangle2D3Node_Stress(E,NU,0,1,0,0,1,1,u1,ID)S2=Triangle2D3Node_Stress(E,NU,0,0,1,0,1,1,u2,ID)S3=Triangle2D3Node_Stress(E,NU,1,1,1,0,2,0,u3,ID)S4=Triangle2D3Node_Stress(E,NU,2,0,2,1,1,1,u4,ID)2、求刚度矩阵程序function k=Triangle2D3Node_Stiffness(E,NU,t,xi,yi,xj,yj,xm,ym,ID)%该函数计算单元的刚度矩阵%输入弹性模量E,泊松比NU,厚度t%输入三个节点i、j、m的坐标xi,yi,xj,yj,xm,ym%输入平面问题性质指示参数ID(1为平面应力,2为平面应变)%输出单元刚度矩阵k(6X6)%---------------------------------------------------------------A = (xi*(yj-ym) + xj*(ym-yi) + xm*(yi-yj))/2;betai = yj-ym;betaj = ym-yi;betam = yi-yj;gammai = xm-xj;gammaj = xi-xm;gammam = xj-xi;B = [betai 0 betaj 0 betam 0 ;0 gammai 0 gammaj 0 gammam ;gammai betai gammaj betaj gammam betam]/(2*A);if ID == 1D = (E/(1-NU*NU))*[1 NU 0 ; NU 1 0 ; 0 0 (1-NU)/2];elseif ID == 2D = (E/(1+NU)/(1-2*NU))*[1-NU NU 0 ; NU 1-NU 0 ; 0 0 (1-2*NU)/2]; endk= t*A*B'*D*B;3、求整体刚度矩阵function z = Triangle2D3Node_Assembly(KK,k,i,j,m)%该函数进行单元刚度矩阵的组装%输入单元刚度矩阵k%输入单元的节点编号I、j、m%输出整体刚度矩阵KK%---------------------------------------------------------------DOF(1)=2*i-1;DOF(2)=2*i;DOF(3)=2*j-1;DOF(4)=2*j;DOF(5)=2*m-1;DOF(6)=2*m;for n1=1:6for n2=1:6KK(DOF(n1),DOF(n2))= KK(DOF(n1),DOF(n2))+k(n1,n2);endendz=KK;4、求应变程序function strain=Triangle2D3Node_Strain(xi,yi,xj,yj,xm,ym,u)%该函数计算单元的应变%输入三个节点i、j、m的坐标xi,yi,xj,yj,xm,ym%输入单元的位移列阵u(6X1)%输出单元的应力strain(3X1),由于它为常应变单元,则单元的应变分量为SNx,SNy,SNz%---------------------------------------------------------------A = (xi*(yj-ym) + xj*(ym-yi) + xm*(yi-yj))/2;betai = yj-ym;betaj = ym-yi;betam = yi-yj;gammaj = xi-xm;gammam = xj-xi;B = [betai 0 betaj 0 betam 0 ;0 gammai 0 gammaj 0 gammam ;gammai betai gammaj betaj gammam betam]/(2*A);strain = B*u;5、求应力程序function stress=Triangle2D3Node_Stress(E,NU,xi,yi,xj,yj,xm,ym,u,ID)%该函数计算单元的应力%输入弹性模量E,泊松比NU,厚度t%输入三个节点i、j、m的坐标xi,yi,xj,yj,xm,ym%输入平面问题性质指示参数ID(1为平面应力,2为平面应变),单元的位移列阵u(6X1)%输出单元的应力stress(3X1),由于它为常应力单元,则单元的应力分量为Sx,Sy,Sxy%---------------------------------------------------------------A = (xi*(yj-ym) + xj*(ym-yi) + xm*(yi-yj))/2;betai = yj-ym;betaj = ym-yi;betam = yi-yj;gammai = xm-xj;gammam = xj-xi;B = [betai 0 betaj 0 betam 0 ;0 gammai 0 gammaj 0 gammam ;gammai betai gammaj betaj gammam betam]/(2*A);if ID == 1D = (E/(1-NU*NU))*[1 NU 0 ; NU 1 0 ; 0 0 (1-NU)/2];elseif ID == 2D = (E/(1+NU)/(1-2*NU))*[1-NU NU 0 ; NU 1-NU 0 ; 0 0 (1-2*NU)/2]; endstress = D*B*u;二、1、四边形单元总程序:E=1e7;NU=1/6;h=1;ID=1;%调用Quad2D4Node_Stiffness函数,求出单元刚度矩阵k1= Quad2D4Node_Stiffness(E,NU,h,0,1,0,0,1,0,1,1,ID)k2= Quad2D4Node_Stiffness(E,NU,h,1,0,2,0,2,1,1,1,ID)%调用Quad2D4Node_Assembly函数,求出求出总体刚度矩阵KK=zeros(12,12);KK= Quad2D4Node_Assembly(KK,k1,1,2,3,4);KK= Quad2D4Node_Assembly(KK,k2,3,5,6,4)% 边界条件的处理及刚度方程求解k=KK(5:12,5:12)p=[0;0;0;0;0;0;0;2000]u=k\p%支反力的计算U=[0;0;0;0;u] %为节点位移P=KK*U%调用Quad2D4Node_Stress函数,求出单元应力中的的S1、S2、S3分别为Sx,Sy,Sxy应力分量u1=[U(1);U(2);U(3);U(4);U(5);U(6);U(7);U(8)];u2=[U(5);U(6);U(9);U(10);U(11);U(12);U(7);(8)];S1= Quad2D4Node_Stress(E,NU,0,1,0,0,1,0,1,1,u1,ID)S2= Quad2D4Node_Stress(E,NU,1,0,2,0,2,1,1,1,u2,ID)2、求刚度矩阵程序function k= Quad2D4Node_Stiffness(E,NU,h,xi,yi,xj,yj,xm,ym,xp,yp,ID) %该函数计算单元的刚度矩阵%输入弹性模量E,泊松比NU,厚度h%输入4个节点i、j、m、p的坐标xi,yi,xj,yj,xm,ym,xp,yp%输入平面问题性质指示参数ID(1为平面应力,2为平面应变)%输出单元刚度矩阵k(8X8)%---------------------------------------------------------------syms s t;a = (yi*(s-1)+yj*(-1-s)+ym*(1+s)+yp*(1-s))/4;b = (yi*(t-1)+yj*(1-t)+ym*(1+t)+yp*(-1-t))/4;c = (xi*(t-1)+xj*(1-t)+xm*(1+t)+xp*(-1-t))/4;d = (xi*(s-1)+xj*(-1-s)+xm*(1+s)+xp*(1-s))/4;B1 = [a*(t-1)/4-b*(s-1)/4 0 ; 0 c*(s-1)/4-d*(t-1)/4 ;c*(s-1)/4-d*(t-1)/4 a*(t-1)/4-b*(s-1)/4];B2 = [a*(1-t)/4-b*(-1-s)/4 0 ; 0 c*(-1-s)/4-d*(1-t)/4 ;c*(-1-s)/4-d*(1-t)/4 a*(1-t)/4-b*(-1-s)/4];B3 = [a*(t+1)/4-b*(s+1)/4 0 ; 0 c*(s+1)/4-d*(t+1)/4 ;c*(s+1)/4-d*(t+1)/4 a*(t+1)/4-b*(s+1)/4];B4 = [a*(-1-t)/4-b*(1-s)/4 0 ; 0 c*(1-s)/4-d*(-1-t)/4 ;c*(1-s)/4-d*(-1-t)/4 a*(-1-t)/4-b*(1-s)/4];Bfirst = [B1 B2 B3 B4];Jfirst = [0 1-t t-s s-1 ; t-1 0 s+1 -s-t ;s-t -s-1 0 t+1 ; 1-s s+t -t-1 0];J = [xi xj xm xp]*Jfirst*[yi ; yj ; ym ; yp]/8;B = Bfirst/J;if ID == 1D = (E/(1-NU*NU))*[1 NU 0 ; NU 1 0 ; 0 0 (1-NU)/2];elseif ID == 2D = (E/(1+NU)/(1-2*NU))*[1-NU NU 0 ; NU 1-NU 0 ; 0 0 (1-2*NU)/2]; endBD = J*transpose(B)*D*B;r = int(int(BD, t, -1, 1), s, -1, 1);z = h*r;k = double(z);3、求总体刚度矩阵程序function z = Quad2D4Node_Assembly(KK,k,i,j,m,p)%该函数进行单元刚度矩阵的组装%输入单元刚度矩阵k,单元的节点编号i、j、m、p%输出整体刚度矩阵KK%---------------------------------------------------------------DOF(1)=2*i-1;DOF(2)=2*i;DOF(3)=2*j-1;DOF(4)=2*j;DOF(5)=2*m-1;DOF(6)=2*m;DOF(7)=2*p-1;DOF(8)=2*p;for n1=1:8for n2=1:8KK(DOF(n1),DOF(n2))= KK(DOF(n1),DOF(n2))+k(n1,n2);endendz=KK;4、求应力程序function stress= Quad2D4Node_Stress(E,NU,xi,yi,xj,yj,xm,ym,xp,yp,u,ID) %该函数计算单元的应力%输入弹性模量E,泊松比NU,厚度h,%输入4个节点i、j、m、p的坐标xi,yi,xj,yj,xm,ym,xp,yp,%输入平面问题性质指示参数ID(1为平面应力,2为平面应变)%输入单元的位移列阵u(8X1)%输出单元的应力stress(3X1)%由于它为常应力单元,则单元的应力分量为Sx,Sy,Sxy%---------------------------------------------------------------syms s t;a = (yi*(s-1)+yj*(-1-s)+ym*(1+s)+yp*(1-s))/4;b = (yi*(t-1)+yj*(1-t)+ym*(1+t)+yp*(-1-t))/4;c = (xi*(t-1)+xj*(1-t)+xm*(1+t)+xp*(-1-t))/4;d = (xi*(s-1)+xj*(-1-s)+xm*(1+s)+xp*(1-s))/4;B1 = [a*(t-1)/4-b*(s-1)/4 0 ; 0 c*(s-1)/4-d*(t-1)/4 ;c*(s-1)/4-d*(t-1)/4 a*(t-1)/4-b*(s-1)/4];B2 = [a*(1-t)/4-b*(-1-s)/4 0 ; 0 c*(-1-s)/4-d*(1-t)/4 ;c*(-1-s)/4-d*(1-t)/4 a*(1-t)/4-b*(-1-s)/4];B3 = [a*(t+1)/4-b*(s+1)/4 0 ; 0 c*(s+1)/4-d*(t+1)/4 ;c*(s+1)/4-d*(t+1)/4 a*(t+1)/4-b*(s+1)/4];B4 = [a*(-1-t)/4-b*(1-s)/4 0 ; 0 c*(1-s)/4-d*(-1-t)/4 ;c*(1-s)/4-d*(-1-t)/4 a*(-1-t)/4-b*(1-s)/4];Bfirst = [B1 B2 B3 B4];Jfirst = [0 1-t t-s s-1 ; t-1 0 s+1 -s-t ;s-t -s-1 0 t+1 ; 1-s s+t -t-1 0];J = [xi xj xm xp]*Jfirst*[yi ; yj ; ym ; yp]/8;B = Bfirst/J;if ID == 1D = (E/(1-NU*NU))*[1 NU 0 ; NU 1 0 ; 0 0 (1-NU)/2];elseif ID == 2D = (E/(1+NU)/(1-2*NU))*[1-NU NU 0 ; NU 1-NU 0 ; 0 0 (1-2*NU)/2]; endstr1 = D*B*u;str2 = subs(str1, {s,t}, {0,0});stress = double(str2);。
三角形单元有限元法

x a2 , y y a5 , xy a3 a5 a2 a6
选取位移函数应考虑的问题
(1)位移函数的个数 等于单元中任意一点的位移分量个数。本单元中 有u和v,与此相应,有2个位移函数;
(2)位移函数是坐标的函数 本单元的坐标系为:x、y;
(3)位移函数中待定常数个数 待定常数个数应等于单元节点自由度总数,以 便用单元节点位移确定位移函数中的待定常数。本 单元有6个节点自由度,两个位移函数中共包含6个 待定常数。
1 E ,换为 2
1
。
{ } [ D]{ }
(1-8)
各种类型结构的弹性物理方程都可用式(1-8)描 述。但结构类型不同,力学性态 (应力分量、应变分 量)有区别, 弹性矩阵[D]的体积和元素是不同的。
1.3 位移函数和形函数
• 1、位移函数概念 由于有限元法采用能量原理进行单元分析,因而 必须事先设定位移函数。 “位移函数”也称 “位移 模式”,是单元内部位移变化的数学表达式,设为坐 标的函数。 一般而论,位移函数选取会影响甚至严重影响 计算结果的精度。在弹性力学中,恰当选取位移函数 不是一件容易的事情;但在有限元中,当单元划分得 足够小时,把位移函数设定为简单的多项式就可以获 得相当好的精确度。这正是有限单元法具有的重要优 势之一。
P
① 1 2 ②
3
l/2
l/2
单元的 节点上 有位移 和力F
②
2、F2
1
①
2
l/2
4、F4
2、F2
2
3
l/2
4、F4
1、F1
3、F3
1、F1
3、F3
(2)单元集合:把所有离散的有限个单元集合起来 代替原结构,形成离散结构节点平衡方程。
【工程力学】FEM-06 平面问题有限元(三角形)

求解方法一般是根据总刚的特性,选取高斯消去法(高斯循序消去法,三角 分解法,高斯—约当消去法)、迭代法(雅可比迭代法,高斯—赛德尔迭代 法,超松弛迭代法,共轭梯度法)等。
讨论:
直接解法的优点在于对于给定的方程组,一种选定了的直接解法可以在规定 步骤之内完成计算,操作数可以预先计算,方法简单。不足之处在于需要保 存系数矩阵中夹杂在非零元素之中的零元素,因为计算中要使用,因此,增 加了对计算机存储的要求,影响计算效率。同时,不能对解的误差进行检查 和控制。
• 单元的特性分析
在分析连续体问题时,必须对单元中的位移分布进行假设,假定位移是坐标 的某种简单函数,称之为位移函数。位移法有限元采用节点位移作为未知 量,在每一个单元内部用该单元的节点位移插值多项式表示单元内的近似位 移函数,{f}=[N]{ }e 根据所选用的单元位移函数,对单元进行力学特性分析: { }=[B]{ }e;{ }=[D][B]{ }e;{F}e=[k]e{ }e
腰三角形误差较小。
4. 采用三角形单元,应使一个单元的顶点必须同时又是相邻三角形单元的顶 点,而不是处于某一边上的内点。
5. 尽可能使每个内节点同时为六个三角形单元的顶点,且六个角度应相差不 大。
6. 厚度有突变或者材料性质变化的地方,应把突变线当作单元的界线。 7. 划分单元后,要进行统一的单元和节点编号:
位移函数(cont.)
u(x, y) 1 2x 3 y v(x, y) 4 5x 6 y
为了将位移的广义坐标表达式转换为节
f (x, y)
u(x, y) v(x, y)
点的位移值表达式,将三个节点的位移
代入上述位移表达式,
1
u i
三角形单元有限元程序设计

三角形单元有限元程序设计%*******************************************************************% NNODE 单元节点数NPION 总结点数% NELEM 单元数NVFIX 受约束边界点数% FIXED 约束信息数组NFORCE 节点力数% FORCE 节点力数组COORD 结构节点坐标数组% LNODS 单元定义数组% YOUNG 弹性模量POISS 泊松比% THICK 厚度 B 单元应变矩阵(3*6)% D 单元弹性矩阵(3*3) S 单元应力矩阵(3*6)% A 单元面积ESTIF 单元刚度矩阵% ASTIF 总体刚度矩阵ASLOD 总体荷载向量% ASDISP 节点位移向量ELEDISP 单元节点位移向量% STRESS 单元应力FP1 数据文件指针%*******************************************************************format short e %设定输出类型clear %清除内存变量FP1=fopen('1-1.txt','rt'); %打开输入数据文件存放初始数据%读入控制数据NELEM=fscanf(FP1,'%d',1), %单元个数(单元编码总数)NPION=fscanf(FP1,'%d',1), %结点个数(结点编码总数)NVFIX=fscanf(FP1,'%d',1) %受约束边界点数NFORCE=fscanf(FP1,'%d',1), %结点荷载个数YOUNG=fscanf(FP1,'%e',1), %弹性模量POISS=fscanf(FP1,'%f',1), %泊松比THICK=fscanf(FP1,'%f',1) %厚度LNODS=fscanf(FP1,'%d',[3,NELEM])' %单元定义数组(单元结点号)%相应为单元结点号(编码)、按逆时针顺序输入COORD=fscanf(FP1,'%f',[2,NPION])' %结点坐标数组%坐标:x,y坐标(共NPOIN组)FORCE=fscanf(FP1,'%f',[3,NFORCE])' %结点力数组%(n,3) n:受力结点数目,(n,1):作用点,(n,2):x方向,(n,3):y方向FIXED=fscanf(FP1,'%d',[3,NVFIX])' %约束信息数组% (n,1):约束点(n,2)与(n,3)分别为约束点x方向和y方向的约束情况,受约束为1否则为0%*******************************************************************%生成单元刚度矩阵并组成总体刚度矩阵ASTIF=zeros(2*NPION,2*NPION); %生成特定大小总体刚度矩阵并置0%*******************************************************************for i=1:NELEM%生成弹性矩阵DD= [1 POISS 0;POISS 1 0;0 0 (1-POISS)/2]*YOUNG/(1-POISS^2)%*******************************************************************%计算当前单元的面积A=det([1 COORD(LNODS(i,1),1) COORD(LNODS(i,1),2);1 COORD(LNODS(i,2),1) COORD(LNODS(i,2),2);1 COORD(LNODS(i,3),1) COORD(LNODS(i,3),2)])/2%*******************************************************************%生成应变矩阵Bfor j=0:2b(j+1)= COORD(LNODS(i,(rem((j+1),3))+1),2)-COORD(LNODS(i,(rem((j+2),3))+1),2);c(j+1)=-COORD(LNODS(i,(rem((j+1),3))+1),1)+COORD(LNODS(i,(rem((j+2),3))+1),1); endB=[b(1) 0 b(2) 0 b(3) 0;...0 c(1) 0 c(2) 0 c(3);...c(1) b(1) c(2) b(2) c(3) b(3)]/(2*A);B1( :,:,i)=B;%*******************************************************************%求应力矩阵S=D*BS=D*B;ESTIF=B'*S*THICK*A; %求解单元刚度矩阵a=LNODS(i,:); %临时向量,用来记录当前单元的节点编号for j=1:3for k=1:3ASTIF((a(j)*2-1):a(j)*2,(a(k)*2-1):a(k)*2)...=ASTIF((a(j)*2-1):a(j)*2,(a(k)*2-1):a(k)*2)+ESTIF(j*2-1:j*2,k*2-1:k*2);%根据节点编号对应关系将单元刚度分块叠加到总刚矩阵中endendend%**************************************************************************%将约束信息加入总体刚度矩阵(对角元素改一法)for i=1:NVFIXif FIXED(i,2)==1ASTIF(:,(FIXED(i,1)*2-1))=0; %一列为零ASTIF((FIXED(i,1)*2-1),:)=0; %一行为零ASTIF((FIXED(i,1)*2-1),(FIXED(i,1)*2-1))=1;%对角元素为1endif FIXED(i,3)==1ASTIF( :,FIXED(i,1)*2)=0; %一列为零ASTIF(FIXED(i,1)*2,:)=0; %一行为零ASTIF(FIXED(i,1)*2 ,FIXED(i,1)*2)=1; %对角元素为1 endend%************************************************************************** %生成荷载向量ASLOD(1:2*NPION)=0; %总体荷载向量置零for i=1:NFORCEASLOD((FORCE(i,1)*2-1):FORCE(i,1)*2)=FORCE(i,2:3);end%************************************************************************** %求解内力ASDISP=ASTIF\ASLOD' %计算节点位移向量ELEDISP(1:6)=0; %当前单元节点位移向量for i=1:NELEMfor j=1:3ELEDISP(j*2-1:j*2)=ASDISP(LNODS(i,j)*2-1:LNODS(i,j)*2);%取出当前单元的节点位移向量endiSTRESS=D*B1(:, :, i)*ELEDISP' %求内力endfclose(FP1); %关闭数据文件程序应用举例 134212yxFF F=100NF=100N如上图所示,矩形平板,一端固支,一端受集中力,划分为两个三角形单元,共4个结点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形单元程序
%------------------------------------------------%compute element matrices and vectors and assemble %------------------------------------------------for iel=1:nel %loop for the total number of element
nd(1)=nodes(iel,1); nd(2)=nodes(iel,2); nd(3)=nodes(iel,3);
%1st connected node for (iel)-th element %2nd connected node for (iel)-th element %3rd connected node for (iel)-th element
%coord values of 1st node %coord values of 2nd node %coord values of 3rd node %extract system dofs for the element
x1=x0(nd(1),1); y1=x0(nd(1),2); x2=x0(nd(2),1); y2=x0(nd(2),2); x3=x0(nd(3),1); y3=x0(nd(3),2); index=feeldof(nd,nnel,ndof);
Ni,x
area=0.5*(x1*y2+x2*y3+x3*y1-x1*y3-x2*y1-x3*y2); %area of triangula area2=area*2; dhdx=(1/area2)*[(y2-y3) (y3-y1) (y1-y2)]; dhdy=(1/area2)*[(x3-x2) (x1-x3) (x2-x1)]; %derivatives w.r.t x %derivatives w.r.t y %kinematic matrice %element stiffness matrice
三角形单元程序设计
Байду номын сангаас
问题描述
考虑一个平面应力问题如图所示,假设厚度h=1,材料为各项 同性,杨氏模量为 E=1,泊松比为 ν=0,相关力和位移边界条 件如图中所示,问题左端为固定约束。试用两个三角形单元 分析此问题,三角形单元的网格划分如图所示。试求问题各 节点位移u、v和应力σx,σy和σxy。
1 T e de K de 2
16:51
-0.5*lengthy*(1+(lx+1-i)/lx)*(1-(j-1)/ly)];
三角形单元程序
%---------------------------------------------------------------------%input data for nodal connectivity for each element %nodes(i,j) where i->element no. and j->connected nodes %---------------------------------------------------------------------nodes=[]; for i=1:lx for j=1:ly nodes=[nodes; (ly+1)*(i-1)+j (ly+1)*i+j (ly+1)*(i-1)+j+1;]; nodes=[nodes; (ly+1)*i+j (ly+1)*i+j+1 (ly+1)*(i-1)+j+1;]; end end
16:51
三角形单元程序
%---------------------------------%input data for boundary conditions %---------------------------------bcdof=[]; bcval=[]; for i=1:ly+1 bcdof=[bcdof 1+2*(i-1) 2+2*(i-1)]; bcval=[bcval 0 0]; end
A(0, 0) D(4, 0)
F 1
fload=-1;
% the total load
B(0, 2)
C (4, 1)
16:51
三角形单元程序
lx=16; % number of element in x-axis ly=8; % number of element in y-axis nel=2*lx*ly; % number of element nnel=3; %number of nodes per element ndof=2; %number of dofs per node nnode=(lx+1)*(ly+1); %total number of nodes in system sdof=nnode*ndof; %total system dofs edof=nnel*ndof; %degrees of freedom per element %------------------------------------------------------%input data for nodal coordinate values %------------------------------------------------------x0=[]; for i=1:lx+1 for j=1:ly+1 x0=[x0; (i-1)*lengthx/lx end end 16:51
Ni, y
kinmtx2=fekine2d(nnel,dhdx,dhdy); k=kinmtx2'*matmtx*kinmtx2*area;
K e BT DBhdxdy BT DBA
A
kk=feasmb_2(kk,k,index); end
%assemble element matrics
16:51
三角形单元程序
%--------------------------------------%find the derivatives of shape functions %---------------------------------------
1 Ni ai bi x ci y 2A
A(0, 0) D(4, 0)
C (4, 1)
B(0, 2)
16:51
三角形单元程序
%------------------------------------------------%initialization of matrices and vectors %------------------------------------------------ff=sparse(sdof,1); %system force vector k=sparse(edof,edof); %initialization of element matrix kk=sparse(sdof,sdof); %system matrix disp=sparse(sdof,1); %system displacement vector eldisp=sparse(edof,1); %element displacement vector stress=zeros(nel,3); %matrix containing stress components strain=zeros(nel,3); %matrix containing strain components index=sparse(edof,1); %index vector kinmtx=sparse(3,edof); %kinematic matrix matmtx=sparse(3,3); %constitutive matrix %------------------------------------------------%compute material matrices %------------------------------------------------matmtx=fematiso(1,emodule,poisson); %constitutive matrice 16:51
A(0, 0) D(4, 0)
F 1
C (4, 1)
B(0, 2)
16:51
三角形单元程序
clear all first_time=cputime; format long %-------------------------------------------%input data for control parameters %-------------------------------------------lengthx=4; %length of x-axis side of problem lengthy=2; %length of y-axis side of problem emodule=1.0; poisson=0.0; %elastic modulus %Poisson's ratio
16:51
三角形单元程序
kk1=kk; %-------------------------------------------------------------------------% force vector %-------------------------------------------------------------------------ff(sdof,1)=fload; %-----------------------% apply boundary condition %-----------------------[kk,ff]=feaplyc2(kk,ff,bcdof,bcval); %------------------------% solve the matrix equation %------------------------%disp=kk\ff; [LL UU]=lu(kk); utemp=LL\ff; disp=UU\utemp;
