题1:在一个10类的模式识别问题中,有3类单独满足多类情况1,其余的
操作系统教程习题答案

1.单项选择题
(1)进程创建原语的任务是。
A、为进程编制程序B、为进程建立PCB表
C、为进程分配CPU D、为进程分配所需的各种资源
(2)进程从执行状态变为阻塞态的原因可能是。
A、D、某个进程被唤醒
(3)进程由执行态变化到就绪态的可能原因是。
A、等待的事件发生B、高优先级进程到来
3.基本概念的解释和辨析
(1)进程和程序
a.进程是动态的,程序是静态的
b.进程是暂时的,程序是永久的
c.进程与程序的组合结构不同
(2)进程和作业
一个正在执行的进程称为作业,作业可包含一个或多个进程
(3)进程和线程
a.地址空间资源:不同的进程地址空间是相互独立的,而统一进程的各线程共享同一地址空间
b.并发性:引入线程的操作系统中,不仅进程之间可以并发执行,而且一个进程的多个线程之间亦可并发执行
单项选择题1以下关于死锁的必要条件的叙述中错误的是a只要具备了死锁的必要条件就一定发生死锁现象b解决死锁问题可以从死锁的必要条件出发c一旦出现死锁处于死锁状态的进程一定同时具备死锁的必要条件d死锁的四个必要条件之间不是完全独立的但也不是等价的2以下关于死锁检测的叙述中错误的是a只要检测出死锁尚未解除则再申请该类资源的进程一定会卷入死锁b只要检测出死锁尚未解除则使用该类资源的所有进程一定卷入了死锁c死锁检测方法对系统资源的分配不加限制只要有剩余资源就可以分配d死锁检测中系统需要反复检测各进程资源申请和分配情况3以下关于死锁问题的说法中正确的是a死锁问题是无法解决的但可以避免b死锁的预防是通过破坏进程进入不安全状态来实现的c通过避免死锁四个必要条件中的任何一个就可以实现死锁避免d死锁的检测和解除是配合使用的当系统检测到出现死锁时就通过死锁解除方法解除死锁4以下关于系统的安全状态的描述中正确的是a系统处于不安全状态一定会发生死锁b系统处于不安全状态可能会发生死锁c系统处于安全状态时也可能会发生死锁d不安全状态是死锁状态的一个特例?5资源的静态分配算法在解决死锁问题中用于??a死锁预防b死锁避免c死锁检测d死锁解除?6有3个进程共享个同类资源为使系统不会发生死锁每个进程最多可以申请个资源
模式识别习题集答案解析

模式识别习题集答案解析1、PCA和LDA的区别?PCA是⼀种⽆监督的映射⽅法,LDA是⼀种有监督的映射⽅法。
PCA只是将整组数据映射到最⽅便表⽰这组数据的坐标轴上,映射时没有利⽤任何数据部的分类信息。
因此,虽然做了PCA后,整组数据在表⽰上更加⽅便(降低了维数并将信息损失降到了最低),但在分类上也许会变得更加困难;LDA在增加了分类信息之后,将输⼊映射到了另外⼀个坐标轴上,有了这样⼀个映射,数据之间就变得更易区分了(在低纬上就可以区分,减少了很⼤的运算量),它的⽬标是使得类别的点距离越近越好,类别间的点越远越好。
2、最⼤似然估计和贝叶斯⽅法的区别?p(x|X)是概率密度函数,X是给定的训练样本的集合,在哪种情况下,贝叶斯估计接近最⼤似然估计?最⼤似然估计把待估的参数看做是确定性的量,只是其取值未知。
利⽤已知的样本结果,反推最有可能(最⼤概率)导致这样结果的参数值(模型已知,参数未知)。
贝叶斯估计则是把待估计的参数看成是符合某种先验概率分布的随机变量。
对样本进⾏观测的过程,把先验概率密度转化为后验概率密度,利⽤样本的信息修正了对参数的初始估计值。
当训练样本数量趋于⽆穷的时候,贝叶斯⽅法将接近最⼤似然估计。
如果有⾮常多的训练样本,使得p(x|X)形成⼀个⾮常显著的尖峰,⽽先验概率p(x)⼜是均匀分布,此时两者的本质是相同的。
3、为什么模拟退⽕能够逃脱局部极⼩值?在解空间随机搜索,遇到较优解就接受,遇到较差解就按⼀定的概率决定是否接受,这个概率随时间的变化⽽降低。
实际上模拟退⽕算法也是贪⼼算法,只不过它在这个基础上增加了随机因素。
这个随机因素就是:以⼀定的概率来接受⼀个⽐单前解要差的解。
通过这个随机因素使得算法有可能跳出这个局部最优解。
4、最⼩错误率和最⼩贝叶斯风险之间的关系?基于最⼩风险的贝叶斯决策就是基于最⼩错误率的贝叶斯决策,换⾔之,可以把基于最⼩错误率决策看做是基于最⼩风险决策的⼀个特例,基于最⼩风险决策本质上就是对基于最⼩错误率公式的加权处理。
模式识别习题及答案

模式识别习题及答案第⼀章绪论1.什么是模式具体事物所具有的信息。
模式所指的不是事物本⾝,⽽是我们从事物中获得的___信息__。
2.模式识别的定义让计算机来判断事物。
3.模式识别系统主要由哪些部分组成数据获取—预处理—特征提取与选择—分类器设计/ 分类决策。
第⼆章贝叶斯决策理论1.最⼩错误率贝叶斯决策过程答:已知先验概率,类条件概率。
利⽤贝叶斯公式得到后验概率。
根据后验概率⼤⼩进⾏决策分析。
2.最⼩错误率贝叶斯分类器设计过程答:根据训练数据求出先验概率类条件概率分布利⽤贝叶斯公式得到后验概率如果输⼊待测样本X ,计算X 的后验概率根据后验概率⼤⼩进⾏分类决策分析。
3.最⼩错误率贝叶斯决策规则有哪⼏种常⽤的表⽰形式答:4.贝叶斯决策为什么称为最⼩错误率贝叶斯决策答:最⼩错误率Bayes 决策使得每个观测值下的条件错误率最⼩因⽽保证了(平均)错误率最⼩。
Bayes 决策是最优决策:即,能使决策错误率最⼩。
5.贝叶斯决策是由先验概率和(类条件概率)概率,推导(后验概率)概率,然后利⽤这个概率进⾏决策。
6.利⽤乘法法则和全概率公式证明贝叶斯公式答:∑====m j Aj p Aj B p B p A p A B p B p B A p AB p 1)()|()()()|()()|()(所以推出贝叶斯公式7.朴素贝叶斯⽅法的条件独⽴假设是(P(x| ωi) =P(x1, x2, …, xn | ωi)= P(x1| ωi) P(x2| ωi)… P(xn| ωi))8.怎样利⽤朴素贝叶斯⽅法获得各个属性的类条件概率分布答:假设各属性独⽴,P(x| ωi) =P(x1, x2, …, xn | ωi) = P(x1| ωi) P(x2| ωi)… P(xn| ωi)后验概率:P(ωi|x) = P(ωi) P(x1| ωi) P(x2| ωi)… P(xn| ωi)类别清晰的直接分类算,如果是数据连续的,假设属性服从正态分布,算出每个类的均值⽅差,最后得到类条件概率分布。
模式识别作业题(1)

m 2 mn ] 是奇异的。 mn n 2
1
2、参考参考书 P314“模式识别的概要表示”画出第二章的知识结构图。 答:略。 3、现有两类分类问题。如下图所示, (1,
1 1 3 ) 、 ( , ) 、 (1, 3 ) 、 (1,-tan10°)为 3 2 2 3 3 ,- * tan 10° ) 、 (2,0)为 W2 类。 5 5
W1 类,其中(1,-tan10°)已知为噪声点; (1,0) 、 ( 自选距离度量方法和分类器算法,判别(
6 ,0)属于哪一类? 5
答:度量方法:根据题意假设各模式是以原点为圆心的扇状分布,以两个向量之间夹角(都 是以原点为起点)的余弦作为其相似性测度,P22。 然后使用 K 近邻法,K 取 3,求已知 7 个点与(
2
答: (1)×,不一定,因为仅仅是对于训练样本分得好而已。 (2)×,平均样本法不需要。 (3)√,参考书 P30,将 r 的值代入式(2.26)即得。 (4)√,参考书 P34,三条线线性相关。 ( 5 ) √ ,就是说解区是 “ 凸 ” 的,参考书 P37 ,也可以证明,设 W1T X’=a, W2T X’=b, 则 a≤λW1+(1-λ)W2≤b(设 a≤b) 。 (6)√,参考书 P38。 (7)×,前一句是错的,参考书 P46。 (8)×,是在训练过程中发现的,参考书 P51。 (9)×,最简单的情况,两个点(0,0)∈w1,(2,0)∈w2,用势函数法求出来的判决界面是 x1=1。 (10)√,一个很简单的小证明, 设 X1=a+K1*e,X2= a-K1*e,X3=b+K2*e,X4= b-K2*e, Sw=某系数*e*e’,设 e=[m n],则 e *e’= [
方法三:参照“两维三类问题的线性分类器的第二种情况(有不确定区域) ”的算法,求 G12,G23,G13。 G12*x1>0, G12*x2<0, G12=(-1,-1,-1)’ G23*x2>0, G23*x3<0, G23=(-1,-1,1)’ G13*x1>0, G13*x3<0, G12=(-1,-1,1)’ 有两条线重合了。
大学模式识别考试题及答案详解

大学模式识别考试题及答案详解Last revision on 21 December 2020一、填空与选择填空(本题答案写在此试卷上,30分)1、模式识别系统的基本构成单元包括:模式采集、特征提取与选择和模式分类。
2、统计模式识别中描述模式的方法一般使用特真矢量;句法模式识别中模式描述方法一般有串、树、网。
3、聚类分析算法属于(1);判别域代数界面方程法属于(3)。
(1)无监督分类 (2)有监督分类(3)统计模式识别方法(4)句法模式识别方法4、若描述模式的特征量为0-1二值特征量,则一般采用(4)进行相似性度量。
(1)距离测度(2)模糊测度(3)相似测度(4)匹配测度5、下列函数可以作为聚类分析中的准则函数的有(1)(3)(4)。
(1)(2) (3)(4)6、Fisher线性判别函数的求解过程是将N维特征矢量投影在(2)中进行。
(1)二维空间(2)一维空间(3)N-1维空间7、下列判别域界面方程法中只适用于线性可分情况的算法有(1);线性可分、不可分都适用的有(3)。
(1)感知器算法(2)H-K算法(3)积累位势函数法8、下列四元组中满足文法定义的有(1)(2)(4)。
(1)({A, B}, {0, 1}, {A01, A 0A1 , A 1A0 , B BA , B 0}, A)(2)({A}, {0, 1}, {A0, A 0A}, A)(3)({S}, {a, b}, {S 00S, S 11S, S 00, S 11}, S)(4)({A}, {0, 1}, {A01, A 0A1, A 1A0}, A)二、(15分)简答及证明题(1)影响聚类结果的主要因素有那些(2)证明马氏距离是平移不变的、非奇异线性变换不变的。
答:(1)分类准则,模式相似性测度,特征量的选择,量纲。
(2)证明:(2分)(2分)(1分)设,有非奇异线性变换:(1分)(4分)三、(8分)说明线性判别函数的正负和数值大小在分类中的意义并证明之。
设计模式考试复习试题[含答案解析]
![设计模式考试复习试题[含答案解析]](https://img.taocdn.com/s3/m/df74e5c7551810a6f52486ad.png)
一、1. 设计模式一般用来解决什么样的问题: A.同一问题的不同表相2. 下列属于面向对象基本原则的是: C.里氏代换3. Open-Close原则的含义是一个软件实体:A.应当对扩展开放,对修改关闭.4. 当我们想创建一个具体的对象而又不希望指定具体的类时,使用(A)模式。
A.创建型5. 要依赖于抽象不要依赖于具体。
即针对接口编程不要针对实现编程:(D)依赖倒转原则6. 依据设计模式思想,程序开发中应优先使用的是( A )关系实现复用。
A, 委派7. 设计模式的两大主题是( D ) D.系统复用与系统扩展8. 单体模式中,两个基本要点(AB)和单体类自己提供单例A .构造函数私有 B.唯一实例9. 下列模式中,属于行为模式的是( B ) B观察者10. “不要和陌生人说话”是( D )原则的通俗表述 D.迪米特1. 软件体系结构是指一个系统的有目的的设计和规划,这个设计规划既不描述活动,也不描述系统怎样开发,它只描述系统的组成元素及其相互的交互协作。
2.一个UML模型只描述了一个系统要做什么,它并没告诉我们系统是怎么做。
3.接口是可以在整个模型中反复使用的一组行为,是一个没有属性而只有方法的类。
4.多重性指的是,某个类有多个对象可以和另一个类的一对象关联。
5.当一个类的对象可以充当多种角色时,自身关联就可能发生。
6.在泛化关系中,子类可以替代父类。
后前者出现的可以相同地方。
反过来却不成立。
7.最通常的依赖关系是一个类操作的形构中用到了另一个类的定义。
8.组成是强类型的聚集,因为聚集中的每个部分体只能属于一个整体。
9.实现的符号和继承的符号有相似之处,两者的唯一差别是实现关系用虚线表示,继承关系用实线表示。
10. 设计模式中应优先使用对象组合而不是类继承。
1.适配器模式属于创建型模式结构型( F )2.在设计模式中,“效果”只是指“原因和结果”( T )3.设计模式使代码编制不能真正工程化( T )4.面向对象语言编程中的异常处理,可以理解为责任链模式(T )5.反模式就是反对在软件开发过程中使用设计模式分析:反模式用来解决问题的带有共性的不良方法(F )1.什么是设计模式?设计模式目标是什么?答:设计模式是一套被反复使用、多数人知晓的、经过分类编目的、代码设计经验的总结。
GB4706.1-1998家用和类似用途电器的安全 第一部分:通用要求.

家用和类似用途电器的安全 第一部分:通用要求GB 4706.1-1998国家标准局批准 1999-06-01实施前言本标准为家用和类似用途电器的安全通用要求。
本标准等效采用国际电工委员会IEC 335-1(1991)第3版《家用和类似用途电器的安全 第1部分:通用要求》和其第1修正件(1994)。
本标准中,作为规范性标准而引用的IEC 标准和对应的国家标准在附录A 列出。
有对应国家标准的,以引用的国家标准作为规范使用;暂无对应国家标准的,则以所列的IEC 标准作为规范使用。
本标准与IEC 出版物 335-1(1991)第3版主要差异如下:1)24.1中,将“符合有关IEC 标准中规定的安全要求”替换为“符合有关国家标准或IEC 标准中规定的安全要求”。
2)IEC 335-1(1991)凡涉及引用IEC 标准的地方,如有对应该IEC 标准的国家标准时,本标准则写入对应的国家标准。
3)7.12.4第6项,将“除非为器具提供一个符合24.3的开关”替换为“除非器具带有一个符合24.3的开关”。
由于GB 4706.1-1992为等同采用IEC 出版物 335-1(1976)第2版,及其第1、2、3、4、5、6号修正件,所以本标准与GB 4706.1-1992属两个不同的版本,在编辑方面完全不同。
为使IEC 出版物335-1的第3版与其第2版在章标题和附录标题上有对应关系,所以该出版物制定时,采用了列空章、列空附录的编辑方法。
在技术内容方面,本标准与GB 4706.1-1992有下列主要不同:——本标准在IEC 前言后有一重要引言,而GB 4706.1-1992无此引言。
——本标准第1章对非单相器具规定的最大额定电压为480V ,而不是GB 4706.1-1992第5章所规定的440V 。
——本标准第5章取消了M 连接的术语,GB 4706.1-1992第2章中的M 连接纳入X 连接的概念。
——本标准第2章增加了Ⅱ类结构和Ⅲ类结构的定义,GB 4706.1-1992第2章中没有这些定义。
模式识别习题解答第三章

题1:在一个10类的模式识别问题中,有3类单独满足多类情况1,其余的类别满足多类情况2。
问该模式识别问题所需判别函数的最少数目是多少?答:将10类问题可看作4类满足多类情况1的问题,可将3类单独满足多类情况1的类找出来,剩下的7类全部划到4类中剩下的一个子类中。
再在此子类中,运用多类情况2的判别法则进行分类,此时需要7*(7-1)/2=21个判别函数。
故共需要4+21=25个判别函数。
题2:一个三类问题,其判别函数如下:d1(x)=-x1, d2(x)=x1+x2-1, d3(x)=x1-x2-11.设这些函数是在多类情况1条件下确定的,绘出其判别界面和每一个模式类别的区域。
2.设为多类情况2,并使:d12(x)= d1(x), d13(x)= d2(x), d23(x)= d3(x)。
绘出其判别界面和多类情况2的区域。
3.设d1(x), d2(x)和d3(x)是在多类情况3的条件下确定的,绘出其判别界面和每类的区域。
答:三种情况分别如下图所示:1.2.3.题3:两类模式,每类包括5个3维不同的模式,且良好分布。
如果它们是线性可分的,问权向量至少需要几个系数分量?假如要建立二次的多项式判别函数,又至少需要几个系数分量?(设模式的良好分布不因模式变化而改变。
)答:(1)若是线性可分的,则权向量至少需要14N n =+=个系数分量; (2)若要建立二次的多项式判别函数,则至少需要5!102!3!N ==个系数分量。
题4:用感知器算法求下列模式分类的解向量w : ω1: {(0 0 0)T, (1 0 0)T, (1 0 1)T, (1 1 0)T} ω2: {(0 0 1)T, (0 1 1)T, (0 1 0)T, (1 1 1)T}解:将属于2w 的训练样本乘以(1)-,并写成增广向量的形式x1=[0 0 0 1]',x2=[1 0 0 1]',x3=[1 0 1 1]',x4=[1 1 0 1]';x5=[0 0 -1 -1]',x6=[0 -1 -1 -1]',x7=[0 -1 0 -1]',x8=[-1 -1 -1 -1]';迭代选取1C =,(1)(0,0,0,0)w '=,则迭代过程中权向量w 变化如下:(2)(0 0 0 1)w '=;(3)(0 0 -1 0)w '=;(4)(0 -1 -1 -1)w '=;(5)(0 -1 -1 0)w '=;(6)(1 -1 -1 1)w '=;(7)(1 -1 -2 0)w '=;(8)(1 -1 -2 1)w '=;(9)(2 -1 -1 2)w '=; (10)(2 -1 -2 1)w '=;(11)(2 -2 -2 0)w '=;(12)(2 -2 -2 1)w '=;收敛所以最终得到解向量(2 -2 -2 1)w '=,相应的判别函数为123()2221d x x x x =--+。
模式识别复习资料

(4)如果 Z j( k 1 ) Z j( k )j 1 ,2 , ,K ,则回到(2),将模式 样本逐个重新分类,重复迭代计算。
.
15
例2.3:已知20个模式样本如下,试用K-均值算法分类。
X1 0,0T X2 1,0T X3 0,1T X4 1,1T X5 2,1T X6 1,2T X7 2,2T X8 3,2T
x1
20
8 聚类准则函数Jj与K的关系曲线
上述K-均值算法,其类型数目假定已知为K个。当K未知时,
可以令K逐渐增加, 此时J j 会单调减少。最初减小速度快,但当 K 增加到一定数值时,减小速度会减慢,直到K =总样本数N 时,
Jj = 0。Jj-K关系曲线如下图:
Jj
曲线的拐点 A 对应着接近最优
④ 判断:
Zj(2)Zj(1)
j 1,2 ,故返回第②步。 .
17
② 从新的聚类中心得:
X 1: D D12||||X X11ZZ12((22))|||| X1S1(2) ┋
X 20:D D12||||X X2200Z Z12((22))|||| X20S2(2) 有: S 1 ( 2 ) { X 1 ,X 2 , ,X 8 } N 1 8
(2)将最小距离 3 对应的类 G1(0) 和G2 (0) 合并为1类,得 新的分类。
G 1( 1 2 ) G 1 ( 0 )G , 2 ( 0 ) G 3(1)G 3(0) G 4(1 )G 4(0 ) G 5(1)G 5(0) G 6(1 )G 6(0)
计算聚类后的距离矩阵D(1): 由D(0) 递推出D(1) 。
3)计算合并后新类别之间的距离,得D(n+1)。
4)跳至第2步,重复计算及合并。
高中物理最常考查的10类难题,解题思维模板

高中物理最常考查的10类难题,解题思维模板题型1:直线运动问题题型概述:直线运动问题是高考的热点,可以单独考查,也可以与其他知识综合考查.单独考查若出现在选择题中,则重在考查基本概念,且常与图像结合;在计算题中常出现在第一个小题,难度为中等,常见形式为单体多过程问题和追及相遇问题.思维模板:解图像类问题关键在于将图像与物理过程对应起来,通过图像的坐标轴、关键点、斜率、面积等信息,对运动过程进行分析,从而解决问题;对单体多过程问题和追及相遇问题应按顺序逐步分析,再根据前后过程之间、两个物体之间的联系列出相应的方程,从而分析求解,前后过程的联系主要是速度关系,两个物体间的联系主要是位移关系.例题:题型2:物体的动态平衡问题题型概述:物体的动态平衡问题是指物体始终处于平衡状态,但受力不断发生变化的问题.物体的动态平衡问题一般是三个力作用下的平衡问题,但有时也可将分析三力平衡的方法推广到四个力作用下的动态平衡问题.思维模板:常用的思维方法有两种.(1)解析法:解决此类问题可以根据平衡条件列出方程,由所列方程分析受力变化;(2)图解法:根据平衡条件画出力的合成或分解图,根据图像分析力的变化.例题:题型3:运动的合成与分解问题题型概述:运动的合成与分解问题常见的模型有两类.一是绳(杆)末端速度分解的问题,二是小船过河的问题,两类问题的关键都在于速度的合成与分解.思维模板:(1)在绳(杆)末端速度分解问题中,要注意物体的实际速度一定是合速度,分解时两个分速度的方向应取绳(杆)的方向和垂直绳(杆)的方向;如果有两个物体通过绳(杆)相连,则两个物体沿绳(杆)方向速度相等.(2)小船过河时,同时参与两个运动,一是小船相对于水的运动,二是小船随着水一起运动,分析时可以用平行四边形定则,也可以用正交分解法,有些问题可以用解析法分析,有些问题则需要用图解法分析.例题:题型概述:抛体运动包括平抛运动和斜抛运动,不管是平抛运动还是斜抛运动,研究方法都是采用正交分解法,一般是将速度分解到水平和竖直两个方向上.思维模板:(1)平抛运动物体在水平方向做匀速直线运动,在竖直方向做匀加速直线运动,其位移满足x=v0t,y=gt2/2,速度满足vx=v0,vy=gt;(2)斜抛运动物体在竖直方向上做上抛(或下抛)运动,在水平方向做匀速直线运动,在两个方向上分别列相应的运动方程求解。
第五讲《中图法》类目的复分与仿分-文档资料

世界种族与民族表分为种族、民族两部分,民族部分先 按地区划分,再按民族划分(演示)。P1127页
世界种族与民族表的使用要点(2点)
◆ 主表中注明“依世界种族与民族表分”时,直接使用本 表复分,方法:将有关复分号加在主类号之后即可。如: 《吉普赛人的民族心理》 C955.510.5 ◆ 主表中未注明“依世界种族与民族表分”时,需依本表 复分的,将有关复分号用民族区分号“”引起,加在主类号 之后。如:《澳大利亚土著人的骨骼》Q983.3“611.1”
● 世界种族与民族表
● 通用时间、地点复分表
back
2
■ 总论复分表的结构 P1113 将各学科门类的共性区分内容编列入此,内容包括关于学科及 专业与事物的总论性类目,关于著作类型等方面内容两部分,复分 号由“-”加数字组成(演示)。如: 《图书馆学辞典》 G25-61 ■ 总论复分表的使用要点 (4个)+ 练习
如:J309 雕塑艺术史 类下注释“依世界地区表分”, (P182页),《法国雕塑艺术史》 J309.565
◆ 若未注明依该表分,但需要据本表复分时,须将复分号 用地区区分号“()”括起,加在主类号后。如:
《美国海军军服》TS941.733(712)
5
◆ 凡使用本表中“洲”、“地区”概括性地区号码复分 后,还需要再依其它标准进行细分的,必须在概括性地区 号码后加“0”,再进行复分,以便于该地区所属国家号码 区别开来。 如:《西欧小说选》 I560.4 否则: I564(比利时文学)!!!! 练习:《美国外交政策》(D871.20)
back
4
世界地区表的结构
本表主要依据自然区划编列,还分别采用依行政区划以及语 种、人种、宗教、集团、古代地区作划分标准。(演示,见 《中图法》P1116页)
机器学习题目

d12(x)= d1(x)-d2(x) = -2x1 + 1 = 0 d13(x)= d1(x)-d3(x) = -x1 + 2x2 = 0 属于 ω2 类的区域应满足 d2(x)>d1(x)且 d2(x)>d3(x), ω2 类的判别界面为: d21(x)= d2(x)-d1(x) = 2x1 - 1 = 0, 可看出 d21(x)=-d12(x) d23(x)= d2(x)-d3(x) = x1 + 2x2 - 1= 0 同理可得 ω3 类的判别界面为: d31(x) = -d13(x) = x1 - 2x2 = 0 d32(x) = -d23(x) = -x1 - 2x2 + 1= 0 若有模式样本 x=(1, 1)T,则: d1(x) = 0,d2(x) = 1,d3(x) = -1 从而:d2(x)>d1(x)且 d2(x)>d3(x),
如果要建立二次的多项式判别函数,则至少需要������
=
������52
=
5! 2!3!
=
10个系数分量。
d(x)总项数的讨论:对于 n 维 x 向量,若用 r 次多项式,d(x)的权系数的总项数为:
Nw
C
r n
r
(n r)! r!n!
作业 3.4 用感知器算法求下列模式分类的解向量 w: ω1: {(0 0 0)T, (1 0 0)T, (1 0 1)T, (1 1 0)T} ω2: {(0 0 1)T, (0 1 1)T, (0 1 0)T, (1 1 1)T}
高考物理10类难题解题模板

高考物理10类难题解题模板题型1:直线运动问题直线运动问题是高考的热点,可以单独考查,也可以与其他知识综合考查.单独考查若出现在选择题中,则重在考查基本概念,且常与图像结合;在计算题中常出现在第一个小题,难度为中等,常见形式为单体多过程问题和追及相遇问题.解图像类问题关键在于将图像与物理过程对应起来,通过图像的坐标轴、关键点、斜率、面积等信息,对运动过程进行分析,从而解决问题;对单体多过程问题和追及相遇问题应按顺序逐步分析,再根据前后过程之间、两个物体之间的联系列出相应的方程,从而分析求解,前后过程的联系主要是速度关系,两个物体间的联系主要是位移关系.题型2:物体的动态平衡问题物体的动态平衡问题是指物体始终处于平衡状态,但受力不断发生变化的问题.物体的动态平衡问题一般是三个力作用下的平衡问题,但有时也可将分析三力平衡的方法推广到四个力作用下的动态平衡问题.常用的思维方法有两种.(1)解析法:解决此类问题可以根据平衡条件列出方程,由所列方程分析受力变化;(2)图解法:根据平衡条件画出力的合成或分解图,根据图像分析力的变化.题型3:运动的合成与分解问题题型概述:运动的合成与分解问题常见的模型有两类.一是绳(杆)末端速度分解的问题,二是小船过河的问题,两类问题的关键都在于速度的合成与分解.思维模板:(1)在绳(杆)末端速度分解问题中,要注意物体的实际速度一定是合速度,分解时两个分速度的方向应取绳(杆)的方向和垂直绳(杆)的方向;如果有两个物体通过绳(杆)相连,则两个物体沿绳(杆)方向速度相等.(2)小船过河时,同时参与两个运动,一是小船相对于水的运动,二是小船随着水一起运动,分析时可以用平行四边形定则,也可以用正交分解法,有些问题可以用解析法分析,有些问题则需要用图解法分析.例题:题型4:抛体运动问题题型概述:抛体运动包括平抛运动和斜抛运动,不管是平抛运动还是斜抛运动,研究方法都是采用正交分解法,一般是将速度分解到水平和竖直两个方向上.(1)平抛运动物体在水平方向做匀速直线运动,在竖直方向做匀加速直线运动,其位移满足x=v0t,y=gt2/2,速度满足vx=v0,vy=gt;(2)斜抛运动物体在竖直方向上做上抛(或下抛)运动,在水平方向做匀速直线运动,在两个方向上分别列相应的运动方程求解。
2021年首都师范大学应用心理347心理学专业综合考研试题及答案解析版

2021年首都师范大学应用心理347心理学专业综合考研试题及参考答案解析说明:信息来源网络整理,准确性有待考量,仅供参考一、名词解释1、神经系统答案:神经系统由外周神经系统和中枢神经系统组成。
中枢神经系统位于颅腔和椎管内,包括脑和脊髓,主要由神经元及神经胶质细胞构成。
位于颅腔和椎管以外的神经组织属于外周神经系统,主要由神经干和神经节组成。
神经系统发挥调节作用主要依赖于中枢神经系统。
解析:本题主要考察神经系统的进化一章中的知识掌握。
属于《普通心理学》中考点。
2.感受性答案:感受性是感觉器官对某种刺激的感受能力,又称为感觉的灵敏度。
解析:人类的各个感觉器官均有相应的适宜刺激,不同感觉器官能够探测的刺激不同,每个感觉器官所能够探测到的物理能量也是有限的。
只有处在特定限度内的刺激才能引起人类的感觉。
这就是感官对刺激的选择性,即感受性和感觉阈限的问题。
感受性是指各感受器对适宜刺激的感觉能力,用感觉阈限的大小来度量。
感受性与感觉阈限之间成反比关系,阈限低表明感受性高,感觉敏锐;反之,阈限高表明感受性低,感觉迟钝。
本题主要考察感觉一章中的知识点的掌握。
属于《普通心理学》中的考点。
3.成就动机答案:成就动机,是指个体希望从事对他有重要意义的、有一定困难的、具有挑战性的活动,且在活动中能获得优异结果或能超过他人的心理倾向。
美国心理学家阿特金森在1963年提出了具有广泛影响的成就动机模型。
该模型认为,成就动机包含追求成功的动机和回避失败的动机,个体的成就行为是这两种动机力量相互抗衡的结果。
解析:成就动机是指一个人所具有的试图追求和达到目标的驱动力。
成就动机是个体追求自认为重要的有价值的工作,并使之达到完美状态的动机,即一种以高标准要求自己力求取得活动成功为目标的动机。
如:具有这种动机因素的学生就能刻苦努力,战胜学习中的种种困难和障碍,取得优良成绩。
本题主要考察动机认知理论的第四个理论:成就动机理论。
属于《普通心理学》中考点。
软考UML题
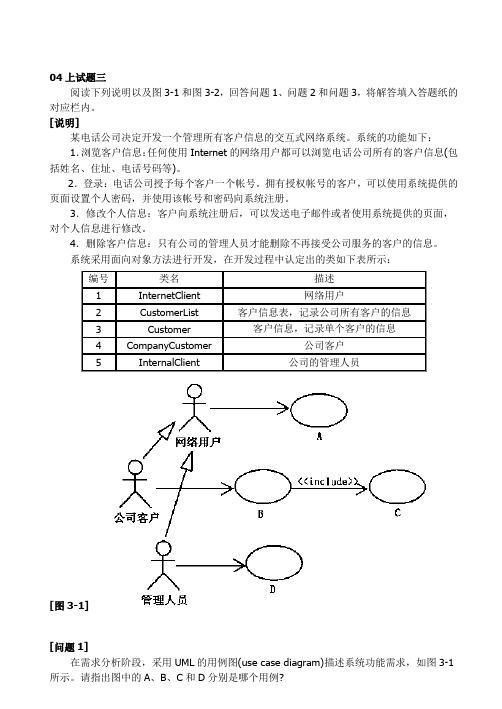
04上试题三阅读下列说明以及图3-1和图3-2,回答问题1、问题2和问题3,将解答填入答题纸的对应栏内。
[说明]某电话公司决定开发一个管理所有客户信息的交互式网络系统。
系统的功能如下:1.浏览客户信息:任何使用Internet的网络用户都可以浏览电话公司所有的客户信息(包括姓名、住址、电话号码等)。
2.登录:电话公司授予每个客户一个帐号。
拥有授权帐号的客户,可以使用系统提供的页面设置个人密码,并使用该帐号和密码向系统注册。
3.修改个人信息:客户向系统注册后,可以发送电子邮件或者使用系统提供的页面,对个人信息进行修改。
4.删除客户信息:只有公司的管理人员才能删除不再接受公司服务的客户的信息。
系统采用面向对象方法进行开发,在开发过程中认定出的类如下表所示:编号类名描述1 InternetClient 网络用户2 CustomerList 客户信息表,记录公司所有客户的信息3 Customer 客户信息,记录单个客户的信息4 CompanyCustomer 公司客户5 InternalClient 公司的管理人员[图3-1][问题1]在需求分析阶段,采用UML的用例图(use case diagram)描述系统功能需求,如图3-1所示。
请指出图中的A、B、C和D分别是哪个用例?[问题2]在UML 中,重复度(Multiplicity)定义了某个类的一个实例可以与另一个类的多少个实例相关联。
通常把它写成一个表示取值范围的表达式或者一个具体的值。
例如图3-2 中的类InternetClient 和CustomerList,InternetClient 端的“0..*”表示:一个Custo~erList 的实例可以与0 个或多个InternetClient 的实例相关联;CustomerList 端的“1”表示:一个InternetClient的实例只能与一个CustomerList的实例相关。
请指出图3-2中(1)到(4)处的重复度分别为多少?[问题3]类通常不会单独存在,因此当对系统建模时,不仅要识别出类,还必须对类之间的相互关系建模。
模式识别

模式识别[填空题]1模式识别系统的基本构成单元包括()()()参考答案:模式采集;特征选择与提取;模式分类[填空题]2统计模式识别中描述模式的方法一般使用();句法模式识别中模式描述方法一般有()、()、()。
参考答案:特征矢量;串;树;网[填空题]3影响层次聚类算法结果的主要因素有()()()()参考答案:计算模式距离的测度;聚类准则;类间距离门限;预定的类别数目[填空题]4线性判别函数的正负和数值大小的几何意义是()()参考答案:正(负)表示样本点位于判别界面法向量指向的正(负)半空间中;绝对值正比于样本点到判别界面的距离[填空题]5感知器算法适用于()的情况参考答案:线性可分[填空题]6在统计模式分类问题中,聂曼-皮尔逊判决准则主要用于()情况;最小最大判别准则主要用于()情况。
参考答案:某一种判决错误较另一种判决错误更为重要;先验概率未知的[多项选择题]7、影响聚类算法结果的主要因素有()。
A. 已知类别的样本质量B. 分类准则C. 特征选取D. 模式相似性测度参考答案:B,C,D[多项选择题]8、影响基本K-均值算法的主要因素有()。
A. 样本输入顺序B. 模式相似性测度C. 聚类准则D. 初始类中心的选取参考答案:A,B,D[多项选择题]9、在统计模式分类问题中,当先验概率未知时,可以使用()。
A. 最小损失准则B. 最小最大损失准则C. 最小误判概率准则D. N-P判决参考答案:B,D[单项选择题]10、散度是根据()构造的可分性判据。
A. 先验概率B. 后验概率C. 类概率密度D. 信息熵E. 几何距离参考答案:C[多项选择题]11、如果以特征向量的相关系数作为模式相似性测度,则影响聚类算法结果的主要因素有()。
A.已知类别样本质量B.分类准则C.特征选取D.量纲参考答案:B,D[多项选择题]12、欧式距离具有()A.平移不变性B.旋转不变性C.尺度缩放不变性D.不受量纲影响的特性参考答案:A,B[多项选择题]13、马式距离具有()。
2020高考排列组合难题21种题型及方法_

4
个不同的盒内有
A
4 4
种方法,根据分步计数
原理装球的方法共有
C52
A
4 4
解决排列组合混合问题,先选后排是最基本的指导思想.此法与相邻元素捆绑策略相似吗?
练习题:一个班有 6 名战士,其中正副班长各 1 人现从中选 4 人完成四种不
同的任务,每人完成一种任务,且正副班长有且只有 1 人参加,则不同
个复合元素,再与其它元素进行排列,同时对相邻元素内部进行自排。 由分步计数原理可得共有 A55 A22 A22 480 种不同的排法
甲乙 丙丁
要求某几个元素必须排在一起的问题,可以用捆绑法来解决问题.即将需要相邻的元素合并 为一个元素,再与其它元素一起作排列,同时要注意合并元素内部也必须排列.
练习题:某人射击 8 枪,命中 4 枪,4 枪命中恰好有 3 枪连在一起的情形的不 同种数为 20
2020 高考数学排列组合难题 21 种方法
排列组合问题联系实际生动有趣,但题型多样,思路灵活,因此解决排 列组合问题,首先要认真审题,弄清楚是排列问题、组合问题还是排列与组 合综合问题;其次要抓住问题的本质特征,采用合理恰当的方法来处理。
1.分类计数原理(加法原理)
完成一件事,有 n 类办法,在第 1 类办法中有 m1 种不同的方法,在第 2 类
置。若有多个约束条件,往往是考虑一个约束条件的同时还要兼顾其它条件
第1页共9页
练习题:7 种不同的花种在排成一列的花盆里,若两种葵花不种在中间,也不 种在两端的花盆里,问有多少不同的种法?
二.相邻元素捆绑策略 例 2. 7 人站成一排 ,其中甲乙相邻且丙丁相邻, 共有多少种不同的排法. 解:可先将甲乙两元素捆绑成整体并看成一个复合元素,同时丙丁也看成一
软件工程课件复习试题

【试题实例】《软件工程》试题一、从供选择的答案中选出应填入下列叙述中()内的正确答案。
Strong软件设计中划分程序模块通常遵循的原则是使各模块间的耦合尽可能( A )。
三种可能的模块耦合是:( B ),例如,一个模块直接引用另一个模块中的数据。
( C ),例如,一个模块把开关量作为参数传送给另一个模块。
( D ),例如,一个模块通过公共数据结构把数据传送给另一个模块。
其中, ( E )的耦合性最强。
【供选择的答案】A:①强②适中③弱B~E:①公共耦合②数据耦合③逻辑耦合④外部耦合⑤内容耦合⑥控制耦合二、为高质量地开发软件项目,在软件结构设计时必须遵循( A )的原则,( B )建立软件系统的模块结构。
并且应根据( C )评价系统模块划分的质量。
此外在模块设计时,应从5种基本的( D )出发,利用它们组合成一个模块的程序块结构。
要求每个( E )的结构应是单入口和单出口。
【供选择的答案】A:①质量控制②程序优化③信息隐蔽④数据共享⑤模块通信B:①自底向上②自顶向下③衍变的自顶向下④随机⑤回归C:①数据独立性②程序独立性③模块独立性④可修改性⑤可理解性D:①数据结构②处理结构③功能结构④成份⑤控制结构E:①程序块②公共块③数据块④记录块⑤通信块三、从下列叙述中选出5条关于好的程序设计风格的正确叙述。
(在对的前面打√)(1) 使用括号以改善表达式的清晰性。
(2) 对递归定义的数据结构不要使用递归过程。
(3) 尽可能对程序代码进行优化。
(4) 不要修补不好的程序, 要重新写。
(5) 不要进行浮点数的相等比较。
(6) 应尽可能多地输出中间结果。
(7) 利用数据类型对数据值进行防范。
(8) 用计数方法而不是用文件结束符或输入序列结束符来判别输入的结束。
(9) 程序中的注释是可有可无的。
(10) 使用有意义的标识符。
四、从下列叙述中选出5条关于软件测试的正确叙述。
(在对的前面打√)(1) 为了使得软件容易测试, 应该使用高级的程序设计语言编制程序。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题1:在一个10类的模式识别问题中,有3类单独满足多类情况1,其余的类别满足多类情况2。
问该模式识别问题所需判别函数的最少数目是多少?答:将10类问题可看作4类满足多类情况1的问题,可将3类单独满足多类情况1的类找出来,剩下的7类全部划到4类中剩下的一个子类中。
再在此子类中,运用多类情况2的判别法则进行分类,此时需要7*(7-1)/2=21个判别函数。
故共需要4+21=25个判别函数。
题2:一个三类问题,其判别函数如下:d1(x)=-x1, d2(x)=x1+x2-1, d3(x)=x1-x2-11.设这些函数是在多类情况1条件下确定的,绘出其判别界面和每一个模式类别的区域。
2.设为多类情况2,并使:d12(x)= d1(x), d13(x)= d2(x), d23(x)= d3(x)。
绘出其判别界面和多类情况2的区域。
3.设d1(x), d2(x)和d3(x)是在多类情况3的条件下确定的,绘出其判别界面和每类的区域。
答:三种情况分别如下图所示:1.2.3.题3:两类模式,每类包括5个3维不同的模式,且良好分布。
如果它们是线性可分的,问权向量至少需要几个系数分量?假如要建立二次的多项式判别函数,又至少需要几个系数分量?(设模式的良好分布不因模式变化而改变。
)答:(1)若是线性可分的,则权向量至少需要14N n =+=个系数分量; (2)若要建立二次的多项式判别函数,则至少需要5!102!3!N ==个系数分量。
题4:用感知器算法求下列模式分类的解向量w : ω1: {(0 0 0)T, (1 0 0)T, (1 0 1)T, (1 1 0)T} ω2: {(0 0 1)T, (0 1 1)T, (0 1 0)T, (1 1 1)T}解:将属于2w 的训练样本乘以(1)-,并写成增广向量的形式x1=[0 0 0 1]',x2=[1 0 0 1]',x3=[1 0 1 1]',x4=[1 1 0 1]';x5=[0 0 -1 -1]',x6=[0 -1 -1 -1]',x7=[0 -1 0 -1]',x8=[-1 -1 -1 -1]';迭代选取1C =,(1)(0,0,0,0)w '=,则迭代过程中权向量w 变化如下:(2)(0 0 0 1)w '=;(3)(0 0 -1 0)w '=;(4)(0 -1 -1 -1)w '=;(5)(0 -1 -1 0)w '=;(6)(1 -1 -1 1)w '=;(7)(1 -1 -2 0)w '=;(8)(1 -1 -2 1)w '=;(9)(2 -1 -1 2)w '=; (10)(2 -1 -2 1)w '=;(11)(2 -2 -2 0)w '=;(12)(2 -2 -2 1)w '=;收敛所以最终得到解向量(2 -2 -2 1)w '=,相应的判别函数为123()2221d x x x x =--+。
题5:用多类感知器算法求下列模式的判别函数: ω1: (-1 -1)T ,ω2: (0 0)T ,ω3: (1 1)T解:采用一般化的感知器算法,将模式样本写成增广形式,即1231011,0,1111x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=-== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭取初始值123000w w w ⎛⎫⎪=== ⎪ ⎪⎝⎭,取1C =,则有第一次迭代:以1x 为训练样本,123(1)(1)(1)0d d d ===,故123111(2)1,(2)1,(2)1111w w w -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=-== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭第二次迭代:以2x 为训练样本,123(2)1,(2)1,(2)1d d d ==-=-,故123111(3)1,(3)1,(3)1002w w w -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=-== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭第三次迭代:以3x 为训练样本,123(3)2,(3)2,(3)0d d d =-==,故123102(4)1,(4)0,(4)2011w w w -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=-== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭第四次迭代:以1x 为训练样本,123(4)2,(4)1,(4)5d d d ==-=-,故112233(5)(4),(5)(4),(5)(4)w w w w w w ===第五次迭代:以2x 为训练样本,123(5)0,(5)1,(5)1d d d ==-=-,故123102(6)1,(6)0,(6)2102w w w -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=-== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭第六次迭代:以3x 为训练样本,123(6)3,(6)0,(6)2d d d =-==,故112233(7)(6),(7)(6),(7)(6)w w w w w w ===第七次迭代:以1x 为训练样本,123(7)1,(7)0,(7)6d d d ===-,故112233(8)(7),(8)(7),(8)(7)w w w w w w ===第八次迭代:以2x 为训练样本,123(8)1,(8)0,(8)2d d d =-==-,故112233(9)(8),(9)(8),(9)(8)w w w w w w ===由于第六、七、八次迭代中对312,,x x x 均以正确分类,故权向量的解为:1231021,0,2102w w w -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=-== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭,可得三个判别函数为:112231210222d x x d d x x =---==+-题6: 采用梯度法和准则函数2(,,)21()8t tw x b J w x b w x b x⎡⎤=---⎣⎦,式中实数b 〉0,试导出两类模式的分类算法。
解:)]sgn(*[*|]|)[(||||412b x w x x b x w b x w x w J tt t -----=∂∂ 其中:⎩⎨⎧≤-->-=-0,10,1)sgn(b x w b x w b x w tt t得迭代式:2(1)()[(())|()|]*[*sgn(())]4||||t t tC w k w k w k x b w k x b x x w k x b x +=+----- 200(1)()()t t t w x b w k w k C b w x x w x b x ⎧->⎪+=+-⎨-≤⎪⎩题7:用LMSE 算法求下列模式的解向量: ω1: {(0 0 0)T , (1 0 0)T , (1 0 1)T , (1 1 0)T }ω2: {(0 0 1)T , (0 1 1)T , (0 1 0)T , (1 1 1)T }解:写出模式的增广矩阵X :00011001101111010011011101011111X ⎛⎫⎪ ⎪ ⎪⎪⎪= ⎪--⎪--- ⎪ ⎪-- ⎪ ⎪----⎝⎭#11000110010111000110110111000100010111110100010111()()001011010011001011011111111101111111111101011111t tX X X X --⎛⎫⎪ ⎪⎪--⎛⎫⎛⎫⎪ ⎪ ⎪------ ⎪⎪ ⎪== ⎪ ⎪ ⎪--------⎪ ⎪ ⎪----------- ⎪⎝⎭⎝⎭⎪-- ⎪ ⎪----⎝⎭=121121212(2)11222224-⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭01110001000101110010110111111111-⎛⎫ ⎪--- ⎪⎪--- ⎪----⎝⎭ 200102011002141112-⎛⎫ ⎪- ⎪=⎪- ⎪---⎝⎭01110001000101110010110111111111-⎛⎫⎪--- ⎪⎪--- ⎪----⎝⎭1111111111111111111111111421001011--⎛⎫ ⎪------ ⎪=⎪------ ⎪--⎝⎭取(1)(11111111)t b 和1C第一次迭代:#(1)(1)(1110.5)t X w b(1)(1)(1)(0.50.50.50.50.50.50.50.5)t X e w b#(2)(1)(1)(1.5 1.51.50.75)t CX w w e(2)(1)[(1)(1)](12111211)t C b b e e第二次迭代:e w b(2)(2)(2)(0.250.250.250.250.250.250.250.25)tX#w w eCX(3)(2)(2)(1.75 1.75 1.750.875)tb b e e(3)(2)[(2)(2)](1 2.5111 2.511)tC第三次迭代:e w bX(3)(3)(3)(0.1250.1250.1250.1250.1250.1250.1250.125)t#w w eCX(4)(3)(3)(1.875 1.875 1.8750.9375)tCb b e e(4)(3)[(3)(3)](1 2.75111 2.7511)t第四次迭代:e w b(4)(4)(4)(0.06250.06250.06250.06250.06250.06250.06250.0625)tX#(5)(4)(4)(1.9375 1.9375 1.93750.9688)tw w eCXb b e e(5)(4)[(4)(4)](1 2.875111 2.87511)tC第五次迭代:e w b(5)(5)(5)(0.03130.03130.03130.03130.03130.03130.03130.0313)tX#w w eCX(6)(5)(5)(1.9688 1.9688 1.96880.9844)tb b e e(6)(5)[(5)(5)](1 2.9375111 2.937511)tC第六次迭代:e w bX(6)(6)(6)(0.01560.01560.01560.01560.01560.01560.01560.0156)t#w w eCX(7)(6)(6)(1.9844 1.9844 1.98440.9922)tb b e e(7)(6)[(6)(6)](1 2.9688111 2.968811)tC第七次迭代:e w bX(7)(7)(7)(0.00780.00780.00780.00780.00780.00780.00780.0078)t#w w eCX(8)(7)(7)(1.9922 1.9922 1.99220.9961)tCb b e e(8)(7)[(7)(7)](1 2.9844111 2.984411)t第八次迭代:e w b(8)(8)(8)(0.00390.00390.00390.00390.00390.00390.00390.0039)tX#(9)(8)(8)(1.9961 1.99611.99610.9980)t CX w w e(9)(8)[(8)(8)](1 2.9922111 2.992211)t C b b e e第九次迭代:(9)(9)(9)(0.00200.00200.00200.00200.00200.00200.00200.0020)tX e w b#(10)(9)(9)(1.9980 1.99801.99800.9990)t CX w w e(10)(9)[(9)(9)](1 2.9961111 2.996111)t C b b e e第十次迭代:3(10)(10)(10) 1.010(0.97660.97660.97660.980.980.980.980.98)tX e w b#(11)(10)(10)(1.9990 1.99901.99900.9995)t CX w w e(11)(10)[(10)(10)](1 2.9980111 2.998011)t C b b e e由于31.010e,可以认为此时权系数调整完毕,最终的权系数为:(2221)t w相应的判别函数为:1231()222d x x x x题8:用二次埃尔米特多项式的势函数算法求解以下模式的分类问题ω1: {(0 1)T , (0 -1)T } ω2: {(1 0)T , (-1 0)T }111201022212011222331201222441211021551211121226612112212()(,)()()1()(,)()()2()(,)()()42()(,)()()2()(,)()()4()(,)()()2(4x x x H x H x x x x H x H x x x x x H x H x x x x x H x H x x x x x H x H x x x x x x H x H x x x ϕϕϕϕϕϕϕϕϕϕϕϕ=========-=========2771221021288122112212299122122122)()(,)()()42()(,)()()2(42)()(,)()()(42)(42)x x x H x H x x x x x H x H x x x x x x H x H x x x ϕϕϕϕϕϕ-===-===-===--所以,势函数91(,)()()k iiki K x x x x ϕϕ==∑第一步:取1101X w ⎛⎫=∈ ⎪⎝⎭,故2222212211212()152040243264K X x x x x x x x =-+++-- 第二步:取2101X w ⎛⎫=∈⎪-⎝⎭,12()50K X =>,故21()()K X K X = 第三步:取3210X w ⎛⎫=∈ ⎪⎝⎭,23()90K X =>,故223232211()()(,)20162016K X K X K X X x x x x =-=+--第四步:取4210X w -⎛⎫=∈ ⎪⎝⎭,34()40K X =>,故222224342121212()()(,)152********K X K X K X X x x x x x x x =-=+---+ 第五步:取5101X w ⎛⎫=∈ ⎪⎝⎭,45()270K X =>,故54()()K X K X =第六步:取6101X w ⎛⎫=∈ ⎪-⎝⎭,56()130K X =-<,故2265612()()(,)3232K X K X K X X x x =+=-+ 第七步:取7210X w ⎛⎫=∈ ⎪⎝⎭,67()320K X =-<,故76()()K X K X =第八步:取8210X w -⎛⎫=∈⎪⎝⎭,78()320K X =-<,故 87()()K X K X =第九步:取9101X w ⎛⎫=∈ ⎪⎝⎭,89()320K X =>,故98()()K X K X =第十步:取10101X w ⎛⎫=∈ ⎪-⎝⎭,910()320K X =>,故109()()K X K X =从第七步到第十步的迭代过程中,全部模式都已正确分类,故算法已经收敛于判别函数:221012()()3232d X K X x x ==-+ 题9:用下列势函数2||||(,)k X X k K X X eα--=求解以下模式的分类问题ω1: {(0 1)T, (0 -1)T}ω2: {(1 0)T, (-1 0)T}选取1α=,在二维情况下,势函数为1222212(,)exp{||||}exp{[()()]}k k k k K X X X X x x x x =--=--+-以下为势函数迭代算法:第一步:取1101X w ⎛⎫=∈ ⎪⎝⎭,故22112()exp{(1)}K X x x =---第二步:取2101X w ⎛⎫=∈⎪-⎝⎭,12()exp{4}0K X =->,故21()()K X K X = 第三步:取3210X w ⎛⎫=∈ ⎪⎝⎭,23()exp{1}0K X =->,故22223231212()()(,)exp{(1)}exp{(1)}K X K X K X X x x x x =-=-------第四步:取4210X w -⎛⎫=∈ ⎪⎝⎭,34()exp{2}exp{4}0K X =--->,故222222434121212()()(,)exp{(1)}exp{(1)}exp{(1)}K X K X K X X x x x x x x =-=---------+-第五步:取5101X w ⎛⎫=∈ ⎪⎝⎭,45()1exp{2}exp{2}0K X =---->,故54()()K X K X =第六步:取6101X w ⎛⎫=∈⎪-⎝⎭,56()exp{4}exp{2}exp{2}0K X =-----<,故 2222656121222221212()()(,)exp{(1)}exp{(1)} exp{(1)}exp{(1)}K X K X K X X x x x x x x x x =+=--++---------+-第七步:取7210X w ⎛⎫=∈ ⎪⎝⎭,67()exp{2}exp{2}1exp{4}0K X =-+----<,故76()()K X K X =第八步:取8210X w -⎛⎫=∈⎪⎝⎭,78()exp{2}exp{2}exp{4}10K X =-+----<,故 87()()K X K X =第九步:取9101X w ⎛⎫=∈ ⎪⎝⎭,89()exp{4}1exp{2}exp{2}0K X =-+---->,故98()()K X K X =第十步:取10101X w ⎛⎫=∈⎪-⎝⎭,910()1exp{4}exp{2}exp{2}0K X =+----->,故 109()()K X K X =从第七步到第十步的迭代过程中,全部模式都已正确分类,故算法已经收敛于判别函数:222210121222221212()()exp{(1)}exp{(1)} exp{(1)}exp{(1)}d X K X x x x x x x x x ==--++---------+-。
