完全平方数的性质
完全平方数整理

完全平方数一、完全平方数常用性质1.主要性质 1.完全平方数的尾数只能是0,1,4,5,6,9。
不可能是2,3,7,8。
2.在两个连续正整数的平方数之间不存在完全平方数。
3.完全平方数的约数个数是奇数,约数的个数为奇数的自然数是完全平方数。
4.若质数p 整除完全平方数2a ,则p 能整除a 。
2.重点公式回顾:平方差公式:22()()a b a b a b -=+-模块一、完全平方数基本性质和概念基础练习、指出下列哪些是平方数?1156,5487,5329,8008。
1. 在3240,8972,2116,2475,2400这五个数中,哪几个是完全平方数?2.正整数的平方按大小排成1 4 9 16 25 36 49 …,那么第85 个位置上的数字是几【例 1】 写出从360到630的自然数中有奇数个约数的数.1、在50~400中,有多少个平方数?2、在50~761中有多少个平方数?例题精讲 知识点拨3、123×134的积是平方数吗?4、一个数的完全平方有39个约数,求该数的约数个数是多少?【例2】从1到2008的所有自然数中,乘以72后是完全平方数的数共有多少个?【巩固】1016与正整数a的乘积是一个完全平方数,则a的最小值是________.2、46035乘以一个自然数a,积是一个整数的平方,求最小的a及这个整数。
3、已知3528a恰是自然数b的平方数,a的最小值是。
【例3】已知自然数n满足:12!除以n得到一个完全平方数,则n的最小值是。
1、(04南京冬令营)一个数与2940的积是完全平方数,那么这个数最小是()。
2、(03甘肃冬令营)祖孙三人,孙子和爷爷的年龄的乘积是1512,而爷爷、父亲、孙子三人的年龄之积是完全平方数,则父亲的年龄是()岁。
3.求一个能被180整除的最小完全平方数.【例4】一个数减去100是一个平方数,减去63也是一个平方数,问这个数是多少?1、能否找到这么一个数,它加上24,和减去30所得的两个数都是完全平方数?2、三个自然数,它们都是完全平方数,最大的数减去第二大的数的差为80,第二大的数减去最小的数的差为60,求这三个数.3、一个自然数减去45及加上44都仍是完全平方数,求此数。
奥数数论:完全平方数要点及解题技巧

奥数数论:完全平方数要点及解题技巧一、完全平方数的定义:一个数如果是另一个整数的完全平方,那么我们就称这个数为完全平方数,也叫做平方数。
二、完全平方数特征:1.末位数字只能是:0、1、4、5、6、9;反之不成立。
2.除以3余0或余1;反之不成立。
3.除以4余0或余1;反之不成立。
4.约数个数为奇数;反之成立。
5.奇数的平方的十位数字为偶数;反之不成立。
6.奇数平方个位数字是奇数;偶数平方个位数字是偶数。
7.两个相临整数的平方之间不可能再有平方数。
平方差公式:X2-Y2=(X-Y)(X+Y)完全平方和公式:(X+Y)2=X2+2XY+Y2完全平方差公式:(X-Y)2=X2-2XY+Y2三、完全平方数的性质:性质1:完全平方数的末位数只能是0,1,4,5,6,9。
性质2:奇数的平方的个位数字为奇数,十位数字为偶数。
性质3:如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数。
性质4:偶数的平方是4的倍数;奇数的平方是4的倍数加1。
性质5:奇数的平方是8n+1型;偶数的平方为8n或8n+4型。
性质6:平方数的形式必为下列两种之一:3k,3k+1。
性质7:不能被5整除的数的平方为5k±1型,能被5整除的数的平方为5k型。
性质8:平方数的形式具有下列形式之一:16m,16m+1,16m+4,16m+9。
性质9:完全平方数的数字之和只能是0,1,4,7,9。
性质10:为完全平方数的充要条件是b为完全平方数。
性质11:如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数。
性质12:在两个相邻的整数的平方数之间的所有整数都不是完全平方数,即若n^2<k^2<(n+1)^2,则k一定不是整数。
性质13:一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n本身)。
完全平方数

完全平方数完全平方即用一个整数乘以自己例如1*1,2*2,3*3等,依此类推。
若一个数能表示成某个整数的平方的形式,则称这个数为完全平方数。
完全平方数是非负数,而一个完全平方数的项有两个。
注意不要与完全平方式所混淆。
完全平方数性质推论例如:0,1,4,9,16,25,36,49,64,81,100,121,144,169,196,225,256,289,324,361,400,441,484,529…观察这些完全平方数,可以获得对它们的个位数、十位数、数字和等的规律性的认识。
下面我们来研究完全平方数的一些常用性质:性质1:末位数只能是0,1,4,5,6,9。
(此为完全平方数的必要不充分条件,且定义为“一个数如果是另一个整数的完全平方,那么我们就称这个数为完全平方数”,0为整数,故0是完全平方数)性质2:奇数的平方的个位数字一定是奇数,偶数的平方的个位数一定是偶数。
证明奇数必为下列五种形式之一:10a+1,10a+3,10a+5,10a+7,10a+9分别平方后,得综上各种情形可知:奇数的平方,个位数字为奇数1,5,9;十位数字为偶数。
性质3:如果十位数字是奇数,则它的个位数字一定是6;反之也成立证明已知,证明k为奇数。
因为k的个位数为6,所以m的个位数为4或6,于是可设m=10n+4或10n+6。
则或即或∴k为奇数。
推论1:如果一个数的十位数字是奇数,而个位数字不是6,那么这个数一定不是完全平方数。
推论2:如果一个完全平方数的个位数字不是6,则它的十位数字是偶数。
性质4:偶数的平方是4的倍数;奇数的平方是4的倍数加1。
这是因为性质5:奇数的平方是8n+1型;偶数的平方为8n或8n+4型。
(奇数:n比那个所乘的数-1;偶数:n比那个所乘的数-2)在性质4的证明中,由k(k+1)一定为偶数可得到是8n+1型的数;由为奇数或偶数可得(2k)2为8n型或8n+4型的数。
性质6:形式必为下列两种之一:3k,3k+1。
1.3 完全平方数

1.3 完全平方数【知识精讲】1.定义:一个数如果是另一个整数的完全平方,那么我们就称这个数为完全平方数,也叫做平方数.例如:0,1,4,9,16,25,36,49,64,81,100,121,144,169,196,225,256,…,分析和比较这些完全平方数,可以获得对它们个位数、十位数、各位数字和等的规律性的认识.2.完全平方数的性质性质1:完全平方数的末位数只能是0,1,4,5,6,9.推论:末位数是2,3,7,8的整数一定不是完全平方数.性质2:奇数的平方的个位数字为奇数,十位数字为偶数.证明:奇数必为下列五种形式之一:10a+1,10a+3,10a+5,10a+7,10a+9.分别平方后,得(10a+1)2=100 a 2+20a+1=20a (5a+1)+1,(10a+3)2=100 a 2+60a+9=20a (5a+3)+9,(10a+5)2=100 a 2+100a+25=20(5a+5a+1)+5,(10a+7)2=100 a 2+140a+49=20(5a+7a+2)+9,(10a+9)2=100 a 2+180a+81=20(5a+9a+4)+1.综上各种情形可知:奇数平方的个位数字为奇数1,5,9;十位数字为偶数.性质3:如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数.证明:∵222(10)10020x y x xy y +=++,∴如果完全平方数2210020x xy y ++的十位数字是奇数,则2y 的十位数字是奇数,∴y =4或6,由此知2210020x xy y ++的个位数字是6.反之,若m 2=10k +6,则k 为奇数.∵m 2的个位数为6,∴m 的个位数为4或6,于是可设m =10n+4或10n+6,从而有10k+6=(10n+4)2=100n 2+10(8n +1)+6,或10k +6=(10n+6)2=100n 2+10(12n+3)+6,即k =10n 2+8n +1=2(5n 2+4n )+1,或k =10n 2+12n +3=2(5n 2+6n )+3,∴k 为奇数.推论1:如果完全平方数的十位数字是偶数,则它的个位数字一定不是6;反之,如果完全平方数的个位数字不是6,则它的十位数字一定是偶数.推论2:如果一个数的十位数字是奇数,而个位数字不是6,那么这个数一定不是完全平方数.推论3:如果一个数的个位数字是6,而十位数字是偶数,那么这个数一定不是完全平方数.注:一个数的十位数字是奇数,个位数字是6,这个数未必是完全平方数;一个数的十位数字是偶数,个位数字不是6,这个数也未必是完全平方数.性质4:偶数的平方是4的倍数;奇数的平方是4的倍数加1(更确切地说是8的倍数加1,即是8n+1型).这是因为(2k)2=4k2,(2k+1)2=4k(k+1)+1.推论:形如4n+2和4n+3型的整数一定不是完全平方数.性质5:完全平方数的形式必为下列两种之一:3k,3k+1.这是因为自然数被3除按余数的不同可以分为三类:3m,3m+1,3m+2.平方后,分别得(3m)2=9m2=3k,(3m+1)2=9m2+6m+1=3k+1,(3m+2)2=9m2+12m+4=3k+1.推论:形如3n+2型的整数一定不是完全平方数.性质6:不能被5整除的数的平方为5k±1型,能被5整除的数的平方为5k型.推论:形如5n±2型的整数一定不是完全平方数.性质7:完全平方数的各位数字之和被9除的余数只可能是0,1,4,7.证明:易知,一个数的各位数字之和被9除的余数等于这个数被9除的余数.因为一个整数被9除只能是9k,9k±1,9k±2,9k±3,9k±4这几种形式,而(9k)2=9(9k2)+0,(9k±1)2=9(9k2±2k)+1,(9k±2)2=9(9k2±4k)+4,(9k±3)2=9(9k2±6k+1)+0,(9k±4)2=9(9k2±8k+1)+7.故知所证结论成立.推论:各位数字和被9除的余数是2,3,5,6,8的整数一定不是完全平方数.性质8:如果质数p能整除a,但不能整除ap,则a不是完全平方数.性质9:在两个相邻的整数的平方数之间的所有整数都不是完全平方数,即若n 2<k<(n +1)2,则k 一定不是完全平方数. 【应用举例】例1.一个自然数减去45及加上44都仍是完全平方数,求此数.解:设此自然数为x ,依题意可得x -45=m 2(1)x +44=n 2(m ,n 为自然数) (2)(2)-(1)可得:89=n 2-m 2,∴n>m .但89为质数,它的正因子只能是1与89,于是n+m =89,n-m =1.解之,得n =45,代入(2),得x =1981.故所求的自然数是1981.例2.求证:四个连续的整数的积加上1,等于一个奇数的平方.(1954年基辅数学竞赛试题).分析:设四个连续的整数为n -1,n ,n +1,n +2,其中n 为整数.欲证(n -1)n (n +1)(n +2)+1是一奇数的平方,只需将它通过因式分解而变成一个奇数的平方即可.证明:设这四个整数之积加上1为m ,则m =(n -1)n (n +1)(n +2)+1=[n (n +1)-1]2,而n (n +1)是两个连续整数的积,所以是偶数;因而n (n +1)-1是奇数.这就证明了m 是一个奇数的平方.例3.求证:11,111,1111,… …这串数中没有完全平方数.(1972年基辅数学竞赛试题)分析:形如11…1的数若是完全平方数,必是末位为1或9的数的平方,即2(101)a +(a ∈N )或2(109)b +(N b ∈),在两端同时减去1即推出矛盾.证明:若211...1(101) (N)a a =+∈,则211...1010020 (N)a a a =+∈,即211...1102 (N)a a a =+∈.因为左端为奇数,右端为偶数,所以左右两端不相等.若211...1(109) (N)b b =+∈,则211...1010018080 (N)b b b =++∈,即211...110188 (N)b b b =++∈.因为左端为奇数,右端为偶数,所以左右两端不相等.综上所述,11…1不可能是完全平方数.另证:由11…1为奇数知,若它为完全平方数,则只能是奇数的平方.但已证过,奇数的平方其十位数字必是偶数,而十位上的数字为1,所以不是完全平方数.例4.矩形四边的长度都是小于10的整数(单位:公分),这四个长度数可构成一个四位数,这个四位数的千位数字与百位数字相同,并且这四位数是一个完全平方数,求这个矩形的面积.(1986年缙云杯初二数学竞赛试题)解:设矩形的边长为x ,y ,则四位数N =1100x +11y ,∵N 是完全平方数,11为质数,∴100x+y 能被11整除.又100x+y =99x+(x+y ), ∴x+y 能被11整除,而18x y +≤,∴x+y =11.∴100x+y =11(9x +1),∴9x +1是一个完全平方数,而x<10,验算知x =7满足条件. 又由x+y =11得y =4.故所求面积为28(cm 2).例5.甲、乙两人合养了n 头羊,而每头羊的卖价又恰为n 元,全部卖完后,两人分钱方法如下:先由甲拿十元,再由乙拿十元,如此轮流,拿到最后,剩下不足十元,轮到乙拿去.为了平均分配,甲应该补给乙多少元?(第2届“祖冲之杯”初中数学邀请赛试题)解:n 头羊的总价为n 2元,由题意知n 2元中含有奇数个10元,即完全平方数的十位数字是奇数.如果完全平方数的十位数字是奇数,则它的个位数字一定是6.所以,n 2的末位数字为6,即乙最后拿的是6元,从而为平均分配,甲应补给乙2元.例6.设2392N x y =+为完全平方数,且N 不超过2392,则满足上述条件的正整数对(,)x y 共_________对. (2002年全国初中数学联赛试题)解:239223(4)N x y x y =+=+ ,23为质数,N 为不超过2392的完全平方数,∴2423(x y m m +=⋅为正整数),且22232392N m =⋅≤. ∴22239210452323m ≤=<, ∴21m =或4. 当21m =时,423x y +=,得1,2,3,4,5y =;19,15,11,7,3x =.当24m =时,得492x y +=,1,2,3,...,22y =;88,84,80,...,4x =.故共有(1,19),(2,15),(3,11)及(1,88),(2,84),...,(22,4),即共有5+22=27对.例7.要使610222x ++为完全平方数,那么非负整数x 是________(要求写出x 的3个值).(2001年第十六届江苏省初中数学竞赛试题)解:61032355293529222(2)222(2)22(22)22x x x ++=+⨯⨯++-=++- , 9x ∴=. 又4610323210222222(2)222(2)22xx x x +++=+⨯⨯++-4321022(22)22x x +=++-,12x ∴=. 又661052526222222(2)222(2)22x x x x +++=+⨯⨯++-652622(22)22x x +=++-,0x ∴=. 此外,将x =1,2,3,4,5,6,7,8,10,11逐个检验可知,x =11时,6106462222(122)x x -++=++=3136=562.注:当x 为大于12的偶数时,因为6103222222(22)x x x <++<+,即66246222(2)122(12)x x x ---<++<+,所以610222x ++不可能是完全平方数.例8.把1,2,…,30这30个数分成k 个组(每个数只能在一个组中出现),使得每一个组中任意两个不同的数的和都不是完全平方数.求k 的最小值.(2006年青少年数学国际城市邀请赛个人赛试题)解:先考虑6,19,30.∵6+19=25,6+30=36,19+30=49,∴这3个数必须属于3个不同组.于是3k ≥.再把1,2,…,30这30个数分成如下3组:1{3,7,11,15,19,23,27,4,8,16,24}A =,2{1,5,9,13,17,21,25,29,6,14,18,26}A =,3{2,10,12,20,22,28,30}A =.由于完全平方数除以4的余数只能是0或1,容易验证123,,A A A 满足题设条件.【巩固练习】1.试证:数列49,4489,444889,…的每一项都是完全平方数.2.用300个2和若干个0组成的整数有没有可能是完全平方数?3.证明:不存在x ,y ,使等式x 2+y 2=1995(x ,y ∈Z )成立.4.求一个四位数,使它等于它的四个数字和的四次方,并证明此数是唯一的.5.已知直角三角形的两直角边长分别为l 厘米、m 厘米,斜边长为n 厘米,且l ,m ,n 均为正整数,l 为质数.证明:2(l +m +1)是完全平方数.(1985年上海初中数学竞赛试题)6.求所有四位数m ,满足2006m <,且存在正整数n ,使得m n -为质数,mn 是一个完全平方数.(2006年青少年数学国际城市邀请赛团体赛试题)练习1.3参考答案:1.证明:44…488…89=4(11…1)×10k +8(11…1)+1=4(11…1)×(99…9+1)+8(11…1)+1=36(11…1)2+12(11…1)+1=(66…6+1)2.2.解:设由300个2和若干个0组成的数为A ,则其数字和为600.∵3︱600,∴3︱A .此数有因数3,若为完全平方数,必有9︱A ,但9†600,∴矛盾,故不可能为完全平方数.3.证明:假设有整数x ,y 存在,使x 2+y 2=1995成立.∵x 2,y 2被4除余数为0或1.∴x 2+y 2被4除余数为0,1或2.又∵1995被4除余数为3.∴矛盾,假设不成立.故没有整数x ,y 存在,使x 2+y 2=1995成立.4.解:设符合题意的四位数为1234x a a a a =,则41234()x a a a a =+++, 41010000= 为五位数,54=625为三位数,∴1234510a a a a <+++<.经计算知,符合题意的只有2401一个.5.解:∵l 2+m 2=n 2,∴l 2=(n+m )(n-m ) .∵l 为质数,且n+m >n-m >0,∴n+m =l 2,n-m =1。
第九讲____完全平方数
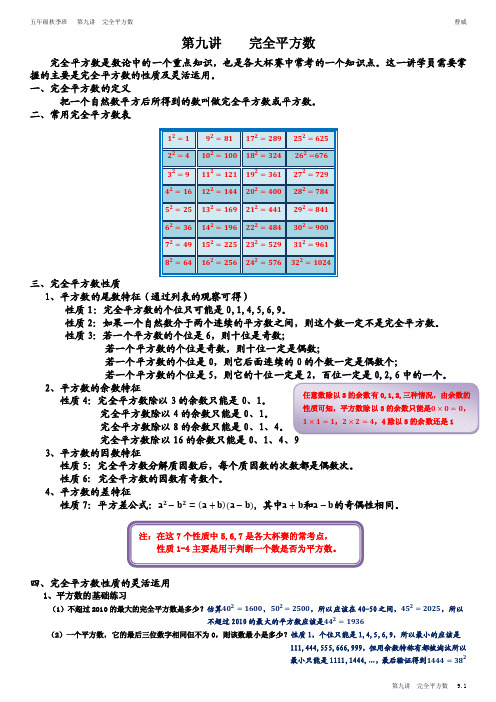
第九讲 完全平方数完全平方数是数论中的一个重点知识,也是各大杯赛中常考的一个知识点。
这一讲学员需要掌握的主要是完全平方数的性质及灵活运用。
一、完全平方数的定义把一个自然数平方后所得到的数叫做完全平方数或平方数。
二、常用完全平方数表三、完全平方数性质1、平方数的尾数特征(通过列表的观察可得)性质1:完全平方数的个位只可能是0,1,4,5,6,9。
性质2:如果一个自然数介于两个连续的平方数之间,则这个数一定不是完全平方数。
性质3:若一个平方数的个位是6,则十位是奇数;若一个平方数的个位是0 若一个平方数的个位是52、平方数的余数特征 性质4:完全平方数除以3的余数只能是0、1。
完全平方数除以4的余数只能是0、1。
完全平方数除以8的余数只能是0、1、4。
完全平方数除以16的余数只能是0、1、43、平方数的因数特征性质5 性质6: 完全平方数的因数有奇数个。
4、平方数的差特征性质7:平方差公式: , 其中 和 的奇偶性相同。
四、完全平方数性质的灵活运用1、平方数的基础练习(1)不超过2010的最大的完全平方数是多少?估算 , ,所以应该在40-50之间, ,所以不超过2010的最大的平方数应该是(2)一个平方数,它的最后三位数字相同但不为0,则该数最小是多少?性质1,个位只能是1,4,5,6,9,所以最小的应该是111,444,555,666,999,但用余数特称有都被淘汰所以最小只能是1111,1444,…,最后验证得到注:在这7个性质中5,6,7是各大杯赛的常考点, 性质1-4主要是用于判断一个数是否为平方数。
2、平方数的例题讲解例1、分析:肯定是发错了。
作业本的总数量如果是个完全平方数的话由性质1可知,平方数的个位只能是0、1、4、5、6、9,所以除以5的余数只能是0、1、4,而题每人5本最后余3本,所以不可能。
拓展练习:(1)1+1×2+1×2×3+1×2×3×4+1×2×3×4×5+1×2×3×4×5×6的结果是完全平方数吗?提示:不是,该式子的结果个位为1+2+6+4+0+0=3,(性质1)(2)我们知道:,,都是完全平方数,那么121+12321+1234321+ …+12345678987654321是不是完全平方数?提示:不是。
完全平方数

第二十四课完全平方数一个自然数与它本身相乘,乘积叫做完全平方数,或叫做平方数.例如1×1=1,2×2=4,3×3=9,…,那么1、4、9、…就是完全平方数.完全平方数有一些有趣而且重要的性质:(1)完全平方数的尾数只能是0,1,4,5,6,9.因为任何一个完全平方数的尾数,只能等于02,12,22,32,…,92的尾数,而这些数的尾数只有0,1,4,5,6,9.(2)完全平方数的约数个数是奇数个.因为完全平方数a2,a是自然数,则a=a1×a2×a3×…×ar,a1,a2,a3,…,ar是a的质因数.尾数一定是奇数,所以a2的约数个数是奇数个.(3)一个完全平方数被3除的余数是0或1.因为一个自然数被3除的余数只能是0,1,2这3个数中的一个.如果这个自然数被3除余数是0,那么这个数的完全平方数被3除余数也是0;如果这个自然数被3除余数是1,那么这个数的完全平方数被3除的余数是12,也是1;如果这个自然数被3除余数是2,那么这个数的完全平方数被3除余数是22被3除的余数是1;所以一个完全平方数被3除的余数只能是0或1.(4)偶数的平方数能被4整除,奇数的平方被4或8除的余数是1.因为偶数表示为2n,n是整数.那么偶数的平方为(2n)2=4n2,能被4整除.奇数表示为2n+1,n是整数,那么奇数的平方为(2n+1)2=4n2+4n+1=4(n+1)n+1,所以奇数的平方被4除的余数是1;又因为n+1,n是两个连续整数,必有一个是偶数,所以4(n+1)n能被8整除,也就是4(n+1)n+1被8除的余数是1,故奇数的平方被8除的余数是1.(5)一个完全平方数的末位数如果是0,那么它的末两位数也一定都是0. 1,4,9,16,25,36,49,64,81,100,121,144,169,196,225,289,324,361,400.完全平方数的末位数如果是0,那么它的末两位数也一定都是0.(6)末位数是5的正整数的平方数的末两位数一定是25.这是因为,末位数是5的正整数都可以写成10a +5的形式(其中a 为正整数),它的平方数是=+2)510(a 2100a .25)1(10025100++=++a a a 其中一个加数是100a(a +1),它的末两位数都是0,另一个加数是25,它们的和的末两位数一定是25.例:判断1369是否为完全平方数,可作如下分析:1369如果是完全平方数,它的算术平方根一定是二位整数.又它的末位数是9,所以它的算术平方根的末位数只可能是3或7.因为160040,9003022==,而900<1369<1600,所以1369的算术平方根只可能是33或37.经计算验证得136937,10893322==.因此,1369是一个完全平方数,它的算术平方根是37.“”例:如果判断1214是否完全平方数,可以仿照前面对1369的分析,得到它的算术平方根只可能是32或38.验算得1214144438,121410243222≠=≠=,因此可以判断出1214不是完全平方数. 例:如果判断237,4323,1348等末位数是3,7,8的数是否完全平方数,则结果是显然的.因为末位是3,7,8的正整数不可能是完全平方数.另外,个位数是0而十位数不是0的数(如38060)一定不是完全平方数.下面举一个可以用完全平方数来解的例子问题 22y x +如果为正整数,则在下面的四组数值中x 和y 只能取( )A.x =25530,y =29464B .x =37615,y =26855C .x =15123,y =32477D .x =28326,y =28614思路启迪: 把题中所给的四组x 、y 的值分别代入22y x +进行计算,就可以得到正确答案.但这种方法运算量太大.可以用筛选法.对所给四组值分别进行分析、筛选,看哪一组数能使22y x +是完全平方数,哪些组数不能使22y x +是完全平方数.如果能使22y x +是完全平方数的只有一组,显然这一组就是正确答案.规范解法对于A :x =25530,y =29464,,y ,x 6022的末位数是的末位数是.22是完全平方数中的一组数有可能使y x A +∴对于B:x =37615,y =26855.2222,25,25y x y x +是末两位数是的末两位数是 的末两位数是50,由于末位数是0时,只有末两位都是0时才能为完全平方数,.y ,x :C .y x B 324771512322==+∴对于为完全平方数中的一组数不可能使,.y x ,y ,x 是完全平方数的数不可能而末位数是的末位数是的末位数也是的末位数是88992222+∴.22为完全平方数中的一组数不可能使y x C +∴ 对于D:x =28326,y =28614.2222,9,6y x y x +∴的末位数也是是末位数是 的末位数是8.而末位数是8的数不可能是完全平方数,.y x D 为完全平方数中的一组数不可能使22+∴根据前面对四组数的分析可知,只有(A)中的一组数有可能使22y x +是完全平方数,其余三组数都没有这个可能.而此题有且只有一个正确答案,所以应选A性质1:完全平方数的末位数只能是0,1,4,5,6,9。
小学奥数 完全平方数 知识点+例题+练习 (分类全面)

二、完全平方数的等价条件:奇数个因数
注:计算一个数的因数先把这个数分解质因数,然后把不同质因数的个数加1以后再相乘所得的乘积就是因数的个数
例如:12=2×2×3
12的质因数2有2个,质因数3有1个因数个数:(2+1)×(1+1)=6个
180=2×2×3×3×5
2.完全平方数的约数一定有奇数个;有奇数个约数的数一定是完全平方数。
3. 奇数的平方是奇数,偶数的平方是偶数
完全平方数除以3的余数只可能为为0或1;
完全平方数除以4的余数只可能为为0或1;
偶数的平方是4的倍数,奇数的平方除以4余1。
(二)一些推论
1.任何偶数的平方一定能被4整除;任何奇数的平方被4(或8)除余1.即被4除余2或3的数一定不是完全平方数。
巩固、已知m,n都是自然数,且n2 126m,则n的最小值为。
四、“平方族”成员典型特征二:除以3或4只能余0或1
注:奇数的平方是奇数,偶数的平方为偶数,而奇数的平方除以4余1,偶数的平方能被4整除
例1、形如11,111,1111,11111,…的数中有没有完全平方数?
巩固、A是由2018个“4”组成的多位数,即444444……(2018个4),A是不是某个自然数B的平方?如果是,写出B;如果不是,请说明理由.
961、 3364、1111111、1521、 1234321、 1849、 89234
2.一个完全平方数被3除的余数是0或1.即被3除余2的数一定不是完全平方数。
3.自然数的平方末两位只有:00,01,21,41,61,81,04,24,44,64,84,25,09,29,49,69,89,16,36,56,76,96。
小学奥数25完全平方数

2、7完全平方数2、7、1相关概念完全平方即用一个整数乘以自己例如1*1,2*2,3*3等等,依此类推。
若一个数能表示成某个整数得平方得形式,则称这个数为完全平方数。
完全平方数就是非负数。
2、7、2性质推论例如:0,1,4,9,16,25,36,49,64,81,100,121,144,169,196,225,256,289,324,361,400,441,484,529…观察这些完全平方数,可以获得对它们得个位数、十位数、数字与等得规律性得认识。
下面我们来研究完全平方数得一些常用性质:性质1:末位数只能就是0,1,4,5,6,9。
此为完全平方数得必要不充分条件,且定义为“一个数如果就是另一个整数得完全平方,那么我们就称这个数为完全平方数”,0为整数,故0就是完全平方数性质2:奇数得平方得个位数字一定就是奇数,十位数字为偶数;偶数得平方得个位数字一定就是偶数。
证明奇数必为下列五种形式之一:10a+1,10a+3,10a+5,10a+7,10a+9分别平方后,得)10a+3)2=100a2+60a+9=20a(5a+3)(10a+1)2=100a2+20a+1=20a(5a+1)+1ﻫ+9ﻫ(10a+5)2=100a2+100a+25=20(5a+5a+1)+5(10a+7)2=100a2+140a+49=20 (5a+7a+2)+9(10a+9)2=100a2+180a+81=20(5a+9a+4)+1综上各种情形可知:奇数得平方,个位数字为奇数1,5,9;十位数字为偶数。
性质3:如果完全平方数得十位数字就是奇数,则它得个位数字一定就是6;反之,如果完全平方数得个位数字就是6,则它得十位数字一定就是奇数。
证明已知m2=10k+6,证明k为奇数。
因为k得个位数为6,所以m得个位数为4或6,于就是可设m=10n+4或10n+6。
则10k+6=(10n+4)2=100+(8n+1)x10+6或10k+6=(10n+6)2=100+(12n+3)x10+6即 k=10+8n+1=2(5+4n)+1或 k=10+12n+3=2(5+6n)+3∴k为奇数。
完全平方数2

一个数如果是另一个整数的完全平方,那么我们就称这个数为完全平方数,也叫做平方数。
例如:0,1,4,9,16,25,36,49,64,81,100,121,144,169,196,225,256,289,324,361,400,441, 484,…观察这些完全平方数,可以获得对它们的个位数、十位数、数字和等的规律性的认识。
下面我们来研究完全平方数的一些常用性质:性质1:完全平方数的末位数只能是0,1,4,5,6,9。
性质2:奇数的平方的个位数字为奇数,十位数字为偶数。
证明奇数必为下列五种形式之一:10a+1, 10a+3, 10a+5, 10a+7, 10a+9分别平方后,得(10a+1)²=100a²+20a+1=20a(5a+1)+1(10a+3)²=100a²+60a+9=20a(5a+3)+9(10a+5)²=100a²+100a+25=20 (5a+5a+1)+5(10a+7)²=100a²+140a+49=20 (5a+7a+2)+9(10a+9)²=100a²+180a+81=20 (5a+9a+4)+1综上各种情形可知:奇数的平方,个位数字为奇数1,5,9;十位数字为偶数。
性质3:如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数。
证明已知m²=10k+6,证明k为奇数。
因为的个位数为6,所以m的个位数为4或6,于是可设m=10n+4或10n+6。
则10k+6=(10n+4)^2=100+(8n+1)x10+6或 10k+6=(10n+6)^2=100+(12n+3)x10+6即 k=10+8n+1=2(5+4n)+1或 k=10+12n+3=2(5+6n)+3∴ k为奇数。
推论1:如果一个数的十位数字是奇数,而个位数字不是6,那么这个数一定不是完全平方数。
4.完全平方数

第四节完全平方数当自然数N 恰好是另一自然数M 的平方时,我们称自然数N 为完全平方数。
完全平方数有下面重要性质:(1)平方数的末位数字只可能是0,1,4,5,6,9。
(2)在完全平方数的质因数分解中,每个质因数的幂指数都是偶数。
(3)完全平方数的末位数字是奇数时,起十位数字必为偶数;末位数字为偶数时,起十位数字有奇数,有偶数;当末位数字为6时,它的十位数字必为奇数。
证:设n 是奇数的平方,即2a n =,a 总可以表示为r q a +=10,其中=r 1,3,5,7,9。
∴222220100)10(r qr q r q a n ++=+==∵2r 只可能是1,9,25,49,81。
而)210(102010022qr q qr q +=+但∵2222)210(1020100r qr q r qr q ++=++的十位数字为qr q 2102+的个位数字(偶数)与2r 的十位数字(显然是0,2,4,8中的一个)之和,因此也为偶数,即完全平方数的末位数字是奇数时,起十位数字必为偶数。
类似地,可证另两个结论。
换句话说,如果一个整数的个位与十位数字都是奇数那么这个整数不是完全平方数,如果一个整数的末位数字为6而十位数字为偶数,那么这个整数不是完全平方数。
下面来看一些与完全平方数有关的问题。
例1、一个自然数减去55后是一个完全平方数,这个自然数加上34,仍是一个完全平方数,试求这个自然数。
解:设这个自然数为x ,则⎩⎨⎧=+=-)2(34)1(5522n x m x (n m ,都是自然数,显然n m <) ②-①得:89))((=+-m n m n③ ∵89是质数,∴⎩⎨⎧=+=-891m n m n ,解得⎩⎨⎧==4445m n ,∴19913422=-=n x 。
例2、用300个2和若干个0组成的整数有没有可能是完全平方数?试说明原因。
分析:设用300个2和若干个0组成的整数为,其位数至少是301位。
完全平方式的定义

完全平方式的定义完全平方式是一个数学概念,它指的是一个数可以被平方数整除。
换句话说,如果一个数n能够表示成m的形式,那么n就是一个完全平数。
例如,4、9、16、25等都是完全平数。
在数学中,完全平数是一个重要的概念,它与平方数、因数、素数等数学知识密切相关。
因此,我们有必要深入了解完全平方式的定义及其相关内容。
一、完全平方式的定义完全平方式的定义非常简单,它是指一个数n可以表示成m的形式,其中m为整数。
例如,16=4,25=5,36=6等都是完全平数。
完全平数也可以用另一种方式来表示,即n可以表示成p1^a1 * p2^a2 * … * pn^an的形式,其中p为素数,a为正整数,并且每个a都是偶数。
例如,36=2 * 3,100=2 * 5等都是完全平数。
二、完全平数的性质完全平数有许多有趣的性质,下面列举一些常见的性质。
1. 完全平数的个数是无限的。
证明:假设完全平数的个数有限,那么我们可以将它们按照大小排序,设最大的完全平数为N。
由于完全平数是无限的,所以一定存在一个更大的完全平数M>M,且M<N,这与N是最大的完全平数矛盾,因此假设不成立,完全平数的个数是无限的。
2. 完全平数的奇数次方根是无理数。
证明:假设√n是一个有理数,即√n=p/q,其中p和q互质。
那么n=p/q,即nq=p。
由于p是完全平数,所以p也是完全平数。
设p=m,那么nq=m,即n可以表示成m/q的形式,而这与n是完全平数矛盾,因此假设不成立,完全平数的奇数次方根是无理数。
3. 完全平数的因数个数是奇数。
证明:假设n是一个完全平数,即n=m。
那么n的因数可以表示成m的因数的平方。
设m的因数个数为k,那么n的因数个数为k。
由于k是奇数,所以k也是奇数,因此完全平数的因数个数是奇数。
4. 完全平数的因数和是完全平数。
证明:假设n是一个完全平数,即n=m。
那么n的因数可以表示成m的因数的平方。
设m的因数为p1、p2、…、pk,那么n的因数可以表示成p1、p2、…、pk的形式。
完全平方数

完全平方数一、完全平方数的性质最重要的4个性质:1.完全平方数的尾数只能是0,1,4,5,6,9。
不可能是2,3,7,8。
2.除以4只能余0或者余1。
不可能余2或3。
3.完全平方数分解质因数后,指数都是偶数,指数是偶数的数是完全平方数。
4.完全平方数的约数个数是奇数,约数的个数为奇数的自然数是完全平方数。
其他性质:性质1:在两个连续正整数的平方数之间不存在完全平方数。
性质2:如果一个完全平方数的个位是0,则它后面连续的0的个数一定是偶数性质3:完全平方数被3,4,5,8,16除的余数一定是完全平方数.性质4:如果一个完全平方数的个位是5,则其十位一定是2,且其百位一定是0,2,6中的一个.性质5:完全平方数的个位是6,那么它的十位是奇数.性质6:若质数p整除a的平方,则p能被a整除。
例题1:下面是一个算式:112123123412345123456+⨯+⨯⨯+⨯⨯⨯+⨯⨯⨯⨯+⨯⨯⨯⨯⨯,这个算式的得数能否是某个数的平方?【考点】平方数特征之平方数的尾数特征【难度】3星【题型】解答【关键词】华杯赛【答案】判断一个数是否是某个数的平方,首先要观察它的个位数是多少.平方数的个位数只能是0,1,4,5,6,9,而2,3,7,8不可能是平方数的个位数.这个算式的前二项之和为3,中间二项之和的个位数为0,后面二项中每项都有因子2和5,个位数一定是0,因此,这个0算式得数的个位数是3,不可能是某个数的平方.例题2:证明:形如11,111,1111,11111,…的数中没有完全平方数。
【考点】平方数特征之平方数的整除特性【难度】2星【题型】解答【答案】由于奇数的平方是奇数,偶数的平方为偶数,而奇数的平方除以4余1,偶数的平方能被4整除.现在这些数都是奇数,它们除以4的余数都是3,所以不可能为完全平方数.例题3:已知自然数n满足:12!除以n得到一个完全平方数,则n的最小值是。
【考点】完全平方数计算及判断【难度】3星【题型】填空【关键词】2008年,学而思杯,6年级,第9题【答案】(法1)先将12!分解质因数:1052=⨯⨯⨯⨯,由于12!除以n得到一个12!235711完全平方数,那么这个完全平方数是12!的约数,那么最大可以为1042⨯⨯,所以n最小235为104212!2353711÷⨯⨯=⨯⨯231=。
完全平方数

完全平方数若一个数是一个整数的平方,则称这个数是完全平方数,简称平方数。
完全平方数有下列性质:(1)平方数的末位数只能是0,1,4,5,6,9;(2)偶平方数能被4整除,奇平方数被8除余1;(3)平方数只能是形如3k或3k+1的数;(4)奇平方数的十位数一定是偶数;(5)若平方数的末位数是奇数时,则其十位数字必为偶数例1、设N=23x+92y为完全平方数,且N不超过2392,则满足上述条件的一切正整数对(x,y)共有对。
因N=23x+92y=23(x+4y),且23为质数,故x+4y=23m2(m为正整数)例2、使n5-5n3+4n+7成为完全平方数的自然数n的取值()A.有且只有一个B.有有限多个,但多于一个C.有无穷多个D.不存在将原式分解因式,分析个位数例3、已知a是正整数,且a2+2004a是一个正整数的平方,求a的最大值解题思路设a2+2004a=m2,其中m是正整数,通过引入参数、配方将问题转化为解不定方程。
例4、若一个整数能够表示成x2+2xy+2y2(x,y是整数)的形式,则称该数为“好数”(1)判断29是否为好数(2)写出80,81,…,100中的好数;(3)如果m,n都是好数,证明:mm也是好数解题思路x2+2xy+2y2=(x+y)2+y2,即一个好数可表示成两个完全平方数的和,这是好数的特征,亦是解本例的关键。
例5、某正整数的平方,其末三位是非0的相同数字,求具有该性质的最小正整数.解:设所求数为p,p>0,p2即具有末三位数,则p2至少有三位数,p至少有两位数。
设p =10a士b(a,b为正整数,1≤b≤5),则p2=100a2±20ab+b2=100a2+10(±2ab)+b2。
验证知当b=1,3,4,5时,p2的十位和个位数字奇偶性相反;当b=2时,p2的末两位数字奇偶性相同.所以所求数必须形如10a±2,而p=12时,p2=144,末两位数字为4.又注意(50n士x)2=2500n2士100nx+x2=100(25n2士nx)+x2。
完全平方数的性质

完全平方数的性质
完全平方数是指一个正整数能够表示成某个整数的平方的形式,即一个数的平方根是另一个整数。
例如:
4=2×2,9=3×3,16=4×4,25=5×5,36=6×6,
49=7×7,64=8×8,81=9×9……
完全平方数一般有以下性质:
1. 任何一个数都可以分解成素因子的平方,而完全平方数就是这些素因子只有一个或者相同的数的乘积。
2. 完全平方数的奇偶性和它的平方根的奇偶性是一致的。
3. 所有的完全平方数都是非负数,而且所有的非负数都不一定是完全平方数。
4. 对于任意一个数n,如果n+1是一个完全平方数,则n必然是一个奇数;如果n+1不是一个完全平方数,则n 必然是一个偶数。
完全平方数

性质1:完全平方数的末位数只能是0,1,4,5,6,9。
性质2:奇数的平方的个位数字为奇数,十位数字为偶数。
性质3:如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数。
性质4:偶数的平方是4的倍数;奇数的平方是4的倍数加1。
性质5:奇数的平方是8n+1型;偶数的平方为8n或8n+4型。
性质6:平方数的形式必为下列两种之一:3k,3k+1。
性质7:不能被5整除的数的平方为5k±1型,能被5整除的数的平方为5k型。
性质8:平方数的形式具有下列形式之一:16m,16m+1, 16m+4,16m+9。
性质9:完全平方数的数字之和只能是0,1,4,7,9。
完全平方数一个自然数与它本身相乘,乘积叫做完全平方数,或叫做平方数.例如1×1=1,2×2=4,3×3=9,…,那么1、4、9、…就是完全平方数.完全平方数有一些有趣而且重要的性质:(1)完全平方数的尾数只能是0,1,4,5,6,9.因为任何一个完全平方数的尾数,只能等于02,12,22,32,…,92的尾数,而这些数的尾数只有0,1,4,5,6,9.(2)完全平方数的约数个数是奇数个.因为完全平方数a2,a是自然数,则a=a1×a2×a3×…×ar,a1,a2,a3,…,ar是a的质因数.尾数一定是奇数,所以a2的约数个数是奇数个.(3)一个完全平方数被3除的余数是0或1.因为一个自然数被3除的余数只能是0,1,2这3个数中的一个.如果这个自然数被3除余数是0,那么这个数的完全平方数被3除余数也是0;如果这个自然数被3除余数是1,那么这个数的完全平方数被3除的余数是12,也是1;如果这个自然数被3除余数是2,那么这个数的完全平方数被3除余数是22被3除的余数是1;所以一个完全平方数被3除的余数只能是0或1.(4)偶数的平方数能被4整除,奇数的平方被4或8除的余数是1. 因为偶数表示为2n ,n 是整数.那么偶数的平方为(2n )2=4n 2,能被4整除.奇数表示为2n+1,n 是整数,那么奇数的平方为(2n+1)2=4n 2+4n+1=4(n+1)n+1,所以奇数的平方被4除的余数是1;又因为n+1,n 是两个连续整数,必有一个是偶数,所以4(n+1)n 能被8整除,也就是4(n+1)n+1被8除的余数是1,故奇数的平方被8除的余数是1.(5)一个完全平方数的末位数如果是0,那么它的末两位数也一定都是0. 1,4,9,16,25,36,49,64,81,100,121,144,169,196,225,289,324,361,400.完全平方数的末位数如果是0,那么它的末两位数也一定都是0.(6)末位数是5的正整数的平方数的末两位数一定是25.这是因为,末位数是5的正整数都可以写成10a +5的形式(其中a 为正整数),它的平方数是=+2)510(a 2100a.25)1(10025100++=++a a a 其中一个加数是100a(a +1),它的末两位数都是0,另一个加数是25,它们的和的末两位数一定是25.例:判断1369是否为完全平方数,可作如下分析:1369如果是完全平方数,它的算术平方根一定是二位整数.又它的末位数是9,所以它的算术平方根的末位数只可能是3或7.因为160040,9003022==,而900<1369<1600,所以1369的算术平方根只可能是33或37.经计算验证得136937,10893322==.因此,1369是一个完全平方数,它的算术平方根是37.“”例:如果判断1214是否完全平方数,可以仿照前面对1369的分析,得到它的算术平方根只可能是32或38.验算得1214144438,121410243222≠=≠=,因此可以判断出1214不是完全平方数. 例:如果判断237,4323,1348等末位数是3,7,8的数是否完全平方数,则结果是显然的.因为末位是3,7,8的正整数不可能是完全平方数.另外,个位数是0而十位数不是0的数(如38060)一定不是完全平方数.下面举一个可以用完全平方数来解的例子问题 22y x +如果为正整数,则在下面的四组数值中x 和y 只能取( )A.x =25530,y =29464B .x =37615,y =26855C .x =15123,y =32477D .x =28326,y =28614思路启迪: 把题中所给的四组x 、y 的值分别代入22y x +进行计算,就可以得到正确答案.但这种方法运算量太大.可以用筛选法.对所给四组值分别进行分析、筛选,看哪一组数能使22y x +是完全平方数,哪些组数不能使22y x +是完全平方数.如果能使22y x +是完全平方数的只有一组,显然这一组就是正确答案.规范解法对于A :x =25530,y =29464,,y ,x 6022的末位数是的末位数是.22是完全平方数中的一组数有可能使y x A +∴对于B:x =37615,y =26855.2222,25,25y x y x +是末两位数是的末两位数是 的末两位数是50,由于末位数是0时,只有末两位都是0时才能为完全平方数,.y ,x :C .y x B 324771512322==+∴对于为完全平方数中的一组数不可能使,.y x ,y ,x 是完全平方数的数不可能而末位数是的末位数是的末位数也是的末位数是88992222+∴ .22为完全平方数中的一组数不可能使y x C +∴对于D:x =28326,y =28614.2222,9,6y x y x +∴的末位数也是是末位数是 的末位数是8.而末位数是8的数不可能是完全平方数,.y x D 为完全平方数中的一组数不可能使22+∴根据前面对四组数的分析可知,只有(A)中的一组数有可能使22y x +是完全平方数,其余三组数都没有这个可能.而此题有且只有一个正确答案,所以应选A性质1:完全平方数的末位数只能是0,1,4,5,6,9。
完全平方数与配方法

完全平方数与配方法配方法(也称为“分解因式法”)是指将一个数按照一定的规则分解成两个因数的乘积。
在配方法中,完全平方数扮演着重要的角色。
下面就来详细讨论完全平方数与配方法之间的关系。
首先,我们来看一下完全平方数的性质。
对于一个完全平方数x^2,它可以表示成(x-a)(x+a)的形式,其中a是一个小于等于x的正整数。
这个性质可以通过展开(x-a)(x+a)来验证:(x-a)(x+a)=x^2-a^2可以看到,这个展开式的结果是一个完全平方数。
因此,可以得出结论:任意一个完全平方数都可以表示成两个因数的乘积。
接下来,我们来看一下配方法。
对于一个一般的整数y,我们要将其分解成两个因数的乘积,可以采用以下的配方法步骤:1.找到y的一个约数d。
2.将y除以d,得到商q。
3.如果q=d,说明找到了完全平方数,即y是一个完全平方数。
4.如果q不等于d,继续进行第1、2、3步骤,直到找到完全平方数或者无解。
举个例子来说明配方法的过程。
假设我们要将24分解成两个因数的乘积。
按照配方法的步骤:1.找到24的一个约数,例如22.将24除以2,得到商123.商12不等于除数2,继续进行下一步。
4.找到商12的一个约数,例如35.将12除以3,得到商46.商4不等于除数3,继续进行下一步。
7.找到商4的一个约数,例如28.将4除以2,得到商29.商2等于除数2,说明找到了完全平方数,即24是一个完全平方数。
在配方法中,找到完全平方数其实就是找到了原数的两个因数。
对于24来说,我们可以将其分解成4和6的乘积:24=4×6通过配方法,我们可以将一个数分解成两个因数的乘积,其中一个因数就是一个完全平方数。
这个方法在因式分解、求积因数、求约数等数学问题中有广泛的应用。
特别是在解决二次方程、求解立方根等问题时,配方法是一个非常有用的工具。
总结起来,完全平方数与配方法是数学中非常重要的概念和工具。
通过配方法,我们可以将一个数分解成两个因数的乘积,其中一个因数就是一个完全平方数。
数字的特殊性质完全平方数和立方数

数字的特殊性质完全平方数和立方数数字的特殊性质:完全平方数和立方数在数学的世界里,数字有着各种各样的性质,其中一些特殊性质备受研究与关注。
本文将介绍其中两种特殊性质,即完全平方数和立方数,并探讨它们的相关性质和应用。
一、完全平方数完全平方数指的是某个整数的平方,例如1、4、9、16等。
我们可以通过一个简单的公式来判断一个数字是否为完全平方数:对于一个非负整数n,如果存在一个非负整数m,使得m * m = n,则n为一个完全平方数。
完全平方数具有以下几个显著的特点:1. 完全平方数的结尾数字只能是0、1、4、5、6或9。
这是因为一个数字的平方的结尾数字只会受到原数字结尾数字的影响。
例如,如果一个数字的结尾是2,那么其平方的结尾数字将是4,依次类推。
2. 完全平方数可以表示为连续奇数之和。
以完全平方数9为例,可以表示为1+3+5=9。
这是因为每个完全平方数n都可以表示为以1开始的连续奇数之和,而奇数序列的和可以通过公式n^2来计算得出。
3. 完全平方数是一种特殊的数学模式。
当我们在平方数序列中观察数字的个位和十位数字时,会发现它们按照一定的模式循环出现。
例如,平方数序列的个位数字将按照0、1、4、9、6、5的循环重复出现。
完全平方数在现实生活中也具有广泛的应用,例如:1. 在几何学中,完全平方数与正方形的面积密切相关。
一个正方形的面积等于其边长的平方,因此可以通过判断一个数字是否为完全平方数来确定它是否为正方形的面积。
2. 完全平方数在计算机科学中也有重要的应用。
例如,在某些加密算法中,完全平方数的性质被用于生成公钥和私钥。
二、立方数立方数是指某个整数的立方,例如1、8、27等。
立方数同样具有一些独特的性质:1. 立方数的个位数字只能是0、1、4、5、6或9。
与完全平方数类似,立方数的个位数字受到原数字个位数字的影响。
2. 立方数可以表示为连续奇数之和的乘积。
以立方数27为例,可以表示为3 * 3 * 3,其中3为奇数。
如何判断一个数是不是完全平方数

如何判断一个数是不是完全平方数下面是一些关于完全平方数的数学性质,对排除完全平方数有一定的加速作用。
性质1:完全平方数的末位数只能是0,1,4,5,6,9。
性质2:奇数的平方的个位数字为奇数,十位数字为偶数。
证明奇数必为下列五种形式之一:10a+1, 10a+3, 10a+5, 10a+7, 10a+9分别平方后,得(10a+1)^2=100+20a+1=20a(5a+1)+1(10a+3)^2=100+60a+9=20a(5a+3)+9(10a+5)^2=100+100a+25=20 (5a+5a+1)+5(10a+7)^2=100+140a+49=20 (5a+7a+2)+9(10a+9)^2=100+180a+81=20 (5a+9a+4)+1综上各种情形可知:奇数的平方,个位数字为奇数1,5,9;十位数字为偶数。
性质3:如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数。
证明已知=10k+6,证明k为奇数。
因为的个位数为6,所以m的个位数为4或6,于是可设m=10n+4或10n+6。
则10k+6=(10n+4)=100+(8n+1)x10+6或10k+6=(10n+6)=100+(12n+3)x10+6即k=10+8n+1=2(5+4n)+1或k=10+12n+3=2(5+6n)+3∴ k为奇数。
推论1:如果一个数的十位数字是奇数,而个位数字不是6,那么这个数一定不是完全平方数。
推论2:如果一个完全平方数的个位数字不是6,则它的十位数字是偶数。
性质4:偶数的平方是4的倍数;奇数的平方是4的倍数加1。
证明这是因为 (2k+1)=4k(k+1)+1(2k)=4性质5:奇数的平方是8n+1型;偶数的平方为8n或8n+4型。
证明在性质4的证明中,由k(k+1)一定为偶数可得到(2k+1)是8n+1型的数;由为奇数或偶数可得(2k)为8n型或8n+4型的数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
完全平方数及其性质能表示为某个整数的平方的数称为完全平方数,简称平方数。
例如:0,1,4,9,16,25,36,49,64,81,100,121,144,169,196,225,256,289,324,361,400,441,484,…观察这些完全平方数,可以获得对它们的个位数、十位数、数字和等的规律性的认识。
一、平方数有以下性质:【性质1】完全平方数的末位数只能是0,1,4,5,6,9。
【性质2】奇数的平方的个位数字为奇数,十位数字为偶数。
【性质3】如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数。
推论1:如果一个数的十位数字是奇数,而个位数字不是6,那么这个数一定不是完全平方数。
推论2:如果一个完全平方数的个位数字不是6,则它的十位数字是偶数。
【性质4】(1)凡个位数字是5,但末两位数字不是25的自然数不是完全平方数;(2)末尾只有奇数个“0”的自然数(不包括0本身)不是完全平方数;100,10000,1000000是完全平方数,10,1000,100000等则不是完全平方数。
(3)个位数字为1,4,9而十位数字为奇数的自然数不是完全平方数。
需要说明的是:个位数字为1,4,9而十位数字为奇数的自然数一定不是完全平方数,如:11,31,51,74,99,211,454,879等一定不是完全平方数一定不是完全平方数。
但个位数字为1,4,9而十位数字为偶数的自然数不都是完全平方数。
如:21,44,89不是完全平方数,但49,64,81是完全平方数。
【性质5】偶数的平方是4的倍数;奇数的平方是4的倍数加1。
这是因为 (2k+1)^2=4k(k+1)+1 (2k)^2=4k^2【性质6】奇数的平方是8n+1型;偶数的平方为8n或8n+4型。
【性质7】平方数的形式一定是下列两种之一:3k,3k+1。
【注意:具备以上条件的不一定是完全平方数(如13,21,24,28等)】【性质8】不能被5整除的数的平方为5k±1型,能被5整除的数的平方为5k型。
【性质9】平方数的形式具有下列形式之一:16m,16m+1,16m+4,16m+9。
除了上面关于个位数,十位数和余数的性质之外,还可研究完全平方数各位数字之和。
例如,256它的各位数字相加为2+5+6=13,13叫做256的各位数字和。
如果再把13的各位数字相加:1+3=4,4也可以叫做256的各位数字的和。
下面我们提到的一个数的各位数字之和是指把它的各位数字相加,如果得到的数字之和不是一位数,就把所得的数字再相加,直到成为一位数为止。
关于完全平方数的数字和有下面的性质:【性质10】完全平方数的各位数字之和只能是0,1,4,7,9。
证明因为一个整数被9除只能是9k,9k±1, 9k±2, 9k±3, 9k±4这几种形式,而(9k)^2=9(9k^2)+0(9k±1)^2=9(9k^2±2k)+1 (9k±2)^2=9(9k^2±4k)+4(9k±3)^2=9(9k^2±6k)+9 (9k±4)^2=9(9k^2±8k+1)+7除了以上几条性质以外,还有下列重要性质:【性质11】a^2b为完全平方数的充要条件是b为完全平方数。
【性质12】如果质数p能整除a,但p^2不能整除a,则a不是完全平方数。
证明由题设可知,a有质因子p,但无因子p^2,可知a分解成标准式时,p的次方为1,而完全平方数分解成标准式时,各质因子的次方均为偶数,可见a不是完全平方数。
【性质13】在两个相邻的整数的平方数之间的所有整数都不是完全平方数,即【性质14】一个正整数n是完全平方数的充分必要条件是n有奇数个因子(包括1和n本身)。
【性质15】完全平方数的约数个数是奇数个。
约数的个数为奇数个的自然数是完全平方数。
【性质16】若质数p整除完全平方数a,则p^2|a。
【性质17】任何四个连续整数的乘积加1,必定是一个平方数。
二、重要结论(不是完全平方数的特点)1.个位数是2,3,7,8的整数一定不是完全平方数;2.个位数和十位数都是奇数的整数一定不是完全平方数;3.个位数是6,十位数是偶数的整数一定不是完全平方数;4.形如3n+2型的整数一定不是完全平方数;5.形如4n+2和4n+3型的整数一定不是完全平方数;6.形如5n±2型的整数一定不是完全平方数;7.形如8n+2, 8n+3, 8n+5, 8n+6,8n+7型的整数一定不是完全平方数;8.数字和是2,3,5,6,8的整数一定不是完全平方数三、个位数与正整数幂正整数幂的个位与其底数的个位有周期性关系。
【性质1】和的个位数字是诸加项个位数字之和的个位数字.【性质2】积的个位数字是诸因数个位数字之积的个位数字.四、例题剖析【例1】有一个1000位的数,它由888个1和112个0组成,这个数是否可能是一个平方数?解法一:这个1000位数的各位数字和为:888→24→6,根据各位数字和是2,3,5,6,8的整数一定不是完全平方数判定,此数不是完全平方数。
解法二:设这个1000位数=A,是a的平方的完全平方数,因为A能被3整除,所以也能被3整除,即A能被9整除,但9不能整除888,所以A不是完全平方数。
【例2】如果m是整数,那么m的平方+1的个位数可能是()。
解:因为完全平方数的个位数只能是0,1,4,5,6,9,所以m的平方+1的个位数可能是1,2,5,6,7,0【例3】有4个不同的数字可共组成18个不同的4位数。
将这18个不同的4位数由小到大排成一排,其中第一个是完全平方数,倒数第二个也是完全平方数。
那么这18个数的平均数是多少?解:(1)由4个不同的数字可以构成:4*3*2*1=24个不同的4位数,只能构成18个4位数说明含有一个数字“0”,即:3*3*2*1=18。
(2)这些4位数中,最小的为a0bc,次大的为cb0a(其中0<a<b<c)。
(3)完全平方数的个位数只能是0,1,4,5,6,9,令c=9,则b必须为偶数(试取8),a取1(1+0+8+9=18→9,☆完全平方数的各位数字之和只能是0,1,4,7,9),得:1089=33的平方,9801=99的平方。
(4)平均数的千位数:(1+8+9)*6/18=6百、十、个位数:(1+8+9+0)*4/18=4所求:6444【例4】1987的1987次幂乘以1988的1988次幂乘以1989的1989次幂的个位数是几?解:先要确定高次幂的个位数周期1987的1,2,3,...1987次幂的个位数分别是7,9,3,1,7,9...,周期为7,9,3,1这4个个位数循环,1987÷4...3,所以的个位数为3;1988的1,2,3,...1988次幂的个位数分别是8,4,2,6,8,4...,周期为8,4,2,6这4个个位数循环,1988÷4...0,所以的个位数为6;1989的1,2,3,...1989次幂的个位数分别是9,1,9,1,...,周期为9,1这2个个位数循环,1989÷2...1,所以的个位数为9;所求:个位数是3×6×9的个位数即为2.总结:(1)和的余数等于余数的和;(2)差的余数等于余数的差;(3)积的余数等于余数的积。
【例5】12345678987654321是否是完全平方数.解:12345678987654321的个位数字和为:36+9+36=81→9所求:是一个完全平方数数学解题能力展示读者评选活动07年六年级组第11题有4不同的数字共可组成18个不同的4位数。
将这18个不同的4位数由小到大排成一排,其中第一个是一个完全平方数,倒数第二个也是完全平方数。
那么这18个数的平均数是:。
分析与解答:一,首先涉及到排列组合与乘法原理:当没有0时,4个不同的数字共可组成4!=24个不同的4位数。
如果只能组成18个不同的4位数,说明其中必有0,即按3×3!=18算出来的。
二,在这四个不同的数中,设最小的数(小0中大)=A2,倒数第二个则是(大中0小)=B2,两数正好是一对反序数。
根据完全平方数的尾数特点,“小”、“大”两数必是1,4,6,9之中的两个。
且中数在小大之间。
三,分类讨论,使用枚举法一一验证,但是注意使用平方数的判断技巧。
1,先判断小数,再用大数验证。
2,利用平方数的整除特征:是2的倍数必是4的倍数,是3的倍数必是9的倍数,是5的倍数必是25的倍数。
3,利用高位估算法与尾数特点确定。
例如平方数为1056,那么肯定是34或者36的平方,然后再验算即可。
四,可以分为以下3类:(1)当“大”=4,那么只有1024,1034符合,1024=32*32,但4201不成立。
1034是2的倍数不是4的倍数。
(2)当“大”=6, 那么1026,1036,1046,1056,4056符合。
1026,1046是2的倍数不是4的倍数,排除。
4056是3的倍数,不是9的倍数,排除。
32*32<1036,1056<33*33,排除1036与1056,其实也可以排除1026,1046。
(3)当“大”=9,在(10中9)的数中,取332=1089, 而9801可以用992来试算,知9801=992.符合。
在(40中9)的数中,取632,672不成立。
在(50中9)的数中,取672,732不成立。
在(60中9)的数中,取732,772不成立。
所以,符合条件的数只能是由1089开始的四位数。
五,求这18个数的和,有两种方法,一种是枚举法,当然要结合找规律,但是也很难计算;另一种是计数法,即根据每一位上的数字出现的次数来统一计算。
又分两种思路:1,直接计算:千位上1,8,9出现的次数为3!=6次,百位十位个位上出现1,8,9的次数为2*2!=4次,所以18个数的总和为(1+8+9)*6444,所以平均数为6444。
2,利用排除法:假设0也可以作为高位,例如0189也算符合要求的,那么这24个数的总和应该是(0+1+8+9)*6666。
那么多加的6个数用同样的方法可知总和为(1+8+9)*222,所以18个数的总和为18*6666-18*222,所以平均数为6444。
点评:1,此题也是难度非常大的一道综合题型,涉及到排列组合计数原理的考察,有数字大小的排列,然后主要是平方数的判断,其实都是奥数课程里面的基本内容,但是组合起来之后就难度变很大了。
2,第一步思路是根据18个数判断出其中必有一个为0,这个一般同学都能判断出,但是这一步离最后答案还相差十万八千里,所以可以看出,计数原理都是作为附属考察内容渗透进每道试题,难度不大,但是不过关又无从下手。
