小学三年级奥数 竞赛班 最短路线
小学奥数习题版三年级三大原理最短路线学生版

知识要点快乐热身【例 1】 如下图所示,小虎家在A 地,姥姥家在B 地。
一天,他要去看望姥姥,但不知有几条路可走,走哪条路最短,热心的小朋友们快帮帮他吧?最短路线【例2】如下图所示,从甲地到乙地一共有两条路可走,请问哪条路长?哪条路短?【例3】观察下图,若黑猫与白猫奔跑速度相同,那么哪只猫先捉到老鼠?白猫黑猫鼠【例4】直线AB是一条公路,公路两侧有甲、乙两个村庄。
现在要在公路上建一个汽车站,让两个村子的人到汽车站的路线之和最短,问汽车站建在哪儿最好?乙甲BA走格子边【例5】一只蚂蚁在长方形格纸上的A点,它想去B点玩,但是不知走哪条路最近。
小朋友们你能给它找到几条这样的最短路线呢?BA【例6】如果A、B 两点变成下面两图这样的位置关系,那么从A到B的最短路线有几条呢?BA【例7】方格纸上取一点A作为起点,再在A的右上方任取一点B作为终点,画一条由A到B的最短路线,聪明的小朋友,你能画出来吗?总共能画出几条呢?【例8】小明和小强到少年宫参加2010上海世博会志愿者培训,少年宫和学校之间的地图如下。
如果他们从学校出发,共有多少种不同的最短路线?学校少年宫【例9】小虎和小羊是好朋友,它们居住的小区的平面图如下。
星期天,两人相约去博物馆看展览,现在小虎要先去小羊家和小羊会和,请问小虎去小羊家的最短路线有多少条?【例10】小聪明想从北村到南村上学,可是他不知道最短路线的走法共有几种?小朋友们,快帮帮忙呀!北村南村【例11】如图,从F点出发到G点,走最短的路程,有多少种不同的走法?GF【例12】“五一”长假就要到了,小新和爸爸决定去黄山玩。
聪明的小朋友请你找找看从北京到黄山的最短路线共有几条呢?北京黄山【例13】下图是小明家和学校的示意图,亲爱的同学们,你们觉得小明从家到学校共有几条最短路线呢?学校小明家【例14】小海龟在小猪家玩,它们想去游乐场坐碰碰车,爱动脑筋的小朋友,请你想一想,从小猪家到游乐场共有几条最短路线呢?游乐场小猪家【例15】学校组织三年级的小朋友去帮助农民伯伯锄草,大家从学校乘车出发,去往的李家村(如图)。
三年级奥数学习计划

三年级奥数学习计划
简介
三年级是孩子们接触奥数的起步阶段,建立学习兴趣和基础知识至关重要。
一个详细的三年级奥数学习计划,帮助家长和老师规划孩子的奥数学习路线,促进孩子全面发展。
目标
• 帮助孩子建立数学学习的兴趣和信心
• 引导孩子掌握基本的奥数解题技巧
• 培养孩子逻辑思维和解决问题的能力
时间安排
• 每周至少安排2-3次奥数学习时间,每次1小时
• 根据孩子的学习状态适时调整学习强度和时间分配学习内容
1. 奥数基础知识
• 熟练掌握加减乘除等基本数学运算
• 了解各种图形的性质和计算方法
• 掌握奇偶性、质数等基本数论知识
2. 奥数解题技巧
• 学习奥数解题的常用方法和技巧
• 练习解决奥数常见类型的题目,如找规律、分类讨论等
3. 逻辑思维训练
• 注重培养孩子的逻辑思维能力
• 练习逻辑推理、问题分解和综合分析能力
学习方法
1. 综合练习
• 每周安排一次奥数综合练习,包括不同难度和类型的题目• 鼓励孩子独立思考和解决问题,培养解决问题的能力
2. 辅导指导
• 定期与孩子进行讨论和答疑,解决学习中遇到的问题
• 有针对性的辅导和指导,帮助学生克服学习难点
3. 奥数小组学习
• 组织奥数小组学习,让孩子们相互交流和合作
• 通过小组学习,促进孩子互相学习和提高
学习评估
• 每学期末进行一次奥数学习成绩评估,记录孩子的学习进展• 根据评估结果调整学习计划,制定下一个学期的学习目标。
小学三年级奥数 第22讲最短路线
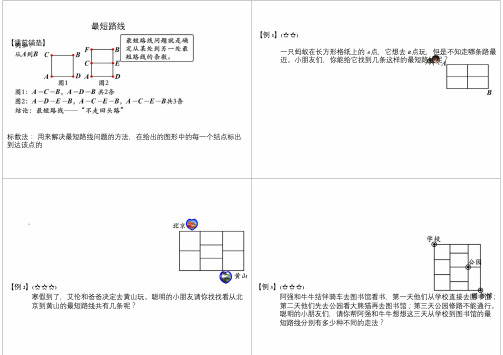
最短路线
【例1】(☆☆)
【课前铺垫】
一只蚂蚁在长方形格纸上的A点,它想去B点玩,但是不知走哪条路最
近。
小朋友们,你能给它找到几条这样的最短路线呢?
标数法:用来解决最短路线问题的方法,在给出的图形中的每一个结点标出
到达该点的
,。
【例2】(☆☆☆)【例3】(☆☆☆)
寒假到了,艾伦和爸爸决定去黄山玩。
聪明的小朋友请你找找看从北京到黄山的最短路线共有几条呢?阿强和牛牛结伴骑车去图书馆看书,第一天他们从学校直接去图书馆;第二天他们先去公园看大熊猫再去图书馆;第三天公园修路不能通行。
聪明的小朋友们,请你帮阿强和牛牛想想这三天从学校到图书馆的最短路线分别有多少种不同的走法?
1
【例4】(☆☆☆☆)【例5】(☆☆☆☆☆)
图中的“我爱史老师”有多少种不同的读法。
一只密蜂从A处出发,A回到家里B处,每次只能从一个蜂房爬向右侧
邻近的蜂房而不准逆行,共有多少种回家的方法?
【例6】(☆☆☆☆☆)
城市街道如下图所示,有几处街区有积水不能通行,那么从A到B的最
短路线有几条?
【本讲总结】
最短路线
宗旨:不走冤枉路,就要朝着目标走
方法:标数法
标数法四步:
1.找目标、定方向
2.从起点标数,起点标1
3.按顺序每个点都要标到
4.某点数字=指向该点箭头
尾巴上的数字相加
注意:
.坏点可以划去或看成
2.必须经过,分段标出
2。
三年级思维拓展- 最短路线

最短路线☜知识要点在日常生活中,我们经常会遇到关于行程的路线问题。
比如从一个地方到另一个地方,两地之间有许多条路,我们就需要选择哪一条路最近,也就是要选择一条最短路线,这样可以省时省力,这就是最短路线问题。
本讲我们就一起来学习怎样找最短路线。
☜精选例题【例1】:如图,甲、乙两个村庄分别在公路的两侧,现在要在公路旁建造一个汽车站,使甲、乙两个村庄到车站的距离之和最短,那么,车站应建在公路何处?☝思路点拨:根据两点之间线段最短,连接甲、乙两点,如图,这条线段与公路有一个交点O,在O点处建一个车站,就能使甲、乙两个村庄到车站的距离之和最短。
☝标准答案:活学巧用1.小明和小强分别住在河岸的两边,现在要修一条路,让小明和小强能去河岸旁取水,并要求这条路使小明和小强去取水的距离之和最短,这条路应该怎么修?小明河岸小强2.如下图,在一条河的两边有A、B两个小区,为了方便两个小区的居民出行,准备在河上建一座桥,请问,这座桥建在何处,使两个小区的居民来往的路程最短?河【例2】:小华、小明两家分别住在河岸边的A、B两地,如图,如果两家想在河边合修一个取水码头,请问,这个码头的点选在何处,才能使小华、小明两家取水时所走的路程之和最短?河☝思路点拨:如图,先在河对岸找到以河为对称轴的对称点A’,再连接A’B,线段A’B与河的交点在O点处,A’O=AO。
因为两个点之间线段最短,所以A’B是两点间最短的距离,而A’B=A’O+OB =AO+OB。
所以应把取水码头的点选在O点,这样小华和小明两家取水时所走的路程之和最短。
☝标准答案:河✌活学巧用1.古希腊有一位著名的学者,名叫海伦。
有一天,一位将军不远千里专程前来向海伦求教一个百思不得其解的问题:从甲地出发到河边饮马(如图),然后再去乙地,走什么样的路线最短呢?这就是后来被人们称为“将军饮马”的问题。
小朋友,你来回答这位将军提出的问题,好吗?2.在公路一边有A、B两个小区,为了方便两个小区居民出行,准备在公路边安放一个汽车站牌,问应该安放在何处才能使两个小区的居民所走的路程之和最短。
三年级奥数最短路线同步练习

三年级奥数最短路线同步练习
(答题时间:30分钟)
1. 图中,从A点沿实线走最短路径到B点,且经过F、D两点,共有多少条不同路线?
2. 沿图中箭头所指的方向从A点到B点共有多少种不同的走法?
3. 如图,从X点到Y点走最短路径共有几种走法?
4. 小君家到学校的道路如图所示。
从小君家到学校走最短路径有多少种不同的走法?
三年级奥数通用版最短路线(二)参考答案
1. 解:我们可以从左下角A点开始,按对角线法,依次向上、向右写出到F、D两点的走法数,最后得到共有8条不同路线。
2. 解:如图所示,先标出到C点的走法数,再标出到D点和E点的走法数,然后标出到F 点的走法数,最后标出到B点的走法数,共有8种不同的走法。
3. 解:用标号法,如图所示,共有716种走法。
4. 解:用标号法,如图所示,共12种走法。
5. 解:先找到甲村关于直线AB的对称点C,连结点C和乙村交直线AB的那一点即为汽车站。
小学奥数之最短路线
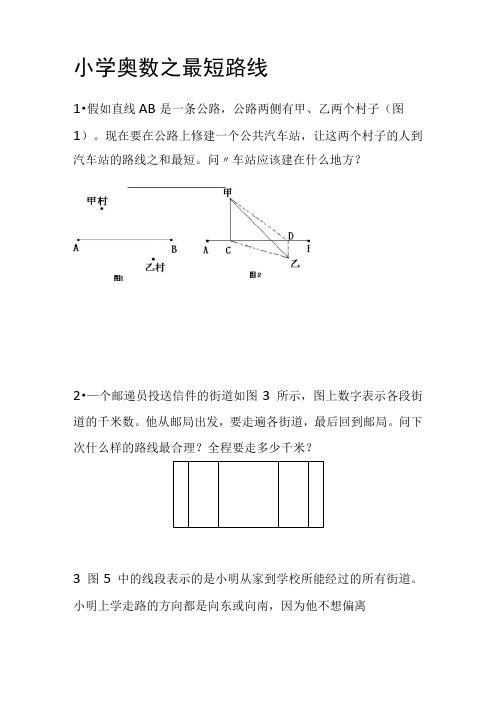
小学奥数之最短路线1•假如直线AB是一条公路,公路两侧有甲、乙两个村子(图1)。
现在要在公路上修建一个公共汽车站,让这两个村子的人到汽车站的路线之和最短。
问〃车站应该建在什么地方?2•—个邮递员投送信件的街道如图3所示,图上数字表示各段街道的千米数。
他从邮局出发,要走遍各街道,最后回到邮局。
问下次什么样的路线最合理?全程要走多少千米?3图5中的线段表示的是小明从家到学校所能经过的所有街道。
小明上学走路的方向都是向东或向南,因为他不想偏离小明家△4.如图8,从甲地到乙地最近的道路有几条?甲学校的方向而走冤枉路。
那么小明从家到学校可以有我少条不同的路线?学校5.某城市的街道非常整齐,如图10所示。
从本南角A 处人匕到东北角B处要求走最近的路并且不能通过十字路口C(正在修路),共有多少种不同的走法?B—6图13是一个街区街道的平面图。
邮递员从邮局出发,跑遍所有街道投送信件。
请你为他安排一条最短的路线,并按图中标出的千米数算出这条路线的长度(单位:千米)。
3邮局14是一个街道平面图。
王宏处到B处,在不走回头路,不走重复路的条件下,可以有多少种不同的路线?请你用交叉点上标数的方法计算一下。
8.从学校到少年宫有4条东西向的马路和3条南北向的马路相通。
如图15,李楠从学校出发,步行到少年宫(只放向9•如图16,从P到Q共有多少咱不同的最短路线?10•如图17所示,某城市的街道图,若从AZ走到B(只能由北向南、由西向东),则共有多少种不同的走法?11.如图18所示,从甲地到乙地,最近的道路有几条?能通车,12•图19为某城市的街道示意图,C处正在挖下水道,不13.如图20所示是一个街道的平面图,在不走回头路、不走重复路和条件下,可以有多少种不同的走法?B。
精品三年级奥数b第二章 最短路线

【方法点拨 】
最短路线问题我们一般用画“树形 图”或“对角求和法”解决。对角求和 口诀:边上一条路,其余对角加。
(3b) 第二章 最短路线
【技巧感悟 】
例1: 小马要把麦子驼到磨坊去,有几种走法?
分析:我们可以这样表示路线图: 小马从A地到B地有2条路线,这2条路线从B地到C地又分别有3种走 法,所以一共有2 X 3 = 6种不同的路线。 解答:小马把麦子驼到磨坊去,共有2 X 3 = 6种走法。
金杯数学(3b)
(3b) 第二章 最短路线 天津科学技术出版社
同学们看了这幅图之 后有什么感觉?…是 不是觉得山路十八弯, 那你们在生活中还有 见过类似弯弯的东西?
(3b) 第二章 最短路线
河流也好弯吧? 那 大家有没有想过:如果 我们走路、开车、坐船 是沿着弯曲的道路走快 点还是沿着直线走快呢?
(3b) 第二章 最短路线
【热身演练 】
1、小兔邀松鼠一起去山羊家做客,小兔有几条路线可以走?
(3b) 第二章 最短路线
【技巧感悟 】
例2、 乔乔要去上课,有哪些最短线路?
分析:乔乔要去学校,只能向上走或 向右走,为了方便分析,我们在道路的交 叉点标上字母,可以把每一步的走法用右 面的树形图表示出来:
分析:在图中的各点标上字母,小牛要从A点回到B点,只能向右走或向上走。 解答:
(3b) 第二章 最短路线
【热身演练 】
3、根据对角求和的方法标出图1、图2中从A点到B点的路线一共 有多少条。
(3b) 第二章 最短路线
【技巧感悟 】
例4: 蚂蚁要把食物从A洞运往B洞处,最近 的路线有几条?
分析:怎样计数从A到B的最短路线的条数 呢?我们将介绍一种非常巧妙的方法--对角求和 法。
三年级奥数三大原理最短路线教师版

知识要点快乐热身【例 1】 如下图所示,小虎家在A 地,姥姥家在B 地。
一天,他要去看望姥姥,但不知有几条路可走,走哪条路最短,热心的小朋友们快帮帮他吧?FEDCBA【分析】可走的路有5条,即:AFB 、AB 、AEB 、ADB 、ACB ,其中最短的路是AB 。
本讲主要学习数最短路线的总条数,通过本节课的学习: 1.掌握“解决最短路线条数问题”的两注意:不重、不漏。
2.准确运用“标数法”解决问题。
3.培养学生的实际操作能力。
1.两点之间,线段最短。
2.标数法计算最短路线的总条数。
最短路线【例 2】 如下图所示,从甲地到乙地一共有两条路可走,请问哪条路长?哪条路短?乙甲【分析】一样长。
【例 3】 观察下图,若黑猫与白猫奔跑速度相同,那么哪只猫先捉到老鼠?白猫黑猫鼠横 竖 斜 黑 1 5 2 白243【例 4】 直线AB 是一条公路,公路两侧有甲、乙两个村庄。
现在要在公路上建一个汽车站,让两个村子的人到汽车站的路线之和最短,问汽车站建在哪儿最好?乙甲B AC乙甲BA【分析】 根据“两点之间,线段最短”这个道理,甲、乙两村的连线与AB 有一个交点C ,这个交点就是所选定的汽车站(如图)。
走格子边【例 5】 一只蚂蚁在长方形格纸上的A 点,它想去B 点玩,但是不知走哪条路最近。
小朋友们 你能给它找到几条这样的最短路线呢?A31211A【分析】如右上图所示,根据标数法可得最短路线有6条。
【例 6】 如果A 、B 两点变成下面两图这样的位置关系,那么从A 到B 的最短路线有几条呢?BA BA【分析】根据上题原理,图中从A 到B 的最短路线都为6条。
【例 7】 方格纸上取一点A 作为起点,再在A 的右上方任取一点B 作为终点,画一条由A 到B 的最短路线,聪明的小朋友,你能画出来吗?总共能画出几条呢?【分析】如右上图所示,根据“标数法”可知共有10条最短路线,其中一条如右上图中粗线所示。
【例 8】 小明和小强到少年宫参加2010上海世博会志愿者培训,少年宫和学校之间的地图如下。
三年级奥数详解答案-第十九讲-最短路线问题

三年级奥数详解答案-第十九讲-最短路线问题第十九讲最短路线问题在日常工作、生活和娱乐中,经常会遇到有关行程路线的问题.在这一讲里,我们主要解决的问题是如何确定从某处到另一处最短路线的条数。
例1 下图4—1中的线段表示的是汽车所能经过的所有马路,这辆汽车从A走到B处共有多少条最短路线?分析为了叙述方便,我们在各交叉点都标上字母.如图4—2.在这里,首先我们应该明确从A到B的最短路线到底有多长?从A点走到B 点,不论怎样走,最短也要走长方形AHBD的一个长与一个宽,即AD+DB.因此,在水平方向上,所有线段的长度和应等于AD;在竖直方向上,所有线段的长度和应等于DB.这样我们走的这条路线才是最短路线.为了保证这一点,我们就不应该走“回头路”,即在水平方向上不能向左走,在竖直方向上不能向上走.因此只能向右和向下走。
有些同学很快找出了从A到B的所有最短路线,即:A→C→D→G→B A→C→F→G→BA→C→F→I→B A→E→F→G→BA→E→F→I→B A→E→H→I→B通过验证,我们确信这六条路线都是从A到B的最短路线.如果按照上述方法找,它的缺点是不能保证找出所有的最短路线,即不能保证“不漏”.当然如果图形更复杂些,做到“不重”也是很困难的。
现在观察这种题是否有规律可循。
1.看C点:由A、由F和由D都可以到达C,而由F→C是由下向上走,由D→C是由右向左走,这两条路线不管以后怎样走都不可能是最短路线.因此,从A到C只有一条路线。
同样道理:从A到D、从A到E、从A到H也都只有一条路线。
我们把数字“1”分别标在C、D、E、H这四个点上,如图4—2。
2.看F点:从上向下走是C→F,从左向右走是E→F,那么从A点出发到F,可以是A→C→F,也可以是A→E→F,共有两种走法.我们在图4—2中的F点标上数字“2”.2=1+1.第一个“1”是从A→C的一种走法;第二个“1”是从A→E的一种走法。
3.看G点:从上向下走是D→G,从左向右走是F→G,那么从A→G我们在G点标上数字“3”.3=2+1,“2”是从A→F的两种走法,“1”是从A→D的一种走法。
小学三年级奥数最短路线问题(下学期教案)

小学三年级奥数最短路线问题(下学期教案) -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN小学三年级奥数最短最短路线问题(下学期教案)在日常工作、生活和娱乐中,经常会遇到有关行程路线的问题.在这一讲里,我们主要解决的问题是如何确定从某处到另一处最短路线的条数。
例1 下图4—1中的线段表示的是汽车所能经过的所有马路,这辆汽车从A走到B处共有多少条最短路线?分析为了叙述方便,我们在各交叉点都标上字母.如图4—2.在这里,首先我们应该明确从A到B的最短路线到底有多长?从A点走到B点,不论怎样走,最短也要走长方形AHBD的一个长与一个宽,即AD+DB.因此,在水平方向上,所有线段的长度和应等于AD;在竖直方向上,所有线段的长度和应等于DB.这样我们走的这条路线才是最短路线.为了保证这一点,我们就不应该走“回头路”,即在水平方向上不能向左走,在竖直方向上不能向上走.因此只能向右和向下走。
有些同学很快找出了从A到B的所有最短路线,即:A→C→D→G→B A→C→F→G→BA→C→F→I→B A→E→F→G→BA→E→F→I→B A→E→H→I→B通过验证,我们确信这六条路线都是从A到B的最短路线.如果按照上述方法找,它的缺点是不能保证找出所有的最短路线,即不能保证“不漏”.当然如果图形更复杂些,做到“不重”也是很困难的。
现在观察这种题是否有规律可循。
1.看C点:由A、由F和由D都可以到达C,而由F→C是由下向上走,由D→C是由右向左走,这两条路线不管以后怎样走都不可能是最短路线.因此,从A 到C只有一条路线。
同样道理:从A到D、从A到E、从A到H也都只有一条路线。
我们把数字“1”分别标在C、D、E、H这四个点上,如图4—2。
2.看F点:从上向下走是C→F,从左向右走是E→F,那么从A点出发到F,可以是A→C→F,也可以是A→E→F,共有两种走法.我们在图4—2中的F点标上2数字“2”.2=1+1.第一个“1”是从A→C的一种走法;第二个“1”是从A→E的一种走法。
三年级下册数学试题-竞赛思维能力训练:03最短路线(三年级竞赛)学生版

从一个地方到另外一个地方,两地之间有许多条路,就有许多种走法,如果你能从中选择一条最短的路线走,这样你就可以节省许多时间了,那么如何能选上最短的路线呢?亲爱的小朋友们,你要记住两点:(1)两点之间线段最短.(2)尽量不走回头路和重复路,这样的话,你就做到了省时省力。
准确运用“标数法”解决题目。
一只蚂蚁在长方形格纸上的A点,它想去B点玩,但是不知走哪条路最近.小朋友们,你能给它找到几条这样的最短路线呢?BA阿呆和阿瓜到少年宫参加2010上海世博会志愿者培训.如果他们从学校出发,共有多少种不同的最短路线?少年宫学校下图是一个街道平面图,从甲地到乙地最近的道路有几条?“十一”长假就要到了,小新和爸爸决定去黄山玩.聪明的小朋友请你找找看从北京到黄山的最短路线共有几条呢?黄山北京大熊和美子准备去看望养老院的李奶奶,可是市中心在修路(城市的街道如图所示),他们从学校到养老院最短路线共有几条呢?聪明的小朋友,请你们快想想吧!养老院市中心学校如图,从A 到B 沿网格线不经过线段CD 和EF 的最短路径的条数是多少条?AC DE F B下图是一个街道平面图,每段长度都是300米。
现在有一辆汽车要从甲地到乙地,要走最近的路,但不能通过十字路口A 、B 、C (正在修路),问共有多少条最短的路线?从甲地到乙地最少要行多少米?乙CBA甲某城市的街道非常整齐,如下图所示,并且每段长度都是400米,现在有一个人要从西南角A 处骑自行车到东北角B 处,要走最近的路,并且不能通过十字路口C 、D 、E (正在修路)。
问:共有多少条最短路线?从A 地到B 地最少要行多少米?EDCBA【标数法发散】一只密蜂从A 处出发,A 回到家里B 处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法?BA864297531在图中,用水平或垂直的线段连接相邻的字母,当沿着这些线段行走时,正好拼出“APPLE ”的路线共有多少条?AAPPLELPPA A P L P P P A A P P P A A P A下图是一个街道平面图,纵横各有5条和4条路,某人要从A处走到B处,问共有多少条最短路线?AB下面是一个街道的平面图,从街道的A地出发到B地,问有多少条最短路线?下图为某城市的街道示意图,C处正在挖下水道,不能通车,从A到B处的最短路线共有多少条?BCA下图是一个街道平面图,C处正在挖下水道,不能通车,一辆汽车从A地到B地的最短路线共有多少条?如果横的每段200米,竖的每段150米,那么从A地到B地至少要行多少米?BCA。
小学奥数全国推荐三年级奥数通用学案附带练习题解析答案24最短路线(二)

年级三年级学科奥数版本通用版课程标题最短路线(二)上一讲我们已经学习了标号法,但是有些类型的最短路线问题更为复杂,比如有些需要我们分步计算,有些需要舍去一些点再考虑,等等。
本讲我们就继续学习一些更复杂的最短路线问题。
复杂的最短路线问题的分类:1. 中间必须经过某些点2. 中间不能经过某些点3. 图形变化问题4. 求最短折线的问题例1下图是某街区的道路图。
从A点沿最短路线到B点,其中经过C点和D点的不同路线共有多少条?分析与解:方法一:题中要求的最短路线是必须经过A、C、D、B,只能是向上或向右,还是利用对角线法标数,如图,满足题意的不同路线共有72条。
方法二:本题可将从A到B分为三段,先是从A到C,再从C到D,最后从D到B。
利用对角线法标数时,前一段的终点看成下一段的起点,再找到这段中需标1的点,依次标数。
如图所示,从A到C有3种走法,从C到D有4种走法,从D到B有6种走法。
因为从A到B是分段走的,从A到C的每种走法又对应从C到D的4种走法,依此类推,所以不同的路线共有3×4×6=72(条)。
例2 大熊和美子准备去看望养老院的李奶奶,可是市中心在修路(城市的街道如图所示),他们从学校到养老院的最短路线共有几条呢?聪明的同学们,请你们快想想吧!分析与解:学校到养老院(也就是说可以经过市中心、也可以不经过市中心)的路线由对角线法可得共有126条,再减去必经过市中心的60 条,即得不经过市中心从学校到养老院的最短路线共有126-60=66(条)。
例3小新和爸爸决定去黄山玩,请你找找看,从北京到黄山的最短路线共有几条?分析与解:我们采用对角线法(如图)来解。
这道题的图形与前几题的图形又有所区别,在解题时要格外注意D、G、K、E、H、L这样的点共有几条最短路线,具体是怎么走的,即由哪两点的数之和来确定另一点(或和哪点的数相同),D点由A点确定,标1;E点由点B、D确定,标1+1=2;H点由E点确定,标2;G点由点A、F确定,标1+1=2;K 点由G点确定,标2;L点由点E、K确定,标2+2=4。
小学奥数知识讲解-最短路线问题

最短路线在日常生活、工作中,经常会遇到有关行程路线的问题。
比如:邮递员送信,要穿遍所有的街道,为了少走冤枉路,需要选择一条最短的路线;旅行者希望寻求最佳旅行路线,以求能够走最近的路而达到目的地,等等。
这样的问题,就是我们所要研究学习的“最短路线问题”。
典型例题例 [1] 假如直线 AB 是一条公路,公路两旁有甲乙两个村子,如下图 1。
现在要在公路上修建一个公共汽车站,让这两个村子的人到汽车站的路线之和最短。
问:车站应该建在什么地方?甲甲A B A B乙乙图1图2分析如果只考虑甲村的人距离公路AB 最近,只要由甲村向公路 AB 画一条垂直线,交 AB 于 C 点,那么 C 点是甲村到公路AB 最近的点,但是乙村到 C 点就较远了。
反过来,由乙村向公路 AB 画垂线,交 AB 于 D 点,那么 D 点是乙村到公路 AB 最近的点。
但是这时甲村到公路 AB 的 D 点又远了。
因为本题要求我们在公路 AB 上取的建站点,能够兼顾甲村和乙村的人到这个车站来不走冤枉路(既路程之和最短),根据我们的经验:两个地点之间走直线最近,所以,只要在甲村乙村间连一条直线,这条直线与公路 AB 交点 P,就是所求的公共汽车站的建站点了(图 2)。
解用直线把甲村、乙村连起来。
因为甲村乙村在公路的两侧,所以这条连线必与公路AB 有一个交点,设这个交点为P,那么在P 点建立汽车站,就能使甲村乙村的人到汽车站所走的路程之和最短。
例 [2] 一个邮递员投送信件的街道如图 3 所示,图上数字表示各段街道的千米数。
他从邮局出发,要走遍各街道,最后回到邮局。
问:走什么样的路线最合理?全程要走多少千米?124213分析选择最短的路线最合理。
那么,什么路线最短呢?一笔画路线应该是最短的。
邮递员从邮局出发,还要回到邮局,按一笔画问题,就是从偶点出发,回到偶点。
因此,要能一笔把路线画出来,必须途径的各点全是偶点。
但是图中有 8 个奇点,显然邮递员要走遍所有街道而又不走重复的路是不可能的。
小学奥数最短路线问题(有答案)

小学六年级奥数教案—运筹学初步本讲主要讲统筹安排问题、排队问题、最短路线问题、场地设置问题等。
这些都是人们日常生活、工作中经常碰到的问题,怎样才能把它们安排得更合理,多快好省地办事,就是这讲涉及的问题。
当然,限于现有的知识水平,我们仅仅是初步探索一下。
1.统筹安排问题例1星期天妈妈要做好多事情。
擦玻璃要20分钟,收拾厨房要15分钟,洗脏衣服的领子、袖口要10分钟,打开全自动洗衣机洗衣服要40分钟,晾衣服要10分钟。
妈妈干完所有这些事情最少用多长时间?分析与解:如果按照题目告诉的几件事,一件一件去做,要95分钟。
要想节约时间,就要想想在哪段时间里闲着,能否利用闲着的时间做其它事。
最合理的安排是:先洗脏衣服的领子和袖口,接着打开全自动洗衣机洗衣服,在洗衣服的40分钟内擦玻璃和收拾厨房,最后晾衣服,共需60分钟(见下图)。
例1告诉我们,当有许多事要做时,科学地安排好先后顺序,就能用较少的时间完成较多的事情。
2.排队问题例2理发室里有甲、乙两位理发师,同时来了五位顾客,根据他们所要理的发型,分别需要10,12,15,20和24分钟。
怎样安排他们的理发顺序,才能使这五人理发和等候所用时间的总和最少?最少要用多少时间?分析与解:一人理发时,其他人需等待,为使总的等待时间尽量短,应让理发所需时间少的人先理。
甲先给需10分钟的人理发,然后15分钟的,最后24分钟的;乙先给需12分钟的人理发,然后20分钟的。
甲给需10分钟的人理发时,有2人等待,占用三人的时间和为(10×3)分;然后,甲给需 15分钟的人理发,有 1人等待,占用两人的时间和为(15×2)分;最后,甲给需 24分钟的人理发,无人等待。
甲理发的三个人,共用(10×3+15×2+24)分,乙理发的两个人,共用(12×2+20)分。
总的占用时间为(10×3+15×2+24)+(12×2+20)=128(分)。
