工程力学例题解析
《工程力学》参考习题解析

2011年课程考试复习题及参考答案工程力学计算题:1.梁结构尺寸、受力如图所示,不计梁重,已知q=10kN/m,M=10kN·m,求A、B、C处的约束力。
2.铸铁T梁的载荷及横截面尺寸如图所示,C为截面形心。
已知I z=60125000mm4,y C=157.5mm,材料许用压应力[σc]=160MPa,许用拉应力[σt]=40MPa。
试求:①画梁的剪力图、弯矩图。
②按正应力强度条件校核梁的强度。
3.传动轴如图所示。
已知F r=2KN,F t=5KN,M=1KN·m,l=600mm,齿轮直径D=400mm,轴的[σ]=100MPa。
试求:①力偶M的大小;②作AB轴各基本变形的内力图。
③用第三强度理论设计轴AB的直径d。
4.图示外伸梁由铸铁制成,截面形状如图示。
已知I z=4500cm4,y1=7.14cm,y2=12.86cm,材料许用压应力[σc]=120MPa,许用拉应力[σt]=35MPa,a=1m。
试求:①画梁的剪力图、弯矩图。
②按正应力强度条件确定梁截荷P。
5.如图6所示,钢制直角拐轴,已知铅垂力F1,水平力F2,实心轴AB的直径d,长度l,拐臂的长度a。
试求:①作AB轴各基本变形的内力图。
②计算AB轴危险点的第三强度理论相当应力。
6.图所示结构,载荷P=50KkN,AB杆的直径d=40mm,长度l=1000mm,两端铰支。
已知材料E=200GPa,σp=200MPa,σs=235MPa,a=304MPa,b=1.12MPa,稳定安全系数n st=2.0,[σ]=140MPa。
试校核AB杆是否安全。
7.铸铁梁如图5,单位为mm,已知I z=10180cm4,材料许用压应力[σc]=160MPa,许用拉应力[σt]=40MPa,试求:①画梁的剪力图、弯矩图。
②按正应力强度条件确定梁截荷P。
8.图所示直径d=100mm的圆轴受轴向力F=700kN与力偶M=6kN·m的作用。
工程力学答案解析

3-5四连杆机构在图示位置平衡。
已知OA=60cm , BC=40cm ,作用BC 上的力偶的力偶矩大小为 M 2=1N.m ,试求作用在 OA上力偶的力偶矩大小 M l 和AB 所受的力F AB 所受的力。
各杆重量不计。
列平衡方程:M =0- F A OA M ^0解: (1)研究BC 杆,受力分析,画受力图:列平衡方程:F B=0 F B BC sin 30°-M 2=01o =5N0.4 sin30°-BC sin30°(2)研究AB (二力杆),受力如图:F'B可知:F A = F B = F B 二 5 N(3)研究OA 杆,受力分析,画受力图:3-8 在图示结构中,各构件的自重都不计,在构件M 产F A OA = 5 0.6 =3 NmBC 上作用一力偶矩为 M 的力偶,各尺寸如图。
求支座MA 的约束力。
lB(2)取DAC为研究对象,受力分析,画受力图;' M =0 -F C l M =0 F C画封闭的力三角形;解得4-5 AB梁一端砌在墙内, 求固定端的约束力。
DCFDA在自由端装有滑轮用以匀速吊起重物F Ccos45°D,设重物的重量为G,又AB长为b,斜绳与铅垂线成:•角,解:(1)研究AB杆(带滑轮),受力分析,画出受力图(平面任意力系);xx(2)选坐标系Bxy ,列出平衡方程;' F x 二 0: - F AX G sin > - 0 F AX = G sin:' F y = 0:F A y -G -G cos : = 0 F Ay 二 G (1 COS :)'M B (F )=0: M A -F Ay b G R-G R 二 0M A =G(1 cos )b4-16由AC 和CD 构成的复合梁通过铰链 C 连接,它的支承和受力如题4-16图所示。
已知均布载荷集度q =10 kN/m ,力偶M =40 kN m ,a =2 m ,不计梁重,试求支座 A 、B 、D 的约束力和铰链 C 所受的力。
工程力学__习题详解_第二章

解: ①选碾子为研究对象
②取分离体画受力图 ∵当碾子刚离地面时NA=0,拉力F最大,这时 由平衡的几何条件,力多边形封闭,故
拉力F和自重及支反力NB构成一平衡力系。
NB P cos r 2 (r h) 2 又由几何关系:tg 0.577 r h
F Ptg
10
所以
F=11.5kN , NB=23.1kN
为该力系的汇交点
三、平面汇交力系合成与平衡的解析法
从前述可知:平面汇交力系平衡的必要与充分条件是该力系 的合力为零。 即:
Rx X 0 R y Y 0
为平衡的充要条件,也叫平衡方程
14
静力学
例题 3
平面汇交力系与平面力偶系
利用铰车绕过定滑轮B的 绳子吊起一货物重P = 20 kN,
由力的平行四边形法则作, 也可用力的三角形来作。 由余弦定理:
R F1 F2 2 F1 F2 cos
2 2
为力多边形
R 1 合力方向由正弦定理: sin sin(180 )
F
4
力三角形规则
F F1 F2 F2 F1
力多边形规则
5
FR1 F1 F2
30
P C
不计并忽略摩擦和滑轮的大小, 试求平衡时杆AB和BC所受的力。
27
静力学
平面汇交力系与平面力偶系
解:
A
60
取滑轮B为研究对象,忽略滑轮的 大小,画受力图。 列写平衡方程
D
B
Fx 0,
30
FAB F1 cos 60 F2 cos 30 0 FBC F1 cos 30 F2 cos 60 0
电气工程力学习题与答案

电气工程力学习题与答案
本文档包含一系列电气工程力研究题及其答案。
以下是一些例题和解答供参考:
1. 题目:一条杆长为L的铁杆,质量为m,静止在弗林斯克级台阶上,杆的一端借由一条轻绳悬挂,另一端连结一质量为M的盒子。
求弗林斯克级台阶的反作用力与盒子的重量之间的关系。
解答:根据受力分析,弗林斯克级台阶的反作用力与盒子的重量之和等于杆的重量。
因此,反作用力与盒子的重量之间的关系可表示为: F反作用力 + Mg = mg ,其中F反作用力为反作用力,M 为盒子的质量,g为重力加速度。
2. 题目:一辆质量为m的小车在水平地面上以速度v做匀速直线运动,小车上的一个物体质量为M。
求物体对小车的反作用力。
解答:根据牛顿第三定律,物体对小车的反作用力与小车对物体的反作用力大小相等,方向相反。
因此,物体对小车的反作用力
的大小可表示为: F反作用力 = -Mv ,其中M为物体的质量,v为速度。
以上是一些电气工程力学习题的例题和解答。
希望能对你有帮助。
工程力学考试题及答案解析
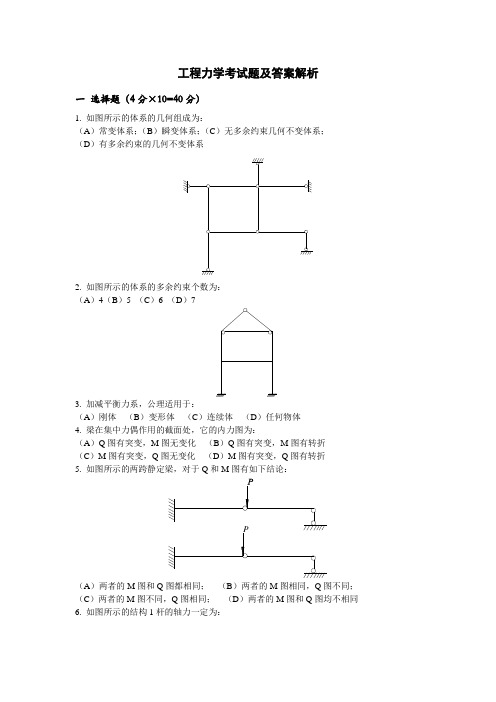
工程力学考试题及答案解析一选择题(4分×10=40分)1. 如图所示的体系的几何组成为:(A)常变体系;(B)瞬变体系;(C)无多余约束几何不变体系;(D)有多余约束的几何不变体系2. 如图所示的体系的多余约束个数为:(A)4(B)5 (C)6 (D)73. 加减平衡力系,公理适用于:(A)刚体(B)变形体(C)连续体(D)任何物体4. 梁在集中力偶作用的截面处,它的内力图为:(A)Q图有突变,M图无变化(B)Q图有突变,M图有转折(C)M图有突变,Q图无变化(D)M图有突变,Q图有转折5. 如图所示的两跨静定梁,对于Q和M图有如下结论:(A)两者的M图和Q图都相同;(B)两者的M图相同,Q图不同;(C)两者的M图不同,Q图相同;(D)两者的M图和Q图均不相同6. 如图所示的结构1杆的轴力一定为:(A)0 (B)2P(拉力)(C)2P(压力)(D)P(拉力)7. 如图所示结构K截面的弯矩(下侧受拉取正)为:(A)0 (B)M (C)2M (D)—M8. 一三铰拱有均布铅垂荷载,受力图如图示,试判断其是否正确:(A)正确,无水平荷载,A、B处反力应无水平分量(B)错误,受力图中未画出铰链C的反力(C)错误,AC和BC构件均为二力构件,A、B反力应有水平分量(D)错误,A、B处有水平分力,受力图中未画出AB9. 请选择正确结论:图形对其对称轴的:(A)静矩为零,惯性矩不为零,惯性积为零(B)静矩不为零,惯性矩和惯性积均为零(C)静矩、惯性矩及惯性积均为零(D)静矩、惯性矩及惯性积均不为零10. 如图所示的桁架结构,零杆的个数为:aaP1(A )1 (B )3 (C )6 (D )7二 求图示悬臂梁最大正应力和最大剪应力,要求写明步骤(10分)10kN40kNC AB Dd =200mm三 绘制刚架弯矩图,要求写明简要步骤(10分×2=20分)(1)(2)q qq qqll四 如图所示结构为预应力钢筋混凝土墙板起吊过程中的计算图。
工程力学(例题)

1.如图2-4所示为一曲柄摇杆机构。
机构中各构件自重不计,圆轮上的销子A 在摇杆BC 的光滑导槽内,圆轮上作用一力偶,其力偶矩大小为M 1=2kN·m,OA =r =0.5m 。
在图示位置时OA 与OB 相互垂直,α=30°,且系统处于平衡状态。
求作用于在摇杆BC 上的力偶矩M 2及铰链O 、B 处的约束力。
解(1)取圆轮为研究对象,画受力图如图2-4b 所示。
A 点的约束力FA 与摇杆的导槽垂直,根据力偶只能用力偶平衡的性质,铰链O 处的约束力FO 必定与FA 形成一个力偶,其转向与M 1转向相反,由此可以确定FA 指向如图2-4b 所示。
ΣMi =0 M 1-FAr sin α=0(2)取摇杆BC 为研究对象,画受力图如图2-4c 所示。
F'A (与FA 互为作用力与反作用力)和FB 形成一力偶,且与M 2平衡。
解之得 M 2=4 M 1=8 kN·m 由此求得2.在图4-8a 所示的杆件中,已知F 1=20kN ,F 2=50kN ,AB 段的直径d 1=20mm ,BC 段的直径d 2=30mm ,试计算各段杆件横截面上的正应力。
解 (1)采用轴力图的简易画法,从左至右作图,可以在不求出固定端约束力和情况下,直接根据外力情况画出轴力图。
(2)确定各横截面的轴力F N 。
采用轴力图的简易画法直接画出轴力图如图解得1sin 30A M F r =ΣM i =020sin ArM F α-+=18kNsin 30O A B M F F F r ====4-8b 所示。
从轴力图上可以看出,各横截面的轴力分别为F N1=20kN ,F N2=-30kN 。
(3)计算各横截面上的正应力。
由式(4-3),AB 段横截面上的正应力为BC 段横截面上的正应力为3.如图4-14a 所示,杆件受轴向载荷作用。
已知:F 1=30kN ,F 2=10kN ,AC 段横截面 面积A 1=500mm2,CD 段横截面面积A 2=200mm2,材料的弹性模量E =200GPa试计算各段杆件横截面上的应力和杆的 总变形Δl 。
工程力学---材料力学(第七章- 梁弯曲时位移计算与刚度设计)经典例题及详解

得: D 0
Pl 2 得: C 16
AC段梁的转角方程和挠曲线方程分别为:
P 2 2 (4 x l ) 16 EI Px y (4 x 2 3 l 2 ) 48 EI
y
P
B
A
x
l 2
C
l 2
x
最大转角和最大挠度分别为:
max A B
ymax y
q 7qa 8k 384 EI
3
q/2
B C
q/2
A B C
顺时针
q/2
例16:图示梁B处为弹性支座,弹簧刚 度
EI k 求C端挠度fC。 2a 3
q
A
EI k
B
C
2a
a
解:(1)梁不变形,仅弹簧变形引起的C点挠度为 4 3 qa 3qa B处反力=qa fC 1 2 k EI
q
B
x
l
由边界条件: x 0时,y 0
x l时,y 0
得:
ql 3 C , D0 24
梁的转角方程和挠曲线方程分别为:
y
q 2 3 3 (6lx 4 x l ) 24 EI
q
x
A qx y (2lx 2 x 3 l 3 ) 24 EI
ql 3 24 EI
A a a
q
B C
a
qa 12 EI
顺时针
3 3
P=qa
A B
P=qa
m=qɑ²/2
qa qa C B 6 EI 4 EI
4
顺时针
B
q
C
qa 5qa fC B a 8EI 24 EI
工程力学课后习题答案解析
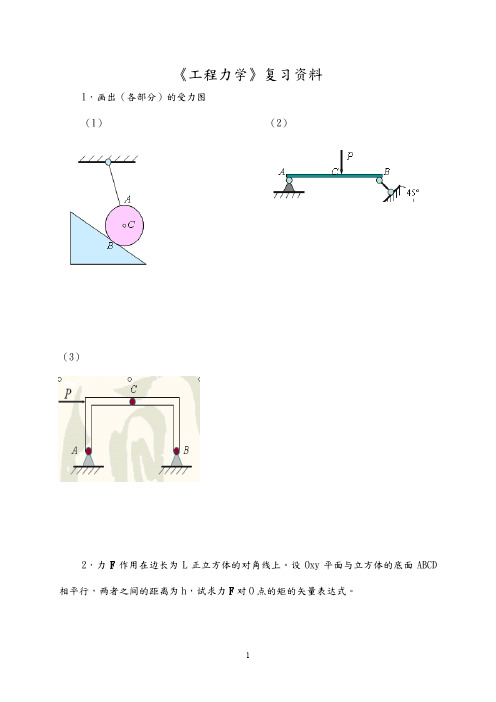
《工程力学》复习资料1.画出(各部分)的受力图(1)(2)(3)2.力F作用在边长为L正立方体的对角线上。
设Oxy平面与立方体的底面ABCD 相平行,两者之间的距离为h,试求力F对O点的矩的矢量表达式。
解:依题意可得:ϕθcos cos ⋅⋅=F F xϕθsin cos ⋅⋅=F F y θsin ⋅=F F z 其中33sin =θ 36cos =θ 45=ϕ 点坐标为:()h l l ,, 则()3)()(3333333j i h l F k F j F i F F M +⋅+=-+-= 3.如图所示力系由F 1,F 2,F 3,F 4和F 5组成,其作用线分别沿六面体棱边。
已知:的F 1=F 3=F 4=F 5=5kN, F 2=10 kN ,OA=OC/2=1.2m 。
试求力系的简化结果。
解:各力向O 点简化 0.0.0.523143=-==-==+-=C O F A O F M C B F A O F M C O F C O F M Z Y X 即主矩的三个分量 kN F F Rx 55==kN F F Ry 102==kN F F F F RZ 5431=+-=即主矢量为: k j i 5105++合力的作用线方程 Z y X ==24.多跨梁如图所示。
已知:q=5kN ,L=2m 。
试求A 、B 、D 处的约束力。
取CD 段0=∑ci M 0212=-⋅ql l F D 解得 kN F D 5=取整体来研究,0=∑iy F02=+⋅-+D B Ay F l q F F 0=∑ix F 0=Ax F0=∑iAM 032=⋅+⋅-⋅l F l ql l F D B 联合以上各式,解得 kN F F Ay A 10-== kN F B 25=5.多跨梁如图所示。
已知:q=5kN ,L=2m ,ψ=30°。
试求A 、C 处的约束力。
(5+5=10分)取BC 段0=∑iy F0cos 2=⋅+⋅-ϕC B F l q F 0=∑ix F 0sin =⋅-ϕC Bx F F0=∑icM 022=⋅⋅+⋅-l l q l F By联合以上各式,解得 kN F Bx 77.5= kN F By 10= kN F C 574.11=取整体研究0=∑ix F0sin =⋅-ϕC Ax F F 0=∑iy F 0cos 2=⋅+⋅-ϕC Ay F l q F0=∑iAM 04cos 32=⋅⋅+⋅⋅-l F l l q M C A ϕ 联合以上各式,解得 kN F Ax 774.5= kN F Ay 10= m kN M A ⋅=406.如图无底的圆柱形容器空筒放在光滑的固定地面上,内放两个重球。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(Φ )8,9 ,10 (Φ ) 3, 4 ,3 Fh.
第五章
用差分法和变分法解平面问题
⑷ 对内结点1、2、3、4分别列出下列类型
的方程:
0点: 20Φ 0 8Φ1, 2,3, 4 2Φ 5,6, 7 ,8 Φ 9,10,11,12 0. 对结点1, 20Φ1 16Φ2 8Φ3 16Φ4 2 Fh, 对结点2, 8Φ1 22Φ2 16Φ3 4Φ4 4 Fh,
第五章
用差分法和变分法解平面问题
例题
例题7 图中所示的薄板,厚度 1,三边 固定,一边受到均布压力q的作用。试用瑞 利-里茨的位移变分法求解,其中 0。 取 a b,
第五章
用差分法和变分法解平面问题
y
q
b
a a
x
第五章
用差分法和变分法解平面问题
解:在瑞利-里茨法中, 设定位移试函数应 满 足位移边界条件,并 应反映图示问题的 对称性。取
例题
(a) AB切开后,仍然处于闭合状态,不发生 张开。这是不稳定的平衡状态;
(b) AB线张开,出现裂纹。这是稳定的平 衡状态。由于系统的稳定平衡状态与邻 近的状态相比,总势能处于极小值,而 (a)、(b)两种状态的外力势能不变,因 此,(b)的形变势能小于(a),即形变势 题
(c )
第五章
用差分法和变分法解平面问题
例题
从式⑶可见,在平面应变情况下,形变势 能 U 中的第一、二、三项均大于平面应
1 μ 2 γ xy 不变。因 力情况下的值,而第四项 2
此,平面应变的形变势能 U大于平面应力 的形变势能U 。
第五章
用差分法和变分法解平面问题
例题
例题5 图中表示一板块,受到铅直方向 均布拉力作用下发生拉伸变形,并使之 两端固定下来,若在其中切开一小口AB 时,试说明板的形变势能将发生什么变 化?
Φ B ( y B y ) fx d s ( x x B ) fy d s ,
A A
B
B
(其中 ΦB 即AB之间面力对B点的力矩,图 中以顺时针方向为正)。
第五章
用差分法和变分法解平面问题
求出边界上各结点的值,如下图所示。 结点 A B CDEGH I
Φ y Φ x
对于平面应变情况,只需将上式中 , E 变换为 μ E μ .(b) E , 1 μ 1 μ2
第五章
用差分法和变分法解平面问题
2
例题
2
1 E E E 1 ( )( )[ ]( )[ ], 2 2 2 2 2 1 1 1 1 1 2
a
b
22
22
20
17
第五章
用差分法和变分法解平面问题
解:对a,b列出方程如下:
4Ta 32 35 22 Tb 0,
4Tb Ta 30 20 22 0.
解出
Ta 28.53,
Tb 25.13(度) .
第五章
用差分法和变分法解平面问题
例题2 用差分法计算图中A和B点的应力分量。 F
u A1u1 A1 ( x a ) xy,
2 2
2 2
由于体力 f x f y 0 ,面力只存在于AB边 ( y b ),因此求解 A1, B1 的位移变分方程 为:
a
6
B
3 a 1
F x
a
a
A 5 .7y
(Z向厚度 ) 1
第五章
用差分法和变分法解平面问题
解:为反映对称性,取A为基点。令
Φ Φ Φ A ( ) A ( ) A 0. x y
边界点的应力函数值: Φ2 Φ3 Φ4 ΦB 0.
Φ Φ 边界点的导数值: ( )3 0, ( ) B F . x y
11 H 10 9 8 G E D C I 3 4 3 B
F
12 J 2 1 2 A 3 4 3 h h h h
x
F
7 6
y
h=l/4 1
第五章
用差分法和变分法解平面问题
解:⑴本题具有的两个对称轴,为了反映对 称性,在 y 向外荷载作用下,取
Φ Φ ΦA ( ) A ( ) A 0 x y
1 6 qa A1 B1 . 5 5 E
由此解出 位移分量的解答是 2 qa x xy u 1.3125 (1 2 ) 2 , E a a 2 qa x v 1.4625 (1 2 ). E a
qa qa , B1 1.4625 . A1 1.3125 E E
u ( x a ) xy[ A1 A2 y A3 x ],
2 2 2
v ( x a ) y[ B1 B2 y B3 x ].
2 2 2
第五章
用差分法和变分法解平面问题
例题
上式已反映了位移对称于y轴的要求:v为x的 偶函数,u为x的奇函数。 仅取各一项进行运算,
J
0
0
0
0 F/2 -Fh/2 F/2 -Fh
0
0
0
0
F/2 -Fh/2
Φ
读者可检验,上述的值反映了边界结点 和边界外一行虚结点上 Φ 值的对称性。
第五章
用差分法和变分法解平面问题
⑶ 计算边界外一行结点的 Φ 值。
Φ 由 ( ) A, B , I , J 0, 得到 y (Φ ) 6 , 7 ,11,12 (Φ ) 2 , 3, 3, 2 ,
C D
A
l
B
E
F
第五章
用差分法和变分法解平面问题
例题
解: ⑴当AB线切开时,AB线上的应力趋于 0。而形变势能是正定的,U 0 ,当这部 应力 0 时,相应的形变势能也失去因 此,板的总的形变势能减少。 ⑵ 当AB线切开后,边界CD和EF仍是固 定的,我们可以比较两种状态:
第五章
用差分法和变分法解平面问题
第五章
⑸按照应力公式 (σ x ) 0 1 (Φ 2Φ ), 2
h 1 (σ y ) 0 2 (Φ1, 3 2Φ0 ), h
2, 4 0
用差分法和变分法解平面问题
及 h l ,求得AJ及EI截面上的应力分量: 4
F (σ x ) J 1.4984 , l F F (σ x ) 2 0.4424 , (σ x )1 0.6136 ; l l F (σ y ) E 0.1648 , l F F (σ y ) 4 0.8912 , (σ y )1 2.0528 . l l
例题
例题6 单位厚度 ( 1) 的深梁,两侧边 固定,上下边受均布荷载q作用,如图所 示。试用位移变分法求解其位移。 (取 a b , y 0 . 2 并设 )。
b u v
b a
o
a
q
q
x
第五章
用差分法和变分法解平面问题
解:在图示荷载作用下,深梁的位移应对 称于y轴,而反对称于x轴。 因此,位移分量u应为 x 、 y 的奇函数, 而v为 x 、y 的偶函数, 如图所示。可以设定位移试函数如下:
第五章
用差分法和变分法解平面问题
例题
再积分求 U , a b
0 0
8 a 2 2E 4 b 2 1 4 b 2 8 A1 B1 A1 ]}. { A1 [ B 1 2 15 7 15 b 1 15 a 2 3a
U 4 U1dxdy
在本题中体力 f x f y 0 ,在 y b边界上 只有 f y q的均布荷载,f x 0 。由此,瑞 利-里茨方程成为
x xy 2 2 u (1 2 ) [ A1 A2 x A3 y ], a ab
x 2 2 v (1 2 )[ B1 B2 x B3 y ]. a
2
2
第五章
用差分法和变分法解平面问题
例题
上式已满足两端的约束边界条件,
x a,
(u, v) 0,
第五章
用差分法和变分法解平面问题
例题
例题1 例题3 例题5 例题7
例题2 例题4 例题6
第五章
用差分法和变分法解平面问题
例题1
40
35
30
25
设图中的矩形域 32 为 6m 4m ,取网 格间距为h=2m,布 置网格如图,各边 24 界点的已知温度值 (度)如图所示, 试求内结点a,b的稳 定温度值。
以及对称和反对称性条件。以下按瑞利里茨法进行计算。
第五章
用差分法和变分法解平面问题
例题
假设只取u,v中一项,即
2 x x xy v B1v1 B1 (1 2 ). u A1u1 A1 (1 2 ) , a a ab 将u和v代入形变势能公式(平面应力问
2
题),得:
2 2 4 E y x x 2 U1 { A (1 6 2 9 4 ) 1 2 2 2 2(1 ) ab a a 2 2 4 2 2 x x 1 2 x x x 2 x [4 B1 4 4 A1 B1 3 (1 2 ) A1 2 2 (1 2 2 4 )]}. 2 a ab a ab a a
网格结点编号如图所示。
第五章
用差分法和变分法解平面问题
Φ Φ ⑵ 计算各边界结点处的 Φ 、 、 值。
F 在A点及J点,各取 布置于两侧,以 2
x
y
反映荷载的对称性,按公式
B B Φ Φ ( ) B f x d s ,( ) B fy d s , A A y x
显然,方括号内
