代数体函数与常微分方程(何育赞,萧修治著)思维导图
微分方程 09.6.15

上
下
停
积分因子: ( x, y) 0, 使
M( x, y)dx N ( x, y)dy 0
为恰当方程.
找 的方法:① 分项组合法
② 公式法
M( x, y)dx N ( x, y)dy 0 有积分因子 ( x)
1 (M N ) ( x), 且 ( x) e ( x)dx .
第十二章
微分方程
一、知识网络关系图
一阶方程
类型 1.可分离 变量方程 2.齐次方程 3.线性方程 4.伯努利方程 5.全微分方程
基本概念
高阶方程
二阶常系数线性 方程解的结构
特征方程法
待 特征方程的根
定 系
及其对应项
数
法 f(x)的形式及其
特解形式
可降阶方程
线性微分 方程
解的结构
欧拉方程
目
回
上
下
停
一阶显示微分方程的初等积分法
(若已知其一个特解 y1( x)) (令 z y y1( x),化为z的n 2的伯努利方程)
目
回
上
下
停
5º全微分方程: M( x, y)dx N ( x, y)dy 0
( 恰当)
u u( x, y), 使
d u(x, y) M(x, y)dx N(x, y)dy (x, y) G
N y x
目
回
上
下
停
可降阶微分方程
1. y(n) = f (x) 型的微分方程
令 z y(n1),
因此
z f ( x)dx C1
即
同理可得 y(n2) f ( x)dx C1dx C2 f ( x)dx dx C1x C2
微分方程PPT(罗兆富等编)第一章 常微分方程的基本概念

,y )0
( n)
(1.1.09)
10
机动 目录 上页 下页 返回 结束
y ( n) f ( x, y, y, y,
, y ( n 1) )
从这两个例子可见, 常微分方程的解可以不包含任何 常数, 也可以包含几个任意常数. 若n阶常微分方程(1.1.09)的解 y ( x, C1 , C2 ,
( x))
F ( x, y, y, y,
,y )0
( n)
(1.1.09)
9
机动 目录 上页 下页 返回 结束
y ( n) f ( x, y, y, y,
, y ( n 1) )
常微分方程的主要问题之一是求方程的解. 所谓求 方程的解就是在某区间I内寻求满足方程 (1.1.09)
,y )0
( n)
(1.1.09)
12
机动 目录 上页 下页 返回 结束
y ( n) f ( x, y, y, y,
, y ( n 1) )
二、数学问题:初值问题
一个常微分方程的通解的用途不是很广, 而真正有用 的是特解, 特解就是满足事先给出的某些附加条件的确 定了任意常数的解, 这样的附加条件称为初始条件, 一个 常微分方程配上初始条件就构成一个初值问题, 初值问 题也称为柯西问题(Cauchy problem).
如果自变量的个数为两个或两个以上, 即未知函数 是多元函数的这种微分方程称为偏微分方程. 常微分方程的一般形式是
F ( x, y, y, y,
,y )0
( n)
机动 目录
(1.1.09)
2
上页 下页 返回 结束
方 程 的 阶
未 自 知 变 函 量 数
未 知 函 数 的 一 阶 导 数
常微分方程的一般概念.ppt

条件为:
1 dP k P dt P t 0(1790 年 ) P0
20
从而得出人口按指数规律增加:
P P0e kt
评价 l相对增长率等于常数这一假设只在一
个较短的时间间隔对问题的模拟较好;
l按指数模型,人口将无限增长下去, 但这是不可能的。
21
2. Logistic 模型(人口增长模型 )
32
Ž C 0 情况,对应
R 2GM0 , R
设初:条 t0件 时 R0,
通过解这个一阶方程, 得
2R2 3 3
2GM 0 tC,
再利用初条件, R3 得 92G到M 0t2
33
这个公式被称为“扁平宇宙模型” (flat universe model) , 试问此 模型就宇宙膨胀可以给出什么预言?
二、近代以来交通、通讯工具的进步对人们社会生活的影 响
(1)交通工具和交通事业的发展,不仅推动各地经济文化交 流和发展,而且也促进信息的传播,开阔人们的视野,加快 生活的节奏,对人们的社会生活产生了深刻影响。
(2)通讯工具的变迁和电讯事业的发展,使信息的传递变得 快捷简便,深刻地改变着人们的思想观念,影响着人们的社 会生活。
请见以下各种微分方程:
(1) dy f(x) dx
(2) dd22 xtad dx tbx0
11
(3) m d d22 ythyd d y tk yF (t) ( 4 )y P (x )y Q (x ) (5 ) xd ys xixnd 0y
( 6 )x 3 y x 2 y 4 x y 3 x 2 (7 ) (y)2 4 y 3 x 0
dt
k
分离变量并积分
rdt
dx
x(1
高中数学最全的思维导图

高中数学最全的思维导图小数老师2015-11-23 11:08很多同学一轮复习已经过半,但还不知道该怎么总结,小数老师给大家提个建议,要想总结,主要还是首先梳理出脉络来,提到某个知识点,那么关于这个知识点相关的所有知识你都要弄明白,这样你就成功了一半!下面是8张思维导图,先研究下看看吧!夷示方法元表、隼合之闾的关系集台「1f映射i I 函数三要妄性质表示定义定义域值域单调性周期性性质対称性基本初等函数分段国数运算:交、弃、补确定性、互异性、无序性解析达列表法使解析式有意义丿对应关采[」换元法求解析式JA连意应用函数的单调在求值域圏象法u函薮破个区圈MlWt减I与曲谒国直是秃亍区减占鱼乂耒冒:2,征阴尊讶*勒査『斷人导披追;儿麗舍弼戴的鱼调性亘塑」是乂填黄于旗点时歌氐L©社有盘文的奇證戳弋r如即)r的奇圈埶詡⑵二呻书⑹=£)最值—C环酩变拱)—f皑拦变彗)—{棒编变箕)亘合函数二次函巍、基本不等式、打崗(耐克)函〕数、三角函数有界性、数形结台、异数.L —次、二次函数、反比例函數一幕函数指数函数对数函数三甬函埶亘台III埶的单调性:同潸异减I哦值法、典型的函数1抽象函数函数与方程函埶的应用图象V性质和应用二分注、图象迭、二次展三次方程根的分布)空间几何体liii台区梭怪梭台L囲台Sfe-正枝{王,长方体、正方体EW.四面体、正四面体一l点在Mh±点与线纬与面一面勻面点在面內点在面外竝面岂強-直线在平窗内厂平行—相乂—f平行关系的]A 转化J i ■■-平厅J垂直曲罕的]线线1相互轉化J垂嵐L相父L平行L三视團•r直观團长对正-喜平齐卞伯隼」一刚面积.表面理体段口高—个公共点没有缺旦漫有有公扛耳------------------ 厂W T 厂直线在平面外-^―---------------- L相交亠线面- "平行「面直垂畳线面甜r-J_ -面面■乎行價耕角的畫化与糾率的变化)位臭关养相立I—C且必:-今血芒:)狂童:战距可正A可员,也可为0. J注at:栽距可正可员,也可訂oj直迭万程茹形式直迭万程茹形式两亶线的交点两亶线的交点圧意若种开式的辕化和运用范圈圧意若种开式的辕化*□运用范围不等式群三即T通项会式等比数列一1(样。
常微分方程的基本概念ppt课件

1 2 1 y2 1 C
2
3x
通解
1 y2 1 C 3x
注 意 : y2 1 ,即y 1也 是 方 程 的 解! 奇异解
例
设降落伞从跳伞塔下落后所受空气阻力与速度
成正比, 并设降落伞离开跳伞塔时( t = 0 ) 速度为0, 求
降落伞下落速度与时间的函数关系.
或写成 u ln | xu | C ,
再将 u y 代入,得通解为 y ln | y | C ;
x
x
再由初始条件 y(1) 1 , 得 C 1 ,
于是得所求特解为 y ln | y | 1 . x
例 在制造探照灯反射镜面时,要求点光源的光线反
射出去有良好的方向性 , 试求反射镜面的形状.
但未知函数的导数必须出现.
未知函数是多元函数,含有未知函数的 偏导数的微分方程称为偏微分方程.
定义2: ( 微分方程的阶 )未知函数的导数的最高 阶数称为微分方程的阶.
例如 dy 4x2 ,
dx
一阶
d 2
dt 2
m
d
dt
g
l
0
二阶
二阶及二阶以上的微分方程称为高阶微分方程.
定义3: ( 微分方程的解)
gt C1,
再积一次分得:S
1 2
gt2
C1t
C2 , 其中C1,C2为任意常数.
5.1 微分方程的基本概念
定义1: 含有未知函数的导数的方程称为微
分方程.
未知函数是一元函数,含有未知函数的导数的微
分方程称为常微分方程.
高等数学各章知识结构
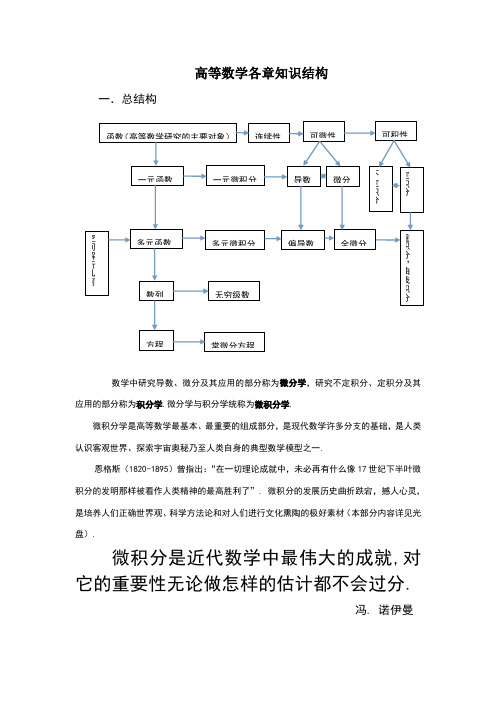
高等数学各章知识结构一.总结构数学中研究导数、微分及其应用的部分称为微分学,研究不定积分、定积分及其应用的部分称为积分学.微分学与积分学统称为微积分学.微积分学是高等数学最基本、最重要的组成部分,是现代数学许多分支的基础,是人类认识客观世界、探索宇宙奥秘乃至人类自身的典型数学模型之一.恩格斯(1820-1895)曾指出:“在一切理论成就中,未必再有什么像17世纪下半叶微积分的发明那样被看作人类精神的最高胜利了”. 微积分的发展历史曲折跌宕,撼人心灵,是培养人们正确世界观、科学方法论和对人们进行文化熏陶的极好素材(本部分内容详见光盘).微积分是近代数学中最伟大的成就,对它的重要性无论做怎样的估计都不会过分.冯. 诺伊曼注:冯. 诺依曼(John von Neumann,1903-1957,匈牙利人),20世纪最杰出的数学家之一,在纯粹数学、应用数学、计算数学等许多分支,从集合论、数学基础到量子理论与算子理论等作多方面,他都作出了重要贡献. 他与经济学家合著的《博弈论与经济行为》奠定了对策论的基础,他发明的“流程图”沟通了数学语言与计算机语言,制造了第一台计算机,被人称为“计算机之父”.微积分中重要的思想和方法:1.“极限”方法,它是贯穿整个《微积分》始终。
导数是一种特殊的函数极限;定积分是一种特殊和式的极限;级数归结为数列的极限;广义积分定义为常义积分的极限;各种重积分、曲线积分、曲面积分都分别是某种和式的极限。
所以,极限理论是整个《微积分》的基础。
尽管上述各种概念都是某种形式的极限,但是它们都有各自独特和十分丰富深刻的内容,这是《微积分》最有魅力的地方之一。
2.“逼近”思想,它在《微积分》处处体现。
在近似计算中,用容易求的割线代替切线,用若干个小矩形面积之和代替所求曲边梯形面积;用折线段的长代替所求曲线的长;用多项式代替连续函数等。
这种逼近思想在理论和实际中大量运用。
3.“求极限、求导数和求积分”是最基本的方法。
常微分方程总结 PPT

8
机动 目录 上页 下页 返回 结束
3. 解微分方程应用题的方法和步骤
(1) 找出事物的共性及可贯穿于全过程的规律列方程. 常用的方法: 1) 根据几何关系列方程 ( 如: P263,5(2) ) 2) 根据物理规律列方程 ( 如: 例4 , 例 5 )
线性无关概念.
23
机动 目录 上页 下页 返回 结束
定义: 设 y1 ( x), y2 ( x),, yn ( x) 是定义在区间 I 上的
n 个函数, 若存在不全为 0 的常数 使得
则称这 n个函数在 I 上线性相关, 否则称为线性无关. 例如, 在( , )上都有
故它们在任何区间 I 上都线性相关;
微分方程的基本概念
含未知函数及其导数的方程叫做微分方程 . 常微分方程 (本章内容)
分类
偏微分方程
方程中所含未知函数导数的最高阶数叫做微分方程
的阶. 一般地 , n 阶常微分方程的形式是
F ( x, y, y,, y ( n ) ) 0
或
y ( n ) f ( x, y, y,, y ( n 1) ) ( n 阶显式微分方程)
y p( x) y q( x) y f ( x) ,
y
( n) ( n 1)
为二阶线性微分方程.
n 阶线性微分方程的一般形式为
a1 ( x) y an 1 ( x) y an ( x) y f ( x) f ( x) 0 时, 称为非齐次方程 ;
f ( x) 0 时, 称为齐次方程.
若 Q(x) 0, 称为非齐次方程 . dy P( x) y 0 1. 解齐次方程 dx
高数强化第四章《常微分方程》(思维导图)

第四章常微分方程
常微分方程基本概念
微分方程微分方程的阶
微分方程的解
通解
特解
初始条件积分曲线
一阶微分方程
可分离变量的方程
齐次微分方程一阶线性微分方程
高阶线性微分方程
线性微分方程的解的结构
齐次特解+齐次特解(线性无关)=齐次通解两个线性无关齐次特解+非齐次特解=非齐次通解非齐次特解-非齐次特解=齐次解
非齐次特解1+非齐次特解2=方程(1+2)的特解
k个非齐特解相加=非齐次解⇔k系数之和=1k个非齐特解相加=齐次解⇔k系数之和=0
常系数齐次线性微分方程
两个不等实特征根r1≠r2二重实特征根r1=r2共轭复根r=α±iβ常系数非齐次线性微分方程
f(x)=x^k·Qm(x)·e^λx
f(x)=x^k·e^αx·[Rm ₁(x)·cosβx+Rm ₂(x)·sinβx]
常见题型
微分方程求解
可分离变量线性齐次
x,y对调变量代换
判别类型,选择方法微分方程所有解≥通解
综合题应用题差分方程
差分方程
一阶常系数线性齐次差分方程
yt+1+a·yt=0
通解=C·(-a)^t 一阶常系数线性非齐次差分方程
yt+1+a·yt=f(t)
f(t)=Pm(t)a≠-1;a=1f(t)=d^t·Pm(t)
a+d≠0;a+d=0。
数学高一下知识点思维导图

数学高一下知识点思维导图数学是一门理科学科,是一门需要逻辑思维的学科。
在高一下学期,学生会接触到更深入的数学知识,并需要掌握更多的数学技巧。
下面是高一下学期数学知识点的思维导图,帮助学生整理和梳理学习内容。
1. 代数- 线性方程组- 高斯消元法- 初等变换- 二次函数- 顶点坐标- 对称轴- 判别式- 不等式- 解不等式- 图像表示2. 几何- 平面几何- 平行线与垂直线 - 四边形性质- 三角形面积- 空间几何- 空间直线和平面 - 空间向量- 空间几何关系 - 三角函数- 正弦定理- 余弦定理- 向量叉乘3. 概率与统计- 随机事件- 概率的定义- 加法规则和乘法规则 - 统计分布- 频数分布- 直方图- 折线图- 抽样调查- 抽样方法- 数据分析- 推论统计4. 数列与数学归纳法- 等差数列- 公差和通项公式- 前n项和- 等比数列- 公比和通项公式- 前n项和- 数学归纳法- 原理与应用- 数学归纳证明5. 导数与微分- 导数的定义- 函数导数的定义与性质 - 高阶导数- 函数的求导法则- 乘积法则- 商法则- 链式法则- 函数的应用- 切线与法线- 最值问题- 凹凸性与拐点以上就是高一下学期数学知识点的思维导图。
通过这样的整理,学生可以更加清晰地了解数学知识点之间的联系和重点内容。
同时,思维导图也能够帮助学生在复习时更加高效地回顾相关知识。
希望这个思维导图能对学生的学习有所帮助!。
微分方程ppt课件

F(x, y, y) 0
(1.8)
如果在(1.8)中能将 y 解出,则得到方程
y f (x, y)
(1.9)
或
M (x, y)dx N(x, y)dy 0
(1.10)
(1.8)称为一阶隐式方程,(1.9)称为一阶显式方程,(1.10)称为微 分形式的一阶方程.
14
机动 目录 上页 下页 返回 结束
推得
c1 v0
c2 H
于是,得到满足上述初值条件的特解为
xx(t()t)H12gt122 gt2c1t v0ct 2
(1.14)
22
机动 目录 上页 下页 返回 结束
它描述了初始高度为H,初始速度为v0的自由落体运 动规律.
求微分方程满足初值条件的解的问题称为初值 问题.
于是我们称(1.14)是初值问题
4
机动 目录 上页 下页 返回 结束
目
录
第一章 初等积方法 第二章 基本定理 第三章 一阶线性微分方程组 第四章 n阶线性微分方程 第五章 定性与稳定性理论简介 第六章 一阶偏微分方程初步
5
机动 目录 上页 下页 返回 结束
第一讲
第一章 初等积分法
1.1 微分方程和解
300多年前,由牛顿(Newton,1642-1727)和 莱布尼兹(Leibniz,1646-1716)所创立的微积分学, 是人类科学史上划时代的重大发现,而微积分 的产生和发展,又与求解微分方程问题密切相 关.这是因为,微积分产生的一个重要动因来自 于人们探求物质世界运动规律的需求.
12
机动 目录 上页 下页 返回 结束
例如下面的方程都是常微分方程
dy 2x dx
(1.4)
高一必修一必修二知识点思维导图

高一必修一必修二知识点思维导图高中是每个学生学习的重要阶段,必修一和必修二是高中生的基础课程,其中包含了许多重要的知识点。
为了更好地理解和掌握这些知识点,下面给出了高一必修一和必修二知识点的思维导图。
一、必修一知识点思维导图1. 数与代数- 实数的概念和性质- 代数式和多项式的基本概念- 一元一次方程与一元一次不等式- 进一步认识二次根式与一元二次方程- 二次根式及其运算- 一元二次方程的解法与应用- 一次函数及其表示- 一次函数图象和性质2. 几何- 平面直角坐标系及其应用- 直线与圆的方程- 三角形的基本概念和性质- 三角形的成立条件及分类- 三角形的相似性质和判定- 三角形的面积与余弦定理- 圆的基本性质- 圆的切线与切线定理3. 数与空间- 点、直线、平面的基本性质和关系- 空间几何体的投影及其应用- 空间几何体的相交和平行关系- 空间的坐标表示和平面方程- 空间几何体的视图与真形的关系4. 数据与统计- 统计基础知识与统计调查- 统计图形的应用和解读- 数据的初步分析和数据的概率解释- 抽样调查与统计规律的探究二、必修二知识点思维导图1. 数与代数- 整式的计算与因式分解- 二次函数及其图像- 平方根与实数的四则运算- 分式及其运算- 幂与指数函数- 对数与指数方程2. 几何- 平面向量及其运算- 点和圆的位置关系- 圆锥曲线的定义和性质- 球与球面的位置关系与球的欧拉公式- 空间直角坐标系及其应用3. 数与空间- 集合及其运算- 命题与证明- 概率初步- 排列与组合- 三角函数的概念和关系- 三角函数的图像变换和性质4. 数据与统计- 随机事件的概率与统计- 正态分布与抽样调查- 综合统计应用与误差分析通过以上的思维导图,可以清晰地了解高一必修一和必修二的知识点,有助于学生对这些知识点的整体把握和深入理解。
每个知识点都包含了具体的内容,同学们可以结合教材进行更加深入的学习和探索。
希望同学们在高一的学习中取得优异的成绩!。
几何画板迭代全解

是运算消耗内存较大。我们先来了解下面这几个最基本的概念。 迭代:按一定的迭代规则,从原象到初象的反复映射过程。 原象:产生迭代序列的初始对象,通常称为“种子” 。 初象:原象经过一系列变换操作而得到的象。与原象是相对概念。 更具体一点,在代数学中,如计算数列 1,3,5,7,9......的第 n 项。我们 知道 an an1 2 ,所以迭代的规则就是后一项等于前一项加 2。以 1 作为原像, 3 作为初像,迭代一次后得到 5,再迭代一次得到 7,如此下去得到以下数值序 列 7 , 9,11, 13, 15......如图 1.1 所示。
4
《几何画板迭代全解》
5. 如何改变参数 n 呢?有两种方法,第一种是双击参数 n,然后在对话框 中输入值。第二种是单击参数 n ,按键盘的‘+’ 、 ‘-’ ,系统默认变 化量为 1。右键单击可以修改变化量的大小。
注意:迭代时,作为迭代深度的参数 n 一定要在最后面选择,这是系统的 规定。
第 4 步
第 5 步
5. 单击迭代框的【显示】按钮【最终迭代】 ,得到的图像仅是最后一条边。 6. 点击迭代框【结构】按钮,我们可以设置创建的对象,选择“仅没有点 的对象”则迭代的像只有正多边形的各条边,而没有顶点,反之则有。
3
《几何画板迭代全解》
选择迭代像,我们可以修改他们的属性,比如颜色和粗细等,但是细心的 你会发现, 线段的迭代像是不能够度量其长度的, 当然也就不能取中点之类的操 作。迭代的点是不能够度量他们的横纵坐标,但是我们可以得到迭代的终点,方 法是选择迭代的点,然后单击【变换】 【终点】 ,可以发现最后的那个点变成实点 了,这个功能在函数映射里面会用到。 上述方法在增加后减少迭代次数时比较麻烦,而且迭代规则限定了,即每 次都是旋转同样的角度。迭代次数和迭代规则能不能用带参数来控制呢?可以 的,这就是深度迭代。 【例 2】画圆的任意 n 边形 【步骤】 1. 新建圆 O 并在圆上任取一点 A。双击圆心 O 作为旋转中心。 2. 新建参数 n=7,计算
高数下册同济六版知识网络图
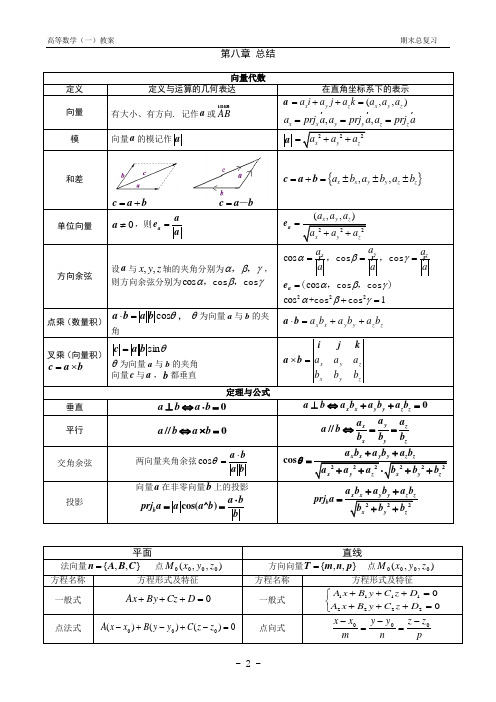
第八章总结=-c a b第十章 总结2()(cos ,sin )(cos ,sin )Df d d d f d βϕθρθρθρρθθρθρθρρ=⎰⎰⎰⎰02θπ≤≤ 0θπ≤≤ 2πθπ≤≤ (3)利用积分区域的对称性与被积函数的奇偶性当D 关于y 轴对称时,(关于x 轴对称时,有类似结论)0(,)f x y x ⎧对于是奇函数,第十一章总结所有类型的积分:○1定义:四步法——分割、代替、求和、取极限;○2性质:对积分的范围具有可加性,具有线性性;○3对坐标的积分,积分区域对称与被积函数的奇偶性。
无穷级数常数项级数傅立叶级数幂级数一般项级数正项级数用收敛定义,nns∞→lim存在常数项级数的基本性质常数项级数的基本性质○1若级数收敛,各项同乘同一常数仍收敛.○2两个收敛级数的和差仍收敛.注:一敛、一散之和必发散;两散和、差必发散.○3去掉、加上或改变级数有限项,不改变其收敛性.○4若级数收敛,则对这级数的项任意加括号后所成的级数仍收敛,且其和不变。
推论:如果加括号后所成的级数发散,则原来级数也发散.注:收敛级数去括号后未必收敛.○5(必要条件)如果级数收敛,则0lim=→nnu莱布尼茨判别法若1+≥nnuu且0lim=∞→nnu,则∑∞=--11)1(nnn u收敛nu∑和nv∑都是正项级数,且nnvu≤.若nv∑收敛,则nu∑也收敛;若nu∑发散,则nv∑也发散.比较判别法比较判别法的极限形式nu∑和nv∑都是正项级数,且lvunnn=∞→lim,则○1若+∞<<l0,nu∑与nv∑同敛或同散;○2若0=l,nv∑收敛,nu∑也收敛;○3如果+∞=l,nv∑发散,nu∑也发散。
比值判别法根值判别法nu∑是正项级数,ρ=+∞→nnn uu1lim,ρ=∞→nnnulim,则1<ρ时收敛;1>ρ(ρ=+∞)时发散;1=ρ时可能收敛也可能发散.收敛性和函数展成幂级数nnnxa∑∞=0,ρ=+∞→nnn aa1lim,1,0;,0;0,.R R Rρρρρ=≠=+∞===+∞缺项级数用比值审敛法求收敛半径)(xs的性质○1在收敛域I上连续;○2在收敛域),(RR-内可导,且可逐项求导;○3和函数)(xs在收敛域I上可积分,且可逐项积分.(R不变,收敛域可能变化).直接展开:泰勒级数间接展开:六个常用展开式11(11)1nnx xx∞==-<<-∑11()!x nne x xn∞==-∞<<+∞∑22TT lπ==∑∞=++=10)sincos(2)(nnnnxbnxaaxf⎰-=πππdxxfa)(1⎰-=πππnxdxxfancos)(1⎰-=πππnxdxxfbnsin)(1收敛定理x是连续点,收敛于)(xf;x是间断点,收敛于)]()([21+-+xfxf周期延拓)(xf为奇函数,正弦级数,奇延拓;)(xf为偶函数,余弦级数、偶延拓.交错级数。
高中数学必修全思维导图

5 、 若 函 数 f (x) 的 定 义 域 关 于 原 点 对 称 , 则 f (x) 可 以 表 示 为
f (x) 1 [ f (x) f (x)] 1 [ f (x) f (x)] ,该式的特点是:右端为一个奇函数
2
2
和一个偶函数的和。
零点与根的关系
零点:对于函数y f(x), 我们把使f ( x ) 0的实数x叫做函数y f ( x )的零点。 定理:如果函数y f ( x ) 在区间[ a , b ]上的图象是连续不断的一条曲线,并且有f ( a ) f ( b ) 0,
在集合B中都有唯一确定的元素y与之对应,那么就称对应f : B为从集合A到集合B的一个映射
传统定义:如果在某变化中有两个变量x , y , 并且对于x在某个范围内的每一个确定的值,
定义
按照某个对应关系f , y都有唯一确定的值和它对应。那么y就是x的函数。记作y f ( x ).
近代定义:函数是从一个数集到另一个数集的映射。
ab
表2
p q
0
p为奇数 q为奇数
ab
ab
ab
幂函数 y x ( R)
0 1
1
1
奇函数
p为奇数 q为偶数
p为偶数 q为奇数
第一象限 性质
减函数
增函数
偶函数
过定点
(0,1)
高中数学必修 2
一、直线与方程
(1)直线的倾斜角
定义:x 轴正向与直线向上方向之间所成的角叫直线的倾斜角。特别地,当直线与 x 轴平行
定义域 函数及其表示 函数的三要素 值域 对应法则
解析法
函数的表示方法 列表法
函数
图象法
单调性导 传数 统定 定义 义: :则在 在 递f 区 区 增( x间 间 区) 在间aa,,a;bb,b上 上如上, ,f 递 (若 若x1减fa)(,xxfa1)(,bxx02是2,),的则 b ,则递 如f (f减 fx(()区 xx在1)间 在 )a。f,ab(,b上 x2上递),递增则减,fa,(,abx,)b是在是递a的增,b递区上减间递区;增间如,。af ,(bx是)0
常微分方程常见形式及解法课件PPT

2021/3/10
11
谢谢观看
2021/3/10
12
常微分方程常见形式及解法
2021/3/10
知行1301 13275001
毕文彬
1
微分方程指描述未知函数的导数与自变量之间的关系 的方程。微分方程的解是一个符合方程的函数。而在 初等数学的代数方程,其解是常数值。 常微分方程(ODE)是指一微分方程的未知数是单一 自变数的函数。最简单的常微分方程,未知数是一个 实数或是复数的函数,但未知数也可能是一个向量函 数或是矩阵函数,后者可对应一个由常微分方程组成 的系统。微分方程的表达通式是:
非齐次一阶常系数线性微分方程:
齐次二阶线性微分方程:
描述谐振子的齐次二阶常系数线性微分方程:
非齐次一阶非线性微分方程:
描述长度为L的单摆的二阶非线性微分方程:
3
2021/3/10
微分方程的解
微分方程的解通常是一个函数表达式(含一 个或多个待定常数,由初始条件确定)。例如 : dy/dx=sinx, 的解是 y=-cosx+C, 其中C是待定常数; 例如,如果知道 y=f(π)=2, 则可推出 C=1, 而可知 y=-cosx+1,
4
简易微分方程的求解方法
01
一阶线性常微分方程
02
二阶常系数齐次常微分方程
2021/3/10
5
01 一阶线性常微分方程
对于一阶线性常微分方程,常用的方法是常 数变易法: 对于方程:
可知其通解:
然后将这个通解代回到原式中,即可求出 C(x)的值
2021/3/10
6
02 二阶常系数齐次常微分方程
对于二阶常系数齐次常微分方程,常 用方法是求出其特征方程的解 对于方程: 可知其通解: 其特征方程: 根据其特征方程,判断根的分布情况 ,然后得到方程的通解 一般的通解形式为(在r1=r2的情况下):
高等数学各章知识结构

高等数学各章知识结构一.总结构数学中研究导数、微分及其应用的部分称为微分学,研究不定积分、定积分及其应用的部分称为积分学.微分学与积分学统称为微积分学.微积分学是高等数学最基本、最重要的组成部分,是现代数学许多分支的基础,是人类认识客观世界、探索宇宙奥秘乃至人类自身的典型数学模型之一.恩格斯(1820-1895)曾指出:“在一切理论成就中,未必再有什么像17世纪下半叶微积分的发明那样被看作人类精神的最高胜利了”. 微积分的发展历史曲折跌宕,撼人心灵,是培养人们正确世界观、科学方法论和对人们进行文化熏陶的极好素材(本部分内容详见光盘).微积分是近代数学中最伟大的成就,对它的重要性无论做怎样的估计都不会过分.冯. 诺伊曼注:冯. 诺依曼(John von Neumann,1903-1957,匈牙利人),20世纪最杰出的数学家之一,在纯粹数学、应用数学、计算数学等许多分支,从集合论、数学基础到量子理论与算子理论等作多方面,他都作出了重要贡献. 他与经济学家合著的《博弈论与经济行为》奠定了对策论的基础,他发明的“流程图”沟通了数学语言与计算机语言,制造了第一台计算机,被人称为“计算机之父”.微积分中重要的思想和方法:1.“极限”方法,它是贯穿整个《微积分》始终。
导数是一种特殊的函数极限;定积分是一种特殊和式的极限;级数归结为数列的极限;广义积分定义为常义积分的极限;各种重积分、曲线积分、曲面积分都分别是某种和式的极限。
所以,极限理论是整个《微积分》的基础。
尽管上述各种概念都是某种形式的极限,但是它们都有各自独特和十分丰富深刻的内容,这是《微积分》最有魅力的地方之一。
2.“逼近”思想,它在《微积分》处处体现。
在近似计算中,用容易求的割线代替切线,用若干个小矩形面积之和代替所求曲边梯形面积;用折线段的长代替所求曲线的长;用多项式代替连续函数等。
这种逼近思想在理论和实际中大量运用。
3.“求极限、求导数和求积分”是最基本的方法。
