8字型比例线段的证明过程
谈谈比例线段证明的方法

谈谈比例线段证明的方法比例线段证明是一种常用的数学证明方法,它可以用来证明两条线段之间的比例关系。
比例线段证明的基本思想是:如果两条线段的长度之比等于两个数之比,则这两条线段之间存在比例关系。
比例线段证明的步骤如下:首先,在平面直角坐标系中绘制两条线段,其中一条线段的长度为a,另一条线段的长度为b。
然后,在两条线段之间绘制一条新的线段,其长度为c,使得a:b=c:d,其中d为新线段的长度。
最后,证明a:b=c:d,即证明两条线段之间存在比例关系。
比例线段证明的关键在于证明a:b=c:d,即证明两条线段之间存在比例关系。
可以使用数学归纳法来证明,即从一般情况出发,逐步推导出特殊情况,最终证明a:b=c:d。
比例线段证明是一种简单而有效的数学证明方法,它可以用来证明两条线段之间的比例关系。
它的基本思想是:如果两条线段的长度之比等于两个数之比,则这两条线段之间存在比例关系。
比例线段证明的关键在于证明a:b=c:d,即证明两条线段之间存在比例关系。
可以使用数学归纳法来证明,即从一般情况出发,逐步推导出特殊情况,最终证明a:b=c:d。
比例线段证明是一种简单而有效的数学证明方法,它可以用来证明两条线段之间的比例关系。
它的优点在于,可以通过简单的图形操作来证明两条线段之间的比例关系,而不需要复杂的数学推理。
此外,比例线段证明也可以用来证明其他几何图形之间的比例关系,比如三角形、圆形等。
总之,比例线段证明是一种简单而有效的数学证明方法,它可以用来证明两条线段之间的比例关系,也可以用来证明其他几何图形之间的比例关系。
它的基本思想是:如果两条线段的长度之比等于两个数之比,则这两条线段之间存在比例关系。
比例线段证明的关键在于证明a:b=c:d,。
8字模型例题

8字模型例题
8字模型是一种数学模型,通常用于描述物理系统中的对称性或周期性。
以下是一个简单的8字模型例题:
题目:一个圆在平面内旋转一圈,经过的时间为T。
在这个圆上任取一点P,当圆旋转一圈时,点P在圆上移动的路径是一个8字形。
求这个8字形的
长度。
答案:8字形的长度等于圆的周长,即2πr,其中r是圆的半径。
解释:当圆旋转一圈时,点P在圆上移动的路径是一个8字形。
由于点P
在圆上任意取,因此这个8字形实际上是由无数个点P的轨迹组成的。
每个点P的轨迹都是一个圆周长,因此这个8字形的长度等于圆的周长,即2πr。
中考专题6,A字型,8字型相似教师版

似,那么 BF 的长度是
.
【分析】①由折叠可知 BF=B’F;②文字相似要分类讨论
【答案】:
①当 B' FC∽ ABC 时,有 B ' F = CF AB BC
∵
AB
=
AC
=
3, BC
=
4, BF
=
B'F
,∴
BF 3
=
4 − BF 4
,解得
BF
=
12 7
②当 B 'CF∽ BCA 时, B = C = CB ' F ,∴ B ' F = FC
2. 如图 OA =12,OB = 6 ,点 P 从点 O 开始沿 OA 边向 A 匀速移动,点 Q 从点 B 开始沿 OB 边向 O 匀速移动,它们的速度都是每秒 1 个单位,如果 P,Q 同时出发,用 t (秒)表示移
动的时间 (0 t 6) , t 为何值时,以 P、Q、O 三点为顶点的三角形与 AOB 相似?
【答案】: t = 4 或 2 3. 如右图,作 DH / /BF 交 AC 于 H , ∵AD 是的中线,FH = HC
DH / /BF, AF : FH = AE : DE = 1: 3, AF : FC = 1: 6
【答案】:D
10
【B 组】
1. (1) EF / /BC ,AEF∽ABC , AG = EF ,即 AG = x ,
∴ CDF∽ CFA , CF = CD ,即 5 = CD ,
CA CF
85
CD = 25 8
【总结】 ①折叠性质:折痕垂直平分对应点连线; ②反 A 字型,选择对应边成比例关系时,选择有公共边的比例.
7
证明线段比例式或等积式的方法

证明线段比例式或等积式的方法(一)比例的性质定理:(二)平行线中的比例线段:①平行线分线段成比例定理:三条平行线截两条直线所得对应线段成比例(图1、2)。
②平行于三角形的一边的直线截其他两边(或两边的延长线)所得的对应线段成比例(图3、4)。
③平行于三角形的一边,且与其他两边(或两边的延长线)相交的直线所截得的三角形的三边与原三角形的三边对应成比例(图3、4)。
(三)三角形中比例线段:①相似三角形中一切对应线段(对应边、对应高、对应中线、对应角平分线、对应周长…)的比都相等,等于相似比。
②相似三角形中一切对应面积的比都相等,等于相似比的平方。
③勾股定理:直角三角形斜边的平方等于两直角边的平方和(图5)。
④射影定理:直角三角形斜边上的高是两直角边在斜边上射影的比例中项(图5)。
直角三角形上任一直角边是它在斜边上的射影与斜边的比例中项(图5)。
⑤正弦定理:三角形中,每一边与对角的正弦的比相等(图6)。
即/sinA=b/sinB=c/sinC⑥余弦定理:三角形中,任一边的平方等于另两边的平方和减去这两边及其夹角余弦乘积的二倍(图6)。
如a2 = b2+c2 - 2 b·c·cosA(四)圆中的比例线段:圆幂定理:①相交弦定理圆内的两条相交弦,被交点分成的两条线段的积相等(图7)。
(推论:若弦与直径垂直相交,则弦的一半为它分直径所成两线段的比例中项。
图8)②切割线定理从圆外一点引圆的切线和割线,切线长为这点到割线与圆交点的两线段长的比例中项(图9)。
③割线定理从圆外一点引圆的两条割线,这一点到每条割线与圆交点的两线段长的积相等(图10)。
(五)比例线段的运算:①借助等比或等线段代换。
②运用比例的性质定理推导。
③用代数或三角方法进行计算。
平行线分线段成比例定理

5
17
2 1
)
)
(3) S△AGE=( 2
4
课堂小结
作业 4
已知AD // ED // BC,AD=15,BC=21,2AE = EB,求EF的长
A D E
H
F
解法(一)
作AG // CD交EF于H AD // EF // BC AD=15, BC=21
B
G
C
AD = HF = GC =15 ,BG = 6 EH AE = BG AB 2AE = EB
A
3k 3m 2m
E
D
2k
G
4m 2a
F
a
B
C
应用1—求线段长度(比值)
如图,△ABC中,D是AB上的点,E是AC上的点,延长ED与射线 CB交于点F.若AE∶EC=1∶2,AD∶BD=3∶2. 求:FB∶FC的值.
A
3k 3m
E
6m
H
2m
D
2k
F
a
B
3a
C
应用1—求线段长度(比值)
如图,△ABC中,D是AB上的点,E是AC上的点,延长ED与射线 CB交于点F.若AE∶EC=1∶2,AD∶BD=3∶2. 求:FB∶FC的值.
A
y
D
x
x
E C
B
5
应用4 — 建立函数关系式
2. 已知:如图,BC = 4, AC = 2 3 ∠C=60°,P为BC上 一点,DP//AB,设BP = x,S△APD= y.
(1)求y关于x的函数关系式; (2)若S△APD =
2 S△APB,求:BP的长. 3
A
D
H
B
平行线分线段成比例8

答案(2)
DB/AD=EC/FE (下/上=下/上) AB/AD=FC/FE (全/上=全/上) AB/DB=FC/EC (全/下=全/下)
A D F E L1 L2
B L4 图1
C L3 L5
教学设计(1)
1.观察图2、图3,说出它们分别是由图1怎样变化得 到的?且写出图2、图3中有关的比例式?
C
B 图4
(1)三条平行线剩下两条,且变 为三角形的一边和截三角形另两 E 边或两边延长线的线段。其中图4 中DE∥BC,图5中AF∥BC (2)结论没变,所得的对应线段 C 成比例。
部分线擦去, 取一部分 F
D(E) 一般到特殊 B C B
(3)推论:平行于三角形一边的 直线截其他两边(或两边的延长 D (E) 线),所得的对应线段成比例。 A C
字母
X型
能力目标小结
1、平行线分线段成比例定理是研究相似形 最重要、最基本的理论基础,而字母A型、字 母X型又是解决相似三角形一章有关计算和证 明的模具,可构造或寻找字母A型、字母X型 解决问题,把它称为三角形相似问题“奠基 法” 。 2、学会用“动态”的观点去解决研究问 题。 3、欣赏模型“字母A型、字母X型”的理 性美、结构美,诱发学习数学的激情,感受数 学的美学文化,培养学生“自主实践、自主探 索、大胆猜想、归纳创新”的数学理念。
1.定理名称: 2.文字语言: 3.图形语言:
D B
平行线分线段成比例定理的推论或三角形 一边平行线的性质定理 平行于三角形一边的直线截其它两边(或 两边的延长线),所得的对应线段成比例。
A E C 图4 B F D C A
图5
4.符号语言:
5.模型语言:
若DE∥BC 则:
相似三角形几何模型-X型图(知识讲解)九年级数学上册基础知识讲与练(北师大版)

专题4.34 相似三角形几何模型-X 型图(知识讲解) 0//A AOBO AB A B DC B CO DO CD ∆⇔==模型一:平行X 字型如图一,在中,D 、C 分别是AO 、BO 延长线上的点,AO BO AB AOB A D DO CO DC∆∠=∠⇔==模型二:非平行X 字型(也称为反X 字型)如图二,在中,DC 分别为AOBO 延长线上的点,AE BF ED FC ⇔=模型三:双(多)X 字型如图三,AD//BC ,AB 、CD 相交于点O ,过点O 的线段EF 交AD 、BC 于E 、F图一 图二 图三类型一、平行X 字型(也称为8字型)1.如图,在ABC 中,点D ,E 分别在边AB 、AC 上,DC 与BE 相交于点O ,且2DO =,6BO DC ==,3OE =.求证:DOE COB △∽△.【分析】利用比例线段来证明相似三角形即可.解:2DO =,6DC =,624OC CD DO ∴=-=-=,2142OD OC ∴==,3162OE OB ==, OD OE OC OB∴=, DOE BOC ∠=∠,DOE COB ∴∆∆∽.【点拨】本题主要考查三角形相似的判定,掌握三角形相似的判定定理是解题的关键.举一反三【变式1】如图,∠1=∠2=∠3,试找出图中两对相似三角形,并说明为什么?【答案】∠AFD∠∠EFB,∠ABC∠∠ADE;理由见分析.【分析】根据两个三角形的两组角对应相等,那么这两个三角形互为相似三角形证明即可.解:∠AFD∠∠EFB,∠ABC∠∠ADE.理由如下:∠∠2=∠3,∠AFD=∠EFB∠∠AFD∠∠EFB,∠∠B=∠D.∠∠1=∠2,∠12=,∠+∠∠+∠EAF EAF∠∠BAC=∠DAE,∠∠ABC∠∠ADE.【点拨】本题考查相似三角形的判定定理,熟记判定定理,本题用到了两组角对应相等的两个三角形互为相似三角形.【变式2】如图,直线a∥b,点M、N分别为直线a和直线b上的点,连接M,N,∠1=70°,点P是线段MN上一动点,直线DE始终经过点P,且与直线a,b分别交于点D、E,设∠NPE=α.(1)证明∠MPD∠∠NPE.(2)当∠MPD与∠NPE全等时,直接写出点P的位置.(3)当∠NPE是等腰三角形时,求α的值.【答案】(1)见分析;(2)点P是MN的中点;(3)40° 或70° 或55°【分析】(1)利用相似三角形的判定定理证明即可;(2)根据全等三角形对应边相等得到MP =NP ,即点P 是MN 的中点;(3)需要分类讨论:PN =PE 、PE =NE 、PN =NE ,再根据三角形内角和计算即可.(1)证明:∠a∥b ,∠∠MPD ∠∠NPE .(2)∠a∥b ,∠∠MDP =∠NEP ,∠当∠MPD 与∠NPE 全等时, MP =NP ,即点P 是MN 的中点;(3)∠a∥b ,∠∠1=∠PNE =70°,∠若PN =PE 时,∠∠PNE =∠PEN =70°.∠a =180°﹣∠PNE ﹣∠PEN =180°﹣70°﹣70°=40°.∠∠a =40°;∠若EP =EN 时,则a =∠PNE =70°;∠若NP =NE 时,则∠PEN =α,此时2α=180°﹣∠PNE =110°,∠α=∠PEN ═55°;综上所述,α的值是40° 或70° 或55°.【点拨】本题考查了相似三角形的判定、全等三角形的性质、等腰三角形的性质,解题关键是熟知相关性质,会根据等腰三角形底边不同进行分类讨论.类型二、非平行X 字型(也称为反8字型)2.在∠DP PB CP PA ⋅=⋅,∠BAP CDP ∠=∠,∠DP AB CD PB ⋅=⋅这三个条件中选择其中一个,补充在下面的问题中,使命题正确,并证明.问题:如图,四边形ABCD 的两条对角线交于P 点,若 (填序号)求证:ABP DCP △△.【答案】∠,证明见分析或∠,证明见分析.【分析】若选择条件∠,可利用两边成比例且夹角相等的两个三角形相似;若选择条件∠,可利用两角相等的两个三角形相似.解:选择条件∠的证明为:∠DP PB CP PA ⋅=⋅, ∠=PA PB DP CP, 又∠APB DPC ∠=∠,∠ABP DCP ∽△△;选择条件∠的证明为:∠APB DPC ∠=∠,BAP CDP ∠=∠∠ABP DCP ∽△△.【点拨】本题考查相似三角形的判定定理,能熟记相似三角形的判定定理,并正确识图是解题关键.举一反三【变式1】如图,在ABC 中,90ACB ∠=︒,CD 是边AB 上的中线,EF 垂直平分CD ,分别交AC ,BC 于E ,F ,连接DE ,DF .(1)求证:OCE OFD ∽△△.(2)当7AE =,24BF =时,求线段EF 的长.【答案】(1)见分析 (2)25EF =【分析】(1)如图(见分析),先根据线段垂直平分线的性质可得90EOC DOF ∠=∠=︒,ED EC =,FD FC =,再根据三角形全等的判定定理证出EDF ECF ≅,根据全等三角形的性质可得12∠=∠,从而可得421∠=∠=∠,然后根据相似三角形的判定即可得证;(2)如图(见分析),延长FD 至G ,使DG DF =,连接AG ,EG ,先根据线段垂直平分线的判定与性质可得EG EF =,再根据三角形全等的判定定理证出ADG BDF ≅△△,根据全等三角形的性质可得24AG BF ==,7B ∠=∠,然后根据平行线的判定与性质可得90EAG ∠=︒,最后在Rt AEG △中,利用勾股定理即可得.(1)证明:∠EF 垂直平分CD ,∠90EOC DOF ∠=∠=︒,ED EC =,FD FC =,在EDF 和ECF △中,ED EC FD FC EF EF =⎧⎪=⎨⎪=⎩,∠()EDF ECF SSS ≅,∠12∠=∠,∠90ACB ∠=︒,90EOC ∠=︒,∠233490∠+∠=∠+∠=︒,∠421∠=∠=∠,在OCE △和OFD △中,9014EOC DOF ∠=∠=︒⎧⎨∠=∠⎩, ∠OCE OFD .(2)解:如图,延长FD 至G ,使DG DF =,连接AG ,EG .则ED 垂直平分FG ,EG EF ∴=, CD 是边AB 上的中线,∠AD BD =,在ADG 和BDF 中,65DG DF AD BD =⎧⎪∠=∠⎨⎪=⎩,∠()ADG BDF SAS ≅△△,∠24AG BF ==,7B ∠=∠,∠AG BC ,∠18090EAG ACB ∠=︒-∠=︒,∠25EG =,∠25EF =.【点拨】本题考查了相似三角形的判定、三角形全等的判定定理与性质、线段垂直平分线的判定与性质等知识点,较难的是题(2),构造全等三角形和直角三角形是解题关键.【变式2】如图,AC ,BD 相交于的点O ,且∠ABO =∠C .求证:∠AOB ∠∠DOC .【分析】利用对顶角相等得到∠AOB =∠COD ,再结合已知条件及相似三角形的判定定理即可求解.证明:∠AC ,BD 相交于的点O ,∠∠AOB =∠DOC ,又∠∠ABO =∠C ,∠∠AOB ∠∠DOC .【点拨】本题考查了相似三角形的判定定理:若一对三角形的两组对应角相等,则这两个三角形相似,由此即可求解.类型三、A、X字型综合3.如图,在∠ABCD中,AC,BD交于点O,点M是AD的中点,连接MC交BD 于点N,ON=1.(1)求证:∠DMN∠∠BCN;(2)求BD的长;(3)若∠DCN的面积为2,直接写出四边形ABNM的面积.【答案】(1)见分析(2) 6 (3) 5【分析】(1)根据平行四边形的性质可得AD∥BC,从而证明8字模型相似三角形△DMN∠∠BCN;(2)由△DMN∠∠BCN,可得到DN:BN=1:2,设OB=OD=x,表示出BN与DN,求出x的值,即可确定出BD的长;(3)根据△MND∠∠CNB且相似比为1:2,得到CN=2MN,BN=2DN.已知△DCN的面积,则由线段之比,得到△MND与△CNB的面积,从而得到S△ABD=S△BCD=S△BCN+S△CND,最后由S四边形ABNM=S△ABD-S△MND求解.(1)证明:∠四边形ABCD是平行四边形,∠AD∥BC,∠∠DMN=∠BCN,∠MDN=∠NBC,∠∠DMN∠∠BCN;(2)解:∠四边形ABCD是平行四边形,∠AD=BC,OB=OD=12BD,∠∠DMN∠∠BCN,∠DM DN BC BN,∠M为AD中点,∠AD=2DM,∠BC=2DM,∠BN=2DN,设OB=OD=x,∠BD=2x,∠BN=OB+ON=x+1,DN=OD-ON=x-1,∠x+1=2(x-1),解得:x=3,∠BD=2x=6,∠BD的长为6;(3)解:∠∠MND∠∠CNB,∠DM:BC=MN:CN=DN:BN=1:2,∠∠DCN的面积为2,∠S∠MND=12S∠CND=1,S∠BNC=2S∠CND=4,∠S∠ABD=S∠BCD=S∠BCN+S∠CND=4+2=6,∠S四边形ABNM=S∠ABD-S∠MND=6-1=5,∠四边形ABNM的面积为5.【点拨】本题考查了相似三角形的判定与性质,平行四边形的性质,熟练掌握相似三角形的面积比等于相似比的平方,等高三角形面积的比等于其对应底的比是解题的关键.举一反三【变式1】如图,在矩形ABCD中,E为AD的中点,EF∠EC交AB于F,延长FE与直线CD相交于点G,连接FC(AB>AE).(1)求证:∠AEF∠∠DCE;(2)∠AEF与∠ECF是否相似?若相似,证明你的结论;若不相似,请说明理由;(3)设ABkBC=,是否存在这样的k值,使得∠AEF与∠BFC相似?若存在,证明你的结论并求出k的值;若不存在,请说明理由.【答案】(1)见分析(2)相似,证明见分析(3)存在,k【分析】(1)由题意可得∠AEF+∠DEC=90°,又由∠AEF+∠AFE=90°,可得∠DEC=∠AFE,据此证得结论;(2)根据题意可证得Rt∠AEF∠Rt∠DEG(ASA),可得EF=EG,∠AFE=∠EGC,可得CE 垂直平分FG,∠CGF是等腰三角形,据此即可证得∠AEF与∠ECF相似;(3)假设∠AEF与∠BFC相似,存在两种情况:∠当∠AFE=∠BCF,可得∠EFC=90°,根据题意可知此种情况不成立;∠当∠AFE=∠BFC,使得∠AEF与∠BFC相似,设BC=a,则AB=ka,可得AF=13ka,BF=23ka,再由∠AEF∠∠DCE,即可求得k值.(1)证明:∠EF∠EC,∠∠FEC=90°,∠∠AEF+∠DEC=90°,∠∠AEF+∠AFE=90°,∠∠DEC=∠AFE,又∠∠A=∠EDC=90°,∠∠AEF∠∠DCE;(2)解:∠AEF∠∠ECF.理由:∠E为AD的中点,∠AE=DE,∠∠AEF=∠DEG,∠A=∠EDG,∠∠AEF∠∠DEG(ASA),∠EF=EG,∠AFE=∠EGC.又∠EF∠CE,∠CE垂直平分FG,∠∠CGF是等腰三角形.∠∠AFE=∠EGC=∠EFC.又∠∠A=∠FEC=90°,∠∠AEF∠∠ECF;(3)解:存在k∠AEF与∠BFC相似.理由:假设∠AEF与∠BFC相似,存在两种情况:∠当∠AFE=∠BCF,则有∠AFE与∠BFC互余,于是∠EFC=90°,因此此种情况不成立;∠当∠AFE=∠BFC,使得∠AEF与∠BFC相似,设BC=a,则AB =ka,∠∠AEF∠∠BCF,∠12AFAE BF BC , ∠AF =13ka ,BF =23ka , ∠∠AEF ∠∠DCE , ∠AE AF DC DE =,即113212ka a ka a =,解得,k =.∠存在k 使得∠AEF 与∠BFC 相似. 【点拨】本题考查了矩形的性质,相似三角形的判定及性质,全等三角形的判定与及性质,等腰三角形的判定及性质,采用分类讨论的思想是解决本题的关键.【变式2】如图,四边形ABCD 为正方形,且E 是边BC 延长线上一点,过点B 作BF ∠DE 于F 点,交AC 于H 点,交CD 于G 点.(1)求证:∠BGC ∠∠DGF ;(2)求证:GD AB DF BG ⋅=⋅;(3)若点G 是DC 中点,求GF CE的值.【答案】(1) 见分析 (2) 见分析(3)GF CE =【分析】 (1)由正方形性质和题干已知垂直条件得直角相等,后由对顶角相等,进而得到∠BGC ∠∠DCF .(2)由第一问的结论可得到相似比,既有DG BC DF BG ⋅=⋅,然后因为正方形四边相等,进行等量代换即可求出证明出结论.(3)通过ASA 判定出∠BGC ∠∠DEC ,进而根据第一问结论可得∠BGC ∠∠DGF ,然后通过相似比设未知数,赋值CG x =,即可求出GF CE的值. (1)证明:∠四边形ABCD 是正方形∠90BCD ADC ∠=∠=︒∠BF DE ⊥∠90GFD ∠=︒∠BCD GFD ∠=∠,又∠BGC DGF ∠=∠,∠∠BGC∠∠DCF .(2)证明:由(1)知∠BGC ∠∠DGF , ∠BG BC DG DF=, ∠DG BC DF BG ⋅=⋅∠四边形ABCD 是正方形,∠AB BC =∠DG AB DF BG ⋅=⋅.(3)解:由(1)知∠BCC ∠∠DGF ,∠FDG CBG ∠=∠,在∠BGC 与∠DEC 中,,{,=,CBG CDE BCG DCE BC CD ∠=∠∠=∠∠∠BGC∠∠DEC (ASA )∠CG EC =∠G 是CD 中点∠CG DG =∠::GF CE CF DC =∠∠BGC∠∠DGF∠::GF DG CG BG =在Rt∠BGC 中,设CG x =,则2BC x =,BC =∠CG BG =∠GF CE =【点拨】本题主要考查了正方形的性质,全等三角形判定和性质,相似三角形判定和性质等知识点,熟练运用相似三角形判定和性质是解题的关键.【变式3】已知:如图,两个DAB 和EBC 中,DA DB =,EB EC =,ADB BEC ∠=∠,且点A 、B 、C 在一条直线上.联结AE 、ED ,AE 与BD 交于点F .(1) 求证:DF AB BF BC=; (2) 如果2BE BF BD =⋅,求证:DF BE =.【分析】(1)利用等腰三角形的性质,证DAB DBA EBC ECB ∠=∠=∠=∠,从而证得AD BE ,BD CE ∥,再利用平行线分线段成比例即可得出结论.(2)证明EBF DBE △△∽,得DEB BFE ∠=∠,继而利用DAF BDE ≌△△,即可得出结论.(1)证明:DA DB =,EB EC =,DAB DBA ∴∠=∠,EBC ECB ∠=∠,ADB BEC ∠=∠,DAB DBA EBC ECB ∴∠=∠=∠=∠,AD BE ∴∥,BD CE ∥,DF AF BF EF ∴=,AF AB EF BC =, DF AB BF BC∴=. (2)证明:2BE BF BD =⋅,BE BD BF BE∴=, EBF DBE ∠=∠,EBF DBE ∴△△∽,DEB BFE ∴∠=∠,AFD BFE ∠=∠,AFD DEB ∴∠=∠,AD BE ,ADF DBE ∴∠=∠又AD BD =,DAF BDE ∴≌△△,DF BE ∴=.【点拨】本题考查等腰三角形的性质,三角形相似的判定与性质,全等三角形的判定与性质,平行线分线段成比例,熟练掌握三角形相似的判定与性质、全等三角形的判定与性质、等腰三角形的性质是解题的关键.。
浙教版数学九年级上册4.1《比例线段》说课稿4

浙教版数学九年级上册4.1《比例线段》说课稿4一. 教材分析《比例线段》是浙教版数学九年级上册4.1的内容,本节课的主要目标是让学生理解比例线段的定义,掌握比例线段的性质和应用。
在教材中,通过引入实际问题,引导学生探究比例线段的关系,从而让学生体会数学与实际生活的联系。
教材内容由浅入深,逐步引导学生掌握比例线段的知识,为后续学习相似三角形打下基础。
二. 学情分析九年级的学生已经掌握了初中阶段的基本数学知识,对图形的认识有一定的基础。
但是,对于比例线段这一概念,学生可能较为陌生,需要通过具体的实例和引导,让学生逐步理解和掌握。
此外,学生可能对实际问题中的比例关系有一定的了解,但如何将实际问题转化为数学问题,运用比例线段解决问题,还需要在本节课中进行引导和培养。
三. 说教学目标1.知识与技能目标:让学生理解比例线段的定义,掌握比例线段的性质,能运用比例线段解决实际问题。
2.过程与方法目标:通过观察、操作、猜想、验证等数学活动,培养学生的动手能力、观察能力和推理能力。
3.情感态度与价值观目标:让学生感受数学与实际生活的联系,激发学生学习数学的兴趣,培养学生的合作意识。
四. 说教学重难点1.教学重点:比例线段的定义及其性质。
2.教学难点:比例线段在实际问题中的应用。
五. 说教学方法与手段1.教学方法:采用问题驱动法、合作学习法、探究学习法等,引导学生主动参与,积极思考。
2.教学手段:利用多媒体课件、实物模型、几何画板等辅助教学,提高学生的学习兴趣和效果。
六. 说教学过程1.导入新课:通过展示实际问题,引导学生关注比例线段的概念,激发学生的学习兴趣。
2.探究新知:引导学生通过观察、操作、猜想、验证等过程,发现并总结比例线段的性质。
3.应用拓展:让学生运用比例线段解决实际问题,巩固所学知识,提高解决问题的能力。
4.课堂小结:总结本节课的主要内容,强调比例线段的概念和性质。
5.布置作业:设计具有针对性的练习题,让学生巩固所学知识,提高解题能力。
证明线段的比例式或等积式的方法

证明线段的比例式或等积式的方法要证明线段的比例式或等积式,有多种方法可以使用。
下面我们将介绍几个常用的方法。
方法一:向量法利用向量的性质可以很方便地证明线段的比例式或等积式。
假设有线段AB和CD,要证明它们的比例式或等积式,可以先求出向量AB和向量CD,然后判断它们是否平行或共线,再比较它们的模长大小。
如果向量AB和向量CD平行或共线,我们可以根据向量的定义得知它们的比例式:AB:CD=,AB,:,CD如果向量AB和向量CD不平行或不共线,但线段AB与线段CD的比例式或等积式成立,我们也可以利用向量的性质推导出它们的比例关系。
具体的推导过程需要根据具体的题目条件来确定。
方法二:相似三角形法利用相似三角形的性质也可以方便地证明线段的比例式或等积式。
相似三角形是指两个或多个三角形的对应角相等且对应边成比例。
如果有线段AB和CD,我们可以通过构造相似三角形来证明它们的比例式。
假设我们可以找到一个三角形ABC与三角形CDE相似,那么根据相似三角形的性质有:AB:CD=AC:CE这样我们就证明了线段AB和CD的比例式。
方法三:重心法利用重心的性质也可以证明线段的比例式或等积式。
重心是指一个几何图形的平衡点,即重心到图形上各点的距离乘以图形上各点的质量(或面积)之和为零。
对于线段AB和CD,我们可以找到它们的重心O,并将线段AO和BO 延长到与CD相交于点E和F。
那么根据重心的性质,线段AO与线段OD 以及线段BO与线段OC的比例关系可以推导出:AO:OC=BO:OD进一步地,根据线段分线段外部点定理,我们可以得出:AO:OD=AB:CD这样我们就证明了线段AB和CD的比例式。
方法四:三角形面积法利用三角形面积的性质也可以证明线段的比例式或等积式。
假设有线段AB和CD,我们可以构造三角形AOB与三角形COD,其中O为点A和C 的连接线与BC的交点。
根据三角形面积的性质,有:三角形AOB的面积:三角形COD的面积=AB:CD这样我们就证明了线段AB和CD的比例式。
第07讲:提供比例线段的几种常见形式

提供比例线段的几种常见形式一、平行线截割:通过寻找或者构建平行线可以得到一组比例线段.(平行线分线段成比例)二、相似三角形对应边成比例:通过寻找或构建相似三角形的对应边提供比例线段。
(在寻找或构建过程中抓住能使三角形相似成立的几个条件) 三、面积等式变换:底×高=底×高⇔高底高底;高高底底==,这样也可以为我们提供不少比例线段。
四、线段等积式变形:当原题已知中提供了线段积相等,如:ab=cd 的条件时,我们也可以通过这四条线段的关系进行变形得到不少比例式。
五、角平分线的性质:遇到提供了角平分线时,可以通过反向延长被平分角一边构造“A 字型”将问题化归为“平行线截割问题或相似三角形问题”来解决。
六、圆中相交的两条弦:圆中两条相交的弦被交点所截线段对应成比例。
针对性例题:1. 平行线截三角形两边或两边的延长线所构成的A 字形或8字形,能为我们提供大量的成比例的线段,可以将线段之间的比值关系互相转化。
例如:如图,已知菱形ABCD 的边长为4,延长CD 至点E ,使DE =3DC ,连结EA 并延长,交CB 的延长线于点F .求FC 的长.例2、如图,在梯形ABCD 中,AB ∥CD ,∠B =90°,E 为BC 上一点,且AE ⊥ED 于点E .若BC =12,DC =7,BE :EC =1:2,求AB 的长.例3、如图,PN ∥BC ,AD ⊥BC 交PN 于点E ,交BC 于点D .(1)若AP :PB =1:2,S ⊿ABC =18cm 2,求⊿APN 的面积;(2)若S ⊿APN :S 四边形PBCN =1:2,求AE :AD 的值.例4、已知,如图,在四边形ABCD 中,AC 平分∠BAD ,AC2=AB·AD.求证:⊿ABC∽⊿ACD .5.已知如图,AD是△ABC中∠A的平分线,求证:=..随堂作业:6.如图,A、B、C、D是⊙O上的点,AD与BC交于点E.请判断下列关系是否一定正确,并说明理由:(1)S⊿AEB:S⊿DCE=AE2:DE 2;(2)S⊿ACD:S⊿DCE=AD2:CD2;(3)AC·AB=AE·AD.1.平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形________. 2.有两角对应_______的两个三角形相似.3.如图在△ABC中,D 、E分别是AB、AC上的点,且DE//BC则下列比例中,不成立的是()A.B.C.D.4.如图,已知DE∥BC,DF∥AC,则图中与⊿ADE 相似的有__________________________.5.如图,在⊿ABC中,∠1=∠B,AD=BD=6.(1)证明:⊿ACD∽⊿ABC;(2)求AC的长.6.已知△ABC中,D为BC中点,E是AB上的一点,AE:EB=2:3,CE交AD与点F,则求AF:FD. 7.已知:如图AD//BE//CF,EG//FH求证:8.如图,已知⊿ABC中,DE∥BC,且S⊿ADE:S⊿CDE=1:3,求S⊿ADE:S⊿DBC的值.9.已知:平行四边形ABCD中,对角线AC=a ,BD=b,四边形EFGH为内接菱形,且菱形的边分别与平行四边形ABCD的对角线平行,求菱形的边长。
比例线段的证明

三、比例线段的证明常用的证明思路有:1、利用有关定理与比例有关的定理甚多,常用的有如下几个方面:平行线截割比例线段.为此,有时需要引出适当的平行线,使欲证的比例线段相应于截割部分.相似形的利用.造就相似形,使比处于对应边或对应元素(如对应的中线、高……).其它如内、外角平分线造成的比,直角三角形中几个比例中项……,都可直接利用或作过渡之用.2、转化比例也可转化成乘积形式,因而可利用圆的相交弦定理、切割线定理…….线段的比也可转化成面积比,然后利用面积公式促使问题易于解决.有时也可设法转化成学过的例题或做过的习题.3、计算利用正、余弦定理或其它有关计算公式,分别计算两端的比,从而来判断它们是否相等.例3.7 在△ABC中,D为BC之中点,过D作一直线分别与AB、AC的延长线交于E、F,如图3-60.求证:AE AF EB CF=.证法1:造就平行线(1)为使AE∶EB处于平行线截割部位,过B引EF的平行线交AC的延长线于G,如图3-61.则有:EF∥BG⇒AE AFEB FG=,CF CDFG DB=.又CD DB=,∴CF FG=.∴AE AF EB CF=.证法2:造就平行线(2)为使AF∶CF处于平行线截割部位,过C引EF的平行线交AB于G,如图3-62.则有:GC∥EF⇒AE AFGE CF=,GE CDEB DB=.又CD DB=,∴GE EB=.∴AE AF EB CF=.证法3:构造相似形(1)如图3-63,作CG∥AB交EF于G,则:△AEF∽△CGF⇒AE AF CG CF=,△BDE≌△CDG⇒EB GC=.F图 3-60图 3-61F 图 3-62F 图 3-63∴AE AFEB CF=. 证法4:构造相似形(2)如图3-64,作BG ∥AF 交FE 的延长线于G ,则: △AEF ∽△BEG ⇒AE AFEB BG=, △BDG ≌△CDF ⇒BG CF =. ∴AE AFEB CF=. 证法5:构造相似形(3)如图3-65,作DG ∥AB 交AF 于G ,则有: △GDF ∽△AEF ⇒GD GFAE AF =, 11()22GD AB AE EB ==+,AG GC =⇒111()()222GF GC CF AC CF AF CF CF AF CF =+=+=-+=+. ∴AE EB AF CF AE AF ++=⇒AE AFEB CF =. 证法6:构造相似形(4)过D 作AF 的平行线,仿证法5也可获证,具体过程略.证法7:构造相似形(5)如图3-66,作EG ∥BC 交AF 于G ,则有: AE AG EB GC =, △AEG ∽△ABC ,△EGF ∽△DCF ⇒22AG EG EG GFAC BC DC CF===. 由合分比定理,2AG GF AC AG CF GF =--,即AG GFGC CF GC =-. 再由等比定理,AG GF AG GF AFGC CF GC GC CF GC CF+===-+-. ∴AE AFEB CF=. 证法8:构造相似形(6)过F 作CB 的平行线,仿证法7也可获证,具体过程略. 本题利用计算也十分简便,现介绍如下. 证法9:计算(1)——利用正弦定理如图3-60,由正弦定理,在△AEF 中,有: sin sin AE AF F AEF =∠⇒sin sin AE FAF AEF =∠, △BDE 、△CDF 中,分别有:sin sin EB DB EDB DEB =∠∠,sin sin DC CFF CDF=∠, 两式相乘,并由DB DC =,EDB CDF ∠=∠,得:F图 3-64F图 3-65F 图3-66F图 3-60sin sin EB CF F DEB =∠⇒sin sin sin sin EB F FCF DEB AEF ==∠∠, ∴AE EB AF CF =,即AE AFEB CF=. 证法10:计算(2)——利用面积 如图3-67,连结AD ,则有:sin sin AED BED S AE AD DE ADEEB S BD DE BDE ∆∆⋅⋅∠==⋅⋅∠, sin sin AFD CFD S AF AD DF ADFCF S CD DF CDF ∆∆⋅⋅∠==⋅⋅∠, 注意到BD CD =,BDE CDF ∠=∠,sin sin ADE ADF ∠=∠,∴AE AFEB CF=. 此例虽不算难,但对利用平行、相似和计算来证比例却有代表性.进一步分析,还会发现以上各个方法皆适用于推广的情形,为说明这一点,先将本例作如下变换:由证法1中的AE AF EB FG =、CF CDFG DB=,若D 不是BC 的中点,则有11CDFG CF DB=⋅,从而有: AE AF CD EB CF DB =⋅,即1AE BD CFEB DC FA⋅⋅=.这正是该例的一般情形.对于更一般地情形,我们有:例3.8 已知:直线l 分别交△ABC 的三边AB 、BC 、CA (或其延长线)于点E 、D 、F ,如图3-68.求证:1AE BD CFEB DC FA⋅⋅=. 证法1:以上各种证法都适用于本例,仿上证法1证之,有:过B 引l 的平行线交AC 于G ,则:AE AF EB FG =,BD FGDC CF=, 两式相乘,得AE BD AFEB DC CF⋅=, 即 1AE BD CF EB DC FA ⋅⋅=.证法2:利用面积AEF BED S AE EFS EB ED ∆∆⋅=⋅(E 处顶角互补), BED CDF S BD EDS DC DF∆∆⋅=⋅(D 处顶角相同), CDF AEF S CF DFS EF FA∆∆⋅=⋅(F 处顶角相对). 三式相乘,即得:1AE BD CFEB DC FA⋅⋅=. 注1:本例正是著名的梅涅劳斯(Menelaus)定理的必要性,用其可以证明某些比例和相等线段.梅涅劳斯定理若用有向线段表示,则为F图 3-67图 3-681AE BD CF EB DC FA⋅⋅=- .因此,梅涅劳斯定理常表述为: 梅涅劳斯定理:在△ABC 中,设X 、Y 、Z 分别是BC 、CA 、AB 所在直线上的点.则:X 、Y 、Z 共线的充要条件是:1BX CY AZXC YA ZB⋅⋅=-. 注2:梅涅劳斯定理的充分性是判别共线点的锐利武器.注3:伟大的科学家爱因斯坦十分钟爱证法2,并给它以“优雅的证明”之美名(见《中等数学》1993年第1期第7页).2例3.9 已知正△ABC ,D 在BC 的延长线上,且=CD BC ,过D 任作一直线分别交AB 、AC 于M 、N ,设=BDM ∠α,如图3-69.求证:=2BMCN.分析:由C 是中点,容易想到利用中位线把2CN 转化成某一条线段,这样就能化简左端.利用比例的性质,也能化简右端.证法1:化简两端利用C 是中点,延长DN 至E ,使N E D N =,如图3-70.则BE 2CN .于是要证等式变为BM BE =,再由合分比定理,等式又变为B E B M B E B M +=-为作出左端,延长EB 至M ',使B M B M '=.再作MF ∥BD 交EB 于F ,易知△BMF是正三角形.这样又转化成证EM EF '=. 为证后式,再作BG ∥MM '分别交MF 、DE 于H 、G .由于MM '⊥BD ,因此BG ⊥MF ⇒2M M BH '=.∴o tan 60BH MH ==,tan GHMHα=⇒BH GH =. 又 BG ∥MM '⇒2EM MM BH EB GB GB ''==. MF ∥BD ⇒2EB BD BD EF FM MH ==,GH MH GB BD=∴ EM BH BD BH BD BH EF GB MH GH BD GH'⋅⋅===⋅⋅, ∴ EM EF '=.证毕. 为简化所证等式并完成证明,该证法作了多条辅助线,反映了证明人超强的逻辑思维能力和深厚的功底.若以BE 代换2CN 后,直接去作出两端,会简捷许多.即:证法2:直接构造如图3-71,作BE ∥AC 交DM 的延长线于E ⇒2BE CN =. 作MP ∥AC 交BD 于P ⇒△BMP 是正△.∥ = 图 3-69图 3-70作MH ⊥BD 于H ⇒BH HP =o tan 60MH BH =,tan MHHDα=. ∴HD BH PDHD BH BD-==+.又 2BM BM PM PDCN BE BE BD ===(∵MP ∥BE )∴2BM CN =tan α时,因取公共的对边MH ,才使得它们的和、差得以简化.于是,又让人想到,若取公共的邻边,则分母相同,分式的和、差更便于表示.依此又有下列证法.证法3:如图3-72,作BE ∥AC 交DM 的延长线于E ,则有:2BE CN=,BM AMBE AN =⇒2BM AM CE AN=. 取BC 的中点P ⇒AP ⊥BC ,PB PC =. 作CQ ∥DM 交AP 于Q ⇒AQ AC AF AN =,tan tan PQPCQ PCα=∠=. 作BQ '∥DM 交AP 延长线于Q '⇒AF AM AMAQ AB AC ==',PQ PQ '=. ∴AQ AMAQ AN='. 又otan60PA PAPB PC ===, ∴PA PQ AQPA PQ AQ -=='+.∴2BM CN = 以上各条思路,皆偏重于几何方面,即以几何方式构造等式两端之量,因而沟通它们就较为费事.如果以α二量,那就不过只是计算而已.即有: 证法4:借助计算(1)自M 、N 分别作BC 的垂线,设垂足分别为E 、F ,如图3-73,设△ABC 之边长为a ,则有:12BE BM =,ME =, ∴ 2tan 1222ME ME ED a BE a BMα===-- ⇒BM =图 3-71图 3-72图 3-73同理,CN =.∴2BM CN = 本例因含有三角函数,故三角函数的有关公式若应用的恰当,就可能不用引任何辅助线,且更能直接的达到目标,现介绍如下:证法5:借助计算(2) 如图2-67,由正弦定理,在△BMD 中,o 2sin sin sin(60)BM BD aBMD αα==∠+. 在△CND 中,o sin sin sin(60)CN CD aCND αα==∠-. 两式相比,则得:o o o o o o sin(60)sin 60cos cos60sin 2sin(60)sin 60cos cos60sin BM CN αααααα--==++o o tan 60tan tan 60tan αα-==+.tan α都可以化成两个线段之比,故可看成纯几何问题而用几何方法;又因含有三角函数,故又可用代数和三角的方法,因而集几何、代数和三角于一体,又方法多样,实为初等数学中一道很好的综合题.它实际上是由1978年全国高等院校统一招生考试的一道试题稍加改编而来的,原题是求证:“BM =CN =(其中a 是正△ABC 的边长)”.上面证法4正是高考题的参考答案.例3.10 在△ABC 中,BM 、BD 分别为中线、内角平分线,BN 是中线关于角平分线的对称线,M 、D 、N 皆在BC 上,如图3-74.求证:=22AN AB NC CB. 分析:比的一端是线段的平方之比,与此有关的是:相似三角形的面积之比等于相似比的平方,依此则有:证法1:构造相似形(1) 因ABNNBCS AN NC S ∆∆=, 故构造相似形既应以AB 、CB 为一双对应边,也应联系着上式,为此自C 作BCE A ∠=∠,其中E 在BM 上,如图3-75,则容易看出△ABN ∽△CBE ⇒22ABN CBE S AB S CB ∆∆=, 故只需再证NBC CBE S S ∆∆=即可,为此再看一下这两个三角形有何关系,容易发现图 3-74△ABN ∽△CBE ⇒ANB BEC ∠=∠,即△NBC 与△CBE 在N 、E 处的顶角互补,故有NBC CBE S S NB NC EB EC ∆∆=⇔⋅=⋅.现来证后者,为此,延长BM 至F ,使MF BM =,则有ABCF 是平行四边形⇒F ABM CBN ∠=∠=∠,CF AB =.又 ANB BEC ∠=∠⇒CEF CNB ∠=∠.∴ △CEF ∽△CNB ⇒EC CF ABNC CB CB ==. 又 △ABN ∽△CBE ⇒NB ABEB CB=, ∴1EB ECNB NC⋅=⋅⇒NBC CBE S S ∆∆=.证毕.上述证明过程曲折了一些,究其原因,乃是为平方而造就相似,造相似倒不难办,可为证等积却费了不少周折.回顾证明过程,又可看出NBC CBE S S ∆∆=⇔NE ∥CB .既然证等积颇费周折,先作NE ∥CB ,可得到等积,然后再去证相似形,因此有:证法2:构造相似形(2)如图3-76,作NE ∥CB 交BM 于E ⇒NBC CBE S S ∆∆=. 延长BM 至F ,使M F BM =,则有ABCF 是平行四边形⇒F ABM CBN ∠=∠=∠,CF AB =.∵ CBE NBC EFC EFC S S EB NB CBEF S S EF CF ∆∆∆∆⋅===⋅, ∴EB CB CBNB CF AB==⇒△CBE ∽△ABN (∵CBE ABN ∠=∠),∴ 22ABN ABN NBC CBE S S AN AB NC S S CB ∆∆∆∆===.证毕. 若再发挥平行四边形ABCF 的特性,还可避开等积,即有: 证法3:构造相似形(3)如图3-77,延长BM 至F ,使M F BM =⇒ABCF 是平行四边形. 作FG ∥NB 交AC 于G ⇒△AFG ≌△CBN ⇒AG CN =. 作FAE BAC ∠=∠,其中E 在BF 上,易知:△ABN ∽△AFE ⇒AN ABAE AF =, △ABE ∽△AFG ⇒AE ABAG AF=. 两式相乘,得 22AN ABAG AF =, 即 22AN AB NC CB=.证毕. 本例的重要特征是有两组等角关系,而前两种证法却没有很好地利图 3-75图 3-76图 3-77用,证法3利用了其中一组.因此,充分发挥它们的作用,是寻求简便证法的关键.此外,还有一个不可忽视的条件——中线,巧用中线平分面积的性质,就可得到出一个不用引辅助线又十分简便的证法.即有:证法4:巧用面积比由ABN MBC ∠=∠、NBC ABM ∠=∠及ABM MBC S S ∆∆=,得ABN ABN ABMNBC MBC NBCS S S AN NC S S S ∆∆∆∆∆∆==⋅ 22AB BN AB BM AB MB BC NB BC CB ⋅⋅=⋅=⋅⋅.证毕. 多么简捷!不过,等角关系的发挥,也可通过正弦定理,故又有: 证法5:利用正弦定理如图3-78,记ABM NBC α∠=∠=,MBD NBD β∠=∠=,由正弦定理,在△ABN 中有,sin(2)sin AN AB ANBαβ+=∠, 在△CBN 中有,sin sin CB CNBNC α∠=, 在△ABM 中有,sin sin AM AB AMB α=∠, 在△MBC 中有,sin sin(2)CB CMBCM αβ∠=+, 四式相乘,并注意到∠ANB 和∠CNB 互补、∠AMB 和∠CMB 互补、AM CM =,得221AN CB NC AB ⋅=⇒22AN AB NC CB =.证毕. 这里我们又没引任何辅助线,不过,若延长BM 至F ,使M F BM =,则证明过程可以简化.如图3-79,有在△ABN 中有,sin(2)sin AN AB ANBαβ+=∠, 在△CBN 中有,sin sin CB CNBNC α∠=, 在△ABF 中有,sin sin(2)AF AB ααβ=+, 三式相乘,并由AF CB =即得所证.证法6:利用梅涅劳斯定理为使欲证等式中的ABCB出现两次,宜作两个全等三角形.为此,延长AB 至E ,使B E B C =;再连EC ,分别交直线BM 、BN 于P 、Q ,如图3-80,则有:在△AEC 中,B 、Q 、N 共线,∴ 1AB EQ CN BE QC NA⋅⋅=⇒AN AB EQ NC CB QC =⋅又在△AEC 中,B 、P 、M 共线,∴1AB EP CM BE PC MA ⋅⋅=⇒PC ABPE CB =. ∵ PBE ABM QBC ∠=∠=∠,图 3-78图 3-79BE BC =⇒PEB QCB ∠=∠,∴ △PEB ≌△QCB ⇒PE QC =,进而有PC EQ =.∴ 22AN AB NC CB =.证毕. 注1:本例原是西班牙第27届数学竞赛题.注2:由后两种证法容易看出:22AN AM AB NC MC CB ⋅=.这就驱散了笼罩在结论上的一层迷雾——为什么一端是线段之比,另一端却是平方之比!此式表明,原来两端都是二比之积,只不过有一个是“1”而被略去而已.注3:由角平分线的性质知,AB ADCB DC=,因此结论可改为AN AB ADNC CB DC=⋅.另外,角平分线保证了ABM CBN ∠=∠.把此推广即有: 例3.11 在△ABC 中,若M 、N 在BC 上,且=ABM CBN ∠∠,如图3-81.则=22AN AM AB NC MC CB ⋅. 由于等角关系还保留着,上述证法完全适用于例3.11.注4:如果等角关系用有向角代替,则M 、N 分别在AC 之两端的延长线上,如图3-82,推广的例3.11依然成立.注5:利用《射影几何》中交比的性质,不但容易证明结论(这里从略),更便于发现、洞察其中的奥秘,也就是说,高等几何对初等几何具有指导作用.所以中学数学教师学习高等几何以及其它高等数学是很有益的.图 3-81图 3-82。
相似三角形中的“8”字模型(3种题型)-2023年九年级数学核心知识点与常见题型(沪教版)(解析版)

重难点专项突破:相似三角形中的“8”字模型(3种题型)【知识梳理】8字_平行型条件:CD∥AB,结论:ΔPAB∼ΔPCD(上下相似);左右不一定相似,不一定全等,但面积相等;四边形ABCD为一般梯形.条件:CD∥AB,PD=PC.结论:ΔPAB∼ΔPCD∼ΔPDC(上下相似)ΔPAD≅ΔPBC左右全等;四边形ABCD为等腰梯形;8字_不平行型条件:∠CDP =∠BAP .结论:ΔAPB∼ΔDPC (上下相似);ΔAPD ∼ΔBPC (左右相似);【考点剖析】题型一:8字-平行型(1)直接利用“8”字型解题例1.如图,在平行四边形ABCD 中,点E 在边DC 上,若:1:2DE EC =,则:BF BE =.【答案】3:5.【解析】:1:2DE EC =,可知23CE CE CD AB ==, 由//CE AB ,可知32BF AB EF CE ==,故:3:5BF BE =. 【总结】初步认识相似三角形中的“8”字型.例2.如图,P 为ABCD 对角线BD 上任意一点.求证:PQ PI PR PS =.【解析】证明:四边形ABCD 为平行四边形,////AB CD AD BC ∴,,////RB DI SD BQ ∴,.根据三角形一边平行线的性质定理,则有PI PD PSPR PB PQ==,PQ PI PR PS∴⋅=⋅.【总结】初步认识相似三角形中的“8”字型,一个图形中存在往往不只一个,可用来进行等比例转化.例3.如图,在平行四边形ABCD中,CD的延长线上有一点E,BE交AC于点F,交AD于点G.求证:2BF FG EF=.【解析】证明:四边形ABCD为平行四边形,////AB CD AD BC∴,,////AB CE AG BC∴,.根据三角形一边平行线的性质定理,则有:EF CF BFBF AF FG==,∴2BF FG EF=.【总结】初步认识相似三角形中的“8”字型,一个图形中存在往往不只一个,可用来进行等比例转化.例4.如图,点C在线段AB上,AMC∆和CBN∆都是等边三角形.求证:(1)MD AMDC CN=;(2)MD EB ME DC=.【解析】证明:(1)AMC∆和CBN∆是等边三角形,60ACM NCB AMC∴∠=∠=∠=︒.∵点C在线段AB 上,18060MCN ACM NCB AMC∴∠=︒−∠−∠=︒=∠.//AM CN∴,∴MD AMDC CN=.(2)同(1)易证得//CM BN,则有ME MCEB NB=.AMC∆和CBN∆是等边三角形,MC AM NB CN∴==,,MD MEDC EB∴=,∴MD EB ME DC=.【总结】初步认识相似三角形中的“8”字型,一个图形中存在往往不只一个,可用来进行等比例转化.例5.如图,已知////AB CD EF.AB m=,CD n=,求EF的长.(用m、n的代数式表示).【答案】mnm n+.【解析】由////AB CD EF,则有EF CF EF BFAB BC CD BC==,,即1EF EFm n+=,得mnEFm n=+.【总结】考查相似三角形中“8”字型的综合应用,得到比例关系.例6.如图,E为平行四边形ABCD的对角线AC上一点,13AEEC=,BE的延长线交CD的延长线于点G,交AD于点F,求:BF FG的值.【答案】1:2.【解析】由//AF BC,可得13AF AEBC EC==,即13AFAD=,故12AFFD=,由//AB DG,可得:::1:2BF FG AF FD==.【总结】考查相似三角形中“8”字型的综合应用,得到比例关系.例7.如图,12//l l,:2:5AF FB=,:4:1BC CD=,求:AE EC的值.【答案】2:1.【解析】由12//l l,得:25AG AFBD FB==,又:4:1BC CD=,可得21AGCD=,故::2:1AE EC AG CD==.【总结】考查相似三角形中“8”字型的综合应用,得到比例关系.(2)添加辅助线构造“8”字模型解题例8.过ABC∆的顶点C任作一直线,与边AB及中线AD分别交于点F、E.求证:2AE AFED FB=.【解析】过点D作//DG AB交CF于点G.//DG AB∴AE AFED GD=,DG CDBF CB=;AD是中线,∴2BC CD=,∴12DGBF=;∴2AE AFED BF=.【总结】题考查三角形一边的平行线知识,要学会构造平行基本模型.AB CDEF例9.如图,AD 是ABC ∆的内角平分线.求证:AB BD AC DC=.【解析】过点C 作//CM AB 交AD 的延长线于点M .//CM AB∴AB BD CM DC =,BAD M ∠=∠AD 是角平分线∴BAD DAC ∠=∠;∴M DAC ∠=∠ ∴AC CM =∴AB BD AC DC =. 【总结】本题考查了三角形一边的平行线、角平分线及等腰三角形的相关知识.题型二:8字-不平行型例10.如图,∠BEC =∠CDB ,下列结论正确的是( )A .EF •BF =DF •CFB .BE •CD =BF •CFC .AE •AB =AD •AC D .AE •BE =AD •DC AB CD M【分析】结合图形利用8字模型相似三角形证明△EFB∽△DFC,然后利用等角的补角相等得出∠AEC=∠ADB,最后证明△ABD∽△ACE,利用相似三角形的对应边成比例逐一判断即可.【解答】解:∵∠BEC=∠CDB,∠EFB=∠DFC,∴△EFB∽△DFC,∴EFDF =FBFC,∴EF•FC=DF•FB,故A不符合题意:∵△EFB∽△DFC,∴BECD =BFFC,∴BE•CF=CD•BF,故B不符合题意;∵∠BEC=∠CDB,∠BEC+∠AEC=180°,∠BDC+∠ADB=180°,∴∠AEC=∠ADB,∴△ABD∽△ACE,∴ABAC =ADAE,∴AB•AE=AD•AC,故C符合题意;因为:AE,BE,AD,CD组不成三角形,也不存在比例关系,故D不符合题意;故选:C.【点评】本题考查了相似三角形的判定与性质,根据题目的已知条件并结合图形分析是解题的关键.【过关检测】一.选择题(共3小题)1.(2023•静安区校级一模)如图,在△ABC中,中线AD与中线BE相交于点G,联结DE.下列结论成立的是()A.B.C.D.【分析】由AD,BE是△ABC的中线,得到DE是△ABC的中位线,推出△DEG∽△ABG,△CDE∽△CBA,由相似三角形的性质即可解决问题.【解答】解:AD,BE是△ABC的中线,∴DE是△ABC的中位线,∴DE∥AB,DE=AB,∴△DEG∽△ABG,∴DG:AG=DE:AB=1:2,BG:EG=AB:DE,==,∴DG=AG,∵BG:EG=AB:DE=2:1,∴GB:BE=2:3,∴S△AGB:S△AEB=2:3,∵AE=EC,∴S△AEB=S△ABC,∴S△AGB=S△ABC,∵△CDE∽△CBA,∴==,∴S△CDE=S△ABC,∴=,结论成立的是=,故选:C.【点评】本题考查相似三角形的判定和性质,关键是掌握相似三角形的性质.2.(2023•徐汇区一模)如图,点D在△ABC边AB上,∠ACD=∠B,点F是△ABC的角平分线AE与CD 的交点,且AF=2EF,则下列选项中不正确的是()A.B.C.D.【分析】过C作CG∥AB交AE延长线于G,由条件可以证明△ACF≌△GCE(ASA),得到AF=EG,CF=CE,由△ADF∽△GCF,再由平行线分线段成比例,即可解决问题.【解答】解:过C作CG∥AB交AE延长线于G,∴∠G=∠BAE,∵AE平分∠BAC,∴∠BAE=∠CAE,∴∠G=∠CAE,∴CG=CA,∵∠ACD=∠B,∠ECG=∠B,∴∠ACF=∠ECG,∴△ACF≌△GCE(ASA),∴CF=CE,AF=EG,∵AF=2FE,∴EG=2FE,令EF=k,则AF=EG=2k,AE=GF=3k,∵△ADF∽△GCF,∴AD:CG=AF:FG=2k:(3k)=2:3,∴=,故A正确.∵AB∥CG,∴CE:BE=GE:AE=2k:(3k)=2:3,∴=,故B正确.∵∠ACD=∠B,∠DAC=∠BAC,∴△ACD∽△ABC,∴==,故C正确.∵=,AC和BD不一定相等,∴不一定等于.故选:D.【点评】本题考查角的平分线,相似三角形的判定和性质,关键是通过辅助线构造相似三角形.3.(2022秋•闵行区期末)如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB.如果==3,且量得CD=4cm,则零件的厚度x为()A.2cm B.1.5cm C.0.5cm D.1cm【分析】根据相似三角形的判定和性质,可以求得AB的长,再根据某零件的外径为10cm,即可求得x的值.【解答】解:∵==3,∠COD=∠AOB,∴△COD∽△AOB,∴AB:CD=2,∵CD=4cm.∴AB=8cm.∵某零件的外径为10cm,∴零件的厚度x为:(10﹣8)÷2=1(cm),故选:D.【点评】本题考查相似三角形的应用,解答本题的关键是求出AB的值.二.填空题(共8小题)4.(2022秋•奉贤区期中)如图,已知点D为△ABC中AC边的中点,AE∥BC,ED交AB于点G,交BC 的延长线于点F,若,BC=8,则AE的长为.【分析】由AE∥BC,可得△AEG∽△BFG,△AED∽△CFD推出==,又有BC的值,再由==1,得出AE=CF,代入即可求解AE的长.【解答】解:∵AE∥BC,∴△AEG∽△BFG,△AED∽△CFD,∴==,==1,即AE=CF,又BC=8,∴=AE=4.故答案为:4.【点评】本题主要考查了平行线分线段成比例的性质问题,应熟练掌握.5.(2022•浦东新区校级模拟)如图,已知点D、E分别在△ABC的边CA、BA的延长线上,DE∥BC.DE:BC=2:3,设=,试用向量表示向量,=.【分析】由DE∥BC可得△ADE∽△ACB,由DE:BC=2:3,可得DA=CD,即可表示,从而得出答案.【解答】解:∵DE∥BC,∴△ADE∽△ACB,∵DE:BC=2:3,∴DA:CA=DE:BC=2:3,∵CD=DA+CA,∴DA=CD,∵=,∴=,∴=﹣,故答案为:﹣.【点评】本题考查向量的运算,相似三角形的判定与性质,熟练掌握相似三角形的性质和向量的运算的解题的关键.6.(2022•静安区二模)如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,点E、F分别是边AB、CD的中点,AO:OC=1:4,设=,那么=.(用含向量的式子表示)【分析】由相似三角形性质可得=4=4,再根据梯形中位线定理即可求得答案.【解答】解:∵AD∥BC,∴△AOD∽△COB,∴==,∴=4=4,∵点E、F分别是边AB、CD∴=(+)=(+4)=,故答案为:.【点评】本题考查了相似三角形的判定和性质,梯形中位线定理,平面向量等,熟练掌握相似三角形的判定和性质是解题关键.7.(2023•静安区校级一模)在矩形ABCD内作正方形AEFD(如图所示),矩形的对角线AC交正方形的边EF于点P.如果点F恰好是边CD的黄金分割点(DF>FC),且PE=2,那么PF=.【分析】先根据黄金分割的定义可得=,再利用正方形的性质可得:DF∥AE,DF=AE,从而可得=,然后证明8字模型相似三角形△CFP∽△AEP,从而利用相似三角形的性质进行计算即可解答.【解答】解:∵点F恰好是边CD的黄金分割点(DF>FC),∴==,∵四边形AEFD是正方形,∴DF∥AE,DF=AE,∴=,∵DC∥AB,∴∠FCP=∠PAE,∠CFP=∠AEP,∴△CFP∽△AEP,∴==,∵PE=2,∴PF=﹣1,故答案为:﹣1.8字模型相似三角形是解题的关键.8.(2022春•浦东新区校级期中)如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,如果△BCD 的面积是△ABD面积的2倍,那么△BOC与△BDC的面积之比是.【分析】过点D作DM⊥BC,垂足为M,过点B作BN⊥AD,交DA的延长线于点N,根据已知易得DM=BN,再根据S△BCD=2S△ABD,从而可得BC=2AD,然后再证明8字模型相似三角形△AOD∽△COB,利用相似三角形的性质可得==,从而可得=,最后根据△BOC与△BDC的高相等,即可解答.【解答】解:过点D作DM⊥BC,垂足为M,过点B作BN⊥AD,交DA的延长线于点N,∵AD∥BC,∴BN=DM,∵S△BCD=2S△ABD,∴BC•DM=2×AD•BN,∴BC=2AD,∵AD∥BC,∴∠ADB=∠DBC,∠DAC=∠ACB,∴△AOD∽△COB,∴==,∴=,∵△BOC与△BDC的高相等,∴==,故答案为:2:3.【点评】本题考查了平行线间的距离,相似三角形的判定与性质,梯形,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.9.(2022秋•虹口区校级月考)如图,梯形ABCD中,AD∥BC,,点E为边BC的中点,点F在边CD上且3CF=CD,EF交对角线AC于点G,则AG:GC=.【分析】如图,连接DE,交AC于M,过M作MH∥EF交CD于H,首先利用AD∥BC,,点E为边BC的中点,可以得到AD:EC=AM:CM=DM:ME=3:2,然后利用MH∥EF,DH:HF=DM:ME=3:2=6:4,最后利用又3CF=CD即可求解.【解答】解:如图,连接DE,交AC于M,过M作MH∥EF交CD于H,∵AD∥BC,,点E为边BC的中点,∴△ADM∽△CME,∴AD:EC=AM:CM=DM:ME=3:2,∵MH∥EF,∴DH:HF=DM:ME=3:2=6:4,又3CF=CD,∴DF=2CF,∴CF:HF=5:4,∴CG:MG=5:4,∴CG=CM,MG=CM,而AM:CM=3:2,∴AM=CM,∴AG=AM+MG=CM,∴AG:GC=CM:CM=7:2.故答案为:7:2.【点评】此题主要考查了相似三角形的性质于判定,同时也利用了平行线的性质,解题的关键是会进行比例线段的转换,有一定的难度.10.(2022秋•黄浦区期末)如图是一个零件的剖面图,已知零件的外径为10cm,为求出它的厚度x,现用一个交叉卡钳(AC和BD的长相等)去测量零件的内孔直径AB.如果==,且量得CD的长是3cm,那么零件的厚度x是cm.【分析】根据相似三角形的判定和性质,可以求得AB的长,再根据某零件的外径为10cm,即可求得x的值.【解答】解:∵==,∠COD=∠AOB,∴△COD∽△AOB,∴AB:CD=3,∵CD=3cm.∴AB=9cm.∵某零件的外径为10cm,∴零件的厚度x为:(10﹣9)÷2=0.5(cm),故答案为:0.5.AB的值.11.(2022春•闵行区校级月考)如图,梯形ABCD中,∠D=90°,AB∥CD,将线段CB绕着点B按顺时针方向旋转,使点C落在CD延长线上的点E处.联结AE、BE,设BE与边AD交于点F,如果AB=4,且=,那么梯形ABCD的中位线等于.【分析】过点B作BG⊥EC,利用同高的两个三角形的面积的比先求出EF:BF,再利用相似三角形的性质求出ED、EG,最后利用梯形中位线与上下底的关系得结论.【解答】解过点B作BG⊥EC,垂足为G∵=,∴=.∵AB∥CD,∴△EDF∽△BAF.∴==,∴ED=2,=.∵AD∥BG,∴=.∴EG=6.∵CB绕着点B按顺时针方向旋转,点C落在CD延长线上的点E处,∴BE=BC.∵BG⊥EC,∴EG=GC=6.∴DC=DG+CG=4+6=10.∴梯形ABCD的中位线=(AB+CD)=(4+10)=7.故答案为:7.【点评】本题主要考查了相似三角形的性质和判定,掌握等腰三角形的三线合一、等高的两个三角形的面积比等于底边的比、梯形的中位线等于上下底的和的一半是解决本题的关键.三.解答题(共12小题)12.(2023•普陀区一模)如图,已知梯形ABCD中,AD∥BC,E是BC上一点,AE∥CD,AE、BD相交于点F,EF:CD=1:3.(1)求的值;(2)联结FC,设,,那么=,=.(用向量、表示)【分析】(1)根据题意可证明四边形AECD为平行四边形,得到AE=CD,则EF:AE=1:3,EF:AF=1:2,易证明△BEF∽△DAF,由相似三角形的性质即可求解;(2)由AF=2EF得,,由三角形法则求出和,再求出,最后利用三角形法则即可求出.【解答】解:∵AD∥BC,AE∥CD,∴四边形AECD为平行四边形,∴AE=CD,∵EF:CD=1:3,∴EF:AE=1:3,EF:AF=1:2,∵AD∥BC,∴△BEF∽△DAF,∴;(2)联结FC,如图,由(1)可得AF=2EF,∵,∴,,∴=,=,∵,AD=EC,∴,∴==,∴==.故答案为:,.【点评】本题主要考查平行四边形的判定与性质、相似三角形的判定与性质、平面向量,熟练三角形法则是解题关键.13.(2023•奉贤区一模)已知:如图,在梯形ABCD中,AD∥BC,点E在对角线BD上,∠EAD=∠BDC.(1)求证:AE•BD=AD•DC;(2)如果点F在边DC上,且,求证:EF∥BC.【分析】(1)利用平行线的性质证明∠ADB=∠DBC,然后利用已知条件可以证明△ADE∽△DBC,由此即可解决问题;(2)利用(1)的结论和已知条件可以证明△DEF∽△DBC,接着利用相似三角形的在即可求解.【解答】证明:(1)∵AD∥BC,∴∠ADB=∠DBC,又∵∠EAD=∠BDC,∴△ADE∽△DBC,∴AE:AD=DC:BD,∴AE•BD=AD•DC;(2)∵AE:AD=DC:BD,且,∴=,而∠EDF=∠BDC,∴△DEF∽△DBC,∴∠DEF=∠DBC,∴EF∥BC.【点评】此题主要考查了相似三角形的性质与判定,同时也利用了平行线的性质,比例的基本性质,有一定的综合性.14.(2023•青浦区一模)如图,在平行四边形ABCD中,点F在边AD上,射线BA、CF相交于点E,DF =2AF.(1)求EA:AB的值;(2)如果,,试用、表示向量.【分析】(1)根据平行四边形的性质可得AB∥CD,AB=CD,易证△AEF∽△DCF,则=,由DF =2AF即可求解;(2)先算出,再根据即可求解.【解答】解:(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴△AEF∽△DCF,∴,∴,∵DF=2AF,∴,∴;(2)∵四边形ABCD是平行四边形,∵DF=2AF,∴,∵,,∴,,∴.【点评】本题主要考查相似三角形的判定与性质、平行四边形的性质、平面向量,熟练掌握平面向量的运算法则是解题关键.15.(2022秋•金山区校级期末)已知:如图,在△ABC中,点D在边BC上,AE∥BC,BE与AD、AC分别相交于点F、G,AF2=FG•FE.(1)求证:△CAD∽△CBG;(2)联结DG,求证:DG•AE=AB•AG.【分析】(1)通过证明△FAG∽△可得∠FAG=∠E,由平行线的性质可得∠E=∠EBC=∠FAG,且∠ACD =∠BCG,可证△CAD∽△CBG;(2)由相似三角形的性质可得=,且∠DCG=∠ACB,可证△CDG∽△CAB,可得=,由平行线分线段成比例可得=,可得结论.【解答】证明:(1)∵AF2=FG⋅FE.∴=,∵∠AFG=∠EFA,∴△FAG∽△FEA,∴∠FAG=∠E,∵AE∥BC,∴∠E=∠EBC,∵∠ACD=∠BCG,∴△CAD∽△CBG;(2)∵△CAD∽△CBG,∴=,∵∠DCG=∠ACB,∴△CDG∽△CAB,∴=,∵AE∥BC,∴=,∴=,∴=,∴DG•AE=AB•AG.【点评】本题考查了相似三角形的判定和性质,解题的关键是正确寻找相似三角形解决问题,属于中考常考题型.16.(2022•松江区二模)已知:如图,两个△DAB和△EBC中,DA=DB,EB=EC,∠ADB=∠BEC,且点A、B、C在一条直线上,联结AE、ED,AE与BD交于点F.(1)求证:;(2)如果BE2=BF•BD,求证:DF=BE.【分析】(1)根据已知易证△DAB∽△EBC,然后利用相似三角形的性质可得∠DAB=∠EBC,=,从而可得AD∥EB,进而证明8字模型相似三角形△ADF∽△EBF,最后利用相似三角形的性质可得=,即可解答;(2)根据已知易证△BFE∽△BED,从而利用相似三角形的性质可得∠BEF=∠BDE,进而可得∠DAF=∠BDE,然后利用(1)的结论可证△ADF≌△DBE,再利用全等三角形的性质即可解答.【解答】证明:(1)∵DA=DB,EB=EC,∴=,∵∠ADB=∠BEC,∴△DAB∽△EBC,∴∠DAB=∠EBC,=,∴AD∥EB,∴∠DAF=∠AEB,∠ADF=∠DBE,∴△ADF∽△EBF,∴=,∴;(2)∵BE2=BF•BD,∴=,∵∠DBE=∠EBF,∴△BFE∽△BED,∴∠BEF=∠BDE,∵∠DAF=∠AEB,∴∠DAF=∠BDE,∵∠ADF=∠DBE,AD=DB,∴△ADF≌△DBE(ASA),∴DF=BE.【点评】本题考查了全等三角形的判定与性质,相似三角形的判定与性质,熟练掌握全等三角形的判定与性17.(2023•宝山区二模)如图,四边形ABCD中,AD∥BC,AC、BD交于点O,OB=OC.(1)求证:AB=CD;(2)E是边BC上一点,联结DE交AC于点F,如果AO2=OF•OC,求证:四边形ABED是平行四边形.【分析】(1)由等腰三角形的性质和判定及平行线的性质,说明△AOB和△DOC全等,利用全等三角形的性质得结论;(2)先说明△AOB∽△FOD,再说明AB∥DE,结合已知由平行四边形的判定可得结论.【解答】证明:(1)∵OB=OC,∴∠DBC=∠ACB.∵AD∥BC,∴∠DAC=∠ACB,∠ADB=∠DBC.∴∠DAC=∠ADB.∴OA=DO.在△AOB和△DOC中,,∴△AOB≌△DOC(SAS).∴AB=CD.(2)∵AO2=OF•OC,OA=OD,OC=OB,∴AO•OD=OF•OB,即.∵∠AOB=∠DOC,∴△AOB∽△FOD.∴∠BAO=∠DFO.∴AB∥DE.∴四边形ABED是平行四边形.【点评】本题主要考查了三角形全等和相似,掌握全等三角形的性质和判定、相似三角形的判定和性质、平行线的性质、等腰三角形的判定和性质及平行四边形的判定是解决本题的关键.18.(2022秋•徐汇区期中)如图,在四边形ABCD中,对角线AC与BD交于点E,DB平分∠ADC,且AB2=BE•BD.(1)求证:△ABE∽△DCE;(2)AE•CD=BC•ED.【分析】(1)根据相似三角形的判定可得△ABE∽△DBA;所以∠BAC=∠BDC,由此可得出△ABE∽△DCE;(2)由(1)中的相似可得出AE:DE=BE:CE,再由∠BEC=∠AED可得△ADE∽△BCE,所以∠EAD=∠EBC,∠ADE=∠BDC=∠BCE,可得△BCD∽△ADE,进而可得结论.【解答】证明:(1)∵AB2=BE•BD,∴AB:BE=BD:AB,∵∠ABE=∠DBA,∴△ABE∽△DBA,∴∠BAC=∠BDC,∵BD平分∠ADC,∴∠ADB=∠BDC=∠BAC,∴△ABE∽△DCE;(2)由(1)中相似可得,AE:DE=BE:CE,∵∠BEC=∠AED,∴△ADE∽△BCE,∴∠EAD=∠EBC,∠ADE=∠BDC=∠BCE,∴△BCD∽△AED,AE•CD=BC•ED.【点评】本题主要考查相似三角形的性质与安定,涉及A字型相似,8字型相似等相关内容,熟练掌握相关判定是解题关键.19.(2022春•杨浦区校级期中)如图1,在△ABC中,点E在AC的延长线上,且∠E=∠ABC.(1)求证:AB2=AC•AE;(2)如图2,D在BC上且BD=3CD,延长AD交BE于F,若=,求的值.【分析】(1)利用两角相等的两个三角形相似,证明△ABC∽△AEB,然后利用相似三角形的性质即可解答;(2)过点E作EH∥CB,交AF的延长线于点H,利用(1)的结论可得===,先AC=2a,AB=3a,从而求出AE的长,进而求出的值,再根据已知设CD=m,BD=3m,从而求出BC,BE的长,然后证明A字模型相似三角形△ACD∽△AEH,利用相似三角形的性质可得EH=m,再证明8字模型相似三角形△BDF∽△EHF,利用相似三角形的性质可得=,从而求出EF的长,进行计算即可解答.【解答】(1)证明:∵∠E=∠ABC,∠A=∠A,∴△ABC∽△AEB,∴=,∴AB2=AC•AE;(2)解:过点E作EH∥CB,交AF的延长线于点H,∵△ABC∽△AEB,∴设AC=2a,AB=3a,∴=,∴AE=a,∴==,∵BD=3CD,∴设CD=m,则BD=3m,∴BC=CD+BD=4m,∴=,∴EB=6m,∵EH∥CD,∴∠ACD=∠AEH,∠ADC=∠AHE,∴△ACD∽△AEH,∴==,∴EH=m,∵EH∥BD,∴∠BDF=∠DHE,∠DBF=∠FEH,∴△BDF∽△EHF,∴===,∴EF=BE=m,∴==,∴的值为.【点评】本题考查了相似三角形的判定与性质,平行线分线段成比例,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.20.(2023•崇明区二模)已知:如图,在平行四边形ABCD中,对角线AC、BD交于E,M是边DC延长线上的一点,联结AM,与边BC交于F,与对角线BD交于点G.(1)求证:AG2=GF•GM;(2)联结CG,如果∠BAG=∠BCG,求证:平行四边形ABCD是菱形.【分析】(1)由平行线的性质和相似三角形的平行判定法,可得到△ABG∽△MDG、△ADG∽△FBG,再利用相似三角形的性质得结论;(2)利用“两角对应相等”先说明△GCF∽△GMC,再利用等腰三角形的三线合一说明BD⊥AC,最后利用菱形的判定方法得结论.【解答】证明:(1)∵四边形ABCD是平行四边形,∴AB∥DM,AD∥BC.∴△ABG∽△MDG,△ADG∽△FBG.∴=,=.∴=.∴AG2=GF•GM.(2)∵AB∥DM,∴∠BAG=∠M.∵∠BAG=∠BCG,∴∠M=∠BCG.∵∠MGC=∠FGC,∴△GCF∽△GMC.∴=,即CG2=GF•GM.∴CG2=AG2.∴CG=AG.∵四边形ABCD是平行四边形,∴AE=CE.∴GE⊥AC,即BD⊥AC.∴平行四边形ABCD是菱形.【点评】本题主要考查了相似三角形的性质和判定,掌握相似三角形的判定和性质、平行四边形的性质、菱形的判定方法、等腰三角形的判定和性质等知识点是解决本题的关键.21.(2021秋•虹口区期末)如图,在梯形ABCD中,∠ABC=90°,AD∥BC,BC=2AD,对角线AC与BD 交于点E.点F是线段EC上一点,且∠BDF=∠BAC.(1)求证:EB2=EF•EC;(2)如果BC=6,sin∠BAC=,求FC的长.【分析】(1)先由AD∥BC得到△EAD∽△ECB,从而得到,然后由∠BDF=∠BAC、∠AEB=∠DEF得证△EAB∽△EDF,进而得到,最后得到结果;(2)先利用条件得到AC、AB的长,然后利用BC=2AD得到AD、BD的长,再结合相似三角形的性质得到EB、EC的长,进而得到EF的长和FC的长.∴△EAD∽△ECB,∴,即,∵∠BDF=∠BAC,∠AEB=∠DEF,∴△EAB∽△EDF,∴,∴,∴EB2=EF•EC.(2)解:∵BC=6,sin∠BAC==,BC=2AD∴AC=9,AD=3,∵∠ABC=90°,AD∥BC,∴∠BAD=90°,∴AB===3,∴BD===3,∵△EAD∽△ECB,∴,∴EC=AC=×9=6,EB=BD=×3=2,∵EB2=EF•EC,即(2)2=6EF,∴EF=4,∴FC=EC﹣EF=6﹣4=2.【点评】本题考查了直角梯形的性质、相似三角形的判定与性质、勾股定理,解题的关键是熟知“8”字模型相似三角形的判定与性质.22.(2021秋•嘉定区期末)如图,在梯形ABCD中,AD∥BC,点E在线段AD上,CE与BD相交于点H,CE与BA的延长线相交于点G,已知DE:AE=2:3,BC=4DE,CE=10.求EH、GE的长.【分析】根据题目的已知并结合图形分析8字型模型相似三角形和A字型模型相似三角形,然后进行计算即可解答.【解答】解:∵AD∥BC,∴∠ADB=∠DBC,∠DEC=∠ECB,∴△DEH∽△BCH,∴,∵BC=4DE,∴,∵CE=10,∴HC=10﹣EH,∴,∴EH=2,∵BC=4DE,DE:AE=2:3,∴,∵AD∥BC,∴∠GAE=∠GBC,∠GEA=∠GCB∴△GAE∽△GBC,∴,∵CE=10,∴GC=10+GE,∴,∴GE=6.【点评】本题考查了相似三角形的判定与性质,梯形,熟练掌握8字型模型相似三角形和A字型模型相似三角形是解题的关键.23.(2021秋•杨浦区期末)如图,已知在Rt△ABC中,∠ACB=90°,AC=BC=5,点D为射线AB上一动点,且BD<AD,点B关于直线CD的对称点为点E,射线AE与射线CD交于点F.(1)当点D在边AB上时,①求证:∠AFC=45°;②延长AF与边CB的延长线相交于点G,如果△EBG与△BDC相似,求线段BD的长;(2)联结CE、BE,如果S△ACE=12,求S△ABE的值.【分析】(1)①如图1,连接CE,根据轴对称的性质可得:EC=BC,∠ECF=∠BCF,设∠ECF=∠BCF=α,则∠BCE=2α,∠ACE=90°﹣2α,再利用等腰三角形性质即可证得结论;②如图2,连接BE,CE,由△EBG∽△BDC,可得出∠G=∠BCD=22.5°,过点D作DH⊥AB交BC于点H,则△BDH是等腰直角三角形,推出CH=DH=BD,再根据CH+BH=BC=5,建立方程求解即可;(2)分两种情况:Ⅰ.当点D在AB上时,如图3,过点C作CM⊥AE于点M,连接BF,利用勾股定理、三角形面积建立方程求解即可;Ⅱ.当点D在AB的延长线上时,如图4,过点C作CM⊥AE于点M,连接BF,利用勾股定理、三角形面积建立方程求解即可.【解答】解:(1)①证明:如图1,连接CE,∵点B关于直线CD的对称点为点∴EC=BC,∠ECF=∠BCF,设∠ECF=∠BCF=α,则∠BCE=2α,∴∠ACE=90°﹣2α,∵AC=BC,∴AC=EC,∴∠AEC=∠EAC=[180°﹣(90°﹣2α)]=45°+α,∵∠AEC=∠AFC+∠ECF=∠AFC+α,∴∠AFC=45°;②如图2,连接BE,CE,∵B、E关于直线CF对称,∴CF垂直平分BE,由(1)知:∠AFC=45°,∴∠BEF=45°,∵△EBG与△BDC相似,∠BEG=∠DBC=45°,∵∠EBG与∠BDC均为钝角,∴△EBG∽△BDC,∴∠G=∠BCD=∠BAG,∵∠G+∠BAG=∠ABC=45°,∴∠G=∠BCD=22.5°,过点D作DH⊥AB交BC于点H,则△BDH是等腰直角三角形,∴DH=BD,BH=BD,∠BHD=45°,∵∠CDH=∠BHD﹣∠BCD=45°﹣22.5°=22.5°=∠BCD,∴CH=DH=BD,∵CH+BH=BC=5,∴BD+BD=5,∴BD==5﹣5,∴线段BD的长为5﹣5;(2)Ⅰ.当点D在AB上时,如图3,过点C作CM⊥AE于点M,连接BF,∵AC=EC=BC=5,∴AM=EM=AE,∴①AM2+CM2=AC2=25,∵S△ACE=AE•CM=12,∴②AM•CM=12,①+②×2,得:(AM+CM)2=49③,①﹣②×2,得:(AM﹣CM)2=49③,∵CM>AM>0,∴AM=3,CM=4,∴AE=6,由(1)知:∠AFC=45°,BE⊥CF,∴∠BEF=45°,∵∠AFC=∠ABC=45°,∴A、C、B、F四点共圆,∴∠AFB+∠ACB=180°,∴∠AFB=90°,∴△BEF是等腰直角三角形,∴EF=BF,设EF=BF=x,则AE=x+6,在Rt△ABF中,AF2+BF2=AB2,∴(x+6)2+x2=50,解得:x=1或x=﹣7(舍去),∴BF=1,∴S△ABE=AE•BF=×6×1=3;Ⅱ.当点D在AB4,过点C作CM⊥AE于点M,连接BF,由(1)知:∠AFC=45°,CF垂直平分BE,∴∠BEF=45°,BF=EF,∴∠EBF=∠BEF=45°,∴∠BFE=90°,∵AC=EC=BC=5,∴AM=EM=AE,与Ⅰ同理可得:AM=EM=4,CM=3,AE=8,设BF=EF=y,则AF=8﹣y,在Rt△ABF中,AF2+BF2=AB2,∴(8﹣y)2+y2=50,解得:y=1或y=7(舍去),∴BF=1,∴S△ABE=AE•BF=×8×1=4;综上,S△ABE的值为3或4.【点评】本题考查了三角形面积,等腰直角三角形性质和判定,相似三角形的判定和性质,轴对称变换的性质,勾股定理等,解题关键是添加辅助线构造直角三角形,运用分类讨论思想和方程思想解决问题.。
沪教版 九年级(上)数学 秋季课程 第1讲 相似性与比例线段(解析版)

相似形与比例线段内容分析放缩与相似形是九年级上学期第一章第一节的内容,主要对相似多边形的概念和性质进行讲解,重点是理解相似形的相关概念和相似多边形性质的运用.通过对相似多边形的学习,为后面学习相似三角形的知识奠定基础.比例线段是九年级上学期第一章第二节的内容,主要讲解比例线段的有关概念和性质,以及三角形一边的平行线的相关性质和判定.比例线段的知识点,重点在于理解不同概念和性质之间的联系和区别,熟练比例线段之间的转换,并能结合具体图形,运用比例线段的性质进行解题.对比例线段的学习之后,我们进一步学习三角形一边的平行线分线段成比例的相关性质和判定.三角形一边的平行线是九年级数学上学期第一章第二节的内容,本讲主要讲解三角形一边平行线性质定理及推论和三角形一边平行线判定定理及推论,以及平行线分线段成比例定理.重点是掌握这两个定理及其推论,分清两个定理及其推论之间的区别和联系,难点是理解该定理和推论的推导过程中所蕴含的分类讨论思想和转化思想,并认识“A”字型和“X”字形这两个基本图形,最后灵活运用本节的三个定理及两个推论,理解和掌握“作平行线”这一主要的作辅助线的方法,为学习相似三角形的性质和判定做好准备.知识结构模块一:放缩与相似形知识精讲1、相似形的概念相似形:我们把形状相同的两个图形称为相似的图形,简称相似形.2、相似多边形的性质如果两个多边形是相似形,那么这两个多边形的对应角相等,对应边的长度成比例.当两个相似的多边形是全等形时,它们对应边的长度的比值为1.例题解析【例1】下列说法中错误的是()A.同一底片先后两次冲印出的照片是相似形B.同一颗树在太阳光下先后两次形成的影子是相似形C.放在投影仪上的图片及其在屏幕上显示的图片是相似形D.放在复印件上的图片及其复印后得到的图片是相似形【答案】B【解析】不同的时刻下,阳光与树射入的夹角不同,形成的影子大小不同,即不是相似形.【总结】考查相似形的定义,抓住相似形的基本定义即形状完全相同才是相似形.【例2】有以下命题:1邻边之比为2 : 3的两个平行四边形相似;2有一个角是40°的两个菱形相似;3两个矩形相似;4两个正方形相似,其中正确的是()A.1和2B.2和4C.3和4D.1和3【答案】B【解析】邻边之比固定,但邻边的夹角不确定,形状不一定相同,①错误;矩形每个角都是90度,但长宽之比不确定,即对应边不一定成比例,③错误;故选B.【总结】考查相似形的定义,根据相似形的性质可知对应角相等,对应边成比例才是相似形.【例3】如果两个矩形相似,已知一个矩形的两边长分别为5 cm和4 cm,另一边矩形的边长为6 cm,则另一边长为______.2/ 29a 甲b 乙【答案】4.8cm或7.5cm.【解析】设矩形另一边长为xcm,根据相似形的定义,对应边成比例,可知546x=或546x=,解得: 4.8x=或7.5x=.【总结】考查相似图形的性质,对应边成比例,但要注意好对应关系,题目未指明的要进行分类讨论.【例4】在平面内,两个形状相同、大小不一定相同的图形称作相似形.我们可以把这一概念推广到空间:如果两个几何体的形状完全相同,大小不一定相同,我们称它们为相似体.如图,甲乙两个不同的正方体,它们是相似体.若两个正方体的棱长分别为a和b,则称这两个相似体的相似比为a : b.我们不难发现它们的一些基本性质:设S甲、S乙分别表示这两个正方体的表面积,则2226=6S a aS b b⎛⎫= ⎪⎝⎭甲乙;设V甲、V乙分别表示这两个正方体的体积,则333V a aV b b⎛⎫== ⎪⎝⎭甲乙.(1)下列几何体中,一定属于相似体的是()A.两个圆柱体B.两个圆锥体C.两个球体D.两个长方体(2)请归纳出相似体的三条主要性质:①两个相似体的对应线段或对应弧长的比等于______;②两个相似体表面积的比等于______;③两个相似体体积的比等于______.(3)某海岛周围海域出产一种鱼,在体长10厘米之后的生长过程中,体型可以近似地看作相似体.若体长20厘米的鱼质量为0.2千克,则体长为60厘米的鱼质量为多少?当地市场上出售这种鱼价格与体长成正比,购买哪种鱼更划算?【答案】(1)C;(2)相似比,相似比的平方,相似比的立方;(3)5.4kg,60cm划算【解析】(1)和圆一样,球只有一个基本量,即半径,所有球体都是相似体,类似所有圆都是相似形,其它的几何体都是至少两个基本量,不能确定相似;(2)表面积是进行平方运算,体积是进行立方运算,由正方体相似进行归纳总结,由此可得相似体对应线段比是相似比,表面积比是相似比的平方,体积比是相似比的立方;(3)鱼的体型可看作相似体,可知其体积比即为相应相似比的立方,即鱼体长比的立方,设60cm长鱼体重mkg,则有30.22060m⎛⎫= ⎪⎝⎭,解得 5.4m=,这种鱼的价格与体长成正比,可知体型越大,这种鱼的单价越低,由此可知60cm体长的鱼划算.【总结】阅读题,主要考查归纳总结的能力,要用题目中的条件分析清楚,进行类比,即可解决问题.4/ 291、比和比例一般来说,两个数或两个同类的量a 与b 相除,叫做a 与b 的比,记作:a b (或表示为a b); 如果::a b c d =(或a cb d=),那么就说a 、b 、c 、d 成比例. 2、比例的性质(1)基本性质:如果a cb d =,那么ad bc =;如果a cb d =,那么b d ac =,a b cd =,c da b=. (2)合比性质: 如果a c b d =,那么a b c db d ++=;如果a cb d =,那么a bc db d--=. (3)等比性质: 如果a c k b d ==,那么a c a ck b d b d +===+(如果是实数运算,要注意强调0b d +≠). 3、比例线段的概念对于四条线段a 、b 、c 、d ,如果::a b c d =(或表示为a cb d=),那么a 、b 、c 、d 叫做成比例线段,简称比例线段. 4、黄金分割如果点P 把线段AB 分割成AP 和PB (AP PB >)两段(如下图),其中AP 是AB 和PB 的比例中项,那么称这种分割为黄金分割,点P 称为线段AB 的黄金分割点.其中,510.6182AP AB -=≈,称为黄金分割数,简称黄金数.模块二:比例线段知识精讲APB6 / 29【例5】把12ab cd =写成比例式,不正确的写法是( )A .2a dc b= B .2a d c b= C .2a d c b= D .2c ab d= 【答案】B【解析】应用比例的基本性质,可知B 选项即为2ab cd =,与原条件不符,故选B . 【总结】考查比例式的变形,应用比例的基本性质转化为等积式,看能不能得到原本题目条件乘积式即可.【例6】已知线段x 、y 满足()():3:1x y x y +-=,那么x : y 等于( ) A .3 : 1 B .2 : 3 C .2 : 1 D .3 : 2【答案】C【解析】令3x y k x y k +=⎧⎨-=⎩,可解得2x ky k =⎧⎨=⎩,即得:2:2:1x y k k ==.【总结】比例运算中,可应用设“k ”法计算相应字母比例关系.【例7】等腰直角三角形中,一直角边与斜边的比是______. 【答案】2:2.【解析】设三角形直角边长为a ,根据勾股定理可知斜边长为2a ,直角边与斜边比为:21:22:2a a ==.【总结】考查应用勾股定理解决等腰直角三角形三边比,注意结果要进行化简.【例8】已知a cb d=,则下列式子中正确的是( ) A .22::a b c d =B .::a d c b =例题解析C .()()::a b a c b d =++D .()()::a b a d b d =--【答案】C【解析】根据比例的合比性,可知C 正确.【总结】考查比例的性质的变形应用,本题根据合比性即可很快得出答案.【例9】若a = 8 cm ,b = 6 cm ,c = 4cm ,则a 、b 、c 的第四比例项d = ______cm ;a 、c 的比例中项x = ______cm .【答案】3,【解析】根据第四比例项和比例中项的基本定义,可得a c b d =,a xx c=,代入即可分别求得3d cm =,x =.【总结】考查比例定义中的相关基本概念.【例10】已知点C 是线段AB 的黄金分割点,5AC =,且AC > BC ,则线段AB =______,BC =______.【答案】10,15-【解析】根据黄金分割点的概念,且AC > BC ,可知AC AB =,5AC =代入可得10AB =,则15BC AB AC =-=-【总结】考查黄金分割点的概念,以及相关的黄金比.【例11】已知三个数2、5,填一个数,使这四个数能组成比例,这个数可能是____________.【解析】设这个数是x ,根据比例的基本性质,转化后,可以得到三种情况,即2x =,8 / 29352x =⨯,523x =,分别解得53x ,103x =23x =. 【总结】考查对比例基本性质的应用,一定要注意题目条件的说明是否需要进行分类讨论的情况,通过转换为乘积的形式,可以做到不重不漏.【例12】已知实数a 、b 、c 满足b c c a a b a b c +++==,求b ca+的值. 【答案】2或1-【解析】当0a b c ++≠时,根据比例的等比性质,可得2b c b c c a a ba ab c++++++==++; 当0a b c ++=时,则有b c a +=-,由此1b c aa a+-==-.故b ca+的值为2或1-. 【总结】考查比例的等比性质,注意等比性质在实数运算中运用的条件,要根据分母是否为0进行分类讨论.1、三角形一边的平行线性质定理平行于三角形一边的直线截其他两边所在的直线,截得的对应线段成比例.如图,已知ABC ∆,直线l // BC ,且与AB 、AC 所在直线交于点D 和点E ,那么AD AEDB EC =.2、三角形一边的平行线性质定理推论平行于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例.如图,点D 、E 分别在ABC ∆的边AB 、AC 上,DE // BC ,那么DE AD AEBC AB AC ==.3、三角形的重心定义:三角形三条中线交于一点,三条中线交点叫三角形的重心.性质:三角形重心到一个顶点的距离,等于它到这个顶点对边中点的距离的两倍. 4、三角形一边的平行线判定定理如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边.5、三角形一边的平行线判定定理推论如果一条直线截三角形的两边的延长线(这两边的延长线在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边.如图,在ABC ∆中,直线l 与AB 、AC 所在直线交于点D 和点E ,如果AD AEDB EC=,那么l //BC .模块三:三角形一边的平行线知识精讲lA B CDEABCDEABCDE ll ABC D E10 / 296、平行线分线段成比例定理两条直线被三条平行的直线所截,截得的对应线段成比例. 如图,直线1l //2l //3l ,直线m 与直线n 被直线1l 、2l 、3l 所截,那么DF EGFB GC=.7、平行线等分线段定理两条直线被三条平行的直线所截,如果一条直线上截得的线段相等,那么另一条直线上截得的线段也相等.【例13】如图,DE // BC ,AD = 5,BD = 2,AE = 3,BC = 8,求线段AC 、DE 的长.【答案】215AC =,407DE =. 【解析】AD = 5,BD = 2,可得7AB AD BD =+=,由DE // BC ,根据三角形一边平行线性质定理的推论,可得AE DE ADAC BC AB ==,即3587DE AC ==,可求得:215AC =,407DE =. 【总结】考查三角形一边平行线性质定理推论的应用,注意解题中适当应用边的关系和相关比例的性质.【例14】如图,ABC ∆中,DE // BC ,AD = EC ,BD = 4 cm ,AE = 3 cm ,则AB =______.例题解析ABCDEABCDEABCDEB CDE F GABC DE【答案】()423cm +.【解析】设AD xcm =,由DE // BC ,可得AD AEAB AC=,又AD EC =, 则该式即为343x x x=++,整理得212x =,由此得23x =, ()423AB AD BD cm =+=+.【总结】考查三角形一边平行线性质定理的应用,注意好题目中对相关条件的应用,改写成比例式解决问题.【例15】ABC ∆中,90A ∠=︒,点D 在AB 上,点E 在BC 上,若DE BDAC BA=,那么DE ______平行于AC .(填“一定”、“不一定”或者“一定不”)【答案】不一定.【解析】根据三角形一边平行线的判定定理,可知一条直线截三角形两边所得的线段对应成 比例,可判定平行,本题中对应成比例的并不是截三角形两边所得线段对应成比例,即 不可判定平行,在AB 上固定一点D ,作ED AB ⊥交BC 于点E ,以点D 为圆心,ED 长为半径画圆,与边AB 还会有另外一个交点,即不一定能判定平行.【总结】考查三角形一边平行线判定定理的条件,只能根据所截得的两边线段对应成比例判定平行,而不能根据这条直线对应成比例关系判定平行.【例16】如图,两条相交于点O 的直线被另外三条直线所截,交点分别为A 、B 、C 和D 、E 、F ,则下列说法中正确的有( )ABCDE12 / 29A B CDE FO (1)若AD // BE // FC ,则AB BCDE EF=; (2)若AD // BE // FC ,则OF ACOC DF =; (3)若AB DEBC EF =,则AD // FC ; (4)若BC BOEF EO=,则BE // FC ; (5)若BE BOFC OC=,则BE // FC .A .1个B .2个C .3个D .4个【答案】B【解析】根据平行线分线段成比例定理,知(1)正确;同时OF OD OF OD DFOC OA OC OA AC+===+, 知(2)错误;根据平行线分线段成比例定理,由于题目中没有给出有直线与BE 平行的条件,则不能证明平行,(3)错误;根据三角形一边平行线的判定定理,BC BOEF EO =, 根据比例的基本性质变形可得BO OEOC OF=,即可证平行,可知(4)正确,(5)错误. 【总结】考查平行线分线段成比例相关的性质定理和判定,注意前提条件再进行判断.【例17】如图,ABC ∆,DE // BC ,若23AD DB =,则:CDE BDC S S ∆∆=( ) A .2 : 3B .2 : 5C .4 : 15D .6:15【答案】B【解析】根据DE // BC ,可得23AE AD EC DB ==,三角形为同高三角形,则有23ADE CDE S AE S EC ∆∆==,可设2ADE S a ∆=,则有3CDE S a ∆=,5ACD S a ∆=,同理23ACD BCD S AD S BD ∆∆==,可得152BCD S a ∆=,则有15:3:2:52CDE BDC S S a a ∆∆==.【总结】结合三角形一边平行线性质定理,考查三角形中的同高三角形,面积比即为其底边长度之比.【例18】如图,DF // AC ,DE // BC ,下列各式正确的是( )A .AD BE BC CF =B .AE CE DE BC = C .AE BD CE AD = D .AD AB DE BC=A B CDE【答案】D【解析】由DE // BC ,根据三角形一边平行线的性质定理的推论,可得AD DE AB BC =,变形即为AD ABDE BC =,D 正确. 【总结】考查三角形一边平行线性质定理的应用,利用比例变形可以将对应边成比例转化为一个三角形中对应边的比例关系,利用相关性质等积转化即可进行判断.【例19】如图,阳光通过窗口照到室内,在地上留下2.7米宽的亮区DE ,如果亮区一边到 窗下墙脚的距离CE = 8.7,窗口高AB = 1.8米,那么窗口底边离地面的高度BC =______.【答案】4m .【解析】射入的光线平行,则有AB DEAC CE =,代入可求得 5.8AC m =,4BC AC AB m =-=.【总结】考查三角形一边平行线性质定理的应用,在路灯、太阳光线中经常用到.【例20】如图,AD // EG // BC ,AF = 12,FC =3,BC = 10,AD = 5,那么EG 的长是______. 【答案】9【解析】由AD // EG // BC ,根据三角形一边平行线的性质定理的推论,可得AF EF AC BC =,CF FGAC AD =,代入即为 121015EF =,3515FG =,求得8EF =,1FG =,即得:9EG EF FG =+=.【总结】考查三角形一边平行线性质定理推论的综合应用,通过比例转化解决问题.【例21】如图,已知ABCD 是梯形,其中AB // CD ,对角线AC 与BD 交于O ,过O 作AB的平行线交AD 于点ABCDEFA B CDE AB C DEFGA BC D EFO14 / 29E ,交BC 于点F ,若AO : OC = 2 : 1,且CD = 1.8,CF = 0.8,那 么AB = ______,BC=______.【答案】 3.6,2.4.【解析】由////AB CD EF ,根据三角形一边平行线的性质定理及推论,可得2AB AO OB BFCD OC OD CF====,由此可求得:AB =3.6, 1.6BF =,故 2.4BC BF CF =+=.【总结】考查三角形一边平行线性质定理推论的综合应用,通过比例转化解决问题.【例22】如图,已知梯形ABCD 中,AD // BC ,MN // BC ,且交对角线BD 于O ,AD = DO = p ,BC = BO = q ,则MN 为( )A .pq p q +B .2pq p q +C .p qpq+ D .2p qpq+ 【答案】B【解析】由AD // MN // BC ,根据三角形一边平行线的性质定理的推论,可得MO BOAD BD =, ON DOBC BD =,由AD = DO = p ,BC = BO = q ,代入即为MO q p p q =+,ON p q p q =+,求得:pq MO p q =+,pq ON p q =+,即得:2pqMN MO ON p q=+=+. 【总结】考查三角形一边平行线性质定理推论的综合应用,通过比例转化解决问题.【例23】如图,直角ABC ∆中两条直角边CA = 4,CB = 3,点E 为斜边AB 上的一个动点,ED ⊥BC 于D ,设AE = x ,BD = y ,则y 关于x 的函数解析式为________________.A B CD ONMAB CD EFG【答案】335y x =-.【解析】由勾股定理,可得225AB AC BC =+=,AE = x , 则5BE x =-,由ED ⊥BC ,90C ∠=︒,可得//DE AC ,根据三角形一边平行线性质定理,则有BD BEBC AB =,即535y x -=,即可得335y x =-. 【总结】考查三角形一边平行线性质定理推论的综合应用,通过比例转化解决问题.【例24】如图,在平行四边形ABCD 中,E 是AB 延长线上的一点,求证: (1)AE AB AD CF =;(2)2GD GF GE =. 【答案】略【解析】证明:(1)四边形ABCD 是平行四边形, //AB CD ∴,//AD BC ,AB CD =DC GC CFAE AG AD∴==AB CFAE AD ∴=即得AE ABAD CF=(2)同样地,由//AD CF ,//DC AE ,可得:GD AG GEGF GC GD==. ∴2GD GF GE =.【总结】考查三角形一边平行线性质定理的基本应用,考查在有平行线的图形中的基本图形,“A ”字型和“8”字型,“A ”字型和“8”字型有叠合的时候可进行等比例转化.【例25】如图,在ABC ∆中,AB > AC ,AD ⊥BC 于D ,点F 是BC 中点,过点F 作BC 垂线交AB 于点E ,BD : DC = 3 : 2,则BE : EA =______.【答案】5:1.【解析】由BD : DC = 3 : 2,F 为BC 中点,即可得ABCDEA B CD EF16 / 2932BF FD BF FD +=-,则5BF FD =,由EF BC ⊥,AD ⊥BC ,可得://EF AD ,根据三角形一边平行线性质定理, 即可得:::5:1BE EA BF FD ==.【总结】考查三角形一边平行线性质定理的综合应用,过程中注意比例转化.【例26】如图,在ABC ∆中,E 、F 分别是BC 、AC 的中点,AE 、BF 交于点G ,过G 作GD // AC 交BC 于点D ,若ED = 5,则BC 的长为______.【答案】30.【解析】∵E 、F 分别是BC 、AC 的中点, ∴G 是ABC ∆的重心.∴13GE AE =.∵GD // AC ,∴可得13ED GE EC AE ==,由此315EC ED ==,230BC EC ==.【总结】考查重心性质的证明,构造平行线,结合三角形一边平行线性质定理即可解决问题.【例27】如图,AD // OM // BC ,AC 、BD 相交于点O .求证:111AD BC OM +=. 【答案】略【解析】证明:////AD OM BC ,OM BM AD AB ∴=,OM AM BC AB=. ABCDOM ABCDE FG1OM OM BM AMAD BC AB AB∴+=+=. 即得:111AD BC OM+=. 【总结】考查三角形一边平行线性质定理的应用,尤其图形中“A ”字型等基本图形有部分叠加图形的情况下可进行等比例转化.【例28】如图,已知:在ABC ∆中,13BD CD =,2AF DF =,求AEAC的值. 【答案】13.【解析】过点D 作//DG BE 交AC 于点G , 根据三角形一边平行线的性质定理,可得13EG BD GC CD ==,2AE AF EG DF ==,则有23AE GC =,则有21132AE EC ==+,根据比例的合比性,则有13AE AC =. 【总结】考查三角形一边平行线性质定理的应用,构造平行线,构造出“A ”字型等相关基本图形进行等比例转化解决问题.【例29】如图,已知AM 是ABC ∆的中线,P 是BC 边上的一个动点,过点P 作AM 的平行线分别交AB 、AC 所在直线与点Q 、R ,求证:PQ + PR 为定值.【答案】略.【解析】证明://PR AM ,PQ BP AM BM ∴=,PR PCAM MC =. BM CM =,2PQ PR BP PC BC AM BM BM++∴===.ABC DEFABCR MP QG18 / 29ABCD E P Q 图1R A B C DO PN MS即得:2PQ PR AM +=,即证PQ + PR 为定值.【总结】考查三角形一边平行线性质定理推论的应用,注意观察图形中的基本图形,本题中即用到两个“A ”字型.【例30】如图,在四边形ABCD 中,AC 与BD 相交于点O ,直线l 平行于BD ,且与AB 、 DC 、BC 、AD 及AC 的延长线分别相交于点M 、N 、R 、S 和P .求证:PM PN PR PS =.【答案】略【解析】证明://BD MSBO AO MP AP ∴=,DO AOPS AP =BO DOPM PS ∴=PS DOPM BO∴=同时由//OB PR ,//OD PN , OB OC PR CP ∴=,OD OCPN CP=OB ODPR PN ∴=PN DO PSPR BO PM∴==即证PM PN PR PS =【总结】考查三角形一边平行线性质定理的应用,找准图形中的“A ”字型和“8”字型等基本图形进行等比例转化即可.【例31】(1)如图1,在ABC ∆中,点D 、E 分别在AB 、AC 上满足DE // BC ,点P 为BC上的任意一点,AP 交DE 于点Q ,求证:DQ BPQE PC =. (2)试参考(1)的方法解决下列问题:如图2,M 、N 为边BC 上的两点,且满足BM = MN = NC ,一条平行于AC 的直线分别交AB 、AM 和AN 的延长线于点D 、E 和F . 求EF : DE 的值.PN M FEDCBA【答案】(1)略;(2)3:1. 【解析】(1)证明://DE BC ,DQ AQ BP AP ∴=,QE AQPC AP =. DQ QEBP PC ∴=.DQ BPQE PC ∴=. (2)过点B 作//BQ DF 交AF 延长线于点Q ,交AM 延长线于点P , 则有////BQ DF AC ,BM MN NC ==, 12BP BM AC MC ∴==,2BQ BN AC NC ==. 14BP BQ ∴=,即得:13BP PQ =.由(1)的结论即可得::3:1EF DE PQ BP ==.【总结】考查三角形一边平行线的应用,“8”字型的叠合,可以进行相应等量转化确定相关线段之间的比例关系解决问题.20 / 29【习题1】如果图形A 与图形B 相似,图形B 与图形C 相似,那么图形A 与图形C ______相似.(填“一定”、“不一定”或“一定不”)【难度】★ 【答案】一定.【解析】根据相似形定义,可知图形A 与图形B 形状相同,图形B 与图形C 形状相同,则必有图形A 与图形C 形状相同,即两图形相似.【总结】考查相似形具有传递性.【习题2】若():8:3x y y +=,则:x y =_____. 【难度】★ 【答案】5:3.【解析】令83x y k y k +=⎧⎨=⎩,可解得:53x ky k =⎧⎨=⎩,即得:5:35:3x y k k ==.【总结】比例运算中,可应用设“k ”法计算相应字母比例关系,也可直接利用比例的合比性质进行求解.【习题3】如图,DE // BC ,下列比例式成立的是( ) A .AD AC AB AE = B .DE DA BC AB = C .EA DA AB AC =D .DA AEAB AC =【难度】★ 【答案】C【解析】根据三角形一边平行线性质定理的推论,由DE // BC ,可得:DA EAAC AB =,可知C 正确. 【总结】考查三角形一边平行线的性质定理.随堂检测BCDEA【习题4】有以下命题,其中正确的判断有( )个(1)如果线段d 是线段a 、b 、c 的第四比例项,则有a cb d =;(2)如果点C 是线段AB 的中点,那么AC 是AB 、BC 的比例中项;(3)如果点C 是线段AB 的黄金分割点,且AC > BC ,那么AC 是AB 与BC 的比例中项; (4)如果点C 是线段AB 的黄金分割点,AC > BC ,且AB = 2,则51AC =-. A .1B .2C .3D .4【答案】C【解析】根据比例相关定义,可知(1)正确;C 是AB 中点时,则有12AC BC AB ==,此 时AB ACAC BC≠,(2)错误;根据黄金分割点的基本定义,可知(3)正确,同时黄金比 为512-,即512AC AB -=,可得51AC =-,(4)正确;(1)(3)(4)正确.综上所述,故选C .【总结】考查比例中的相关概念,以及黄金分割等基本知识.【习题5】如图,已知菱形BEDF 内接于ABC ∆,点E 、D 、F 分别在AB 、AC 和BC 上,若AB = 15 cm ,BC = 12 cm ,则菱形边长为______.【答案】203cm .【解析】根据三角形一边平行线的性质定理,则有DE AEBC AB=, 则有1BE AE BE DEAB AB AB BC+=+=,由AB = 15 cm ,BC = 12 cm ,DE BE =,即为11512DE DE +=,解得:203DE =,即菱形边长.【总结】考查三角形一边平行线性质定理的应用.【习题6】如图,在ABC ∆中,DE // BC ,EF // CD ,AF = 3,FD = 2,求AB 的长.ABCDEF22 / 29【答案】253. 【解析】AF = 3,FD = 2,可得5AD AF FD =+=,由DE // BC ,EF // CD ,可得AF AE AD AD AC AB ==,即得355AB =,求得253AB =. 【总结】考查三角形一边平行线性质定理的应用,注意利用基本“A ”字型,尤其有叠合的图形进行等比例转化.【习题7】如图,在平行四边形ABCD 中,AB = 24,X 、Y 是对角线AC 上的三等分点,联结DX 并延长,交AB 于P ,再联结PY 并延长,交DC 于Q ,则CQ 的长为______【答案】6.【解析】由四边形ABCD 是平行四边形,可知 //AB CD ,根据三角形一边平行线的性质定理,可得2DC XC AP AX ==,12CQ CY AP AY ==,由此可得14CQ CD =,即得11644CQ CD AB ===. 【总结】考查三角形一边平行线性质定理的应用,注意找到图形中的“X ”字型.【习题8】如图,在矩形ABCD 中,截去一个矩形ABFE (图中阴影部分),余下的矩形DEFC与原矩形ABCD 相似.(1)设AB = 6 cm ,BC = 8 cm ,求矩形DEFC 的面积;ABCDE FAB CDPQXYA BCDEF GHO(2)若截去的矩形ABFE 是正方形,求ABBC的值. 【答案】(1)227cm ;(2)512-. 【解析】(1)余下矩形与原矩形相似,根据相似形的性质,则有DE EF AB BC =,代入即为668DE =,求得 4.5DE cm =,则有227DEFC S DE EF cm =⋅=矩形;(2)同(1)有DE EF AB BC =,设原矩形宽为a ,则有AE EF BF a ===,代入即为BC a aa BC-=,整理得:220a aBC BC +-=,两边同除以2BC ,即得210a a BC BC ⎛⎫+-= ⎪⎝⎭,解方程得512a BC -=,即512AB BC -=,此时为黄金比. 【总结】考查相似形的基本性质的应用.【习题9】如图,平行四边形ABCD 中,对角线交点为O ,E 为AD 延长线上一点,OE 交CD 于F ,交AB 于G ,交CB 的延长线与H ,试求AB ADDF DE-的值. 【答案】2.【解析】由平行四边形的性质,则有DO OB =,由此可得 DF GB =,又//DC AB ,则有AG AEDF DE=,则有112AB AD AG GB AE DE AG AE DF DE DF DE DF DE +-⎛⎫⎛⎫-=-=+--= ⎪ ⎪⎝⎭⎝⎭. 【总结】考查三角形一边平行线性质定理的应用,注意找准图形中的“A ”字型和“8”字型等基本图形进行比例转化,同时应用好平行四边形的相关性质.【习题10】如图,已知在ABC ∆中,90C ∠=︒,以BC 为边向外作正方形BCDE ,联结AE交BC 于F ,作FG // AC ,交AB 于G .(1)试判断FCG ∆的形状,并加以证明;(2)若正方形BCDE 边长为1,30AEB ∠=︒,求AB 的长.ABCDEF24 / 29【答案】(1)等腰直角三角形;(2)523-.【解析】(1)FCG ∆是等腰直角三角形. 证明:四边形BCDE 是正方形, //BC DE ∴,////BE CD FG .CF AF DE AE ∴=,FG AFBE AE=. CF FGDE BE∴=. CF FG ∴=. //FG AC ,90CFG ACB ∴∠=∠=︒.即证FCG ∆是等腰直角三角形.(2)1BE BC ==,30AEB ∠=︒,333BE BF ∴==. 313FG CF ∴==-. 由//FG AC ,可得33FG BF AC BC ==,则331AC FG ==-,根据勾股定理,即可得()2222311523AB AC BC =+=-+=-.【总结】考查三角形一边平行线性质定理的应用,结合归纳猜想进行解题.ABCDEFGA B C DEFO【作业1】下列说法正确的是( ) A .边数相同的多边形相似 B .对应边成比例的多边形相似 C .对应角相等的多边形相似D .全等的多边形相似【难度】★ 【答案】D【解析】根据相似形的概念和性质,形状大小完全相同,即对应角相等,对应边对应成比例同时满足,可知ABC 错误,全等的图形是特殊的相似形,可知D 正确.【总结】考查相似形的基本概念和性质.【作业2】已知137x y y-=,则x y y +的值为______. 【答案】277. 【解析】由137x y y -=,则有137x y y -=,根据比例的合比性,13772777x y x +++==. 【总结】考查相关比例的转化,可利用比例的性质进行求解.【作业3】如图,已知AD // BE // CF ,下列比例式成立的有( )(1)AB AC DE DF =;(2)AB DE EF BC =;(3)AC DF EF BC =;(4)BC EFAC DF =. A .1个B .2个C .3个D .4个【答案】B【解析】根据平行线分线段成比例定理,可得AB DEBC EF=, 结合比例的合比性,即得AB DE AC DF =,BC EFAC DF=, (1)正确,(2)错误,(3)错误,(4)正确,综上所述,故选B .【总结】考查平行线分线段成比例定理,结合比例基本性质进行等比例转化.【作业4】已知P 、Q 是线段AB 的两个黄金分割点,且AB = 10 cm ,则PQ 长为( ) A .()551-B .()551+C .()1052-D .()535-课后作业26 / 29D RQPCBA【答案】C【解析】假设P 在Q 左侧,根据黄金分割点的性质,可知512AQ AB -=,5112AP AB -=-,由10AB cm =,可得()551AQ =-,()535AP =-,则()1052PQ AQ AP =-=-.【总结】考查线段的黄金分割点和黄金分割比的应用.【作业5】已知578a b c==,且a + b + c = 20,求2a b c +-的值. 【答案】9.【解析】根据比例的等比性,可得1578578a b c a b c ++====++,由此可得5a =,7b =,8c =,所以225789a b c +-=⨯+-=.【总结】考查比例的等比性基本知识的应用,应用在部分方程题中可以使题目简便易于计算,当然也可以用设“k ”法.【作业6】如图,小华是个爱动脑筋的小朋友,他发现可以通过如下的方法测得路灯的高度; 晚上他由路灯下的B 处走到C 处时,测得影子CD 的长为1米,继续往前走3米到达E 处时,测得影子EF 的长度为2米,已知小华的身高是1.5米,那么路灯A 的高度AB等于( ) A .4.5米 B .6米 C .7.2米D .8米【答案】B【解析】设小明身高为h , 1.5h m =,依题意可得,h CD AB BD =,h EF AB BF =,即得12123BC BC =+++,求得3BC m =,则4BD m =,1.514AB =,即可求得6AB m =,故选B . 【总结】考查三角形一边平行线性质的实际应用,注意把握好“A ”字型等比例转化. 【作业7】如图,ABC ∆中,在BC 上取一点P ,CA 上取一点Q ,使得BP : PC = 2 : 5,CQ : QA = 3 : 4,AP 与BQ 交于点R ,则AR : RP =______.【答案】14:3.【解析】过点P 作//PD BQ 交AC 于D ,根据三角形一边平行线性质定理,则有AR AQPR QD=, ABC DEF。
平行线分线段成比例八大题型

【变式】如图,已知点 F 在 AB 上,且 AF:BF=1:2,点 D 是 BC 延长线上一点,BC:CD =2:1,连接 FD 与 AC 交于点 M,则 FN:ND= .
解:过点 F 作 FE∥BD,交 AC 于点 E,
∴=,
∵AF:BF=1:2,
∴ = 1,
3
∴ = 1,
3
即 FE= 13BC, ∵BC:CD=2:1,
C l3
【小结】若将所截出的小线段位置靠上的(如 AB )称为上,位置靠下的称为下,两条线段
上上 上上 下下
合成的线段称为全,则可以形象的表示为 下 下 , 全 全 , 全 全 .
【题型1 “井”字型】
【例 1】如图,直线 l1∥l2∥l3,直线 AC 和 DF 被 l1,l2,l3 所截,如果 AB=2,BC=3,EF =2,那么 DE 的长是( )
A.2
B
.4
3
C.1
D.34
【分析】根据平行线分线段成比例定理得出比例式,代入求出即可. 【解答】解:∵直线 l1∥l2∥l3, ∴=,
∵AB=2,BC=3,EF=2,
∴2 = ,
32
∴DE=
4,
3
故选:B.
【变式】如图,a∥b∥c,两条直线与这三条平行线分别交于点 A,B,C 和 D,E,F.已知 AB=3,BC=2,DE=6,则 DF 等于( )
∵ = = 1,
2
∴BG=2DG, ∵BE=4DG, ∴ = 1,
4
故 D 错误,符合题意; 故选:D.
【变式】已知,在△ABC 中,点 D 为 AB 上一点,过点 D 作 DE∥BC,DH∥AC 分别交 AC、 BC 于点 E、H,点 F 是 BC 延长线上一点,连接 FD 交 AC 于点 G,则下列结论中错误的 是( )
2023年中考数学常见几何模型全归纳之模 相似模型-母子型(共角共边模型)和A(X)字型(解析版)

∴∠BCD=∠ACD=45°,∠BCE=∠ACF= 90°,∴∠DCE=∠DCF= 135°
∵在△DCE与△DCF中,
,∴ ,∴DE=DF;
(2)证明∶∵∠DCE= ∠DCF= 135°∴∠CDF+∠F=180°-135°=45°,
∵∠CDF+∠CDE=45°,∴∠F=∠CDE,
【详解】∵∠B=∠ACD,∠A=∠A,
∴△ACD∽△ABC,∴ ,
∵ ,∴ ,
∴ ,
∴△ADC与△ACB的周长比1:2,故选:B.
【点睛】本题主要考查了相似三角形的判定与性质,证明△ACD∽△ABC是解答本题的关键.
2.(2022·陕西汉中·九年级期末)如图, 是等腰直角 斜边 的中线,以点 为顶点的 绕点 旋转,角的两边分别与 、 的延长线相交,交点分别为点 、 , 与 交于点 , 与 交于点 ,且 .(1)如图1,若 ,求证: ;(2)如图2,若 ,求证: ;
1.(2022·湖南怀化·中考真题)如图,△ABC中,点D、E分别是AB、AC的中点,若S△ADE=2,则S△ABC=_____.
【答案】8
【分析】根据三角形中位线定理求得DE∥BC, ,从而求得△ADE∽△ABC,然后利用相似三角形的性质求解.
【详解】解:∵D、E分别是AB、AC的中点,则DE为中位线,
∴ ,∴ ∴ ,
∵ ,DE=BF,∴ ,
∴ ,∴ ,
∵ , ,∴ ,
∵ ,∴ ,
∴ .
【点睛】本题考查了相似三角形,熟练掌握相似三角形的面积比等于相似比的平方、灵活运用平行条件证明三角形相似并求出相似比是解题关键.
3.(2022·浙江宁波·中考真题)(1)如图1,在 中,D,E,F分别为 上的点, 交 于点G,求证: .
平行线分线段成比例上课用
A A B (D) E L1 (D) L1
B
L2 C L3
E
L2
C
F
F
L3
结论:在∆ACF中,因为BE//CF,所以所得的对应线段成 比例。 结论:平行于三角形一边的直线截其他两边,所得的对应 线段成比例
.如图2:△ABC中,DE ∥BC,如果 AE :EC=7 :3,则DB :AB=( )
在ABC中,DE // BC
DB : AB EC : AC AE : EC 7 : 3 EC : AC 3 : 10 DB : AB 3 : 10
B
图2 D
A
E
C
三、平行线分线段成比例定理的主要知识点:
1 平行线分线段成比例定理(x型):
三条平行线截两条直线,所得的对应线段成比例
二、平行线分线段成比例定理
A D L1
B
E
L2
C
F
L3
A B
D E
L1
A (D) B E
L1 L2 2、A字型 L3
L2
F 1、八字型 C L3
C
F
D
A
L1 L2
D B (E)
A
L1 L2 4、X型 L3
B
C
E
F
L3
3、X型
C
F
三、平行线分线段成比例定理的主要知识点:
1 平行线分线段成比例定理(八字型):
AB 9
DE 3 ,则AB=( 9 (1)已知BC=3, ) EF
A
D
L1
B C
E F
L2 L3
三、平行线分线段成比例定理的主要知识点:
比例与相似高级教程
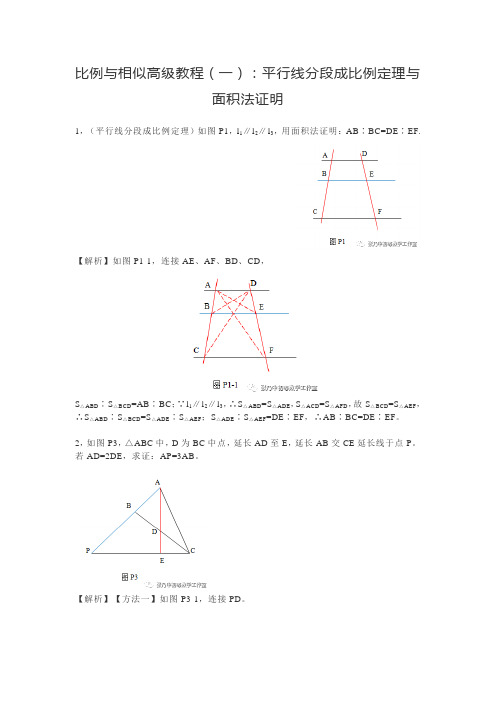
比例与相似高级教程(一):平行线分段成比例定理与面积法证明1,(平行线分段成比例定理)如图P1,l1∥l2∥l3,用面积法证明:AB∶BC=DE∶EF.【解析】如图P1-1,连接AE、AF、BD、CD,S△ABD∶S△BCD=AB∶BC;∵l1∥l2∥l3,∴S△ABD=S△ADE,S△ACD=S△AFD,故S△BCD=S△AEF,∴S△ABD∶S△BCD=S△ADE∶S△AEF;S△ADE∶S△AEF=DE∶EF,∴AB∶BC=DE∶EF。
2,如图P3,△ABC中,D为BC中点,延长AD至E,延长AB交CE延长线于点P。
若AD=2DE,求证:AP=3AB。
【解析】【方法一】如图P3-1,连接PD。
设S△ABD=1,则S△ACD=1,∵AD=2DE,∴S△ECD=1/2,设S△PBD=x,则S△P CD=x,S△PDE=x-1/2,∵PE∶EC= S△APE∶S△ACE= S△PDE∶S△CDE,∴(1+x+x-1/2)∶(1+1/2)=(x-1/2)∶1/2,解得:x=2,∴S△APD=3;AP∶AB= S△APD∶S△ABD=3∶1,即AP=3AB。
【方法二】如图P3-2,过点C作CF∥AB,与AE延长线交于点F。
则△ABD≌△FCD,CF=AB,FD=AD,∵AD=2DE,∴FD=2DE, FE=DE,FE∶EA =1∶3;CF∶AP=FE∶EA=1∶3,∴AP=3AB。
【平行4】如图P4,已知平行四边形ABCD中,E、F分别为边AB、AD上的点,EF与对角线AC交于点P。
若AE∶EB=a∶b,AF∶FD=m∶n(a,b,m,n均为正数),求AP∶PC的值(用a,b,m,n表示)【解析】如图P4-1,过点F作FG∥AB,交AC于点G。
则△AFG∽△ADC,△APE∽△GPF,∴FG∶CD=AF∶AD=m∶(m+n)AG∶AC=AF∶AD=m∶(m+n),AC=(m+n)AG/m,FG∶AE=PG∶AP=(AG-AP)∶AP=(AG∶AP)-1即:FG∶aCD/(a+b)=(AG∶AP)-1,AG∶AP=1+m(a+b)/a(m+n),AG=(2ma+mb+na)AP/[a(m+n)]AC=(m+n) /m·(2ma+mb+na)AP/[a(m+n)]= (2ma+mb+na)AP/am,PC=AC-AP=(2ma+mb+na)AP/am-AP=(ma+mb+na)AP/am,∴AP∶PC=am∶(ma+mb+na)【练习1】如图,已知:P为△ABC中位线MN上任意一点,BP、CP的延长线分别交对边AC、AB于D、E,求证:AD∶DC+AE∶EB=1【提示】过点A作BC的平行线,则MP、NP分别为△ABF和△ACG的中位线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8字型比例线段的证明过程
一、引言
比例线段是数学中常见的概念,它描述了两个线段之间的比例关系。
而8字型比例线段是一种特殊的比例线段,它具有特殊的几何性质。
本文将从基本概念出发,逐步证明8字型比例线段的性质。
二、基本概念
我们需要明确比例线段的定义。
在数学中,如果两个线段AB和CD 的比值等于线段EF和GH的比值,即AB/CD=EF/GH,那么我们称线段AB和CD与线段EF和GH成比例。
三、证明过程
1. 假设有两个线段AB和CD,它们与线段EF和GH成比例。
2. 过点A和C分别作线段EF和GH的平行线,分别与线段CD和AB相交于点I和J。
3. 根据平行线的性质,我们可以得知线段AI与线段CJ成比例,即AI/CJ=EF/GH。
4. 同样地,过点B和D分别作线段EF和GH的平行线,分别与线段CD和AB相交于点K和L。
5. 根据平行线的性质,我们可以得知线段BK与线段DL成比例,即BK/DL=EF/GH。
6. 由于线段AB和CD与线段EF和GH成比例,可以得知
AI/CJ=BK/DL。
7. 根据等比例关系,我们可以得知AI·DL=BJ·CK。
8. 由于四边形AIJK是一个平行四边形,所以AI=JK,BJ=IK,CK=KJ,DL=LI。
9. 结合以上等式,我们可以得知AI·DL=BJ·CK可以转化为JK·LI=IK·KJ。
10. 根据平行四边形的性质,我们可以得知IK·KJ=JK·LI。
11. 由于等式JK·LI=IK·KJ成立,可以得知四边形IKJL是一个平行四边形。
12. 根据平行四边形的性质,我们可以得知线段IJ平分线段KL。
13. 由于线段IJ平分线段KL,我们可以得知线段IJ与线段KL成比例,即IJ/KL=1/1。
14. 综上所述,线段AB和CD与线段EF和GH成比例的条件下,线段IJ与线段KL成比例,比例为1:1。
四、结论
通过以上证明过程,我们可以得出结论:在线段AB和CD与线段EF和GH成比例的条件下,线段IJ与线段KL成比例,比例为1:1。
这就是8字型比例线段的性质。
五、应用
8字型比例线段的性质在实际问题中有广泛的应用。
例如,在工程设计中,我们可以利用8字型比例线段的性质来确定建筑物的尺寸
比例,使其更加协调美观。
在地图绘制中,我们可以利用8字型比例线段的性质来放大或缩小地图的比例尺。
总之,掌握8字型比例线段的性质对于解决实际问题具有重要意义。
六、总结
通过本文的证明过程,我们深入了解了8字型比例线段的性质。
通过合理运用这一性质,我们可以解决实际问题,提高解决问题的效率。
同时,本文也展示了证明过程的逻辑性和严谨性,希望读者通过本文的阅读,对8字型比例线段有更深入的理解。
