指数函数和对数函数历年高考题汇编附答案
(完整版)指数函数对数函数专练习题(含答案).docx
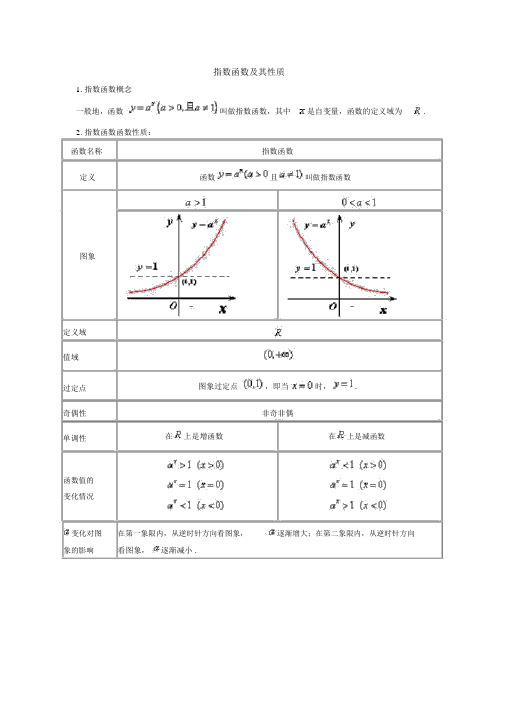
指数函数及其性质1.指数函数概念一般地,函数叫做指数函数,其中是自变量,函数的定义域为.2.指数函数函数性质:函数名称定义图象定义域值域过定点奇偶性单调性函数值的变化情况变化对图象的影响指数函数函数且叫做指数函数图象过定点,即当时,.非奇非偶在上是增函数在上是减函数在第一象限内,从逆时针方向看图象,逐渐增大;在第二象限内,从逆时针方向看图象,逐渐减小 .对数函数及其性质1.对数函数定义一般地,函数叫做对数函数,其中是自变量,函数的定义域.2.对数函数性质:函数名称定义函数对数函数且叫做对数函数图象定义域值域过定点奇偶性图象过定点,即当非奇非偶时,.单调性在上是增函数在上是减函数函数值的变化情况变化对图象的影响在第一象限内,从顺时针方向看图象,看图象,逐渐减小 .逐渐增大;在第四象限内,从顺时针方向指数函数习题一、选择题aa ≤ b,则函数 f ( x ) =1?2x 的图象大致为 ()1.定义运算 a ?b =>b a b2.函数 f ( x ) = x 2-bx + c 满足 f (1 + x ) =f (1 - x ) 且 f (0) =3,则 f ( b x ) 与 f ( c x ) 的大小关系是()xxA . f ( b ) ≤ f ( c ) x xB . f ( b ) ≥ f ( c )xxC . f ( b )> f ( c )D .大小关系随 x 的不同而不同3.函数 y = |2 x - 1| 在区间A . ( - 1,+∞ )C . ( - 1,1)( k - 1, k + 1) 内不单调,则 k 的取值范围是 ()B . ( -∞, 1)D . (0,2)4.设函数 f ( x ) =ln [( x -1)(2 -x)] 的定义域是 ,函数 ( ) = lg(x - 2x -1) 的定义域是 ,Ag xaB若 ?,则正数a 的取值范围 ()ABA . a >3B . a ≥ 3C . a > 5D . a ≥ 5.已知函数 f (x = 3- a x -3, x ≤ 7,若数列 { a n 满足 a n = f (n )(n ∈ * ,且 {a n }是递5 ) a x - 6, x >7. } N) 增数列,则实数a 的取值范围是 ()A . [ 9, 3)B . ( 9, 3) 44C . (2,3)D . (1,3)2x16.已知 a >0 且 a ≠ 1,f ( x ) = x - a ,当 x ∈ ( - 1,1) 时,均有 f ( x )< 2,则实数 a 的取值范围 是( )1 1 A . (0 , 2] ∪ [2 ,+∞ ) B . [ 4, 1) ∪ (1,4]11C . [ 2, 1) ∪ (1,2]D . (0 , 4) ∪ [4 ,+∞ )二、填空题xa7.函数 y = a ( a >0,且 a ≠ 1) 在 [1,2] 上的最大值比最小值大 2,则 a 的值是 ________.8.若曲线 | y | = 2 x + 1 与直线 y =b 没有公共点,则b 的取值范围是 ________.| x|的定义域为9. (2011 ·滨州模拟 ) 定义:区间 [x 1,x 2 ]( x 1<x 2) 的长度为 x 2- x 1. 已知函数 y = 2 [a , b] ,值域为 [1,2] ,则区间 [a , b] 的长度的最大值与最小值的差为 ________.三、解答题10.求函数y=2x2 3x 4 的定义域、值域和单调区间.11.(2011 ·银川模拟 ) 若函数y=a2x+ 2a x-1( a>0 且a≠ 1) 在x∈ [- 1,1]上的最大值为14,求a 的值.12.已知函数f (x) = 3x,(a+ 2) = 18, (x) =λ·3ax-4x的定义域为 [0,1] .f g(1)求 a 的值;(2) 若函数g( x) 在区间 [0,1] 上是单调递减函数,求实数λ的取值范围.1. 解析:由? = a a≤ b x2x x≤0,b a>b x>0 .1答案: A2. 解析:∵f (1 +x) =f (1 -x) ,∴f ( x) 的对称轴为直线x=1,由此得 b=2.又 f (0)=3,∴c=3.∴f ( x)在(-∞,1)上递减,在(1,+∞)上递增.x≥2x≥ 1,∴ (3 x) ≥(2 x) .若 x≥0,则3f f若 x<0,则3x<2x<1,∴f (3x)> f (2x).∴f (3x)≥ f (2x).答案: A3.解析:由于函数 y=|2x-1|在(-∞,0)内单调递减,在(0,+∞)内单调递增,而函数在区间 ( k- 1,k+ 1) 内不单调,所以有答案: Ck-1<0<k+1,解得-1<k<1.4.解析:由题意得: A=(1,2)x x>1x x>1在(1,2)上恒成立,即,a- 2且 a>2,由 A? B知 a- 2x x上恒成立,令x x xln a-2xln2>0 ,所以函数a-2 - 1>0 在 (1,2)u( x)=a- 2- 1,则u′( x) =au ( x ) 在 (1,2) 上单调递增,则 u ( x )> u (1) = a - 3,即 a ≥ 3.答案: B*f ( n ) 为增函数,5. 解析: 数列 { a } 满足 a = f ( n )( n ∈ N ) ,则函数nna >18- 6- ) × 7- 3,所以 3- a >0注意 a>(3,解得 2<a <3.aa8-6> 3- a × 7-3答案: C1 2x1 21 x x21的图象,6. 解析: f ( x )<? x -a < ? x - <a ,考查函数 y = a与 y =x - 2222当 a >1 时,必有 a-1≥1,即 1<a ≤ 2,21 1当 0<a <1 时,必有 a ≥ ,即 ≤a <1,2 2 1 综上, 2≤ a <1 或 1<a ≤ 2. 答案: C7. 解析: 当 a >1 时, y x在 [1,2] 上单调递增,故 2a3x= a a - a = ,得 a = . 当 0<a <1 时, y = a2 22a在 [1,2] 上单调递减,故 a -a = 2,得 a = 2. 故 a =2或 2.1131 3答案: 2或28. 解析: 分别作出两个函数的图象,通过图象的交点个数来判断参数的取值范围.x+1 与直线 y = b 的图象如图所示,由图象可得:如果x+ 1 与直线 y = b曲线 | y | = 2 | y | = 2没有公共点,则 b 应满足的条件是 b ∈ [- 1,1] .答案: [- 1,1]9. 解析: 如图满足条件的区间 [a , b] ,当 a =- 1, b = 0 或 a = 0, b = 1 时区间长度最小,最小值为 1,当 a =- 1,b = 1 时区间长度最大,最大值为2,故其差为 1.答案: 110. 解: 要使函数有意义,则只需- x 2-3x + 4≥ 0,即 x 2+ 3x -4≤ 0,解得- 4≤ x ≤ 1.∴函数的定义域为 { x | -4≤ x ≤ 1} .223225 令 t =- x - 3x + 4,则 t =- x - 3x + 4=- ( x + ) +4,2253∴当-4≤ x ≤ 1 时, t max = 4 ,此时 x =- 2, t min = 0,此时 x =- 4 或 x =1.∴0≤t ≤ 25 . ∴0≤ -x 2- 3x + 4≤ 5 .4 2∴函数 y = ( 1)x 23 x4的值域为 [ 2 , 1] .8223 225由 t =- x - 3x + 4=- ( x + )+4( - 4≤ x ≤ 1) 可知,23当- 4≤ x ≤- 2时, t 是增函数,3当- 2≤ x ≤1 时, t 是减函数.根据复合函数的单调性知:y = ( 1 )x 23 x 4在 [ - 4,- 3 3] 上是减函数,在 [ - ,1] 上是增函数.22 233∴函数的单调增区间是 [ - 2, 1] ,单调减区间是 [ - 4,- 2] . 11. 解: 令x22tt >0y= t+ 2t1= ( t+ 1)2,其对称轴为t =- 1.该二次函数a = ,∴ ,则--在[ - 1,+ ∞ ) 上是增函数.x12①若 a >1,∵x ∈ [ - 1,1] ,∴t = a ∈ [ a , a ] ,故当 t = a ,即 x =1 时, y max =a + 2a - 1=14,解得 a = 3( a =- 5 舍去 ) .②若 0<a <1,∵x ∈ [ - 1,1] ,∴ = x∈1 1=-时,a [ a , ] ,故当 t = ,即 1t a ax12y max = (a + 1) - 2= 14.11∴a =3或- 5( 舍去 ) .1综上可得 a = 3 或 3.12. 解: 法一: (1) 由已知得 a2 aa =log 32.3 += 18? 3 = 2?(2) 此时 g ( x ) = λ·2x - 4 x ,设 0≤ x 1<x 2≤ 1,因为 g ( x ) 在区间 [0,1] 上是单调减函数,所以 g ( x ) - g ( x ) = (2 x - 2x )( λ- 2x - 2x )>0 恒成立,即 λ<2x + 2x 恒成立.1 2 1 2 2 1 2 1由于 2x 2+ 2x 1>2 + 2 = 2,所以实数 λ的取值范围是λ≤ 2.法二: (1) 同法一.(2) 此时 g ( x ) = λ·2x - 4x ,因为 g ( x ) 在区间 [0,1] 上是单调减函数,所以有 g ′( x ) = λln2 ·2x - ln4 ·4x = ln2 [- 2 ·(2x )2+ λ·2x] ≤0 成立.x2 设 2 = u ∈ [1,2] ,上式成立等价于-2u+ λu ≤0 恒成立.因为 u ∈ [1,2] ,只需 λ≤2u 恒成立,所以实数 λ的取值范围是λ≤ 2.对数与对数函数同步练习一、选择题1、已知 3a2 ,那么 log3 8 2log 3 6 用 a 表示是()A 、 a 2B 、 5a2C 、 3a (1 a)2D 、 3a a 22、 2log a (M 2N ) log a Mlog a N ,则M的值为()A 、1NB 、4C 、1D 、 4 或 1413 、 已 知 x 2 y 2 1, x0, y 0 , 且 log a (1 x) m,log a n,则 log a y 等 于1 x()A 、 m nB 、 m nC 、 1m nD 、 1m n224、如果方程 lg 2 x (lg5lg 7)lgx lg5 glg 7 0 的两根是 ,,则 g的值是()A 、 lg5 glg 7B 、 lg35C 、 35D 、13515、已知 log 7[log 3 (log 2 x)] 0,那么 x2等于( )A 、1B 、13 C 、1D 、1322 2336、函数 ylg2 1 的图像关于()1 xA 、 x 轴对称B 、 y 轴对称C 、原点对称D 、直线 yx 对称7、函数 ylog (2 x 1) 3x2 的定义域是()A 、 2,1 U 1,B 、 1,1 U 1,32C 、 2,D 、 1,328、函数 ylog 1 (x 2 6x17) 的值域是()2A 、 RB 、 8,C 、, 3D 、 3,9、若 log m 9 log n 9 0 ,那么 m, n 满足的条件是( )A 、 m n 1B 、 n m 1C 、 0 n m 1D 、 0 m n 110、 log a 2 1,则 a 的取值范围是()3A 、 0, 2U 1,B 、 2,C 、 2,1D 、 0, 2U 2,3333 311、下列函数中,在 0,2 上为增函数的是()A 、 ylog 1 ( x1)B 、 y log 2 x 2 12C 、 ylog 2 1D 、 ylog 1 ( x 2 4x 5)x212、已知 g( x) log a x+1 ( a 0且a 1) 在 10, 上有 g( x)0 ,则 f ( x)a x 1 是( )A 、在 ,0上是增加的 B 、在 ,0 上是减少的C 、在, 1 上是增加的D 、在,0 上是减少的二、填空题13、若 log a 2 m,log a 3 n, a 2 m n 。
(精选试题附答案)高中数学第四章指数函数与对数函数真题

(名师选题)(精选试题附答案)高中数学第四章指数函数与对数函数真题单选题1、设a=log2π,b=log6π,则()A.a−b<0<ab B.ab<0<a−bC.0<ab<a−b D.0<a−b<ab答案:D分析:根据对数函数的性质可得a−b>0,ab>0,1b −1a<1,由此可判断得选项.解:因为a=log2π>log22=1,0=log61<b=log6π<log66=1,所以a>1,0<b<1,所以a−b>0,ab>0,故排除A、B选项;又1b −1a=a−bab=logπ6−logπ2=logπ3<logππ<1,且ab>0,所以0<a−b<ab,故选:D.2、若函数f(x)=x3+x2−2x−2的一个正零点附近的函数值用二分法计算,其参考数据如下:那么方程x3+x2−2x−2=0的一个近似根(精确度0.1)为().A.1.2B.1.4C.1.3D.1.5答案:B分析:根据二分法求零点的步骤以及精确度可求得结果.解:因为f(1)<0,f(1.5)>0,所以f(1)f(1.5)<0,所以函数在(1,1.5)内有零点,因为1.5−1=0.5>0.1,所以不满足精确度0.1;因为f(1.25)<0,所以f(1.25)f(1.5)<0,所以函数在(1.25,1.5)内有零点,因为1.5−1.25=0.25>0.1,所以不满足精确度0.1;因为f(1.375)<0,所以f(1.375)f(1.5)<0,所以函数在(1.375,1.5)内有零点,因为1.5−1.375=0.125>0.1,所以不满足精确度0.1;因为f(1.4375)>0,所以f(1.4375)f(1.375)<0,所以函数在(1.375,1.4375)内有零点,因为1.4375−1.375=0.0625<0.1,所以满足精确度0.1;所以方程x 3+x 2−2x −2=0的一个近似根(精确度0.05)是区间(1.375,1.4375)内的任意一个值(包括端点值),根据四个选项可知选B . 故选:B3、已知55<84,134<85.设a =log 53,b =log 85,c =log 138,则( ) A .a <b <c B .b <a <c C .b <c <a D .c <a <b 答案:A分析:由题意可得a 、b 、c ∈(0,1),利用作商法以及基本不等式可得出a 、b 的大小关系,由b =log 85,得8b =5,结合55<84可得出b <45,由c =log 138,得13c =8,结合134<85,可得出c >45,综合可得出a 、b 、c 的大小关系.由题意可知a 、b 、c ∈(0,1),a b =log 53log 85=lg3lg5⋅lg8lg5<1(lg5)2⋅(lg3+lg82)2=(lg3+lg82lg5)2=(lg24lg25)2<1,∴a <b ;由b =log 85,得8b =5,由55<84,得85b <84,∴5b <4,可得b <45; 由c =log 138,得13c =8,由134<85,得134<135c ,∴5c >4,可得c >45.综上所述,a <b <c . 故选:A.小提示:本题考查对数式的大小比较,涉及基本不等式、对数式与指数式的互化以及指数函数单调性的应用,考查推理能力,属于中等题.4、已知函数f (x )={a +a x ,x ≥03+(a −1)x,x <0(a >0 且a ≠1),则“a ≥3”是“f (x )在R 上单调递增”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件答案:A分析:先由f(x)在R 上单调递增求得a 的取值范围,再利用充分条件,必要条件的定义即得. 若f(x)在R 上单调递增, 则{a >1a −1>0a +1≥3 , 所以a ≥2,由“a ≥3”可推出“a ≥2”,但由“a ≥2”推不出 “a ≥3”, 所以“a ≥3”是“f(x)在R 上单调递增”的充分不必要条件. 故选:A.5、已知9m =10,a =10m −11,b =8m −9,则( ) A .a >0>b B .a >b >0C .b >a >0D .b >0>a 答案:A分析:法一:根据指对互化以及对数函数的单调性即可知m =log 910>1,再利用基本不等式,换底公式可得m >lg11,log 89>m ,然后由指数函数的单调性即可解出. [方法一]:(指对数函数性质) 由9m =10可得m =log 910=lg10lg9>1,而lg9lg11<(lg9+lg112)2=(lg992)2<1=(lg10)2,所以lg10lg9>lg11lg10,即m >lg11,所以a =10m −11>10lg11−11=0.又lg8lg10<(lg8+lg102)2=(lg802)2<(lg9)2,所以lg9lg8>lg10lg9,即log 89>m ,所以b =8m −9<8log 89−9=0.综上,a >0>b . [方法二]:【最优解】(构造函数) 由9m =10,可得m =log 910∈(1,1.5).根据a,b 的形式构造函数f(x)=x m −x −1(x >1) ,则f ′(x)=mx m−1−1, 令f ′(x)=0,解得x 0=m11−m,由m =log 910∈(1,1.5) 知x 0∈(0,1) .f(x)在(1,+∞)上单调递增,所以f(10)>f(8),即a>b,又因为f(9)=9log910−10=0,所以a>0>b .故选:A.【整体点评】法一:通过基本不等式和换底公式以及对数函数的单调性比较,方法直接常用,属于通性通法;法二:利用a,b的形式构造函数f(x)=x m−x−1(x>1),根据函数的单调性得出大小关系,简单明了,是该题的最优解.6、已知函数f(x)={2,x>mx2+4x+2,x≤m,若方程f(x)−x=0恰有三个根,那么实数m的取值范围是()A.[−1,2)B.[−1,2]C.[2,+∞)D.(−∞,−1]答案:A分析:由题意得,函数y=f(x)与函数y=x有三个不同的交点,结合图象可得出结果.解:由题意可得,直线y=x与函数f(x)=2(x>m)至多有一个交点,而直线y=x与函数f(x)=x2+4x+2(x≤m)至多两个交点,函数y=f(x)与函数y=x有三个不同的交点,则只需要满足直线y=x与函数f(x)=2(x>m)有一个交点直线y=x与函数f(x)=x2+4x+2(x≤m)有两个交点即可,如图所示,y=x与函数f(x)=x2+4x+2的图象交点为A(−2,−2),B(−1,−1),故有m≥−1.而当m≥2时,直线y=x和射线y=2(x>m)无交点,故实数m的取值范围是[−1,2).故选:A.7、已知x ,y ,z 都是大于1的正数,m >0,log x m =24,log y m =40,log xyz m =12,则log z m 的值为( ) A .160B .60C .2003D .320答案:B分析:根据换底公式将log x m =24,log y m =40,log xyz m =12,化为log m x =124,log m y =140,log m xyz =112,再根据同底数的对数的加减法运算即可得解. 解:因为log x m =24,log y m =40,log xyz m =12, 所以log m x =124,log m y =140,log m xyz =112,即log m x +log m y +log m z =112,∴log m x =112−log m y −log m z =112−124−140=160, ∴log z m =60. 故选:B .8、下列函数中是增函数的为( )A .f (x )=−xB .f (x )=(23)xC .f (x )=x 2D .f (x )=√x 3答案:D分析:根据基本初等函数的性质逐项判断后可得正确的选项. 对于A ,f (x )=−x 为R 上的减函数,不合题意,舍. 对于B ,f (x )=(23)x为R 上的减函数,不合题意,舍. 对于C ,f (x )=x 2在(−∞,0)为减函数,不合题意,舍.对于D,f(x)=√x3为R上的增函数,符合题意,故选:D.9、已知函数f(x)={a x,x<0(a−3)x+4a,x≥0满足对任意x1≠x2,都有(x1-x2)[f(x1)-f(x2)]<0成立,则a的取值范围为()A.(0,14]B.(0,1)C.[14,1)D.(0,3)答案:A分析:根据给定不等式可得函数f(x)为减函数,再利用分段函数单调性列出限制条件求解即得.因对任意x1≠x2,都有(x1-x2)[f(x1)-f(x2)]<0成立,不妨令x1<x2,则f(x1)>f(x2),于是可得f(x)为R上的减函数,则函数y=a x在(−∞,0)上是减函数,有0<a<1,函数y=(a−3)x+4a在[0,+∞)上是减函数,有a−3<0,即a<3,并且满足:a0≥f(0),即4a≤1,解和a≤14,综上得0<a≤14,所以a的取值范围为(0,14].故选:A10、如图所示,函数y=|2x−2|的图像是()A.B.C.D.答案:B分析:将原函数变形为分段函数,根据x=1及x≠1时的函数值即可得解.∵y=|2x−2|={2x−2,x≥12−2x,x<1,∴x=1时,y=0,x≠1时,y>0. 故选:B.填空题11、化简:(1+1232)(1+1216)(1+128)(1+124)(1+122)(1+12)=________.答案:2−1263分析:分析式子可以发现,若在结尾乘以一个(1−12),则可以从后到前逐步使用平方差公式进行计算,为保证恒等计算,在原式末尾乘以(1−12)×2即可﹒原式=(1+1232)(1+1216)(1+128)(1+124)(1+122)(1+12)×(1−12)×2=(1+1232)(1+1216)(1+128)(1+124)(1+122)×(1−122)×2 =(1+1232)(1+1216)(1+128)(1+124)×(1−124)×2=(1+1232)(1+1216)(1+128)×(1−128)×2=(1+1232)(1+1216)×(1−1216)×2=(1+1232)×(1−1232)×2=(1−1264)×2=2−1263所以答案是:2−1263﹒12、不等式log4x≤12的解集为___________.答案:(0,2]分析:根据对数函数的单调性解不等式即可. 由题设,可得:log 4x ≤log 4412,则0<x ≤412=2, ∴不等式解集为(0,2]. 所以答案是:(0,2].13、在用二分法求函数f (x )的零点近似值时,若第一次所取区间为[−2,6],则第三次所取区间可能是______.(写出一个符合条件的区间即可) 答案:[−2,0]或[0,2]或[2,4]或[4,6](写一个即可). 分析:根据二分法的概念,可求得结果.第一次所取区间为[−2,6],则第二次所取区间可能是[−2,2],[2,6];第三次所取区间可能是[−2,0],[0,2],[2,4],[4,6].所以答案是:[−2,0]或[0,2]或[2,4]或[4,6](写一个即可).14、设函数f(x)={2x +1,x ≤0|lgx |,x >0,若关于x 的方程f 2(x )−af (x )+2=0恰有6个不同的实数解,则实数a 的取值范围为______. 答案:(2√2,3)分析:作出函数f(x)的图象,令f(x)=t ,结合图象可得,方程t 2−at +2=0在(1,2]内有两个不同的实数根,然后利用二次函数的性质即得;作出函数f(x)={2x +1,x ≤0|lgx |,x >0的大致图象,令f (x )=t ,因为f 2(x )−af (x )+2=0恰有6个不同的实数解, 所以g (t )=t 2−at +2=0在区间(1,2]上有2个不同的实数解,∴{Δ=a 2−8>01<a2<2g (1)=3−a >0g (2)=6−2a ≥0 , 解得2√2<a <3,∴实数a 的取值范围为(2√2,3). 所以答案是:(2√2,3).15、函数y =log a (kx −5)+b (a >0且a ≠1)恒过定点(2,2),则k +b =______. 答案:5分析:根据对数函数的图象与性质,列出方程组,即可求解. 由题意,函数y =log a (kx −5)+b 恒过定点(2,2),可得{2k −5=1b =2 ,解得k =3,b =2,所以k +b =3+2=5.所以答案是:5. 解答题16、(1)计算:(1100)−12−√(1−√2)2−8×(√5−√3)0+816;(2)已知x +x −1=4,求x 12+x −12. 答案:(1)3;(2)x 12+x −12=√6.分析:(1)根据指数幂的运算法则进行计算,求得答案; (2)先判断出x >0,然后将x 12+x −12平方后结合条件求得答案. (1)原式=[(100)−1]−12−(√2−1)−8+(23)16,=10012−√2+1−8+212=10+1−8=3.(2)由于x +x−1=4>0,所以x >0,(x 12+x −12)2=x +x −1+2=6,所以x 12+x −12=√6.17、(1)证明对数换底公式:log b N =log a N log a b(其中a >0且a ≠1,b >0且b ≠1,N >0)(2)已知log 32=m ,试用m 表示log 3218. 答案:(1)证明见解析;(2)log 3218=2+m 5m.分析:(1)将对数式转化为指数式,然后两边取对数,利用对数函数的应算法则,即可证明. (2)利用换底公式将等号左边化为以3为底的对数,然后根据对数运算法则化简即得. (1)设log b N =x ,写成指数式b x =N . 两边取以a 为底的对数,得xlog a b =log a N .因为b >0,b ≠1,log a b ≠0,因此上式两边可除以log a b ,得x =log a N log a b.所以,log b N =log a N log a b.(2)log 3218=log 318log 332=log 332+log 32log 325=2+log 325log 32=2+m 5m.小提示:本题考查换底公式的证明和应用,属基础题,关键是将对数式转化为指数式,然后两边取对数,利用对数函数的应算法则,即可证明. 18、已知函数f (x )=a x −1a x +1(a >0,且a ≠1). (1)若f (2)=35,求f (x )解析式; (2)讨论f (x )奇偶性.答案:(1)f (x )=2x −12x +1;(2)奇函数.分析:(1)根据f (2)=35,求函数的解析式;(2)化简f (−x ),再判断函数的奇偶性. 解:(1)∵f (x )=a x −1a x +1,f (2)=35.即a 2−1a 2+1=35,∴a =2.即f (x )=2x −12x +1.(2)因为f (x )的定义域为R ,且f (−x )=a −x −1a −x +1=1−a x1+a x =−f (x ),所以f (x )是奇函数.19、如图,某中学准备在校园里利用院墙的一段,再砌三面墙,围成一个矩形花园ABCD ,已知院墙MN 长为25米,篱笆长50米(篱笆全部用完),设篱笆的一面AB 的长为x 米.(1)当AB 的长为多少米时,矩形花园的面积为300平方米?(2)若围成的矩形ABCD 的面积为 S 平方米,当 x 为何值时, S 有最大值,最大值是多少?答案:(1)15米;(2)当 x 为12.5米时, S 有最大值,最大值是312.5平方米.分析:(1)设篱笆的一面AB 的长为 x 米,则BC =(50−2x)m ,根据“矩形花园的面积为300平方米”列一元二次方程,求解即可;(2)根据题意,可得S =x(50−2x),根据二次函数最值的求法求解即可.(1)设篱笆的一面AB 的长为 x 米,则BC =(50−2x)m ,由题意得,x(50−2x)=300,解得x 1=15,x 2=10,∵50−2x ≤25,∴x ≥12.5,∴x=15,所以,AB的长为15米时,矩形花园的面积为300平方米;(2)由题意得,S=x(50−2x)=−2x2+50x=−2(x−12.5)2+312.5,12.5≤x<25∴x=12.5时,S取得最大值,此时,S=312.5,所以,当x为12.5米时,S有最大值,最大值是312.5平方米.。
历年高考真题分类汇编---指数、对数、幂函数.doc

温馨提示:此题库为Word 版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,关闭Word 文档返回原板块。
考点7 指数函数、对数函数、幂函数一、选择题1. (2013·大纲版全国卷高考文科·T6)与(2013·大纲版全国卷高考理科·T5)相同函数)0)(11(log )(2>+=x xx f 的反函数()1=f x -( )A.()1021x x >- B.()1021xx ≠- C.()21x x R -∈ D.()210xx -> 【解题指南】首先令)11(log 2xy +=求出x ,然后将y x ,互换,利用反函数的定义域为原函数的值域求解.【解析】选A.由)11(log 2xy +=,0>x ,得函数的值域为0>y ,又x y 112+=,解得121-=y x ,所以()1=f x -121-x )0(>x 2.(2013·北京高考理科·T5)函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=e x 关于y 轴对称,则f(x)= ( )A.e x+1B.e x-1C.e -x+1D.e -x-1 【解题指南】把上述变换过程逆过来,求出y=e x 关于y 轴对称的函数,再向左平移1个单位长度得到f(x).【解析】选D.与y=e x 关于y 轴对称的函数应该是y=e -x ,于是f(x)可由y=e -x 向左平移1个单位长度得到,所以f(x)=e -(x+1)=e -x-1. 3.(2013·广东高考文科·T2)函数lg(1)()1x f x x +=-的定义域是( )A .(1,)-+∞B .[1,)-+∞C .(1,1)(1,)-+∞D .[1,1)(1,)-+∞ 【解题指南】函数的定义域有两方面的要求:分母不为零,真数大于零,据此列不等式即可获解.【解析】选C. 解不等式10,10x x +>-≠可得1,1x x >-≠是定义域满足的条件.4.(2013·山东高考文科·T5)函数()f x =( )A.(-3,0]B.(-3,1]C.(,3)(3,0]-∞--D.(,3)(3,1]-∞--【解题指南】定义域的求法:偶次根式为非负数,分母不为0.【解析】选A. ⎩⎨⎧>+≥-03021x x ,解得03≤<-x .5.(2013·陕西高考文科·T3)设a, b, c 均为不等于1的正实数, 则下列等式中恒成立的是 ( ) A .·log log log a c c b a b =B. b a b c c a log log log =⋅C. c b bc a a a log log )(log ⋅=D.()log g og o l l a a a b b c c +=+【解题指南】a, b,c ≠1,掌握对数两个公式:abb y x xyc c a a a a log log log ,log log log =+= 并灵活转换即可得解.【解析】选B.对选项A: bab a b bc c a c c a log log log log log log =⇒=⋅,显然与第二个公式不符,所以为假。
指数函数与对数函数高考题(含答案)

指数函数与对数函数高考题1、(2009湖南文)2log )A .BC .12-D . 122、(2012安徽文)23log 9log 4⨯=( )A .14B .12C .2D .43、(2009全国Ⅱ文)设2lg ,(lg ),lg a e b e c === ( )A.a b c >>B.a c b >>C.c a b >>D.c b a >>4、(2009广东理)若函数()y f x =是函数(0,1)x y a a a =>≠且的反函数,其图像经过点)a ,则()f x =( )A. 2log xB. 12log x C.12x D. 2x 5、(2009四川文)函数)(21R x y x ∈=+的反函数是( )A. )0(log 12>+=x x yB. )1)(1(log 2>-=x x yC. )0(log 12>+-=x x yD. )1)(1(log 2->+=x x y6、(2009全国Ⅱ理)设323log ,log log a b c π=== )A. a b c >>B. a c b >>C. b a c >>D. b c a >>7、(2009天津文)设3.02131)21(,3log ,2log ===c b a ,则( )A.c b a <<B. b c a <<C. a c b << D .c a b <<8、(2009湖南理) 若2log a <0,1()2b >1,则 ( )A .a >1,b >0B .a >1,b <0 C. 0<a <1, b >0 D. 0<a <1, b <09、(2009江苏)已知集合{}2log 2,(,)A x x B a =≤=-∞,若A B ⊆则实数a 的取值范围是(,)c +∞,其中c =10、(2010辽宁文)设25a b m ==,且112a b+=,则m =( )11、(2010全国文)函数)1)(1ln(1>-+=x x y 的反函数是( )A.y=1x e +-1(x>0)B. y=1x e -+1(x>0)C. y=1x e +-1(x ∈R)D.y=1x e -+1 (x∈R)12、(2012上海文)方程03241=--+x x 的解是_________ .13、(2011四川理)计算21100)25lg 41(lg -÷-_______ . 14、(2011江苏)函数)12(log )(5+=x x f 的单调增区间是__________ 。
指数函数与对数函数高考题(含标准答案)

指数函数与对数函数高考题1、(2009湖南文)2log )A .BC .12-D . 122、(2012安徽文)23log 9log 4⨯=( )A .14B .12C .2D .43、(2009全国Ⅱ文)设2lg ,(lg ),lg a e b e c === ( )A.a b c >>B.a c b >>C.c a b >>D.c b a >>4、(2009广东理)若函数()y f x =是函数(0,1)x y a a a =>≠且的反函数,其图像经过点)a ,则()f x =( )A. 2log xB. 12log x C.12x D. 2x 5、(2009四川文)函数)(21R x y x ∈=+的反函数是( )A. )0(log 12>+=x x yB. )1)(1(log 2>-=x x yC. )0(log 12>+-=x x yD. )1)(1(log 2->+=x x y6、(2009全国Ⅱ理)设323log ,log log a b c π=== )A. a b c >>B. a c b >>C. b a c >>D. b c a >>7、(2009天津文)设3.02131)21(,3log ,2log ===c b a ,则( )A.c b a <<B. b c a <<C. a c b << D .c a b <<8、(2009湖南理) 若2log a <0,1()2b >1,则 ( )A .a >1,b >0B .a >1,b <0 C. 0<a <1, b >0 D. 0<a <1, b <09、(2009江苏)已知集合{}2log 2,(,)A x x B a =≤=-∞,若A B ⊆则实数a 的取值范围是(,)c +∞,其中c =10、(2010辽宁文)设25a b m ==,且112a b+=,则m =( )11、(2010全国文)函数)1)(1ln(1>-+=x x y 的反函数是( )A.y=1x e +-1(x>0)B. y=1x e -+1(x>0)C. y=1x e +-1(x ∈R)D.y=1x e -+1 (x∈R)12、(2012上海文)方程03241=--+x x 的解是_________ .13、(2011四川理)计算21100)25lg 41(lg -÷-_______ .14、(2011江苏)函数)12(log )(5+=x x f 的单调增区间是__________ 。
指数函数和对数函数历年高考习题汇编附答案

欢迎共阅历届高考中的“指数函数和对数函数”试题汇编大全一、选择题1、已知⎩⎨⎧≥<+-=1,log 1,4)13()(x x x a x a x f a是(,)-∞+∞上的减函数,那么a 的取值范围是(A )(0,1) (B )1(0,)3 (C )11[,73 (D )1[,1)72.、函数y=㏒x(x ﹥1)的反函数是3、设A.,(-044、函数5A.C.6A .2ln (0)x x >C .ln 2(x x +>7、已知函数()ln 1(0)f x x x =+>,则()f x 的反函数为(A )1()x y e x R +=∈ (B )1()x y e x R -=∈(C )1(1)x y e x +=> (D )1(1)x y e x -=>8、函数y =f (x )的图像与函数g (x )=log 2x (x >0)的图像关于原点对称,则f (x )的表达式为 (A )f (x )=(x >0)(B )f (x )=log 2(-x )(x <0)(C )f (x )=-log 2x (x >0)(D )f (x )=-log 2(-x )(x <0) 9、函数y=1+a x (0<a <1)的反函数的图象大致是(A )(B )(C )(D )10、设f (x )=1232,2,log (1),2,x e x x x -⎧<⎪⎨-≥⎪⎩则不等式f (x )>2的解集为 (A)(1,2)⋃(3,+∞)(B)(10,+∞) (C)(1,2)⋃(10,+∞)(D)(1,2)16.(2006陕西理)设函数f(x)=log a (x+b)(a>0,a ≠1)的图象过点(2,1),其反函数的图像过点(2,8),则a+b等于()A.6B.5C.4D.319、(2006天津理)已知函数)(x f y =的图象与函数x a y =(0>a 且1≠a )的图象关于直线xy =是( A .,2[22.((A)1<n 23、(A.(1.A .(2. A 4.(2005天津理科)若函数)1,0( )(log )(≠>-=a a ax x x f a 在区间)0,2(-内单调递增,则a 的取值范围是 ()A .)1,41[B .)1,43[C .),49(+∞D .)49,1(5.(2005天津理科)设)(1x f -是函数)1( )(21)(>-=-a a a x f x x 的反函数,则使1)(1>-x f 成立的x 的取值范围为 ()A .),21(2+∞-a aB .)21,(2a a --∞C .),21(2a aa - D .),[+∞a8.(2005上海理、文)若函数121)(+=x x f ,则该函数在()+∞∞-,上是 ()A .单调递减无最小值B .单调递减有最小值C .单调递增无最大值D .单调递增有最大值 9.(2005湖南理、文)函数f (x )=x 21-的定义域是( ) A .(-∞,0] B .[0,+∞)C .(-∞,0) D .(-∞,+∞)18.(2005湖北卷理、文)函数|1|||ln --=x e y x 的图象大致是()19.(2005湖北理、文)在x y x y x y y x 2cos ,,log ,222====这四个函数中,当1021<<<x x 时,使2)()()2(2121x f x f x x f +>+恒成立的函数的个数是() A .0 B .1 C .2 D .320.(2005山东文、理)下列函数中既是奇函数,又是区间[]1,1-上单调递减的是(A )()sin f x x =(B)()1f x x =-+(C)1()()2x x f x a a -=+(D)2()2xf x ln x-=+21.(2005山东理、文)函数⎪⎩⎪⎨⎧≥<<-=-0,01,)sin()(12x ex x x f x π,若2)()1(=+a f f ,则a 的所有可能值为( )A.1 B.1,22-C.22- D.1,22 22.(2005山东理科)01a <<,下列不等式一定成立的是()A .B .C .D .3.(20064.(6][()27f n +,则(f m +6.(7、(。
指数函数与对数函数高考题及答案
指数函数与对数函数(一)选择题(共15题)1.(安徽卷文7)设232555322555a b c ===(),(),(),则a ,b ,c 的大小关系是 (A )a >c >b (B )a >b >c (C )c >a >b (D )b >c >a【答案】A【解析】25y x =在0x >时是增函数,所以a c >,2()5xy =在0x >时是减函数,所以c b >。
【方法总结】根据幂函数与指数函数的单调性直接可以判断出来.2.(湖南卷文8)函数y=ax2+ bx 与y= ||log b ax(ab ≠0,| a |≠| b |)在同一直角坐标系中的图像可能是【答案】D【解析】对于A 、B 两图,|b a |>1而ax2+ bx=0的两根之和为 -b a ,由图知0<-b a <1得-1<ba <0,矛盾,对于C 、D 两图,0<|b a |<1,在C 图中两根之和-b a <-1,即ba >1矛盾,选D 。
3.(辽宁卷文10)设525bm ==,且112a b +=,则m =(A(B )10 (C )20 (D )100 【答案】D解析:选A.211log 2log 5log 102,10,m m m m a b +=+==∴=又0,m m >∴=4.(全国Ⅰ卷理8文10)设a=3log 2,b=In2,c=125-,则A. a<b<cB. b<c<aC. c<a<b D . c<b<a 【答案】C【解析】 a=3log 2=21log 3, b=In2=21log e ,而22log 3log 1e >>,所以a<b,c=125-=,而222log 4log 3>=>,所以c<a,综上c<a<b.【命题意图】本小题以指数、对数为载体,主要考查指数函数与对数函数的性质、实数大小的比较、换底公式、不等式中的倒数法则的应用.5.(全国Ⅰ卷理10)已知函数F(x)=|lgx|,若0<a<b,且f(a)=f(b),则a+2b 的取值范围是(A))+∞(B))+∞ (C)(3,)+∞ (D)[3,)+∞【答案】A【命题意图】本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a 的取值范围,而利用均值不等式求得a+2b 2a a =+>,从而错选A,这也是命题者的用苦良心之处.【解析】因为 f(a)=f(b),所以|lga|=|lgb|,所以a=b(舍去),或1b a =,所以a+2b=2a a +又0<a<b,所以0<a<1<b ,令2()f a a a =+,由“对勾”函数的性质知函数()f a 在a ∈(0,1)上为减函数,所以f(a)>f(1)=1+21=3,即a+2b 的取值范围是(3,+∞).6.(全国Ⅰ卷文7)已知函数()|lg |f x x =.若a b ≠且,()()f a f b =,则a b +的取值范围是(A)(1,)+∞ (B)[1,)+∞ (C) (2,)+∞ (D) [2,)+∞【答案】C【命题意图】本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a 的取值范围,而利用均值不等式求得a+b=12a a +≥,从而错选D,这也是命题者的用苦良心之处. 7.(山东卷文3)函数()()2log 31x f x =+的值域为A.()0,+∞ B. )0,+∞⎡⎣ C. ()1,+∞ D. )1,+∞⎡⎣ 【答案】A【解析】因为311x+>,所以()()22log 31log 10x f x =+>=,故选A 。
指数函数与对数函数高考题及答案精编版
指数函数与对数函数(一)选择题(共15题)1.(安徽卷文7)设232555322555a b c ===(),(),(),则a ,b ,c 的大小关系是 (A )a >c >b (B )a >b >c (C )c >a >b (D )b >c >a【答案】A【解析】25y x =在0x >时是增函数,所以a c >,2()5xy =在0x >时是减函数,所以c b >。
【方法总结】根据幂函数与指数函数的单调性直接可以判断出来.2.(湖南卷文8)函数y=ax2+ bx 与y= ||log b ax(ab ≠0,| a |≠| b |)在同一直角坐标系中的图像可能是【答案】D【解析】对于A 、B 两图,|b a |>1而ax2+ bx=0的两根之和为 -b a ,由图知0<-b a <1得-1<ba <0,矛盾,对于C 、D 两图,0<|b a |<1,在C 图中两根之和-b a <-1,即ba >1矛盾,选D 。
3.(辽宁卷文10)设525bm ==,且112a b +=,则m =(A(B )10 (C )20 (D )100 【答案】D解析:选A.211log 2log 5log 102,10,m m m m a b +=+==∴=又0,m m >∴=4.(全国Ⅰ卷理8文10)设a=3log 2,b=In2,c=125-,则A. a<b<cB. b<c<aC. c<a<b D . c<b<a 【答案】C【解析】 a=3log 2=21log 3, b=In2=21log e ,而22log 3log 1e >>,所以a<b,c=125-=,而222log 4log 3>=>,所以c<a,综上c<a<b.【命题意图】本小题以指数、对数为载体,主要考查指数函数与对数函数的性质、实数大小的比较、换底公式、不等式中的倒数法则的应用.5.(全国Ⅰ卷理10)已知函数F(x)=|lgx|,若0<a<b,且f(a)=f(b),则a+2b 的取值范围是(A))+∞(B))+∞ (C)(3,)+∞ (D)[3,)+∞【答案】A【命题意图】本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a 的取值范围,而利用均值不等式求得a+2b 2a a =+>,从而错选A,这也是命题者的用苦良心之处.【解析】因为 f(a)=f(b),所以|lga|=|lgb|,所以a=b(舍去),或1b a =,所以a+2b=2a a +又0<a<b,所以0<a<1<b ,令2()f a a a =+,由“对勾”函数的性质知函数()f a 在a ∈(0,1)上为减函数,所以f(a)>f(1)=1+21=3,即a+2b 的取值范围是(3,+∞).6.(全国Ⅰ卷文7)已知函数()|lg |f x x =.若a b ≠且,()()f a f b =,则a b +的取值范围是(A)(1,)+∞ (B)[1,)+∞ (C) (2,)+∞ (D) [2,)+∞【答案】C【命题意图】本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a 的取值范围,而利用均值不等式求得a+b=12a a +≥,从而错选D,这也是命题者的用苦良心之处. 7.(山东卷文3)函数()()2log 31x f x =+的值域为A.()0,+∞ B. )0,+∞⎡⎣ C. ()1,+∞ D. )1,+∞⎡⎣ 【答案】A【解析】因为311x+>,所以()()22log 31log 10x f x =+>=,故选A 。
指数函数与对数函数高考题及答案
指数函数与对数函数之相礼和热创作(一)选择题(共15题)1.(安徽卷文7a,b,c的大小关系是(A)a>c>b (B)a>b>c (C)c>a>b (D)b>c>a【答案】A【方法总结】根据幂函数与指数函数的单调性直接可以判别出来.2.(湖南卷文8)函数y=ax2+ bx与(ab ≠0,| a |≠| b |)在同不停角坐标系中的图像可能是【答案】D【解析】对于A、B两图,而ax2+ bx=0的两根之和为由图知得矛盾,对于C、D两图,在C图中两根之和矛盾,选D.3.(辽宁卷文10(A(B)10 (C)20 (D)100【答案】D解析:选4.(天下Ⅰ卷理8文10)设则A. a<b<cB.b<c<aC. c<a<b D .c<b<a 【答案】C【解析】以是a<b,以是c<a,综上c<a<b.【命题意图】本小题以指数、对数为载体,次要考查指数函数与对数函数的性子、实数大小的比较、换底公式、不等式中的倒数法则的使用.5.(天下Ⅰ卷理10)已知函数F(x)=|lgx|,若0<a<b,且f(a)=f(b),则a+2b的取值范围是【答案】A【命题意图】本小题次要考核对数函数的性子、函数的单调性、函数的值域,考生在做本小题时极易忽视a的取值范围,而利用均值不等式求得从而错选A,这也是命题者的用苦良心之处.【解析】由于f(a)=f(b),以是|lga|=|lgb|,以是a=b(舍往),或又0<a<b,以是0<a<1<b,由“对勾”函数的性子知上为减函数,以是即a+2b的取值范围是(3,+∞).6.(天下Ⅰ卷文7(C)【答案】C【命题意图】本小题次要考核对数函数的性子、函数的单调性、函数的值域,考生在做本小题时极易忽视a的取值范围,而利用均值不等式求得从而错选D,这也是命题者的用苦良心之处.7.(山东卷文3A. B. C. D.【答案】AA.【命题意图】本题考核对数函数的单调性、函数值域的求法等根底学问.8.(陕西卷文7)下列四类函数中,个有性子“对恣意的x>0,y>0,函数f(x)满足f(x+y)=f(x)f(y)”的是 [ ](A)幂函数(B)对数函数(C)指数函数(D)余弦函数【答案】Cf(x+y)=f(x)f(y).9.(上海卷理17【答】()10.(上海卷文17间[答]()(A)(0,1). (B)(1,1.25). (C)(1.25,1.75)(D)(1.75,2)11.(四川卷理3(A)0 (B)1 (C)2 (D)4=log525=2答案:C12.(四川卷文2)函数y=log2x的图象大致是高^考#资*源^网(A) (B) (C) (D)解析:本题考核对数函数的图象和基赋性子.答案:C13.(天津卷文6(A)a<c<b (B) b<c<a (C) a<b<c (D) b<a<c【答案】D【解析】由于以是c最大,清除A、B;又由于a、选D.【命题意图】本题考核对数函数的单调性,属根底题.14.(浙江卷文2(A)0 (B)1 (C)2 (D)3,选B,本题次要调查了对数函数概念及其运算性子,属容易题15.(重庆卷文4(A(D)【答案】Cx>∴40,(二)填空题(共4题)1. (福建卷理15)已知定义域为(0)+∞,的函数()f x 满足:(1)对恣意(0)x ∈+∞,,恒有(2)2()f x f x =成立;(2)当(12]x ∈,时()2f x x =-.给出结论如下:①对恣意m Z ∈,有(2)0m f =; ②函数()f x 的值域为[0)+∞,; ③存在n Z∈,使得(21)9n f +=; ④“函数()f x 在区间()a b ,上单调递减”的充要条件是“存在k Z ∈,使得1()(22)k k a b +⊆,,”.其中全部正确结论的序号是. 【答案】①②④ 【解析】○10)2(2)2(2)22()2(111====⋅=---f f f f m m m m ,正确;○2取]2,2(1+∈m m x ,则]2,1(2∈m x ;m m xx f 22)2(-=,从而xxf x f x f m m m -====+12)2(2)2(2)( ,其中,,2,1,0=m ,从而),0[)(+∞∈x f ,正确;○3122)12(1--=++n m n f ,假设存在n使9)12(=+n f 即存..,,21t s x x 102221=-x x 又x2更如下:2,4,8,16,32,……,显然不存在,以是该命题错误;○4根据后面的分析容易晓得该选项正确;综合有正确的序号是○1○2○4. 【命题意图】本题经过笼统函数,考查了函数的周期性,单调性,以及门生的综合分析才能,难度不大.2.(上海卷理8)对恣意不等于1的负数a ,函数f(x)=log (3)a x +的反函数的图像都经过点P ,则点P 的坐标是 解析:f(x)=log (3)a x +的图像过定点(-2,0),以是其反函数的图像过定点(0,-2)3.(上海卷文9交点坐标是.解析:考查反函数相关概念、性子法一:另x=0,有y=-2x轴交点为(-2,0),利用对称性可知,(0,-2)4.(浙江卷文16)某商家一月份至五月份累计贩卖额达3860万元,预测六月份贩卖额为500万元,七月份贩卖额比六月份递增x%,八月份贩卖额比七月份递增x%,九、十月份贩卖总额与七、八月份贩卖总额相称,若一月至十月份贩卖总额至多至多达7000万元,则,x 的最小值.解析:20;化简【命题意图】本题次要调查了用一元二次不等式处理实践成绩的才能,属中档题。
(完整word版)指数函数与对数函数高考题(含答案),推荐文档

指数函数与对数函数高考题1、 (2009湖南文) Iog 2 .; 2的值为 ()A . ,2B .22、(2012安徽文) Iog 2 9 Iog 3 4 ()A. 1B.1c.423、 (2009全国U 文:)设aIg e,b(Ige)2,cA. a b c B a c b C. c 4、( 2009广东理)若函数y f (x ) 是C .12D.-2D. Ig e,则() a b D.c b a〔y a x (a0,且a 1)的反函数,其图像经过点(、,a,a),则 f (x)()(c,),其中 c= ----------------------10、(2010 辽宁文)设 2a 5b1 1m,且a b 2,则mA. B.10 C.20 D.100A. log 2 xB. log-I x2C. 12xD. x 25、(2009四川文)函数X1y 2 (xR )的反函数是(A. y 1 log 2 x(x0) B . y Iog 2(x 1)(x 1) C . y1 log2 x(x0)D . yIog 2(x 1)(x1)6 ( 2009全国U 理)设 a Iog 3 ,b Iog 2 3,c log^ 2 ,A. a b cB. a c bC. b a cD.7、(2009天津文)设a0.3则(A. a b cB.C.a cb 8、(2009 湖南理)若Iog 2av0, g)b > 1,贝U ( A . a > 1,b > 0B . a > 1,b v 0C.0v a v 1, b > 0D.0v a v 1, b9、(2009江苏)已知集合A x log 2 x 2 ,B,a ),若A B 则实数a 的取值范围是11、(2010全国文)函数y 1 ln(x 1)(x 1)的反函数是()A.y= e x 1-1(x>0)B. y= e x 1+1(x>0)C. y= e x1-1(x R)D.y= e x 1+1 (x R)12、(2012上海文)方程4x2x 1 3 0的解是13、(2011四川理)计算(lg14 lg25)1100 214、(2011江苏)函数f(x)log5(2x 1)的单调增区间是15、(2012北京文)已知函数 f (x) lgx ,若f(ab) 1, f(a2) f(b2)16、(2010安徽文)(7)设a(3),b5(2), c (352)525,则a, b,c的大小关系是17、18、19、20、A.a > c > b(2010四川理)A.0B.a > b> cC.c > a> bD.b > c> a2log510 log 5 0.25B.1C. 2D.4(2010天津文)设a 2log5 4,b (log53), c log 45,则(A. a c bB.C.D.b c a1y (2)x1的图象关于直线y=x对称的图象像大致是((2011四川文)函数(2012四川文)函数21、(2009广东文)若函数y f (x)是函数y a(a 0,且a 1)的反函数,且f (2)1,则C . log i x 2x 322、 (2009北京理)为了得到函数y lg 「的图像,只需把函数y lg x 的图像上所有的10点( )A.向左平移3个单位长度,再向上平移1个单位长度 B .向右平移3个单位长度,再向上平移1个单位长度 C .向左平移3个单位长度,再向下平移1个单位长度 D .向右平移3个单位长度,再向下平移1个单位长度2 x23、 (2009全国U 文)函数y log 2 的图像( )2 xA.关于原点对称B.关于直线y x 对称C.关于y 轴对称D.关于直线y x 对称124、(2009 辽宁文)已知函数 f (x)满足:x > 4,则 f (x) = (-)x ;当 x v 4 时 f(x) = f (x 1), 则 f(2 log 2 3)二()f(x)( )B .29、 (2012 重庆文)设函数 f(x) x 2 4x 3,g(x) 3x 2,集合 M {x R|f(g(x)) 0},N {x R|g(x) 2},则 MIN 为( )A. (1, )B. (0,1)C. (-1,1)D. ( ,1)430、 (2012上海春)函数y log ?x ------------------ (x [2,4])的最大值是log 2 x31、 (2011重庆文)若实数£ ,T 满足」」-'',贝听的最大是 ________ .32、 (2012 北京文)已知 f(x) m(x 2m)(x m 3) , g(x) 2x 2 .若 x R, f(x) 0 或g(x) 0,则m 的取值范围是 ____________ — 33、 (2012上海文理)已知函数f(x) lg(x 1).(1)若0f(12x) f(x) 1 ,求x 的取值范围;A.—B.— C.1 D.-241288log 2 x,x 0,25、 (2010天津理) 若函数f (x )= log 1( x), x 02,若 f(a) f(a ),则实数 a 的取值范围是()A. (-1,0)U(0,1) B. (- x ,-1 ) U (1,+ x)C .(-1,0)U(1,+ %)D. (- x ,-1 ) U (0,1)log 3 x,x 0r ,126(2010湖北已知函数f (x ),则 PL))( )2x,x 09A.4B. 1C.-4D- 144 27、 (2011安徽文)若点(a, b )在ylg x 图像上, a 1,则下列点也在此图像上的是( )1 A. (— ,b)B.(10a,b)C.(®,b 1) D.(a 2,2b)aa21x,x 1f(x)28、 (2011辽宁理)设函数 1 log 2 x, x 1 则满足f (x ) 2的x 的取值范围是 ()A . [ 1,2]B . [0,2]C . [1, )[1,+ ]D . [0,)⑵若g(x)是以2为周期的偶函数,且当0 x 1时,有g(x) f (x),求函数y g(x) (x [1,2])的反函数.5指数函数与对数函数参考答案11-log 22 —,易知D 正确.222、 【解析】选D log 29 log 34 他 S 塑 如 4lg 2 lg3 lg 2 lg313、 【解析】本题考查对数函数的增减性,由1>lge>0,知a>b,又c=- lge,作商比较知c>b, 选B o5、【解析】由y 2X 1 x 1 log 2 y x 1 log 2 y ,又因原函数的值域是y 0 ,二其反函数是y 1 log 2 x(x 0)6【解析】Qlog 3 2 log 2 .2 log 2 3 b c log 2 3 log 2 2 Iog 3 3 Iog 3a b a b c7、【解析】由已知结合对数函数图像和指数函数图像得到 a 0,0 c 1,而b log 2 3 1, 因此选D o【考点定位】本试题考查了对数函数和指数函数的性质运用,考查了基本的运算能力。
指数函数与对数函数试题(含详解)

指数函数与对数函数试题(含详解)————————————————————————————————作者:————————————————————————————————日期:指数函数1.指数函数概念 一般地,函数叫做指数函数,其中是自变量,函数的定义域为.2.指数函数函数性质: 函数名称 指数函数 定义函数且叫做指数函数图象定义域 值域过定点 图象过定点,即当时,.奇偶性 非奇非偶单调性在上是增函数在上是减函数函数值的 变化情况变化对图象的影响在第一象限内,从逆时针方向看图象,逐渐增大;在第二象限内,从逆时针方向看图象,逐渐减小.对数函数及其性质1.对数函数定义 一般地,函数叫做对数函数,其中是自变量,函数的定义域.2.对数函数性质: 函数名称 对数函数定义函数且叫做对数函数图象定义域值域 过定点 图象过定点,即当时,.奇偶性 非奇非偶单调性在上是增函数 在上是减函数函数值的 变化情况变化对图象的影响 在第一象限内,从顺时针方向看图象,逐渐增大;在第四象限内,从顺时针方向看图象,逐渐减小.指数函数习题一、选择题1.定义运算a ⊗b =⎩⎨⎧a a ≤bb a >b,则函数f (x )=1⊗2x 的图象大致为( )2.函数f (x )=x 2-bx +c 满足f (1+x )=f (1-x )且f (0)=3,则f (b x )与f (c x )的大小关系是( ) A .f (b x )≤f (c x ) B .f (b x )≥f (c x ) C .f (b x )>f (c x )D .大小关系随x 的不同而不同3.函数y =|2x -1|在区间(k -1,k +1)内不单调,则k 的取值范围是( ) A .(-1,+∞) B .(-∞,1) C .(-1,1) D .(0,2)4.设函数f (x )=ln[(x -1)(2-x )]的定义域是A ,函数g (x )=lg(a x -2x -1)的定义域是B ,若A ⊆B ,则正数a 的取值范围( ) A .a >3 B .a ≥3 C .a > 5D .a ≥ 55.已知函数f (x )=⎩⎨⎧3-a x -3,x ≤7,a x -6,x >7.若数列{a n }满足a n =f (n )(n ∈N *),且{a n }是递增数列,则实数a 的取值范围是( )A .[94,3)B .(94,3)C .(2,3)D .(1,3)6.已知a >0且a ≠1,f (x )=x 2-a x ,当x ∈(-1,1)时,均有f (x )<12,则实数a 的取值范围是( )A .(0,12]∪[2,+∞)B .[14,1)∪(1,4]C .[12,1)∪(1,2]D .(0,14)∪[4,+∞)二、填空题7.函数y =a x(a >0,且a ≠1)在[1,2]上的最大值比最小值大a2,则a 的值是________.8.若曲线|y |=2x +1与直线y =b 没有公共点,则b 的取值范围是________.9.(2011·滨州模拟)定义:区间[x 1,x 2](x 1<x 2)的长度为x 2-x 1.已知函数y =2|x |的定义域为[a ,b ],值域为[1,2],则区间[a ,b ]的长度的最大值与最小值的差为________.三、解答题 10.求函数y =2342x x ---+的定义域、值域和单调区间.11.(2011·银川模拟)若函数y =a 2x +2a x-1(a >0且a ≠1)在x ∈[-1,1]上的最大值为14,求a 的值.12.已知函数f (x )=3x ,f (a +2)=18,g (x )=λ·3ax -4x 的定义域为[0,1]. (1)求a 的值;(2)若函数g (x )在区间[0,1]上是单调递减函数,求实数λ的取值范围.1.解析:由a ⊗b =⎩⎨⎧a a ≤bb a >b得f (x )=1⊗2x=⎩⎨⎧2xx ≤01x >0.答案:A2. 解析:∵f (1+x )=f (1-x ),∴f (x )的对称轴为直线x =1,由此得b =2. 又f (0)=3,∴c =3.∴f (x )在(-∞,1)上递减,在(1,+∞)上递增.若x ≥0,则3x ≥2x ≥1,∴f (3x )≥f (2x). 若x <0,则3x <2x <1,∴f (3x )>f (2x ). ∴f (3x )≥f (2x ). 答案:A3.解析:由于函数y =|2x-1|在(-∞,0)内单调递减,在(0,+∞)内单调递增,而函数在区间(k -1,k +1)内不单调,所以有k -1<0<k +1,解得-1<k <1. 答案:C4. 解析:由题意得:A =(1,2),a x -2x >1且a >2,由A ⊆B 知a x -2x>1在(1,2)上恒成立,即a x -2x -1>0在(1,2)上恒成立,令u (x )=a x -2x -1,则u ′(x )=a x ln a -2x ln2>0,所以函数u (x )在(1,2)上单调递增,则u (x )>u (1)=a -3,即a ≥3. 答案:B5. 解析:数列{a n }满足a n =f (n )(n ∈N *),则函数f (n )为增函数,注意a 8-6>(3-a )×7-3,所以⎩⎨⎧a >13-a >0a 8-6>3-a7-3,解得2<a <3.答案:C6. 解析:f (x )<12⇔x 2-a x <12⇔x 2-12<a x ,考查函数y =a x 与y =x 2-12的图象,当a >1时,必有a -1≥12,即1<a ≤2,当0<a <1时,必有a ≥12,即12≤a <1,综上,12≤a <1或1<a ≤2.答案:C7. 解析:当a >1时,y =a x 在[1,2]上单调递增,故a 2-a =a 2,得a =32.当0<a <1时,y=a x 在[1,2]上单调递减,故a -a 2=a 2,得a =12.故a =12或32.答案:12或328. 解析:分别作出两个函数的图象,通过图象的交点个数来判断参数的取值范围.曲线|y |=2x +1与直线y =b 的图象如图所示,由图象可得:如果|y |=2x +1与直线y =b 没有公共点,则b 应满足的条件是b ∈[-1,1]. 答案:[-1,1]9. 解析:如图满足条件的区间[a ,b ],当a =-1,b =0或a =0,b =1时区间长度最小,最小值为1,当a =-1,b =1时区间长度最大,最大值为2,故其差为1. 答案:110. 解:要使函数有意义,则只需-x 2-3x +4≥0,即x 2+3x -4≤0,解得-4≤x ≤1. ∴函数的定义域为{x |-4≤x ≤1}.令t =-x 2-3x +4,则t =-x 2-3x +4=-(x +32)2+254,∴当-4≤x ≤1时,t max =254,此时x =-32,t min =0,此时x =-4或x =1.∴0≤t ≤254.∴0≤-x 2-3x +4≤52.∴函数y =2341()2x x ---+的值域为[28,1]. 由t =-x 2-3x +4=-(x +32)2+254(-4≤x ≤1)可知,当-4≤x ≤-32时,t 是增函数,当-32≤x ≤1时,t 是减函数.根据复合函数的单调性知:y =2341()2x x ---+在[-4,-32]上是减函数,在[-32,1]上是增函数.∴函数的单调增区间是[-32,1],单调减区间是[-4,-32].11. 解:令a x =t ,∴t >0,则y =t 2+2t -1=(t +1)2-2,其对称轴为t =-1.该二次函数在[-1,+∞)上是增函数.①若a >1,∵x ∈[-1,1],∴t =a x ∈[1a,a ],故当t =a ,即x =1时,y max =a 2+2a -1=14,解得a =3(a =-5舍去). ②若0<a <1,∵x ∈[-1,1],∴t =a x ∈[a ,1a ],故当t =1a,即x =-1时,y max =(1a+1)2-2=14.∴a =13或-15(舍去).综上可得a =3或13.12. 解:法一:(1)由已知得3a +2=18⇒3a=2⇒a =log 32. (2)此时g (x )=λ·2x -4x , 设0≤x 1<x 2≤1,因为g (x )在区间[0,1]上是单调减函数,所以g (x 1)-g (x 2)=(2x 1-2x 2)(λ-2x 2-2x 1)>0恒成立,即λ<2x 2+2x 1恒成立.由于2x 2+2x 1>20+20=2,所以实数λ的取值范围是λ≤2. 法二:(1)同法一.(2)此时g (x )=λ·2x -4x ,因为g (x )在区间[0,1]上是单调减函数,所以有g ′(x )=λln2·2x -ln4·4x =ln2[-2·(2x )2+λ·2x ]≤0成立.设2x =u ∈[1,2],上式成立等价于-2u 2+λu ≤0恒成立. 因为u ∈[1,2],只需λ≤2u 恒成立, 所以实数λ的取值范围是λ≤2.对数函数同步练习一、选择题1、已知32a =,那么33log 82log 6-用a 表示是( )A 、2a -B 、52a -C 、23(1)a a -+D 、 23a a -2、2log (2)log log a a a M N M N -=+,则NM的值为( ) A 、41 B 、4 C 、1 D 、4或1 3、已知221,0,0x y x y +=>>,且1log (1),log ,log 1y a a a x m n x+==-则等于( )A 、m n +B 、m n -C 、()12m n +D 、()12m n - 4、如果方程2lg (lg5lg 7)lg lg5lg 70x x +++=的两根是,αβ,则αβ的值是( )A 、lg5lg7B 、lg35C 、35D 、351 5、已知732log [log (log )]0x =,那么12x -等于( ) A 、13B 、123C 、122D 、1336、函数2lg 11y x ⎛⎫=-⎪+⎝⎭的图像关于( ) A 、x 轴对称 B 、y 轴对称 C 、原点对称 D 、直线y x =对称7、函数(21)log 32x y x -=-的定义域是( )A 、()2,11,3⎛⎫+∞ ⎪⎝⎭B 、()1,11,2⎛⎫+∞ ⎪⎝⎭C 、2,3⎛⎫+∞ ⎪⎝⎭D 、1,2⎛⎫+∞ ⎪⎝⎭8、函数212log (617)y x x =-+的值域是( )A 、RB 、[)8,+∞C 、(),3-∞-D 、[)3,+∞ 9、若log 9log 90m n <<,那么,m n 满足的条件是( )A 、 1 m n >>B 、1n m >>C 、01n m <<<D 、01m n <<< 10、2log 13a <,则a 的取值范围是( )A 、()20,1,3⎛⎫+∞ ⎪⎝⎭B 、2,3⎛⎫+∞ ⎪⎝⎭C 、2,13⎛⎫⎪⎝⎭D 、220,,33⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭11、下列函数中,在()0,2上为增函数的是( ) A 、12log (1)y x =+ B 、22log 1y x =-C 、21log y x= D 、212log (45)y x x =-+12、已知()log x+1 (01)a g x a a =>≠且在()10-,上有()0g x >,则1()x f x a+=是( )A 、在(),0-∞上是增加的B 、在(),0-∞上是减少的C 、在(),1-∞-上是增加的D 、在(),0-∞上是减少的 二、填空题13、若2log 2,log 3,m n a a m n a +=== 。
(完整版)指数函数与对数函数高考题(含答案)

指数函数与对数函数高考题1、(2009湖南文)2log )A .BC .12-D . 122、(2012安徽文)23log 9log 4⨯=( )A .14B .12C .2D .43、(2009全国Ⅱ文)设2lg ,(lg ),lg a e b e c === ( )A.a b c >>B.a c b >>C.c a b >>D.c b a >>4、(2009广东理)若函数()y f x =是函数(0,1)x y a a a =>≠且的反函数,其图像经过点)a ,则()f x =( )A. 2log xB. 12log x C.12xD. 2x 5、(2009四川文)函数)(21R x y x ∈=+的反函数是( )A. )0(log 12>+=x x yB. )1)(1(log 2>-=x x yC. )0(log 12>+-=x x yD. )1)(1(log 2->+=x x y6、(2009全国Ⅱ理)设323log ,log log a b c π=== )A. a b c >>B. a c b >>C. b a c >>D. b c a >>7、(2009天津文)设3.02131)21(,3log ,2log ===c b a ,则( )A.c b a <<B. b c a <<C. a c b << D .c a b <<8、(2009湖南理) 若2log a <0,1()2b >1,则 ( )A .a >1,b >0B .a >1,b <0 C. 0<a <1, b >0 D. 0<a <1, b <09、(2009江苏)已知集合{}2log 2,(,)A x x B a =≤=-∞,若A B ⊆则实数a 的取值范围是(,)c +∞,其中c =10、(2010辽宁文)设25a b m ==,且112a b+=,则m =( )11、(2010全国文)函数)1)(1ln(1>-+=x x y 的反函数是( )A.y=1x e +-1(x>0)B. y=1x e -+1(x>0)C. y=1x e +-1(x ∈R)D.y=1x e -+1 (x∈R)12、(2012上海文)方程03241=--+x x 的解是_________ .13、(2011四川理)计算21100)25lg 41(lg -÷-_______ .14、(2011江苏)函数)12(log )(5+=x x f 的单调增区间是__________ 。
指数函数与对数函数高考题(含答案)

指数函数与对数函数高考题1、(2009湖南文)2log )A .BC .12-D . 122、(2012安徽文)23log 9log 4⨯=( )A .14B .12C .2D .43、(2009全国Ⅱ文)设2lg ,(lg ),lg a e b e c === ( )A.a b c >>B.a c b >>C.c a b >>D.c b a >>4、(2009广东理)若函数()y f x =是函数(0,1)x y a a a =>≠且的反函数,其图像经过点)a ,则()f x =( )A. 2log xB. 12log x C.12xD. 2x 5、(2009四川文)函数)(21R x y x ∈=+的反函数是( )A. )0(log 12>+=x x yB. )1)(1(log 2>-=x x yC. )0(log 12>+-=x x yD. )1)(1(log 2->+=x x y6、(2009全国Ⅱ理)设323log ,log log a b c π===,则( )A. a b c >>B. a c b >>C. b a c >>D. b c a >>7、(2009天津文)设3.02131)21(,3log ,2log ===c b a ,则( )A.c b a <<B. b c a <<C. a c b << D .c a b <<8、(2009湖南理) 若2log a <0,1()2b >1,则 ( )A .a >1,b >0B .a >1,b <0 C. 0<a <1, b >0 D. 0<a <1, b <09、(2009江苏)已知集合{}2log 2,(,)A x x B a =≤=-∞,若A B ⊆则实数a 的取值范围是(,)c +∞,其中c =10、(2010辽宁文)设25a b m ==,且112a b+=,则m =( )11、(2010全国文)函数)1)(1ln(1>-+=x x y 的反函数是( )A.y=1x e +-1(x>0)B. y=1x e -+1(x>0)C. y=1x e +-1(x ∈R)D.y=1x e -+1 (x∈R)12、(2012上海文)方程03241=--+x x 的解是_________ .13、(2011四川理)计算21100)25lg 41(lg -÷-_______ .14、(2011江苏)函数)12(log )(5+=x x f 的单调增区间是__________ 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
历届高考中的“指数函数和对数函数”试题汇编大全一、选择题 1、已知⎩⎨⎧≥<+-=1,log 1,4)13()(x x x a x a x f a是(,)-∞+∞上的减函数,那么a 的取值范围是(A )(0,1) (B )1(0,)3(C )11[,)73(D )1[,1)72.、函数y=㏒21-x x(x ﹥1)的反函数是 =122-x x (x >0) = 122-x x (x <0) =x x 212- (x >0) D. .y =xx 212- (x <0) 3、设f(x)=x x -+22lg,则)2()2(xf x f +的定义域为 A. ),(),(-4004Y B.(-4,-1)Y (1,4) C. (-2,-1)Y (1,2) D. (-4,-2)Y (2,4)4、函数y =( )A.(3,+∞)B.[3, +∞)C.(4, +∞)D.[4, +∞)5、与方程221(0)xx y ee x =-+≥的曲线关于直线y x =对称的曲线的方程为( )A.ln(1y =+ B.ln(1y =C.ln(1y =-+D.ln(1y =--6、已知函数xy e =的图象与函数()y f x =的图象关于直线y x =对称,则A .()22()xf x e x R =∈ B .()2ln 2ln (0)f x x x =>gC .()22()xf x e x R =∈ D .()2ln ln 2(0)f x x x =+>7、已知函数()ln 1(0)f x x x =+>,则()f x 的反函数为(A )1()x y e x R +=∈ (B )1()x y e x R -=∈ (C )1(1)x y e x +=> (D )1(1)x y e x -=> 8、函数y =f (x )的图像与函数g (x )=log 2x (x >0)的图像关于原点对称,则f (x )的表达式为 (A )f (x )=1log 2x (x >0) (B )f (x )=log 2(-x )(x <0)(C )f (x )=-log 2x (x >0) (D )f (x )=-log 2(-x )(x <0) 9、函数y=1+a x (0<a <1)的反函数的图象大致是(A ) (B ) (C ) (D )10、设f (x )= 1232,2,log (1),2,x e x x x -⎧<⎪⎨-≥⎪⎩ 则不等式f (x )>2的解集为 (A)(1,2)⋃(3,+∞) (B)(10,+∞) (C)(1,2)⋃ (10 ,+∞) (D)(1,2)16. (2006陕西理)设函数f(x)=log a (x+b)(a>0,a ≠1)的图象过点(2,1),其反函数的图像过点(2,8),则a+b 等于( )19、(2006天津理)已知函数)(x f y =的图象与函数xa y =(0>a 且1≠a )的图象关于直线x y =对称,记]1)2(2)()[()(-+=f x f x f x g .若)(x g y =在区间]2,21[上是增函数,则实数a 的取值范围是( ) A .),2[+∞ B .)2,1()1,0(Y C .)1,21[ D .]21,0( 22.(2006浙江理)已知0<a <1,log 1m <log 1n <0,则 (A)1<n <m (B) 1<m <n (C)m <n <1 (D) n <m <1 23、(2006广东)函数2()lg(31)f x x ++的定义域是A.1(,)3-+∞B. 1(,1)3-C. 11(,)33-D. 1(,)3-∞-(2005年)1.(2005全国卷Ⅰ理、文)设10<<a ,函数)22(log )(2--=xx a a a x f ,则使0)(<x f 的x 的取值范围是( )A .()0,∞-B .()+∞,0C .()3log ,a ∞-D .()+∞,3log a 2.(2005全国卷Ⅲ理、文)若ln 2ln 3ln 5,,235a b c ===,则( )A .a <b<cB .c<b<aC .c<a <bD .b<a <c4.(2005天津理科)若函数)1,0( )(log )(3≠>-=a a ax x x f a 在区间)0,21(-内单调递增,则a 的取值范围是 ( )A .)1,41[B . )1,43[C .),49(+∞D .)49,1(5.(2005天津理科)设)(1x f-是函数)1( )(21)(>-=-a a a x f x x的反函数,则使1)(1>-x f 成立的x 的取值范围为( )A .),21(2+∞-a aB . )21,(2a a --∞C . ),21(2a aa - D . ),[+∞a8.(2005上海理、文)若函数121)(+=x x f ,则该函数在()+∞∞-,上是( )A .单调递减无最小值B .单调递减有最小值C .单调递增无最大值D .单调递增有最大值9.(2005湖南理、文)函数f (x )=x21-的定义域是( )A .(-∞,0]B .[0,+∞)C .(-∞,0)D .(-∞,+∞))函数y=|log 2x|()>,112.(2005辽宁卷)函数1ln(2++=x x y )的反函数是( )A .2xx e e y -+= B .2x x e e y -+-=C .2xx e e y --= D .2x x e e y ---=13.(2005辽宁卷)若011log 22<++aa a,则a 的取值范围是 ( )A .),21(+∞B .),1(+∞C .)1,21(D .)21,0(14.(2005江西理、文)已知实数a , b 满足等式,)31()21(ba=下列五个关系式①0<b <a ②a <b <0 ③0<a <b ④b <a <0 ⑤a =b 其中不可能...成立的关系式有 ( ) A .1个 B .2个 C .3个 D .4个A .)3,0(B .)2,3(C .)4,3(D .)4,2(17、(2005江苏)函数)(321R x y x∈+=-的反函数的解析表达式为( )A .32log 2-=x y B .23log 2-=x y C .23log 2x y -= D .xy -=32log 2 18.(2005湖北卷理、文)函数|1|||ln --=x ey x 的图象大致是( )19.(2005湖北理、文)在x y x y x y y x2cos ,,log ,222====这四个函数中,当1021<<<x x 时,使2)()()2(2121x f x f x x f +>+恒成立的函数的个数是( )A .0B .1C .2D .320.(2005山东文、理)下列函数中既是奇函数,又是区间[]1,1-上单调递减的是(A )()sin f x x = (B) ()1f x x =-+ (C) 1()()2x x f x a a -=+ (D) 2()2xf x lnx-=+ 21.(2005山东理、文)函数⎪⎩⎪⎨⎧≥<<-=-0,01,)sin()(12x ex x x f x π,若2)()1(=+a f f ,则a 的所有可能值为( ) A.1 B.1,22-C.22- D. 1,22 22.(2005山东理科) 01a <<,下列不等式一定成立的是 ( )A .(1)(1)log (1)log (1)2a a a a +--++>B .(1)(1)log (1)log (1)a a a a +--<+C .(1)(1)log (1)log (1)a a a a +--++<(1)(1)log (1)log (1)a a a a +--++D .(1)(1)log (1)log (1)a a a a +---+<(1)(1)log (1)log (1)a a a a +---+ 二、填空题(2006年)3.(2006江苏)不等式3)61(log 2≤++xx 的解集为 _______ 4.(2006江西文、理)设3()log (6)f x x =+的反函数为1()f x -,若11[()6][()6]27f m f n --++=g,则()f m n +=.6.(2006辽宁文、理)设,0.(),0.x e x g x lnx x ⎧≤=⎨>⎩ 则1(())2g g =__________7、(2006上海文、理)若函数()(0,1)xf x a a a =>≠且的反函数的图像过点(2,1)-,则___a =。
10.(2006重庆理)设a >0,a ≠1,函数)32lg(2)(+-=x x a x f 有最大值.则不等式log a (x 2-5x +7) >0的解集为_______.(2005年)2.(2005北京文理)对于函数f (x )定义域中任意的x 1,x 2(x 1≠x 2),有如下结论: ①f (x 1+x 2)=f (x 1)·f (x 2);② f (x 1·x 2)=f (x 1)+f (x 2); ③1212()()f x f x x x -->0;④1212()()()22x x f x f x f ++<.当f (x )=l gx 时,上述结论中正确结论的序号是 .3.(2005广东卷)函数xex f -=11)(的定义域是 .5.(2005江苏卷)函数)34(log 25.0x x y -=的定义域为_____________________.6.(2005年江苏卷)若618.03=a,)1,[+∈k k a ,则k =______________. 7.(2005天津文科)设函数x x x f -+=11ln)(,则函数)1()2()(xf x f xg +=的定义域为__________. 8.(2005上海理、文)函数)1(log )(4+=x x f 的反函数)(1x f-=__________.9.(2005上海理、文)方程0224=-÷xx的解是__________. 10.(2005江西理、文)若函数)2(log )(22a x x x f n ++=是奇函数,则a = .11.(2005春考·上海)方程2lg lg(2)0x x -+=的解集是 .。
