优化问题与先进算法-课件PPT(讲义演示稿)
合集下载
网络优化及实例ppt课件

…
运价 20 23 26 29
精品课件
32
…
20
精品课件
21
钢管运输问题(CUMCM-
2000B)
常用解法: 二次规划
先计算最小运费矩阵
➢ 两种运输方式(铁路/公路)混合最短路问题 ➢ 是普通最短路问题的变种,需要自己设计算法
精品课件
22
钢管运输问题(CUMCM-
2000B)
fi表示钢厂i是否使用;xij是从钢厂i运到节点j的钢管量 yj是从节点j向左铺设的钢管量;zj是向右铺设的钢管量
Min
i, j
(
pi
c ij
) xij
0.1 2
15
[(1
j 1
y j ) y j (1 z j ) z j ]
15
s.t. 500 f i xij S i f i , i 1,..., 7. j 1
7
xij y j z j ,
j 1,..., 15 .
cumcm2000b.lg4
性规划模型除了可以利用数学软件求解 外,讨论问题推广时应设计快速近似算法 3.一题多解讨论算法性能比较与分析
应
精品课件
24
大规模数据处理是近年竞赛题的 倾如:向
1. 04年A题:奥运会临时超市网点设计 2. 05年A题:长江水质的评价和预测 3. 05年B题:DVD的在线租赁
难 度逐年增大
•单向? •双向?
精品课件
2
欧拉把哥尼斯堡七桥问题转化为一个 图论上的问题:
精品课件
3
七桥问题 的
顶因
答案是 否定的 点 为
图
中
没
有
偶
度
精品课件
《算法设计与分析》课件

常见的贪心算法包括最小生成树算法 、Prim算法、Dijkstra算法和拓扑排 序等。
贪心算法的时间复杂度和空间复杂度 通常都比较优秀,但在某些情况下可 能需要额外的空间来保存状态。
动态规划
常见的动态规划算法包括斐波那契数列、背包 问题、最长公共子序列和矩阵链乘法等。
动态规划的时间复杂度和空间复杂度通常较高,但通 过优化状态转移方程和状态空间可以显著提高效率。
动态规划算法的时间和空间复杂度分析
动态规划算法的时间复杂度通常为O(n^2),空间复杂度为O(n)。
04 经典问题与算法实现
排序问题
冒泡排序
通过重复地遍历待排序序列,比较相邻元素的大小,交换 位置,使得较大的元素逐渐往后移动,最终达到排序的目 的。
快速排序
采用分治策略,选取一个基准元素,将比基准元素小的元 素移到其左边,比基准元素大的元素移到其右边,然后对 左右两边的子序列递归进行此操作。
动态规划是一种通过将原问题分解为若干个子 问题,并从子问题的最优解推导出原问题的最 优解的算法设计方法。
动态规划的关键在于状态转移方程的建立和状态 空间的优化,以减少不必要的重复计算。
回溯算法
01
回溯算法是一种通过穷举所有可能情况来求解问题的算法设计方法。
02
常见的回溯算法包括排列组合、八皇后问题和图的着色问题等。
空间换时间 分治策略 贪心算法 动态规划
通过增加存储空间来减少计算时间,例如使用哈希表解决查找 问题。
将问题分解为若干个子问题,递归地解决子问题,最终合并子 问题的解以得到原问题的解。
在每一步选择中都采取当前状态下最好或最优(即最有利)的 选择,从而希望导致结果是最好或最优的。
通过将问题分解为相互重叠的子问题,并保存子问题的解,避 免重复计算,提高算法效率。
优化算法讲座.ppt

题目: 优化算法
Optimization Algorithms
内容
§1 绪 论
§2 最佳食品搭配问题
§3 选址问题VRP
§4 最短路线问题 §5 分派问题 §6 最小费用流和最大流量问题 §7 钢管的订购和运输 §8 赛跑数据的二次规划问题 §9 交通运输问题
2
图: GPS基站安排
3
第一节: 绪 论
x47 x57 x67 v
4
8
7 5
8
1
14
3
13
6
31
例7:钢管的订购和运输
要铺设一条从A1 A2 A15的输送天然气的主管道, 如图1 所示. 经筛选, 可以生产这种主管道钢管的钢厂有S1, S2 ,S7. 图中粗 线表示铁路, 单细线表示公路, 双细线表示要铺设的管道(假设沿管 道线或者原来有公路或者建有施工公路). 圆圈表示火车站, 每段铁 路公路和管道旁的阿拉伯数字表示里程(单位km).
14
Matlab求解
Return
1. 线性规划问题:
linprog
2. 有约束的一元函数的最小值: fminbnd
min f (x) s.t. x1 x x2
3. 无约束多元函数最小值:
fminsearch
4. 有约束的多元函数最小值: fmincon
5. 二次规划问题 :
quadprog
aij x j
bi , i
1, 2,..., n.
xi 0, i 1, 2,..., n.
10
11
4. 根据设计变量的允许值
整数规划(0-1规划)和实数规划。
5. 根据变量具有确定值还是随机值
Optimization Algorithms
内容
§1 绪 论
§2 最佳食品搭配问题
§3 选址问题VRP
§4 最短路线问题 §5 分派问题 §6 最小费用流和最大流量问题 §7 钢管的订购和运输 §8 赛跑数据的二次规划问题 §9 交通运输问题
2
图: GPS基站安排
3
第一节: 绪 论
x47 x57 x67 v
4
8
7 5
8
1
14
3
13
6
31
例7:钢管的订购和运输
要铺设一条从A1 A2 A15的输送天然气的主管道, 如图1 所示. 经筛选, 可以生产这种主管道钢管的钢厂有S1, S2 ,S7. 图中粗 线表示铁路, 单细线表示公路, 双细线表示要铺设的管道(假设沿管 道线或者原来有公路或者建有施工公路). 圆圈表示火车站, 每段铁 路公路和管道旁的阿拉伯数字表示里程(单位km).
14
Matlab求解
Return
1. 线性规划问题:
linprog
2. 有约束的一元函数的最小值: fminbnd
min f (x) s.t. x1 x x2
3. 无约束多元函数最小值:
fminsearch
4. 有约束的多元函数最小值: fmincon
5. 二次规划问题 :
quadprog
aij x j
bi , i
1, 2,..., n.
xi 0, i 1, 2,..., n.
10
11
4. 根据设计变量的允许值
整数规划(0-1规划)和实数规划。
5. 根据变量具有确定值还是随机值
2024年算法优化与应用成果展示 PPT模版

算法应用于医疗诊断
在肿瘤识别领域,使用深度学习算 法优化诊断模型,准确率提升至 95%,减少漏诊率。
算法助力金融风控
金融公司利用机器学习算法进行信 贷风险评估,成功识别高风险借款 者,降低违约率20%。
--------->
影响与影响范围
1.算法优化推动产业变革
算法优化技术提升了生产效率,预计2024年将推动全球经济增长2.5%,涉 及行业众多。
4.算法优化的伦理和隐私问题
在算法优化过程中,需关注数据隐私保护,并考虑算法决策可能带来的伦理问题,确保技术的健康发展。
数据质量与多样性
数据质量影响算法效能
据研究表明,数据质量每提升10%,算法准 01
确率可提高5%,突显数据质量对算法优化 的关键作用。
数据多样性促进算法创新
02 实际案例表明,使用多样性数据集训练的算
法,其泛化能力提高30%,证明了数据多样 性对算法创新的积极推动作用。
算法适应性与灵活性
1.算法适应性提升效率
2024年研究显示,适应性强的算法在处理复杂任务时,相比传统算法效率提升30%。
2.算法灵活性增强适应性
灵活性强的算法能更好地适应不同场景,如自适应推荐算法在电商平台上点击率提升 20%。
多领域应用广泛
在医疗、金融、物流等领域,算法优 化技术广泛应用,提高决策准确性和 响应速度。
挑战与机遇并存
随着算法优化技术的不断发展,将面 临数据隐私、伦理等挑战,但也为创 新和发展带来新机遇。
算法优化技术路线图:潜在问题识别
1.优化算法的重要性
优化算法提升效率20%,减少资源浪费10%。
2.实际应用的挑战
Logo/Company
2024年算法优化 与应用成果展示
算法的优化ppt课件

快速排序法:先从这堆书中随便挑出一本,把比它编号小 的放左边,比它编号大的放右边。分成两堆后,再分步直 到所有的书都按序号排好。最后把从小到大排序后的书按 照书架顺序归类,每个书架跑一次,这样并不需要跑很多 次就完成了。
“分治”思想,先保证列表的前半部分都小于后半部分,然 后分别对前半部分和后半部分排序。
群体智能优化算法主要模拟了昆虫、兽群、鸟群 和鱼群的群集行为,这些群体按照一种合作的方 式寻找食物,群体中的每个成员通过学习它自身 的经验和其他成员的经验来不断地改变搜索的方 向。群体智能优化算法的突出特点就是利用了种 群的群体智慧进行协同搜索,从而在解空间内找 到最优解。 模拟生物理想自由分布模型的萤火虫算法 ………
解决方法
• 首先,刷锅; • 然后,煮鸡蛋的同时,叠被,洗脸,刷牙; • 最后,吃早点。(共21分钟)
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
材料四:
• 某车间只有一台高精 度的机床,常常出现 很多零件同时要求用 这台机床加工的情况。 现有6个零件要求加工, 每个零件加工耗时如 下表所示。
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
材料一
• 孙膑是战国时期著名的军事家。齐国的将军田忌 经常同齐威王赛马。马分上、中、下三等,在比 赛时,总是以上等马对上等马,中等马对中等马, 下等马对下等马。齐威王每一个等级的马都要比 田忌的强,所以田忌总是输。孙膑给田忌出了个 主意,比赛时,让他以下等马对齐威王的上等马, 再以上等马对他的中等马,最后以中等马对他的 下等马。比赛结束,田忌以三局两胜的战绩取得 了胜利。同样的马匹,仅仅调换了比赛顺序,就 得到了反败为胜的结果。从算法角度讲,孙膑的 策略是一种经过优化的算法。
“分治”思想,先保证列表的前半部分都小于后半部分,然 后分别对前半部分和后半部分排序。
群体智能优化算法主要模拟了昆虫、兽群、鸟群 和鱼群的群集行为,这些群体按照一种合作的方 式寻找食物,群体中的每个成员通过学习它自身 的经验和其他成员的经验来不断地改变搜索的方 向。群体智能优化算法的突出特点就是利用了种 群的群体智慧进行协同搜索,从而在解空间内找 到最优解。 模拟生物理想自由分布模型的萤火虫算法 ………
解决方法
• 首先,刷锅; • 然后,煮鸡蛋的同时,叠被,洗脸,刷牙; • 最后,吃早点。(共21分钟)
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
材料四:
• 某车间只有一台高精 度的机床,常常出现 很多零件同时要求用 这台机床加工的情况。 现有6个零件要求加工, 每个零件加工耗时如 下表所示。
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
材料一
• 孙膑是战国时期著名的军事家。齐国的将军田忌 经常同齐威王赛马。马分上、中、下三等,在比 赛时,总是以上等马对上等马,中等马对中等马, 下等马对下等马。齐威王每一个等级的马都要比 田忌的强,所以田忌总是输。孙膑给田忌出了个 主意,比赛时,让他以下等马对齐威王的上等马, 再以上等马对他的中等马,最后以中等马对他的 下等马。比赛结束,田忌以三局两胜的战绩取得 了胜利。同样的马匹,仅仅调换了比赛顺序,就 得到了反败为胜的结果。从算法角度讲,孙膑的 策略是一种经过优化的算法。
最优化方法全部ppt课件

解法:Lagrange乘子法
1.2 实例
数据拟合问题 原料切割问题 运输问题 营养配餐问题 分配问题
1.3 基本概念
1. 最优化问题的向量表示法
设 xvx1,x2,L,xnT 则
m i n fx 1 ,x 2 ,L ,x n m i n fx v (1)
以向量为变量的实值函数 定义向量间的序关系(定义1.1):
②取 c0,1,4,9,L并画出相应的曲线(称之为等值线).
③确定极值点位置,并用以往所学方法求之。
易知本题的极小值点 xv* 2,1T。
再复杂点的情形见P13上的例1.7。 虽然三维及以上的问题不便于在平面上画图,图解 法失效,但仍有相应的等值面的概念,且等值面具有以 下性质:
①有不同函数值的等值面互不相交(因目标函数是单值 函数的缘故);
其中
g1 xv0
x1
g2 xv0
x1
L
gv
xv0
g1 xv0
x2
g2 xv0
x2
L
M
g1 xv0
xn
M
g2 xv0
xn
称为向量值函数 gv xv 在点
L
xv 0
g
m xv0
x1
g
m
xv0
x2
g
M
m xv0
xn
处的导数,
而gv xv0 T 称为向量值函数 gv xv 在点 xv 0 处的Jacobi矩阵。
称为最优化方法。最优化方法是在第二次世界大战前后,
在军事领域中对导弹、雷达控制的研究中逐渐发展起来 的。
最优化方法解决问题一般步骤: (1)提出需要进行最优化的问题,开始收集有关资 料和数据; (2)建立求解最优化问题的有关数学模型,确定变 量,列出目标函数和有关约束条件; (3)分析模型,选择合适的最优化方法; (4)求解方程。一般通过编制程序在电子计算机上 求得最优解; (5)最优解的验证和实施。 随着系统科学的发展和各个领域的需求,最优化方 法不断地应用于经济、自然、军事和社会研究的各个领 域。
1.2 实例
数据拟合问题 原料切割问题 运输问题 营养配餐问题 分配问题
1.3 基本概念
1. 最优化问题的向量表示法
设 xvx1,x2,L,xnT 则
m i n fx 1 ,x 2 ,L ,x n m i n fx v (1)
以向量为变量的实值函数 定义向量间的序关系(定义1.1):
②取 c0,1,4,9,L并画出相应的曲线(称之为等值线).
③确定极值点位置,并用以往所学方法求之。
易知本题的极小值点 xv* 2,1T。
再复杂点的情形见P13上的例1.7。 虽然三维及以上的问题不便于在平面上画图,图解 法失效,但仍有相应的等值面的概念,且等值面具有以 下性质:
①有不同函数值的等值面互不相交(因目标函数是单值 函数的缘故);
其中
g1 xv0
x1
g2 xv0
x1
L
gv
xv0
g1 xv0
x2
g2 xv0
x2
L
M
g1 xv0
xn
M
g2 xv0
xn
称为向量值函数 gv xv 在点
L
xv 0
g
m xv0
x1
g
m
xv0
x2
g
M
m xv0
xn
处的导数,
而gv xv0 T 称为向量值函数 gv xv 在点 xv 0 处的Jacobi矩阵。
称为最优化方法。最优化方法是在第二次世界大战前后,
在军事领域中对导弹、雷达控制的研究中逐渐发展起来 的。
最优化方法解决问题一般步骤: (1)提出需要进行最优化的问题,开始收集有关资 料和数据; (2)建立求解最优化问题的有关数学模型,确定变 量,列出目标函数和有关约束条件; (3)分析模型,选择合适的最优化方法; (4)求解方程。一般通过编制程序在电子计算机上 求得最优解; (5)最优解的验证和实施。 随着系统科学的发展和各个领域的需求,最优化方 法不断地应用于经济、自然、军事和社会研究的各个领 域。
第3课-算法的优化PPT课件

7
.
排序算法的优化
所谓 “排序” ,就是使 一串记录按照其
中的某个或某些关键字的大小递增或递减排 列的操作。
例 :将12 -3 4 8 -5顺序排
列出来,人工是如何排序的呢?
请用自然语言说一说排序的算法过程。
8
.
排序:
第1轮排序后 12
第2轮排序后 12
第3轮排序后 12
第4轮排序后
10
.
快速排序法
是冒泡排序法的一种改进。 它的基本思 想是:
1.把一组需要排序的数据分成两部分,
让其中一部分的所有数据都比另外一部分的所
有数据小。
2.按第1步方法对这两部分数据分别进行
多次快速排序,直到完全将数据按要求排序。
11
.
12
.
活动三 查找的算法优化
一、顺序查找 二、二分查找
13
.
我实践我创新
4
.
加油站
达到同一目的可以用多种不同的方法。 但方 法不同, 解决问题的效率也会有差别。 在解 决实际问题时, 我们要尽可能选择高效的算 法。
5
.
试一试:
一位商人有9枚银币,其中有一枚略轻,是假银币, 你能用天平(不用砝码)将假银币找出来吗? 请给出最优化的算法。
6
.
读一读
蚂蚁的视力较差,但却能在黑暗的世界中快速找到食物, 而且可以找到从洞穴到食物的最短路径。蚂蚁是如何做到 的呢? 研究表明:蚂蚁在行走过程中会释放种称为 “信息素” 的挥发性化学物质,用来标识自己的行走路 径。在寻找食物的过程中,蚂蚁会根据信息素的浓度选择 行走的方向,并最终到达食物所在的地方。
第3课 算法的优化
1
.
SEO站内优化课件PPT

SEO站内优化课件
contents
目录
• SEO基础知识 • 站内优化策略 • SEO工具与技术 • SEO实战案例 • SEO常见问题与解决方案 • SEO未来趋势
01 SEO基础知识
SEO定义
SEO定义
SEO(搜索引擎优化)是一种通过优化网站结构和内容, 提高网站在搜索引擎结果页排名的方法,从而吸引更多潜 在用户访问网站,提高网站流量和知名度。
SEMrush
一款付费的关键词研究工具,提供了全面的关键词分析、竞争对手分析、流量预 测等功能,适合专业人士使用。
网站结构优化
URL结构优化
合理的URL结构能够提高网站的SEO效果,建议使用简洁的 URL,包含关键词,并保持一致的结构。
内容优化
优质的内容是吸引用户和搜索引擎的重要因素。建议定期 更新内容,保持内容的质量和原创性,并合理使用关键词 。
更新频率
保持内容更新频率,定期发布新内容,提高网站 活跃度和权重。
内部链接
合理设置内部链接,引导搜索引擎爬虫深入抓取 网站内容。
链接优化
外部链接
建立高质量的外部链接, 提高网站权威性和权重。
内部链接
优化内部链接结构,提高 页面之间的关联度和用户 体验。
链接质量
避免低质量或违规链接, 以免对网站造成负面影响。
流量来源追踪
Google Analytics能够追踪网站的流量来源,包括自然搜索、广告投 放、社交媒体等,帮助网站管理员了解不同推广渠道的效果。
SEO插件
SEOMOZ
一款知名的SEO插件,提供了网站分析、关键词排名监测、竞争对手分析等功能,帮助网 站管理员提高网站的SEO效果。
Yoast SEO
一款功能强大的SEO插件,支持WordPress等平台,提供了关键词优化、元标签管理、内 容优化等功能。
contents
目录
• SEO基础知识 • 站内优化策略 • SEO工具与技术 • SEO实战案例 • SEO常见问题与解决方案 • SEO未来趋势
01 SEO基础知识
SEO定义
SEO定义
SEO(搜索引擎优化)是一种通过优化网站结构和内容, 提高网站在搜索引擎结果页排名的方法,从而吸引更多潜 在用户访问网站,提高网站流量和知名度。
SEMrush
一款付费的关键词研究工具,提供了全面的关键词分析、竞争对手分析、流量预 测等功能,适合专业人士使用。
网站结构优化
URL结构优化
合理的URL结构能够提高网站的SEO效果,建议使用简洁的 URL,包含关键词,并保持一致的结构。
内容优化
优质的内容是吸引用户和搜索引擎的重要因素。建议定期 更新内容,保持内容的质量和原创性,并合理使用关键词 。
更新频率
保持内容更新频率,定期发布新内容,提高网站 活跃度和权重。
内部链接
合理设置内部链接,引导搜索引擎爬虫深入抓取 网站内容。
链接优化
外部链接
建立高质量的外部链接, 提高网站权威性和权重。
内部链接
优化内部链接结构,提高 页面之间的关联度和用户 体验。
链接质量
避免低质量或违规链接, 以免对网站造成负面影响。
流量来源追踪
Google Analytics能够追踪网站的流量来源,包括自然搜索、广告投 放、社交媒体等,帮助网站管理员了解不同推广渠道的效果。
SEO插件
SEOMOZ
一款知名的SEO插件,提供了网站分析、关键词排名监测、竞争对手分析等功能,帮助网 站管理员提高网站的SEO效果。
Yoast SEO
一款功能强大的SEO插件,支持WordPress等平台,提供了关键词优化、元标签管理、内 容优化等功能。
最优化理论与算法完整版课件

几何规划 动态规划 不确定规划:随机规 划、模糊规划等
多目标规划 对策论等
随机过程方法
统计决策理论 马氏过程 排队论 更新理论 仿真方法 可靠性理论等
TP SHUAI
统计学方法
回归分析 群分析 模式识别 实验设计 因子分析等
6
优化树
TP SHUAI
7
•最优化的发展历程
2E d 2 B2 p L2 h2 0
8 L2 h2
dhB
6.结构设计问题
另外还要考虑到设计变量d和h有界。 从而得到两杆桁架最优设计问题的数学模型:
min 2dB L2 h2
s.t.
p L2 h2 0 dhB
2E d 2 B2
则称x0为极小化问题min f(x),x S的局部最优解
TP SHUAI
30
优化软件 / /neos/solvers/index.html
TP SHUAI
23
6.结构设计问题
p1
p2
h
2p
2L
B
d
受力分析图
圆杆截面图
2p
h
2L
桁杆示意图
TP SHUAI
24
6.结构设计问题
解:桁杆的截面积为 : S dB
桁杆的总重量为:W 2dB L2 h2
负载2p在每个杆上的分力为:p1
p
cos
p
L2 h2 h
20
5负载平衡(1)
实例: 网络G(V,E) 及一组m 个数的集合{s,d>0},表示 连接源点 s与汇点d 之间的流量
解: {s,d>0}的一组路由, 即G(V,E) 中m 条s 与 d间的路, 表示连接s与d 的负载流量的路径。
多目标规划 对策论等
随机过程方法
统计决策理论 马氏过程 排队论 更新理论 仿真方法 可靠性理论等
TP SHUAI
统计学方法
回归分析 群分析 模式识别 实验设计 因子分析等
6
优化树
TP SHUAI
7
•最优化的发展历程
2E d 2 B2 p L2 h2 0
8 L2 h2
dhB
6.结构设计问题
另外还要考虑到设计变量d和h有界。 从而得到两杆桁架最优设计问题的数学模型:
min 2dB L2 h2
s.t.
p L2 h2 0 dhB
2E d 2 B2
则称x0为极小化问题min f(x),x S的局部最优解
TP SHUAI
30
优化软件 / /neos/solvers/index.html
TP SHUAI
23
6.结构设计问题
p1
p2
h
2p
2L
B
d
受力分析图
圆杆截面图
2p
h
2L
桁杆示意图
TP SHUAI
24
6.结构设计问题
解:桁杆的截面积为 : S dB
桁杆的总重量为:W 2dB L2 h2
负载2p在每个杆上的分力为:p1
p
cos
p
L2 h2 h
20
5负载平衡(1)
实例: 网络G(V,E) 及一组m 个数的集合{s,d>0},表示 连接源点 s与汇点d 之间的流量
解: {s,d>0}的一组路由, 即G(V,E) 中m 条s 与 d间的路, 表示连接s与d 的负载流量的路径。
第三章求解优化问题的智能算法PPT课件

2020/8/1
4
3.1 概述——最优化方法的研究起源和意义 2/2
随着近代科学技术发展的需要,特别是由于计算机技术的飞速 发展,促进了最优化方法的迅速发展,并很快渗透到各个领域。
20世纪70年代,最优化方法这门应用技术科学又开始产生出最 优设计、最优控制与最优管理等分支。到20世纪80年代,最优 化技术又在这些分支中发展出了新的更细的分支,比如,工程 技术领域的机械优化设计、建筑结构优化设计以及化工石油领 域的优化设计等。
(1)枚举法。
枚举出可行解集合内的所有可行解,以求出精确最优解。对于连 续函数,该方法要求先对其进行离散化处理,这样就有可能产生 离散误差而永远达不到最优解。另外,当枚举空间比较大时,该 方法的求解效率比较低,有时甚至在目前最先进的计算工具上都 无法求解。
(2)启发式算法。
寻求一种能产生可行解的启发式规则,以找到一个最优解或近似 最优解。该方法的求解效率虽然比较高,但对每一个需要求解的 问题都必须找出其特有的启发式规则,这个启发式规则无通用性, 不适合于其他问题。
第三章 求解优化问题的智能算法
2020/8/1
1
整体概况
概况一
点击此处输入 相关文本内容
01
概况二
点击此处输入 相关文本内容
02
概况三
点击此处输入 相关文本内容
03
2
3.1 概述
2020/8/1
3
3.1 概述——最优化方法的研究起源和意义 1/2
最优化问题是指在一定的约束条件下,决定某个或某些可控制 的因素应有的合理取值,使所选定的目标达到最优的问题。解 决最优化问题的方法称为最优化方法。它具有高度应用性和技 术性的特点。
2020/8/1
工程最优化设计理论、方法和应用PPT课件

∆Xk = αk dk 即 Xk+1=Xk+αk dk 满足f(Xk+1) < f(Xk)
于是 变成求
f(Xk+1)=f(Xk+αk dk )
的极值点问题
这里的核心问题是确定
?dk ?αk
1.解析法:可以确定dk(目标函数的负梯度方向),也可求出
一元函数的极值确定一最佳搜索步长αk,即φ(αk ) = f(Xk+αk dk ),应有φ’(αk )=0
min f (x1,..., xn )
s.t. gk (x1,..., xn ) 0 k 1,..., n
Eular,Lagrange, Problems in infinite dimensions, calculus of variations
1950s-, 数学规划法, 即:数值计算法(迭代法)—通过计算求得最优解。
供应量
360
300
200
?
分析:设每天生产甲产品 x1 件, 乙产品 x2 件,于是该生产计划问题可归结为
求变量 x1, x2 使函数 f(x1,x2)=60x1+120x2 极大化
需满足条件
g1(x1, x2 ) 9x1 4x2 360
g2 (x1, x2 ) 3x1 10x2 300
g3 (x1, x2 ) 4x1 5x2 200
Fe
2EI
L2
其中,I钢管截面惯性矩
I (R4 r4 ) A (T 2 D2 )
4
8
1
刚好满足强度约束条 件 时,有
F1 A
F(B2 h2 ) 2
TDh
y
其中 A是钢管截面面积 A=π(R2-r2)= πTD
于是 变成求
f(Xk+1)=f(Xk+αk dk )
的极值点问题
这里的核心问题是确定
?dk ?αk
1.解析法:可以确定dk(目标函数的负梯度方向),也可求出
一元函数的极值确定一最佳搜索步长αk,即φ(αk ) = f(Xk+αk dk ),应有φ’(αk )=0
min f (x1,..., xn )
s.t. gk (x1,..., xn ) 0 k 1,..., n
Eular,Lagrange, Problems in infinite dimensions, calculus of variations
1950s-, 数学规划法, 即:数值计算法(迭代法)—通过计算求得最优解。
供应量
360
300
200
?
分析:设每天生产甲产品 x1 件, 乙产品 x2 件,于是该生产计划问题可归结为
求变量 x1, x2 使函数 f(x1,x2)=60x1+120x2 极大化
需满足条件
g1(x1, x2 ) 9x1 4x2 360
g2 (x1, x2 ) 3x1 10x2 300
g3 (x1, x2 ) 4x1 5x2 200
Fe
2EI
L2
其中,I钢管截面惯性矩
I (R4 r4 ) A (T 2 D2 )
4
8
1
刚好满足强度约束条 件 时,有
F1 A
F(B2 h2 ) 2
TDh
y
其中 A是钢管截面面积 A=π(R2-r2)= πTD
《优化算法讲》PPT课件 (2)
2020/11/22
23
4.4.2 遗传算法中小生境的实现方法
• 1.基于预选择机制的小生境实现方法(Cavicchio ,1970年) • 2.基于排挤的小生境实现方法( De Jong,1975年) • 3.基于共享函数(Sharing Function)的小生境实现方法( Goldberg和Richardson,
ik是所描述的基因在原常规染色体中的基因座编号, vk为对应的基因值。
2020/11/22
4.3.1 变长度染色体遗传算法的编码 与解码
• 若常规遗传算法中一个个体的基因型是:
X:1 0 0 1 0 1 其染色体长度为L=6。使用变长度染色体编码,该个体就可表 示为:
Xm:(1,1)(2,0)(3,0)(4,1)(5,0)(6,1)
在这种变长度染色体遗传算法中,允许染色体的长度可长可短。 如:
Xm:(1,1)(2,0)(3,0)(4,1)(5,0)(6,1)(3,1)(1,0) Xm:(1,1)(3,0)(5,0)(6,1)
前者称为过剩指定,后者称为缺省指定。而当个体的所有基因 都能在编码串中得到唯一的描述时,这种描述称为正常指定。
它在常规遗传算法中所对应的个体为: X:1 0 0 1 0 1
2020/11/22
19
4.3.1 变长度染色体遗传算法的编码 与解码
(2)描述不足时的解码方法。可规定它们取某 一项先设定的标准值(或缺省值)。 例如,对于变长度染色体遗传算法中的个体
Xm:(1,1)(3,0)(5,0)(6,1) 若取缺省值为0的话,则它在常规遗传算法中
2020/11/22
21
4.3.3 变长度染色体遗传算法的算法 结构
• 算法MessyGA
优化方法的数学基础PPT课件
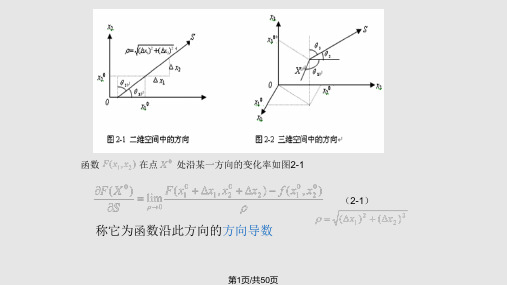
第26页/共50页
2.
处取得极值充分条件
x*
2F
x12
2F
2
F
(
x*
)
x2x1
2F
xnx1
2F x1x2 2F
x22
2F xnx2
2F
x1xn
2F
x2xn
正定或负定
2F
xn2 x*
第27页/共50页
各阶主子式均大于零:
,
,
,..
则海色(Hessian)矩阵H(x) 是正定 则X*为极小点。 的,
第30页/共50页
§2-4 有约束优化问题的极值条件
• 不等式约束的多元函数极值的必要条件是著名 的库恩--塔克(Kuhn-Tucker)条件,它是非线 性优化问题的重要理论Байду номын сангаас
1 库恩—塔克条件 (K-T条件)
• 对于多元函m数in 不F等( x式) 的约束优化问题:
•
s.t. g j (x) 0 ( j 1, 2, , m)
f
( x(1) )
2x1 4
2 x2
x(1)
2 4
第11页/共50页
例2-3:试求目标函数 f x1, x2 3x12 4x1x2 x22 在点X 0 0,1T 处
的最速下降方向。
解: 由于
f X
f X
x1 6x1 4x2 , x2 4x1 2x2
则函数在 X 0 0,1T 处的最速下降方向是
3)任何一组凸集的积(或交)仍是凸集。
第15页/共50页
二、凸函数
具有凸性(表现为单峰性)或只有唯一的局部最优值 亦即全域最优值的函数,称为凸函数或单峰函数。其数学 定义是:
2.
处取得极值充分条件
x*
2F
x12
2F
2
F
(
x*
)
x2x1
2F
xnx1
2F x1x2 2F
x22
2F xnx2
2F
x1xn
2F
x2xn
正定或负定
2F
xn2 x*
第27页/共50页
各阶主子式均大于零:
,
,
,..
则海色(Hessian)矩阵H(x) 是正定 则X*为极小点。 的,
第30页/共50页
§2-4 有约束优化问题的极值条件
• 不等式约束的多元函数极值的必要条件是著名 的库恩--塔克(Kuhn-Tucker)条件,它是非线 性优化问题的重要理论Байду номын сангаас
1 库恩—塔克条件 (K-T条件)
• 对于多元函m数in 不F等( x式) 的约束优化问题:
•
s.t. g j (x) 0 ( j 1, 2, , m)
f
( x(1) )
2x1 4
2 x2
x(1)
2 4
第11页/共50页
例2-3:试求目标函数 f x1, x2 3x12 4x1x2 x22 在点X 0 0,1T 处
的最速下降方向。
解: 由于
f X
f X
x1 6x1 4x2 , x2 4x1 2x2
则函数在 X 0 0,1T 处的最速下降方向是
3)任何一组凸集的积(或交)仍是凸集。
第15页/共50页
二、凸函数
具有凸性(表现为单峰性)或只有唯一的局部最优值 亦即全域最优值的函数,称为凸函数或单峰函数。其数学 定义是:
相关主题
