【创新设计】2015高考数学(人教通用,文科)二轮专题训练：大题综合突破练2

合集下载

2015届高三下文科数学综合训练二参考答案

2015届高三（下）文科数学综合训练二参考答案一、选择题：（本大题共12小题，每小题5分，共60分）二、填空题：（本大题共4小题，每小题4分，共16分）13．8； 14． 15．1； 16．1(0,]3．三、解答题：（第22题14分，其他每题12分，共74分）17. 本题主要考等差数列、数列求和等基础知识；考查推理论证与运算求解能力，满分12分．解：（I ）∵点(,)n n S 在函数2()f x x =的图象上，∴2.n S n = ················································································································ 1分∴当1n =时，111a S ==, ······················································································· 2分当2n ≥时，1n n n a S S -=- ··················································································· 3分22(1)21n n n =--=- ································································· 4分又11a =满足21,n a n =- ························································································ 5分 ∴2 1.n a n =- ·········································································································· 6分(II) ∵111(21)(21)n n n b a a n n +==⋅-⋅+ ·································································· 7分111()22121n n =--+，············································································ 9分 ∴12n n T b b b =++⋅⋅⋅+111111[(1)()()]23352121n n =-+-+⋅⋅⋅+--+ ·················································· 11分 11(1)221n =-+.21nn =+ ················································································ 12分 18．本题主要考查概率、统计等基础知识，考查数据处理能力、抽象概括能力、运算求解能力以及应用意识，考查或然与必然思想、化归与转化思想．满分12分．解：（I ）从统计的5年发电量中任取2年的基本事件为(7.4,7.0),(7.4,9.2),(7.4,7.9),(7.4,10.0),(7.0,9.2),(7.0,7.9),(7.0,10.0),(9.2,7.9),(9.2,10.0),(7.9,10.0) 共10个． ······························ 3分（说明：若列出不足6个，不给分；若列出6个，不足10个且所列均正确者得1分）其中2年发电量都低于8.0（亿千瓦时）的基本事件为 (7.4,7.0),(7.4,7.9),(7.0,7.9),共3个． ······························································· 5分所以这2年发电量都低于8.0（亿千瓦时）的概率3.10P = ·································· 6分（II ）∵1500140019001600210085001700,55x ++++=== ································ 7分 7.47.09.27.910.041.58.3.55y ++++=== ····························································· 8分又直线 0.004y x a =+ 过点(,)x y ， ····································································· 9分 ∴8.30.0041700,a =⨯+ 解得 1.5a =，∴0.004 1.5y x =+． ······························································································· 10分当1800x =时，0.0041800 1.58.79.0y =⨯+=<,··················································· 11分所以不能完成发电任务，缺口量为0.3（亿千瓦时）． ········································· 12分 19．本题主要考查空间线与线、线与面、面面的位置关系等基础知识；考查空间想象能力、推理论证能力，满分12分．证法一：（I ）连接1AC 交1A C 于点N ，则N 为1A C 的中点．……1分∵M 为AB 的中点，∴1//MN BC ．……………………………………………3分又∵1MN ACM ⊂平面， ………………………………4分 11BC ACM ⊄平面， ……………………………………5分 ∴11//BC ACM 平面．……………………………………6分（II ）∵CA CB =，M 为AB 的中点，∴CM AB ⊥． …………………………………………7分 ∵1A 在平面ABC 的射影为M ，∴1A M ACB ⊥平面，……………………………………8分 ∴1A M AB ⊥，…………………………………………9分又1CMA M M =，∴1AB ACM ⊥平面，…………………………………10分又11AB ABB A ⊂平面，………………………………11分 ∴111.ACM ABB A ⊥平面平面 …………………………12分证法二：（I ）取11A B 中点N ，连结1,BN C N ，………1分∵M 为AB 的中点，∴1A N MB =，1A N //MB∴四边形1A MBN 为平行四边形，∴1//BN A M ．…………………………………………2分同理可得1//C N CM ，又11C N ACM ⊄平面，1CM ACM ⊂平面，…………3分 ∴11//C N ACM 平面．…………………………………4分同理1//BN ACM 平面． ∵1C NBN N =，∴11//BC N ACM 平面平面，……………………………5分 ∵11BC BC N ⊂平面，A 1ABC 1CMB 1N证法二图B 1 A 1 ABC 1 C MN证法一图∴11//BC ACM 平面． …………………………………6分（II ）同解法一．20．本题主要考查三角恒等变换、三角函数的图象与性质、解三角形等基础知识；考查运算求解能力，考查函数与方程思想、数形结合思想．满分12分．解：（I ）依题意得：1()2cos 222f x x x x ωωω=+- ····························································· 2分12cos 22x x ωω=+ ················································································· 3分 sin(2)6x πω=+， ···························································································· 4分 ∵0ω>，∴222T ππω==，∴12ω=， ··············································································································· 5分∴()sin()6f x x π=+． ······························································································ 6分（II ）∵0A π<<， ∴7666A πππ<+<． ∵()sin()6f x x π=+在x A =时取得最值，∴,623A A πππ+==． ···························································································· 8分∵1sin 2ABC S bc A ∆===，∴6bc =． ··············································································································· 9分 ∵5b c +=，∴2222cos a b c bc A =+- ·························································································· 10分22b c bc =+- 2()3b c bc =+- 2518=-7=， ·································································································· 11分∴a = ················································································································· 12分 21．本题主要考查函数、导数、不等式等基本知识；考查运算求解能力、推理论证能力；考查化归转化思想、函数方程的思想、数形结合思想．满分12分．解法一：（I ）()1,x f x e '=- ···················································································· 1分由()0f x '>可得0,x >；由()0f x '<可得0,x < ············································ 2分 ∴()f x 在(,0)-∞上单调递减，在(0,)+∞上单调递增． ······································ 3分(II) (),x g x e x '=- ································································································· 4分由（I ）知()g x '在(,0)-∞上单调递减，在(0,)+∞上单调递增， ∴()(0)10,g x g ''≥=> ······························································································ 5分∴()g x 在[0,)+∞上单调递增， ··············································································· 6分 ∴[0,)x ∈+∞时，min ()(0)0.g x g == ······································································· 7分（III ）由(II) 知当0x >时，()0,g x >即0x >时，211,2x e x >+ ····················································································· 8分设函数221311()1(ln )ln ,2222h x x x x x =+-+=--则211()(0),x h x x x x x-'=-=> ············································································· 9分由()0h x '>可得1x >；由()0h x '<可得01,x <<∴()h x 在(0,1)上单调递减，在(1,)+∞上单调递增． ··········································· 10分 ∴()(1)0,h x h ≥=∴0x >时，2131ln ,22x x +≥+ ·············································································· 11分∴3ln .2x e x >+ ······································································································ 12分解法二：（I ）(II)同解法一．（III ）设3()ln ,2x h x e x =--则1()(0),x h x e x x '=-> ························································································· 8分∵1()x h x e x '=-在 (0,)+∞上单调递增，且121()20,(1)10,2h e h e ''=-<=-> ()h x 在1(,1)2上连续， ·································· 9分∴存在唯一01(,1)2x ∈，使得0()0h x '=，即00001,ln ,x e x x x ==-························· 10分∴0(0,)x x ∈时，()0,h x '<()h x 在0(0,)x 上单调递减，0(,)x x ∈+∞时，()0,h x '>()h x 在0(,)x +∞上单调递增， …………………………11分∴0000031331()()ln 20,2222x h x h x e x x x ≥=--=+->-=>∴()0h x >，即3ln .2x e x >+················································································ 12分 22．本题主要考查直线、抛物线、椭圆等基础知识及直线与抛物线的位置关系；考查运算求解、抽象概括能力，化归与转化思想．满分14分．解法一：（I ）∵抛物线22(0)x py p =>的焦点为(0,).2pF ···································· 1分椭圆22143y x +=的焦点为(0,1)± ············································································ 2分 ∴1,2,2pp == ∴抛物线的方程为24.x y = ····················································································· 3分（II ）（ⅰ）联立21,4y kx x y=+⎧⎨=⎩得2440,x kx --=······················································ 4分 216160,k ∆=+>设1122(,),(,)A x y B x y则12124,4x x k x x +=⋅=-， ···················································································· 5分由24x y =，得2,,42x x y y '==所以过A 的切线PA 的方程为：1111(),2y y x x x -=- 整理得： 2111124y x x x =- ⋅⋅⋅① …………………………………6分同理切线PB 的方程为：2221124y x x x =- ⋅⋅⋅②联立①②解得122,1,2P P x xx k y +===-即(2,1).P k - ········································ 7分当0k =时，(0,1),(0,1),P F -有.PF AB ⊥……………………………………………8分当0k ≠时，1(1)1,02PF k k k--==--有.PF AB ⊥所以0PF AB ⋅=为定值． ······················································································ 9分（ⅱ）由（ⅰ）可设直线PF 的方程为：11(0)y x k k=-+≠．…………………10分由211,4y x k x y ⎧=-+⎪⎨⎪=⎩得2440,x x k +-= 设223434(,),(,)44x x C x D x则34344,4,x x x x k+=-⋅=-…………………11分∵(2,1)P k -，(0,1).F∴PC FD PD CF ⋅-⋅2222334444331111(2,1)(,1)(2,1)(,1)4444x k x x x x k x x x =-+⋅---+⋅--2222343443431111(2)(1)(1)(2)(1)(1)4444x k x x x x k x x x =-⋅++⋅-+-++⋅-………12分22343434122()28x x k x x x x =-++-24182()(4)28k k =---+⋅--=0∴PC FD PD CF ⋅=⋅， ·························································································· 13分又,,,P C F D 共线，∴||||||||.PC FD PD CF ⋅=⋅ ···················································································· 14分。

2015届高考数学(文科,通用)二轮复习突破练高考中档大题规范练(四) Word版含答案

高考中档大题规范练(四)——概率与统计(推荐时间：70分钟)1．(2014·湖南)某企业有甲、乙两个研发小组．为了比较他们的研发水平，现随机抽取这两个小组往年研发新产品的结果如下：(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )．其中a ，a 分别表示甲组研发成功和失败；b ，b 分别表示乙组研发成功和失败．(1)若某组成功研发一种新产品，则给该组记1分，否则记0分．试计算甲、乙两组研发新产品的成绩的平均数和方差，并比较甲、乙两组的研发水平；(2)若该企业安排甲、乙两组各自研发一种新产品，试估计恰有一组研发成功的概率．解 (1)甲组研发新产品的成绩为 1,1,1,0,0,1,1,1,0,1,0,1,1,0,1，其平均数为x 甲＝1015＝23；方差为s 2甲＝115⎣⎡⎦⎤⎝⎛⎭⎫1－232×10＋⎝⎛⎭⎫0－232×5＝29. 乙组研发新产品的成绩为 1,0,1,1,0,1,1,0,1,0,0,1,0,1,1，其平均数为x 乙＝915＝35；方差为s 2乙＝115⎣⎡⎦⎤⎝⎛⎭⎫1－352×9＋⎝⎛⎭⎫0－352×6＝625. 因为x 甲>x 乙，s 2甲<s 2乙，所以甲组的研发水平优于乙组． (2)记事件E ＝{恰有一组研发成功}．在所抽得的15个结果中，恰有一组研发成功的结果是(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )共7个．故事件E 发生的频率为715.将频率视为概率，则得所求概率为P (E )＝715.即恰有一组研发成功的概率为715.2．先后随机投掷2枚正方体骰子，其中x 表示第1枚骰子出现的点数，y 表示第2枚骰子出现的点数．(1)求点P (x ，y )在直线y ＝x －2上的概率； (2)求点P (x ，y )满足y 2<2x 的概率．解每枚骰子出现的点数都有6种情况，所以基本事件总数为6×6＝36(个)．(1)记“点P (x ，y )在直线y ＝x －2上”为事件A ，则事件A 有4个基本事件：(3,1)，(4,2)，(5,3)，(6,4)，所以P (A )＝436＝19.(2)记“点P (x ，y )满足y 2<2x ”为事件B ，则事件B 有12个基本事件：(1,1)，(2,1)，(3,1)，(3,2)，(4,1)，(4,2)，(5,1)，(5,2)，(5,3)，(6,1)，(6,2)，(6,3)，所以P (B )＝1236＝13.3．有编号为1,2,3的三个白球，编号为4,5,6的三个黑球，这六个球除编号和颜色外完全相同，现从中任意取出两个球．(1)求取得的两个球颜色相同的概率； (2)求取得的两个球颜色不相同的概率．解从六个球中取出两个球的基本事件有(1,2)，(1,3)，(1,4)，(1,5)，(1,6)，(2,3)，(2,4)，(2,5)，(2,6)，(3,4)，(3,5)，(3,6)，(4,5)，(4,6)，(5,6)共计15个基本事件．(1)记事件A 为“取出的两个球是白球”，则这个事件包含的基本事件的是(1,2)，(1,3)，(2,3)，共计3个基本事件，故P (A )＝315＝15.记事件B 为“取出的两个球是黑球”，同理可得P (B )＝15.记事件C 为“取出的两个球的颜色相同”，则C ＝A ＋B ，且A ，B 互斥，根据互斥事件的概率加法公式，得P (C )＝P (A ＋B )＝P (A )＋P (B )＝25.(2)记事件D 为“取出的两个球的颜色不相同”，则事件C ，D 互斥，根据互斥事件概率之间的关系，得P (D )＝1－P (C )＝1－25＝35.4．(2014·辽宁)某大学餐饮中心为了解新生的饮食习惯，在全校一年级学生中进行了抽样调查，调查结果如下表所示：(1)面有差异”；(2)已知在被调查的北方学生中有5名数学系的学生，其中2名喜欢甜品，现在从这5名学生中随机抽取3人，求至多有1人喜欢甜品的概率．附：P (2≥k ) 解 (1)将2×22＝n (n 11n 22－n 12n 21)2n 1＋n 2＋n ＋1n ＋2＝100×(60×10－20×10)270×30×80×20＝10021≈4.762. 因为4.762>3.841，所以有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”．(2)从5名数学系学生中任取3人的一切可能结果所组成的基本事件空间Ω＝{(a 1，a 2，b 1)，(a 1，a 2，b 2)，(a 1，a 2，b 3)，(a 1，b 1，b 2)，(a 1，b 2，b 3)，(a 1，b 1，b 3)，(a 2，b 1，b 2)，(a 2，b 2，b 3)，(a 2，b 1，b 3)，(b 1，b 2，b 3)}．其中a i 表示喜欢甜品的学生，i ＝1,2；b j 表示不喜欢甜品的学生，j ＝1,2,3.Ω由10个基本事件组成，且这些基本事件的出现是等可能的．用A 表示“3人中至多有1人喜欢甜品”这一事件，则事件A ＝{(a 1，b 1，b 2)，(a 1，b 2，b 3)，(a 1，b 1，b 3)，(a 2，b 1，b 2)，(a 2，b 2，b 3)，(a 2，b 1，b 3)，(b 1，b 2，b 3)}．事件A 是由7个基本事件组成，因而P (A )＝710.5．某商场为吸引顾客消费，推出一项优惠活动．活动规则如下：消费每满100元可以转动如图所示的圆盘一次，其中O 为圆心，且标有20元，10元，0元的三部分区域面积相等．假定指针停在任一位置都是等可能的．当指针停在某区域时，返相应金额的优惠券．例如：某顾客消费了218元，第一次转动获得了20元，第二次获得了10元，则其共获得了30元优惠券．顾客甲和乙都到商场进行了消费，并按照规则参与了活动．(1)若顾客甲消费了128元，求他获得的优惠券金额大于0元的概率； (2)若顾客乙消费了280元，求他总共获得的优惠券金额不低于20元的概率．解 (1)设“甲获得的优惠券金额大于0元”为事件A .因为指针停在任一位置都是等可能的，而题中所给的三部分区域的面积相等，所以指针停在20元，10元，0元区域内的概率都是13.根据互斥事件的概率，有P (A )＝13＋13＝23，所以“顾客甲获得的优惠券金额大于0元”的概率是23.(2)设“乙获得的优惠券金额不低于20元”为事件B .因为顾客乙转动转盘两次，设乙第一次转动转盘获得优惠券的金额为x 元，第二次获得优惠券的金额为y 元，则基本事件空间可以表示为Ω＝{(20,20)，(20,10)，(20,0)，(10,20)，(10,10)，(10,0)，(0,20)，(0,10)，(0,0)}，即Ω中含有9个基本事件，每个基本事件发生的概率都为19.而乙获得的优惠券金额不低于20元，是指x ＋y ≥20，所以事件B 中包含的基本事件有6个．所以乙获得的优惠券金额不低于20元的概率为 P (B )＝69＝23.6．已知关于x 的一元二次方程9x 2＋6ax －b 2＋4＝0，a ，b ∈R .(1)若a 是从1,2,3三个数中任取的一个数，b 是从0,1,2三个数中任取的一个数，求已知方程有两个不相等实根的概率；(2)若a 是从区间[0,3]内任取的一个数，b 是从区间[0,2]内任取的一个数，求已知方程有实数根的概率．解设事件A 为“方程9x 2＋6ax －b 2＋4＝0有两个不相等的实数根”；事件B 为“方程9x 2＋6ax －b 2＋4＝0有实数根”．(1)由题意，知基本事件共9个，即(1,0)，(1,1)，(1,2)，(2,0)，(2,1)，(2,2)，(3,0)，(3,1)，(3,2)，其中第一个数表示a 的取值，第二个数表示b 的取值．由Δ＝36a 2－36(－b 2＋4)＝36a 2＋36b 2－36×4>0，得a 2＋b 2>4.事件A 要求a ，b 满足条件a 2＋b 2>4，可知包含6个基本事件，即(1,2)，(2,1)，(2,2)，(3,0)，(3,1)，(3,2)，则事件A 发生的概率为P (A )＝69＝23.(2)a ，b 的取值所构成的区域如图所示，其中0≤a ≤3,0≤b ≤2.构成事件B 的区域为{(a ，b )|0≤a ≤3,0≤b ≤2，a 2＋b 2≥4}(如图中阴影部分)，则所求的概率为P (B )＝2×3－14×π×222×3＝1－π6.。

【三维设计】2015年高考数学总复习创新问题专项训练(二)文北师大版

创新问题专项训练(二)一、选择题 1．用C (A )表示非空集合A 中的元素个数，定义A *B ＝⎩⎪⎨⎪⎧C A －C B ，C A C B ，C B －C A ，C AC B ，若A ＝{x |x 2－ax －1＝0，a ∈R }，B ＝{x ||x 2＋bx ＋1|＝1，b ∈R }，设S ＝{b |A *B ＝1}，则C (S )等于( )A ．4B ．3C ．2D ．12．已知集合A ＝{(x ，y )||x －2|＋|y －3|≤1}，集合B ＝{(x ，y )|x 2＋y 2＋Dx ＋Ey ＋F ≤0，D 2＋E 2－4F >0}，若集合A ，B 恒满足“A ⊆B ”，则集合B 中的点所形成的几何图形面积的最小值是( )A.22πB ．πC.12πD.2π3．已知数组(x 1，y 1)，(x 2，y 2)，…，(x 10，y 10)满足线性回归方程y ^＝b ^x ＋a ^，则“(x 0，y 0)满足线性回归方程y ^＝b ^x ＋a ^”是“x 0＝x 1＋x 2＋ … ＋x 1010，y 0＝y 1＋y 2＋…＋y 1010”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件4．给出定义：若函数f (x )在D 上可导，即f ′(x )存在，且导函数f ′(x )在D 上也可导，则称f (x )在D 上存在二阶导函数，记f ″(x )＝(f ′(x ))′，若f ″(x )<0在D 上恒成立，则称f (x )在D 上为凸函数．以下四个函数在(0，π2)上不是凸函数的是( )A ．f (x )＝sin x ＋cos xB ．f (x )＝ln x －2xC ．f (x )＝－x 3＋2x －1D ．f (x )＝x ·e x5．定义：若函数f (x )的图像经过变换T 后所得图像对应函数的值域与f (x )的值域相同，则称变换T 是f (x )的同值变换．下面给出四个函数及其对应的变换T ，其中T 不属于f (x )的同值变换的是( )A ．f (x )＝(x －1)2，T 将函数f (x )的图像关于y 轴对称 B ．f (x )＝2x －1－1，T 将函数f (x )的图像关于x 轴对称C ．f (x )＝2x ＋3，T 将函数f (x )的图像关于点(－1,1)对称D ．f (x )＝sin(x ＋π3)，T 将函数f (x )的图像关于点(－1，0)对称二、填空题6．对于非空实数集A ，记A *＝{y |任意x ∈A ，y ≥x }．设非空实数集合M ，P ，满足M ⊆P .给出以下结论：①P *⊆M *；②M *∩P ≠∅；③M ∩P *＝∅.其中正确的结论是________(写出所有正确结论的序号)．7．已知[x ]表示不超过实数x 的最大整数，如[1.8]＝1，[－1.2]＝－2.x 0是函数f (x )＝ln x －2x的零点，则[x 0]等于________．8．某同学为研究函数f (x )＝1＋x 2＋1＋－x2(0≤x ≤1)的性质，构造了如图所示的两个边长为1的正方形ABCD 和BEFC ，点P 是边BC 上的一个动点，设CP ＝x ，则AP ＋PF ＝f (x )．请你参考这些信息，推知函数f (x )的极值点是______；函数f (x )的值域是________．9.(1)如图，矩形ABCD 的三个顶点A ，B ，C 分别在函数y ＝x ，y ＝x 12，y ＝(22)x的图像上，且矩形的边分别平行于两坐标轴．若点A 的纵坐标为2，则点D 的坐标为________．(2)若存在实常数k 和b ，使得函数f (x )和g (x )对其定义域上的任意实数x 分别满足：f (x )≥kx ＋b 和g (x )≤kx ＋b ，则称直线l ：y ＝kx ＋b 为f (x )和g (x )的“隔离直线”．已知h (x )＝x 2，φ(x )＝2eln x (其中e 为自然对数的底数)，根据你的数学知识，推断h (x )与φ(x )间的隔离直线方程为________．三、解答题10．已知二次函数f (x )＝ax 2＋bx ＋c 和g (x )＝ax 2＋bx ＋c ·ln x (abc ≠0)． (1)证明：当a <0时，无论b 为何值，函数g (x )在定义域内不可能总为增函数； (2)在同一函数图像上取任意两个不同的点A (x 1，y 1)，B (x 2，y 2)，线段AB 的中点C (x 0，y 0)，记直线AB 的斜率为k ，若f (x )满足k ＝f ′(x 0)，则称其为“K 函数”．判断函数f (x )＝ax 2＋bx ＋c 与g (x )＝ax 2＋bx ＋c ·ln x (abc ≠0)是否为“K 函数”？并证明你的结论．11．如图，两个圆形飞轮通过皮带传动，大飞轮O 1的半径为2r (r 为常数)，小飞轮O 2的半径为r ，O 1O 2＝4r .在大飞轮的边缘上有两个点A ，B ，满足∠BO 1A＝π3，在小飞轮的边缘上有点C .设大飞轮逆时针旋转，传动开始时，点B ，C 在水平直线O 1O 2上．(1)求点A 到达最高点时A ，C 间的距离； (2)求点B ，C 在传动过程中高度差的最大值．答案1．选B 显然集合A 的元素个数为2，根据A *B ＝1可知，集合B 的元素个数为1或3，即方程|x 2＋bx ＋1|＝1有1个根或有3个根．结合函数y ＝|x 2＋bx ＋1|的图象可得，b ＝0或4－b 24＝－1，即b ＝0或b ＝±2 2.2．选B 集合A 可以看作是由区域{(x ，y )||x |＋|y |≤1}向右平移2个单位长度、向上平移3个单位长度得到的，这是一个边长为2的正方形区域，集合B 是一个圆形区域，如果A ⊆B 且集合B 中的点形成的几何图形的面积最小，则圆x 2＋y 2＋Dx ＋Ey ＋F ＝0是|x －2|＋|y －3|＝1所表示正方形的外接圆，其面积是π×12＝π.3．选B 由于线性回归方程恒过样本点的中心(x ，y )，则由“x 0＝x 1＋x 2＋…＋x 1010，y 0＝y 1＋y 2＋…＋y 1010”一定能推出“(x 0，y 0)满足线性回归方程y ^＝b ^x ＋a ^”，反之不一定成立．4．选D 由凸函数的定义可得该题即判断f (x )的二阶导函数f ″(x )的正负．对于A ，f ′(x )＝cos x －sin x ，f ″(x )＝－sin x －cos x ，在x ∈(0，π2)上，恒有f ″(x )<0；对于B ，f ′(x )＝1x －2，f ″(x )＝－1x 2，在x ∈(0，π2)上，恒有f ″(x )<0；对于C ，f ′(x )＝－3x 2＋2，f ″(x )＝－6x ，在x ∈(0，π2)上，恒有f ″(x )<0；对于D ，f ′(x )＝e x ＋x e x ，f ″(x )＝e x ＋e x ＋x e x ＝2e x ＋x e x，在x ∈(0，π2)上，恒有f ″(x )>0.5．选B 选项B 中，f (x )＝2x －1－1的值域为(－1，＋∞)，将函数f (x )的图象关于x轴对称变换后所得函数的值域为(－∞，1)，值域改变，不属于同值变换．经验证，其他选项正确．6．解析：对于①，由M ⊆P 得知，集合M 中的最大元素m 必不超过集合P 中的最大元素p ，依题意有P *＝{y |y ≥p }，M *＝{y |y ≥m }，又m ≤p ，因此有P *⊆M *，①正确；对于②，取M ＝P ＝{y |y <1}，依题意得M *＝{y |y ≥1}，此时M *∩P ＝∅，因此②不正确；对于③，取M ＝{0，－1,1}，P ＝{y |y ≤1}，此时P *＝{y |y ≥1}，M ∩P *＝{1}≠∅，因此③不正确．综上所述，其中正确的结论是①.答案：①7．解析：∵函数f (x )的定义域为(0，＋∞)，∴函数f ′(x )＝1x ＋2x2>0，即函数f (x )在(0，＋∞)上单调递增．由f (2)＝ln 2－1<0，f (e)＝ln e －2e >0，知x 0∈(2，e)，∴[x 0]＝2.答案：28．解析：显然当点P 为线段BC 的中点时，A ，P ，F 三点共线，此时AP ＝PF ，且函数f (x )取得最小值5，函数f (x )的图象的对称轴为x ＝12；当x ∈[0，12]时，函数f (x )单调递减，且值域为[5，2＋1]；当x ∈[12，1]时，函数f (x )单调递增，且值域为[5，2＋1]，∴函数f (x )的值域为[5，2＋1]．答案：x ＝12[5，2＋1]9．解析：(1)由A 点的纵坐标为2，得点A 的横坐标是⎝⎛⎭⎪⎫222＝12，由矩形的边平行于坐标轴，得B 点的纵坐标是2，从而横坐标是22＝4，所以C 点的横坐标是4，纵坐标是(22)4＝14，所以点D 的横坐标等于A 点的横坐标12，点D 的纵坐标等于C 点的纵坐标14，即D 点的坐标是(12，14)．(2)容易观察到h (x )和φ(x )有公共点(e ，e)，又(x －e)2≥0，即x 2≥2e x －e ，所以猜想h (x )和φ(x )间的隔离直线为y ＝2e x －e ，下面只需证明2eln x ≤2e x －e 恒成立即可，构造函数λ(x )＝2eln x －2e x ＋e.由于λ′(x )＝2e e －xx(x >0)，即函数λ(x )在区间(0，e)上递增，在(e ，＋∞)上递减，故λ(x )≤λ(e)＝0，即2eln x －2e x ＋e≤0，得2eln x ≤2e x －e.故猜想成立，所以两函数间的隔离直线方程为y ＝2e x －e.答案：(1)(12，14)(2)y ＝2e x －e10．解：(1)假设g (x )在定义域(0，＋∞)上为增函数，则有g ′(x )＝2ax ＋b ＋c x ＝2ax 2＋bx ＋cx>0对于一切x >0恒成立，从而必有2ax 2＋bx ＋c >0对于一切x >0恒成立．又a <0，由二次函数的图象可知：2ax 2＋bx ＋c >0对于一切x >0恒成立是不可能的．因此当a <0时，无论b 为何值，函数g (x )在定义域内不可能总为增函数．(2)函数f (x )＝ax 2＋bx ＋c 是“K 函数”，g (x )＝ax 2＋bx ＋c ·ln x (abc ≠0)不是“K 函数”．证明如下：对于二次函数f (x )＝ax 2＋bx ＋c ，k ＝f x 1－f x 2x 1－x 2＝a x 22－x 21＋b x 2－x 1x 2－x 1＝a (x 2＋x 1)＋b ＝2ax 0＋b .又f ′(x 0)＝2ax 0＋b ，故k ＝f ′(x 0)．故函数f (x )＝ax 2＋bx ＋c 是“K 函数”．对于函数g (x )＝ax 2＋bx ＋c ·ln x (abc ≠0)(x >0)，不妨设x 2>x 1>0，则k ＝g x 1－g x 2x 1－x 2＝a x 21－x 22＋b x 1－x 2＋c ln x 1x 2x 1－x 2＝2ax 0＋b ＋c lnx 1x 2x 1－x 2.又g ′(x 0)＝2ax 0＋b ＋c x 0，若g (x )为“K 函数”，则必满足k ＝g ′(x 0)，即有2ax 0＋b ＋c ln x 1x 2x 1－x 2＝2ax 0＋b ＋cx 0，也即c ln x 1x 2x 1－x 2＝2c x 1＋x 2(c ≠0)，所以lnx 1x 2x 1－x 2＝2x 1＋x 2.设t ＝x 1x 2，则0<t <1，ln t ＝t －1＋t.①设s (t )＝ln t －t －1＋t，则s ′(t )＝t －2t＋t2>0，所以s (t )在t ∈(0,1)上为增函数，s (t )<s (1)＝0，故ln t ≠t －1＋t.②①与②矛盾，因此，函数g (x )＝ax 2＋bx ＋c ·ln x (abc ≠0)不是“K 函数”． 11．解：(1)以O1为坐标系的原点，O 1O 2所在直线为x 轴，建立如图所示的直角坐标系．当点A 到达最高点时，点A 绕O 1转过π6，则点C 绕O 2转过π3.此时A (0,2r )，C (92r ，32r )．∴AC ＝－92r 2＋r －32r 2＝25－23·r .(2)由题意，设大飞轮转过的角度为θ，则小飞轮转过的角度为2θ，其中θ∈[0,2π]．此时B (2r cos θ，2r sin θ)，C (4r ＋r cos 2θ，r sin 2θ)．记点B ，C 的高度差为d ，则d ＝|2r sin θ－r sin 2θ|，即d ＝2r |sin θ－sin θcos θ|.设f (θ)＝sin θ－sin θcos θ，θ∈[0,2π]，则f ′(θ)＝(1－cos θ)(2cos θ＋1)．令f ′(θ)＝(1－cos θ)(2cos θ＋1)＝0，得cos θ＝－12或1，则θ＝2π3，4π3，0或2π.f (θ)和f ′(θ)随θ的变化情况如下表：综上所述，点B ，C 在传动过程中高度差的最大值d max ＝332r .。

全国通用2015年高考文科数学二轮复习突破练大题部分10份

目录高考中档大题规范练 (1)高考中档大题规范练(一) ........................................................................................................ 1 高考中档大题规范练(二) ........................................................................................................ 6 高考中档大题规范练(三) ...................................................................................................... 11 高考中档大题规范练(四) ...................................................................................................... 16 高考压轴大题突破练 .. (20)高考压轴大题突破练(一) ...................................................................................................... 20 高考压轴大题突破练(二) ...................................................................................................... 25 高考压轴大题突破练(三) ...................................................................................................... 32 高考压轴大题突破练(四) ...................................................................................................... 36 高考大题纵横练 . (42)高考大题纵横练(一) .............................................................................................................. 42 高考大题纵横练(二) .. (47)高考中档大题规范练高考中档大题规范练(一) ——三角函数与平面向量(推荐时间：60分钟)1．(2014·江苏)已知α∈⎝⎛⎭⎫π2，π，sin α＝55. (1)求sin ⎝⎛⎭⎫π4＋α的值；(2)求cos ⎝⎛⎭⎫5π6－2α的值．解 (1)因为α∈⎝⎛⎭⎫π2，π，sin α＝55，所以cos α＝－1－sin 2α＝－255.故sin ⎝⎛⎭⎫π4＋α＝sin π4cos α＋cos π4sin α ＝22×⎝⎛⎭⎫－255＋22×55＝－1010. (2)由(1)知sin 2α＝2sin αcos α ＝2×55×⎝⎛⎭⎫－255＝－45， cos 2α＝1－2sin 2α＝1－2×⎝⎛⎭⎫552＝35，所以cos ⎝⎛⎭⎫5π6－2α＝cos 5π6cos 2α＋sin 5π6sin 2α ＝⎝⎛⎭⎫－32×35＋12×⎝⎛⎭⎫－45＝－4＋3310.2．已知函数f (x )＝3sin 2x ＋2cos 2x ＋a . (1)求函数f (x )的最小正周期以及单调递增区间；(2)当x ∈[0，π4]时，函数f (x )有最大值4，求实数a 的值．解 f (x )＝3sin 2x ＋2cos 2x ＋a ＝cos 2x ＋3sin 2x ＋1＋a ＝2sin(2x ＋π6)＋a ＋1.(1)函数f (x )的最小正周期为2π2＝π，由2k π－π2≤2x ＋π6≤2k π＋π2(k ∈Z )，解得k π－π3≤x ≤k π＋π6(k ∈Z )．∴函数f (x )的单调递增区间为[k π－π3，k π＋π6](k ∈Z )．(2)∵x ∈[0，π4]，∴2x ＋π6∈[π6，2π3]，从而sin(2x ＋π6)∈[12，1]．∴f (x )＝2sin(2x ＋π6)＋a ＋1∈[a ＋2，a ＋3]，∵f (x )有最大值4，即a ＋3＝4，∴a ＝1.3．在△ABC 中，角A ，B ，C 所对的边分别是a ，b ，c ，已知c ＝2，C ＝π3.(1)若△ABC 的面积等于3，求a ，b ；(2)若sin C ＋sin(B －A )＝2sin 2A ，求△ABC 的面积．解 (1)由余弦定理及已知条件得，a 2＋b 2－ab ＝4，又△ABC 的面积等于3，所以12ab sin C ＝3，得ab ＝4，联立方程⎩⎪⎨⎪⎧a 2＋b 2－ab ＝4，ab ＝4，解得a ＝2，b ＝2.(2)由题意得sin(B ＋A )＋sin(B －A )＝4sin A cos A ，即sin B cos A ＝2sin A cos A .当cos A ＝0时，A ＝π2，B ＝π6，a ＝433，b ＝233，则△ABC 的面积S ＝12bc ＝233；当cos A ≠0时，得sin B ＝2sin A ，由正弦定理得b ＝2a ，联立方程⎩⎪⎨⎪⎧a 2＋b 2－ab ＝4，b ＝2a ，解得a ＝233，b ＝433.则△ABC 的面积S ＝12ab sin C ＝233，综上，△ABC 的面积为233.4．(2014·山东)已知向量a ＝(m ，cos 2x )，b ＝(sin 2x ，n ), 函数f (x )＝a ·b ，且y ＝f (x )的图象过点(π12，3)和点(2π3，－2)． (1)求m ，n 的值；(2)将y ＝f (x )的图象向左平移φ(0<φ<π)个单位后得到函数y ＝g (x )的图象，若y ＝g (x )图象上各最高点到点(0,3)的距离的最小值为1，求y ＝g (x )的单调递增区间．解 (1)由题意知f (x )＝a ·b ＝m sin 2x ＋n cos 2x . 因为y ＝f (x )的图象过点(π12，3)和(2π3，－2)，所以⎩⎨⎧3＝m sin π6＋n cos π6，－2＝m sin 4π3＋n cos 4π3，即⎩⎨⎧3＝12m ＋32n ，－2＝－32m －12n ，解得⎩⎨⎧m ＝3，n ＝1.(2)由(1)知，f (x )＝3sin 2x ＋cos 2x ＝2sin(2x ＋π6)．由题意知，g (x )＝f (x ＋φ)＝2sin(2x ＋2φ＋π6)．设y ＝g (x )的图象上符合题意的最高点为(x 0,2)，由题意知x 20＋1＝1，所以x 0＝0，即到点(0,3)的距离为1的最高点为(0,2)．将其代入y ＝g (x )，得sin(2φ＋π6)＝1，因为0<φ<π，所以φ＝π6，因此g (x )＝2sin(2x ＋π2)＝2cos 2x .由2k π－π≤2x ≤2k π，k ∈Z ，得k π－π2≤x ≤k π，k ∈Z ，所以函数y ＝g (x )的单调递增区间为[k π－π2，k π]，k ∈Z .5．(2014·上海) 如图，某公司要在A 、B 两地连线上的定点C 处建造广告牌CD ，其中D 为顶端，AC 长35米，CB 长80米，设A 、B 在同一水平面上，从A 和B 看D 的仰角分别为α和β.(1)设计中CD 是铅垂方向，若要求α≥2β，问CD 的长至多为多少(结果精确到0.01米)? (2)施工完成后，CD 与铅垂方向有偏差，现在实测得α＝38.12°，β＝18.45°，求CD 的长(结果精确到0.01米)?解 (1)令DC ＝h ，则tan α＝h AC ＝h 35，tan β＝h CB ＝h80. 因为90°>α≥2β>0°，所以tan α≥tan 2β＝2tan β1－tan 2β>0，即h 35≥2·h 801－(h 80)2＝2·80h802－h2>0，解得0<h ≤202≈28.28，所以，CD 的最大长度是28.28米．(2)设CD ＝h ，BD ＝m ，在△ABD 中，由正弦定理得，msin 38.12°＝35＋80sin (38.12°＋18.45°)，解得m ＝35＋80sin (38.12°＋18.45°)·sin 38.12°≈85.064.在△BCD 中，由余弦定理得，h 2＝802＋m 2－2·80·m ·cos 18.45°，解得h ≈26.93，所以，CD 的长是26.93米．6．已知函数f (x )＝sin 2(x 2＋π12)＋3sin(x 2＋π12)cos(x 2＋π12)－12.(1)在△ABC 中，若sin C ＝2sin A ，B 为锐角且有f (B )＝32，求角A ，B ，C ； (2)若f (x )(x >0)的图象与直线y ＝12交点的横坐标由小到大依次是x 1，x 2，…，x n ，求数列{x n }的前2n 项和，n ∈N *.解 (1)因为f (x )＝1－cos (x ＋π6)2＋32sin(x ＋π6)－12＝32sin(x ＋π6)－12cos(x ＋π6)＝sin(x ＋π6－π6)＝sin x ，又f (B )＝32，故sin B ＝32. 又B 为锐角，所以B ＝π3.由sin C ＝2sin A ，得c ＝2a ，所以b 2＝a 2＋4a 2－2a ·2a cos π3＝3a 2.所以c 2＝a 2＋b 2.所以△ABC 为直角三角形，C ＝π2，A ＝2π3－π2＝π6.综上，A ＝π6，B ＝π3，C ＝π2.(2)由正弦曲线的对称性、周期性，可知 x 1＋x 22＝π2，x 3＋x 42＝2π＋π2，…， x 2n －1＋x 2n 2＝2(n －1)π＋π2，所以x 1＋x 2＋…＋x 2n －1＋x 2n＝π＋5π＋9π＋…＋(4n －3)π＝n π＋12n (n －1)·4π＝(2n 2－n )π.高考中档大题规范练(二)——数列(推荐时间：60分钟)1．已知{a n }为等差数列，且a 2＝－1，a 5＝8. (1)求数列{|a n |}的前n 项和； (2)求数列{2n ·a n }的前n 项和．解 (1)设等差数列{a n }的公差为d ，因为a 2＝－1，a 5＝8，所以⎩⎪⎨⎪⎧a 1＋d ＝－1，a 1＋4d ＝8，解得a 1＝－4，d ＝3，所以a n ＝－4＋3(n －1)＝3n －7，因此|a n |＝|3n －7|＝⎩⎪⎨⎪⎧－3n ＋7，n ＝1，2，3n －7，n ≥3记数列{|a n |}的前n 项和为S n ，当n ＝1时，S 1＝|a 1|＝4，当n ＝2时，S 2＝|a 1|＋|a 2|＝5，当n ≥3时，S n ＝S 2＋|a 3|＋|a 4|＋…＋|a n |＝5＋(3×3－7)＋(3×4－7)＋…＋(3n －7) ＝5＋(n －2)[2＋3n －7]2＝32n 2－112n ＋10.又当n ＝2时满足此式，综上，S n ＝⎩⎪⎨⎪⎧4，n ＝1，32n 2－112n ＋10，n ≥2.(2)记数列{2n ·a n }的前n 项和为T n ，则T n ＝2a 1＋22a 2＋23a 3＋…＋2n a n ， 2T n ＝22a 1＋23a 2＋24a 3＋…＋2n a n －1＋2n ＋1a n ，所以－T n ＝2a 1＋d (22＋23＋…＋2n )－2n ＋1a n .由(1)知，a 1＝－4，d ＝3，a n ＝3n －7，所以－T n ＝－8＋3×4(1－2n －1)1－2－(3n －7)×2n ＋1＝－20－(3n －10)×2n ＋1，故T n ＝20＋(3n －10)×2n ＋1.2．已知函数f (x )＝14x ＋2(x ∈R )．(1)证明：f (x )＋f (1－x )＝12；(2)若数列{a n }的通项公式为a n ＝f (nm )(m ∈N *，n ＝1,2，…，m )，求数列{a n }的前m 项和S m ；(3)设数列{b n }满足b 1＝13，b n ＋1＝b 2n ＋b n ，T n ＝1b 1＋1＋1b 2＋1＋…＋1b n ＋1，若(2)中的S m 满足对不小于2的任意正整数m ，S m <T n 恒成立，试求m 的最大值． (1)证明因为f (x )＝14x ＋2，所以f (1－x )＝141－x ＋2＝4x 4＋2·4x ＝4x2(4x ＋2).所以f (x )＋f (1－x )＝14x ＋2＋4x2(4x ＋2)＝2＋4x 2(4x ＋2)＝12. (2)解由(1)，知f (x )＋f (1－x )＝12，所以f (k m )＋f (1－k m )＝12(1≤k ≤m －1)(k ∈N *)，即f (k m )＋f (m －k m )＝12.由题设知，a n ＝f (n m )，所以a k ＋a m －k ＝12，a m ＝f (m m )＝f (1)＝16.又S m ＝a 1＋a 2＋…＋a m －1＋a m ，① S m ＝a m －1＋a m －2＋…＋a 1＋a m ，②由①＋②，得2S m ＝(m －1)×12＋2a m ＝m 2－16，即S m ＝m 4－112(m ∈N *)．(3)解由b 1＝13，b n ＋1＝b 2n ＋b n ＝b n (b n ＋1)，显然对任意n ∈N *，b n >0，则1b n ＋1＝1b n (b n ＋1)＝1b n －1b n ＋1，即1b n ＋1＝1b n －1b n ＋1，所以T n ＝(1b 1－1b 2)＋(1b 2－1b 3)＋…＋(1b n －1b n ＋1)＝1b 1－1b n ＋1＝3－1b n ＋1. 因为b n ＋1－b n ＝b 2n >0，所以b n ＋1>b n ，即数列{b n }是单调递增数列．所以T n 关于n 递增，所以当n ∈N *时，T n ≥T 1.因为b 1＝13，b 2＝(13)2＋13＝49，所以T n ≥T 1＝3－1b 2＝34.由题意，知S m <34，即m 4－112<34，解得m <103，所以m 的最大值为3.3．设数列{a n }的前n 项和为S n ，满足2S n ＝a n ＋1－2n ＋1＋1，n ∈N *，且a 1＝1，设数列{b n }满足b n ＝a n ＋2n .(1)求证数列{b n }为等比数列，并求出数列{a n }的通项公式； (2)若数列c n ＝6n －3b n，T n 是数列{c n }的前n 项和，证明T n <3.(1)解当n ≥2时，由⎩⎪⎨⎪⎧2S n ＝a n ＋1－2n ＋1＋12S n －1＝a n －2n＋1⇒2a n ＝a n ＋1－a n －2n ，所以a n ＋1＝3a n ＋2n ，从而b n ＋1＝a n ＋1＋2n ＋1＝3(a n ＋2n )＝3b n ，故{b n }是以3为首项，3为公比的等比数列， b n ＝a n ＋2n ＝3×3n －1＝3n ，a n ＝3n －2n (n ≥2)，因为a 1＝1也满足，于是a n ＝3n －2n . (2)证明 c n ＝6n －3b n ＝2n －13n －1，则T n ＝130＋331＋532＋…＋2n －33n －2＋2n －13n －1，①13T n ＝131＋332＋533＋…＋2n －33n －1＋2n －13n ，② ①－②得，23T n ＝130＋231＋232＋…＋23n －1－2n －13n ＝1＋23·1－13n －11－13－2n －13n ＝2－13n －1－2n －13n ＝2－2(n ＋1)3n，故T n ＝3－n ＋13n －1<3.4．已知单调递增数列{a n }的前n 项和为S n ，满足S n ＝12(a 2n ＋n )．(1)求数列{a n }的通项公式；(2)设c n ＝⎩⎪⎨⎪⎧1a 2n ＋1－1，n 为奇数，3×2a n －1＋1，n 为偶数，求数列{c n }的前n 项和T n .解 (1)n ＝1时，a 1＝12(a 21＋1)，得a 1＝1，当n ≥2时，S n －1＝12(a 2n －1＋n －1)，得a n ＝S n －S n －1＝12(a 2n －a 2n －1＋1)，化简得(a n －1)2－a 2n －1＝0，a n －a n －1＝1或a n ＋a n －1＝1(n ≥2)，又{a n }是单调递增数列，故a n －a n －1＝1，所以{a n }是首项为1，公差为1的等差数列，故a n ＝n . (2)c n ＝⎩⎪⎨⎪⎧1a 2n ＋1－1，n 为奇数，3×21n a -＋1，n 为偶数，当n 为偶数时，T n ＝(c 1＋c 3＋…＋c n －1)＋(c 2＋c 4＋…＋c n ) ＝(122－1＋142－1＋…＋1n 2－1)＋3×(21＋23＋…＋2n －1)＋n 2＝11×3＋13×5＋…＋1(n －1)×(n ＋1)＋3×2(1－42n)1－4＋n 2＝12×(11－13＋13－15＋…＋1n －1－1n ＋1)＋2×(42n－1)＋n 2＝2n ＋1＋n 2－2n －42(n ＋1). 当n 为奇数时，T n ＝(c 1＋c 3＋…＋c n )＋(c 2＋c 4＋…＋c n －1) ＝[122－1＋142－1＋…＋1(n ＋1)2－1]＋3×(21＋23＋…＋2n －2)＋n －12 ＝12×(11－13＋13－15＋…＋1n －1n ＋2)＋2×(412n -－1)＋n －12＝2n ＋n 2－2n －92(n ＋2).所以T n＝⎩⎪⎨⎪⎧2n＋n 2－2n －92(n ＋2)，n 为奇数，2n ＋1＋n 2－2n －42(n ＋1)，n 为偶数.5．已知函数f (x )＝2x ＋33x ，数列{a n }满足a 1＝1，a n ＋1＝f (1a n )，n ∈N *.(1)求数列{a n }的通项公式；(2)令b n ＝1a n －1a n (n ≥2)，b 1＝3，S n ＝b 1＋b 2＋…＋b n ，若S n <m －2 0142对一切n ∈N *成立，求最小正整数m .解 (1)∵a n ＋1＝f (1a n )＝2a n ＋33a n ＝2＋3a n 3＝a n ＋23，∴{a n }是以1为首项，23为公差的等差数列．∴a n ＝1＋(n －1)×23＝23n ＋13.(2)当n ≥2时，b n ＝1a n －1a n ＝1(23n －13)(23n ＋13) ＝1(2n －1)(2n ＋1)9＝92(12n －1－12n ＋1)，又b 1＝3＝92(1－13)，∴S n ＝b 1＋b 2＋…＋b n ＝92(1－13＋13－15＋…＋12n －1－12n ＋1)＝92(1－12n ＋1)＝9n2n ＋1，∵S n <m －2 0142对一切n ∈N *成立，即9n 2n ＋1<m －2 0142对一切n ∈N *成立，又9n 2n ＋1<92，∴m －2 0142≥92，即m ≥2 023.∴最小正整数m 为2 023.6．某工厂为扩大生产规模，今年年初新购置了一条高性能的生产线，该生产线在使用过程中的维护费用会逐年增加，第一年的维护费用是4万元，从第二年到第七年，每年的维护费用均比上年增加2万元，从第八年开始，每年的维护费用比上年增加25%. (1)设第n 年该生产线的维护费用为a n ，求a n 的表达式；(2)若该生产线前n 年每年的平均维护费用大于12万元时，需要更新生产线．求该生产线前n 年每年的平均维护费用，并判断第几年年初需要更新该生产线？解 (1)由题意知，当n ≤7时，数列{a n }是首项为4，公差为2的等差数列， ∴a n ＝4＋(n －1)×2＝2n ＋2.当n ≥8时，数列{a n }从a 7开始构成首项为a 7＝2×7＋2＝16，公比为1＋25%＝54的等比数列，则此时a n ＝16×⎝⎛⎭⎫54n －7，∴a n ＝⎩⎪⎨⎪⎧2n ＋2，n ≤7，16×⎝⎛⎭⎫54n －7，n ≥8.(2)设S n 为数列{a n }的前n 项和，当1≤n ≤7时，S n ＝4n ＋n (n －1)2×2＝n 2＋3n ，当n ≥8时，由S 7＝70，则S n ＝70＋16×54×1－⎝⎛⎭⎫54n －71－54＝80×⎝⎛⎭⎫54n －7－10， ∴该生产线前n 年每年的平均维护费用为 S nn ＝⎩⎨⎧n ＋3，1≤n ≤7，80×⎝⎛⎭⎫54n －7－10n，n ≥8.当1≤n ≤7时，⎩⎨⎧⎭⎬⎫S n n 为递增数列，当n ≥8时，∵S n ＋1n ＋1－S nn ＝80×⎝⎛⎭⎫54n －6－10n ＋1－80×⎝⎛⎭⎫54n －7－10n＝80×⎝⎛⎭⎫54n －7·⎝⎛⎭⎫n 4－1＋10n (n ＋1)>0，∴S n ＋1n ＋1>S n n.∴⎩⎨⎧⎭⎬⎫S n n 也为递增数列．又∵S 77＝10<12，S 88＝80×54－108＝11.25<12，S 99＝80×⎝⎛⎭⎫542－109≈12.78>12， ∴第9年年初需要更新生产线．高考中档大题规范练(三)——立体几何(推荐时间：70分钟)1．(2014·江苏)如图，在三棱锥P －ABC 中，D ，E ，F 分别为棱PC ，AC ，AB 的中点．已知P A ⊥AC ，P A ＝6，BC ＝8，DF ＝5. 求证：(1)直线P A ∥平面DEF ； (2)平面BDE ⊥平面ABC .证明 (1)因为D ，E 分别为棱PC ，AC 的中点，所以DE ∥P A .又因为P A ⊄平面DEF ，DE ⊂平面DEF ，所以直线P A ∥平面DEF .(2)因为D ，E ，F 分别为棱PC ，AC ，AB 的中点，P A ＝6，BC ＝8，所以DE ∥P A ，DE ＝12P A ＝3，EF ＝12BC ＝4.又因为DF ＝5，故DF 2＝DE 2＋EF 2，所以∠DEF ＝90°，即DE ⊥EF . 又P A ⊥AC ，DE ∥P A ，所以DE ⊥AC .因为AC ∩EF ＝E ，AC ⊂平面ABC ，EF ⊂平面ABC ，所以DE ⊥平面ABC ，又DE ⊂平面BDE ，所以平面BDE ⊥平面ABC .2．(2014·江西)如图，三棱柱ABC －A 1B 1C 1中，AA 1⊥BC ，A 1B ⊥BB 1. (1)求证：A 1C ⊥CC 1；(2)若AB ＝2，AC ＝3，BC ＝7，问AA 1为何值时，三棱柱ABC －A 1B 1C 1体积最大，并求此最大值． (1)证明由AA 1⊥BC ，知BB 1⊥BC .又BB 1⊥A 1B ，BC ⊂平面BCA 1，A 1B ⊂平面BCA 1，故BB 1⊥平面BCA 1，所以BB 1⊥A 1C . 又BB 1∥CC 1，所以A 1C ⊥CC 1. (2)解方法一设AA 1＝x ，在Rt △A 1BB 1中，A 1B ＝A 1B 21－BB 21＝4－x 2. 同理A 1C ＝A 1C 21－CC 21＝3－x 2，在△A 1BC 中，cos ∠BA 1C ＝A 1B 2＋A 1C 2－BC 22A 1B ·A 1C＝－x 2(4－x 2)(3－x 2)，sin ∠BA 1C ＝12－7x 2(4－x 2)(3－x 2)，所以S △A 1BC ＝12A 1B ·A 1C ·sin ∠BA 1C ＝12－7x 22.从而三棱柱ABC －A 1B 1C 1的体积V ＝S 直·l ＝S △A 1BC ·AA 1＝x 12－7x 22.因为x 12－7x 2＝12x 2－7x 4＝－7(x 2－67)2＋367，故当x ＝67＝427，即AA 1＝427时，体积V 取到最大值377.方法二如图所示，过A 1作BC 的垂线，垂足为D ，连接AD . 由AA 1⊥BC ，A 1D ⊥BC ，故BC ⊥平面AA 1D ，BC ⊥AD . 又AB ＝2，AC ＝3，BC ＝7，所以AB 2＋AC 2＝BC 2，故∠BAC ＝90°，所以S △ABC ＝12AD ·BC ＝12AB ·AC ，所以AD ＝2217.设AA 1＝x ，在Rt △AA 1D 中，A 1D ＝AD2－AA 21＝127－x 2，S △A 1BC ＝12A 1D ·BC ＝12－7x 22. 从而三棱柱ABC －A 1B 1C 1的体积V ＝S 直·l ＝S △A 1BC ·AA 1＝x 12－7x 22.因为x 12－7x 2＝12x 2－7x 4 ＝－7(x 2－67)2＋367，故当x ＝67＝427，即AA 1＝427时，体积V 取到最大值377.3．如图所示，已知三棱锥A －BPC 中，AP ⊥PC ，AC ⊥BC ，M 为AB 的中点，D 为PB 的中点，且△PMB 为正三角形． (1)求证：MD ∥平面APC ； (2)求证：平面ABC ⊥平面APC ；(3)若BC ＝4，AB ＝20，求三棱锥D －BCM 的体积． (1)证明由已知，得MD 是△ABP 的中位线，所以MD ∥AP .又MD ⊄平面APC ，AP ⊂平面APC ，故MD ∥平面APC .(2)证明因为△PMB 为正三角形，D 为PB 的中点，所以MD ⊥PB .所以AP ⊥PB .又AP ⊥PC ，PB ∩PC ＝P ，所以AP ⊥平面PBC . 因为BC ⊂平面PBC ，所以AP ⊥BC .又BC ⊥AC ，AC ∩AP ＝A ，所以BC ⊥平面APC . 因为BC ⊂平面ABC ，所以平面ABC ⊥平面APC . (3)解由题意，可知MD ⊥平面PBC ，所以MD 是三棱锥D －BCM 的一条高，在Rt △ABC 中，AB ＝20，BC ＝4，则CM ＝12AB ＝10，又在正三角形PMB 中，DM ＝53，所以DC ＝MC 2－DM 2＝102－(53)2＝5，所以cos ∠DBC ＝25＋16－252×5×4＝25，则S △BCD ＝12·BD ·BC ·sin ∠DBC ＝12×5×4×215＝221，所以V D －BCM ＝V M －DBC ＝13×S △BCD ×MD＝13×221×53＝107. 4．在四棱锥P －ABCD 中，底面ABCD 是边长为a 的正方形，PD ⊥底面ABCD ，且PD ＝a ，P A ＝PC ＝2a ，若在这个四棱锥内放一球，求此球的最大半径．解当球内切于四棱锥，即与四棱锥各面均相切时球半径最大，设球的半径为r ，球心为O ，连接OP 、OA 、OB 、OC 、OD ，则把此四棱锥分割成四个三棱锥和一个四棱锥，这些小棱锥的高都是r ，底面分别为原四棱锥的侧面和底面，则V P －ABCD ＝13r (S △P AB ＋S △PBC ＋S △PCD ＋S △P AD ＋S 正方形ABCD )＝13r (2＋2)a 2.由题意，知PD ⊥底面ABCD ， ∴V P －ABCD ＝13S 正方形ABCD ·PD ＝13a 3.由体积相等，得13r (2＋2)a 2＝13a 3，解得r ＝12(2－2)a .5．(2014·课标全国Ⅰ)如图，三棱柱ABC －A 1B 1C 1中，侧面BB 1C 1C 为菱形，B 1C 的中点为O ，且AO ⊥平面BB 1C 1C . (1)证明：B 1C ⊥AB ；(2)若AC ⊥AB 1，∠CBB 1＝60°，BC ＝1，求三棱柱ABC －A 1B 1C 1的高．(1)证明连接BC 1，则O 为B 1C 与BC 1的交点．因为侧面BB 1C 1C 为菱形，所以B 1C ⊥BC 1. 又AO ⊥平面BB 1C 1C ，所以B 1C ⊥AO ，由于AB ⊂平面ABO ，故B 1C ⊥AB .(2)解作OD ⊥BC ，垂足为D ，连接AD . 作OH ⊥AD ，垂足为H .由于BC ⊥AO ，BC ⊥OD ，AO ∩OD ＝O ，故BC ⊥平面AOD ，所以OH ⊥BC .又OH ⊥AD ，BC ∩AD ＝D ，所以OH ⊥平面ABC . 因为∠CBB 1＝60°，所以△CBB 1为等边三角形．又BC ＝1，可得OD ＝34. 由于AC ⊥AB 1，所以OA ＝12B 1C ＝12.由OH ·AD ＝OD ·OA ，且AD ＝OD 2＋OA 2＝74，得OH ＝2114. 又O 为B 1C 的中点，所以点B 1到平面ABC 的距离为217，故三棱柱ABC －A 1B 1C 1的高为217.6．如图，四边形ABCD 为正方形，EA ⊥平面ABCD ，EF ∥AB ，AB ＝4，AE ＝2，EF ＝1. (1)求证：BC ⊥AF ；(2)若点M 在线段AC 上，且满足CM ＝14CA ，求证：EM ∥平面FBC ；(3)试判断直线AF 与平面EBC 是否垂直？若垂直，请给出证明；若不垂直，请说明理由． (1)证明因为EF ∥AB ，所以EF 与AB 确定平面EABF . 因为EA ⊥平面ABCD ，所以EA ⊥BC . 由已知，得AB ⊥BC 且EA ∩AB ＝A ，又AF ⊂平面EABF ，所以BC ⊥AF .(2)证明如图所示，过M 作MN ⊥BC ，垂足为N ，连接FN ，则MN ∥AB . 又CM ＝14AC ，所以MN ＝14AB .又EF ∥AB 且EF ＝14AB ，所以EF ∥MN ，且EF ＝MN .所以四边形EFNM 为平行四边形，所以EM ∥FN . 又FN ⊂平面FBC ，EM ⊄平面FBC ，所以EM ∥平面FBC . (3)解 AF ⊥平面EBC . 证明如下：由(1)，可知AF ⊥BC .在四边形ABFE 中，AB ＝4，AE ＝2，EF ＝1，∠BAE ＝∠AEF ＝90°，所以tan ∠EBA ＝AE AB ＝12，tan ∠F AE ＝EF AE ＝12，即tan ∠EBA ＝tan ∠F AE ，则∠EBA ＝∠F AE . 设AF ∩BE ＝P ，因为∠P AE ＋∠P AB ＝90°，故∠PBA ＋∠P AB ＝90°. 则∠APB ＝90°，即EB ⊥AF . 又EB ⊂平面EBC ，BC ⊂平面EBC ，且EB ∩BC ＝B ，所以AF ⊥平面EBC .高考中档大题规范练(四)——概率与统计(推荐时间：70分钟)1．(2014·湖南)某企业有甲、乙两个研发小组．为了比较他们的研发水平，现随机抽取这两个小组往年研发新产品的结果如下：(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )．其中a ，a 分别表示甲组研发成功和失败；b ，b 分别表示乙组研发成功和失败． (1)若某组成功研发一种新产品，则给该组记1分，否则记0分．试计算甲、乙两组研发新产品的成绩的平均数和方差，并比较甲、乙两组的研发水平；(2)若该企业安排甲、乙两组各自研发一种新产品，试估计恰有一组研发成功的概率．解 (1)甲组研发新产品的成绩为 1,1,1,0,0,1,1,1,0,1,0,1,1,0,1，其平均数为x 甲＝1015＝23；方差为s 2甲＝115⎣⎡⎦⎤⎝⎛⎭⎫1－232×10＋⎝⎛⎭⎫0－232×5＝29.乙组研发新产品的成绩为 1,0,1,1,0,1,1,0,1,0,0,1,0,1,1，其平均数为x 乙＝915＝35；方差为s 2乙＝115⎣⎡⎦⎤⎝⎛⎭⎫1－352×9＋⎝⎛⎭⎫0－352×6＝625.因为x 甲>x 乙，s 2甲<s 2乙，所以甲组的研发水平优于乙组． (2)记事件E ＝{恰有一组研发成功}．在所抽得的15个结果中，恰有一组研发成功的结果是(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )，(a ，b )共7个．故事件E 发生的频率为715.将频率视为概率，则得所求概率为P (E )＝715.即恰有一组研发成功的概率为715.2．先后随机投掷2枚正方体骰子，其中x 表示第1枚骰子出现的点数，y 表示第2枚骰子出现的点数．(1)求点P (x ，y )在直线y ＝x －2上的概率； (2)求点P (x ，y )满足y 2<2x 的概率．解每枚骰子出现的点数都有6种情况，所以基本事件总数为6×6＝36(个)．(1)记“点P (x ，y )在直线y ＝x －2上”为事件A ，则事件A 有4个基本事件：(3,1)，(4,2)，(5,3)，(6,4)，所以P (A )＝436＝19.(2)记“点P (x ，y )满足y 2<2x ”为事件B ，则事件B 有12个基本事件：(1,1)，(2,1)，(3,1)，(3,2)，(4,1)，(4,2)，(5,1)，(5,2)，(5,3)，(6,1)，(6,2)，(6,3)，所以P (B )＝1236＝13.3．有编号为1,2,3的三个白球，编号为4,5,6的三个黑球，这六个球除编号和颜色外完全相同，现从中任意取出两个球． (1)求取得的两个球颜色相同的概率； (2)求取得的两个球颜色不相同的概率．解从六个球中取出两个球的基本事件有(1,2)，(1,3)，(1,4)，(1,5)，(1,6)，(2,3)，(2,4)，(2,5)，(2,6)，(3,4)，(3,5)，(3,6)，(4,5)，(4,6)，(5,6)共计15个基本事件．(1)记事件A 为“取出的两个球是白球”，则这个事件包含的基本事件的是(1,2)，(1,3)，(2,3)，共计3个基本事件，故P (A )＝315＝15.记事件B 为“取出的两个球是黑球”，同理可得P (B )＝15.记事件C 为“取出的两个球的颜色相同”，则C ＝A ＋B ，且A ，B 互斥，根据互斥事件的概率加法公式，得P (C )＝P (A ＋B )＝P (A )＋P (B )＝25.(2)记事件D 为“取出的两个球的颜色不相同”，则事件C ，D 互斥，根据互斥事件概率之间的关系，得P (D )＝1－P (C )＝1－25＝35.4．(2014·辽宁)某大学餐饮中心为了解新生的饮食习惯，在全校一年级学生中进行了抽样调查，调查结果如下表所示：(1)方面有差异”；(2)已知在被调查的北方学生中有5名数学系的学生，其中2名喜欢甜品，现在从这5名学生中随机抽取3人，求至多有1人喜欢甜品的概率．附：P (2≥k ) 解 (1)将2×22＝n (n 11n 22－n 12n 21)2n 1＋n 2＋n ＋1n ＋2＝100×(60×10－20×10)270×30×80×20＝10021≈4.762. 因为4.762>3.841，所以有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”．(2)从5名数学系学生中任取3人的一切可能结果所组成的基本事件空间Ω＝{(a 1，a 2，b 1)，(a 1，a 2，b 2)，(a 1，a 2，b 3)，(a 1，b 1，b 2)，(a 1，b 2，b 3)，(a 1，b 1，b 3)，(a 2，b 1，b 2)，(a 2，b 2，b 3)，(a 2，b 1，b 3)，(b 1，b 2，b 3)}．其中a i 表示喜欢甜品的学生，i ＝1,2；b j 表示不喜欢甜品的学生，j ＝1,2,3.Ω由10个基本事件组成，且这些基本事件的出现是等可能的．用A 表示“3人中至多有1人喜欢甜品”这一事件，则事件A ＝{(a 1，b 1，b 2)，(a 1，b 2，b 3)，(a 1，b 1，b 3)，(a 2，b 1，b 2)，(a 2，b 2，b 3)，(a 2，b 1，b 3)，(b 1，b 2，b 3)}．事件A 是由7个基本事件组成，因而P (A )＝710.5．某商场为吸引顾客消费，推出一项优惠活动．活动规则如下：消费每满100元可以转动如图所示的圆盘一次，其中O 为圆心，且标有20元，10元，0元的三部分区域面积相等．假定指针停在任一位置都是等可能的．当指针停在某区域时，返相应金额的优惠券．例如：某顾客消费了218元，第一次转动获得了20元，第二次获得了10元，则其共获得了30元优惠券．顾客甲和乙都到商场进行了消费，并按照规则参与了活动． (1)若顾客甲消费了128元，求他获得的优惠券金额大于0元的概率； (2)若顾客乙消费了280元，求他总共获得的优惠券金额不低于20元的概率．解 (1)设“甲获得的优惠券金额大于0元”为事件A .因为指针停在任一位置都是等可能的，而题中所给的三部分区域的面积相等，所以指针停在20元，10元，0元区域内的概率都是13.根据互斥事件的概率，有P (A )＝13＋13＝23，所以“顾客甲获得的优惠券金额大于0元”的概率是23.(2)设“乙获得的优惠券金额不低于20元”为事件B .因为顾客乙转动转盘两次，设乙第一次转动转盘获得优惠券的金额为x 元，第二次获得优惠券的金额为y 元，则基本事件空间可以表示为Ω＝{(20,20)，(20,10)，(20,0)，(10,20)，(10,10)，(10,0)，(0,20)，(0,10)，(0,0)}，即Ω中含有9个基本事件，每个基本事件发生的概率都为19.而乙获得的优惠券金额不低于20元，是指x ＋y ≥20，所以事件B 中包含的基本事件有6个．所以乙获得的优惠券金额不低于20元的概率为 P (B )＝69＝23.6．已知关于x 的一元二次方程9x 2＋6ax －b 2＋4＝0，a ，b ∈R .(1)若a 是从1,2,3三个数中任取的一个数，b 是从0,1,2三个数中任取的一个数，求已知方程有两个不相等实根的概率；(2)若a 是从区间[0,3]内任取的一个数，b 是从区间[0,2]内任取的一个数，求已知方程有实数根的概率．解设事件A 为“方程9x 2＋6ax －b 2＋4＝0有两个不相等的实数根”；事件B 为“方程9x 2＋6ax －b 2＋4＝0有实数根”．(1)由题意，知基本事件共9个，即(1,0)，(1,1)，(1,2)，(2,0)，(2,1)，(2,2)，(3,0)，(3,1)，(3,2)，其中第一个数表示a 的取值，第二个数表示b 的取值．由Δ＝36a 2－36(－b 2＋4)＝36a 2＋36b 2－36×4>0，得a 2＋b 2>4.事件A 要求a ，b 满足条件a 2＋b 2>4，可知包含6个基本事件，即(1,2)，(2,1)，(2,2)，(3,0)，(3,1)，(3,2)，则事件A 发生的概率为P (A )＝69＝23.(2)a ，b 的取值所构成的区域如图所示，其中0≤a ≤3,0≤b ≤2. 构成事件B 的区域为{(a ，b )|0≤a ≤3,0≤b ≤2，a 2＋b 2≥4}(如图中阴影部分)，则所求的概率为P (B )＝2×3－14×π×222×3＝1－π6.高考压轴大题突破练高考压轴大题突破练(一) ——直线与圆锥曲线(1)(推荐时间：70分钟)1．(2014·课标全国Ⅰ)已知点A (0，－2)，椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为32，F 是椭圆E 的右焦点，直线AF 的斜率为233，O 为坐标原点．(1)求E 的方程；(2)设过点A 的动直线l 与E 相交于P ，Q 两点，当△OPQ 的面积最大时，求l 的方程．解 (1)设F (c,0)，由条件知，2c ＝233，得c ＝ 3.又e ＝c a ＝32，所以a ＝2，b 2＝a 2－c 2＝1.故E 的方程为x 24＋y 2＝1.(2)当l ⊥x 轴时，不合题意，故设l ：y ＝kx －2，P (x 1，y 1)，Q (x 2，y 2)，将y ＝kx －2代入x 24＋y 2＝1得(1＋4k 2)x 2－16kx ＋12＝0. 当Δ＝16(4k 2－3)>0，即k 2>34时，x 1,2＝8k ±24k 2－34k 2＋1.从而|PQ |＝k 2＋1|x 1－x 2|＝4k 2＋1·4k 2－34k 2＋1.又点O 到直线PQ 的距离d ＝2k 2＋1，所以△OPQ 的面积S △OPQ ＝12d |PQ |＝44k 2－34k 2＋1.设4k 2－3＝t ，则t >0，S △OPQ ＝4t t 2＋4＝4t ＋4t .因为t ＋4t ≥4，当且仅当t ＝2，即k ＝±72时等号成立，且满足Δ>0，所以，当△OPQ 的面积最大时l 的方程为y ＝72x －2或y ＝－72x －2.2．(2014·陕西)如图，曲线C 由上半椭圆C 1：y 2a 2＋x 2b 2＝1(a >b >0，y ≥0)和部分抛物线C 2：y ＝－x 2＋1(y ≤0)连接而成，C 1与C 2的公共点为A ，B ，其中C 1的离心率为32. (1)求a ，b 的值；(2)过点B 的直线l 与C 1，C 2分别交于点P ，Q (均异于点A ，B )，若AP ⊥AQ ，求直线l 的方程．解 (1)在C 1，C 2的方程中，令y ＝0，可得b ＝1，且A (－1,0)，B (1,0)是上半椭圆C 1的左，右顶点．设C 1的半焦距为c ，由c a ＝32及a 2－c 2＝b 2＝1，得a ＝2.∴a ＝2，b ＝1.(2)由(1)知，上半椭圆C 1的方程为y 24＋x 2＝1(y ≥0)．易知，直线l 与x 轴不重合也不垂直，设其方程为y ＝k (x －1)(k ≠0)，代入C 1的方程，整理得(k 2＋4)x 2－2k 2x ＋k 2－4＝0.(*) 设点P 的坐标为(x p ，y p )，∵直线l 过点B ，∴x ＝1是方程(*)的一个根．由根与系数的关系，得x p ＝k 2－4k 2＋4，从而y p ＝－8kk 2＋4，∴点P 的坐标为(k 2－4k 2＋4，－8kk 2＋4)．同理，由⎩⎪⎨⎪⎧y ＝k (x －1)(k ≠0)，y ＝－x 2＋1(y ≤0)得点Q 的坐标为(－k －1，－k 2－2k )． ∴AP →＝2k k 2＋4(k ，－4)，AQ →＝－k (1，k ＋2)．∵AP ⊥AQ ，∴AP →·AQ →＝0，即－2k 2k 2＋4[k －4(k ＋2)]＝0.∵k ≠0，∴k －4(k ＋2)＝0，解得k ＝－83.经检验，k ＝－83符合题意．∴直线l 的方程为y ＝－83(x －1)，即直线l 的方程为y ＝－83x ＋83.3．已知抛物线C ：y ＝mx 2(m >0)，焦点为F ，直线2x －y ＋2＝0交抛物线C 于A ，B 两点，P 是线段AB 的中点，过P 作x 轴的垂线交抛物线C 于点Q . (1)求抛物线C 的焦点坐标；(2)若抛物线C 上有一点R (x R,2)到焦点F 的距离为3，求此时m 的值；(3)是否存在实数m ，使△ABQ 是以Q 为直角顶点的直角三角形？若存在，求出m 的值；若不存在，说明理由．解 (1)∵抛物线C ：x 2＝1m y ，∴它的焦点F (0，14m )．(2)∵|RF |＝y R ＋14m ，∴2＋14m ＝3，得m ＝14. (3)存在，联立方程⎩⎪⎨⎪⎧y ＝mx 2，2x －y ＋2＝0，消去y 得mx 2－2x －2＝0，依题意，有Δ＝(－2)2－4×m ×(－2)>0⇒m >－12.设A (x 1，mx 21)，B (x 2，mx 22)，则⎩⎨⎧x 1＋x 2＝2m，x 1·x 2＝－2m，(*)∵P 是线段AB 的中点，∴P (x 1＋x 22，mx 21＋mx 222)，即P (1m ，y P )，∴Q (1m ，1m)．得QA →＝(x 1－1m ，mx 21－1m )，QB →＝(x 2－1m ，mx 22－1m )，若存在实数m ，使△ABQ 是以Q 为直角顶点的直角三角形，则QA →·QB →＝0，即(x 1－1m )·(x 2－1m )＋(mx 21－1m )(mx 22－1m )＝0，结合(*)化简得－4m 2－6m＋4＝0，即2m 2－3m －2＝0，∴m ＝2或m ＝－12，而2∈(－12，＋∞)，－12∉(－12，＋∞)．∴存在实数m ＝2，使△ABQ 是以Q 为直角顶点的直角三角形．4．已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左，右焦点分别为F 1，F 2，点M (0,2)是椭圆的一个顶点，△F 1MF 2是等腰直角三角形． (1)求椭圆的方程；(2)过点M 分别作直线MA ，MB 交椭圆于A ，B 两点，设两直线的斜率分别为k 1，k 2，且k 1＋k 2＝8，证明：直线AB 过定点⎝⎛⎭⎫－12，－2. (1)解由已知，可得b ＝2，a 2＝(2b )2＝8，所求椭圆方程为x 28＋y 24＝1.(2)证明设A ，B 两点的坐标分别为(x 1，y 1)，(x 2，y 2)，若直线AB 的斜率存在，设方程为y ＝kx ＋m ，由⎩⎪⎨⎪⎧x 28＋y 24＝1，y ＝kx ＋m ，得(1＋2k 2)x 2＋4kmx ＋2m 2－8＝0. 则x 1＋x 2＝－4km 1＋2k 2，x 1x 2＝2m 2－81＋2k 2.由k 1＋k 2＝8，得y 1－2x 1＋y 2－2x 2＝8，所以kx 1＋m －2x 1＋kx 2＋m －2x 2＝8，即2k ＋(m －2)·x 1＋x 2x 1x 2＝8.所以k －mk m ＋2＝4，整理得m ＝12k －2.故直线AB 的方程为y ＝kx ＋12k －2，即y ＝k ⎝⎛⎭⎫x ＋12－2. 所以直线AB 过定点⎝⎛⎭⎫－12，－2. 若直线AB 的斜率不存在，设AB 的方程为x ＝x 0，设A (x 0，y 0)，B (x 0，－y 0)，由已知y 0－2x 0＋－y 0－2x 0＝8，得x 0＝－12.此时AB 的方程为x ＝－12，显然过点⎝⎛⎭⎫－12，－2. 综上，直线AB 过定点⎝⎛⎭⎫－12，－2. 5．已知椭圆的一个顶点为A (0，－1)，焦点在x 轴上，中心在原点．若右焦点到直线x －y ＋22＝0的距离为3. (1)求椭圆的标准方程；(2)设直线y ＝kx ＋m (k ≠0)与椭圆相交于不同的两点M ，N .当|AM |＝|AN |时，求m 的取值范围．解 (1)依题意可设椭圆方程为x 2a 2＋y 2＝1，则右焦点F (a 2－1，0)，由题设|a 2－1＋22|2＝3，解得a 2＝3.∴所求椭圆的方程为x 23＋y 2＝1.(2)设P (x P ，y P )，M (x M ，y M )，N (x N ，y N )， P 为弦MN 的中点，由⎩⎪⎨⎪⎧y ＝kx ＋m ，x 23＋y 2＝1得(3k 2＋1)x 2＋6mkx ＋3(m 2－1)＝0， ∵直线与椭圆相交，∴Δ＝(6mk )2－4(3k 2＋1)×3(m 2－1)>0 ⇒m 2<3k 2＋1.① ∴x P ＝x M ＋x N 2＝－3mk3k 2＋1，从而y P ＝kx P ＋m ＝m3k 2＋1，∴k AP ＝y P ＋1x P ＝－m ＋3k 2＋13mk ，又∵|AM |＝|AN |，∴AP ⊥MN ，则－m ＋3k 2＋13mk ＝－1k ，即2m ＝3k 2＋1.②把②代入①，得m 2<2m ，解得0<m <2；由②，得k 2＝2m －13>0，解得m >12.综上求得m 的取值范围是12<m <2.高考压轴大题突破练(二)——直线与圆锥曲线(2)(推荐时间：70分钟)1．设椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左，右焦点分别为F 1，F 2.点P (a ，b )满足|PF 2|＝|F 1F 2|.(1)求椭圆的离心率e ；(2)设直线PF 2与椭圆相交于A ，B 两点．若直线PF 2与圆(x ＋1)2＋(y －3)2＝16相交于M ，N 两点，且|MN |＝58|AB |，求椭圆的方程．解 (1)设F 1(－c,0)，F 2(c,0)(c >0)，因为|PF 2|＝|F 1F 2|，所以(a －c )2＋b 2＝2c . 整理得2(c a )2＋ca －1＝0，解得c a ＝－1(舍)，或c a ＝12.所以e ＝12.(2)由(1)知a ＝2c ，b ＝3c ，可得椭圆方程为3x 2＋4y 2＝12c 2，直线PF 2的方程为y ＝3(x －c )．A ，B 两点的坐标满足方程组⎩⎨⎧3x 2＋4y 2＝12c 2，y ＝3(x －c ).消去y 并整理，得5x 2－8cx ＝0. 解得x 1＝0，x 2＝85c .得方程组的解⎩⎨⎧x 1＝0，y 1＝－3c ，⎩⎨⎧x 2＝85c ，y 2＝335c .不妨设A (85c ，335c )，B (0，－3c )，所以|AB |＝(85c )2＋(335c ＋3c )2＝165c . 于是|MN |＝58|AB |＝2c .圆心(－1，3)到直线PF 2的距离 d ＝|－3－3－3c |2＝3|2＋c |2.因为d 2＋(|MN |2)2＝42，所以34(2＋c )2＋c 2＝16.整理得7c 2＋12c －52＝0，得c ＝－267(舍)，或c ＝2.16122．已知椭圆的中心在原点，焦点在x 轴上，焦距为215，且经过点M (4,1)，直线l ：x －y ＋m ＝0交椭圆于不同的两点A ，B . (1)求m 的取值范围；(2)若直线l 不经过点M ，求证：直线MA ，MB 的斜率互为相反数．(1)解设椭圆的方程为x 2a 2＋y 2b 2＝1(a >b >0)，因为2c ＝215，所以a 2＝b 2＋c 2＝b 2＋15，又因为椭圆过点M (4,1)，所以16a 2＋1b 2＝1，解得b 2＝5，a 2＝20，故椭圆方程为x 220＋y 25＝1，将y ＝x ＋m 代入x 220＋y 25＝1，整理得5x 2＋8mx ＋4m 2－20＝0， Δ＝(8m )2－20(4m 2－20)>0，解得－5<m <5. (2)证明设直线MA ，MB 的斜率分别为k 1和k 2，设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝－8m5，x 1x 2＝4m 2－205.k 1＋k 2＝y 1－1x 1－4＋y 2－1x 2－4＝(y 1－1)(x 2－4)＋(y 2－1)(x 1－4)(x 1－4)(x 2－4)，则(y 1－1)(x 2－4)＋(y 2－1)(x 1－4) ＝(x 1＋m －1)(x 2－4)＋(x 2＋m －1)(x 1－4) ＝2x 1x 2＋(m －5)(x 1＋x 2)－8(m －1) ＝2(4m 2－20)5－8m (m －5)5－8(m －1)＝0.所以k 1＋k 2＝0，即直线MA ，MB 的斜率互为相反数．3．已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为12，以原点为圆心，椭圆的短半轴为半径的圆与直线x －y ＋6＝0相切，过点P (4,0)且不垂直于x 轴的直线l 与椭圆C 相交于A 、B 两点． (1)求椭圆C 的方程； (2)求OA →·OB →的取值范围．解 (1)由题意知e ＝c a ＝12，∴e 2＝c 2a 2＝a 2－b 2a 2＝14，即a 2＝43b 2，又b ＝61＋1＝3，∴a 2＝4，b 2＝3，43(2)由题意知直线AB 的斜率存在，设直线PB 的方程为y ＝k (x －4)，由⎩⎪⎨⎪⎧y ＝k (x －4)，x 24＋y 23＝1，得(4k 2＋3)x 2－32k 2x ＋64k 2－12＝0，由Δ＝(－32k 2)2－4(4k 2＋3)(64k 2－12)>0，得k 2<14，设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝32k 24k 2＋3，x 1x 2＝64k 2－124k 2＋3，①∴y 1y 2＝k (x 1－4)k (x 2－4)＝k 2x 1x 2－4k 2(x 1＋x 2)＋16k 2，∴OA →·OB →＝x 1x 2＋y 1y 2＝(1＋k 2)·64k 2－124k 2＋3－4k 2·32k 24k 2＋3＋16k 2＝25－874k 2＋3，∵0≤k 2<14，∴－873≤－874k 2＋3<－874，∴－4≤25－874k 2＋3<134，∴OA →·OB →∈[－4，134)，即OA →·OB →的取值范围是[－4，134)．4．在平面直角坐标系xOy 中，已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率e ＝23，且椭圆C 上的点到点Q (0,2)的距离的最大值为3. (1)求椭圆C 的方程．(2)在椭圆C 上，是否存在点M (m ，n )，使得直线l ：mx ＋ny ＝1与圆O ：x 2＋y 2＝1相交于不同的两点A 、B ，且△OAB 的面积最大？若存在，求出点M 的坐标及对应的△OAB 的面积；若不存在，请说明理由．解 (1)∵e 2＝c 2a 2＝a 2－b 2a 2＝23，∴a 2＝3b 2，∴椭圆方程为x 23b 2＋y 2b 2＝1，即x 2＋3y 2＝3b 2.设椭圆上的点到点Q (0,2)的距离为d ，则 d ＝(x －0)2＋(y －2)2＝x 2＋(y －2)2＝3b 2－3y 2＋(y －2)2＝－2(y ＋1)2＋3b 2＋6， ∴当y ＝－1时，d 取得最大值，且d max ＝3b 2＋6＝3，解得b 2＝1，∴a 2＝3. ∴椭圆C 的方程为x 23＋y 2＝1.(2)假设存在点M (m ，n )满足题意，则m 23＋n 2＝1，即m 2＝3－3n 2.设圆心到直线l 的距离为d ′，则d ′<1， d ′＝|m ·0＋n ·0－1|m 2＋n 2＝1m 2＋n 2.∴|AB |＝212－d ′2＝2 1－1m 2＋n 2. ∴S △OAB ＝12|AB |d ′＝12·21－1m 2＋n 2·1m 2＋n2 ＝1m 2＋n 2⎝⎛⎭⎫1－1m 2＋n 2. ∵d ′<1，∴m 2＋n 2>1， ∴0<1m 2＋n 2<1， ∴1－1m 2＋n 2>0.∴S △OAB ＝1m 2＋n 2⎝⎛⎭⎫1－1m 2＋n 2 ≤⎝ ⎛⎭⎪⎪⎫1m 2＋n 2＋1－1m 2＋n 222＝12，当且仅当1m 2＋n 2＝1－1m 2＋n 2，即m 2＋n 2＝2>1时，S △OAB 取得最大值12.由⎩⎪⎨⎪⎧m 2＋n 2＝2，m 2＝3－3n2得⎩⎨⎧m 2＝32，n 2＝12，∴存在点M 满足题意，M 点坐标为⎝⎛⎭⎫62，22，⎝⎛⎭⎫62，－22，⎝⎛⎭⎫－62，22或⎝⎛⎭⎫－62，－22，此时△OAB 的面积为12.5．(2014·山东)已知抛物线C ：y 2＝2px (p >0)的焦点为F ，A 为C 上异于原点的任意一点，过点A 的直线l 交C 于另一点B ，交x 轴的正半轴于点D ，且有|F A |＝|FD |.当点A 的横坐标为3时，△ADF 为正三角形． (1)求C 的方程．(2)若直线l 1∥l ，且l 1和C 有且只有一个公共点E ， ①证明直线AE 过定点，并求出定点坐标．②△ABE 的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．解 (1)由题意知F (p2，0)．设D (t,0)(t >0)，则FD 的中点为(p ＋2t4，0)．因为|F A |＝|FD |，由抛物线的定义知3＋p2＝⎪⎪⎪⎪t －p 2，解得t ＝3＋p 或t ＝－3(舍去)．由p ＋2t4＝3，解得p ＝2.所以抛物线C 的方程为y 2＝4x . (2)①由(1)知F (1,0)．设A (x 0，y 0)(x 0y 0≠0)，D (x D,0)(x D >0)．因为|F A |＝|FD |，则x 0＋1＝|x D －1|，由x D >0，x 0>0，得x D ＝x 0＋2，故D (x 0＋2,0)，故直线AB 的斜率k AB ＝－y 02.因为直线l 1和直线AB 平行，设直线l 1的方程为y ＝－y 02x ＋b ，代入抛物线方程得y 2＋8y 0y －8by 0＝0，由题意Δ＝64y 20＋32b y 0＝0，得b ＝－2y 0.设E (x E ，y E )，则y E ＝－4y 0，x E ＝4y 20.当y 20≠4时，k AE ＝y E －y 0x E －x 0＝－4y 0＋y 04y 20－y 204＝4y 0y 20－4，可得直线AE 的方程为y －y 0＝4y 0y 20－4(x －x 0)．。

(完整word版)2015年全国新课标2卷高考文科数学答案

2015普通高等学校招生全国统一考试Ⅱ卷文科数学第一卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

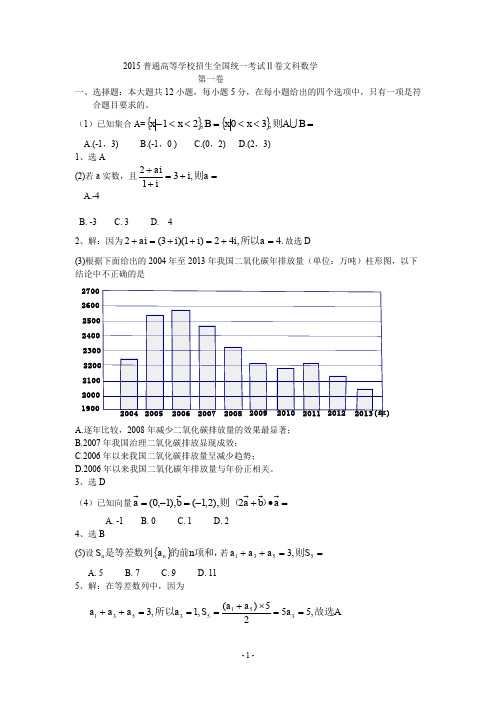
（1）已知集合A={}{}=<<=<<-B A x x B x x 则,30,21 A.(-1，3) B.(-1，0 ) C.(0，2) D.(2，3) 1、选A (2)若a 实数，且=+=++a i iai则,312 A.-4B. -3C. 3D. 42、解：因为.4,42)1)(3(2=+=++=+a i i i ai 所以故选D(3)根据下面给出的2004年至2013年我国二氧化碳年排放量（单位：万吨）柱形图，以下结论中不正确的是2700260025002400210020001900)A.逐年比较，2008年减少二氧化碳排放量的效果最显著；B.2007年我国治理二氧化碳排放显现成效；C.2006年以来我国二氧化碳排放量呈减少趋势；D.2006年以来我国二氧化碳年排放量与年份正相关。

3、选D（4）已知向量=∙+-=-=则（2),2,1(),1,0( A. -1 B. 0 C. 1 D. 2 4、选B(5)设{}项和，的前是等差数列n a S n n 若==++5531,3S a a a 则A. 5B. 7C. 9D. 115、解：在等差数列中，因为.,5525)(,1,335153531A a a a S a a a a 故选所以==⨯+===++(6)一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为A.81 B.71 C. 61 D. 51 6、解：如图所示，选D.(7)已知三点)32()30(),01(，，，，C B A ,则ABC ∆外接圆的圆心到原点的距离为A.35B. 321C. 352D. 34 7、解：根据题意，三角形ABC 是等边三角形，设外接圆的圆心为D ，则D （1，332）所以， .32137341==+=OD 故选B. (8)右边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”。

【创新设计】2015高考数学(人教通用,文科)二轮专题训练：大题综合突破练4

页眉内容突破练(四)1．已知函数f (x )＝2cos 2x ＋3sin 2x ，x ∈R . (1)求函数f (x )的单调递增区间；(2)将函数f (x )图象上所有点的横坐标伸长为原来的2倍，纵坐标不变得到函数h (x )的图象，再将h (x )的图象向右平移π3个单位得到g (x )的图象，求函数g (x )的解析式，并求g (x )在[0，π]上的值域．解 (1)∵f (x )＝2cos 2x ＋3sin 2x ＝1＋cos 2x ＋3sin 2x ， ∴f (x )＝2sin (2x ＋π6)＋1.由2k π－π2≤2x ＋π6≤2k π＋π2，k ∈Z ，得k π－π3≤x ≤k π＋π6，k ∈Z .∴f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π－π3，k π＋π6，k ∈Z . (2)∵f (x )＝2sin (2x ＋π6)＋1―――――――――――→横坐标伸长为原来的2倍纵坐标不变h (x )＝2sin ⎝ ⎛⎭⎪⎫x ＋π6＋1，∵x ∈[0，π]， ∴x －π6∈[－π6，5π6]． ∴sin (x －π6)∈[－12，1]． ∴g (x )在[0，π]上的值域为[0,3]．2．某出租车公司为了解本公司出租车司机对新法规的知晓情况，随机对100名出租车司机进行调查．调查问卷共10道题，答题情况如下表：答对题目数[0,8) 8 9 10 女 2 13 12 8 男337169(1)如果出租车司机答对题目数大于等于9，就认为该司机对新法规的知晓情况比较好，试估计该公司的出租车司机对新法规知晓情况比较好的概率； (2)从答对题目数少于8的出租车司机中任选出2人做进一步的调查，求选出的2人中至少有一名女出租车司机的概率．解 (1)答对题目数小于9的人数为55，记“答对题目数大于等于9”为事件A ， P (A )＝1－55100＝0.45.(2)设答对题目数小于8的司机为A 、B 、C 、D 、E ，其中A 、B 为女司机，任选出2人包含AB 、AC 、AD 、AE 、BC 、BD 、BE 、CD 、CE 、DE ，共10种情况，至少有一名女出租车司机的事件为AB 、AC 、AD 、AE 、BC 、BD 、BE ，共7种．记“选出的2人中至少有一名女出租车司机”为事件M ，则P (M )＝710＝0.7. 3．已知四棱锥P －ABCD 中，PC ⊥底面ABCD ，PC ＝2，且底面ABCD 是边长为1的正方形．E 是最短的侧棱PC 上的动点．(1)求证：P 、A 、B 、C 、D 五点在同一个球面上，并求该球的体积； (2)如果点F 在线段BD 上，DF ＝3BF ，且EF ∥平面P AB ，求PEEC 的值． (1)证明设P A 的中点为M ，连接AC ，CM ，则△P AC 为直角三角形， ∴CM ＝PM ＝AM ＝62.设正方形ABCD 的中心为点O ，连接OM ，则OM ∥PC ，OM ＝1，∵PC ⊥底面ABCD ，∴OM ⊥底面ABCD ，又O 为BD 的中点，连接BM ，DM ，则BM ＝DM ＝1＋(22)2＝62，∴CM ＝PM ＝AM ＝BM ＝DM ，故点P 、A 、B 、C 、D 在以M 为球心，半径为62的球上，且V 球M ＝43π(62)3＝6π. (2)解连接CF 并延长交AB 于K ，连接PK . ∵EF ∥平面P AB ，EF ⊂平面PCK ，平面PCK ∩平面P AB ＝PK ，∴EF ∥PK ，∵DF ＝3BF ，又AB ∥CD ，∴CF ＝3KF . ∵EF ∥PK ，∴CE ＝3PE ，∴PE EC ＝13.4．已知数列{a n }的前n 项和S n ＝a n ＋n 2－1，数列{b n }满足3n ·b n ＋1＝(n ＋1)a n ＋1－na n ，且b 1＝3. (1)求a n ，b n ；(2)设T n 为数列{b n }的前n 项和，求T n .解 (1)当n ≥2时，S n ＝a n ＋n 2－1，S n －1＝a n －1＋(n －1)2－1，两式相减，得a n ＝a n －a n －1＋2n －1，∴a n －1＝2n －1， ∴a n ＝2n ＋1，∴3n ·b n ＋1＝(n ＋1)(2n ＋3)－n (2n ＋1)＝4n ＋3， ∴b n ＋1＝4n ＋33n .∴当n ≥2时，b n ＝4n －13n －1，又b 1＝3适合上式，∴b n ＝4n －13n －1.(2)由(1)知，b n ＝4n －13n －1， ∴T n ＝31＋73＋1132＋…＋4n －53n －2＋4n －13n －1，①13T n ＝33＋732＋1133＋…＋4n －53n －1＋4n －13n ，② ①－②，得23T n ＝3＋43＋432＋…＋43n －1－4n －13n＝3＋4×13(1－13n －1)1－13－4n －13n ＝5－4n ＋53n ， ∴T n ＝152－4n ＋52×3n －1.5．已知点M (－1,0)，N (1,0)，动点P (x ，y )满足：|PM |＋|PN |＝2 3. (1)求P 的轨迹C 的方程；(2)是否存在过点N (1,0)的直线l 与曲线C 相交于A 、B 两点，并且曲线C 上存在点Q ，使四边形OAQB 为平行四边形？若存在，求出直线l 的方程．解 (1)由|PM |＋|PN |＝23知道曲线C 是以M ，N 为焦点的椭圆，且a ＝3，c ＝1，b ＝2，所以曲线C 的方程为x 23＋y 22＝1.(2)设A (x 1，y 1)、B (x 2，y 2)，由题意知l 的斜率一定不为0，故不妨设l ：x ＝my ＋1，代入椭圆方程整理得 (2m 2＋3)y 2＋4my －4＝0，显然Δ＞0，则⎩⎪⎨⎪⎧y 1＋y 2＝－4m2m 2＋3，y 1y 2＝－42m 2＋3，①假设存在点Q ，使得四边形OAQB 为平行四边形，其充要条件为OQ →＝OA →＋OB →，则点Q 的坐标为(x 1＋x 2，y 1＋y 2)．由点Q 在椭圆上，即(x 1＋x 2)23＋(y 1＋y 2)22＝1.整理得2x 21＋3y 21＋2x 22＋3y 22＋4xx 21＋6y 1y 2＝6. 又A 、B 在椭圆上，即2x 21＋3y 21＝6,2x 22＋3y 22＝6.故2x 1x 2＋3y 1y 2＝－3，②所以x 1x 2＝(my 1＋1)(my 2＋1)＝m 2y 1y 2＋m (y 1＋y 2)＋1，将①②代入上式解得m ＝±22.即直线l的方程是：x＝±22y＋1，即2x±2y－2＝0.6．已知f(x)＝e x＋ax－1(e为自然对数)(1)当a＝1时，求过点(1，f(1))处的切线与坐标轴围成的三角形的面积；(2)若f(x)≥x2在(0,1)上恒成立，求实数a的取值范围．解(1)当a＝1时，f(x)＝e x＋x－1，f(1)＝e，f′(x)＝e x＋1，f′(1)＝e＋1，∴函数f(x)在点(1，f(1))处的切线方程为y－e＝(e＋1)(x－1)，即y＝(e＋1)x－1，设切线与x、y轴的交点分别为A，B，令x＝0，得y＝－1；令y＝0，得x＝1e＋1.∴A(1e＋1，0)，B(0，－1)．∴S△OAB ＝12×1e＋1×1＝12(e＋1).(2)由f(x)≥x2得a≥1＋x2－e xx，令h(x)＝1＋x2－e xx＝1x＋x－e xx，则h′(x)＝1－1x2－e x(x－1)x2＝(x－1)(x＋1－e x)x2，令k(x)＝x＋1－e x，k′(x)＝1－e x，∵x∈(0,1)，∴k′(x)＝1－e x＜0，k(x)在x ∈(0,1)为减函数，∴k(x)＜k(0)＝0，又∵x－1＜0，x2＞0，∴h′(x)＝(x－1)(x＋1－e x)x2>0，∴h(x)在x∈(0,1)为增函数，h(x)＜h(1)＝2－e，因此只需a≥2－e.。

2015届全国新课标Ⅱ卷高考压轴卷文科数学试题及答案

（第5题图）2015年考前押题试卷（全国新课标II 卷）文科数学第I 卷（选择题，共60分）一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求） 1．若复数3()1x i z x R i+=∈-是实数，则x 的值为A ．-3B ．3C ．0 D2．设集合2{|3100}M x R xx =∈--<，{|||2}N x Z x =∈<，则MN =A ．(2,2)-B ．(1,2)C ．{1,0,1}-D．{2,1,0,1,2}--3．24sin 225α=，02πα<<cos()4πα-的值为A ．15B ．15- C ．75D ．15±4．下列判断错误．．的是 A ．“22ambm <”是“a < b ”的充分不必要条件B ．命题“x R ∀∈，3210xx --≤”的否定是“0xR ∃∈，3210x x -->”假命题C ．若p ,q 均为假命题，则p q ∧为D ．若~(4,0.25)B ξ，则1D ξ=5．在右图的算法中，如果输入A=138,B=22,则输出的结果是A ．2B ．4C ．128 D．06．若椭圆22221(0)x y a b a b +=>>，则双曲线22221x y a b-=的渐近线方程为A ．B ．C ．D ．A ．x y 2±=B ．x y 21±=C ．x y 4±=D ．x y 41±= 7．已知等差数列{}na 中，111a=，前7项的和735S=，则前n 项和S n 中A ．前6项和最大B ．前7项和最大C ．前6项和最小D ．前7项和最小8．已知二项式2(n x （n N +∈）展开式中，前三项的二项式系数和是56，则展开式中的常数项为A ．45256B ．47256C ．49256D ．512569．已知某个几何体的三视图如图（主视图中的弧线是半圆），根据图中标出的尺寸，可得这个几何体的体积是A ．8 + πB ．283π+C ．12 + πD ．2123π+10．某五所大学进行自主招生，同时向一所重点中学的五位学习成绩优秀，并在某些方面有特长的学生发出提前录取通知单.若这五名学生都乐意进这五所大学中的任意一所就读，则仅有两名学生录取到同一所大学（其余三人在其他学校各选一所不同大学）的概率是A ．15B ．24125C ．96125D ．4812511．如图，设平面EF αβ=，AB ⊥α，CD ⊥α，垂足分别为B 、D ，若增加个一αAEB D第9题条件，就能推出BD ⊥EF 。

2015届高考数学(文科,通用)二轮复习突破练高考中档大题规范练(二) Word版含答案

高考中档大题规范练(二)——数列(推荐时间：60分钟)1．已知{a n }为等差数列，且a 2＝－1，a 5＝8. (1)求数列{|a n |}的前n 项和； (2)求数列{2n ·a n }的前n 项和．解 (1)设等差数列{a n }的公差为d ，因为a 2＝－1，a 5＝8，所以⎩⎪⎨⎪⎧a 1＋d ＝－1，a 1＋4d ＝8，解得a 1＝－4，d ＝3，所以a n ＝－4＋3(n －1)＝3n －7，因此|a n |＝|3n －7|＝⎩⎪⎨⎪⎧－3n ＋7，n ＝1，2，3n －7，n ≥3记数列{|a n |}的前n 项和为S n ，当n ＝1时，S 1＝|a 1|＝4，当n ＝2时，S 2＝|a 1|＋|a 2|＝5，当n ≥3时，S n ＝S 2＋|a 3|＋|a 4|＋…＋|a n |＝5＋(3×3－7)＋(3×4－7)＋…＋(3n －7) ＝5＋(n －2)[2＋3n －7]2＝32n 2－112n ＋10.又当n ＝2时满足此式，综上，S n ＝⎩⎪⎨⎪⎧4，n ＝1，32n 2－112n ＋10，n ≥2.(2)记数列{2n ·a n }的前n 项和为T n ，则T n ＝2a 1＋22a 2＋23a 3＋…＋2n a n ， 2T n ＝22a 1＋23a 2＋24a 3＋…＋2n a n －1＋2n ＋1a n ，所以－T n ＝2a 1＋d (22＋23＋…＋2n )－2n ＋1a n .由(1)知，a 1＝－4，d ＝3，a n ＝3n －7，所以－T n ＝－8＋3×4(1－2n －1)1－2－(3n －7)×2n ＋1＝－20－(3n －10)×2n ＋1，故T n ＝20＋(3n －10)×2n ＋1.2．已知函数f (x )＝14x ＋2(x ∈R )．(1)证明：f (x )＋f (1－x )＝12；(2)若数列{a n }的通项公式为a n ＝f (nm )(m ∈N *，n ＝1,2，…，m )，求数列{a n }的前m 项和S m ；(3)设数列{b n }满足b 1＝13，b n ＋1＝b 2n ＋b n ，T n ＝1b 1＋1＋1b 2＋1＋…＋1b n ＋1，若(2)中的S m 满足对不小于2的任意正整数m ，S m <T n 恒成立，试求m 的最大值． (1)证明因为f (x )＝14x ＋2，所以f (1－x )＝141－x ＋2＝4x 4＋2·4x ＝4x2(4x ＋2).所以f (x )＋f (1－x )＝14x ＋2＋4x2(4x ＋2)＝2＋4x 2(4x ＋2)＝12. (2)解由(1)，知f (x )＋f (1－x )＝12，所以f (k m )＋f (1－k m )＝12(1≤k ≤m －1)(k ∈N *)，即f (k m )＋f (m －k m )＝12.由题设知，a n ＝f (n m )，所以a k ＋a m －k ＝12，a m ＝f (m m )＝f (1)＝16.又S m ＝a 1＋a 2＋…＋a m －1＋a m ，① S m ＝a m －1＋a m －2＋…＋a 1＋a m ，②由①＋②，得2S m ＝(m －1)×12＋2a m ＝m 2－16，即S m ＝m 4－112(m ∈N *)．(3)解由b 1＝13，b n ＋1＝b 2n ＋b n ＝b n (b n ＋1)，显然对任意n ∈N *，b n >0，则1b n ＋1＝1b n (b n ＋1)＝1b n －1b n ＋1，即1b n ＋1＝1b n －1b n ＋1，所以T n ＝(1b 1－1b 2)＋(1b 2－1b 3)＋…＋(1b n －1b n ＋1)＝1b 1－1b n ＋1＝3－1b n ＋1. 因为b n ＋1－b n ＝b 2n >0，所以b n ＋1>b n ，即数列{b n }是单调递增数列．所以T n 关于n 递增，所以当n ∈N *时，T n ≥T 1.因为b 1＝13，b 2＝(13)2＋13＝49，所以T n ≥T 1＝3－1b 2＝34.由题意，知S m <34，即m 4－112<34，解得m <103，所以m 的最大值为3.3．设数列{a n }的前n 项和为S n ，满足2S n ＝a n ＋1－2n ＋1＋1，n ∈N *，且a 1＝1，设数列{b n }满足b n ＝a n ＋2n .(1)求证数列{b n }为等比数列，并求出数列{a n }的通项公式； (2)若数列c n ＝6n －3b n，T n 是数列{c n }的前n 项和，证明T n <3.(1)解当n ≥2时，由⎩⎪⎨⎪⎧2S n ＝a n ＋1－2n ＋1＋12S n －1＝a n －2n＋1⇒2a n ＝a n ＋1－a n －2n ，所以a n ＋1＝3a n ＋2n ，从而b n ＋1＝a n ＋1＋2n ＋1＝3(a n ＋2n )＝3b n ，故{b n }是以3为首项，3为公比的等比数列， b n ＝a n ＋2n ＝3×3n －1＝3n ，a n ＝3n －2n (n ≥2)，因为a 1＝1也满足，于是a n ＝3n －2n . (2)证明 c n ＝6n －3b n ＝2n －13n －1，则T n ＝130＋331＋532＋…＋2n －33n －2＋2n －13n －1，①13T n ＝131＋332＋533＋…＋2n －33n －1＋2n －13n ，② ①－②得，23T n ＝130＋231＋232＋…＋23n －1－2n －13n ＝1＋23·1－13n －11－13－2n －13n ＝2－13n －1－2n －13n ＝2－2(n ＋1)3n，故T n ＝3－n ＋13n －1<3.4．已知单调递增数列{a n }的前n 项和为S n ，满足S n ＝12(a 2n ＋n )．(1)求数列{a n }的通项公式；(2)设c n ＝⎩⎪⎨⎪⎧1a 2n ＋1－1，n 为奇数，3×2a n －1＋1，n 为偶数，求数列{c n }的前n 项和T n .解 (1)n ＝1时，a 1＝12(a 21＋1)，得a 1＝1，当n ≥2时，S n －1＝12(a 2n －1＋n －1)，得a n ＝S n －S n －1＝12(a 2n －a 2n －1＋1)，化简得(a n －1)2－a 2n －1＝0，a n －a n －1＝1或a n ＋a n －1＝1(n ≥2)，又{a n }是单调递增数列，故a n －a n －1＝1，所以{a n }是首项为1，公差为1的等差数列，故a n ＝n . (2)c n ＝⎩⎪⎨⎪⎧1a 2n ＋1－1，n 为奇数，3×21n a -＋1，n 为偶数，当n 为偶数时，T n ＝(c 1＋c 3＋…＋c n －1)＋(c 2＋c 4＋…＋c n ) ＝(122－1＋142－1＋…＋1n 2－1)＋3×(21＋23＋…＋2n －1)＋n 2＝11×3＋13×5＋…＋1(n －1)×(n ＋1)＋3×2(1－42n)1－4＋n 2＝12×(11－13＋13－15＋…＋1n －1－1n ＋1)＋2×(42n－1)＋n 2＝2n ＋1＋n 2－2n －42(n ＋1). 当n 为奇数时，T n ＝(c 1＋c 3＋…＋c n )＋(c 2＋c 4＋…＋c n －1) ＝[122－1＋142－1＋…＋1(n ＋1)2－1]＋3×(21＋23＋…＋2n －2)＋n －12 ＝12×(11－13＋13－15＋…＋1n －1n ＋2)＋2×(412n -－1)＋n －12＝2n ＋n 2－2n －92(n ＋2).所以T n＝⎩⎪⎨⎪⎧2n＋n 2－2n －92(n ＋2)，n 为奇数，2n ＋1＋n 2－2n －42(n ＋1)，n 为偶数.5．已知函数f (x )＝2x ＋33x ，数列{a n }满足a 1＝1，a n ＋1＝f (1a n )，n ∈N *.(1)求数列{a n }的通项公式；(2)令b n ＝1a n －1a n (n ≥2)，b 1＝3，S n ＝b 1＋b 2＋…＋b n ，若S n <m －2 0142对一切n ∈N *成立，求最小正整数m .解 (1)∵a n ＋1＝f (1a n )＝2a n ＋33a n ＝2＋3a n 3＝a n ＋23，∴{a n }是以1为首项，23为公差的等差数列．∴a n ＝1＋(n －1)×23＝23n ＋13.(2)当n ≥2时，b n ＝1a n －1a n ＝1(23n －13)(23n ＋13) ＝1(2n －1)(2n ＋1)9＝92(12n －1－12n ＋1)，又b 1＝3＝92(1－13)，∴S n ＝b 1＋b 2＋…＋b n ＝92(1－13＋13－15＋…＋12n －1－12n ＋1)＝92(1－12n ＋1)＝9n2n ＋1，∵S n <m －2 0142对一切n ∈N *成立，即9n 2n ＋1<m －2 0142对一切n ∈N *成立，又9n 2n ＋1<92，∴m －2 0142≥92，即m ≥2 023.∴最小正整数m 为2 023.6．某工厂为扩大生产规模，今年年初新购置了一条高性能的生产线，该生产线在使用过程中的维护费用会逐年增加，第一年的维护费用是4万元，从第二年到第七年，每年的维护费用均比上年增加2万元，从第八年开始，每年的维护费用比上年增加25%. (1)设第n 年该生产线的维护费用为a n ，求a n 的表达式；(2)若该生产线前n 年每年的平均维护费用大于12万元时，需要更新生产线．求该生产线前n 年每年的平均维护费用，并判断第几年年初需要更新该生产线？解 (1)由题意知，当n ≤7时，数列{a n }是首项为4，公差为2的等差数列， ∴a n ＝4＋(n －1)×2＝2n ＋2.当n ≥8时，数列{a n }从a 7开始构成首项为a 7＝2×7＋2＝16，公比为1＋25%＝54的等比数列，则此时a n ＝16×⎝⎛⎭⎫54n －7，∴a n ＝⎩⎪⎨⎪⎧2n ＋2，n ≤7，16×⎝⎛⎭⎫54n －7，n ≥8.(2)设S n 为数列{a n }的前n 项和，当1≤n ≤7时，S n ＝4n ＋n (n －1)2×2＝n 2＋3n ，当n ≥8时，由S 7＝70，则S n ＝70＋16×54×1－⎝⎛⎭⎫54n －71－54＝80×⎝⎛⎭⎫54n －7－10， ∴该生产线前n 年每年的平均维护费用为 S nn ＝⎩⎨⎧n ＋3，1≤n ≤7，80×⎝⎛⎭⎫54n －7－10n，n ≥8.当1≤n ≤7时，⎩⎨⎧⎭⎬⎫S n n 为递增数列，当n ≥8时，∵S n ＋1n ＋1－S nn ＝80×⎝⎛⎭⎫54n －6－10n ＋1－80×⎝⎛⎭⎫54n －7－10n＝80×⎝⎛⎭⎫54n －7·⎝⎛⎭⎫n 4－1＋10n (n ＋1)>0，∴S n ＋1n ＋1>S n n.∴⎩⎨⎧⎭⎬⎫S n n 也为递增数列．又∵S 77＝10<12，S 88＝80×54－108＝11.25<12，S 99＝80×⎝⎛⎭⎫542－109≈12.78>12， ∴第9年年初需要更新生产线．。

人教版通用2015年高考数学文科大题部分专练11份

目录中档大题规范练——导数的应用 ........................................................................................... 1 中档大题规范练——概率与统计 ........................................................................................... 7 中档大题规范练——立体几何 ............................................................................................. 11 中档大题规范练——三角函数 ............................................................................................. 15 中档大题规范练——数列 ..................................................................................................... 18 中档大题规范练——圆锥曲线 ............................................................................................. 24 中档大题规范练——直线与圆 ............................................................................................. 31 压轴大题突破练——函数与导数(一) .................................................................................. 35 压轴大题突破练——函数与导数(二) .................................................................................. 40 压轴大题突破练——直线与圆锥曲线(一) .......................................................................... 44 压轴大题突破练——直线与圆锥曲线(二) .. (47)中档大题规范练——导数的应用1．已知函数f (x )＝x 3－2x ＋1，g (x )＝ln x . (1)求F (x )＝f (x )－g (x )的单调区间和极值；(2)是否存在实常数k 和m ，使得x >0时，f (x )≥kx ＋m 且g (x )≤kx ＋m ？若存在，求出k 和m 的值；若不存在，说明理由．解 (1)由F (x )＝x 3－2x ＋1－ln x (x >0)，得F ′(x )＝3x 3－2x －1x(x >0)，令F ′(x )＝0得x ＝1，易知F (x )在(0,1)上单调递减，在(1，＋∞)上单调递增，从而F (x )的极小值为F (1)＝0.(2)易知f (x )与g (x )有一个公共点(1,0)，而函数g (x )在点(1,0)处的切线方程为y ＝x －1，下面只需验证⎩⎪⎨⎪⎧f (x )≥x －1g (x )≤x －1都成立即可．设h (x )＝x 3－2x ＋1－(x －1)(x >0)，则h ′(x )＝3x 2－3＝3(x ＋1)(x －1)(x >0)．易知h (x )在(0,1)上单调递减，在(1，＋∞)上单调递增，所以h (x )的最小值为h (1)＝0，所以f (x )≥x －1恒成立．设k (x )＝ln x －(x －1)，则k ′(x )＝1－x x(x >0)．易知k (x )在(0,1)上单调递增，在(1，＋∞)上单调递减，所以k (x )的最大值为k (1)＝0，所以g (x )≤x －1恒成立．故存在这样的实常数k ＝1和m ＝－1，使得x >0时，f (x )≥kx ＋m 且g (x )≤kx ＋m .2．设函数f (x )＝ax 3＋bx 2＋cx 在区间[0,1]上单调递增，在区间(－∞，0)，(1，＋∞)上单调递减，又f ′(12)＝32. (1)求f (x )的解析式．(2)若在区间[0，m ](m >0)上恒有f (x )≤x 成立，求m 的取值范围．解 (1)f ′(x )＝3ax 2＋2bx ＋c ，由已知f ′(0)＝f ′(1)＝0，即⎩⎪⎨⎪⎧c ＝0，3a ＋2b ＋c ＝0，解得⎩⎪⎨⎪⎧b ＝－32a ，c ＝0.所以f ′(x )＝3ax 2－3ax ，所以f ′(12)＝3a 4－3a 2＝32，所以a ＝－2，b ＝3，所以f (x )＝－2x 3＋3x 2.(2)令f (x )≤x ，即－2x 3＋3x 2－x ≤0，所以x (2x －1)(x －1)≥0，所以0≤x ≤12或x ≥1.又f (x )≤x 在区间[0，m ]上恒成立，所以0<m ≤12.3．已知函数f (x )＝ax 3＋x 2＋bx (其中常数a ，b ∈R )，g (x )＝f (x )＋f ′(x )是奇函数．(1)求f (x )的表达式；(2)讨论g (x )的单调性，并求g (x )在区间[1,2]上的最大值与最小值．解 (1)由题意得f ′(x )＝3ax 2＋2x ＋b ，因此g (x )＝f (x )＋f ′(x )＝ax 3＋(3a ＋1)x 2＋(b ＋2)x ＋b . 因为函数g (x )是奇函数，所以g (－x )＝－g (x )，即对任意实数x ，有a (－x )3＋(3a ＋1)(－x )2＋ (b ＋2)(－x )＋b ＝－[ax 3＋(3a ＋1)x 2＋(b ＋2)x ＋b ]，从而3a ＋1＝0，b ＝0，解得a ＝－13，b ＝0，因此f (x )的表达式为f (x )＝－13x 3＋x 2.(2)由(1)知g (x )＝－13x 3＋2x ，所以g ′(x )＝－x 2＋2.令g ′(x )＝0，解得x 1＝－2，x 2＝2，则当x <－2或x >2时，g ′(x )<0，从而g (x )在区间(－∞，－ 2 )，(2，＋∞)上是减函数；当－2<x <2时，g ′(x )>0，从而g (x )在区间(－2，2)上是增函数．由上述讨论知，g (x )在区间[1,2]上的最大值与最小值只能在x ＝1，2，2时取得，而g (1)＝53，g (2)＝423，g (2)＝43，因此g (x )在区间[1,2]上的最大值为g (2)＝423，最小值g (2)＝43.4．甲方是一农场，乙方是一工厂．由于乙方生产需占用甲方的资源，因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入，在乙方不赔付甲方的情况下，乙方的年利润x (元)与年产量t (吨)满足函数关系x ＝2 000t .若乙方每生产一吨产品必须赔付甲方S 元(以下称S 为赔付价格)．(1)将乙方的年利润ω(元)表示为年产量t (吨)的函数，并求出乙方获得最大利润的年产量；(2)甲方每年受乙方生产影响的经济损失金额y ＝0.002t 2(元)，在乙方按照获得最大利润的产量进行生产的前提下，甲方要在索赔中获得最大净收入，应向乙方要求的赔付价格S 是多少？解 (1)因为赔付价格为S 元/吨，所以乙方的实际年利润为ω＝2 000t －St . ω′＝1 000t －S ＝1 000－S t t ，令ω′＝0，得t ＝t 0＝(1 000S)2.当t <t 0时，ω′>0；当t >t 0时，ω′<0，所以t ＝t 0时，ω取得最大值．因此乙方获得最大利润的年产量t 0＝(1 000S )2(吨)．(2)设甲方净收入为v 元，则v ＝St －0.002t 2 将t ＝(1 000S )2代入上式，得到甲方净收入v 与赔付价格S 之间的函数关系式． v ＝1 0002S －2×1 0003S 4.又v ′＝－1 0002S 2＋8×1 0003S 5＝1 0002×(8 000－S 3)S 5，令v ′＝0，得S ＝20.当S <20时，v ′>0；当S >20时，v ′<0，所以S ＝20时，v 取得最大值．因此甲方向乙方要求的赔付价格S ＝20(元/吨)时，获得最大净收入． 5．已知函数f (x )＝ln x ＋2ax，a ∈R .(1)若函数f (x )在[2，＋∞)上是增函数，求实数a 的取值范围； (2)若函数f (x )在[1，e]上的最小值为3，求实数a 的值．解 (1)∵f (x )＝ln x ＋2a x ，∴f ′(x )＝1x －2a x 2.∵f (x )在[2，＋∞)上是增函数，∴f ′(x )＝1x －2ax 2≥0在[2，＋∞)上恒成立，即a ≤x2在[2，＋∞)上恒成立．令g (x )＝x2，则a ≤g (x )min ，x ∈[2，＋∞)，∵g (x )＝x2在[2，＋∞)上是增函数，∴g (x )min ＝g (2)＝1.∴a ≤1.所以实数a 的取值范围为(－∞，1]． (2)由(1)得f ′(x )＝x －2ax2，x ∈[1，e]．①若2a <1，则x －2a >0，即f ′(x )>0在[1，e]上恒成立，此时f (x )在[1，e]上是增函数．所以f (x )min ＝f (1)＝2a ＝3，解得a ＝32(舍去)．②若1≤2a ≤e ，令f ′(x )＝0，得x ＝2a . 当1<x <2a 时，f ′(x )<0，所以f (x )在(1,2a )上是减函数，当2a <x <e 时，f ′(x )>0，所以f (x )在(2a ，e)上是增函数．所以f (x )min ＝f (2a )＝ln(2a )＋1＝3，解得a ＝e 22(舍去)．③若2a >e ，则x －2a <0，即f ′(x )<0在[1，e]上恒成立，此时f (x )在[1，e]上是减函数．所以f (x )min ＝f (e)＝1＋2ae＝3，得a ＝e.适合题意．综上a ＝e.6．已知函数f (x )＝a ln x ＋12ax 2＋bx (a ≠0)．(1)若函数f (x )的图象在x ＝1处的切线方程为y ＝3x －32b ，求a 、b 的值；(2)若a ＝2时，函数f (x )是增函数，求实数b 的取值范围； (3)设函数g (x )＝lnx 的图象C 1与函数h (x )＝f (x )－ag (x )的图象C 2交于点P 、Q ，过线段PQ 的中点R 作x 轴的垂线分别交C 1、C 2于点M 、N ，问是否存在点R ，使C 1在M 处的切线与C 2在N 处的切线平行？若存在，求出R 的横坐标；若不存在，请说明理由．解 (1)函数f (x )＝a ln x ＋12ax 2＋bx 的定义域为(0，＋∞)，f ′(x )＝ax ＋ax ＋b ＝ax 2＋bx ＋a x，当x ＝1时，f ′(1)＝2a ＋b ＝3，f (1)＝12a ＋b ，所以函数f (x )的图象在x ＝1处的切线方程为y －(12a ＋b )＝3(x －1)，即y ＝3x ＋(12a ＋b －3)，所以12a ＋b －3＝－32b ，解方程组⎩⎪⎨⎪⎧2a ＋b ＝3，12a ＋b －3＝－32b ，得a ＝b ＝1. (2)由(1)知，f ′(x )＝2x ＋2x ＋b ，则f ′(x )≥0在(0，＋∞)上恒成立，即b ≥－2x－2x 在(0，＋∞)上恒成立，因为2x ＋2x ≥22x·2x ＝4(当且仅当x ＝1时等号成立)，所以－2x －2x ≤－4，所以b ≥－4，故实数b 的取值范围为[－4，＋∞)．(3)设点P 、Q 的坐标分别为(x 1，y 1)、(x 2，y 2)，且0<x 1<x 2，则点M 、N 的横坐标均为x ＝x 1＋x 22.C 1在点M 处的切线斜率为k 1＝1x |x ＝x 1＋x 22＝2x 1＋x 2.C 2在点N 处的切线斜率为k 2＝(ax ＋b )|x ＝x 1＋x 22＝a (x 1＋x 2)2＋b . 假设C 1在点M 处的切线与C 2在点N 处的切线平行，则k 1＝k 2，则2x 1＋x 2＝a (x 1＋x 2)2＋b ，即2(x 2－x 1)x 1＋x 2＝a (x 22－x 21)2＋b (x 2－x 1)＝(a 2x 22＋bx 2)－(a 2x 21＋bx 1) ＝y 2－y 1＝ln x 2－ln x 1＝lnx 2x 1，所以ln x 2x 1＝2(x 2－x 1)x 1＋x 2＝2(x 2x 1－1)1＋x 2x 1，令u ＝x 2x 1>1，则ln u ＝2(u －1)1＋u ，u >1，①令r (u )＝ln u －2(u －1)1＋u ，u >1，则r ′(u )＝1u －4(1＋u )2＝(u －1)2u (u ＋1)2.因为u >1，所以r ′(u )>0，所以r (u )在(1，＋∞)上单调递增，故r (u )>r (1)＝0，则ln u >2(u －1)1＋u，这与①矛盾，故假设不成立．即不存在满足题意的点R .中档大题规范练——概率与统计1.第12届全运会已于2013年8月31日在辽宁沈阳举行，组委会在沈阳某大学招募了12名男志愿者和18名女志愿者，将这30名志愿者的身高编成如图所示的茎叶图(单位：cm)，身高在175 cm 以上(包括175 cm)定义为“高个子”，身高在175 cm 以下(不包括175 cm)定义为“非高个子”．(1)如果用分层抽样的方法从“高个子”和“非高个子”中共抽取5人，再从这5人中选2人，求至少有一人是“高个子”的概率；(2)若从身高180 cm 以上(包括180 cm)的志愿者中选出男、女各一人，求这2人身高相差5 cm 以上的概率．解 (1)根据茎叶图知，“高个子”有12人，“非高个子”有18人，用分层抽样的方法，每个人被抽中的概率是530＝16，所以抽取的5人中，“高个子”有12×16＝2人，“非高个子”有18×16＝3人．“高个子”用A ，B 表示，“非高个子”用a ，b ，c 表示，则从这5人中选2人的情况有(A ，B )，(A ，a )，(A ，b )，(A ，c )，(B ，a )，(B ，b )，(B ，c )，(a ，b )，(a ，c )，(b ，c )，共10种，至少有一名“高个子”被选中的情况有(A ，B )，(A ，a )，(A ，b )，(A ，c )，(B ，a )，(B ，b )，(B ，c )，共7种．因此，至少有一人是“高个子”的概率是P ＝710.(2)由茎叶图知，有5名男志愿者身高在180 cm 以上(包括180 cm)，身高分别为181 cm,182 cm,184 cm,187 cm,191 cm ；有2名女志愿者身高为180 cm 以上(包括180 cm)，身高分别为180 cm,181 cm.抽出的2人用身高表示，则有(181,180)，(181,181)，(182,180)，(182,181)，(184,180)，(184,181)，(187,180)，(187,181)，(191,180)，(191,181)，共10种情况，身高相差5 cm 以上的有(187,180)，(187,181)，(191,180)，(191,181)，共4种情况，故这2人身高相差5 cm 以上的概率为410＝25.2．(2013·北京)如图是某市3月1日至14日的空气质量指数趋势图，空气质量指数小于100表示空气质量优良，空气质量指数大于200表示空气重度污染．某人随机选择3月1日至3月13日中的某一天到达该市，并停留2天．(1)求此人到达当日空气质量优良的概率；(2)求此人在该市停留期间只有1天空气重度污染的概率；(3)由图判断从哪天开始连续三天的空气质量指数方差最大？(结论不要求证明)解 (1)在3月1日至3月13日到达这13天中，1日，2日，3日，7日，12日，13日共6天的空气质量优良．所以，此人到达当日空气质量优良的概率P ＝613.(2)事件“此人在该市停留期间只有1天空气重度污染”发生，则该人到达日期应在4日，5日，7日或8日．所以，只有一天空气重度污染的概率P ＝413.(3)从3月5日开始连续三天的空气质量指数方差最大．3．先后随机投掷2枚正方体骰子，其中x 表示第1枚骰子出现的点数，y 表示第2枚骰子出现的点数． (1)求点P (x ，y )在直线y ＝x －2上的概率； (1)求点P (x ，y )满足y 2<2x 的概率．解每枚骰子出现的点数都有6种情况，所以，基本事件总数为6×6＝36(个)．(1)记“点P (x ，y )在直线y ＝x －2上”为事件A ，则事件A 有4个基本事件：(3,1)，(4,2)，(5,3)，(6,4)，所以，P (A )＝436＝19.(2)记“点P (x ，y )满足y 2<2x ”为事件B ，则事件B 有12个基本事件：(1,1)，(2,1)，(3,1)，(3,2)，(4,1)，(4,2)，(5,1)，(5,2)，(5,3)，(6,1)，(6,2)，(6,3)，所以，P (B )＝1236＝13.4．(2013·福建)某工厂有25周岁以上(含25周岁)工人300名，25周岁以下工人200名．为研究工人的日平均生产量是否与年龄有关，现采用分层抽样的方法，从中抽取了100名工人，先统计了他们某月的日平均生产件数，然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组，再将两组工人的日平均生产件数分成5组：[50,60)，[60,70)，[70,80)，[80,90)，[90,100]分别加以统计，得到如图所示的频率分布直方图．(1)从样本中日平均生产件数不足60件的工人中随机抽取2人，求至少抽到一名“25周岁以下组”工人的概率； (2)规定日平均生产件数不少于80件者为“生产能手”，请你根据已知条件完成2×2列联表，并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”？附：χ2＝n (n 11n 22－n 12n 21)2n 1＋n 2＋n ＋1n ＋2P (χ2≥k )0.100 0.050 0.010 0.001 k2.7063.8416.63510.828(注：此公式也可以写成 K 2＝n (ad －bc )2(a ＋b )(c ＋d )(a ＋c )(b ＋d ))解 (1)由已知得，样本中有25周岁以上组工人60名，25周岁以下组工人40名．所以，样本中日平均生产件数不足60件的工人中，25周岁以上组工人有60×0.05＝3(人)，记为A 1，A 2，A 3；25周岁以下组工人有40×0.05＝2(人)，记为B 1，B 2.从中随机抽取2名工人，所有的可能结果共有10种，它们是(A 1，A 2)，(A 1，A 3)，(A 2，A 3)，(A 1，B 1)，(A 1，B 2)，(A 2，B 1)，(A 2，B 2)，(A 3，B 1)，(A 3，B 2)，(B 1，B 2)．其中，至少有1名“25周岁以下组”工人的可能结果共有7种，它们是(A 1，B 1)，(A 1，B 2)，(A 2，B 1)，(A 2，B 2)，(A 3，B 1)，(A 3，B 2)，(B 1，B 2)．故所求的概率P ＝710.(2)由频率分布直方图可知，在抽取的100名工人中，“25周岁以上组”中的生产能手60×0.25＝15(人)，“25周岁以下组”中的生产能手40×0.375＝15(人)，据此可得2×2列联表如下：生产能手非生产能手合计 25周岁以上组 15 45 60 25周岁以下组15 25 40 合计3070100所以得K 2＝n (ad －bc )2(a ＋b )(c ＋d )(a ＋c )(b ＋d )＝100×(15×25－15×45)260×40×30×70＝2514≈1.79. 因为1.79<2.706.所以没有90%的把握认为“生产能手与工人所在的年龄组有关”．5．有编号为1,2,3的三个白球，编号为4,5,6的三个黑球，这六个球除编号和颜色外完全相同，现从中任意取出两个球．(1)求取得的两个球颜色相同的概率； (2)求取得的两个球颜色不相同的概率．解从六个球中取出两个球的基本事件有(1,2)，(1,3)，(1,4)，(1,5)，(1,6)，(2,3)，(2,4)，(2,5)，(2,6)，(3,4)，(3,5)，(3,6)，(4,5)，(4,6)，(5,6)共计15个基本事件．(1)记事件A 为“取出的两个球是白球”，则这个事件包含的基本事件的是(1,2)，(1,3)，(2,3)，共计3个基本事件，故P (A )＝315＝15.记事件B 为“取出的两个球是黑球”，同理可得P (B )＝15.记事件C 为“取出的两个球的颜色相同”，则C ＝A ＋B ，且A ，B 互斥，根据互斥事件的概率加法公式，得P (C )＝P (A ＋B )＝P (A )＋P (B )＝25.(2)记事件D 为“取出的两个球的颜色不相同”，则事件C ，D 互斥，根据互斥事件概率之间的关系，得P (D )＝1－P (C )＝1－25＝35.6．(2014·福建)根据世行2013年新标准，人均GDP 低于1 035美元为低收入国家；人均GDP 为1035～4085美元为中等偏下收入国家；人均GDP 为4085～12616美元为中等偏上收入国家；人均GDP 不低于12616美元为高收入国家．某城市有5个行政区，各区人口占该城市人口比例及人均GDP 如下表：行政区区人口占城市人口比例区人均GDP(单位：美元) A 25% 8 000 B 30% 4 000 C 15% 6 000 D 10% 3 000 E20%10 000(1)判断该城市人均GDP 是否达到中等偏上收入国家标准；(2)现从该城市5个行政区中随机抽取2个，求抽到的2个行政区人均GDP 都达到中等偏上收入国家标准的概率．解 (1)设该城市人口总数为a ，则该城市人均GDP 为1a (8 000×0.25a ＋4 000×0.30a ＋6000×0.15a ＋3 000×0.10a ＋10 000×0.20a )＝6 400. 因为6 400∈[4 085,12 616)，所以该城市人均GDP 达到了中等偏上收入国家标准．(2)“从5个行政区中随机抽取2个”的所有的基本事件是{A ，B}，{A ，C}，{A ，D}，{A ，E}，{B ，C}，{B ，D}，{B ，E}，{C ，D}，{C ，E}，{D ，E}，共10个．设事件“抽到的2个行政区人均GDP 都达到中等偏上收入国家标准”为M ，则事件M 包含的基本事件是：{A ，C}，{A ，E}，{C ，E}，共3个，所以所求概率为P (M )＝310.中档大题规范练——立体几何1．如图所示，已知三棱锥A －BPC 中，AP ⊥PC ，AC ⊥BC ，M 为AB 的中点，D 为PB 的中点，且△PMB 为正三角形．(1)求证：DM ∥平面APC ；(2)求证：平面ABC ⊥平面APC ；(3)若BC ＝4，AB ＝20，求三棱锥D －BCM 的体积．(1)证明由已知，得MD 是△ABP 的中位线，所以MD ∥AP .又MD ⊄平面APC ，AP ⊂平面APC ，故MD ∥平面APC .(2)证明因为△PMB 为正三角形，D 为PB 的中点，所以MD ⊥PB .所以AP ⊥PB .又AP ⊥PC ，PB ∩PC ＝P ，所以AP ⊥平面PBC .因为BC ⊂平面PBC ，所以AP ⊥BC .又BC ⊥AC ，AC ∩AP ＝A ，所以BC ⊥平面APC .因为BC ⊂平面ABC ，所以平面ABC ⊥平面APC .(3)解由(2)知，可知MD ⊥平面PBC ，所以MD 是三棱锥D －BCM 的一条高，又AB ＝20，BC ＝4，△PMB 为正三角形，M ，D 分别为AB ，PB 的中点，经计算可得MD ＝53，DC ＝5，S △BCD ＝12×BC ×BD ×sin ∠CBD ＝12×5×4×215＝221. 所以V D －BCM ＝V M －DBC ＝13×S △BCD ×MD ＝13×221×53＝107. 2．如图，在Rt △ABC 中，AB ＝BC ＝4，点E 在线段AB 上．过点E 作EF ∥BC 交AC 于点F ，将△AEF 沿EF 折起到△PEF 的位置(点A 与P 重合)，使得∠PEB ＝30°.(1)求证：EF ⊥PB ；(2)试问：当点E 在何处时，四棱锥P —EFCB 的侧面PEB 的面积最大？并求此时四棱锥P —EFCB 的体积．(1)证明 ∵EF ∥BC 且BC ⊥AB ，∴EF ⊥AB ，即EF ⊥BE ，EF ⊥PE .又BE ∩PE ＝E ，∴EF ⊥平面PBE ，又PB ⊂平面PBE ，∴EF ⊥PB .(2)解设BE ＝x ，PE ＝y ，则x ＋y ＝4.∴S △PEB ＝12BE ·PE ·sin ∠PEB ＝14xy ≤14⎝⎛⎭⎫x ＋y 22＝1. 当且仅当x ＝y ＝2时，S △PEB 的面积最大．此时，BE ＝PE ＝2.由(1)知EF ⊥平面PBE ，∴平面PBE ⊥平面EFCB ，在平面PBE 中，作PO ⊥BE 于O ，则PO ⊥平面EFCB .即PO 为四棱锥P —EFCB 的高．又PO ＝PE ·sin 30°＝2×12＝1. S 梯形EFCB ＝12×(2＋4)×2＝6. ∴V P —BCFE ＝13×6×1＝2.3.如图，在矩形ABCD 中，AB ＝2BC ，P 、Q 分别是线段AB 、CD 的中点，EP ⊥平面ABCD .(1)求证：DP ⊥平面EPC ；(2)问在EP 上是否存在点F ，使平面AFD ⊥平面BFC ？若存在，求出FP AP的值；若不存在，说明理由．(1)证明 ∵EP ⊥平面ABCD ，∴EP ⊥DP .又ABCD 为矩形，AB ＝2BC ，P 、Q 分别为AB 、CD 的中点，连接PQ ，则PQ ⊥DC 且PQ ＝12DC . ∴DP ⊥PC .∵EP ∩PC ＝P ，∴DP ⊥平面EPC .(2)解假设存在F 使平面AFD ⊥平面BFC ，∵AD ∥BC ，BC ⊂平面BFC ，AD ⊄平面BFC ，∴AD ∥平面BFC .∴AD 平行于平面AFD 与平面BFC 的交线l .∵EP ⊥平面ABCD ，∴EP ⊥AD ，而AD ⊥AB ，AB ∩EP ＝P ，∴AD ⊥平面EAB ，∴l ⊥平面F AB .∴∠AFB 为平面AFD 与平面BFC 所成二面角的平面角．∵P 是AB 的中点，且FP ⊥AB ，∴当∠AFB ＝90°时，FP ＝AP .∴当FP ＝AP ，即FP AP ＝1时，平面AFD ⊥平面BFC .4．(2013·课标全国Ⅱ)如图，直三棱柱ABC －A 1B 1C 1中，D ，E 分别是AB ，BB 1的中点．(1)证明：BC 1∥平面A 1CD ；(2)设AA 1＝AC ＝CB ＝2，AB ＝22，求三棱锥C －A 1DE 的体积．(1)证明连接AC 1交A 1C 于点F ，则F 为AC 1中点．又D 是AB 中点，连接DF ，则BC 1∥DF .因为DF ⊂平面A 1CD ，BC 1⊄平面A 1CD ，所以BC 1∥平面A 1CD .(2)解因为ABC －A 1B 1C 1是直三棱柱，所以AA 1⊥CD .又因为AC ＝CB ，D 为AB 的中点，所以CD ⊥AB .又AA 1∩AB ＝A ，于是CD ⊥平面ABB 1A 1.由AA 1＝AC ＝CB ＝2，AB ＝22，得∠ACB ＝90°，CD ＝2，A 1D ＝6，DE ＝3，A 1E ＝3，故A 1D 2＋DE 2＝A 1E 2，即DE ⊥A 1D .所以1C A DE V －＝13×S △A 1ED ×CD ＝13×12×6×3×2＝1.5．(2013·辽宁)如图，AB 是圆O 的直径，P A 垂直圆O 所在的平面，C 是圆O 上的点．(1)求证：BC ⊥平面P AC ；(2)设Q 为P A 的中点，G 为△AOC 的重心，求证：QG ∥平面PBC .证明 (1)由AB 是圆O 的直径，得AC ⊥BC ，由P A ⊥平面ABC ，BC ⊂平面ABC ，得P A ⊥BC .又P A ∩AC ＝A ，P A ⊂平面P AC ，AC ⊂平面P AC ，所以BC ⊥平面P AC .(2)连接OG 并延长交AC 于M ，连接QM ，QO ，由G 为△AOC 的重心，得M 为AC 中点．由Q 为P A 中点，得QM ∥PC ，又O 为AB 中点，得OM ∥BC .因为QM ∩MO ＝M ，QM ⊂平面QMO ，MO ⊂平面QMO ，BC ∩PC ＝C ，BC ⊂平面PBC ，PC ⊂平面PBC .所以平面QMO ∥平面PBC .因为QG ⊂平面QMO ，所以QG ∥平面PBC .6．(2014·四川)在如图所示的多面体中，四边形ABB 1A 1和ACC 1A 1都为矩形．(1)若AC ⊥BC ，证明：直线BC ⊥平面ACC 1A 1；(2)设D ，E 分别是线段BC ，CC 1的中点，在线段AB 上是否存在一点M ，使直线DE ∥平面A 1MC ？请证明你的结论．(1)证明因为四边形ABB 1A 1和ACC 1A 1都是矩形，所以AA 1⊥AB ，AA 1⊥AC .因为AB ∩AC ＝A ，AB ⊂平面ABC ，AC ⊂平面ABC ，所以AA 1⊥平面ABC .因为直线BC ⊂平面ABC ，所以AA 1⊥BC .又由已知，AC ⊥BC ，AA 1∩AC ＝A ，AA 1⊂平面ACC 1A 1，AC ⊂平面ACC 1A 1，所以BC ⊥平面ACC 1A 1.(2)解取线段AB 的中点M ，连接A 1M ，MC ，A 1C ，AC 1，设O 为A 1C ，AC 1的交点．由题意知，O 为AC 1的中点．连接MD ，OE ，OM ，则MD ，OE 分别为△ABC ，△ACC 1的中位线，所以MD 綊12AC ，OE 綊12AC ，因此MD 綊OE .从而四边形MDEO 为平行四边形，则DE ∥MO .因为直线DE ⊄平面A 1MC ，MO ⊂平面A 1MC ，所以直线DE ∥平面A 1MC .即线段AB 上存在一点M (线段AB 的中点)，使直线DE ∥平面A 1MC .中档大题规范练——三角函数1．已知函数f (x )＝(sin x －cos x )sin 2x sin x. (1)求f (x )的定义域及最小正周期；(2)求f (x )的单调递增区间．解 (1)由sin x ≠0得x ≠k π(k ∈Z )，故f (x )的定义域为{x ∈R |x ≠k π，k ∈Z }．因为f (x )＝(sin x －cos x )sin 2x sin x＝2cos x (sin x －cos x )＝sin 2x －2cos 2x＝sin 2x －(1＋cos 2x ) ＝2sin ⎝⎛⎭⎫2x －π4－1，所以f (x )的最小正周期T ＝2π2＝π. (2)函数y ＝sin x 的单调递增区间为⎣⎡⎦⎤2k π－π2，2k π＋π2(k ∈Z )．由2k π－π2≤2x －π4≤2k π＋π2，x ≠k π(k ∈Z )，得k π－π8≤x ≤k π＋3π8，x ≠k π(k ∈Z )．所以f (x )的单调递增区间为⎣⎡⎭⎫k π－π8，k π和⎝⎛⎦⎤k π，k π＋3π8(k ∈Z )． 2．已知△ABC 的三个内角A ，B ，C 成等差数列，角B 所对的边b ＝3，且函数f (x )＝23sin 2x ＋2sin x cos x －3在x ＝A 处取得最大值．(1)求f (x )的值域及周期；(2)求△ABC 的面积．解 (1)因为A ，B ，C 成等差数列，所以2B ＝A ＋C ，又A ＋B ＋C ＝π，所以B ＝π3，即A ＋C ＝2π3. 因为f (x )＝23sin 2x ＋2sin x cos x － 3 ＝3(2sin 2x －1)＋sin 2x ＝sin 2x －3cos 2x＝2sin ⎝⎛⎭⎫2x －π3，所以T ＝2π2＝π. 又因为sin ⎝⎛⎭⎫2x －π3∈[－1,1]，所以f (x )的值域为[－2,2]．(2)因为f (x )在x ＝A 处取得最大值，所以sin ⎝⎛⎭⎫2A －π3＝1. 因为0<A <23π，所以－π3<2A －π3<π，故当2A －π3＝π2时，f (x )取到最大值，所以A ＝512π，所以C ＝π4. 由正弦定理，知3sin π3＝c sin π4⇒c ＝ 2. 又因为sin A ＝sin ⎝⎛⎭⎫π4＋π6＝2＋64，所以S △ABC ＝12bc sin A ＝3＋34. 3．已知函数f (x )＝3sin 2x ＋2cos 2x ＋a .(1)求函数f (x )的最小正周期以及单调递增区间；(2)当x ∈[0，π4]时，函数f (x )有最大值4，求实数a 的值．解 f (x )＝3sin 2x ＋2cos 2x ＋a＝cos 2x ＋3sin 2x ＋1＋a＝2sin(2x ＋π6)＋a ＋1. (1)函数f (x )的最小正周期为2π2＝π，由2k π－π2≤2x ＋π6≤2k π＋π2，k ∈Z ，解得k π－π3≤x ≤k π＋π6，k ∈Z .故函数f (x )的单调递增区间为[k π－π3，k π＋π6](k ∈Z )． (2)∵x ∈[0，π4]，∴2x ＋π6∈[π6，2π3]，从而sin(2x ＋π6)∈[12，1]． ∴f (x )＝2sin(2x ＋π6)＋a ＋1∈[a ＋2，a ＋3]， ∵f (x )有最大值4，∴a ＋3＝4，故a ＝1.4．设向量a ＝(3sin x ，sin x )，b ＝(cos x ，sin x )，x ∈[0，π2]． (1)若|a |＝|b |，求x 的值；(2)设函数f (x )＝a ·b ，求f (x )的最大值．解 (1)由|a |2＝(3sin x )2＋(sin x )2＝4sin 2x ，|b |2＝(cos x )2＋(sin x )2＝1，由|a |＝|b |，得4sin 2x ＝1.又x ∈[0，π2]，从而sin x ＝12，所以x ＝π6. (2)f (x )＝a ·b ＝3sin x ·cos x ＋sin 2x ＝32sin 2x －12cos 2x ＋12＝sin(2x －π6)＋12. 当x ＝π3∈[0，π2]时，sin(2x －π6)取最大值1，所以f (x )的最大值为32. 5．已知函数f (x )＝4cos ωx ·sin(ωx －π6)＋1(ω>0)的最小正周期是π. (1)求f (x )的单调递增区间；(2)求f (x )在[π8，3π8]上的最大值和最小值．解 (1)f (x )＝4cos ωx ·sin(ωx －π6)＋1 ＝23sin ωx cos ωx －2cos 2ωx ＋1＝3sin 2ωx －cos 2ωx ＝2sin(2ωx －π6)．最小正周期是2π2ω＝π，所以，ω＝1，从而f (x )＝2sin(2x －π6)．令－π2＋2k π≤2x －π6≤π2＋2k π，k ∈Z . 解得－π6＋k π≤x ≤π3＋k π，k ∈Z . 所以函数f (x )的单调递增区间为[－π6＋k π，π3＋k π](k ∈Z )． (2)当x ∈[π8，3π8]时，2x －π6∈[π12，7π12]， f (x )＝2sin(2x －π6)∈[6－22，2]，所以f (x )在[π8，3π8]上的最大值和最小值分别为2，6－22. 6.在斜度一定的山坡上的一点A 测得山顶上一建筑物顶端对于山坡的斜度为15°，如图所示，向山顶前进100 m 后，又从B 点测得斜度为45°，设建筑物的高为50 m ．求此山对于地平面的斜度θ的余弦值．解在△ABC 中，∠BAC ＝15°，∠CBA ＝180°－45°＝135°，AB ＝100 m ，所以∠ACB ＝30°. 由正弦定理，得100sin 30°＝BC sin 15°，即BC ＝100sin 15°sin 30°. 在△BCD 中，因为CD ＝50，BC ＝100sin 15°sin 30°，∠CBD ＝45°，∠CDB ＝90°＋θ，由正弦定理，得50sin 45°＝100sin 15°sin 30°sin (90°＋θ)，解得cos θ＝3－1.因此，山对地面的斜度的余弦值为3－1.中档大题规范练——数列1．已知公差大于零的等差数列{a n }的前n 项和S n ，且满足：a 2a 4＝64，a 1＋a 5＝18.(1)若1<i <21，a 1，a i ，a 21是某等比数列的连续三项，求i 的值．(2)设b n ＝n (2n ＋1)S n，是否存在一个最小的常数m 使得b 1＋b 2＋…＋b n <m 对于任意的正整数n 均成立，若存在，求出常数m ；若不存在，请说明理由．解 (1)数列{a n }为等差数列，因为a 1＋a 5＝a 2＋a 4＝18，又a 2a 4＝65，所以a 2，a 4是方程x 2－18x ＋65＝0的两个根，又公差d >0，所以a 2<a 4，所以a 2＝5，a 4＝13.所以⎩⎪⎨⎪⎧a 1＋d ＝5，a 1＋3d ＝13，① 所以a 1＝1，d ＝4.所以a n ＝4n －3.由1<i <21，a 1，a i ，a 21是某等比数列的连续三项，所以a 1a 21＝a 2i ，即1×81＝(4i －3)2，解得i ＝3.(2)由(1)知，S n ＝n ×1＋n (n －1)2×4＝2n 2－n ，所以b n ＝1(2n －1)(2n ＋1)＝12(12n －1－12n ＋1)，② 所以b 1＋b 2＋…＋b n＝12(1－13＋13－15＋…＋12n －1－12n ＋1)＝n 2n ＋1，因为n 2n ＋1＝12－12(2n ＋1)<12，③ 所以存在m ＝12使b 1＋b 2＋…＋b n <m 对于任意的正整数n 均成立． 2．设S n 为数列{a n }的前n 项和，已知a 1≠0,2a n －a 1＝S 1·S n ，n ∈N *.(1)求a 1，a 2，并求数列{a n }的通项公式；(2)求数列{na n }的前n 项和．解 (1)令n ＝1，得2a 1－a 1＝a 21，即a 1＝a 21.因为a 1≠0，所以a 1＝1.令n ＝2，得2a 2－1＝S 2＝1＋a 2，解得a 2＝2.当n ≥2时，由2a n －1＝S n,2a n －1－1＝S n －1，两式相减得2a n －2a n －1＝a n ，即a n ＝2a n －1.于是数列{a n }是首项为1，公比为2的等比数列．因此，a n ＝2n －1. 所以数列{a n }的通项公式为a n ＝2n －1. (2)由(1)知，na n ＝n ·2n －1. 记数列{n ·2n －1}的前n 项和为B n ，于是 B n ＝1＋2×2＋3×22＋…＋n ×2n －1.① 2B n ＝1×2＋2×22＋3×23＋…＋n ×2n .②①－②，得－B n ＝1＋2＋22＋…＋2n －1－n ·2n ＝2n －1－n ·2n . 从而B n ＝1＋(n －1)·2n .即数列{na n }的前n 项和为1＋(n －1)·2n .3．设数列{a n }的前n 项和为S n ，满足2S n ＝a n ＋1－2n ＋1＋1，n ∈N *，且a 1＝1，设数列{b n }满足b n ＝a n ＋2n .(1)求证数列{b n }为等比数列，并求出数列{a n }的通项公式；(2)若数列c n ＝6n －3b n，T n 是数列{c n }的前n 项和，证明：T n <3. (1)解当n ≥2时，由⎩⎪⎨⎪⎧2S n ＝a n ＋1－2n ＋1＋1，2S n －1＝a n －2n ＋1 ⇒2a n ＝a n ＋1－a n －2n⇒a n ＋1＝3a n ＋2n ，从而b n ＋1＝a n ＋1＋2n ＋1＝3(a n ＋2n )＝3b n ，故{b n }是以3为首项，3为公比的等比数列，b n ＝a n ＋2n ＝3×3n －1＝3n ， a n ＝3n －2n (n ≥2)，因为a 1＝1也满足，于是a n ＝3n －2n .(2)证明 c n ＝6n －3b n ＝2n －13n －1，则T n ＝130＋331＋532＋…＋2n －33n －2＋2n －13n －1，① 13T n ＝131＋332＋533＋…＋2n －33n －1＋2n －13n ，② ①－②，得23T n ＝130＋231＋232＋…＋23n －1－2n －13n ＝1＋23·1－13n －11－13－2n －13n ＝2－13n －1－2n －13n ＝2－2(n ＋1)3n，故T n ＝3－n ＋13n －1<3. 4．已知单调递增数列{a n }的前n 项和为S n ，满足S n ＝12(a 2n＋n )． (1)求数列{a n }的通项公式；(2)设c n ＝⎩⎪⎨⎪⎧ 1a 2n ＋1－1，n 为奇数，3×2a n －1＋1，n 为偶数，求数列{c n }的前n 项和T n .解 (1)n ＝1时，a 1＝12(a 21＋1)，得a 1＝1，由S n ＝12(a 2n ＋n )，① 则当n ≥2时，S n －1＝12(a 2n －1＋n －1)，② ①－②得a n ＝S n －S n －1＝12(a 2n －a 2n －1＋1)，化简得(a n －1)2－a 2n －1＝0，a n －a n －1＝1或a n ＋a n －1＝1(n ≥2)，又{a n }是单调递增数列，故a n －a n －1＝1，所以{a n }是首项为1，公差为1的等差数列，故a n ＝n .(2)c n ＝⎩⎪⎨⎪⎧1a 2n ＋1－1，n 为奇数，3×2a n －1＋1，n 为偶数，当n 为偶数时，T n ＝(c 1＋c 3＋…＋c n －1)＋(c 2＋c 4＋…＋c n )＝(122－1＋142－1＋…＋1n 2－1)＋3×(21＋23＋…＋2n －1)＋n 2 ＝11×3＋13×5＋…＋1(n －1)×(n ＋1)＋3×2(1－4n 2)1－4＋n 2 ＝12×(11－13＋13－15＋…＋1n －1－1n ＋1)＋2×(4n 2－1)＋n 2 ＝2n ＋1＋n 2－2n －42(n ＋1). 当n 为奇数时，T n ＝(c 1＋c 3＋…＋c n )＋(c 2＋c 4＋…＋c n －1)＝[122－1＋142－1＋…＋1(n ＋1)2－1]＋3×(21＋23＋…＋2n －2)＋n －12 ＝12×(11－13＋13－15＋…＋1n －1n ＋2)＋2×(4n －12－1)＋n －12＝2n＋n 2－2n －92(n ＋2). 所以T n ＝⎩⎪⎨⎪⎧ 2n ＋n 2－2n －92(n ＋2)(n 为奇数)，2n ＋1＋n 2－2n －42(n ＋1)(n 为偶数).5．已知函数f (x )＝2x ＋33x ，数列{a n }满足a 1＝1，a n ＋1＝f (1a n)，n ∈N *. (1)求数列{a n }的通项公式；(2)令b n ＝1a n －1a n (n ≥2)，b 1＝3，S n ＝b 1＋b 2＋…＋b n ，若S n <m －2 0142对一切n ∈N *恒成立，求最小正整数m .解 (1)∵a n ＋1＝f (1a n )＝2a n ＋33a n＝2＋3a n 3＝a n ＋23， ∴{a n }是以1为首项，23为公差的等差数列． ∴a n ＝1＋(n －1)×23＝23n ＋13. (2)当n ≥2时，b n ＝1a n －1a n ＝1(23n －13)(23n ＋13) ＝1(2n －1)(2n ＋1)9＝92(12n －1－12n ＋1)，又b 1＝3＝92(1－13)， ∴S n ＝b 1＋b 2＋…＋b n ＝92(1－13＋13－15＋…＋12n －1－12n ＋1)＝92(1－12n ＋1)＝9n 2n ＋1， ∵S n <m －2 0142对一切n ∈N *恒成立，即9n 2n ＋1<m －2 0142对一切n ∈N *恒成立，又9n 2n ＋1<92，∴m －2 0142≥92，即m ≥2 023.∴最小正整数m 为2 023.6．某工厂为扩大生产规模，今年年初新购置了一条高性能的生产线，该生产线在使用过程中的维护费用会逐年增加，第一年的维护费用是4万元，从第二年到第七年，每年的维护费用均比上年增加2万元，从第八年开始，每年的维护费用比上年增加25%.(1)设第n 年该生产线的维护费用为a n ，求a n 的表达式；(2)若该生产线前n 年每年的平均维护费用大于12万元时，需要更新生产线．求该生产线前n 年每年的平均维护费用，并判断第几年年初需要更新该生产线？解 (1)由题意知，当n ≤7时，数列{a n }是首项为4，公差为2的等差数列，所以a n ＝4＋(n －1)×2＝2n ＋2.当n ≥8时，数列{a n }从a 7开始构成首项为a 7＝2×7＋2＝16，公比为1＋25%＝54的等比数列，则此时a n ＝16×⎝⎛⎭⎫54n －7，所以a n ＝⎩⎪⎨⎪⎧ 2n ＋2，n ≤7，16×⎝⎛⎭⎫54n －7，n ≥8. (2)设S n 为数列{a n }的前n 项和，当1≤n ≤7时，S n ＝4n ＋n (n －1)2×2＝n 2＋3n ，当n ≥8时，由S 7＝72＋3×7＝70，则S n ＝70＋16×54×1－⎝⎛⎭⎫54n －71－54＝80×⎝⎛⎭⎫54n －7－10， ∴该生产线前n 年每年的平均维护费用为S n n ＝⎩⎨⎧ n ＋3，1≤n ≤7，80×⎝⎛⎭⎫54n －7－10n ，n ≥8.当1≤n ≤7时，⎩⎨⎧⎭⎬⎫S n n 为递增数列，当n ≥8时，∵S n ＋1n ＋1－S n n ＝80×⎝⎛⎭⎫54n －6－10n ＋1－80×⎝⎛⎭⎫54n －7－10n ＝80×⎝⎛⎭⎫54n －7·⎝⎛⎭⎫n 4－1＋10n (n ＋1)>0， ∴S n ＋1n ＋1>S n n. ∴⎩⎨⎧⎭⎬⎫S n n 也为递增数列．又∵S 77＝10<12，S 88＝80×54－108＝11.25<12， S 99＝80×⎝ ⎛⎭⎪⎫542－109≈12.78>12，则第9年年初需更新生产线．中档大题规范练——圆锥曲线1．已知中心在原点的双曲线C 的右焦点为(2,0)，实半轴长为3.(1)求双曲线C 的方程；(2)若直线l ：y ＝kx ＋2与双曲线C 的左支交于A ，B 两点，求k 的取值范围；(3)在(2)的条件下，线段AB 的垂直平分线l 0与y 轴交于M (0，b )，求b 的取值范围．解 (1)设双曲线方程为x 2a 2－y 2b 2＝1 (a >0，b >0)，由已知，得a ＝3，c ＝2，b 2＝c 2－a 2＝1，故双曲线方程为x 23－y 2＝1. (2)设A (x A ，y A )，B (x B ，y B )，将y ＝kx ＋2代入x 23－y 2＝1，得(1－3k 2)x 2－62kx －9＝0.由题意，知⎩⎪⎨⎪⎧ 1－3k 2≠0，Δ＝36(1－k 2)>0，x A ＋x B ＝62k 1－3k2<0，x A x B ＝－91－3k 2>0，解得33<k <1. 所以当33<k <1时，直线l 与双曲线C 的左支有两个交点． (3)由(2)，得x A ＋x B ＝62k 1－3k 2，所以y A ＋y B ＝(kx A ＋2)＋(kx B ＋2)＝k (x A ＋x B )＋22＝221－3k 2，所以AB 中点P 的坐标为⎝ ⎛⎭⎪⎫32k 1－3k 2，21－3k 2. 设l 0的方程为y ＝－1k x ＋b ，将P 点的坐标代入l 0的方程，得b ＝421－3k 2， ∵33<k <1，∴－2<1－3k 2<0，∴b <－2 2. ∴b 的取值范围是(－∞，－22)．2．已知离心率为12的椭圆C 1的左，右焦点分别为F 1，F 2，抛物线C 2：y 2＝4mx (m >0)的焦点为F 2，设椭圆C 1与抛物线C 2的一个交点为P (x 0，y 0)，|PF 1|＝73. (1)求椭圆C 1的标准方程及抛物线C 2的标准方程；(2)直线x ＝m 与椭圆C 1在第一象限的交点为Q ，若存在过点A (4,0)的直线l 与椭圆C 1相交于不同的两点M ，N ，使得36|AQ |2＝35|AM |·|AN |，求出直线l 的方程．解 (1)∵在椭圆C 1中c ＝m ，e ＝12， ∴a ＝2m ，b 2＝3m 2，设椭圆C 1的方程为x 24m 2＋y 23m 2＝1，联立x 24m 2＋y 23m 2＝1与y 2＝4mx ，得3x 2＋16mx －12m 2＝0，即(x ＋6m )·(3x －2m )＝0，得x ＝2m 3或－6m (舍去)，代入y 2＝4mx 得y ＝±26m 3， ∴设点P 的坐标为(2m 3，26m 3)， |PF 2|＝2m 3＋m ＝5m 3， |PF 1|＝2a －5m 3＝7m 3＝73， ∴m ＝1，此时，椭圆C 1的标准方程为x 24＋y 23＝1，抛物线C 2的标准方程为y 2＝4x .(2)由题设知直线l 的斜率存在，设直线l 的方程为y ＝k (x －4)，由⎩⎪⎨⎪⎧y ＝k (x －4)，x 24＋y 23＝1，消去y 整理，得(3＋4k 2)x 2－32k 2x ＋64k 2－12＝0.由题意知Δ＝(32k 2)2－4(3＋4k 2)(64k 2－12)>0，解得－12<k <12. 设M (x 1，y 1)，N (x 2，y 2)，则x 1＋x 2＝32k 23＋4k 2，x 1x 2＝64k 2－123＋4k 2.由(1)知m ＝1，∴⎩⎪⎨⎪⎧ x ＝1，x 24＋y 23＝1，解得⎩⎪⎨⎪⎧x ＝1，y ＝±32， ∴点Q 的坐标是(1，32)． ∴|AQ |2＝454，由已知条件可知|AM |·|AN |＝3635×454＝817. 又|AM |·|AN |＝(4－x 1)2＋y 21·(4－x 2)2＋y 22 ＝(4－x 1)2＋k 2(4－x 1)2·(4－x 2)2＋k 2(4－x 2)2＝(k 2＋1)·(4－x 1)·(4－x 2)＝(k 2＋1)[x 1x 2－4(x 1＋x 2)＋16]＝(k 2＋1)(64k 2－123＋4k 2－4×32k 23＋4k 2＋16) ＝(k 2＋1)·363＋4k 2. ∴(k 2＋1)·363＋4k 2＝817，解得k ＝±24，经检验成立． ∴直线l 的方程为x －22y －4＝0或x ＋22y －4＝0.3．(2013·课标全国Ⅱ)平面直角坐标系xOy 中，过椭圆M ：x 2a 2＋y 2b2＝1(a >b >0)右焦点的直线x ＋y －3＝0交M 于A ，B 两点，P 为AB 的中点，且OP 的斜率为12. (1)求M 的方程；(2)C ，D 为M 上的两点，若四边形ACBD 的对角线CD ⊥AB ，求四边形ACBD 面积的最大值．解 (1)设A (x 1，y 1)，B (x 2，y 2)，则x 21a 2＋y 21b2＝1，① x 22a 2＋y 22b2＝1，② ①－②，得(x 1－x 2)(x 1＋x 2)a 2＋(y 1－y 2)(y 1＋y 2)b 2＝0. 因为y 1－y 2x 1－x 2＝－1，设P (x 0，y 0)，因为P 为AB 的中点，且OP 的斜率为12，所以y 0＝12x 0，即y 1＋y 2＝12(x 1＋x 2)．所以可以解得a 2＝2b 2，即a 2＝2(a 2－c 2)，即a 2＝2c 2，又因为右焦点(c,0)在直线x ＋y －3＝0上，解得c ＝3，所以a 2＝6，所以M 的方程为x 26＋y 23＝1. (2)因为CD ⊥AB ，直线AB 方程为x ＋y －3＝0，所以设直线CD 方程为y ＝x ＋m ，将x ＋y －3＝0代入x 26＋y 23＝1得： 3x 2－43x ＝0，即A (0，3)，B ⎝⎛⎭⎫433，－33，所以可得|AB |＝463；将y ＝x ＋m 代入x 26＋y 23＝1得： 3x 2＋4mx ＋2m 2－6＝0，设C (x 3，y 3)，D (x 4，y 4)，则|CD |＝2(x 3＋x 4)2－4x 3x 4＝22318－2m 2，又因为Δ＝16m 2－12(2m 2－6)>0，即－3<m <3，所以当m ＝0时，|CD |取得最大值4，所以四边形ACBD 面积的最大值为12|AB |·|CD |＝863. 4．已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)，⊙O ：x 2＋y 2＝b 2，点A ，F 分别是椭圆C 的左顶点和左焦点，点P 是⊙O 上的动点．(1)若P (－1，3)，P A 是⊙O 的切线，求椭圆C 的方程．(2)是否存在这样的椭圆C ，使得|P A ||PF |恒为常数？如果存在，求出这个常数及C 的离心率e ；如果不存在，说明理由．解 (1)由P (－1，3)在⊙O ：x 2＋y 2＝b 2上，得b 2＝1＋3＝4.直线P A 的斜率k P A ＝3－0－1－(－a )＝3a －1，而直线P A 的斜率k P A ＝－1k OP ＝13，所以3a －1＝13，解得a ＝4.所以a 2＝16，所以椭圆C 的方程为x 216＋y 24＝1. (2)假设存在椭圆C ，使得|P A ||PF |恒为常数．设椭圆C 的半焦距为c ，当P (－b,0)时，则有|P A ||PF |＝a －b |c －b |；当P (b,0)时，|P A ||PF |＝a ＋b b ＋c. 依假设有a －b |c －b |＝a ＋b b ＋c. ①当c －b >0时，有a －b c －b ＝a ＋b b ＋c，所以(a －b )(b ＋c )＝(a ＋b )(c －b )，化简整理得a ＝c ，这是不可能的．②当c －b <0时，有a －b b －c ＝a ＋b b ＋c. 所以(a －b )(b ＋c )＝(a ＋b )(b －c )，化简整理得ac －b 2＝0.所以c 2－a 2＋ac ＝0，两边同除以a 2，得e 2＋e －1＝0.解得e ＝－1＋52，或e ＝－1－52∉(0,1)(舍去)．可见，若存在椭圆C 满足题意，只可能离心率e ＝－1＋52. 设P (x ，y )为⊙O ：x 2＋y 2＝b 2上任意一点，则|P A ||PF |＝(x ＋a )2＋y 2(x ＋c )2＋y 2|P A |2|PF |2＝(x ＋a )2＋b 2－x 2(x ＋c )2＋b 2－x 2＝2ax ＋a 2＋b 22cx ＋c 2＋b 2＝2ax ＋2a 2－c 22cx ＋a 2.(*) 由上c 2－a 2＋ac ＝0，得a 2－c 2＝ac ，所以2a 2－c 2a 2·c a ＝a 2＋ac a 2·c a＝a ＋c a 2·c ＝ac ＋c 2a 2＝a 2a 2＝1，从而2a 2－c 2a 2＝a c. 代入(*)式得|P A |2|PF |2＝a c ＝5＋12，所以存在满足题意的椭圆C ，这个常数为5＋12，椭圆C 的离心率为e ＝－1＋52. 5．已知平面内一动点P 到点F (1,0)的距离与点P 到y 轴的距离的差等于1.(1)求动点P 的轨迹C 的方程；(2)过点F 作两条斜率存在且互相垂直的直线l 1，l 2，设l 1与轨迹C 相交于点A ，B ，l 2与轨迹C 相交于点D ，E ，求AD →·EB →的最小值．解 (1)设动点P 的坐标为(x ，y )，由题意有(x －1)2＋y 2－|x |＝1. 化简得y 2＝2x ＋2|x |.当x ≥0时，y 2＝4x ；当x <0时，y ＝0.所以，动点P 的轨迹C 的方程为y 2＝4x (x ≥0)和y ＝0 (x <0)．(2)由题意知，直线l 1的斜率存在且不为0，设为k ，则l 1的方程为y ＝k (x －1)．由⎩⎪⎨⎪⎧y ＝k (x －1)，y 2＝4x ，得k 2x 2－(2k 2＋4)x ＋k 2＝0. 设A (x 1，y 1)，B (x 2，y 2)，则x 1，x 2是上述方程的两个实根，于是x 1＋x 2＝2＋4k2，x 1x 2＝1. 因为l 1⊥l 2，所以l 2的斜率为－1k. 设D (x 3，y 3)，E (x 4，y 4)，则同理可得x 3＋x 4＝2＋4k 2，x 3x 4＝1.故AD →·EB →＝(AF →＋FD →)·(EF →＋FB →)＝AF →·EF →＋AF →·FB →＋FD →·EF →＋FD →·FB →＝|AF →|·|FB →|＋|FD →|·|EF →|＝(x 1＋1)(x 2＋1)＋(x 3＋1)(x 4＋1)。

2015年高考文科数学(全国通用)二轮复习突破练小题部分10份

目录高考小题综合练 (1)高考小题综合练(一) ................................................................................................................ 1 高考小题综合练(二) ................................................................................................................ 6 高考小题综合练(三) .............................................................................................................. 12 高考小题综合练(四) .............................................................................................................. 18 高考小题分项练 .. (27)高考小题分项练(一) .............................................................................................................. 27 高考小题分项练(二) .............................................................................................................. 33 高考小题分项练(三) .............................................................................................................. 39 高考小题分项练(四) .............................................................................................................. 46 高考小题分项练(五) .............................................................................................................. 53 高考小题分项练(六) .. (60)高考小题综合练高考小题综合练(一)(推荐时间：40分钟)1．已知集合A ＝{－1,1}，B ＝{x |ax ＋2＝0}，若B ⊆A ，则实数a 的所有可能取值的集合为( ) A ．{－2} B ．{2} C ．{－2,2} D ．{－2,0,2}答案 D解析当a ＝0时，B ＝∅⊆A ，合乎题意；当a ≠0时，B ＝{x |ax ＋2＝0}＝⎩⎨⎧⎭⎬⎫－2a ，∵B ⊆A ，∴－2a ＝1或－2a ＝－1，解得a ＝±2，综上所述，实数a 的所有可能取值的集合为{－2,0,2}．2．(2014·上海)设a ，b ∈R ，则“a ＋b >4”是“a >2，且b >2”的( ) A ．充分非必要条件 B ．必要非充分条件 C ．充要条件D ．既非充分也非必要条件答案 B解析显然，a ＋b >4，无法推出a >2且b >2，∴不是充分条件，若a >2且b >2，则a ＋b >4成立，∴是必要条件，∴必要不充分条件，所以选B. 3．i 是虚数单位，则ii (1＋i )的模为( )A.12B.22C. 2 D ．2答案 B 解析i i (1＋i )＝11＋i ＝12－12i ，故其模为22.4．将函数f (x )＝cos(π＋x )(cos x －2sin x )＋sin 2x 的图象向左平移π8个单位长度后得到函数g (x )，则g (x )具有性质( )A ．最大值为2，图象关于直线x ＝π2对称B ．周期为π，图象关于(π4，0)对称C ．在(－π2，0)上单调递增，为偶函数D ．在(0，π4)上单调递增，为奇函数答案 D解析 f (x )＝－cos x (cos x －2sin x )＋sin 2x ＝2sin x cos x －(cos 2x －sin 2x ) ＝sin 2x －cos 2x ＝2sin(2x －π4)，所以g (x )＝2sin[2(x ＋π8)－π4]＝2sin 2x .结合正弦函数的性质，可知D 正确．5．已知各项不为零的等差数列{a n }的前n 项和为S n ．若m ∈N *，且a m －1＋a m ＋1－a 2m ＝0，S 2m －1＝38，则m ＝( )A ．10B ．20C ．30D ．40答案 A解析 a m －1＋a m ＋1＝2a m ，得2a m －a 2m ＝0，又a m ≠0，所以a m ＝2，则S 2m －1＝(2m －1)(a 1＋a 2m －1)2＝(2m －1)a m ＝2(2m －1)＝38，所以m ＝10.6．在△ABC 中，AB ＝2，BC ＝1.5，∠ABC ＝120°(如图所示)，若将△ABC 绕BC 边所在直线旋转一周，则所形成的旋转体的体积是( ) A.92π B.72π C.52π D.32π 答案 D解析如图所示，该旋转体的体积为圆锥CD 与圆锥BD 的体积之差，由已知求得BD ＝1.所以V ＝V 圆锥CD －V 圆锥BD ＝13×π×3×52－13×π×3×1＝32π. 7．双曲线y 2a 2－x 2b 2＝1(a >0，b >0)的渐近线与抛物线y ＝x 2＋1相切，则该双曲线的离心率等于( ) A.52 B. 5 C. 6 D.62答案 A解析可以设切点为(x 0，x 20＋1)，由y ′＝2x ， ∴切线方程为y －(x 20＋1)＝2x 0(x －x 0)，即y ＝2x 0x －x 20＋1，∵已知双曲线的渐近线为y ＝±a b x ，∴⎩⎪⎨⎪⎧1－x 20＝0，±a b ＝2x 0，∴x 0＝±1，∴ab ＝2， ∴e ＝c a＝c 2a 2＝ a 2＋b 2a 2＝ 4b 2＋b 24b 2＝52. 8．(2014·辽宁)若将一个质点随机投入如图所示的长方形ABCD 中，其中AB ＝2，BC ＝1，则质点落在以AB 为直径的半圆内的概率是( )A.π2B.π4C.π6D.π8答案 B解析设质点落在以AB 为直径的半圆内为事件A ，则P (A )＝阴影面积长方形面积＝12π·121×2＝π4.9．(2014·湖南)执行如图所示的程序框图，如果输入的t ∈[－2,2]，则输出的S 属于( )A ．[－6，－2]B ．[－5，－1]C ．[－4,5]D ．[－3,6]答案 D解析由程序框图知，当0≤t ≤2时，输出S ＝t －3，此时S ∈[－3，－1]；当－2≤t <0时，执行t ＝2t 2＋1后1<t ≤9，执行1<t ≤9时，输出S ＝t －3，此时S ∈(－2,6]．因此输出S 的值属于[－3,6]．10．某班级有50名学生，其中有30名男生和20名女生，随机询问了该班五名男生和五名女生在某次数学测验中的成绩，五名男生的成绩分别为86,94,88,92,90，五名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是( ) A ．这种抽样方法是一种分层抽样 B ．这种抽样方法是一种系统抽样C ．这五名男生成绩的方差大于这五名女生成绩的方差D ．该班男生成绩的平均数大于该班女生成绩的平均数答案 C解析 x 男＝15(86＋94＋88＋92＋90)＝90， x女＝15(88＋93＋93＋88＋93)＝91， s 2男＝15[(86－90)2＋(94－90)2＋(88－90)2＋(92－90)2＋(90－90)2]＝8，s 2女＝15[(88－91)2＋(93－91)2＋(93－91)2＋(88－91)2＋(93－91)2]＝6.11．(2014·浙江)在3张奖券中有一、二等奖各1张，另1张无奖．甲、乙两人各抽取1张，两人都中奖的概率是________．答案 13解析设中一、二等奖及不中奖分别记为1,2,0，那么甲、乙抽奖结果有(1,2)，(1,0)，(2,1)，(2,0)，(0,1)，(0,2)，共6种．其中甲、乙都中奖有(1,2)，(2,1)，2种，所以P (A )＝26＝13.12．抛物线x 2＝2py (p >0)的焦点为F ，其准线与双曲线x 23－y 23＝1相交于A 、B 两点，若△ABF为等边三角形，则p ＝________. 答案 6解析因为△ABF 为等边三角形，所以由题意知B ⎝⎛⎭⎫p 3，－p 2，代入方程x 23－y 23＝1得p ＝6.13．已知定义在R 上的函数y ＝f (x )满足以下三个条件：①对于任意的x ∈R ，都有f (x ＋1)＝1f (x )；②函数y ＝f (x ＋1)的图象关于y 轴对称；③对于任意的x 1，x 2∈[0,1]，且x 1<x 2，都有f (x 1)>f (x 2)，则f (32)，f (2)，f (3)从小到大的关系是________．答案 f (3)<f (32)<f (2)解析由①得f (x ＋2)＝f (x ＋1＋1)＝1f (x ＋1)＝f (x )，所以函数f (x )的周期为2.因为函数y ＝f (x＋1)的图象关于y 轴对称，将函数y ＝f (x ＋1)的图象向右平移一个单位即得y ＝f (x )的图象，所以函数y ＝f (x )的图象关于x ＝1对称；根据③可知函数f (x )在[0,1]上为减函数，又结合②知，函数f (x )在[1,2]上为增函数．因为f (3)＝f (2＋1)＝f (1)，在区间[1,2]上，1<32<2，所以f (1)<f (32)<f (2)，即f (3)<f (32)<f (2)．14．在△ABC 中，已知D 是边AB 上的一点，若AD →＝2DB →，CD →＝13CA →＋λCB →，则λ＝________.答案 23解析因为AD →＝2DB →，所以AD →＝23AB →，又CD →＝CA →＋AD →＝CA →＋23AB →＝CA →＋23(CB →－CA →)＝13CA →＋23CB →，所以λ＝23.15．已知某几何体的三视图如图所示，其中，正视图、侧视图均是由三角形与半圆构成的，俯视图由圆与内接三角形构成，根据图中的数据可得此几何体的体积为_________________．答案2π6＋16解析据三视图可知，该几何体是一个半球(下部)与一个四面体(上部)的组合体，其直观图如图所示，其中BA ，BC ，BP 两两垂直，且BA ＝BC ＝BP ＝1，∴(半)球的直径长为AC ＝2，∴该几何体的体积为 V ＝V 半球＋V P －ABC ＝12×43π(AC 2)3＋13×12×BA ·BC ·PB ＝2π6＋16.高考小题综合练(二)(推荐时间：40分钟)1．全集U＝R，A＝{x|x2－2x≤0}，B＝{y|y＝cos x，x∈R}，则右图中阴影部分表示的集合()A．{x|x<－1或x>2} B．{x|－1≤x≤2}C．{x|x≤1} D．{x|0≤x≤1}答案 D解析阴影部分表示的集合是A∩B.依题意知，A＝{x|0≤x≤2}，B＝{y|－1≤y≤1}，所以A∩B＝{x|0≤x≤1}，故选D.2．复数1＋i4＋3i的虚部是()A.125i B.1 25C．－125D．－125i 答案 B解析1＋i4＋3i＝(1＋i)(4－3i)(4＋3i)(4－3i)＝725＋i25，所以虚部为125.3．(2014·陕西)原命题为“若z1，z2互为共轭复数，则|z1|＝|z2|”，关于其逆命题，否命题，逆否命题真假性的判断依次如下，正确的是()A．真，假，真B．假，假，真C．真，真，假D．假，假，假答案 B解析原命题正确，所以逆否命题正确．模相等的两复数不一定互为共轭复数，同时因为逆命题与否命题互为逆否命题，所以逆命题和否命题错误．故选B.4．(2014·湖南)某市生产总值连续两年持续增加．第一年的增长率为p ，第二年的增长率为q ，则该市这两年生产总值的年平均增长率为( ) A.p ＋q 2B.(p ＋1)(q ＋1)－12C.pqD.(p ＋1)(q ＋1)－1答案 D解析设年平均增长率为x ，则(1＋x )2＝(1＋p )(1＋q )，所以x ＝(1＋p )(1＋q )－1.5．设数列{a n }是首项为1，公比为4的等比数列，把{a n }中的每一项都减去3后，得到一个新数列{b n }，{b n }的前n 项和为S n ，对任意的n ∈N *，下列结论正确的是( ) A ．4b n ＝b n ＋1且S n ＝13(4n －1)B ．4b n －6＝b n ＋1且S n ＝13(4n －1)C ．4b n ＋9＝b n ＋1且S n ＝13(4n －1)－3nD ．4b n －9＝b n ＋1且S n ＝13(4n －1)－3n答案 C解析由已知得b n ＝4n －1－3，故有4b n ＋9＝4(4n －1－3)＋9＝4n －3＝b n ＋1，S n ＝(1＋4＋42＋…＋4n －1)－3n ＝13(4n －1)－3n .6．已知x ，y 满足约束条件⎩⎪⎨⎪⎧x －y ≥0，x ＋y ≤1，0≤y ≤12，若目标函数z ＝ax ＋y (其中a 为常数)仅在点⎝⎛⎭⎫12，12处取得最大值，则实数a 的取值范围是( )A ．(－2,2)B ．(0,1)C ．(－1,1)D ．(－1,0)答案 C解析由x ，y 满足约束条件⎩⎪⎨⎪⎧x －y ≥0，x ＋y ≤1，0≤y ≤12，画出此不等式组表示的平面区域如图中阴影部分所示．由目标函数z ＝ax ＋y ，得y ＝－ax ＋z ，因为z 仅在点⎝⎛⎭⎫12，12处取得最大值，所以得－1<－a <1，得实数a 的取值范围是(－1,1)．7．一个半径为2的球体经过切割后，剩余部分几何体的三视图如图所示，则该几何体的表面积为( )A ．15πB ．16πC ．17πD ．18π答案 B解析该几何体是从一个球体中挖去14个球体后剩余的部分，所以该几何体的表面积为34×(4π×22)＋2×π×222＝16π. 8．(2014·课标全国Ⅱ)若函数f (x )＝kx －ln x 在区间(1，＋∞)单调递增，则k 的取值范围是( ) A ．(－∞，－2] B ．(－∞，－1] C ．[2，＋∞) D ．[1，＋∞)答案 D解析由于f ′(x )＝k －1x ，f (x )＝kx －ln x 在区间(1，＋∞)单调递增⇔f ′(x )＝k －1x ≥0在(1，＋∞)上恒成立．由于k ≥1x ，而0<1x <1，所以k ≥1.即k 的取值范围为[1，＋∞)．9．已知锐角A ，B 满足2tan A ＝tan(A ＋B )，则tan B 的最大值为( )A.22 B.24C. 2 D ．2 2 答案 B解析 tan B ＝tan[(A ＋B )－A ]＝tan (A ＋B )－tan A 1＋tan (A ＋B )tan A ＝tan A 1＋2tan 2A ＝11tan A＋2tan A ，又tan A >0，则1tan A＋2tan A ≥22，当且仅当tan A ＝22时取等号．所以tan B ≤122＝24.故选B.10．当x ＝π4时，函数f (x )＝A sin(x ＋φ)(A >0)取得最小值，则函数y ＝f ⎝⎛⎭⎫3π4－x 是( ) A ．奇函数且图象关于点⎝⎛⎭⎫π2，0对称 B ．偶函数且图象关于点(π，0)对称C ．奇函数且图象关于直线x ＝π2对称D ．偶函数且图象关于点⎝⎛⎭⎫π2，0对称答案 C解析由题意得，sin ⎝⎛⎭⎫π4＋φ＝－1， ∴φ可取－3π4.∴f ⎝⎛⎭⎫3π4－x ＝A sin ⎝⎛⎭⎫3π4－x －3π4＝－A sin x ， ∴选C.11．设直线x －my －1＝0与圆(x －1)2＋(y －2)2＝4相交于A ，B 两点，且弦AB 的长为23，则实数m 的值是______．答案 ±33解析由条件可知圆心(1,2)到直线x －my －1＝0的距离d ＝4－3＝1，即|1－2m －1|1＋m2＝1，解得m ＝±33.12．(2014·天津)某大学为了解在校本科生对参加某项社会实践活动的意向，拟采用分层抽样的方法，从该校四个年级的本科生中抽取一个容量为300的样本进行调查，已知该校一年级、二年级、三年级、四年级的本科生人数之比为4∶5∶5∶6，则应从一年级本科生中抽取________名学生．答案 60解析根据题意，应从一年级本科生中抽取的人数为44＋5＋5＋6×300＝60.13．(2014·上海)为强化安全意识，某商场拟在未来的连续10天中随机选择3天进行紧急疏散演练，则选择的3天恰好为连续3天的概率是________(结果用最简分数表示)．答案11514．设D ，E 分别是△ABC 的边AB ，BC 上的点，AD ＝12AB ，BE ＝23BC .若DE →＝λ1AB →＋λ2AC→(λ1，λ2为实数)，则λ1＋λ2的值为________．答案 12解析 DE →＝DB →＋BE →＝12AB →＋23BC →＝12AB →＋23(BA →＋AC →)＝－16AB →＋23AC →，所以λ1＝－16，λ2＝23，即λ1＋λ2＝12.15．已知数列{a n }满足a n ＝n ·k n (n ∈N *,0<k <1)，下面说法正确的是____________________． ①当k ＝12时，数列{a n }为递减数列；②当12<k <1时，数列{a n }不一定有最大项；③当0<k <12时，数列{a n }为递减数列；④当k 1－k 为正整数时，数列{a n }必有两项相等的最大项．答案 ③④ 解析a n ＋1a n ＝n ＋1nk ，因为0<k <1，所以当n <k1－k 时，a n ＋1a n >1，即a n ＋1>a n ；当n >k1－k 时，a n ＋1a n <1，即a n ＋1<a n .①当k ＝12时，a 1＝12，a 2＝2×(12)2＝12，a 1＝a 2，故数列{a n }不是递减数列．故①不正确．②当12<k <1时，k1－k∈(1，＋∞)，所以数列{a n }先减后增，有最大值，故②不正确．③当0<k <12时，k1－k ∈(0,1)，所以数列{a n }是递减数列，故③正确．④当k 1－k 为正整数时，令k 1－k ＝n ∈N *，所以k ＝n n ＋1∈[12，1)．k ＝12时，a 1＝a 2＝12，数列{a n }从第二项起递减，所以此时数列{a n }有两项相等的最大值； 12<k <1时，数列从第一项到第n －1项递增，从第n ＋1项起递减． a n a n －1＝n n －1k ＝n n －1×n n ＋1＝n 2n 2－1>1，所以a n >a n －1，a n ＋1a n ＝n ＋1n k ＝n ＋1n ×nn ＋1＝1，所以a n ＝a n ＋1，所以此时数列{a n }有两项相等的最大值，故④正确．高考小题综合练(三)(推荐时间：40分钟)1．(2014·大纲全国)设集合M ＝{x |x 2－3x －4<0}，N ＝{x |0≤x ≤5}, 则M ∩N 等于( ) A ．(0,4] B ．[0,4) C ．[－1,0) D ．(－1,0]答案 B解析 ∵集合M ＝{x |x 2－3x －4<0}＝{x |－1<x <4}． N ＝{x |0≤x ≤5}，∴M ∩N ＝{x |0≤x <4}．2．已知l ，m 是两条不同的直线，α是一个平面，且l ∥α，则下列命题正确的是( ) A ．若l ∥m ，则m ∥α B ．若m ∥α，则l ∥m C ．若l ⊥m ，则m ⊥α D ．若m ⊥α，则l ⊥m 答案 D解析由l ∥α，l ∥m ，可得m ⊂α或m ∥α，A 不正确；由l ∥α，m ∥α，可得l ∥m 或l ，m 相交或l ，m 互为异面直线，B 不正确；由l ∥α，l ⊥m ，可得m ∥α或m ，α相交，C 不正确；由l ∥α，m ⊥α，可得l ⊥m ，D 正确．3．已知函数f (x )＝⎩⎪⎨⎪⎧|sin x |，x ∈[－π，π]，lg x ，x >π，x 1，x 2，x 3，x 4，x 5是方程f (x )＝m 的五个不等的实数根，则x 1＋x 2＋x 3＋x 4＋x 5的取值范围是( ) A ．(0，π) B ．(－π，π) C ．(lg π，1) D ．(π，10)答案 D解析函数f (x )的图象如图所示，结合图象可得x 1＋x 2＝－π，x 3＋x 4＝π，若f (x )＝m 有5个不等的实数根，需lg π<lg x 5<1，得π<x 5<10，又由函数f (x )在[－π，π]上对称，所以x 1＋x 2＋x 3＋x 4＝0，故x 1＋x 2＋x 3＋x 4＋x 5的取值范围为(π，10)． 4．(2014·陕西)原命题为“若a n ＋a n ＋12<a n ，n ∈N ＋，则{a n }为递减数列”，关于其逆命题，否命题，逆否命题真假性的判断依次如下，正确的是( ) A ．真，真，真 B ．假，假，真 C ．真，真，假 D ．假，假，假答案 A 解析a n ＋a n ＋12<a n ⇔a n ＋1<a n ⇔{a n }为递减数列．原命题与其逆命题都是真命题，所以其否命题和逆否命题也都是真命题，故选A. 5．在区间[0，π]上随机取一个数x ，则事件“sin x ＋cos x ≥62”发生的概率为( ) A.14 B.13 C.12 D.23 答案 B解析因为⎩⎪⎨⎪⎧sin x ＋cos x ≥62，0≤x ≤π，所以⎩⎪⎨⎪⎧sin (x ＋π4)≥32，0≤x ≤π，即π12≤x ≤5π12.根据几何概型的计算方法，所以所求的概率为P ＝5π12－π12π＝13. 6．下列不等式中，一定成立的是( ) A ．lg ⎝⎛⎭⎫x 2＋14>lg x (x >0) B ．sin x ＋1sin x ≥2(x ≠k π，k ∈Z )C ．x 2＋1≥2|x |(x ∈R ) D.1x 2＋1>1(x ∈R ) 答案 C解析取x ＝12否定A ，取x ＝－π4否定B ，取x ＝0否定D ，故选C.7．已知x 、y 取值如下表：从所得的散点图分析可知：y 与x 线性相关，且y ＝0.95x ＋a ，则a 等于( ) A ．1.30 B ．1.45 C ．1.65 D ．1.80答案 B解析代入样本点中心(x ，y )，可知a ＝1.45.8．定义在R 上的函数y ＝f (x )在(－∞ ，a )上是增函数，且函数y ＝f (x ＋a )是偶函数，当x 1<a ，x 2>a ，且|x 1－a |<|x 2－a |时，有( )A ．f (x 1)>f (x 2)B ．f (x 1)≥f (x 2)C ．f (x 1)<f (x 2)D ．f (x 1)≤f (x 2)答案 A解析因为函数y ＝f (x ＋a )是偶函数，其图象关于y 轴对称，把这个函数图象平移|a |个单位(a <0左移，a >0右移)可得函数y ＝f (x )的图象，因此函数y ＝f (x )的图象关于直线x ＝a 对称，此时函数y ＝f (x )在(a ，＋∞)上是减函数．由于x 1<a ，x 2>a 且|x 1－a |<|x 2－a |，说明x 1与对称轴的距离比x 2与对称轴的距离小，故f (x 1)>f (x 2)．9．已知双曲线的顶点与焦点分别是椭圆x 2a 2＋y 2b 2＝1(a >b >0)的焦点和顶点，若双曲线的两条渐近线与椭圆的焦点构成的四边形恰为正方形，则椭圆的离心率为( ) A.13 B.12 C.33 D.22 答案 D解析设椭圆的焦点F 1(－c,0)，F 2(c,0)，由题意可知双曲线方程为x 2c 2－y 2b 2＝1，其渐近线方程为y ＝±bc x ，又双曲线的两条渐近线与椭圆的焦点构成的四边形恰为正方形，所以由椭圆的对称性知双曲线的渐近线方程为y ＝±x ，即b ＝c ，所以a ＝b 2＋c 2＝2c ，所以椭圆的离心率为22. 10．在平面上，AB 1→⊥AB 2→，|OB →1|＝|OB 2→|＝1，AP →＝AB 1→＋AB 2→.若|OP →|<12，则|OA →|的取值范围是( ) A ．(0，52] B ．(52，72] C ．(52，2] D ．(72，2] 答案 D解析根据条件知A ，B 1，P ，B 2构成一个矩形AB 1PB 2，以AB 1，AB 2为坐标轴建立直角坐标系，设|AB 1|＝a ，|AB 2|＝b ，点O 的坐标为(x ，y )，则点P 的坐标为(a ，b )，由|OB 1→|＝|OB 2→|＝1得⎩⎪⎨⎪⎧ (x －a )2＋y 2＝1，x 2＋(y －b )2＝1，则⎩⎪⎨⎪⎧(x －a )2＝1－y 2，(y －b )2＝1－x 2，又由|OP →|<12，得(x －a )2＋(y －b )2<14，则1－x 2＋1－y 2<14，即x 2＋y 2>74①又(x －a )2＋y 2＝1，得x 2＋y 2＋a 2＝1＋2ax ≤1＋a 2＋x 2，则y 2≤1；同理，由x 2＋(y －b )2＝1，得x 2≤1，即有x 2＋y 2≤2② 由①②知74<x 2＋y 2≤2，所以72<x 2＋y 2≤ 2.而|OA →|＝x 2＋y 2，所以72<|OA →|≤ 2. 11．设x ，y 满足约束条件⎩⎪⎨⎪⎧x －y ≥－1，x ＋y ≤3，x ≥0，y ≥0，则z ＝x －2y 的取值范围为________．答案 [－3,3]解析如右图，阴影部分为不等式组表示的平面区域，易知点A (1,2)，B (3,0)分别为目标函数取得最小值和最大值的最优解，即z min ＝1－2×2＝－3，z max ＝3－2×0＝3，故z ＝x －2y 的取值范围是[－3,3]．12．执行下面的程序框图，则输出的S 的值是________．答案 63解析由程序框图知，当n ＝1时，S ＝1＋21＝3；当n ＝2时，S ＝3＋22＝7；当n ＝3时，S ＝7＋23＝15；当n ＝4时，S ＝15＋24＝31；当n ＝5时，S ＝31＋25＝63>33，循环结束，故输出S 的值是63.13.如图所示，ABCD —A 1B 1C 1D 1是棱长为a 的正方体，M 、N 分别是下底面的棱A 1B 1、B 1C 1的中点，P 是上底面的棱AD 上的点，AP ＝a3，过P 、M 、N 的平面交上底面于PQ ，Q 在CD 上，则PQ ＝________. 答案223a 解析如图所示，连接AC ，易知MN ∥平面ABCD ， ∴MN ∥PQ .又∵MN ∥AC ，∴PQ ∥AC . 又∵AP ＝a3，∴PD AD ＝DQ CD ＝PQ AC ＝23， ∴PQ ＝23AC ＝223a .14．设A ，B 为双曲线x 2a 2－y 2b 2＝λ(a >0，b >0，λ≠0)同一条渐近线上的两个不同的点，已知向量m ＝(1,0)，|AB →|＝6，AB →·m |m |＝3，则双曲线的离心率为________．答案 2或233解析设AB →与m 的夹角为θ，则AB →·m |m |＝6cos θ＝3，所以cos θ＝12.所以双曲线的渐近线与x 轴成60°角，可得ba ＝ 3.当λ>0时，此时e ＝ca ＝1＋(ba)2＝2；当λ<0时，e ＝cb＝1＋(a b )2＝233.15．定义域为R 的函数f (x )满足f (x ＋2)＝2f (x )，当x ∈[0,2)时，f (x )＝⎩⎪⎨⎪⎧x 2－x ，x ∈[0，1)，－(12)3||2x -，x ∈[1，2)，若x ∈[－4，－2)时，f (x )≥t 4－12t 恒成立，则实数t 的取值范围是________．答案 (－∞，－2]∪(0,1]解析当－4≤x <－3时，0≤x ＋4<1，f (x )＝12f (x ＋2)＝14f (x ＋4)＝14[(x ＋4)2－(x ＋4)]，即f (x )＝14(x ＋4)(x ＋3)．此时，－116≤f (x )≤0.当－3≤x <－2时，1≤x ＋4<2， f (x )＝12f (x ＋2)＝14f (x ＋4)＝(－14)·(12)3|4|2x +-＝(－14)·(12)5||2x +.此时，－14≤f (x )≤－28.所以f (x )在[－4，－2)上的最小值为－14.f (x )≥t 4－12t 恒成立，则t 4－12t ≤－14，即t 2＋t －2t ≤0，(t ＋2)(t －1)t≤0，即t ≤－2或0<t ≤1. 高考小题综合练(四)(推荐时间：40分钟)1．(2014·福建)复数z ＝(3－2i)i 的共轭复数z 等于( ) A ．－2－3i B ．－2＋3i C ．2－3i D ．2＋3i答案 C解析因为z ＝(3－2i)i ＝3i －2i 2＝2＋3i ，所以z ＝2－3i ，故选C.2．“m ＝1”是“直线x －y ＝0和直线x ＋my ＝0互相垂直”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件答案 C解析因为m ＝1时，两直线分别是直线x －y ＝0和直线x ＋y ＝0，两直线的斜率分别是1和－1.所以两直线垂直，所以充分性成立；当直线x －y ＝0和直线x ＋my ＝0互相垂直，则1×1＋(－1)m＝0，所以m＝1，所以必要性成立．故选C. 3．(2014·湖南)若0<x1<x2<1，则()A．e2x－e1x>ln x2－ln x1B．e1x－e2x<ln x2－ln x1C．x2e1x>x1e2xD．x2e1x<x1e2x答案 C解析设f(x)＝e x－ln x(0<x<1)，则f′(x)＝e x－1x ＝x e x－1x.令f′(x)＝0，得x e x－1＝0.根据函数y＝e x与y＝1x的图象可知两函数图象交点x0∈(0,1)，因此函数f(x)在(0,1)上不是单调函数，故A，B选项不正确．设g(x)＝e xx(0<x<1)，则g′(x)＝e x(x－1)x2.又0<x<1，∴g′(x)<0.∴函数g(x)在(0,1)上是减函数．又0<x1<x2<1，∴g(x1)>g(x2)，∴x2e x1>x1e x2.4．(2014·新课标Ⅰ)如图，圆O的半径为1，A是圆上的定点，P是圆上的动点，角x的始边为射线OA，终边为射线OP，过点P作直线OA的垂线，垂足为M，将点M到直线OP的距离表示成x的函数f(x)，则y＝f(x)在[0，π]的图象大致为()答案 B解析如图所示，当x ∈(0，π2)时，则P (cos x ，sin x )，M (cos x,0)，作MM ′⊥OP ，M ′为垂足，则|MM ′||OM |＝sin x ，∴f (x )cos x＝sin x ，∴f (x )＝sin x cos x ＝12sin 2x ，则当x ＝π4时，f (x )max ＝12；当x ∈(π2，π)时，有f (x )|cos x |＝sin(π－x )，f (x )＝－sin x cos x ＝－12sin 2x ，当x ＝3π4时，f (x )max ＝12.只有B 选项的图象符合．5．(2014·四川)已知F 为抛物线y 2＝x 的焦点，点A ，B 在该抛物线上且位于x 轴的两侧，OA →·OB →＝2(其中O 为坐标原点)，则△ABO 与△AFO 面积之和的最小值是( ) A ．2 B ．3 C.1728D.10答案 B解析设直线AB 的方程为x ＝ny ＋m (如图)， A (x 1，y 1)，B (x 2，y 2)， ∵OA →·OB →＝2， ∴x 1x 2＋y 1y 2＝2.联立⎩⎪⎨⎪⎧y 2＝x ，x ＝ny ＋m ，得y 2－ny －m ＝0，∴y 1y 2＝－m ＝－2， ∴m ＝2，即点M (2,0)．又S △ABO ＝S △AMO ＋S △BMO ＝12|OM ||y 1|＋12|OM ||y 2|＝y 1－y 2， S △AFO ＝12|OF |·|y 1|＝18y 1，∴S △ABO ＋S △AFO ＝y 1－y 2＋18y 1＝98y 1＋2y 1≥298y 1·2y 1＝3，当且仅当y 1＝43时，等号成立．6．若不等式(a －a 2)·(x 2＋1)＋x ≤0对一切x ∈(0,2]恒成立，则a 的取值范围为( ) A.⎝ ⎛⎦⎥⎤－∞，1－32B.⎣⎢⎡⎭⎪⎫1＋32，＋∞C.⎝ ⎛⎦⎥⎤－∞，1－32∪⎣⎢⎡⎭⎪⎫1＋32，＋∞D.⎣⎢⎡⎦⎥⎤1－32，1＋32答案 C解析 ∵x ∈(0,2]，∴a 2－a ≥x x 2＋1＝1x ＋1x.要使a 2－a ≥1x ＋1x在x ∈(0,2]时恒成立，则a 2－a ≥⎝ ⎛⎭⎪⎫1x ＋1x max ，由基本不等式得x ＋1x ≥2，当且仅当x ＝1时，等号成立，即⎝ ⎛⎭⎪⎫1x ＋1x max＝12. 故a 2－a ≥12，解得a ≤1－32或a ≥1＋32.故选C.7．某程序框图如图所示，现输入如下四个函数，则可以输出的函数是( )A ．f (x )＝|x |xB ．f (x )＝12x －1＋12C ．f (x )＝e x －e －xe x ＋e －xD ．f (x )＝cos x答案 C解析第一个判断框的目的是判断输入的函数是否为奇函数，第二个判断框的目的是判断输入的函数是否存在零点．结合选项，知函数f (x )＝e x －e －x e x ＋e －x为奇函数，且存在零点．8．已知点O ，N ，P 在△ABC 所在平面内，且|OA →|＝|OB →|＝|OC →|，NA →＋NB →＋NC →＝0，P A →·PB →＝PB →·PC →＝PC →·P A →，则点O ，N ，P 依次是△ABC 的( ) A ．重心、外心、垂心 B ．重心、外心、内心 C ．外心、重心、垂心D ．外心、重心、内心(注：三角形的三条高线交于一点，此点称为三角形的垂心) 答案 C解析由|OA →|＝|OB →|＝|OC →|知O 为△ABC 的外心．∵P A →·PB →＝PB →·PC →，∴(P A →－PC →)·PB →＝CA →·PB →＝0，同理AB →·PC →＝0，BC →·P A →＝0，∴点P 是△ABC 的垂心，由NA →＋NB →＋NC →＝0知NA →＋NB →＝－NC →，结合向量加法的平行四边形法则知N 为△ABC 的重心．故选C.9．函数y ＝xsin 2x，x ∈⎝⎛⎭⎫－π2，0∪⎝⎛⎭⎫0，π2的图象可能是下列图象中的( )答案 C解析由函数y ＝xsin 2x，x ∈⎝⎛⎭⎫－π2，0∪⎝⎛⎭⎫0，π2是偶函数，排除A ；又由函数y ＝sin 2x ，y ＝2x ，x ∈⎝⎛⎭⎫0，π2的图象可知恒有2x >sin 2x ，x ∈⎝⎛⎭⎫0，π2，所以y ＝x sin 2x >12，x ∈⎝⎛⎭⎫0，π2，排除B 和D ，故选C.10．函数f (x )在[a ，b ]上有定义，若对任意x 1，x 2∈[a ，b ]，有f (x 1＋x 22)≤12[f (x 1)＋f (x 2)]，则称f (x )在[a ，b ]上具有性质P .设f (x )在[1,3]上具有性质P ，现给出如下命题：①f (x )在[1,3]上的图象是连续不断的；②f (x 2)在[1，3]上具有性质P ；③若f (x )在x ＝2处取得最大值1，则f (x )＝1，x ∈[1,3]；④对任意x 1，x 2，x 3，x 4∈[1,3]，有f (x 1＋x 2＋x 3＋x 44)≤14[f (x 1)＋f (x 2)＋f (x 3)＋f (x 4)]．其中真命题的序号是( ) A ．①② B ．①③ C ．②④ D ．③④答案 D解析 ①中，反例：取函数f (x )＝⎩⎪⎨⎪⎧(x －1)2，x ∈[1，2]∪(2，3]，2，x ＝2，则函数f (x )满足题设条件具有性质P ，但函数f (x )的图象不是连续的．②中，反例：f (x )＝－x 在[1,3]上具有性质P ，f (x 2)＝－x 2在[1，3]上不具有性质P . ③中，在[1,3]上，f (2)＝f (x ＋(4－x )2)≤12[f (x )＋f (4－x )]⇒⎩⎪⎨⎪⎧f (x )＋f (4－x )≥2，f (x )≤f (x )max＝f (2)＝1，f (4－x )≤f (x )max＝f (2)＝1⇒f (x )＝1，所以，对于任意x 1，x 2∈[1,3]，f (x )＝1. ④中，f (x 1＋x 2＋x 3＋x 44)＝f ((x 1＋x 2)＋(x 3＋x 4)4)≤12[f (x 1＋x 22)＋f (x 3＋x 42)] ⇒12[12(f (x 1)＋f (x 2))＋12(f (x 3)＋f (x 4))] ≤14[f (x 1)＋f (x 2)＋f (x 3)＋f (x 4)]．由以上推断可知①②错误，③④正确．11．如图，在棱长为2的正方体ABCD －A 1B 1C 1D 1中，E 为BC 的中点，点P 在线段D 1E 上，点P 到直线CC 1的距离的最小值为________．答案255解析过点P 作PH 垂直上底面A 1B 1C 1D 1，过点E 作线段EE 1垂直底面A 1B 1C 1D 1，E 1在线段B 1C 1上，点P 到线段CC 1的距离PP 1＝HC 1.当点P 在线段ED 1上运动时，其最小值为点C 1到线段D 1E 1的距离，所以最小值就是△C 1D 1E 1的高为255.12．已知集合A ＝{x ，xy ，lg(xy )}，B ＝{0，|x |，y }，若A ＝B ，则x ＝________，y ＝________. 答案－1 －1解析由A ＝B 知需分多种情况进行讨论，由lg(xy )有意义，则xy >0.又0∈B ＝A ，则必有lg(xy )＝0，即xy ＝1. 此时，A ＝B ，即{0,1，x }＝{0，|x |，y }． ∴⎩⎪⎨⎪⎧ x ＝|x |，xy ＝1，y ＝1，或⎩⎪⎨⎪⎧x ＝y ，xy ＝1，|x |＝1，解得x ＝y ＝1或x ＝y ＝－1.当x ＝y ＝1时，A ＝B ＝{0,1,1}与集合元素的互异性矛盾，应舍去；当x ＝y ＝－1时，A ＝B ＝{0，－1,1}满足题意，故x ＝y ＝－1.13．若正实数x ，y ，z 满足x ＋y ＋z ＝1，则1x ＋y ＋x ＋y z 的最小值是________．答案 3解析 ∵x ＋y ＋z ＝1，且x ，y ，z 都是正实数，∴1x ＋y ＋x ＋y z ＝x ＋y ＋z x ＋y ＋x ＋y z ＝1＋zx ＋y ＋x ＋y z ≥3.14．已知三棱柱ABC －A 1B 1C 1的侧棱垂直于底面，各项点都在同一球面上，若该棱柱的体积为3，AB ＝2，AC ＝1，∠BAC ＝60°，则此球的表面积等于________．答案 8π解析由已知条件得：12×2×1×sin 60°×AA 1＝3，∴AA 1＝2，∵BC 2＝AB 2＋AC 2－2AB ×AC ×cos 60°，∴BC ＝3，设△ABC 的外接圆的半径为R ，则BC sin 60°＝2R ，∴R ＝1， ∴外接球的半径为1＋1＝2，∴球的表面积等于4π(2)2＝8π.15．若函数f (x )＝x n ＋1(n ∈N *)的图象与直线x ＝1交于点P ，且在点P 处的切线与x 轴交点的横坐标为x n ，则log 2 013x 1＋log 2 013x 2＋log 2 013x 3＋…＋log 2 013x 2 012的值为________．答案－1解析将x ＝1代入函数式得f (1)＝1n ＋1＝1，即P (1,1)，对函数求导得f ′(x )＝(n ＋1)x n ，则f ′(1)＝(n ＋1)×1n ＝n ＋1，则在点P (1,1)处的切线为y －1＝(n ＋1)(x －1)，y ＝(n ＋1)x －n ，令y ＝0得x n ＝nn ＋1，又log 2013x 1＋log 2 013x 2＋log 2 013x 3＋…＋log 2 013x 2 012＝log 2013(x 1·x 2·x 3·…·x 2 012)＝log 2 013(12·23·34·…·2 0122 013)＝log 2 013(12 013)＝－1.高考小题分项练高考小题分项练(一)(推荐时间：40分钟)1．(2014·课标全国Ⅰ)已知集合A＝{x|x2－2x－3≥0}，B＝{x|－2≤x<2}，则A∩B等于() A．[－2，－1] B．[－1,2)C．[－1,1] D．[1,2)答案 A解析∵A＝{x|x≥3或x≤－1}，B＝{x|－2≤x<2}，∴A∩B＝{x|－2≤x≤－1}＝[－2，－1]，故选A.2．(2014·湖南)已知命题p：若x>y，则－x<－y；命题q：若x>y，则x2>y2.在命题①p∧q；②p∨q；③p∧(綈q)；④(綈p)∨q中，真命题是()A．①③B．①④C．②③D．②④答案 C解析当x>y时，－x<－y，故命题p为真命题，从而綈p为假命题．当x>y时，x2>y2不一定成立，故命题q为假命题，从而綈q为真命题．由真值表知，①p∧q为假命题；②p∨q为真命题；③p∧(綈q)为真命题；④(綈p)∨q为假命题．故选C.3．已知函数f (x )是定义在(－∞，＋∞)上的奇函数，若对于任意的实数x ≥0，都有f (x ＋2)＝f (x )，且当x ∈[0,2)时，f (x )＝log 2(x ＋1)，则f (－2 015)＋f (2 016)的值为( ) A ．－1 B ．－2 C ．2 D ．1答案 A解析由已知f (x )为R 上奇函数且周期为2，对于任意的实数x ≥0，都有f (x ＋2)＝f (x )，∴f (－2 015)＋f (2 016)＝－f (2 015)＋f (2 016)＝－f (2×1 007＋1)＋f (2×1 008＋0)＝－f (1)＋f (0)＝－log 22＋log 21＝－1.4．已知命题p 、q ，“綈p 为真”是“p ∧q 为假”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件答案 A解析因为綈p 为真，所以p 为假，那么p ∧q 为假，所以“綈p 为真”是“p ∧q 为假”的充分条件；反过来，若“p ∧q 为假”，则“p 真q 假”或“p 假q 真”或“p 假q 假”，所以由“p ∧q 为假”不能推出綈p 为真．综上可知，“綈p 为真”是“p ∧q 为假”的充分不必要条件．5．已知f (x ＋1)＝f (x －1)，f (x )＝f (－x ＋2)，方程f (x )＝0在[0,1]内有且只有一个根x ＝12，则f (x )＝0在区间[0,2 013]内根的个数为( ) A ．2 011 B ．1 006 C ．2 013 D ．1 007答案 C解析由f (x ＋1)＝f (x －1)，可知f (x ＋2)＝f (x )，所以函数f (x )的周期是2，由f (x )＝f (－x ＋2)可知函数f (x )关于直线x ＝1对称，因为函数f (x )＝0在[0,1]内有且只有一个根x ＝12，所以函数f (x )＝0在区间[0，2 013]内根的个数为2 013个，选C. 6．“φ＝π”是“曲线y ＝sin(2x ＋φ)过坐标原点”的( ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件D ．既不充分也不必要条件答案 A解析当φ＝π时，y ＝sin(2x ＋φ)＝－sin 2x 过原点．当曲线过原点时，φ＝k π，k ∈Z ，不一定有φ＝π.所以“φ＝π”是“曲线y ＝sin(2x ＋φ)过原点”的充分不必要条件． 7．设函数f (x )满足x 2f ′(x )＋2xf (x )＝e x x ，f (2)＝e 28，则x ＞0时，f (x )( )A ．有极大值，无极小值B ．有极小值，无极大值C ．既有极大值又有极小值D ．既无极大值也无极小值答案 D 解析由x 2f ′(x )＋2xf (x )＝e xx，得f ′(x )＝e x －2x 2f (x )x 3，令g (x )＝e x －2x 2f (x )，x ＞0，则g ′(x )＝e x －2x 2f ′(x )－4xf (x )＝e x －2·ex x ＝(x －2)e x x.令g ′(x )＝0，得x ＝2.当x ＞2时，g ′(x )＞0；当0＜x ＜2时，g ′(x )＜0， ∴g (x )在x ＝2时有最小值g (2)＝e 2－8f (2)＝0，从而当x ＞0时，f ′(x )≥0，则f (x )在(0，＋∞)上是增函数，所以函数f (x )无极大值，也无极小值．8．已知函数f (x )＝x (1＋a |x |)．设关于x 的不等式f (x ＋a )<f (x )的解集为A .若⎣⎡⎦⎤－12，12⊆A ，则实数a 的取值范围是( ) A.⎝ ⎛⎭⎪⎫1－52，0B.⎝⎛⎭⎪⎫1－32，0C.⎝⎛⎭⎪⎫1－52，0∪⎝⎛⎭⎪⎫0，1＋32 D .⎝⎛⎭⎪⎫－∞，1－52答案 A解析 ∵⎣⎡⎦⎤－12，12⊆A ，∴f (a )<f (0)， ∴a (1＋a |a |)<0，解得－1<a <0，可排除C. ∵f ⎝⎛⎭⎫－12＋a <f ⎝⎛⎭⎫－12，∴⎝⎛⎭⎫－12＋a ⎝⎛⎭⎫1＋a ⎪⎪⎪⎪－12＋a <－12⎝⎛⎭⎫1＋a 2， ∴a ⎝⎛⎭⎫－12＋a ⎪⎪⎪⎪－12＋a <－54a . ∵－1<a <0，∴⎝⎛⎭⎫－12＋a ⎪⎪⎪⎪－12＋a >－54， ∴－⎝⎛⎭⎫－12＋a 2>－54，∴⎝⎛⎭⎫－12＋a 2<54， ∴1－52<a <0.排除B ，D.应选A.9．若变量x ，y 满足|x |－ln 1y＝0，则y 关于x 的函数图象大致是( )答案 B解析由|x |－ln 1y ＝0，有y ＝1e |x |＝⎩⎪⎨⎪⎧e －x，x ≥0，e x ，x <0，利用指数函数图象可知答案选B.10．已知f (x )＝⎩⎪⎨⎪⎧a ＋x 2＋2x ，x <0，f (x －1)，x ≥0，且函数y ＝f (x )＋x 恰有3个不同的零点，则实数a 的取值范围是( ) A ．(－∞，1] B ．(0,1] C ．(－∞，0] D ．(－∞，2]答案 A解析当x <0时，f (x )＝(x ＋1)2＋a －1，把函数f (x )在[－1,0)上的图象向右平移一个单位即得函数y ＝f (x )在[0,1)上的图象，继续右移可得函数f (x )在[0，＋∞)上的图象．如果函数y ＝f (x )＋x 恰有3个不同的零点，即函数y ＝f (x )，y ＝－x 的图象有三个不同的公共点，实数a 应满足最小值a －1≤0，即可，即a ≤1.11．已知集合A ＝{(x ，y )|x 2＋y 2＝1}，B ＝{(x ，y )|kx －y －2≤0}，其中x ，y ∈R .若A ⊆B ，则实数k 的取值范围是________．答案 [－3， 3 ]解析要使A ⊆B ，只需直线kx －y －2＝0与圆相切或相离，所以d ＝21＋k 2≥1，解得－3≤k ≤ 3.12．已知函数f (x )＝ln x ，若任意x 1、x 2∈[2,3]且x 2>x 1，t ＝f (x 2)－f (x 1)x 2－x 1，则实数t 的取值范围是________．答案 (13，12)解析对函数求导得f ′(x )＝1x，可得当x ∈[2,3]时f ′(x )>0，函数在x ∈[2,3]上单调递增，又f ′(2)＝12，f ′(3)＝13，根据题意得f ′(3)<t <f ′(2)，13<t <12. 13．函数f (x )＝ln x ＋ax (a ∈R )存在与直线2x －y ＝0平行的切线，则实数a 的取值范围是________．答案 (－∞，2)解析 f ′(x )＝1x ＋a ，∵函数f (x )存在与直线2x －y ＝0平行的切线，∴1x ＋a ＝2，即a ＝2－1x <2.14．在平面直角坐标系xOy 中，设定点A (a ，a )，P 是函数y ＝1x (x >0)图象上一动点，若点P ，A 之间的最短距离为22，则满足条件的实数a 的所有值为________．答案10，－1解析 |P A |2＝(x －a )2＋⎝⎛⎭⎫1x －a 2＝x 2＋1x 2－2ax －2ax ＋2a 2＝⎝⎛⎭⎫x ＋1x 2－⎝⎛⎭⎫x ＋1x 2a ＋2a 2－2 ＝⎝⎛⎭⎫x ＋1x －a 2＋a 2－2 由x >0，得x ＋1x≥2，由已知条件⎩⎪⎨⎪⎧ a ≥2，a 2－2＝8或⎩⎪⎨⎪⎧a <2，(2－a )2＋a 2－2＝8，解得a ＝10或a ＝－1.15．如果对定义在R 上的函数f (x )，对任意两个不相等的实数x 1，x 2，都有x 1f (x 1)＋x 2f (x 2)>x 1f (x 2)＋x 2f (x 1)，则称函数f (x )为“H 函数”．给出下列函数①y ＝－x 3＋x ＋1；②y ＝3x －2(sin x －cos x )；③y ＝e x＋1；④f (x )＝⎩⎪⎨⎪⎧ln|x |，x ≠0，0， x ＝0.以上函数是“H 函数”的所有序号为________．答案 ②③解析 x 1f (x 1)＋x 2f (x 2)>x 1f (x 2)＋x 2f (x 1)，即(x 1－x 2)[f (x 1)－f (x 2)]>0，所以函数f (x )在R 上是增函数．对于①，由y ′＝－3x 2＋1>0得－33<x <33，即函数在区间(－33，33)上是增函数，其不是“H 函数”；对于②，由y ′＝3－2(cos x ＋sin x )＝3－22sin(x ＋π4)>0恒成立，所以其为“H 函数”；对于③，由y ′＝e x >0恒成立，所以其为“H 函数”；对于④，由于其为偶函数，所以其不可能在R 上是增函数．所以不是“H 函数” 综上知，是“H 函数”的有②③.高考小题分项练(二)(推荐时间：40分钟)1．(2013·课标全国Ⅱ改编)设θ为第二象限角，若tan ⎝⎛⎭⎫θ＋π4＝12，则sin θ＋cos θ等于( ) A ．－105B.105C.255 D ．－255答案 A解析 ∵tan ⎝⎛⎭⎫θ＋π4＝12，∴tan θ＝－13，即⎩⎪⎨⎪⎧3sin θ＝－cos θ，sin 2θ＋cos 2θ＝1且θ为第二象限角，解得sin θ＝1010，cos θ＝－31010. ∴sin θ＋cos θ＝－105. 2．已知A 、B 、C 是圆O ：x 2＋y 2＝1上三点，OA →＋OB →＝OC →，则AB →·OA →等于( ) A.32 B ．－32C ．－32D.12答案 C解析 ∵OA →＋OB →＝OC →， ∴OA →2＋OB →2＋2OA →·OB →＝OC →2， ∴OA →·OB →＝－12，∴AB →·OA →＝(OB →－OA →)·OA →＝OA →·OB →－OA →2＝－32.3．函数y ＝x cos x ＋sin x 的图象大致为( )答案 D解析函数y ＝x cos x ＋sin x 为奇函数，排除B.取x ＝π2，排除C ；取x ＝π，排除A ，故选D.4．已知三个向量m ＝(a ，cos A 2)，n ＝(b ，cos B 2)，p ＝(c ，cos C2)共线，其中a ，b ，c ，A ，B ，C 分别是△ABC 的三条边及相对三个角，则△ABC 的形状是( ) A ．等腰三角形 B ．等边三角形 C ．直角三角形D ．等腰直角三角形答案 B解析在三角形中，cos A 2，cos B 2，cos C 2均不为0，故由题意可得a cos A 2＝b cos B 2＝ccos C2.由正弦定理得2sin A 2cos A 2cos A 2＝2sin B 2cos B 2cos B 2＝2sin C 2cosC2cos C 2⇒sin A 2＝sin B 2＝sin C2，即A ＝B ＝C ，所以△ABC 为等边三角形． 5．函数y ＝11－x的图象与函数y ＝2sin πx (－2≤x ≤4)的图象所有交点的横坐标之和等于( )A ．2B ．4C ．6D ．8 答案 D解析作出函数y ＝11－x及y ＝2sin πx (－2≤x ≤4)的图象，发现共有8个交点(x i ，y i )(i ＝1,2，…，8并令x 1<x 2<…<x 8)，且这些点构成了四对关于点(1,0)对称的点，则每对点的横坐标和为x 1＋x 8＝2，x 2＋x 7＝2，x 3＋x 6＝2，x 4＋x 5＝2.所以所有交点的横坐标和为8.6．(2014·浙江)记max{x ，y }＝⎩⎪⎨⎪⎧ x ，x ≥y ，y ，x <y ，min{x ，y }＝⎩⎪⎨⎪⎧y ，x ≥y ，x ，x <y ，设a ，b 为平面向量，则( )A ．min{|a ＋b |，|a －b |}≤min{|a |，|b |}B ．min{|a ＋b |，|a －b |}≥min{|a |，|b |}C ．max{|a ＋b |2，|a －b |2}≤|a |2＋|b |2D ．max{|a ＋b |2，|a －b |2}≥|a |2＋|b |2 答案 D解析由于|a ＋b |，|a －b |与|a |，|b |的大小关系与夹角大小有关，故A ，B 错．当a ，b 夹角为锐角时，|a ＋b |>|a －b |，此时，|a ＋b |2>|a |2＋|b |2；当a ，b 夹角为钝角时，|a ＋b |<|a －b |，此时，|a －b |2>|a |2＋|b |2；当a ⊥b 时，|a ＋b |2＝|a －b |2＝|a |2＋|b |2，故选D.7．已知函数y ＝A sin(ωx ＋φ)＋k 的最大值为4，最小值为0，最小正周期为π2，直线x ＝π3是其图象的一条对称轴，则符合条件的解析式为( ) A ．y ＝2sin(4x ＋π6)＋2B ．y ＝2sin(2x ＋π3)＋2C ．y ＝2sin(4x ＋π3)＋2D ．y ＝4sin(4x ＋π6)答案 A解析由题意可得A ＋k ＝4，-A +k ＝0，解得A ＝2，k ＝2，再由最小正周期为π2，可得2πω＝π2，解得ω＝4，所以函数y ＝A sin(ωx ＋φ)＋k ＝2sin(4x ＋φ)＋2，再由x ＝π3是其图象的一条对称轴，可得4×π3＋φ＝k π＋π2，k ∈Z ，即φ＝k π－5π6，k ∈Z ，当k ＝1时，φ＝π6，故符合条件的函数解析式是y ＝2sin(4x ＋π6)＋2，故选A.8．函数f (x )＝A sin(ωx ＋ωπ)(A >0，ω>0)在区间⎣⎡⎦⎤－3π2，－3π4上单调递增，则ω的最大值是( ) A.12B.34C ．1D ．2答案 C解析函数f (x )＝A sin(ωx ＋ωπ)的图象向右平移π个单位得函数f (x )＝A sin ωx 的图象，问题等价于函数f (x )＝A sin ωx 在区间⎣⎡⎦⎤－π2，π4上单调递增，故只要2πω≥2π，即ω≤1. 9．函数y ＝tan(πx 4－π2)(0<x <4)的图象如图所示，A 为图象与x 轴的交点，过点A 的直线l 与函数的图象交于C 、B 两点．则(OB →＋OC →)·OA →＝( )A ．－8B ．－4C ．4D ．8答案 D解析因为函数y ＝tan(πx 4－π2)(0<x <4)的图象对称中心是(2k ＋2,0)(k ∈Z )．所以点A 的坐标是(2,0)．因为点A 是对称中心，所以点A 是线段BC 的中点，所以OC →＋OB →＝2OA →.所以(OB →＋OC →)·OA →＝2OA →·OA →＝2(OA →)2＝2×4＝8.故选D.10．(2014·重庆)已知△ABC 的内角A ，B ，C 满足sin 2A ＋sin(A －B ＋C )＝sin(C －A －B )＋12，面积S 满足1≤S ≤2，记a ，b ，c 分别为A ，B ，C 所对的边，则下列不等式一定成立的是( ) A ．bc (b ＋c )>8 B ．ab (a ＋b )>16 2 C ．6≤abc ≤12 D ．12≤abc ≤24 答案 A解析由sin 2A ＋sin(A －B ＋C )＝sin(C －A －B )＋12，得sin 2A ＋sin(A －B ＋C )－sin(C －A －。

(完整word版)2015年全国新课标2卷高考文科数学及答案

2015年普通高等学校招生全国统一考试(新课标Ⅱ卷)数学(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分，考试时间120分钟．第Ⅰ卷一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知集合{}{}30|,21|<<=<<-=x x B x x A ，则=⋃B A ( )A ．(－1,3)B ．(－1,0)C ．(0,2)D ．(2,3)2．若a 为实数，且i iai +=++312，则=a ( ) A ．－4 B ．－3 C ．3 D ．43．根据下面给出的2004年至2013年我国二氧化硫年排放量(单位：万吨)柱形图，以下结论中不正确的是( )A ．逐年比较，2008年减少二氧化硫排放量的效果最显著B ．2007年我国治理二氧化硫排放显现成效C ．2006年以来我国二氧化硫年排放量呈减少趋势D ．2006年以来我国二氧化硫年排放量与年份正相关4．向量()1,1-=a ，()2,1-=b ，则()=⋅+a b a 2 ( )A ．－1B ．0C ．1D ．25．设n S 是等差数列{}n a 的前n 项和，若3531=++a a a ，则=5S ( )A ．5B ．7C ．9D ．11 6.第6题图一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为( )A.18B.17C.16D.157．已知三点()01，A ()30，B ，()32，C ，则ABC ∆外接圆的圆心到原点的距离为( )A.53B.213C.253D.438.第8题图右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入的a ，b 分别为14,18，则输出的=a ( )A ．0B ．2C ．4D ．149．已知等比数列{}n a 满足411=a ，()14453-=a a a ，则=2a ( ) A ．2 B ．1 C.12 D.1810．已知A ，B 是球O 的球面上两点，∠AOB ＝90°，C 为该球面上的动点．若三棱锥O ABC 体积的最大值为36，则球O 的表面积为( )A ．36πB ．64πC ．144πD ．256π 11.如图，长方形ABCD 的边AB ＝2，BC ＝1，O 是AB 的中点．点P 沿着边BC ，CD 与DA 运动，记∠BOP ＝x ，将动点P 到A ，B 两点距离之和表示为x 的函数f (x )，则y ＝f (x )的图象大致为( )12.设函数()()2111ln x x x f +-+=，则使得()()12->x f x f 成立的x 的取值范围是( )A.⎝ ⎛⎭⎪⎫13，1B.()∞+⋃⎪⎭⎫ ⎝⎛∞，，131- C.⎝ ⎛⎭⎪⎫－13，13 D.⎪⎭⎫ ⎝⎛∞+⋃⎪⎭⎫ ⎝⎛∞，，3131-- 第Ⅱ卷二、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上)13．已知函数()x ax x f 23-=的图象过点()4,1-，则=a ________.14．若x ，y 满足约束条件⎩⎨⎧ x ＋y －5≤0，2x －y －1≥0，x －2y ＋1≤0，则y x z +=2的最大值为________． 15．已知双曲线过点()34，，且渐近线方程为x y 21±=，则该双曲线的标准方程为________．16．已知曲线x x y ln +=在点()1,1处的切线与曲线()122+++=x a ax y 相切，则=a ________. 三、解答题(解答应写出文字说明，证明过程或演算步骤)17．(本小题满分12分) ABC ∆中，D 是BC 上的点，AD 平分BAC ∠，DC BD 2=(1)求CB sin sin (2)若︒=∠60BAC ，求B ∠18.(本小题满分12分)某公司为了解用户对其产品的满意度，从A ，B 两地区分别随机调查了40个用户，根据用户对产品的满意度评分，得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表．图①B地区用户满意度评分的频数分布表2015·新课标Ⅱ卷第4页(1)在图②中作出B地区用户满意度评分的频率分布直方图，并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值，给出结论即可)．图②(2)根据用户满意度评分，将用户的满意度分为三个等级：估计哪个地区用户的满意度等级为不满意的概率大？说明理由．19.(本小题满分12分)如图，长方体1111D C B A ABCD -中，16=AB ，10=BC ,81=AA ，点E ,F 分别在11B A ,11C D 上，411==F D E A .过点E ,F 的平面α与此长方体的面相交，交线围成一个正方形．(1)在图中画出这个正方形(不必说明画法和理由)；(2)求平面α把该长方体分成的两部分体积的比值．20.(本小题满分12分)已知椭圆C ：12222=+by a x ()0.>>b a 的离心率为22，点()22，在C 上．(1)求C 的方程；(2)直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点A ,B ，线段AB 的中点为M .证明：直线OM 的斜率与直线l 的斜率的乘积为定值．21.(本小题满分12分)已知函数()()x a x x f -+=1ln ．(1)讨论()x f 的单调性；(2)当()x f 有最大值，且最大值大于22-a 时，求a 的取值范围．请考生在第22、23、24题中任选一题作答，如果多做，则按所做的第一题计分．作答时请写清题号．22. （本小题满分10分）选修4-1：几何证明选讲如图O 是等腰三角形AB C 内一点, ⊙O 与△ABC 的底边BC 交于M ,N 两点,与底边上的高交于点G ,且与AB ,AC 分别相切于E ,F 两点.（I ）证明EF ∥BC .（II ）若AG 等于⊙O 的半径,且AE MN ==,求四边形EDCF 的面积23.（本小题满分10分）选修4-4：坐标系与参数方程在直角坐标系xOy 中,曲线1cos ,:sin ,x t C y t αα=⎧⎨=⎩ （t 为参数,且0t ≠ ）,其中0απ≤<,在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线23:2sin ,:.C C ρθρθ== （I ）求2C 与3C 交点的直角坐标；（II ）若1C 与 2C 相交于点A ,1C 与3C 相交于点B ,求AB 最大值24.(本小题满分10分)选修4－5：不等式选讲设a ，b ，c ，d 均为正数，且a ＋b ＝c ＋d .证明：(1)若ab >cd ，则a ＋b >c ＋d ；N M G OFE D C B A(2)a＋b>c＋d是|a－b|<|c－d|的充要条件．2015·新课标Ⅱ卷第8页1、选A2、故选D3、选D4、选B5、解：在等差数列中，因为.,5525)(,1,335153531A a a a S a a a a 故选所以==⨯+===++6、解：如图所示，选D.7、选B.8、故选B.9、解：因为{}),1(4,414531-==a a a a a n 满足所以， .21241,2,2),1(4123144424=⨯=====-=q a a q q a a a a a 所以，所以又解得故选C.10、解：因为A,B 都在球面上，又为该球面上动点，C AOB ,90︒=∠所以三棱锥的体积的最大值为3661213132==⨯⨯R R R ，所以R=6，所以球的表面积为 S=14442=R ππ，故选C.11、解：如图，当点P 在BC 上时， ,tan 4tan ,tan 4,tan ,22x x PB PA x PA x PB x BOP ++=+∴+===∠ 当4π=x 时取得最大值51+，以A,B 为焦点C,D 为椭圆上两定点作椭圆，显然，当点P 在C,D 之间移动时PA+PB<51+. 又函数)(x f 不是一次函数，故选B.xP O DC B A12、解：因为函数时函数是增函数是偶函数，),0[,11)1ln()(2+∞∈+-+=x x x x f .131,)12(,12)12()(22<<->∴->∴->x x x x x x f x f 解得故选A.第二卷一、填空题：本大题共4个小题，每小题5分 13、答：a=-214、解：当x=3,y=2时，z=2x+y 取得最大值8.15、解：设双曲线的方程为.43,4),0(422=≠=-k k k y x ）代入方程，解得，点（1422=-∴y x 双曲线的标准方程为16、解：.122,11'-=∴+=x y xy ，切线方程为切线的斜率为 .8120.08,08,021)2(12222=+=====-=∆=+++++=-=a x y a a a a a ax ax x a ax y x y 所以与切线平行，不符。

2015年普通高等学校招生全国统一考试(全国新课标II卷)数学试题 (文科)解析版

2015年普通高等学校招生全国统一考试全国新课标 II 卷文科数学一、选择题：本大题共12道小题,每小题5分,共60分. 1．已知集合{}|12A x x =-<<,{}|03B x x =<<,则A B =（）A ．()1,3-B ．()1,0-C ．()0,2D ．()2,3【答案】A考点：集合运算.2. 若为a 实数,且2i3i 1ia +=++,则a =( ) A ．4- B ．3- C ．3 D ．4【答案】D【解析】试题分析：由题意可得()()2i 1i 3i 24i 4a a +=++=+⇒= ,故选D.考点：复数运算.3. 根据下面给出的2004年至2013年我国二氧化碳年排放量（单位：万吨）柱形图,以下结论中不正确的是（）A ．逐年比较,2008年减少二氧化碳排放量的效果最显著B ．2007年我国治理二氧化碳排放显现成效C ．2006年以来我国二氧化碳年排放量呈减少趋势D ．2006年以来我国二氧化碳年排放量与年份正相关【答案】 D考点：柱形图4. 已知()1,1=-a ,()1,2=-b ,则(2)+⋅=a b a （）A ．1-B ．0C ．1D ．2【答案】C 【解析】试题分析：由题意可得22=a ,3,⋅=-a b 所以()222431+⋅=+⋅=-=a b a a a b .故选C.考点：向量数量积.5. 设n S 是等差数列{}n a 的前n 项和,若1353a a a ++=,则5S =（） A ．5 B ．7 C ．9 D ．11【答案】A 【解析】试题解析：13533331a a a a a ++==⇒=,()15535552a a S a +===.故选A. 考点：等差数列6. 一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为（）1A.8 1B.7 1C.6D.15【答案】D【解析】试题分析：截去部分是正方体的一个角,其体积是正方体体积的16,所以截去部分体积与剩余部分体积的比值为15 ,故选D.考点：三视图7. 已知三点(1,0),A B C ,则△ABC 外接圆的圆心到原点的距离为（）5A.3 4D.3 【答案】B考点：直线与圆的方程.8. 右边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的,a b 分别为14,18,则输出的a 为（）A.0B. 2C.4D.14【答案】B 【解析】试题分析：由题意输出的a 是18,14的最大公约数2,故选B. 考点：1. 更相减损术；2.程序框图.9．已知等比数列{}n a 满足114a =,()35441a a a =-,则2a =（）A.2B.1C.12 1D.8【答案】C【解析】试题分析：由题意可得()235444412a a a a a ==-⇒=,所以34182a q q a ==⇒= ,故2112a a q ==,选C.考点：等比数列.10. 已知B A ,是球O 的球面上两点,︒=∠90AOB ,C 为该球面上的动点.若三棱锥ABC O -体积的最大值为36,则球O 的表面积为（）A.π36B. π64C.π144D. π256【答案】C考点：球与几何体的切接.11. 如图,长方形的边AB =2,BC =1,O 是AB 的中点,点P 沿着边BC ,CD 与DA 运动,记BOP x ∠= ,将动点P 到A ,B 两点距离之和表示为x 的函数()f x ,则的图像大致为（）A ．B ．C ．D ．【答案】B考点：函数图像12. 设函数21()ln(1||)1f x x x =+-+,则使得()(21)f x f x >-成立的x 的取值范围是（）A ．1,13⎛⎫ ⎪⎝⎭B ．()1,1,3⎛⎫-∞+∞ ⎪⎝⎭C ．11,33⎛⎫-⎪⎝⎭ D ．11,,33⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭【答案】A 【解析】试题分析：由21()ln(1||)1f x x x=+-+可知()f x 是偶函数,且在[)0,+∞是增函数,所以 ()()()()121212113f x f x f x f x x x x >-⇔>-⇔>-⇔<< .故选A.考点：函数性质二、填空题：本大题共4小题,每小题5分,共20分13. 已知函数()32f x ax x =-的图像过点（-1,4）,则a = ．【答案】-2 【解析】试题分析：由()32f x ax x =-可得()1242f a a -=-+=⇒=- .考点：函数解析式14. 若x ,y 满足约束条件50210210x y x y x y +-≤⎧⎪--≥⎨⎪-+≤⎩,则z =2x +y 的最大值为．【答案】8考点：线性规划15. 已知双曲线过点(,且渐近线方程为12y x =±,则该双曲线的标准方程为．【答案】2214x y -=考点：双曲线几何性质16. 已知曲线ln y x x =+在点()1,1 处的切线与曲线()221y ax a x =+++ 相切,则a = ．【答案】8 【解析】试题分析：由11y x'=+可得曲线ln y x x =+在点()1,1处的切线斜率为2,故切线方程为21y x =-,与()221y ax a x =+++ 联立得220ax ax ++=,显然0a ≠,所以由2808a a a ∆=-=⇒=.考点：导数的几何意义.三、解答题17（本小题满分12分）△ABC 中D 是BC 上的点,AD 平分∠BAC ,BD =2DC .（I ）求sin sin BC∠∠ ；（II ）若60BAC ∠=,求B ∠.【答案】（I ）12；30.考点：解三角形试题解析：（I ）由正弦定理得,,sin sin sin sin AD BD AD DCB BADC CAD==∠∠∠∠ 因为AD 平分∠BAC ,BD =2DC ,所以sin 1.sin 2B DC C BD ∠==∠.（II ）因为()180,60,C BAC B BAC ∠=-∠+∠∠=所以()1sin sin sin .2C BAC B B B ∠=∠+∠=∠+∠ 由（I ）知2sin sin B C ∠=∠,所以tan 30.B B ∠=∠= 考点：解三角形18. （本小题满分12分）某公司为了了解用户对其产品的满意度,从A ,B 两地区分别随机调查了40个用户,根据用户对其产品的满意度的评分,得到A 地区用户满意度评分的频率分布直方图和B 地区用户满意度评分的频率分布表.A 地区用户满意度评分的频率分布直方图（I ）在答题卡上作出B 地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分散程度.（不要求计算出具体值,给出结论即可）B 地区用户满意度评分的频率分布直方图（II）根据用户满意度评分,将用户的满意度评分分为三个等级：估计那个地区的用户的满意度等级为不满意的概率大,说明理由.【答案】（I）见试题解析（II）A地区的用户的满意度等级为不满意的概率大.考点：1.频率分布直方图；2.概率估计.19. （本小题满分12分）如图,长方体1111ABCD A B C D -中AB =16,BC =10,18AA =,点E ,F 分别在1111,A B D C 上,11 4.A E D F ==过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.（I ）在图中画出这个正方形（不必说明画法与理由）；（II ）求平面α把该长方体分成的两部分体积的比值. 【答案】（I ）见试题解析（II ）97 或79考点：1.几何体中的截面问题；2.几何体的体积20. （本小题满分12分）已知椭圆()2222:10x y C a b a b +=>> ,点(在C 上.（I ）求C 的方程；（II ）直线l 不经过原点O ,且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 中点为M ,证明：直线OM 的斜率与直线l 的斜率乘积为定值.【答案】（I ）2222184x y +=（II ）见试题解析考点：直线与椭圆21. （本小题满分12分）已知()()ln 1f x x a x =+-. （I ）讨论()f x 的单调性；（II ）当()f x 有最大值,且最大值大于22a -时,求a 的取值范围. 【答案】（I ）0a ≤,()f x 在()0,+∞是单调递增；0a >,()f x 在10,a ⎛⎫⎪⎝⎭单调递增,在1,a ⎛⎫+∞ ⎪⎝⎭单调递减；（II ）()0,1. 【解析】考点：导数的应用.请考生在22、23、24题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号22. （本小题满分10分）选修4-1：几何证明选讲如图O是等腰三角形AB C内一点,圆O与△ABC的底边BC交于M,N两点,与底边上的高交于点G,且与AB,AC分别相切于E,F两点.（I）证明EF BC；（II）若AG等于圆O半径,且AE MN【答案】（I）见试题解析；（II考点：1.几何证明；2.四边形面积的计算.23. （本小题满分10分）选修4-4：坐标系与参数方程在直角坐标系xOy 中,曲线1cos ,:sin ,x t C y t αα=⎧⎨=⎩ （t 为参数,且0t ≠ ）,其中0απ≤<,在以O为极点,x 轴正半轴为极轴的极坐标系中,曲线23:2sin ,:.C C ρθρθ== （I ）求2C 与3C 交点的直角坐标；（II ）若1C 与 2C 相交于点A ,1C 与3C 相交于点B ,求AB 最大值.【答案】（I ）()30,0,2⎫⎪⎪⎭；（II ）4. 【解析】试题分析：（I ）把2C 与3C 的方程化为直角坐标方程分别为2220x y y +-=,220x y +-=,联立解考点：参数方程、直角坐标及极坐标方程的互化.24. （本小题满分10分）选修4-5：不等式证明选讲设,,,a b c d 均为正数,且a b c d +=+.证明：（I ）若ab cd > ,+>；（II ）>是a b c d -<-的充要条件. 【答案】【解析】试题分析：（I ）由a b c d +=+及ab cd >,可证明22>,开方即得>（II ）本小题可借助第一问的结论来证明,但要分必要性与充分性来证明. 试题解析：解：（I ）因为22a b c d =++=++考点：不等式证明.。

【创新设计】2015高考数学(人教通用,文科)二轮专题训练：小题综合限时练3

限时练(三)(建议用时：40分钟)一、选择题1．已知i 为虚数单位，复数z 满足i z ＝1＋i ，则z ＝( )． A ．1＋i B ． 1－i C. －1＋iD ．－1－i解析由题意z ＝1＋i i ＝(1＋i )ii 2＝1－i ，则z ＝1＋i. 答案 A2．设集合A ＝{1,2}，则满足A ∪B ＝{1,2,3}的集合B 的个数是( )． A ．1 B ．3 C ．4D ．6解析符合题意的B 有{3}，{1,3}，{2,3}，{1,2,3}，共4个．答案 C3．函数f (x )＝log 2(4x ＋1)的值域为( )． A ．[0，＋∞) B ．(0，＋∞) C ．[1，＋∞)D ．(1，＋∞)解析因为4x ＋1＞1，所以f (x )＝log 2(4x ＋1)＞0. 答案 B4．已知函数f (x )为偶函数，当x ＜0时，f (x )＝sin x ＋cos x ，则f ⎝ ⎛⎭⎪⎫π4＝( )．A ．0B ． 2C ．－ 2D ．1解析由题意f ⎝ ⎛⎭⎪⎫π4＝f ⎝ ⎛⎭⎪⎫－π4＝sin ⎝ ⎛⎭⎪⎫－π4＋cos ⎝ ⎛⎭⎪⎫－π4＝－22＋22＝0.答案 A5．圆(x ＋2)2＋y 2＝4与圆x 2＋y 2－2x －2y ＋1＝0( )． A ．内切 B ．相交 C ．外切D ．相离解析两圆圆心分别是(－2,0)，(1,1)，圆心距为d ＝10，而两圆半径分别为2,1，显然10＞2＋1，故两圆相离．答案 D6．已知数列{a n }满足1＋log 3a n ＝log 3a n ＋1(n ∈N ＋)，且a 2＋a 4＋a 6＝9，则log 13(a 5＋a 7＋a 9)的值是( )． A.15 B ．－15 C ．5D ．－5解析由1＋log 3a n ＝log 3a n ＋1(n ∈N ＋)可以推出a n ＋1＝3a n ，数列{a n }是以3为公比的等比数列，故a 5＋a 7＋a 9＝27(a 2＋a 4＋a 6)＝35，故log 13(a 5＋a 7＋a 9)＝－5. 答案 D7．从装有3个红球、2个白球的袋中任取3个球，则所取的3个球中至少有1个白球的概率是( )． A.110 B ．310 C.35D ．910解析由题意可知从5个球中任取3个球的所有情况有10种，所取的3个球至少有1个白球的情况有(10－1)种，根据古典概型公式得所求概率P ＝10－110＝910. 答案 D8．某企业2014年2月份生产A ，B ，C 三种产品共6 000件，根据分层抽样的结果，该企业统计员制作了如下的统计表格：产品分类 A B C 产品数量 2 600 样本容量260由于不小心，表格中B ，C 产品的有关数据已被污染看不清楚，统计员记得B 产品的样本容量比C 产品的样本容量多20，根据以上信息，可得C 产品数量是( )． A ．160B ．180C ．1 600D ．1 800解析记B ，C 两种产品的样本容量分别为x ，y ，则⎩⎨⎧x ＋y ＝600－260，x －y ＝20，解得⎩⎨⎧x ＝180，y ＝160，因此C 产品数量为1 600. 答案 C 9．函数y ＝cos πxx 的图象大致为( )．解析考虑函数的性质，它是奇函数，排除C ，D ；当x 从正方向趋向于0时，cos πxx →＋∞，排除B ，故选A. 答案 A10．如图为长方体与圆柱构成的组合体的三视图，则该几何体的体积为( )．A ．64＋32πB ．64＋64πC ．256＋64πD ．256＋128π解析由题意，V ＝8×8×4＋π×42×4＝256＋64π. 答案 C11．已知△ABC 是边长为4的等边三角形，点D ，E 分别满足DC →＝－AC →，BE →＝EC →，则AB →·DE →＝( )． A ．8 B ．4 C ．－8D ．－4解析 AB →·DE →＝AB →·(DC →＋CE →)＝AB →·⎝ ⎛⎭⎪⎫－AC →＋12CB →＝－AB →·AC →＋12AB →·CB →＝－4×4×cos π3＋12×4×4×cos π3＝－4. 答案 D12．定义在R 上的函数f (x )满足：f ′(x )＞f (x )恒成立，若x 1＜x 2，则e x 1f (x 2)与e x 2f (x 1)的大小关系为( )． A ．e x 1f (x 2)＞e x 2f (x 1) B ．e x 1f (x 2)＜e x 2f (x 1) C ．e x 1f (x 2)＝e x 2f (x 1)D ．e x 1f (x 2)与e x 2f (x 1)的大小关系不确定解析设g (x )＝f (x )e x ，则g ′(x )＝f ′(x )e x－f (x )e x(e x )2＝f ′(x )－f (x )e x ，由题意g ′(x )＞0，所以g (x )单调递增，当x 1＜x 2时，g (x 1)＜g (x 2)，则f (x 1)e x 1＜f (x 2)e x 2，所以e x 1f (x 2)＞e x 2f (x 1)．答案 A 二、填空题13．若实数x ，y 满足不等式组⎩⎨⎧x ≥1，y ≥1，x ＋2y ≤5，则yx 的最大值是________．解析作出不等式组表示的平面区域(可行域)，如图△ABC 内部(含边界)，yx 表示可行域内点与原点连线的斜率，最大值在A (1,2)处取得，y x ＝21＝2.答案 214．执行如图的程序框图，则输出的S 的值为________．解析 S ，T ，n 的值依次为3,1,2；6,4,3；9,11,4，此时有T ＞S ，因此执行语句S ＝S －n ＝5，输出S ＝5. 答案 515．设P 是双曲线x 2a 2－y 2b 2＝1上的点，它的一条渐近线方程为y ＝32x ，两焦点间距离为213，F 1，F 2分别是该双曲线的左、右焦点，若|PF 1|＝3，则|PF 2|＝________. 解析由题意b a ＝32，又2c ＝2a 2＋b 2＝213，所以a ＝2，b ＝3，由双曲线定义得||PF 2|－|PF 1||＝2a ＝4，故|PF 2|＝7. 答案 716．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若其面积S ＝b 2＋c 2－a 216，则cos A ＝________.解析因为b 2＋c 2－a 2＝2bc cos A ，由S ＝b 2＋c 2－a 216得b 2＋c 2－a 2＝16S ，即2bc cos A ＝16×12bc sin A ，cos A ＝4sin A ，所以cos A ＝41717. 答案41717。

【创新设计】(江苏专用)2015高考数学二轮复习专题整合突破练2 理(含最新原创题,含解析)

【创新设计】（江苏专用）2015高考数学二轮复习专题整合突破练2理（含最新原创题，含解析）1．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，设向量m ＝(a ，c )，n ＝(cos C ，cos A )． (1)若m ∥n ，c ＝3a ，求角A ；(2)若m ·n ＝3b sin B ，cos A ＝45，求cos C 的值．解 (1)∵m ∥n ，∴a cos A ＝c cos C . 由正弦定理得sin A cos A ＝sin C cos C ，化简得sin 2A ＝sin 2C .∵A ，C ∈(0，π)，∴2A ＝2C (舍)或2A ＋2C ＝π， ∴A ＋C ＝π2，∴B ＝π2，在Rt △ABC 中，tan A ＝ac ＝33，A ＝π6. (2)∵m ·n ＝3b cos B ，∴a cos C ＋c cos A ＝3b sin B . 由正弦定理得sin A cos C ＋sin C cos A ＝3sin 2B ，从而sin(A ＋C )＝3sin 2B .∵A ＋B ＋C ＝π，∴sin(A ＋C )＝sin B ，从而sin B ＝13，∵cos A ＝45>0，A ∈(0，π)，∴A ∈⎝ ⎛⎭⎪⎫0，π2，sin A ＝35.∵sin A >sin B ，∴a >b ，从而A >B ，B 为锐角， cos B ＝223.∴cos C ＝－cos(A ＋B )＝－cos A cos B ＋sin A sin B ＝－45×223＋35×13＝3－8215.2．如图，在正三棱柱ABC －A 1B 1C 1中，E ，F 分别为BB 1，AC 的中点． (1)求证：BF ∥平面A 1EC ； (2)求证：平面A 1EC ⊥平面ACC 1A 1.证明 (1)连接AC 1并交A 1C 于点O ，连接OE ，OF ，在正三棱柱ABC －A 1B 1C 1中，四边形ACC 1A 1为平行四边形，所以OA ＝OC 1. 又因为F 为AC 的中点，所以OF ∥CC 1且OF ＝12CC 1.因为E 为BB 1的中点，所以BE ∥CC 1且BE ＝12CC 1，所以BE ∥OF 且BE ＝OF ，所以四边形BEOF 是平行四边形，所以BF ∥OE . 又BF ⊄平面A 1EC ，OE ⊂平面A 1EC ，所以BF ∥平面A 1EC . (2)由(1)知BF ∥OE ，因为AB ＝CB ，F 为AC 的中点，所以BF ⊥AC ，所以OE ⊥AC .又因为AA 1⊥底面ABC ，而BF ⊂底面ABC ，所以AA 1⊥BF .由BF ∥OE 得OE ⊥AA 1，而AA 1，AC ⊂平面ACC 1A 1，且AA 1∩AC ＝A ，所以OE ⊥平面ACC 1A 1.因为OE ⊂平面A 1EC ，所以平面A 1EC ⊥平面ACC 1A 1.3. 若两个椭圆的离心率相等，则称它们为“相似椭圆”．如图，在直角坐标系xOy 中，已知椭圆C 1：x 26＋y 23＝1，A 1，A 2分别为椭圆C 1的左、右顶点．椭圆C 2以线段A 1A 2为短轴且与椭圆C 1为“相似椭圆”．(1)求椭圆C 2的方程；(2)设P 为椭圆C 2上异于A 1，A 2的任意一点，过P 作PQ ⊥x 轴，垂足为Q ，线段PQ 交椭圆C 1于点H .求证：H 为△PA 1A 2的垂心．(垂心为三角形三条高的交点) (1)解由题意可知A 1(－6，0)，A 2(6，0)，椭圆C 1的离心率e ＝22. 设椭圆C 2的方程为y 2a 2＋x 2b2＝1(a ＞b ＞0)，则b ＝ 6.因为b a＝1－e 2＝22，所以a ＝2 3. 所以椭圆C 2的方程为y 212＋x 26＝1.(2)证明设P (x 0，y 0)，y 0≠0，则y 2012＋x 206＝1，从而y 20＝12－2x 20.将x ＝x 0代入x 26＋y 23＝1得x 206＋y 23＝1，从而y 2＝3－x 202＝y 204，即y ＝±y 02.因为P ，H 在x 轴的同侧，所以取y ＝y 02，即H (x 0，y 02)．所以kA 1P ·kA 2H ＝y 0x 0－6·12y 0x 0＋6＝y 20x 20－＝12－2x 2x 20－＝－1，从而A 1P ⊥A 2H .又因为PH ⊥A 1A 2，所以H 为△PA 1A 2的垂心．4．如图，某园林单位准备绿化一块直径为BC 的半圆形空地，△ABC 外的地方种草，△ABC 的内接正方形PQRS 为一水池，其余的地方种花，若BC ＝a ，∠ABC ＝θ，设△ABC 的面积为S 1，正方形的PQRS 面积为S 2.(1)用a ，θ表示S 1和S 2；(2)当a 固定，θ变化时，求S 1S 2的最小值．解 (1)S 1＝12a sin θ·a cos θ＝14a 2sin 2θ，设正方形边长为x ，则BQ ＝xtan θ，RC ＝x tan θ，∴xtan θ＋x tan θ＋x ＝a ，∴x ＝a1tan θ＋tan θ＋1＝a sin 2θ2＋sin 2θ， S 2＝⎝ ⎛⎭⎪⎫a sin 2θ2＋sin 2θ2＝a 2sin 22θ4＋sin 22θ＋4sin 2θ， (2)当a 固定，θ变化时，S 1S 2＝14⎝ ⎛⎭⎪⎫4sin 2θ＋sin 2θ＋4，令sin 2θ＝t ，则S 1S 2＝14⎝ ⎛⎭⎪⎫4t ＋t ＋4(0＜t ≤1)，利用单调性求得t ＝1时，⎝ ⎛⎭⎪⎫S 1S 2min ＝94.5．已知函数f (x )＝a ln x －1x(a 为常数)．(1)若曲线y ＝f (x )在点(1，f (1))处的切线与直线x ＋2y －5＝0垂直，求a 的值； (2)求函数f (x )的单调区间；(3)当x ≥1时，f (x )≤2x －3恒成立，求a 的取值范围．解 (1)函数f (x )的定义域为{x |x ＞0}，f ′(x )＝ax ＋1x 2. 又曲线y ＝f (x )在点(1，f (1))处的切线与直线x ＋2y －5＝0垂直，所以f ′(1)＝a ＋1＝2，即a ＝1. (2)由f ′(x )＝ax ＋1x 2(x ＞0)，当a ≥0时， f ′(x )＞0恒成立，所以f (x )的单调增区间为(0，＋∞)．当a ＜0时，由f ′(x )＞0，得0＜x ＜－1a，所以f (x )的单调增区间为⎝ ⎛⎭⎪⎫0，－1a ；由f ′(x )＜0，得x ＞－1a，所以f (x )的单调减区间为⎝ ⎛⎭⎪⎫－1a，＋∞.(3)设g (x )＝a ln x －1x－2x ＋3，x ∈[1，＋∞)，则g ′(x )＝a x ＋1x 2－2＝－2x 2＋ax ＋1x 2.令h (x )＝－2x 2＋ax ＋1，考虑到h (0)＝1＞0，当a ≤1时，h (x )＝－2x 2＋ax ＋1的对称轴x ＝a4＜1，h (x )在[1，＋∞)上是减函数，h (x )≤h (1)＝a －1≤0，所以g ′(x )≤0，g (x )在[1，＋∞)上是减函数，所以g (x )≤g (1)＝0，即f (x )≤2x 2－3恒成立．当a ＞1时，令h (x )＝－2x 2＋ax ＋1＝0，得x 1＝a ＋a 2＋84＞1，x 2＝a －a 2＋84＜0，当x ∈[1，x 1)时，h (x )＞0，即g ′(x )＞0，g (x )在[1，x 1)上是增函数；当x ∈(x 1，＋∞)时，h (x )＜0，即g ′(x )＜0，g (x )在(x 1，＋∞)上是减函数．所以0＝g (1)＜g (x 1)，即f (x 1)＞2x 1－3，不满足题意．综上，a 的取值范围为a ≤1.6．已知无穷数列{a n }的各项均为正整数，S n 为数列{a n }的前n 项和．(1)若数列{a n }是等差数列，且对任意正整数n 都有S n 3＝(S n )3成立，求数列{a n }的通项公式；(2)对任意正整数n ，从集合{a 1，a 2，…，a n }中不重复地任取若干个数，这些数之间经过加减运算后所得数的绝对值为互不相同的正整数，且这些正整数与a 1，a 2，…，a n 一起恰好是1至S n 全体正整数组成的集合． (ⅰ)求a 1，a 2的值； (ⅱ)求数列{a n }的通项公式．解 (1)设无穷等差数列{a n }的公差为d ，因为S 3n ＝(S n )3对任意正整数n 都成立，所以分别取n ＝1，n ＝2时，则有：⎩⎪⎨⎪⎧a 1＝a 31，8a 1＋28d ＝a 1＋d3.因为数列{a n }的各项均为正整数，所以d ≥0. 可得a 1＝1，d ＝0或d ＝2.当a 1＝1，d ＝0时，a n ＝1，S n 3＝(S n )3成立；当a 1＝1，d ＝2时，S n ＝n 2，所以S n 3＝(S n )3.因此，共有2个无穷等差数列满足条件，通项公式为a n ＝1或a n ＝2n －1. (2)(ⅰ)记A n ＝{1,2，…，S n }，显然a 1＝S 1＝1.对于S 2＝a 1＋a 2＝1＋a 2，有A 2＝{1,2，…，S n }＝{1，a 2，1＋a 2，|1－a 2|}＝{1,2,3,4}，故1＋a 2＝4，所以a 2＝3.(ⅱ)由题意可知，集合{a 1，a 2，…，a n }按上述规则，共产生S n 个正整数．而集合{a 1，a 2，…，a n ，a n ＋1}按上述规则产生的S n ＋1个正整数中，除1,2，…，S n 这S n个正整数外，还有a n －1，a n ＋1＋i ，|a n ＋1－i |(i ＝1,2，…，S n )，共2S n ＋1个数．所以，S n ＋1＝S n ＋(2S n ＋1)＝3S n ＋1.又S n ＋1＋12＝3⎝ ⎛⎭⎪⎫S n ＋12，所以S n ＝⎝ ⎛⎭⎪⎫S 1＋12·3n －1－12＝12·3n －12.当n ≥2时，a n ＝S n －S n －1 ＝12·3n －12－⎝ ⎛⎭⎪⎫12·3n －1－12＝3n －1.而a 1＝1也满足a n ＝3n －1.所以，数列{a n }的通项公式是a n ＝3n －1.。

【创新设计】2015高考数学(人教通用,文科)二轮专题训练：小题综合限时练1

限时练(一)(建议用时：40分钟)一、选择题1．已知集合A ＝{－1,0,1}，B ＝{x |－1≤x ＜1}，则A ∩B ＝( )． A ．{0} B ．{0,1} C ．{－1,0}D ．{－1,0,1}解析 A ∩B ＝{－1,0}．答案 C2．若(1＋2a i)i ＝1－b i ，其中a ，b ∈R ，则|a ＋b i|＝( )． A.12＋i B ． 5 C.52D ．54 解析因为(1＋2a i)i ＝1－b i ，所以－2a ＋i ＝1－b i ，a ＝－12，b ＝－1，|a ＋b i|＝|－12－i|＝52. 答案 C3．设a ＝log 123，b ＝(13)0.2，c ＝213，则( )． A ．a ＜b ＜cB ．c ＜b ＜aC ．c ＜a ＜bD ．b ＜a ＜c解析由函数的性质得到a ＝log 123＜0，b ＝(13)0.2∈(0,1)，c ＝213＞1，所以，a ＜b ＜c . 答案 A4．等差数列{a n }的前n 项和为S n ，若a 2＋a 4＋a 6＝12，则S 7的值是( )． A ．21B ．24C ．28D ．7解析 ∵a 2＋a 4＋a 6＝3a 4＝12，∴a 4＝4， ∴S 7＝a 1＋a 72×7＝7a 4＝28. 答案 C5．设a ，b ∈R ，则“(a －b )·a 2＜0”是“a ＜b ”的( )． A ．充分非必要条件 B ．必要非充分条件 C ．充要条件D ．既不充分也不必要条件解析由(a －b )·a 2＜0，得a ≠0且a ＜b ；反之，由a ＜b ，不能推出(a －b )·a 2＜0，即“(a －b )·a 2＜0”是“a ＜b ”的充分非必要条件．答案 A6．抛物线y 2＝4x 的焦点到双曲线x 2－y 23＝1的渐近线的距离是( )．A.12 B ．32 C ．1D ． 3解析抛物线y 2＝4x 的焦点为(1,0)，双曲线x 2－y 23＝1的渐近线为x ±33y ＝0，所以抛物线y 2＝4x 的焦点到双曲线x 2－y 23＝1的渐近线的距离是|1±33×0|1＋⎝ ⎛⎭⎪⎫332＝32. 答案 B7．某程序框图如图所示，若输出的S ＝57，则判断框内应填入( )．A ．k ＞7?B ．k ＞6?C ．k ＞5?D ．k ＞4?解析由程序框图可知，程序在运行过程中各变量值变化如下表：k S 是否满足条件循环前 1 1 否第一次循环 2 4 否第二次循环 3 11 否第三次循环 4 26 否第四次循环557是所以退出循环的条件应为k ＞4. 答案 D8．已知函数f (x )＝A sin(ωx ＋φ)⎝ ⎛⎭⎪⎫A ＞0，ω＞0，|φ|＜π2的图象如图所示，则f (x )的解析式为( )．A ．f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π3B ．f (x )＝sin ⎝ ⎛⎭⎪⎫2x －π3C ．f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π6D ．f (x )＝sin ⎝ ⎛⎭⎪⎫2x －π6解析由图象可知A ＝1，且14T ＝14×2πω＝7π12－π3＝π4， ∴ω＝2，f (x )＝sin(2x ＋φ)．把⎝ ⎛⎭⎪⎫7π12，－1代入得：－1＝sin ⎝ ⎛⎭⎪⎫2×7π12＋φ，又∵|φ|＜π2， ∴7π6＋φ＝3π2， ∴φ＝π3， ∴f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π3. 答案 A9．已知O 是坐标原点，点A (－2,1)，若点M (x ，y )为平面区域⎩⎨⎧x ＋y ≥2，x ≤1，y ≤2上的一个动点，则O A →·OM →的取值范围是( )． A ．[－1,0] B ．[－1,2] C ．[0,1]D ．[0,2]解析 ∵A (－2,1)，M (x ，y )，∴z ＝O A →·OM →＝－2x ＋y ，作出不等式组对应的平面区域及直线－2x ＋y ＝0，如图所示．平移直线－2x ＋y ＝0，由图象可知当直线经过点N (1,1)时，z min ＝－2＋1＝－1；经过点M (0,2)时，z max ＝2. 答案 B10．如图F 1，F 2是双曲线C 1：x 2－y23＝1与椭圆C 2的公共焦点，点A 是C 1，C 2在第一象限的公共点．若|F 1F 2|＝|F 1A |，则C 2的离心率是( )．A.13 B ．23 C.15D ．25解析由题意知，|F 1F 2|＝|F 1A |＝4， ∵|F 1A |－|F 2A |＝2，∴|F 2A |＝2， ∴|F 1A |＋|F 2A |＝6， ∵|F 1F 2|＝4， ∴C 2的离心率是46＝23. 答案 B11．已知某几何体的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形，则此几何体的体积V 为( )．A.323 B ．403 C.163D ．40解析观察三视图可知，该几何体为四棱锥，底面为直角梯形，两个侧面与底面垂直，棱锥的高为4，由图中数据得该几何体的体积为13×4＋12×4×4＝403.答案 B12．已知定义在R 上的函数f (x )是奇函数且满足f ⎝ ⎛⎭⎪⎫32－x ＝f (x )，f (－2)＝－3，数列{a n }满足a 1＝－1，且S n n ＝2×a nn ＋1(其中S n 为{a n }的前n 项和)，则f (a 5)＋f (a 6)＝( )． A ．－3 B ．－2 C ．3D ．2解析 ∵函数f (x )是奇函数， ∴f (－x )＝－f (x )，∵f (32－x )＝f (x )， ∴f (32－x )＝－f (－x )，∴f (3＋x )＝f (x )， ∴f (x )是以3为周期的周期函数． ∵S n n ＝2×a nn ＋1，∴S n ＝2a n ＋n ，S n －1＝2a n －1＋(n －1)(n ≥2)．两式相减并整理得出a n ＝2a n －1－1，即a n －1＝2(a n －1－1)，∴数列{a n －1}是以2为公比的等比数列，首项为a 1－1＝－2， ∴a n －1＝－2·2n －1＝－2n ，a n ＝－2n ＋1， ∴a 5＝－31，a 6＝－63.∴f (a 5)＋f (a 6)＝f (－31)＋f (－63)＝f (2)＋f (0)＝f (2)＝－f (－2)＝3. 答案 C 二、填空题13．曲线f (x )＝e x 在x ＝0处的切线方程为__________．解析 ∵f ′(x )＝e x ，∴f ′(0)＝1.又f (0)＝1， ∴切线方程为：y －1＝x ，即x －y ＋1＝0.答案 x －y ＋1＝014．已知向量p ＝(2，－1)，q ＝(x,2)，且p ⊥q ，则|p ＋λq |的最小值为__________．解析 ∵p ·q ＝2x －2＝0，∴x ＝1， ∴p ＋λq ＝(2＋λ，2λ－1)，∴|p ＋λq |＝(2＋λ)2＋(2λ－1)2＝5λ2＋5≥ 5. 答案515．在△ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，若a ＝2，b ＝2，sin B ＋cos B ＝2，则角A 的大小为________．解析由sin B ＋cos B ＝2，得2sin ⎝ ⎛⎭⎪⎫B ＋π4＝2，sin ⎝ ⎛⎭⎪⎫B ＋π4＝1，而B ∈(0，π)，所以B ＝π4.由正弦定理得，sin A ＝a sin B b ＝12，又A ＋B ＋C ＝π，A ∈⎝ ⎛⎭⎪⎫0，3π4，∴A ＝π6. 答案 π616．已知a ＞0，b ＞0，方程为x 2＋y 2－4x ＋2y ＝0的曲线关于直线ax －by －1＝0对称，则3a ＋2bab 的最小值为______．解析该曲线表示圆心为(2，－1)的圆，直线ax －by －1＝0经过圆心，则2a ＋b －1＝0，即2a ＋b ＝1，所以 3a ＋2b ab ＝3b ＋2a ＝(3b ＋2a )(2a ＋b )＝6a b ＋2ba ＋7≥26a b ·2ba ＋7＝7＋43(当且仅当a ＝2－3，b ＝23－3时等号成立)．答案 7＋4 3。

【创新设计】2015高考数学(鲁闽皖京渝津,文科)大二轮总复习：大题综合突破练2Word版含解析

^ 所求回归直线方程为： y＝ 6.5x＋17.5，
^ 当广告支出为 12 时，销售额 y＝6.5×12＋ 17.5＝95.5.
(2)实际值和预测值对应表为
x2
45 6
8
y 30 40 60 50 70
(1)试预测当广告费支出为 12 万元时，销售额是多少？
(2)在已有的五组数据中任意抽取两组，求至少有一组数据其预测值与实际值之
差的绝对值不超过 5 的概率．
2＋ 4＋ 5＋ 6＋8
解 (1) x ＝
5
＝5，
y
30＋40＋＝
50＋60＋ 5
70 ＝
50，
因为点 (5,50)在回归直线上，代入回归直线方程求得 a＝17.5，
(1)设公比为
q.∵aa42＝
1 9＝
q2，
∴q＝13或
q＝－
1 3.
1 又数列 { an} 为正项等比数列，∴ q＝ 3.
又∵
a2＝
1 9.
∴ a1＝13，
∴an＝
1 3
n， n∈ N * .
(2)∵ bn＝log3an·log3an＋1，n∈N*，
∴ bn＝ n( n＋ 1) ， n∈ N * .
解 (1)由题意知周期 T＝π，∴ ω＝ 2，
π
π
因为 f 4 ＝ 3，所以 A＝2，f(x)＝2sin (2x－ 6)，
由π2＋2kπ≤2x－ π6≤ 32π＋2kπk（∈ Z)，得 π3＋kπ≤x≤ 56π＋ kπk（∈Z )，
π
5π
所以 f(x)的单调递减区间为 [3＋kπ， 6 ＋ kπ]k(∈ Z)．
突破练二
π 1．已知函数 f(x)＝Asin (ωｘ－6)(ω＞ 0)相邻两个对称轴之间的距离是

2015届高三第二次模拟突破冲刺数学(文)试题 Word版含答案

高三第二次模拟突破冲刺数学（文）试题（五）高三文数备课组一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．集合 U = {1,2,3,4,5,6} , N = {1,4,5} , M= {2,3,4} ,则 N ∩（M C U ）A ．{1 ,4 ,5}B ．{4}C ．{1 ,5}D ．{ 1 ,2 ,3 ,4 ,5}2.已知复数iiz +-=11i (为虚数单位)，则z 的共轭复数是( ) A. i +1 B. i C.i - D.i -13．下列有关命题的说法正确的是( ) A ．p 是q 的必要不充分条件，则p ⌝是q ⌝的充分不必要条件B ．对于命题p ：x R∃∈，使得210x x +-<，则p ⌝：x R ∀∈，均有210x x +->C ．线性回归方程y = bx ∧+ a 对应的直线一定经过其样本数据点(x 1 , y 1)、(x 2 , y 2)、…, （x n , y n ) 中的一个D ．“1m =-”是“直线l 1：(21)10mx m y +-+=与直线l 2：330x my ++=垂直”的充要条件4 ．过点M(1 ,2）的直线l 与圆25)4()3(:22=-+-y x C 交于A 、B 两点,C 为圆心,当∠ACB 最小时, 直线l 的方程是( )A ．x-2y+3=0B ．2x+y-4=0C ．x-y+1=0D ．x+y-3=05. 已知()f x 是定义在R 上周期为4的奇函数，当(0,2]x ∈时，2()2log x f x x =+，则(2015)f =( )A ．-2B ．21C ．2 D ． 56. 已知点),(y x M 的坐标满足⎪⎩⎪⎨⎧≤≥+≥+-3005x y x y x ，)3,1(-N ，点O 为坐标原点，则⋅的最小值是( )A. 12B. -21C. -6D. 5 7．设n m l ,,表示不同的直线，γβα,,表示不同的平面，给出下列四个命题： ①若m ∥l ，且α⊥m ，则α⊥l ； ②若m ∥l ，且m ∥α，则l ∥α；③若α∩,l =ββ∩,m =γγ∩n =α，则l ∥m ∥n ； ④若α∩,m =ββ∩,l =γγ∩n =α，且n ∥β，则l ∥m . 其中正确命题的个数是( ) A ．1B ．2C ．3D ．48. 某几何体的三视图如图所示，则它的表面积为( ) A ． B ．C ．D ． (2+π9.如果执行如图的程序框图，那么输出的值是( ) A. 2016B. 1-C.12D. 210. 函数14)62sin(2-+=xx x y π的图象大致为( )11、坐标平面上的点集S 满足2442{(,)|log (2)2sin 2cos [,]}84S x y x x y y y =-+=+∈,-ππ，将点集S 中的所有点向x 轴作投影，所得投影线段的长度为( ).A 1 .B 2 .C .D 12.已知点A 是抛物线y x 42=的对称轴与准线的交点，点B 为抛物线的焦点，P 在抛物线上且满足PB m PA =，当m 取最大值时，点P 恰好在以B A ,为焦点的双曲线上，则双曲线的离心率为( )A ．212+ B ．12+ C ．215- D ．15-二、填空题：本大题共4小题，每小题5分，共20分．把答案填写在答题卡的相应位置． 13．向量a ，b 满足||1=a ，||=b ，()(2)+⊥-a b a b ，则向量a 与b 的夹角为__________。

2015高考数学(人教通用,文科)二轮专题训练：大题综合

突破练(三)1．设函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx ＋π6＋2sin 2ωx 2(ω＞0)，已知函数f (x )的图象的相邻对称轴的距离为π.(1)求函数f (x )的解析式；(2)若△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c (其中b ＜c )，且f (A )＝32，△ABC 的面积为S ＝63，a ＝27，求b ，c 的值．解 (1)f (x )＝32sin ωx ＋12cos ωx ＋1－cos ωx ＝32sin ωx －12cos ωx ＋1 ＝sin (ωx －π6)＋1.∵函数f (x )的图象的相邻两对称轴间的距离为π. ∴函数f (x )的周期为2π.∴ω＝1.∴函数f (x )的解析式为f (x )＝sin (x －π6)＋1. (2)由f (A )＝32，得sin (A －π6)＝12. 又∵A ∈(0，π)，∴A ＝π3. ∵S ＝12bc sin A ＝6 3. ∴12bc sin π3＝63，bc ＝24.由余弦定理，得a 2＝(27)2＝b 2＋c 2－2bc cos π3＝b 2＋c 2－24.∴b 2＋c 2＝52.又∵b ＜c ，解得b ＝4，c ＝6.2．已知等差数列{a n }的公差为2，其前n 项和为S n ＝pn 2＋2n ，n ∈N *， (1)求p 的值及a n ；(2)在等比数列{b n }中，b 3＝a 1，b 4＝a 2＋4，若等比数列{b n }的前n 项和为T n ，求证：数列{T n ＋16}为等比数列．(1)解由已知a 1＝S 1＝p ＋2，S 2＝4p ＋4即a 1＋a 2＝4p ＋4.∴a 2＝3p ＋2. 由已知a 2－a 1＝2，∴p ＝1，∴a 1＝3，又公差为2， ∴a n ＝2n ＋1，n ∈N *.(2)证明在等比数列{b n }中，设公比为q ，∵b 3＝a 1＝3，b 4＝a 2＋4＝9，∴q ＝3.由b 3＝b 1·32，即3＝b 1·32，解得b 1＝13. ∴{b n }是以13为首项，3为公比的等比数列． ∴T n ＝13(1－3n )1－3＝16·(3n－1)．即T n ＋16＝16·3n ＝12·3n －1. 又∵T 1＋16＝12，T n ＋16T n －1＋16＝3，n ≥2，n ∈N *. ∴数列{T n ＋16}是以12为首项，公比为3的等比数列．3．为了响应政府“节能、降耗、减排、增效”的号召，某工厂决定转产节能灯，现有A 、B 两种型号节能灯的生产线供选择．从这两种生产线生产的大量节能灯中各随机抽取100个进行质量评估，经检测，综合得分情况如下面的频率分布直方图：产品级别划分以及利润如下表：(1)估计生产A型节能灯的一级品率；(2)估计生产一个B型节能灯的利润大于0的概率，并估计生产100个B型节能灯的平均利润．解(1)由频率分布直方图知，A型节能灯的一级品的频率为0.044×5＋0.016×5＝0.3，所以生产A型节能灯的一级品率的估计值为0.3.(2)由条件知，生产B型节能灯一个产品的利润大于0的概率当且仅当k≥75，由频率分布直方图知，k≥75的频率为0.96，所以生产B型节能灯一个产品的利润大于0的概率估计值为0.96.生产100个B型节能灯的平均利润为1100×[4×(－2)＋54×2＋42×4]＝2.68(元)．4．已知三棱柱ABC－A1B1C1中，∠BCA＝90°，AA1＝AC＝BC＝2，A1在底面ABC 上的射影恰为AC的中点D.(1)求证：AC1⊥BA1；(2)求四棱锥A1－BCC1B1的体积．(1)证明∵A1在底面ABC上的射影恰为AC的中点D，∴A1D⊥平面ABC.∵A1D⊂平面A1AC，∴平面A1AC⊥平面ABC.∵BC⊥AC，平面A1AC∩平面ABC＝AC，∴BC⊥平面A1AC.∵AC1⊂平面A1AC，∴BC⊥AC1.易知四边形ACC1A1为平行四边形．又∵AA1＝AC，∴四边形ACC1A1为菱形，A1C⊥AC1，BC⊥AC1，又∵A1C∩BC＝C，∴AC1⊥平面A1CB.又∵BA1⊂平面A1CB，∴AC1⊥BA1.(2)解 ∵VA 1－ABC ＝13S △ABC ·A 1D ＝13×12×2×2×3＝233， VA 1B 1C 1－ABC ＝S △ABC ·A 1D ＝12×2×2×3＝23，∴VA 1－BCC 1B 1＝VA 1B 1C 1－ABC －VA 1－ABC ＝23－233＝433.5．在圆x 2＋y 2＝8上任取一点P ，过点P 作x 轴的垂线PD ，D 为垂足，M 为垂线段PD 上的点，且满足|MD |＝22|DP |. (1)求点M 的轨迹方程；(2)若直线l 与(1)中轨迹E 相交于不同两点A ，B ，且满足OA →⊥OB →(O 为坐标原点)，求线段AB 长度的取值范围．解 (1)设M (x ，y )，P (x 1，y 1)．由|MD |＝22|DP |，得{ x 1＝x ， y 1＝2y ，又∵P (x 1，y 1)在圆x 2＋y 2＝8上，∴x 21＋y 21＝8，即x 2＋(2y )2＝8.∴点M 的轨迹E 的方程为x 28＋y 24＝1.(2)(ⅰ)假设直线l 的斜率存在，其方程为y ＝kx ＋m .联立{ y ＝kx ＋m ， x 2＋2y 2＝8，可得(1＋2k 2)x 2＋4kmx ＋2m 2－8＝0.∴⎩⎪⎨⎪⎧Δ＝64k 2－8m 2＋32＞0，x 1＋x 2＝－4km 1＋2k 2，x 1x 2＝2m 2－81＋2k 2，(*)∵OA →·OB →＝0，∴x 1x 2＋(kx 1＋m )(kx 2＋m )＝0. 化简，可得(k 2＋1)x 1x 2＋km (x 1＋x 2)＋m 2＝0. 将(*)式代入，化简可得3m 2＝8k 2＋8. 又∵|AB |＝1＋k 2|x 1－x 2|＝1＋k264k2－8m2＋321＋2k2.将m2＝83(k2＋1)代入，可得|AB|＝1＋k22×64k23＋3231＋2k2＝323(1＋k2)(4k2＋1)(1＋2k2)2＝3231＋k21＋4k4＋4k2＝3231＋11k2＋4k2＋4≤2 3.∴当且仅当k2＝12，即k＝±22时等号成立．又由k21＋4k4＋4k2≥0，∴|AB|≥323＝463.∴463≤|AB|≤2 3.(ⅱ)若直线l的斜率不存在，则易得|AB|＝46 3.综上，得463≤|AB|≤2 3.6．已知函数f(x)＝(x2－2ax＋a2)ln x，a∈R，(1)当a＝0时，求函数f(x)的单调区间；(2)当a＝－1时，令F(x)＝f(x)x＋1＋x－ln x，证明：F(x)≥－e－2(其中e为自然对数的底数)；(3)若函数f(x)不存在极值点，求实数a的取值范围．解(1)当a＝0时，f(x)＝x2ln x(x＞0)，此时f′(x)＝2x ln x＋x＝x(2ln x＋1)．令f′(x)＞0，解得x＞e－12；令f′(x)<0，解得0<x<e－12.∴函数f(x)的单调递增区间为(e－12，＋∞)，单调递减区间为(0，e－12)．(2)F(x)＝f(x)x＋1＋x－ln x＝x ln x＋x.由F′(x)＝2＋ln x，得F(x)在(0，e－2)上单调递减，在(e－2，＋∞)上单调递增．∴F(x)≥F(e－2)＝－e－2.(3)f′(x)＝2(x－a)ln x＋(x－a)2x＝x－ax·(2x ln x＋x－a)．令g(x)＝2x ln x＋x－a，则g′(x)＝3＋2ln x.∴函数g(x)在(0，e－32)上单调递减，在(e－32，＋∞)上单调递增．∴g(x)≥g(e－32)＝－2e－32－a.①当a≤0时，∵函数f(x)无极值，∴－2e－32－a≥0.解得a≤－2e－3 2.②当a＞0时，g(x)min＝－2e－32－a＜0，即函数g(x)在(0，＋∞)存在零点，记为x0.由函数f(x)无极值点，易知x＝a为方程f′(x)＝0的重根，即x＝a也是2x ln x ＋x－a＝0的根．∴2a ln a＋a－a＝0，即2a ln a＝0，a＝1.当0＜a＜1时，x0＜1且x0≠a，函数f(x)的极值点为a和x0；当a＞1时，x0＞1，且x0≠a，函数f(x)的极值点为a和x0；当a＝1时，x0＝1，此时函数f(x)无极值．综上，a≤－2e－32或a＝1.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

突破练(二)
1．已知函数f (x )＝A sin (ωx －π6)(ω＞0)相邻两个对称轴之间的距离是π2，且满足f (π
4)＝ 3.
(1)求f (x )的单调递减区间；
(2)在钝角△ABC 中，a 、b 、c 分别为角A 、B 、C 的对边，sin B ＝3sin C ，a ＝2，f (A )＝1，求△ABC 的面积．解 (1)由题意知周期T ＝π，∴ω＝2，
因为f ⎝ ⎛⎭
⎪⎫
π4＝3，所以A ＝2，f (x )＝2sin (2x －π6)，
由π2＋2k π≤2x －π6≤3π2＋2k π(k ∈Z )，得π3＋k π≤x ≤5π
6＋k π(k ∈Z )，所以f (x )的单调递减区间为[π3＋k π，5π
6＋k π](k ∈Z )． (2)由题意b ＝3c ，f (A )＝2sin (2A －π
6)＝1， ∴sin (2A －π6)＝1
2，
∵ －π6＜2A －π6＜11π6，∴A ＝π6或π2，
因为△ABC 为钝角三角形，所以A ＝π2舍去，故A ＝π
6， ∵a 2＝b 2＋c 2－2bc cos A ， ∴4＝3c 2＋c 2－23c 2×3
2＝c 2，
所以c ＝2，b ＝23，S △ABC ＝12×23×2×1
2＝ 3. 2．已知正项等比数列{a n }满足a 2＝19，a 4＝1
81，n ∈N *
(1)求数列{a n }的通项公式；(2)设数列{b n }满足b n ＝log 3a n log 3a n ＋1，求数列⎩⎨⎧⎭
⎬⎫
1b n 的
前n 项和T n ，
解 (1)设公比为q .∵a 4a 2
＝1
9＝q 2，
∴q ＝13或q ＝－13.
又数列{a n }为正项等比数列，∴q ＝1
3. 又∵a 2＝19. ∴a 1＝1
3， ∴a n ＝⎝ ⎛⎭
⎪⎫13n
，n ∈N *.
(2)∵b n ＝log 3a n ·log 3a n ＋1，n ∈N *， ∴b n ＝n (n ＋1)，n ∈N *. ∴1b n
＝
1n (n ＋1)＝1n －1
n ＋1
.
∴T n ＝1－12＋12－13＋…＋1n －1n ＋1＝1－1n ＋1＝n n ＋1
.
3．某种产品的广告费支出x 与销售额y (单位：万元)之间有如下对应数据：
x 2 4 5 6 8 y
30
40
60
50
70
若广告费支出x 与销售额y 回归直线方程为y ^
＝6.5x ＋a (a ∈R )． (1)试预测当广告费支出为12万元时，销售额是多少？
(2)在已有的五组数据中任意抽取两组，求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率．解 (1)x ＝2＋4＋5＋6＋85＝5，
y ＝
30＋40＋50＋60＋70
5
＝50，
因为点(5,50)在回归直线上，代入回归直线方程求得a ＝17.5，所求回归直线方程为：y ^
＝6.5x ＋17.5，
当广告支出为12时，销售额y ^
＝6.5×12＋17.5＝95.5. (2)实际值和预测值对应表为
x 2 4 5 6 8 y
30
40
60
50
70
y ^
30.5 43.5 50 56.5 69.5
在已有的五组数据中任意抽取两组的基本事件：(30,40)，(30,60)，(30,50)，(30,70)，(40,60)，(40,50)，(40,70)，(60,50)，(60,70)，(50,70)共10个，两组数据其预测值与实际值之差的绝对值都超过5的有(60,50)，
所以至少有一组数据其预测值与实际值之差的绝对值不超过5的概率为P ＝1－110＝910.
4．如图，三棱柱ABC －A 1B 1C 1的侧棱AA 1⊥平面ABC ，△ABC 为等边三角形，侧面AA 1CC 1是正方形，E 是A 1B 的中点，F 是棱CC 1上的点．
(1)若F 是棱CC 1的中点时，求证：AE ⊥平面A 1FB ； (2)当V E －ABF ＝93时，求正方形AA 1C 1C 的边长． (1)证明取AB 的中点为M ，连接EF ，EM ，CM ，
因为E 是A 1B 的中点，F 是棱CC 1中点，所以EM ∥AA 1，FC ∥AA 1，EM ＝FC ＝1
2AA 1，则四边形EMCF 是平行四边形，所以EF ∥CM ，又因为△ABC 为正三角形，侧面AA 1C 1C 是正方形， ∴AA 1＝AB ，所以AE ⊥A 1B ，CM ⊥AB ，因为侧棱AA 1⊥平面ABC ，所以CM ⊥AA 1，
∴CM ⊥平面A 1AB ，∴EF ⊥平面A 1AB ，所以EF ⊥AE ，又因为AE ⊥A 1B ，A 1B ∩EF ＝E ，所以AE ⊥平面A 1FB .
(2)解设正方形AA 1C 1C 的边长为x ，由于E 是A 1B 的中点，△EAB 的面积为定值，
∵CC 1∥平面AA 1B ，∴点F 到平面EAB 的距离为定值，即为点C 到平面AA 1B 的距离，
又V E －ABF ＝V F －ABE ，且V F －ABE ＝1
3S △ABE ·h ＝9 3. 即13·12·x ·
x 2·32x ＝93，
∴x 3＝216，∴x ＝6.所以正方形的边长为6.
5．已知圆C 1的圆心在坐标原点O ，且恰好与直线l 1：x －2y ＋35＝0相切，点A 为圆上一动点，AM ⊥x 轴于点M ，且动点N 满足ON →＝33OA →＋(1－33)OM →
，设动点N 的轨迹为曲线C . (1)求曲线C 的方程；
(2)直线l 与直线l 1垂直且与曲线C 交于B 、D 两点，求△OBD 面积的最大值．解 (1)设动点N (x ，y )，A (x 0，y 0)，因为AM ⊥x 轴于M ，所以M (x 0,0)，设圆C 1的方程为x 2＋y 2＝r 2，由题意得r ＝|35|
1＋4
＝3，所以圆C 1的方程为x 2＋y 2＝9，由题意，ON →＝33OA →＋(1－33)OM →，得(x ，y )＝33(x 0，y 0)＋(1－3
3)(x 0,0)，
所以⎩⎨⎧
x ＝x 0，y ＝3
3y 0，
即⎩⎨⎧
x 0＝x ，
y 0
＝3y . 将A (x ，3y )代入x 2
＋y 2
＝9，得动点N 的轨迹方程x 29＋y 2
3＝1.
(2)由题意可设直线l ：2x ＋y ＋m ＝0，设直线l 与椭圆x 29＋y 2
3＝1交于B (x 1，y 1)，D (x 2，y 2)，
联立方程⎩⎨⎧
y ＝－2x －m ，
x 2＋3y 2
＝9
得13x 2＋12mx ＋3m 2－9＝0，
Δ＝144m 2－13×4(3m 2－9)＞0，解得m 2＜39， x 1,2＝－12m ±468－12m 226＝－6m ±117－3m 2
13，
又因为点O 到直线l 的距离d ＝
|m |
5
， BD ＝5·|x 1－x 2|＝5·2117－3m 2
13，
所以S △OBD ＝12·|m |
5
·5·2117－3m 213
＝m 2(117－3m 2)13＝3m 2(39－m 2)13≤332(当且仅当m 2＝39－m 2即m 2＝392时取
到最大值)．
所以△OBD 面积的最大值为33
2. 6．设函数f (x )＝ln x －14x 2－1
2x . (1)求f (x )的单调区间和极值；
(2)若g (x )＝x ⎣⎢⎡⎦⎥⎤f (x )＋14x 2＋1，当x ＞1时，g (x )在区间(n ，n ＋1)内存在极值，求整数n 的值．
解 (1)f ′(x )＝1x －12x －12＝－x 2
－x ＋2
2x
(x ＞0)，
令f ′(x )＝0，解得x ＝1(－2舍去)，根据x ，f ′(x )，f (x )的变化情况列出表格：
x (0,1) 1 (1，＋∞)
f ′(x ) ＋ 0 － f (x )
递增
极大值－3
4
递减
由上表可知函数f (x )的单调增区间为(0,1)，递减区间为(1，＋∞)，在x ＝1处取得极大值－3
4，无极小值． (2)g (x )＝x ⎣⎢⎡⎦⎥⎤
f (x )＋14x 2＋1＝x ln x －12x 2＋x ，
g ′(x )＝ln x ＋1－x ＋1＝ln x －x ＋2，
令h(x)＝ln x－x＋2，∴h′(x)＝1
x－1＝
1－x
x，
因为x＞1，∴h′(x)＜0恒成立，所以h(x)在(1，＋∞)为单调递减函数，
因为h(1)＝1＞0，h(2)＝ln 2＞0，h(3)＝ln 3－1＞0，h(4)＝ln 4－2＜0.
所以h(x)在区间(3,4)上有零点x0，且函数g(x)在区间(3，x0)和(x0,4)上单调性相反，因此，当n＝3时，g(x)在区间(n，n＋1)内存在极值，所以n＝3.。