明渠梯形断面临界水深计算公式的推求

合集下载

03 渠道临界水深计算

临界水深
Q2 Ak3
g Bk
临界水深对应的过水断面面积
临界水深对应的水面宽度
式中： A (b mh)h
B b 2mh
计算思路：不断假设水深h，当假设的水深使临界流方程成立时，该假
设水深即临界水深hk。
/ 水利水电建筑工程
水力分析与计算子项目
/ 水利水电建筑工程
水力分析与计算子项目
3.Excel试算临界水深
需要用到的公式和需要注意的问题： ①基本变量的单元格符号应加“$”加以固定；
②常用的excel计算符号：求和 sum函数；求差 “—”号；求积 “ * ”号；求商 “ / ”号；平均数 average 函数；开方 “sqrt”或“power（a，0.5）”函数；幂函数 “^”或 power（a，b）=ab 三角函数相应的三角函数（注意：默认的格式是弧度制）。
水力分析与计算子项目
用excel计算临界水深
/ 水利水电建筑工程
水力分析与计算子项目
四课下练习
某梯形断面渠道，底宽b=2.5.0m，边坡系数m=2.0。当通过流量Q=7.0m3/s时，试计算渠道的临界水深hk。
要求：编写excel公式，并用单变量求解的方法计算结果。
/ 水利水电建筑工程
水力分析与计算子项目
A
B
B7=($B$4+$C$4 *A7)*A7
C7=$B$4+2*$C$4* A7
A (b mh)h B b 2mh
D4=A4^2/9.8
A3 / B
D7=B7^3/C7
/ 水利水电建筑工程
/ 水利水电建筑工程
在编制计算程序时，应注意这些参数在计算过程中始终不变，应当使用“$”符号加以控制。

梯形渠道水力半径公式

梯形渠道水力半径公式摘要：一、引言二、梯形渠道水力半径公式的概念和原理三、梯形渠道水力最佳断面设计的方法四、梯形渠道水力半径公式的应用实例五、结论正文：一、引言梯形渠道是水利工程中非常常见的一种渠槽形式，它具有占地少、施工简单、运行可靠等优点。

在水利工程设计中，如何确定梯形渠道的水力最佳断面，以达到过水面积最大或流量最大的目的，是一个重要的研究课题。

而梯形渠道水力半径公式则是解决这一问题的关键。

二、梯形渠道水力半径公式的概念和原理梯形渠道的水力半径公式是指，在梯形渠道内，水流的半径与渠道的宽度和深度之间存在着一定的关系。

这个关系可以用一个公式来表示，即：R = (b + h) / 2，其中，R 表示水力半径，b 表示梯形渠道的宽度，h 表示梯形渠道的深度。

根据水力半径公式，我们可以知道，当梯形渠道的宽度和深度确定时，水力半径也就确定了。

而水力半径的大小直接影响到梯形渠道的水力性能，如过水面积、流量等。

三、梯形渠道水力最佳断面设计的方法要确定梯形渠道的水力最佳断面，可以采用以下步骤：1.根据工程需要，确定梯形渠道的宽度b 和深度h。

2.根据水力半径公式，计算出对应的水力半径R。

3.利用梯形渠道的水力最佳断面设计方法，求解出最佳断面的水深。

4.根据求解出的最佳断面水深，设计出梯形渠道的水力最佳断面。

四、梯形渠道水力半径公式的应用实例假设某水利工程需要设计一条梯形渠道，宽度为4 米，深度为2 米。

根据水力半径公式，可以计算出该梯形渠道的水力半径为：R = (4 + 2) / 2 = 3 米。

然后，利用梯形渠道的水力最佳断面设计方法，可以求解出最佳断面的水深。

假设该渠道的设计流量为10 立方米/秒，通过计算可得，最佳断面的水深为0.6 米。

根据求解出的最佳断面水深，可以设计出梯形渠道的水力最佳断面，以达到过水面积最大或流量最大的目的。

五、结论梯形渠道水力半径公式在水利工程设计中具有重要作用，它可以帮助我们确定梯形渠道的水力最佳断面，从而达到过水面积最大或流量最大的目的。

水力学习题解析(吴持恭4)

《水力学》（吴持恭主编）习题解析绪论（P12）0.1 解：2000221.00337.0101775.0tt ++=ν，当C t ︒=35,25,15,9,7,3时，代入公式得相应温度下的运动粘滞系数：0.016091、0.014237、0.013435、0.011413、0.008962、0.007244cm 2/s 。

0.2 解：32⎪⎭⎫ ⎝⎛=H y u u m ，dy y H Hu dy yHH Hu dy y Hu H y u d du m m m m 313132313232323232)(⎪⎪⎭⎫ ⎝⎛=⋅==⎪⎭⎫⎝⎛=--- 将5.0,25.0=Hy分别代入上式得：H u H u y H H u dy du m m m 84.0,058.13231=⎪⎪⎭⎫⎝⎛= 0.3 解：X=0，Y=0，Z=-g0.4 解：[][]L LT ML MT L g p h =⎥⎦⎤⎢⎣⎡⋅=⎥⎦⎤⎢⎣⎡=----2321ρ 0.5 解：根据牛顿内摩擦定律有：dydu μτ= 由于两板之间的距离非常小m mm 001.01==δ，故两板之间的速度分布可近似地看作线性分布，从而有：δμμτu dy du == 又：δμτuAA F =⋅=将已知数据：m s m u m A s Pa 001.0,1,2.08.0,15.12==⨯=⋅=δμ 代入得：KN uA F 184001.012.08.015.1=⨯⨯⨯==δμ 0.6 解：（1）dp V dVk -=，34m V =，3001.01m L dV ==，a p dp 5=，故a p dp V dV k 00005.054001.0-=-=-=，a p k K 2000000005.011-=-==（2）a p kV dV dp 25.0100014001.0=--=-=水静力学（P52-59）1.1 解：由等压面条件有：γγγac c a c p p h p p h p p -=−−−−→−⎭⎬⎫⨯+=+=联立求解30 从而：()Kpa p c 4.10738.978=⨯+=()m p p h ac 96.08.99810734=-=-=γ1.2 解：已知：()()()⎪⎭⎪⎬⎫=⨯===⨯===⨯==33300/28.1331000/8.913600/10.111000/8.96.1132/50.81000/8.93.867m KN g m KN g m KN g m m ργργργ m cm h m cm h m cm s 04.04,2.020,05.051======由等压面条件有：()()1010110100gh h h p p x h p p x h p p A B B A γγγγγγγ-=-=-−−−−→−⎭⎬⎫++=++=联立求解代入已知数据得：()()()Kpa h p p A B 52.00.28.5-11.110=⨯=-=-γγ由U 型比压计等压面条件有：()Kpa h s p h s p m A m A 35.504.028.13305.01.110-=⨯-⨯-=--=⇒=++γγγγ()Kpa p p A B 83.452.035.552.0-=+-=+=由计算可知，A 与B 两点均存在真空。

梯形断面明渠临界水深计算方法新探

梯形断面明渠临界水深计算方法新探李兴印卢军启杨玲霞（郑州大学水利与环境学院中国郑州 450001)摘要：临界水深是水力学计算中的一个很重要的参数，在水力计算及水工设计中应用非常广泛。

在实际工程中，梯形断面渠道较为常见，故梯形断面明渠临界水深的求解就显得尤为重要。

本文在临界流方程的基础上，通过引进无量纲参数，导出了临界水深的近似计算公式。

通过算例证明了所得公式的计算精度较高。

公式为显式，可直接应用计算，且形式简单，使用方便，可为相关水力计算提供便利。

关键词：梯形明渠；临界水深；近似计算1．引言临界水深是梯形断面明渠水力计算中一个很重要的水力要素，在水利水电工程、农田灌溉、城市给排水工程中应用十分广泛，鉴于梯形断面形式的复杂性，对临界水深的基本方程无论通过怎样的数学变换，也无法得到临界水深的显函数精确解析解，其临界水深只有借助迭代理论、最优逼近拟合理论及先进的数学工具进行求解。

很多专家和科技人员从20世纪50 年代甚至更早就对临界水深问题进行探讨和研究。

特别是80 年代以来，关于梯形断面临界水深的计算方法的研究已取得大量的成果，他们相继提出了许多计算方法，都具有很好的参考价值，为相关工程实践提供参考，同时也为相关工程问题提出了许多宝贵的意见和建议。

对于梯形断面明渠临界水深的计算问题，常见的求解方法有试算法、图解法、迭代法、近似求解法等。

笔者对目前几种常见的临界水深计算方法进行总结和分析，并采用无量纲参数进而推出一种新的临界水深近似计算公式，并对其举例探讨，分析其精度，以期为相关工程设计提供参考。

2．临界水深计算的基本方程引述众所周知，在梯形断面渠道的流量、断面尺寸均确定的情况下，相应于断面比能最小值E smin 的水深，称为临界水深。

断面比能E s 的公式为：E s = h + g v 22α = h + 222gAQ α (1) 由临界水深的定义可得，令dhdE s = 1 - 222gA Q α = 0 得到临界流方程亦临界水深计算的基本方程：=gQ 2αkk B A 3 (2) 式中 Q ——过水断面的流量，m 3/s ； α——动能修正系数，常取1.0～1.05； g ——重力加速度，常取9.8m /s 2； A k ——临界水深时过水断面面积，m 2； B k ——临界水深时水面宽度，m 。

梯形明渠正常水深的直接计算方法

梯形明渠正常水深的直接计算方法赵延风;祝晗英;王正中;张宽地;芦琴【摘要】[目的]寻求梯形明渠正常水深的直接计算方法.[方法]针对梯形明渠正常水深计算时需求解高次隐函数方程,以及传统的查图表法或试算法计算复杂、误差大、适用范围小的缺点,通过引入无量纲水面宽度,根据数值计算方法,对梯形明渠均匀流的基本方程进行了恒等变形,得到了快速收敛的迭代公式,并与合理的迭代初值进行配合使用.[结果]提出了梯形明渠正常水深的直接计算公式.误差分析及实例计算表明,在工程最常用范围内,即无量纲水深x∈[0.1,2.0],梯形断面边坡系数m∈[0.5,4.0]时,正常水深的最大相对误差仅为0.78%.[结论]与现有公式相比,该直接计算公式物理概念明确、计算简捷、精度高、适用范围广.【期刊名称】《西北农林科技大学学报（自然科学版）》【年(卷),期】2009(037)004【总页数】5页(P220-224)【关键词】梯形明渠;正常水深;直接计算方法;无量纲水深;无量纲水面宽度【作者】赵延风;祝晗英;王正中;张宽地;芦琴【作者单位】西北农林科技大学,水利与建筑工程学院,陕西,杨凌712100;西安市水务局,渭浐河管理中心,陕西,西安,710015;西北农林科技大学,水利与建筑工程学院,陕西,杨凌712100;西北农林科技大学,水利与建筑工程学院,陕西,杨凌712100;西北农林科技大学,水利与建筑工程学院,陕西,杨凌712100【正文语种】中文【中图分类】TV131.4梯形明渠的正常水深是梯形明渠均匀流水力计算中一个基本的水力要素，在水利水电、灌溉排水、城市供水等生产实践中广泛应用。

由于其计算时需要求解一元高次方程，故无法直接求解，而传统的求解方法，如查图表法或者试算法，既费时又费力，而且精度不高。

近20年来，国内外相继提出了许多新的计算方法[1-13]，这些方法在工程实践中发挥了重要作用，但仍存在公式形式复杂、适用范围小、计算精度低等问题，至今尚没有一种集简捷、准确、适用范围广于一体的计算公式。

用诺谟图快速求解梯形断面渠道的临界水深

将式（）子和分母同时除以ｂ，简化后得：１分经
≈ — — Ｌ）（４
等式两边取对数后得：
ｌｈ＝ｌｇｊｇ，２＋ｌ＾一（／）ｌｂ＋（／）ｌＥｇｒ１３ｇ１３ ‘ ｇ
—
ｌ（＋Ｅｂｇ１／）
角度制作一张诺谟图，为该公式法的补充。同时作结合文章中的公式，制作诺谟图的最基本原理之把
（）９
式（）９在双对数坐标纸上均为直线方程６～（）式。若将因变量作为纵坐标，则式（）６表示参变量，为一定值时，自变量为ｂ的直线方程式；（）式７表示参变量Ｅ为一定值时，自变量为的直线方
年第４期上。由于一般在水力学中，确地求解梯精形断面渠道的临界水深值，了有公式试算法以外，除还有诺谟图查表计算法。笔者读了张工的快速求解梯形断面渠道临界水深近似值文章后，图从另一试
（）６
（）７（）８
２诺谟图制作及其应用
２１数学原理．
ｌＴ＝一（／）ｌＥ＋ｌｇＩ１３ ‘ ｇｇｌＴ＝ｌＴ一ｌ（＋Ｅｂｇ３ｇ２ｇ１／）
张文倬梯形断面渠道的ｆ界水深近似计算式：晦
（）１
则有
ｌＴ＝ｌｈ —ｌｇ３ｇｋｇ２
维普资讯
２期水电站设计第２卷第３
ＤＨＰＳ
２０６年９月０
用诺谟图快速求解梯形断面渠道的临界水深

03 渠道临界水深计算

专题3. 临界水深的计算从比能曲线可知，在水深由零增加到无穷大的过程中，断面比能也在随着水深而改变，但其中有一个最小值存在。

我们把在渠道流量、断面尺寸确定的情况下，相应断面比能Es 最小的水深，称为临界水深，用hk 表示。

计算临界水深的基本方程式临界流方程，其形式如下：kk B Ag Q 32=α (式3-1) 式中：A k 为临界水深对应的过水断面面积，m 2；Bk 为临界水深对应的水面上宽，m ；对于等腰梯形断面渠道，过水断面面积A 与水深h 之间的关系复杂，不易由临界流方程直接求解出临界水深h k ，需用试算法求解。

试算法的基本思路：当给定渠道断面形状、形状及流量时，临界流方程（式3-1）左端的gQ 2α可直接求出，而右端的B A 3仅是水深的函数，可假设若干个水深，分别求出其B A 3值，当该值与g Q 2α相等时，此水深即所求的临界水深。

也可只假设几个水深，绘制BA h 3—关系曲线，在曲线上查出满足临界流方程式的水深，即所求临界水深h k 。

【工程任务】某梯形断面渠道，底宽b=2.0m ，边坡系数m=1.5。

当通过流量Q=4.0m 3/s 时，渠道中实际的水深为h=1.0m ，试计算渠道的临界水深h k 。

【分析与计算】1. 试算法求解这是一个典型的计算梯形断面临界水深的问题。

由式子3-1可知，当Q 已知时，由可解出临界流方程左端的值，然后不断试算方程右端的值，即可解出临界水深。

先设h 1=0.5m ，63.18.94122=⨯=g Q α 过水断面面积38.15.0)5.05.12()(=⨯⨯+=+=h mh b A （m 2）水面上宽5.35.05.1222=⨯⨯+=+=mh b B （m ）74.05.338.133==B A 该值与已知的gQ 2α不符，故需重新代数计算。

将h 代0.5、0.6、0.7、0.8m 时，得到B A 3值分别为0.74、1.39、2.37、3.81。

梯形断面水力半径计算公式

梯形断面水力半径计算公式以梯形断面水力半径计算公式为标题，我将为大家介绍梯形断面水力半径的计算方法。

梯形断面是水力学中常见的一种河道断面形状，其计算方法较为复杂。

水力半径是梯形断面的一个重要参数，它可以反映水流在断面中的流动情况。

下面将详细介绍梯形断面水力半径的计算公式和计算步骤。

我们需要了解梯形断面的几何特征。

梯形断面由上底宽度b1、下底宽度b2、高度h和两个斜边组成。

根据梯形的几何特征，我们可以得到梯形断面的面积和湿周。

梯形断面的面积可以通过上底宽度b1、下底宽度b2和高度h计算得到，其计算公式为：A = (b1 + b2) * h / 2梯形断面的湿周可以通过上底宽度b1、下底宽度b2和高度h计算得到，其计算公式为：P = b1 + b2 + 2 * √(h^2 + (b2 - b1)^2)有了梯形断面的面积和湿周，我们就可以计算梯形断面的水力半径了。

水力半径R是梯形断面的面积与湿周之比，其计算公式为：R = A / P在实际计算中，我们可以先计算出梯形断面的面积和湿周，然后再通过这两个值计算出水力半径。

下面以一个具体的例子来说明梯形断面水力半径的计算步骤。

假设一个梯形断面的上底宽度b1为4米，下底宽度b2为6米，高度h为3米。

我们先利用上述公式计算出梯形断面的面积和湿周：A = (4 + 6) * 3 / 2 = 15平方米P = 4 + 6 + 2 * √(3^2 + (6 - 4)^2) = 20.39米然后，我们可以利用面积和湿周的值计算出水力半径：R = 15 / 20.39 = 0.73米通过这个例子，我们可以看到梯形断面的水力半径计算并不复杂，只需要根据梯形的几何特征，利用相应的公式进行计算即可。

在实际工程中，我们可以根据梯形断面的水力半径来评估水流的流动情况，为水利工程的设计和建设提供参考依据。

梯形断面的水力半径是一个重要的水力学参数，它可以反映水流在梯形断面中的流动情况。

经验公式简化计算梯形渠道断面

经验公式简化计算梯形渠道断面
梯形渠道断面是水力学计算中的重要求解内容，它的计算精度直接影响流体流动状态和所获得水力性能参数，是工程计算必不可少的实用技术工作。

梯形渠道断面分析定义为由不同宽度、不同深度和角度构成的渠道，空间上有两个断面，
只有两个断间距离：上断量S_up，下断量S_down。

梯形渠道断面形状按平均底宽B_mid、上平宽B_up（靠后平）和下平宽B_down（靠前平）的组合来决定的。

由于梯形渠道断面的形状复杂，昂贵的计算资源被消耗，空间受限，所以为了提高效率，
必须采用一种更简单的计算方法。

为此，会根据历史经验公式来简化计算梯形渠道断面。

历史经验公式据说是采用跨江宗淼在19世纪中叶建立的，原先是将渠道总断面积分成底
宽与高之比所形成的矩形沟渠及其边坡底宽之比，即两个断面形状的定义：其一是上断面形式下的矩形，其二是下断面
的梯形。

由此，在计算梯形渠道断面时，可以利用上述历史经验公式来简化计算，通过查表，可以
通过计算渠道总断面积来计算出上断面、下断面、比例系数等参数，也可以直接输入渠道总断面积来进行计算，从而提高梯形渠道断面计算的效率。

众所周知，历史经验公式只是用来简化计算梯形渠道断面，而不足以代替高度精确的计算，如果要求较高的精度，则建议采用更精确的计算方法，比如采用椭圆形方程解或双底面方
程解来计算梯形渠道断面。

从以上可以看出，梯形渠道断面的计算是一件十分重要的和复杂的工作，历史经验公式已经为我们提供了较为方便的实用方式，加以不断发展和改进，可以满足我们在实际工程计算中对梯形渠道断面计算的要求，从而减少计算时间和节省计算资源。

渠道底宽和水深的直接计算

渠道底宽和水深的直接计算水力学计算?肇遣.趱,诳一(-力钟渠道底宽和水深的直接计算④坚I一(米易县水幸『J电力局)1问题的提出在渠道底坡i,渠床糙率n卡口断面形状已经确定的情况下,水力计算的任务就是确定通过设计流量的断面尺寸,即底宽b和水深h.根据流量公式Q—or:cv和谢才公式v=,雨,可以得到计算渠道均匀流的流量公式:Q一,一Ri(1)式中,C为谢才系数,c=*--R”….将CR”代入式(1),经整理后得Q;∞R,2.(2)对于梯形断面渠道,面积一(b+mh)h,水力半径R—,则式(2)可变为:.=1(b+mh)h[㈤对于矩形断面渠道,面积~o=bh,水力半径R,则式(2)变为:Q=Mfj㈨由式(3)和式(4)可见,在渠道底坡i,渠床糙率系数n,渠道边坡系数iTl已经确定的情况下,渠道的流量仍与底宽b和水深h两个条件有关.在渠道设计流量已经确定的情况下,要计算确定底宽b和水深h,常采用试算法和图解法,而试算法或图解法都比较麻烦.为此,本文提出求解底宽和水深的直接计算法.算法就是首先根据渠道的稳定条件和力求节省工程量,施工难度小,运行维护方便等要求,选用合适的宽深比B=b/h.然后直接算出相应的水深h和底宽b.2计算公式的推求由宽深比B=b/h得bah(5)将式(5)代入式(3),得梯形断面渠道的流量公式:Q={c+m[j_::!]0“+)…丽由式(6)司得梯形断面渠道水探的计算公式:一rL(口+m)J(nQ)”(a+2,1+辨)拈r”一+m).运行维护的原则.小型莱,衬砌渠道,边坡系数一般较小.水力最优断面属宽浅式,宽深比宜靠近最优断面的宽深比选择,即a=b/h≈2,T一m.大型渠道或不衬砌的渠道,边坡一般都比较平缓,即边坡系数m直较大,当m>0.75时,水力最优断面为窄深式宽深比过小的窄深式渠道,施工运行维护都比较困难, 因此.宜在最优断面宽深比的基础上适当加大,即:=6/>2,]矛一山区傍山渠道,多为小型渠道,且山洪侵蚀严重,多为全挖方渠道,且石方要占相当太的比例,挖方量是工程量的主体.为了减少工水力学计算?程量,节省投资,宽深比宜在最优断面宽深比的基础上适当降低,即:口=blh<2,I+m～m4算铡米易县晃桥水库南干渠届山区傍山渠道,首段O+000~0+500,设计流量I.4mIS,底坡i=I/1000,断面型式为梯形,边坡系数m一0.5;软骨料混凝土衬砌,糙率系数n=O.018,求该段渠道的水深h和底宽b.该渠道属于山区傍山衬砌小型渠道,水力最优断面的宽深比a=;省学会五届理事会二次全会在成都召开; ;1998年2月llEl,四JIj省水荆学喜在1副省长敬正书关于辞击学喜理事长的信{专成都召开了五届理事喜第二次全体喜议,与函,并一致通过了推荐水电厅厅长陈德静同;;备代表近80人.会议由副理事长赵文廉教志为理事长的建议,通过1推选谢成蒙和州;;授主持.太喜首先听取了常务副理事长谢成纪华两同志为中国水利学会七届理事喜的毒蒙同志所作的.五太讲末的工作回顾和伞理事候选人的提议.};年的工作布暑的报告.题目是”高举邓小平新任[标签:快照]。

梯形明渠临界水深简易计算法

梯形明渠临界水深简易计算法
韩会玲
【期刊名称】《海河水利》
【年(卷),期】1995(000)002
【摘要】回归分析的方法，给出一个具有足够精度、只用函数计算器就可以计算的梯形断面临界水深计算公式。

大量计算结果表明，用建议公式计算的结果与精确解非常接近，能满足工程计算上的要求。

【总页数】2页(P33-34)
【作者】韩会玲
【作者单位】无
【正文语种】中文
【中图分类】TV133
【相关文献】
1.梯形明渠临界水深的模式搜索算法求解 [J], 张宽地;吕宏兴;赵延风;杨艳
2.弧底梯形明渠临界水深的简化计算法 [J], 滕凯;张丽伟
3.弧底梯形明渠临界水深的直接算法 [J], 王正中;申永康;彭元平;陈涛;赵颖
4.基于优化拟合的梯形明渠临界水深简化算法 [J], 滕凯
5.蚁群算法在梯形明渠临界水深计算中的应用 [J], 刘思韬;王慧斌
因版权原因，仅展示原文概要，查看原文内容请购买。

梯形断面明渠临界水深计算方法新探

在实际工程中，梯形断面渠道较为常见，故梯形断面明渠临界水深的求解就显得尤为重要。

本文在临界流方程的基础上，通过引进无量纲参数，导出了临界水深的近似计算公式。

通过算例证明了所得公式的计算精度较高。

公式为显式，可直接应用计算，且形式简单，使用方便，可为相关水力计算提供便利。

很多专家和科技人员从20世纪50 年代甚至更早就对临界水深问题进行探讨和研究。

对于梯形断面明渠临界水深的计算问题，常见的求解方法有试算法、图解法、迭代法、近似求解法等。

2．临界水深计算的基本方程引述众所周知，在梯形断面渠道的流量、断面尺寸均确定的情况下，相应于断面比能最小值E smin 的水深，称为临界水深。

梯形类渠道水力最佳断面统一公式的推求

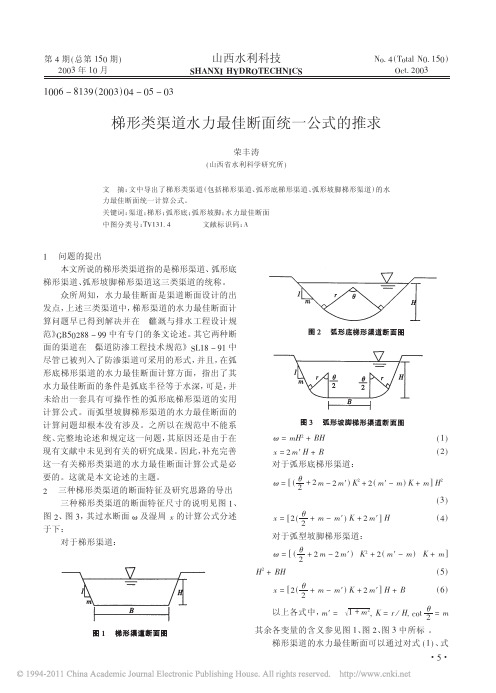
" ! < = ’ # ; # 7 #> & ( ; ’ #> ? $ ’ % ’
" 以上各式中， <# #> < $$ ; #’A ( " ) * $+ 1*’ 其余各变量的含义参见图 $、图 ’、图 ( 中所标。梯形渠道的水力最佳断面可以通过对式 # $ & 、式・ !・
第 " 期 # 总第 $%& 期 ’ (&&) 年 $& 月 #(’ 求
* ( ’・ & !N
# ($ ’
$ S # " #T E " # E " ’ # ’ E $ ’ ( W # " W ( # ’ U &( # (( ’ (
!"#$%&’$() (* +)$*$", -./&’$() *(# 0"1’ 23,#&/4$5 6"5’$() (* 7#&8"9($, : ’38", ;<&))"4 3+45 6745./+ =>1’#&5’? -89: ;/;7< =7<9>7: .87 ?49@97= 7A?/.9+4 @+< .87 B7:. 8C=<?092 :72.9+4 +@ .</;7D+9= E .C;7= 28/4470F G8928 9420?=7 .87 :./4=/<= .</;7D+9=/0 28/4470F .</;7D+9=/0 28/4470 G9.8 2?<>7= B+..+H /4= .</;7D+9=/0 28/4470 G9.8 2?<>7= :0+;7.+7, @"3 A(#,1I J8/4470 -</;7D+9= J?<>7= K+..+H J?<>7= L0+;7 -+7 K7:. MC=</?092 L72.9+4

水力学常用计算公式

1、明渠均匀流计算公式： Q=Aν=AC RiC=n 1R y （一般计算公式）C=n1R 61（称曼宁公式) 2、渡槽进口尺寸（明渠均匀流）gZ 2bh Q ＝z ：渡槽进口的水位降（进出口水位差）ε：渡槽进口侧向收缩系数，一般ε＝0。

8～0。

9 b ：渡槽的宽度（米) h ：渡槽的过水深度（米） φ：流速系数φ＝0。

8～0.95 3、倒虹吸计算公式:Q=mA z g 2(m 3/秒）4、跌水计算公式：跌水水力计算公式：Q ＝εmB 2/30g 2H ，式中：ε—侧收缩系数，矩形进口ε＝0.85～0.95；，B —进口宽度（米）；m —流量系数5、流量计算公式：Q=Aν式中Q ——通过某一断面的流量,m 3／s ；ν—-通过该断面的流速,m ／h A ——过水断面的面积，m 2。

6、溢洪道计算1）进口不设闸门的正流式开敞溢洪道（1）淹没出流：Q ＝εσMBH 23＝侧向收缩系数×淹没系数×流量系数×溢洪道堰顶泄流长度×溢洪水深23 （2）实用堰出流：Q=εMBH23=侧向收缩系数×流量系数×溢洪道堰顶泄流长度×溢洪水深23 2)进口装有闸门控制的溢洪道（1）开敞式溢洪道。

Q ＝εσMBH 23＝侧向收缩系数×淹没系数×流量系数×溢洪道堰顶泄流长度×溢洪水深23 （2）孔口自由出流计算公式为Q=MωH=堰顶闸门自由式孔流的流量系数×闸孔过水断面面积×H 其中：ω=be7、放水涵管（洞）出流计算 1）、无压管流Q=μA 02gH=流量系数×放水孔口断面面积×02gH 2）、有压管流Q ＝μA 02gH=流量系数×放水孔口断面面积×02gH8、测流堰的流量计算——薄壁堰测流的计算 1）三角形薄壁测流堰，其中θ＝90°,即自由出流：Q ＝1.4H 25或Q ＝1.343H 2。

梯形明渠临界水深的计算解法

梯形明渠临界水深的计算解法
徐焕文;孙慕群
【期刊名称】《中国农村水利水电》
【年(卷),期】2002()12
【总页数】2页(P57-58)
【关键词】计算;梯形断面;临界水深;渠道
【作者】徐焕文;孙慕群
【作者单位】湖南省长沙电力学院;湖北省水利水电科学研究所
【正文语种】中文
【中图分类】TV135.3
【相关文献】
1.计算梯形明渠临界水深与共轭水深的优化方法 [J], 卢泰山
2.一种弧底梯形明渠临界水深的快速解法 [J], 杨茂松;马子普
3.梯形明渠临界水深解法新探 [J], 王正中;沙际德
4.梯形明渠正常水深和临界水深的迭代计算法 [J], 杨伟;刘宗健
5.梯形明渠正常水深和临界水深的达代计算法 [J], 杨伟; 刘宗健
因版权原因，仅展示原文概要，查看原文内容请购买。