C语言求素数问题算法
c语言求素数个数方法超时

c语言求素数个数方法超时(原创版2篇)目录(篇1)I.素数定义及性质II.常见的求素数个数方法III.C语言求素数个数方法IV.优化C语言求素数个数方法正文(篇1)I.素数定义及性质-----------素数又称质数,是指只能被1和自身整除的正整数。
例如,2、3、5、7等都是素数。
素数具有许多独特的性质,如素数无限性、素数间的关系、素数的应用等。
II.常见的求素数个数方法-------------1.试除法:通过不断试除每个整数,判断是否能被整除来判断该数是否为素数。
但效率较低,对于大数可能超时。
2.埃拉托色尼筛选法:通过筛选掉2、3、5等合数,缩小素数的搜索范围,但依然存在效率问题。
3.筛法:利用素数分布定理,先预处理出一部分素数,再用剩余的数除以已预处理的素数的余数来判断是否为素数。
但需要预处理,且对于大数仍存在超时问题。
III.C语言求素数个数方法-------------C语言求素数个数的方法主要有试除法和筛法两种。
试除法可以通过循环遍历每个整数,判断是否能被整除来判断该数是否为素数。
但效率较低,对于大数可能超时。
筛法可以利用预处理过的素数表来快速判断一个数是否为素数。
但需要预处理,且对于大数仍存在超时问题。
为了解决这些问题,我们可以使用摩尔投票筛法来优化C语言求素数个数的方法。
摩尔投票筛法的基本思想是利用试除法筛选掉大部分合数,再用剩余的合数除以已筛选的合数的余数来判断是否为素数。
具体实现步骤如下:1.初始化一个数组p,p[i]表示第i个合数的因子个数。
例如,p[2]=1,p[3]=2,p[5]=1,p[7]=2,p[11]=3,p[13]=2,p[17]=3,p[19]=2,p[31]=4等。
2.初始化一个数组t,t[i]表示第i个合数的因子个数是否大于等于p[i]。
例如,t[2]=0,t[3]=0,t[5]=0,t[7]=0,t[11]=0,t[13]=0,t[17]=0,t[19]=0,t[3 1]=0等。
C语言求素数问题算法

1.自然数是0,1,2……2.素数是2,3,5……(不包括1的只能背1和它本身整除的自然数)【1】求10000以内的所有素数。
素数是除了1和它本身之外再不能被其他数整除的自然数。
由于找不到一个通项公式来表示所有的素数,所以对于数学家来说,素数一直是一个未解之谜。
像著名的哥德巴赫猜想、孪生素数猜想,几百年来不知吸引了世界上多少优秀的数学家。
尽管他们苦心钻研,呕心沥血,但至今仍然未见分晓。
自从有了计算机之后,人们借助于计算机的威力,已经找到了2216091以内的所有素数。
求素数的方法有很多种,最简单的方法是根据素数的定义来求。
对于一个自然数N,用大于1小于N的各个自然数都去除一下N,如果都除不尽,则N为素数,否则N为合数。
但是,如果用素数定义的方法来编制计算机程序,它的效率一定是非常低的,其中有许多地方都值得改进。
第一,对于一个自然数N,只要能被一个非1非自身的数整除,它就肯定不是素数,所以不必再用其他的数去除。
第二,对于N来说,只需用小于N的素数去除就可以了。
例如,如果N能被15整除,实际上就能被3和5整除,如果N不能被3和5整除,那么N也决不会被15整除。
第三,对于N来说,不必用从2到N一1的所有素数去除,只需用小于等于√N(根号N)的所有素数去除就可以了。
这一点可以用反证法来证明:如果N是合数,则一定存在大于1小于N的整数d1和d2,使得N=d1×d2。
如果d1和d2均大于√N,则有:N=d1×d2>√N×√N=N。
而这是不可能的,所以,d1和d2中必有一个小于或等于√N。
基于上述分析,设计算法如下:(1)用2,3,5,7逐个试除N的方法求出100以内的所有素数。
(2)用100以内的所有素数逐个试除的方法求出10000以内的素数。
首先,将2,3,5,7分别存放在a[1]、a[2]、a[3]、a[4]中,以后每求出一个素数,只要不大于100,就依次存放在A 数组中的一个单元中。
C语言常用数值计算算法(素数、公约数、级数、方程根和定积分)
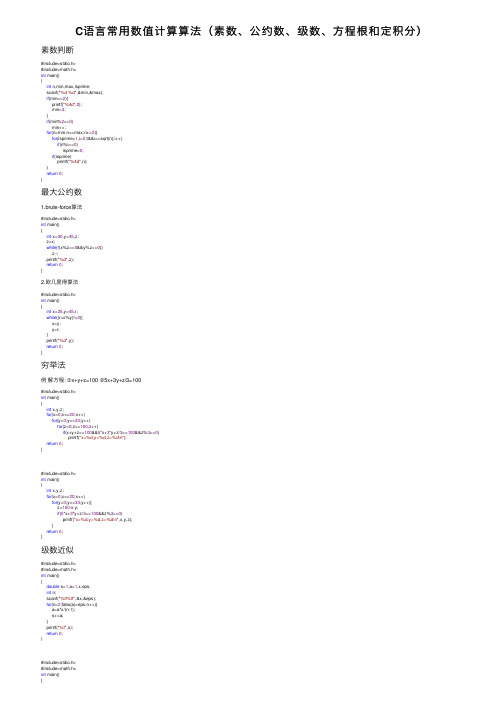
C语⾔常⽤数值计算算法(素数、公约数、级数、⽅程根和定积分)素数判断#include<stdio.h>#include<math.h>int main(){int n,min,max,isprime;scanf("%d %d",&min,&max);if(min<=2){printf("%4d",2);min=3;}if(min%2==0)min++;for(n=min;n<=max;n+=2){for(isprime=1,i=2;t&&i<=sqrt(n);i++)if(n%i==0)isprime=0;if(isprime)printf("%4d",n);}return0;}最⼤公约数1.brute-force算法#include<stdio.h>int main(){int x=30,y=45,z;z=x;while(!(x%z==0&&y%z==0))z--;printf("%d",z);return0;}2.欧⼏⾥得算法#include<stdio.h>int main(){int x=35,y=45,r;while((r=x%y)!=0){x=y;y=r;}printf("%d",y);return0;}穷举法例解⽅程: ①x+y+z=100 ②5x+3y+z/3=100#include<stdio.h>int main(){int x,y,z;for(x=0;x<=20;x++)for(y=0;y<=33;y++)for(z=0;z<=100;z++)if(x+y+z==100&&5*x+3*y+z/3==100&&z%3==0)printf("x=%d,y=%d,z=%d\n");return0;}#include<stdio.h>int main(){int x,y,z;for(x=0;x<=20;x++)for(y=0;y<=33;y++){z=100-x-y;if(5*x+3*y+z/3==100&&z%3==0)printf("x=%d,y=%d,z=%d\n",x,y,z);}return0;}级数近似#include<stdio.h>#include<math.h>int main(){double s=1,a=1,x,eps;int n;scanf("%lf%lf",&x,&eps);for(n=2;fabs(a)>eps;n++){a=a*x/(n-1);s+=a;}printf("%f",s);return0;)#include<stdio.h>#include<math.h>int main(){double sum,x,eps=1e-6,fn,tn;int s=1,n=2;scanf("%lf",&x);s=fn=x;do{s=-s;fn=fn*(2*n-3)/(2*n-2)*x*x;tn=sign*fn/(2*n-1);sum=sum+tn;n++;}while(fabs(tn)>eps);printf("%f",sum);⼀元⾮线性⽅程求根⼀、⽜顿迭代法 1.基本概念:如果函数连续,且待求零点孤⽴,那么在零点周围存在⼀个区域,当初值在这个邻域内时,⽜顿法收敛。
统计素数并求和c语言

统计素数并求和c语言素数的定义是,除了1和其自身可以被整除的数。
它们只能被1和自身整除,这种数叫做素数。
素数是自然数中的一种特殊的数,在数学中有许多素数的抽象理论。
在实际的编程应用中,统计素数及其求和是一个非常简单的操作,在c语言中,有两种方式可以实现这种功能:一种是通过“埃拉托斯特尼筛法”来求出一定范围内的素数,所谓“筛法”,是指将一定范围内的数字(从2开始)一个个“筛掉”,带被被筛当然都是素数,但是也可能会被2,3,5,7,11等素数筛掉。
然后再将剩下的数字全部相加,就可以得到该范围内的素数的和。
另一种是通过线性排序的方法来求解,将一定范围内的数字从小到大依次排列,然后将每一个数字除以它的前一个数字,如果出现余数。
则说明这个数字是一个素数,将所有的素数相加,就可以得到该范围内的素数的和。
总的来说,c语言中统计素数并求和有以上两种方法,下面将介绍利用埃拉托斯特尼筛法实现统计素数及求和的编程实例,以便读者能够更好地理解两种方法的应用。
编程实例:利用“埃拉托斯特尼筛法”统计素数并求和//求出从1~N的素数并求和#include <stdio.h>int main(void) {int N=1000; //要求求出从1~N的素数int prime[N+1],sum=0; //prime[N+1]用来标记是否为素数for(int i=0;i<N+1;i++) //初始化,全部初始化为1prime[i]=1;for(int i=2;i<=N;i++) { //从2开始筛选if(prime[i]==0) continue; //如果不是素数,则跳过for(int j=2*i;j<=N;j+=i) //将i倍数筛掉prime[j]=0;sum+=i;//求和}printf(从1~%d的素数和为:%dN,sum);return 0;}上面的程序中,首先用一个数组prime[N+1]来标记是否为素数,全部初始化为1,然后从2开始进行筛选,找出所有的素数,并将素数求和。
素数对猜想c语言

素数对猜想c语言素数对猜想是一个数学问题,它要求找到两个素数,它们的差是唯一的偶数。
在 C 语言中,可以通过编写程序来搜索符合条件的素数对。
以下是一个简单的实现方法:1. 先定义一个数组,其中存储着所有小于给定规模的素数。
2. 然后定义一个变量表示当前已知的最小素数,它每次被找到时都会被更新。
3. 在循环中,每次迭代都会检查当前已知的最小素数是否等于当前数值,如果是,那么它就被更新为当前数值减去 2。
4. 如果当前数值是偶数,那么就需要检查是否存在已知的素数对,如果存在,那么就需要更新这些素数对中任意一对的数值。
5. 重复执行循环,直到找到符合条件的素数对或者确定不存在符合条件的素数对。
以下是一个示例代码,它使用上述方法搜索符合条件的素数对: ```c#include <stdio.h>#include <stdbool.h>// 存储所有小于给定规模的素数的数组int prime_array[100001];// 初始化所有素数void initialize_prime_array() {for (int i = 2; i <= sqrt(prime_array[0]); i++) {if (prime_array[i] == 0) {prime_array[i] = 1;}}}// 查找符合条件的素数对bool find_prime_pair(int min_prime, int max_prime) { bool found_pair = false;// 更新最小素数int current_prime = min_prime;while (current_prime != max_prime) {if (prime_array[current_prime] == 0) {current_prime = prime_array[current_prime] + 2;found_pair = true;break;}current_prime++;}return found_pair;}int main() {initialize_prime_array();bool found_pair = find_prime_pair(2, 100000);if (found_pair) {printf("The prime pair is %d and %d", found_pair ? 2 : 1, found_pair + 2);} else {printf("No prime pair is found");}return 0;}```该程序使用 `prime_array` 数组来存储所有小于给定规模的素数,`initialize_prime_array` 函数用于初始化所有素数,`find_prime_pair` 函数用于查找符合条件的素数对,`main` 函数是程序的主函数。
最大素数c语言

最大素数的求解1. 什么是素数?素数是指只能被1和自身整除的正整数。
在数学中,素数也被称为质数。
素数是数字领域中的基本概念,对于很多数论问题都起到了至关重要的作用。
2. 如何判断一个数是否为素数?判断一个数是否为素数有多种方法,下面介绍两种常用的判断素数的方法。
2.1 蛮力法蛮力法是一种最简单直接的判断素数的方法,其基本思想是对待判断的数从2开始,逐个除以所有小于它的自然数,如果能被除尽,则该数不是素数;如果不能被除尽,则该数是素数。
蛮力法的C语言代码如下:#include <stdio.h>int isPrime(int num) {if (num < 2) {return 0;}for (int i = 2; i * i <= num; i++) {if (num % i == 0) {return 0;}}return 1;}int main() {int n;printf("请输入一个正整数: ");scanf("%d", &n);if (isPrime(n)) {printf("%d是素数\n", n);} else {printf("%d不是素数\n", n);}return 0;}2.2 埃氏筛法埃氏筛法是一种更高效的判断素数的方法,其基本思想是从2开始,将每个素数的倍数标记为合数,直到遍历完所有小于等于待判断数的自然数,剩下的未被标记的数即为素数。
埃氏筛法的C语言代码如下:#include <stdio.h>#include <stdbool.h>void sieveOfEratosthenes(int n) {bool isPrime[n+1];for (int i = 2; i <= n; i++) {isPrime[i] = true;}for (int i = 2; i * i <= n; i++) {if (isPrime[i]) {for (int j = i * i; j <= n; j += i) {isPrime[j] = false;}}}printf("小于等于%d的素数有: ", n);for (int i = 2; i <= n; i++) {if (isPrime[i]) {printf("%d ", i);}}printf("\n");}int main() {int n;printf("请输入一个正整数: ");scanf("%d", &n);sieveOfEratosthenes(n);return 0;}3. 求解最大素数有了判断素数的方法,我们可以通过遍历一定范围内的数,找到其中的最大素数。
素数c语言程序编写

素数c语言程序编写素数是指只能被1和自身整除的正整数,如2、3、5、7等。
在计算机编程中,判断一个数是否为素数是一个常见的问题。
下面我们来介绍一下如何用C语言编写素数程序。
首先,我们需要明确一个概念:质数。
质数是指除了1和本身之外,不能被其他正整数整除的正整数。
因此,素数和质数是同义词。
接下来,我们来看一下如何用C语言编写素数程序。
下面是一个简单的示例代码:```#include <stdio.h>int main(){int n, i, flag = 0;printf("Enter a positive integer: ");scanf("%d", &n);for(i=2; i<=n/2; ++i){if(n%i == 0){flag = 1;break;}}if (n == 1){printf("1 is not a prime number.\n");}else{if (flag == 0)printf("%d is a prime number.\n", n);elseprintf("%d is not a prime number.\n", n); }return 0;}```这个程序的作用是判断输入的正整数是否为素数。
程序首先要求用户输入一个正整数,然后通过for循环从2开始到n/2进行遍历,判断n是否能被i整除。
如果能被整除,则说明n不是素数,将flag标记为1,跳出循环。
最后根据flag的值输出结果。
需要注意的是,1不是素数,因此需要特殊处理。
如果输入的是1,则直接输出“1 is not a prime number.”。
此外,还有一些优化的方法可以提高程序的效率。
比如,可以只遍历到sqrt(n)即可,因为如果n能被大于sqrt(n)的数整除,那么一定能被小于sqrt(n)的数整除。
C语言求质数

【C语言】求解素数(质数)的N种境界★试除法:首先要介绍的,当然非"试除法"莫属。
"试除",顾名思义,就是不断地尝试能否整除。
比如要判断自然数x 是否质数,就不断尝试小于x 且大于1的自然数,只要有一个能整除,则x 是合数;否则,x 是素数。
显然,试除法是最容易想到的思路。
不客气地说,也是最平庸的思路。
不过呢,这个最平庸的思路,也有好多种境界。
不信请看下文:◎境界1假设要判断x 是否为质数,就从2 一直尝试到x-1。
这种做法,其效率应该是最差的1.#include<stdio.h>2.#include<Windows.h>3.int main()4.{5. int i = 0,k = 0;6. int count = 0;7. for(i=100; i<=200; i++)8. {9. for(k=2; k<i; k++)10. {11. if(i%k == 0)12. break;13. }14. if(k == i)15. printf("%d是素数\n",i);16. count++;17. }18. printf("\n%4d",count);19. system("pause");20. return 0;}◎境界2所有素数都是偶数,因此可以加快步长1.#include<stdio.h>2.#include<Windows.h>3.int main()4.{5. int i = 0, k = 0;6. int count = 0;7. for(i=101; i<=200; i+=2)8. {9. for(k=2; k<i; k++)10. {11. if(i%k == 0)12. break;13. }14. if(k==i)15. printf("%d是素数\n",i);16. count++;17. }18. printf("\n%4d",count);19. system("pause");20. return 0;21.}◎境界3除了2以外,所有可能的质因数都是奇数。
C语言判断素数

注意,这个示例中的判断素数的算法是一种简单但有效的方法,但对于大数可能不够高效。 如果需要处理大数的素数判断,可以考虑使用更高级的算法,如 Miller-Rabin 算法或 AKS 素数测试算法。
}
rHale Waihona Puke turn 1; // 是素数 }int main() { int num; printf("请输入一个正整数: "); scanf("%d", &num);
if (isPrime(num)) { printf("%d 是素数\n", num);
} else { printf("%d 不是素数\n", num);
判断一个数是否为素数是一个常见的数学问题。素数是指只能被 1 和自身整除的正整数。下 面是一个使用 C 语言判断素数的示例:
c 复制代码
#include <stdio.h>
int isPrime(int num) { if (num <= 1) { return 0; // 不是素数 }
for (int i = 2; i * i <= num; i++) { if (num % i == 0) { return 0; // 不是素数 }
}
return 0; }
在这个示例中,我们定义了一个函数 isPrime 来判断一个数是否为素数。首先,我们判断 如果数小于等于 1,则不是素数。然后,我们使用一个循环从 2 开始,逐个判断是否能整除 该数。如果能整除,则不是素数。循环的终止条件是 i 的平方大于等于该数,这是因为如果 存在大于 i 的因子,那么必然存在小于等于 i 的因子。最后,如果循环结束仍未找到能整除 的因子,则该数是素数。 在 main 函数中,我们从用户输入中获取一个正整数,并调用 isPrime 函数来判断是否为素 数,然后输出结果。
C语言判断素数(求素数)(两种方法)

C语言判断素数(求素数)(两种方法)素数又称质数。
所谓素数是指除了 1 和它本身以外,不能被任何整数整除的数,例如17就是素数,因为它不能被 2~16 的任一整数整除。
思路1):因此判断一个整数m是否是素数,只需把 m 被 2 ~ m-1 之间的每一个整数去除,如果都不能被整除,那么 m 就是一个素数。
思路2):另外判断方法还可以简化。
m 不必被 2 ~ m-1 之间的每一个整数去除,只需被 2 ~ 之间的每一个整数去除就可以了。
如果 m 不能被 2 ~ 间任一整数整除,m 必定是素数。
例如判别 17 是是否为素数,只需使 17 被 2~4 之间的每一个整数去除,由于都不能整除,可以判定 17 是素数。
原因:因为如果 m 能被 2 ~ m-1 之间任一整数整除,其二个因子必定有一个小于或等于,另一个大于或等于。
例如16 能被 2、4、8 整除,16=2*8,2 小于 4,8 大于 4,16=4*4,4=√16,因此只需判定在 2~4 之间有无因子即可。
两种思路的代码请看解析。
思路1) 的代码:#include <stdio.h>int main(){int a=0; // 素数的个数int num=0; // 输入的整数printf("输入一个整数:");scanf("%d",&num);for(int i=2;i<num;i++){if(num%i==0){a++; // 素数个数加1}}if(a==0){printf("%d是素数。
\n", num);}else{printf("%d不是素数。
\n", num);}return 0;}思路2)的代码:#include <stdio.h>#include <math.h>void main(){int m; // 输入的整数int i; // 循环次数int k; // m 的平方根printf("输入一个整数:");scanf("%d",&m);// 求平方根,注意sqrt()的参数为 double 类型,这里要强制转换m的类型k=(int)sqrt( (double)m );for(i=2;i<=k;i++)if(m%i==0)break;// 如果完成所有循环,那么m为素数// 注意最后一次循环,会执行i++,此时 i=k+1,所以有i>kif(i>k)printf("%d是素数。
c语言求素数个数方法超时

c语言求素数个数方法超时【实用版3篇】篇1 目录1.素数概念及求解方法2.C 语言实现求素数个数的方法3.求素数个数的算法复杂度4.避免算法超时的方法篇1正文1.素数概念及求解方法素数是指在大于 1 的自然数中,除了 1 和该数自身,不能被其他自然数整除的数。
求解素数的方法有很多,其中较为常见的有埃拉托斯特尼筛法(Sieve of Eratosthenes)和试除法等。
2.C 语言实现求素数个数的方法这里我们以埃拉托斯特尼筛法为例,介绍如何用 C 语言实现求素数个数的方法。
```c#include <stdio.h>#include <stdbool.h>bool is_prime(int num, int* primes) {for (int i = 0; primes[i] <= sqrt(num); i++) {if (num % primes[i] == 0) {return false;}}return true;}int count_primes(int n) {int* primes = (int*)malloc(n * sizeof(int)); int prime_count = 0;for (int i = 2; i <= n; i++) {if (is_prime(i, primes)) {primes[prime_count++] = i;}}for (int i = 0; i < prime_count; i++) {printf("%d ", primes[i]);}free(primes);return prime_count;}int main() {int n;printf("请输入整数 n:");scanf("%d", &n);int prime_count = count_primes(n);printf("小于等于%d的素数个数为:%d", n, prime_count);return 0;}```3.求素数个数的算法复杂度上述算法的时间复杂度主要取决于筛法的迭代次数,为 O(n *log(log(n))),空间复杂度为 O(n)。
c语言两个数之间的素数

以下是一个C语言程序,用于查找两个数之间的素数:
```c
#include <stdio.h>
#include <stdbool.h>
// 判断一个数是否为素数
bool is_prime(int n) {
if (n <= 1) {
return false;
}
for (int i = 2; i * i <= n; i++) {
if (n % i == 0) {
return false;
}
}
return true;
}
int main() {
int a, b;
printf("请输入两个数:");
scanf("%d %d", &a, &b);
printf("在 %d 和 %d 之间的素数有:", a, b);
for (int i = a; i <= b; i++) {
if (is_prime(i)) {
printf("%d ", i);
}
}
printf("\n");
return 0;
}
```
在上述代码中,我们定义了一个is_prime函数,用于判断一个数是否为素数。
该函数使用试除法,从2开始遍历到该数的平方根,判断是否存在能够整除该数的因子。
如果存在,则该数不是素数;否则,该数是素数。
在主函数中,我们使用scanf函数从标准输入中读取两个整数a和b,然后使用for循环遍历a到b之间的所有整数,判断每个整数是否为素数。
如果是素数,则输出该整数。
c语言判断素数的函数程序

c语言判断素数的函数程序一、题目背景素数是指只能被1和自身整除的正整数。
在计算机编程中,判断一个数是否为素数是一项基础且常见的操作。
本文将介绍如何用C语言编写一个判断素数的函数程序。
二、函数原型判断素数的函数原型如下:int is_prime(int n);其中,n为待判断的正整数,函数返回值为1表示n是素数,返回值为0表示n不是素数。
三、算法思路判断一个正整数是否为素数的方法有很多种,本文将介绍两种常见的方法:试除法和埃氏筛法。
1. 试除法试除法是最简单直观的一种方法。
它的基本思路是:将待判断的正整数n分别除以2到sqrt(n)之间的每个正整数m,如果存在任意一个m使得n能够被m整除,则n不是素数;否则n是素数。
2. 埃氏筛法埃氏筛法又称“爱氏筛法”,它可以在O(nloglogn)时间复杂度内求出小于等于n(其中n为正整数)的所有素数。
该方法基于以下性质:如果一个正整数x不是素数,则它可以表示成两个较小正整数p和q(x=pq)的乘积形式。
如果p和q均大于sqrt(x),则它们的乘积也一定大于x,这与x=pq矛盾。
因此,只需要考虑sqrt(n)以内的正整数是否为素数即可。
四、函数实现1. 试除法实现下面是一个使用试除法判断素数的C语言函数实现:int is_prime(int n){if (n < 2) // 小于2的数不是素数return 0;for (int i = 2; i * i <= n; i++) // 只需循环到sqrt(n)即可if (n % i == 0)return 0;return 1;}2. 埃氏筛法实现下面是一个使用埃氏筛法判断素数的C语言函数实现:int is_prime(int n){if (n < 2) // 小于2的数不是素数return 0;int prime[n + 1]; // 标记数组,用来记录每个数字是否为素数 memset(prime, 1, sizeof(prime));for (int i = 2; i * i <= n; i++) // 只需循环到sqrt(n)即可if (prime[i]) // 如果i是素数,则将i的倍数都标记为非素数 for (int j = i * i; j <= n; j += i)prime[j] = 0;return prime[n];五、函数测试下面是一个使用上述函数判断素数的示例程序:#include <stdio.h>int is_prime(int n);int main(){int n;printf("请输入一个正整数:");scanf("%d", &n);if (is_prime(n))printf("%d是素数。
求出200——1000之间所有的素数

C语言程序设计综合实验报告学院:信息科学与工程学院专业:自动化1002班学号:201004134070 姓名:吴君指导老师:2011年6月25日武汉科技大学求出200——1000之间所有的素数,要求1)调用函数判断某数是不是素数;2)输出结果,每行输出十个;程序:#include<stdio.h>#include<math.h>int judge(int n)//定义一个函数{int i,k;k=sqrt(n);for(i=2;i<=k;i++)//判断I是否是素数{if(n%i==0){ break;}}if (i>k){return 1;//返回一个函数值}return 0;}void main(){int i,m,k;for(i=201;i<1000;i=i+2){m=judge(i);//调用自定义函数if (m==1){printf("%4d",i); //输出结果k++;if(k%10==0)//大于10换行printf("\n");}}}输出结果:211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641643 647 653 659 661 673 677 683 691 701709 719 727 733 739 743 751 757 761 769773 787 797 809 811 821 823 827 829 839853 857 859 863 877 881 883 887 907 911919 929 937 941 947 953 967 971 977 983991 997Press any key to continue利用随机函数产生200个正整数,统计这200个正整数中相同的个数。
使用函数求素数和c语言

使用函数求素数1. 素数的定义在数学中,素数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的数。
换句话说,素数只能被1和它自己整除,不能被其他数整除。
例如,2、3、5、7、11、13等都是素数。
而4、6、8、9、10、12等不是素数。
2. 求素数的一般方法要判断一个数是否为素数,一般的方法是逐个除以2到该数的平方根之间的所有整数,如果能整除则不是素数。
这种方法的时间复杂度较高,特别是对于大数来说,计算会很慢。
而更高效的方法是采用筛选法。
简单来说,筛选法的基本思想是从2开始,将每个素数的倍数标记为合数,直到没有合数为止。
这样剩下的都是素数。
3. 使用函数求素数的过程在C语言中,我们可以编写一个函数来实现求素数的功能。
下面是一个例子:#include <stdio.h>#include <stdbool.h>bool isPrime(int number);int main() {int n;printf("请输入一个正整数:");scanf("%d", &n);printf("小于等于%d的素数有:\n", n);for (int i = 2; i <= n; i++) {if (isPrime(i)) {printf("%d ", i);}}return 0;}bool isPrime(int number) {if (number <= 1) {return false;}for (int i = 2; i * i <= number; i++) {if (number % i == 0) {return false;}}return true;}以上代码中,isPrime函数用于判断一个数是否为素数。
它接受一个参数number,表示需要判断的数,返回一个bool值,表示是否为素数(true表示是素数,false表示不是素数)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.自然数是0,1,2……2.素数是2,3,5……(不包括1的只能背1和它本身整除的自然数)【1】求10000以内的所有素数。
素数是除了1和它本身之外再不能被其他数整除的自然数。
由于找不到一个通项公式来表示所有的素数,所以对于数学家来说,素数一直是一个未解之谜。
像著名的哥德巴赫猜想、孪生素数猜想,几百年来不知吸引了世界上多少优秀的数学家。
尽管他们苦心钻研,呕心沥血,但至今仍然未见分晓。
自从有了计算机之后,人们借助于计算机的威力,已经找到了2216091以内的所有素数。
求素数的方法有很多种,最简单的方法是根据素数的定义来求。
对于一个自然数N,用大于1小于N的各个自然数都去除一下N,如果都除不尽,则N为素数,否则N为合数。
但是,如果用素数定义的方法来编制计算机程序,它的效率一定是非常低的,其中有许多地方都值得改进。
第一,对于一个自然数N,只要能被一个非1非自身的数整除,它就肯定不是素数,所以不必再用其他的数去除。
第二,对于N来说,只需用小于N的素数去除就可以了。
例如,如果N能被15整除,实际上就能被3和5整除,如果N不能被3和5整除,那么N也决不会被15整除。
第三,对于N来说,不必用从2到N一1的所有素数去除,只需用小于等于√N(根号N)的所有素数去除就可以了。
这一点可以用反证法来证明:如果N是合数,则一定存在大于1小于N的整数d1和d2,使得N=d1×d2。
如果d1和d2均大于√N,则有:N=d1×d2>√N×√N=N。
而这是不可能的,所以,d1和d2中必有一个小于或等于√N。
基于上述分析,设计算法如下:(1)用2,3,5,7逐个试除N的方法求出100以内的所有素数。
(2)用100以内的所有素数逐个试除的方法求出10000以内的素数。
首先,将2,3,5,7分别存放在a[1]、a[2]、a[3]、a[4]中,以后每求出一个素数,只要不大于100,就依次存放在A 数组中的一个单元中。
当我们求100—10000之间的素数时,可依次用a[1]-a[2]的素数去试除N,这个范围内的素数可以不保存,直接打印。
【2】用筛法求素数。
简单介绍一下厄拉多塞筛法。
厄拉多塞是一位古希腊数学家,他在寻找素数时,采用了一种与众不同的方法:先将2-N的在2的上面画一个圆圈,然后划去2的其他倍数;第一个既未画圈又没有被划去的数是3,将它画圈,再划去3的其他倍数;现在既未画圈又没有被划去的第一个数是5,将它画圈,并划去5的其他倍数……依次类推,一直到所有小于或等于N 的各数都画了圈或划去为止。
这时,表中画了圈的以及未划去的那些数正好就是小于N的素数。
这很像一面筛子,把满足条件的数留下来,把不满足条件的数筛掉。
由于这种方法是厄拉多塞首先发明的,所以,后人就把这种方法称作厄拉多塞筛法。
在计算机中,筛法可以用给数组单元置零的方法来实现。
具体来说就是:首先开一个数组:a[i],i=1,2,3,…,同时,令所有的数组元素都等于下标值,即a[i]=i,当i不是素数时,令a[i]=0 。
当输出结果时,只要判断a[i]是否等于零即可,如果a[i]=0,则令i=i+1,检查下一个a[i]。
筛法是计算机程序设计中常用的算法之一。
【3】用6N±1法求素数。
任何一个自然数,总可以表示成为如下的形式之一:6N,6N+1,6N+2,6N+3,6N+4,6N+5 (N=0,1,2,…)显然,当N≥1时,6N,6N+2,6N+3,6N+4都不是素数,只有形如6N+1和6N+5的自然数有可能是素数。
所以,除了2和3之外,所有的素数都可以表示成6N±1的形式(N为自然数)。
根据上述分析,我们可以构造另一面筛子,只对形如6 N±1的自然数进行筛选,这样就可以大大减少筛选的次数,从而进一步提高程序的运行效率和速度。
在程序上,我们可以用一个二重循环实现这一点,外循环i按3的倍数递增,内循环j为0-1的循环,则2(i+j)-1恰好就是形如6N±1的自然数。
代码:时间复杂度O(n).代码:时间复杂度O(n/2), 速度提高一倍.定理: 如果n不是素数, 则n有满足1<d<=sqrt(n)的一个因子d.证明: 如果n不是素数, 则由定义n有一个因子d满足1<d<n.如果d大于sqrt(n), 则n/d是满足1<n/d<=sqrt(n)的一个因子.代码: 时间复杂度O(sqrt(n)/2), 速度提高O((n-sqrt(n))/2).例如: 11%3 != 0 可以确定11%(3*i) != 0.定理: 如果n不是素数, 则n有满足1<d<=sqrt(n)的一个"素数"因子d.证明:I1. 如果n不是素数, 则n有满足1< d <=sqrt(n)I2. 如果d是素数, 则定理得证, 算法终止.I3. 令n=d, 并转到步骤I1.由于不可能无限分解n的因子, 因此上述证明的算法最终会停止.代码:假设n范围内的素数个数为PI(n), 则时间复杂度O(PI(sqrt(n))).函数PI(x)满足素数定理: ln(x)-3/2 < x/PI(x) < ln(x)-1/2, 当x >= 67时.因此O(PI(sqrt(n)))可以表示为O(sqrt(x)/(ln(sqrt(x))-3/2)),O(sqrt(x)/(ln(sqrt(x))-3/2))也是这个算法的空间复杂度.5. 构造素数序列primes[i]: 2, 3, 5, 7, ...由4的算法我们知道, 在素数序列已经被构造的情况下, 判断n是否为素数效率很高; 但是, 在构造素数序列本身的时候, 是否也可是达到最好的效率呢?事实上这是可以的! -- 我们在构造的时候完全可以利用已经被构造的素数序列!假设我们已经我素数序列: p1, p2, .. pn现在要判断pn+1是否是素数, 则需要(1, sqrt(pn+1)]范围内的所有素数序列,而这个素数序列显然已经作为p1, p2, .. pn的一个子集被包含了!代码:在一定的应用范围内, 我们可以把近似认为makePrimes需要常数时间.在后面的讨论中, 我们将探讨一种对计算机而言更好的makePrimes方法.6. 更好地利用计算机资源...当前的主流PC中, 一个整数的大小为2^32. 如果需要判断2^32大小的数是否为素数,则可能需要测试[2, 2^16]范围内的所有素数(2^16 == sqrt(2^32)).由4中提到的素数定理我们可以大概确定[2, 2^16]范围内的素数个数.由于2^16/(ln(2^16)-1/2) = 6138, 2^16/(ln(2^16)-3/2) = 6834,我们可以大概估计出[2, 2^16]范围内的素数个数6138 < PI(2^16) < 6834.在对[2, 2^16]范围内的素数进行统计, 发现只有6542个素数:p_6542: 65521, 65521^2 = 4293001441 < 2^32, (2^32 = 4294967296)p_6543: 65537, 65537^2 = 4295098369 > 2^32, (2^32 = 4294967296)在实际运算时unsigned long x = 4295098369;将发生溢出, 为131073.在程序中, 我是采用double类型计算得到的结果.分析到这里我们可以看到, 我们只需要缓冲6543个素数, 我们就可以采用4中的算法高效率地判断[2, 2^32]如此庞大范围内的素数!(原本的2^32大小的问题规模现在已经被减小到6543规模了!)虽然用现在的计算机处理[2, 2^16]范围内的6542个素数已经没有一点问题,虽然makePrimes只要被运行一次就可以, 但是我们还是考虑一下是否被改进的可能?!我想学过java的人肯定想把makePrimes作为一个静态的初始化实现, 在C++中也可以模拟java中静态的初始化的类似实现:#define NELEMS(x) ((sizeof(x)) / (sizeof((x)[0])))static int primes[6542+1];static struct _Init { _Init(){makePrimes(primes, NELEMS(primes);} } _init;如此, 就可以在程序启动的时候自动掉用makePrimes初始化素数序列.但, 我现在的想法是: 为什么我们不能在编译的时候调用makePrimes函数呢?完全可以!!! 代码如下:有点不可思议吧, 原本makePrimes需要花费的时间复杂度现在真的变成O(1)了!(我觉得叫O(0)可能更合适!) 7. 二分法查找现在我们缓存了前大约sqrt(2^32)/(ln(sqrt(2^32)-3/2))个素数列表, 在判断2^32级别的素数时最多也只需要PI(sqrt(2^32))次判断(准确值是6543次), 但是否还有其他的方式判断呢?当素数比较小的时候(不大于2^16), 是否可以直接从缓存的素数列表中直接查询得到呢?答案是肯定的! 由于primes是一个有序的数列, 因此我们当素数小于2^16时, 我们可以直接采用二分法从primes中查询得到(如果查询失败则不是素数).代码:时间复杂度:if(n <= primes[NELEMS(primes)-1] && n >= 67): O(log2(NELEMS(primes))) < 13;if(n > primes[NELEMS(primes)-1]): O(PI(sqrt(n))) <= NELEMS(primes).8. 素数定理+2分法查找在7中, 我们对小等于primes[NELEMS(primes)-1]的数采用2分法查找进行判断.我们之前针对2^32缓冲的6453个素数需要判断的次数为13次(log2(1024*8) == 13).对于小的素数而言(其实就是2^16范围只内的数), 13次的比较已经完全可以接受了.不过根据素数定理: ln(x)-3/2 < x/PI(x) < ln(x)-1/2, 当x >= 67时, 我们依然可以进一步缩小小于2^32情况的查找范围(现在是0到NELEMS(primes)-1范围查找).我们需要解决问题是(n <= primes[NELEMS(primes)-1):如果n为素数, 那么它在素数序列可能出现的范围在哪?---- (n/(ln(n)-1/2), n/(ln(n)-3/2)), 即素数定理!上面的代码修改如下:时间复杂度:if(n <= primes[NELEMS(primes)-1] && n >= 67): O(log2(hi-lo))) < ???;if(n > primes[NELEMS(primes)-1]): O(PI(sqrt(n))) <= NELEMS(primes).9. 打包成素数库(给出全部的代码)到目前为止, 我已经给出了我所知道所有改进的方法(如果有人有更好的算法感谢告诉我).这里需要强调的一点是, 这里讨论的素数求法是针对0-2^32范围的数而言, 至于像寻找成百上千位大小的数不在此讨论范围, 那应该算是纯数学的内容了.代码保存在2个文件: prime.h, prime.cpp.代码:到这里, 关于素数的讨论基本告一段落. 回顾我们之前的求解过程, 我们会发现如果缺少数学的基本知识会很难设计好的算法; 但是如果一味地只考虑数学原理,而忽律了计算机的本质特征, 也会有同样的问题.一个很常见的例子就是求Fibonacci数列. 当然方法很多, 但是在目前的计算机中都没有实现的必要!因为Fibonacci数列本身是指数增长的, 32位的有符号整数所能表示的位置只有前46个:因此, 我只需要把前46个Fibonacci数保存到数组中就可以搞定了!比如: F(int i) = {return Fibonacci[i];} 非常简单, 效率也非常好.。
