盖斯定律应用
盖斯定律及其应用

盖斯定律及其应用盖斯定律化学反应的反应热只与反应的始态(各反应物)和终态(各生成物)有关,而与具体反应进行的途径无关,如果一个反应可以分几步进行,则各分步及反应的反应热之和与该反应一步完成的反应热是相同的,这就是盖斯定律。
例如:122(g)2(g)2(l)H 2(g)2(g)2(l)H 2(g)H 1H O H O 21H O H O 2H O ∆∆∆+=+−−→ 可以通过两种途径来完成。
如上图表:已知: 2(g)2(g)2(g)11H O H O ;H 241.8kJ /mol 2+=∆=- 2g 2l 2H O H O H 44.0kJ /mol =∆=()();- 根据盖斯定律,则12H H H 241.8kJ /mol 44.0kJ /mol 285.8kJ /mol ∆=∆∆=+=+-(-)- 其数值与用量热计测得的数据相同。
盖斯定律的应用盖斯定律:当某一物质在定温定压下经过不同的反应过程,生成同一物质时,无论反应是一步完成还是分几步完成,总的反应热是相同的。
即反应热只与反应始态(各反应物)和终态(各生成物)有关,而与具体反应的途径无关。
应用盖斯定律进行简单计算,关键在于设计反应过程,同时注意:⑴ 当反应式乘以或除以某数时,△H 也应乘以或除以某数。
⑵ 反应式进行加减运算时,△H 也同样要进行加减运算,且要带“+”、“-”符号,即把△H 看作一个整体进行运算。
⑶ 通过盖斯定律计算比较反应热的大小时,同样要把△H 看作一个整体。
⑷ 在设计的反应过程中常会遇到同一物质固、液、气三态的相互转化,状态由固→液→气变化时,会吸热;反之会放热。
⑸ 当设计的反应逆向进行时,其反应热与正反应的反应热数值相等,符号相反。
【例1】.已知⑴ ()()()2221g g g 1H O H O H akJ /mol 2+=∆;= ⑵ ()()()2222g g g 2H O 2H O H bkJ /mol +=∆;=⑶ ()()()2223g g l 1H O H O H ckJ /mol 2+=∆;= ⑷ ()()()2224g g l 2H O 2H O H dkJ /mol +=∆;=下列关系式中正确的是( )A .a <c <0B .b >d >0C .2a =b <0D .2c =d >0【解析】:⑴、⑵式反应物、生成物的状态均相同,⑴×2=⑵,即2△H 1=△H 2,2a =b ,又H 2的燃烧反应为放热反应,故2a =b <0,C 项符合题意。
盖斯定律的原理及应用

盖斯定律的原理及应用1. 引言盖斯定律是流体力学中的基本定律之一,描述了管道中流体的流动行为。
它由爱尔兰工程师亨利·盖斯于1799年提出,是流体力学领域中的重要原理。
本文将介绍盖斯定律的基本原理以及其在实际应用中的作用。
2. 盖斯定律的原理盖斯定律表述了液体或气体通过管道时的流量与压力之间的关系。
根据盖斯定律,管道内流体的流量Q与压力差△P之间呈线性关系。
具体可以用以下公式表示:Q = kA△P其中,Q表示流量,A表示管道的横截面积,△P表示压力差,k 为比例常数。
该公式可以简化为Q ∝△P。
盖斯定律的基本原理可以通过流体的动量守恒和能量守恒来推导。
根据动量守恒定律,流体在管道中的动量变化等于施加在其上的力乘以时间。
而根据能量守恒定律,单位时间内流过管道某一截面的功率等于管道前后的压力差。
基于这两个定律,可以推导出盖斯定律的数学表达式。
3. 盖斯定律的应用盖斯定律在很多实际应用中起着重要作用,以下列举几个常见的应用场景:3.1 水管系统的设计在设计水管系统时,盖斯定律可以用于确定不同管段的管径。
通过测量进水口和出水口处的压力差,可以根据盖斯定律计算出流量,然后根据流量要求确定相应的管径。
这有助于确保水流的稳定性和高效性。
3.2 汽车制动系统盖斯定律在汽车制动系统中有广泛应用。
制动系统中的刹车片通过液压系统施加力来减速汽车。
根据盖斯定律,当刹车踏板施加的力增大时,液压系统中的压力增加,从而提高了制动力。
这使得汽车的制动更加可控和安全。
3.3 喷气发动机的燃烧室设计盖斯定律在喷气发动机的燃烧室设计中也起着重要作用。
喷气发动机中的燃油通过喷射和燃烧产生高温高压的气体,从而产生推力。
盖斯定律可以用于确定燃烧室中燃气的流动速度和压力分布,有助于提高燃烧效率和推力。
3.4 水力发电站的设计盖斯定律在水力发电站的设计中也有重要应用。
水力发电利用水流的动能来驱动发电机,产生电能。
通过应用盖斯定律,可以计算出水流的流量和压力,从而设计合适的水轮机和水管系统,以提高发电效率。
盖斯定律的例题及解析

盖斯定律的例题及解析盖斯定律的例题及解析引言:盖斯定律,又被称为95/5定律,是指在许多事物中,相对较少的因素或个体对结果的影响最为显著。
这一定律在很多领域都有应用,尤其在经济学、商业管理和社会科学中被广泛运用。
在本文中,我们将通过几个例题深入探讨盖斯定律,并解析相关的概念和原理。
第一部分:盖斯定律的例子1. 企业中的盖斯定律假设在一家企业中,只有5%的员工占据了整个企业利润的95%。
这意味着少数高效能的员工对企业的利润贡献最大。
例如,销售团队中,只有少数销售人员创造了绝大部分的销售额。
此例子展示了盖斯定律在组织内的应用,即少数关键个体对整个组织的影响最为显著。
2. 人口统计中的盖斯定律在人口统计中,盖斯定律也可以得到验证。
例如,在世界范围内,只有5%的人口拥有了95%的财富。
这表明,富裕资源的分配非常不平等。
盖斯定律在人群中的应用,展示了少数人对整个社会或群体的影响力远大于其它大多数。
第二部分:解析盖斯定律的概念和原理1. 基于深度和广度的评估通过对盖斯定律的例子进行评估,我们可以发现这一法则的深度和广度。
盖斯定律强调了少数重要因素或个体对结果的巨大影响,因此可以说具有较大的深度。
而在不同的领域,无论是企业中的盈利、人口的财富分布,还是其他方面的现象,盖斯定律都有着普遍的适用性,这体现了它的广度。
2. 由简到繁、由浅入深的讨论为了更好地理解盖斯定律,我们可以从简单的例子开始,比如企业中的影响力分配或财富分布,逐渐深入探讨更广泛的应用领域,如产品市场份额的分布、人口文化的传播等。
这种由简到繁、由浅入深的探讨方式可以帮助我们更全面地理解盖斯定律,并将其应用到更多的实际问题中。
第三部分:总结和回顾通过对盖斯定律的讨论,我们可以得出以下几个总结和回顾性的内容:1. 盖斯定律强调少数因素或个体对结果的显著影响,这种不平衡的分布在许多领域都有普遍存在。
2. 盖斯定律的深度和广度使其成为一个强有力的理论框架,可以用于解释和预测各种现象。
--考点四盖斯定律的三大应用(共45张PPT)

化学键 C—H C—F H—F F—F
键能
414
489
565
158
根据键能数据计算以下反应的反应热 ΔH: CH4(g)+4F2(g)===CF4(g)+4HF(g) ΔH=__________。 (3)发射卫星用 N2H4 气体为燃料,NO2 气体为氧化剂,两者 反应生成 N2 和水蒸气,已知: N2(g)+2O2(g)===2NO2(g) ΔH1=+67.7 kJ·mol-1; 2H2(g)+O2(g)===2H2O(g) ΔH2=-484 kJ·mol-1; N2H4(g)+O2(g)===N2(g)+2H2O(g) ΔH3=-534 kJ·mol-1; H2O(l)===H2O(g) ΔH4=+44.0 kJ·mol-1。
ΔH=+66.0 kJ·mol-1
WO2(g)+2H2(g)
W(s)+2H2O(g) ΔH=-137.9 kJ·mol-1
则 WO2(s) WO2(g)的 ΔH=__________________。
解析:将反应①WO2(s)+2H2(g) W(s)+2H2O(g) ΔH = + 66.0 kJ·mol - 1 和 ②WO2(g) + 2H2(g) W(s) + 2H2O(g) ΔH = - 137.9 kJ·mol - 1 作 如 下 处 理 : ① - ② 可 得 WO2(s) WO2(g) ΔH=+203.9 kJ·mol-1。
第六章
化学反应与能量
第一节 化学能与热能
考点四 盖斯定律的三大应用
精讲精练考能
重点讲解 提升技能
盖斯定律的内容 对于一个化学反应,无论是一步完成还是分几步完成,其反 应热是相同的。即:化学反应的反应热只与反应体系的始态和终 态有关,而与反应的途径无关。
盖斯定律及其应用

人 教 版 化 学
C( 石墨 ) + O2(g)= CO2(g)
H 2(g) + 1/2O 2(g) = H 2O(l)
ΔH2=- 393.5 kJ· mol
-1
-1
ΔH 3 =- 285.8 kJ ·mol
②
③ 根据盖斯定律求反应 C(石墨)+2H 2(g)= CH 4(g) ④ 的ΔH 4
化学反应原理
已知 25 ℃、101 kPa 下,1 g C8H18(辛烷)燃烧生成二 氧化碳和液态水时放出 48.40 kJ 热量。则 C8H18 的燃烧 热为 ________________。
人 教 版 化 学
化学反应原理
第1章 第三节
[解析 ] 注意燃烧热为燃烧 1 mol 物质所放出的热 量。 1 g C8H18 燃烧生成二氧化碳和液态水时放出 48.40 kJ 热量,则 1 mol C8H18 完全燃烧放出的热量为 48.40 kJ· g
第1章 第三节
[解析 ] 方法一: 因为反应式①②③和④ 之间有以下 关系: ②+③×2-①=④ 所以 ΔH4= ΔH2+ 2ΔH3-ΔH1 =- 393.5+ 2×(- 285.8)- (- 890.3) =- 74.8(kJ· mol 1)
-
人 教 版 化 学
化学反应原理
第1章 第三节
方法二:也可以设计一个途径,使反应物经过一些 中间步骤最后回复到产物:
-1
C.- 244.15 kJ· mol-1
D.+ 244.15 kJ· mol-1
化学反应原理
第1章 第三节
[解析 ] ①×2 得:2C(s)+ 2O2(g)===2CO2(g) =- 787.0 kJ· mol
-1
ΔH4
盖斯定律及其应用-高二化学(人教版2019选择性必修1)

④H2Sg+H2SO4aq===Ss+SO2g+
2H2Ol ΔH4=+61 kJ·mol-1
(3)加和调整好的热化学方程式 (4)求焓变ΔH (5)检查 系统(Ⅰ):①+②+③可得出H2O(l)===H2(g)+1/2O2(g) ΔH=ΔH1+ΔH2+ΔH3
【答案】 H2O(l)===H2(g)+1/2O2(g) ΔH=+286 kJ·mol-1 H2S(g)===H2(g)+S(s) ΔH=+20 kJ·mol-1
系统(Ⅰ) H2SO4aq ΔH2=-151 kJ·mol-1 ③2HIaq===H2g+I2s
ΔH3=+110 kJ·mol-1
系统(Ⅱ)
②SO2g+I2s+2H2Ol===2HIaq +H2SO4aq ΔH2=-151 kJ·mol-1 ③2HIaq===H2g+I2s ΔH3=+110 kJ·mol-1
C.ΔH3=ΔH1-2ΔH2 答案:A
D.ΔH3=ΔH1-ΔH2
解析:热化学方程式①、②和③之间存在关系:①+2×②=③,故有
ΔH1+2ΔH2=ΔH3。
突破点二:盖斯定律的应用
应用一 利用盖斯定律计算反应热
[方法归纳] 有些反应进行得很慢,有些反应不容易直接发生,有些反应的产品不纯,
这给测定反应热造成了困难,此时若应用盖斯定律,就可以间接把它们的反应热计算
解析: 将已知的热化学方程式依次编号为①、②、③、④,将方程式 ③×2-①-④×4得 2N2H4(g)+2NO2(g)===3N2(g)+4H2O(l),所以反应的ΔH=2×(-534 kJ·mol-1)-67.7 kJ·mol-1-4×(+44.0 kJ·mol-1)=-1 311.7 kJ·mol-1。
出来。
盖斯定律的应用

1、盖斯定律的涵义:对于一个化学反应,无论是一步完成还是分几步完成,其反应焓变是一样的的。
这就是盖斯定律。
也就是说,化学反应的反应热只与反应体系的始态和终态有关,而与具体的反应进行的途径无关。
2、盖斯定律的应用盖斯定律在科学研究中具有重要意义。
因为有些反应进行的很慢,有些反应不容易直接发生,有些反应的产品不纯(有副反应发生),这给测定反应热造成了困难。
此时如果应用盖斯定律,就可以间接的把它们的反应热计算出来。
例如:C(S)+0.5O2(g)=CO(g)上述反应在O2供应充分时,可燃烧生成CO2、O2供应不充分时,虽可生成CO,但同时还部分生成CO2。
因此该反应的△H无法直接测得。
但是下述两个反应的△H却可以直接测得:C(S)+O2(g)=CO2(g) ;△H1= - 393.5kJ/molCO(g)+0.5 O2(g)=CO2(g) ;△H2=- 283.0kJ/mol根据盖斯定律,就可以计算出欲求反应的△H3。
分析上述反应的关系,即知△H1=△H2+△H3△H3=△H1-△H2=-393.5kJ/mol-(-283.0kJ/mol)=-110.5kJ/mol 例5图由以上可知,盖斯定律的实用性很强。
3、反应热计算根据热化学方程式、盖斯定律和燃烧热的数据,可以计算一些反应的反应热。
反应热、燃烧热的简单计算都是以它们的定义为基础的,只要掌握了它们的定义的内涵,注意单位的转化即可。
热化学方程式的简单计算的依据:(1)热化学方程式中化学计量数之比等于各物质物质的量之比;还等于反应热之比。
(2)热化学方程式之间可以进行加减运算。
例1:按照盖斯定律,结合下述反应方程式,回答问题,已知:(1)NH3(g)+HCl(g)===NH4Cl(s)△H1=-176kJ/mol(2)NH3(g)+H2O(l)===NH3.H2O(aq) △H2=-35.1kJ/mol(3)HCl(g) +H2O(l)===HCl(aq) △H3=-72.3kJ/mol(4)NH3(aq)+ HCl(aq)===NH4Cl(aq) △H4=-52.3kJ/mol(5)NH4Cl(s)+2H2O(l)=== NH4Cl(aq) △H5=?则第(5)个方程式中的反应热△H是____。
利用盖斯定律计算反应热的方法

利用盖斯定律计算反应热的方法【最新版3篇】篇1 目录1.引言2.盖斯定律及其应用3.利用盖斯定律计算反应热的方法4.结论篇1正文一、引言盖斯定律是一种广泛应用于化学反应能量计算的定律,它揭示了一个化学反应的焓变与反应步骤之间的关系。
本章节将介绍盖斯定律的基本原理以及其在实际应用中的价值。
二、盖斯定律及其应用盖斯定律是指在一个包含多个步骤的化学反应中,各步反应的焓变之和等于该总反应的焓变。
换句话说,我们可以利用已知的反应步骤计算出总反应的焓变,而不必进行实际实验。
这一理论为我们提供了一种高效计算反应热的方法。
三、利用盖斯定律计算反应热的方法利用盖斯定律计算反应热的方法可以分为以下几个步骤:1.确定初始和目标反应。
根据题目中的条件,确定初始和目标反应,以及它们的焓变。
2.确定中间步骤。
根据题目中的条件,确定初始反应和目标反应之间的中间步骤,以及每个中间步骤的焓变。
3.计算总反应的焓变。
根据初始反应、目标反应和中间步骤的焓变,利用盖斯定律计算总反应的焓变。
4.确定温度和压力。
根据题目中的条件,确定计算反应热所需的温度和压力。
5.利用公式计算反应热。
根据总反应的焓变、温度和压力,利用公式计算反应热。
四、结论利用盖斯定律计算反应热的方法是一种高效、简便的方法,可以大大减少实验误差和实验时间。
篇2 目录1.引言2.盖斯定律及其应用3.利用盖斯定律计算反应热的方法4.结论篇2正文一、引言盖斯定律是一种广泛应用于化学反应能量计算的定律,它揭示了一个化学反应的焓变只与反应物和产物的相对焓变有关,而与反应的具体途径无关。
本文将介绍利用盖斯定律计算反应热的方法。
二、盖斯定律及其应用盖斯定律是指一个化学反应的焓变只与反应物和产物的相对焓变有关,而与反应的具体途径无关。
也就是说,一个化学反应的焓变可以通过加和各个反应物和产物的焓变来计算。
三、利用盖斯定律计算反应热的方法1.确定反应物和产物:首先,我们需要确定要计算反应热的化学反应。
利用盖斯定律计算反应热的方法

利用盖斯定律计算反应热的方法盖斯定律(Gibbs' Law)是热力学中非常重要的定律之一,它可以用来计算化学反应的热力学热变化。
该定律可以表示为以下方程式:ΔG=ΔH-TΔS其中,ΔG表示反应的自由能变化,ΔH表示反应的焓变化,ΔS表示反应的熵变化,T表示温度。
1.确定反应物和生成物:首先确定化学反应中的反应物和生成物。
这些物质在反应方程式中是明确的。
例如,对于A+B→C+D的反应,A和B 是反应物,C和D是生成物。
2.确定反应的热化学方程式:根据反应物和生成物,建立反应的热化学方程式。
这些方程式描述了反应物与生成物之间的化学反应关系,同时还包括反应的系数和状态标识。
3.确定反应的焓变化:利用已知的标准生成焓(ΔH°)值,计算反应的焓变化。
标准生成焓是指在标准状态下,1摩尔物质形成的过程中放出或吸收的热量。
通过查阅化学手册或热化学数据库确定反应物和生成物的标准生成焓,然后根据反应方程中的系数计算反应的焓变化。
4.确定反应的熵变化:确定反应的熵变化也需要一些信息。
从反应物到生成物的熵变可以通过已知的标准摩尔熵(ΔS°)值计算得出。
标准摩尔熵是指在标准状态下,1摩尔物质的熵变。
5. 确定温度:在应用盖斯定律计算反应热时,还需要确定反应发生的温度。
温度的单位通常是Kelvin(K)。
6.应用盖斯定律计算反应热:根据以上确定的ΔH,ΔS和温度值,应用盖斯定律进行计算。
7.解释结果:根据计算所得的反应热ΔG值,可以判断反应是自发进行的还是不自发进行的。
当ΔG<0时,反应是自发进行的,反应具有较大的发生倾向性。
当ΔG>0时,反应是不自发进行的,需要提供能量才能发生。
需要注意的是,在进行计算时要确保所有物质的标准生成焓和标准摩尔熵都是在相同温度下进行计算的。
此外,这种计算方法适用于理想气体和溶液的状态,对于其他复杂的体系可能需要考虑更多因素。
总而言之,利用盖斯定律计算反应热的方法是根据盖斯定律的方程式和已知的物质的焓变化和熵变化,应用热力学原理进行计算,以确定反应的自发性和热力学热变化。
盖斯定律的例题及解析

盖斯定律的例题及解析一、什么是盖斯定律?盖斯定律,也称为网络效应定律或马太效应,是指在某个系统中,一些优势节点会越来越优势,而一些弱势节点则会越来越弱。
这种现象在社交网络、经济市场等领域都有体现。
二、盖斯定律的例题下面以社交网络为例,解释盖斯定律的具体运作方式。
假设有一个社交网络平台,其中有1000个用户,他们之间可以互相关注和互动。
其中有一个用户A拥有1000个粉丝,而其他用户只拥有10-20个粉丝。
根据盖斯定律,用户A的影响力将会越来越大,而其他用户的影响力则会逐渐减小。
三、盖斯定律的解析1. 原因分析这种现象可以通过以下原因进行解释:首先是“富者愈富”的原因。
在社交网络中,受欢迎的用户更容易获得更多的关注和互动机会。
这些机会进一步增加了他们的影响力和受欢迎程度。
相反地,在社交网络中不那么受欢迎的用户则很难获得这些机会,从而导致他们的影响力逐渐减小。
其次是“弱者愈弱”的原因。
在社交网络中,用户之间的关注和互动是基于一定的兴趣相似性。
因此,那些不受欢迎的用户可能会被忽视或被边缘化,他们很难获得更多的关注和互动机会。
这种边缘化进一步削弱了他们的影响力和受欢迎程度。
2. 盖斯定律的应用盖斯定律在许多领域都有广泛的应用。
例如:在商业领域中,盖斯定律可以解释为什么大公司越来越大,而小公司则越来越小。
大公司拥有更多的资源和市场份额,这使得它们更容易获得更多的客户和利润,并进一步扩大规模。
在科学研究领域中,盖斯定律可以解释为什么少数科学家拥有更多的发表论文、引用次数和奖项。
这些科学家通常可以获得更多资金、资源和合作机会,这使得他们能够进行更深入、更广泛的研究,并获得更多的成就。
在教育领域中,盖斯定律可以解释为什么一些学生比其他学生更容易获得好成绩。
这些学生通常拥有更多的资源、支持和机会,这使得他们能够更好地发挥自己的潜力并取得更好的成绩。
四、如何应对盖斯定律?虽然盖斯定律在许多领域都有广泛应用,但我们仍然可以采取一些措施来缓解其影响。
盖斯定律应用

⑤=④+③+②-①,
即△H5 = +16.3kJ/mol
你知道神六的火箭燃料是什么吗?
复习:
1、已知:H2(g)+Cl2(g)=2HCl(g) △H=-184.6kJ/mol 则反应HCl(g)=1/2H2(g)+1/2Cl2(g)的△H为( D ) A. +184.6 kJ/mol B. -92.3 kJ/mol C. -369.2 kJ/mol D. +92.3 kJ/mol 规律: “正逆”反应的反应热效应数值相等,符号相反 2、甲硅烷(SiH4)是一种无色气体,遇到空气能发
【解】:根据盖斯定律,反应④不论是一步完成还是分几步完成, 其反应热效应都是相同的。下面就看看反应④能不能由①②③三 个反应通过加减乘除组合而成,也就是说,看看反应④能不能分 成①②③几步完成。 ①×2 + ②×4 - ③ = ④ 所以,ΔH=ΔH1×2 +ΔH2×4 -ΔH3 =-283.2×2 -285.8×4 +1370 =-339.2 kJ/mol
C(s)+1/2O2(g)=CO(g) △H=-110.35kJ/mol
H CO(g)+1/2O2(g)=CO2(g) △H=-282.57kJ/mol
与这些碳完全燃烧相比,损失的热量是(C )
• 392.92 kJ B. 2489.44 kJ
C. 784.92 kJ
D. 3274.3 kJ
《盖斯定律及应用》课件

对可逆过程的依赖性
总结词
盖斯定律的应用依赖于可逆过程,但实 际反应往往难以达到可逆状态。
VS
详细描述
盖斯定律仅适用于可逆过程,但在实际反 应中,由于各种因素的限制,如反应动力 学、热力学ቤተ መጻሕፍቲ ባይዱ化学平衡等,反应很难完全 达到可逆状态。因此,在应用盖斯定律时 需要考虑这些因素的影响。
对热力学过程的依赖性
详细描述
盖斯定律表明,一个系统的热力学状态变化只取决于起始和 最终状态,而与变化过程中所经历的中间状态无关。这意味 着,通过不同的反应路径,可以达到相同的最终状态,这些 路径的热力学行为是等效的。
盖斯定律的发现与起源
总结词
盖斯定律由苏格兰物理学家和数学家詹姆斯·克拉克·盖斯于19世纪提出。
详细描述
盖斯定律的发展趋势与展望
盖斯定律的理论研究进展
盖斯定律基本原理的完善
随着理论物理学的发展,盖斯定律的基本原理得到进一 步明确和阐述,为相关领域的研究提供更坚实的理论基 础。
盖斯定律与其他理论的融合
盖斯定律与热力学、统计力学等理论相互渗透,形成更 广泛的理论体系,推动相关领域的发展。
盖斯定律在交叉学科中的应用
要点二
详细描述
盖斯定律在多个领域中具有重要意义。在化学反应计算中 ,盖斯定律可以用于计算不同反应路径的能量变化,有助 于理解化学反应的本质和过程。在能源利用方面,盖斯定 律有助于优化能源转换过程,提高能源利用效率。此外, 在环境保护领域,盖斯定律可以帮助我们更好地理解和控 制环境污染物的生成和转化过程。
总结词
盖斯定律的应用受到热力学过程的限制,不 适用于非热力学平衡过程。
详细描述
盖斯定律适用于等温、等压或绝热过程,但 不适用于非热力学平衡过程。在非平衡过程 中,化学反应的热效应不仅与反应途径有关 ,还与反应条件有关。因此,在应用盖斯定 律时需要确保所研究的反应过程符合热力学 的基本原理。
第六章-第一节-第3课时-盖斯定律及其应用

反应热间的关系 ΔH1=aΔH2 ΔH1=-ΔH2
ΔH=ΔH1+ΔH2 =ΔH3+ΔH4+ΔH5
4
归纳总结:
推论一:若某化学反应从始态(S)到终态(L)其焓变为△H1, 而从终态(L)到始态(S)的焓变为△H 2,这两者和为0。
即△H1+ △H 2 = 0 推论二:若某一化学反应可分为多步进行,则其总焓变为各步反 应的焓变之和。 盖斯定律的重要意义:间接地计算某些反应的反应热
②定侧向
H2(g)+I2(g)===2HI(g) ΔH2=-11.0 kJ·mol-1② ③调系数
对应反应:
(g)+I2(g)===
(g)+2HI(g) ④求焓变
ΔH3=__+__8_9_.3__kJ·mol-1。 ③
6
盖斯定律的应用1
新坐标P139-3
★★ 3.(1)(2018·全国卷Ⅰ,节选)已知:2N2O5(g)===2N2O4(g)+O2(g)
高三化学备课组
盖斯定律在 ΔH 求算中的应用 ——变化观念与证据推理
盖斯定律充分体现了能量守恒定律,在近几年高考试题中出现 率 100%,难度中档。呈现形式主要是根据两个或三个已知热化学方 程式推导目标反应的热化学方程式或其 ΔH。体现了变化观念与证据 推理的化学核心素养。
2
一、盖斯定律
化学反应不管是一步完成还是分几步完成,其反应热是相同的,
即化学反应的反应热只与反应体系的始态和终态有关,而与反应的
途径无关。体现了能量守恒定律。
△H1 < 0
(始态)S
△H1 +△H2 = 0
ΔH、ΔH1、ΔH2之间有何关系?
ΔH
A
B
ΔH1ΔH2Fra bibliotekL(终态)
盖斯定律用xyz计算的例子

盖斯定律用xyz计算的例子以盖斯定律用xyz计算的例子为题,列举一下1. 例子一:小明每天都会花三个小时玩电脑游戏。
根据盖斯定律,我们可以得出结论:小明的时间分配中,电脑游戏占据了绝大部分,而其他活动的时间很少,如学习、运动、社交等。
这个例子中,x 代表小明的时间,y代表玩电脑游戏的时间,z代表其他活动的时间。
可以通过xyz的比例来判断小明的时间分配情况。
2. 例子二:某公司的销售额为100万,其中10%来自于某个产品的销售。
根据盖斯定律,我们可以得出结论:该产品的销售额占据了整体销售额的很小比例,而其他产品的销售额占据了绝大部分。
这个例子中,x代表总销售额,y代表某个产品的销售额,z代表其他产品的销售额。
可以通过xyz的比例来判断该产品在整体销售额中的重要性。
3. 例子三:某城市的交通事故率为每年100起,其中90%是由于超速行驶引起的。
根据盖斯定律,我们可以得出结论:超速行驶是造成交通事故的主要原因,而其他原因所引发的交通事故很少。
这个例子中,x代表交通事故总数,y代表超速行驶引起的交通事故数,z代表其他原因引起的交通事故数。
可以通过xyz的比例来判断超速行驶在交通事故中的占比情况。
4. 例子四:某学校的学生人数为1000人,其中80%的学生都是来自本省的。
根据盖斯定律,我们可以得出结论:本省学生占据了学校学生人数的绝大部分,而其他省份的学生很少。
这个例子中,x 代表学校的学生总数,y代表本省学生的人数,z代表其他省份学生的人数。
可以通过xyz的比例来判断本省学生在学校中的比例。
5. 例子五:某公司的利润为100万,其中50%来自于某个部门的业绩。
根据盖斯定律,我们可以得出结论:该部门的业绩对整体利润的贡献很大,而其他部门的业绩贡献较少。
这个例子中,x代表总利润,y代表某个部门的业绩贡献,z代表其他部门的业绩贡献。
可以通过xyz的比例来判断该部门在公司利润中的占比情况。
6. 例子六:某国家的电力消耗为1000万千瓦时,其中70%来自于化石燃料的发电。
盖斯定律的应用及反应热 的计算和大小比较 新高考化学专题讲解 考点详细分析深入讲解 最新版

盖斯定律的应用及反应 热 的计算和大小比较
详细分析与深入讲解
必备知识通关
1.盖斯定律 不管化学反应是一步完成还是分几步完成,其反应热是相同的。即反应 热只与反应体系的始态和终态有关,而与反应途径无关。如:
途径一:A→B 途径二:A→C→B 则ΔH1、ΔH2、ΔH的关系为ΔH=ΔH1+ΔH2。
2.根据反应进行程度的大小比较反应焓变大小
③C(s)+ 1 O2(g) 2
④C(s)+O2(g)
CO(g) ΔH3 CO2(g) ΔH4
反应④,C完全燃烧,放热更多,|ΔH3|<|ΔH4|,但ΔH3<0,ΔH4<0,故ΔH3>ΔH4。
解题能力提升
3.根据反应物或生成物的状态比较反应焓变大小
⑤S(g)+O2(g) ⑥S(s)+O2(g) 方法一:图像法
ΔH3。则下列判断正确的是
A.ΔH2>ΔH3
B.ΔH1<ΔH3
C.ΔH1+ΔH3=ΔH2
D.ΔH1+ΔH2>ΔH3
解题能力提升
SO2(g)+2OH-(aq)
S(aq)+H2O(l) ΔH1
ClO-(aq)+SO32-(aq)
SO42-(aq)+Cl-(aq) ΔH2
CaSO4(s)
Ca2+(aq)+SO42-(aq) ΔH3
则反应SO2(g)+Ca2+(aq)+ClO-(aq)+2OH-(aq)
CaSO4(s)+H2O(l)+Cl-(aq)的ΔH=
。
解题能力提升
解析:(1)将已知热化学方程式依次编号为①、②,根据盖斯定律,由①×3+
盖斯定律的例题及解析

盖斯定律的例题及解析一、什么是盖斯定律盖斯定律(Gauss’s Law),也称高斯定理,是电磁学中的基本定律之一,用于描述电场的性质。
根据盖斯定律,通过任何闭合曲面的电通量等于该闭合曲面内的电荷总量除以真空电容率。
数学公式表示为:其中,S为闭合曲面,E为电场强度,dS为曲面上的面元,Q为闭合曲面内的电荷总量,ε₀为真空电容率。
二、盖斯定律的应用1. 理解电场盖斯定律可以帮助我们理解电场的分布情况。
通过计算电通量,可以确定电场是从正电荷向外发散还是向内收敛。
当闭合曲面内没有电荷时,电通量为零,表示电场无源。
而当闭合曲面内有电荷时,电通量不为零,表示电场有源。
2. 计算电场强度通过盖斯定律,可以利用已知的电荷分布计算出电场强度。
首先选择一个合适的闭合曲面,使得计算电通量相对简便。
然后根据所选曲面的形状和对称性,确定哪些面元的电通量可以直接求得。
最后,根据高斯定律公式计算出电场强度。
3. 研究电荷分布盖斯定律也可用于研究电荷的分布情况。
通过观察闭合曲面内的电通量,可以推断出曲面内的电荷分布情况。
例如,如果电通量是正的,表示闭合曲面内存在正电荷;如果电通量是负的,表示闭合曲面内存在负电荷。
通过这种方式,我们可以了解电荷在空间中的分布情况。
三、盖斯定律的例题分析1. 球形电荷分布假设有一个半径为R的均匀带电球体,其电荷密度为ρ。
求球心处的电场强度。
解析:1.选择一个球形闭合曲面,以球心为球心,半径为r(r > R)。
2.根据球对称性,球面上的所有面元的电通量都相等。
由于电场和面元的夹角为零度,电通量可直接求得。
3.根据盖斯定律公式,电通量等于在球体内的电荷总量除以真空电容率。
公式表示为:4.解方程得到电场强度E。
2. 无限长均匀带电线假设有一条无限长均匀带电线,线密度为λ。
求距离线上一点P距离为r处的电场强度。
解析:1.选择一个以点P为球心的球形闭合曲面,半径为r。
2.根据线对称性,球面上的所有面元的电通量都相等。
高中化学 盖斯定律
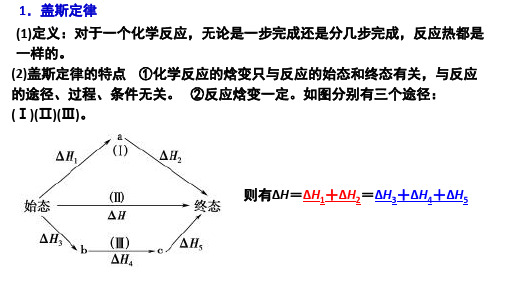
不能很好的控制反应的程度,故不能直接通过实验测得△H1
CO(g)+1/2O2(g) = CO2(g) △H2=-283.0 kJ/mol
C(s)+O2(g) = CO2(g)
△H3=-393.5 kJ/mol
(1)消元法 写出目标方程式确定“多余物质”(要消去的物质)然后用消元法逐一消去 “多余物质”,导出“四则运算式”
分析: CO(g) △H1 + △H2 = △H3
H1
H2
C(s)
H3 CO2(g)
C(s)+O2(g) = CO2(g)
△H3=-393.5 kJ/mol
— CO(g)+1/2O2(g) = CO2(g) △H2=-283.0 kJ/mol
C(s)+1/2O2(g) = CO(g) △H1=?
∴△H1 = △H3 - △H2 = -393.5 kJ/mol -(-283.0 kJ/mol)= -110.5 kJ/mol
ΔH2
C
ΔH3=ΔH1+ΔH2 ΔH1=ΔH3- ΔH2
(2)唯一法:对于比较复杂的几步反应,可以换个角度: 找唯 一,调方向,改倍数,不多余
测定 C(s)+1/2O2(g)=CO(g) 的焓变△H1
CO(g)+1/2O2(g) = CO2(g) △H2=-283.0 kJ/mol
C(s)+O2(g) = CO2(g)
△H3=-393.5 kJ/mol
盖斯定律的应用 (1)科学意义:对于无法或较难通过实验测定的反应的焓变,可应用盖斯定律 计算求得。 (2)方法——“叠加法”若一个化学反应的化学方程式可由另外几个化学反 应的化学方程式相加减而得到,则该化学反应的焓变即为另外几个化学反 应焓变的代数和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 2.已知下列热化学方程式: 2H2(g)+O2(g)=2H2O(g); ΔH=-483.6 kJ/mol • H2(g)+O2(g)=H2O(g); • ΔH=-241.8 kJ/mol • H2(g)+O2(g)=H2O(I); • ΔH=-285.8 kJ/mol • 则氢气的燃烧热为 (C ) • A.-438.6 kJ/mol B.-241.8 kJ/mol • C.-285.8 kJ/mol D.无法确定
①C(s)+1/2O2(g)==CO(g) ΔH1=? ②CO(g)+1/2O2(g)== CO2(g) ΔH2=-283.0kJ/m ol ③C(s)+O2(g)==CO2(g) ΔH3=-393.5kJ/m ol
•①
+
②
=
③
,
则 ΔH1 + ΔH2 =ΔH3 • 所以, ΔH1 =ΔH3- ΔH2 = -393.5kJ/m 283.0kJ/m olol =-110.5kJ/m ol
3.已知 ① CO(g) + 1/2 O2(g) =CO2(g)
② H2(g) + 1/2 O2(g) =H2O(l)
ΔH1= -283.0 kJ/mol ΔH2= -285.8 kJ/mol
③C2H5OH(l) + 3 O2(g) = 2 CO2(g) + 3 H2O(l) ΔH3=-1370 kJ/mol 试计算④2CO(g)+ 4 H2(g)= H2O(l)+ C2H5OH(l) 的ΔH
3、已知H+(aq)+OH-(aq)=H2O(l) △H=-57.3kJ/mol,计算
下列反应中放出的热量。
(1)用20g NaOH 配成稀溶液跟足量稀盐酸反应,放出热 28.65 量为 kJ。
(2)用0.1molBa(OH)2配成稀溶液跟足量稀硝酸反应,放 出热量为 11.46 kJ。 (3)用1mol醋酸稀溶液和足量NaOH溶液反应,放出的热
如何测出这个反应的反应热: (1)C(s)+1/2O2(g)==CO(g) ΔH1=?
①C(s)+1/2O2(g)==CO(g) ΔH1=? ②CO(g)+1/2O2(g)== CO2(g) ΔH2=-283.0kJ/m ol ③C(s)+O2(g)==CO2(g) ΔH3=-393.5kJ/m ol
选修4第一章 第三节化学反应热的计算盖斯定律应用
教学目标:
• 掌握盖斯定律,并学会应用盖斯定律进行 化学反应热的计算;进一步巩固对化学反 应本质的理解。
复习:
1、已知:H2(g)+Cl2(g)=2HCl(g) △H=-184.6kJ/mol 则反应HCl(g)= 1 2(g)+ 1Cl2(g)的△H为( D ) H
【解】:根据盖斯定律,反应④不论是一步完成还是分几步完成, 其反应热效应都是相同的。下面就看看反应④能不能由①②③三 个反应通过加减乘除组合而成,也就是说,看看反应④能不能分 成①②③几步完成。①×2 + ②×4 - ③ = ④ 所以,ΔH=ΔH1×2 +ΔH2×4 -ΔH3 =-283.2×2 -285.8×4 +1370 =-339.2 kJ/mol
• 练习 • 1.按照盖斯定律,结合下述反应方程式,回答问题,已 知: • (1)NH3(g)+HCl(g)=NH4Cl(s) △H1=-176kJ/mol • (2)NH3(g)+H2O(l)=NH3·H2O(aq) △H2=-35.1kJ/mol • (3)HCl(g) +H2O(l)=HCl(aq) △H3=-72.3kJ/mol • (4)NH3(aq)+ HCl(aq)=NH4Cl(aq) △H4=-52.3kJ/mol • (5)NH4Cl(s)+2H2O(l)= NH4Cl(aq) △H5=? • 则第(5)个方程式中的反应热△H是________。 • 根据盖斯定律和上述反应方程式得: • (4)+ (3)+ (2)- (1)= (5),即△H5 = +16.3kJ/mol
A. 392.92 kJ B. 2489.44 kJ
C. 784.92 kJ
D. 3274.3 kJ
二.反应热的计算:
利用反应热的概念、盖斯定律、热化 学方程式进行有关反应热的计算
课本P14 例1: Na(s) + 1/2Cl2(g)= NaCl (s) 23g/mol △H 1.0g -17.87kJ △H=23g/mol×(-17.87kJ)÷ 1.0g =-411kJ/mol 答:
2
2
A.+184.6 kJ/mol
B.-92.3 kJ/mol
C.-369.2 kJ/mol
D.+92.3 kJ/mol
2、甲硅烷(SiH4)是一种无色气体,遇到空气能发生爆 炸性自燃,生成SiO2和水。已知室温下1g甲硅烷自燃 放出44.6kJ热量,其热化学方程式为:
SiH4(g)+O2(g)=SiO2(s)+H2O(l) △H=-1427.2kJ/mol _____________________________________________
【解】钠与氯气起反应的化学方程式如下
课本P14 例2:
【解】 设1kg乙醇燃烧后放出的热量为X C2H6O(l) + 3O2(g)= 2CO2(g) +3H2O (l) 46g/mol -1366.8kJ/mol 1000g X
X=(-1366.8kJ/mol × 1000g)/ 46g/mol =-29710kJ 答:1kg乙醇燃烧后放出29710kJ热量
A
ΔH1
ΔH ΔH2
B
C
ΔH、ΔH1、ΔH2 之间有何关系?
ΔH=ΔH1+ΔH2
例1:写出石墨变成金刚石的热化学方程式 (25℃,101kPa时) • 说明: (1)可以在书中查找需要的数据 • (2)并告诉大家你设计的理由。
查燃烧热表知:
①C(石墨,s)+O2(g)=CO2(g) △H1=-393.5kJ/m ol ②C(金刚石,s)+O2(g)=CO2(g) △H2=-395.0kJ/m ol
• 3.已50 kJ/mol,则1 g Zn在氧气中燃烧放 出的热量约为 ( A) • A.5.4 kJ B.350 KJ • C.3.5 kJ D.8.5 Kj • 350÷65=5.4(KJ)
• 4.根据热化学方程式(在25℃、101 kPa时):S(s) +O2(g)=SO2(g);ΔH=-297.23 kJ/mol,分 析下列说法中不正确的是( C ) • A.S的燃烧热为297.23 kJ/mol • B.S(g)+O2(g)=SO2(g)放出的热量大于 297.23 kJ • C.S(g)+O2(g)=SO2(g)放出的热量小于 297.23 kJ • D.形成1 mol SO2的化学键所释放的总能量大于断裂1 mol S(s)和1 mol O2(g)的化学键所吸收的总能量
2.盖斯定律的应用
有些化学反应进行很慢或不易直接发生, 很难直接测得这些反应的反应热,可通过盖 斯定律获得它们的反应热数据。
关键:目标方程式的“四则运算式”的导出。
方法:写出目标方程式确定“过渡物质”(要消去的物质) 然后用消元法逐一消去“过渡物质”,导出“四则运算式”
练习
1.已知石墨的燃烧热:△H=-393.5kJ/mol (1)写出石墨的完全燃烧的热化学方程式 (2)二氧化碳转化为石墨和氧气的热化学方程式 C(石墨,s)+O2(g)=CO2(g) △H1=-393.5kJ/mol CO2(g) =C(石墨,s)+O2(g) △H1=+393.5kJ/mol
正逆反应的反应热效应数值相等,符号相反。 “+”不能省去。 思考:为什么在热化学反应方程式中通常可 不表明反应条件?
热化学方程式还可以表示理论可进行实际难进行的化学反应
2.已知25℃、101kPa下,石墨、金刚石燃烧的热化学方程式分 别为 C(石墨)+O2(g)=CO2(g) △H=-393.51kJ· mol-1 C(金刚石)+O2(g)=CO2(g) △ H=-395.41kJ· mol-1 据此判断,下列说法中正确的是( A ) A、由石墨制备金刚石是吸热反应;等质量时,石墨的能量比金 刚石的低 B、由石墨制备金刚石是吸热反应;等质量时,石墨的能量比金 刚石的高 C、由石墨制备金刚石是放热反应;等质量时,石墨的能量比金 刚石的低 D、由石墨制备金刚石是放热反应;等质量时,石墨的能量比金 刚石的高
所以, ①- ②得: C(石墨,s)= C(金刚石,s) △H=+1.5kJ/mol 观察该热化学方程式,回答:金刚石能自 动变成石墨吗?需要什么条件?
你知道神六的火箭燃料是什么吗?
例2:某次发射火箭,用N2H4(肼)在NO2中燃烧,生 成N2、液态H2O。已知: N2(g)+2O2(g)==2NO2(g) △H1=+67.2kJ/mol N2H4(g)+O2(g)==N2(g)+2H2O(l) △H2=-534kJ/mol 假如都在相同状态下,请写出发射火箭反应的热化学 方程式。
量
小于
(大于、小于、等于)57.3kJ,理
。
由是 醋酸是弱电解质,只是少部分电离,发生电 离时要吸热,中和时放热较少
燃烧热
研究的条件
燃烧物的量
在25℃、101kPa时,1mol纯物质完全燃烧生成
稳定的化合物时所放出的热量
反应程度
反应程度
单位一般用kJ/mol
表示的意义
C的燃烧热为393.5kJ/mol, 表示在101kPa时,1molC完全燃烧放出393.5kJ的热量 表示为:△H =-393.5kJ/mol
应用了什么规律?
