14带参数的方法(二)
TP14 带参数的方法(二) ACCP 6.0 S1-1-使用Java理解程序逻辑 PPT课件

Score sc=new Score();
public float getAvg(Students stu){
float avg=0;
float avg=0;
stu.java=80;
avg=(stu.java +stu.database
stu.database=95;
+stu.html )/3;
stu.html=77;
练习——查找会员积分
需求说明:
循环输入多个会员的信息,根据会员编号,查找 会员积分
完成时间:25分钟
共性问题集中讲解
共性问题集中讲解
常见调试问题及解决办法 代码规范问题
总结
基本数据类型和引用数据类型作为方法参数,
public class 在Tes传tSc递ore时{ 有什么不同之处?
public static void main(String[] args省p)u{略bl内ic存cl分as配s Score {
三门课成绩 Score scr=enteuwrnSacvogr;e();
float }avg=0;
s}tu.java=80; 返回调结用果方法,传递参数,
stu.database=95;
返回结果
stu.html=77;
avg=sc.getAvg(stu);
System.out.println("该学生的平均分为:"+avg);
Students stu=new Students();
//计算平均分,对象作为参数
Score sc=new Score();
public float getAvg(Students stu){
float avg=0;
《无线局域网技术与实践》第14课 大型WLAN优化(二)
(3 )尽管系统功能受损,但能够快速恢复。
这一级别的需求应在WLAN部署环节中,根据WLAN架构和业务特点采用相应技术实现,包括故障检测、诊断、隔离和恢复技术等。
2. WLAN可靠性指标衡量WLAN可靠性的指标通常包括平均故障间隔时间和平均故障修复时间两种,通常以小时为单位。
(I )平均故障间隔时间(mean time between failures, MTBF ) . MTBF 越长,WLAN 可靠性越高。
(2 )平均故障修复时间(mean time to repair, MTTR ),故障修复时间是指故障检测时间、硬件更换时间、系统初始化时间、链路恢复时间、路由覆盖时间、转发恢复时间等的总和。
MTTR越短,WLAN 可靠性越高。
小【教师】提出问题,课堂互动什么是WLAN可靠性?A【学生】聆听、思考、回答问题■【学生】聆听、记录、理解二、AC备份技术■【教师】结合教材讲解大型WLAN面临的挑战相关知识在采用"AC+瘦AP"组网方式的WLAN中,AC的可靠性至关重要.当AC或CAPWAP 链路发生故障时,其管理的所有AP都会受到影响,从而造成大量用户的WLAN业务中断。
AC备份技术可以很好地解决这一问题.AC备份技术可为一台AP部署两台AC,当负责管理AP的AC (称为主用AC )发生故障时,另一台AC(称为备用AC )可接管其所有工作, 从而保证WLAN业务不中断,提高WLAN的可靠性。
福一扫吁小【教师】提出问题,课堂互动如果不为WLAN中的AC设置备份,会有什么影响?*>【学生】聆听、思考、回答问题中【教师】总结学生回答古代著名学者朱柏庐在《朱子家训》一书中提到,"宜未雨而绸缪,毋临渴而掘井",意思是说,做事情要早做准备,不要事到临头才想办法。
AC备份技术就体现了古人这种“未雨绸缪"的智慧。
如果不为WLAN中的AC设置备份,那么一旦该AC发生故障,在故障排除之前,其负责管理的所有WLAN业务都将中断,这会带来不小的麻烦和损失。
采煤方法之14采区车场

(二)石门装车式下部车场
1、在石门里布置装车站
Ⅰ7
采煤方法之14采区车场
4、采区车场施工设计
•线路设计 线路总体布置,绘草图; 计算各线段和联接点尺寸; 计算线路总尺寸;
作线路布置的平、剖面图。 •硐室设计 按线路设计,定巷道或硐室断面大小; 确定硐室位置
一、采区上部车场形式 采区上部车场 — 采区上山 与采区上部区段回风平巷 或阶段回风大巷之间一组 联络巷道和硐室。
易跑车。
2、逆向平车场 当绞车房距轨上变坡点较远; 煤层联合布置采区;操作安全;通过能力小。
3、采区上部甩车场 优点:调车省力;通过能力大,可减少工程 量。 绞车房高,不易维护,绞车房有下行风。
选上部车场解决的关键问题? 选用:采区上部围岩稳定。
二、采区中部车场形式
采区中部车场—联结上山和中部区段平巷的 一组巷道和硐室。
3、线路表示方法:
用两根轨道中心线作为线路的标志, 采用单线表示。 单轨线路 — 单线(细实线); 双轨线路 — 双线(细实线)。
(二)轨道曲线线路
Concept:
δ=
R=
车场线路=直线段线路+联
T= K=
接点线路(圆曲线)
1、曲线半径R及弯道转角
曲线半径R见表18-4,机车 最小值12m
1)单轨线路联接系统参数
7
8
5
3
6
2
ⅠⅠ
1 3
5 2
14经典液相色谱法2-平面色谱分析 (1)

在分离一些极性较小的物质,为了增加 其在固定相中的溶解度,常用甲酰胺或二 甲基甲酰胺、丙二醇等作为固定相。分离 酸、碱性物质,常将纸条浸过缓冲溶液。
展开剂的选择 选择依据:根据被分离物质在两相中的
溶解度和展开剂的极性来考虑。 在流动相中的溶解度较大的物质将会移
动得快,具有较大的比移值;对极性物质, 增加展开剂中极性溶剂的比例,可以增大比 移值,增加非极性溶剂的比例,可以减少比 移值。
保留。
K趋近∞,Rf趋近0,组分停留在原点, 完全被固定相保留。
✓讨论
Rf与K有关,即与组分性质(溶解度) 以及薄层板和展开剂的性质有关。
色谱条件一定,Rf只与组分性质有关, 是薄层色谱基本定性参数,说明组分的色 谱保留行为。
• 分离参数 分离度
R 2l2 l1/W1 W2 2d /W1 W2
2、用薄层色谱法分离某样品,先用氯仿展开, 各组分的Rf太大,可在氯仿中加入一定比例 的( c ),以使Rf值在合适的范围。 A. 甲醇 B.丙酮 C.环己烷 D. 氨水
分离原理: 纸色谱法可以看成是溶质在固定相和流
动相之间连续萃取的过程。依据溶质在两相 间分配系数的不同而达到分离的目的。常用 比移值Rf来表示各组分在色谱中的位置。
Rf值与化学结构的关系
化合物极性大或亲水性强 分配系数大 Rf 值小(水为固定相)
化合物极性小或亲水脂强 分配系数小 Rf 值大(水为固定相)
c.点样方法 吸取一定量的样液,轻轻接触于薄层的
点样线上,点样线一般距薄层底边 1.5~2cm, 点间距约0.8~1.5cm(新药典规定为1.5~2.0 cm)。点样后形成的原点面积越小越好,一 般原点直径不超过2~4mm为宜。
展开和展开剂的流速
快速入门篇十四:运动控制器基础轴参数与基础运动控制指令

快速⼊门篇⼗四:运动控制器基础轴参数与基础运动控制指令今天,我们来讲解⼀下正运动技术运动控制器的基础轴参数与基础运动控制指令。
视频——正运动技术基础运动控制指令⼀材料准备与控制器接线参考控制器接线参考⼆常⽤轴参数的设置1、BASE——轴选择语法:BASE(轴1,轴2,轴3,...)最⼤可⽤轴数根据控制器实际硬件决定。
BASE指令⽤于导向下⼀个运动指令轴的参数读/写⼊特定轴或轴组。
每⼀个过程有其⾃⼰的BASE基本轴组,每个程序能单独赋值。
ZBasic 程序与控制轴运动的运动发⽣器分开。
每个轴的运动发⽣器有其独⽴的功能,因此每个轴能以⾃⼰的速度、加速度等进⾏编程。
轴可以通过叠加运动、同步运动或者通过插补链接在⼀起,插补运动的速度等参数采⽤主轴的参数,默认BASE选择的第⼀个轴例⼦:BASE(0,1,2,3) '轴列表选择:0,1,2,3,轴0为主轴BASE(3,2,5) '轴列表选择:3,2,5,轴3为主轴2、ATYPE——轴类型语法:ATYPE=类型值设置轴的类型,提供轴类型列表,只能设置为当前轴具备的特性。
在程序初始化的时候就设置好ATYPE,ATYPE若不匹配会导致程序⽆法正常运⾏。
⽀持不同类型的轴混合插补。
例⼦:BASE(0,1,2) '主轴为轴0ATYPE=1,1,1 '按轴列表匹配,设为脉冲轴类型ATYPE AXIS(4)=3 '轴4设为正交编码器类型ATYPE(3)=65 '轴3设为ECAT周期位置模式653、UNITS——脉冲当量语法:UNITS=脉冲数 UNITS(轴号)=脉冲数控制器以UNITS作为基本单位,指定每单位发送的脉冲数,⽀持5位⼩数精度。
UNITS是⽤户单位与脉冲单位之间的纽带,UNITS=10000,MOVE(2) 等效给电机20000个脉冲。
若电机不带机械负载,电机转的圈数取决于电机转⼀圈需要的脉冲数:例1:电机转⼀圈需要10000脉冲数,MOVE(3)想让电机转3圈,则UNITS=10000。
使用导数来解决含参函数单调性的讨论方法的总结

155使用导数来解决含参函数单调性的讨论方法的总结蓝荣升作者发现,使用导数来解决函数的单调性,它在高中数学试卷中占有相当大的份额。
函数的单调性是求解函数极值,最值(范围)以及零点个数问题的基础,它经常出现在压轴题的第一问,并且存在一定的困难。
求函数单调性的最困难的部分是含参函数的分类讨论,而分类讨论的思想又是高中阶段着重培养的思想方法。
因此,利用分类讨论来解决带参数的函数单调性问题已成为近年来高考的重点和热点。
这类问题的难点在于学生不懂得如何讨论,或者讨论不全面,这里总结了带参函数单调性的分类讨论的一般步骤,在学会之后,没有不知道如何讨论或讨论不全面的情况。
以下是对单调性一般步骤的讨论(解决了讨论的大部分单调性问题):第一步:求定义域,单调区间是定义域的子集,因此求单调区间必须先求定义域,定义域有三种常见的情况需要讨论。
(1)偶次根式,根号下整体不小于0。
(2)分式,分母不等于0。
(3)对数,真数大于0。
第二步:求函数导数,令0)('=x f ,求出它的根21,x x ,根的个数一般有三种情况:无根、一个根,两个根。
导函数是分式一般先通分,并且还要考虑能不能因式分解。
第三步:如果方程有两根,则要考虑4种情况;如果只有一根则只需考虑第一种情况;如果根不能被求解,并且导数不能被判断出正的或负的,那么我们就需要求函数的二阶导数,利用二阶导数的正负来确定一阶导数的单调性,然后利用最值得到一阶导数的正负,进而判断出原函数的单调性。
(1)是否存在根(判断根是否在定义域中),得到参数的讨论点。
(2)21x x =,得到参数的讨论点。
(3)21x x >,得到参数的讨论点。
(4)21x x <,得到参数的讨论点。
第四步:判断21,x x 分定义域的每个区间的导数的正负情况,如果导数大于0,则函数单调递增,如果导数小于0,则函数单调递减。
以下三种常见方法可用来判断导数的正负:(1)数轴穿根法:(2)函数图像法:(3)区域判断法:只需要判断每个因式的正负。
三相电压型PWM整流器PI调节器参数整定的原理和方法

三相电压源型PWM整流器PI调节器参数整定的原理和方法1引言1.1 PID调节器简介在工程实际中,应用最为广泛的调节器控制规律为比例、积分、微分控制,简称PID控制,又称PID调节。
PID控制器问世至今已有近70年历史,它以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制的主要技术之一。
目前,在工业过程控制中,95%以上的控制回路具有PID结构。
当被控对象的结构和参数不能完全掌握,或得不到精确的数学模型,控制理论的其它技术难以采用时,系统控制器的结构和参数必须依靠经验和现场调试来确定,这时应用PID控制技术最为方便。
PID控制,实际中也有PI和PD控制。
PID控制器就是根据系统的误差,利用比例、积分、微分计算出控制量进行控制的,其原理图如图1-1所示。
图1-1 PID控制系统原理图PID控制器传递函数常见的表达式有以下两种:(1)()ip dKG s K K ss=++,Kp代表比例增益,Ki代表积分增益,Kd代表微分增益;(2)1()p diG s K T sT s=++(也有表示成1()(1)p diG s K T sT s=++),Kp代表比例增益,Ti代表积分时间常数,Td代表微分时间常数。
这两种表达式并无本质区别,在不同的仿真软件和硬件电路中也都被广泛采用。
⏹比例(P,Proportion)控制比例控制是一种最简单的控制方式,其控制器的输出与输入误差信号成比例关系,能及时成比例地反映控制系统的偏差信号,偏差一旦产生,调节器立即产生控制作用,以减少偏差。
当仅有比例控制时系统输出存在稳态误差(Steady-state error)。
⏹积分(I,Integral)控制在积分控制中,控制器的输出与输入误差信号的积分成正比关系。
对一个自动控制系统,如果在进入稳态后存在稳态误差,则称这个控制系统是有稳态误差的或简称有差系统(System with Steady-state Error)。
为了消除稳态误差,在控制中必须引入“积分项”。
C语言复习题(2)答案

{ 4; } A.1--2--3--4 --3--2…… B.1--2--3--4--3--2-4…… C.1--2--4--3--2--4…… D.1--2--4--3---2---1--4…… 21.对下以下系统函数,以下说法错误的是( B)。 A.time()函数的头文件是:time.h B.stdlib.h 头文件中,有 printf(),scanf()函数 C.函数分为两大类,一类是系统函数,一类是用户自定义函数
B.18 C.45 D.9 24. 有以下程序 void main( ) { int i; for (i=0;i<3;i++ ) switch(i) { case 1: printf("%d ", i);
case 2: printf("%d ", i); default: printf("%d ", i); } } 执行后输出结果是( A)。 A.011122 B.012 C.012020 D.120 25..在 C 语言中,假设所有变量均为整型,则下列代码执行后 c 的值 是( D )。
D.! 28. 在 C 语言中,10%2 的值为(C)。 A.5 B.2 C.0 D.-1 29.在 C 语言中,下面( B )转义序列表示换行。 A.\a B.\n C.\r D.\f
30. 在 C 语言中,定义带参数的方法时,参数可以为一个或多个,多 个参数之间使用(B )符号进行分隔。 A.;(分号) B.,(逗号) C.空格符 D.-(连字符) 31.C 语言中,scanf()函数可以使用( C)格式说明符接受单精度浮 点型变量的值。 A.%c B.%d C.%f D.%s
C.必须在程序的最后 D.可以在任意位置 3..表达式 a+=a-=a=9 的值是(D)。 A.9 B.-9 C.18 D.0 4. 设有定义:int a=10;则表达式 a+=a*=a 的值是( C )。 A.10 B.100 C.200
java编程题

java编程题1、(1)编写一个圆类Circle,该类拥有:①一个成员变量Radiu(私有,浮点型);//存放圆的半径;②两个构造方法Circle()//将半径设为0Circle(doubler)//创建Circle对象时将半径初始化为r③三个成员方法doublegetArea()//获取圆的面积doublegetPerimeter()//获取圆的周长voidhow()//将圆的半径、周长、面积输出到屏幕编写应用程序,创建类的对象,分别设置圆的半径,计算并分别显示圆半径、圆面积、圆周长。
2、定义一个表示学生信息的类Student,要求如下:(1)类Student的成员变量:NO表示学号;Name表示姓名;Se某表示性别;Age表示年龄;Java:表示Java课程成绩。
(2)类Student带参数的构造方法:在构造方法中通过形参完成对成员变量的赋值操作。
(3)类Student的方法成员:getNo():获得学号;getName():获得姓名;getSe某():获得性别;getAge()获得年龄;getJava():获得Java课程成绩(4)根据类Student的定义,创建五个该类的对象,输出每个学生的信息,计算并输出这五个学生Java语言成绩的平均值,以及计算并输出他们Java语言成绩的最大值和最小值。
3、输入一行字符,分别统计出其中英文字母、空格、数字和其它字符的个数。
4、用Java语言定义一个员工类Employee(1)员工类Employee属性有:id:String型,代表员工ID号name:String型,代表姓名age:int型,代表年龄5、题目:企业发放的奖金根据利润提成。
利润(I)低于或等于10万元时,奖金可提10%;利润高于10万元,低于20万元时,低于10万元的部分按10%提成,高于10万元的部分,可可提成7.5%;20万到40万之间时,高于20万元的部分,可提成5%;40万到60万之间时高于40万元的部分,可提成3%;60万到100万之间时,高于60万元的部分,可提成1.5%,高于100万元时,超过100万元的部分按1%提成,从键盘输入当月利润,求应发放奖金总数?6、题目:给一个不多于5位的正整数,要求:一、求它是几位数,二、逆序打印出各位数字。
Multisim14电子电路仿真方法和样例

Multisim14电⼦电路仿真⽅法和样例Multisim14电⼦电路仿真⽅法和样例2019年9⽉本⼿册基于Multisim14仿真环境,从最基本的仿真电路图的建⽴开始,结合实际的例⼦,对模拟和数字电路中常⽤的测试⽅法进⾏介绍。
这些应⽤⽰例包括:常⽤半导体器件特性曲线的测试、放⼤电路静态⼯作点和动态参数的测试、电压传输特性的测试、波形上升时间的测试、逻辑函数的转换与化简、逻辑分析仪的使⽤⽅法等。
此外,本⼿册侧重于测试⽅法的介绍,仅对主要步骤进⾏说明,如碰到更细节的问题,可参阅《Multisim 14教学版使⽤说明书》或其它帮助⽂档。
1.MULTISIM14主界⾯简介 (4)2.仿真电路图的建⽴ (4)3.常⽤半导体器件特性曲线的测试⽅法 (5)3.1晶体三极管特性曲线的测试 (5)3.1.1 IV分析仪测试⽅法 (5)3.1.2 直流扫描分析⽅法 (5)3.2结型场效应管特性曲线的测试 (6)3.2.1 IV分析仪测试⽅法 (6)3.2.2 直流扫描分析⽅法 (7)3.3⼆极管、稳压管伏安特性曲线的测试 (7)4.放⼤电路静态⼯作点的测试⽅法 (7)4.1虚拟仪器测试⽅法 (7)4.2静态⼯作点分析⽅法 (8)5.放⼤电路动态参数的测试⽅法 (8)5.1电压放⼤倍数的测试 (8)5.1.1瞬态分析测试⽅法 (8)5.1.2 虚拟仪器测试⽅法 (9)5.2输⼊电阻的测试 (9)5.3输出电阻的测试 (10)5.4频率响应的测试 (10)5.4.1交流分析⽅法 (10)5.4.2 波特图仪测试⽅法 (10)6.电压传输特性的测试⽅法 (11)7.上升时间的测试⽅法 (12)8.逻辑函数的转换与化简 (13)8.1逻辑函数转换为真值表 (13)8.2真值表转换为逻辑函数 (13)9.逻辑分析仪的使⽤⽅法 (14)图2.1 ⽰例电路1. Multisim14主界⾯简介运⾏Multisim14,⾃动进⼊电路图编辑界⾯。
实验十四TTL、CMOS门电路参数及逻辑特性的测试

实验十四TTL、CMOS门电路参数及逻辑特性的测试大学通信工程系林XX一.实验目的:1、掌握TTL、CMOS与非门参数的测量方法;2、掌握TTL、CMOS与非门逻辑特性的测量方法;3、掌握TTL与CMOS门电路接口设计方法。
二.实验原理:(一)TTL门电路:TTL门电路是标准的集成数字电路,其输入、输出端均采用双极型三极管结构:凡是TTL器件特性均与TTL门电路具有相同特性,故需了解TTL门电路的主要参数。
7400是TTL型中速二输入端四与非门。
图1是它的部电路原理图和管脚排列图。
1、TTL与非门的主要参数:(1)输入短路电流:I IS:与非门某输入端接地时,该输入端接入地的电流。
(2)输入高电平电流I IH:与非门某输入端接V CC(5V),其他输入端悬空或接V CC时,流入该输入端的电流。
TTL与非门特性如图2所示:(3)开门电平V ON:使输出端维持低电平V OL所需的最小输入高电平,通常以V O=0.4V时的Vi定义。
(4)关门电平V OFF:使输出端保持高电平V OH所允许的最大输入低电平,通常以Vo=0.9V OH时的Vi定义。
阀值电平V T:V T=(V OFF+V ON)/2(5)开门电阻R ON:某输入端对地接入电阻(其他悬空),使输出端维持低电平(通常以V O=0.4V)所需的最小电阻值。
(6)关门电阻R OFF:某输入端对地接入电阻(其他悬空),使输出端保持高电平V OH(通常以V O=0.9V OH 所允许的最大电阻值)。
TTL与非门输入端的电阻负载特性曲线如图3所示。
(7)输出低电平负载电流I OL:输出保持低电平V O=0.4V时允许的最大灌流(如图4);(8)输出高电平负载电流I OH:输出保持高电平V O=0.9V OH时允许的最大拉流;(9)平均传输延迟时间tpd:○1开通延迟时间t OFF:输入正跳变上升到1.5V相对输出负跳变下降到1.5V的时间间隔;○2关闭延迟时间t ON:输入负跳变上升到1.5V相对输出正跳变下降到1.5V的时间间隔;○3平均传输延迟时间:开通延迟时间与关闭延迟时间的算术平均值。
高中(必修一)数学口诀

高中数学口诀人教A 版必修一第一章 集合篇1、集合三个特性:确定性、互异性、无序性(互异性:求出答案记得带回去检验看是否出现重复)2、常见数集表示方法:(1)、N ——自然数数集(自然的英语nature) (2)、Z ——整数集(拼音zheng )(3)、Q ——有理数集 (4)、R ——实数集3、一个集合有n 个元素,则其子集的个数为n 2,真子集个数为12-n ,非空子集个数为12-n ,非空真子集个数为22-n .4、元素与集合之间用∉∈或,集合于集合之间用⊆。
5、空集是任何集合的子集,是任何非空集合的真子集。
6、口诀:看到子集,首先考虑空集,然后才是画数轴列不等式。
7、两个重要公式:∁U (A ∪B )=(∁U A )∩(∁U B );∁U (A ∩B )=(∁U A )∪(∁U B ).(口诀:拆开变号)人教A 版必修一第一章 函数篇1、区间是一种特殊的数集表达形式,只能用于表示数集,而且不管开闭,必须左小右大。
2、形成函数的三个要求:每一性、唯一性、允许多对一不能一对多。
3、函数三要素:定义域、值域和对应关系(函数问题,不管啥题定义域优先)4、函数的表示方法:解析法、图像法、列表法5、判断两个函数是否相等只需要判断定义域和对应关系是否相等即可。
6、求定义域口诀(1)、先求定义域再化简; (2)、分式要求分母不为0.(3)、偶次根式要求被开方数≥0; (4)、0次方和负数次方要求底数不为0;(5)、指数要求底数>0且≠1; (6)、对数(log )要求真数>0,底数>0且≠1;(7)、复合函数定义域的求法:(口诀:简单算复杂“放”,复杂算简单“代”。
) 若()x f 定义域为[]b a , ,则复合函数()[]x g f 定义域由()b x g a ≤≤解出; 若()[]x g f 定义域为[]b a , ,则()x f 定义域相当于[]b a x ,∈时()x g 的值域.7、函数值域的求法(求值域也要先求定义域)(1)、图像法:能画图的坚决画图(2)、单调性法:有增减就可以代两端求最值得到值域;(3)、换元法:(口诀:次方出现两倍关系就可以使用换元法,设低次为t )操作步骤:第一步:求定义域并设t ; 第二步:马上求出t 的范围;第三步:用t 表示出x ; 第四步:求出新函数值域即为原函数的值域。
带参数的方法

带参数的⽅法如何使⽤带参数的⽅法1定义带参数的⽅法2语法: <访问修饰符> 返回类型 <⽅法名>(<形式参数列表>) {3//⽅法的主体4 }5// 访问修饰符: 该⽅法允许被访问调⽤的权限范围6返回类型: ⽅法返回值的类型7形式参数列表: 传送给⽅法的形参列表8调⽤带参数的⽅法9语法: 对象名.⽅法名(参数1, 参数2,……,参数n)10定义带参数的⽅法11public class ZhazhiJi {12public String zhazhi ( String fruit ) { //参数列表:(数据类型参数1,数据类型参2…)13 String juice = fruit + "汁";14return juice;15 }16 }17调⽤带参数的⽅法18/*调⽤zhazhi⽅法*/19 ZhazhiJi myZhazhiji = new ZhazhiJi();20 String myFruit = "苹果";21 String myJuice = myZhazhiji.zhazhi(myFruit);//调⽤⽅法,传递的参数要与参数列表⼀⼀对应22 System.out.println(myJuice);调⽤带参⽅法时,有哪些注意事项?1带参⽅法的调⽤2对象名. ⽅法名( 变量 1, 变量 2,......, 变量 n);3调⽤⽅法时,需要注意以下两点。
4 1·先实例化对象,再调使⽤⽅法。
5 2·实参的类型、数量、顺序都要与形参⼀⼀对应。
名词解释:形参、实参1形参代表定义⽅法时括号内的参数(参数列表)public void xc(形参)2实参代表在调⽤⽅法时⽅法括号内的参数(参数列表) .xc(实参);⼀个⽅法可以有多少个参数,多少个返回值?--- 注意:当携带多个参数时,实参列表需要和形参列表的顺序和数据类型保持⼀致1带多个参数的⽅法2问题: 在保存了多个学⽣姓名的数组中,指定查找区间,查找某个学⽣姓名并显⽰是否查找成功3设计⽅法,通过传递三个参数(开始位置、结束位置、查找的姓名)来实现4⽰例:5public boolean searchName (int start,int end,String name){/*返回值类型 boolean带有三个形参 {int start,int end,String name} */6boolean find = false; // 是否找到标识7// 指定区间数组中,查找姓名8for(int i=start-1;i<end;i++) {9if(names[i].equals(name)) {10 find=true;11break;12 }13 }14return find; // 返回结果:boolean类型15 }1617if(st.searchName(s,e,name)) { //传递三个实参 {s,e,name}18 System.out.println("找到了!");19 }else{20 System.out.println("没找到该学⽣!");21 }包 --- Package1 java中的包(package)2 1. 包,对应到磁盘中的⽂件夹3 2 新建⼀个class,默认保存在缺省包中4 3 声明包的关键字:package5 package语句,置顶位置6 4. 导⼊包的关键字:import7import包名.类名(*表⽰所有);8 5. 作⽤:分类存放、⽅便查找和管理;防⽌同名冲突;9在更⼴的范围内保护类、数据和⽅法10 6. 命名规范11 Java包名通常由⼩写字母组成,不能以圆点开头或结尾。
2016新编同步皮带规格参数

同步皮带、同步齿轮型号规格表机械工程类2009-11-18 12:18:12 阅读711 评论0 字号:大中小订阅这里的资料应该对机械设计的网友有益吧——同步皮带、同步齿轮型号规格表第一部份同步皮带主要型号:一、3M 节距是3.00mm. 带高2.40mm, 齿高1.17mm. (120-3M-1800-3M)二、5M 节距是5.00mm. 带高3.80mm, 齿高2.06mm. (180-5M-2100-5M)三、8M 节距是8.00mm. 带高6.00mm, 齿高3.36mm. (368-8M-5600-8M)四、14M节距是14.00mm. 带高10.00mm, 齿高6.02mm. (966-14M-4760-14M)五、20M节距是20.00mm. 带高13.20mm, 齿高9.00mm. (20-20M-5600-20M)六、MXL 节距是2.032mm. 带高1.14mm, 齿高0.51mm. (32-MXL-1170-MXL)七、XXL 节距是3.175mm. 带高1.52mm, 齿高0.76mm. (B80-XXL-B463-XXL)八、XL 节距是5.080mm. 带高2.30mm, 齿高1.27mm. (54-XL-1300-XL)九、L 节距是9.525mm. 带高3.60mm, 齿高1.91mm. (98-L-1043-L)十、H 节距是12.700mm. 带高4.30mm, 齿高2.29mm. (185-H-2360-H)十一、XH 节距是22.225mm. 带高11.20mm, 齿高6.35mm. (464-XH-1800-XH)十二、XXH 节距是31.750mm. 带高15.70mm, 齿高9.53mm.十三、S2M 节距是2.00mm. 带高1.36mm, 齿高0.76mm. (130-S2M-30-S2M)十四、S3M 节距是3.00mm. 带高1.90mm, 齿高1.14mm. (150-S2M-3210-S2M)十五、S4.5M 节距是4.50mm. 带高2.81mm, 齿高1.71mm. (180-S4.5M-950-S4.5M)十六、S5M 节距是5.00mm. 带高3.40mm, 齿高1.91mm. (150-S5M-20-S5M)十七、S8M 节距是8.00mm. 带高5.30mm, 齿高3.05mm. (480-S8M-3200-S8M)十八、S14M 节距是14.00mm. 带高10.20mm, 齿高5.30mm. (966-S14M-4326-S14M)十九、P3M 节距是3.00mm. 带高1.90mm, 齿高1.15mm. (110-P3M-1569-P3M)二十、P5M 节距是5.00mm. 带高3.50mm, 齿高1.95mm. (225-P5M-2525-P5M)二十一、P8M 节距是8.00mm. 带高5.50mm, 齿高3.20mm. (376-P8M-2800-P8M)二十二、P14M 节距是14.00mm. 带高10.00mm, 齿高.00mm.(966-P14M-4578-P14M)二十三、T2.5 节距是2.50mm. 带高1.30mm, 齿高0.70mm. (145-T2.5-400-T2.5)二十四、T5 节距是5.00mm. 带高2.20mm, 齿高1.20mm. (150-T5-20-T5)二十五、T10 节距是10.00mm. 带高4.50mm, 齿高2.50mm. (340-T10-2800-T10)二十六、T20 节距是20.00mm. 带高8.00mm, 齿高5.00mm. (1240-T20-2760-T20)第二部份同步齿轮主要型号一、AS型(平面式无挡板)二、BS型(有台阶无挡板)三、AF型(平面式有挡板)四、BF型(有台阶有挡板)五、W型(两面凹形无挡板)带及同步带轮的选用同步带传动是一种带齿与带轮齿槽的啮合传动。
信长之野望14各项参数修改方法

信长之野望14 各项参数修改⽅法 《信长之野望14:创造》各项参数是可以修改的,相信很多新⼿玩家都还不知道吧。
那么各项参数该怎么修改呢?下⾯就和⼩编⼀起来看看《信长之野望14:创造》各项参数修改的⽅法吧。
说明:修改p a r a m.n14很简单,不过⾸先必须备份⼀下。
修改有两个⽅法: ⼀使⽤记事本打开p a r a m.n14(双击该⽂件然后选“从⼀安装列表中选择程序”,选择记事本打开即可);然后根据提供的字串搜索(提供的字串搜索结果都是唯⼀的),然后就可以进⾏数值上的修改;注意不要删掉空格 ⼆将p a r a m.n14改名p a r a m.n13,然后使⽤天道v a n修改器的p a r a m修改器来修改;优点是提供了参数的序号,可以直接根据参数序号修改,更加安全 直辖范围修改: 刚刚找到了两个直辖范围相关的参数,分别是31号参数(100000)和32号参数(40)。
这两个值之间是貌似有相互制约,就是必须两个值都增⼤才⾏。
⽅法: ⽤记事本打开p a r a m.n14,搜索“17010000040670”字串(这个字串只出现⼀次),⾥⾯的100000和40就是需要修改的参数。
第⼀个参数建议不要超过900000,第⼆个参数不要超过900;把他们设置为500000和500应该完全⾜够了。
注意:是否有副作⽤尚且不知。
新筑城参数修改: “20222500050”中的5000是新筑城的初始⼈⼜,50是新筑城的民忠,他们分别为1127号和1128号参数 忠诚度参数修改: 搜索字串“-1-2400-33310”,可以得到唯⼀结果,这些应该是忠诚度的修正值。
(973到981号参数) 经过测试确认的有: 其中的4是任命城主时的忠诚度修正(975号参数) 最后的10是长期作为家⾂的忠诚奖励最⼤值(这个奖励可以提供+1到+10的忠诚修正)(981号参数) -3是灭国后登⽤的忠诚度修正(978号参数) -3后⾯的3是⼀门众带来的忠诚度修正(979号参数) 初始民忠修改: 从1036号到1111号参数(共76个)是76分国与民忠相关的参数,是76分国各国民忠最⼤值的基准值,实际最⼤民忠值还会受到政策等的影响 费⽤修改: 966项是筑城所需资⾦搜索“30005001008000300300”字串,其中的8000就是筑城资⾦ 556是外交⼯作所需资⾦,这个不⽤测其实就能看出来搜索“200090 60050”⾥⾯的600就是外交费⽤ 81号参数和82号参数分别是整备和设营费⽤。
昌吉市第十四小学纳米黑板设备参数
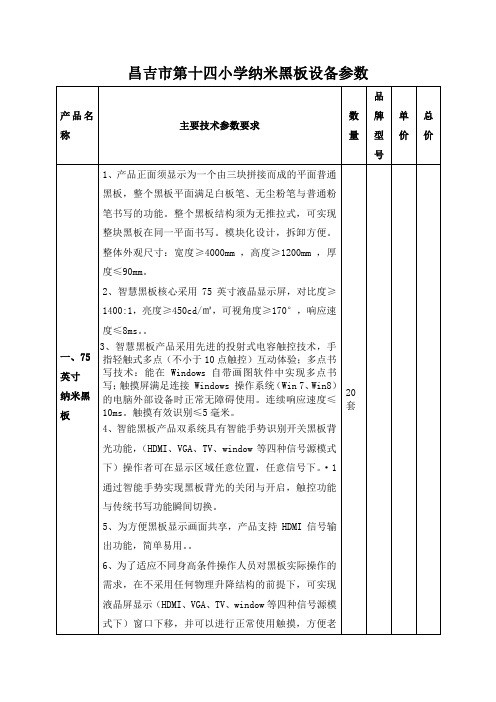
(7)区域监看:学校数量和黑板数量变化趋势图、常用软件使用前10名、学校活跃排名、最近一个月的黑板在线数量。
(8)设备信息查看:可在控制端网页查看互动黑板的基本信息,如:系统、cpu、硬盘、内存等信息。
3、内置有线网卡,支持无线WiFi:IEEE 802.11n/b/g 标准,保证足够的信号强度;
4、为保证系统兼容性及后期升级维护的便利性,智慧黑板内置电脑与智慧黑板同一品牌
20套
四、智能
无线麦克风
1、智慧黑板支持无线MIC功能,智慧黑板整机具有无线MIC接收功能,可以将无线MIC音频输出到内置音箱;智慧黑板整机支持无线MIC和本机声音混音功能;可以同时录制MIC和本机电脑音频;
2、智慧黑板核心采用75英寸液晶显示屏,对比度≥1400:1,亮度≥450cd/㎡,可视角度≥170°,响应速度≤8ms。。
1. 3、智慧黑板产品采用先进的投射式电容触控技术,手指轻触式多点(不小于10点触控)互动体验;多点书写技术:能在 Windows 自带画图软件中实现多点书写;触摸屏满足连接 Windows 操作系统(Win 7、Win8)的电脑外部设备时正常无障碍使用。连续响应速度≤10ms。触摸有效识别≤5毫米。
(20)资源管理及共享:老师和学校管理员可上传资源到服务器,老师可在智慧黑板端登录后下载、上传文件。
(21)日志管理:记录平台操作历史,方便管理员进行管理。
七、配套教学管资源
1.功能简述
(1)电子教学辅助资源:放在云资源平台,可下载到本地使用,
(2)电子资源读取方式:U盘方式或电脑本地相结合
药物分析 第14章 气相色谱法(优选.)

(2)按组分主要差别选择
极性差别为主要矛盾——极性固定液 沸点差别为主要矛盾——非极性固定液
例1:苯(80.1 0C),环己烷(80.7 0C) 选非极性柱——分不开; 选中强极性柱——较好分离,环己烷先出柱
例2:分离胺类:一甲胺 二甲胺 三甲胺
形成氢键能力
CH3-NH2> CH3-NHCH3>CH3-N(CH3)2
吸收了塔板理论的有效成果——H, 并从动力学角度较好地解释了影响柱效的因素
H = A + B/u + Cu
塔板 高度
涡流 扩散 项
纵向 扩散 项
传质 阻抗 项
1、涡流扩散项(多径扩散项):A
产生原因:载气携样品进柱,遇到来自固定相颗粒的 阻力→路径不同→涡流扩散
A = 2λdp
dp:填充物的平均颗粒直径 λ:填充物的填充不规则因子 固体颗粒越小,填充越均匀,A项越小,H↓,柱效↑。
第14章 气相色谱法
一 概述 二 气相色谱理论 三 色谱柱 四 检测器 五 分离条件的选择 六 定性定量分析 七 应用与示例
第一节 概述
气相色谱法(GC):以气体为流动相的色谱法。
一、分类:
1 按固定相分
气-固 (GSC) 吸附
气-液 (GLC) 分配
2 按柱的粗细分 填充柱 Ф 2~4mm,L2~4m
实际:tm不参与柱内分配
neff
5.54(
t
' R
)2
w1/ 2
16(tR' )2 w
H eff
L n e ff
讨论: neff和Heff扣除了死时间,更能真实的反映柱效
例: 在柱长为2m的5%的阿皮松柱、柱温为 1000C,记录纸速度为2.0cm/min的色谱条件下, 测定苯的保留时间为1.5min,半峰宽为0.20cm, 求理论塔板数和理论塔板高度。
2024中考复习重难点02 含参类方程与不等式问题(解析版)

重难点突破02 含参类方程与不等式问题目录题型01 根据分式方程解的情况求字母的值或取值范围题型02 整式方程(组)与一元一次不等式组结合求参数的问题题型03 同解方程组题型04 根据二元一次方程组解满足的情况求参数题型05 二元一次方程组整数解问题题型06 利用相反数求二元一次方程组参数题型07 已知方程的解求参数题型08 根据一元二次方程根的情况求参数题型09 根据一元一次不等式组的整数解求参数的取值范围题型10 根据一元一次不等式组的解集的情况求参数的取值范围题型11 整式方程(组)与一元一次不等式结合求参数的问题题型01 根据分式方程解的情况求字母的值或取值范围1.(2023·山东淄博·中考真题)已知x=1是方程m2−x −1x−2=3的解,那么实数m的值为()A.−2B.2C.−4D.4【答案】B【分析】将x=1代入方程,即可求解.【详解】解:将x=1代入方程,得m2−1−11−2=3解得:m=2故选:B.【点睛】本题考查分式方程的解,解题的关键是将x=1代入原方程中得到关于m的方程.2.(2023·黑龙江牡丹江·中考真题)若分式方程ax+2=1−3x+2的解为负数,则a的取值范围是()A.a<−1且a≠−2B.a<0且a≠−2 C.a<−2且a≠−3D.a<−1且a≠−3【答案】D【分析】直接解分式方程,进而得出a的取值范围,注意分母不能为零.【详解】解:去分母得:a=x+2−3,解得:x=a+1,∵分式方程ax+2=1−3x+2的解是负数,∵a+1<0,x+2≠0,即a+1+2≠0,解得:a<−1且a≠−3,故选:D.【点睛】此题主要考查了分式方程的解,正确解分式方程是解题关键.3.(2023·山东日照·中考真题)若关于x的方程xx−1−2=3m2x−2解为正数,则m的取值范围是()A.m>−23B.m<43C.m>−23且m≠0D.m<43且m≠234.(2023·四川巴中·中考真题)关于x的分式方程x+mx−2+12−x=3有增根,则m=.【答案】−1【分析】等式两边同时乘以公因式(x−2),化简分式方程,然后根据方程有增根,求出x的值,即可求出m.【详解】x+mx−2+12−x=3,解:方程两边同时乘以(x−2),得x+m+(−1)=3(x−2),∴m=2x−5,∵原方程有增根,∴x−2=0,∴x=2,∴m=2x−5=−1,故答案为:−1.【点睛】本题考查分式方程的知识,解题的关键是掌握分式方程的增根.5.(2020·黑龙江牡丹江·中考真题)若关于x的分式方程2x−1=mx有正整数解,则整数m的值是()A.3B.5C.3或5D.3或4【答案】D【分析】解带参数m的分式方程,得到x=mm−2=1+2m−2,即可求得整数m的值.【详解】解:2x−1=mx,两边同时乘以x(x−1)得:2x=m(x−1),去括号得:2x=mx−m,移项得:2x−mx=−m,合并同类项得:(2−m)x=−m,系数化为1得:x=mm−2=1+2m−2,若m为整数,且分式方程有正整数解,则m=3或m=4,当m=3时,x=3是原分式方程的解;当m=4时,x=2是原分式方程的解;故选:D.【点睛】本题考查分式方程的解,始终注意分式方程的分母不为0这个条件.题型02 整式方程(组)与一元一次不等式组结合求参数的问题6.(2020·重庆·中考真题)若关于x的一元一次不等式结{3x−12≤x+3x≤a的解集为x≤a;且关于y的分式方程y−ay−2+3y−4y−2=1有正整数解,则所有满足条件的整数a的值之积是()A.7B.-14C.28D.-56【答案】A【分析】不等式组整理后,根据已知解集确定出a的范围,分式方程去分母转化为正整数方程,由分式方程有非负整数解,确定出a的值,求出之和即可.【详解】解:解不等式3x−12≤x+3,解得x≤7,∵不等式组整理的{x≤7x≤a,由解集为x≤a,得到a≤7,分式方程去分母得:y−a+3y−4=y−2,即3y−2=a,解得:y=a+23,由y为正整数解且y≠2,得到a=1,7,1×7=7,故选:A.【点睛】此题考查了分式方程的解,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.7.(2023·重庆·中考真题)若关于x的一元一次不等式组{x+32≤42x−a≥2,至少有2个整数解,且关于y的分式方程a−1y−2+42−y=2有非负整数解,则所有满足条件的整数a的值之和是.即a−12≥0且a−12≠2,解得:a ≥1且a ≠5∵a 的取值范围是1≤a ≤6,且a ≠5 ∵a 可以取:1,3, ∵1+3=4, 故答案为:4.【点睛】本题考查了分式方程的解,以及解一元一次不等式组,熟练掌握运算法则是解题关键. 8.(2024·重庆·模拟预测)已知关于x 的一元一次不等式组{2(3−x )+1<−x x +a −2<0有解且最多5个整数解,且关于y 的分式方程y+a y−3−3=43−y的解为正整数,则满足条件的所有整数a 的和为 .【答案】−20【分析】本题考查了分式方程的解,解一元一次不等式组,以及一元一次不等式组的整数解,熟练掌握解一元一次不等式组以及解分式方程是解本题的关键.首先求出不等式组的解集为7<x <2−a ,然后根据有解且最多5个整数解得到−11≤a <−5,然后解分式方程为y =a+132,结合解为正整数且解有意义,得出a 的另一个范围,从而得出所有整数a 的和.【详解】{2(3−x )+1<−x①x +a −2<0②解∵得,x >7 解∵得,x <2−a∵关于x 的一元一次不等式组{2(3−x )+1<−x x +a −2<0有解且最多5个整数解,∵7<2−a ≤13 解得−11≤a <−5y +a y −3−3=43−y去分母得,y +a −3y +9=−4 解得y =a+132∵关于y 的分式方程y+ay−3−3=43−y 的解为正整数, ∵y =a+132是正整数,且y =a+132≠3,即a ≠−7∵a =−11或−9,∵−11+(−9)=−20.∵满足条件的所有整数a的和为−20.故答案为:−20.9.(2024·重庆开州·二模)若关于x的方程x+22−x +axx−2=−2有正整数解,且关于y的不等式组{2y−43<22a−y−1≤0至少有两个整数解,则符合条件的所有整数a的和为.【答案】1【分析】本题考查了解分式方程和分式方程的解,一元一次不等式组的整数解,熟练掌握运算法则是解本题的关键.由分式方程有正整数解,确定出满足条件a的值,将不等式组整理后,由不等式组至少有两个整数解确定出a的范围,综合求解即可.【详解】解:x+22−x +axx−2=−2去分母得:−x−2+ax=−2(x−2),去括号得:−x−2+ax=−2x+4,移项,合并同类项得:(a+1)x=6,∵x=6a+1.∵分式方程有可能产生增根2,∵6a+1≠2,∵a≠2.∵关于x的分式方程x+22−x +axx−2=−2有正整数解,∵a=0,1,5,{2y−43<2①2a−y−1≤0②,解∵得:y<5,解∵得:y≥2a−1,∵不等式组的解集为:2a−1≤y<5,∵关于y的不等式组{2y−43<22a−y−1≤0至少有两个整数解,∵2a−1≤3,∵a ≤2.综上,整数a =1,0.∵满足条件的整数a 的和为1+0=1. 故答案为:1.10.(2024·四川成都·模拟预测)若整数a 使得关于x 的分式方程ax−122−x+3=xx−2有整数解,且使得二次函数y =(a −2)x 2+2(a −1)x +a +1的值恒为非负数,则所有满足条件的整数a 的值之和是 . 【答案】15 【分析】本题考查了二次函数与x 轴的交点问题,解不等式组及分式方程,正确理解二次函数的值恒为非负数的性质是解题关键.根据二次函数的性质,得到一元一次不等式组,求得a ≥3,再解分式方程,得到x =6a−2,再根据a 、x 均为整数,找出满足条件的a 的值,求和即可.【详解】解:∵二次函数y =(a −2)x 2+2(a −1)x +a +1的值恒为非负数, ∴{a −2>0Δ=4(a −1)2−4(a −2)(a +1)≤0, 解得:a ≥3, 解分式方程ax−122−x+3=xx−2得:x =6a−2,∵x ≠2, ∴a ≠5,∵a 、x 均为整数,∴a =3时,x =6;a =4时,x =3;a =8时,a =1; ∴所有满足条件的整数a 的值之和是3+4+8=15, 故答案为:15.题型03 同解方程组11.(2020·广东·中考真题)已知关于x ,y 的方程组{ax +2√3y =−10√3x +y =4与{x −y =2x +by =15 的解相同.(1)求a ,b 的值;(2)若一个三角形的一条边的长为2√6,另外两条边的长是关于x 的方程x 2+ax +b =0的解.试判断该三角形的形状,并说明理由.12.(2021·广东·二模)解关于x 、y 的方程组时,小明发现方程组{ax +by =2x −y =8的解和方程组{5x +2y =b 2x +3y =−9 的解相同. (1)求方程组的解;(2)求关于t 的方程(at ﹣b )2+2(at ﹣b )﹣3=0的解. 【答案】(1){x =3y =−5(2)t =23或29【分析】(1 )根据二元一次方程组的解相同,可得新方程组,根据解方程组,可得x 、y 的值;(2 )根据方程组的解满足方程,把方程组的解代入,可得关于a 、b 的二元一次方程组,根据解方程组,可得a 、b 的值;然后利用换元法解该方程.【详解】(1)由方程组{ax +by =2x −y =8 的解和方程组{5x +2y =b 2x +3y =−9的解相同知,{x −y =8①2x +3y =−9②.由∵×3+∵,得5x =15.则x =3. 将x =3代入∵,得3﹣y =8,则y =﹣5. ∵方程组的解为:{x =3y =−5;(2)把{x =3y =−5 分别代入ax +by =2和5x +2y =b 可得方程组{3a −5b =2b =5,解得:{a =9b =5,设at ﹣b =n ,则方程(at ﹣b )2+2(at ﹣b )﹣3=0可变为n 2+2n ﹣3=0, ∵(n +3)(n ﹣1)=0, ∵n =﹣3或1, ∵at ﹣b =﹣3或1,把{a =9b =5 代入得:9t ﹣5=﹣3或1, 解得:t =23或29;【点睛】本题考查了二元一次方程组和一元二次方程的解法,理解方程组解相同的含义是解决问题的关键.题型04 根据二元一次方程组解满足的情况求参数13.(2023·四川眉山·中考真题)已知关于x,y 的二元一次方程组{3x −y =4m +1x +y =2m −5的解满足x −y =4,则m 的值为( ) A .0 B .1C .2D .3【答案】B【分析】将方程组的两个方程相减,可得到x −y =m +3,代入x −y =4,即可解答. 【详解】解:{3x −y =4m +1①x +y =2m −5②,①−②得2x −2y =2m +6, ∴x −y =m +3,代入x −y =4,可得m +3=4, 解得m =1,故选:B .【点睛】本题考查了根据解的情况求参数,熟练利用加减法整理代入是解题的关键.14.(2022·山东聊城·中考真题)关于x ,y 的方程组{2x −y =2k −3x −2y =k的解中x 与y 的和不小于5,则k 的取值范围为( )A .k ≥8B .k >8C .k ≤8D .k <8 【答案】A【分析】由两式相减,得到x +y =k −3,再根据x 与 y 的和不小于5列出不等式即可求解.【详解】解:把两个方程相减,可得x +y =k −3,根据题意得:k −3≥5,解得:k ≥8.所以k 的取值范围是k ≥8.故选:A .【点睛】本题考查二元一次方程组、不等式,将两式相减得到x 与y 的和是解题的关键.15.(2023·四川泸州·中考真题)关于x ,y 的二元一次方程组{2x +3y =3+a x +2y =6的解满足x +y >2√2,写出a 的一个整数值 . 【答案】7(答案不唯一)【分析】先解关于x 、y 的二元一次方程组的解集,再将x +y >2√2代入,然后解关于a 的不等式的解集即可得出答案.【详解】将两个方程相减得x +y =a −3,∵x +y >2√2,∵a −3>2√2,∵a >3+2√2,∵4<8<9,∵2<2√2<3,∵5<2√2+3<6,∵a 的一个整数值可以是7.故答案为:7(答案不唯一).【点睛】本题主要考查了解二元一次方程组和解一元一次不等式,整体代入的思想方法是解答本题的亮点.16.(2024·浙江宁波·模拟预测)若关于x,y的方程组{2x−y=5kx+y=4k+3的解满足x−y≤5,则k的取值范围是.【答案】k≤3【分析】本题主要考查二元一次方程组和一元一次不等式的解法,把方程组的解求出,即用k表示出x、y,代入不等式x−y≤5,转化为关于k的一元一次不等式,可求得k的取值范围.【详解】解:{2x−y=5k①x+y=4k+3②由①+②可得:3x=9k+3,所以:x=3k+1③把③代入②得:3k+1+y=4k+3,解得:y=k+2,代入x−y≤5可得:3k+1−(k+2)≤5,解得:k≤3,故答案为:k≤3.题型05 二元一次方程组整数解问题17.(2022·广东揭阳·模拟预测)如果关于x,y的方程组{4x−3y=66x+my=26的解是整数,那么整数m的值为()A.4,−4,−5,13B.4,−4,−5,−13C.4,−4,5,13D.−4,5,−5,13【答案】B【分析】先将m看作已知量,解二元一次方程组,用m表示出y,再结合x,y为整数,得出y的整数解,然后把y的整数解代入①,得出x的解,再把方程组的整数解代入②,即可得出m的值.【详解】解:{4x−3y=6①6x+my=26②,由②×2−①×3,可得:y=342m+9,∵x,y为整数,∵当(2m+9)为−34,−17,−2,−1,34,17,2,1时,y为整数,18.(23-24八年级上·重庆沙坪坝·期末)关于x ,y 的二元一次方程组{kx +y =43x +y =0的解为整数,关于z 的不等式组{3z >z −44z −2k−13≤1有且仅有2个整数解,则所有满足条件的整数k 的和为( ) A .6B .7C .11D .12 【答案】A【分析】本题考查了解含参数的二元一次方程组整数解,含参数的不等式组整数解问题;解出方程组,根据整数解确定k 的取值,解出不等式组,由整数解的个数确定k 的取值范围,即可求解;能正确解出含参数的方程组和不等式组,并确定k 的取值范围是解题的关键.【详解】解:解方程组{kx +y =43x +y =0得: {x =4k−3y =123−k, ∵关于x ,y 的二元一次方程组的解为整数,∵k 可取−1,1,2,4,5,7,解关于z 的不等式组得{z >−2z ≤1+k 6 ,∵关于z 的不等式组有且仅有2个整数解,∴0≤1+k6<1,解得:−1≤k <5,∵整数k 为−1,1,2,4,其和为−1+1+2+4=6,故选:A.19.(22-23七年级下·重庆·阶段练习)已知关于x,y的二元一次方程组{ax+2y=612x−y=1的解为整数,且关于z的方程z−a2−z3=1的解为非负数,求满足条件的所有整数a的和为()A.2B.4C.9D.11题型06 利用相反数求二元一次方程组参数20.(2022·四川南充·二模)已知x 、y 满足方程组{x +2y =2m −12x +y =5,且x 与y 互为相反数,则m 的值为( )A .m =−2B .m =2C .m =−3D .m =3 【答案】A【分析】根据题意可得x +y =0,由方程组的解法可得3x +3y =2m +4,代入计算即可.【详解】解:{x +2y =2m −1①2x +y =5② , ∵+∵得,3x +3y =2m +4,即3(x +y )=2m +4,又∵x 与y 互为相反数,∵x +y =0,即2m +4=0,解得m =-2,故选:A .【点睛】本题考查二元一次方程组的解,掌握二元一次方程组的解法以及相反数的定义是正确解答的前提.21.(2020·浙江杭州·模拟预测)已知关于x ,y 的方程组{3x −5y =2a x −2y =a −5则下列结论中正确的是( ) ∵当a =5时,方程组的解是{x =10y =20;∵当x ,y 的值互为相反数时,a =20; ∵当2x ⋅2y =212时,a =14;∵不存在一个实数a ,使得x =y .A .∵∵∵B .∵∵∵C .∵∵∵D .∵∵【答案】C【分析】∵把a=5代入方程组求出解,即可做出判断;∵根据题意得到x+y=0,代入方程组求出a 的值,即可做出判断;∵根据题中方程组得到{x =25−a y =15−a,再得到x+y=12,代入求出a 的值,即可做出判断; ∵假如x=y ,得到a 无解,本选项正确.【详解】解:∵把a=5代入方程组得:{3x −5y =10x −2y =0, 解得:{x =20y =10,本选项错误;∵由x 与y 互为相反数,得到x+y=0,即y=-x ,代入方程组得:{3x +5x =2a x +2x =a −5, 解得:a=20,本选项正确;∵方程组解得:{x =25−a y =15−a, 由题意得:x+y=12,把{x =25−a y =15−a代入得:25-a+15-a =12, 解得:a=14,本选项正确;∵若x=y ,则有{−2x =2a −x =a −5,可得a=a -5,矛盾, 故不存在一个实数a 使得x=y ,本选项正确.则正确的选项有∵∵∵,故选:C . 【点睛】本题考查二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.22.(2021·内蒙古包头·二模)若满足方程组{4x +y =3m +32x −y =m −1的x 与y 互为相反数,则m 的值为( ) A .2B .−2C .11D .−11 【答案】B【分析】由x 与y 互为相反数,得到y =-x ,代入方程组计算即可求出m 的值.【详解】解:由题意得:y =-x ,代入方程组得:{4x −x =3m +3①2x +x =m −1②, 消去x 得:3m +3=m −1,解得:m =-2,故选:B .【点睛】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法. 题型07 已知方程的解求参数23.(2023·湖南永州·中考真题)关于x 的一元一次方程2x +m =5的解为x =1,则m 的值为( )A .3B .−3C .7D .−7【答案】A【分析】把x=1代入2x+m=5再进行求解即可.【详解】解:把x=1代入2x+m=5得:2+m=5,解得:m=3.故选:A.【点睛】本题主要考查了一元一次方程的解,以及解一元一次方程,解题的关键是掌握使一元一次方程左右两边相等的未知数的值是一元一次方程的解,以及解一元一次方程的方法和步骤.24.(2021·浙江金华·中考真题)已知{x=2y=m是方程3x+2y=10的一个解,则m的值是.【答案】2【分析】把解代入方程,得6+2m=10,转化为关于m的一元一次方程,求解即可.【详解】∵{x=2y=m是方程3x+2y=10的一个解,∵6+2m=10,解得m=2,故答案为:2.【点睛】本题考查了二元一次方程的解,一元一次方程的解法,灵活运用方程的解的定义,转化为一元一次方程求解是解题的关键.25.(2023·江苏镇江·中考真题)若x=1是关于x的一元二次方程x2+mx−6=0的一个根,则m的值为.【答案】5【分析】:把x=1代入方程x2+mx−6=0,求出关于m的方程的解即可.【详解】把x=1代入方程x2+mx−6=0,得1+m−6=0,解得m=5.故答案为:5.【点睛】本题考查了一元二次方程的解.能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.26.(2023·四川内江·中考真题)已知a、b是方程x2+3x−4=0的两根,则a2+4a+b−3=.【答案】−2【分析】利用一元二次方程的解的定义和根与系数的关系,可得a+b=−3,a2+3a−4=0,从而得到a2+3a=4,然后代入,即可求解.【详解】解:∵a,b是方程x2+3x−4=0的两根,∵a+b=−3,a2+3a−4=0,∵a2+3a=4,∵a2+4a+b−3=a2+3a+a+b−3=4+(−3)−3=−2.故答案为:−2.【点睛】本题主要考查了一元二次方程的解的定义和根与系数的关系,熟练掌握一元二次方程的解的定义和根与系数的关系是解题的关键.题型08 根据一元二次方程根的情况求参数27.(2023·广东广州·中考真题)已知关于x的方程x2−(2k−2)x+k2−1=0有两个实数根,则√(k−1)2−(√2−k)2的化简结果是()A.−1B.1C.−1−2k D.2k−3【答案】A【分析】首先根据关于x的方程x2−(2k−2)x+k2−1=0有两个实数根,得判别式△=[−(2k−2)]2−4×1×(k2−1)≥0,由此可得k≤1,据此可对√(k−1)2−(√2−k)2进行化简.【详解】解:∵关于x的方程x2−(2k−2)x+k2−1=0有两个实数根,∵判别式△=[−(2k−2)]2−4×1×(k2−1)≥0,整理得:−8k+8≥0,∵k≤1,∵k−1≤0,2−k>0,∵√(k−1)2−(√2−k)2=−(k−1)−(2−k)=−1.故选:A.【点睛】此题主要考查了一元二次方程根的判别式,二次根式的性质,熟练掌握二次根式的性质,理解一元二次方程根的判别式是解答此题的关键.28.(2023·江苏连云港·中考真题)若关于x的一元二次方程x2−2x+m=0有两个不相等的实数根,则m的取值范围是.【答案】m<1【分析】此题考查了根的判别式,熟练掌握根的判别式与方程解的情况之间的关系是解本题的关键.根据方程有两个不相等的实数根,得到根的判别式大于0,求出m的范围即可.【详解】解:∵关于x的一元二次方程x2−2x+m=0有两个不相等的实数根,∵Δ=4−4m>0,解得:m<1.故答案为:m<1.29.(2021·四川内江·中考真题)若关于x的一元二次方程ax2+4x−2=0有实数根,则a的取值范围为.【答案】a≥−2且a≠0【分析】利用一元二次方程根的定义和判别式的意义得到a≠0且Δ=42−4a×(−2)≥0,然后求出两不等式的公共部分即可.【详解】解:根据题意得a≠0且Δ=42−4a×(−2)≥0,解得a≥−2且a≠0.故答案为∶a≥−2且a≠0.【点睛】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2−4ac有如下关系:当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.30.(2023·湖北襄阳·中考真题)关于x的一元二次方程x2+2x+3−k=0有两个不相等的实数根.(1)求k的取值范围;(2)若方程的两个根为α,β,且k2=αβ+3k,求k的值.【答案】(1)k >2(2)k =3【分析】(1)根据一元二次方程有两个不相等的实数根,得出b 2−4ac >0,把字母和数代入求出k 的取值范围;(2)根据两根之积为:ca ,把字母和数代入求出k 的值. 【详解】(1)解:b 2−4ac =22−4×1×(3−k )=−8+4k ,∵有两个不相等的实数,∵−8+4k >0,解得:k >2;(2)∵方程的两个根为α,β,∵αβ=ca =3−k ,∵k 2=3−k +3k ,解得:k 1=3,k 2=−1(舍去).即:k =3.【点睛】本题主要考查根与系数的关系、根的判别式,解题的关键是掌握x 1,x 2是方程ax 2+bx +c =0的两根时,x 1+x 2=−b a ,x 1⋅x 2=ca . 题型09 根据一元一次不等式组的整数解求参数的取值范围31.(2023·广东潮州·二模)如果关于x 的不等式组{6x −m ≥05x −n <0的整数解仅为1,2,3,那么适合这个不等式组的整数对(m,n )共有( )A .42对B .36对C .30对D .11对 【答案】C【分析】本题考查了解一元一次不等式组,不等式组的整数解的应用,先求出不等式组的解集,根据已知得出关于m 、n 的不等式组,求出整数解即可,解此题的关键是求出m 、n 的值.【详解】解:{6x −m ≥0①5x −n <0②, 解不等式∵得:x ≥m 6,解不等式∵得:x <n5,∵不等式组的解集是m 6≤x <n 5, ∵关关于x 的不等式组{6x −m ≥05x −n <0的整数解仅为1,2,3, ∵0<m6≤1,3<n5≤4,∵m 、n 为整数,∵m =1、2、3、4、5、6,n =16、17、18、19、20, 6×5=30,所以适合这个不等式组的整数对(m,n )共有30对,故选:C .32.(2024·河南安阳·一模)已知不等式组{2(x −1)>3x+12x <a,有四个整数解,则a 的取值范围为 . 【答案】9<a ≤10【分析】本题考查根据不等式组的解集的情况,求出参数的范围,先求出不等式组的解集,根据解集得到关于a 的不等式组,求解即可.【详解】解:解{2(x −1)>3x+12x <a,得:{x >5x <a, ∵不等式组有四个整数解,∵5<x <a ,∵不等式组的整数解为6,7,8,9,∵9<a ≤10;故答案为:9<a ≤10.33.(2023·四川宜宾·中考真题)若关于x 的不等式组{2x +1>x +a①x 2+1≥52x −9② 所有整数解的和为14,则整数a 的值为 .【答案】2或−1【分析】根据题意可求不等式组的解集为a −1<x ≤5,再分情况判断出a 的取值范围,即可求解.【详解】解:由∵得:x >a −1,由∵得:x ≤5,∴不等式组的解集为:a −1<x ≤5,∵所有整数解的和为14,∵整数解为:2、3、4、5,∴1≤a −1<2,解得:2≤a <3,∵ a 为整数,∴a =2.∵整数解为:−1,0,1,2、3、4、5,∴−2≤a −1<−1,解得:−1≤a <0,∵ a 为整数,∴a =−1.综上,整数a 的值为2或−1故答案为:2或−1.【点睛】本题考查了含参数的一元一次不等式组的整数解问题,掌握一元一次不等式组的解法,理解参数的意义是解题的关键.题型10 根据一元一次不等式组的解集的情况求参数的取值范围34.(2023·湖北鄂州·中考真题)已知不等式组{x −a >2x +1<b的解集是−1<x <1,则(a +b )2023=( ) A .0B .−1C .1D .2023【答案】B【分析】按照解一元一次不等式组的步骤进行计算,可得2+a <x <b −1,再结合已知可得2+a =−1,b −1=1,然后进行计算可求出a ,b 的值,最后代入式子中进行计算即可解答.【详解】解:{x −a >2①x +1<b② , 解不等式∵得:x >2+a ,解不等式∵得:x <b −1,∵原不等式组的解集为:2+a <x <b −1,∵不等式组的解集是−1<x <1,∵2+a =−1,b −1=1,∵a =−3,b =2,∵(a +b )2023=(−3+2)2023=(−1)2023=−1,故选:B .【点睛】本题考查了根据一元一次不等式组的解集求参数,准确熟练地进行计算是解题的关键.35.(2023·湖北黄石·中考真题)若实数a 使关于x 的不等式组{−2<x −1<3x −a >0的解集为−1<x <4,则实数a 的取值范围为 . 【答案】a ≤−1/−1≥a【分析】根据不等式的性质解一元一次不等组,再根据不等式组的取值方法即可且求解. 【详解】解:{−2<x −1<3①x −a >0②, 由∵得,−1<x <4;由∵得,x >a ;∵解集为−1<x <4,∵a ≤−1,故答案为:a ≤−1.【点睛】本题主要考查解不等式组,求不等式组解集,掌握解不等式组的方法,不等组的取值方法等知识是解题的关键.36.(2023·山东聊城·中考真题)若不等式组{x−12≥x−232x −m ≥x 的解集为x ≥m ,则m 的取值范围是 . 【答案】m ≥−1/−1≤m 【分析】分别求出两个不等式的解集,根据不等式组的解集即可求解.【详解】解:{x−12≥x−23①2x −m ≥x② , 解不等式∵得:x ≥−1,解不等式∵得:x ≥m ,∵不等式组的解集为:x ≥m ,∵m ≥−1.故答案为:m ≥−1.【点睛】本题考查了解一元一次不等式组,根据不等式的解求参数的取值范围,熟练掌握解不等式组解集的口诀:同大取大,同小取小大小小大中间找,大大小小找不到(无解)是解题的关键.题型11 整式方程(组)与一元一次不等式结合求参数的问题37.(2022·四川泸州·中考真题)若方程x−3x−2+1=32−x的解使关于x的不等式(2−a)x−3>0成立,则实数a的取值范围是.【答案】a<−1【分析】先解分式方程得x=1,再把x=1代入不等式计算即可.【详解】x−3x−2+1=32−x去分母得:x−3+x−2=−3解得:x=1经检验,x=1是分式方程的解把x=1代入不等式(2−a)x−3>0得:2−a−3>0解得a<−1故答案为:a<−1【点睛】本题综合考查分式方程的解法和一元一次不等式的解法,解题的关键是熟记相关运算法则.38.(2023·四川泸州·一模)已知方程3−aa−4−a=14−a,且关于x的不等式a≤x<b只有3个整数解,则b的取值范围是.【答案】1<b≤2【分析】此题考查了解分式方程,以及一元一次不等式的整数解.分式方程去分母转化为整式方程,求出整式方程的解得到a的值,经检验确定出分式方程的解,根据已知不等式只有3个整数解,即可确定出b 的范围.【详解】解:分式方程去分母得:3−a−a(a−4)=−1,整理,得:a2−3a−4=0,即(a−4)(a+1)=0,解得:a=4或a=−1,经检验a=4是增根,故分式方程的解为a=−1,∵不等式a≤x<b只有3个整数解,∵1<b≤2,故答案为:1<b≤2.39.(2021·湖北荆州·中考真题)已知:a是不等式5(a−2)+8<6(a−1)+7的最小整数解,请用配方法解关于x的方程x2+2ax+a+1=0.【答案】x1=2+√5,x2=2-√5【分析】先解不等式,结合已知得出a的值,然后利用配方法解方程即可【详解】解:∵5(a−2)+8<6(a−1)+7;∵5a−10+8<6a−6+7;∵−a<3;∵a>-3;∵a是不等式5(a−2)+8<6(a−1)+7的最小整数解,∵a=-2;∵关于x的方程x2-4x-1=0;∵x2-4x+4=5;∵(x-2)2=5;∵x-2=±√5;∵x1=2+√5,x2=2-√5.【点睛】本题考查了解不等式以及解一元二次方程,熟练掌握相关的运算方法是解题的关键.40.(2022·江苏苏州·一模)若不等式3x+2≤4x−1的最小整数解是方程23x−13mx=1的解,求m的值.【答案】m=1【分析】解出一元一次不等式的解,求出x的最小整数值,然后将x的最小整数值代入方程求解即可.【详解】解:由3x+2≤4x−1,解得x≥3,∵x的最小整数值为x=3,∵x=3是方程23x−13mx=1的解,∵2 3×3−13m×3=1,解得m=1,∵m的值为1.【点睛】本题考查了解一元一次不等式,一元一次方程的解.解题的关键在于找出x的最小整数值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
回顾与作业点评
• 纠正代码中的错误,输出“早上好!”
//方法定义 public void addName(name){ //方法体 } 必须指定形参类型 方法没有返回值 //方法调用 int n = 对象名.addName("张三");
• 包(package)的作用有哪些?
预习检查
• 训练要点:
指导——增加会员
• 需求说明:
• 实现思路:
– 带参方法的定义及调用 – 对象类型的参数 – 创建包com.wxws.sms,增加会员类和会员操 作类,实现MyShopping系统的增加会员功能 1、创建会员类 2、创建会员操作类 3、进行测试 – 增加会员方法
完成时间:25分钟 讲解需求说明
内存分配图
对象类型的参数3-3
public class TestScore { public static void main(String[] args)省略内存分配 { public class Score { Students stu=new Students(); //计算平均分,对象作为参数 Score sc=new Score(); public float getAvg(Students stu){ float avg=0; float avg=0; stu.java=80; avg=(stu.java +stu.database stu.database=95; +stu.html )/3; stu.html=77; return avg; avg=sc.getAvg(stu); } System.out.println("该学生的平均分为: } "+avg); } main:stu 0x2a486c } main:avg getAvg:stu getAvg:avg 0 84.0 0x2a486c 0 84.0
• 基本数据类型和引用数据类型作为方法参 数,在传递时有什么不同之处?
本章目标
• 会使用数组作为方法的参数和返回值 • 会使用对象作为方法的参数
数组类型的方法返回值2-1
1、编写方法,实现学生的姓名排序
• 使用Arrays类提供的sort()方法实现 • 定义一个独立的方法来实现姓名排序, 该方法的返回值为数组类型
• 画出在本章“计算学生平均分 ”问题中, 程序执行时的内存分配过程图
0.0 80 0.0 95
}
0.0 77
数组类型的方法返回值2-2
public class StudentsBiz { public class TestSort { String[ ] names = w String[5]; // 学生姓名数组 public static void main(String[ ] args) { public void inputNames(){ StudentsBiz st = new StudentsBiz(); 调用方法,返回结果 //接收用户输入的5个学生姓名,存放于 names 中 st.inputNames(); } 返回字符串数组 ] namesbysort =st.getNames(); //字符串数组作为返回值 String[ System.out.println("****排序后****"); public String[ ] getNames(){ Arrays.sort(names); for(int i =0;i< namesbysort.length;i++){ if(namesbysort [i]!=null){ return names; System.out.print(namesbysort [i]+"\t"); } } } 处理返回结果 } } } 演示示例1:数组类型的方法返回值
0.0 80 0.0 95
0.0 77
对象数组类型的参数2-1
3、计算学生的平均身高
• Students类中定义身高属性 • Height类中定义方法,传递学生对象数组,求平均身高 • 测试类调用Height类的方法
对象数组类型的参数2-2
对象数组作为参数 public class Height { public float getAvgHeight( Students[ ] stu){ float avgHeight=0; float all=0;//所有学生的总身高 int count=0;//学生计数 for(int i=0; i<stu.length; i++){ public class TestHeight{ if(stu[i].height != 0){ public static void main(String[ ] args) { all=all+stu[i].height; count++; Students[ ] stu = new Students[5]; Height h=new Height(); 调用方法,传递对象数组 } … } float avgheight=h.getAvgHeight(stu); avgHeight=all/count; System.out.println("平均身高:"+avgheight+"cm"); return avgHeight; } } } 演示示例3:对象数组类型的参数
public class Score { public static void main(String[] args)省略内存分配 { Students stu=new Students(); //计算平均分,对象作为参数 public float getAvg(Students stu){ Score sc=new Score(); float avg=0; float avg=0; avg=(stu.java +stu.database stu.java=80; +stu.html )/3; stu.database=95; return avg; stu.html=77; } avg=sc.getAvg(stu); } System.out.println("该学生的平均分为: "+avg); } main:stu 0x2a486c main:avg getAvg:stu getAvg:avg 0 84.0 0x2a486c 0 84.0
• 难点指导:
练习——查找会员积分
• 需求说明:
– 循环输入多个会员的信息,根据会员编号, 查找会员积分
完成时间:25分钟
共性问题集中讲解
共性问题集中讲解
常见调试问题及解决办法 代码规范问题
总结
• 基本数据类型和引用数据类型作为方法 public class TestScore { 参数,在传递时有什么不同之处?
对象类型的参数3-1
2、编写学生成绩计算类,计算学生平均分
• 定义学生类,添加属性:三门课的成绩 • 定义学生成绩计算类,添加方法,传递对象参数 • 定义测试类
对象类型的参数3-2
public class Students { //定义三门课成绩属性 对象类型的参数 float java=0; public class Score { float database=0; //计算平均分,对象作为参数 public float float html=0; public class TestScore { getAvg(Students stu){ floatmain(String[] avg=0; } public static void args) { +stu.database +stu.html )/3; Students avg=(stu.java stu=new Students(); return avg; Score sc=new Score(); 三门课成绩 float } avg=0; } 返回结果 stu.java=80; 调用方法,传递参数, 返回结果 stu.database=95; stu.html=77; avg=sc.getAvg(stu); System.out.println("该学生的平均分为:"+avg); } } 演示示例2:对象类型的参数
