理论力学下册第二章碰撞
高中物理课件《碰撞》
弹性碰撞
退出
目录
上一页
下一页
练习反馈
在细线下吊着一个质量为M的木块, 构成一个单摆,摆长为 l。一颗质量为 m的子弹水平射入木块,最后留在木 块中,随木块一起摆动。已知木块摆 动时摆线的最大偏角是θ。求子弹射 入木块前的速度。
退出
目录
上一页
下一页
拓展延伸
α粒子散射
退出
目录
上一页
ቤተ መጻሕፍቲ ባይዱ
下一页
16.4 碰撞
目录
牛顿摆 碰撞种类 弹性碰撞 练习反馈 拓展延伸
退出
目录
上一页
下一页
牛顿摆
退出
目录
上一页
下一页
碰撞种类
弹性碰撞
动量守恒 机械能守恒
退出
目录
上一页
下一页
碰撞种类
非弹性碰撞
动量守恒 机械能有损失
退出
目录
上一页
下一页
碰撞种类
完全非弹性碰撞
动量守恒 机械能损失最大
退出
目录
上一页
下一页
理论力学碰撞实验报告

一、实验目的1. 了解碰撞现象的特点及研究方法;2. 掌握碰撞实验的基本原理和实验步骤;3. 通过实验验证动量守恒定律和动能守恒定律;4. 提高动手操作能力和实验数据处理能力。
二、实验原理1. 动量守恒定律:如果一个系统所受的合外力为零,那么该系统总动量保持不变。
2. 动能守恒定律:在一个孤立系统中,如果只有重力或弹力做功,系统的总动能保持不变。
3. 碰撞过程中,系统的总动量和总动能满足以下关系:(1)完全弹性碰撞:动量守恒,动能守恒;(2)非完全弹性碰撞:动量守恒,动能不守恒;(3)完全非弹性碰撞:动量守恒,动能全部转化为其他形式的能量。
三、实验仪器与设备1. 气垫导轨:用于实现无摩擦滑动,保证实验结果的准确性;2. 滑块:用于实现碰撞实验;3. 数显计时器:用于测量碰撞时间;4. 量角器:用于测量碰撞前后的角度;5. 计算器:用于数据处理和计算。
四、实验步骤1. 将气垫导轨放置在实验桌上,确保导轨水平;2. 将滑块放置在导轨的一端,调整滑块与导轨的接触面,使其能够正常滑动;3. 使用数显计时器测量滑块在导轨上自由滑动的距离和时间,记录数据;4. 将滑块放置在导轨的另一端,调整滑块与导轨的接触面,使其能够正常滑动;5. 观察滑块在碰撞过程中的运动状态,记录碰撞前后的角度;6. 重复步骤3-5,进行多次实验,记录数据;7. 根据实验数据,计算碰撞前后的动量和动能,验证动量守恒定律和动能守恒定律。
五、实验结果与分析1. 实验数据:(1)自由滑动距离:L1 = 1.2m,L2 = 1.3m,L3 = 1.1m;(2)自由滑动时间:t1 = 0.5s,t2 = 0.6s,t3 = 0.4s;(3)碰撞前角度:θ1 = 30°,θ2 = 40°,θ3 =25°;(4)碰撞后角度:φ1 = 35°,φ2 = 45°,φ3 = 30°。
2. 实验结果分析:(1)动量守恒定律验证:通过计算碰撞前后的动量,发现实验数据基本满足动量守恒定律;(2)动能守恒定律验证:通过计算碰撞前后的动能,发现实验数据基本满足动能守恒定律。
理论力学17.碰撞

动量守恒定律
动量守恒定律指出,在碰撞过程中,总动量始终保持不变。无论是理想弹性 碰撞还是非弹性碰撞,总动量都会在碰撞前后保持相等。
碰撞的应用
碰撞的概念在物理学、工程学和运动学中有许多应用。例如,汽车碰撞测试和台球运动中的撞球现象都是碰撞 的应用。
理论力学17.碰撞
在本节中,我们将探讨碰撞的基本原理、理想弹性碰撞和非弹性碰撞。我们 还将研究碰撞中的能量守恒定律和动量守恒定律,并介绍碰撞的一些应用。
碰撞的定义
碰撞是物体之间发生的相互作用,其中两个或多个物体产生相互接触并相互 响。它是研究理论力学中重要的一部分。
碰撞的基本原理
碰撞的基本原理涉及到动量和能量的转移。在碰撞过程中,物体的动量和能 量可能会发生变化,这取决于碰撞的类型。
理想弹性碰撞
理想弹性碰撞是指碰撞过程中动能丧失最小的碰撞。在这种碰撞中,物体之 间发生的相互作用是完全弹性的,动量和能量都得到保持。
非弹性碰撞
非弹性碰撞是指碰撞过程中动能丧失的碰撞。在这种碰撞中,物体之间发生 的相互作用会导致动能的损失,部分动能会转化为其他形式的能量。
能量守恒定律
能量守恒定律指出,在碰撞过程中,总能量始终保持不变。无论是理想弹性 碰撞还是非弹性碰撞,总能量都会在碰撞前后保持相等。
理论力学碰撞习题及答案
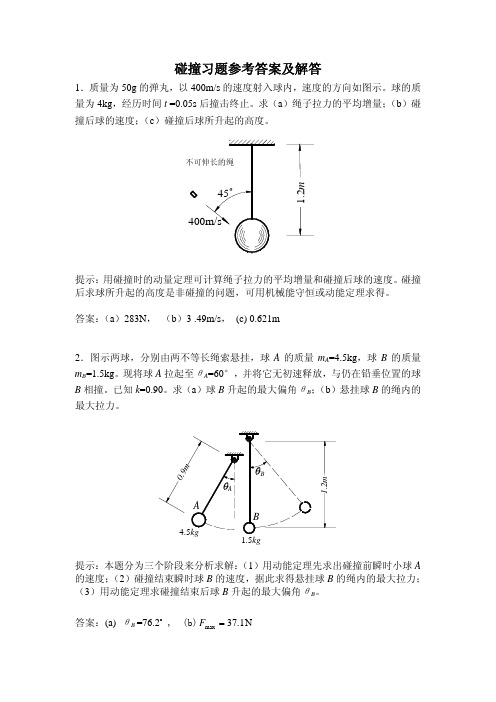
碰撞习题参考答案及解答1.质量为50g 的弹丸,以400m/s 的速度射入球内,速度的方向如图示。
球的质量为4kg ,经历时间t =0.05s 后撞击终止。
求(a )绳子拉力的平均增量;(b )碰撞后球的速度;(c )碰撞后球所升起的高度。
提示:用碰撞时的动量定理可计算绳子拉力的平均增量和碰撞后球的速度。
碰撞后求球所升起的高度是非碰撞的问题,可用机械能守恒或动能定理求得。
答案:(a )283N , (b )3 .49m/s , (c) 0.621m2.图示两球,分别由两不等长绳索悬挂,球A 的质量m A =4.5kg ,球B 的质量m B =1.5kg 。
现将球A 拉起至θA =60°,并将它无初速释放,与仍在铅垂位置的球B 相撞。
已知k =0.90。
求(a )球B 升起的最大偏角θB ;(b )悬挂球B 的绳内的最大拉力。
提示:本题分为三个阶段来分析求解:(1)用动能定理先求出碰撞前瞬时小球A 的速度;(2)碰撞结束瞬时球B 的速度,据此求得悬挂球B 的绳内的最大拉力;(3)用动能定理求碰撞结束后球B 升起的最大偏角θB 。
答案:(a) θB =76.2o , (b)1.37max =F N3.撞击机的摆,由钢铸圆盘A 和圆杆B 组成。
钢铸圆盘的半径为10cm ,厚为5cm 。
圆杆B 的半径为2cm ,长为90cm 。
问用该机器击打碎石,其所在水平面与转轴O 的距离l 应多大方能使轴不受碰撞?碰撞的方向可视为水平。
答案:cm 90.6 , 18842250 , 207995 , cm 77=====maJ l J ma a OO ρρ a 为质心距转轴O 的距离,J O 为摆对转轴O 的转动惯量,ρ为材料密度。
4.质量为m 1的滑块A 置于光滑的水平面上,它与质量为m 2长为l 的均质杆AB 铰接,如图所示,系统初始静止,杆AB 铅垂,m 1=2m 2。
今有一冲量为I 的水平碰撞力作用于杆的B 端。
【理论力学2】第二章碰撞

1
2
m11
m1
m22
m2
即碰撞结束时 两物体速度相同 一起运动
以 T1 和 T2 分别表示此两物体组成的质点系在碰撞过程
开始和结束时的动能 则有
T1
1 2
m112
1 2
m2
2 2
,T2
1 2
m112
1 2
m222
在碰撞过程中质点系损失的动能为
T
T1
T2
1 2
m1
(12
12 )
1 2
m2
(1
k )1
代入1 的数值 得
I 2ma (1 k) 6ag 3l
根据冲量定理 有
m(2a 1a) IOx I ,IOy 0
则
IOx ma(1 2 ) I I (1 k)am1
(1 k)m( 2a 1) 6ag 3l 2
由上式可见 当 2a 1 0 时 3l 2
物体在弹性碰撞结束时 变形不能完全恢复
动能有损失
k=1称为完全弹性碰撞 k=0称为非弹性碰撞或塑性碰撞 由式(2-7)和(2-8)有
k I2 I1
即恢复因数又等于正碰撞的两个阶段中作用于物体的碰 撞冲量大小的比值
如图所示 此为斜碰撞 此时定义恢复因数为 k n n
式中 n 和 n 分别是速度 和 在法线方向的投影
(e) i
i1
i1
积分 或
得
LO 2 LO1
dLO
n i1
t 0 ri
dI
(e) i
n
LO2 LO1
t 0 ri
dI
(e) i
n
ri
t 0
dI
(e) i
【理论力学2】第二章碰撞

积分 或
得
LO 2 dLO LO1
i 1
n
t
0
(e) ri dI i
n t n (e) t (e) LO 2 LO1 ri dI i ri dI i i 1 0 i 1 0
n n (e) (e) LO 2 LO1 ri I i M O (I i ) (2-4) i 1 i 1 ( e) 称 ri I i 为冲量矩 其中不计普通力的冲量矩 (2-4)是用于碰撞过程的动量矩定理 又称为冲量矩定理: 质点系在碰撞开始和结束时对点O的动量矩的变化 等于作用于质点系的外碰撞冲量对同一点的主矩
i 1 i 1 i 1 i 1
1.用于碰撞过程的动量定理——冲量定理
(e) 因为 I i 0 于是得
i i 1
(e) mii mii I i
n
n
n
i 1
i 1
i 1
(2-2)
式(2-2)是用于碰撞过程的质点系动量定理 因此又称为冲量定理: 质点系在碰撞开始和结束时动量的变化 等于作用于质点系的外碰撞冲量的主矢 (2-2)可写成 n mC I i(e) mC (2-3) i 1 分别是碰撞开始和结束时质心的速度 式中 C 和 C
2gh2
于是得恢复因数 h2 k h1 几种材料的恢复因数见表
碰撞物体 铁对铅 木对胶 木对 的材料 木 木 恢复因数 0.14 0.26 0.50 钢对 钢 0.56 象牙对象 牙 0.89 玻璃对 玻璃 0.94
对于各种实际的材料 均有0<k<1 由这些材料做成的物体发生的碰撞称为弹性碰撞 物体在弹性碰撞结束时 变形不能完全恢复 动能有损失 k=1称为完全弹性碰撞 k=0称为非弹性碰撞或塑性碰撞
大学物理碰撞

1 2
mv
2 A
1 2
mvB2
v0 vA vB
v02 vA2 vB2
(vA
vB )2
v
2 A
vB2
2vAvB
cos
v A2
vB2
900
—— 碰撞后两质点运动的方向相互垂直
04_08_碰撞 —— 力学
5/12
06 质量为MA的小球A沿光滑的弧形轨道滑下,与放 在轨道端点P处(该处轨道的切线方向为水平方向)的 质量为MB的静止小球B发生弹性正碰撞,A,B小球碰撞 后同时落在水平地面上。如果A、B两球的落地点距P点 正下方O的距离之比为
4.8 碰撞 —— 两个物体之间发生相互作用的过程 碰撞的时间很短 —— 两个物体之间的冲力很大,忽略其它的力:重力 、摩擦力等 —— 碰撞过程中,物体来不及发生位移,系统的机械 能为物体动能之和
碰撞过程分为三个阶 段1) 压缩形变 —— 冲力做负功,机械能转变为系统的内能 2) 达到最大形变 —— 机械能全部转变为系统的内能 3) 恢复形变 —— 冲力做正功,系统的内能转化为机械能
MA 5 MB
8/12
07 地面固定一半径为R的光滑球面,球面正上方放
置一质量为M的滑块。一质量为m的油灰以速度v0射向 滑块,并粘在滑块上一起沿球面运动,计算(1)它们
滑至多大的角度时脱离球面;(2)如果油灰和滑块在A
点就脱离球面,则油灰的入射速率至少为多少?
1)研究系统为油灰和滑 块,系统在水平方向不受外 力,水平方向上动量守恒
3) 非弹性碰撞
—— 碰撞结束后,物体的形变只有部分恢复,系统的 动量守恒,动能不守恒
04_08_碰撞 —— 力学
4/12
05 速度为 v0 的质点A和另一质点B发生非对心弹性
碰撞 课件

C. pA'=-2kg·m/s,pB'=14kg·m/s
分D.析p:A碰'=-撞4动kg量·m守/s恒,p,pB'=A17kgp·mB/s pA 'pB '知:A·B·C都满足.
VA ' VB' ,知:A·B·C也都满足.
总动能不能增加,即 PA2 PB2
PA2
PB2
2m 2m 2m 2m
得:只有A正确了
练习2.用轻弹簧相连的质量均为m=2㎏的A、 B两物体都以v=6m/s的速度在光滑的水平地面 上运动,弹簧处于原长,质量M = 4㎏的物体C 静止在前方,如图所示。B与C碰撞后二者粘 在一起运动,在以后的运动中,求:
(1)当弹簧的弹性势能最大时物体A的速度。 (2)弹性势能的最大值是多大?
v
A
B
C
③若 m2>>m1 , 则v1’= -v1 , v2’=0 .
④ 若 m1 >> m2 , 则v1’= v1,v2’=2v1 .
3、非弹性碰撞:
V1
V2
光滑
m1 v1 m2 v2 m1v1' m2 v'2
1 2
m1 v12
1 2
m
2
v
2 2
1 2
m1 v1'2
1 2
m2
v'22
Ek
4、完全非弹性碰撞:
V1
V2
光滑
m1v1 m2v2 (1 2
m
2
v
2 2
1 2
(m1
m2 )v2
Ek max
粒子散射后,速度方向向着各个方向.散 射是研究物质微观结构的重要方法.— —卢瑟福做α粒子散射实验,提出了原 子的核式结构学说。
2(7)碰撞

e v2第十v五1 章 机械波 v10 v20
m1v10 m2v20 m1v1 m2v2 …(1)
e v2 v1 ……(2) v10 v20
v1
v10
(1
e)m2 (v10 m1 m2
v20 )
v2
v20
(1
e)m1(v10 v20 ) m1 m2
结论:有能量损耗.
152、–完8全弹多性碰普撞勒效应
第十五章 机械波
v v v v v 10
O m1 m1
m110 mm22 2200 m1
1
2
m2 X
碰撞前
碰撞后
依动量守恒、能量守恒列方程:
m1v10 m2v20 m1v1 m2v2
1 2
m1v102
1 2
m2v202
1 2
m1v12
v
m1 m2
X
碰撞后
m1v10 m2v20 m1v1 m2v2
…(1)
v1 v2 v
…(2)
讨论: A)碰撞后速度 v m1v10 m2v20 m1 m2
…(3)
B)能量:
碰撞前
Ek1
1 2
m1v120
1 2
m2v220
…(4)
1B5)能–量8: 多普勒效应
第十五章 机械波
碰撞前
Ek1
1 2
m1v120
1 2
m2v220
v ……m(1vm1401)
m2v20 m2
碰撞后
Ek 2
1 2
最新理论力学-碰撞教学讲义ppt课件

18
对于两物体正碰撞的情况,恢复系数等于两物体在碰撞 结束与碰撞开始时,质心的相对速度大小的比值。)
联立(1),(2)式,解得:
u1
v1
(1k) m2 m1 m2
(v1
v2
)
u2 v2 (1k)m1m1m2 (v1v2) 对于完全弹性碰撞(k=1):
20
由正碰撞结束时两质心的速度公式知: v 1 u 1 ( 1 k ) m 1 m 2 m 2 ( v 1 v 2 );v 2 u 2 ( 1 k ) m 1 m 1 m 2 ( v 1 v 2 )
n
n
miui mivi
Si(e)
冲量定理
i1
i1
(19-2)
设质点系总运动定理,上式可写成:
M uCM vC Si(e)
(19-3)
9
碰撞时质点系动量的改变等于作用在质点系上所有外碰
撞冲量的矢量和。
式(19-1)、(19-2)和(19-3)都写成投影形式,形式上与普 通的动量定理相同,所不同的是在这里都不计普通力的冲量。
应用冲量定理在y 轴投影
式
0(m)vS1
第二阶段:由弹性变形开始恢复到脱离接触。该阶段中,
小球动能增大,变形(弹性)逐渐恢复。设碰撞冲量为 S 2 ,
则:
mu0S2
u S2 v S1
13
对于给定材料,|u|与|v|的比值是不变的,该比值称为恢复系数。
k
u v
——由实验测定
一般0<k<1,各种材料的恢复系数,可查阅书中表。 k=1 理想情况——完全弹性碰撞。 k=0 极限情况——非弹性碰撞或塑性碰撞。
理论力学第二章:碰撞

碰撞前、后系统动能的变化
1 1 T=T1-T2 mA v A vA v A vA mB vB v B vB vB 2 2
mA mA vA vB , vB vB 1 k vA vB vA v A 1 k m A mB m A mB
m A mB 2 2 T= 1 k v A vB 2m A mB 两种特殊情形下,碰撞前、后系统动能的变化
完全弹性碰撞 —— k=1, T=T2-T1=0。 碰撞过程中没有能量损失。
23
塑性碰撞 —— k=0, 动能损失为
m A mB v A v B 2 T= 2m A mB
第 二 章【下册】
碰
撞
1
碰
撞
※ 碰撞现象 · 碰撞力 ※ 几个工程实际问题 ※ 动力学普遍定理在碰撞问题中的应用 ※ 恢复系数 ※ 碰撞问题举例
※ 撞击中心
※ 结论与讨论
2
§15-1 碰撞现象· 碰撞力
碰撞 — 物体与物体之间,在极短的时间内,速度发生 突然改变,并发生有限量的动量传递与能量转换,同时 伴随有极大的撞击力的动力学过程。 碰撞主要研究碰撞物与被碰撞物在碰撞后的运动效应。 例:铁锤打击钢板 锤重 4.45N ; 碰撞前锤的速度 457.2 mm/s ; 碰撞的时间间隔 0.00044s ; 撞击力峰值 1491 N , 塑料 是静载作用的 335 倍 。
§15-3 恢复系数(因数)
考察两个球的正碰撞的变形阶段与恢复阶段 I I 1 1 mB mA F 变形阶段 I1 I2 t1 tm t2
tm t1
t
vA vAB vB vAB I2 I2 mB 恢复阶段 mA vAB v'A v v' AB B 变形阶段的碰撞冲量 恢复阶段的碰撞冲量
物体的碰撞.ppt

第一节 物体的碰撞
美国公布的答案是:被撞破的鸡蛋多半是“运 动着的蛋”,即去撞的那一只。 解释是:“鸡蛋壳的形状是曲面的,在碰撞时 对那只不动的鸡蛋所加的压力,是作用在蛋壳 外面的。蛋壳像一切拱形的物体一样,很能承 受住从外面来的压力(外撞力),但是,作用 在运动着的蛋上的力,情形就完全两样了,运 动着的蛋黄和蛋白,在碰撞的那一霎那,要从 内部压向蛋壳。而拱形的物体抗受这种压力( 内撞力)的能力是比抗受外来压力的能力(外 撞力)要低得多的,因此蛋壳就破碎了。”
第一节 物体的碰撞 研究撞蛋问题很有现实意义:因为在交通事故中人脑 的损伤状态,与那只“运动着的蛋”颇为相似:若将 人的头颅比鸡蛋,则颅骨就像蛋壳,脑浆就像蛋清, 脑髓就像蛋黄。一旦头部受到强烈冲击,脑髓就要撞 击头盖骨内侧,因此很容易引起脑震荡或者脑血冲; 即使颅骨不破裂,脑髓也会受到损伤。一些骑摩托车 的人以为只要戴上安全头盔,脑袋就不会受损伤了。 然而,据推算当车速超过20公里/小时,一旦撞车,即 使头盔完好无损,强大的惯性也会使乘员脑袋突然前 倾而遭受激烈振荡,在振荡的瞬间(仅千分之几秒) ,头的转动角加速度将超过1600转/秒 而引起脑震荡 。
A碰前 B碰前 A碰后 B碰后
第1次 10J
5J
5J
10J
弹性碰撞
第2次 10J
5J
4J
9J
非弹性碰撞
第3次 15J
5J
不成立
7J
14J
第一节 物体的碰撞
四.碰撞的规律
①… …?
②碰撞后系统的总动能不大于碰撞前系统的总动能。
③碰撞时的速度关系必须满足实际情景。
第一节 物体的碰撞
问题:一个质量为m的静止物体,在力F 的作用下开 始运动,经过时间t 将获得多大的速度? 解:物体在力F作用下得到的加速度为: a F
2-7两体碰撞

解 尘埃与飞船作完全 非弹性碰撞, 把它们作为 一种系 统, 则 动量守恒 .
m
v
即 m0v0 mv
得
dm
m0 v0 v2
dv
Svdt
第二章 质点力学
2–7 两体碰撞
已知 m0 , v0 , .
求
v 与 t 旳关系 .
m
v
解
dm
m0 v0 v2
dv
Svdt
v dv S
v v0 3 m0 v0
第二章 质点力学
2–7 两体碰撞
完全弹性碰撞
(五个小球质量全同)
第二章 质点力学
2–7 两体碰撞
2. 完全非弹性碰撞 两物体碰撞后,以同一速度运动。
动能不再守恒,只有动量守恒!
v1
v2
m1
v10 m2 v20 m1 m2
非弹性碰撞 因为非保守力旳作用 ,两物体碰撞
后,使部分机械能转换为热能、声能,化学能等其他
第二章 质点力学
2–7 两体碰撞
碰撞 两物体相互接触时间极短而互作用力较大
旳相互作用。
F
exFin源自piCi对心碰撞:碰撞前、后两个物体旳
速度均沿两个物体中心旳连线!
碰前
m1
v10
m2
v20
动量 守恒:
m1 v10 m2 v20 m1 v1 m2 v2
或写成标量式:
AB
碰后 v1
v2
1 2
m2v22
m1(v120 - v12 ) m2 (v22 v220 )
碰前
m1
v10
m2
v20
AB
碰后 v1 v2
AB
v10 v1 v2 v20
碰撞 课件

3. 当甲车的速度为零时,乙车速度为___1__米/秒, 方向___向__右____。
V1
S
N
甲
V2
N
S
乙
碰撞问题的解应同时遵守三个原则:
1. 系统动量守恒的原则
mv1 mv2 mv1 mv2
2. 不违背能量守恒的原则
1 2
mv12
1 2
mv22
1 2
mv12
1 2
mv22
3. 物理情景可行性原则
碰撞
一.不同类型的碰撞:
1. 完全弹性碰撞——动量守恒,动能守恒
2. 完全非弹性碰撞——动量守恒,动能损失 最大(以共同速度运动),动能转化为其它能量,
如内能、重力势能、弹性势能、磁场能、电场能等。
3. 非弹性碰撞——动量守恒,动能有损失
碰撞的特征和基本假定 1. 碰撞的特征:物体的运动速度或动量在极短的时间内发生极巨的改变。碰撞 时间之短往往以千分之一秒甚至万分之一秒来度量。因此加速度非常大,作用力 的数值也非常大。
例2 在竖直向上的匀强磁场中有两根光滑水平 平行导轨,其上放置两根平行导体棒a、b,质量分别 为m1 ` m2, b棒开始静止,a棒以初速度V0向右运动, 求最后两棒的速度各是多少?
解:两棒只受相互作用的磁场力,且始终大小相等,
方向相反,因此动量守恒。
B
由 m1V0= (m1+m2) V
b
a
得 V=m1V0 / (m1+m2)
2m1 m1 m2
V0
1. 若 m1 = m2
2. 若 m1 << m2
V2 V0 V1 0
质量相等的两物体
V1 V0 V2 0
弹性碰撞后交换速度
理论力学:碰撞与冲击的实例

假设:摩擦力均匀分布
JCAB MC (F)
2020/12/9
IL
2JC aC
AB
20
理论力学
§7-3 碰撞与冲击
思考题:(1)长为L的均质杆AB放在光滑水平面上(2)边长为 L均质板放在光滑的水平面上,若在这两个物体上分别作用一个 冲量I。冲量作用在何位置时,冲击后,物体获得的动能最大。
基本公式
求杆碰撞后的角速度、质心速度和碰撞冲量。 muC mvC I
n
B
LC2 LC1
M
C
(
I
(*) i
)
i1
A
e I2 u1n u2n
I1
v1n v2n
h
解:取杆为研究对象
1、求碰撞前的质心速
度和碰撞点的速度
vC
vA
2020/12/9
vA vC 2gh
13
理论力学
§7-3 碰撞与冲击
1
理论力学
夯 击 与 锻 造
碰撞与冲击的实例
2020/12/9
2
理论力学
台 球 中 的 碰 撞 问 题
2020/12/9
碰撞与冲击的实例
台球特技实例
3
理论力学
碰撞与冲击的实例
足球运动的碰撞问题
2020/12/9
4
理论力学
碰撞与冲击的实例
2020/12/9
5
理论力学
碰撞与冲击的实例
飞行员座椅弹射装置
T-T 公共切平面 T
碰撞前碰撞点的速度 v1, v2
碰撞后碰撞点的速度 u1, u2 压缩冲量(大小):I1 恢复冲量(大小):I 2
I
II
u1
u2 n
下册第2章 碰撞

又
u1 u2 k (v1 v2 ) m1m2 T T1 T2 (1 k 2 )(v1 v2 ) 2 2(m1 m2 )
21
(1) 对于完全弹性碰撞(k =1): T T1 T2 0 ( T T1 T2
m1m2 (1 k 2 )( v1 v2 ) 2 ) 2(m1 m2 ) 系统动能没有损失,可以利用机械能守恒定律求碰撞后的速度。 (2) 对于塑性碰撞 (k =0):T T T m1m2 (v v ) 2 1 2 2(m1 m2 ) 1 2
结束与碰撞开始时,质心的相对速度大小的比值。)
联立(1),(2)式,解得:
u1 v1 (1 k 1 u2 v2 (1 k ) ( v1 v2 ) m1 m2 对于完全弹性碰撞(k=1):
2 m2 2m1 u1 v1 (v1 v2 ) ; u2 v2 (v1 v2 ) m1 m2 m1 m2
v k v
'n r n r
(e)
27
§2-5 碰撞冲量对绕定轴转动刚体的作用 撞击中心
1. 角速度的改变:
J z1 J z2 mz ( Si( e ) )
i 1
n
2 1
m (S
i 1 z
n
(e) i
)
Jz
28
2. 支座的反碰撞冲量,撞击中心:
设刚体有对称面,绕垂直此平
2 因 v2 0 , T1 1 m1v1 ,故 2
T
T1
m2 (1 k 2 )T1 T m1 m2
于是
m2 15000 (1 0.62 ) 0.6 60% (1 k 2 ) m1 m2 1000 15000
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(e) Lz1 M z ( I i )
n i 1 n
(e) J z 2 J z 1 M z ( I i )
i 1
角速度的变化为
2 1
(e) M z (I i ) Jz
(2-10)
2.支座的反碰撞冲量· 撞击中心
第一阶段碰撞冲量为 I 1 0 (m ) I1 第二阶段碰撞冲量为 I 2
于是得
§ 2-3 质点对固定面的碰撞· 恢复因数
(m 0) I 2
I2 (2-7) I1 k (2-8) 常数k恒取正值 称为恢复因数
恢复因数需要用试验测定
2gh1
例 2-2 如图所示为一测量子弹速度的装置 称为射击摆 其是一个悬挂于水平轴O的填满砂土的筒 当子弹水平射入砂筒后 使筒绕轴O转过一偏角 测量偏角的大小即可求出子弹的速度 已知摆的质量为 m1 对于轴O的转动惯量为 J O 摆的重心C到轴O的距离为h 子弹的质量为 m2 子弹射入砂筒时 子弹到轴O的距离为d 悬挂索的重量不计 求子弹的速度
1 1 1 1 2 2 2 m2 2 2 T1 m11 m2 2 ,T2 m11 2 2 2 2Βιβλιοθήκη 在碰撞过程中质点系损失的动能为
1 1 2 2 2 ) m2 ( 2 2 ) T T1 T2 m1 (1 1 2 2 2 1 1 )( 2 2 ) m1 (1 1 )(1 1 ) m2 ( 2 2 2 2
(e) (f) (g)
l 2 sin 由(f)(g)两式消去I 得 Cy 6 cos
6 sin 2 代入式(e) 解得 2 (1 3 cos2 )l
§ 2-5 碰撞冲量对绕定轴转动刚体的作 用· 撞击中心
1.定轴转动刚体受碰撞时角速度的变化
Lz 2
即
m1m2 (1 k 2 )(1 2 ) 2 2(m1 m2 )
(d)
在理想情况下 k=1 T T1 T2 0 在塑性碰撞时 k=0 动能损失为 m1m2 T T1 T2 (1 2 ) 2 2(m1 m2 ) 如果第二个物体在塑性碰撞开始时处于静止 即 2 0 则动能损失为 m1m2 T T1 T2 12 2(m1 m2 ) 1 2 T m 上式可改写为 注意到 1 1 1 2 m2 1 T T1 T2 T1 T1 (e) m m1 m2 1 1 m2 可见 在塑性碰撞过程中 损失的动能与两物体质量比有关 当 m2 m1时 T T1 当 m2 m1时 T 0
求碰撞结束时各自质心的速度和碰撞过程中动能的损失
解:有
m2 2 m11 m2 2 m11
(a )
由恢复因数定义 由式(2-9) 有 1 2 k 1 2
(b)
联立(a)和(b)二式 解得 m2 1 (1 k ) 1 (1 2 ) m1 m2 (c) m1 2 (1 k ) 2 (1 2 ) m1 m2 在理想情况下 k=1 有 2m2 2m1 1 2 1 (1 2 ) , 2 (1 2 ) m1 m2 m1 m2
在不考虑摩擦的一般情况下 碰撞前后的两个物体都在运动 此时恢复因数定义为
r n k n r
n n
(2-9)
和 r 分别为碰撞后和碰撞前两物体接触点沿 式中 r 接触面法线方向的相对速度
§ 2-4 碰撞问题举例
例 2-1 两物体的质量分别为 m1和 m2 恢复因数为k 产生对心正碰撞 如图所示
解: 设碰撞开始时子弹速度为 则 LO1 m2 d 设碰撞结束时摆的角速度为ω 则 LO2 J O m2 d 2 ( J O m2 d 2 ) 因 LO1 LO2 解得 J O m2 d 2 m2 d 碰撞结束后 摆与子弹一起绕轴O转过角度 应用动能定理 有
解:
mCy I y mCy ( e) J C 2 J C 1 M C ( I )
Cx sin Cx
选质心为基点 沿y轴投影 有 有
mCx I x mCx
(a)
(b)
(c) 有
地面光滑 杆只受有y方向的碰撞冲量I I x 0
§ 2-2 用于碰撞过程的基本定理
碰撞过程开始瞬时的速度为 设质点的质量为m 结束时的速度为 则质点的动量定理为 t m m Fdt I (2-1) 0 式中 I 为碰撞冲量 普通力的冲量忽略不计 质点系 ( e ) (i ) mii mii I i I i 设质点系有n个质点 对于每个质点都可列出如上的方程 将n个方程相加 得 n n n n (e) (i ) m m I I i i i i i i
由于碰撞时碰撞力极大而碰撞时间极短 在研究一般的碰撞问题时 通常做如下两点简化
(1)在碰撞过程中 由于碰撞力非常大 重力 弹性力 等等普通力远远不能与之相比 因此这些普通力的冲量忽略不计 (2)由于碰撞过程非常短促 碰撞过程中 速度变化为有限值 物体在碰撞开始和碰撞结束时的位置变化很小 因此在碰撞过程中 物体的位移忽略不计
1 1 2 0 ( J O m2 d 2 2 ) m1 g (h h cos ) m2 g (d d cos ) 2 2
即
1 ( J O m2 d 2 ) 2 (m1h m2 d )(1 cos ) g 2
2 因 1 cos 2 sin
由式(2-7)和(2-8)有 I2 k I1 即恢复因数又等于正碰撞的两个阶段中作用于物体的碰 撞冲量大小的比值
n 如图所示 此为斜碰撞 此时定义恢复因数为 k n 和 n 分别是速度 和 在法线方向的投影 式中 n
由于不计摩擦 和 在切线方向的投影相等 由图可见 tan n tan n 于是 n tan k n tan 对于实际材料有k<1 由上式可见 当碰撞物体表面光滑时 应有
将式(c)代入上式 得两物体在正碰撞过程中损失的动能 m1m2 1 ) ( 2 2 )] T T1 T2 (1 k ) (1 2 )[(1 1 2 m1 m2 由式(b)得
2 k (1 2 ) 1
于是得 T T1 T2
第二章
碰
撞
§ 2-1 碰撞的分类· 碰撞问题的简化
1.碰撞的分类
对心碰撞 偏心碰撞 正碰撞 斜碰撞 碰撞时两物体间的相互作用力称为碰撞力 光滑碰撞与非光滑碰撞 完全弹性碰撞 弹性碰撞 塑性碰撞
2.对碰撞问题的两个简化
碰撞现象的特点是 碰撞时间极短(一般为103 ~ 104 s ) 速度变化为有限值 加速度变化相当巨大 碰撞力极大
2gh2
于是得恢复因数 h2 k h1 几种材料的恢复因数见表
碰撞物体 铁对铅 木对胶 木对 的材料 木 木 恢复因数 0.14 0.26 0.50 钢对 钢 0.56 象牙对象 牙 0.89 玻璃对 玻璃 0.94
对于各种实际的材料 均有0<k<1 由这些材料做成的物体发生的碰撞称为弹性碰撞 物体在弹性碰撞结束时 变形不能完全恢复 动能有损失 k=1称为完全弹性碰撞 k=0称为非弹性碰撞或塑性碰撞
积分 或
得
LO 2 dLO LO1
i 1
n
t
0
(e) ri dI i
n t n (e) t (e) LO 2 LO1 ri dI i ri dI i i 1 0 i 1 0
n n (e) (e) LO 2 LO1 ri I i M O (I i ) (2-4) i 1 i 1 ( e) 称 ri I i 为冲量矩 其中不计普通力的冲量矩 (2-4)是用于碰撞过程的动量矩定理 又称为冲量矩定理: 质点系在碰撞开始和结束时对点O的动量矩的变化 等于作用于质点系的外碰撞冲量对同一点的主矩
2.用于碰撞过程的动量矩定理——冲量矩定理
质点系动量矩定理
n n (e) d (e) LO M O ( Fi ) ri Fi dt i 1 i 1
上式可写成
n n (e) ( e) dLO ri Fi dt ri dI i i 1 i 1
LC J C
式(2-5)可写为 式中 1 ,2 分别为平面运动刚体碰撞前后的角速度 上式中不计普通力的冲量矩 式(2-6)与(2-3)结合起来 可用来分析平面运动刚体的碰撞问题 称为刚体平面运动的碰撞方程
( e) J C 2 J C 1 M C (I i )
(2-6)
A C AC
1 cos 2 Ay Cy 2
(d)
Ay Ay 1 由恢复因数 k Ay sin 1 2 cos 代入式(d) 得 sin Cy 2
m sin I 由(b)和(c)两式得 mCy 1 l 2 ml 2 I cos 12 2
2
代入上式中 解得
m1h m2 d J O m2 d
2
g 2 sin
2
于是得子弹射入砂筒前的速度为
2 sin
( J O m2 d 2 )(m1h m2 d ) g
2 m2 d
例 2-3 速度为 平行于杆 均质细杆长l 质量为m 杆与地面成θ角 斜撞于光滑地面 如图所示 如为完全弹性碰撞 求撞后杆的角速度
或
3.刚体平面运动的碰撞方程
(用于刚体平面运动碰撞过程中的基本定理) 用于碰撞过程的质点系相对于质心的动量矩定理 n ( e) LC 2 LC1 M C (I i ) (2-5)
