六年级数学上册组合图形的周长和面积[1]汇编
六年级数学上册组合图形的周长和面积讲解

六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
六年级数学上册组合图形的周长和面积[1]汇编
![六年级数学上册组合图形的周长和面积[1]汇编](https://img.taocdn.com/s3/m/2640e421a58da0116d17496f.png)
六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法: 1圆面积减去等腰直角三角形的面积,4拓-2 X1=1.14 (平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)£解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以?=7,所以阴影部分的面积为:7- ^「=7-丨X7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)£解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积, 所以阴影部分的面积:2X2- n= 0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16- n()=16-4n=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为叶形”,是用两个圆减去一个正方形,n() >2-16=8n -16=9.12 平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)n :-n()=100.48 平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长 >对角线长煜,求)正方形面积为:5X5^2=12.5(5)2所以阴影面积为:n ^4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)£解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,£所以阴影部分面积为:n()=3.14平方厘米例9.求阴影部分的面积。
5、组合图形的周长与面积

O'
A
O
C
小结:
我们学过的公式总汇:
d ( 1 )d 2r ,r 2 (2)C = d,C = 2 r
C C (3)r = ,d = 2
C半圆 (4)C半圆 ( +2)r,r = +2 n n n (5)l C r d 360 180 360
180l 180l (6)r ,n n r
小结:
常用结论 (1)周长相等的正方形、圆和长方形中,圆的 面积最大。 (2)在正方形中剪一个最大的圆的直径等于正 方形的边长。 (3)在长宽不等的长方形中剪一个最大的圆的 直径等于较小边的长度。 (4)在圆中剪一个最大的正方形的对角线长等 于圆的直径。
方法一:分割法
求阴影部分的面积
3 S阴 S圆 S正 4
4dm
练习:
求下列图形的面积
(1)
1cm 3cm
45°
2cm
练习:
求下列图形的面积
(2)
4dm
Hale Waihona Puke 练习:求下列图形的面积
(3)
20cm
练习:
求下列图形的面积
(4)
4m
练习:
求下列图形的面积
(5)
练习:
求下列图形的面积
(6)
6 10
单位:厘米
练习:
求下列图形的面积
(7)
B
左图中圆O与圆O’ 的半径都等于9厘 米,而扇形ABC的 圆心角是30度。
r=5cm
方法二:补缺法
求阴影部分的面积
S 阴=S正 – S半圆
10m
方法三:割补法
求阴影部分的面积
S阴= S三角形
六年级总复习《组合图形面积》经典习题汇编

组合图形1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求三角形AEF 的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)
部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S阴。
部分12平方厘米,求阴影部分面积。
(完整版)六年级数学上册组合图形的周长和面积

六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
《组合图形的面积》六年级上册
两个内圆面积:
5×5×3.14+2×2×3.14 =78.5+12.56
4 10
3 求阴影部分周长和面积(单位:dm)
温馨提示
(1)阴影的周长=大圆周长的一半 + 两
个小圆周长的一半
(2)阴影的面积=大圆面积的一半 — 两
个小圆面积的一半
3
5
阴影的周长:8×3.14÷2+3×3.14÷2+5×3.14÷2=25.12(dm)
阴影面积=(扇形面积 – 三角形 面积形面积)×2
10cm
13 求阴影部分面积。(单位:cm)
温馨提示:
1)正方形面积 – 圆面积=等于4
角的空白面积。
8
2)正方形面积 – 4个角的扇形
面积(也就是一个圆的面积)=
圆中间的空白面积。
8
14 跑道长多少米?(两端各是半圆)跑道 面积是多少?
跑道长: 10×2×3.14+100×2 =62.8+200 =262.8(米)
100米
15 求阴影部分面积。
温馨提示:
(1)做辅助线把圆心连起来呈现
出一个正方形,正方形的边长
是半径的2倍。
(2)正方形的面积 - 4个空白扇形
2cm
的面积(也就是一个圆面积)=
中间的阴影面积
16 求阴影部分面积。
温馨提示:
(1)正方形面积-外圆面积
=4个角的阴影面积
4cm
(2)4个角的阴影面积+小
=9×4.5÷2 =20.25(平方厘米)
阴影面积:
42-20.25 =21.75(平方厘米)
30 求阴影部分面积。(单位:厘米)
温馨提示:
六年级数学上册组合图形的周长和面积

六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积.(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1。
505平方厘米例3。
求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2—π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16—π()=16-4π=3.44平方厘米例5。
求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形",是用两个圆减去一个正方形,π()×2-16=8π—16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100。
48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积.(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4—12.5=7。
125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积.(单位:厘米)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10。
六年级数学组合图形“面积周长”训练

六年级数学组合图形“面积周长”训练
对于数学这门学科,很多孩子还是觉得特别难的,先不说压轴题和应用题,就拿几何题来说,就是孩子们学习的一个重难点。
所有积累的知识都是在平常的学习过程中积累得来的,只有当量变发展到一定程度时才有可能产生质变。
因此,孩子们在平时的学习过程中,特别是刚接触这一学科时,一定要将它所包含的每一个概念、理论等熟练掌握,分清它们的用途,并且对其进行分类,从而为以后的学习打下基础。
鉴于此,下面是老师专门整理的小学六年级的组合图形面积+周长训练,非常的全面经典,建议为孩子打印一份,吃透了,考试名列前茅。
六年级数学上册组合图形的周长和面积

六年级数学上册组合图形的周长和面积21、如图12,已经半圆的直径为10㎝,求阴部分的面积及阴影弧线长的和。
22、如下图,已知AB=12厘米,且阴影部分甲的面积比阴影部分乙的面积大12平方厘米。
求BC的长是多少厘米?23、如下图,求出阴影部分的周长和面积。
(单位:㎝)24、如下图,已知AC=CD=DB=2㎝,求阴影部分的周长和面积。
25、已经半圆的直径为9㎝,求阴影部分的面积。
26、如下图,求阴影部分的周长与面积。
(单位:㎝)27、如图所示,圆的周长为12.56厘米,AC 两点把圆分成相等的两段弧,阴影部分(1)的面积与阴影部分(2)的面积相等,求平行四边形ABCD 的面积。
28、如图所示,直径BC =8厘米,AB =AC ,D 为AC 的重点,求阴影部分的面积。
DACB12ACDC29、 如图所示,AB =BC =8厘米,求阴影部分的面积。
30、 如图所示,求四边形ABCD 的面积。
(单位:厘米)31、如图19-16所示,BE 长5厘米,长方形AEFD 面积是38平方厘米。
求CD 的长度。
32.图19-17是两个完全一样的直角三角形重叠在一起,按照图中的已知条件求阴影部分的面积(单位:厘米)。
B45○7 C ABBC AE3819-1633、如图19-19所示,∠1=15度,圆的周长位62.8厘米,平行四边形的面积为100平方厘米。
求阴影部分的面积(得数保留两位小数)。
34、如图19-20所示,三角形ABC 的面积是31.2平方厘米,圆的直径AC =6厘米,BD :DC =3:1。
求阴影部分的面积。
35、如图19-21所示,求阴影部分的面积(单位:厘米。
得数保留两位小数)。
D304019-17 120519-1919-2030AB12 19-21三角形面积计算【例题1】已知如图,三角形ABC的面积为8平方厘米,AE=ED,BD=2/3BC,求阴影部分的面积。
【思路导航】阴影部分为两个三角形,但三角形AEF的面积无法直接计算。
人教版六年级上册组合图形

六年级上册组合图形的周长和面积(单位:厘米)
1. 求阴影部分的面积。
2.正方形面积是7平方厘米,求阴影部分的面积。
3.求图中阴影部分的面积。
4.求阴影部分的面积。
(单位:厘米)
5.求阴影部分的面积。
6、求阴影部分的面积。
(单位:厘米)
7、求阴影部分的面积。
(单位:厘米) 8.求阴影部分的
面积和周长。
(
单位
:厘米
)
9.求阴影部分的面积。
(单位:厘米)
10.求阴影部分的面积。
(单位:厘米)
11.求阴影部分的面积。
(单位:厘米)
12.求阴影部分的面积。
(单位:厘米)
13.求阴影部分的面积。
(单位:厘米)
14.求阴影部分的面积。
(单位:厘米)。
(基础版)第16讲 组合图形的周长与面积—小升初数学精讲精练专题汇编
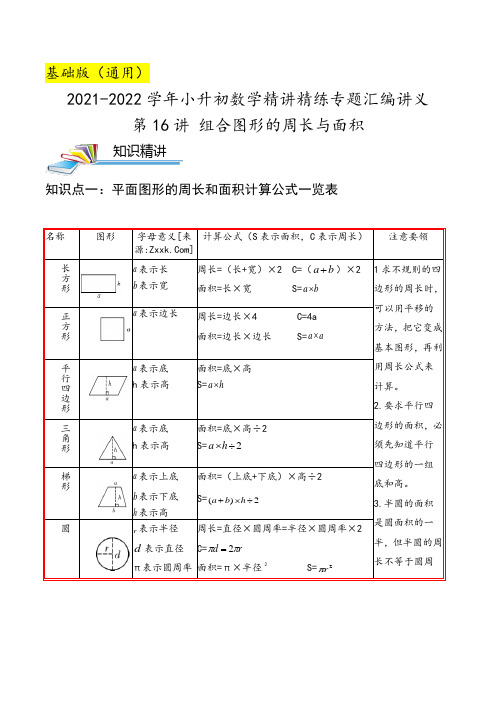
基础版(通用)2021-2022学年小升初数学精讲精练专题汇编讲义第16讲组合图形的周长与面积知识点一:平面图形的周长和面积计算公式一览表名称图形字母意义[来源:]计算公式(S表示面积,C表示周长)注意要领长方形a表示长b表示宽周长=(长+宽)×2 C=(ba+)×2面积=长×宽 S=ba⨯1求不规则的四边形的周长时,可以用平移的方法,把它变成基本图形,再利用周长公式来计算。
2.要求平行四边形的面积,必须先知道平行四边形的一组底和高。
3.半圆的面积是圆面积的一半,但半圆的周长不等于圆周正方形a表示边长周长=边长×4 C=4a面积=边长×边长 S=aa⨯平行四边形a表示底h表示高面积=底×高S=ha⨯三角形a表示底h表示高面积=底×高÷2S=2÷⨯ha梯形a表示上底b表示下底h表示高面积=(上底+下底)×高÷2S=2)(÷⨯+hba圆r表示半径d表示直径π表示圆周率周长=直径×圆周率=半径×圆周率×2 C=rdππ2=面积=π×半径 2 S=2rπ知识精讲知识点二:组合图形的周长和面积实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施平移、旋转、割补、等量代换等方法将它们转化为基本图形的和、差关系,问题就能解决了.一、精挑细选(共5题;每题2分,共10分)1.下面三幅图中,正方形一样大,则三个阴影部分的面积( )A .一样大B .第一幅图最大C .第二幅图最大D .第三幅图最大2.(2021·坪山)如图,甲和乙的周长相比,( )。
A .甲长B .乙长C .同样长3.(2021六上·海安期末)一个木匠用32米木围栏材料把一块花园围起来,花园有四种可能圆环r表示小圆半径R 表示大圆半径圆环面积=大圆面积-小圆面积 )(22r R S -=π环长的一半。
6年级上册数学圆形组合图形周长和面积计算图形汇总

6-组合图形周长长方形周长=
正方形周长=
圆的周长=
【方法】1、数边2、爱拼才会赢 3.加法
【隐藏完整圆】求阴影部分周长
单位:dm单位:m
单位:dm
单位:m
单位:m
2、求下图的周长(单位:米)
【二分之一圆
】求阴影部分周长
←6dm
6dm
2cm
单位:m
单位:cm
单位:cm 单位:cm
单位:cm
【四分之一圆
】求阴影部分周长
cm
单位:cm
单位:cm
单位:cm
6-4组合图形面积
【基础准备】1、图形面积公式2、求不完整面积的方法
【拼凑变完整】求阴影部分面积。
2cm
单位:cm
【陈年旧事】
计算下面图形面积。
单位:cm
单位:m
【挖空图:大减小】求阴影部分的面积。
单位:m
单位:cm
【叶子形:对半分】求阴影部分面积(单位:厘米)。
cm。
六年级上册数学 几何公式周长面积体积公式

六年级上册数学
几何公式周长面积体积公式
长方形的周长=(长+宽)×2 C=(a+b)×2
正方形的周长=边长×4 C=4a
长方形的面积=长×宽S=ab
正方形的面积=边长×边长S=a×a=a2
三角形的面积=底×高÷2 S=ah÷2
平行四边形的面积=底×高S=ah
梯形的面积=(上底+下底)×高÷2 S=(a+b)h÷2
直径=半径×2d=2r半径=直径÷2 r=d÷2
圆的周长=圆周率×直径=圆周率×半径×2 c=πd=2πr
长方体的体积=长×宽×高V=abh
长方体(或正方体)的体积=底面积×高V=abh
正方体的体积=棱长×棱长×棱长V=aaa
圆的周长=直径×πC=πd=2πr
圆的面积=半径×半径×πS=πr2
圆柱的表(侧)面积:圆柱的表(侧)面积等于底面的周长乘高
S=ch=πdh=2πrh
圆柱的表面积:圆柱的表面积等于底面的周长乘高再加上两头的圆的面积S=ch+2s=ch+2πr2
圆柱的体积:圆柱的体积等于底面积乘高V=Sh
圆锥的体积=1/3底面×高V=1/3Sh。
六年级数学上册组合图形的周长和面积+六年级数学易错题

六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。
(单位:厘米) 解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米) 解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米) 解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米) 解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求) 正方形面积为:5×5÷2=12.5 所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
六年级数学上册组合图形的周长和面积+六年级数学易错题

六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。
(单位:厘米) 解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米) 解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米) 解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米) 解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求) 正方形面积为:5×5÷2=12.5 所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
(单位:厘米)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10.求阴影部分的面积。
(单位:厘米)解:同上,平移左右两部分至中间部分,则合成一个长方形,所以阴影部分面积为2×1=2平方厘米(注: 8、9、10三题是简单割、补或平移)例11.求阴影部分的面积。
(单位:厘米)解:这种图形称为环形,可以用两个同心圆的面积差或差的一部分来求。
(π-π)×=×3.14=3.66平方厘米例12.求阴影部分的面积。
(单位:厘米)解:三个部分拼成一个半圆面积.π()÷2=14.13平方厘米例13.求阴影部分的面积。
(单位:厘米)解: 连对角线后将"叶形"剪开移到右上面的空白部分,凑成正方形的一半.所以阴影部分面积为:8×8÷2=32平方厘米例14.求阴影部分的面积。
(单位:厘米)解:梯形面积减去圆面积,(4+10)×4-π=28-4π=15.44平方厘米 .例15.已知直角三角形面积是12平方厘米,求阴影部分的面积。
分析: 此题比上面的题有一定难度,这是"叶形"的一个半.解: 设三角形的直角边长为r,则=12,=6圆面积为:π÷2=3π。
圆内三角形的面积为12÷2=6,阴影部分面积为:(3π-6)×=5.13平方厘米例16.求阴影部分的面积。
(单位:厘米)解:[π+π-π]=π(116-36)=40π=125.6平方厘米例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)解:上面的阴影部分以AB为轴翻转后,整个阴影部分成为梯形减去直角三角形,或两个小直角三角形AED、BCD面积和。
所以阴影部分面积为:5×5÷2+5×10÷2=37.5平方厘米例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
解:阴影部分的周长为三个扇形弧,拼在一起为一个半圆弧,所以圆弧周长为:2×3.14×3÷2=9.42厘米例19.正方形边长为2厘米,求阴影部分的面积。
解:右半部分上面部分逆时针,下面部分顺时针旋转到左半部分,组成一个矩形。
所以面积为:1×2=2平方厘米例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
解:设小圆半径为r,4=36, r=3,大圆半径为R,=2=18,将阴影部分通过转动移在一起构成半个圆环,所以面积为:π(-)÷2=4.5π=14.13平方厘米例21.图中四个圆的半径都是1厘米,求阴影部分的面积。
解:把中间部分分成四等分,分别放在上面圆的四个角上,补成一个正方形,边长为2厘米,所以面积为:2×2=4平方厘米例22.如图,正方形边长为8厘米,求阴影部分的面积。
解法一: 将左边上面一块移至右边上面,补上空白,则左边为一三角形,右边一个半圆.阴影部分为一个三角形和一个半圆面积之和. π()÷2+4×4=8π+16=41.12平方厘米解法二: 补上两个空白为一个完整的圆.所以阴影部分面积为一个圆减去一个叶形,叶形面积为:π()÷2-4×4=8π-16所以阴影部分的面积为:π()-8π+16=41.12平方厘米例23.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少?解:面积为4个圆减去8个叶形,叶形面积为:π-1×1=π-1所以阴影部分的面积为:4π-8(π-1)=8平方厘米例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。
如果圆周π率取3.1416,那么花瓣图形的的面积是多少平方厘米?分析:连接角上四个小圆的圆心构成一个正方形,各个小圆被切去个圆,这四个部分正好合成3个整圆,而正方形中的空白部分合成两个小圆.解:阴影部分为大正方形面积与一个小圆面积之和.为:4×4+π=19.1416平方厘米例25.如图,四个扇形的半径相等,求阴影部分的面积。
(单位:厘米)分析:四个空白部分可以拼成一个以2为半径的圆.所以阴影部分的面积为梯形面积减去圆的面积,4×(4+7)÷2-π=22-4π=9.44平方厘米例26.如图,等腰直角三角形ABC和四分之一圆DEB,AB=5厘米,BE=2厘米,求图中阴影部分的面积。
解: 将三角形CEB以B为圆心,逆时针转动90度,到三角形ABD位置,阴影部分成为三角形ACB面积减去个小圆面积,为: 5×5÷2-π÷4=12.25-3.14=9.36平方厘米例27.如图,正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,求阴影部分的面积。
解: 因为2==4,所以=2以AC为直径的圆面积减去三角形ABC面积加上弓形AC面积,π-2×2÷4+[π÷4-2]=π-1+(π-1)=π-2=1.14平方厘米例28.求阴影部分的面积。
(单位:厘米)解法一:设AC中点为B,阴影面积为三角形ABD面积加弓形BD的面积,三角形ABD的面积为:5×5÷2=12.5弓形面积为:[π÷2-5×5]÷2=7.125所以阴影面积为:12.5+7.125=19.625平方厘米解法二:右上面空白部分为小正方形面积减去小圆面积,其值为:5×5-π=25-π阴影面积为三角形ADC减去空白部分面积,为:10×5÷2-(25-π)=π=19.625平方厘米例29.图中直角三角形ABC的直角三角形的直角边AB=4厘米,BC=6厘米,扇形BCD所在圆是以B为圆心,半径为BC的圆,∠CBD=,问:阴影部分甲比乙面积小多少?解: 甲、乙两个部分同补上空白部分的三角形后合成一个扇形BCD,一个成为三角形ABC,此两部分差即为:π×-×4×6=5π-12=3.7平方厘米例30.如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米。
求BC的长度。
解:两部分同补上空白部分后为直角三角形ABC,一个为半圆,设BC长为X,则40X÷2-π÷2=28所以40X-400π=56 则X=32.8厘米例31.如图是一个正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,求阴影部分的面积。
解:连PD、PC转换为两个三角形和两个弓形,两三角形面积为:△APD面积+△QPC面积=(5×10+5×5)=37.5两弓形PC、PD面积为:π-5×5所以阴影部分的面积为:37.5+π-25=51.75平方厘米例32.如图,大正方形的边长为6厘米,小正方形的边长为4厘米。
求阴影部分的面积。
解:三角形DCE的面积为:×4×10=20平方厘米梯形ABCD的面积为:(4+6)×4=20平方厘米从而知道它们面积相等,则三角形ADF面积等于三角形EBF面积,阴影部分可补成圆ABE的面积,其面积为:π÷4=9π=28.26平方厘米例33.求阴影部分的面积。
(单位:厘米)解:用大圆的面积减去长方形面积再加上一个以2为半径的圆ABE面积,为(π+π)-6=×13π-6=4.205平方厘米例34.求阴影部分的面积。
(单位:厘米)解:两个弓形面积为:π-3×4÷2=π-6阴影部分为两个半圆面积减去两个弓形面积,结果为π+π-(π-6)=π(4+-)+6=6平方厘米例35.如图,三角形OAB是等腰三角形,OBC是扇形,OB=5厘米,求阴影部分的面积。
解:将两个同样的图形拼在一起成为圆减等腰直角三角形[π÷4-×5×5]÷2=(π-)÷2=3.5625平方厘米。
