物质结构——晶体分类及空间利用率的计算
晶体空间利用率计算

混合物晶体空间利用率计算
总结词
混合物晶体空间利用率是指混合物晶体中不同组分原子的堆积密度之和,即单位 体积内所包含的不同组分原子的数目之和。
详细描述
混合物晶体空间利用率计算需要考虑不同组分原子的半径、配位数以及不同组分 之间的相互作用等因素。例如,在铜锌合金中,铜和锌的半径不同,导致它们在 晶体中的排列方式不同,从而影响空间利用率。
引入掺杂元素或分子
有机掺杂
通过引入有机分子或小分子掺杂剂,可以改变晶体的生长过程和 结构,从而提高空间利用率。
无机掺杂
引入无机离子或分子掺杂剂可以调整晶体的能带结构和物理性能, 同时也有助于提高空间利用率。
金属原子掺杂
金属原子掺杂可以改变晶体的导电性和磁性等性质,同时也有助于 优化晶体的空间利用率。
06
未来展望与研究方向
深入研究晶体结构与空间利用率的关系
总结词
深入理解晶体结构与空间利用率的关系是关键,需要进一步研究晶体结构的特点和规律,以及它们对空间利用率 的影响。
详细描述
晶体结构是影响空间利用率的重要因素之一。为了更好地理解空间利用率,需要深入研究晶体结构的组成、排列 方式和相互关系,以及它们对晶体空间利用率的影响。这有助于揭示晶体结构的本质特征,为提高空间利用率提 供理论支持。
意义
空间利用率的高低直接影响到晶体的 物理和化学性质,如熔点、硬度、热 导率等。空间利用率高的晶体具有更 好的机械性能和化学稳定性。
计算方法简介
几何法
通过计算晶体中原子或分子的几 何排列来计算空间利用率。具体 方法包括最近邻法、次近邻法等 。
统计法
通过统计晶体中原子或分子的分 布概率来计算空间利用率。这种 方法考虑了晶体中的涨落效应, 计算结果更为准确。
晶体密度、空间利用率的通用计算方法

晶体密度、空间利用率的通用计算方法以金属晶体为例进行分析,计算方法如下:第一步,确定晶胞含有的微粒数。
若1个晶胞中含有x 个微粒,则: (1)1个晶胞中原子利用的体积 = x ·4 π r 3 / 3 ,其中r 表示金属原子半径。
(2)1个晶胞质量 = x ·M / N A ,其中M 表示金属的摩尔质量,N A 表示阿伏加德罗常数。
若计算对象是离子晶体,该式亦然成立,M 则表示离子化合物的摩尔质量。
第二步,计算晶胞体积。
不同类型晶胞的体积有不同计算方法,用a 表示晶胞棱长,a 3表示晶胞的体积,r 表示金属原子半径,归纳总结如下:(1)简单立方结构,晶胞体积a 3 =(2r ) 3 =8r 3 ;侧面形状及数据为:,(2)体心立方结构,晶胞体积a 3 =64√3r 3 / 9 ;(3)六方堆积结构,晶胞体积a 3 = 8√2 r 3 ;晶胞相关数据为为:(4)面心立方结构,晶胞体积a 3 =16√2 r 3 ;a√2a√3a4r= 2r(1)有关晶体密度的计算通用关系式:x·M /N A=ρ·a3,依据是晶体密度等于晶胞密度,具体计算时把各类型晶胞的体积,代入关系式即可,下式亦同。
(2)有关空间利用率的计算通用关系式:x·4 πr3 / 3=w%·a3,其中w% 表示晶胞空间利用率。
注意事项:(1)在实际计算时要注意长度单位换算,晶胞棱长及原子半径单位常用pm,而密度中的体体积单位常用(cm)3,存在换算关系1pm=10-10cm。
(2)若计算离子晶体密度,方法大同小异,需要综合考虑阴、阳离子半径来求晶胞体积。
常见金属晶胞结构与性质归纳一览表:。
晶体空间利用率计算PPT课件

Ba:1×1 Ti:8× (1/8) O:12× (1/4)
化学式为:BaTiO3
-
9
2:某离子晶体晶胞结构如 图所示,X位于立方体的 顶点,Y位于立方体的中 心。试分析:
(1)在一个晶胞中有 1/2个X, 1 个Y,所以 该晶体的化学式为__X_Y_2_
(2)晶体中距离最近的2 个X与一个Y所形成的夹角 ∠XYX角度为__1_0_9_._5_°_(填 角的度数)
V晶胞
2r
2 4r3
h
2r
3 100% 8 2r3
=74%
-
16
4、面心立方最密堆积
a2 2r
V球
4
4r3
3
4r
V 晶 胞 a3(22 r)3 16 2 r3
a 空间利用率= V球 100 %
V晶胞
4 4r3
3 100% 16 2r3
=74%
-
17
【堆积方式及性质小结】
堆积方式 晶胞类型 空间利 配位数 用率
位于顶点的微粒,晶胞完全拥有其1/8。 位于面心的微粒,晶胞完全拥有其1/2。 位于棱上的微粒,晶胞完全拥有其1/4。 位于体心上的微粒,微粒完全属于该晶胞。
-
6
计算:NaCl晶胞、CsCl晶胞中含有 的阴、阳离子数目分别是多少?
NaCl晶胞
钠离子:1+12×1/4 = 4 氯离子:8 ×1/8+6×1/2 =- 4
比为—————————1。:2:3
乙晶胞中所含金属原子数为8×1/8+6×1/2=4
晶胞中所含金属原子数为12×1/6+2×1/2+3=6
-
12
二、空间利用率的计算
1、空间利用率:指构成晶体的原子、离
晶体配位数_空间利用率计算
解析:
① Ni原子的配位数为: Ni原子的数目为: 8×1/8 + 6×1/2 =4 ②晶体的密度为: m= 4M/NA ; V= a3 ,a2+a2+a2 = (4r)2 3a2=16r2→a=4d/3 p=m/v=4M/NA/4d/3= 3M/dNA
探究3:已知铜晶胞是面心立方晶胞,该晶胞的 边长为3.6210-10m ,每一个铜原子的质量为 1.05510-25kg ,试回答下列问题: (1)一个晶胞中“实际”拥有的铜原子数是多 少? (2)该晶胞的体积是多大? (3)利用以上结果计算金属铜的密度。 (4)计算空间利用率。
探究1:单质晶体中原子的堆积方式
如下图所示,其晶胞特征如下图乙所示,原子之间 相互位置关系的平面图如下图丙所示。
甲
乙
丙
若已知Ni的原子半径为d,NA代表阿伏加德罗常数,Ni的 相对原子质量为M,请回答: ①晶胞中Ni原子的配位数为___ ___ _ ,一个晶胞中Ni 原子的数目为_ _; ②该晶体的密度为______ _ (用字母表示)。
a
3
100 %
晶胞的有关计算
1) 利用晶胞参数可计算晶胞体积(V),根据相对分子 质量(M)、晶胞中粒子数(Z)和阿伏伽德罗NA,可计算 晶体的密度 :M·Z/NA·V 2)已知棱长,求某线段。晶胞中各线段间的关系如下:
3 )空间利用率:指构成晶体的微粒在整个晶体空间中 所占有的体积百分比。 球体积 空间利用率 = ———— 100% 晶胞体积
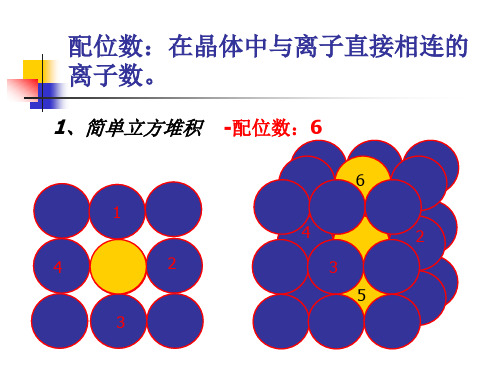
配位数:在晶体中与离子直接相连的 离子数。
1、简单立方堆积
-配位数:6
6 1 4 3 2 1 4 3 5 2
2、钾型(体心立方堆积)
晶胞空间利用率公式

晶胞空间利用率公式晶胞空间利用率公式是描述晶体结构中原子或离子排列紧密程度的一个重要参数。
晶体结构是由一定数量的原子或离子按照一定的规律排列而成的,晶胞是晶体中最小的重复单元,晶胞空间利用率是指晶胞中实际占据的原子或离子体积与晶胞总体积之比,是描述晶体结构紧密程度的一个重要参数。
晶胞空间利用率公式为:V = (n × Vm) / Vc其中,V表示晶胞空间利用率,n表示晶胞中实际占据的原子或离子数,Vm表示一个原子或离子的摩尔体积,Vc表示晶胞的体积。
晶胞空间利用率是晶体结构中一个重要的物理量,它反映了晶体中原子或离子排列的紧密程度。
晶体结构中原子或离子的排列方式决定了晶体的物理性质,如硬度、密度、热膨胀系数等。
因此,晶胞空间利用率是研究晶体结构和性质的重要参数。
晶胞空间利用率的大小与晶体结构有关。
对于紧密堆积的晶体结构,晶胞空间利用率较大,如钻石、金刚石等;对于松散堆积的晶体结构,晶胞空间利用率较小,如石墨、石英等。
晶胞空间利用率还与晶体中原子或离子的大小有关,原子或离子越大,晶胞空间利用率越小。
晶胞空间利用率的计算需要知道晶体结构中原子或离子的排列方式和晶胞的大小。
晶体结构可以通过X射线衍射、电子衍射等方法进行测定,晶胞的大小可以通过晶体的晶胞参数计算得到。
因此,晶胞空间利用率的计算需要先确定晶体结构和晶胞参数,然后根据公式进行计算。
晶胞空间利用率的大小对晶体的物理性质有重要影响。
晶胞空间利用率较大的晶体结构通常具有较高的密度和硬度,如钻石、金刚石等;晶胞空间利用率较小的晶体结构通常具有较低的密度和硬度,如石墨、石英等。
晶胞空间利用率还与晶体的热膨胀系数有关,晶胞空间利用率较大的晶体结构通常具有较小的热膨胀系数,如钻石、金刚石等;晶胞空间利用率较小的晶体结构通常具有较大的热膨胀系数,如石墨、石英等。
晶胞空间利用率的大小还与晶体的稳定性有关。
晶胞空间利用率较大的晶体结构通常比较稳定,如钻石、金刚石等;晶胞空间利用率较小的晶体结构通常比较不稳定,如石墨、石英等。
晶体空间利用率计算

V球 空间利用率= 100% V晶胞 4 3 r 3 3 100% =52% 8r
1个晶胞中平均含有1个原子 4 3 V =(2r)3=8r3 V球= r 晶胞 3
2、体心立方堆积 a b a
b a a 2 2 2 2 (4r ) a b 3a
2 2 2
4 a r 3
【堆积方式及性质小结】
堆积方式 晶胞类型 空间利 配位数 用率 简单立方 简单立方 体心立方 体心立方 六方堆积 六方 52% 68% 74% 74% 6 8 12 实例
Po Na、K、Fe
Cu、Ag、Au Mg、Zn、Ti
面心立方 面心立方
12
空间利用率= 4 3 2 r 3 100% 3 a
4 3 2 r 3 100% 4 3 ( r) 3
3 100% 68% 8
3、六方最密堆积 hs
s 2r 3r 2 3r
2
s
V球 100% 空间利用率= V晶胞
4 3 V球 2 r 2r 3 2 6 2 V晶胞 s 2h 2 3r 2 r 8 2r 3 3
【例题1】现有甲、乙、丙、丁四种晶胞,可推 1:1 知甲晶体中与的粒子个数比为——————;乙 DC2 或C2D 晶体 的化学式为—————— ————;丙晶体的 化学式为EF或FE ;丁晶体的化学式为XY Z —————— ———。
2
B
A
Z D C F E X
甲乙丙Fra bibliotek丁Y
甲
乙
丙
【例题2】上图甲、乙、丙三种结构单元中,金属 1:2:3 原子个数比为—————————。 乙晶胞中所含金属原子数为8×1/8+6×1/2=4 晶胞中所含金属原子数为12×1/6+2×1/2+3=6
金属晶体四类晶胞空间利用率的计算知识讲解

金属晶体四类晶胞空间利用率的计算金属晶体四类晶胞空间利用率的计算高二化学·唐金圣在新课标人教版化学选修3《金属晶体》一节中,给出了金属晶体四种堆积方式的晶胞空间利用率。
空间利用率就是晶胞上占有的金属原子的体积与晶胞体积之比。
下面就金属晶体的四种堆积方式计算晶胞的空间利用率。
一、简单立方堆积:在简单立方堆积的晶胞中,晶胞边长a等于金属原子半径r的2倍,晶胞的体积V晶胞=(2r)3。
晶胞上占有1个金属原子,金属原子的体积V原子=4πr3/3 ,所以空间利用率V原子/V晶胞 = 4πr3/ (3×(2r)3)=52.33﹪。
二、体心立方堆积:在体心立方堆积的晶胞中,体对角线上的三个原子相切,体对角线长度等于原子半径的4倍。
假定晶胞边长为a ,则a2 + 2a2 = (4r)2, a=4 r/√3 ,晶胞体积V晶胞 =64r3/ 3√3 。
体心堆积的晶胞上占有的原子个数为2,原子占有的体积为V原子=2×(4πr3/3)。
晶胞的空间利用率等于V原子/V晶胞 =(2×4πr3×3√3)/(3×64r3)= 67.98﹪。
三、面心立方最密堆积在面心立方最密堆积的晶胞中,面对角线长度是原子半径的4倍。
假定晶胞边长为a,则a2 + a2 = (4r)2 ,a = 2√2r ,晶胞体积V晶胞=16√2r3。
面心立方堆积的晶胞上占有的原子数为4,原子占有的体积为V原子 = 4×(4πr3/3)。
晶胞的空间利用率等于V原子/V晶胞 =(4×4πr3)/(3×16√2r3)= 74.02﹪.四、六方最密堆积六方最密堆积的晶胞不再是立方结构。
晶胞上、下两个底面为紧密堆积的四个原子中心连成的菱形,边长a = 2r ,夹角分别为60°、120°,底面积s = 2r×2r×sin(60°) 。
晶体空间利用率计算

晶体空间利用率计算晶体空间利用率(Crystal Packing Efficiency)是指晶体中原子或离子占据晶胞体积的比例,是晶体内部空间的紧密程度的量化指标之一、晶体空间利用率的计算是晶体学中一个重要的概念,可以帮助我们理解晶体结构的紧密程度和稳定性。
在计算晶体空间利用率时,需要考虑晶胞的体积和晶体中原子或离子的体积。
晶体是由晶胞(unit cell)重复堆积而成的,晶胞是晶体的最小重复单元。
晶胞是三维空间中的一个平行六面体,具有一定的形态和尺寸。
晶体中的原子或离子分布在晶胞的特定位置上。
晶胞的体积可以通过晶胞的各个边长(a、b、c)及夹角(α、β、γ)来计算。
晶胞的体积(V)可以用以下公式表示:V = a * b * c * sin(α) * sin(β) * sin(γ)在计算晶体空间利用率时,我们需要考虑晶体中原子或离子的体积。
原子或离子的体积可以通过元素的晶胞中原子或离子数(Z)及原子或离子的半径(r)来计算。
原子或离子的体积(V_atom)可以用以下公式表示:V_atom = (4/3) * π * r^3 * Zη = (V_atom / V) * 100%晶体空间利用率通常介于0到100%之间。
当晶体空间利用率接近100%时,表示晶体中的原子或离子堆积非常紧密,晶体结构稳定性较高。
而当晶体空间利用率较低时,表示晶体中的原子或离子之间存在较多的空隙或间隙,晶体结构相对较松散。
计算晶体空间利用率的一个重要应用是对晶体的密度进行估计。
晶体的密度可以通过晶体的分子量(M)及晶胞的体积(V)来计算。
晶体的密度(ρ)可以用以下公式表示:ρ=(M/V)*10^24通过计算晶体的密度,可以帮助我们研究晶体的物理特性、确定其材料的性质,并且在材料科学和工程领域中具有重要的应用价值。
总结起来,晶体空间利用率是一个衡量晶体内部空间紧密程度的重要指标,可以通过晶胞的体积和晶体中原子或离子的体积来计算。
晶体空间利用率计算PPT课件

晶胞中的不同位置的微粒是被一个或几个 相邻晶胞分享的,因此一个晶胞所包含的 实际内容是“切割”以后的部分
计算方法:切割法
氯化钠晶体
顶点 棱上
钠离子 氯离子
体心 面心
思考:氯化钠 晶体中钠离子 和氯离子分别 处于晶胞的什
么位置?
方法小结(对于立方体结构)
位于顶点的微粒,晶胞完全拥有其1/8。 位于面心的微粒,晶胞完全拥有其1/2。 位于棱上的微粒,晶胞完全拥有其1/4。 位于体心上的微粒,微粒完全属于该晶胞。
The foundation of success lies in good habits
19
结束语
当你尽了自己的最大努力时,失败也是伟大的, 所以不要放弃,坚持就是正确的。
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End 演讲人:XXXXXX 时 间:XX年XX月XX日
分比。
球体积
空间利用率 =
100%
晶胞体积
2、空间利用率的计算步骤:
(1)计算晶胞中的微粒数 (2)计算晶胞的体积
三、金属晶体空间利用率计算
1.简单立方堆积 立方体的棱长为2r,球的半径为r
过程:
1个晶胞中平均含有1个原子
2r
V球= 4 r3 V晶胞=(2r)3=8r
3
空间利用率= V球 100%
3r
r 3 2 3r2
2
2
3r 2
2 3
h
6r
2 6r 3
8 2r3
空间利用率= V球 100%
V晶胞
2r
高中化学微课-《空间利用率和空隙填充率》

空间利用率为:
3、六方最密堆积(hcp)
特征:晶胞为底面为菱形的平行六面体, 晶胞含有2个原子。
4、面心立方最密堆积(ccp)
特征:晶胞含有4个原子,在面对角线相切。 即
空间利用率:
二、空隙填充率
空隙填充一般用来看待离子晶体的形成,主 要认为阳离子填入阴离子形成的空隙中。针对 不同的离子晶体结构,有不同的空隙类型(八 面体或四面体)与填充率(填充的正四面体 (正八面体)空隙数/总正四面体(正八面体) 空隙数)。
6、六方ZnS型(纤维锌矿)
阴离子以hcp堆积, 阳离子占据所有正 四面体空隙的一半, 填充率为50%。
4、CaF2 型
阳离子以ccp堆积, 阴离子占据所有 的阳离子形成的 正四面体空隙, 填充率100%。
5、 TiO2 型(金红石)
Ti离子占据晶胞顶点和体心 位置,6个O离子构成八面 体将Ti离子包围起来,Ti的 配位数为6,O的配位数为 3。阳离子占据了一半的阴 离子围成的八面体空隙,填 充率是50%。
一、空间利用率
空间利用率:指构成晶体的原子、离子或分 子在整个晶体空间中积/晶胞体积×100%。
1、简单立方堆积(SCP)
特征:棱上相切,即 a = 2r 此种晶胞只含有一个原子,空间利用率是
即:
说明:立方晶胞的边长为a,金属圆球的半径是r。
2、体心立方(bcp)
1、NaCl型
氯离子以ccp堆积, 钠离子填充在氯 离子形成的正八 面体空隙中,填 充率是100%
2、CsCl型
阴离子(Cl-)以 scp堆积,阳离 子填充在阴离子 形成的立方体空 隙中,填充率为 100%.
3、立方ZnS型(闪锌矿)
晶体空间利用率的计算公式

晶体空间利用率的计算公式晶体空间利用率是指晶体中原子或离子所占据的空间与晶体总空间的比值,是评价晶体紧密程度的重要指标。
晶体空间利用率的计算公式为:V = V_atom / V_cell其中,V表示晶体空间利用率,V_atom表示晶体中原子或离子所占据的空间,V_cell表示晶胞的体积。
晶体空间利用率的计算方法晶体空间利用率的计算方法需要先确定晶体的晶胞类型和晶胞参数,然后计算出晶胞的体积和晶体中原子或离子所占据的空间,最后将两者相除即可得到晶体空间利用率。
以简单立方晶体为例,其晶胞类型为P,晶胞参数为a,晶胞体积为V_cell = a^3。
假设晶体中只有一个原子,其半径为r,则原子所占据的空间为V_atom = (4/3)πr^3。
将V_atom和V_cell代入晶体空间利用率的计算公式中,即可得到简单立方晶体的晶体空间利用率:V = V_atom / V_cell = (4/3)πr^3 / a^3同样的,对于其他晶体类型,也可以根据其晶胞类型和晶胞参数计算出晶胞体积和原子或离子所占据的空间,从而得到晶体空间利用率。
晶体空间利用率的意义晶体空间利用率是评价晶体紧密程度的重要指标,其数值越大,表示晶体中原子或离子所占据的空间越大,晶体越紧密。
晶体空间利用率的大小还与晶体的物理性质密切相关,如密度、硬度、热膨胀系数等,因此晶体空间利用率的计算对于研究晶体的物理性质具有重要意义。
晶体空间利用率还可以用于比较不同晶体之间的紧密程度,从而为晶体的合成和应用提供参考。
例如,在材料科学中,晶体空间利用率可以用于评价材料的结构性能,指导新材料的设计和合成。
晶体空间利用率是评价晶体紧密程度的重要指标,其计算公式简单易懂,可以用于比较不同晶体之间的紧密程度,具有重要的理论和应用价值。
晶体的空间利用率

2 6 a 2 6 a
3
3
V球243 r3 (晶胞2个 中)球 有
V球V晶胞 10% 074.05%
【例题1】现有甲、乙、丙、丁四种晶胞,可推
知甲晶体中与的粒子个数比为———1—:1——;乙 晶体 的化学式为——D—C—2——或—C—2—D—;丙晶体的 化学式为E—F—或——F—E— ;丁晶体的化学式为X——Y—2Z。
BA
甲
DC
乙
F
E
丙
Z X
Y
丁
甲
乙
丙
【例题2】上图甲、乙、丙三种结构单元中,金属
原子个数比为———1—:2—:—3———。
乙晶胞中所含金属原子数为8×1/8+6×1/2=4 晶胞中所含金属原子数为12×1/6+2×1/2+3=6
【堆积方式及性质小结】
堆积方式 晶胞类型 空间利 配位数 用率
实例
简单立方 简单立方 52% 6
/3 空间利用率:(2r)3
= 52.36%
(2)体心立方:在立方体顶点的微粒为8个
晶胞共享,处于体心的金属原子全部属于该晶 胞。
1个晶胞所含微粒数为:8×1/8 + 1 = 2
请计算:空间利用率?
(3)面心立方:在立方体顶点的微粒为8个晶
胞共有,在面心的为2个晶胞共有。
晶体的空间利用率
河南省太康县第一高级中学 乔纯杰
一、空间利用率的计算
1、空间利用率:指构成晶体的原子、离
子或分子在整个晶体空间中所占有的体积百
分比。
球体积
空间利用率 =
100%
晶胞体积
2、空间利用率的计算步骤:
(1)计算晶胞中的微粒数 (2)计算晶胞的体积
晶体配位数,空间利用率计算
3a 2 16r 2
r 3a 4
空间利用率
= 晶胞含有原子的体积 / 晶胞体积 100%
2 4 r3 2 4 ( 3 a)3
=
3 a3
34 a3
100% 68%
空间利用率计算
例2:求面心立方晶胞的空间利用率.
解:晶胞边长为a,原子半径为r. 由勾股定理: a 2 + a 2 = (4r)2
a = 2.83 r
每个面心立方晶胞含原子数目: 8 1/8 + 6 ½ = 4
= (4 4/3 r 3) / a 3 = (4 4/3 r 3) / (2.83 r ) 3 100 %
= 74 %
配位数:12
7 1 9
6
5
8 2
3 4
10
11
12
空间利用率计算
例1:计算体心立方晶胞中金属原子的空间利用率。
解:体心立方晶胞:中心有1个原子, 8个顶点各1个原子,每个 原子被8个 晶胞共享。每个晶胞含有几个原子:1 + 8 × 1/8 = 2
空间利用率计算
设原子半径为r 、晶胞边长为a ,根据勾股定理,
配位数配位数怎么算面心立方的配位数设备利用率如何计算资产利用率怎么计算配位数和配位多面体资产利用率计算公式晶体计算介电常数计算晶体晶体空间群
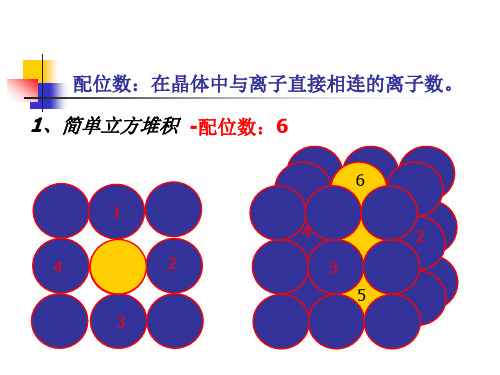
配位数:在晶体中与离子直接相连的离子数。
1、简单立方堆积 -配位数:6
1
4
2
3
6
1
4
2
3
5
6
8
7
1
2
4
3
3. 镁型(六方紧密堆积)
物质结构与性质 晶胞空间利用率的计算

=74.05%
四、六方晶胞
60° 120°
c h
ab
a=b=2r, c=2h
四、六方晶胞
D
D
h
C
A
B
Ca a
h
a
C
S底
A
60°
OEA
F
B
B
OA=
2
3 AE
=
32AB·sin60°=
3 3
a
OD2 = AD2 - OA2
6
h= 3 a
c
=
2h
=
26 3
a
3
CF=AC·sin60°= a
2
S底 = AB·CF =
3 a2
2
V晶胞 = S底·2h = 2 a3
四、六方晶胞
1 2
×1 3
=
1 6
1 2
×
1 6
=
1 12
晶胞中原子总数:
4
×
1 6
+
4
×
1 12
+1 =2
四、六方晶胞
边长与半径的关系:
c
a = b = 2r,c = 2 6 a = 4 6 r
33Biblioteka 原子总体积:V原子=
4 r3 ×2
3
=
8 r3
二、体心立方晶胞
边长与半径的关系: a = 4 r 3
原子总体积:
V原子
=
2×
4 3
r3
晶胞体积: V晶胞 = a3 = (
4 3
r )3
空间利用率
V原子 =
×100% =
V晶胞
2× 4 r3
物质结构——晶体分类及空间利用率的计算

如:干冰、O2、I2、C60 等分子 (4)若分子间靠氢键形成的晶体,则不采取密堆积结构,每个分子周围紧邻的分子数要小于 12 个。因为氢键有方向性和饱和性,一
个分子周围其他分子的位置和数目是一定的。如:冰晶体、苯甲酸晶体
1
4、常见原子晶体的晶胞 【硼晶体、金刚石、晶体硅、锗、SiO2、SiC(金刚砂)、BN(氮化硼)、Si3N4】 (1)金刚石
c、每个 Si 原子被 12 个十二元环共用,每个 O 原子被 6 个十二元环共用
d、每个 SiO2 晶胞中含有 8 个 Si 原子,含有 16 个 O 原子
e、硅原子与 Si—O 共价键之比为 1:4,1mol Si O2 晶体中有 4mol 共价键 (4)SiC:将金刚石晶胞中的一个 C 原子周围与之连接的 4 个 C 原子全部换成 Si 原子,键长稍长些便可得到 SiC 的晶胞。(其中晶胞
凡处于立方体顶点的微粒同时为8个晶胞共有属于该晶胞的为18凡处于立方体棱上的微粒同时为4个晶胞共有属于该晶胞的为14凡处于立方体面上的微粒同时为2个晶胞共有属于该晶胞的为12凡处于立方体体心的微粒完全属于该晶胞2四种晶体类型的比较类型比较分子晶体原子晶体金属晶体离子晶体概念只含分子的晶体即分子构成的晶体或者说分子间以分子间作用力相结合形成的晶体相邻原子间以共价键相互结合形成空间网状结构的晶体由金属阳离子和自由电子通过金属键键形成的具有一定几何外形的晶体由阴阳离子通过离子键结合而成的晶体构成粒子分子原子金属阳离子自由电子阴阳离子粒子间的相互作用范德华力某些含氢键共价键金属键离子键硬度较小很大有的很大有的很小较大熔沸点较低很高有的很高有的很低较高溶解性相似相溶难溶于任何溶剂难溶于常见溶剂大多易溶于水等极性溶剂导电传热性一般不导电溶于水后有的能导电一般不具有导电性电和热的良导体晶体不导电水溶液或熔融态导电物质类别及举例大多数非金属单质气态氢化物酸非金属氧化物sio2除外绝大多数有机物有机盐除外部分非金属单质如金刚石硅晶体硼部分非金属化合物如sicsio2金属单质与合金如naalfe青铜金属氧化物如k2ona2o强碱如kohnaoh绝大部分盐如nacl3常见分子晶体的晶胞1co2晶体晶胞
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d、碳原子与共价键之比为 1:2,12g 金刚石中有 2 mol 共价键 (2)Si:由于 Si 与碳同主族,晶体 Si 的结构同金刚石的结构。将金刚石晶胞中的 C 原子全部换成 Si 原子,健长稍长些便可得到晶
体硅的晶胞
(3)SiO2:在晶体硅的晶胞中,在每 2 个 Si 之间插入 1 个 O 原子,便可得到 SiO2 晶胞 a、SiO2 晶体中最小的环为 12 元环,即 6 个 O,6 个 Si b、每个 Si 与 4 个 O 以共价键结合,形成正四面体结构,每个正四面体占有 1 个 Si,4 个“1O”,n(Si)∶n(O)=1∶2 2
墨晶体是层状结构的,每一层内部碳原子间是共价键相维系,层内的碳原子的核间距为 142pm 层间距离为 335pm,说明层间没
水分子周围只有 4 个紧邻的水分子,虽然氢键不属于化学键,却也具有方向性,即氢键的存在迫使在正四面体中心的水分子与四
面体顶点方向的 4 个相邻的水分子相互吸引
(3)若分子间只有范德华力,则分子晶体采取分子密堆积,每个分子周围有 12 个紧邻的分子。在分子晶体中,原子先以共价键形成
分子,分子再以分子间作用力形成晶体。由于分子间作用力没有方向性和饱和性,分子间尽可能采取密堆积的排列方式
如:干冰、O2、I2、C60 等分子 (4)若分子间靠氢键形成的晶体,则不采取密堆积结构,每个分子周围紧邻的分子数要小于 12 个。因为氢键有方向性和饱和性,一
个分子周围其他分子的位置和数目是一定的。如:冰晶体、苯甲酸晶体
1
4、常见原子晶体的晶胞 【硼晶体、金刚石、晶体硅、锗、SiO2、SiC(金刚砂)、BN(氮化硼)、Si3N4】 (1)金刚石
c、每个 Si 原子被 12 个十二元环共用,每个 O 原子被 6 个十二元环共用
d、每个 SiO2 晶胞中含有 8 个 Si 原子,含有 16 个 O 原子
e、硅原子与 Si—O 共价键之比为 1:4,1mol Si O2 晶体中有 4mol 共价键 (4)SiC:将金刚石晶胞中的一个 C 原子周围与之连接的 4 个 C 原子全部换成 Si 原子,键长稍长些便可得到 SiC 的晶胞。(其中晶胞
物质类别及举例
大多数非金属单质、气态氢化
物、酸、非金属氧化物(SiO2 除外)、绝大多数有机物(有机
盐除外)
部分非金属单质
(如金刚石、硅、 晶体硼)、部分非
金属化合物(如 SiC、SiO2)
金属单质与合金(如 Na、 Al、Fe、青铜)
金属氧化物(如 K2O、Na2O)、强碱 (如 KOH、NaOH)、
(3)晶胞概念:描述晶体结构的基本单元
(4)晶体中晶胞的排列——无隙并置
①无隙:相邻晶胞之间没有任何间隙
②并置:所有晶胞平行排列、取向相同
(5)用均摊法确定晶胞中的粒子数和晶体的化学式:均摊是指每个结构单元(晶胞)平均拥有的粒子数目。在晶体中,一个粒子同时为
1
n 个结构单元(晶胞)所共有,那么对一个结构单元(晶胞)来讲,该粒子只能算作 。 以立方体晶胞为例:
的 8 个顶点和 6 个面心为 Si 原子,4 个互不相邻的立方体体心的为 C 原子,反之亦可)
a、每个 SiC 晶胞中含有 4 个硅原子,含有 4 个碳原子
b、1mol SiC 晶体中有 4mol Si—C 共价键
5、石墨晶体的结构——混合晶体
(1)结构:石墨不同于金刚石,它的碳原子不像金刚石的碳原子那样呈 sp3 杂化,而是呈 sp2 杂化,形成平面六元并环结构,因此石
n
①凡处于立方体顶点的微粒,同时为 8 个晶胞共有,属于该晶胞的为 1/8
②凡处于立方体棱上的微粒,同时为 4 个晶胞共有,属于该晶胞的为 1/4
③凡处于立方体面上的微粒,同时为 2 个晶胞共有,属于该晶胞的为 1/2
④凡处于立方体体心的微粒,完全属于该晶胞
2、四种晶体类型的比较
比较
类型
分子晶体
原子晶体
绝大部分盐(如 NaCl)
3、常见分子晶体的晶胞
(1)CO2 晶体晶胞:CO2 分子间存在分子间作用力,CO2 的晶胞呈面心立方体,立方体的每个顶点有一个 CO2 分子,每个面上也有一
个 CO2 分子,因此,每个晶胞中有 4 个 CO2 分子。在干冰晶体中,每个 CO2 分子距离最接近且相等的 CO2 分子有 12 个 (在三个
粒子间的相互作用 硬度
范德华力(某些含氢键) 较小
共价键 很大
金属键 有的很大,有的很小
离子键 较大
熔、沸点
较低
很高
有的很高,有的很低
较高
溶解性
相似相溶
难溶于任何溶剂
难溶于常见溶剂
大多易溶于水等极 性溶剂
导电、传热性
一般不导电,溶于水后有的能 一般不具有导电
导电
性
电和热的良导体
晶体不导电,水溶 液或熔融态导电
a、每个碳与相邻 4 个碳以共价键结合,形成正四面体结构,键角均为 109°28′ b、每个金刚石晶胞中含有 8 个碳原子,最小的碳环为 6 元环,并且不在同一平面(实际为椅式结构),碳原子为 sp3 杂化
1
c、每个碳原子被 12 个六元环共用,每个共价键被 6 个六元环共用,一个六元环实际拥有 个碳原子
金属晶体
离子晶体
概念
只含分子的晶体(即分子构成 的晶体)或者说分子间以分子 间作用力相结合形成的晶体
相邻原子间以共 价键相互结合形 成空间网状结构 的晶体
由金属阳离子和自由电子 通过金属键键形成的具有 一定几何外形的晶体
由阴、阳离子通过 离子键结合而成的 晶体
构成粒子
分子
原子
金属阳离子、)
(CO2 晶体晶胞)
(碘晶体的晶胞)
(冰晶体)
(2)冰晶体:水分子之间的相互作用除了范德华力还有氢键,而冰晶体水分子之间主要是依靠氢键形成的。由于氢键具有一定的方向
性,中央的水分子与周围的四个水分子结合,边缘的四个水分子也按照同样的规律再与其他的水分子结合。在冰的晶体中,每个
常见的晶体结构及密度、空间利用率的计算
一、四大晶体比较 1、晶体常识 (1)晶体与非晶体的比较
晶体
非晶体
结构特征
结构微粒周期性有序排列
结构微粒无序排列
自范性
有
无
性质特 征
熔点 异同表
现
固定 各向异性
不固定 各向同性
二者区别方法
间接方法 科学方法
看是否有固定的熔点 对固体进行 X射线衍射实验
(2)得到晶体的途径:①熔融态物质凝固;②气态物质冷却不经液态直接凝固(凝华);③溶质从溶液中析出
