外圆内方与内圆外方

内圆外方和外圆内方相关问题的些许思考

＝三角形 ABD ＋三角形 BCD ＝r ＋r ＝２
２
分的面积＝圆的面积－正方形面积＝ π
r －２
r２＝ (
π－
２
２)
r.
现把各类情况列表展示.
以上两种情况较为简单直观,在与学生探究的过程中基
本是以学生的合作讨论为基础,教师稍加总结即可得出
２
２
２
２
a２＝ d２ ,又由 d
＋ AD ＝a ＋a ＝ BD ＝直径 d ,所以２
２
r 可知d２＝ (
２
r)
r２＝２a２ ,进一步得出r２＝
＝２
＝４
Hale Waihona Puke a２,所２a２
以圆的面积＝π
r２＝π ,阴影部分面积＝圆的面积－正方
２
a２
π
２
形面积＝ π －a２＝
－１ a . 这类问题利用了勾股
大家交流一下.
数学问题的解决进行公式化处理是学生最易理解和接
受的学习方式,如长方形、正方形面积、周长公式化,三角形
面积公式化等,那么内圆外方与外圆内方相关问题能否公式
化处理,在教学过程中我和我班同学进行了一番探讨,情况
知道三角形 ABD ＝三角形 BCD ,线段 OC 垂直于线段BD ,
所以 OC 是三角形 BCD 的高,由此可知三角形 BCD 的面积
BD ＝d ＝２
r,所
＝ OC ×BD ÷２,前面我们知道了 OC ＝r,
以 OC ×BD ÷２＝r×d ÷２＝r×２

人教版六年级上册第五单元《圆的面积——外圆内方和外方内圆》教案

（2）计算过程的逻辑推理：在计算外圆内方和外方内圆的面积时，需要学生具备一定的逻辑推理能力，理解面积计算的先后顺序和逻辑关系。
举例：引导学生分析外圆内方和外方内圆的面积计算步骤，明确先求哪个图形的面积，再进行相应的运算。
（3）解决实际问题的应用：将所学知识应用于解决生活中的实际问题，是学生需要突破的难点。
五、教学反思
在今天的教学过程中，我发现学生们对外圆内方和外方内圆的概念掌握得还不错，但在实际运用面积公式进行计算时，部分学生还是显得有些吃力。这让我意识到，在今后的教学中，我需要更加关注学生对公式运用的熟练程度。
在导入新课环节，通过提问生活中的实例，学生们能够很快地进入学习状态，这表明实例导入法对于激发学生的学习兴趣是相当有效的。但在新课讲授过程中，我发现有些学生对理论知识的接受程度并不高，可能是我讲授的方式不够生动形象，也有可能是学生对这部分内容的理解还不够深入。
举例：通过画图、剪裁、拼接等实际操作，让学生直观地感受外圆内方和外方内圆的面积计算方法。
2.教学难点
（1）空间观念的建立：对于六年级学生来说，空间观念正在逐步形成，如何让学生在脑海中构建出外圆内方和外方内圆的图形，是本节课的一个难点。
举例：利用教具、模型或多媒体展示，帮助学生建立空间观念，更好地理解图形的面积计算。
二、核心素养目标
本节课的核心素养目标旨在培养学生的以下能力：1.空间观念与几何直观：通过外圆内方和外方内圆的学习，提高学生对图形面积的认识，增强空间观念和几何直观能力；2.逻辑思维与问题解决：培养学生运用圆的面积公式进行推理和计算，解决实际问题的能力，提高逻辑思维水平；3.数学抽象与模型构建：使学生能够从具体实例中抽象出数学模型，构建外圆内方和外方内圆的面积计算方法，提升数学抽象和模型构建能力。通过本节课的学习，让学生在实际问题中体会数学的价值，培养数学素养。

《外圆内方和外方内圆》

研究主题教学内容《外方内圆和外圆内方》杨冰飞教学年级六年级课时安排 1把握教材《外方内圆和外圆内方》是人教版六年级上册第五单元《圆》新增内容，是在学习了各平面图形的面积、圆的认识、圆的周长、圆的面积及圆环的面积的基础上学习的。

教材的文字和图片分析，由欣赏古代建筑物的图片引入，抽象出图形提出问题：你能求出正方形和圆之间部分的面积吗？针对圆内方的图形，书上出现分割法，借助图形直观帮助学生突破“圆内方”难点。

最后，在学生反思验证过程中通过推理得到一般性规律，培养学生严谨的数学意识。

研究学生前置学习单：课前有对学生进行访谈以及前测， 95％的学生可以看出并且画图表达大正方形面积是小正方形面积的2倍。

100％的学生能理解圆的直径就是正方形的边长并区分圆的周长和面积的计算方法。

对于画圆内最大的正方形，约50％的学生利用对折绘制；有30％的学生利用外切正方形绘制。

可以看出，对于外方内圆的面积，学生已经掌握，但是学生对观察组合图形间的关系经验比较欠缺，认识有限。

教学目标预设整体教学目标上限目标下限目标适合学生1.结合具体情境，学生通过画图、分析、推理等活动过程探究圆和正方通过画图、分析、推理等活动，在探究过程中掌握知识，建立数学模型，能掌握计算此类图形面积的方法，并能准确计算。

形的组合图形的面积差和面积比的关系，掌握计算此类图形面积的方法，并能准确计算。

灵活解决此类图形计算问题。

2、通过数学建模的过程，得到一般性结论，渗透分割法，借助图形旋转的动态方式帮助学生积累经验，发展几何直观，培养学生发现问题、提出问题、分析问题和解决问题的能力。

积累活动经验，发展几何直观，串联沟通已有的知识经验和活动经验，能方法迁移，解决类似数学问题，可以用动态的眼光看数学图形。

在小组讨论，全班交流的过程中，推理出一般性结论，应用结论，解决简单的外圆内方和外方内圆的问题。

3、结合例题渗透传统文化的教育，通过体验图形和生活的联系感受数学的价值，提高学生对数学的兴趣。

六年级上册数学内圆外方和外圆内方教学设计表格式

六年级上册数学内圆外方和外圆内方教学设计表格式一、引言在数学教学中，内圆外方和外圆内方是六年级上册的重要知识点之一。

通过深入理解和掌握这一知识点，学生可以更好地理解几何图形之间的关系，培养几何思维能力和数学解决问题的能力。

本教学设计旨在帮助学生全面、深入地理解内圆外方和外圆内方的概念和性质。

二、教学目标1. 理解内圆外方和外圆内方的定义及性质。

2. 掌握内圆外方和外圆内方的计算方法。

3. 能够运用内圆外方和外圆内方的相关知识解决实际问题。

三、教学内容及安排1. 内圆外方和外圆内方的定义和性质介绍（1课时）：a. 内圆外方的定义和性质b. 外圆内方的定义和性质2. 内圆外方和外圆内方的计算方法（2课时）：a. 内圆外方的计算方法b. 外圆内方的计算方法3. 内圆外方和外圆内方的综合运用（2课时）：a. 解决与内圆外方和外圆内方相关的实际问题四、教学方法1. 案例分析法：通过具体案例引导学生理解内圆外方和外圆内方的概念和性质。

2. 教师讲解法：结合示意图和具体计算步骤，讲解内圆外方和外圆内方的计算方法。

3. 互动讨论法：组织学生进行小组讨论，共享彼此的解题思路和方法。

五、教学过程1. 第一课时：引入内圆外方和外圆内方的概念，通过具体图形示意图引导学生理解定义和性质。

2. 第二至第三课时：分别介绍内圆外方和外圆内方的计算方法，以及相关综合运用的案例分析。

3. 第四课时：组织学生进行小组讨论，解决与内圆外方和外圆内方相关的实际问题，并进行汇报和讨论。

六、教学评价1. 定期进行课堂练习和作业，检测学生对内圆外方和外圆内方的掌握程度。

2. 结合学生讨论和汇报的情况，及时对学生的理解和运用能力进行评价和指导。

七、个人观点和理解内圆外方和外圆内方作为数学中的基本几何图形，不仅具有一定的理论意义，更能够帮助学生培养几何思维和解决实际问题的能力。

作为教师，应该注重引导学生深入理解内圆外方和外圆内方的概念，注重培养学生的数学思维和实际运用能力。

外方内圆和外圆内方知识点的探究

外方内圆和外圆内方知识点的探究外方内圆和外圆内方是中国古代哲学家孔子提出的两个重要概念，它们代表了一种思考和认识世界的方式。

在本文中，我们将深入探讨外方内圆和外圆内方的含义及其在思维方式和知识领域中的应用。

让我们来了解外方内圆的概念。

外方代表了人类对外界事物的感知和认识，它是我们对世界的直接观察和理解。

外方包括我们通过感官来获取的各种信息，如视觉、听觉、触觉等。

外方是我们对外界事物进行客观观察和分析的过程，类似于从外部了解一个事物的表面现象。

而内圆则代表了我们对内在本质和深层含义的认识和理解。

内圆是我们通过思考、分析和推理来深入了解事物的本质和内在联系的过程。

内圆是我们对外界事物进行主观思考和探索的过程，类似于从内部探寻一个事物的本质和内在规律。

外方内圆的思维方式强调了综合和平衡，它要求我们既要注重对外界事物的客观观察和分析，又要注重对其内在本质和深层含义的主观思考和探索。

外方内圆的思维方式不仅能够帮助我们更全面、深入地认识世界，还能够帮助我们形成更深刻、灵活的思考和判断能力。

外方内圆在知识领域中也有重要的应用。

在学习和研究的过程中，我们通常会首先通过外方的方式进行输入和积累知识，然后再通过内圆的方式对知识进行整合、分析和运用。

外圆内方知识点的探究是一种由浅入深的学习方法，它要求我们从基础概念出发，逐渐向深层次和复杂的知识拓展。

这种学习方式可以帮助我们建立起扎实的知识基础，并且能够更好地理解和应用知识。

总结回顾一下，外方内圆是一种思考和认识世界的方式，它强调了综合和平衡。

外方代表了对外界事物的客观观察和分析，内圆代表了对事物本质和内在联系的主观思考和探索。

在知识领域中，外方内圆的思维方式可以帮助我们形成更全面、深入的理解，而外圆内方的知识点的探究方法能够帮助我们建立起扎实的知识基础。

通过对外方内圆和外圆内方的探究，我们可以更好地认识世界和自我，提高我们的思维和认知能力。

作为一个思考和写作的工具，外方内圆可以帮助我们更好地理解和表达自己的观点，并且帮助我们探究和发现更多的知识和真理。

《外圆内方内圆外方》教案

“外圆内方”和“外方内圆”教学设计主讲人课题“外圆内方”和“外方内圆”授课内容课本第69页的例3及相关的练习题教学目标1.认识“外圆内方”和“外方内圆”的图形，掌握这两类问题的解题方法。

2.应用圆的面积的计算公式解决生活中的相关实际问题，培养学生灵活、综合运用知识的能力。

3.体验数学与生活的联系，感受平面图形的学习价值。

教学重点掌握“外圆内方”和“内方外圆”图形的面积计算方法。

教学难点培养综合运用知识的能力。

课前准备课件、三角板、圆规教学活动过程备注一、复习旧知1. 一个圆的周长是12.56cm，求它的半径？2. 一个圆形茶几面的半径是3dm ，它的面积是多少平方分米？二、探究新知1.展示课本p69页的例3中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。

上图中的两个圆半径都是1m，你能求出正方形和圆之间部分的面积吗？2.阅读与理解（阅读题目，观察图形，理解题意。

）已知条件：左图外面是正方形，里面是圆;右图外面是圆，里面是正方形。

两个圆的半径都是1米。

所求的问题: 左图求得是正方形比圆多的面积；右图求得是圆比正方形多的面积3.分析与解答“外圆内方”和“外方内圆”教学设计(1)左图--外方内圆提问①图中的正方形于圆有什么关系（正方形的边长就是圆的直径。

）。

②谁能说说解决问题的思路？独立解答。

③组织交流汇报（见课件）（2）右图--外圆内方提问①图中的正方形于圆有什么关系（正方形的对角线就是圆的直径。

）。

②怎样求正方形的面积呢？谁能说说解决问题的思路？（在图上作辅助线，把图中的正方形分成两个三角形，它的底是2米，高是1米。

）。

③组织交流汇报。

（见课件）4.回顾与反思（1）小组讨论。

如果两个圆的半径都是r，结果又是怎样的？左图：（2r）²－3.14×r²＝0.86r²右图：3.14×r²－（1/2×2r×r）×2＝1.14r²(2)代入求值当r＝1 m时，计算出0.86r²和1.14r²的值。

《外圆内方和外方内圆》

研究主题教学内容《外方内圆和外圆内方》杨冰飞教学年级六年级课时安排 1把握教材《外方内圆和外圆内方》是人教版六年级上册第五单元《圆》新增内容，是在学习了各平面图形的面积、圆的认识、圆的周长、圆的面积及圆环的面积的基础上学习的。

教材的文字和图片分析，由欣赏古代建筑物的图片引入，抽象出图形提出问题：你能求出正方形和圆之间部分的面积吗？针对圆内方的图形，书上出现分割法，借助图形直观帮助学生突破“圆内方”难点。

最后，在学生反思验证过程中通过推理得到一般性规律，培养学生严谨的数学意识。

研究学生前置学习单：课前有对学生进行访谈以及前测， 95％的学生可以看出并且画图表达大正方形面积是小正方形面积的2倍。

100％的学生能理解圆的直径就是正方形的边长并区分圆的周长和面积的计算方法。

对于画圆内最大的正方形，约50％的学生利用对折绘制；有30％的学生利用外切正方形绘制。

可以看出，对于外方内圆的面积，学生已经掌握，但是学生对观察组合图形间的关系经验比较欠缺，认识有限。

教学目标预设整体教学目标上限目标下限目标适合学生1.结合具体情境，学生通过画图、分析、推理等活动过程探究圆和正方通过画图、分析、推理等活动，在探究过程中掌握知识，建立数学模型，能掌握计算此类图形面积的方法，并能准确计算。

形的组合图形的面积差和面积比的关系，掌握计算此类图形面积的方法，并能准确计算。

灵活解决此类图形计算问题。

2、通过数学建模的过程，得到一般性结论，渗透分割法，借助图形旋转的动态方式帮助学生积累经验，发展几何直观，培养学生发现问题、提出问题、分析问题和解决问题的能力。

积累活动经验，发展几何直观，串联沟通已有的知识经验和活动经验，能方法迁移，解决类似数学问题，可以用动态的眼光看数学图形。

在小组讨论，全班交流的过程中，推理出一般性结论，应用结论，解决简单的外圆内方和外方内圆的问题。

3、结合例题渗透传统文化的教育，通过体验图形和生活的联系感受数学的价值，提高学生对数学的兴趣。

外方内圆和外圆内方知识点

外方内圆和外圆内方知识点外方内圆和外圆内方是数学中的两个几何形状，它们具有一些特殊的性质和应用。

在本文中，我们将详细介绍外方内圆和外圆内方的知识点。

一、外方内圆1. 定义：外方内圆是指一个正方形的四个顶点分别与一个圆相切。

2. 性质：a. 外接圆：外方内圆的四个顶点共同确定了一个圆，称为外接圆。

b. 对角线：正方形的对角线经过外接圆的直径。

c. 角度关系：正方形的对角线与边长之比为√2，即对角线长度为边长乘以√2。

d. 面积关系：正方形的面积等于外接圆面积的两倍。

3. 应用：a. 工程设计：在建筑设计中，外方内圆常用于构造具有稳定性和美观性的结构。

b. 地理测量：测量地球表面时，可以使用正方形和其外接圆来近似表示地球的形状。

二、外圆内方1. 定义：外圆内方是指一个圆与一个正方形相切，且该正方形的四条边都与圆相切。

2. 性质：a. 内切圆：外圆内方的四个顶点共同确定了一个圆，称为内切圆。

b. 对角线：正方形的对角线是内切圆的直径。

c. 角度关系：正方形的对角线与边长之比为√2，即对角线长度为边长乘以√2。

d. 面积关系：正方形的面积等于内切圆面积的两倍。

3. 应用：a. 工程设计：外圆内方常用于设计具有良好流动性和稳定性的物体，如水泵叶轮、风力发电机桨叶等。

b. 制造业：在制造过程中，外圆内方可以用来精确定位和测量工件。

三、外方内圆和外圆内方的区别1. 形状：外方内圆是一个正方形加一个内切圆，而外圆内方是一个正方形加一个外接圆。

2. 圈数：在外方内圆中，正方形围绕着内切圆旋转一周；而在外圆内方中，正方形围绕着外接圆旋转一周。

3. 应用场景：外方内圆常用于建筑和地理测量等领域，而外圆内方常用于工程设计和制造业等领域。

总结：外方内圆和外圆内方是两个几何形状，它们具有一些相似的性质和应用。

外方内圆是一个正方形加一个内切圆，而外圆内方是一个正方形加一个外接圆。

它们在角度关系、面积关系和对角线等方面有一些共同的特点。

外圆内方内圆外方

外方内圆和外圆内方教学设计武汉市恒大嘉园学校杨玲教学目标：1．结合具体情境认识与圆相关的组合图形的特征，掌握计算此类图形面积的方法，并能准确计算。

2．在解决实际问题的过程中，通过独立思考、合作探究、讨论交流等活动，培养学生分析问题和解决问题的能力。

3．结合例题渗透传统文化的教育，通过体验图形和生活的联系感受数学的价值，提升学习的兴趣。

教学重点：掌握计算组合图形面积的方法，并能准确计算。

教学难点：对组合图形进行分析。

教学准备：课件、学具、作业纸。

教学过程：一、创设情景，谈话引入1．师：古时候，由于人们的活动范围狭小，往往凭自己的直觉认识世界，看到眼前的地面是平的，以为整个大地是平的，并且把天空看作是倒扣着的一口巨大的锅。

我国古代有“天圆如张盖，地方如棋局”的说法。

（结合课件出示）虽然这种说法是错误的，却产生了深远的影响，尤其体现在建筑设计上。

2．课件展示：鸟巢和水立方等建筑，精美的雕窗。

二、探究新知，解决问题1．实践操作（课件出示教材例3中的雕窗插图）师：谁能说说这两种设计有什么联系和区别？预设1：左边的雕窗外面是方的里面是圆的；右边的雕窗外面是圆的里面是方的。

师：我们可以将上述特征分别概括地称为外方内圆、外圆内方。

预设2：都是由圆和正方形这两个图形组成的。

师：也就是我们以前学过的什么图形？（组合图形）你能用学具组合出这两个图形吗？学生操作，作品展示。

2．解决问题（1）阅读与理解师：怎样计算正方形和圆之间部分的面积？需要什么条件？先想一想，再同桌交流。

预设1：正方形的面积减去圆的面积；圆的面积减去正方形的面积。

预设2：需要知道正方形的边长和圆的半径。

师：只告诉你这两个圆的半径都是1米，你能计算出这两部分的面积吗？学生思考，尝试练习。

（2）分析与解答师：谁来说说你是怎么计算左图中正方形和圆之间部分的面积的？预设：正方形的面积是2×2=4（m），减去圆的面积(3.14 m)，等于0.86 m。

外圆内方与内圆外方

三、知识应用
（一）解决问题。
右图是一面我国唐代外圆内方的铜镜。铜镜的直径是24.8 cm。外面的圆与内部的正方形之间的面积是多少？
Байду номын сангаас
操作练习： 1、先画一个边长为4厘米的正方形，然后在正方形中画一个最大的圆。
提示：1、用什么画正方形比较标准？怎么找圆心？半径是多少？
2、先画一个直径为4厘米的圆，然后在圆中画一个最大的正方形。
“外方内圆”和“外圆内方”
探究新知
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。上图中的两个圆半径都是1m，你能求出正方形和圆之间部分的面积吗？
二、探究新知
外方内圆
r=1m
图（1）
二、探究新知
外圆内方
r=1m
看你有多敢想
图（2）
S正=2S三
二、探究新知
外圆内方
r=1m
S正=d²÷2
提示：怎样找到正方形的四个顶点？
四、布置作业
作业：第72页练习十五，第9题。第73页练习十五，第10题～第14题。

5.4外圆内方和外方内圆问题及扇形(导学案)人教版六年级上册数学

5.4 外圆内方与外方内圆问题及扇形（导学案）引言在六年级上册数学的教学中，圆和扇形的相关概念及计算是基础几何知识的重要组成部分。

学生在掌握了圆的基本属性之后，将面临更为复杂的问题，如外圆内方和外方内圆问题。

本导学案旨在通过引导学习，帮助学生深化对圆和扇形知识的理解，培养其几何思维和解决实际问题的能力。

一、外圆内方问题1.1 概念引入外圆内方问题指的是一个正方形完全位于一个圆内部，圆的直径等于正方形的对角线。

这种情况下，圆的半径（r）与正方形的边长（a）之间存在特定的关系。

1.2 解题步骤步骤一：理解正方形的对角线首先，学生需要理解正方形对角线的性质，即对角线将正方形分为两个等腰直角三角形。

在等腰直角三角形中，边长与对角线的关系为 $ a\sqrt{2} $。

步骤二：建立圆和正方形的关系由于圆的直径等于正方形的对角线，可以得出圆的直径 $ d = a\sqrt{2} $。

因此，圆的半径 $ r = \frac{d}{2} = \frac{a\sqrt{2}}{2} $。

步骤三：计算圆的面积和正方形的面积圆的面积 $ A_{\text{圆}} = \pi r^2 $，正方形的面积 $ A_{\text{正方形}} = a^2 $。

代入半径的表达式，可以得到圆的面积 $ A_{\text{圆}} = \pi \left(\frac{a\sqrt{2}}{2}\right)^2 $。

1.3 实际应用外圆内方问题在工程制图、设计等领域有着广泛的应用。

例如，在设计圆形广场时，如果需要在广场中心布置一个正方形的花园，了解外圆内方的关系对于计算所需的空间大小至关重要。

二、外方内圆问题2.1 概念引入外方内圆问题则是指一个圆完全位于一个正方形内部，圆的直径等于正方形的边长。

在这种情况下，圆的半径（r）与正方形的边长（a）之间的关系与外圆内方问题不同。

2.2 解题步骤步骤一：理解圆的直径与正方形边长的关系在外方内圆问题中，圆的直径 $ d = a $，因此圆的半径 $ r = \frac{d}{2} = \frac{a}{2} $。

外圆内方和外方内圆的公式

外圆内方和外方内圆的公式外圆内方和外方内圆都是特殊的图形，它们都拥有自己的公式。

在几何学中，这些公式被用来计算这些图形的面积以及其他相关的特征。

在本文中，我们将深入探讨外圆内方和外方内圆的公式及其应用。

一、外圆内方的公式外圆内方，简称外接正方形，是如图所示的以圆的直径为对角线的正方形。

此时，正方形的边长就是圆的直径。

因为外圆内方是一个正方形，因此可以使用正方形的面积公式计算其面积。

外圆内方的面积等于正方形的边长的平方，即S=a²。

其中，a代表正方形的边长，这也是圆的直径。

二、外方内圆的公式外方内圆，简称内切圆，是如图所示的刚好与正方形相切的圆形。

内切圆的半径r等于正方形边长a的一半。

因为内切圆是一个圆形，所以我们需要使用圆形的面积公式来计算其面积。

外方内圆的面积等于圆的面积，公式为S=πr²。

其中，π是一个常数，约等于3.14。

因此，外方内圆的面积可以表示为S=π(a/2)²，S=π(a²/4)。

三、如何应用这些公式？了解了外圆内方和外方内圆的公式后，我们可以运用它们来计算相关的几何问题。

以下是一些例子。

例一：已知一个圆的半径为10cm，求它的外圆内方和外方内圆的面积。

答案：首先，外圆内方的边长等于圆的直径，即20cm。

因此，外圆内方的面积为S=20²=400cm²。

其次，内切圆的半径等于10cm，因此其面积为S=π(10/2)²=25π≈78.5cm²。

例二：已知一个正方形的面积为36cm²，求它的外圆内方和外方内圆的面积。

答案：首先，正方形的边长等于根号下面积，即a=√36=6cm。

因此，外圆内方的面积为S=6²=36cm²。

其次，内切圆的半径等于正方形边长的一半，即r=3cm。

因此，其面积为S=π(3/2)²=2.25π≈7.07cm²。

结论：外圆内方和外方内圆是重要的几何图形，我们可以使用它们的公式来计算它们的面积和其他相关的特征。

(2015年新)外圆内方和外方内圆

Fra bibliotek外方内圆
外圆内方
1、外方内圆的面积是0.86r² 2、外圆内方的面积是1.14r²
计算阴影部分的面积：
右图中的铜钱直径22.5mm，中间的正方形边长为6mm。这外铜钱的面积是多少？
圆的面积 – 正方形面积
一个运动场如右图，两端是半圆形，中间是长方形。这个运动场的周长是多少厘米？面积是多少平方厘米？
周长：3.14×8
复习：
（3）一块圆环的花坛，外直径是20m,内半径是5m，这块花坛的面积是多少？外半径： 20÷2=10（cm）
花坛面积： 3.14 ×（10²- 5² ）
观察下面两个图形相同和不同？
外方内圆
外圆内方
圆的半径都是 1m r 圆的半径都是
算出正方形和圆之间的面积正方形面积 - 圆的面积 2×2 = 4（m² ） 2×2 = 4（m² ）
感谢聆听!
Thanks for your time
爱是什么？一个精灵坐在碧绿的枝叶间沉思。风儿若有若无。一只鸟儿飞过来，停在枝上，望着远处将要成熟的稻田。精灵取出一束黄澄澄的稻谷问道：“你爱这稻谷吗？” “爱。” “为什么？” “它驱赶我的饥饿。” 鸟儿啄完稻谷，轻轻梳理着光润的羽毛。 “现在你爱这稻谷吗？”精灵又取出一束黄澄澄的稻谷。鸟儿抬头望着远处的一湾泉水回答：“现在我爱那一湾泉水，我有点渴了。” 精灵摘下一片树叶，里面盛了一汪泉水。鸟儿喝完泉水，准备振翅飞去。 “请再回答我一个问题，”精灵伸出指尖，鸟儿停在上面。 “你要去做什么更重要的事吗？我这里又稻谷也有泉水。” “我要去那片开着风信子的山谷，去看那朵风信子。” “为什么？它能驱赶你的饥饿？” “不能。” “它能滋润你的干渴？” “不能。”爱是什么？一个精灵坐在碧绿的枝叶间沉思。风儿若有若无。一只鸟儿飞过来，停在枝上，望着远处将要成熟的稻田。精灵取出一束黄澄澄的稻谷问道：“你爱这稻谷吗？” “爱。” “为什么？” “它驱赶我的饥饿。” 鸟儿啄完稻谷，轻轻梳理着光润的羽毛。 “现在你爱这稻谷吗？”精灵又取出一束黄澄澄的稻谷。鸟儿抬头望着远处的一湾泉水回答：“现在我爱那一湾泉水，我有点渴了。” 精灵摘下一片树叶，里面盛了一汪泉水。鸟儿喝完泉水，准备振翅飞去。 “请再回答我一个问题，”精灵伸出指尖，鸟儿停在上面。 “你要去做什么更重要的事吗？我这里又稻谷也有泉水。” “我要去那片开着风信子的山谷，去看那朵风信子。” “为什么？它能驱赶你的饥饿？” “不能。” “它能滋润你的干渴？” “不能。”

方圆有道(内方外方,内方外圆,内圆外圆,内圆外方)

方圆有道,广结善缘现实生活中,有些人内心方正,有些人内心圆滑,有些人对外方正,有些人对外圆滑。

从这个角度来看,人的个性呈现四种形态:内方外方,内方外圆,内圆外圆,内圆外方。

"到什么山上唱什么歌",和不同性情的人物来往,要用不同的交际之道。

1.对内方外方的人要诚实委婉有些人直来直去,有棱有角。

他们往往个性太直,情太真,血太热,气太傲。

他们处世认真,不留余地;做事投入,过于突出;活力四射,难免张扬;才华过人,忘记平衡。

他们坚持"是我的错,我就承认,绝不东推西挡:是你的错,就是你的错,想赖也赖不掉"。

这种人便是内方外方的人。

表里如一、秉公立世,是对这些人的美丽评价。

忠心耿耿的屈原、刚直无私的包拯,是这类人的典型代表。

如果社会上缺乏这种人,那是不堪设想的,因为他们是空气的清新器,丑行的绊脚石。

同这种品性的人交往,一要诚实。

内方外方的人不会口蜜腹剑,不会阳奉阴违,是个值得信赖、值得尊重的人物,所以要待之以诚,关心爱护。

如果对他们虚伪猜忌,会使他们产生强烈反感,他们还会把这种不满表现在脸上,使你们之间的心理距离扩大。

二要委婉。

内方外方的人做事不灵活,言辞不变通,往往会使人陷入难堪境地,所以和他们来往,要注意婉转。

看到内方外方的人口无遮拦、尖锐抨击时,要采用合适的方式转移主题或者幽上一默,赞扬一句,巧妙地加以引导。

内方外方的人是心地纯正、刚直无私的人,不应该因为他们曾经"刺伤"过你,就对他们计较、发火。

有位内方外方的大作家在如日中天的时候,接到一位青年的来信。

这位青年说,想同他合写一部小说。

大作家看后,心中有点生气,他在信中毫无保留地写道:"先生,你怎么如此胆大包天呢?竟然想把一匹高贵的马和一头卑贱的驴子套在同一辆车上。

"这位青年灵机一动,在回信的开头写道:"尊敬的阁下,您怎么这样抬举我呢,竟然把我比作马。

"在信的后半部分,这位青年将自己的写作特长、潜力、合作的必要性、可行性以及对青年成长的影响等一五一十地写出来。

人教版六年级上册第五单元《圆的面积——外圆内方和外方内圆》教学设计

人教版六年级上册第五单元《圆的面积——外圆内方和外方内圆》教学设计在教学设计中，我会详细阐述教学内容、教学目标、教学难点与重点、教具与学具准备、教学过程、板书设计、作业设计以及课后反思与拓展延伸。

一、教学内容我打算用人教版六年级上册第五单元的《圆的面积——外圆内方和外方内圆》作为教学内容。

我会引导学生回顾之前学过的平面图形的面积计算方法，如正方形、长方形等。

然后，我会引入圆的面积的概念，并讲解圆的面积的计算公式。

接着，我会通过具体例题，让学生掌握外圆内方和外方内圆的面积计算方法。

二、教学目标通过这节课的学习，我希望学生能够理解并掌握圆的面积的概念和计算方法，能够灵活运用到实际问题中。

同时，我也希望学生能够理解并掌握外圆内方和外方内圆的面积计算方法，能够解决相关的实际问题。

三、教学难点与重点本节课的重点是让学生理解并掌握圆的面积的计算方法，以及外圆内方和外方内圆的面积计算方法。

而教学难点则是让学生理解并掌握圆的面积的概念，以及如何将圆的面积运用到实际问题中。

四、教具与学具准备我会准备多媒体课件、黑板、粉笔等教具，以及练习题、计算器等学具。

五、教学过程1. 实践情景引入：我会通过展示一些实际问题，如计算自行车轮胎的面积，引入圆的面积的概念。

2. 讲解圆的面积的概念和计算方法：我会用多媒体课件展示圆的面积的计算过程，并讲解圆的面积的计算公式。

3. 例题讲解：我会通过具体的例题，让学生掌握外圆内方和外方内圆的面积计算方法。

4. 随堂练习：我会给出一些练习题，让学生当场练习，巩固所学知识。

5. 板书设计：我会设计简洁明了的板书，突出圆的面积的计算公式和外圆内方、外方内圆的面积计算方法。

6. 作业设计：我会布置一些有关圆的面积计算的作业题，让学生课后巩固所学知识。

六、板书设计板书设计主要包括圆的面积的计算公式，以及外圆内方和外方内圆的面积计算方法。

七、作业设计1. 计算自行车轮胎的面积。

2. 计算一个直径为10厘米的圆的面积。

外方内圆,外圆内方说课稿

外方内圆,外圆内方说课稿说课稿：外方内圆、外圆内方的艺术之美尊敬的各位评委、亲爱的同仁们，大家好！我今天将为大家分享一种古代文学艺术批评中的修辞手法——"外方内圆"，以及如何在文学作品中体现这一手法。

我所选的作品是一篇散文，它巧妙地运用了外方内圆的结构，展现了一种独特的艺术之美。

一、什么是外方内圆？"外方内圆"是古代文学艺术批评的一个概念，用以描述作品的结构。

"外方"指的是整体的布局和结构，而"内圆"则是在整体中突出的主题或情感。

这种结构上的对比营造了一种独特的艺术张力，使整体更具深度和内涵。

二、作品选取及结构分析所选散文《梦回大唐》是一篇以描写盛唐风华为主题的文章。

在整体结构上，文章通过外方内圆的手法展现了盛唐的辉煌和人物的梦幻之美。

* 外方：描绘盛唐盛世风采* 在整篇文章中，通过丰富的历史描写、盛唐风貌的瑰丽描绘，形成了宏伟的"外方"结构。

读者仿佛走进了盛唐的繁华之境，感受到了那个辉煌的时代。

* 内圆：突出梦幻之美* 通过一位普通人物的视角，作者在"内圆"中展现了梦幻之美。

在盛唐的背景下，普通人物的梦境成为整篇文章的情感高潮，同时凸显了盛唐时代的独特魅力。

三、艺术之美的体现"外方内圆"的结构使得整篇文章在表达盛唐盛世风采的同时，通过内圆的梦幻之美，呈现了一种更深刻、更抽象的情感。

这种对比使得作品更具层次感，引发读者对历史和人物的深思。

四、总结通过对《梦回大唐》的分析，我们更好地理解了"外方内圆"这一修辞手法在文学作品中的运用。

这种结构的形成，不仅使整体更加完整和有序，同时也为作品赋予了更深刻的内涵和情感。

在欣赏这篇散文时，我们仿佛也走进了一个"外方"璀璨的盛唐，又沉浸在一个"内圆"梦幻的美妙世界中。

内圆外方和外圆内方的面积公式

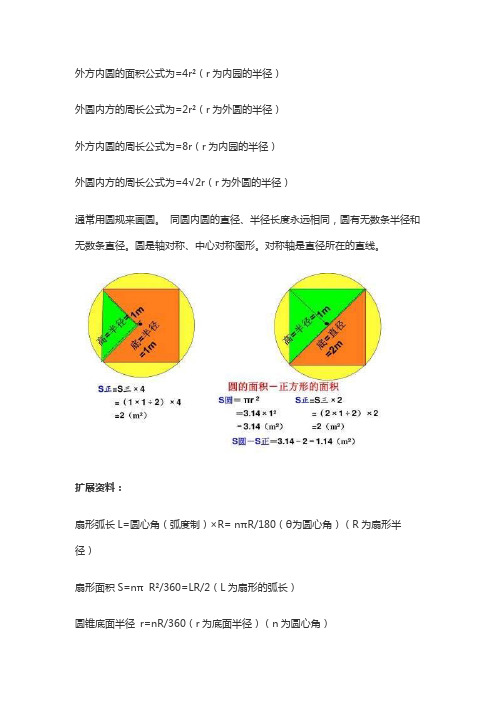
外方内圆的面积公式为=4r²（r为内园的半径）
外圆内方的周长公式为=2r²（r为外圆的半径）
外方内圆的周长公式为=8r（r为内园的半径）
外圆内方的周长公式为=4√2r（r为外圆的半径）
通常用圆规来画圆。

同圆内圆的直径、半径长度永远相同，圆有无数条半径和无数条直径。

圆是轴对称、中心对称图形。

对称轴是直径所在的直线。

扩展资料：
扇形弧长L=圆心角（弧度制）×R= nπR/180（θ为圆心角）（R为扇形半径）
扇形面积S=nπR²/360=LR/2（L为扇形的弧长）
圆锥底面半径r=nR/360（r为底面半径）（n为圆心角）
圆形一周的长度，就是圆的周长。

能够重合的两个圆叫等圆，等圆有无数条对称轴。

圆是一个正n边形（n为无限大的正整数），边长无限接近0但永远无法等于0。

优弧一般用三个字母表示，劣弧一般用两个字母表示。

优弧是所对圆心角大于180度的弧，劣弧是所对圆心角小于180度的弧。