静力学习题课
合集下载
静力学-刚体系统平衡习题课2
p
FGy
G
3、再研究AG杆，求出 FGy
0 FGy
刚体系平衡求解
1、研究对象
2、受力分析
3、平衡条件 4、列方程、求解 尽量一个方程解一个未知量！
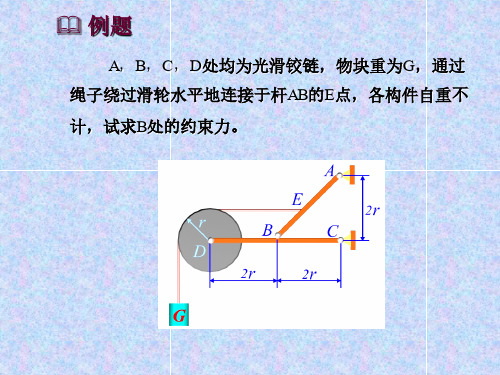
例：已知 F，求 AG 杆上的约束力。
A
a
C
F
2a E
a
B
a
a
a
D
a
解：1、研究AG杆， 画受力图. H
A
F
FDx FGx
G
O
FDy
D
M
D
(F ) 0
FGxa Fa 0
G
FGy
FGx F FDx 2F
G
M
(F ) 0
FDxa F 2a 0
A
a D
F
2a E
x
FDy
D
FGx F FGy 3F
FGy 3F
[AG]:
Fy 0
FDy 3F
FGy
G
A C a D a G
F
2a a
B E a H
研究图示构件，画受力图 B C
FDx D
a 2a
E a
H
O
a
O
FCG FDy
方法3 A
F
FDx FGx
求出
FDy
p
FH
FDy
D
M F
y
0 FDy
13 G G F A sin 45 8
D A
K C B Ⅰ
2. [DEC] 受力分析如图所示
列平衡方程
E
Ⅱ
M
其中
静力学习题课
3-6：对空间任意两个力，一定能找到一根轴，使这两个力在该轴上
的投影分别为零，对否？
正确
精品资料
静力学习题课
3-7：空间任意(rènyì)力系向两个不同的点简化，试问下述情况是 否可能。
（1）主矢相等(xiāngděng) 可能 （，2主）矩主相矢等不(相xiā等n，g主dě矩n相g)等。。 不可能
力2-2偶：吗平？面力偶系向作用面内任一点简化的结果可能是什么？
一个力偶或平衡
2-3：平面任意力系向作用面内任一点简化的结果可能是什么？
一个力、一个力偶、一个力和一个力偶、平衡
2-4：平面平行力系向作用面内任一点简化的结果可能是什么？
一个力、一个力偶、一个力和一个力偶、平衡 2-5：平面任意力系向作用面内任一点简化，一般情况下，主矢和 主矩是否与简化中心的选择有关？
下述三种情况下，物块B、C将发生怎样的运动
？
A.F1<F<F2
B. F2<F<F1 C. F<F2<F1
B和C一起运动 C运动、B不动
B、C均不运动
精品资料
mg θ
F
C
B
A
D.对于任意平面平行力系，一定存在某平面汇交力系与之等效。 错 E.对于任意平面汇交力系，一定存在某平面平行力系与之等效。 对
F.对于任意平面汇交力系，一定存在某平面力偶系与之等效。 错
2-10：图示平面结构，AB//CD，各构件自重不计
F
，在刚体上作用一力偶，试判断下述说法的正误：
M
E
A.这是平面力偶系问题，因为平面力偶系只
的关C系为_______。
M
A θ
P θB
A.FNA=FNB
静力学1-2章习题课
1.压立体的绘制是求解曲面上液体总压力的关键。压力体的绘 制方法与方向的判断原则。
1.压力体的绘制是求解曲面上液体总压力的关键。压力体的绘 制方法与方向的判断原则。
2.绘压力体图
p0 A B
pa
1、图算法 2、重力场中流体静压强
的分布规律 3、压力体的绘制
2.答案：
p0 A
B
pa
1、图算法 2、重力场中流体静压强
v 1.075m s
0.4cm
D=12cm L=14cm
牛顿内摩擦定律
第一、第二章 （流体静力学） 习题课
一、流体的主要物理性质 二、重力场中流体静压强的分布规律
z p c
p p0 gh
三、液体的相对平衡 四、液体作用在平面上的总压力 五、液体作用在曲面上的总压力
第一、第二章 （流体静力学） 习题课
8.压立体的绘制是求解曲面上液体总压力的关键。压力体的绘 制方法与方向的判断原则。
习题： 1.液体的粘滞性只有在流动时才表现出来。（ ） 2.在相对静止的同种、连通、均质液体中，等压面就是水平面。 （） 3.某点的真空度为65000Pa，当地大气压为0.1MPa，该点的 绝对压强为（ ）
(a)65000Pa (b)55000Pa (c) 35000Pa （d）165000Pa
5.
1、等压面 2、重力场中流体静压强的分布规律
5.
1、等压面 2、重力场中流体静压强的分布规律
3.计算举例
1.
静止流体中应力的特性
静止流体中应力的特性
2.如图：
已知h1=20mm，
h2=240mm，
h3
h3=220mm， 求水深H。
水银
静力学习题课答案
【1】 梁AB 一端为固定端支座，另一端无约束，这样的梁称为悬臂梁。
它承受均布荷载q 和一集中力P 的作用，如图4－9（a ）所示。
已知P =10kN ， q =2kN/m ，l =4m ，︒=45α，梁的自重不计，求支座A 的反力。
【解】：取梁AB 为研究对象，其受力图如图4－9（b ）所示。
支座反力的指向是假定的，梁上所受的荷载和支座反力组成平面一般力系。
在计算中可将线荷载q 用作用其中心的集中力2qlQ =来代替。
选取坐标系，列平衡方程。
)(kN 07.7707.010cos 0cos - 0A A →=⨯====∑ααP X P X X)(kN 07.11707.010242sin 2 0sin 2 0A A ↑=⨯+⨯=+==--=∑ααP ql Y P qlY Y )( m kN 28.404707.0108423sin 83 0sin 422ql 022A A ⋅=⨯⨯+⨯⨯=⋅+==⋅-⎪⎭⎫⎝⎛+-=∑l P ql m l P l l m M A αα力系既然平衡，则力系中各力在任一轴上的投影代数和必然等于零，力系中各力对任一点之矩的代数和也必然为零。
因此，我们可以列出其它的平衡方程，用来校核计算有无错误。
校核028.40407.114424242A A B =+⨯-⨯⨯=+⋅-⨯=∑m l Y l ql M 可见，Y A 和m A 计算无误。
【2】 钢筋混凝土刚架，所受荷载及支承情况如图4－12（a ）所示。
已知kN 20 m,kN 2 kN,10 kN/m,4=⋅===Q m P q ，试求支座处的反力。
【解】：取刚架为研究对象，画其受力图如图4－12（b ）所示，图中各支座反力指向都是假设的。
本题有一个力偶荷载，由于力偶在任一轴上投影为零，故写投影方程时不必考虑力偶，由于力偶对平面内任一点的矩都等于力偶矩，故写力矩方程时，可直接将力偶矩m 列入。
设坐标系如图4－12（b ）所示，列三个平衡方程)(kN 3446106 06 0A A ←-=⨯--=--==++=∑q P X q P X X)(kN 296418220310461834 036346 0B B A ↑=⨯++⨯+⨯=+++==⨯--⨯-⨯-⨯=∑q m Q P Y q m Q P Y M)(kN 92920 00B A B A ↓-=-=-==-+=∑Y Q Y Q Y Y Y校核3462203102)9(6)34(6363266 C=⨯⨯+-⨯+⨯+-⨯--⨯=⨯+-++-=∑qmQPYXMAA说明计算无误。
5静力学习题课
a
a
A
a
a
静定构件
a
20
例5:
一梁由支座A以及BE、CE、DE三杆支撑.
已知:q = 0.5kN/m，a = 2m，梁与支撑杆的重量不计. 求:各杆内力。
寻找二力构件！ DE CE BE
整体静定结构
21
1、整体上看，由于DE是二力杆，D的约束反力只
有一个，因此，整体为静定问题。
可求得：
FED
YC 5000 (N)
X 0 XC S FG cos450
整体静定结构
X C 10000 (N)
由m A 0 S DE sin451Q 2 0 S DE 14140 (N)
10
例1 一组合梁ABC 的支承及载荷如图示。已知 F＝1 kN，M＝0.5 kNm，求固定端A 的约束力。
② 力矩和力偶矩的区别： 力矩:是力对那一点的转矩, 与取矩点有关, 且不能在平面内 任意移动。 力偶矩: 它是在平面内和平行它自身平面内可任意移动,与取矩
点无关。
6
(二) 基本方程
平面
X 0 Y 0
空间
mA 0
X 0,m x ( F ) 0 Y 0,m y ( F ) 0 Z 0,m z ( F ) 0
B
FBy FBx
图(c)
29
整体静定结构
30
1.5m
1.5m
例8 已知 P=1200N，各杆与滑轮 自重不计, 轮的半径为r ； 求 支承A，B处的约束反力及杆 BC的内力
2m
2m
解 整体受力如图,有 XA
X 0, X A T 0 Y 0, YA P YB 0
YA
静力学习题课
解： 在图a和图b中总压力P的大小是相同的，仅作用 方向相反而已。 由于AB是个圆弧面，所以面上各点的静水压 强都沿半径方向通过圆心点，因而总压力P也必 通过圆心。
（1）先求总压力P的水平分力。
铅垂投影面的面积 Ax bh 1 2 2m2 投影面形心点淹没深度 hc h / 2 1m
2
2
（3）闸门上的合力作用中心（对闸门下端之矩）
lc P
b 2
gh1h1
/
s in
1 3
h1
/
s in
b 2
gh2 h2
/
s in
1 3
h2
/ sin
lc
1 P
b 6
g
/ sin 2 (h13
h23 )
lc
1 34.65
1 1 9.8 / sin 2 (45) (33 6
BD
lD
lc
d 2
0.514 m
重力作用线距转动轴B点的距离
l1
d 2
cos60
0.25m
启门力T到B点的距离 l2 2l1 0.5m
由力矩平衡方程 T l2 P BD G l1 解得 T 32.124KN
l1 P
D l2
lC lD
5.平面闸门AB倾斜放置，已知α ＝45°，门宽b＝1m，
1P
y2 h1 h2 e
3
2.45m 0.72m 21.73m 2.45m
1P 3
3 2.11m
1.73m 2.45m 1 P
3
同理， y3 2.72m
习题课_静力学
解：研究对象： 起重机 分析力：
Gb
ea
满载时
P, W, G, NA , NB
AP B
W
mB(F) NAd PeWa G(b d) 0
NA d NB
不向右翻倒，有NA 0
Pe Wa G(b d )
NA
d
0
解不等式得
G Wa Pe 54kN bd
Gb
e
空载时 P, G, NA , NB 不向左翻倒
mo (F) m SABr sin[180 ( )] 0
XO
m
NB A
整体考虑
m
S AB r
sin(
)
Prsin( ) cos
O
SAB’
YO
X XO P 0 XO P Y YO N B 0 YO Ptg
p.16
例题
例题
例17. 图示连续梁，载荷和尺寸如图，各杆的自重不计，A端
NB
Tc
sin (h d ) Tc
2b
cosb
1.67kN
代入第二式解得 N A TC cos NB 2.19kN
或利用两矩式
mE (F) NA 2b Tc sin (h d) Tc cosb 0
p.12
例题
例题
例13. 已知：图示L形杆AOBC自重不计，O处挂一重物重为P，
X
80
p.8
例题
例题
例8. 重力坝受力情况如图，长度单位为m, AB = 5.7m, G1 =
450kN, G2 = 200kN, P1=300kN, P2 = 70kN, =16o40’。
求力系向A点简化的结果,以及力系的最终简化结果。
解：先求力系向A点简化的主矢
理论力学第I篇 静力学习题课
F
y
0, FAy FRB W 0, FAy 150N #
附录： 习题解答
3－15
C F Ay F Ax A FT D B FR B FT
C F Dy D F BC F Dx
r E W
E W
对象：CE杆和滑轮 受力：如右图 方程：
3 M F 0 , F 2 FT 1.5 r W r 0, FBC 1500 N # D BC 5
FB 87.5 kN
F1 125 kN
F2 53 kN
F3 FB 87.5 kN#
（d）
附录： 习题解答
4－9
4－9 在平面曲柄连杆滑块机构中，曲柄OA长r,作用有一矩为M的力偶，小滑 块B于水平面之间的摩擦因数为f。OA水平。连杆与铅垂线的夹角为，力与 水平面成角，求机构在图示位置保持平衡时力FP的值。（不计机构自重， ＞ m=arctanf ）
M sin( m ) M sin( m ) FP r cos cos( m ) r cos cos( m )
第一篇 静力学
静力学习题课
第I篇 静力学习题课
例题1
结构由杆AB与BC在B处铰接而成。结构A处为固定端，C处为 辊轴支座。结构在DE段承受均布载荷作用，载荷集度为q；E处作 用有外加力偶，其力偶矩为M。若q、l、M等均为已知，试求A、C 二处的约束力。
第I篇 静力学习题课
F
FAx 0# Fy 0, FAy q 2l FRC 0
x
(1) (2) M A F 0, M A q 2l 2l M FRC 4l 0 (3) 对象：杆BC 受力：图（b） 方程：
《流体力学》第二章流体静力学习题课
G
B
空 气 石 油
9.14m
7.62 3.66
1 1
p1 1 g(9.14 3.66) pG 2 g(7.62 3.66)
5.481 g pG 3.96 2 g
pG 5.481 g 3.96 2 g
甘 油
1.52
A
12.25 5.48 8.17 3.96
习题课
3 例题1:如 图 所 示 容 器， 上 层 为 空 气， 中 层 为 石油 8170 N m 的 石 油， 下 层 为 3 甘油 12550 N m 的 甘 油， . m时 压 力 表 的 读 数。 试 求： 当 测 压 管 中 的 甘 油 表 面 高 程 为 914
解： 设 甘 油 密 度 为 1 ， 石 油 密 度 为 2 做 等 压 面 1--1， 则 有
p1 1 gh1 p 2 1 g (h2 h1 h) 2 gh
由于两边密度为ρ1的液体容量相等，所以D2h2=d2h，代 入上式得 d2 p1 p 2 2 g 1 2 1 g h
0.012 1000 9.806 0.03 13600 9.806 1 0.12 4 =3709.6(pa)
34.78k N/m2
1
习题课 【例2-1】 如图1所示测量装置，活塞直径d=35㎜， 油的相对密度d油=0.92 ，水银的相对密度dHg=13.6，活 塞与缸壁无泄漏和摩擦。当活塞重为15Ｎ时，h=700㎜， 试计算Ｕ形管测压计的液面高差Δh值。 【解】 重物使活塞单位面积上承受的压强为
p 15 15 （Pa） 15590 2 d 0.0352 4 4
静力学习题课
B. F2 F1
C. F1 F2
。
，
自由矢量 C. 定位矢量 D. 滑动矢量
。
，
5
题型二：选择题
3、重 W 80 kN 的物体自由地放在倾角为 30 的斜面上， 若物体与斜面间的静摩擦系数 f 3 4 ，动摩擦系数
f d 0.4 ，则作用在物体上的摩擦力的大小为： C
静力学习题课
1
题型一：判断题
1、力可以沿着作用线移动而不改变它对物体的运动效应。 （×）
2、作用于刚体的力可沿其作用线移动而不改变其对刚体的 运动效应。 （√ ）
3、若作用在刚体上的三个力的作用线汇交于同一点，则 该刚体必处于平衡状态。 （×） 4、凡是受到两个力作用的刚体都是二力杆。 （×）
5、用解析法求平面汇交力系的平衡问题时，所建立的坐标 系x，y轴一定要相互垂直。 (× )
A. 27.7kN B. 40kN
。
C. 30kN D. 0
，
6
题型二：选择题
α 4、一重W 的物体置于倾角为 的斜面上，若摩擦因数为f， A 且 tgα < f , 则物体 ;
若增加物体重量，则物体 A ；
若减轻物体重量，则物体
A. 静止不动； B. 向下滑动；
A
。
，
C. 运动与否取决于平衡条件。
7
题型三：填空题
1、沿边长为 a=2m 的正方形各边分别作用有 F1, F 2 , F 3 , F 4 ,
主矢大小为 , 主矩大小为 16 kN· m 。
且 F 1 F 2 F 3 F 4 4kN , 该力系向B点简化的结果为：
0
m 向D点简化的结果是什么？ FR=0; MD=16 kN·
习题课-静力学
习题课-静力学
3.图示力偶中等效的是（B）
NEFU- Junkai Lu
(A) a和c (B) a和b (C) b和c (D) b和d
36Fd顺
36Fd顺
36Fd逆
48Fd顺
4.关于力对点之矩的说法，下列哪个是错误的（B）
(A) 互相平衡的两个力，对同一点之矩的代数和等于零。
(B) 力对点之矩与力的大小和方向有关，而与矩心位置无关。
4.关于力对点之矩的说法，下列哪个是错误的（ ） (A) 互相平衡的两个力，对同一点之矩的代数和等于零。 (B) 力对点之矩与力的大小和方向有关，而与矩心位置无关。 (C) 力的数值为零、或力的作用线通过矩心时，力矩均为零。 (D) 力对点之矩不会因为力矢沿其作用线移动而改变。
10
School of Civil Engineering
习题课-静力学
NEFU- Junkai Lu
10. 力系的平衡
平面任意力系
Fx 0
Fy 0
M o 0
Fx 0
M A 0
M B 0
A、B两点 连线不得 与投影轴 x轴垂直
空间任意力系
Fix 0 Fiy 0 Fiz 0
(C) 力的数值为零、或力的作用线通过矩心时，力矩均为零。
(D) 力对点之矩不会因为力矢沿其作用线移动而改变。
力有关，力偶无关
11
School of Civil Engineering
习题课-静力学
NEFU- Junkai Lu
5.图示正方体顶角上作用着六个大小相等的力，此力系向任一点简化的结 果是（ ）
D
F3
理论力学 静力学部分习题课
AC 1 MAy 0,FCz AC P 2 2 0, FCz 2 P 2 AC 1 MCy ' 0,( P1 FAz) AC P 2 2 0, FAz P1 2 P 2
Fx 0,F
Ax
FCx 0
（2）杆AB 为研究对象，受力及坐标如图所 示
取曲杆为研究对象受力及坐标如图列平衡方程fxayazazaydzazdyaydxdzdydxayazfxayazdzdydzazdyaydxdzdydxayaz方法二321和bc分别重p1和p2其端点a用球铰固定在水平面上另1端b由球铰链相连接靠在光滑的铅直墙上墙面与ac平行如图的支座约束力以及墙上点b所受的压力
12.图示三铰刚架受力 F 作用，则A支座约束力的大小 为___________，B支座约 束力的大小为__________。
2 F 2
2 F 2
13.正三棱柱的底面为等腰三角形， 已知OA=OB=a，在平面ABED内有 沿对角线AE的一个力，图中，此 力对各坐标轴之矩 M (F ) 0 为： ； 2 M (F ) Fa 。 2
解：AB 和BC 两杆为研究对象，受力及坐标如图所示。 由于未知力较多，尽可能用 轴矩式平衡方程（需保证方 程独立）求解，力求使取矩 轴与较多的未知力相交和平 行，从而使方程中所含未知 量最少。
1 MCz ' ' 0,( FN FAy) AC 0, FAy FN 2 ( P1 P 2)
x
y
结束
题2-46图 (a)所示结构AC、DF、BF及EC四杆组成，其中A、B、 C、D，E及F均为光滑铰链。各杆自重不计。试求支座A、D的 反力及杆BF、EC所受的力。
《理论力学》静力学典型习题+答案
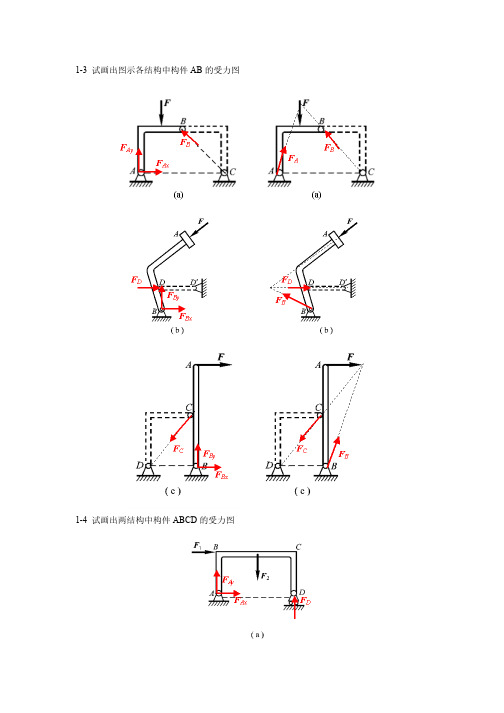
1-3 试画出图示各结构中构件AB的受力图的受力图1-4 试画出两结构中构件ABCD的受力图的受力图1-5 试画出图a和b所示刚体系整体各个构件的受力图所示刚体系整体各个构件的受力图1-5a 1-5b 在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2，机构在图示位置平衡。
为二力杆，受力方向分别沿着各杆端点连线的方向。
为二力杆，受力方向分别沿着各杆端点连线的方向。
6F 2 F BCF ABB45oy x F BCF CD C60o F 130ox y 力构成封闭的力多边形，如图所示。
力构成封闭的力多边形，如图所示。
为二力杆为二力杆((受力如图所示受力如图所示))，故曲杆10a F BC60o F 130o F 2 F BCAB45o 解：机构中AB杆为二力杆，点A,B出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件，点O,C处的约束力方向也可确定，各杆的受力如图所示。
对BC杆有：0=åM30sin20=-××MCBFB对AB杆有：杆有：ABFF=对OA杆有：杆有： 0=åM01=×-AOFMA求解以上三式可得：mNM×=31，NFFFCOAB5===，方向如图所示。
，方向如图所示。
////2-6求最后简化结果。
解：解：2-6a2-6a坐标如图所示，各力可表示为坐标如图所示，各力可表示为: :j Fi FF23211+=，i FF=2，j Fi FF23213+-=先将力系向A点简化得（红色的）：j Fi FFR3+=，kFaMA23=方向如左图所示。
由于AR MF^，可进一步简化为一个不过A点的力点的力((绿色的绿色的))，主矢不变，其作用线距A点的距离ad43=，位置如左图所示。
，位置如左图所示。
2-6b同理如右图所示，可将该力系简化为一个不过A点的力（绿色的），主矢为：，主矢为：i F F R2-= 其作用线距A 点的距离a d43=，位置如右图所示。
理论力学静力学部分习题课
理论力学静力学部分习题课
1、 四块相同的均质板，各重Q ，长2b ，叠放如图，在板1的右端A 挂着重物P ，其重P=2Q 。
欲使各板都平衡，求每块板可伸出的最大距离。
2、 梯子两部分AB 和AC 在A 点铰接，又在D ，
E 两点用水平绳连接，如图。
梯子放在
3、梯子AB 重为P ，上端靠在光滑的墙上，下端搁在粗糙的地面上，摩擦系数为f ，试问当梯子与地面的夹角α为何值时，体重Q 的人才能爬到梯子的顶点。
4、重物A 与B 用一不计重量的连杆铰接后放置如图示。
已知B 重kN 1，A 与水平面、B 与斜面间的摩擦角均为
15。
不计铰链中的摩擦力，求平衡时A 的最小重量。
5、平面构架由曲杆AB 铰接直杆BC ，CD ，DE 和DG 组成如图示，曲杆AB 的垂直部分受有水平三角形分布载荷。
N/m 10=q ，水平直杆BC 上作用一力偶m N 20⋅=M ，BC CD ⊥，DG DE =，不计自重。
求杆CD 的内力及插入端A 的约束力。
静力学习题课概论
YB
Y 0 YA YD YB 0
YA YD YB P 0 P
∴ X D 2P （→） X A P （←） X B P （←） YD P （↑） YA P （ ↓ ） YB 0
静力学习题课
静力学习题课
静力学习题课
力系
空间力系
平面力系
汇 交 力 系
力 偶 系
平
任
行
意
力
力
系
系
静力学习题课
静力学主要内容
受力分析 力系的等效 力系的简化 力系的平衡
静力学习题课
一 受力分析 1、取研究对象（分离体）——将所要研究的物体 从周围物体中单独拿出来，
2、在其上画出所有的主动力和所有的约束反力。
注意：不论采用哪种 形式的平衡方程，其 独立的平衡方程的个 数只有三个，对一个 物体来讲,只能解三个 未知量,不得多列！
A、B、C 不共线
静力学习题课
平面平行力系的平衡方程
平面平行力系的平衡方程为： Y 0
mO (Fi )0
一矩式
mA (Fi ) 0 二矩式
mB (Fi ) 0
条件：AB连线不能平行 于力的作用线
MA
FAy
AM
FAx a
B
F
F 600
C
C
a
Fx 0
FAx
2、研究BC杆，画受力图
3、再研究整体
FBy
B
F
600
FC
C
FBx a
MB 0
FC
Fy 0
FAy
MA 0
MA
静力学习题课
[例] 已知:构架ABC由AB、AC 、AF三杆组成，受力及尺寸
如图所示。DF杆上的销子E可在 AC
静力学习题课
定研究对象：梁BCD 定问题性质：平面 建立参考坐标系： 受力分析 主动力简化
约束力正向
平衡方程
y
O
F
q C
M D
A
B a a F1 F
x
F2 qa
圆柱铰 动铰支座
a
FOy
FAy
a
FCy
M
未知数与方程个数的分析: 3/3
FOx
a M B ( Fi ) 0, FCy a M F2 0
M=284.9N.m
FAx’
▲ FAy’
方法三：
M
FAy
⑴ 研究 AB 杆与推板 O1C 组成 的局部，受力如图，列平衡方程求 解(间接应用三力平衡汇交定理或二 力平衡公理确定FO 的指向):
1
FAx FO
1
M
K
( F ) 0,
FAy
M FOy FOx
⑵ 研究轮 O
M
( F ) 0, ② M=284.9N.m
M FOy F qa a
力系的平衡/刚体系平衡/解
讨论：
定研究对象：梁BCD
主动力的处理
y
O
F
q C
M D
A
B a a
x
M
a
a
M
F
M
F1 F
M
M
■
14、图所示一结构由AB、BC 与CE 三个构件构成，E 处有一滑轮，细 绳通过该轮悬挂一重为 12 kN 的重 物，A为固定铰支座，B 为滑动铰支 座，C、D 与E 为圆柱铰，AD = BD = l1= 2m，CD = DE = l2= 1.5m，不 计杆件与滑轮的重量。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
FCy2
工 程 力 学
FCx2
静力学习题课
FCy2
M
F
F
C
( F ) 0,
0,
0,
FBx b FBy a M 0
工 程 力 学
FCx2
x
FBx FCx 2 0
y
FBy FCy 2 0
FCx 2 Pa M 1 qb 2b 2b 4
Pa M 1 FBx qb 2b 2b 4
工 程 力 学
Q 1 q a 2 2
FAx
MA
FBx
把分布力转换成集中力Q´，作用在E´点
1 BE a 3
静力学习题课
再以左半段为研究对象（含铰链B） FBy Q´ E´ FAy
工 程 力 学
FAx
MA
FBx
1 1 M B (F) 0 M A 4 q a 3 a FAy 2a 0
1 FAy FC F q 2a 0 Fy 0 2 1 7 M A (F) 0 M A FC 3a F 2a 2 q 2a 3 a 0
静力学习题课
再以左半段为研究对象（含铰链B）
工 程 力 学
静力学习题课
再以左半段为研究对象（含铰链B） FBy Q´ E´ FAy
解题过程： 起重机
Y A 48.33(kN)
系统整体
梁 CD
x
FAy FBy P 0
FAx FBx qb 0
P M qb 2 FAy 2 2a 4a
P M qb 2 FBy P FAy 2 2a 4a
静力学习题课
2. 再取AC为研究对象，受力分析如图所示。
1
工 程 力 学
1
静力学习题课
1
1
b M C ( F ) 0, FAx b qb 2 FAy a 0
工 程 力 学
解：BC杆为二力杆，以整体为 研究对象，其受力如图。 列平衡方程：
M
A
(F ) 0
T AD sin q FBl P AD cosq 0
T P
FB 2 ( P P) 0
静力学习题课
F
工 程 力 学
x
0
FAx FB cos q P 0
解：以整体为研究对象，受力如图： Q
工 程 力 学
1 Q q 2a 2
FAx FAy
MA
E
FC
把分布力转换成集中力Q，作用在E点
2 7 AE a 2a a 3 3
静力学习题课
解：以整体为研究对象，受力如图：
工 程 力 学
FAx
MA E
FAy
FC
Fx 0
FAx 0
FCy 2
P M qb 2 2 2a 4a
静力学习题课
• 例 9 : 刚架结构如图所示， 其中C处光滑铰链。结构的 尺寸和载荷如图所示。试
工 程 力 学
求A，B处的约束力。
静力学习题课
解: 1. 取整体为研究对象，受力如图所示。
工 程 力 学
静力学习题课
•
例10: 已知连续梁上，P=10kN, Q=50kN, CE 铅垂, 不
工 程 力 学
示。试求 A ， B 铰链处的约
束力及销钉 C对 AC 杆、 BC
杆的作用力。
静力学习题课
解: 1. 取整体为研究对象，受力如图所示。
工 程 力 学
静力学习题课
M B (F ) 0,
工 程 力 学
b M P a FAy 2a qb 0 2
y
F 0, F 0,
FAx P
F
y
0 FAy P FB sin q 0
FAy P FAx FAy P, FB 0
静力学习题课
• 例7：组合梁 ABC上作用一集中力 F和三角形分布载 荷，最大载荷集度为，其支承及载荷如图所示，求A、 C处的约束反力。
工 程 力 学
静力学习题课
由mC 0
' YD 6 YG 1 0
50 YD 8.33( kN ) 6
静力学习题课
③ 再研究整体
X 0 , XA 0
工 mA 0,YB 3 YD 12 P 10 Q 6 0 程 力 YB 100(kN) 学
Y 0, YA YB YD Q P 0
j力系的主矢、主矩都会改变 k力系的主矢不会改变，主矩一般都会改变 l力系的主矢会改变、主矩一般不改变 m力系的主矢、主矩都不会改变，力系简化时与简化
中心无关。
静力学习题课
• 例4: 带有不平行二槽的矩形平板上
工 程 力 学
作用一力偶M,今在槽内插入两个固 定于地面的销钉，若不计摩擦则： j平板保持平衡 k平板不能平衡 l无法判断
1 BS1 a 2 2 BS 2 a 3
静力学习题课
也可以以右半段为研究对象。（不含铰链B） T1 T2 FBx
工 程 力 学
S1S2 FBy
FC
1 1 1 2 M B (F) 0 FC a 2 q a 2 a 4 qa 3 a 0
静力学习题课
• 例 8 : 刚架结构如图所示， 其中 A ， B 和 C 都是铰链。 结构的尺寸和载荷如图所
静力学习题课
• 例 5:
重 W=80kN 的物体自由地放
工 程 力 学
在倾角为 30o 的斜面上，若物体与 斜面间的静摩擦系数 f=0.433, 动 摩擦系数fd=0.4,则作用在物体上的 摩擦力的大小为： j30kN k40kN l27.7kN m0。
静力学习题课
• 例6：图示结构，各杆自重不计。 已知 l,r,P,q=45°。试确定A、B处 约束反力。
静力学习题课
再以左半段为研究对象（含铰链B）
工 程 力 学
1 q 2
静力学习题课
也可以以右半段为研究对象。（不含铰链B） T1 T2 FBx
工 程 力 学
S1S2 FBy
FC
把分布力转换成集中力T1，T2，分别作用在S1、S2点。
1 T1 q a 2 1 1 1 T2 q a qa 2 2 4
力F41、F3、F2组成的力三角形自行封闭。表明它们 组成平衡力系。
静力学习题课
• 例2: 在三种情况下,力F沿其作用线滑移到D点,并不改变B处
受力的情况是:
F
D A
(a) √ D
F A
C
D B
工 程 力 学
B
(b)
C A B
√
(c)
静力学习题课
• 例3: 力系简化时若取不同的简化中心，则
工 程 力 学
计梁重,求A ,B和D点的约束反力。
工 程 力 学
静力学习题课
工 程 力 学
分析： 系统整体
梁 CD
起重机
静力学习题课
工 程 力 学
ቤተ መጻሕፍቲ ባይዱ
解：①研究起重机
由mF 0
YG 2 Q 1 P 5 0
50 510 YG 50( kN ) 2
静力学习题课
工 程 力 学
② 再研究梁CD
静力学习题课
• 例1: 已知F1 、 F2 、 F3 、 F4 为 作用于刚体上的平面共点力系，其 力系关系如图所示，由此可知： (1) 力系可合成为一个力偶 (2) 力系可合成为一个力 (3) 力系简化为一个力和一个力偶 (4) 力系的合力为零，力系平衡。
工 程 力 学
F41
√
力F4、F1的合矢量是F41。
工 程 力 学
FAx
F
F
x
0,
0,
FAx FCx1 qb 0
y
FAy FCy1 0
FCx1 Pa M 1 qb 2b 2b 4
Pa M 3 qb 2b 2b 4
P M qb 2 FCy1 2 2a 4a
静力学习题课
3. 再取BC为研究对象，受力分析如图所示。
工 程 力 学
FCx2
静力学习题课
FCy2
M
F
F
C
( F ) 0,
0,
0,
FBx b FBy a M 0
工 程 力 学
FCx2
x
FBx FCx 2 0
y
FBy FCy 2 0
FCx 2 Pa M 1 qb 2b 2b 4
Pa M 1 FBx qb 2b 2b 4
工 程 力 学
Q 1 q a 2 2
FAx
MA
FBx
把分布力转换成集中力Q´，作用在E´点
1 BE a 3
静力学习题课
再以左半段为研究对象（含铰链B） FBy Q´ E´ FAy
工 程 力 学
FAx
MA
FBx
1 1 M B (F) 0 M A 4 q a 3 a FAy 2a 0
1 FAy FC F q 2a 0 Fy 0 2 1 7 M A (F) 0 M A FC 3a F 2a 2 q 2a 3 a 0
静力学习题课
再以左半段为研究对象（含铰链B）
工 程 力 学
静力学习题课
再以左半段为研究对象（含铰链B） FBy Q´ E´ FAy
解题过程： 起重机
Y A 48.33(kN)
系统整体
梁 CD
x
FAy FBy P 0
FAx FBx qb 0
P M qb 2 FAy 2 2a 4a
P M qb 2 FBy P FAy 2 2a 4a
静力学习题课
2. 再取AC为研究对象，受力分析如图所示。
1
工 程 力 学
1
静力学习题课
1
1
b M C ( F ) 0, FAx b qb 2 FAy a 0
工 程 力 学
解：BC杆为二力杆，以整体为 研究对象，其受力如图。 列平衡方程：
M
A
(F ) 0
T AD sin q FBl P AD cosq 0
T P
FB 2 ( P P) 0
静力学习题课
F
工 程 力 学
x
0
FAx FB cos q P 0
解：以整体为研究对象，受力如图： Q
工 程 力 学
1 Q q 2a 2
FAx FAy
MA
E
FC
把分布力转换成集中力Q，作用在E点
2 7 AE a 2a a 3 3
静力学习题课
解：以整体为研究对象，受力如图：
工 程 力 学
FAx
MA E
FAy
FC
Fx 0
FAx 0
FCy 2
P M qb 2 2 2a 4a
静力学习题课
• 例 9 : 刚架结构如图所示， 其中C处光滑铰链。结构的 尺寸和载荷如图所示。试
工 程 力 学
求A，B处的约束力。
静力学习题课
解: 1. 取整体为研究对象，受力如图所示。
工 程 力 学
静力学习题课
•
例10: 已知连续梁上，P=10kN, Q=50kN, CE 铅垂, 不
工 程 力 学
示。试求 A ， B 铰链处的约
束力及销钉 C对 AC 杆、 BC
杆的作用力。
静力学习题课
解: 1. 取整体为研究对象，受力如图所示。
工 程 力 学
静力学习题课
M B (F ) 0,
工 程 力 学
b M P a FAy 2a qb 0 2
y
F 0, F 0,
FAx P
F
y
0 FAy P FB sin q 0
FAy P FAx FAy P, FB 0
静力学习题课
• 例7：组合梁 ABC上作用一集中力 F和三角形分布载 荷，最大载荷集度为，其支承及载荷如图所示，求A、 C处的约束反力。
工 程 力 学
静力学习题课
由mC 0
' YD 6 YG 1 0
50 YD 8.33( kN ) 6
静力学习题课
③ 再研究整体
X 0 , XA 0
工 mA 0,YB 3 YD 12 P 10 Q 6 0 程 力 YB 100(kN) 学
Y 0, YA YB YD Q P 0
j力系的主矢、主矩都会改变 k力系的主矢不会改变，主矩一般都会改变 l力系的主矢会改变、主矩一般不改变 m力系的主矢、主矩都不会改变，力系简化时与简化
中心无关。
静力学习题课
• 例4: 带有不平行二槽的矩形平板上
工 程 力 学
作用一力偶M,今在槽内插入两个固 定于地面的销钉，若不计摩擦则： j平板保持平衡 k平板不能平衡 l无法判断
1 BS1 a 2 2 BS 2 a 3
静力学习题课
也可以以右半段为研究对象。（不含铰链B） T1 T2 FBx
工 程 力 学
S1S2 FBy
FC
1 1 1 2 M B (F) 0 FC a 2 q a 2 a 4 qa 3 a 0
静力学习题课
• 例 8 : 刚架结构如图所示， 其中 A ， B 和 C 都是铰链。 结构的尺寸和载荷如图所
静力学习题课
• 例 5:
重 W=80kN 的物体自由地放
工 程 力 学
在倾角为 30o 的斜面上，若物体与 斜面间的静摩擦系数 f=0.433, 动 摩擦系数fd=0.4,则作用在物体上的 摩擦力的大小为： j30kN k40kN l27.7kN m0。
静力学习题课
• 例6：图示结构，各杆自重不计。 已知 l,r,P,q=45°。试确定A、B处 约束反力。
静力学习题课
再以左半段为研究对象（含铰链B）
工 程 力 学
1 q 2
静力学习题课
也可以以右半段为研究对象。（不含铰链B） T1 T2 FBx
工 程 力 学
S1S2 FBy
FC
把分布力转换成集中力T1，T2，分别作用在S1、S2点。
1 T1 q a 2 1 1 1 T2 q a qa 2 2 4
力F41、F3、F2组成的力三角形自行封闭。表明它们 组成平衡力系。
静力学习题课
• 例2: 在三种情况下,力F沿其作用线滑移到D点,并不改变B处
受力的情况是:
F
D A
(a) √ D
F A
C
D B
工 程 力 学
B
(b)
C A B
√
(c)
静力学习题课
• 例3: 力系简化时若取不同的简化中心，则
工 程 力 学
计梁重,求A ,B和D点的约束反力。
工 程 力 学
静力学习题课
工 程 力 学
分析： 系统整体
梁 CD
起重机
静力学习题课
工 程 力 学
ቤተ መጻሕፍቲ ባይዱ
解：①研究起重机
由mF 0
YG 2 Q 1 P 5 0
50 510 YG 50( kN ) 2
静力学习题课
工 程 力 学
② 再研究梁CD
静力学习题课
• 例1: 已知F1 、 F2 、 F3 、 F4 为 作用于刚体上的平面共点力系，其 力系关系如图所示，由此可知： (1) 力系可合成为一个力偶 (2) 力系可合成为一个力 (3) 力系简化为一个力和一个力偶 (4) 力系的合力为零，力系平衡。
工 程 力 学
F41
√
力F4、F1的合矢量是F41。
工 程 力 学
FAx
F
F
x
0,
0,
FAx FCx1 qb 0
y
FAy FCy1 0
FCx1 Pa M 1 qb 2b 2b 4
Pa M 3 qb 2b 2b 4
P M qb 2 FCy1 2 2a 4a
静力学习题课
3. 再取BC为研究对象，受力分析如图所示。