第四章-数字图像处理中的基本运算
《数字图像处理》教学大纲

《数字图像处理》教学大纲
一、课程简介
数字图像处理是机器视觉、模式识别、医学图像处理等的基础,本课程为工程专业的学生提供数字图像处理的基本知识,是理论性和实践性都很强的综合性课程。
课程内容广泛涵盖了数字图像处理的基本原理,包括图像采样和量化、图像算术运算和逻辑运算、直方图、图像色彩空间、图像分割、图像形态学、图像频域处理、图像分割、图像降噪与图像复原、特征提取与识别等。
二、课程目标
通过本课程学习,学生可以掌握数字图像处理的基本方法,具备一定的解决图像处理应用问题的能力,培养解决复杂工程问题的能力。
具体目标如下:
1.掌握数字图像处理的基本原理、计算方法,能够利用专业知识并通过查阅资
料掌握理解相关新技术,对检测系统及处理流程进行创新性设计;
2.能够知晓工程领域中涉及到的数字图像处理技术,理解其适用场合、检测对
象及条件的限制,能根据给定的目标要求,针对工业检测中的工程问题选择和使用合适的技术和编程,进行仿真和分析;
3.能够知晓工程领域中所涉及的现代工具适用原理及方法,根据原理分析和仿
真结果,进行方案比选,确定设计方案,具有检测算法的设计能力;
4.通过校内外资源和现代信息技术,了解数字图像处理发展趋势,提高解决复
杂工程问题的能力。
三、课程目标对毕业要求的支撑关系
四、理论教学内容及要求
四、实验教学内容及要求
五、课程考核与成绩评定
六、教材及参考书。
数字图像处理-图像基本运算
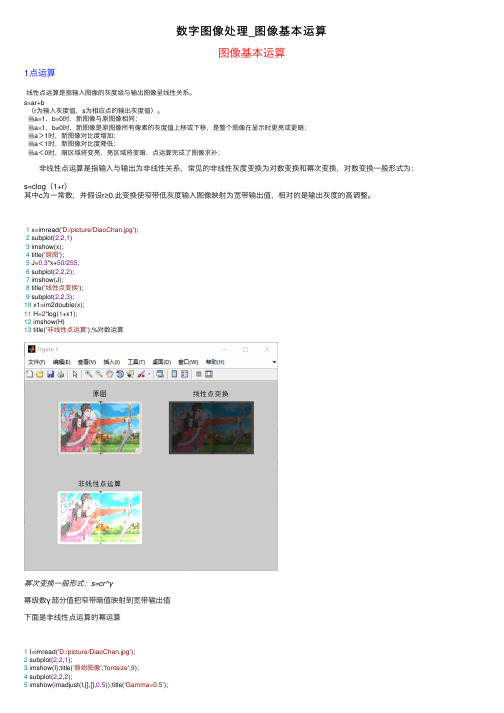
数字图像处理_图像基本运算图像基本运算1点运算线性点运算是指输⼊图像的灰度级与输出图像呈线性关系。
s=ar+b(r为输⼊灰度值,s为相应点的输出灰度值)。
当a=1,b=0时,新图像与原图像相同;当a=1,b≠0时,新图像是原图像所有像素的灰度值上移或下移,是整个图像在显⽰时更亮或更暗;当a>1时,新图像对⽐度增加;当a<1时,新图像对⽐度降低;当a<0时,暗区域将变亮,亮区域将变暗,点运算完成了图像求补; ⾮线性点运算是指输⼊与输出为⾮线性关系,常见的⾮线性灰度变换为对数变换和幂次变换,对数变换⼀般形式为:s=clog(1+r)其中c为⼀常数,并假设r≥0.此变换使窄带低灰度输⼊图像映射为宽带输出值,相对的是输出灰度的⾼调整。
1 x=imread('D:/picture/DiaoChan.jpg');2 subplot(2,2,1)3 imshow(x);4 title('原图');5 J=0.3*x+50/255;6 subplot(2,2,2);7 imshow(J);8 title('线性点变换');9 subplot(2,2,3);10 x1=im2double(x);11 H=2*log(1+x1);12 imshow(H)13 title('⾮线性点运算');%对数运算幂次变换⼀般形式:s=cr^γ幂级数γ部分值把窄带暗值映射到宽带输出值下⾯是⾮线性点运算的幂运算1 I=imread('D:/picture/DiaoChan.jpg');2 subplot(2,2,1);3 imshow(I);title('原始图像','fontsize',9);4 subplot(2,2,2);5 imshow(imadjust(I,[],[],0.5));title('Gamma=0.5');7 imshow(imadjust(I,[],[],1));title('Gamma=1');8 subplot(2,2,4);9 imshow(imadjust(I,[],[],1.5));title('Gamma=1.5');2代数运算和逻辑运算加法运算去噪处理1 clear all2 i=imread('lenagray.jpg');3 imshow(i)4 j=imnoise(i,'gaussian',0,0.05);5 [m,n]=size(i);6 k=zeros(m,n);7for l=1:1008 j=imnoise(i,'gaussian',0,0.05);9 j1=im2double(j);10 k=k+j1;11 End12 k=k/100;13 subplot(1,3,1),imshow(i),title('原始图像')14 subplot(1,3,2),imshow(j),title('加噪图像')15 subplot(1,3,3),imshow(k),title(‘求平均后的减法运算提取噪声1 I=imread(‘lena.jpg’);2 J=imnoise (I,‘lena.jpg’,0,0.02);3 K=imsubtract(J,I);4 K1=255-K;5 figure;imshow(I);7 figure;imshow(K1);乘法运算改变图像灰度级1 I=imread('D:/picture/SunShangXiang.jpg')2 I=im2double(I);3 J=immultiply(I,1.2);4 K=immultiply(I,2);5 subplot(1,3,1),imshow(I);subplot(1,3,2),imshow(J);6 subplot(1,3,3);imshow(K);逻辑运算1 A=zeros(128);2 A(40:67,60:100)=1;3 figure(1)4 imshow(A);5 B=zeros(128);6 B(50:80,40:70)=1;7 figure(2)8 imshow(2);9 C=and(A,B);%与10 figure(3);11 imshow(3);12 D=or(A,B);%或13 figure(4);14 imshow(4);15 E=not(A);%⾮16 figure(5);17 imshow(E);3⼏何运算平移运算实现图像的平移1 I=imread('lenagray.jpg');2 subplot(1,2,1);3 imshow(I);4 [M,N]=size(I);g=zeros(M,N);5 a=20;b=20;6for i=1:M7for j=1:N8if((i-a>0)&(i-a<M)&(j-b>0)&(j-b<N)) 9 g(i,j)=I(i-a,j-b);10else11 g(i,j)=0;12 end13 end14 end15 subplot(1,2,2);imshow(uint8(g));⽔平镜像变换1 I=imread('lena.jpg');2 subplot(121);imshow(I);3 [M,N]=size(I);g=zeros(M,N);4for i=1:M5for j=1:N6 g(i,j)=I(i,N-j+1);7 end8 end9 subplot(122);imshow(uint8(g));垂直镜像变换1 I=imread('lena.jpg');2 subplot(121);imshow(I);3 [M,N]=size(I);g=zeros(M,N);4for i=1:M5for j=1:N6 g(i,j)=I(M-i+1,j);7 end8 end9 subplot(122);imshow(uint8(g));图像的旋转1 x=imread('D:/picture/DiaoChan.jpg');2 imshow(x);3 j=imrotate(x,45,'bilinear');4 k=imrotate(x,45,'bilinear','crop');5 subplot(1,3,1),imshow(x);6 title(‘原图')7 subplot(1,3,2),imshow(j);8 title(‘旋转图(显⽰全部)')9 subplot(1,3,3),imshow(k);10 title(‘旋转图(截取局部)')⼏种插值法⽐较1 i=imread('lena.jpg');2 j1=imresize(i,10,'nearest');3 j2=imresize(i,10,'bilinear');4 j3=imresize(i,10,'bicubic');5 subplot(1,4,1),imshow(i);title(‘原始图像')6 subplot(1,4,2),imshow(j1);title(‘最近邻法')7 subplot(1,4,3),imshow(j2);title(‘双线性插值法')8 subplot(1,4,4),imshow(j3);title(‘三次内插法')放缩变换1 x=imread('D:/picture/ZiXia.jpg')2 subplot(2,3,1)3 imshow(x);4 title('原图');5 Large=imresize(x,1.5);6 subplot(2,3,2)7 imshow(Large);8 title('扩⼤为1.5');9 Small=imresize(x,0.1);10 subplot(2,3,3)11 imshow(Small);12 title('缩⼩为0.3');13 subplot(2,3,4)14 df=imresize(x,[600700],'nearest');15 imshow(df)16 title('600*700');17 df1=imresize(x,[300400],'nearest');18 subplot(2,3,5)19 imshow(df1)20 title('300*400');后记:(1)MATLAB基础知识回顾1:crtl+R是对选中的区域注释,ctrl+T是取消注释2:有的代码中点运算如O=a.*I+b/255 ,其中b除以255原因是:灰度数据有两种表式⽅法:⼀种是⽤unit8类型,取值0~255;另⼀种是double类型,取值0~1。
数字图像处理基本知识

数字图像处理基本知识数字图像处理基木知识图像处理最早出现于20世纪50年代,当时的电子计算机己经发展到一定水平,人们开始利用计算机来处理图形和图像信息。
数字图像处理作为一门学科大约形成于20世纪60年代初期。
早期的图像处理的目的是改善图像的质量,它以人为对象,以改善人的视觉效果为目的。
图像处理中,输入的是质量低的图像,输出的是改善质量后的图像,常用的图像处理方法有图像增强、复原、编码、压缩等。
数字图像处理常用方法:1)图像变换:由于图像阵列很大,直接在空间域中进行处理,涉及计算量很大。
因此,往往采用各种图像变换的方法,如傅立叶变换、沃尔什变换、离散余弦变换等间接处理技术,将空间域的处理转换为变换域处理,不仅可减少计算量,而且可获得更有效的处理(如傅立叶变换可在频域中进行数字滤波处理)。
目前新兴研究的小波变换在时域和频域中都具有良好的局部化特性,它在图像处理中也有着广泛而有效的应用。
2)图像编码压缩:图像编码压缩技术可减少描述图像的数据量(即比特数),以便节省图像传输、处理时间和减少所占用的存储器容量。
压缩可以在不失真的前提下获得,也可以在允许的失真条件下进行。
编码是压缩技术中最重要的方法,它在图像处理技术中是发展最早且比较成熟的技术。
3)图像增强和复原:图像增强和复原的目的是为了提高图像的质量,如去除噪声,提高图像的清晰度等。
图像增强不考虑图像降质的原因,突出图像中所感兴趣的部分。
如强化图像高频分量,可使图像中物体轮廓清晰,细节明显;如强化低频分量可减少图像中噪声影响。
图像复原要求对图像降质的原因有一定的了解,一般讲应根据降质过程建立“降质模型”,再采用某种滤波方法,恢复或重建原来的图像。
4)图像分割:图像分割是数字图像处理中的关键技术之一。
图像分割是将图像中有意义的特征部分提取出来,其有意义的特征有图像中的边缘、区域等,这是进一步进行图像识别、分析和理解的基础。
虽然目前己研究出不少边缘提取、区域分割的方法,但还没有一种普遍适用于各种图像的有效方法。
第四章-数字图像处理中的基本运算

非线性拉伸实例3
第4章 图像处理中的基本运算
第4章 图像处理中的基本运算
非线性拉伸实例4
第4章 图像处理中的基本运算 非线性拉伸实例5
第4章 图像处理中的基本运算
非线性拉伸实例6
第4章 图像处理中的基本运算
非线性拉伸实例7
第4章 图像处理中的基本运算
4.2.2 点运算与直方图
点运算是一种确定的函数关系下所进行的像素变换 运算,因此,点运算之后输出图像和输入图像之间 的直方图也具有与变换函数相关联的对应关系。 从图4-3中可以找到它们之间的关系,即灰度级小区 间内输入像素的个数,等于输出像素的个数,而且 输入、输出图像的阴影部分面积可以用小矩形的面 积近似替代(替代积分式)。 HB(DB)ΔDB=HA(DA)ΔDA 最后输出的直方图的值为(详细推导见P73-74)
H A (DA ) H B ( DB ) df ( D A ) dDA
第4章 图像处理中的基本运算
4.2.3. 点运算的应用
(1) 对比度增强 在一些数字图像中,技术人员所关注的特征 可能仅占据整个灰度级非常小的一个范围。点 运算可以扩展所关注部分的灰度信息的对比度, 使之占据可显示灰度级的更大部分。又称为对 比度拉伸。
第4章 图像处理中的基本运算
4.3 代数运算
1、概念 2、运算类型及应用
第4章 图像处理中的基本运算
1. 代数运算概念
代数运算是指两幅输入图像之间进行点 对点的加、减、乘、除运算得到输出图像的 过程。如果记输入图像为A(x,y)和B(x,y), 输出图像为C(x,y),则有如下四种形式:
(1) (2) (3) (4) C(x,y) C(x,y) C(x,y) C(x,y) = = = = A(x,y)+ B(x,y) A(x,y)- B(x,y) A(x,y)×B(x,y) A(x,y)/B(x,y)
数字图像处理各章要求必做题及参考答案
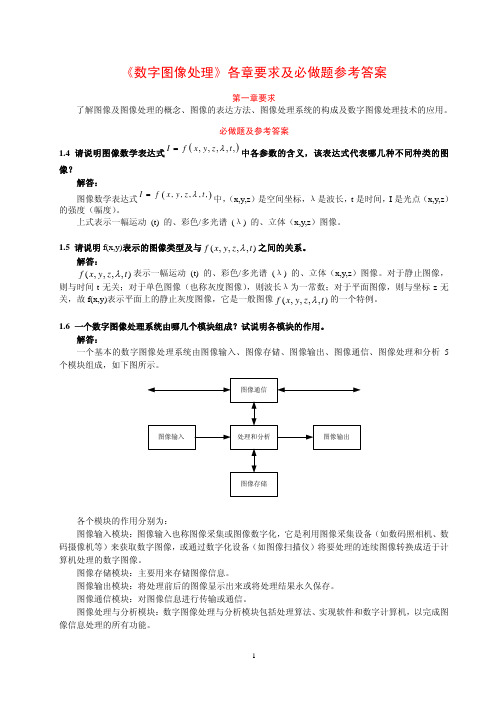
图像通信
图像输入
处理和分析
图像输出
图像存储
各个模块的作用分别为: 图像输入模块:图像输入也称图像采集或图像数字化,它是利用图像采集设备(如数码照相机、数 码摄像机等)来获取数字图像,或通过数字化设备(如图像扫描仪)将要处理的连续图像转换成适于计 算机处理的数字图像。 图像存储模块:主要用来存储图像信息。 图像输出模块:将处理前后的图像显示出来或将处理结果永久保存。 图像通信模块:对图像信息进行传输或通信。 图像处理与分析模块:数字图像处理与分析模块包括处理算法、实现软件和数字计算机,以完成图 像信息处理的所有功能。
2.10(1) 存储一幅 1024×768,256 个灰度级的图像需要多少 bit? (2) 一幅 512×512 的 32 bit 真彩图像的容量为多少 bit? 解答:
(1)一幅 1024×768,256 个灰度级的图像的容量为: b=1024× 768×8 = 6291456 bit (2)一幅 512×512 的 32 位真彩图像的容量为: b=512 × 512 × 32=8388608 bit
的图像具有如题表 4.4.2 所示的灰度级分布。
题表 4.4.1
灰度级
0
1
2
3
4
5
6
7
各灰度级概率分布
0.14 0.22 0.25 0.17 0.10 0.06 0.03 0.03
题表 4.4.2
灰度级
0
1
2
3
4
5
6
7
各灰度级概率分布
0
0
0
0.19 0.25 0.21 0.24 0.11
解答: (1)直方图均衡化结果如下表所示
数字图像处理各章要求必做题及参考答案

−a
v
−a
v
∫ ( ) =
2E v
⎡ ⎢⎣
0 −a
e− jux − e jux
sin v(x + a)dx⎤⎥⎦
∫ =
−4 jE v
⎡ ⎢⎣
0 −a
sin
ux
sin
v(
x
+
a)dx
⎤ ⎥⎦
( ) = 4 jE (u sin va − v sin ua) v u2 − v2
3
第三章要求 1. 了解图像的几何变换; 2. 了解图像的离散傅立叶变换,掌握其重要性质; 3. 了解变换的一般表示形式; 4. 了解图像的离散余弦变换的原理 ; 5. 掌握图像的离散沃尔什-哈达玛变换; 6. 了解 K-L 变换的原理。
4 4
4 4
4⎥⎥ 4⎥
⎢⎣1 4 4 1⎥⎦
⎢⎣4 4 1 1⎥⎦
⎢⎣4 4 4 4⎥⎦
解答:
由H2 =
1 ⎡1 2 ⎢⎣1
1⎤ -1⎥⎦
和H
2
N
=
1 ⎡HN 2 ⎢⎣HN
HN -H N
⎤ ⎥⎦
得
⎡1 1 1 1 ⎤
H4
=
1 2
⎢⎢1 ⎢1
-1 1
1 -1
-1⎥⎥ -1⎥
⎢⎣1
-1
-1
1
⎥ ⎦
⎡10 0 0 −6⎤
X = ⎡⎣x1
x 2
x3 ⎤⎦T 的协方差矩阵 CX 。
解答:
⎧⎡1⎤ ⎡1⎤ ⎡1⎤⎫ ⎡3⎤
∑ 根据式 mx
=
1 M
M
xk
k =1
得 mX
=
1 3
MATLAB数字图像处理实验--图像基本运算

MATLAB数字图像处理实验--图像基本运算一、实验目的1.理解图像点运算、代数运算、几何运算的基本定义和常见方法;2.掌握在MTLAB中对图像进行点运算、代数运算、几何运算的方法;3.掌握在MATLAB中进行插值的方法4.运用MATLAB语言进行图像的插值缩放和插值旋转5.进一步熟悉了解MATLAB语言的应用。
二、实验设备与软件1.PC计算机系统2.MATLAB软件,包括图像处理工具箱(Image Processing Toolbox)3.实验图片三、实验内容及结果分析3.1图像的点运算选择pout.tif作为实验图像,实验原理及内容参照《MATLAB图像处理编程及应用》程序代码:I=imread('pout.tif');figure;subplot(1,3,1);imshow(I);title('原图');J=imadjust(I,[0.3;0.6],[0.1;0.9]);subplot(1,3,2);imshow(J);title('线性扩展');I1=double(I);I2=I1/255;C=2;K=C*log(1+I2);subplot(1,3,3);imshow(K);title('非线性扩展');M=255-I;figure;subplot(1,3,1);imshow(M);title('灰度倒置');N1=im2bw(I,0.4);N2=im2bw(I,0.7);subplot(1,3,2);imshow(N1);title('二值化阈值0.4');subplot(1,3,3);imshow(N2);title('二值化阈值0.7');执行结果:原图线性扩展非线性扩展灰度倒置二值化阈值0.4二值化阈值0.7实验1结果图3.2图像的代数运算选择两幅图像,一幅是原图像,一幅为背景图像,采用正确的图像代数运算方法,分别实现图像叠加、混合图像的分离和图像的局部显示效果。
数字图像处理04章04

第4章 图像处理中的基本运算
双线性插值的特点
➢ 计算量大,但缩放后图像质量高,不会出 现图像不连续的情况。 ➢ 具有低通滤波器的性质,使高频分量减弱, 所以使图像的轮廓在一定程度上受损。
第4章 图像处理中的基本运算
双线性插值
根据点P(x0,y0)的四个相邻点的灰度值, 通过两次插值计算出灰度值f(x0,y0)
✓双线性插值(一阶插值):采用在(x ,y)
周围四个网格点的灰度值进行内插
第4章 图像处理中的基本运算
双线性插值公式
f (x0 , y0 )
f (x, y) [ f (x 1, y) f (x, y)] [ f (x, y 1) f (x, y)] [ f (x 1, y 1) f (x, y)
第4章 图像处理中的基本运算
四. 灰度插值
图像的比例缩放、 旋转变换时等,变换过程需要两 个独立的算法:
一个算法完成几何变换; 一个算法用于灰度级插值.
第4章 图像处理中的基本运算
灰度插值的概念
数字图像处理只能对坐标网格点(离散点) 的值进行变换。而坐标变换后产生的新坐标 值同网格点值往往不重合,因此需要通过内 插的方法将非网格点的灰度值变换成网格点 的灰度值,这种算法称为灰度内插。
✓最邻近插值法 ✓双线性插值(一阶插值)
第4章 图像处理中的基本运算
最邻近插值法
计算与点P(x0,y0)临近的四个点; 将与点P(x0,y0)最近的整数坐标点(x,y)
的灰度值取为P(x0,y0) 点灰度近似值。
最邻近插值法实质 就是最临近点重复
第4章 图像处理中的基本运算
图像加减运算的基本原理与应用

图像加减运算的基本原理与应用1. 概述图像加减运算是数字图像处理中常用的一种操作,通过对图像的像素进行加法或减法运算,可以实现对图像的亮度、对比度等特征的调整,以及实现图像的融合、背景减除等应用。
2. 图像加法运算图像加法运算是将两幅图像的对应像素值相加得到新的像素值的过程。
具体步骤如下:1.读取两幅待加图像A和B,获取它们的像素矩阵。
2.确保两幅图像的尺寸相同,如果尺寸不同,可以通过插值等方法将它们调整至相同尺寸。
3.对于每个像素,将待加图像A和B对应位置的像素值相加,得到新的像素值。
4.将得到的新像素值存储在新的图像中,得到加法运算后的图像C。
图像加法运算常用于图像的亮度调整、对比度增强等应用,例如将两张曝光不同的照片进行加法运算,可以得到更好的曝光效果。
3. 图像减法运算图像减法运算是将两幅图像的对应像素值相减得到新的像素值的过程。
具体步骤如下:1.读取两幅待减图像A和B,获取它们的像素矩阵。
2.确保两幅图像的尺寸相同,如果尺寸不同,可以通过插值等方法将它们调整至相同尺寸。
3.对于每个像素,将待减图像A和B对应位置的像素值相减,得到新的像素值。
4.将得到的新像素值存储在新的图像中,得到减法运算后的图像C。
图像减法运算常用于图像的背景减除、运动目标检测等应用,通过减去背景图像,可以突出运动目标的轮廓。
4. 图像加减运算的应用图像加减运算可以应用于多个领域,下面列举了几个常见的应用场景:1.图像融合:通过将两幅图像进行加权相加,实现图像的融合效果,常用于全景图像拼接、HDR图像合成等应用。
2.背景减除:通过将背景图像与待减图像进行减法运算,得到仅包含目标物体的图像,常用于运动目标检测、视频监控等应用。
3.图像增强:通过将图像与增强滤波器进行加法运算,可以增强图像的对比度、边缘等特征,常用于图像增强、边缘检测等应用。
4.图像修复:通过将待修复图像与修复模板进行减法运算,可以去除图像中的噪声、伪影等干扰,常用于图像复原、去噪等应用。
3.数字图像基本运算

C x, y = A x, y /B(x, y) OpenCV 函 数 表 示 : void cvDiv(constCvArr* src1, constCvArr* src2, CvArr* dst, doublescale=1);//scale*src1(i)/src2(i),如果 src1=NULL,则计算 scale/src2(i)。 主要用法: 1. 去除数字化器灵敏度随空间变化造成的影响; 2. 用于产生对多光谱分析十分有用的比率图像。
dst,doublescale=1);//一个简单的乘法函数。 它将 src1 中的元素与 src2 中相对应的元素相乘, 然后把结果赋给 dst。如果 mask 是空,那么与其中 0 元素相对应的 dst 元素都不会因此操 作而改变; double cvGEMM(constCvArr* src1,constCvArr* src2,double alpha, constCvArr* src3, double beta, CvArr* dst, inttABC = 0);//广义矩阵乘法(generalized matrix multiplicatipm, GEMM)在 OpenCV 中是由 cvGEMM()来实现的,可实现矩阵乘法、转置后相乘、比例缩放 等; void cvMatMul(constCvArr* src1,const CvArr* src2,CvArr* dst);//用于矩阵乘法。 主要用法: 1. 得到一个局部图像; 2. 去除图像的某些部分 d)图像除法
数字图像处理 第四章图像增强

Pr(rk) 0.19 0.25 0.21 0.16 0.08 0.06
0.03
0.02
计算每个sk对应的像素数目 计算均衡化后的直方图
Tr
Sk并
sk
nsk Ps(sk)
0.19
1/7
0.44
3/7
S0=1/7 S1=3/7 S2=5/7
790 0.19 1023 0.25 850 0.21
0.65
✓ 校正后的原始图像 f (i, j) C g(i, j) gc(i, j)
9
灰度级校正注意问题:
对降质图像进行逐点灰度级校正所获得的图像, 其中某些像素的灰度级值有可能要超出记录器 件或显示器输入灰度级的动态范围,在输出时 还要采用其他方法来修正才能保证不失真地输 出。
降质图像在数字化时,各像素灰度级都被量化 在离散集合中的离散值上,但经校正后的图像 各像素灰度极值并不一定都在这些离散值上, 因此必须对校正后的图像进行量化。
),使得结果图像s的直方图Ps(s)为一个常数
Pr(r)
Ps(s)
直方图均衡化 T(r)
r
s
26
直方图均衡化理论基础
-1 由概率论可知,若Pr(r)和变换函数s=T(r)已知,r=T (s)是单 调增长函数,则变换后的概率密度函数Ps(s)可由Pr(r)得到:
分 布 函 数 Fs(s)sp( s s) ds=rp( r r) dr
✓ 计算均衡后的直方图
s k 计
T( rk)
k
=
i 0
P(r
r
)
i
k i 0
ni n
s k并
round( sk计 * (L L 1
1))
j
数字图像处理CH4点运算

线性点运算的定义
01
线性点运算是数字图像处理中的 一种基本运算,它通过对图像中 的每个像素应用线性函数来改变 图像的像素值。
02
线性点运算通常用于调整图像的 对比度和亮度,以及进行图像的 缩放和旋转等变换。
非线性点运算的示例
对比度拉伸
通过非线性函数将图像的对比度进行拉伸,增强图 像的细节和清晰度。
伽玛校正
通过非线性函数校正图像的伽玛值,以实现图像的 亮度和对比度的调整。
直方图均衡化
通过非线性函数对图像的直方图进行均衡化处理, 以提高图像的对比度和清晰度。
05
点运算的优缺点
点运算的优点
80%
高效性
图像分割
通过点运算中的图像分割 技术,将图像分割成不同 的区域或对象,用于对象 识别和场景理解。
THANK YOU
感谢聆听
点运算的缺点
细节丢失
缺乏空间信息
由于点运算通常会对像素值进行线性 或非线性变换,可能会导致图像细节 的丢失或失真。
点运算主要关注像素值的变化,忽略 了像素之间的空间关系,可能会丢失 重要的空间信息。
不符合人眼视觉特性
点运算的某些操作可能与人类视觉系 统的特性不符,导致处理后的图像看 起来不自然。
点运算的改进方向
无损压缩
通过特定的编码方式,对 图像数据进行压缩,同时 保持原始数据的完整性和 准确性。
压缩感知
利用点运算中的压缩感知 理论,对图像进行稀疏表 示和压缩,实现高效的图 像处理和传输。
图像识别
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d c
g(x, y)
[ f (x, y) a] c a f (x, y) b ba
c
f (x, y) a
宽 窄
第4章 图像处理中的基本运算
(2)分段线性点运算 将感兴趣的灰度范围线性扩展,抑制不感兴趣
的灰度区域,就要使用分段线性点运算。
设f(x,y)灰度范围为[0,Mf],g(x,y)灰度范围 为[0,Mg],分段线性点运算如下图所示:
像设备的非线性和图像记录设备动态范围太窄 等因素,都会产生对比度不足的弊病,使图像中 的细节分辨不清.
这时可通过点运算将灰度范围线性扩展. 设f(x,y)灰度范围为[a,b],g(x,y)灰度范 围为[c,d]. 则线性点运算公式为:
第4章 图像处理中的基本运算
线性点运算公式
d
f (x, y) b
度: 暗(不变):中(增加):亮(不变) 暗(降低):中(增加):亮(降低) 暗(加强):中(压低):亮(加强) 公式见下页。
第4章 图像处理中的基本运算
(1) DB=f(DA)=DA+CDA(DM-DA)
(2)
f
(DA )
Dm 2
1
1 απ sin( )
s
in[απ(
DA DB
1 2
第4章 图像处理中的基本运算
差值法的应用举例
(a)差影法可以用于混合图像的分离
-
=
第4章 图像处理中的基本运算
(b) 检测同一场景两幅图像之间的变化
设:
时刻1的图像为T1(x,y), 时刻2的图像为T2(x,y) g(x,y) = T2 (x,y) - T1(x,y)
=
-
g(x,y)
T1(x,y)
)]
2
(3)
f
(DA )
Dm 2
1
1 απ tan( )
tan[απ( DA DB
12 )]
2
第4章 图像处理中的基本运算
255
255
218
输出DB
输出DB
128 255
输入DA
加亮-减暗图像
32
128 255
输入DA
加暗-减亮图像
亮度调整
第4章 图像处理中的基本运算
非线性拉伸实例1 对比度拉伸
拉伸效果:图像加亮、减暗
第4章 图像处理中的基本运算
非线性拉伸实例2
第4章 图像处理中的基本运算 非线性拉伸实例3
第4章 图像处理中的基本运算
第4章 图像பைடு நூலகம்理中的基本运算
非线性拉伸实例4
第4章 图像处理中的基本运算
非线性拉伸实例5
第4章 图像处理中的基本运算
非线性拉伸实例6
第4章 图像处理中的基本运算
255 142
DB
0
255
DA
降低对比度
第4章 图像处理中的基本运算
降低对比度举例
255
DB
0
255
DA
第4章 图像处理中的基本运算
③ 如果a=1,b≠0,操作仅使所有像素的 灰度值上移或下移,其效果是使整个图像 更暗或更亮
255
255
DB
DB
0
整个图像DA 更亮
0
DA
255
整个图像更暗
255
(2) 光度学标定 点运算可消除图像传感器的非线性的影响。
第4章 图像处理中的基本运算
(3) 显示标定 一些显示设备不能保持数字图像上像素的灰
度值和显示屏幕上相应点的亮度之间的线性关系。 这一缺点可以通过点运算予以克服,即在图像显 示之前,先设计合理的点运算关系,可将点运算 和显示非线性组合起来互相抵消,以保持在显示 图像时的线性关系。 (4) 轮廓线
(1) C(x,y) = A(x,y)+ B(x,y) (2) C(x,y) = A(x,y)- B(x,y) (3) C(x,y) = A(x,y)×B(x,y) (4) C(x,y) = A(x,y)/B(x,y)
第4章 图像处理中的基本运算
2. 运算类型及应用
(1)加运算 (2)减运算 (3)乘运算 (4)除运算
点运算。即:
DB f (DA) aDA b
255
输出DB b
f(DA)=aDA+b
0
输入DA
255
第4章 图像处理中的基本运算
① 如果a>1,输出图像的对比度增大
255
DB
0 48
218 255
DA
提高对比度
第4章 图像处理中的基本运算
提高对比度举例
第4章 图像处理中的基本运算
② 如果a<1,输出图像的对比度减小
第4章 图像处理中的基本运算
4.2 点运算
在图像处理中,点运算是一类简单却非常 具有代表性的重要算法之一,也是其他图 像处理运算的基础。运用点运算可以改变 图像像素占据的灰度值范围,但不会改变 图像内的空间位置关系。
点运算包括以下内容: 1.定义 2:分类
3:应用
第4章 图像处理中的基本运算
HB(DB)ΔDB=HA(DA)ΔDA 最后输出的直方图的值为(详细推导见P73-74)
H B (DB )
H A (DA ) df (DA )
dDA
第4章 图像处理中的基本运算
4.2.3. 点运算的应用
(1) 对比度增强 在一些数字图像中,技术人员所关注的特征
可能仅占据整个灰度级非常小的一个范围。点 运算可以扩展所关注部分的灰度信息的对比度, 使之占据可显示灰度级的更大部分。又称为对 比度拉伸。
点运算可为图像加上轮廓线。 (5) 剪裁
对于8bit图像,通过点运算,在每个像素值 被存储之前,输出灰度级一定要剪裁到0~255 的范围内。
第4章 图像处理中的基本运算
4.3 代数运算
1、概念 2、运算类型及应用
第4章 图像处理中的基本运算
1. 代数运算概念
代数运算是指两幅输入图像之间进行点 对点的加、减、乘、除运算得到输出图像的 过程。如果记输入图像为A(x,y)和B(x,y), 输出图像为C(x,y),则有如下四种形式:
在银行金库内,摄像头每隔一固定时间拍摄一 幅图像,并与上一幅图像做差影,如果图像差 别超过了预先设置的阈值,则表明可能有异常 情况发生,应自动或以某种方式报警;
用于遥感图像的动态监测,差值图像可以发现 森林火灾、洪水泛滥,监测灾情变化等;
也可用于监测河口、海岸的泥沙淤积及监视江 河、湖泊、海岸等的污染;
第4章 图像处理中的基本运算
④如果a=1,b=0时,输出、输入图像相同
255
DB
0
DA
255
第4章 图像处理中的基本运算
⑤ 如果a为负值,暗区域将变亮,亮区域将变暗
255
DB
0
DA
255
第4章 图像处理中的基本运算
255
DB
0
DA
255
第4章 图像处理中的基本运算
线性点运算公式 当图象成像时曝光不足或过度, 或由于成
第4章 图像处理中的基本运算
第4章 图像处理中的基本运算
分段线性点运算公式
宽
g(x, y)
Mg d [ f (x, y) b] d
Mf b
d c b a [ f (x, y) a] c
c f (x, y)
a
窄
b f (x, y) M f
a f (x, y) b
0 f (x, y) a
第4章 图像处理中的基本运算
第四章:数字图像处理中的基本运算
第4章 图像处理中的基本运算
图像处理基本运算概述
图像处理中,经常要采用各种各样的算法。根 据数字图像处理运算中输入信息与输出信息的 类型,图像处理典型算法从功能上具有以下几 种:
(1)单幅图像 (2)多幅图像 (3)单幅或多幅图像
单幅图像 单幅图像
1. 定义
所谓点运算是指像素值(像素点的灰度值)通 过运算之后,可以改善图像的显示效果。这是一 种像素的逐点运算。
点运算与相邻的像素之间没有运算关系,是原 始图像与目标图像之间的影射关系。是一种简单 但却十分有效的图像处理方法。
点运算又称为“对比度增强”、“对比度拉 伸”、“灰度变换”
第4章 图像处理中的基本运算
K=2
K=4
K=16
第4章 图像处理中的基本运算
生成图象叠加效 果:可以得到各种 图像合成的效果, 也可以用于两张图 片的衔接
第4章 图像处理中的基本运算
(2)减法运算
C(x,y) = A(x,y) - B(x,y)
主要应用
消除背景影响
差影法(检测同一场景两幅图像之间的 变化)
第4章 图像处理中的基本运算
第4章 图像处理中的基本运算
(3)非线性点运算:输出灰度级与输入灰度级呈 非线性关系的点运算。
255 输出
0
输入
255
非线性点运算灰度变换函数的斜率处处为正, 这类函数保留了图像的基本外貌。
第4章 图像处理中的基本运算
非线性点运算的函数形式可以表示为: DB = f (DA)
同灰样度,值D。A为f表输示入非点线的性灰函度数值。,DB为相应输出点的 有三种典型的非线性点运算函数,可以改变对比
g(x,y) = 1/M (g0(x,y)+g1(x,y)+…+ g M (x ,y))
前提:噪音h(x,y)i为互不相关,且均值为0时, 上述图象均值将降低噪音的影响。
第4章 图像处理中的基本运算
相加
图例:求平均消除加性随
机噪声,k=1,2,3,4,16,
K=1
表示1幅图像平均、2幅
图像相加后求平均…
