05 电磁学:第15章 电容器和静电场中的电介质
静电场中的电介质,电容器

静电场中的电介质、电容器1、分子的正负电荷中心重合的电介质叫 无极分子 电介质,在外电场的作用下,分子正负电荷中心发生相对位移,形成 电偶极子 。
2、电介质在电容器中的作用是:(1) 增加电容器的电容量 ,(2) 提高耐压能力 。
3、在两板间距为d 的平行板电容器中,平行地插入一块厚度为d/2的金属大平板,则电容变为原来的 2 倍;如果插入的是厚度为d/2的相对电容率为εr =4的大介质平板,则电容变为原来的 1.6 倍。
4、一平板电容器始终与端电压一定的电源相联,当电容器两极板间为真空时,电场强度为0E ,电位移为0D ,而当极板间充满相对电容率为r ε的各向同性均匀电介质时,电场强度为E ,电位移为D ,则( B )(A)00 , /D D E E r ==ε (B)00 , D D E E r ε== (C)000/ , /εεD D E E r == (D)00 , D D E E ==5、两个完全相同的电容器,把一个电容器充电,然后与另一个未充电的电容器并联,那么总电场能量将( C )(A)增加 (B)不变 (C)减少 (D)无法确定6、一空气平行板电容器,接电源充电后电容器中储存的能量为W 0,在保持电源接通的条件下,在两极板间充满相对电容率为r ε的各向同性均匀电介质,则该电容器中储存的能量W 为( A )(A) 0W W r ε= (B) r W W ε/0=(C) 0)1(W W r ε+= (D) 0W W =7、一球形电容器,内球壳半径为R 1外球壳半径为R 2,两球壳间充满了相对电容率为r ε的各向同性均匀电介质,设两球壳间电势差为U 12,求:(1)电容器的电容;(2)电容器储存的能量。
解:(1) 24r D s d D s π⋅=⋅⎰ , ∑=Q qQ q r D s d D s ==⋅=⋅∑⎰24π , 24rQD π= 2004r Q DE r rεπεεε== 21012124)(21R R R R Q dr E U r R Rεπε-=⋅=⎰ , 12122104R R U R R Q r -=επε 12210124R R R R U Q C r -==επε (2) 12212210212221R R U R R CU W r -==επε 8、求图中所示组合的等值电容,并求各电容器上的电荷。
5静电场中的电介质、电容(45学时)

串联电容器总电容的倒数等于 各串联电容倒数之和。
当电容器的耐压能力不被满足时,常用串并联 使用来改善。如串联使用可用在稍高的电压中, 从而提高耐压能力。并联使用可以提高容量。 有介质后电容增大
C r C0
电容器的性能主要由其电容和耐压来标定。在 使用电容器时,所加电压不能超过耐压值,否则就 会因场强过大使电介质的绝缘性能遭到破坏而烧坏 电容器(击穿)。 击穿场强:电介质所能承受的不被击穿的最大场强
U AB
B
A
E dl
2 0l RA q q 2 0l 电容 C q RB RB U AB ln ln RA 求电容步骤: 2 0l RA
A)让两极板带等量异性电荷并求其电场分布;
q
ln
dr l Edr 2 r 0 R
RB RA
RB RA
场 强 分 布 曲 线
普遍结论: 当电介质充满两 个等势面之间的空间 时,该空间的场强等 于真空时场强的 1/ r 倍。
2 q0 (4 π 0 R2 )
q0 (4 π 0 r R )
2 1
E
2 q0 (4 π 0 r R2 )
0 r R1 R2 在带电面两侧的场强都发生突变,这是面电荷 分布的电场的一个共同特点(有普遍性)。
1 1 1 1 C C1 C2 Cn
电容器串联后,等效 电容比每个电容器的 电容都小,但耐压能 力增加了。
电容器串联后,等效电容的 倒数是各电容的倒数之和。
2.电容器的并联
q1 C1 q2 C2
UB
UA
特点:
等效
UA
C
UB
qi
Ci
q q1 q2 qn
教学PPT静电场中的电介质

-
P E
D
P(R)
球表面的油面上的束缚电荷:
q
4P(RR2)(rˆ) (1(111rr))q4qR2
q总与 q 反号,数值小于q 。
另一解法:用 E 的高斯定理
E
0
P (rˆ) 0(r 1)E
(1
1
r
)
q(1
1
r
)q
练习五
-
q' +q
-+
S
-
+
+
- +' + +-
+-
+-
R
+
-+
r
*四、静电场的边界条件 在两种介质的分界面上
一、电介质的电结构
电中性的分子中,带负电的电子(或负离 子)与带正电的原子核(或正离子)束缚得很 紧,不能自由运动-束缚电荷或极化电荷。
电偶极子模型: 每一个分子中的正电荷集中于一点,称为 正电荷重心;负电荷集中于另一点,称为负 电荷重心 — 两者构成电偶极子
二、有极分子和无极分子 1、有极分子(Polar molecule) — 极性电介质
ds
-电位移通量
s
DdS
q0
S
注:1)E与电介质有关,
D0E P
而D与电介质无关。
2)E 线与所有电荷有关,从正电荷出发终止
与负电荷。
D线与自由电荷有关,从自由正电荷出发终止
与自由负电荷。
++ + + + + +
- - -
+
+ +
--
第15章静电场中的电介质-文档资料

一、电介质对电场的影响 1. 实验事实 金属平板两极板间的电压
为 U0 ,此时维持极板上的
电荷 Q 不 变,使两极板间 充满均匀的各向同性的电 介质,由实验可测得两极 板间电压。
U Uo
r
一、电介质对电场的影响 2. 相对介电常数(相对电容率)
U
Uo
r
r 是一个没有单位的、大于1的纯数,称为
-q +q
H
H
H+
H+
甲烷分子CH4 无极分子
水分子H2O 有极分子
无极分子
有极分子
无电场时: 热运动---紊乱
电中性
有电场时:电介质分子的极化
位移极化 产生感生电矩
取向极化
位移极化
取向极化
结论:极化的总效果是介质边缘出现电荷分布。 称呼:由于这些电荷仍束缚在每个分子中,所 以称之为面束缚电荷或面极化电荷。 电介质内的电场强度:
第 15 章 静电场中的电介质
第 15 章
静电场中的电介质
一、电介质对电场的影响
二、电介质的极化
三、 D 的高斯定律
四、电容器和它的电容
五、电容器的能量
一、电介质对电场的影响
电介质也即绝缘体
特点是分子中正负电荷束缚得很紧,内 部几乎没有自由电荷,不导电,但在电场中会 受到电场的影响,反过来也会影响原有电场的 分布。
电介质的相对介电常数或相对电容率,是
表征电介质电学性质的。
一、电介质对电场的影响
3.对电场的影响
把
U
Uo
r
两边同除以 d , 有
Uo U d r d
即
E
Eo
r
一、电介质对电场的影响
静电场中的电介质通用课件

多功能材料
探索具有多种功能的电介 质材料,如压电、热电、 铁电等。
介电性能的优化
介电常数与损耗
通过材料设计和制备工艺优化, 降低电介质的介电损耗,提高介
电常数。
温度稳定性
提高电介质材料的温度稳定性,使 其在宽温度范围内保持稳定的介电 性能。
耐电压强度
提高电介质材料的耐电压强度,确 保其在高压环境下能够稳定工作。
电位移矢量与电场强度的关系
总结词
电位移矢量描述了电场中电介质内的电场分布,与电场强度之间存在密切关系。
详细描述
在静电场中,电位移矢量D与电场强度E之间存在线性关系,即D=εE,其中ε为电介质材料的介电常数。这一关系 描述了电场中电介质内的电场分布特性。
电极化与电场强度的关系
总结词
电极化现象是电介质在电场作用下产生电荷 位移的现象,与电场强度有直接关系。
静电场与电介质相互作用的深入研究
电介质极化机制
多场耦合效应
深入研究静电场对电介质极化的影响 机制,揭示其微观结构和宏观性能之 间的关系。
研究静电场与其他物理场(如机械力 场、温度场等)的耦合效应,探索多 场作用下的电介质性能演变规律。
界面效应
关注静电场中电介质界面效应的研究, 探索界面电荷、极化现象及其对整体 性能的影响。
复合电介质是指由有机和 无机材料混合构成的电介 质,如复合绝缘材料等。
PART 02
电介质在静电场中的表现
电极化现象
总结词
电极化现象是电介质在静电场中因电场作用而产生的极化状态,表现为电介质 内部正负电荷的相对位移。
详细描述
当电介质置于静电场中,其内部的分子或原子在电场的作用下发生相对位移, 使得电介质整体呈现出宏观的极化状态。这种极化状态使得电介质内部的正负 电荷中心不再重合,形成电偶极矩。
静电场中的电介质PPT资料(正式版)

—— 描述介质的极化程度
两类电介质分子结构: + 无极 §3-6 有电介质时的静电场方程
H+
C--
H+
P103例1、半径为R、电荷 为的金属球,放在介电常数为 的均匀无限大介质中, 求电介质中的电场强度
- 分子 介质中的高斯定理:在任何静电场中,通过任意闭合曲面的电位移通量等于该曲面所包围的自由电荷(free charge)的代数和。
p0
定义:P
pi
极化时:
-
+
E0
p0
实(各验向规同性律电:介质)P Ve0E
e与E无关,取决
于电介质的种类。
电极化率 总场 EE0E
§3-4 极化电荷
一、极化电荷 q 与极化强度P 的关系
P n
S
q sP d S sP d S C o s
二、极化电荷体密度与极化强度关系 q sPdS
4.
特例:真空
——
特殊介质
真空中:P0
所以:D 0E P 0E
S D d SS0 E d S q i
真空
EdS
S
1
0
qi
D与 E 的关系
对于D 各向同0E 性的P 电 介 质0E : Pe 0E e0 E1 e0E
令r 1e D 0rEE
相对介电常数
DE
=0r:介电常数
注: D 0EP是定义式,普遍成立。
静电场中的电介质
§3-2 偶极子
• 偶极子:两个相距很近而且等值异号的 点电荷组成一个偶极子。
•
偶极子激发的电场如何?P87-8E8
p r3
电偶极矩
p ql
• 偶极子在外电场作用下如何变化?
大学物理课件介质及电容

二、静电场的能量
1 2 2 1 0 r S S S ( Ed ) W CU C 2d 2 d 1 2 1 2 E Sd E V d 2 2 W 1 2 电位移矢量: 能量密度: w E V 2 D E 1 2 1 静电场能量密度: we E we D E 2 2 1 2 1 静电场能量: W e V 2 E dV We V 2 D EdV
R
Q
Q 4 0 R
Q C U
4 0 R
由孤立导体作 电容不经济!
3
欲得到 1F 的电容 孤立导体球的半径 R=?
由孤立导体球电容公式知:
R
1 4 0
910 m 1.5 10 RE
9
二.导体组的电容
导体壳内部的场只由腔内的电量 Q 和 几何条件决定 (相当于孤立导体) 几何条件 腔内导体表面与壳的内表面 形状及相对位置 定义
电介质的 介电常数
五. 有介质存在时的Gauss定理
自由电荷电场中的高斯定理:
E0 dS
S
q
0
0
考虑所有电荷产生的场:
S
S
E0
r
dS
q
0
r 0
E dS
S
q
0
称为:电位移矢量 令:D ε0 εr E D dS q0
三、电容器的串联和并联
1. 并联电容器的电容:
C1
UA
C2
Ci
UB
等效
UA
C
UB
令U
U A U B q1 C1U q2 C2U
第十五讲§5.5 静电场中的介质

第十五讲 §5.5 静电场中的介质—不导电的物质(绝缘体) 一、电介质的极化1、电介质对电容的影响 相对电容率 ①Q 不变,加入电介质()r ε 0r C C ε= 0r 00r 0C U QU Q C εε===②Q 不变,加入电介质()r ε r0E E ε=000r 0U U εεεE E d E Ed r =⇒=⇒=2、电介质的电结构:电介质的分子都处在束缚状态,没有自由电荷。
3、电极化现象:电介质在外场中其两端出现极化电荷(束缚电荷)的现象。
4、无机分子电介质的极化:分子的正负电荷的中心是重合的。
比如:H ;CH 4均为无机分子电介质,即电矩为零。
在外场中,无机分子电介质中的正负电荷中心被拉开,形成分子电矩、分子电矩在外场的作用下进行有序排列,对外显示电性。
5、有机分子电介质的极化:分子的正负电荷的中心不重合,有电矩,是杂乱无章的,对外不显电性。
比如:H 2O 为有机分子电介质。
在外场中,有机分子电介质中无序排列的电矩在外场的作用下进行有序排列,对外显示电性。
二、电介质中的电场 1、电极化强度和极化电荷⑴电极化强度(P ):是描述电介质极化强弱的物理量。
单位体积内分子电偶极矩的矢量和。
①VP P i∆=∑ 其中iP 为单个分子的电偶极矩 r q P =②`P σ=··SS P σσ=∆∆= ‘σ为极化电荷的面密度③E P χε0= E E rr r rχεεχεεσεεεσεχ0001000`1P =−−→−-==-= χ 为电介质的极化率⑵极化电荷与自由电荷①0`1Q Q r r εε-= ``00;S Q S Q ==σσ ②0`1σεεσr r -= 0``000;εσεσ==E E2、电介质中的电场强度0`E 1E r r εε-= ⎪⎪⎭⎫ ⎝⎛-=⇒=-=⇒+=r r E E EE E E E E E εε110`0`0`0三、电位移 电介质中的高斯定理1、电位移矢量:是人为引入的一个辅助量,其好处是只需考虑自由电荷,而无需考虑极化电荷。
大学物理课件:15-2 静电场中的电介质
P cos
Pn
P en
( 极化电荷面密度)
dS
P L
均匀电介质表面产生的极化电荷面密度等于该处电极化强度 沿表面外法线方向的投影。
穿出S面的总电量:
q外
PdS
S
q内 q外
PdS
S
第15章 静电场中的导体和电介质
9
大学
15-2 静电场中的电介质
物理
【例15-6】求均匀极化的电介质球表面上极 化电荷 的分布。已知电极化强度为 P
S 0E dS qi
P dS
S
S 0E P dS qi
第15章 静电场中的导体和电介质
11
大学
15-2 静电场中的电介质
物理
S 0E P dS qi
定义电位移矢量:D
0E
P
单位:C m2
介质中的高斯定理: 在静电场中,通过任意封闭
曲面的电位移通量等于该曲面所包围的自由电荷的
r 1 2πrr
1'
( r
1) 0E1
( r 1) 2 π r R1
2'
( r
1) 0E2
( r 1) 2 π r R2
r
R2 R1
第15章 静电场中的导体和电介质
19
大学
15-2 静电场中的电介质
物理
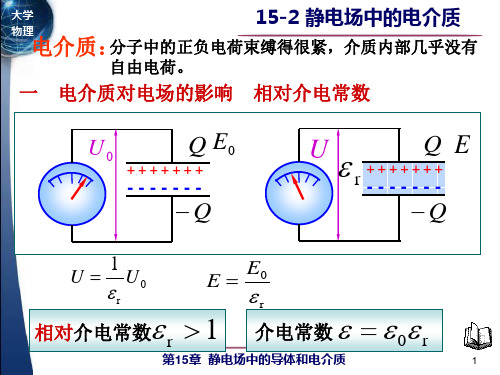
电介质:分子中的正负电荷束缚得很紧,介质内部几乎没有
自由电荷。
一 电介质对电场的影响 相对介电常数
U0
Q E0
+++++++
-------
Q
U
QE
r
+
-
大学物理电场静电场中的介质以及电容和电容器共32页

56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左来自1、不要轻言放弃,否则对不起自己。
2、要冒一次险!整个生命就是一场冒险。走得最远的人,常是愿意 去做,并愿意去冒险的人。“稳妥”之船,从未能从岸边走远。-戴尔.卡耐基。
梦 境
3、人生就像一杯没有加糖的咖啡,喝起来是苦涩的,回味起来却有 久久不会退去的余香。
大学物理电场静电场中的介质以及电容和 4、守业的最好办法就是不断的发展。 5、当爱不能完美,我宁愿选择无悔,不管来生多么美丽,我不愿失 去今生对你的记忆,我不求天长地久的美景,我只要生生世世的轮 回里有你。 电容器
大学物理_4静电场中的电介质

S
i
自由电荷
各向同性 线性介质
P 0r 1E
D 0r E E 介质方程
r 0 称介质的介电常数(电容率)
在 斯具 定有 理某出种发对解称出性D的情况下,可以首先由高
即 D E P q
说明:
1.电位移在闭合面上的通量只和闭合面内的自
第十五章 静电场中的电介质
(Dielectric In Electrostatic Field)
§15.1 电介质对电场的影响 §15.2 电介质的极化 §15.3 D的高斯定律 §15.4 电容器及其电容 §15.5 电容器的能量
§15.1 电介质对电场的影响 电介质的特点:无自由电荷,不导电。 电场中置入各向同性均匀电介质时的影响
定义 C Q 单位:法拉 F
U
电容只与几何因素和介质有关 固有的容电本领
【例1】求真空中孤立导体球的电容
解:设球带电为 Q
导体球电势 U Q
4 0 R
导体球电容 C Q
U
4 0 R
问题
欲得到 1F的电容, 孤立导体球的半径R
由孤立导体球电容公式知
R
1
4 0
9109 m
R3
4π 0r 2
(r (r
R) R)
q2r2
we
0E2
2
32π2
q2
0
R
6
32π2 0 r 4
(r R) (r R)
静电能:We
V wedV
0
we
4πr
2dr
静电场电容电介质课件.ppt

U
电容的计算 设Q E
U AB
内表面
Q
AQ
B
C Q U
典型的电容器 球形
R1 R2
柱形
R1
R2
平行板 d
例 求柱形电容器单位长度的电容 柱形
解:设单位长度带电量为
R1< r< R2
E 2 0r
R2
U
R1
2
0
r
dr
ln R2 2 0 R1
C
U
2 0
ln R2
R1
r
宏观上无限小 微观上无限大
定义
P lim
i
pi
V
的体积元 V
pi
每个分子的 电偶极矩
量纲
SI
单位
c m2
P L2TI
三.极化强度P 与极化电荷的关系
在已极化的介质内任意作一闭合面S S 将把位于S 附近的电介质分子分为两部分
一部分在 S 内 一部分在 S 外
电偶极矩穿过S 的分子对S 内的极化电荷有贡献
dS
S
1.小面元dS对面S内极化电荷的贡献
外场
在dS附近薄层内认为介质均匀极化
l
dS P
dq
qnl
dS
cos
PdScos
分子数
P dS
密度 n
如果 /2 落在面内的 是负电荷
如果 > /2 落在面内的 是正电荷
dS
l dS P V
所以小面元ds对面内极化
电荷的贡献
dq Pnds P ds
例 求真空中孤立导体球的电容(如图)
解:设球带电为 Q
R
导体球电势 U Q
《静电场中的电介质》课件

电介质的极化机制可以分为电子式极化、离子式极化和取向式极化三种。电子式极化是由于电介质中的电子受到 电场作用而产生的位移;离子式极化是由于电介质中的离子受到电场作用而产生的位移;取向式极化是由于电介 质中的分子或分子的取向受到电场作用而产生的改变。
02 静电场中的电介质
电介质在静电场中的表现
压电材料的研究涉及晶体、陶瓷、复合材料等多个领域,研究者通过优化材料成分、结 构及制备工艺,提高压电材料的性能,如压电常数、机电耦合系数等,以拓展其应用范
围。
新型电介质材料的研究
总结词
新型电介质材料在能源、环保、医疗等领域 具有广阔的应用前景。
详细描述
随着科技的发展,新型电介质材料不断涌现 ,如铁电材料、弛豫铁电体、多铁性材料等 。这些材料在储能、传感、信息处理等方面 展现出独特的优势,为相关领域的技术创新
VS
详细描述
压电材料中的电介质在受到外力作用时, 会发生形变导致分子间的电荷重新分布, 产生电压。这种现象称为压电效应。利用 压电效应可以制作传感器和换能器等器件 ,广泛应用于声学、电子学和物理学等领 域。
05 电介质在静电场中的研究进展
高介电常数材料的研究
总结词
高介电常数材料在静电场中表现出优异的电 学性能,是当前研究的热点之一。
电介质的极化机制包括电子极化、离子极化和取向极化等,这些机制在不同频率和 强度的电场中表现不同。
电介质的极化状态会影响其在静电场中的行为,如介电常数和电导率等,这些性质 在电子设备和电磁波传播等领域有重要应用。
电介质极化对电场的影响
01
电介质的极化状态会改变静电场的分布,因为电介质的存在会 导致电场畸变。
02
电介质在静电场中的行为可以用Maxwell方程组描述,通过求
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C U B
C = ∑ Ci
i
本章内容
电容器串联
Zhang Shihui
2.串联电容器的电容
UA
C1
C2
Ci
令 U = UA −UB ,U =U +U 1 2
+Ui
UB
等效
q q C1 = , C2 = U1 U2 q q ∵C = = U U1 +U2 +
q Ci = Ui
+Ui
1 1 =∑ C i Ci
3.电介质的极化
Zhang Shihui
3.有外电场存在时电介质的变化 1) 极化
无极分子的极化·位移极化 电场 有极分子的极化 ·取向极化 电场
E0
电子发生位移
E0
电偶极子取向发生偏转
由于热运动,这种取向只能是部分发生,遵守统计规律。
取向极化 本章内容
极化强度
Zhang Shihui
2)极化强度 极化 ∑ i pi 强度 P = Δ V
单位体积内电偶极子矢量和, pi 反映了电介质极化的程度。
= qli
很明显,电介质的极化程度和电偶极子有关。 无外场时,电介质中任 pi = 0 一体积元ΔV内电偶极子 i 的矢量和等于零
∑ ∑
有外场时,电介质被极 pi ≠ 0 化, ΔV 内电偶极子的 E0 i 矢量和不再为零 外场越强,极化程度越高;ΔV内电偶极子矢量和越大。
1)球形电容器 Q ˆ E= r ( R1 ≤ r ≤ R2 ) 2 4πε 0 r R2 Q ⎛ 1 1 ⎞ Δ U = ∫ Edr = − ⎜ ⎟ R1 4πε 0 ⎝ R1 R2 ⎠
4πε 0 R1 R2 Q = 球形电容器 C = R2 − R1 ΔU
本章内容
平行板电容器
Zhang Shihui
充入电介质后的电容和电场
Zhang Shihui
充入电介质前 ΔU 0 充入电介质后 U =
真空中的值
U0
εr
电势差变小,电量不变,导致电容器 的电容变大
Qd ΔU 0 = E0 d = ε0S
Q Q C= = εr = ε C0 ΔU ΔU 0
此外,极板间距和几何条件也没有变, 电势差变小。意味着,场强变弱。 如平行板电容器 E =
本章内容
UA
C
UB
Ui 1 U1 U2 = + + + C q q q
学习指导· P131·第14、15章·习作题6
Zhang Shihui
两只电容器,C1 = 8μF, C2 = 2μF,分别把它们充电到 1000V,然后将它们反接,此时两极板间的电势差为 (A)0V (B)200V (C)600V (D)1000V 解:反接前C1、C2分别带电 C1U 、C2U 反接后 Q′ = C1U − C2U 反接后,设极板间电势差为 U ′ + + - C1 C2 - + +
Q′ = C1U ′ + C2U ′ ⇒ C1U ′ + C2U ′ = C1U − C2U
C1 − C 2 8−2 U = ⇒U′= ⋅ 1000 = 600(V ) C1 + C 2 8+2
本章内容
学习指导· P132·第14、15章·习作题9
Zhang Shihui
C1、C2两个电容器,分别标有200pF(电容)、500V(耐压 值)和300pF、900V。把它们串联起来在两端加上1000V 电压,则 (A) C1被击穿,C2不被击穿; (B) C2被击穿,C1不被击穿; (C) 两者都被击穿;(D) 两者都不被击穿。 解:串联,两电容器带电量相等
Q
−Q
ε
d
真空中静电场能量
S
本章内容
学习指导· P132·第14、15章·习作题8
Zhang Shihui
电容器储存的能量
Zhang Shihui
1.电容器储存的能量
某瞬间,搬运的电量为dq;此时极 板已储存电量q,板间电势差为U。 搬运dq的电量,抵抗电容器极板间 电场力做功为 dA = Udq = ( q C )dq 若最终搬运的总电量为Q,则总功
B
C
K A
ε
电容器在充电过程中获 得能量。充电过程中, 电源将电子从电容器正 极板搬运到负极板;期 间,抵抗电容器极板间 的电场力做功。电容器 能量增加。
1.孤立导体的电容
从有导体存在时的电荷分布和场强分析, 可以看出,无论是孤立的导体,还是多 个导体组成的导体组,都能携带净电荷。
以孤立导体球壳为例
Q
R
U= Q 4πε 0 R
定义
q C= U
升高单位电压所需的 电量为该导体的电容。
表示导体固有的容电本领。 单位:法拉1F = 1C/V 1μ F (微法 ) = 10−6 F
d 1 储能 W = CU 2 2
有电介质存在时的静电场能量 本章内容
例1
Zhang Shihui
例1. 一个导体球半径为R,带电Q。试求, 此带电球体系统的静电能。
Q
R
E=
Q
4πε 0r
2
( r > R) , E = 0 ( r < R)
∞
1 2 2 We = ∫ we dV = ∫ 2 ε 0 E dV = ∫ 32π 2 ε0 r 4 4π r dr R ⎛ all space ⎞ ⎜ ⎟
S
电位移矢量用途
Zhang Shihui
电位移矢量的用途 用于计算有电介质存在的电场 ΔS ∫ D ⋅ dS = S Q ΔS E0 ⇒ D ∫ dS = Q S Q ΔS E' Q⇒D= ⇒ DΔS = ΔS S S E D Q ⇒E= = ε εS 分析平行板间电场 Qd (ε = ε ε > ε ) ⇒ U = Ed = 0 r 0 εS
除颤和频闪 本章内容
A = ∫ Udq = ∫
Q 0
Q
0
q 1 Q2 dq = C 2 C
2
1Q 1 2 = CU 电容器储能 W = 2 2 C
该能量存在于两极板之间的电场中。
静电场的能量
Zhang Shihui
2.静电场的能量 1 ⎛ ε0 ⎞ 1 2 )2 W = CU = ⎜ S ⎟ (Ed 2⎝ d ⎠ 2 1 1 2 = ε 0 E 2V = ε 0 E Sd 2 2
d
平行板电容器
ε0S
d
圆柱形电容器
Zhang Shihui
3)柱形电容器
Q 设单位长度带电量为 λ = h
R2
R1
h
λ E= 2πε 0 r
R2 R1
( R1 ≤ r ≤ R2 )
ΔU = ∫
R2 Q λ dr = ln 2πε 0 r 2πε 0 h R1
R2 R1 Q r
高斯面
−Q
2 πε 0 h 圆柱形电容器 C = ln ( R 2 R1 )
E = E0 + E′, | E |=| E0 | − | E′ |
E0
E′
E0
E′
电介质电泳 本章内容
极化电场
Zhang Shihui
实验发现,对于各项同向的电介质,其极化后的合电场
E = E0 εr
P = ε 0 χ E = ε 0 (ε r −1) E
χ 为电介质的极化率,无量纲;对于均匀介质,是常数。
例. 无限大均匀电介质中,带电量为q的球壳外的场强
ε r 为电介质相对介电常数。ε = ε 0ε r 电介质的介电常数。
E=
E0
εr
=
q 4πε0εr r
2
=
q 4π ε r
2
水的相对介电常数为80
1 E = E0 80
本章内容
4.有电介质时的高斯定理
Zhang Shihui
7.有电介质时的高斯定律
= 9 ×10 m ≈ 1.5 ×10 RE
9 3
直径1cm,电容仅10-15法拉,太小。
太阳直径是地球直径 的109倍;1F的电容 相当于十五个太阳。
本章内容
球形电容器
Zhang Shihui
2.导体组的电容
孤立导体电容很小,作电容器不合适。 那么,转而观察一下导体组的电容。
−Q Q R1
R2
R2、R1大小越接近, 电容越大,易实现。
静电场 能量密度
以平行板电容器为例,分 析电容器能量与电场能量 之间的关系: 设电容为C, 电量为Q; 极板间距为d, 电势差为U,场强为E, 板 间电介质介电常数为ε0。
Q
d
−Q
S
W 1 we = = ε 0 E 2 V 2
U = Ed , C =
ε0S
1 2 静电场能量 We = ∫V ε 0 E dV 2
电介质中
∫∫
S
E0
∑ ⋅ dS =
S
ε0
S
q0
=
∫∫ ε E ⋅ dS
r S S
即
∫∫ ε ε E ⋅ dS = ∑
0 r
S
q0 ⇔
∫∫ ε E ⋅ dS = ∑
S
q0
电位移矢量 有电介质存在 的高斯定理
D =εE
ε = ε 0ε r
质存在时的电场
本章内容
∫∫
S
D ⋅ dS = ∑ q0 用来计算有电介
⎝ of field ⎠
Q2
We =
Q2
8πε 0 R
本章内容
15.4 静电场中的电介质
Zhang Shihui
本章内容
1.充入介质的电容器
Zhang Shihui
1.充入介质的电容器
