控制系统计算机仿真课后答案
《控制系统数字仿真》练习题及答案

《控制系统数字仿真》练习题及答案1. 单选题1. 某系统的函数关系式为y=1/(x3-2x+4),绘制x在0至10之间变化的图形,正确的是()。
A. fplot('1/(x*3-2*x+4)',[0 10])B. fplot('1/(x.^3-2*x+4)',[0 10])C. plot('1/(x.^3-2*x+4)',[0 10])D. plot('1/(x*3-2*x+4)',[0 10])正确答案:B2. 绘制系统零极点图的命令是()。
A. stepB. pzmapC. rlocusD. sgrid正确答案:B3. 将系统零极点形式变换为传递函数形式的命令是()。
A. tf2zpB. ss2tfC. ss2zpD. zp2tf正确答案:D4. AUTOCAD的坐标体系,包括世界坐标和()坐标系。
A. 绝对坐标B. 平面坐标C. 相对坐标D. 用户坐标正确答案:D5. 在MATLAB工作空间中,表示圆周率的特殊变量是()。
A. piB. ansC. iD. eps正确答案:A6. 下列哪条指令是求矩阵的行列式的值()。
A. invB. diagC. detD. eig正确答案:C7. 在CAD网络系统中,以下说法不正确的是()。
A. 设计资料可以共享B. 硬件可以共享C. 电脑文件可以共享D. 可以方便管理设计进度正确答案:C8. i=2; a=2i;b=2*i;c=2*sqrt(-1);程序执行后;a, b, c的值分别是()。
A. a=4,b=4,c=2.0000iB. a=4,b=2.0000i, c=2.0000iC. a=2.0000i, b=4,c=2.0000iD. a=2.0000i,b=2.0000i,c=2.0000i正确答案:C9. 在循环结构中跳出循环,执行循环后面代码的命令为()。
A. returnB. breakC. continueD. keyboard正确答案:B10. figure命令的作用是()。
控制系统仿真matlab第六章习题答案汇总
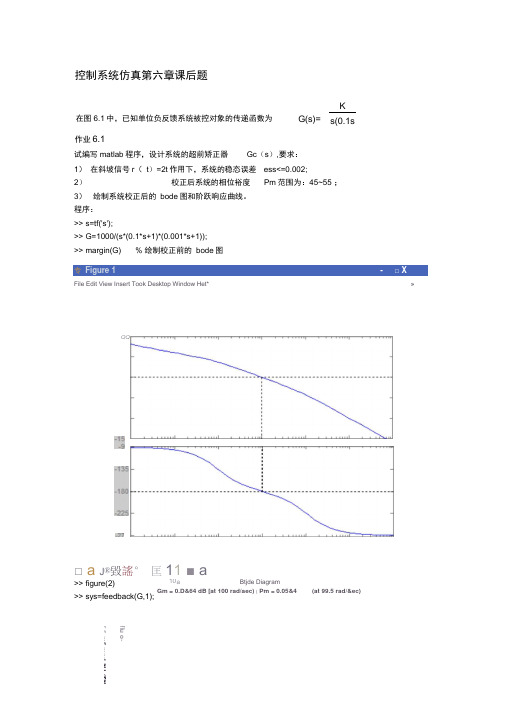
控制系统仿真第六章课后题作业6.1试编写matlab 程序,设计系统的超前矫正器 Gc (s ),要求:1) 在斜坡信号r ( t )=2t 作用下,系统的稳态误差 ess<=0.002;2)校正后系统的相位裕度 Pm 范围为:45~55 ; 3) 绘制系统校正后的 bode 图和阶跃响应曲线。
程序:>> s=tf('s');>> G=1000/(s*(0.1*s+1)*(0.001*s+1));>> margin(G)% 绘制校正前的 bode 图 专 Figure 1 - □ X File Edit View Insert Took Desktop Window Het* »□ a J ®毀謠° 匡11 ■ a >> figure(2)>> sys=feedback(G,1); 在图6.1中,已知单位负反馈系统被控对象的传递函数为G(s)= Ks(0.1s 1)(0.0QQo oBtjde Diagram Gm = 0.D&64 dB [at 100 rad/aec) ( Pm = 0.05&4 (at 99.5 rad/&ec)flu o-5 5 mE mprl 左一6『左 a 10>> step(sys) %绘制校正前的单位阶跃响应曲线Figure 2File Edit 过ew Insert Tools Window Help□已鸟|罠4紗®悬乙| 口目| ■回Step Response1.3>> [Gm,Pm]=margin(G); %该句值计算bode图的增益裕量Gm和相位裕量Pm >> [mag,phase,w]=bode(G); %该句只计算bode图上多个频率点w对应的幅值和相位>> QWPm=50; %取矫正后的相位为50>> Flm=QWPm-Pm+5;>> Flm=Flm*pi/180;>> alfa=(1-si n(FIm))/(1+si n( FIm));>> adb=20*log10(mag);>> am=10*log10(alfa);>> wc=spli ne(adb,w,am);>> T=1/(wc*sqrt(alfa));>> alfat=alfa*T;>> Gc=tf([T 1],[alfat 1]) %校正器的传递函数Tran sfer function:0.01794 s + 1Time 330.00179 s + 1>> figure(3)>> margin(Gc*G) %系统矫正后的bode图Ffgure 3Filt gdit yisw ifisert Hcdt Mfimdcw title】I ■回Bode DiagramGm = 17.6 dB (st 69B rad/sec) s Pm = 4S.2 deg (at 176 rad/sec)"I 0 0 N -- 1 1 I I I ! 1 ! | ! ■' I I ' ' I J I I ........... | I I « i i i | i | i f ■ J !!|!|>> figure(4)>> step(feedback(Gc*G ,1)) % 校正后的单位阶跃响应曲线Figure 4n xl Fie Edit 辺足w Insert Tools Desktop Window HelpO t3 J -S □ S ■ Q1010°ID1 1 孑10Frequency (r&fh'see)作业6.2在图6.1中,已知单位负反馈系统被控对象的传递函数为试编写matlab 程序,设计系统的滞后校正器 Gc ( s ),要求:1) 在斜坡信号r(t)=t 作用下,系统的稳态误差ess 乞0.01 ; 2) 校正后系统的相位裕度 Pm 范围为:40~50 ;3) 绘制系统矫正前后的 bode 图和阶跃响应曲线。
(完整版)计算机控制系统课后习题答案

1-1 什么是计算机控制系统?画出一个实际计算机控制系统原理结构图,并说明一个计算机控制系统由哪些部分组成及各部分的作用。
利用计算机参与控制的系统称为计算机控制系统。
1-2 简述计算机控制系统的控制过程。
实时数据采样实时计算控制量实时控制实时管理1-3 实时、在线方式和离线方式的含义是什么?(1)实时:所谓“实时”,是指信号的输入、计算和输出都是在一定时间范围内完成的,超出了这个时间就会失去控制时机,控制也就失去了意义。
(2)“在线”方式:生产过程和计算机系统直接连接,并接受计算机直接控制的方式称为在线或联机方式。
(3)“离线”方式:若生产过程设备不直接与计算机相连接,其工作不直接受计算机的控制的方式叫做“脱机”方式或“离线”方式。
1-4 计算机控制系统的硬件由哪几部分组成?各部分的作用是什么?主机:这是微型计算机控制系统的核心,通过接口它可以向系统的各个部分发出各种命令,同时对被控对象的被控参数进行实时检测及处理。
输入输出通道:这是微机和生产对象之间进行信息交换的桥梁和纽带。
(3)外部设备:这是实现微机和外界进行信息交换的设备,简称外设,包括人机联系设备(操作台)、输入输出设备(磁盘驱动器、键盘、打印机、显示终端等)和外存贮器(磁盘)。
(4)生产过程装置a.测量变送单元:为了测量各种参数而采用的相应检测元件及变送器。
b.执行机构:要控制生产过程,必须有执行机构。
1.5 计算机控制系统的软件由哪几部分组成?各部分的作用是什么?就功能来分,软件可分为系统软件、应用软件及数据库。
系统软件:它是由计算机设计者提供的专门用来使用和管理计算机的程序。
系统软件包括:a.操作系统:即为管理程序、磁盘操作系统程序、监控程序等;b.诊断系统:指的是调节程序及故障诊断程序;c.开发系统:包括各种程序设计语言、语言处理程序(编译程序)、服务程序(装配程序和编辑程序)、模拟主系统(系统模拟、仿真、移植软件)、数据管理系统等;d.信息处理:指文字翻译、企业管理等。
计算机控制技术与系统仿真答案

第一章绪论1.什么是计算机控制系统?它主要有哪几部分组成?各部分的作用是什么?计算机控制系统是利用计算机(包括其他多种控制器)来实现生产过程或运动对象自动控制的系统。
计算机控制系统主要由控制系统和被控生产过程对象两大部分组成。
控制系统又包括硬件和所匹配的软件。
2.简述计算机控制系统的控制过程。
实时数据采集:利用检测、变送装置,实时地对被控制量的瞬时值进行采集和输入。
实时控制决策:对采集、输入的数据进行比较、分析和处理,并按照预定的控制策略(算法)进行运算,产生决策信号。
实时控制输出:根据决策信号实时控制执行机构,实现对被控制对象的控制任务。
3.计算机控制系统的典型形式有几种?各有什么特点?(1)操作指导控制系统QICS:优点:结构简单、控制灵活和安全。
缺点:由人工控制,速度受到限制,不能控制对象。
(2)直接数字控制系统DDCS:优点:实时性好、可靠性高和适应性强。
(3)监督控制系统SCCS:优点:生产过程始终处于最有工况。
(4)集散控制系统:优点:分散控制、集中操作、分级管理、分而自治和综合协调。
(5)现场总线控制系统:优点:与DOS相比降低了成本,提高了可靠性。
(6)计算机集成制造系统4.试列举计算机控制系统的最新发展趋势,说明研究计算机控制系统的重要性。
大规模及超大规模集成电路的发展,提高了计算机的可靠性和性价比,从而使计算机控制系统的应用也越来越广泛,并逐渐向智能化、网络化和集成化的方向发展。
5.略6.略第三章硬件设计基础1.请说出计算机控制系统常用的主控制器有哪些?各有什么特点?在计算机控制系统中,常用主控制器包括:工业控制计算机(IPC)、可编程序控制器(PLC)、智能工业调节器、数字信号处理器(DSP)、单片机(MCU)、ARM处理器等。
IPC:性能可靠、软件丰富、价格低廉。
PLC:可靠性高,抗干扰嫩力强,硬件配套齐全,功能完善,易学易用:系统的设计、安装、调试工作量小,维护方便,容易改造;体积小,重量轻,能耗低。
控制系统的MATLAB仿真与设计课后答案

控制系统的MATLAB 仿真与设计课后答案第二章1>>x=[15 22 33 94 85 77 60]>>x(6)>>x([1 3 5])>>x(4:end)>>x(find(x>70))2>>T=[1 -2 3 -4 2 -3] ;>>n=length(T);>>TT=T';>>for k=n-1:-1:0>>B(:,n-k)=TT.^k;>>end>>B>>test=vander(T)3>>A=zeros(2,5);>>A(:)=-4:5>>L=abs(A)>3>>islogical(L)>>X=A(L)4>>A=[4,15,-45,10,6;56,0,17,-45,0] >>find(A>=10&A<=20)5>>p1=conv([1,0,2],conv([1,4],[1,1]));>>p2=[1 0 1 1];>>[q,r]=deconv(p1,p2);>>cq='商多项式为 '; cr='余多项式为 ';>>disp([cq,poly2str(q,'s')]),disp([cr,poly2str(r,'s')]) 6>>A=[11 12 13;14 15 16;17 18 19];>>PA=poly(A)>>PPA=poly2str(PA,'s')第三章1>>n=(-10:10)';>>y=abs(n);>>plot(n,y,'r.','MarkerSize',20)>>axis equal>>grid on>>xlabel('n')2>>x=0:pi/100:2*pi;>>y=2*exp(-0.5*x).*sin(2*pi*x);>>plot(x,y),grid on;3>>t=0:pi/50:2*pi;>>x=8*cos(t);>>y=4*sqrt(2)*sin(t);>>z=-4*sqrt(2)*sin(t);>>plot3(x,y,z,'p');>>title('Line in 3-D Space');>>text(0,0,0,'origin');>>xlabel('X'),ylable('Y'),zlable('Z');grid;4>>theta=0:0.01:2*pi;>>rho=sin(2*theta).*cos(2*theta); >>polar(theta,rho,'k');5>>[x,y,z]=sphere(20);>>z1=z;>>z1(:,1:4)=NaN;>>c1=ones(size(z1));>>surf(3*x,3*y,3*z1,c1);>>hold on>>z2=z;>>c2=2*ones(size(z2));>>c2(:,1:4)=3*ones(size(c2(:,1:4))); >>surf(1.5*x,1.5*y,1.5*z2,c2);>>colormap([0,1,0;0.5,0,0;1,0,0]); >>grid on>>hold off第四章1>>for m=100:999m1=fix(m/100);m2=rem(fix(m/10),10);m3=rem(m,10);if m==m1*m1*m1+m2*m2*m2+m3*m3*m3 disp(m)endend2M文件:function[s,p]=fcircle(r)s=pi*r*r;p=2*pi*r;主程序:[s,p]=fcircle(10)3>>y=0;n=100;for i=1:ny=y+1/i/i;end>>y4 M文件:function f=factor(n)if n<=1f=1;elsef=factor(n-1)*n; end主程序:>>s=0;for i=1:5s=s+factor(i);end>>s5>>sum=0;i=1;while sum<sum=sum+i;i=i+1;end;>>n=i-26for循环M文件:function k=jcsum(n) k=0;for i=0:nk=k+2^i;end主程序:>>jcsum(63)While循环M文件:function k=jcsum1(n)k=0;i=0;while i<=nk=k+2^i;i=i+1;end主程序:>>jcsum1(63)第五章1>>A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4]; >>b=[13,-9,6,0]';>>x=A\b2M文件:function f=fxyz(u)x=u(1);y=u(2);z=u(3);f=x+y.^2./x/4+z.^2./y+2./z;主程序:[U,fmin]=fminsearch('fxyz',[0.5,0.5,0.5]) 3>>X=linspace(0,2*pi,50);。
《自动控制系统计算机仿真》习题参考答案

3 0 1 0 X 2 3 0 X 2 u 6 6 1 0
解:1)求特征值法,输入命令
计算结果为 可见,矩阵 A 的特征值实部均为负,因此系统稳定。 2)采用李亚普诺夫第二法, 输入命令
计算结果
显然,P 阵的各阶主子式均为正定,系统稳定。 6-2 某单位负反馈系统的开环控制系统的传递函数为
试求该系统状态空间表达式的对角线标准形。 解:输入语句
计算结果
表明该系统状态空间表达式的对角线标准形为
6
3 0 0 7.762 0 2 0 X 9.798 u X 0 0 1 2.872
4-3 求出以下系统的传递函数
11
运行后,计算出
G C (s)
0.3162s 1 0.1044s 1 5.692 s 1 0.04888s 1
于是,校正后的系统开环传递函数为
GC ( s )G ( s )
0.033s 2 0.4206s 1 200 2 0.2782 s 5.741s 1 s (0.1s 1)(0.01s 1)
, 3-5
,
,
已知某系统的闭环传递函数 ( s ) 如下,试用 roots()命令来判断系统的稳定性。
( s)
解:输入命令
3s 2 2s 5 s 5 2 s 4 4 s 3 5s 2 7 s 6
计算结果如下,系统不稳定
3-6
求复数矩阵 C
1 3i 5 i 7 3i 的转置 C1 与共轭转置 C2。 6 2i 3 2i 4 3i
《自动控制系统计算机仿真》
习题参考答案
控制系统仿真答案
控制系统仿真答案一.选择题二.名词解释及简答题1.系统的三个属性是什么?请解释其具体含义。
答:系统的三个属性:整体性、相关性、隶属性。
整体性:各部分(子系统)不能随意分割。
相关性:各部分(子系统) 以一定的规律或方式相联系,由此决定了其特有的性能。
隶属性:不能清楚的分出系统“内部”与“外部”,常常需要根据研究的问题来确定哪些属于系统的内部因素,哪些属于外部环境,其界限也是随不同的研究目的而变化,将这一特性称之为隶属性。
2.试利用图形表示仿真的基本内容以及其相互关系。
答:3.简述传统的设计流程以及基于虚拟样机的设计流程的区别(可用图形表示)。
答:三.判断题,正确的在括号内打“√”,错误的打“╳”,并改正错误结论重新阐述。
1.(√)为了限制所研究问题涉及的范围,一般用系统边界把被研究的系统与系统环境区分开来。
2.(╳)模型按数学模型的形式分为:物理仿真、数学仿真、数学-物理混合仿真或半实物仿真。
改1:按模型的性质分为:物理仿真、数学仿真、数学-物理混合仿真或半实物仿真。
改2:按数学模型的形式分为:连续系统仿真、离散事件系统仿真、离散—连续系统仿真。
3.(√)series函数可以将两个系统按串联方式连接,它即适合于连续时间系统,也适合于离散时间系统。
4.(√)S-函数为Simulink的“系统”函数,它是能够响应Simulink求解器命令的函数,采用非图形化的方法实现一个动态系统。
5.(╳)Matlab在执行运算符的优先级的时候,逻辑运算符“<”的优先级要高于矩阵乘法运算“*”的优先级。
改:Matlab在执行运算符的优先级的时候,逻辑运算符“<”的优先级要低于矩阵乘法运算“*”的优先级。
四、2、main(){float x,money;Scanf(“%f/n”,&x);If(x<50) then money=2.5*xElse if(x>=50 and x<100)Else if (x>=100)Then money=2.5*x*(1-0.2) ;Printf(“money=%f”,money);}五.综合题1.编程实现以下图形绘制。
《控制系统数字仿真与CAD》张晓华版课后答案doc

2-2.用MATLAB语言求下列系统的状态方程(1)状态方程模型参数:编写matlab 程序如下>>num=[1 7 24 24];>>den=[1 10 35 50 24];>>[AB C D]=tf2ss(num,den)(2) 零极点增益:编写程序>> num=[1 7 24 24];>> den=[1 10 35 50 24];>> [ZPK]=tf2zp(num,den)得到结果Z= -2.7306 + 2.8531 , -2.7306 -2.8531i ,-1.5388P=-4, -3 ,-2 ,-1K=1(3) 部分分式形式:编写程序>> num=[1 7 24 24];>> den=[1 10 35 50 24];>> [R PH]=residue(num,den)得到结果R= 4.0000 ,-6.0000, 2.0000, 1.0000P= -4.0000, -3.0000 , -2.0000 ,-1.0000H=[](2)解:(1)传递函数模型参数:编写程序>>A=[2.25 -5 -1.25 -0.5;2.25 -4.25 -1.25 -0.25;0.25 -0.5 -1.25 -1;1.25 -1.75 -0.25 -0.75];>> B=[4 2 2 0];>> C=[0 2 0 2];>> D=[0];>> [num den]=ss2tf(A,B,C,D)得到结果num = 0 4.0000 14.0000 22.0000 15.0000den=1.0000 4.0000 6.2500 5.2500 2.2500(2) 零极点增益模型参数:A=[2.25 -5 -1.25 -0.5: 2.25 -4.25 -1.25 -0.25 :0.25 -0.5 -1.25 -1: 1.25 -1.75 -0.25 -0.75];B=[4 2 2 0];C=[0 2 0 2];D=[0];[Z,P,K]=ss2zp(A,B,C,D)(3)部分分式形式的模型参数:A=[2.25 -5 -1.25 -0.52.25 -4.25 -1.25 -0.250.25 -0.5 -1.25 -11.25 -1.75 -0.25 -0.75];B=[4 2 2 0]';C=[0 2 0 2];D=[0];[num den]=ss2tf(A,B,C,D)[R,P,H]=residue(num,den)2-6(1)解:m 文件程序为h=0.1;disp('函数的数值解为'); %显示‘’中间的文字%disp('y='); %同上%y=1;fort=0:h:1m=y;disp(y); %显示y 的当前值%y=m-m*h;end保存文件da2.m在matalb 命令行中键入>> da得到结果函数的数值解为y= 1 0.9000 0.8100 0.7290 0.6561 0.5905 0.5314 0.4783 0.4305 0.3874 0.3487 (2)另建一个m文件求解y=e在t∈[0,1]的数值程序为h=0.1;disp('函数的离散时刻解为');disp('y=');fort=0:h:1y=exp(-t);disp(y);end 保存文件da3.m在matalb 命令行中键入>> da3函数的离散时刻解为y= 1 0.9048 0.8187 0.7408 0.6703 0.6065 0.5488 0.4966 0.4493 0.4066 0.3679 2-5.解:(1)编辑m 文件程序h=0.1;disp('四阶龙格-库塔方法求解函数数值解为');disp('y=');y=1;fort=0:h:1disp(y);k1=-y;k2=-(y+k1*h/2);k3=-(y+k2*h/2);k4=-(y+k3*h);y=y+(k1+2*k2+2*k3+k4)*h/6;end 保存文件q5.m在matlab 命令行里键入>> q5得到结果四阶龙格-库塔方法求解函数数值解为y= 1 0.9048 0.8187 0.7408 0.6703 0.6065 0.5488 0.4966 0.4493 0.4066 0.36792-7>>a=[1 0];>> b=[14.6];>> c=[1 3.4 16.35];>> d=conv(a,b);>> e=conv(d,c)e= 1.0000 8.0000 31.9900 75.2100 0>> f=[00 0 5 100];>> g=e+fg= 1.0000 8.0000 31.9900 80.2100 100.0000%以上是计算闭环传递函数的特征多项式以上是计算闭环传递函数的特征多项式以上是计算闭环传递函数的特征多项式以上是计算闭环传递函数的特征多项式%>> p=roots(g) %计算特征多项式的根计算特征多项式的根计算特征多项式的根计算特征多项式的根,,,就是闭环,就是闭环就是闭环就是闭环传递函数的极点传递函数的极点传递函数的极点传递函数的极点%p=-0.9987 + 3.0091i-0.9987 -3.0091i-3.0013 + 0.9697i-3.0013 -0.9697i>> m=[5 100];>> z=roots(m)z= -20 %计算零点计算零点计算零点计算零点%3-2.进行下列计算,给出不使用for 和while 等循环语句的计算方法。
张晓华 控制系统数字仿真与CAD课后答案

质量的技术。
控制系统 CAD 可以解决以频域法为主要内容的经典控制理论和以时域法为
kh
现代控制测略都可利用 CAD 技术实现有效的分析与设计。
答:虚拟现实技术是一种综合了计算机图形技术,多媒体技术,传感器技术,显 示技术以及仿真技术等多种学科而发展起来的高新技术。 1-7 什么是离散系统?什么是离散事件系统?如何用数学的方法描述它们? 答:本书所讲的“离散系统”指的是离散时间系统,即系统中状态变量的变化仅 发生在一组离散时刻上的系统。它一般采用差分方程,离散状态方程和脉冲 传递函数来描述。
(2) 零极点增益: 编写程序
7
24
24 ],D=[0]
w .c
7
24
w w
得到结果 num = 0 den =1.0000 4.0000 14.0000 4.0000 6.2500
w
G( s ) =
若侵犯了您的版权利益,敬请来信通知我们! ℡
kh
(2) 零极点增益模型参数:编写程序>> A=[2.25 -5 -1.25 -0.5 2.25 -4.25 -1.25 -0.25
案 网
.c
om
课后答案网
行非实时仿真。 (5) 易于和实物相连。 1-5 什么是 CAD 技术?控制系统 CAD 可解决那些问题? 答:CAD 技术,即计算机辅助设计(Computer Aided Design),是将计算机高速
断以及创造性思维结合起来,用以快速设计进程,缩短设计周期,提高设计
om
得到结果 Z =-1.0000 + 1.2247i -1.0000 - 1.2247i
P= -0.5000 + 0.8660i K = 4.0000 -0.5000 - 0.8660i
控制系统数字仿真与CAD 全习题答案

第一章习题1-1什么是仿真?它所遵循的基本原则是什么?答:仿真是建立在控制理论,相似理论,信息处理技术和计算技术等理论基础之上的,以计算机和其他专用物理效应设备为工具,利用系统模型对真实或假想的系统进行试验,并借助专家经验知识,统计数据和信息资料对试验结果进行分析和研究,进而做出决策的一门综合性的试验性科学。
它所遵循的基本原则是相似原理。
1-2在系统分析与设计中仿真法与解析法有何区别?各有什么特点?答:解析法就是运用已掌握的理论知识对控制系统进行理论上的分析,计算。
它是一种纯物理意义上的实验分析方法,在对系统的认识过程中具有普遍意义。
由于受到理论的不完善性以及对事物认识的不全面性等因素的影响,其应用往往有很大局限性。
仿真法基于相似原理,是在模型上所进行的系统性能分析与研究的实验方法。
1-3数字仿真包括那几个要素?其关系如何?答: 通常情况下,数字仿真实验包括三个基本要素,即实际系统,数学模型与计算机。
由图可见,将实际系统抽象为数学模型,称之为一次模型化,它还涉及到系统辨识技术问题,统称为建模问题;将数学模型转化为可在计算机上运行的仿真模型,称之为二次模型化,这涉及到仿真技术问题,统称为仿真实验。
1-4为什么说模拟仿真较数字仿真精度低?其优点如何?。
答:由于受到电路元件精度的制约和容易受到外界的干扰,模拟仿真较数字仿真精度低但模拟仿真具有如下优点:(1)描述连续的物理系统的动态过程比较自然和逼真。
(2)仿真速度极快,失真小,结果可信度高。
(3)能快速求解微分方程。
模拟计算机运行时各运算器是并行工作的,模拟机的解题速度与原系统的复杂程度无关。
(4)可以灵活设置仿真试验的时间标尺,既可以进行实时仿真,也可以进行非实时仿真。
(5)易于和实物相连。
1-5什么是CAD技术?控制系统CAD可解决那些问题?答:CAD技术,即计算机辅助设计(Computer Aided Design),是将计算机高速而精确的计算能力,大容量存储和数据的能力与设计者的综合分析,逻辑判断以及创造性思维结合起来,用以快速设计进程,缩短设计周期,提高设计质量的技术。
控制系统的Matlab仿真与设计课后答案

控制系统的Matlab仿真与设计课后答案第一篇:控制系统的Matlab仿真与设计课后答案MATLAB课后习题答案 2.1 x=[15 22 33 94 85 77 60] x(6)x([1 3 5])x(4:end)x(find(x>70))2.3 A=zeros(2,5);A(:)=-4:5L=abs(A)>3 islogical(L)X=A(L)2.4 A=[4,15,-45,10,6;56,0,17,-45,0] find(A>=10&A<=20)2.5 p1=conv([1,0,2],conv([1,4],[1,1]));p2=[1 0 1 1];[q,r]=deconv(p1,p2);cq='商多项式为';cr='余多项式为';disp([cq,poly2str(q,'s')]),disp([cr,poly2str(r,'s')])2.6 A=[11 12 13;14 15 16;17 18 19];PA=poly(A)PPA=poly2str(PA,'s')3.1 n=(-10:10)';y=abs(n);plot(n,y,'r.','MarkerSize',20)axis equal grid on xlabel('n')3.2 x=0:pi/100:2*pi;y=2*exp(-0.5*x).*sin(2*pi*x);plot(x,y),grid on;3.3 t=0:pi/50:2*pi;x=8*cos(t);y=4*sqrt(2)*sin(t);z=-4*sqrt(2)*sin(t);plot3(x,y,z,'p');title('Line in 3-D Space');text(0,0,0,'origin');xlabel('X'),ylable('Y'),zlable('Z');grid;3.4theta=0:0.01:2*pi;rho=sin(2*theta).*cos(2*theta);polar(theta,rho,'k');3.5[x,y,z]=sphere(20);z1=z;z1(:,1:4)=NaN;c1=ones(size(z1));surf(3*x,3*y,3*z1,c1);hold on z2=z;c2=2*ones(size(z2));c2(:,1:4)=3*ones(size(c2(:,1:4)));surf(1.5*x,1.5*y,1.5*z2,c2);col ormap([0,1,0;0.5,0,0;1,0,0]);grid on hold off 第四章function f=factor(n)if n<=1 f=1;elsef=factor(n-1)*n;endfunction[s,p]=fcircle(r)s=pi*r*r;p=2*pi*r;function k=jcsum1(n)k=0;i=0;while i<=n k=k+2^i;i=i+1;end function k=jcsum(n)k=0;for i=0:n k=k+2^i;end4.1for m=100:999m1=fix(m/100);m2=rem(fix(m/10),10);m3=rem(m,10);ifm==m1*m1*m1+m2*m2*m2+m3*m3*m3 disp(m)end end4.2[s,p]=fcircle(10)4.3y=0;n=100;for i=1:ny=y+1/i/i;end y4.4s=0;for i=1:5s=s+factor(i);end s4.5sum=0;i=1;while sum<2000 sum=sum+i;i=i+1;end;n=i-2 4.6jcsum(63)jcsum1(63)4.1 for m=100:999m1=fix(m/100);m2=rem(fix(m/10),10);m3=rem(m,10);if m==m1*m1*m1+m2*m2*m2+m3*m3*m3disp(m)end end 4.3 y=0;n=100;for i=1:ny=y+1/i/i;end y 4.4 s=0;for i=1:5s=s+factor(i);end s 4.5sum=0;i=1;while sum<2000sum=sum+i;i=i+1;end;n=i-2 4.6i=0;k=0;while i<=63k=k+2^i;i=i+1;end k ii=0;k=0;for i=0:63k=k+2^i;end i k第五章functionf=fxyz(u)x=u(1);y=u(2);z=u(3);f=x+y.^2./x/4+z.^2./y+2./z;5.1A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];b=[13,-9,6,0]';x=Ab5.2[U,fmin]=fminsearch('fxyz',[0.5,0.5,0.5])5.3X=linspace(0,2*pi,50);Y=sin(X);P=polyfit(X,Y,3)AX=linspace(0,2*pi,50);Y=sin(X);Y1=polyval( P,X)plot(X,Y,':O',X,Y1,'-*')5.4x=0:2.5:10;h=[0:30:60]';T=[95,14,0,0,0;88,48,32,12,6;67,64,54,48,41];xi=[0:0.5:10];hi= [0:10:60]';temps=interp2(x,h,T,xi,hi,'cubic');mesh(xi,hi,temps);5.1 A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];b=[13,-9,6,0]';x=Ab 5.3X=linspace(0,2*pi,50);Y=sin(X);P=polyfit(X,Y,3)AX=linspace(0,2*p i,50);Y=sin(X);Y1=polyval(P,X)plot(X,Y,':O',X,Y1,'-*')6.1syms x y=finverse(1/tan(x))6.2syms x yf=1/(1+x^2);g=sin(y);fg=compose(f,g)6.3syms xg=(exp(x)+x*sin(x))^(1/2);dg=diff(g)6.4F=int(int('x*exp(-x*y)','x'),'y')6.5syms xF=ztrans(x*exp(-x*10))6.6a=[0 1;-2-3];syms sinv(s*eye(2)-a);6.7 f=solve('a*x^2+b*x+c')6.8 f=solve('x+y+z=1','x-y+z=2','2*x-y-z=1')6.9y=dsolve('D2y+2*Dy+2*y=0','y(0)=1','Dy(0)=0')ezplot(y), grid on6.10a=maple('simplify(sin(x)^2+cos(x)^2);')6.11f=maple('laplace(exp(-3*t)*sin(t),t,s);')6.12 syms t xF=sin(x*t+2*t);L=laplace(F)第七章function[sys,x0,str,ts]=ww(t,x,u,flag)%¶¨ÒåÁ¬ÐøϵͳµÄSº¯Êý A=[0,1;-0.4,-0.2];B=[0;0.2];C=[1,0];D=0;switch flag, case 0,[sys,x0,str,ts]=mdlInitializeSizes(A,B,C,D);case 1,sys=mdlDerivatives(t,x,u,A,B,C,D);case 2,sys=mdlUpdate(t,x,u);case 3,sys=mdlOutputs(t,x,u,A,B,C,D);case 4,sys=mdlGetTimeOfNextVarHit(t,x,u);case 9,sys=mdlTerminate(t,x,u);otherwiseerror(['Unhandled flag = ',num2str(flag)]);end%=============================== function [sys,x0,str,ts]=mdlInitializeSizes(A,B,C,D)sizes = simsizes;sizes.NumContStates = 2;sizes.NumDiscStates = 0;sizes.NumOutputs = 1;sizes.NumInputs = 1;sizes.DirFeedthrough = 1;sizes.NumSampleTimes = 1;sys = simsizes(sizes);x0 = [0;0];str = [];ts = [0 0];%=============================== function sys=mdlDerivatives(t,x,u,A,B,C,D)sys = A*x+B*u;%===============================function sys=mdlUpdate(t,x,u)sys = [];%=============================== functionsys=mdlOutputs(t,x,u,A,B,C,D)sys = C*x+D*u;%=============================== function sys=mdlGetTimeOfNextVarHit(t,x,u)sampleTime = 1;sys = t + sampleTime;%===============================function sys=mdlT erminate(t,x,u)sys = [];7.17.27.37.47.57.67.7第八章8.1num=[5];den=[1,2,2];sys=tf(num,den)8.1.2s = tf('s');H = [5/(s^2+2*s+2)];H.inputdelay =28.1.3h=tf([0.5,0],[1,-0.5,0.5],0.1)8.2num=2*[1,0.5];den=[1,0.2,1.01];sys=tf(num,den)[z,p,k]=tf2zp(num,den);zpk(z,p,k)[A,B,C,D]=tf2ss(num,den);ss(A,B,C,D)8.3 num=[1,5];den=[1,6,5,1];ts=0.1;sysc=tf(num,den);sysd=c2d(sysc,ts,'tustin')8.4.08.4.1 %¶Ôϵͳ·½¿òͼÿ¸ö»·½Ú½øÐбàºÅ,ÓÐ8¸öͨµÀ,ÁÐдÿ¸öͨµÀ´«µÝº¯Êý r1=1;r2=2;c1=3;c2=4;G1=r1;G2=tf(1,[c1,0]);G3=1;%ÊÇ·ÖÀëµãºÍ»ãºÏµãµÄÁ¬Ïß,²»Äܺϲ¢,´«º¯Îª1 G4=-1;G5=1/r2;G6=tf(1,[c2,0]);G7=-1;G8=-1;%½¨Á¢ÎÞÁ¬½ÓµÄ״̬¿Õ¼äÄ£ÐÍG=append(G1,G2,G3,G4,G5,G6,G7,G8)%д³öϵͳµÄÁ¬½Ó¾ØÕóQ=[1 4 0 %ͨµÀ1µÄÊäÈëÊÇͨµÀ4 2 1 7 %ͨµÀ2µÄÊäÈëÊÇͨµÀ1,7 3 2 02 0 53 8 6 5 0 7 5 060];%¸ººÅÔÚ´«º¯ÖÐÌåÏÖ %ÁгöϵͳµÄ×ܵÄÊäÈëºÍÊä³ö¶ËµÄ±àºÅinputs=1;outputs=6;%Éú³É×éºÏºóϵͳµÄ״̬¿Õ¼äÄ£ÐÍsys=connect(G,Q,inputs,outputs)8.4.2r1=1;r2=2;c1=3;c2=4;[A,B,C,D]=linmod('x84');[num,den ]=ss2tf(A,B,C,D);sys=tf(num,den)8.5A=[1,1,0;0,1,0;0,0,2];B=[0,0;1,0;0,-2];n=size(A)Tc=ctrb(A,B);if n==rank(T c)disp('ϵͳÍêÈ«ÄÜ¿Ø');elsedisp('ϵͳ²»ÍêÈ«ÄÜ¿Ø');end 第九章function [rtab,info]=routh(den)info=[];vec1=den(1:2:length(den));nrT=length(vec1);vec2=den(2:2:length(den)-1);rtab=[vec1;vec2,zeros(1,nrT-length(vec2))];for k=1:length(den)-2, alpha(k)=vec1(1)/vec2(1);for i=1:length(vec2),a3(i)=rtab(k,i+1)-alpha(k)*rtab(k+1,i+1);endif sum(abs(a3))==0 a3=polyder(vec2);info=[info,'All elements in row ',...int2str(k+2)' are zeros;'];elseif abs(a3(1))info=[info,'Replaced first element;'];endrtab=[rtab;a3, zeros(1,nrT-length(a3))];vec1=vec2;vec2=a3;end9.1num=[2,5,1];den=[1,2,3];bode(num,den);grid on;figure;nyquist(num,den);9.2num=5*[1,5,6];den=[1,6,10,8];step(num,den);gridon;figure;impulse(num,den);grid on;9.3kosi=0.7;wn=6;num=wn^2;den=[1,2*kosi*wn,wn^2];step(num,den);grid on;figure;impulse(num,den);gridon;9.4den=[1,2,8,12,20,16,16];[rtab,info]=routh(den)a=rtab(:,1) if all(a>0)disp('ϵͳÊÇÎȶ¨µÄ');elsedisp('ϵͳÊDz»Îȶ¨µÄ');end9.5num=7*[1,5];den=conv([1,0,0],conv([1,10],[1,1]));[gm,pm,wg,wc]=margin(num,den)9.1 >> sys=tf([2,5,1],[1,2,3])Transfer function: 2 s^2 + 5 s + 1---------------s^2 + 2 s + 3>> rlocus(sys)>> nyquist(sys)>> bode(sys)9.2>> G=tf(conv([5],[1,5,6]),[1,6,10,8]);>> step(G)>> impulse(G) sys=tf([5,25,30],[1,6,10,8]);>> step(sys)>> impulse(sys)9.4>> GH=tf(conv([7],[1,5]),conv([1,0,0],conv([1,10],[1,1])));>> [Gm,Pm,Wcg,Wcp]=margin(GH)Gm =0 Pm =-47.2870 Wcg =0 Wcp = 1.4354 >>GH=tf(conv([7],[1,5]),conv([1,0,0],conv([1,10],[1,1])));>>[Gm,Pm,Wcg,Wcp]=margin(GH)GH_close=feedback(GH,1)step( GH_close),grid on Gm =0 Pm =-47.2870 Wcg =0 Wcp =1.4354 第十章function s=bpts2s(bp,ts,delta)kosi=sqrt(1-1./(1+((1./pi).*log(1./bp)).^2));wn=-log(delta.*sqrt(1-kosi.^2))/(kosi.*ts);s=-kosi.*wn+j.*wn.*sqrt(1-kosi.^2);function[ngc,dgc]=fa_lead(ng0,dg0,Pm,wc,w)ngv=polyval(ng0,j*wc);dgv=polyval(dg0,j*wc);g=ngv/dgv;thetag=angle(g);mg=abs(g);thetar=Pm*pi/180;tz=(1+mg*cos(thetar-thetag))/(-wc*mg*sin(thetar-thetag));tp=(cos(thetar-thetag)+mg)/(wc*sin(thetar-thetag));ngc=[tz,1];dgc=[tp,1];function[ngc,dgc]=fg_lag_pm(ng0,dg0,w,Pm)[mu,pu]=bode(ng0,dg0,w);wgc=spline(pu,w,Pm+5-180);%²åÖµÇóÈ¡Âú×ãÏà½ÇÔ£¶ÈµÄ½ÇƵÂÊ×÷ΪÆÚÍûµÄ¼ôÇÐƵÂÊngv=polyval(ng0,j*wgc);dgv=polyval(dg0,j*wgc);g=ngv/dgv;alph=abs(1/g);T=10/alph*wgc, ngc=[alph*T,1];dgc=[T,1];function[ngc,dgc]=fg_lag_wc(ng0,dg0,w,wc)ngv=polyval(ng0,j*wc);dgv=polyval(dg0,j*wc);g=ngv/dgv;alph=abs(1/g);T=10/(alph*wc);ngc=[alph*T,1];dgc=[T,1];function[ngc,dgc]=fg_lead_pd(ng0,dg0,wc)ngv=polyval(ng0,j*wc);dg v=polyval(dg0,j*wc);g=ngv/dgv;mg0=abs(g);t=sqrt(((1/mg0)^2-1)/(wc^2));%·ùÖµÏà¼ÓΪÁãngc=[t,1];dgc=[1];%Gc(s)=1+Tsfunction[ngc,dgc]=fg_lead_pm(ng0,dg0,Pm,w)[mu,pu]=bode(ng0,dg0,w);%¼ÆËãÔ-ϵͳµÄ¶ÔÊýƵÂÊÏìÓ¦Êý¾Ý[gm,pm,wcg,wcp]=margin(mu,pu,w);%ÇóÈ¡Ô-ϵͳµÄÏà½ÇÔ£¶ÈºÍ¼ôÇÐƵÂÊalf=ceil(Pm-pm+5);%¼ÆËã¿ØÖÆÆ÷ÌṩµÄ×î´ó³¬Ç°½Ç¶È£¬phi=(alf)*pi/180;%½«×î´ó³¬Ç°½Çת»»Îª»¡¶Èµ¥Î»a=(1+sin(phi))/(1-sin(phi));%¼ÆËãaÖµdbmu=20*log10(mu);%ϵͳµÄ¶ÔÊý·ùÖµmm=-10*log10(a);%wm´¦µÄ¿ØÖÆÆ÷¶ÔÊý·ùÖµwgc=spline(dbm u,w,mm);%²îÖµÇóÈ¡wm£¬ÈÏΪwm£½wcT=1/(wgc*sqrt(a));%¼ÆËãTngc=[a*T,1];dgc=[T,1];function[ngc,dgc]=fg_lead_pm_wc(ng0,dg0,Pm,wc,w)[mu,pu]=bode(ng0,dg0,w);ngv=polyval(ng0,j*wc);dgv=poly val(dg0,j*wc);g=ngv/dgv;%ÇóÔ-ϵͳÔÚÆÚÍûµÄ¼ôÇÐƵÂÊ´¦µÄƵÂÊÏìÓ¦Êý¾ÝG0(jwc) theta=180*angle(g)/pi;%Ô-ϵͳÔÚÆÚÍûµÄ¼ôÇÐƵÂÊ´¦µÄÏà½ÇÔ£¶È£¬µ¥Î»Îª¶Èalf=ceil(Pm-(theta+180)+5);%×î´ó³¬Ç°½Ç phi=(alf)*pi/180;a=(1+sin(phi))/(1-sin(phi));dbmu=20*log10(mu);mm=-10*log10(a);wgc=spline(dbmu,w,mm);T=1/(wgc*sqrt(a));KK=128;s1=-2+i*2*sqrt(3);a=2ng0=[10];dg0=conv([1,0],conv([1,2],[1,8]));g0=tf(ng0,dg0);[ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a);gc=tf(ngc,dgc)function s=kw2s(kosi,wn)s=-kosi.*wn+j*wn.*sqrt(1-kosi.^2);10.1ng0=[1];dg0=10000*[1 0-1.1772];g0=tf(ng0,dg0);%Âú×㿪»·ÔöÒæµÄΪУÕýϵͳµÄ´«µÝº¯Êýs=kw2s(0.7,0.5)%ÆÚÍûµÄ±Õ»·Ö÷µ¼¼«µãngc=rg_lead(ng0,dg0,s);gc=tf(ngc,1)g0c=tf(g0*gc);rlocus(g0 ,g0c);b1=feedback(g0,1);%δУÕýϵͳµÄ±Õ»·´«µÝº¯Êýb2=feedback(g0c,1);%УÕýºóϵͳµÄ±Õ»·´«µÝº¯Êýfigure,step(b1,'r--',b2,'b');gridon %»æÖÆУÕýÇ°ºóϵͳµÄµ¥Î»½×Ô¾KK=20;s1=-2+i*sqrt(6);a=1ng0=[10];dg0=conv([1,0],[1,4]);g0=tf(ng0,dg0);[ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a);gc=tf(ngc,dgc)g0c=tf(K K*g0*gc);b1=feedback(k*g0,1);b2=feedback(g0c,1);step(b1,'r--',b2,'b');grid ong0c=tf(KK*g0*gc);rlocus(g0,g0c);b1=feedback(k*g0,1);b2=feedback(g0c,1);figure,step(b1,'r--',b2,'b');grid onng0=[1];dg0=conv([1,0,0],[1,5]);g0=tf(ng0,dg0);w=logspace (-3,3);KK=1;Pm=50;[ngc,dgc]=lead4(ng0,dg0,KK,Pm,w);gc=tf(ngc,dgc);g0c=tf(KK*g0*gc);bode(KK*g0,w);holdon,bode(g0c,w);grid on,hold off [gm,pm,wcg,wcp]=margin(g0c)Kg=20*log10(gm)g1=feedback( g0c,1);bode(g1),grid on, [mag,phase,w]=bode(g1);a=find(mag<=0.707*mag(1));wb=w(a( 1))max(mag)b=find(mag==max(mag))wr=w(b)KK=40;Pm=50;ng0= KK *[1];dg0=conv([1,0],conv([1,1],[1,4]));g0=tf(ng0,dg0);w=logspace(-2,4);[ngc,dgc]=fg_lead_pm(ng0,dg0,Pm,w)gc=tf(ngc,dgc),g0c=tf(g0*gc);b1=feedback(g0,1);b2=feedback(g0c,1);step(b1,'r--', b2,'b');grid on figure, bode(g0,'r--',g0c,'b',w), grid on,[gm,pm,wcg,wcp]=margin(g0c), Km=20*log10(gm) KK=200;bp=0.3;ts=0.7;delta=0.05;ng0=[1];dg0=conv([1,0],conv([0.1,1],conv([0.021],conv([0.01,1],[0.005 1]))));g0=tf(ng0,dg0);w=logspace(-4,3);t=[0:0.1:3];[mag,phase]=bode(KK*g0,w);[gm0,pm0,wg0,wc0] =margin(mag,phase,w),gm0=20*log10(gm0)%gm0 =-15.6769 %2¡¢È·¶¨ÆÚÍûµÄ¿ª»·´«µÝº¯Êý mr=0.6+2.5*bp;wc=ceil((2+1.5*(mr-1)+2.5*(mr-1)^2)*pi/ts), h=(mr+1)/(mr-1)w1=2*wc/(h+1), w2=h*w1 w1=wc/10;w2=25;ng1=[1/w1,1];dg1=conv([1/w2,1],conv([1,0],[1 ,0]));g1=tf(ng1,dg1);g=polyval(ng1,j*wc)/polyval(dg1,j*wc);K=abs(1/g);%¼ôÇÐƵÂÊ´¦·ùֵΪ1£¬ÇóKÖµ g1=tf(K*g1)%3¡¢È·¶¨·´À¡»·½Ú´«µÝº¯Êýh=tf(dg1,ng1);Kh=1/K;h=tf(Kh*h)%ÆÚÍûƵÂÊÌØÐԵĵ¹ÌØÐÔ%4¡¢ÑéËãÐÔÄÜÖ¸±êg2=feedback(KK*g0,h);%УÕýºó£¬ÏµÍ³µÄ¿ª»·´«µÝº¯Êýb1=feedback(KK*g0,1);b2=feedback(g2,1);bode(KK*g0,'r--',g2,'b',h,'g',w);grid onfigure,step(b1, 'r--',b2, 'b',t);grid on,[pos,tr,ts,tp]=stepchar(b2,delta)function[ngc,dgc]=lag2(ng0,dg0,w,KK,Pm)[mu,pu]=bode(KK*ng0,dg 0,w);wgc=spline(pu,w,Pm+5-180),ngv=polyval(KK*ng0,j*wgc);dgv=polyval(dg0,j*wgc);g=ngv/dgv;alph=abs(1/g), T=10/alph*wgc, ngc=[alph*T,1];dgc=[T,1];function[ngc,dgc]=lead4(ng0,dg0,KK,Pm,w)[mu,pu]=bode(KK*ng0,d g0,w);[gm,pm,wcg,wcp]=margin(mu,pu,w);alf=ceil(Pm-pm+5);phi=(alf)*pi/180;a=(1+sin(phi))/(1-sin(phi)), dbmu=20*log10(mu);mm=-10*log10(a);wgc=spline(dbmu,w,mm), T=1/(wgc*sqrt(a)),ngc=[a*T,1];dgc=[T,1];function[ngc,dgc]=ra_lead(ng0,dg0,s1)ngv=polyval(ng0,s1);dgv=pol yval(dg0,s1);g=ngv/dgv;thetag=angle(g);mg=abs(g);thetas=ang le(s1);ms=abs(s1);tz=(sin(thetas)-mg*sin(thetag-thetas))/(mg*ms*sin(thetag));tp=-(mg*sin(thetas)+sin(thetag+thetas))/(ms*sin(thetag));ngc=[tz,1]; dgc=[tp,1];function[ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a)ngv=polyval(ng0,s1);dgv=polyval(dg0,s1);g=dgv/ngv;k=abs(g);%ÆÚÍûÖ÷µ¼¼«µã´¦µÄ¸ù¹ì¼£ÔöÒæ beta=k/KK;[kosi1,wn1]=s2kw(s1);zc=-wn1*sin(a*pi/180)/sin(pi-atan(sqrt(1-kosi1^2)/kosi1)-(a*pi/180));%ÀûÓÃÕýÏÒ¶¨Àí pc=beta*zc;ngc=beta*[1,-zc];dgc=[1,-pc];functionvarargout=rg_lead(ng0,dg0,s1)if nargout==1ngv=polyval(ng0,s1);dgv=polyval(dg0,s1);g=ngv/dgv;thetal=pi-angle(g);zc=real(s1)-imag(s1)/tan(thetal);t=-1/zc;varargout{1}=[t,1];elseif nargout==2 ngv=polyval(ng0,s1);dgv=polyval(dg0,s1);g=ngv/dgv;theta=angle(g);phi=angle(s1);if theta>0 phi_c=pi-theta;endif theta<0;phi_c=-thetaendtheta_z=(phi+phi_c)/2;theta_p=(phi-phi_c)/2;z_c=real(s1)-imag(s1)/tan(theta_z);p_c=real(s1)-imag(s1)/tan(theta_p);nk=[1-z_c];varargout{2}=[1-p_c];kc=abs(p_c/z_c);if theta<0 kc=-kcendvarargout{1}=kc*nk;elseerror('Êä³ö±äÁ¿ÊýÄ¿²»ÕýÈ·£¡');endfunction [bp,ts]=s2bpts(s,delta)[kosi,wn]=s2kw(s);bp=exp(-kosi.*pi./sqrt(1-kosi.^2));ts=-1./(kosi.*wn)*log(delta.*sqrt(1-kosi.^2));function[kosi,wn]=s2kw(s)kosi=1./sqrt(1+(imag(s)/real(s)).^2);wn=-real(s)./kosi;%Èç¹ûwnΪ¸ºÖµ£¬ÔòwnÈ¡Õý£¬²¢ÇÒkosiÈ¡·´iwn=(wn<0);wn(iwn)=-wn(iwn);kosi(iwn)=-kosi(iwn);function[pos,tr,ts,tp]=stepchar(g0,delta)[y,t]=step(g0);[mp,ind]=max(y);dimt=length(t);yss=y(dimt);pos=100*(mp-yss)/yss;tp=t(ind);for i=1:dimtif y(i)>=1 tr=t(i);break;end end;for i=1:length(y)ify(i)<=(1-delta)*yss|y(i)>=(1+delta)*yss ts=t(i);end end第十一章11.1a=[0 1 0;0 0 1;-1-5-6];b=[0 0 1]';p=[-2+4j;-2-4j;-10];K=acker(a,b,p)eig(a-b*K)11.2a=[0 1 0;0 0 1;-6-11-6];b=[1,0,0]';p=[-2+2*sqrt(3)*j;-2-2*sqrt(3)*j;-10];K=acker(a,b,p)eig(a-b*K)11.6A=[-1 0 0;0-2-3;0 0-3];B=[1 0;2 3;-3-3];C=[1 0 0;1 1 1 ];[G,K,L]=decoupling(A,B,C)11.8A=[0 20.6;1 0];b=[0 1]';c=[0 1];d=0;G=ss(A,b,c,d);Q=diag([1,0,0,0,0]);R=1;p=[-1.8+2.4j;-1.8-2.4j];[k,P]=lqr(A,b,Q,R);l=(acker(A',c',p))' Gc=-reg(G,k,l);zpk(Gc), eig(Gc.a), t=0:0.05:2;G_1=feedback(G*Gc,1);a1=eig(G_1.a), y_1=step(G_1,t);第十二章function[t,xx]=diffstate(G,H,x0,u0,N,T)xk=x0;u=u0;t=0 for k=1:N xk=G*xk+H*u;x(:,k)=xk;t=[t,k*T];end;xx=[x0,x];12.1function sys=M601(t,x)u=1;sys=[x(2);x(3);-800*x(1)-80*x(2)-24*x(3)+u];function[t,y]=ode4(A,B,C,D,x0,h,r,v,t0,tf)Ab=A-B*v*C;B=B;C=C;x=x0';y=0;t=t0;N=round((tf-t0)/h);for i=1:N k1=Ab*x+B*r;k2=Ab*(x+h*k1/2)+B*r;k3=Ab*(x+h*k2/2)+B*r;k4=Ab*(x+h *k3)+B*r;x=x+h*(k1+2*k2+2*k3+k4)/6;y=[y,C*x];t=[t,t(i)+h];end 12.1tspan=[0,10];x0=[0,0,0]';[t,y]=ode45('M601',tspan,x0);y1=800*y(:,1);plot(t,y1);12.2 num=10;den=conv([1,0],conv([1,2],[1,3]));[A,B,C,D]=tf2ss(num,den);x0=[0,0,0];v=1;t0=0;tf=10;h=0.01; r=1;[t,y]=ode4(A,B,C,D,x0,h,r,v,t0,tf);plot(t,y),grid12.3 12.4 g=[-2.8-1.4 0 0;1.4 0 0 0;-1.8-0.3-1.4-0.6;0 0 0.6 0];h=[1 0 1 0]';c=[0 0 0 1];d=0;x0=[0 0 0 0]';u=1;N=30;T=0.1;[t,xx]=diffstate(g,h,x0,u,N,T);plot(t,xx);y=c*xx;figurestairs(t,y)grid on12.6 第十四章14.1clear all;load optcar.mat;t=signals(1,:);p=signals(2,:);v=signals(3,:);a=signals(4,:);theta =signals(5,:);subplot(4,1,1);plot(t,p);gridon;ylabel('λÖÃ(m)');subplot(4,1,2);plot(t,v);gridon;ylabel('ËÙ¶È(m/s)');subplot(4,1,3);plot(t,a);gridon;ylabel('¼ÓËÙ¶È(m/s2)');subplot(4,1,4);plot(t,theta);gridon;ylabel('½Ç¶È(¶È)');14.1clear all loadcar.mat %½«µ¼Èëµ½car.matÖеķÂÕæʵÑéÊý¾Ý¶Á³ö t=signals(1,:);x=signals(2,:);theta=signals(3,:);x1=signals(4,:);thet a1=signals(5,:);plot(t,x,t,x1);ylabel('С³µÎ»ÖÃ(m)'),grid on;%»æÖÆ¿ØÖÆÁ¦×÷ÓÃϽüËÆÄ£Ðͺ;«È·Ä£ÐÍxµÄµ¥Î»½×Ô¾ÏìÓ¦ÇúÏß figure % »æÖÆ¿ØÖÆÁ¦×÷ÓÃϽüËÆÄ£Ðͺ;«È·Ä£ÐÍthetaµÄµ¥Î»½×Ô¾ÏìÓ¦ÇúÏßplot(t,theta,t,theta1);ylabel('°Ú½ÇÖµ(rad)'),grid on;第二篇:控制系统的MATLAB仿真与设计课后答案第二章1>>x=[15 22 33 94 85 77 60] >>x(6)>>x([1 3 5])>>x(4:end)>>x(find(x>70))2>>T=[1-2 3-4 2-3];>>n=length(T);>>TT=T';>>for k=n-1:-1:0 >>B(:,n-k)=TT.^k;>>end >>B >>test=vander(T)3>>A=zeros(2,5);>>A(:) =-4:5 >>L=abs(A)>3 >>islogical(L)>>X=A(L)4>>A=[4,15,-45,10,6;56,0,17,-45,0] >>find(A>=10&A<=20)5>>p1=conv([1,0,2],conv([1,4],[1,1 ]));>>p2=[1 0 1 1];>>[q,r]=deconv(p1,p2);>>cq='商多项式为';cr='余多项式为';>>disp([cq,poly2str(q,'s')]),disp([cr,poly2str(r,'s')])6>>A=[11 12 13;14 15 16;17 18 19];>>PA=poly(A)>>PPA=poly2str(PA,'s')第三章1>>n=(-10:10)';>>y=abs(n);>>plot(n,y,'r.','MarkerSize',20)>>axisequal >>grid on>>xlabel('n')2>>x=0:pi/100:2*pi;>>y=2*exp(-0.5*x).*sin(2*pi*x);>>plot(x,y),gridon;3>>t=0:pi/50:2*pi;>>x=8*cos(t);>>y=4*sqrt(2)*sin(t);>>z=-4*sqrt(2)*sin(t);>>plot3(x,y,z,'p');>>title('Line in 3-D Space');>>text(0,0,0,'origin');>>xlabel('X'),ylable('Y'),zlable('Z');gr id;4>>theta=0:0.01:2*pi;>>rho=sin(2*theta).*cos(2*theta);>>po lar(theta,rho,'k');5>>[x,y,z]=sphere(20);>>z1=z;>>z1(:,1:4)=NaN ;>>c1=ones(size(z1));>>surf(3*x,3*y,3*z1,c1);>>holdon >>z2=z;>>c2=2*ones(size(z2));>>c2(:,1:4)=3*ones(size(c2(:,1 :4)));>>surf(1.5*x,1.5*y,1.5*z2,c2);>>colormap([0,1,0;0.5,0,0;1,0,0 ]);>>grid on >>hold off第四章1>>for m=100:999 m1=fix(m/100);m2=rem(fix(m/10),10);m3=rem(m,10);ifm==m1*m1*m1+m2*m2*m2+m3*m3*m3 disp(m)end end M文件:function[s,p]=fcircle(r)s=pi*r*r;p=2*pi*r;主程序:[s,p]=fcircle(10)3>>y=0;n=100;for i=1:n y=y+1/i/i;end >>y M文件:function f=factor(n)if n<=1 f=1;elsef=factor(n-1)*n;end主程序:>>s=0;for i=1:5 s=s+factor(i);end >>s5>>sum=0;i=1;while sum<2000 sum=sum+i;i=i+1;end;>>n=i-26 for循环M文件:function k=jcsum(n)k=0;for i=0:n k=k+2^i;end主程序: >>jcsum(63)While循环M文件: function k=jcsum1(n)k=0;i=0;while i<=n k=k+2^i;i=i+1;end主程序:>>jcsum1(63)第五章1>>A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];>>b=[13,-9,6,0]';>>x=Ab M文件:functionf=fxyz(u)x=u(1);y=u(2);z=u(3);f=x+y.^2./x/4+z.^2./y+2./z;主程序:[U,fmin]=fminsearch('fxyz',[0.5,0.5,0.5])3>>X=linspace(0,2*p i,50);>>Y=sin(X);>>P=polyfit(X,Y,3)>>AX=linspace(0,2*pi,50);>>Y=sin(X);>>Y1=polyval(P,X)>>plot(X,Y,':O',X,Y1,'-*')4>>x=0:2.5:10;>>h=[0:30:60]';>>T=[95,14,0,0,0;88,48,32,12,6; 67,64,54,48,41];>>xi=[0:0.5:10];>>hi=[0:10:60]';>>temps=interp 2(x,h,T,xi,hi,'cubic');>>mesh(xi,hi,temps);第六章1>>syms x>>y=finverse(1/tan(x))2>>syms x y>>f=1/(1+x^2);g=sin(y);>>fg=compose(f,g)3>>syms x>>g=(exp(x)+x*sin(x))^(1/2);>>dg=diff(g)4>>F=int(int('x*e xp(-x*y)','x'),'y')5>>syms x>>F=ztrans(x*exp(-x*10))6>>a=[0 1;-2-3];>>syms s>>inv(s*eye(2)-a);7>>f=solve('a*x^2+b*x+c')8>>f=solve('x+y+z=1','x-y+z=2','2*x-y-z=1')9>>y=dsolve('D2y+2*Dy+2*y=0','y(0)=1','Dy(0)=0')>>ezpl ot(y),grid on10>>a=maple('simplify(sin(x)^2+cos(x)^2);')11>>f=maple(' laplace(exp(-3*t)*sin(t),t,s);')12>>syms t x>>F=sin(x*t+2*t);>>L=laplace(F)第七章第八章1-1>>h=tf([5,0],[1,2,2])1-2>>s = tf('s');>>H = [5/(s^2+2*s+2)];>>H.inputdelay =2 1-3>>h=tf([0.5,0],[1,-0.5,0.5],0.1)2>>num=2*[1,0.5];den=[1,0.2,1.01];>>sys=tf(num,d en)>>[z,p,k]=tf2zp(num,den);>>zpk(z,p,k)>>[A,B,C,D]=tf2ss(nu m,den);>>ss(A,B,C,D)3 >>num=[1,5];den=[1,6,5,1];ts=0.1;>>sys c=tf(num,den);>>sysd=c2d(sysc,ts,'tustin')>>r1=1;r2=2;c1=3;c2=4;>>[A,B,C,D]=linmod('x84');>>[num ,den]=ss2tf(A,B,C,D);>>sys=tf(num,den)5>>A=[1,1,0;0,1,0;0,0,2]; B=[0,0;1,0;0,-2];>>n=size(A)>>Tc=ctrb(A,B);if n==rank(Tc)disp('系统完全能控');elsedisp('系统不完全能控');end第九章1>>num=[2,5,1];den=[1,2,3];>>bode(num,den);grid on;>>figure;>>nyquist(num,den);2>>num=5*[1,5,6];den=[1,6,1 0,8];>>step(num,den);gridon;>>figure;>>impulse(num,den);gridon;3>>kosi=0.7;wn=6;>>num=wn^2;den=[1,2*kosi*wn,wn^2]; >>step(num,den);grid on;>>figure;>>impulse(num,den);grid on;4 M文件:function[rtab,info]=routh(den)info=[];vec1=den(1:2:length(den));nrT=len gth(vec1);vec2=den(2:2:length(den)-1);rtab=[vec1;vec2,zeros(1,nrT-length(vec2))];for k=1:length(den)-2, alpha(k)=vec1(1)/vec2(1);for i=1:length(vec2), a3(i)=rtab(k,i+1)-alpha(k)*rtab(k+1,i+1);endif sum(abs(a3))==0 a3=polyder(vec2);info=[info,'All elements in row ',...int2str(k+2)' are zeros;'];elseif abs(a3(1)) rtab=[rtab;a3, zeros(1,nrT-length(a3))];vec1=vec2;vec2=a3;end主程序:>>den=[1,2,8,12,20,16,16];>>[rtab,info]=routh(den)>>a=rt ab(:,1)if all(a>0)disp('系统是稳定的');elsedisp('系统是不稳定的');end5>>num=7*[1,5];den=conv([1,0,0],conv([1,10],[1,1]));>>[gm ,pm,wg,wc]=margin(num,den)第十章 M文件:。
控制系统数字仿真与CAD习题全答案

2-2.用 matlab 语言求下列系统的状态方程、传递函数、零极点增益、和部分分 式形式的模型参数,并分别写出其相应的数学模型表达式:
(1)
G(s)=
s3 + 7s2 + 24s + 24 s4 +10s3 + 35s2 + 50s + 24
2.25 -5 -1.25 -0.5 4
(2)
.
X
=
(3)部分分式形式的模型参数:编写程序>> A=[2.25 -5 -1.25 -0.5 2.25 -4.25 -1.25 -0.25 0.25 -0.5 -1.25 -1 1.25 -1.75 -0.25 -0.75];
>> B=[4 2 2 0]'; >> C=[0 2 0 2]; >> D=[0]; >> [num den]=ss2tf(A,B,C,D) >> [R,P,H]=residue(num,den)
指令与控制台指令与控制台指令与控制台指令与控制台角度读角度读角度读角度读出装置出装置出装置出装置转台电子转台电子转台电子转台电子驱动器驱动器驱动器驱动器陀螺陀螺陀螺陀螺力矩器力矩器力矩器力矩器星敏感器星敏感器星敏感器星敏感器地球模拟器地球模拟器地球模拟器地球模拟器指令译码器指令译码器指令译码器指令译码器星光模拟器星光模拟器星光模拟器星光模拟器姿态控制系统电子装置姿态控制系统电子装置姿态控制系统电子装置姿态控制系统电子装置射频敏感器射频敏感器射频敏感器射频敏感器太阳敏感器太阳敏感器太阳敏感器太阳敏感器混合计算机混合计算机混合计算机混合计算机太阳模拟器太阳模拟器太阳模拟器太阳模拟器数字部分数字部分数字部分数字部分接口接口接口接口卫星动力学卫星动力学卫星动力学卫星动力学三轴机械转台三轴机械转台三轴机械转台三轴机械转台模拟部分模拟部分模拟部分模拟部分地球敏感器地球敏感器地球敏感器地球敏感器8888卫星姿态控制仿真试验系统卫星姿态控制仿真试验系统卫星姿态控制仿真试验系统卫星姿态控制仿真试验系统第二章习题第二章习题第二章习题第二章习题21212121思考题思考题思考题思考题
控制系统仿真期末考试题及答案

《自动控制系统计算机仿真》习题参考答案1-1什么是仿真?它的主要优点是什么?它所遵循的基本康JM是什么?答:所谓仿耳,畝是使用其它相似的系统来樓仿曳实的需要研究的系统.计算机仿真是指以数字计算机为主要工具,编写并且运行反映真实系统运行状况的程序.对计算机■出的信息进行分析和研究,从而对实际系统运行状杏和演化规律进行編合评估与预测.它是非的设计自动控制系统或甘评价系统性能和功能的一种技术手段.仿真的主要优点是,方便快捷、成本低巌、工作效車和计算II度都很高.它所遵循的基本原则是相似性原理.1-2你认为计算机仿真的发展方向是什么?各;向模型更加准确的方向发展,向虐拟现实技术,以及高技术智能化、一体化方向发尺.向更加广■的时空发展.1-3计算机敷字仿真包括■些要素?它们的关系如何?答,计算机仿真的三要素是:系一丸的对象、模一系统的抽象、计算机一真的工具和手段.它<1的关系是相互依存.2-1控制算法的步长应该如何选择?«:控制算法步长的选择应该怡当.如果步长太小,就会增加迭代次数,增加计算量;如果步长太大,计算碳養将显著堆加,甚至造成计算结杲失真.2-2通常控制系统的建模有■几种方法?4t. i\ *»、1、绘厶2-2通常控制系统的建模有■几种方法?I)机理建模法,2)实鲨麓模法;3)综合建模法.2-3用欧拉法求以下系统的■出响应)•(/)在0W/W1上"0.1时的效值解・y + y = 0, y(0) = 0.8解,输入以下语句dt=0. 1; X set stepy=0.8; % set initial valuefor 1=1:10;尸y-y拿dt; yl (i+l)=y;endt=0:0. 1:1; yl (1)=0. 8;plot (t,yl)2-4用二阶龙格库塔法对2・3恳求敬值解.并且比较两种方法的结杲.解:•入以下语句 dt=O. 1: X set rtopy=0. 8. kl=-0. 8; k2=-0. 8. X set initial value for i«l: 10;y=y+(dt/2)•(kl+k2); k2=-y. yl(i*l)=y; endt=0:0. 1:1, yl (1)=0. 8.plot (t^yl) 经过比较两种方法的结杲•发现它们几乎汉有什么差别•2<X)3-1編写两个m 文件.分别使用for 和Mhile 循环语句计算工mi解:■入语句A=(l 0 2;1 1 3;3 1 2); B=(2;l;l]; X=inv(A) *B3-3已知矩阵"0 1 3'■ ■2 1 8A= 1 2 1,B= 4 1 4.5 4 23 3 2 ■ ■试分别求出A 阵和B 阵的秩、转豪、行列式.逆矩阵以及特征值.解■第1个m 文件,尸0;for k=l:200;尸s+k'3;enddispCThe SUM is*), s5=0; k=l;Th© sum iswhile k<=200;s=s+k"3; k=k+l; s =enddispCThe is 9), s 4040100003- 2求解以下钱性代敷方程:计算结果0.4000 -1.80000. 8000 绘制的曲践图第2个m 文件 运行结果祁是求矩阵的秩、行列式.逆矩阵、特征值的函效分别为* rank(), det( ), inv( ), ei R ( )•求矩阵转覽的命令为S0 1 5求出A 阵的秩为3、转事为A = 1 2 4 、行列式为-15、逆矩阵3 1 2 ■ ■■ 0 -0.6667 0.3333"6.1926'A'* = -0.21 -0.2 以及转征值eig(A) =-30.4033330.06670.8074 ■ ■2 4 3求出 R 阵的秩为3、转■为B r = 113、行列式为56、逆矩阵8 4 23-4对于3・3題中的A 阵和B 阵.在Command 窗口中分别求出C 二AS D 矩阵为A 中每个元 素平方俎成的矩阵、E 矩阵为A 阵杲以B 阵、F 矩阵为A 阵和B 阵敷组桑积(即,对应元素分别 相桑的积构成的矩阵). 解:输入命令,:=A '2 ,XA.・2 , E=A*B , F=A. »B ,计算结果为 c =D =E =F =16 14 7 0 1 9 13 1010 0 1 24 7 9 7 14 1 13 a18 4 2 4 14212392516♦321560,151243- 5已知某系统的闭环传逼函效①(S)如下,试用mots (〉命令来判斷系统的稳定性.3r + 23 + 5<j>( $)= ----------------------------s 5 + 2/ +4$' +5/ + 7$+ 6解*输入命令R=roots([1 2 4 5 7 6]) 计算结果如下.礙统不■定0.4477 + 1.390810.4477 ・ 1. 3908丄 -0. 8749 + 1.29921 -0. 8749 ・ l ・2992i -1. 1457-0.1786 B> 0.07140.1607 0.3929-0.0714-0.3571 0.4286-0.0536 -0.0357以及特征值eig(B)91606-2.0803+1.3363/ -2.0803-1.3363]3.6求期矩阵3 6+—的转置口与共純转置5解・输入语句C=[l+3<i 5-i 7+3»i;6+2<i 3+2“ 4-3<i];C1=C・‘C2=C计算结果Cl =C2 =1. 0000+ 3. OOOOi 6. 0000 +2. OOOOi 1.0000 -3. OOOOi 6.0000 - 2.OOOOi5. 0000-1.OOOOi 3. 0000 + 2. OOOOi 5.0000 + 1.00001 3.0000 - 2.000017. 0000+ 3.OOOOi 4.0000 - 3.OOOOi7.0000 - 3.00001 4.0000 + 3.000014-1某系统的传址函效为l・3y' + 2s + 3^"?+0.5?+1.2J +1使用MATLAB求出状杏空间表达式和零极点模型.解:■入语句sy»=tf(I1.3 2 3Ml 0.5 1.2 1]);|/VB.CJ)]-tCss(11.3 2 3].[1 0.5 1.2 1])i乙P.K)=lCzp([l・3 2 3).(1 0.5 1.2 ID计算机返回1.3000表明该系统的状杏空间表达式为该系统的手极点模型为C(・)_ 13(s + 0 7692 -1.311)(5 + 0.7692 +131/)(3 - 0」153 -1」6427)(5 — 0」1534 1」642/)(y + 0.7307)-0.5000 ・ 1.2000 -1.00001.0000 0 00 1.0000 0 -0.7692 十1.3100!•0.7092 ・ l.JlOOiP«0.1153^1.164210.1153 ・ l」642i•0.7307-0.5 1-1.2-「0X +丁0■1■■UMXX) 2.0000 3.0000 QX =4-2某单■入单输出系统* y + 6y+lly + 6y = 6//试求该系统状杰空间表达式的对角域标准形. 解,输入语句G-tf (⑹ J16116D ; G1=cimorUG ,'mod 汕)计算结果表明该系统状杰空间表达式的对角线标准形为n-d =A-[«l 0 1;1 -2 0;0 0 ・3]; B-(0;0;l]; 0(1 1 [fkdHrftflABC.D)0 -0.0000 1.0000 3.0000i 6 1165- 1基一单位负反馈控制系统.其开环传递函数为它的输入信号为r(/) = 2x|(/-o.5),试便用Shmilink 构造其仿真模型,并且观農其响应曲枚. 解:在Simulink 环境下构造仿真模型如下阶跃信号(Step)的设覽如下xl x2 X3 xl -3 0 0 X2 0 -2 0 x3 0 0 -1xl -7.762 x2 -9.798 X3 2.872Xl X2 X3yl 03865 0.61241.044■-3 0■ 0 -7.762"x0 一2 0 X + -9.7980 ■ 0-1 ■2.872 ■ ■y = [-0.3865 0.6124 L044]X■-1 0 1■()■1 -2 0 X +0 0■-3 ■1 •解:输入语句>• = [1 1 ()]X计算结果表明该系统的传递函效为G(S)=£ + 3f +6J 2+ 丨 ls +6s(s + l)4-3咬出以下系统的传遥函数响应曲找如下Step (hitput ■plilalexpiet vector pat&retcis <: l-£ .J• ■ ■• ■■.■■■■..■■■■•■••■■■■•■■■■■■■■■■■■■■■■■•■■■■・/ EmbU “ro crocstntd«t«eUon5-2 *5-1 fl 中的闭环控制系统封装成一个子系统.解:按住飢标右犍拖拽,方框包括了闭环系统部分.松开右键后.透择-create subsystem*,建立了系统模塑以及子系统模型如下.6- 1分别采用求取特征值的方法和李亚普诺夫第二法判别下面系统的稳定性•■_3 0 ■1■■ 一。
控制系统的Matlab仿真与设计课后答案

end
end
4.2[s,p]=fcircle(10)
4.3y=0;n=100;
fori=1:n
y=y+1/i/i;
end
y
4.4s=0;
fori=1:5
s=s+factor(i);
end
s
4.5sum=0;i=1;
whilesum<2000
sum=sum+i;
i=i+1;
end;
n=i-2
y=2*exp(-0.5*x).*sin(2*pi*x);
plot(x,y),grid on;
3.3
t=0:pi/50:2*pi;
x=8*cos(t);
y=4*sqrt(2)*sin(t);
z=-4*sqrt(2)*sin(t);
plot3(x,y,z,'p');
title('Line in 3-D Space');
text(0,0,0,'origin');
xlabel('X'),ylable('Y'),zlable('Z');grid;
3.4
theta=0:0.01:2*pi;
rho=sin(2*theta).*cos(2*theta);
polar(theta,rho,'k');
3.5
[x,y,z]=sphere(20);
fg=compose(f,g)
6.3symsx
g=(exp(x)+x*sin(x))^(1/2);
Y=sin(X);
P=polyfit(X,Y,3)
控制系统的MATLAB仿真与设计课后答案

第二章1>>x=[15 22 33 94 85 77 60]>>x(6)>>x([1 3 5])>>x(4:end)>>x(find(x>70))2>>T=[1 -2 3 -4 2 -3] ;>>n=length(T);>>TT=T';>>for k=n-1:-1:0>>B(:,n-k)=TT.^k;>>end>>B>>test=vander(T)3>>A=zeros(2,5);>>A(:)=-4:5>>L=abs(A)>3>>islogical(L)>>X=A(L)4>>A=[4,15,-45,10,6;56,0,17,-45,0] >>find(A>=10&A<=20)5>>p1=conv([1,0,2],conv([1,4],[1,1]));>>p2=[1 0 1 1];>>[q,r]=deconv(p1,p2);>>cq='商多项式为'; cr='余多项式为';>>disp([cq,poly2str(q,'s')]),disp([cr,poly2str(r,'s')]) 6>>A=[11 12 13;14 15 16;17 18 19];>>PA=poly(A)>>PPA=poly2str(PA,'s')第三章1>>n=(-10:10)';>>y=abs(n);>>plot(n,y,'r.','MarkerSize',20)>>axis equal>>grid on>>xlabel('n')2>>x=0:pi/100:2*pi;>>y=2*exp(-0.5*x).*sin(2*pi*x);>>plot(x,y),grid on;3>>t=0:pi/50:2*pi;>>x=8*cos(t);>>y=4*sqrt(2)*sin(t);>>z=-4*sqrt(2)*sin(t);>>plot3(x,y,z,'p');>>title('Line in 3-D Space');>>text(0,0,0,'origin');>>xlabel('X'),ylable('Y'),zlable('Z');grid;4>>theta=0:0.01:2*pi;>>rho=sin(2*theta).*cos(2*theta); >>polar(theta,rho,'k');5>>[x,y,z]=sphere(20);>>z1=z;>>z1(:,1:4)=NaN;>>c1=ones(size(z1));>>surf(3*x,3*y,3*z1,c1);>>hold on>>z2=z;>>c2=2*ones(size(z2));>>c2(:,1:4)=3*ones(size(c2(:,1:4))); >>surf(1.5*x,1.5*y,1.5*z2,c2);>>colormap([0,1,0;0.5,0,0;1,0,0]); >>grid on>>hold off第四章1>>for m=100:999m1=fix(m/100);m2=rem(fix(m/10),10);m3=rem(m,10);if m==m1*m1*m1+m2*m2*m2+m3*m3*m3 disp(m)endend2M文件:function[s,p]=fcircle(r)s=pi*r*r;p=2*pi*r;主程序:[s,p]=fcircle(10)3>>y=0;n=100;for i=1:ny=y+1/i/i;end>>y4 M文件:function f=factor(n)if n<=1elsef=factor(n-1)*n; end主程序:>>s=0;for i=1:5s=s+factor(i); end>>s5>>sum=0;i=1; while sum<2000sum=sum+i;i=i+1;end;>>n=i-26for循环M文件:function k=jcsum(n) k=0;for i=0:nk=k+2^i;end>>jcsum(63)While循环M文件:function k=jcsum1(n)k=0;i=0;while i<=nk=k+2^i;i=i+1;end主程序:>>jcsum1(63)第五章1>>A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4]; >>b=[13,-9,6,0]';>>x=A\b2M文件:function f=fxyz(u)x=u(1);y=u(2);z=u(3);f=x+y.^2./x/4+z.^2./y+2./z;[U,fmin]=fminsearch('fxyz',[0.5,0.5,0.5])3>>X=linspace(0,2*pi,50);>>Y=sin(X);>>P=polyfit(X,Y,3)>>AX=linspace(0,2*pi,50);>>Y=sin(X);>>Y1=polyval(P,X)>>plot(X,Y,':O',X,Y1,'-*')4>>x=0:2.5:10;>>h=[0:30:60]';>>T=[95,14,0,0,0;88,48,32,12,6;67,64,54,48,41]; >>xi=[0:0.5:10];>>hi=[0:10:60]';>>temps=interp2(x,h,T,xi,hi,'cubic');>>mesh(xi,hi,temps);第六章1>>syms x>>y=finverse(1/tan(x))2>>syms x y>>f=1/(1+x^2); g=sin(y);>>fg=compose(f,g)>>g=(exp(x)+x*sin(x))^(1/2);>>dg=diff(g)4>>F=int(int('x*exp(-x*y)','x'),'y')5>>syms x>>F=ztrans(x*exp(-x*10))6>>a=[0 1;-2 -3];>>syms s>>inv(s*eye(2)-a);7>>f=solve('a*x^2+b*x+c')8>>f=solve('x+y+z=1','x-y+z=2','2*x-y-z=1')9>>y=dsolve('D2y+2*Dy+2*y=0','y(0)=1','Dy(0)=0') >>ezplot(y),grid on10>>a=maple('simplify(sin(x)^2+cos(x)^2);')11>>f=maple('laplace(exp(-3*t)*sin(t),t,s);')12>>syms t x>>F=sin(x*t+2*t);>>L=laplace(F)第七章12 34 56 7第八章1-1>>h=tf([5,0],[1,2,2])1-2>>s = tf('s');>>H = [5/(s^2+2*s+2) ];>>H.inputdelay =21-3>>h=tf([0.5,0],[1,-0.5,0.5],0.1) 2>>num=2*[1,0.5];den=[1,0.2,1.01]; >>sys=tf(num,den)>>[z,p,k]=tf2zp(num,den);>>zpk(z,p,k)>>[A,B,C,D]=tf2ss(num,den);>>ss(A,B,C,D)3 >>num=[1,5]; den=[1,6,5,1]; ts=0.1; >>sysc=tf(num,den);>>sysd=c2d(sysc,ts,'tustin')4>>r1=1;r2=2;c1=3;c2=4;>>[A,B,C,D]=linmod('x84');>>[num,den]=ss2tf(A,B,C,D);>>sys=tf(num,den)5>>A=[1,1,0;0,1,0;0,0,2];B=[0,0;1,0;0,-2]; >>n=size(A)>>Tc=ctrb(A,B);if n==rank(Tc)disp('系统完全能控');elsedisp('系统不完全能控');end第九章1>>num=[2,5,1];den=[1,2,3];>>bode(num,den);grid on ;>>figure;>>nyquist(num,den);2>>num=5*[1,5,6];den=[1,6,10,8];>>step(num,den);grid on ;>>figure;>>impulse(num,den);grid on ;3>>kosi=0.7;wn=6;>>num=wn^2;den=[1,2*kosi*wn,wn^2]; >>step(num,den);grid on ;>>figure;>>impulse(num,den);grid on ;4 M文件:function [rtab,info]=routh(den)info=[];vec1=den(1:2:length(den)); nrT=length(vec1); vec2=den(2:2:length(den)-1);rtab=[vec1; vec2, zeros(1,nrT-length(vec2))];for k=1:length(den)-2,alpha(k)=vec1(1)/vec2(1);for i=1:length(vec2),a3(i)=rtab(k,i+1)-alpha(k)*rtab(k+1,i+1);endif sum(abs(a3))==0a3=polyder(vec2);info=[info,'All elements in row ',...int2str(k+2) ' are zeros;'];elseif abs(a3(1))<epsa3(1)=1e-6;info=[info,'Replaced first element;'];endrtab=[rtab; a3, zeros(1,nrT-length(a3))];vec1=vec2; vec2=a3;end主程序:>>den=[1,2,8,12,20,16,16];>>[rtab,info]=routh(den)>>a=rtab(:,1)if all(a>0)disp('系统是稳定的');elsedisp('系统是不稳定的');end5>>num=7*[1,5];den=conv([1,0,0],conv([1,10],[1,1])); >>[gm,pm,wg,wc]=margin(num,den)第十章1 M文件:function varargout=rg_lead(ng0,dg0,s1)if nargout==1ngv=polyval(ng0,s1);dgv=polyval(dg0,s1);g=ngv/dgv;thetal=pi-angle(g);zc=real(s1)-imag(s1)/tan(thetal);t=-1/zc;varargout{1}=[t,1];elseif nargout==2ngv=polyval(ng0,s1); dgv=polyval(dg0,s1);g=ngv/dgv; theta=angle(g); phi=angle(s1);if theta>0phi_c=pi-theta;endif theta<0;phi_c=-thetaendtheta_z=(phi+phi_c)/2; theta_p=(phi-phi_c)/2;z_c=real(s1)-imag(s1)/tan(theta_z);p_c=real(s1)-imag(s1)/tan(theta_p);nk=[1 -z_c]; varargout{2}=[1 -p_c]; kc=abs(p_c/z_c);if theta<0kc=-kcendvarargout{1}=kc*nk;elseerror('输出变量数目不正确!');end主程序:>> ng0=[1]; dg0=10000*[1 0 -1.1772];>>g0=tf(ng0,dg0); %满足开环增益的为校正系统的传递函数>>s=kw2s(0.7,0.5) %期望的闭环主导极点>>ngc=rg_lead(ng0,dg0,s);>>gc=tf(ngc,1)>>g0c=tf(g0*gc);>>rlocus(g0,g0c);>>b1=feedback(g0,1); %未校正系统的闭环传递函数>>b2=feedback(g0c,1); %校正后系统的闭环传递函数>>figure,step(b1,'r--',b2,'b'); grid on%绘2M文件:function [ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a)ngv=polyval(ng0,s1);dgv=polyval(dg0,s1);g=dgv/ngv;k=abs(g); %期望主导极点处的根轨迹增益beta=k/KK;[kosi1,wn1]=s2kw(s1);zc=-wn1*sin(a*pi/180)/sin(pi-atan(sqrt(1-kosi1^2)/kosi1)-(a*pi/180)); %利用正弦定理pc=beta*zc;ngc=beta*[1,-zc];dgc=[1,-pc];主程序:>>KK=20;s1=-2+i*sqrt(6);a=1>>ng0=[10];dg0=conv([1,0],[1,4]);>>g0=tf(ng0,dg0);>>[ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a);>>g0c=tf(KK*g0*gc);>>b1=feedback(k*g0,1);>>b2=feedback(g0c,1);>>step(b1,'r--',b2,'b');grid on3M文件:function [ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a)ngv=polyval(ng0,s1);dgv=polyval(dg0,s1);g=dgv/ngv;k=abs(g); %期望主导极点处的根轨迹增益beta=k/KK;[kosi1,wn1]=s2kw(s1);zc=-wn1*sin(a*pi/180)/sin(pi-atan(sqrt(1-kosi1^2)/kosi1)-(a*pi/180)); %利用正弦定理pc=beta*zc;ngc=beta*[1,-zc];dgc=[1,-pc];主程序:>>KK=128;s1=-2+i*2*sqrt(3);a=2>>ng0=[10];dg0=conv([1,0],conv([1,2],[1,8]));>>g0=tf(ng0,dg0);>>[ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a);>>g0c=tf(KK*g0*gc);>>rlocus(g0,g0c);>>b1=feedback(k*g0,1);>>b2=feedback(g0c,1);>>figure,step(b1,'r--',b2,'b');grid on4M文件:function [ngc,dgc]=lead4(ng0,dg0,KK,Pm,w)[mu,pu]=bode(KK*ng0,dg0,w); [gm,pm,wcg,wcp]=margin(mu,pu,w); alf=ceil(Pm-pm+5); phi=(alf)*pi/180;a=(1+sin(phi))/(1-sin(phi)), dbmu=20*log10(mu);mm=-10*log10(a); wgc=spline(dbmu,w,mm), T=1/(wgc*sqrt(a)),ngc=[a*T,1]; dgc=[T,1];主程序:>>ng0=[1];dg0=conv([1,0,0],[1,5]);>>g0=tf(ng0,dg0);>>w=logspace(-3,3);>>KK=1;Pm=50;>>[ngc,dgc]=lead4(ng0,dg0,KK,Pm,w);>>gc=tf(ngc,dgc);g0c=tf(KK*g0*gc);>>bode(KK*g0,w);hold on,bode(g0c,w);grid on,hold off>>[gm,pm,wcg,wcp]=margin(g0c)>>Kg=20*log10(gm)>>g1=feedback(g0c,1);>>bode(g1),grid on,>>[mag,phase,w]=bode(g1);>>a=find(mag<=0.707*mag(1));>>wb=w(a(1))>>max(mag)>>b=find(mag==max(mag))>>wr=w(b)5M文件:function [ngc,dgc]=fg_lead_pm(ng0,dg0,Pm,w)[mu,pu]=bode(ng0,dg0,w); %计算原系统的对数频率响应数据[gm,pm,wcg,wcp]=margin(mu,pu,w); %求取原系统的相角裕度和剪切频率alf=ceil(Pm-pm+5); %计算控制器提供的最大超前角度,phi=(alf)*pi/180; %将最大超前角转换为弧度单位a=(1+sin(phi))/(1-sin(phi)); %计算a值dbmu=20*log10(mu); %系统的对数幅值mm=-10*log10(a); %wm处的控制器对数幅值wgc=spline(dbmu,w,mm); %差值求取wm,认为wm=wcT=1/(wgc*sqrt(a)); %计算Tngc=[a*T,1]; dgc=[T,1];主程序:>>KK=40; Pm=50;>>ng0= KK *[1]; dg0=conv([1,0],conv([1,1],[1,4])); >>g0=tf(ng0,dg0) ;>>w=logspace(-2,4);>>[ngc,dgc]=fg_lead_pm(ng0,dg0,Pm,w)>>gc=tf(ngc,dgc),g0c=tf(g0*gc);>>b1=feedback(g0,1); b2=feedback(g0c,1);>>step(b1,'r--', b2,'b'); grid on>>figure, bode(g0,'r--',g0c,'b',w), grid on,>>[gm,pm,wcg,wcp]=margin(g0c), Km=20*log10(gm)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
控制系统计算机仿真课后答案参考答案说明:1( 对于可以用文字或数字给出的情况,直接给出参考答案。
2( 对于难以用文字或数字给出的情况,将提供MATLAB程序或Simulink模型。
第 1 章1.1 系统是被研究的对象,模型是对系统的描述,仿真是通过模型研究系统的一种工具或手段。
1.2 数学仿真的基本工具是数字计算机,因此也称为计算机仿真或数字仿真。
将数学模型通过一定的方式转变成能在计算机上实现和运行的数学模型,称之为仿真模型。
1.3 因为仿真是在模型上做试验,是一种广义的试验。
因此,仿真基本上是一种通过试验来研究系统的综合试验技术,具有一般试验的性质。
而进行试验研究通常是需要进行试验设计。
1.4 解析法又称为分析法,它是应用数学推导、演绎去求解数学模型的方法。
仿真法是通过在模型上进行一系列试验来研究问题的方法。
利用解析法求解模型可以得出对问题的一般性答案,而仿真法的每一次运行则只能给出在特定条件下的数值解。
,解析法常常是围绕着使问题易于求解,而不是使研究方法更适合于问题,常常因为存在诸多困难而不能适用。
从原则上讲,仿真法对系统数学模型的形式及复杂程度没有限制,是广泛适用的,但当模型的复杂程度增大时,试验次数就会迅速增加,从而影响使用效率。
1.5 仿真可以应用于系统分析、系统设计、理论验证和训练仿真器等方面。
1.6,8,20,71,,,,,,,,,x,100x,0u,,,, ,,,,0100,,,,y,,,002x注:本题答案是用MATLAB中tf2ss()函数给出的,是所谓“第二能控标准型”(下同)。
11.7,3,3,11,,,,,,,,,x,100x,0u,,,, ,,,,0100,,,,y,,,013x1.82s,3s,3G(s), 32s,4s,5s,21.91.368,0.36801,,,,,,,,x(k,1),100x(k),0u(k),,,, ,,,,0100,,,,y(k),,,00.3680.264x(k)1.10 仿真模型见praxis1_10_1.mdl;MATLAB程序见praxis1_10_2.m。
第 2 章 2.1 仿真模型见praxis2_1.mdl。
欧拉法:1.22RK4法:1.2428解析解:1.2428造成差异的原因是截断项数不同。
2.2 仿真模型见praxis2_2.mdl。
RK4法:1.7173欧拉法:1.252.3 因为方程中有参数k,因此序号用m。
欧拉法:hkhyy ,(1,),m,1mTTRK2法:222hhkhkhy(1)y ,,,,,m,m122TT2T2T1显然,当时,数值解将发散。
系统的特征值,若,则,超,,,h,2,h,2Th,2TT 出稳定性范围。
2.4 仿真模型见praxis2_4.mdl。
令, x,y,x,y12则系统状态方程和输出方程为,xxx(0)011,,,,,,,,,,111,,,,,,,,,,,,,,xxx(0)2,0.50222,,,,,,,,,,y,x1欧拉法:x,x,hx1,11,02,0x,x,h(2x,0.5x) 2,12,01,02,0y(0.1),1RK4法(过程略):y(0.1),1.00992.5 仿真模型见praxis2_5.mdl。
y(0.5),0.22012.6 仿真模型见praxis2_6.mdl,分析自己完成。
2.7 K=2.5时仿真模型见praxis2_7.mdl。
2.8 p = 1时仿真模型见praxis2_8_1.mdl,praxis2_8_5.mdl。
2.9(1)仿真模型见praxis2_9_1.mdl。
(2)仿真模型见praxis2_9_2.mdl;MATLAB程序见time_frac.m。
2.10仿真模型见praxis2_10.mdl。
2.11仿真模型见praxis2_11.mdl。
2.12(1)、(2)、(3)仿真模型见praxis2_11_1.mdl。
(4) 仿真模型见praxis2_11_2.mdl。
32.13仿真模型见praxis2_13.mdl。
2.14仿真模型见praxis2_14.mdl。
2.15仿真模型见praxis2_15.mdl。
2.16 (1) 仿真模型见praxis2_16_1.mdl。
(2) 仿真模型见praxis2_16_2.mdl。
2.17仿真模型见praxis2_17.mdl。
2.18仿真模型见praxis2_18.mdl。
1)、(2)仿真模型见praxis2_19_1.mdl。
2.19 ((3)仿真模型见praxis2_19_2.mdl。
2.20 (1) 离散化模型的MATLAB程序见praxis2_20.m,结果在ad和bd中。
(2)、(3)自己完成。
2.21 (1)离散化模型的MATLAB程序见praxis2_21_1.m,结果在ad和bd中。
(2)离散化模型的MATLAB程序见praxis2_21_2.m,结果在ad、bd和c中。
2.22 系统的系统状态方程和输出方程为,x,,ax,u y,(b,a)x,uRK2法:22ahhhx(k,1),(1,ah,)x(k),(1,ah)u(k),u(k,1)22222ahy(k,1),(b,a)(1,ah,)x(k) 2hh,(b,a)(1,ah)u(k),[1,(b,a)]u(k,1)2220,h,系统的特征值为,因此,步长的取值范围是。
,,,aa离散相似法(): h,T1,ah,ahx(k,1),ex(k),(1,e)u(k)a 1,ah,ahy(k,1),(b,a)ex(k),(b,a)(1,e)u(k),u(k,1)a步长的取值范围是,因为算法是无条件稳定的。
h,02.23 由于对输入信号采用了零阶保持器,因此必须根据u (t)的变化情况选择步长T。
如4果u(t)的变化比较剧烈,则应选择较小的T值;反之,可选得大一些。
然而,不管T如何选择,都不会发生计算不稳定的情况。
2.24 零阶保持器可以较好地重构呈现阶跃和分段阶梯特性的信号;三角保持器可以较好地重构呈现阶跃、分段阶梯和线性特性的信号。
2.25 两环节间没有采样开关时,系统的方程为,x,,10x,u11, x,x21y,x2离散化方程为1010,T,Tx(k,1),ex(k),0.1(1,e)u(k)111010,T,Tx(k,1),0.1(1,e)x(k),x(k),0.1(T,0.1,0.1e)u(k) 212y(k,1),x(k,1)2有,10T,1,0.1(1e)z,X(z)U(z)1,10T,1,1ez ,10T,1,10T2,2,,,,0.1(T0.10.1e) z0.01(1e)z,X(z)U(z)2,1,10T,1,,(1z)(1ez)脉冲传递函数为,10T,1,10T,2Y(z)0.1(T,0.1,0.1e)z,[0.01,(0.1T,0.01)e]zG(z),, ,1,10T,1U(z)(1,z)(1,ez)两环节间有采样开关时,系统的方程为,y,u1 y,,10y,y1离散化方程为y(k,1),y(k),Tu(k)1111010,T,Ty(k,1),ey(k),(1,e)y(k)110脉冲传递函数为,10T,2Y(z)T(1,e)z G(z),,,10T,1,1U(z)10(1,ez)(1,z)52.26 采用双线性变换法2,1,2Y(z)T(1,2z,z) G(z),,22,12,2U(z)(T,1.2T,4),(2T,8)z,(T,1.2T,4)z采用根匹配法Y(z)1,a,bG(z),, ,1,2U(z)1,az,bz其中,,0.3Ta,eT2cos0.9539 ,0.6Tb,e2.27,T,2T,1Y(z)(1,e)(1,e)1,z G(z),,,T,2T,1,3T,2U(z)2T1,(e,e)z,ez2.28 实时仿真算法一般应该是快速仿真算法,但并不是所有的快速算法都适用于实时仿真,因为它们不一定满足实时性需求。
第 3 章3.1 系统的状态是随时间连续变化的,这类系统称为连续时间系统;可以用差分方程或离散状态方程来描述的系统称为离散时间系统;采样系统是既有连续信号又有离散信号的混合系统。
采样系统按采样周期T重复工作。
采样控制系统实际存在的采样开关的采样周期,这有异于连续系统离散化时人为引入虚拟的采样开关和保持器,使得计算步长必须与采样周期相匹配。
3.2 步长h与采样周期T必须满足条件h,T/N其中,N为正整数。
3.3 采样控制系统仿真通常有差分方程递推求解法、双重循环方法、应用MATLAB控制工具箱时域响应分析函数法和Simulink仿真法。
第1种方法简单易行且仿真精度高;适合于连续部分不要求计算内部状态变量或不含非线性环节的场合。
第2种方法通用性较强;6适合于要求得到控制系统的输出值,或要求得到受控对象内部状态变量的响应,或被控对象中具有典型非线性环节的非线性系统的场合。
第3种方法非常简单;适合于系统整体闭环脉冲传递函数可以写出的场合。
第4种方法通用性最强;适合于用框图描述的采样控制系统仿真。
3.4 (1) MATLAB程序见praxis3_4_1.m和praxis3_4_2.m;仿真模型见praxis3_4_3.mdl。
(2) 自己完成。
3.5 MATLAB程序见praxis3_5_1.m;仿真模型见praxis3_5_2.mdl。
3.6 仿真模型见praxis3_6.mdl。
3.7 仿真模型见praxis3_7_1.mdl和praxis3_7_2.mdl。
3.8 仿真模型见praxis3_8.mdl。
3.9 (1) 仿真模型见praxis3_9.mdl。
(2) 自己完成。
第 4 章4.1 动态优化问题也称为函数优化问题。
在这类问题中,控制器的结构并不知道,需要设计出满足某种优化条件的控制器。
在数学上,此类问题属于泛函问题,即所谓寻找最优函数的问题。
在控制理论中,这通常属于最优控制的范畴。
静态优化问题也称为参数优化问题。
在这类问题中,控制器的结构、形式已经确定,而需要调整或寻找控制器的参数,使得系统性能在某种指标意义下达到最优。
可以将动态优化问题转化为静态优化问题。
4.2 间接寻优法是按照普通极值存在的充分必要条件来进行寻优的方法;直接寻优法是按照一定的寻优规律改变寻优参数,并且直接计算目标函数值的方法。
间接寻优法是一种解析方法,能根据充分必要条件确定寻优参数的准确极值,但需要能将目标函数写成解析形式。
直接寻优法不需要将目标函数写成解析形式,但寻优过程是一系列试探步骤,不能保证能求出寻优参数的准确极值。
由于在控制系统的参数优化问题中,目标函数一般很难写成解析形式,而只能在对系统进行仿真的过程中将其计算出来,并且目标函数的求导也不易实现,所以一般采用直接寻优法。
