三维图形变换3DTransformation
基于Directx的三维图形立体变换的实现

西南科技大学毕业设计(论文)题目名称:基于Directx的三维图形立体变换的实现年级:2003级■本科□专科学生学号:20035247学生姓名:宋彦宾指导教师:蒋体钢学生单位:信息工程学院技术职称:副研究员学生专业:通信专业教师单位:信息工程学院西南科技大学教务处制基于Directx的三维图形立体变换的实现摘要:目前在世界上三维图形大量的被应用到日常生活中,它是许多媒体应用程序和游戏的主体部分,所以掌握最新的三维技术是很有必要的。
本文首先研究了利用C#和Directx9编程以及立体几何技术,数学变换和几何图形技术来制作三维立体图形的方法,掌握了利用API接口创建窗口实现消息传递以及对坐标系,缓存,矩阵坐标变换的知识。
其次,利用3DS Max创建三维立体图形,加载到所编写的三位图形立体变换程序中,并进行调试。
设计主要完成了对绘制出来的电视机的平移,旋转和缩放技术的处理,最后通过程序对图形进行渲染使其更具有可观性。
关键词:API;Visual C#.Net;Direct3D;3DS MaxThe Realization of Three-Dimensional Graph Three-Dimensional Transformation Based on DirectxAbstract:In the world of nowadays, the three -dimensional graphics are applying to daily life in a large number. It is the main part of the game and applications of many media. So, it's necessary to master the latest 3-D technology.Firstly, this thesis researches on using C # and the Directx9 programming as well as the three-dimensional geometric technology, the mathematical manipulation and the geometric figure technology to manufacture the three-dimensional graphics. Mastering the use of the API interfaces to create a window that can realize message transmission. Acquainting the knowledge on the coordinate system, the texture and the matrix coordinate transformation. Secondly, the 3D models of the system were created by 3dsmax, then prepared to load the stereo 3D graphics transformation process, and debugging. The translation, the rotation and scaling of TV which have mapped out were completed in this design. Finally, by embroidering in procedure, the graphics were more arresting.Key words:API, Visual C#.Net, Direct3D, 3DS Max目录第1章绪论 (1)1.1 三维技术的现状 (1)1.2 编程语言简介 (2)1.3 三维图形立体变换的设计分析 (2)1.3.1 设计需求分析 (2)1.3.2 设计性能要求 (2)第2章DirectX9.0技术 (3)2.1 DirectX9.0的概念 (3)2.1.1 Direct3D的构架 (3)2.1.2 设计规划 (4)2.2 DirectX 9.0函数简介 (5)2.2.1 窗口类的处理 (6)2.2.2 创建IDirect3D接口 (7)2.2.3 创建IDirect3DDevice界面 (8)2.2.4 开始渲染 (9)2.2.5 顶点属性与顶点格式 (10)2.2.6 顶点缓冲 (10)2.2.7 索引缓冲 (12)2.2.8 D3D中的图元简介 (13)2.2.9 向量 (14)2.2.10 矩阵的操作 (15)第3章主体程序的设计与实现 (19)3.1 三维图形立体变换的设计 (19)3.2 三维图形立体变换设计具体实现 (19)3.2.1 利用.X文件图像获取 (19)3.2.2 利用画点画线函数生成图像 (23)3.2.3 图像的缩放 (33)3.2.4 图像的旋转 (34)3.2.5 图像保存为.TXT文挡 (37)3.2.6 渲染功能实现 (38)3.2.7 光源和观察矩阵的实现 (39)3.2.8 键盘的控制 (39)3.3 程序运行的调试 (40)总结 (41)4.1 设计开发小结 (41)4.2 项目改进方向和未来展望 (41)致谢 (42)参考文献 (43)附录 (44)第1章绪论1.1 三维技术的现状在计算机屏幕上绘图的最基本单位是点,点构成线,线又构成多边形,还可以朝空间发展,构成立体图行,如正方体、立方体、锥体、球等。
深入理解CSS变形transform(3d)

深⼊理解CSS变形transform(3d)前⾯的话 本⽂将详细介绍关于transform变形3D的内容,但需以了解为基础。
3D变形涉及的属性主要是transform-origin、transform、transform-style、perspective、perspective-origin、backface-visibility坐标轴 在了解透视之前,⾸先要先了解坐标轴。
3D变形与2D变形最⼤的不同就在于其参考的坐标轴不同。
2D变形的坐标轴是平⾯的,只存在x轴和y轴,⽽3D变形的坐标轴则是x、y、z三条轴组成的⽴体空间,x轴正向、y轴正向、z轴正向分别朝向右、下和屏幕外透视 透视是transform变形3D中最重要的内容。
如果不设置透视,元素的3D变形效果将⽆法实现。
//下⾯以rotateX()旋转函数为例,rotateX(45deg)表⽰元素以X轴⽅向为轴沿顺时针旋转45⾓度//左图是⽆变形和透视样式的原始效果,中图是设置变形和透视样式的效果,右图是设置变形但未设置透视样式的效果 由以上三个图可说明,如果不设置透视,那么浏览器会将元素的3D变形操作投射垂直到2D视平⾯上,最终呈现出来的只是元素的宽⾼变化 要深⼊了解透视,需要了解观察者、被透视元素和变形元素这⼏个概念。
⾸先是变形元素,顾名思义,就是进⾏transform3D变形的元素,主要进⾏transform、transform-origin、backface-visibility等属性的设置 观察者是浏览器模拟出来的⽤来观察被透视元素的⼀个没有尺⼨的点,观察者发出视线,类似于⼀个点光源发出光线 被透视元素也就是被观察者观察的元素,根据属性设置的不同,它有可能是变形元素本⾝,也可能是它的⽗级或祖先元素(后⾯会详细介绍),主要进⾏perspective、perspective-origin等属性的设置透视距离 透视距离perspective是指观察者沿着平⾏于z轴的视线与屏幕之间的距离,简称视距perspective 值: none | <length> 初始值: none 应⽤于: ⾮inline元素(包括block、inline-block、table、table-cell等) 继承性: ⽆ [注意]透视perspective不可为0和负数,因为观察者与屏幕距离为0时或者在屏幕背⾯时是不可以观察到被透视元素的正⾯的 [注意]透视perspective不可取百分⽐,因为百分⽐需要相对的元素,但z轴并没有可相对的元素尺⼨【1】⼀般地,物体离得越远,显得越⼩。
计算机图形学之图形变换

4 T
3
2 p
1
0
012 34 567 8
线段和多边形的平移可以通过顶点的
平移来实现。同样线段和多边形的其它几 何变换也可以通过对顶点的几何变换来实 现。
2. 旋转变换(Rotation) 二维旋转有两个参数:
旋转中心: 旋转角:
?
6 P’
5
4
3
P
2
1
0
012 34 567 8
设OP与x轴的夹角为 则:
由于采用齐次坐标矩阵表示几何变换, 多个变换的序列相应地可以用矩阵链乘来表 示。
需要注意:先作用的变换其矩阵在右边, 后作用的变换其矩阵在左边。
变换函数
平移变换 void glTanslate{fd}(TYPE x, TYPE y, TYPE z);
旋转变换 void glRotate{fd}(TYPE angle, TYPE x, TYPE y, TYPE z); 绕矢量v=(x,y,z)T逆时针方向旋转angle指定的角度。 旋转角度的范围是0~360度。当angle=0时, glRotate()不起作用。
二维旋转有两个参数: 旋转中心: 旋转角:
上述变换可以分解为三个基本变换:
•平移:
•旋转:
•平移: 回原位。
使旋转中心移到坐标原点; 使旋转中心再移
二维旋转有两个参数: 旋转中心: 旋转角:
因此上述变换可以写成矩阵乘积形式:
4. 5 基本三维几何变换(Basic three-dimensional geometric transformation)
1. 矩阵表示(Matrix representation) 前面三种变换都可以表示为如下的矩
阵形式
6.2三维图形投影变换技术1

P(x,y,z)
(x y z 1)*
0 1 0
=(x’y’z’1)
0 0 1 0 0 0 0 1
平行投影方向为Y轴 投影面为 平行投影方向为 轴,投影面为o-xz面, 面
则空间中任意一点P(x,y,z)投影到 投影到o-xz面上获 则空间中任意一点 投影到 面上获 得点P’(x’,y’,z’)的关系是 得点 的关系是
•x’=x •y’=y •z’=0 用矩阵表示: 用矩阵表示:
1 0 0 0 0
(x y z 1)*
三维坐标
0 1 0
=(x’y’z’1)
投影后的 二维坐标
0 0 0 0 0 0 0 1
变换矩阵
•投影方向:x轴,投影面 面 投影方向: 轴 投影面yz面 投影方向 •投影方向:y轴,投影面 面 投影方向: 轴 投影面xz面 投影方向 •投影矩阵为多少? 投影矩阵为多少? 投影矩阵为多少
投影视点E-观察者的眼睛 投影面xy面 透视投影(投影视点 观察者的眼睛 投影面 面) 投影视点 观察者的眼睛,投影面
投影方法:从视点E经过形体的各个点,向投影平 投影方法 视点 经过形体的各个点, 经过形体的各个点
画射线,这些射线和投影面o-xy的交点形成投影像 的交点形成投影像 面画射线,这些射线和投影面 的交点 (也就是具有真实立体感的二维图形)。
前面讲的内容解决了如何在计算机中定义一个立体形体, 前面讲的内容解决了如何在计算机中定义一个立体形体 ,下面 我们来解决第二个问题: 我们来解决第二个问题:
•如何将三维形体作为二维图像 如何将三维形体作为二维图像 如何将三维形体作为二 •在图像显示器等输出装置上 在图像显示器等输出装置上 在图像显示器 •表示出来? 表示出来? 表示出来
transformation的翻译

transformation的翻译
transformation是指一个过程,它可以改变位置、形状、大小或明
暗的影像的任何几个特征,也可以改变它的属性。
在数学中,transformation可以指投影、旋转、尺度变换、反射以及更多其他的变换。
它也可以被称为形状变换、几何变换或者几何变形。
它实际上就是通
过改变元素的坐标或大小来改变形状或大小的过程。
它可以用来量化图像
的形状,也可以用来计算图像之间的相似性。
Transformation可以被用于许多用途,如图像检索,地图投影,三
维重建,计算机视觉,物体检测和分类等。
它的应用在数字图像处理中也
有很大的推动作用,如图像压缩,图像全景,图像去噪,图像合成,图像
滤波和图像分割等。
简而言之,transformation指的是一个过程,通过改变特征,如位置、形状、大小和明暗程度来改变图像的属性,进而实现图像处理的目的。
它是数字图像处理领域中常用的方法,在某些应用中也可以通过transformation来提高效率和质量。
三维空间旋转变换公式

三维空间旋转变换公式摘要:一、引言二、三维空间旋转变换的概念1.旋转变换的定义2.三维空间旋转变换的分类三、三维空间旋转变换公式1.欧拉角公式2.旋转矩阵公式3.旋转四元数公式四、三维空间旋转变换的应用1.坐标变换2.刚体运动五、结论正文:一、引言在三维空间中,物体的运动不仅仅包括平移,还包括旋转。
旋转变换是描述物体在三维空间中围绕某个轴旋转的变换。
了解三维空间旋转变换的公式,对于研究和分析物体在三维空间中的运动具有重要意义。
二、三维空间旋转变换的概念1.旋转变换的定义三维空间旋转变换,是指将一个向量从一个坐标系旋转到另一个坐标系的变换。
这种变换可以通过一个旋转矩阵或四元数来表示。
2.三维空间旋转变换的分类根据旋转轴的不同,三维空间旋转变换可以分为以下三种:(1)绕x轴旋转(2)绕y轴旋转(3)绕z轴旋转三、三维空间旋转变换公式1.欧拉角公式欧拉角公式是一种常用的表示三维空间旋转变换的方法,它用三个角度来描述旋转。
以绕x、y、z轴分别为旋转轴的旋转变换为例:(1)绕x轴旋转:Rx = |cosθ| |0, 0, 1| + |sinθ| |1, 0, 0|(2)绕y轴旋转:Ry = |cosφ| |0, 1, 0| + |sinφ| |0, 0, -1|(3)绕z轴旋转:Rz = |cosψ| |1, 0, 0| + |sinψ| |0, -1, 0|2.旋转矩阵公式旋转矩阵是一种更简洁的方式来表示三维空间旋转变换。
以绕x、y、z轴分别为旋转轴的旋转变换为例:(1)绕x轴旋转:Rx = |1, 0, 0||0, cosθ, -sinθ||0, sinθ, cosθ|(2)绕y轴旋转:Ry = |cosφ, 0, sinφ||0, 1, 0||-sinφ, 0, cosφ|(3)绕z轴旋转:Rz = |cosψ, -sinψ, 0||sinψ, cosψ, 0||0, 0, 1|3.旋转四元数公式四元数是一种更简洁的表示三维空间旋转变换的方法。
计算机图形学 专业术语中英对照表

计算机图形学专业术语中英对照表2 manifolds 二维流形2D Transformation 二维坐标变换3D Entity 3D实体3D geometric modeling 三维几何造型3D Transformation 三维坐标变换3D Viewing 三维观察4-connected Area 四连通区域4-connected Neighbourhood 四连通邻域8-connected Area 八连通区域8-connected Neighbourhood 八连通邻域A set of pixels 像素集合A set of voxels 体素集合Accumulation Buffer 累积缓存(区存储RGBA颜色数据,用来累积一系列图像,形成一个最终的合成图像)Active Edge List-AEL 活化边表Active Polygon Table 活化多边形表Affine Transformations 仿射变换Algorithm ['ælɡəriðəm] 算法aliasing 走样Alpha Value 阿尔法通道值(用来存储透明度信息)Ambiguity 二义性Anti-aliasing ['ænti 'eiliəsiŋ]反走样Antialiasing 反走样API=Application Programming Interface 应用程序接口Area Subdivision Method 区域细分算法Argument=Parameter 参数Axis 轴Back face detection背面剔除Binary Region Codes 二进制区域编码bintree 二叉树Boundary Fill Algorithm 边界填充算法Boundary points 边界点Boundary Representations 边界表示法Bounding Box 包围盒Bounding rectangles 包围盒Bresenham’s Circle Algorithm Bresenham圆弧插补算法BSP Tree Method BSP树算法(半空间分割法)Callback Function 回调函数Cartesian coordinate 笛卡尔坐标Cathode Ray Tube 阴极射线管Cell decomposition 单元分解表示法Center of Projection 投影中心Chapter 2 Overview of display systemChapter 3 Graphics output primitiveChapter 4 TransformationChapter 5 Introduction to OpenGLchapter 6 Visible-Surface Detection Methods(可见面判别)Chapter 7 Solid Modeling 实体造型Circle Generating Algorithms 圆弧插补算法Clip window 剪裁窗口Clipping 剪裁Cohen-Sutherland Line Clipping 科恩-苏特算法,利用编码的剪裁算法coherence连贯的Color Buffers 颜色缓冲区Color CRT 彩色阴极射线管complement 取余Composite Transformation 级联变换Constructive Solid Geometry 构造实体几何或称CSG树体素构造法Operating code 操作码Convex Polygon 凸多边形Coordinate origin 坐标原点Coordinate 坐标Coordinate 坐标Counterclockwise 逆时针cyclically overlap each other 相互循环遮挡dangling edge 悬边dangling face 悬面Data Gloves 数据手套DDA Algorithm(Digital Differential Analyzer) 数字微分分析法Depth Buffer Method 深度缓冲器算法Depth Buffers 深度缓冲区(存储每个像素的深度值)Depth overlaps checking 深度重叠测试depth overlap深度重叠Depth Sorting Method 深度排序法(画家算法)Diameter 直径Difference of two objects 两个物体的差Differential Scaling 差值缩放Digitizers 数字化仪Direct View Storage Tubes 直视存储管Display Hardware 显示硬体(eg.显卡)Display lists 显示列表Display Mode 显示模式Display System 显示系统Double Buffer 双缓冲区(前端可视缓冲区与后台可绘制缓冲区的组合.它可以使得在显示一幅图像的同时绘制另一幅图像)Driving Programmes 驱动程序Drum Plotter 鼓式绘图仪Edge Fill Algorithm 边缘填充算法Edge Table 边表edge 边enclosed boundary封闭边界Enlargement 放大Euler Operation 欧拉运算Euler’s Formula 欧拉公式Event processing loop 事件处理环exterior point 外部点face 面facets in the scene 场景中面片Far plane 远裁剪面Fence Fill Algorithm 栅栏填充算法Finite Time 有限时间Fixed Point 固定点Flood Fill Algorithm 泛滥填充算法Force Feedback力反馈Frame Buffer 帧缓存器Frame Rate 帧频Frame 帧Framebuffer 帧缓冲器GDI=Graphic Devices Interface 图形设备接口General sweep 广义SweepGeometrical information 几何信息,包括顶点、棱边、表面的大小、尺寸、位置、形状等信息glue 粘合Graphics Software 图形软件Half-Edge Data Structure 半边结构Hard-Copy Devices 硬拷贝设备Header files 头文件Homogeneous Coordinates 齐次坐标——Homogeneous Parameter 齐次参量Image-Space Methods图象空间算法Initialize 初始化Inkjet Plotter 绘图仪Input Devices 输入设备Input Events 输入事件Inside-Outside Tests 内外测试integer values 整数值Interface 接口interior point 内部点Interior points 内点Intersection calculation 求交计算Intersection of two objects 两个物体的交Intersection point 交点intersection 交点Invalid object 无效物体Iterative 反复的Joysticks 操纵杆Keyboard 键盘Left Child 左子树Liang-Barsky Line Clipping 梁友栋-巴斯基剪裁算法Light Pen 光笔Lighting 灯光Line Clipping 线段的裁剪Line Drawing Algorithms 直线插补算法Line Rate 行频Line Stipple 点划线Linear Octree 线性八叉树Map 映射Material properties材料特征如硬度、密度、热处理方法等。
三维空间旋转变换公式

三维空间旋转变换公式摘要:1.三维空间的基本概念2.三维空间的旋转变换公式3.旋转变换公式的应用4.总结正文:一、三维空间的基本概念三维空间是一个由三个相互垂直的维度组成的空间,通常用长、宽、高三个参数来表示。
在三维空间中,每个点都具有三个坐标值,即x、y、z,它们分别表示该点在三个维度上的位置。
三维空间广泛应用于物理、数学、工程等领域,对于研究和解决实际问题具有重要意义。
二、三维空间的旋转变换公式在三维空间中,旋转变换是一种基本的几何变换,它可以将一个点或一个物体从一个位置旋转到另一个位置。
旋转变换公式可以用来描述这种变换。
假设有一个点P(x, y, z) 在一个以原点为中心,长、宽、高分别为a、b、c 的三维空间中,现在将这个点围绕原点逆时针旋转α角度,那么旋转后的点P"(x", y", z") 可以通过以下公式计算:x" = xco sα - zsinαy" = ycosα + xsinαz" = zcosα + ysinα其中,α表示旋转的角度,x、y、z 表示点P 的坐标,x"、y"、z"表示旋转后点P"的坐标。
三、旋转变换公式的应用旋转变换公式在实际应用中具有广泛的应用,例如在计算机图形学中,利用旋转变换公式可以将一个图形从一个位置旋转到另一个位置,从而实现图形的变换;在物理学中,旋转变换公式可以用来描述物体的旋转运动,从而研究物体的运动规律;在工程领域,旋转变换公式可以用来解决各种实际问题,如机械设备的旋转、建筑物的倾斜等。
四、总结三维空间的旋转变换公式是一种基本的几何变换公式,它可以描述一个点或一个物体在一个三维空间中的旋转变换。
三维霍夫变换

三维霍夫变换三维霍夫变换(3D Hough Transform)是一种图像处理技术,用于在三维空间中检测物体的形状和位置。
它是二维霍夫变换的扩展,可以应用于三维模型重建、目标检测和姿态估计等领域。
本文将介绍三维霍夫变换的原理、算法以及应用。
一、原理三维霍夫变换的原理基于极坐标的转换。
在三维空间中,一个点的位置可以由它的坐标表示,即(x, y, z)。
而霍夫变换则将点的位置表示为参数空间中的一个点,该点与待检测物体的某个参数相关联。
对于三维空间中的线段,可以通过其在参数空间上的投影进行检测。
二、算法三维霍夫变换的算法与二维霍夫变换类似,主要包括以下几个步骤:1. 确定参数空间:根据待检测物体的特性选择适当的参数空间,为每个参数建立对应的投票矩阵。
2. 构建投票矩阵:遍历图像中的每个点,将每个点在参数空间上的投票结果累加到对应的投票矩阵中。
3. 提取特征:根据投票矩阵的结果,提取出具有较高得票数的参数组合,作为待检测物体的特征。
4. 检测与定位:根据提取的特征,对图像进行检测和定位,获取待检测物体的形状和位置信息。
三、应用三维霍夫变换在许多领域中有广泛的应用。
1. 三维模型重建:三维霍夫变换可以用于从多个二维视图中重建三维模型。
通过在不同视角下进行三维霍夫变换,可以将多个二维投票矩阵叠加得到最终的三维投票矩阵,从而估计出物体的三维形状。
2. 目标检测:三维霍夫变换可以用于目标检测,特别是对于三维物体的检测。
通过在参数空间中查找具有较高得票数的参数组合,可以准确地定位图像中的目标物体。
3. 姿态估计:三维霍夫变换可以用于姿态估计,即确定物体在三维空间中的方向和角度。
通过分析在不同姿态下的霍夫变换结果,可以获得物体的姿态信息。
四、总结三维霍夫变换是一种有效的图像处理技术,可以用于三维模型重建、目标检测和姿态估计等应用。
它通过将图像点的位置转换为参数空间中的投票,实现对待检测物体的形状和位置的准确提取。
随着计算机视觉技术的不断发展,三维霍夫变换在各个领域中将发挥更重要的作用。
三维空间旋转变换公式

三维空间旋转变换公式(原创版)目录1.三维空间旋转变换公式的概念2.三维空间旋转变换公式的分类3.三维空间旋转变换公式的应用4.三维空间旋转变换公式的举例正文一、三维空间旋转变换公式的概念三维空间旋转变换公式是一种在三维空间中对物体进行旋转变换的数学公式。
在物理学、工程学、计算机图形学等学科中,对物体的旋转变换有着广泛的应用。
通过三维空间旋转变换公式,可以实现对物体在三维空间中的平移、旋转等操作,从而实现物体在不同空间位置和方向的变换。
二、三维空间旋转变换公式的分类三维空间旋转变换公式主要分为以下三种:1.欧拉角旋转变换公式:欧拉角是一种用来描述物体三维空间旋转的三个角度,通常用φ、θ、ψ表示。
欧拉角旋转变换公式能够将一个物体从一个方向旋转到另一个方向。
2.四元数旋转变换公式:四元数是一种用来表示三维空间中物体旋转的矩阵,通常用 q 表示。
四元数旋转变换公式具有计算简便、表达式紧凑等特点,广泛应用于计算机图形学中。
3.旋转矩阵旋转变换公式:旋转矩阵是一种用来描述物体在三维空间中旋转的矩阵,通常用 R 表示。
旋转矩阵旋转变换公式可以通过矩阵乘法实现物体的旋转变换。
三、三维空间旋转变换公式的应用三维空间旋转变换公式在许多领域都有着广泛的应用,例如:1.物理学:在物理学中,研究物体在三维空间中的运动规律,常常需要用到三维空间旋转变换公式,以便分析物体在不同方向和位置的运动状态。
2.工程学:在工程学中,例如机器人学、自动化技术等领域,三维空间旋转变换公式可以用来实现对机器人的控制,使其能够完成各种复杂的动作。
3.计算机图形学:在计算机图形学中,三维空间旋转变换公式可以用来实现对物体在三维空间中的渲染和显示,从而提高图形图像的质量和视觉效果。
四、三维空间旋转变换公式的举例假设有一个长方体,其在三维空间中的初始位置为 (x1, y1, z1),绕着 x 轴旋转 90 度后,其位置变为 (x1, y1, z2)。
三维坐标变换ppt课件

x, y, z,1 x, y, z,1T x0, y0,z0 R
说明:变换矩阵TR将一个直角坐标系变换为另一个 坐标系。即使一个坐标系是右手坐标系,另一个为 左手坐标系,结论依然成立。
26
习题7
7-1 对于点P(x,y,z) ,(1) 写出它绕x 轴旋转 角,然后再绕y轴旋 转 角的变换矩阵。 (2)写出它绕 y 轴旋转 角,然后再绕 x 轴 旋转 角的变换矩阵。所得到的变换矩阵的结果一样吗? 7-2 写出绕空间任意轴旋转的变换矩阵。
0 a
1 0
a2 b2 c2
0
0
a
0
a2 b2 c2
0
0
b2 c2
0
a2 b2 c2
ห้องสมุดไป่ตู้
0
1
AV Rx Ry
17
利用这一结果,则绕任意轴旋转的变换矩阵可表示为:
y
P2 •
P1 • x
z
y
• P’2
P• ’1
x
z
1) T
y
P• ’1
0 sz
0 0
0 0 0 1
x y
x xsx , y ysy , z zsz 其中 sx , sy , sz 为正值。
4
(2) 相对于所选定的固定点的比例变换
z
z
(xf,yf,zf)
(1)
(xf,yf,zf)
y (2)
y
x z
x yz
(3) (xf,yf,zf)
0
0
0 0 1 0
tx ty tz 1
C++3D图形变换(含源码,下载后可复制黏贴使用)

实验三 3D图形变换一.实验目的:掌握3D图像的变换,了解多数的3D变换,平移,旋转等几何变换,还有投影变换等知识。
二.实验原理:3D图像的移动,比例变化,旋转等几何变换算法原理及各种投影变换算法原理。
三.实验步骤:一.建立MFC单文档程序,用来编写3D变换。
二.建立Mainframe,并设计,添加相应的ID及映射函数。
三.实验的主要代码:1、设计3维图形平移变换算法的实现程序;void CMyView::OnTranslation(){m_Select=SEL_TS;m_str="平移";CBaseClass my1; //构造新的CBaseClass对象int i,j;for ( i=1;i<=4;++i){for ( j=1;j<=4;++j)my1.A[i][j]=0;}my1.A[1][1]=1;my1.A[2][2]=1;my1.A[4][4]=1;my1.A[3][3]=1;my1.A[4][1]=20; //x轴方向上平移my1.A[4][2]=28; //y轴方向上平移my1.A[4][3]=28; //z轴方向上平移my1.Draw();}2、设计3维图形缩放变换算法的实现程序;void CMyView::OnScalingS(){m_Select=SEL_MO;m_str="整体变比";CBaseClass my1; //构造新的CBaseClass对象int i,j;for ( i=1;i<=4;++i){for ( j=1;j<=4;++j)my1.A[i][j]=0;}my1.A[1][1]=1;my1.A[2][2]=1;my1.A[3][3]=1;my1.A[4][4]=0.5;my1.Draw();}void CMyView::OnScalingXyz(){m_Select=SEL_MO;m_str="XYZ变比";CBaseClass my1; //构造新的CBaseClass对象int i,j;for ( i=1;i<=4;++i){for ( j=1;j<=4;++j)my1.A[i][j]=0;}my1.A[1][1]=2; //x轴方向上比例my1.A[2][2]=1; //y轴方向上比例my1.A[3][3]=2; //z轴方向上比例my1.A[4][4]=1;my1.Draw();}3、设计3维图形旋转变换算法的实现程序。
三维坐标系的旋转变换

三维坐标系的旋转变换三维坐标系的旋转变换是计算机图形学和几何学中一个非常重要的概念。
它能够将一个物体在三维空间中绕着指定的轴进行旋转,从而改变它相对于其他物体的位置和方向。
本文将介绍三维坐标系的旋转变换的原理、方法和应用,并提供一些指导意义的实例。
一、三维坐标系的基本概念在介绍旋转变换之前,我们先来了解一下三维坐标系的基本概念。
三维坐标系由三个相互垂直的坐标轴组成:X轴、Y轴和Z轴。
X轴代表左右方向,Y轴代表前后方向,Z轴代表上下方向。
每个点在三维空间中都可以由三个坐标值来表示,分别表示其在X轴、Y轴和Z轴上的位置。
二、旋转变换的原理旋转变换是通过改变坐标系的方向和角度来实现的。
在三维坐标系中,我们可以选择一条旋转轴,将其视为一个固定不动的轴,然后将其他点围绕着这个轴进行旋转。
旋转角度可以是正数(顺时针方向)或负数(逆时针方向),单位通常是弧度或角度。
三、旋转变换的方法通过旋转变换,我们可以在三维空间中实现各种各样的变换效果,例如旋转、翻转、缩放等。
以下是几种常见的旋转变换方法:1. 绕X轴旋转:围绕X轴进行旋转变换时,我们可以通过改变Y 轴和Z轴的坐标值,来实现点在平面上的旋转效果。
2. 绕Y轴旋转:围绕Y轴进行旋转变换时,我们可以通过改变X 轴和Z轴的坐标值,来实现点在平面上的旋转效果。
3. 绕Z轴旋转:围绕Z轴进行旋转变换时,我们可以通过改变X 轴和Y轴的坐标值,来实现点在平面上的旋转效果。
四、旋转变换的应用旋转变换在计算机图形学和几何学中有广泛的应用。
它可以用来进行三维模型的角度调整,实现刚体变换,以及修正物体在三维空间中的位置和方向。
例如,在计算机游戏中,我们可以通过旋转变换来实现角色的动画效果,使其在三维空间中做出各种各样的动作。
五、旋转变换的指导意义掌握三维坐标系的旋转变换对于计算机图形学和几何学的研究和应用都非常重要。
它可以帮助我们理解和分析三维空间中的物体运动和变化,并通过数学方法实现对其的控制和调整。
三维空间旋转变换公式

三维空间旋转变换公式在三维空间中,旋转变换是一种常见的操作,它允许我们将物体绕指定的轴进行旋转。
为了实现这一操作,我们需要使用旋转变换公式。
下面是三维空间旋转变换公式的描述。
在三维空间中,旋转变换可以由旋转矩阵来表示。
对于一个给定的点P(x, y, z),通过旋转变换,我们可以得到旋转后的点P'(x', y', z')。
旋转变换公式如下:x' = cosθ * (cosβ * cosγ) * x + (cosθ * sinβ * cosγ - sinθ * sinγ) * y + (cosθ * sinβ * sinγ + sinθ * cosγ) * zy' = sinθ * (cosβ * cosγ) * x + (sinθ * sinβ * cosγ + cosθ * sinγ) * y + (sinθ * sinβ * sinγ - cosθ * cosγ) * zz' = -sinβ * cosγ * x + sinβ * sinγ * y + cosβ * z其中,θ表示绕x轴的旋转角度,β表示绕y轴的旋转角度,γ表示绕z轴的旋转角度。
通过这个公式,我们可以将三维空间中的点进行绕任意轴的旋转。
根据旋转矩阵的性质,我们可以将多个旋转进行组合,以实现复杂的旋转效果。
需要注意的是,旋转角度值使用弧度制表示。
若需要使用角度制,需要进行相应的转换。
总结起来,三维空间旋转变换公式允许我们通过旋转矩阵将一个给定的点绕指定的轴进行旋转。
这个公式给出了旋转后的点在三维坐标系中的新坐标。
通过合理使用旋转角度,我们可以实现在三维空间中的各种旋转变换。
计算机图形学2010_06三维图形变换
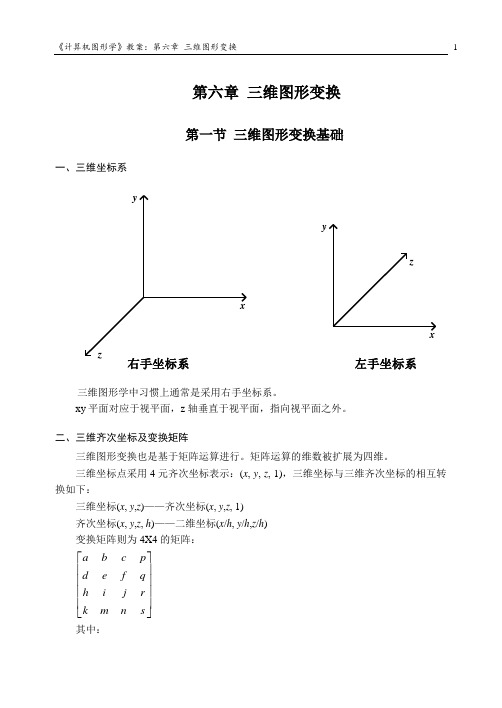
第六章 三维图形变换第一节 三维图形变换基础一、三维坐标系xyzxyz右手坐标系左手坐标系三维图形学中习惯上通常是采用右手坐标系。
xy 平面对应于视平面,z 轴垂直于视平面,指向视平面之外。
二、三维齐次坐标及变换矩阵三维图形变换也是基于矩阵运算进行。
矩阵运算的维数被扩展为四维。
三维坐标点采用4元齐次坐标表示:(x , y , z , 1),三维坐标与三维齐次坐标的相互转换如下:三维坐标(x , y ,z )——齐次坐标(x , y ,z , 1) 齐次坐标(x , y ,z , h )——二维坐标(x /h , y /h ,z /h ) 变换矩阵则为4X4的矩阵:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡s nm kr j i h q f e d p c b a 其中:平移变换第二节 三维几何变换一、三维基本变换 1. 平移变换⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1010000100001nmk T )1,,,()1,,,(n z m y k x T z y x +++=⋅2. 比例变换)1,,,()1,,,(1000000000000jz ey ax T z y x j e a T =⋅⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡= 3. 旋转变换三维的基本旋转变换分为三种,即绕三个坐标轴的旋转变换。
(1)绕z 轴旋转γ角旋转后z 值不变,x,y 值将发生改变,x,y 值的计算公式与平面旋转相同,即:zz y x y y x x ='+='-='γγγγcos sin sin cos 则变换矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=1000010000cos sin 00sin cos γγγγT 有:)1,1,cos sin ,sin cos ()1,,,(γγγγy x y x z y x +-=T(2)绕x 轴旋转α角则旋转后x 的坐标值不变,y 和z 的坐标值将改变,相当于在yz 平面上绕平面原点进行旋转变换。
平面转转变换的公式为:ααααcos sin sin cos y x y y x x +='-='对应而来,这里y 对应于x ,z 对应y ,有:ααααcos sin sin cos z y z z y y +='-='则变换矩阵为:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=10000cos sin 00sin cos 00001ααααT )1,cos sin ,sin cos ,()1,,,(ααααz y z y x z y x +-=T(3)绕y 轴旋转β角这时,z 对应于x ,x 对应于y 。
三维图形的几何变换讲课文档

先平移后旋转
先旋转后平移
第二十三页,共64页。
三、三维图形的几何变换
三维图形的变换是二维图形变换的简单扩展,变换的 原理还是把齐次坐标点(x,y,z,1)通过变换矩阵变换成新 的齐次坐标点(x’,y’,z’,1),即
x ' y ' z '1 x y z 1 T
其中T为三维基本(齐次)变换矩阵:
1 0 0
T1
0
1
0
c / a 0 1
第十四页,共64页。
(2)将直线与平面图形一起按逆时针反向旋转
θ=arctan(-b/a),使直线与轴重合。即作旋转变换。
cos sin 0
T2
sin
cos
0
0
0 1
第十五页,共64页。
(3)将旋转之后的图形对y轴作对称变换,相当于对y轴 进行对称变换。其变换矩阵为:
透视投影的图形与眼睛观察景物的原理及效果是一致的, 因而常用于图形的真实效果显示。由于平行投影后直线 间的平行关系不变,因而它常用于三维图形交互和生成 工程图的视图。
第三十四页,共64页。
投影变换分类:
正交投影 正平行
正等测投影
投影
平行 投影
正轴测 投影
正二测 正三测
斜平行 斜等测
投
投影
影
斜二测
一点透视
1001 0001
1000 窗口
0000
0101 0100
1010 0010 0110
第四十四页,共64页。
对线段的两端点分别进行编码。然后根据线段两端点编 码就能方便地判断出线段相对于窗口的位置关系:
第四十五页,共64页。
《维图形变换》课件

DirectX是微软公司开发的一套多媒体应用程序编 程接口(API),主要用于游戏和多媒体应用程序 的开发。它包含了一系列用于渲染图形、处理声 音、输入设备等的组件。
硬件加速
DirectX充分利用了计算机的硬件资源,特别是显 卡和声卡,来提高渲染和音频处理的速度。这使 得DirectX在性能上具有优势。
云计算与大数据技术
云计算和大数据技术将为维图形变换提供更强大的计算能力和数据处理 能力,使得大规模的图形计算和数据处理成为可能,进一步拓展维图形 变换的应用领域。
对课程内容的反思与建议
课程内容深度与广度
建议在课程内容上增加一些高级主题和案例,以帮助学生 更好地理解和掌握维图形变换的原理和应用。
实践环节的加强
维图形变换的优化
性能优化
减少冗余计算
通过减少不必要的计算和 重复计算,提高程序运行 效率。
使用缓存机制
将计算结果缓存起来,避 免重复计算,提高运行速 度。
优化数据结构
选择合适的数据结构,以 便更高效地存储和访问数 据。
渲染优化
使用合适的渲染算法
选择适合图形变换的渲染算法,如双缓冲技术、多重采样抗锯齿 等。
图形变换的实现
在DirectX中,图形变换同样通过矩阵运算实现。 与OpenGL不同的是,DirectX使用固定管线渲染 ,这意味着开发者需要编写特定的代码来处理图 形的渲染过程。
游戏开发
由于DirectX在游戏开发领域的广泛应用,许多知 名的游戏引擎都支持DirectX,使得开发者能够快 速地构建高质量的游戏。
WebGL实现
WebGL简介
图形变换的实现
跨平台兼容性
实时渲染
WebGL(Web Graphics Library)是一种基于OpenGL ES 2.0的图形渲染API,用于在 Web浏览器中创建3D图形。 它不需要任何插件,即可在浏 览器中实现高性能的3D渲染。
图形学名词解释

图形学名词解释3D三维(three dimension)。
客观世界中静止的物体都是三维的,在计算机图形学中常在一定的坐标系中用(x,y,z)坐标系列表示物体。
3D modeling 3D建模。
用三维坐标来描述物体的形状。
在各种计算机图形应用领域中有不同的三维建模方法,用不同的算法来描述这些领域中的物体和对象。
3D transformation 3D变换。
在三维空间中把物体的三维坐标从一个位置变换至另一位置,或者从一个坐标系变换至另一坐标系。
这是一种对物体的三维坐标(x,y,z)进行数据操作的一种形式。
3D transformation sequence 3D变换序列。
把客观世界中的物体在计算机屏幕上显示,通常需要进行一系列坐标变换,如从物体的相对坐标系变换至计算机屏幕需要经过平移、旋转、视点投影变换等一系列坐标变换。
4D四维(four dimension)。
在计算机图形学中描述客观世界除了用三维坐标来描述物体的形状外,还用时间t作为第四维来描述过程,通常用(x,y,z,t)表示。
6D六维(six dimension)。
在计算机图形学三维应用过程中(例如:模拟仿真、虚拟现实应用等)用六个自由度(x,y,z坐标、偏角、倾角、仰角)来描述物体的运动。
a stream一段流AABB沿坐标轴的包围盒(axis-aligned bounding boxes)ABI二进制接口Absorption吸收Accumulation Buffer累积缓存。
累积缓存同颜色缓存一样也保存颜色数据,但它只保存RGBA颜色数据,而不能保存颜色索引数据(因为在颜色表方式下使用累积缓存其结果不确定)。
这个缓存一般用于累积一系列图像,从而形成最后的合成图像。
利用这种方法,可以进行场景反走样操作。
action mapping动作映射algorithm算法。
一般指在用电脑软件解决问题时所用的数学方法或程序实现过程。
通常用数学公式或程序框图来描述。
三维坐标系旋转变换公式

三维坐标系旋转变换公式三维坐标系旋转变换公式是在几何中常用的一种数学变换,它既可以描述平面的旋转,又可以根据旋转角度和旋转轴,表达把物体从一个坐标系移动到另一个坐标系的变换。
本文重点介绍三维坐标系旋转变换公式的含义及其计算方法,并结合实例对其应用进行讨论。
一、三维坐标系旋转变换公式的含义三维坐标系,也称空间坐标系,是指三个坐标轴构成的坐标系,包括X轴、Y轴和Z轴,直观上它仿佛是一个立方体,其中每个方向上的坐标变化都可以依据三维坐标系旋转变换公式表达出来。
三维坐标系旋转变换公式定义为:$$x =cos(θ)x-sin(θ)y$$$$y=sin(θ)x+cos(θ)y$$$$z =z,$$其中θ表示坐标系旋转变换时所采用的旋转角度,x和y表示原坐标系中的坐标,x和y表示变换后的坐标。
二、三维坐标系旋转变换公式的计算在三维坐标系中,当给定旋转角度和旋转轴时,可以根据三维坐标系旋转变换公式计算坐标变换。
旋转轴的方向可以用单位向量描述,单位向量的方向是指该向量在原点指向的方向,以及该向量的大小。
计算坐标变换时,首先需要计算旋转矩阵,旋转矩阵定义为:$$R=begin{bmatrix}cos(θ) & sin(θ) & 0-sin(θ) & cos(θ) & 00 & 0 & 1end{bmatrix}$$旋转矩阵可以表示坐标系旋转时的线性变换,在坐标变换时,可以将坐标矩阵与旋转矩阵进行乘积运算,即可得到变换后的坐标。
三、三维坐标系旋转变换实例假设存在一个三维坐标系,其中的坐标为(1,2,3),且坐标系旋转角度为90度,旋转轴方向为(1,0,0),则可以用三维坐标系旋转变换公式计算变换后的坐标。
首先,计算旋转矩阵,根据旋转变换公式可知,当θ=90°时,旋转矩阵为:$$R=begin{bmatrix}0 & 1 & 0-1 & 0 & 00 & 0 & 1end{bmatrix}$$然后,将待变换的坐标(1,2,3)与旋转矩阵进行乘积,可以得到变换后的坐标(2,-1,3)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
aa12xx
b1 y c1z d1 0 b2 y c2z d2 0
参数形式 :
p(t) p0 t v or p(t) p0 t ( p1 p0 )
or : p(t) (1 t) p0 t p1 (linear interpolation)
课堂上:理解概念
课后:阅读相关资料、书籍
最好是自己去推导一遍: 我们课程主页上公布每次课的资料
参考书
计算机游戏程序设计。电子工业出版社。 计算机图形学算法基础 科学出版社 真实感图形学算法基础 科学出版社 OpenGL教材
颜色
可见光的波长 400-780 nm 三色原理用三种颜色表示:R,G,B. 减法颜色系统: Cyan, Magenta,
一般的,矩阵乘法不满足交换率,即 AxB BxA
如果I是单位阵,则AxI = IxA = A I具有如下形式:
方阵的逆和行列式的值
方阵A的逆记为A-1:A-1A=AA-1=I 如果方阵对应的行列式的值det(A)=0,
则A不可逆 如果A是3x3的方阵,则
游戏中的矩阵
三维图形学中一般使用4x4矩阵
空间坐标系到齐次坐标系的转换
点的齐次坐标表示
齐次向量!坐标形式(w0)
几何求交
线段求交 ◦ 平行? ◦ 求交点的计算
通过三个点的园: 主要任务是计算中心点
线与线求交、线与面求交: ◦ 参数解 ◦ 可用于裁剪
线与多边形求交 ◦ 边界计算 ◦ 光线与多边形求交
矩阵
矩阵是n个向量的并列表示
then: a
a a ;
(aayb, ax
)
b
a
向量几何:投影
向量投影:
p v1 v2 / v2
v1 v2
P>0
投影与坐标系
v1 v2
P<0
k
j i
向量几何:叉积
V1和v2的叉积是一个新的向量v,它与 v1和 v2都垂直,其范数 为:
a a a 2
向量之间的夹角:
q
d
a
b
a
b
cos(q
);
thus:
cos(q )
aa
b b
a b
if d 0 : q 90; if d 0 : q 90; if d 0 : q 90
垂直向量:
a (ax , ay ) a a 0;
float IN_41, float IN_42, float IN_43, float IN_44) {
_11=IN_11; _12=IN_12; _13=IN_13; _14=IN_14;
_21=IN_21; _22=IN_22; _23=IN_23; _24=IN_24;
_31=IN_31; _32=IN_32; _33=IN_33; _34=IN_34;
x2 y2
a
b
b
a
a
(b
c)
a
b
a
c
z2 axb
b
area=|axb|
a
b
a
2
b
2
(a
b)2
a
叉积与点积的区别
两个向量的点积是一个数 两个向量的叉积仍然是一个向量
点与向量的坐标系统
坐标系统由三个正交的向量 i, j, k 以及原点O组成.
点:
xi
y
j
zk
(i ,
j,
k,
O)
x y
0z
pO
统一的形式:
x
i
y
j
z
k
(i ,
j,
k ,O)
x y
1z
x x/ w
y
y
/
w
z z / w
w
//带参构造函数
//… 更多 };
Plane3数据结构
struct Plane3 { Point3 n; float d;
// 平面法向 //原点垂直法向距离
Plane3() {} //缺省构造函数
plane3(float nX,float nY, float nZ, float D) { n(nX, nY, nZ); d=D}
or :
v1 v2
v1 v2
v1 v2
sin(q ),
whereq
v1, v2
( y1z2 z1 y2 ) i (z1x2 x1z2 ) j (x1 y2 y1x2 ) k
属性:
i jk i.e. v1 v2 x1 y1 z1
Point3数据结构
struct Point3 { Union { struct { float x,y,z; //分量形式 }; float v[3]; // 数组形式 };
Point3() {};
//缺省构造函数
Point3 (float X, float Y, float Z) {x = X; y=Y; z=Z}
(x1x2 )2 ( y1 y2 )2 (z1 z2 )2
w v v i.e. w 1
向量几何:点积
定义: 属性:
d v1 v2 x1x2 y1 y2 z1z2
a
b
b
a
(a
c)
b
a
b
c
b
向量的表示:
v
i
x,
v
j
y,
v
k
z
v
x
i
y
j
z
ห้องสมุดไป่ตู้
k
x
y z
k
点的表示:
O
j
i
p
O
x
i
y
j
z
k
x
y z
线的表示方法
二维解析表达形式 :
ax by c 0
三维解析表达形式 :
_41=IN_41; _42=IN_42; _43=IN_43; _44=IN_44;
}
};
三维变换
一个变换通常用4x4矩阵表示.
对一个点或者向量进行变换等价于将一个矩阵乘以该点或向量的齐 次坐标.
向量的嵌套: 如矩阵乘法
m00 m01 m02 m03 p0 m00 p0 m01 p1 m02 p2 m03
};
//分量表示
float m[4][4];
//矩阵表示
};
//带参构造函数
matrix4 (float IN_11, float IN_12, float IN_13, float IN_14,
float IN_21, float IN_22, float IN_23, float IN_24,
float IN_31, float IN_32, float IN_33, float IN_34,
v2v2 p0
v1
p4 p1
p3 p2
平面与法向
三点决定一个平面,法向是垂直平面的 向量
平面方程
给定垂直平面的法向N=(A,B,C)T,以 及平面上任意一点(x0,y0,z0),我们能够 得到未知系数D,并确定相应的平面方 程
齐次坐标
一个统一的点与向量表示方法 ◦ 向量:
◦
v
矩阵的加法
将矩阵对应的元素直接相加
矩阵减法
将矩阵对应的元素直接相减
矩阵与向量的乘法
矩阵与向量相乘
注意:矩阵的列数必须与向量的行数相 等
矩阵乘法
两个矩阵的乘法可以分解为第一个矩阵 与第二个矩阵中的每一列向量的乘法
矩阵乘法
如果A和B分别为mxp以及pxn大小的 矩阵,则AxB为mxn矩阵
线段
t [t1, t2 ]
平面表示
解析表达式
参数ax表达by式 cz d 0
p(s, t )
平面法向
p0
sv1
tv2
◦ 解析形式n: (a,b, c)
◦ 参数形式: n v1 v2
多边形法向:
n ( p2 p1) ( p3 p2 )
Z
V
V
P
Y
X
向量
向量是一列数字,表示如下:
向量几何:基本操作
加法:
v1
v2
x1 x2
y1
y2
x1 x2
y1
y
2
z1 z2 z1 z2
点与向量的加法:
q
p
v
1
齐次坐标
非齐次坐标
齐次坐标
