2019-05-21-21-系统建模与动力学分析-信号流图和状态空间模型
2018线性系统理论课件03-第1章(2)由系统机理和框图建立状态空间模型

3. 一阶微分惯性环节 其传递函数为 G(s) Y (s) s b 1 b a
n1 r 0
s nr 1
f
(r)
(0)
(1.2.6)
式中 f (r) (0) 是 r 阶导数 dr f (t) 在 t 0 时的值。 dt r
特别地,如果 f (t) 及其各阶导数的所有初始值全都等于零,则有
L
dn f dt
(t)
n
sn
F
(s)
(1.2.7)
1.2.2.3 积分性质
试列写以电枢电压u(t)为输入,轴的角位移(t)为
输出的状态空间模型。
+
Ra
ia
La
u
M
J, f
f
-
图1-4 电枢控制的直流电动机原理图
解 :设电动机励磁电流不变,铁心工作在非饱和区。
按照图1-4所描述的电动机系统,可以写出如下主 回路电压方程和轴转动动力学方程
u
Raia
La
dia dt
J
0
Ce La
1
La
0 1 x 0 u
0
f
0
J
y [0 1 0]x
1.2由系统框图建立状态空间描述
首先复习补充有关积分变换的知识。 拉氏变换的定义 拉氏变换的微分性质 拉氏变换的积分性质
1.2.1拉普拉斯变换的定义
本次课主要内容
1.2由系统框图建立状态空间描述 1.3由系统机理建立状态空间描述
为了讲解问题方便,我们先讲1.3 的内容,然后再介绍1.2的内容。 下面先复习上节课的主要内容。
信号与系统复习题

信号与系统试题库一、填空题绪论:1.离散系统的激励与响应都是____离散信号 __。
2.请写出“LTI ”的英文全称___线性非时变系统 ____。
3.单位冲激函数是__阶跃函数_____的导数。
4.题3图所示波形可用单位阶跃函数表示为()(1)(2)3(3)t t t t εεεε+-+---。
5.如果一线性时不变系统的输入为f(t),零状态响应为y f (t )=2f (t-t 0),则该系统的单位冲激响应h(t)为____02()t t δ-_________。
6. 线性性质包含两个容:__齐次性和叠加性___。
7. 积分⎰∞∞-ω--δ-δdt )]t t ()t ([e 0t j =___01j t e ω--_______。
8.已知一线性时不变系统,当激励信号为f(t)时,其完全响应为(3sint-2cost )ε(t);当激励信号为2f(t)时,其完全响应为(5sint+cost)ε(t),则当激励信号为3f(t)时,其完全响应为___7sint+4cost _____。
9. 根据线性时不变系统的微分特性,若:f(t)−−→−系统y f (t) 则有:f ′(t)−−→−系统_____ y ′f (t)_______。
10. 信号f(n)=ε(n)·(δ(n)+δ(n-2))可_____δ(n)+δ(n-2)_______信号。
11、图1所示信号的时域表达式()f t =()(1)(1)tu t t u t --- 。
12、图2所示信号的时域表达式()f t =()(5)[(2)(5)]u t t u t u t +----。
13、已知()()()2f t t t t εε=--⎡⎤⎣⎦,则()f t '=()(2)2(2)u t u t t δ----。
14、[]2cos32td ττδτ-∞⎛⎫+ ⎪⎝⎭⎰=8()u t 。
15、[]()1td τδττ-∞'-⎰=()()u t t δ+。
第二章-1-建模基本概念-电路-传递函数-方块图

2
1 RCs RC 1
电路及组成
例2:电阻电感电容(RLC)串联电路
1 LDi Ri ie CD
uR
L 1 DuR uR e R RCD
d 2uc (t ) duc (t ) T1T2 T2 uc (t ) e 2 dt dt
• 上述方程是线性定常微分方程。由这种方程描述的系统又称为 线性时不变( linear time-invariant, LTI )系统。由二阶微 分方程描述的系统称为二阶系统。
的方块图。
U
ei
i
R
U
o
I
1
Cs
e0
1 U0 I , Cs
U
i
Ui Uo I R
I
1 Cs
1 R
U
o
传递函数
U o (s) 1 U i(s) RCs 1
电路及组成
一阶系统的阶跃响应
考察标号为***的方程( 称为一阶微分方程 )
de0 T e0 ei dt
控制轨迹
***
19
电路及组成
一阶系统的阶跃响应
y x
A KA 0.632KA
de0 T e0 ei d dt
***
y (t ) KA(1 e
T1 T2
t
T
)
t 时域响应分析: 当 t=0, y(0)=0, 当 t=T, , 当
t
dy dt
t
t 0
KA T dy dt 0
y (T ) KA(1 e 1 ) 0.632 KA
图 2.1
va
LD R LD
vb
16
自动控制原理-第二章 控制系统的数学模型

t
f (t)dt 0
t
f ( )d
n
ki .L[ f (t )]
i 1
sF (s) f (0 )
s2F (s) sf (0 ) f (0 )
snF (s) sn1 f (0 ) sn2 f (0 ) f (n1) (0 )
电枢回路方程为
La
dia (t) dt
Raia (t)
Ea (t)
ua (t)
电磁转矩方程 M m Cmia (t)
电动机轴上转矩平衡方程
Jm
dm (t)
dt
fmm (t)
Mm
MC
(t)
若以角速度 m 为输出量、电枢电压 ua 为输入量,
消去中间变量,直流电动机的微分方程为
(s2+s+1)Uc(s)= Ur(s)+0.1(s+2)
即 U S 1 U S 0.1S 2
C
S2 S 1 r
S2 S 1
通电瞬间, ur(t)=1 或 Ur(s)=L[ur(t)]=1/S
故 U S 1 1 0.1S 2
C
S2 S 1 S S2 S 1
再对上式两边求反拉氏变换:
u c
t
L1 U C
S
L1
S
2
1 S
1
1 S
S
2
1 S
1
=1+1.15e-0.5tSin(0.866t-120°)+ 0.2e-0.5tSin(0.866t+30°)
现代控制理论基础-第2章-控制系统的状态空间描述精选全文完整版

(2-18)
解之,得向量-矩阵形式的状态方程
(2-19)
输出方程为
(2-20)
(5) 列写状态空间表达式
将式(2-19)和式(2-20)合起来即为状态空间表达式,若令
则可得状态空间表达式的一般式,即
(2-21)
例2.2 系统如图
取状态变量:
得:
系统输出方程为:
写成矩阵形式的状态空间表达式为:
1.非线性系统
用状态空间表达式描述非线性系统的动态特性,其状态方程是一组一阶非线性微分方程,输出方程是一组非线性代数方程,即
(2-7)
2. 线性系统的状态空间描述
若向量方程中 和 的所有组成元都是变量 和 的线性函数,则称相应的系统为线性系统。而线性系统的状态空间描述可表示为如下形式: (2-8) 式中,各个系数矩阵分别为 (2-9)
4.线性定常系统的状态空间描述
式中的各个系数矩阵为常数矩阵
当系统的输出与输入无直接关系(即 )时,称为惯性系统;相反,系统的输出与输入有直接关系(即 )时,称为非惯性系统。大多数控制系统为惯性系统,所以,它们的动态方程为
(2-11)
1.系统的基本概念 2. 动态系统的两类数学描述 3. 状态的基本概念
2.2 状态空间模型
2.2.1状态空间的基本概念
1.系统的基本概念
■系统:是由相互制约的各个部分有机结合,且具有一定功能的整体。 ■静态系统:对于任意时刻t,系统的输出惟一地取决于同一时刻的输入,这类系统称为静态系统。静态系统亦称为无记忆系统。静态系统的输入、输出关系为代数方程。 ■动态系统:对任意时刻,系统的输出不仅与t时刻的输入有关,而且与t时刻以前的累积有关(这种累积在t0(t0<t)时刻以初值体现出来),这类系统称为动态系统。由于t0时刻的初值含有过去运动的累积,故动态系统亦称为有记忆系统。动态系统的输入、输出关系为微分方程。
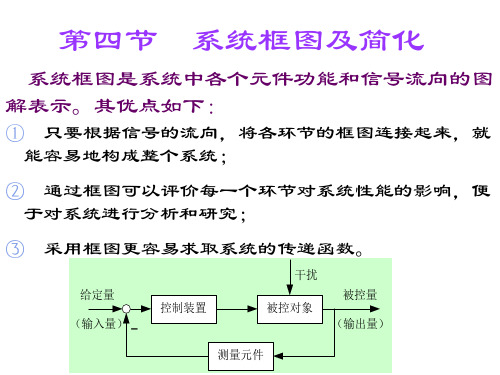
第三章(第四节) 系统框图及简化
X o (s)
X i (s)
G1 ( s) G2 ( s )
X o (s)G2(s) 来自)X 2 (s)b)
X 0 ( s ) X 1 ( s ) X 2 ( s ) G1 ( s ) X i ( s ) G 2 ( s ) X i ( s ) (G1 ( s ) G2 ( s )) X i ( s ) X 0 (s) G1 ( s ) G2 ( s ) X i (s)
X i (s)
G (s) 1 G (s) H (s)
X o (s)
H(s) a)
b)
闭环传递函数 X 0 ( s ) = G ( s) E ( s)
E ( s ) = X i ( s) B ( s)
消去E (s) (s)得 ﹑B X 0 (s )= G (s ) 轾i (s ) ± H (s ) X 0 (s ) X 臌 轾 G (s ) H (s ) X 0 (s )=G (s ) X i (s ) 1 臌
Y ( s) YN ( s) YX ( s)
G2 (s) G1 (s) X (s) N ( s) 1 G1 (s)G2 (s) H (s)
若设计控制系统时,使
G1 ( s) H ( s) 1,且 G1 ( s)G2 ( s) H ( s) 1
1 则:Y ( s) G1 (s) X (s) N (s) G1 ( s) H ( s)
为便于绘制框图,将上式表示为 1轾 I(s) = 犏 i ( s)- U 0 ( s) U R臌 1 U0 (s ) = I ( s) Cs
U i (s)
1轾 I(s) = 犏 i (s)- U 0 (s) U 臌 R
1 U 0 (s ) = I (s ) Cs
系统动力学及Vensim建模与模拟技术
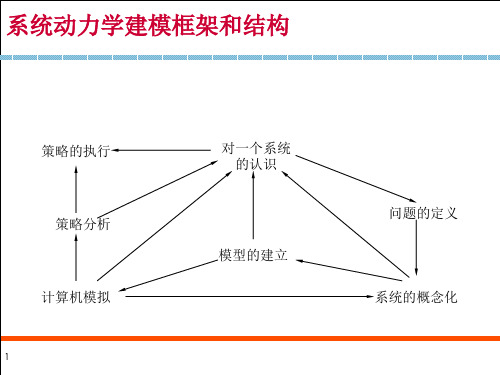
R1 实际库存 发货 满足顾客订货时间 结存订单 发货2
顾客订货速率
20
变量与方程建立
Page 21
变量
状态变量
Level或积分量 是单位时间变化量 是单位时间变化量
速率变量
辅助变量
21
应用例举(库存与劳动力模型)
Page 22
确定问题
问题的定义 参考模式 构模目的与使用模型的用户持点(关注两者的变化关系) 系统的界限 (库存、劳动力) 系统的反馈结构 (以库存和劳动力为主的因果反馈回路分析)
Vensim软件的界面
Page 9
标题栏:Titel Bar 菜单栏: Menu 工具栏 :Tools Bar
Main Tools Simulation Tools Analysis Tools Sketch Tools
状态栏 :Status Bar 流图区
9
Vensim软件的界面
订货增加
库存减少
订货 -
减少交 货延迟
库存增加
16
因果回路图分析(分析的基本技巧)
Page 17
因果链极性
因果链A→+ B:连接A与B的因果链取正号,
– (1)若增加A使B也增加,或 – (2)若A的变化使B在同一方向上发生变化。
因果链A→- B:连接A与B的因果链取负号,
– (1)若A的增加使B减少,或 – (2)若A的变化使B在相反方向上发生变化。
水位差 + 决定添水
18
流图构建(模型的实质性)
Page 19
系统动力学认为反馈系统中包含连续的,类似流体流动与积累过程。 速率或称变化率,随着时间的推移,使状态变量的值增或减。
状态、状态变量、状态空间、状态方程和动态方程

如式(2-2)所示。
其中,G=(g1,g2,…,gm ),G 是一个函数矢量。
第2章 状态空间分析法
在现代控制理论中,用系统的状态方程和输出方程来描
述系统的动态行为,状态方程和输出方程合起来称作系统的
状态空间表达式或动态方程。
根据函数向量F 和G 的不同情况,一般控制系统可以分
取每个积分器的输出端信号为状态变量x1 和x2,积分器的输
入端即ሶ 1 和ሶ 2,从图可得系统状态方程:
第2章 状态空间分析法
第2章 状态空间分析法
例2-6 求如图2-10(a)所示系统的动态方程。
图2-10 方块图
第2章 状态空间分析法
第2章 状态空间分析法
第2章 状态空间分析法
2.4 由系统的微分方程或传递函数求其动态方程
第2章 状态空间分析法
第2章 状态空间分析法
第2章 状态空间分析法
例2-2-电路如图2-6所示。以ei 作为系统的控制输入u(t),
eo 作为系统输出y(t)。建立系统的动态方程。
图2-6 RLC 电路
第2章 状态空间分析法
解 该RLC 电路有两个独立的储能元件L 和C,我们可以
取电容C 两端电压和流过电感L 的电流作为系统的两个状态
性,因此会产生一定程度上的结构差异,这也会导致动态方程
差异的产生;从系统微分方程或传递函数出发的系统实现问
题,更是会导致迥然不同的系统内部结构的产生,因而也产生
了不同的动态方程。所以说系统动态方程是不唯一的。
第2章 状态空间分析法
例如图2-11所示的传递函数的直接法实现,按照图上所
示各状态变量的取法,我们有式(2-24)所示动态方程。如果将
状态空间模型

Ce La 1
f
x1 x2 x3
1 La 0 0
u
J
x1
Y 0
1
0
x2
x3
最后根据上述状态方程和输出方程可画出结构图
u(t) 1
La
Ra
+++
x1 L
dt
x1
Ca
L
x2
x2
Y(t)
dt
1
1
Cm
J
+ x3
+
dt
x3
f J
F3
第2讲
状态空间模型
数学模型:描述系统动态行为的数学表达式, 称为控制系统的数学模型。
经典理论模型:用一个高阶微分方程或传递函 数描述。系统的动态特性仅仅由一个单输出对给定 输入的响应来表征。
实际上,系统内部还有若干其他变量,他们之 间(包含输出变量在内)是相互独立的。关于他们 对输入的响应是不易相互导出的,必须重新分别建 模求解。由此可见,单一的高阶微分方程,是不能 完全揭示系统内全部运动状态的。
x(t ) f x(t ) u(t )
y(t )
g
x(t
)
u(t )
5.非线性时变系统:
x(t) f x(t), u(t), t
y(t )
g
x(t ),
u(t), t
6.线性系统状态空间表达式的简便写法:
由上可知,对任意阶次的线性系统,其状态 空间表达式的基本形式是一样的,区别在于四个 矩阵不同,故可用四联矩阵来简单表示:
﹡完全描述:若给定 t=t0 时刻这组变量的值(初 始状态)又已知t≥t0 时系统的输入u(t),则系统在 t≥t0 时,任何瞬时的行为就完全且唯一被确定。
系统动力学简介

尽可能确定变量的量纲,必要时可自己创
造一些。例如某些心理学方面的变量,不 得不采用诸如精神上的“压力”单位。确 定量纲有助于突出因果图中文字叙述的涵 义。
因果关联图应用指南(二)
尽可能定义变量本身为正值,不把诸如
“衰减”、“衰退”、“降低”一类定 义为变量。由于“衰退”的增长或“降 低”的上升的说法将令人费解,而且当 检验因果链的极性与确定回路的极性时, 将使人目眩。 如果某因果链需加以扩充,以便于更详 尽地反映反馈结构的机制,则毫不犹豫 地将其扩充为一组因果链。 反馈结构应形成闭合问路。
的系统是复杂系统。 反馈系统俯拾皆是,生物的、环境的、生态的、 工业的、农业的、经济的和社会的系统都是反 馈系统。 开环系统是相对于闭环系统(即反馈系统)而言 的,因其内部未形成闭合的反馈环,像是被断 开的环,故称为开环系统。
1)正反馈回路
回路上的因果链全是正极性的,或者负极性的 因果链个数是偶数,则称为正反馈。
系统动力学基本理论
1、因果关联图 定义:反映系统各要素之间因果关系的图就称 为因果关系图。用箭线表示要素之间的因果 关系。
(1)因果链
如果A的增加使B也增加,则称为正极性,记作:
A
+
B
如果A的增加使B减少,则称为负极性,记作: A
-
B
例如,年出生人数增加导致人口总数增加,年死亡人数增 加导致人口总数减少。 BRTH + POP
Romeo and Juliet by William Shakespeare
罗密欧与朱丽叶相爱的二阶系统模型
Romeo's Love for Juliet change in Romeo's love ROMEO'S REACTION
系统动力学及Vensim建模与模拟技术

系统有一定的输入: U=(u1, u2, ..,um): 控制量 系统是通过相互作用而发展变化的:X’=f(X,U,t)
X`(x 1`,x 2`,. . . ,x n`)
X( x1, x2 ,. . ,x n)
U( u1, u2, . . ., um)
系统由多个子系统组成,最小的子系统是一阶反馈回路,它包含:状 态量,速率量,及辅助变量,是一个多元一阶微分方程
系统的未来发展取决于其结构及初始条件: U, f(X,U,t)) 系统动力学的模型,相当于这组微分方程组: X’=f(X,U,t)
16
基本理论知识
Page 1
系统动力学及Vensim
建模与模拟技术
1
系统动力学简介
Page 2
理论概述 发展简史 应用领域 基本理论知识 SD结构模型化原理 建模举例
2
理论概述
Page 3
系统动力学(简称SD—system dynamics)的 出现于1956年,创始人为美国麻省理工学院 (MIT)的福瑞斯特(J.W.Forrester)教授。系统 动力学是福瑞斯特教授于1958年为分析生产管 理及库存管理等企业问题而提出的系统仿真方法, 最初叫工业动态学。
系统为相互作用诸单元的复合体
从系统动力学的观点看,一个系统包含物质,信息和运动(可以包 括人及活动)三部分,系统动力学研究的范围可大可小,其种类可 分为:天然的或人工的;社会的或工程的;经济的或者政治的;心 理学的、医学的或生态的。
7
基本理论知识
2.什么是反馈
Page 8
系统内同一单元或同一子块其输入与输出的关系 称之为“反馈”
State-Space-Model-状态空间模型 共119页

为的完整描述,称为系统的状态空间表达式。
x Ax Bu
y
Cx
Du
状态空间表达式的结构图为:
26
现代控制理论基础讲义 龚道雄
一、状态空间模型
D
u
x
B+
∫
x
+ +
y
C
重点:
+
A
定常线性系统!
x Ax Bu
10
现代控制理论基础讲义 龚道雄
一、状态空间模型
11
现代控制理论基础讲义 龚道雄
一、状态空间模型
回顾:线性方程组的矩阵表示:
a11x1 a12 x2 a21x1 a22 x2 am1x1 am2 x2
a1n xn b1 a2n xn b2 ,
9
现代控制理论基础讲义 龚道雄
一、状态空间模型
用一阶微分方程组表示系统模型!
x1m2l2g1(Iml2)u 1(Mm)mgl1mlu
引入新的变量
小车状态:y, y
x1 x x2 x x3 x4
摆的状态: ,
x1 x2 x2 {1m2l2g}x3 {1(I ml2)}u x3 x4 x4 {1(M m)mgl}x3 {1ml}u
因此,本章内容为现代控制理论的基础知识。
一、状态空间模型
小车-倒立摆例子
V
u
H
7
现代控制理论基础讲义 龚道雄
一、状态空间模型
小车-倒立摆例子 V
小 车 的 水 平 运 动 : Md dt22 xuH
State-Space-Model-状态空间模型

B
m n×m m r×m
C
D
现代控制理论基础讲义 龚道雄
一、状态空间模型
状态空间表达式与传递函数 表示的比较
信号表示的不同
传递函数为频域信号
状态空间模型为时域信号 反映系统的信息不同 传递函数只描述输入输出信息 状态空间模型还描述系统内部 状态信息
Ax b
12 现代控制理论基础讲义 龚道雄
一、状态空间模型
质量—弹簧—阻尼模型
13
现代控制理论基础讲义 龚道雄
一、状态空间模型
质量—弹簧—阻尼模型 0
0
14
现代控制理论基础讲义 龚道雄
一、状态空间模型
小车-倒立摆
x1 x2 x2 { 1m 2l 2 g}x3 { 1 ( I ml 2 )}u x3 x4 x4 { 1 ( M m)mgl}x3 { 1ml}u
2 2 U L ( s ) L C2 s U ( s ) ( R C s 1)( LC s R C s 1) R C s 1 1 1 2 2 2 1 2 2 2 U ( s ) R L C s L 1 2 U 2 ( s ) ( R1C1s 1)( LC2 s R2C2 s 1) R1C2 s
d 2 摆绕重心的转动: I 2 Vl sin Hl cos dt
8 现代控制理论基础讲义 龚道雄
一、状态空间模型
d 2x M 2 uH dt d2 m 2 ( x l sin ) H dt d2 m 2 (l cos ) V mg dt d 2 I 2 Vl sin Hl cos dt
x Ax Bu y Cx Du
第一章-状态空间表达式

现代控制理论Model Control Theory前言1.胚胎萌芽期(1945年以前)•十八世纪以后,蒸汽机的使用提出了调速稳定等问题1765年俄国人波尔祖诺夫发明了锅炉水位调节器1784年英国人瓦特发明了调速器,蒸汽机离心式调速器1877年产生了劳斯稳定判据•十九世纪前半叶,动力使用了发电机、电动机促进了水利、水电站的遥控和程控的发展以及电压、电流的自动调节技术的发展•十九世纪末,二十世纪初,使用内燃机促进了飞机、汽车、船舶、机器制造业和石油工业的发展,产生了伺服控制和过程控制•二十世纪初第二次世界大战,军事工业发展很快飞机、雷达、火炮上的伺服机构,总结了自动调节技术及反馈放大器技术,搭起了经典控制理论的架子,但还没有形成学科。
2.经典控制理论时期(1940-1960)1945年美国贝尔实验室的Bode和Nyqusit提出频率响应法,奠定了控制理论的基础。
美国MIT的N. Wiener在研究随机过程的预测问题中,提出Wiener滤波理论.50年代趋于成熟.主要内容对单输入单输出系统进行分析,采用时域、频率法(频域)、根轨迹法(复数域)、相平面法、描述函数法;讨论系统稳定性的代数和几何判据以及校正网络等。
面临的挑战:被控对象日益复杂化、控制性能要求不断提高。
wiener3.现代控制理论时期(50年代末-60年代初)空间技术的发展提出了许多复杂控制问题,用于导弹、人造卫星和宇宙飞船上。
取得的成就1:1957年发射人造地球卫星;2:工业机器人产品;3:1961年载人航天;4:1969年登月;4.大系统和智能控制时期(70年代)各学科相互渗透,要分析的系统越来越大,越来越复杂。
例如:人工智能、模拟人的人脑功能、机器人等。
应用举例本课程内容•状态空间模型;•基于状态空间模型的系统分析(Analysis):运动分析、能控性、能观性、稳定性•基于状态空间模型的系统综合(Synthesis):极点配置、控制器设计、观测器设计、最优控制器设计。
系统动力学模型SD2

2.73 LEV(0)
当T(或1/CONST)大时, 相应的LEV(t) 为较平缓的增长曲线; 反之,LEV(t)为较陡峭的变化曲线。
时间常数T与倍增时间Td的关系
正反馈系统——重要参数
2. 倍增时间Td 变量由初始值增至二倍的初始值时所需的时间。 每经过一个Td ,LEV的值的状态变量INC再细分成若干状态变量。 假设 TSS=3天 INC→→ INC1, INC2, INC3。
延迟环节
疾病蔓延模型的三阶物质延迟
三阶物质延迟(DELAY3) R SYMP.KL=DELAY3(INF.JK, TSS)
DELAYP
打印隐含的状态变量功能
3.1 DYNAMO语言概述
DYNAMO是一种计算机模拟语言系列。取名来自Dynamic Models(动态模型)的混合缩写。 顾名思义,DYNAMO的涵义在于建立真实系统的模型,并借助 于计算机进行系统结构、功能与动态行为的模拟。 DYNAMO系列是伴随系统动力学,相辅相成地发展起来的。 DYNAMOⅠ、 DYNAMO Ⅱ、 DYNAMO Ⅲ、 DYNAMO Ⅳ…… DYNAMO是特地为模拟动态反馈系统而设计的专用语言。它能 够方便地以表格、图形等形式输出数据型的模拟结果。
令t=T=1/CONST t=2T
LEV(T) = LEV(0)e =2.73 LEV(0) LEV(2T) =2.73 LEV(T)=LEV(0)e 2=7.45LEV(0)
正反馈系统——重要参数
1. 时间常数T 定义:时间常数为CONST的倒数。 T=1/CONST
7.45 LEV(0)
涵义:T决定正反馈系统中增长或减少的 速度。
2001 0.1
第一章线性系统的状态空间描述

则有 x1 x2
x2 x3
x3 a0 x1 a1x2 a2 x3 b0u
写成矩阵形式
x1 0 1 0 x1 0
x2
0
0
1
x2
0
u
x3 a0 a1 a2 x3 b0
x1
y 1
0
0
x2
x3
状态图如下:
一般情况下,n 阶微分方程为: y(n) an1 y(n1) a1 y a0 y b0u
选择 n 个状态变量为 系统方程为
x1 y 0u x2 x1 1u x3 x2 2u
xn xn1 n1u
x1
x2
xn
0
0
0
a0
1 0 0 a1
0 1 0 a2
0 0 0 a3
0 0 1 an1
x1 x2
xn
1
x3 x4
0 0 0
0 0 0
mg M
0
(M m)g Ml
0
x2
1 M
u
;
1 0
x3 x4
0
1 Ml
x1
y 1
0
0
0
x2
x3 x4
状态图为
1.2 由微分方程求状态空间表达式
一个系统,用线性定常微分方程描述其输入和输出的关系。通过选 择合适的状态变量,就可以得到状态空间表达式。
设小球的重心坐标为: ( yG , zG )
则 yG y l sin
zG l cos
在水平方向,应用牛顿第二定律:
M
d2 y dt2
m
d2 dt2
(y
l
sin )
u
转动方向的力矩平衡方程式:
系统动力学及Vensim建模与模拟技术

12
系统动力学的学科基础
Page 13
系统动力学的学科基础可划分为三个层次:
方法论。系统动力学的方法论是系统方法论,其基本原则是将所研究对象 置于系统的形式中加以考察。系统方法论目前还不很完善,系统动力学自 身的发展也将会丰富、充实系统方法论。
8
系统及其构成和结构
Page 9
系统:一个由相互区别、相互作用的各部分有机地联结一 起,为同一目的而完成某种功能的集合体。
系统动力学是认识系统问题和解决系统问题的有效工具之 一。
系统的结构:所谓结构是指单元的秩序。它包含两层意思 ,首先是指组成系统的各单元,其次是指诸单元间的作用 与关系。系统的结构标志着系统构成的特征。例:
2
主要内容
(1)系统动力学简介 系统动力学发展历史 系统动力学主要应用领域 系统动力学学科基础 系统动力学建模基本过程
(2)Vensim 软件简介 软件配置 基本功能 用户界面 模型库及辅助知识
(3)系统动力学及Vensim建模基础 因果链与反馈 因果回路图构建 流图构建
3
Page 3
(ALLOC P)
Reality Check
主要开发者:Bob Eberlein
Ph.D in MIT 前国际系统动力学学会主席 2007国际系统动力学大会主席
25
Page 25
Vensim 软件功能
Vensim PLE
个人学习版。具有一般建模模拟功能,多视窗, 原因追踪, 复合模拟等功能。
技术科学和基础理论。主要有反馈理论、控制理论、控制论、信息沦、非 线性系统理论,大系统理论和正在发展中的系统学。
9-1 连续系统状态空间方程建立.ppt
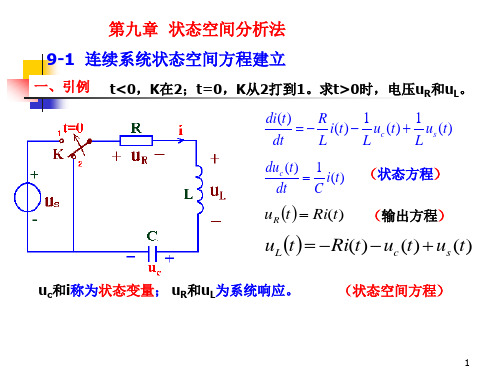
8、离散系统状态空间方程建立
1) 选状态变量:独立、完备 一般可选信号流图中延迟器的输出;
2) 列写初始方程,消去非状态变量、整理化 简方程为标准型方程:
X(k 1) AX(k) Bf(k) 3) 列写输出方程,并整理为标准型方程:
Y(k) CX(k) Df(k)
14
例1: 已知: y(k) 3y(k 1) 7 y(k 2) 5y(k 3 ) 6 f(k),
X(s)φ(s)X(0- )φ(s)BF(s) Y(s) CX(s) DF(s)
φ(s) [s1 A]1
Cφ(s)X(0- ) H(s)F(s)
状态预解矩阵 H(s) Cφ(s)B D 系统函数矩阵
零输入分量:Xzi(s)φ(s)X(0- ) 零输入响应:Yzi(s) Cφ(s)X(0- )
零状态分量:Xzs(s)φ(s)BF(s) 零状态响应:Yzs(s) H(s)F(s)
18
3、系统函数矩阵与单位冲激响应矩阵
1)系统函数矩阵
H11(s)
H(
s)
H
21(s)
H
q1
(s)
H(s) Cφ(s)B D
H12(s) H1m (s) H22(s) H2m (s)
Hq2 (s) Hqm (s)
4
例1、图示电路, 1、 选择状态变量
iL,uc
2、以 x1= uc,x2= iL作为状态变 量列写系统的状态方程;
0.5
dx1 dt
i s iR
x2
2
dx2 dt
x1
2x2
3、写出uL、 iR为响应的输出方程。
5
2、已知系统模型列写(间接列写法)
1) 已知系统微分方程列写状态空间方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
状态空间表达式的建立
首先,根据梅森公式由传递函数得到相应的信号流图,在信号流图中 定义每个积分器的输出为状态变量;
然后,根据信号流图中信号传递关系,列写状态空间表达式。 例题:假设4阶系统传递函数为:
或
G(s)s4b 3a s3 3s 3b 2sa2 2s2b 1sa 1sb 0a0
G (s)1 b3 a s3 s1 1 b2 a s2 s2 2 b 1a s1 s3 3 b0a s0 s 4 4
M 2 d d 2 v t f k 2 ( y 2 y 1 ) B 2 d d 2 y t d d 1 y t
( 2 )
将状态变量代入上两式,整理后得
x1 x3
x2 x4 x 3 M 1 1 ( k 1 k 2 ) x 1 M k 2 1 x 2 M 1 1 ( B 1 B 2 ) x 3 M B 2 1 x 4 x 4 M k 2 2x 1 M k 2 2x 2 M B 2 2x 3 M B 2 2x 4 M 1 2f
上述方法可推广到n阶系统。其参数为
0 1 0 0 00来自01A
0
0
0
0,b0 ,cb0 b1 bn1
1
0
d0
a0 a1 a2 an1
1
状态空间表达式的建立
按直接分解法得到的状态空间模型称为能控标准型,或者相变量型状 态空间表达式。
输入前馈形式的信号 流图如右图所示。 其各状态变量间的 关系为。
P 1 G 1 G 2 G 3 G 4 G 5 G 6 ;P 2 G 1 G 2 G 7 G 6 ;P 3 G 1 G 2 G 3 G 4 G 8
8个回路,各回路增益分别为
L 1G 2G 3G 4G 5H 2; L 2G 5G 6H 1; L 3G 8H 1 L 4G 7H 2G 2; L 5G 4H 4; L 6G 1G 2G 3G 4G 5G 6H 3 L 7G 1G 2G 7G 6H 3; L 8G 1G 2G 3G 4G 8H 3
状态空间表达式的建立
根据系统的输入输出模型-传递函数建立状态空间表达式
由传递函数建立状态空间表达式的过程称为“实现”。 由于状态变量选取的非唯一性,系统的实现也不是唯一的。 其中维数最低的实现称为该系统的最小实现。
直接分解法
这种方法适用于传递函数的分子、分母多项式没有分解成因式的 情况。具体步骤如下:
信号流图
前向通路与前向通路增益: 信号从输入节点到输出节点传递时,对任何 节点只通过一次的通路,称为前向通路。而前向通路上的各支路增益 之积称为前向通路增益。
回路与回路增益: 任何信号传递通路的起点和终点在同一节点上,且通 过任何节点不多于一次的闭合通路称为回路。回路中各支路增益的乘 积称为回路增益。
如果要利用(1)式确定混合节点与输入节点之间的传递函数,需要 从混合节点增加一条增益为1的支路,将混合节点变为输出节点。
实际上(1)式的P就是闭环系统的传递函数,而△就是闭环系统的特
征多项式。
信号流图
例题:一系统的信号 流图如右图所示。试 利用梅森增益公式确定 系统的传递函数。 解: 由图可知,系统有3 条前向通路,分别为
x1 a 3 x 1 x 2 b 3 u
x2 a 2 x 1 x 3 b 2 u x3 a 1 x 1 x 4 b1u x4 a 0 x 1 b 0 u y x1
a3 1 0 0 b3
x a2
0
1
0
x
b2
u
(t
)
a1 a0
0 0
0 0
1 0
bb10
矩阵形式的状态空间表达式为: y 1 0 0 0x
状态空间表达式的建立
写成矩阵形式的系统方程为
0
xx 12k10k2
xx 43
M1 k2
M2
0
0 k2
M1 k2
M2
1
0 B1B2
M1 B2
M2
M BM 00B2122xxxx1432M 00012f
输出方程为
x1
y1 y2
1 0
0 1
0 0
0 0
x2 x3 x4
系统矩阵;
B(t)是n×r 维的矩阵,称为输入矩阵。
状态空间模型
输出方程: 描述输出变量、状态变量和输入变量之间关系的代数方程 组,称为输出方程,其矩阵形式表示为:
yC (t)xD (t)u
式中:
y,C(t),D(t)分别是m维输出向量(m表示输出变量的个数), m×n 维的输出矩阵, n×r 维的前馈矩阵。
第一段,描述的是系统输入对系统内部变量即状态变量的影响;
第二段,描述的是系统的输入和内部变量对输出变量的影响。这种模 型表征了系统的所有动力学特征,是对系统的一种完全描述。
状态空间模型
状 态 动态系统的状态是指完全描述系统时域行为的一个最 小变量组。“最小变量组”是指这组变量之间是相互独立的。
状态空间模型
状态方程: 描述系统状态变量与输入变量之间关系的一阶微分方程, 称为系统的状态方程。状态方程表征了系统由输入引起的内部状态变 化,其矩阵形式为:
x & A (t)xB (t)u
式中:
x,u分别是n维状态向量(n是系统的阶数)和r维输入向量(r是输入
变量的维数);
A(t)是n×n维的方阵,它表明了系统内部状态变量之间的联系,称为
当然,也可以从微分方程开始,绘制系统的信号流图。
信号流图
信号流图
梅森增益公式 计算从输入节点到输出节点之间总增益的 梅森公式,可以表示为
P1 k
Pkk
(1)
式中: Pk是第k条前向通路的增益;
△称为信号流图的特征式,具体有
1 La LbLc Ld LeLf
a
b,c
d ,e, f
于是可得到系统的传递函数为
G(s)Y(s)P1P22P3
R(s)
状态空间模型
通常,系统的数学模型有两种类型:
一种是系统的输入输出模型,它描述的是系统的外部特性,即输入与 输出之间的关系,如微分方程和传递函数等。
另一种是状态空间模型,它不仅描述了系统的外特性,而且也给出了 系统的内部信息。
这种模型分两段来描述输入与输出之间的信号传递。
(1)
状态空间表达式的建立
如果令积分器的输出为状态变量,则积分器的输入自然就是状态变 量的导数。
由梅森公式
G (s)Y(s)1
U (s) k
P k k
(2)
可知,分子是前向通道参数,分母是反馈回路参数。当所有的反馈 回路相互接触,以及所有前向通路与反馈回路接触时,
Pkk 前向通路增益之和 G(s)1 k Lq1-反馈回路增益(3之 ) 和
状态空间模型
状态空间表达式: 状态方程和输出方程的组合,称为状态空间表达式 或动态方程。
x A(t)xB(t)u y C(t)xD(t)u
对于线性定常连续系统,其状态空间表达式为
x Ax Bu y Cx Du
线性系统的方块图 线性连续系统的状态 空间表达式常用右图 所示的方块图来表示。
如果回路之间没有任何公共节点,则称此种回路为互不接触回路。 如果已经有了系统的方块图,可以很方便地画出对应的信号流图。
信号流图
注意:
(1)节点所表示的变量等于流入该节点的信号之和。 (2)从节点流出的每一支路信号都等于该节点所表示的变量。
由此可知, 1、信号流图中的节点起到了方块图中的相加点和分支点的作用。 2、支路增益相当于方块图中的方块中的函数。
状态变量 最小变量组中的变量称为状态变量。 状态向量 由状态变量构成的向量称为系统的状态向量或简称状
态。 状态空间 状态向量的取值空间称为状态空间,状态空间的维
数等于系统的阶数。 状态轨迹 对于某一时刻,状态向量表示为状态空间中的一个
点,状态向量随时间变化将构成状态空间中的一条轨迹,即状态 轨迹。
写成矩阵形式为:
x1 0 1 0 0 x1 0
x2
0
0
1
0 x20u
xx 43
0 a0
0 a1
0 a2
1a3xx43
0 1
x1
y b0
b1
b2
b3
x2 x3 x4
状态空间表达式的建立
在上面的信号流图中,节点 x i,xi1,i1,2,3可分别合并为一个节点
。于是,可直接由(1)式得到如下图所示的被称为相变量型信号 流图。
nC为纯电容回路数(包括由电容和
独立电压源组成的回路数);
nL为纯电感割集数(包括由电感和
独立电流源组成的割集数)。
状态空间表达式的建立
例题:一机械系统如下图所示。试建立以力f为输入,两质量 块的位移y1,y2为输出的状态空间表达式。
解:该系统有4个储能元件,它们是相互独立的。因此,可以选择这 4个储能元件的变量(弹簧的位移和质量块的速度)作为状态变量。 即y1,y2 ,v1,v2.
状态空间表达式的建立
建立状态空间表达式的方法主要有两种: 一是根据物理机理直接建立状态空间表达式; 二是由已知的系统输入输出模型,如微分方程、传递函数、方块图等
,转化为系统的状态空间表达式。
根据系统物理机理建立状态空间表达式
通常选取独立的储能元件的变量作为系统的状态变量。如弹簧的位移 、质量块的运动速度、电感的电流和电容的电压等。
系统建模与动力学分析
学 时 数:48 学 分:3 任 课 教 师:连峰 工 作 单 位:电信学院综合自动化研究所 办公室地点:西一楼117房间 办公室电话:82663948-801
信号流图
信号流图是一种表示一组线性代数方程的图示方法。 像方块图一样,它也是一种描述系统内部信号传递关系的数学
图示模型。 信号流图比方块图更简便明了,不用进行简化,就可利用梅森
