等体积法求线面角测试题(含答案)

合集下载

平面向量多选题(讲义及答案)及解析

平面向量多选题(讲义及答案)及解析一、平面向量多选题1．下列条件中，使点P 与A ，B ，C 三点一定共面的是（） A ．1233PC PA PB =+ B ．111333OP OA OB OC =++ C ．QP QA QB OC =++ D ．0OP OA OB OC +++=【答案】AB 【分析】根据四点共面的充要条件，若A ，B ，C ，P 四点共面(1)PC xPA yPB x y ⇔=++=()1OP xOA yOB zOC x y z ⇔=++++=，对选项逐一分析，即可得到答案. 【详解】对于A ，由1233PC PA PB =+，12133+=，所以点P 与A ，B ，C 三点共面.对于B ，由111333OP OA OB OC =++，1111333++=，所以点P 与A ，B ，C 三点共面.对于C ，由OP OA OB OC =++，11131++=≠，所以点P 与A ，B ，C 三点不共面. 对于D ，由0OP OA OB OC +++=，得OP OA OB OC =---，而11131---=-≠，所以点P 与A ，B ，C 三点不共面. 故选：AB 【点睛】关键点睛：本题主要考查四点共面的条件，解题的关键是熟悉四点A ，B ，C ，P 共面的充要条件(1)PC xPA yPB x y ⇔=++=()1OP xOA yOB zOC x y z ⇔=++++=，考查学生的推理能力与转化思想，属于基础题.2．如图所示，设Ox ，Oy 是平面内相交成2πθθ⎛⎫≠⎪⎝⎭角的两条数轴，1e ，2e 分别是与x ，y 轴正方向同向的单位向量，则称平面坐标系xOy 为θ反射坐标系中，若12OM xe ye =+，则把有序数对(),x y 叫做向量OM 的反射坐标，记为(),OM x y =.在23πθ=的反射坐标系中，()1,2a =，()2,1b =-.则下列结论中，正确的是（）A ．()1,3a b -=-B ．5a =C ．a b ⊥D ．a 在b 上的投影为37【答案】AD 【分析】123a b e e -=-+，则()1,3a b -=-，故A 正确；3a =，故B 错误；32a b ⋅=-，故C 错误；由于a 在b 上的投影为33727a b b-⋅==，故D 正确.【详解】()()121212223a b e e e e e e -=+--=-+，则()1,3a b -=-，故A 正确；()2122254cos33a e e π=+=+=B 错误；()()22121211223222322a b e e e e e e e e ⋅=+⋅-=+⋅-=-，故C 错误；由于()22227b e e =-=a 在b 上的投影为3372147a b b-⋅==-，故D 正确。

第8章立体几何专题7 线面角的求解常考题型专题练习——【含答案】

线面角的求解【方法总结】1、线面角的范围：[0°,90°]2、线面角求法（一）：先确定斜线与平面，找到线面的交点A为斜足；找线在面外的一点B，过点B向平面α做垂线，确定垂足O；连结斜足与垂足为斜线AB在面α上的投影；投影AO与斜线AB之间的夹角为线面角；把投影AO与斜线AB归到一个三角形中进行求解（可能利用余弦定理或者直角三角形）。

注意：以上第二步过面外一点向平面做垂线的方法有一下几种：1）线在面外的一点B与平面上某点的连线正垂直于面α，无需再做辅助线；2）题中已知有与面α垂直的直线，过线在面外的一点B直接做此垂线的平行线；3）过线在面外的一点B做两垂直平面交线的垂线，利用面面垂直的性质证明OB⊥面α（这两个垂直平面一个是面α，另一个是过点B且与α垂直的平面）。

3、线面角求法（二）用等体积法，求出斜线PA在面外的一点P到面的距离，利用三角形的正弦公式进行求解。

114、线面角求法（三）利用空间向量进行求解，高二再学。

人教版高中数学必修第二册第三单元《立体几何初步》测试题(答案解析)(1)

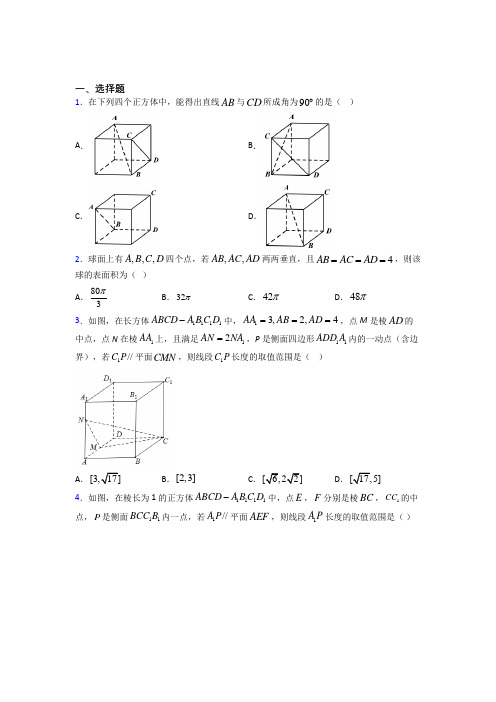
一、选择题1．在下列四个正方体中，能得出直线AB 与CD 所成角为90︒的是（）A ．B ．C ．D ．2．球面上有,,,A B C D 四个点，若,,AB AC AD 两两垂直，且4AB AC AD ===，则该球的表面积为（）A ．803πB ．32πC ．42πD ．48π3．如图，在长方体1111ABCD A B C D -中，13,2,4AA AB AD ===，点M 是棱AD 的中点，点N 在棱1AA 上，且满足12AN NA =，P 是侧面四边形11ADD A 内的一动点（含边界），若1//C P 平面CMN ，则线段1C P 长度的取值范围是（）A ．17]B ．[2,3]C ．6,22]D ．[17,5] 4．如图，在棱长为1的正方体1111ABCD A B C D -中，点E ，F 分别是棱BC ，1CC 的中点，P 是侧面11BCC B 内一点，若1//A P 平面AEF ，则线段1A P 长度的取值范围是（）A ．[2,3]B ．5,22⎡⎤⎢⎥⎣⎦C ．325,42⎡⎤⎢⎥⎣⎦D ．51,2⎡⎤⎢⎥⎣⎦ 5．如图所示，在棱长为a 的正方体1111ABCD A B C D -中，E 是棱1DD 的中点，F 是侧面11CDD C 上的动点，且1//B F 面1A BE ，则F 在侧面11CDD C 上的轨迹的长度是（）A ．aB ．2aC ．2aD ．22a 6．如图，在长方体1111ABCD A B C D -中，若,,,E F G H 分别是棱111111,,,A B BB CC C D 的中点，则必有（）A ．1//BD GHB ．//BD EFC ．平面//EFGH 平面ABCDD ．平面//EFGH 平面11A BCD7．菱形ABCD 的边长为3，60B ∠=，沿对角线AC 折成一个四面体，使得平面ACD ⊥平面ABC ，则经过这个四面体所有顶点的球的表面积为（）A ．15πB ．12πC ．8πD ．6π8．鲁班锁运用了中国古代建筑中首创的榫卯结构，相传由春秋时代各国工匠鲁班所作，是由六根内部有槽的长方形木条，按横竖立三方向各两根凹凸相对咬合一起，形成的一个内部卯榫的结构体.鲁班锁的种类各式各样，千奇百怪.其中以最常见的六根和九根的鲁班锁最为著名.下图1是经典的六根鲁班锁及六个构件的图片，下图2是其中的一个构件的三视图（图中单位：mm ），则此构件的表面积为（）A ．27600mmB ．28400mmC ．29200mmD ．210000mm 9．将表面积为36π的圆锥沿母线将其侧面展开，得到一个圆心角为23π的扇形，则该圆锥的轴截面的面积为（）A ．3B ．2C ．3D ．310．在长方体1111ABCD A B C D -中，23AB AD ==12CC =1C BD C --的大小是（）A ．30ºB ．45ºC ．60ºD ．90º 11．αβ、是两个不同的平面，m n 、是平面α及β之外的两条不同直线，给出四个论断：①m n ⊥；②αβ⊥；③n β⊥；④.m α⊥以其中三个论断作为条件，余下一个作为结论，其中正确命题的个数是（）A ．1个B ．2个C ．3个D ．4个12．已知四棱锥的各个顶点都在同一个球的球面上，且侧棱长都相等，高为4，底面是边长为32 ）A ．75518πB ．62516πC ．36πD ．34π13．长方体1111ABCD A B C D -的8个顶点都在球O 的表面上，E 为AB 的中点，3CE =，53cos 9ACE ∠=，且四边形11ABB A 为正方形，则球O 的直径为（） A ．4 B 51C ．451D ．4或514．垂直于同一条直线的两条直线的位置关系是（）A ．平行B ．相交C ．异面D ．A 、B 、C 均有可能二、解答题15．如图，在三棱锥V-ABC 中，VC ⊥底面ABC ，AC BC ⊥，D 是棱AB 的中点，且AC BC VC ==.（1）证明：平面VAB ⊥平面VCD ；（2）若22AC =，且棱AB 上有一点E ，使得线VD 与平面VCE 所成角的正弦值为1515，试确定点E 的位置，并求三棱锥C-VDE 的体积. 16．如图所示，在四棱锥P ABCD -中，90CAD ABC ∠=∠=，30BAC ADC ∠=∠=，PA ⊥平面ABCD ，E 为PD 中点，2AC =.（1）求证：//AE 平面PBC .（2）若四面体PABC 的体积为33，求PCD 的面积. 17．如图三棱柱111ABC A B C －中，11,,60CA CB AB AA BAA ∠︒＝＝＝，（1）证明1AB A C ⊥；（2）若16AC ＝，2ABCB ＝＝，求三棱柱111ABC A B C －的体积S .18．如图甲，平面四边形ABCD 中，已知45A ︒∠=，90︒∠=C ，105ADC ︒∠=，2AB BD ==，现将四边形ABCD 沿BD 折起，使得平面ABD ⊥平面BDC (如图乙)，设点E ，F 分别是棱AC ，AD 的中点.（1）求证：DC ⊥平面ABC ；（2）求三棱锥A BEF -的体积.19．如图，在底面半径为2、母线长为4的圆锥中内接一个高为3的圆柱，求圆柱的体积及表面积．20．在四棱锥P ABCD -中，//AD BC ，BC CD ⊥，120ABC ∠=︒，4=AD ，3BC =，=2AB ，3=CD CE ，⊥AP ED ．（1）求证：DE ⊥面PEA ；（2）已知点F 为AB 中点，点P 在底面ABCD 上的射影为点Q ，直线AP 与平面ABCD 所成角的余弦值为3，当三棱锥-P QDE 的体积最大时，求异面直线PB 与QF 所成角的余弦值．21．如图，在正三棱柱111ABC A B C -（侧棱垂直于底面，且底面是正三角形）中，16AC CC ==，M 是棱1CC 的中点.（1）求证：平面1AB M ⊥平面11ABB A ；（2）求1A M 与平面1AB M 所成角的正弦值.22．如图，在直三棱柱111ABC A B C -中，1AC CC =，AC BC ⊥，D 为1BC 中点，1AC 与1A C 交于点O .（1）求证：//OD 平面111A B C ；（2）求证：平面1AC B ⊥平面1A BC .23．如图，AB 是圆O 的直径，CA 垂直圆O 所在的平面，D 是圆周上一点.（1）求证：平面ADC ⊥平面CDB ；（2）若1AC =，12AD =，BD AD =，求二面角A BC D --的余弦值. 24．如图，四面体ABCD 中，点E ，F 分别为线段AC ，AD 的中点，平面EFNM ⋂平面BCD MN =，90CDA CDB ∠=∠=︒，DH AB ⊥，垂足为H .（1）求证：//EF MN ；（2）求证：平面CDH ⊥平面ABC .25．如图，在四棱锥P ABCD -中，PA ⊥平面ABC ，//,90AD BC ABC ︒∠=，2AD =，23AB =，6BC =．（1）求证：平面PBD ⊥平面PAC ；（2）PA 长为何值时，直线PC 与平面PBD 所成角最大？并求此时该角的正弦值． 26．如图所示，在四棱锥P ABCD -中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD DC =，E 是PC 的中点，过E 点作EF PB ⊥交PB 于点F .求证：（1）//PA 平面EDB ；（2）PB ⊥平面EFD .【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】根据线面垂直的性质以及判定定理判断A ，平移直线结合异面直线的定义，判断BCD.【详解】对于A ，如下图所示，连接,AE GB由于,CD BE CD BG ⊥⊥，根据线面垂直判定定理得CD ⊥平面AEBG ，再由线面垂直的性质得出AB CD ⊥，则A 正确；对于B ，如下图所示，连接,BF AF因为ABF 为正三角形，//CD AF ，所以直线AB 与CD 所成角为60︒，则B 错误；对于C ，如图所示，连接HD因为在CDH △中，45HDC ∠=︒，//AB HD ，所以直线AB 与CD 所成角为45︒，则C 错误；对于D ，如下图所示，连接GB因为//AG CD ，所以直线AB 与CD 所成角为90GAB ∠≠︒，则D 错误；故选：A【点睛】本题主要考查了求异面直线的夹角，属于中档题.2．D解析：D【分析】分析：首先求得外接球半径，然后求解其表面积即可.详解：由题意可知，该球是一个棱长为4的正方体的外接球，设球的半径为R ，由题意可得：()22222444R =++,据此可得：212R =，外接球的表面积为：2441248S R πππ==⨯=.本题选择D 选项.点睛：与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径. 3．C解析：C【分析】首先找出过点1C 且与平面CMN 平行的平面，然后可知点P 的轨迹即为该平面与侧面四边形11ADD A 的交线段，进而可以利用解三角形的知识求出线段1C P 长度的取值范围．【详解】如图所示：，取11A D 的中点G ，取MD 的中点E ，1A G 的中点F ，1D D 的三等分点H 靠近D ，并连接起来．由题意可知1//C G CM ，//GH MN ，所以平面1//C GH 平面CMN ．即当点P 在线段GH 上时，1//C P 平面CMN ．在1H C G 中，2212222C G =+=2212222C H =+=22GH =，所以1H C G 为等边三角形，取GH 的中点O ，1226C O ==故线段1C P 长度的取值范围是6,22]．故选：C ．【点睛】本题主要考查线面平行，面面平行的判定定理和性质定理的应用，以及解三角形，意在考查学生的逻辑推理能力和数学运算能力，属于中档题．4．C解析：C【分析】分别取111,BB B C 的中点,N M ,可得平面1//A MN 平面AEF ，从而点P 的轨迹为线段MN ，然后计算出线段1A P 的范围.【详解】分别取111,BB B C 的中点,N M ,则1//A M AE ,1A M ⊄平面AEF ，AE ⊂平面AEF ，则1//A M 平面AEF . //EF NM ,MN ⊄平面AEF ，EF ⊂平面AEF ，则//MN 平面AEF又1MN A M M ⋂=,所以平面1//A MN 平面AEF又平面1A MN ⋂面11BCC B MN =所以点P 的轨迹为线段MN当P 为线段MN 的端点M （或N ）时，1A P 最长，此时1122111522P M A B A BB A ⎛⎫==+= ⎪⎝⎭当P 为线段MN 的中点时，1A P 最短，此时22111322P A N MN A ⎛⎫=-= ⎪⎝⎭所以325,42AP ⎡⎤∈⎢⎥⎣⎦，故选：C ．【点睛】本题考查利用向量法解决线面平面的探索问题，本题也可以构造面面平面得出动点的轨迹，从而求解，属于中档题.5．D解析：D【分析】解：设G ，H ，I 分别为CD 、1CC 、11C D 边上的中点，证明平面1//A BGE 平面1B HI ，得到1//B F 面1A BE ，则F 落在线段HI 上，求出1122HI CD ==【详解】解：设G ，H ，I 分别为CD 、1CC 、11C D 边上的中点，1//A B EG ,则1A BEG 四点共面，11//,//EG HI B H A E , 平面1//A BGE 平面1B HI ，又1//B F 面1A BE ，F ∴落在线段HI 上，正方体1111ABCD A B C D -中的棱长为a ，1122HI CD a ∴==，即F 在侧面11CDD C 上的轨迹的长度是22a ．故选：D ．【点睛】本题考查利用线面平行求线段长度，找到动点的运动轨迹是解题的关键，属于基础题. 6．D解析：D【分析】根据“过直线外一点有且只有一条直线与已知直线平行”来判断AB 选项的正确性，根据平行直线的性质判断C 选项的正确性，根据面面平行的判定定理判断D 选项的正确性.【详解】选项A:由中位线定理可知：1//GH D C ，因为过直线外一点有且只有一条直线与已知直线平行，所以1,BD GH 不可能互相平行，故A 选项是错误的；选项B: 由中位线定理可知：1//EF A B ，因为过直线外一点有且只有一条直线与已知直线平行，所以,BD EF 不可能互相平行，故B 选项是错误的；选项C: 由中位线定理可知：1//EF A B ，而直线1A B 与平面ABCD 相交，故直线EF 与平面ABCD 也相交，故平面EFGH 与平面ABCD 相交，故C 选项是错误的；选项D:由三角形中位线定理可知：111//,//EF A B EH A D ，EF ⊄平面11A BCD ，1A B ⊂平面11A BCD ，EH ⊄平面11A BCD ，11A D ⊂平面11A BCD ,所以有//EF 平面11A BCD ，//EH 平面11A BCD ，而EF EH E =，因此平面//EFGH 平面11A BCD .所以D 选项正确.故本选：D【点睛】本小题主要考查面面平行的判定定理，考查线线平行的性质，属于中档题.7．A解析：A【分析】首先根据已知条件找到四面体外接球的球心，再求出半径，即可得到球体的表面积.【详解】如图所示，1O ，2O 分别为ABC 和DAC △的外接圆圆心，因为菱形ABCD ，60B ∠=，所以ABC 和DAC △为等边三角形.设E 为AC 的中点，连接DE ，BE ，则DE AC ⊥，BE AC ⊥，又因为平面ACD ⊥平面ABC AC =，所以DE ⊥平面ABC .分别过1O ，2O 作垂直平面ABC 和平面ACD 的直线，则交点O 为四面体ABCD 外接球的球心.因为2233332⎛⎫==-= ⎪⎝⎭EB DE ，四边形12OO EO 为矩形，所以123==O B DO ，1213===O E O E OO . 所以外接圆半径为()223153=22⎛⎫+⎪ ⎪⎝⎭，表面积为15π. 故选：A【点睛】本题主要考查四面体外接球的表面积，根据题意确定外接球的球心为解题关键，属于中档题.8．B解析：B【分析】由三视图可知，该构件是长为100，宽为20，高为20的长方体的上面的中间部分去掉一个长为40，宽为20，高为10的小长方体的一个几何体，进而求出表面积即可.【详解】由三视图可知，该构件是长为100，宽为20，高为20的长方体的上面的中间部分去掉一个长为40，宽为20，高为10的小长方体的一个几何体，如下图所示，其表面积为：()210020220202100204010210202840m 0m S =⨯⨯+⨯⨯+⨯-⨯⨯+⨯⨯=.故选：B.【点睛】本题考查几何体的表面积的求法，考查三视图，考查学生的空间想象能力与计算求解能力，属于中档题.9．B解析：B【分析】如图所示，设此圆锥的底面半径为r ，高为h ，母线长为l .可得πr 2+πrl ＝36π，2πr ＝l •23π，联立解得：r ，l ，h 22l r =-即可得出该圆锥的轴截面的面积S 12=•2r •h ＝rh . 【详解】如图所示，设此圆锥的底面半径为r ，高为h ，母线长为l .则πr 2+πrl ＝36π，化为：r 2+rl ＝36，2πr ＝l •23π，可得l ＝3r . 解得：r ＝3，l ＝9，h 22l r =-=2.该圆锥的轴截面的面积S 12=•2r •h ＝rh ＝2=2. 故选：B.【点睛】本题考查了圆锥的表面积、弧长的计算公式，考查了推理能力与计算能力，属于中档题. 10．A解析：A【分析】取BD 中点为O ，1CC ⊥平面ABCD ，所以C 即1C 在平面ABCD 上的投影，易知CO BD ⊥，再利用线面垂直证明1BD C O ⊥，得到1COC ∠即二面角1C BD C --，再计算二面角大小即可.【详解】由题意，作出长方体1111ABCD A B C D -的图象，取BD 中点为O ，连接CE 、1C E ，因为1CC ⊥平面ABCD ，所以C 即1C 在平面ABCD 上的投影，又BD ⊂平面ABCD ，所以1CC BD ⊥，因为23AB AD ==ABCD 是正方形，O 为BD 中点，所以CO BD ⊥，又1CO CC C =，所以BD ⊥平面1COC ，又1C O ⊂平面1COC ，所以1BD C O ⊥，1COC ∠即二面角1C BD C --，又12CC =()()2223236CO +==所以123tan 36COC ∠==，130COC ∠=.故选：A【点睛】本题主要考查二面角的求法和线面垂直的判定定理和性质，考查学生空间想象能力，属于中档题.11．B解析：B【分析】分别以①②③④作为结论，另外三个作条件，根据线面垂直和面面垂直的判定定理依次判断真假.【详解】若m n ⊥，αβ⊥，n β⊥，则m 与α可能平行可能相交，即①②③不能推出④；同理①②④不能推出③；若m n ⊥，n β⊥，m α⊥，两个平面的垂线互相垂直则这两个平面垂直，则αβ⊥，即①③④能够推出②；若αβ⊥，n β⊥，m α⊥，两个平面互相垂直，则这两个平面的垂线互相垂直，即m n ⊥，所以②③④能够推出①.所以一共两个命题正确.故选：B【点睛】此题考查空间直线与平面位置关系的辨析，根据选择的条件推出结论，关键在于熟练掌握空间垂直关系的判定和证明.12．B解析：B【分析】如图所示，设四棱锥P ABCD -中，球的半径为R ，底面中心为O '且球心为O ，可得OP ⊥底面ABCD ．3AO '=，4PO '=，在Rt AOO ∆'中，利用勾股定理解得R ，即可得出球的表面积．【详解】如图所示，设球的半径为R ，底面中心为O '且球心为O .∵四棱锥P ABCD -中，32AB =， ∴3AO '=.∵4PO '=，∴Rt AOO ∆'中，|4|OO R '=-，222AO AO OO ''=+，∴2223(4)R R =+-，解得258R =， ∴该球的表面积为222562544816R πππ⎛⎫=⨯= ⎪⎝⎭.故选：B .【点睛】本题考查几何体的外接球问题，此类问题常常构造直角三角形利用勾股定理进行求解，属于中等题.13．C解析：C【分析】设2AB x =，则AE x =，29BC x =-，由余弦定理可得222539392393x x x =++-⨯⨯+⨯，求出x ，即可求出球O 的直径. 【详解】根据题意，长方体内接于球O 内，则球的直径为长方体的体对角线，如图作出长方体1111ABCD A B C D -：设2AB x =，则AE x =，29BC x =-，由余弦定理可得：222539392393x x x =++-⨯+，∴1x =6，∴2AB =，22BC =，球O 的直径为4484++=；或26AB =，3BC =，球O 的直径为2424351++=.故选：C ．【点睛】本题考查球的直径的计算方法，考查余弦定理，考查计算能力和分析能力，属于常考题. 14．D解析：D【分析】结合公理及正方体模型可以判断：A ，B ，C 均有可能，可以利用反证法证明结论，也可以从具体的实物模型中去寻找反例证明．【详解】解：如图，在正方体1AC 中，1A A ⊥平面ABCD ，1A AAD ，1A A BC ⊥，又//AD BC ，∴选项A 有可能； 1A A ⊥平面ABCD ，1A A AD ，1A A AB ⊥，又AD AB A =，∴选项B 有可能；1A A ⊥平面ABCD ，1A A ⊥平面1111D C B A ，AC ⊂平面ABCD ，11A D ⊂平面1111D C B A ，1A A AC ∴⊥，111A A A D ⊥，又AC 与11A D 不在同一平面内，∴选项C 有可能．故选：D ．【点睛】本题主要考查了空间中直线与直线之间的位置关系，考查空间想象能力和思维能力，属于中档题．二、解答题15．（1）证明见解析；（2）点E 位于线段AD 的中点或线段BD 22. 【分析】（1）易得CD AB ⊥，再根据VC ⊥底面ABC ，得到 VC AB ⊥，进而AB ⊥平面VCD ，再利用面面垂直的判定定理证明.（2）过点D 在平面ABC 内作DF CE ⊥于F ，DF ⊥平面VCE ，则DVF ∠就是直线VD 与平面VCE 所成的角，在Rt VFD 中，由15sin DF DVF VD ∠==，求得DF ，然后在Rt DCE 中，求出1DE =，然后由三棱锥C-VDE 的体积为13CDE V S VC =⋅⋅求解. 【详解】（1）因为AC BC =，D 是AB 的中点，所以CD AB ⊥.又VC ⊥底面ABC ，AB 平面ABC ，所以VC AB ⊥，而VC CD C ⋂=，所以AB ⊥平面VCD .又AB 平面VAB ，所以平面VAB ⊥平面VCD .（2）过点D 在平面ABC 内作DF CE ⊥于F ，则由题意知DF ⊥平面VCE .，连接VF ，于是DVF ∠就是直线VD 与平面VCE 所成的角.在Rt VFD 中，1515DF VD =. 又因为3VD =55DF =. 在Rt DCE 中，1DE =.故知点E 位于线段AD 的中点或线段BD 的中点，三棱锥C-VDE 的体积为1112221223323CDE S VC ⋅⋅=⨯⨯⨯⨯=. 【点睛】方法点睛：(1)证明平面和平面垂直的方法：①面面垂直的定义；②面面垂直的判定定理(a ⊥β，a ⊂α⇒α⊥β)．(2)已知两平面垂直时，一般要用性质定理进行转化，在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直．16．（1）证明见解析；（2）7【分析】（1）取CD 中点F ，连接EF ，AF ，利用面面平行的判定定理证明平面//AEF 平面PBC ，再用面面平行的性质可得//AE 平面PBC ；（2）根据体积求出PA ，过A 作AQ CD ⊥于Q ，连接PQ ，AQ ，求出PQ 和CD 后，根据三角形面积公式可求得结果.【详解】（1）取CD 中点F ，连接EF ，AF ，则//EF PC ，又120BCD AFD ∠=∠=︒，∴//BC AF ，∴平面//AEF 平面PBC ，∴//AE 平面PBC .（2）因为90CAD ABC ∠=∠=，30BAC ADC ∠=∠=，2AC =，所以1,3BC AB == 由已知得：113323P ABC V AB BC PA -=⋅⋅⋅=，即11331323PA ⨯⨯⨯⨯=，可得2PA =.过A 作AQ CD ⊥于Q ，连接PQ ，AQ ，∵PA ⊥平面ABCD ，∴PA AQ ⊥，PA CD ⊥，∴CD PQ ⊥，ACD △中，2AC =，90CAD ∠=，30ADC ∠=，∴4CD =，23AD =22334AC AD AQ CD ⋅⨯===， 222237PQ PA AQ =+=+=，∴11742722PCD S PQ CD =⋅=⨯⨯=△. 【点睛】关键点点睛：掌握面面平行的判定定理和面面平行的性质是解题关键.17．（1）证明见解析；（2）3.【分析】（1）取AB 中点E ，连接11,,CE A B A E ，根据已知条件，利用等腰三角形的性质得到1A E AB ⊥，,CE AB ⊥利用线面垂直的判定定理证得AB ⊥面1,CEA 即可得到1AB A C ⊥ ；（2）在1CEA 中可以证明1A E CE ⊥，结合1A E AB ⊥，利用线面垂直判定定理得到1A E ⊥平面ABC ,作为三棱柱的高，进而计算体积.【详解】(1)取AB 中点E ，连接11,,CE A B A E ，11,60AB AA BAA ∠︒＝＝，1BAA ∴是等边三角形，1A E AB ∴⊥，CA CB ＝，,CE AB ∴⊥1,CE A E E ⋂＝AB ∴⊥面1,CEA 1AB A C ∴⊥.(2)由于CAB ∆为等边三角形，3CE ∴＝1123322S AB CE ⨯⨯⨯=底面积＝＝1CEA 中，3CE ＝13EA ＝16AC =1A E CE ∴⊥，结合1A E AB ⊥，又,,AB CE E AB CE ⋂=⊂平面ABC ,1A E ∴⊥平面ABC ,13h A E ∴＝＝3V Sh =＝.【点睛】本题考查线面垂直的判定与证明，考查棱柱的体积计算，属基础题，为证明线线垂直，常常先证线面垂直，为证明线面垂直，又常常需要先证明线线垂直，这是线面垂直关系常用的证明与判定方式，要熟练掌握.18．（1）证明见解析；（2. 【分析】（1）在图甲中先证AB BD ⊥，在图乙中由面面垂直的性质定理先证AB CD ⊥，由条件可得DC BC ⊥，进而可判定DC ⊥平面AB C ；（2）利用等体积法进行转化计算即可.【详解】（1）图甲中，∵AB BD =且45A ︒∠=，45ADB ︒∴∠=， ()()180180454590ABD ADB A ︒︒︒︒︒∴∠=-∠+∠=-+=，即AB BD ⊥，图乙中，∵平面ABD ⊥平面BDC ，且平面ABD 平面BDC BD =，∴AB ⊥平面BDC ，又CD ⊂平面BDC ，∴AB CD ⊥，又90DCB ︒∠=，∴DC BC ⊥，且AB BC B ⋂=，又AB ，BC ⊂平面AB C ，∴DC ⊥平面AB C ；（2）因为点E ，F 分别是棱AC ，AD 的中点，所以//EF DC ，且12EF DC =，所以EF ⊥平面ABC ，由（1）知，AB ⊥平面BDC ，又BC ⊂平面BDC ，所以AB BC ⊥，105ADC ︒∠=，45ADB ︒∠=，1054560CDB ADC ADB ︒︒︒∴∠=∠-∠=-=， 90906030CBD CDB ︒︒︒︒∴∠=-∠=-=，cos3022BC BD ︒∴=⋅=⨯=1sin 30212DC BD ︒=⋅=⨯=，所以12ABC S AB BC =⨯⨯△12ABE ABC S S ==△△1122EF DC ==，所以111332A BEF F ABE ABE V V EF S --==⋅⋅=⋅=△ 【点睛】方法点睛：计算三棱锥体积时，常用等体积法进行转化，具体的方法为：①换顶点，换底面；②换顶点，不换底面；③不换顶点，换底面.19．体积V ；表面积(21π+．【分析】由已知计算出圆柱的底面半径，代入圆柱表面积和体积公式，即可得到答案.【详解】解：设圆柱的底面半径为r ，高为'h ，圆锥的高h ='3h ＝，1'2h h ∴＝，则122r =，1r ∴＝． ∴圆柱的体积2V r h π'=＝；表面积(22221S r rh πππ=+='．【点睛】本题考查的知识点求圆柱的表面积和体积，其中根据已知条件，求出圆柱的底面半径，是解答本题的关键.20．（1）证明见解析；（2．【分析】（1）在直角梯形ABCD 中先求出,,CD CE BE ，然后可求得,DE AE ，从而可证明DE AE ⊥，由线面垂直判定定理证明线面垂直；（2）由（1）得面面垂直，知Q 在AE 上，PAQ ∠为直线AP 与平面ABCD 所成的角，cos AQ PAQ AP ∠==AQ x =（0x <≤-P QDE 的体积，由二次函数知识求得最大值，及此时x 的值，得Q 为AE 中点，从而有//FQ BE ，PBE ∠为异面直线PB 与QF 所成角（或补角），由余弦定理可得．【详解】（1）证明：//AD BC ，BC CD ⊥，120ABC ∠=︒，4=AD ，3BC =，=2AB ，∴CD ===CD ，∴1CE =，CD =2BE =，由余弦定理得AE ===又2DE ===，∴222DE AE AD ，∴AD DE ⊥，∵AP DE ⊥，又AP AE A =，AP AE ⊂、平面APE ，∴DE ⊥平面APE ．（2）由（1）DE ⊥平面APE ．DE ⊂平面ABCD ，∴平面ABCD ⊥平面PAE ，∴Q 点在AE 上，PAQ ∠为直线AP 与平面ABCD 所成的角，cos 3AQ PAQ AP ∠==，设AQ x =（0x <≤PQ =，QE x =，12(23)232QDE S x x =⨯⨯-=-△， 212(23)33P QDE QDE V PQ S x x -=⋅=--△22(3)223x =--+≤，当且仅当3x =时等号成立，则当P QDE V -最大时，3AQ =，∴Q 为AE 中点，∵F 为AB 中点，∴//FQ BC ，∴PBE ∠为异面直线PB 与QF 所成角（或补角），1,3QB QE ==，则由PQ ⊥平面ABCD 得3,7PE PB ==，又2BE =，则2227cos 2PB BE PE PBE PB BE +-∠==⋅， ∴异面直线PB 与QF 所成角的余弦值为714．【点睛】本题考查线面垂直的判定定理，考查直线与平面所成的角，异面直线所成的角，三棱锥的体积等，旨在考查学生的空间想象能力，运算求解能力，逻辑推理能力．属于中档题． 21．（1）证明见解析；（210 【分析】（1）连接1A B 交1AB 于O ，连接MO ，证明1MO AB ⊥，1MO A B ⊥，然后得到MO ⊥平面11ABB A 即可；（2）首先证明1A O ⊥平面1AB M ，然后可得1A MO ∠即为1A M 与平面1AB M 所成的角，然后利用111sin A O MO MA A ∠=算出答案即可. 【详解】（1）证明：连接1A B 交1AB 于O ，连接MO ，易得O 为1A B ，1AB 的中点∵1CC ⊥平面ABC ，AC ⊂平面ABC∴1CC AC ⊥又M 为1CC 中点，16AC CC == ∴223635AM =+=同理可得135B M =∴1MO AB ⊥连接MB ，同理可得135A M BM ==1MO A B ∴⊥又11AB A B O ⋂=，1AB ，1A B ⊂平面11ABB A∴MO ⊥平面11ABB A又MO ⊂平面1AB M∴平面1AB M ⊥平面11ABB A（2）解：易得11A O AB ⊥又由（1）平面1AB M ⊥平面1ABB A平面1AB M 平面111ABB A AB =，1AO ⊂平面11ABB A ∴1A O ⊥平面1AB M∴1A MO ∠即为1A M 与平面1AB M 所成的角在11Rt AA B △中，22111663222AB AO ==+=在1Rt AOM 中，1113210sin 35AO MO A A M ∠=== 故1A M 与平面1AB M 10【点睛】方法点睛：几何法求线面角的步骤：（1）作：作出辅助线，构成三角形；（2）证：利用线面角的定义证明作出的角即为所求角；（3）求：在直角三角形中求解即可. 22．（1）证明见解析；（2）证明见解析.（1）连接1B C ，可知点D 为1B C 的中点，利用中位线的性质可得出11//OD A B ，利用线面平行的判定定理可证得结论成立；（2）证明出四边形11AAC C 为菱形，可得出11AC AC ⊥，证明出BC ⊥平面11AAC C ，可得出1AC BC ⊥，利用线面垂直和面面垂直的判定定理可证得结论成立.【详解】（1）如下图所示，连接1B C ，在三棱柱111ABC A B C -中，11//BB CC 且11BB CC =，则四边形11BB C C 为平行四边形， D 为1BC 的中点，则D 为1B C 的中点，同理可知，点O 为1A C 的中点，11//OD A B ∴， OD ⊄平面111A B C ，11A B ⊂平面111A B C ，因此，//OD 平面111A B C ；（2）在直三棱柱111ABC A B C -中，1CC ⊥平面ABC ，11//AA CC 且11AA CC =，所以四边形11AAC C 为平行四边形，1AC CC =，所以，平行四边形11AAC C 为菱形，则11AC AC ⊥，1CC ⊥平面ABC ，BC ⊂平面ABC ，1BC CC ∴⊥，BC AC ⊥，1AC CC C =，BC ∴⊥平面11AAC C ，1AC ⊂平面11AAC C ，1AC BC ∴⊥，1AC BC C =，1AC ∴⊥平面1A BC ，1AC ⊂平面1AC B ，因此，平面1AC B ⊥平面1A BC .【点睛】方法点睛：证明面面垂直的常用方法：（1）面面垂直的定义；（2）面面垂直的判定定理.在证明面面垂直时，可假设两个平面垂直成立，利用面面垂直的性质定理转化为线面垂直，即可找到所要证的线面垂直，然后组织论据证明即可.23．（1）证明见解析；（2）105.（1）证明,BD AC BD AD ⊥⊥后得BD ⊥平面ADC ，然后可得面面垂直；（2）连结OD ，作OE BC ⊥于E ，连结DE ，证得OED ∠为二面角A BC D --的平面角，在三角形中可得其余弦值．【详解】证明：（1）∵CA ⊥平面ADB ，BD ⊂平面ADB ，∴CA BD ⊥，.又D 是圆周上一点，AB 是圆O 的直径，DA DB ⊥，又CA ⊂平面CAD ，DA ⊂平面CAD ，ADCA A =，∴BD ⊥平面CAD ，而BD ⊂平面ACD ，∴平面ADC ⊥平面CDB ；（2）连结OD ，作OE BC ⊥于E ，连结DE ，∵CA ⊥平面ADB ，CA ⊂平面ABC ，∵平面ABC ⊥平面ADB ，∵BD AD =，∴⊥OD AB ，又∵OD ⊂平面ADB ，∵平面ABC平面ADB AB =， ∴OD ⊥平面ABC ，∵BC ⊂面ABC ，∴BC OD ⊥.又∵BC OE ⊥，OE DE E =，∴BC ⊥平面ODE ，∴BC DE ⊥，∴OED ∠为二面角A BC D --的平面角.又1AC =，12AD =，BD AD =， ∴2OD =，3OE =，30DE =，所以cos OE OED DE ∠==10所以二面角A BC D --的余弦值为105. 【点睛】方法点睛：本题考查证明面面垂直，求二面角．求二面角的方法：（1）定义法：根据定义作出二面角的平面角（并证明）然后在相应三角形中求角．（2）向量法：建立空间直角坐标系，用二面角的两个面的法向量的夹角与二面角相等或互补计算．24．（1）证明见解析；（2）证明见解析.【分析】本题考查线面平行与线面垂直的判定，难度不大.（1）利用线面平行的判定定理证得//EF 平面BCD ，进而利用线面平行的性质定理证得；（2）利用线面垂直的判定定理证得CD ⊥平面ADB ，进而证得AB ⊥平面CDH ，然后由面面垂直判定定理证得结论.【详解】证明：（1）因为点E 、F 分别为线段AC 、AD 的中点，EF ∴为ACD △的中位线，则//EF CD ，CD ⊂平面BCD ，EF ⊄平面BCD ，//EF ∴平面BCD ，又EF ⊂平面EFNM ，平面EFNM ⋂平面BCD MN =，//EF MN ∴；（2）90CDA CDB ∠=∠=︒，CD DA ∴⊥，CD DB ⊥，DA DB D ⋂=，DA ⊂平面ADB ，DB ⊂平面ADB ， CD 平面ADB ，CD AB ∴⊥又DH AB ⊥，DH CD D ⋂=，DC ⊂平面DCH ，DH ⊂平面DCH ，AB ∴⊥平面CDH ，AB ⊂平面ABC ，∴平面CDH ⊥平面ABC.【点睛】要证线线平行，常常先证线面平行，综合利用线面平行的判定与性质进行证明；要证面面垂直，常常先证线面垂直，而要证线面垂直，又常常先证另一个线面垂直.25．（1）证明见解析；（2）PA =PC 与平面PBD 所成角最大，此时该角的正弦值为35. 【分析】（1）根据已知条件，得到BD PA ⊥，再利用正切函数的性质，求得0030,BAC 60ABD ∠=∠=，得到BD AC ⊥，进而可证得平面PBD ⊥平面PAC ；（2）建立空间坐标系，得到()BD =-，()0,2,DP t =-，()2PC t =-，进而得到平面PBD 的一个法向量为1,3,n ⎛= ⎝⎭，进而可利用向量的公式求解【详解】（1）∵PA ⊥平面,ABCD BD ⊂平面ABCD ，∴BD PA ⊥，又3tan ,tan 33AD BC ABD BAC AB AB ∠==∠==， ∴0030,BAC 60ABD ∠=∠=，∴090AEB ∠=，即BD AC ⊥（E 为AC 与BD 交点）．又PA AC ，∴BD ⊥平面PAC ，又因为BD ⊂平面PBD ，所以，平面PAC ⊥平面PBD（2）如图，以AB 为x 轴，以AD 为y 轴，以AP 为z 轴，建立空间坐标系，如图，设AP t =，则()()()()23,0,0,23,6,0,0,2,0,0,0,B C D P t ，则()23,2,0BD =-，()0,2,t DP =-，()23,6,PC t =-，设平面PBD 法向量为(),,n x y z =，则00n BD n DP ⎧⋅=⎨⋅=⎩，即232020x y y tz ⎧-+=⎪⎨-+=⎪⎩，取1x =，得平面PBD 的一个法向量为231,3,n t ⎛⎫= ⎪ ⎪⎝⎭，所以22226333cos ,1214448451PC nPC n PC n t t t t ⋅===++++，因为22221441445151275t t t t +++=≥，当且仅当23t =时等号成立，所以5c 33353os ,PC n ≤=，记直线PC 与平面PBD 所成角为θ，则sin cos ,PC n θ=，故3sin 5θ≤，即23t =时，直线PC 与平面PBD 所成角最大，此时该角的正弦值为35．【点睛】关键点睛：解题关键在于利用定义和正切函数的性质，得到BD ⊥平面PAC ，进而证明平面PAC ⊥平面PBD ；以及建立空间直角坐标系，求出法向量，进行求解直线PC 与平面PBD 所成角的最大值，难度属于中档题26．（1）证明见解析；（2）证明见解析.【分析】（1）连结AC 、BD ，交于点O ，连结OE ，通过//OE PA 即可证明；（2）通过PD BC ⊥， CD BC ⊥可证BC ⊥平面PDC ，即得DE BC ⊥，进而通过DE ⊥平面PBC 得DE PB ⊥，结合EF PB ⊥即证.【详解】证明：（1）连结AC 、BD ，交于点O ，连结OE ，底面ABCD 是正方形，∴O 是AC 中点，点E 是PC 的中点，//OE PA ∴.OE ⊂平面EDB ， PA ⊄平面EDB ，∴//PA 平面EDB .（2）PD DC =，点E 是PC 的中点，DE PC ∴⊥.底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，∴PD BC ⊥， CD BC ⊥，且 PD DC D ⋂=，∴BC ⊥平面PDC ，∴DE BC ⊥，又PC BC C ⋂=，∴DE ⊥平面PBC ，∴DE PB ⊥，EF PB ⊥，EF DE E ⋂=，PB ∴⊥平面EFD .【点睛】本题考查线面平行和线面垂直的证明，属于基础题.。

立体几何(7大题型)(解析版)2024年高考数学立体几何大题突破

立体几何立体几何是高考数学的必考内容，在大题中一般分两问，第一问考查空间直线与平面的位置关系证明；第二问考查空间角、空间距离等的求解。

考题难度中等，常结合空间向量知识进行考查。

2024年高考有很大可能延续往年的出题方式。

题型一：空间异面直线夹角的求解1(2023·上海长宁·统考一模)如图，在三棱锥A-BCD中，平面ABD⊥平面BCD,AB=AD,O为BD的中点.(1)求证：AO⊥CD；(2)若BD⊥DC,BD=DC,AO=BO，求异面直线BC与AD所成的角的大小.【思路分析】(1)利用面面垂直的性质、线面垂直的性质推理即得.(2)分别取AB,AC的中点M,N，利用几何法求出异面直线BC与AD所成的角.【规范解答】(1)在三棱锥A-BCD中，由AB=AD,O为BD的中点，得AO⊥BD，而平面ABD⊥平面BCD，平面ABD∩平面BCD=BD，AO⊂平面ABD，因此AO⊥平面BCD，又CD⊂平面BCD，所以AO⊥CD.(2)分别取AB,AC的中点M,N，连接OM,ON,MN，于是MN⎳BC,OM⎳AD，则∠OMN是异面直线BC与AD所成的角或其补角，由(1)知，AO ⊥BD ，又AO =BO ，AB =AD ，则∠ADB =∠ABD =π4，于是∠BAD =π2，令AB =AD =2，则DC =BD =22，又BD ⊥DC ，则有BC =BD 2+DC 2=4，OC =DC 2+OD 2=10，又AO ⊥平面BCD ，OC ⊂平面BCD ，则AO ⊥OC ，AO =2，AC =AO 2+OC 2=23，由M ,N 分别为AB ,AC 的中点，得MN =12BC =2,OM =12AD =1,ON =12AC =3，显然MN 2=4=OM 2+ON 2，即有∠MON =π2，cos ∠OMN =OM MN =12，则∠OMN =π3，所以异面直线BC 与AD 所成的角的大小π3.1、求异面直线所成角一般步骤：(1)平移：选择适当的点，线段的中点或端点，平移异面直线中的一条或两条成为相交直线．(2)证明：证明所作的角是异面直线所成的角．(3)寻找：在立体图形中，寻找或作出含有此角的三角形，并解之．(4)取舍：因为异面直线所成角θ的取值范围是0,π2，所以所作的角为钝角时，应取它的补角作为异面直线所成的角．2、可通过多种方法平移产生，主要有三种方法：(1)直接平移法(可利用图中已有的平行线)；(2)中位线平移法；(3)补形平移法(在已知图形中，补作一个相同的几何体，以便找到平行线)．3、异面直线所成角：若n 1 ,n 2分别为直线l 1,l 2的方向向量，θ为直线l 1,l 2的夹角，则cos θ=cos <n 1 ,n 2 > =n 1 ⋅n 2n 1 n 2.1(2023·江西萍乡·高三统考期中)如图，在正四棱台ABCD -A 1B 1C 1D 1中，E ,F 分别是BB 1,CD 的中点.(1)证明：EF ⎳平面AB1C 1D ；(2)若AB =2A 1B 1，且正四棱台的侧面积为9，其内切球半径为22，O 为ABCD 的中心，求异面直线OB 1与CC 1所成角的余弦值.【答案】(1)证明见解析；(2)45【分析】(1)根据中位线定理，结合线面平行判定定理以及面面平行判定定理，利用面面平行的性质，可得答案；(2)根据题意，结合正四棱台的几何性质，求得各棱长，利用线线角的定义，可得答案.【解析】(1)取CC 1中点G ，连接GE ,GF ，如下图：在梯形BB 1C 1C 中，E ,G 分别为BB 1,CC 1的中点，则EG ⎳B 1C 1，同理可得FG ⎳C 1D ，因为EG ⊄平面AB 1C 1D ，B 1C 1⊂平面AB 1C 1D ，所以EG ⎳平面AB 1C 1D ，同理可得GF ⎳平面AB 1C 1D ，因为EG ∩FG =G ，EG ,FG ⊆平面EFG ，所以平面EFG ⎳平面AB 1C 1D ，又因为EF ⊆平面EFG ，所以EF ⎳平面AB 1C 1D ；(2)连接AC ,BD ，则AC ∩BD =O ，连接A 1O ,A 1C 1,B 1O ,在平面BB 1C 1C 中，作B 1N ⊥BC 交BC 于N ，在平面BB 1D 1D 中，作B 1M ⊥BD 交BD 于M ，连接MN ，如下图：因为AB =2A 1B 1，则OC =A 1C 1，且OC ⎳A 1C 1，所以A 1C 1CO 为平行四边形，则A 1O ⎳CC 1，且A 1O =CC 1，所以∠A 1OB 1为异面直线OB 1与CC 1所成角或其补角，同理可得：B 1D 1DO 为平行四边形，则B 1O =D 1D ，在正四棱台ABCD -A 1B 1C 1D 1中，易知对角面BB 1D 1D ⊥底面ABCD ，因为平面ABCD ∩平面BB 1D 1D =BD ，且B 1M ⊥BD ，B 1M ⊂平面BB 1D 1D ，所以B 1M ⊥平面ABCD ，由内切球的半径为22，则B 1M =2，在等腰梯形BB 1C 1C 中，BC =2B 1C 1且B 1N ⊥BC ，易知BN =14BC ，同理可得BM =14BD ，在△BCD 中，BN BC=BM BD =14，则MN =14CD ，设正方形ABCD 的边长为4x x >0 ，则正方形A 1B 1C 1D 1的边长为2x ，MN =x ，由正四棱台的侧面积为9，则等腰梯形BB 1C 1C 的面积S =94，因为B 1M ⊥平面ABCD ，MN ⊂平面ABCD ，所以B 1M ⊥MN ，在Rt △B 1MN ，B 1N =B 1M 2+MN 2=2+x 2，可得S =12⋅B 1N ⋅B 1C 1+BC ，则94=12×2+x 2×4x +2x ，解得x =12，所以BC =2，B 1C 1=1，BN =14BC =12，B 1N =32，则A 1B 1=1，在Rt △BB 1N 中，BB 1=B 1N 2+BN 2=102，则CC 1=DD 1=102，所以在△A 1OB 1中，则cos ∠A 1OB 1=A 1O 2+B 1O 2-A 1B 212⋅A 1O ⋅B 1O=1022+102 2-12×102×102=45，所以异面直线OB 1与CC 1所成角的余弦值为45.2(2023·辽宁丹东·统考二模)如图，平行六面体ABCD -A 1B 1C 1D 1的所有棱长都相等，平面CDD 1C 1⊥平面ABCD ，AD ⊥DC ，二面角D 1-AD -C 的大小为120°，E 为棱C 1D 1的中点．(1)证明：CD ⊥AE ；(2)点F 在棱CC 1上，AE ⎳平面BDF ，求直线AE 与DF 所成角的余弦值．【答案】(1)证明见解析；(2)37【分析】(1)根据面面垂直可得线面垂直进而得线线垂直，由二面角定义可得∠D 1DC =120°，进而根据中点得线线垂直即可求；(2)由线面平行的性质可得线线平行，由线线角的几何法可利用三角形的边角关系求解，或者建立空间直角坐标系，利用向量的夹角即可求解.【解析】(1)因为平面CDD 1C 1⊥平面ABCD ，且两平面交线为DC ,AD ⊥DC ，AD ⊂平面ABCD , 所以AD ⊥平面CDD 1C 1，所以AD ⊥D 1D ,AD ⊥DC ，∠D 1DC 是二面角D 1-AD -C 的平面角，故∠D 1DC =120°．连接DE ，E 为棱C 1D 1的中点，则DE ⊥C 1D 1,C 1D 1⎳CD ，从而DE ⊥CD ．又AD ⊥CD ，DE ∩AD =D ，DE ,AD ⊂平面AED ，所以CD ⊥平面AED ，ED ⊂平面AED ,因此CD ⊥AE ．(2)解法1：设AB =2，则DE =D 1D 2-12D 1C 1 2=3，所以CE =AE =AD 2+DE 2=7．连AC 交BD 于点O ，连接CE 交DF 于点G ，连OG ．因为AE ⎳平面BDF ，AE ⊂平面AEC ,平面AEC ∩平面BDF =OG ，所以AE ∥OG ，因为O 为AC 中点，所以G 为CE 中点，故OG =12AE =72．且直线OG 与DF 所成角等于直线AE 与DF 所成角．在Rt △EDC 中，DG =12CE =72，因为OD =2，所以cos ∠OGD =722+72 2-(2)22×72×72=37．因此直线AE 与DF 所成角的余弦值为37．解法2；设AB =2，则DE =D 1D 2-12D 1C 1 2=3，所以CE =AE =AD 2+DE 2=7．取DC 中点为G ，连接EG 交DF 于点H ，则EG =DD 1=2．连接AG 交BD 于点I ，连HI ，因为AE ⎳平面BDF ，AE ⊂平面AGE ，平面AGE ∩平面BDF =IH ，所以AE ∥IH ．HI 与DH 所成角等于直线AE 与DF 所成角．正方形ABCD 中，GI =13AG ，DI =13DB =223，所以GH =13EG ，故HI =13AE =73．在△DHG 中，GH =13EG =23，GD =1，∠EGD =60°，由余弦定理DH =1+49-1×23=73．在△DHI 中，cos ∠DHI =732+73 2-223 22×73×73=37．因此直线AE 与DF 所成角的余弦值为37．解法3:由(1)知DE ⊥平面ABCD ，以D 为坐标原点，DA为x 轴正方向，DA为2个单位长，建立如图所示的空间直角坐标系D -xyz ．由(1)知DE =3，得A 2,0,0 ,B 2,2,0 ,C 0,2,0 ,E (0,0,3)，C 1(0,1,3)．则CC 1=(0,-1,3)，DC =(0,2,0)，AE =(-2,0,3)，DB =(2,2,0)．由CF =tCC 1 0≤t ≤1 ，得DF =DC +CF =(0,2-t ,3t )．因为AE ⎳平面BDF ，所以存在唯一的λ，μ∈R ，使得AE =λDB +μDF=λ2,2,0 +μ(0,2-t ,3t )=2λ,2λ+2μ-tμ,3μt ，故2λ=-2,2λ+2μ-tμ=0,3μt =3，解得t =23，从而DF =0,43,233 ．所以直线AE 与DF 所成角的余弦值为cos AE ,DF =AE ⋅DF|AE ||DF |=37．题型二：空间直线与平面夹角的求解2(2024·安徽合肥·统考一模)如图，三棱柱ABC -A 1B 1C 1中，四边形ACC 1A 1,BCC 1B 1均为正方形，D ,E 分别是棱AB ,A 1B 1的中点，N 为C 1E 上一点.(1)证明：BN ⎳平面A 1DC ；(2)若AB =AC ,C 1E =3C 1N，求直线DN 与平面A 1DC 所成角的正弦值.【思路分析】(1)连接BE ,BC 1,DE ,则有平面BEC 1⎳平面A 1DC ，可得BN ⎳平面A 1DC ；(2)建立空间直角坐标系，利用空间向量进行计算即可.【规范解答】(1)连接BE ,BC 1,DE .因为AB ⎳A 1B 1，且AB =A 1B 1，又D ,E 分别是棱AB ,A 1B 1的中点，所以BD ⎳A 1E ，且BD =A 1E ，所以四边形BDA 1E 为平行四边形，所以A 1D ⎳EB ，又A 1D ⊂平面A 1DC ,EB ⊄平面A 1DC ，所以EB ⎳平面A 1DC ，因为DE ⎳BB 1⎳CC 1，且DE =BB 1=CC 1，所以四边形DCC 1E 为平行四边形，所以C 1E ⎳CD ，又CD ⊂平面A 1DC ,C 1E ⊄平面A 1DC ，所以C 1E ⎳平面A 1DC ，因为C 1E ∩EB =E ,C 1E ,EB ⊂平面BEC 1，所以平面BEC 1⎳平面A 1DC ，因为BN ⊂平面BEC 1，所以BN ⎳平面A 1DC .(2)四边形ACC 1A 1,BCC 1B 1均为正方形，所以CC 1⊥AC ,CC 1⊥BC ，所以CC 1⊥平面ABC .因为DE ⎳CC 1，所以DE ⊥平面ABC ，从而DE ⊥DB ,DE ⊥DC .又AB =AC ，所以△ABC 为等边三角形.因为D 是棱AB 的中点，所以CD ⊥DB ，即DB ,DC ,DE 两两垂直.以D 为原点，DB ,DC ,DE 所在直线为x ,y ,z 轴，建立如图所示的空间直角坐标系D -xyz .设AB =23，则D 0,0,0 ,E 0,0,23 ,C 0,3,0 ,C 10,3,23 ,A 1-3,0,23 ，所以DC =0,3,0 ,DA 1=-3,0,23 .设n=x ,y ,z 为平面A 1DC 的法向量，则n ⋅DC=0n ⋅DA 1 =0，即3y =0-3x +23z =0 ，可取n=2,0,1 .因为C 1E =3C 1N ，所以N 0,2,23 ,DN =0,2,23 .设直线DN 与平面A 1DC 所成角为θ，则sin θ=|cos ‹n ,DN ›|=|n ⋅DN ||n |⋅|DN |=235×4=1510，即直线DN 与平面A 1DC 所成角正弦值为1510.1、垂线法求线面角(也称直接法)：(1)先确定斜线与平面，找到线面的交点B 为斜足；找线在面外的一点A ，过点A 向平面α做垂线，确定垂足O ；(2)连结斜足与垂足为斜线AB 在面α上的投影；投影BO 与斜线AB 之间的夹角为线面角；(3)把投影BO 与斜线AB 归到一个三角形中进行求解(可能利用余弦定理或者直角三角形)。

新高考数学重难点培优专题讲义——立体几何小题专练(含详细答案解析)

立体几何小题培优讲义高考规律立体几何是高考的热点内容，属于高考的必考内容之一.从近几年的高考情况来看，高考对该部分的考查，小题主要体现在三个方面：一是有关空间线面位置关系的判断；二是空间几何体的体积和表面积的计算，难度较易；三是常见的一些经典常考压轴小题，涉及到空间角、空间距离与轨迹问题等，难度中等或偏上．知识梳理【知识点1 空间几何体表面积与体积的常见求法】1.求几何体体积的常用方法(1)公式法：直接代入公式求解.(2)等体积法：四面体的任何一个面都可以作为底面，只需选用底面面积和高都易求出的形式即可.(3)补体法：将几何体补成易求解的几何体，如棱锥补成棱柱，三棱柱补成四棱柱等.(4)分割法：将几何体分割成易求解的几部分，分别求体积.2.求组合体的表面积与体积的一般方法求组合体的表面积的问题，首先应弄清它的组成部分，其表面有哪些底面和侧面，各个面的面积应该怎样求，然后根据公式求出各个面的面积，最后相加或相减.求体积时也要先弄清各组成部分，求出各简单几何体的体积，再相加或相减.【知识点2 几何体与球的切、接问题的解题策略】1.常见的几何体与球的切、接问题的解决方案：常见的与球有关的组合体问题有两种：一种是内切球，另一种是外接球.常见的几何体与球的切、接问题的解决方案：2.空间几何体外接球问题的求解方法：空间几何体外接球问题的处理关键是确定球心的位置，常见的求解方法有如下几种：(1)涉及球与棱柱、棱锥的切、接问题时，一般过球心及多面体的特殊点(一般为接、切点)或线作截面，把空间问题转化为平面问题求解.(2)若球面上四点P,A,B,C构成的三条线段P A,PB,PC两两垂直，且P A=a，PB=b，PC=c，一般把有关元素“补形”成为一个球内接长方体，根据4R2=a2+b2+c2求解.(3)利用平面几何体知识寻找几何体中元素间的关系，或只画内切、外接的几何体的直观图，确定球心的位置，弄清球的半径(直径)与该几何体已知量的关系，列方程(组)求解.【知识点3 几何法与向量法求空间角】1.几何法求异面直线所成的角(1)求异面直线所成角一般步骤：①平移：选择适当的点，线段的中点或端点，平移异面直线中的一条或两条成为相交直线；②证明：证明所作的角是异面直线所成的角；③寻找：在立体图形中，寻找或作出含有此角的三角形，并解之；④取舍：因为异面直线所成角的取值范围是，所以所作的角为钝角时，应取它的补角作为异面直线所成的角.2.用向量法求异面直线所成角的一般步骤：(1)建立空间直角坐标系；(2)用坐标表示两异面直线的方向向量；(3)利用向量的夹角公式求出向量夹角的余弦值；(4)注意两异面直线所成角的范围是，即两异面直线所成角的余弦值等于两向量夹角的余弦值的绝对值.3.几何法求线面角(1)垂线法求线面角(也称直接法)；(2)公式法求线面角(也称等体积法)：用等体积法，求出斜线P A在面外的一点P到面的距离，利用三角形的正弦公式进行求解.，其中是斜线与平面所成的角，h是垂线段的长，l是斜线段的长.4.向量法求直线与平面所成角的主要方法:(1)分别求出斜线和它在平面内的射影直线的方向向量，将题目转化为求两个方向向量的夹角(或其补角)；(2)通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角或钝角的补角，取其余角就是斜线和平面所成的角.5.几何法求二面角作二面角的平面角的方法：作二面角的平面角可以用定义法，也可以用垂面法，即在一个半平面内找一点作另一个半平面的垂线，再过垂足作二面角的棱的垂线，两条垂线确定的平面和二面角的棱垂直，由此可得二面角的平面角.6.向量法求二面角的解题思路:用法向量求两平面的夹角：分别求出两个法向量，然后通过两个平面的法向量的夹角得到两平面夹角的大小.【知识点4 立体几何中的最值问题及其解题策略】1.立体几何中的几类最值问题立体几何中的最值问题有三类：一是空间几何体中相关的点、线和面在运动，求线段长度、截面的面积和体积的最值；二是空间几何体中相关点和线段在运动，求有关角度和距离的最值；三是在空间几何体中，已知某些量的最值，确定点、线和面之间的位置关系．2.立体几何中的最值问题的求解方法解决立体几何中的最值问题主要有两种解题方法：一是几何法，利用几何体的性质，探求图形中点、线、面的位置关系；二是代数法，通过建立空间直角坐标系，利用点的坐标表示所求量的目标函数，借助函数思想方法求最值；通过降维的思想，将空间某些量的最值问题转化为平面三角形、四边形或圆中的最值问题．【知识点5 立体几何中的轨迹问题及其解题策略】1.立体几何中的轨迹问题立体几何中的轨迹问题，这是一类立体几何与解析几何的交汇题型，既考查学生的空间想象能力，即点、线、面的位置关系，又考查用代数方法研究轨迹的基本思想，培养学生的数学运算、直观想象等素养．2.立体几何中的轨迹问题的求解方法解决立体几何中的轨迹问题有两种方法：一是几何法：对于轨迹为几何体的问题，要抓住几何体中的不变量，借助空间几何体（柱、锥、台、球）的定义；对于轨迹为平面上的问题，要利用降维的思想，熟悉平面图形（直线、圆、圆锥曲线）的定义．二是代数法：在图形中，建立恰当的空间直角坐标系，利用空间向量进行求解．【知识点6 以立体几何为载体的情境题的求解策略】1.以立体几何为载体的几类情境题以立体几何为载体的情境题大致有三类：(1)以数学名著为背景设置问题，涉及中外名著中的数学名题名人等；(2)以数学文化为背景设置问题，包括中国传统文化，中外古建筑等；(3)以生活实际为背景设置问题，涵盖生产生活、劳动实践、文化精神等．2.以立体几何为载体的情境题的求解思路以立体几何为载体的情境题都跟图形有关，涉及在具体情境下的图形阅读，需要通过数形结合来解决问题.此类问题的求解过程主要分四步：一是要读特征，即从图形中读出图形的基本特征；二是要读本质，即要善于将所读出的信息进行提升，实现“图形→文字→符号”的转化；三是要有问题意识，带着问题阅读图形，将研究图形的本身特征和关注题目要解决的问题有机地融合在一起；四是要有运动观点，要“动手”去操作，动态地去阅读图形．【题型1 求几何体的体积与表面积】【例1】（2023·江苏徐州·沛县湖西中学模拟预测）在三棱锥P−ABC中，三条侧棱P A，PB，PC两两垂直，且PA=PB=PC=2，若三棱锥P−ABC的所有顶点都在同一个球的表面上，则该球的体积是（）A．4√3πB．4√2πC．6πD．12π【变式1-1】（2023·陕西铜川·统考一模）我国古代数学名著《数书九章》中有“天池盆测雨”题：在下雨时，用一个圆台形的天池盆接雨水，天池盆盆口直径为二尺八寸，盆底直径为一尺二寸，盆深一尺八寸，若盆中积水深九寸，则平地降雨量是（）（注：①平地降雨量等于盆中积水体积除以盆口面积；②一尺等于十寸；③V台=13(S上+S下+√S上⋅S下)ℎ）A．6寸B．4寸C．3寸D．2寸【变式1-2】（2023·全国·模拟预测）如图，已知正四棱台ABCD−A1B1C1D1的高为2,AB=2A1B1,P,Q分别为B1C1,C1D1的中点，若四边形PQDB的面积为152，则该四棱台的体积为（）A．563B．56C．283D．28【变式1-3】（2023·山东·统考一模）陀螺起源于我国，在山西夏县新石器时代的遗址中，就出土了目前发现的最早的石制陀螺因此，陀螺的历史至少也有四千年，如图所示为一个陀螺的立体结构图，若该陀螺底面圆的直径AB=12cm，圆柱体部分的高BC=6cm，圆锥体部分的高CD=4cm，则这个陀螺的表面积是（）A．(144+12√13)πcm2B．(144+24√13)πcm2C．(108+12√13)πcm2D．(108+24√13)πcm2【题型2 与球有关的截面问题】【例2】（2023·陕西咸阳·武功县普集高级中学校考模拟预测）已知球O的一个截面的面积为2π，球心O到该截面的距离比球的半径小1，则球O的表面积为（）A．8πB．9πC．12πD．16π【变式2-1】（2023·全国·校联考模拟预测）上、下底面均为等边三角形的三棱台的所有顶点都在同一球面上，若三棱台的高为3，上、下底面边长分别为√15，2√6，则该球的表面积为（）A．32πB．36πC．40πD．42π【变式2-2】（2023·河南·信阳高中校联考模拟预测）如图，在三棱锥A−BCD中，AB,AC,AD两两垂直，且AB=AC=AD=3，以A为球心，√6为半径作球，则球面与底面BCD的交线长度的和为（）A．2√3πB．√3πC．√3π2D．√3π4【变式2-3】（2023·江西南昌·江西师大附中校考三模）已知正方体ABCD−A1B1C1D1的棱长为2，E为棱CC1上的一点，且满足平面BDE⊥平面A1BD，则平面A1BD截四面体ABCE的外接球所得截面的面积为（）A．136πB．2512πC．83πD．23π【题型3 体积、面积、周长、距离的最值与范围问题】【例3】（2023·福建莆田·莆田一中校考一模）如图，在边长为a的正三角形的三个角处各剪去一个四边形.这个四边形是由两个全等的直角三角形组成的，并且这三个四边形也全等，如图①.若用剩下的部分折成一个无盖的正三棱柱形容器，如图②.则这个容器的容积的最大值为（）A．a327B．a336C．a354D．a372【变式3-1】（2023·全国·模拟预测）在直三棱柱ABC−A1B1C1中，∠BAC=60°，侧面BCC1B1的面积为2√3，则直三棱柱ABC−A1B1C1外接球的表面积的最小值为（）A．4πB．8πC．4√3πD．8√3π【变式3-2】（2023·山东·山东省实验中学校考二模）正四棱柱ABCD−A1B1C1D1中，AB=2，P为底面A1B1C1D1的中心，M是棱AB的中点，正四棱柱的高ℎ∈[√2,2√2]，点M到平面PCD的距离的最大值为（）A．2√63B．83C．4√23D．329【变式3-3】（2023·湖南长沙·长沙一中校考模拟预测）已知A，B，C，D是体积为20√53π的球体表面上四点，若AB=4，AC=2，BC=2√3，且三棱锥A－BCD的体积为2√3，则线段CD长度的最大值为（）A．2√3B．3√2C．√13D．2√5【题型4 几何体与球的切、接问题】【例4】（2023·河北邯郸·统考三模）三棱锥S−ABC中，SA⊥平面ABC，AB⊥BC，SA=AB=BC．过点A分别作AE⊥SB，AF⊥SC交SB、SC于点E、F，记三棱锥S−FAE的外接球表面积为S1，三棱锥S−ABC的外接球表面积为S2，则S1S2=（）A．√33B．13C．√22D．12【变式4-1】（2023·福建龙岩·统考模拟预测）如图，已知正方体的棱长为2，以其所有面的中心为顶点的多面体为正八面体，则该正八面体的内切球表面积为（）A．π6B．πC．4π3D．4π【变式4-2】（2023·全国·模拟预测）为了便于制作工艺品，某工厂将一根底面半径为6cm，高为4cm的圆柱形木料裁截成一个正四棱台木料，已知该正四棱台上底面的边长不大于4√2cm，则当该正四棱台的体积最大时，该正四棱台外接球的表面积为（）A．128πcm2B．145πcm2C．153πcm2D．160πcm2【变式4-3】（2023·浙江温州·乐清市知临中学校考二模）如今中国被誉为基建狂魔，可谓是逢山开路，遇水架桥.公路里程､高铁里程双双都是世界第一.建设过程中研制出用于基建的大型龙门吊､平衡盾构机等国之重器更是世界领先.如图是某重器上一零件结构模型，中间最大球为正四面体ABCD的内切球，中等球与最大球和正四面体三个面均相切，最小球与中等球和正四面体三个面均相切，已知正四面体ABCD棱长为2√6，则模型中九个球的表面积和为（）A．6πB．9πC．31π4D．21π【题型5 空间线段以及线段之和最值问题】【例5】（2023·湖南长沙·长郡中学校联考模拟预测）已知底面边长为a的正四棱柱ABCD−A1B1C1D1内接于半径为√3的球内，E，F分别为B1C1，C1D1的中点，G，H分别为线段AC1，EF上的动点，M为线段AB1的中点，当正四棱柱ABCD−A1B1C1D1的体积最大时，|GH|+|GM|的最小值为（）A．√2B．3√22C．2D．1+√2【变式5-1】（2023·安徽合肥·合肥市第六中学校考模拟预测）已知在长方体ABCD−A1B1C1D1中，AB=BC= 1，AA1=√3，在线段A1D上取点M，在CD1上取点N，使得直线MN//平面ACC1A1，则线段MN长度的最小值为（）A．√33B．√213C．√37D．√217【变式5-2】（2023·四川绵阳·模拟预测）如图，棱长为2的正方体ABCD−A1B1C1D1中，点P在线段AD1上运动，以下四个命题：；④|C1P|+①三棱锥D−BPC1的体积为定值；②C1P⊥CB1；③直线DC1与平面ABC1D1所成角的正弦值为12|DP|的最小值为√10．其中真命题有（）A．1个B．2个C．3个D．4个【变式5-3】（2023·天津和平·耀华中学校考二模）粽子，古称“角黍”，早在春秋时期就已出现，到晋代成为了端午节的节庆食物．现将两个正四面体进行拼接，得到如图所示的粽子形状的六面体，其中点G在线，则下列说法正确的是（）段CD（含端点）上运动，若此六面体的体积为163A．EF=2B．EF=4C．EG+FG的最小值为3√2D．EG+FG的最小值为2√6【题型6 空间角问题】【例6】（2023·全国·模拟预测）已知正三棱柱ABC−A1B1C1的侧面积是底面积的6√3倍，点E为四边形ABB1A1的中心，点F为棱CC1的中点，则异面直线BF与CE所成角的余弦值为（）A．2√3913B．√3913C．√3926D．3√3926【变式6-1】（2023·河北保定·统考二模）如图，在长方体ABCD−A1B1C1D1中，AB=BC=1，AA1=2，对角线B1D与平面A1BC1交于E点．则A1E与面AA1D1D所成角的余弦值为（）A．13B．√33C．23D．√53【变式6-2】（2023·全国·模拟预测）在正方体ABCD−A1B1C1D1中，若点N是棱BB1上的动点，点M是线段A1C1（不含线段的端点）上的动点，则下列说法正确的是（）A．存在直线MN，使MN//B1C B．异面直线CM与AB所成的角可能为π3C．直线CM与平面BND所成的角为π3D．平面BMC//平面C1NA【变式6-3】（2023·四川遂宁·统考三模）如图，正方体ABCD−A1B1C1D1的棱长为2，线段B1D1上有两个动点E,F（E在F的左边），且EF=√2．下列说法不正确的是（）A．当E运动时，二面角E−AB−C的最小值为45∘B．当E,F运动时，三棱锥体积B−AEF不变C．当E,F运动时，存在点E,F使得AE//BFD．当E,F运动时，二面角C−EF−B为定值【题型7 翻折问题】【例7】（2023·四川泸州·统考一模）已知菱形ABCD的边长为6，∠BAD=60°，将△BCD沿对角线BD翻折，使点C到点P处，且二面角A−BD−P为120°，则此时三棱锥P−ABD的外接球的表面积为（）A．21πB．28√21πC．52πD．84π【变式7-1】（2023·福建福州·福建省福州第一中学校考模拟预测）在矩形ABCD中，AB=3,AD=4，将△ABD 沿对角线BD翻折至△A′BD的位置，使得平面A′BD⊥平面BCD，则在三棱锥A′−BCD的外接球中，以A′C为直径的截面到球心的距离为（）A．√43510B．6√25C．√23910D．√11310【变式7-2】（2023·湖北恩施·校考模拟预测）如图，矩形ABCD中，E、F分别为BC、AD的中点，且BC=2AB=2，现将△ABE沿AE向上翻折，使B点移到P点，则在翻折过程中，下列结论不正确的是（）A．存在点P，使得PE∥CFB．存在点P，使得PE⊥EDC．三棱锥P−AED的体积最大值为√26D．当三棱锥P−AED的体积达到最大值时，三棱锥P−AED外接球表面积为4π【变式7-3】（2023·四川·校联考模拟预测）如图，已知△ABC是边长为4的等边三角形，D,E分别是AB,AC 的中点，将△ADE沿着DE翻折，使点A到点P处，得到四棱锥P−BCED，则下列命题错误的是（）A．翻折过程中，该四棱锥的体积有最大值为3B．存在某个点P位置，满足平面PDE⊥平面PBCC．当PB⊥PC时，直线PB与平面BCED所成角的正弦值为√33πD．当PB=√10时，该四棱锥的五个顶点所在球的表面积为523【题型8 立体几何中的轨迹问题】【例8】（2023·全国·模拟预测）如图，正方体ABCD−A1B1C1D1的棱长为3，点P是平面ACB1内的动点，M，N分别为C1D1，B1C的中点，若直线BP与MN所成的角为θ，且sinθ=√55，则动点P的轨迹所围成的图形的面积为（）A．3π4B．π2C．π3D．π4【变式8-1】（2023·海南省直辖县级单位·文昌中学校考模拟预测）已知四棱柱ABCD−A1B1C1D1的底面ABCD 为正方形，侧棱与底面垂直，点P是侧棱DD1上的点，且DP=2PD1,AA1=3,AB=1.若点Q在侧面BCC1B1（包括其边界）上运动，且总保持AQ⊥BP，则动点Q的轨迹长度为（）A．√3B．√2C．2√33D．√52【变式8-2】（2023·河北·统考模拟预测）已知正四棱锥（底面为正方形，且顶点在底面的射影为正方形的中心的棱锥为正四棱锥）P－ABCD的底面正方形边长为2，其内切球O的表面积为π3，动点Q在正方形ABCD 内运动，且满足OQ=OP，则动点Q形成轨迹的周长为（）A．2π11B．3π11C．4π11D．5π11【变式8-3】（2023·全国·校联考模拟预测）如图，已知正方体ABCD−A1B1C1D1的棱长为2，P为空间中一点且满足∠APB1=∠ADB1，则以下说法正确的有（）A．若P在面AB1C1D上，则其轨迹周长为8√6π9B．若A1P⊥AB1，则D1P的最小值为√3+1−√6C．P的轨迹围成的封闭曲面体积为32√6π227+4√3πD．四棱锥P-ABCD体积最大值为4(2√6+√2+3)9【题型9 以立体几何为载体的情境题】【例9】（2023·云南大理·统考一模）我国古代数学名著《数书九章》中有“天池盆测雨”题，在下雨时，用一个圆台形的天池盆接雨水，天池盆盆口直径为36寸，盆底直径为12寸，盆深18寸.若某次下雨盆中积水的深度恰好是盆深的一半，则该天池盆中水的体积为（）A．1404π立方寸B．1080π立方寸C．756π立方寸D．702π立方寸【变式9-1】（2023·广东广州·广东实验中学校考一模）阿基米德多面体是由边数不全相同的正多边形为面的多面体．如图所示的阿基米德多面体有四个全等的正三角形面和四个全等的正六边形面，该多面体是由过正四面体各棱的三等分点的平面截去四个小正四面体得到．若该多面体的所有顶点都在球O的表面上，且点O到正六边形面的距离为√62，则球O的体积为（）A．7√1424πB．7√143πC．11√2224πD．11√223π【变式9-2】（2023·河南·校联考模拟预测）如图1所示，宫灯又称宫廷花灯，是中国彩灯中富有特色的汉民族传统手工艺品之一．图2是小明为自家设计的一个花灯的直观图，该花灯由上面的正六棱台与下面的正六棱柱组成，若正六棱台的上、下两个底面的边长分别为4dm和2dm，正六棱台与正六棱柱的高分别为1dm 和6dm，则该花灯的表面积为（）A．(108+30√3)dm2B．(72+30√3)dm2C．(64+24√3)dm2D．(48+24√3)dm2【变式9-3】（2023·河南郑州·统考模拟预测）《九章算术·商功》：“斜解立方，得两堑堵，斜解堑堵，其一为阳马，其一为鳖臑”.意思是一个长方体沿对角面斜解（图1），得到一模一样的两个堑堵（图2），再沿一个堑堵的一个顶点和相对的棱斜解（图2），得一个四棱锥称为阳马（图3），一个三棱锥称为鳖臑（图4）.若长方体的体积为V，由该长方体斜解所得到的堑堵、阳马和鳖臑的体积分别为V1，V2，V3，则下列等式错误的是（）A．V1+V2+V3=V B．V1=2V2C．V2=2V3D．V2−V3=V61．（2023·北京·统考高考真题）坡屋顶是我国传统建筑造型之一，蕴含着丰富的数学元素．安装灯带可以勾勒出建筑轮廓，展现造型之美．如图，某坡屋顶可视为一个五面体，其中两个面是全等的等腰梯形，两个面是全等的等腰三角形．若AB=25m,BC=AD=10m，且等腰梯形所在的平面、等腰三角形所在的平，则该五面体的所有棱长之和为（）面与平面ABCD的夹角的正切值均为√145A．102m B．112mC．117m D．125m2．（2023·全国·统考高考真题）已知△ABC为等腰直角三角形，AB为斜边，△ABD为等边三角形，若二面角C−AB−D为150°，则直线CD与平面ABC所成角的正切值为（）A．15B．√25C．√35D．253．（2023·全国·统考高考真题）已知圆锥PO的底面半径为√3，O为底面圆心，P A，PB为圆锥的母线，∠AOB=120°，若△PAB的面积等于9√34，则该圆锥的体积为（）A．πB．√6πC．3πD．3√6π4．（2023·天津·统考高考真题）在三棱锥P−ABC中，点M,N分别在棱PC,PB上，且PM=13PC，PN=23PB，则三棱锥P−AMN和三棱锥P−ABC的体积之比为（）A．19B．29C．13D．495．（2021·浙江·统考高考真题）如图已知正方体ABCD−A1B1C1D1，M，N分别是A1D，D1B的中点，则（）A．直线A1D与直线D1B垂直，直线MN//平面ABCDB．直线A1D与直线D1B平行，直线MN⊥平面BDD1B1C．直线A1D与直线D1B相交，直线MN//平面ABCDD．直线A1D与直线D1B异面，直线MN⊥平面BDD1B16．（2023·全国·统考高考真题）下列物体中，能够被整体放入棱长为1（单位：m）的正方体容器（容器壁厚度忽略不计）内的有（）A．直径为0.99m的球体B．所有棱长均为1.4m的四面体C．底面直径为0.01m，高为1.8m的圆柱体D．底面直径为1.2m，高为0.01m的圆柱体7．（2023·全国·统考高考真题）已知圆锥的顶点为P，底面圆心为O，AB为底面直径，∠APB=120°，PA=2，点C在底面圆周上，且二面角P−AC−O为45°，则（）．A．该圆锥的体积为πB．该圆锥的侧面积为4√3πC．AC=2√2D．△PAC的面积为√38．（2023·全国·统考高考真题）已知点S,A,B,C均在半径为2的球面上，△ABC是边长为3的等边三角形，SA⊥平面ABC，则SA=．9．（2023·全国·统考高考真题）在正方体ABCD−A1B1C1D1中，AB=4,O为AC1的中点，若该正方体的棱与球O的球面有公共点，则球O的半径的取值范围是．10．（2023·全国·统考高考真题）在正方体ABCD−A1B1C1D1中，E，F分别为AB，C1D1的中点，以EF为直径的球的球面与该正方体的棱共有个公共点．11．（2023·全国·统考高考真题）在正四棱台ABCD−A1B1C1D1中，AB=2,A1B1=1,AA1=√2，则该棱台的体积为．12．（2023·全国·统考高考真题）底面边长为4的正四棱锥被平行于其底面的平面所截，截去一个底面边长为2，高为3的正四棱锥，所得棱台的体积为．立体几何小题【题型1 求几何体的体积与表面积】 (4)【题型2 与球有关的截面问题】 (7)【题型3 体积、面积、周长、距离的最值与范围问题】 (10)【题型4 几何体与球的切、接问题】 (13)【题型5 空间线段以及线段之和最值问题】 (18)【题型6 空间角问题】 (23)【题型7 翻折问题】 (30)【题型8 立体几何中的轨迹问题】 (35)【题型9 以立体几何为载体的情境题】 (40)立体几何是高考的热点内容，属于高考的必考内容之一.从近几年的高考情况来看，高考对该部分的考查，小题主要体现在三个方面：一是有关空间线面位置关系的判断；二是空间几何体的体积和表面积的计算，难度较易；三是常见的一些经典常考压轴小题，涉及到空间角、空间距离与轨迹问题等，难度中等或偏上．【知识点1 空间几何体表面积与体积的常见求法】1.求几何体体积的常用方法(1)公式法：直接代入公式求解.(2)等体积法：四面体的任何一个面都可以作为底面，只需选用底面面积和高都易求出的形式即可.(3)补体法：将几何体补成易求解的几何体，如棱锥补成棱柱，三棱柱补成四棱柱等.(4)分割法：将几何体分割成易求解的几部分，分别求体积.2.求组合体的表面积与体积的一般方法求组合体的表面积的问题，首先应弄清它的组成部分，其表面有哪些底面和侧面，各个面的面积应该怎样求，然后根据公式求出各个面的面积，最后相加或相减.求体积时也要先弄清各组成部分，求出各简单几何体的体积，再相加或相减.【知识点2 几何体与球的切、接问题的解题策略】1.常见的几何体与球的切、接问题的解决方案：常见的与球有关的组合体问题有两种：一种是内切球，另一种是外接球.常见的几何体与球的切、接问题的解决方案：2.空间几何体外接球问题的求解方法：空间几何体外接球问题的处理关键是确定球心的位置，常见的求解方法有如下几种：(1)涉及球与棱柱、棱锥的切、接问题时，一般过球心及多面体的特殊点(一般为接、切点)或线作截面，把空间问题转化为平面问题求解.(2)若球面上四点P,A,B,C构成的三条线段P A,PB,PC两两垂直，且P A=a，PB=b，PC=c，一般把有关元素“补形”成为一个球内接长方体，根据4R2=a2+b2+c2求解.(3)利用平面几何体知识寻找几何体中元素间的关系，或只画内切、外接的几何体的直观图，确定球心的位置，弄清球的半径(直径)与该几何体已知量的关系，列方程(组)求解.【知识点3 几何法与向量法求空间角】1.几何法求异面直线所成的角(1)求异面直线所成角一般步骤：①平移：选择适当的点，线段的中点或端点，平移异面直线中的一条或两条成为相交直线；②证明：证明所作的角是异面直线所成的角；③寻找：在立体图形中，寻找或作出含有此角的三角形，并解之；④取舍：因为异面直线所成角的取值范围是，所以所作的角为钝角时，应取它的补角作为异面直线所成的角.2.用向量法求异面直线所成角的一般步骤：(1)建立空间直角坐标系；(2)用坐标表示两异面直线的方向向量；(3)利用向量的夹角公式求出向量夹角的余弦值；(4)注意两异面直线所成角的范围是，即两异面直线所成角的余弦值等于两向量夹角的余弦值的绝对值.3.几何法求线面角(1)垂线法求线面角(也称直接法)；(2)公式法求线面角(也称等体积法)：用等体积法，求出斜线P A在面外的一点P到面的距离，利用三角形的正弦公式进行求解.是斜线与平面所成的角，h是垂线段的长，l是斜线段的长.4.向量法求直线与平面所成角的主要方法:(1)分别求出斜线和它在平面内的射影直线的方向向量，将题目转化为求两个方向向量的夹角(或其补角)；(2)通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角或钝角的补角，取其余角就是斜线和平面所成的角.5.几何法求二面角作二面角的平面角的方法：作二面角的平面角可以用定义法，也可以用垂面法，即在一个半平面内找一点作另一个半平面的垂线，再过垂足作二面角的棱的垂线，两条垂线确定的平面和二面角的棱垂直，由此可得二面角的平面角.6.向量法求二面角的解题思路:用法向量求两平面的夹角：分别求出两个法向量，然后通过两个平面的法向量的夹角得到两平面夹角的大小.【知识点4 立体几何中的最值问题及其解题策略】1.立体几何中的几类最值问题立体几何中的最值问题有三类：一是空间几何体中相关的点、线和面在运动，求线段长度、截面的面积和体积的最值；二是空间几何体中相关点和线段在运动，求有关角度和距离的最值；三是在空间几何体中，已知某些量的最值，确定点、线和面之间的位置关系．2.立体几何中的最值问题的求解方法解决立体几何中的最值问题主要有两种解题方法：一是几何法，利用几何体的性质，探求图形中点、线、面的位置关系；二是代数法，通过建立空间直角坐标系，利用点的坐标表示所求量的目标函数，借助函数思想方法求最值；通过降维的思想，将空间某些量的最值问题转化为平面三角形、四边形或圆中的最值问题．【知识点5 立体几何中的轨迹问题及其解题策略】1.立体几何中的轨迹问题立体几何中的轨迹问题，这是一类立体几何与解析几何的交汇题型，既考查学生的空间想象能力，即点、线、面的位置关系，又考查用代数方法研究轨迹的基本思想，培养学生的数学运算、直观想象等素养．2.立体几何中的轨迹问题的求解方法解决立体几何中的轨迹问题有两种方法：一是几何法：对于轨迹为几何体的问题，要抓住几何体中的不变量，借助空间几何体（柱、锥、台、球）的定义；对于轨迹为平面上的问题，要利用降维的思想，熟悉平面图形（直线、圆、圆锥曲线）的定义．二是代数法：在图形中，建立恰当的空间直角坐标系，利用空间向量进行求解．【知识点6 以立体几何为载体的情境题的求解策略】1.以立体几何为载体的几类情境题以立体几何为载体的情境题大致有三类：(1)以数学名著为背景设置问题，涉及中外名著中的数学名题名人等；(2)以数学文化为背景设置问题，包括中国传统文化，中外古建筑等；(3)以生活实际为背景设置问题，涵盖生产生活、劳动实践、文化精神等．。

(压轴题)高中数学必修二第一章《立体几何初步》测试(包含答案解析)(1)

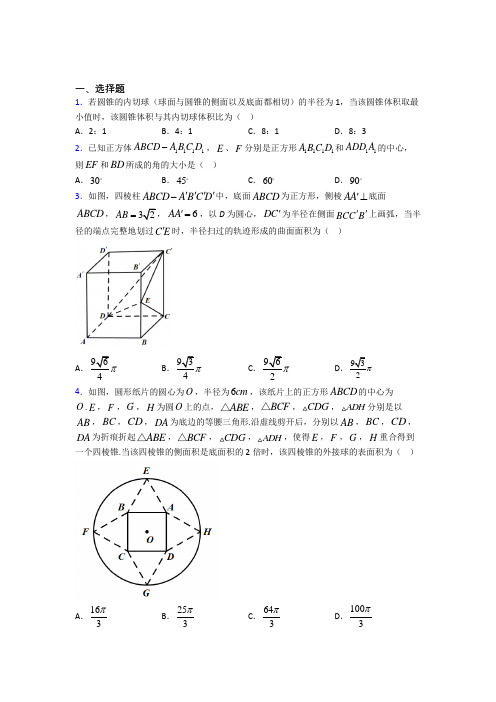
一、选择题1．若圆锥的内切球（球面与圆锥的侧面以及底面都相切）的半径为1，当该圆锥体积取最小值时，该圆锥体积与其内切球体积比为（） A ．2：1B ．4：1C ．8：1D ．8：32．已知正方体1111ABCD A B C D -，E 、F 分别是正方形1111D C B A 和11ADD A 的中心，则EF 和BD 所成的角的大小是（） A ．30B ．45C ．60D ．903．如图，四棱柱ABCD A B C D ''''-中，底面ABCD 为正方形，侧棱AA '⊥底面ABCD ，32AB =，6AA '=，以D 为圆心，DC '为半径在侧面BCC B ''上画弧，当半径的端点完整地划过C E '时，半径扫过的轨迹形成的曲面面积为（）A ．96π B ．93π C ．96π D ．93π 4．如图，圆形纸片的圆心为O ，半径为6cm ，该纸片上的正方形ABCD 的中心为O .E ，F ，G ，H 为圆O 上的点，ABE △，BCF △，CDG ，ADH 分别是以AB ，BC ，CD ，DA 为底边的等腰三角形.沿虚线剪开后，分别以AB ，BC ，CD ，DA 为折痕折起ABE △，BCF △，CDG ，ADH ，使得E ，F ，G ，H 重合得到一个四棱锥.当该四棱锥的侧面积是底面积的2倍时，该四棱锥的外接球的表面积为（）A ．163πB ．253πC ．643πD ．1003π5．如图，在四棱锥E ABCD -中，底面ABCD 是正方形，且平面ABCD ⊥平面AEB ，则（）A ．DEC ∠可能为90︒B ．若AEB △是等边三角形，则DEC 也是等边三角形C ．若AEB △是等边三角形，则异面直线DE 和AB 所成角的余弦值为24D ．若AEB △是直角三角形，则BE ⊥平面ADE6．在棱长为2的正方体ABCD ﹣A 1B 1C 1D 1中，点E ，F 分别是棱C 1D 1，B 1C 1的中点，P 是上底面A 1B 1C 1D 1内一点，若AP ∥平面BDEF ，则线段AP 长度的取值范围是（） A ．[322，5] B ．[5，22]C ．[324，6] D ．[6，22]7．如图，在四棱锥P ABCD -中，底面ABCD 是矩形.其中3AB =，2AD =，PAD △是以A ∠为直角的等腰直角三角形，若60PAB ∠=︒，则异面直线PC 与AD 所成角的余弦值是（）A 22B ．22C 27D 2118．三个平面将空间分成n 个部分，则n 不可能是（） A ．5B ．6C ．7D ．89．正三棱柱111ABC A B C -各棱长均为1，M 为1CC 的中点，则点1B 到面1A BM 的距离为（） A 2B ．22C ．12D ．3210．已知四面体ABCD ，AB ⊥平面BCD ，1AB BC CD BD ====，若该四面体的四个顶点都在球O 的表面上，则球O 的表面积为（）A ．73π B ．7π C ．712π D ．79π 11．空间四边形PABC 的各边及对角线长度都相等，D 、E 、F 外别是AB 、BC 、CA 的中点，下列四个结论中不成立的是（） A ．//BC 平面PDF B ． DF ⊥平面PAE C ．平面PDE ⊥平面ABCD ．平面PAE ⊥平面ABC12．如果一个水平放置的平面图形的斜二测直观图是如图所示的直角梯形，其中2O A ''=，45B A O '''∠=,//B C O A ''''.则原平面图形的面积为（）A ．32B ．62C ．322D ．34二、填空题13．已知直三棱柱111ABC A B C -，14AB BC AA ===，42AC =，若点P 是上底面111 A B C 所在平面内一动点，若三棱锥P ABC -的外接球表面积恰为41π，则此时点P 构成的图形面积为________．14．已知正三棱锥A BCD -的四个顶点在球O 的球面上，2AB =，且π2BAC ∠=，则球O 的表面积为_______．15．如图，在矩形ABCD 中，2AB =，1AD =，点E 为CD 的中点，F 为线段CE （端点除外）上一动点．现将DAF △沿AF 折起，使得平面ABD ⊥平面ABC ．设直线FD 与平面ABCF 所成角为θ，θ的取值范围为__________．16．如图，四边形ABCD 是矩形，且有2AB BC =，沿AC 将ADC 翻折成AD C '，当二面角D AC B '--的大小为3π时，则异面直线D C '与AB 所成角余弦值是______.17．正四面体ABCD 棱长为2，AO ⊥平面BCD ，垂足为O ，设M 为线段AO 上一点，且90BMC ︒∠=则二面角M BC O --的余弦值为________．18．已知棱长为4的正方体ABCD -A 1B 1C 1D 1中，点M 是棱AD 的中点，点N 是棱AA 1的中点，P 是侧面四边形ADD 1A 1内一动点（含边界），若C 1P ∥平面CMN ，则线段C 1P 长度的取值范围是________.19．已知四面体P ﹣ABC 的外接球的球心O 在AB 上，且PO ⊥平面ABC ，2AC 3=AB ，若四面体P ﹣ABC 的体积为32，则该球的体积为_____． 20．在三棱锥P ABC -中，PA ⊥平面ABC ，60BAC ∠=︒，23AB AC ==，2PA =，则三棱锥P ABC -外接球的半径为____________.三、解答题21．如图，在直三棱柱111ABC A B C -中，1,2AC BC AC BC CC ⊥===.（1）求三棱柱111ABC A B C -的体积；（2）求异面直线1CB 与1AC 所成角的大小；（3）求二面角1B AC C --的平面角的余弦值.22．如图，四棱锥P ABCD -的底面为正方形，PA ⊥底面ABCD ，E ，F ，H 分别为AB ，PC ，BC 的中点.（1）求证：DE ⊥平面PAH ；（2）若2PA AD ==，求直线PD 与平面PAH 所成线面角的正弦值.23．如图，在四棱锥P ABCD -中，底面ABCD 为菱形，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =，3BAD π∠=，E 是线段AD 的中点，连结BE ．（1）求证：BE PA ⊥；（2）求二面角A PD C --的余弦值；（3）在线段PB 上是否存在点F ，使得//EF 平面PCD ？若存在，求出PFPB的值；若不存在，说明理由．24．如图，在三棱锥M 中，M 为BC 的中点，3PA PB PC AB AC =====，26BC =.（1）求二面角P BC A --的大小；（2）求异面直线AM 与PB 所成角的余弦值. 25．如图，在三棱锥P ABC -中，1,2,135AB AC BAC ︒==∠=，1cos ,3BAP AP BC ∠=-⊥．（1）若23BM MC =，求证：PM BC ⊥；（2）当3AP =，且N 为BC 中点时，求AN 与平面PBC 所成角的正弦值．26．在三棱锥P ABC -中，AE BC ⊥于点,E CF AB ⊥于点F ，且AE CF O ⋂=，若点P 在平面ABC 上的射影为点O ．（1）证明：AC PB ⊥；（2）若ABC 是正三角形，点,G H 分别为,PA PC 的中点．证明：四边形EFGH 是矩形．【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】根据三角形相似得出圆锥的底面半径和高的关系，根据体积公式和基本不等式得出答案．【详解】设圆锥的高为h ，底面半径为r ，则当球面与圆锥的侧面以及底面都相切时，轴截面如图，由~AOE ACF 可得：22(1)11h r --=，即22r h h =-， ∴圆锥的体积22148[(2)4]33(2)323h V r h h h h ππππ===-++--．当且仅当22h -=，即4h =时取等号．∴该圆锥体积的最小值为83π．内切球体积为43π．该圆锥体积与其内切球体积比2:1．故选：A ．【点睛】方法点睛：在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”（即条件要求中字母为正数）、“定”（不等式的另一边必须为定值）、“等”（等号取得的条件）的条件才能应用，否则会出现错误.2．C解析：C 【分析】作出图形，连接1AD 、11B D 、1AB ，推导出1//EF AB ，11//BD B D ，可得出异面直线EF 和BD 所成的角为11AB D ∠，分析11AB D 的形状，即可得出结果. 【详解】如下图所示，连接1AD 、11B D 、1AB ，设正方体1111ABCD A B C D -的棱长为1，则11112AD AB B D === 所以，11AB D 为等边三角形，则1160AB D ∠=，因为E 、F 分别是正方形1111D C B A 和11ADD A 的中心，则E 、F 分别是11B D 、1AD 的中点，所以，1//EF AB ，在正方体1111ABCD A B C D -中，11//BB DD 且11BB DD =，所以，四边形11BB D D 为平行四边形，则11//BD B D ，所以，异面直线EF 和BD 所成的角为1160AB D ∠=. 故选：C. 【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下：（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角；（3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．3．A解析：A 【分析】先确定曲面面积占以点D 为顶点， DC '为母线在平面 BCC B ''所形成的圆锥的侧面积的18，利用圆锥的侧面积S rl π=即可得出结论. 【详解】由题意 6,32CE CC AA BC AB ''=====22361832BE CE CB -=-=，所以45BCE ∠=， 45ECC '∠=，所以曲面面积占以点D 为顶点， DC '为母线在平面 BCC B ''所形成的圆锥的侧面积的18，所以圆锥的侧面积 636186S rl CC DC ππππ'==⨯⨯=⨯⨯=，所以曲面面积为1961868ππ⨯=. 故选：A. 【点睛】方法点睛：本题考查曲面面积，考查圆锥的侧面积，确定曲面面积占以点D 为顶点， DC '为母线在平面 BCC B ''所形成的圆锥的侧面积的18是关键，考查系数的空间想象力. 4．D解析：D 【分析】连接OE 交AB 于点I ，设E ，F ，G ，H 重合于点P ，正方形的边长为x （0x >）cm ，则2x OI =，62xIE =-，求出x 的值，再利用勾股定理求R ，代入球的表面积公式，即可得答案. 【详解】连接OE 交AB 于点I ，设E ，F ，G ，H 重合于点P ，正方形的边长为x （0x >）cm ，则2x OI =，62x IE =-，因为该四棱锥的侧面积是底面积的2倍，所以246222x x x ⎛⎫⨯⨯-= ⎪⎝⎭，解得4x =. 设该四棱锥的外接球的球心为Q ，半径为R ，如图，则QP QC R ==，22OC =16423OP =-=所以()(222RR =+，解得R =所以外接球的表面积为210043S ππ==（2cm ）. 故选：D . 【点睛】关键点点睛：本题考查平面图形的折叠，四棱锥外接球的半径，解题关键在于平面图形折叠成立体图形后，要明确变化的量和没有变的量，以及线线的位置，线面的位置关系，对于几何体的外接球的问题，关键在于确定外接球的球心的位置.5．C解析：C 【分析】对A ，直角三角形的斜边大于直角边可判断；对B ，由>=EC EB DC 可判断；对C ，可得CDE ∠即异面直线DE 和AB 所成角，即可求出；对D ，EAB ∠（或EBA ∠）为直角时，BE 与平面ADE 不垂直. 【详解】对A ，由题意，若90DEC ∠=︒，则DC EC >，但EC BC CD >=，故A 不正确；对B ，若AEB △是等边三角形，显然有>=EC EB DC ，所以DEC 不会是等边三角形，故B 不正确；对C ，若AEB △是等边三角形，设边长为2，则DE EC ==//AB CD ，则CDE ∠即异面直线DE 和AB 所成角，易求cos4CDE ∠==，故C 正确；对D ，当AEB △是以AEB ∠为直角的直角三角形时，BE ⊥平面ADE ，当AEB △是以EAB ∠（或EBA ∠）为直角的直角三角形时，BE 与平面ADE 不垂直，故D 不正确．故选：C. 【点睛】本题考查四棱锥的有关位置关系的判断，解题的关键是正确理解长度关系，正确理解位置关系的变化.6．A解析：A 【分析】分别取棱A 1B 1、A 1D 1的中点M 、N ，连接MN ，可证平面AMN ∥平面BDEF ，得P 点在线段MN 上．由此可判断当P 在MN 的中点时，AP 最小；当P 与M 或N 重合时，AP 最大．然后求解直角三角形得答案．【详解】如图所示，分别取棱A 1B 1、A 1D 1的中点M 、N ，连接MN ，连接B 1D 1， ∵M 、N 、E 、F 为所在棱的中点，∴MN ∥B 1D 1，EF ∥B 1D 1，∴MN ∥EF ，又MN ⊄平面BDEF ，EF ⊂平面BDEF ，∴MN ∥平面BDEF ；连接NF ，由NF ∥A 1B 1，NF ＝A 1B 1，A 1B 1∥AB ，A 1B 1＝AB ，可得NF ∥AB ，NF ＝AB ，则四边形ANFB 为平行四边形，则AN ∥FB ，而AN ⊄平面BDEF ，FB ⊂平面BDEF ，则AN ∥平面BDEF ．又AN ∩NM ＝N ，∴平面AMN ∥平面BDEF ．又P 是上底面A 1B 1C 1D 1内一点，且AP ∥平面BDEF ，∴P 点在线段MN 上．在Rt △AA 1M 中，AM 222211215AA A M =+=+=，同理，在Rt △AA 1N 中，求得AN 5=，则△AMN 为等腰三角形．当P 在MN 的中点时，AP 最小为222322()2+=，当P 与M 或N 重合时，AP 最大为5．∴线段AP 长度的取值范围是32,52⎡⎤⎢⎥⎣．故选：A ．【点睛】本题主要考查了空间中点、线、面间的距离问题，其中解答中通过构造平行平面寻找得到点P 的位置是解答的关键，意在考查空间想象能力与运算能力，属于中档试题.7．D解析：D 【分析】在图形中找到（并证明）异面直线所成的角，然后在三角形中计算．【详解】因为//AD BC ，所以PCB ∠是异面直线PC 与AD 所成角（或其补角），又PA AD ⊥，所以PA BC ⊥，因为AB BC ⊥，AB PA A ⋂=，,AB PA ⊂平面PAB ，所以BC ⊥平面PAB ，又PB ⊂平面PAB ，所以PB BC ⊥．由已知2PA AD ==，所以22222cos 23223cos607PB PA AB PA AB PAB =+-⋅∠=+-⨯⨯︒=22211cos 11(7)2BC PCB PC ∠===+，所以异面直线PC 与AD 所成角的余弦值为21111．故选：D ．【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下：（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角；（3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．8．A解析：A 【分析】三个平面不重合，先按其中平行的平面的个数分类：三个平面两两平行，两个平面平行，没有平行的平面(两两相交)，对两两相交的情况，再根据三条交线互相平行，重合，交于一点，分别讨论. 【详解】按照三个平面中平行的个数来分类：（1）三个平面两两平行，如图1，可将空间分成4部分；（2）两个平面平行，第三个平面与这两个平行平面相交，如图2，可将空间分成6部分；（3）三个平面中没有平行的平面：（i ）三个平面两两相交且交线互相平行，如图3，可将空间分成7部分；（ii ）三个平面两两相交且三条交线交于一点，如图4，可将空间分成8部分.（iii ）三个平面两两相交且交线重合，如图5，可将空间分成6部分；综上，可以为4，6，7，8部分，不能为5部分，故选：A.9．B解析：B 【分析】连接11A N B AB =，根据已知条件先证明11B A A B ⊥、1⊥MN AB ，再通过线面垂直的判定定理证明1AB ⊥平面1A BM ，由此确定出1B N 的长度即为点1B 到面1A BM 的距离，最后完成求解. 【详解】连接1B A 交1A B 于N ，连接11,,,,MB MN MB MA MA ，如图所示：因为11A ABB 为正方形，所以11B A A B ⊥，又因为22111115142MB MC C B =+=+=2215142MA MC CA =+=+=，所以1MB MA =且N 为1AB 中点，则MN 为等腰三角形1AMB 的中垂线， ∴1⊥MN AB 且1MNA B N =，∴1AB ⊥平面1A BM ，∴1B N 就是点1B 到截面1A BM 的距离，又因为111121122B N AB ==+=，所以点1B 到截面1A BM 2，故选：B. 【点睛】方法点睛：求解平面外一点A 到平面α的距离的方法：（1）几何方法：通过线面垂直的证明，找到A 在平面α内的投影点A '，则AA '即为A 到平面α的距离；（2）向量方法：①建立合适空间直角坐标系，在平面α内取一点B ；②求解出AB 和平面α的法向量n ；③根据AB n d n⋅=即可求解出点A 到平面α的距离.10．A解析：A 【分析】本题首先可根据题意将四面体ABCD 看作底面是等边三角形的直三棱柱的一部分，然后求出直三棱柱的外接球的半径，最后根据球的表面积计算公式即可得出结果. 【详解】因为AB ⊥平面BCD ，1AB BC CD BD ====，所以可将四面体ABCD 看作底面是等边三角形的直三棱柱的一部分，如图所示：则四面体ABCD 的外接球即直三棱柱的外接球，因为底面三角形BCD 的外心到三角形BCD 的顶点的长度为222131323，所以直三棱柱的外接球的半径221372312r，则球O 的表面积2277π4π4π123S r ，故选：A. 【点睛】关键点点睛：本题考查四面体的外接球的表面积的计算，能否将四面体ABCD 看作底面是等边三角形的直三棱柱的一部分是解决本题的关键，考查直三棱柱的外接球的半径的计算，是中档题.11．C解析：C 【分析】由线面平行的判定定理可判断A ；由线面垂直的判定定理可判断B ；反证法可说明C ；由面面垂直的判定定理可判断D. 【详解】对于A ，D ，F 外别是AB ，CA 的中点，//BC DF ∴，DF ⊂平面PDF ，∴//BC 平面PDF ，故A 正确，不符合题意；对于B ，各棱长相等，E 为BC 中点，,BC AE BC PE ∴⊥⊥，PEAE E =，BC ∴⊥平面PAE ，//BC DF ，∴DF ⊥平面PAE ，故B 正确，不符合题意；对于C ，假设平面PDE ⊥平面ABC ，设DE BF O ⋂=，连接PO ，则O 是DE 中点，PO DE ∴⊥，平面PDE平面ABC DE =，PO ∴⊥平面ABC ，BF ⊂平面ABC ，PO BF ∴⊥，则PB PF =，与PB PF ≠矛盾，故C 错误，符合题意；对于D ，由B 选项 DF ⊥平面PAE ， DF ⊂平面ABC ，∴平面PAE ⊥平面ABC ，故D 正确，不符合题意. 故选：C. 【点睛】本题考查线面关系和面面关系的判定，解题的关键是正确理解判断定理，正确理解垂直平行关系.12．A解析：A 【分析】作出原平面图形，然后求出面积即可．【详解】45B A O '''∠=B O A '''=∠，则O A B '''△是等腰直角三角形，∴2A B OB '''==又O C C B ''''⊥，45C O B '''∠=︒，∴1B C ''=，在直角坐标系中作出原图形为：梯形OABC ，//OA BC ，2,1OA BC ==，高22OB = ∴其面积为1(21)22322S =+⨯= 故选：A 【点睛】方法点睛：本题考查斜二测法画平面图形直观图，求原图形的面积，可能通过还原出原平面图形求得面积，也可以通过直观图到原图形面积的关系求解：直观图面积为S '，原图形面积为S ，则2S S '=二、填空题13．【分析】确定是等腰直角三角形的中点分别是和的外心由直棱柱性质得的外接球的球心在上外接球面与平面的交线是圆是以为圆心为半径的圆求出可得面积【详解】则设分别是的中点则分别是和的外心由直三棱柱的性质得平面解析：4π【分析】确定ABC 是等腰直角三角形，11,AC A C 的中点1,D D 分别是ABC 和111A B C △的外心，由直棱柱性质得P ABC -的外接球的球心O 在1DD 上，外接球面与平面111A B C 的交线是圆，是以1D 为圆心，1D P 为半径的圆，求出1PD 可得面积．【详解】4,2AB BC AC ===90ABC ∠=︒，设1,D D 分别是11,AC A C 的中点，则1,D D 分别是ABC 和111A B C △的外心，由直三棱柱的性质得1DD ⊥平面ABC ，所以P ABC -的外接球的球心O 在1DD 上，如图，24()41OA ππ=，则41OP OA ==，2222413(22)22OD OA AD ⎛⎫=-=-= ⎪ ⎪⎝⎭，所以11135422OD DD OD AA OD =-=-=-=， 222211415222PD OP OD ⎛⎫⎛⎫=-=-= ⎪⎪ ⎪⎝⎭⎝⎭， P ABC -的外接球面与平面111A B C 的交线是圆，是以1D 为圆心，1D P 为半径的圆，其面积为224S ππ=⨯=．故答案为：4π．【点睛】关键点点睛：本题考查立体几何中动点轨迹问题的求解，重点考查了几何体的外接球的有关问题的求解，关键是根据外接球的性质确定球心位置，结合勾股定理得出动点所满足的具体条件，结论：三棱锥的外接球的球心在过各面外心且与此面垂直的直线上．14．【分析】经分析正三棱锥是以△BCD 底面的三棱锥可以把看出以AB 为边长的正方体切割下来的可借助于正方体的外接球求解【详解】正三棱锥中所以△BCD 为底面且所以正三棱锥是以AB 为边长的正方体切割下来的所以解析：6π【分析】经分析，正三棱锥A BCD -是以△BCD 底面的三棱锥，可以把看出以AB 为边长的正方体切割下来的，可借助于正方体的外接球求解. 【详解】正三棱锥A BCD -中，π2BAC ∠=，所以△BCD 为底面，且π2BAD DAC BAC ∠=∠=∠=, 所以正三棱锥A BCD -是以AB 为边长的正方体切割下来的，所以正三棱锥A BCD -的外接球就是正方体的外接球.设外接球的半径为R ,所以2R =所以外接球的表面积为246S R ππ==．故答案为：6π 【点睛】多面体的外接球问题解题关键是找球心和半径，求半径的方法有：(1)公式法；(2) 多面体几何性质法；(3)补形法；(4)寻求轴截面圆半径法；(5)确定球心位置法．15．【分析】在矩形中作交于交于在翻折后的几何体中证得平面平面从而平面得是直线与平面所成的角设C 求得的范围后可得范围【详解】在矩形中作交于交于设由图易知∴即∴则在翻折后的几何体中又平面∴平面又平面∴平面平解析：(0,]6π【分析】在矩形ABCD 中作DO AF ⊥，交AF 于O ，交AB 于M ，在翻折后的几何体中，证得平面ODM ⊥平面ABCF ，从而DM ⊥平面ABCF ，得DFM ∠是直线FD 与平面ABCF 所成的角．设(01)CF x x =<<C ，求得sin θ的范围后可得θ范围．【详解】在矩形ABCD 中作DO AF ⊥，交AF 于O ，交AB 于M ，设(01)CF x x =<<，AM t =，由图易知DAM FDA △△，∴AM AD DA DF =，即112t x =-，∴12t x=-，01x <<，则112t <<．在翻折后的几何体中，AF OD ⊥，AF OM ⊥，又OD OM O =，,OD OM ⊂平面ODM ，∴AF ⊥平面ODM ，又AF ⊂平面ABCF ，∴平面ODM ⊥平面ABCF ，又平面ABD ⊥平面ABC AB =．平面ODM平面ABD DM =，∴DM ⊥平面ABCF ，连接MF ，则DFM ∠是直线FD 与平面ABCF 所成的角．DFM θ∠=，而DM =12DF x t=-=，∴2422211sin 1()24DM t t t t t DF θ==-=-+=--+， ∵112t <<，∴2114t <<，∴10sin 2θ<≤，即06πθ<≤．故答案为：(0,]6π．【点睛】方法点睛：本题考查求直线与平面所成的角，求线面角常用方法：（1）定义法：作出直线与平面所成的角并证明，然后在直角三角形中计算可得；（2）向量法：建立空间直角坐标系，由直线的方向向量与平面的法向量夹角的余弦的绝对值等于直线与平面所成角的正弦值计算．16．【分析】作于于可得等于二面角的平面角从而可得然后求得而因此可得是异面直线与所成角（或补角）这样在求解可得【详解】如图作于于则连接根据二面角平面角的定义知与的夹角等于二面角的平面角所以因为所以设则在矩解析：12．【分析】作DM AC ⊥于M ，BN AC ⊥于N ，可得,MD NB '<>等于二面角D AC B '--的平面角，从而可得DMD '∠，然后求得DD '，而//AB CD ，因此可得D CD '∠是异面直线D C '与AB 所成角（或补角）．这样在DCD '求解可得．【详解】如图，作DM AC ⊥于M ，BN AC ⊥于N ，则//DM BN ，连接,D M DD ''，根据二面角平面角的定义知MD '与NB 的夹角等于二面角D AC B '--的平面角，所以,3MD NB π'<>=，因为//DM BN ，所以23DMD π'∠=，设1BC =，则22AB BC ==ABCD 中，3AC =1263DM ⨯==， 63D M DM '==，则222222666612cos 22333332DD DM D M DM D M π⎛⎫⎛⎫⎛⎫'''=+-⋅=+-⨯⨯⨯-= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以2DD '=，因为//AB CD ，所以D CD '∠是异面直线D C '与AB 所成角（或补角）．DCD '是正三角形，3D CD π'∠=，1cos 2D CD '∠=．所以异面直线D C '与AB 所成角余弦值是12．故答案为：12．【点睛】关键点点睛：本题考查求异面直线所成的角，解题方法根据异面直线所成角定义作出它们所成的角，然后解三角形可得，解题关键是利用图中MD '与NB 的夹角等于二面角D AC B '--的平面角，从而求得DMD '∠，只要设1BC =，可求得DD '，从而求得结论．17．【分析】连接延长交于则是中点可得是二面角的平面角求出可得结论【详解】由已知是中心连接延长交于则是中点连接则而∴平面平面∴∴是二面角的平面角由对称性又由平面平面得∴故答案为：【点睛】关键点点睛：本题考 3 【分析】连接DO 延长交BC 于E ，则E 是BC 中点，可得MEO ∠是二面角M BC O --的平面角．求出,ME OE 可得结论．【详解】由已知O 是BCD △中心，连接DO 延长交BC 于E ，则E 是BC 中点，连接AE ，则BC AE ⊥，BC DE ⊥，而AEDE E =，∴BC ⊥平面AED ，ME ⊂平面AED ，∴BC ME ⊥，∴MEO ∠是二面角M BC O --的平面角．2BC =，90BMC ︒∠=，由对称性2BM CM ==，112ME BC ==，又1133233EO DE ==⨯⨯=，由AO ⊥平面BCD ，EO ⊂平面BCD ，得AO EO ⊥， ∴3cos 3EO MEO ME ∠==．故答案为：33．【点睛】关键点点睛：本题考查求二面角，解题关键是作出二面角的平面角．这可根据平面角的定义作出（并证明），然后在直角三角形中求角即得．注意一作二证三计算三个步骤．18．【分析】分别取棱的中点连接易证平面平面由题意知点必在线段上由此可判断在或处时最长位于线段中点处时最短通过解直角三角形即可求得【详解】如下图所示连分别为所在棱的中点则又平面平面平面四边形为平行四边形又解析：[32,25]【分析】分别取棱1BB 、11B C 的中点M 、N ，连接MN ，易证平面1//A MN 平面AEF ，由题意知点P 必在线段MN 上，由此可判断P 在M 或N 处时1A P 最长，位于线段MN 中点处时最短，通过解直角三角形即可求得．【详解】如下图所示，连MN ，EF ，1A D ，EMM ，N ，E ，F 分别为所在棱的中点，则1//MN A D ，1//EF A D ，//EF MN ∴，又MN ⊂平面1C EF ，EF ⊂平面1C EF ，//MN ∴平面1C EF ．11//,C C EM C C EM =， ∴四边形1C CME 为平行四边形，1//C E CM ，又CM ⊄平面1C EF ，1C E ⊂平面1C EF ，//CM ∴平面1C EF ，又NMCM M =，∴平面//NMC 平面1C EF ．P 是侧面四边形ADD 1A 1内一动点，且C 1P ∥平面CMN ， ∴点P 必在线段EF 上．在Rt △11C D E 中，222211114225C E C D D E =+=+=同理，在Rt △11C D F 中，可得125C F =，∴△1C EF 为等腰三角形．当点P 为EF 中点O 时，1C P EF ⊥，此时1C P 最短；点P 位于,E F 处时，1C P 最长．()222211(25)232C O C E OE =-=-=1125C E C F ==∴线段1C P 长度的取值范围是[32,25]．故答案为：[32,25] 【点睛】本题考查点、线、面间的距离问题，考查学生的运算能力及推理转化能力，属中档题，解决本题的关键是通过构造平行平面寻找P 点位置．19．【分析】根据四面体是球的内接四面体结合位置关系可得棱锥的形状以及棱长之间的关系利用体积公式即可代值计算【详解】设该球的半径为R 则AB ＝2R2ACAB2R ∴ACR 由于AB 是球的直径所以△ABC 在大圆所解析：【分析】根据四面体是球的内接四面体，结合位置关系，可得棱锥的形状，以及棱长之间的关系，利用体积公式即可代值计算. 【详解】设该球的半径为R ，则AB ＝2R ，2AC ==2R ， ∴AC=，由于AB 是球的直径，所以△ABC 在大圆所在平面内且有AC ⊥BC ，在Rt △ABC 中，由勾股定理，得：BC 2＝AB 2﹣AC 2＝R 2，所以R t △ABC 面积S 12=⨯BC ×AC =2，又PO ⊥平面ABC ，且PO ＝R ，四面体P ﹣ABC 的体积为32，∴VP ﹣ABC 13=⨯R R 232=3＝9，R 3＝所以：球的体积V 43=⨯πR 343=⨯=．故答案为：. 【点睛】本题考查三棱锥外接球体积的计算，属基础题；本题的重点是要根据球心的位置去推导四面体的几何形态，从而解决问题.20．【分析】先在等边三角形中求出外接圆半径从而可求该三棱锥的外接球的半径【详解】详解：因为所以为等边三角形所以等边外接圆的半径为如图三棱锥外接球球心为半径为设球心到平面的距离为外接圆圆心为连接则平面取中【分析】先在等边三角形ABC 中求出BC =，外接圆半径2r ，从而可求该三棱锥的外接球的半径. 【详解】详解：因为060AB AC BAC ==∠=，所以ABC 为等边三角形，所以BC =ABC 外接圆的半径为23r，如图，三棱锥P ABC -外接球球心为O ，半径为R ，设球心O 到平面ABC 的距离为d ，ABC 外接圆圆心为'O ，连接,','AO AO OO ，则'OO ⊥平面ABC ，取PA 中点,D OP OA =，所以OD PA ⊥，又PA ⊥平面ABC ，所以//PA OO '，则四边形'ADOO 是矩形，所以在PDO △和'OAO △中，由勾股定理可得()222222222R d R d ⎧=+⎪⎨=+-⎪⎩，解得：1,5d R ==. 故答案为：5.【点睛】本题主要考查了三棱锥外接球的表面积，其中根据几何体的结构特征和球的性质，求得三棱锥的外接球的半径是解答的关键，着重考查了空间想象能力，以及推理与运算能力.三、解答题21．（1）4；（2）60︒；（33【分析】（1）根据棱锥的体积公式求解即可；（2）作辅助线，利用平行得出异面直线1CB 与1AC 所成角就是COE ∠，再结合等边三角形的性质得出夹角；（3）过C 作1CF AC ⊥于点F ，连接,CF BF ，由11,CF AC BF AC ⊥⊥结合定义得出二面角1B AC C --的平面角，再由直角三角形的边角关系得出平面角的余弦值. 【详解】（1）三棱柱111ABC A B C -的体积1122242ABC V SCC ⎛⎫=⋅=⨯⨯⨯= ⎪⎝⎭（2）记1BC 与1B C 的交点为O ，作AB 的中点E ，连接,OE CE ，异面直线1CB 与1AC 所成角就是COE ∠2CO OE CE ===60COE ︒∴∠=（3）过C 作1CF AC ⊥于点F ，连接,CF BF11,CF AC BF AC BFC ⊥⊥⇒∠为所求角3tan 2,cos 32BC BFC BFC FC ∠===∠=【点睛】关键点睛：在求异面直线的夹角时，关键是利用中位线定理得出平行，从而得出异面直线的夹角.22．（1）证明见解析；（2）105. 【分析】（1）由PA ⊥底面ABCD ，得PA DE ⊥，由Rt ABH Rt DAE ≌△△，得DE AH ⊥，可得答案.（2）由可知DE ⊥平面PAH ，连接PG ，则DPG ∠即为直线PD 与平面PAH 所成线面角，在Rt PDG △中，由sin DPG ∠可得答案. 【详解】（1）因为PA ⊥底面ABCD ，DE ⊂底面ABCD ，所以PA DE ⊥，因为E ，H 分别为正方形ABCD 的边AB ，BC 的中点，,,AB DA BH AE HBAEAD ，所以Rt ABH Rt DAE ≌△△，所以BAH ADE ∠=∠，由90AED ADE ∠+∠=所以90BAH AED ∠+∠=，所以DE AH ⊥，因为PA ⊂平面PAH ，AH ⊂平面PAH ，PA AH A ⋂=，所以DE ⊥平面PAH .（2）由（1）可知DE ⊥平面PAH ，设AH DE G ⋂=，如图，连接PG ，则DPG ∠即为直线PD 与平面PAH 所成线面角，因为2PA AD ==，所以22PD =，5DE =，在Rt DAE 中，由于AG DE ⊥，所以2AD DG DE =⋅，所以45DG =⋅，所以5DG =，所以在Rt PDG △中，105sin 22DG DPG PD ∠===，即直线PD 与平面PAH 所成线面角的正弦值为10.【点睛】本题主要考查线面垂直的证明、线面角的求法，对于线面角的求法的步骤,作：作（或找）出斜线在平面上的射影，证：证明某平面角就是斜线与平面所成的角；算：通常在垂线段、斜线段和射影所组成的直角三角形中计算. 23．（1）证明见解析；（2）73）存在；12PF PB =．【分析】（1）首先证明BE AD ⊥，再由面面垂直的性质定理可得BE ⊥平面PAD ，即证. （2）连结PE ，以E 为坐标原点，EP ，EA ，EB 为,,x y z 轴，建立空间直角坐标系，(0,3,0)EB a =是平面PAD 的一个法向量，再求出平面PCD 的一个法向量，利用空间向量的数量积即可求解.（3）根据题意可得EF 与平面PCD 的法向量垂直，假设线段PB 上存在点F 使得//EF 平面PCD ，再利用向量的数量积即可求解. 【详解】解：（1）因为四边形ABCD 为菱形，所以AB AD =．。

线面角、面面角强化训练(含答案)

线面角、面面角强化训练一．解答题（共24小题）1．（2012•浙江）如图，在侧棱垂直底面的四棱柱ABCD﹣A1B1C1D1中，AD∥BC，AD⊥AB，AB=．AD=2，BC=4，AA1=2，E是DD1的中点，F是平面B1C1E与直线AA1的交点．（1）证明：（i）EF∥A1D1；（ii）BA1⊥平面B1C1EF；（2）求BC1与平面B1C1EF所成的角的正弦值．2．（2010•湖南）如图所示，在正方体ABCD﹣A1B1C1D1中，E是棱DD1的中点．（Ⅰ）求直线BE与平面ABB1A1所成的角的正弦值；（Ⅱ）在棱C1D1上是否存在一点F，使B1F∥平面A1BE？证明你的结论．3．（2009•湖南）如图，在正三棱柱ABC﹣A1B1C1中，AB=4，AA1=，点D是BC的中点，点E在AC上，且DE⊥A1E．（1）证明：平面A1DE⊥平面ACC1A1；（2）求直线AD和平面A1DE所成角的正弦值．4．（2008•上海）如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，E是BC1的中点．求直线DE与平面ABCD所成角的大小（结果用反三角函数值表示）．5．（2005•黑龙江）如图，四棱锥P﹣ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD=PD，E，F分别为CD，PB的中点．（1）求证：EF⊥面PAB；（2）若，求AC与面AEF所成的角．6．如图，四棱锥S﹣ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1．（Ⅰ）证明：SD⊥平面SAB；（Ⅱ）求AB与平面SBC所成的角的大小．7．（2011•北京）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．（Ⅰ）求证：BD⊥平面PAC；（Ⅱ）若PA=AB，求PB与AC所成角的余弦值；（Ⅲ）当平面PBC与平面PDC垂直时，求PA的长．8．（2008•安徽）如图，在四棱锥O﹣ABCD中，底面ABCD四边长为1的菱形，∠ABC=，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC的中点．（Ⅰ）证明：直线MN∥平面OCD；（Ⅱ）求异面直线AB与MD所成角的大小；（Ⅲ）求点B到平面OCD的距离．9．（2005•北京）如图，在直三棱柱ABC﹣A1B1C1中，AC=3，BC=4，AB=5，AA1=4，点D为AB的中点．（Ⅰ）求证AC⊥BC1；（Ⅱ）求证AC1∥平面CDB1；（Ⅲ）求异面直线AC1与B1C所成角的余弦值．10．（2009•江西）在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2．以AC的中点O为球心、AC为直径的球面交PD于点M，交PC于点N（1）求证：平面ABM⊥平面PCD；（2）求直线CD与平面ACM所成的角的大小；（3）求点N到平面ACM的距离．11．（2008•海南）如图，已知点P在正方体ABCD﹣A′B′C′D′的对角线BD′上，∠PDA=60°．（Ⅰ）求DP与CC′所成角的大小；（Ⅱ）求DP与平面AA′D′D所成角的大小．12．如图，四棱锥P﹣ABCD中，底面ABCD为菱形，PA⊥底面ABCD，，PA=2，E是PC上的一点，PE=2EC．（Ⅰ）证明：PC⊥平面BED；（Ⅱ）设二面角A﹣PB﹣C为90°，求PD与平面PBC所成角的大小．13．（2012•重庆）如图，在直三棱柱ABC﹣A1B1C1中，AB=4，AC=BC=3，D为AB的中点．（Ⅰ）求异面直线CC1和AB的距离；（Ⅱ）若AB1⊥A1C，求二面角A1﹣CD﹣B1的平面角的余弦值．14．（2012•重庆）如图，在直三棱柱ABC﹣A1B1C1中，AB=4，AC=BC=3，D为AB的中点（Ⅰ）求点C到平面A1ABB1的距离；（Ⅱ）若AB1⊥A1C，求二面角A1﹣CD﹣C1的平面角的余弦值．15．（2012•浙江）如图，在四棱锥P﹣ABCD中，底面是边长为的菱形，∠BAD=120°，且PA⊥平面ABCD，PA=，M，N分别为PB，PD的中点．（1）证明：MN∥平面ABCD；（2）过点A作AQ⊥PC，垂足为点Q，求二面角A﹣MN﹣Q的平面角的余弦值．16．（2012•四川）如图，在三棱锥P﹣ABC中，∠APB=90°，∠PAB=60°，AB=BC=CA，点P在平面ABC内的射影O在AB上．（Ⅰ）求直线PC与平面ABC所成的角的大小；（Ⅱ）求二面角B﹣AP﹣C的大小．17．（2012•山东）在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF．（Ⅰ）求证：BD⊥平面AED；（Ⅱ）求二面角F﹣BD﹣C的余弦值．18．（2011•辽宁）如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=PD．（I）证明：平面PQC⊥平面DCQ（II）求二面角Q﹣BP﹣C的余弦值．19．如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD．（Ⅰ）证明：PA⊥BD；（Ⅱ）若PD=AD，求二面角A﹣PB﹣C的余弦值．20．如图，已知正三棱柱ABC﹣A1B1C1的，底面边长是侧棱长2倍，D、E分别是AC、A1C1的中点；（Ⅰ）求证：直线AE∥平面BDC1；（Ⅱ）求证：直线A1D⊥平面BDC1；（Ⅲ）求直线A1C1与平面BDC1所成的角．21．已知斜三棱柱ABC﹣A1B1C1中，∠BCA=90°，AC=BC=2，A1在底面ABC上的射影恰为AC的中点D，又知BA1⊥AC1．（Ⅰ）求证：AC1⊥平面A1BC；（Ⅱ）求C1到平面A1AB的距离；（Ⅲ）求二面角A﹣A1B﹣C的余弦值．22．已知在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=1，AB=2，E、F分别是AB、PD 的中点．（Ⅰ）求证：AF∥平面PEC；（Ⅱ）求PC与平面ABCD所成角的大小；（Ⅲ）求二面角P一EC一D的大小．23．如图，ABCD﹣A1B1C1D1是棱长为6的正方体，E、F分别是棱AB、BC上的动点，且AE=BF．（1）求证：A1F⊥C1E；（2）当A1、E、F、C1共面时，求：①D1到直线C1E的距离；②面A1DE与面C1DF所成二面角的余弦值．24．如图，在直三棱柱ABC﹣A1B1C1中，AC=BC=CC1=2，AC⊥BC，点D是AB的中点．（Ⅰ）求证：AC1∥平面CDB1；（Ⅱ）求点B到平面CDB1的距离；（Ⅲ）求二面角B﹣B1C﹣D的大小．线面角、面面角强化训练参考答案与试题解析一．解答题（共24小题）1．（2012•浙江）如图，在侧棱垂直底面的四棱柱ABCD﹣A1B1C1D1中，AD∥BC，AD⊥AB，AB=．AD=2，BC=4，AA1=2，E是DD1的中点，F是平面B1C1E与直线AA1的交点．（1）证明：（i）EF∥A1D1；（ii）BA1⊥平面B1C1EF；（2）求BC1与平面B1C1EF所成的角的正弦值．B=B=，即∠，BH=，H=，2．（2010•湖南）如图所示，在正方体ABCD﹣A1B1C1D1中，E是棱DD1的中点．（Ⅰ）求直线BE与平面ABB1A1所成的角的正弦值；（Ⅱ）在棱C1D1上是否存在一点F，使B1F∥平面A1BE？证明你的结论．BE=中，所成的角的正弦值为3．（2009•湖南）如图，在正三棱柱ABC﹣A1B1C1中，AB=4，AA1=，点D是BC的中点，点E在AC上，且DE⊥A1E．（1）证明：平面A1DE⊥平面ACC1A1；（2）求直线AD和平面A1DE所成角的正弦值．），，﹣，，﹣所成角的正弦值为4．（2008•上海）如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，E是BC1的中点．求直线DE与平面ABCD所成角的大小（结果用反三角函数值表示）．EF=（5．（2005•黑龙江）如图，四棱锥P﹣ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD=PD，E，F分别为CD，PB的中点．（1）求证：EF⊥面PAB；（2）若，求AC与面AEF所成的角．EF DGa所成角的正弦值为所成角为，∴）解：由，得，∴所成的角为所成的角为．6．如图，四棱锥S﹣ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1．（Ⅰ）证明：SD⊥平面SAB；（Ⅱ）求AB与平面SBC所成的角的大小．的法向量为锐角时，所求的角即为它的余角；当=MD=SM=（，y==，，＞==，＞arcsin7．（2011•北京）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．（Ⅰ）求证：BD⊥平面PAC；（Ⅱ）若PA=AB，求PB与AC所成角的余弦值；（Ⅲ）当平面PBC与平面PDC垂直时，求PA的长．，则，代入公式可求的法向量的法向量，，﹣，，，=|）知，设的法向量令的法向量所以的法向量=0t=PA=8．（2008•安徽）如图，在四棱锥O﹣ABCD中，底面ABCD四边长为1的菱形，∠ABC=，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC的中点．（Ⅰ）证明：直线MN∥平面OCD；（Ⅱ）求异面直线AB与MD所成角的大小；（Ⅲ）求点B到平面OCD的距离．ADC=DP=利用勾股定理求得等于，，的坐标表示．设平面的法向量为，，表示出和在向量的距离为，∴，所成角的大小为．的距离为．，，•=0•=0•（，﹣，．在向量=）上的投影的绝对值，的距离为9．（2005•北京）如图，在直三棱柱ABC﹣A1B1C1中，AC=3，BC=4，AB=5，AA1=4，点D为AB的中点．（Ⅰ）求证AC⊥BC1；（Ⅱ）求证AC1∥平面CDB1；（Ⅲ）求异面直线AC1与B1C所成角的余弦值．=λ，与AC，AB=，CE=CBCED==所成角的余弦值（（Ⅰ）∵=0⊥，，=∥（Ⅲ）∵=，＞所成角的余弦值为10．（2009•江西）在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2．以AC的中点O为球心、AC为直径的球面交PD于点M，交PC于点N（1）求证：平面ABM⊥平面PCD；（2）求直线CD与平面ACM所成的角的大小；（3）求点N到平面ACM的距离．距离的的一个法向量，结合然后求出距离的，再利用向量的射影公式直接求点的中点可得即，则，，由PN=（．）可知所求距离为．的一个法向量，由可得：，所以所求角的大小为，所以，则距离的，设点．11．（2008•海南）如图，已知点P在正方体ABCD﹣A′B′C′D′的对角线BD′上，∠PDA=60°．（Ⅰ）求DP与CC′所成角的大小；（Ⅱ）求DP与平面AA′D′D所成角的大小．（Ⅰ）利用，求出．即可．．通过，得到．求出，，由已知，．解得，所以（Ⅰ）因为．即．，所以．．则，）则，则，由已知，，解得，∴（Ⅰ）因为，．即．，所以12．如图，四棱锥P﹣ABCD中，底面ABCD为菱形，PA⊥底面ABCD，，PA=2，E是PC上的一点，PE=2EC．（Ⅰ）证明：PC⊥平面BED；（Ⅱ）设二面角A﹣PB﹣C为90°，求PD与平面PBC所成角的大小．，（2），﹣=，（）•==0•=0），（的法向量为，则，=，则，﹣），∴•﹣，（﹣，﹣，＞==13．（2012•重庆）如图，在直三棱柱ABC﹣A1B1C1中，AB=4，AC=BC=3，D为AB的中点．（Ⅰ）求异面直线CC1和AB的距离；（Ⅱ）若AB1⊥A1C，求二面角A1﹣CD﹣B1的平面角的余弦值．=．=，得D=，D=2=．=，﹣得=0，2，）=，=，则⊥，⊥取=（=，则⊥，，即取得，＞==．14．（2012•重庆）如图，在直三棱柱ABC﹣A1B1C1中，AB=4，AC=BC=3，D为AB的中点（Ⅰ）求点C到平面A1ABB1的距离；（Ⅱ）若AB1⊥A1C，求二面角A1﹣CD﹣C1的平面角的余弦值．=，从而D=．所以=，，，从而，，﹣，故，2，，=，则有⊥，⊥•且•，即，取=，=，则⊥，⊥，即且=0，＞=，所以二面角的平面角的余弦值15．（2012•浙江）如图，在四棱锥P﹣ABCD中，底面是边长为的菱形，∠BAD=120°，且PA⊥平面ABCD，PA=，M，N分别为PB，PD的中点．（1）证明：MN∥平面ABCD；（2）过点A作AQ⊥PC，垂足为点Q，求二面角A﹣MN﹣Q的平面角的余弦值．的法向量，AQ=2AC=AB=中，（﹣，（），的平面角的余弦值为BD=AM=PB=AE=AQ=2BPC=MQ=．QE=，∴AEQ=的平面角的余弦值为16．（2012•四川）如图，在三棱锥P﹣ABC中，∠APB=90°，∠PAB=60°，AB=BC=CA，点P在平面ABC内的射影O在AB上．（Ⅰ）求直线PC与平面ABC所成的角的大小；（Ⅱ）求二面角B﹣AP﹣C的大小．OP=与平面OP=，，OC====．为原点，建立空间直角坐标系．则）=2=，则由得出，取﹣，所以（﹣===．OP=，，，所以=2 =）为平面==arcsin（Ⅱ）由（Ⅰ）知，，，=，则由得出，，则，所以=，的一个法向量为==arccos17．（2012•山东）在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF．（Ⅰ）求证：BD⊥平面AED；（Ⅱ）求二面角F﹣BD﹣C的余弦值．，﹣，，因此（，﹣==，则•，•y=z，则==，＞=，所以二面角CB=CGFGC=的余弦值为18．（2011•辽宁）如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=PD．（I）证明：平面PQC⊥平面DCQ（II）求二面角Q﹣BP﹣C的余弦值．求出则、、由向量积的运算易得•，•、、的坐标，的法向量法向量，==••=即因此可取，=，＞﹣的余弦值为﹣19．如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD．（Ⅰ）证明：PA⊥BD；（Ⅱ）若PD=AD，求二面角A﹣PB﹣C的余弦值．的坐标，求出向量，和平面BD=，，，，=的法向量为，则因此可取（，=，==﹣的余弦值为：﹣20．如图，已知正三棱柱ABC﹣A1B1C1的，底面边长是侧棱长2倍，D、E分别是AC、A1C1的中点；（Ⅰ）求证：直线AE∥平面BDC1；（Ⅱ）求证：直线A1D⊥平面BDC1；（Ⅲ）求直线A1C1与平面BDC1所成的角．D=21．已知斜三棱柱ABC﹣A1B1C1中，∠BCA=90°，AC=BC=2，A1在底面ABC上的射影恰为AC的中点D，又知BA1⊥AC1．（Ⅰ）求证：AC1⊥平面A1BC；（Ⅱ）求C1到平面A1AB的距离；（Ⅲ）求二面角A﹣A1B﹣C的余弦值．，求，））=的法向量=，则，）∴的距离为的法向量（，的法向量，的余弦值为22．已知在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=1，AB=2，E、F分别是AB、PD 的中点．（Ⅰ）求证：AF∥平面PEC；（Ⅱ）求PC与平面ABCD所成角的大小；（Ⅲ）求二面角P一EC一D的大小．FO=中，中，所成的角大小为，可得的大小为23．如图，ABCD﹣A1B1C1D1是棱长为6的正方体，E、F分别是棱AB、BC上的动点，且AE=BF．（1）求证：A1F⊥C1E；（2）当A1、E、F、C1共面时，求：①D1到直线C1E的距离；②面A1DE与面C1DF所成二面角的余弦值．坐标，代入向量数量积公式，易得满足，的一个法向量为，的一个法向量为24．如图，在直三棱柱ABC﹣A1B1C1中，AC=BC=CC1=2，AC⊥BC，点D是AB的中点．（Ⅰ）求证：AC1∥平面CDB1；（Ⅱ）求点B到平面CDB1的距离；（Ⅲ）求二面角B﹣B1C﹣D的大小．（Ⅰ）求出通过，相关向量，计算，求二面角，∴，的距离是，．的大小是。

北京市西城区2024-2025学年高二上学期期中测验数学试题含解析

2024-2025学年度第一学期期中试卷高二数学（答案在最后）2024年11月本试卷共4页，共150分．考试时长120分钟．考生务必将答案答在答题卡上，在试卷上作答无效．考试结束后，将本试卷和答题卡一并交回．第一部分（选择题，共40分）一、选择题共10小题，每小题4分，共40分，在每小题列出的四个选项中，选出符合题目要求的一项．1.直线的倾斜角是23π，则斜率是（）A.33-B.33C.D.【答案】C 【解析】【分析】由直线的倾斜角与斜率的关系即得.【详解】∵直线的倾斜角是23π，∴直线的斜率为2tan tan()tan 333ππππ=-=-=故选：C.2.已知点P 在椭圆22132x y +=上，点()11,0F ，()21,0F -，则12PF PF +=（）A.2B.C.D.【答案】C 【解析】【分析】根据题意由椭圆标准方程以及椭圆定义即可得出结果.【详解】由椭圆方程为22132x y +=可知1a c ==，则()11,0F ，()21,0F -即为椭圆的左、右焦点，由椭圆定义可得122PF PF a +==.故选：C3.已知圆222610x y x y +-++=关于直线0x y m ++=对称，则实数m =（）A.－2B.－1C.1D.2【答案】D 【解析】【分析】根据圆关于直线对称即圆心在直线上得到答案.【详解】将222610x y x y +-++=化成标准方程为()()22139x y -++=，圆心为()1,3-，半径为3，因为圆222610x y x y +-++=关于直线0x y m ++=对称，所以圆心()1,3-在直线上，即130m -+=，解得2m =.故选：D.4.以点()2,1A 为圆心，且与x 轴相切的圆的标准方程为（）A.()()22211x y -+-= B.()()22214x y -+-=C.()()22211x y +++= D.()()22214x y +++=【答案】A 【解析】【分析】根据圆心和半径可得圆的方程.【详解】以点()2,1A 为圆心，且与x 轴相切的圆的半径为1．故圆的标准方程是()()22211x y -+-=．故选:A ．5.已知Q 为直线:210l x y ++=上的动点，点P 满足()1,3QP =-，记P 的轨迹为E ，则（）A.E的圆 B.E 是一条与l 相交的直线C.E 上的点到l D.E 是两条平行直线【答案】C 【解析】【分析】设(),P x y ，由()1,3QP =-可得Q 点坐标，由Q 在直线上，故可将点代入坐标，即可得P 轨迹E ，结合选项即可得出正确答案.【详解】设(),P x y ，由()1,3QP =-，则()1,3Q x y -+，由Q 在直线:210l x y ++=上，故()12310x y -+++=，化简得260x y ++=，即P 的轨迹为E 为直线且与直线l 平行，E 上的点到l的距离d ==，故A 、B 、D 错误，C 正确.故选：C .6.如图，三棱锥D-ABC 中，DC ⊥平面ABC ，DC=1，且为边长等于2的正三角形，则DA 与平面DBC所成角的正弦值为A.5B.5C.5D.25【答案】B 【解析】【分析】先过A 点作出高线，利用等体积法先求高线，再计算线面角．【详解】过点A 作垂直于平面BCD 的直线，垂足为O ，利用等体积法求解AO ．011131V DC S 60221V AO S 33233D ABC ABC A BCD BCD sin --=⨯=⨯⨯⨯⨯===⨯，由此解得AO =，DA 与平面DBC 所成角为ADO ∠，所以15sin ADO 5AO AD ∠==,故选B 【点睛】本题考查了等体积法和线面角的基本求法，综合性强，在三棱锥中求高线，利用等体积法是一种常见处理手段，计算线面角，先找线面角，要找线面角必找垂线，而求解垂线的基本方法为等体积法或者点到平面的距离公式．7.点M 是直线250x y -+=上的动点，O 是坐标原点，则以OM 为直径的圆经过定点（）．A.(0,0)和(1,1)-B.(0,0)和(2,2)-C.(0,0)和(1,2)-D.(0,0)和(2,1)-【答案】D 【解析】【分析】过点O 作OP 垂直于直线250x y -+=，根据圆的性质可得以OM 为直径的圆过定点O 和P ，得解.【详解】如图，过点O 作OP 垂直于直线250x y -+=，垂足为P ，则以OM 为直径的圆过定点O 和P ，易知直线OP 的方程为12y x =-，联立25012x y y x -+=⎧⎪⎨=-⎪⎩，解得21x y =-⎧⎨=⎩，即()2,1P -.所以以OM 为直径的圆经过定点()0,0和()2,1-.故选：D.8.“3m =”是“椭圆2214x y m+=的离心率为12”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A 【解析】【分析】根据椭圆2214x y m+=的离心率为12求出m ，进而求得答案.【详解】椭圆2214x y m +=的离心率为12，当04m <<时，4122=，得3m =；当4m >时，12=，得163m =．即“3m =”是“椭圆2214x y m+=的离心率为12”的充分不必要条件．故选：A.9.布达佩斯的伊帕姆维泽蒂博物馆收藏的达·芬奇方砖，在正六边形上画了具有视觉效果的正方体图案（如图1），把三片这样的达·芬奇方砖形成图2的组合，这个组合表达了图3所示的几何体．若图3中每个正方体的棱长为1，则点P 到平面QGC 的距离是（）A.12B.22C.32D.1【答案】B 【解析】【分析】根据题意，建立空间直角坐标系，结合向量法求解点到面的距离，即可得到结果.【详解】建立如图所示空间直角坐标系，则()()()()0,2,0,0,0,2,1,0,2,2,0,1C G Q P ，则()()()1,0,0,0,2,2,2,2,1GQ GC CP ==-=-，设平面QGC 的一个法向量为(),,n x y z =，则0220GQ n x GC n y z ⎧⋅==⎪⎨⋅=-=⎪⎩ ，取1z =，得()0,1,1n = ，所以点P 到平面QGC 的距离是22n CP n ⋅== .故选：B10.如图，已知正方体1111ABCD A B C D -的棱长为1，点M 为棱AB 的中点，点P 在正方形11BCC B 的边界及其内部运动．以下四个结论中错误的是（）A.存在点P满足1PM PD +=B.存在点P 满足1π2D PM ∠=C.满足1AP D M ⊥的点P 的轨迹长度为π4D.满足1MP D M ⊥的点P的轨迹长度为4【答案】C 【解析】【分析】建立空间直角坐标系，利用空间向量解决此题，对于A ，利用两个特殊点求出1PM PD +的值，在此范围内即可；对于B ，利用向量垂直数量积等于零解方程即可求P 点坐标；对于C ，D 利用向量垂直数量积等于零可求P 点的轨迹方程，根据图形找到P 点的轨迹求长度即可．【详解】如图所示，建立空间直角坐标系，则(1A ,0,0)，1(0D ,0,1)，1(1,,0)2M ，1(0C ,1,1)，动点P 设为(P x ,1,)z ，对于A ，点M 关于平面11BCB C 的对称点为13(1,,0)2M ，当动点P 在点1M时，此时1min 11()2PM PD D M +===<，当动点P 在点1C时，此时111135122PM PD C D C M +=+=+=>，所以存在点P满足1PM PD +=，所以A 正确；对于B ，1(1,,)2PM x z =--- ，1(,1,1)PD x z =--- ，若1π2D PM ∠=，则11(1)(1)02PM PD x x z z ⋅=--+--= ，化简得：2211()(022x z -+-=，解得1212x z ⎧=⎪⎪⎨⎪=⎪⎩，即11(,1,)22P ，满足题意，所以B 正确；对于C ，(1,1,)AP x z =- ，11(1,,1)2D M =- ，若1AP D M ⊥，则11102AP D M x z ⋅=-+-= ，即12z x =-，取BC 中点E ，1BB 中点F ，则点P 的轨迹为线段EF ，长度为22，所以C 错误；对于D ，1(1,,)2MP x z =- ，11(1,,1)2D M =- ，若1MP D M ⊥，则11104MP D M x z ⋅=-+-= ，即34z x =-，取BF 中点H ，BE 中点K ，则点P 的轨迹为线段HK ，长度为24，所以D 正确．故选：C ．第二部分（非选择题，共110分）二、填空题共5小题，每小题5分，共25分．11.椭圆22194x y +=的离心率是_________．【答案】53【解析】【分析】利用标准方程，求出a ，b ，然后求解c ，即可求解离心率．【详解】椭圆22194x y +=的长半轴为a ＝3，短半轴为b ＝2，则半焦距为c ==．所以椭圆的离心率为：e 53c a ==．故答案为53．【点睛】本题考查椭圆的简单性质的应用，离心率的求法，是基础题．12.已知直线1l ：()210m x y +++=，2l ：()5210x m y +-+=．若12l l ∥，则实数m 的值为______．【答案】－3【解析】【分析】根据两直线平行的条件列式求解即可.【详解】若12l l ∥，则()()2250m m +--=，解得3m =或3m =-，当3m =时，直线1l ：510x y ++=与2l ：5310x y ++=重合，不符合题意；当3m =-时，直线1l ：10x y -++=与2l ：5510x y -+=，符合题意，综上，3m =-故答案为：－3.13.在正三棱柱111ABC A B C -中，2AB =，1AA =，则异面直线1AB 与1BC 所成角的大小为______．【答案】π2【解析】【分析】利用异面直线夹角的向量求法建立空间直角坐标系计算可得结果.【详解】分别取11,BC B C 的中点1,O O ，连接1,AO OO ，由正三柱性质可知11,,AO BC OO BC AO OO ⊥⊥⊥，以O 为坐标原点，1,,OA OB OO 所在直线分别为,,x y z 轴建立空间直角坐标系，如下图所示：由2AB =，12AA =可得)()((113,0,0,0,1,0,0,1,2,0,1,2AB BC -，所以((113,1,2,0,2AB BC ==-，又111111022cos ,066AB BC AB BC AB BC ⋅===⨯，且[]11,0,πAB BC ∈ ；所以11π,2AB BC = .故答案为：π214.已知点P 是圆()2211x y -+=上的动点，直线1l ：3470x y -+=，2l ：340x y m -+=，记P 到直线1l ，2l 的距离分别为1d ，2d （若P 在直线上，则记距离为0），（1）1d 的最大值为______；（2）若当点P 在圆上运动时，12d d +为定值，则m 的取值范围是______．【答案】①.3②.(],8∞--【解析】【分析】（1）根据圆上点到直线的距离最大值为圆心到直线的距离加半径求解即可；（2）根据12d d +为定值，分析得到圆的位置，结合直线与圆的位置关系求解.【详解】（1）圆()2211x y -+=，圆心 th ，半径为1，圆心到直线1l 的距离()2231407234d ⨯-⨯+==+-，所以P 到直线1l 的距离1d 的最大值为13d +=；（2）当7m =时，两直线重合，不符题意；当7m ≠时，直线1l ，2l 平行，若当点P 在圆上运动时，12d d +为定值，所以圆在两平行线之间，此时直线2l 与圆相离，所以()223140134m d ⨯-⨯+=≥+-，解得2m ≥或8m ≤-，又因为当2m ≥时，直线1l ，2l 在圆同侧，不符合题意，所以8m ≤-，故答案为：3，(],8∞--.15.伯努利双纽线（简称双纽线）是瑞士数学家伯努利（1654-1705）在1694年提出的．伯努利将椭圆的定义作了类比处理，指出是到两个定点距离之积为定值的点的轨迹是双纽线．在平面直角坐标系xOy 中，到定点(),0A a -，(),0B a 的距离之积为()20a a >的点的轨迹C 就是伯努利双纽线，C 的方程为()()2222222x y a x y +=-，其形状类似于符号∞，若点()00,P x y 是轨迹C 上一点，给出下列四个结论：①曲线C 关于原点中心对称；②00y x ≤恒成立；③曲线C 2a ；④当0x a =时，0y 取得最大值或最小值．其中所有正确结论的序号是______．【答案】①②③【解析】【分析】根据曲线的方程，结合对称性的判定方法，联立方程组，以及不等式和三角形面积，逐项判定，即可求解.【详解】在曲线C 上任取一点(),M x y ，关于原点的对称点为(),M x y '--，代入曲线C 的方程，可知M '在曲线C 上，所以曲线C 关于原点中心对称，故①正确；因为点()00,P x y 是轨迹C 上一点，所以()()22222200002x y a x y +=-，因为()222000x y +≥，所以()()222222000020x y a x y +=-≥，即2200y x ≤，所以00y x ≤，故②正确；因为()()()22222222222x y a x x y y a +=-+≤，所以2222x y a +≤，≤，所以曲线C ，故③正确；因为()00,P x y ，所以12121212011||||sin ||||22PF F S PF PF F PF F F y =⋅⋅∠=⋅ ，又212||||PF PF a ⋅=，所以2120sin 2||a F PF a y ∠=⋅，即012||sin 22a a y F PF =∠≤，所以022a a y -≤≤，当12π2F PF ∠=时等号成立，故④错误，故答案为：①②③【点睛】方法点睛：本题考查曲线的轨迹及其性质的问题，同时需要结合解三角形的方法对所给信息进行辨析.三、解答题共6小题，共85分．解答题应写出文字说明、验算步骤或证明过程．16.已知直线l ：()()211510x y λλλ++---=，R λ∈．（1）当直线l 与直线20x y +=垂直时，求λ的值；（2）设直线l 恒过定点P ，求P 的坐标；（3）若对任意的实数λ，直线l 与圆()2220x y r r +=>总有公共点，直接写出r 的取值范围．【答案】（1）14λ=（2）()2,1P（3）r ≥【解析】【分析】（1）根据直线与直线垂直关系列方程即可求得λ的值；（2）将直线方程转化为()1250x y x y λ--++-=，列方程组解得定点坐标即可；（3）根据直线与圆位置关系结合点与圆位置关系求解即可.【小问1详解】当直线l ：()()211510x y λλλ++---=与直线20x y +=垂直时，可得()()21112410λλλ+⨯+-⨯=-=，解得14λ=；【小问2详解】直线l ：()()211510x y λλλ++---=方程整理得()1250x y x y λ--++-=，令10,250x y x y --=⎧⎨+-=⎩，解得2,1,x y =⎧⎨=⎩即直线l 恒过定点()2,1P ；【小问3详解】对任意的实数λ，直线l 与圆()2220x y rr +=>总有公共点，则直线l 恒过定点()2,1P 在圆上或者圆内，则OP r =≤，即r ≥17.已知C 经过点()0,2A -，()3,1B ，并且圆心C 在直线28y x =-上，（1）求C 的方程；（2）设过点()2,0P 的直线l 与C 交于M ，N 两点，若MN =l 的方程．【答案】（1）()()22329x y -++=（2）2x =或3460x y +-=．【解析】【分析】（1）根据圆的几何性质确定线段AB 的垂直平分线方程，从而联立直线可得圆心坐标，根据圆的定义得半径，从而得圆的方程；（2）根据直线与圆相交弦长公式，分直线斜率存在与不存在两种情况验证求解直线方程即可.【小问1详解】因为()0,2A -，()3,1B ，则1AB k =，且线段AB 中点为31,22⎛⎫- ⎪⎝⎭，则线段AB 的垂直平分线的斜率为1-，故其方程为1322y x ⎛⎫+=-- ⎪⎝⎭，即10x y +-=，由圆的对称性知点C 在AB 的垂直平分线上，因此联立10,28,x y y x +-=⎧⎨=-⎩解得3,2,x y =⎧⎨=-⎩即点()3,2C -，又因为3r AC ==，所以圆C ：()()22329x y -++=．【小问2详解】圆心()3,2C -，半径3r =当1l 的斜率不存在时，1l ：2x =，则圆心C 到直线1l 的距离为1d =，此时相交弦长MN ==当1l 的斜率存在时，设1l ：()2y k x =-，即20kx y k --=，因为相交弦长MN ==所以C 到1l的距离为1d ==，解得34k =-，此时，直线1l ：3460x y +-=，综上，直线1l 的方程为2x =或3460x y +-=．18.已知椭圆C ：()222210+=>>x y a b a b的左、右焦点分别为()1F和)2F ，长轴长为4．（1）求椭圆C 的方程；（2）设P 为椭圆C 上一点，()1,0M ．若存在实数λ使得12PF PF PM λ+=，求λ的取值范围．【答案】（1）2214x y +=（2）4,3⎡⎢⎣．【解析】【分析】（1）根据椭圆,,a b c 的关系列方程组求得,,a b c 的值，即可得椭圆方程；（2）根据椭圆的定义可得124PF PF +=，再根据两点距离公式结合点在椭圆上求解PM 的取值范围，即可得所求.【小问1详解】由题知22224,,c a a b c ⎧=⎪=⎨⎪=+⎩解得2,1,a b c ⎧=⎪=⎨⎪=⎩所以，C 的方程为2214x y +=．【小问2详解】由椭圆的定义可知124PF PF +=，设点 h t h ，其中220014x y +=，则220014x y =-，所以()222020200033421224433PM x y x x x ⎛⎫=-+=-+=-+ ⎪⎝⎭，因为022x -≤≤，所以2293PM ≤≤，即633PM ≤≤当且仅当043x =时，63PM =，02x =-时，3PM =，因为12PF PF PM λ+=，则12PF PF PM λ+=，所以4,3λ⎡∈⎢⎣．综上所述，λ的取值范围是4,3⎡⎢⎣．19.如图，在三棱台111ABC A B C -中，若1A A ⊥平面1,,2ABC AB AC AB AC AA ⊥===，111,A C N =为AB 中点，M 为棱BC 上一动点（不包含端点）.（1）若M 为BC 的中点，求证：1//A N 平面1C MA .（2）是否存在点M ，使得平面1C MA 与平面11ACC A 所成角的余弦值为66？若存在，求出BM 长度；若不存在，请说明理由.【答案】（1）证明见解析（2）23【解析】【分析】（1）利用三角形中位线定理，结合平行四边形的判定定理和性质、线面平行的判定定理进行证明即可；（2）利用空间向量夹角公式进行求解即可.【小问1详解】连接NM ，因为N 为AB 中点，M 为BC 的中点，所以1//,2NM AC NM AC =，因为111ABC A B C -是正三棱台，111,2A C AC ==，所以11111//,2AC AC AC AC =，于是有11111//,2NM A C NM A C =，因此四边形11NMC A 是平行四边形，所以111//,A N C M A N ⊄平面1C MA ，1C M ⊂平面1C MA ，所以1//A N 平面1C MA【小问2详解】假设存在点M ，使得平面1C MA 与平面11ACC A 所成角的余弦值为66，因为1A A ⊥平面,,ABC AB AC ⊂平面ABC ，所以11,A A AB AA AC ⊥⊥，而AB AC ⊥，所以建立如图所示的空间直角坐标系，()()()()()10,0,0,0,1,2,2,0,0,0,2,0,,,A C B C M x y z ，设()()()()()0,12,,2,2,022,2,0BM BC x y z M λλλλλ=∈⇒-=-⇒-，设平面1C MA 的法向量为(),,m a b c =，()()1220,1,2,0,,2,AC AM λλ=-=，所以有()1202,2,112220m AC b c m m AM a b λλλλ⎧⋅=+=⎪⎛⎫⇒=-⎨ ⎪-⎝⎭⋅=-+=⎪⎩，因为1A A AB ⊥，AB AC ⊥，11,,AA AC A AA AC A == ，所以AB ⊥平面11ACC A ，所以平面11ACC A 的法向量为()2,0,0AB =，所以41cos ,66m AB m AB m ABλ⋅==⇒⋅ ，解得13λ=，1λ=-舍去，即42,,033M ⎛⎫ ⎪⎝⎭，223BM ==，即BM 长度为223.20.平面直角坐标系xOy 中，点M 到点()0,1F 的距离比它到x 轴的距离多1，记点M 的轨迹为C ．（1）求轨迹C 的方程；（2）设斜率为k 的直线l 过定点()1,0P ，若直线l 与轨迹C 恰好有一个公共点，求实数k 的取值范围．【答案】（1）24,00,0y y x y ≥⎧=⎨<⎩（2）[)0,1．【解析】【分析】（1）根据题意列出等量关系并整理即可得出轨迹C 的方程；（2）分情况将曲线C 与直线方程联立，根据方程根的个数求得实数k 的取值范围．【小问1详解】设点 t1y =+，两边平方，并整理得24,0220,0y y x y y y ≥⎧=+=⎨<⎩,所以轨迹C 的方程为24,00,0y y x y ≥⎧=⎨<⎩.【小问2详解】易知直线():1l y k x =-，当0y ≥时，如下图所示：联立()214y k x x y⎧=-⎨=⎩，消去y 得2440x kx k -+=，21616k k ∆=-，当0∆=，即0k =或1k =时，有且仅有一个公共点且满足题意；当0∆<，即01k <<时，无公共点；当0y <时，令0x =，yk =-，当0k ≤时，无公共点；当0k >时，有一个公共点；综合以上可知当01k ≤<时，有且仅有一个公共点，故k 的取值范围是[)0,1．21.用一个矩形铁皮制作成一个直角圆形弯管（如图1）：将该矩形铁皮围成一个圆柱体（如图2），再用一个与圆柱底面所成45︒的平面截圆柱，将圆柱截成两段，再将这两段重新拼接就可以得到直角圆形弯管．现使用长为2π，宽为π的矩形铁皮制作一个直角圆形弯管，当得到的直角圆形弯管的体积最大时（不计拼接损耗部分），解答下列问题．（1）求该直角圆形弯管的体积；（2）已知在制造直角圆形弯管时截得的截口是一个椭圆，求该椭圆的离心率；（3）如图3，若将圆柱被截开的一段的侧面沿着圆柱的一条母线剪开，并展成平面图形（如图4），证明：该截口展开形成的图形恰好是某正弦型函数的部分图象，并指出该正弦型函数的最小正周期与振幅．【答案】（1）2π（2）22（3）证明见解析，最小正周期为2π，振幅为1【解析】【分析】（1）易知直角圆形弯管的体积即为切割前圆管体积，且当矩形的长或宽作为圆柱的高时，体积最大，分别求两种情况的体积；（2）根据圆柱截面的性质可得a =，即可得离心率；（3）以椭圆的短轴所在直线在底面的投影为x 轴建立平面直角坐标系，设对于底面圆上一点()cos ,sin P αα，则()1,0与P 所连接的弧长为α，假设短轴对应的高度为0，可得点P 对应到椭圆上的点的高度，即可得截口展开形成的图形的函数，进而可得最小正周期与振幅.【小问1详解】易知直角圆形弯管的体积即为切割前圆管体积，且当矩形的长或宽作为圆柱的高时，体积最大，当矩形的长作为圆柱的高时，圆柱体的底面圆周长为π，则底面半径为12，高为2π，体积为221π2ππ22⎛⎫⨯= ⎪⎝⎭；当矩形的宽作为圆柱的高时，圆柱体的底面圆周长为2π，则底面半径为1，高为π，体积为222ππ1ππ2⨯=>；所以体积为2π；【小问2详解】设该椭圆为()222210+=>>x y a b a b，因此22a b =，即a =，所以22c e a ===；【小问3详解】以椭圆的短轴所在直线在底面的投影为x 轴建立平面直角坐标系，设对于底面圆上一点()cos ,sin P αα，则()1,0与P 所连接的弧长为α，假设短轴对应的高度为0，则点P 对应到椭圆上的点的高度为sin tan 45sin αα︒=，所以，截口展开形成的图形的函数解析式为sin y x =，最小正周期为2π，振幅为1.。

等体积法求线面角测试题(含答案)

等体积法求线面角测试题(含答案)等体积法求线面角1.如图，三棱柱ABC-A1B1C1的侧棱与底面垂直，底面是边长为a的正三角形，体积为V，若P为底面A1B1C1的中心，则直线PA与平面ABC所成角的大小为多少度？答案：60°解题思路：根据题目条件，三棱柱的底面积为a^2*√3/4，高为2V/a^2，底面中心为P，连接PA，得到PA的长度为√(a^2+(2V/a^2)^2)，再根据勾股定理求得PA与底面的距离，即√(3/4*a^2+(V/a^2)^2)，由此得到PA与平面ABC的夹角正弦值为1/2，即60°。

2.如图，在正四棱锥P-ABCD中，已知PA=AB=PAD所成角的正弦值为x，若M为PA的中点，则直线BM与平面ABCD所成角的正弦值为多少？答案：√(1-x^2)解题思路：连接MB，由于PA=AB=PAD，所以∠PAB=∠PBA，∠PAD=∠PDA，即三角形PAB和三角形PDA全等，所以∠APB=∠DPB，又因为M是XXX的中点，所以MB⊥PA，即∠BMP=90°，故∠BMA=∠PMA-∠PMB=arcsin(x)-90°，所以BM与平面ABCD所成角的正弦值为sin(arcsin(x)-90°)=√(1-x^2)。

3.如图，在三棱锥中，已知平面与侧棱BC垂直，侧棱AB和AC的夹角为α，BC的长度为a，则与平面所成角的正弦值为多少？答案：cos(α)解题思路：连接BA和CA，由于平面与侧棱BC垂直，所以平面与三角形ABC的高重合，故平面与三角形ABC的底面面积相等，即平面与三角形ABC的底面BC所成的角相等，即∠ABC=90°-α，所以平面与三角形ABC的夹角为α，其正弦值为sin(α)，而cos(α)=BC/AB=a/√(a^2+(2a*sin(α))^2)=a/√(a^2+4a^2*sin^2(α))=a/√(a^2*(1+4*sin^2(α)))=1/√(1+4*sin^2(α))，故答案为cos(α)。

(压轴题)高中数学必修二第一章《立体几何初步》测试卷(有答案解析)(3)

一、选择题1．设1l 、2l 、3l 是三条不同的直线，α、β、γ是三个不同的平面，则下列命题是真命题的是（）A ．若1//l α，2//l α，则12l l //B ．若1l α⊥，2l α⊥，则12l l ⊥C ．若12//l l ，1l α⊂，2l β⊂，3l αβ⋂=，则13//l lD ．若αβ⊥，1l αγ=，2l βγ⋂=，则12l l //2．如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，四边形ABCD 为正方形，PA AB =，E 为AP 的中点，则异面直线PC 与DE 所成的角的正弦值为（）．A ．2B ．5C ．155D ．1053．在底面为正方形的四棱锥P ABCD -中，侧面PAD ⊥底面ABCD ，PA AD ⊥，PA AD =，则异面直线PB 与AC 所成的角为（）A ．30B ．45︒C ．60︒D ．90︒4．在三棱锥P ABC -中，PA ⊥平面ABC ，120224BAC AP AB AC ∠====，，则三棱锥P ABC -的外接球的表面积是（）A ．18πB ．36πC ．40πD ．72π5．已知m ，n 是两条直线，α，β是两个平面，则下列命题中错误的是（） A ．若m n ⊥，m α⊥，n β⊥，则αβ⊥B ．若m α⊂，//αβ，则//m βC ．若m n ⊥，m α⊥，βn//，则αβ⊥D ．若l αβ=，//m α，//m β，则//m l6．已知正方体1111ABCD A B C D -，点,E F 分别是棱11B C ，11A D 的中点，则异面直线BE ，DF 所成角的余弦值为（）A ．55B ．35C ．45D ．2557．已知正三棱柱111ABC A B C -中，1AB AA =，M 是1CC 的中点，则异面直线AM 与1A B 所成角的大小为（）A ．π6B ．π4C ．π3D ．π28．如图，正三棱柱111ABC A B C -的高为4，底面边长为43，D 是11B C 的中点，P 是线段1A D 上的动点，过BC 作截面AP α⊥于E ，则三棱锥P BCE -体积的最小值为（）A ．3B ．23C ．43D ．129．某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：3cm ）是（）A ．24B ．30C ．47D ．710．在下面四个正方体ABCD A B C D ''''-中，点M 、N 、P 均为所在棱的中点，过M 、N 、P 作正方体截面，则下列图形中，平面MNP 不与直线A C '垂直的是（）A ．B ．C ．D ．11．在四棱锥P -ABCD 中，//AD BC ，2AD BC =，E 为PD 中点，平面ABE 交PC 于F ，则PF FC=（） A ．1 B ．32 C ．2 D ．3 12．在正方体1111ABCD A B C D -中，M 和N 分别为11A B ，和1BB 的中点．，那么直线AM 与CN 所成角的余弦值是（）A ．25B 10C ．35D 3二、填空题13．已知正三棱锥A BCD -的四个顶点在球O 的球面上，2AB =，且π2BAC ∠=，则球O 的表面积为_______．14．如图在菱形ABCD 中，2AB =，60A ∠=，E 为AB 中点，将AED 沿DE 折起使二面角A ED C '--的大小为90，则空间A '、C 两点的距离为________；15．如图，在正方体1111ABCD A B C D -中，E ，F ，G 分别是棱11A B ，1BB ，11B C 的中点，则下列结论中：①FG BD ⊥； ②1B D ⊥面EFG ；③面//EFG 面11ACC A ； ④//EF 面11CDD C ．正确结论的序号是________.16．在棱长为2的正方体1111ABCD A B C D -中，P 是11A B 的中点，过点1A 作与平面1PBC 平行的截面，则此截面的面积是_______________．17．在三棱锥P ABC -中，P 在底面ABC 的射影为ABC 的重心，点M 为棱PA 的中点，记二面角P BC M --的平面角为α，则tan α的最大值为___________.18．已知某几何体的三视图如图所示，则该几何体的体积是__________．19．如图，已知正四面体D ABC -，P 为线段AB 上的动点（端点除外），则二面角D PC B --的平面角的余弦值的取值范围是___________．20．棱长为a 的正四面体的外接球的表面积为______．三、解答题21．如图，该多面体由底面为正方形ABCD 的直四棱柱被截面AEFG 所截而成，其中正方形ABCD 的边长为4，H 是线段EF 上（不含端点）的动点，36==FC EB ．（1）证明：//GH 平面ABCD ；（2）求H 到平面AEC 的距离．22．如图，正四棱锥P ABCD -中，底面ABCD 的边长为4，4PD =，E 为PA 的中点.（1）求证：//PC 平面EBD .（2）求三棱锥E ABD -的体积.23．在如图所示的几何体中，四边形BCED 为直角梯形，//DE CB ，BC EC ⊥，90AED ∠=︒.（1）证明：平面ABC ⊥平面ACE .（2）若P ，Q 分别是AE ，CD 的中点，证明：//PQ 平面ABC .24．如图，在三棱锥M 中，M 为BC 的中点，3PA PB PC AB AC =====，26BC =.（1）求二面角P BC A --的大小；（2）求异面直线AM 与PB 所成角的余弦值.25．如图，在三棱锥P ABC -中，1,2,135AB AC BAC ︒==∠=，1cos ,3BAP AP BC ∠=-⊥．（1）若23BM MC =，求证：PM BC ⊥；（2）当3AP =，且N 为BC 中点时，求AN 与平面PBC 所成角的正弦值． 26．如图，已知在三棱锥P ABC -中，ABC 是边长为2的正三角形，PAC △是以AC 为斜边的等腰直角三角形，若直线PB 与平面ABC 所成的角为6π．（Ⅰ）若PB PC >，求证：平面PAC ⊥平面ABC ；（Ⅱ）若PB PC <，求直线AB 与平面PAC 所成角的正弦值．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】利用已知条件判断1l 与2l 的位置关系，可判断AD 选项的正误；利用线面垂直的性质定理可判断B 选项的正误；利用线面平行的性质定理可判断C 选项的正误.【详解】对于A 选项，若1//l α，2//l α，则1l 与2l 平行、相交或异面，A 选项错误；对于B 选项，若1l α⊥，2l α⊥，由线面垂直的性质定理可得12//l l ，B 选项错误；对于C 选项，12//l l ，1l α⊂，2l β⊂，α、β不重合，则1l β⊄，1//l β∴， 1l α⊂，3l αβ⋂=，13//l l ∴，C 选项正确；对于D 选项，若αβ⊥，1l αγ=，2l βγ⋂=，则1l 与2l 相交或平行，D 选项错误.故选：C.【点睛】方法点睛：对于空间线面位置关系的组合判断题，解决的方法是“推理论证加反例推断”，即正确的结论需要根据空间线面位置关系的相关定理进行证明，错误的结论需要通过举出反例说明其错误，在解题中可以以常见的空间几何体（如正方体、正四面体等）为模型进行推理或者反驳． 2．D解析：D【分析】先取正方形的中心O ，连接OE ，由PC//OE 知OED ∠为异面直线PC 与DE 所成的角，再在OED 中求OED ∠的正弦即可.【详解】连AC ，BD 相交于点O ，连OE 、BE ，因为E 为AP 的中点，O 为AC 的中点，有PC//OE ，可得OED ∠为异面直线PC 与DE 所成的角，不妨设正方形中，2AB =，则2PA =，由PA ⊥平面ABCD ，可得,PA AB PA AD ⊥⊥，则145BE DE ==+=，1122222OD BD ==⨯=，因为BE DE =，O 为BD 的中点，所以90EOD ∠=︒，210sin 55OD OED DE ∠===．故选：D.【点睛】方法点睛：求空间角的常用方法：（1）定义法，由异面直线所成角、线面角、二面角的定义，结合图形，作出所求空间角，再结合题中条件，解对应三角形，即可求出结果；（2）向量法：建立适当的空间直角坐标系，通过计算向量夹角（直线方向向量与直线方向向量、直线方向向量与平面法向量，平面法向量与平面法向量）余弦值，即可求出结果. 3．C解析：C【分析】由已知可得PA ⊥平面ABCD ，底面ABCD 为正方形，分别过P ，D 点作AD ，AP 的平行线交于M ，连接CM ，AM ，因为PB ∥CM ，所以ACM 就是异面直线PB 与AC 所成的角,再求解即可.【详解】由题意：底面ABCD 为正方形，侧面PAD ⊥底面ABCD ，PA AD ⊥，面PAD 面ABCD AD =，PA ⊥平面ABCD ，分别过P ，D 点作AD ，AP 的平行线交于M ，连接CM ，AM ，∵PM ∥AD ，AD ∥BC ，PM ＝AD ，AD ＝BC ．∴ PBCM 是平行四边形，∴ PB ∥CM ，所以∠ACM 就是异面直线PB 与AC 所成的角．设PA ＝AB ＝a ，在三角形ACM 中，2,2,2AM a AC a CM a ===， ∴三角形ACM 是等边三角形．所以∠ACM 等于60°，即异面直线PB 与AC 所成的角为60°．故选：C.【点睛】思路点睛：先利用面面垂直得到PA ⊥平面ABCD ，分别过P ，D 点作AD ，AP 的平行线交于M ，连接CM ，AM ，得到∠ACM 就是异面直线PB 与AC 所成的角． 4．D解析：D【分析】先找出ABC 的外接圆的半径，然后取ABC 的外接圆的圆心N ，过N 作平面ABC 的垂线NG ，作PA 的中垂线，交NG 于O ，则O 是外接球球心， OA 为外接球半径，求解半径并求表面积即可.【详解】如图所示，1204BAC AB AC ∠===，，取BC 中点M ，连接AM 并延长到N 使AM =MN ，则四边形ABNC 是两个等边三角形组成的菱形，AN =BN =CN ，点N 是ABC 的外接圆圆心，过N 作平面ABC 的垂线NG ，则球心一定在垂线NG 上，因为PA ⊥平面ABC ，则PA //NG ，PA 与NG 共面，在面内作PA 的中垂线，交NG 于O ，则O 是外接球球心，半径R =OA ，Rt AON 中，122ON AP ==，4AN =，故()224232R =+=，故外接球的表面积2441872S R πππ==⨯=.故选:D.【点睛】求空间多面体的外接球半径的常用方法：①补形法：侧面为直角三角形，或正四面体，或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；②利用球的性质：几何体中在不同面均对直角的棱必然是球大圆直径，也即球的直径； ③定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可.本题就是采用这个方法.本题使用了定义法.5．C解析：C【分析】利用直二面角可判断A 的正误，利用面面平行或线面平行性质定理即判断定理可判断BD 的正误，从而可得正确的选项，利用反例可判断C 是错误的.【详解】对于A ，如图，设l αβ=，空间中取一点O （O 不在平面,αβ内，也不在直线,m n上），过O 作直线,a b ，使得,////a m b n ，且,a A b B αβ⋂=⋂=，故a b ⊥.因为m α⊥，故a α⊥，而l α⊂，故a l ⊥，同理b l ⊥,因为a b O ⋂=，故l ⊥平面OAB .设平面OAB 交l 与C ，连接,AC BC ，因为,AC BC ⊂平面OAB ，故,,l AC l BC ⊥⊥所以ACB ∠为l αβ--的平面角. 因为a α⊥，AC α⊂，故OA AC ⊥，同理OB BC ⊥，而OA OB ⊥，故在四边形OACB 中，90ACB ∠=︒即αβ⊥，故A 正确.对于B ，由面面平行的性质可得若m α⊂，//αβ，则//m β，故B 正确. 对于D ，如图，过m 作平面γ，使得a γα=，过m 作平面η，使得b ηβ⋂=，因为//m α，m γ⊂，故//a m ，同理//b m ，故//a b ，而a β⊄，b β⊂，故//a β，而a α⊂，l αβ=，故//a l ，所以//m l ，故D 正确.对于C ，在如图所示的正方体中，//AD 平面11A D CB ，1AA ⊥平面ABCD ，1AD AA ⊥，但是平面11A D CB 与平面ABCD 不垂直，故C 错误.故选：C. 【点睛】思路点睛：对于立体几何中与位置有关的命题的真假判断，一般根据性质定理和判定定理来处理，反例一般可得正方体中寻找.6．B解析：B 【分析】证明//BE AF ，得AFD ∠是异面直线BE ，DF 所成角或其补角，在三角形中求解即可．【详解】连接,AF EF ，∵,E F 分别是棱11B C ，11A D 的中点，∴//EF AB ，EF AB =， ∴ABEF 是平行四边形，∴//BE AF ，∴AFD ∠是异面直线BE ，DF 所成角或其补角，设正方体的棱长为2，则111A F D F ==，22215AF DF ==+=，2223cos 25255AF DF AD AFD AF DF +-∠===⋅⨯⨯，异面直线BE ，DF 所成角的余弦值为35．故选：B ．【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下：（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角；（3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．7．D解析：D 【分析】取AC 中点E ，连接1,A E BE ，先通过BE ⊥平面11ACC A 可得BE AM ⊥，再由1ACM A AE ≅可得1AM A E ⊥，即可得出AM ⊥平面1A BE ，即1AM A B ⊥.【详解】取AC 中点E ，连接1,A E BE ，ABC 为正三角形，BE AC ∴⊥，正三棱柱111ABC A B C -中，1CC ⊥平面ABC ，BE ⊂平面ABC ，1CC BE ∴⊥，1ACCC C =，BE ∴⊥平面11ACC A ，AM ⊂平面11ACC A ，BE AM ∴⊥，在直角三角形ACM 和直角三角形1A AE 中，1,AC A A CM AE ==,1ACM A AE ∴≅， 1CAM AA E ∴∠=∠，12CAM A EA π∴∴∠+∠=，则1AM A E ⊥，1BE A E E ⋂=，AM ∴⊥平面1A BE ，1A B ⊂平面1A BE ，1AM A B ∴⊥，故异面直线AM 与1A B 所成角的大小为2π.【点睛】本题考查异面直线所成角的求解，解题的关键是通过证明AM ⊥平面1A BE 判断出1AM A B ⊥.8．C解析：C 【分析】因为P BCE P ABC E ABC V V V ---=-则当E ABC V -取最大值时，三棱锥P BCE -体积有最小值，建立坐标系求得当点E 的高为3时，问题得解. 【详解】以点O 为原点，,,OA OD OB 分别为,,x y z 轴建立空间直角坐标系，如图所示：设点(),0,E x z ，依题意得()6,0,0A ，则()6,0,AE x z =- ，(),0,OE x z = 因为过BC 作截面AP α⊥于E ，所以AE OE ⊥则0AE OE ⋅=，故()2600x x z -++= 所以()6z x x =-3x =时max 3z =又()143P BCE P ABC E ABC ABCV V V S z ---=-=-因为max 3z =所以三棱锥P BCE -体积的最小值()1114343643332P BCE ABC V S-=-=⋅⋅=故选：C 【点睛】关键点点晴：本题的解题关键是将问题转化为求E ABC V -的最大值，通过建系求得三棱锥E ABC -的高的最大值即可.9．D解析：D 【分析】先找到几何体的原图，再求出几何体的高，再求几何体的体积得解. 【详解】由三视图可知几何体为图中的四棱锥1P CDD E -，由题得22437AD =-=，所以几何体的高为7. 所以几何体的体积为11(24)676732⋅+⋅⋅=. 故选：D 【点睛】方法点睛：通过三视图找几何体原图常用的方法有：（1）直接法；（2）拼凑法；（3）模型法.本题利用的就是模型法.要根据已知条件灵活选择方法求解.10．A解析：A 【分析】利用线面垂直的判定定理可判断BCD 选项，利用假设法推出矛盾，可判断A 选项. 【详解】对于A 选项，连接B C '，假设A C '⊥平面MNP ，在正方体ABCD A B C D ''''-中，A B ''⊥平面BB C C ''，B C '⊂平面BB C C ''，A B B C '''∴⊥，所以，A B C ''为直角三角形，且A CB ''∠为锐角，因为M 、N 分别为BB '、BC 的中点，则//MN B C '，所以，MN 与A C '不垂直，这与A C '⊥平面MNP 矛盾，故假设不成立，即A C '与平面MNP 不垂直；对于B 选项，连接B D ''、A C ''，如下图所示：因为四边形A B C D ''''为正方形，则A C B D ''''⊥，CC '⊥平面A B C D ''''，B D ''⊂平面A B C D ''''，CC B D '''∴⊥， A C CC C ''''=，B D ''∴⊥平面A CC ''，A C '⊂平面A CC ''，A CB D '''∴⊥，M 、P 分别为A B ''、A D ''的中点，则//MN B D ''，可得MP A C '⊥，同理可证A C MN '⊥，MP MN M ⋂=，A C '∴⊥平面MNP ；对于C 选项，连接C D '、A N '、CN 、A P '、PC ，取A B ''的中点E ，连接C E '、PE ，因为四边形CC D D ''为正方形，则CD C D ''⊥，A D ''⊥平面CC D D ''，C D '⊂平面CC D D ''，C D A D '''∴⊥， CD A D D ''''=，C D '∴⊥平面A CD ''，A C '⊂平面A CD ''，A C C D ''∴⊥，M 、N 分别为DD '、C D ''的中点，//MN C D '∴，A C MN '∴⊥，在正方形A B C D ''''中，E 、N 分别为A B ''、C D ''的中点，//A E C N ''∴且A E C N ''=，所以，四边形A EC N ''为平行四边形，所以，//A N C E ''且A N C E ''=，同理可证四边形CC EP '为平行四边形，//C E CP '∴且C E CP '=，所以，//A N CP '且A N CP '=，所以，四边形A PCN '为平行四边形，易得A N CN '=，所以，四边形A PCN '为菱形，所以，A C PN '⊥，MN PN N =，A C '∴⊥平面MNP ；对于D 选项，连接AC 、BD ，因为四边形ABCD 为正方形，则AC BD ⊥，AA '⊥平面ABCD ，BD ⊂平面ABCD ，AA BD '∴⊥， AC AA A '⋂=，BD ∴⊥平面AA C '，A C '⊂平面AA C '，AC BD '∴⊥，M 、N 分别为CD 、BC 的中点，则//MN BD ，A C MN '∴⊥，同理可证A C MP '⊥，MN MP M ⋂=，A C '∴⊥平面MNP .故选：A. 【点睛】方法点睛：证明线面垂直的方法：一是线面垂直的判定定理；二是利用面面垂直的性质定理；三是平行线法（若两条平行线中一条垂直于这个平面，则另一条也垂直于这个平面），解题时，注意线线、线面与面面关系的相互转化；另外，在证明线线垂直时，要注意题中隐含的垂直关系，如等腰三角形的底边上的高、中线和顶角的角平分线三线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形（或给出线段长度，经计算满足勾股定理）、直角梯形等等．11．C解析：C 【分析】首先通过延长直线,DC AB ，交于点G ，平面BAE 变为GAE ，连结PG ，EG 交于点F ，再根据三角形中线的性质，求PFFC的值. 【详解】延长,DC AB ，交于点G ，连结PG ，EG 交PC 于点F ，//AD BC ，且2AD BC =，可得点,B C 分别是,AG DG 的中点，又点E 是PD 的中点，PC ∴和GE 是△PGD 的中线，∴点F 是重心，得2PFFC=故选：C 【点睛】关键点点睛：本题的关键是找到PC 与平面BAE 的交点，即将平面BAE 转化为平面GAE 是关键. 12．A解析：A 【分析】作出异面直线AM 和CN 所成的角，然后解三角形求出两条异面直线所成角的余弦值. 【详解】设,E F 分别是1,AB CC 的中点，由于,M N 分别是111,A B BB 的中点，结合正方体的性质可知11//,//B E AM B F CN ，所以1EB F ∠是异面直线AM 和CN 所成的角或其补角，设异面直线AM 和CN 所成的角为θ，设正方体的边长为2，2211125B E B F ==+=，2221216EF =++=，则1cos cos EB F θ=∠=55625255+-=⨯⨯.故选：A.【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下：（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角；（3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．二、填空题13．【分析】经分析正三棱锥是以△BCD 底面的三棱锥可以把看出以AB 为边长的正方体切割下来的可借助于正方体的外接球求解【详解】正三棱锥中所以△BCD 为底面且所以正三棱锥是以AB 为边长的正方体切割下来的所以解析：6π【分析】经分析，正三棱锥A BCD -是以△BCD 底面的三棱锥，可以把看出以AB 为边长的正方体切割下来的，可借助于正方体的外接球求解. 【详解】正三棱锥A BCD -中，π2BAC ∠=，所以△BCD 为底面，且π2BAD DAC BAC ∠=∠=∠=, 所以正三棱锥A BCD -是以AB 为边长的正方体切割下来的，所以正三棱锥A BCD -的外接球就是正方体的外接球. 设外接球的半径为R ,所以232R =所以外接球的表面积为246S R ππ==．故答案为：6π 【点睛】多面体的外接球问题解题关键是找球心和半径，求半径的方法有：(1)公式法；(2) 多面体几何性质法；(3)补形法；(4)寻求轴截面圆半径法；(5)确定球心位置法．14．【分析】由二面角的大小为可得平面平面得到平面由勾股定理可得答案【详解】连接所以是等边三角形所以因为为中点所以所以即所以因为平面平面平面平面所以平面平面所以所以故答案为：【点睛】对于翻折问题解题时要认解析：22. 【分析】由二面角A ED C '--的大小为90，可得平面A ED '⊥平面EDCB ，得到A E '⊥平面EDCB ，由勾股定理可得答案. 【详解】连接DB CE 、，2AB AD ==，60A ∠=，所以ABD △、CBD 是等边三角形，所以2AD BD CD ===，因为E 为AB 中点，1AE A E '==，所以DE AB ⊥，DE A E ⊥'，3DE =，30EDB ∠=，所以90EDC ∠=，即DE CD ⊥，所以222347EC ED CD =+=+=，因为平面A ED '⊥平面EDCB ，DE A E ⊥'，平面A ED'平面EDCB DE =，所以A E '⊥平面EDCB ，EC ⊂平面EDCB ，所以A E EC '⊥，所以221722A C A E EC ''=+=+=.故答案为：22.【点睛】对于翻折问题，解题时要认真分析图形，确定有关元素间的关系及翻折前后哪些量变了，哪些量没有变，根据线线、线面、面面关系正确作出判断，考查了学生的空间想象力..15．②④【分析】由是正三角形可判断①；判断出平面平面平面可判断②；假设面面则可以推出可判断③；由平面平面平面可判断④【详解】连接分别是的中点对于①因方是正三角形所以与不垂直；对于②连接因为且所以平面平面解析：②④. 【分析】由1//FG BC ，1BDC 是正三角形，可判断①；判断出1DB ⊥平面11A C B ，平面11//AC B 平面EFG ，可判断②；假设面//EFG 面11ACC A ，则可以推出1//AA EF 可判断③；由平面11//ABB A 平面11DCC D ，EF ⊂平面11ABB A ，可判断④. 【详解】连接11A C ，1A B ，1BC ，BD ，1B D ，E ，F ，G 分别是1A B ，1BB ，11B C 的中点．对于①，因方1//FG BC ，1BDC 是正三角形，所以FG 与BD 不垂直；对于②，连接11D B ，因为1111111AC B D ,AC BB ⊥⊥，且1111B D BB B ⋂=，所以11A C ⊥平面11BDD B ，1DB ⊂平面11BDD B ，所以111AC DB ⊥，同理11BC DB ⊥，且1111A C BC C ，所以1DB ⊥平面11A C B ，因为1//A B EF ，11//AC EG ，且111A B AC A ⋂=，EF EG E =，所以平面11//AC B 平面EFG ，所以1B D ⊥平面EFG ．正确；对于③，如果面//EFG 面11ACC A ，由平面EFG 平面11ABB A EF =，平面11CC A A平面111BB A A A A =，则1//AA EF ，显然不正确；对于④，因为平面11//ABB A 平面11DCC D ，EF ⊂平面11ABB A ，所以//EF 平面11CDD C ，正确故选：②④. 【点睛】方法点睛：本题主要考查了正方体中垂直与平行关系，考查了线线垂直、线面垂直的判定、线面平行的判断、面面平行的判断与性质，对于证明线线关系、线面关系，面面关系等方面的问题，必须在熟练掌握有关的定理和性质的前提下，再利用已知来进行证明，属于中档题.16．【分析】取的中点分别为连接先证明四边形是平行四边形再利用面面平行的判断定理证明平面平面可得平行四边形即为所求的截面再计算其面积即可【详解】取的中点分别为连接因为所以四边形是平行四边形所以因为所以四边解析：6【分析】取AB ，11D C 的中点分别为,M N ，连接11,,,,A M MC CN A N PM ，先证明四边形1A MCN 是平行四边形，再利用面面平行的判断定理证明平面1//PBC 平面1A MCN ，可得平行四边形1A MCN 即为所求的截面，再计算其面积即可. 【详解】取AB ，11D C 的中点分别为,M N ，连接11,,,,A M MC CN A N PM ，因为11A P NC ，所以四边形11A PC N 是平行四边形，所以11A N PC ，因为1PM CC 所以四边形1PMCC 是平行四边形，所以1MC PC ，所以1A N MC ，所以四边形1A MCN 是平行四边形，因为11//PC A N ，1PC ⊄平面1A MCN ，1A N ⊂平面1A MCN ，所以1//PC 平面1A MCN ，同理可证//PB 平面1A MCN ，因为1PC PB P ⋂=，所以平面1//PBC 平面1A MCN ，因此过点1A 作与平面1PBC 平行的截面，即是平行四边形1A MCN ，连接MN ，作1A H MN ⊥于点H ，由115AM A N ==，22MN = 可得()()221523A H =-=所以1111223622A MNSMN A H =⨯⨯=⨯=，所以平行四边形1A MCN 的面积为1226A MNS =故答案为：26【点睛】关键点点睛：本题的关键点是找出过点1A 与平面1PBC 平行的截面，所以想到作平行线，利用面面平行的判断定理证明所求的截面即是平行四边形1A MCN ，先求四边形一半的面积，乘以2即可得所求平行四边形的面积，也可以直接求菱形的面积.17．【分析】取中点为过分别作底面的垂线根据题中条件得到；过分别作的垂线连接由二面角的定义结合线面垂直的判定定理及性质得到为二面角的平面角；为二面角的平面角得出令进而可求出最值【详解】取中点为过分别作底面解析：34【分析】取BC 中点为E ，过P 、M 分别作底面的垂线PO 、MN ，根据题中条件，得到AN NO OE ==，2PO MN =；过O 、N 分别作BC 的垂线OG 、NH ，连接MH ，PG ，由二面角的定义，结合线面垂直的判定定理及性质，得到MHN ∠为二面角M BC A--的平面角；PGO ∠为二面角A BC P --的平面角，得出tan 4tan PGO MHN ∠=∠，()23tan tan tan 14tan MHNPGO MHN MHNα∠=∠-∠=+∠，令tan 0x MHN =∠>，进而可求出最值. 【详解】取BC 中点为E ，过P 、M 分别作底面的垂线PO 、MN ，则O 为ABC 的重心，MN ⊥平面ABC ；PO ⊥平面ABC ；由于点M 为棱PA 的中点，所以有AN NO OE ==，2PO MN =；过O 、N 分别作BC 的垂线OG 、NH ，连接MH ，PG ，因为BC ⊂平面ABC ，所以MN BC ⊥，同理PO BC ⊥；又MN NH N ⋂=，MN ⊂平面MNH ，NH ⊂平面MNH ，所以BC ⊥平面MNH ；因为MH ⊂平面MNH ，所以BC MH ⊥，所以MHN ∠为二面角MBC A --的平面角；同理BC PG ⊥，所以PGO ∠为二面角A BC P --的平面角，所以tan PO PGO OG ∠=，tan MNMHN HN∠=，因为NO OE =，//OG NH ，所以12OG NH =；因此2tan4tan12PO MNPGOMHNOG HN∠===∠，所以()2tan tan3tan tan tan1tan tan14tanPGO MHN MHNPGO MHNPGO MHN MHN α∠-∠∠=∠-∠==+∠⋅∠+∠，令tan0x MHN=∠>，则2333tan1444x xx xα=≤=+，当且仅当214x=，即12x=时，等号成立.故答案为：34.【点睛】关键点点睛：求解本题的关键在于确定二面角M BC A--、A BC P--以及P BC M--三者之间的关系，由题中条件得出二面角A BC P--是二面角M BC A--的4倍，进而可求得结果. 18．【分析】先根据三视图得到几何体是底面是直角三角形的一个三棱锥再根据锥体的体积计算公式求解即可【详解】利用正方体法还原三视图如图所示根据三视图可知该几何体是底面直角边为2的等腰直角三角形高为2的三棱锥解析：43.【分析】先根据三视图得到几何体是底面是直角三角形的一个三棱锥，再根据锥体的体积计算公式求解即可.【详解】利用正方体法还原三视图，如图所示，根据三视图，可知该几何体是底面直角边为2的等腰直角三角形，高为2的三棱锥S-ABC，故其体积114222323V=⨯⨯⨯⨯=.故答案为：43. 【点睛】本题主要考查三视图还原几何体，锥体的体积公式，考查考生的观察分析能力与空间想象能力及运算能力，属于中档题.19．【分析】当点从点运动到点时二面角的平面角逐渐增大二面角的平面角最小趋于二面角的平面角最大趋于二面角的平面角的补角求出二面角的平面角和二面角的平面角即可【详解】当点从点运动到点时二面角的平面角逐渐增大解析：11,33⎛⎫- ⎪⎝⎭【分析】当点P 从点A 运动到点B 时，二面角D PC B --的平面角逐渐增大，二面角D PC B --的平面角最小趋于二面角D AC B --的平面角，最大趋于二面角D BC A --的平面角的补角，求出二面角D AC B --的平面角和二面角D BC A --的平面角即可. 【详解】当点P 从点A 运动到点B 时，二面角D PC B --的平面角逐渐增大，二面角D PC B --的平面角最小趋于D AC B --的平面角，最大趋于二面角D BC A --的平面角的补角，设正四面体的棱长为2a ，如图所示，取AC 的中点E ，连接DE 、BE ，易知DEB ∠为二面角D AC B --的平面角，DE BE ==，所以()22221cos 3a DEB +-∠==，同理可得：二面角D BC A --的平面角的补角的余弦值为13-，故二面角D PC B --的平面角的余弦值的取值范围是11,33⎛⎫- ⎪⎝⎭，故答案为：11,33⎛⎫- ⎪⎝⎭【点睛】本题主要考查了二面角的平面角的求解，考查空间想象能力，属于中档题.20．【分析】由正四面体性质可知球心在棱锥高线上利用勾股定理可求出半径R 即可求出球的面积【详解】正四面体的棱长为：底面三角形的高：棱锥的高为：设外接球半径为R 解得所以外接球的表面积为：；故答案为：【点睛】解析：232a π 【分析】由正四面体性质可知，球心在棱锥高线上，利用勾股定理可求出半径R ，即可求出球的面积. 【详解】正四面体的棱长为：a ，底面三角形的高：3322a a =， 22236()323a a a -⨯⨯=，设外接球半径为R ，22263)()R R a =-+，解得6R =，所以外接球的表面积为：2263442a a ππ⎛⎫⨯= ⎪ ⎪⎝⎭；故答案为：232a π．【点睛】本题考查球的表面积的求法，解题的关键是根据球心的位置，在正四面体中求出球的半径．三、解答题21．（1）证明见解析；（26．（1）取BC 的中点M ，连接HM ，DM ．证明四边形DGHM 是平行四边形，可得线面平行；（2）由H 到平面AEC 的距离为F 到平面AEC 的距离的一半，先求出F 到平面AEC 的距离，用体积法可求得F 到平面AEC 的距离．【详解】（1）证明：取BC 的中点M ，连接HM ，DM ．因为该多面体由底面为正方形ABCD 的直四棱柱被截面AEFG 所截而成，所以截面AEFG 是平行四边形，则4=-=DG CF EB ．因为36==FC EB ，所以1(26)42=⨯+=HM ，且DG//FC//HM ，所以四边形DGHM 是平行四边形，所以GH //DM ．因为DM ⊂平面ABCD ，GH ⊄平面ABCD ，所以//GH 平面ABCD ．（2）解：连接HA ，HC ，AF ，记F 到平面ACE 的距离为d ，则H 到平面ACE 的距离为2d ．在CEF △中，6EF =，高为4，所以CEF △的面积为164122⨯⨯=．因为三棱锥A CEF -的高为4，所以A CEF -的体积为1124163⨯⨯=．在ACE 中，42AC =，25AE CE ==，所以ACE 的面积为22142(25)(22)462⨯⨯-=．因为A CEF -的体积与F ACE -的体积相等，所以146163⨯⨯=d ，所以26d =．故H 到平面ACE 的距离为6．方法点睛：本题考查证明线面平行，考查求点到平面的距离．求点到平面的距离的常用方法：（1）定义法：作出点到平面的垂线段，求出垂线段的长；（2）用体积法计算；（3）空间向量法：求出平面外的点到平面内任一点连线的向量在平面的法向量方向上投影的绝对值．22．（1）证明见解析；（2）82 3.【分析】（1）连接AC交BD于点O，连接EO，利用三角形中位线定理可得//EO PC，再由线面平行的判定定理可得结论；（2）先证明PO⊥面ABCD，由E是PA的中点，可得E到面ABCD的距离12PO=，再利用棱锥的体积公式可得答案.【详解】（1）连接AC交BD于点O，连接EO.四边形ABCD为正方形，所以O为AC中点，又E为PA中点，//EO PC∴，又EO⊂面EBD，PC⊄面EBD，//PC∴面EBD.（2）正四棱锥P ABCD-中,PA PC=，O是AC的中点PO AC∴⊥，PD PB=，O是BD的中点PO BD∴⊥，又AC与BD在平面ABCD内相交，所以PO⊥面ABCDE是PA的中点，E∴到面ABCD的距离12PO =，221822,2ABD S AB AD PO PD DO ∆=⋅⋅==-=，182323E ABD ABD PO V S -∆=⋅⋅=【点睛】方法点睛：证明线面平行的常用方法：①利用线面平行的判定定理，使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线，可利用几何体的特征，合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质，即两平面平行，在其中一平面内的直线平行于另一平面. 23．（1）证明见解析；（2）证明见解析. 【分析】（1）由DE EC ⊥，AE DE ⊥，利用线面垂直的判定定理可得DE ⊥平面ACE ，再由//DE CB ，利用面面垂直的判定定理证明.（2）取CE 的中点O ，连接OP ，OQ ，由三角形中位线可得.//OQ DE ，//OP AC ，再利用线面平行和面面平行的判定定理证明. 【详解】（1）在直角梯形BCED 中，BC EC ⊥，//DE CB ，则DE EC ⊥.因为90AED ∠=︒，所以AE DE ⊥. 因为AE EC E ⋂=，所以DE ⊥平面ACE ，所以BC ⊥平面ACE . 因为BC ⊂平面ABC ，所以平面ABC ⊥平面ACE .（2）取CE 的中点O ，连接OP ，OQ .因为O ，P 分别为CE ，AE 的中点，所以//OP AC ,又OP ⊄平面ABC ，AC ⊂平面ABC ，//OP 平面ABC ，同理//OQ 平面ABC ，。

第8章立体几何专题7 线面角的求解常考题型专题练习——【含答案】

3、线面角求法（二）用等体积法，求出斜线PA在面外的一点P到面的距离，利用三角形的正弦公式进行求解。

114、线面角求法（三）利用空间向量进行求解，高二再学。

【巩固练习】1、已知正方体1111ABCD A B C D -的体积为162，点P 在正方形1111D C B A 上，且1,A C 到P 的距离分别为2,23，则直线CP 与平面11BDD B 所成角的正切值为( )A.2 B.3 C.12D.13【答案】A【解析】易知22AB =；连接1C P ，在直角1CC P ∆中，可计算22112C P CP CC =-=；又1112,4A P A C ==，所以点P 是11A C 的中点；连接AC 与BD 交于点O ，易证AC ⊥平面11BDD B ，直线CP 在平面11BDD B 内的射影是OP ，所以CPO ∠就是直线CP 与平面11BDD B 所成的角，在直角CPO ∆中，2tan 2CO CPO PO ∠== .2、把正方形沿对角线折起,当以四点为顶点的三棱锥体积最大时，直线和平面所成的角的大小为A．B．C．D．[来源网ZXXK]【答案】C【解析】如图所示，当平面平面时，三棱锥的体积最大，取的中点，则平面，故直线和平面所成的角为，则，所以，故选C.3、如图，在三棱锥P-ABC中，,PA AB⊥PC BC⊥，,AB BC⊥22,AB BC==5PC=，则PA与平面ABC所成角的大小为_______.【答案】45︒【解析】如图，作平行四边形ABCD，连接PD，由AB BC⊥，则平行四边形ABCD是矩形．由BC CD⊥，BC PC⊥，PC CD C=，∴BC⊥平面PCD，而PD⊂平面PCD，∴BC PD⊥，同理可得AB PD⊥，又AB BC B⋂=，∴PD⊥平面11ABCD ．,PD CD PD AD ⊥⊥，PAD ∠是PA 与平面ABC 所成角．由2,5CD AB PC ===得1PD =，又1AD BC ==，∴45PAD ∠=︒．∴PA 与平面ABC 所成角是45︒．4、已知三棱柱ABC －A 1B 1C 1的侧棱与底面边长都相等，A 1在底面ABC 内的射影为△ABC 的中心O ，则AB 1与底面ABC 所成角的正弦值为（）A ．23B ．13C ．33D ．23【答案】A【解析】作1A H ⊥面ABC 于点H ,延长11B A 到D ,延长BA 到E 使得111B A A D =，,BA AE =如图则有11A EAB ，又因为1A O ⊥面ABC ，故1A EO ∠为所求角，且111sin AO A EO A E∠=已知底面为正三角形，且O为底面中点，解三角形可知：111336,333AO AB AA A O AA==∴=又在AEO∆中运用余弦定理，150EAO∠=︒则()()22212cos3EO EA AO EA AO EAO AB=+-⋅∠=故由勾股定理可得22113A E AO EO AB=+=则1623sin33A EO∠==故选A5、如图所示，已知AB为圆O的直径，且AB＝4，点D为线段AB上一点，且13AD DB=，点C为圆O上一点，且3BC AC=.点P在圆O所在平面上的正投影为点D，PD＝DB.(1)求证：CD⊥平面PAB；(2)求直线PC与平面PAB所成的角．【答案】（1）见解析；（2）301旗开得胜1【解析】(1)证明：连接CO ，由3AD ＝DB 知，点D 为AO 的中点．又因为AB 为圆O 的直径，所以AC ⊥CB. 由3AC ＝BC 知，∠CAB ＝60°，所以△ACO 为等边三角形．故CD ⊥AO. 因为点P 在圆O 所在平面上的正投影为点D ，所以PD ⊥平面ABC ，又CD ⊂平面ABC ，所以PD ⊥CD ，由PD ⊂平面PAB ，AO ⊂平面PAB ，且PD ∩AO ＝D ，得CD ⊥平面PAB.(2)由(1)知∠CPD 是直线PC 与平面PAB 所成的角，又△AOC 是边长为2的正三角形，所以CD ＝3. 在Rt △PCD 中，PD ＝DB ＝3，CD ＝3，所以3tan 3CD CPD PD ∠==，∠CPD ＝30°，即直线PC 与平面PAB 所成的角为30°.16、如图，在四棱锥P -ABCD 中，AP ⊥平面PCD ，//AD BC ，AB BC ⊥，12AP AB BC AD ===，E 为AD 的中点，AC 与BE 相交于点O .（1）证明：PO ⊥平面ABCD .（2）求直线BC 与平面PBD 所成角的正弦值.【答案】（1）证明见解析（2）2211【解析】（1）证明：AP ⊥平面PCD ，CD ⊂平面PCD ，AP CD ∴⊥，//,AD BC 12BC AD =，E 为AD 的中点，则//BC DE 且BC DE =. ∴四边形BCDE 为平行四边形，//BE CD ∴，AP BE ∴⊥.1又,AB BC⊥12AB BC AD ==，且E 为AD 的中点，∴四边形ABCE 为正方形，BE AC ∴⊥，又,AP AC A =BE ∴⊥平面APC ，PO ⊂平面APC ，则BE PO ⊥.AP ⊥平面,PCD PC ⊂平面PCD ，AP PC ∴⊥，又22AC AB AP ==，PAC ∴∆为等腰直角三角形，O 为斜边AC 上的中点，PO AC ∴⊥且,ACBE O =PO ∴⊥平面ABCD .（2）高一学生可以用等体积法求解。

求线面角的三种方法

试题研究SHI TI Y ANJIU本文介绍求线面角的三种常见方法，并对其作比较分析.例如图1，在正三棱柱ABC -A 1B 1C 1中，AB =2AA 1，点D 是A 1B 1的中点，点E 在A 1C 1上，且DE ⊥AE ．求直线AD 和平面ABC 1所成角的正弦值．A 1ABCDE C 1B 1A 1AB C D E C 1B 1FH 图1图2方法1直接作出线面角求解分析因为本题几何图形是特殊的几何体——正三棱柱，点D 在特殊位置上——线段A 1B 1的中点，所以本题比较容易作出线面角.解如图2，设F 是AB 的中点，连结DF ，DC 1，C 1F ．由正三棱柱ABC -A 1B 1C 1的性质及D 是A 1B 1的中点知，A 1B 1⊥C 1D ，A 1B 1⊥DF ．又C 1DDF =D ，所以A 1B 1⊥平面C 1DF ．而AB ∥A 1B 1，所以AB ⊥平面C 1DF ．又AB 平面ABC 1，故平面ABC 1⊥平面C 1DF ．过点D 作DH 垂直C 1F 于点H ，则DH ⊥平面ABC 1．连结AH ，则∠HAD 是AD 和平面ABC 1所成的角．由已知AB =2AA 1，不妨设AA 1=2，则AB =2，DF =2，DC 1=3，C 1F =5，AD =AA 21+A 1D 2=3，DH =DF ·DC 1C 1F=305．所以sin ∠HAD =DHAD=105．方法2用等体积法求出点D 到面ABC 1的距离h ，h AD为所求线面角的正弦值分析如图3，连结C 1D ，BD ，即得四棱锥D -ABC 1．用等体积法，即V D -ABC 1=V C 1-DAB，容易求出点D 到平面ABC 1的距离h ．解如图3，连结C 1D ，BD.因为平面A 1B 1C 1⊥平面AB 1，C 1D ⊥A 1B 1，所以C 1D ⊥平面AB 1．不妨设AA 1=2，则AB =2，DC 1=3，AC 1=BC 1=6，AD =BD =3.易求S ΔA DB =2，S ΔABC 1=5．设D 在平面ABC 1内的射影为H ，DH =h ，连结AH ，则∠HAD 是AD 和面ABC 1所成的角.因为V D -A B C 1=V C 1-DA B，所以13×h ×S ΔA B C 1=13×C 1D ×S ΔABD ，h =305．所以sin ∠HAD =DHAD=105．A 1AB C DE C 1B 1图3H ⊙潜江舒云水五胡十六国标志中国正式成为具有相似生活习惯和同一文化观念的多民族国家。

(压轴题)高中数学必修二第一章《立体几何初步》检测题(包含答案解析)(2)

A． B． C． D．
3．设，为两条不同的直线，，为两个不同的平面，给出下列命题：
①若，，则；
②若，，则；
③若，，，则；
④若，，则与所成的角和与所成的角相等．
其中正确命题的序号是）
A．①②B．①④C．②③D．②④
4．《九章算术》与《几何原本》并称现代数学的两大源泉.在《九章算术》卷五商功篇中介绍了羡除（此处是指三面为等腰梯形，其他两侧面为直角三角形的五面体）体积的求法.在如图所示的羡除中，平面是铅垂面，下宽，上宽，深，平面BDEC是水平面，末端宽，无深，长（直线到的距离），则该羡除的体积为（）
D. ，与所成的角，转化为的大小，的最小角是与平面所成的角，即，此时，所以的最小角大于，故D正确.
故选：C
【点睛】
关键点点睛：本题考查利用几何的综合应用，包含线线，线面角，垂直关系，首先会作图，关键选项是C和D，C选项的关键是平面，点是等边三角形的中心，D选项的关键是知道先与平面中线所成角中，其中线面角是其中的最小角.
C．，，则 D．，，则
12．在正方体中，和分别为，和的中点．，那么直线与所成角的余弦值是（）
A． B． C． D．
二、填空题
13．如图，在矩形中，，，点E为的中点，F为线段（端点除外）上一动点．现将沿折起，使得平面平面．设直线与平面所成角为，的取值范围为__________．
【详解】
依题意，，而，
解得，记的中心为О，的中心为О1，则，
取的中点，因为，，由勾股定理得，同理可得，
所以正三棱柱的外接球的球心为即，为外接球的半径，

几何法求线线角,线面角,二面角的10类题型(教师版)

几何法求线线角、线面角、二面角常考题型题型一平行四边形平移法求线线角 4题型二中位线平移法求线线角 6题型三补形平移法求线线角 8题型四作垂线法求线面角 10题型五等体积法求线面角 13题型六定义法求二面角 15题型七三垂线法求二面角 17题型八垂面法求二面角 19题型九补棱法求二面角 22题型十射影面积法求二面角 25知识梳理一、线线角的定义与求解线线角主要是求异面直线所成角。

1、线线角的定义：①定义：设a,b是两条异面直线，经过空间任一点O作直线a ⎳a，b ⎳b，把a 与b 所成的锐角或直角叫做异面直线a,b所成的角(或夹角)②范围：0,π22、求异面直线所成角一般步骤：(1)平移：选择适当的点，线段的中点或端点，平移异面直线中的一条或两条成为相交直线．(2)证明：证明所作的角是异面直线所成的角．(3)寻找：在立体图形中，寻找或作出含有此角的三角形，并解之．(4)取舍：因为异面直线所成角θ的取值范围是0,π2，所以所作的角为钝角时，应取它的补角作为异面直线所成的角．3、可通过多种方法平移产生，主要有三种方法：①平行四边形平移法；②中位线平移法；③补形平移法(在已知图形中，补作一个相同的几何体，以便找到平行线)．二、线面角的定义与求解1、线面角的定义：平面的一条斜线和它在平面上的射影所成的锐角，取值范围：[0°，90°]2、垂线法求线面角(也称直接法)：(1)先确定斜线与平面，找到线面的交点B为斜足；找线在面外的一点A，过点A向平面α做垂线，确定垂足O；(2)连结斜足与垂足为斜线AB在面α上的投影；投影BO与斜线AB之间的夹角为线面角；(3)把投影BO与斜线AB归到一个三角形中进行求解(可能利用余弦定理或者直角三角形)。

3、公式法求线面角(也称等体积法)：用等体积法，求出斜线P A在面外的一点P到面的距离，利用三角形的正弦公式进行求解。

公式为：sinθ=h，其中θ是斜线与平面所成的角，h是垂线段的长，l是斜线段的长。

(压轴题)高中数学高中数学选修2-1第二章《空间向量与立体几何》检测题(有答案解析)(4)

一、选择题1．在四面体OABC 中，空间的一点OM 满足1126OM OA OB OC λ=++，若MA ，MB ，MC 共面，则λ=（）A ．12B ．13C ．512D ．7122．长方体1111ABCD A B C D -，110AB AA ==，25AD =，P 在左侧面11ADD A 上，已知P 到11A D ､1AA 的距离均为5，则过点P 且与1A C 垂直的长方体截面的形状为（）A ．六边形B ．五边形C ．四边形D ．三角形3．已知向量(2,0,2)a =-，则下列向量中与a 成45的夹角的是（） A ．(0,0,2)B ．(2,0,0)C ．(2,2D ．)2,2,0-4．在正方体ABCD-A 1B 1C 1D 1中，E 为棱CC 1的中点，则异面直线AE 与CD 1所成角的余弦值为（） A ．26B ．36C ．56D ．135．如图，已知正三棱柱111ABC A B C -的棱长均为2，则异面直线1A B 与1B C 所成角的余弦值是( )A ．3B ．12C ．14D ．06．如图是由16个边长为1的菱形构成的图形，菱形中的锐角为,3π=,,a AB b CD =则=a b ⋅A ．5-B ．1-C ．3-D ．6-7．已知菱形ABCD 中，∠60ABC =︒，沿对角线AC 折叠之后,使得平面BAC ⊥平面DAC ，则二面角B CD A --的余弦值为（）.A ．2B ．12C 3D 5 8．记动点P 是棱长为1的正方体1111-ABCD A B C D 的对角线1BD 上一点，记11D PD Bλ=．当APC ∠为钝角时，则λ的取值范围为( ) A ．(0,1)B ．1(,1)3C ．1(0,)3D ．(1,3)9．在直三棱柱111ABC A B C -中，90ABC ∠=︒，2AB =，11BC CC ==，则异面直线1AB 与1BC 所成角的余弦值为（）A ．1010-B ．1510-C ．1010D ．151010．已知a =（λ+1，0，6），b =（2λ+1，2μ﹣1，2）．若//a b ，则λ与μ的值分别为（） A ．﹣5，﹣2B ．1152--，C ．5，2D ．2152-，11．如图，在长方体ABCD ﹣A 1B 1C 1D 1中，DC ＝2，DA ＝DD 1＝1，点M 、N 分别为A 1D 和CD 1上的动点，若MN ∥平面AA 1C 1C ，则MN 的最小值为（）A ．53B ．23C ．56D ．5212．在长方体1111ABCD A B C D -中，若13AC =，则111()AB AC AD AC ++⋅=（） A ．0B ．3C ．3D ．6二、填空题13．如图，四边形ABCD 和ADPQ 均为正方形，它们所在的平面互相垂直，动点M 在线段PQ 上，E 、F 分别为AB 、BC 的中点．设异面直线EM 与AF 所成的角为，则的最大值为 .14．在空间直角坐标系中，点()2,1,4-关于x 轴对称的点的坐标是______． 15．在平面直角坐标系中，点(1,0,2)A 到点(3,4,0)B -之间的距离为__________． 16．已知四棱锥P ABCD -的底面ABCD 是边长为2的正方形，5PA PD ==ABCD ⊥平面PAD ，M 是PC 的中点，O 是AD 的中点，则直线BM 与平面PCO 所成角的正弦值是__________.17．已知平面α的一个法向量()2,2,1n =--，点()1,3,0A --在平面α内，则点()2,1,4P -到平面α的距离为_________.18．如图，四棱锥P ABCD -中，ABCD 是矩形，PA ⊥平面ABCD ，1==PA AB ，2BC =，四棱锥外接球的球心为O ，点E 是棱AD 上的一个动点.给出如下命题：①直线PB 与直线CE 是异面直线；②BE 与PC 一定不垂直；③三棱锥E BCO -的体积为定值；④CE PE +的最小值为22.其中正确命题的序号是______________.（将你认为正确的命题序号都填上）19．已知向量=211a -（，，），(,1,1)b λ=-，若a 与b 的夹角为钝角，则λ的取值范围是______.20．已知棱长为1的正方体1111ABCD A B C D -中，E ，F 分别是11B C 和11C D 的中点，点1A 到平面DBEF 的距离为________________．三、解答题21．如图，在四棱锥P ABCD -中，6π∠=CAD ，且321,2AD CD PA ABC ===，和PBC 均是等边三角形，O 为BC 的中点.（I ）求证：PO ⊥平面ABCD ；（Ⅱ）求CB 与平面PBD 所成角的正弦值.22．如图，AE ⊥平面ABCD ，//CF AE ，//AD BC ，AD AB ⊥，1AB AD ==，2AE BC ==，87CF =（1）求直线CE 与平面BDE 所成角的正弦值；（2）求平面BDE 与平面BDF 夹角的余弦值．23．如图，四棱锥S ABCD -中，底面ABCD 是梯形，//AB CD ，90ADC ∠=︒，3AD =，22SD CD AB ===，点E ，F 分别是BC ，SD 的中点.（1）求证：//EF 平面SAB ；（2）若SB SC =，2EF =，求二面角B SC D --的余弦值.24．如图，四边形ABCD 与四边形BDEF 均为菱形，60DAB DBF ∠=∠=︒，且FA FC =（1）求证：平面ACF ⊥平面ABCD ；（2）求二面角A FC B --的余弦值.25．如图，在三棱台111ABC A B C -中，1AA ⊥平面ABC ，90BAC ∠=︒，4AB =，11112A B A C ==，11AB BC ⊥.（1）求1AA 的长；（2）求二面角11B AC C --的正弦值.26．如图，在四棱锥P ABCD -中，PD ⊥平面ABCD ，四边形ABCD 是等腰梯形//,2,4,,AB DC BC CD AD AB M N ====分别是,AB AD 的中点.（1）证明：平面PMN ⊥平面PAD ；（2）若二面角C PN D --的大小为60°，求四棱锥P ABCD -的体积.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】根据向量共面定理求解．【详解】由题意1126MA OA OM OA OB OC λ=-=--， 1526MB OB OM OA OB OC λ=-=-+-，11(1)26MC OC OM OA OB OC λ=-=--+-，∵MA ，MB ，MC 共面，∴在在实数唯一实数对(,)m n ，使得MA mMB nMC =+，1126OA OB OC λ--1511(1)2626m OA OB OC n OA OB OC λλ⎛⎫⎡⎤=-+-+--+- ⎪⎢⎥⎝⎭⎣⎦，∴111222511666(1)m n m n m n λλλ⎧--=⎪⎪⎪-=-⎨⎪-+-=-⎪⎪⎩，解得132313m n λ⎧=-⎪⎪⎪=-⎨⎪⎪=⎪⎩．故选：B ．【点睛】结论点睛：本题考查空间向量共面定理．空间上任意三个不共面的向量都可以作为一个基底，其他向量都可用基底表示，且表示方法唯一．,,OA OB OC 是不共面的向量，OM xOA yOB zOC =++，则,,,M A B C 共面⇔1x y z ++=．2．B解析：B 【分析】以D 为坐标原点建立如图所示的空间直角坐标系，先利用向量找出截面与11A D 、AD 和AB 的交点，再过Q 作//QF MN 交11B C 于F ，过F 作//EF QM ，交1BB 于E ，即可判断截面形状. 【详解】以D 为坐标原点建立如图所示的空间直角坐标系，则()()()120,0,5,25,0,10,0,10,0P A C ，()125,10,10AC ∴=--，设截面与11A D 交于(),0,10Q Q x ，则()20,0,5Q PQ x =-，()12520500Q AC PQ x ∴⋅=---=，解得18Qx =，即()18,0,10Q ，设截面与AD 交于(),0,0M M x ，则()20,0,5M PM x =--，()12520500M AC PM x ∴⋅=--+=，解得22Mx =，即()22,0,0M ，设截面与AB 交于()25,,0N N y ，则()3,,0N MN y =，1253100N AC MN y ∴⋅=-⨯+=，解得7.5Ny =，即()25,7.5,0N ，过Q 作//QF MN ，交11B C 于F ，设(),10,10F F x ，则()18,10,0F QF x =-，则存在λ使得QF MN λ=，即()()18,10,03,7.5,0F x λ-=，解得22F x =，故F 在线段11B C 上，过F 作//EF QM ，交1BB 于E ，设()25,10,E E z ，则()3,0,10E EF z =--，则存在μ使得EF QM μ=，即()()3,0,104,0,10E z μ--=-，解得 2.5E z =，故E 在线段1BB 上，综上，可得过点P 且与1A C 垂直的长方体截面为五边形QMNEF . 故选：B.【点睛】本题考查截面的形状的判断，解题的关键是先利用向量找出截面与11A D 、AD 和AB 的交点，即可利用平面的性质找出其它点的位置.3．B解析：B 【分析】根据空间向量数量积的坐标公式，即可得到答案【详解】根据夹角余弦值cos a b a b θ⋅=对于A 若()b 0,0,2,=则-222=222a b a b ⋅⨯，而2cos 452︒=，故不符合条件对于B 若()b 20,0,=，则222==222a b a b⋅⨯，而2cos 452︒=，故符合条件对于C 若(b 0,22,=，则-21==-cos 45222a b a b ⋅≠︒⨯，故不符合条件对于D 若()b 2-2=，，则21==cos 45222a b a b⋅≠︒⨯，故不符合条件故选B 【点睛】本题考查了向量的数量积，运用公式代入进行求解，较为简单4．A解析：A 【分析】以D 为坐标原点，分别以DA ，DC ，DD 1 所在直线为x ，y ，z 轴建立空间直角坐标系，利用空间向量求异面直线AE 与CD 1所成角的余弦值为2 ．【详解】以D 为坐标原点，分别以DA ，DC ，DD 1 所在直线为x ，y ，z 轴建立空间直角坐标系，设正方体棱长为2，则A （2，0，0），E （0，2，1），D 1（0，0，2），C （0，2，0），()2,2,1AE =-,()10,2,2D C =- ,∵cos ＜1,AE D C ＞26922=⋅ ∴异面直线AE 与CD 1所成角的余弦值为26．故选A ．【点睛】本题主要考查异面直线所成的角的求法，意在考查学生对该知识的理解掌握水平和分析推理能力.5．C解析：C 【分析】建立空间直角坐标系，结合空间向量的结论求解异面直线所成角的余弦值即可. 【详解】以AC 的中点O 为坐标原点，建立如图所示的空间直角坐标系O xyz -，则：()10,1,2A -,)3,0,0B，)13,0,2B ，()0,1,0C ，向量()13,1,2A B =-,()13,1,2B C =--，11cos ,A B B C <>1111A B B C A B B C⋅=⨯2222=⨯14=.本题选择C 选项.【点睛】本题主要考查异面直线所成的角的求解，空间向量的应用等知识，意在考查学生的转化能力和计算求解能力.6．B解析：B 【解析】设菱形中横向单位向量为,m 纵向单位向量为n ，则111,1122m n m n ==⋅=⨯⨯=，2a AB m n ==+，32b CD m n ==-+，()()232a b m n m n ⋅=+-+=223443421m n m n -+-⋅=-+-=-，故选B. 7．D解析：D 【分析】取AC 的中点E ，分别以EA ，ED ，EB 为x 轴，y 轴，z 轴建立空间直角坐标系，利用空间向量求二面角B CD A --的余弦值．【详解】解：如图取AC 的中点E ，分别以EA ，ED ，EB 为x 轴，y 轴，z 轴建立空间直角坐标系，令棱形ABCD 的边长为2，则()1,0,0A ，()1,0,0C -，()0,3,0D ，()0,0,3B 设平面BCD 的法向量为(),,n x y z =，()1,0,3BC =--，()0,3,3BD =-30330x z y z ⎧--=⎪⎨-=⎪⎩令3z =则3y =，3x =- 即()3,3,3n =-平面ACD 的法向量为()0,0,1m = 令二面角B CD A --的夹角为θ35cos 115n m n mθ===⨯ 因二面角B CD A --为锐二面角5cos θ=故选D【点睛】本题考查求二面角二余弦值，关键是准确的建立空间直角坐标系，属于中档题．8．B解析：B 【分析】建立空间直角坐标系，利用∠APC 不是平角，可得∠APC 为钝角等价于cos ∠APC ＜0，即，从而可求λ的取值范围．【详解】由题设，建立如图所示的空间直角坐标系D-xyz ，则有A （1，0，0），B （1，1，0），C （0，1，0），1D （0，0，1） ∴ =（1，1，-1），∴ =（λ，λ，-λ），∴=+=（-λ，-λ，λ）+（1，0，-1）=（1-λ，-λ，λ-1） =+ =（-λ，-λ，λ）+（0，1，-1）=（-λ，1-λ，λ-1）显然∠APC 不是平角，所以∠APC 为钝角等价于cos ∠APC ＜0 ∴ 0PA PC ⋅<∴（1-λ）（-λ）+（-λ）（1-λ）+（λ-1）（λ-1）=（λ-1）（3λ-1）＜0，得＜λ＜1 因此，λ的取值范围是（，1），故选B.点评：本题考查了用空间向量求直线间的夹角，一元二次不等式的解法，属于中档题．9．C解析：C 【分析】本题首先可以根据题意建立空间直角坐标系，然后根据2AB =以及11BC CC ==得出12,0,1AB 、()10,1,1BC =，最后根据1111cos θAB BC AB BC 即可得出结果.【详解】因为三棱柱111ABC A B C -是直三棱柱，且90ABC ∠=︒，所以可以以B 为原点、AB 为x 轴、BC 为y 轴、1BB 为z 轴构建空间直角坐标系，如图：因为2AB =，11BC CC ==，所以()2,0,0A ，()10,0,1B ，()0,0,0B ，()10,1,1C ，故12,0,1AB ，()10,1,1BC =，设异面直线1AB 与1BC 所成角为θ，则1111110cosθ1052AB BC AB BC ，故选：C. 【点睛】本题考查异面直线所成角的求法，可借助空间向量来求解，能否合理的构建空间直角坐标系是解决本题的关键，考查计算能力，考查数形结合思想，是中档题.10．D解析：D 【分析】利用共线向量的性质直接求解．【详解】(1a λ=+，0，6)，(21b λ=+，21μ-，2)，//a b ，∴6(21)2(1)λλ+=+，且021μ=-，解得25λ=-，12μ=． λ∴与μ的值分别为21,52-．故选：D ．【点睛】本题主要考查了空间中共线向量的性质等基础知识，考查运算求解能力，是基础题．11．A解析：A 【分析】先建立空间坐标系，设出(),0,M m m ，()0,22,N n n -+，转化条件得1m n +=，利用函数即可得解. 【详解】如图建系，由题意可设(),0,M m m ，()0,22,N n n -+，∴(),22,MN m n n m =---，又 ()10,0,1AA =，()1,2,0AC =-，∴平面11AAC C 的法向量()2,1,0n =，又 //MN 面11AA CC ，∴=0MN n ⋅即1m n +=，∴()()2222222941MN m n n m m m =+-+-=-+， ∴MN 最小值为5.故选：A. 【点睛】本题考查了空间向量的应用，考查了转化化归和函数思想，属于中档题.12．D解析：D 【分析】建立空间直角坐标系，利用向量的坐标运算即可求解. 【详解】如图建立空间直角坐标系A xyz -，设1,,AB a AD b AA c ===，则111(,0,),(,,0),(0,,),(,,)AB a c AC a b AD b c AC a b c ====. 则111(2,2,2)2AB AC AD a b c AC ++==，所以21111()2()6AB AC AD AC AC ++⋅==. 故选：D 【点睛】本题主要考查了向量的坐标运算，向量的模的概念，属于容易题.二、填空题13．【详解】建立坐标系如图所示设则设则由于异面直线所成角的范围为所以令则当时取等号所以当时取得最大值考点：1空间两直线所成的角；2不等式解析：25【详解】建立坐标系如图所示.设1AB =，则11(1,,0),(,0,0)22AF E =.设(0,,1)(01)M y y ≤≤，则1(,,1)2EM y =-，由于异面直线所成角的范围为(0,]2π，所以221122cos 115451144yy y θ-+==⋅++⋅++.22281[]14545y y y +=-++，令81,19y t t +=≤≤，则281161814552y y t t+=≥++-，当1t =时取等号. 所以2211222cos 511555451144yy y θ-+==≤⨯=⋅++⋅++，当0y =时，取得最大值.考点：1、空间两直线所成的角；2、不等式.14．【分析】根据对称关系确定点的坐标【详解】∵在空间直角坐标系中点关于轴对称的点的坐标为∴点关于轴对称的点的坐标为【点睛】本题考查空间直角坐标系点对称关系考查基本分析求解能力属基础题解析：()2,1,4---【分析】根据对称关系确定点的坐标. 【详解】∵在空间直角坐标系中，点(),,x y z 关于x 轴对称的点的坐标为(),,x y z --， ∴点()2,1,4-关于x 轴对称的点的坐标为()2,1,4---．【点睛】本题考查空间直角坐标系点对称关系，考查基本分析求解能力，属基础题.15．【解析】故的距离为故答案为解析：26【解析】222(13)(04)(20)26AB =-+++-=，故AB 的距离为26，故答案为26. 16．【详解】以O 为坐标原点建立空间直角坐标系设因此设平面一个法向量为取因此直线与平面所成角的正弦值是解析：885【详解】以O 为坐标原点建立空间直角坐标系，设1(1,2,0),(1,2,0),(0,0,2)(,1,1)2B C P M -∴- 因此3(,1,1)2BM =-- ,设平面PCO 一个法向量为(,,)(0,0,2)00(,,)(,,)(1,2,0)02x y z z n x y z x y z x y ⋅==⎧⎧=∴∴⎨⎨⋅-==⎩⎩，取(2,1,0)n =因此直线BM 与平面PCO 所成角的正弦值是31885cos ,1754BM n --==⨯17．【分析】由题意算出根据向量是平面的一个法向量算出向量在上的投影的绝对值即可得到到的距离【详解】解：根据题意可得又平面的一个法向量点A在内到的距离等于向量在上的投影的绝对值即故答案为:【点睛】本题给出解析：23【分析】由题意算出()1,4,4AP =-，根据向量()2,2,1n =--是平面α的一个法向量，算出向量AP 在n 上的投影的绝对值，即可得到P 到α的距离. 【详解】解：根据题意，可得()()1,3,0,1,4,2A P ---， ()1,4,4AP =-，又平面α的一个法向量()2,2,1n =--，点A 在α内，()2,1,4P ∴-到α的距离等于向量AP 在n 上的投影的绝对值， ()()1242412P n A -⨯-+⨯-∴⨯=-=+即(232AP nd n ===- 故答案为:23【点睛】本题给出平面的法向量和平面上的一点，求平面外一点到平面的距离；着重考查了向量的数量积公式和点到平面的距离计算等知识，属于中档题.18．①③④【分析】由题意画出图形由异面直线的概念判断①；利用线面垂直的判定与性质判断②；找出球心由棱锥底面积与高为定值判断③；设列出关于的函数式结合其几何意义求出最小值判断④【详解】解：对于①直线经过平解析：①③④ 【分析】由题意画出图形，由异面直线的概念判断①；利用线面垂直的判定与性质判断②；找出球心，由棱锥底面积与高为定值判断③；设AE x =，列出PE EC +关于x 的函数式，结合其几何意义求出最小值判断④．【详解】解：对于①，直线PB 经过平面ABCD 内的点B ，而直线CE 在平面ABCD 内不过C ，∴直线PB 与直线CE 是异面直线，故①正确；对于②，当E 与D 重合时，BE AC ⊥，因为PA ⊥平面ABCD ，BE ⊂平面ABCD ，所以PA BE ⊥，又PAAC A =，PA ⊂平面PAC ，AC ⊂平面PAC ，BE ∴⊥平面PAC ，则BE 垂直AC ，故②错误；对于③，由题意知，四棱锥P ABCD -的外接球的球心为O 是PC 的中点，则△BCE 的面积为定值，且O 到平面ABCD 的距离为定值，∴三棱锥E BCO -的体积为定值，故③正确；对于④，设AE x =，则2DE x =-，2211(2)PE EC x x ∴+=+++-．由其几何意义，即平面内动点(,1)x 与两定点(0,0)，(2,0)距离和的最小值知，其最小值为22，故④正确．故答案为：①③④．【点睛】本题考查命题的真假判断与应用，考查空间想象能力和思维能力，属于中档题．19．【解析】即解析：12λλ<≠-且【解析】0a b a b ⋅<且与不共线，即212110,1λλ---<≠⇒ 12λλ<≠-且 20．1【分析】以D 点为原点的方向分别为轴建立空间直角坐标系求出各顶点的坐标进而求出平面的法向量代入向量点到平面的距离公式即可求解【详解】以为坐标原点的方向分别为轴的正方向建立空间直角坐标系则所以设是平解析：1 【分析】以D 点为原点，1,,DA DC DD 的方向分别为,,x y z 轴建立空间直角坐标系，求出各顶点的坐标，进而求出平面BDEF 的法向量，代入向量点到平面的距离公式，即可求解．【详解】以D 为坐标原点，DA ，DC ，1DD 的方向分别为x ，y ，z 轴的正方向，建立空间直角坐标系Dxyz ，则1(1,0,1)A ，(1,1,0)B ，1(0,,1)2F ，所以(1,1,0)DB =，1(0,,1)2DF，1(1,0,1)A D =--，设 (,,)x y z =m 是平面BDFE 的法向量，则m DB m DF ⎧⊥⎨⊥⎩，即0102m DB x y m DF y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩，令1y =，可得112x z =-⎧⎪⎨=-⎪⎩，故1(1,1,)2m =--，设点A 在平面BDFE 上的射影为H ，连接1A D ，则1A D 是平面BDFE 的斜线段，所以点1A 到平面BEFE的距离1111A D m d m+⋅===．【点睛】本题主要考查了空间向量在求解距离中的应用，对于利用空间向量求解点到平面的距离的步骤通常为：①求平面的法向量；②求斜线段对应的向量在法向量上的投影的绝对值，即为点到平面的距离．空间中其他距离问题一般都可转化为点到平面的距离求解．着重考查了推理与运算能力，属于基础题.三、解答题21．（Ⅰ）证明见解析；（Ⅱ. 【分析】（Ⅰ）根据题中的边长以及垂直关系，可求出,OA OP ，利用勾股定理判断OP OA ⊥，再根据等边三角形三线重合，判断OP BC ⊥，即可证明PO⊥平面ABCD ；（Ⅱ）根据垂直关系，以O 为坐标原点，建立空间直角坐标系，利用向量的坐标公式求CB 与平面PBD 所成角的正弦值.【详解】（Ⅰ）证明：在ACD △中，由已知得AC =,ABC PBC O 为BC 的中点,OA BC OP BC ∴⊥⊥，且32OA OP ==.在PAO 中，已知PA =则有222,PO OA PA OP OA +=∴⊥. 又,OA BC O OA ⋂=⊂平面,ABCD BC ⊂平面,ABCD OP ∴⊥平面ABCD .（Ⅱ）以O 为坐标原点，,,OA OC OP 分别为x 轴，y 轴，z 轴的正方向，建立如图所示的空间直角坐标系，则3330,0,,0,,0,,0222P B C ⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，31,2D ⎛⎫ ⎪ ⎪⎝⎭. (0,3,0)(1,3,0)BC BD ∴==，，3333)2BP ⎛⎫== ⎪ ⎪⎝⎭.设平面PBD 的法向量为(,,)n x y z =，则00n BP n BD ⎧⋅=⎨⋅=⎩即3030x y z ⎧=⎪⎨=⎪⎩，令1z =.则3,3y x ==.∴平面PBD 的一个法向量为(3,3,1)n =-，39sin |cos ,|BC n θ∴=<>=.39sin θ∴= 【点睛】方法点睛：1.利用面面垂直的性质定理，得到线面垂直，进而确定线面角中的垂足，明确斜线在平面内的射影，即可确定线面角；2.在构成线面角的直角三角形中，可利用等体积法解垂线段的长度h ，而不必画出线面角，利用sin h θ= /斜线段长，进行求角；3.建立空间直角坐标系，利用向量法求解，设a 是直线l 的方向向量，n 是平面的法向量，利用公式sin cos ,a n θ=<>求解. 22．（1）49；（2）13．【分析】首先以A 为原点，建立空间直角坐标系，（1）求平面BDE 的法向量m ，利用公式sin cos ,CE m θ=<>求解；（2）求平面BDF 的法向量n ，利用公式cos ,m n <> 求解.【详解】以A 为原点，,,AB AD AE 分别为,,x y z 轴的正方向，建立空间直角坐标系，()1,0,0B ，()0,1,0D ，()0,0,2E ，()1,2,0C ，81,2,7F ⎛⎫ ⎪⎝⎭ （1）设平面BDE 法向量(),,m x y z =，()1,1,0BD =-，()1,0,2BE =-，则020x y x z -+=⎧⎨-+=⎩，令1z =，则2,2x y ==，∴()2,2,1m =，()1,2,2CE =--，2424sin cos ,339CE m θ--+=<>==⨯ （2）设平面BDF 法向量(),,n x y z =，()1,1,0BD =-，80,2,7BF ⎛⎫= ⎪⎝⎭，则82070y z x y ⎧+=⎪⎨⎪-+=⎩，令4x =，则4,7y z ==-∴()4,4,7n =-，8871cos cos ,393m n θ+-=<>==⋅，因为平面BDE 与平面BDF 夹角是锐二面角，所以二面角的余弦值是13.【点睛】关键点点睛：本题是比较典型的向量坐标法解决空间角，关键是计算准确，23．（1）证明见解析；（27. 【分析】（1）取AD 中点I ，推出//FI SA ，//IE AB ，证明//FI 平面SAB ，//IE 平面SAB ，推出平面//EFI 平面SAB ，然后证明//EF 平面SAB ；（2）以D 为原点，DA ，DC 所在直线为x ，y 轴，过D 垂直于平面ABCD 的直线为z 轴建立空间直角坐标系，设(, , )S x y z ，通过2SD =，SB SC =2EF =，求出()0,0,2S ，得出(3,1,2)SB =-，(0,2,2)SC =-，求出平面SBC 的法向量，然后利用空间向量的数量积可求出答案.【详解】（1）取AD 中点I ，∵E ，F 分别是BC ，SD 的中点，∴//FI SA ，//IE AB ，且FIEI I =， ∵SA ⊂平面SAB ， FI ⊄平面SAB ，∴//FI 平面SAB ，同理AB平面SAB ，IE ⊄平面SAB ，//IE ∴平面SAB ，又∵FI EI I =， ∴平面//EFI 平面SAB ，又∵FI ，IE ⊂平面FIE ，FIIE I =， ∴平面//EFI 平面SAB ，∵EF ⊂平面EFI ，∴//EF 平面SAB .（2）以D 为原点，DA ，DC 所在直线为x ，y 轴，过D 垂直于平面ABCD 的直线为z 轴建立空间直角坐标系，设(, , )S x y z ，则,,222x y z F ⎛⎫ ⎪⎝⎭，因为2SD =，SB SC =，2EF =，所以2222222222224((1)(2)3422x y z x y z x y z y z ⎧⎪++=⎪⎪-+-+=+-+⎨⎪-⎛⎫⎛⎫⎪++= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎩，求得0x y ==，24z =，不妨取()0,0,2S ， ∴(3,1,2)SB =-，(0,2,2)SC =-，设(,,)n x y z =⊥平面SBC ，∴320220n SB x y z nSC y z ⎧⋅=+-=⎪⎨⋅=-=⎪⎩，令1y =，则1,3z x ==，所以3,1,13n ⎛⎫= ⎪⎪⎝⎭，因为AD ⊥平面SCD ，所以取(1,0,0)m =为平面SCD 的法向量， ∴cos |cos ,|71m nm nm n θ⋅=〈〉===⋅+，所以二面角B SC D--的余弦值为7. 【点睛】方法点睛：本题考查直线与平面平行的判定定理、二面角平面角的求法，第二问关键点是建立空间直角坐标系，求出S 点坐标，考查了空间想象力及计算能力.24．（1）证明见解析；（2. 【分析】（1）AC 与BD 交于点O ，连接FO ､FD ，证明FO AC ⊥，FO BD ⊥，然后得到FO ⊥平面ABCD 即可；（2）以O 为原点，OA ､OB 、OF 分别为x ､y ､z 轴建立空间直角坐标系，然后求出平面BFC 和平面ACF 的法向量，然后可算出答案.【详解】（1）证明：AC 与BD 交于点O ，连接FO ､FD ，∵FA FC =，O 是AC 中点，且O 是BD 中点，∴FO AC ⊥，∵四边形BDEF 为菱形，60DBF ∠=︒，∴FD FB =，∴FO BD ⊥，又AC BD O =，∴FO ⊥平面ABCD ，∵FO ⊂平面ACF ，∴平面ACF ⊥平面ABCD（2）易知OA ，OB ，OF 两两垂直以O 为原点，OA ､OB 、OF 分别为x ､y ､z 轴建立如图所示的空间直角坐标系设2AB =，∵四边形ABCD 为菱形，60DAB ∠=︒则2BD =，∴1OB =，3OA OF ==故(0,0,0)O ，(0,1,0)B ，()3,0,0C -，(3F ∴(3,0,3CF =，3,1,0CB ，()0,1,0OB =设平面BFC 的一个法向量为(,,)n x y z = 则33030n CF x z n CB x y ⎧⋅=+=⎪⎨⋅=+=⎪⎩，取1x =，得()1,3,1n =-- 显然，()0,1,0OB =为平面ACF 的一个法向量 ∴15cos ,OB nOB n OB n ⋅<>==-⋅ 由图知，二面角A FC B --的平面角为锐角∴二面角A FC B --的余弦值为155 【点睛】关键点睛：用向量法求解空间角的问题时，解题的关键是建立适当的空间直角坐标系，准确地写出点的坐标和算出直线的方向向量、平面的法向量.25．（1）22）155. 【分析】（1）连接1A B ，先证得11A C ⊥平面11ABB A ，得111AC AB ⊥，然后由已知得1AB ⊥平面11A BC ，1A B ⊂平面11A BC ，∴11AB A B ⊥，在直角梯形11AA B B 中，可求得1AA ；（2）以A 为原点，AB ，AC ，1AA 方向为x 轴､y 轴､z 轴的正方向，建立空间直角坐标系A xyz -，然后求得二面角11B AC C --的两个面的的法向量，由法向量的余弦值得二面角的正弦值．【详解】解：（1）如图，连接1A B .1AA ⊥平面111A B C ，11A B ⊂平面111A B C ，则111AC A A ⊥，又1111AC A B ⊥，1111AA A B A =，∴11A C ⊥平面11ABB A ，而1AB ⊂平面11ABB A ，故111AC AB ⊥.又11AB BC ⊥，1111A C BC C ，可得1AB ⊥平面11A BC ，1A B ⊂平面11A BC ，∴11AB A B ⊥，故1111111112tan tan 224AA A BA A AB A BA A AB AA AA ∠=∠⇒∠=∠⇒=⇒=（2）如图，以A 为原点，AB ，AC ，1AA 方向为x 轴､y 轴､z 轴的正方向，建立空间直角坐标系A xyz -，则(12,0,22B ，(10,2,22C ()4,0,0AB =为平面1AC C 的一个法向量.设(),,n x y z =为平面11B AC 的一个法向量，则112220002220x z n AB n AC y z ⎧⎧+=⋅=⎪⎪⇒⎨⎨⋅=+=⎪⎪⎩⎩，取1z =，得()2,2,1n =--，则4210cos ,545n AB -〈〉==- ∴15sin ,n AB 〈〉=. 15．【点睛】方法点睛：本题考查线面垂直的判定，考查空间向量法求二面角．求二面角的常用方法是空间向量法，即建立空间直角坐标系，求出二面角两个面的法向量，由法向量的夹角与二面角相等或互补求解．26．（1）证明见解析；（2）1.【分析】（1）连接DM ，证出MN AD ⊥，PD MN ⊥，再利用面面垂直的判定定理即可证明. （2）连接BD ，以点D 为坐标原点，以,,DA DB DP 为,,x y z 轴，建立空间直角坐标系，设(0,0,)(0)P m m >，根据空间向量的数量积求出m ，再根据锥体的体积公式即可求解.【详解】（1）连接DM ，显然//DC BM 且DC BM =，∴四边形BCDM 为平行四边形，//DM BC ∴且DM BC =，AMD ∴△是正三角形，MN AD ∴⊥，又PD ⊥平面,ABCD MN ⊂平面,ABCD PD MN ∴⊥,,PD AD D MN ⋂=∴⊥平面PAD ，又MN ⊂平面PMN ，∴平面PMN ⊥平面PAD .（2）连接BD ，易知//,,BD MN BD AD BD PD ∴⊥⊥. 建立如图所示的空间直角坐标系，则(0,0,0),(1,0,0),(1,3,0)D N C -，设(0,0,)(0)P m m>，(1,0,),(2,3,0)PN m CN ∴=-=-.设平面PNC 的法向量为(,,)a x y z =，00a PN a CN ⎧⋅=∴⎨⋅=⎩，即0,230,x mz x y -=⎧⎪⎨-=⎪⎩ 令3,(3,2,3)z a m m ==，而平面PND 的一个法向量为(0,1,0)b =，221|cos ,|cos 602343a b m m ︒〈〉===++ 解得33m =，所以113(24)31323V =⨯⨯+⨯⨯=.【点睛】方法点睛：证明面面垂直的常用方法：证明两平面垂直常转化为线面垂直，利用线面垂直的判定定理来证明，也可作出二面角的平面角，证明平面角为直角，利用定义证明.解决二面角相关问题通常用向量法，具体步骤为：（1）建坐标系，建立坐标系的原则是尽可能的使得已知点在坐标轴上或在坐标平面内；（2）根据题意写出点的坐标以及向量的坐标，注意坐标不能出错.（3）利用数量积验证垂直或求平面的法向量.（4）利用法向量求距离、线面角或二面角.。

线面角、二面角练习(含答案)

(D) 证明 , 4B L PD; G)若 P4 = PD = AB, /APD = 90“, 设 Q 为 PB 中点 , 求直线 4Q 与平面 PBC 所成角的余弦值
.(10分 ) 如图 , 在四楂锥 P 一 4BC 丁中 , 底面 4BC是D矩形 ,M7 是 P4 的中点 ,PD 平 _ 面 4L BCD,
心的 M L DN, 即异面直线 4M 与 DN 所成角大小为 90., 故选 D.
2. ( AP4D 为直角三角形 , 且 P4 = 4D, …LP4D 二 90., 即 P4 L 4D, 四边形 4B8为C正 D方形 , - DA L BA, N PANBA= 4, P4 c 面 P4B,PB C 面 P4B,
A. 307
B. 45°
二、解答题 ( 共 14 小题 , 每小题 10 分 , 共 140分 )
C. 60°
D. 90°
2.(分1) 0如图 , 平面 P4D L 平面 4BCD,4B为 C正D方形 ,AP 是 4 直角D 三角形 , 且 P4 = 4D 二 2, E
、友、G 分别是线段 P4、PD、CD 的中点。
(D) 证明 , PB平 |面 4BC ) 设二面角 D - 4F - C 为 60“,=4P 1,4一Dv, 求三棒锥丁一 4CD 的体积 .
三、填空题 ( 共 1 小题 ,每小题 5 分 , 共 5 分 )
16.(5 分 ) 已知长方体 A4BCD 一 4 BCLD 中 ,4B 万 2,4D = AA; 三 1, 则的线 BDu 与平面

等体积法求线面角

苏艺伟（福建省龙海第一中学新校区３６３１００）苏艺伟中学二级教师。

工作以来认真钻研教材，积极写作，发表两篇ＣＮ级、多篇漳州市级文章，获得过漳州市论文比赛一等奖。

一般地，对于三棱锥求体积问题，经常用等体积法求解．事实上，借助等体积法还可以求直线与平面所成角的正弦值．对于较为复杂的线图１面角问题，有时候很难直接找出该角，此时可以借助等体积法先求出直线上某点到平面的距离．如图１所示，设点Ｐ到α的距离为ｈ，首先借助等体积法求出ｈ，再利用ｓｉｎθ＝ｈＰＡ求解．图２例１如图２所示，四棱锥Ｐ－ＡＢＣＤ的底面ＡＢＣＤ是矩形，ＡＢ＝２，ＰＡ＝ＰＢ＝ＢＣ＝槡１０，ＰＤ＝ＰＣ＝槡２．（１）求证：面ＰＡＢ⊥面ＰＣＤ；（２）求直线ＰＡ与面ＰＢＣ所成角的正弦值．解（１）取ＣＤ中点Ｆ，ＡＢ中点Ｅ，连接ＰＥ，ＰＦ，ＥＦ．由ＰＦ＝１，ＰＥ＝３，得ＰＦ２＋ＰＥ２＝ＥＦ２．所以ＰＥ⊥ＰＦ．由ＰＦ⊥ＣＤ，ＡＢ∥ＣＤ，得ＰＦ⊥ＡＢ．由ＰＦ⊥ＰＥ，ＰＦ⊥ＡＢ，ＡＢ∩ＰＥ＝Ｅ，得ＰＦ⊥面ＰＡＢ．又ＰＦ面ＰＣＤ，所以面ＰＡＢ⊥面ＰＣＤ．（２）设点Ａ到面ＰＢＣ的距离为ｈ，则ｓｉｎθ＝ｈ槡１０，ＶＡ－ＰＢＣ＝ＶＣ－ＰＡＢ，Ｓ△ＰＢＣ＝１２×槡２　×槡１９槡２＝槡１９２．因为ＣＤ∥面ＰＡＢ，点Ｃ到面ＰＡＢ的距离即为点Ｆ到面ＰＡＢ的距离．因为ＦＰ⊥面ＰＡＢ，所以点Ｆ到面ＰＡＢ的距离为１，即１３×槡１９２ｈ＝１３×３×１，解得ｈ＝６１槡９．所以ｓｉｎθ＝ｈ槡１０＝槡６　１９０１９０＝槡３　１９０９５．图３例２如图３所示，在三棱锥Ｐ－ＡＢＣ中，ＰＡ⊥面ＡＢＣ，ＡＣ⊥ＢＣ，Ｄ为ＰＣ中点，Ｅ为ＡＤ中点，ＰＡ＝ＡＣ＝２，ＢＣ＝１．（１）求证：ＡＤ⊥面ＰＢＣ；（２）求ＰＥ与面ＡＢＤ所成角的正弦值．解由已知可得ＰＣ＝槡２　２，ＡＤ＝槡２，ＤＥ＝槡２２，ＰＤ＝槡２，ＰＤ⊥ＡＤ，ＰＥ＝槡１０２，ＰＢ＝３，·１１·２０２０年第１２期数学中的思想和方法《数理天地》高中版ＰＣ⊥ＢＣ，ＢＤ＝槡３，ＡＤ＝槡２，ＡＢ＝槡５，ＡＤ⊥ＢＤ．（１）因为ＰＡ⊥面ＡＢＣ，ＰＡ面ＰＡＣ，所以面ＰＡＣ⊥面ＡＢＣ．由ＢＣ⊥ＡＣ，面ＰＡＣ⊥面ＡＢＣ，面ＰＡＣ∩面ＡＢＣ＝ＡＣ，得ＢＣ⊥面ＰＡＣ，所以ＢＣ⊥ＡＤ．由ＡＤ⊥ＰＣ，ＡＤ⊥ＢＣ，ＰＣ∩ＢＣ＝Ｃ，得ＡＤ⊥面ＰＢＣ．（２）设点Ｐ到面ＡＢＤ距离为ｈ，ＶＰ－ＡＢＤ＝ＶＢ－ＰＡＤ，Ｓ△ＡＢＤ＝槡６２，Ｓ△ＰＡＤ＝１，ＢＣ⊥面ＰＡＣ，即ＢＣ⊥面ＰＡＤ，点Ｂ到面ＰＡＤ距离为ＢＣ＝１．所以１３ｈ　×槡６２＝１３×１×１，解得ｈ　＝槡６３，所以ｓｉｎθ＝ｈ槡１０２＝槡６３槡１０２＝槡２　１５１５．图４例３如图４所示，在四棱锥Ｐ－ＡＢＣＤ中，△ＰＡＤ为等边三角形，ＡＢ＝ＡＤ＝１２ＣＤ＝２，∠ＢＡＤ＝∠ＡＤＣ＝９０°，∠ＰＤＣ＝６０°，Ｅ为ＢＣ中点．（１）证明：ＡＤ⊥ＰＥ；（２）求直线ＰＡ与面ＰＤＥ所成角的大小．解（１）取ＡＤ中点Ｏ，连接ＯＰ，ＯＥ，则ＡＤ⊥ＰＯ，ＡＤ⊥ＯＥ，所以ＡＤ⊥面ＰＯＥ，ＡＤ⊥ＰＥ．（２）作ＰＱ⊥ＣＤ，ＰＨ⊥ＯＥ，连接ＨＱ．因为ＡＤ⊥面ＰＯＥ，ＰＨ面ＰＯＥ，所以ＡＤ⊥ＰＨ．由ＰＨ⊥ＡＤ，ＰＨ⊥ＯＥ，ＡＤ∩ＯＥ＝Ｏ，得ＰＨ⊥面ＡＢＣＤ．又ＣＤ⊥ＰＱ，所以ＣＤ⊥ＨＱ，故四边形ＤＯＨＱ为矩形．又ＤＱ＝１，ＤＯ＝１，所以ＯＨ＝ＱＨ＝１，ＰＯ＝槡３，ＯＨ＝１，ＰＨ＝槡２．设点Ａ到面ＰＤＥ距离为ｈ，则ＶＡ－ＰＤＥ＝ＶＰ－ＡＤＥ．Ｓ△ＰＥＤ＝槡６，Ｓ△ＡＥＤ＝３，１３×槡６×ｈ＝１３×槡２×３，ｈ　＝槡３．所以ｓｉｎθ＝ｈ２＝槡３２，θ＝６０°．图５例４如图５所示，在边长为４的正方形ＡＢＣＤ中，Ｅ，Ｆ分别为边ＡＢ，ＡＤ中点，以ＣＥ和ＣＦ为折痕把△ＤＦＣ和△ＢＥＣ折起，使点Ｂ，Ｄ重合于点Ｐ位置，连接ＰＡ，得到四棱锥Ｐ－ＡＥＣＦ．（１）在线段ＰＣ上是否存在一点Ｇ，使ＰＡ与面ＥＦＧ平行若存在，求出ＰＧＧＣ；（２）求直线ＡＰ与面ＰＥＣ所成角的正弦值．解（１）连接ＥＦ，ＡＣ交于点Ｏ，则ＡＣ⊥ＥＦ，ＡＯＯＣ＝１３．当ＰＧＧＣ＝１３时，ＰＡ与面ＥＦＧ平行．因为ＡＯＯＣ＝ＰＧＧＣ＝１３，·２１·《数理天地》高中版数学中的思想和方法２０２０年第１２期所以ＰＡ∥ＯＧ．故ＰＡ与面ＥＦＧ平行．（２）设点Ａ到面ＰＥＣ的距离为ｈ，ＶＡ－ＰＥＣ＝ＶＰ－ＡＥＣ，Ｓ△ＰＥＣ＝４，Ｓ△ＡＥＣ＝４．因为ＰＣ⊥ＰＥ，ＰＣ⊥ＰＦ，所以ＰＣ⊥面ＰＥＦ，ＰＣ⊥ＯＰ．又ＥＦ⊥ＯＣ，ＥＦ⊥ＯＰ，所以ＥＦ⊥面ＯＰＣ．又ＥＦ面ＡＥＣ，所以面ＡＥＣ⊥面ＯＰＣ．作ＰＴ⊥ＯＣ，则ＰＴ⊥面ＡＥＣ，ＰＴ＝４３，所以１３×４ｈ＝１３×４×４３，解得ｈ＝４３．因为ＰＣ＝４，ＰＴ＝４３，ＣＴ＝槡８　２３，ＡＴ＝槡４　２３，ＡＰ＝槡４　３３．所以ｓｉｎθ＝４３４３槡３＝槡３３．借助等体积法求线面角，可以避开找角的难点，降低思维难度，其关键在于求出直线上某点到平面的距离．在实际解题中，要充分运用立体几何中的判定定理，性质定理，并善于结合题目条件挖掘隐含的信息，沟通各个几何元素之间的关系，不断转化，实现解题的高效．（上接第１０页）即Ｆ（ｘ）在［０，１］上单调递减，所以Ｆ（ｘ）ｍａｘ＝Ｆ（０），即Ｆ（ｘ）≤Ｆ（０）＝１－ｔ≤０，得ｔ≥１．１１．正难则反，利用补集思想例１２关于ｘ的方程ｘ２＋２ｍｘ＋２ｍ２－１＝０至少有１个负实数根，求实数ｍ的取值范围．解设全集Ｕ＝｛ｍ｜Δ≥０｝＝｛ｍ｜－１≤ｍ≤１｝．设方程没有负实数根，即只有正实数根或零根时ｍ的范围为集合Ａ．由Δ≥０，ｘ１＋ｘ２≥０，ｘ１ｘ２≥０，烅烄烆得－１≤ｍ≤１，２ｍ≤０，２ｍ２－１≥０，烅烄烆所以－１≤ｍ≤－槡２２，即Ａ＝ｍ｜－１≤ｍ≤－槡２２｛｝，所以集合Ａ的补集是ｍ｜－槡２２＜ｍ≤１｛｝，故ｍ的取值范围是－槡２２＜ｍ≤１．１２．根据函数的奇偶性、周期性、对称性等性质例１３若ｆ（ｘ）＝ｓｉｎ（ｘ＋α）＋ｃｏｓ（ｘ－α）为偶函数，求α的值．解由题得ｆ（－ｘ）＝ｆ（ｘ）对一切ｘ∈Ｒ恒成立，所以ｓｉｎ（－ｘ＋α）＋ｃｏｓ（－ｘ－α）＝ｓｉｎ（ｘ＋α）＋ｃｏｓ（ｘ－α），ｓｉｎ（ｘ＋α）＋ｓｉｎ（ｘ－α）＝ｃｏｓ（ｘ＋α）－ｃｏｓ（ｘ－α），２ｓｉｎｘ·ｃｏｓα＝－２ｓｉｎｘ·ｓｉｎα，即ｓｉｎｘ（ｓｉｎα＋ｃｏｓα）＝０对一切ｘ∈Ｒ恒成立，所以只需也必须ｓｉｎα＋ｃｏｓα＝０．故α＝ｋπ－π４（ｋ∈Ｚ）．·３１·２０２０年第１２期数学中的思想和方法《数理天地》高中版。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

等体积法求线面角
一、单选题(共6道，每道16分)
1.如图，三棱柱ABC-A1B1C1的侧棱与底面垂直，体积为，底面是边长为的正三角形，若P为底面A1B1C1的中心，则直线PA与平面ABC所成角的大小为( )
A.60°
B.75°
C.45°
D.30°
答案：A
解题思路：
试题难度：三颗星知识点：直线与平面所成的角
2.如图，在正四棱锥P-ABCD中，已知PA=AB=，若M为PA的中点，则直线BM与平面PAD所成角的正弦值是( )
A. B.
C. D.
答案：C
解题思路：
试题难度：三颗星知识点：直线与平面所成的角
3.如图，在三棱锥中，已知平面，，，则
与平面所成角的正弦值是( )
A. B.
C. D.
答案：C
解题思路：
试题难度：三颗星知识点：直线与平面所成的角
4.如图，在三棱锥S-ABC中，底面ABC是边长为2的等边三角形，SA⊥底面ABC，SA=3，则直线AB与平面SBC所成角的正弦值为( )
A. B.
C. D.
答案：D
解题思路：
试题难度：三颗星知识点：直线与平面所成的角
5.如图，已知PA=PB=PC，且PA，PB，PC两两垂直，则PA与平面ABC所成角的正弦值为( )
A. B.
C. D.
答案：C
解题思路：
试题难度：三颗星知识点：直线与平面所成的角
6.如图，已知P是正四面体ABCD的棱AC的中点，则直线PD与平面BCD所成角的正弦值为( )
A. B.
C. D.
答案：A
解题思路：
试题难度：三颗星知识点：直线与平面所成的角。